Prerpints.org logo
Preprint
Article

Anomalous Ferromagnetic Phase in the Gd1-xErxB4 Series: Crystal Growth, Thermal and Magnetic Properties

Altmetrics

Downloads

100

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

05 July 2023

Posted:

07 July 2023

You are already at the latest version

Alerts
Abstract
Rare-earth tetraborides RB4 are of great interest due to the occurrence of geometric magnetic frustration and corresponding unusual magnetic properties. While the Gd3+ spins in GdB4 align along the ab plane, Er3+ spins in the isomorphic ErB4 are confined to the c–axis. The magnetization in the latter exhibits a plateau at the midpoint of the saturation magnetization. Therefore, solid solutions of (Gd, Er)B4 provide an excellent playground for exploring the intricate magnetic behavior in these compounds. Single crystals of Gd(1-x)Erx B4 (x = 0, 0.2, and 0.4) were grown in aluminum flux. X-ray diffraction scans revealed single phase materials, and a drop in the unit cell volume with increasing Er content, suggesting the partial substitution of Er at the Gd sites. Heat capacity measurements indicated a systematic decrease of the Néel temperature (TN) with increasing Er content. The effective magnetic moment determined from the magnetization measurement agreed with the calculated free-ion values for Gd3+ and Er3+, providing further evidence for the successful substitution of Er for Gd. The partial substitution resulted in an anomalous ferromagnetic phase below TN, exhibiting significant anisotropy, predominantly along the c-axis. This intriguing behavior merits further studies of the magnetism in the Gd(1-x)ErxB4 borides.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

Motivated by their interesting magnetic properties, the rare earth tetraborides with general formula RB4 (R = Rare earth) have been studied for many years [1,2,3]. These compounds are metallic conductors and show antiferromagnetic (AF) ordering, except for R = Pr, which is ferromagnetic (FM) [2]. The indirect coupling between the magnetic ions is of the Ruderman-Kittel-Kasuya-Yosida type (RKKY) [2]. The crystal structure is tetragonal belonging to the symmetry group P4/mbm. Due to the nature of the crystal structure, these compounds exhibit strongly anisotropic magnetic and electrical properties [4,5].
The magnetic sublattice of R ions in RB4 consists of 2d orthogonal R–R dimers in the ab-plane, forming squares and triangles [6]. The bond length between the rare earth Nearest Neighbor dimmer (NN) is very close to the Next Nearest Neighbor (NNN). Therefore, one can presume that the corresponding magnetic interactions J1 and J2, as shown in Figure 1, are also close to each other. If the magnetic interaction between the rare-earth ions is antiferromagnetic, it is likely that the system should exhibit geometrically frustrated magnetic interactions, consistently with the theoretical approach described in the Shastry–Sutherland lattice (SSL) [6,7,8].
There are some noteworthy differences between GdB4 and ErB4. All heavy RB4 (R = Tb, Dy, Ho, Er, Tm) display strong Ising-like anisotropies, resulting in the rare-earth magnetic moments being oriented preferably along the c-axis or along the ab-plane. The Er3+ ions in ErB4 have a large total angular moment J = 15/2; the compound shows an antiferromagnetic transition at TN = 15.4 K, and the M × H curve exhibits a plateau region at the midpoint of the saturation magnetization (MS) value, a feature attributed to the competition between the Zeeman effect and magnetic frustration [9]. The Er3+ magnetic moments align along the c-axis, and they were previously determined to be 8.2 ± 0.6 μ B [10].
In contrast, the Gd3+ magnetic moments in GdB4 align perpendicularly to the c-axis, i.e., along the basal ab-plane [11]. No plateau is observed in M x H curves, and the antiferromagnetic ordering temperature for GdB4 is TN = 42 K [2,12]. Spherical neutron polarimetry revealed that the magnetic spins order non-collinearly (see Figure 1), in a structure with the Shubnikov magnetic space group P4/m’b’m’. The magnetic moment of Gd3+ was determined to be 7.14 ± 0.17 μ B , quite close to the free ion value [11].
The goal of this work is to probe the thermal and magnetic properties of Gd1-xErxB4 (x = 0 – 0.4). Single crystals were grown from aluminum flux, and analyzed by means of Laue X-ray images, and powder X-ray diffraction (XRD). Measurements of magnetization [M(T, H)] and heat capacity [Cp(T, H)] were carried out with magnetic fields applied parallel and perpendicular to the c-axis. These measurements permitted monitoring the fast evolution of the magnetic properties upon the partial substitution of Er for Gd in GdB4.

2. Materials and Methods

Stoichiometric amounts of high purity Gd (Merch 99.9%), Er (Merch 99.9%) and B (Alfa Aesar 99,99%) corresponding to the G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4) compositions, and high purity aluminum shots (Alfa Aesar 99.99%) were placed in 70 ml alumina crucibles, in 5% - 95% amounts by weight, respectively. The alumina crucibles were loaded on a vertical tube furnace under flowing ultra-high pure argon gas, heated and maintained at 1500 °C for one hour, cooled slowly to 1000 °C, and fast-cooled to ambient temperature by turning the furnace off. The G d 1 − x E r x B 4 crystals were separated from the flux by dissolving the aluminum in a saturated NaOH solution. Laue photographs were taken by back-reflection methodology to assess the quality of the single crystals and determine the crystallographic orientation [13]. The open-source software QLaue was used to simulate the diffraction spots [14].
Ambient temperature X-ray powder diffraction was carried out on a few crystals crushed in an agate mortar, using the CuKα radiation of a D-8 Discovery diffractometer in the 15 ≤ 2θ ≤ 120° range. The characterization of the GdB4 single crystal is described elsewhere [15]. The grown crystals had plate-like polyhedral morphology; the largest dimension could reach ≈ 1.5 mm, and the larger facets corresponded to the (110) and (001) planes.
Specific heat Cp(T) and magnetization M(T, H) measurements of the G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4) crystals were obtained with a Physical Property Measurement System (PPMS) from Quantum Design. The Cp(T) data were collected in the 2 - 100 K temperature range. The M(T, H) data were collected in the 2 - 300 K temperature range in applied magnetic fields up to 9 T applied both parallel and perpendicular to the c-direction.

3. Results and Discussion

3.1. Samples and X-ray diffraction

The flux growth method for the synthesis of G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4) crystals yielded platelets with typical dimensions of ≈ 1.5 × 1.5 × 0.5 mm3, as shown in Figure 2. The X-ray Laue images displayed in Figure 3 and Figure 4 indicate that the larger facets are perpendicular to the crystallographic c-direction. The orientation of the crystals was determined from the Laue images using the QLaue software. The lack of distortion or smearing in the diffraction spots of Figure 3 and Figure 4 is suggestive of high crystallinity, with absence of defects or twining. The crystal morphology was suitable for assembling and measuring the physical properties parallel and perpendicular to the c-axis, as discussed in the following sections.
Structural refinement of the G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4) crystals was carried out using the General Structure Analysis System (GSAS) software based on the Rietveld methodology [16], and the results are shown in Figure 5. The XRD patterns do not show the presence of additional phases, and the lattice parameters resulting from the refinement are listed in Table 1. These compounds crystallize in a tetragonal structure at room temperature, P4/mbm (No. 127). The (001) Bragg reflection shifts towards higher 2θ values upon the partial substitution of Er for Gd, as show in the inset of Figure 5b, a result consistent with the smaller ionic radius of Er [17], and in turn a drop of the unit cell volume.
Given the different magnetic structures of GdB4 and ErB4, the progressive substitution of Er for Gd in the G d 1 − x E r x B 4 is quite likely to affect the magnetic and thermal properties. We monitored these changes by means of measurements of Cp(T) and M(T, H).

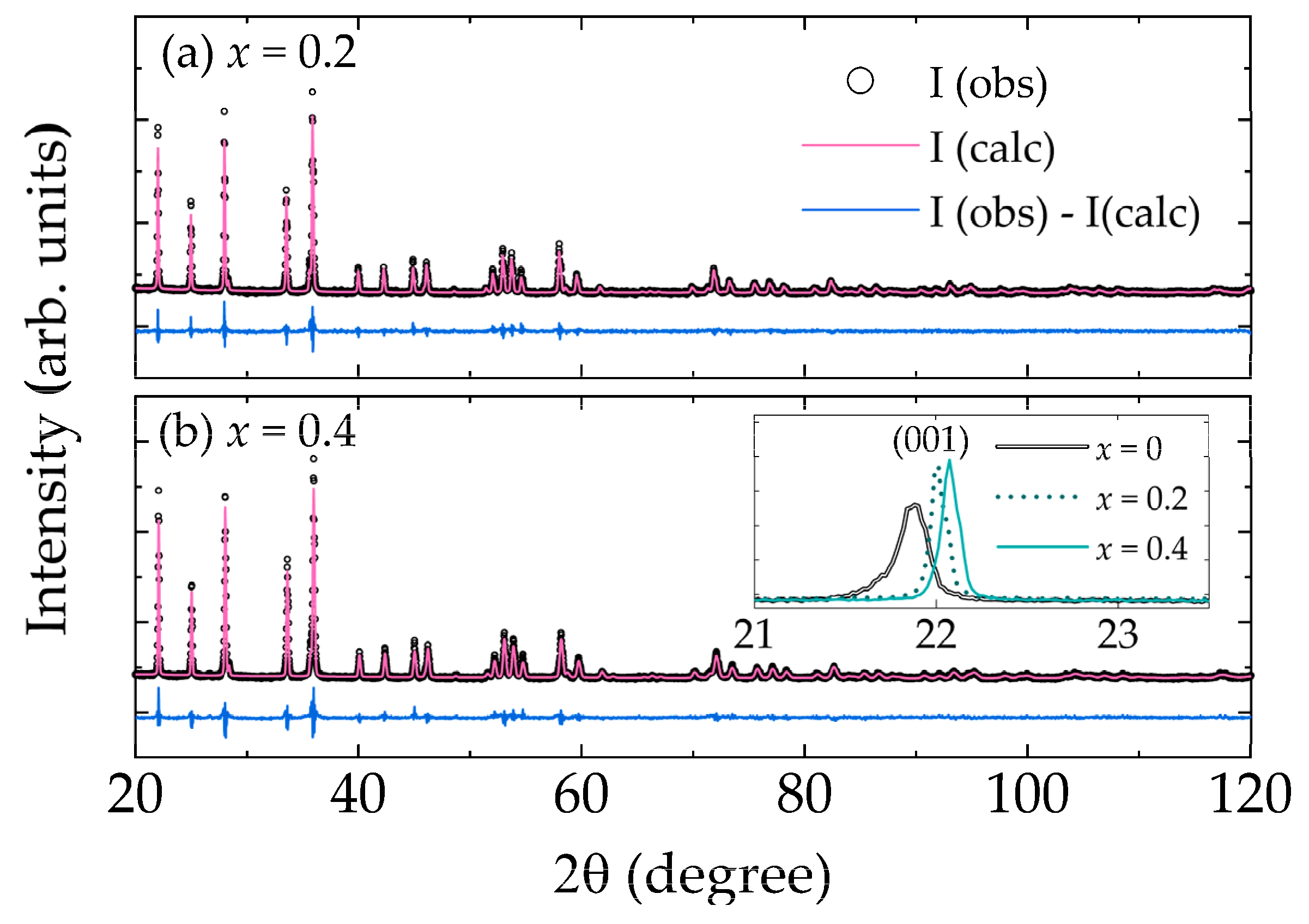
3.2. Specific heat

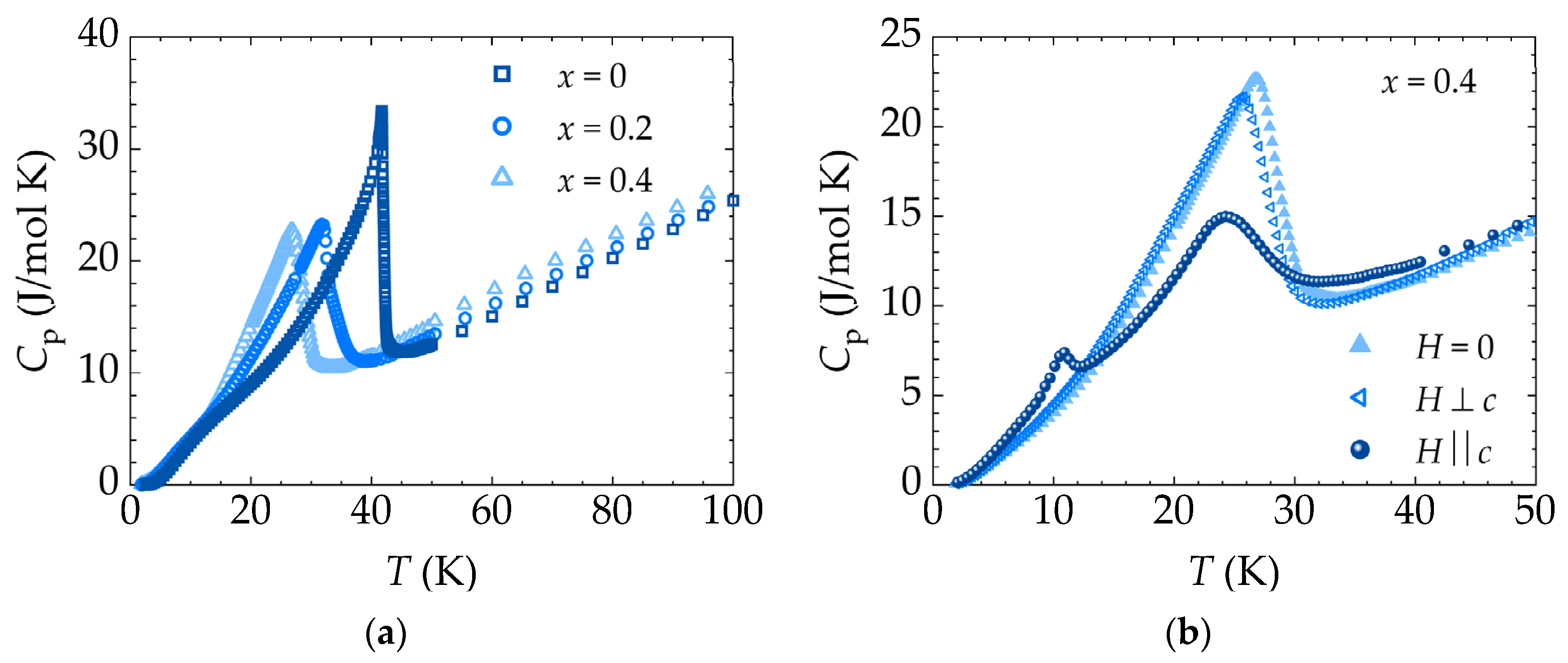
The zero-field specific heat Cp(T) data for the G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4) crystals are shown in Figure 6a. The Cp(T) curve for the undoped GdB4 clearly shows a pronounced peak at the Néel temperature TN = 41.8 K, indicating a transition from a paramagnetic (PM) to an antiferromagnetic (AFM) phase. Upon the partial substitution of Er for Gd, the magnetic ordering feature shifts to lower temperatures, reaching 31.8 and 26.8 K for Gd0.8Er0.2B4 and Gd0.6Er0.4B4, respectively. A small bump centered near T ≈ 10 K is observed in GdB4, a feature frequently observed in other lanthanide compounds and attributed to the Schottky contribution to the heat capacity [18]. The occurrence of this feature remains in the x = 0.2 sample but is much more suppressed in x = 0.4 crystal. Previous studies have shown that the Schottky contribution to the heat capacity in ErB4 occurs at higher temperatures [19].
At low temperatures, the heat capacity can be approximated by the relation Cp = Cel + Clatt + CSch + Cm, where Cel, Clatt, CSch, and Cm are the contributions due to the electron system, phonon, Schottky anomaly, and magnetic subsystem, respectively. To probe the effect of the partial change of Er for Gd in the sample magnetism, the magnetic contribution Cm for each composition was estimated, as depicted in Figure 7b. The phonon contribution Clatt was estimated using the method described by Stout and Catalano [20], which relies on measuring the heat capacity Cp of a nonmagnetic isomorph, which in this case was YB4.
The heat capacity of YB4 at low temperatures can be expressed as Cp:YB4 = Cel + Clatt = aT + bT3, where a = 12⋅10-4 J/mol K2 and b = 2.1⋅10-5 J/mol K4, values obtained by fitting. Comparable values of a and b have been reported for GdB4 (a = 5.96⋅10-4 J/mol K2 and b = 4.89⋅10-5 J/mol K4) and ErB4 (a = 8.46⋅10-4 J/mol K2 and b = 6.82⋅10-5 J/mol K4) in previous studies [18,19]. Therefore, it is reasonable to assume that the contributions of Cel and Clatt to the heat capacity of the G d 1 − x E r x B 4 series are like those of YB4. Consequently, the specific heat of YB4 was subtracted from the specific heat of the G d 1 − x E r x B 4 series, enabling the determination of the specific heat associated with the Schottky and magnetic anomalies.
The contribution to the specific heat due to the Schottky anomaly CSch for a system with n levels, separated by energies ε n and with degeneracy g n , is given by
C s c h = R g 1 ε 1 T 2 e − ε 1 / T + g 2 ε 2 T 2 e − ε 2 / T + … g 0 + g 1 e − ε 1 / T + g 2 e − ε 2 / T + … − R g 1 ε 1 T e − ε 1 T + g 2 ε 2 T e − ε 2 T + … g 0 + g 1 e − ε 1 T + g 2 e − ε 2 T + … 2 ,
where R is the ideal gas constant and ε n is given in kelvin. The CSch curve for all samples was obtained by fitting the data below TN using the equation C = AT α + CSch, where AT α represents the magnetic specific heat contribution, with α = 3 for AFM systems. As initial parameters for the Schottky anomaly, the data from Ref. [18] for Gd3+ were used, where g 0 = 2 , g 1 = 2 , g 2 = 4 , ε 1 = 30 K , and ε 2 = 75 K . For Er3+, the data from Ref. [19] are g 0 = 2 , g 1 = 4 , g 2 = 6 , g 3 = 4 , ε 1 = 85 K , ε 2 = 240 K , and ε 3 = 700 K . For the fitting procedure, only ε 1 and ε 2 for Gd3+ were free parameters. The parameters for Er3+ were kept fixed since initial fits indicated their values did not vary significantly. Thus, Cm was obtained by subtracting the fitted CSch, considering the proportional contribution due to the Gd3+ and Er3+.
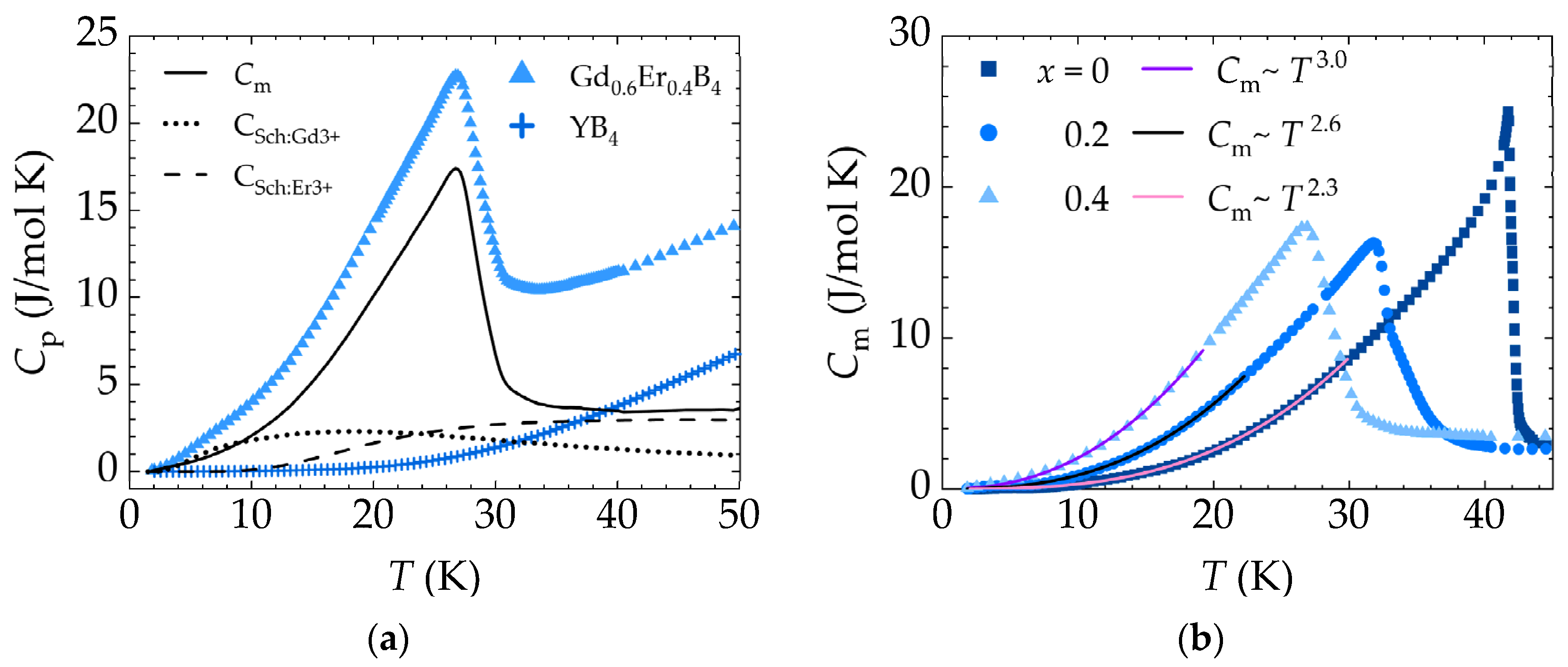
The different contributions to the total specific heat is exemplified in Figure 7a, for the x = 0.4 sample. After isolating the Cm curve, its temperature dependence was investigated by fitting to the equation A T α for temperatures up to 0.7TN, as shown in Figure 7b. For GdB4, α = 3, as expected for antiferromagnetic systems. The exponent α decreases to 2.6 and 2.3 for the samples with x = 0.2 and 0.4, respectively, approaching the 1.5 value, expected for ferromagnetic systems. This is an indication of a change in the system's ordering, due to the possible competition between magnetic anisotropies.
In order to probe the competition between magnetic anisotropies, we have performed measurements of Cp(T) in magnetic fields H up to 9 T. Shown in Figure 6b is the effect of a magnetic field H = 5 T applied along the two different crystallographic directions in Gd0.6Er0.4B4, resulting in a drop in the temperature of the Cp peak at TN, and a significant change in morphology for H//c. In general, for fields in the -9 T ≤ H ≤ +9 T range, the value of TN drops by ~ 15% and ~7% for fields applied parallel and perpendicular to the c-axis, respectively. In contrast, Cp(T) for the Gd0.8Er0.2B4 is nearly insensitive to the magnetic field (data not shown), with the value of TN dropping but staying within 3% of the zero-field value, for both orientations.
In addition to the main feature at TN, the Cp(T) data for Gd0.6Er0.4B4, shown in Figure 6b, presents a second feature at low temperatures, centered near 10 K, when a 5 T magnetic field is applied parallel to the c-axis. This peak, observed only in Gd0.6Er0.4B4, is possibly due to a metamagnetic transition, occurring exclusively along the c-axis, as suggested by the magnetization data.

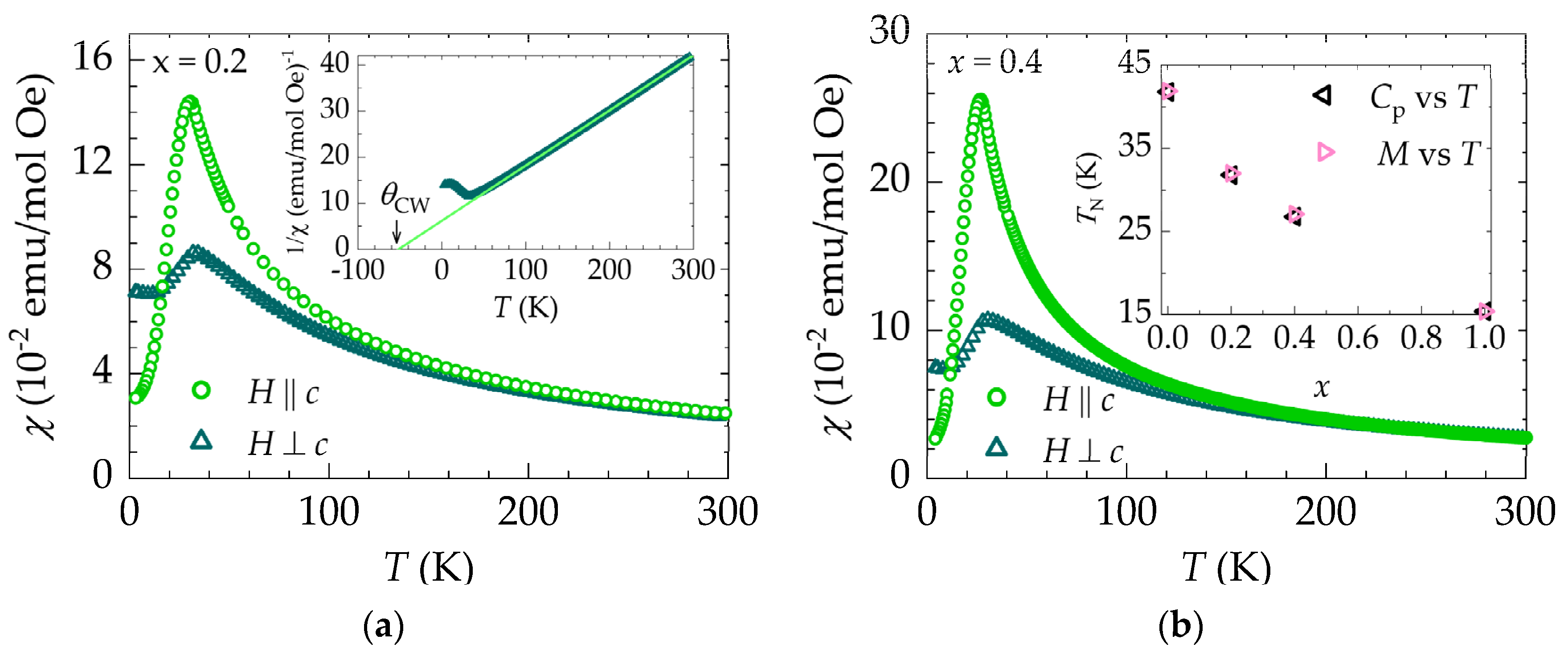
3.3. Magnetization

The temperature-dependent magnetic susceptibility curves χ (= Μ / H) × T for G d 1 − x E r x B 4 (x = 0.2 and 0.4), taken in 0.5 T magnetic fields parallel or perpendicular to the c-axis, are shown in Figure 8. The maximum value of χ occurs approximately at the same TN determined from the Cp(T) measurements of Figure 6. The value of TN was taken from the minimum of the second derivatives d 2 χ / d T 2 . Consistently with the Cp(T) data, TN drops with the Er concentration, as shown in the inset of Figure 8b.
For both x = 0.2 and x = 0.4 samples, χ (T) exhibits anisotropic behavior up to ~ 150 K, a temperature considerably higher than TN. In contrast, the undoped GdB4 displays anisotropic χ (T) behavior only below TN. Notably, the partial substitution of 20% Er seems to be sufficient to induce this anisotropic behavior, reminiscent of the behavior in ErB4 [9]. To gauge the magnitude of the anisotropy at 4 K, we calculated the ratio of the susceptibilities perpendicular and parallel to the c-axis and obtained 2.3 and 2.8 for x = 0.2 and 0.4, respectively. On the other hand, the susceptibilities parallel to the c-axis are higher near TN, exhibiting a magnitude of 1.7 and 2.8 times greater than the perpendicular susceptibility for the x = 0.2 and x = 0.4 samples, respectively. The magnetic susceptibility data for Gd0.8Er0.2B4 show that the substitution of 20% of Er favors the c-axis for spins alignment, since χ tends to lower values with decreasing temperature, while the perpendicular susceptibility shows a small temperature dependence.
As shown in the inset of Figure 8a for Gd0.8Er0.2B4, the magnetic susceptibility ( χ ) in the PM region follows the Curie-Weiss law [21]
χ = C T − θ C W ,
where θ C W is the Curie-Weiss constant, which is usually associated with the magnetic interactions between PM ions, expressed in units of temperature, and C is the Curie constant, given by
C = N a μ e f f 2 3 k B .
Here N a is the Avogadro’s number, k B the Boltzmann constant, and μ e f f the effective magnetic moment, calculated from
μ e f f = g J J J + 1 1 / 2 μ B ,
where g J is the Landé g-factor, J the total quantum number, and μ B the Bohr magneton. The theoretical values of μ e f f calculated for Gd3+ and Er3+ are 7.94 and 9.58 μ B , respectively.
For the G d 1 − x E r x B 4 solid solutions the theoretical values of μ e f f can be approximately obtained from
μ e f f = 1 − x μ e f f G d 2 + x μ e f f E r 2 1 / 2 .
On the other hand, the experimental values of μ e f f can be obtained by fitting the 1 / χ vs T data to the expression
1 χ = 8 T − θ C W μ e f f 2 ,
resulting from combining Equations (2) and (3), with N a = 6.022⋅1023 mol-1, k B = 1.381 · 10 − 16 erg/K, and μ B = 9.274⋅10-21 emu, as shown in the inset of Figure 8a. The experimental values of μ e f f obtained from fits of the experimental data to Equation (6) at temperatures above 100 K, are displayed in Table 2. The μ e f f values obtained from the χ ( T ) data with field along the two crystallographic directions are consistent with the calculated μ e f f values for the Gd3+ and Er3+ free ions, providing additional evidence for the effective partial substitution of Er for Gd within this series.
The data displayed in Table 2 indicate that the effective magnetic moments μ e f f e x p for GdB4 and Gd0.8Er0.2B4 are only slightly different for the two orientations of the magnetic field, suggesting that the magnetic anisotropy in these two compositions is very small. Upon normalization with respect to parameters associated with the c-axis, the difference between these values amounts to 0.5% and 0.7% for x = 0 and x = 0.2, respectively. On the other hand, there is a marked difference of 4.6% between the two values for the x=0.4 composition, a value close to the increased magnetic anisotropy in the Gd0.6Er0.4B4 crystal.
The magnetic anisotropic behavior of χ(T) is also noted in the Curie-Weiss constant for the x = 0.2 and 0.4 samples. The difference between θ C W values obtained along directions parallel and perpendicular to the c-axis also increases with x. These differences are 5.7%, 46%, and 220% for crystals with x = 0, 0.2, and 0.4, respectively.
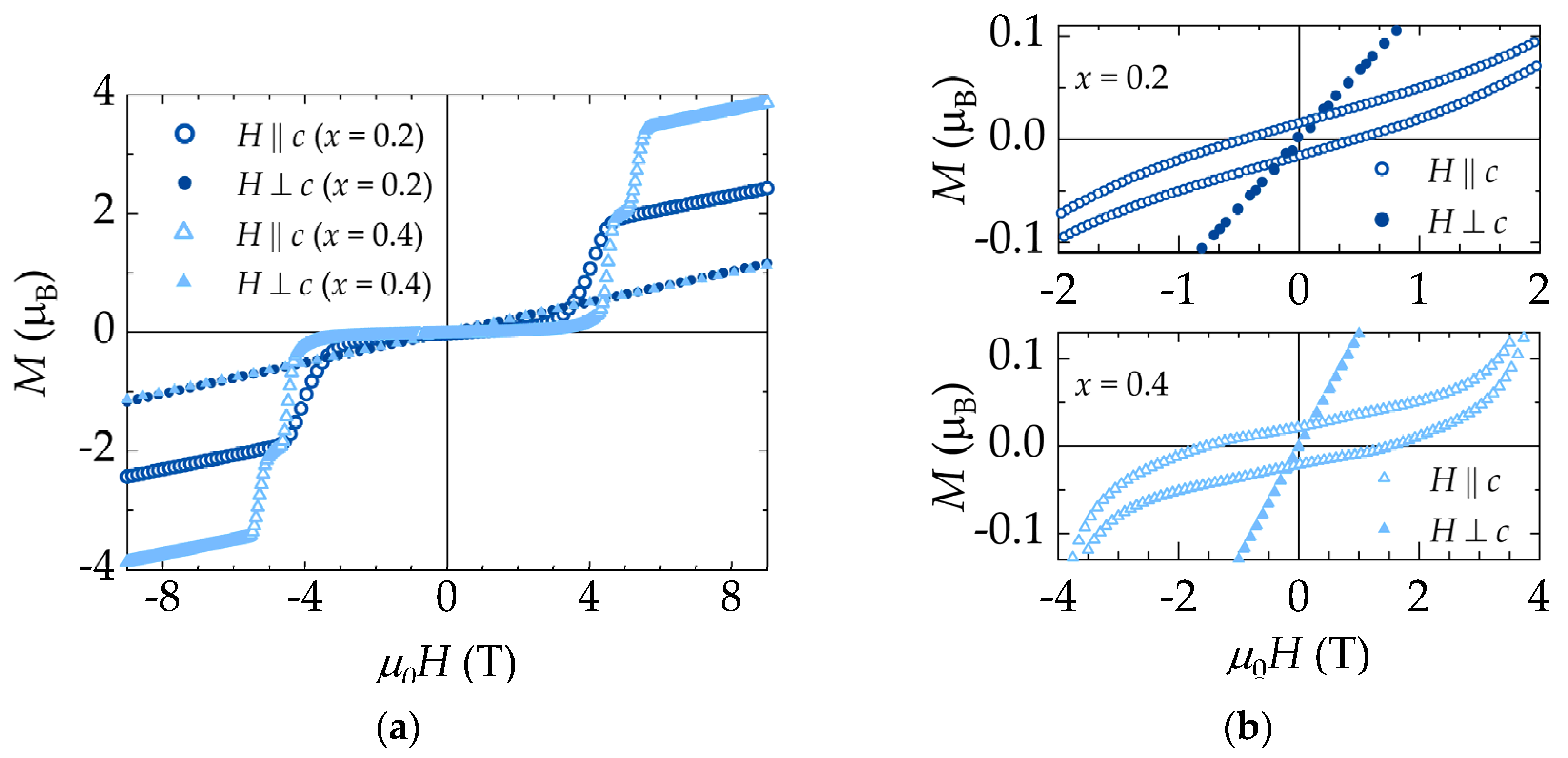
The occurrence of appreciable magnetic anisotropy in the G d 1 − x E r x B 4 series is also noticeable in the isothermal magnetization curves for x = 0.2 and 0.4 samples, as shown in Figure 9, provided that the magnitudes of magnetization differ significantly when measured along two distinct crystallographic directions. Also, a careful examination of Figure 9b clearly shows an increase in anisotropy with the Er content.
Although GdB4 and ErB4 are antiferromagnetic systems that exhibit magnetization curves without hysteresis, the x = 0.2 and 0.4 composition show anomalous remnant magnetization behavior. As shown in Figure 9b, these samples display an appreciable coercive field at 5 K, with HC values of ~ 0.46 T and ~ 1.53 T for x = 0.2 and 0.4, respectively. This anomaly is also significantly anisotropic, i.e., it is more pronounced for H applied along the c-axis. In the x = 0.2 sample, a minor hysteresis is observed along the direction perpendicular to the c-axis, with an HC value of ~ 0.025 T. In addition, for the x = 0.4 sample, the coercive field and remnant magnetization are negligibly small along the (001) plane.
As the applied magnetic field along the c-axis increases, Gd0.6Er0.4B4 displays two magnetic transitions for H ≤ 9 T, as shown in Figure 9a. The first (near 4.5 T) is suggestive of a metamagnetic transition, characterized by a magnetization plateau state occurring at M/MS = ½, where MS is the saturation magnetization of the Er3+ ions. The second transition corresponds to the full alignment of the Er3+ ions along the c-axis. The theoretical value of the saturation magnetization per Er3+ ion is M S = g J μ B = 9 μ B . Based on this value, the saturation magnetization for the Er3+ ions in the x = 0.4 sample corresponds to 3.6 μ B .
Immediately after a magnetic field of 5.6 T, the transition to the total magnetization of the system reaches a value close to 3.46 μ B . By subtracting the contribution of the Gd3+ ions, the experimental saturation magnetization corresponding to the Er3+ ions is 94% of the theoretical value. In this procedure, as a first approximation, we assume that the Gd3+ ions contribute linearly to the system's magnetization with H, corresponding to the initial slope of the virgin magnetization curve up to the considered magnetic field of 5.6 T.
Only one field-induced transition is observed for the Gd0.8Er0.2B4 composition, as shown in Figure 9a. Using the same procedure applied for the x = 0.4 composition to subtract the contribution of the Gd3+ ions, the magnetization attributed to the Er3+ ions amount to 99% of the theoretical value of the expected saturation magnetization. These results reveal that the transition to the plateau state only takes place in the x = 0.4 sample, while the transition to the field-induced paramagnetic state, corresponding to the full alignment of the magnetic moments of Er3+, occurs for both x = 0.2 and x = 0.4 compositions.
In contrast, M × H curves with field applied perpendicular to the c-axis do not show field induced transitions in fields up to 9 T, as shown in Figure 9. This finding is consistent with the specific heat data of Figure 6b, where a metamagnetic transition is detected as a second peak occurring at low temperatures for a 5 T magnetic field also applied along the c-axis. When the same magnitude of magnetic field is applied perpendicular to the c-axis, only a single maximum is observed in the Cp × T curve, corresponding to the transition to the AF state. Similar findings are observed for magnetic fields up to 9 T applied perpendicular to the c-axis (data not shown). According to studies conducted in ErB4 [9], two field-induced transitions occur for fields applied parallel and perpendicular to the c-axis. At 1.5 K, the plateau state is maintained between 2 and 4 T along the c-axis and between 11.5 and 13.0 T along the a-axis. Therefore, if these magnetic transitions exist along the direction perpendicular to the c-axis, they were not observed in our lightly Er-doped materials, as our experimental measurements were conducted up to a maximum applied magnetic field of 9 T. When comparing the M × H curves along the c-axis for Gd0.6Er0.4B4 with pure ErB4, the transition to the plateau state in the x = 0.4 sample occurs at relatively higher magnetic fields, and this state is maintained within a narrow range of 4.5 to 5.3 T.
It is interesting to note that GdB4 and TbB4 are the only members of the RB4 family that have the easy axis along the ab-plane. In the case of GdB4, Gd´s 4f shell is half filled, with L = 0, so the ions are in the s-state, and the anisotropy in the ordered phase comes mainly from the exchange interaction [23], which is small. It is suggested that this small magnetic anisotropy is the reason why no plateaus are observed in the M × H curves [24]. Therefore, the doping with Er seems to be a convenient way to induce anisotropy in the magnetic properties GdB4. Our findings suggest that 40% of substitution of Er for Gd is already enough to provoke the appearance of a plateau phase in the M × H curves.

4. Conclusions

In conclusion, we carried out a study of the thermal and magnetic properties of flux-grown G d 1 − x E r x B 4 single crystals. This study revealed detailed magnetic transitions in both x = 0.2 and 0.4 compositions, including the full alignment of Er3+ magnetic moments for magnetic field applied along the c-axis, and a metamagnetic transition corresponding to a plateau phase observed in the x = 0.4 sample.
While GdB4 and ErB4 compounds exhibit antiferromagnetic behavior with reversible magnetization isotherms and no magnetic hysteresis, the partial substitution of Er for Gd in the GdB4 lattice induced an anomalous ferromagnetic phase below the ordering temperature TN of the materials. This ferromagnetic phase exhibited significant anisotropy, with a pronounced manifestation along the c-axis. It is worth noting that the c-axis and the [110] direction correspond to the easy magnetization axes of ErB4 and GdB4 compounds, respectively.
Despite the lower Er content in the G d 1 − x E r x B 4 (x = 0.2 and 0.4) samples, we observed moderately high values for the coercive field and remnant magnetization along the c-axis, which coincides with the easy axis for ErB4. These intriguing features are likely due to the competing anisotropies. To further elucidate the origins of these interesting behavior, a comprehensive investigation of the physical properties of these single crystals is currently underway.

Author Contributions

Conceptualization, R.F.J.; formal analysis, S.H.M. and V.B.B.; investigation, S.H.M., F.A., R.F.J. and M.S.T; resources, R.F.J.; writing—original draft preparation, S.H.M. and V.B.B.; writing—review and editing, F.A., R.F.J. and M.S.T.; supervision, R.F.J.; funding acquisition, R.F.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by FAPESP (Grants No. 2013/07296–2, 2019/26141–6, 2022/02691–0, and 2022/10874–7), CNPq (Grant No. 301463/2019–0), and CAPES (Finance Code 001).

Data Availability Statement

The data presented in this study are available on request.

Acknowledgments

The authors thank the Laboratory of Crystallography, Instituto de Física, Universidade de São Paulo, Brazil, for the x-ray Laue diffraction work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Post, B.; Moskowitz, D.; Glaser, F.W. Borides of Rare Earth Metals. J. Am. Chem. Soc. 1956, 78, 1800–1802. [Google Scholar] [CrossRef]
  2. Buschow, K.H.J.; Creyghton, J.H.N. Magnetic Properties of Rare Earth Tetraborides. The Journal of Chemical Physics 1972, 57, 3910–3914. [Google Scholar] [CrossRef]
  3. Bae, J.H.; Cho, K.K.; Lee, J.W.; Han, S.H.; Cho, B.K. Magnetic Entropy Changes for the Rotating Magnetocaloric Effect in RB4 (R = Gd, Tb, Dy, Ho, Er, and Tm). Journal of Magnetism and Magnetic Materials 2023, 576, 170767. [Google Scholar] [CrossRef]
  4. Kim, J.Y.; Cho, B.K.; Han, S.H. Anisotropic Magnetic Phase Diagrams of HoB4 Single Crystal. J. Appl. Phys. 2009. [Google Scholar] [CrossRef]
  5. Ye, L.; Suzuki, T.; Checkelsky, J.G. Electronic Transport on the Shastry-Sutherland Lattice in Ising-Type Rare-Earth Tetraborides. Phys. Rev. B 2017, 95, 174405. [Google Scholar] [CrossRef]
  6. Yoshii, S.; Yamamoto, T.; Hagiwara, M.; Shigekawa, A.; Michimura, S.; Iga, F.; Takabatake, T.; Kindo, K. High-Field Magnetization of TmB4. J. Phys.: Conf. Ser. 2006, 51, 59–62. [Google Scholar] [CrossRef]
  7. Iga, F.; Shigekawa, A.; Hasegawa, Y.; Michimura, S.; Takabatake, T.; Yoshii, S.; Yamamoto, T.; Hagiwara, M.; Kindo, K. Highly Anisotropic Magnetic Phase Diagram of a 2-Dimensional Orthogonal Dimer System TmB4. Journal of Magnetism and Magnetic Materials 2007, 310, e443–e445. [Google Scholar] [CrossRef]
  8. Sriram Shastry, B.; Sutherland, B. Exact Ground State of a Quantum Mechanical Antiferromagnet. Physica B+C 1981, 108, 1069–1070. [Google Scholar] [CrossRef]
  9. Michimura, S.; Shigekawa, A.; Iga, F.; Sera, M.; Takabatake, T.; Ohoyama, K.; Okabe, Y. Magnetic Frustrations in the Shastry–Sutherland System ErB4. Physica B: Condensed Matter 2006, 378–380, 596–597. [Google Scholar] [CrossRef]
  10. Will, G.; Schäfer, W.; Pfeiffer, F.; Elf, F.; Etourneau, J. Neutron Diffraction Studies of TbB4 and ErB4. Journal of the Less Common Metals 1981, 82, 349–355. [Google Scholar] [CrossRef]
  11. Blanco, J.A.; Brown, P.J.; Stunault, A.; Katsumata, K.; Iga, F.; Michimura, S. Magnetic Structure of GdB4 from Spherical Neutron Polarimetry. Phys. Rev. B 2006, 73, 212411. [Google Scholar] [CrossRef]
  12. Fisk, Z.; Maple, M.B.; Johnston, D.C.; Woolf, L.D. Multiple Phase Transitions in Rare Earth Tetraborides at Low Temperature. Solid State Communications 1981, 39, 1189–1192. [Google Scholar] [CrossRef]
  13. Cullity, B.D.; Stock, S.R. Elements of X-Ray Diffraction, 3rd ed.; Pearson: USA, 2014; ISBN 978-1-292-04054-7. [Google Scholar]
  14. QLaue. Available online: https://sourceforge.net/projects/qlaue/ (accessed on 5 June 2023).
  15. Masunaga, S.H.; Barbeta, V.B.; Jardim, R.F.; Becerra, C.C.; Torikachvili, M.S.; Rosa, P.F.S.; Fisk, Z. Anomalous Remnant Magnetization in Dilute Antiferromagnetic Gd1-XYxB4. Phys. Rev. Mater. 2018, 2, 084415. [Google Scholar] [CrossRef]
  16. Toby, B.H. EXPGUI, a Graphical User Interface for GSAS. J Appl Cryst 2001, 34, 210–213. [Google Scholar] [CrossRef]
  17. Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst A 1976, 32, 751–767. [Google Scholar] [CrossRef]
  18. Novikov, V.V.; Mitroshenkov, N.V.; Morozov, A.V.; Matovnikov, A.V.; Avdashchenko, D.V. Heat Capacity and Thermal Expansion of Gadolinium Tetraboride at Low Temperatures. Journal of Applied Physics 2012, 111, 063907. [Google Scholar] [CrossRef]
  19. Novikov, V.V.; Мorozov, А.V.; Мatovnikov, А.V.; Мitroshenkov, N.V.; Аvdashchenko, D.V.; Kuznetsov, S.V.; Kornev, B.I.; Маrakhina, О.А.; Novikova, V.V.; Bordacheva, Е.О. The Properties of Lattice, Electronic and Magnetic Subsystems of Erbium Tetraboride Based on Calorimetric Data at Temperatures of 2–300 K. Journal of Alloys and Compounds 2013, 581, 431–434. [Google Scholar] [CrossRef]
  20. Stout, J.W.; Catalano, E. Heat Capacity of Zinc Fluoride from 11 to 300°K. Thermodynamic Functions of Zinc Fluoride. Entropy and Heat Capacity Associated with the Antiferromagnetic Ordering of Manganous Fluoride, Ferrous Fluoride, Cobaltous Fluoride, and Nickelous Fluoride. The Journal of Chemical Physics 2004, 23, 2013–2022. [Google Scholar] [CrossRef]
  21. Carlin, R.L. Magnetochemistry; Springer: Berlin, Heidelberg, 1986; ISBN 978-3-642-70735-3. [Google Scholar]
  22. Song, M.S.; Cho, K.K.; Lee, J.W.; Cho, B.K. Abnormal Field-Dependence of Magnetocaloric Effect in ErB4 and TmB4. AIP Advances 2020, 10, 025219. [Google Scholar] [CrossRef]
  23. Lovesey, S.W.; Rodríguez, J.F.; Blanco, J.A.; Brown, P.J. Phase Transitions, Noncollinear Magnetism, and Magnetoelectric Symmetry in Gadolinium Tetraboride. Phys. Rev. B 2004, 70, 172414. [Google Scholar] [CrossRef]
  24. Baranovskiy, A.; Grechnev, A. Electronic Structure and Exchange Interactions in GdB4. Journal of Magnetism and Magnetic Materials 2015, 375, 96–99. [Google Scholar] [CrossRef]
Preprints 78721 g001
Figure 1. Exchange interactions J1 and J2 between NN and NNN rare-earth (R) ions in RB4. The arrows indicate the spin projection in the ab-plane of the non-collinear magnetic structure of GdB4.
Figure 1. Exchange interactions J1 and J2 between NN and NNN rare-earth (R) ions in RB4. The arrows indicate the spin projection in the ab-plane of the non-collinear magnetic structure of GdB4.
Preprints 78721 g001
Preprints 78721 g002
Figure 2. Images of (a) Gd0.8Er0.2B4 and (b) Gd0.6Er0.4B4 single crystals grown by the flux method, placed on a 1 mm grid paper.
Figure 2. Images of (a) Gd0.8Er0.2B4 and (b) Gd0.6Er0.4B4 single crystals grown by the flux method, placed on a 1 mm grid paper.
Preprints 78721 g002
Preprints 78721 g003
Figure 3. Laue X-ray diffraction photograph and the simulated pattern showing the (001) plane for Gd0.8Er0.2B4.
Figure 3. Laue X-ray diffraction photograph and the simulated pattern showing the (001) plane for Gd0.8Er0.2B4.
Preprints 78721 g003
Preprints 78721 g004
Figure 4. Laue X-ray diffraction photograph and the simulated pattern showing the (001) plane for Gd0.6Er0.4B4.
Figure 4. Laue X-ray diffraction photograph and the simulated pattern showing the (001) plane for Gd0.6Er0.4B4.
Preprints 78721 g004
Preprints 78721 g005
Figure 5. Ambient temperature XRD patterns (symbols) for (a) Gd0.8Er0.2B4, and (b) Gd0.6Er0.4B4. Corresponding calculated patterns are shown in solid red lines and the difference between experimental and calculated intensities in solid blue lines. The inset displays an expanded view of the (001) reflection for G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4).
Figure 5. Ambient temperature XRD patterns (symbols) for (a) Gd0.8Er0.2B4, and (b) Gd0.6Er0.4B4. Corresponding calculated patterns are shown in solid red lines and the difference between experimental and calculated intensities in solid blue lines. The inset displays an expanded view of the (001) reflection for G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4).
Preprints 78721 g005
Preprints 78721 g006
Figure 6. (a) Zero-field temperature dependence of the specific heat Cp(T) for G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4); (b) Cp(T) for x = 0.4 measured in H = 0 and H = 5 T, with field applied parallel and perpendicular to the c-axis.
Figure 6. (a) Zero-field temperature dependence of the specific heat Cp(T) for G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4); (b) Cp(T) for x = 0.4 measured in H = 0 and H = 5 T, with field applied parallel and perpendicular to the c-axis.
Preprints 78721 g006
Preprints 78721 g007
Figure 7. (a) Specific heat for Gd0.6Er0.4B4, YB4, and estimated values of Cm, and CSch.; (b) Cp(T) Magnetic heat capacity for G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4). Solid lines are fits to AT α.
Figure 7. (a) Specific heat for Gd0.6Er0.4B4, YB4, and estimated values of Cm, and CSch.; (b) Cp(T) Magnetic heat capacity for G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4). Solid lines are fits to AT α.
Preprints 78721 g007
Preprints 78721 g008
Figure 8. Temperature dependence of the magnetic susceptibility for (a) Gd0.8Er0.2B4 and (b) Gd0.6Er04B4. The applied magnetic field parallel or perpendicular to the c-axis was 0.5 T. The inset in (a) shows 1/χ(T) for a field perpendicular to the c-axis, and the corresponding value of θ CW. The inset in (b) displays the Néel temperature for different Er concentrations at zero applied field (TN for x = 1.0 was obtained from Ref. [9]).
Figure 8. Temperature dependence of the magnetic susceptibility for (a) Gd0.8Er0.2B4 and (b) Gd0.6Er04B4. The applied magnetic field parallel or perpendicular to the c-axis was 0.5 T. The inset in (a) shows 1/χ(T) for a field perpendicular to the c-axis, and the corresponding value of θ CW. The inset in (b) displays the Néel temperature for different Er concentrations at zero applied field (TN for x = 1.0 was obtained from Ref. [9]).
Preprints 78721 g008
Preprints 78721 g009
Figure 9. (a) Field-dependent magnetization at 5 K for G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4) with field parallel (open symbols) and perpendicular (closed symbols) to the c-axis; (b) Expanded view of magnetization curves near H = 0 for x = 0.2 on the upper panel and for x = 0.4 on the lower panel.
Figure 9. (a) Field-dependent magnetization at 5 K for G d 1 − x E r x B 4 (x = 0, 0.2, and 0.4) with field parallel (open symbols) and perpendicular (closed symbols) to the c-axis; (b) Expanded view of magnetization curves near H = 0 for x = 0.2 on the upper panel and for x = 0.4 on the lower panel.
Preprints 78721 g009
Table 1. Crystal structure data and refinement for G d 1 − x E r x B 4 (x = 0, 0.2, 0.4, and 1.0).
Table 1. Crystal structure data and refinement for G d 1 − x E r x B 4 (x = 0, 0.2, 0.4, and 1.0).
x a , b Å c Å χ 2
0 1 7.1421(2) 4.0467(2) 1.7
0.2 7.1298(2) 4.0377(2) 2.9
0.4 7.1133(7) 4.0264(5) 4.1
1.0 2 7.071(3) 4.000(1) −
1 Data from Ref. [15]. 2 Data from Ref. [10].
Table 2. Calculated and experimental values of effective magnetic moment ( μ e f f ) and Curie-Weiss constant ( θ C W ) for G d 1 − x E r x B 4 (x = 0, 0.2, 0.4, and 1.0). μ e f f c a l c values are calculated using equation (5) and μ e f f e x p values are obtained from the fittings of ( 1 / χ ) vs T data to Equation (6).
Table 2. Calculated and experimental values of effective magnetic moment ( μ e f f ) and Curie-Weiss constant ( θ C W ) for G d 1 − x E r x B 4 (x = 0, 0.2, 0.4, and 1.0). μ e f f c a l c values are calculated using equation (5) and μ e f f e x p values are obtained from the fittings of ( 1 / χ ) vs T data to Equation (6).
x μ e f f c a l c μ B μ e f f e x p μ B
( H ∥ c )		 θ C W K
( H ∥ c )		 μ e f f e x p μ B
( H ⊥ c )		 θ C W K
( H ⊥ c )
0 7.94 7.98 -70 7.94 -66
0.2 8.29 8.20 -39 8.26 -57
0.4 8.63 8.34 -15 8.72 -48
1.0 9.58 9.27* +11.24* 9.50* -23.26*
*Data from Ref. [22].
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated