Prerpints.org logo
Preprint
Article

Numerical Investigation of a Combustible Polymer in a Rectangular Stockpile: A Spectral Approach

Altmetrics

Downloads

81

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 July 2023

Posted:

07 July 2023

You are already at the latest version

Alerts
Abstract
Despite the immense application of combustion in reactive materials, one of the challenges people are facing globally is the auto-ignition of such materials, resulting in fire and explosion hazards if proper measures are not considered. To avoid this unfortunate occurrence, a mathematical model describing the thermal decomposition of combustible polymer material in a rectangular stockpile is formulated. A nonlinear momentum equation is provided with the assumption that the combustible polymer follows Carreau constitutive relation. The chemical reaction of the polymer material is assumed exothermic; therefore, Arrhenius’s kinetic theory is considered in the energy balance equation. The bivariate spectral local linearization Scheme (BSLLS) is utilized to provide a numerical solution for the dimensionless equations governing the problem. The obtained results are validated by the collocation weighted residual method (CWRM) and a good agreement is achieved. Dimensionless velocity, temperature, and thermal stability results are presented and explained comprehensively with suitable applications.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

In engineering and industry, the burning of combustible materials in a slab is important for storing cellulosic materials, solids combustion, refuse cremation, heavy oil recovery, and other processes [1,2,3]. Polymers can undergo combustion and release a large amount of energy, which can then be used for transportation, generating electric power, and providing heat for various applications. Compared to other energy sources like solar cells, wind generators, and turbines, polymers are quite inexpensive. However, there are some difficulties with polymer burning, such as fire ignitions brought on by a combination of human negligence and the physical characteristics of hydrocarbon polymers. This has caused extensive property destruction and claimed the lives of an unknown number of people. From this perspective, several authors have been prompted to study the causes of fire ignition in the combustion process and how it can be controlled.
Drysdale [4] described ignition as the process of initiating a fast exothermic reaction, which then propagates and causes changes in the materials involved, generating temperatures greatly in excess of ambient. The same author distinguished between two kinds of ignition: piloted ignition, in which a flammable mixture is ignited by a pilot such as an electrical spark or an autonomous flame, and auto-ignition, in which flaming develops spontaneously within the mixture. Shi and Chew [5] studied polymers’ response to fire under auto-ignition conditions within a cone shape calorimeter and concluded that C O and C O 2 production process for polymers is a two-step reaction. In the first step reaction, C O and other flammable substances are generated following Arrhenius law. The second stage is the oxidation reaction of C O in the presence of air. The whole process is expressed as follows
{ S t e p 1 : P o l y m e r + O 2 → H 2 O + C O + o t h e r s   p r o d u c t S t e p 2 : C O + 0.5 O 2 → C O 2 .
Shi and Chew also discovered that the C O and C O 2 emissions from flaming combustions are greater than those from non-flaming combustion.
Combustion of polyethylene and polyvinyl chloride has been examined in [6,7,8]. These investigations used experimental settings, allowing researchers to acquire more information and factors for pyrolysis, ignition, and combustion. Geschwindner et al [9] used a mix of high-speed-planar laser-induced fluorescence of the HO radical (OH-PLIF) and a thermal decomposition analysis to examine the combustion of micrometer-sized polypropylene (PP) particles. They found that the highest density of flame-retardant polymer particles decreases during ignition and the early stage of burning. Lohrer et al [10,11] investigated the effects of physical factors like material wetness, atmospheric humidity, and concentration of oxygen on the combustion of reactive materials and discovered that water in the reactive material increases auto-ignition.
Some mathematical theoretical methods that are less expensive and faster than experimental approaches have been implemented in the literature to explain the auto-ignition of combustible materials in a stockpile. For instance, a one-step combustion process of heat transfer in a spherical channel was investigated in [12,13]. According to their reports, the system maintains stability as heat is lost to the atmosphere. In addition, enhancement in the chemical reaction rate leads to an increase in heat generation in the stockpile, resulting in a quick auto-ignition. Lebelo et al [14,15,16] examined the two-step thermal decomposition of combustible materials in a sphere, and they found that elevation in the two-step kinetic parameter diminishes the heat loss rate at the sphere’s surface, which in turn speeds up auto-ignition.
In the above-reviewed literature, the authors did not consider flow behaviour in their studies. However, an increase or decrease in flow speed contributes to the heat transfer performance of combustible materials. It has been discovered in the literature that the Carreau fluid model well describes the flow behavior of polymeric solution due to the inclusion of very small or very large shear rates in the model [17]. Several studies on Carreau fluid constitutive relations have been documented in the literature. For instance, Siska et al. [18] examined the terminal velocity of non-spherical particles falling through a Carreau fluid and concluded that the Carreau fluid model can well characterize the rheology of various polymeric solutions, such as 1% methylcellulose tylose in glycerol solution and 3% hydroxyethylcellulose Natrosol HHX in glycerol solution. [19] reported an intriguing study on the entropy production of Carreau fluid in the presence of infinite shear rate viscosity. Also, the behavior of a Carreau fluid flow past a stretching sheet is widely analysed in [20,21]. In addition, the peristaltic movement of a Carreau fluid is extensively studied in [22,23,24]. For more on the Carreau fluid model with different configurations, see [25,26,27].
Motivated by the reviewed literature in [12,13,14,22,28], this study focuses on the investigation of the thermal decomposition of Carreau fluid in a rectangular stockpile with variable thermophysical properties. The authors believe that this present study has not been reported in the literature. The outcome of this study would be found useful by engineers, dealing with the combustion of polymers, to determine conditions necessary for explosion and how to control them. The rest of the article is structured as follows: Mathematical model for the unsteady fully developed flow and temperature of the polymer is presented in section two; Section three deals with the application of BSLLM on the dimensionless initial-boundary value problem; In section four, extensive discussion of the obtained findings is provided, and concluding remarks are given in section five.

2. Mathematical Analysis

A transient laminar flow of a reactive incompressible Carreau fluid material in a combustible stockpile positioned at a distance 2 h apart is considered. x ^ − a x i s is parallel to the flow direction and y ^ − a x i s traversed to the flow direction. Initially, the fluid is assumed fully developed in the stockpile of temperature, T 0 , and the material’s viscosity and thermal conductivity are assumed as μ = μ 0 and κ = κ 0 respectively. At time t ^ > 0 , the combustion process begins, and the material properties become temperature dependent, μ = μ ( T ) and κ = κ ( T ) . We also assumed that the means of heat loss to the environment is mainly by radiation and convection. The influence of density variation with temperature is approximated following Boussinesque approximation. The equations governing the momentum and energy balance under the assumptions above are [14,15,16,20,26]:
ρ ∂ u ^ ∂ t ^ = − ∂ P ^ ∂ x ^ + ∂ ∂ y ^ μ ( T ⁡ ) 1 + Γ 2 ∂ u ^ ∂ y ^ 2 n − 1 2 ∂ u ^ ∂ y ^ + ρ g β T − T 0 ,
ρ c p ∂ T ∂ t ^ = ∂ ∂ y ^ κ ( T ⁡ ) ∂ T ∂ y ^ + μ ( T ⁡ ) 1 + Γ 2 ∂ u ^ ∂ y ^ 2 n − 1 2 ∂ u ^ ∂ y ^ 2 + Q 1 A 1 C 1 e − E 1 R T + Q 2 A 2 C 2 e − E 2 R T − ε σ T 4 − T 0 4 ,
With the initial-boundary conditions
u ^ y ^ , 0 = 0 , ​ ​ ​ ​ ​ ​ ​ ​ T y ^ , 0 = T 0 ∂ u ^ ∂ y ^ 0 , ​ ​ ​ ​ ​ t ^ = 0 , ∂ T ∂ y ^ 0 , ​ ​ ​ ​ ​ t ^ = 0 , f o r t ^ > 0 u ^ h , ⁡ ​ ​ ​ ​ ​ t ^ = 0 , − κ ( T ) ∂ T ∂ y ^ ( h , t ^ ) = h t [ T ( h , t ^ ) − T a ] , f o r t ^ > 0
Here, u ^ − axial velocity, P ^ − modified pressure, T − absolute temperature, T a − ambient temperature, T 0 − initial temperature of the stockpile, μ 0 − material’s dynamic viscosity at temperature T 0 , κ 0 − material’s thermal conductivity at temperature T 0 , ρ − material’s density, Q 1 , Q 2 − first and second step heat of reaction, A 1 , A 2 − first and second step rate constant, C 1 , C 2 − first and second step reactant’s concentration, α 0 , α 1 − heat transfer coefficients, ε − stockpile’s emissivity ( 0 < ε < 1 ) , σ − Stefan-Boltzmann constant, β − volumetric coefficient, g − gravitational acceleration, h t − coefficient of heat transfer, Γ − time constant, n − dimensionless power law index. n < 1 represents shear-thinning fluids, n = 0 represents Newtonian fluids, and n > 1 is for shear-thickening fluids The variable viscosity and thermal conductivity, μ ( T ) and κ ( T ) are given respectively:
μ ̄ ( T ⁡ ) = μ 0 e − b 1 ( T ⁡ − T 0 ⁡ )   and   κ ̄ ( T ⁡ ) = κ 0 e − b 2 ( T ⁡ − T 0 ⁡ ) ,
where b 1 and b 2 are dynamic viscosity and thermal conductivity variation parameters. We introduce the below dimensionless parameters into equations (1)-(3).
y = y ̄ h , x ⁡ = x ̄ h , t = ν t ̄ h 2 , u = u ^ h ν , μ = μ ^ μ 0 , κ = κ ^ κ 0 , ν = μ 0 ρ , P = P ^ h 2 ν 2 , θ = E 1 T − T 0 R T 0 2 , θ a = E 1 T a − T 0 R T 0 2 , β 1 = b 1 R T 0 2 E 1 , β 2 = b 2 R T 0 2 E 1 , W e = Γ ν h 2 , Pr ⁡ = μ 0 c p κ 0 , A = − ∂ P ^ ∂ x ̄ , λ = Q 1 E 1 A 1 h 2 C 1 e − E 1 R T 0 T 0 2 R κ 0 , G r = g β R T 0 2 h 3 ρ 2 E 1 μ 0 2 , ϵ 1 = R T 0 E 1 , ϵ 2 = E 2 E 1 , V d = μ 0 3 e E 1 R T 0 ρ 2 Q 1 A 1 h 4 C 1 , R a = ε σ h 2 E 1 T 0 2 R κ 0 , ω = Q 2 A 2 E 2 Q 1 A 1 E 1 e E 1 − E 2 R T 0 , B i = h h t κ 0 .
The following dimensionless equations are then obtained:
∂ u ∂ t = A + ∂ ∂ y e − β 1 θ 1 + W e 2 ∂ u ∂ y 2 n − 1 2 ∂ u ∂ y + G r θ ,
Pr ⁡ ∂ θ ∂ t = ∂ ∂ y e − β 2 θ ∂ θ ∂ y + λ e θ 1 + ϵ 1 θ + ω e ϵ 2 θ 1 + ϵ 1 θ + V d e − β 1 θ 1 + W e 2 ∂ u ∂ y 2 n − 1 2 ∂ u ∂ y 2 − R a ϵ 1 θ + 1 4 − 1 ,
u y , 0 = 0 , ​ ​ ​ ​ ​ ​ ​ ​ θ y , 0 = 0 , ∂ u ∂ y 0 , ​ ​ ​ ​ ​ t = 0 , ∂ θ ∂ y 0 , ​ ​ ​ ​ ​ t = 0 , f o r t > 0 u 1 , ​ ​ ​ ​ ​ t = 0 , ∂ θ ∂ y ( 1 , t ) = − B i e β 2 θ [ θ ( 1 , t ) − θ a ] , f o r t > 0
where β 1 , β 2 , W e , Pr , ⁡ λ , ϵ 1 , ϵ 2 , A , Gr , V d ⁡ , R a , ω , B i , θ a are respectively variable viscosity parameter, variable thermal conductivity parameter, material parameter, Prandtl number, Frank-Kamenetskii parameter, activation energy parameter, activation energy ratio parameter, pressure gradient, Buoyancy parameter, viscous heating parameter, radiation parameter, two-step exothermic reaction parameter, Biot number, ambient temperature parameter.
In the next section, a robust numerical method, Bivariate spectral local linearisation scheme (BSLLS) is adopted to provide a solution for dimensionless equations (6)-(8).

3. Method of Solution

In this section, BSLLS is implemented to provide numerical solution for Equations (6)-(8) as outlined in [29,30]. For further studies on the convergence analysis of BSLLS, see [31]. To adopt BSLLS, the nonlinear equations (6) , (7), and nonlinear convective boundary conditions (8) are respectively represented by F , Θ , and B c .
F = A + ∂ ∂ y e − β 1 θ 1 + W e 2 ∂ u ∂ y 2 n − 1 2 ∂ u ∂ y + G r θ − ∂ u ∂ t ,
Θ = ∂ ∂ y e − β 2 θ ∂ θ ∂ y + λ e θ 1 + ϵ 1 θ + ω e ϵ 2 θ 1 + ϵ 1 θ + V d e − β 1 θ 1 + W e 2 ∂ u ∂ y 2 n − 1 2 ∂ u ∂ y 2                   − R a ϵ 1 θ + 1 4 − 1 − Pr ⁡ ∂ θ ∂ t ,
B c = ∂ θ ∂ y ( 1 , t ) + B i e β 2 θ [ θ ( 1 , t ) − θ a ]
The iteration technique (Quasi-linearization method) is applied independently on Equation (9)-(11) to arrive at
α 0 , r ( y , t ) ∂ 2 u r + 1 ∂ y 2 + α 1 , r ( y , t ) ∂ u r + 1 ∂ y + α 2 , r ( y , t ) ∂ u r + 1 ∂ t = R 1 , r ( y , t ) ,
β 0 , r ( y , t ) ∂ 2 θ r + 1 ∂ y 2 + β 1 , r ( y , t ) ∂ θ r + 1 ∂ y + β 2 , r ( y , t ) θ r + 1 + β 3 , r ( y , t ) ∂ θ r + 1 ∂ t = R 2 , r ( y , t ) ,
c 0 , r ( 1 , t ) ∂ θ r + 1 ∂ y + c 1 , r ( 1 , t ) θ r + 1 = d r ( 1 , t ) ,
where,
α 0 , r ( y , t ) = ∂ F ∂ ∂ 2 u ∂ y 2 = e − β 1 θ 1 + n W e 2 ∂ u ∂ y 2 1 + W e 2 ∂ u ∂ y 2 n − 3 2 , α 1 , r ( y , t ) = ∂ F ∂ ∂ u ∂ y = e − β 1 θ n − 1 W e 2 ∂ u ∂ y 3 + n W e 2 ∂ u ∂ y 2 ∂ 2 u ∂ y 2 − β 1 1 + W e 2 ∂ u ∂ y 2 1 + n W e 2 ∂ u ∂ y 2 ∂ θ ∂ y 1 + W e 2 ∂ u ∂ y 2 n − 5 2 , α 2 , r ( y , t ) = ∂ F ∂ ∂ u ∂ t = − 1 , β 0 , r ( y , t ) = ∂ T ∂ ∂ 2 θ ∂ y 2 = e − β 2 θ , β 1 , r ( y , t ) = ∂ T ∂ ∂ θ ∂ y = − 2 β 2 e − β 2 θ ∂ θ ∂ y , β 2 , r ( y , t ) = ∂ T ∂ θ = λ β 2 V d ∂ u ∂ y 2 − e − β 2 θ ϵ 1 θ + 1 2 W e 2 ∂ u ∂ y 2 + 1 n − 1 2 + ω ϵ 2 e ϵ 2 θ ϵ 1 θ + 1 + e θ ϵ 1 θ + 1 ϵ 1 θ + 1 2 + β 2 2 e − β 2 θ ∂ θ ∂ y 2 − β 2 e − β 2 θ ∂ 2 θ ∂ y 2 − 4 Ra ϵ 1 ϵ 1 θ + 1 3 , β 3 , r ( y , t ) = ∂ T ∂ ∂ θ ∂ t = − Pr , ⁡ c 0 , r ( 1 , t ) = ∂ B c ∂ ∂ θ ∂ y = 1 , c 1 , r ( 1 , t ) = ∂ B c ∂ θ = β 2 B i θ r ( 1 , t ) + B i e β 2 θ r ( 1 , t ) − β 2 B i θ a e β 2 θ r ( 1 , t ) , d r ( 1 , t ) = c 0 , r ( 1 , t ) ∂ θ r ∂ y + c 1 , r ( 1 , t ) θ r − B c r ( 1 , t ) , R 1 , r ( y , t ) = α 0 , r ( y , t ) ∂ 2 u r ∂ y 2 + α 1 , r ( y , t ) ∂ u r ∂ y + α 2 , r ( y , t ) ∂ u r ∂ t − F r ( y , t ) , R 2 , r ( y , t ) = β 0 , r ( y , t ) ∂ 2 θ r ∂ y 2 + β 1 , r ( y , t ) ∂ θ r ∂ y + β 2 , r ( y , t ) θ r + β 3 , r ( y , t ) ∂ θ r ∂ t − Θ r ( y , t ) .
The next step is to transform the physical domains t ∈ [ 0 , T ] and y ∈ [ 0 , 1 ] respectively into domains τ ∈ [ − 1 , 1 ] and x ∈ [ − 1 , 1 ] using transformations t = T ( τ + 1 ) 2 and y = ( x + 1 ) 2 ,
with collocation points
x i = c o s ( π i N x ) i = 0 N x and τ j = c o s ( π j N τ ) j = 0 N τ .
Assumed that solutions for u ( τ , x ) and θ ( τ , x ) in the form of bivariate Lagrange’s interpolating polynomials are defined as:
u ( x , τ ) ≈ ∑ p = 0 N y ∑ q = 0 N t u ( x i , τ j ) L p ( x ) L q ( τ ) , θ ( x , τ ) ≈ ∑ p = 0 N y ∑ q = 0 N t θ ( x i , τ j ) L p ( x ) L q ( τ ) ,
where function L p ( x ) represents Lagrange cardinal polynomial of the Chebyshev-Gaus-Lobatto grid points
L p ( x ) = ∏ p = 0 p ≠ i N x x − x i x p − x i ,
with L p ( x i ) = δ i p = { 0 , i ≠ p 1 , i = p .
The function L q ( τ ) is defined similarly. The derivative values at Chebyshev-Gaus-Lobatto points ( x i , τ j ) are computed as follows:
∂ r u ∂ x r ( x i , τ j ) = 2 r ∑ p = 0 N x D i , p r u ( x p , τ j ) = D r u j , ∂ u ∂ τ ( x i , τ j ) = 2 T ∑ q = 0 N τ d j , q u ( x i , τ q ) = 2 T ∑ q = 0 N τ d j , q u q , ∂ r θ ∂ x r ( x i , τ j ) = 2 r ∑ p = 0 N x D i , p r θ ( x p , τ j ) = D r θ j ,
∂ θ ∂ τ ( x i , τ j ) = 2 T ∑ q = 0 N τ d j , q θ ( x i , τ q ) = 2 T ∑ q = 0 N τ d j , q θ q ,
where,
r is the order of the derivative, D r = 2 r D i , p r and d ^ j , q = 2 T d j , q   are Chebyshev differentiation matrices ( N x + 1 ) × ( N x + 1 ) and ( N τ + 1 ) × ( N τ + 1 ) respectively. u j and θ j are defined as
u j = [ u ( x 0 , τ j ) , u ( x 1 , τ j ) , u ( x 2 , τ j ) , … , u ( x N x , τ j ) ] T , f o r j = 0,1 , 2 , … , N τ , θ j = [ θ ( x 0 , τ j ) , θ ( x 1 , τ j ) , θ ( x 2 , τ j ) , . . . , θ ( x N x , τ j ) ] T , f o r j = 0,1 , 2 , . . . , N τ ,
with superscript T denotes transpose. Substituting Eq. (17) and (18) into (12) and (13) yield
α 0 , r ( x , τ j ) D 2 u r + 1 , j + α 1 , r ( x , τ j ) D u r + 1 , j + α 2 , r ( x , τ j ) ∑ q = 0 N τ d ^ j , q u r + 1 , q = R 1 , r ( x , τ j ) , β 0 , r ( x , τ j ) D 2 θ r + 1 , j + β 1 , r ( x , τ j ) D θ r + 1 , j + β 2 , r ( x , τ j ) I + β 3 , r ( x , τ j ) ∑ q = 0 N τ d ^ j , q θ r + 1 , q = R 2 , r ( x , τ j ) ,
where, α k , r ( x , τ j )   ( k = 0 , 1 , 2 ) = ( α k , r ( x 0 , τ j ) ⋱ α k , r ( x N x , τ j ) ) , β k , r ( x , τ j )   ( k = 0 , 1 , 2 , 3 ) = ( β k , r ( x 0 , τ j ) ⋱ β k , r ( x N x , τ j ) ) ,
R 1 , r ( x , τ j ) = α 0 , r ( x , τ j ) D 2 u r , j + α 1 , r ( x , τ j ) D u r , j + α 2 , r ( x , τ j ) ∑ q = 0 N τ d ^ j , q u r , q − F r ( x , τ j ) , R 2 , r ( x , τ j ) = β 0 , r ( x , τ j ) D 2 θ r , j + β 1 , r ( x , τ j ) D θ r , j + β 2 , r ( x , τ j ) θ r , j + β 3 , r ( x , τ j ) ∑ q = 0 N τ d ^ j , q θ r , q − Θ r ( x , τ j ) , and I is an identity matrix. Applying spectral collocation on boundary conditions (8) and convective boundary condition (14) we have:
∑ p = 0 N x 2 D N x , p u r + 1 ( x p , τ j ) = 0 ,     u r + 1 ( x 0 , τ j ) = 0 , ∑ p = 0 N x 2 D N x , p θ r + 1 ( x p , τ j ) = 0 ,     c 0 , r ( x 0 , τ j ) ∑ p = 0 N x 2 D 0 , p θ r + 1 ( x p , τ j ) + c 1 , r ( x 0 , τ j ) θ r + 1 ( x 0 , τ j ) = d r ( x 0 , τ j ) . Imposing boundary conditions on Equation (19) for j = 0 , 1 , ... , N τ − 1 , we obtain the following N τ ( N x + 1 ) × N τ ( N x + 1 ) system of matrices
A 1 ( 0,0 ) A 1 ( 0,1 ) … A 1 ( 0 , N τ − 1 ) A 1 ( 1,0 ) A 1 ( 1,1 ) … A 1 ( 1 , N τ − 1 ) ⋮ ⋮ ⋮ ⋮ A 1 ( N τ − 1,0 ) A 1 ( N τ − 1,1 ) … A 1 ( N τ − 1 , N τ − 1 ) u r + 1,0 u r + 1,1 ⋮ u r + 1 , N τ − 1 = R 1 ( x , 0 ) R 1 ( x , 1 ) ⋮ R 1 ( x , N τ − 1 ) , A 2 ( 0,0 ) A 2 ( 0,1 ) … A 2 ( 0 , N τ − 1 ) A 2 ( 1,0 ) A 2 ( 1,1 ) … A 2 ( 1 , N τ − 1 ) ⋮ ⋮ ⋮ ⋮ A 2 ( N τ − 1,0 ) A 2 ( N τ − 1,1 ) … A 2 ( N τ − 1 , N τ − 1 ) θ r + 1,0 θ r + 1,1 ⋮ θ r + 1 , N τ − 1 = R 2 ( x , 0 ) R 2 ( x , 1 ) ⋮ R 2 ( x , N τ − 1 ) ,
with
A 1 ( j , j ) = α 0 , r ( x , τ j ) D 2 + α 1 , r ( x , τ j ) D + α 2 , r ( x , τ j ) d ^ j , j I = , j = 0,1 , ⋯ , N τ − 1 , A 1 ( j , i ) = α 2 , r ( x , τ j ) d ^ j , i I , w h e n j ≠ i , R 1 ( x , τ j ) = R 1 , r ( x , τ j ) − α 2 , r ( x , τ j ) d ^ j , N τ u r + 1 , N τ ,   f o r   j = 0,1 , ⋯ , N τ − 1 , A 2 ( j , j ) = β 0 , r ( x , τ j ) D 2 + β 1 , r ( x , τ j ) D + β 2 , r ( x , τ j ) I + β 3 , r ( x , τ j ) d ^ j , j I ,   j = 0,1 , ⋯ , N τ − 1 , A 2 ( j , i ) = β 3 , r ( x , τ j ) d ^ j , i ,   w h e n   j ≠ i , R 2 ( x , τ j ) = R 2 , r ( x , τ j ) − β 3 , r ( x , τ j ) d ^ j , N τ θ r + 1 , N τ ,   f o r   j = 0,1 , ⋯ , N τ − 1 ,
The vector u r + 1 , N τ and θ r + 1 , N τ correspond to the initial condition given in Equation (8). Matrices (20) are solved iteratively until suitable results are obtained.

3.1. Convergence Analysis

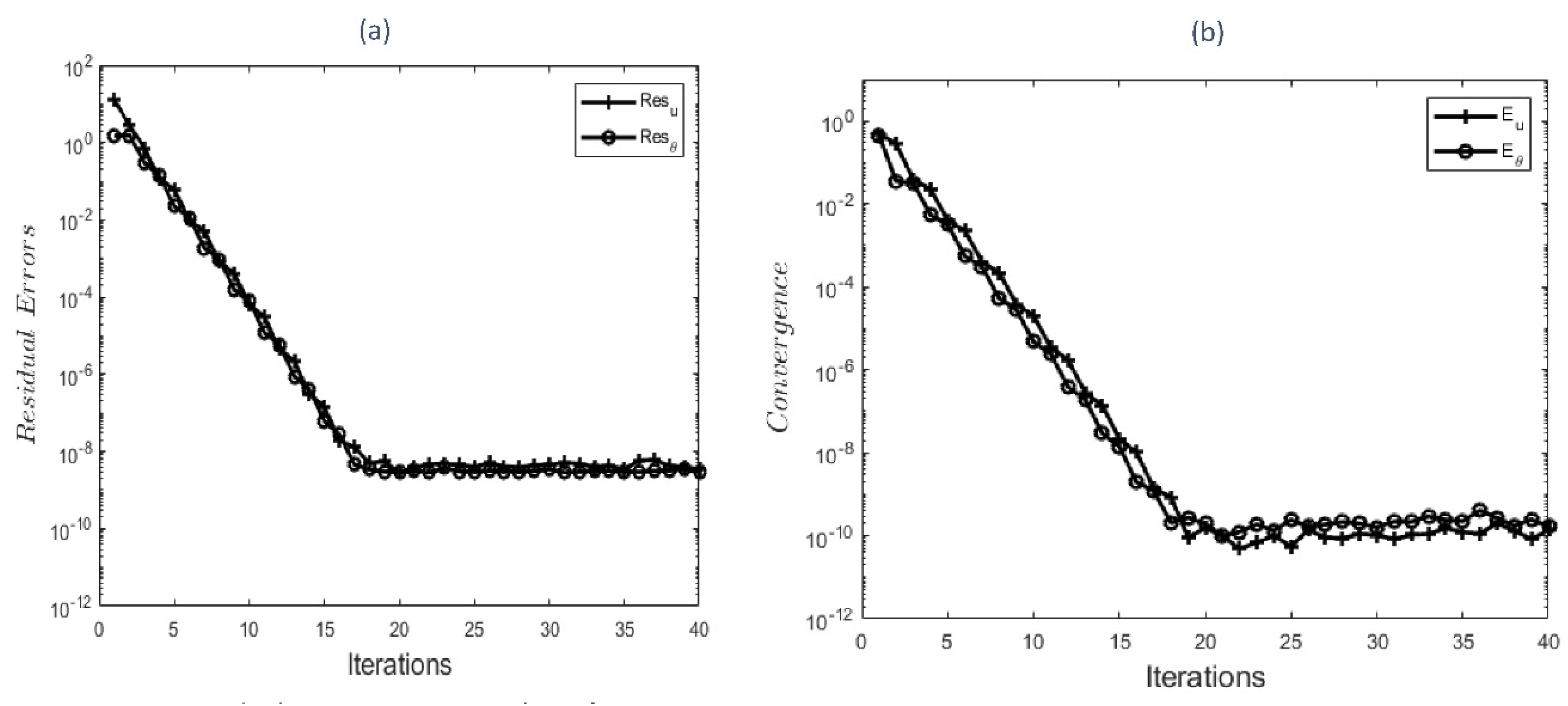
The convergence of BSLLS is evaluated by considering the error norms between two successive iterations. Error norms are defined as
E u = max 0 < i < N t ‖ u r + 1 , i − u r , i ‖ , E θ = max 0 < i < N t ‖ θ r + 1 , i − θ r , i ‖ ,
E u and E θ decrease swiftly as the number of iterations increases (see Figure 1b). This shows that BSLLS converges within a few iterations. Also, residual error norms are computed to show the accuracy of BSLLS. Residual error norms are given as
R u = max 0 < i < N t ‖ ∂ u ( F ) ‖ , R θ = max 0 < i < N t ‖ ∂ θ ( Θ ) ‖ ,
where ∂ u and ∂ θ are corresponding nonlinear partial differential equations (9) and (10) respectively. Figure 1a depicts residual error R u and R θ against the number of iterations. Residual errors are found to decrease rapidly with an increasing number of iterations.

4. Results and Discussion

In this section, we employed the parameter values, n = 0.5 ,   W e = 0.5 ,   A = 1 ,   β 1 = 0.1 ,   β 2 = 0.1 ,   λ = 0.1 ,   ϵ 1 = 0.1 ,     ϵ 2 = 0.1 ,   ω = 1 ,   R a = 0.1 ,   Pr = 10 ,   G r = 1 ,   V d = 0.5 ,     θ a = 0.1 ,   A = 1 , T = 120 , as default values, unless otherwise stated in graphs and tables. The results obtained by BSLLS are validated with the ones obtained using the collocation weighted residual method (see Table 1) and a good agreement is achieved.

4.1. Transient profiles for velocity and temperature

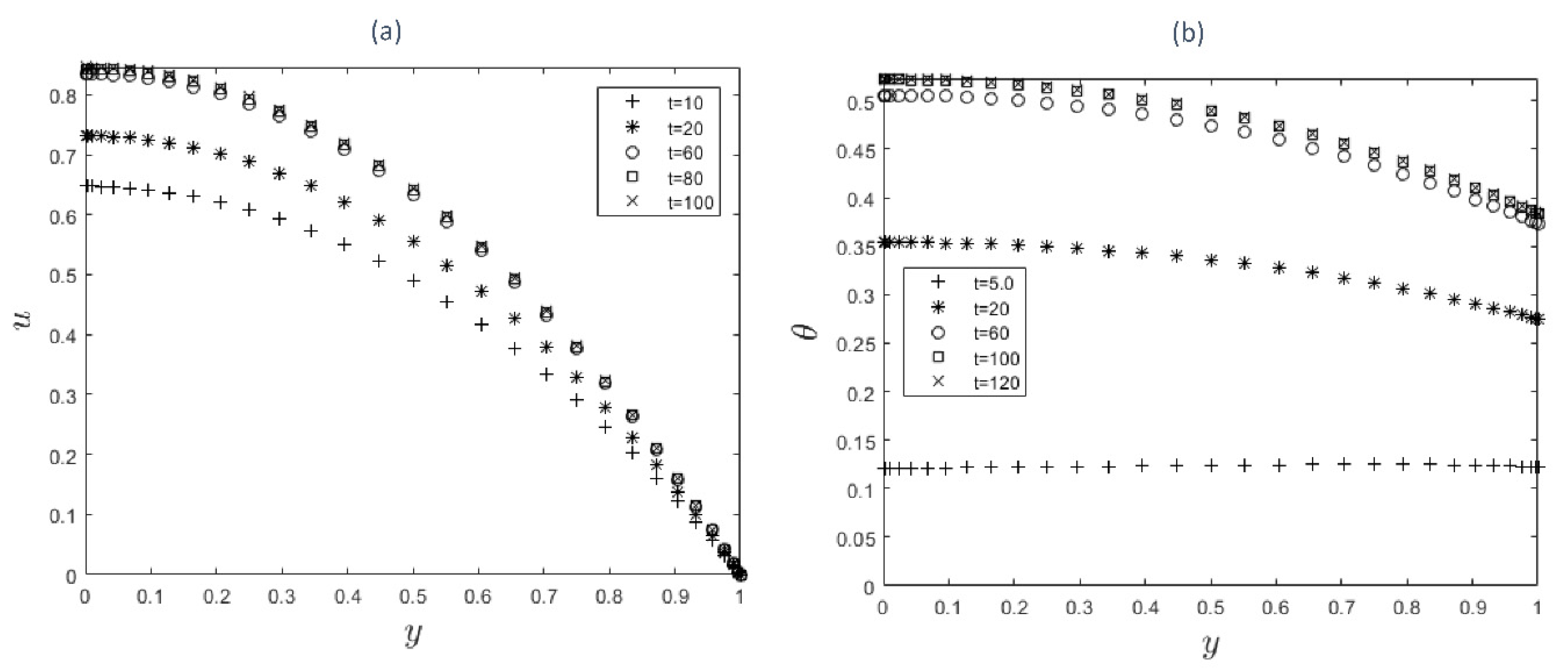
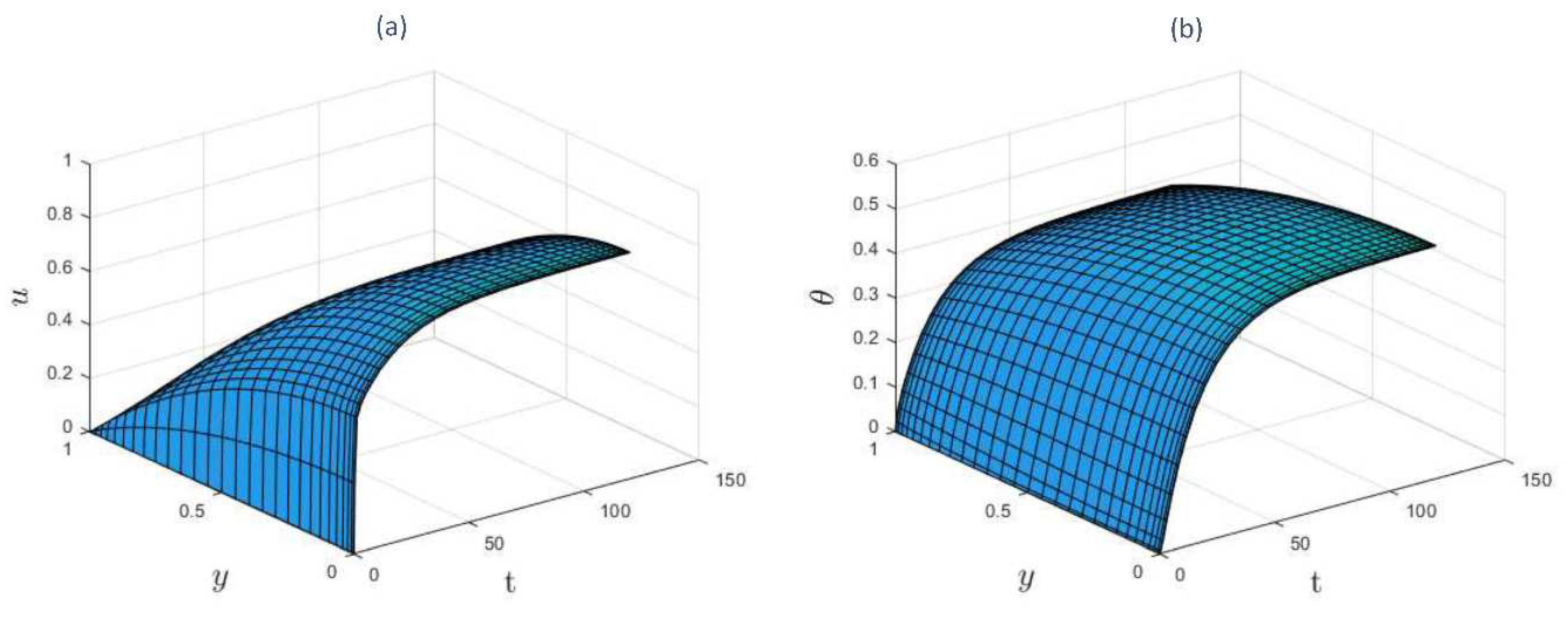
Figures 2a to 3b show the time development of the velocity and temperature profiles. As time passes, velocity (see Figure 2a) and temperature (see Figure 2b) profiles rise until they reach steady state maximum values. Furthermore, the velocity profile achieves a steady state sooner the han temperature profile. This is to be expected since velocity acts as a source of heat for the combustion and hence increases the temperature profile.

4.2. Solution blow-up profile

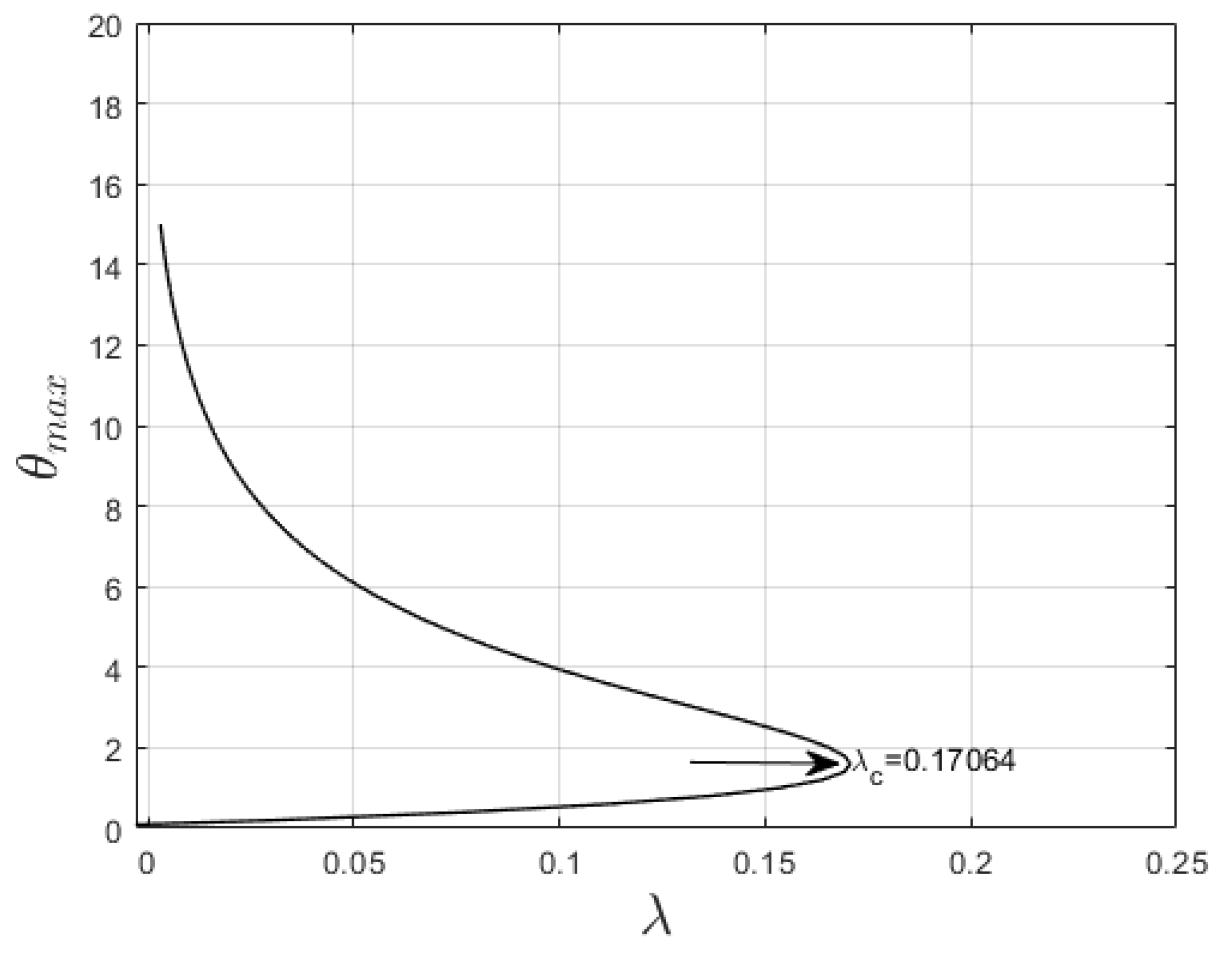
The plot of maximum temperature, ( θ ( 0 ) ) versus reaction rate, λ is provided in Figure 4 to examine the thermal criticality condition of the system. The critical value of Frank-Kamenetskii parameter, λ c is computed at steady state (when combustion is independent of time) to explain auto-ignition during the combustion process. In thermal explosion theory, the solution for Eqn. (10), at steady state, is finite for λ between interval 0 and λ c as depicted in Figure 4. Auto-ignition is then defined at the upper limit of the interval, λ c , and a real solution does not exist when λ > λ c .
To prevent or control spontaneous ignition, we examine the impact of thermophysical parameters on the thermal criticality in Table 2. An improvement in the values of parameters such as power law index ( n ) , radiation ( R a ) , and Biot number ( B i ) enhances thermal criticality. This implies that these factors are important in reducing auto-ignition. In other words, for thermal stability to be maintained in the combustion process, the values of n , R a , and B i should be made very high. However, lower values should be kept for parameters β 1 , β 2 and W e to achieve thermal stability.

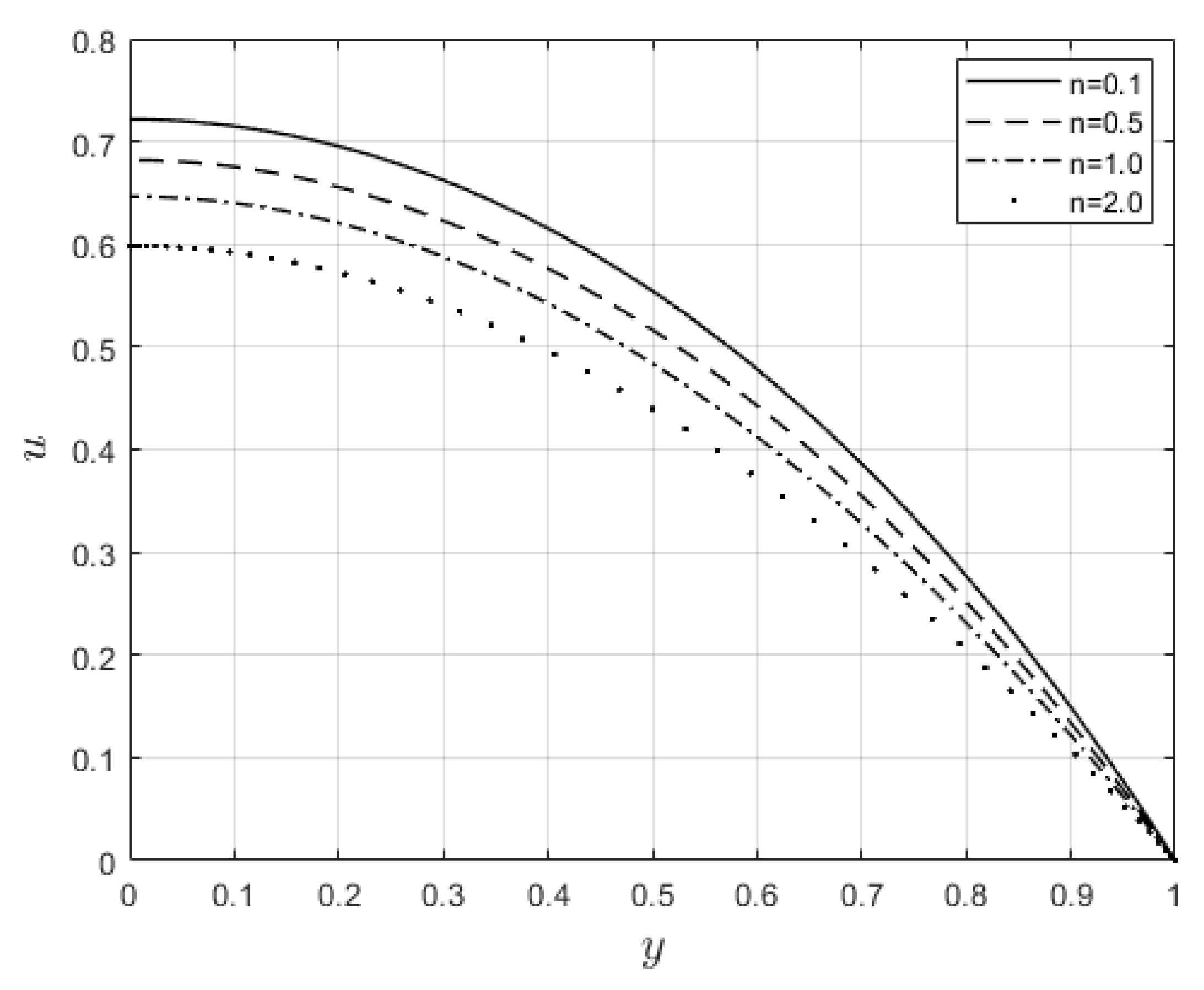
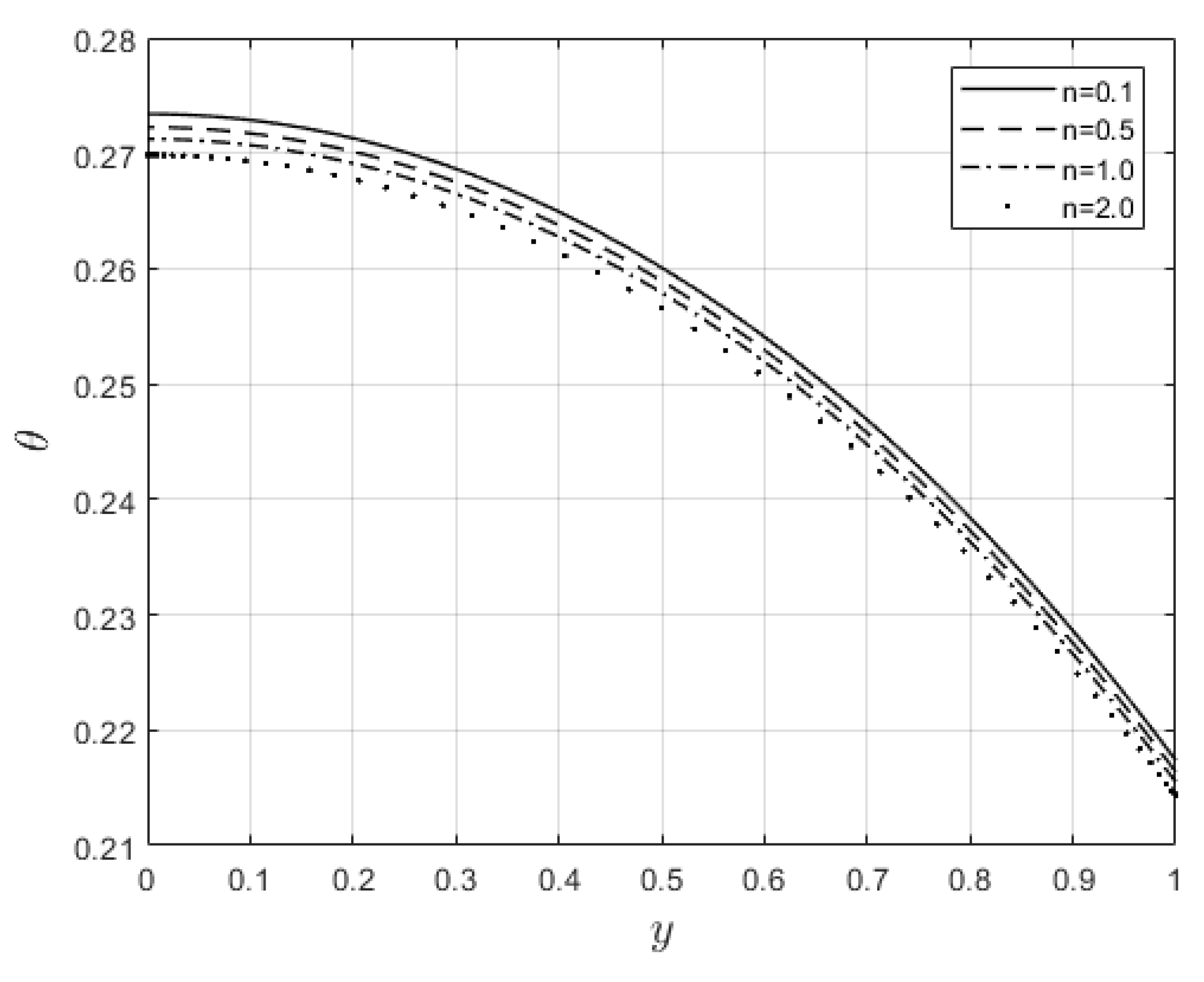
4.3. Velocity and temperature profiles’ dependence on flow parameters

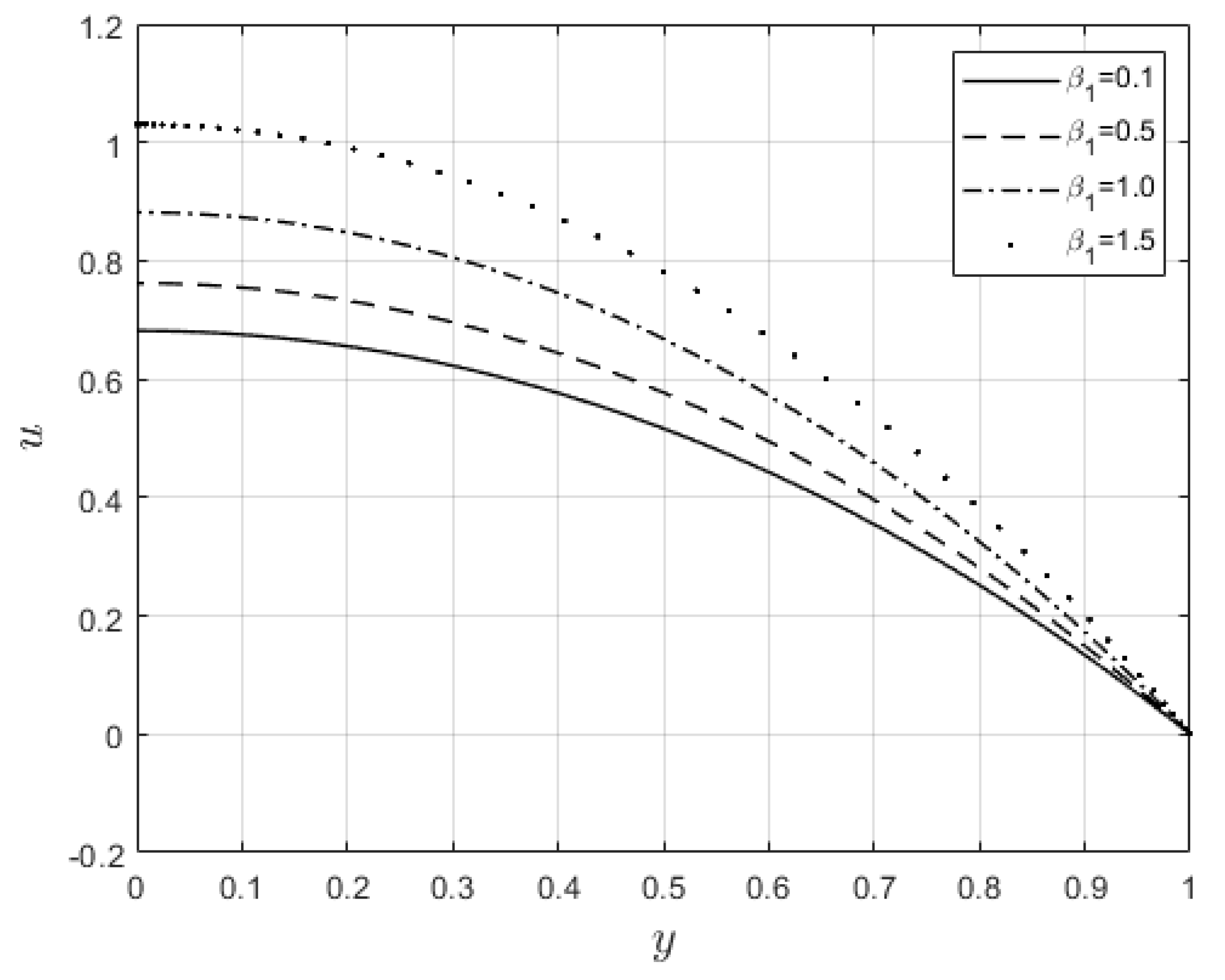
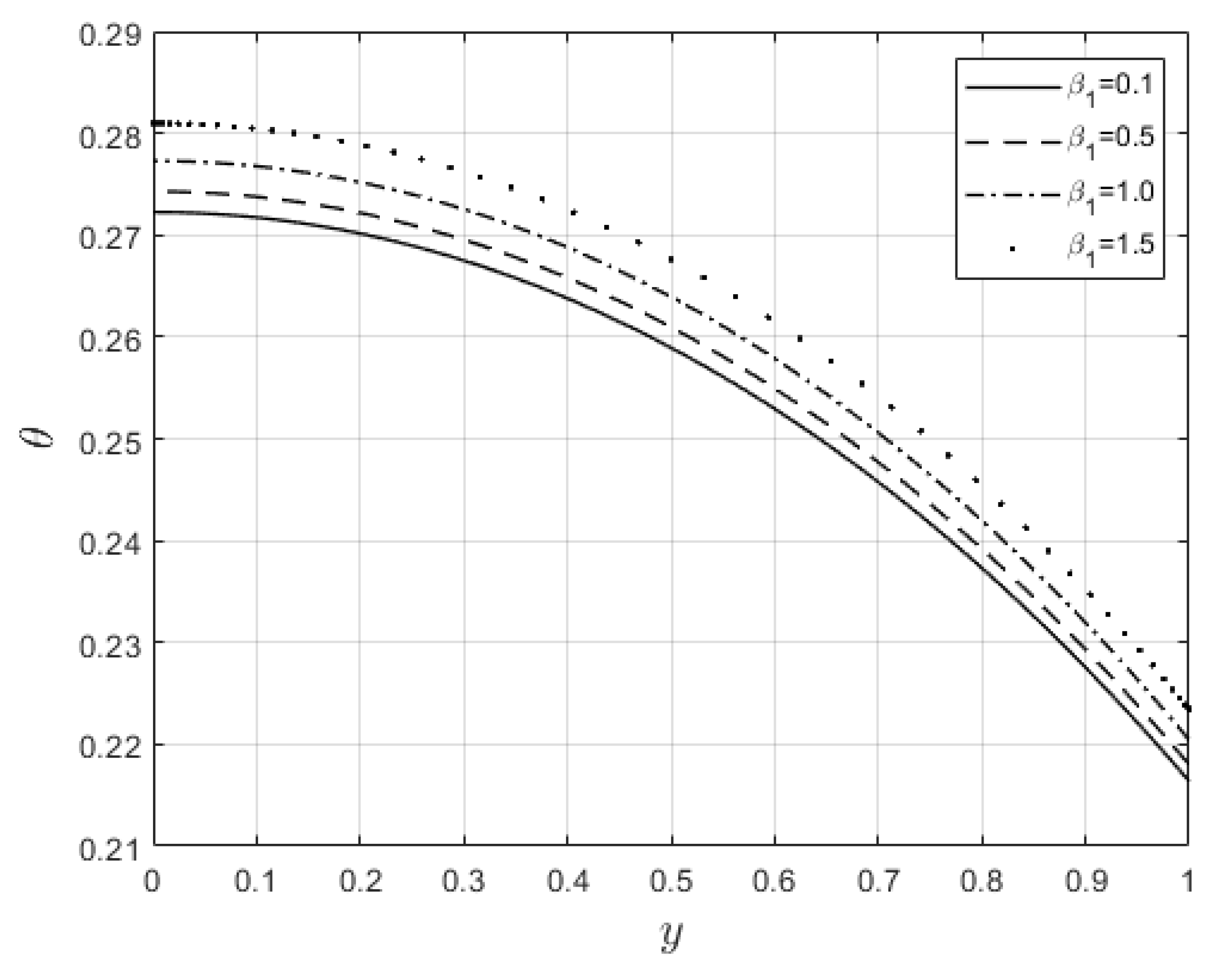
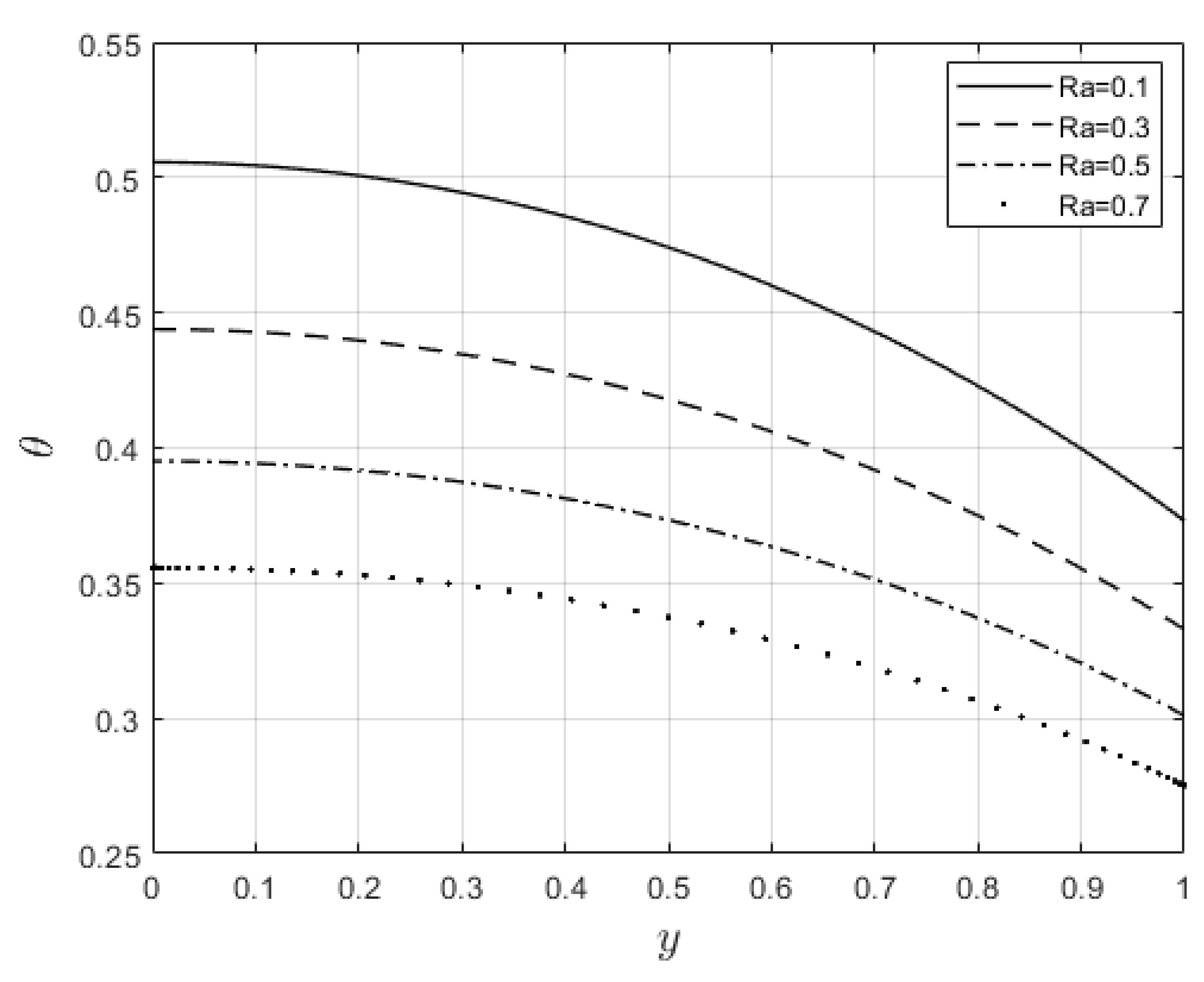
Figure 5 and Figure 6 depict the impacts of W e on velocity and temperature profiles respectively. Both profiles are elevated as the W e values increase. This is ascribed to the fact that when W e increases the fluid becomes thinner, and the resistance force to the flow decreases, hence the velocity profile increases. Furthermore, internal heat generation, because of viscous term, is high when W e increases. This leads to an enhancement in the temperature profile. 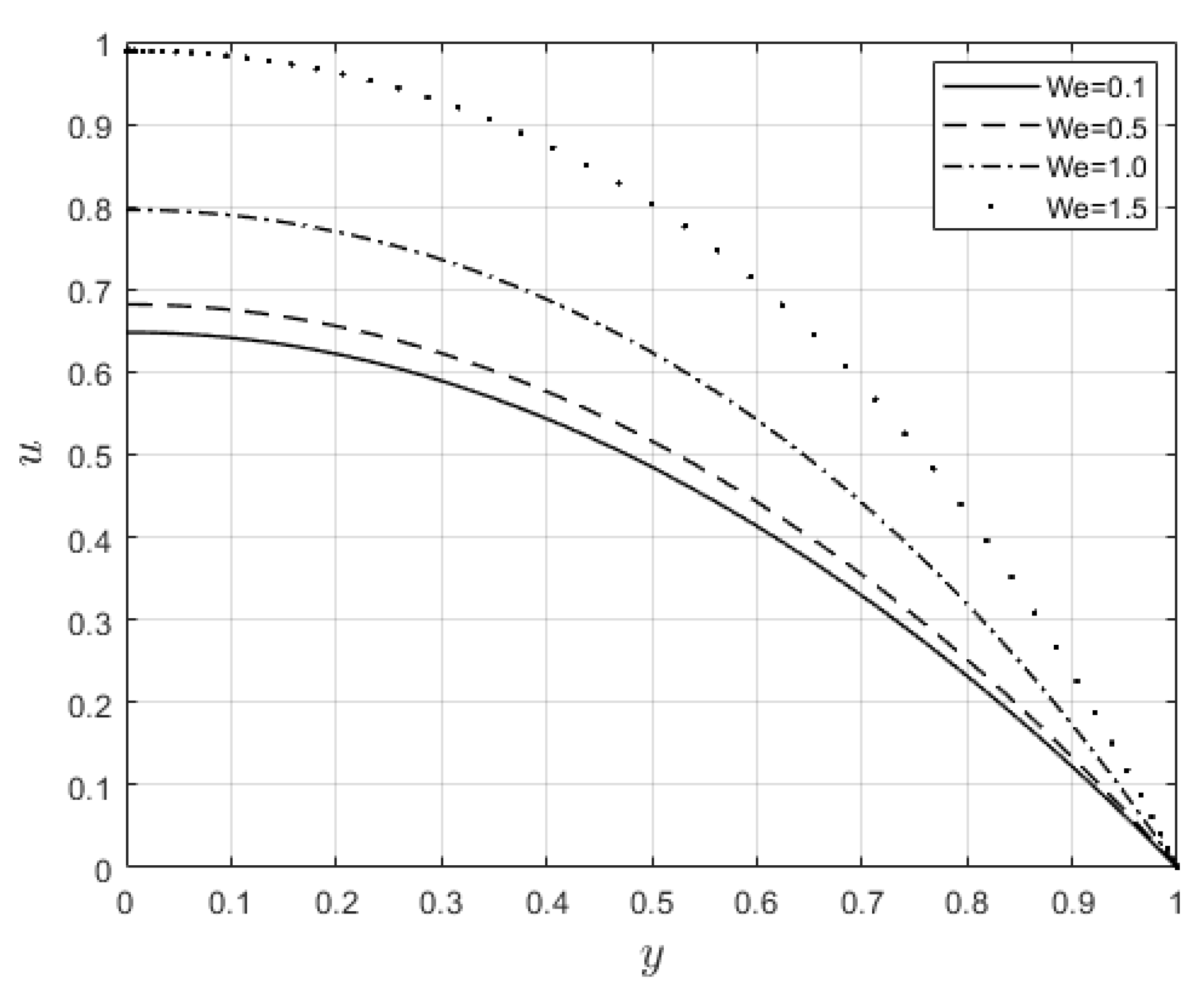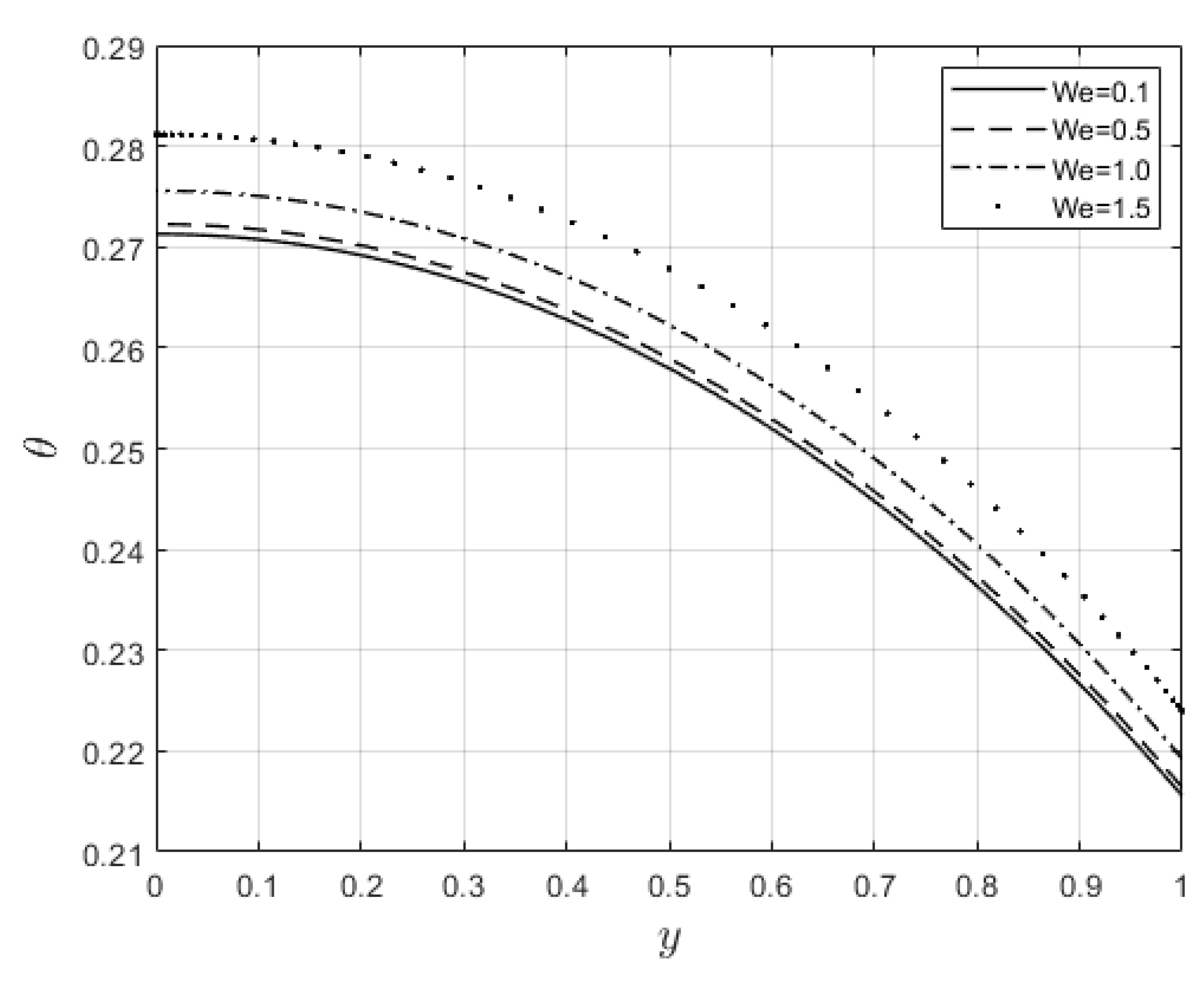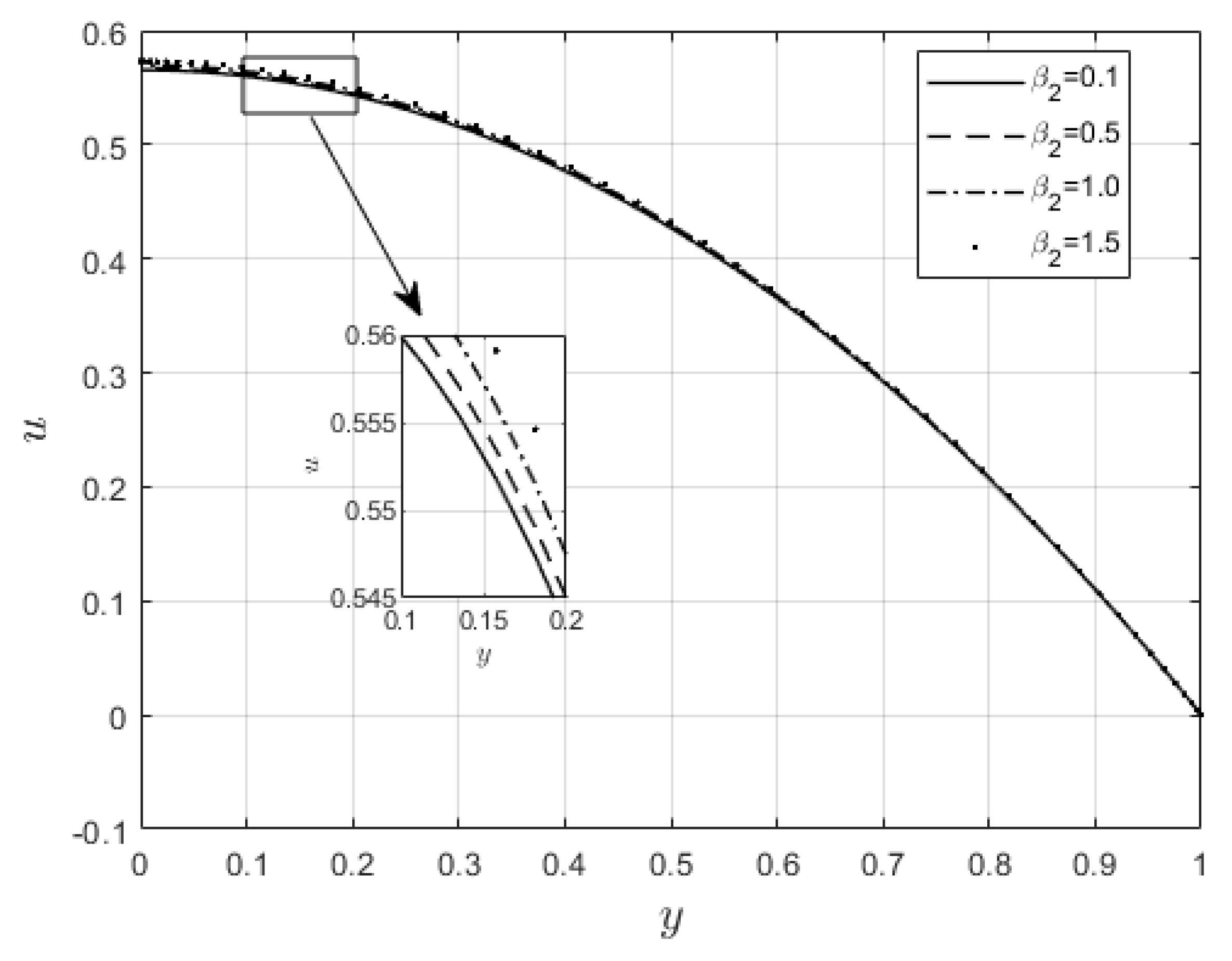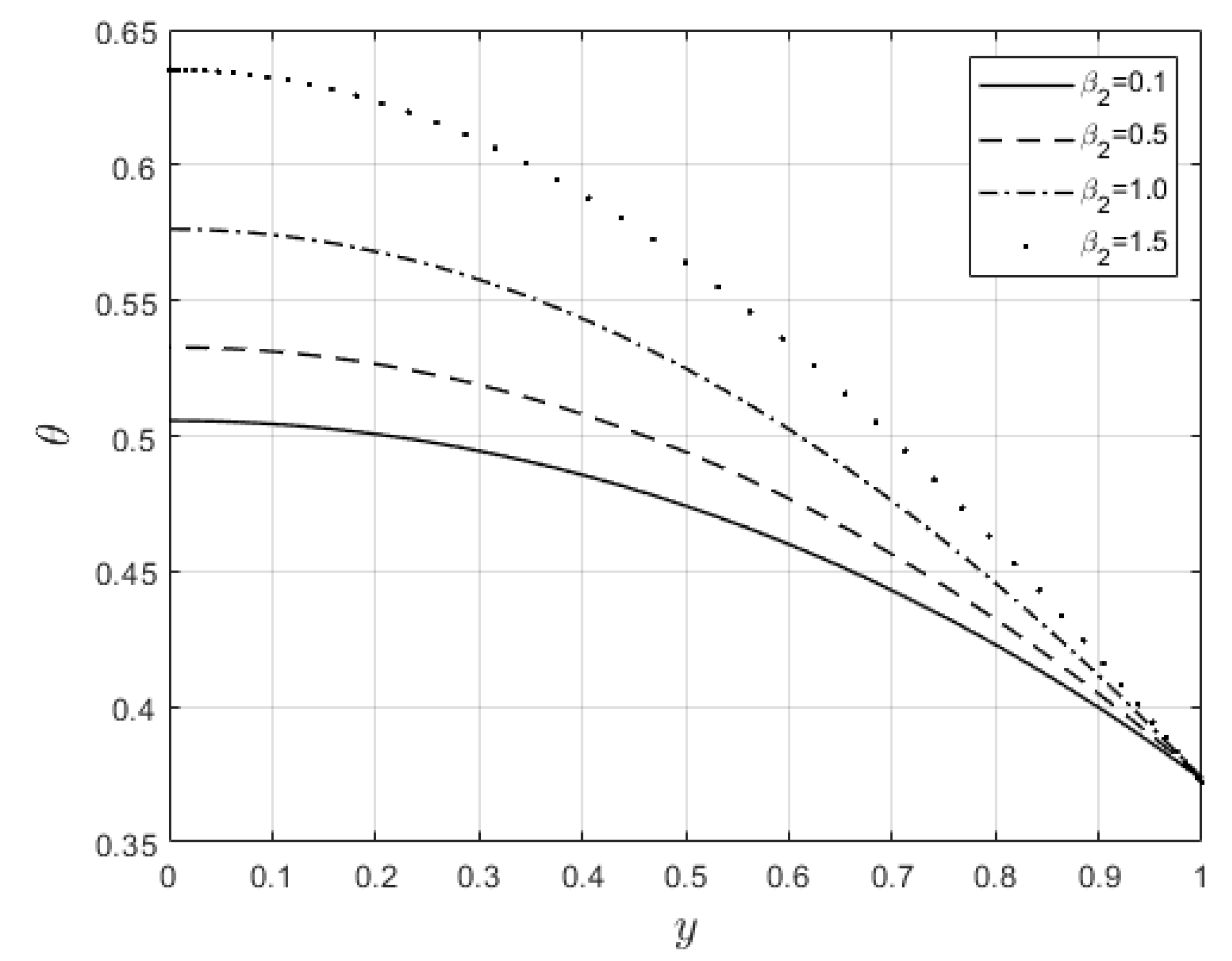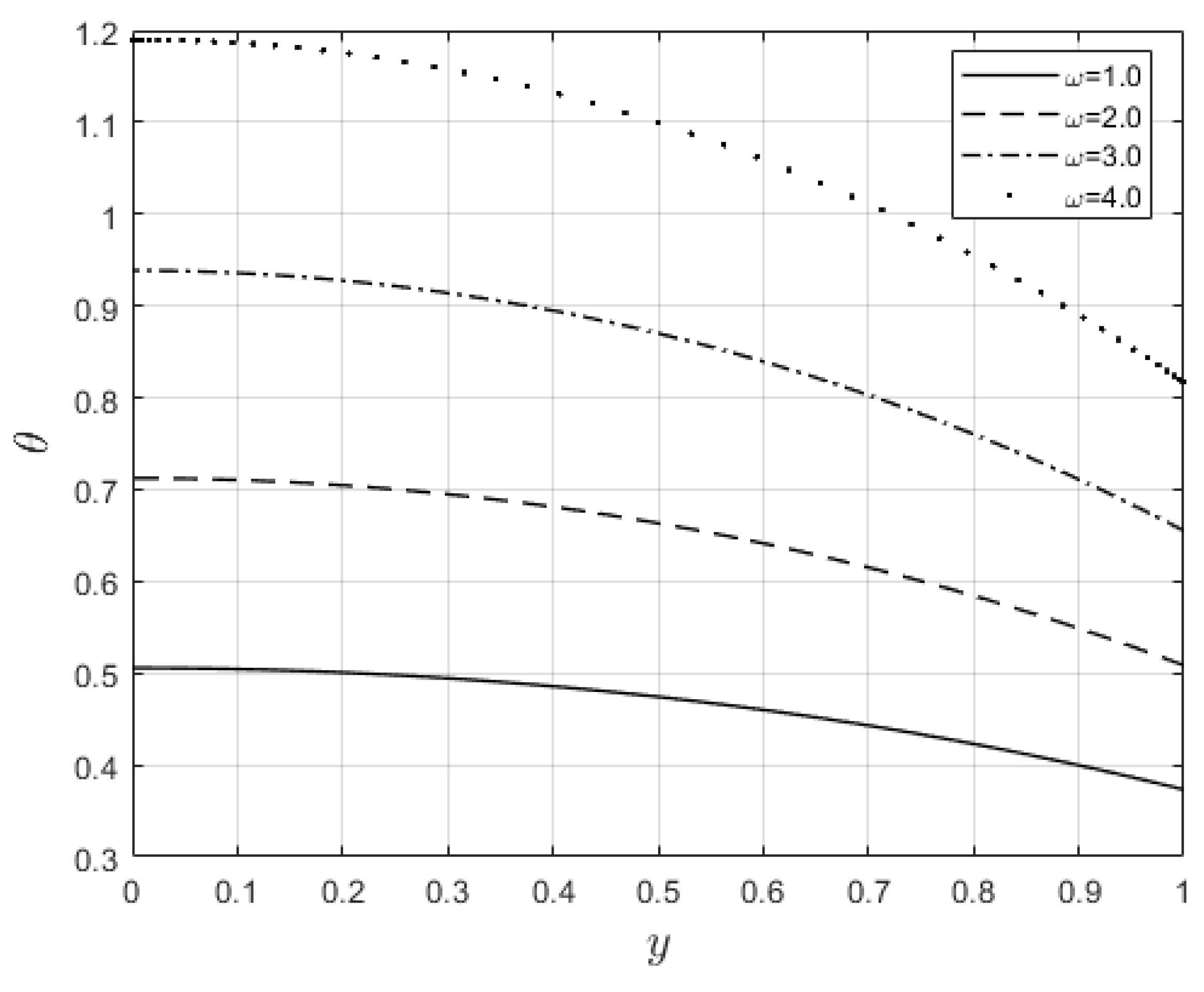Figure 7 and Figure 8 show the power law index’s, n , effect on the velocity and temperature distributions, respectively. The velocity distribution decreases with increasing n values. When n > 1 , the resistance force to the flow for shear thickening fluids becomes maximal, and the velocity profile decreases (see Figure 7). A decrease in fluid speed results in a decrease in viscous heating, and the temperature profile reduces significantly (see Figure 8).
Figures 9 & 10 examine the behavior of velocity and temperature distributions subjected to variable viscosity parameter, β 1 . The velocity profile seems elevated with increasing values of β 1 as observed in Figure 9. The reason for this is that fluid viscosity reduces as β 1 increases, leading to an enhancement in the velocity profile. An increase in the velocity profile naturally enhances heat source term in the energy equation, resulting in an elevation in temperature profile. Variable thermal conductivity’s, β 2 , impact on the magnitude of velocity and temperature is explained in Figure 11 & 12 respectively. An increase in the values of β 2 increases temperature profile (see Figure 12). This is attributed to the fact that, as the values of β 2 increase, the thermal conductivity term e − β 2 θ reduces. This leads to the slow random movement of fluid molecules and thus facilitates heat transfer through the fluid and consequently enhances temperature profile. The significant temperature rises in response to β 2 means that the fluid viscosity is reduced, and the flow speed appreciated (see Figure 11). 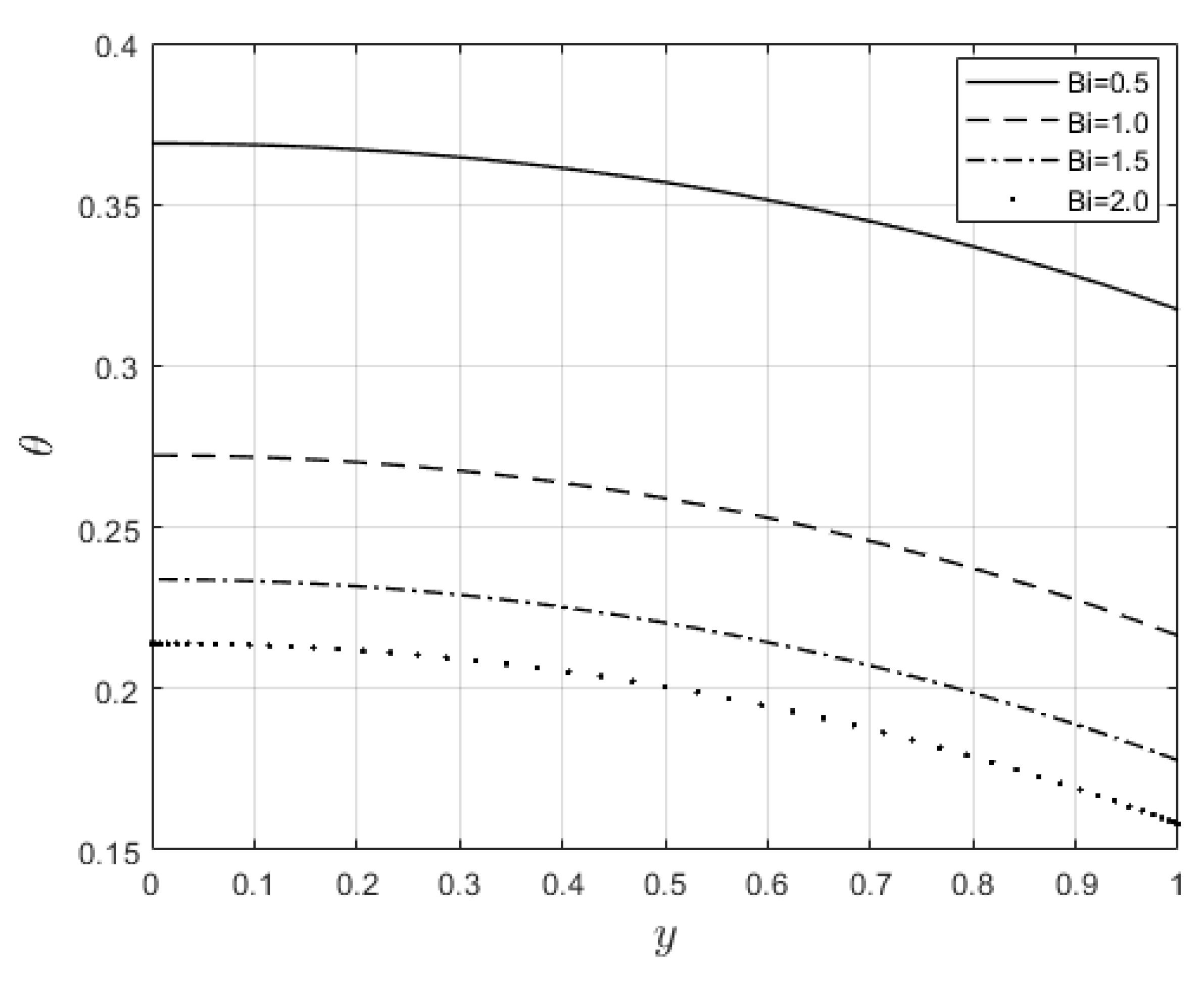Figure 13 depicts the effect of radiation parameter, R a on the fluid temperature. It is observed that the temperature profile reduces as R a values rise. This indicates that more heat exits the stockpile through radiation and thus reduces the fluid temperature profile. The same scenario is seen in Figure 14 as the temperature profile reduces with increasing Biot number, B i , because more heat escapes the stockpile through the walls. Enhancement in temperature profile is observed in Figure 15 as two-step parameter, ω , values increase. This is due to extra heating created by higher values of ω .

5. Concluding Remarks

This article considers the combustion of polymer material in a rectangular stockpile. The rheology of the polymer is assumed to follow the Carreau fluid constitutive relation. The spectral local linearization method is implemented to provide a numerical solution for the problem. The impacts of various thermokinetic factors on the flow and thermal behaviors were examined. From the obtained results, it has been found that some parameters W e ,   B i ,   β 2 ,   a n d   ω improve the combustion process since the temperature profiles increase as the values of these parameters increase. This may speed up thermal ignition and thus lead to an explosion. The opposite scenario was observed as the values of n ,   R a ,   a n d   B i increase. This slows down chemical reaction and thus minimizes the combustion process.

Data Availability Statement

No data associated in this manuscript.

References

  1. 1. Q. Xiong and S. Kong, Modelling effect of interphase transport coefficients on biomass pyrolysis in fluidized beds, Power Technology, 262, 96-105, 2014.
  2. Q. Xiong, S. Kong and Passalacqua, Development of a generalized numerical frame work for simulating biomass fast pyrolysis in fluidized-bed reactors, Chemical Engineering Science, 99,305-313, 2013.
  3. Z. Tan, G. Su and J. Su, Improved lumped models for combined convective and radiative cooling of a wall, Applied Thermal Engineering, 29,2439-2443, 2009.
  4. D. Drysdale, Ignition: The initiation of flaming combustion, In: An introduction to fire dynamics, (Third Edition), Wiley, 225-275, [Chapter 6].
  5. L. Shi and M. Y. L. Chew, A review of fire processes modeling of combustible materials under external heat flux, Fuel, 106, 30-50, 2013.
  6. Sener and E. Demirhan, The investigation of using magnesium hydroxide as a flame retardant in the cable insulation material by cross-linked polyethylene, Mater. Des., 29, 1376-1379, 2008.
  7. T. Gong, Q. Xie and X. Huang, Fire behaviors of flame-retardant cable part decomposition, swelling and spontaneous ignition, Fire Saf. J., 95, 113-121, 2018.
  8. Q. Xie, T. Gong and X. Huang, Fire zone diagram of flame-retardant cables: Ignition and upward flame spread, Fire Technol., 57, 2643-2659, 2021.
  9. C. Geschwindner, D. Goedderz, T. Li, J. Koser, et al., Investigation of flame retarded Polypropylene by high-speed planar laser-induced fluorescence of OH radicals combined with a thermal decomposition analysis, Exp. Fluids, 61, 30, 2020.
  10. C. Lohrer, U. Krause and J. Steinbach, Self-ignition of combustible bulk materials under various ambient conditions, Inst. Che.Eng. Trans IChemE, 83, 145-150, 2000.
  11. C. Lohrer, M. Schmidt and U. Krause, A study on the influence of liquid water and water vapor on the self-ignition of lignite coal-experiments and numerical simulations J. Prev. Process. Ind., 18, 167-177, 2005.
  12. R. S. Lebelo, Thermal stability investigation in a reactive sphere of combustible material, Adv. Math. Phys., Article ID 9384541, 2016.
  13. R. S. Lebelo, O. D. Makinde and T. Chinyoka, Thermal decomposition analysis in a sphere of combustible materials, Adv. Mech. Eng., 9(2), 1-14, 2017.
  14. R. S. Lebelo, A. T. Adeosun, J. A. Gbadeyan, S. O. Akindeinde, On the heat transfer stability for a convective reactive material of variable thermal conductivity in a sphere, Gorteria Journal, 34(11), 62-74, 2021.
  15. R. S. Lebelo et al., Two-step low temperature oxidation for thermal stability analysis of a combustible sphere, Alexandrial Engineering Journal, 57, 2829-2835, 2018.
  16. R. S. Lebelo, M. Waetzel, R. K. Mahlobo, K. C. Moloi and S. O. Adesanya, On transient heat analysis of a two-step convective reactive cylinder, Journal of Physics: Conference Series, 1730 (012141), 1-5, 2021.
  17. M. Khan and Hashim, Boundary layer flow and heat transfer to Carreau fluid over a nonlinear stretching sheet, AIP Advances, 5 (107203), 1-14, 2015.
  18. B. Siska, H. Bendova and I. MacHak, Terminal velocity of non-spherical particles falling through a Carreau model fluid, Chem. Eng. Process, 44(12), 1312-1319, 2005.
  19. S. Reedy, P. Srihari, F. Ali, K. Naikoti, Numerical analysis of Carreau fluid flow over a vertical porous microchannel with entropy generation, Partial Differential Equations in Applied Mathematics, 5,100304, 2022.
  20. T. Abbas, S. Rehman, R. A. Shah, M. Idrees and M. Qayyum, Analysis of MHD Carreau fluid flow over a stretching permeable sheet with variable viscosity and thermal conductivity, Physical A, 551, 124225, 2020.
  21. M. Megahed, Carreau fluid flow due to nonlinearly stretching sheet with thermal radiation, heat flux, and variable thermal conductivity, Applied Mathematics and Mechanics, 40, 1615-1624, 2019.
  22. Peristatic motion of Carreau fluid in a channel with convective boundary conditions, Applied Bionics and Biomechanics, 11, 157-168, 2014.
  23. M. M. Alqarni, A. Riaz, M. Firdous, et al, Hall currents and EDL effects on multiphase wavy flow of Carreau fluid in a microchannel having oscillating walls: A numerical study, DOI:10.3389/fphy.2022.984277, 2022.
  24. S. Noreen, T. Kausar, D. Tripathi, Q. U. Ain and D. C. Li, Heat transfer analysis on creeping flow Carreau fluid driven by peristaltic pumping in an inclined asymmetric channel. Therm Sci Eng Prog, 17, 100486, Doi: 10.1016/j.tsep.2020.100486, 2020.
  25. S. K. Asha and J. Beleri, Peristatic flow of Carreau nanofluid in presence of joule heat effect in an inclined asymmetric channel by multi-step differential transformation method, World Scientific News: An International Journal, 164, 44-63, 2022.
  26. M. Qayyum, T. Abass, S. Afzal, S. T. Saeed, A. Akgul, M. Inc, K. H. Mahmoud and A. S Alsubaie, Heat transfer analysis of unsteady MHD Carreau fluid flow over a stretching/shrinking sheet, Coatings, 12, 1661, 2022.
  27. Y. Shao, A. Wu, S. Z. Abbas, W. A. Khan, I. M. Ashraf, Thermal management for the shear-rate driven flow of Carreau fluid in a ciliated channel, 139, 106473, 2022.
  28. M. S. Tshehla, The flow of a Carreau fluid down an inclined with a free surface. International Journal of the Physical Sciences, 6(16), 3896-3910, 2011.
  29. Y. O. Tijani, S. D. Oloniiju, K. B. Kasali and M. T. Akolade, Nonsimilar solution of a boundary layer flow of a Reiner-Philippoff fluid with nonlinear thermal convection. Heat Transfer, 51, 5659-5678, 2022.
  30. T. M. Agbaje, S. Mondal, S. S. Motsa, and Sibada, P., A numerical study of unsteady non-Newtonian Powell-Eyring nanofluid flow over a shrinking sheet with heat generation and thermal radiation. Alexandria Engineering Journal, 56(1), 81-91, (2017).
  31. V. M. Magagula, On the multidomain bivariate spectral local linearization method for solving systems of nonlinear boundary layer partial differential equations. International Journal of Mathematics and Mathematical Sciences, Article ID 6423294, 2019.
Preprints 78764 g001
Figure 1. (a): Residual errors against number of iterations. (b): Solution convergence against number of iterations.
Figure 1. (a): Residual errors against number of iterations. (b): Solution convergence against number of iterations.
Preprints 78764 g001
Preprints 78764 g002
Figure 2. (a): Velocity steady state condition. (b): Temperature steady state condition.
Figure 2. (a): Velocity steady state condition. (b): Temperature steady state condition.
Preprints 78764 g002
Preprints 78764 g003
Figure 3. (a): 3D Velocity profile. (b): 3D Temperature profile.
Figure 3. (a): 3D Velocity profile. (b): 3D Temperature profile.
Preprints 78764 g003
Preprints 78764 g004
Figure 4. Bifurcation curve.
Figure 4. Bifurcation curve.
Preprints 78764 g004
Preprints 78764 g005
Figure 5. Velocity distributions for W e .
Figure 5. Velocity distributions for W e .
Preprints 78764 g005
Preprints 78764 g006
Figure 6. Temperature distribution for W e .
Figure 6. Temperature distribution for W e .
Preprints 78764 g006
Preprints 78764 g007
Figure 7. Velocity profiles for n
Figure 7. Velocity profiles for n
Preprints 78764 g007
Preprints 78764 g008
Figure 8. Temperature profiles for n
Figure 8. Temperature profiles for n
Preprints 78764 g008
Preprints 78764 g009
Figure 9. Velocity graph for variation in β 1 .
Figure 9. Velocity graph for variation in β 1 .
Preprints 78764 g009
Preprints 78764 g010
Figure 10. Temperature graph for variation in β 1 .
Figure 10. Temperature graph for variation in β 1 .
Preprints 78764 g010
Preprints 78764 g011
Figure 11. β 2 effect on velocity profiles.
Figure 11. β 2 effect on velocity profiles.
Preprints 78764 g011
Preprints 78764 g012
Figure 12. β 2 effect on temperature profiles.
Figure 12. β 2 effect on temperature profiles.
Preprints 78764 g012
Preprints 78764 g013
Figure 13. Impact of R a on temperature distribution.
Figure 13. Impact of R a on temperature distribution.
Preprints 78764 g013
Preprints 78764 g014
Figure 14. Influence of B i on temperature profiles.
Figure 14. Influence of B i on temperature profiles.
Preprints 78764 g014
Preprints 78764 g015
Figure 15. Temperature profiles with change in ω
Figure 15. Temperature profiles with change in ω
Preprints 78764 g015
Table 1. Validation of Bivariate Spectral Local Linearization Method with Chebyshev Collocation Method.
Table 1. Validation of Bivariate Spectral Local Linearization Method with Chebyshev Collocation Method.
y u B S L L M u C W R M θ B S L L M θ C W R M
0.00 0.8472544166 0.8472544291 0.5231137461 0.5231137500
0.25 0.7969166162 0.7969166280 0.5149631360 0.5149631391
0.50 0.6436905650 0.6436905747 0.4901023867 0.4901023899
0.75 0.3812086637 0.3812086696 0.4472855132 0.4472855163
1.00 - 9 . 59276 × 10 − 14 - 1 . 12618 × 10 − 23 0.3843857453 0.3843857480
Table 2. Variations in Criticality values for: A = 1 ,   ω = 1 ,   G r = 1 ,   Pr = 10 , ϵ 1 = 0.1 ,     ϵ 2 = 0.1 ,     V d = 0.5 , T = 120 .
Table 2. Variations in Criticality values for: A = 1 ,   ω = 1 ,   G r = 1 ,   Pr = 10 , ϵ 1 = 0.1 ,     ϵ 2 = 0.1 ,     V d = 0.5 , T = 120 .
β 1 β 2 W e n R a B i λ c
0.1 0.1 0.5 0.5 0.1 1.0 0.17064
0.3 0.1 0.5 0.5 0.1 1.0 0.15603
0.5 0.1 0.5 0.5 0.1 1.0 0.14231
0.1 0.1 0.5 0.5 0.1 1.0 0.17064
0.1 0.3 0.5 0.5 0.1 1.0 0.15942
0.1 0.5 0.5 0.5 0.1 1.0 0.14860
0.1 0.1 0.1 0.5 0.1 1.0 0.18038
0.1 0.1 0.3 0.5 0.1 1.0 0.17695
0.1 0.1 0.5 0.5 0.1 1.0 0.17064
0.1 0.1 0.5 0.5 0.1 1.0 0.17064
0.1 0.1 0.5 1.0 0.1 1.0 0.18081
0.1 0.1 0.5 1.5 0.1 1.0 0.18591
0.1 0.1 0.5 0.5 0.1 1.0 0.17064
0.1 0.1 0.5 0.5 0.3 1.0 0.19447
0.1 0.1 0.5 0.5 0.5 1.0 0.21836
0.1 0.1 0.5 0.5 0.1 0.5 0.10362
0.1 0.1 0.5 0.5 0.1 1.0 0.17064
0.1 0.1 0.5 0.5 0.1 1.5 0.22120
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated