Submitted:
06 July 2023
Posted:
10 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Model and Notation
3. Bayesian estimation of joint model
3.1. Prior specification
3.2. Bayesian analysis of joint model
4. Simulation Studies
5. An Example
6. Concluding Remarks
Appendix A
References
- Faucett, C.L.; Thomas, D.C. Simultaneously modelling censored survival data and repeatedly measured covariates: a gibbs sampling approach. Stat. Med. 1996, 15, 1663–1685. [Google Scholar] [CrossRef]
- Wulfsohn, M.S.; Tsiatis, A.A. A Joint model for survival and longitudinal data measured with error. Biometrics 1997, 53, 330–339. [Google Scholar] [CrossRef] [PubMed]
- Schluchter, M.D. Methods for the analysis of informatively censored longitudinal data. Stat. Med. 1992, 11, 1861–1870. [Google Scholar] [CrossRef] [PubMed]
- Tsiatis, A.A.; Degruttola, V.; Wulfsohn, M.S. Modeling the relationship of survival to longitudinal data measured with error: applications to survival and CD4 counts in patients with AIDS. J. Am. Stat. Assoc. 1995, 90, 27–37. [Google Scholar] [CrossRef]
- Tsiatis, A.A.; Davidian, M. Joint modeling of longitudinal and time-to-event data: an overview. Stat. Sin. 2004, 14, 809–834. [Google Scholar] [CrossRef]
- Yu, M.; Law, N.J.; Taylor, J.M.G.; Sandler, H.M. Joint longitudinal-survival-cure models and their application to prostate cancer. Stat. Sin. 2004, 14, 835–862. [Google Scholar] [CrossRef]
- Diggle, P.J.; Sousa, I.; Chetwynd, A.G. Joint modelling of repeated measurements and time-to-event outcomes: the fourth armitage lecture. Stat. Med. 2008, 27, 2981–2998. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, A.; Gould, *!!! REPLACE !!!*; et al. Joint modeling of survival and longitudinal non-survival data: current methods and issues. Stat. Med. 2015, 34, 2181–2195. [Google Scholar] [CrossRef]
- Henderson, R.; Diggle, P.; Dobson, A. Joint modelling of longitudinal measurements and event time data. Biostatistics 2000, 1, 465–480. [Google Scholar] [CrossRef]
- Zeng, D.; Cai, J. Simultaneous modelling of survival and longitudinal data with an application to repeated quality of life measures. Lifetime Data Analysis 2005, 11, 151–174. [Google Scholar] [CrossRef]
- Tang, A.; Zhao, X.; Tang, N. Bayesian variable selection and estimation in semiparametric joint models of multivariate longitudinal and survival data. Biom. J. 2017, 59, 57–78. [Google Scholar] [CrossRef] [PubMed]
- Song, P.X.; Tan, M. Marginal models for longitudinal continuous proportional data. Biometrics 2000, 56, 496–502. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Park, T.; Casella, G. The Bayesian Lasso. J. Am. Stat. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Hans, C. Bayesian lasso regression. Biometrika 2009, 96, 835–845. [Google Scholar] [CrossRef]
- Guo, R.; Zhu, H.; Chow, S.M.; Ibrahim, J.G. Bayesian Lasso for semiparametric sructural equation models. Biometrics 2012, 68, 567–577. [Google Scholar] [CrossRef]
- Tang, A.; Zhao, X.; Tang, N. Bayesian variable selection and estimation in semiparametric joint models of multivariate longitudinal and survival data. Biom. J. 2017, 59, 57–78. [Google Scholar] [CrossRef]
- Ohlssen, D.I.; Sharples, L.D.; Spiegelhalter, D.J. Flexible random effects models using Bayesian semiparametric models: applications to institutional comparisons. Stat. Med. 2007, 26, 2088–2112. [Google Scholar] [CrossRef]
- Yang, M.; Dunson, D.B.; Baird, D. Semiparametric bayes hierarchical models with mean and variance constraints. Comput. Stat. Data. Anal. 2010, 54, 2172–2186. [Google Scholar] [CrossRef]
- Ishwaran, H.; Zarepour, M. Markov chain monte carlo in approximate dirichlet and beta two-parameter process hierarchical models. Biometrika 2000, 87, 371–390. [Google Scholar] [CrossRef]
- Chow, S.; Tang, N.; Yuan, Y.; Song, X.; Zhu, H. Bayesian estimation of semiparametric nonlinear dynamic factor analysis models using the Dirichlet process prior. Br. J. Math. Stat. Psychol. 2011, 64, 69–106. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Peng, Y.; Tu, D. Jointly modeling longitudinal proportional data and survival times with an application to the quality of life data in a breast cancer trial. Lifetime Data Analysis 2017, 23, 183–206. [Google Scholar] [CrossRef] [PubMed]
- Levine, M.; Bramwell, V.; Pritchard, K.; et al. Randomized trial of intensive cyclophosphamide, epirubicin, and fluorouracil chemotherapy compared with cyclophosphamide, methotrexate, and fluorouracil in premenopausal women with node-positive breast cancer. J. Clini. Oncol. 1998, 16, 2651–2658. [Google Scholar] [CrossRef] [PubMed]
- Tang, A.; Duan, X.; Zhao, Y. Bayesian variable selection and estimation in semiparametric simplex mixed-effects models with longitudinal proportional data. Entropy 2022, 24, 1466. [Google Scholar] [CrossRef]

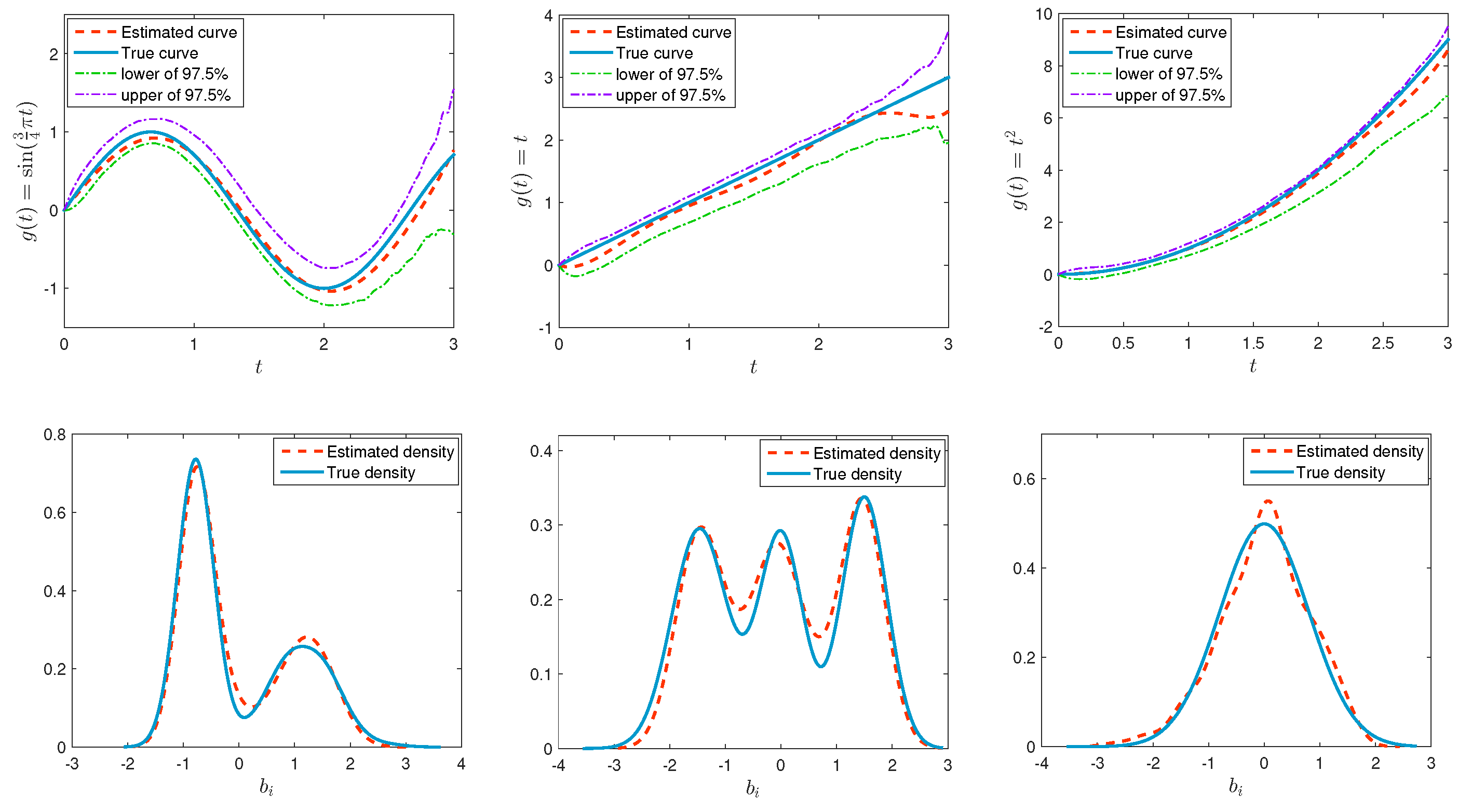
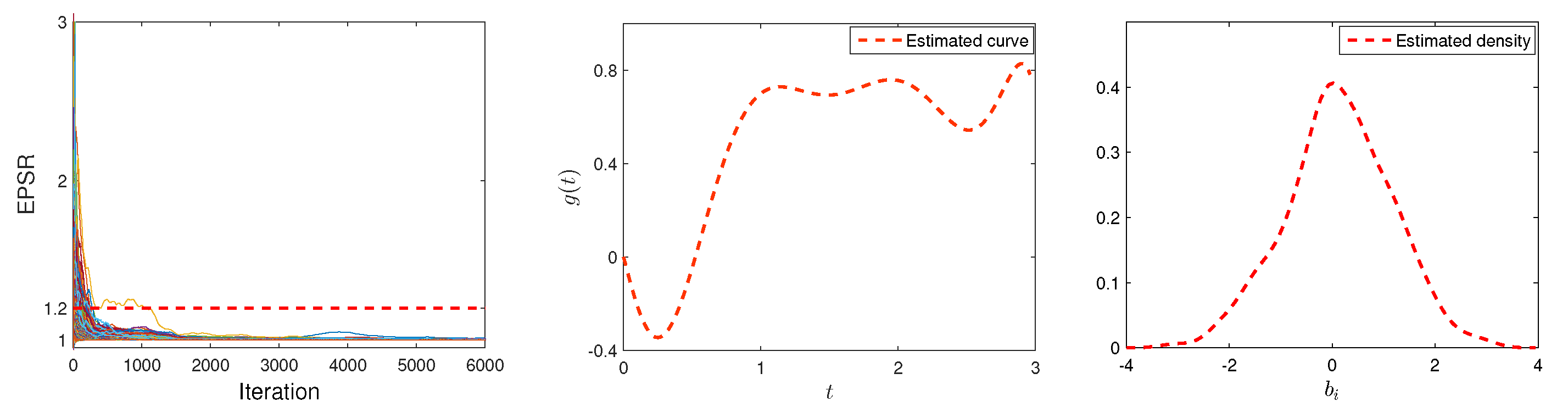
| Pra. | True | Simulation I | Simulation II | Simulation III | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias | RMS | F0(%) | Bias | RMS | F0(%) | True | Bias | RMS | F0(%) | ||
| 1.00 | -0.005 | 0.058 | 0.0 | -0.080 | 0.112 | 0.0 | 1.00 | -0.015 | 0.104 | 0.0 | |
| 0.00 | 0.002 | 0.036 | 99.0 | 0.001 | 0.049 | 98.0 | 0.50 | -0.009 | 0.077 | 0.0 | |
| 0.00 | -0.002 | 0.033 | 99.0 | 0.005 | 0.042 | 99.5 | -0.50 | 0.011 | 0.085 | 0.0 | |
| -0.50 | 0.005 | 0.041 | 0.0 | 0.003 | 0.056 | 0.0 | -0.50 | 0.001 | 0.079 | 0.0 | |
| 0.50 | -0.001 | 0.037 | 0.0 | -0.009 | 0.063 | 0.0 | 0.50 | 0.000 | 0.083 | 0.0 | |
| -1.00 | 0.013 | 0.066 | 0.0 | 0.006 | 0.091 | 0.0 | -1.00 | 0.028 | 0.136 | 0.0 | |
| 0.00 | 0.010 | 0.120 | 95.5 | -0.004 | 0.105 | 98.0 | -0.50 | 0.002 | 0.125 | 0.5 | |
| 1.00 | 0.001 | 0.148 | 0.0 | -0.052 | 0.144 | 0.0 | 1.00 | -0.008 | 0.141 | 0.0 | |
| -0.50 | 0.018 | 0.138 | 5.0 | 0.039 | 0.136 | 6.5 | -0.50 | 0.008 | 0.127 | 2.5 | |
| 0.00 | -0.002 | 0.197 | 97.0 | 0.010 | 0.178 | 97.5 | 1.00 | -0.007 | 0.191 | 0.0 | |
| 0.60 | 0.006 | 0.106 | 0.0 | -0.019 | 0.088 | 0.0 | 0.60 | -0.002 | 0.145 | 1.0 | |
| 0.36 | -0.002 | 0.018 | – | -0.001 | 0.019 | – | 0.36 | 0.005 | 0.020 | – | |
| Est of random effects | Quantile of RASE | ||||||
|---|---|---|---|---|---|---|---|
| Mean | Est mean | SD | Est SD | 25% | 50% | 75% | |
| Simulation I | -0.011 | -0.007 | 1.004 | 0.961 | 0.091 | 0.115 | 0.138 |
| Simulation II | -0.023 | 0.014 | 1.268 | 1.202 | 0.135 | 0.181 | 0.239 |
| Simulation III | -0.001 | -0.001 | 0.879 | 0.797 | 0.109 | 0.152 | 0.227 |
| Par. | Est | SD | CI |
|---|---|---|---|
| 0.241 | 0.038 | ( 0.171, 0.321) | |
| 0.309 | 0.050 | ( 0.214, 0.414) | |
| 0.263 | 0.046 | ( 0.168, 0.344) | |
| -0.334 | 0.142 | (-0.608,-0.057) | |
| 0.719 | 0.143 | ( 0.452, 0.999) | |
| 0.600 | 0.145 | ( 0.315, 0.880) | |
| 0.259 | 0.135 | ( 0.003, 0.542) | |
| 0.180 | 0.003 | ( 0.174, 0.186) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





