Prerpints.org logo
Preprint
Article

Magnetic Properties and Reminiscent Rare Earth-Cobalt Coupling in RCo3B2 Compounds

Altmetrics

Downloads

1534

Views

69

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 July 2023

Posted:

10 July 2023

You are already at the latest version

Alerts
Abstract
The magnetic properties of RCo3B2 compounds, with heavy rare earths, are investigated by using magnetic measurements and electronic structure calculations. The cobalt sublattice magnetizations are very small and antiparallel oriented to rare earths moments. Contributions of cobalt moments to the Curie constants were also shown. The cobalt magnetic behavior has been analyzed in spin fluctuations model. The presence of short-range order above the Curie temperatures in RCo3B2 compounds with R=Tb, Dy, and Ho has been attributed to reminiscent R5d-Co3d interactions.
Keywords: 
Subject: Chemistry and Materials Science  -   Metals, Alloys and Metallurgy

1. Introduction

The RCo3B2 compounds, at ambient conditions, crystallize in a CeCo3B2-type structure, space group P6/mmm. This is derived from CaCu5-type lattice, by replacing Co atoms by B at 2c site. The R atoms are located on 1a site, Co in 3g and B on 2c positions [1]. At T<Tc=27 K, the TbCo3B2 crystallizes in orthorhombic type structure, space group Cmmm [2].
The RCo3B2 compounds show interesting physical properties. An anomaly in the temperature dependence of the magnetic susceptibility, at T≅150 K, was shown in YCo3B2 [3]. Small magnetic moments were also determined, at T=4.2 K, in this compound [4,5]. Anomalies in the magnetic susceptibilities of TbCo3B2 at T=150 K, were also shown and attributed to the collapse of cobalt sublattice magnetization [6,7]. The careful analysis of the magnetic properties of the YCo3B2 compound evidenced that really it is a paramagnet [8,9]. The magnetic susceptibility, χ, at T<10 K follows a T2 dependence, then the χ values increase with temperature up to a maximum located at T≅150 K. For T>300 K, the magnetic susceptibility follows a Curie-Weiss type dependence. A similar behavior has been shown in RCo2 compounds with R=Y or Lu [10]. The cobalt magnetic behavior in these compounds, can be well analyzed in the spin fluctuations model [11].
The RCo3B2 borides with magnetic heavy rare earths, R= Gd [5,9,12,13,14,15,16,17], Tb [5,14,15,18,19,20], Dy [5,8,14,15,17,21,22,23], Ho [24] and Er [12,14] are magnetically ordered. Starting from magnetic measurements was assumed that cobalt, at T<Tc, either has a small cobalt ordered moment [5,6,15,16,21] or the cobalt moment is nil [12,19]. The presence of a small cobalt moment, in DyCo3B2, antiparallel oriented to Dy one, was shown by magnetic Compton profile analysis [25]. A parallel alignment of Ho and Co moments in HoCo3B2 was also reported [7], in contradiction with general trend of magnetic properties of heavy rare earth-transition metal-boron compounds [26]. The band structure calculations on GdCo3B2 also showed the presence of a cobalt moment, MCo≅0.1 μB/atom, antiparallel oriented to gadolinium one [27]. The Curie temperatures of RCo3B2 compounds are rather low, below 53 K. Crystalline electric fields (CEF) at R sites were evidenced. The Tb moment in TbCo3B2 was assumed to be induced in the singlet ground state by a component of exchange field perpendicular to the crystalline electric field, which admixes higher lying states into singlet ground state [19].
The magnetic susceptibilities. χ, of RCo3B2 compounds with heavy rare earths, were investigated in a limited temperature range, mainly at Tc < T< 300 K. The experimental data were fitted assuming a Curie-Weiss type behavior. A change of χ vs T slopes, at T ≅ 300 K, was shown in case of RCo3B2 compounds with R = Gd and Dy, the Curie constants being determined only from the data obtained at T < 300 K [5]. The reported effective moments per formula unit, were assumed to be close to those of R3+ free ions [5,6,7,12,18,20,24]. A nonlinear temperature dependence of the magnetic susceptibilities was later shown in ferrimagnetic GdxY1-xCo3B2 system with x > 0.2. The effective cobalt moments, μ ≅ 1.4μB/Co atom, determined at 350 K< T < 700 K, where linear temperature dependences of susceptibilities were shown, are little dependent on composition [8]. By magnetic diffuse scattering on TbCo3B2, the clusters of aligned moments which fluctuate over time, was shown at T > Tc [19]. The above behavior has been attributed to the existence of a nonmagnetic singlet ground state, well separated from the first excited state by an energy gap, which leads to rapidly fluctuating magnetic exchange fields (MEFs). The minimum of the correlation length was found to be ξ=6.5(2.5) nm. The short-range order, above Tc, was also reported in DyCo3B2 [22] and HoCo3B2 [24] compounds, as well as in RCo2 series [28], where the R moments are close to gJ values.
In this paper, the magnetic behavior of heavy rare-earths RCo3B2 compounds, in a large temperature range as well as their electronic structures, have been investigated. A small cobalt moment was shown in magnetic ordered state, as well as their contributions to the Curie constants. The magnetic behavior of cobalt has been analyzed in the spin fluctuations model. No magnetic phase transition was shown, at T≅150 K. The presence of short-range order, above the Curie temperatures, in some RCo3B2 compounds was correlated with reminiscent R5d-Co3d magnetic coupling.

2. Materials and Methods

The RCo3B2 samples with heavy rare earths were prepared by arc melting the constituent elements in purified argon atmosphere and re-melting several times to ensure a good homogeneity [8,9]. A little higher rare earth content, of about 1%, than corresponding to stoichiometric sample, was used to compensate their loss during the melting and to avoid the formation of phases with higher Curie points. The samples were treated under vacuum at 1000 oC, for ten days.
Magnetic measurements were performed in temperature range 4.2 K - 700 K or 800 K and fields up to 7 T. In the temperature range Tc <T < 200 K, the magnetic susceptibilities were determined from their field dependence, according to Honda-Owen plot [29], χ m = χ + c M i / H , by extrapolating the measured values χm to H-1→0. By c is denoted a presumed magnetic ordered impurity content and Mi is their magnetization. By this method the possible alteration of magnetic susceptibilities is avoided, even if some magnetic ordered impurities are present. Very small amounts of impurities were shown, in some samples, in a limited temperature range above Tc.
The ground state electronic structure and magnetic properties of RCo3B2 compounds have been determined by means of the tight binding linear muffin-tin orbital (TB-LMTO) method in its atomic sphere approximation (ASA) [30,31]. The standard combined correction terms have been used to compensate the errors due to ASA [32]. The local spin density approximation (LSDA) has been employed for the exchange and correlation potential of the electronic gas, assuming the Von Barth and Hedin parameterization [33]. The valence band consists of s-, p- and d- orbitals whereas the 4f orbitals of R atoms have been considered as open core states that do not hybridize with conduction electrons but having the polarizations calculated self-consistently. All electronic structure calculations have been performed for the experimental values of the lattice spacings. Due to the non-closed-packed structure of CeCo3B2-type lattice, an empty sphere was inserted at appropriate interstitial position, without breaking the crystals symmetry, in order to fulfill ASA space filling requirement. The atomic radii used have been chosen such that the overlapping maintains within permissible ASA limit. The analysis of the data has been made starting from 4f-5d-3d exchange interaction model [34].

3. Results and Discussions

The X-ray analysis, at ambient conditions, showed the presence of only one phase having hexagonal structure, P6/mmm space group. The lattice parameters, including those for GdCo3B2 compound [8] are given in Table1. The a lattice constants decrease according to lanthanide contraction while the c ones are little dependent of R partner. In the structure, the R atoms have (2R, 2Co, 6B) and cobalt (4R, 6Co, 4B) nearest neighbors, their physical properties, particularly of cobalt, being determined by their local environments. The distances between Co atoms are of about 0.252 nm and those between Tb and Co of about 0.2935 nm. The distance between cobalt and boron, of about 0.209 nm, is smaller than the sum of metallic radius of Co (0.125 nm) and B (0.088 nm), and consequently a strong hybridization of Co3d and B2p orbitals occurs [1].
The total and partial densities of states of Ho1a, Co3g and B2c atoms in HoCo3B2 compound, are given as example in Figure 1. There is a strong hybridization of Co3d and B2p bands, resulting in an induced magnetic moment of about 0.002 μB/B atom. A hybridization of Co3d and R5d states is also shown. The R5d band polarization, M5d, as previously stated [35], is induced by both local 4f-5d exchange, M5d(f), as well as by R5d-Co3d short range interactions, M5d(d), M 5 d = M 5 d d + M 5 d ( f ) with M5d(d)=-0.04 μB and M5d(f) = - αG, where G is the De Gennes factor, G = g J − 1 2 J J + 1 -Figure 2. The rate, α =1.1*10-2 μB/G, is similar with that determined in RNi2 series and somewhat smaller than that obtained in RCo2 compounds (1.9*10-2 μB/G) [35]. The M5d(d) is the induced polarization by the R5d interactions with the zi cobalt atoms situated in their environment. As previously stated, the R5d band polarization is a measure of the exchange interactions between R and Co moments, as already evidenced in RCo2 [36] as well as RFe2 [37] series.
The computed cobalt moments in RCo3B2 compounds with R= Gd, Tb, Dy, Ho and Er are antiparallel oriented to those of rare earths and decrease from 0.09 μB/atom (R=Gd) down to 0.03 μB/atom for R=Er, The small cobalt moments, as already mentioned, are the result of strong hybridization of Co3d and B2p bands. The contributions of cobalt sublattice to the RCo3B2 magnetizations, decrease from about 4%, (R=Gd), down to about 1% (R=Er). There is a linear dependence of cobalt moments on the R5d band polarizations, with a rate of 0.58, confirming their induction by 4f-5d-3d exchange path -Figure 3. The ratio M 5 d ( d ) / ∑ i z i M C o i ≅ 10 − 1 , determined in RCo3B2 series, is by one order of magnitude higher than that in RCo2 compounds [35]. The exchange interactions between cobalt atoms are of short range. The radius of R5d orbitals, of 0.533 nm [38] is sensitively higher than the distances between neighboring R-Co or R-R atoms and consequently there are R5d-Co3d and R5d-R5d exchange interactions, in addition to those through conduction electrons [35,39].
The magnetization isotherms at T=4.2 K, for RCo3B2 (R=Gd to Er) compounds having small anisotropies are nearly saturated in fields up to 7 T -Figure 4. High anisotropies are evidenced in case of compounds with R=Tb, Dy and Ho, their magnetizations, being far from saturation in field of 7 T. The Curie temperatures are rather low and follow a nearly linear dependence on R5d band polarization M5d, De Gennes factor, respectively -Figure 3. The Tc value for TbCo3B2 is smaller than the predicted trend, probably due to peculiar terbium magnetism. The Curie temperatures of RCo3B2 with R=Tb, Dy and Ho increase when increasing external field, with a rate of about 0.6-0.7 K/T, as also estimated from magnetocaloric investigations [18,21,24].
The magnetizations determined at T=4.2 K, correspond to those at reduced temperatures T/Tc=0.34 (R=Er), 0.25 (R=Ho), 0.19 (R=Dy), 0.155 (R= Tb), 0.073 (R=Gd) and thus corrections for thermal variations of magnetizations must to be taken into account, in order to obtain their values in fundamental state, Ms(0). In addition, the saturation magnetizations of compounds having high anisotropy, can be obtained only by extrapolation of experimentally determined values at H-1→ 0, according to the approach to saturation law. The magnetizations, at T=4.2 K, in field of 7 T, as well those obtained by extrapolation at H-1→ 0, taking into account the thermal variation of magnetizations assuming Brillouin type dependences with J value characteristic for each rare earth, are listed in Table 1. The Ms(0) values, thus determined, except for TbCo3B2 are by 0.1-0.5 μB smaller than the gJJ values of rare earths, as expected for a ferrimagnetic type ordering. The estimated ordered cobalt moments from magnetic measurements, are thus in the range 0.07-0.16 μB/atom, in roughly agreement with the data obtained from band structure calculations. In the case of TbCo3B2, the CEF-only ground state of Tb ion is a non-magnetic singlet and at the magnetic ordered transition, the Tb moment is induced into the singlet ground state by a component of exchange field and consequently can be smaller than predicted by the gJJ value [19].
The thermal variations of reciprocal susceptibilities of RCo3B2 compounds with R=Gd, Tb, Dy, Ho and Er are given in Figure 5a,b. These are little nonlinear, and can be approximated with linear trend, with a change in slope, at temperatures T≅300 K. The deviations from a linear trend, decrease as the relative contributions of cobalt sublattice, CCo/Ctot, to the Curie constant, Ctot, diminishes. According to the addition law of magnetic susceptibilities and assuming that the effective R moments, are given by their free ions values, the effective cobalt moments were determined. These are in the range of 1.13-1.84 μB/Co atom, close to those previously determined in GdCo3B2 [8] or YCo3B2 [9] compounds -Table 1. The ratio r between the number of cobalt spins Sp, determined in paramagnetic range and S0, obtained from saturation measurements (band structures), r = S p / S 0 = 8 − 12 , is very high, showing a high degree of itinerancy.
The magnetic behavior of cobalt in heavy rare earths RCo3B2 compounds, as well as in YCo3B2, can be analyzed in spin fluctuations model [11]. The model considers the balance between the frequencies of longitudinal spin fluctuations, which are determined by their lifetime and of transverse fluctuations that are of thermal origin, the concept of temperature induced cobalt moment, respectively. For an exchange enhanced paramagnet as YCo3B2, or a weak ferromagnet, as cobalt in RCo3B2 series with magnetic heavy rare earths, the wave number dependent susceptibility, χq , has a large enhancement due to electron-electron interactions, for small q values. The average amplitude of spin fluctuations, < S l o c 2 > = 3 k B T ∑ χ q increases with temperature and reaches an upper limit determined by the charge neutrality condition, at a temperature T*. At T>T*, when the frequency of thermal fluctuations is higher than of longitudinal ones, a Curie-Weiss behavior is evidenced, as in systems having local moments. The moments are localized in q space. Similar behavior was shown already, for cobalt in RCo2 series [10,40].
No magnetic ordered phase, having a Curie temperature at T≅150 K, was shown in the investigated RCo3B2 series. The same conclusion can be obtained by the analysis of the temperature dependences of volume thermal expansion [2] and electronic specific heat [2,18,41], in TbCo3B2. The Grüneisen ratio [42], Γ T ∝ β ( T ) / C ( T ) , where β(T) and C(T) denote the contributions of volume thermal expansion and electronic specific heat, respectively, diverges at the approach to the quantum critical point (QCP), according to a 1/Tε law [43,44]. The volume thermal expansion coefficient, β(T), in the temperature range 70 < T < 200 K is well described by the relation predicted by the three-dimensional Gaussian scenario [43,44], with rates β(T)/T = 0.7·10-7/T1/2 K-1.5 and the electronic contribution to the specific heat by C(T)/T = -0.061T1/2 J/mol·K1.5. There is only one divergence of Γ(T), by approaching to Tc = 37 K. No others QCP points were evidenced at higher temperatures, confirming that the compound is in paramagnetic state at T>Tc. The observed anomaly, at T ≅ 150 K, already reported in some RCo3B2 compounds, can be attributed to the presence of magnetic ordered impurity content or due to location of small cobalt content at B2c site, during sample preparation. Since β ( T ) ∝ T 1 / 2 and C ( T ) ∝ T 3 / 2 , respectively it results that Γ∝1/T. The Gruneisen exponent, ε=1, suggests that the magnetic behavior of TbCo3B2 follows the 3D Spin Density Wave (SDW), QPC prediction, in agreement with the neutron diffraction study [19].
The presence of a short range order (SRO) of the Tb sublattice, extending up to T≅160 K, was reported in TbCo3B2 and attributed to the fluctuating magnetic exchange fields, created by induction of Tb moment in singlet ground state [19]. Accordingly, these lead to formation of clusters of Tb ions with partially admixed levels which tend to align. The short-range order, above Tc, was also reported in DyCo3B2 up to 100 K [41] and HoCo3B2 up to T=50 K [24], where no such mechanism for induced R moment is present.
The short-range order, at T>Tc, as in case of RCo2 compounds [45,46], can be analyzed starting from the 4f-5d-3d interaction model [34,35]. The short-range exchange interactions between cobalt atoms cancel at the Curie point, as well as the M5d(d) contribution to R5d band polarization. Since of large extension of R5d orbitals, there are reminiscent R-Co and R-R magnetic couplings [39,45,46] and consequently cluster formation. In such a cluster the R and Co moments are still antiparallel aligned in a limited temperature range above Tc [28,46]. As function of temperature and external field, different arrangements of R and Co are possible [28,46]. The exchange interactions, strongly connected with R5d band polarizations [36,37], are diminished. The R5d-Co3d magnetic coupling cannot be observed in RCo3B2 compounds, at T>Tc, since the cobalt moment is very small and cannot be determined by neutron diffraction. Such a magnetic coupling was found in RCo2 series, with R=Tb, Ho and Er, in the presence of magnetic field, when MCo is by one order of magnitude higher than in RCo3B2 series [47,48,49,50]. The paramagnetic clusters have been ascribed to reminiscent rare earth-cobalt magnetic coupling [45,46]. The intensities of R5d-Co3d interactions, although present, are not enough to induce a magnetic order, as confirmed by polarized neutron diffraction studies at Tc < T < 300 K, on RCo2 compounds with R=Tb, Ho, Er and Tm [45,46,48,49,50]. There is a linear dependence of the projections of cobalt on the rare earths moments, with rates dependent on the intensities of R5d-Co3d magnetic coupling [45,46]. Although the compounds were in paramagnetic state, the observed cluster has been attributed, in early studies, to the presence of a Griffits phase, a kind of low temperature remnant magnetic order of undiluted system [28]. The polarized neutron diffraction study, on the exchange enhanced LuCo2 paramagnet, at T=100 K, in field of 5.72 T, evidenced an induced cobalt moment of 0.016 μB, as well as an antiparallel oriented Lu5d band polarization [51], confirming the presence of Co3d-Lu5d coupling in paramagnetic state
In high fields and close to Tc, a deviation from linear trend of the field dependence of magnetization was also shown, in RCo2 series, in agreement with the increase of Curie temperature, when increasing external field [36].
The presence of short-range order in TbCo3B2 extends up to T=160 K [19], 100 K in DyCo3B2 compound [41] and 50 K in HoCo3B2 one [24]. A higher thermal energy, as compared to that corresponding at Tc it is necessary for magnetic decoupling of atoms situated in a cluster and to achieve classical paramagnetic state with fluctuating single moments. These interactions can be also influenced by the cobalt magnetic behavior which increases with temperature and saturates at T*>300 K. The thermal energies (Et) for breaking the reminiscent R5d-Co3d coupling, determined from the maximum temperatures, where short range interactions are present, were estimated in RCo3B2 and RCo2 compounds -Figure 6. These decrease linearly with de Gennes factor, the intensities of magnetic coupling, respectively with a higher rate in RCo3B2 series. The difference can be correlated to a higher reminiscent R5d-Co3d interactions in RCo2 series, than in RCo3B2 system.

4. Conclusions

The RCo3B2 compounds with R=Gd, Tb, Dy, Ho and Er are ferrimagnetic. When magnetization is determined at 4.2 K, corrections for their thermal variation must be made in order to obtain their value in fundamental state. High external fields are necessary to overcome the anisotropy in compounds with R= Tb, Dy and Ho. The cobalt sublattice magnetization is rather small, due to the strong hybridization of Co3d and B2p states, as evidenced from band structures analysis. Low values of effective cobalt moments are evidenced in paramagnetic regions. No magnetic transitions at T=150 K are observed. The itinerancy degree of cobalt is rather high, showing a weak ferromagnetism. The magnetic behavior of cobalt can be well described by spin fluctuations model. The short-range order evidenced in RCo3B2 compounds with R=Tb, Dy and Ho, above the Curie temperatures, were attributed to reminiscent R5d-Co3d magnetic coupling, whose intensities are not enough to induce magnetic order. The energies necessary for breaking these interactions decrease linearly with the R5d-Co3d-R5d magnetic coupling, band polarizations, respectively. This behavior seems to characterize the systems with low Curie points, where the Co-Co interactions cancel at the Curie point, those of R5d-Co3d type, being still present at higher temperatures.

Author Contributions

Conceptualization, E.B.; investigation, E.B, P.V. formal analysis, E.B., P.V..; writing—original draft preparation E.B.; writing—review and editing, E.B, P.V.; supervision,. All authors have read and agreed to the published version of the manuscript.

Funding

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Niihara, Koichi; Yajima, S. The Preparation and Crystal Structure of Ternary Rare Earth Borides, RCo3B2. Bull. Chem. Soc. Jpn. 1973, 46, 770–774. [Google Scholar] [CrossRef]
  2. Dubman, M.; Caspi, E.N.; Ettedgui, H.; Keller, L.; Melamud, M.; Shaked, H. Magnetic Ordering and Spin-Reorientation Transitions in Tb Co3 B2. Phys. Rev. B - Condens. Matter Mater. Phys. 2005, 72, 024446. [Google Scholar] [CrossRef]
  3. Sigalov, O.; Shames, A.I.; Caspi, E.N.; Dubman, M.; Ettedgui, H.; Goren, S.D.; Shaked, H. Magnetic Phase Transition in YCo3B2 Studied by Magnetic Resonance. J. Appl. Phys. 2005, 98, 74105. [Google Scholar] [CrossRef]
  4. Ido, H.; Yamauchi, H.; Cheng, S.F.; Sankar, S.G.; Wallace, W.E. Magnetic Properties of the Y1−xGdxCo3B2 System. J. Appl. Phys. 1991, 70, 6540–6542. [Google Scholar] [CrossRef]
  5. Ido, H.; Nanjo, M.; Yamada, M. Magnetic Susceptibility of RCo3B2 (R=Y, Sm, Gd, and Dy). J. Appl. Phys. 1994, 75, 7140–7142. [Google Scholar] [CrossRef]
  6. Caspi, E.N.; Pinto, H.; Kuznietz, M.; Ettedgui, H.; Melamud, M.; Felner, I.; Shaked, H. Magnetic Properties of TbCo3B2 Studied by Neutron Diffraction, Magnetization, and Ac-Susceptibility Measurements. J. Appl. Phys. 1998, 83, 6733–6735. [Google Scholar] [CrossRef]
  7. Caspi, E.N.; Dubman, M.; Ettedgui, H.; Shakedb, H.; Short, S.; Jorgensen, J.D. . Magnetic and Crystallographic Properties of HoCo3B2. Phys. B Condens. Matter 2005, 359–361, 944–946. [Google Scholar]
  8. Ballou, R.; Burzo, E.; Pop, V. Magnetic Properties of (GdxY1 − x)Co3B2 Compounds. J. Magn. Magn. Mater. 1995, 140–144, 945–946. [Google Scholar] [CrossRef]
  9. Burzo, E.; Vlaic, P. , Pop, V.; Creanga, I.. Magnetic Properties and Electronic Structures of YCo3-XNixB2 Compounds. J. Optoelectron. Adv. Mater. 2006, 8, 484–486. [Google Scholar]
  10. Burzo, E.; Lemaire, R. On the Magnetic Behaviour of RCo2 Compounds Where R Is Yttrium or a Rare-Earth. Solid State Commun. 1992, 84, 1145–1148. [Google Scholar] [CrossRef]
  11. Moriya, T. Recent Progress in the Theory of Itinerant Electron Magnetism. J. Magn. Magn. Mater. 1979, 14, 1–46. [Google Scholar] [CrossRef]
  12. Oesterreicher, H.; Parker, F.T.; Misroch, M. Magnetic Studies on RCo3B2 (R=Sm, Gd, Er). Appl. Phys. 1977, 12, 287–292. [Google Scholar] [CrossRef]
  13. Kapusta, C.; Rosenberg, M.; Buschow, K.H.J. Nuclear Magnetic Resonance Study of the RE(Co, B)5-Type Compounds (RE  Y, Gd). J. Alloys Compd. 1992, 187, 409–422. [Google Scholar] [CrossRef]
  14. Ido, H.; Nashima, O.; Ito, T.; Kaneda, T.; Saito, Y.; Konno, K.; Yoshida, H.; Motokawa, M. Magnetic Properties of RCo3B2 (R=rare Earth) Compounds. J. Appl. Phys. 1999, 85, 4865–4867. [Google Scholar] [CrossRef]
  15. Li, L.; Nishimura, K.; Huo, D.; Qian, Z.; Namiki, T. Critical Behaviour of the RCo3B2 (R = Gd, Tb and Dy) Compounds. J. Alloys Compd. 2013, 572, 205–208. [Google Scholar] [CrossRef]
  16. Li, L.; Nishimura, K.; Igawa, H.; Huo, D. Magnetic Properties and Magnetocaloric Effect in GdCo3B2 Compound. J. Alloys Compd. 2011, 509, 4198–4200. [Google Scholar] [CrossRef]
  17. Malik, S.K.; Umarji, A.M.; Shenoy, G.K. Magnetic and Mössbauer Studies on GdCo3B2 and DyCo3B2. J. Appl. Phys. 1985, 57, 3252–3254. [Google Scholar] [CrossRef]
  18. Li, L.; Huo, D.; Igawa, H.; Nishimura, K. Large Magnetocaloric Effect in TbCo3B2 Compound. J. Alloys Compd. 2011, 509, 1796–1799. [Google Scholar] [CrossRef]
  19. Rivin, O.; Shaked, H.; Gukasov, A.; Caspi, E.N. Long-Range and Short-Range Magnetic Order in the Singlet Ground State System TbCo 3 B 2. Phys. Rev. B 2014, 89, 174423. [Google Scholar] [CrossRef]
  20. Wolfson, E.J.; Caspi, E.N.; Ettedgui, H.; Shaked, H.; Avdeev, M. The Effect of Non-Magnetic Dilution of the Tb Sublattice in TbCo 3 B 2. J. Phys. Condens. Matter 2010, 22, 026001. [Google Scholar] [CrossRef]
  21. Toliński, T.; Falkowski, M.; Kowalczyk, A.; Synoradzki, K. Magnetocaloric Effect in the Ternary DyCo3B2 Compound. Solid State Sci. 2011, 13, 1865–1868. [Google Scholar] [CrossRef]
  22. Li, L.; Igawa, H.; Nishimura, K.; Huo, D. Study of the Magnetic Transition and Large Magnetocaloric Effect in DyCo3B2 Compound. J. Appl. Phys. 2011, 109, 83901. [Google Scholar] [CrossRef]
  23. Smardz, L.; Jezierski, A.; Kowalczyk, A. Electronic Properties of DyCo3B2 Compound. J. Magn. Magn. Mater. 1999, 205, 209–214. [Google Scholar] [CrossRef]
  24. Zheng, X.Q.; Xu, J.W.; Zhang, H.; Zhang, J.Y.; Wang, S.G.; Zhang, Y.; Xu, Z.Y.; Wang, L.C.; Shen, B.G. Magnetic Properties and Magnetocaloric Effect of HoCo3B2 Compound. AIP Adv. 2018, 8, 56432. [Google Scholar] [CrossRef]
  25. Miyagawa, H. . W.Y.; H.N.. S.Y.. N.S.. Magnetic Compton Profiles of DyCo4B and DyCo3B 2. J. Phys. IV Fr. 2003, 104, 503–506. [Google Scholar]
  26. Burzo, E. Rare Earths-Transition Metals-Boron Compounds; Switzerland, S.N., Ed.; 2023; ISBN 978-3-030-99245-3.
  27. “Vlaic, P.; “Burzo Babes-Bolyai Univ., 3400 Cluj-Napoca (Romania)],” E. [Faculty of P. Electronic Structures and Magnetic Properties of RN+1Co3n+5B2n (n=0, 1, 2, 3 and ∞) Compounds with R=Y and Gd. 2002, 1. https://doi.org/2. Eur. Phys. J. B 2013, 86, 489. [CrossRef]
  28. Bartolomé, F.; Bonilla, C.M.; Herrero-Albillos, J.; Calvo-Almazán, I.; Castán, C.; Weschke, E.; Schmitz, D.; Paudyal, D.; Mudryk, Y.; Pecharsky, V.; et al. Short-Range Magnetic Correlations and Parimagnetism in RCo2. Eur. Phys. J. B 2013, 86, 489. [CrossRef]
  29. Bates, L.F. Modern Magnetism, Cambridge Univ.Press, Cambridge. 1951. [Google Scholar]
  30. Andersen, O.K. Linear Methods in Band Theory. Phys. Rev. B 1975, 12, 3060–3083. [Google Scholar] [CrossRef]
  31. Andersen, O.K.; Jepsen, O. Explicit, First-Principles Tight-Binding Theory. Phys. Rev. Lett. 1984, 53, 2571–2574. [Google Scholar] [CrossRef]
  32. Skriver, H.L. The LMTO Method: Muffin-Tin Orbitals and Electronic StructureNo Title; The LMTO Method, Springer, N.Y., Ed. 1984. [Google Scholar]
  33. Barth, U. von; Hedin, L. A Local Exchange-Correlation Potential for the Spin Polarized Case. I. J. Phys. C Solid State Phys. 1972, 5, 1629–1642. [Google Scholar] [CrossRef]
  34. Campbell, I.A. Indirect Exchange for Rare Earths in Metals. J. Phys. F Met. Phys. 1972, 2, L47–L50. [Google Scholar] [CrossRef]
  35. Burzo, E.; Chioncel, L.; Tetean, R.; Isnard, O. On the R 5d Band Polarization in Rare-Earth–Transition Metal Compounds. J. Phys. Condens. Matter 2011, 23, 026001. [Google Scholar] [CrossRef]
  36. Burzo, E.; Vlaic, P.; Kozlenko, D.P.; Rutkauskas, A. V High-Pressure Neutron Diffraction Study of RCo2 Compounds. J. Phys. Chem. Solids 2022, 160, 110330. [Google Scholar] [CrossRef]
  37. Brooks, M.S.S.; Gasche, T.; Auluck, S.; Nordström, L.; Severin, L.; Trygg, J.; Johansson, B. Ab Initio Calculation of Molecular Field Interactions in Rare-earth Transition-metal Intermetallics (Invited). J. Appl. Phys. 1991, 70, 5972–5976. [Google Scholar] [CrossRef]
  38. Vonsovski, G.V. Magnetism Vol. 2. In; Wiley and Sons Publ., N.Y., Ed.; 1974; p. 626.
  39. Burzo, E.; Chioncel, L.; Costina, I.; Chiuzbăian, S.G. Electronic Structure and Magnetic Properties of Gd x La 1− x Ni 5 System. J. Phys. Condens. Matter 2006, 18, 4861–4877. [Google Scholar] [CrossRef]
  40. Burzo, E.; Chioncel, L. . Reminiscent Rare-Earth Cobalt Magnetic Couplings above the Curie Temperature and Spin Fluctuations in RCo2 Compounds. Rom. Repts. Phys. 2022, 74, 501. [Google Scholar]
  41. Perthold, W.; Hong, N.M.; Michor, H.; Hilscher, G.; Ido, H.; Asano, H. Specific Heat of RCo3B2 (R = Y, Sm, Gd, Dy, Lu). J. Magn. Magn. Mater. 1996, 157–158, 649–650. [Google Scholar] [CrossRef]
  42. Grüneisen, E. Theorie Des Festen Zustandes Einatomiger Elemente. Ann.Phys 1912, 39, 257–306. [Google Scholar] [CrossRef]
  43. Zhu, L.; Garst, M.; Rosch, A.; Si, Q. Universally Diverging Grüneisen Parameter and the Magnetocaloric Effect Close to Quantum Critical Points. Phys. Rev. Lett. 2003, 91, 066404. [Google Scholar] [CrossRef]
  44. Küchler, R.; Gegenwart, P.; Geibel, C.; Steglich, F. Systematic Study of the Grüneisen Ratio near Quantum Critical Points. Sci. Technol. Adv. Mater. 2007, 8, 428–433. [Google Scholar] [CrossRef]
  45. Burzo, E. Exchange Interactions in Heavy Rare-Earths RCo 2 Compounds. J. Phys. Conf. Ser. 2017, 848, 012004. [Google Scholar] [CrossRef]
  46. Burzo, E.; Chioncel, L. . On the Magnetic Behavior of Heavy Rare-Earths RCo2 Compounds. Rom J. Phys. 2018, 62, 601. [Google Scholar]
  47. Herrero-Albillos, J.; Bartolomé, F.; García, L.M.; Young, A.T.; Funk, T.; Campo, J.; Cuello, G.J. Observation of a Different Magnetic Disorder in ErCo 2. Phys. Rev. B 2007, 76, 094409. [Google Scholar] [CrossRef]
  48. Gignoux, D.; Givord, F. Polarised Neutron Study of TbCo2. J. Phys. F Met. Phys. 1979, 9, 1409–1419. [Google Scholar] [CrossRef]
  49. Gignoux, D.; Givord, F.; Koehler, W.C. Determination of Cobalt Behavior in TmCo2 and HoCo2 by Means of Polarized Neutron Diffraction. Phys. B+C 1977, 86–88, 165–166. [Google Scholar] [CrossRef]
  50. Gignoux, D.; Givord, D.; Givord, F.; Koehler, W.C.; Moon, R.M. Polarized-Neutron Study of Tm Co 2. Phys. Rev. B 1976, 14, 162–171. [Google Scholar] [CrossRef]
  51. Gignoux, D.; Givord, F.; Koehler, W.C.; Moon, R.M. . Field Induced Magnetic Density in the Paramagnetic Compound LuCo2. J. Magn. Magn. Mater. 1977, 5, 172–175. [Google Scholar] [CrossRef]
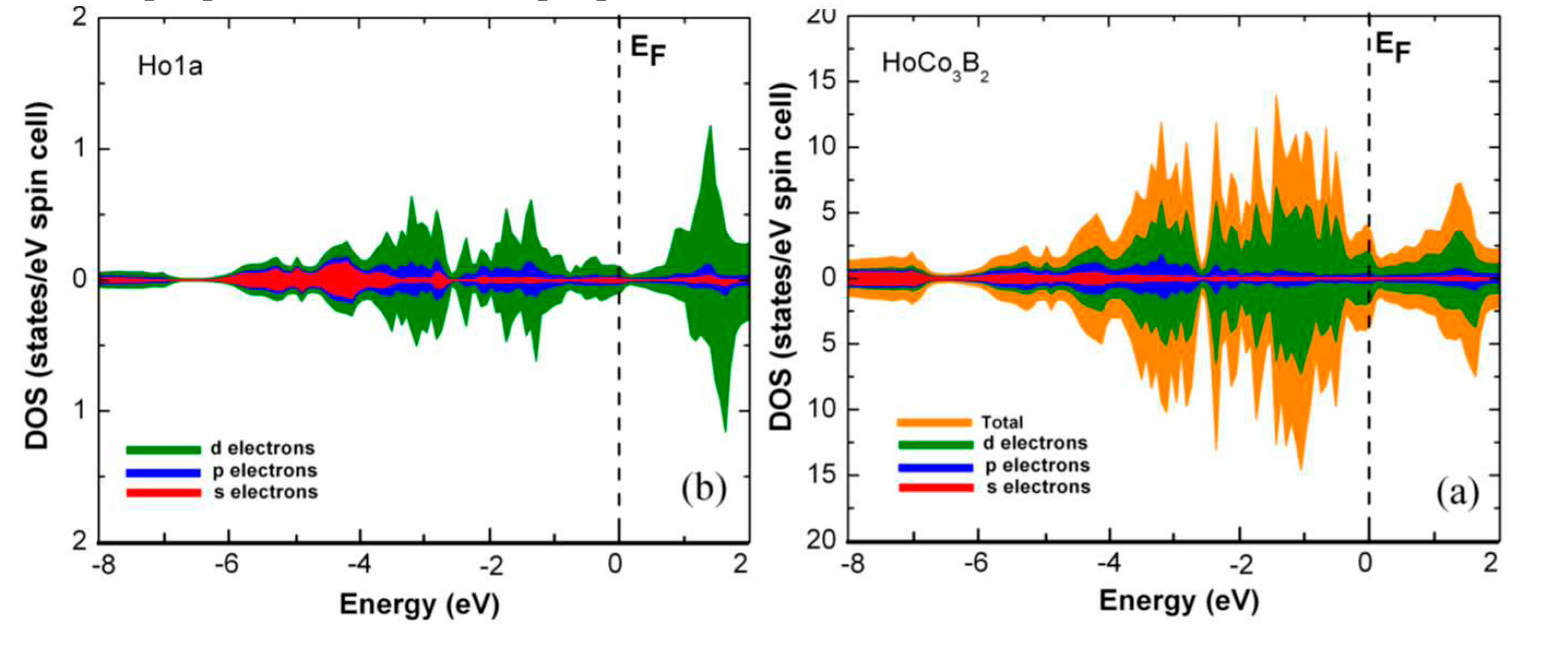
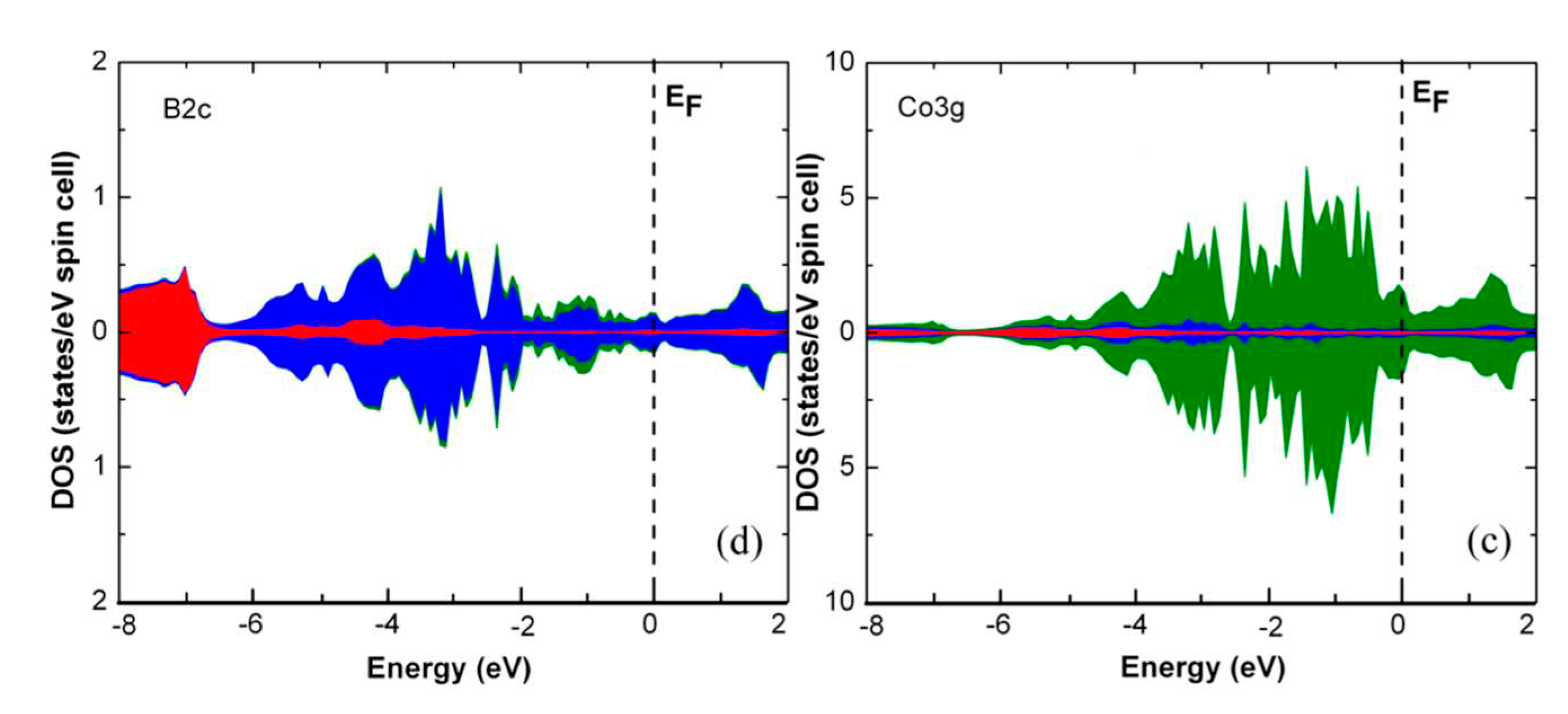
Preprints 78874 g001aPreprints 78874 g001b
Figure 1. Orbital decomposed total (a) and partial (b-d) densities of states of Ho, Co and B atoms in HoCo3B2 compound.
Figure 1. Orbital decomposed total (a) and partial (b-d) densities of states of Ho, Co and B atoms in HoCo3B2 compound.
Preprints 78874 g001aPreprints 78874 g001b
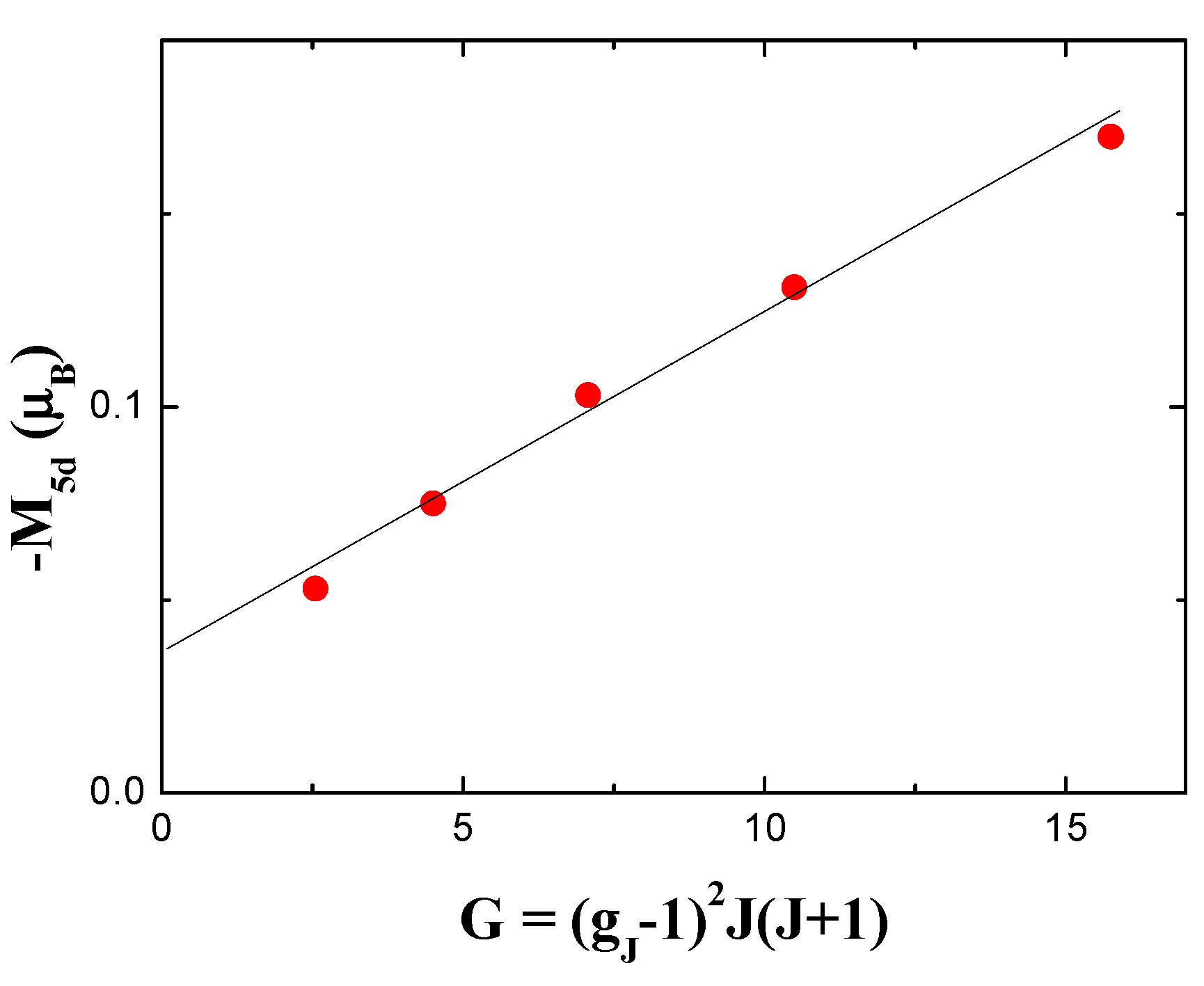
Preprints 78874 g002
Figure 2. The dependence of R5d band polarizations on de Gennes factor in RCo3B2 series.
Figure 2. The dependence of R5d band polarizations on de Gennes factor in RCo3B2 series.
Preprints 78874 g002
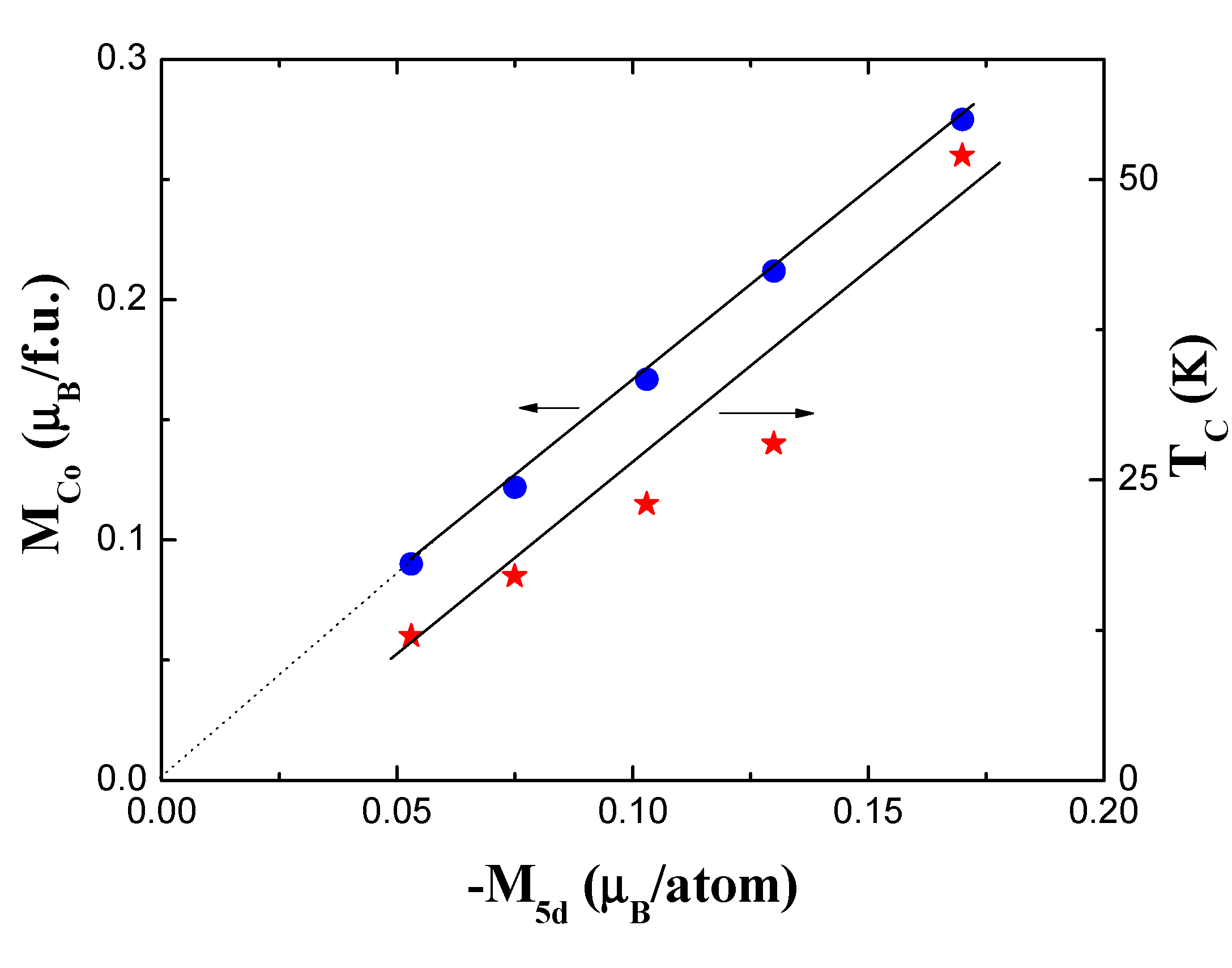
Preprints 78874 g003
Figure 3. Cobalt magnetizations and Curie temperatures as function of R5d band polarizations in RCo3B2 compound.
Figure 3. Cobalt magnetizations and Curie temperatures as function of R5d band polarizations in RCo3B2 compound.
Preprints 78874 g003
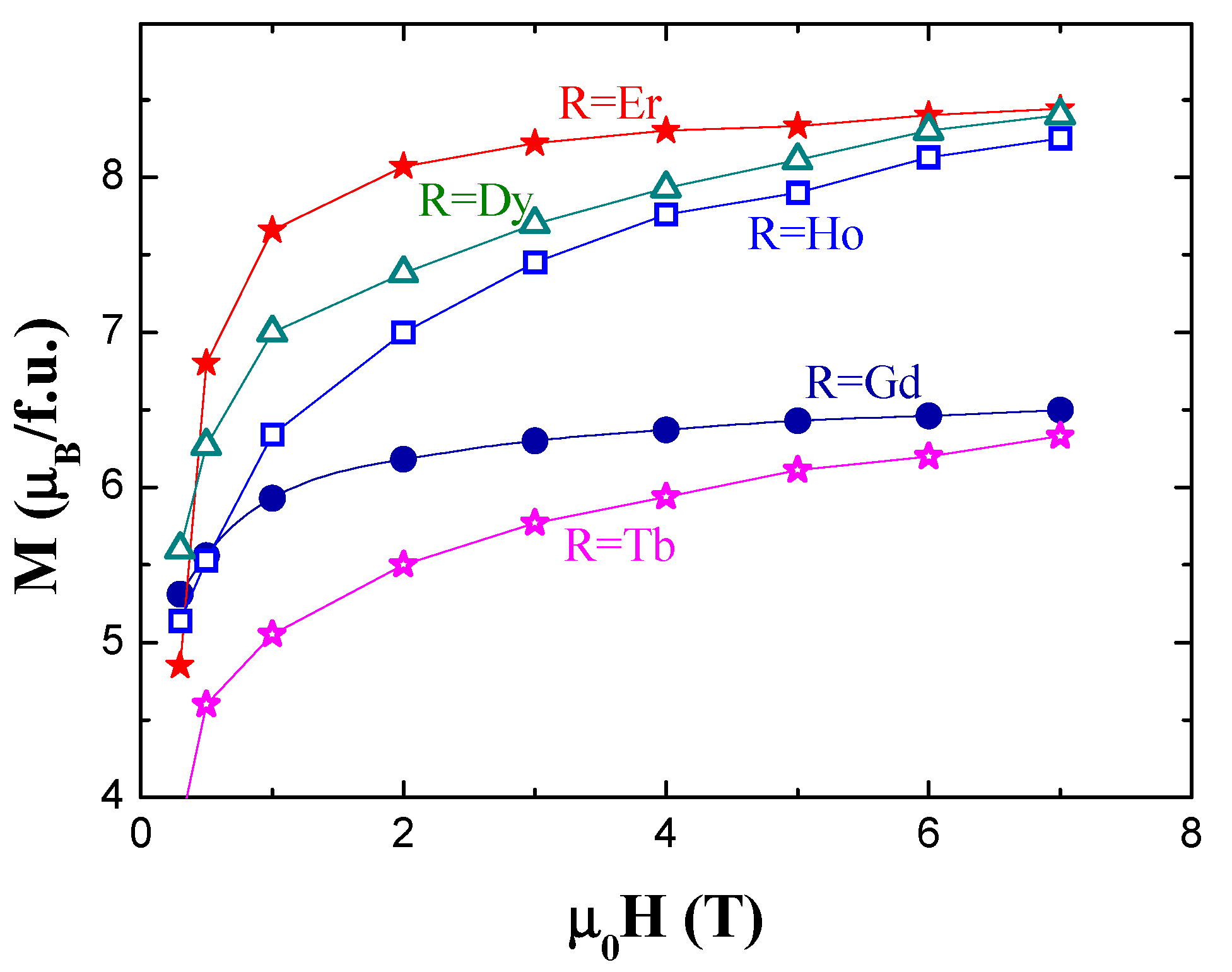
Preprints 78874 g004
Figure 4. Magnetization isotherms at T=4.2 K.
Figure 4. Magnetization isotherms at T=4.2 K.
Preprints 78874 g004
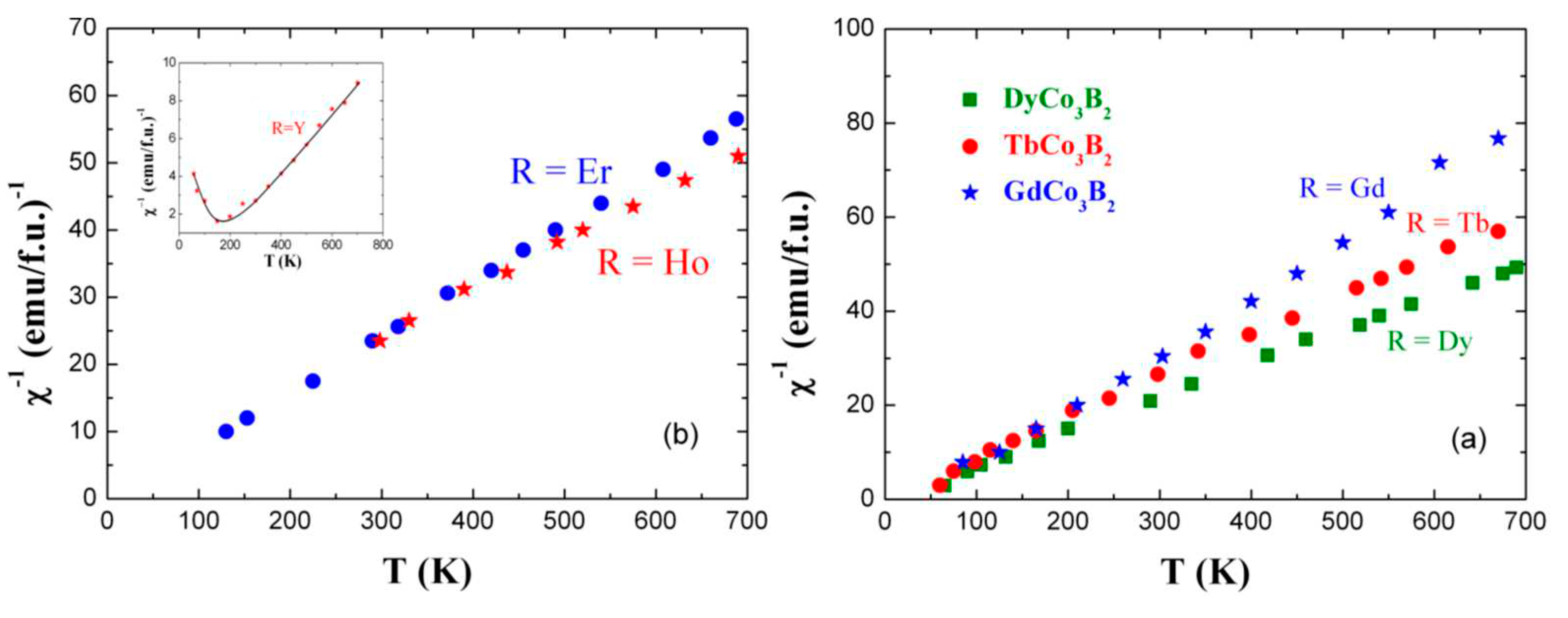
Preprints 78874 g005
Figure 5. Thermal variations of reciprocal susceptibilities for RCo3B2 compounds with R=Gd, Tb, Dy (a) and R=Ho, Er, Y (b).
Figure 5. Thermal variations of reciprocal susceptibilities for RCo3B2 compounds with R=Gd, Tb, Dy (a) and R=Ho, Er, Y (b).
Preprints 78874 g005
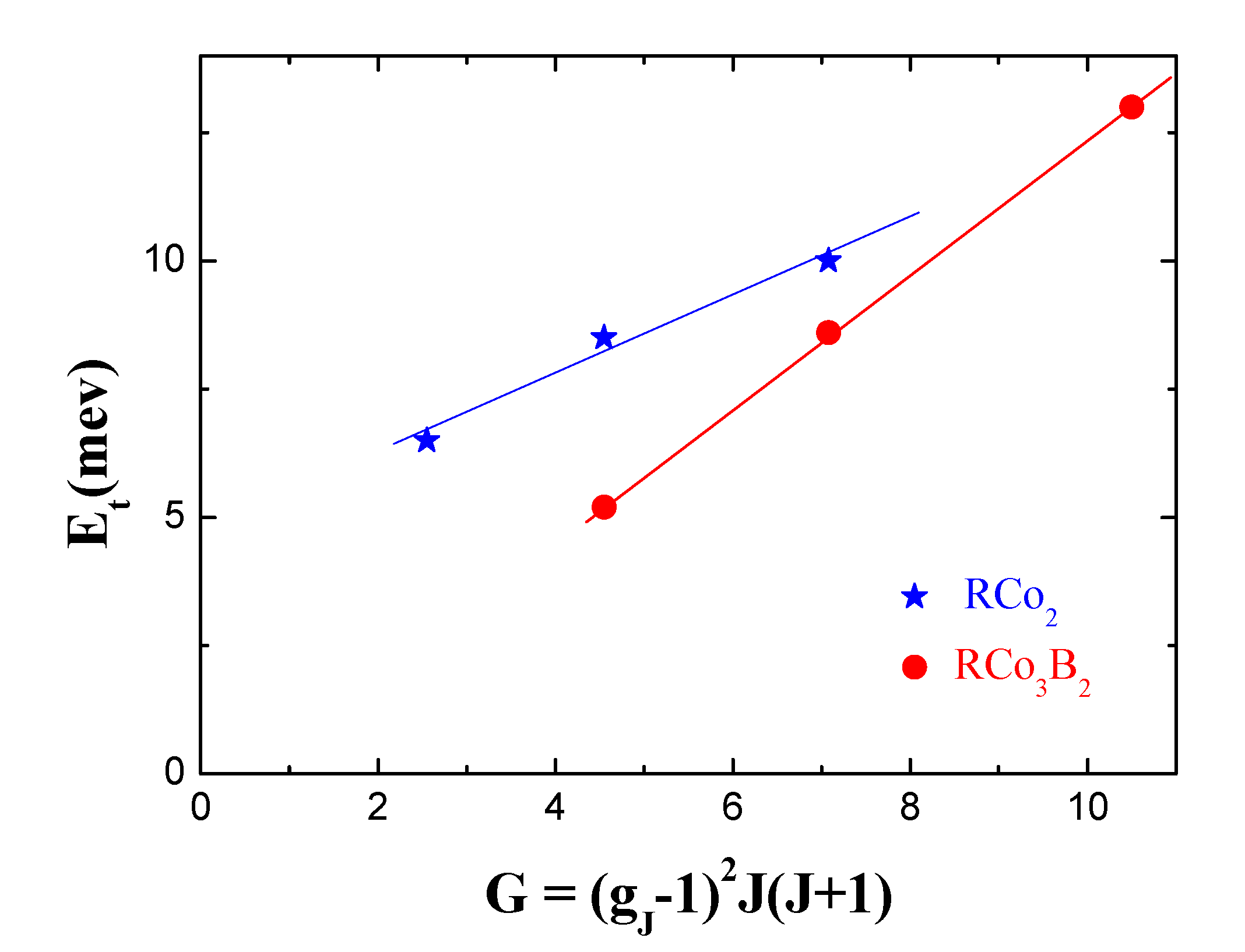
Preprints 78874 g006
Figure 6. The thermal energy for decoupling the interactions in the paramagnetic clusters in some RCo3B2 and RCo2 compounds.
Figure 6. The thermal energy for decoupling the interactions in the paramagnetic clusters in some RCo3B2 and RCo2 compounds.
Preprints 78874 g006
Table 1. Lattice parameters and magnetic data.
Table 1. Lattice parameters and magnetic data.
R Lattice parameters (nm) Magnetization (μB/f.u.) C
(emuK/f.u.)		 Meff (Co) (μB/atom)
a c M4.2a) M0b) Ctotal CCo
Gd 0.5058 0.3020 6.42 6.54 8.63 0.74 1.40
Tb 0.5051 0.3007 6.03 7.73 12.70 0.88 1.53
Dy 0.5029 0.3020 8.23 9.44 15.10 0.96 1.60
Ho 0.520 0.3023 8.57 9.76 14.61 0.48 1.13
Er 0.5004 0.3023 8.37 8.90 12.72 1.28 1.84
Y 0.5032 0.3025 - - 0.674 0.674 1.34
a) at T = 4.2 K, H =7 T; b) extrapolated at T = 0 K and H → ∞.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated