On \Sigma-classes in E^8. IV. The neighbourhood of F_{22}

Preprint

Article

On \Sigma-classes in E^8. IV. The neighbourhood of F_{22}

Altmetrics

Downloads

Views

Comments

Peter Engel^*

This version is not peer-reviewed

Submitted:

12 July 2023

Posted:

13 July 2023

You are already at the latest version

Alerts

Abstract

In the cone of positive quadratic forms C^{8 x 8}, it is shown that there exists in the neighbourhood of the quadratic form Q_{F_{22}} a large cluster of non-equivalent \Sigma_0-subcones of positive volume which are as well minimal as maximal.

Keywords:

Subject: Chemistry and Materials Science - Physical Chemistry

1. Introduction

In d-dimensional Euclidean space

E^{d}

, a bounded, convex body of finite volume congruent copies of which can be juxtaposed by translations such that they fill space without gaps, and overlap only in border points, is denoted by Fedorov [10] as parallelohedron. A special kind of parallelohedron, the Dirichlet parallelohedron is obtained by applying Dirichlet’s famous construction [1] to a lattice of translations

Λ^{d}

. Voronoï [12,13] thoroughly investigated general properties of parallelohedra in spaces of arbitrary dimensions d. That is why they are often referred to as Voronoï parallelohedra.

Quadratic forms, translation lattices and parallelohedra play a predominant role in the geometry of numbers, but also in crystallography, where the lattice-like arrangement of atomic building blocks is a fundamental property of regular crystals. In crystallography, the discovery of quasicrystals, the structure of which can be viewed as projected from higher dimensional translation lattices, has greatly stimulated the investigation of lattices and parallelohedra in arbitrary dimensions.

In Euclidean space

E^{8}

, the collective of all lattices in the open cone

C^{8 \times 8}

of positive definite quatratic forms is considered by studying its subdivision into

Σ

-subcones.

Voronoï proposed that each parallelohedron

\tilde{P}

is affinely equivalent to a Dirichlet parallelohedron

P

, but he proved it for primitive parallelohedra only [12], §44. Primitive means that at each vertex of a parallelohedron

P

in its tiling exactly the minimal number

d + 1

of parallelohedra meet. These are the generic parallelohedra, for under small perturbations the combinatorial type remains fixed.

By using affinely invariant operations only, the zone contraction and zone extension, it becomes obvious that each combinatorial type of totally contracted Dirichlet parallelohedron is sufficient to prove that its complete contraction family can be represented by affine Dirichlet parallelohedra too. In dimensions

d \geq 0

there exist totally contracted parallelohedra which are also referred to as minimal. But in dimensions

d \geq 6

there exist parallelohedra which are as well minimal as maximal that is they allow no extension. This makes these parallelohedra particularly interesting.

In order to find

Σ_{0}

-classes in

C^{8 \times 8}

, the parallelohedra of the maximal finite irreducible subgroups of

G L_{8} (Z Z)

given by Plesken and Pohst [11] are of importance. The five types viz.:

F_{5}

F_{8}

F_{15}

F_{22}

, and

F_{26}

, respectively, are as much minimal as maximal.

In previous papers the neighbourhood of the quadratic form

Q_{F_{5}}

[7],

Q_{F_{8}}

[8]

Q_{F_{15}}

[9] were investigated. In this note, the neighbourhood of

Q_{F_{22}}

will be looked at.

Table 1. The parallelohedra of the maximal finite irreducible subgroups of

G L_{8} (Z Z)

Table 1. The parallelohedra of the maximal finite irreducible subgroups of

G L_{8} (Z Z)

No.	Group	Order	Comb. Type	Zones	Belts
$F_{1}$	$B_{8}$	$2^{8} 8!$	16.256	8(8)	$4_{28}$
$F_{2}$	$D_{8}$	$2^{8} 8!$	112.272	136(0)	$6_{224}$
$F_{3}$		$2 \cdot 1152^{2}$	48.576	24(0)	$4_{114} 6_{32}$
$F_{4}$	$D_{8}^{*}$	$2^{8} 8!$	272.1120	56(0)	$4_{28} 6_{512}$
$F_{5}$	$E_{8}$	$2^{14} 3^{5} 5^{2} 7$	240.19449	8760(0)	$6_{1120}$
$F_{6}$		$3! \cdot 1152$	264.5304	36(0)	$4_{108} 6_{972}$
$F_{7}$		$12^{4} 4!$	24.1296	12(12)	$4_{54} 6_{4}$
$F_{8}$		$2 \cdot 6^{4} 4!$	348.3588	93(0)	$6_{1386}$
$F_{9}$		$2 \cdot 144^{2}$	60.10404	18(18)	$4_{2} 256_{48}$
$F_{10}$	$A_{8}$	$2 \cdot 9!$	72.510	9(9)	$6_{84}$
$F_{11}$		$2 \cdot 6^{4} 4!$	186.5940	174(0)	$4_{54} 6_{544}$
$F_{12}$		$2 \cdot 6^{3} 3!$	402.94254	1497(0)	$6_{2259}$
$F_{13}$	$A_{8}^{*}$	$2 \cdot 9!$	510.362880	36(36)	$6_{3025}$
$F_{14}$		$2 \cdot 240^{2}$	40.900	10(10)	$4_{100} 6_{20}$
$F_{15}$		$2^{7} \cdot 15^{2}$	360.3840	180(0)	$6_{1700}$
$F_{16}$		$2 \cdot 240^{2}$	60.14400	20(20)	$4_{225} 6_{50}$
$F_{17}$		${(2 \cdot 5!)}^{2}$	290.43310	1195(0)	$6_{1370}$
$F_{18}$		$2 \cdot 3! \cdot 5!$	390.106200	450(0)	$6_{2160}$
$F_{19}$		$2 \cdot 3! \cdot 5!$	180.6510	15(15)	$4_{90} 6_{400}$
$F_{20}$		1152	296.13696	580(0)	$4_{66} 6_{1168}$
$F_{21}$		1152	200.2992	304(0)	$4_{48} 6_{564}$
$F_{22}$		$3 \cdot 1152$	456.28632	264(0)	$6_{2260}$
$F_{23}$		672	398.90384	297(0)	$6_{2192}$
$F_{24}$		672	426.37638	21(21)	$4_{24} 6_{1428}$
$F_{25}$		672	308.8028	1011(0)	$4_{21} 6_{1386}$
$F_{26}$		672	398.127848	1036(0)	$6_{2227}$

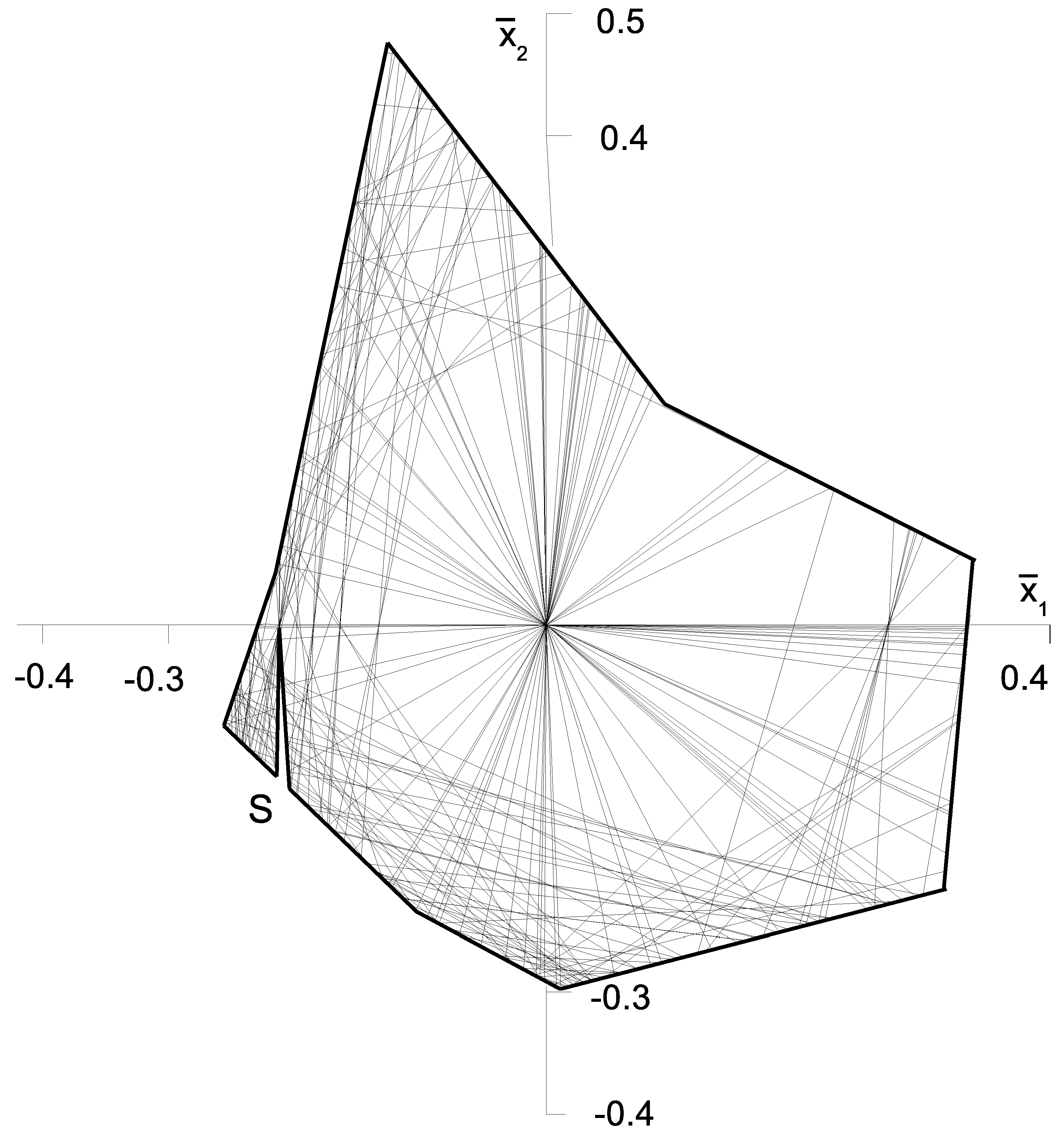
2. The Irreducible Subgroup $F_{22}$

Notations and methods developed in previous papers [3,4,5,6] will be applied.

Referred to an optimal basis the following Gram matrix is obtained.

Q_{F_{22}} : = (\begin{matrix} 6 & - 3 & 2 & 3 & 2 & - 1 & 1 & 0 \\ - 3 & 6 & - 1 & - 3 & 1 & 0 & - 3 & - 3 \\ 2 & - 1 & 6 & 3 & 2 & 1 & - 1 & 2 \\ 3 & - 3 & 3 & 6 & - 1 & 1 & 2 & 3 \\ 2 & 1 & 2 & - 1 & 6 & - 3 & - 3 & - 2 \\ - 1 & 0 & 1 & 1 & - 3 & 6 & 3 & 3 \\ 1 & - 3 & - 1 & 2 & - 3 & 3 & 6 & 3 \\ 0 & - 3 & 2 & 3 & - 2 & 3 & 3 & 6 \end{matrix}) .

The corresponding parallelohedron is computed by half-space intersections,

P (Q_{F_{22}}) : = ⋂_{\forall t \in Λ^{d} ∖ {O}} H_{t} .

(1)

P (Q_{F_{22}})

has 456 facets, 28’632 vertices, and 264 zones all of which are open. Therefore,

P (Q_{F_{22}})

is minimal. The 228 pairs of facet vectors

\pm f_{i}

are listed in Table 2. The set of facet vectors is denoted by

F_{F_{22}}

The condition for a zone vector

z_{k}^{*}

to be extendable is given by

L_{i} (z_{k}^{*}) : = f_{j} z_{k}^{*}, i \in {- 1, 0, 1}, \forall f_{j} \in F_{F_{22}}

(2)

It is readily verified that for all zone vectors

z_{k}^{*}

with components

∣ z_{l} ∣ \leq 4

l = 1, . . ., 8

, the facet vectors

f_{j} \in F_{F_{22}}

belong to layers

L_{i} (z_{k}^{*})

- n \leq i \leq n

, where

n \geq 2

. Therefore,

P (Q_{F_{22}})

is as much minimal as maximal.

The 456 facet vectors of

P (Q_{F_{22}})

belong to three equivalence classes of norm 6, 8, and 10, respectively. In order to obtain the group

G_{F_{22}}

, the unified polytope scheme, described in [2], was used. Each identical scheme induces a permutation

S

of the facet vectors under their automorphism group. There exists an isomorphism between the class of identical schemes and the group of automorphisms of

P (Q_{F_{22}})

Below are given generating rotations of order 6 (

S_{1}

), 8 (

S_{2}

), and 12 (

S_{3}

), respectively, which generate the group

G_{F_{22}}

of order 3’456. The group contains only pure rotations.

S_{1} : = (\begin{matrix} 0 & - 1 & 0 & 0 & - 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & - 1 & 1 & 0 & 0 \\ - 1 & 1 & 0 & - 1 & 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & 0 & 0 & - 1 & 0 & - 1 \\ 0 & 0 & - 1 & 0 & 0 & 0 & 1 & 0 \\ - 1 & 1 & 0 & - 1 & 0 & 0 & - 1 & - 1 \\ 1 & - 1 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}),

S_{2} : = (\begin{matrix} 0 & 0 & 1 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & - 1 & 1 & 1 & 0 & 0 & 0 & 1 \\ - 1 & 1 & - 1 & - 1 & 0 & - 1 & - 1 & - 1 \\ - 1 & 1 & - 1 & - 1 & 0 & 0 & 0 & 0 \\ - 1 & 0 & - 1 & - 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & - 1 & 1 & 1 & 0 \end{matrix}),

S_{3} : = (\begin{matrix} 0 & 0 & 0 & - 1 & 1 & - 1 & - 1 & - 1 \\ 0 & 1 & 0 & - 1 & 1 & - 1 & - 1 & - 1 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ - 1 & 1 & 0 & 0 & - 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & - 1 & 0 & 0 & 0 \\ - 1 & 0 & - 1 & 0 & - 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & - 1 & - 1 & 0 \end{matrix}) .

It holds:

S_{i}^{t} Q_{F_{22}} S_{i} = Q_{F_{22}}, \forall S_{i} \in G_{F_{22}} .

(3)

3. The Neighbourhood of $Q_{F_{22}}$

In the neighourhood of

Q_{F_{22}}

, a form

Q_{1}

was found, whose parallelohedron is primitive and therefore, has the maximal number 510 of facets, as well as 362’304 vertices, and 761 zones all of which are open:

Q_{1} : =

(\begin{matrix} 6.05228 & - 3.02808 & 1.83912 & 2.92092 & 1.83868 & - 0.86624 & 0.86536 & - 0.10748 \\ - 3.02808 & 6.05256 & - 0.86504 & - 2.92108 & 1.08004 & - 0.10812 & - 2.81348 & - 2.91876 \\ 1.83912 & - 0.86504 & 6.05272 & 2.81244 & 2.05364 & 0.97484 & - 0.86644 & 2.05432 \\ 2.92092 & - 2.92108 & 2.81244 & 6.05292 & - 0.97332 & 0.86608 & 1.83976 & 2.81120 \\ 1.83868 & 1.08004 & 2.05364 & - 0.97332 & 6.05352 & - 3.02916 & - 2.92188 & - 1.94620 \\ - 0.86624 & - 0.10812 & 0.97484 & 0.86608 & - 3.02916 & 6.05368 & 2.91984 & 2.92224 \\ 0.86536 & - 2.81348 & - 0.86644 & 1.83976 & - 2.92188 & 2.91984 & 6.05396 & 3.02740 \\ - 0.10748 & - 2.91876 & 2.05432 & 2.81120 & - 1.94620 & 2.92224 & 3.02740 & 6.05412 \end{matrix}) .

The Gram matix

Q_{1}

defines the

Σ_{0}^{1}

-subcone. For each

Q

in the open

Σ_{0}^{1}

-subcone, the set of facet vectors

F_{Q_{1}}

is an invariant of

Σ_{0}^{1}

and it is denoted by

F_{Σ_{0}^{1}}

. The facet vectors are given in Table 4. Since

P (Q_{1})

is generic it has the maximal number of facets. Verifying equation (2) for all zone vectors

z_{k}^{*}

with components

∣ z_{l} ∣ \leq 4

, it results that the facet vectors

f_{j} \in F_{Σ_{0}^{1}}

, lie in layers

L_{i} (z_{k}^{*})

i \in {- n \leq i \leq n}

, where

n \geq 2

. Thus,

P (Q_{1})

is as much minimal as maximal.

In order to calculate the

Σ_{0}^{1}

-subcone, all tripletts

f_{i} + f_{j} + f_{k} = 0, f_{i}, f_{j}, f_{k} \in F_{Σ_{0}^{1}},

are determined. Their number is

N_{b}

=3’793 and the number of half-spaces

H_{i}

becomes

3 N_{b}

. The closed subcone

Σ_{0}^{1}

with apex in

\tilde{O}

becomes

Σ_{0}^{1} : = ⋂_{i = 1}^{3 N_{b}} H_{i} .

(4)

Because of the heigh complexity of the

Σ_{0}^{1}

-subcone, the direct computation of

Σ_{0}^{1}

as well as of its

Φ

-subcones is not practicable with small computers. Instead, existence charts may be defined which intersect the

Σ_{0}^{1}

-subcone.

Using condition

n_{i}^{t} q > 0, i = 1, \dots, 3 N_{b} .

(5)

any further form

Q_{2} \in Σ_{0}^{1}

can be found viz.:

Q_{2} : =

(\begin{matrix} 6.05104 & - 3.02844 & 1.83868 & 2.78892 & 1.82188 & - 0.87588 & 0.86456 & - 0.10868 \\ - 3.02844 & 6.07416 & - 0.86660 & - 2.87348 & 1.07004 & - 0.11692 & - 2.81192 & - 2.91592 \\ 1.83868 & - 0.86660 & 6.14472 & 2.83496 & 2.06568 & 0.96604 & - 0.86968 & 2.05112 \\ 2.78892 & - 2.87348 & 2.83496 & 6.17292 & - 0.96612 & 0.85528 & 1.83936 & 2.81088 \\ 1.82188 & 1.07004 & 2.06568 & - 0.96612 & 6.05596 & - 3.03876 & - 2.92208 & - 1.94636 \\ - 0.87588 & - 0.11692 & 0.96604 & 0.85528 & - 3.03876 & 6.06728 & 2.90464 & 2.91460 \\ 0.86456 & - 2.81192 & - 0.86968 & 1.83936 & - 2.92208 & 2.90464 & 6.06596 & 3.02140 \\ - 0.10868 & - 2.91592 & 2.05112 & 2.81088 & - 1.94636 & 2.91460 & 3.02140 & 6.04612 \end{matrix}) .

The parallelohedron

P (Q_{2})

is primitive and therefore, has the maximal number 510 of facets, as well as 362’160 vertices, and 778 zones all of which are open, and it proves that

Q_{F_{22}}

lies on the boundary of

Σ_{0}^{1}

The three forms

Q_{F_{22}}, Q_{1}, Q_{2} \in Σ_{0}^{1}

determine a 2-section

Π^{2}

through the

Σ_{0}^{1}

-subcone. with origin in

Q_{F_{22}}

and cartesian coordinates

{\bar{x}}_{1}

, and

{\bar{x}}_{2}

, respectively. Each

Q \in Π^{2}

is obtained by

Q = Q_{F_{22}} + \sum_{i = 1}^{2} λ_{i} {\bar{x}}_{i}, λ_{i} \in I R .

The condition (5) is used to decide if

Q

is interior to a

Σ_{0}^{k}

-subcone. Considering that

F_{Σ_{0}^{k}}

is an invariant for

Σ_{0}^{k}

, the parallelohedron

P (Q)

is easily computed.

In what follows, the surrounding of the

Σ_{0}^{1}

-subcone in the section

Π^{2}

is investigated.

First, all walls

W_{k}

containing

Q_{F_{22}}

are determined along the four straight line segments

\begin{matrix} 0.1 {\bar{x}}_{1} + λ_{2} {\bar{x}}_{2} \\ - 0.1 {\bar{x}}_{1} + λ_{2} {\bar{x}}_{2} \\ λ_{1} {\bar{x}}_{1} + 0.1 {\bar{x}}_{2} \\ λ_{1} {\bar{x}}_{1} - 0.1 {\bar{x}}_{2} \end{matrix} - 0.1 \leq λ_{1}, λ_{2} \leq 0.1,

forming a quadrangle arround the center

Q_{F_{22}}

. Applying the method of nested intervals, the border point

Q_{k}

between two neighbouring

Σ_{0}^{k}

- and

Σ_{0}^{k + 1}

-subcones is easily determind within an

ϵ

-limit. The value of

ϵ

is chosen to be

ϵ = d e t (Q) 10^{- 10} .

The border point

Q_{k}

corresponds to a limiting parallelohedron

P (Q_{k})

which is characterized by haveing some vertex

v \in P (Q_{k})

where at least d+1 facets meet. The wall

W_{k}

contains

Q_{k}

and the origin

\tilde{O}

. Thus, the wall normal

n_{k}

is easily calculated.

It proves that there exists a highly complex cluster

C_{F_{22}}

Σ_{0}^{k}

-subcones. In Figure 1 is shown the section through the

C_{F_{22}}

-cluster. Only the border lines of the

Σ_{0}^{k}

-subcones are drawn. Each border line corresponds to a wall

W_{h}

having wall normal

n_{h}

of some

Σ_{0}^{k}

-subcone, and therefore, has a representation as a tensor product

n_{h} = f_{a} \otimes f_{b}, f_{a}, f_{b} \in F_{Σ_{0}^{k}} .

There exist two kinds of walls. Walls

W^{(i)}

that separate two adjacent

Σ_{0}

-subcones, and walls

W^{(a)}

that separate a

Σ_{0}

-subcone from a adjacent

Σ_{1}

-subcone. In order to determine all walls, it would require to compute a huge number of

Φ

-subcones which at present is far out of reach.

The walls containing the center

Q_{F_{22}}

belong to three non-equivalent wall classes

W_{h}

h = 1, 2, 3

, under the group

G_{F_{22}}

which are shown in Table 6.

A representative wall normal

n_{j}

W_{j} \in W_{h}

is given by a tensor product

n_{j} : = (f_{a} \otimes f_{b}), f_{a}, f_{b} \in F_{Σ_{0}^{k}} .

Although the walls

W_{i} \in W_{h}

are equivalent, the

Σ_{0}^{i}

-subcones in the

C_{F_{22}}

-cluster are not equivalent because the section

Π^{2}

generally contains only one element of the orbit of some

Q \in Σ_{0}^{1}

under the group

G_{F_{22}}

. Altogether there exist 684 walls containing

Q_{F_{22}}

, whereof 102 intersect the

C_{F_{22}}

-cluster.

For fixing the outer border of the

C_{F_{22}}

-cluster further walls along suitable straight line segments were determined in order to find the walls which separate a

Σ_{0}^{i}

-subkone from a

Σ_{1}^{j}

-subcone. Thereby, the border lines avoiding the center

Q_{F_{22}}

were found which are shown in Figure 1. Remarkable in the Figure is the spike S of

Σ_{1}^{j}

-subcones entering into the

C_{F_{22}}

-cluster. In the

Π^{2}

-section, the border lines do not necessarily extend over the whole cluster. When several border lines intersect then some border lines may end in the point of intersection. In Figure 1 it is seen that many of the walls

W_{i} \in W^{(i)}

end in the center

Q_{F_{22}}

. We don’t have further investigated this behaviour.

A rough estimate for the number of non-equivalent

Σ_{0}^{k}

-subcones within the

C_{F_{22}}

-cluster in

E^{8}

could amount up to

10^{10}

References

P.G.L. Dirichlet, Über die Reduction der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen, J. reine angew. Math. 40 (1850) 209-227; [Oeuvre Vol. II, p. 41-59].
P. Engel, On the enumeration of four-dimensional polytopes, Discrete Math 91 (1991) 9-31.
P. Engel, The contraction types of parallelohedra in E⁵, Acta Cryst. A 56 (2000) 491-496.
P. Engel, On Fedorov’s parallelohedra - a review and new results, Cryst. Res. Technol. 50, No. 12 (2015) 929-943.
P. Engel, On the Σ-classes in E⁶, Acta Cryst. A 76 (2020) 622-626.
P. Engel, On Σ-classes in E⁷, JSODS (2023), Vol. 1 No. 1.
P. Engel, On Σ-classes in E⁸. I. The neighbourhood of F₅, Crystals (2023) 13(2),246.
P. Engel, On Σ-classes in E⁸. II. The neighbourhood of F₈, IJMSOR (2023), Vol. 3 No. 1.
P. Engel, On Σ-classes in E⁸. III. The neighbourhood of F₁₅, to be published.
E.S. Fedorov, Nachala ucheniya o figurah, Verhandlungen der russisch-kaiserlichen mineralogischen Gesellschaft zu St. Petersburg 21 (1885), 1-279; [Reprint: Akad. Nauk SSSR, 1953; Résumé in German, E.S. Fedorov, Elemente der Gestaltungslehre, Z. Kristallogr. 21 (1893), 679-694].
W. Plesken, M. W. Plesken, M. Pohst, The eight dimensional case and complete description of dimensions less than ten, Math. Comp. 34 (1980) 277-301.
G.M. Voronoï, Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. recherches sur les paralléloèdres primitifs, J. reine angew. Math. 134 (1008) 198-287.
G.M. Voronoï, Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. recherches sur les paralléloèdres primitifs, J. reine angew. Math. 135 (1909) 67-181.

Figure 1. Existence chart through the

C_{F_{22}}

-cluster in

E^{8}

Figure 1. Existence chart through the

C_{F_{22}}

-cluster in

E^{8}

Table 2. The facet vectors

\pm f_{i}

P (Q_{F_{22}})

Table 2. The facet vectors

\pm f_{i}

P (Q_{F_{22}})

$f_{1}$	1 0 0 0 0 0 0 0	$f_{3}$	0 1 0 0 0 0 0 0	$f_{5}$	1 1 0 0 0 0 0 0
$f_{7}$	0 0 1 0 0 0 0 0	$f_{9}$	0 1 1 0 0 0 0 0	$f_{11}$	1 0 -1 0 0 0 0 0
$f_{13}$	1 1 -1 0 0 0 0 0	$f_{15}$	0 0 0 1 0 0 0 0	$f_{17}$	0 1 0 1 0 0 0 0
$f_{19}$	0 1 -1 1 0 0 0 0	$f_{21}$	1 1 -1 1 0 0 0 0	$f_{23}$	1 0 0 -1 0 0 0 0
$f_{25}$	0 0 1 -1 0 0 0 0	$f_{27}$	1 0 1 -1 0 0 0 0	$f_{29}$	0 0 0 0 1 0 0 0
$f_{31}$	0 0 0 1 1 0 0 0	$f_{33}$	0 1 -1 1 1 0 0 0	$f_{35}$	1 0 0 0 -1 0 0 0
$f_{37}$	0 1 0 0 -1 0 0 0	$f_{39}$	1 1 0 0 -1 0 0 0	$f_{41}$	0 0 1 0 -1 0 0 0
$f_{43}$	0 1 1 0 -1 0 0 0	$f_{45}$	1 1 1 0 -1 0 0 0	$f_{47}$	1 0 0 -1 -1 0 0 0
$f_{49}$	1 1 0 -1 -1 0 0 0	$f_{51}$	0 0 1 -1 -1 0 0 0	$f_{53}$	1 0 1 -1 -1 0 0 0
$f_{55}$	1 1 1 -1 -1 0 0 0	$f_{57}$	1 0 1 -2 -1 0 0 0	$f_{59}$	0 0 0 0 0 1 0 0
$f_{61}$	1 0 0 0 0 1 0 0	$f_{63}$	1 1 0 0 0 1 0 0	$f_{65}$	1 0 -1 0 0 1 0 0
$f_{67}$	1 0 0 -1 0 1 0 0	$f_{69}$	0 0 0 0 1 1 0 0	$f_{71}$	1 0 -1 0 1 1 0 0
$f_{73}$	0 1 -1 1 1 1 0 0	$f_{75}$	0 0 1 0 0 -1 0 0	$f_{77}$	0 0 0 1 0 -1 0 0
$f_{79}$	0 1 0 1 0 -1 0 0	$f_{81}$	1 0 0 0 -1 -1 0 0	$f_{83}$	0 1 0 0 -1 -1 0 0
$f_{85}$	1 1 0 0 -1 -1 0 0	$f_{87}$	0 0 1 0 -1 -1 0 0	$f_{89}$	0 1 1 0 -1 -1 0 0
$f_{91}$	1 1 1 0 -1 -1 0 0	$f_{93}$	0 1 0 1 -1 -1 0 0	$f_{95}$	1 0 0 -1 -1 -1 0 0
$f_{97}$	0 0 1 -1 -1 -1 0 0	$f_{99}$	1 0 1 -1 -1 -1 0 0	$f_{101}$	1 1 1 -1 -1 -1 0 0
$f_{103}$	1 0 1 -1 -2 -1 0 0	$f_{105}$	1 1 1 -1 -2 -1 0 0	$f_{107}$	0 0 0 0 0 0 1 0
$f_{109}$	0 1 0 0 0 0 1 0	$f_{111}$	1 1 0 0 0 0 1 0	$f_{113}$	0 0 1 0 0 0 1 0
$f_{115}$	0 1 1 0 0 0 1 0	$f_{117}$	0 1 0 1 0 0 1 0	$f_{119}$	1 0 0 -1 0 0 1 0
$f_{121}$	1 1 0 -1 0 0 1 0	$f_{123}$	0 0 1 -1 0 0 1 0	$f_{125}$	0 1 1 -1 0 0 1 0
$f_{127}$	1 1 1 -1 0 0 1 0	$f_{129}$	0 0 0 0 1 0 1 0	$f_{131}$	0 1 0 0 1 0 1 0
$f_{133}$	0 1 0 1 1 0 1 0	$f_{135}$	0 1 -1 1 1 0 1 0	$f_{137}$	1 1 1 -1 -1 0 1 0
$f_{139}$	0 1 0 0 0 -1 1 0	$f_{141}$	1 1 0 0 0 -1 1 0	$f_{143}$	0 0 1 0 0 -1 1 0
$f_{145}$	0 1 1 0 0 -1 1 0	$f_{147}$	0 1 0 1 0 -1 1 0	$f_{149}$	0 0 1 -1 0 -1 1 0
$f_{151}$	0 1 1 -1 0 -1 1 0	$f_{153}$	0 1 0 0 -1 -1 1 0	$f_{155}$	1 1 0 0 -1 -1 1 0
$f_{157}$	0 0 1 0 -1 -1 1 0	$f_{159}$	0 1 1 0 -1 -1 1 0	$f_{161}$	1 1 1 0 -1 -1 1 0
$f_{163}$	0 0 1 -1 -1 -1 1 0	$f_{165}$	1 0 1 -1 -1 -1 1 0	$f_{167}$	0 1 1 -1 -1 -1 1 0
$f_{169}$	1 1 1 -1 -1 -1 1 0	$f_{171}$	0 0 2 -1 -1 -1 1 0	$f_{173}$	0 1 2 -1 -1 -1 1 0
$f_{175}$	0 1 1 0 -1 -2 1 0	$f_{177}$	1 0 0 0 0 0 -1 0	$f_{179}$	1 0 -1 0 0 0 -1 0
$f_{181}$	0 0 0 1 0 0 -1 0	$f_{183}$	1 0 0 0 -1 0 -1 0	$f_{185}$	1 1 0 0 -1 0 -1 0
$f_{187}$	0 0 1 0 -1 0 -1 0	$f_{189}$	1 0 -1 0 -1 0 -1 0	$f_{191}$	0 0 0 1 -1 0 -1 0
$f_{193}$	1 0 0 -1 -1 0 -1 0	$f_{195}$	1 -1 0 -1 -1 0 -1 0	$f_{197}$	1 0 1 -1 -1 0 -1 0
$f_{199}$	0 0 0 0 0 1 -1 0	$f_{201}$	1 0 0 0 0 1 -1 0	$f_{203}$	1 0 -1 0 0 1 -1 0
$f_{205}$	1 -1 -1 0 0 1 -1 0	$f_{207}$	0 0 0 1 0 1 -1 0	$f_{209}$	1 0 -1 1 0 1 -1 0
$f_{211}$	1 0 0 -1 0 1 -1 0	$f_{213}$	1 -1 0 -1 0 1 -1 0	$f_{215}$	1 0 0 0 -1 1 -1 0
$f_{217}$	1 0 0 -1 -1 1 -1 0	$f_{219}$	0 1 1 0 0 -1 2 0	$f_{221}$	0 1 1 -1 0 -1 2 0
$f_{223}$	0 0 0 0 0 0 0 1	$f_{225}$	0 1 0 0 0 0 0 1	$f_{227}$	1 1 0 0 0 0 0 1
$f_{229}$	1 0 -1 0 0 0 0 1	$f_{231}$	0 1 -1 0 0 0 0 1	$f_{233}$	1 1 -1 0 0 0 0 1
$f_{235}$	0 1 -1 1 0 0 0 1	$f_{237}$	1 0 0 -1 0 0 0 1	$f_{239}$	1 1 0 -1 0 0 0 1
$f_{241}$	0 0 1 -1 0 0 0 1	$f_{243}$	1 0 -1 -1 0 0 0 1	$f_{245}$	0 0 0 0 1 0 0 1
$f_{247}$	0 1 0 0 1 0 0 1	$f_{249}$	0 1 -1 0 1 0 0 1	$f_{251}$	1 1 -1 0 1 0 0 1
$f_{253}$	0 1 -1 1 1 0 0 1	$f_{255}$	1 1 0 0 -1 0 0 1	$f_{257}$	1 0 0 -1 -1 0 0 1
$f_{259}$	1 1 0 -1 -1 0 0 1	$f_{261}$	2 1 0 -1 -1 0 0 1	$f_{263}$	1 1 1 -1 -1 0 0 1
$f_{265}$	0 1 0 0 0 -1 0 1	$f_{267}$	1 1 0 0 0 -1 0 1	$f_{269}$	1 1 -1 0 0 -1 0 1
$f_{271}$	0 1 0 1 0 -1 0 1	$f_{273}$	0 1 -1 1 0 -1 0 1	$f_{275}$	1 0 0 -1 0 -1 0 1
$f_{277}$	1 1 0 -1 0 -1 0 1	$f_{279}$	0 0 1 -1 0 -1 0 1	$f_{281}$	0 1 0 0 -1 -1 0 1
$f_{283}$	1 1 0 0 -1 -1 0 1	$f_{285}$	1 2 0 0 -1 -1 0 1	$f_{287}$	0 1 1 0 -1 -1 0 1
$f_{289}$	1 0 0 -1 -1 -1 0 1	$f_{291}$	1 1 0 -1 -1 -1 0 1	$f_{293}$	2 1 0 -1 -1 -1 0 1
$f_{295}$	0 0 1 -1 -1 -1 0 1	$f_{297}$	1 0 1 -1 -1 -1 0 1	$f_{299}$	0 1 1 -1 -1 -1 0 1
$f_{301}$	1 1 1 -1 -1 -1 0 1	$f_{303}$	1 0 1 -2 -1 -1 0 1	$f_{305}$	1 1 1 -1 -2 -1 0 1
$f_{307}$	1 1 0 -1 0 0 1 1	$f_{309}$	0 1 0 0 1 0 1 1	$f_{311}$	0 1 0 0 0 -1 1 1
$f_{313}$	1 1 0 0 0 -1 1 1	$f_{315}$	1 2 0 0 0 -1 1 1	$f_{317}$	0 1 1 0 0 -1 1 1
$f_{319}$	0 1 0 -1 0 -1 1 1	$f_{321}$	1 1 0 -1 0 -1 1 1	$f_{323}$	0 0 1 -1 0 -1 1 1
$f_{325}$	0 1 1 -1 0 -1 1 1	$f_{327}$	1 1 1 -1 0 -1 1 1	$f_{329}$	0 1 0 0 1 -1 1 1
$f_{331}$	1 1 0 -1 -1 -1 1 1	$f_{333}$	0 1 1 -1 -1 -1 1 1	$f_{335}$	1 1 1 -1 -1 -1 1 1
$f_{337}$	1 2 1 -1 -1 -1 1 1	$f_{339}$	1 1 1 -2 -1 -1 1 1	$f_{341}$	0 1 1 -1 -1 -2 1 1
$f_{343}$	1 1 1 -1 -1 -2 1 1	$f_{345}$	1 0 0 0 0 0 -1 1	$f_{347}$	1 1 0 0 0 0 -1 1
$f_{349}$	1 0 -1 0 0 0 -1 1	$f_{351}$	1 1 -1 0 0 0 -1 1	$f_{353}$	0 1 -1 1 0 0 -1 1
$f_{355}$	1 1 -1 1 0 0 -1 1	$f_{357}$	1 0 0 -1 0 0 -1 1	$f_{359}$	1 0 -1 -1 0 0 -1 1
$f_{361}$	1 0 0 0 -1 0 -1 1	$f_{363}$	1 1 0 0 -1 0 -1 1	$f_{365}$	1 0 -1 0 -1 0 -1 1
$f_{367}$	1 1 -1 0 -1 0 -1 1	$f_{369}$	1 0 0 -1 -1 0 -1 1	$f_{371}$	1 1 0 -1 -1 0 -1 1
$f_{373}$	2 1 0 -1 -1 0 -1 1	$f_{375}$	1 0 -1 0 0 1 -1 1	$f_{377}$	1 1 -1 0 0 1 -1 1
$f_{379}$	1 0 0 -1 0 1 -1 1	$f_{381}$	1 0 -1 -1 0 1 -1 1	$f_{383}$	1 0 -1 0 1 1 -1 1
$f_{385}$	1 1 0 0 -1 -1 -1 1	$f_{387}$	1 0 0 -1 -1 -1 -1 1	$f_{389}$	1 0 -1 0 0 1 -2 1
$f_{391}$	0 0 1 0 0 0 0 -1	$f_{393}$	0 0 0 1 0 0 0 -1	$f_{395}$	1 0 0 0 -1 0 0 -1
$f_{397}$	0 0 1 0 -1 0 0 -1	$f_{399}$	0 0 0 1 -1 0 0 -1	$f_{401}$	0 0 1 -1 -1 0 0 -1
$f_{403}$	1 0 1 -1 -1 0 0 -1	$f_{405}$	0 0 0 0 0 1 0 -1	$f_{407}$	1 0 0 0 0 1 0 -1
$f_{409}$	0 0 1 0 0 1 0 -1	$f_{411}$	0 0 0 1 0 1 0 -1	$f_{413}$	0 0 0 0 1 1 0 -1
$f_{415}$	0 0 0 1 1 1 0 -1	$f_{417}$	0 0 1 0 -1 -1 0 -1	$f_{419}$	0 0 0 0 0 0 1 -1
$f_{421}$	0 0 1 0 0 0 1 -1	$f_{423}$	0 1 1 0 0 0 1 -1	$f_{425}$	0 0 0 1 0 0 1 -1
$f_{427}$	0 1 0 1 0 0 1 -1	$f_{429}$	0 0 1 -1 0 0 1 -1	$f_{431}$	0 0 0 0 1 0 1 -1
$f_{433}$	0 0 1 0 -1 0 1 -1	$f_{435}$	0 0 1 -1 -1 0 1 -1	$f_{437}$	0 0 0 0 1 1 1 -1
$f_{439}$	0 0 1 0 0 -1 1 -1	$f_{441}$	0 0 1 0 -1 -1 1 -1	$f_{443}$	0 1 1 0 -1 -1 1 -1
$f_{445}$	0 0 1 -1 -1 -1 1 -1	$f_{447}$	0 0 2 -1 -1 -1 1 -1	$f_{449}$	0 0 0 1 0 1 -1 -1
$f_{451}$	1 1 0 -1 0 -1 0 2	$f_{453}$	1 1 0 -1 -1 -1 0 2	$f_{455}$	1 1 -1 0 0 0 -1 2

Table 3. The facet vectors

\pm f_{i}

P (Q_{1})

Table 3. The facet vectors

\pm f_{i}

P (Q_{1})

$f_{1}$	1 0 0 0 0 0 0 0	$f_{3}$	0 1 0 0 0 0 0 0	$f_{5}$	1 1 0 0 0 0 0 0
$f_{7}$	0 0 1 0 0 0 0 0	$f_{9}$	0 1 1 0 0 0 0 0	$f_{11}$	1 0 -1 0 0 0 0 0
$f_{13}$	1 1 -1 0 0 0 0 0	$f_{15}$	0 0 0 1 0 0 0 0	$f_{17}$	0 1 0 1 0 0 0 0
$f_{19}$	1 1 0 1 0 0 0 0	$f_{21}$	0 1 -1 1 0 0 0 0	$f_{23}$	1 1 -1 1 0 0 0 0
$f_{25}$	1 0 0 -1 0 0 0 0	$f_{27}$	0 0 1 -1 0 0 0 0	$f_{29}$	1 0 1 -1 0 0 0 0
$f_{31}$	0 0 0 0 1 0 0 0	$f_{33}$	0 0 0 1 1 0 0 0	$f_{35}$	0 1 -1 1 1 0 0 0
$f_{37}$	1 0 0 0 -1 0 0 0	$f_{39}$	0 1 0 0 -1 0 0 0	$f_{41}$	1 1 0 0 -1 0 0 0
$f_{43}$	0 0 1 0 -1 0 0 0	$f_{45}$	0 1 1 0 -1 0 0 0	$f_{47}$	1 1 1 0 -1 0 0 0
$f_{49}$	0 1 0 1 -1 0 0 0	$f_{51}$	1 0 0 -1 -1 0 0 0	$f_{53}$	1 1 0 -1 -1 0 0 0
$f_{55}$	0 0 1 -1 -1 0 0 0	$f_{57}$	1 0 1 -1 -1 0 0 0	$f_{59}$	1 1 1 -1 -1 0 0 0
$f_{61}$	1 0 1 -2 -1 0 0 0	$f_{63}$	0 0 0 0 0 1 0 0	$f_{65}$	1 0 0 0 0 1 0 0
$f_{67}$	0 1 0 0 0 1 0 0	$f_{69}$	1 1 0 0 0 1 0 0	$f_{71}$	1 0 -1 0 0 1 0 0
$f_{73}$	1 1 -1 0 0 1 0 0	$f_{75}$	1 0 0 -1 0 1 0 0	$f_{77}$	0 0 0 0 1 1 0 0
$f_{79}$	1 0 -1 0 1 1 0 0	$f_{81}$	0 0 0 1 1 1 0 0	$f_{83}$	0 1 -1 1 1 1 0 0
$f_{85}$	0 0 1 0 0 -1 0 0	$f_{87}$	0 0 0 1 0 -1 0 0	$f_{89}$	0 1 0 1 0 -1 0 0
$f_{91}$	1 0 0 0 -1 -1 0 0	$f_{93}$	0 1 0 0 -1 -1 0 0	$f_{95}$	1 1 0 0 -1 -1 0 0
$f_{97}$	0 0 1 0 -1 -1 0 0	$f_{99}$	0 1 1 0 -1 -1 0 0	$f_{101}$	1 1 1 0 -1 -1 0 0
$f_{103}$	0 1 0 1 -1 -1 0 0	$f_{105}$	1 0 0 -1 -1 -1 0 0	$f_{107}$	0 0 1 -1 -1 -1 0 0
$f_{109}$	1 0 1 -1 -1 -1 0 0	$f_{111}$	1 1 1 -1 -1 -1 0 0	$f_{113}$	0 0 1 -1 -2 -1 0 0
$f_{115}$	1 0 1 -1 -2 -1 0 0	$f_{117}$	1 1 1 -1 -2 -1 0 0	$f_{119}$	0 0 0 0 0 0 1 0
$f_{121}$	0 1 0 0 0 0 1 0	$f_{123}$	1 1 0 0 0 0 1 0	$f_{125}$	0 0 1 0 0 0 1 0
$f_{127}$	0 1 1 0 0 0 1 0	$f_{129}$	0 1 0 1 0 0 1 0	$f_{131}$	1 0 0 -1 0 0 1 0
$f_{133}$	1 1 0 -1 0 0 1 0	$f_{135}$	0 0 1 -1 0 0 1 0	$f_{137}$	1 0 1 -1 0 0 1 0
$f_{139}$	0 1 1 -1 0 0 1 0	$f_{141}$	1 1 1 -1 0 0 1 0	$f_{143}$	0 0 0 0 1 0 1 0
$f_{145}$	0 1 0 0 1 0 1 0	$f_{147}$	1 1 -1 0 1 0 1 0	$f_{149}$	0 1 0 1 1 0 1 0
$f_{151}$	0 1 -1 1 1 0 1 0	$f_{153}$	1 1 1 -1 -1 0 1 0	$f_{155}$	0 0 0 0 1 1 1 0
$f_{157}$	0 1 0 0 0 -1 1 0	$f_{159}$	1 1 0 0 0 -1 1 0	$f_{161}$	0 0 1 0 0 -1 1 0
$f_{163}$	0 1 1 0 0 -1 1 0	$f_{165}$	0 1 0 1 0 -1 1 0	$f_{167}$	0 0 1 -1 0 -1 1 0
$f_{169}$	0 1 1 -1 0 -1 1 0	$f_{171}$	0 1 0 0 -1 -1 1 0	$f_{173}$	1 1 0 0 -1 -1 1 0
$f_{175}$	0 0 1 0 -1 -1 1 0	$f_{177}$	0 1 1 0 -1 -1 1 0	$f_{179}$	1 1 1 0 -1 -1 1 0
$f_{181}$	0 0 1 -1 -1 -1 1 0	$f_{183}$	1 0 1 -1 -1 -1 1 0	$f_{185}$	0 1 1 -1 -1 -1 1 0
$f_{187}$	1 1 1 -1 -1 -1 1 0	$f_{189}$	0 0 2 -1 -1 -1 1 0	$f_{191}$	0 1 2 -1 -1 -1 1 0
$f_{193}$	0 1 1 0 -1 -2 1 0	$f_{195}$	1 0 0 0 0 0 -1 0	$f_{197}$	1 0 -1 0 0 0 -1 0
$f_{199}$	0 0 0 1 0 0 -1 0	$f_{201}$	1 0 0 0 -1 0 -1 0	$f_{203}$	1 1 0 0 -1 0 -1 0
$f_{205}$	0 0 1 0 -1 0 -1 0	$f_{207}$	1 0 -1 0 -1 0 -1 0	$f_{209}$	0 0 0 1 -1 0 -1 0
$f_{211}$	1 0 0 -1 -1 0 -1 0	$f_{213}$	1 -1 0 -1 -1 0 -1 0	$f_{215}$	0 0 1 -1 -1 0 -1 0
$f_{217}$	1 0 1 -1 -1 0 -1 0	$f_{219}$	0 0 0 0 0 1 -1 0	$f_{221}$	1 0 0 0 0 1 -1 0
$f_{223}$	1 0 -1 0 0 1 -1 0	$f_{225}$	1 -1 -1 0 0 1 -1 0	$f_{227}$	0 0 0 1 0 1 -1 0
$f_{229}$	1 0 -1 1 0 1 -1 0	$f_{231}$	1 1 -1 1 0 1 -1 0	$f_{233}$	1 0 0 -1 0 1 -1 0
$f_{235}$	1 -1 0 -1 0 1 -1 0	$f_{237}$	1 0 -1 0 1 1 -1 0	$f_{239}$	1 0 0 0 -1 1 -1 0
$f_{241}$	1 0 0 -1 -1 1 -1 0	$f_{243}$	0 1 1 0 0 -1 2 0	$f_{245}$	0 1 1 -1 0 -1 2 0
$f_{247}$	0 0 0 0 0 0 0 1	$f_{249}$	1 0 0 0 0 0 0 1	$f_{251}$	0 1 0 0 0 0 0 1
$f_{253}$	1 1 0 0 0 0 0 1	$f_{255}$	1 0 -1 0 0 0 0 1	$f_{257}$	0 1 -1 0 0 0 0 1
$f_{259}$	1 1 -1 0 0 0 0 1	$f_{261}$	0 1 0 1 0 0 0 1	$f_{263}$	0 1 -1 1 0 0 0 1
$f_{265}$	1 1 -1 1 0 0 0 1	$f_{267}$	1 0 0 -1 0 0 0 1	$f_{269}$	1 1 0 -1 0 0 0 1
$f_{271}$	0 0 1 -1 0 0 0 1	$f_{273}$	1 0 -1 -1 0 0 0 1	$f_{275}$	0 0 0 0 1 0 0 1
$f_{277}$	0 1 0 0 1 0 0 1	$f_{279}$	1 0 -1 0 1 0 0 1	$f_{281}$	0 1 -1 0 1 0 0 1
$f_{283}$	1 1 -1 0 1 0 0 1	$f_{285}$	0 1 -1 1 1 0 0 1	$f_{287}$	1 1 0 0 -1 0 0 1
$f_{289}$	1 0 0 -1 -1 0 0 1	$f_{291}$	1 1 0 -1 -1 0 0 1	$f_{293}$	2 1 0 -1 -1 0 0 1
$f_{295}$	1 1 1 -1 -1 0 0 1	$f_{297}$	1 1 -1 0 1 1 0 1	$f_{299}$	0 1 0 0 0 -1 0 1
$f_{301}$	1 1 0 0 0 -1 0 1	$f_{303}$	0 1 -1 0 0 -1 0 1	$f_{305}$	1 1 -1 0 0 -1 0 1
$f_{307}$	0 1 0 1 0 -1 0 1	$f_{309}$	0 1 -1 1 0 -1 0 1	$f_{311}$	1 0 0 -1 0 -1 0 1
$f_{313}$	1 1 0 -1 0 -1 0 1	$f_{315}$	0 0 1 -1 0 -1 0 1	$f_{317}$	1 0 -1 -1 0 -1 0 1
$f_{319}$	0 1 0 0 -1 -1 0 1	$f_{321}$	1 1 0 0 -1 -1 0 1	$f_{323}$	1 2 0 0 -1 -1 0 1
$f_{325}$	0 1 1 0 -1 -1 0 1	$f_{327}$	1 0 0 -1 -1 -1 0 1	$f_{329}$	1 1 0 -1 -1 -1 0 1
$f_{331}$	2 1 0 -1 -1 -1 0 1	$f_{333}$	0 0 1 -1 -1 -1 0 1	$f_{335}$	1 0 1 -1 -1 -1 0 1
$f_{337}$	0 1 1 -1 -1 -1 0 1	$f_{339}$	1 1 1 -1 -1 -1 0 1	$f_{341}$	1 0 1 -2 -1 -1 0 1
$f_{343}$	1 1 1 -1 -2 -1 0 1	$f_{345}$	1 1 0 -1 0 0 1 1	$f_{347}$	0 1 0 0 1 0 1 1
$f_{349}$	0 1 -1 0 1 0 1 1	$f_{351}$	0 1 0 0 0 -1 1 1	$f_{353}$	1 1 0 0 0 -1 1 1
$f_{355}$	1 2 0 0 0 -1 1 1	$f_{357}$	0 1 1 0 0 -1 1 1	$f_{359}$	0 1 0 -1 0 -1 1 1
$f_{361}$	1 1 0 -1 0 -1 1 1	$f_{363}$	0 0 1 -1 0 -1 1 1	$f_{365}$	0 1 1 -1 0 -1 1 1
$f_{367}$	1 1 1 -1 0 -1 1 1	$f_{369}$	0 1 0 0 1 -1 1 1	$f_{371}$	1 1 0 -1 -1 -1 1 1
$f_{373}$	0 1 1 -1 -1 -1 1 1	$f_{375}$	1 1 1 -1 -1 -1 1 1	$f_{377}$	1 2 1 -1 -1 -1 1 1
$f_{379}$	1 1 1 -2 -1 -1 1 1	$f_{381}$	0 1 1 -1 -1 -2 1 1	$f_{383}$	1 1 1 -1 -1 -2 1 1
$f_{385}$	1 0 0 0 0 0 -1 1	$f_{387}$	0 1 0 0 0 0 -1 1	$f_{389}$	1 1 0 0 0 0 -1 1
$f_{391}$	1 0 -1 0 0 0 -1 1	$f_{393}$	1 1 -1 0 0 0 -1 1	$f_{395}$	0 1 -1 1 0 0 -1 1
$f_{397}$	1 1 -1 1 0 0 -1 1	$f_{399}$	1 0 0 -1 0 0 -1 1	$f_{401}$	1 0 -1 -1 0 0 -1 1
$f_{403}$	1 0 0 0 -1 0 -1 1	$f_{405}$	1 1 0 0 -1 0 -1 1	$f_{407}$	1 0 -1 0 -1 0 -1 1
$f_{409}$	1 1 -1 0 -1 0 -1 1	$f_{411}$	1 0 0 -1 -1 0 -1 1	$f_{413}$	1 1 0 -1 -1 0 -1 1
$f_{415}$	2 1 0 -1 -1 0 -1 1	$f_{417}$	1 0 -1 0 0 1 -1 1	$f_{419}$	1 1 -1 0 0 1 -1 1
$f_{421}$	1 0 0 -1 0 1 -1 1	$f_{423}$	1 0 -1 -1 0 1 -1 1	$f_{425}$	1 0 -1 0 1 1 -1 1
$f_{427}$	1 0 0 0 -1 -1 -1 1	$f_{429}$	1 1 0 0 -1 -1 -1 1	$f_{431}$	1 0 0 -1 -1 -1 -1 1
$f_{433}$	1 0 -1 0 0 1 -2 1	$f_{435}$	0 0 1 0 0 0 0 -1	$f_{437}$	0 0 0 1 0 0 0 -1
$f_{439}$	1 0 0 0 -1 0 0 -1	$f_{441}$	0 0 1 0 -1 0 0 -1	$f_{443}$	0 0 0 1 -1 0 0 -1
$f_{445}$	0 0 1 -1 -1 0 0 -1	$f_{447}$	1 0 1 -1 -1 0 0 -1	$f_{449}$	0 0 0 0 0 1 0 -1
$f_{451}$	1 0 0 0 0 1 0 -1	$f_{453}$	0 0 1 0 0 1 0 -1	$f_{455}$	0 0 0 1 0 1 0 -1
$f_{457}$	0 0 0 0 1 1 0 -1	$f_{459}$	0 0 0 1 1 1 0 -1	$f_{461}$	0 0 1 0 -1 -1 0 -1
$f_{463}$	0 0 0 0 0 0 1 -1	$f_{465}$	0 0 1 0 0 0 1 -1	$f_{467}$	0 1 1 0 0 0 1 -1
$f_{469}$	0 0 0 1 0 0 1 -1	$f_{471}$	0 1 0 1 0 0 1 -1	$f_{473}$	0 0 1 -1 0 0 1 -1
$f_{475}$	0 0 0 0 1 0 1 -1	$f_{477}$	0 0 0 1 1 0 1 -1	$f_{479}$	0 0 1 0 -1 0 1 -1
$f_{481}$	0 0 1 -1 -1 0 1 -1	$f_{483}$	1 0 1 -1 -1 0 1 -1	$f_{485}$	0 0 0 0 0 1 1 -1
$f_{487}$	0 0 0 0 1 1 1 -1	$f_{489}$	0 1 0 1 1 1 1 -1	$f_{491}$	0 0 1 0 0 -1 1 -1
$f_{493}$	0 0 1 0 -1 -1 1 -1	$f_{495}$	0 1 1 0 -1 -1 1 -1	$f_{497}$	0 0 1 -1 -1 -1 1 -1
$f_{499}$	0 0 2 -1 -1 -1 1 -1	$f_{501}$	0 0 0 1 0 1 -1 -1	$f_{503}$	1 1 0 -1 0 -1 0 2
$f_{505}$	1 1 0 -1 -1 -1 0 2	$f_{507}$	1 1 -1 0 0 0 -1 2	$f_{509}$	1 1 0 -1 -1 -1 -1 2

Table 4. The wall classes

W_{h}

h = 1, 2, 3

, of walls containing

Q_{F_{22}}

Table 4. The wall classes

W_{h}

h = 1, 2, 3

, of walls containing

Q_{F_{22}}

Class	Representative wall normal $n_{j}$	Order	Intersecting $Π^{2}$
$W_{1}$	(1 0 0 0 0 0 0 0) ⊗ (0 0 0 0 0 0 0 1)	288	84
$W_{2}$	(0 1 0 -1 1 -1 1 1) ⊗ (0 0 0 0 1 0 0 0)	288	13
$W_{3}$	(1 0 -1 0 0 0 0 0) ⊗ (0 0 0 1 0 1 0 -1)	108	5
Total		684	102

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On \Sigma-classes in E^8. IV. The neighbourhood of F_{22}

Abstract

1. Introduction

2. The Irreducible Subgroup F 22

3. The Neighbourhood of Q F 22

References

MDPI Initiatives

Important Links

Subscribe

2. The Irreducible Subgroup $F_{22}$

3. The Neighbourhood of $Q_{F_{22}}$