Mathematical Modelling of Virus Spreading in COVID-19

Preprint

Article

Mathematical Modelling of Virus Spreading in COVID-19

Altmetrics

Downloads

109

Views

Comments

A peer-reviewed article of this preprint also exists.

Liaofu Luo^*

Jun Lv^*

Liaofu Luo^*

Jun Lv^*

This version is not peer-reviewed

This preprints belongs to the Collection

Preprints on COVID-19 and SARS-CoV-2

Submitted:

13 July 2023

Posted:

14 July 2023

You are already at the latest version

Alerts

Abstract

A mathematical model is proposed to analyze the spreading dynamics of COVID-19. By using the parameters of the model, namely the basic reproduction number (R0) and the attenuation constant (k), the daily number of infections (DNI) and the cumulative number of infections (CNI) are deduced and shown to be in good agreement with experimental data. This model effectively addresses three key issues: explaining the waveform pattern of DNI, predicting the occurrence of the second wave of infection, and understanding the competitive spread of two viruses in a region. The findings demonstrate that these significant challenges can be comprehensively tackled using a simple mathematical framework. The theoretical insights derived from this model hold potential in guiding the estimation of the severity of an infection wave and formulating effective strategies for the control and mitigation of epidemic outbreaks.

Keywords:

Subject: Biology and Life Sciences - Life Sciences

1. Introduction

The ongoing COVID-19 pandemic has posed several unresolved questions. Firstly, our aim is to understand the reason behind the waveform pattern observed in the Daily Number of Infections (DNI) and to predict the scale and duration of an infection wave, including the Cumulative Number of Infections (CNI) and the time for infection ending. Secondly, we investigate why the second wave of infection typically follows the first wave and how to predict its occurrence. Lastly, we explore how virus spreading in a region is influenced by the emergence of new strains and develop methods to control their spread. Existing epidemic models have limitations in addressing these problems comprehensively. Firstly, since the 1920s the differential equations were used to model the population distribution of disease spread, including susceptible, infected, and recovered/dead pools [1,2]. Such models could not examine important social and behavioural factors, such as the behavioural responses of individuals to policy measures, and the effect of heterogeneous social contacts on diffusion patterns. Secondly, since the 1990s agent-based simulations were proposed that include some important sources of population heterogeneity and explore the structure and dynamics of transmission networks. However, none of the agent-based models are based on explicit empirical/theoretical assumptions of individual behaviour, social transmission mechanisms and social structure constraints [3-5]. Recently, several network models simulating the spread of epidemics in the population were proposed, such as the Susceptible-Infectious-Susceptible model on random networks [6], and the epidemic spreading on modular networks [7]. Although these specific models have solved some aspects of the complexity of infectious diseases and obtained meaningful results, they still fail to comprehensively answer the aforementioned unresolved questions.

As the Chinese idiom goes, "The greatest truths are the simplest". Starting from the principle of natural selection - the interaction and compromise between the virus and its host (human) - we propose a mathematical model based on insights from experimental data. The model is based on two fundamental assumptions. First, each viral strain has a basic reproduction number (R₀), which represents the average number of infections caused by an initial infectious person in a completely susceptible population [8]. R₀ is a measure of the transmission potential of a particular infectious disease. Second, virus infections undergo a series of events in m steps that weaken with each step, described by an attenuation constant k (k<1). The parameter k is influenced by social contacts and policy measures, where looser contacts and measures result in higher values of k. Based on two parameters R₀ and k we can deduce the general formula for the Daily Number of Infections (DNI) and the Cumulative Number of Infections (CNI) over m steps. The CNI is denoted by F(R₀,k;m). These formulas are in good agreement with experiments and provide a generalized framework to simulate single and multiple virus infections. By introducing F₁ and F₂ we can also study the competitive spread of two viruses in a region, including scenarios with the introduction of a new virus strain. It is worth noting that the loosening of public health measures and/or the emergence of new viruses can lead to subsequent waves of virus transmission.

2. Materials and Methods

The data of daily virus infections of COVID-19 are taken from WHO (https://covid19.who.int/data) for the UK and from the public database (https://ourworldindata.org/coronavirus) for Hong Kong. Since Gauss discovered the least square method and successfully applied it to astronomical observation, the ordinary Least Square is recognized as one of the best methods for curvilinear regression. In the present study, we use the Least Square simulation of observational data of the virus infection to determine the parameters in each COVID-19 pandemic. The goodness of the nonlinear Least Square fitting (NLLSF) is tested by R², i.e.

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - {\hat{π}}_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}},

where y_i are the observation values,

\bar{y}

their average and

{\hat{π}}_{i}

the predictions of the model. The goodness R² and the p-value of Prob(F-statistic) are calculated for each simulation. Define F-statistic as

F - s t a t i s t i c = \frac{(\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2} - \sum_{i = 1}^{n} {(y_{i} - {\hat{π}}_{i})}^{2}) / (k - 1)}{\sum_{i = 1}^{n} {(y_{i} - {\hat{π}}_{i})}^{2} / (n - k)},

(n – number of samples, ν - number of parameters) that can be calculated from the experimental data. The p-value is decided by the percentile of the Fisher’s F-distribution F_ν_-1,n-ν(z), namely,

p - v a l u e = t h e p r o b a b i l i t y o f F_{ν - 1, n - ν} (z > F - s t a t i s t i c) .

The goodness R², the p-value and the root mean squared error (RMSE) for each simulation are given in the figures.

3. Results

3.1. Derivation of formulas for Cumulative Number of Infections (CNI) and Daily Number of Infections (DNI)

The potential for infection of a given virus strain is determined by the basic reproduction number known as R₀. For the virus to spread, it must continually re-infect the host population. However, countermeasures by humans must aim to limit these subsequent infections. Essentially, this implies that the interaction and compromise between the virus and host (humans) necessitates the j-th reproduction number R_j to be smaller than the (j-1)-th reproduction R_j_-1, as expressed in the equation

R_{j} = k R_{j - 1}, (k < 1) .

The attenuation constant 'k' in this scenario is influenced by social contact rates and policy measures. After m-1 rounds of infection spread, the total number of infections in a specific area can be represented as

F (R_{0}, k; m) = R_{0} + R_{0} R_{1} + \dots + R_{0} R_{1} R_{2} \dots R_{m - 1} = R_{0} + k R_{0}^{2} + \dots + k^{m (m - 1) / 2} R_{0}^{m} .

(1)

This function F(R₀,k;m) describes the Cumulative Number of Infections (CNI), which is an increasing function of m. Assuming the total infected individuals as N, solving the equation F(R₀,k;m)=N will produce 'm', the transmission number of the virus strain. The parameter m grows with time t. Assuming each transmission takes place every q days, we have

m = (t + t_{0}) / q,

(2)

where t₀ is a time shift parameter linked to the start of infection (the time of m=1). Inserting (2) into (1) we obtain a formula of CNI vs t represented by four parameters R₀, k, q and t₀ that can be used to simulate the change of a cumulative number of infections with time in a region. As seen in Figure 1, our simulations of the UK-alpha strain (November 2020 to April 2021) and the Hong Kong-delta/omicron strain (February 2022 to April 2022) spreading are well fitted to the data obtained from COVID-19 pandemic updates.

Applying Equations (1) and (2), the Daily Number of Infections (DNI) is derived:

\{\begin{array}{l} d F / d t = (d F / d m) / q \\ d F / d m = k^{m (m - 1) / 2} R_{0}^{m} \end{array} .

(3)

From Eq (3), it is easy to understand why DNI first rises then falls, considering that R₀>1 (for most infectious viruses) and k<1. Zero DNI is arrived when dF/dm =0, which requires m to be large enough such that

k^{(m - 1) / 2} R_{0} < 1 o r R_{0} < {(1 / k)}^{(m - 1) / 2} .

(4)

This is a condition for the end of an infection wave.

3.2. Insights from typical figures of CNI vs m

Utilizing Eq (1), we plotted the change of CNIs with variables k and m for the given R₀ (Figure 2). Figures 2A-E show typical cases that help in understanding the development and termination of an infection wave.

From Figure 2, one can observe that the curve of F(R₀,k;m) increases with m and approaches a stable value when m>m_st for each k<k_th. We denote F(R₀,k_th;m_st) as N_th. Calculating for m_st =15 in Figure 2A to 2E, we obtained the threshold k_th and the corresponding CNI, N_th, for each given R₀ (each virus strain). On the other hand, CNI attaining a stable value means DNI approaching zero. By defining

E_{k m} = {(1 / k_{t h})}^{(m_{s t} - 1) / 2}

Eq (4) can be written as R₀<E_km. The threshold k_th, the corresponding CNI N_th and the parameter E_km are listed in Table 1. We found the relation R₀<E_km to hold well across all data.

The daily increasing number dF/dm=0 means the virus infection dies out. The above result shows the higher the basic reproduction number R₀, the more strict public health measure is required to increase E_km to satisfy Eq (4) and terminate the wave of virus infection effectively. From Table 1 we found the cumulative infection numbers N_th of many virus strains (except Omicron with R₀=18.6) are lower than 10⁵ if appropriate k (lower than k_th) is introduced.

For the virus strain of given R₀, if F(R₀,k;m) (for all m) exceeds a threshold N_max, then the spread of this strain would lead to a wave of COVID-19 pandemic in a region with population larger than N_max. In order to end this spread, the necessary condition would be

F (R_{0}, k; m) < N_{m a x} (f o r a l l m) .

(5)

Equation (5) provides a constraint on k for strains with R₀. The critical value of k is denoted as k_cr. Taking N_max= 10⁷ the values of k_cr are also listed in Table 1. Note that the parameter k_th is the threshold value of k required for ending the spread in 15^th generation, but the parameter k_cr is that value for ending the spread in arbitrary generation. The latter constraint is looser than the former. Therefore, k_cr is larger than k_th.

Virus strains with low R₀ values have higher k_cr and k_th values. As a result, they can spread in regions with smaller populations under looser public health measures. This theoretical prediction can explain why strains like SARS-CoV in 2003 only spread in restricted regions and soon disappeared globally. On the contrary, virus strains with high R₀ values, such as Omicron, have lower k_cr and k_th values. To satisfy Equations (4) and (5), the parameter k needs to meet very strict constraints. In cases where social management measures are not stringent enough, the number of infected individuals will quickly surpass the N_max limit, triggering a global pandemic wave, possibly culminating in a type of coexistence between viruses and humans.

In summary, the termination of an infection wave is determined by the condition dF/dm =0 on the CNI diagram (Figure 2), which requires a sufficiently large m and the condition in Equation (4) satisfied, i.e. R₀<E_km=(1/k_th)⁷. Additionally, the necessary condition for a pandemic to die out in a population of N_max is expressed by Equation (5), imposing a limitation on k, namely k<k_cr.

3.3. Prediction on the Second Wave of pandemics

Early models based on previous pandemics such as SARS, MERS, and the 2009 H1N1 outbreak can effectively predict the occurrence of the first wave of a disease. However, their predictive power decreases when it comes to anticipating the possibility of a second wave [9]. This raises the question: Why does the second wave of COVID-19 infections often follow the first wave? The present model aims to address this issue.

As shown in Figure 2, there are multiple curves (F versus m) for a given R₀ value. These curves differ from each other by the parameter k. When the number of daily new infections (DNI) approaches zero, any fluctuation in k significantly influences the spread of the virus. Therefore, changes in public health measures can induce variations in virus spread along different curves. Generally, as public health measures are relaxed, the parameter k increases, causing the virus to transition from one curve of F to another steeper curve. This signifies the onset of a new wave of virus spread. For instance, in Figure 2A, the spread of the Omicron variant (with an R₀ of 18.6) is plotted. Assuming the initial spread is along the curve with k equal to 0.613, a stable state is reached at m=15. At this point, the k value increases to 0.722. In response to this change, the virus begins spreading along a new curve with k=0.722, starting from m=4, as the value of F(18.6, 0.722; m=4) is equal to the original CNI value, F(18.6, 0.613; m=15). This example explains how the second wave of virus infection occurs. However, in cases where the parameter k decreases when DNI approaches zero, the curve of F will transition to a flatter one. This indicates that the first wave of viral infection will end soon and no second wave will occur.

By examining Figure 2A to Figure 2E, we can analyze how the occurrence of a second wave depends on the R₀ value of the virus. For instance, as k changes from 0.85 to 0.9, the CNI (at m=15) for high R₀ viruses increases hundreds of times, whereas it only increases tens of times for low R₀ viruses. Therefore, our model predicts that multi-wave infections are more likely to occur with viruses that have high R₀ values.

In the aforementioned discussions, we have assumed that no virus mutation occurs and that only one type of virus is spreading. In reality, changes in public health measures may be accompanied by virus mutations. In this case, the change in public health measures would cause the jump of F not only between different curves with a given R₀ but also between different R₀ values, providing more opportunities for the occurrence of a second wave during virus spread.

Another crucial point to consider is that the change in k can simultaneously induce a change in q, as the eigen-time (inherent time) m depends on q (Equation (2)). In the case of a single wave, the parameter m can be used to represent time dependence, and q can be simply set to 1 (known as normalization). However, when studying two continuous waves, the dependence on q should be clearly indicated due to the different eigen-times m. We have mentioned that the dependence of F on the change in k results in a jump from one curve to another. Meanwhile, the dependence of F on the change in q only affects the lengthening or shortening of the abscissa of the graph without altering the shape of the curve. When the public health measures change and a jump between curves occurs, the abscissa of the graph of the second wave simultaneously lengthens or shortens.

The occurrence of the second wave of infection is more likely when public health measures are relaxed. This change in the second wave is accompanied by a change in the q value. These predictions align with experimental data. For example, in the UK from May to September 2021, public health measures were relaxed, and a second wave of infection followed the first wave (Figure 1A). Similarly, in Hong Kong several months after May 2022, the looser public health measures led to a second wave occurring after the first wave (Figure 1B). (The data on the change of public health measures can be found at https://www.bsg.ox.ac.uk/research/covid-19-government-response-tracker)

In summary, the dependence of CNI on k (given a specific R₀) is determined by the jump between different curves on the graph F(R₀,k;m) versus m, referred to as k-transformation. The dependence of CNI on the duration of m is obtained by stretching the abscissa m on the graph, known as q-transformation. The k-transformation and q-transformation, occurring when the first wave is nearing its end, are the causes of a continuous second wave. The change in k is attributed to the modification of public health measures, while the modification of q is due to the change in physical time within a unit of m. The changes in k and q provide an explanation for the experimental data on continuous multi-wave infections.

3.4. Cross-Spread of Two Viruses: Discriminant Function

Viral infections often involve the simultaneous presence of two or more viruses. To accurately simulate the cross-spread of two viruses, it is necessary to consider the differences in eigen-times (m₁ and m₂) between these viruses and their relationship with the physical time t. Consequently, additional parameters q and t₀ (as given in Eq (2)) must be taken into account. By utilizing the four parameters R₀, k, q and t₀, the CNI F(R₀,k;m) can be expressed as:

F (R_{0}, k; m (t)) = F (t; a, b, c, d), (a = R_{0}, b = k, c = q, d = t_{0})

(6)

When the CNIs of two virus strains F₁(t;a₁,b₁,c₁,d₁) and F₂(t;a₂,b₂,c₂,d₂) intersect at t_cr,

F_{1} (t_{c r}; a_{1}, b_{1}, c_{1}, d_{1}) = F_{2} (t_{c r}; a_{2}, b_{2}, c_{2}, d_{2}),

(7)

and

\{\begin{matrix} F_{1} (t; a_{1}, b_{1}, c_{1}, d_{1}) > F_{2} (t; a_{2}, b_{2}, c_{2}, d_{2}) (t < t_{c r}) \\ F_{1} (t; a_{1}, b_{1}, c_{1}, d_{1}) < F_{2} (t; a_{2}, b_{2}, c_{2}, d_{2}) (t > t_{c r}) \end{matrix} .

This represents a transition in the population of virus strains from F₁ to F₂. As it is challenging to directly solve the intersection equation (Eq (7)), we introduce a function:

D_{21} = l o g [(d F_{2} / d t) / (d F_{1} / d t)],

(8)

which satisfies:

\{\begin{matrix} D_{21} > 0 a s d F_{2} / d t > d F_{1} / d t \\ D_{21} < 0 a s d F_{2} / d t < d F_{1} / d t \end{matrix} .

(9)

By utilizing Eqs (2)(3)(6) and (8) D₂₁ can be formulated as a simple quadratic function of time

D_{21} = α t^{2} + β t + γ,

(10)

where

\{\begin{array}{l} α = \log b_{2} / (2 c_{2}^{2}) - \log b_{1} / (2 c_{1}^{2}) \\ β = (2 d_{2} - c_{2}) \log b_{2} / (2 c_{2}^{2}) - (2 d_{1} - c_{1}) \log b_{1} / (2 c_{1}^{2}) + \log a_{2} / c_{2} - \log a_{1} / c_{1} \\ γ = d_{2} (d_{2} - c_{2}) \log b_{2} / (2 c_{2}^{2}) - d_{1} (d_{1} - c_{1}) \log b_{1} / (2 c_{1}^{2}) + d_{2} \log a_{2} / c_{2} - d_{1} \log a_{1} / c_{1} + \log (c_{1} / c_{2}) \end{array}

In order to determine if a real root of D21 exists, we define:

∆ = β^{2} - 4 α γ .

(11)

The value of Δ determines the existence of the real root in the quadratic form D₂₁. This form, known as the discriminant function, serves as a tool to identify the occurrence of t_cr and the domain of its existence. The prediction rules can be summarized as follows:

Rule 1:

When Δ>0, the quadratic form intersects with t axis at t_s and t_m (t_m>t_s),

t_{s} = \{\begin{matrix} \frac{- β - \sqrt{∆}}{2 α} (f o r α > 0) \\ \frac{- β + \sqrt{∆}}{2 α} (f o r α < 0) \end{matrix}, t_{m} = \{\begin{matrix} \frac{- β + \sqrt{∆}}{2 α} (f o r α > 0) \\ \frac{- β - \sqrt{∆}}{2 α} (f o r α < 0) \end{matrix} .

These values partition the time into three distinct domains: t<t_s in the first domain, t_s<t<t_m in the second domain and t>t_m in the third domain.

Rule 2:

In the first domain, t_a=qm₀-t₀ is defined as the initial time where m₀>>1, indicating m_1,2=(t+d_1,2)/c_1,2>>1. If D₂₁>0, there will be no intersection of F₁(t) and F₂(t) in the domain between t_a and t_s when the initial values of F at t_a satisfy F₁(t_a)<F₂(t_a), but there may be one t_cr (the number of t_cr is either 1 or 0) in the domain when F₁(t_a)>F₂(t_a). If D₂₁<0, there will be no intersection of F₁(t) and F₂(t) in the domain when the initial values satisfy F₁(t_a)>F₂(t_a), but there may be one t_cr (the number of t_cr is either 1 or 0) when F₁(t_a)<F₂(t_a).

Rule 3:

In the second domain, if D₂₁>0 there will be no intersection of F₁(t) and F₂(t) in the domain when the F-values at t=t_s satisfy F₁(t_s)<F₂(t_s), but there may be one t_cr (the number of t_cr is either 1 or 0) when F₁(t_s)>F₂(t_s). If D₂₁<0 there will be no intersection of F₁(t) and F₂(t) in the domain when the F-values at t=t_s satisfy F₁(t_s)>F₂(t_s), but there may be one t_cr (i.e. the number of t_cr is either 1 or 0) when F₁(t_s)<F₂(t_s). The F-values at t=t_s are determined by F₁(t) and F₂(t) in the first domain.

Rule 4:

In the third domain, if D₂₁>0 there will be no intersection of F₁(t) and F₂(t) in the domain when the F-values at t=t_m satisfy F₁(t_m)<F₂(t_m), but there may be one t_cr (the number of t_cr is either 1 or 0) when F₁(t_m)>F₂(t_m). If D21<0 there will be no intersection of F₁(t) and F₂(t) in the domain when the F-values at t=t_m satisfy F₁(t_m)>F₂(t_m), but there may be one t_cr (i.e. the number of t_cr is either 1 or 0) when F₁(t_m)<F₂(t_m). The F-values at t=t_m are determined by F₁(t) and F₂(t) in the second domain.

Rule 5:

There can be at most one tcr in a given domain because the symbol of D₂₁ is definite in any domain. The magnitude of the domain is an important factor to predict the occurrence of a t_cr. For example, in the second domain the magnitude is t_m-t_s=Δ^1/2/(2|α|), and the necessary condition for the occurrence of t_cr is a large enough (t_m-t_s) or Δ.

Rule 6:

When Δ < 0, the quadratic form D₂₁ does not intersect with t axis. In this case, there is only one domain and the rule is the same as that in the first domain given by Rule 2.

Figure 3 presents examples of cross-spread of two virus strains, 1 and 2. The left panel shows the discriminant function, and the right panel displays the cross-spread of the two strains. The influence of the change in parameters (as an example, we only assume the R₀ value of strain 1 changes) on the intersection of two strains is shown in the figure. In Figure 3A, there is no intersection. In Figure 3B and 3C, there are two intersections in the second and third domain, respectively. In Figure 3D, there is one intersection in the second domain. These intersection occurrences are in agreement with aforementioned prediction rules.

In the first domain we have introduced t_a =qm₀-t₀ as the initial time. To study the cross spread in the time interval between m=1 and t_a where dF/dt in D₂₁ is difficult to be defined one should use F(t)-ladder method as follows:

The step size of CNIs of the first few steps in two ladders 1 and 2 are given by

a_{1}

b_{1} a_{1}^{2}

b_{1}^{3} a_{1}^{3}

b_{1}^{6} a_{1}^{4}

b_{1}^{10} a_{1}^{5}

b_{1}^{15} a_{1}^{6}

b_{1}^{21} a_{1}^{7}

b_{1}^{28} a_{1}^{8}

b_{1}^{36} a_{1}^{9}

, etc., and

a_{2}

b_{2} a_{2}^{2}

b_{2}^{3} a_{2}^{3}

b_{2}^{6} a_{2}^{4}

b_{2}^{10} a_{2}^{5}

b_{2}^{15} a_{2}^{6}

b_{2}^{21} a_{2}^{7}

b_{2}^{28} a_{2}^{8}

b_{2}^{36} a_{2}^{9}

, etc., respectively (Eq (1)). Strain 1 spreads from the 1^st step a₁ at t=c₁-d₁ on ladder 1 and strain 2 spreads from the 1^st step a₂ at t=c₂-d₂ on ladder 2. The CNI and arrival time t of the two strains on their respective ladders are listed in Table 2. For example, let’s take c₁=7, d₁=15, c₂=5, d₂=10. The earlier arrival times, in turn, are t= c₁-d₁ =-8, c₂-d₂ =-5, 2c₁-d₁ =-1, 2c₂-d₂ =0, 3c₂-d₂ =5, 3c₁-d₁ =6, etc. By using Table 2, one can easily calculate the CNI at each arrival time as the parameters a₁, b₁, a₂, b₂ are given, compare the CNI values on two ladders and obtain the information on the cross spread of two strains.

3.5. Examples of the Cross-Spread of Two Viruses

The epidemics that occurred in the UK from November 2020 to February 2022 provide a clear demonstration of the cross-spread phenomenon involving multiple viruses. This process can be divided into five stages, namely: (A) the alpha epidemic, (B) the delta invasion and cross-spread of two strains, (C) the delta dominant stage, (D) the omicron invasion and cross-spread of delta and omicron, and (E) the omicron dominant stage. In this section, we will specifically focus on studying the cross-spread of two strains during stage B and D.

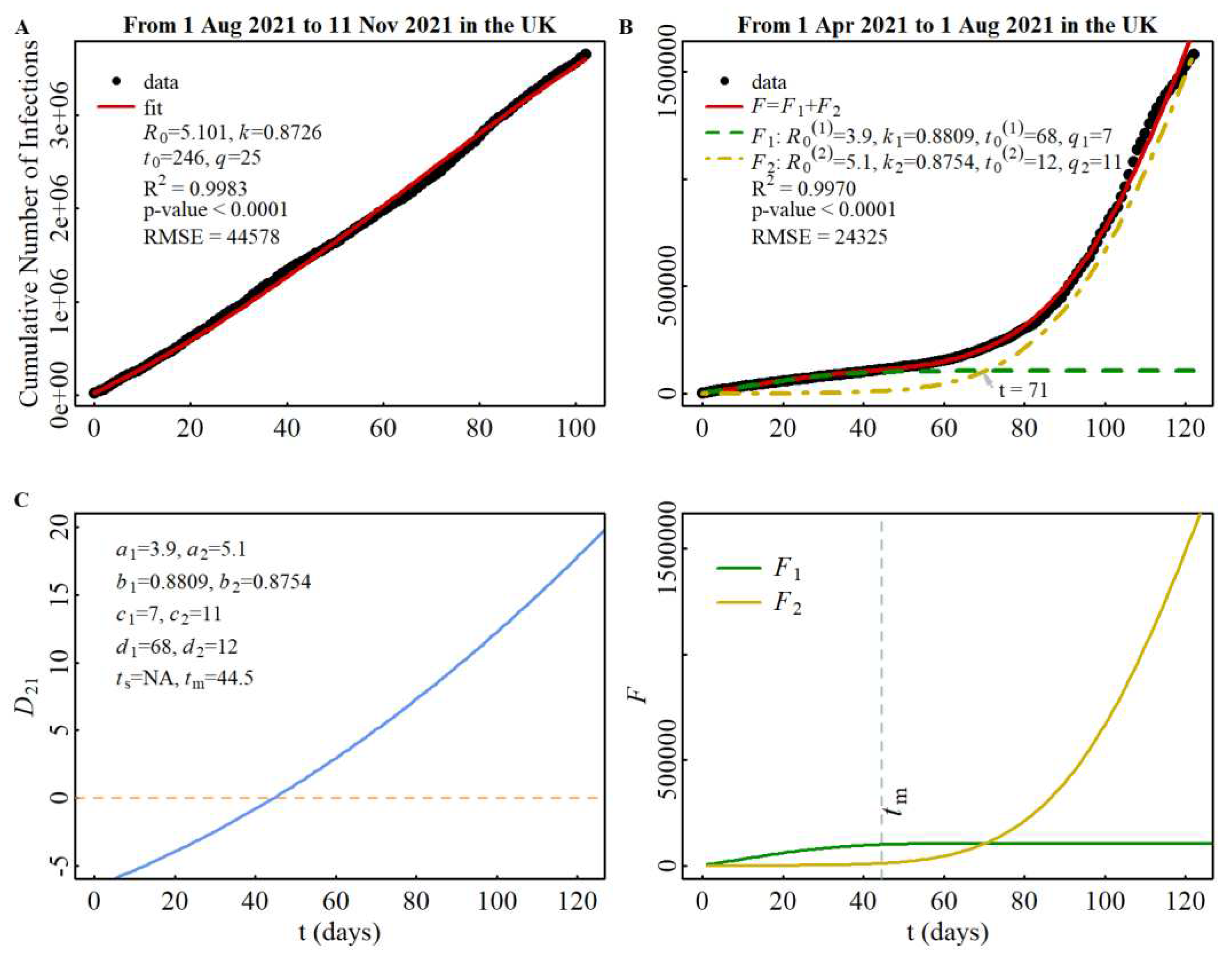
Firstly, let us examine the cross-spread between the alpha strain (designated as strain 1) and the delta strain (designated as strain 2) during stage B. The spread of the alpha strain during stage A has been represented in Figure 1A, where we obtained the parameter a₁=R₀⁽¹⁾=3.9. The spread of the delta strain during stage C has been illustrated in Figure 4A, and we derived the parameter a₂=R₀⁽²⁾=5.1 based on this data. By using R₀⁽¹⁾ and R₀⁽²⁾ as inputs, we simulated the cross-spread of the two strains, as depicted in Figure 4B. Furthermore, utilizing all the parameters a_i, b_i, c_i, d_i (i=1,2) obtained from Figures 1A, 4A, and 4B, we constructed the discriminant function of the cross-spread and plotted the intersection of the two strains during stage B in Figure 4C. Interestingly, we discovered that one t_cr occurs at t=71 in the region where t>t_m (t_m=44.5), which is consistent with the prediction outlined in Rule 4.

Similarly, we investigated the cross-spread between the delta strain (strain 1) and the omicron strain (strain 2) during stage D. The results of this analysis are shown in Figures 5A, 5B, and 5C. From Figure 5C, we observed that a t_cr appears at t=42 in the region where t>t_m (t_m=28.5), which is in agreement with the prediction made by Rule 4.

In both simulations, we assumed April 1 as the initial time for stage B, and November 11 as the initial time for stage D. Due to the uncertainty surrounding the exact timing of the delta invasion in stage B and the omicron invasion in stage D, we shifted the initial times t of stages B and D by several days. Remarkably, we found that the same values of k₁, k₂, q₁, q₂, t₀⁽¹⁾ were obtained, and only t₀⁽²⁾ varied while still maintaining the invariant t+ t₀⁽²⁾.

4. Discussion

4.1. On the Simulation of COVID-19 Cases

The traditional SIR-type epidemic models depict the exponential growth of the number of infected individuals. However, empirical data has demonstrated that COVID-19 outbreaks do not exhibit exponential growth, but rather follow a three-parameter Gompertz growth function [10,11]. A new compartment model, known as the broken link model, has been proposed in the literature to explain the mechanism of Gompertz growth [12]. In our proposed model, we suggest that the spread of the virus depends on four parameters: R₀, k, q and t₀. R₀ describes the inherent infectious ability of the virus, k represents the strictness of social management, q represents the time needed for one step of infection, and t₀ is an additional parameter that aligns with the starting date of the experimental data. By incorporating these four parameters, our four-parameter simulation accurately fits all COVID-19 epidemic data involving a single strain of the virus. Consequently, the mechanism of Gompertz growth has been elucidated by our model and contributes to the prediction of future outbreaks.

4.2. On the Mutation of the SARS-CoV-2 Virus

The SARS-CoV-2 virus continuously undergoes mutations, giving rise to new strains. This ongoing mutation process is the reason why the pandemic has persisted for more than three years. As a result of natural selection, these new mutant strains possess higher infectious ability but lower lethality rates. Although the lethality rate of the new strains may be lower, it still results in a significant number of deaths. Therefore, since mutation occurrence is inevitable and costly, the key focus should be on reducing the epidemic probability of mutants. While humans cannot prevent the virus from mutating, they can hinder the mutant strains from dominating the competition. According to six prediction rules on cross-spread of two strains, it is highly unlikely for the intersection point t_cr to manifest under the following conditions: 1. when Δ>0, there are three domains and in this case there will be no occurrence of t_cr within a domain if the period of this domain is short enough (i.e. t_s-t_a small, Δ small, or t_m large) or if the symbol of D₂₁ within a domain does not align with the symbol of F₁-F₂ at the initial time of this domain; 2. when Δ<0, there is only one domain and in this case there will be no t_cr if the period of virus spread is short enough or if the symbol of D₂₁ does not align with the symbol of F₁-F₂ at the initial time.

An example to highlight the phenomenon of no occurrence of t_cr is the winter epidemic in China in 2022. Among tens of millions of SARS-CoV-2 cases in one city, no new mutant strain emerged or triumphed over the competition, with the exception of the original omicron strand. This suggests that the pandemic was effectively terminated within a short period, lasting only one month.

In conclusion, the strategies proposed by our model to control an epidemic have two main aspects. First, it is critical to prevent the occurrence of a second wave. Second, one should aim to avoid competition among mutant strains. In the latter scenario, minimizing the duration of virus spread is an efficient approach.

4.3. Dependence of Virus Infection Potential on Temperature and Humidity

The conformational equilibrium between the open and closed conformations of the receptor binding domain (RBD) of the spike (S) protein can be analyzed using first-principle techniques for a susceptible individual. The RBD can exist in either the open or closed position, known as the up or down conformation, respectively. The population of conformational states can be determined based on the free energy change during conformational transitions of the S protein. Let us denote the closed conformation as state A and the open conformation as state B. The Gibbs free energies of states A and B are represented by GA and GB, respectively. Generally, if GA is lower than GB, the RBD will primarily assume the inactive conformation A. Conversely, in order to initiate the infectious process, the equilibrium should shift towards the open conformation, implying that GB should be lower than GA [13]. The free energy G in a given conformation is related to the partition function Z, which can be expressed as follows:

G = - k_{B} T l n Z, Z = \sum_{n} e^{- β E_{n}} (β = \frac{1}{k_{B} T}) .

(12)

Here E_n represents the energy level of a given conformation,

{(E_{n})}_{A, B} = V_{A, B} + (n + 1 / 2) ℏ ω_{A, B},

(13)

V_A,B represents two minima of conformational potential respectively and (n+1/2)ħω_A,B the corresponding vibrational energy around the minimum of conformational potential. By the summation of Boltzmann factor over vibration states one has

\frac{Z_{A}}{Z_{B}} = e^{- β (V_{A} - V_{B})} Y_{A / B}, Y_{A / B} = \frac{e^{\frac{1}{2} β ℏ ω_{B}} - e^{- \frac{1}{2} β ℏ ω_{B}}}{e^{\frac{1}{2} β ℏ ω_{A}} - e^{- \frac{1}{2} β ℏ ω_{A}}} .

(14)

Let T_C represent the phase transition temperature, which can be determined by ΔG=G_B-G_A=0. From Eqs (12) and (14) we obtain a simplified equation for T_C

\frac{2 (V_{B} - V_{A})}{ℏ {(ω}_{A} - ω_{B})} = c o t h \frac{ℏ ω_{A}}{2 k_{B} T_{C}} (a s |\frac{ω_{A} - ω_{B}}{ω_{A}}| ≪ 1)

(15)

and ΔG>0 for T>T_C, ΔG<0 for T<T_C. Therefore, if the environmental temperature decreases to T<T_C, the conformational transition from the closed conformation to the open conformation occurs rapidly. This explains why the virus has higher transmission rates during the winter and the entrance to host cells is prioritized. Conversely, the summer season provides the most favorable conditions for virus elimination. In addition to temperature, the conformational equilibrium is influenced by humidity. The virus can be modeled as a charged sphere, and through the application of electrostatics principles to salty solutions, one can derive an expression for the potential at the surface of the charged sphere, where the dielectric constant ε is incorporated [14]. This implies that the elastic frequency ω² should be replaced by ω²/ε. Considering water has a dielectric constant of ε=80, the frequency parameter takes a reduced value of ω/9 in the presence of a fully salty solution rather than ω in a vacuum. Consequently, this provides a quantitative estimation of the virus's infection potential, which is strongly dependent on humidity.

The above discussions on the susceptible individual can be extended to the population level, providing evidence that R₀ is influenced by temperature and humidity.

Author Contributions

Conceptualization, L.L.; validation, J.L., and L.L.; investigation, J.L.; writing—original draft preparation, L.L.; writing—review and editing, J.L.; visualization, J.L.; supervision, L.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
Murray, J.D. Mathematical biology, 2nd ed.; Springer-Verlag Berlin Heidelberg GmbH: New York, USA, 1993; pp. 1–92. [Google Scholar] [CrossRef]
Squazzoni, F.; Polhill, J.G.; Edmonds, B.; Ahrweiler, P.; Antosz, P.; Scholz, G.; Chappin, E.; Borit, M.; Verhagen, H.; Giardini, F.; et al. Computational models that matter during a global pandemic outbreak: A call to action. JASSS 2020, 23, 10. [Google Scholar] [CrossRef]
Adam, D. Special report: The simulations driving the world's response to COVID-19. Nature 2020, 580, 316–318. [Google Scholar] [CrossRef] [PubMed]
Sridhar, D.; Majumder, M.S. Modelling the pandemic. BMJ 2020, 369, m1567. [Google Scholar] [CrossRef] [PubMed]
Parshani, R.; Carmi, S.; Havlin, S. Epidemic threshold for the susceptible-infectious-susceptible model on random networks. Phys. Rev. Lett. 2010, 104, 258701. [Google Scholar] [CrossRef] [PubMed]
Valdez, L.D.; Braunstein, L.A.; Havlin, S. Epidemic spreading on modular networks: The fear to declare a pandemic. Phys. Rev. E 2020, 101, 032309. [Google Scholar] [CrossRef] [PubMed]
Wan, S.; Liu, J.; Liu, M. Progress on the basic reproduction number of SARS-CoV-2. Chin. Sci. Bull. 2020, 65, 2334–2341. [Google Scholar] [CrossRef]
Costris-Vas, C.; Schwartz, E.J.; Smith, R. Predicting COVID-19 using past pandemics as a guide: how reliable were mathematical models then, and how reliable will they be now? Math. Biosci. Eng. 2020, 17, 7502–7518. [Google Scholar] [CrossRef] [PubMed]
Levitt, M.; Scaiewicz, A.; Zonta, F. Predicting the trajectory of any COVID19 epidemic from the best straight line. MedRxiv 2020. [CrossRef]
Ohnishi, A.; Namekawa, Y.; Fukui, T. Universality in COVID-19 spread in view of the Gompertz function. Prog. Theor. Exp. Phys. 2020, 12, 123J01. [Google Scholar] [CrossRef]
Ikeda, Y.; Sasaki, K.; Nakano, T. A new compartment model of COVID-19 transmission: The broken-link model. Int. J. Environ. Res. Public. Health 2022, 19, 6864. [Google Scholar] [CrossRef] [PubMed]
Luo, L.F.; Zuo, Y.C. Spike conformation transition in SARS-CoV-2 infection. ArXiv 2021. Available online: https://arxiv.org/abs/2009.11288v2.
Phillips, R.; Kondev, J.; Theriot, J.; Garcia, H.G. Physical Biology of the Cell, 2nd ed.; Garland Science: New York, USA, 2012; pp. 355–382. [Google Scholar]

Figure 1. COVID-19 pandemics in the UK (A) and Hong Kong (B).

Figure 2. CNI functions F(R₀,k;m) for several typical R₀ values. Panel A: R₀=18.6 (for Omicron BA.4, BA.5 in South Africa, 2022-1), panel B: R₀=9.5 (for Omicron B.1.1.529 in many countries, 2021-11), panel C: R₀=6.5 (for Delta in India, R0=5-8, 2020-10), panel D: R₀=4.5 (for Alpha in the UK, 2020-9, Beta in South Africa, 2020-5, Gamma in Brazil, 2020-11, R₀=4-5), and panel E: R₀=2 (for SARS-CoV 2003, R₀=2-3).

Figure 3. Discriminant Function and intersection occurrence.

Figure 4. CNI simulation in the UK from November 2020 to November 2021. Panel A: CNI simulation of delta spread in stage C, panel B: CNI simulation of alpha/delta spread in stage B, and panel C: discriminant function and intersection of alpha/delta spread in stage B (left panel gives discriminant function and right panel the cross-spread of two strains). Note: CNI simulation of alpha spread in stage A from November 2020 to April 2021 has been plotted in Figure 1A.

Figure 5. CNI simulation in the UK from November 2021 to February 2022. Panel A: CNI simulation of omicron spread in stage E (only the data of first omicron peak is used.); panel B: CNI simulation of delta/omicron spread in stage D; and panel C: Discriminant function and intersection of delta/omicron spread in stage D (left panel gives discriminant function and right panel the cross-spread of two strains).

Table 1. Parameters related to virus infection dying out.

R₀	k_th(m_st=15)	E_km=(1/k_th)⁷	N_th	k_cr(N_max=10⁷)
18.6	0.613	30.7	10⁵	0.722
9.5	0.722	9.78	∼10⁵	0.8
6.5	0.75	7.49	∼10⁴	0.85
4.5	0.8	4.77	∼10³	0.9
2	0.9	2.09	∼10²	>0.95

Table 2. CNI and arrival time t of two strains on F(t)-ladder.

t	CNI
c_i-d_i ¹	a_i
2c_i-d_i	a_i+b_ia_i²
3c_i-d_i	a_i+b_ia_i²+ b_i³a_i³
4c_i-d_i	a_i+b_ia_i²+ b_i³a_i³+ b_i⁶a_i⁴
5c_i-d_i	a_i+b_ia_i²+ b_i³a_i³+ b_i⁶a_i⁴+ b_i¹⁰a_i⁵
6c_i-d_i	a_i+b_ia_i²+ b_i³a_i³+ b_i⁶a_i⁴+ b_i¹⁰a_i⁵+ b_i¹⁵a_i⁶

¹ i=1, 2 refer to two strains respectively, to save space only six steps of the F(t)-ladder are listed.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Mathematical Modelling of Virus Spreading in COVID-19

Abstract

1. Introduction

2. Materials and Methods

3. Results

3.1. Derivation of formulas for Cumulative Number of Infections (CNI) and Daily Number of Infections (DNI)

3.2. Insights from typical figures of CNI vs m

3.3. Prediction on the Second Wave of pandemics

3.4. Cross-Spread of Two Viruses: Discriminant Function

3.5. Examples of the Cross-Spread of Two Viruses

4. Discussion

4.1. On the Simulation of COVID-19 Cases

4.2. On the Mutation of the SARS-CoV-2 Virus

4.3. Dependence of Virus Infection Potential on Temperature and Humidity

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe