Analyses of Subsample Averaging of Single Trials for Event-Related Potential Classification

Preprint

Article

Analyses of Subsample Averaging of Single Trials for Event-Related Potential Classification

Altmetrics

Downloads

120

Views

Comments

This version is not peer-reviewed

Submitted:

13 July 2023

Posted:

17 July 2023

You are already at the latest version

Alerts

Abstract

Event-related potentials (ERPs) are estimated by averaging time-locked single trial electroencephalography (EEG) signals in response to specific events or stimuli. Classifying ERPs accurately is a challenge because (a) single trials have poor signal-to-noise-ratios (SNRs) and (b) it is difficult to collect large single trial ensembles to generate high SNR ERPs for classifier training and testing. The m-subsample averaging (m-SA) strategy which generates small-sample ERPs by repeated averaging of a small number of single trials drawn without replacement, has been proposed as a solution to the two problems. An ERP formed by averaging m single trials is referred to as an m-ERP where m is referred to as the averaging parameter. In this study, we conduct thorough analyses of m-SA and focus on issues not addressed in previous studies to better understand the beneficial properties of m-SA and to further support its application for ERP classification. Specifically, we (a) analyze the improvement in SNR as a function of m using the mean-root-mean-square SNR and visual analyses of m-ERP plots with confidence intervals, (b) analyze the improvement in interclass separation as a function of m, (c) determine how the SNR and interclass separation analyses can help to select the averaging parameter m, (d) determine the number of distinct m-ERPs that can be drawn from a single-trial ensemble, and (e) determine several probabilities related to the generation of distinct m-ERPs. Furthermore, an extensive set of experiments are designed to analyze the performance of support vector machine and convolution neural network classifiers employing m-SA with various combinations of the averaging parameters used for generating the training and test sets. The results confirm that ERPs can be classified accurately using small subsample averaging. Most importantly, it is concluded that m-SA can be deployed in practice to accurately classify ERPs in brain activity research and in clinical applications without having to collect a prohibitively large number of single trials.

Keywords:

Subject: Computer Science and Mathematics - Signal Processing

1. Introduction

Event-related potentials (ERPS), which are the brain responses to specific sensory, cognitive, or motor events [1,2,3,4], are widely used to diagnose neurological disorders in clinical evaluations [5,6,7,8,9,10,11] and to study brain functioning in neuroscience and cognitive psychology research [12,13,14,15,16,17,18,19]. The response to an event, referred to as a single trial, is modeled as the additive superposition of the ERP (signal of interest) and the ongoing electroencephalogram (EEG) activity (noise). The ERP is not discernible in the single trial because it is much smaller than the EEG in which it is embedded. That is, the signal-to-noise ratio (SNR) of single trials is poor. The standard method for improving the SNR is through averaging multiple single trials acquired through repeated presentations of the same stimulus [20,21,22,23,24,25,26]. Including more single trials in the average is expected to lead to better SNR improvements, therefore, it is not unusual in practice to attempt collecting hundreds of single trials to generate a single ERP. However, collecting a large number of single trials from participants is problematic because they have trouble paying attention to the tasks, become restless, and experience fatigue during lengthy experiments. As a result, the noise level in the single trials increases and the SNR decreases even further. An interesting study [27] explored the effect of the number of trials on statistical power and asked the following question: how many trials does it take to get a significant ERP effect? It was determined that there is no simple answer to the question but recommended that the sample size, the anticipated effect magnitude, and the noise level should be considered. The study also offered two practical conclusions. First, unless power is near floor or ceiling, increasing the number of trials almost always produces appreciable increases in power. Second, the extent to which power can be increased by increasing the number of trials appears to be greater in within-participant designs than in between-groups designs.

In this study related to ERP classifier design, we pose a similar question: how many single trials are needed to design a practical ERP classifier yielding acceptable classification accuracies? The term “design” encompasses the training and testing operations which require training and test sets. It is impossible to train and test an ERP classifier if all single trials are used to generate a single ERP. Furthermore, it would be impractical to collect an enormously large number of single trials to generate large ensembles of high SNR ERPs to form training and test sets. The most obvious solution is to use single trails directly, without averaging, as attempted in the design of customized brain computer interfaces (BCIs) which are typically controlled by the presentation of a single stimulus, that is, by single trials [28,29,30,31,32,33]. In general, irrespective of the application, high classification accuracies cannot be expected with single trials due to the poor SNR. Classifying ERPs accurately, therefore, is a challenge primarily because (a) single trials have poor SNRs and (b) it is difficult to collect large single trial ensembles in practice to generate high SNR ERP ensembles for classifier training and testing. The question as to how many single trials are needed to design ERP classifiers can be rephrased as: is it possible to design high accuracy ERP classifiers from a practical-sized single trial ensemble? We have proposed subsample averaging as answer to the rephrased question and demonstrated, empirically, that it facilitates the design of ERP classifiers [34,35]. Since detailed analyses of subsample averaging are the main focus of this study, a concise description of the procedure is presented next.

1.1. Subsample Averaging

The method to generate subsample ERPs is called

m

-Subsample Averaging (

m

-SA) in which

m

, referred to as the averaging parameter, is the subsample size [34,35]. The goal of

m

-SA is to enable the design of ERP classifiers that yield high accuracies for small values of

m

so that a large number of single-trials do not have to be collected for classifier design. Given a single trial ensemble of size

S_{0}

m

-SA generates subsample ERP ensembles for classifier design by:

(a): Drawing a random subsample of single trials, without replacement, of size $m,$ $m < S_{0}$ .
(b): Averaging the $m$ single trials to obtain a subsample ERP which is called an $m$ -ERP.
(c): Replacing the $m$ single trials of the subsample into the single trial ensemble.
(d): Repeating steps (a)–(c) $q$ times to generate an ensemble of $S_{q}$ $m$ -ERPs.

Steps (a)–(d) are repeated

Q

times to yield

Q

m

-ERP ensembles, each of size

S_{q}

. The generation of each ensemble is referred to as a “run.”. For each run, the single trial ensemble is first randomly partitioned into a training set and a test set to prevent the same single trials being used in both sets. The

m

-ERPs of the training and test sets are generated independently from the single trials in their respective sets. The

m

-ERP ensembles of each channel are generated from the single trials of the corresponding channel. A large number of

m

-ERPs can be generated by

m

-SA for ERP classifier design from a practical sized single trial ensemble. Furthermore,

m

-SA is highly flexible and can be used to generate large

m

-ERP ensembles for customized classifier design for individual subjects as well as group-based classifier design involving multiple subjects [35]. For convenience, single trials are referred to as 1–ERPs.

1.2. Aim of the Study

The aim of this study is to conduct detailed analyses of

m

-SA to answer the following important questions not addressed in the previous studies:

(a): What is the relationship between the SNR and the averaging parameter $m$ ? This question will be answered with the help of the ERP averaging model. The SNR will be analyzed as a function of $m$ objectively using the mean-root-mean-square SNR and subjectively by comparing plots of $m$ -ERPs with the full sample ERP. The 95% confidence intervals (CIs) will be included in the plots to compare the variations within the generated $m$ -ERPs against the variations within the single trials.
(b): What is the relationship between the interclass separation and the averaging parameter $m$ ? A measure of the interclass separation will be analyzed as a function of $m$ to answer this question. The interclass separation will be plotted for various values of $m$ to observe how the measure is affected by increasing $m$ . Furthermore, an example involving 2-dimensional Gaussian clusters will be used to illustrate the improvements that can be expected by increasing $m$ .
(c): How can the SNR and interclass separation analyses conducted in (a) and (b) help with the selection of the averaging parameter $m$ ?
(d): What is the number of distinct $m$ -ERPs that can be drawn from a single-trial ensemble? Combinatorial analyses will be conducted to develop a relationship between $m$ and the number of distinct $m$ -ERPs that can be generated by $m$ -SA.
(e): Given an ensemble of 1-ERPs, what is the probability of generating (a) a distinct $m$ -ERP, (b) duplicates of an $m$ -ERP, and (c) an ensemble of distinct $m$ -ERPs? Through probability analyses, relationships will be derived to determine these probabilities as functions of $m$ .

The answers to the above set of questions will offer valuable insights into the properties of

m

-SA and support the suitability of

m

-SA for ERP classifier design. In addition, a set of experiments are designed to systematically analyze the performance trends as a function of the averaging parameters used for generating the training and test sets and to show the improvements over single trial classification. An appearance of some overlap of this study with our two previous studies described in [34,35] is inevitable because

m

-SA is employed in those studies simply to facilitate classifier design. Furthermore, the ERP data used are the same as in the previous studies. Consequently, some issues related to the development of

m

-SA, description of the ERP data, and related terminology will overlap. However, the goals of this study are totally different from those of the previous studies which focused on exploiting the cone-of-influence of the continuous wavelet transform for the development of unichannel and multidomain ERP classifiers. Most importantly, none of the analyses related questions listed above are covered in the previous studies or in other reported studies.

2. Methods

In this section we (a) describe the single-trial data used in this study, (b) analyze the variability of

m

-ERP as a function of

m

using plots with confidence intervals (c) analyze the SNR as a function of

m

using the mean-root-mean-square SNR, (d) analyze the interclass separation as a function of

m

, (e) determine several probabilities related to the generation of distinct

m

-ERPs, and (f) describe the experiments using SVM and CNN classifiers to evaluate classifier performance as a function of various combinations of the averaging parameters used for training and testing.

2.1. Single trial data

The EEG/ERP data used in this study, which was also used in the two previous studies [34,35], was downloaded from: https://eeglab.org/tutorials/10_Group_analysis/study_creation.html#description-of-the-5-subject-experiment-tutorial-data (accessed on May 1, 2023).

This binary data set was selected because it is compact and serves the purpose of demonstrating the aims outlined in Section 1.2. Complete details of the data can be found on the listed website and the details of the single trials extracted from the EEG can be found in [34]. Details of the single trial data pertinent to this study are:

Task: Auditory binary semantic task requiring subjects to distinguish between synonymous and non-synonymous word pairs.
Number of ERP classes: Two (synonymous, non-synonymous).
Number of subjects: 5.
Number of channels: 64.
Sampling rate: 200 Hz; Single trial duration: 1 s; Number of samples in single trials: 200
Number of single trials for each subject: 195 synonymous and 195 non-synonymous.

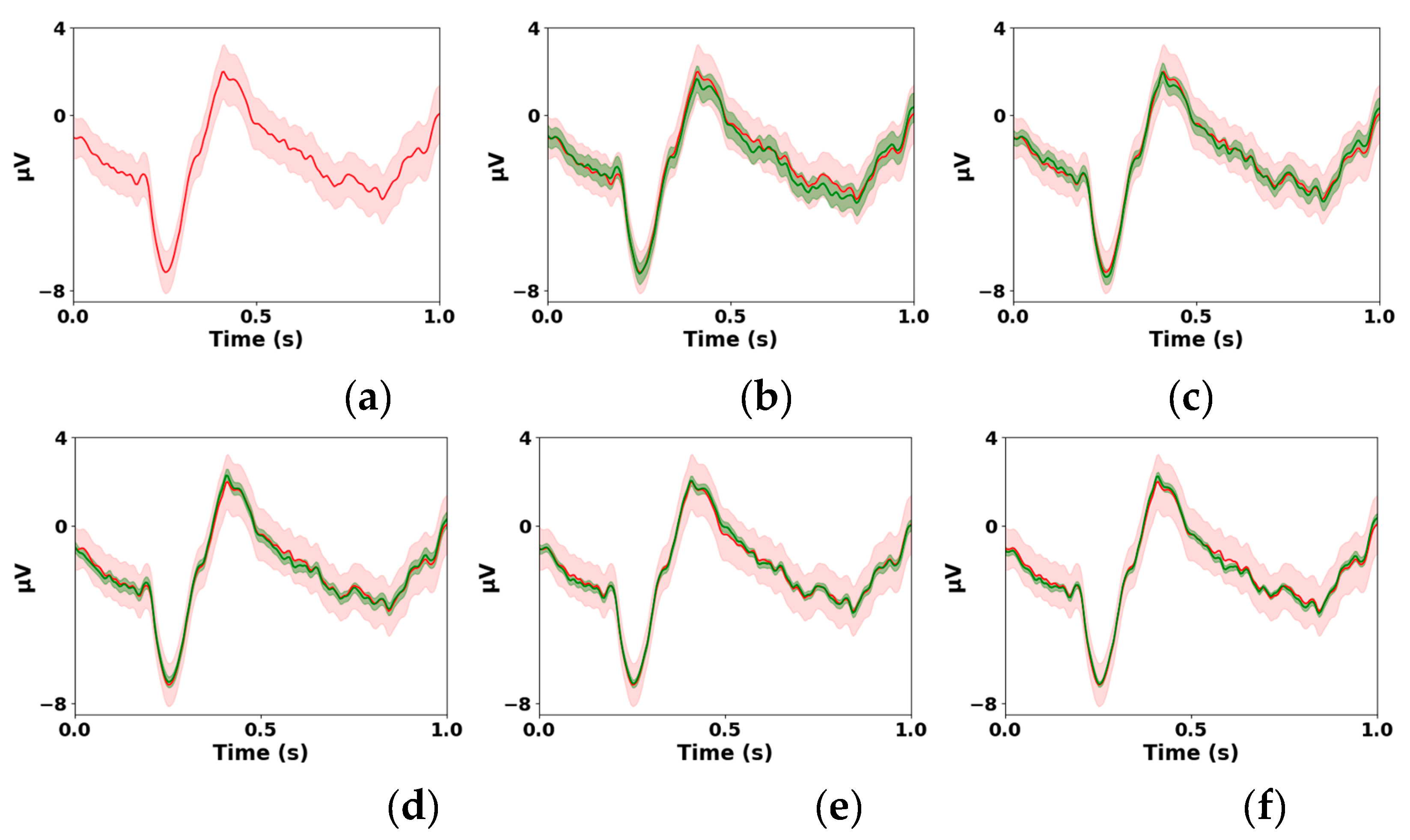
2.2. Visual Analyses of $m$ -ERPs

The most straightforward way to analyze real subsample

m

-ERPs is to compare them subjectively with the full sample ERPs through visual examination. The full sample ERP estimated by averaging all

S_{0}

single trials will be referred to as the gold standard ERP (GS-ERP). To avoid cluttering plots with

S_{0}

m

-ERPs, the mean of the

m

-ERPs, referred to as the mean

m

-ERP (M

m

-ERP) is plotted together with the GS-ERP. Figure 1 shows examples of GS-ERPs estimated from a single trial ensemble of size

S_{0} = 195

and the M

m

-ERPs determined from the 195

m

-ERPs generated using

m

-SA for

m

= 8, 16, 32, 64, 128. The GS-ERP and M

m

-ERPs are displayed in red and green, respectively. The plots also contain the superimposed 95% CIs to reflect the variations across the

S_{0}

1-ERPs and

S_{0}

m

-ERPs. The CIs of the GS-ERP and M

m

-ERPs are shaded in light red and green, respectively. The plots show that (a) the similarity between the M

m

-ERPs and GS-ERPs increases when

m

is increased and (b) the variations in the

m

-ERPs decrease when

m

is increased.

2.3. SNR Analyses

The improvement in the SNRs of

m

-ERPs generated by

m

-SA can be determined by first considering the following model most often used to describe the brain’s response to an external stimulus or event [20,21,22,23,24,25,26]:

g = f + η,

(1)

in which,

g

is the single trial recording,

f

is the stimulus induced signal of interest, and

η

is the ongoing EEG (noise). In this signal plus noise model, it is assumed that

f

is deterministic,

f

and

η

are independent, and

η

is zero-mean with variance

σ^{2}

. An

m

-ERP is the signal formed by averaging

m

time-locked single trials in the 1-ERP ensemble which is given by

g_{m} = (1 / m) \sum_{i = 1}^{m} (f + η_{i}),

(2)

= (1 / m) \sum_{i = 1}^{m} f + (1 / m) \sum_{i = 1}^{m} η_{i} .

(3)

That is,

g_{m} = f + η_{m},

(4)

where

η_{m}

is the average of the

m

single trial EEGs in

g_{m}

. It follows that

E [g_{m}] = f and

(5)

V a r [g_{m}] = (\frac{1}{m}) σ^{2} .

(6)

where

E [.]

and

V a r [.]

are the expectation and variance operators, respectively. That is, the variance of the zero-mean noise in

g_{m}

decreases by a factor of

m

resulting in an improvement in the SNR. Furthermore, because the

E [g_{m}] = f

g_{m}

approaches

f

as the number of single trials

m

in the averaging process increases.

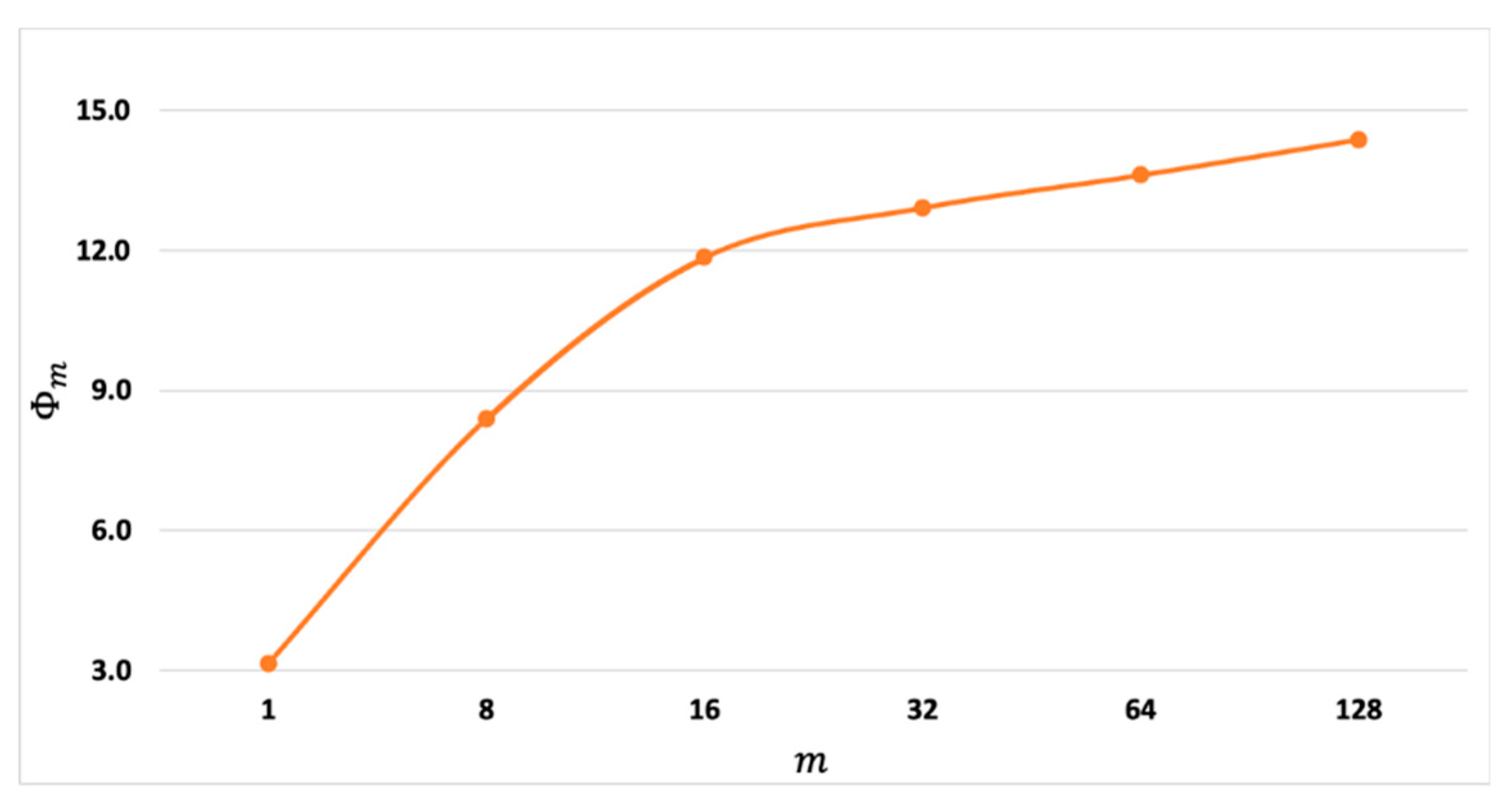
Given an ensemble of

m

-ERPs, the improvement in the SNR as a function of

m

can be measured objectively using the mean-root-mean-square SNR which is denoted by

Φ_{m}

and is given by

Φ_{m} = {[\frac{1}{S_{q}} \sum_{ω = 1}^{S_{q}} \frac{\sum_{q = 1}^{Q} {[G_{G S} (q)]}^{2}}{\sum_{q = 1}^{Q} {[G_{G S} (q) - G_{m, ω} (q)]}^{2}}]}^{1 / 2},

(7)

where,

Q

is the duration of the ERPs,

S_{q}

is the number of

m

-ERPs generated,

G_{G S} (q)

represents the gold standard ERP, and

G_{m, ω} (q)

represents the

ω^{t h}

m

-ERP.

Φ_{m}

was computed for the

m

-ERPs using the 1-ERP ensemble that was used to generate the plots in Figure 1. Note the unequal spacings of the x-axis tick values in Figure 1 and in the figures to follow. The results, presented in Figure 2 for

m

=1,8,16,32,64, and 128, confirm that

Φ_{m}

increases when

m

is increased.

2.4. Interclass separation Analyses

Interclass separation measures are useful for determining the separation between a pair of clusters in feature space. Clusters with high interclass separations are generally easier to classify thus facilitating classifiers design. If

G_{x m}

and

G_{y m}

are the

m

-ERPs of the feature clusters belonging to classes

x

and

y

, respectively, and

d_{E} (A, B)

is the Euclidean distance between vectors

A

and

B

in feature space, the inter-class separation between the

x

and

y

clusters of the

m

-ERPs can be measured by

ρ_{(x, y) m} = \frac{d_{E} (\bar{G_{x m}}, \bar{G_{y m}})}{(1 / N_{x}) \sum_{k = 1}^{N_{x}} d_{E} (G_{x m, k}, \bar{G_{x m}}) + (1 / N_{y}) \sum_{k = 1}^{N_{y}} d_{E} (G_{y m, k}, \bar{G_{y m}})},

(8)

where,

G_{x m, k}

and

G_{y m, k}

are the

k^{t h}

m

-ERPs in the respective ensembles;

\bar{G_{x m}}

and

\bar{G_{y m}}

are the cluster means; and

N_{x}

and

N_{y}

are the number of

m

-ERPs in the

x

and

y

m

-ERP ensembles, respectively. The numerator in Equation (8) is the Euclidean distance between the cluster centroids and the denominator is the total compactness because each term in the denominator is a measure of the respective cluster compactness.

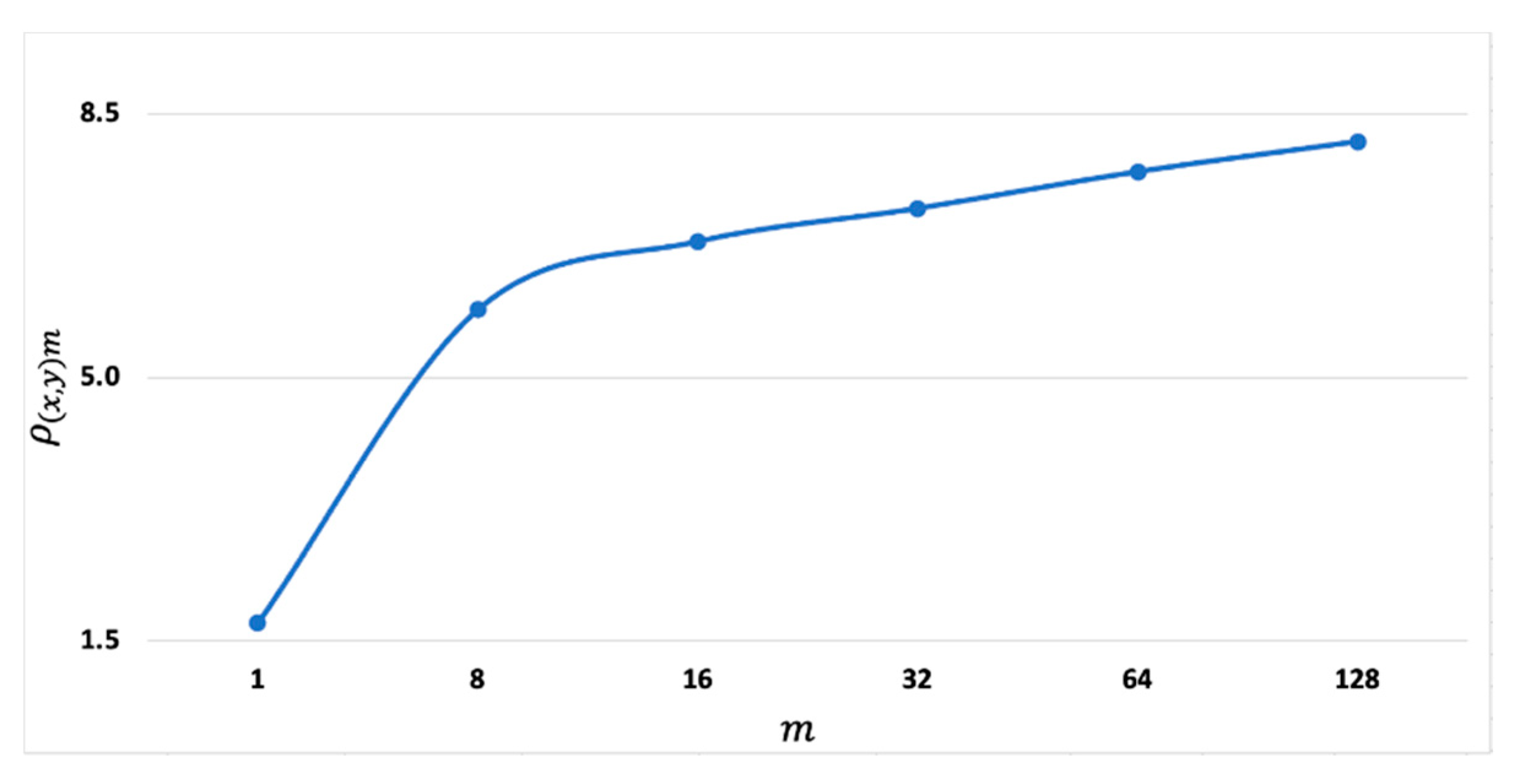
Figure 3 shows a plot of the interclass separation as a function of

m

using the 2-class single trials of channel O2 of the first subject. It is clear that

ρ_{(x, y) m}

increases because the denominator of Equation (8) decreases when

m

increases. Although the analyses have focused only on a single trial ensemble of one channel collected from a single subject, similar results can be expected from the single-trial ensembles across subjects and across channels.

Further insights into the increase in the inter-class separation as

m

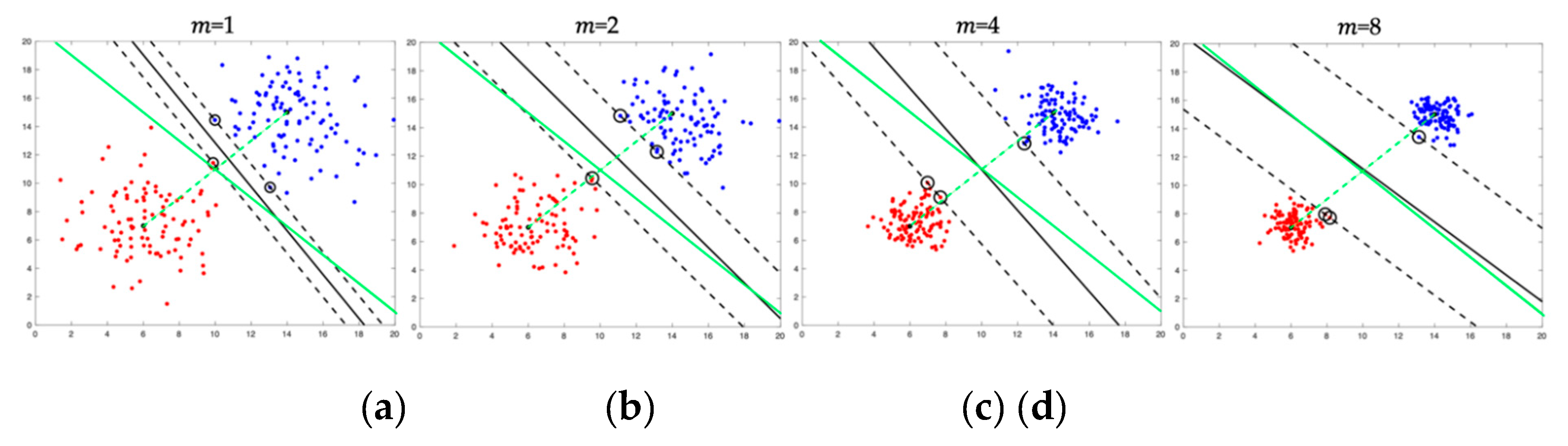
is increased can be demonstrated by using a toy dataset consisting of clusters of two-dimensional feature vectors instead of real high-dimensional ERP clusters which cannot be visualized in feature space. The conclusions drawn from the demonstration can be generalized to higher dimensional clusters, including ERP clusters. Figure 4a illustrates two 100-point clusters drawn from two bivariate Gaussian distributions with different means and identical covariance matrices of the form

σ^{2} I

where

σ^{2}

is the variance of each feature and

I

is the identity matrix. That is, the features are statistically independent. The features vectors in the two clusters are regarded as the original single-trial 1-ERP training vectors belonging to two classes. Figure 4b–d show examples of 100-point

m

-ERP clusters, generated from the original clusters using

m

-SA, for

m

= 2, 4, and 8. The vectors in the resulting clusters are regarded as

m

-ERPs generated from the single trial vectors. It will be assumed that the a priori probabilities of the two classes are equal. For the choice of cluster parameters with equal prior class probabilities, the Bayes optimal classifier reduces to the nearest mean classifier [36] whose decision boundary is the perpendicular bisector (solid green line) of the line joining the two means (green dashed line). The linear SVM classifier is also specifically chosen for this illustration because it can be used to elegantly demonstrate the effects of

m

-SA on the decision boundaries as a function of

m

. Each figure shows the cluster means (black filled circles), support vectors (black circles), SVM margins (black dashed lines), and the SVM decision boundary (solid black line). The following conclusions can be drawn from the figures: when

m

is increased, the (a) the inter-class scatter separation increases due to the increase in the cluster compactness, (b) the width of the SVM margins increase, and (c) the SVM decision boundary approaches the optimal decision boundary. Based on these conclusions, it can be expected that classification accuracies will, in general, increase as the subsampling parameter

m

is increased. Furthermore, classifier complexity is reduced because the shrinking of the clusters makes them more easily separable when

m

is increased.

2.5. Selection of the Averaging Parameter

An important question that must be addressed is the selection of the averaging parameter

m

for classifier design. The results from the SNR and interclass separation analyses can help provide answers to the question. It is clear from Figure 2 and Figure 3 that increasing

m

will improve the SNR and increase the interclass separation, respectively, which should in turn improve the classifier performance. However, it is also clear from Figure 1 and Figure 4 that the variations decrease in the

m

-ERPs and the shapes of the clusters are not preserved as

m

is increased, respectively. As a result, the risk of overfitting increases especially for non-linearly separable clusters which can have adverse effects on the classifier performance. Therefore, the selection of

m

involves a tradeoff between improving SNR and interclass separation against the risk of overfitting. Other factors influencing the selection of

m

include the size of the single-trial ensemble

S_{0}

, the SNRs of the single trials, and the number of

m

-ERPs needed in the training and test sets. An empirical approach using a validation set can be used in practice to determine the smallest value of

m

that yields the desired level of performance for a particular classification problem.

The averaging parameter does not have to be the same for the training and test sets, that is, the classifier can be trained with

m

-ERPs and tested on

n

-ERPs. Although it is desirable to keep both

m

and

n

small in practice, it is especially important to be able to obtain high accuracies for small values of

n

so that a large number of single trails does not have to be collected to get test results. A classifier labelled “CL” which is trained and tested with

m

-ERPs and

n

-ERPs, respectively, will be denoted by

m

-CL-

n

. It is also possible to train classifiers with

m

-ERPs taking multiple values of

m

to reduce overfitting and thus improve generalization.

2.6. Probability Analyses

In order to gain a better understanding of

m

-SA, this subsection focuses on answering the following questions: (a) what is the number of distinct

m

-ERPs that can be generated? (b) what is the probability of generating distinct

m

-ERPs? (c) what is the probability of generating duplicates of an

m

-ERPs? and (d) what is the probability of generating an ensemble consisting entirely of distinct

m

-ERPs?

2.6.1. Number of Distinct $m$ ERPs

For the

m

-SA method to be an effective method for generating ensembles of

m

-ERPs for classifier design, it is important that the ensembles contain

m

-ERPs that are distinct (not identical). An

m

-ERP in an ensemble is defined as being distinct if no other

m

-ERP in the ensemble is generated by averaging exactly the same

m

single-trials. That is, a pair of

m

-ERPs are distinct even if they differ by one single trial in the averaging operation. This issue can be investigated by first determining the number of distinct

m

-ERPs which is given by the number of combinations (order of single-trials does not matter in the averaging operation) of

S_{0}

single-trials taken

m

at a time. That is, the number

K_{m}

of distinct

m

-ERPs is given by

K_{m} = \frac{S_{0}!}{(S_{0} - m)! m!}

(9)

2.6.2. Probability of Generating a Distinct $m$ -ERP

Because the distinct

m

-ERPs are equally likely, the probability

P_{m}

of a distinct

m

-ERP is

(1 / K_{m})

. For practical values of

S_{0}

and

m

K_{m}

tends to be quite large. Consequently,

P_{m}

tends to be quite small. For example, when

S_{0} =

128 and

m = 8

K_{8}

= 1.4297e+12 and

P_{8}

= 6.9945e-13. The maximum number of distinct

m

-ERPs occurs when

m = S_{0} / 2

for which case

P_{m}

takes on its least value. Low values of

P_{m}

are desirable to avoid generating duplicates of

m

-ERPs.

2.6.3. Probability of Generating Duplicates of $m$ -ERPs

The probability of generating

x

duplicates of an

m

-ERP from

R

subsamples of size

m

drawn from an ensemble of

S_{0}

single trials is given by the binomial probability

P_{m, R, x} = \frac{R!}{(R - x)! x!} P_{m}^{x} {(1 - P_{m})}^{(R - x)} .

(10)

The probabilities of generating duplicates of

m

-ERPs using

m

-SA is extremely small which is beneficial in practice. For example, the probability

P_{8, 100, 2}

of obtaining 2 identical

8

-ERPs from

R = 100

subsamples of size 8 generated from an ensemble of

S_{0} = 128

single-trials is 2.4217e-21. Furthermore, for a fixed

m

, the probability of generating identical

m

-ERPs decreases as

S_{0}

is increased.

2.6.4. Probability of Generating a Distinct $m$ -ERP ensemble

The probability that an

m

-ERP ensemble generated from

R

subsamples of size

m

drawn from an ensemble of

S_{0}

single trials is distinct is given by

P_{m, R} = \frac{K_{m}!}{(K_{m} - R)! {(K_{m})}^{R}} .

(11)

For practical values of

K_{m}

and

R

P_{m, R}

tends to be high which is also a desirable property of

m

-SA. That is, it is very likely that all

m

-ERPs in the ensemble are different. For example, if

S_{0} =

128,

m = 4

, and R

= 1000

, then,

K_{m} = 10668000

and

P_{4, 1000} \approx 0.9543.

2.7. Classification Experiments

The goal of the experiments described in this section is to demonstrate how

m

-SA enables the design of ERP classifiers and to observe the performance trends as the training and testing averaging parameters are varied systematically. Although m-SA can be used in conjunction with most ERP classifiers, classical SVM [37] and deep learning CNN classifiers [38] are selected because they are quite diverse from each other. Furthermore, SVMs [39,40,41,42] and CNNs [43,44,45,46,47,48,49,50] and have proven to be quite effective in numerous classification problems including EEG and ERP classification. The performance trends as functions of the averaging parameters observed from these two classifiers should hold for most other classifiers.

For the purpose of this study, classifiers were designed for the ERPs of each channel independently. The four top-ranked channels (Cz, C2, T8, C6) as determined in [35] according to their interclass separations were selected from each subject to give a total of 4x5=20 data sets to design the classifiers. These 20 data sets are more than adequate for demonstrating the goals of this study. Increasing the number of channels will simply increase the already large number of tables used to present the results without any additional benefits. For each value of

m

, the number of

m

-ERPs generated for designing the classifier of each channel was equal to the number of single trials, that is, 195/class. Five-fold cross validation was used to evaluate the performance of the classifiers. Therefore, the number of

m

-ERPs tested for a run was (195/class)(2 classes)=390. The final classification accuracies were averaged over 50 runs, that is the average of testing (390)(50)=19,500

m

-ERPs.

2.7.1. 𝑚-SVM- $n$ and $m$ -CNN- $n$ Classifiers

The SVM and CNN classifiers trained with

m

-ERPs and tested on

m

-ERPs will be referred to as

m

-SVM-

n

and

m

-CNN-

n

, respectively. The inputs to both classifier types were the min-max normalized

m

-ERPs. That is, no feature extraction was involved in order to analyze the performance independent of the choice of the feature sets. However, the same performance trends can be expected if features sets are used. The classifiers were implemented using the PyTorch library. Details of the implementations are as follows:

m

-SVM-

n

classifiers: The Gaussian radial basis function kernel was used to implement the

m

-SVM-

n

classifiers. An exhaustive grid search was applied to select the best combinations of the regularization parameter

C

and influence parameter

γ

m

-CNN-

n

classifiers: The architecture of the CNN classifiers consisted of a sequence of a convolution layer, pooling layer, convolution layer, pooling layer, and a fully connected network (FCN) consisting of 3 layers of neurons. The activation functions were ReLU in the convolution layers, sigmoidal in the first 2 layers in the FCN, and softmax in last FCN layer. The “same” operation was used in the convolution layers. The dimensions of the filters in both convolution layers were filters

(9 \times 1)

and the number of filters in both layers was 32. The pooling layer used a (

2 \times 1)

max pooling filter with a stride of

2

. The FCN had 1024, 256, and 2 neurons in the 3 layers. The training options used were: initialization = min-max, optimizer = Adam, learning rate = 0.001, number of epochs = 50, drop out probabilities =0.15.

3. Results and Discussion

The complete set of results for the 20 data sets are presented in Table A1, Table A2, Table A3 and Table A4 in Appendix A for combinations of

m

and

n

taking values 1, 4, 8, 16, and 32. The tables show the results for each of the 4 channels selected. Each entry in the tables is an average of testing 19,500

m

-ERPs. Note that except for the case in which the training averaging parameter

m

is equal to one, the testing averaging parameter

n

takes values that are less than, equal to, and greater than

m

. The 1-SVM-1 and 1-CNN-1 are single trial classifiers, that is, the classifiers trained and tested solely with single trials. These single trial classifiers serve as the baseline for performance comparisons with the

m

-SVM-

n

and

m

-CNN-

n

classifiers. The averages across the 4 channels are summarized in Table 1 and Table 2. That is, each entry in Table 1 and Table 2 is the average of the 4 corresponding values in the Tables in Appendix A. The average accuracies across the 5 subjects are also presented in Table 1 and Table 2.

3.1. Discussion

It is of interest to analyze the trends in the tables in Appendix A as well as Table 1 and Table 2. It is clear that the

m

-SVM-

n

and

m

-CNN-

n

classifiers outperform the 1-SVM-1 and 1-CNN-1 baseline single trial classifiers, respectively. The

m

-SVM-

n

and

m

-CNN-

n

results in the tables in Appendix A show that:

(a): for a fixed $m$ , the accuracies increase when $n$ is increased (across the rows of each channel),
(b): for a given $n$ the accuracies increase when $m$ is increased (along the columns of each channel),
(c): the accuracies increase when $m$ and $n$ and are increased together (across the diagonals of each channel), and
(d): for the same increases in $m$ and $n$ , the improvements in classification accuracies are larger for smaller values of $m$ and $n$ .

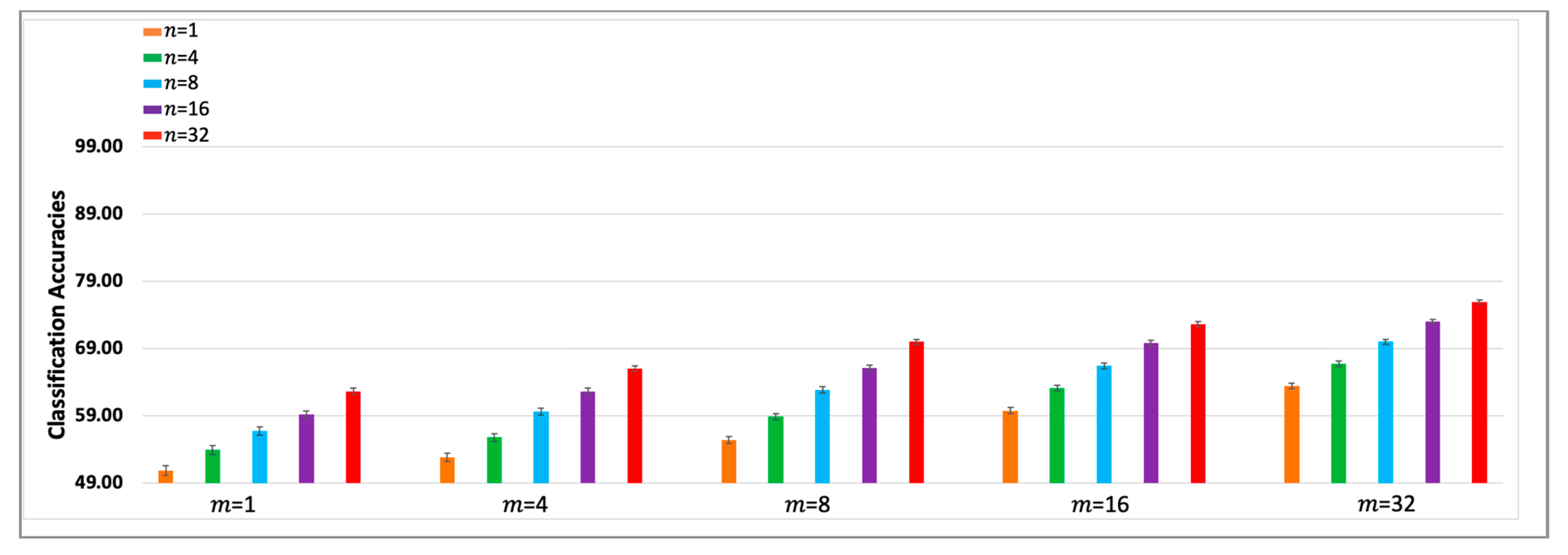
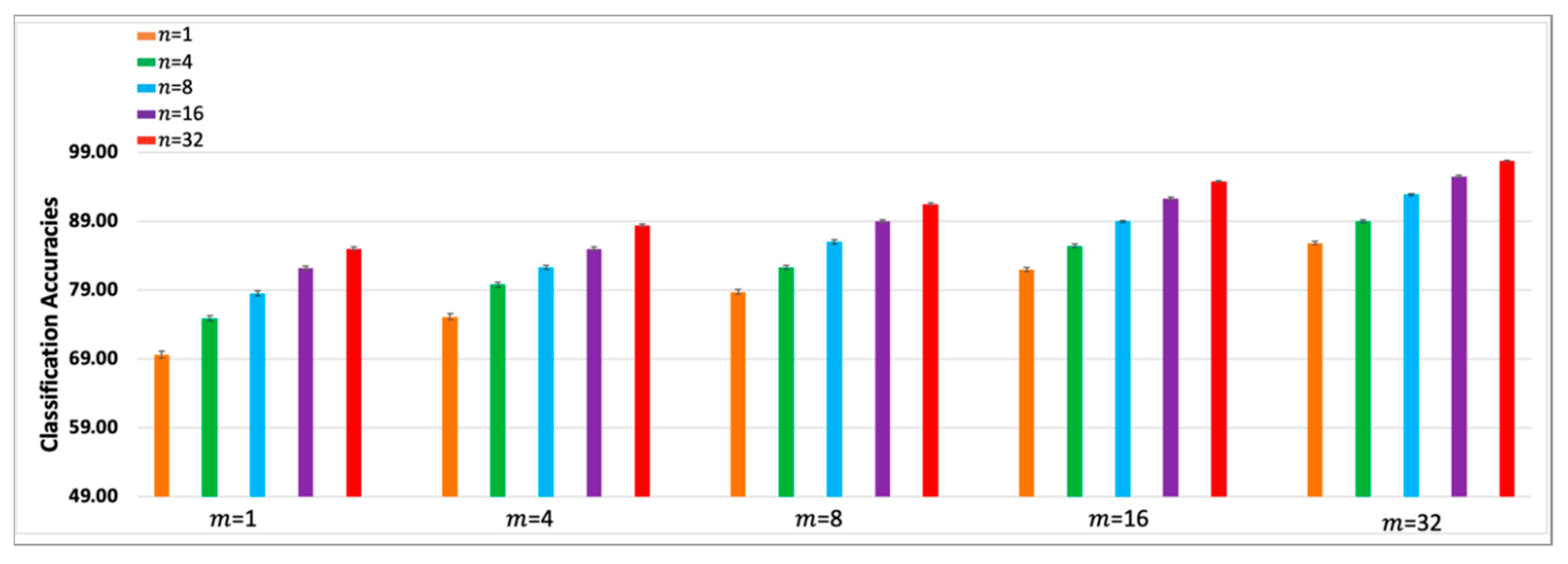
To facilitate trend analyses, Figure 5 and Figure 6 show bar graphs of the subject averages of the

m

-SVM-

n

and

m

-CNN-

n

classifiers, that is, the last columns of Table 1 and Table 2. The first bar in each figure depicts the accuracy of the baseline single trial classifier. The error bars represent +/-1 standard error of the mean. The improvement trends in the accuracies as

n

is increased can be observed within each sub-bar graph and the improvements as

m

is increased is observed across the sub-bar graphs. The two tables and bar graphs also reveal the diminishing improvements in the classification accuracies for higher

m

and

n

values. The CNN classifiers outperform SVM classifiers, however, the key point to note is that the performance trends of both types of classifiers are remarkably similar. Most importantly, the results indicate that high classification accuracies can be obtained using small values of

m

and

n

. That is,

m

-SA can be used to design ERP classifiers using small subsampled ERPs from a practical sized single trial ensemble.

4. Conclusions

Previous studies have empirically shown that

m

-subsample averaging is an effective method for facilitating the design of ERP classifiers. This study focused on analyzing

m

-SA to have a better understanding of the properties of subsample averaging that support its suitability for ERP classifier design. The analyses showed that (a) the SNR improves by increasing the averaging parameter

m

, (b) the inter-class separation increases by increasing

m

, (c) a large number of distinct

m

-ERPs can be generated by

m

-SA, (d) the probability of generating a distinct

m

-ERP is small, (e) the probability of generating duplicates of

m

-ERPs is small, and (f) the probability of generating an ensemble consisting of distinct

m

-ERPs is high. These analyses results offer important insights into the favorability of

m

-SA for ERP classifier design. The extensive set of classification experiments showed that the

m

-SVM-

n

and

m

-CNN-

n

classifiers outperformed the baseline single trial classifiers and most importantly, confirmed that high classification accuracies can be obtained using small-average

m

-ERPs generated from practical sized single trial ensembles. Consequently, prohibitively large numbers of single trials do not have to be collected in practice for the design and deployment of ERP classifiers in numerous applications related to brain activity research and clinical applications. Finally, it must be emphasized that

m

-SA is not restricted to SVM and CNN classifiers and can be used in conjunction with most ERP classifiers. Furthermore, although

m

-SA is specifically developed for ERP classification, it can be exploited to improve the performance in other signal classification problems where repeated time-locked trials can be collected or where repeated trials can be synchronized prior to averaging.

Author Contributions

Conceptualization, L.G. and X.C.; methodology, L.G. and X.C.; software, X.C.; validation, L.G. and X.C.; writing-original draft preparation, L.G. and X.C.; writing-review and editing, L.G. and X.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Publicly available data were used in this study. The data can be found here: https://eeglab.org/tutorials/10_Group_analysis/study_creation.html#description-of-the-5-subject-experiment-tutorial-data (accessed on May 1, 2023).

Appendix A

Table A1. Accuracies of the

m

-SVM-

n

classifiers for channels Cz and C2.

Table A1. Accuracies of the

m

-SVM-

n

classifiers for channels Cz and C2.

		Channel Cz					Channel C2
$m$	$n$	Subjects					Subjects
$m$	$n$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$
1	1	50.77	50.39	51.11	52.19	50.68	51.63	50.00	51.43	50.00	51.25
	4	54.83	54.86	54.21	54.62	53.69	53.26	53.62	54.47	53.07	54.53
	8	57.18	58.28	57.88	58.05	57.24	56.76	56.53	56.96	56.78	57.59
	16	60.73	61.06	60.58	60.54	61.04	59.30	58.65	58.48	59.99	59.10
	32	63.20	63.73	63.64	63.48	64.32	62.85	62.20	62.58	63.41	62.49
4	1	53.15	52.31	52.16	52.54	52.50	52.31	51.54	52.23	52.31	52.31
	4	56.61	55.68	55.89	56.77	55.64	55.66	55.17	55.84	55.40	55.74
	8	59.69	58.46	59.85	58.79	58.28	58.06	58.18	59.43	59.56	59.67
	16	62.65	62.61	62.30	61.15	62.98	62.10	62.27	62.47	62.09	61.30
	32	66.54	65.85	66.08	66.60	65.45	65.53	65.54	66.77	66.68	66.48
8	1	56.11	54.66	56.41	55.05	56.62	55.73	55.96	55.11	56.96	55.67
	4	60.80	59.34	59.92	60.44	60.91	58.91	57.85	58.27	58.55	58.27
	8	63.27	63.32	64.91	65.34	63.39	62.89	60.60	62.64	62.07	63.89
	16	67.22	68.85	66.15	65.70	66.25	65.67	65.42	66.49	65.79	66.96
	32	71.98	70.77	69.53	70.20	70.00	69.51	68.76	69.71	69.93	68.48
16	1	60.76	59.99	59.89	60.03	59.74	60.33	60.53	60.69	61.56	60.24
	4	63.89	64.55	64.84	60.22	64.05	63.33	63.68	63.13	65.24	63.51
	8	67.42	66.45	66.81	67.45	66.34	66.67	67.63	67.51	66.17	66.73
	16	70.04	71.15	70.85	71.79	70.12	70.76	69.48	69.84	71.93	68.63
	32	73.12	72.86	73.61	73.56	71.34	73.01	73.16	74.47	73.06	72.43
32	1	63.60	62.20	61.82	61.73	63.30	63.31	64.69	63.75	65.33	65.08
	4	67.06	66.94	67.11	65.08	67.00	66.92	67.56	67.93	67.08	66.33
	8	70.36	71.53	70.68	70.33	70.58	70.45	69.20	70.96	69.77	69.49
	16	74.27	73.05	74.92	73.38	74.34	72.09	73.70	73.25	72.94	73.62
	32	76.26	76.61	76.33	78.00	76.57	75.78	75.37	76.37	75.28	75.30

Table A2. Accuracies of the

m

-SVM-

n

classifiers for channels T8 and C6.

Table A2. Accuracies of the

m

-SVM-

n

classifiers for channels T8 and C6.

		Channel T8					Channel C6
$m$	$n$	Subjects					Subjects
$m$	$n$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$
1	1	50.68	50.77	50.42	51.57	51.63	50.51	50.39	50.00	50.43	50.00
	4	54.88	54.83	53.94	54.20	54.12	52.31	53.65	52.53	53.69	52.14
	8	56.12	57.12	57.74	57.76	56.99	54.08	55.01	55.75	54.63	54.90
	16	58.33	59.71	59.38	58.42	59.88	57.26	57.00	58.94	56.53	57.88
	32	61.41	61.24	63.74	66.19	64.22	60.72	60.62	60.84	61.02	60.52
4	1	52.70	52.31	52.23	53.41	53.74	52.92	52.94	53.53	53.13	54.88
	4	56.26	56.00	55.70	55.99	56.85	55.35	54.65	54.12	55.24	56.11
	8	61.40	62.05	61.61	60.30	61.80	58.62	58.84	59.55	58.69	58.78
	16	64.26	66.42	64.26	64.97	63.55	60.18	62.10	62.43	61.69	60.69
	32	66.19	67.22	67.24	66.12	67.24	63.82	65.24	65.29	64.73	64.23
8	1	54.46	55.20	54.66	55.19	55.28	54.87	54.42	54.44	54.25	55.62
	4	57.89	58.14	56.70	58.89	57.89	58.84	57.84	58.94	58.48	59.70
	8	63.85	63.70	63.84	65.08	63.29	60.58	60.59	60.72	60.54	61.78
	16	66.85	66.70	65.84	67.08	66.29	65.62	65.20	64.53	64.91	64.05
	32	69.61	70.36	71.43	69.77	71.95	69.08	71.06	68.75	68.70	69.58
16	1	58.08	59.32	59.70	59.08	58.79	58.51	59.09	59.73	59.89	57.94
	4	62.77	63.52	63.40	65.17	65.88	60.34	61.05	61.18	61.02	60.97
	8	66.36	68.81	68.68	65.21	67.95	65.23	65.02	63.51	62.86	65.16
	16	69.15	68.36	70.30	70.73	70.19	68.99	69.30	69.16	67.27	68.14
	32	72.47	73.44	73.22	72.31	73.21	72.19	70.86	71.57	71.11	71.62
32	1	63.72	62.67	63.56	65.08	63.59	62.78	62.97	62.22	63.46	63.00
	4	66.36	66.45	66.55	68.71	67.98	66.00	66.62	66.38	63.93	66.12
	8	69.45	69.96	68.06	69.54	68.35	70.35	70.69	69.58	69.43	70.62
	16	71.15	73.22	72.19	72.88	72.89	72.98	72.00	71.92	72.80	72.44
	32	75.63	75.52	75.27	73.04	74.38	76.22	75.08	76.97	76.45	76.65

Table A3. Accuracies of the

m

-CNN-

n

classifiers for channels Cz and C2.

Table A3. Accuracies of the

m

-CNN-

n

classifiers for channels Cz and C2.

		Channel Cz					Channel C2
$m$	$n$	Subjects					Subjects
$m$	$n$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$
1	1	72.66	70.63	73.66	70.63	71.56	71.56	69.53	72.69	71.92	70.39
	4	74.40	73.81	76.89	72.31	76.35	78.46	76.54	76.72	77.69	76.25
	8	78.13	79.22	79.69	82.34	81.88	79.23	80.31	79.23	79.31	77.69
	16	82.33	82.42	82.57	82.67	84.48	81.21	82.72	83.91	83.95	81.25
	32	85.44	85.74	85.94	85.44	86.73	85.67	86.82	85.79	84.29	83.94
4	1	75.81	77.66	77.69	74.88	76.09	76.15	75.39	76.29	76.54	75.00
	4	79.05	81.15	80.79	78.08	80.44	81.04	80.19	80.67	80.41	82.10
	8	82.47	82.95	81.16	81.83	83.00	83.02	84.05	83.52	82.36	83.32
	16	86.15	85.66	85.86	87.06	87.27	85.11	85.62	84.14	83.44	85.30
	32	89.08	88.40	89.71	90.58	89.59	88.51	89.20	89.94	90.56	89.20
8	1	80.92	81.76	80.75	79.62	82.89	80.73	78.53	80.89	78.44	78.47
	4	83.61	83.47	85.82	82.35	84.09	83.19	81.95	83.08	81.58	81.09
	8	86.82	86.55	87.21	88.92	85.16	87.86	85.73	86.78	87.03	85.73
	16	90.23	89.59	90.25	91.12	89.35	90.68	91.03	91.59	90.30	89.74
	32	93.66	92.83	92.23	93.25	92.66	92.61	93.93	93.61	92.48	90.62
16	1	82.62	83.97	83.44	86.15	85.08	82.95	82.36	83.08	83.42	81.43
	4	85.47	86.34	85.47	88.48	86.74	85.65	86.68	88.18	87.31	86.76
	8	90.92	90.83	91.13	89.52	90.77	91.53	90.64	93.03	90.24	90.63
	16	93.98	91.90	93.24	91.68	92.62	94.19	93.94	94.73	95.47	94.20
	32	96.83	95.89	94.84	94.70	95.31	96.22	96.00	95.60	96.66	96.01
32	1	86.56	85.94	85.94	88.25	88.56	85.18	84.95	86.12	84.37	85.62
	4	88.85	88.46	87.31	89.46	91.81	88.26	86.27	88.26	88.16	88.41
	8	93.56	93.54	93.46	93.47	92.92	93.85	90.15	93.48	92.68	91.22
	16	96.82	96.65	95.87	95.50	96.24	95.49	93.95	96.71	94.32	95.07
	32	97.90	98.13	97.78	98.04	98.13	98.74	97.43	99.73	96.40	97.96

Table A4. Accuracies of the

m

-CNN-

n

classifiers for channels T8 and C6.

Table A4. Accuracies of the

m

-CNN-

n

classifiers for channels T8 and C6.

		Channel T8					Channel C6
$m$	$n$	Subjects					Subjects
$m$	$n$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$
1	1	69.53	67.34	66.72	65.47	67.97	69.62	64.23	68.44	69.38	67.97
	4	73.13	74.15	74.78	74.00	74.14	72.22	72.71	74.65	73.32	75.59
	8	78.14	77.05	76.33	76.87	77.59	78.37	77.24	78.42	76.39	76.78
	16	80.23	82.09	81.34	80.70	80.84	82.98	82.95	82.25	80.74	82.39
	32	83.62	85.70	83.87	83.65	84.42	84.29	84.97	84.22	85.77	84.05
4	1	75.50	73.08	72.83	74.26	74.56	73.78	72.50	73.96	75.41	74.54
	4	78.21	78.29	78.35	81.19	81.77	78.71	79.59	78.54	78.12	78.76
	8	80.15	82.69	81.72	81.81	82.44	81.20	80.54	80.85	84.19	83.99
	16	84.57	83.94	82.61	85.13	83.40	84.79	84.37	85.23	85.82	84.41
	32	87.86	85.73	86.78	87.03	85.73	87.98	88.33	89.19	87.25	86.19
8	1	76.35	76.92	77.19	78.35	76.18	77.23	78.46	75.00	78.46	77.15
	4	80.37	80.03	81.69	82.62	82.49	81.26	83.09	82.79	80.50	80.52
	8	85.62	84.44	86.74	84.75	85.06	83.52	84.58	86.19	85.11	86.23
	16	88.20	88.15	90.16	89.08	89.57	85.31	86.11	86.31	85.66	87.22
	32	90.11	91.33	91.24	91.33	91.46	90.23	89.35	88.35	87.89	90.79
16	1	80.56	79.32	80.62	81.00	80.33	80.96	78.94	80.94	81.88	79.95
	4	83.80	84.69	84.10	84.16	83.22	82.65	85.74	85.49	82.98	84.60
	8	86.03	88.01	85.91	85.26	88.07	87.68	87.86	87.57	86.68	86.56
	16	91.02	91.54	92.80	90.78	90.24	91.47	90.52	89.42	91.99	89.90
	32	94.61	94.42	93.55	92.57	92.10	93.68	92.74	94.90	93.48	95.37
32	1	84.42	84.45	87.14	85.17	86.41	84.64	86.04	86.10	85.00	85.57
	4	88.05	88.37	88.23	90.67	87.93	89.97	91.26	88.92	89.14	91.44
	8	92.61	92.15	92.91	93.50	92.83	92.83	93.38	91.48	93.92	93.39
	16	95.17	95.51	94.82	96.92	95.90	95.23	96.09	94.25	95.72	94.36
	32	98.37	98.69	98.08	97.17	96.51	97.82	97.92	95.90	96.08	97.69

References

Blackwood, D. H. R. , and Walter J. Muir. “Cognitive brain potentials and their application.” The British Journal of Psychiatry 157, no. S9 (1990): 96-101. [CrossRef]
Coles, Michael GH, and Michael D. Rugg. Event-related brain potentials: An introduction. Oxford University Press, 1995.
Handy, Todd C., ed. Event-related potentials: A methods handbook. MIT press, 2005.
Luck, Steven J. An introduction to the event-related potential technique. MIT press, 2014.
Sur, Shravani, and Vinod Kumar Sinha. “Event-related potential: An overview.” Industrial psychiatry journal 18, no. 1 (2009): 70. [CrossRef]
Verleger, Rolf. “Alterations of ERP components in neurodegenerative diseases.” The Oxford handbook of event-related potential components (2012).
Landa, Leos, Zdenek Krpoun, Martina Kolarova, and Tomas Kasparek. “Event-related potentials and their applications.” Activitas Nervosa Superior 56 (2014): 17-23. [CrossRef]
Seer, Caroline, Florian Lange, Sebastian Loens, Florian Wegner, Christoph Schrader, Dirk Dressler, Reinhard Dengler, and Bruno Kopp. “Dopaminergic modulation of performance monitoring in Parkinson’s disease: An event-related potential study.” Scientific Reports 7, no. 1 (2017): 41222. [CrossRef]
Sowndhararajan, Kandhasamy, Minju Kim, Ponnuvel Deepa, Se Jin Park, and Songmun Kim. “Application of the P300 event-related potential in the diagnosis of epilepsy disorder: a review.” Scientia pharmaceutica 86, no. 2 (2018): 10. [CrossRef]
Hajcak, Greg, Julia Klawohn, and Alexandria Meyer. “The utility of event-related potentials in clinical psychology.” Annual review of clinical psychology 15 (2019): 71-95. [CrossRef]
Rokos, Alexander, Richard Mah, Rober Boshra, Amabilis Harrison, Tsee Leng Choy, Stefanie Blain-Moraes, and John F. Connolly. “Eliciting and recording Event Related Potentials (ERPs) in behaviourally unresponsive populations: a retrospective commentary on critical factors.” Brain Sciences 11, no. 7 (2021): 835. [CrossRef]
Coles, Michael GH, and Michael D. Rugg, eds. Electrophysiology of Mind: Event-related brain potentials and Cognition. Oxford University Press, 1996.
Hillyard, Steven A., and Lourdes Anllo-Vento. “Event-related brain potentials in the study of visual selective attention.” Proceedings of the National Academy of Sciences 95, no. 3 (1998): 781-787. [CrossRef]
Picton, Terence W., S. Bentin, P. Berg, Emanuel Donchin, S. A. Hillyard, R. Johnson, G. A. Miller et al. “Guidelines for using human event-related potentials to study cognition: recording standards and publication criteria.” Psychophysiology 37, no. 2 (2000): 127-152.
Rugg, Michael D., and Tim Curran. “Event-related potentials and recognition memory.” Trends in cognitive sciences 11, no. 6 (2007): 251-257. [CrossRef]
Luck, Steven J., and Emily S. Kappenman. “ERP components and selective attention.” The Oxford handbook of event-related potential components (2012): 295-327.
Woodman, Geoffrey F. “A brief introduction to the use of event-related potentials in studies of perception and attention.” Attention, Perception, & Psychophysics 72 (2010): 2031-2046.
Gupta, Resh S., Autumn Kujawa, and David R. Vago. “A preliminary investigation of ERP components of attentional bias in anxious adults using temporospatial principal component analysis.” Journal of psychophysiology (2021). [CrossRef]
Vurdah, Nydia, Julie Vidal, and Arnaud Viarouge. “Event-Related Potentials Reveal the Impact of Conflict Strength in a Numerical Stroop Paradigm.” Brain Sciences 13, no. 4 (2023): 586. [CrossRef]
Woody, Charles D. “Characterization of an adaptive filter for the analysis of variable latency neuroelectric signals.” Medical and biological engineering 5 (1967): 539-554. [CrossRef]
Wastell, D. G. “Statistical detection of individual evoked responses: an evaluation of Woody’s adaptive filter.” Electroencephalography and Clinical Neurophysiology 42, no. 6 (1977): 835-839. [CrossRef]
Möucks, Joachim, Walter Köuhler, Theo Gasser, and Dinh Tuan Pham. “Novel approaches to the problem of latency jitter.” Psychophysiology 25, no. 2 (1988): 217-226. [CrossRef]
Aunon, Jorge I., Clare D. McGillem, and Donald G. Childers. “Signal processing in evoked potential research: averaging and modeling.” Critical reviews in bioengineering 5, no. 4 (1981): 323-367.
McGillem, Clare D., Jorge I. Aunon, and Carlos A. Pomalaza. “Improved waveform estimation procedures for event-related potentials.” IEEE transactions on biomedical engineering 6 (1985): 371-379. [CrossRef]
Gevins, Alan S., Nelson H. Morgan, Steven L. Bressler, Joseph C. Doyle, and Brian A. Cutillo. “Improved event-related potential estimation using statistical pattern classification.” Electroencephalography and clinical neurophysiology 64, no. 2 (1986): 177-186. [CrossRef]
Gupta, Lalit, Dennis L. Molfese, Ravi Tammana, and Panagiotis G. Simos. “Nonlinear alignment and averaging for estimating the evoked potential.” IEEE transactions on biomedical engineering 43, no. 4 (1996): 348-356.
Boudewyn, Megan A., Steven J. Luck, Jaclyn L. Farrens, and Emily S. Kappenman. “How many trials does it take to get a significant ERP effect? It depends.” Psychophysiology 55, no. 6 (2018): e13049. [CrossRef]
Jochumsen, Mads, Hendrik Knoche, Troels Wesenberg Kjaer, Birthe Dinesen, and Preben Kidmose. “EEG headset evaluation for detection of single-trial movement intention for brain-computer interfaces.” Sensors 20, no. 10 (2020): 2804. [CrossRef]
Wirth, Christopher, Jake Toth, and Mahnaz Arvaneh. ““You Have Reached Your Destination”: A Single Trial EEG Classification Study.” Frontiers in neuroscience 14 (2020): 66. [CrossRef]
Chailloux Peguero, Juan David, Omar Mendoza-Montoya, and Javier M. Antelis. “Single-option P300-BCI performance is affected by visual stimulation conditions.” Sensors 20, no. 24 (2020): 7198. [CrossRef]
De Venuto, Daniela, and Giovanni Mezzina. “A single-trial P300 detector based on symbolized EEG and autoencoded-(1D) CNN to improve ITR performance in BCIs.” Sensors 21, no. 12 (2021): 3961. [CrossRef]
Leoni, Jessica, Silvia Carla Strada, Mara Tanelli, Alessandra Brusa, and Alice Mado Proverbio. “Single-trial stimuli classification from detected P300 for augmented Brain–Computer Interface: A deep learning approach.” Machine Learning with Applications 9 (2022): 100393. [CrossRef]
Fernández-Rodríguez, Álvaro, Ricardo Ron-Angevin, Francisco Velasco-Álvarez, Jaime Diaz-Pineda, Théodore Letouzé, and Jean-Marc André. “Evaluation of Single-Trial Classification to Control a Visual ERP-BCI under a Situation Awareness Scenario.” Brain Sciences 13, no. 6 (2023): 886. [CrossRef]
Chen, Xiaoqian, Resh S. Gupta, and Lalit Gupta. “Exploiting the Cone of Influence for Improving the Performance of Wavelet Transform-Based Models for ERP/EEG Classification.” Brain Sciences 13, no. 1 (2022): 21. [CrossRef]
Chen, Xiaoqian, Resh S. Gupta, and Lalit Gupta. “Multidomain Convolution Neural Network Models for Improved Event-Related Potential Classification.” Sensors 23, no. 10 (2023): 4656. [CrossRef]
Hart, Peter E., David G. Stork, and Richard O. Duda. Pattern classification. Hoboken: Wiley, 2000.
Cortes, Corinna, and Vladimir Vapnik. “Support-vector networks.” Machine learning 20 (1995): 273-297.
LeCun, Yann, Yoshua Bengio, and Geoffrey Hinton. “Deep learning.” nature 521, no. 7553 (2015): 436-444.
Stewart, Andrew X., Antje Nuthmann, and Guido Sanguinetti. “Single-trial classification of EEG in a visual object task using ICA and machine learning.” Journal of neuroscience methods 228 (2014): 1-14. [CrossRef]
Parvar, Hossein, Lauren Sculthorpe-Petley, Jason Satel, Rober Boshra, Ryan CN D’Arcy, and Thomas P. Trappenberg. “Detection of event-related potentials in individual subjects using support vector machines.” Brain informatics 2, no. 1 (2015): 1-12. [CrossRef]
Yasoda, K., R. S. Ponmagal, K. S. Bhuvaneshwari, and K. Venkatachalam. “Automatic detection and classification of EEG artifacts using fuzzy kernel SVM and wavelet ICA (WICA).” Soft Computing 24 (2020): 16011-16019. [CrossRef]
Buriro, Abdul Baseer, Bilal Ahmed, Gulsher Baloch, Junaid Ahmed, Reza Shoorangiz, Stephen J. Weddell, and Richard D. Jones. “Classification of alcoholic EEG signals using wavelet scattering transform-based features.” Computers in biology and medicine 139 (2021): 104969. [CrossRef]
Lawhern, Vernon J., Amelia J. Solon, Nicholas R. Waytowich, Stephen M. Gordon, Chou P. Hung, and Brent J. Lance. “EEGNet: a compact convolutional neural network for EEG-based brain–computer interfaces.” Journal of neural engineering 15, no. 5 (2018): 056013. [CrossRef]
Khan, Aisha, Jee Eun Sung, and Je-Won Kang. “Multi-channel fusion convolutional neural network to classify syntactic anomaly from language-related ERP components.” Information Fusion 52 (2019): 53-61. [CrossRef]
Lee, Hyeon Kyu, and Young-Seok Choi. “Application of continuous wavelet transform and convolutional neural network in decoding motor imagery brain-computer interface.” Entropy 21, no. 12 (2019): 1199. [CrossRef]
Craik, Alexander, Yongtian He, and Jose L. Contreras-Vidal. “Deep learning for electroencephalogram (EEG) classification tasks: a review.” Journal of neural engineering 16, no. 3 (2019): 031001. [CrossRef]
Santamaria-Vazquez, Eduardo, Victor Martinez-Cagigal, Fernando Vaquerizo-Villar, and Roberto Hornero. “EEG-inception: a novel deep convolutional neural network for assistive ERP-based brain-computer interfaces.” IEEE Transactions on Neural Systems and Rehabilitation Engineering 28, no. 12 (2020): 2773-2782. [CrossRef]
Liu, Tianjun, and Deling Yang. “A three-branch 3D convolutional neural network for EEG-based different hand movement stages classification.” Scientific Reports 11, no. 1 (2021): 10758.
Zang, Boyu, Yanfei Lin, Zhiwen Liu, and Xiaorong Gao. “A deep learning method for single-trial EEG classification in RSVP task based on spatiotemporal features of ERPs.” Journal of Neural Engineering 18, no. 4 (2021): 0460c8. [CrossRef]
Liang, Xinbin, Yaru Liu, Yang Yu, Kaixuan Liu, Yadong Liu, and Zongtan Zhou. “Convolutional Neural Network with a Topographic Representation Module for EEG-Based Brain—Computer Interfaces.” Brain Sciences 13, no. 2 (2023): 268. [CrossRef]

Figure 1. GS-ERPs (red) and M

m

-ERPs (green) (a)

m

=1; (b)

m

=1 and

m

=8; (c)

m

=1 and

m

=16; (d)

m

=1 and

m

=32; (e)

m

=1 and

m

=64; (f)

m

=1 and

m

=128. The 95% CIs of the 1-ERPs and

m

-ERPs are shaded in light red and green, respectively.

Figure 1. GS-ERPs (red) and M

m

-ERPs (green) (a)

m

=1; (b)

m

=1 and

m

=8; (c)

m

=1 and

m

=16; (d)

m

=1 and

m

=32; (e)

m

=1 and

m

=64; (f)

m

=1 and

m

=128. The 95% CIs of the 1-ERPs and

m

-ERPs are shaded in light red and green, respectively.

Figure 2. The mean-root-mean square SNR

Φ_{m}

as a function of

m

Φ_{1}

=3.14,

Φ_{8}

=8.39,

Φ_{16}

=11.84,

Φ_{32}

=12.9,

Φ_{64}

=13.6,

Φ_{128}

=14.36

Figure 2. The mean-root-mean square SNR

Φ_{m}

as a function of

m

Φ_{1}

=3.14,

Φ_{8}

=8.39,

Φ_{16}

=11.84,

Φ_{32}

=12.9,

Φ_{64}

=13.6,

Φ_{128}

=14.36

Figure 3. Interclass separation as a function of

m

ρ_{(x, y) 1} = 1.73

ρ_{(x, y) 8} = 5.9

ρ_{(x, y) 16} = 6.81

ρ_{(x, y) 32} = 7.25

ρ_{(x, y) 64} = 7.74

ρ_{(x, y) 128} = 8.14

Figure 3. Interclass separation as a function of

m

ρ_{(x, y) 1} = 1.73

ρ_{(x, y) 8} = 5.9

ρ_{(x, y) 16} = 6.81

ρ_{(x, y) 32} = 7.25

ρ_{(x, y) 64} = 7.74

ρ_{(x, y) 128} = 8.14

Figure 4. Illustration of the interclass separation and decision boundaries as a function of

m

(a) single-trial clusters (b) 2-ERP clusters (c) 4-ERP clusters (d) 8-ERP clusters.

Figure 4. Illustration of the interclass separation and decision boundaries as a function of

m

(a) single-trial clusters (b) 2-ERP clusters (c) 4-ERP clusters (d) 8-ERP clusters.

Figure 5. The classification accuracies of the

m

-SVM-

n

classifiers averaged across the 5 subjects.

Figure 5. The classification accuracies of the

m

-SVM-

n

classifiers averaged across the 5 subjects.

Figure 6. The classification accuracies of the

m

-CNN-

n

classifiers averaged across the 5 subjects.

Figure 6. The classification accuracies of the

m

-CNN-

n

classifiers averaged across the 5 subjects.

Table 1. Accuracies of the

m

-SVM-

n

classifiers averaged across the 4 channels.

Table 1. Accuracies of the

m

-SVM-

n

classifiers averaged across the 4 channels.

$m$	$n$	Subjects					Subject Avg
$m$	$n$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$	Subject Avg
1	1	50.90	50.39	50.74	51.05	50.89	50.79
	4	53.82	54.24	53.79	53.90	53.62	53.87
	8	56.03	56.73	57.08	56.80	56.68	56.66
	16	58.90	59.10	59.35	58.87	59.47	59.14
	32	62.04	61.95	62.70	63.53	62.89	62.62
4	1	52.77	52.27	52.54	52.85	53.36	52.76
	4	55.97	55.38	55.39	55.85	56.08	55.73
	8	59.44	59.38	60.11	59.34	59.63	59.58
	16	62.30	63.35	62.87	62.48	62.13	62.63
	32	65.52	65.96	66.34	66.03	65.85	65.94
8	1	55.30	55.06	55.15	55.36	55.80	55.33
	4	59.11	58.29	58.46	59.09	59.19	58.83
	8	62.65	62.05	63.03	63.26	63.09	62.82
	16	66.34	66.54	65.75	65.87	65.89	66.08
	32	70.04	70.24	69.86	69.65	70.00	69.96
16	1	59.42	59.73	60.00	60.14	59.18	59.69
	4	62.58	63.20	63.14	62.91	63.60	63.09
	8	66.42	66.98	66.63	65.42	66.54	66.40
	16	69.74	69.57	70.04	70.43	69.27	69.81
	32	72.70	72.58	73.22	72.51	72.15	72.63
32	1	63.35	63.13	62.84	63.90	63.74	63.39
	4	66.59	66.89	66.99	66.20	66.85	66.70
	8	70.15	70.34	69.82	69.77	69.76	69.97
	16	72.62	72.99	73.07	73.00	73.32	73.00
	32	75.97	75.65	76.24	75.70	75.73	75.86

Table 2. Accuracies of the

m

-CNN-

n

classifiers averaged across the 4 channels.

Table 2. Accuracies of the

m

-CNN-

n

classifiers averaged across the 4 channels.

$m$	$n$	Subjects					Subject Avg
$m$	$n$	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$	Subject Avg
1	1	70.84	67.93	70.38	69.35	69.47	69.59
	4	74.55	74.30	75.76	74.33	75.58	74.91
	8	78.47	78.45	78.42	78.73	78.49	78.51
	16	81.69	82.55	82.52	82.01	82.24	82.20
	32	84.75	85.81	84.95	84.79	84.78	85.02
4	1	75.31	74.65	75.19	75.27	75.05	75.10
	4	79.25	79.81	79.59	79.45	80.77	79.77
	8	81.71	82.56	81.81	82.54	83.19	82.36
	16	85.15	84.90	84.46	85.36	85.10	84.99
	32	88.36	87.91	88.91	88.86	87.68	88.34
8	1	78.81	78.92	78.46	78.72	78.67	78.71
	4	82.11	82.14	83.34	81.76	82.05	82.28
	8	85.96	85.33	86.73	86.45	85.55	86.00
	16	88.60	88.72	89.58	89.04	88.97	88.98
	32	91.65	91.86	91.36	91.24	91.38	91.50
16	1	81.77	81.15	82.02	83.11	81.70	81.95
	4	84.39	85.86	85.81	85.73	85.33	85.43
	8	89.04	89.34	89.41	87.92	89.01	88.94
	16	92.67	91.98	92.55	92.48	91.74	92.28
	32	95.34	94.76	94.72	94.35	94.70	94.77
32	1	85.20	85.34	86.32	85.70	86.54	85.82
	4	88.78	88.59	88.18	89.36	89.90	88.96
	8	93.21	92.30	92.83	93.39	92.59	92.87
	16	95.68	95.55	95.41	95.61	95.39	95.53
	32	98.21	98.04	97.87	96.92	97.57	97.72

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Analyses of Subsample Averaging of Single Trials for Event-Related Potential Classification

Abstract

1. Introduction

1.1. Subsample Averaging

1.2. Aim of the Study

2. Methods

2.1. Single trial data

2.2. Visual Analyses of m -ERPs

2.3. SNR Analyses

2.4. Interclass separation Analyses

2.5. Selection of the Averaging Parameter

2.6. Probability Analyses

2.6.1. Number of Distinct m ERPs

2.6.2. Probability of Generating a Distinct m -ERP

2.6.3. Probability of Generating Duplicates of m -ERPs

2.6.4. Probability of Generating a Distinct m -ERP ensemble

2.7. Classification Experiments

2.7.1. 𝑚-SVM- n and m -CNN- n Classifiers

3. Results and Discussion

3.1. Discussion

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Appendix A

References

MDPI Initiatives

Important Links

Subscribe

2.2. Visual Analyses of $m$ -ERPs

2.6.1. Number of Distinct $m$ ERPs

2.6.2. Probability of Generating a Distinct $m$ -ERP

2.6.3. Probability of Generating Duplicates of $m$ -ERPs

2.6.4. Probability of Generating a Distinct $m$ -ERP ensemble

2.7.1. 𝑚-SVM- $n$ and $m$ -CNN- $n$ Classifiers