Submitted:
18 July 2023
Posted:
19 July 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Background
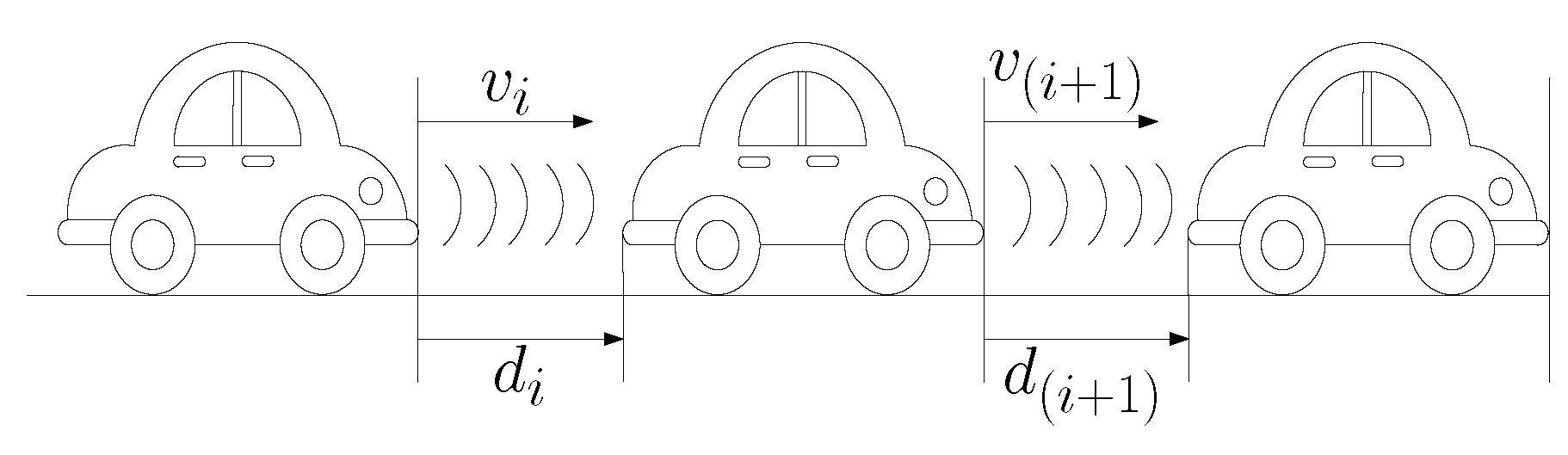
2.1. Cooperative Cruise Control
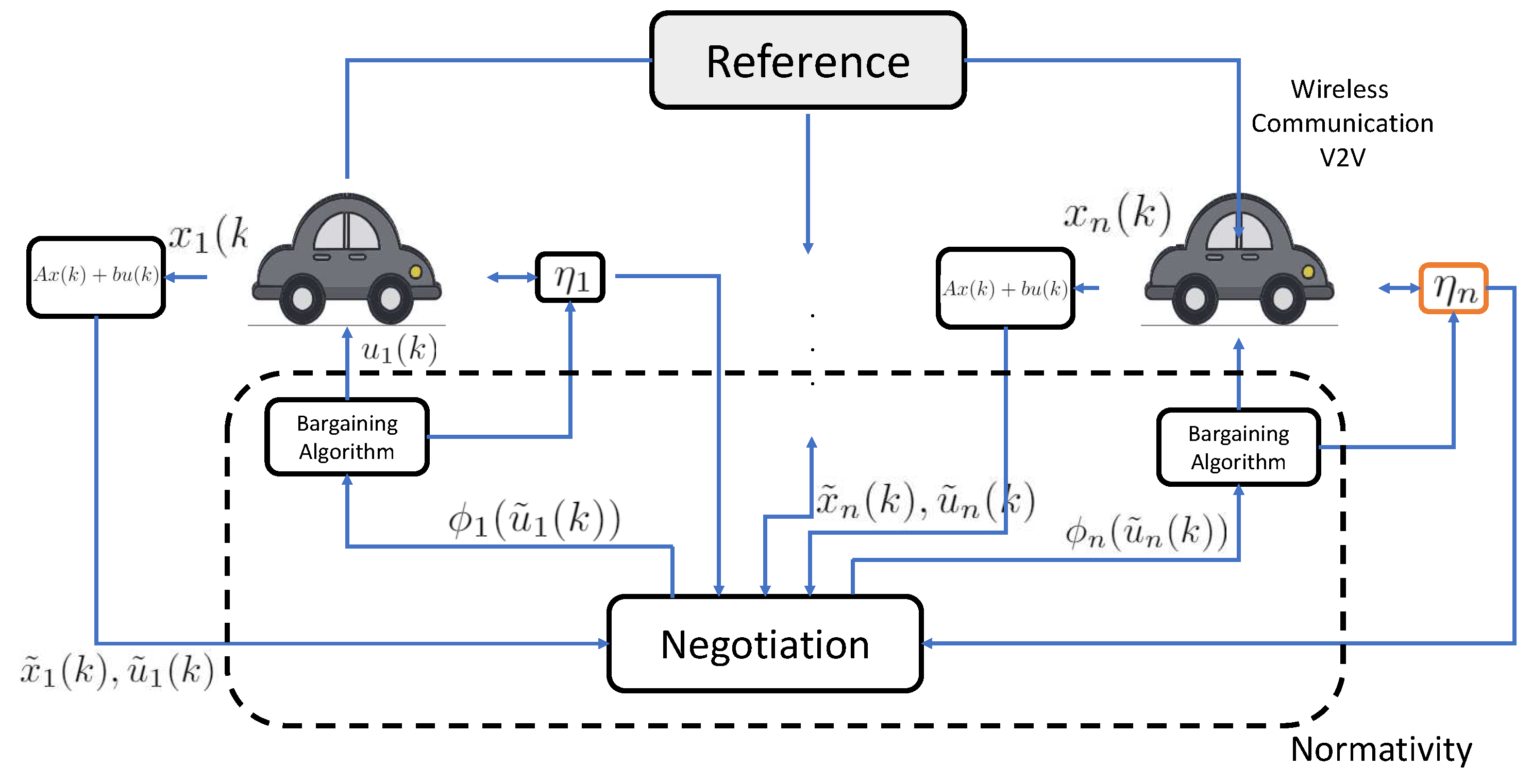
2.2. Distributed Model Predictive Control with Bargaining Games
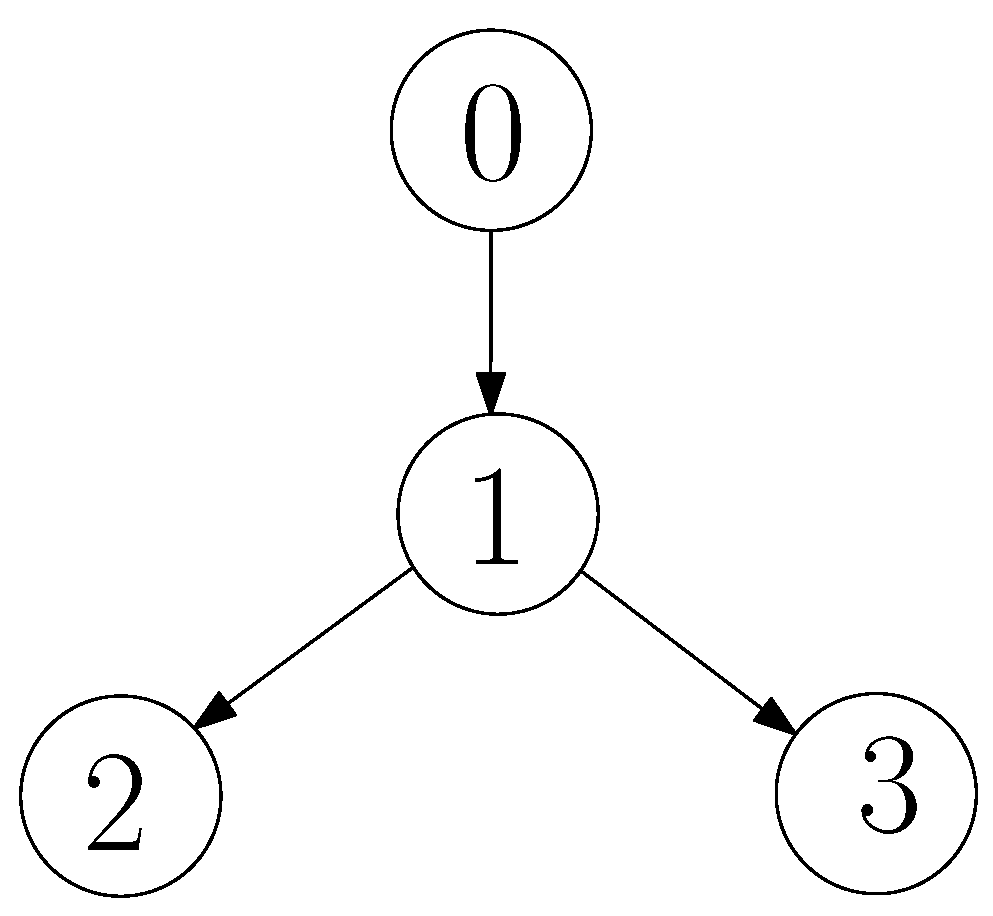
3. Cooperative Cruise Control as a Bargaining Game
| Algorithm 1:Distributed bargaining algorithm |
 |
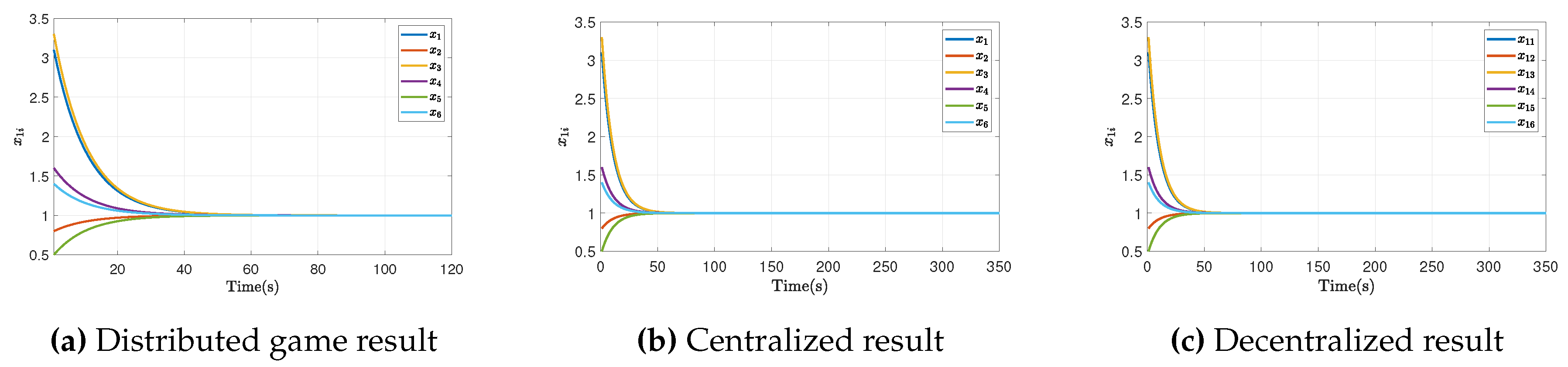
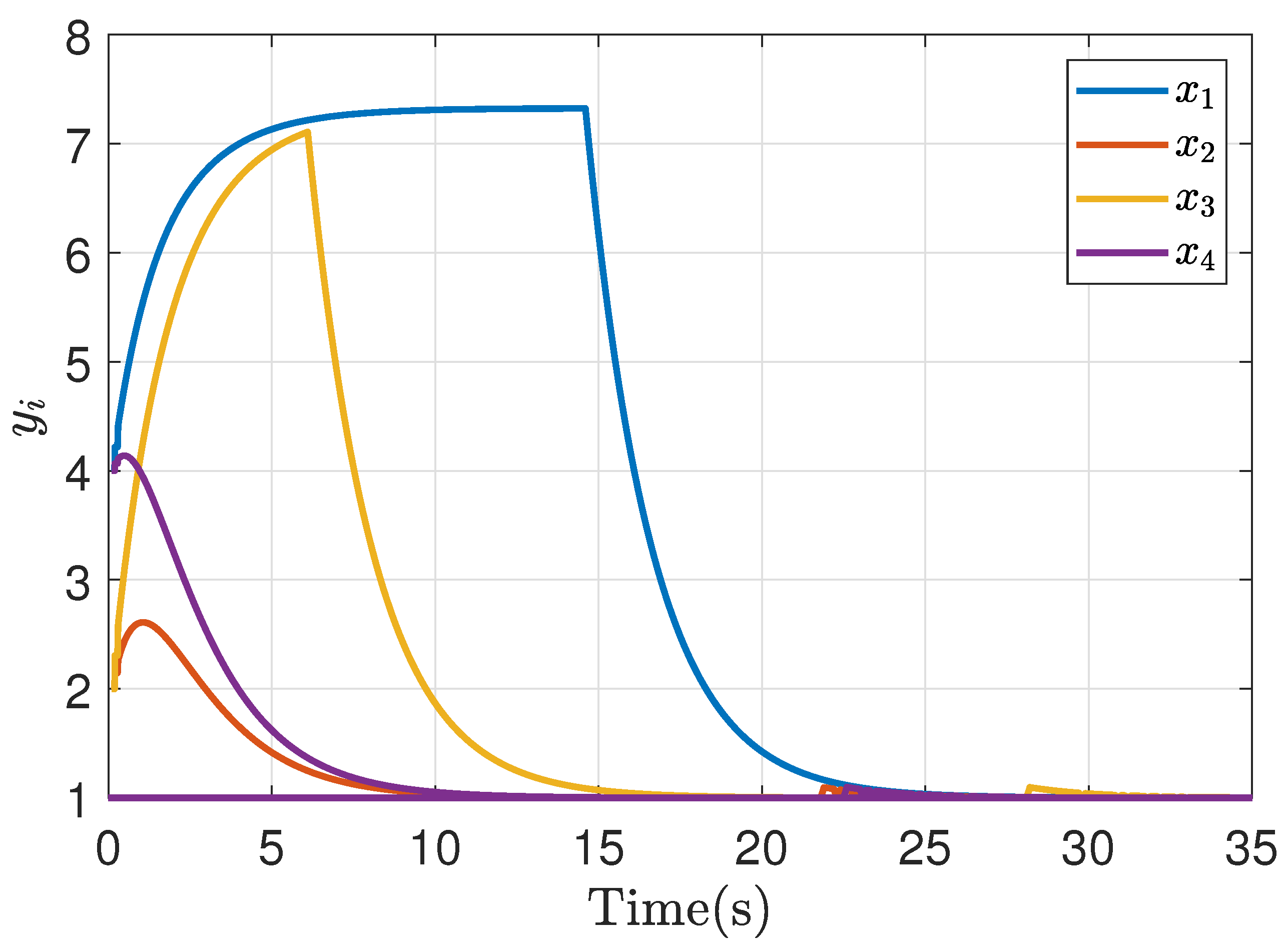
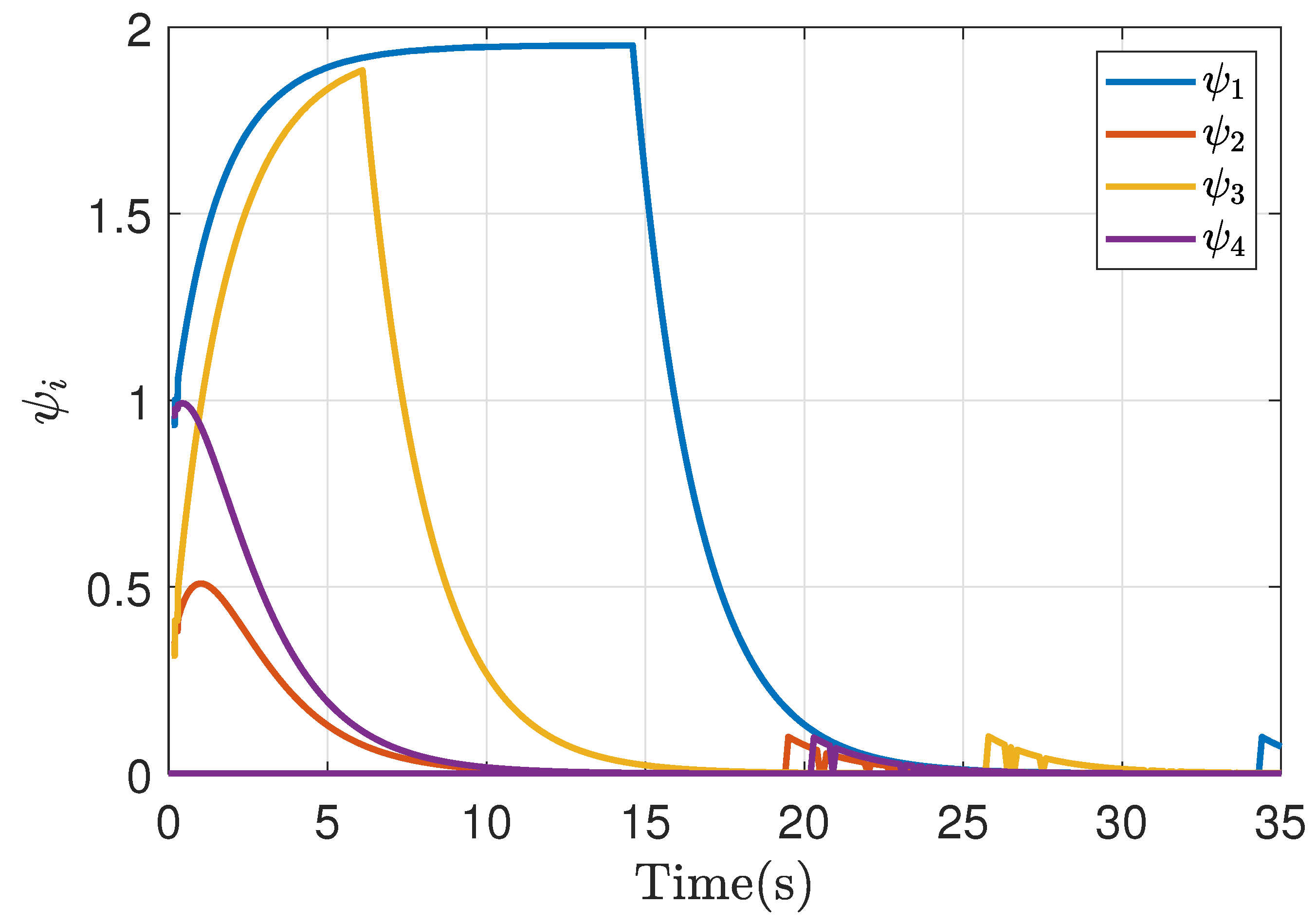
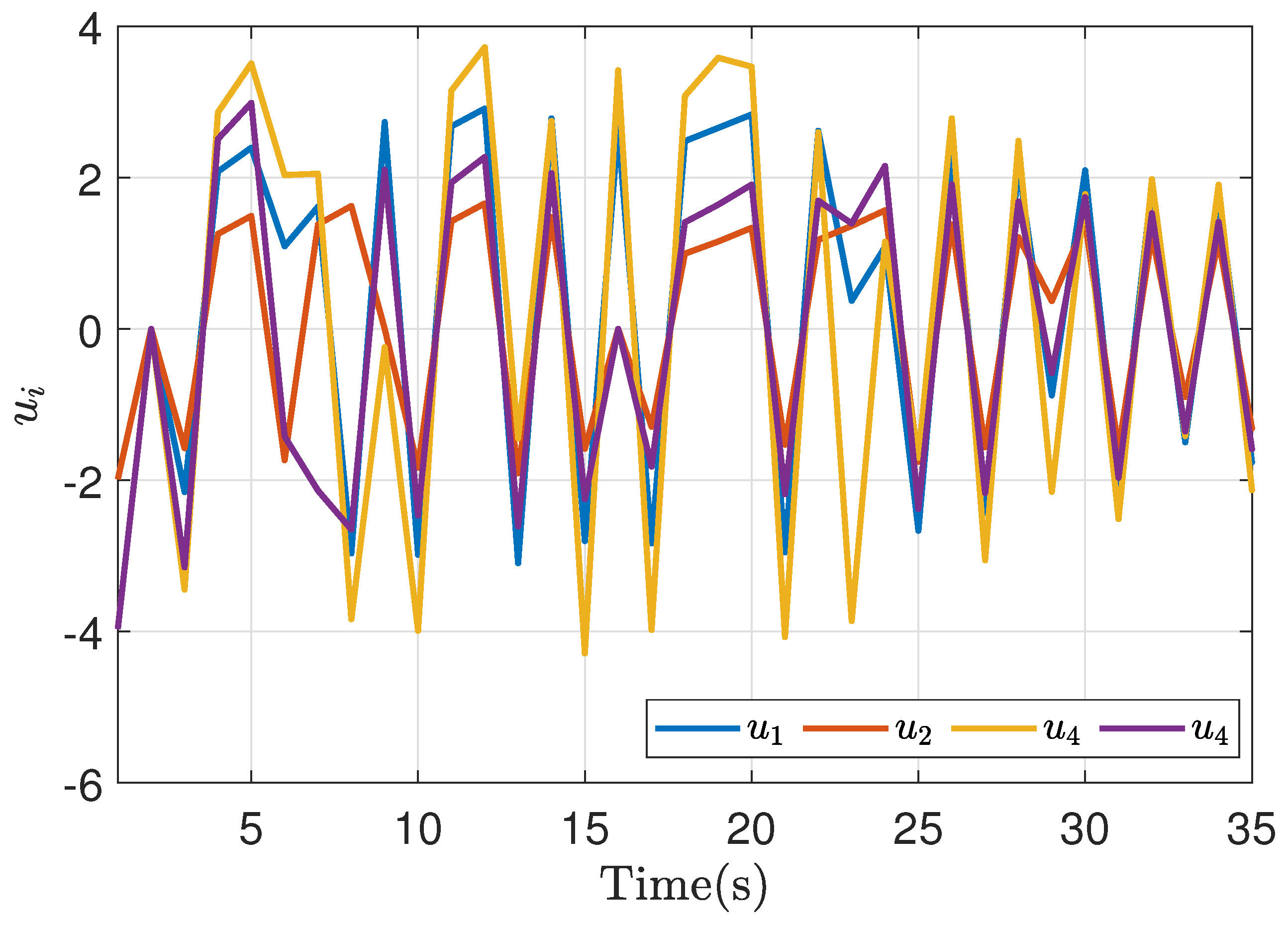
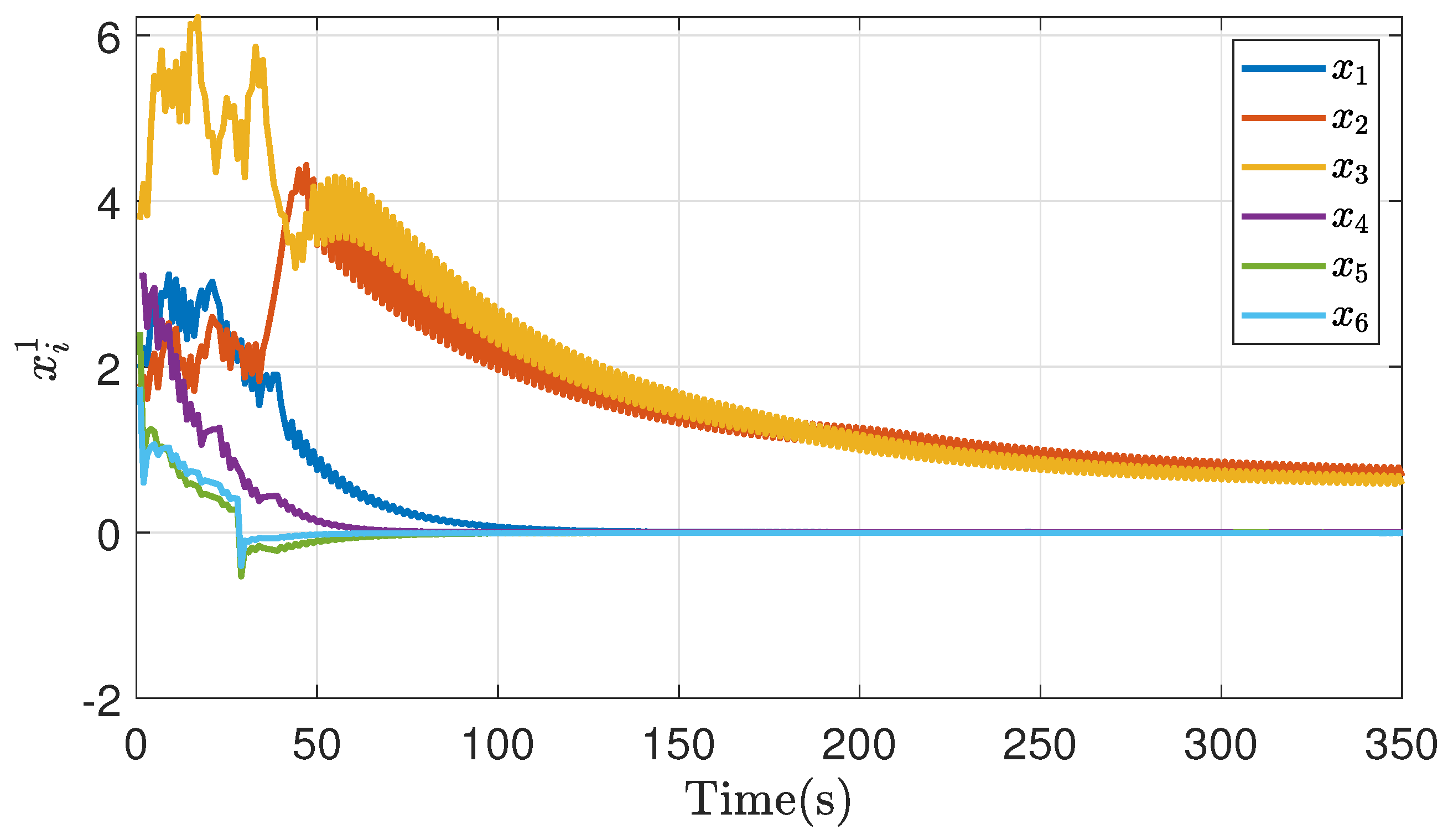
4. Simulation Results
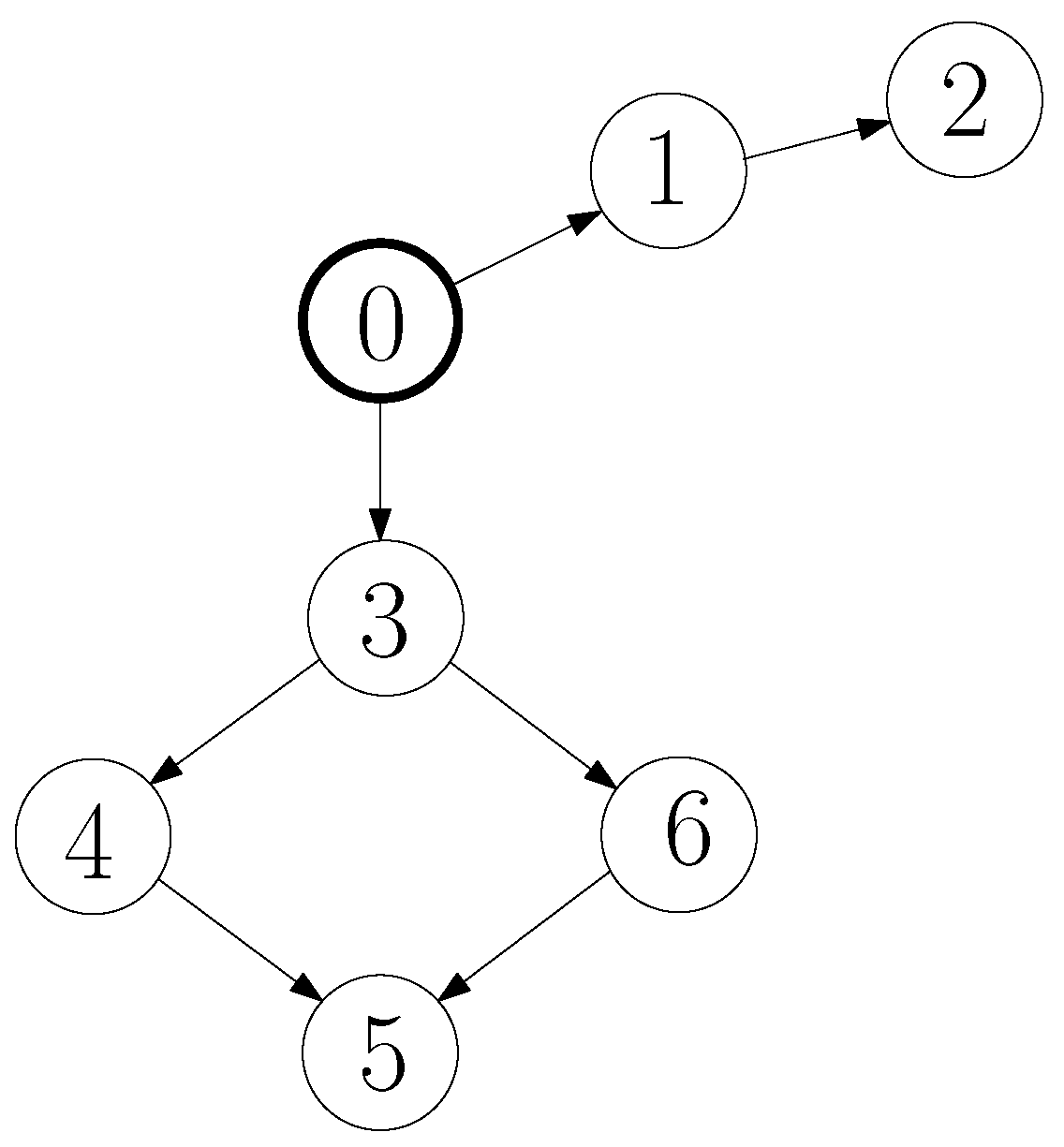
4.1. Symmetric Game
4.2. Non-Symmetric Game
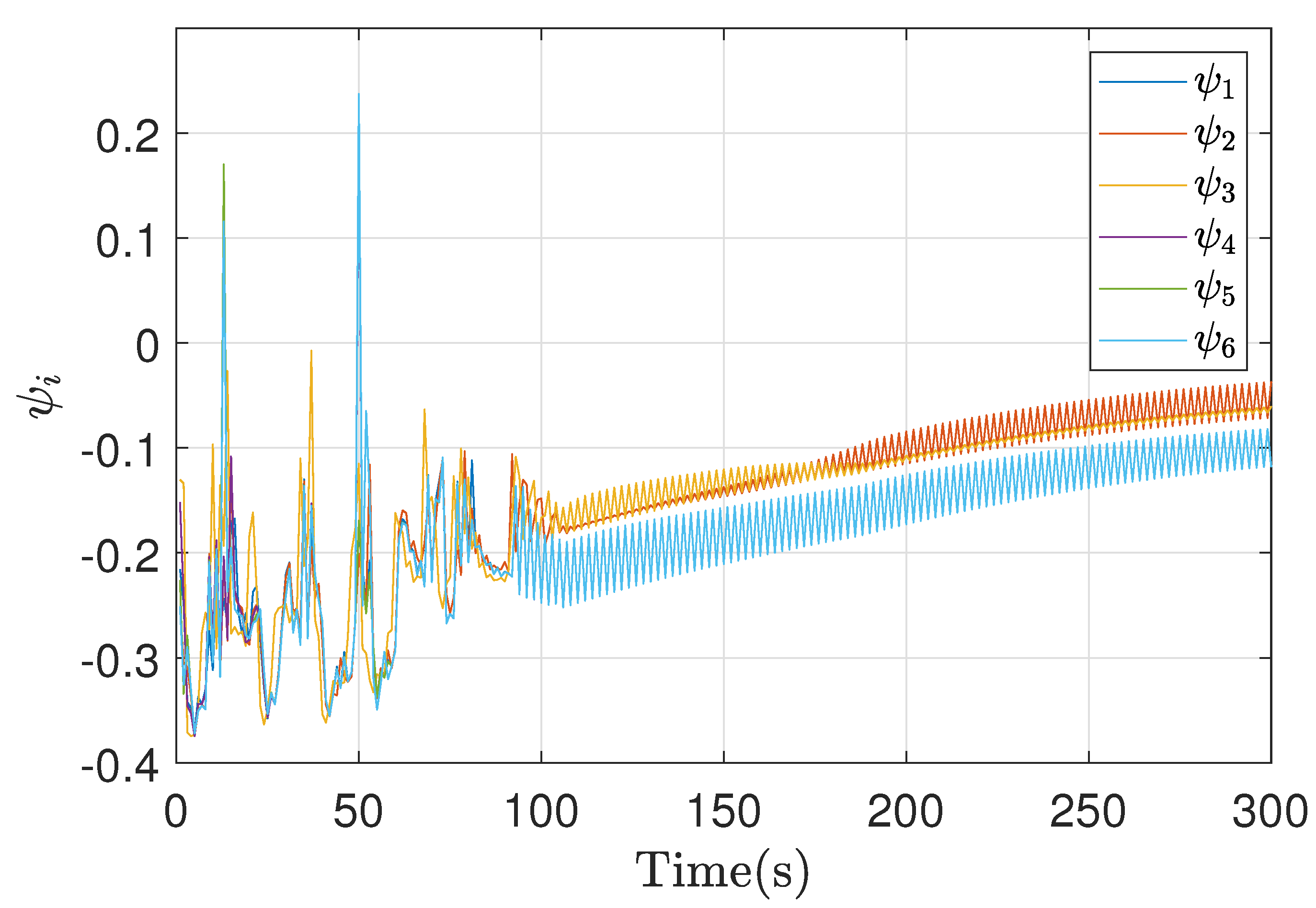
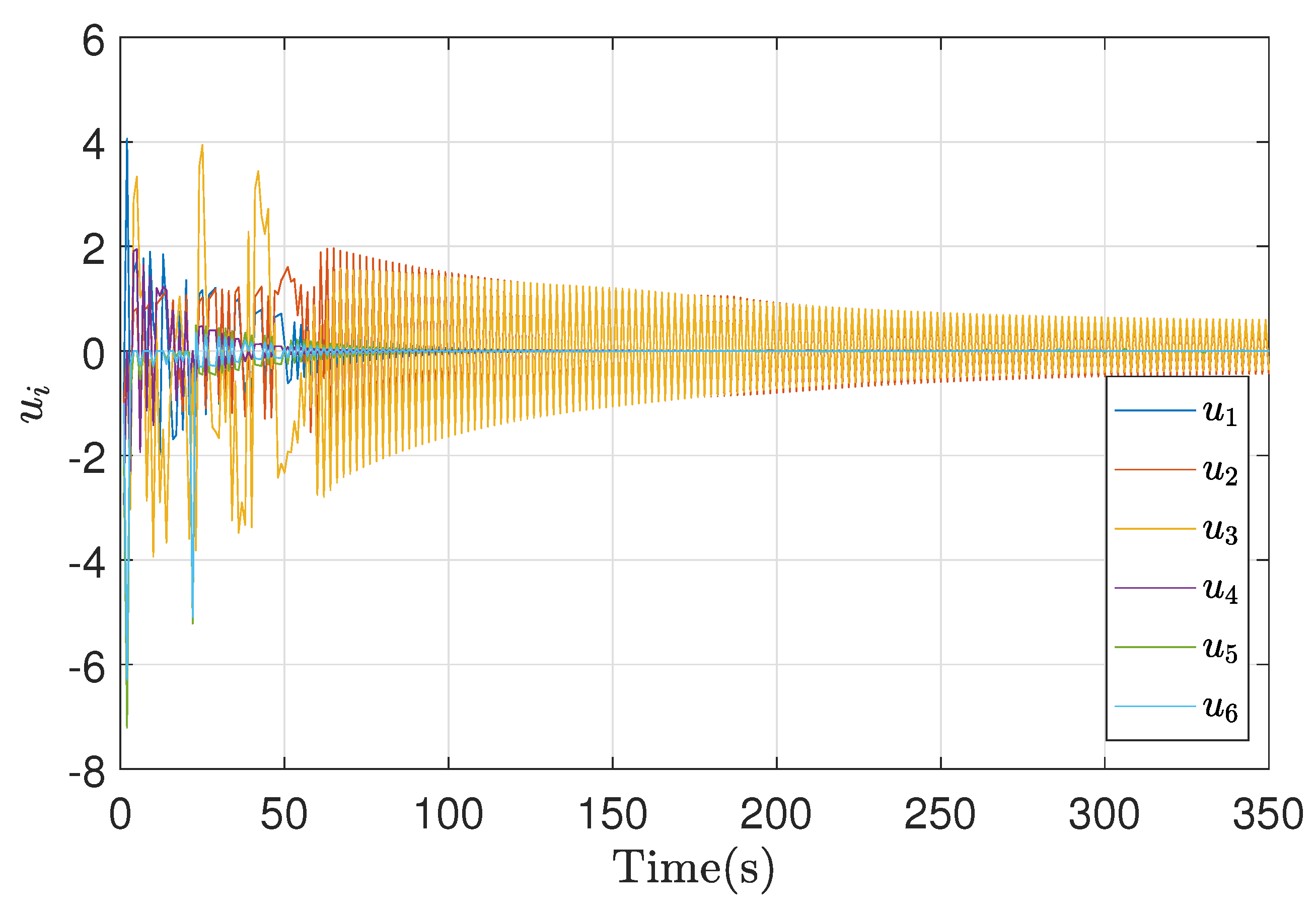
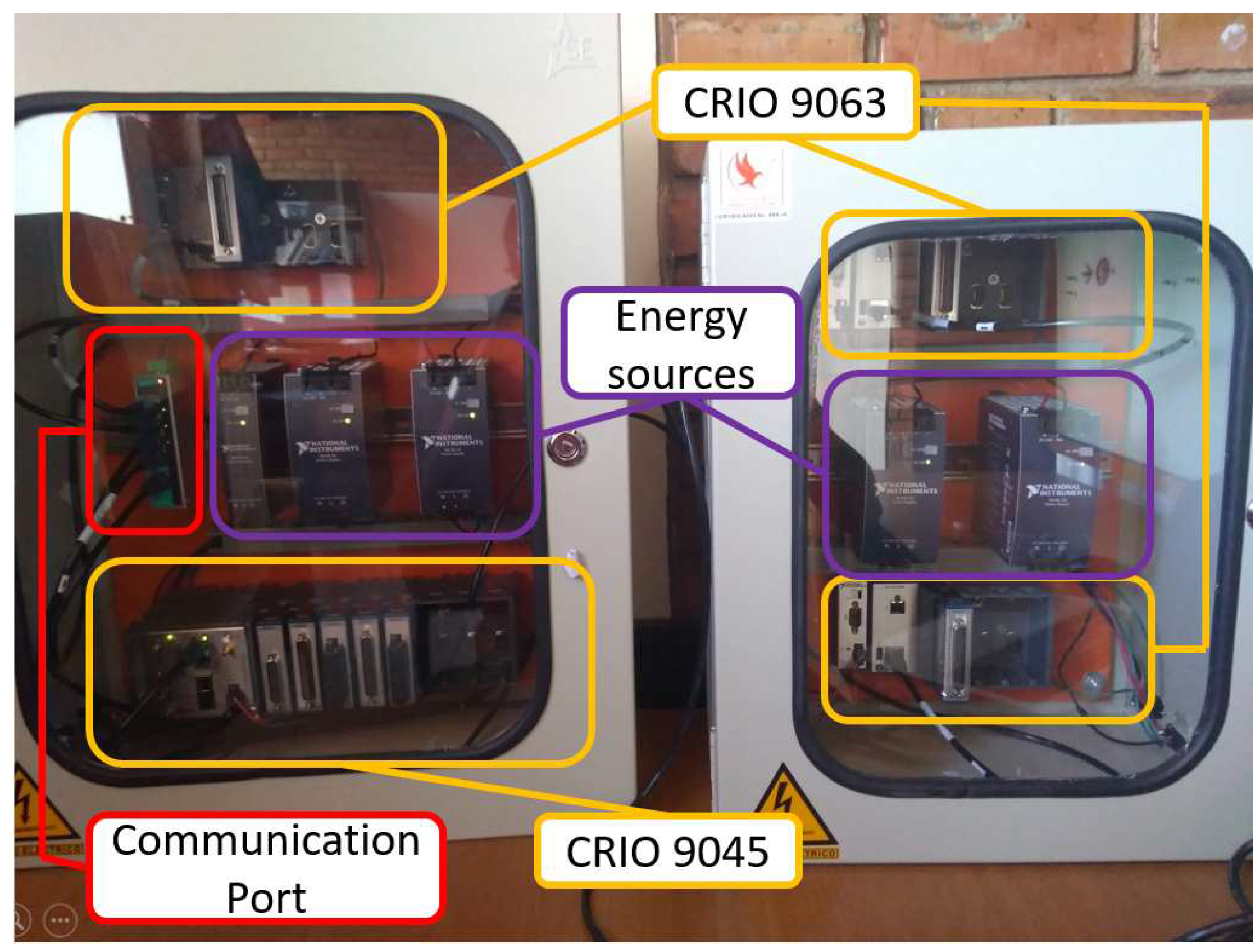
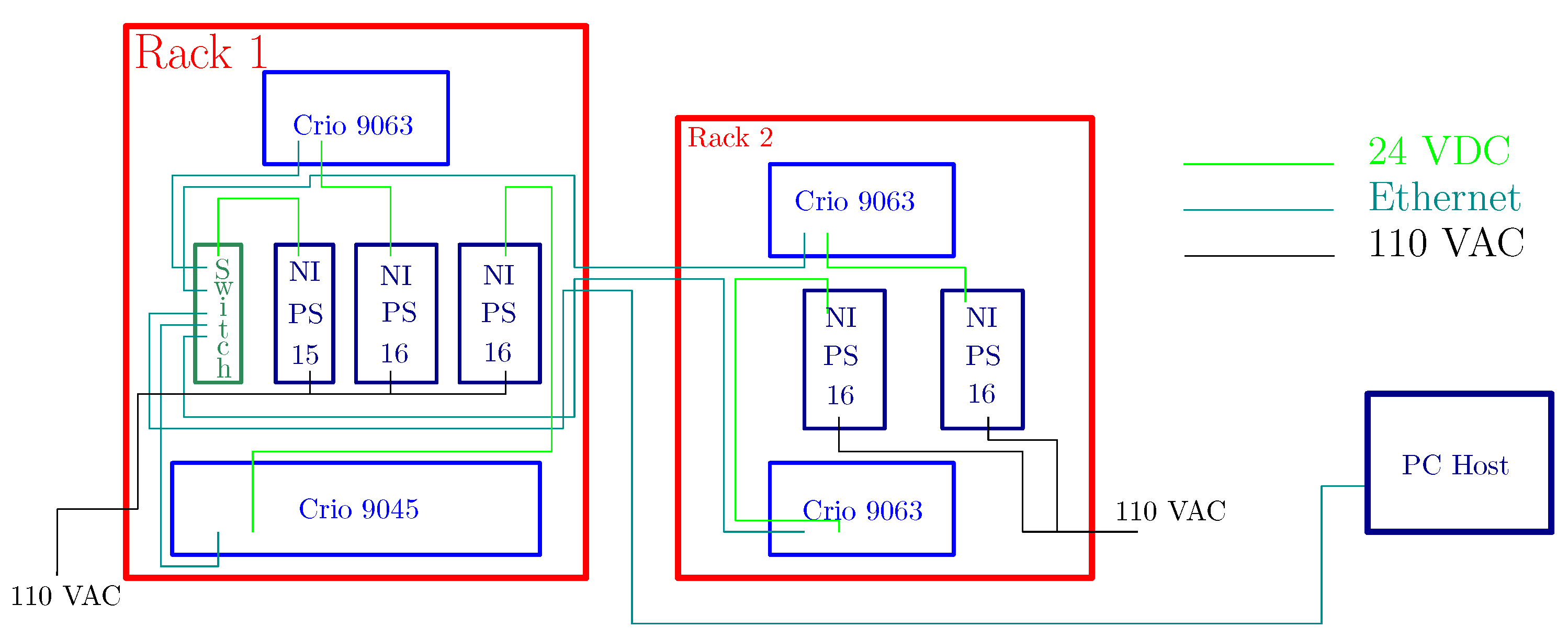
5. Implementation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CAV | Connected and Autonomous Vehicle |
| CCAC | Cooperative Cruise Adaptive Control |
| DMPC | Distributed Model Predictive Control |
| HIL | Hardware-in-the-Loop |
| ITS | Intelligent Transportation Systems |
| MPC | Model Predictive Control |
| V2V | Vehicle to Vehicle |
References
- Ballinger, B.; Stringer, M.; Schmeda-Lopez, D.R.; Kefford, B.; Parkinson, B.; Greig, C.; Smart, S. The vulnerability of electric vehicle deployment to critical mineral supply. Applied Energy 2019, 255, 113844. [Google Scholar] [CrossRef]
- Jia, D.; Lu, K.; Wang, J.; Zhang, X.; Shen, X. A Survey on Platoon-Based Vehicular Cyber-Physical Systems. IEEE Communications Surveys Tutorials 2016, 18, 263–284. [Google Scholar] [CrossRef]
- van Arem, B.; van Driel, C.J.G.; Visser, R. The Impact of Cooperative Adaptive Cruise Control on Traffic Flow Characteristics. IEEE Transactions on Intelligent Transportation Systems 2006, 7, 429–436. [Google Scholar] [CrossRef]
- Lee, J.; Park, B.B.; Malakorn, K.; So, J.J. Sustainability assessments of cooperative vehicle intersection control at an urban corridor. Transportation Research Part C: Emerging Technologies 2013, 32, 193–206. [Google Scholar] [CrossRef]
- Kovačić, M.; Mutavdžija, M.; Buntak, K. New Paradigm of Sustainable Urban Mobility: Electric and Autonomous Vehicles: A Review and Bibliometric Analysis. Sustainability 2022, 14. [Google Scholar] [CrossRef]
- Kaffash, S.; Nguyen, A.T.; Zhu, J. Big data algorithms and applications in intelligent transportation system: A review and bibliometric analysis. International Journal of Production Economics 2021, 231, 107868. [Google Scholar] [CrossRef]
- Eskandarian, A.; Wu, C.; Sun, C. Research Advances and Challenges of Autonomous and Connected Ground Vehicles. IEEE Transactions on Intelligent Transportation Systems 2021, 22, 683–711. [Google Scholar] [CrossRef]
- Mcdonald, A.; McGehee, D.; Chrysler, S.; Angell, L.; Askelson, N.; Seppelt, B. National Survey Identifying Gaps in Consumer Knowledge of Advanced Vehicle Safety Systems. Transportation Research Record Journal of the Transportation Research Board 2016, 2559. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z. Cooperative control of multi-agent systems: a consensus region approach; CRC Press, 2017.
- Shladover, S.E.; Su, D.; Lu, X.Y. Impacts of cooperative adaptive cruise control on freeway traffic flow. Transportation Research Record 2012, 2324, 63–70. [Google Scholar] [CrossRef]
- Zohdy, I.H.; Rakha, H.A. Intersection management via vehicle connectivity: The intersection cooperative adaptive cruise control system concept. Journal of Intelligent Transportation Systems 2016, 20, 17–32. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zhu, H. Theory and Experiment of Cooperative Control at Multi-Intersections in Intelligent Connected Vehicle Environment: Review and Perspectives. Sustainability 2022, 14. [Google Scholar] [CrossRef]
- Yang, H.; Rakha, H.; Ala, M.V. Eco-cooperative adaptive cruise control at signalized intersections considering queue effects. IEEE Transactions on Intelligent Transportation Systems 2016, 18, 1575–1585. [Google Scholar] [CrossRef]
- Farina, M.; Scattolini, R. Distributed predictive control: A non-cooperative algorithm with neighbor-to-neighbor communication for linear systems. Automatica 2012, 48, 1088–1096. [Google Scholar] [CrossRef]
- Trodden, P.A.; Maestre, J.M. Distributed predictive control with minimization of mutual disturbances. Automatica 2017, 77, 31–43. [Google Scholar] [CrossRef]
- Grammatico, S. Proximal Dynamics in Multiagent Network Games. IEEE Transactions on Control of Network Systems 2018, 5, 1707–1716. [Google Scholar] [CrossRef]
- Valencia, F.; López, J.D.; Patino, J.A.; Espinosa, J.J. Bargaining game based distributed MPC. In Distributed Model Predictive Control Made Easy; Springer, 2014; pp. 41–56.
- Oszczypała, M.; Ziółkowski, J.; Małachowski, J.; Lęgas, A. Nash Equilibrium and Stackelberg Approach for Traffic Flow Optimization in Road Transportation Networks—A Case Study of Warsaw. Applied Sciences 2023, 13, 3085. [Google Scholar] [CrossRef]
- Dixit, V.V.; Denant-Boemont, L. Is equilibrium in transport pure Nash, mixed or Stochastic? Transportation Research Part C: Emerging Technologies 2014, 48, 301–310. [Google Scholar] [CrossRef]
- Chu, H.; Guo, L.; Gao, B.; Chen, H.; Bian, N.; Zhou, J. Predictive cruise control using high-definition map and real vehicle implementation. IEEE Transactions on Vehicular Technology 2018, 67, 11377–11389. [Google Scholar] [CrossRef]
- Lin, Y.; Wu, C.; Eskandarian, A. Integrating odometry and inter-vehicular communication for adaptive cruise control with target detection loss. In Proceedings of the 2018 IEEE Intelligent Vehicles Symposium (IV). IEEE; 2018; pp. 1848–1853. [Google Scholar] [CrossRef]
- Rayamajhi, A.; Biron, Z.A.; Merco, R.; Pisu, P.; Westall, J.M.; Martin, J. The impact of dedicated short range communication on cooperative adaptive cruise control. In Proceedings of the 2018 IEEE International Conference on Communications (ICC). IEEE; 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Isermann, R.; Schaffnit, J.; Sinsel, S. Hardware-in-the-loop simulation for the design and testing of engine-control systems. Control Engineering Practice 1999, 7, 643–653. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Shen, W. Lithium-ion battery pack state of charge and state of energy estimation algorithms using a hardware-in-the-loop validation. IEEE Transactions on Power Electronics 2016, 32, 4421–4431. [Google Scholar] [CrossRef]
- Maniatopoulos, M.; Lagos, D.; Kotsampopoulos, P.; Hatziargyriou, N. Combined control and power hardware in-the-loop simulation for testing smart grid control algorithms. IET Generation, Transmission & Distribution 2017, 11, 3009–3018. [Google Scholar]
- Wei, W.; Wu, Q.; Wu, J.; Du, B.; Shen, J.; Li, T. Multi-agent deep reinforcement learning for traffic signal control with Nash Equilibrium. In Proceedings of the 2021 IEEE 23rd Int Conf on High Performance Computing &, Cloud & Big Data Systems & Application (HPCC/DSS/SmartCity/DependSys). IEEE, 2021, Communications; 7th Int Conf on Data Science & Systems; 19th Int Conf on Smart City; 7th Int Conf on Dependability in Sensor; pp. 1435–1442.
- Valencia, F.; Patiño, J.; López, J.D.; Espinosa, J. Game Theory Based Distributed Model Predictive Control for a Hydro-Power Valley Control. IFAC Proceedings Volumes 2013, 46, 538–544. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Guillo-Sansano, E.; Syed, M.H.; Nguyen, V.H.; Blair, S.M.; Reguera, L.; Tran, Q.T.; Caire, R.; Burt, G.M.; Gavriluta, C.; et al. Multi-agent system with plug and play feature for distributed secondary control in microgrid—Controller and power hardware-in-the-loop Implementation. Energies 2018, 11, 3253. [Google Scholar] [CrossRef]
- Filho, C.M.; Wolf, D.F.; Grassi, V.; Osório, F.S. Longitudinal and lateral control for autonomous ground vehicles. In Proceedings of the 2014 IEEE Intelligent Vehicles Symposium Proceedings; 2014; pp. 588–593. [Google Scholar] [CrossRef]
- Baldi, S.; Frasca, P. Adaptive synchronization of unknown heterogeneous agents: An adaptive virtual model reference approach. Journal of the Franklin Institute 2019, 356, 935–955. [Google Scholar] [CrossRef]
- Nash Jr, J.F. The Bargaining Problem. Econometrica 1950, 18, 155–162. [Google Scholar] [CrossRef]
- Peters, H. Axiomatic bargaining game theory. In Proceedings of the Theory and decision library C; 1992. [Google Scholar]
- Nash, J.F. Equilibrium points in n-person games. Proceedings of the National Academy of Sciences 1950, 36, 48–49. [Google Scholar] [CrossRef]
- Peters, H.; Van Damme, E. Characterizing the Nash and Raiffa bargaining solutions by disagreement point axioms. Mathematics of Operations Research 1991, 16, 447–461. [Google Scholar] [CrossRef]
- Börgers, T.; Sarin, R. Learning through reinforcement and replicator dynamics. Journal of Economic Theory 1997, 77, 1–14. [Google Scholar] [CrossRef]
- Zou, Y.; Su, X.; Li, S.; Niu, Y.; Li, D. Event-triggered distributed predictive control for asynchronous coordination of multi-agent systems. Automatica 2019, 99, 92–98. [Google Scholar] [CrossRef]
- Zoccali, P.; Loprencipe, G.; Lupascu, R.C. Acceleration measurements inside vehicles: passengers’ comfort mapping on railways. Measurement 2018, 129, 489–498. [Google Scholar] [CrossRef]
- Baldi, S.; Rosa, M.R.; Frasca, P.; Kosmatopoulos, E.B. Platooning merging maneuvers in the presence of parametric uncertainty. IFAC-PapersOnLine 2018, 51, 148–153. [Google Scholar] [CrossRef]
- Arevalo-Castiblanco, M.F.; Tellez-Castro, D.; Sofrony, J.; Mojica-Nava, E. Adaptive synchronization of heterogeneous multi-agent systems: A free observer approach. Systems & Control Letters 2020, 146, 104804. [Google Scholar] [CrossRef]
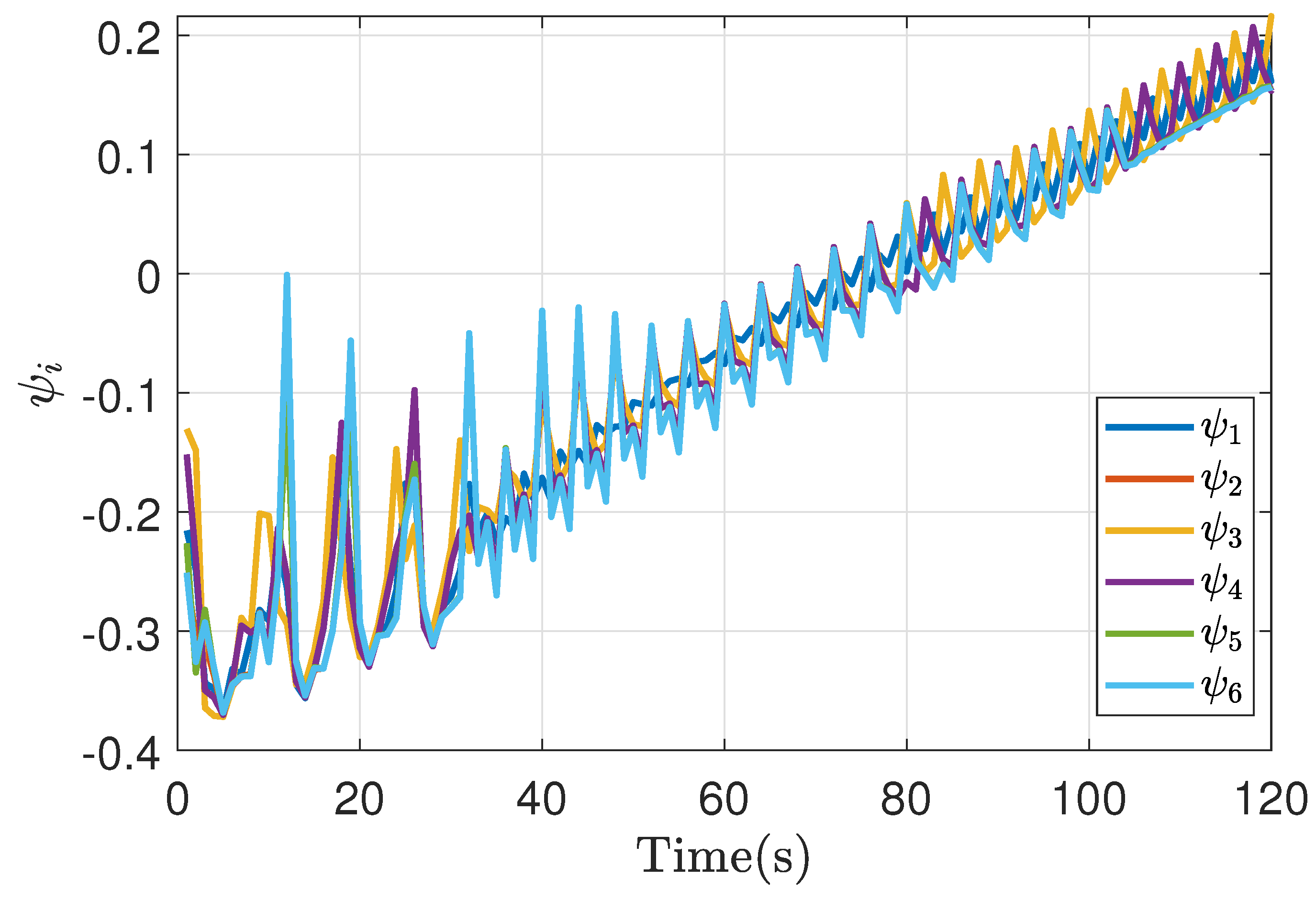
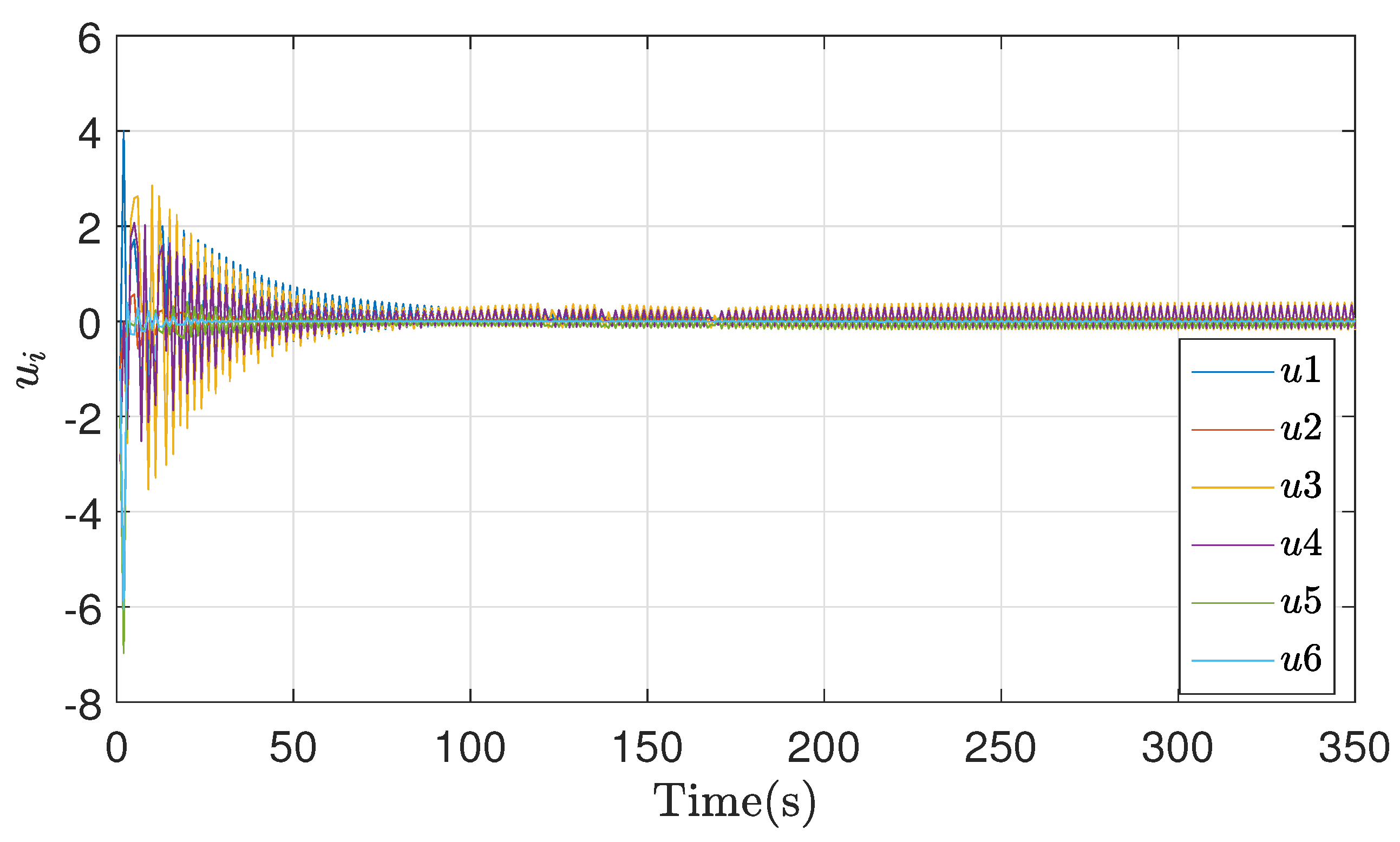
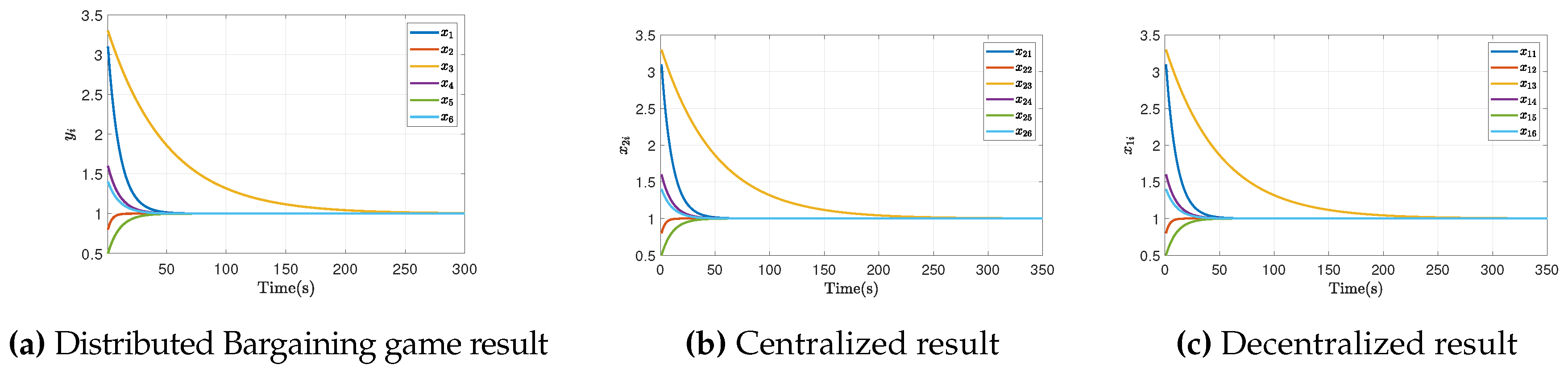
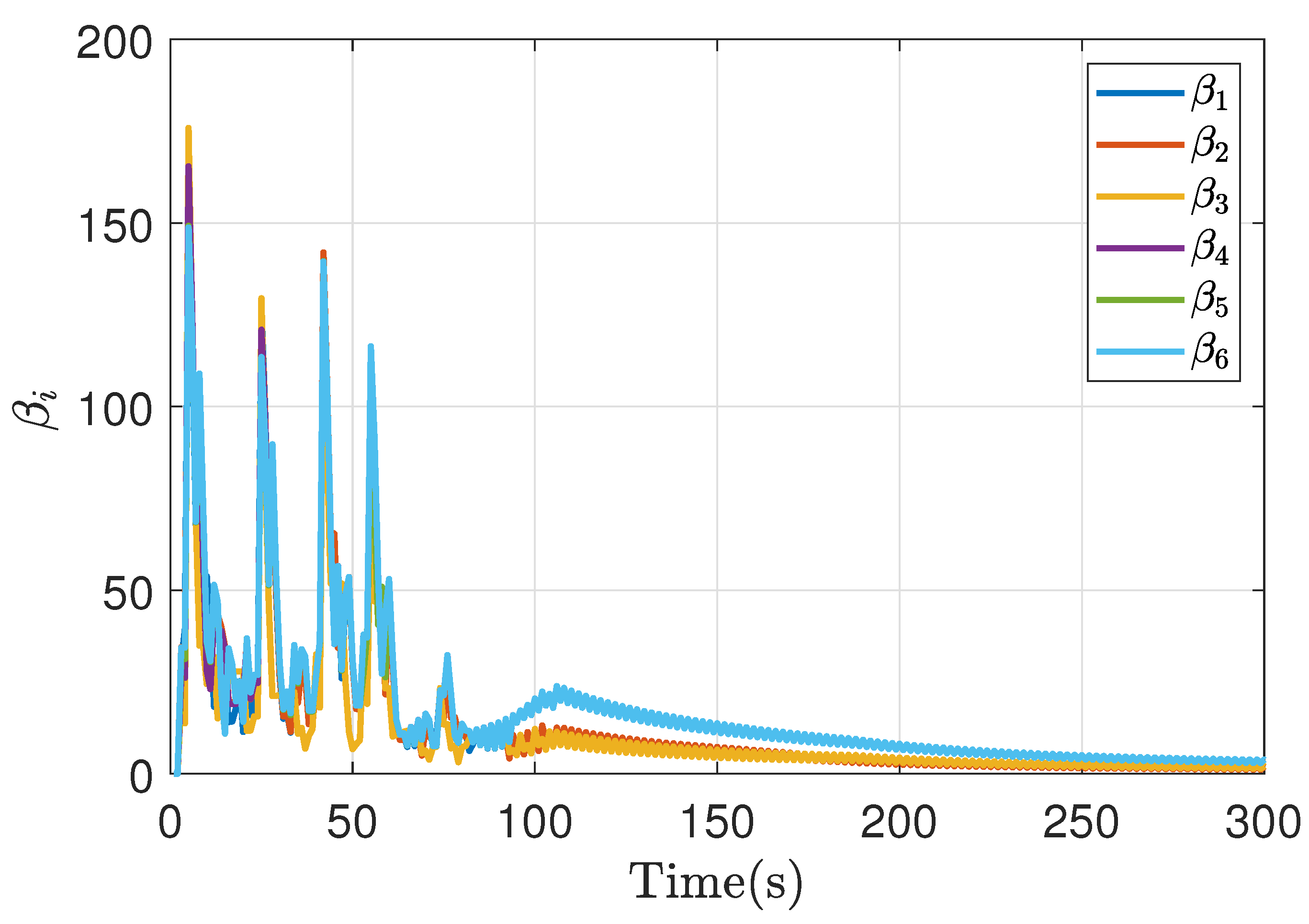
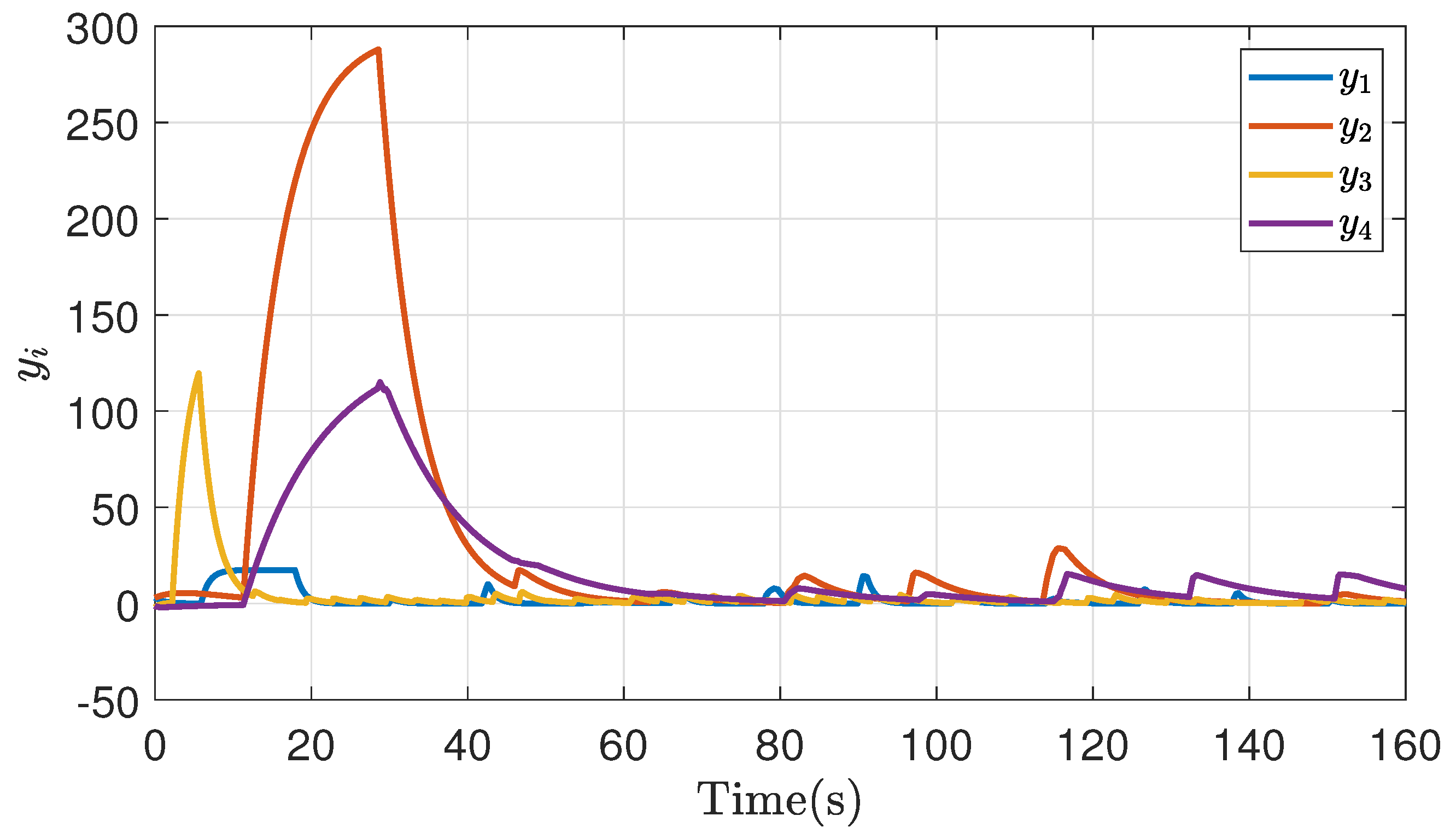
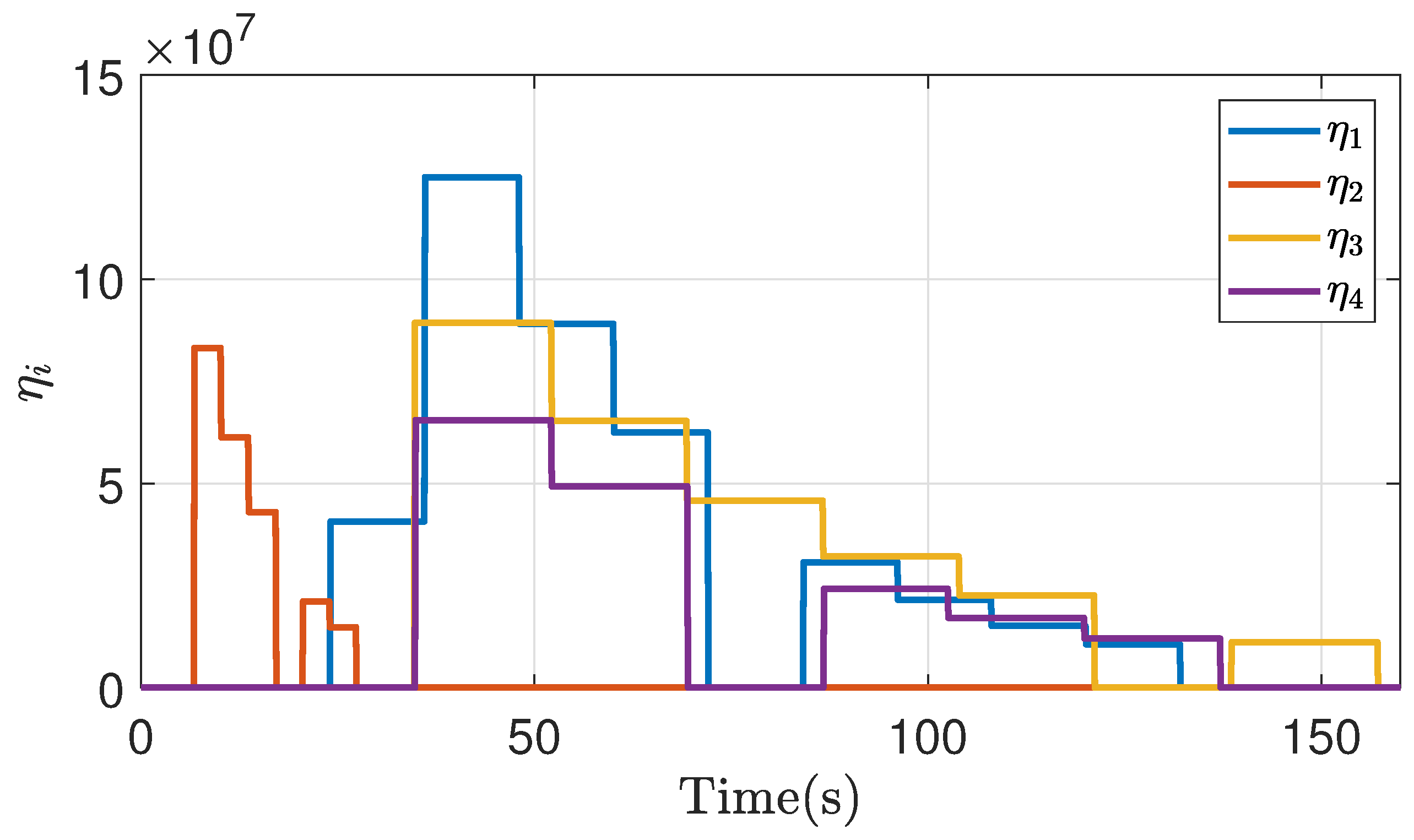
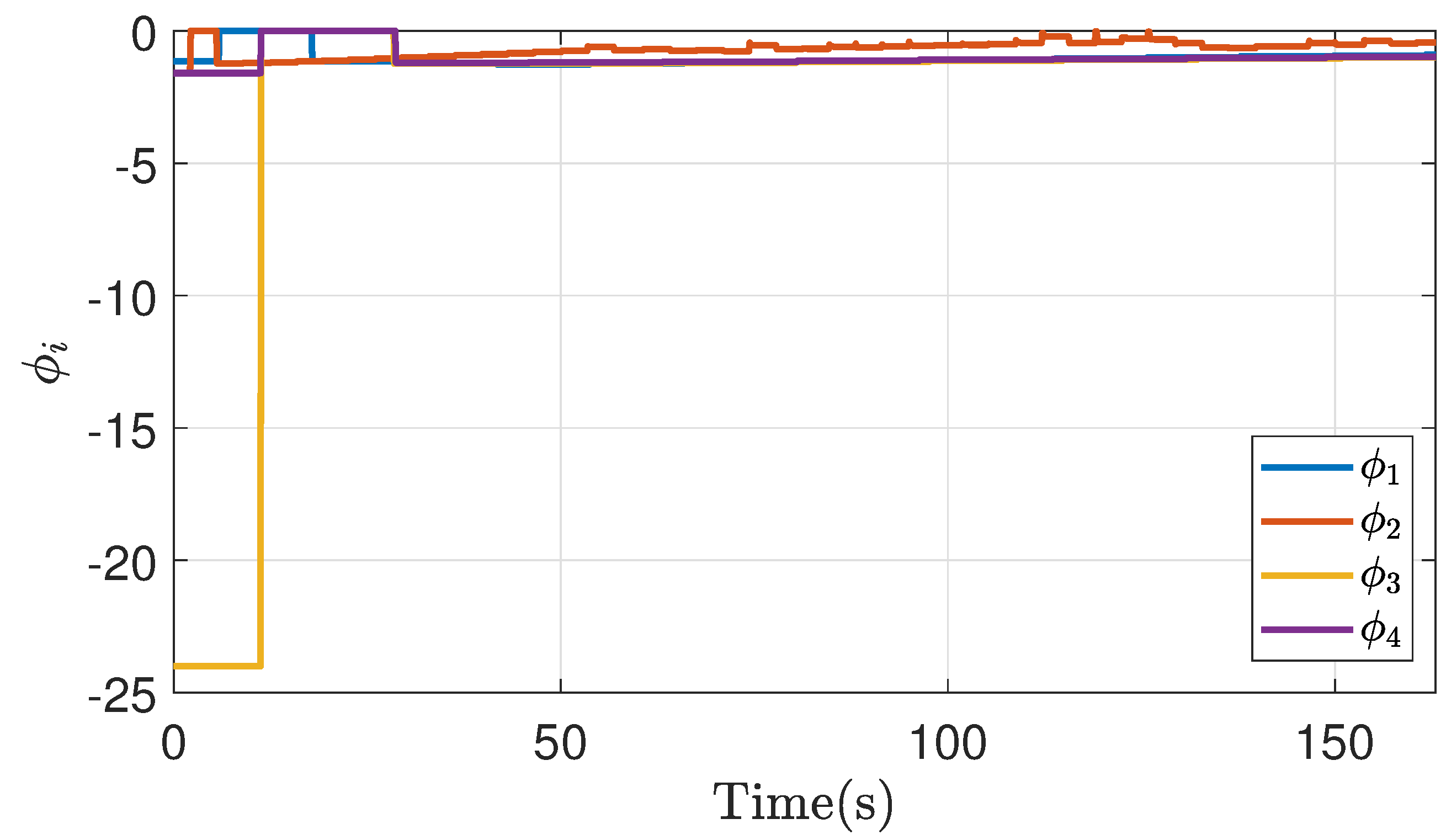
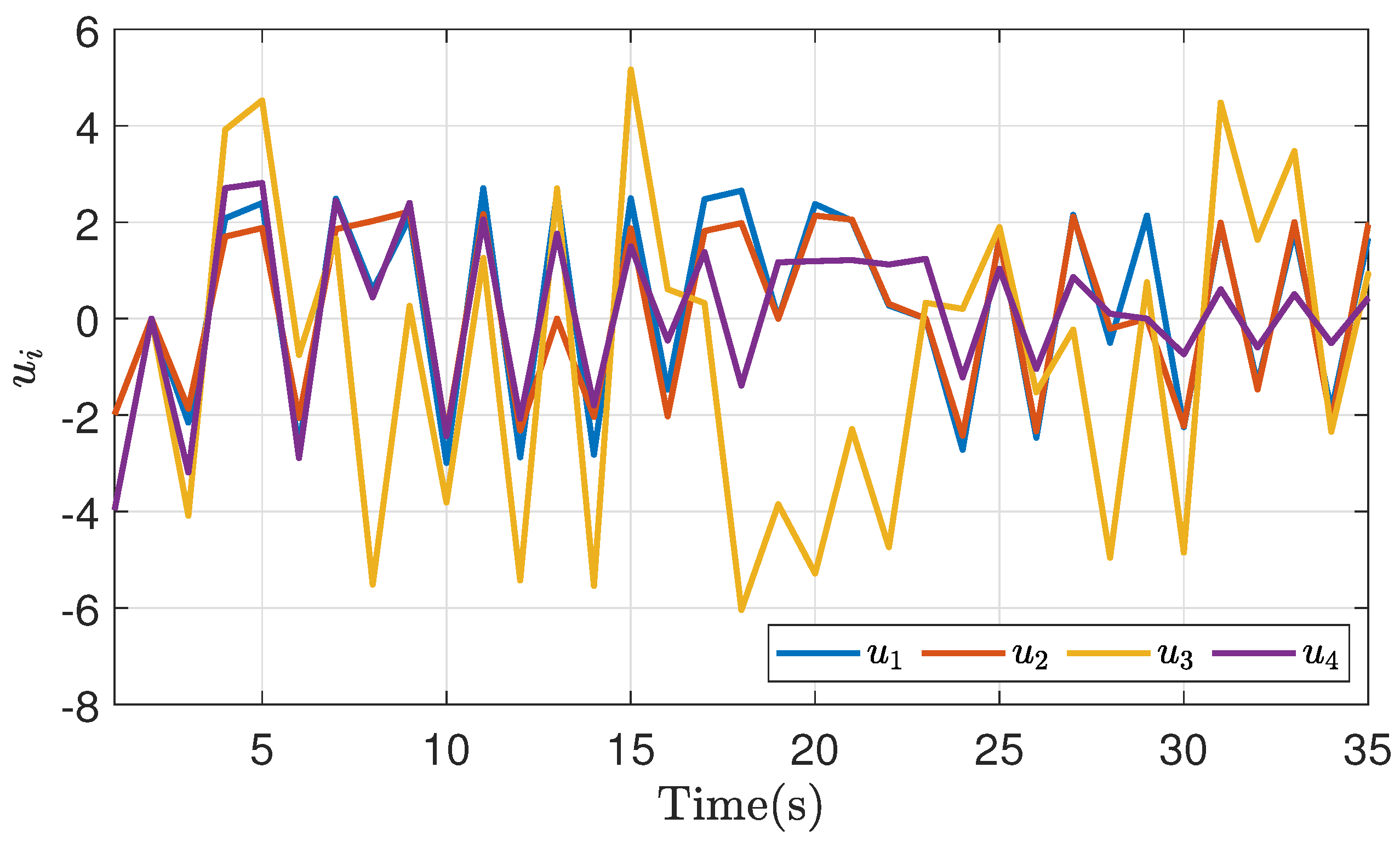
| -0.25 | -0.5 | 1 | ||
| -1.25 | 1 | 0.5 | ||
| -0.5 | 2.5 | 0.75 | ||
| -0.75 | 2 | 1.5 | ||
| -1.5 | 2.5 | 1 | ||
| -1 | 2 | 1 | ||
| -0.75 | 1 | 0.5 |
| -0.25 | -0.5 | 1 | ||
| -1.25 | 1 | 0.5 | ||
| -0.5 | 2.5 | 0.75 | ||
| -0.75 | 2 | 1.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





