Prerpints.org logo
Preprint
Article

Deflection of Null and Time-like Geodesics in Topological Defects Space-time Geometry

This version is not peer-reviewed.

Submitted:

19 July 2023

Posted:

20 July 2023

Read the latest preprint version here

Abstract
In this work, we study the deflection of photon light and/or time-like geodesics in the background of the topological defects in four-dimensional space-time geometry. These topological defects geometries are cosmic string space-time with screw dislocation, spiral dislocation, and spacelike dislocation. We derive the deflection of light-like and time-like geodesics and show the effects of cosmic string parameter, screw dislocation parameter, and spacelike dislocation parameter on them. Our derivation technique is based on the fact that the photon rays (light-like) and/or time-like geodesics is along the path parallel to the z-axis with constant radius of the cylinder.
Keywords: 
Subject: 
Physical Sciences  -   Theoretical Physics

1. Introduction

The general relativity is a theory connecting the space-time geometry with matter-energy within it. The presence of matter-energy causes the space-time to be curved and this curved geometry determines the motion of a test body (or light-like geodesics) [1,2,3,4,5,6]. General relativity has been developed into an essential tool in modern astrophysics. It provides the foundation for the current understanding of black holes, regions of space where the gravitational effect is strong enough that even light cannot escape. Their strong gravity is thought to be responsible for the intense radiation emitted by certain types of astronomical objects (such as active galactic nuclei or micro-quasars). This theory predicts the novel effects of gravity, such as gravitational waves, gravitational lensing and an effect of gravity on time known as gravitational time dilation. Many of these predictions have been confirmed by experiment or observation, most recently gravitational waves. The distance between two points in curved space-time is described by the line element
d s 2 = g μ ν ( x μ ) d x μ d x ν ,   ( μ , ν = 0 , 1 , 2 , 3 ) .
The shortest distance between two points is a straight line. This seemingly universally true statement is actually a consequence of the flat Euclidean geometry that describes most human scale concerns. In non-flat space, a truly ‘straight line’ will no longer be the shortest distance between two points. The more general concept that describes the shortest distance in curved space is called a geodesic and is described by
x ¨ μ + Γ α β μ x ˙ α x ˙ β = 0 ,
where dot represent derivative w. r. t. λ, proper time. In the case of flat Euclidean geometry, the Christoffel symbols are all zero which reduces the expression to the first term equaling zero which is just the equation of a straight line.
The Lagrangian of a system in relativity theory is defined by
L = 1 2 g μ ν x ˙ μ x ˙ ν
For geodesics motion,
g μ ν x ˙ μ x ˙ ν = ε ,
Where ε = 0 (light-like geodesics), -1 (time-like geodesics) and +1 (spacelike geodesics) in the metric signature − , + , + , +   o r + 2 .
Deflection of light in a curved space-time background is the phenomenon that predicted by the general relativity theory, which states that the path of light can be curved or deflected by the presence of massive objects in its vicinity. This phenomenon is also called as gravitational lensing and the first experimental observation in Ref. [11] predicates the correctness of this theory. Gravitational lensing is a helpful technique to understand galaxies, dark matter, dark energy and the universe [11]. A lot of works on gravitational lensing have been investigated for black holes, wormholes, cosmic strings and other massive objects. These includes, optical properties of gravitational lens galaxies as a probe of galaxy structure and evolution [12], by a charged black hole of string theory [13], by braneworld black holes [14], in the deformed Horava-Lifshitz black hole [15], by wormholes [16], Reissner-Nordstorm black hole [17], by double stars and planetary systems [18], properties of galaxy dark matter halos from weak lensing [19], by naked singularities space-times [20,21,22,23,24], by Schwarzschild black hole [25], optical scalars in terms of energy-momentum distribution [26], expressions for optical scalars and deflection angle at second order in terms of curvature scalars [27], in non-commutative wormholes [28], effect of the Brane-Dicke coupling parameter on weak lensing by wormholes and naked singularities [29], applications of the Gauss-Bonnet theorem to gravitational lensing [30], in the Kerr-Randers optical geometry [31], bending angle of light for finite distance and the Gauss-Bonnet theorem [32], weak lensing in a plasma medium and gravitational deflection of massive particles using the Gauss-Bonnet theorem [33], light deflection by a rotating global monopole space-time [34], Hawking radiation and deflection of light from Rindler Modified Schwarzschild black hole [35], lensing by rotating wormholes[36], gravito-magnetic bending angle of light with finite-distance corrections in stationary axisymmetric space-times[37], light deflection by charged wormholes in Einstein-Maxwell-dilaton theory[38], weak lensing by phantom black holes and phantom wormholes using the Gauss-Bonnet theorem [39], effect of Lorentz symmetry breaking on the deflection of light in a cosmic string space-time [40], light deflection and Gauss-Bonnet theorem[41], light deflection by a quantum improved Kerr black hole pierced by a cosmic string [42], deflection angle of light for an observer and source at finite distance from a rotating wormhole [43], effect of the cosmological constant on the deflection angle by a rotating cosmic string [44], deflection of light by rotating regular black holes using the Gauss-Bonnet theorem [45], light deflection by Damour-Solodukhin wormholes and Gauss-Bonnet theorem [46], lensing under the effect of Weyl and bumblebee gravities [47], lensing by wormholes supported by electromagnetic, scalar, and quantum effects [48], deflection angle of photon through dark matter by black holes/wormholes using the Gauss-Bonnet theorem [49], finite distance corrections to the light deflection in a gravitational field with a plasma medium [50], weak gravitational lensing by Kerr-MOG black hole and Gauss-Bonnet theorem [51], shadow cast and deflection angle of Kerr-Newman-Kasuya space-time [52], deflection angle of light for an observer and source at finite distance from a rotating global monopole [53], weak Gravitational lensing by phantom black holes and phantom wormholes using the Gauss-Bonnet theorem [54], Exact geometric optics in a Morris-Thorne wormhole space-time [55], gravitational lens equation in spherically symmetric and static space-time [56], Bronnikov-Kim wormhole in weak-field approximation [57], the light deflection by an Ellis wormhole [58], weak gravitational lensing effect using the Gauss-Bonnet theorem (GBT) in asymptotically conical Morris-Thorne wormhole solution [59], deflection of light under the effects of topologically charged Ellis-Bronnikov-type wormhole space-time [60], in Morris-Thorne-type wormhole with cosmic string [61], deflection of light due to the gravitational field of global monopole in Eddington-inspired Born-Infeld theory using strong field approach [62], and gravitational lensing caused by a topologically charged Monopole/Wormhole, both in the weak field limit and in the strong field limit [63]. In Eddington-inspired Born-Infeld wormhole space-time with cosmic string [64], by the Ellis Wormhole [65], Wave Effect in Gravitational Lensing by the Ellis Wormhole[66], Strong deflection limit analysis and gravitational lensing of an Ellis wormhole[67], Light curves of light rays passing through a wormhole[68], and strong gravitational lensing by wormholes [69], and many more in the literature.
Topological defects are produced during phase transitions in the early universe. Several types of topological defects stated above arise in most unified particle physics models of strong, weak and electromagnetic interactions [70, 71]. Although, until now, these objects have not yet been observed in the laboratory, but studies of these defects have took place in different branches of physics and chemistry. The topological defects more known in the literature are domain walls [72,73], cosmic string [74,75,76], and the global monopole [77]. The latter two are the strongest candidates to be observed [72]. Topological defect plays important role in condensed matter systems, cosmology, and particle physics. Topological defects in the context of symmetry breaking were first extensively discussed by Nielsen and Olesen [78], who discovered the possibility of string-like topological defects due to symmetry breaking. The line of discoveries was continued by ’t Hooft [79] and Polyakov [80] who showed that the existence of monopole-like topological defects is highly possible. This area of research was then further developed by Kibble, Coleman, Hindmarsh, among others. The topological defects play a crucial role in structure formation in the early universe because it is believed that these defects carry energy. This energy leads to an extra attractive gravitational force, and hence, these defects can acts as seeds for cosmic structure. In particular, cosmic strings, and global textures can lead to attractive scenarios for the formation of galaxies and large scale structure [81].
Our motivation in this work is to study the deflection of light-like and time-like geodesics in curved space-time background under the effects of cosmic strings. In fact, we derive the deflection angle through an interesting method and analyze the effects, such as screw dislocation, cosmic string, and spacelike dislocation on them. In this analysis, we follow the procedure done in Ref. [82] to calculate the deflection of photon rays or time-like geodesics in the background of the topological defect geometries. This method states that the radius of the cylinder is assuming constant r = a and time-like geodesics or photon rays is along travelling along the path parallel to the z-axis with a speed z ˙ = v (v=c for light-like geodesics).

2. Deflection of Lightlike and Timelike Geodesics in Topologicaldefects Background:

In this section, we study the deflection of light-like and time-like geodesics in various curved space-time background in the presence of topological defect produced by cosmic string. We see that the topological defect modified the results.

2.1. Cosmic String Space-Time with Screw Dislocation

Let us consider a cosmic string space-time, where screw dislocation is present given by the following line-element [83,84,85,86]:
d s 2 = − c 2 d t 2 + d r 2 + α 2 r 2 d φ 2 − 2 β   d z d φ + d z 2 ,
where β = b 4   π   r   with b is the Z-component of the Burger vector. The Burger vector of the screw dislocation has components b x = b y =0; b z =b and α is the topological defect parameter.
The Lagrangian of the system is defined by
L = 1 2 g μ ν x ˙ μ x ˙ ν
For light-like or time-like geodesics, we have
ε = − c 2 + r ˙ 2 + α 2   r 2 φ ˙ 2 − 2 β z ˙ φ ˙ + z ˙
2.
In this analysis, we follow the procedure done in Ref. [82] to calculate the deflection angle of photon rays or time-like geodesics in the topological defect background. Let us suppose that the motion of particle (or light) is in the direction of the z-axis, or we can say;
r = a   ( constant ) ;   z ˙ = v (velocity of massive or massless objects)
Thereby, we get from Equation (7)
α 2   a 2   φ ˙ 2   - 2 β   v   φ ˙ + ( v 2   – c 2 ) = ε .
Let us consider the solution of the above equation is of the form
φ = A   t .
Then, we get for the constant A in the following quadratic equation
α 2   a 2 A 2   - 2   β   v   A + ( v 2   – c 2 ) = ε .
The solution of this equation gives us
A = 1 2 2 β v α 2 a 2 ± 4 β 2 v 2 α 4 a 4 − 4 v 2 − c 2 − ∈ α 2 a 2 .
Using approximation, v   ≈ c   (for light-like geodesic i.e.   ε = 0   ), we get,
A ≈ 2 β c α 2 a 2
Which gives the function φ in the form:
φ   ( t ) ≈ 2   β   c α 2 a 2 t .
Now, we choose the interval z 2 − z 1 = ∆ z = l; the distance between two points on the line parallel to z-axis, then ∆ t   = l c   ; where c being the velocity of light. For the deflection angle ∆ φ , we get
∆ φ ≈ 2 β l a 2 α 2
Now, we discuss the same deflection for time-like geodesic; ε = − 1 and v < c .
Therefore, from Equation (12), we have
A = 1 2 2 β v α 2 a 2 ± 4 β 2 v 2 + 4 α 2 a 2 c 2 γ 2 − 1 α 2 a 2 ,   where   γ = 1 1 − v 2 c 2 .
So; the function φ can be written in the following form
φ t = 1 2 2 β V α 2 a 2 c ± 4 β 2 v 2 c 2 + 4 α 2 a 2 1 γ 2 − 1 c 2 α 2 a 2   c   t
Now, as stated earlier, considering ∆ t   = l c   ; where c being the velocity of light. The deflection angle ∆ φ of time-like geodesics will be
∆ φ = β v α 2 a 2 c ± β 2 v 2 c 2 + α 2 a 2 1 γ 2 − 1 c 2 α 2 a 2   l .
We see that the deflection angle of photon rays and/or time-like geodesics is directly proportional to the screw dislocation parameter ( β ) and depends on the cosmic string parameter α . We plot Figure 1 and Figure 2 of the deflection angle of photon rays Equation (15) with cosmic string parameter α keeping fixed β = 0.5 , a = 1 . In Figure 3, we plot this deflection angle for different values of screw dislocation parameter β keeping fixed l = 1 = a .

2.2. Cosmic String Space-Time with Spiral Dislocation

In this part, we consider geometry of space-time defined by the following line-element [85, 87]
d s 2 = − c 2 d t 2 + d r + β d φ 2 + α 2 r 2 d φ 2 + d z 2 = − c 2 d t 2 + d r 2 + α 2 r 2 + β 2 d φ 2 + 2 β   d r   d φ + d z 2
For the time-like or light-like geodesics, using the space-time (19), we obtain
− c 2 + r ˙ 2 + φ ˙ 2 α 2 r 2 + β 2 + 2 β r ˙ φ ˙ + z ˙ 2 = ε
Let us consider r= a (constant), z ˙ = v , then we get,
− c 2 + φ ˙ 2 α 2 a 2 + β 2 + v 2 = ε   ⇒ α 2 a 2 + β 2 φ ˙ 2 = ε + c 2 1 − v 2 c 2 ⇒ φ ˙ 2 = ε + c 2 γ 2 α 2 a 2 + β 2 ,   where   1 γ 2 = 1 − v 2 c 2
Let as consider the solution of the form
φ = A t
Therefore, φ ˙ = A From Equation (21), we obtain the constant A as follows:
A 2 = ε α 2 a 2 + β 2 + c 2 γ 2 α 2 a 2 + β 2
Therefore, from Equation (22), we obtain the angular coordinate as follows
φ t = ε α 2 a 2 + β 2 + c 2 γ 2 α 2 a 2 + β 2 1 / 2 t
Defining ∆ t = l / c . Therefore, the deflection angle will become
∆ φ = ε α 2 a 2 + β 2 + c 2 γ 2 α 2 a 2 + β 2 1 / 2 ∆ t ∆ φ = 1 c ε α 2 a 2 + β 2 + c 2 γ 2 1 α 2 a 2 + β 2 1 / 2 l
For photon light, we have
v ≈ c , 1 γ 2 → 0 , ε = 0 .
Therefore, the deflection angle from Equation (25) will be
∆ φ = 0
For time-like geodesics, we have
v < c ,   ε = − 1
Therefore, the deflection angle of time-like geodesics will be
∆ φ t i m e − l i k e = 1 c − 1 ( α 2 a 2 + β 2 ) + c 2 γ 2 1 α 2 a 2 + β 2 1 / 2 l = l 1 γ 2 − 1 c 2 α 2 a 2 + β 2 .
So, we can say that for spiral dislocation by the cosmic string metric of (19), the deflection angle of photon light caused by such dislocation is zero, and for time-like geodesics, it will be non-zero given by the Equation (29) which depends on the parameter β , the cosmic string parameter α and changes with change in the length l .

2.3. Cosmic String Space-Time with Spacelike Dislocation

Let us consider a metric of the cosmic string space time with space-like dislocation by the following line-element [88,89,90,91]
d s 2 = − c 2 d t 2 + d r 2 + α 2 r 2 d φ 2 + d z − χ   d φ 2 = − c 2 d t 2 + d r 2 + α 2 r 2 + χ 2 d φ 2 − 2 χ d z d φ + d z 2
For light-like or time-like geodesics, we have
− c 2 + r ˙ 2 + α 2 r 2 + χ 2 φ 2 ˙ − 2 χ z ˙ φ ˙ + z ˙ = ε
Let the motion of light-like or time-like geodesics is in the direction of z-axis. We can write
r = a ;   z ˙ = v .
Therefore, we get the equation of   φ from (4.4)
α 2 a 2 + χ 2 φ ˙ 2 − 2   χ   v   φ ˙ + v 2 − c 2 = ε
Suppose the solution of the above equation is of the form
φ = A   t
Substituting this into the Equation (33), we get the following quadratic equation for the constant A given by
α 2 a 2 + χ 2 A 2 − 2   χ   v A + v 2 − c 2 = ε
The solution will be
A = χ   v ± χ 2   v 2 − α 2 a 2 + χ 2 ( v 2 − c 2 − ε ) ( α 2 a 2 + χ 2 )
For photon light, we use the approximation   v ≈ c ,   ε =0, we get
A = 2   χ   c ( α 2 a 2 + χ 2 )
This gives the function φ in the following form
φ t ≈ 2   χ   c ( α 2 a 2 + χ 2 ) t .
We choose the distance between two points in the z-axis, z 2 − z 1 = ∆ z = l then, ∆ t = l c , c being the velocity of light. For light-like geodesics, we obtain the deflection angle
∆ φ ≈ 2   χ ( α 2 a 2 + χ 2 ) l .
For time-like geodesics, ε = − 1 . Therefore, from Equation (36), we obtain
A = χ v ± χ 2 v 2 − α 2 a 2 + χ 2 ( v 2 − c 2 + 1 ) ( α 2 a 2 + χ 2 )
This gives us the function φ in the following form
φ t ≈ χ v ± χ 2 v 2 − α 2 a 2 + χ 2 ( v 2 − c 2 + 1 ) ( α 2 a 2 + χ 2 ) t
Following the previous procedure, we obtain the deflection angle of massive objects
∆ φ ≈ χ v ± χ 2 v 2 − α 2 a 2 + χ 2 ( v 2 − c 2 + 1 ) α 2 a 2 + χ 2 l c
So, we can say that if we define the spacelike dislocation by the metric of Equation (30), then the deflection angle of the light rays and time-like geodesics caused by such dislocation is given by Equations (39) and (42). This deflection angle depends on the spacelike dislocation parameter χ as well as the cosmic string parameter α . We plot the deflection angle for photon rays Equation (39) with cosmic string parameter α in Figure 4 and Figure 5. We also plot this deflection angle (photon rays) with cosmic dislocation parameter χ for fixed values of cosmic string parameter α = 0.5 in Figure 6 and for different values of l in Figure 7.

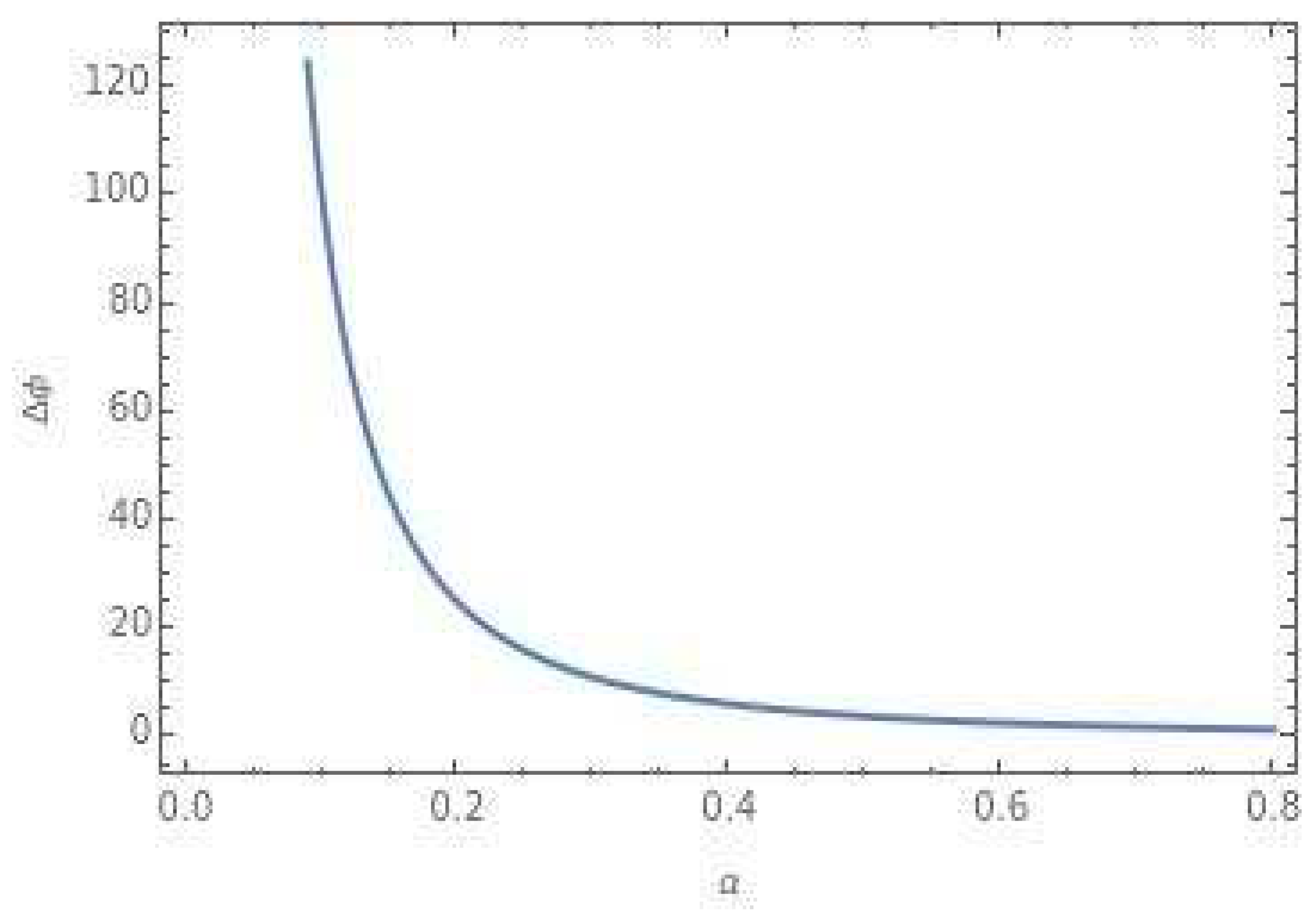
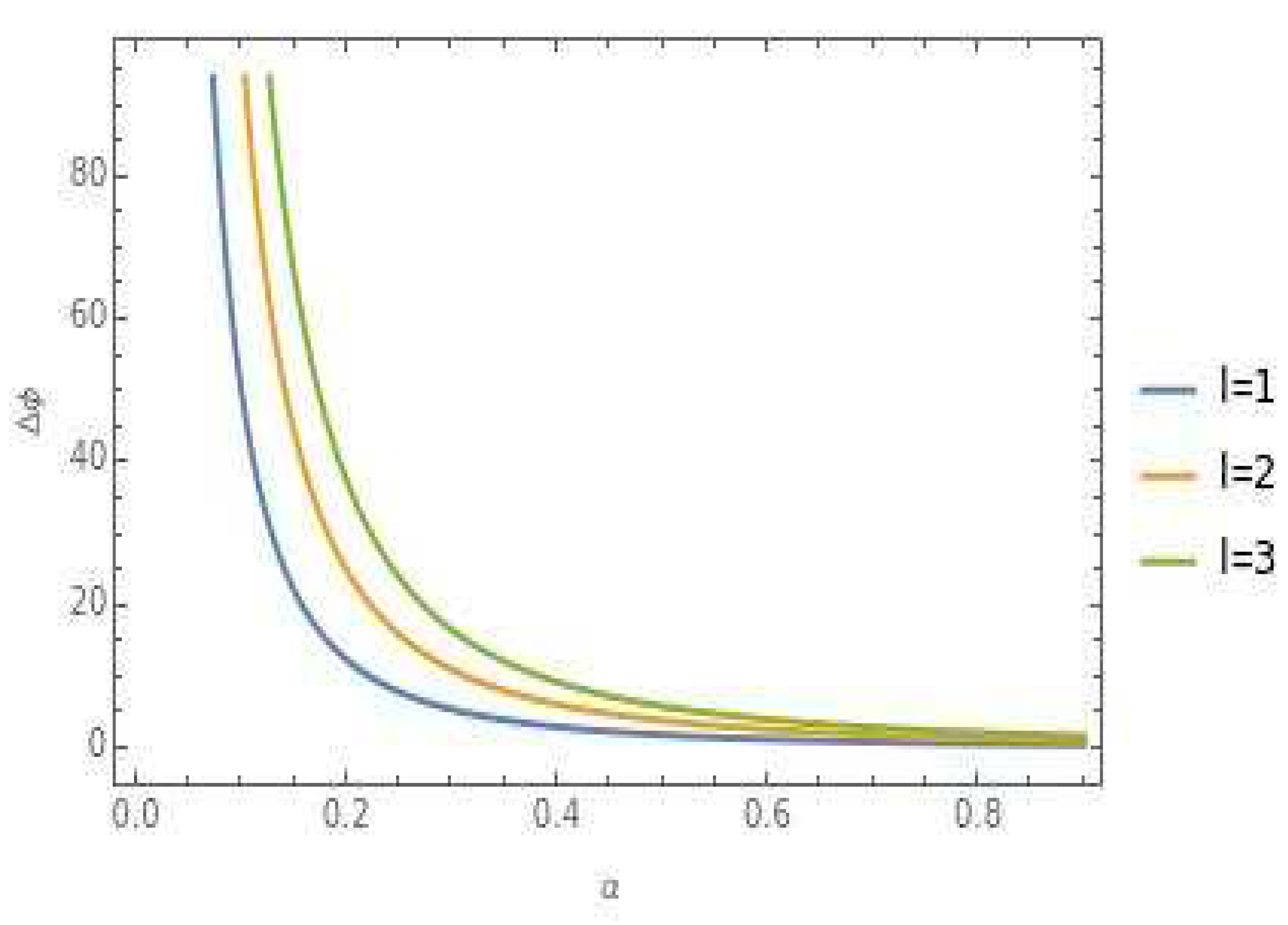
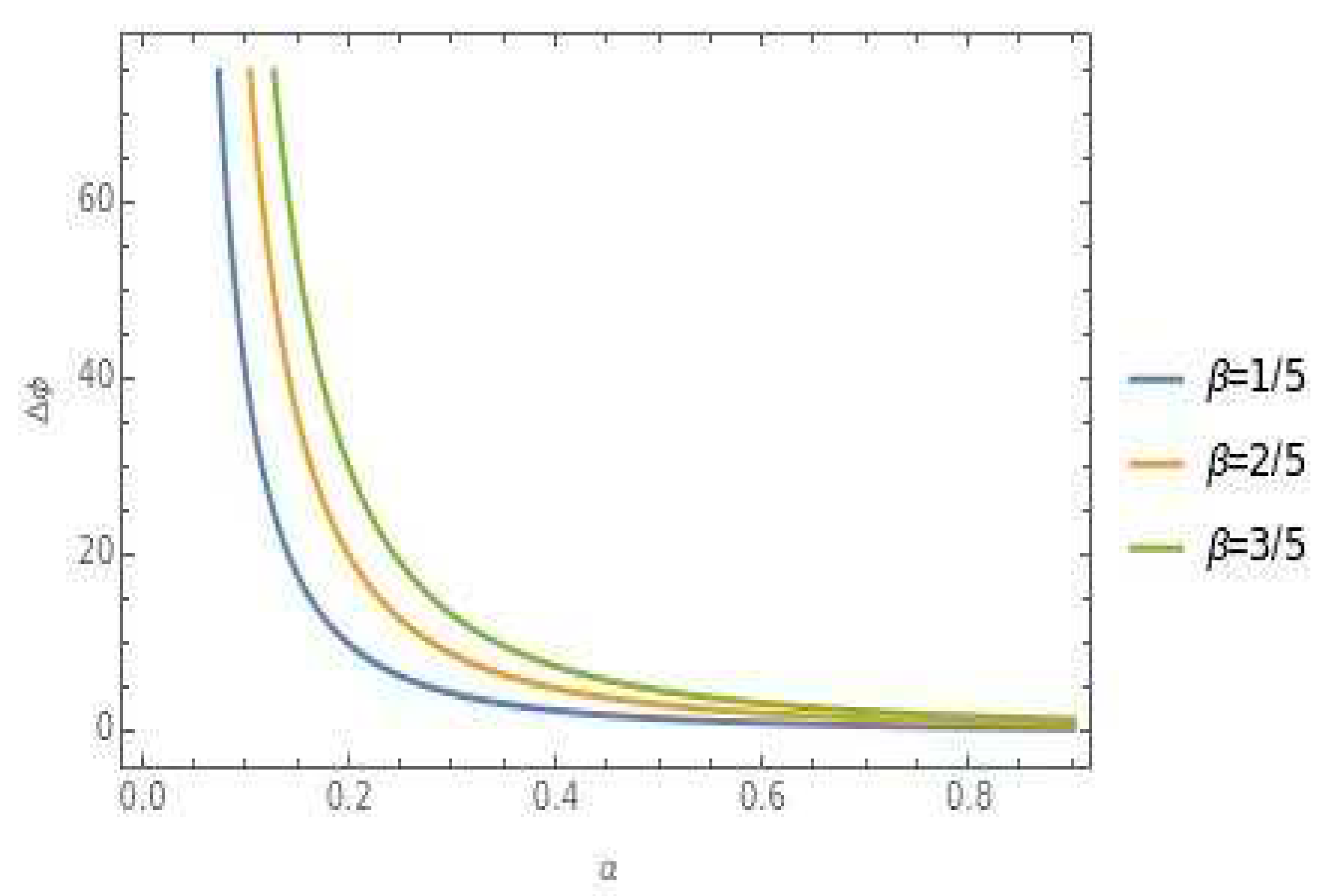
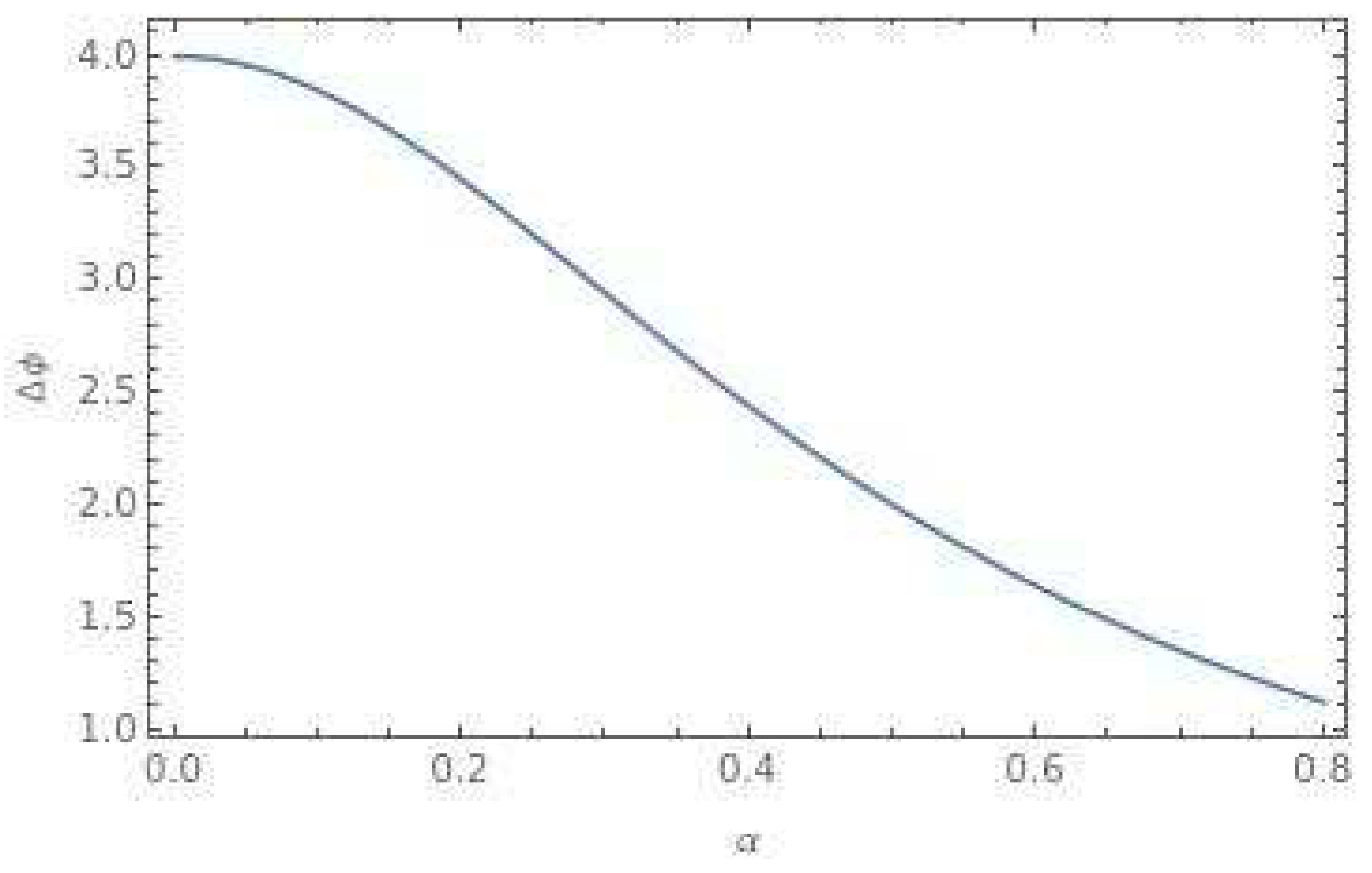
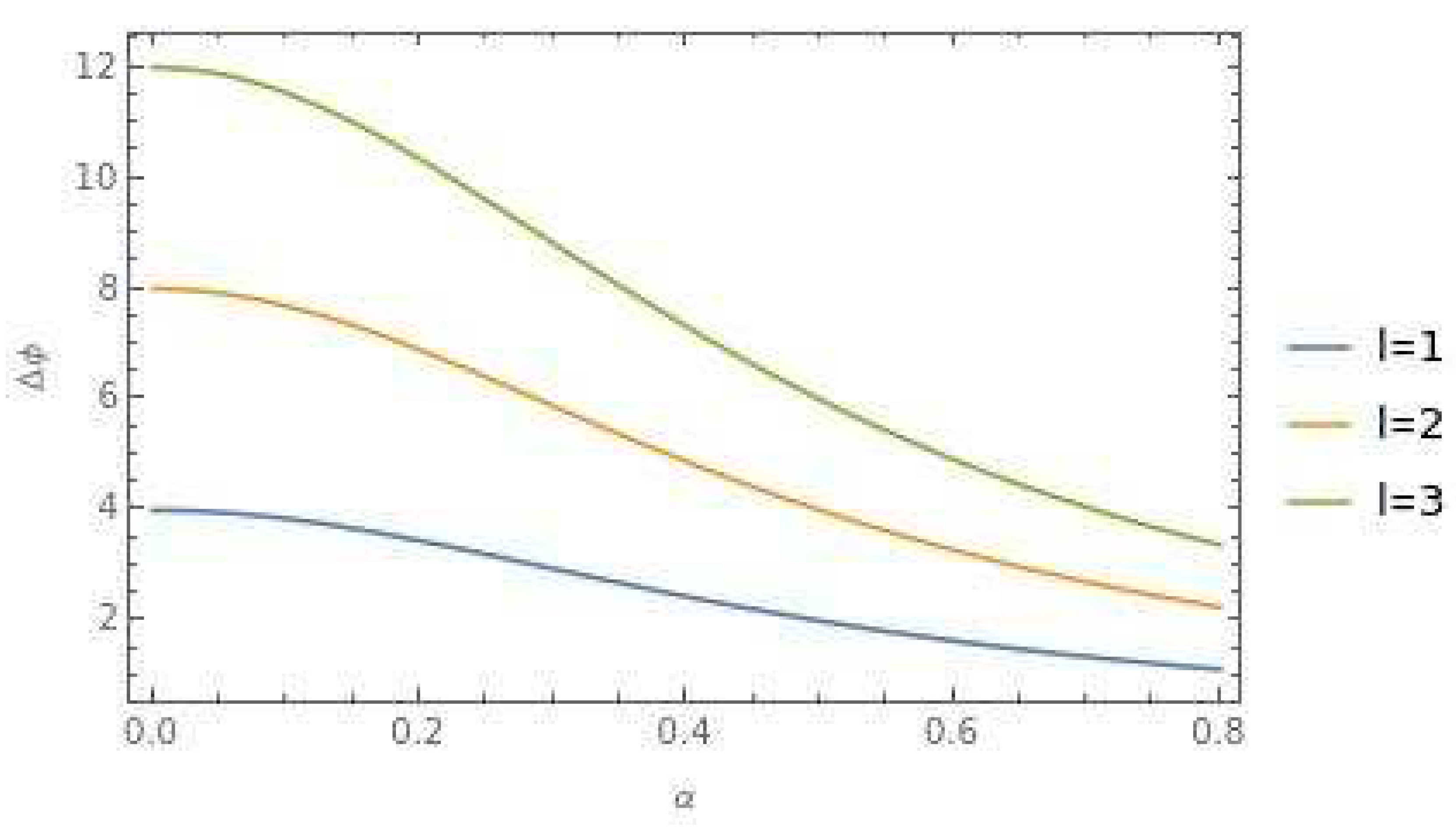
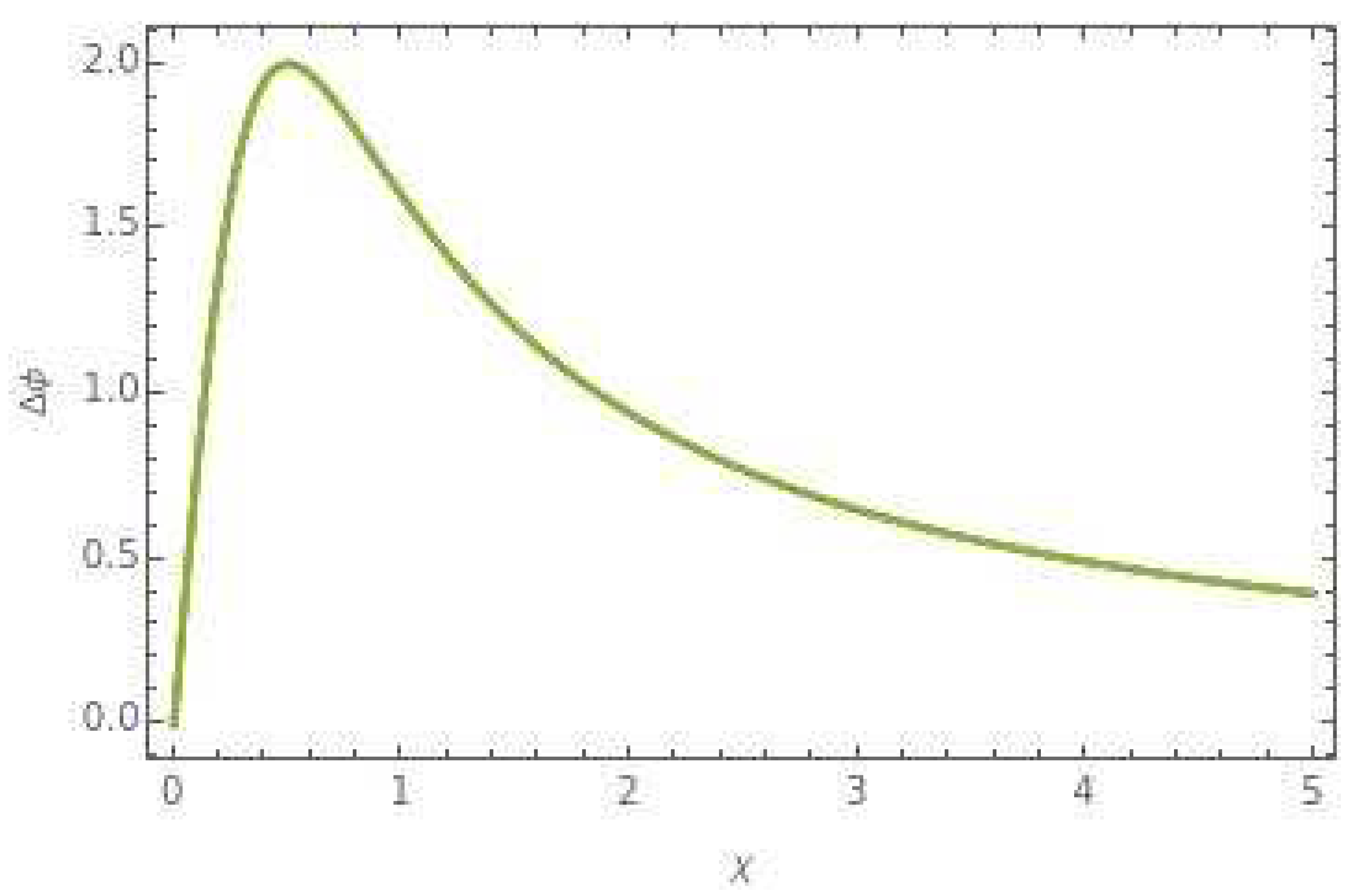
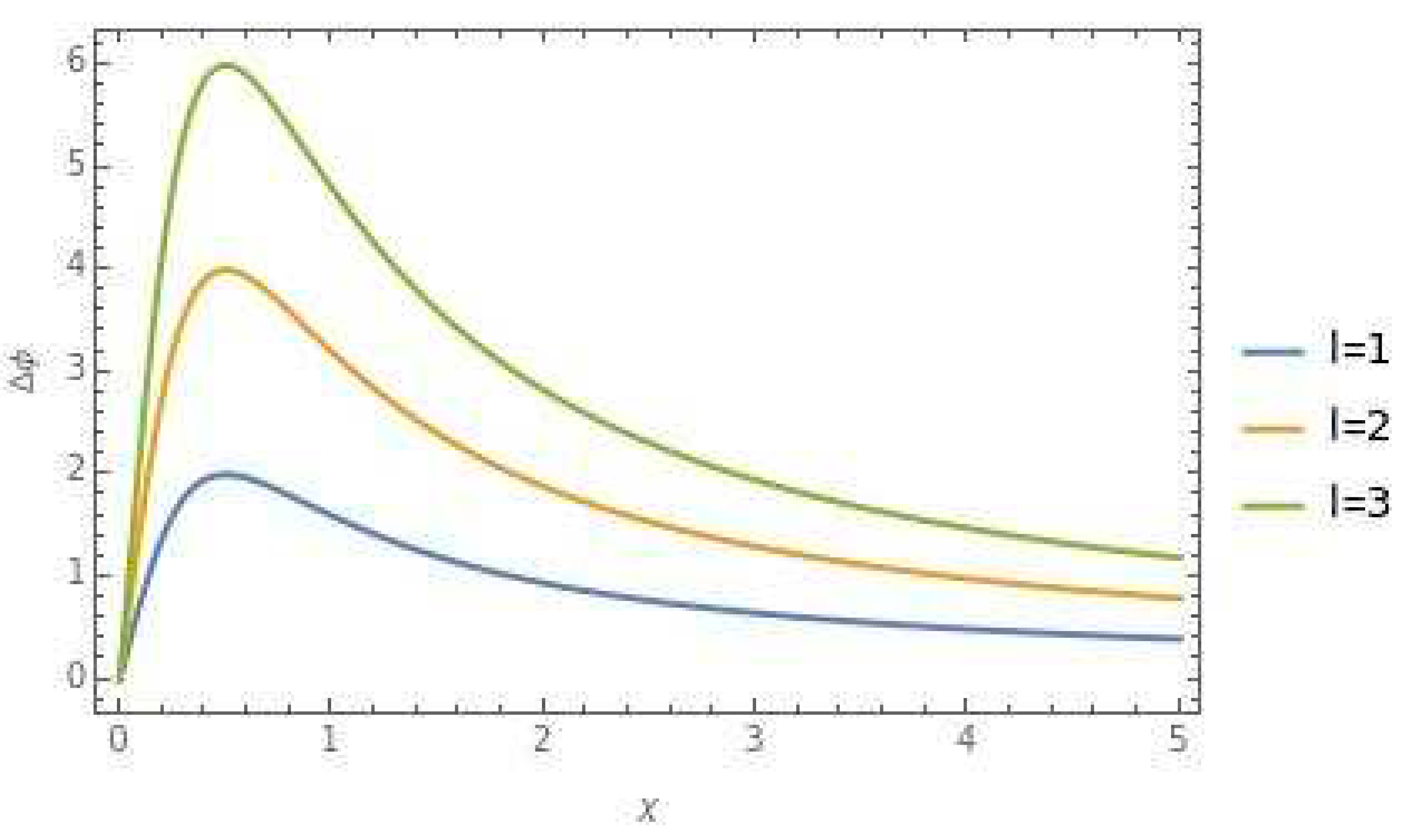
3. Discussions:

In this analysis, we have studied the deflection of time-like or null geodesics in the background of the topological defects produced by cosmic string space-times, with screw dislocation, spiral dislocation, and space-like dislocation. We derived the deflection angle for photon rays as well as for time-like geodesics and have seen that the cosmic string parameter α , the torsion (screw) parameter β , and spacelike dislocation parameter χ influences this deflection angle when the massless particles and/or massive objects travelling along the path parallel to the z-axis.

Author Contributions

M.A. Choudhury: Writing (Section 2.1), A. Kayum: Writing (Section 2.2), M. Hassan: Writing (Section 2.3), F. Ahmed: Supervision, Formal analysis, Investigation, Conceptualization, Writing-original & draft, Reviewing. All authors have read and agreed to the published version of the manuscript.

Funding

No fund has received for this article.

Data Availability Statement

No new data generated or analyzed in this work.

Conflicts of Interest

There are no conflicts of interest.

References

  1. B. F. Schutz, A First Course in General Relativity, Cambridge University Press, Cambridge (2015).
  2. W. Rindler, Relativity: Special, General, and Cosmological, Oxford University Press, Oxford (2006).
  3. J. G. Williams and D. E. Vincent, General Relativity and Relativistic Astrophysics, World Scientific Publishing (1992).
  4. S. Carroll, Space-time and Geometry: An Introduction to General Relativity, Cambridge University Press, Cambridge (2019).
  5. Robert M. Wald, General Relativity, University of Chicago Press, UK (1984).
  6. R. K. Sachs and H.- H. Wu, General Relativity for Mathematicians, Springer (2012). [CrossRef]
  7. K. Schwarzschild, arXiv: physics/9905030.
  8. R. P. Kerr, Phys. Rev. Lett. 11 (5): 237–238 (1963).
  9. L. Bergström and A. Goobar, Cosmology and Particle Astrophysics, Springer Berlin, Heidelberg (2006).
  10. G. F. R. Ellis and van H. Elst, arXiv: gr-qc/9812046.
  11. A. S. Eddington, Mathematical Theory of Relativity, Cambridge University Press, Cambridge (1922).
  12. C. R. Keeton, C. S. Kochanek and E. E. Falco, Astrophys. J. 509, 561 (1998).
  13. A. Bhadra, Phys. Rev. D 67, 103009 (2003).
  14. R. Whisker, Phys. Rev. D 71, 064004 (2005).
  15. S. B. Chen and J. I. Jing, Phys. Rev. D 80, 024036 (2009).
  16. K. K. Nandi, Y. Z. Zhang and A. V. Zakharov, Phys. Rev. D 74, 024020 (2006).
  17. E. F. Eiroa, G. E. Romero and D. F. Torres, Phys. Rev. D 66, 024010 (2002).
  18. S. Mao and B. Paczynski, Astrophys. J. 374, L37 (1991).
  19. H. Hoekstra, H. K. C. Yee and M. D. Gladders, Astrophys. J. 606, 67 (2004).
  20. K. S. Virbhadra and G. F. R. Ellis, Phys. Rev. D 65, 103004 (2002).
  21. F. Ahmed, Adv. High Energy Physics 2017, 3587018 (2017).
  22. F. Ahmed, Progress of Theoretical and Experimental Physics 2017, 083E03 (2017).
  23. F. Ahmed and F. Rahaman, Adv. High Energy Physics 2018, 7839619 (2018).
  24. F. Ahmed and F. Rahaman, Eur. Phys. J. A 54, 52 (2018).
  25. K. S. Virbhadra and G. F. R. Ellis, Phys. Rev. D 62, 084003 (2000).
  26. E. Gallo and O. M. Moreschi, Phys. Rev. D 83, 083007 (2011).
  27. G. Crisnejo and E. Gallo, Phys. Rev. D 97, 084010 (2018).
  28. M. Sharif and S. Iftikhar, Astrophys. Space Sci. 357, 85 (2015).
  29. W. Javed, R. Babar and A. Ovgun, Phys. Rev. D 99, 084012 (2019).
  30. G. W. Gibbons and M. C. Werner, Class. Quant. Grav. 25, 235009 (2008).
  31. M. C. Werner, Gen Relativity Grav. 44, 3047 (2012).
  32. A. Ishihara, Y. Suzuki, T. Ono, T. Kitamura and H. Asada, Phys. Rev. D 94, 084015 (2016).
  33. G. Crisnejo and E. Gallo, Phys. Rev. D 97, 124016 (2018).
  34. K. Jusufi, M. C. Werner, A. Banerjee and A. Ovgün, Phys. Rev. D 95, 104012 (2017).
  35. I. Sakalli and A. Ovgun, EPL 118, 60006 (2017).
  36. K. Jusufi and A. Ovgun, Phys. Rev. D 97, 024042 (2018).
  37. T. Ono, A. Ishihara and H. Asada, Phys. Rev. D 96, 104037 (2017).
  38. K. Jusufi, A. Ovgun and A. Banerjee, Phys. Rev. D 96, 084036 (2017),.
  39. A. Ovgun, G. Gyulchev and K. Jusuf, doi:10.1016/j.aop.2019.04.007.
  40. K. Jusufi, I. Sakalli and A. Ovgun, Phys. Rev. D 96, 024040 (2017).
  41. H. Arakida, Gen. Rel. Grav. 50, 48 (2018).
  42. K. Jusufi and A. Ovgun, arXiv:1707.02824 [gr-qc].
  43. T. Ono, A. Ishihara and H. Asada, Phys. Rev. D 98, 044047 (2018).
  44. K. Jusufi and A. Ovgun,, Phys. Rev. D 97, 064030 (2018).
  45. K. Jusufi, A. Ovgun, J. Saavedra, Y. Vasquez and P. A. Gonzalez, Phys. Rev. D 97, 124024 (2018).
  46. A. Ovgun, Phys. Rev. D 98, 044033 (2018).
  47. A. Ovgun, K. Jusufi and I. Sakalli, Ann. Phys. 399, 193 (2018).
  48. K. Jusufi, A. Ovgun, A. Banerjee and I. Sakalli, Eur. Phys. J. Plus (2019) 134: 428.
  49. A. vgun, http://arxiv.org/abs/1806.05549.
  50. G. Crisnejo, E. Gallo and A. Rogers, http://arxiv.org/abs/1807.00724.
  51. A. övgun, I. Sakalli and J. Saavedra, http://arxiv.org/abs/1806.06453.
  52. A. övgun, I. Sakalli and J. Saavedra, JCAP 1810, 041 (2018).
  53. T. Ono, A. Ishihara and H. Asada, http://arxiv.org/abs/1811.01739.
  54. A. Övgün, G. Gyulchev, K. Jusufi, Ann. Phys. 406 (2019) 152.
  55. T. Müller, Phys. Rev. D 77, 044043 (2008).
  56. V. Perlick, Phys. Rev. D 69, 064017 (2004).
  57. N. Tsukamoto, Phys. Rev. D 105, 064013 (2022); Phys. Rev. D 104, 124016 (2021); Phys. Rev. D 104, 064022 (2021); Phys. Rev. D 103, 024033 (2021); Phys. Rev. D 102, 104029 (2020); Phys. Rev. D 101, 104021 (2020); N. Tsukamoto, T. Kitamura, K Nakajima, H Asada, Phys. Rev. D 90, 064043 (2014); N. Tsukamoto, T. Kitamura, K. Nakajima and H. Asada, Phys. Rev. D 90, 064043 (2014); Phys. Rev. D 95, 084021 (2017); Phys. Rev. D 97, 084051 (2018); EPJC 83, 284 (2023).
  58. K. Nakajima and H. Asada, Phys. Rev. D 85, 107501 (2012).
  59. K. Jusufi, Phys. Rev. D 98, 044016 (2018).
  60. H. Aounallah, A. R. Soares and R. L. L. Vitória , EPJC 80, 447 (2020).
  61. F. Ahmed, EPL 142, 39002 (2023).
  62. I. N. Huda and H. S. Ramadhan, J. Phys.: Conf. Ser. 1816, 012021 (2021).
  63. A. R. Soares, R. L. L. Vitoria and C. F. S. Pereira, arXiv:2305.11105[gr-qc].
  64. F. Ahmed, https://arxiv.org/abs/2306.12455.
  65. F. Abe, ApJ 725 (2010) 787.
  66. C.-M. Yoo, T. Harada, N. Tsukamoto, Phys. Rev. D 87, 084045 (2013).
  67. N. Tsukamoto, Phys. Rev. D 94, 124001 (2016).
  68. N. Tsukamoto, T. Harada, Phys. Rev. D 95, 024030 (2017).
  69. R. Shaikh, P. Banerjee, S. Paul, T. Sarkar, JCAP 07 (2019) 028.
  70. T. W. B. Kibble, J. Phys. A: Meth. Gen. 9, 1387 (1976).
  71. T. W. B. Kibble, Phys. Rep. 67, 183 (1980).
  72. A. Vilekin and E. P. S. Shellard, Strings and Other Topological Defects, Cambridge University Press, Cambridge (1994).
  73. A . Vilekin, Phys. Rep. 121, 263 (1985).
  74. A. Vilekin, Phys. Lett. B 133, 177 (1983).
  75. W. A Hiscock, Phys. Rev. D 31, 3288 (1985).
  76. B. Linet, Gen. Relativ. Gravit. 17, 1109 (1985).
  77. M. Barriola and A Vilekin, Phys. Rev. Lett. 63, 341 (1989).
  78. H. B. Nielsen and P. Olesen, Nucl. Phys. B 61, 45 91973).
  79. G’t Hooft, Nucl. Phys. B 79, 276 (1974).
  80. A. M. Polyakov, JETP Lett. 20, 194 (1974).
  81. R. H. Brandenberger, Int. J Mod. Phys. A 9, 2117 (1994).
  82. M. Pardy, https://doi.org/10.48550/arXiv.gr-qc/0106019.
  83. H. Kleinert, Gauge Fields in Condensed Matter, vol. 2, World Scientific Publishing Co, Singapore, 1989.
  84. M. O. Katanaev and I. V. Volovich, Ann. Phys. (NY) 216, 1 (1992).
  85. K. C. Valanis and V. P. Panoskaltsis, Acta Mech. 175, 77 (2005).
  86. C. Furtado and F. Moraes, EPL 45, 279 (1999).
  87. K. Bakke and C. Furtado, Phys. Rev. A 87, 012130 (2013).
  88. R. A. Puntigam and H. H. Soleng, Classical and Quantum Gravity 14, 1129 (1997).
  89. V. B. Bezerra, J. Math. Phys. 38, 2553 (1997).
  90. F. Ahmed, Advances in High Energy Physics 2020, 5691025 (2020).
  91. F. Ahmed, Advances in High Energy Physics 2020, 4832010 (2020).
Preprints 79968 g001
Figure 1. The deflection angle of photon light with cosmic string parameter keeping fixed l . Here β = 0.5 , l = 1 = a .
Figure 1. The deflection angle of photon light with cosmic string parameter keeping fixed l . Here β = 0.5 , l = 1 = a .
Preprints 79968 g001
Preprints 79968 g002
Figure 2. The deflection angle of photon light with cosmic string parameter for fixed value of l . Here β = 0.5 , a = 1 .
Figure 2. The deflection angle of photon light with cosmic string parameter for fixed value of l . Here β = 0.5 , a = 1 .
Preprints 79968 g002
Preprints 79968 g003
Figure 3. The deflection angle of photon light with cosmic string parameter for different values of screw dislocation parameter β . Here l = 1 = a .
Figure 3. The deflection angle of photon light with cosmic string parameter for different values of screw dislocation parameter β . Here l = 1 = a .
Preprints 79968 g003
Preprints 79968 g004
Figure 4. The deflection angle of photon light with cosmic string parameter α for l = 1 = a , χ = 0.5 .
Figure 4. The deflection angle of photon light with cosmic string parameter α for l = 1 = a , χ = 0.5 .
Preprints 79968 g004
Preprints 79968 g005
Figure 5. The deflection angle of photon light with cosmic string parameter α for different l with χ = 0.5 , a = 1 .
Figure 5. The deflection angle of photon light with cosmic string parameter α for different l with χ = 0.5 , a = 1 .
Preprints 79968 g005
Preprints 79968 g006
Figure 6. The deflection angle of photon light with cosmic dislocation parameter χ for α = 0.5 , l = 1 = a .
Figure 6. The deflection angle of photon light with cosmic dislocation parameter χ for α = 0.5 , l = 1 = a .
Preprints 79968 g006
Preprints 79968 g007
Figure 7. The deflection angle of photon light with cosmic dislocation parameter χ for different l with α = 0.5 , a = 1 .
Figure 7. The deflection angle of photon light with cosmic dislocation parameter χ for different l with α = 0.5 , a = 1 .
Preprints 79968 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated