Prerpints.org logo
Preprint
Article

Deflection of Null and Time-like Geodesics in Topological Defects Space-Time Geometry

This version is not peer-reviewed.

Submitted:

21 July 2023

Posted:

25 July 2023

You are already at the latest version

Abstract
In this research, we investigate the bending of photon light and/or time-like geodesics within the context of four-dimensional space-time geometry, specifically in the presence of topological defects. These topological defects manifest as cosmic string space-time configurations, encompassing screw dislocation, spiral dislocation, and spacelike dislocation. Our primary objective is to determine the extent of deflection experienced by light-like and time-like geodesics and analyze how this deflection is affected by the cosmic string parameter, screw dislocation parameter, and spacelike dislocation parameter. To accomplish this, we employ a derivation technique that centers on the observation that photon rays (light-like geodesics) and/or time-like geodesics follow paths parallel to the z-axis while maintaining a constant radius along the cylinder.
Keywords: 
Subject: 
Physical Sciences  -   Theoretical Physics

1. Introduction

General relativity is a fundamental theory that establishes a profound connection between the geometry of space-time and the distribution of matter-energy within it. According to this theory, the presence of matter and energy influences the curvature of space-time, and this curvature, in turn, governs the motion of objects within it, including the trajectory of test bodies and the propagation of light along light-like geodesics [1,2,3,4,5,6].
The theory of general relativity has made several remarkable predictions about the nature of gravity, introducing novel effects such as gravitational waves and gravitational lensing. Over time, many of these predictions have been experimentally validated or observed, providing substantial evidence for the validity of the theory. One of the most notable recent successes of general relativity is the detection of gravitational waves, which provided further confirmation of the theory's predictive power.
In essence, general relativity provides a comprehensive framework for understanding the intricate interplay between matter-energy and the curvature of space-time, unveiling profound insights into the nature of gravity and its far-reaching implications in the universe.
The distance between two points in curved space-time is described by the line element
d s 2 = g μ ν ( x μ ) d x μ d x ν ,   ( μ , ν = 0 ,   1 ,   2 ,   3 )
.
The geodesics equation is given by
x ¨ μ + Γ α β μ x ˙ α x ˙ β = 0 ,
where dot represent derivative w. r. t. λ, proper time.
The Lagrangian of a system in relativity theory is defined by
L = 1 2 g μ ν x ˙ μ x ˙ ν
For geodesics motion,
g μ ν x ˙ μ x ˙ ν = ε ,
where ε = 0 (light-like geodesics), -1 (time-like geodesics) and +1 (spacelike geodesics) in the metric signature − , + , + , +   o r + 2 .
In the context of general relativity, the phenomenon known as the deflection of light is a crucial prediction of the theory. It proposes that the path of light can be curved or bent due to the gravitational influence of massive objects present in its vicinity. This effect is commonly referred to as gravitational lensing, and its first experimental observation, documented in Reference [11], served as a significant validation of the correctness of the general relativity theory.
Gravitational lensing offers a valuable and powerful technique for studying various astronomical phenomena, such as galaxies, dark matter, dark energy, and the structure of the universe itself [11]. Extensive research on gravitational lensing has been conducted, exploring its implications for diverse massive objects like black holes, wormholes, cosmic strings, and more (see References [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69]).
Through the study of gravitational lensing, scientists gain essential insights into the behavior of light in the presence of massive gravitational fields, providing a deeper understanding of the fundamental workings of the cosmos and enabling investigations into the nature of elusive entities like dark matter and dark energy. This research has significant implications for astrophysics and cosmology, contributing to our comprehension of the universe's large-scale structure and evolution.
In the early universe, topological defects emerged as a consequence of the spontaneous symmetry breaking mechanism. These defects manifest in various unified particle physics models, encompassing strong, weak, and electromagnetic interactions [70,71]. While direct observation of these objects in a laboratory setting has not been achieved so far, studies of topological defects have been conducted in diverse fields of physics and chemistry. The topological defects comprise several types, among which are domain walls [72,73], cosmic strings [74,75,76], and global monopoles [77]. Among these, cosmic strings and global monopoles stand out as the most promising candidates for potential observation [72].
Despite not yet being directly detected, the investigation of topological defects holds significant scientific interest. These studies shed light on the fundamental physics that governs the early universe and may provide crucial insights into the structure and evolution of our cosmos. Furthermore, understanding topological defects has implications beyond cosmology, with applications in different branches of physics and chemistry. As research in this field continues, it has the potential to uncover novel phenomena and enrich our understanding of the universe at its most fundamental levels.
Our primary goal in this study is to investigate the bending or deflection of light-like and time-like geodesics within a curved space-time background influenced by cosmic strings. To achieve this, we utilize an intriguing method to derive the deflection angle, and then we proceed to analyze the effects of various factors, including screw dislocation, cosmic string, and spacelike dislocation, on these geodesics.
The method we adopt in this analysis is based on the approach presented in Reference [73], which allows us to calculate the deflection of photon rays and time-like geodesics in the presence of topological defect geometries. In this method, we assume a constant radius of the cylinder, with the value denoted as "a", and the time-like geodesics or photon rays are considered to travel parallel to the z-axis with a speed of "z ̇=v" (where "v=c" for light-like geodesics, corresponding to the speed of light).
By employing this approach, we aim to gain valuable insights into the behavior of light-like and time-like geodesics in the vicinity of cosmic strings and other topological defects. This investigation will shed light on the intricate interplay between these defects and the curved space-time background, providing crucial information about the deflection of geodesics and the effects of various parameters involved

2. Deflection of Lightlike and Timelike Geodesics in Topological Defects Background

In this section, we study the deflection of light-like and time-like geodesics in various curved space-time background in the presence of topological defect produced by cosmic string. We see that the topological defect modified the results.

2.1. Cosmic String Space-Time with Screw Dislocation

Let us consider a cosmic string space-time, where screw dislocation is present given by the following line-element [74,75,76,77]:
d s 2 = − c 2 d t 2 + d r 2 + α 2 r 2 d φ 2 − 2 β   d z d φ + d z 2 ,
where β = b 4   π   r   with b is the Z-component of the Burger vector. The Burger vector of the screw dislocation has components b x = b y =0; b z =b and α is the topological defect parameter.
The Lagrangian of the system is defined by
L = 1 2 g μ ν x ˙ μ   x ˙ ν
For light-like or time-like geodesics, we have
ε = − c 2 + r ˙ 2   + α 2   r 2   φ ˙ 2   − 2   β   z ˙   φ ˙ + z ˙ 2
In this analysis, we follow the procedure done in Ref. [73] to calculate the deflection angle of photon rays or time-like geodesics in the topological defect background. Let us suppose that the motion of particle (or light) is in the direction of the z-axis, or we can say;
r = a   ( constant ) ;   z ˙
=v (velocity of massive or massless objects)
Thereby, we get from Equation (7)
α 2   a 2   φ ˙ 2     - 2 β   v   φ ˙ + ( v 2   – c 2 ) = ε .
Let us consider the solution of the above equation is of the form
𝜑=𝐴 𝑡.
Then, we get for the constant A in the following quadratic equation
α 2   a 2 A 2   - 2   β   v   A + ( v 2   – c 2 ) = ε .
The solution of this equation gives us
A = 1 2 2 β   v α 2 a 2 ± 4 β 2 v 2 α 4 a 4 − 4 v 2 − c 2 − ∈ α 2 a 2 .
Using approximation, v   ≈ c   (for light-like geodesic i.e.   ε = 0   ), we get,
A ≈ 2 β c α 2 a 2
Which gives the function φ in the form:
φ   ( t ) ≈ 2   β   c α 2 a 2 t .
Now, we choose the interval z 2 − z 1 = ∆ z = l; the distance between two points on the line parallel to z-axis, then ∆ t   = l c   ; where c being the velocity of light. For the deflection angle ∆ φ , we get
∆ φ ≈ 2 β l a 2 α 2 .
Now, we discuss the same deflection for time-like geodesic; ε = − 1 and v < c .
Therefore, from Equation (12), we have
A = 1 2 2 β v α 2 a 2 ± 4 β 2 v 2 + 4 α 2 a 2 c 2 γ 2 − 1 α 2 a 2   ,   where   γ = 1 1 − v 2 c 2 .
So; the function φ can be written in the following form
φ ( t ) = 1 2 2 β V α 2 a 2 c ± 4 β 2 v 2 c 2 + 4 α 2 a 2 1 γ 2 − 1 c 2 α 2 a 2   c   t
Now, as stated earlier, considering ∆ t   = l c   ; where c being the velocity of light. The deflection angle ∆ φ of time-like geodesics will be
∆ φ = β v α 2 a 2 c ± β 2 v 2 c 2 + α 2 a 2 1 γ 2 − 1 c 2 α 2 a 2   l .
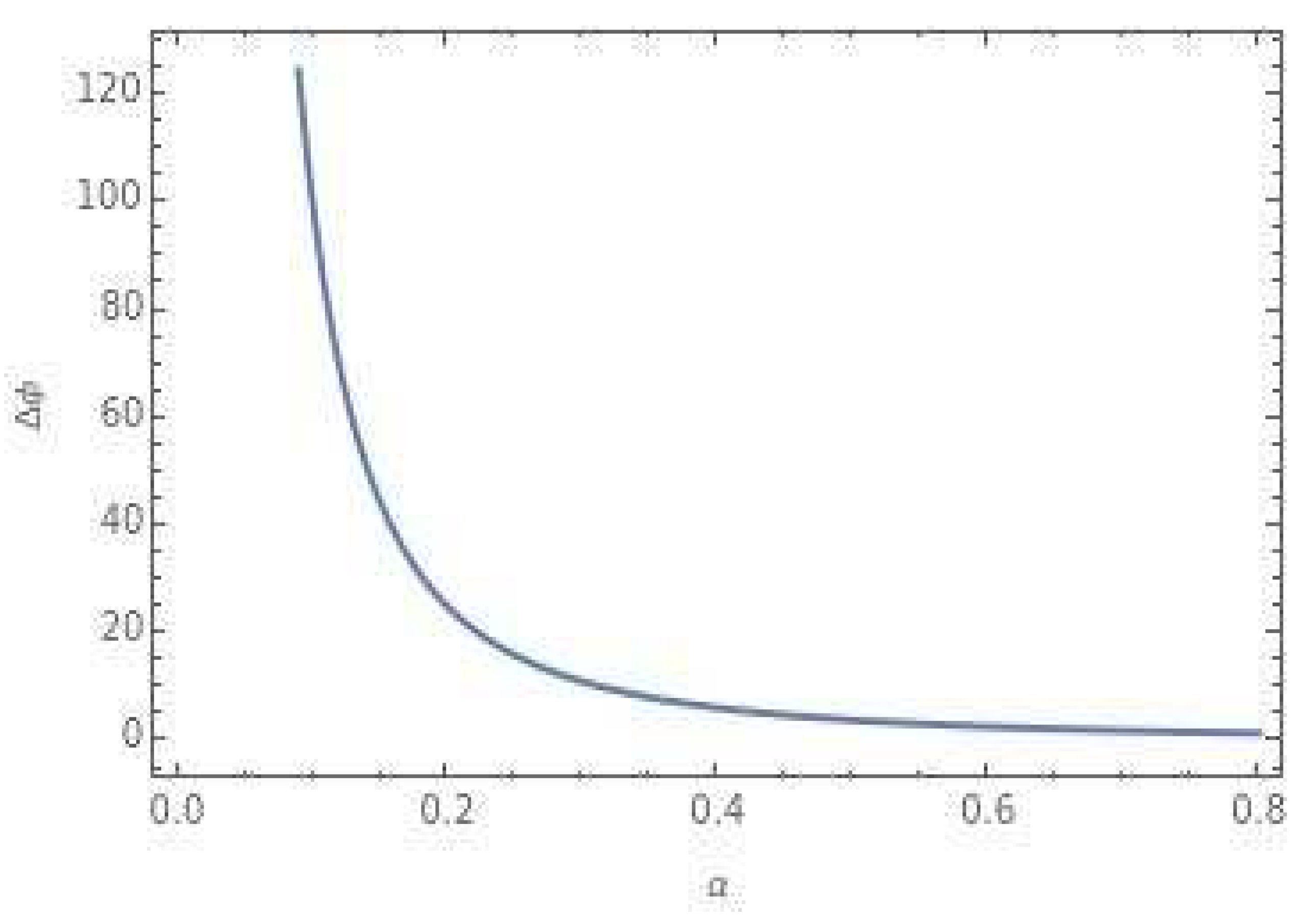
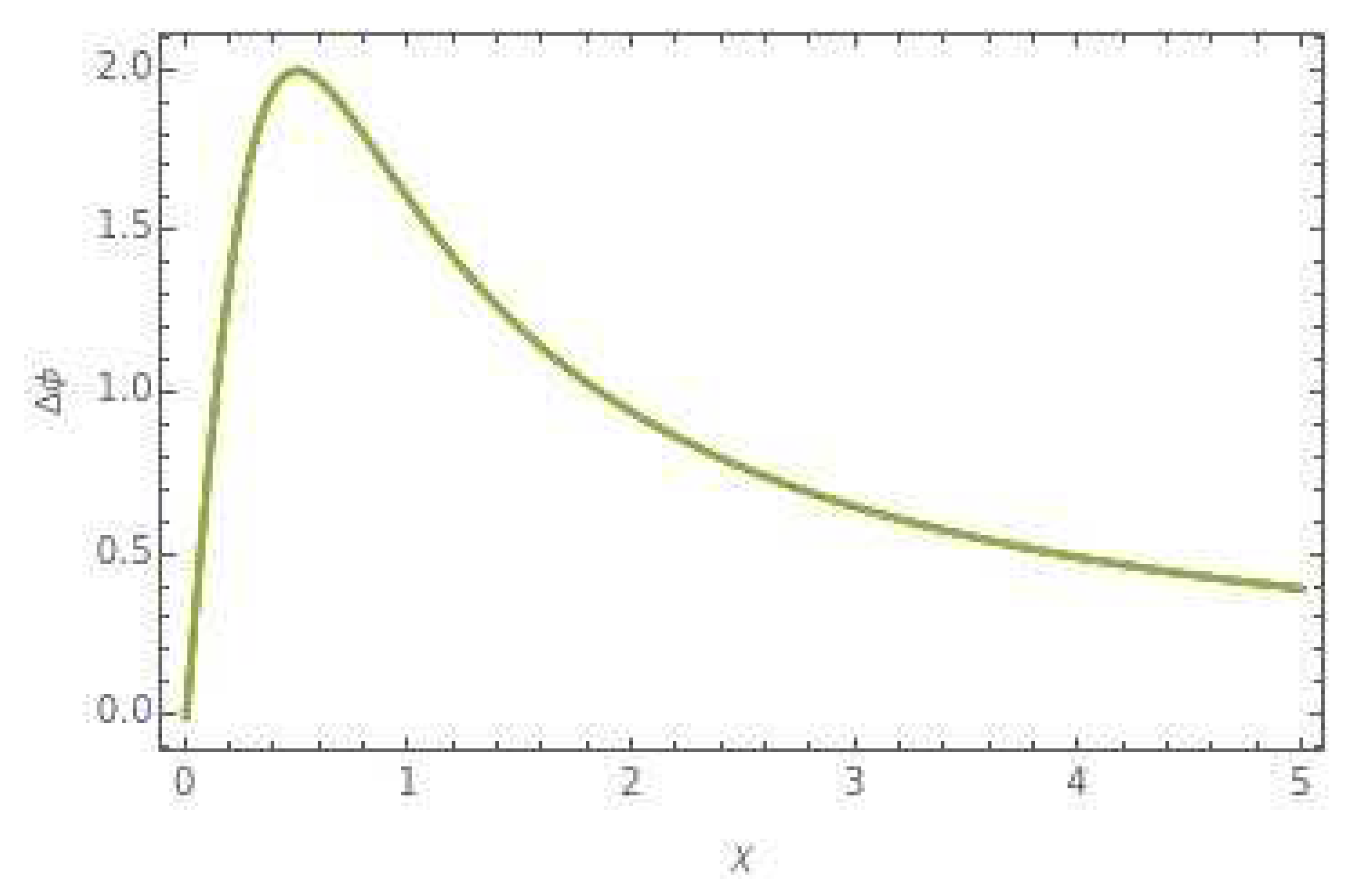
In our observations, we find that the deflection angle of photon rays and/or time-like geodesics exhibits a direct proportionality to the screw dislocation parameter (β) and also depends on the cosmic string parameter (α). To visualize these relationships, we present Figure 1 and Figure 2, showcasing the deflection angle of photon rays given by Equation (15), with the cosmic string parameter α fixed at a specific value, and β set at 0.5, while keeping a constant value of "a" at 1.
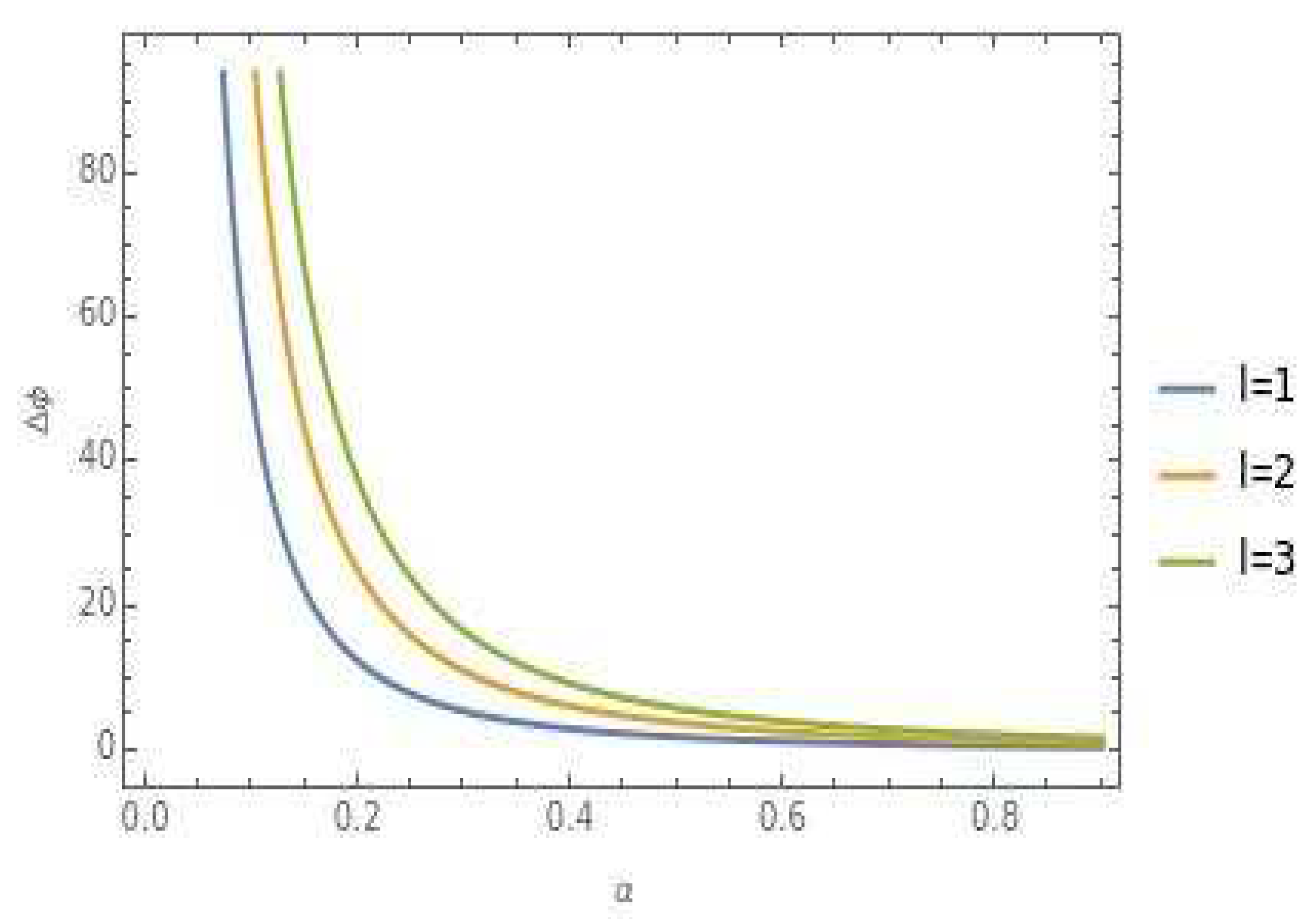
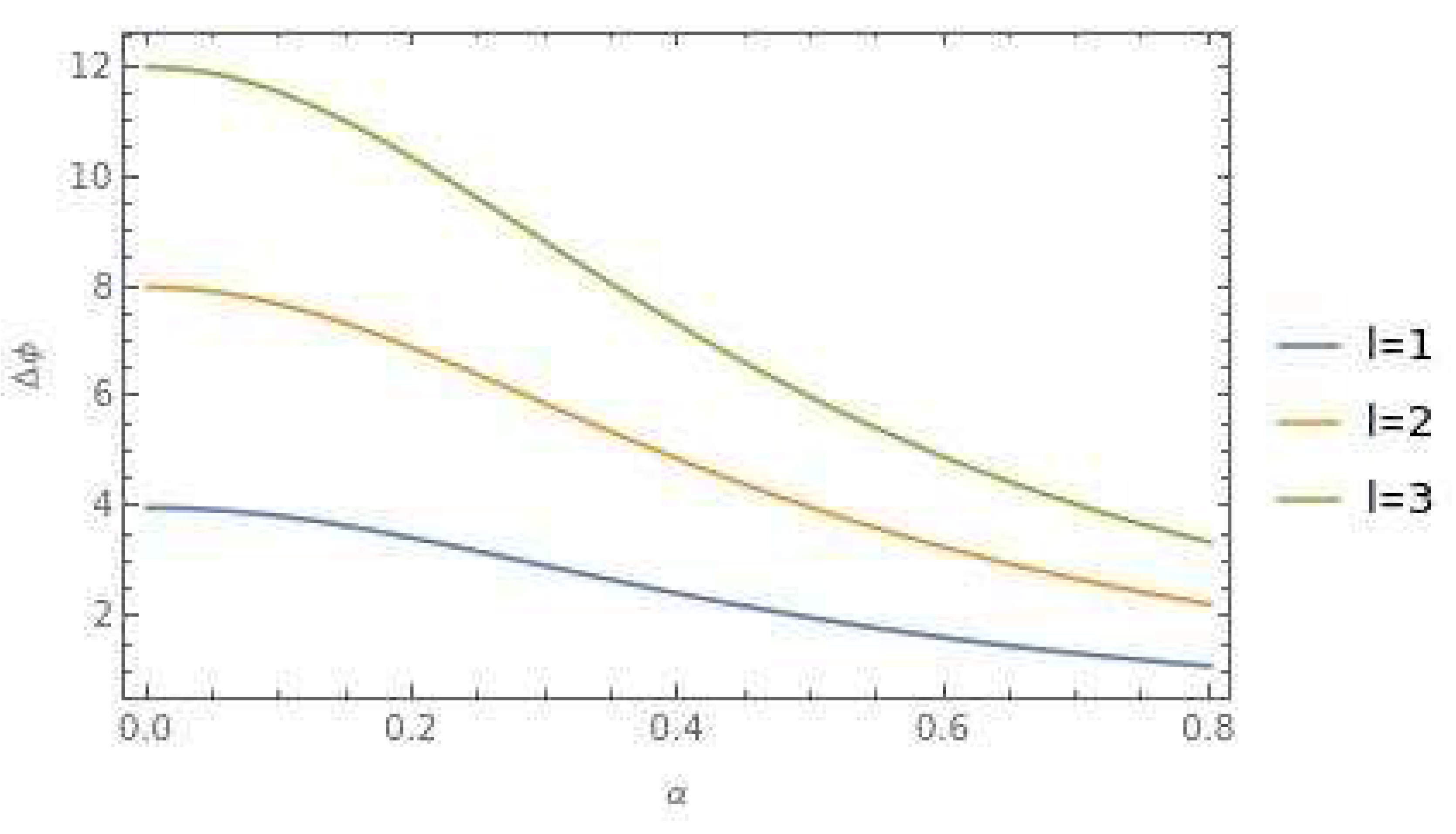
In Figure 3, we further explore the deflection angle by plotting it for various values of the screw dislocation parameter β, while maintaining fixed values for "l" and "a" at 1.
These plotted figures provide valuable insights into the behavior of the deflection angle of photon rays and/or time-like geodesics under the influence of cosmic strings and screw dislocations. They illustrate the dependency of the deflection angle on the parameters α and β, enabling a better understanding of the effects of these topological defect parameters on the geodesic paths in the curved space-time background.

2.2. Cosmic String Space-Time with Spiral Dislocation

In this part, we consider geometry of space-time defined by the following line-element [76,78]
d s 2 = − c 2 d t 2 + d r + β d φ 2 + α 2 r 2 d φ 2 + d z 2 = − c 2 d t 2 + d r 2 + α 2 r 2 + β 2 d φ 2 + 2 β   d r   d φ + d z 2
For the time-like or light-like geodesics, using the space-time (19), we obtain
− c 2 + r ˙ 2 + φ ˙ 2 α 2 r 2 + β 2 + 2   β   r ˙   φ ˙ + z ˙ 2 = ε
Let us consider r= a (constant), z ˙ = v , then we get,
− c 2 + φ ˙ 2 α 2 a 2 + β 2 + v 2 = ε   ⇒ α 2 a 2 + β 2 φ ˙ 2 = ε + c 2 1 − v 2 c 2
⇒ φ ˙ 2 = ε + c 2 γ 2 α 2 a 2 + β 2 ,   where   1 γ 2 = 1 − v 2 c 2
Let as consider the solution of the form
φ = A t
Therefore, φ ˙ = A From Equation (21), we obtain the constant A as follows:
A 2 = ε α 2 a 2 + β 2 + c 2 γ 2 α 2 a 2 + β 2
Therefore, from Equation (22), we obtain the angular coordinate as follows
φ t = ε α 2 a 2 + β 2 + c 2 γ 2 α 2 a 2 + β 2 1 / 2 t
Defining ∆ t = l / c . Therefore, the deflection angle will become
∆ φ = ε α 2 a 2 + β 2   + c 2 γ 2   α 2 a 2 + β 2   1 / 2 ∆ t
∆ φ = 1 c   ε α 2 a 2 + β 2   + c 2 γ 2 1 α 2 a 2 + β 2   1 / 2 l
For photon light, we have
v ≈ c ,   1 γ 2 → 0 ,   ε = 0 .
Therefore, the deflection angle from Equation (25) will be
∆ φ = 0
For time-like geodesics, we have
v < c ,   ε = − 1
Therefore, the deflection angle of time-like geodesics will be
∆ φ t i m e − l i k e = 1 c − 1 ( α 2   a 2 + β 2 )   + c 2 γ 2 1   α 2   a 2 + β 2   1 / 2 l = l 1 γ 2 − 1 c 2 α 2   a 2 + β 2
Indeed, based on the cosmic string metric presented in Equation (19), we can infer that the deflection angle of photon light caused by the spiral dislocation is zero. This result suggests that spiral dislocations, as described by the given metric, do not induce any bending or deflection in the path of photon rays.
However, for time-like geodesics, the situation is different. The deflection angle for time-like geodesics, as derived from Equation (29), is non-zero and depends on several factors. It is influenced by the parameter β, which represents the screw dislocation, as well as the cosmic string parameter “α”.Additionally, the deflection angle changes with variations in the length parameter "l".
This outcome implies that time-like geodesics are indeed affected by the presence of cosmic strings and screw dislocations, leading to deflection in their trajectory. The deflection angle's dependence on β, α, and l highlights the complex interplay between these parameters in determining the path followed by time-like geodesics in the curved space-time background described by the cosmic string metric.

2.3. Cosmic String Space-Time with Spacelike Dislocation

Let us consider a metric of the cosmic string space time with space-like dislocation by the following line-element [79,80,81,82]
d s 2 = − c 2 d t 2 + d r 2 + α 2 r 2 d φ 2 + d z − χ   d φ 2 = − c 2 d t 2 + d r 2 + α 2 r 2 + χ 2 d φ 2 − 2   χ   d z   d φ + d z 2
For light-like or time-like geodesics, we have
− c 2 + r ˙ 2 + α 2 r 2 + χ 2 φ 2 ˙ − 2   χ   z   ˙ φ ˙ + z ˙ = ε
Let the motion of light-like or time-like geodesics is in the direction of z-axis. We can write
r = a ;   z ˙ = v .
Therefore, we get the equation of   φ from (4.4)
α 2 a 2 + χ 2 φ ˙ 2 − 2   χ   v   φ ˙ + v 2 − c 2 = ε
Suppose the solution of the above equation is of the form
φ = A   t
Substituting this into the Equation (33), we get the following quadratic equation for the constant A given by
α 2 a 2 + χ 2 A 2 − 2   χ   v A + v 2 − c 2 = ε
The solution will be
A = χ   v ± χ 2   v 2 − α 2 a 2 + χ 2 ( v 2 − c 2 − ε ) ( α 2 a 2 + χ 2 )
For photon light, we use the approximation   v ≈ c ,   ε =0, we get
A = 2   χ   c ( α 2 a 2 + χ 2 ) .
This gives the function φ in the following form
φ t ≈ 2   χ   c ( α 2 a 2 + χ 2 ) t .
We choose the distance between two points in the z-axis, z 2 − z 1 = ∆ z = l then, ∆ t = l c , c being the velocity of light. For light-like geodesics, we obtain the deflection angle
∆ φ ≈ 2   χ ( α 2 a 2 + χ 2 ) l .
For time-like geodesics, ε = − 1 . Therefore, from Equation (36), we obtain
A = χ v ± χ 2   v 2 − α 2 a 2 + χ 2 ( v 2 − c 2 + 1 ) ( α 2 a 2 + χ 2 )
This gives us the function φ in the following form
φ t ≈ χ v ± χ 2   v 2 − α 2 a 2 + χ 2 ( v 2 − c 2 + 1 ) ( α 2 a 2 + χ 2 ) t
Following the previous procedure, we obtain the deflection angle of massive objects
∆ φ ≈     χ v ± χ 2   v 2 − α 2 a 2 + χ 2 ( v 2 − c 2 + 1 ) α 2 a 2 + χ 2   l c
Absolutely, if we consider spacelike dislocation as defined by the metric presented in Equation (30), the deflection angle experienced by both light rays and time-like geodesics can be described by Equations (39) and (42), respectively. In this scenario, the deflection angles are determined by the spacelike dislocation parameter χ and the cosmic string parameter α.
For light rays, the deflection angle is expressed by Equation (39), which incorporates the spacelike dislocation parameter χ and the cosmic string parameter α. This deflection angle quantifies how the presence of spacelike dislocation modifies the path of photon rays.
Similarly, for time-like geodesics, the deflection angle is given by Equation (42). This angle is also influenced by the spacelike dislocation parameter χ and the cosmic string parameter α. It illustrates how the spacelike dislocation affects the trajectory of time-like geodesics in the curved space-time background established by the cosmic string metric.
By analyzing these equations, we gain a comprehensive understanding of the intricate dependencies between the deflection angles and the spacelike dislocation parameter χ and cosmic string parameter α. These results provide valuable insights into the behavior of light rays and time-like geodesics in the presence of spacelike dislocation, enhancing our understanding of the effects of these parameters on the geodesic motion within the curved space-time geometry.
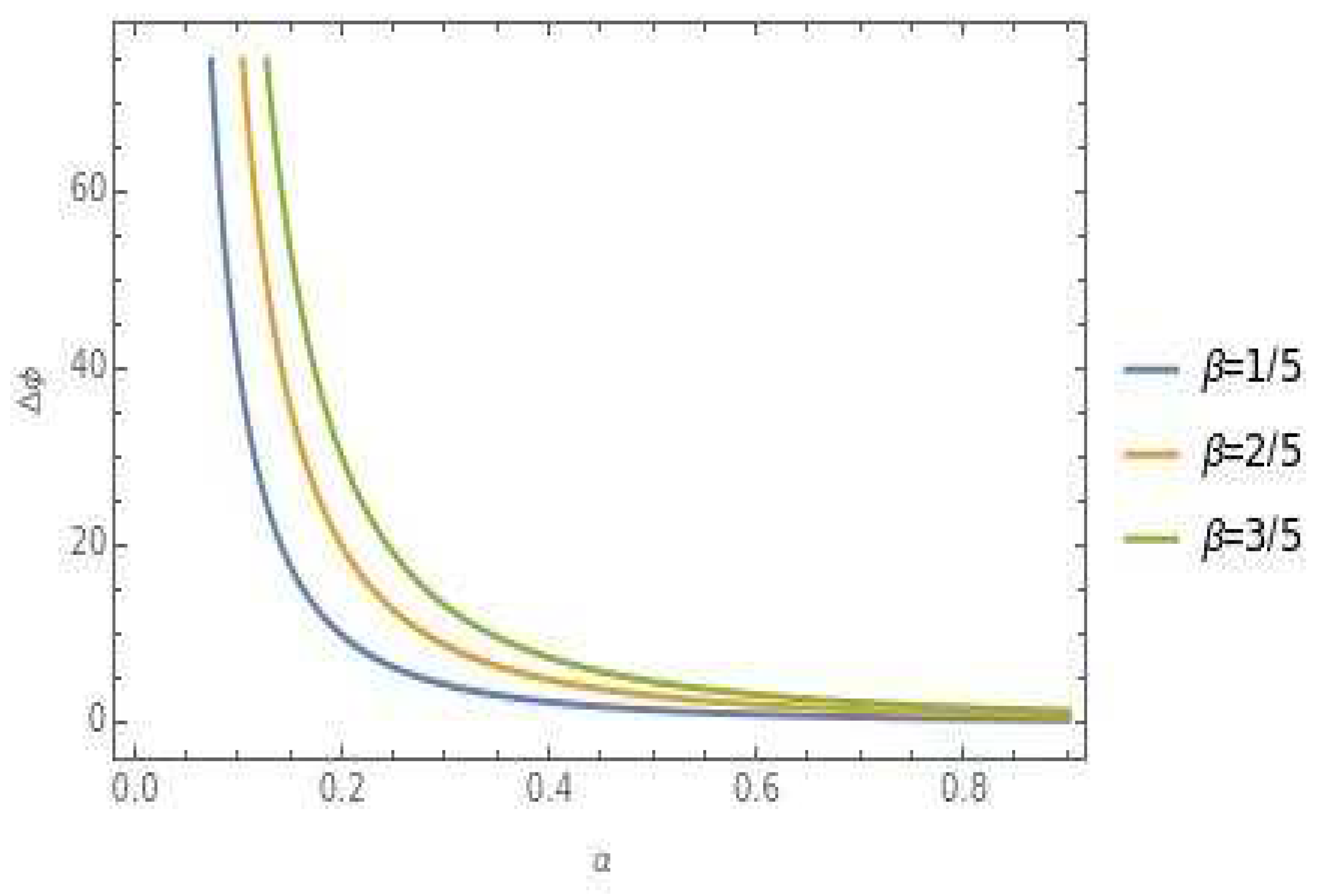
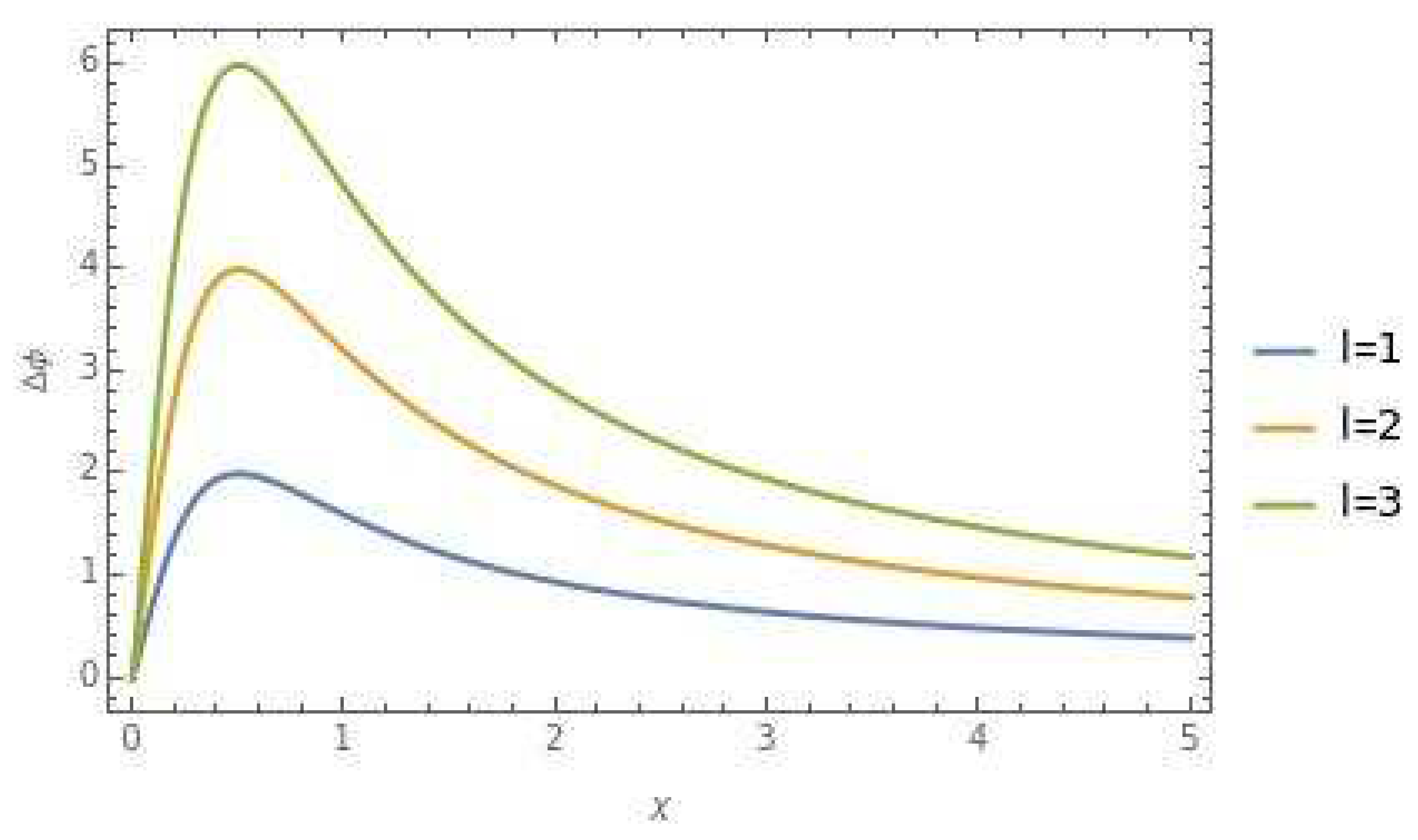
In Figure 4 and Figure 5, we showcase the plotted deflection angle for photon rays, as given by Equation (39), while varying the cosmic string parameter α. These figures provide a visual representation of how the deflection angle changes with different values of α, allowing us to observe the relationship between the cosmic string parameter and the deflection angle experienced by photon rays.
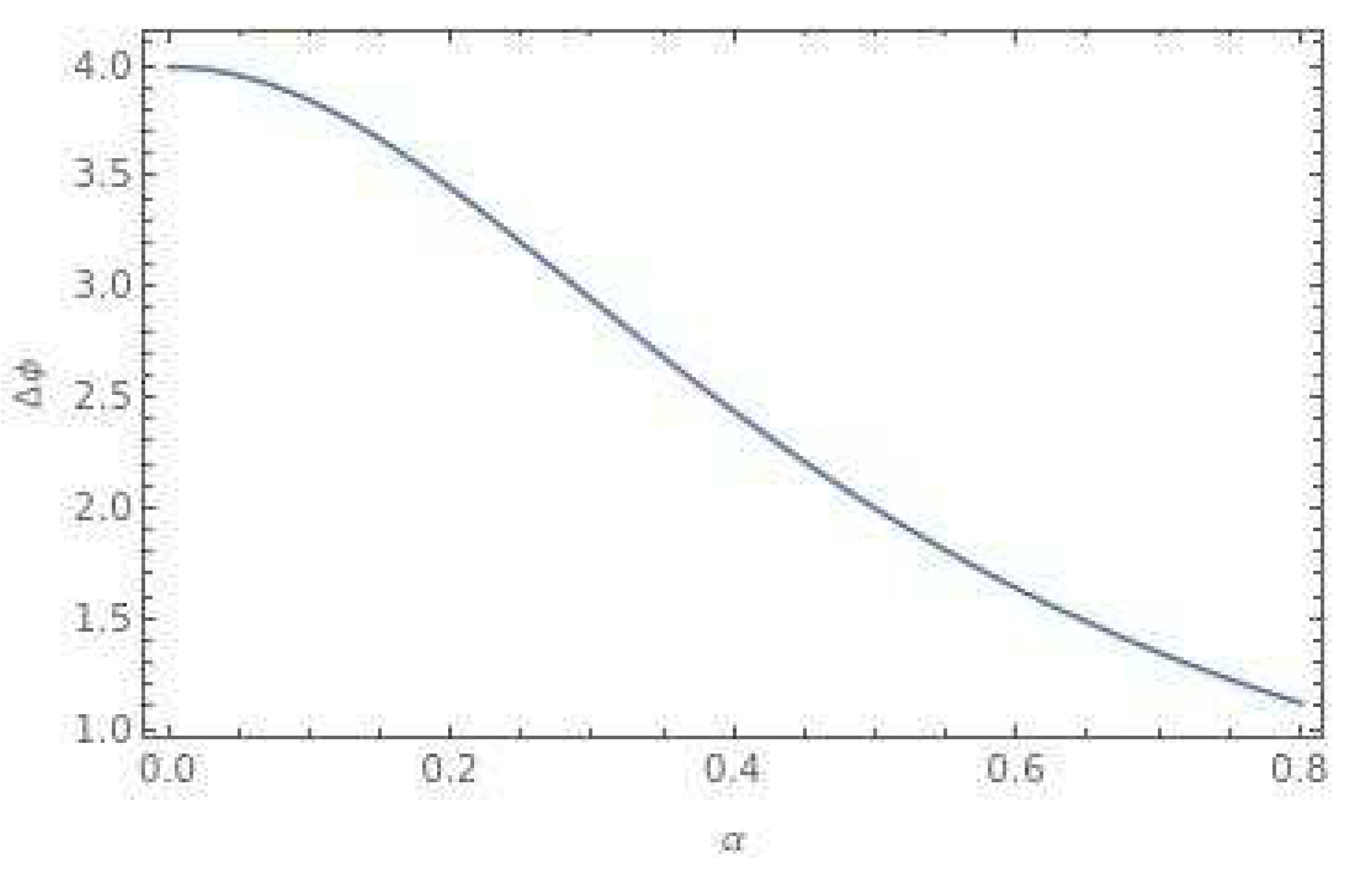
Furthermore, in Figure 6, we present the plotted deflection angle for photon rays as a function of the cosmic dislocation parameter χ, while keeping the cosmic string parameter fixed at α=0.5. This plot helps us understand how the deflection angle changes with variations in the cosmic dislocation parameter, while the cosmic string parameter remains constant.
In Figure 7, we investigate the deflection angle for photon rays with different values of the length parameter l, while maintaining a fixed cosmic string parameter α. This plot illustrates the impact of varying the length parameter on the deflection angle of photon rays.
By analyzing these plotted figures, we gain valuable insights into how the deflection angle of photon rays is influenced by changes in the cosmic string parameter α, the cosmic dislocation parameter χ, and the length parameter l. These plots offer a visual representation of the complex relationships between these parameters and the deflection of photon rays, enhancing our understanding of the effects of cosmic strings and spacelike dislocations on the bending of light rays in the curved space-time background.

3. Discussions

In this comprehensive analysis, our focus has been on examining the deflection of time-like and null geodesics within the framework of topological defects formed by cosmic string space-times, incorporating screw dislocation, spiral dislocation, and spacelike dislocation.
Throughout our investigation, we successfully derived the deflection angle for both photon rays and time-like geodesics. Notably, we observed that the deflection angle is significantly affected by three crucial parameters: the cosmic string parameter α, the torsion (screw) parameter β, and the spacelike dislocation parameter χ. These parameters play a pivotal role in influencing the deflection angle when dealing with either massless particles (photon rays) or massive objects traveling parallel to the z-axis.
Our analysis reveals the intricate relationship between these parameters and the deflection of geodesics, providing valuable insights into how cosmic string space-times and the presence of topological defects impact the trajectory of light rays and particles. By understanding the effects of α, β, and χ on geodesic motion, we gain a deeper comprehension of the interplay between curvature in space-time and the influence of these defect parameters. These findings contribute significantly to our understanding of the underlying physics involved in the deflection of geodesics in the presence of cosmic strings and topological defects, enriching our knowledge of the universe's early evolution and its impact on light and matter.

Author Contributions

M. A. Choudhury: Writing (Section 2.1), A. Kayum: Writing (Section 2.2), M. Hassan: Writing (Section 2.3), F. Ahmed: Supervision, Formal analysis, Investigation, Conceptualization, Writing-original & draft, Reviewing.

Funding

This research received no external funding.

Data Availability Statement

No new data generated or analyzed in this work.

Conflicts of Interest

There are no conflicts of interest.

References

  1. B. F. Schutz, A First Course in General Relativity, Cambridge University Press, Cambridge (2015).
  2. W. Rindler, Relativity: Special, General, and Cosmological, Oxford University Press, Oxford (2006).
  3. J. G. Williams and D. E. Vincent, General Relativity and Relativistic Astrophysics, World Scientific Publishing (1992).
  4. S. Carroll, Space-time and Geometry: An Introduction to General Relativity, Cambridge University Press, Cambridge (2019).
  5. Robert, M. Wald, General Relativity, University of Chicago Press, UK (1984).
  6. R. K. Sachs and H.- H. Wu, General Relativity for Mathematicians, Springer (2012).
  7. K. Schwarzschild, arXiv: physics/9905030.
  8. R. P. Kerr, Phys. Rev. Lett. 11 (5): 237–238 (1963).
  9. L. Bergström and A. Goobar, Cosmology and Particle Astrophysics, Springer Berlin, Heidelberg (2006).
  10. G. F. R. Ellis and van H. Elst, arXiv: gr-qc/9812046.
  11. A. S. Eddington, Mathematical Theory of Relativity, Cambridge University Press, Cambridge (1922).
  12. C. R. Keeton, C. S. C. R. Keeton, C. S. Kochanek and E. E. Falco, Astrophys. J. 509, 561 (1998).
  13. A. Bhadra, Phys. Rev. D 67, 103009 (2003).
  14. R. Whisker, Phys. Rev. D 71, 064004 (2005).
  15. S. B. Chen and J. I. Jing, Phys. Rev. D 80, 024036 (2009).
  16. K. K. Nandi, Y. Z. K. K. Nandi, Y. Z. Zhang and A. V. Zakharov, Phys. Rev. D 74, 024020 (2006).
  17. E. F. Eiroa, G. E. E. F. Eiroa, G. E. Romero and D. F. Torres, Phys. Rev. D 66, 024010 (2002).
  18. S. Mao and B. Paczynski, Astrophys. J. 374, L37 (1991).
  19. H. Hoekstra, H. K. C. H. Hoekstra, H. K. C. Yee and M. D. Gladders, Astrophys. J. 606, 67 (2004).
  20. K. S. Virbhadra and G. F. R. Ellis, Phys. Rev. D 65, 103004 (2002).
  21. F. Ahmed, Adv. High Energy Physics 2017, 3587018 (2017).
  22. F. Ahmed, Progress of Theoretical and Experimental Physics 2017, 083E03 (2017).
  23. F. Ahmed and F. Rahaman, Adv. High Energy Physics 2018, 7839619 (2018).
  24. F. Ahmed and F. Rahaman, Eur. Phys. J. A 54, 52 (2018).
  25. K. S. Virbhadra and G. F. R. Ellis, Phys. Rev. D 62, 084003 (2000).
  26. E. Gallo and O. M. Moreschi, Phys. Rev. D 83, 083007 (2011).
  27. G. Crisnejo and E. Gallo, Phys. Rev. D 97, 084010 (2018).
  28. M. Sharif and S. Iftikhar, Astrophys. Space Sci. 357, 85 (2015).
  29. W. Javed, R. W. Javed, R. Babar and A. Ovgun, Phys. Rev. D 99, 084012 (2019).
  30. G. W. Gibbons and M. C. Werner, Class. Quant. Grav. 25, 235009 (2008).
  31. M. C. Werner, Gen Relativity Grav. 44, 3047 (2012).
  32. A. Ishihara, Y. A. Ishihara, Y. Suzuki, T. Ono, T. Kitamura and H. Asada, Phys. Rev. D 94, 084015 (2016).
  33. G. Crisnejo and E. Gallo, Phys. Rev. D 97, 124016 (2018).
  34. K. Jusufi, M. C. K. Jusufi, M. C. Werner, A. Banerjee and A. Ovgün, Phys. Rev. D 95, 104012 (2017).
  35. I. Sakalli and A. Ovgun, EPL 118, 60006 (2017).
  36. K. Jusufi and A. Ovgun, Phys. Rev. D 97, 024042 (2018).
  37. T. Ono, A. T. Ono, A. Ishihara and H. Asada, Phys. Rev. D 96, 104037 (2017).
  38. K. Jusufi, A. K. Jusufi, A. Ovgun and A. Banerjee, Phys. Rev. 0840; 96. [Google Scholar]
  39. A. Ovgun, G. A. Ovgun, G. Gyulchev and K. [CrossRef]
  40. K. Jusufi, I. K. Jusufi, I. Sakalli and A. Ovgun, Phys. Rev. D 96, 024040 (2017).
  41. H. Arakida, Gen. Rel. Grav. 50, 48 (2018).
  42. K. Jusufi and A. arXiv:1707.02824 [gr-qc].
  43. T. Ono, A. T. Ono, A. Ishihara and H. Asada, Phys. Rev. D 98, 044047 (2018).
  44. K. Jusufi and A. Ovgun,, Phys. Rev. D 97, 064030 (2018).
  45. K. Jusufi, A. K. Jusufi, A. Ovgun, J. Saavedra, Y. Vasquez and P. A. Gonzalez, Phys. Rev. D 97, 124024 (2018).
  46. A. Ovgun, Phys. Rev. D 98, 044033 (2018).
  47. A. Ovgun, K. A. Ovgun, K. Jusufi and I. Sakalli, Ann. Phys. 399, 193 (2018).
  48. K. Jusufi, A. K. Jusufi, A. Ovgun, A. Banerjee and I. Sakalli, Eur. Phys. J. Plus (2019) 134: 428.
  49. A. Övgun, http://arxiv.org/abs/1806.05549.
  50. G. Crisnejo, E. G. Crisnejo, E. Gallo and A. Rogers, http://arxiv.org/abs/1807.00724.
  51. A. Övgun, I. A. Övgun, I. Sakalli and J. Saavedra, http://arxiv.org/abs/1806.06453.
  52. A. Övgun, I. A. Övgun, I. Sakalli and J. Saavedra, JCAP 1810, 041 (2018).
  53. T. Ono, A. T. Ono, A. Ishihara and H. Asada, http://arxiv.org/abs/1811.01739.
  54. A. Övgün, G. A. Övgün, G. Gyulchev, K. Jusufi, Ann. Phys. 406 (2019) 152.
  55. T. Müller, Phys. Rev. D 77, 044043 (2008).
  56. V. Perlick, Phys. Rev. D 69, 064017 (2004).
  57. N. Tsukamoto, Phys. Rev. D 105, 064013 (2022); Phys. Rev. D 104, 124016 (2021); Phys. Rev. D 104, 064022 (2021); Phys. Rev. D 103, 024033 (2021); Phys. Rev. D 102, 104029 (2020); Phys. Rev. D 101, 104021 (2020); N. Tsukamoto, T. Kitamura, K Nakajima, H Asada, Phys. Rev. D 90, 064043 (2014); N. Tsukamoto, T. Kitamura, K. Nakajima and H. Asada, Phys. Rev. D 90, 064043 (2014); Phys. Rev. D 95, 084021 (2017); Phys. Rev. D 97, 084051 (2018); EPJC 83, 284 (2023).
  58. K. Nakajima and H. Asada, Phys. Rev. D 85, 107501 (2012).
  59. K. Jusufi, Phys. Rev. D 98, 044016 (2018).
  60. H. Aounallah, A. R. H. Aounallah, A. R. Soares and R. L. L. Vitória, EPJC 80, 447 (2020).
  61. F. Ahmed, EPL 142, 39002 (2023).
  62. I. N. Huda and H. S. Ramadhan, J. Phys.: Conf. Ser. 1816, 012021 (2021).
  63. A. R. Soares, R. L. L. A. R. Soares, R. L. L. Vitoria and C. F. S. arXiv:2305.11105[gr-qc].
  64. F. Ahmed, https://arxiv.org/abs/2306.12455.
  65. F. Abe, ApJ 725 (2010) 787.
  66. C.-M. Yoo, T. C.-M. Yoo, T. Harada, N. Tsukamoto, Phys. Rev. D 87, 084045 (2013).
  67. N.Tsukamoto, Phys. Rev. D 94, 124001 (2016).
  68. N. Tsukamoto, T. N. Tsukamoto, T. Harada, Phys. Rev. D 95, 024030 (2017).
  69. R. Shaikh, P. R. Shaikh, P. Banerjee, S. Paul, T. Sarkar, JCAP 07 (2019) 028.
  70. T. W. B. Kibble, J. T. W. B. Kibble, J. Phys. A: Meth. Gen. 9, 1387 (1976).
  71. T. W. B. Kibble, Phys. Rep. 67, 183 (1980).
  72. A. Vilekin and E. P. S. Shellard, Strings and Other Topological Defects, Cambridge University Press, Cambridge (1994).
  73. M. [CrossRef]
  74. H. Kleinert, Gauge Fields in Condensed Matter, vol. 2, World Scientific Publishing Co, Singapore, 1989.
  75. M. O. Katanaev and I. V. Volovich, Ann. Phys. (NY) 216, 1 (1992).
  76. K. C. Valanis and V. P. Panoskaltsis, Acta Mech. 175, 77 (2005).
  77. C. Furtado and F. Moraes, EPL 45, 279 (1999).
  78. K. Bakke and C. Furtado, Phys. Rev. A 87, 012130 (2013).
  79. R. A. Puntigam and H. H. Soleng, Classical and Quantum Gravity 14, 1129 (1997).
  80. V. B. Bezerra, J. V. B. Bezerra, J. Math. Phys. 38, 2553 (1997).
  81. F. Ahmed, Advances in High Energy Physics 2020, 5691025 (2020).
  82. F. Ahmed, Advances in High Energy Physics 2020, 4832010 (2020).
Preprints 80239 g001
Figure 1. The deflection angle of photon light with cosmic string parameter keeping fixed l . Here β = 0.5 , l = 1 = a .
Figure 1. The deflection angle of photon light with cosmic string parameter keeping fixed l . Here β = 0.5 , l = 1 = a .
Preprints 80239 g001
Preprints 80239 g002
Figure 2. The deflection angle of photon light with cosmic string parameter for fixed value of l . Here β = 0.5 , a = 1 .
Figure 2. The deflection angle of photon light with cosmic string parameter for fixed value of l . Here β = 0.5 , a = 1 .
Preprints 80239 g002
Preprints 80239 g003
Figure 3. The deflection angle of photon light with cosmic string parameter for different values of screw dislocation parameter β . Here l = 1 = a .
Figure 3. The deflection angle of photon light with cosmic string parameter for different values of screw dislocation parameter β . Here l = 1 = a .
Preprints 80239 g003
Preprints 80239 g004
Figure 4. The deflection angle of photon light with cosmic string parameter α for l = 1 = a , χ = 0.5 .
Figure 4. The deflection angle of photon light with cosmic string parameter α for l = 1 = a , χ = 0.5 .
Preprints 80239 g004
Preprints 80239 g005
Figure 5. The deflection angle of photon light with cosmic string parameter α for different l with χ = 0.5 , a = 1 .
Figure 5. The deflection angle of photon light with cosmic string parameter α for different l with χ = 0.5 , a = 1 .
Preprints 80239 g005
Preprints 80239 g006
Figure 6. The deflection angle of photon light with cosmic dislocation parameter χ for α = 0.5 , l = 1 = a .
Figure 6. The deflection angle of photon light with cosmic dislocation parameter χ for α = 0.5 , l = 1 = a .
Preprints 80239 g006
Preprints 80239 g007
Figure 7. The deflection angle of photon light with cosmic dislocation parameter χ for different l with α = 0.5 , a = 1 .
Figure 7. The deflection angle of photon light with cosmic dislocation parameter χ for different l with α = 0.5 , a = 1 .
Preprints 80239 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated