Prerpints.org logo
Preprint
Article

Research on Application of Fractional Calculus Operator in Image Underlying Processing

Altmetrics

Downloads

132

Views

49

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 July 2023

Posted:

20 July 2023

You are already at the latest version

Alerts
Abstract
The theory of fractional calculus extends the order of classical integer calculus from integer to non-integer. As a new engineering application tool, it has made many important research achievements in many fields, including image processing. This paper mainly studies the application of fractional calculus theory in image enhancement and denoising, including the basic theory of fractional calculus and its amplitude frequency characteristics, the application of fractional differential operator in image enhancement, and the application of fractional integral operator in image denoising. The experimental results show that the fractional calculus theory has more special advantages in image enhancement and denoising. Compared with the existing integer order image enhancement operators, the fractional differential operator can more effectively enhance the "weak edge" and "strong texture" details of the image. The fractional order integral image denoising operator can not only improve the signal-to-noise ratio of the image compared to traditional denoising methods, but also better preserve detailed information such as edges and textures of the image.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The fractional calculus theory has been born for about three hundred years, but in this long period of time, the fractional calculus theory is only the analysis and derivation of pure mathematical theory by mathematicians, and engineering technicians are unfamiliar with it[1,2]. It was not until Mandelbrot first proposed the fractal theory [3,4,5] and described Riemann-Liouville fractional calculus as Brownian motion in fractal media that fractional calculus was first applied to the field of engineering technology. Therefore, fractional calculus theory, as a mathematical description method for analyzing complex systems, gradually developed into a modeling tool for engineering technology. In recent decades, many scholars at home and abroad have found that fractional calculus operators have memory and nonlocality, which is very suitable for describing materials with memory and genetic properties in the real world. Therefore, fractional calculus theory has been increasingly applied in basic science and engineering and other fields, and its practical value has also been initially reflected [6]. In recent ten years, many scholars at home and abroad have found that fractional calculus has a broad application prospect in the field of signal analysis and processing. They have applied the theory of fractional calculus to traditional memristor elements and proposed different types of fractional impedance in natural realization forms [7,8,9]. In recent years, scholars at home and abroad have tried to integrate fractional calculus theory with classical swarm intelligence algorithm, and proposed fractional neural network algorithm and fractional ant colony algorithm based on Fractional Steepest Descent Approach. These new algorithms have achieved good application results [10,11,12,13,14]. The application of fractional calculus theory in image processing originates from Pu Yifei and other researchers who found that fractional differentiation has such characteristics as "nonlocality" and "Weak derivative". They tentatively applied fractional calculus theory to digital image underlying processing and achieved good simulation results, and proposed six basic fractional differential operator for digital image processing, The application of fractional calculus theory in image processing is gradually emerging [15] [16].Meriem Hacini built a bi-directional fractional-order derivative mask for image processing applications[17]. It has been applied in edge detection and de-noising problems using real and synthetic images by the proposed method used the gradient computation properties. Xuefeng Zhang proposed image enhancement method based on rough set and fractional order differentiator [18]. In the image enhancement process, 2D Fourier transform is employed to turn gray levels into a gradient, then an adaptive fractional order differential operator based on entropy is proposed to enhance the information of images. Meng-Meng Li proposed a novel active contour method for noisy image segmentation using adaptive fractional order differentiation [19], and the fractional differentiation with an adaptively defined order is incorporated into the fitting term to deal with noise during the evolution of curves. Since then many scholars have proposed many new image processing methods based on fractional calculus theory and partial differential equations [20,21,22]. Jian Bai proposed a new variational model for image denoising and decomposition using the fractional-order bounded variation space to capture cartoon patterns [23]. Through the combination of fractional calculus theory and partial differential equation theory, A. Abirami studied the variable-order fractional diffusion model for medical image denoising using the Caputo finite difference scheme for the proposed problem [24]. Based on the PU operator theory, many scholars have expanded and improved it, and proposed a new classical image processing model incorporating fractional calculus theory [25,26,27,28,29], including image enhancement methods based on fractional Contrast Limited Adaptive Histogram Equalization, image denoising methods based on fractional order NLM, and image denoising methods based on fractional order BM3D.
This paper is mainly about the application of fractional calculus theory in digital image processing. The remaining structure of this article is as follows. Section 2 introduces mathematical and physical knowledge of fractional calculus theory. Section 3 introduces the construction of fractional order differential operator and the simulation contrast experiment in image enhancement. Section 4 proposes the construction of fractional order integral operators and simulation experiments in image denoising. Finally, the conclusions are given in Section6..

2. Basic Theory of Fractional Calculus

In this section, we briefly introduce three contents. First, three basic definitions of fractional calculus theory and their practical scenarios. Second, amplitude frequency characteristics of fractional differential operator and fractional integral operator. At last, the amplitude frequency characteristics of fractional calculus of common signals.

2.1. Fractional Calculus Theory

Different definitions of fractional calculus can be obtained by analyzing the problem from different application angles. Up to now, there is still no unified time domain definition expression of fractional calculus. Among the numerous definitions, there are mainly three classical definitions of fractional calculus, which are Grümwald-Letnikov definition, Riemann-Liouville definition and Capotu definition. They are respectively Equation (1), Equation (2), and Equation (3) [1] [2].
  • Grümwald-Letnikov of fractional calculus is defined as follows,
D a G t v f ( x ) = lim h → 0 h v ∑ j = 0 t − a h Γ ( v + j ) j ! Γ ( v ) f ( x − j h ) v ∈ R
  • The definition of Riemann-Liouville for fractional order integration and Riemann Liouville for fractional order differentiation are as follows,
{ D a R t − v f ( x ) = − 1 Γ （ v ） ∫ a t f ( y ) ( x − y ) 1 − v d y D a R t v f ( x ) = − 1 Γ （ n − v ） d n d t n ∫ a t f ( y ) ( x − y ) 1 + v − n d y
  • Caputo of fractional calculus is defined as follows,
D a C t v f ( x ) = D a R t v f ( x ) − ∑ j = 0 m − 1 f ( j ) ( a ) Γ ( j − v + 1 ) ( t − a ) k − v
The three definitions of fractional calculus are closely related and can be transformed under certain conditions. Both Riemann Liouville definition of fractional calculus and Caputo definition of fractional calculus are improvements to Grümwald-Letnikov definition of fractional calculus. Grümwald-Letnikov definition of fractional calculus can be converted into convolution operation form in numerical implementation, so it is very suitable for application in signal processing. The Riemann- Liouville definition of fractional calculus is mainly used to calculate the analytical solutions of some relatively simple functions. The Caputo definition of fractional calculus is applicable to the analysis of the initial boundary value problems of fractional differential equations, so it is very suitable for application in the engineering field.

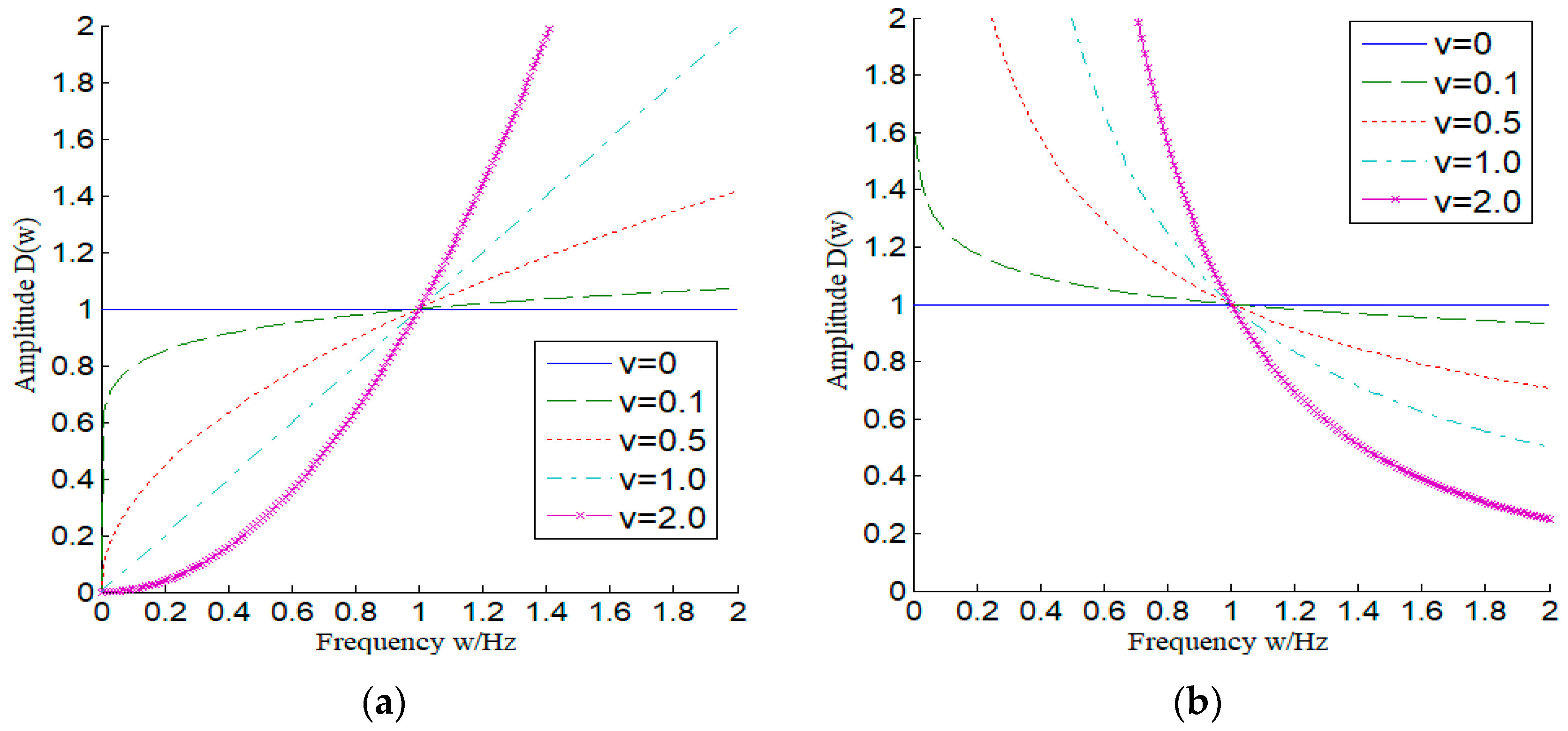
2.2. Amplitude Frequency Characteristics of Fractional Calculus Operators

2.2.1. Fractional Order Differential Operator

Let the square integrable energy signal  f ( x ) ∈ L 2 ( R ) , whose Fourier transform is  f ( ω ) ∧ = ∫ R f ( x ) e − i ω x d x . The n-th derivative of the signal  f ( x )  is  f n ( x )  ( n ∈ Z + ), and according to the properties of the Fourier transform, Equation (4) can be obtained.
D n f ( x ) ⇔ F T ( D f ∧ ) n ( ω ) = ( i ω ) n ⋅ f ( ω ) ∧ = d n ( ω ) ∧ f ( ω ) ∧
By extending the positive integer n to the positive real number v ( v ∈ R + ), the fractional order derivative of the signal  f ( x )  can be obtained as  f v ( x ) . According to the properties of fractional order Fourier transform [30,31,32], Equation (5) can be obtained, where  d v ( ω ) ∧ can be further expanded to obtain Equation (6).
D v f ( x ) ⇔ F T ( D f ∧ ) v ( ω ) = ( i ω ) v ⋅ f ( ω ) ∧ = d   v ( ω ) ∧ ⋅ f ( ω ) ∧
{ d v ( ω ) ∧ = ( i ω ) v = α v ( w ) ⋅ ∧ e i θ v ( ω ) α v ( w ) ∧ = | ω | v , θ v ( ω ) ∧ = v π 2 sgn ( ω )
According to Equation (5) and Equation (6), the amplitude frequency characteristic curve of fractional order differential operator of one-dimensional signal can be obtained, as shown in Figure 1 (a). It can be seen from direct observation that firstly fractional order differential operator has a strengthening effect on medium and high frequency signals, and the amplitude of the strengthening increases nonlinearly and sharply with the increase of frequency and differential order. Secondly, fractional order differential order  v ∈ [ 0 , 1 ] , in the very low frequency part ( ω < 1 ) of the signal, the fractional order differential operator improves the amplitude of the signal to a certain extent, and the amplitude of the increase is slightly greater than that of the first and second order differential operator. In the end, the fractional order differential order v ∈ [ 0 , 1 ] , in the middle and high frequency part ( ω > 1 )of the signal, the fractional order differential operator improves the amplitude of the signal to a certain extent, but the amplitude of the increase is also significantly less than the first and second order differential operator. The above properties show that the fractional order differential operator has the property of "Weak derivative", and the fractional order differential operator not only strengthens the high frequency component of the signal, but also retains the very low frequency component of the signal nonlinearly. In addition, by analyzing the physical meaning of fractional calculus operator from the perspective of signal processing, it can be seen that fractional differential operator can be understood as generalized amplitude and phase modulation. Its amplitude changes exponentially with frequency in fractional order, and its phase is the generalized Hilbert change of frequency [15].

2.2.2. Fractional Order Integral Operator

Let the square integrable energy signal  f ( t ) ∈ L 2 ( R ) , whose Fourier transform is  f ( ω ) ∧ = ∫ R f ( t ) e − i ω t d t . When v ∈ R − , I = D − 1 and  v ' = − v can be assumed to obtain the Fourier transform form of the fractional order integral operator based on the G-L definition, as shown in Equation (7). Further expand the expression ( i ω ) v ' to obtain Equation (8).
I v ' f ( t ) ⇔ F T ( I f ∧ ) v ' ( ω ) = ( i ω ) v ' ⋅ f ( ω ) ∧ = i v ' ( ω ) ∧ ⋅ f ( ω ) ∧
{ i v ' ( ω ) ∧ = α v ' ( w ) ⋅ ∧ e i θ v ' ( ω ) α v ' ( w ) ∧ = | ω | − v ' , θ v ‘ ( ω ) ∧ = − v ' π 2 sgn ( ω )
According to Equations (7) and (8), the amplitude frequency characteristic curve of the fractional order integration operator for one-dimensional signals can be obtained, as shown in Figure 1 (b). By direct observation, it can be seen that firstly fractional order integration operators have an attenuation effect on both medium and high frequency signals, and they rapidly decay nonlinearly with increasing frequency and integration order. Secondly, fractional order integration order  v ' ∈ [ 0 , 1 ] , in the frequency ω < 1 region of the signal, the fractional order integration operator improves the amplitude of the signal to a certain extent, but the amplitude of the improvement is much smaller than that of the first and second order integration operators. At last, fractional order integration order  v ' ∈ [ 0 , 1 ] , in the frequency ω > 1 region of the signal, the fractional order integration operator weakens the amplitude of the signal to a certain extent, but the amplitude of the weakening is also significantly smaller than that of the first and second order integration operators. The above properties indicate that the fractional order integral operator not only weakens the high-frequency part of the signal, but also preserves the highest frequency part nonlinearly. The fractional order integration operator not only weakens the low-frequency part of the signal, but also preserves the lowest frequency part.

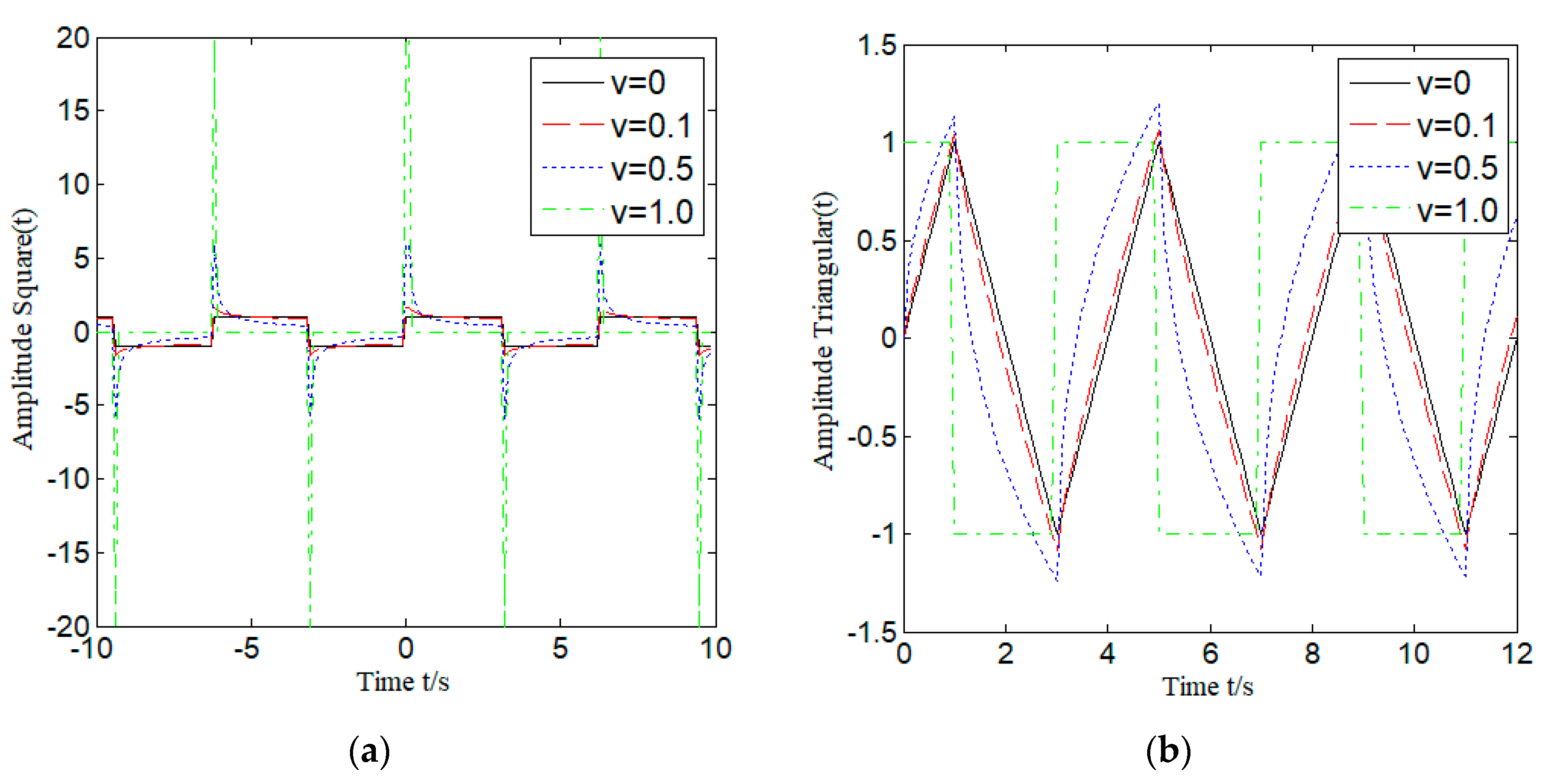
2.3. Fractional Order Calculus Processing and Analysis of Common Signals

Figure 2a–d show the amplitude frequency characteristic curve of fractional calculus after processing square wave signal (Equation 9), triangular signal (Equation 10), sinusoidal signal ( sin ( t ) ) and Gaussian signal (Equation 11) respectively. It can be seen from direct observation that firstly when the order increases from 0 to 1, the fractional calculus result of the square wave signal increases sharply at its sudden change, and the fractional calculus result of the triangular wave signal gradually becomes a rectangular wave. Secondly, when the fractional derivative order  v = 1 is used, it represents the first derivative of the sine and Gaussian signals, which can be understood that the direction of change of the signal at that point is the fastest. When the fractional order differential order  v ∈ [ 0 , 1 ] is reached, it indicates that the sine and Gaussian signals are fractional order continuous interpolation between the value of the function itself and the direction of the fastest change.
s q u a r e ( t ) = { 1 0 ≤ t ≤ T − 1 T < t ≤ 2 T
Triangular ( t ) = ∑ n = 1 ∞ 4 E n π 2 sin 2 ( n π 2 ) cos ( n ω t )
g a u s s   ( t ) = 1 2 π e − t 2 2
The above properties indicate that the integer order differential of the signal at stationary is zero, while the fractional order differential at stationary is not zero. The integer order differential value of the signal along the slope is constant, while the fractional order differential value of the signal along the slope is variable, but exhibits nonlinear changes over time. The characteristics of fractional calculus operator can make it retain some low-frequency weak texture information to a certain extent while strengthening the details of image high-frequency edges and textures. Therefore, the image processing method based on fractional calculus is better than the traditional image processing method based on integer order, which is not only conducive to extracting the edge and texture of the image, but also can retain the contour information of the image to a certain extent.

3. Research on the Application of Fractional Differential in Image Enhancement

In this section, we mainly introduce two contents, the characteristics of fractional differential operator of image signals and the image enhancement experiment of fractional order. The characteristic of fractional differential operator of image signal mainly analyzes the relationship between the differential order of fractional differential operator and the high pass strength of two-dimensional signal. The image enhancement experiment of fractional order differential operator mainly proves the advantages of fractional order differential image enhancement algorithm compared with integral order image enhancement operator after image processing.

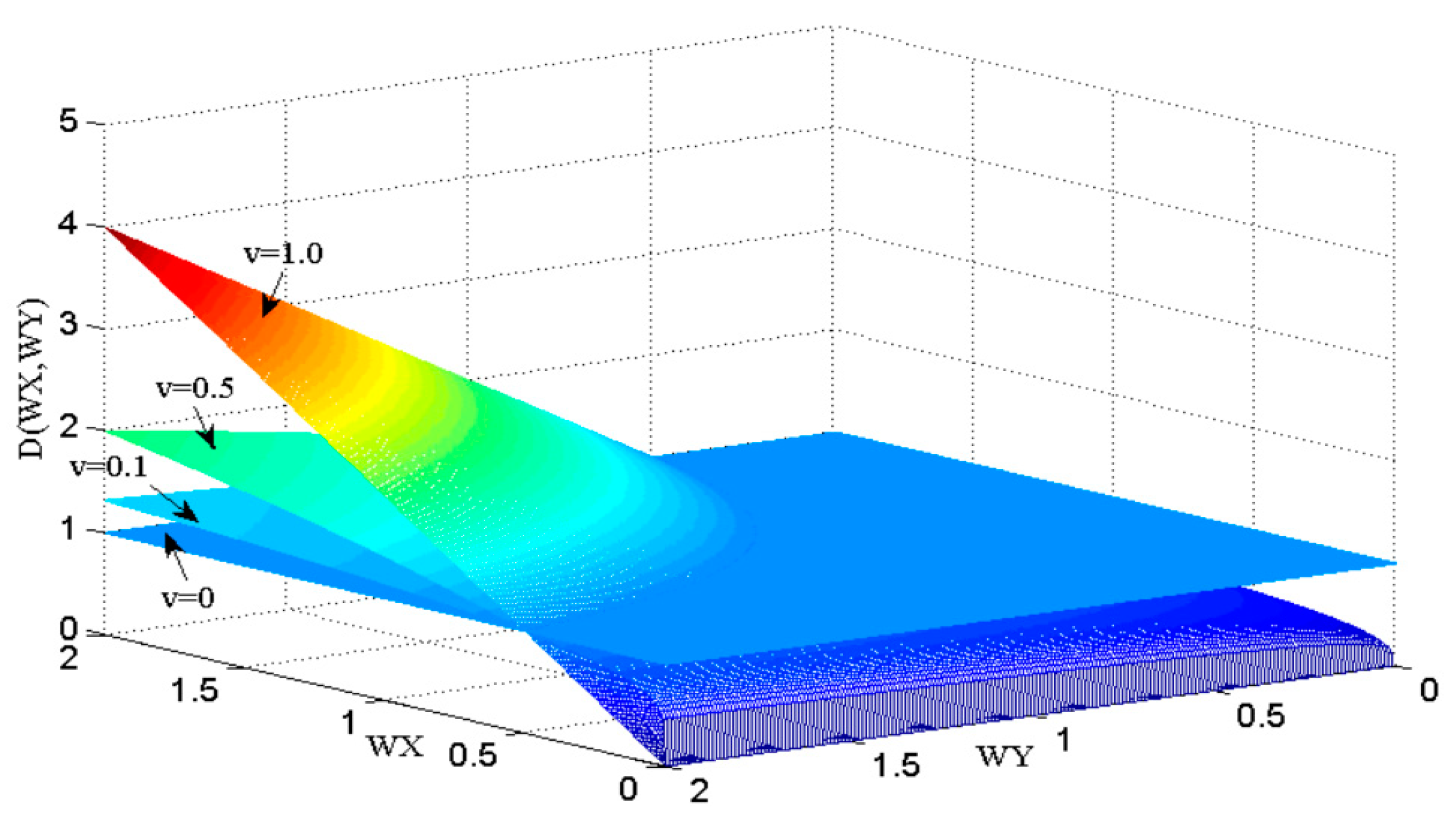
3.1. Amplitude Frequency Characteristics of Fractional Order Differential Image Enhancement Operators

Let the fractional order v derivative of the two-dimensional energy function  f ( x , y ) be  f v ( x , y ) ( v ∈ R + ). Because of the separability of the fractional Fourier transform, it can be considered that the fractional order differential filter of the two-dimensional energy function  f v ( x , y ) is separable. Therefore, the fractional order differential filter function of the two-dimensional energy function  f ( x , y ) can be obtained by expanding on the basis of Equation (5), as shown in Equation (12).
( D f ∧ ) v ( ω x , ω y ) = ω x v e i v π 2 sgn ⁡ ( ω x ) * ω y v e i v π 2 sgn ⁡ ( ω y )
The amplitude frequency characteristic surface of different order fractional differential operator of two-dimensional signals can be obtained from equation (12), as shown in Figure (3). The figure shows the amplitude frequency characteristic surface of fractional differential operator with order  v ∈ { 0 , 0.1 , 0.5 , 1.0 } respectively. It can be seen from direct observation that the fractional differential operator belongs to a high pass filter, and its cut-off frequency is related to the fractional differential order. With the increase of the differential order, the fractional differential operator's high frequency filtering performance is stronger, that is, the fractional differential operator has the attenuation effect on the low-frequency signal of the image, and the degree of attenuation increases with the increase of the differential order.

3.2. Image Enhancement Experiment and Analysis of Fractional Differential Operator

Under certain conditions, it can be considered that the fractional differentiation of two-dimensional image signals  I ( x , y ) in the X and Y directions is separable, thus obtaining a normalized 8-direction fractional differentiation image enhancement operator. The duration  [ a , t ] of the image signal  I ( x , y ) is divided equally by the step size  h = 1 , that is, n = [ t − a h ] = h = 1 [ t − a ] , and the numerical calculation expression of the fractional differential operator along the X and Y axes can be obtained, as shown in Equations (13) and (14), where  R x v ( x , y ) and  R y v ( x , y ) represent the fractional differential remainder in the horizontal and vertical direction. (13)
D a G t v I ( x , y ) x = Δ I ( x , y ) + ( − v ) I ( x − 1 , y ) + ( − v ) ( − v + 1 ) 2 I ( x − 2 , y ) + ( − v ) ( − v + 1 ) ( − v + 2 ) 6 I ( x − 3 , y ) + R x v ( x , y )
D a G t v I ( x , y ) y = Δ I ( x , y ) + ( − v ) I ( x , y − 1 ) + ( − v ) ( − v + 1 ) 2 I ( x , y − 2 ) + ( − v ) ( − v + 1 ) ( − v + 2 ) 6 I ( x , y − 3 ) + R y v ( x , y )
Figure 4 represents the fractional order differential image enhancement mask operator  W D . This operator extends Equations (13) and (14) to the other directions of the image to obtain an image enhancement operator in the 8 direction. This operator has anisotropic rotation invariance and its filtering coefficient is shown in Equation (15).
{ W D 0 = 1 ， W D 1 = − v ， W D 2 = − v ( − v + 1 ) 2 ， W D 3 = − v ( − v + 1 ) ( − v + 2 ) 6 ， … ， W D m = − v ( − v + 1 ) ( − v + 2 ) ... ( − v + m − 1 ) m ! }
As shown in Figure 5, in order to facilitate visual observation, Figure (b) to (f) respectively represent the inverted images filtered by different order ( v ∈ { 0.1 , 0.5 , 0.8 , 1.0 , 2.0 } ) differential operator on the Barbara images. It can be seen from direct observation that the image is filtered by fractional differential operator of order v=0.1, which improves the high frequency information of the image to a certain extent, while retaining a large amount of low frequency information of the image. As the differential order increases, the fractional order filtering operator attenuates a large amount of low-frequency information in the image, while non-linear enhancing the high-frequency information in the image. After the image is filtered by fractional differential operator with differential order v=2.0, a large amount of low-frequency information of the image is removed, and the high-frequency part of the image is nonlinear enhanced.
Figure 6 shows the contrast diagram of Barbara image enhanced by different order ( v ∈ { 0.1 , 0.5 , 0.8 , 1.0 , 2.0 } ) differential operator.It can be seen from direct observation that after the image is enhanced by fractional differential operator of order v=0.1, because the low order differential filter operator retains a large amount of low-frequency contour information and weak texture information, and at the same time, the edge and texture information of the image are properly improved, the image after filtering and fusion by the low order fractional differential operator will appear overall bright and overexposure. After the image is enhanced by fractional differential operator with the order of v=2.0, because the higher-order differential operator removes all low-frequency information of the image, and at the same time greatly improves the high-frequency edge and strong texture information of the image, the overall contrast of the image after filtering and fusion by higher-order fractional differential operator will not be greatly improved, and edge jitter occurs.
As shown in Figure 7, Figure (b) and Figure (c) respectively represent images enhanced by fractional order differential operator of order v=0.5 and v=0.8, Figure (d), Figure (e) and Figure (f) represent images enhanced by classical integer order differential enhancement operators sobel, prewitt and laplacian, and Figure 8 represents histograms corresponding to each image in Figure 7. Direct observation shows that the fractional differential operator of order v=0.5 and v=0.8 can not only improve the weak texture feature information in the smooth area of the image as much as possible, but also can nonlinearly enhance the strong texture detail information in the image with relatively small gray value change amplitude and frequency, and can also nonlinearly enhance the high-frequency edge information in the image with relatively large gray value change amplitude. The histogram contrast diagram (8) obtained by image enhancement methods of different methods shows that the fractional order differential enhancement operator has better gray level equalization distribution and better overall image contrast than the image processed by the integer order differential operator.

4. Research on the Application of Fractional Integral in Image Denoising

This section mainly elaborates on the characteristics of fractional order integration operators for image signals and the experiments on image denoising using fractional order integration operators. The former mainly analyzes the relationship between the integration order of fractional order integral operators and the low-pass intensity of two-dimensional signals. The latter demonstrates the advantages of fractional order integral image denoising operators over integer order image denoising operators in processing noisy images from both subjective visual comparison and objective indicator performance.

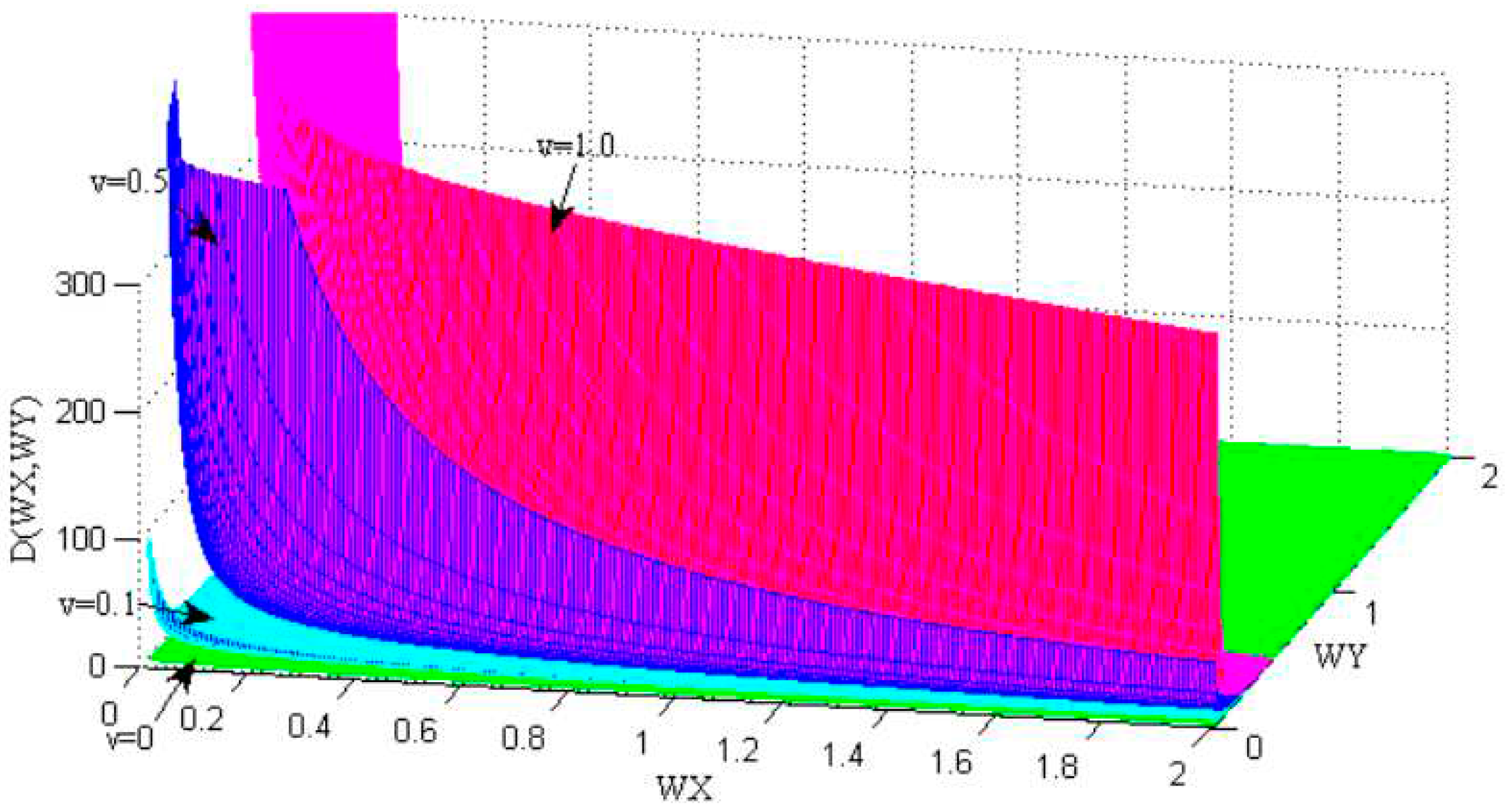
4.1. The Amplitude Frequency Characteristics of Fractional Order Integral Operator Image Denoising Operator

Let the fractional integral of the two-dimensional energy function  f ( x , y ) be  f v ' ( x , y ) ( v ' ∈ R − ). Because of the separability of the fractional Fourier transform, it can be considered that the fractional integral filter of the two-dimensional energy function f ( x , y ) is separable. Therefore, the fractional integral filter function of the two-dimensional energy function  f ( x , y ) can be obtained by expanding on the basis of Equation (7), as shown in Equation (16).
( I f ∧ ) v ' ( ω x , ω y ) = ( | ω x | − v ' e i − v ' π 2 sgn ( ω x ) ) ∗ ( | ω y | − v ' e i − v ' π 2 sgn ( ω y ) )
Figure 9 shows the amplitude frequency characteristic surface of different order ( v ∈ { 0.1 , 0.5 , 0.8 , 1.0 , 2.0 } ) fractional integration operators for two-dimensional signals obtained from Equation (16) .Direct observation shows that fractional order integration operators belong to low-pass filters, and their cutoff frequency is related to the fractional order of integration. As the order of integration increases, the low-pass performance of fractional order integration operators becomes stronger, that is, the fractional order integration operator has a attenuation effect on the high-frequency signal of the image, and the degree of attenuation increases nonlinearly with the increase of integration order.

4.2. Experiment and Analysis of Fractional Order Integral Operator for Image Denoising

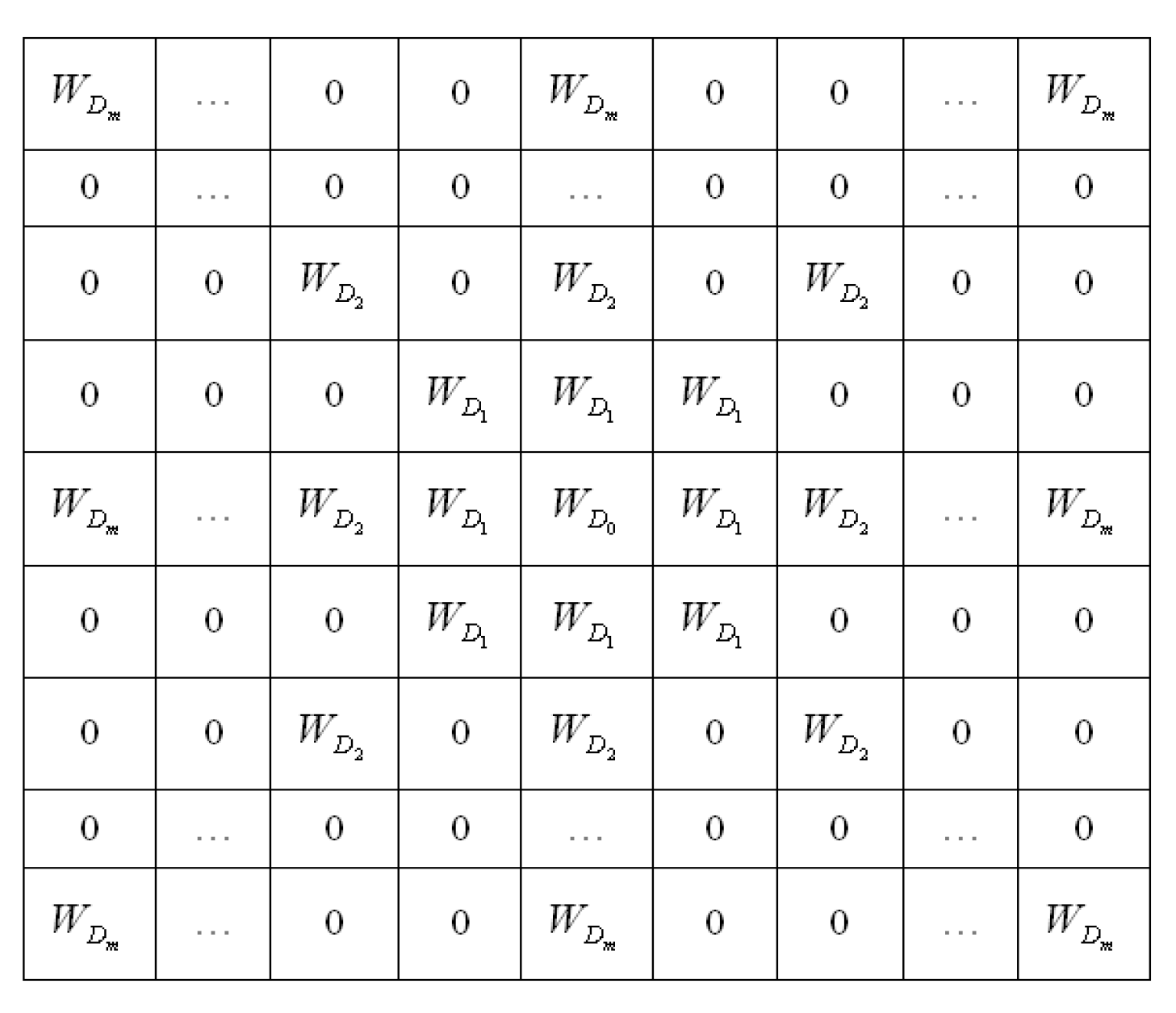
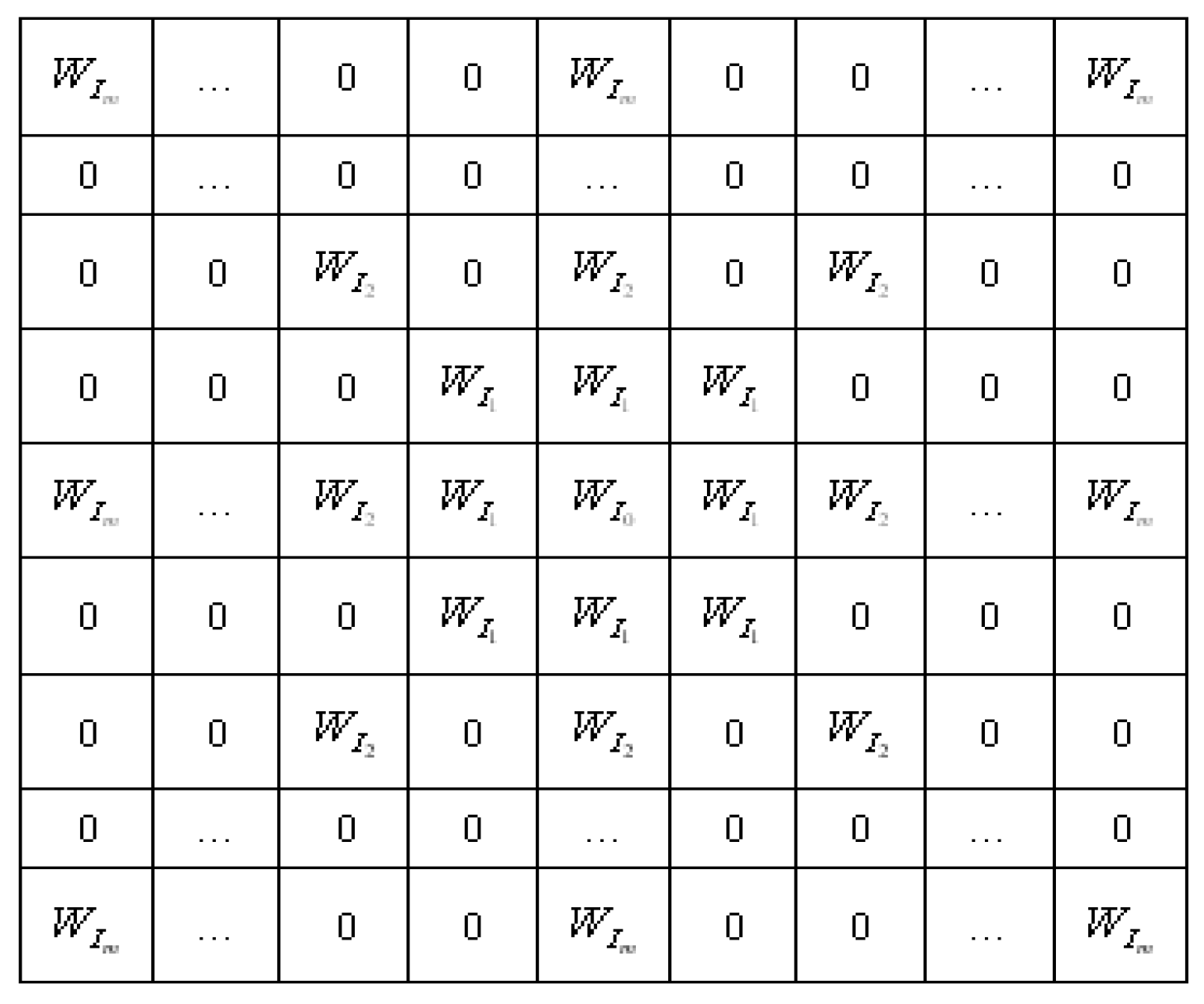
4.2.1. Construction of Fractional Order Integral Operators

As mentioned above, it can be considered that the fractional integration of two-dimensional image signals  I ( x , y ) in the X-axis and Y-axis directions is separable under certain conditions. We can use the normalized 8-direction fractional order integration operator to denoise the images separately. By dividing the duration  [ a , t ] of image signal  I ( x , y ) into equal steps  h = 1 , i.e.  n = [ t − a h ] = h = 1 [ t − a ] , the numerical expression for the fractional order integration operator along the X and Y axes defined by G-L can be obtained, as shown in Equations (17) and (18), where  R x v ‘ ( x , y ) and  R x v ’ ( x , y ) represent the residual terms of the fractional order integration in the horizontal and vertical directions.
I a G t v ' I ( x , y ) x = Δ I ( x , y ) + v ' I ( x − 1 , y ) + v ' ( v ' + 1 ) 2 I ( x − 2 , y ) + v ' ( v ' + 1 ) ( v ' + 2 ) 6 I ( x − 3 , y ) + R x v ( x , y )
I a G t v ' I ( x , y ) y = Δ I ( x , y ) + v ' I ( x , y − 1 ) + v ' ( v ' + 1 ) 2 I ( x , y − 2 ) + v ' ( v ' + 1 ) ( v ' + 2 ) 6 I ( x , y − 3 ) + R y v ( x , y )
Figure 10 shows the fractional order integral denoising operator  W I . This operator extends Equations (19) and (20) to the remaining 6 directions of the image, resulting in an 8-direction denoising operator. This operator has anisotropic rotation invariance and its filtering coefficient is shown in Equation (19).
{ W I 0 = 1 ， W I 1 = v ， W I 2 = v ( v + 1 ) 2 ， W I 3 = v ( v + 1 ) ( v + 2 ) 6 ， ... , W I m = v ( v + 1 ) ( v + 2 ) ... ( v + m − 1 ) m ! }

4.2.2. Evaluation Criterion

1. Subjective Evaluation
Subjective evaluation refers to the subjective evaluation of the enhanced image by directly applying the human eye to it, striving to truly reflect human visual perception. Subjective visual evaluation is more vivid and vivid because it directly affects images with the human eye [33] [34]. Due to the sensitivity of the human eye to the texture details and edge parts of the image, this experiment adopts direct observation of the overall visual effect of the denoised image, with a focus on observing the edges and texture features of the image.
2. Objective Evaluation
The objective indicator evaluation method constructs mathematical functions based on certain objective image evaluation features that can reflect the subjective perception of the human eye, and obtains calculation results based on certain image features based on the evaluation function. This article uses average gradient, edge preservation coefficient, and signal-to-noise ratio to compare and analyze the processing effects of image denoising operators [35].
  • Average Gradient (AG)
The average gradient value of an image can represent the contrast of details and texture changes in the image, and can to some extent reflect the clarity of the image. The calculation formula for the average gradient value is shown in Equation (20).
A G = 1 M * N ∑ i = 1 r o w ∑ j = 1 c o l Δ horizontal f ( i , j ) 2 + Δ vertical f ( i , j ) 2
  • Edge Preservation Index (EPI)
The edge preservation index represents the situation where the filtering operator maintains the horizontal or vertical edges of the image. The higher the EPI value, the higher the operator's ability to preserve edges. The formula for the edge preservation coefficient is shown in Equation (21).
E P I = ∑ i = 1 row ∑ j = 1 c o l | Δ horizontal f a f t e r ( i , j ) + Δ vertical f a f t e r ( i , j ) | ∑ i = 1 row ∑ j = 1 c o l | Δ horizontal f b e f o r ( i , j ) + Δ vertical f b e f o r ( i , j ) |
  • Signal-Noise Ratio(SNR)
Image signal-to-noise ratio is an important indicator to measure the quality of an image, representing the ratio of the size of the image signal to the noise signal. The calculation formula for image signal-to-noise ratio is shown in Equation (22).
S N R = 10 × l g ( ∑ i = 1 r o w ∑ j = 1 c o l f ( i , j ) 2 ∑ i = 1 r o w ∑ j = 1 c o l | f ( i , j ) − f d e n o i s e ( i , j ) | 2 )

4.2.3. Experimental Results and Comparative Analysis

As shown in Figure 11, it represents the image denoised by fractional integral image denoising operators of different orders for the Barbara image with Gaussian white noise of mean  μ = 0 and variance  σ = 0.1 . By direct observation, it can be seen that the denoising operator with a fractional integration order of v=0.1 has weak denoising ability, but almost no loss of image edge and texture information is caused. The denoising operator with a fractional integration order of v=1.0 has good denoising ability, but it results in severe loss of image edge and texture information, and poor visual effect. From this, it can be seen that as the order of the fractional integration operator increases, the performance of noise removal improves. However, the high-frequency information attenuation of the denoised image also increases, resulting in a more severe degree of image blur.
As shown in Figure 12, it represents the image denoised by image denoising operators of different methods for the Barbara image with Gaussian white noise of mean  μ = 0 and variance  σ = 0.1 . As shown in Figure 12, Figure 12c represents the image processed using the mean method, Figure 12d represents the image processed using the Gaussian method, Figure 12e represents the image processed using the Wiener method, and Figure 12f represents the image processed using the fractional integration low order iteration method. As shown in Figure 13, Figure 13a represents the inverse image of the residual image between the average method processed image and the original image (the inverse image is for visual observation), Figure 13b represents the inverse image of the residual image between the Gaussian method processed image and the original image, and Figure 13c represents the inverse image of the residual image between the Wiener method processed image and the original image, Figure 13d represents the inverse image of the residual image between the image processed by the fractional order integration low order iteration method and the original image. From direct observation, it can be seen that the proposed method in this article is a low order fractional order integral iterative denoising method. Due to setting a smaller integration order, in each iteration of denoising, compared to integer order integration denoising methods, this method can to some extent preserve the edge and texture information of the image, thus achieving "micro denoising" of noisy images. Table 1 shows the comparison of average gradient values, edge preservation coefficients, and signal-to-noise ratio values after processing images using different denoising methods. By direct observation, it can be seen that the low order fractional order integral iterative denoising method proposed in this article preserves detailed information such as edges and textures of the image while ensuring a higher signal-to-noise ratio as much as possible compared to integer order denoising methods.

5. Conclusions

Fractional calculus is to extend the calculus order of classical integer calculus from integer to non-integer or even complex numbers. Integer calculus theory has obtained many classical image processing models in image underlying processing. This paper mainly studies the image enhancement and denoising methods based on the single theory of fractional calculus, without using the self-similarity and local feature information of the image. First, the paper introduces three classical definitions of fractional calculus and the application fields of different definitions. Secondly, the paper discusses the amplitude frequency characteristics of the fractional calculus operator in detail, and deeply studies the nonlinear relationship between the high pass and low-pass performance of the fractional calculus operator of one-dimensional and two-dimensional signals and the order of calculus. On this basis, the paper constructs the image enhancement model based on the fractional differential operator and the image denoising model based on the fractional calculus operator. Finally, the experimental data shows that the fractional order calculus image processing method proposed in this paper has better contrast and clarity enhancement effect than the integer order calculus method in image enhancement, and has better edge preserving and denoising ability in image enhancement. The fractional order calculus theory is the extension and continuation of integer order calculus. Attempting to apply the fractional order calculus theory to the underlying image processing has broad development prospects. At present, the research focus of scholars at home and abroad is to build new image processing methods based on the fractional order calculus theory and classic intelligent algorithms. It is believed that with the further improvement of computer hardware performance, the classic intelligent algorithms will be further optimized, the new method of fractional order image processing will definitely play an important role in future practical applications.

References

  1. K. B. Ordham; J. Spanier. The Fractional Calculus, Academic Press, New York, NY, USA, 1974.
  2. K. S. Miller; B. Ross. An Introduction to the Fractional Calculus and Fractional Differential Equations, John Willey, New York, NY, USA, 1993.
  3. Petras, I. Fractional derivatives, fractional integrals, and fractional differential equations in Matlab, in ‘Engineering education and research using MATLAB’ vol. 10 (In-TechOpen, London, 2011), pp. 239–264.
  4. Mandelbrot; B.B.; van Ness; J.W.: ‘Factional Brownian motion, fractional noises and applications’, Geophys. J. R. Astron. SIAM Rev., 1968,10, (4), pp.422–437.
  5. Manderlbrot; B.B.; Wallis; J.R. Computer experiments with fractional Gaussian noises. Water Resour. Res., 1969, 5, (1), pp. 228–267.
  6. Huang Guo; XuLi; Pu Yi-fei.Summary of research on image processing using fractional calculus J. Application Research of Com- puters, 2012,29(02):414-420+426.
  7. Yi-Fei Pu, Bo Yu, Qiu-Yan He, and Xiao Yuan. Fracmemristor Oscillator: Fractional-Order Memristive Chaotic Circuit. IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 69, no. 12, pp. 5219 – 5232, 2022. [CrossRef]
  8. Yi-Fei Pu, Bo Yu, Qiu-Yan He, and Xiao Yuan. “Fractional-Order Memristive Neural Synaptic Weighting Achieved by Pulse-Based Fracmemristor Bridge Circuit,” Frontiers of Information Technology & Electronic Engineering, vol. 22, no. 6, pp. 862-876, 2021. [CrossRef]
  9. Qiu-Yan He;Yi-Fei Pu ; Bo Yu;Xiao Yuan.Electrical Characteristics of Quadratic Chain Scaling Fractional-Order Memristor IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—II: EXPRESS BRIEFS, VOL. 69, NO. 11, NOVEMBER 2022.
  10. Yi-Fei Pu; Patrick SIARRY;Wu-Yang ZHU et al. Fractional-Order Ant Colony Algorithm: A Fractional Long Term Memory Based Cooperative Learning Approach. Swarm and Evolutionary Computation, vol. 69, Article ID 101014, 18 pages, 2022. [CrossRef]
  11. Hq A;Xuan L A ;Zs A . Neural network method for fractional-order partial differential equations.J. Neurocomputing, 2020, 414:225-237.
  12. Yi-Fei Pu, Zhang Yi, and Ji-Liu Zhou. “Fractional Hopfield Neural Networks: Fractional Dynamic Associative Recurrent Neural Networks,” IEEE Transactions on Neural Networks and Learning Systems, vol. 28, no. 10, pp. 2319-2333, 2017. [CrossRef]
  13. Dong Y, Liao W, Wu M, et al. Convergence analysis of Riemann-Liouville fractional neural network[J]. Mathematical Methods in the Applied Sciences, 2022(10):45.
  14. Li X; Zhan Y; Tong S. Adaptive neural network decentralized fault-tolerant control for nonlinear interconnected fractional-order systems.J. Neurocomputing, 2022, 488:14-22. [CrossRef]
  15. Yi-Fei Pu; Ji-Liu Zhou; Xiao Yuan. Fractional Differential Mask: A Fractional Differential Based Approach for Multi-scale Texture Enhancement, IEEE Transactions on Image Processing, vol.19, no.2, pp. 491-511, 2010.
  16. Pu; Y.-F.; Siarry; P. Chatterjee, A., et al.: ‘A fractional-order variational framework for retinex: fractional-order partial differential equation-based formulation for multi-scale nonlocal contrast enhancement with texture preserving’, IEEE Trans. Image Process., 2018, 27, (3), pp. 1214–1229. [CrossRef]
  17. Hacini M ;Hachouf F; Charef A. A new Bi-Directional Fractional-Order Derivative Mask for Image Processing Applications[J]. IET Image Processing, 2020, 14(11): 2512-2524.
  18. Zhang, X., Dai, L. Image Enhancement Based on Rough Set and Fractional Order Differentiator. Fractal Fract., 2022, 6, 214. [CrossRef]
  19. Meng-Meng Li, Bing-Zhao Li. A novel active contour model for noisy image segmentation based on adaptive fractional order differentiation. IEEE Transactions on Image Processing, vol. 29, pp.9520-9531, 2020. [CrossRef]
  20. Nandal S , Kumar S . Single image fog removal algorithm in spatial domain using fractional order anisotropic diffusion[J]. Multimedia Tools and Applications, (2019) 78: 10717–10732.
  21. A. Abirami, “A new fractional order total variational model for multiplicative noise removal,” Journal of Applied Science and Computations, vol. 6, no. 3, pp. 483–491, 2019.
  22. A. Abirami, P. Prakash, and K. -angavel, “Fractional diffusion equation-based image denoising model using CN-GL scheme,” International Journal of Computer Mathematics, vol. 95, no. 6-7, pp. 1222–1239, 2018.
  23. Bai J, Feng X C. Image decomposition and denoising using fractional-order partial differential equations[J]. IET Image Processing, 2020, 14(7).
  24. Abirami A, Prakash P, Ma Y K. Variable-Order Fractional Diffusion Model-Based Medical Image Denoising[J]. Mathematical Problems in Engineering: Theory, Methods and Applications, 2021(Pt.51):2021.
  25. Xu L, Huang G, Chen Q L, et al. An improved method for image denoising based on fractional-order integration[J]. Frontiers of Information Technology & Electronic Engineering, 2020, 21(10):1485-1493.
  26. Xiuhong, Y., Baolong, G.: ‘Fractional-order tensor regularization for image inpainting’, IET Image Process., 2017, 11, (9), pp. 734–745.
  27. WANG Yong-xing;PU Yi-fei;GONG Xiao-qian;ZHOU Ji-liu. Fractional block matching three-dimensional filter.J. Application Ｒesearch of Computers.2015,32(1),287-290.
  28. FENG Chenbo;QIN Yali;CHEN Hui;CHANG Liping;XUE Linlin. Fractional Total Variation Algorithm Based on Improved Non-local Means. J.Computer Engineering.2019,45(4),241-247.
  29. Liu, K.; Tian, Y. Research and analysis of deep learning image enhancement algorithm based on fractional differential. Chaos Solitons Fractals 2020, 131, 109507. [Google Scholar] [CrossRef]
  30. Kaur, K.; Jindal, N.; Singh, K. Fractional Fourier Transform based Riesz fractional derivative approach for edge detection and its application in image enhancement. Signal Process. 2021, 180, 107852. [Google Scholar] [CrossRef]
  31. A Téllez-Velázquez, Cruz-Barbosa R. On the Feasibility of Fast Fourier Transform Separability Property for Distributed Image Processing[J]. Scientific Programming, 2021.
  32. RanTao;Feng Zhang;Yue Wang.Research progress on discretization of fractional Fourier transform.J. Chinese Science Series E: Information Science. 2008 38(4), 481- 503.
  33. K. Gu, J. Zhou, J. F. Qiao, G. Zhai, W. Lin, and A. C. Bovik, “No-reference quality assessment of screen content pictures,” IEEE Trans. Image Process., vol. 26, no. 8, pp. 4005–4018, Aug. 2017.
  34. K. Gu et al., “Blind quality assessment of tone-mapped images via analysis of information, naturalness and structure,” IEEE Trans. Multimedia, vol. 18, no. 3, pp. 432–443, Mar. 2016.
  35. HUANG Guo, XU Li, CHEN Qingli, et al. Research on Non-local Multi-scale Fractional Differential Image Enhancement Algorithm[J].Journal of Electronics & Information Technology,2019,41(12):2972-2979.
Preprints 79884 g001
Figure 1. Amplitude frequency characteristic curve of fractional calculus operator. (a) fractional differential; (b) fractional integral.
Figure 1. Amplitude frequency characteristic curve of fractional calculus operator. (a) fractional differential; (b) fractional integral.
Preprints 79884 g001
Preprints 79884 g002aPreprints 79884 g002b
Figure 2. Fractional Calculus Amplitude Frequency Diagram of Common Signals. (a) Square Wave; (b) Triangular Wave; (c) Sine Wave; (d) Gaussian Signal.
Figure 2. Fractional Calculus Amplitude Frequency Diagram of Common Signals. (a) Square Wave; (b) Triangular Wave; (c) Sine Wave; (d) Gaussian Signal.
Preprints 79884 g002aPreprints 79884 g002b
Preprints 79884 g003
Figure 3. Amplitude frequency characteristic surface of two-dimensional signal fractional differentiation.
Figure 3. Amplitude frequency characteristic surface of two-dimensional signal fractional differentiation.
Preprints 79884 g003
Preprints 79884 g004
Figure 4. Fractional order differential augmentation operator.
Figure 4. Fractional order differential augmentation operator.
Preprints 79884 g004
Preprints 79884 g005
Figure 5. Fractional Differential Operator of Different Orders. (a) Original image; (b) v=0.1; (c) v=0.5; (d) v=0.8; (e) v=1.0; (f) v=2.0.
Figure 5. Fractional Differential Operator of Different Orders. (a) Original image; (b) v=0.1; (c) v=0.5; (d) v=0.8; (e) v=1.0; (f) v=2.0.
Preprints 79884 g005
Preprints 79884 g006
Figure 6. Fractional differential operator of different orders. (a) Original image; (b) v=0.1; (c) v=0.5; (d) v=0.8; (e) v=1.0; (f) v=2.0.
Figure 6. Fractional differential operator of different orders. (a) Original image; (b) v=0.1; (c) v=0.5; (d) v=0.8; (e) v=1.0; (f) v=2.0.
Preprints 79884 g006
Preprints 79884 g007aPreprints 79884 g007b
Figure 7. Differential Image Enhancement Method. (a) Original image;(b) v=0.5;(c) v=0.8;(d) Sobel ; (e) Prewitt;(f) Laplacian.
Figure 7. Differential Image Enhancement Method. (a) Original image;(b) v=0.5;(c) v=0.8;(d) Sobel ; (e) Prewitt;(f) Laplacian.
Preprints 79884 g007aPreprints 79884 g007b
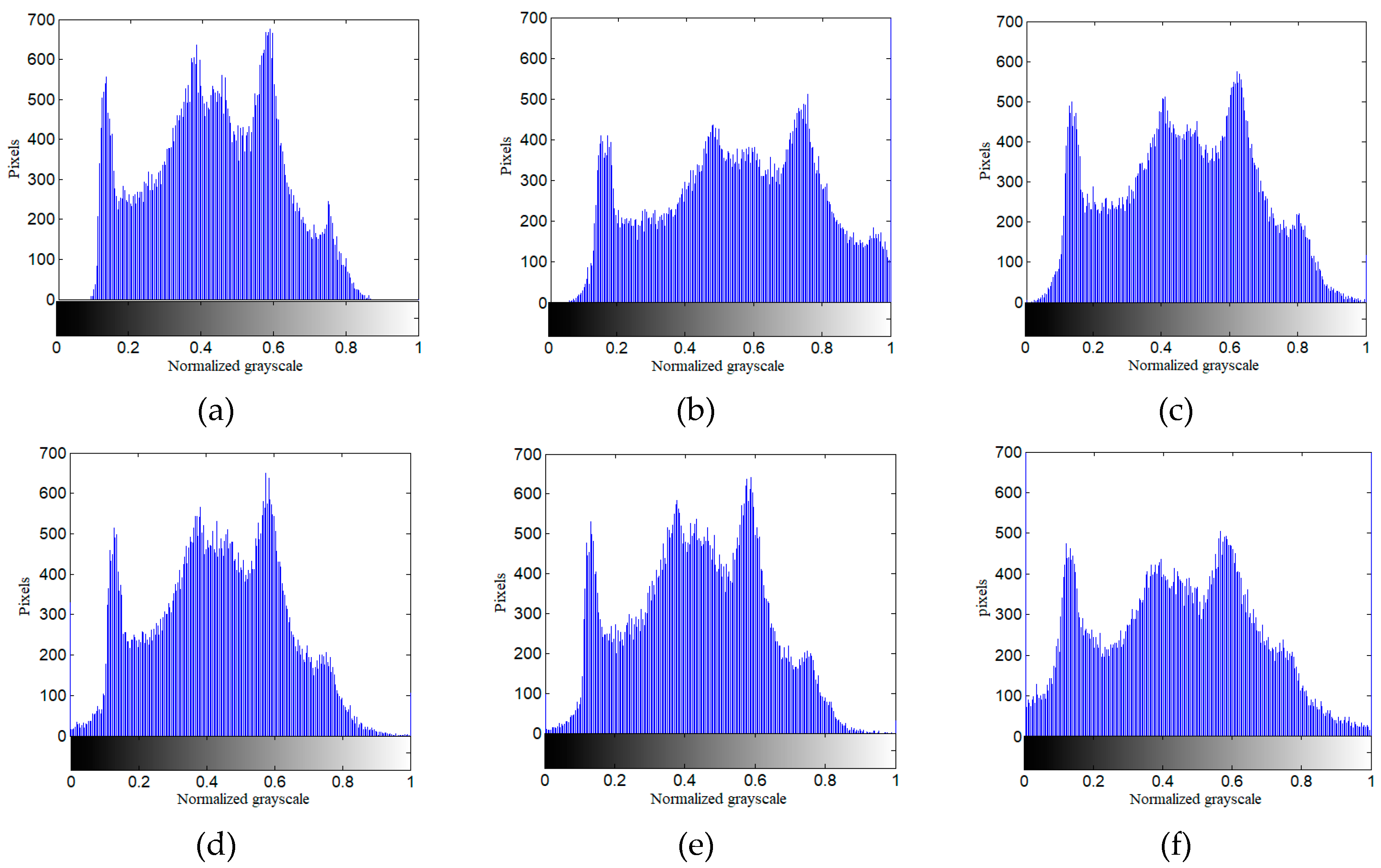
Preprints 79884 g008
Figure 8. Grayscale histogram. (a) Original image; (b) v=0.5; (c) v=0.8; (d) Sobel; (e) Prewitt; (f) Laplacian.
Figure 8. Grayscale histogram. (a) Original image; (b) v=0.5; (c) v=0.8; (d) Sobel; (e) Prewitt; (f) Laplacian.
Preprints 79884 g008
Preprints 79884 g009
Figure 9. Amplitude frequency characteristic surface of two-dimensional signal fractional integration.
Figure 9. Amplitude frequency characteristic surface of two-dimensional signal fractional integration.
Preprints 79884 g009
Preprints 79884 g010
Figure 10. Fractional order integral denoising mask operator.
Figure 10. Fractional order integral denoising mask operator.
Preprints 79884 g010
Preprints 79884 g011
Figure 11. Fractional order integration operators of different orders. (a) Original image;(b) Noisy image;(c) v=0.01;(d) v=0.1;(e) v=0.5;(f) v=1.0.
Figure 11. Fractional order integration operators of different orders. (a) Original image;(b) Noisy image;(c) v=0.01;(d) v=0.1;(e) v=0.5;(f) v=1.0.
Preprints 79884 g011
Preprints 79884 g012
Figure 12. Images after denoising using different methods. (a) Original image;(b) Noisy image; (c) Mean denoising; (d) Gaussian denoising;(e) Wiener denoising;(f) Fractional integral denoising.
Figure 12. Images after denoising using different methods. (a) Original image;(b) Noisy image; (c) Mean denoising; (d) Gaussian denoising;(e) Wiener denoising;(f) Fractional integral denoising.
Preprints 79884 g012
Preprints 79884 g013aPreprints 79884 g013b
Figure 13. Residual images of denoised images using different methods. (a) Mean denoising; (b) Gaussian denoising;(c) Wiener denoising;(d) Fractional integral denoising.
Figure 13. Residual images of denoised images using different methods. (a) Mean denoising; (b) Gaussian denoising;(c) Wiener denoising;(d) Fractional integral denoising.
Preprints 79884 g013aPreprints 79884 g013b
Table 1. Comparison of experimental data of image denoising algorithms using different methods.
Table 1. Comparison of experimental data of image denoising algorithms using different methods.
Denoising average gradient method Edge retention coefficient Signal to Noise Ratio
mean value
Gaussian
Wiener
fractional order		 0.0138
0.0186
0.0165
0.0208		 0.3547
0.5388
0.4356
0.7084		 18.2964
19.3706
19.2437
19.8679
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated