Prerpints.org logo
Preprint
Article

Simulation Study of the Lunar Spectral Irradiances and the Earth-Based Moon Observation Geometry

Altmetrics

Downloads

91

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

21 July 2023

Posted:

21 July 2023

You are already at the latest version

Alerts
Abstract
As a radiant light source within the dynamic range of most spacecraft payloads, the moon pro-vides an excellent reference for on-orbit radiometric calibration. This research hinges on the pre-cise simulation of lunar spectral irradiances and the Earth-based Moon observation geometry. The paper leverages the Hapke model to simulate the temporal changes in lunar spectral irradi-ances, utilizing datasets obtained from Lunar Reconnaissance Orbiter Camera (LROC). The re-search also details the transformation process from the lunar geographic coordinate system to the instantaneous projection coordinate system, thereby delineating the necessary observational geometry. The insights offered by this study have the potential to enhance future in-orbit space-craft calibration procedures, thereby boosting the fidelity of data gathered from satellite obser-vations.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Satellite radiometric calibration is the basis and key to remote sensing quantification. Countries around the world attach great importance to satellite calibration and have developed a variety of calibration methods, such as laboratory calibration, field calibration, and cross-calibration [1,2]. Laboratory calibration cannot represent the operation of satellites in orbit. Field calibration is affected by atmospheric scattering and absorption, geometric differences between ground measurements and satellite observations, and scale differences between ground measurement points and satellite measurement points. In addition, for remote sensing, the influence of the atmosphere on the calibration is relartive large. Unlike the Earth, the Moon has essentially no atmosphere and its reflectance is very stable hence it is good radiance source for the calibration of space crafts. For visible spectral remote sensing, the reflectance of the moon is very stable, and the spectral curve is smooth. For thermal infrared remote sensing, the specific emissivity of the moon is very large, similar to a black body. Therefore, whether it is short-wave or long-wave remote sensing, the moon is a good light source for on-orbit radiation calibration and stability monitoring [3,4] .
There has been a great deal of research on lunar calibration [5,6,7,8,9]. At present, many satellites have carried out observation experiments on the moon with various payloads, such as MODIS [10], Hyperion [11], GOES [12], SeaWiFS [13,14], S-NPP [15], Hodoyoshi-1 [16] and FY meteorological satellite [17], etc. These observations have laid a good foundation for satellite calibration using the moon as a calibration source. In this paper, we simulatethe distribution of the lunar spectral irradiances at the observation time, which is influenced by the phase of the Moon, the libration, and the distance between the Sun, Earth and the Moon. There are two key main question in our research question including the lunar spectral irradiances simulation and a projection transformation from the lunar geographic coordinate system to an instantaneous projection coordinate system. The Hapke bidirectional reflectance function can be used to simulate the lunar spectral irradiances at the observation time by using Lunar Reconnaissance Orbiter Camera (LROC) products. The projection in an instantaneous projection coordinate system can establish a mapped relationship between transformation from the lunar geographic coordinate system and the instantaneous projection coordinate system at the observation time. It is expected that the conclusion drawn in this paper support for on-orbit calibration of spacecraft in the future.

2. Materials and Methods

2.1. Data and Coordination System

2.1.1. Data Collection

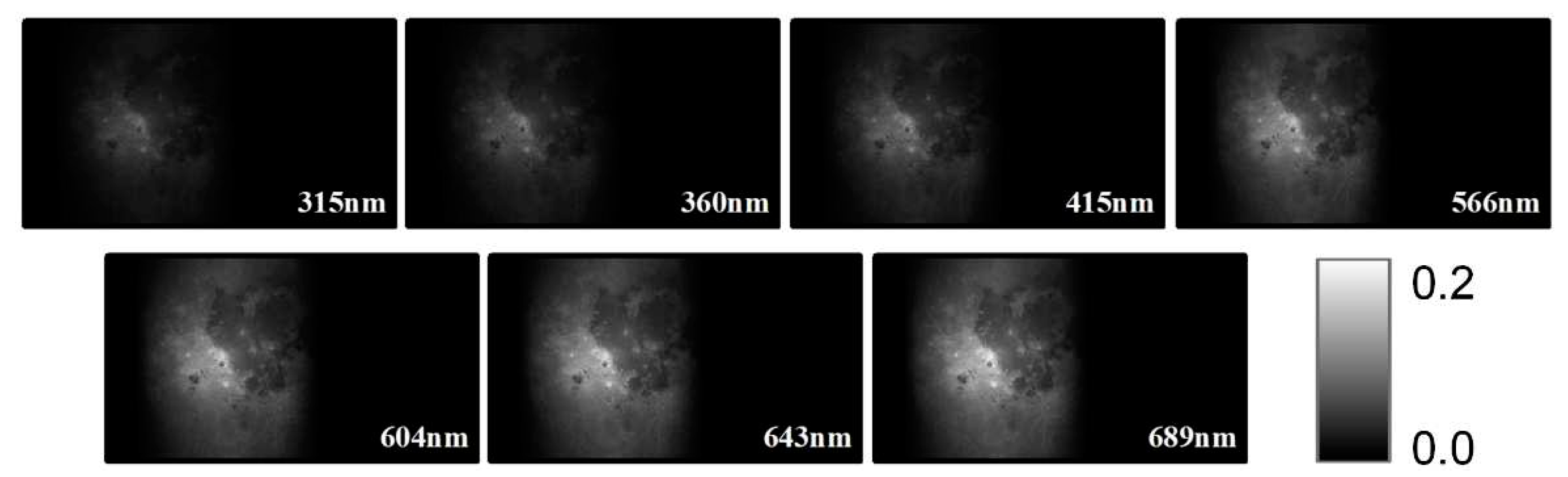
In June 2009, NASA launched the Lunar Reconnaissance Orbiter(LRO), a robotic spacecraft, now orbiting the Moon at an altitude of 50-200 km. The LROC, one of the instruments on board LRO, is provided to construct the lunar global multi-spectral map[18] including 321, 360, 415, 566, 604, 643, and 689 nm. Global multispectral observations in seven wavelengths could be used to characterize lunar resources, in particular ilmenite. Some products of LROC including LROC Empirically Normalized Wide Angle Camera Mosaic Data Record (MDREMP), LROC Special Data Record Hapke Photometric Parameter Maps (SDWHAP) would be used in our research.
The SDWHAP consisted of 9 Hapke parameters (w, b, c, Bc0, hc, Bs0, hs, theta, phi) for each of the 7 bands of the Wide Angle Camera (WAC) in Equirectangular projection (centered at 0°N, 0°E; 1° by 1° pixel scale)[19]. Spatially resolved near-global Hapke photometric parameter maps of the Moon from ~66,000 LROC WAC multispectral observations acquired from February 2010 to October 2011. Maps extend 0°E-360°E, 70°N-70°S. These maps could be used to normalize the simulated reflectance at standard angles in 1° latitude by 1° longitude tiles in this research.
The MDREMP empirically normalized WAC mosaic was constructed from 137,400 colour WAC images acquired from January 21, 2010, to January 31, 2013, over a broad range of lighting and viewing geometries[20]. Each pixel from the WAC observations was photometrically normalized to a standard geometry of 30-degree incidence angle, 0-degree emission angle, and 30-degree phase angle using an empirically derived global photometric function. Normalized WAC pixels for each location were combined using the median (average n=142), so each mosaic value is using information from many observations.
The SORCE SIM Solar Spectral Irradiance (SSI) data product SORCE SIM Level 3 Solar Spectral Irradiance Daily Means V027 (SOR3SIMD) would be used in the research as the estimation product of solar radiation energy[21]. The SOR3SIMD is constructed using measurements from the SIM instruments, which are combined into merged daily solar spectra over the spectral range from 240 to 2416 nm at a spectral resolution ranging from 1 to 27 nm. Irradiances are reported at a mean solar distance of 1 AU and zero relative line-of-sight velocity to the Sun. The SIM absolute uncertainty is about 2%. All of the SOR3SIMD data are arranged in a single file in a tabular ASCII text file which can be easily read into a spreadsheet application. The columns contain the date, Julian day, minimum wavelength, maximum wavelength, instrument mode, data version number, irradiance value, irradiance uncertainty, and data quality. The rows are arranged with data at each wavelength over the full SIM wavelength range, repeating each day for the length of the measurement period.

2.1.2. The Basic Coordinate System

  • The lunar geographic coordinate system;
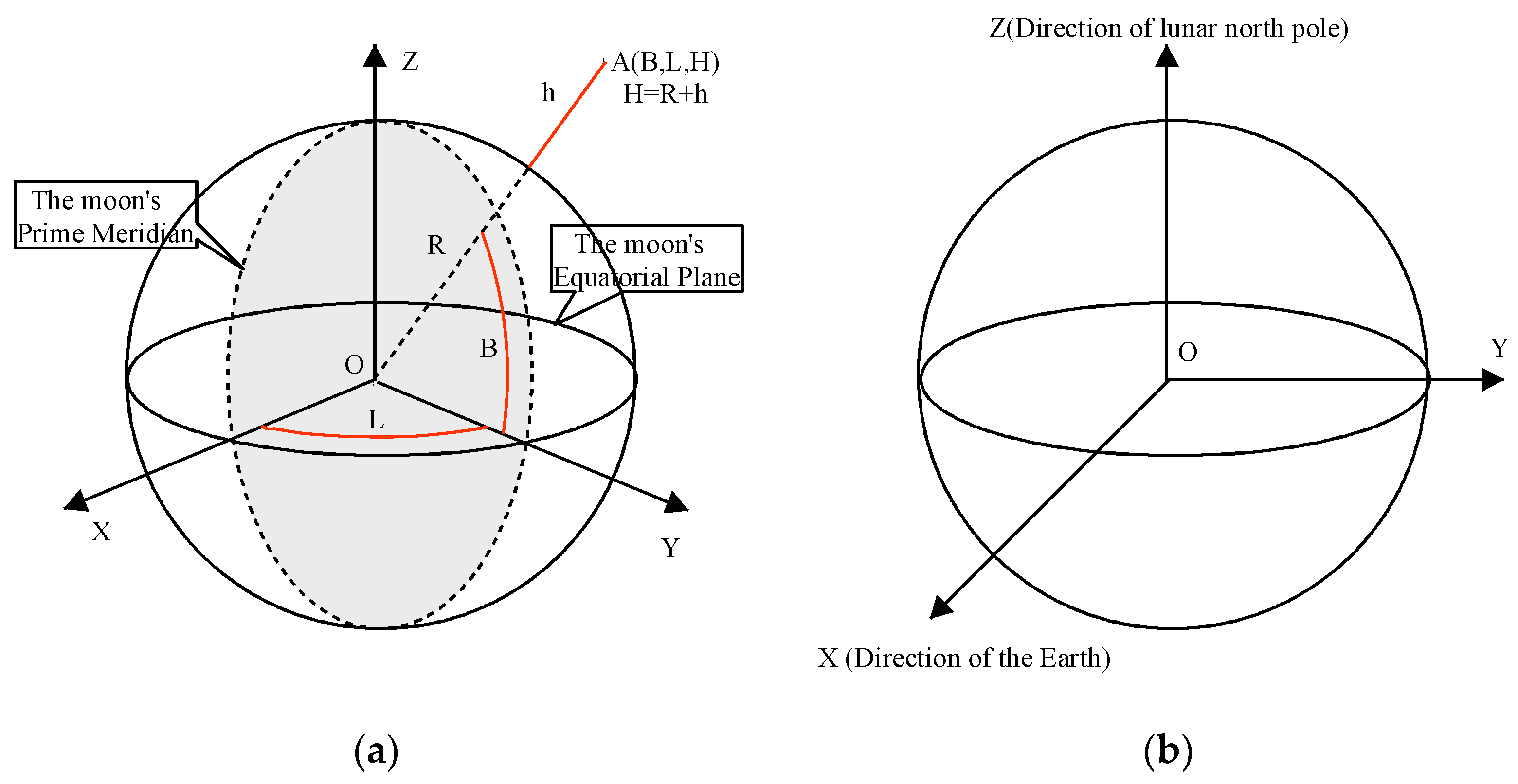
The lunar geographic coordinate system is commonly used for lunar mapping, similar to the Earth's geographic coordinate system. The lunar geographic coordinate system uses a three-dimensional spherical surface to define locations on the moon. The lunar geographic coordinate system includes an angular unit of measure, a prime meridian, and a datum (based on a spheroid). The origin of the coordinates is the centre of the lunar reference ellipsoid and the reference plane is the spherical reference ellipsoid sphere. The basic plane includes the lunar prime meridian and the equatorial plane. Latitude values (B) are measured relative to the equator and range from –90° at the south pole to +90° at the north pole. Longitude values (L) are measured relative to the prime meridian and range from –180° when travelling west to 180° when travelling east. The elevation (H) is defined by the distance from the reference point of the reference ellipsoid normal to the reference ellipsoid. The position of any point (A) on the moon is referenced by its longitude, latitude and elevation values in the lunar geographic coordinate system (Figure 1(a)) as ( B , L , H ) .
2.
The lunar-fixed system;
The lunar-fixed system describes the location of a station on the lunar surface. The lunar-fixed system coordinate system is a right-handed Cartesian system (X, Y, Z; Figure 1(b)). The origin is at the lunar centre of mass, the Z-axis is on the line between the North and South Poles, with positive values increasing northward and the X and Y axes are on the plane of the Equator. The X-axis is found by extending from 180 degrees longitude at the Equator (negative) to 0 degrees longitude (prime meridian) at the Equator (positive). The Y-axis is found by extending from 90 degrees west longitude at the Equator (negative) to 90 degrees east longitude at the Equator (positive).
3.
Instantaneous coordinate system;
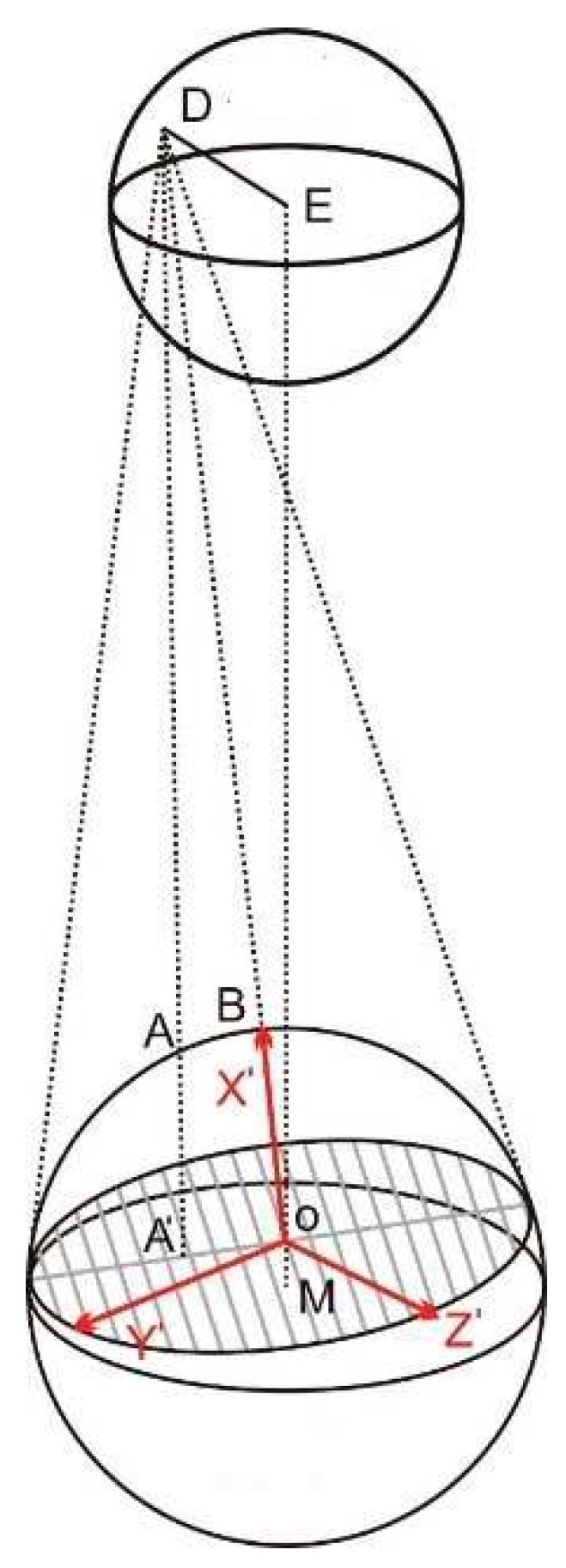
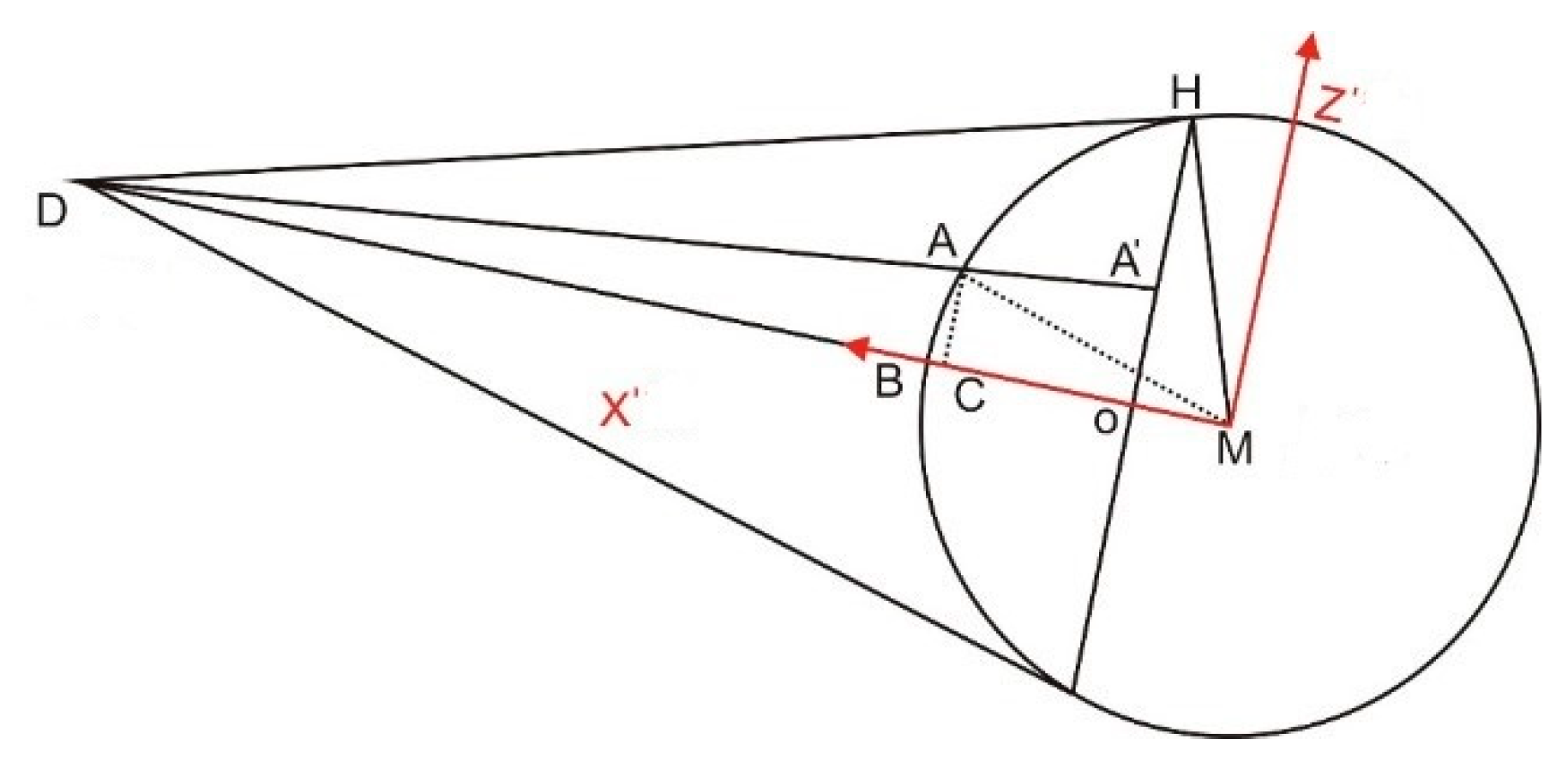
The instantaneous coordinate system is included in the instantaneous projection coordinate system (O-Y’Z’) and three-dimensional instantaneous coordinate system (O-X’Y’Z’; Figure 2). The pointE is the centroid of the earth, the point M is the centroid of the moon, the point D is an arbitrary observation point on the surface of the earth, and the shaded portion is the projection plane at the observation time (Figure2). The origin of the instantaneous coordinate system is O which is the intersection of the observation direction vector DM and the projection surface OY’Z’. The X-axis (OX’) is in the opposite of the observation direction. The Y-axis (OY’) and the Z-axis (OZ’) axes are in the projection plane. The Y-axis is the Normal vector to the plane ODE. The Z-axis could be defined using the right-hand corkscrew rule based on the direction of the X-axis and the Y-axis.

2.2. Methods

In this paper, we focus on observation simulation based on two key information sources: the lunar surface reflectance simulation and a projection transformation from the lunar geographic coordinate system to the instantaneous projection coordinate system that produced fine temporal and high-frequency resolution Lunar reflectance images. The Hapke model is determined for lunar surface reflectance simulation in specific frequency channels and at a specific time. The projection in an instantaneous projection coordinate system can establish a mapped relationship between transformation from the lunar geographic coordinate system and the instantaneous projection coordinate system at the observation time.

2.2.1. Hapke Model

The Hapke bidirectional reflectance model has been widely used for soil modelling. Through this model, the solution of the reflectivity in the direction of the whole moon at the observation time can be realized. I/F, which is also called the radiance factor [22], is the ratio of the radiance observed from a surface to that of a perfectly white Lambertian surface illuminated by the same light, but at normal incidence. I is the radiance data observed from the scene and F is the incident solar irradiance from above the Martian surface. Assuming that the shadow effect is not considered, the equation [19,23] is written as:
I F = L S i e , e e K w 4 p g 1 + B S 0 B S g + M i e , e e [ 1 + B C 0 B C g ]
where L S i e , e e is the Lommel-Seeliger function, i e and e e are the effective angle of incidence and emission respectively, K is the porosity factor, w is the single scattering albedo, p(g) is the phase function, B S 0 is the amplitude of Shadow Hiding Opposition Effect (SHOE), B S g is SHOE function, M i e , e e is Isotropic Multiple-Scattering Approximation (IMSA) [24,25], B C 0 is the amplitude of Coherent Backscatter Opposition Effect (CBOE), B C g is Coherent Backscatter Opposition function.
The Lommel-Seeliger function (LS) is given by
L S i e , e e = c o s ⁡ ( i e ) cos ⁡ i e + c o s ⁡ ( e e )
The phase function p(g) is given by
p g = 1 + c 2 1 − b 2 ( 1 − 2 b c o s g + b 2 ) 3 / 2 + 1 − c 2 1 − b 2 ( 1 + 2 b c o s g + b 2 ) 3 / 2
where b (0 ≤ b ≤ 1) is the shape-controlling parameter, and c (−1 ≤ c ≤ 1) is the relative strength of backward and forward lobes. The SHOE function B S g is given by
B S g = 1 / [ 1 + t a n ⁡ ( g 2 ) / h S ]
where h S is the angular width parameter of SHOE. The IMSA function M i e , e e is given by
M i e , e e = H cos ⁡ i e K , w H cos ⁡ e e K , w − 1
where H ( x , w ) is Ambartsumian-Chandrasekhar H function, which is approximated by
H x , w ⋍ { 1 − w x [ r 0 + 1 − 2 r 0 x 2 l n ⁡ ( 1 + x x ) ] } − 1
where r 0 is diffusive reflectance, given by
r 0 = 1 − 1 − w 1 + 1 − w
The CBOE function B C g is given by
B C g = 1 + 1 − e x p ⁡ [ − t a n ⁡ ( g 2 ) / h C ] tan ⁡ g 2 / h C 2 [ 1 + t a n ⁡ ( g 2 ) / h C ] 2
where h C is the angular width of CBOE.

2.2.2. The transformation relationship of the basic coordinate systems

The conversion relationship between the instantaneous projection and lunar geographic coordinate systems was obtained based on using the lunar fixed coordinate system as an auxiliary. The accurate conversion of lunar geographic coordinates to instantaneous projection coordinates was obtained by rotation transformation. This method involves a process of transforming lunar geodetic coordinates to lunar fixed coordinates, lunar fixed coordinates to three-dimensional instantaneous coordinates and, finally, three-dimensional instantaneous coordinates to instantaneous projection coordinates.
  • Transformation of lunar geodetic coordinates to lunar fixed coordinates;
The transformation from the lunar geodetic coordinate system (B, L, H) to the lunar fixed coordinate system (X, Y, Z) to which both can be defined in the lunar ellipsoid is:
{ X = ( R + h ) ⋅ cos B ⋅ cos L Y = ( R + h ) ⋅ cos B ⋅ sin L Z = ( R + h ) ⋅ sin B
where X, Y, Z is the coordinate value corresponding to the lunar point in the lunar fixed system, R is the lunar radius, L, B, h represent the coordinate value of the lunar point in the lunar geographic coordinate system, where L is the longitude and B is the latitude, and h is the elevation.
2.
Transformation of lunar fixed coordinates to three-dimensional instantaneous coordinates;
The triaxial vector direction of the instantaneous coordinate system can be expressed in the lunar fixed coordinate system.
The component along the X-axis ( M D → ):
( X X ′ , Y Y ′ , Z Z ′ ) = ( X D , Y D , Z D )
The component along the Y-axis ( O Y ′ → ):
O Y ′ → = M D → × M E → ( X Y ′ , Y Y ′ , Z Y ′ ) = ( Y D Z E − Z D Y , E X E Z D − X D Z E , X D Y E − X E Y D )
The component along the Z-axis ( O Z ′ → ):
O Z ′ → = M B → × O Y ′ → ( X Z ′ , Y Z ′ , Z Z ′ ) = ( Y E Z Y ′ − Z E Y , Y ′ X Y ′ Z E − X E Z Y ′ , X E Y Y ′ − X Y ′ Y E )
The origin of the instantaneous coordinate system in the lunar fixed coordinate system is derived from:
| M O | | M H | = | M H | | M D | | M O | = | M H | * | M H | | M D |
where DH is the tangent line to the moon which passes through the observation station, OH is the radius of the lunar projection circle from the observation station at observation time, and MO is the distance of the Lunar centroid and point M (Figure 3). Point O and B are both on the vector MD, then the point O in the lunar fixed coordinate system is written as:
O ( O x , O y , O z ) = ( | M O | , 0 , 0 )
The instantaneous coordinate system is defined as taking the site O for origin, (Xox, Yox, Zox) for X-axis, (Xoy, Yoy, Zoy) for Y-axis, (Xoz, Yoz, Zoz) for Z-axis. Here the triaxial unit vector of the lunar fixed coordinate system is written as:
X o x = X X ′ X X ′ 2 + Y X ′ 2 + Z X ′ 2 , Y o x = Y X ′ X X ′ 2 + Y X ′ 2 + Z X ′ 2 , Z o x = Z X ′ X X ′ 2 + Y X ′ 2 + Z X ′ 2 X o y = X Y ′ X Y ′ 2 + Y Y ′ 2 + Z Y ′ 2 , Y o y = Y Y ′ X Y ′ 2 + Y Y ′ 2 + Z Y ′ 2 , Z o y = Z Y ′ X Y ′ 2 + Y Y ′ 2 + Z Y ′ 2 X o z = X z ′ X z ′ 2 + Y z ′ 2 + Z z ′ 2 , Y o z = Y z ′ X z ′ 2 + Y z ′ 2 + Z z ′ 2 , Z o z = Z z ′ X z ′ 2 + Y z ′ 2 + Z z ′ 2
There is simple translation relation between the instantaneous coordinate system and the lunar fixed coordinate system. M was obtained as the rotation matrix in equation (15) from the rotation matrix:
M = [ X o x   Y o x   Z o x   O x X o y   Y o y   Z o y   O y X o z   Y o z   Z o z   O z 0       0     0     1 ]
According to the definition of the rotation matrix, it can be converted to the lunar fixed coordinate system by rotation transformation in equation (16):
( x ′ , y ′ , z ′ , 1 ) = ( x , y , z , 1 ) ⋅ M
where ( x , y , z ) is the target point at the lunar fixed coordinate and ( x ′ , y ′ , z ′ ) is the target point at the instantaneous coordinate system.
3.
Transformation of three-dimensional instantaneous coordinates to instantaneous projection plane coordinates;
The corresponding three-dimensional instantaneous coordinates can be projected to the instantaneous projection coordinates at the observation time by a perspective projection which is a linear projection where there are three-dimensional objects on a projection plane. In the three-dimensional instantaneous coordinate system, the linear equation of each lunar surface site at the observation time was determined to calculate the two-dimensional instantaneous projection coordinate of the target point. The linear equation of the arbitrary sampling point, A, on the lunar surface and the observation point, D, was determined to calculate the intersection coordinates of DA and the projection surface (X=0; Figure 2). The three-dimensional instantaneous coordinate of the intersection point is ( 0 ,   Y ,   Z ) , with an instantaneous projection coordinate of ( Y ,   Z ) .

3. Results and Discussion

3.1. Observation Environment

The simulated observation site in the study is set in Inner Mongolia, China (115º15´1.8"east, 42º12´42.6" north, 1365 m altitude), which is mainly to facilitate the comparative observation requirements later. Different simulation observation points also could be selected according to different observation requirements, and the selection of observation positions here would not affect the accuracy of the research. The coordinates of the observation station in the lunar fixed coordinate system are the basis for the research of the lunar observation geometry. The fundamental ephemerides are the bases for computing the planetary and lunar positions and other related phenomena that are listed in the Astronomical Almanac. The fundamental planetary and lunar ephemerides of the Astronomical Almanac, starting in the year 2003, are DE405/LE405 of Caltech’s Jet Propulsion Laboratory (JPL). The coordinates of the observation and the sun are obtained by DE405 during February 2019 (Table 1).
This study used observations from February 10, 2019, and February 19, 2019, as examples. The coordinates of the ground observation are (395850181.233, −40592333.726, 52381084.201) and (357730461.395, −8793065.875, −11557451.723) and the coordinates of the sun are (−68763558072.833, 130348136839.307, −1647761867.411) and (146594202092.887, 21709548884.399, −2268854787.204) (Table 1).
The equation of the transformation from rectangular coordinates to spherical coordinates is written as:
α = a r c t a n ⁡ ( Y / X ) δ = a r c t a n ⁡ ( Z X 2 + Y 2 )
where α is the latitude of the subsolar point on the moon, and δ is the longitude of the subsolar point on the moon. Therefore, the spherical coordinates of the subsolar points are (−62.2182, −0.6409) on February 10, 2019, and (8.4281, −0.8776) on February 19, 2019.

3.2. Lunar Spectral Irradiances Simulation

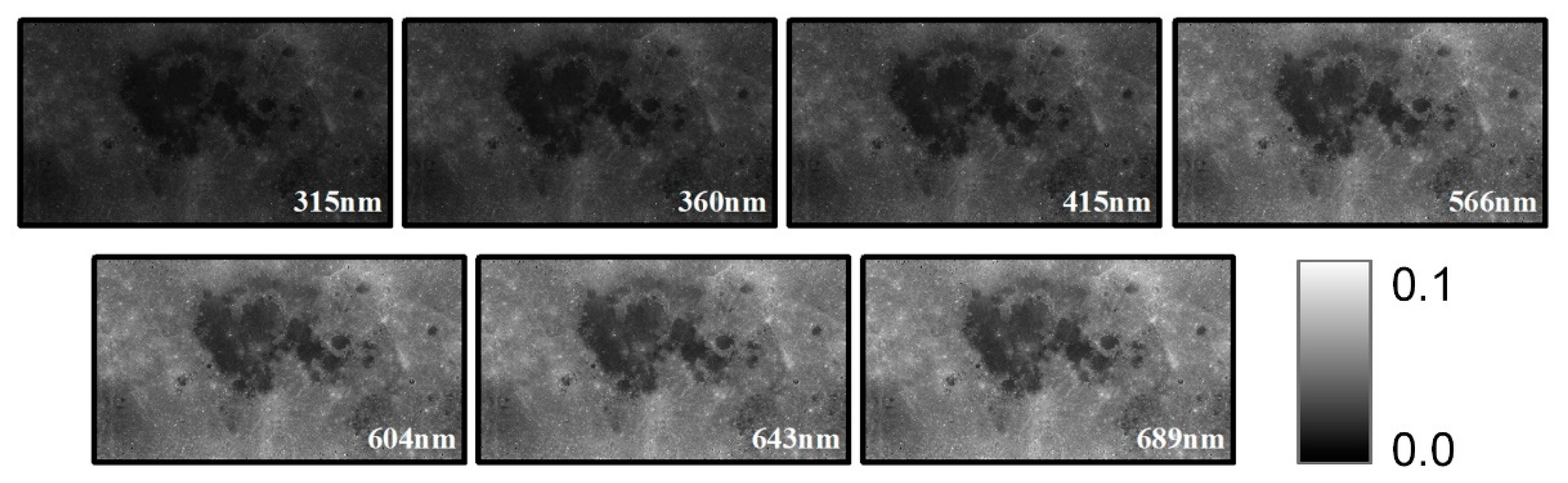
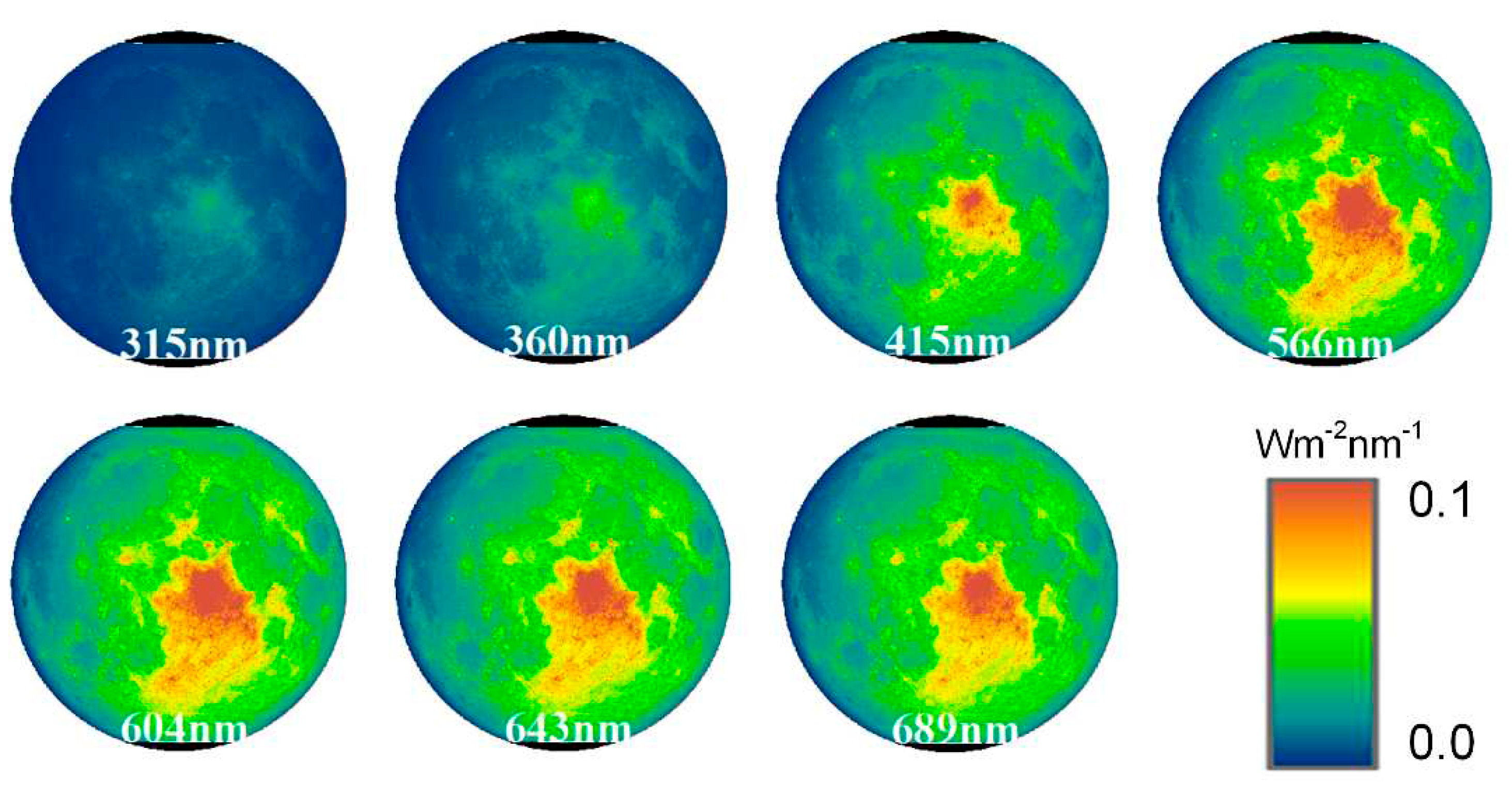
To extract the distribution of instantaneous lunar spectral radiance, the directional reflectance at the observation moment must be obtained first. We would use the MDREMP which gives the directional reflectance of a 30-degree incidence and 0-degree emission angle as the basic data of reflectance simulation in this research. On this basis, we calculated the radiance factor in the standard angle of phase (g) = incidence (i) = 30°, emission (e) = 0° and the radiance factor of each pixel at the observation time by Hapke bidirectional reflectance function using SDRPHO. The standared directional reflectance and the standard radiance factor are shown based on the GCS_MOON_2000 coordinate system in Figure 4 and Figure 5.
The directional reflectance of each pixel at the observation time is affected by the observation parameters mainly including the incident angle and the emission angle. Since the distance between the earth and the moon is relatively large relative to the radius of the earth, the emission angle is can be approximately 0°, and the function of the incident angle is given by
s i n h = s i n φ ∗ s i n δ + c o s φ ∗ c o s δ ∗ c o s t
where δ is the solar declination (equal to the latitude of the subsolar point), φ is the latitude and t is the local time which can be obtained from the subsolar point and the longitude. The distribution of the radiance factor on February 19, 2019, and February 10, 2019, is shown in Figure S1. On February 19, 2019, the subsolar point is close to the prime meridian. Therefore, the lunar phase is close to the full moon and the brightness temperature is high on the near side of the moon. On February 10, 2019, the longitude of the subsolar point is −62.2182 which is also the point of the highest physical temperature.
The lunar spectral reflectance at the observation time is given by
R e f o b s e r v a t i o n = I / F o b s e r v a t i o n I / F s t d ∗ R e f s t d
where I/Fstd is the radiance factor in the angle of phase (g) = incidence (i) = 30°, emission (e) = 0°, I/Fobservation is the radiance factor of each pixel at the time of observation and Refstd is the directional reflectivity of 30-degree incident angle and 0-degree emission angle. The solar irradiance at the observation time is written as:
I o b s e r v a t i o n = I s t d ∗ ( 1 A U / d S u n − M o o n ) 2
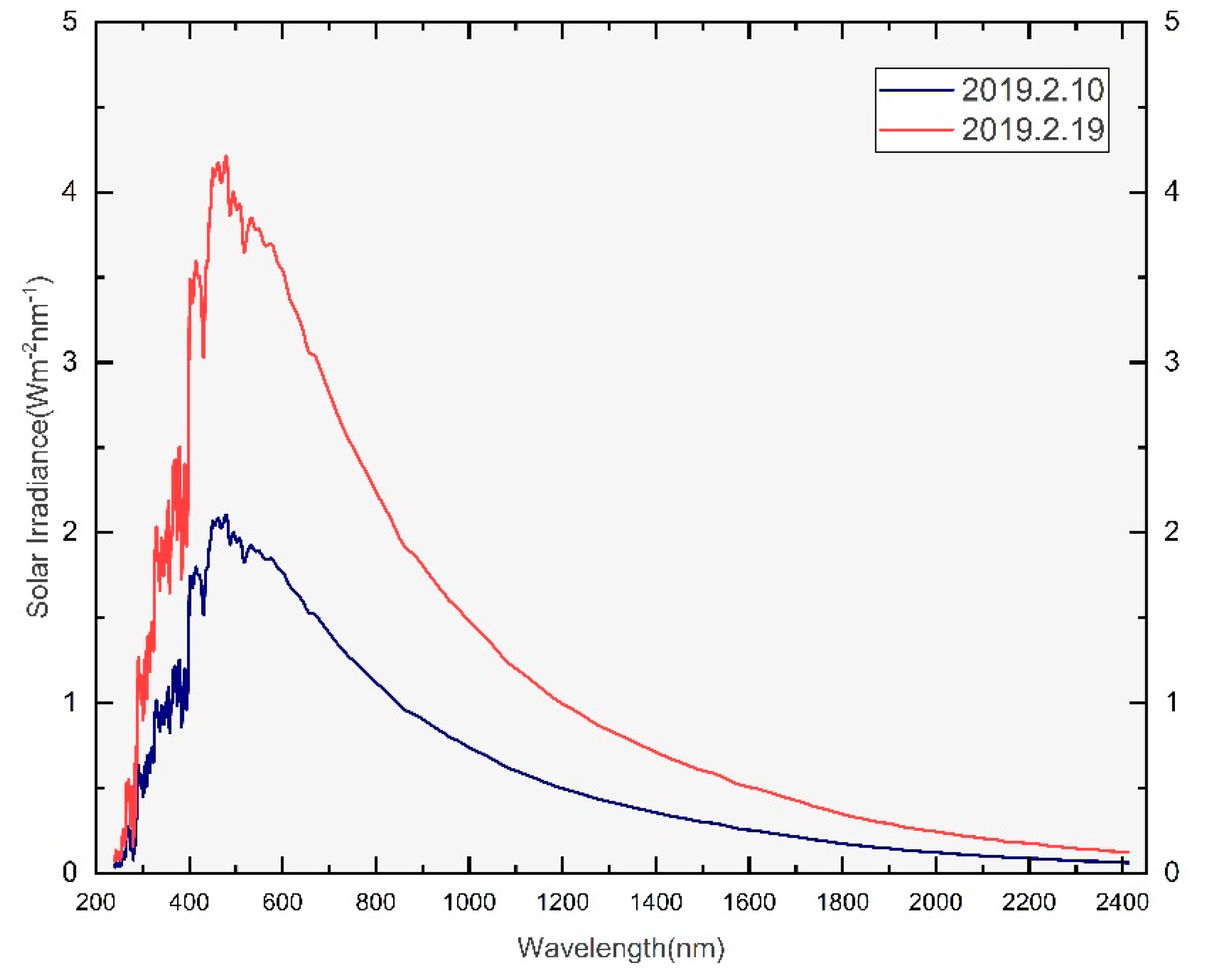
where d S u n − M o o n is the distance between the sun and the moon at the observation time, and I s t d is the solar irradiance at standardized distances of 1 AU for the Sun and Moon distance. 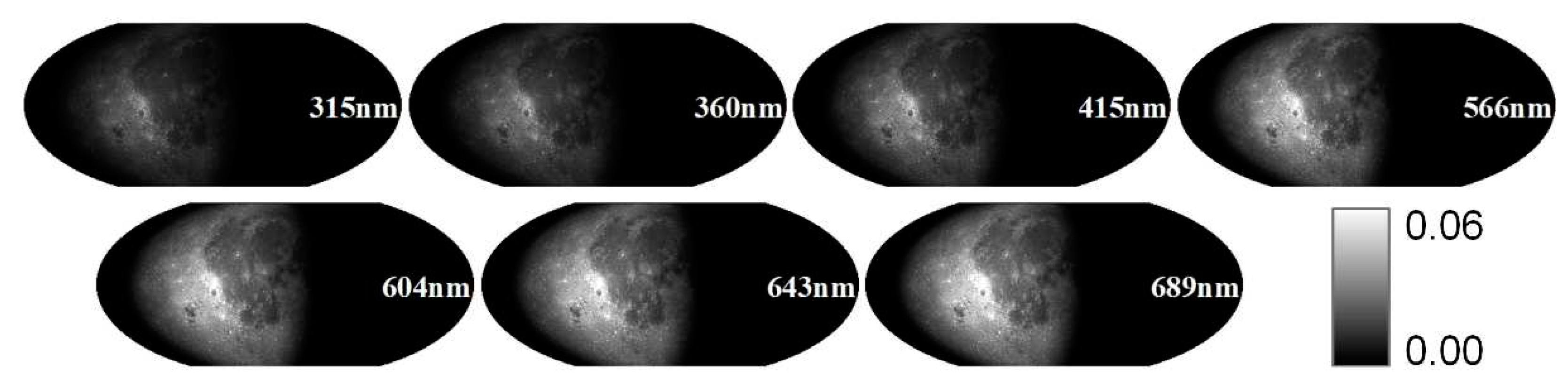The SOR3SIMD shows that the solar irradiances in 321, 360, 415, 566, 604, 643 and 689nm on February 19, 2019, are 0.6032033, 0.9699519, 1.78526, 1.843822, 1.751854, 1.598708, 1.453432 and the ones on February 10, 2019, are 0.6004955, 0.9693273, 1.785617, 1.843921, 1.752042, 1.598314, 1.453312 in Figure A3. We multiply the solar irradiance by the lunar directional reflectance at the observation time to get the distribution of the lunar surface irradiance at the observation time(Figure 6 and Figure 7 ).

3.3. The Earth-based Moon observation geometry

The emission angle of the lunar directional reflectance varies little on each pixel of the moon, for the distance between the earth and the moon is much greater than the radius of the moon. To reduce the computational complexity of the model, the numerical simulation process in this study is approximately vertical observation, that is, the emission angle is 0°. We only need to consider the influence of the observation position and field of view in the simulation. The projection at the observation time in the instantaneous projection coordinate system can be obtained based on transformation from lunar geographic and instantaneous projection coordinate systems on February 10, 2019(Figure 8) and February 19, 2019 (Figure 9). The simulated observation on February 19, 2019, is high at a full moon while most of the Moon's disc is illuminated (Figure 9). While the longitude of the subsolar point is −62.2182 on February 10, 2019, more than half of the moon’s disc is unilluminated and the simulated lunar spectral irradiances show low values at the west side of the moon (Figure 8).

4. Conclusions

In this study, we simulated the distribution of the instantaneous lunar spectral irradiances and established a geometric model for earth-based moon observation. We simulated the lunar observation environment at a specific time point and a specific observation location to obtain the lunar spectral irradiances distribution within the observation field of view. This research can provide technical support for earth-based moon exploration and satellite radiometric calibration. The main conclusions include:
(1) We obtained the lunar bidirectional spectral reflectance at the observation based on the standard reflectance data and reflection factors from product MDRHAP, and product SDRPHO by the Hapke bidirectional reflectance function. And the distribution of the lunar spectral irradiances at the observation time could be achieved based on the lunar bidirectional spectral reflectance and product SOR3SIMD to establish, and finally obtained the product of the lunar albedo at the observation time.
(2) Based on obtaining the distribution of the lunar irradiances at the observation, the conversion relationship between the lunar geographic coordinate system and the lunar fixed coordinate system, the conversion relationship between the lunar fixed coordinate system and the instantaneous coordinate system, and the conversion relationship between the instantaneous coordinate system and the two-dimensional instantaneous projection plane coordinate system was established. Following this, The distribution of the lunar irradiances in the lunar projection plane at the observation time could be obtained quickly, conveniently and accurately. The geometric model for the earth-based moon observation was established in this study.

Author Contributions

YL-Software, Formal analysis, Methodology, Writing - Original Draft, Visualization, Funding acquisition; QR- Conceptualization, Methodology, Visualization, Supervision, Writing - Review & Editing, Funding acquisition; TT, HZ, WL, HG- Data Curation, Formal analysis; JP, ZM - Methodology, Writing - Review & Editing.

Funding

Please add: This study was funded by National Natural Science Foundation of China (Grant No. 41971306), the Foundation of Tianjin Normal University (52XB1502, 043-135202XK1604), National key research and development program of China(2021YFA0715100, 2021YFA0715101).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Preprints 80155 g0a1
Figure A1. The distribution of the spectral radiance factor on February 10, 2019.
Figure A1. The distribution of the spectral radiance factor on February 10, 2019.
Preprints 80155 g0a1
Preprints 80155 g0a2
Figure A2. The distribution of the spectral radiance factor on February 19, 2019.
Figure A2. The distribution of the spectral radiance factor on February 19, 2019.
Preprints 80155 g0a2
Preprints 80155 g0a3
Figure A3. SOR3SIMD SORCE Spectral Irradiance at the observation time.
Figure A3. SOR3SIMD SORCE Spectral Irradiance at the observation time.
Preprints 80155 g0a3

References

  1. Green, P.D.; Lobb, D. 2015. The traceable radiometry underpinning terrestrial and helio studies (truths) mission//Proceedings of SPIE 9639, Sensors, Systems, and Next-Generation Satellites XIX. Toulouse: SPIE: 96391C. [CrossRef]
  2. Leckey, J. 2015. Climate absolute radiance and refractivity observatory (CLARREO). International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, XL-7/W3: 213–217. [CrossRef]
  3. Kieffer, H.H.; Wildey, R.L. Absolute calibration of landsat instruments using the moon. Photogrammetric Engineering and Remote Sensing 1985, 51, 1391–1393. [Google Scholar]
  4. Kieffer, H.H. Photometric stability of the lunar surface. Icarus 1997, 130, 323–327. [Google Scholar] [CrossRef]
  5. Kouyama, T.; Yokota, Y.; Ishihara, Y.; et al. Development of an application scheme for the SELENE SP lunar reflectance model for radiometric calibration of hyperspectral and multispectral sensors. Planetary and Space Science, 2016, 124, 76–83. [Google Scholar] [CrossRef]
  6. Kieffer, H.H.; Wildey, R.L. Establishing the Moon as a Spectral Radiance Standard. Journal of Atmospheric and Oceanic Technology 1996, 13, 360–375. [Google Scholar] [CrossRef]
  7. Kieffer, H.H.; Stone, T.C. The spectral irradiance of the moon. Astronomical Journal 2005, 129, 2887. [Google Scholar] [CrossRef]
  8. Stone, T.C. Radiometric calibration stability and inter-calibration of solar-band instruments in orbit using the moon. Proceedings of SPIE -The International Society for Optical Engineering 2008, 7081, 70810X–70810X. [Google Scholar]
  9. Zhang, L.; Zhang, P.; Hu, X.; et al. A novel hyperspectral lunar irradiance model based on ROLO and mean equigonal albedo. Optik - International Journal for Light and Electron Optics 2017, 142, 657–664. [Google Scholar] [CrossRef]
  10. Sun, J.Q.; Xiong, X.; Barnes, W.L.; et al. MODIS Reflective Solar Bands On-Orbit Lunar Calibration[J]. IEEE Transactions on Geoscience & Remote Sensing, 2007, 45, 2383–2393. [Google Scholar]
  11. Kieffer, H.H.; Jarecke, P.J.; Pearlman, J. Initial lunar calibration observations by the EO-1 Hyperion imaging spectrometer. Proceedings of SPIE - The International Society for Optical Engineering, 2002, 4480, 43–253. [Google Scholar]
  12. tone, T.C.; Kieffer, H.H.; Grant, I.F. Potential for calibration of geostationary meteorological satellite imagers using the Moon. Proc. Of SPIE - The International Society for Optical Engineering 2005, 5882, 58820P–1. [Google Scholar]
  13. Barnes, R.A.; Eplee, R.E.; Patt, F.S., Jr.; et al. Changes in the radiometric sensitivity of SeaWiFS determined from lunar and solar-based measurements. Applied Optics 1999, 38, 4649–4664. [Google Scholar] [CrossRef] [PubMed]
  14. Barnes, W.; Xiong, M.X.; Eplee, M.R.; et al. Use of the Moon for Calibration and Characterization of MODIS, SeaWiFS, and VIRS. Neuropharmacology 2006, 30, 1269–1274. [Google Scholar]
  15. Xiong, X.; Butler, J.; Chiang, K.; et al. Assessment of S-NPP VIIRS On-Orbit Radiometric Calibration and Performance. Remote Sensing 2016, 8. [Google Scholar] [CrossRef] [PubMed]
  16. Kouyama, T.; Kato, S.; Miyashita, N. One-year lunar calibration result of Hodoyoshi-1, Moon as an ideal target for small satellite radiometric calibration[C]. 32nd Annual AIAA/USU Conference on Small Satellites, 2018.
  17. Wu, R.; Zhang, P.; Yang, Z.; et al. Monitor the radiance calibration of the remotesensing instrument by using the reflected lunar irradiance. Journal of Remote Sensing 2016, 20, 278–289. [Google Scholar]
  18. Robinson, M.S.; Brylow, S.M.; Tschimmel, M.; et al. Lunar reconnaissance orbiter camera (LROC) instrument overview. Space science reviews 2010, 150, 81–124. [Google Scholar] [CrossRef]
  19. Sato, H.; Robinson, M.S.; Hapke, B.; Denevi, B.W.; Boyd, A.K. Resolved Hapke parameter maps of the Moon. Journal of Geophysical Research Planets 2014, 119, 1775–1805. [Google Scholar] [CrossRef]
  20. Boyd, A.K.; Robinson, M.S.; Sato, H. Lunar Reconnaissance Orbiter wide angle camera photometry: An empirical solution[C]//Lunar and planetary science conference. 2012 (1659): 2795.
  21. Cahalan, R.F.; Ajiquichí, P.; Yatáz, G. Solar Temperature Variations Computed from SORCE SIM Irradiances Observed During 2003–2020. Solar Physics 2022, 297, 1–37. [Google Scholar] [CrossRef]
  22. Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge Univ. Press: New York, 1993; Volume 262. [Google Scholar]
  23. Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge Univ. Press: New York, 2012. [Google Scholar]
  24. Hapke, B. (1981), Bidirectional reflectance spectroscopy: 1. Theory, J. Geophys. Res., 86(B4), 3039–3054. [CrossRef]
  25. Hapke, B. Scattering and diffraction of light by particles in planetary regoliths. J. Quant. Spectrosc. Radiat. Transfer 1999, 61, 565–581. [Google Scholar] [CrossRef]
Preprints 80155 g001
Figure 1. Spatial schematic map of lunar geographic coordinate system(a) and lunar fixed coordinate system(b).
Figure 1. Spatial schematic map of lunar geographic coordinate system(a) and lunar fixed coordinate system(b).
Preprints 80155 g001
Preprints 80155 g002
Figure 2. Spatial schematic diagram of the instantaneous coordinate system.
Figure 2. Spatial schematic diagram of the instantaneous coordinate system.
Preprints 80155 g002
Preprints 80155 g003
Figure 3. A schematic diagram of the O coordinates for the centre of the projection plane.
Figure 3. A schematic diagram of the O coordinates for the centre of the projection plane.
Preprints 80155 g003
Preprints 80155 g004
Figure 4. The standard spectral directional reflectance in the angle of phase (g) = incidence (i) = 30°, emission (e) = 0°.
Figure 4. The standard spectral directional reflectance in the angle of phase (g) = incidence (i) = 30°, emission (e) = 0°.
Preprints 80155 g004
Preprints 80155 g005
Figure 5. The spectral radiance factor in the angle of phase (g) = incidence (i) = 30°, emission (e) = 0°.
Figure 5. The spectral radiance factor in the angle of phase (g) = incidence (i) = 30°, emission (e) = 0°.
Preprints 80155 g005
Preprints 80155 g006
Figure 6. the lunar spetral directional reflectance on February 10, 2019.
Figure 6. the lunar spetral directional reflectance on February 10, 2019.
Preprints 80155 g006
Preprints 80155 g007
Figure 7. the lunar spetral directional reflectance on February 19, 2019.
Figure 7. the lunar spetral directional reflectance on February 19, 2019.
Preprints 80155 g007
Preprints 80155 g008
Figure 8. The lunar projection of simulated lunar spectral irradiances on February 10, 2019.
Figure 8. The lunar projection of simulated lunar spectral irradiances on February 10, 2019.
Preprints 80155 g008
Preprints 80155 g009
Figure 9. The lunar projection of simulated lunar spectral irradiances on February 19, 2019.
Figure 9. The lunar projection of simulated lunar spectral irradiances on February 19, 2019.
Preprints 80155 g009
Table 1. Coordinates of observation station and sun in the lunar fixed coordinate system.
Table 1. Coordinates of observation station and sun in the lunar fixed coordinate system.
Data Coordinates of ground observation station Coordinates of the sun
X Y Z X Y Z
2019/2/1 395639321.307 38266042.153 -15849967.443 -99334958891.534 -108485879852.694 -1171442964.620
2019/2/2 399640093.024 30777392.101 -6563094.663 -119974203729.788 -85057374185.770 -1231368074.096
2019/2/3 402685070.881 22136782.712 3300020.343 -135216339462.342 -57802203851.536 -1288816108.819
2019/2/4 404693614.330 12731899.257 13281732.483 -144374909882.550 -27942575832.102 -1344004947.971
2019/2/5 405640480.936 2928981.481 22929598.868 -147036292818.152 3181752374.513 -1397161309.976
2019/2/6 405541552.787 -6930590.156 31810331.329 -143078435155.000 34173595168.771 -1448580728.712
2019/2/7 404440889.456 -16525313.441 39523064.133 -132676493008.997 63641084625.959 -1498682229.099
2019/2/8 402402105.046 -25543546.654 45711628.386 -116295112933.068 90260214900.542 -1548047213.407
2019/2/9 399505457.430 -33672735.027 50075703.091 -94667693940.652 112834367682.262 -1597433863.658
2019/2/10 395850181.233 -40592333.726 52381084.201 -68763558072.833 130348136839.307 -1647761867.411
2019/2/11 391559903.599 -45974249.023 52469735.772 -39744503333.340 142013026479.114 -1700064966.986
2019/2/12 386787918.572 -49493363.868 50270509.901 -8912690818.860 147302963299.864 -1755411786.303
2019/2/13 381719057.508 -50849055.971 45811310.726 22347792041.978 145978021923.941 -1814797129.357
2019/2/14 376566083.558 -49796904.064 39232712.489 52633065902.452 138095292018.467 -1879008847.484
2019/2/15 371560773.505 -46188109.262 30801448.213 80582499483.860 124006394512.285 -1948480187.702
2019/2/16 366942382.327 -40012367.109 20919690.691 104939820676.515 104341757089.059 -2023149071.275
2019/2/17 362947605.099 -31437617.178 10123197.305 124609551347.494 79982360586.191 -2102357053.840
2019/2/18 359804790.386 -20837224.395 -940149.502 138706228121.825 52020241616.223 -2184840665.057
2019/2/19 357730461.395 -8793065.875 -11557451.723 146594202092.887 21709548884.399 -2268854787.204
2019/2/20 356920641.971 3935406.505 -21021437.531 147916241856.587 -9589629379.677 -2352435667.788
2019/2/21 357528505.274 16478337.064 -28710924.878 142609676191.742 -40472151539.559 -2433736968.225
2019/2/22 359627293.264 27949141.862 -34159777.298 130909369199.958 -69550729352.054 -2511328325.223
2019/2/23 363169664.415 37545333.070 -37096038.251 113337395800.903 -95518093425.997 -2584351169.953
2019/2/24 367961943.748 44635701.859 -37445541.630 90679860686.103 -117205674881.443 -2652508169.417
2019/2/25 373667897.489 48819362.226 -35307649.051 63951866322.691 -133636184478.287 -2715928989.419
2019/2/26 379844747.389 49950975.964 -30917152.876 34352166533.880 -144067710609.959 -2774991214.582
2019/2/27 386002345.951 48133405.680 -24604863.636 3209512005.569 -148027322897.020 -2830157031.899
2019/2/28 391670335.457 43683136.367 -16764082.161 -28076922033.176 -145332636386.792 -2881855373.510
2019/3/1 396458241.465 37076022.056 -7825065.961 -58100360361.126 -136100336125.527 -2930415269.263
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated