Prerpints.org logo
Preprint
Article

Optical Super‐Resonances in Mesoscale Dielectric Cenosphere: Giant Magnetic Field Generations

Altmetrics

Downloads

139

Views

37

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (11.26MB )

This version is not peer-reviewed

Submitted:

24 July 2023

Posted:

25 July 2023

You are already at the latest version

Alerts
Abstract
Resonant light scattering by mesoscale dielectric spheres has received enormous attention and found many interesting applications. The recently emerged field of Mesotronics provides novel opportunities for wavelength-scaled optics and new fundamental aspects are still being uncovered. It has recently been demonstrated that high-order Mie resonances can be excited in homogeneous low-dissipation mesoscale dielectric spheres, leading to the generation of intense magnetic fields. This Letter describes a simple and effective way to drastically enhance the superresonance effect. Proof-of-principle results for the first time show that yet one more novel phenomenon of increasing the intensity of the magnetic field without changing the resonant Mie size parameter of the sphere by introducing an air cavity. In such a dielectric cenosphere (from two Greek words “kenos” - hollow and “sphaira” - sphere), by correct choosing of the air cavity size, it is possible to increase the intensity of the electromagnetic fields at the poles of the sphere by an order of magnitude due to increasing of amplitude of resonant partial wave coefficient.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics
According to Maxwell equations, in a vacuum energies of electric and magnetic fields are equal [1]. For example, as the Earth’s magnetic field [2] as interstellar medium [3] has an average magnitude of about 30 μTesla (T).
The problem of generating strong magnetic fields has a long history and has been studied for a long time [4,5]. P. Kapitsa conducted the first experiments with very strong magnetic fields (up to 50-100 Tesla in a coil of 1 mm inner diameter during a few milliseconds) with the high magnetic energy density (B2/2µo=40 kJ/cm3 at 100 T) at the beginning of the 20th century [6,7,8]. The magneto-cumulative generators, suggested by A. Sakharov almost 30 years later, allows obtaining magnetic fields around 3000 T [9,10,11]. In 1958, at the newly created Novosibirsk Institute of Hydrodynamics, V.F. Minin began work on the generation of megagauss magnetic fields and electromagnetic acceleration of microparticles up to several km/s. The methods of the magnetic fields generation (including laser light interaction with a conical target for plasma jet formation in a hypercumulative mode) up to about 100 MG, higher than that in flux-compression generators, were discussed in [12,13,14,15]. The history of high magnetic field generation are reviewed in [5,11,16,17].
Electromagnetic fields with large values of the magnetic induction strength can be observed in intense optical beams [18,19,20,21], where the magnetic induction amplitude can be reached about of 109 T, which is 2 orders of magnitude smaller than the amplitude of the magnetic induction in magnetar neutron stars [22,23]. This is due to the size of the star itself and the size of the smallest vortices that can be created in a given structure. Now a laboratory record for pulsed magnetic inductions strength are above 3000 T [5,16,22]. Nevertheless, new physical principles are required to generate giant magnetic fields.
The effect of the photonic nanojet [24,25] (PNJ) is based on the field localization in the shadow side of dielectric mesoscale particle of arbitrary 3D shape [26]. In the context of the generation of localized magnetic fields, this non-resonant effect is important because the magnetic field in the PNJ can be enhanced more than the electric one, for example, both for spherical [25] and cubic [27] mesoscale particles. On the other hand, in a dielectric sphere, the resonances are size-dependent and defined by the Mie size parameter q (q=2πR/λ, where R is the radius of particle and λ the incident wavelength). For the lowest order resonance, the particle radius R is in order of λ/n, where n is a refractive index of a sphere material [28].
The fundamental role of magnetic and electric low-index (less than 5) modes in determining the resonant properties of dielectric nanoparticles is well-known. Recently, we showed that homogeneous dielectric mesoscale spheres for specific values of the size parameter q~10 could support high-order Fano resonance, associated with internal Mie modes (so-called super-resonance modes, SR). Such resonance can generate the magnetic and electric field intensity enhancement about 104- 107 [29,30]. From the Bio-Savart low one can followed that reducing the size of the coil one can increase the magnetic field amplitude [29,31]. In the near-field one can possible to localize electromagnetic field below the classical diffraction limit and, thus, for the focused optical wave the minimum size of the equivalent coil will be much less than the wavelength. Such extremely high values of the electromagnetic fields enhancement [29,30] are due to the possibility of creating small optical vortices similar to superoscillation effect [32,33,34], which is associated with the formation of regions having extremal high values of the local wavenumber vectors [35] and origination of other recently discovered peculiarities of the Poynting vector field [36]. Usually optical vortices and Fano resonances are independent due to interference phenomena of different types [37]. We emphasize that the vortices are not due to the features of the incident radiation, but arise during the scattering of a plane linearly polarized wave, which has no features. For SR conditions, these phenomena are mutually dependent. This provides a new mechanism to obtain extreme field localization with giant field enhancement. An important feature of these high-order Fano resonances in mesoscale dielectric homogeneous spheres is the field space localization, which is below the diffraction limit near its poles [29,30,40,41,42]. Noteworthy this effect was extended to the acoustic domain [38]. However, the small values of dissipation in the particle material can suppress the SR effect [29,39]. Therefore, the search for dielectrics with low dissipation is an urgent problem. Borosilicate glass, for example, can be one of such material in optics [40]. We also find that SR resonances are very sensitive to a refraction index change in the surrounding medium, which could be useful for sensing [41]. It also could be noted that the resonant size parameter q must be smaller for particles with a high refractive index [29] and higher for the particles having a low refractive index [30]. For example, for materials with extremely high refractive index (n>10) and small Mie size parameter (q<1), SR resonances with giant enhancement of magnetic fields can be observed in the range of the first Fano resonances [42] (see Supplementary).
As we noted above, in a dielectric sphere the SR resonances are size-dependent. An obvious way to increase the intensity of the resonant values of the magnetic field is to increase the size of the sphere. However, this is not always possible both from a practical and technological point of view. Therefore, the question is relevant: is it possible to further increase the intensity of the resonant peak of the magnetic field without changing the resonant value of Mie size parameter q?
In this paper using a recently found solution for a high-order Fano resonance in homogeneous mesoscale dielectric spheres [29,30,40,41], we analyze the magnetic and electric fields intensities with giant enhancement near a resonant sphere with concentric air cavity (so-called cenosphere [43]). To the best of our knowledge, no study has yet been proposed demonstrating the effect of amplification of superresonance in a dielectric sphere with an increase in the intensity of resonant peaks of magnetic and electric fields. Based on Lorentz-Mie theory [44] for the first time we show that it is possible to increase by an order of magnitude the intensity of the resonant peak of the magnetic field without changing the resonant value of Mie size parameter q by introducing the air cavity. As before, we reveal the contribution of an individual mode at SR. In our study, we use a low loss sphere with a refractive index of 1.5, which is characteristic of dielectrics in the optical range.
Aden and Kerker firstly considered the theory of light scattering from two concentric spheres including hollow sphere [45]. The whispering gallery mode (WGM) resonance properties inside the liquid-filled hollow glass microsphere with different refractive index and diameter less than wavelength were studied in [46]. Retsch et al. studied the hollow silica spheres with extremely thin low refractive index shells, where the efficiency of Mie resonance is maximized due to significantly reduced multiple scattering while lengthens the mean free path of light inside the sphere [47]. Some achievements of low modes Mie resonances in subwavelength hollow dielectric spheres were discussed in numerous papers; see, e.g., [48,49] and reference therein. As a rule, here only magnetic and electric dipole terms have been considered and other higher order terms (more than 4) have been neglected.

Model

The Mie theory allows identifying multipolar origin and the spectral characteristics of all resonances (both electric and magnetic) observed in the scattering. According to the Lorentz–Mie theory [44], the scattering of a linearly polarized plane electromagnetic wave by a spherical particle is represented as a slowly converging infinite series of partial components. Each partial wave is represented as a sum of two modes, magnetic and electric [44]. The corresponding efficiencies of external and internal scattering are mathematically connected with the equations for two pairs of complex scattering coefficients (al, bl) and (cl, dl), respectively, which, in turn, are expressed as combinations of Bessel and Neumann spherical functions and their derivatives.
The detailed analysis of the amplitudes of the Mie scattering coefficients (cl, dl) carried out earlier for homogeneous spheres shows the strong scattering of a high-order single mode in the internal electric or magnetic field of a particle to be a key factor responsible for the superresonance effect [29,30,39,40,41,42]. In the content of the SR, we are interested in the Mie coefficients associated with the internal scattering of fields in the field component equations, which can be written as [30,40,50,51,52]:
A e l = i l + 1 2 l + 1 l ( l + 1 ) c l , A m l = i l + 1 2 l + 1 l ( l + 1 ) d l ,
where
c l = y ζ l x ψ ′ l x − y ζ ′ l x ψ l x y ζ ′ l x ψ l y − x ζ l x ψ ′ l y ,   d l = y ζ ′ l x ψ l x − y ζ l x ψ ′ l x y ζ l x ψ ′ l y − x ζ ′ l x ψ l y .
Here, x = kma and y = kpa (the subscripts m and p correspond to the medium and the particle),
ζ l ρ = ρ h l 1 ρ = π ρ 2 H l + 1 2 1 ρ ,   ψ l ρ = ρ j l ρ = π ρ 2 J l + 1 2 ρ ,
ζ ′ l ρ = ∂ ζ l ρ ∂ ρ ,   ψ ′ l ρ = ∂ ψ l ρ ∂ ρ ,
It is noteworthy that for theoretical simulation of the superresonances for sphere with Mie size parameter in order of 40, need high resolution to reproduce the high order Mie modes. In our work we follow to [52] in simulations of cenosphere scattering. SR modes are high sensitive to the Mie size parameter q. Here we used a q sampling accuracy of dq=10-4…10-5. Higher accuracies make it possible to localize the position of the resonance and, accordingly, the achievable level of maximum field enhancement, more accurately [53], but the manufacture of such spheres encounters significant difficulties, since simple morphological inconsistencies (e.g. surface roughness, any deviation from a perfect sphere) can lead to significant changes in the mode profiles.

Results and discussion

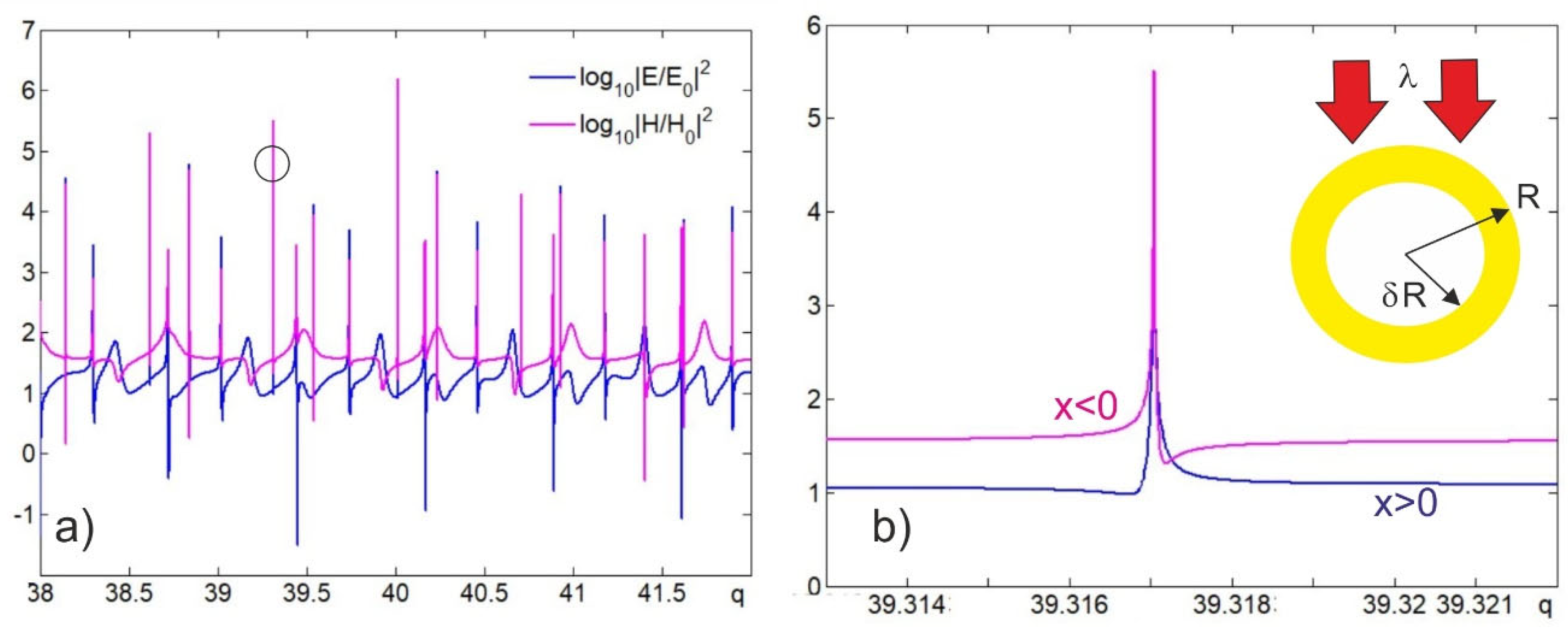
The effect of the SR is illustrated in Figure 1 for a nonabsorbing homogeneous spherical particle with n=1.5 and Mie size parameter near q~40. An asymmetric lineshape of the high-order Fano resonance [37] is observed for the spectra of the magnetic and electric fields intensities in the pole at the shadow side of a sphere (x=0, y=0, z=-R) [29,30,42]. Figure 1a shows the spectrum of field intensity resonances for a homogeneous sphere with the size parameter q range from 38 to 42 at λ=532 nm. In the case under study, the field intensity enhancements can attain giant values on the order of 105–106 for such Fano resonances. As example, the characteristic resonance lines are shown in more detail in Figure 1b for homogeneous sphere with q = 39.31704 (marked in black circle in Figure 1a).
According to Figure 1a, the size parameter q = 39.31704 of a homogeneous spherical particle in the optical range was chosen because the magnetic field intensity of resonance scattering peaks is significantly larger than that for the electric fiend intensity (see Figure 2 below).
Fano resonance, as a nontrivial multimode coupling, occurs when a near-field mode (low-Q) is coupled with a dark mode (high-Q), and as can be seen, all resonance Fano lines are quite narrow. As it well known, the Q factor of a spherical particle can be estimated by the simple formula Q=λ/Δλ [55], where Δλ is the resonance line width at half maximum (FWHM) [56] at the resonance wavelength λ. As follows from Figure 1b (on a logarithmic scale), under the conditions considered Q=4.5×107 at λ=532 nm for a homogeneous sphere. The line FWHM H2 and E2 are approximately the same and, hence, the Q factors for magnetic and electric fields are also equal. Note that zero-intensity frequency is less than ω0 (ω0 correspond to the position of the band [54]) at x>0 (for the electric field intensity) and more than ω0 at x<0 (for the magnetic field intensity) that is clearly seen in Figure 1.
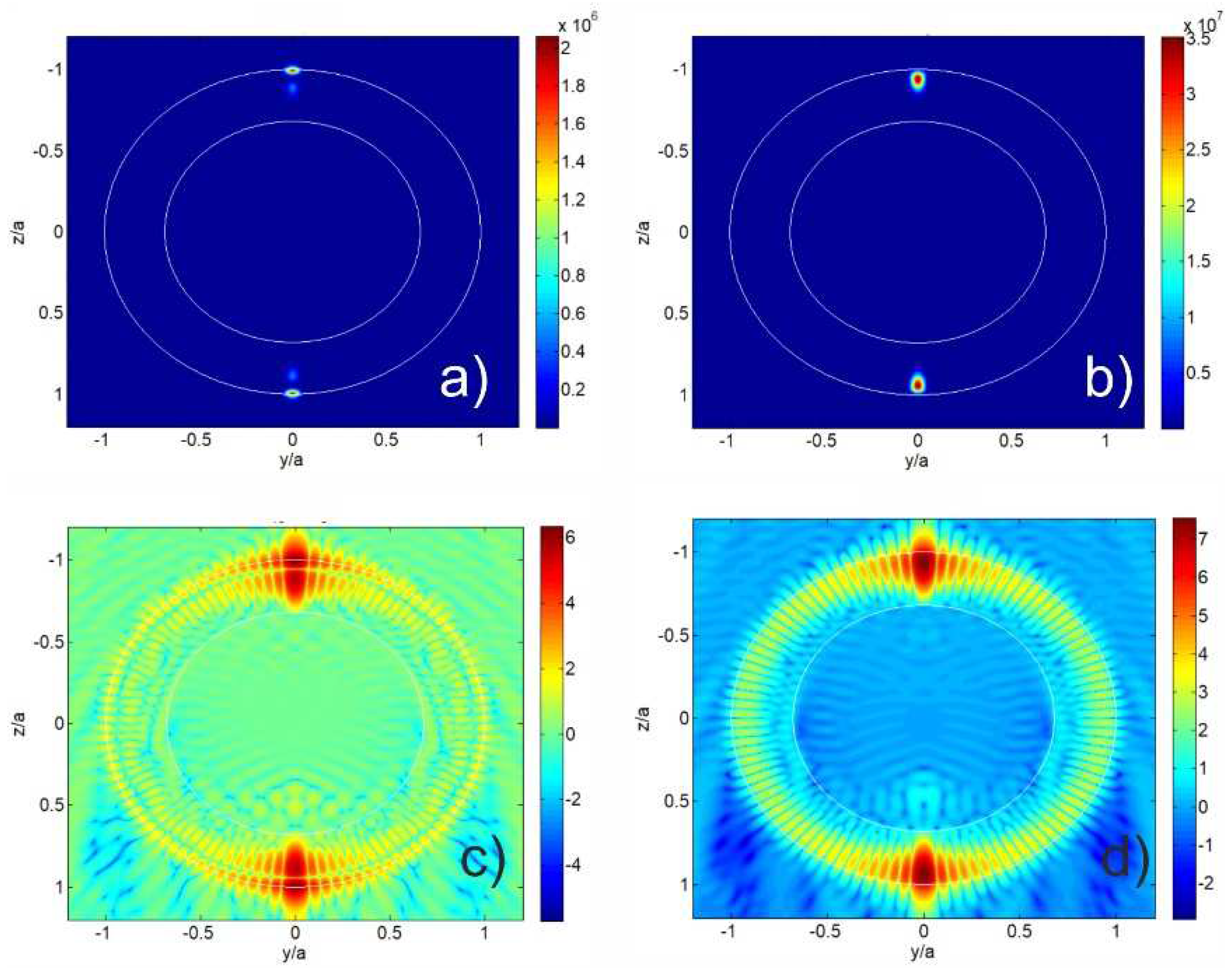
Figure 2 shows the distribution of electric and magnetic fields intensities for homogeneous spherical particle with Mie size parameter q = 39.31704 . Any high-order Mie resonance is the same as the excitation of a WGM [30], which is clear seen from Figure 2. Inside the sphere, for example, in Figure 2d, one can see 104 magnetic field intensity maxima of different magnitude located around near the sphere surface. It corresponds to 52 wavelengths of the standing “creeping” wave, which is an improper eigenwave wave resulting from curvature of the sphere surface and total internal reflection from it. In other words this pattern corresponds to the transverse magnetic mode TM52,0,1, where l=52 is orbital, m=0 is azimuthal and p=1 is the radial mode numbers, respectively [57,58].
The spatial field configuration inside a sphere under SR conditions, which are clear seen from Figure 2, are similar to the spatial field configuration inside a sphere with other Mie size parameter and refractive index [29,30,40,41,42]. Notable, only 2 maxima at the poles of a homogeneous sphere has magnitude about 4-5 order higher than others [30]. According to the Mie theory, this corresponds to a significant predominance of a single term in the series of internal scattering coefficients, which is responsible for the excited resonant mode. As a result, two “hot spots” both for magnetic and electric fields appear at the poles of the spherical particle. One can see that under superresonance conditions, the maximal magnetic field intensity enhancement is an order of magnitude higher than that of the electric field intensity:   E / E 0 max 2 = 2.327 × 10 5 and H / H 0 max 2 = 3.968 × 10 6 for the selected values of q and n. A detailed analysis of the features of the formation of superresonance in a homogeneous sphere was carried out earlier in the works [29,30,40,41,42].
Figure 3 shows the distribution of electric and magnetic fields intensities for the cenosphere with Mie size parameter q = 39.31704 and δ = 0 .6799 . The structure of the field inside the cenosphere is generally similar to the structure of the field for a homogeneous sphere. One can see that under superresonance conditions at the same value of q = 39.31704 as for a homogeneous spherical particle, the maximal both magnetic and electric field intensity enhancement is an order of magnitude higher than that of a homogeneous sphere: E / E 0 max 2 = 2.114 × 10 6 and H / H 0 max 2 = 3.516 × 10 7 .
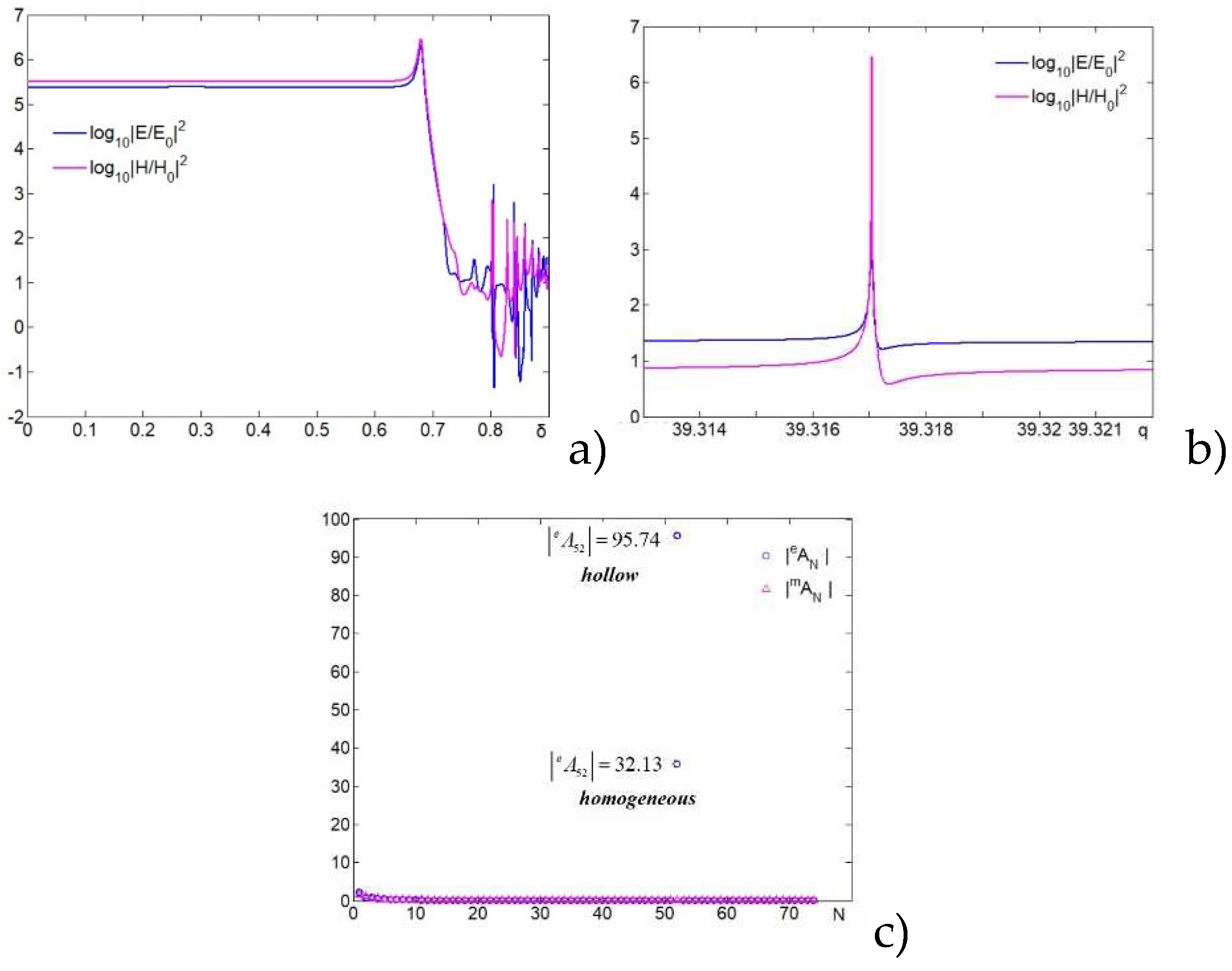
As simulation shown (Figure 4b), under the conditions considered Q factor for the cenosphere is Q=5.1×107 at λ=532 nm. The line FWHM H2 and E2 are approximately the same as for homogeneous sphere and, hence, the Q factors for magnetic and electric fields are also equal.
To understand the effect of increasing the maximum field intensities at superresonance, Figure 4a below shows the dependence of the maximum field intensity at the shadow pole of a cenosphere on the cavity radius defined as R c a v = δ R (see insert in Figure 1b).
Figure 4c shows Mie modes distribution for a homogeneous sphere and cenosphere with δ = 0 .6799 and q = 39.31704 . Such a modes distribution is typical for the Fano resonance: the interaction of all internal low-intensity modes with an individual high-intensity mode [29,30]. The resonance scattering coefficient is evidently much larger (by more than 40 times) than the other coefficients. Such an extreme value is explained by the constructive interference between a partial wave with the high-order mode N=52 and the wide spectrum of all other modes inside both a homogeneous and hollow mesoscale sphere. From the Figure 4c one can see that with the optimal cavity size, the number of the resonant mode does not change, but the amplitude of a single mode, corresponding to the number N=52 increases by about 3 times. The amplitude of a single N=52 mode significantly (by about a hundred times) dominates over other modes for a cenosphere. Thus, we can control the amplitude of the high-order resonant mode by adjusting the size of the internal cavity. As a result, the maximum intensity of the fields in the poles of the cenosphere increases because under SR the internal scattering efficiency is proportional to the square of the Mie scattering coefficients (1): Q l ( e ) ~ A l ( e ) 2 , Q l ( m ) ~ A l ( m ) 2 (see “Methods” in [29]).

Conclusion

Previous work has demonstrated that mesoscale low-loss homogeneous dielectric sphere support high-order Mie resonances in the visible spectral range. As a general trend, the current research pursued an increase the efficiency of the giant magnetic field generation. We show that the maximal field’s intensity enhancement can be controlled by introducing the air cavity into the resonant homogeneous sphere and by changing the wall thickness of the cenosphere. Compared to homogeneous spheres, the air cavity size comprises an additional design parameter to tune the maximal field intensity enhancement. It has been show that it is possible to control the interaction between bright and dark modes in a dielectric mesoscale sphere by adjusting the air cavity radius, and as a result to increase the magnetic and electric field enhancement. For example, an optimal cavity introduced into a resonant sphere makes it possible to increase the intensity of the magnetic and electric fields by an order of magnitude without changing resonant value of the Mie size parameter q. In particular, in optical range the cenosphere with Mie size parameter of q = 39.31704  and refractive index of 1.5 makes it possible to provide a magnetic field enhancement of the order of H / H 0 max 2 = 3.5 × 10 7  which are comparable to those in neutron stars. Also nonlinear optical effects can be enhanced if spherical particles are placed on the surface of materials exhibiting considered nonlinear effects.
These properties make cenospheres ideal for different applications, and their potential in making flexible, angle-independent giant electromagnetic fields generation. However, the SR properties are especially sensitive to morphology; hence, precise control of the hollow sphere is required. The obtained results unravel essential features of the superresonance effect in a mesoscale homogeneous sphere and cenosphere and shed new light on this recently discovered phenomenon.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Acknowledgments

This work was supported by the Natural Science Foundation of the Higher Education Institutions of Jiangsu Province (No. 22KJB460016), and partially supported by TPU development program.

References

  1. Maxwell, J.C. A Dynamical Theory of the Electromagnetic Field. Philos. Trans. R. Soc. Lond. 1865, 155, 459–512. [Google Scholar]
  2. Gillet, N.; Gerick, F.; Jault, D.; Schwaiger, T.; Aubert, J.; Istas, M. Satellite magnetic data reveal interannual waves in Earth’s core. PNAS 2022, 119, e2115258119. [Google Scholar] [CrossRef] [PubMed]
  3. Beck, R. Magnetic fields in spiral galaxies. Astron. Astrophys. Rev. 2016, 24, 4. [Google Scholar] [CrossRef]
  4. Furth, H.P. High Magnetic Field Research. Science, 1960, 132, 387–393. [Google Scholar] [CrossRef] [PubMed]
  5. Knoepfel, H.E. Magnetic Fields. JOHN WILEY & SONS, INC., N.Y., 2000, 619p.
  6. Kapitza, P.L. A method of producing strong magnetic fields. Proc. R. Soc. A 1924, 105, 691–710. [Google Scholar]
  7. Kapitza, P.L. Further developments of the method of obtaining strong magnetic fields. Proc. R. Soc. A 1927, 115, 772. [Google Scholar]
  8. Kapitza, P.L. The study of the magnetic properties of matter strong magnetic fields.—I.—The balance and its properties. Proc. R. Soc. A 1931, 131, 224–243. [Google Scholar]
  9. Sakharov, A.D.; Lyudaev, R.Z.; Smirnov, E.N.; Plyushchev, Y.I.; Pavlovskiĭ, A.I.; Chernyshev, V.K.; Feoktistova, E.A.; Zharinov, E.A. Zysin, Magnetic cumulation. Sov. Phys. Dokl. 1965, 165, 65. [Google Scholar]
  10. Sakharov, A.D. Magnetoimplosive generators. Phys. Uspekhi 1966, 9, 294–304. [Google Scholar] [CrossRef]
  11. Knoepfel, H.; Luppi, R. Very high magnetic fields generated in single-turn solenoids. J. Phys. E: Sci. Instrum. 1972, 5, 1133. [Google Scholar] [CrossRef]
  12. Felber, F.S., M.A. Liberman and A. L. Velikovich. Methods for producing ultrahigh magnetic fields. Appl. Phys. Lett. 1985, 46, 1042. [CrossRef]
  13. Minin, V.F.; Minin, I.V.; Minin, O.V. Cumulative plasma jet formation for acceleration of macroparticles, Proceedings. The 9th Russian-Korean International Symposium on Science and Technology, 2005. KORUS 2005., Novosibirsk, Russia, 2005, pp. 236–238.
  14. Sentoku, Y.; Mima, K.; Ruhl, H.; Toyama, Y.; Kodama, R., T.E. Cowan. Laser light and hot electron micro focusing using a conical target. Physics of Plasmas 2004, 11, 3083–3087. [CrossRef]
  15. P. F. Baranov and I. A. Zatonov. Some pioneering research in laboratory simulation of scaled astrophysical phenomena by Russian physicists. J. Phys. Conf. Ser. 2020, 1709, 1709–012003.
  16. Battesti, R.; Beard, J.; Böser, S.; et al. High magnetic fields for fundamental physics. Physics Reports 2018, 765–766, 1–39. [Google Scholar] [CrossRef]
  17. S. E. Shipilov and V. P. Yakubov. History of technical protection. IOP Conf. Ser. Mater. Sci. Eng. 2018, 363, 012033. [CrossRef]
  18. Longman and R. Fedosejevs. Kilo-Tesla axial magnetic field generation with high intensity spin and orbital angular momentum beams. Phys. Rev. Research 2021, 3, 043180. [CrossRef]
  19. Sederberg, S. ; Kong, F., and P. B. Corkum. Tesla-Scale Terahertz Magnetic Impulses. Phys. Rev. X 2020, 10, 011063.
  20. Murakami, M. ; Honrubia, J.J. ; Weichman, K.V. Arefiev & S. V. Bulanov. Generation of megatesla magnetic fields by intense-laser-driven microtube implosions. Sci Rep. 2020, 10, 16653.
  21. Jiang, K.; Pukhov, A., and C. T. Zhou. Magnetic field amplification to gigagauss scale via hydrodynamic flows and dynamos driven by femtosecond lasers. New J. Phys. 2021, 23, 063054. [CrossRef]
  22. R. A.Treumann, W. Baumjohann and A. Balogh. The strongest magnetic fields in the universe: How strong can they become? Frontiers in Physics 2014, 2, 59.
  23. Beskin; V.S.; Balog; Falanga; M. & Treumann, R.A. Magnetic fields at largest universal strengths: Overview. Space Sci. Rev. 2015, 191, 1–12.
  24. Heifetz; Kong; S.C.; Sahakian; A.V.; et al., “Photonic Nanojets,”. J. Comput. Theor. Nanosci., 2009, 6, 1979–1992.
  25. Luk`yanchuk; et al. Refractive index less than two: Photonic nanojets yesterday, today and tomorrow. Opt. Mater. Express 2017, 7, 1820–1847. [Google Scholar] [CrossRef]
  26. Minin, I.V.; Minin, O.V., Y. Geints. Localized EM and photonic jets from non-spherical and non-symmetrical dielectric mesoscale objects: Brief review. Ann. der Physik 2015, 527, 491–497. [Google Scholar] [CrossRef]
  27. Minin; O.V.; Minin, I.V. Optical Phenomena in Mesoscale Dielectric Particles. Photonics 2021, 8.
  28. Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. , Optically resonant dielectric nanostructures. Science 2016, 354, aag2472. [Google Scholar] [CrossRef]
  29. 29. Wang; Z.B.; Luk'yanchuk; Yue; L.Y.; et al. High order Fano resonances and giant magnetic fields in 80 dielectric microspheres. Sci. Rep. 2019; 9.
  30. Minin; I.V.; Minin; O.V. & Zhou, S. High-Order Fano Resonance in a Mesoscale Dielectric Sphere with a Low Refractive Index. Jetp Lett. 2022, 116, 144–148.
  31. Portugall, O.; et al. Megagauss magnetic field generation in single-turn coils: New frontiers for scientific experiments. J. Phys. D: Appl. Phys. 1999, 32, 32–2354. [Google Scholar] [CrossRef]
  32. Chen; Wen; Z.Q. & Qiu, C.W. Superoscillation: From physics to optical applications. Light Sci Appl 2019, 8, 56.
  33. et al. Roadmap on superoscillations. J. Opt. 2019, 21, 053002. [Google Scholar] [CrossRef]
  34. Minin; I.V.; Minin, O.V. Control of focusing properties of diffraction elements. Sov. J. Quantum Electron. 1990, 20, 198–199. [CrossRef]
  35. Minin, O.V.; Minin, I.V. , Unusual optical effects in dielectric mesoscale particles, Proc. SPIE 12193, 121930E (). 29 April.
  36. Yue, L.; Yan, B.; Monks, J.; et al. Full three-dimensional Poynting vector flow analysis of great field intensity enhancement in specifically sized spherical particles, Sci. Rep. 2019, 9, 20224. [Google Scholar]
  37. Luk’yanchuk, B.; Miroshnichenko, A.; Kivshar, Y. Fano resonances and topological optics: An interplay of far- and near-field interference phenomena, J. Opt. 2013, 15, 073001.
  38. Michavila, C.; et al. Super-resonances in a dielectric mesoscale sphere immersed in water: Effects in extreme field localization of acoustic wave. Proc. Mtgs. Acoust. 2019, 38, 070001. [Google Scholar]
  39. Yue; Wang; Yan et al. Super-Enhancement Focusing of Teflon Spheres, Ann. Phys. (Berl.) 2020, 532, 10.
  40. Minin, O.V.; Minin, I.V.; Zhou, S. Superresonance in Micron Borosilicate Glass Sphere in Optical Range. Optoelectron. Instrument. Proc. 2022, 58, 514–519. [Google Scholar] [CrossRef]
  41. Minin, I.V.; Minin, O.V.; Zhou, S. Features of the Generation of Extreme Electromagnetic Fields in a Mesoscale Dielectric Sphere with Regard to the Environment. Tech. Phys. Lett. 2022, 48, 41–44. [Google Scholar] [CrossRef]
  42. Luk, B.S. ; Bekirov, A. ; Wamg, Z.;et al. Optical Phenomena in Dielectric Spheres Several Light Wavelengths in Size: A Review. Physics of Wave Phenomena 2022, 30, 271–241.
  43. Ranjbar, N.; Cenospheres, C.K. Cenospheres: A review. Fuel 2017, 207, 1–12. [Google Scholar] [CrossRef]
  44. Bohren, C.; Huffman, D. Absorption and Scattering of Light by Small Particles, WILEY-VCH Verlag, N.Y. (1998).
  45. Aden, A.L.; Kerker, M. Scattering of electromagnetic waves from two concentric spheres. J. Appl. Phys. 1951, 22, 1242–1246. [Google Scholar] [CrossRef]
  46. Liu, S.; Shi, B.; Wang, Y.; Cui, L.; Yamg, J.; Sun, W.; Li, H. Whispering gallery modes in a liquid-filled hollow glass microsphere. Optics Letters 2017, 42, 4659. [Google Scholar] [CrossRef] [PubMed]
  47. Retsch, M.; Schmelzeisen, M.; Butt, H.J.; Thomas, E.L. Visible Mie Scattering in Nonabsorbing Hollow Sphere Powders. Nano Lett. 2011, 11, 1389. [Google Scholar] [CrossRef] [PubMed]
  48. Zhong, K.; Song, K.; Clays, K. Hollow spheres: Crucial building blocks for novel nanostructures and nanophotonics. Nanophotonics 2018, 7, 693–713. [Google Scholar] [CrossRef]
  49. Xu, J.; Wu, Y.; Zhang, P.; et al. Resonant Scattering Manipulation of Dielectric Nanoparticles. Adv. Optical Mater. 2021, 2100112. [Google Scholar] [CrossRef]
  50. Ye, Q.-L.; Yoshikawa, H.; Bandow, S.; Awaga, K. Green magnetite (Fe3O4): Unusual optical Mie scattering and magnetic isotropy of submicron-size hollow spheres. Appl. Phys. Lett. 2009, 94, 063114. [Google Scholar] [CrossRef]
  51. S. N. A. Zaine and N. M. Mohamed. MATLAB simulation of Mie scattering by hollow sphere TiO2 for dye solar cell application. AIP Conf. Proc. 2016, 1787, 050026.
  52. Rasskazov, I.L.; Carney, P.S.; Moroz, A. STRATIFY: A comprehensive and versatile MATLAB code for a multilayered sphere. OSA Continuum 2020, 3, 2290–2306. [Google Scholar] [CrossRef]
  53. Chyiek, P.; Pendleton, J.D.; Pinnick, R.G. Internal and near-surface scattered field of a spherical particle at resonant conditions. Appl. Opt. 1985, 24, 3940. [Google Scholar]
  54. Rybin, M.V.; Filonov, D.S.; Belov, P.A.; et al. Switching from Visibility to Invisibility via Fano Resonances: Theory and Experiment. Sci. Rep. 2015, 5, 8774. [Google Scholar] [CrossRef]
  55. E. Green. The story of Q. Am. Scientist 1955, 43, 584–594.
  56. W. V. Houston. A compound interferometer for fine structure work. Phys. Rev. 1927, 29, 0478–0484. [CrossRef]
  57. Chiasera, A.; Dumeige, Y.; Féron, P.; et al. Spherical whispering-gallery-mode microresonators. Laser & Photon. Rev. 2010, 4, 457–482. [Google Scholar]
  58. Klimov, V.; Heydarian, R.; Simovski, C. Spatial Fano resonance of a dielectric microsphere impinged on by a Bessel beam, J. Opt. Soc. Am. B 2021, 38, C84–C93. [Google Scholar] [CrossRef]
Preprints 80342 g001
Figure 1. The spectrum of field intensity resonances for homogeneous sphere vs the size parameter q (a) and resonance lines near q = 39.31704 (b). In the insert on the Figure 1b the geometry of the problem is shown. Here X is the Fano asymmetry parameter [54].
Figure 1. The spectrum of field intensity resonances for homogeneous sphere vs the size parameter q (a) and resonance lines near q = 39.31704 (b). In the insert on the Figure 1b the geometry of the problem is shown. Here X is the Fano asymmetry parameter [54].
Preprints 80342 g001
Preprints 80342 g002
Figure 2. The distribution of electric (left column, a) and c)) and magnetic (right column, b) and d)) fields intensities for a homogeneous spherical particle with q = 39.31704 . Figures a), b) are given in linear intensity scale and c), d) – in log scale.
Figure 2. The distribution of electric (left column, a) and c)) and magnetic (right column, b) and d)) fields intensities for a homogeneous spherical particle with q = 39.31704 . Figures a), b) are given in linear intensity scale and c), d) – in log scale.
Preprints 80342 g002
Preprints 80342 g003
Figure 3. The distribution of electric (left column, a) and c)) and magnetic (right column, b) and d)) fields intensities for hollow spherical particle with q = 39.31704 and δ = 0 .6799 . Figures a), b) are given in linear intensity scale and c), d) – in log scale.
Figure 3. The distribution of electric (left column, a) and c)) and magnetic (right column, b) and d)) fields intensities for hollow spherical particle with q = 39.31704 and δ = 0 .6799 . Figures a), b) are given in linear intensity scale and c), d) – in log scale.
Preprints 80342 g003
Preprints 80342 g004
Figure 4. The maximum field intensities at the shadow pole of hollow particle vs relative cavity radius δ at q = 39.31704 (a). Fano line shape (b). Mie modes distribution for a homogeneous sphere and cenosphere with δ = 0 .6799 (c).
Figure 4. The maximum field intensities at the shadow pole of hollow particle vs relative cavity radius δ at q = 39.31704 (a). Fano line shape (b). Mie modes distribution for a homogeneous sphere and cenosphere with δ = 0 .6799 (c).
Preprints 80342 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated