Surface Quality Evaluation in the Milling Process Using a Ball Nose End Mill

Shaped surfaces are increasingly used in the field of mould making for casting or injection moulding, where future products include shapes with different curvatures. These are surfaces that form convex curves, concave curves, or a combination thereof. Given these machined surfaces, it is important to know the impact of the finishing strategies on these surfaces. This paper deals with the comparison of finishing milling strategies in the production of shaped surfaces and the analysis of different methods for the evaluation of surface topography, surface roughness and the evaluation of deviations. The material used for the experiments was AlCu4Mg aluminium alloy, and Constant Z, Spiral and Spiral circle strategies were chosen for the finishing strategies. The evaluation of surface topography and surface roughness was carried out at three different sample heights with respect to the tool contact with the machined surface. The results showed changes in the toolpaths due to the variation of the effective diameter of the tool cutter to the machined surface as well as the choice of strategy. To produce specimens with corresponding shapes in terms of topography, the Constant Z strategy was the most suitable, in which uniform toolpaths were obtained over the whole height of the sample.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

Nowadays, free form shapes are some of the most difficult surfaces to produce. They are present in various areas of production, such as the automotive industry, the aerospace industry, or the production of dies, moulds, and many others, where the shape corresponds to the shape of the future product [1,2,3].

In this group of future products, we can find different shapes comprising convex, concave, or flat surfaces. In some cases, these surfaces can be described mathematically. Each part must be manufactured to meet the recommended quality and dimensions, so the requirement for the correct selection of milling strategy is justified. To support this requirement, it is necessary to know the effectiveness and influence of strategies in milling free form shapes [4,5,6].

The most frequent use of free-form surfaces is in plastic mouldings. Moulds, whose shape corresponds to the future product, consist mainly of free form shapes. To achieve the required mould shape, the milling process represents the main production operation.

To achieve this, CNC machines are used, which can produce parts in 3 or 5 axes, where the NC program is generated by the CAM system [7].

For the best machining of these complex shapes, different CAM systems are used, where the user can choose the appropriate strategy to match the specific toolpath in accordance with the geometry of the part. The main disadvantage of the CAM system is that the simulation process does not provide the micro surface texture after machining, related to the cutting edge of the tool. Proper selection of the free form milling strategy can improve the surface roughness [8]. When programming with CAM systems, strategies such as zig-zag, radial, raster, or spiral curves are most useful for milling free-form surfaces [9,10]. Many researchers describe the effect of tool path strategies on roughness, but only a few studies address the effect of toolpath strategies on surface topography [11,12]. Currently, many CAD/CAM systems incorporate different strategies to select various milling shapes and to achieve recommended shapes and dimensions [13]. Therefore, it is very important to select the most appropriate strategy considering the relationship between best roughness, higher dimension accuracy, and effective time production.

Cutting tools with ball milling cutters are used in various areas of production. They are most commonly used in mould-making, automotive, aerospace, and other industries. In these areas, it is important to achieve the desired shape of the future part, which can include a variety of shapes ranging from convex, and concave curves to planar surfaces or variously shaped complex surfaces. All of these surfaces must be produced based on production requirements in terms of accuracy, dimensions, and other factors.

Of the three basic machining operations such as roughing, semi-finishing, and finishing operations, ball-end milling tools are used the most in finishing operations. It is very important to keep in mind that the tool-surface contact relationship is different from conventional milling. One of the main characteristics of shaped surface machining is that the contact between the tool and the workpiece is constantly changing. In addition, machining through the centre of the cutting tool can negatively affect the surface quality [14,15]. The contact between the tool and the surface is different when milling freeform surfaces compared to milling simple shapes. In the contact position, the cutting speed varies from the programmed value. These are the areas where contact is made between the tool and the machined surface. In the first region, the tool axis is parallel to the machined surface, and in the second region, the material is cut through the centre of the tool and the position of the tool axis is almost perpendicular to the machined surface [16,17].

The advantage of using a ball end mill for multi-axis milling of free-form surfaces is the ability to change the cutting-edge contact depending on the angle between the machined surface and the tool axis [15]. Therefore, the nominal diameter of the tool changes when in contact with the machined surface [17]. In the case when the cutting speed of the tool is zero (cutting by the centre of the tool), the material is removed not by the shearing process, but as a result of plastic deformation known as ploughing [15]. The contact of the tool with the machined surface in the ascendant and descendant directions is shown in Figure 1a and Figure 1b respectively.

Toh [1] was involved in a free form milling experiment using a ball end mill. He investigated the milling direction and found that better results could be obtained with an ascending milling direction than with a descending one. Milling in the ascending direction avoids the reduction of cutting speeds and the problems that arise in plastic deformation [18,19].

Scandiffio et al. [20] investigated the ascending and descending direction of the tool in the machining process and the relationship between the tool and the surface when using a ball end mill. The results showed that worse surface quality was obtained when using descending milling The research evaluated the roughness parameter, tool wear, machining forces, and tool life. By the experiment conducted, Souza et al. [21] claim that shear cutting or ploughing that occurs during freeform cutting when a ball end mill is used has an effect on the roughness parameter. The reason for the change in the roughness of the machined surface is due to the change in cutting speed during milling, which changes the contact of the tool with the machined surface and therefore the effective diameter of the tool with respect to the position of the tool on the toolpath.

According to Souza et al. [21], when a ball end mill is used, the roughness parameters measured on a free-form surface can be affected by the material cutting mechanism – shearing or ploughing. Machining through the centre of the tool can have a negative effect on the final surface quality in terms of surface roughness or surface topography [22,23]. When the tool centre is used in the milling process, the machined surface can be negatively affected. As a result of plastic deformation, the surface roughness increases [21].

For free-form milling surfaces, the changing contact between the tool and machined surface area depends on the axial depth of the cut and surface geometry [24,25]. In Figure 2a, the cutting edge is in contact with the machined surface. Figure 2b shows the point when the cutting tool descends lower on the machined surface and Figure 2c describes the maximum and minimum effective tool radius at the bottom of the machined surface. When milling a free surface, the contact between the tool and the machined surface changes. The value of the effective tool diameter depends on the curvature of the surface and the depth of the cut.

Boujelbene et al. [18] investigated the effect of tool orientation on cutting speed and tool life. The result was that machining with the centre of the tool, where the cutting speed is zero, leads to worse roughness parameters. Liu et al. [26] studied the changing contact in the tool-workpiece relationship in terms of the predicted geometric deviation from the desired geometry. Aspinwall et al. [27] examined the effect of inclined surface milling when a ball end mill was used. The effects of tool wear, cutting force, and surface roughness were analysed. Wojciechowski et al. [28] verified a method for the estimation of vibration and roughness during free surface milling with a ball end mill. They concluded that the tool overhang length has a significant effect on the roughness parameters. The effect of the tool path on the milling of the convex surface was evaluated by Shaghayegh et al [29] when hardened material was used. The results showed that the radial strategy achieved the best surface texture and the spiral strategy the worst. Boujelbene et al. [18] studied the effect of tool orientation on cutting speed and tool life. They came to the conclusion that machining with the centre of the tool, where the cutting speed is zero, leads to a worse roughness parameter. Käsemodel et al. [30] examined the influence of the cutting direction in free-form surface milling. The result showed that the effective radius of the tool was larger when cutting upwards, resulting in a more favourable value of effective cutting speed. On the other hand, in the opposite direction, in a downward movement, the effective tool radius was found to be much smaller, and the cutting speed may be reduced to a critical value.

A suitable effective cutting speed is usually achieved when the tool cuts approximately tangentially. Changes in cutting speed during full surface milling can cause process instability [27] in terms of roughness parameters [31], dimensional accuracy [28] as well as geometric deviations. In the downward-cutting method of free-form surface milling, elastoplastic deformation of the material in the form of a notched effect [32] may occur on the surface of the part. In the process of cutting through the centre of the tool, where the cutting speed is low, the vibrations are maximum in this area [33,34]. For this reason, the correct selection of the milling strategy is very important [35]. It can affect the contact area in the machining process, which affects the tool wear, surface texture, roughness, and vibration. According to Antoniadis [36], the choice of milling strategy for freeform surfaces has a significant impact because their selection can affect the contact area between the tool and the surface, vibration, roughness parameters, or tool wear. In this case, it is important to understand the relationship between tool-workpiece contact in freeform milling [37].

The surface quality is influenced by various inputs, including feed rate, cutting speed, or depth of cut, which are referred to as controlled inputs, and uncontrolled inputs such as the workpiece, tool usage, or machine vibration [38,39]. Numerous studies, as reported by Toh [40], have investigated the roughness parameters in free surface milling and various geometrical features such as the scallop height, the influence of the toolpath strategy, or the cutting conditions during milling. Abuelnaga and White [41,42] elaborated on the possibilities of freeform surface machining where surface roughness and dimensional accuracy were evaluated. Shajari [43] investigated spiral, raster, radial, and 3D feed strategies in freeform milling of low curvature convex surfaces and evaluated cutting force and surface texture. This experiment concluded that the radial strategy produced the best surface quality and the helical strategy resulted in the worst surface quality. Ikua [44] complemented the results by stating that the poor quality of the sculpted machined surface may be influenced by the lower cutting force. Matras and Kowalczyk [45] analysed the effect of milling strategies on the free surface topography of aluminium alloy when Z-level, radial, offset, and circular strategies were used. It was found that the lowest roughness parameter as required was obtained only when the tool path was circular.

The results obtained by Hao [46] show that surface topography is affected by the plastic deformation of the machined surface and, in the latter case, by cutting vibration generated during machining. A parameter known as cycle time is included in the machining process, which includes the time it takes for the machine to read one line of NC code and then transfer this data to the machine motion. The second aspect is the time in which the control unit needs to correct the machine’s motion such as position, speed, or acceleration [47]. Different toolpaths are generated in the machining process using linear interpolation, which is defined as the path between two successive cutting tool positions (CL). In a CAM system, a tolerance band, also known as chord error, can be defined to modify the toolpath segments. If the user sets the tolerance zone smaller, the toolpath becomes more similar to the CAD model [48]. Yau [49,50] described in more detail the problem of interpolation of linear segments (Figure 3a) and curved toolpaths Figure 3b, where the number of segments increases and the increasing number of segments affects the size of the NC program.

Souza [51] found that the toolpaths in a CAM system appear to be the same, but each CAM system generates a different NC code when processing identical geometry. According to this different NC code, a different machining process is generated, which affects the real machining time, surface roughness, or feed rate oscillation. According to Siller et al. [52], segment length decomposition is used as an indicator of geometric composition. They used histograms to verify the relationship between surface radius and segment length, where they obtained that a small radius of curvature corresponds to a smaller segment length.

2. Materials and Methods / Research Methodology

A parabolic surface was chosen as the modelled surface to be parametrically described. For the shape surface, the following equation was defined:

y = - 0,048 * x^{2} + 30,

(1)

CAD system Solidworks was used to design the model (Figure 4) and the CAM system SolidCAM to select the milling strategy.

For the experimental research, three test specimens were produced. An aluminium alloy (AlCu4Mg) with the following mechanical properties was selected for production: tensile strength = 101.89 MPa; yield strength = 86.69 MPa; hardness = 90.20 HB. The experimental tests were carried out on an EMCO MILL 155 3-axis machine with a maximum spindle speed of 5,000 rpm (EMCO MAIER Ges.m.b.H., Hallein/Austria), which contains a Heidenhain iTNC 530 control system. Roughing, semi-finishing, and finishing operations are mostly used in the machining process for milling free-form surfaces [53,54]. The machining operations con-specifically used in the experimental research are shown in Figure 5.

The roughening and semi-finishing operations were the same for all three samples to achieve the same surface texture. Of all the operations, the finishing operation is the most challenging because the cutting speed of tool-material contact and chip formation change during milling [55,56]. The cutting parameters with a description of the tool used for fabrication are shown in Table 1. A sintered carbide ball-end mill was used for the finishing operation using a fixed BT-40 system with a mechanical collet chuck with a tool overhang of 40 mm. The parameters for each operation were selected based on the tool manufacturer's recommendations. A mineral oil-based emulsion coolant was used for cooling during production. The dimensions of the test specimens were 65 x 65 x 40 mm.

The following input data have been defined for the milling process of shaped surfaces.

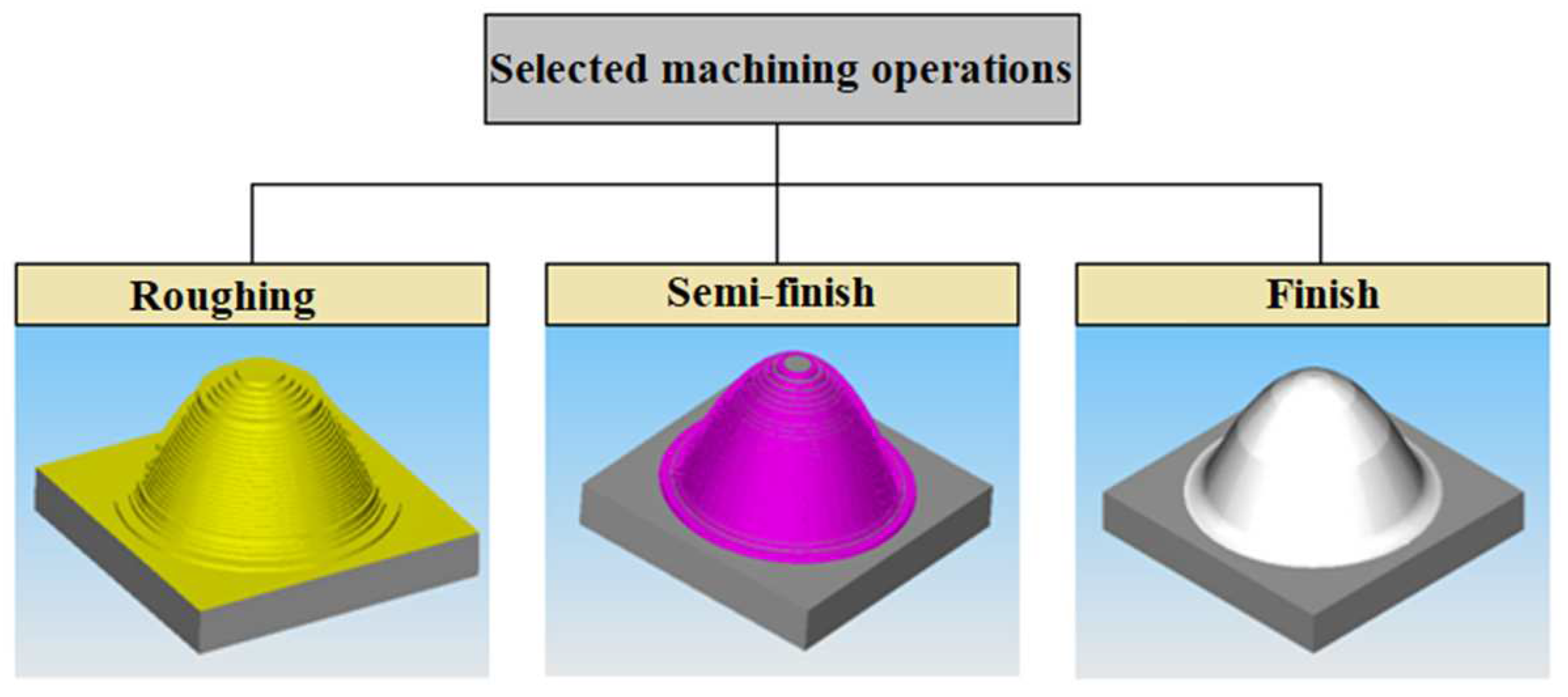
Roughing operation – end mill tool D18 mm, two interchangeable plates marked APXT11T3PDR-MA, manufactured by Korloy, depth of cut a_p = 3 mm, side step a_e = 3 mm, toolpath tolerance T = 0.1 mm, surface allowance P = 0.5 mm
Semi-finish operation – end mill D 8 mm with two-flute cutters marked as 273618.080, cutting material HSS Co8, depth of cut a_p = 0.5 mm, side step a_e = 0.5 mm, strategy Constant Z, toolpath tolerance T = 0.1 mm, surface allowance P = 0.2 mm
Finishing operation - ball end mill D 6 mm with two-flute cutters marked as 511418.060, cutting material HSS Co8, side step a_e = 0.25 mm, toolpath tolerance T = 0.01 mm, scallop height SH = 0.01 mm

The following methods and equipment were used in the experiment:

Comparison and evaluation of surface topography using a Keyence VHX-5000 digital microscope (Keyence International, Mechelen, Belgium).
Roughness evaluation using device Alicona InfiniteFocus G5 (Alicona Imaging GmbH, Raaba/Graz, Austria).
Evaluation of shape deviations using coordinate measuring machine ZEISS Duramax HTG (Carl Zeiss, Jena, Germany).

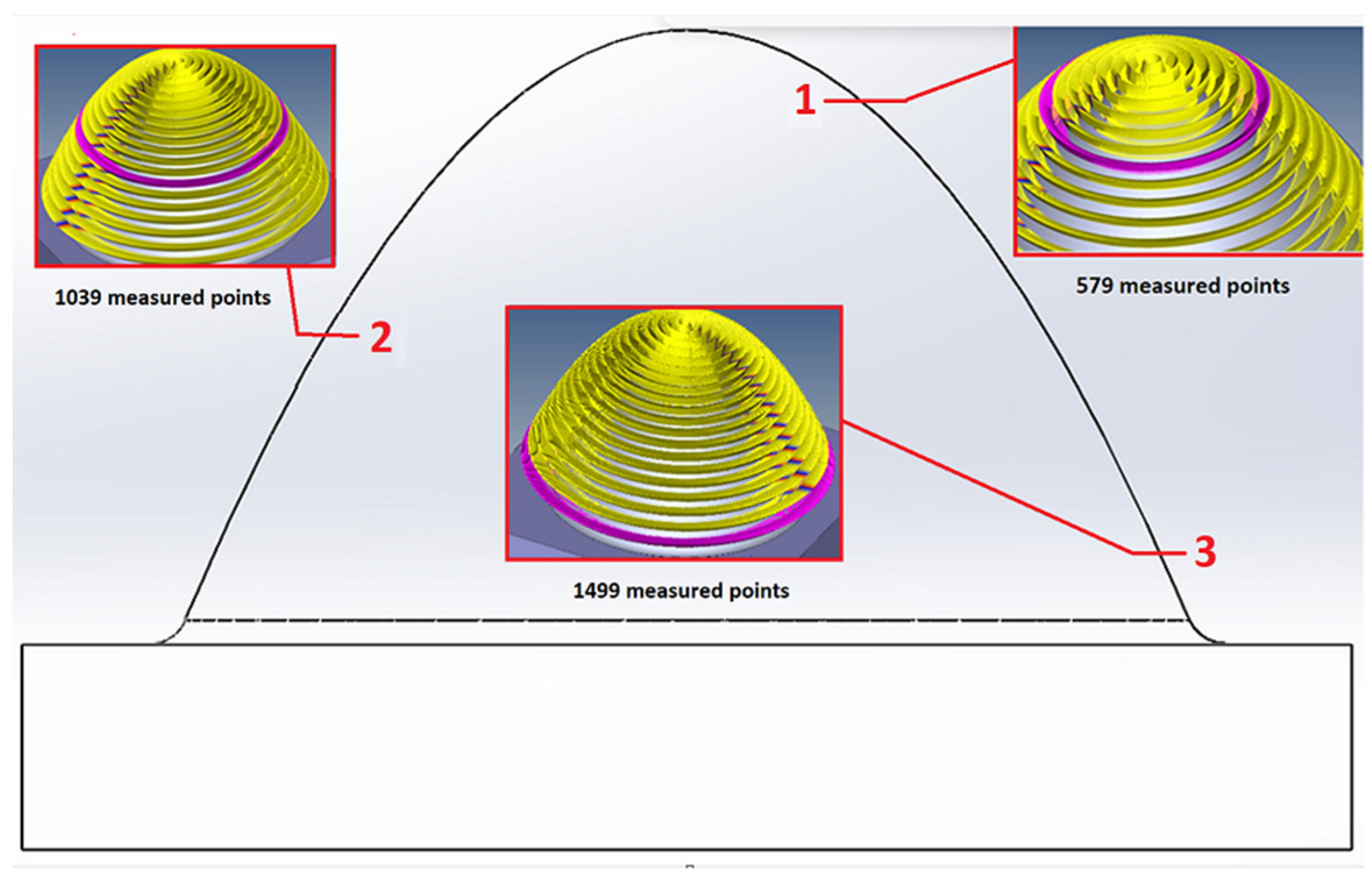
2.1. Topography observation methodology

Surface topography is the result of many factors, including vibration during the cutting process, the relative position of the tool and workpiece, cutting conditions and cutting environment. Surface topography was observed at three heights on each of the samples. These were distances from the highest point of the sample surface downwards of 7.5 mm, 15 mm and 22.5 mm. The effective diameter of the tool varies depending on the depth of cut and the actual curvature of the surface.

2.2. Surface roughness analysis methodology

The values of the observed surface roughness parameters were evaluated (in accordance with ISO 25 178) from the extracted surface after removal of its nominal shape (polynomial function of the paraboloid). Surface extraction was performed using the Alicona Infinite Focus G5 optical measuring instrument, which uses Focus-Variation technology. For the purpose of the analysis, measurements were taken at three locations at specified heights. All measurements were taken at a position of 0 degrees with respect to the sample axis, as shown in Figure 6. The area measured was 6x6 mm.

The following surface roughness parameters were evaluated in the experiment:

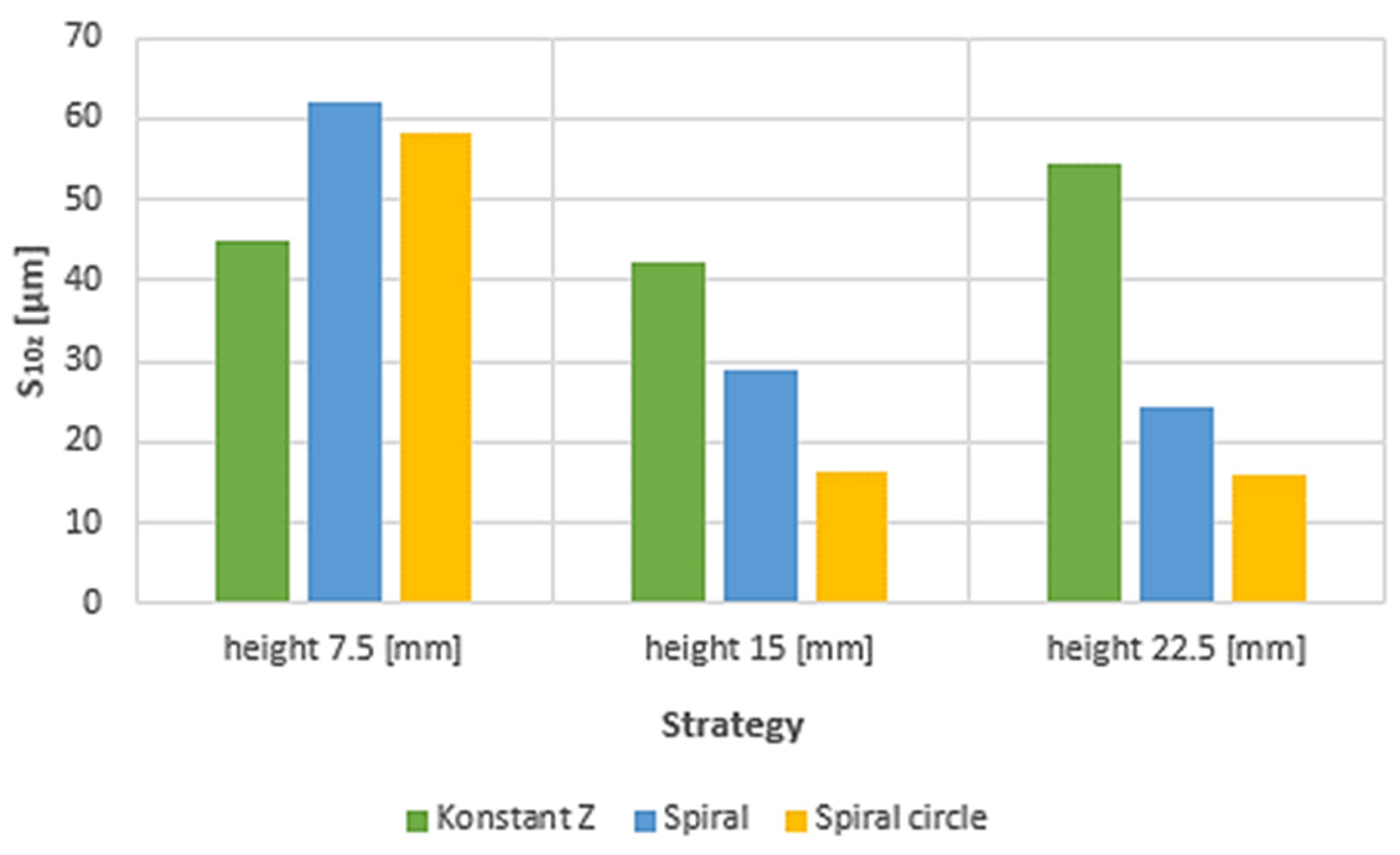
S10z - is sensitive to changes in the topography of the observed surface; an important parameter in evaluating of the surface functionality (affects dimensional accuracy of fitted surfaces, tightness of joints, etc.).
Sa - is a powerful statistical parameter that is used to regulate and control pro-duction.
Ssk - gives us information about the protrusions and depressions of the topography of the observed surface. If it takes a positive value protrusion dominate and if it takes a negative value depressions dominate.

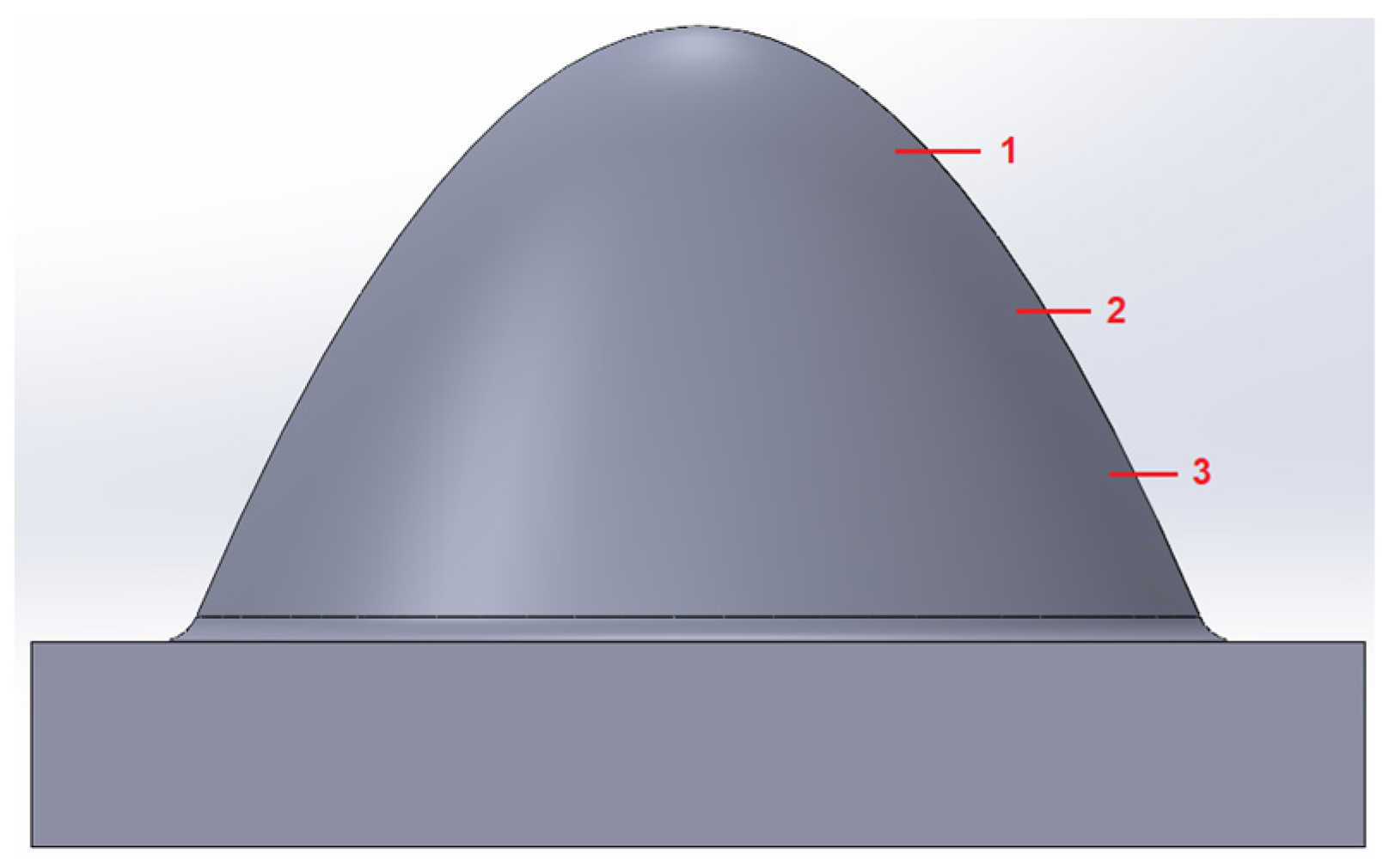
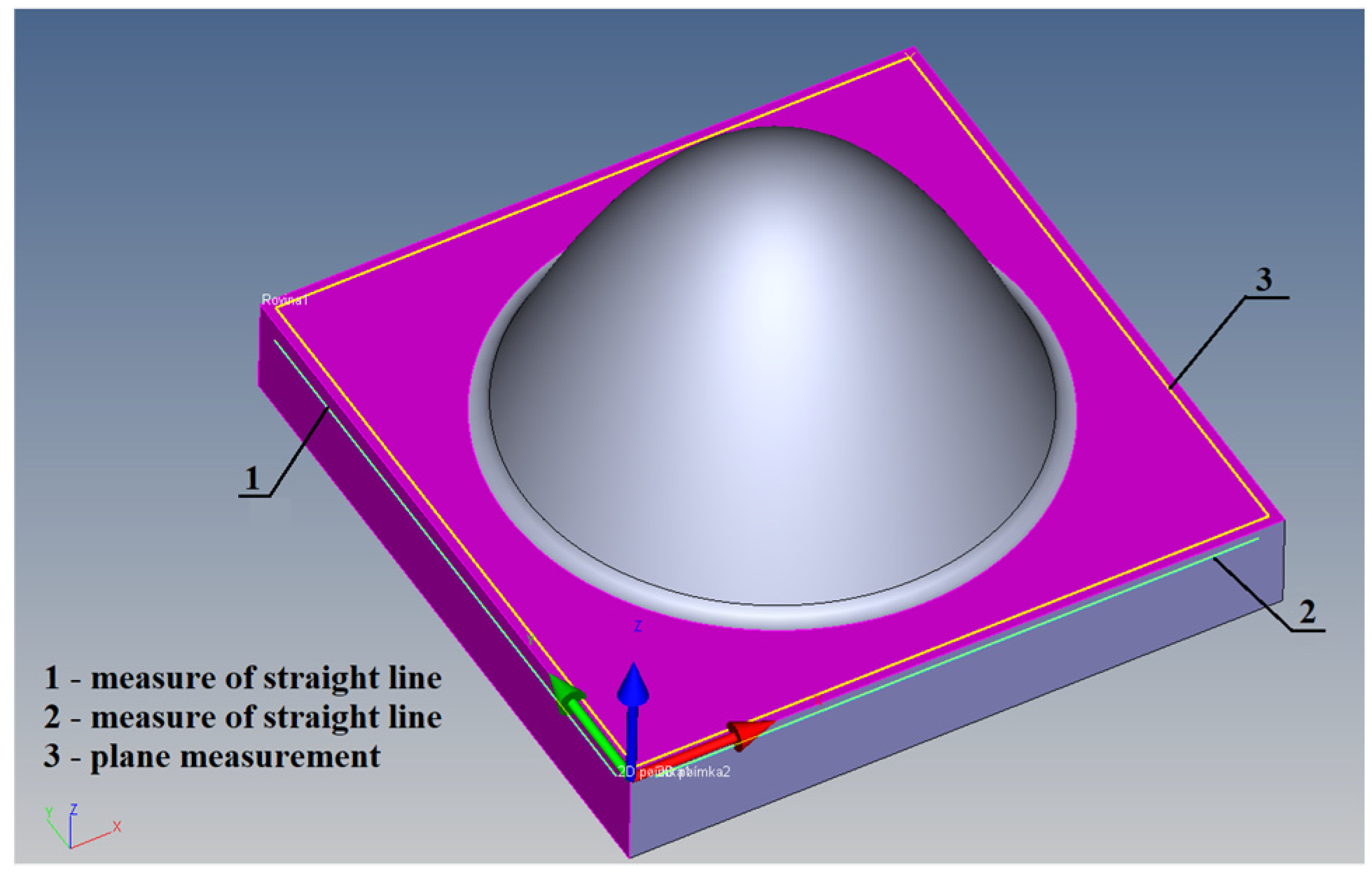
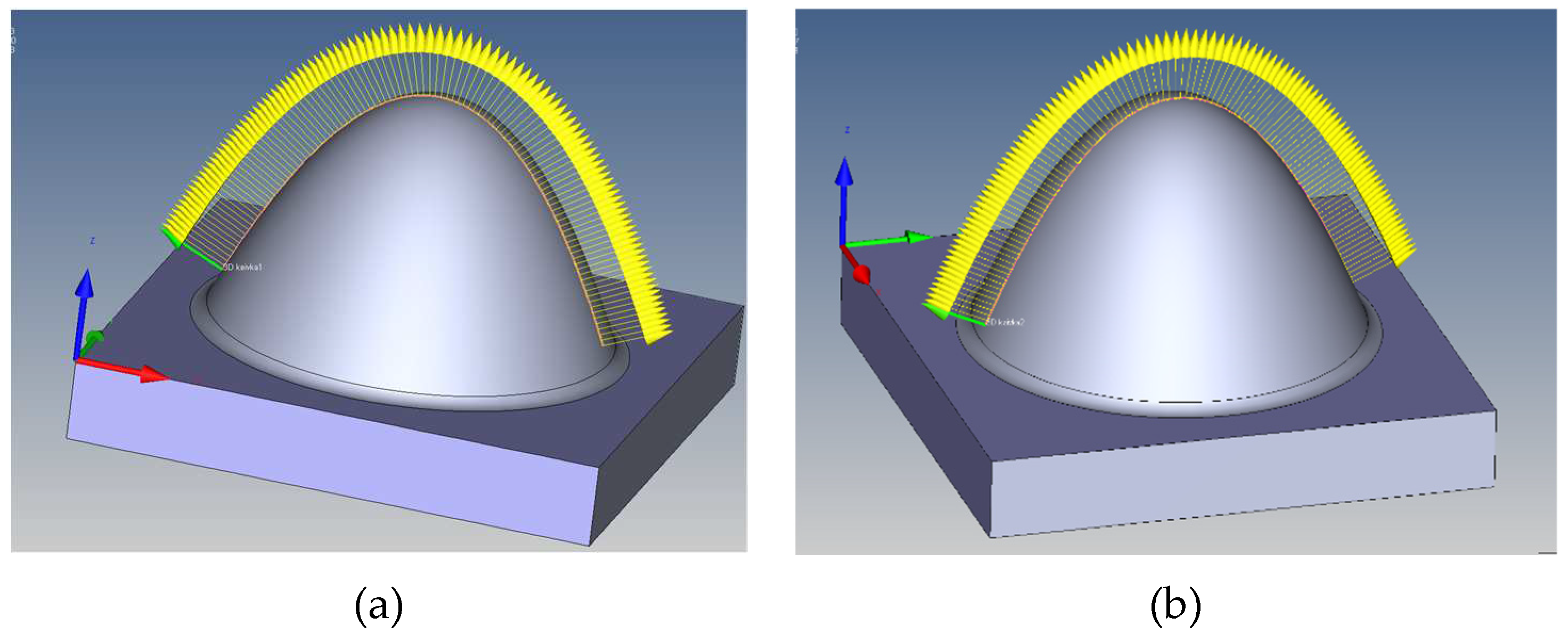
2.3. Methodology of the shape deviation

For better information about the obtained surface shape deviation, a ZEISS Duramax HTG coordinate measuring machine was used. During the evaluation, the research area was evaluated as a whole. At a temperature of 18-22 °C, the measurement error is 2.2 + L/3 (E0 length measurement error in μm). ZEISS Calypso 2021 software and a sensor with a diameter D of 1 mm on a length of 45 mm with a silicon nitride bead particularly suitable for aluminium were used for the measurements. At the beginning of the measurement, it was necessary to establish the basic coordinate system, which consists of a sensing plane and two 2D lines. The determination of the basic coordinate system is shown in Figure 7.

Once the coordinate system was oriented, measurements were taken, denoted as 3D curve 1 and 3D curve 2. Basically, measurements were taken in the two planes: the XZ plane as shown in Figure 8a, and the YZ plane as shown in Figure 8b. The normal vectors from the measurement points are marked in yellow. The scanning step was 0.1 mm so a point on the surface was recorded every 0.1 mm during scanning. A total of 749 measurement points were taken in one plane at a speed of 2 mm/s.

Subsequently, the 3D curve measurements were complemented by surface measurements. Circular paths were taken on the surface of the samples, along which the sensor moved from the highest point to the lowest. The normal vectors from the measurement points are marked in yellow. The scanning step was 0.1 mm and the measurement speed was 3 mm/s. The number of measurement points varied depending on the location, and the height of the measurement on the surface on which the sensor was located. For the highest location, 579 points were recorded, 1039 points were recorded in the middle level and 1499 points were recorded in the lowest location as shown in Figure 9.

3. Results

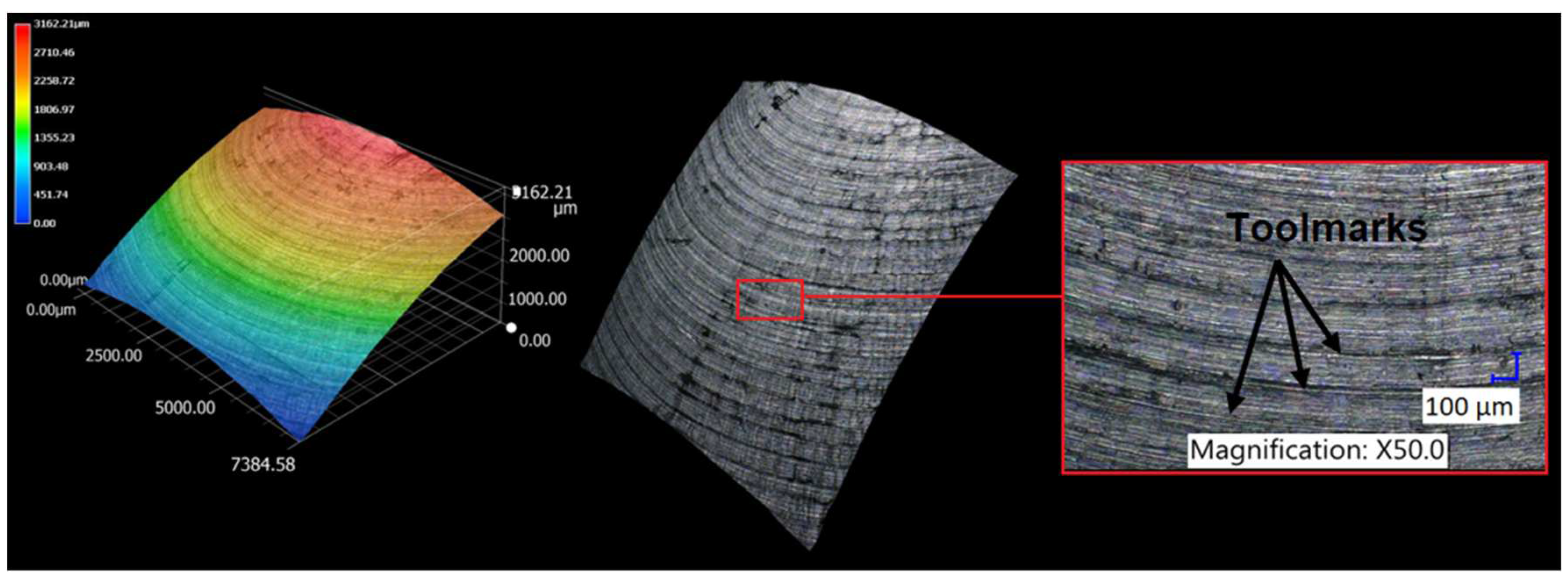
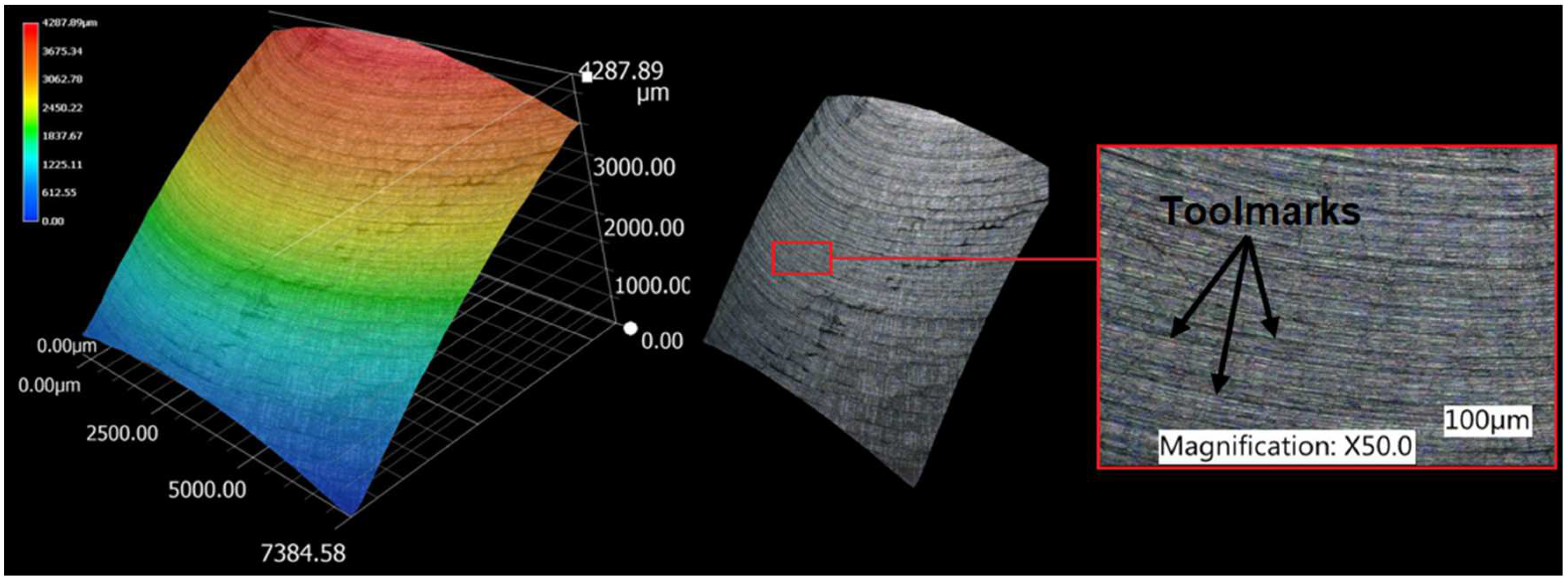
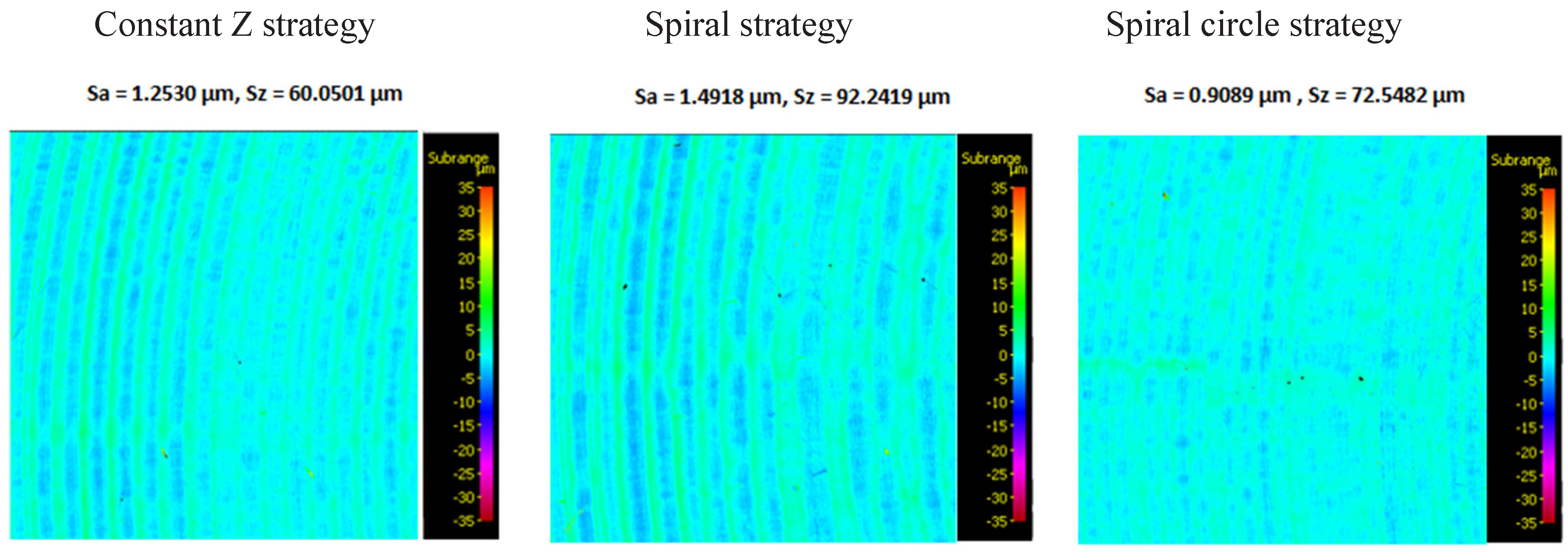
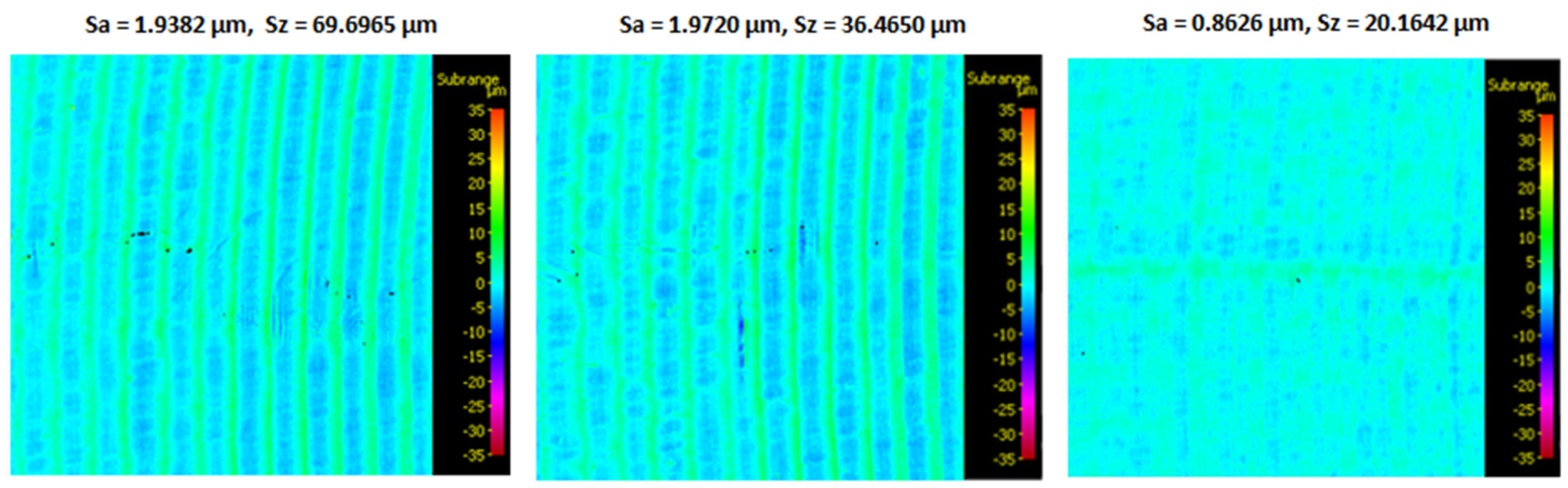
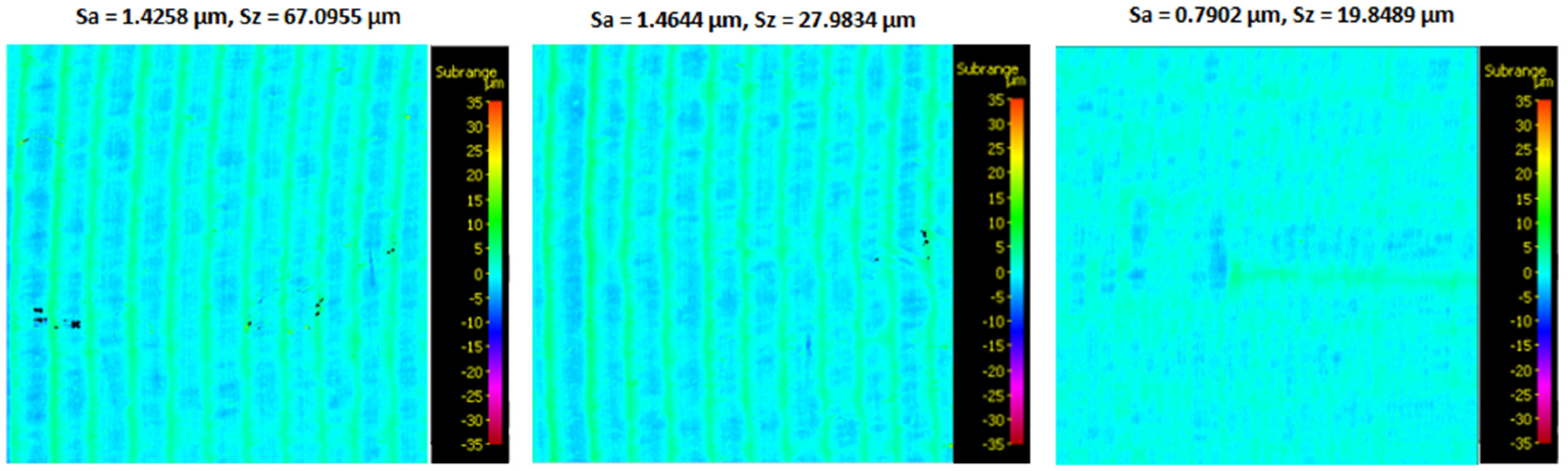
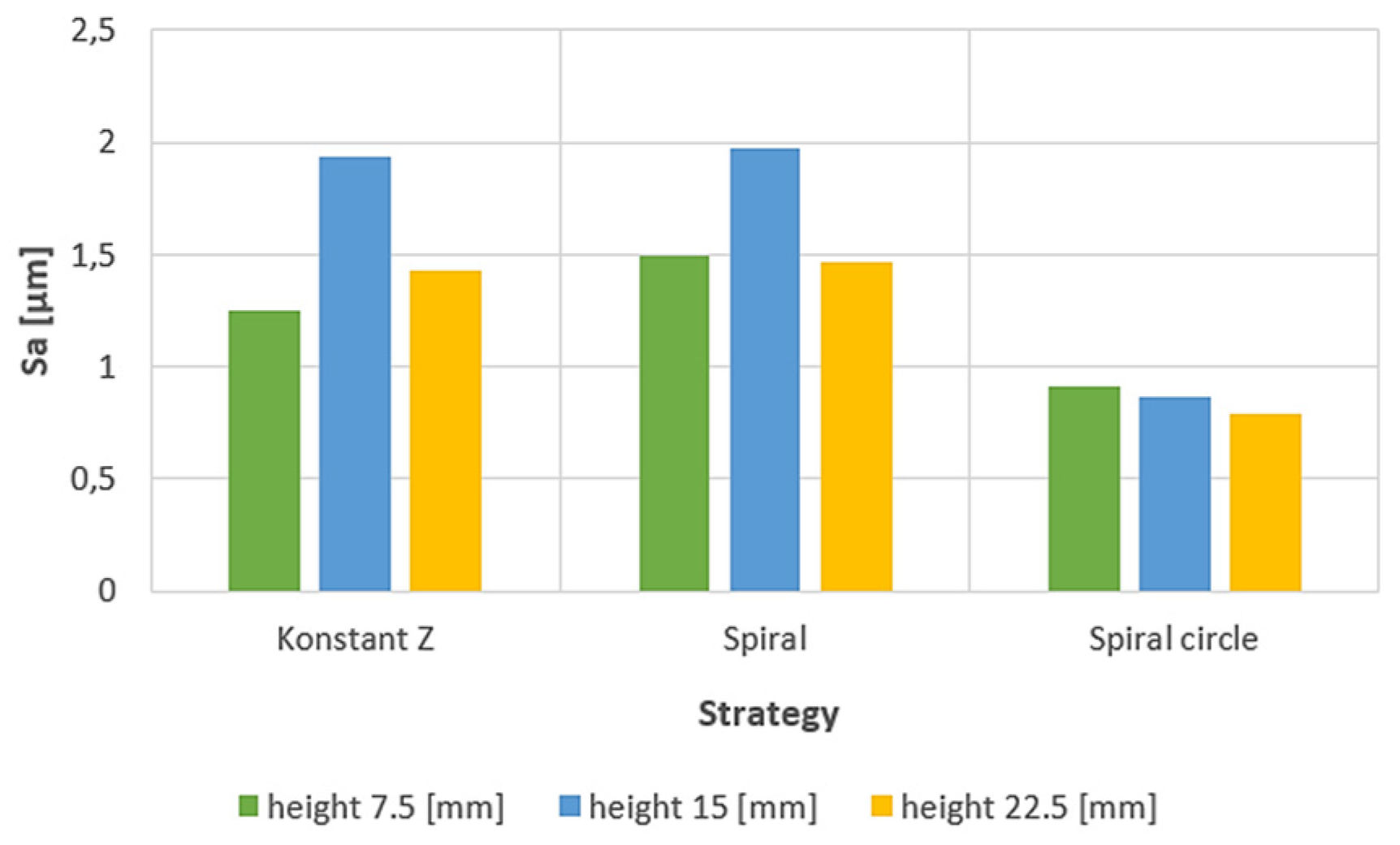
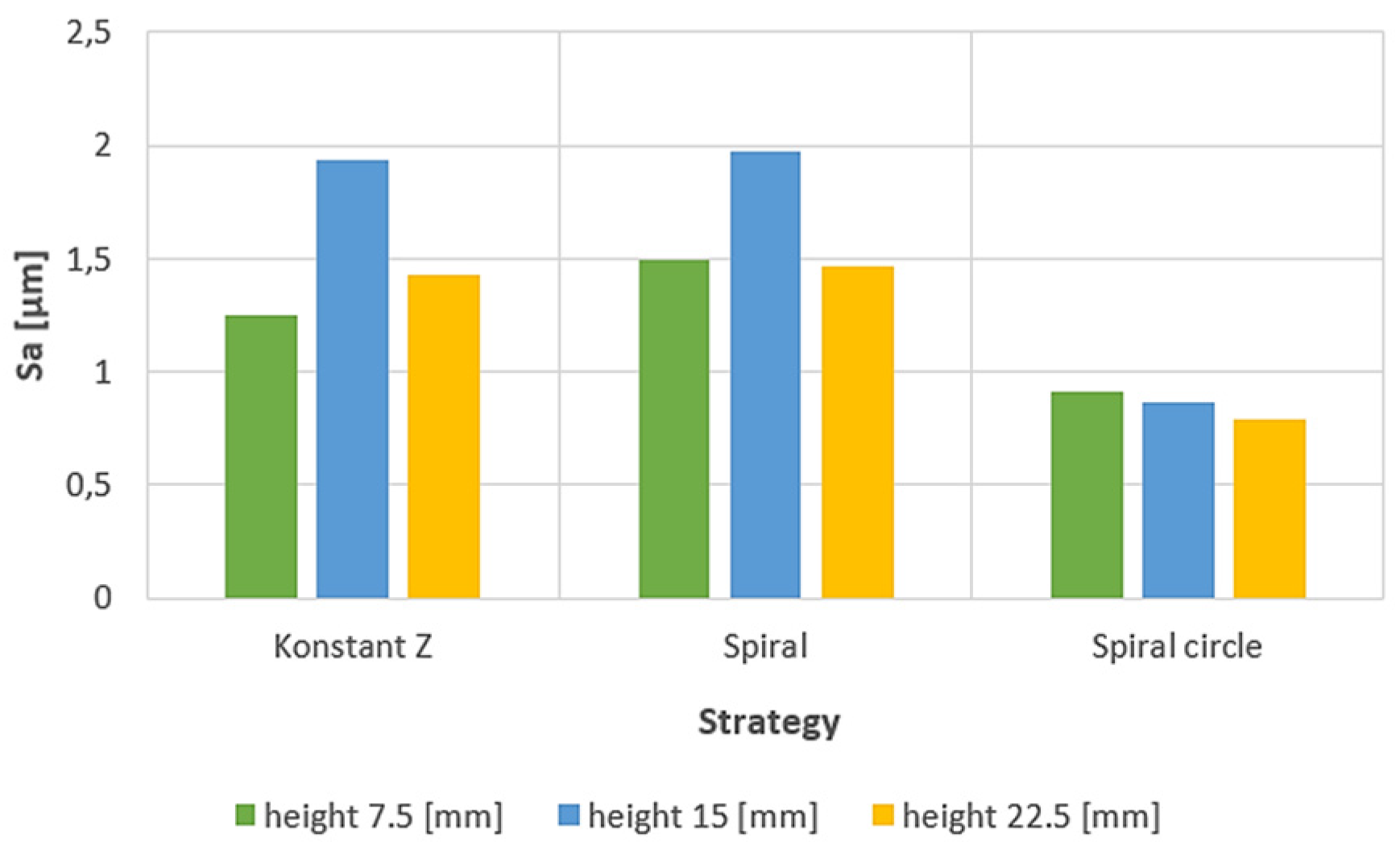
3.1. Surface topography evaluation

Individual surface features were examined with a digital microscope at specified heights. A comparison of the 3D surface topography with respect to the tool-workpiece contact point at a height of 7.5 mm for specific strategies is shown in Figure 10, Figure 11 and Figure 12.

A comparison of the 3D surface topography with respect to the tool-workpiece contact point at 15 mm for specific strategies is shown in Figure 13, Figure 14 and Figure 15. The machined surfaces of the samples are represented by a colour scale defining the contour lines. These contour lines thus give a consistent representation defining the height positioning of the tool marks. A realistic view of the machined surface element is shown in the figure to the right.

The last comparison shows the 3D surface topography (Figure 16, Figure 17 and Figure 18) with respect to the tool-workpiece contact point at a height of 22.5mm for specific strategies.

A comparison of the surface topography details at 50x magnification with respect to the 22.5 mm height at which the machined surface was observed for the Constant Z strategy is documented in Figure 19 and for the Spiral Circle strategy in Figure 20. In Figure 19, the toolpaths can be observed, which are arranged along the contour line and are clearly visible.

Lighter areas on the surface indicate surface defects in the form of dimples, which cause changes in the surface texture. The formation of the defects on the machined surface could have been caused by the irregular vibration of the cutting edge of the tool when using the Spiral circle strategy in the cutting process. Therefore, the tool marks obtained do not achieve the ideal machined surface, which may result in a worse surface quality as is shown in Figure 20.

At each of these heights, there was a change in the effective tool diameter with respect to the machined surface, the value of which depended on the axial depth of the cut and the curvature of the workpiece surface. Grooves separating the individual cuts during the cutting process are visible on all elements of the sample surfaces. It can be assumed that the formation of the individual grooves was determined by the method used to grind the cutting edge of the tool. On this basis, it can be said that the grinding tool was moved in height by a step change in the setting angle. The result in the cutting process approximated a semi-spherical shape due to the number of low conical surfaces.

The sample machined with the Constant Z strategy was the only one to present a surface free of surface defects, resulting in a regular alignment of the tool paths along the contours. For the specimens where the Spiral circle strategy was used, surface defects in the form of dimples were observed at all three heights studied, compared to the Spiral strategy where the formation of dimples was only observed at the height of 22.5 mm.

As part of the evaluation, distance measurements of the radial depth parameter were made when machining in the downward direction. These were the distances from the highest point of the specimen, namely 7.5 mm, 15 mm, and 22.5 mm. A comparison of the individual radial depths of cut a_e at a particular height is shown for the constant Z strategy (Figure 21), the spiral strategy (Figure 22), and the spiral circle strategy in Figure 23. From a general point of view, as the radius of curvature of the surface increases, the contact area of the tool with the workpiece increases and consequently the effective diameter of the tool also increases.

As shown in Figure 21, by applying the Z-constant strategy, the assumption of a larger effect of the effective tool diameter on the machined area was confirmed, where at distances from the highest point, the radial depth of cut a_e increased in the downward direction. However, for the Spiral (Figure 22) and Spiral-circle strategies (Figure 23), this assumption was not proved. The measured values of the radial depth of cut a_e parameter are shown in Table 2, Table 3 and Table 4. A comparison of the measured radial depth of cut a_e values with respect to the selected finishing milling strategy is shown in Figure 24.

3.2. Roughness evaluation

Comparison of surface roughness values for all three strategies at three different heights for a particular strategy is shown in Figure 25, Figure 26 and Figure 27. The nesting index value (Lc = 800 µm) was determined in accordance with ISO 25 178 and taking into account the surface geometry.

For better visualization of the results, the measured surface roughness data is also displayed in the form of a graph, as shown in Figure 28 and Figure 29. Comparison of surface parameter S_10z is shown in Figure 30.

As shown in Figure 28, the lowest values of the surface roughness parameter Sa were obtained for the spiral circle strategy for all three heights evaluated, ranging from 0.7902 µm to 0.9089 µm. The highest values were shown for all three heights evaluated when using the spiral circle strategy in the range from 1.4644 µm to 1.4918 µm. Considering the surface topography, it can be concluded that this parameter decreased with possible increasing tool wear. This decreasing tendency was related to the deterioration of the surface quality and the wear of the tool, which caused "wiping" effects on the machined surface. The original single well visible toolpaths turned into dimples formed after the material was stripped off. Although the Sa parameter was reduced by using the spiral circle strategy, the machined surfaces showed a deterioration phenomenon due to tool wear.

For the spiral circle strategy, a negative value of S_sk = - 0.0534 µm was measured (Figure 29). It can be assumed that a greater number of valleys occur on the milled area with this strategy.

In contrast, the Ssk parameters for the Constant Z and Spiral strategies showed positive values for all three heights. This indicates that the milled surfaces had many peaks and the distribution of heights was skewed below the reference plane. The slope measurement results shown indicate that the slope factor of the profile is positive for the constant Z and spiral strategies. This indicates an increase in the coefficient of friction (due to the more rounded surface roughness).

In the evaluation of the parameter S_10z, the lowest values were measured using the spiral circle milling strategy for the two measured heights of 15 and 22.5 mm (Figure 30). The highest S_10z values were measured with the Constant Z strategy.

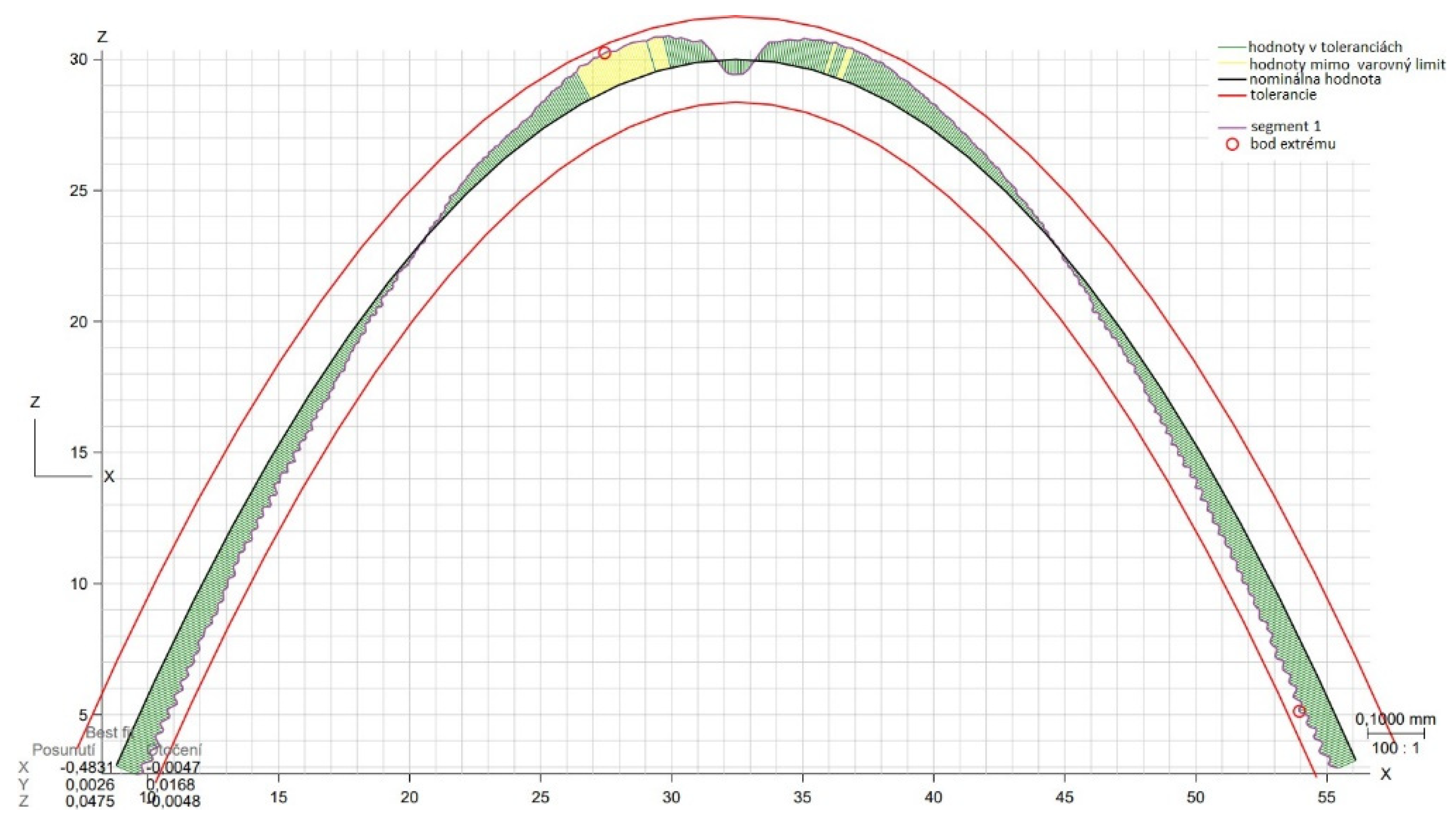
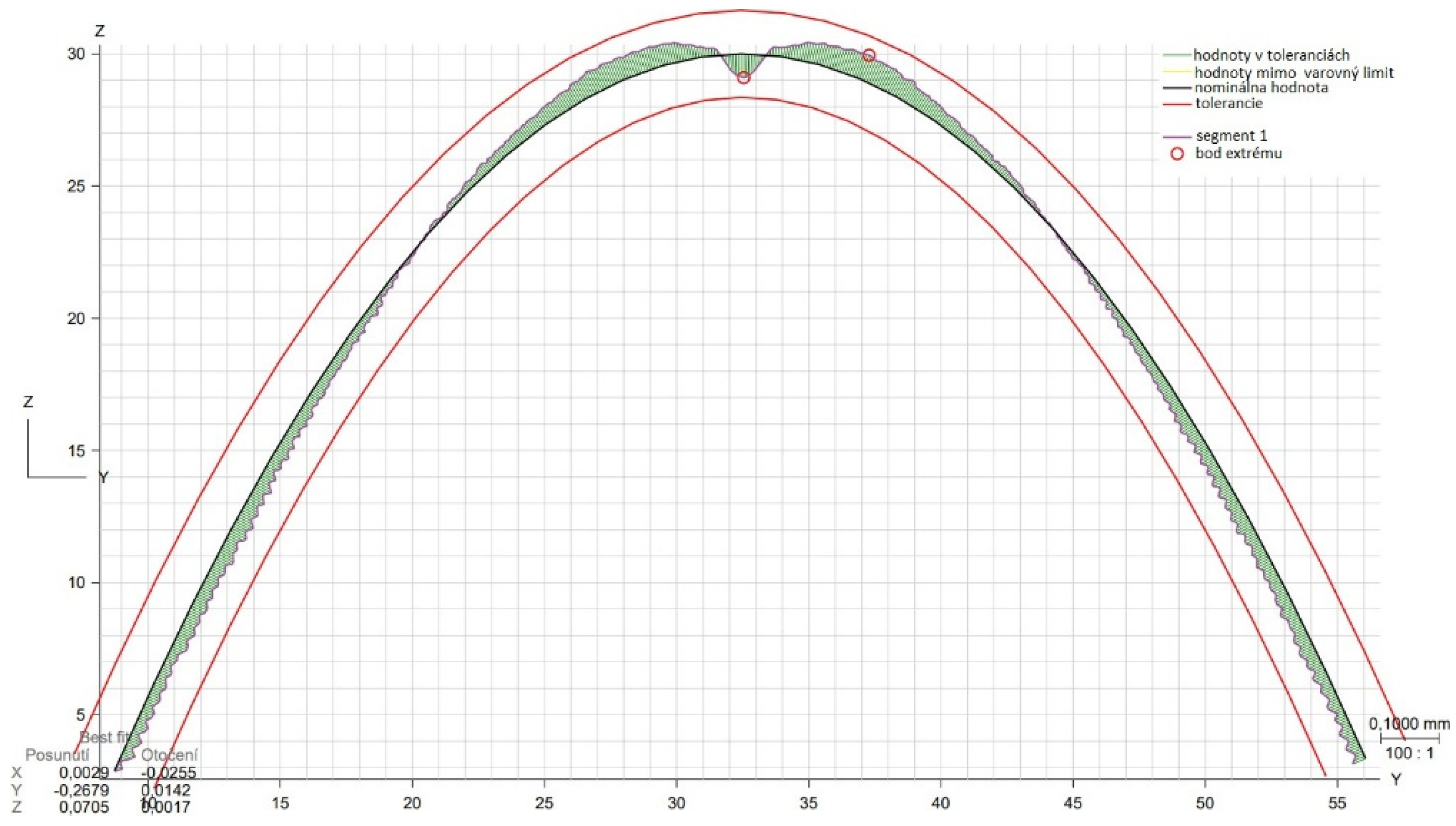
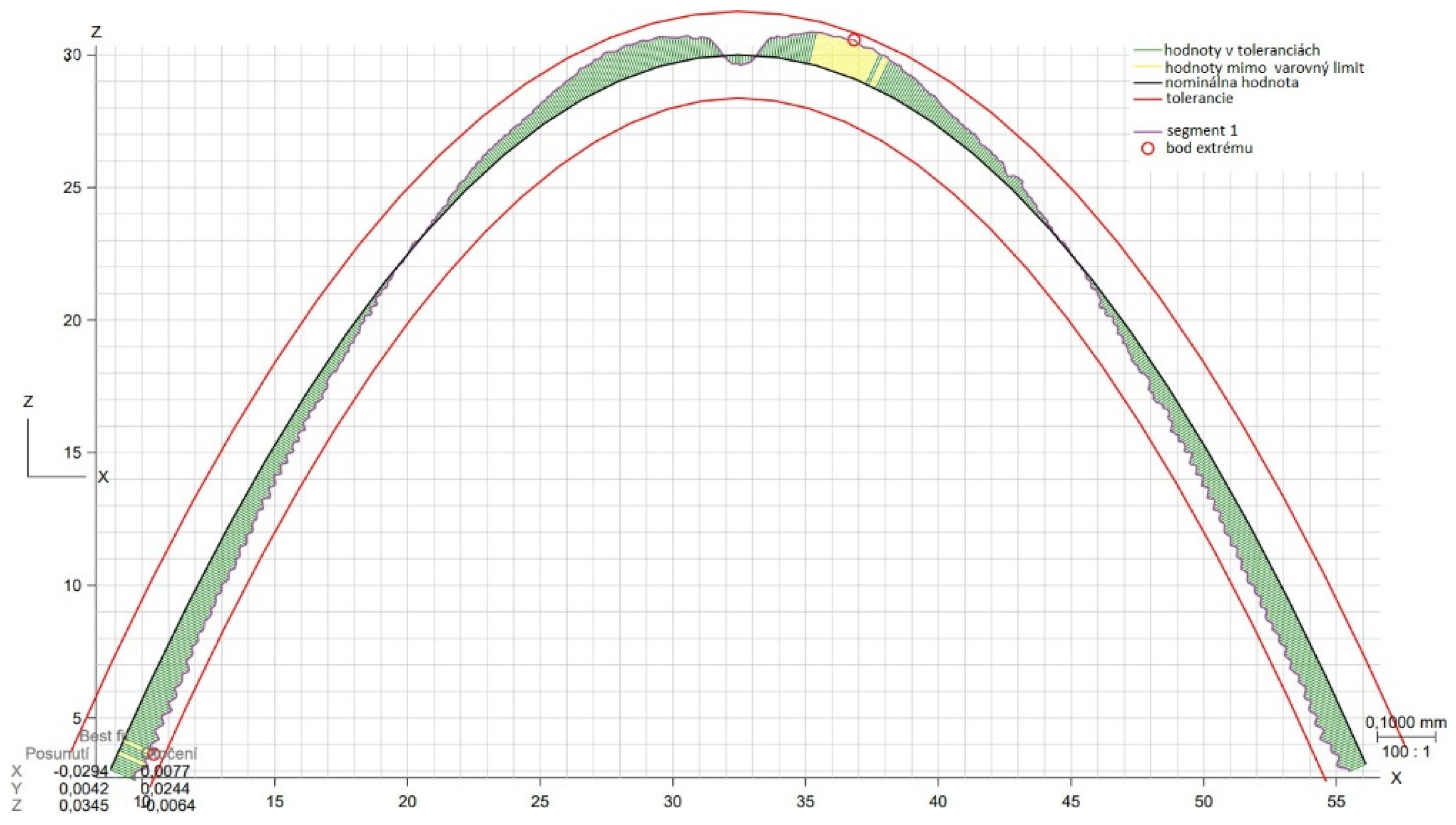
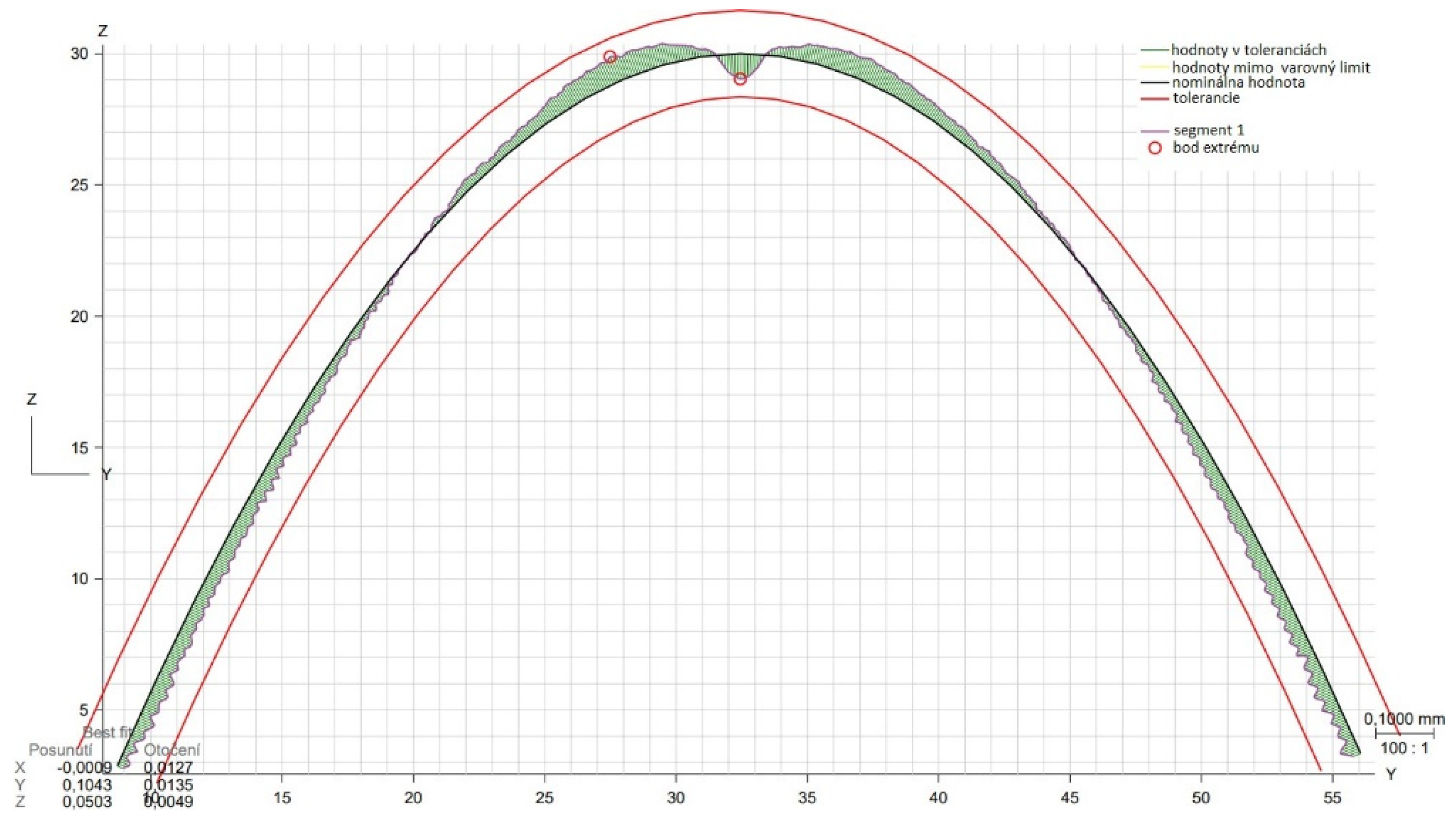
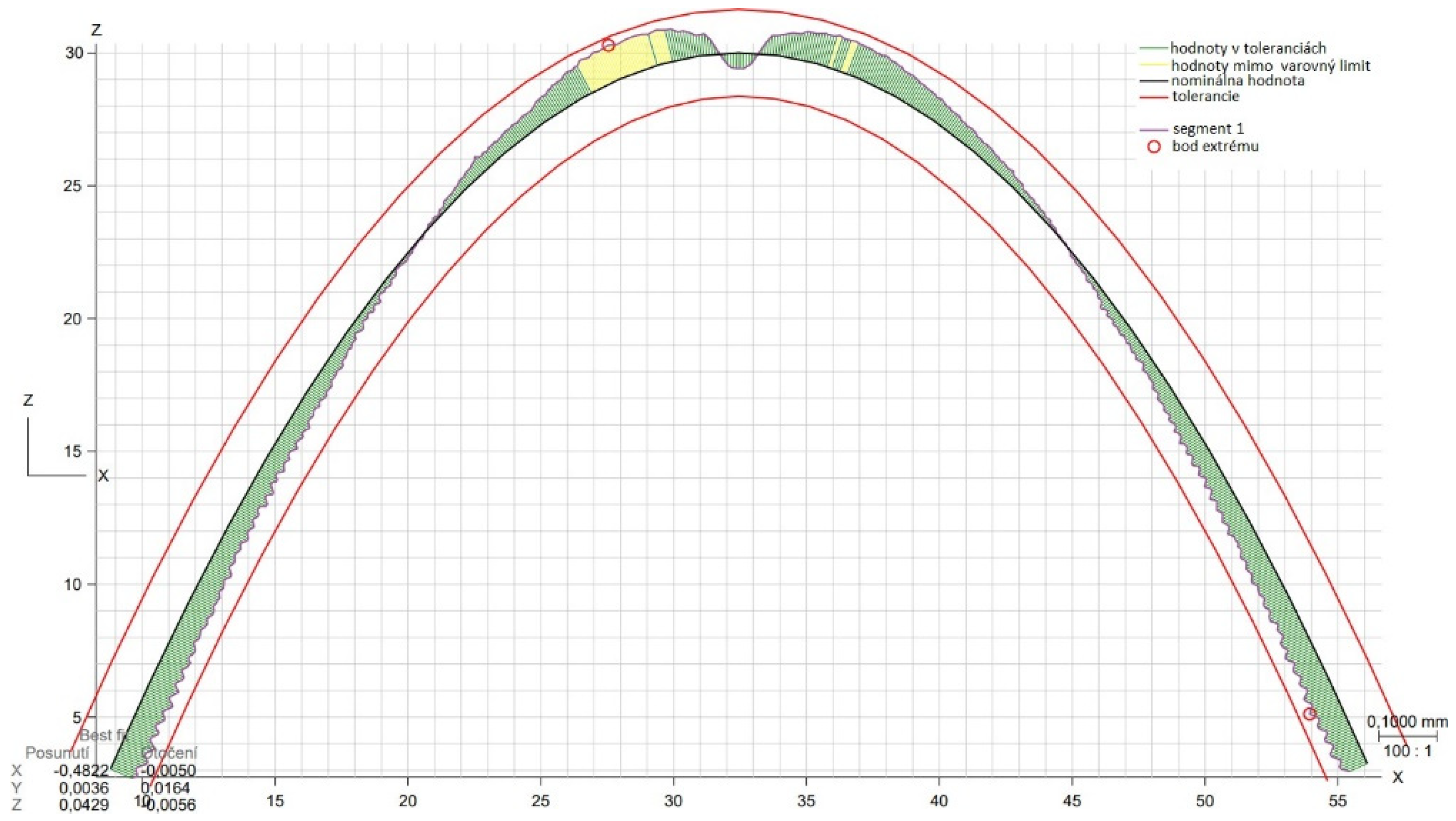
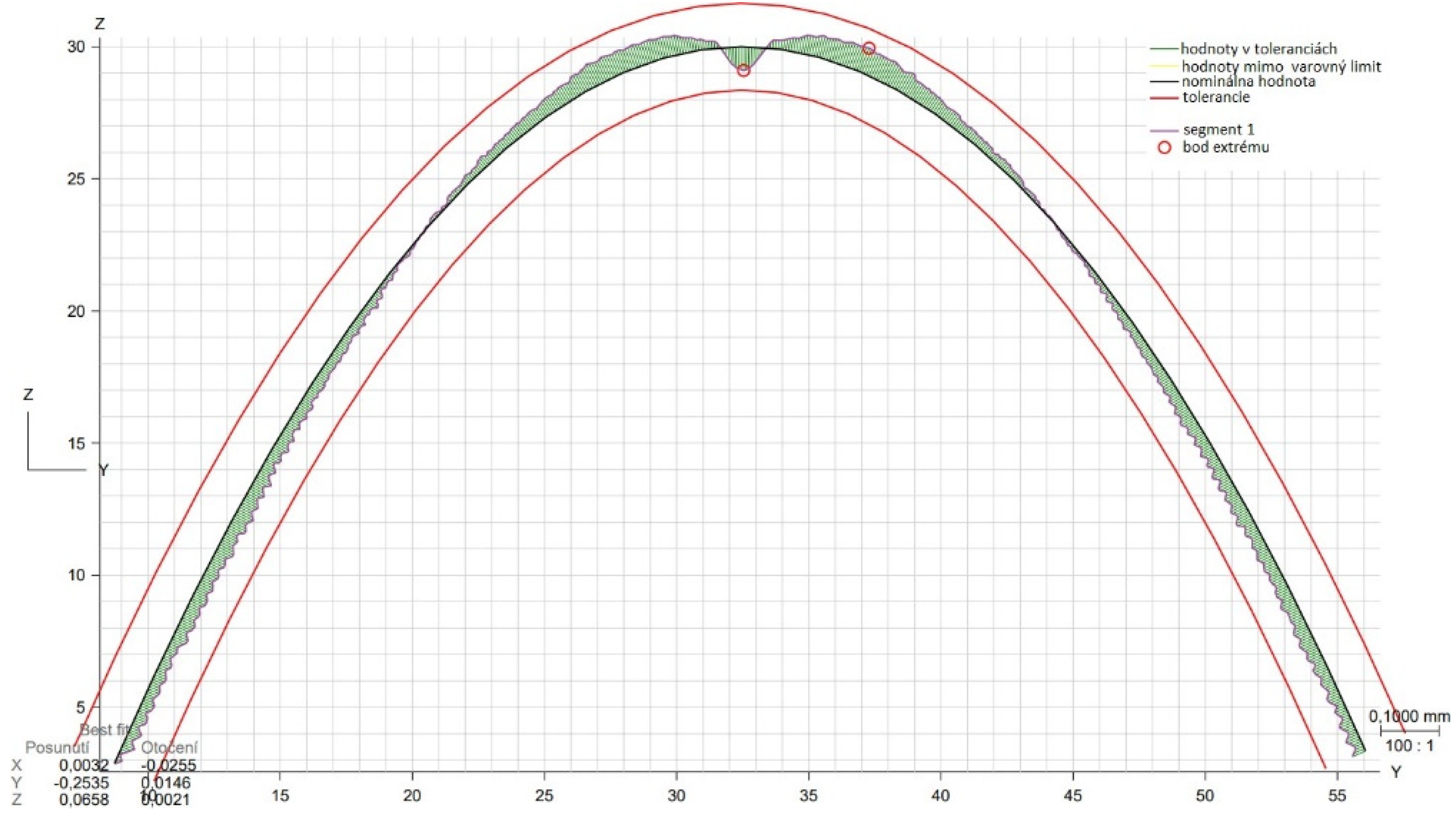
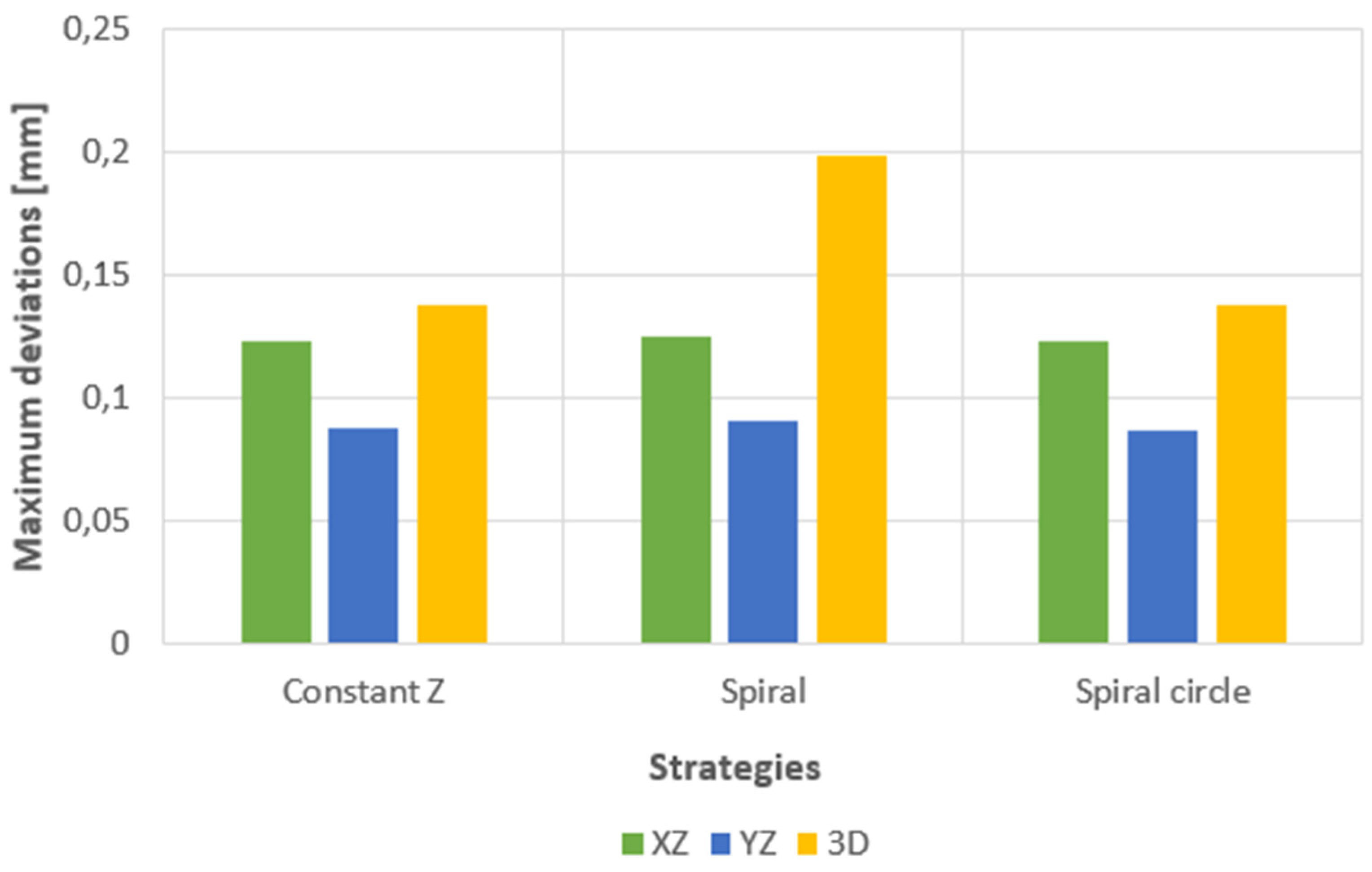
3.3. Shape deviation evaluation

The measured surface deviations from the ideal state are shown in Figure 31, Figure 32, Figure 33, Figure 34, Figure 35 and Figure 36.

At a height of 7 mm below the top, in all cases the positive deviation becomes negative, i.e. non-cutting becomes undercutting. The negative deviation is also present at the top of all samples. The values of the measured deviations for the different strategies are given in Table 5, Table 6 and Table 7.

The graph in Figure 37 compares the maximum shape deviations for all evaluated strategies.

4. Discussion

The machined surface can be identified by several characteristics. The parameters of surface roughness and accuracy of shapes are of paramount importance to the practice of surface forming. The roughness of the machined surface is influenced by a number of technological factors, such as the properties of the material to be machined, the cutting conditions, the cutting environment, the stability of the cutting process, and the condition of the tool. Similarly, the accuracy of the shapes produced depends on a number of factors such as the condition of the machine, the knowledge and experience of the machine operator, the surrounding environment, and the quality of the designed manufacturing process. When designing a manufacturing process, machining strategies must also be considered, as confirmed by a number of literature sources. The strategies are not universal but predetermined for certain surface shapes. For surfaces with vertical walls of rotational shape, as in the case of the presented samples, strategies with contouring in parallel planes or with radial paths are suitable. Zig-zag or raster strategies are not suitable. Evaluation of the surface topography on the machined specimens showed visible grooves separating the individual sections.

The following statements can be assumed:

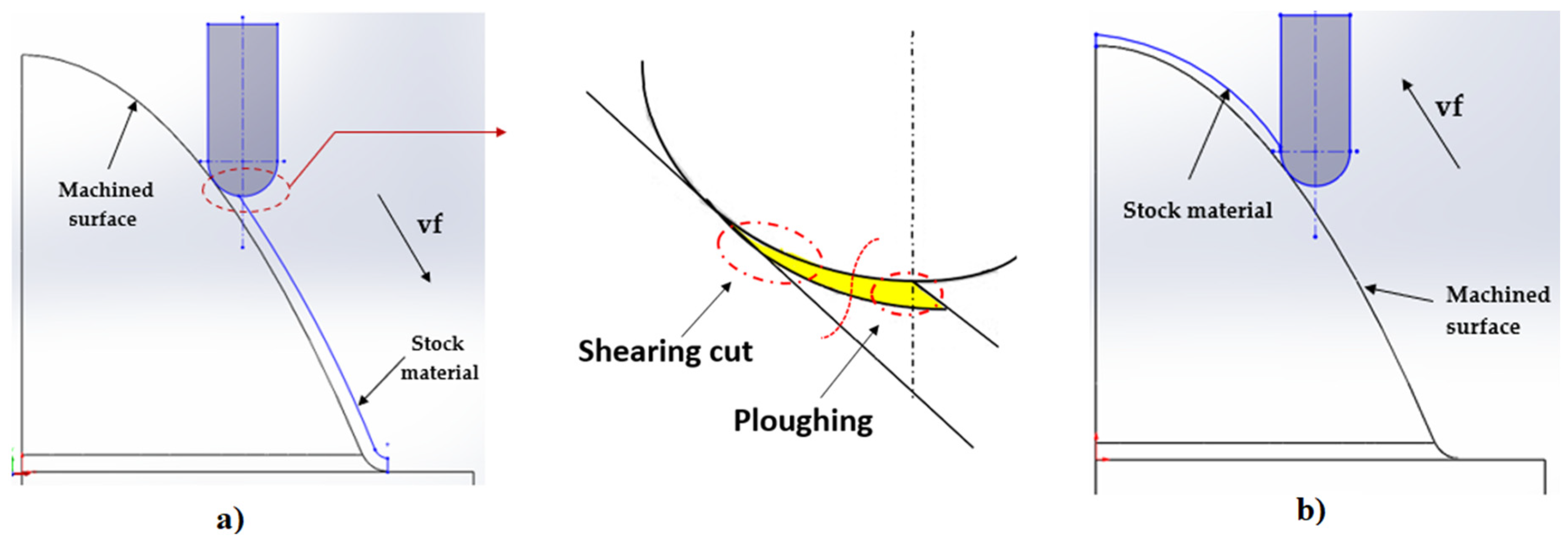
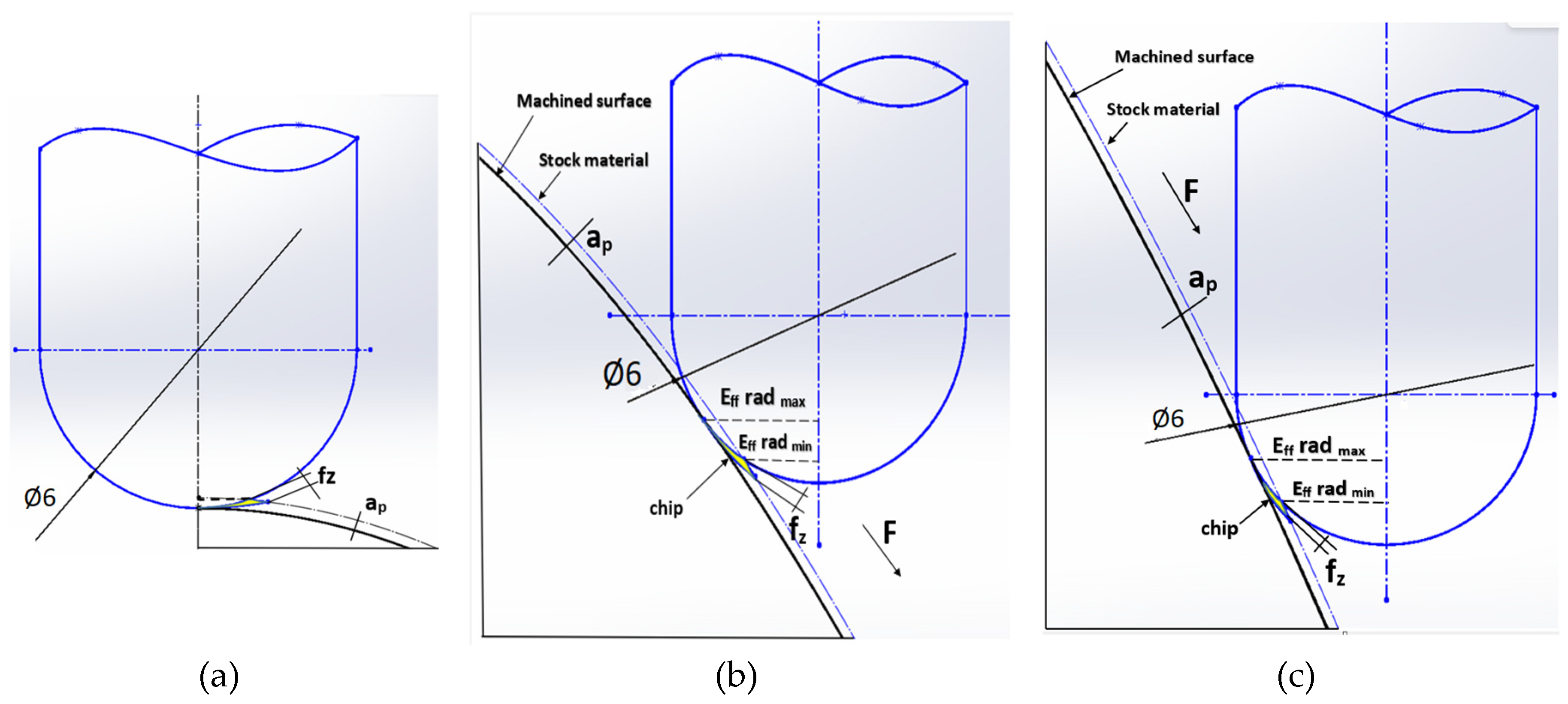
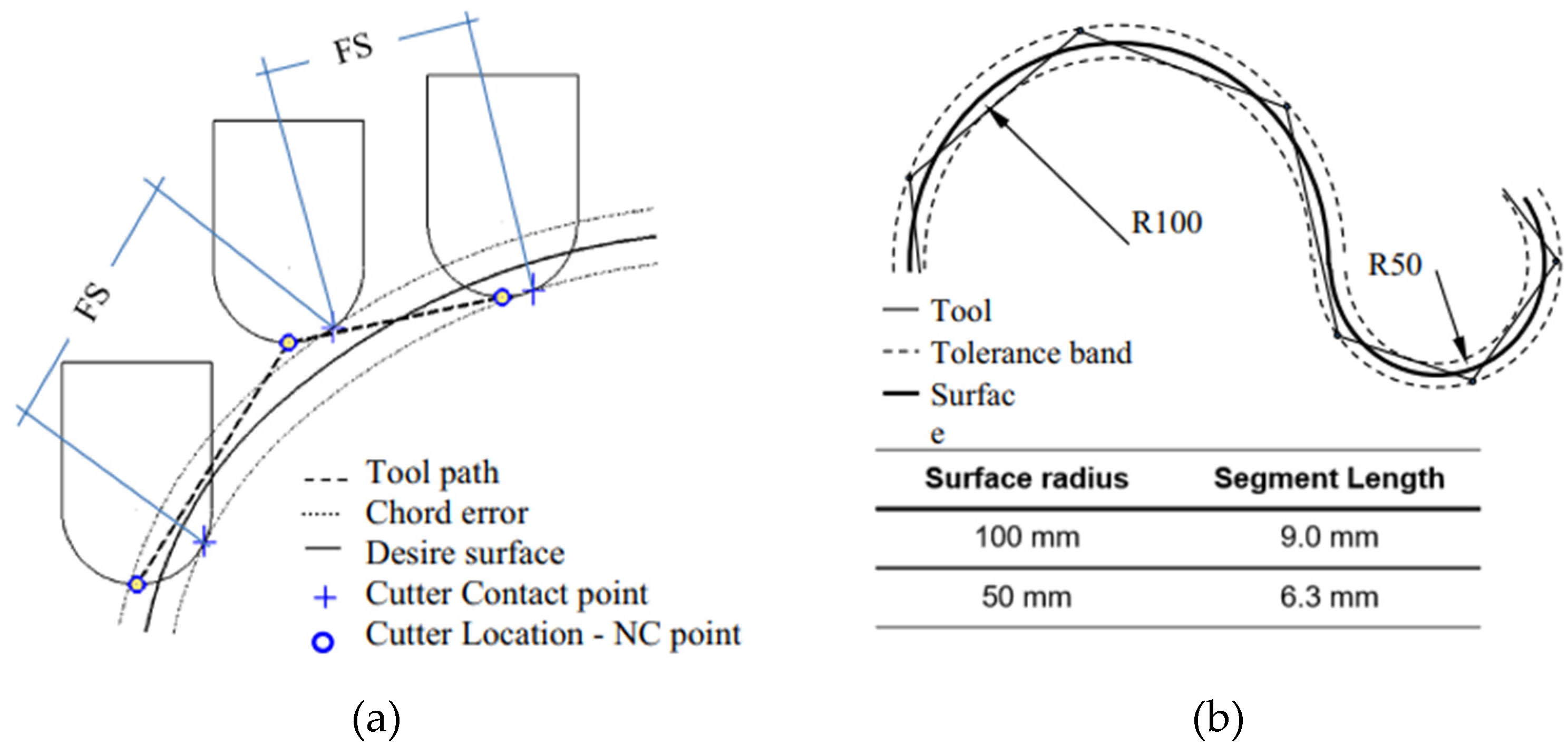
From the details it is possible to see the variation of toolpaths due to the influence of the tool contact in the relationship between the tool and the machined surface. This is due to the changing effective diameter of the tool with respect to the curvature of the surface. The constant Z strategy demonstrated better surface quality with respect to topography than the Spiral circle strategy. The cause of the defects on the machined surface in the form of dimples was due to the vibrations generated in the cutting process, which resulted in repeated deviations from the programmed path.
The individual details indicate that under ideal conditions (no cutting vibration and tool deformation), the toolpath obtained by the Constant Z strategy showed an ideal machined surface, which made it possible to observe uniform surface topography on the surface along the feed. This results in tool grooves aligned along contours that are clearly visible.
The errors in the form of dimples are the result of an inadequate control system of the CNC milling machine. The overall machining process involves a so-called cycle time, in which the control system reads the generated NC code line and then converts this data from the code line into a tool position change. Thus, in the case of creating a toolpath consisting of multiple small segments, the machine control system must recalculate a number of NC blocks in a short time. If the control system is not able to handle a given volume of calculations related to the required toolpaths and the cutting conditions in the cutting process, it will adapt to its calculation capabilities in the form of a reduced feed rate.

From the details of the observed surfaces produced by the three different strategies, it was possible to see the difference in toolpaths due to the influence of tool contact in the relationship between the tool and the machined surface. Better surface topography was obtained with the Constant Z strategy, which is visible and different in relation to the Spiral circle strategy. In the Constant Z strategy, the tool path was in line with the ideal machined surface and produced a uniform and periodic surface topography along the feed. This resulted in highly visible tool grooves aligned along the contours. At distances from the highest point, the radial depth of section a_e increased in a descending direction under the influence of the Constant Z strategy. When using the Spiral-circle strategy, such an increase in the radial depth of cut was not confirmed. This could have been caused by the vibration of the tool in the cutting process.

The evaluation of the surface roughness shows that the Spiral circle strategy gives the most consistent results for the Sa parameter, while the Constant Z strategy has the highest variance. On the other hand, this strategy has the most balanced Sz parameter. The machined surface obtained by the spiral circle strategy showed regular peaks and valleys. The machined surface in micro dimensions was not smooth and presented various distinct properties. Higher degrees of surface deterioration increased significantly when using the spiral circle strategy. Surface defects on the machined surface such as tool feed marks, grooves, plastic flows, stuck material particles, scratch marks, cracks were produced.

Using the Constant Z strategy, it was possible to observe a regular ordering of the tool paths along the contours. In the case of the spiral circle strategy, it was possible to see an increase in tool wear, which led to an increase in the number of dimples. There was an increase in tool wear, which led to an increase in the length of contact between the tool and the machined surface. This also worsened the friction between the tool and the workpiece, resulting in instability of the cutting process and the formation of defects on the surface. The cracks and dimples were caused by plastic deformation at the cutting point due to the pressure between the tool and the machined surface as the tool moved in the feed direction. Due to material extrusion and tool movement, these surfaces were plastically deformed by the blunt rounding of the cutting edges. The adhered material particles could detach and subsequently remove some part of the workpiece material and create a tear on the surface.

Based on the data evaluated by the ZEISS Calypso software, which is shown in Table 5, Table 6 and Table 7, it can be stated that the differences of the measured deviations were in the hundredths of a millimetre. No tolerance deviations were recorded for the Constant Z and Spiral circle methods. For the Spiral method, a tolerance limit was observed when scanning the 3D profile, as can be seen in Table 6 (the red value). Based on the evaluation of the geometric deviations, the Constant Z and Spiral circle methods can be classified as suitable and the Spiral method as not suitable.

Conclusions

The research aimed to present the effect of finishing strategy on surface topography, surface roughness, and variations in machining curved surfaces. The choice of the sample shape was based on the wide occurrence of such surface areas in the machining of injection moulds and other shape tools where it is necessary to achieve the required quality and accuracy of production with respect to the future shape of the product. Three strategies were evaluated – Constant Z, Spiral, and Spiral circle, whose paths were programmed in the CAM system SolidCAM. The material used for the experiments was the aluminium alloy AlCu4Mg. The evaluation of surface topography and surface roughness was carried out at three different sample locations selected to significantly change the effective diameter of the tool on which the tool comes into contact with the machined surface. The results showed changes in the monitored parameters due to a change in the effective diameter of the cutting tool as well as the influence of the strategy used. To produce samples with corresponding shapes in terms of topography, the Constant Z strategy is the most suitable, in which uniform tool paths were achieved over the whole height of the sample.

For better understanding of the relationship between the machined surface and the tool, it might be interesting to investigate the effects of cutting forces and evaluate them in the production of different shaped surfaces. In the future, it would be interesting to perform an experiment that would record cutting forces during the production of differently shaped surfaces and their effect on the component accuracy and tool life, when a ball end mill is used. Another point of future investigation could be the change in the machined material and the influence of different clamping methods, for example, heat chuck or collet chuck, and evaluation of their influence on the surface texture, roughness parameters, and cutting forces. Also, a research study dealing with the application of simultaneous milling of the sculptured surfaces could be considered and a comparison of tool wear using 3-axis and 5-axis machining could be carried out. The research presented in this paper was performed to validate our proposed study and to acquire data for future research.

Author Contributions

Conceptualization, J.V.; methodology, J.V., P.I., and M.D.; validation, J.V., and M.D.; formal analysis, J.V., and L.K.; investigation, J.V.; resources, J.V.; writing—original draft preparation, J.V.; writing—review and editing, J.V. and L.K.; visualization, J.V.; J.B. and L.K.; supervision, L.K.; project administration, P.I. and M.V.; funding acquisition, M.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by The Ministry of Education, Science, Research and Sport of the Slovak Republic, grant number VEGA 1/0457/21, 1/0384/20, KEGA 036TUKE-4/2021.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

Toh, C.K. A study of the effects of cutter path strategies and orientations in milling. J. Mater. Process. Technol. 2004, 152, 346–356. [Google Scholar] [CrossRef]
Daymi, A.; Boujelbene, M.; Linares, J.M.; Bayraktar, E.; Amara, A.B. Influence of workpiece inclination angle on the surface roughness in ball end milling of the titanium alloy Ti-6Al- 4V. J. Achiev. Mater. Manuf. Eng. 2009, 35, 79–86. [Google Scholar]
Václav, Š.; Mareš, A.; Legutko, S.; Košťál, P.; Delgado Sobrino, D.R. Proposal of a system for estimating the assembly time in small and medium-sized enterprises. Tech. Gaz. 2020, 27, 2089–2096. [Google Scholar] [CrossRef]
Razavykia, A.; Iranmanesh, S.; Esmaeilzadeh, A. The Effect of Tool Path Strategy on Surface and Dimension in High-Speed Milling. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2017, 35, 1475–1479. [Google Scholar]
Varga, J.; Spišák, E.; Gajdoš, I.; Mulidrán, P. Comparison of milling strategies in the production of shaped surfaces. Adv. Sci. Technol. Res. J. 2022, 16, 267–274. [Google Scholar] [CrossRef]
Grešová, Z.; Ižol, P.; Vrabeľ, M.; Kaščák, Ľ.; Brindza, J.; Demko, M. Influence of ball-end milling strategy on the accuracy and roughness of free form surfaces. Appl. Sci. 2022, 12, 1–17. [Google Scholar] [CrossRef]
Boujelbene, M.; Moisan, A.; Tounsi, N.; Brenier, B. Productivity enhancement in dies and molds manufacturing by the use of C1 continuous tool path. Int. J. Mach. Tools Manuf. 2004, 44, 101–107. [Google Scholar] [CrossRef]
Ramos, A.M.; Relvas, C.; Simoes, J.A. The influence of finishing milling strategies on texture, roughness and dimensional deviations on the machining of complex surfaces. J. Mater. Process. Technol. 2003, 136, 209–216. [Google Scholar] [CrossRef]
Suresh, B.V.; Raviswaran, N. Tool path generation algorithm and 3D tolerance analysis for free-form surfaces. Ethiop. J. Sci. Technol. 2006, 4, 23–30. [Google Scholar]
Misra, D.; Sundararajan, V.; Wright, P.K. Zig-zag tool path generation for sculptured surface. Geom. Algorithmic Asp. Comput. -Aided Des. Manuf. 2003, 265–280. [Google Scholar] [CrossRef]
Toh, C.K. Surface topography analysis in high speed finish milling inclined hardened steel. Precis. Eng. 2004, 28, 386–398. [Google Scholar] [CrossRef]
Ižol, P.; Brindza, J.; Vrabeľ, M.; Demko, M.; Basilio, S.E. Effect of optimization software on part shape accuracy and production times during rough milling of aluminum alloy. Machines 2022, 10, 1–18. [Google Scholar] [CrossRef]
Asilturk, I.; Akkus, H. Determining the effect of cutting parameters on surface roughness in hard turning using the Taguchi method. Measurement 2011, 44, 1697–1704. [Google Scholar] [CrossRef]
Varga, J.; Tóth, T.; Kaščák, Ľ.; Spišák, E. The effect of the machining strategy on the surface accuracy when milling with a ball end cutting tool of the aluminum alloy AlCu4Mg. Appl. Sci. 2022, 12, 1–16. [Google Scholar] [CrossRef]
Chiang, S.; Tsai, C.; Lee, A. Analysis of cutting forces in ball end milling. J. Mater. Process. Technol. 1995, 47, 231–249. [Google Scholar] [CrossRef]
Varga, J.; Tóth, T.; Frankovský, P.; Dulebová, Ľ.; Spišák, E.; Zajačko, I.; Živčák, J. The influence of automated machining strategy on geometric deviations of machined surfaces. Appl. Sci. 2021, 11, 1–15. [Google Scholar] [CrossRef]
Souza, A.F.; Bodziak, B. Advanced free form manufacturing by computer aided systems Book Mechanical Engineering. April 2012. [CrossRef]
Boujelbene, M.; Moisan, A.; Torbaty, S. Study of the tool inclination in multi-axes milling. In Proceedings of the 15th International Conference on Manufacturing Systems – ICMaS, Bucharest, Romania, 26–27 October 2006. [Google Scholar]
Ozturk, E.; Tunc, L.T.; Budak, E. Investigation of lead and tilt angle effects in 5-axis ball-end milling processes. Int. J. Mach. Tools Manuf. 2009, 49, 1053–1062. [Google Scholar] [CrossRef]
Scandiffio, I.; Diniz, A.E.; Souza, A.F. Evaluating surface roughness, tool life, and machining force when milling free-form shapes on hardened AISI D6 steel. Int. J. Adv. Manuf. Technol. 2015, 82, 1–13. [Google Scholar] [CrossRef]
Souza, A.F.; Berkenbrock, E.; Rodriguez, A.R.; Diniz, A.E. Influences of the tool path strategy on the 75 machining force when milling free form geometries with a ball-end cutting tool. J. Braz. Soc. Mech. Sci. Eng. 2014, 37, 675–687. [Google Scholar] [CrossRef]
Bissacco, G.; Hansen, H.N.; Chiffre, L. Size effect on surface generation in micromilling of hardened tool steel. CIRP Ann. - Manuf. Technol. 2006, 555, 593–596. [Google Scholar] [CrossRef]
Ducobu, F.; Filippi, E.; Rivière, L.E. Chip formation and minimum chip thickness in micro-milling. Processings of the 12th CIRP Conference on modeling of machining operations, Donostia-San Sebastián, Spain, 9−14 September 2009. [Google Scholar]
Tuysuz, O.; Altintas, Y.; Feng, H.Y. Prediction of cutting forces in three and five-axis ball-end milling with tool indentation effect. Int. J. Mach. Tools Manuf. 2013, 66, 66–81. [Google Scholar] [CrossRef]
Chiang, S.T.; Tsai, Ch.M.; Lee, A.Ch. Analysis of cutting forces in ball-end milling. J. Mater. Process. Technol. 1995, 47, 231–249. [Google Scholar] [CrossRef]
Liu, N.; Loftus, M.; Whitten, A. Surface finish visualization in high speed, ball nose milling applications. Int. J. Mach. Tools Manuf. 2005, 45, 1152–1161. [Google Scholar] [CrossRef]
Aspinwall, D.K.; Dewes, R.C.; Ng, E.G.; Sage, C. The influence of cutter orientation and workpiece angle on machinability when high-speed milling Inconel 718 under finishing conditions. Int. J. Mach. Tools Manuf. 2007, 47, 1839–1846. [Google Scholar] [CrossRef]
Wojciechowski, S.; Wiackiewicz, G.M.; Krolczyk, G.M. Study on metrological relations between instant tool displacements and surface roughness during precise ball end milling. Measurement 2018, 129, 686–694. [Google Scholar] [CrossRef]
Shaghayegh, S.; Sadeghi, M.H.; Hassanpour, H. The Influence of Tool Path Strategies on Cutting Force and Surface Texture during Ball End Milling of Low Curvature Convex Surfaces. Sci. World J. 2014, 2014, 1–14. [Google Scholar] [CrossRef]
Käsemodel, R.B.; Souza, A.F.; Voigt, R.; Basso, I.; Rodrigues, A.R. CAD/CAM interfaced algorithm reduces cutting force, roughness, and machining time in free-form milling. Int. J. Adv. Manuf. Technol. 2020, 107, 1883–1900. [Google Scholar] [CrossRef]
Souza, A.F.; Diniz, A.E.; Rodrigues, A.R.; Coelho, R.T. Investigating the cutting phenomena in free-form milling using a ball-end cutting tool for die and mold manufacturing. Int. J. Adv. Manuf. Technol. 2014, 71, 1565–1577. [Google Scholar] [CrossRef]
Tuysuz, O.; Altintas, Y.; Feng, H.Y. Prediction of cutting forces in three and five-axis ball-end milling with tool indentation effect. Int. J. Mach. Tools Manuf. 2013, 66, 66–81. [Google Scholar] [CrossRef]
Kose, E.; Kurt, A.; Şeker, U. The Effects of the Feed Rate on the Cutting Tool Stresses in Machining of Inconel 718. J. Mater. Process. Technol. 2008, 231, 165–173. [Google Scholar] [CrossRef]
Schulz, H.; Hock, S. High-Speed Milling of Dies and Moulds — Cutting Conditions and Technology. J. Mater. Process. Technol. 1995, 44, 35–38. [Google Scholar] [CrossRef]
Cai, Y.; Zhangiang, L.; Shi, Z.; Song, Q. Optimum end milling tool path and machining parameters for micro Laval nozzle manufacturing. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 231, 1–11. [Google Scholar] [CrossRef]
Antoniadis, A.; Bilalis, N.; Balouktsis, A.; Savakis, C. Prediction of Surface Topomorphy and Roughness in Ball-End Milling. Int. J. Adv. Manuf. Technol. 2003, 21, 965–971. [Google Scholar] [CrossRef]
Šimunović, G.; Šimunović, K.; Šarić, T. Modelling and simulation of surface roughness in face milling. Int. J. Simul. Model. 2013, 12, 141–153. [Google Scholar] [CrossRef]
Vukelic, D.; Tadic, B.; Miljanic, D. Novel workpiece clamping method for increased machining performance. Teh. Vjesn. -Tech. Gaz. 2012, 19, 837–846. [Google Scholar] [CrossRef]
Antic, A.; Kozak, D.; Kosec, B.; Šimunović, G.; Šarić, T.; Kovačevič, D.; Čep, R. The influence of tool wear on the chip-forming mechanism and tool vibrations. Teh. Vjesn. -Tech. Gaz. 2013, 20, 105–112. [Google Scholar] [CrossRef]
Toh, C.K. Design, evaluation, and optimization of cutter path strategies when high speed milling hardened mold and die materials. Mater. Des. 2005, 26, 517–533. [Google Scholar] [CrossRef]
Abuelnaga, A.M.; Dardiry, M.A. Optimization methods for metal cutting. Int. J. Mach. Tool Des. Res. 1997, 24, 11–18. [Google Scholar] [CrossRef]
White, B.; Houshyar, A. Quality and optimum parameter selection in metal cutting. Comput. Ind. 1992, 20, 87–98. [Google Scholar] [CrossRef]
Shajari, S.; Sadeghi, M.H.; Hassanpour, H. The Influence of Tool Path Strategies on Cutting Force and Surface Texture during Ball End Milling of Low Curvature Convex Surfaces. Sci. World J. 2014, 2014, 1–14. [Google Scholar] [CrossRef]
Ikua, B.W.; Tanaka, H.; Obata, F.; Sakamoto, S.; Kishi, T.; Ishii, T. Prediction of cutting forces and machining error in ball end milling of curved surfaces—II experimental verification. Precis. Eng. 2002, 26, 69–82. [Google Scholar] [CrossRef]
Matras, A.; Kowalczyk, R. Analysis of machining accuracy during free form surface milling simulation for different milling strategies. Proc. SPIE - Int. Soc. Opt. Eng. 2014, 9290, 1–7. [Google Scholar] [CrossRef]
Hao, X.; Yue, C.; Liu, X.; Wang, L. Modeling of Convex Surface Topography in Milling Process. Met. - Open Access Metall. J. 2020, 10, 1–21. [Google Scholar] [CrossRef]
Pessoles, X.; Landon, Y.; Rubio, W. Kinematic modelling of a 3-axis NC machine tool in linear and circular interpolation. Int. J. Adv. Manuf. Technol. 2010, 47, 5–8. [Google Scholar] [CrossRef]
Monreal, M.; Rodriguez, C.A. Infuence of tool path strategy on the cycle time of high-speed milling. Comput. -Aided Des. 2003, 35, 395–401. [Google Scholar] [CrossRef]
Yau, H.T.; Kuo, M.J. NURBS machining and feed rate adjustment for high-speed cutting of complex sculptured surfaces. Int. J. Prod. Res. 2001, 39, 21–41. [Google Scholar] [CrossRef]
Coelho, R.T.; Souza, A.F.; Roger, A.R. Mechanistic approach to predict real machining time for milling free-form geometries applying high feed rate. Int. J. Adv. Manuf. Technol. 2010, 46, 1103–1111. [Google Scholar] [CrossRef]
Souza, A.F.; Käsemodel, R.B.; Arias, M.; Marin, F.; Rodriguez, A.R. Study of tool paths calculated by diferent commercial CAM systems and infuences on the real machining time and surface roughness for milling free-form geometries. J. Braz. Soc. Mech. Sci. Eng. 2019, 363, 1–12. [Google Scholar] [CrossRef]
Siller, H.; Rodriguez, C.A.; Ahuett, H. Cycle time prediction in high-speed milling operations for sculptured surface finishing. J. Mater. Process. Technol. 2006, 174, 355–362. [Google Scholar] [CrossRef]
Lasemi, A.; Xue, D.; Gu, P. Recent development in CNC machining of freeform surfaces: A state-of-the-art review. Comput. Aided Des. 2010, 42, 641–654. [Google Scholar] [CrossRef]
Václav, Š.; Sivtsev, N.S.; Senderská, K. Investigation of stress-strain state of a workpiece at gauge burnishing of its holes. Adv. Sci. Technol. Res. J. 2017, 11, 211–222. [Google Scholar] [CrossRef]
Kaymakci, M.; Lazoglu, I. Tool path selection strategies for complex sculptured surface machining. Mach. Sci. Technol. 2008, 12, 119–132. [Google Scholar] [CrossRef]
Pokorný, P.; Peterka, J.; Václav, Š. The task of 5-axis milling. Tech. Gaz. 2012, 19, 147–150. [Google Scholar]

Figure 1. Tool contact with machined surface a) ascendant direction b) descendant direction.

Figure 2. Tool contact with machined surface a) ascendant direction b) descendant direction.

Figure 3. Trajectory view calculation for free-shaped toolpath a) forward step b) size length [51].

Figure 4. 3D model of the test sample.

Figure 5. Selected machining operations.

Figure 6. Measured areas for surface roughness assessment.

Figure 7. Focusing of the basic coordinate system - spatial alignment method 3-2-1.

Figure 8. Measurements of 3D curves a) XZ plane b) YZ plane.

Figure 9. Number of points measured depending on the measurement location.

Figure 10. Detail of the investigated surface at 7.5 mm; Constant Z strategy.

Figure 11. Detail of the investigated surface at 7.5 mm; Spiral strategy.

Figure 12. Detail of the investigated surface at 7.5 mm; Spiral circle strategy.

Figure 13. Detail of the investigated surface at 15 mm; Constant Z strategy.

Figure 14. Detail of the investigated surface at 15 mm; Spiral strategy.

Figure 15. Detail of the investigated surface at 15 mm; Spiral circle strategy.

Figure 16. Detail of the investigated surface at 22.5 mm; Constant Z strategy.

Figure 17. Detail of the investigated surface at 22.5 mm; Spiral strategy.

Figure 18. Detail of the investigated surface at 22.5 mm; Spiral circle strategy.

Figure 19. Surface topography for Constant Z strategy.

Figure 20. Surface topography for Spiral circle strategy.

Figure 21. Comparison of the radial depth of cut at a specific height for the Constant Z strategy.

Figure 22. Comparison of the radial depth of cut at a specific height for the Spiral strategy.

Figure 23. Comparison of the radial depth of cut at a specific height for the Spiral circle strategy.

Figure 24. Comparison of radial depth of cut a_e at specific heights for each strategy.

Figure 25. Surface roughness rating for all three strategies, measurement height 7.5 mm.

Figure 26. Surface roughness rating for all three strategies, measurement height 15 mm.

Figure 27. Surface roughness rating for all three strategies, measurement height 22.5 mm.

Figure 28. Comparison of surface roughness Sa [µm] for different heights with respect to the strategies.

Figure 29. Comparison of surface roughness Ssk [µm] for different heights with respect to the strategies.

Figure 30. Comparison of surface roughness S₁₀z [µm] for different heights with respect to the strategies.

Figure 31. Measured deviations plot of the curve in XZ plane for Constant Z strategy.

Figure 32. Measured deviations plot of the curve in YZ plane for Constant Z strategy.

Figure 33. Measured deviations plot of the curve in XZ plane for Spiral strategy.

Figure 34. Measured deviations plot of the curve in YZ plane for Spiral strategy.

Figure 35. Measured deviations plot of the curve in XZ plane for Spiral circle strategy.

Figure 36. Measured deviations plot of the curve in YZ plane for Spiral circle strategy.

Figure 37. Deviations comparison of the evaluated areas for each milling strategy.

Table 1. Cutting parameters with the tool description.

Tool Diameter [mm]	Cutting speed [m.min^{- 1}]	Feed per tooth [mm]	Spindle frequency [RPM]	Tool producer	Tool code
End Mill D 18	270	0.125	4800	Korloy	AMS2018S
End Mill D8	123	0.029	4900	ZPS-FN	273618.080
Ball End Mill D6	92.4	0.022	4900	ZPS-FN	511418.060

Table 2. Radial depth of cut a_e [µm] of 7.5mm.

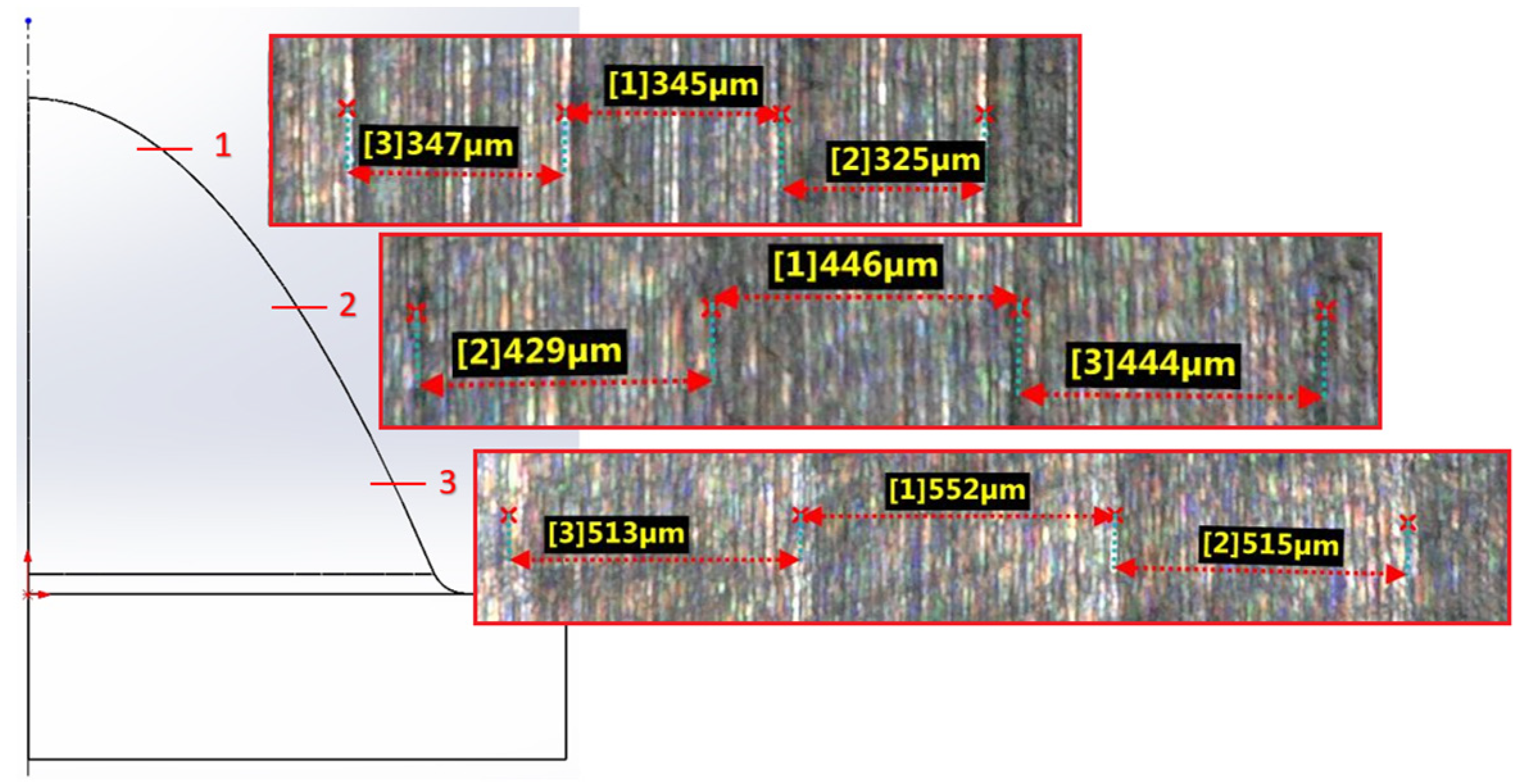
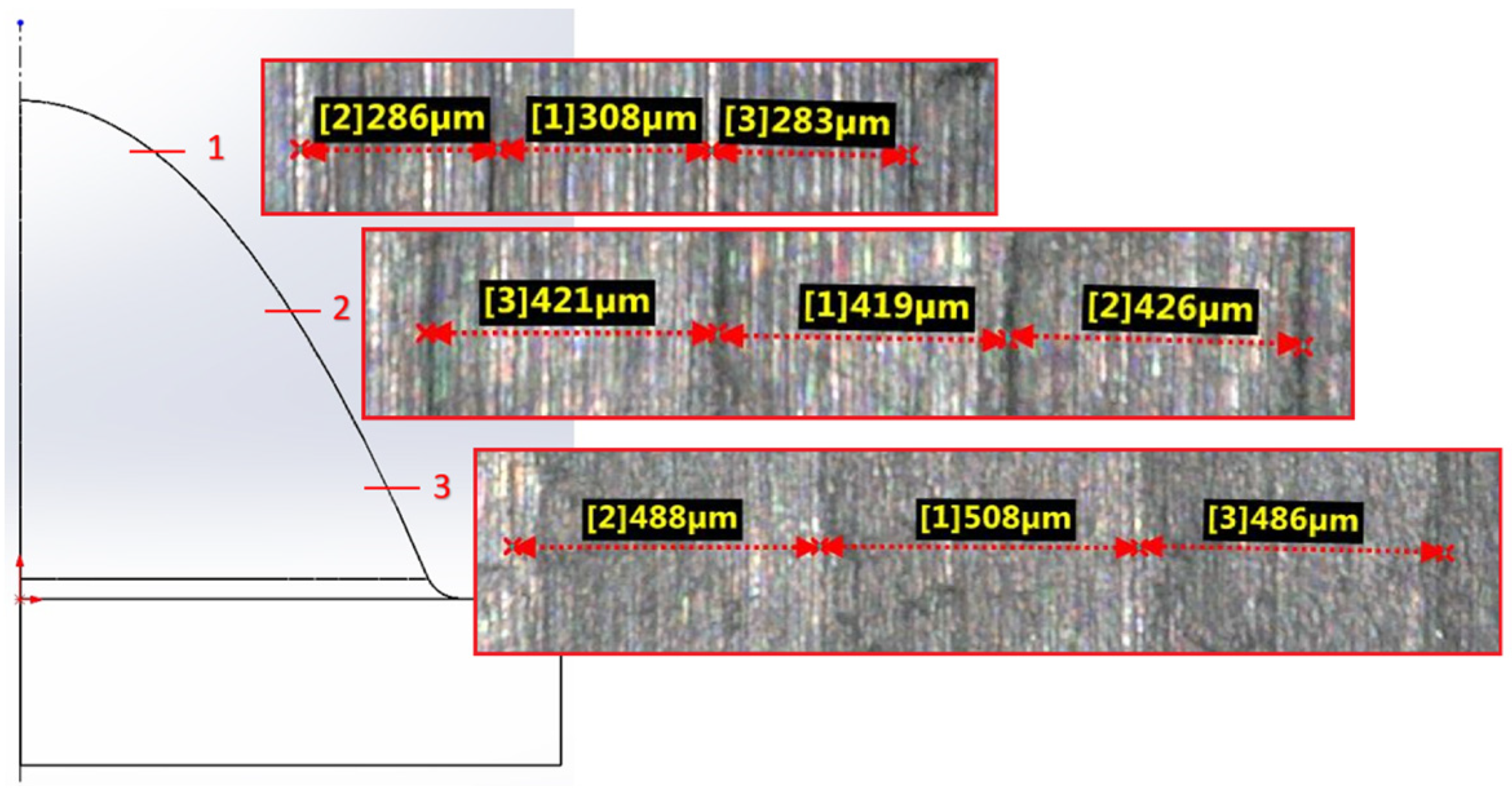
Strategy	Radial depth of cut a_e [µm] of 7.5mm
Strategy	Measurement 1	Measurement 2	Measurement 3
Constant Z	347	345	325
Spiral	286	308	283
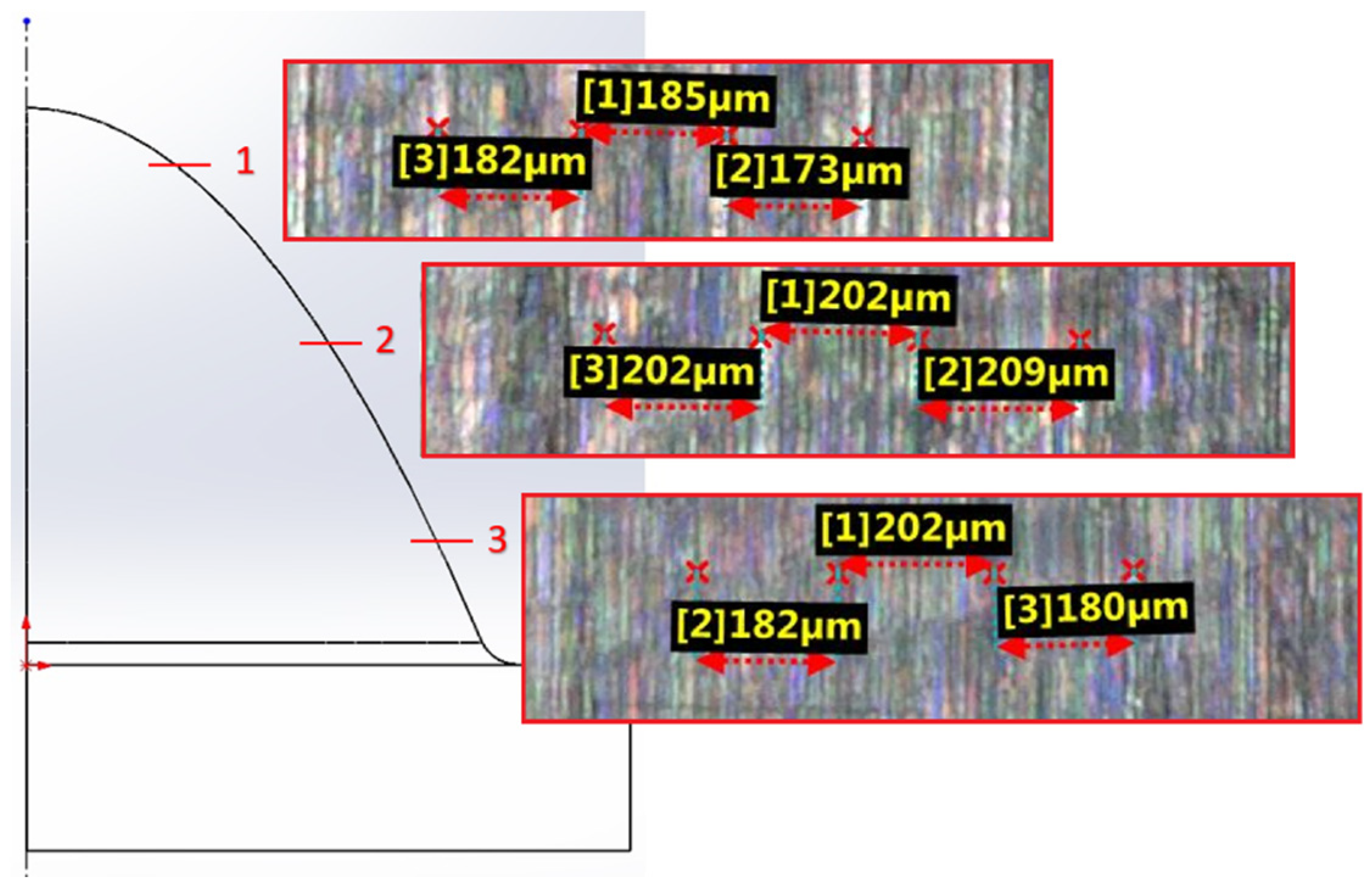
Spiral circle	182	185	173

Table 3. Radial depth of cut a_e [µm] of 15mm.

Strategy	Radial depth of cut a_e [µm] of 15mm
Strategy	Measurement 1	Measurement 2	Measurement 3
Constant Z	429	446	444
Spiral	421	419	426
Spiral circle	202	202	209

Table 4. Radial depth of cut a_e [µm] of 22.5mm.

Strategy	Radial depth of cut a_e [µm] of 22.5mm
Strategy	Measurement 1	Measurement 2	Measurement 3
Constant Z	513	552	515
Spiral	488	508	486
Spiral circle	182	202	180

Table 5. Measured deviation values for Constant Z strategy.

Area evaluated	Calculated deviation [mm]	Set tolerance [mm]	Maximum negative deviation [mm]	Maximum positive deviation [mm]
2D profile XZ	0.1231	0.15	-0.0549	0.0616
2D profile YZ	0.0874	0.15	-0.0411	0.0437
3D area profile	0.1372	0.15	-0.0686	0.0665

Table 6. Measured deviation values for Spiral strategy.

Area evaluated	Calculated deviation [mm]	Set tolerance [mm]	Maximum negative deviation [mm]	Maximum positive deviation [mm]
2D profile XZ	0.1249	0.15	-0.0580	0.0625
2D profile YZ	0.0905	0.15	-0.0440	0.0453
3D area profile	0.1983	0.15	-0.0561	0.0991

Table 7. Measured deviation values for Spiral circle strategy.

Area evaluated	Calculated deviation [mm]	Set tolerance [mm]	Maximum negative deviation [mm]	Maximum positive deviation [mm]
2D profile XZ	0.1228	0.15	-0.0557	0.0614
2D profile YZ	0.0868	0.15	-0.0411	0.0434
3D area profile	0.1371	0.15	-0.0686	0.0670

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer