FEA of Infilled Composite Beam Using Angle Type Shear Connector

1. Introduction

In order to increase the land utilization ratio, modern buildings are undergoing a trend of high-rise construction and longer spans. Consequently, the selection of structural systems that satisfy the economic use of materials and the efficiency of construction methods has become a crucial issue. While using a single material can ensure sufficient strength by increasing the size of the structural elements, the economic feasibility is compromised due to the increased use of materials. As a result, the utilization of composite members, which combine concrete and steel, has been increasing.

Composite beams, among various composite members, utilize shear connectors to leverage the advantages of concrete and steel, achieving efficiency in structural performance. In order to resist the horizontal shear forces at the interface between the steel girder and the concrete slab, stud anchors are commonly used. Currently, the majority of composite beams in use are exposed type, where the concrete slab is placed on top of the steel girder, and extensive research has been conducted on this configuration[1,2,3]. In recent studies, there has been a focus on U-shaped infilled composite beams to increase the bond strength between the concrete and the steel girder [4,5,6,7,8]. When using infilled composite beams, additional spacing elements may be required to withstand the concrete pressure. However, by using angle-type shear connectors, this study expects the shear connectors to serve both as connectors and spacing elements simultaneously. Therefore, angle-type shear connectors were employed in this research.

The existing design equations[9] only provide design equations for channel-type and stud-type shear connectors. There are no design equations available for angle-type shear connectors. Therefore, the strength of angle-type shear connectors is being designed based on design equations for channel-type shear connectors, which have a similar form[10,11,12]. In this paper, we evaluate the flexural capacity of composite beams using angle-type shear connectors and present a corresponding finite element analysis model. Ultimately, through the finite element analysis model, we aim to propose a design method for angle-type shear connectors of a similar configuration to that of this paper.

2. Experiment

2.1. Experiment Plan

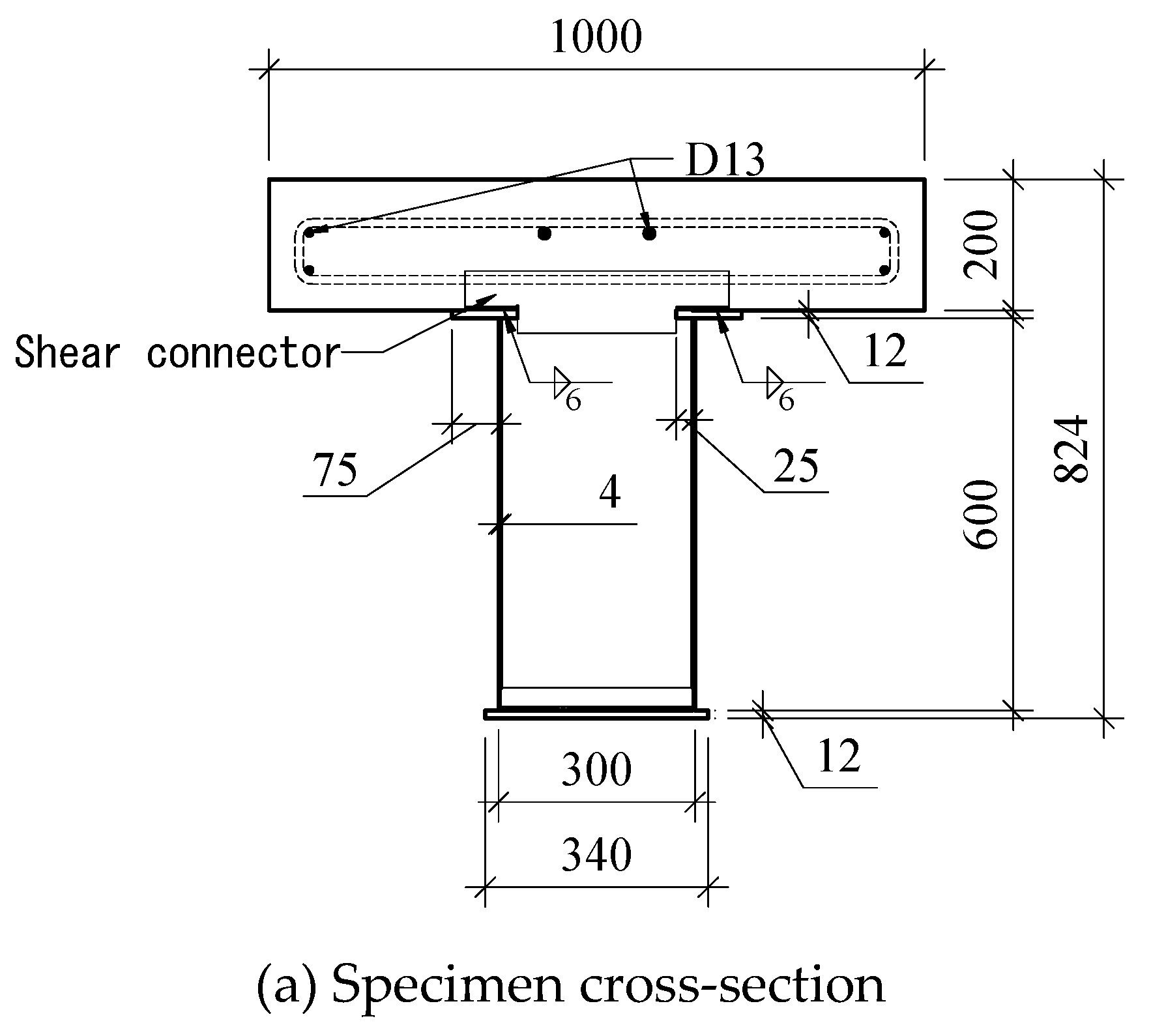
One of the crucial factors determining the maximum strength in composite beams is the degree of composite action between concrete and steel girder. In this paper, the spacing of shear connectors, which directly affects the degree of composite action, was set as a variable. Table 1 summarizes the names of the specimens and their corresponding variables. The height of the steel girder was set to 624mm, and the height of the slab was 200mm, resulting in a total height of 824mm for the specimens. The length of the specimens was set to 8,080mm to match the site conditions. For the distribution of moments, a two-point loading scheme was planned with a distance of 1,150mm, taking into consideration the site conditions. The spacing of the shear connectors was set to 1,000mm, 600mm, and 400mm, respectively. The shear connectors were designed in the form of angle-type shear connectors with a height of 80mm, a width of 400mm, and a thickness of 6mm. The reinforcement for the slab included D13 bars for main reinforcement and D10 bars for tie reinforcement, installed at 200mm intervals. The concrete was designed with a strength of 24MPa. The web of the steel girder was made of SS275 (equivalent to A36), and the flange and shear connectors were made of SM355 (equivalent to A572) steel.

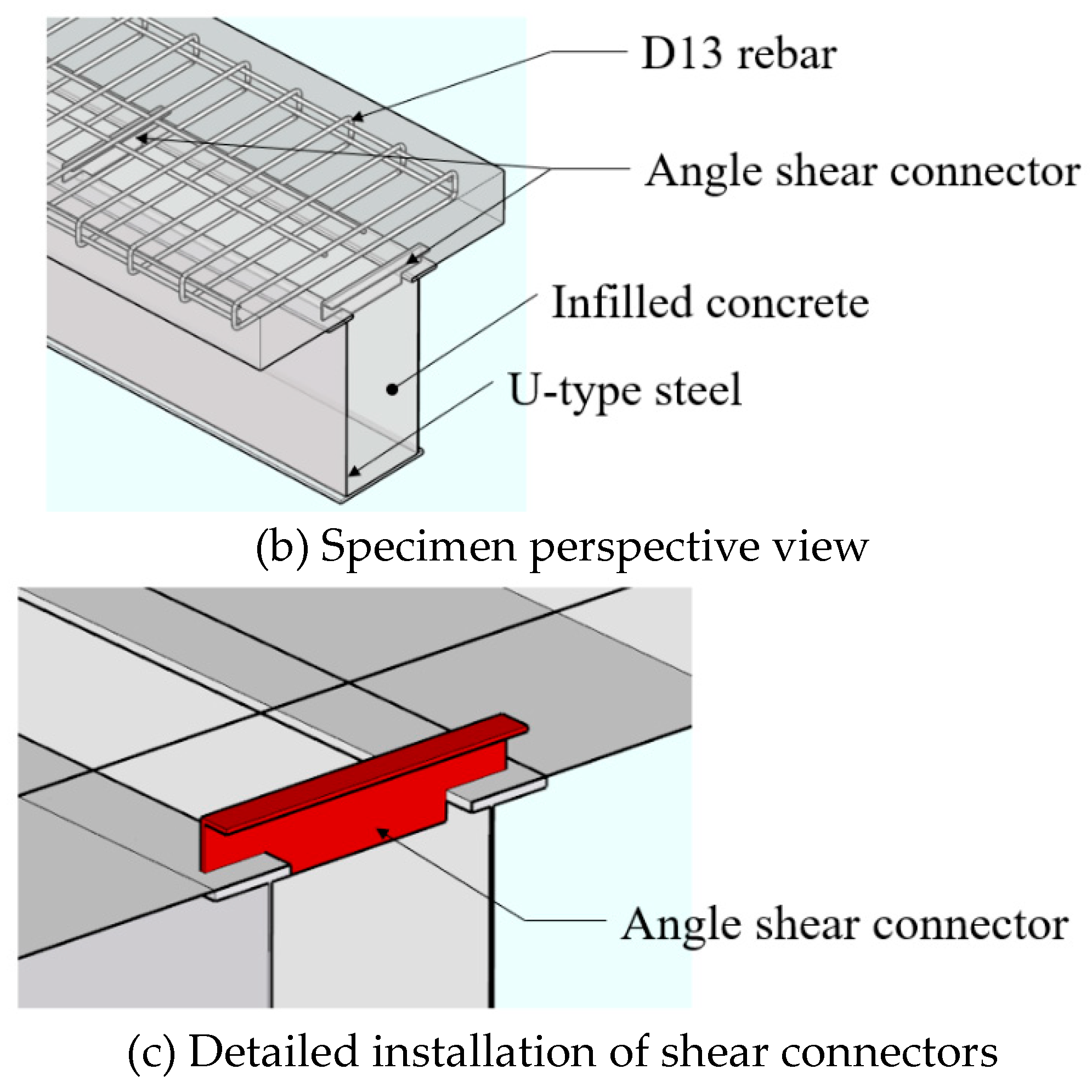
Figure 1(a) shows a cross-section of the composite beam. The size of the concrete slab was set to 1,000×200 (width × thickness), considering the experimental conditions and loading range. The thickness of the steel girder web was set to 4mm, and the width of the bottom flange was planned to be 340mm. Figure 1(b) represents a perspective view of the specimen, showing the appearance of the shear connectors and the reinforcement. The shear connectors were installed at points that do not affect the reinforcement, and their shape was installed in a configuration that connects the upper flange as indicated in Figure 1(c). The shear connectors were oriented in the same direction for ease of installation.

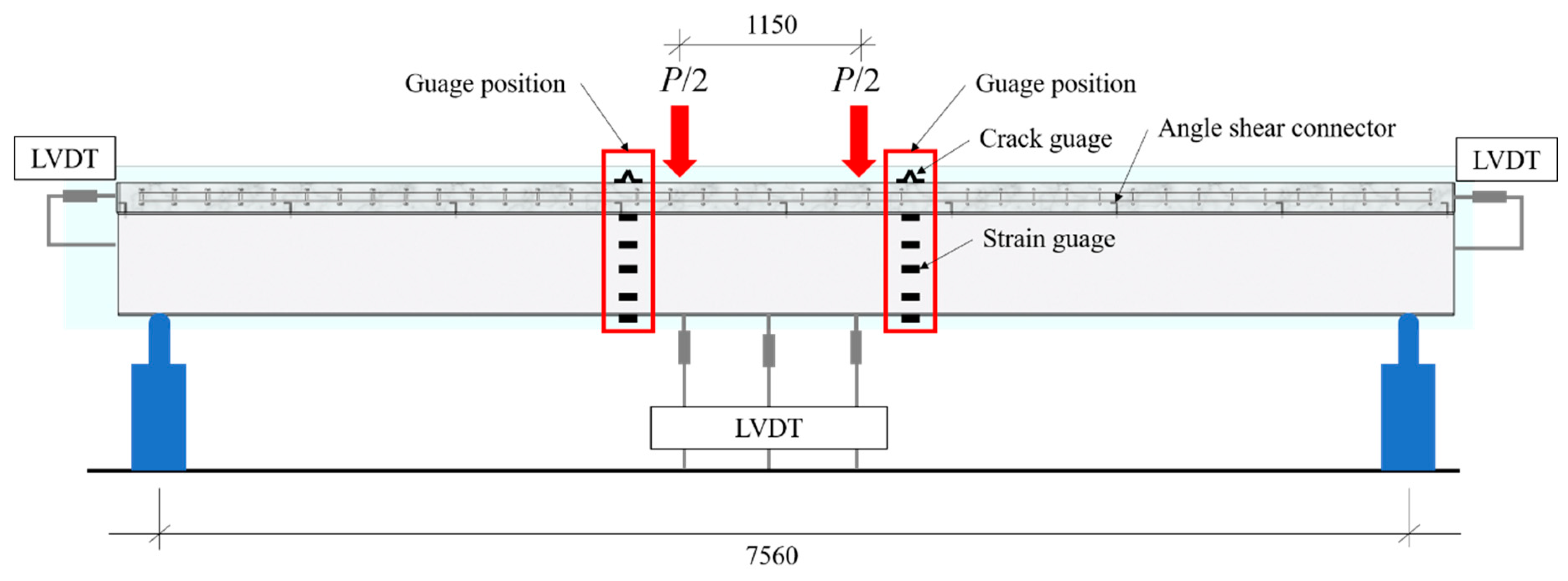
Figure 2 shows the installation of the specimen. The length of the specimen was determined as 7,560mm, considering the site conditions, and the distance between the loading points was 1,150mm. The specimen was subjected to a 2-point loading using a Universal Testing Machine (UTM) with a capacity of 10MN. The loading speed was controlled at 0.05mm/sec. The test was terminated when the strength decreased to 80% of the maximum load after reaching the maximum load.

Displacement gauges were installed at the center of the beam and at the loading points to measure the deflection of the beam. Additional displacement gauges were also installed at both ends to measure the slip between the concrete and the steel beam. Strain gauges were placed near the loading points to locate the neutral axis during yielding. Crack gauges were installed on the top surface of the slab to measure the deformation of the concrete. Furthermore, strain gauges were attached at intervals of 1,000mm near the loading points to assess the yield point of the flange.

2.2. Experiment Results

Table 2 presents the results of material tests conducted following ASTM standards[13]. For A36 4t, the yield strength was measured as 361.25MPa, and the tensile strength was 454.50Mpa. For A36 6t, the yield strength was measured as 356.75Mpa, and the tensile strength was 430.79Mpa. As for the material used for the flange (A572), the yield strength was 383.21Mpa, and the tensile strength was 554.82Mpa. The average compressive strength of the concrete was measured as 21.57Mpa.

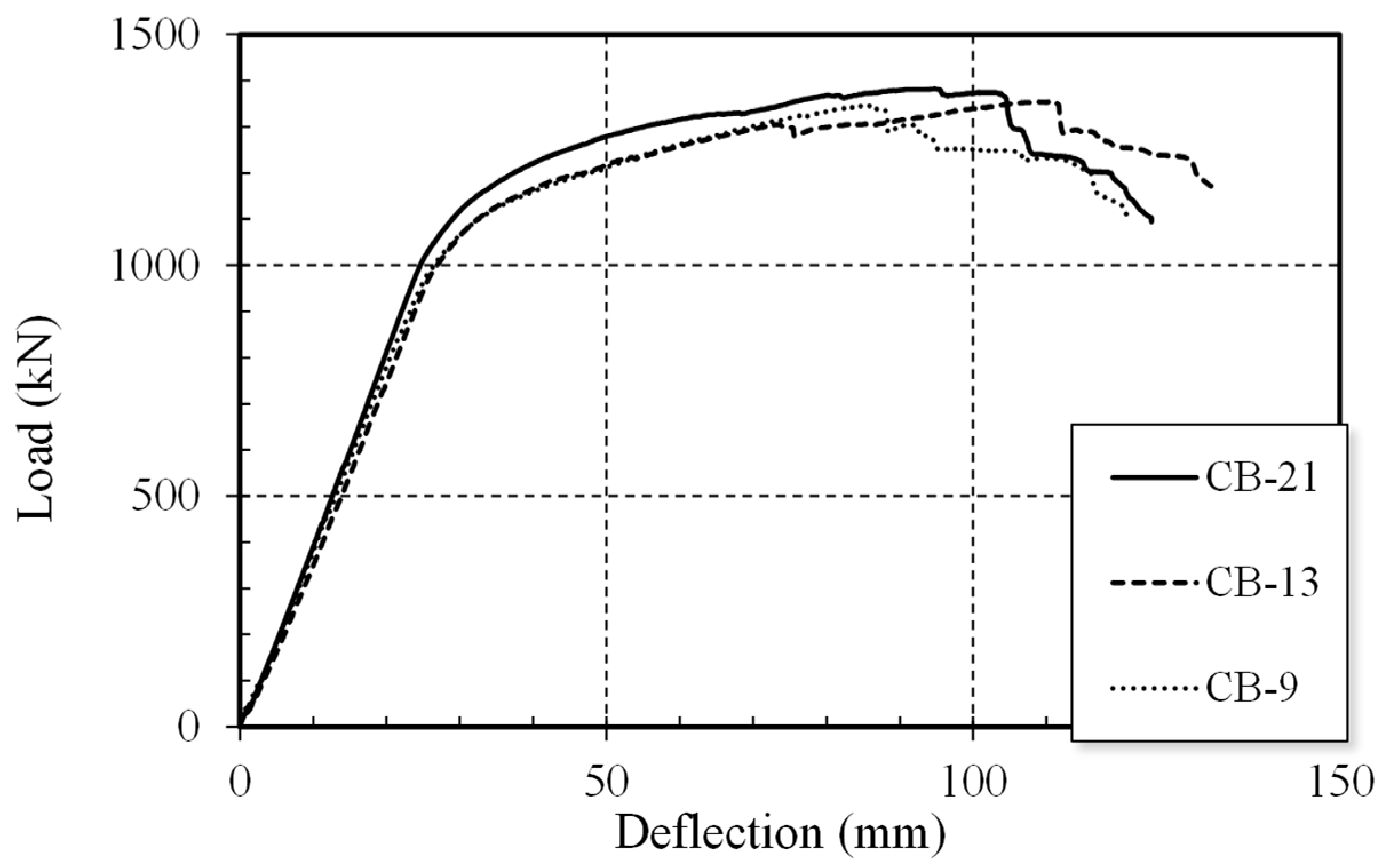
Figure 4 depicts the experimental results of the composite beam. The initial slopes were similar for all cases, and the yield strength and tensile strength exhibited slight variations depending on the composite ratio. The specimen with the narrowest spacing of the shear connectors showed the highest yield strength and ultimate strength. However, there was little difference between the specimens with shear connector spacings of 600mm and 1000mm. This can be attributed to the non-uniform strength distribution within the concrete.

Table 3 summarizes the experimental results. The yield strength and ductility were evaluated following the method suggested by AC495[14]. The yield strengths of the specimens were measured in the order of shear connector spacing as 1165.72kN, 1135.51kN, and 1121.33kN, respectively. The maximum strengths were measured as 1382.09kN, 1353.74kN, and 1346.95kN, respectively. The ductility values were 3.67, 3.69, and 3.51, respectively. Ultimately, it was observed that narrower shear connector spacing resulted in superior yield strength, maximum strength, and ductility.

Figure 4 illustrates the failure modes of the specimens. All specimens experienced the collapse of the upper slab, resulting in a decrease in the strength of the specimens. No slip of the lateral concrete was observed.

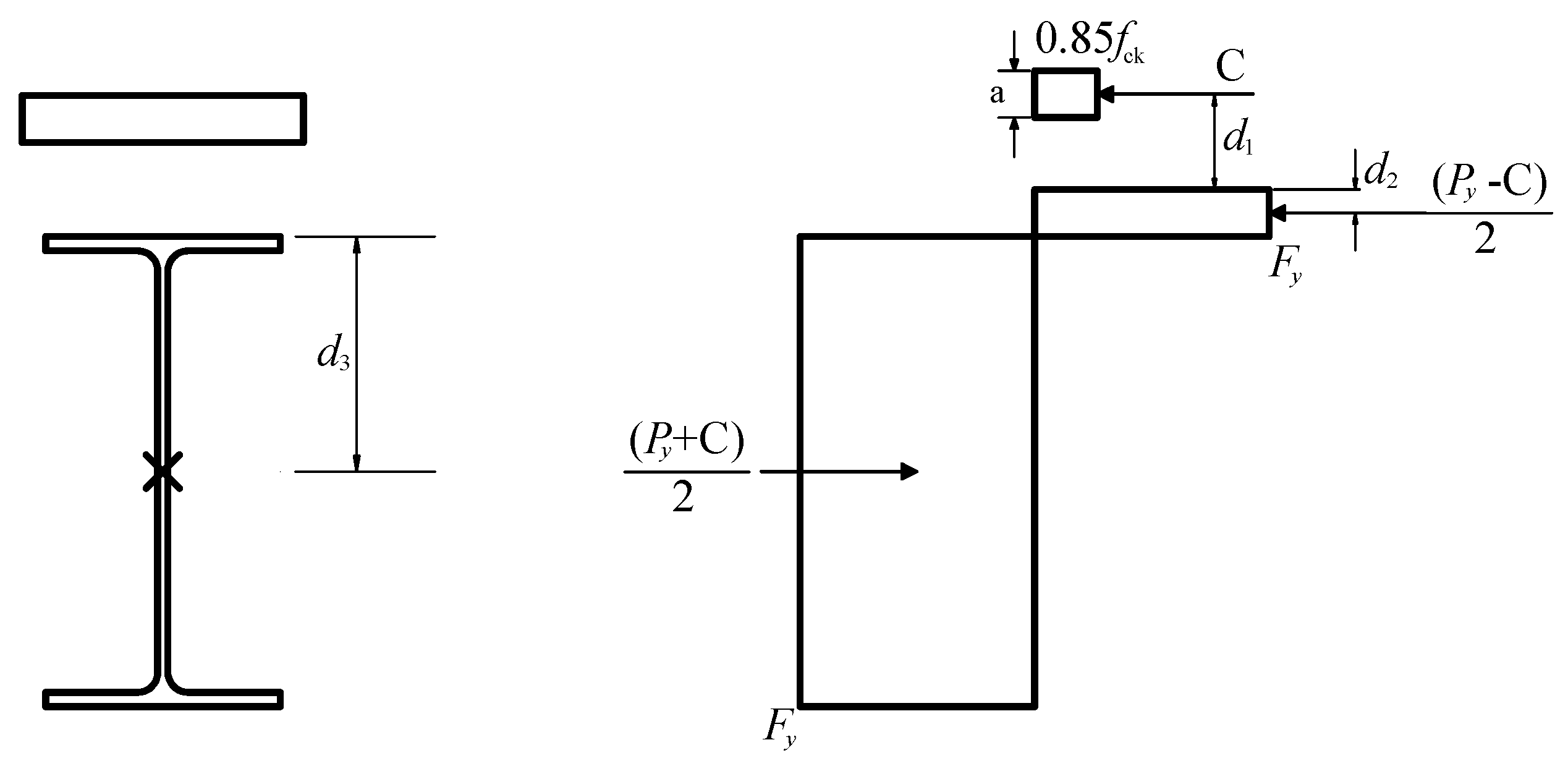
The theoretical calculation of the composite beam is determined based on the stress-strain distribution as shown in Figure 5. Using this stress-strain distribution, the compressive force $C$ acting on the concrete slab of the test specimen is determined as the minimum value among equations (1) to (3). Equation (3) involves the shear strength of the shear connector, denoted as $Q_n$, and in this study, an angled shear connector was used. Therefore, equation (4) for the shear strength of a channel-shaped shear connector was utilized to calculate $Q_n$[9].

$$C=A_s{F}_y$$

(1)

$$C=0.85f_{ck}{A}_c$$

(2)

$$C=\sum Q_n$$

(3)

$$Q_n=0.3\left(t_f+0.5t_w\right)L_a\sqrt{f_{ck}{E}_c}$$

(4)

Here, $A_s$ is the total cross-sectional area of steel section, $F_y$ is the yield strength of steel, $f_{ck}$ is the compressive strength of concrete, $A_c$ is the total cross-sectional area of concrete, $t_f$ is the flange thickness of the angle, $t_w$ is the web thickness of the angle, and $E_c$ is the elasticity modulus of the concrete.

Equation (5) calculates the design flexural strength in the positive moment region, taking into account the composite effect with the slab. After the manifestation of the composite action, it is assumed that no lateral-torsional buckling occurs due to the restraining effect.

$$M_n=C\left(d_1+d_2\right)+P_y\left(d_3-d_2\right)$$

(5)

Here, $d_1$ is the distance from the center of compression force $C$ in the concrete to the top of the steel member, $d_2$ is the distance from the center of compression force in the steel member to the top of the steel member(If there is no compression force on the steel member, $d_2$ is equal to 0), $P_y$ is the tensile strength of the steel member, and $d_3$ is the Distance from the center of action of $P_y$ on the steel member to the top of the steel member.

There is no available equation for the angle-shaped shear connector used in this study. Therefore, assuming a channel-shaped shear connector and calculating based on the existing equation for channel sections, the strength can be estimated to be approximately 802.84 kN, as shown in Table 4. Consequently, all specimens exhibit behavior corresponding to a composite ratio of 100%, resulting in a final strength of 1182.14 kN. However, since a reduction in strength was observed in the experimental results, it is desired to infer the strength of the angle-shaped shear connector through computational analysis.

Table 4. Theoretical Analysis Results of Specimens.

No.	Specimen	$P_{max}$ (kN)	${\mathrm{P}}_{Theory}$ (kN)	$P_{max}/P_{Theory}$
1	CB-21	1382.09	1182.14	1.17
2	CB-13	1353.74		1.15
3	CB-9	1346.95		1.14

Table 4. Theoretical Analysis Results of Specimens.

No.	Specimen	$P_{max}$ (kN)	${\mathrm{P}}_{Theory}$ (kN)	$P_{max}/P_{Theory}$
1	CB-21	1382.09	1182.14	1.17
2	CB-13	1353.74		1.15
3	CB-9	1346.95		1.14

3. Finite Element Analysis

3.1. General Information of the Analysis Model

In the analysis study, the widely used general-purpose nonlinear finite element analysis software ABAQUS was employed[15]. In this paper, a proposed analysis model for the composite beam was developed by referring to various concrete models currently available.

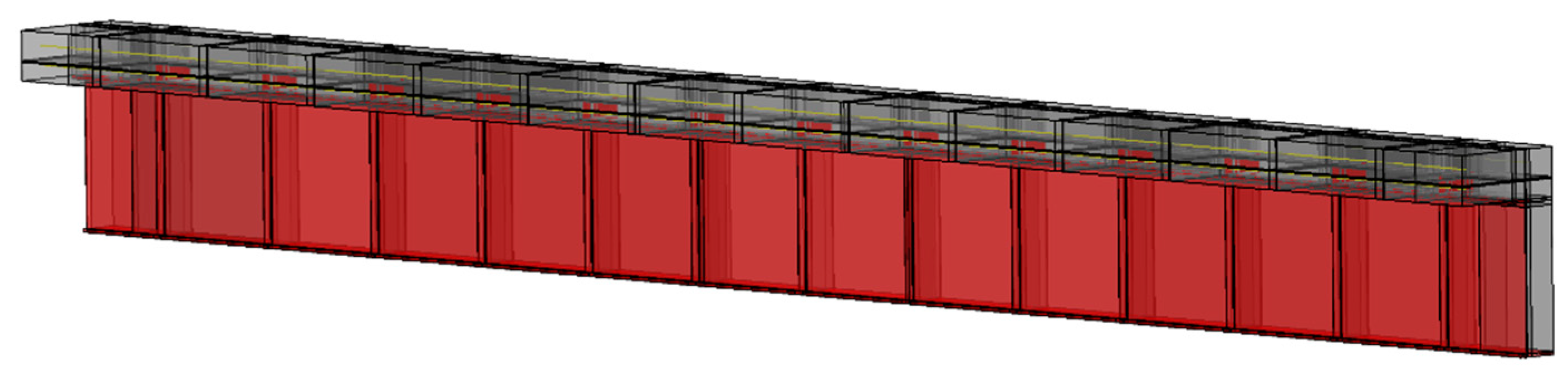
The concrete and steel elements were modeled using reduced integration solid elements (C3D8R) with eight nodal points. Due to the significantly increased analysis speed of concrete, reduced integration elements were used to accelerate the analysis process. The analysis model was created by modeling only half of the composite beam since its shape is symmetric, as shown in Figure 6. The boundary conditions were set to match the actual experiment, and the mesh size was set to 50 throughout the model, except in areas with the shear connectors, where it was set to 10. General contact elements were utilized for contact analysis, and all contact surfaces within the specimen were defined. The contact behavior was defined such that normal direction contact used the Hard Contact feature to prevent penetration under compression and allow separation under tension. The tangential direction contact was defined using the Penalty feature to provide resistance against friction. The friction coefficient between steel and concrete was set to 0.65 for the analysis [16].

For the reinforcement embedded in the concrete, truss elements were used for modeling, and the Embedded Element feature was utilized to integrate them with the concrete behavior.

Finite element analysis can be broadly classified into implicit and explicit methods. Generally, the implicit method involves iterative calculations at each step, resulting in higher accuracy of the solution. However, it is time-consuming and less suitable for analyzing the present study's results due to its lower convergence rate. Therefore, in this research, the explicit method, which has a higher convergence rate, was employed for the analysis.

3.2. Concrete Analysis Model

The stress-strain behavior of concrete, encompassing both tension and compression, was represented using the Concrete Damaged Plasticity feature, which allows for the depiction of stress reduction after reaching the maximum stress. The input values used for this feature are presented in Table 4[17,18].

Table 4. Material properties of concrete.

Concrete Compressive Behavior		Concrete Compression Damage
Yield Stress (MPa)	Inelastic Strain	Damage Parameter	Inelastic Strain
9.59	0	0	0
10.50	4.97E-05	0	4.97E-05
13.86	2.50E-04	0	2.50E-04
16.74	4.50E-04	0	4.50E-04
19.14	6.50E-04	0	6.50E-04
21.06	8.50E-04	0	8.50E-04
22.50	1.05E-03	0	1.05E-03
23.46	1.25E-03	0	1.25E-03
23.94	1.45E-03	0	1.45E-03
24.00	1.55E-03	0	1.55E-03
20.40	3.35E-03	0.2	3.35E-03
Concrete Tensile Behavior		Concrete Tension Damage
Yield Stress (MPa)	Cracking strain	Damage Parameter	Cracking strain
2.4	0	0	0
0.05	9.38E-04	0.97916667	9.38E-04

Table 4. Material properties of concrete.

Concrete Compressive Behavior		Concrete Compression Damage
Yield Stress (MPa)	Inelastic Strain	Damage Parameter	Inelastic Strain
9.59	0	0	0
10.50	4.97E-05	0	4.97E-05
13.86	2.50E-04	0	2.50E-04
16.74	4.50E-04	0	4.50E-04
19.14	6.50E-04	0	6.50E-04
21.06	8.50E-04	0	8.50E-04
22.50	1.05E-03	0	1.05E-03
23.46	1.25E-03	0	1.25E-03
23.94	1.45E-03	0	1.45E-03
24.00	1.55E-03	0	1.55E-03
20.40	3.35E-03	0.2	3.35E-03
Concrete Tensile Behavior		Concrete Tension Damage
Yield Stress (MPa)	Cracking strain	Damage Parameter	Cracking strain
2.4	0	0	0
0.05	9.38E-04	0.97916667	9.38E-04

The Damage Parameter in concrete represents the coefficient that converts the elastic modulus of concrete when there is a decrease in strength after the elastic range. The calculation was carried out based on the abbreviated stress-strain behavior recommended by ABAQUS. The elastic modulus of concrete($E_c$) was calculated using the equation (6) provided by ACI 318, and a Poisson's ratio of 0.2 was used for concrete[19].

$$E_c=4700\sqrt{f_{ck}}$$

(6)

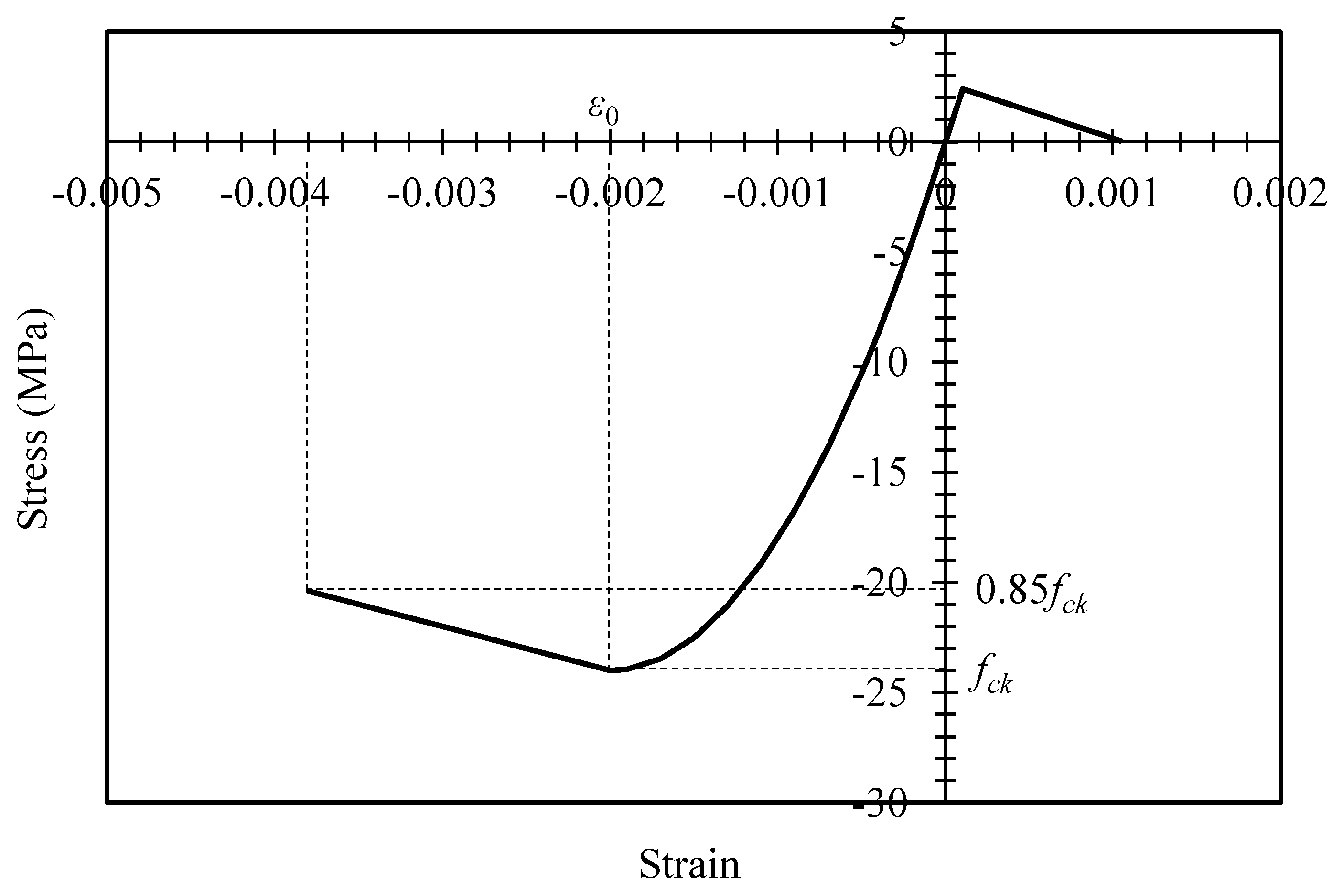
The stress-strain relationship of concrete was modeled using the formulation proposed by Hognestad, as shown in Figure 7. Although various concrete models accounting for strength degradation have been presented, the Hognestad model was selected for its computational speed and convergence characteristics[20,21]. The equations for the Hognestad model are given as follows: (7) and (8)[21].

$$f_c=f_{ck}\left[\frac{2{\epsilon }_c}{{\epsilon }_0}-{\left(\frac{{\epsilon }_c}{{\epsilon }_0}\right)}^2\right]\mathrm{for}{\epsilon }_0\le {\epsilon }_c\le 0$$

(7)

$$f_c=f_{ck}\left[1-0.15\frac{{\epsilon }_c-{\epsilon }_0}{{\epsilon }_{cu}-{\epsilon }_0}\right]\mathrm{for}{\epsilon }_{cu}\le {\epsilon }_c\le {\epsilon }_0$$

(8)

Here, $f_c$ is the stress in concrete, ${\epsilon }_c$ is the strain in concrete, $f_{ck}$ is the compressive strength of concrete, ${\epsilon }_{cu}$ is the ultimate compressive strain of concrete, and ${\epsilon }_0$ is the strain at maximum stress $f_{ck}$. In this analysis, ${\epsilon }_0$ is chosen as 0.002.

In the analysis of concrete beams, tension behavior of concrete has minimal influence. However, ABAQUS requires a tension softening curve for concrete. Therefore, a linear tension behavior was assumed for concrete. The tensile strength of concrete$(f_t)$ was taken as $f_t=0.1f_{ck}$, and the ultimate tensile strain$({\epsilon }_{tu})$ was selected as ${\epsilon }_{tu}=10f_t/E_c$.

In addition, the characteristic and damage variables for concrete compression and tension were generally set to the default values provided by ABAQUS. The dilation angle, which defines the post-peak behavior, was input as 38. The eccentricity, which is a measure of the ratio between compressive and tensile strengths of concrete, was set to 0.1.

The ratio of biaxial compression strength to uniaxial compression strength (ratio) can be calculated based on experimental results. However, in this study, the default value of 1.16 provided by ABAQUS was used. The parameter controls the yield surface of the concrete plasticity model and is known to have a value distribution based on previous research. In this study, the default value of 2/3 provided by ABAQUS was used[15].

The viscosity parameter can be adjusted to improve the convergence of the analysis by modifying the viscosity. However, in this analysis, the convergence was not significantly affected, so a value of 0 was used.

3.3. Steel part analysis model

For the steel component, the stress-strain curve determined from material testing needs to be converted from nominal stress-strain to true stress-strain before inputting into ABAQUS. The following equation was used to perform the conversion, and the resulting values were inputted into ABAQUS[15].

$${\sigma }_{true}={\sigma }_{nom}\left(1+{\epsilon }_{nom}\right)$$

(9)

$${\epsilon }_{ln}^{pl}=\ln \left(1+{\epsilon }_{nom}\right)-\raisebox{1ex}{${\sigma }_{true}$}\!\left/ \!\raisebox{-1ex}{$E$}\right.$$

(10)

Here, ${\sigma }_{true}$ is the true stress, ${\sigma }_{nom}$ is the nominal stress, ${\epsilon }_{nom}$is the nominal strain, ${\epsilon }_{ln}^{pl}$ is the true plastic strain, and $E$ is the elastic modulus.

3.4. Verification and Parameter Analysis of the Analysis Model

Table 5 summarizes the analysis model, where the variables are represented by the number of shear connectors. The initial analysis and verification were conducted on the existing specimens CB-21, 13, and 9. The validated analysis method was then used to analyze the models with varying numbers of shear connectors. Additionally, in order to evaluate the strength in the absence of shear connectors, the analysis was also performed on models with zero shear connectors.

Table 5. Summary of variable analysis.

No.	Specimen	Spacing between stud (mm)	Number of studs (EA)
1	CB-21	400	21
2	CB-13	600	13
3	CB-9	1000	9
4	CB-7	1300	7
5	CB-5	1950	5
6	CB-3	3900	3
7	CB-0	-	0

Table 5. Summary of variable analysis.

No.	Specimen	Spacing between stud (mm)	Number of studs (EA)
1	CB-21	400	21
2	CB-13	600	13
3	CB-9	1000	9
4	CB-7	1300	7
5	CB-5	1950	5
6	CB-3	3900	3
7	CB-0	-	0

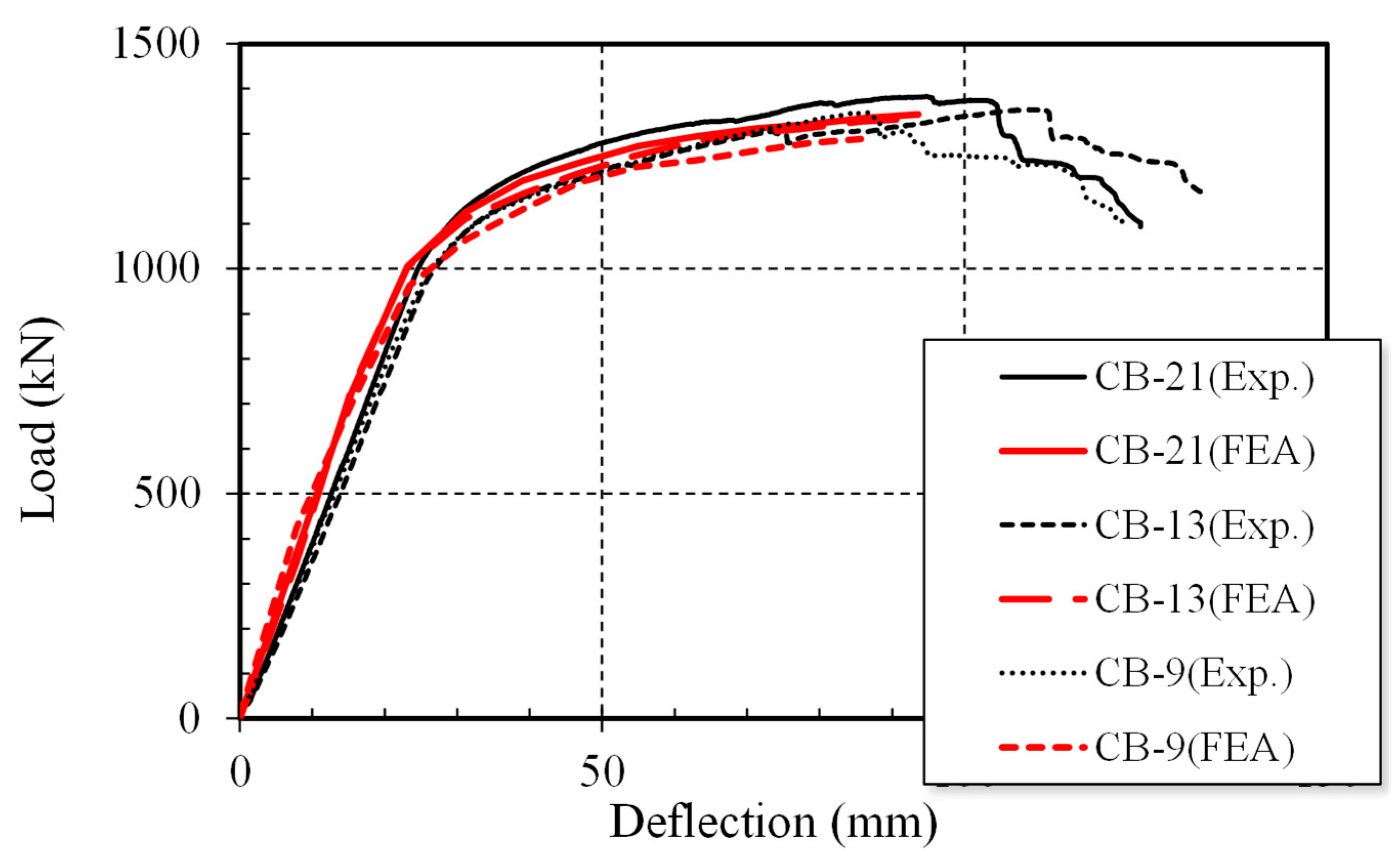
Figure 8 illustrates the results of the analysis for the existing test specimens. The analysis was terminated at the point where overall concrete crushing occurred in the girder section. In the actual experimental results, due to the non-uniformity of concrete strength, there was almost no significant difference in strength according to the spacing of shear connectors. However, the computational analysis represented a uniform concrete strength, resulting in a slight decrease in strength as the spacing of shear connectors increased. The difference in maximum strength and ductility between the experiment and analysis is believed to be due to the non-uniformity of concrete. Considering that the initial stiffness and the actual failure mode are similar between the experiment and analysis, the analysis model is considered reliable. 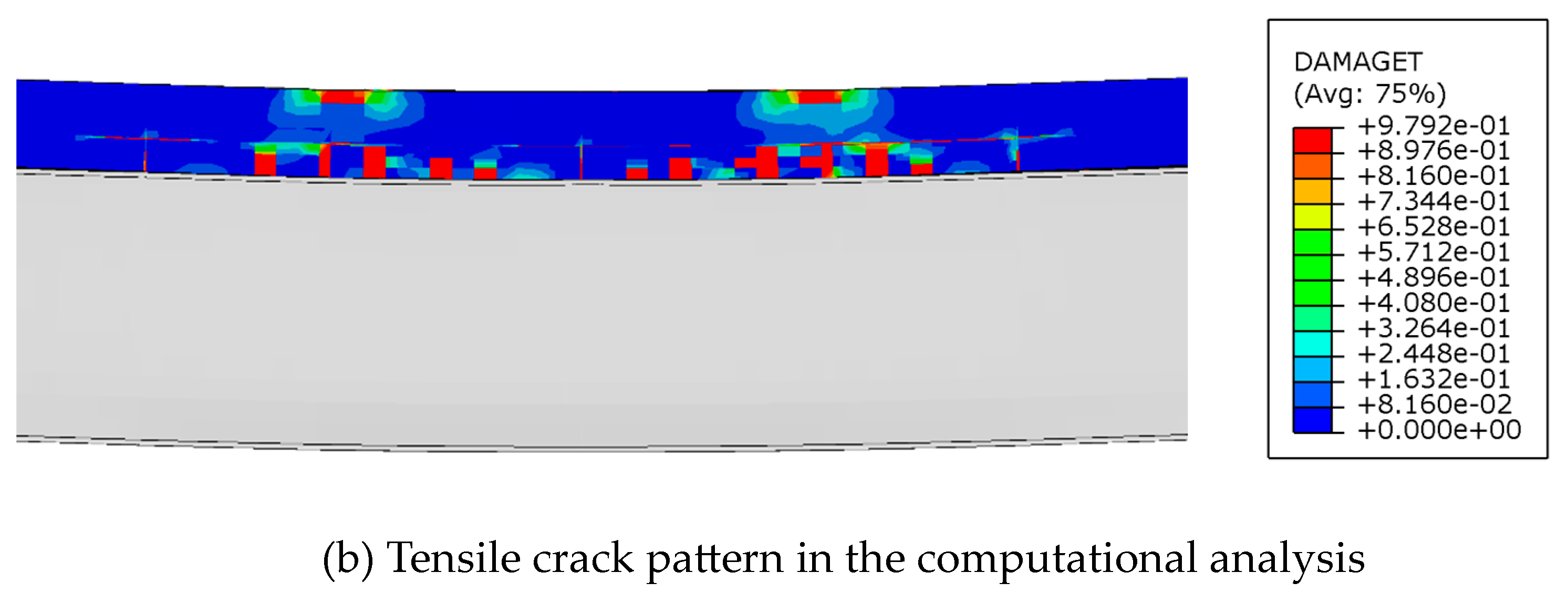Figure 9 compares the failure modes of the experiment and analysis, where Figure 10(b) represents the degree of tensile damage in concrete. A value close to 1 indicates the occurrence of tensile failure in concrete. In the actual test specimen, tensile cracks occurred in the lower part, and the computational analysis is deemed to be similar to the actual experiment.

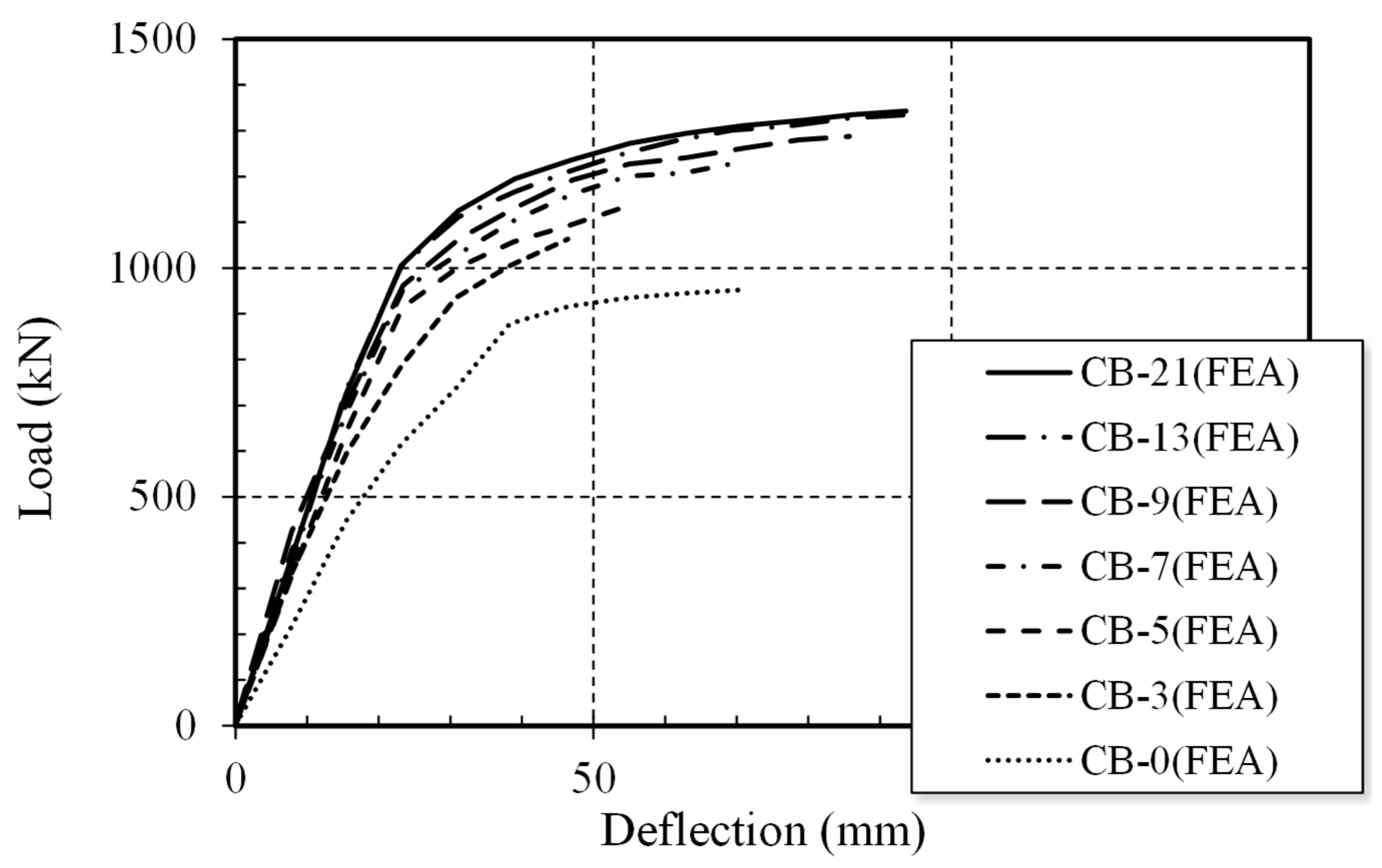
Figure 10 shows the load-displacement curves obtained from the variable analysis. It can be observed that as the number of shear connectors decreases, the maximum strength decreases. Up to 13 shear connectors, the behavior was similar to a composite action with a composite ratio of 100%. In the analysis results, no shear connector failure occurred, and the analysis was terminated based on concrete crushing. From 9 shear connectors or less, high stresses were observed in the shear connector region. Assuming a tensile strength of the weld material as 430 MPa, the analysis was terminated if the stress in the shear connector region exceeded this value.

In the actual experiments, even if concrete crushing occurred, the behavior of partial damage led to the ductile behavior of the composite beam. However, in the analysis, the strength reduction due to concrete crushing was not considered, resulting in no decrease in strength. Furthermore, in this study, the strength of the angle-type shear connectors was analyzed, and an analysis method based on this was proposed. Therefore, it was determined that the analysis method is reliable.

Table 6 compares the maximum strengths obtained from the experimental and analytical results. For the CB-21 specimen, the experimental strength was 1382.09 kN, and the analytical strength was 1359.28 kN. For the CB-13 specimen, the experimental strength was 1353.74 kN, and the analytical strength was 1335.49 kN. Lastly, for the CB-9 specimen, the experimental strength was 1346.95 kN, and the analytical strength was 1287.89 kN. The ratios between the experimental and analytical strengths were very close, with values of 1.02, 1.01, and 1.05, respectively.

Table 6. Results of analysis for existing specimens.

No.	Specimen	$P_{max}$ (kN)	$P_{FEA}$ (kN)	$P_{max}/P_{FEA}$
1	CB-21	1382.09	1359.28	1.02
2	CB-13	1353.74	1335.49	1.01
3	CB-9	1346.95	1287.89	1.05

Table 6. Results of analysis for existing specimens.

No.	Specimen	$P_{max}$ (kN)	$P_{FEA}$ (kN)	$P_{max}/P_{FEA}$
1	CB-21	1382.09	1359.28	1.02
2	CB-13	1353.74	1335.49	1.01
3	CB-9	1346.95	1287.89	1.05

Based on the previous finite element analysis results, it was observed that the capacity of the composite beam varies with the number of shear connectors. This allows us to infer the strength of the angle-type shear connectors used in this study. In order for the composite beam to achieve its maximum composite action, it should be able to transmit all the compressive forces in the concrete, requiring a strength of approximately 4080 kN. Based on the experimental and analytical results, it can be concluded that up to 13 shear connectors exhibited complete composite behavior. Therefore, the individual strength of each shear connector can be calculated as 313.85 kN. Using this information, the resistance of the composite beam can be calculated using the equation provided earlier.

Table 7 compares the finite element analysis results with the inferred values of the shear connectors presented earlier. The ratios between the analysis results and the theoretical calculations range from 1.13 to 1.20, showing a consistent distribution. The higher strength observed in the analysis results can be attributed to a conservative evaluation of the maximum strength during the analysis. When the number of shear connectors is 0, the flexural strength of the steel and the bending strength of the concrete were calculated separately and combined, resulting in a ratio of 1.37. The larger deviation compared to other theoretical values can be attributed to the presence of minor composite behavior due to the friction between the concrete and the steel even in the absence of shear connectors.

Table 7. Results of variable analysis.

No.	Specimen	$P_{FEA}$ (kN)	$P_{Thoery}$ (kN)	$P_{FEA}/P_{Theory}$
1	CB-21	1359.28	1182.14	1.15
2	CB-13	1335.49	1176.82	1.13
3	CB-9	1287.89	1100.12	1.17
4	CB-7	1231.49	1021.73	1.20
5	CB-5	1133.44	947.36	1.19
6	CB-3	1005.17	831.57	1.20
7	CB-0	952.81	706.25	1.37

Table 7. Results of variable analysis.

No.	Specimen	$P_{FEA}$ (kN)	$P_{Thoery}$ (kN)	$P_{FEA}/P_{Theory}$
1	CB-21	1359.28	1182.14	1.15
2	CB-13	1335.49	1176.82	1.13
3	CB-9	1287.89	1100.12	1.17
4	CB-7	1231.49	1021.73	1.20
5	CB-5	1133.44	947.36	1.19
6	CB-3	1005.17	831.57	1.20
7	CB-0	952.81	706.25	1.37

Based on the previous experimental results, numerical analysis, and finite element analysis, the behavior of the composite beam using angle-shaped shear connectors was evaluated. The comparison between the experimental results and numerical analysis provided confidence in the reliability of the numerical analysis, allowing for the inference of the strength of the angle-shaped shear connectors. This inference enabled theoretical calculations, and it is deemed that the strength of the composite beam can be calculated based on this, taking safety into consideration during the design process.

4. Conclusions

The aim of this paper was to evaluate the behavior of a filled composite beam using angle-shaped shear connectors and to propose a design method for such composite beams through numerical analysis. The results obtained from this study are summarized as follows:

1) The design equation for the angle-shaped shear connectors used in this study is not provided, so the design should be conducted based on a similar design equation for the "double-headed" shear connectors. When calculating the strength of the composite beam using the existing design equation, all cases showed complete composite behavior. However, the actual experimental results showed a decrease in strength. Based on this, it is concluded that the existing design equation is not suitable for determining the strength of angle-shaped shear connectors.

2) In order to investigate the influence of the spacing of angle-shaped shear connectors in the composite beam, a numerical analysis was conducted. The experimental results and the numerical analysis results were compared for the validation of the numerical analysis model, and a high reliability was observed with a strength ratio of 1.03. Furthermore, a variable analysis was performed based on the spacing of the shear connectors, and it was confirmed that the strength decreased as the spacing increased.

3) Based on the experimental results and the numerical analysis, it was inferred to the strength of the angle-shaped shear connectors, which was estimated to be approximately 313.85 kN. With this information, it is possible to theoretically calculate the flexural strength of the composite beam and this type of composite beam can be designed.

4) Through the analysis of the composite beam without shear connectors, it was observed that even without shear connectors, the composite beam exhibits composite behavior due to friction. Therefore, it can be concluded that when designing a composite beam using shear connectors, consideration of this frictional composite behavior can potentially lead to a reduction in the number of shear connectors.