Prerpints.org logo
Preprint
Article

An Improved Human-Inspired Algorithm for Distribution Network Stochastic Reconfiguration Considering Multi-Objective Intelligent Framework and Unscented Transformation

Altmetrics

Downloads

140

Views

34

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

26 July 2023

Posted:

28 July 2023

You are already at the latest version

Alerts
Abstract
In this paper, stochastic multi-objective intelligent framework (MOIF) is performed for distribution network reconfiguration to minimize power losses, the number of voltage sags, the system's average RMS fluctuation, the average system interruption frequency (ASIFI), the momentary average interruption frequency (MAIFI), and the system average interruption frequency (SAIFI) considering the network uncertainty. The unscented transformation (UT) approach is applied to model the demand uncertainty due to simplicity to implement and no presumptions to simplify. A human-inspired intelligent method named improved mountaineering team-based optimization (IMTBO) is applied to determine the decision variables defined as the network's optimal configuration. The conventional MTBO is improved using a quasi-opposition-based learning strategy to overcome premature convergence and achieve the optimal solution. The simulation results showed that in single- and double-objective optimization, some objectives are weakened compared to their base value, while the results of the MOIF indicated a fair compromise between different objectives, and all objectives are improved. The results of MOIF based on the IMTBO cleared that the losses are reduced by 30.94%, the voltage sag numbers and average RMS fluctuation are reduced by 33.68% and 33.65%, and also ASIFI, MAIFI, and SAIFI are improved by 6.80%, 44.61%, and 0.73%, respectively. Also, the superior capability of the MOIF based on the IMTBO is proved compared to the conventional MTBO, particle swarm optimization, and artificial electric field algorithm. Moreover, the results of the stochastic MOIF based on the UT showed the power loss increased by 7.62%, voltage sag, and SARFI increased by 5.39% and 5.31%, and ASIFI, MAIFI, and SAIFI weakened by 2.28%, 6.61%, and 1.48%, respectively compared to the deterministic MOIF model.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

1.1. Motivation

Primarily, the distribution system is responsible for ensuring optimal electricity supply and normal consumer consumption. There are significant losses in distribution networks. To reduce losses and improve the characteristics of the distribution network, conventional techniques [1,2] such as capacitors, distributed generation sources (DG), D-FACT tools, and other costly and equipment-intensive techniques have been employed. Reconfiguration is one of the most effective strategies for minimizing distribution line losses. Network reconfiguration is the process of modifying the structure of a network using section switches and connecting lines to minimize power losses and sustain production-consumption equilibrium [4-5]. Regarding power quality and reliability, two additional significant aspects of distribution networks include power quality and reliability. A modern power network should be designed to supply consumers with a sufficient amount of electrical energy that is highly reliable. Voltage declines and other fundamental power quality fluctuations can cause significant economic losses by interfering with power electronic control devices. The electricity supplied to consumers must therefore be of sufficient quality and dependability. Power factor refers to how much the quantity of electricity supplied affects the performance of subscribers' equipment [6-7]. Reliability is the ability of a system to perform its required operations under specified conditions and within a specified timeframe. Therefore, distribution system operation [6-7] is predominantly concerned with improving reliability and electricity quality. As a crucial aspect of network operation, distribution network reconfiguration has a significant impact on enhancing reliability and power quality.

1.2. Literature review and research gap

Numerous studies have been conducted on the subject of distribution network reconfiguration. Numerous solutions revolving around the reconfiguration of distribution networks have been implemented in [8] to eliminate voltage dips and increase network reliability. In [9], a strategy for feeder reconfiguration is used to reduce the propagation of voltage sag in distribution networks. Recently, Genetic Algorithm (GA) [10] has been utilized to minimize losses by implementing encryption, resolving the reconfiguration problem, and determining the new network architecture. In [11], the distributed synchronous static compensator (DSTATCOM) is reconfigured and optimally allocated using a differential evolutionary algorithm in order to reduce power losses and improve the voltage profile in energy distribution networks. In [12], a reconfiguration is made to improve power quality, voltage stability, and system load by reconfiguring the network. Using the genetic algorithm (GA), the distribution network is reconfigured in [13] to minimize energy losses. A golden flower pollination algorithm is utilized in [14] to configure the distribution network so as to minimize power losses. In [15], the branch exchange heuristics are revisited, and a method integrating them with other techniques, such as evolutionary meta-heuristics and cluster analysis, is introduced. Using the genetic algorithm, [16] presents an optimal method for optimizing network reconfiguration problems in a power distribution system in order to increase reliability and decrease power losses. In [17] is presented a novel method for reconfiguring power infrastructures using graph theory after an extreme event, as well as the least expensive solution for connecting all utility consumers using a minimum spanning tree with a radial topology. A defect recovery reconfiguration strategy for DC distribution networks based on a hybrid particle swarm optimizer is presented in [18]. Using teaching-learning-based optimization, [19] proposes a method for effectively restoring service by adjusting the network architecture configuration with optimal tie-switch and section-switch configurations. In [20], a single-optimization technique is used to configure the network in order to minimize voltage losses at each load point, and the quantum-binary firefly algorithm is used to determine the optimal solution. In [21], the optimal distribution network topology is determined using a spanning tree generation algorithm, a matrix of adjacency or fundamental cycle information, and a genetic algorithm. [22] presents an enhanced balancing optimization algorithm and a reuse technique for restructuring power distribution networks with optimal distribution of distributed generators. Incorporated into the recycling strategy is the iterative exploration of the solution space. A novel mathematical optimization strategy for network reconfiguration involving the insertion of soft open points is presented in [23]. In addition, a new soft open point placement allocation index is developed in order to reduce the computational burden imposed by optimization approaches while maintaining control over discrete allocation factors. Using the salp swarm optimization algorithm, [24] presents a novel reconfiguration strategy for radial distribution networks to reduce the cost of power loss and increase reliability. [25] presents a reconfiguration strategy for optimizing network design and spatial margin pricing for DG-connected buses. To ascertain the optimal network configuration while minimizing power losses, pyrotechnics is combined with a game-based, iterative strategy. A method for distribution network reconfiguration is presented in [26] that employs a comprehensive examination of operating scenarios to determine the reconfiguration solution with the highest efficiency over a long-term operation period. A new algorithm based on the coyote algorithm is used in [27] to manage the problem of network reconfiguration and positioning of distributed productions in order to reduce energy losses. In terms of minimizing voltage instability and power imbalance, [28] establishes the optimal distribution network design. The paper [29] proposes a load flow model for configuring distribution networks to provide the optimal starting point and convergence path for search algorithms. It is demonstrated that the optimal universal flow arrangement is unique and optimal. By reconfiguring the distribution network using an enhanced binary cuckoo search algorithm, [30] provides a method for reducing power losses in the distribution network.
- The review of the literature has shown that the operation of the distribution network is based on the optimization of the network configuration with various goals, including the minimization of losses and voltage deviations, as well as the improvement of reliability and power quality in various studies, but the investigation of these goals is scattered and single or double-objective. And it has not been evaluated as a comprehensive objective function.
- From the literature evaluations, it is clear that the lack of a multi-objective optimization structure consisting of various objectives of minimizing power losses, improving reliability indicators and also improving distribution network power quality indicators in solving the reconfiguration problem to achieve the optimal network configuration by creating a compromise between different goals are felt.
- In the previous studies, the reconfiguration of distribution networks has been done using various intelligent optimization methods to determine the optimal configuration of the network. Considering that an optimization method is not able to have a successful performance in all different problems with different objective functions structure, thus presenting an intelligent optimization method with the ability to robust premature convergence to determine the optimal configuration of the network and achieve the best goals.
- Moreover, one of the challenges facing the reconfiguration problem in the distribution network is the uncertainty of the network load, and evaluating its effect on decision-making of the network operators which is not addressed well in the literature integrated with power quality and reliability objectives.

1.3. Contributions

In this research, the distribution network is reconfigured stochastically using a multi-objective intelligent framework (MOIF) to minimize power losses, and improve power quality and reliability indices considering the network load uncertainty using an unscented transformation (UT) [31]. The UT against the monte carlo simulation (MCS) which is very time consuming, has low calculation time and no presumptions to simplify the model. Two power quality indicators are the decline in voltage sags and the system's average RMS fluctuation frequency. The average system interruption frequency index, the instantaneous average interruption frequency index, and the system average interruption frequency index are reliability indices. The number of open network switches is determined by a new improved mountaineering team-based optimization (IMTBO) algorithm and the conventional MTBO [32] is improved based on a quasi-opposition-based learning strategy [33] to avoid premature convergence. A 33-bus electrical distribution network is used to implement the proposed MOIF. Also, the effectiveness of the proposed MOIF has been examined on each of the objectives. To validate the IMTBO, it has been compared to conventional MTBO, particle swarm optimization, and artificial electric field algorithm [34] in solving the reconfiguration problem based on the MOIF. Moreover, the deterministic and stochastic MOIF results are compared to evaluate the effect of the uncertainty consideration to solve the reconfiguration problem.

1.3. Paper structure

In the second section of the study, the constraints for the multi-objective function and reconfiguration problem are discussed. Section 3 explains the proposed meta-heuristic strategy and implementation method for solving the optimization problem. Section 4 describes the outcomes of the suggested procedure, whereas Section 5 summarizes the findings of the study.

2. Problem Statement

In this study, the MOIF is outlined for reconfiguration of the distribution network with an emphasis on decreasing electrical losses, improving power quality, and increasing reliability metrics.

2.1. Objective function

Identification of the ideal network configuration, which is offered in this research with the MOIF with reducing power losses, increasing power quality, and improving reliability indicators, is the goal of distribution network optimization based on reconfiguration. In this research, subscribers are given access to power quality indicators [35,36,37] such as the frequency of the system's average RMS fluctuation and the number of voltage sags ( N s a g ) throughout the assessment period (SARFI). Reliability indices can go by the names Average System Interrupt Frequency Index (ASIFI), Momentary Average Interrupt Frequency Index (MAIFI), and System Average Interrupt Frequency Index (SAIFI). The MOIF based on the weighted coefficients is formulated by
O F = ϑ 1 × P L o s s P L o s s , m a x + ϑ 2 × N s a g N s a g , m a x + ϑ 3 × S A R F I S A R F I m a x + ϑ 4 × A S I F I A S I F I m a x + ϑ 5 × M A I F I M A I F I m a x + ϑ 6 × S A I F I S A I F I m a x
Where, P L o s s , m a x is maximum value of network power losses, N s a g , m a x indicates the maximum number of voltage sags, S A R F I m a x is maximum system average RMS variation frequency, A S I F I m a x ,   M A I F I m a x and S A I F I m a x are maximum value of ASIFI, MAIFI and SAIFI indices. The maximum values mentioned are obtained from network load distribution in non- reconfiguration mode. Also, the set of absolute values of all weight coefficients ( ϑ 1 ,   ϑ 2 ,   ϑ 3 ,   ϑ 4 ,   ϑ 5 ,   a n d   ϑ 6 ) must be equal to 1.
The active power loss ( P L ) of the entire network is defined based on the total loss of all network lines as follows [35-37]:
P L o s s = ∑ i = 1 N b r a n c h R E S i × C U R i 2
Where, R E S i , ، C U R i and N b r a n c h are the resistance, the current passing through the i-th line and the total number of network lines, respectively.
N s a g stands for the total number of subscribers affected throughout the assessment period by all potential mistakes. Monitoring the network's stated bus voltage (Ei) and determining the kind and location of the bus load allow one to calculate N s a g . The location of the defect in a system determines the propagation of voltage dips, and the severity of voltage dips on buses located far from faults. Through fault evaluation, the sag-subjected region at each fault site is able to be found. Nevertheless, recognizing the system element which leads to significant voltage drops spreading throughout a failure is essential for improving power quality and reliability and determining the likelihood of a defect occurring. Voltage reductions are principally brought on by frequent line faults. Thus, fault analysis can identify the system lines responsible for significant slope exposure. If the faulted line fault rate with length L L is μ , then the determined annual quantity of line failures ( ∂ ) is defined by [4, 35]
∂ = ∑ i = 1 N b r a n c h L L i × μ i
N s a g and the total amount of disruptions ( γ ) can be calculated by observing the magnitude of the system's particular bus voltages (Ei) and distinguishing the kind and position of load bus i. According to [35,36,37], the yearly N s a g is as follows [4, 20, 35]:
N s a g = ∑ i = 1 N b u s ∑ ∂ = 1 ∂ t o t a l 1       i f   0.1   p . u < E i < 0.9   p . u 0                                                           O t h e r w i s e
The N s a g that corresponds to sensitive buses is equal to the overall number of continuous interruptions, as the majority of processes involving sensitive equipment experience lengthy interruptions. For non-sensitive loads, the overall number of disruptions annually can be calculated using the following formula [4, 35]:
γ = ∑ i = 1 N b u s ∑ ∂ = 1 ∂ t o t a l 1         i f   E i ≤ 0.1   p . u 0                     O t h e r w i s e
The disruptions emphasized in Eq. (5) may be further subdivided into kept going distractions if the insensitive demand bus is the faulty bus or if it is located downward of the failure, as every one of the other buses is separated while the circuit breaker is opened to eliminate the error. The fault will be eliminated by the safety mechanism once the service is restored, so these outages can be categorized as temporary or transient. Using Eqs. (4)-(5), the aforementioned disruption classifications can be utilized to determine the SARFI annually along with reliability metrics.
The SARFI of the entire network can be determined using the estimated total number of voltage sags, N s a g , caused by faults. The SARFI index is presented as follows [35-37].
S A R F I = N s a g T N C S
Where, TNCS refers to the total number of customers supplied.
The SARFI sags number could be converted into ongoing disruptions, temporary disruptions, and demand disruptions that impact the system's accessibility. Other objective functions related to loading reliability indicators, ie, ASIFI, MAIFI, and SAIFI, respectively; represent indicators related to loading, stable interruptions, and short-term. ASIFI can represent financial losses related to load interruptions, whereas MAIFI is used to indicate subscriber interruptions caused by protection operations. SAIFI can be used to represent the common stable interval. The defined indicators are presented below [20, 35-37].
A S I F I = T Q L I T Q L S
M A I F I = C S T I T N C S
S A I F I = T C C I T N C S
Where, TQLI and TQLS are interrupted and served total connected kVA demand, CSTI is the number of customer short-term interruptions number in total, while TCCI is the total of customer long-term interruptions number caused by each occurrence.

2.2. Constraints

During the optimization process, the problem's objective function should be optimized within certain constraints. The following list of restrictions is provided [35-38].

2.2.1. Power flow

P i = ∑ i = 1 N b u s E i E j Y i j cos ⁡ θ i j − δ i + δ j
Q i = ∑ i = 1 N b u s E i E j Y i j sin ⁡ θ i j − δ i + δ j
In solving the optimization problem, load distribution equations must be established in any situation. P i and δ i are respectively the active and reactive power injected from the network to the bus, E i and δi are the range and angle of the ith bus voltage, respectively, and Y i j and θ i j are the range and admittance angle between the ith and jth nodes of the network, respectively.

2.2.2. Voltage

When addressing the optimization problem, the voltage of the network buses should not exceed the minimum and maximum values permitted.
E m i n ≤ E i ≤ E m a x
Where, E m i n and E m a x are respectively the lowest and highest values of the accepted voltage range for network buses.

2.2.3. Current

The current flowing through the network lines shall not exceed the maximum allowed value and stay within the thermal range of the lines.
C U R f , i ≤ C U R f , i m a x
Where, ، C U R f , i is the current passing through the ith line of the network and C U R f , i m a x   is the maximum allowed current passing through the line

2.2.4. Radiality condition

Each bus in the radial network must take a single route to the main feeder since there are no loops in its configuration. The network branch matrix is created for this purpose. A matrix with the same number of rows, network lines, and columns as network buses is known as a network branch matrix. As a consequence, we will obtain [36-35] for each grid line that lines between two buses i and j.
I n c ( b r i j ) = 1                               n b u s = i − 1                     n b u s = j 0                                               e l s e
After forming the above matrix, if its determinant is zero, the network is radial and otherwise, the matrix is non-radial. In this situation, if the condition of radiality of the network is not respected, a fine or penalty is considered in the value of the objective function, which is thus removed from the competition.

3. Proposed Optimizer

In this research, the MOIF for reconfiguration of the distribution network has been implemented using a new intelligent improved mountaineering team based optimization (IMTBO) and in this section, its formulation and also the implementation method for solving the reconfiguration problem are explained.

3.1. Overview of the MTBO

3.1.1. Inspiration

The primary inspiration for the MTBO algorithm is the team's methodical and coordinated ascent of a mountain, taking into account the possibility of natural calamities, as outlined in the stages provided below.

3.1.2. First phase: coordinated mountaineering

The most seasoned member of a climbing team is always chosen to be the leader and stand in front of the group, which is analogous to the best outcome in the most recent iteration of the algorithm in optimization science. The best member of the algorithm population, or alternatively, the climbing group, fills this job. To climb the mountain peak or, alternatively, to find the finest overall solution, this person guides the best or the complete group toward the aim or objective. Members approach the group leader in the manner described below [32]:
X i new = X i + r a n d × X L e a d e r − X i
In a climbing team, each member is directed by both the group leader and the person in front of them as the movement is planned under the supervision of the group leader. The members are normally grouped from best to worst. to be The population is thought to be ranked from best to worst after each iteration of the MTBO algorithm, and each person is directed by the group leader and the opposing person. Consequently, the following adjustments are made to the equation of normal motion up the mountain peak [32]:
X i new = X i + r a n d × X L e a d e r − X i + r a n d × X i i − X i
In contrast, in the realm of optimization, every action occurs at random, and the phase probability is considered to be equal to Li; so, the pseudo-code of this phase is presented by [32]
i f r a n d < L i X i new = X i + r a n d × X L e a d e r − X i + r a n d × X i i − X i e n d

3.1.3. Second phase: natural catastrophes' impact

Natural calamities often put mountaineers' lives in peril and may keep them from reaching the summit, or, to put it another way, imprison the people in tiny but impending peaks [32]. The frequency of avalanches and cliff fall is the most important factor in the MTBO algorithm. The majority of the MTBO optimization process is based on avalanches, which are a kind of natural catastrophe. The beginning of an avalanche at this point is thus more probable than it would be under other circumstances. Because of this, the critical state in the event of a randomly occurring avalanche in MTBO is seen as being similar to the worst case of the algorithm XWorst or, alternatively, XAvalanche. In the case of an avalanche and other catastrophes, the subject tries to flee the disaster scenario XWorst or equivalently XAvalanche and rescue himself utilizing the inspired equation below. To put it another way, one is freed from being constrained by a local optimum solution and is able to move toward the global optimization of the ideal solution [32].
X i new = X i − r a n d × X Avalanche − X i
It is assumed that the probability of an avalanche occurring is equal to Ai, and the pseudocode for this phase is as follows [32]:
i f r a n d < A i X i new = X i − r a n d × X Avalanche − X i e n d

3.1.4. Third phase: concerted action by many people to prevent catastrophes

Human groups are fundamentally different from other phenomena and creatures in that they cooperate and lead one another in a highly deliberate, planned, and effective way. This kind of interpersonal and teamwork is crucial in a climbing team. Therefore, in a climbing team, in the event of an emergency or someone being trapped, the whole team makes an effort to free the trapped person. Therefore, MTBO draws its inspiration from the group's coordinated and social effort and cooperation to free the imprisoned member, whereby each member's position is equaled to the average position, or Xmean or XTeam. One is toward the Xmean or XTeam position. The following model [32] serves as a representation for this behavior:
X i new = X i + r a n d × X Team − X i
The pseudo code for this phase is as follows [32]: The chance of rescuing a person caught in an avalanche or stuck in the best local solution is equal to Mi.
i f r a n d < M i X i new = X i + r a n d × X Team − X i e n d

3.1.5. Fourth phase: potential members' demise

However, it is well known that sometimes an avalanche's strength results in the death of a member of a climbing team. It is thus probable that the climbers will die in the disaster and that none of the aforementioned precautions will be able to rescue them. The member in question is eliminated from the group at this stage of the MTBO process, and the following equation [32] is used to randomly add a new member to the group:
X i new = X X max − X m i n ( ) m i n
Figure 1 displays the general pseudocode of the MTBO's optimization procedure.

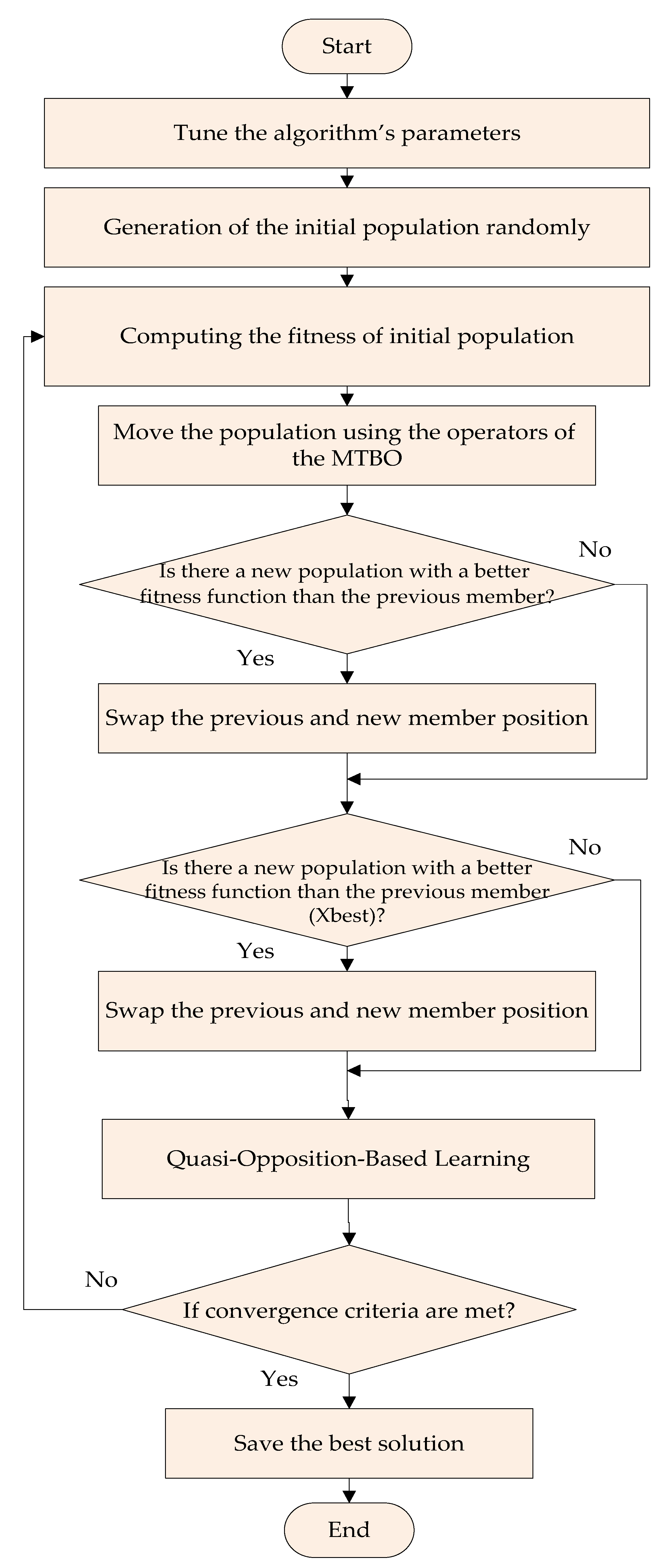
3.2. Overview of the improved MTBO (IMTBO)

Using quasi-opposition-based learning (QOBL) [33], a observing status is stated and evaluated at each iteration in order to avoid the suggested approach from becoming locked in local optimal solutions. There are subsequent stages involved. First, a distance constant is established between the mean and the optimal solution [33]:
φ = ∑ j = 1 n ( X ave , j − X best , j ) 2
The minimal value of the distance under the constant criterion is then determined [33]:
φ m i n = 15 10 ( I t e r / I t e r m a x )
Subsequently, the monitoring condition is evaluated. If D c < D cmin, QOBL is used to expand the variety of the population and increase the convergence range of the algorithm. A portion of the evaluation points are selected at random, and based on this, the opposite evaluation points are produced, as well as evaluated concurrently. The fitness level of the original test points and the quasi-opposite test points are then computed and ranked ascendingly, and the initial NP solutions for the descending leadership motion and the trending leadership motion are selected. To preserve the stochastic nature of IMTBO, a quasi-opposite answer is randomly generated from the center of the search space ( X C S ) and the mirrored position of every point of the test ( X M P ):
X i , j q = X C S + r a n d ( ) × X M P − X C S ,             i f   X M P > X C S , X M P + r a n d ( ) × X C S − X M P ,             O t h e r w i s e i = 1,2 , … ,   N q
X C S = X m a x + X m a x 2
X M P = X m a x + X m a x − X i , j
Where, Nq is the total amount of randomly selected test points for the generation of opposite test points, which in this study has been configured to 5.
Figure 2 depicts the flowchart of the IMTBO in the optimization process.

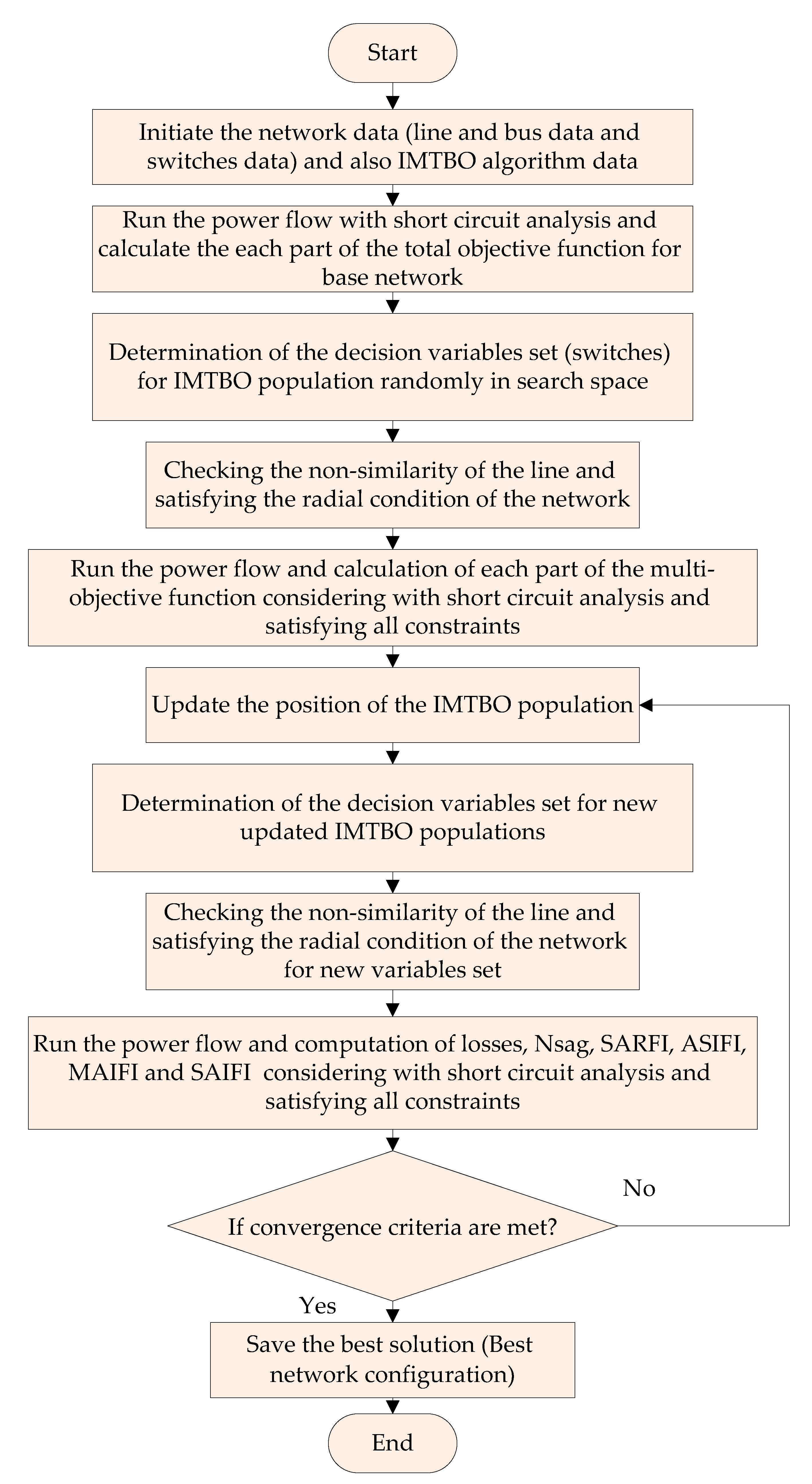
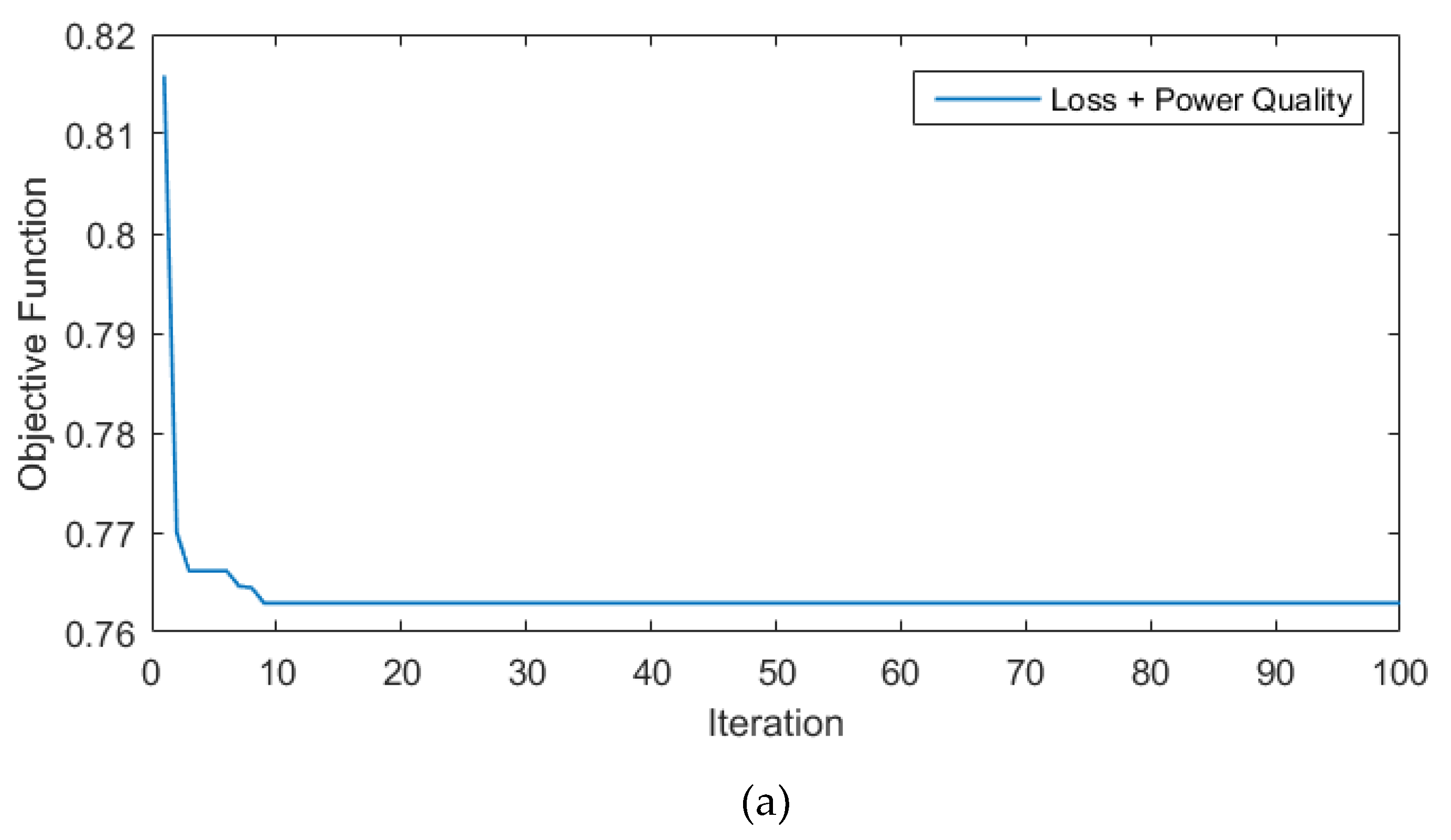
3.3. Implementation of the IMTBO

The reconfiguration of the distribution network may be completed by modifying the preset state of the tie lines, depending on the defined goal functions and constraints. For each modification to a network's design, the N s a g , SARFI, ASIFI, MAIFI, SAIFI, and P L o s s indices are computed in Matlab using a short-circuit evaluation and the stable-state power flow method. The network reconfiguration modifies the distribution feeders' structural organization by modifying ties and sectioning switches' open/closed status. By actuating a switch that connects the two feeders, a feeder can be partially or completely met by an alternative feeder. To maintain radial structures, the sectionalizing switch must be deactivated. In distribution networks, network reconfiguration is frequently employed to minimize network losses, regulate demands, and increase voltage fluctuations. The reconfiguration is additionally feasible to mitigate voltage sag spreading in the system by increasing failure branch connection impedance. Whenever a fault occurs at certain system buses, the voltage on a few system buses may fluctuate. Consequently, the power quality and dependability of the system may be impacted by defects in the weak area. The primary objective of network reconfiguration is to reduce N s a g and reliability indices by isolating the vulnerable area from the primary power source. To avoid increasing system-wide line losses, network reconfiguration should be restricted. There must be a balance within the rise in branch losses and the enhancement of the power quality and dependability of the network. Therefore, optimization techniques are required to find an architecture that can achieve both a small number of voltage dips and a suitable quantity of power loss.
The implementation phases of IMTBO to solve the network reconfiguration problem are depicted in Figure 3. Shown here are the reconfiguration problem's implementation steps. Under typical conditions, the network is radial. The number of network lines should be one less than the total amount of network buses, as the network must be radial. Nevertheless, the network contains communication connections that are typically open and external to the circuit. Therefore, if you take into account the quantity of network buses n and the quantity of network lines m, you must always have m=n-1, which stands for the active lines of the distribution network. The number of network lines that must be removed from the circuit in order to maintain the network's radial state must be determined by the optimization method, and this number must be equal to the number of optimization variables. To preserve the network's radial requirements, 5 lines must be eliminated from the circuit in the typical 33-bus network, where there are 33 buses and a total of 37 lines. This will result in five optimization variables for the nvar optimization problem. After the candidate lines have been identified to be removed from the circuit by cutting them off, it is required to examine the distribution network's restrictions. Proposed lines for deletion must be two-by-two, and line numbers should not be duplicated. If this condition is not satisfied, the associated objective function will be severely penalized and eliminated from the optimization. After confirming the constraints of the radial network, the problem's objective functions were studied. After removing the load from the network with the revised distribution structure, the amount of power loss is then computed. In the following, the network voltage drop has been calculated so that the number of weak buses can be identified and N s a g may be calculated. Afterwards, criteria and indicators for network dependability will be calculated. After calculating the value of the objective function corresponding to each set of optimization variables, including open network switches, all sets of responses were ranked by the objective function values, from lowest to highest. If we have reached the maximum number of allowable repetitions of the problem, the search and optimization are halted; otherwise, the optimization continues.

4. Uncertainty Modeling based on the UT

In the problem outlined in Eqs. (1)–(23), uncertainties include the generation of photovoltaic and wind energy as well as the network demand. In this work, the unknown parameters are modeled using the UT technique [31]. The UT is capable of modeling uncertainty and decision-making hazards well. It was created with the idea that approximating a distribution of probabilities is simpler than approximating a consequence or transformation of an arbitrary nonlinear function [31]. The UT's fundamental idea is the approximation of the PDF by a collection of chosen points known as sigma points and corresponding weights [31]. A weighting of these sigma points will yield metrics on the mean, variance, and other aspects of mapping moments. Low sample size requirements and simplicity of use are benefits of the UT. The parameter n, which is assigned a value of three in this study, denotes the size of the input vector for uncertainty (U) in this method. Additionally, 2n+1 probabilities are generated. Computation time is significantly decreased because no scenario reduction strategy is used for this small set of possibilities. Y = f(x), where y ∈ R r is the uncertain output vector and includes r elements, and x ∈ R n is the uncertain input vector, denotes the problem with its uncertain, nonlinear, and stochastic nature. By μ x and σ x , the mean and covariance of x are displayed. The symmetric and asymmetric portions of x are used to determine the variance and covariance of uncertainty, respectively. The UT method's application tries to determine the outcomes' mean and covariance quantities, or μ y and σ y [62]. The items that follow the steps describe this [31]:
Step 1: Choose 2n+1 samples from the uncertain input data:
x 0 = μ x
x s = μ x ± n 1 − W 0 × σ X ,       ∀ s = 1 , 2 , ... , n
Where, W0 is the weight of the mean value μ x .
Step 2: Assess the weighting factor of individual sample points:
W 0 = W 0
W s = 1 − W 0 2 n ,       ∀ s = 1 , 2 , ... , n
W s + n = 1 − W 0 2 n ,       ∀ s + n = n + 1 , n + 2 , ... , 2 n
∑ s = 1 n W s = 1
Step 3: Sample 2n+1 points to the nonlinear function to obtain output samples as per Eq. (27).
y S = f ( x s )
Step 4: Assess μ y and σ y of the output variable θ.
μ y = ∑ s = 1 n W s θ s
σ y = ∑ s = 1 n W s ( θ s − μ y ) − ( θ s − μ y ) T

5. Results and Discussions

The IMTBO method is used to simulate the MOIF for reconfiguration of the distribution network in this segment with the goal of reducing power losses and improving the indicators of power quality and distribution network dependability. Putting the suggested strategy into practice on the IEEE 33-bus standard distribution network (Figure 4). 33 buses and 37 branches make up this network, which is fed by a 12.6 kV transmission network. Five communication switches between buses 8-21, 9-15, 12-22, 18-33, and 25-29, as well as lines 33 to 37, may be used to alter the network topology in the case of unexpected events or disruptions. The 33-bus network's load and lines, as well as the lines' exit rates and the network's subscriber count, are all covered by the data that has been taken from references [41,40]. The balance of all loads and voltages is taken for granted in the simulation for the best reconfiguration. The primary post is not where the problem originates, and the dependability of each load point within a subscriber group is assessed. When evaluating dependability, the voltage sag problem affects all industrial loads. The superiority of the IMTBO is compared with the conventional MTBO, particle swarm optimization (PSO), and artificial electric field algorithm (AEFA). For a fair comparison of the population size, the maximum number of iteration and repetitions for each algorithm are set to 50, 100, and 25, respectively, and the parameters of the MTBO, PSO, and AEFA algorithms are regarded as the regulatory parameters provided by their authors in the articles, as shown in Table 1. The number of optimization variables equals the number of switchable lines, which is five lines. In addition, line number one, which is the connection line to the main network and the main feeder, cannot be removed or altered; therefore, the optimization variables can be adjusted from line number 2 to line number 37.
To evaluate the effectiveness of the proposed procedure, four simulation cases are provided as follows:
Case 1) Distribution network without reconfiguration
Case 2) Reconfiguration to minimize power losses in addition to improving power quality
Case 3) Reconfiguration with the aim of minimizing power losses in addition to improving reliability
Case 4) Reconfiguration to minimize power losses and improve power quality and reliability
Case 5) Reconfiguration to minimize power losses and improve power quality and reliability considering uncertainties

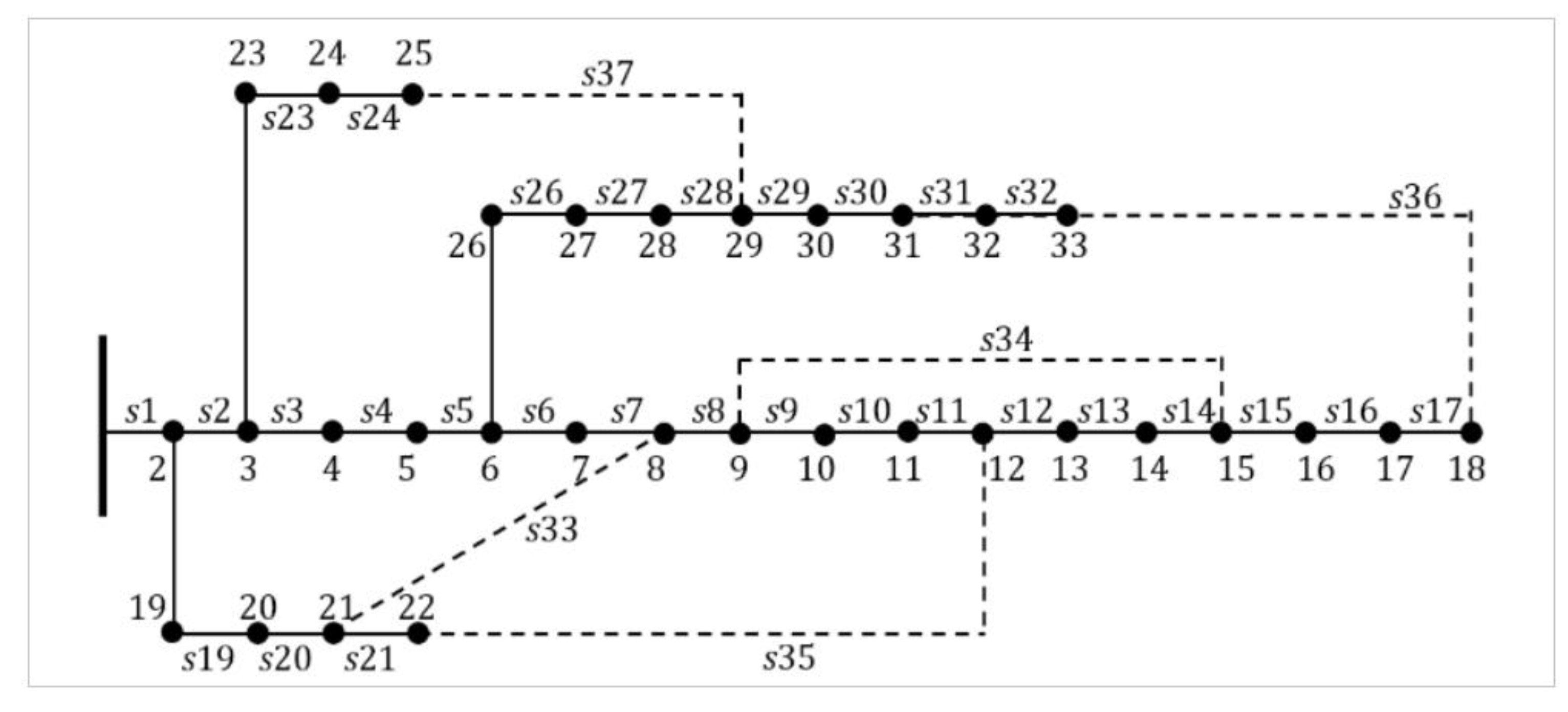
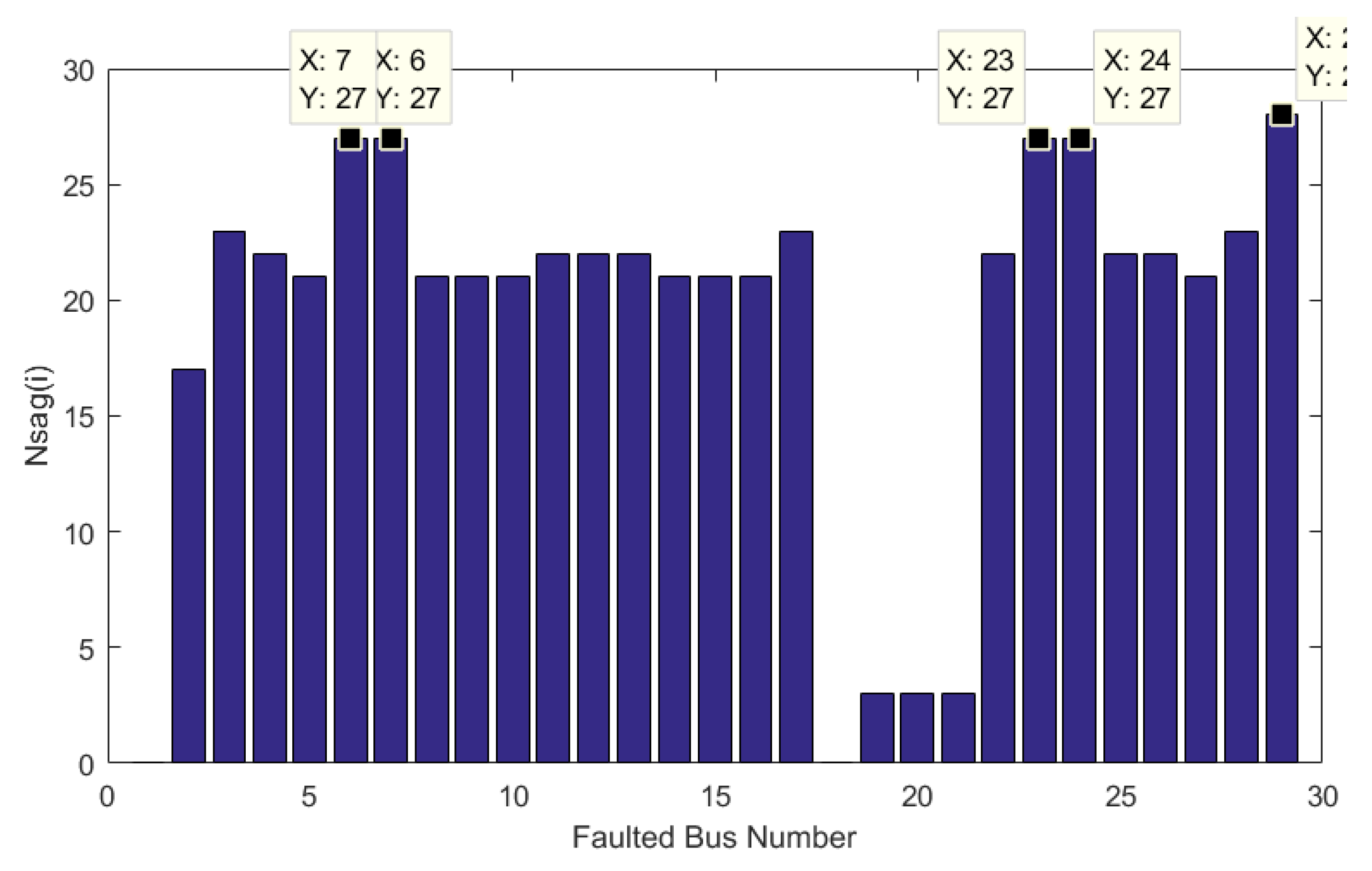
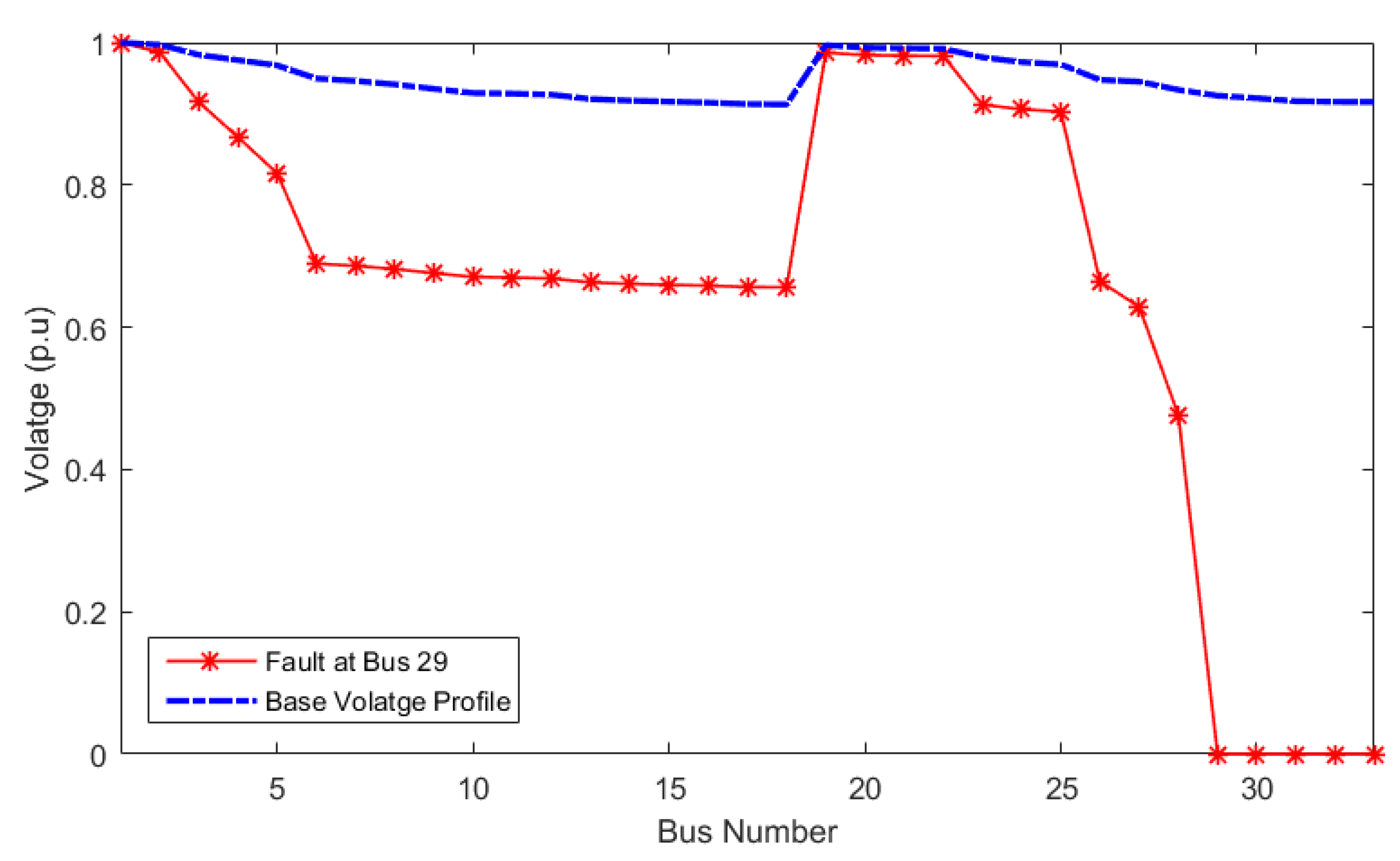
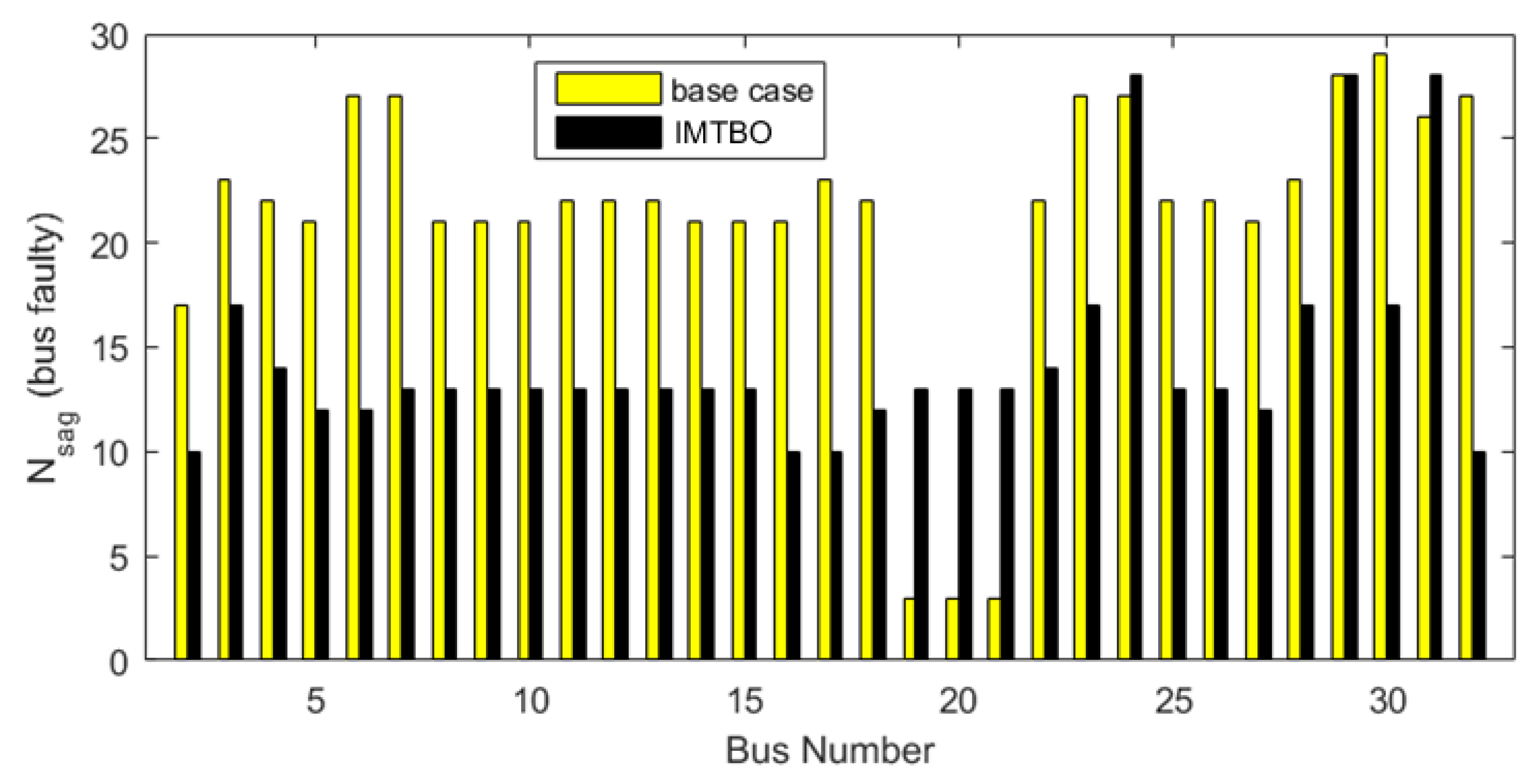
5.1. Results of the base network (Case 1)

In this section, the results of power flow and fault analysis are presented to evaluate the performance of the distribution network of 33 buses before optimal reconfiguration. Except for the main post, fault analysis simulation has been done in all buses. For the basic network, the values of P L o s s , N s a g , SARFI, SAIFI, ASIFI, and MAIFI are 202.68 kW, 16104, 8.2331, 1.3614, 2.3508, and 4.6479, respectively, which are given in Table 2. Lines 33, 34, 35, 36, and 37 are open network switches or tie lines.
The simulation of short circuit fault in all buses except for the main post is done to determine the weak area or the bus that causes the voltage sag in the network. The number of voltage sags of the network buses by the LLL fault is shown in Figure 5.
It is possible to identify buses with the potential to impair power quality and reliability. Buses 6, 7, 23, 24, and 29 are the most sensitive buses to the propagation of voltage drop in the entire network, and bus 29 affects more than the rest of the network buses. Figure 6 shows the network voltage profile in normal conditions and the LLL fault in bus 29.

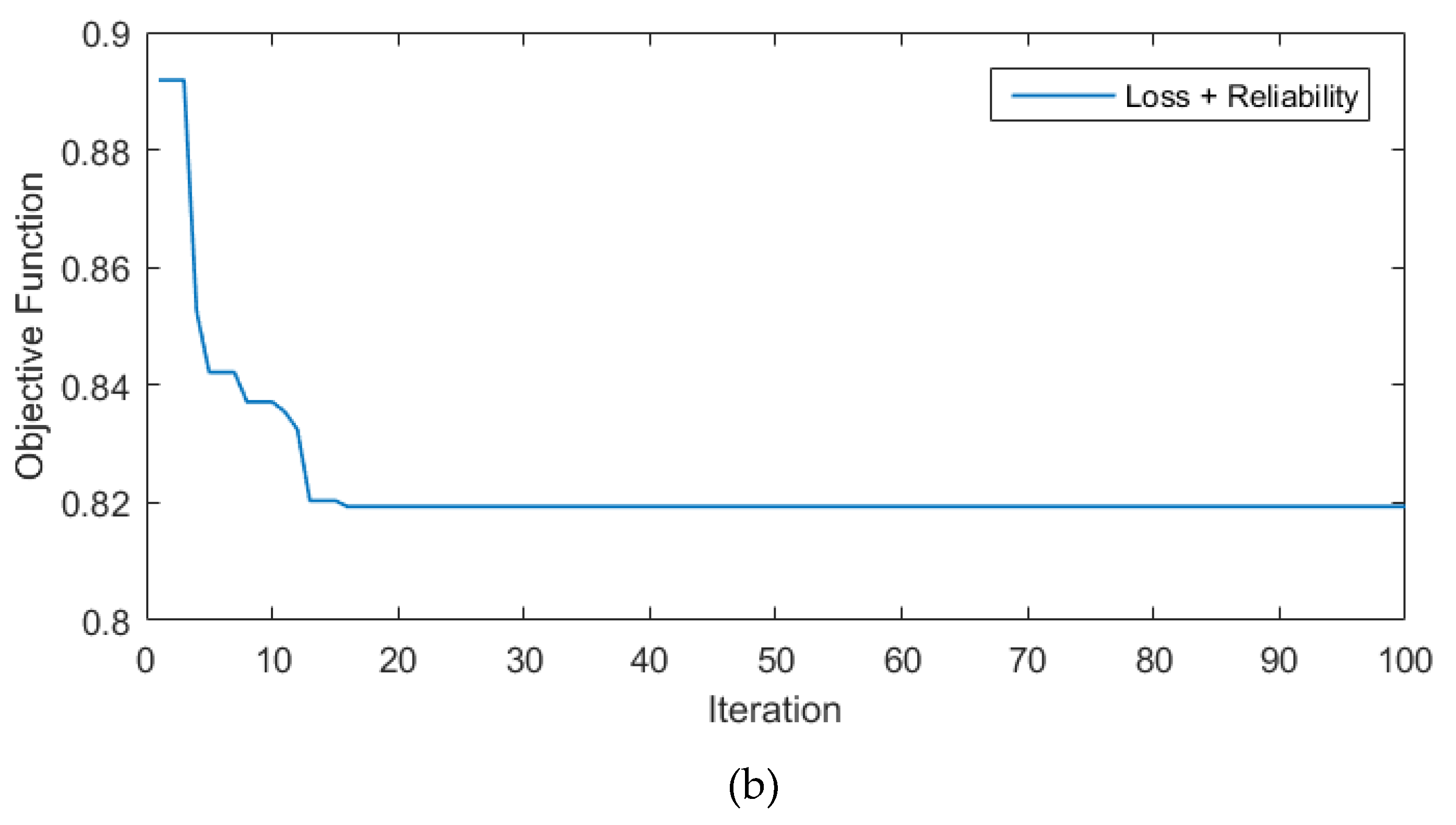
5.2. Results of dual-objective reconfiguration (Cases 2 and 3)

This part uses the IMTBO method to simulate a dual-objective reconfiguration of the distribution network with the goals of reducing power losses and power quality indicators (case 2) as well as power losses and reliability indicators (case 3). The convergence curve of the IMTBO in solving two different problems is shown in Figure 7. It can be seen that the IMTBO has good convergence accuracy in solving problems with different objective functions and found the optimal solution with a suitable convergence speed.
The simulated outcomes of the MOIF for reconfiguration of the distribution network using the IMTBO to reduce power losses are shown in Table 3. For case 1, the IMTBO has determined the optimal arrangement of the network by leaving lines 7, 9, 14, 28, and 32 open, and for case 2 by opening lines 7, 8, 9, 16, and 28. Comparison of the results of cases 2 and 3 shows that case 1 has obtained better power quality indicators, i.e. lower N s a g and SARFI values compared to case 2. Also, the comparison of the results of cases 2 and 3 shows that case 2 has obtained better reliability indices, i.e. lower ASIFI, MAIFI, and SAIFI values compared to case 2. The amount of power loss is also lower in case 3 compared to case 2. The results showed that each of cases 2 and 3 improved the network performance to the maximum from their point of view, and from another point of view, the amount of improvement was not significant, in other words, a suitable compromise between all loss targets and indicators of power quality and reliability was not established.

5.3. Results of MOIF for reconfiguration (Case 4)

This part also uses the IMTBO to simulate the consequences of the MOIF for reconfiguration of the distribution network with the goal of decreasing power losses, power quality indicators, and reliability indicators (case 4). In this section, the IMTBO performance is compared with conventional MTBO, PSO, and AEFA algorithms. The convergence curve of different algorithms in solving case 4 is shown in Figure 8. It can be seen that the IMTBO algorithm has a lower convergence tolerance compared to other algorithms and achieved the optimal solution with a smaller amount of the objective function, which indicates its better performance compared to other algorithms.
The optimization results along with various reliability and power loss indices are presented in Table 4. As can be seen, the IMTBO has obtained a lower value of the objective function compared to other methods. Therefore, the IMTBO algorithm has shown better overall performance in improving each of the objectives compared to the PSO, AEFA, and conventional MTBO methods. The amount of power loss by each of the MTBO, PSO, AEFA, and conventional MTBO methods is 139.97 kW, 166.94 kW, 146.28 kW, and 144.77 kW respectively, and N s a g value is 10680, 11520, 10848, and 10848 respectively, SARFI value is 5.46, 5.88 respectively, 5.54 and 5.54, ASIFI value is 2.19, 2.35, 2.19, and 2.16 respectively, MAIFI value is 2.57, 2.99, 2.95, and 2.81 respectively and SAIFI value is 1.36, 1.36, 1.39 and 1.37 respectively. The results showed that the IMTBO method has shown better performance in improving all objectives compared to other methods.
In this study, the number of buses that have a voltage lower than 0.95 p.u is defined as weak buses. The number of weak basses for the base network without reconfiguration is 21 basses, which after reconfiguration has decreased to 8 basses, i.e., it has decreased by 61.9%. The N s a g criterion in the basic state is equal to 16104 points, which has decreased to 10680 with optimization based on the IMTBO method, which has decreased by 33.68%. The active power loss of the network has also decreased by 30.94% from 202.68 kW to 139.97 kW. SARFI power quality index has also decreased by 33.68% from 8.23 to 5.46. In addition, the ASIFI and MAIFI index decreased by 6.43% and 44.57%, respectively, from 2.35 and 4.64 to 2.19 and 2.57, respectively. Significant financial losses may come from the interruption of heavy loads due to poor network power quality and low reliability, hence these improvements in power quality and reliability indicators are highly desirable. The SAIFI index has changed significantly and reached 1.35 from 1.36 and decreased by 0.74%.
The IMTBO efficiently generates the optimal reconfiguration solution in several iterations. Power quality and network reliability have improved significantly, despite a slight improvement in the system's SAIFI benchmark. Figure 9 shows the number of network bus drops after solving case 3 by IMTBO after the LLL fault in different locations. The voltage sag performance of different network buses has improved significantly compared to the base state.

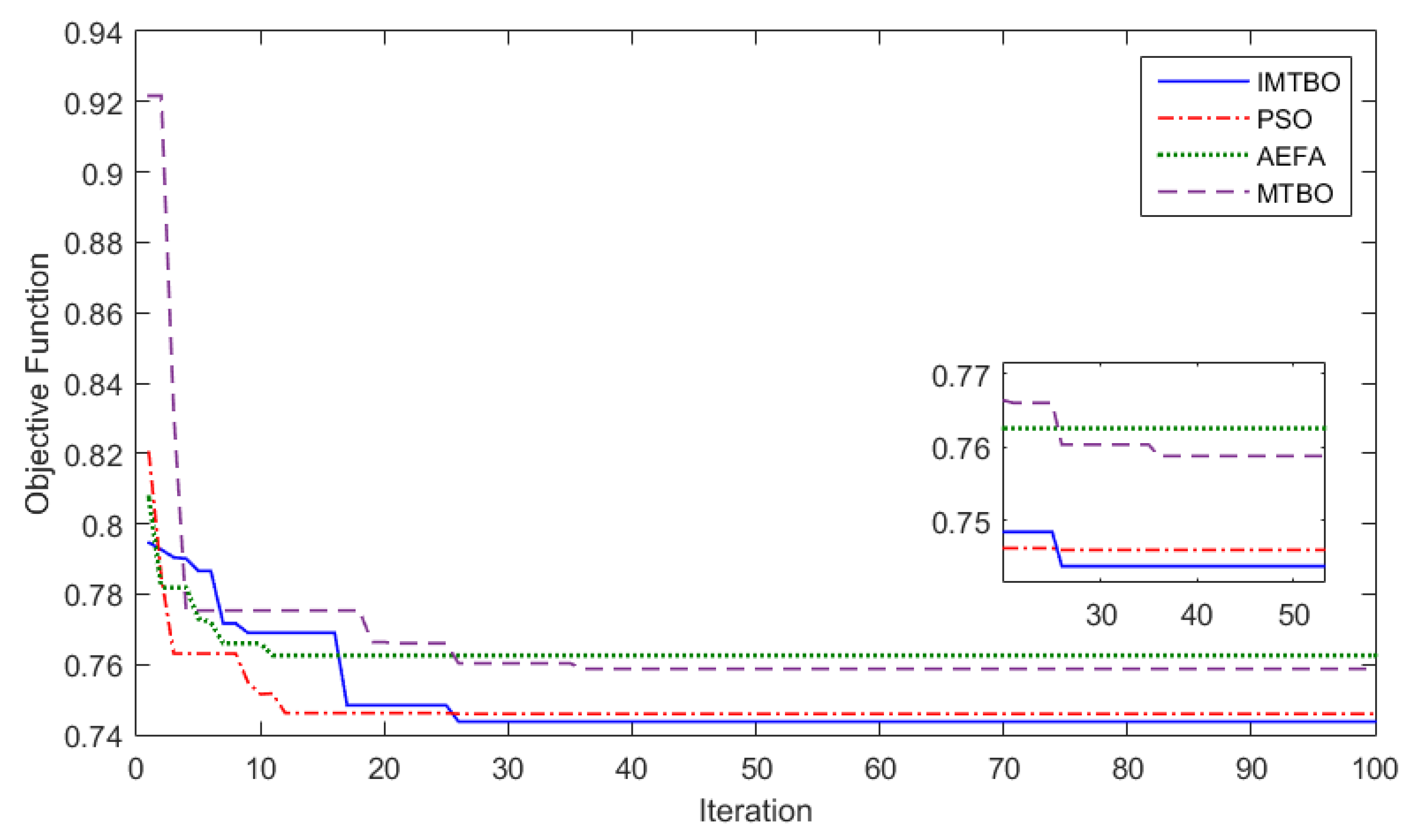
5.4. Analysis of different cases

In Table 5, the results of single objective reconfiguration with different objective functions are presented. The IMTBO method has been run 30 times for each objective function to evaluate the optimal reconfiguration performance. The best optimization results with different objective functions until the last iteration of optimization for each single objective optimization are presented in Table 10. The N s a g objective function is the most appropriate objective function to improve power quality. The results showed that the best value of each goal in single-objective optimization is provided with the same goal. In addition, the results of Table 10 show that in single-objective optimizations, some indicators are even weakened compared to their base state. The results show that when all the indicators of loss, power quality, and reliability are considered as the objective function, a better compromise has been made between all the objectives, and in general, according to Table 3 and Table 4, a lower objective function value has been obtained. 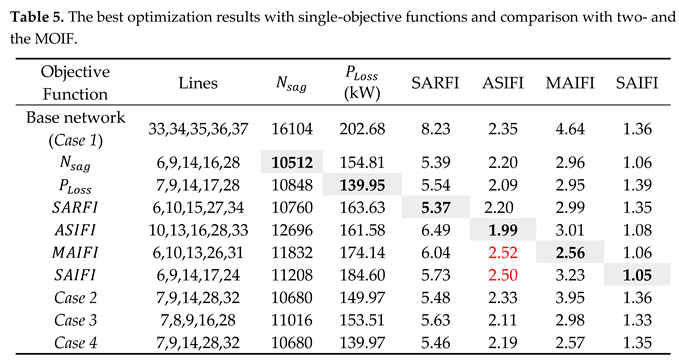Preprints 80618 i001

5.5. Comparison with previous studies

This section compares the performance of the proposed method with that of various prior studies. In [43], the problem of reconfiguration and application of sparse productions to improve reliability has been done using Genetic Algorithm (GA). In [42], the problem with different modes of using the reconfiguration and location of scattered productions considering the reliability indices of the energy supply of subscribers (ENS), the average duration of outages (SAIDI), the average number of outages (SAIFI) and the CAIDI index which It is obtained by dividing SAIDI by SAIFI. In this comparison, the focus is on the reconfiguration mode of the problem. In this study, the SAIFI index is common between the two studies, of course, the optimization problem is done in [43] with different objectives such as ENS minimization, SAIDI minimization, and CAIDI minimization, but the network SIAFI value is extracted in reconfiguration mode. The value of SAIFI in [43], with each of the objectives of SAIDI, ENS, and CAIDI is equal to 1.36 (the value of this index before the optimization is also obtained in the relevant reference) which in the proposed IMTBO method, the value of SIAFI with the objectives N s a g minimization, ASIFI minimization, MAIFI minimization, and SAIFI minimization are obtained as 1.0691, 1.0801, 1.0661 and 1.0504 respectively. Therefore, the proposed method has a good performance in reducing SAIFI with different objective functions.

5.6. Results of MOIF for reconfiguration considering demand uncertainty (Case 5)

In this section, results of the MOIF for distribution network reconfiguration considering the network demand uncertainty are presented in Table 6 and compared with the deterministic results (Case 4). The results showed that considering the uncertainty of the network load demand in the stochastic reconfiguration model, in addition to the increased network power losses, the power quality and reliability indicators were also weakened. Therefore, it is necessary to include the uncertainty of the load in the detailed network reconfiguration for the decision of the network operators. The results showed that in the stochastic model, taking into account the uncertainty of the load, the amount of power loss 7.62%, the number of voltage sag 5.39%, the SARFI index 5.31%, and each of the reliability indices of ASIFI, MAIFI and SAIFI respectively 2.28%, 6.61% and 1.48% have increased compared to the deterministic reconfiguration model. The IMTBO method determined the optimal network configuration by opening switches 7, 10, 28, 32 and 34. In the stochastic reconfiguration model, the UT approach has low calculation time against conventional uncertainty modeling approaches such as Monte Carlo simulation and no presumptions to simplify the model. 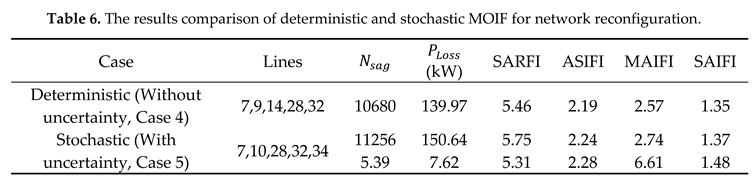Preprints 80618 i002

5. Conclusions

In this study, the network's MOIF for stochastic reconfiguration was investigated to minimize the power losses and enhance the reliability and power quality indices considering demand uncertainty using the UT. The new IMTBO was utilized to find the network optimal configuration to satisfy operational requirements, preserve network radiality. Additionally, the MOIF was resolved using the PSO, AEFA, and conventional MTBO techniques, and the outcomes were compared and investigated to validate the IMTBO. To determine the location or bus responsible for the network's voltage sag, a simulation of short-circuit faults was performed on all buses, excluding the main post. According to the results, buses 6, 7, 23, 24, and 29 were the most sensitive to the spread of voltage sag across the entire network, with bus 29 affecting the plurality of network buses. In terms of power quality and reliability indicators, as well as objective function value, simulation results demonstrated that the IMTBO optimization method was preferable to PSO, AEFA, and conventional MTBO. The results cleared that the success of the proposed MOIF reduced active losses by 30.94%, improved the SARFI index by 33.68%, and enhanced the ASIFI and MAIFI indices by 6.43% and 44.57%, respectively. The MOIF for reconfiguration has enhanced network performance in terms of power quality and reliability in comparison to single-objective reconfiguration, whereas single-objective marketing cannot produce a workable compromise between all objectives. In addition, the superior efficacy of the proposed IMTBO-based method compared to Ref. [43] in terms of increasing the SAIFI index is validated. Moreover, the results of the stochastic reconfiguration based on the MOIF using the UT, cleared that the losses was increased and also the power quality and reliability indices were weakened compared to the deterministic MOIF without uncertainty. The results illustrated that considering the demand uncertainty gives the network operator to make accurate decision to aware the network optimal configuration. The results showed that the UT was simple to model the uncertainty with low number of sampling points.

Author Contributions

Min Zhu: Conceptualization, Methodology, Software, Writing – original draft; Saber Arabi Nowdeh: Methodology, Software, Writing – original draft; Aspassia Daskalopulu: Investigation, Validation, Writing – review & editing.

Funding

This research received no funding.

Data Availability Statement

The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Mohammadi, M., & Akbari Nasab, M. (2011). Voltage sag mitigation with D-STATCOM in distribution systems. Australian Journal of Basic and Applied Sciences, 5(5), 201-207.
  2. Transmission and Distribution Committee. (2003). IEEE Guide for Electric Power Distribution Reliability Indices. IEEE Std 1366™-2003.
  3. Wang, B., Zhu, H., Xu, H., Bao, Y., & Di, H. (2021). Distribution network reconfiguration based on noisynet deep q-learning network. IEEE Access, 9, 90358-90365. [CrossRef]
  4. Chattopadhyay, S., Mitra, M., & Sengupta, S. (2011). Electric power quality. In Electric Power Quality (pp. 5-12). Springer Netherlands.
  5. Tomoiagă, B., Chindriş, M., Sumper, A., Sudria-Andreu, A., & Villafafila-Robles, R. (2013). Pareto optimal reconfiguration of power distribution systems using a genetic algorithm based on NSGA-II. Energies, 6(3), 1439-1455. [CrossRef]
  6. García, J. A. M., & Mena, A. J. G. (2013). Optimal distributed generation location and size using a modified teaching–learning based optimization algorithm. International journal of electrical power & energy systems, 50, 65-75. [CrossRef]
  7. Rao, R. V., Savsani, V. J., & Vakharia, D. P. (2012). Teaching–learning-based optimization: an optimization method for continuous non-linear large scale problems. Information Sciences, 183(1), 1-15. [CrossRef]
  8. Chen, S. L., Chen, G. B., Hsu, S. C., Chen, A. Y. T., Guo, T. Y., Huang, F. F., & Huang, Y. C. (2002, October). Mitigation of voltage sags by network reconfiguration of a utility power system. In Transmission and Distribution Conference and Exhibition 2002: Asia Pacific. IEEE/PES (Vol. 3, pp. 2067-2072). IEEE. [CrossRef]
  9. Yun, S. Y., Oh, J. H., Rim, S. J., & Kim, J. C. (2000). Mitigation of voltage sag using feeder transfer in power distribution system. In Power Engineering Society Summer Meeting, 2000. IEEE (Vol. 3, pp. 1421-1426). IEEE. [CrossRef]
  10. Torres, J., Guardado, J. L., Rivas-Dávalos, F., Maximov, S., & Melgoza, E. (2013). A genetic algorithm based on the edge window decoder technique to optimize power distribution systems reconfiguration. International Journal of Electrical Power & Energy Systems, 45(1), 28-34. [CrossRef]
  11. Jazebi, S., Hosseinian, S. H., & Vahidi, B. (2011). DSTATCOM allocation in distribution networks considering reconfiguration using differential evolution algorithm. Energy Conversion and Management, 52(7), 2777-2783. [CrossRef]
  12. Salman, N., Mohammed, A., & Shareef, H. (2009, November). Reinforcement of power distribution network against voltage sags using graph theory. In Research and Development (SCOReD), 2009 IEEE Student Conference on (pp. 341-344). IEEE. [CrossRef]
  13. Jakus, D., Čađenović, R., Vasilj, J., & Sarajčev, P. (2020). Optimal reconfiguration of distribution networks using hybrid heuristic-genetic algorithm. Energies, 13(7), 1544. [CrossRef]
  14. Swaminathan, D., Rajagopalan, A., Montoya, O. D., Arul, S., & Grisales-Noreña, L. F. (2023). Distribution Network Reconfiguration Based on Hybrid Golden Flower Algorithm for Smart Cities Evolution. Energies, 16(5), 2454. [CrossRef]
  15. Pereira, E. C., Barbosa, C. H., & Vasconcelos, J. A. (2023). Distribution Network Reconfiguration Using Iterative Branch Exchange and Clustering Technique. Energies, 16(5), 2395. [CrossRef]
  16. Kahouli, O., Alsaif, H., Bouteraa, Y., Ben Ali, N., & Chaabene, M. (2021). Power system reconfiguration in distribution network for improving reliability using genetic algorithm and particle swarm optimization. Applied Sciences, 11(7), 3092. [CrossRef]
  17. Quintana, E., & Inga, E. (2022). Optimal reconfiguration of electrical distribution system using heuristic methods with geopositioning constraints. Energies, 15(15), 5317. [CrossRef]
  18. Yang, M., Li, J., Li, J., Yuan, X., & Xu, J. (2021). Reconfiguration strategy for dc distribution network fault recovery based on hybrid particle swarm optimization. Energies, 14(21), 7145. [CrossRef]
  19. Ayalew, M., Khan, B., & Alaas, Z. M. (2022). Optimal Service Restoration Scheme for Radial Distribution Network Using Teaching Learning Based Optimization. Energies, 15(7), 2505. [CrossRef]
  20. Shareef, H., Ibrahim, A. A., Salman, N., Mohamed, A., & Ai, W. L. (2014). Power quality and reliability enhancement in distribution systems via optimum network reconfiguration by using quantum firefly algorithm. International Journal of Electrical Power & Energy Systems, 58, 160-169. [CrossRef]
  21. Čađenović, R., Jakus, D., Sarajčev, P., & Vasilj, J. (2018). Optimal distribution network reconfiguration through integration of cycle-break and genetic algorithms. Energies, 11(5), 1278. [CrossRef]
  22. Shaheen, A. M., Elsayed, A. M., El-Sehiemy, R. A., & Abdelaziz, A. Y. (2021). Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems. Applied Soft Computing, 98, 106867. [CrossRef]
  23. Ali, Z. M., Diaaeldin, I. M., El-Rafei, A., Hasanien, H. M., Aleem, S. H. A., & Abdelaziz, A. Y. (2021). A novel distributed generation planning algorithm via graphically-based network reconfiguration and soft open points placement using Archimedes optimization algorithm. Ain Shams Engineering Journal, 12(2), 1923-1941. [CrossRef]
  24. Fathi, R., Tousi, B., & Galvani, S. (2021). A new approach for optimal allocation of photovoltaic and wind clean energy resources in distribution networks with reconfiguration considering uncertainty based on info-gap decision theory with risk aversion strategy. Journal of Cleaner Production, 295, 125984. [CrossRef]
  25. Azad-Farsani, E., Sardou, I. G., & Abedini, S. (2021). Distribution Network Reconfiguration based on LMP at DG connected busses using game theory and self-adaptive FWA. Energy, 215, 119146. [CrossRef]
  26. Wang, X., Liu, X., Jian, S., Peng, X., & Yuan, H. (2021). A distribution network reconfiguration method based on comprehensive analysis of operation scenarios in the long-term time period. Energy Reports, 7, 369-379. [CrossRef]
  27. Nguyen, T. T., Nguyen, T. T., Nguyen, N. A., & Duong, T. L. (2021). A novel method based on coyote algorithm for simultaneous network reconfiguration and distribution generation placement. Ain Shams Engineering Journal, 12(1), 665-676. [CrossRef]
  28. Anteneh, D., Khan, B., Mahela, O. P., Alhelou, H. H., & Guerrero, J. M. (2021). Distribution network reliability enhancement and power loss reduction by optimal network reconfiguration. Computers & Electrical Engineering, 96, 107518. [CrossRef]
  29. Qu, Y., Liu, C. C., Xu, J., Sun, Y., Liao, S., & Ke, D. (2021). A global optimum flow pattern for feeder reconfiguration to minimize power losses of unbalanced distribution systems. International Journal of Electrical Power & Energy Systems, 131, 107071. [CrossRef]
  30. Abdelkader, M. A., Osman, Z. H., & Elshahed, M. A. (2021). New analytical approach for simultaneous feeder reconfiguration and DG hosting allocation in radial distribution networks. Ain Shams Engineering Journal, 12(2), 1823-1837. [CrossRef]
  31. Nowdeh, S. A., Naderipour, A., Davoudkhani, I. F., & Guerrero, J. M. (2023). Stochastic optimization–based economic design for a hybrid sustainable system of wind turbine, combined heat, and power generation, and electric and thermal storages considering uncertainty: A case study of Espoo, Finland. Renewable and Sustainable Energy Reviews, 183, 113440.
  32. Faridmehr, I., Nehdi, M. L., Davoudkhani, I. F., & Poolad, A. (2023). Mountaineering Team-Based Optimization: A Novel Human-Based Metaheuristic Algorithm. Mathematics, 11(5), 1273. [CrossRef]
  33. Zheng, T., & Luo, W. (2019). An enhanced lightning attachment procedure optimization with quasi-opposition-based learning and dimensional search strategies. Computational Intelligence and Neuroscience, 2019. [CrossRef]
  34. Yadav, A. (2019). AEFA: Artificial electric field algorithm for global optimization. Swarm and Evolutionary Computation, 48, 93-108. [CrossRef]
  35. Moghaddam, M. J. H., Kalam, A., Shi, J., Nowdeh, S. A., Gandoman, F. H., & Ahmadi, A. (2020). A new model for reconfiguration and distributed generation allocation in distribution network considering power quality indices and network losses. IEEE Systems Journal, 14(3), 3530-3538. [CrossRef]
  36. Naderipour, A., Abdullah, A., Marzbali, M. H., & Nowdeh, S. A. (2022). An improved corona-virus herd immunity optimizer algorithm for network reconfiguration based on fuzzy multi-criteria approach. Expert Systems with Applications, 187, 115914. [CrossRef]
  37. Ch, Y., Goswami, S. K., & Chatterjee, D. (2016). Effect of network reconfiguration on power quality of distribution system. International Journal of Electrical Power & Energy Systems, 83, 87-95. [CrossRef]
  38. Moghaddam, M. J. H., Kalam, A., Nowdeh, S. A., Ahmadi, A., Babanezhad, M., & Saha, S. (2019). Optimal sizing and energy management of stand-alone hybrid photovoltaic/wind system based on hydrogen storage considering LOEE and LOLE reliability indices using flower pollination algorithm. Renewable energy, 135, 1412-1434. [CrossRef]
  39. Mahdavi, S., Rahnamayan, S., & Deb, K. (2018). Opposition based learning: A literature review. Swarm and evolutionary computation, 39, 1-23. [CrossRef]
  40. Duan, D. L., Ling, X. D., Wu, X. Y., & Zhong, B. (2015). Reconfiguration of distribution network for loss reduction and reliability improvement based on an enhanced genetic algorithm. International Journal of Electrical Power & Energy Systems, 64, 88-95. [CrossRef]
  41. Mendoza, J. E., Lopez, M. E., Coello, C. C., & Lopez, E. A. (2009). Microgenetic multiobjective reconfiguration algorithm considering power losses and reliability indices for medium voltage distribution network. IET Generation, Transmission & Distribution, 3(9), 825-840. [CrossRef]
  42. Whitley, D. (1994). A genetic algorithm tutorial. Statistics and computing, 4(2), 65-85. [CrossRef]
  43. Boor, Z., & Hosseini, S. M. (2013). Optimal Placement of DG to Improve the Reliability of Distribution Systems Considering Time Varying Loads using Genetic Algorithm.
Preprints 80618 g001
Figure 1. The pseudo code of the MTBO's optimizer.
Figure 1. The pseudo code of the MTBO's optimizer.
Preprints 80618 g001
Preprints 80618 g002
Figure 2. The proposed IMTBO algorithm's flowchart.
Figure 2. The proposed IMTBO algorithm's flowchart.
Preprints 80618 g002
Preprints 80618 g003
Figure 3. Flowchart of the proposed methodology based on IMTBO.
Figure 3. Flowchart of the proposed methodology based on IMTBO.
Preprints 80618 g003
Preprints 80618 g004
Figure 4. IEEE standard 33-bus distribution network.
Figure 4. IEEE standard 33-bus distribution network.
Preprints 80618 g004
Preprints 80618 g005
Figure 5. Number of network bus voltage sags by the LLL fault.
Figure 5. Number of network bus voltage sags by the LLL fault.
Preprints 80618 g005
Preprints 80618 g006
Figure 6. Voltage profile of bus 29 with the LLL problem and the 33-bus network under normal circumstances.
Figure 6. Voltage profile of bus 29 with the LLL problem and the 33-bus network under normal circumstances.
Preprints 80618 g006
Preprints 80618 g007aPreprints 80618 g007b
Figure 7. Convergence curve of IMTBO in solving the problem with different objectives a) Case 2 and b) Case 3.
Figure 7. Convergence curve of IMTBO in solving the problem with different objectives a) Case 2 and b) Case 3.
Preprints 80618 g007aPreprints 80618 g007b
Preprints 80618 g008
Figure 8. Convergence characteristics of different methods in solving the problem (Case 4).
Figure 8. Convergence characteristics of different methods in solving the problem (Case 4).
Preprints 80618 g008
Preprints 80618 g009
Figure 9. Number of network bus voltage drops using IMTBO after LLL error in different buses (Case 4).
Figure 9. Number of network bus voltage drops using IMTBO after LLL error in different buses (Case 4).
Preprints 80618 g009
Table 1. Adjustment parameters of different algorithms.
Table 1. Adjustment parameters of different algorithms.
Algorithm Parameter
MTBO --
PSO [32] C1= C2=2 & Inertia weight= Linearly decline from 0.9 to 0.1
AEFA [33-34] Initial value used in Coulomb’s constant (K0)=100
Table 2. Loss values and indicators of power quality and reliability for the base mode 33-bus network (Case 1).
Table 2. Loss values and indicators of power quality and reliability for the base mode 33-bus network (Case 1).
Item Base Network
Opened Switches 33,34,35,36,37
P L o s s (kW) 202.68
N s a g 16104
S A R F I 8.2331
A S I F I 2.3508
M A I F I 4.6479
S A I F I 1.3614
O F 1
Table 3. Results of solving cases 2 and 3 using the IMTBO.
Table 3. Results of solving cases 2 and 3 using the IMTBO.
Item/Method Base Network Loss + Power Quality$(Case 2) Loss + Reliability$(Case 3)
Opened Switches 33,34,35,36,37 7,9,14,28,32 7,8,9,16,28
P L o s s (kW) 202.68 149.9782 153.5122
N s a g 16104 10680 11016
S A R F I 8.23 5.46 5.63
A S I F I 2.35 2.33 2.11
M A I F I 4.64 3.95 2.98
S A I F I 1.36 1.36 1.33
O F 1 0.7629 0.81934
Table 4. Numerical results of solving case 4 using different algorithms.
Table 4. Numerical results of solving case 4 using different algorithms.
Item/Method Base Network IMTBO PSO AEFA MTBO
Opened Switches 33,34,35,36,37 7,9,14,28,32 7,10,14,28,32 7,9,14,17,28 9,28,32,33,34
P L o s s (kW) 202.68 139.97 166.94 146.28 144.77
N s a g 16104 10680 11520 10848 10848
S A R F I 8.23 5.46 5.88 5.54 5.54
A S I F I 2.35 2.19 2.35 2.19 2.16
M A I F I 4.64 2.57 2.99 2.95 2.81
S A I F I 1.36 1.35 1.36 1.39 1.37
O F 1 0.74372 0.74594 0.76256 0.75876
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated