Prerpints.org logo
Preprint
Article

Digital Grading the Color Fastness to Rubbing of Fabrics Based on Spectral Reconstruction and BP Neural Network

Altmetrics

Downloads

99

Views

54

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

27 July 2023

Posted:

28 July 2023

You are already at the latest version

Alerts
Abstract
To digital grade the color fastness of fabrics after rubbing, an automatic grading method based on spectral reconstruction technology and BP neural network was proposed. Firstly, the modeling samples are prepared by rubbing the fabrics according to the ISO standard of 105-X12. Then, to comply with visual rating standards for color fastness, the modeling samples are professionally graded to obtain the visual rating result. After that, a digital camera is used to capture digital images of the modeling samples inside a closed and uniform lighting box, and the color data values of the modeling samples are obtained through spectral reconstruction technology. Finally, the color fastness prediction model for rubbing was constructed using the modeling samples data and BP neural network. The color fastness level of the testing samples was predicted using the prediction model, and the prediction results were compared with the existing color difference conversion method and curve fitting method. Experimental show that the prediction model of fabric color fastness can be better constructed using the BP neural network, where the root-mean-square error of the prediction for the training sample is 0.30, and the root-mean-square error of the prediction for the test sample is 0.25. The overall performance of the method is slightly better than the color difference conversion method, and it is significantly outperforming the curve fitting method. It can be seen that the digital rating method of fabric color fastness to rubbing based on spectral reconstruction and BP neural network has a high consistency with the visual evaluation, which will help for the automatic color fastness grading.
Keywords: 
Subject: Computer Science and Mathematics  -   Artificial Intelligence and Machine Learning

1. Introduction

Color fastness is the expression of the color of a textile to various effects during the processing and use of the material, and it is a very important indicator when testing the color quality of fabrics[1,2,3]. The color fastness of textile fabrics is usually determined by assessing the discoloration of the sample, or by assessing the staining of the undyed lining fabric. Expressed as a number of grades, the color fastness is usually divided into five grades with a half grade between two adjacent grades, forming five grades and nine steps. Generally, the higher the grade the better the color fastness, and the lower the grade the worse the color fastness.
For color fastness grading, the traditional method mainly uses the artificial visual method[4] referencing the standard grading gray card. The color difference between the sample to be rated and the reference sample is usually visually observed by a specially trained professional in a dark room and under a standard light box. The visually observed color difference of textiles samples is then compared with the standard grading gray card under the same observed conditions. The grade of the standard grading gray card closest to the visually observed color difference of textiles fabrics is assigned as the color fastness grade of it. However, due to the subjective differences in the work experience and physiological state of the professional person, the artificial visual method will inevitably affect the final rating results. In addition, the artificial visual method can only help to estimate the approximate differences of tested samples based on human perception experience, it does not allow for quantitative analysis of visually perceived color differences. More importantly, the practical application of the artificial visual method is also inefficient.
With the development of technology, the grading of color fastness based on color measurement equipment such as spectrophotometers are used for fabric quality evaluation. As one of the precise optical measuring instruments, the spectrophotometer can accurately measure the spectral reflectance of the fabric, and the color data of the fabric can be calculated through colorimetric theory[5,6]. However, the applications of the spectrophotometer are limited to the measurement of flat objects with pure color dyed and by contact way, and the measurement of color using the spectrophotometer should be done manually placing the fabric in front of the measurement hole. Thus, the application of a spectrophotometer in the automatic grading of digital color fastness is restricted.
Recently, digital imaging-based methods are used for digital grading color fastness of fabric[7], where the color fastness is calculated based on the captured images of fabric and the mathematical grading method. In terms of the digital imaging-based methods, the extracted RGB values are firstly converted to the CIEXYZ tristimulus and then converted to the CIELab values. Based on the calculated CIELab values the color difference between the tested and reference fabric can be calculated[8,9]. Hence the color fastness can be graded refer to the calculated color difference.
Two different types of digital color fastness grading methods have been proposed. The first type is called as color difference conversion method, and the second is called as curve fitting method. For the first type of method, using the calculated CIELab values from captured RGB values, the CIEDE2000 color difference is calculated between the tested and reference fabric. And the relationship between the CIEDE2000 color difference and standard color fastness grades are fitted by mathematical algorithms such as linear regression[10,11]. With the established regression model, the color fastness of the newly tested fabric will be predicted. For the curve fitting method, the color image of standard grading gray card of color fastness captured with a digital camera is first converted to the grayscale image. Then, the grayscale difference between a pair of gray patches of each grade is calculated. After that, the grayscale differences are fitted with their corresponding color fastness grades using the curve fitting method. With the fitted curve between the grayscale difference and corresponding grades, the newly tested fabric will be predicted for its color fastness based the gray image difference between rubbed and unrubbed area[12,13].
However, for the digital imaging-based methods, due to the extracted RGB values are imaging condition related, and the calculated CIELab values are not the true color attributes of the tested fabric sample most time, which will inevitably bring grading error to the grading results. Therefore, how to use the more accurate color data for color fastness grading is the key issue. As we all know, spectral reflectance is the ‘fingerprint’ of object color, if spectral reflectance can be acquired with a digital camera, then the color data of fabric will be accurately calculated using the spectral reflectance, the appointed standard illumination and the standard color matching functions[14,15,16,17]. Using the groundtruth color data, the grading of color fastness of fabric will be more accurate and confident.
To deal with the deficiencies of the current digital imaging-based methods, we propose the digital grading method for the color fastness to rubbing of textiles based on spectral reconstruction technology and BP (Backward Propagation) neural network modeling. Different from the existing methods that directly calculate the color data from RGB values, the spectral reconstruction technology can help us to acquire the spectral reflectance of the captured image of fabrics, which will provide the basis to calculate the groundtruth color data of the fabrics. In addition, the BP neural network is selected to model the relationship between the color attributes difference of the tested fabric and the corresponding color fastness grades. Experimental results show that the digital imaging-based color fastness grading method proposed in this paper is significantly efficiency compared to the existing methods.

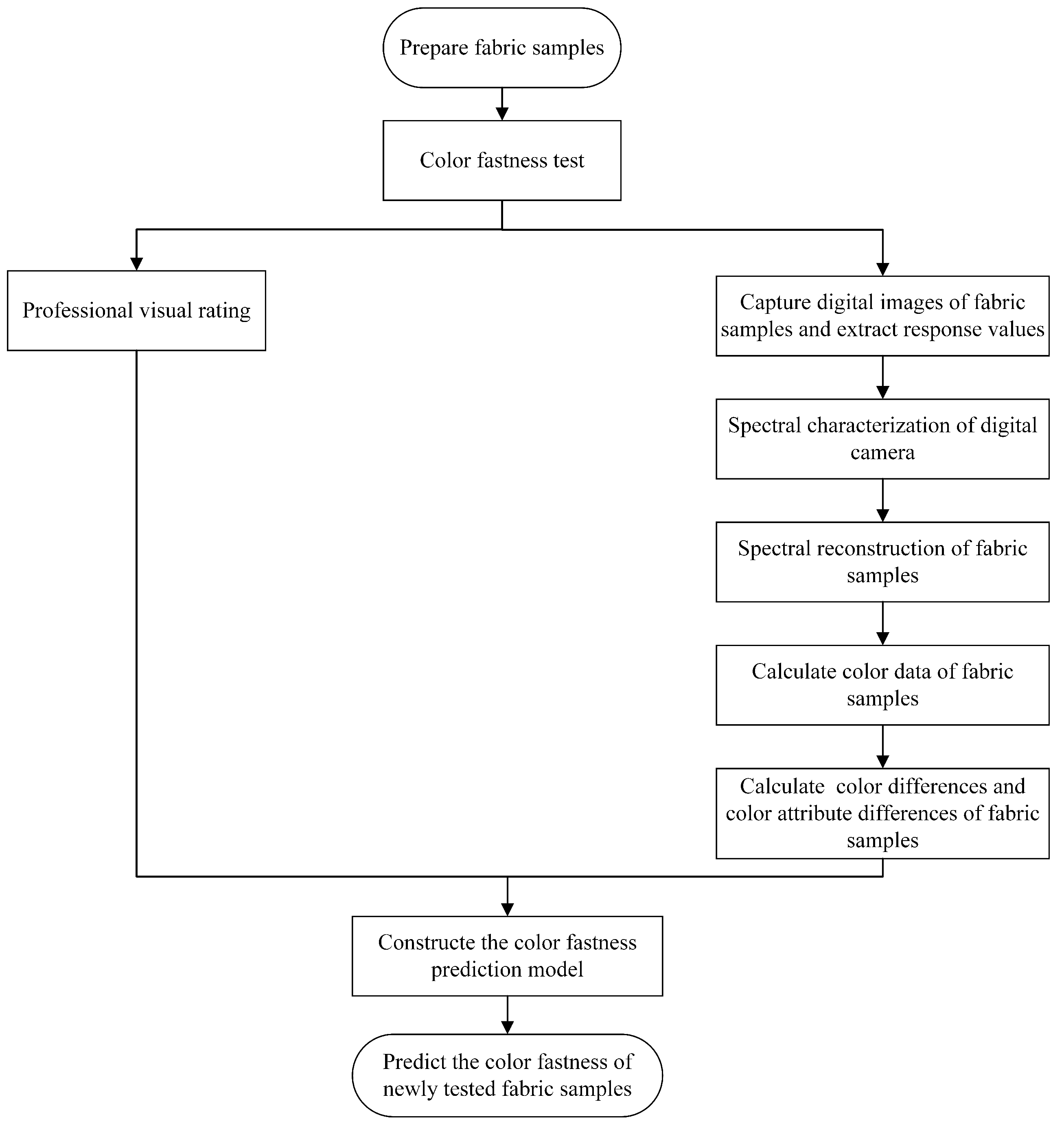
2. Methodology

Conventional color fastness mainly includes color fastness to rubbing, color fastness to washing and color fastness to perspiration[18,19,20], etc. This paper mainly studies the color fastness to rubbing. The overall flowchart of the proposed method is shown in Figure 1. Firstly, the fabric samples are prepared for color fastness modeling. The fabrics are paired samples, one of them will be rubbed as tested and another remains as a reference. After the rubbing test, all the samples will be visually graded by a specially trained professional under standard grading conditions. So, the ground truth of each tested sample is acquired as a reference for digital grading model construction. Then, the spectral reconstruction technology is used to reconstruct the spectral reflectance of the modeling samples, and the color data of the modeling sample is calculated by colorimetry theory. Based on the calculated color data, we can acquire the color difference (such as CIEDE2000) and color attribute difference (such as ΔL, Δa, and Δb) of each paired sample. Finally, the BP neural network is adopted to construct the color fastness model between the input data (color difference and color attribute difference) and the visually graded color fastness result. Using the constructed color fastness prediction model, the color fastness grade of the newly tested samples will be easily predicted.
Details of color data acquisition based on spectral reconstruction technology are presented in Section 2.1, and the construction of the color fastness digital grading model based on the BP neural network is illustrated in Section 2.2. In addition, a brief introduction to the current two types of digital imaging-based methods is also presented in Section 2.2.

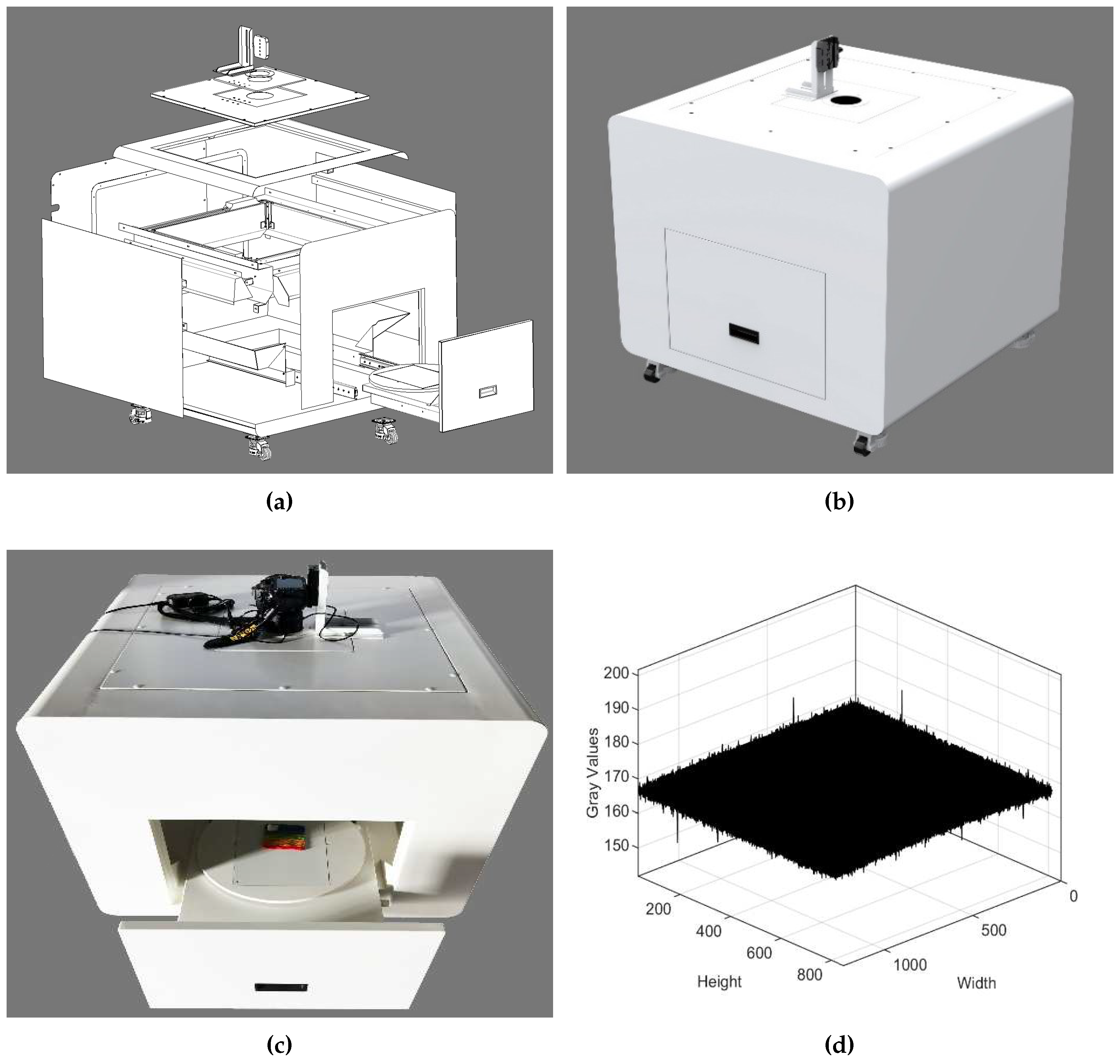
2.1. Color Data Acquisition Based on Spectral Reconstruction

In this study, spectral reconstruction technology was used to calculate the color data of fabric samples. The first step is to take digital images of fabric samples and spectral characterization samples (such as the X-rite ColorChecker color chart or custom fabrics chart) with a digital camera. With uniform illumination of daylight light source in a closed light box of ColorEye, the sample is placed on the sample platform and the optical path of the digital camera is perpendicular to the plane of the platform. The geometric diagram of the uniformly illuminated light box is shown in Figure 2a and the rendering effect of light box is shown in Figure 2b. The real product of light box is presented in Figure 2c and the inner illumination uniformity of the imaging area over the platform that checked with the X-rite gray card and Nikon D7200 digital camera are plotted in Figure 2d. To set the appropriate imaging parameters such as ISO, shutter speed, and aperture size, we make sure the RGB values of the white and black patch in the X-rite ColorChecker 24 color chart are approximately 235 and 35, respectively. Therefore, we set the ISO as 100, the shutter speed as 1/20 second, and the aperture size as f/5.6 with a focal length of 35mm. In the experiment, we use these imaging parameters to capture the samples.
Using the set imaging parameters, the digital images of fabric samples and spectral characterization samples are captured in the light box by a digital camera, and the average RGB values of each fabric sample and each color patch in the modeling samples are extracted. If we set the extract area as m × n pixels, the average RGB response values in the extraction area is calculated as shown in Equation (1),
d = 1 m × n ∑ i = 1 m × n r i , g i , b i ,
where i indicates the ith pixel in the extracted area, r i , g i , and b i are the red, green, and blue channel RGB response values of the ith pixel, and d is the response value vector with the dimension of 1 × 3. It should be noted that the raw format digital response values that without post-processed by the digital camera ISP (Image Signal Processing) module is used in this study. Compared to the normal RGB response values commonly used in current methods, the raw format response values is cleaner and linearity than post-processed RGB values, which will benefit the higher spectral reconstruction accuracy. Because the response of each channel is no longer linear after processing the raw image, but is better represented by a more complex non-linear law. Additionally, the post-processing methods of different camera manufacturers often differ and are difficult to accurately simulate or describe, making it challenging to model post-processing steps accurately[21,22].
The spectral characterization of digital camera is carried out in the second step utilizing a pseudo-inverse technique based on polynomial expansion. As is illustration, the raw response value from the spectral characterization sample is extended into a second-order polynomial, as given in Equation (2), which has a total of 10 expansion items.
d exp = 1 , r , g , b , r g , r b , g b , r 2 , g 2 , b 2 T ,
where d e x p is the vector of digital response values following polynomial expansion, the superscript T denotes the transpose, and r, g, and b are the red, green, and blue channel raw response values of any sample. Equation (3) is the expanded matrix of digital response values of the spectral characterization samples after polynomial expansion.
D train = d exp , 1 , d exp , 2 , … , d exp , j T ( j = 1 , 2 , … , P ) ,
where j is the jth spectral characterization sample, P indicates the total number of spectral characterization samples, d e x p , j stands for the extended vector of numerical response values for the jth sample, and D t r a i n is the extended matrix of spectral modeling samples.
As indicated in Equation (4) to Equation (7), in the proposed method, we use the Tikhonov regularization to regularize the solution of the spectral reconstruction matrix. Firstly, the singular value decomposition (SVD) algorithm is applied to the expanded response matrix D t r a i n of the spectral modeling samples. Then a very small number α is added to the eigenvalues to obtain the constrained eigenvalues to reduce the condition number of the expanded response matrix. After that, we reconstruct the response expansion matrix D t r a i n , r e c . Finally, the spectral reconstruction matrix Q is obtained by solving with pseudo-inverse (PI) algorithm and to obtain the spectral reconstruction model.
D train = USV T ,
P = S + α I ,
D train , rec = UPV T ,
Q = R train · pinv D train , rec ,
where R t r a i n is the spectral matrix of the spectral modeling samples, U and V are the orthogonal decomposition matrices obtained by SVD algorithm, S and P are diagonal matrices containing eigenvalues, I is the unit matrix, and pinv(·) is the mathematical function of pseudo-inverse algorithm.
In the next step, we use the established spectral reconstruction model to reconstruct the spectral reflectance of the newly tested fabric sample. The extracted raw response d t e s t of the newly tested fabric is first expanded using the polynomial as in Equation (1), to get the expanded response vector d t e s t , e x p . Then the spectral reflectance of tested fabric samples are reconstructed using the spectral reconstruction matrix Q, as indicated in Equation (8).
r test = Q · d test , exp ,
where r t e s t is the reconstructed spectral reflectance of the tested fabric sample and matrix Q is the established spectral reconstruction matrix.
Using the constructed spectral reflectance above, the corresponding color data of the fabric samples are calculated based on the colorimetry theory. The tristimulus values of the fabric samples are calculated as indicated in Equation (9) and Equation (10).
X = k ∫ λ x ( λ ) E ( λ ) S ( λ ) d λ Y = k ∫ λ y ( λ ) E ( λ ) S ( λ ) d λ Z = k ∫ λ z ( λ ) E ( λ ) S ( λ ) d λ ,
where,
k = 100 / ∑ λ y ( λ ) E ( λ ) d λ ,
where x(λ), y(λ), and z(λ) are standard observer color matching functions, E(λ) is the fabric samples spectral reflectance, S(λ) is the relative spectral power distribution function of the light source, λ is the wavelength, k is the adjustment factor, and X, Y, and Z are the three stimulus value data of the fabric sample.
Then, the CIELab color data of the fabric samples are calculated from the corresponding tristimulus. According to the theory of chromaticity, the method of calculating the corresponding CIELab color data from the tristimulus value data is shown in formula (11) to formula (12).
L = 116 f Y Y n − 16 a = 500 f X X n − f Y Y n , b = 200 f Y Y n − f Z Z n
where,
f H H n = H H n 1 / 3 if H H n > ( 24 / 116 ) 1 / 3 f H H n = ( 841 / 108 ) H H n + 16 / 116 if H H n ≤ ( 24 / 116 ) 1 / 3 ,
where L, a, and b represent the lightness, red-green, and yellow-blue color values of the fabric sample in the CIELab color space, respectively. X, Y, and Z are the three stimulus value data of the fabric, and X n , Y n , and Z n are the three stimulus value data of the reference light source. In Equation (12), H and H n represent the three stimulus values of the fabric and reference light source, respectively.
With the CIELab color data of fabric samples, the next step is to calculate the color difference and color attribute difference in order to perform the color fastness test. Using the CIELab color data of the fabric sample pair, the CIEDE2000 color difference value of the fabric sample pair and the corresponding ΔL, Δa, and Δb color difference values are calculated. The CIEDE2000 color difference formula is shown in formula (13).
Δ E 2000 = Δ L ′ k L S L 2 + Δ C ′ k C S C 2 + Δ H ′ k H S H 2 + R T Δ C ′ k C S C Δ H ′ k H S H 1 2 ,
where ΔL, ΔC, and ΔH represent the lightness, chroma, and hue differences of the fabric sample pair in the CIELCh color space, which are automatically converted from the CIELab color space when calculating the color difference. k H , k L , and k C are the weights for hue, lightness, and chroma when calculating the color difference. For fabric samples, k L is usually set to 1.5, and k H and k C are set to 1. S L , S C , and S H are the weighting functions for lightness, chroma, and hue, respectively, and R T is the adjustment term for color difference calculation. The calculation of the color differences ΔL, Δa, and Δb are shown in equations (14) to (16).
Δ L = L 1 − L 2 ,
Δ a = a 1 − a 2 ,
Δ b = b 1 − b 2 ,
where (L 1 , a 1 , b 1 ) and (L 2 , a 2 , b 2 ) are the CIELab color data of the reference sample and the color fastness test sample in the fabric sample pair, respectively.

2.2. Color Fastness Prediction Methods

2.2.1. Existing Methods

(1) The color difference conversion method
For the color difference conversion method, the RGB values of the target sample images are firstly extracted as described in Equation (1). Then the RGB values are converted to CIEXYZ stimulus values according to the conversion method between the working RGB color space and CIEXYZ color space. However, since the CIEXYZ is not a perceptually uniform color space, therefore we further transform the CIEXYZ to the device independent and perceptually more uniform CIELab color space, this will benefit to calculate the color difference in accordance with the visual perception. After we have the CIELab color data, the color difference of the paired sample is calculated using the CIE DE2000 color difference equations. Then the color fastness grade of staining is calculated according to the relevant regulations in ISO 105-A11 standard, and the final rating result is obtained[10,11]. The specific algorithm formula is shown in equations (17) to (18):
G R S = − 0.061 Δ E G R S + 2.474 1 + e − 0.191 Δ E G R S ,
where,
Δ E G R S = Δ E 00 − 0.423 Δ E 00 2 − Δ L 00 2 ,
where GRS stands for calculated grade, ΔE 00 is the color difference value calculated using the CIEDE2000 color difference formula.
(2) The curve fitting method
The curve fitting method is proposed based on the concept that the color fastness grade is highly correlated to the gray scale difference of the standard grading gray card[12,13], where the further assumption is that the gray scale difference of the standard grading gray card is highly correlated with their color difference. Based on the above assumptions, one should firstly capture the image of standard grading gray card, and calculated the gray scale difference of the paired gray patches for each color fastness grade. Then, the polynomial-based curve fitting method is applied to the corresponding gray scale difference and the color fastness grade, to construction the color fastness prediction model. With the constructed model, the color fastness grade of the testing paired sample will be predicted through calculating their gray image difference and put it into the prediction model. It should be note that the imaging of the paired testing sample should be captured at the same imaging conditions as the prediction model constructed, or the prediction result will be incorrect.

2.2.2. The Proposed Method

In this study, the BP neural network is used to construct a color fastness prediction model for fabric samples. The BP neural network is a multi-layer feedforward network trained using the backpropagation algorithm. It typically consists of three layers, namely the input layer, hidden layer, and output layer. Each layer of neurons is fully connected to the adjacent layer, but there is no connection among neurons in the same layer. The neurons in different layers are not connected in a feedback manner, forming a hierarchical and feedforward neural network system[23,24,25].
The BP neural network is a useful tool for both classification and regression problems. In the case of color fastness rating, it can be approached as either a classification or regression problem. When we treat the color fastness rating as classification problem, of which the color fastness grade is divided into nine grades ranging from 1 to 5 with 0.5 as the step, we can get the color fastness grade of test samples directly, but it is not benefit for us to evaluate the precision of the prediction model more accurately. Therefore, we treat the color fastness rating as a regression problem in this study, and the prediction model is trained by the BP neural network and prepared training samples. The specific predict color fastness values of the testing paired samples between 0 to 5 will be given out by the prediction model with continue numbers. And based on the predicted color fastness value, the color fastness grade will be determined to the nearest grade level.

2.3. Evaluation Metrics

In this study, the general metric of root-mean-square error (RMSE) is used to measure the deviation between the predicted color fastness grade and the visual grade of fabric samples obtained from the experts. The calculation of RMSE is shown in Equation (19):
R M S E = ∑ i = 1 n y − y 1 2 n ,
where RMSE represents the root mean square error, y represents the predicted color fastness value of the tested samples, y 1 represents the actual value of the tested samples, and n represents the number of tested samples. The smaller the RMSE value, the better the consistency between the model prediction results and the visual rating results.

3. Experiment

To validate the proposed fabric color fastness rating method for rubbing tests, we employed the following instruments and materials in the experiment. They are the Y(B) 571-III color fastness rubbing tester, the pure cotton twill fabric with the size of 10cm×25cm, the white cotton rubbing cloth with the size of 5cm×5cm, the standard gray card for assessing staining of color, the standard colorimetric light box ColorChex N7, the Nikon D7200 digital camera, the X-rite Color Checker classical 24 color chart, and the closed lighting box ColorEye with uniform illumination. Using the above instruments and materials, the experiment aimed to assess the color fastness of the textile fabric after multiple rubbing tests and verify the accuracy of the proposed rating method. The rubbing fastness experiment is carried out in section 3.1, the visual rating experiment is described in section 3.2, the construction of prediction model based on BP neural network is illustrated in section 3.3, and the testing of the existing methods is presented in section 3.4.

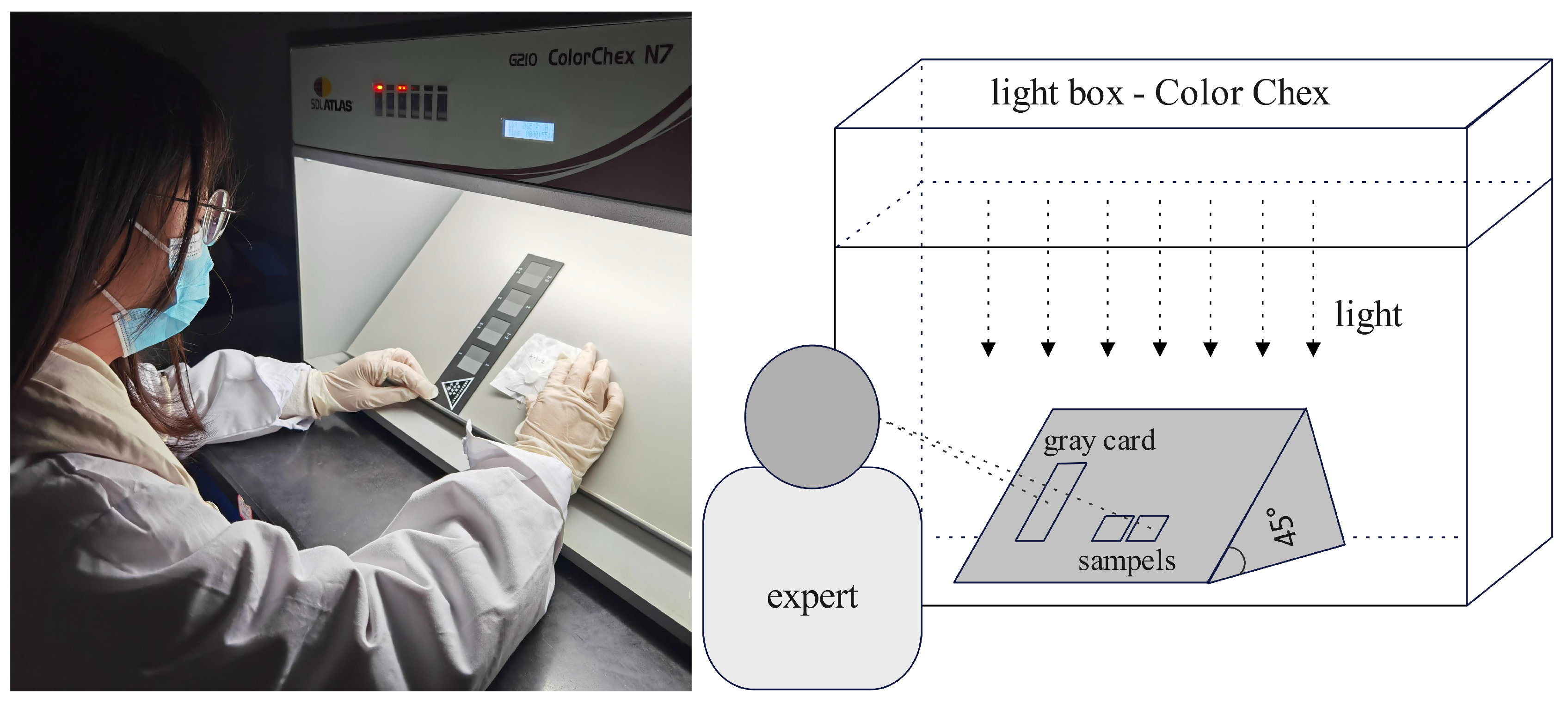
3.1. The Rubbing Color Fastness Experiment

The color fastness to rubbing is an important testing item for fabric. It is the degree of color retention of fabrics after they are subjected to rubbing during use. Usually, the color fastness to rubbing of fabrics is reflected by the staining grade. According to the ISO 105-X12 standard, dry rubbing and wet rubbing tests should be tested simultaneously [26,27]. The testing parameters of the fabric samples are shown in Table 1. During the testing process, the tested fabric samples are fixed to the rubbing platform of the color fastness rubbing tester of Y (B) 571-III, with a dry rubbing cloth on the one rubbing head and a wet rubbing cloth that with a water content of 95%-100% on the other rubbing head. Through adjust the number of rubbing times between 150 ∼ 200 with the pressure of 9N, we can obtain the experiment samples that with the color fastness grades covering all the nine steps from 1 to 5 with the 0.5 as step. Finally, the database including the rubbed samples and their corresponding color-stained rubbing cloth are constructed, some of the samples are shown in Figure 3.

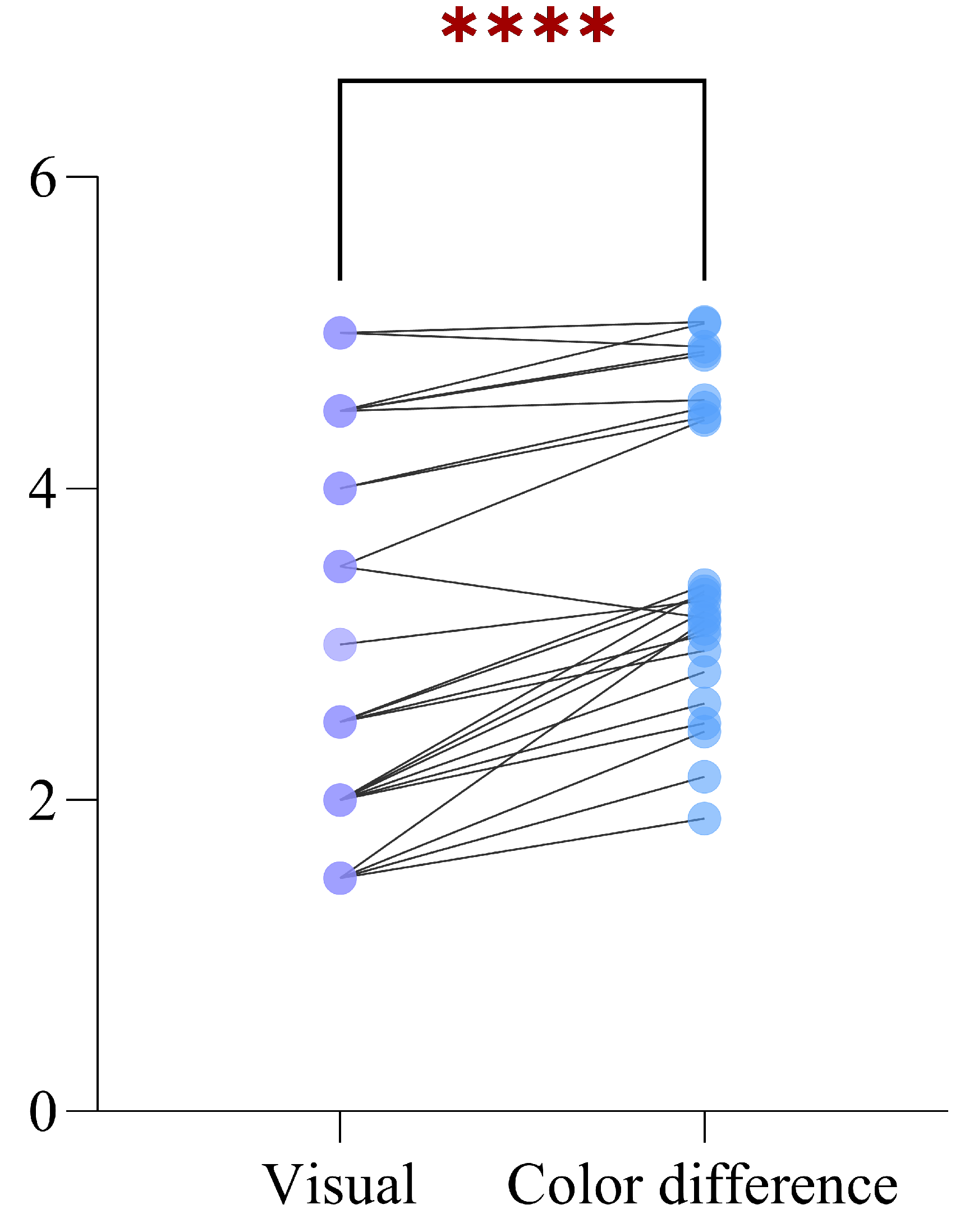
3.2. The Visual Rating Experiment

According to the standard ISO 105-A03, the gray card for staining is used to visually evaluate the rubbered cloth samples. The visual rating experiment is carried out in a dark room and in a professional light box ColorChex N7 (see as in Figure 4). The professional rating person sit in front of the lighting box to visually rating the color fastness grade of the sample. The vertical viewing distance from the eyes to the viewing surface is about 30cm. During the rating, the unstained lining fabric and the stained lining fabric were placed side by side in the same plane, while the gray sample card was also placed nearby on the same plane. The color difference between the unstained lining fabric and the stained lining fabric was visually assessed according to the difference level on the standard grading gray card, and the reference color fastness grade is acquired of all the modeling and testing fabric samples through the visual rating experiment.

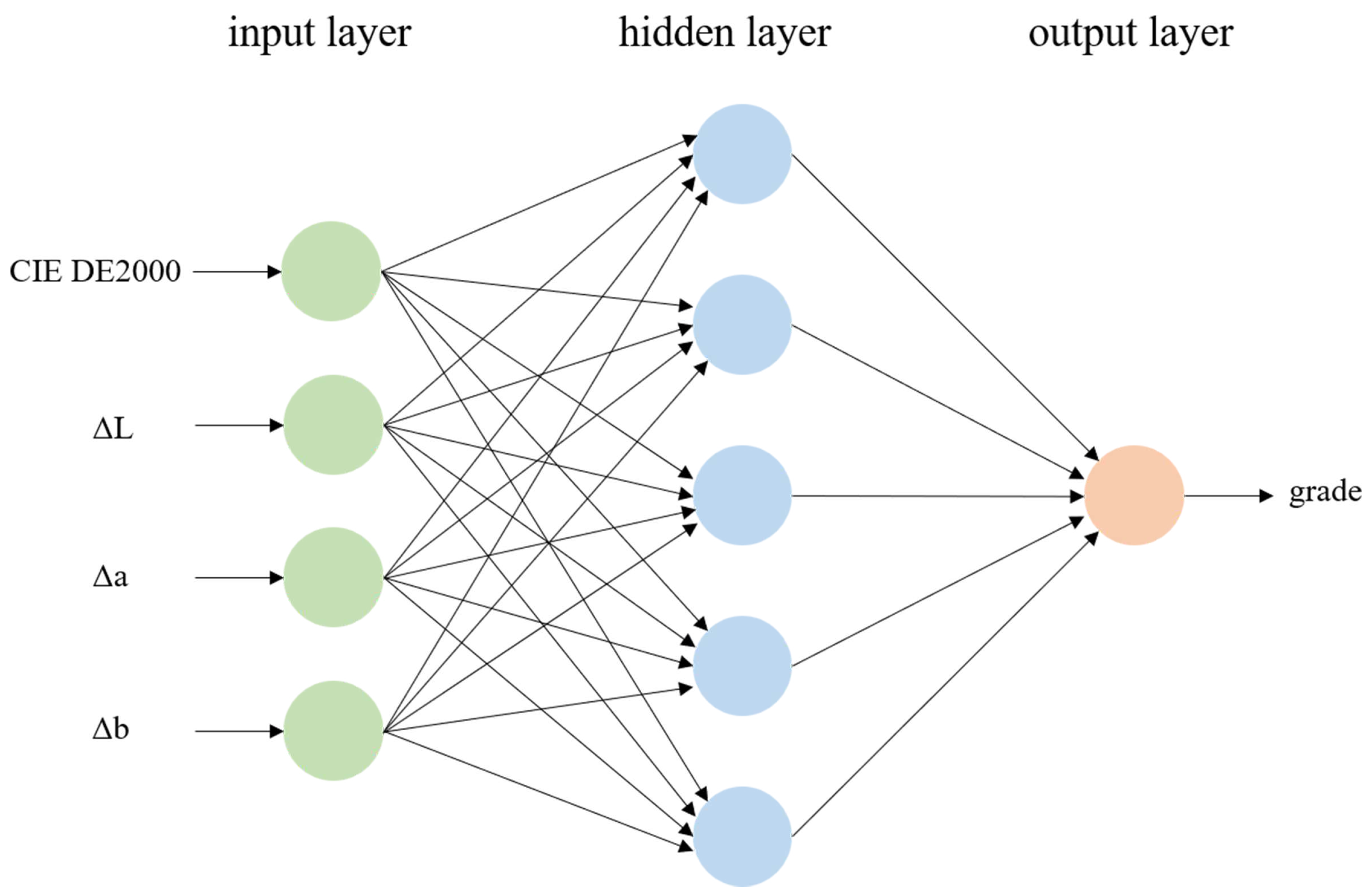
3.3. The BP Neural Network Modeling

In this study, the CIEDE2000 color difference value and the ΔL, Δa, and Δb values of fabric samples are used as input, and the corresponding visual rating results of fabric samples were used as output to train the BP neural network. According to the number of input and output parameters, we set the number of input layer nodes to 4, and the number of output layer nodes to 1. The number of hidden layer nodes is set to 5. The structure diagram of the training model is shown in Figure 5.
In addition, the number of iterations is set to 1000, the learning rate is set to 0.01, and the Sigmoid function is select to as the activation function in the hidden layer neurons, the Sigmoid function is shown in Equation (20).
S ( x ) = 1 1 + e − x ,
where S(·)is the Sigmoid activation function, x is the independent variable, and e is the natural logarithm. The weights between the nodes of the BP neural network were continuously adjusted based on the root mean square error of the modeling samples until the overall average error of the modeling samples reached a stable convergence state. When the BP neural network is reach to the convergence state, the color fastness prediction model is constructed.

3.4. Testing of Existing Methods

(1) Testing of color difference conversion method
The color data of all the fabric samples were extracted using the method described in section 2.1, and the color fastness prediction results were acquired using the color difference conversion method that described in section 2.2.1. To validate the performance of the color difference conversion method, the paired-sample T-test was conducted between the prediction results and the visual results. Firstly, 25 samples are randomly selected from all fabric samples, and they satisfy the normal distribution condition after normal distribution test. Then, the paired-sample T-test was performed to compare whether the prediction results and visual results were significantly different with each other, and the result of paired-sample T-test are shown in Figure 6.
In Figure 6, the purple dot on the left represents the color fastness of the visual rating, the blue dot on the right represents the predicted color fastness of the color difference conversion method, and each line between them connect the same sample. The ‘****’ above the straight line indicate that the p-value of the paired sample T-test is less than 0.0001, which means that there is a significant difference between the prediction results of color difference conversion method and visual rating results. Therefore, a further step is needed to modify the prediction results of color difference conversion method to the visual rating results.
Since the color difference conversion method is proposed base on the calculation of the CIEDE2000 color difference from the color attributes of L, a, and b in the CIELAB color space. To realize the modification from the prediction results of color difference conversion method to the visual rating results, the ΔL, Δa, and Δb were selected to modify the prediction results of color difference conversion method. The modification of the predicted result is based on a linear regression model, where the ΔL, Δa, and Δb are treated as the independent variables, and the grade difference of color fastness between predicted and visual rated is treated as the dependent variable. The results of linear regression analysis between independent and dependent variables are presented in Table 2.
It can be seen from Table 2 that the p-value of the significance analysis of ΔL and Δa is less than 0.05, indicating that both have a significant impact on the grade difference of color fastness between predicted and visual rated result. The p-value of Δb is 0.954 greater than 0.05, and the regression coefficient is not significant, indicating that the Δb has little influence on the grade difference of color fastness. At the same time, the VIFs are all less than 5, indicating that there is no multicollinearity among the independent variables. According to the linear regression analysis results, the multiple linear regression model is constructed as shown in Equation (21).
Y = − 0.292 − 0.042 * X 1 − 0.028 * X 2 ,
where X 1 represents the ΔL, X 2 represents the Δa, and Y represents the grade difference of color fastness between predicted and visual rated result. Therefore, with the established linear regression model, the predicted color fastness based on color difference conversion method can be easily modified to the visual rating grade.
(2) Testing of curve fitting method
For testing of the curve fitting method, the standard grading gray card images were first collected and converted into grayscale images. The grayscale difference between two patches of each grade was extracted, and the grayscale difference was fitted to the corresponding color fastness grade using a curve fitting method. According to the tests, the third-order polynomial curve was found to have the best fitting effect, as shown in Figure 7.
The analysis of the third-order polynomial fitting is presented in Table 3. Based on the fitted parameters, a third-order polynomial fitting equation was obtained, where x represents the grayscale difference of the fabric sample to be evaluated, p1, p2, p3, p4 are the coefficients of the equation, and the predict color fastness grade is denoted as D. The correlation coefficient of the fitting equation of R 2 is 0.99, indicating a good fitting result between the grayscale difference and the color fastness grade. The next step is to convert the testing fabric sample into a grayscale image, and to extract its grayscale value. After that, the color fastness grade of the testing fabric sample will be predicted using the established third-polynomial prediction model.

4. Results and Analysis

In this study, a total of 70 groups of samples were collected and tested, covering all nine color fastness grades from 1.0 to 5.0. We randomly used 49 groups of them as training samples to develop the BP neural network prediction model, and used the remaining 21 groups as test samples to test the accuracy of the constructed model and also to compare the three different methods. The experimental results are shown in Figure 8.
In Figure 8, the red circles represent the referenced true color fastness grades obtained by a visual rating method, while the blue circles represent the predicted color fastness grades by different methods. It is easy to find from Figure 8a and Figure 8b that, for the proposed method based on spectral reconstruction and BP neural network, the RMSE between the predicted and groundtruth are 0.30 and 0.25 for the training and testing set, respectively. As they are smaller than 0.5, the results indicate that a relatively good prediction for both the training and testing sets.
To further compare the performance of different methods, the prediction results of testing set that based on color difference conversion method and curve fitting method are also plotted in Figure 8c and Figure 8d. The RMSE for the color difference conversion method was 0.24, while the RMSE for the curve fitting method was 0.33. It is evident that the BP neural network model constructed in this study has similar prediction result to the color difference conversion method, and is significantly better than the curve fitting method. These results have supported the effectiveness and superiority of the proposed method in this paper for color fastness prediction purpose.
To facilitate a more comprehensive comparison between the three different methods for color fastness prediction, the color fastness grade of each fabric sample in testing sample set are calculated and summarized in Table 4. And the visual rating result is also reported as reference. In addition, to facilitate numerical comparison of the three methods, the root mean square error, the maximum error, the minimum error, and the median error for each of the three methods were also calculated and summarized in Table 5.
It can be seen from Table 5 that the root mean square error of the proposed method is almost the same as that of the color difference conversion method, and both smaller than that of the curve fitting method. The maximum error of BP model is 0.89, the minimum error is 0 and the median error is 0.15, and both the minimum and median error are the smallest. Overall, the BP model show the similar prediction result as the color difference conversion method, but significantly outperform the curve fitting method.
To better visualize the prediction errors distribution of the testing samples of the three methods, the prediction error of each method was boxplot in Figure 9. Where the box plot is a stable method for describing the distribution of data and is not influenced by outliers. For the boxplot of Figure 9, the upper boundary of the box represents the upper quartile of the data, while the lower boundary of the box represents the lower quartile of the data. The line in the middle of the box represents the median value of the data. The upper and lower limits of the box represent the maximum and minimum values of the data. The points outside the box (represented by filled circles in Figure 9) can be considered as outliers, which are typically defined as values that fall below the lower quartile minus 1.5 times the interquartile range or above the upper quartile plus 1.5 times the interquartile range.
It can be observed from Figure 9 that the error distribution of the BP model is more concentrated, while the error distribution of the curve fitting method is more scattered. The distance between the median value and the upper and lower quartiles can be used to evaluate the uniformity of the error distribution. It can be seen that the error distribution of the BP model is the most uniform, while the error distributions of the color difference conversion method and the curve fitting method are less uniform. The position of the median error indicates that, among the three methods, the error of the curve fitting method are generally higher, while the error of the BP model is generally lower.
Furthermore, it is worth noting that the error of the BP model and the color difference conversion method for the fourth sample are both outliers in the dataset. This may due to the uneven coloration of fabric samples. During the rubbing and staining process, the collected data may not accurately represent the real color differences before and after rubbing, and leading to errors in calculating the color fastness grade.
Through the comparative analysis of different methods above, it is concluded that the color fastness prediction method based on spectral reconstruction technology and BP neural network is highly consistent with the professional visual rating result. It also has indicated that the color fastness rating method based on spectral reconstruction and BP neural network can be a good choice in the future to help for digital grading the color fastness to rubbing of fabrics.

5. Conclusions

In this study, the color fastness grading methods was investigated and a new grading method based spectral reconstruction technology and BP neural network modeling is proposed for digital grading the color fastness to rubbing of fabrics. Experiment results have indicated the effective and the superiority of the proposed method. The proposed method have eliminated the subjective differences of traditional visual rating methods for color fastness grading, and also have solved the limitations of spectrophotometer in practical applications. The research outcomes in this paper further enhances the feasibility of applying the digital imaging-based color fastness grading method in the factory in order to improve the evaluation efficiency. In the following works, we will increase the number of experimental samples, and improve the accuracy of color fastness grading. At the same time, other color fastness grading studies, such as color fastness to washing, color fastness to light, color fastness to perspiration, etc., will be carried out to test the adaptability of the proposed method.

Author Contributions

Methodology, validation, writing—review and editing, J.L. and H.L.; methodology, data collection and analysis, writing—original draft preparation, J.Z. and G.C.; investigation, resources, L.L.; funding acquisition, writing—review, X.H.; data curation, K.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Hubei Provincial Natural Science Foundation General Project(No.2022CFB537) and Hubei Provincial Department of Education Science and Technology Research Program Youth Talent(No.Q20221706).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Yu, X.; Wang, H. Support vector machine classification model for color fastness to ironing of vat dyes. Textile Research Journal 2021, 91, 1889–1899. [Google Scholar] [CrossRef]
  2. Popa, S.; Radulescu-Grad, M.E.; Perdivara, A.; Mosoarca, G. Aspects regarding colour fastness and adsorption studies of a new azo-stilbene dye for acrylic resins. Scientific Reports 2021, 11, 5889. [Google Scholar] [CrossRef] [PubMed]
  3. Liu, J.; Yuan, Y.; Zhang, X.; Lixia, S. Development of intelligent grade system for textiles color fastness. Cotton Textile Technology 2019, 47. [Google Scholar]
  4. Huang, S.; Tu, X.; Zhou, S. Application of Kappa Coefficient Consistency test in visual evaluation of color fastness. Knitting Industries 2022, p. 5.
  5. Development of a low-cost UV-Vis spectrophotometer and its applicatiorn for the detection of mercuric ions assisted by chemosensors. Sensors 2020, 20, 906. [CrossRef]
  6. Deidda, R.; Sacre, P.Y.; Clavaud, M.; Coïc, L.; Avohou, H.; Hubert, P.; Ziemons, E. Vibrational spectroscopy in analysis of pharmaceuticals: Critical review of innovative portable and handheld NIR and Raman spectrophotometers. TrAC Trends in Analytical Chemistry 2019, 114, 251–259. [Google Scholar] [CrossRef]
  7. An, Y.; Xue, W.; Ding, Y.; Zhang, S. Evaluation of textile color rubbing fastness based on image processing. Journal of Textile Research 2023, 43, 131–137. [Google Scholar]
  8. Salueña, B.H.; Gamasa, C.S.; Rubial, J.M.D.; Odriozola, C.A. CIELAB color paths during meat shelf life. Meat science 2019, 157, 107889. [Google Scholar] [CrossRef]
  9. Lin, C.J.; Prasetyo, Y.T.; Siswanto, N.D.; Jiang, B.C. Optimization of color design for military camouflage in CIELAB color space. Color Research & Application 2019, 44, 367–380. [Google Scholar]
  10. Cui, G.; Luo, M.; Rhodes, P.; Rigg, B.; Dakin, J. Grading textile fastness. Part 2; Development of a new staining fastness formula. Coloration technology 2003, 119, 219–224. [Google Scholar] [CrossRef]
  11. Cui, G.; Luo, M.; Rigg, B.; Butterworth, M.; Dakin, J. Grading textile fastness. Part 3: Development of a new fastness formula for assessing change in colour. Coloration technology 2004, 120, 226–230. [Google Scholar] [CrossRef]
  12. Zheng, C. Discussion on Evaluation of Color Fastness Grade of Fabrics by Image Method. Light and Textile Industry and Technology 2010, 39, 3. [Google Scholar]
  13. Zhang, Q.; Liu, J.; Gao, W. Grade evaluation of color fastness to laundering based on image analysis. Journal of Textile Research 2013, 34, 100–105. [Google Scholar]
  14. Liang, J.; Xin, L.; Zuo, Z.; Zhou, J.; Liu, A.; Luo, H.; Hu, X. Research on the deep learning-based exposure invariant spectral reconstruction method. Frontiers in Neuroscience 2022, 16, 1031546. [Google Scholar] [CrossRef]
  15. Zhao, Y.; Po, L.M.; Yan, Q.; Liu, W.; Lin, T. Hierarchical regression network for spectral reconstruction from RGB images. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, 2020, pp. 422–423.
  16. Liang, J.; Wan, X. Optimized method for spectral reflectance reconstruction from camera responses. Optics Express 2017, 25, 28273–28287. [Google Scholar] [CrossRef]
  17. Xiao, K.; Zhu, Y.; Li, C.; Connah, D.; Yates, J.M.; Wuerger, S. Improved method for skin reflectance reconstruction from camera images. Optics Express 2016, 24, 14934–14950. [Google Scholar] [CrossRef]
  18. Kert, M.; Gorjanc, M. The study of colour fastness of commercial microencapsulated photoresponsive dye applied on cotton, cotton/polyester and polyester fabric using a pad-dry-cure process. Coloration Technology 2017, 133, 491–497. [Google Scholar] [CrossRef]
  19. Sezgin Bozok, S.; Ogulata, R.T. Effect of silica based sols on the optical properties and colour fastness of synthetic indigo dyed denim fabrics. Coloration Technology 2021, 137, 209–216. [Google Scholar] [CrossRef]
  20. Kumar, R.; Ramratan, K.A.; Uttam, D. To study natural herbal dyes on cotton fabric to improving the colour fastness and absorbency performance. J Textile Eng Fashion Technol 2021, 7, 51–56. [Google Scholar]
  21. Liang, J.; Xiao, K.; Pointer, M.R.; Wan, X.; Li, C. Spectra estimation from raw camera responses based on adaptive local-weighted linear regression. Optics express 2019, 27, 5165–5180. [Google Scholar] [CrossRef]
  22. Liu, Y.; Li, J.; Wang, X.; Li, X.; Song, Y.; Li, R. A study of spectral reflectance reconstruction using the weighted fitting algorithm based on the Sino Colour Book. Coloration Technology 2023. [Google Scholar] [CrossRef]
  23. Han, J.X.; Ma, M.Y.; Wang, K. Product modeling design based on genetic algorithm and BP neural network. Neural Computing and Applications 2021, 33, 4111–4117. [Google Scholar] [CrossRef]
  24. Song, S.; Xiong, X.; Wu, X.; Xue, Z. Modeling the SOFC by BP neural network algorithm. International Journal of Hydrogen Energy 2021, 46, 20065–20077. [Google Scholar] [CrossRef]
  25. Li, Y.; Liu, P.; Zhou, J.; Ren, Y.; Jin, J. Center extraction of structured light stripe based on back propagation neural network. Acta Optica Sinica 2019, 39, 1212005. [Google Scholar]
  26. Luo, Y.; Pei, L.; Zhang, H.; Zhong, Q.; Wang, J. Improvement of the rubbing fastness of cotton fiber in indigo/silicon non-aqueous dyeing systems. Polymers 2019, 11, 1854. [Google Scholar] [CrossRef] [PubMed]
  27. Lei, Z. Study on Test of Color Fastness to Rubbing of Textiles 2020. 793, 012017.
Preprints 80752 g001
Figure 1. The overall flowchart of the proposed color fastness digital grading method.
Figure 1. The overall flowchart of the proposed color fastness digital grading method.
Preprints 80752 g001
Preprints 80752 g002
Figure 2. (a) left up: the geometric diagram of the uniformly illuminated light box, (b) right up: the real rendering effect of light box, (c) left down: the real product of light box, and (d) right down: the inner illumination uniformity over the imaging area over the platform.
Figure 2. (a) left up: the geometric diagram of the uniformly illuminated light box, (b) right up: the real rendering effect of light box, (c) left down: the real product of light box, and (d) right down: the inner illumination uniformity over the imaging area over the platform.
Preprints 80752 g002
Preprints 80752 g003
Figure 3. Digital images of the rubbed samples in the database, for each sample, the rubbed samples and their corresponding color-stained rubbing cloth are presented.
Figure 3. Digital images of the rubbed samples in the database, for each sample, the rubbed samples and their corresponding color-stained rubbing cloth are presented.
Preprints 80752 g003
Preprints 80752 g004
Figure 4. The scene and geometric diagram of visual rating experiment settings.
Figure 4. The scene and geometric diagram of visual rating experiment settings.
Preprints 80752 g004
Preprints 80752 g005
Figure 5. BP neural network structure diagram.
Figure 5. BP neural network structure diagram.
Preprints 80752 g005
Preprints 80752 g006
Figure 6. Result of the paired-sample T-test between prediction results of color difference conversion method and visual rating results using 25 randomly selected fabric samples.
Figure 6. Result of the paired-sample T-test between prediction results of color difference conversion method and visual rating results using 25 randomly selected fabric samples.
Preprints 80752 g006
Preprints 80752 g007
Figure 7. The third-order polynomial curve to fit the relationship between grayscale difference of standard grading gray card and the corresponding color fastness grade.
Figure 7. The third-order polynomial curve to fit the relationship between grayscale difference of standard grading gray card and the corresponding color fastness grade.
Preprints 80752 g007
Preprints 80752 g008
Figure 8. (a) comparison of the prediction results of the training set by BP neural network prediction model, (b) comparison of the prediction results of the testing set by BP neural network prediction model, (c) comparison of the prediction results of the testing set by color difference conversion method, (d) comparison of the prediction results of the testing set by curve fitting method.
Figure 8. (a) comparison of the prediction results of the training set by BP neural network prediction model, (b) comparison of the prediction results of the testing set by BP neural network prediction model, (c) comparison of the prediction results of the testing set by color difference conversion method, (d) comparison of the prediction results of the testing set by curve fitting method.
Preprints 80752 g008
Preprints 80752 g009
Figure 9. Boxplot the prediction error of three different methods.
Figure 9. Boxplot the prediction error of three different methods.
Preprints 80752 g009
Table 1. Parameters to test the fabric samples.
Table 1. Parameters to test the fabric samples.
Texture 100% cotton twill
Size 10*25cm
Yarn count 40 counts
Density 133*72
Color pink, purple, yellow, blue, orange, green
Table 2. The results of linear regression analysis between independent and dependent variables.
Table 2. The results of linear regression analysis between independent and dependent variables.
Model Unstandardized Coefficients Standardized Coefficient t Significance (p-Value) Covariance Statistics
B Standard Error β Tolerance VIF
Constant -0.292 0.048 -6.088 0.000
Δ L -0.042 0.009 -0.550 -4.730 0.000 0.744 1.344
Δ a -0.028 0.014 -0.281 -2.037 0.046 0.527 1.896
Δ b -0.001 0.012 -0.008 -0.057 0.954 0.498 2.010
Table 3. The analysis of the third-order polynomial fitting results.
Table 3. The analysis of the third-order polynomial fitting results.
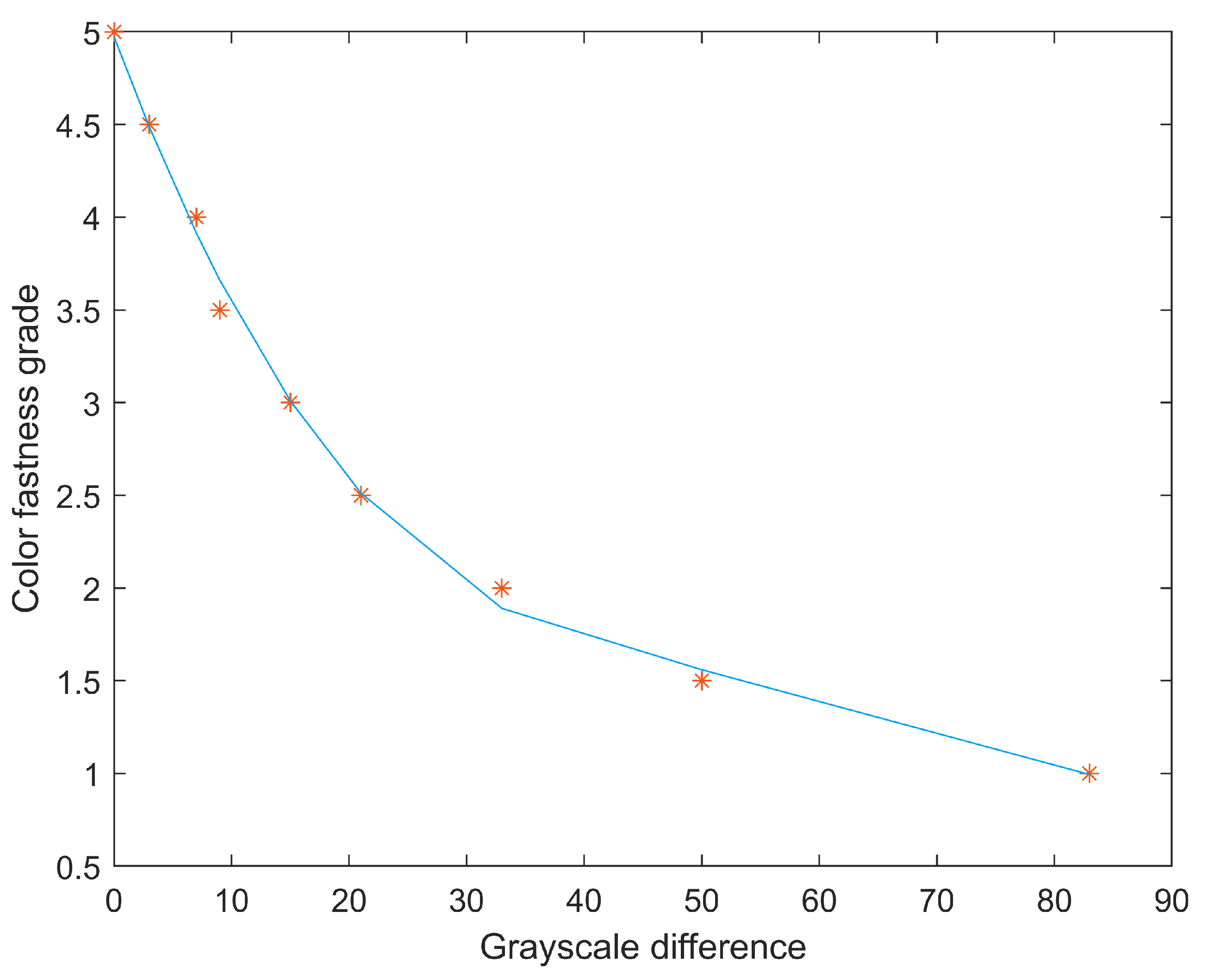
Curve Fitting Fitting Equation Correlation coefficient
third-order polynomial D = p1*x 3 + p2*x 2 + p3*x + p4 R 2 =0.99
p1 = -1.72e-05
p2 = 0.0029
p3 = -0.17
p4 = 4.97
Table 4. Color fastness grade of testing samples acquired from different methods.
Table 4. Color fastness grade of testing samples acquired from different methods.
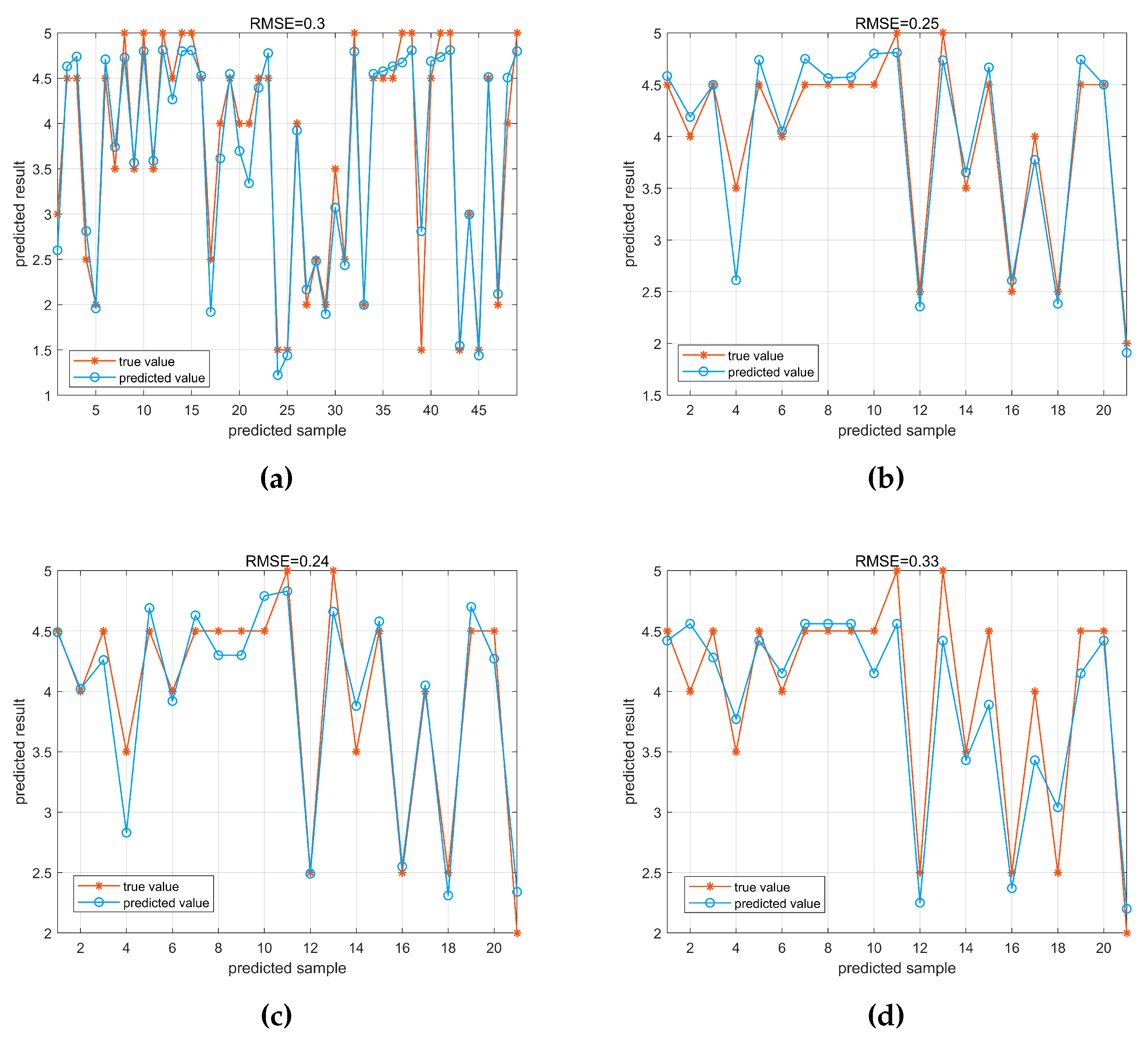
Sample No. Visual result BP Model Color Difference Conversion Curve Fitting
1 4.5 4.58 4.49 4.42
2 4 4.18 4.02 4.56
3 4.5 4.49 4.26 4.28
4 3.5 2.61 2.83 3.77
5 4.5 4.73 4.69 4.42
6 4 4.04 3.92 4.15
7 4.5 4.74 4.63 4.56
8 4.5 4.56 4.3 4.56
9 4.5 4.57 4.3 4.56
10 4.5 4.79 4.79 4.15
11 5 4.81 4.83 4.56
12 2.5 2.35 2.49 2.25
13 5 4.73 4.66 4.42
14 3.5 3.65 3.88 3.43
15 4.5 4.66 4.58 3.89
16 2.5 2.60 2.55 2.37
17 4 3.77 4.05 3.43
18 2.5 2.38 2.31 3.04
19 4.5 4.74 4.7 4.15
20 4.5 4.50 4.27 4.42
21 2 1.91 2.34 2.2
Table 5. Test sample error.
Table 5. Test sample error.
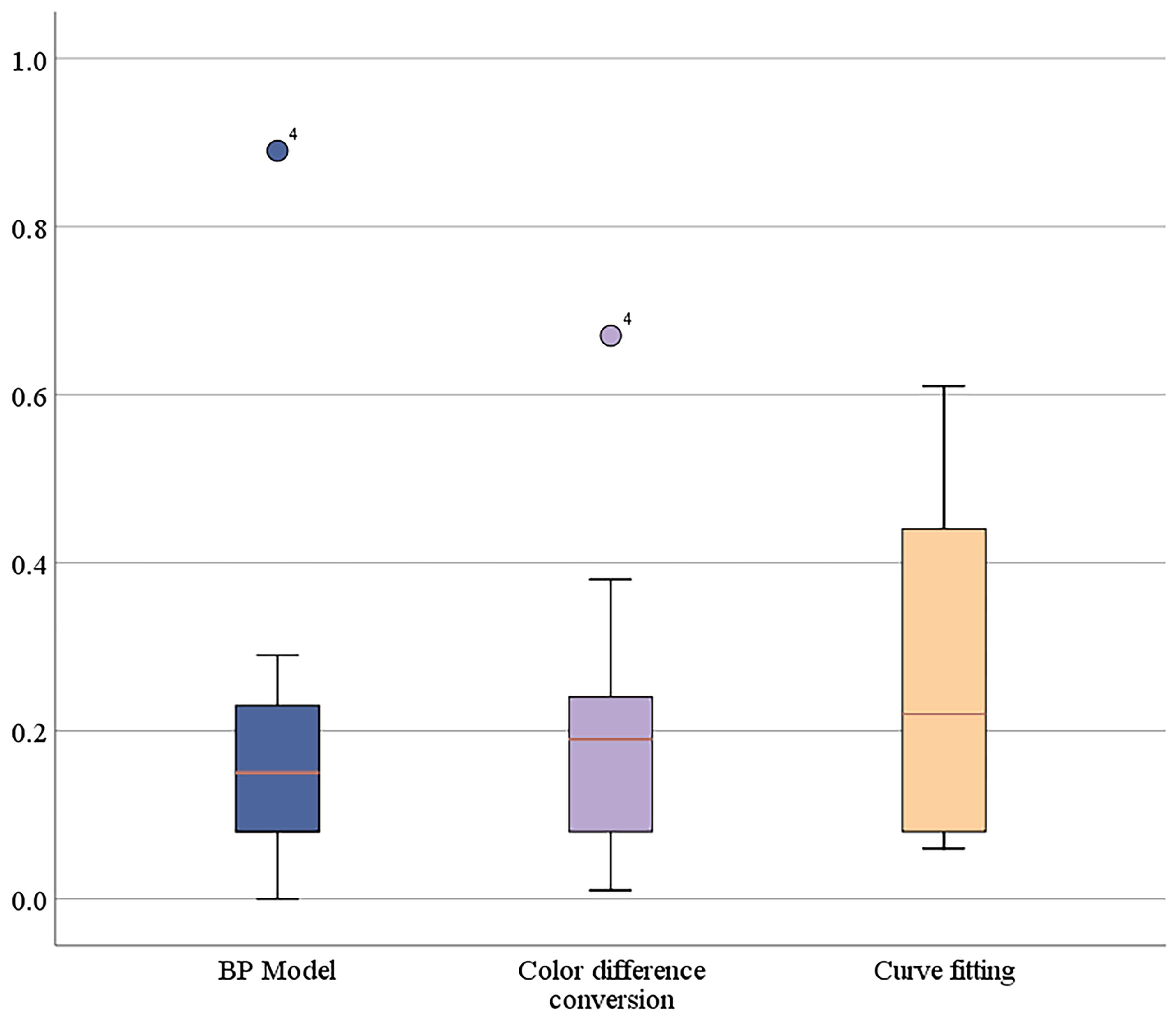
BP Model Color Difference Conversion Curve Fitting
RMSE 0.25 0.24 0.33
Maximum Error 0.89 0.67 0.61
Minimum Error 0 0.01 0.06
Median Error 0.15 0.19 0.22
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated