Aqueous Binary Mixtures of Stearic Acid and Its Hydroxylated Counterpart 12-Hydroxystearic Acid: Fine Tuning of the Lamellar/Micelle Threshold Temperature Transition and of the Micelle Shape

This study examines the behavior of stearic acid (SA) and 12-hydroxystearic acid (12-HSA) aqueous mixtures as a function of temperature and 12-HSA/SA molar ratio (R). Whatever R, the system exhibits a morphological transition at a given threshold temperature, from multilamellar self-assemblies at low temperature towards small micelles at high temperature, as shown by a combination of transmittance measurements, Wide Angle X-ray diffraction (WAXS), small angle neutron scattering (SANS) and differential scanning calorimetry (DSC) experiments. Such transition originates from the melting of the crystallized fatty acids within the lamellar phase. The precise determination of the threshold temperature, which ranges between 20°C and 50°C depending on R, allows for the construction of the whole phase diagram of the system as a function of R. At high temperature the micelles that are formed are oblate for pure SA solutions (R = 0) and prolate for pure 12-HSA solution (R = 1). In the case of mixtures, there is a progressive continuous transition from oblate to prolate shape when increasing R, with micelles that are almost purely spherical for R = 0.33.

Keywords:

Subject: Chemistry and Materials Science - Physical Chemistry

1. Introduction

A current trend in the field of Soft Matter is the design of so-called “smart” stimuli-responsive materials whose macroscopic properties can be tuned over a large range on demand and in a controlled manner. This stems from the fact that the structures of the self-assemblies formed by the elementary bricks of the soft matter systems (surfactants, nanoparticles, polymers, liquid crystals) can strongly reorganize themselves under the effect of slight variations of their environment, which in turn tune their macroscopic properties, in particular the rheological ones. The desired macroscopic changes can then be triggered either by a change of composition (pH, ionic strength, etc…), either by an external stimulus (light, magnetic field, shear, ultrasounds, etc.) or by temperature or pressure.

In such a context, the possibility to design stimuli-responsive foams or emulsions has attracted a lot of interest lately. The goal is to get a fine control of the lifetime of these metastable systems through the physico-chemical parameter(s) chosen to trigger their stability. Depending on the targeted application, this necessitates to either arrest or speed up the three main mechanisms that drives their destabilization, namely the Oswald ripening, the coalescence and the drainage. This passes thus by both a fine control of the elasticity of the layer at the interface (air/water in foams or water/oil in emulsions) and by the viscosity of the aqueous phase for the drainage.

As bio-based, non-toxic and renewable molecules, fatty acids, that are carboxylic acids with an aliphatic chain and that are used since antiquity as surfactants, are tools of choice for the conception of such stimuli-responsive foams or emulsions. The first way to play with is the Krafft temperature, as the formation of a stable non-aqueous foam by a Pickering approach has been achieved by the irreversible adsorption of fatty acids crystals below their melting temperature,^1,2 following a concept originally developed on SDS foams.³ The most common use of fatty acids is however when they are solubilized in aqueous solutions below their Krafft temperature, which necessitates to lower it in the case of fatty acids with long saturated chains (C14 to C22) that are not soluble at room temperature with conventional metallic counterions. Such a solubilization step can be achieved by the use of organic counterions, usually an alkyl amine, that makes ion pairing with the carboxylated heads^4–6 or with cationic surfactants that form catanionic self-assemblies.⁷ In the case of organic counterions, the main physico-chemical parameters that tune both the properties of the monolayers and the morphologies of the self-assembled aggregates in aqueous solution are the pH and the temperature. Both play on the packing parameter of the fatty acid molecules. The pH controls the ionization state of the carboxylated heads, and therefore the competition between H-bonding of the protonated COOH heads and electrostatic repulsions between the deprotonated COO- heads. For its part, temperature controls the state of crystallinity of the fatty chains. Recent studies have then shown that the self-assembled aggregates based on long fatty acid chains display a broad polymorphism as a function of these 2 parameters, mainly lamellar at low pH and/or low temperature (facetted 2D objects, planar lamellar phases, unilamellar or mutilamellar vesicles)^8–11 and spherical micelles at large pH and/or temperature,^8–14 with wormlike aggregates in intermediate regime. Stimuli-responsive foams or emulsions based on long fatty acid chains have thus mostly relied on these two parameters.¹⁵ In the case of pH, its modification often goes through the addition of an additional species within the liquid phase, which is problematic once foams or emulsions are formed. This drawback can be circumvented for fatty acids in presence of CO₂ (gas) that may decrease the solubility of stearic acid and have given rise recently to the design of many CO₂-stimulable systems.^16,17 pH change, and therefore foam stability, can also be triggered through the UV irradiation of a photoacid generator added in aqueous solution from the beginning.¹⁸

Compared to saturated ones, hydroxylated fatty acids with long chains have a huge potential since the hydroxyl function along the alkyl chain bring 3 useful properties to the molecules. First, a second hydrophilic center that enable them to adopt an unconventional conformation at the air/water interface if the OH group is located sufficiently far from the head group.^19–21 Second, the possibility to make an hydrogen bond network within the monolayer and to make it therefore very elastic.²¹ Third, it makes them chiral which enables the formation of self-assemblies with unconventional morphologies in aqueous solution, such as twisted ribbons²² or multi-lamellar tubes that come from the rolling of helical ribbons in the case of 12-hydroxy stearic acid (12-HSA).²³ Such a structure has also been recently described in literature from complexes of ionic surfactants and cyclodextrins.^17,24–27

These multi-lamellar tubes of 12-HSA are made of a few (~3-6) stacked bilayers separated by a lamella of water. These lamellas roll up in tubes of micrometer diameter size and of length 10 µm or more. The tubes swell over a wide range of temperature. They can be obtained from a large set of counterions,^28,29 in various physicochemical conditions³⁰ and they melt into small micelles with a threshold melting temperature²⁸ that depends on the counterion/12-HSA ratio.²⁹ The transition from multi-lamellar tubes to micelles makes them a tool of choice for to the design of thermo-responsive systems since the viscosity in the tubes regime is larger by 3 to 5 orders of magnitude, depending on swelling, than that of the regime of small micelles at high temperature.^29,31 This has enabled to design the first ultra-stable and responsive aqueous foams reported in literature,¹⁵ the drainage being started on demand from the drop of viscosity. The temperature of destabilization is tunable by an appropriate choice of the type of counterion and counterion/12-HSA ratio.³² Besides, it has been demonstrated that the 12-HSA tubes can be loaded by molecules of biomedical interest, which makes them also very appealing for the design of drug release triggered systems.³³.

One step further for the design for the thermostable long-fatty acids chains-based architecture would be the design of a system that would be responsive to both CO₂ and temperature and for which both the rheological surface properties of the monolayers and the rheological bulk properties of the self-assemblies in aqueous solution would be tunable. With this in mind, we have recently studied mixtures of 12-HSA and its counterpart stearic acid (SA), that differ only the hydroxyl on the 12^th carbon of the C18 alkyl chains of 12-HSA, so that the heads have a single state of ionization, which is a prerequisite for a further triggering by pH. Monolayers of mixtures have a rich behavior since their 2D phase, established by surface pressure versus surface area isotherms, show a eutectic point with a good miscibility.³⁴ Even if the surface rheological properties of the mixed monolayers have not yet been established to the best of our knowledge, it is likely that their surface elasticity will be largely dependent on the ratio between the two fatty acids owing to hydrogen bonds that can be formed between 12-HSA molecules. In aqueous solution, when mixtures are solubilized by ethanolamine counterions, we have shown recently that the self-assemblies display a very broad polymorphism depending on the ratio between the two fatty acids.³⁵ When doping the SA molecules by a low content of 12-HSA molecules (less than 25%), the planar lamellar self-assemblies that are formed in pure SA solutions turn into complex multi-lamellar facetted structures with planar domains bounded by spherical curved domains that may result from a local phase separation. When doping the 12-HSA molecules by a low content of SA molecules (less than 25%), the multi-lamellar long tubes that are formed in pure 12-HSA systems are preserved but the length of the tubes decreases upon addition of SA. At intermediate ratios, spectacular long 1-D multilamellar objects made of tubes bounded by helical ribbons solutions are formed. The transition between the different regimes of morphologies is accompanied by a change of their viscoelastic properties. We extend here this first study to a wide range of temperatures in order to elaborate the whole phase diagram of the SA/12-HSA system, focusing on the transition between lamellar self-assemblies and micellar assemblies, coupling macroscopic observations, transmittance measurements, Differential Scanning Calorimetry (DSC) , Wide Angle X-Ray scattering (WAXS) and Small Angle Neutron Scattering (SANS).

2. Results

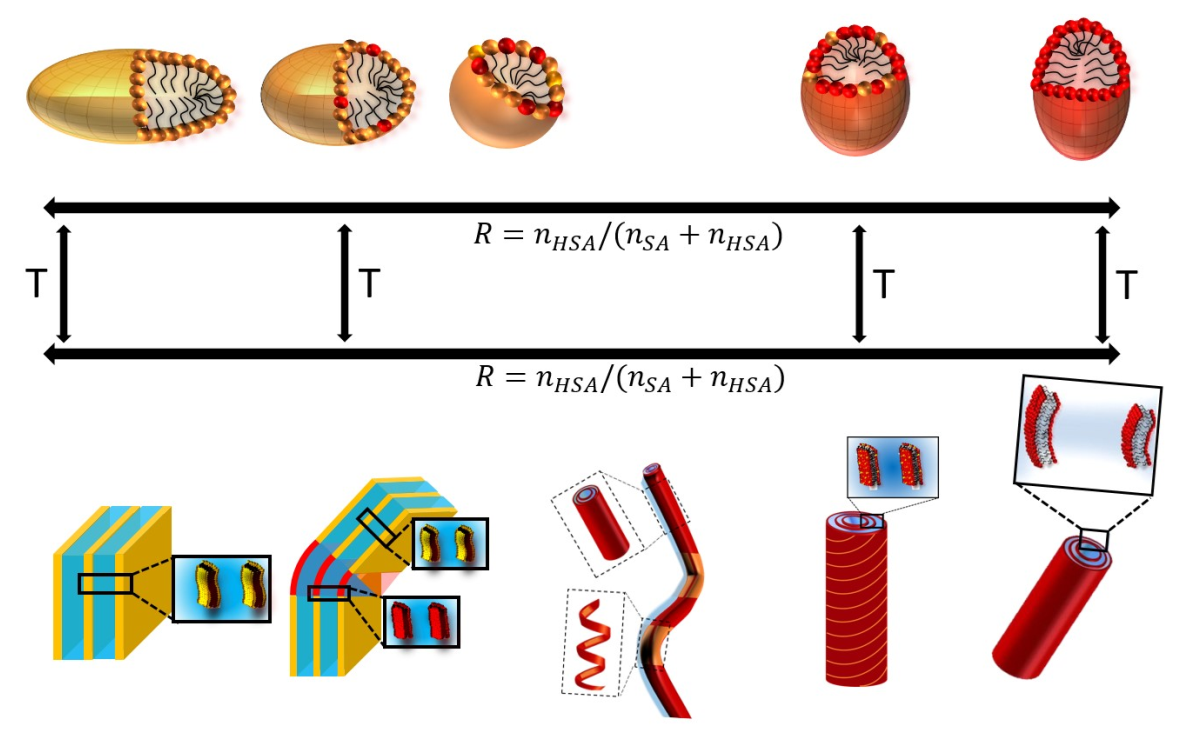
2.1. Macroscopic Behavior and Determination of Threshold Temperature

As in reference,³⁵ we focus on aqueous mixtures of 12-HSA and SA molecules with an overall content of 2wt% of fatty acids that are solubilized in water thanks to the use of ethanolamine as counterion with a molar ratio surfactant/counter ion r of 0.2. The ratio of 12-HSA to the total concentration of fatty acids R defined as R=n_12HSA/(n_SA+n_12HSA) is probed over the full range varying from R = 0 to R = 1. As described in the Materials and Methods section, the protocol enabling the solubilization of stock solutions of both SA and 12-HSA in water in presence of ethanolamine always involve a step where the fatty acid/ethanolamine mixture is heated at 70°C. The pH of the samples is 10.85 ± 0.15 in H₂O, meaning that all the fatty acids bear a carboxylate head.³⁵ The solutions are then macroscopically limpid with an apparent viscosity close to that of water. This behavior is consistent with literature that shows that either SA⁸ or 12-HSA²⁸ are self-assembled in small micelles at such temperature. The stock solutions are then mixed at 70°C to reach the targeted R. The mixtures stay limpid and not viscous after this final mixing step for every R under scrutiny.

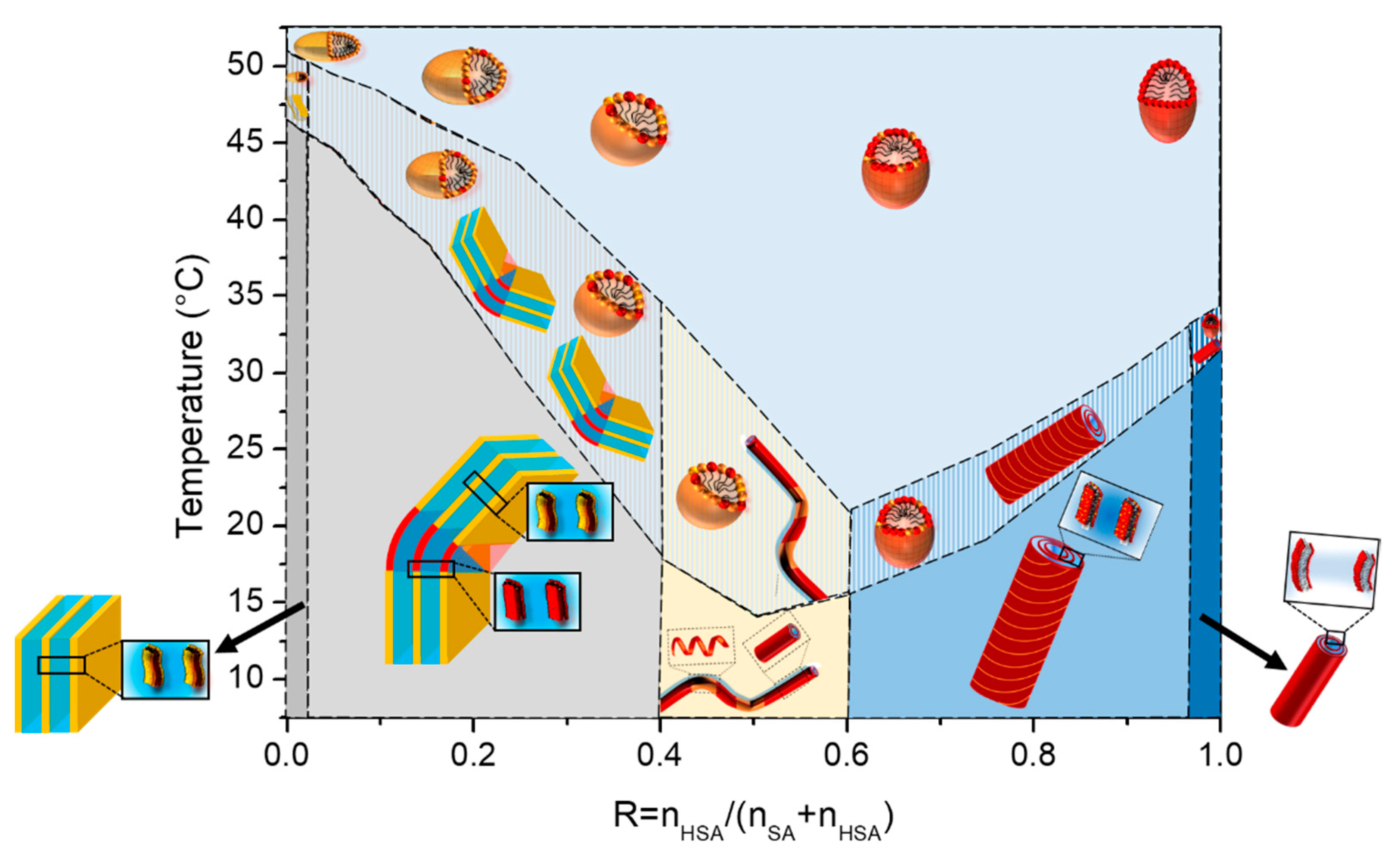
When the mixtures are cooled down to 20°C, they undergo a transition from limpid to turbid, along with an increase of viscosity, at a given temperature that depends on R. 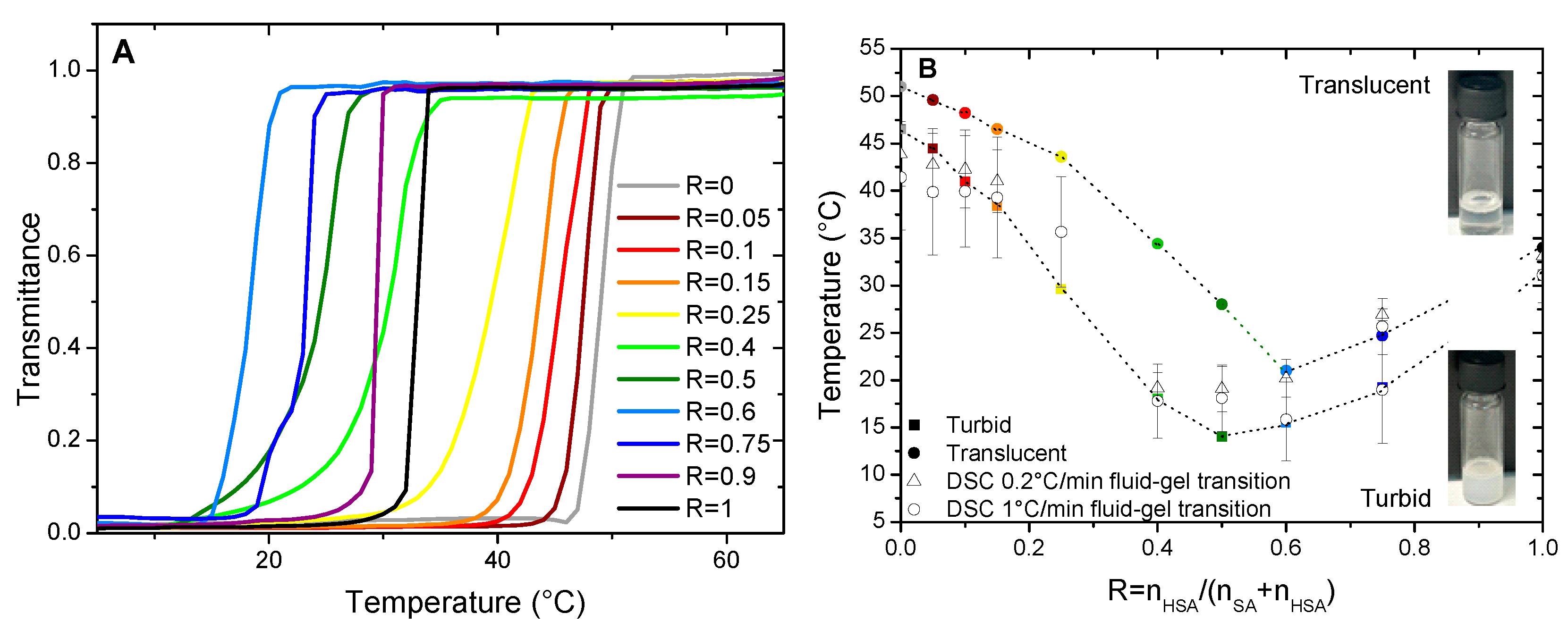The turbidity and change of viscosity arise from the formation of multilamellar self-assemblies of different geometries (planar lamellar phases, multilamellar tubes or supramolecular assemblies containing both of them) that are large enough to scatter visible light.³⁵ The temperature of transition threshold between the limpid and turbid phases, as identified by visual inspection, depends however strongly on R. In order to determine it and establish the macroscopic state diagram of the system, we have measured the transmittance T of the samples at 450 nm on a UV-Vis spectrometer as function of temperature. Whatever the sample, T does not decrease sharply from 100% to 0% at a well-defined temperature upon cooling but over a temperature range of a several degrees with a magnitude that depends on the cooling rate. The lower the cooling rate, the sharper is the transition (compare Figure 1A obtained with the ramp of 0.2°C/min with Figure S1 obtained with the ramp of 1°C/min). Besides, the onset temperature of appearance of turbidity is as high as the cooling rate is low. The measurement of T over a cooling/heating cycle also shows a strong hysteresis with an onset of appearance of turbidity at a lower temperature during the initial cooling step than for the following heating step (see Figure S2). It takes thus an important time for the system to reach a steady state close to equilibrium. The transition appears thus to occur over an extended range of temperature where some self-assembled objects that scatter light coexist with some other ones that do not. The measurements obtained at the lowest cooling rate allow to build a state diagram for the system that is divided into 3 regions (Figure 1B): at low temperature the turbid phase; at intermediate temperature the regime where the phase transition takes place; and the translucent phase at high temperature. It is likely that the intermediate region of coexistence is only a kinetic feature and would vanish it the state diagram would have been built with an infinitely slow cooling rate. The turbid/transition threshold corresponds to the temperature where transmittance T falls to 0 and the transition/translucent one to the temperature where T starts to decrease from 1.

For the pure HSA solution (R = 1), the onset of appearance of turbidity occurs at 35°C, in accordance with reference²⁹ where the temperature of the micelles/multilamellar tube transition was determined at such temperature for an r of 0.2. The temperature threshold occurs by contrary at a much larger temperature close to 51°C for the pure SA system at R = 0 which is consistent with the value obtained by Xu and collaborators⁸ in which the reported temperature of transition is 50°C. In between, three different regimes can be identified as function of R. At large content in SA (from R=0.05 to R=0.25) the transition temperature decreases slightly and continuously from the R = 0 case upon the progressive introduction of HSA molecules, with an overall decrease of about 7°C. Symmetrically, at large content in HSA (from R=0.9 to R=0.75), the transition temperature slightly decreases upon the progressive introduction of SA molecules; with an overall decrease of about 10°C from the R = 1 case. At intermediate R, the transition temperature drops strongly upon increase of R, with a decrease of ~ 15°C from R=0.25 to R=0.4 - R=0.6, in order to bridge the two regimes of temperature threshold where one of the two fatty acids is in large excess. It is worth noting that the phase transition occurs over a much larger temperature range for such regime of intermediate ratio R where it is more difficult for the system to reach equilibrium.

2.2. DSC Measurements

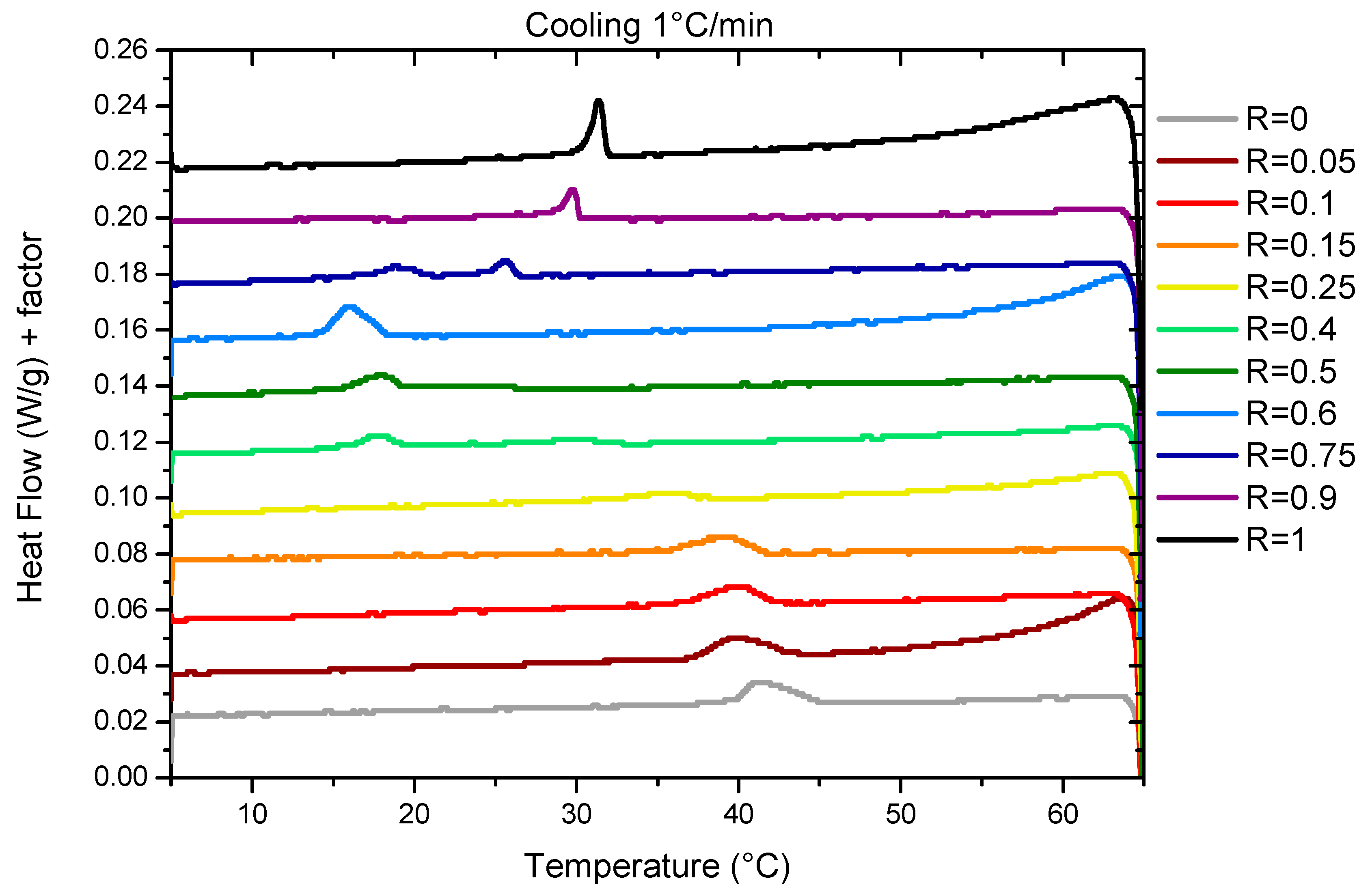
The temperature of transition threshold was also assessed by DSC measurements. Measurements were performed with two different ramps of 0.2°C/min and 1°/min. We represent results obtained during cooling at 1°C/min (Figure 2) for which the thermal events are easier to evidence than those obtained at 0.2°C/min that have a poorer resolution due to experimental limitations (Figure S4). As already explained for transmittance measurements, there is a small temperature offset between both set of data associated to the slow kinetics that is taken by the system to reach equilibrium. The temperature of transitions for the two cooling rates are represented on Figure 1B For the sake of comparison with transmittance, we have chosen to represent here data obtained upon cooling. Heating ramps have been also performed (Figures SI3 and SI5) and evidence a large hysteresis between cooling and heating cycles, as for transmittance measurements.

For R=1 (pure 12-HSA solution), there is one endothermic peak between 30°C and 35°C whose shape and width is similar to those obtained in reference⁷ for an ethanolamine/fatty acid ratio r = 0.2, where it was showed that it is associated to both the Lα-Lβ fluid-gel transition of the fatty acids and the transition of multi-lamellar tubes into micelles. For such an r, when all heads are on their COO^- form, the melting of the fatty acid chains induce then the morphological transition by changing the packing parameter. For larger r, when part of the heads are on their COOH form, it was shown that Lα-Lβ fluid-gel transition and the melting of multi-lamellar tubes into micelles give rise to two distinct endothermic peaks on enthalpograms because H-bonds that remain within fluid fatty acids above the Lα-Lβ fluid-gel transition have to be broken to allow the transition from tubes to micelles.

For R = 0 (pure SA solution) we identify a broad peak between 40 and 45°C (Figure 2). This is consistent with previous results by Xu et al.⁸ for pure SA solutions solubilized by ethanolamine that evidenced a lamella-micelles transition at around 42°C by coupled DSC and cryo-TEM measurements at a SA concentration (1.5wt%), close to that of our current study (2wt%).

In the case of mixtures, there is only one broad peak whatever the R under scrutiny except for R=0.75. This suggests for all these ratio R the presence of a single transition corresponding to the melting of both fatty acids and mesophases, by analogy to the R = 1 and R = 0 cases. When R varies, the intensity of the peaks and their width evolves. The peak broadening is probably associated to the time necessary to reach equilibrium, that differ from one R to another, as we chose to measure all the samples with the same temperature ramp to compare their behaviors in similar conditions. For some ratios the melting temperature can be shifted up to 5°C by reducing the ramp at 1°C/min down to 0.2°C/min. Indeed, the time necessary to reach a turbid steady state after crossing the limpid-turbid transition is very dependent on the ratio R, as shown by turbidity measurements. At the intermediate R, when the peak becomes hardly visible in the DSC experiment, it is much slower than for other R.

Three different regimes can be identified depending on R. Firstly, at low R, (R=0, R=0.05, R=0.1, R=0.15, R=0.25) the peak decreases in intensity and widens at the same time. The transition temperature decreases slightly from 42°C for R=0 to 36°C for R=0.25. At R=0.25, the peak is hardly detectable at a ramp of 1°C/min and not detectable at 0.2°C/min. This may be due to a broadening of the melting peak to such an extent that apparatus is no longer sensitive enough to enable its measurement. At intermediate R (R=0.4, R=0.5, R=0.6), there is a large peak between 15°C and 20°C whose intensity increases with R. At high R (R=0.9, R=1), where mixtures form multi-lamellar tubes at 20°C,³⁵ a rather broad but well-defined melting peak is observed whose intensity increases with R. The transition temperature also increases when the proportion of HSA increases. For all these ratios, the fact that there is only one single transition, as in the case of pure 12-HSA at r=0.2, suggests that it corresponds to both the transition Lα-Lβ and the multilamellar - micellar transition. For R = 0.75 we observe two different peaks. The comparison with other sample at different R tends to indicate that there are two different structures that are melting at different temperature in the sample. At ambient temperature, we already noticed that the solution is a mixture of two different fatty-acids architectures for such ratio,³⁵ with multi-lamellar tubes co-existing with multi-lamellar ribbons. We hypothesize that the sharper peak at 26°C corresponds to the melting of multilamellar tubes, similarly as for the higher R, whereas the broad peak at 20°C may correspond to the melting of ribbons.

Temperatures of transition obtained by DSC do match the threshold temperatures obtained by transmittance measurements, as shown in Figure 1B. It demonstrates that the thermodynamical transition evidenced by DSC corresponds to the melting of large self-assembled structures.

2.3. Wide Angle X-Ray Scattering (WAXS)

WAXS measurements were performed to determine if the fatty acid chains within the bilayers are fluid or in a gelled state for the whole range of HSA/SA mixtures at 36°C and 50°C (Figure 3). For the sake of comparison, they are compared with the data at 20°C we already obtained in³⁵ that showed some Bragg diffraction peaks and demonstrates that the fatty acids are in a crystalline gel state in all cases. At 50°C, whatever R, the diffractograms do no longer show these Bragg peaks, revealing a completely fluid assembly of the different fatty acids. A 36°C, the diffractograms show either the signature of crystalline fatty acid self-assembly with the presence of a Bragg peak or those of fatty acids in a fluid state, as observed at 50°C, depending on the ratio R.

Three different regimes of R can be distinguished. At low R, from R=0 (pure SA) to R=0.25, a Bragg peak is observed at 20°C for q_peak = 1.534 Å^-1. As the temperature is increased to 36°C, it is still present but this position is shifted towards lower q (q_peak = 1.520 Å^-1). When there is a majority of SA in the mixture, the main crystalline structure is the one of the pure SA sample at both 20°C and 36°C. However, there are noticeable changes in the crystalline structures formed when the temperature is increased. This is likely due to a change in the SA crystalline structure, not disturbed by the addition of a small amount of HSA molecules. At 50°C all samples do not longer present any crystalline peak. The crystal-fluid transition of the fatty acids occurs thus between 36°C and 50°C in this regime, exactly in the temperature range where the endothermic peak was observed with DSC measurements. This indicates that the transitions evidenced in the enthalpograms do correspond to the crystal-fluid transitions. As R increases (for R from 0.4 to 0.6), the crystalline structure obtained at 20°C with Bragg peaks of low intensity, i.e. crystalline domains of low size, disappear at 36°C and 50°C. This is again consistent with the temperature transitions obtained by DSC. There are smaller crystalline parts in the mixed fatty acid mixtures. For R≥0.75, the two Bragg peaks present at 20°C, similar to those of the crystalline phase of fatty acids in the pure 12-HSA sample (R = 1) forming the multilamellar tubes, are no longer observed at 36°C and 50°C, in accordance with the temperature transitions thresholds (Figure 1(B)) that are all below 35°C for this regime of R.

In summary, as previously observed for pure SA and 12-HSA solutions, the crystalline structures of the gelled bilayers at 20°C of the mixed solutions melt between 20°C and 50°C depending on R.

2.4. Structure of Samples by SANS

The structure of self-assemblies was determined by SANS. All the samples were prepared in D₂O while the data obtained with other experimental techniques were obtained with samples prepared in H₂O. This isotopic exchange would possibly shift the transition temperatures. We have checked that this is not the case by transmittance measurements (Figure S6) that demonstrates that the transition temperatures are similar in D₂O and H₂O solutions.

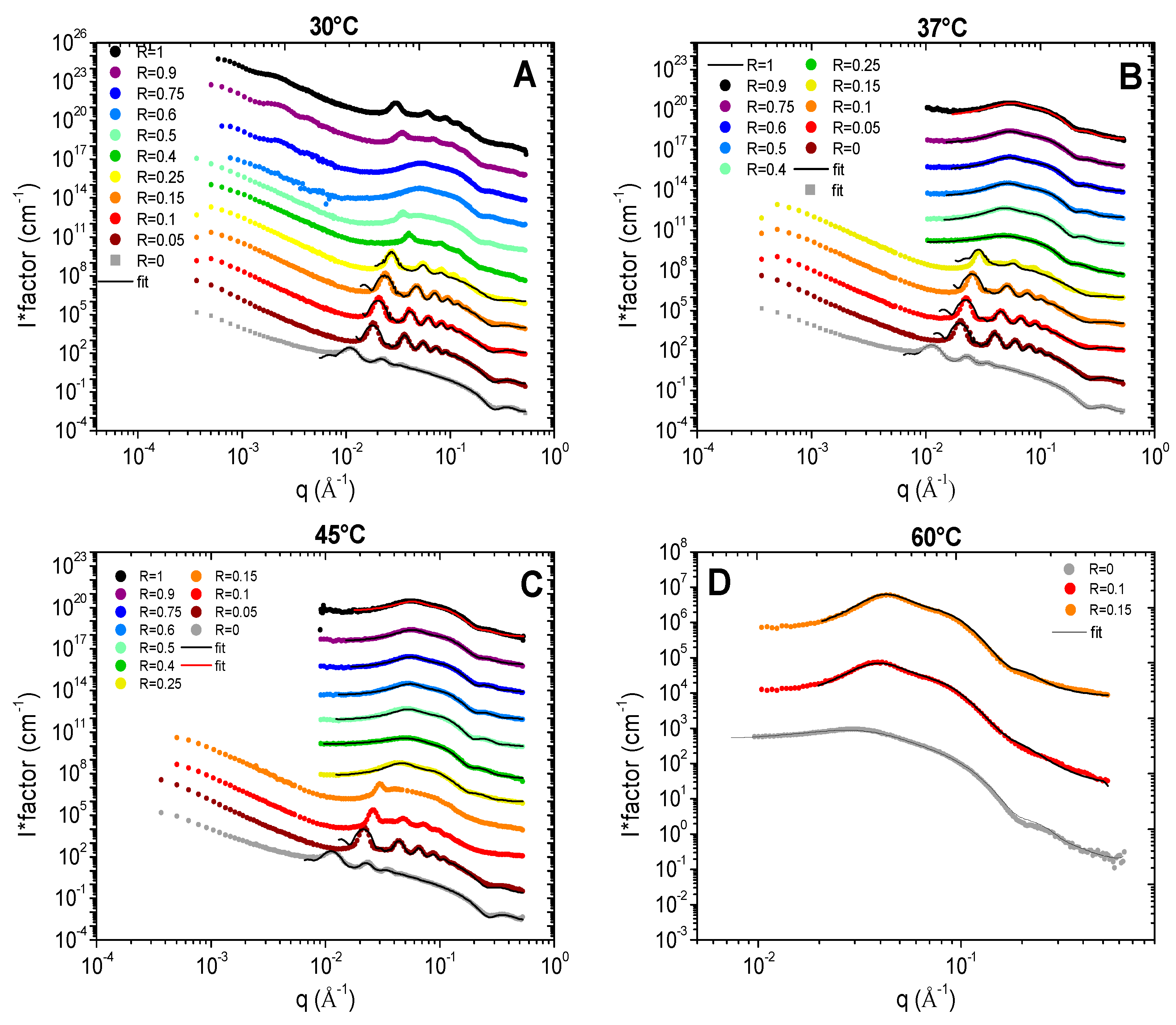
All the results are represented on Figure 4 for each temperature (30, 37, 45, 60°C). Depending on R and/or the temperature, the scattered intensity shows 3 different behaviors: (i) at low temperature, when samples are turbid white, the scattering is characteristic of multilamellar self-assemblies; (ii) at high temperature, for translucent samples, the scattering is characteristic of small micelles interacting through repulsive interactions and (iii) in the transition domain at intermediate temperature, the scattering is typical from the combination of scattering of the two types of objects. The turbidity arises thus from the formation of multi-lamellar objects that have a sufficiently large size to scatter light. When all or most of the surfactant molecules are involved in small micelles, the sample is translucent and starts becoming partially turbid as soon as a few molecules make lamellar objects. The translucent/turbid transition threshold of the state diagram corresponds thus to the onset of formation of these first multi-lamellar objects.

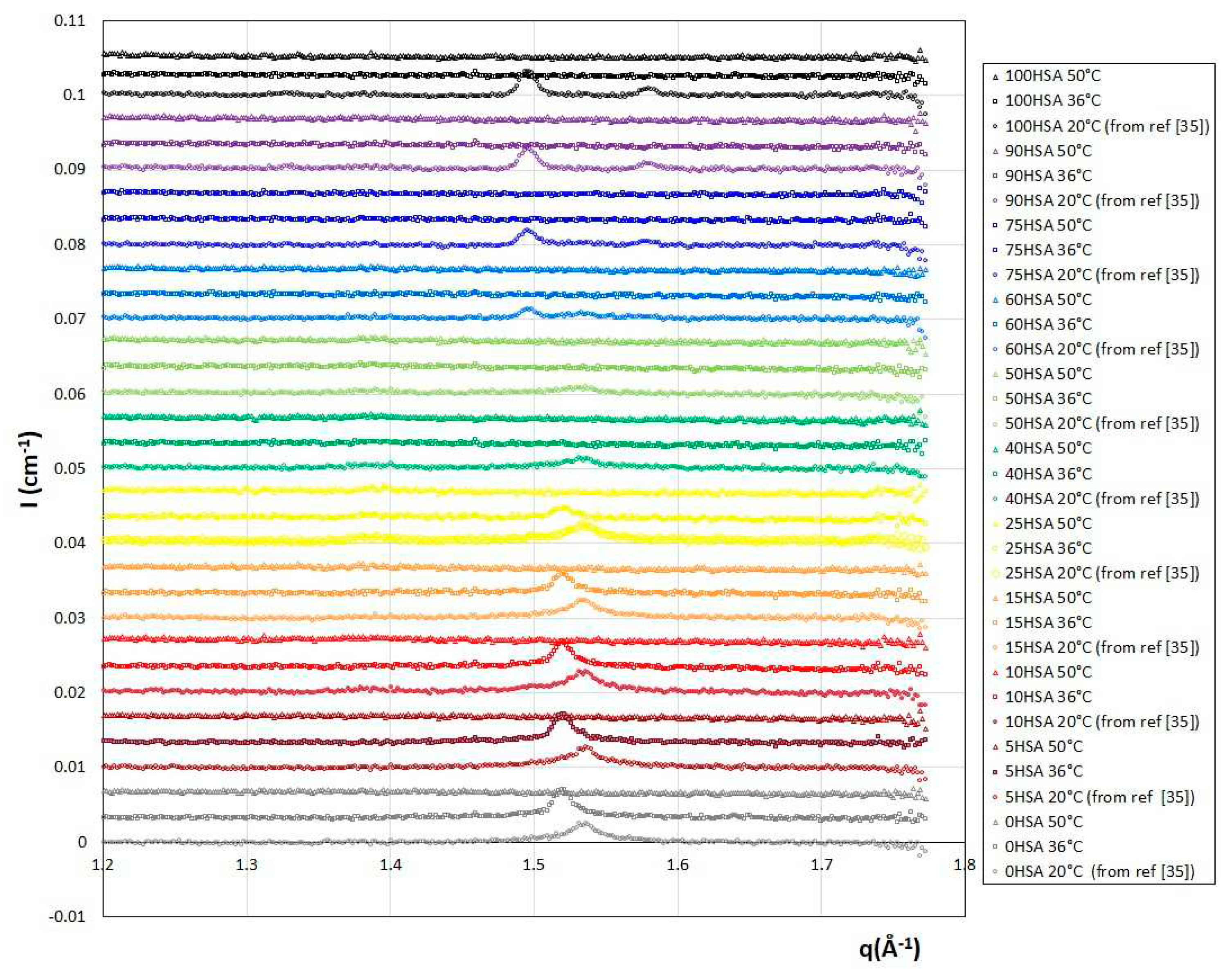
At low temperature, we recover the scattering of the different multilamellar self-assemblies that were obtained at 20°C and exhaustively described in reference.³⁵ For all samples, there are several Bragg peaks associated with the interlamellar distance at intermediate q and an oscillation at q ~ 0.25 Å^-1 originating from the lamella form factor at large q. Only the low q part differs from one self-assembled structure to another: q^-2 for planar lamella at R = 0, q^-4 at low R for lamellar facetted structures with planar domains bounded by spherical curved domains, q^-3 for mixtures of helical ribbons and multilamellar tubes and q^-3 with an oscillation associated radius of the tubular shape for multilamellar tubes. The scattering curves were thus fitted in the intermediate and large q region following the same approach we used in reference³⁵ by a model proposed by Nallet et al³⁶ to determine the structural parameters of lamella (thickness, d-spacing, rigidity represented in Figure 5). It considers a form factor of the lamella and a structure factor between lamella for which both the number of stacked bilayers and the Caillé parameter (η), accounting for the thermal fluctuations of the bilayers, were adjusted. This model enables to fit satisfactorily all the data for which multi-lamellar objects were formed, respectively for all R except from 0.4 to 1 at 30°C (Figure 4(A)), all R ≤ 0.25 at 37°C (Figure 4B) and all R ≤ 0.15 at 45°C (Figure 4C). Although the ratios 1, 0.9 and 0.4 at 30°C present some Bragg peaks that refer to multi-lamellar objects, at intermediate q they start concomitantly to present the curved shape of a micelle, thus showing that solutions are containing both lamellar objects and micelles. For this reason, these scattering curves were not fitted by the sum of a Nallet model for the lamella and of interacting micelles, as there would be too many free parameters in the modelling to provide an unambiguous result.

All the results of these fits are represented on Figure 4. The low q part of the curves was not fitted as it displays different behavior from one sample to another (q^-2 versus q^-3 versus q^-4). Please note that the results obtained at R=0.4 were not analyzed. Indeed, we showed in³⁵ that the sample at 20°C was not homogeneous at the millimetric scale at 20°C, with a possible phase separation, which gives a strong uncertainty on the effective concentration that is actually probed by the neutron beam.

Whatever R, the increase in temperature does not change the morphology of the self-assembly for a given R. As was observed in the case of pure 12-HSA solutions in,²⁸ the increase in temperature is accompanied by a slight decrease in the inter-lamellar distance (Figure 4A) while the Caillé parameter does not evolve much with temperature except for the ratio R=0.25 (Figure 4B). The thickness of the lamella does not evolve with temperature and remains constant around 23 Å for each of the R ratios. This thickness is close to the size of a fatty acid (21 Å)²⁹ and corresponds to interdigitated lamellar phases. This result is noticeable for samples with low R (R ≤ 0.25). Indeed, when self-assemblies are predominantly formed of SA, WAXS measurements reveal that the lattice parameter of the crystallized fatty acids evolve with temperature. This local modification of the structure is not accompanied by a significant change of the thickness of the lamella. Structural reorganization occurs thus in-plane.

Let us now discuss the scattered curves obtained for all R ≥ 0.25 at 45°C and for R=0, R=0.1 and R=0.15 at 60°C for which the Bragg peaks associated to the lamella self-assemblies have completely vanished (Figure 4C,D respectively). They are completely different from those at 20°C and are typical of the one of small micelles interacting through repulsive interactions, consistently with literature. They display three main features: (i) at very low q values (q < 0.01 Å^–1), the scattering intensity decreases when q decreases, showing that the isothermal osmotic compressibility (χ_T ) of the system is very weak due to electrostatic repulsions; (ii) at intermediate q, it shows a strong correlation peak at q^*, ranging between 0.02 Å^–1 and 0.06 Å^–1 depending on the sample, that correspond in direct space to the mean distance between micelles (2π/ q^*); (iii) for q > 0.1 Å^–1, a Porod like decay in q^-4 stemming from the 3-D character of the micelles with a marked oscillation at ~ 0.25 Å^–1 associated with the first minima of the form factor.

We assume in a first time that micelles are spheres. Since they are centrosymmetric objects, the scattering intensity I(q) can be written like:

I (q) = Φ {(ρ_{f a t t y_a c i d} - ρ_{D 2 O})}^{2} V P (q) S (q)

(1)

where Φ is the volume fraction of micelles, ρ_{fatty_acid} and ρ_D2O are the respective neutron scattering length density of the fatty acids (considering in first approximation that it is similar for 12-HSA and SA) and of D₂O, V is the volume of the micelle; P(q) is the normalized micelle form factor; S(q) is the inter-micelles structure factor.

The low compressibility of the samples, associated to a strong correlation peak revealing an homogeneous distribution of self-assembled objects within the sample, highlight the presence of strong repulsions between micelles. Since the pH of all the solutions is around 10.85 ± 015, each fatty acid bears a carboxylate head. The micelles are thus strongly negatively charged, and the repulsions are of electrostatic origin. The structure factor S(q) can thus be fitted by a model proposed by Hayter and Penfold for charged 3D objects,³⁷ that consider a Yukawa potential describing electrostatic interactions following DLVO theory in the mean spherical approximation,³⁸ as will be shown later on.

At large q, S(q)_q→∞ = 1 by principle. In practice S(q) ~ 1 here for q > 0.1 Å^–1, which enables to decouple the structure factor and form factor during fitting procedure and get an accurate description of the form factor without any assumption of the structure factor.

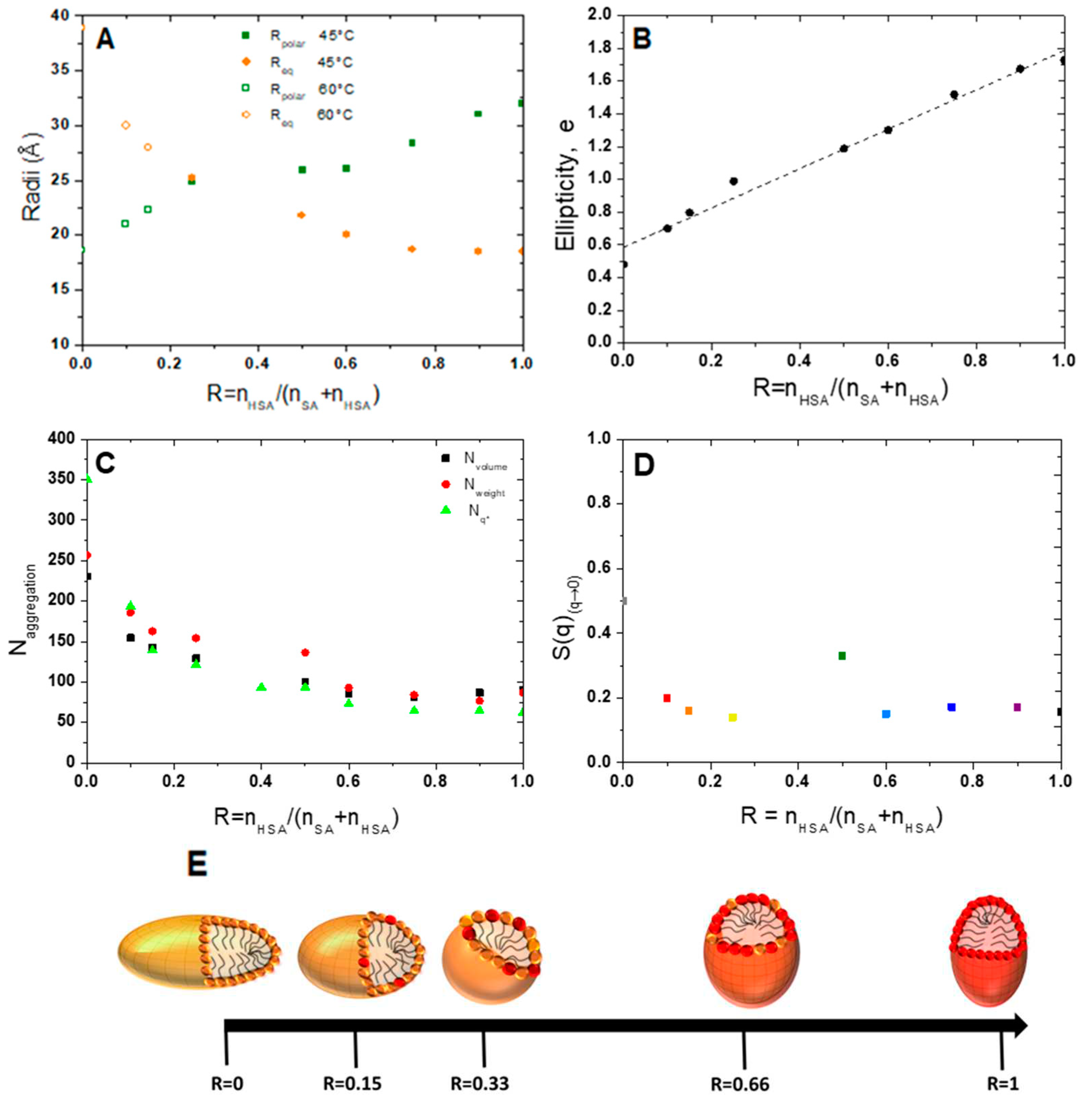
Let us now describe the influence of R on the micelle shape. For R = 1 (pure 12-HSA solution), most studies in the literature have focused on suspensions with a stoichiometric ethanolamine/fatty acid ratio (r = 0.5).²⁹ For this r, the HSA micelles form spherical micelles with a radius of 22 Å at high temperature, which corresponds to the length of the hydrophobic tail.²⁹ We have tested such a form factor model of spheres in our case (r = 0.2) and the best fit gives a micelle radius of 18.5 Å. This result agrees with the literature²⁹ at such r of 0.2 at 72°C but the curve obtained does not fit properly the data.

We therefore chose to refine the model and fit the scattered intensity of the 12-HSA solution at 45°C using an homogeneous ellipsoidal micellar model that is both compatible with the observation of a characteristic length of 18.5 Å and the size of the molecule. For a dispersion of ellipsoids of revolution, the decoupling approximation of the structure factor and of the form factor is not valid. It has however been shown by Green et al³⁹ that the approximation stays valid for either a dilute dispersion and/or low aspect ratios of the ellipsoids. This is the case for the ranges of volume fraction under scrutiny of our study (~ 2%) and aspect ratios (between 0.5 and 1.7, see later), the deviation of the decoupled S(q) being less than 1% from an explicit calculation of S(q) of hard ellipsoids (see e g Figure 2 of reference³⁹). We will then postulate that the decoupling approximation is valid for all data on micelles presented afterwards. The model refines our data well by giving an equatorial radius of 18.5 Å and a polar radius of 32 Å, i.e. an ellipticity of 1.7. HSA micelles are therefore prolate micelles. The fatty acids are thus not interdigitated within micelles, contrarily to the lamellar phase.

For R=0 (pure SA solution) at 60°C (Figure 4), a simple look at the evolution of the intensity with respect to the 12-HSA case shows that the SA micelles have a larger aggregation number N than 12-HSA ones (see Figure S7 that compare all curves in cm^-1 without any multiplication by a pre-factor). Indeed, the q-position of the structure correlation peak q^* shifts towards low q for R = 0. Since q^* is inversely proportional to the distance between scattering objects, this shows that the distance between micelles is larger for R=0 than for R=1. Given that the total fatty acid concentration in solution is constant for both ratios, this implies that N is larger for R = 0. Moreover, at the same time, the q-range where the Porod q^-4 arise shifts towards low q for R = 0 with respect to R = 1. As for pure 12-HSA micelles, it was not possible to fit properly the scattering curve by using a purely spherical form factor and the best modelling was obtained with an elliptical form factor, with a polar radius of 18.9 Å and an equatorial one of 38.5 Å. The shape of the SA micelles is thus oblate, which is strikingly different from the 12-HSA case where they are prolate.

For the other R, the evolution of the intensity as function of R shows that the aggregation number of fatty acid per micelle N decreases varies continuously from one sample to another (see Figure SI7) from R = 0 to R = 1. Indeed, q^* shifts towards large q with an increase of R and the q-range where the Porod q^-4 arise shifts towards large q at the same time. Data were fitted at large q by an ellipsoidal micelles model (detailed in Supplementary Materials) for all R to account for the evolution of shape. Polar and equatorial radii are represented on Figure 6A and ellipticity on Figure 6B. The ellipticity e, defined as 1-(radius polar/radius equatorial), decays linearly when R decreases and takes values lower than 1 for R < 0.25. The system transit from prolate micelles at high R, as for pure 12-HSA micelles, to oblate micelles at low R, as for the pure SA micelles. Spherical micelles are obtained when R is close to 0.33. The ellipticity can be tuned from the choice of R with e = 0.58 + 1.2 R.

The aggregation number, N, was determined in three different ways: one deduced from the mass of the scattering objects, from the extrapolation of the scattered intensity when q tends to 0 I(q) _q→0, taking here the structure factor equal to 1 on the full q-range, which we call N_Weight, one obtained by the ratio between the volume of the ellipsoid and that of a fatty acid molecule, which we call N_volume, and one extracted from the position of the correlation peak, q*, assuming that the repartition of micelles is spatially homogeneous, i.e. the mean distance between micelles is 2π/ q*, that we call N_q*.

N_{w e i g h t} = \frac{N_{a} I_{0}}{V_{f a t t y a c i d}^{2} . ∆ ρ ² . c . M_{f a t t y a c i d}}

(2)

Where

V_{f a t t y a c i d}

is the specific volume of the fatty acid, Δρ is the neutron scattering contrast between fatty acid and D₂0 and c the concentration of both fatty acids, N_a, the Avogadro number and M_{fatty acid} the average molar mass of fatty acids at each ratio (ie M_{fatty acid}=R.M_HSA+(1-R).M_SA).

N_{v o l u m e} = \frac{V_{e l l i p s o i d}}{V_{f a t t y a c i d}}

(3)

The volume of a molecule of fatty acid is approximated by using Tanford’s formula for the alkyl chain volume (V = 27.4 + 26.9n_c, where n_c is the number of alkyl chain carbons).⁴⁰ We have chosen to use the same value whatever the ratio R, the slight error introduced in this calculation being minute.

N_{q *} = \frac{Φ_{v} . {(\frac{2 π}{q^{*}})}^{3}}{V_{f a t t y a c i d}}

(4)

Where

Φ_{v}

is the volume fraction in fatty acid and q* the position of the correlation peak. N_weight and N_volume, N_q* values have the same order of magnitude and vary in the same way. At high R, the values obtained from the three approaches are slightly different which may be due to the value of the volume of a 12-HSA molecule which might be slightly different from the one of pure SA used in this calculation, to the uncertainty one the scattering length density of the micelles as the exact localization of the counter-ion is unknown and to the uncertainty on the different fits. At R=1, N is close to 100 and vary only slightly when decreasing R up to R= 0.5. It then strongly increases and reach value between 250 and 350 molecules at R = 0, depending on the method used to obtain it. The calculation of N_q* is not fit-dependent and is probably more accurate than the others. In particular, it does not depend on the scattering length density of the core of the micelle, that we have considered equal to that of a fatty acid in the fitting, a value that may slightly wrong due to presence of the ethanolamine counterions.

The experimental structure factors were then obtained by dividing the scattered intensity by these adjusted form factors (equation 1). They are represented on Figure S8, which allow to highlight the very low compressibilities of the suspension, and therefore strong repulsions. They were fitted with a model of the Hayter and Penfold,³⁷ fixing all parameters to their known experimental values (temperature, ionic strength calculated from all ions introduced in solution, concentration, dielectric constant), except for the effective charge by micelle Z_micelle. Z_micelle varies from 20 to 50 per micelles depending on R and micelle’s size (see table SI 1). The large values obtained for the effective micellar charge are in agreement with the charged character of the fatty acids.

3. Discussion

The corpus of results gathered from the different experimental techniques (transmittance, WAXS, SANS, and DSC) converges to a consistent picture and demonstrates that the self-assemblies have the same overall behavior for all ratios R with a transition from a multilamellar phase to a micellar phase in solution. Indeed, the temperature of thermodynamic transition evidenced by DSC matches the onset of appearance of turbidity, the fluid/gel transition of the bilayer and the morphological transition at the nanoscale. This allows to build the phase diagram of HSA/SA mixtures as a function of R ratio and temperature (Figure 7).

The fact that the lamellar/micelle transition is driven by the melting of the gelled lamellae of the fatty acids in all mixtures highlights the role of the concentration ratio r between fatty acid and the ethanolamine counter ion on the mechanism of the transition. Indeed, while solutions of pure SA show a single lamellar phase/micelle transition regardless of ethanolamine concentration,⁸ the 12-HSA solutions undergo either only one transition at high ethanolamine concentration (r = 0.2), in accordance with the findings of the current study, or two distinct enthalpic phenomena at lower ethanolamine concentration, i.e. larger r (r = 0.5) that correspond respectively to the melting of the lamellae and to the lamellar self-assembly /micelle transition at larger temperature. The reason invoked to explain such a peculiar behavior at large r, when the fatty acids heads are not all charged, was the necessity to break the H-bonds that remain between heads on their COOH form.²⁹ This is however not sufficient to capture all the subtle mechanisms of the transition, otherwise the same behavior would have also been observed for pure solutions of SA. It has probably to be associated with the ability of the ethanolamine to penetrate/interact within the bilayer, which must be easier in SA bilayers than in 12-HSA ones, given that these latter form H-bonds between fatty chains. Indeed, at r = 0.5, 12-HSA crystallized bilayers are not interdigitated²⁸ while they are interdigitated at r = 0.2.³⁵ We demonstrate here that crystallized bilayers are interdigitated in all mixtures at low r, without temperature shift. Thus, such a temperature shift of the lamellar/micelle transition with respect to the fluid/solid transition of the lamella only occurs when these latter are not interdigitated. We also demonstrate here that the fatty acids are no longer interdigitated once melted when they do form micelles.

If all mixtures display the same overall behavior, the ratio R has an influence on both the threshold temperature of transition and the ability of the system to reach its steady state with time when changing temperature. At intermediate R, the transition temperature passes by a minimum at R = 0.6. At the same time, the transition temperature zone, where micelles and lamellar phase truly co-exist (see SANS data at 37°C in Figure 4A), is broad in this regime of intermediate R, with a DSC peak that is very broad. Such regime of R corresponds to the ratios for which we demonstrated in³⁵ that there is a partitioning at local scales between 12-HSA and SA molecules at 20°C, which is at the origin of the minimum of the temperature threshold. The sizes of crystalline domains in this region of R are indeed smaller, as shown by WAXS data. Given that the melting temperature is a function of the size of the crystal domains, it is logical to have a lowered melting temperature in mixtures with respect to pure 12-HSA and SA solutions. It is worth mentioning that the shape of the phase diagram is comparable to phase diagrams bearing a eutectic point, that would be located at ~ R=0.6. Nicely, this ratio is close to the one where the presence of a eutectic point has been demonstrated by Matuo et al³⁴ (R = 0.75) that built the 2D phase diagram of mixed monolayers of HSA/SA at the air/water interface. In the case of mixed monolayers, this ratio depends on the length of the alkyl chain and is not observed for longer alkyl chains. It is thus interesting to point out that the behavior of HSA/SA mixtures in monolayers mirrors that of mixtures in aqueous solution. It suggests that partitioning probably also occurs in monolayers. The partitioning also explains why the transition zone is larger at intermediate R, since the two types of domains that co-exist in lamellar self-assemblies have to form upon cooling (respectively melt upon heating) within the same sample.

The temperature also influences the morphology of the lamellar self-assemblies formed below the lamellar/micelles transition temperature. For pure 12-HSA solutions (R=0) at r=0.2, the inter-lamellar distance decreases with increasing temperature, in accordance with literature.²⁸ Such a behavior does not happen for pure SA solutions since the interlamellar distance does not vary with temperature (see Figure 5A). However the Caillé parameter as well as the lattice parameter of the crystalline phase slightly vary. The interactions between lamella are thus almost temperature independent, given that they are mainly driven by electrostatic interactions originating from their negatively charged heads, while the rigidity is directly influenced by packing of molecules within the layer. In the case of mixtures, the interlamellar distance decreases slightly with temperature in all cases, as for the pure 12-HSA case at R = 1, even for mixtures containing low amounts of 12-HSA. The presence of 12-HSA molecules play thus a prominent role on this inter-lamellar distance, whether partitioning occurs or not, and whatever the crystalline structure of the fatty acids within the lamella.

Let us now discuss the influence of the ratio R on the structure of the micelles that are formed above the lamellar/micelles threshold temperature. This the first time to the best of our knowledge that it is demonstrated that 12-HSA micelles at r=0.2 are ellipsoidal prolate and not spherical, as many surfactant micelles.^41–43 The most well-known case is that of cetyltrimethylammonium bromide (CTAB) micelles⁴⁴ with an aspect ratio that varies largely as a function of either the ionic strength⁴⁴ or when mixed with small other molecules.^45–47 It is therefore not surprising to observe that HSA micelles, spherical for r=0.5 are prolate when ethanolamine is added at r=0.2. Along the same lines, we also demonstrate for the first time that SA micelles are oblate. The aspect ratio of a micelle is keen to change when a surfactant is mixed with another surfactant, as in the present case for all mixtures. The ellipticity varies continuously when the ratio R is changed. In an excess of 12-HSA, in the regime of high R, the progressive addition of SA decreases the ellipticity of the micelle while maintaining its prolate shape. One can hypothesize, as schematically represented in Figure 6E, that SA molecules are distributed randomly within the of 12-HSA molecules and slightly modify in average the curvature of micelles. Symmetrically, when some 12-HSA molecules are introduced in oblate micelles of SA, the ellipticity increases when increasing R from R = 0 towards more spherical micelles. In the regime of low R (R<0.25,) we have shown in,³⁵ that there is a partitioning between the SA and 12-HSA molecules driven by hydrogen bonds within the facetted lamellar self-assemblies formed at 20°C originating from the formation of H-bonds between the OH functions on the alkyl chains of the 12-HSA fatty acids. Such partitioning could also occur within the micelles at high temperature, but is unlikely since the formation of H-bonds is not favored at large temperature. We have however no direct proof of such possible partitioning within the mixed micelles and have chosen to represent a random distribution of the fatty acids within the micelles at high temperature for the sake of honesty (Figure 6E and Figure 7).

4. Experimental

4.1. Materials and Sample Preparation

12-Hydroxystearic acid (HSA) was purchased from Xilong Chemical Co., Ltd., Shantou, Stearic acid (SA) was purchased from Sigma-Aldrich and ethanolamine from Aldrich Chemistry (≥99.5%). H₂O was provided by a Millipore system and D₂O purchased from Eurisotop.

Aqueous stock-solutions of HSA and SA at a concentration of 100 g/L were prepared as follows. HSA (respectively SA) and ethanolamine were first weighted accurately in a sample tube into which ultrapure water was further added to reach the targeted molar concentration of fatty acid. The mass of ethanolamine was adjusted to set the molar ratio surfactant/counter ion r at 0.2, calculated by r = n_{fatty_acid}/( n_{fatty_acid} + n_ethanolamine). Then, the solutions were stirred and heated to 70 °C in an oven for 2 hours, a temperature at which solutions are non-viscous, and vortexed to ensure homogenization. They all look clear and homogeneous at 70 °C.

The mixture samples were then prepared at a fixed concentration of fatty acid molecules of 20 g/L by mixing stock-solutions and ultrapure water in appropriate dilutions to reach the targeted ratio of the two fatty acids R defined by:

R = \frac{n_{12 H S A}}{(n_{12 H S A} + n_{S A})}

where n_12HSA and n_SA are the moles of the fatty acids. The mixtures were then heated back in an oven at 70 °C for two hours and vortexed for some seconds for homogenization. This concentration was chosen in order to compare the results with literature, where a large corpus of knowledge exists for the pure 12-HSA system.^28–30 In the case of SANS experiments, all samples were prepared in D₂O at the same volume fraction.

We probed the following R values in the paper: 1 (pure sample of HSA fatty acids as reference), 0.9, 0.75, 0.6, 0.5, 0.4, 0.25, 0.1, 0.05 and 0 (reference sample of SA fatty acids).

In the following we systematically heated the samples at 70 °C for homogenization before any kind of measurement.

4.2. UV-Visible Spectroscopy (UV-Vis)

UV-Vis experiments were performed on a Varian Cary 100 spectrometer. For all the measurements, the wavelength used was 450 nm. We used a thermal program with ramp temperatures between 65 °C and 5 °C (heating and cooling cycles) at a rate of 0.2 °C/min and 1 °C/min.

4.3. Differential Scanning Calorimetry (DSC)

The phase transition temperatures were measured on a TA DSC25 calorimeter. For these measurements, we used two stainless steel cells, one containing water used as reference, and the other one containing approximatively 7 mg of sample. The heating and cooling ramps were between 5 °C and 65 °C at a rate of 1 °C/min and 0.2 °C/min.

4.4. Wide Angle X-Ray Scattering (WAXS)

WAXS measurements were carried out on a Xeuss 2.0 instrument from Xenocs, which uses a microfocused Cu Kα source with a wavelength of 1.54 Å and a PILATUS3 detector (Dectris, Switzerland). The experiments were performed at a sample-to-detector distance of 350 mm with a collimated beam size of 0.8 × 0.8 mm to achieve a q-range of 0.038 Å⁻¹ – 1.78 Å⁻¹. The solutions were poured inside 1.5 mm glass capillaries that were placed onto a home-made sample holder thermalized with a circulating water flow coupled with a Huber bath, allowing to control the samples temperature to 36°C and 50°C. The measurements were performed for 35 minutes per sample to achieve a good statistic. The respective scattering from empty beam, empty capillary and dark field were measured independently and subtracted from the sample scattering, taking account their relative transmission, and normalized with incident beam intensity to obtain scattering in absolute units (cm^-1). A reference solvent sample measurement was measured independently and its contribution from the samples scattering was subtracted properly.

4.5. Small Angle Neutron Scattering (SANS)

Small angle neutron scattering experiments were performed at the Institut Laue-Langevin – The European Neutron Source (Grenoble, France) on the diffractometer D11 (DOI: http://dx.doi.org/10.5291/ILL-DATA.9-11-2041). We used four configurations (6 Å at 1.7 m, 6 Å 5.5 m, 6 Å at 20.5 m, and 13 Å at 38 m) to reach a very broad q-range spanning from 5.9 10^-4 Å^-1 to 0.53 Å^-1. The samples were prepared in D₂O in order to optimize neutron contrast with hydrogenated molecules and to reduce as much as possible incoherent scattering. We checked beforehand that the use of deuterated water instead of hydrogenated water does not modify the macroscopic aspect of samples. Samples were held in flat quartz cells (Hellma) with a 2 mm optical path.

All samples were measured at 30 °C, 37°C, 45 °C and samples at R = 0.15 and R = 0.1 were additionally measured at 60 °C. The temperature was set by a circulating bath that thermalizes the sample holder into which samples were placed. Transmissions, scattering of empty cell, sintered ¹⁰B₄C (neutron absorber to estimate the ambient background for the detector), scattering of hydrogenated water (as a flat field) and differential scattering cross section of water (for absolute scale) were measured independently. Subtraction of parasitic contributions and normalization by water to take into account detectors heterogeneities were applied to raw data by the GRASP software (version Grasp Lockdown V.9.22e) to obtain corrected data in absolute units (cm^-1).³⁸ Contributions from solvent and incoherent scattering were then subtracted.

Fitting software used was SasView 5.0.4 (http://www.sasview.org/.). Fitting models are detailed in the supplementary information.

5. Conclusion

The variations of temperature thresholds we evidence for different HSA/SA mixtures suggest that subtle changes in the internal structure of the mixtures can induce significant changes on phase segregations and domain sizes leading do different thermal properties. This observation is important because it highlights the complexity of the interactions in these systems and demonstrate that small changes in the blend composition may enable to tune the material properties over a large extent. In particular, it opens up interesting perspectives for the design of new functional materials with temperature-tunable properties. Indeed, fatty acid mixtures have been widely studied for their ability to form self-assembled structures such as lamellae and micelles for their further use in a variety of applications including the production of foams and gels.^15,32 The establishment of the whole phase diagram of fatty acid mixtures as a function of mixture composition and temperature sets thus the foundations for the design of new fatty acid-based functional materials with stimuli-responsive properties, such as stimulable foams and gels^15,32 or for the design of drug release triggered systems.³³

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org. Figure S1: Transmittance of sample as a function of temperature upon cooling at a cooling rate of 1°C/min; Figure S2: Transmittance of sample as a function of temperature upon heating at a cooling rate of 0.2°C/min; Figure S3: Enthalpograms of samples upon heating at a heating rate of 0.2°C/min. Figure S4: Enthalpograms of samples upon cooling at a cooling rate of 0.2°C/min. Figure S5: Enthalpograms of samples upon heating at a heating rate of 1°C/min. Figure S5: Comparison of transmittance of R=0, R=0.25, R=0.75 and R=1 samples in D2O and in H2O. Figure S7. SANS intensity profiles of all samples in the micelles regime. Figure S8. Structure factors of micelles. Table S1: Values of the micelles’ parameters by fitting the SANS data

Funding

This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union’s Horizon 2020 research and innovation program under the SINE2020 project, grant agreement No 654000.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The raw data will be available from the corresponding authors upon reasonable request.

Acknowledgments

The authors warmly thank Anne-Laure Fameau for fruitful discussions.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds are available from the authors upon reasonable request.

References

Fameau, A.; Marangoni, A. G. Back to the Future: Fatty Acids, the Green Genie to Design Smart Soft Materials. J. Am. Oil Chem. Soc. 2022, 99 (7), 543–558. [Google Scholar] [CrossRef]
Callau, M.; Sow-Kébé, K.; Jenkins, N.; Fameau, A.-L. Effect of the Ratio between Fatty Alcohol and Fatty Acid on Foaming Properties of Whipped Oleogels. Food Chem. 2020, 333, 127403. [Google Scholar] [CrossRef] [PubMed]
Zhang, L.; Mikhailovskaya, A.; Yazhgur, P.; Muller, F.; Cousin, F.; Langevin, D.; Wang, N.; Salonen, A. Precipitating Sodium Dodecyl Sulfate to Create Ultrastable and Stimulable Foams. Angew. Chem. Int. Ed. 2015, 54 (33), 9533–9536. [Google Scholar] [CrossRef] [PubMed]
Novales, B.; Navailles, L.; Axelos, M.; Nallet, F.; Douliez, J.-P. Self-Assembly of Fatty Acids and Hydroxyl Derivative Salts. Langmuir 2008, 24 (1), 62–68. [Google Scholar] [CrossRef] [PubMed]
Douliez, J.-P.; Navailles, L.; Nallet, F. Self-Assembly of Fatty Acid−Alkylboladiamine Salts. Langmuir 2006, 22 (2), 622–627. [Google Scholar] [CrossRef]
Klein, R.; Touraud, D.; Kunz, W. Choline Carboxylate Surfactants: Biocompatible and Highly Soluble in Water. Green Chem. 2008, 10 (4), 433. [Google Scholar] [CrossRef]
Fameau, A.-L.; Zemb, T. Self-Assembly of Fatty Acids in the Presence of Amines and Cationic Components. Adv. Colloid Interface Sci. 2014, 207, 43–64. [Google Scholar] [CrossRef]
Xu, W.; Gu, H.; Zhu, X.; Zhong, Y.; Jiang, L.; Xu, M.; Song, A.; Hao, J. CO ₂ -Controllable Foaming and Emulsification Properties of the Stearic Acid Soap Systems. Langmuir 2015, 31 (21), 5758–5766. [Google Scholar] [CrossRef]
Xu, W.; Zhang, H.; Zhong, Y.; Jiang, L.; Xu, M.; Zhu, X.; Hao, J. Bilayers at High PH in the Fatty Acid Soap Systems and the Applications for the Formation of Foams and Emulsions. J. Phys. Chem. B 2015, 119 (33), 10760–10767. [Google Scholar] [CrossRef]
Arnould, A.; Perez, A. A.; Gaillard, C.; Douliez, J.-P.; Cousin, F.; Santiago, L. G.; Zemb, T.; Anton, M.; Fameau, A.-L. Self-Assembly of Myristic Acid in the Presence of Choline Hydroxide: Effect of Molar Ratio and Temperature. J. Colloid Interface Sci. 2015, 445, 285–293. [Google Scholar] [CrossRef]
Arnould, A.; Cousin, F.; Chabas, L.; Fameau, A.-L. Impact of the Molar Ratio and the Nature of the Counter-Ion on the Self-Assembly of Myristic Acid. J. Colloid Interface Sci. 2018, 510, 133–141. [Google Scholar] [CrossRef]
Zana, R. Partial Phase Behavior and Micellar Properties of Tetrabutylammonium Salts of Fatty Acids: Unusual Solubility in Water and Formation of Unexpectedly Small Micelles. Langmuir 2004, 20 (14), 5666–5668. [Google Scholar] [CrossRef] [PubMed]
Zana, R.; Schmidt, J.; Talmon, Y. Tetrabutylammonium Alkyl Carboxylate Surfactants in Aqueous Solution: Self-Association Behavior, Solution Nanostructure, and Comparison with Tetrabutylammonium Alkyl Sulfate Surfactants. Langmuir 2005, 21 (25), 11628–11636. [Google Scholar] [CrossRef] [PubMed]
Klein, R.; Kellermeier, M.; Drechsler, M.; Touraud, D.; Kunz, W. Solubilisation of Stearic Acid by the Organic Base Choline Hydroxide. Colloids Surf. Physicochem. Eng. Asp. 2009, 338 (1-3), 129–134. [Google Scholar] [CrossRef]
Fameau, A.-L.; Saint-Jalmes, A.; Cousin, F.; Houinsou Houssou, B.; Novales, B.; Navailles, L.; Nallet, F.; Gaillard, C.; Boué, F.; Douliez, J.-P. Smart Foams: Switching Reversibly between Ultrastable and Unstable Foams. Angew. Chem. Int. Ed. 2011, 50 (36), 8264–8269. [Google Scholar] [CrossRef] [PubMed]
Wang, Z.; Ren, G.; Yang, J.; Xu, Z.; Sun, D. CO2-Responsive Aqueous Foams Stabilized by Pseudogemini Surfactants. J. Colloid Interface Sci. 2019, 536, 381–388. [Google Scholar] [CrossRef]
Liu, Y.; Jessop, P. G.; Cunningham, M.; Eckert, C. A.; L. Liotta, C. Switchable Surfactants. Science 2006, 313 (35), 958–960. [CrossRef]
Fameau, A.-L.; Arnould, A.; Lehmann, M.; von Klitzing, R. Photoresponsive Self-Assemblies Based on Fatty Acids. Chem. Commun. 2015, 51 (14), 2907–2910. [Google Scholar] [CrossRef]
Cristofolini, L.; Fontana, M. P.; Boga, C.; Konovalov, O. Microscopic Structure of Crystalline Langmuir Monolayers of Hydroxystearic Acids by X-Ray Reflectivity and GID: OH Group Position and Dimensionality Effect. Langmuir 2005, 21 (24), 11213–11219. [Google Scholar] [CrossRef]
Vollhardt, D.; Siegel, S.; Cadenhead, D. A. Characteristic Features of Hydroxystearic Acid Monolayers at the Air/Water Interface. J. Phys. Chem. B 2004, 108 (45), 17448–17456. [Google Scholar] [CrossRef]
Yim, K. S.; Rahaii, B.; Fuller, G. G. Surface Rheological Transitions in Langmuir Monolayers of Bi-Competitive Fatty Acids. Langmuir 2002, 18 (17), 6597–6601. [Google Scholar] [CrossRef]
Nakagawa, M.; Kawai, T. Tuning Gel–Sol Transition Behavior of a Hydrogel Based on 12-Hydroxystearic Acid and a Long-Chain Amidoamine Derivative. Bull. Chem. Soc. Jpn. 2019, 92 (2), 435–440. [Google Scholar] [CrossRef]
Douliez, J.-P.; Gaillard, C.; Navailles, L.; Nallet, F. Novel Lipid System Forming Hollow Microtubes at High Yields and Concentration. Langmuir 2006, 22 (7), 2942–2945. [Google Scholar] [CrossRef]
Jiang, L.; Peng, Y.; Yan, Y.; Deng, M.; Wang, Y.; Huang, J. “Annular Ring” Microtubes Formed by SDS@2β-CD Complexes in Aqueous Solution. Soft Matter 2010, 6 (8), 1731. [Google Scholar] [CrossRef]
Yang, S.; Yan, Y.; Huang, J.; Petukhov, A. V.; Kroon-Batenburg, L. M. J.; Drechsler, M.; Zhou, C.; Tu, M.; Granick, S.; Jiang, L. Giant Capsids from Lattice Self-Assembly of Cyclodextrin Complexes. Nat. Commun. 2017, 8 (1), 15856. [Google Scholar] [CrossRef] [PubMed]
Landman, J.; Ouhajji, S.; Prévost, S.; Narayanan, T.; Groenewold, J.; Philipse, A. P.; Kegel, W. K.; Petukhov, A. V. Inward Growth by Nucleation: Multiscale Self-Assembly of Ordered Membranes. Sci. Adv. 2018, 4 (6), eaat1817. [Google Scholar] [CrossRef]
Ouhajji, S.; Landman, J.; Prévost, S.; Jiang, L.; Philipse, A. P.; Petukhov, A. V. In Situ Observation of Self-Assembly of Sugars and Surfactants from Nanometres to Microns. Soft Matter 2017, 13 (13), 2421–2425. [Google Scholar] [CrossRef]
Fameau, A.-L.; Cousin, F.; Navailles, L.; Nallet, F.; Boué, F.; Douliez, J.-P. Multiscale Structural Characterizations of Fatty Acid Multilayered Tubes with a Temperature-Tunable Diameter. J. Phys. Chem. B 2011, 115 (29), 9033–9039. [Google Scholar] [CrossRef]
Fameau, A.-L.; Cousin, F.; Saint-Jalmes, A. Morphological Transition in Fatty Acid Self-Assemblies: A Process Driven by the Interplay between the Chain-Melting and Surface-Melting Process of the Hydrogen Bonds. Langmuir 2017, 33 (45), 12943–12951. [Google Scholar] [CrossRef]
Fameau, A.-L.; Houinsou-Houssou, B.; Novales, B.; Navailles, L.; Nallet, F.; Douliez, J.-P. 12-Hydroxystearic Acid Lipid Tubes under Various Experimental Conditions. J. Colloid Interface Sci. 2010, 341 (1), 38–47. [Google Scholar] [CrossRef]
Fameau, A.-L.; Saint-Jalmes, A. Yielding and Flow of Solutions of Thermoresponsive Surfactant Tubes: Tuning Macroscopic Rheology by Supramolecular Assemblies. Soft Matter 2014, 10 (20), 3622. [Google Scholar] [CrossRef]
Fameau, A.-L.; Cousin, F.; Derrien, R.; Saint-Jalmes, A. Design of Responsive Foams with an Adjustable Temperature Threshold of Destabilization. Soft Matter 2018, 14 (14), 2578–2581. [Google Scholar] [CrossRef] [PubMed]
Salerno, C.; Chiappetta, D. A.; Arechavala, A.; Gorzalczany, S.; Scioscia, S. L.; Bregni, C. Lipid-Based Microtubes for Topical Delivery of Amphotericin B. Colloids Surf. B Biointerfaces 2013, 107, 160–166. [Google Scholar] [CrossRef]
Matuo, H.; Mitsui, T.; Motomura, K.; Matuura, R. Eutectic Transformation in Mixed Monolayers of Long Normal Chain Fatty Acids with 12-Hydroxyoctadecanoic Acid. Chem. Phys. Lipids 1981, 29 (1), 55–67. [Google Scholar] [CrossRef]
Almeida, M.; Dudzinski, D.; Amiel, C.; Guigner, J.-M.; Prévost, S.; Le Coeur, C.; Cousin, F. Aqueous Binary Mixtures of Stearic Acid and Its Hydroxylated Counterpart 12-Hydroxystearic Acid: Cascade of Morphological Transitions at Room Temperature. Molecules 2023, 28 (11), 4336. [Google Scholar] [CrossRef]
Nallet, F.; Laversanne, R.; Roux, D. Modelling X-Ray or Neutron Scattering Spectra of Lyotropic Lamellar Phases : Interplay between Form and Structure Factors. J. Phys. II 1993, 3 (4), 487–502. [Google Scholar] [CrossRef]
Hayter, J. B.; Penfold, J. An Analytic Structure Factor for Macroion Solutions. Mol. Phys. 1981, 42 (1), 109–118. [Google Scholar] [CrossRef]
Cousin, F. Small Angle Neutron Scattering. EPJ Web Conf. 2015, 104, 01004. [Google Scholar] [CrossRef]
Greene, D. G.; Ferraro, D. V.; Lenhoff, A. M.; Wagner, N. J. A Critical Examination of the Decoupling Approximation for Small-Angle Scattering from Hard Ellipsoids of Revolution. J. Appl. Crystallogr. 2016, 49 (5), 1734–1739. [Google Scholar] [CrossRef]
Walker, C. H. The Hydrophobic Effect: Formation of Micelles and Biological Membranes: By C. Tanford Wiley; Brisbane, Chichester, New York, Toronto, 1980 x + 233 Pages. £11.75. FEBS Lett. 1981, 124 (1), 127–127. [Google Scholar] [CrossRef]
Ivanović, M. T.; Hermann, M. R.; Wójcik, M.; Pérez, J.; Hub, J. S. Small-Angle X-Ray Scattering Curves of Detergent Micelles: Effects of Asymmetry, Shape Fluctuations, Disorder, and Atomic Details. J. Phys. Chem. Lett. 2020, 11 (3), 945–951. [Google Scholar] [CrossRef] [PubMed]
Iyer, J.; Blankschtein, D. Are Ellipsoids Feasible Micelle Shapes? An Answer Based on a Molecular-Thermodynamic Model of Nonionic Surfactant Micelles. J. Phys. Chem. B 2012, 116 (22), 6443–6454. [Google Scholar] [CrossRef] [PubMed]
De Caro, L.; Giudice, A. D.; Morin, M.; Reinle-Schmitt, M.; Grandeury, A.; Gozzo, F.; Giannini, C. Small Angle X-Ray Scattering Data Analysis and Theoretical Modelling for the Size and Shape Characterization of Drug Delivery Systems Based on Vitamin E TPGS Micelles. J. Pharm. Sci. 2023, 112 (1), 243–249. [Google Scholar] [CrossRef] [PubMed]
Goyal, P. S.; Chakravarthy, R.; Dasannacharya, B. A.; Desa, J. A. E.; Kelkar, V. K.; Manohar, C.; Narasimhan, S. L.; Rao, K. R.; Valaulikar, B. S. SANS from Micellar Solutions of CTAB and Sodium Salicylate. Phys. B Condens. Matter 1989, 156–157, 471–473. [Google Scholar] [CrossRef]
Schmutzler, T.; Schindler, T.; Schmiele, M.; Appavou, M.-S.; Lages, S.; Kriele, A.; Gilles, R.; Unruh, T. The Influence of N- Hexanol on the Morphology and Composition of CTAB Micelles. Colloids Surf. Physicochem. Eng. Asp. 2018, 543, 56–63. [Google Scholar] [CrossRef]
Oliver, R. C.; Lipfert, J.; Fox, D. A.; Lo, R. H.; Kim, J. J.; Doniach, S.; Columbus, L. Tuning Micelle Dimensions and Properties with Binary Surfactant Mixtures. Langmuir 2014, 30 (44), 13353–13361. [Google Scholar] [CrossRef]
Padsala, S.; Dharaiya, N.; Sastry, N. V.; Aswal, V. K.; Bahadur, P. Microstructural Morphologies of CTAB Micelles Modulated by Aromatic Acids. RSC Adv. 2016, 6 (107), 105035–105045. [Google Scholar] [CrossRef]

Figure 1. (A) Transmittance as a function of temperature for HSA/SA mixtures from R=0 to R=1 upon cooling at a cooling rate of 0.2°C/min. (B) Temperatures of transition determined by turbimetry and by DSC as a function of ratio R, where error bars are estimated from the width of the peak.

Figure 2. Enthalpograms obtained for 2wt% mixture in fatty acid at various R ratios upon cooling at a cooling rate of 1°C/min. Data are shifted for clarity.

Figure 3. WAXS diffractograms for the different HSA/SA samples ratio, from pure SA (R=0) to pure HSA (R=1) at 3 different temperatures (20°C from reference,35 36°C and 50°C). The spectra were successively shifted in intensity by an offset of 0.0033 cm-1 for clarity.

Figure 4. SANS intensity profiles at 4 temperatures (A: 30°C, B: 37°C, C: 45°C, D: 60°C) for the different samples in D₂O for different HSA/SA ratios, from pure SA (R=0) to pure HSA (R=1). The spectra are successively shifted by a factor 10 in intensity for clarity (data for R=0 in absolute scale). The black and red continuous lines correspond to the best fit of the data either by a lamellar model or by a model of an elliptical micelles in interactions (see description in supplementary material). Some data showing a combination of scattering of lamellar objects and micelles are not fitted (see explanation in text).

Figure 5. Value of lamellar spacing (A) Caillé Parameter (B) and thickness (C) obtained from fitting of lamellar phase at different temperature. Data at 20°C are already published in³⁵ but are represented for the sake of comparison.

Figure 6. Evolution (A) of polar and equatorial radii obtained from micelles’ fit at 45 and 60°C, (B) of the ellipticity (C) of the number of aggregations N_volume and N_weight as a function of the ratio R. (D) S(q)_(q→0) obtained from division on the scattered intensity by the fitted form factor. (E) Schematic representation of the evolution of micelles shape as a function of the ratio R from prolate micelles to oblate ones. The SA molecules are represented in orange and the 12-HSA molecules in red. .

Figure 7. Schemes of the structures of the self-assembled aggregates as function of R from pure SA (R=0) to pure 12-HSA (R=1). The SA molecules are represented in orange and the 12-HSA molecules in red. .

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer