Prerpints.org logo
Preprint
Article

The Implicit Numerical Method for the Radial Anomalous Subdiffusion Equation

Altmetrics

Downloads

96

Views

14

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

31 July 2023

Posted:

01 August 2023

You are already at the latest version

Alerts
Abstract
This paper presents a numerical method for solving a two-dimensional subdiffusion equation with a Caputo fractional derivative. The problem considered assumes symmetry in both the equation’s solution domain and the boundary conditions, allowing for a reduction of the two-dimensional equation to a one-dimensional one. The proposed method is an extension of the fractional Crank-Nicolson method, based on the discretization of the equivalent integral-differential equation. To validate the method, the obtained results were compared with a solution obtained through Laplace transform. The analytical solution in the image of the Laplace transform was inverted using the Gaver-Wynn-Rho algorithm implemented in the specialized mathematical computing environment, Wolfram Mathematica. The results clearly show the mutual convergence of the solutions obtained by the two methods.
Keywords: 
Subject: Computer Science and Mathematics  -   Computational Mathematics

1. Introduction

Diffusion is a process of spontaneous movement of particles due to collisions with other particles. These collisions can occur between diffusing particles as well as particles of the medium in which diffusion occurs. The fundamental characteristic of this type of movement is that the mean square displacement of the particle (the square of its dispersion), depends non-linearly on time [1,2]
x 2 ( t ) ∼ D α t α , 0 < α ≤ 2 ,
as opposed to the linear dependence ( α = 1 ) that characterizes Brownian motion. In the first case, when the exponent of the power is less than one, it is called subdiffusion, whereas when the diffusion exponent is greater than one, it is called superdiffusion. The second case concerns the so-called Lévy flights which have been observed experimentally [3,4,5]. Subdiffusion is most commonly observed in media such as gels and porous media, where particle movement is extremely difficult [6,7].
The thermal conductivity, which involves the flow of heat through solid substances like metal, is a twin process to diffusion. It is a process where thermal energy is transferred through conduction by the transfer of particle vibrations. The particles in a solid state are close to each other and are held together by intermolecular forces. When one particle gains energy, it transfers it to the neighboring particle through vibration transfer. Mathematical models incorporating fractional-order derivatives are excellent tools for describing thermal conduction in porous materials, such as porous aluminum [8].
Within the framework of subdiffusion or thermal conductivity processes modeled by subdiffusion or the fractional thermal conductivity equation, a subclass of so-called fractional Stefan problems can be distinguished. They are designed to describe the evolution of the boundary between two phases of a material undergoing a phase transition. Examples include the drug release from slab matrices [9,10]. Numerous papers presenting analytical and numerical results have been devoted to this phenomenon [11,12,13,14,15,16,17].
In the papers [18,19], Povstenko et al. consider the two dimensional time-fractional heat conduction equations. In the solution, they use Laplace and Fourier integral transforms, which allow the reduction of higher-degree differential equations to lower-degree equations, which greatly improved the obtaining of the solution. In addition, the paper [19] uses the Gaver-Stehfest algorithm to invert the Laplace transform. A similar approach to those presented in the aforementioned papers is used in this article, based, moreover, on the results presented in the monograph [20], with the difference that the Gaver-Wynn-Rho algorithm [21,22,23] was used to determine the original solution from the Laplace transform image.
Numerous numerical methods have been proposed for solving equations of anomalous diffusion. Ciesielski introduced numerical schemes for various cases in his doctoral dissertation [24], including equations with fractional-order time and spatial derivatives. The discussed cases were limited to one-dimensional problems. Papers [25,26] considered one-dimensional subdiffusion equations with a fractional spatial Riemann-Liouville derivative and provided corresponding numerical schemes. Bhrawy et al. [27] presented a numerical method for a subdiffusion equation with a Caputo time derivative. Błasik [28,29,30] extended the classical Crank-Nicolson method to one-dimensional subdiffusion equations with a Caputo time derivative, considering a variable diffusion coefficient and nonlinear source term. Other variants of the Crank-Nicloson method for the subdiffusion equation are included in the papers [31,32,33]. Noteworthy are also the articles [34,35,36,37,38], in which the authors have developed numerical methods characterized by high accuracy. Numerical results for the two-dimensional subdiffusion equation were presented in papers [39,40], while a more general case involving a source term was discussed in [41,42]. Other numerical approaches related to subdiffusion concern inverse problems [43] and use a non-standard definition of the Caputo derivative [44].
The article was structured as follows. The second section presented the basic definitions and properties of the following: fractional order differential calculus, integral transforms, and numerical methods. These concepts were utilized throughout the rest of the article. In the subsequent section, the problem to be solved was formulated as a two-dimensional sub-diffusion equation, along with uniqueness conditions. Two different methods were employed to solve this problem, each discussed in its respective sub-section. The fourth section showcased the numerical results obtained from the calculations. Finally, the article concluded with a section summarizing the findings and providing additional insights.

2. Preliminaries

Let us begin our consideration by introducing two fractional order operators: the left-sided Riemann-Liouville integral and the left-sided Caputo derivative together with the composition rule of the two mentioned operators [45].
Definition 1. 
The left-sided Riemann-Liouville integral of order α, denoted as I 0 + α , is given by the following formula for R e ( α ) ∈ ( 0 , 1 ] :
I 0 + α f ( t ) : = 1 Γ ( α ) ∫ 0 t f ( τ ) d τ ( t − τ ) 1 − α ,
where Γ is the Euler gamma function.
Definition 2. 
Let R e ( α ) ∈ ( 0 , 1 ] . The left-sided Caputo derivative of order α is given by the formula:
C D 0 + α f ( t ) : = 1 Γ ( 1 − α ) ∫ 0 t f ′ ( τ ) d τ ( t − τ ) α , 0 < R e ( α ) < 1 , d f ( t ) d t , R e ( α ) = 1 .
Property 1 
(Lemma 2.22 in [45]). Let function f ∈ C 1 ( 0 , T ) . Then, the composition rule for the left-sided Riemann-Liouville integral and the left-sided Caputo derivative is given as follows:
I 0 + α C D 0 + α f ( t ) = f ( t ) − f ( 0 ) , R e ( α ) ∈ ( 0 , 1 ] .
The definition of the Laplace integral transform [46], combined with the following property [47], will play an important role in determining the semi-analytical solution of the problem considered in the next section.
Definition 3. 
Let f ( t ) be a real function of the variable t ∈ R . Then the Laplace transform of the function f ( t ) is the function f ^ ( s ) of the complex variable defined by formula
L { f ( t ) } = f ^ ( s ) = ∫ 0 ∞ e − s t f ( t ) d t ,
where R e ( s ) > 0 .
Property 2. 
Let the function f ( t ) be the original, and let L { f ( t ) } = f ^ ( s ) , then the following formula holds
L { C D 0 + α f ( t ) } = s α f ^ ( s ) − f ( 0 ) , R e ( α ) ∈ ( 0 , 1 ] .
Bessel functions of the first and second kind [45,48] present two further definitions.
Definition 4. 
Let z ∈ C ∖ { R − , 0 } and ν ∈ C , then the Bessel function of the first kind denoted by J ν ( z ) is given by the following series:
J ν ( z ) = ∑ l = 0 ∞ ( − 1 ) l ( z / 2 ) 2 l + ν l ! Γ ( ν + l + 1 ) .
Definition 5. 
Let ν ∈ C ∖ Z , then the Bessel function of the second kind denoted by Y ν ( z ) is given by the following formula:
Y ν ( z ) = J ν ( z ) cos ν π − J − ν ( z ) sin ν π .
In the case of integer order m ∈ Z , function is defined in terms of the limit of
Y m ( z ) = lim ν → m Y ν ( z ) .
The numerical scheme proposed in the next section uses a mesh of nodes defined as follows:
Definition 6. 
Let Π = { ( r , t ) : r ∈ 1 2 , 1 ; t ∈ [ 0 , 1 ] } be a continuous region of solutions for the partial differential equation. Then the set Π ¯ = { ( r i , t j ) ∈ Π : r i = 1 2 + i Δ r , i ∈ { 0 , 1 , . . . , m } , Δ r = 1 2 m ; t j = j Δ t , j ∈ { 0 , 1 , . . . , n } ; Δ t = 1 n } we call the rectangular regular mesh described by the set of nodes.
In the further part of the paper, the real order of the left-sided Caputo derivative, and the left-sided Riemann-Liouville integral is considered.

3. Mathematical formulation and solution of the problem

Consider a two-dimensional subdiffusion equation in a region with axial symmetry. Let us also assume an axisymmetric system of boundary and initial conditions. The equation under consideration has the form:
C D 0 + , t α U ( x , y , t ) = D α ∂ 2 U ( x , y , t ) ∂ x 2 + ∂ 2 U ( x , y , t ) ∂ y 2 , 1 4 < x 2 + y 2 < 1 , t > 0 ,
supplemented by boundary conditions on the edges of the circular ring:
U ( x , y , t ) = U b , x 2 + y 2 = 1 , t > 0 ,
U ( x , y , t ) = 0 , x 2 + y 2 = 1 4 , t > 0 ,
and initial condition
U ( x , y , 0 ) = 0 , 1 4 ≤ x 2 + y 2 ≤ 1 ,
where the generalized diffusion coefficient D α is constant.
In the axisymmetric region in which we derive the solution of the differential equation, it is convenient to introduce the polar coordinates given by: x = r cos ϕ , y = r sin ϕ , for which the differential Equation (10) with boundary and initial conditions takes the form of:
C D 0 + , t α U ( r , ϕ , t ) = D α ∂ 2 U ( r , ϕ , t ) ∂ r 2 + 1 r 2 ∂ 2 U ( r , ϕ , t ) ∂ ϕ 2 + 1 r ∂ U ( r , ϕ , t ) ∂ r , 1 2 < r < 1 , 0 ≤ ϕ < 2 π , t > 0 ,
U ( 1 , ϕ , t ) = U b , 0 ≤ ϕ < 2 π , t > 0 ,
U 1 2 , ϕ , t = 0 , 0 ≤ ϕ < 2 π , t > 0 ,
U r , ϕ , 0 = 0 , 1 2 ≤ r ≤ 1 , 0 ≤ ϕ < 2 π .
The assumptions made about symmetry allow us to reduce the dimension of the problem under consideration. Let us note that for a fixed radius r and arbitrary angle ϕ , the diffusion flux in the direction normal to the edge takes the constant values. Thus, the function U does not depend on ϕ , and the second differential term on the right hand side of Equation (14) is equal to zero. As a result, the two-dimensional equation is immediately reduced to the one-dimensional one:
C D 0 + , t α U ( r , t ) = D α ∂ 2 U ( r , t ) ∂ r 2 + 1 r ∂ U ( r , t ) ∂ r , 1 2 < r < 1 , t > 0 ,
U ( 1 , t ) = U b , t > 0 ,
U 1 2 , t = 0 , t > 0 ,
U r , 0 = 0 , 1 2 ≤ r ≤ 1 .
It should be mentioned that in addition to symmetry, there are other ways to reduce the dimensions of differential problems, such as scaling [49,50], and integral transforms [46], which will be shown in the next section.

3.1. A numerical approach

In the paper [28], a generalized Crank-Nicolson method was proposed for the one-dimensional subdiffusion equation. The obtained results were further extended to the more general case, to the equation with a source term [29]. In both cases, obtained results confirmed the accuracy of the proposed methods. Therefore, an analogous approach will be applied to the problem defined by equations (18)-(21).
For some technical reasons, the numerical approximation of the left-sided Caputo derivative is much simpler compared to the approximation of the left-sided Riemann-Liouville integral. Therefore, we apply Property 1 to the Equation (18), which yields an integro-differential equation in the following form:
U ( r , t ) = U ( r , 0 ) + D α Γ ( α ) ∫ 0 t 1 ( t − τ ) 1 − α ∂ 2 U ( r , τ ) ∂ r 2 d τ + D α r Γ ( α ) ∫ 0 t 1 ( t − τ ) 1 − α ∂ U ( r , τ ) ∂ r d τ .
The solution U of the initial boundary value problem considered in the paper fulfills the assumptions of Property 1, and its existence and the uniqueness was proven in the more general case in the paper [51]. Further consideration will be conducted with reference to the mesh of nodes given in Definition 6. For each node of the grid, we determine the discrete form of the integral kernel in the integrals on the right-hand side of Equation (22). For this purpose, we approximate the solution U by a linear function between two consecutive nodes with respect to the variable t:
U ¯ ( r , t ) = U ( r , t j ) t − t j + 1 t j − t j + 1 + U ( r , t j + 1 ) t − t j t j + 1 − t j ,
for t j ≤ t ≤ t j + 1 , j = 0 , . . . , n − 1 .
Subsequently, we discretize the first- and second-order derivatives of the right-hand side of the integro-differential equation (22) using differential quotients approximating the first
∂ U ( r , t ) ∂ r i , j = U i + 1 , j − U i − 1 , j 2 Δ r + O ( ( Δ r ) 2 ) ,
and second derivative
∂ 2 U ( r , t ) ∂ r 2 i , j = U i − 1 , j − 2 U i , j + U i + 1 , j ( Δ r ) 2 + O ( ( Δ r ) 2 ) ,
with respect to the spatial variable r.
Using transformations analogous to those in the paper [29], we obtain the discrete form of integro-differential equation (22) as follows:
U i , k = U i , 0 + D α ∑ j = 0 k w j , k U i − 1 , j − 2 U i , j + U i + 1 , j ( Δ r ) 2 + D α r i ∑ j = 0 k w j , k U i + 1 , j − U i − 1 , j 2 Δ r ,
where the weights corresponding to the integral kernel of the left-sided Riemann-Liouville integrals are of the form:
w j , k : = ( Δ t ) α Γ ( 2 + α ) ( α + 1 − k ) k α + ( k − 1 ) α + 1 , j = 0 ( k − j + 1 ) α + 1 − 2 ( k − j ) α + 1 + ( k − j − 1 ) α + 1 , 0 < j < k 1 , j = k
We transform Equation (26) in such a way that the unknown values of the U function in the k-th time layer are on its left side. Finally, we obtain an implicit numerical scheme, which in node 1 2 + i Δ r , k Δ t takes the form:
− D α ( 2 r i − Δ r ) w k , k 2 r i ( Δ r ) 2 U i − 1 , k + 1 + 2 D α w k , k ( Δ r ) 2 U i , k − D α ( 2 r i + Δ r ) w k , k 2 r i ( Δ r ) 2 U i + 1 , k = U i , 0 + ∑ j = 0 k − 1 D α w j , k ( Δ r ) 2 2 r i − Δ r 2 r i U i − 1 , j − 2 U i , j + 2 r i + Δ r 2 r i U i + 1 , j
Applying the above relationship to each of the m − 2 nodes of the k-th time layer, we obtain a system of linear equations with m − 2 unknown values of the U-function, which can be written in matrix form:
A U k = B ,
where matrix A is defined by
A = 1 + 2 δ − ( 2 r 1 + Δ r ) δ 2 r 1 0 0 ⋯ 0 0 0 − ( 2 r 2 − Δ r ) δ 2 r 2 1 + 2 δ − ( 2 r 2 + Δ r ) δ 2 r 2 0 ⋯ 0 0 0 0 − ( 2 r 3 − Δ r ) δ 2 r 3 1 + 2 δ − ( 2 r 3 + Δ r ) δ 2 r 3 ⋯ 0 0 0 ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ 0 0 0 − ( 2 r i − Δ r ) δ 2 r i 1 + 2 δ − ( 2 r i + Δ r ) δ 2 r i 0 0 ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ ⋮ ⋮ 0 0 0 0 ⋯ − ( 2 r m − 2 − Δ r ) δ 2 r m − 2 1 + 2 δ − ( 2 r m − 2 + Δ r ) δ 2 r m − 2 0 0 0 0 ⋯ 0 − ( 2 r m − 1 − Δ r ) δ 2 r m − 1 1 + 2 δ ,
where δ : = D α w k , k ( Δ r ) 2 . The elements of vector B are defined by
B = b 1 + ( 2 r 1 − Δ r ) δ 2 r 1 U 0 , k b 2 b 3 ⋮ b i ⋮ b m − 2 b m − 1 + ( 2 r m − 1 + Δ r ) δ 2 r m − 1 U m , k ,
where
b i : = U i , 0 + ∑ j = 0 k − 1 D α w j , k ( Δ r ) 2 2 r i − Δ r 2 r i U i − 1 , j − 2 U i , j + 2 r i + Δ r 2 r i U i + 1 , j .

3.2. A semi-analytical approach

The application of the Laplace transform and Property 2 to subdiffusion Equation (18) removes the time variable, thus reducing the considered equation to the form of an ordinary differential equation, which is solved in terms of the space variable r. As a consequence of this treatment, we get the equation:
s α U ^ ( r , s ) = D α ∂ 2 U ^ ( r , s ) ∂ r 2 + 1 r ∂ U ^ ( r , s ) ∂ r , 1 2 < r < 1 ,
supplemented with boundary conditions
U ^ ( 1 , s ) = U b s ,
U 1 2 , s = 0 .
We can write the boundary value problem (30)-(32) as follows, using the notation for ordinary differential equations:
U ^ ′ ′ ( r ) + 1 r U ^ ′ ( r ) − s α D α U ^ ( r ) = 0
U ^ ( 1 ) = U b s ,
U ^ 1 2 = 0 .
The differential equation (33) is the so-called Bessel differential equation, whose general solution is well known in the form of Bessel functions of the first and second kind [48]:
U ^ ( r ) = c 1 J 0 i r s α / 2 D α + c 2 Y 0 − i r s α / 2 D α
Applying the boundary conditions (34) and (35) to Equation (36), we obtain a system of equations:
c 1 J 0 i s α / 2 D α + c 2 Y 0 − i s α / 2 D α = U b s c 1 J 0 i s α / 2 2 D α + c 2 Y 0 − i s α / 2 2 D α = 0
Solving the system of equations (37), we obtain a constant c 1 in the form of:
c 1 = U b Y 0 − i s α / 2 2 D α s J 0 i s α / 2 D α Y 0 − i s α / 2 2 D α − J 0 i s α / 2 2 D α Y 0 − i s α / 2 D α ,
and a constant c 2 in the form of:
c 2 = − U b J 0 i s α / 2 2 D α s J 0 i s α / 2 D α Y 0 − i s α / 2 2 D α − J 0 i s α / 2 2 D α Y 0 − i s α / 2 D α .
Obtaining the original U ( r , t ) by analytical transformations is problematic, therefore this task will be realized in the next section using the Gaver-Wynn-Rho algorithm [21,22,23].

4. Numerical examples

The numerical results presented in the following section assume the following values for the parameters of the initial boundary value problem (18)-(21): U b = 1 , D α = 1 , t ∈ [ 0 , 1 ] , α ∈ { 0.25 , 0.5 , 0.75 , 1 } . Numerical simulations were performed for seventeen mesh variants, which adopted: ( Δ r , Δ t ) ∈ 1 50 , 1 100 , 1 200 , 1 400 × 1 50 , 1 100 , 1 200 , 1 400 ∪ 1 1600 , 1 1600 .
The figures shown below illustrate the results of numerical calculations, which assumed the following values of grid steps: Δ r = 1 100 and Δ t = 1 400 . This choice provides a compromise between good readability of the graphs and accuracy of the presented results.
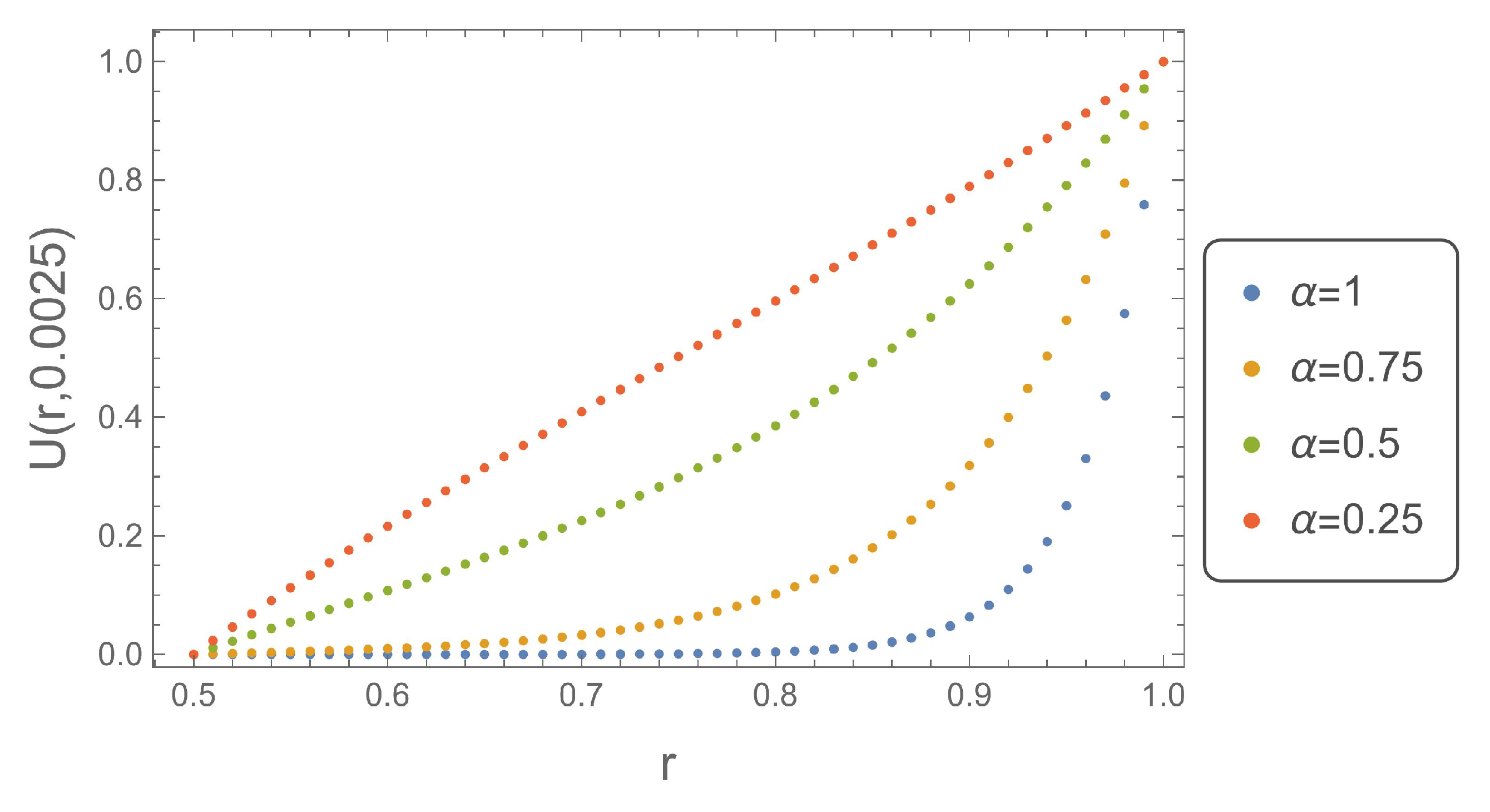
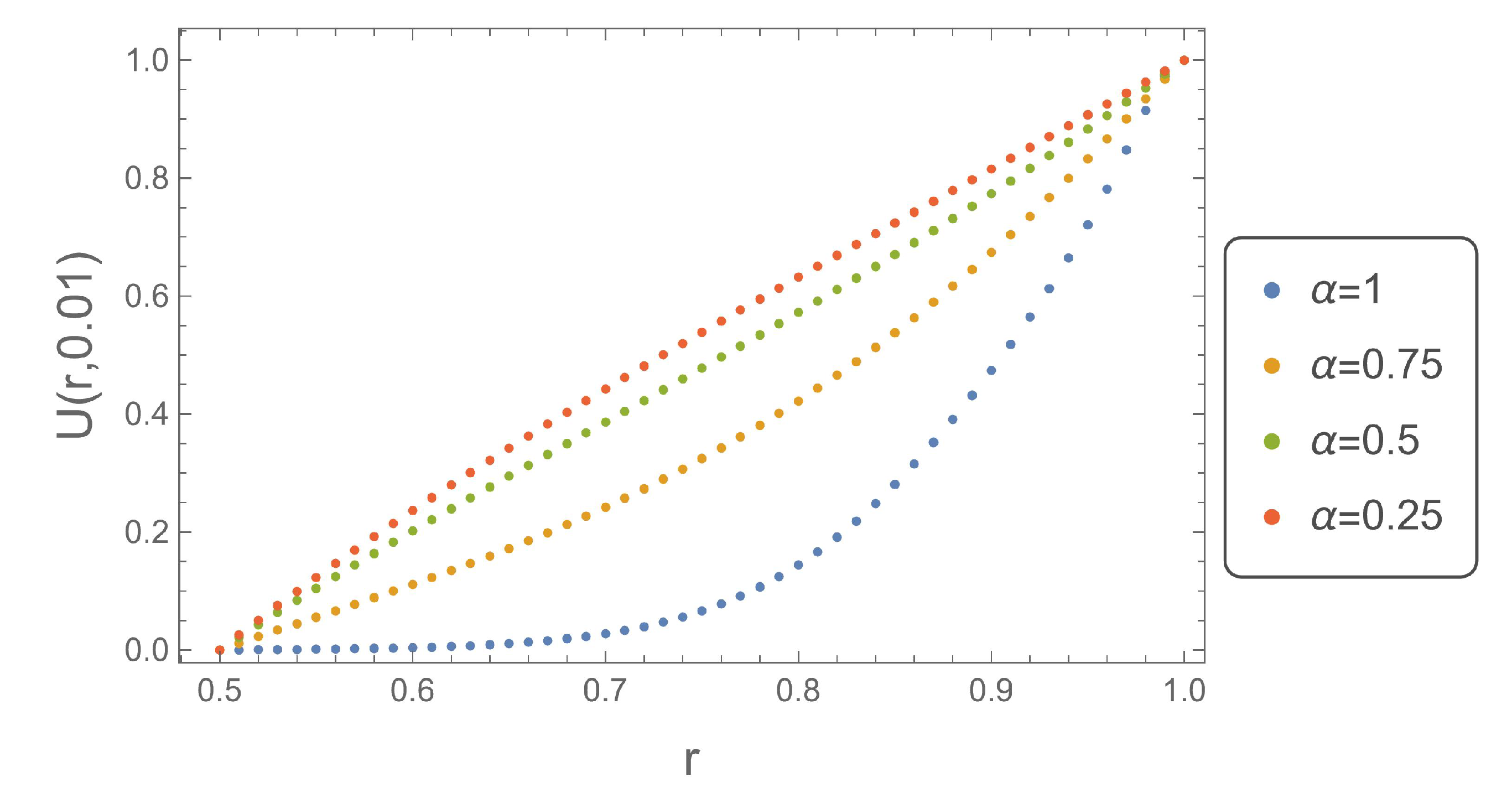
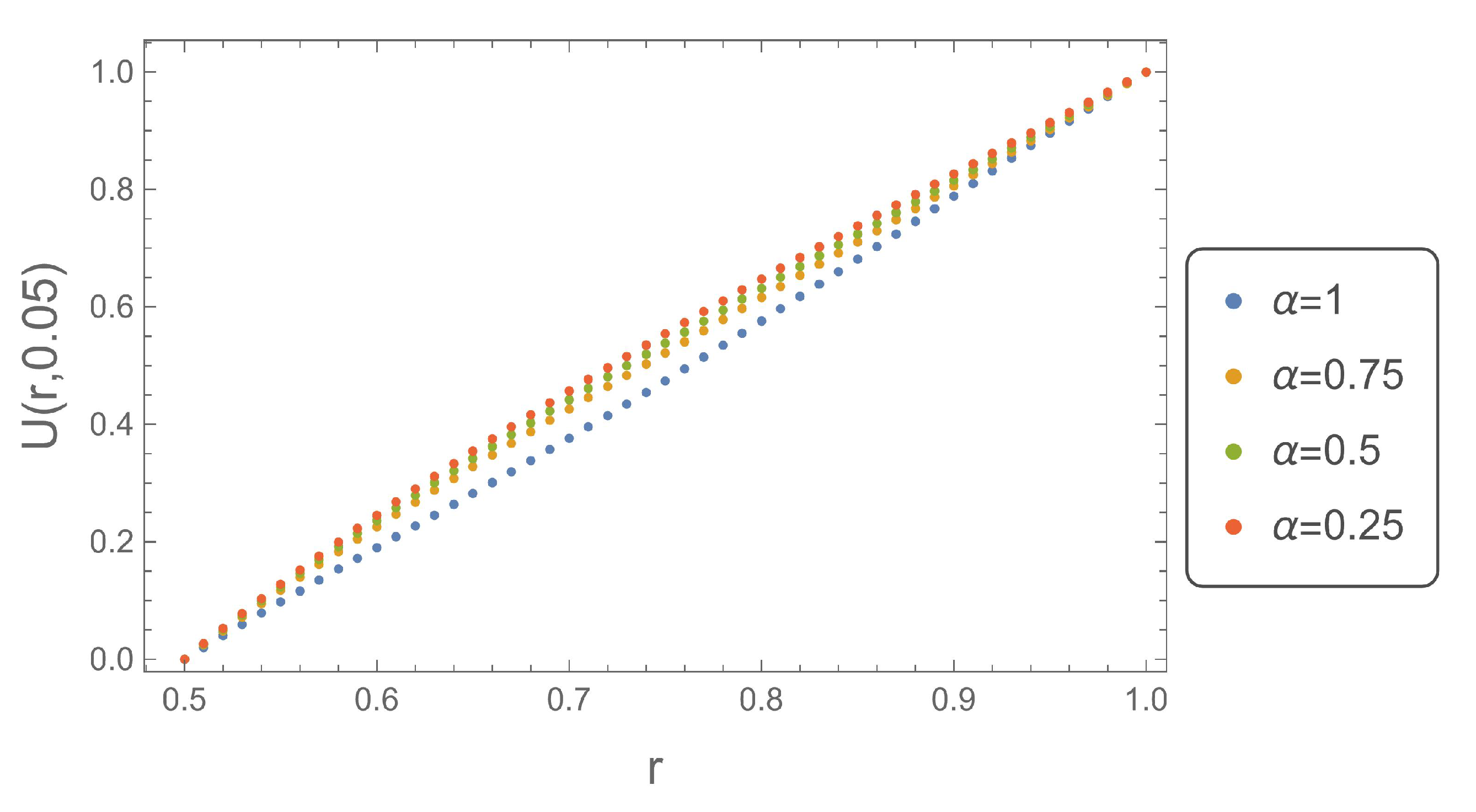
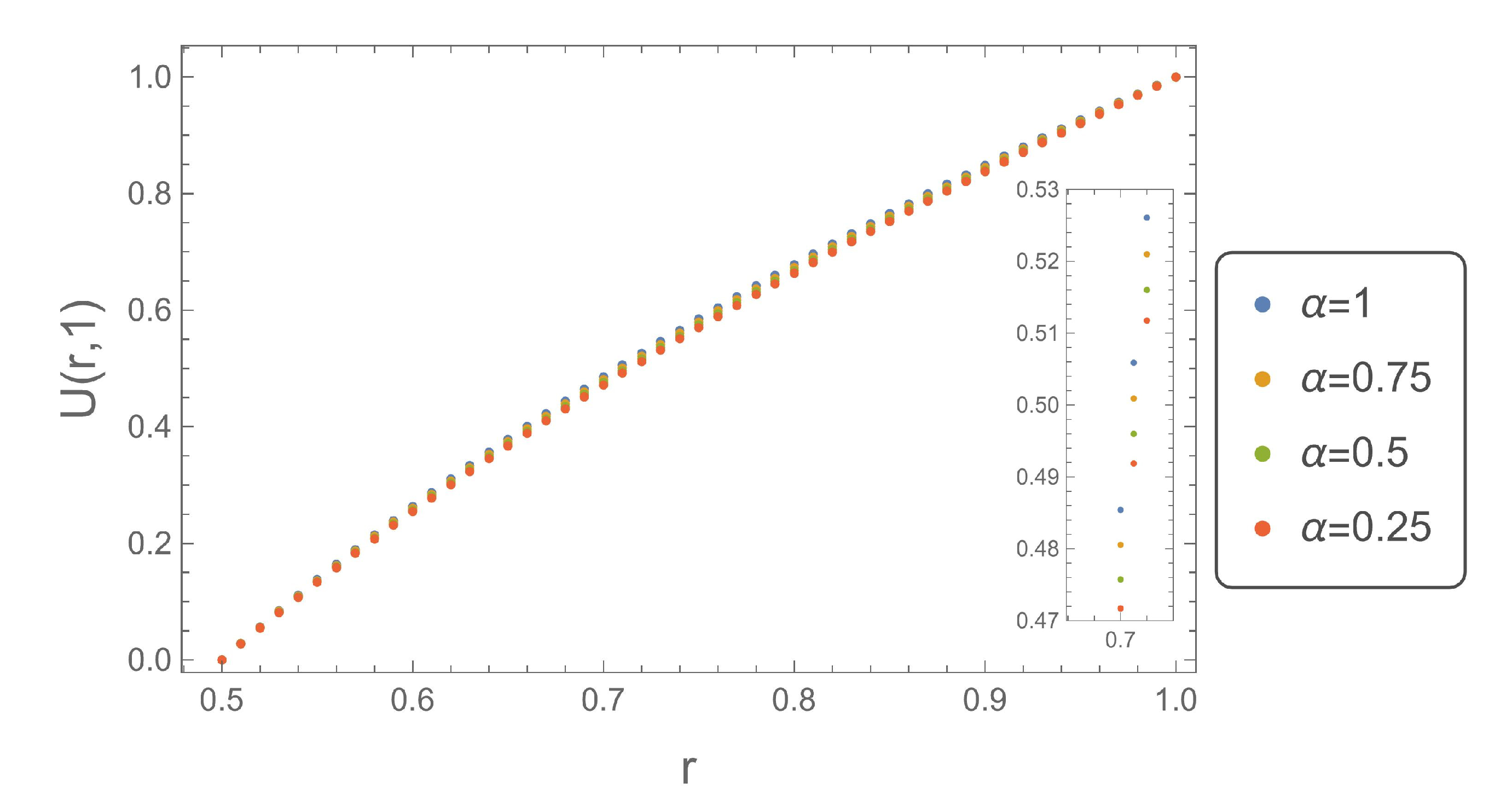
Figure 1, Figure 3, Figure 5 and Figure 7 show the solutions of the subdiffusion Equation (18) depending on the radius r at four different time instants. They clearly demonstrate the nature of the modeled phenomenon. For very early time instants just after the initiation of the process t ≪ 1 , the solution obtained for α = 0.25 reaches the largest values. The disproportion between the solution for α = 0.25 and α = 1 decreases with the increase of time, and this results directly from the relation (1). Figure 7 shows that for t = 1 , the solution obtained for α = 1 takes the largest values.
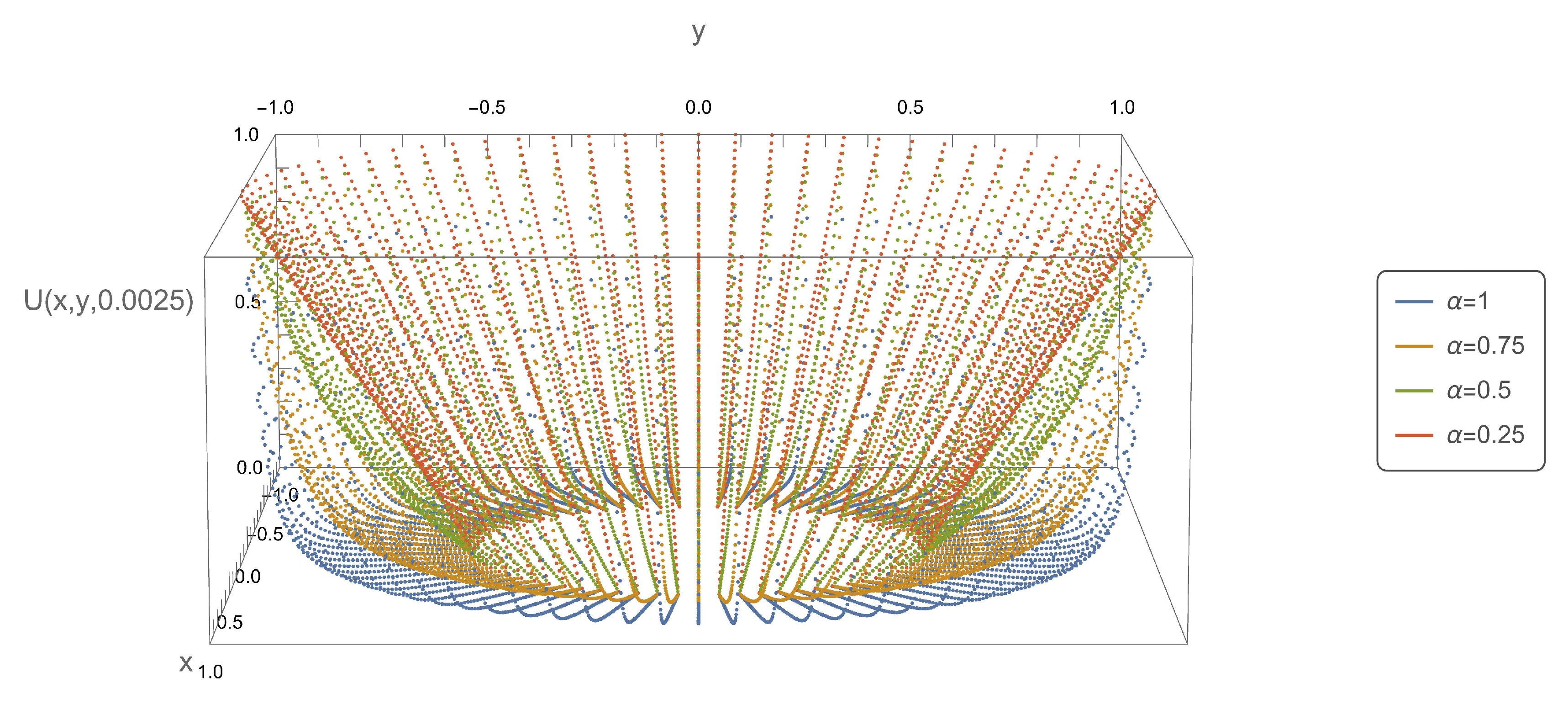
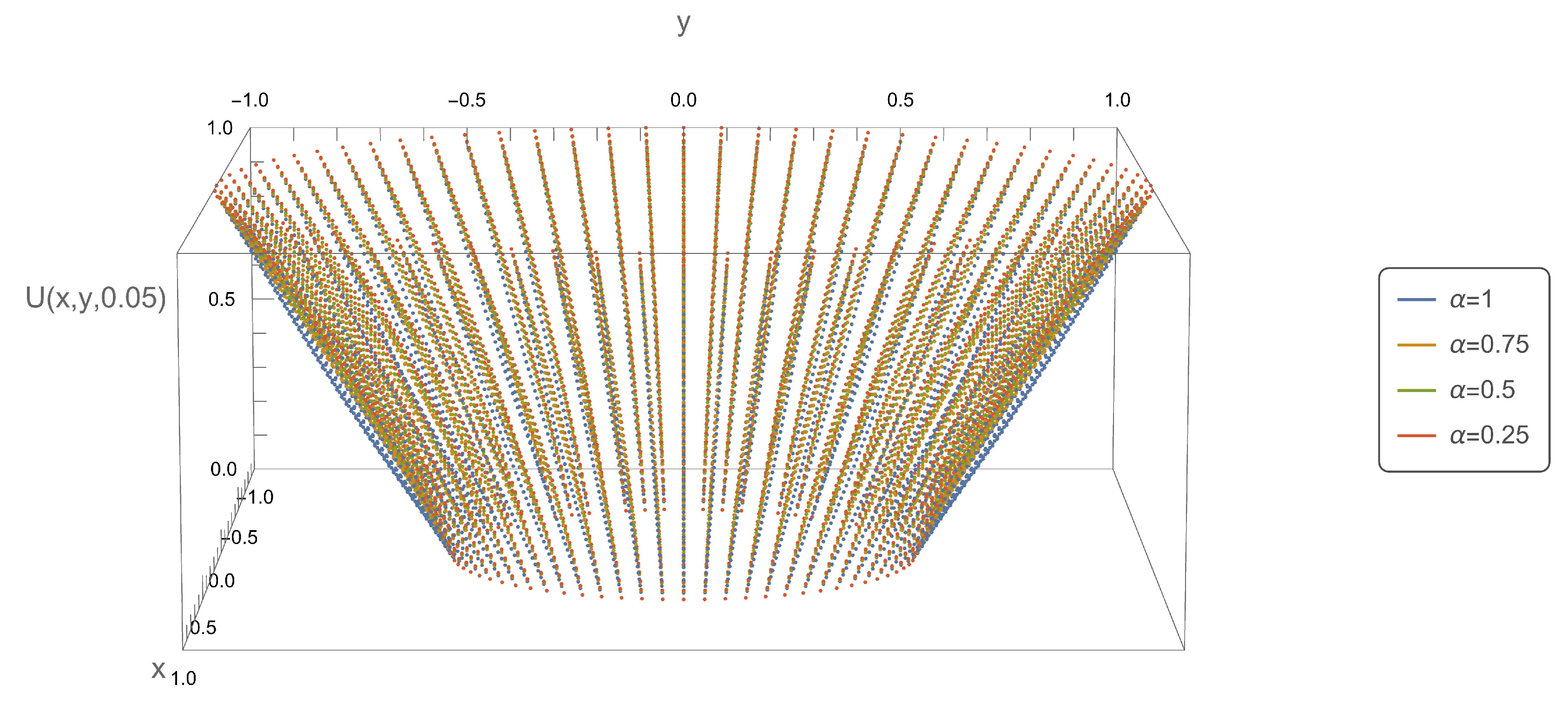
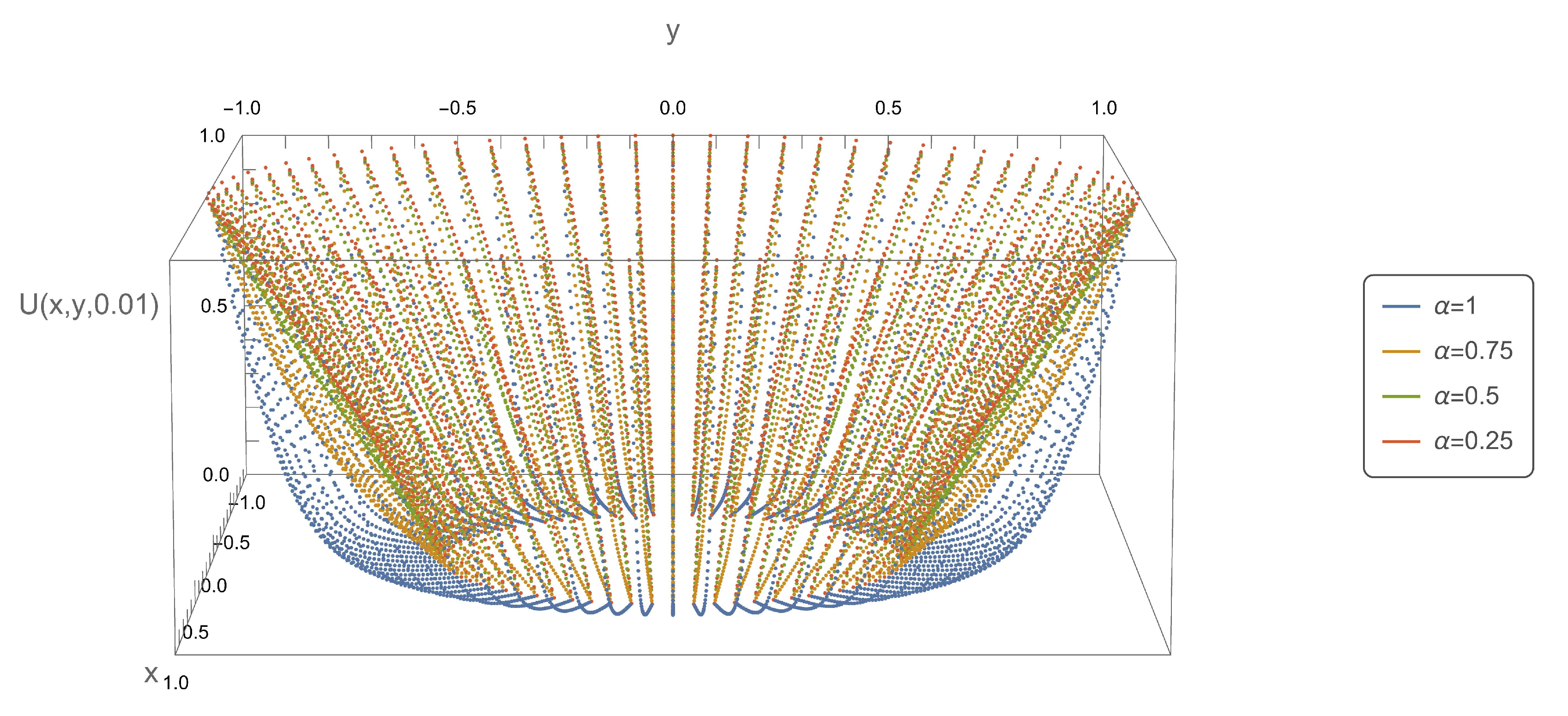
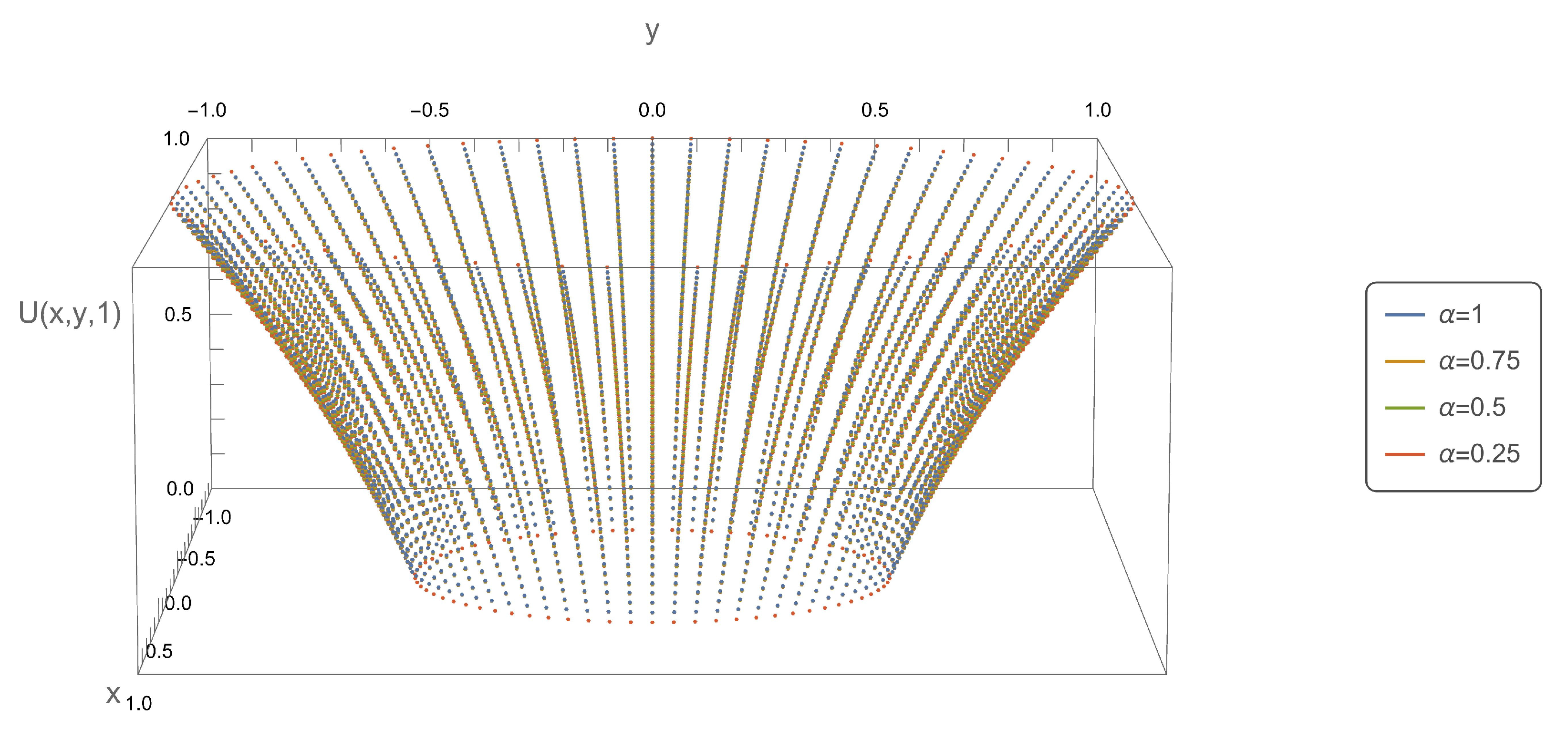
Figure 2, Figure 4, Figure 6 and Figure 8, present the axial symmetry of the obtained solutions in the Cartesian coordinate system. The values of the variable ϕ were determined as follows: ϕ = π i 36 , i = 1 , 2 , . . . , 72 . The x, y coordinates were determined using the relationship x = r cos ϕ , y = r sin ϕ .
Preprints 81019 g001
Figure 1. Plot of U ( r , 1 / 400 ) determined numerically for Δ r = 1 / 100 , Δ t = 1 / 400 .
Figure 1. Plot of U ( r , 1 / 400 ) determined numerically for Δ r = 1 / 100 , Δ t = 1 / 400 .
Preprints 81019 g001
Preprints 81019 g002
Figure 2. Plot of function U ( x , y , 1 / 400 ) .
Figure 2. Plot of function U ( x , y , 1 / 400 ) .
Preprints 81019 g002
Preprints 81019 g003
Figure 3. Plot of U ( r , 1 / 100 ) determined numerically for Δ r = 1 / 100 , Δ t = 1 / 400 .
Figure 3. Plot of U ( r , 1 / 100 ) determined numerically for Δ r = 1 / 100 , Δ t = 1 / 400 .
Preprints 81019 g003
Preprints 81019 g004
Figure 4. Plot of function U ( x , y , 1 / 100 ) .
Figure 4. Plot of function U ( x , y , 1 / 100 ) .
Preprints 81019 g004
Preprints 81019 g005
Figure 5. Plot of U ( r , 1 / 20 ) determined numerically for Δ r = 1 / 100 , Δ t = 1 / 400 .
Figure 5. Plot of U ( r , 1 / 20 ) determined numerically for Δ r = 1 / 100 , Δ t = 1 / 400 .
Preprints 81019 g005
Preprints 81019 g006
Figure 6. Plot of function U ( x , y , 1 / 20 ) .
Figure 6. Plot of function U ( x , y , 1 / 20 ) .
Preprints 81019 g006
Preprints 81019 g007
Figure 7. Plot of U ( r , 1 ) determined numerically for Δ r = 1 / 100 , Δ t = 1 / 400 .
Figure 7. Plot of U ( r , 1 ) determined numerically for Δ r = 1 / 100 , Δ t = 1 / 400 .
Preprints 81019 g007
Preprints 81019 g008
Figure 8. Plot of function U ( x , y , 1 ) .
Figure 8. Plot of function U ( x , y , 1 ) .
Preprints 81019 g008
In order to validate the numerical method proposed in subsection 3.1, the results obtained with it were compared with those received by the inverse Laplace transform of the image (36) using the Gaver-Wynn-Rho algorithm implemented in Wolfram Mathematica. The comparison was made at twenty points ( r , t ) ∈ { 0.6 , 0.7 , 0.8 , 0.9 } × { 0.2 , 0.4 , 0.6 , 0.8 , 1 } , which are common to all tested mesh variants. 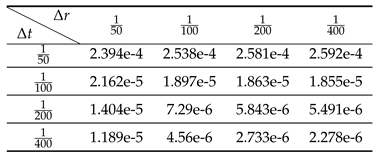Table 1, Table 2, Table 3 and Table 4 collect the average absolute difference between the solution obtained by the proposed numerical method U ( r , t ) and that obtained by the inverse Laplace transform U G W R ( r , t ) . The analysis of all the tables leads to the observation that as the steps of the grid Δ r and Δ t are reduced, then U ( r , t ) converges to U G W R ( r , t ) for all tested values of the order α .

4.1. Convergence analysis

The order of convergence of the proposed numerical scheme was estimated using EOC (experimental order of the convergence) and calculated as follows [35]:
E O C = log 2 | U i , j 1 1600 , 1 1600 − U i , j Δ t , Δ r | | U i , j 1 1600 , 1 1600 − U i , j Δ t / 2 , Δ r / 2 | = log 2 Δ U Δ t , Δ r Δ U Δ t / 2 , Δ r / 2 ,
where by U i , j Δ t , Δ r denoted the numerical solution of the considered equation at nodal points common to all considered meshes ( 1 2 + i 50 , j 50 ) for i = 0 . . 25 , j = 0 . . 50 , with time step Δ t ∈ 1 50 , 1 100 , 1 200 and spatial step Δ r ∈ 1 50 , 1 100 , 1 200 . By U i , j 1 1600 , 1 1600 the reference numerical solution obtained under the fine mesh is denoted. We use the formula (40) only when the closed analytical solution is not available. The calculation results shown in Table 5 and Table 6 indicate that the order of convergence of the proposed method is approximately equal to one. We can come to similar conclusions by comparing the elements on the main diagonal in Table 1, Table 2, Table 3 and Table 4.

5. Conclusions

The method proposed in the article is a generalization of the fractional Crank-Nicolson method to a two-dimensional subdiffusion equation in the polar coordinate system, taking into account the assumed symmetry of the area and boundary conditions. To validate the method, the obtained results were compared with those received using the semi-analytical approach, where the analytical solution in the Laplace transform domain was numerically inverted. It was observed that the method based on the discretization of the integro-differential equation generates solutions that converge to those obtained by the Gaver-Wynn-Rho algorithm. As the time and space steps are decreased, the average absolute difference between the solutions decreases.
Furthermore, it was found that the semi-analytical approach is more effective in determining the solution at specific points within the area, despite the relatively longer time to obtaining a solution at a single point. On the other hand, the generalized Crank-Nicolson method allows for the determination of the solution at all nodal points within the area significantly faster, but with lower accuracy. In the tests, it took approximately 10 seconds to obtain solutions for 10201 nodal points, while the Gaver-Wynn-Rho algorithm generated solutions for 20 points in about 3 seconds.
In a subsequent stage of testing, the plan is to further investigate the convergence analysis of the proposed scheme and reduce the computational cost.

References

  1. Metzler, R.; Klafter, J. The random walk:s guide to anomalous diffusion: a fractional dynamics approach. Physics Reports 2000, 339, 1–77. [Google Scholar] [CrossRef]
  2. Metzler, R.; Klafter, J. The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. Journal of Physics A: Mathematical and General 2004, 37, 161–208. [Google Scholar] [CrossRef]
  3. Weeks, E.; Urbach, J.; Swinney, L. Anomalous diffusion in asymmetric random walks with a quasi-geostrophic flow example. Physica D: Nonlinear Phenomena 1996, 97, 291–310. [Google Scholar] [CrossRef]
  4. Solomon, T.; Weeks, E.; Swinney, H. Observations of anomalous diffusion and Lévy flights in a 2-dimensional rotating flow. Physical Review Letters 1993, 71, 3975–3979. [Google Scholar] [CrossRef]
  5. Humphries, N.E.; Queiroz, N.; Dyer, J.R.M.; Pade, N.G.; Musyl, M.K.; Schaefer, K.M.; Fuller, D.W.; Brunnschweiler, J.M.; Doyle, T.K.; Houghton, J.D.R.; Hays, G.C.; Jones, C.S.; Noble, L.R.; Wearmouth, V.J.; Southall, E.J.; Sims, D.W. Environmental context explains Lévy and Brownian movement patterns of marine predators. Nature 2010, 465, 1066–1069. [Google Scholar] [CrossRef] [PubMed]
  6. Kosztołowicz, T.; Dworecki, K.; Mrówczyński, S. How to Measure Subdiffusion Parameters. Physical Review Letters 2005, 94, 170602. [Google Scholar] [CrossRef]
  7. Kosztołowicz, T.; Dworecki, K.; Mrówczyński, S. Measuring subdiffusion parameters. Physical Review E 2005, 71, 041105. [Google Scholar] [CrossRef]
  8. Brociek, R.; Słota, D.; Król, M.; Matula, G.; Kwaśny, W. Comparison of mathematical models with fractional derivative for the heat conduction inverse problem based on the measurements of temperature in porous aluminum. International Journal of Heat and Mass Transfer 2019, 143. [Google Scholar] [CrossRef]
  9. Xi-cheng, L. Fractional Moving Boundary Problems and Some of Its Applications to Controlled Release System of Drug. PhD thesis, Shandong University, 2009.
  10. Yin, C.; Li, X. Anomalous diffusion of drug release from slab matrix: Fractional diffusion models. International Journal of Pharmaceutics 2011, 418, 78–87. [Google Scholar] [CrossRef]
  11. Voller, V.R. An exact solution of a limit case Stefan problem governed by a fractional diffusion equation. International Journal of Heat and Mass Transfer 2010, 53, 5622–5625. [Google Scholar] [CrossRef]
  12. Voller, V.R. Fractional Stefan problems. International Journal of Heat and Mass Transfer 2014, 74, 269–277. [Google Scholar] [CrossRef]
  13. Chmielowska, A.; Słota, D. Fractional Stefan Problem Solving by the Alternating Phase Truncation Method. Symmetry 2022, 14. [Google Scholar] [CrossRef]
  14. Błasik, M.; Klimek, M. Numerical solution of the one phase 1D fractional Stefan problem using the front fixing method. Mathematical Methods in the Applied Sciences 2015, 38, 3214–3228. [Google Scholar] [CrossRef]
  15. Roscani, S.; Marcus, E. Two equivalent Stefans problems for the time fractional diffusion equation. Fractional Calculus and Applied Analysis 2013, 16, 802–815. [Google Scholar] [CrossRef]
  16. Roscani, S. Hopf lemma for the fractional diffusion operator and its application to a fractional free-boundary problem. Journal of Mathematical Analysis and Applications 2015, 434, 125–135. [Google Scholar] [CrossRef]
  17. Błasik, M. A Numerical Method for the Solution of the Two-Phase Fractional Lamé–Clapeyron–Stefan Problem. Mathematics 2020, 8, 2157. [Google Scholar] [CrossRef]
  18. Povstenko, Y.Z.; Kyrylych, T. Time-Fractional Heat Conduction in a Plane with Two External Half-Infinite Line Slits under Heat Flux Loading. Symmetry 2019, 11. [Google Scholar] [CrossRef]
  19. Povstenko, Y.Z.; Klekot, J. Time-Fractional Heat Conduction in Two Joint Half-Planes. Symmetry 2019, 11. [Google Scholar] [CrossRef]
  20. Povstenko, Y.Z. Linear Fractional Diffusion-Wave Equation for Scientists and Engineers; Birkhäuser, 2015.
  21. Valkó, P.P.; Abate, J. Comparison of sequence accelerators forthe Gaver method of numerical Laplace transform inversion. Computers & Mathematics with Applications 2004, 48, 629–636. [Google Scholar] [CrossRef]
  22. Abate, J.; Valkó, P.P. Multi-precision Laplace transform inversion. International Journal for Numerical Methods in Engineering 2004, 60, 979–993. [Google Scholar] [CrossRef]
  23. Guo, S.; Fan, X.; Gao, K.; Li, H. Precision controllable Gaver-Wynn-Rho algorithm in Laplace transform triple reciprocity boundary element method for three dimensional transient heat conduction problems. Engineering Analysis with Boundary Elements 2020, 114, 166–177. [Google Scholar] [CrossRef]
  24. Ciesielski, M. Frakcjalna metoda roznic skonczonych w zastosowaniu do modelowania anomalnej dyfuzji w obszarze ograniczonym. PhD thesis, Czestochowa University of Technology, 2005.
  25. Liu, F.; Yang, C.; Burrage, K. Numerical method and analytical technique of the modified anomalous subdiffusion equation with a nonlinear source term. Journal of Computational and Applied Mathematics 2009, 231, 160–176. [Google Scholar] [CrossRef]
  26. Zhuang, P.; Liu, F.; Anh, V.; Turner, I. New Solution and Analytical Techniques of the Implicit Numerical Method for the Anomalous Subdiffusion Equation. SIAM Journal on Numerical Analysis 2008, 46, 1079–1095. [Google Scholar] [CrossRef]
  27. Bhrawy, A.H.; Baleanu, D.; Mallawi, F. A new numerical technique for solving fractional sub-diffusion and reaction sub-diffusion equations with a non-linear source term. Thermal Science 2015, 19, 25–34. [Google Scholar] [CrossRef]
  28. Błasik, M. A Generalized Crank-Nicolson Method for the Solution of the Subdiffusion Equation. 23rd International Conference on Methods & Models in Automation & Robotics (MMAR); 2018; pp. 726–729. [Google Scholar]
  29. Błasik, M. The implicit numerical method for the one-dimensional anomalous subdiffusion equation with a nonlinear source term. Bulletin of the Polish Academy of Sciences: Technical Sciences 2021, 69, e138240. [Google Scholar] [CrossRef]
  30. Błasik, M. Numerical methodfor the solution of the one-dimensional anomalous subdiffusion equation with a variable diffusion coefficient. Acta Physica Polonica A 2020, 138. [Google Scholar] [CrossRef]
  31. Zhang, P.; Pu, H. The error analysis of Crank-Nicolson-type difference scheme for fractional subdiffusion equation with spatially variable coefficient. Boundary Value Problems 2017, 2017. [Google Scholar] [CrossRef]
  32. Onal, M.; Esen, A. A Crank-Nicolson Approximation for the time Fractional Burgers Equation. Applied Mathematics and Nonlinear Sciences 2020, 5, 177–184. [Google Scholar] [CrossRef]
  33. Jin, B.; Li, B.; Zhou, Z. An analysis of the Crank–Nicolson method for subdiffusion. IMA Journal of Numerical Analysis 2017, 38, 518–541. [Google Scholar] [CrossRef]
  34. Wang, L.; Stynes, M. An α-robust finite difference method for a time-fractional radially symmetric diffusion problem. Computers and Mathematics with Applications 2021, 97, 386–393. [Google Scholar] [CrossRef]
  35. Gu, X.M.; Sun, H.W.; Zhao, Y.L.; Zheng, X. An implicit difference scheme for time-fractional diffusion equations with a time-invariant type variable order. Applied Mathematics Letters 2021, 120, 107270. [Google Scholar] [CrossRef]
  36. Luo, W.H.; Huang, T.Z.; Wu, G.C.; Gu, X.M. Quadratic spline collocation method for the time fractional subdiffusion equation. Applied Mathematics and Computation 2016, 276, 252–265. [Google Scholar] [CrossRef]
  37. Luo, W.H.; Li, C.; Huang, T.Z.; Gu, X.M.; Wu, G.C. A High-Order Accurate Numerical Scheme for the Caputo Derivative with Applications to Fractional Diffusion Problems. Numerical Functional Analysis and Optimization 2017, 39, 600–622. [Google Scholar] [CrossRef]
  38. Yang, X.; Wu, L.; Zhang, H. A space-time spectral order sinc-collocation method for the fourth-order nonlocal heat model arising in viscoelasticity. Applied Mathematics and Computation 2023, 457, 128192. [Google Scholar] [CrossRef]
  39. Chen, C.M.; Liu, F.; Turner, I.; Anh, V. Numerical schemes and multivariate extrapolation of a two-dimensional anomalous sub-diffusion equation. Numerical Algorithms 2010, 54, 1–21. [Google Scholar] [CrossRef]
  40. Sweilam, N.H.; Ahmed, S.M.; Adel, M. A simple numerical method for two-dimensional nonlinear fractional anomalous sub-diffusion equations. Mathematical Methods in the Applied Sciences 2020, 44, 2914–2933. [Google Scholar] [CrossRef]
  41. Huang, H.; Cao, X. Numerical method for two dimensional fractional reaction subdiffusion equation. The European Physical Journal Special Topics 2013, 222, 1961–1973. [Google Scholar] [CrossRef]
  42. Yu, B.; Jiang, X.; Xu, H. A novel compact numerical method for solving the two-dimensional non-linear fractional reaction-subdiffusion equation. Numerical Algorithms 2015, 68, 923–950. [Google Scholar] [CrossRef]
  43. Krasnoschok, M.; Pereverzyev, S.; Siryk, S.V.; Vasylyeva, N. Determination of the Fractional Order in Semilinear Subdiffusion Equations. Fractional Calculus and Applied Analysis 2020, 23, 694–722. [Google Scholar] [CrossRef]
  44. Krasnoschok, M.; Pata, V.; Siryk, S.V.; Vasylyeva, N. Equivalent definitions of Caputo derivatives and applications to subdiffusion equations. Dynamics of Partial Differential Equations 2020, 17, 383–402. [Google Scholar] [CrossRef]
  45. Kilbas, A.; Srivastava, H.; Trujillo, J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, 2006. [Google Scholar]
  46. Debnath, L.; Bhatta, D. Integral Transforms and Their Applications, 2nd ed.; Chapman and Hall/CRC: New York, 2006. [Google Scholar]
  47. Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, 1999. [Google Scholar]
  48. Zill, D.; Cullen, M. Differential Equations with Boundary-Value Problems; Cengage Learning, 2008.
  49. Barenblatt, G. Scaling, Self-Similarity, and Intermediate Asymptotics; Cambridge University Press: Cambridge, 1996. [Google Scholar]
  50. Barenblatt, G. Scaling; Cambridge University Press: Cambridge, 2003. [Google Scholar]
  51. Luchko, Y. Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation. Computers and Mathematics with Applications 2010, 59, 1766–1772. [Google Scholar] [CrossRef]
Table 1. The value of | U ( r , t ) − U G W R ( r , t ) | for α = 1 .
Table 1. The value of | U ( r , t ) − U G W R ( r , t ) | for α = 1 .
Preprints 81019 i001
Table 2. The value of | U ( r , t ) − U G W R ( r , t ) | for α = 0.75 .
Table 2. The value of | U ( r , t ) − U G W R ( r , t ) | for α = 0.75 .
Preprints 81019 i001
Table 3. The value of | U ( r , t ) − U G W R ( r , t ) | for α = 0.5 .
Table 3. The value of | U ( r , t ) − U G W R ( r , t ) | for α = 0.5 .
Preprints 81019 i001
Table 4. The value of | U ( r , t ) − U G W R ( r , t ) | for α = 0.25 .
Table 4. The value of | U ( r , t ) − U G W R ( r , t ) | for α = 0.25 .
Preprints 81019 i001
Table 5. Convergence order of the proposed numerical scheme for α ∈ { 1 , 0.75 } .
Table 5. Convergence order of the proposed numerical scheme for α ∈ { 1 , 0.75 } .
α = 1 α = 0.75
n m Δ t Δ r Δ U Δ t , Δ r EOC Δ U Δ t , Δ r EOC
50 25 1 50 1 50 4.721e-3 - 2.759e-3 -
100 50 1 100 1 100 1.781e-3 1.406 6.509e-4 2.084
200 100 1 200 1 200 7.416e-4 1.264 2.857e-4 1.188
400 200 1 400 1 400 2.939e-4 1.3353 1.231e-4 1.215
Table 6. Convergence order of the proposed numerical scheme for α ∈ { 0.5 , 0.25 } .
Table 6. Convergence order of the proposed numerical scheme for α ∈ { 0.5 , 0.25 } .
α = 0.5 α = 0.25
n m Δ t Δ r Δ U Δ t , Δ r EOC Δ U Δ t , Δ r EOC
50 25 1 50 1 50 1.15e-3 - 2.836e-4 -
100 50 1 100 1 100 1.788e-4 2.684 7.505e-5 1.918
200 100 1 200 1 200 1.117e-4 0.679 4.03e-5 0.897
400 200 1 400 1 400 4.913e-5 1.186 1.715e-5 1.233
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated