Prerpints.org logo
Preprint
Article

Investigation of oxygen behavior under different melt flow, diffusion boundary layer and crystal-melt interface in a 300mm silicon crystal growth with CUSP magnetic field

Altmetrics

Downloads

145

Views

31

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

31 July 2023

Posted:

02 August 2023

You are already at the latest version

Alerts
Abstract
: The silicon single crystals for semiconductor application is usually grown by Czochralski (CZ) method. This paper researches 300mm silicon Czochralski (CZ) crystal growth with CUSP magnetic field for IGBTs substrate application. The different positions of Zero-Gauss plane (ZGP) under CUSP magnetic field are simulated and compared to numerical analysis, investigated melt convection, melt flow velocity near to quartz crucible wall, diffusion boundary layer and effect of initial oxygen concentration in the silicon crystal, and the shape of solid/liquid interface was discussed. The results show that the change of the ZGP of the CMF mainly affects the convection in the melt, which leads to the difference of the thickness of the boundary layer near to the wall of the quartz crucible, and was found to be the key to reduce the oxygen dissolution from the crucible wall and oxygen diffuse into the crystal, along with the differences in the shape of the crystal-melt interface. In addition, we have carried out actual industrial single crystal production under the three configurations. The results show that the experimental data of oxygen content and shape of the crystal-melt interfaces in silicon crystal are consistent with the numerical results.
Keywords: 
Subject: Chemistry and Materials Science  -   Materials Science and Technology

1. Introduction

In recent decades, with the development of mass-produced electronic components, driven by the huge business opportunities of industrial power control, automotive, photovoltaic and wind-electrical demand. As we know, the insulated gate bipolar transistors (IGBTs) is used to float-zone (FZ) silicon wafer substrate, in order to overcome the cost and high volume products, it’s been moved to large diameter wafer substrate, the expansion plan of IGBTs substrate material is gradually shifted to the more cost-effective 300mm production line. Therefore, the silicon material grown by the Czochraski process with magnetic field equipment to apply for the use as IGBTs substrate. IGBT has been widely applied and is mainly used in high voltage, high current and high power, compared with chip performance, the user pays more attention to the stability and reliability of products that need time verification, but the requirements for impurities in the crystal are relatively important, especially oxygen and carbon atoms in the crystal are easy to form oxygen- and carbon- relative compounds after heat treatment processes, may impact the device performance [1].
Further discussion of relationship between oxygen and IGBTs device, the oxygen concentration of IGBTs wafer is required to be as low as possible, because if the oxygen concentration in the silicon wafer is too high, the excess oxygen will be precipitated into SiOx during the heat treatment process of the device manufacturing process, resulting in the composite life deterioration of the IGBTs [2]. In addition, when silicon wafers containing excessive oxygen are subjected to low temperature at about 450℃ during crystal cooling or process cooling, oxygen thermal donors will be formed, resulting in changes in the electrical property of the substrate, which is one of the important quality characteristics, requiring uniformity and stability. In particular, it is required that the resistivity distribution in the crystal is uniform, and the resistivity does not change after heat treatment in the device manufacturing process.
The oxygen concentration and its uniformity in CZ crystal mainly depend on the flow state in the molten liquid and some process parameters of crystal pulling. With the increase of the diameter of silicon single crystal, the number of silicon crystal growth system in the molten liquid increases, and the heat convection in the crucible becomes more intense [3]. In order to ensure the quality of crystallization, the heat convection in the molten liquid must be suppressed. Applying magnetic field is an effective method to control the liquid flow during silicon growth [4].
The MCZ technique is capable of growing low oxygen, low microdefects and high resistivity CZ silicon. Beginning in 1980, various types of magnetic fields were developed, including magnetic field orientation (VMCZ for longitudinal magnetic field, HMCZ for transverse magnetic field and Cusp magnetic field) [5], and crystal growth studies were conducted. Kakomoto [6] studied the VMCZ magnet and found that the VMCZ magnet field could suppress the radial heat convection, and oxygen concentration decreased with the increase of the longitudinal magnetic field intensity. Liu 's model showed that near to the crucible wall, HMCZ inhibited the longitudinal molten flow caused by heat convection, delaying the oxygen transfer and thus blocking the oxygen transfer [7]. However, the radial magnetic field destroyed the symmetry of the growth system relative to the growth axis, so the effect of magnetic field was also non-axisymmetric, resulting in the appearance of growth fringes at the crystal surface intervals. During the growth of VMCZ, oxygen concentration in the crystal is affected by many variables and cannot be easily controlled. Therefore, CUSP magnetic field is more suitable method for crystal growth in our research, which can reduce the adverse factors of HMCZ and VMCZ from the perspective of controlling the oxygen concentration of silicon single crystal. In past studies, the oxygen concentration of crystal can be improved by application of the magnetic field and changing of crucible rotation, but it is not sufficient to change the crucible rotation parameter only to maintain the oxygen level in the ideal range.
The melt silicon is electrical conductivity, and under the action of magnetic field, the flow of the melt will inevitably cause induced current and thus produce Lorentz force. Under the action of Lorentz force, the heat convection in the silicon melt is inhibited, and the oxygen, point defects and other impurities in the silicon crystal are suppression. Proper distribution of magnetic field can improve the uniformity of single crystal, reduce initial oxygen concentration, boron, aluminum and other impurities from the quartz crucible into the melt, thus improving the quality of silicon. The experimental and theoretical studies show that using CUSP magnetic field to pull crystals can control the convection of molten liquid, the transport of impurities and the formation of defects [8]. CUSP magnetic field is axisymmetric distribution relative to the pulling shaft, and the magnetic field cancels each other at the center point of the magnetic field, and the magnetic field strength in the vertical direction is zero. At the position away from the center of the magnetic field, there is a vertical magnetic field and a horizontal magnetic field is formed along the radius. In this way, by applying a CUSP magnetic field to the molten silicon liquid, the convection of the molten silicon liquid along the direction orthogonal to the magnetic field line can be controlled. As a result, it can not only reduce the amount of oxygen from the silica crucible, but also promote the oxygen evaporation in the silicon molten liquid, so as to stably grow a single crystal with lower oxygen concentration.

2. Experimental setup and Modeling approach

A installation schematic of the industrial CZ system with the CUSP magnet is shown in Figure 1. The system mainly consists of single crystal furnace, heater, graphite crucible, quartz crucible, crystal pulling and rotation equipment. The system is applied to grow 300mm diameter silicon single crystal, the initial charge size of silicon melt is 260Kg, the single crystal growth parameters are shown in Table 1. It is notable that the crystal and crucible rotation are opposite. Argon flow rates and furnace pressure are fixed during crystal growth. The CUSP-magnetic field (CMF) is added to the outside of the single crystal furnace. The coil of the CMF is coaxial with the crystal growth furnace, there are two coils in the cusp-magnetic configuration, upper and lower coils, are used to induce a CMF and the current of the upper and lower coils is opposite. The Zero Gauss plane (ZGP) is determined by gauss-meter and is at the mid-position between the upper and lower coils in the CMF configuration, as shown by the blue line. The reference intensity of the magnetic field is 0.09 T, which is set at the intersection of the ZGP position and the quartz crucible. The intensity remains constant during the growth process.

3. Description of CUSP magnetic field

We conducted numerical simulations on the control of the oxygen concentration using a crystal growth simulator (CGSim). The cusp-magnetic field (CMF) is shown in Figure 2. During crystal growth, the crystal solid-liquid interface is fixed in the symmetric region of two coils. The effective magnetic field composition is the longitudinal magnetic field perpendicular to the bottom of the crucible and the radial magnetic field perpendicular to the wall of the crucible, but there is no orthogonal magnetic field composition on the surface of the molten liquid. The position of ZGP is determined by changing the position of the fixed coil while maintaining a constant magnetic ratio (MR) of upper and lower coils, which means the upper and lower coils have the same distribution.
In this paper, three Zero-Gauss plane models: ZGP located (a) 20 mm above the melt-gas (m-g) interface, (b) on the m-g interface and (c) 20mm below the m-g interface, are studied initial oxygen concentration behavior in the silicon crystal. The Previous studies [9] have detailed numerical simulation methods for temperature, melt flow, and oxygen diffusion boundary conditions at quartz crucible wall. The influence of magnetic field position on oxygen concentration is based on the diffusion boundary conditions of melt flow velocity at the crucible wall and c-m interface respectively, all numerical calculations were performed using CGSim software.

4. Results and discussion

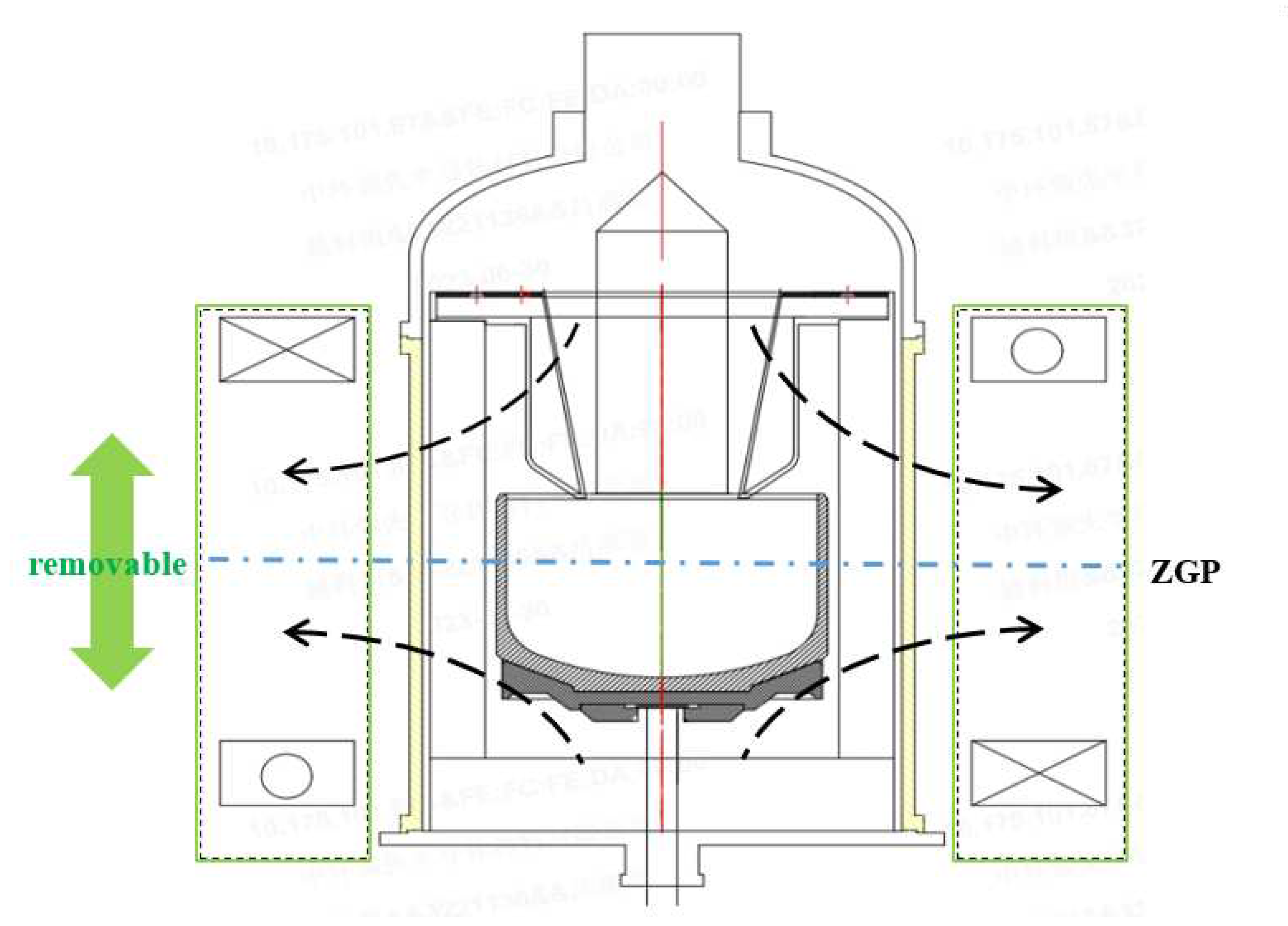
4.1. CMF effects on the silicon melt convection

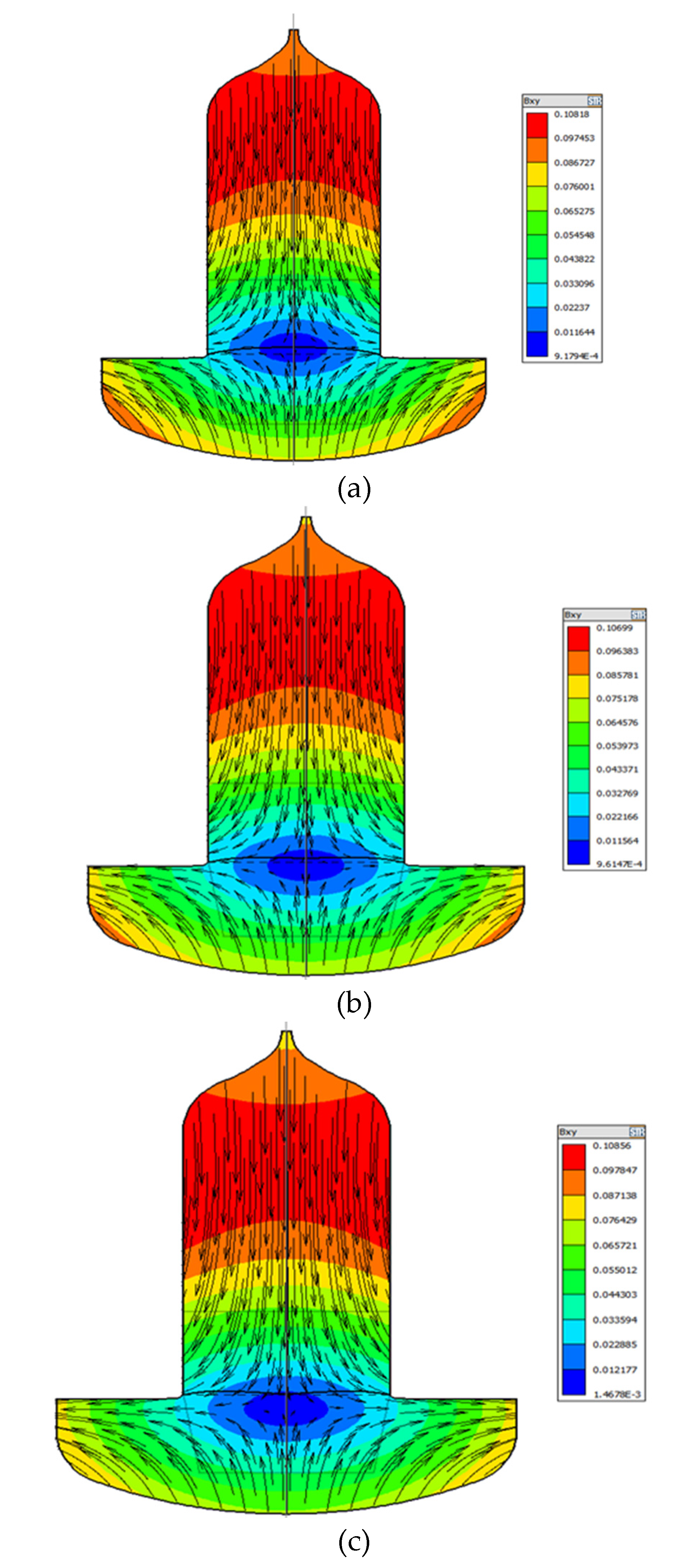
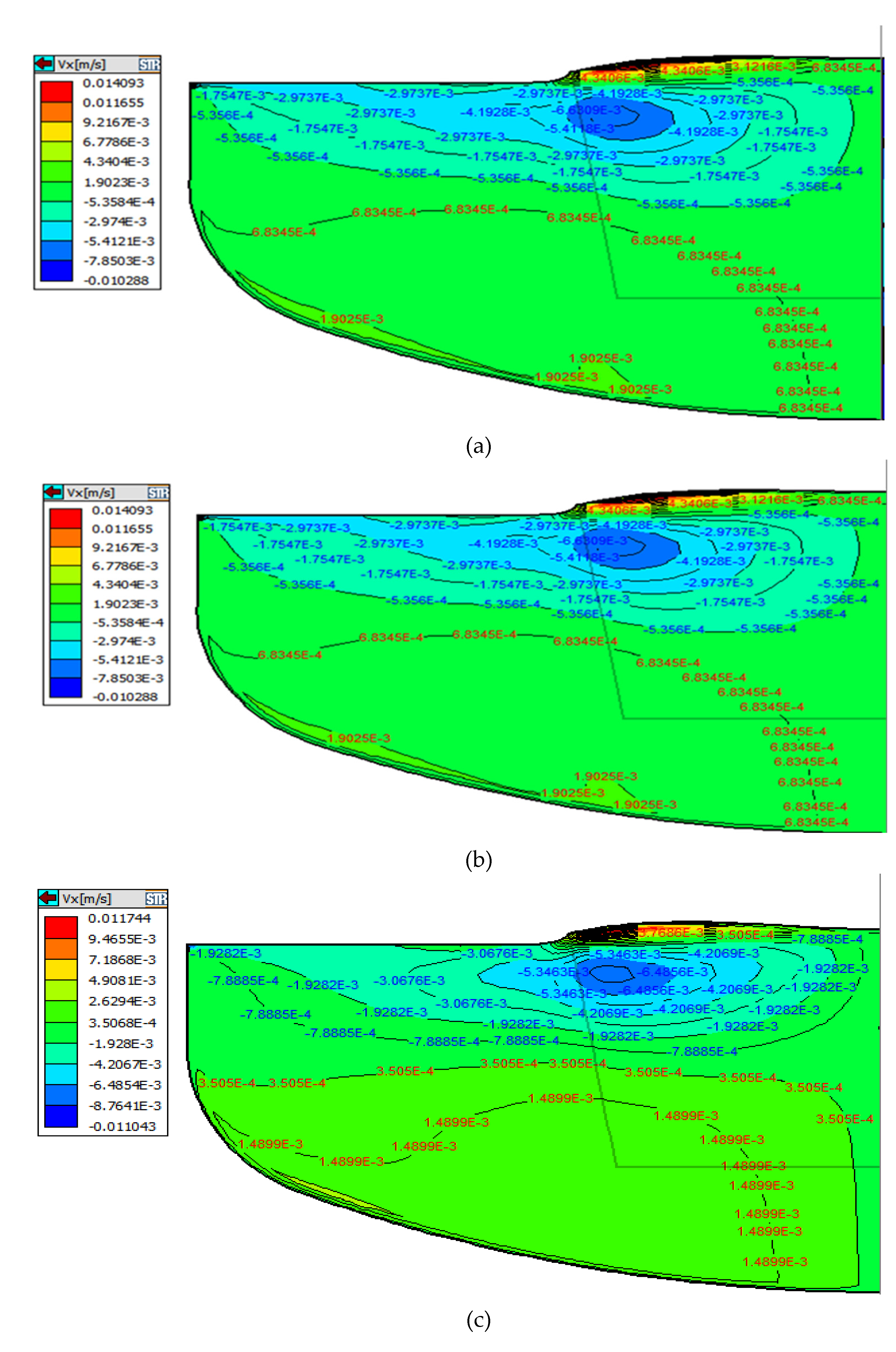
Figure 3 compares the influence of magnetic field intensity and distribution on flow structure under different CMF conditions. As can be seen from Figure 3 that the structure of melt under different CMF conditions consists of two parts, one forming a Taylor-Proudman unit (1) under the ingot and the other forming a buoyancy unit (2) along the crucible wall [10]. Among them, cell (1) is mainly caused by the rotation of the crystal and crucible, and cell (2) is mainly formed by convection driven by buoyancy. Obviously, under the three ZGP models, the distribution area and strength of the two kinds of circulation have obvious changes.
It can be seen from Figure 3 that the Taylor-Proudman vortex (1) is a counter-clockwise flow cycle. As the position of the zero magnetic surface moves down, the horizontal magnetic field near the growth interface gradually increases and dominates, because this direction is contrary to the Taylor-Proudman vortex (1), inhibits the counter-clockwise cell (1) in the crystallization zone. On the contrary, as the zero magnetic surface moved upward, the horizontal magnetic force weakened, and the flow area of the Taylor-Proudman vortex (1) gradually increased. When the ZGP at 20 mm above the m-g interface, the CMF suppresses the buoyancy convection near the crucible wall, a region of high magnetic field intensity. The cell (1) extends from the central part to the outer region of the melt and the flow area is the largest, thus preventing the diffusion of oxygen from the bottom of the crucible wall into the solid-liquid interface, as shown in Figure 3a.
In addition, moving the center of the ZGP above the m-g interface increases the vertical component of the CMF in the direction opposite to the buoyancy cell (2). Especially for ZGP located 20 mm above the m-g interface, this results in a weakening of the cell (2). Moreover, it can be seen from the magnetic induction intensity distribution in Figure 3c that the magnetic induction intensity of the melt at the bottom of the crucible wall is the weakest in this case, so the buoyancy cell (2) is enhanced, and the Taylor-Proudman cell (1) is weakened, resulting in more high oxygen melt at the bottom entering the crystal. Meanwhile, the distribution of the two kinds of flow circulations leads to a W-shaped growth interface geometry in Figure 3c, which is known as a source of dislocation generation [11], which is unfavorable to the single crystal growth process.

4.2. CMF effects on the oxygen transport

It is assumed that oxygen diffusion at all surfaces is of dissolution and volatilization rate Determinants, in the case of steady growth, can establish a simple relationship:
[O]S= [O]m－[O]a
where, [O]S, [O]m and [O]a are respectively the number of oxygen atoms from unit time entering the crystal, melting from the quartz crucible and evaporating from the free surface of the melt.
[O]s=ARvkeCm=AcD(Cc－Cm)/δc－AmD(Ca－Cm)/ δm
where, AR is the cross-sectional area of the crystal rod, Ac is the contact area between quartz crucible and silicon melt, Am is the contact area between silicon melt and external atmosphere, v is the pulling speed, ke is the equilibrium segregation coefficient of oxygen, Cm is the concentration of oxygen in melt. Cc is the concentration of oxygen on the surface of quartz crucible, Ca is the concentration of oxygen in the peripheral atmosphere, δc is the thickness of the diffusion boundary layer between quartz crucible and silicon melt, δm is the thickness of the diffusion boundary layer between silicon melt and the peripheral atmosphere, and D is the diffusion coefficient.
Based on the above discussion, under the certain crystal growth parameters, the oxygen concentration in the crystal depends on the thickness of the two diffusion boundary layers. However, convection in the melt will affect the thickness of the diffusion boundary layer, change the transport of oxygen content, and thus affect the distribution of oxygen content, so it is significant to study the convection in the melt. The theoretical calculation of the thickness of the boundary layer is easily derived. In the previous research, the boundary layer at the crucible wall was discussed [12], there is a substantial theory and calculation method. The habitual force expression of the unit is ρ v ∂ u / ∂ x , ∂ u / ∂ x is proportional to U/l (U is the velocity at the outer edge of the boundary layer), therefore ρ u 2 / l ,the expression of friction force of monolith volume is ∂ τ / ∂ y . Suppose that under the condition of stratified flow, its expression is μ ∂ 2 u / ∂ x 2 , since the magnitude of the velocity ladder perpendicular to the wall is equal to the magnitude of the accumulated friction force of the mono site, the lower relation formula can be obtained as follows,
μ U / δ 2 ~ ρ U 2 / l
The correlation formula of boundary layer thickness is obtained, below:
δ ~ μ l / ρ U = v l / U
The scale factor is 5, taking the length as 1 as the reference length, so can be calculated as follows,
δ = 5 / Re
The common formula of the deduced boundary layer is as follows,
δ （ x ） ∝ vx / U
It can be concluded from formula (6) that the boundary layer is inversely proportional to the axial flow velocity, where is the thickness of the boundary layer, Re is the Reynolds number, and U = V(x,y) is the longitudinal velocity.
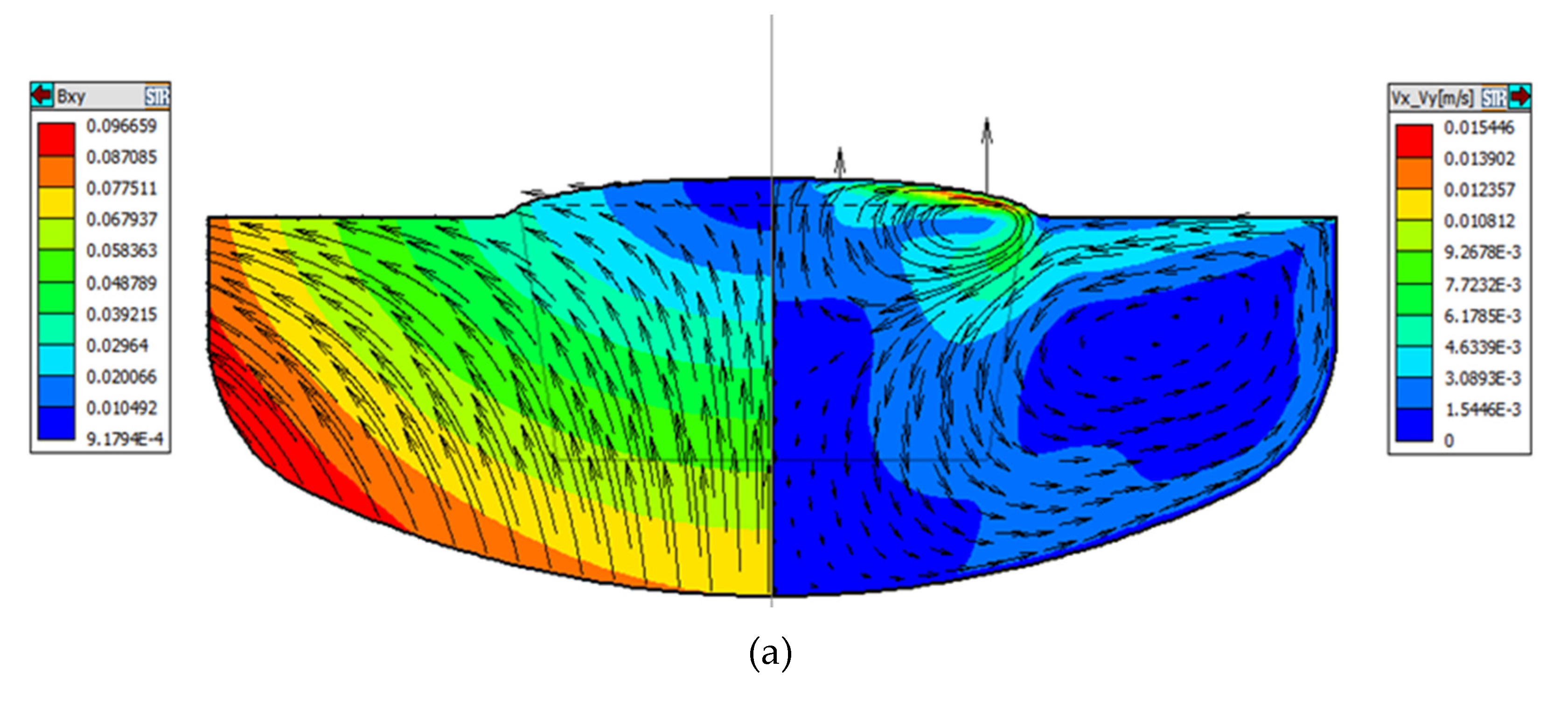
Consequently, to clearly explain the effect on oxygen concentration under the three magnetic field models, we will focus on the convection at the crucible wall, crucible bottom, and free interface. As can be seen from the convection distribution on the right of Figure 3, under the action of buoyancy unit (2), the convection at the crucible wall is dominated by the longitudinal direction, while the convection at the bottom of the crucible and the free interface is radial and opposite. As can be seen from the description of the first section, the convection under different magnetic field conditions is different. In order to clearly explain the oxygen concentration under the three magnetic field models, we show a typical example of the distributions of radial velocity component in the melt, as shown in Figure 4a-c.
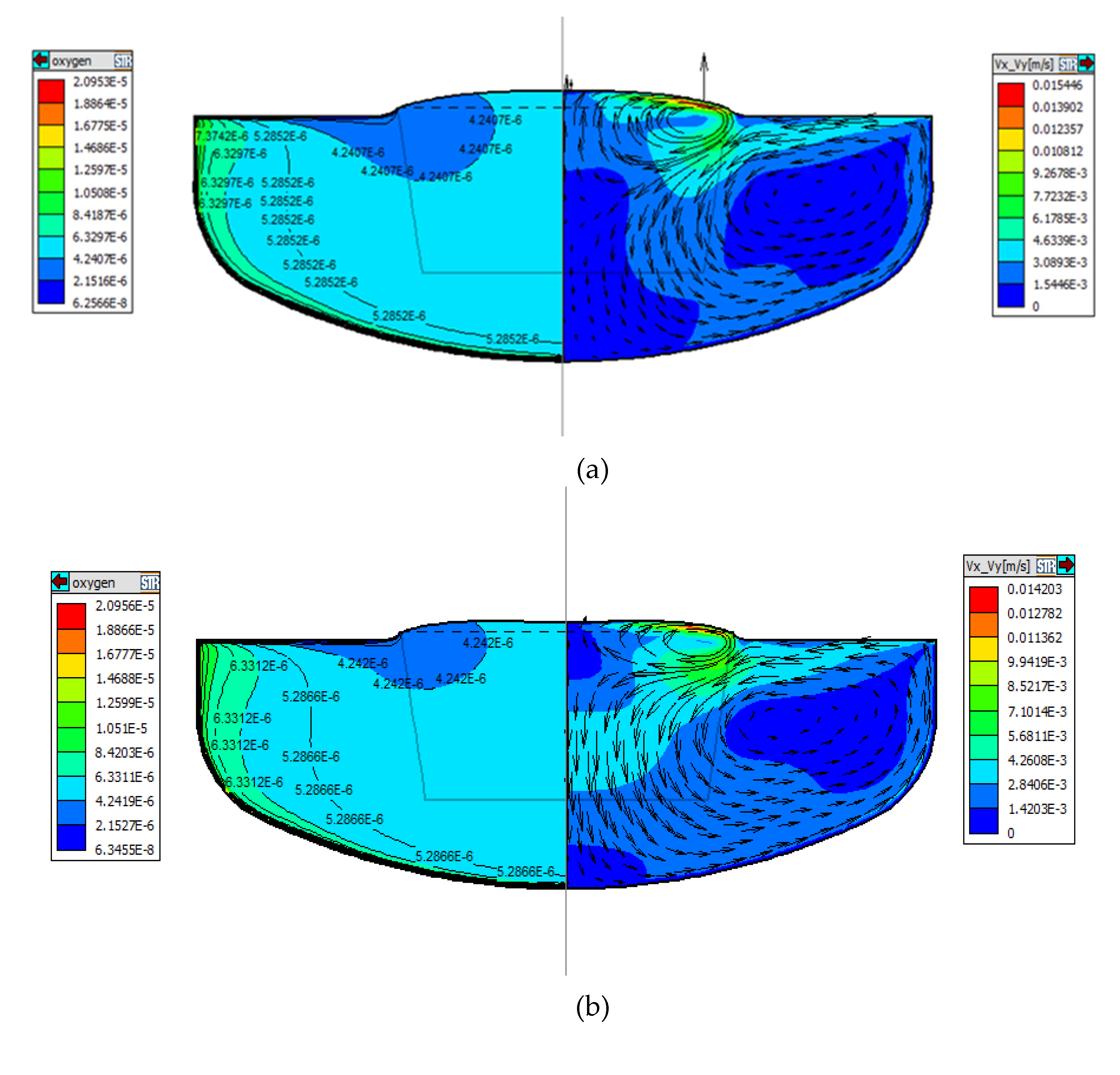
It is generally known that the oxygen in the melt comes from the oxygen dissolution, which occurs at the interface between the silicon melt and crucible. The oxygen is mainly dissolved at the bottom of the crucible and then transferred to the vicinity of solid-liquid interface through the thermal convection. According to previous studies and formula (6), the thickness of the boundary layer is inversely proportional to the velocity at this position. 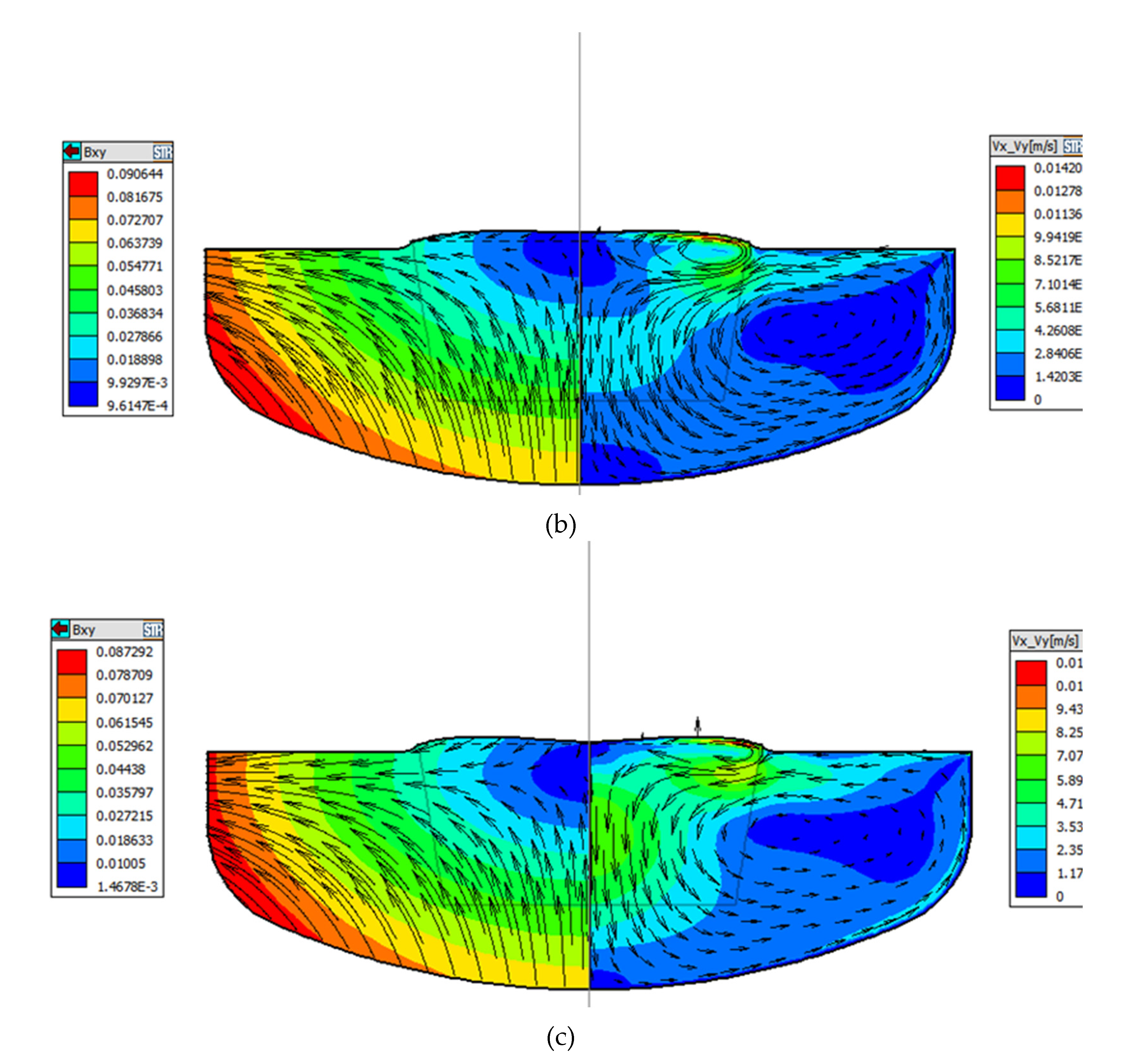As can be seen in Figure 4a-c, the horizontal velocity at the bottom of the crucible and at Angle R gradually increases as the position of ZGP moves down, and the horizontal convective flow rate of melt near the bottom of the crucible is the largest at -20mm position. Therefore, the diffusion boundary layer between the quartz crucible and the silicon melt at this position is thin, the washing of the crucible wall is more intense, resulting in more oxygen impurities entering the melt, and finally a part of the oxygen in the melt is integrated into the crystal. 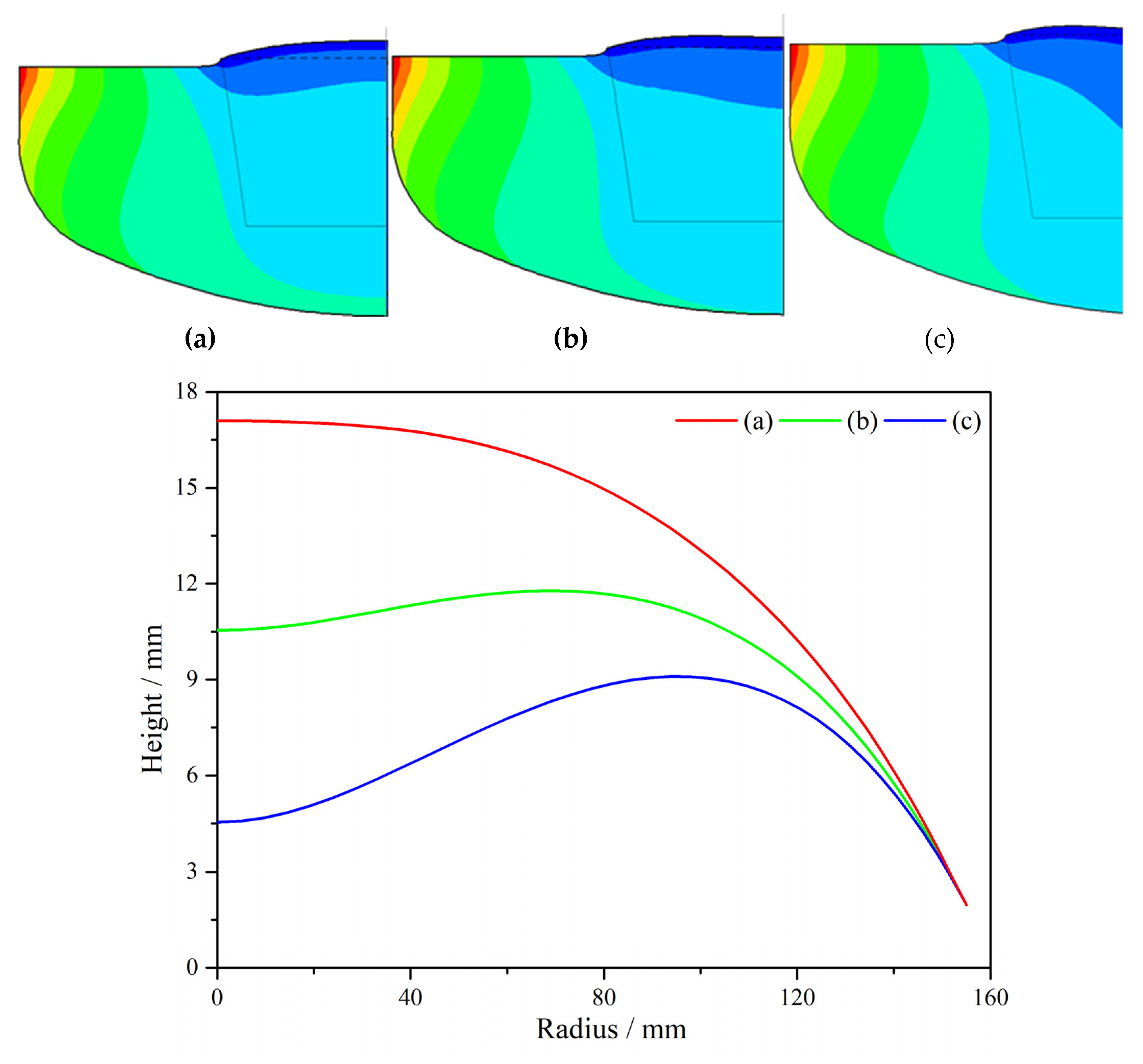The oxygen concentration distribution in the three cases are displayed in Figure 5a-c, through the comparison of the results of oxygen concentration, the oxygen concentration near the bottom of the crucible gradually increases as the position of the ZGP moves down, and it is again verified that the decomposition of the crucible wall is inversely proportional related to the strength of the convection flow (that is the thickness of the boundary layer).
The influence of different CMF configurations on the flow pattern has been studied above and the initial oxygen concentration distribution in the three cases are displayed in Figure 5a-c. In the CMF, most of the oxygen is carried to the free surface evaporates. Only a small amount is transported to the crystallization zone. A small gradient of oxygen concentration is found in the core region of the melt due to the Taylor–Proudman flow.
For the case that ZGP is located 20 mm above the m-g interface, according to the above discussion and VX-Vy overall analysis, the flow rate near to the crucible wall is slow due to the inhibition of melt convection near to the crucible wall, which results in the decrease of dissolved oxygen concentration in the crucible wall and slow corrosion rate of the crucible. Moreover, with the melt convection of cell (2), oxygen in the area near to the crucible wall is transported to the free interface and volatilized. Less oxygen is delivered to the core region of the melt, less and less oxygen diffuse into crystal, so the low-oxygen zone below the solid-liquid interface is larger, as shown in Figure 5a.
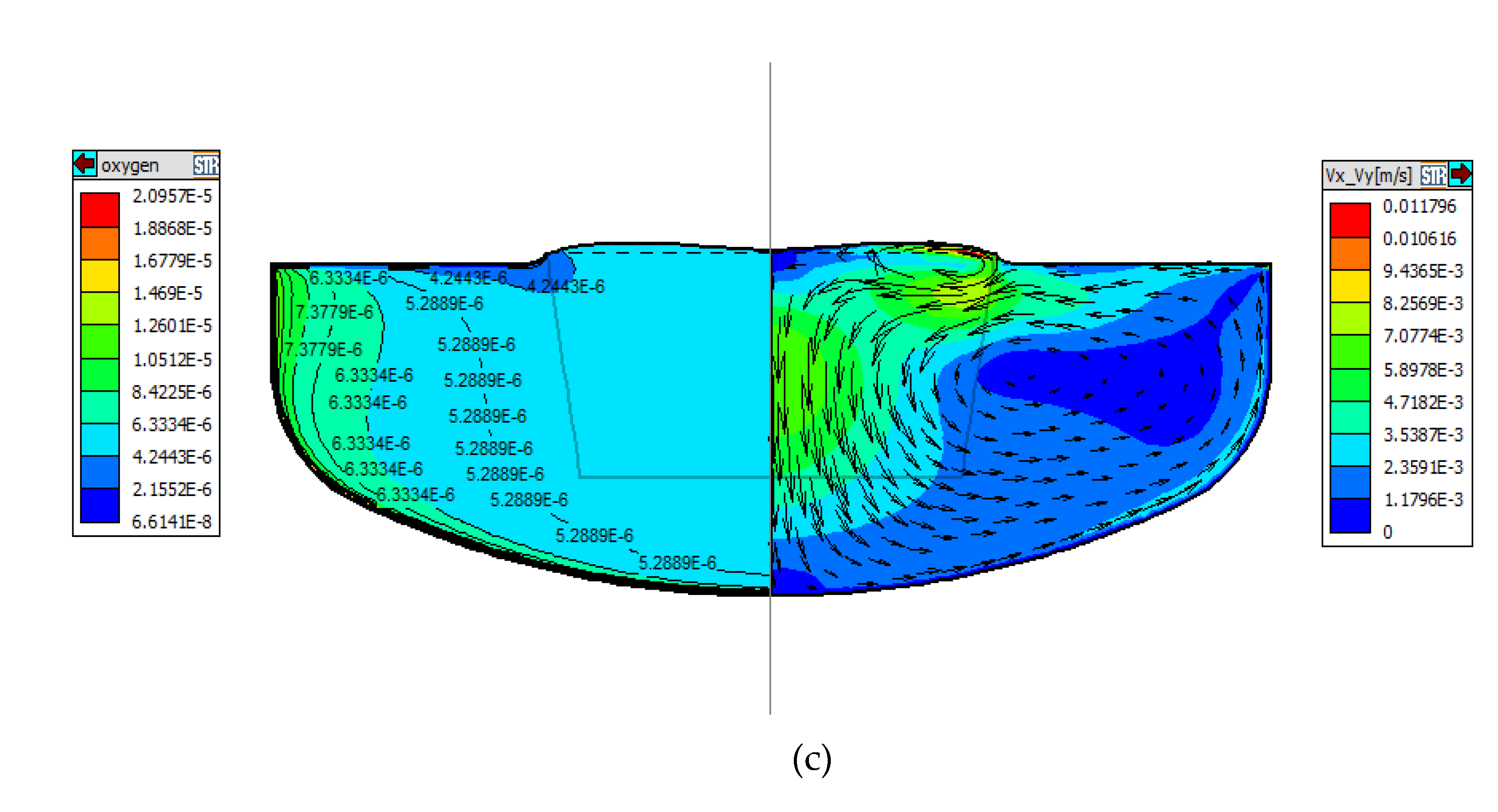
For the case that ZGP is located on the m-g interface, at a given magnetic field strength, the zero magnetic surface enhances the flow of dissolved oxygen from the crucible into the melt, then bring into the crystal. However, the decrease of the axial magnetic intensity in the crystallization zone causes the radial distribution of oxygen on the growth interface to become uniform.
In the ZGP is located 20mm below the m-g interface cases, With the change of the position of the zero magnetic surface, the strength and weakness of the convection flow near the crucible wall changed with it. Under the action of strong convection, the melt convection brushing near the wall of the quartz crucible is stronger, which can also be proved by the melt convection intensity distribution oxygen concentration at the growth interface is increased, greater than the positive of 20 mm above.
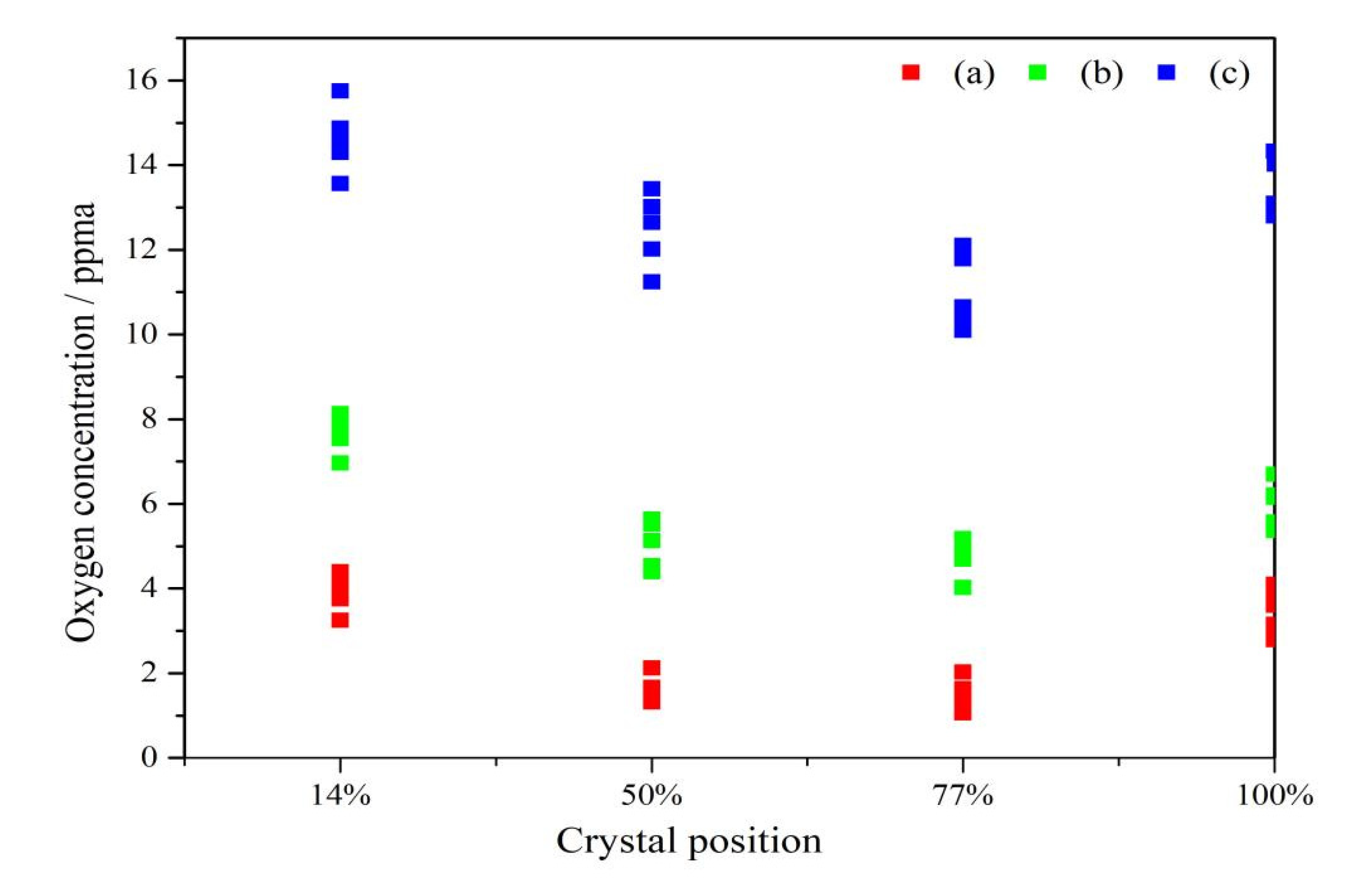
In the above mentioned, the single crystal growth parameters (experiments are carried out with fixed rotation rates for the crucible and crystal), we carried out the actual industrial single crystal pulling process, and the whole single crystal is segmented to test the central oxygen concentration at the head and tail of each crystal segment. The results are shown in the Figure 6. The figure displays the difference of oxygen concentration in the center of the interface at the crystal segment with the crystal length. When the ZGP is located 20 mm above the m-g interface, the overall oxygen concentration shows the lowest level. At the former part of crystal lengths, the axial oxygen concentration decreases slowly as the crystal length increases until it reaches a minimum, the lowest value in the three groups was 1.02 ppma. Then increases continuously as the crystal length increases further. Therefore, the largest oxygen concentration appears in the initial and final stages of the whole crystal growth process. The experimental results and simulation results show the same trend, which further confirms the discussion under numerical simulation in this paper.

4.3. CMF effects on growth interface

Compare the shape of the growth interface under different MF, the simulation results are shown in Figure 7. When the ZGP is located 20 mm above the m-g interface, the interface is convex to crystal. While the ZGP is located on the m-g interface, the interface near the crystal axis is slightly concave to crystal and convex at the right side near the edge of crystal. When the ZGP is located 20mm below the m-g interface cases, the growth interface becomes more convex towards the liquid direction, and a W-shaped growth interface is obtained. The interface shape is absolutely affected by the convection of Taylor-Proudman unit (1) near the growth interface, shown in Figure 3. In addition, it can be seen that the lower the position of the ZGP, the smaller the temperature gradient below the crystal, so the more convex near the crystal axis.
In order to confirm the morphology of the growth interface in the actual crystal growth and verify the guiding significance of the numerical simulation, we tested the growth interface of the single crystal in the actual industrial single crystal pulling process. The results are shown in the Figure 8. The red line is the location of the single crystal length discussed in the simulation. The experiment uses the LP SCAN tool to select a single crystal profile with a range of 50mm above and below the simulated single crystal position for longitudinal scanning. The results show that the growth interface on the surface under the three ZGP position is consistent with the simulation trend, which further confirms that the actual production has a positive matching with the numerical simulation.

5. Conclusion

This paper investigated the effects of CMFs distribution at different positions of Zero-Gauss plane (ZGP) on melt convection, oxygen concentration transfer and crystal-melt interface of 300mm MCZ silicon crystal by numerical simulation. The results shown that when the ZGP moves downward gradually from the melt-gas interface, the melt flow velocity near the quartz crucible wall gradually increases, resulting in a decrease in the thickness of the diffusion boundary layer. Along with the changes in the convection area and intensity, more oxygen concentration is generated and transported to the bottom of the solid-liquid interface, and finally diffuse into the crystal, resulting in a significant increase in oxygen concentration. In the oxygen concentration distribution of the crystal discussed in this paper, the ZGP located +20 mm case is the lowest value in this calculation. In addition, melt convection and temperature gradient at the solid-liquid interface leads to different shapes of the growth interface. When the ZGP is located +20mm, the shape of the interface is convex to crystal, while when the ZGP -20 mm, the interface near the crystal axis is slightly concave to crystal. In addition, the actual industrial crystal growth can be accomplished simulation results and the crystal data were evaluated. The trend of crystal oxygen concentration was consistent with the simulation analysis, and the solid-liquid interface scanning results were in agreement with the simulation results, indicating that the simulation and discussion in this paper provide valuable guidance for the practical production.

Acknowledgments

This work was supported by the project for Science and Technology Correspondent of Tianjin City (Grant No. 20YDTPJC01710) and the Research Foundation of Education Bureau of Hebei (Grant No. QN2021044).

References

  1. -J. Schulze, H. Ofner, F-J. Niedernostheide, F. Lukermann, A. Schulz, IET Power Electron., 2019, 12, 3870–3873.
  2. alaev, V.; Sattler, A.; Kadinski, L. Crystal twisting in Cz Si growth. J. Cryst. Growth 2015, 413, 12–16. [Google Scholar]
  3. im Bok-Cheol, Lee In-Kyoo, Kim Kwang-Hun, and Lee Hong-Woo. 2004. Oxygen concentration in the Czochralski-grown crystals with cusp-magnetic field. J. Cryst. Growth (2004).
  4. in Liu, Lijun Liu, Zaoyang Li, and Yuan Wang. 2012. Effects of cusp-shaped magnetic field on melt convection and oxygen transport in an industrial CZ-Si crystal growth. J. Cryst. Growth 2012, 101-108. [CrossRef]
  5. oichi Kakimoto, Xin Liu, and Satoshi Nakano. 2022. Analysis of the Effect of Cusp-Shaped Magnetic Fields on Heat, Mass, and Oxygen Transfer Using a Coupled 2D/3D Global Model. Crystal research and technology (1979) (2022), 2100092. [CrossRef]
  6. oichi K, Kyung-Woo Y, Minoru E. Oxygen transfer during single silicon crystal growth in Czochralski system with vertical magnetic fields[J]. Journal of Crystal Growth, 1996, 163. [Google Scholar]
  7. iu X, Liu L, Li Z, et al. Effects of static magnetic fields on thermal fluctuations in the melt of industrial CZ-Si crystal growth[J]. Journal of crystal growth, 2012, 360, 38–42. [Google Scholar] [CrossRef]
  8. unling Ding, Yuqing Li, and Lijun Liu. 2021. Effect of cusp magnetic field on the turbulent melt flow and crystal/melt interface during large-size Czochralski silicon crystal growth. Int. J. Therm. Sci. (2021).
  9. C. Chen, P.C. Guo, C.H. Chang, Y.Y. Teng, C. Hsu, H.M. Wang, C.C. Liu, Numerical simulation of oxygen transport during the Czochralski silicon crystal growth with a cusp magnetic field, J. Cryst. Growth 2014, 401, 888–894.
  10. Raufeisen, M. Breuer, T. Botsch, A. Delgado, International Journal of Heat and Mass Transfer 2008, 51, 6219. [Google Scholar] [CrossRef]
  11. V. Smirnova, N.V. Durnev, K.E. Shandrakova, E.L. Mizitov, V.D. Soklakov, Journal of Crystal Growth 2008, 310, 2185.
  12. C Brice, RA Laudise. The Growth of Crystals from Liquids. North-Holland Publishing Company, Amsterdam, 1973, chapter 4.
Preprints 81096 g001
Figure 1. Schematic diagram of the major components of the industrial CZ furnace.
Figure 1. Schematic diagram of the major components of the industrial CZ furnace.
Preprints 81096 g001
Preprints 81096 g002
Figure 2. Distribution of Bxy with CMF (a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Figure 2. Distribution of Bxy with CMF (a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Preprints 81096 g002
Preprints 81096 g003aPreprints 81096 g003b
Figure 3. Distribution of magnetic induction in the melt (left) and fow structure (right) with CMF (a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Figure 3. Distribution of magnetic induction in the melt (left) and fow structure (right) with CMF (a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Preprints 81096 g003aPreprints 81096 g003b
Preprints 81096 g004
Figure 4. Distribution of radial velocity component (Vx) in the melt at (a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Figure 4. Distribution of radial velocity component (Vx) in the melt at (a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Preprints 81096 g004
Preprints 81096 g005aPreprints 81096 g005b
Figure 5. Distribution of oxygen concentration in the melt (left) and flow pattern (right) with CMF(a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Figure 5. Distribution of oxygen concentration in the melt (left) and flow pattern (right) with CMF(a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Preprints 81096 g005aPreprints 81096 g005b
Preprints 81096 g006
Figure 6. Experimental data of oxygen concentration with CMF(a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Figure 6. Experimental data of oxygen concentration with CMF(a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Preprints 81096 g006
Preprints 81096 g007
Figure 7. Comparison between growth interface shape under different CMF in simulation(a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Figure 7. Comparison between growth interface shape under different CMF in simulation(a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Preprints 81096 g007
Preprints 81096 g008
Figure 8. Comparison between growth interface shape under different CMF in experiments(a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Figure 8. Comparison between growth interface shape under different CMF in experiments(a) 20 mm above the m-g interface, (b) on the m-g interface, (c) 20mm below the m-g interface.
Preprints 81096 g008
Table 1. Single crystal growth parameter.
Table 1. Single crystal growth parameter.
Parameter Value
Furnace pressure, Pa 2000
Argon gas flow rate, slpm 95
Crystal pulling rate, mm/h 24.5
Ratio of crystal to crucible rotation rate 6:-1
Magnetic field strength, T 0.09
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated