Prerpints.org logo
Preprint
Article

Application of Shannon Entropy in Assessing Changes in Precipitation Conditions and Temperature Based on Long-Term Sequences Using the Bootstrap Method

Altmetrics

Downloads

257

Views

327

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

29 February 2024

Posted:

01 March 2024

You are already at the latest version

Alerts
Abstract
In this paper, the Shannon entropy measure was used to assess changes in precipitation and temperature conditions. Due to the short, low-volume sequences of precipitation and temperature data analysed, a bootstrap method was used in the procedure for calculating Shannon entropy. The analysis used minimum and maximum values of monthly precipitation totals and monthly mean temperatures for 377 catchments distributed across the globe. A 110-year data series from 1901 to 2010 was analysed. Entropy values for the estimated parameters of the generalised extreme value distribution (GEV) were calculated for the adopted data. Entropy value calculations were performed for the left-hand constraint, based on minimum values, and for the right-hand constraint, based on maximum values. The applicability of Shannon's entropy measure in the analysis of climate change was demonstrated by allowing the degree of disorder and complexity of the distributions describing climate variables in the form of precipitation and temperature to be measured. This made it possible to obtain information on the directions of changes occurring with regard to minimum and maximum values in the field of monthly precipitation and mean temperatures in the analysed catchments. The study demonstrated the existence of Shannon entropy trends. The evaluation of entropy trends for precipitation and temperature sequences was performed using non-parametric tests. Mann -Kendall tests at the 5% significance level were used for trend analyses. The Pettitt test was performed to determine the point of change in trend for the rainfall and temperature data. The performed analysis was supported by graphical presentations.
Keywords: 
Subject: Environmental and Earth Sciences  -   Environmental Science

1. Introduction

Climate extremes such as droughts, floods, extreme temperatures and storms have the potential to make significant impacts on economic sectors that are closely linked to climate, such as water management, agriculture, food security, energy security, forestry, health and tourism. Changes in these sectors can have far-reaching consequences for countries whose economies rely more heavily on these sectors [1,2,3]. Most research work performed to date on climate change unfortunately overlooks or downplays the importance of variability in climate extremes [3]. This is evident in studies on reducing the vulnerability of agriculture due to short-term hydrometeorological events, which compound the challenge [4,5,6]. With regard to the existing needs, climate change adaptation policies are insufficient [7].
The variability of these characteristics is an important aspect of climate change risk assessment, as it affects the intensity and frequency of extreme events. The IPCC report points out [8,9,10] that expected changes in the variability of precipitation and temperature in the future will be characterised by a high degree of uncertainty. In light of the above, there is a need to develop methods and algorithms that can improve the efficiency of predicting and estimating the intensity of climate hazards [3,11]. The Earth’s atmospheric system is too complex to be described deterministically. This means that predicting its future state is difficult or impossible [12]. It is an open system and driven mainly by the continuous influx of solar radiation and the Earth’s rotation. The system is too large to solve deterministically due to the following factors: the amount of data needed to describe its state, incomplete instrumentation to monitor its state, the lack of a correct way to spatially partition the system for long-term analysis, and the lack of accurate historical data prior to 1900. Therefore, stochastic analyses can be useful in assessing the variability of climatic conditions [12]. Analyses of entropy directions show that if global warming were to continue, a decrease in thermodynamic entropy would mean more free energy driving the weather; an increase in informational entropy would mean difficulty in predicting which way the process would go [12]. One potential tool to help with this is the Shannon entropy trend assessment. Entropy analysis can provide information on the degree of irregularity, unpredictability and variability in climate systems, which can be valuable for developing more accurate forecasts and risk-management strategies for extreme climate events [13].
Climate change is a phenomenon that leads to significant spatial and temporal heterogeneity in the impacts of these changes on biological systems, health and sectors of economies [14]. Studies show that global increases in average temperature mask important differences in temperature elevation between land and sea and small areas and large regions [15,16,17]. Climate change also inevitably results in changes in the frequency, intensity, spatial extent, duration and timing of extreme weather and climate events [3,18]. Extreme values can be analysed in terms of changes in the types and parameters of probability distributions and trends in statistical characteristics (e.g., minimum, maximum values) [19]. One can also look at the variability of extreme values through the characteristics of the tails of extreme distributions [20]. An effective tool is time-frequency analysis, which enables the study of changes in time and frequency, which is particularly useful for considering correlations between different characteristics describing climate variability [21,22,23]. It is also possible to monitor the change in Shannon entropy and its trends as a measure of climate variability and the extreme phenomena that result from this variability [13,24,25,26]. Shannon entropy is a measure of the degree of disorder or unpredictability in a system, and an increase in entropy can indicate greater climate variability. Analysis of Shannon entropy and other measures of a statistical nature can be useful for assessing climate variability and extremes.
Projections indicate that climate and weather variability will increase as the planet warms. Changes in the frequency and intensity of climate extremes and in the instability of weather patterns will have significant consequences for both human and natural systems. By the end of this century, the frequency of extreme conditions, such as heat stress, droughts and floods, is projected to increase, with numerous negative impacts beyond those resulting from changes in mean values alone [1,2]. Given the uncertainty associated with forecasts of changes in extremes and the limited confidence in these forecasts, it is important to perform trend analyses and analyses of extreme values based on the longest possible series of measurements. Both the low certainty of the forecasts and the high confidence in the forecasts do not exclude the possibility of extreme changes. In the context of limitations in understanding climate processes in different regions, there is the possibility of extreme changes with low probability, however, with significant impact. Changes in extremes are observed and there is evidence that some of these changes are due to anthropogenic influences [1]. Analysis of historical observations of climate variables indicates anthropogenic climate change [27,28,29]. The study of changes in precipitation and temperature variability [30,31,32] dependent upon the observed period show changes in trends and allow us to assess the form of the directions of these occurring changes [33,34]. However, the attribution of individual extreme events to these influences remains a challenge. An example of this is the analyses performed as part of work on climate variability at different periods and scales within a region (e.g., in the rhythm of multi-decadal oscillations) [35,36]. The observed changes in the magnitude, frequency and timing of extreme events obtained represent one of the first analyses of this under-researched phenomenon in which patterns have been shown to be complex and not always consistent with previous studies [10,27,37,38].
The increase in entropy affects the unpredictability of the weather and makes it difficult to plan adaptation measures. There can be a sudden transition from one extreme state to another in a short period of time. An increase in entropy in the climate system increases the degree of chaos and unpredictability. This, in turn, leads to greater weather variability, more frequent occurrence of extreme climatic events and difficulty in predicting long-term trends. Increased entropy can negatively affect economic sectors such as agriculture, which need stable weather conditions for efficient production. However, increased entropy can also lead to increased biodiversity, as organisms need to adapt to more variable environmental conditions. There is a complex interaction between polarisation feedback [39] and increased entropy in the climate system. Polarisation feedback refers to the change in direction and intensity of climatic phenomena over a short period of time. Abrupt jumps between weather extremes, such as sudden changes from drought to torrential rain or from extreme cold to heat, are examples of polarisation feedback. The implication of polarisation and entropy increase is that phenomena identified by entropy and polarisation reinforce each other. Rapid changes in weather that are characteristic of polarisation can contribute to greater weather variability and an increase in entropy. In turn, an increase in entropy can influence larger jumps between extreme weather states, further intensifying polarisation. Therefore, with regard to understanding positive feedback in the climate system, polarisation and entropy in the climate system may be important to better understand climate change and develop effective management and adaptation strategies. The interactions of climate variables can influence the occurrence of hurricanes, tornadoes and droughts. In addition, these interactions can affect a measure of risk that includes threats to life, livelihoods, health, well-being, ecosystems, species, economic, social and cultural resources, services (including ecosystem services) and infrastructure. Risk results from the interaction between system vulnerability and exposure, and between system exposure and forcing [15,40,41]. As a result, one phenomenon can amplify or weaken another, complicating the process of understanding the scale of climate change. Anthropogenic factors, such as industrial activity, deforestation, land use transformation, pollutant emissions and greenhouse gas emissions [42,43,44], can influence the variability of extreme values and the polarisation of climate factors [15,39,45].

2. Methodology

There is now a growing body of scientific evidence confirming that human activities are influencing climate change, contributing to shorter durations of high-intensity precipitation and longer periods of high temperature and low precipitation. The variability of extreme events, such as floods and droughts, is increasingly apparent and can be attributed to the erratic nature and intensity of human activities. Therefore, investigating the climate variability factors associated with monthly precipitation and mean monthly temperatures is key to understanding climate change at the regional level and developing strategies to manage water resources and reduce the risk of floods and droughts.
Minimum and maximum values of monthly precipitation and minimum and maximum values of mean monthly temperatures over the year were adopted for the analysis. In view of the purpose of the analysis, i.e., assessing long-term climate variability, it is better to perform analyses on averages rather than on extreme values for several reasons. Such analyses are characterised by greater statistical stability. Averages have less variability than extreme values, which means that for the same data, we will obtain a smaller standard error of the average estimator than of the extreme value estimator. Statistical stability is particularly important for long-term analyses, as variability in values can affect the interpretation of results and decision-making. Another argument is the larger number of observations, as the analysis on averages can be conducted for a larger number of observations than the analysis on extreme values, enabling more representative results. It should be noted that analyses on averages are a better reflection of reality, providing information on typical values that are more representative of long-term changes than extreme values. Furthermore, extreme values may be the result of random factors or unpredictable events that do not reflect typical conditions. To summarise, for the search for long-term changes, analysis on averages is more statistically stable, enabling a larger number of observations and a better reflection of typical values, which is important for decision-making and action planning.
Shannon’s entropy variability calculations were performed for the left constraint on the basis of minimum values of monthly precipitation and minimum values of monthly mean temperature. For the right-hand constraint, calculations of Shannon entropy variability were performed on the basis of maximum values of monthly precipitation and maximum values of mean monthly temperature. Due to the small-volume dataset, a bootstrap technique [46,47] was used to assess the extreme distributions of the minimum and maximum values of Shannon entropy variability.

2.1. Bootstrap Resampling Technique

In the present study, a bootstrap resampling technique was used to estimate the parameters of the distribution of extreme precipitation and temperature values.. The main idea of the bootstrap method is to generate large samples with replacement by resampling the original samples based on the assumption that the samples are independent and identically distributed. This method is recommended not only for its computational efficiency but as an easy-to-implement approach that generates bootstrap replications without relying on the assumption of true distribution [48]. It can be implemented by relying only on the information obtained from the sample value.
The steps of the bootstrap method used in this study are described as follows:
  • Population sequences of annual minimum and maximum values from monthly precipitation and annual minimum and maximum values from monthly average temperatures were created:
  • For the estimation of GEV parameters describing minimum values:
P m i n y = min k ⁡ P y , k ⁡ ,   k = 1 , … , 12 ; y = 1901 , … , 2010 T m i n y = min k ⁡ T y , k ⁡ ,   k = 1 , … , 12 ; y = 1901 , … , 2010
  • For the estimation of the GEV parameters describing the maximum values of:
P m a x y = max k ⁡ P y , k ⁡ ,   k = 1 , … , 12 ; y = 1901 , … , 2010 T m a x y = max k ⁡ T y , k ⁡ ,   k = 1 , … , 12 ; y = 1901 , … , 2010
The number of elements in both the precipitation and temperature sequence does not reliably allow an assessment of Shannon entropy values at the 5% significance level. A 1000-fold number of draws from the seventy-element sequence was assumed. For the assessment of Shannon entropy trends, the seventy-element strings were assumed to be created in the following recursive manner:
  • For the estimation of Shannon entropy values based on the GEV distribution describing minimum values:
X P i = P m i n 1901 + i , . . ,   P m i n 1970 + i   ,   i = 1 , … , 40 X T i = T m i n 1901 + i , . . ,   T m i n 1970 + i   ,   i = 1 , … , 40
  • For the estimation of Shannon entropy values based on the GEV distribution describing the maximum values of:
X P i = P m a x 1901 + i , . . ,   P m a x 1970 + i   ,   i = 1 , … , 40 X T i = T m a x 1901 + i , . . ,   T m a x 1970 + i   ,   i = 1 , … , 40
Forty seventy-element strings were arbitrarily obtained in this way. These strings provided a resource for 1000-fold bootstrap draws. In this way, forty 1000-fold bootstrapped strings were created from which Shannon entropy was calculated at the 5% significance level for both precipitation and temperature for minimum and maximum values (Figure 1).
2.
It was assumed that the series of annual minimum and maximum monthly precipitation and average temperature were original samples, the total length of multi-year records.
3.
Bootstrap samples of the minimum and maximum series of precipitation and temperature were drawn using the bootstrapping process, which involves randomly selecting values to replace the original sample.
4.
The above analysis was performed on all analysed catchments.
For each drawn sequence, the Anderson-Darling test (ADT) was performed to confirm the possibility of describing the drawn sequence with the GEV distribution at the 5% significance level (Figure 1). If this possibility was not confirmed, the results of such an experiment were disregarded and proceeded to the next draw. For the estimation of the GEV parameters for the minimum values, the agreement of the ADT test at the 5% significance level was achieved in 91% of occassions and for the maximum values, this level was reached in 99.6% of cases. GEV parameters were estimated using the maximum likelihood method [49,50,51]. The ADT test was adopted due to the priority given to values from the tails of the distribution, which is important in the case of extreme distributions. In subsequent steps, the value of the Shannon entropy estimator was calculated at the 5% significance level [47]. The above methodology was applied to each of the 377 analysed catchments (Figure 1). The analysis code was developed in Matlab software.

2.2. Fitting the GEV Distribution

Modelling the variability of climate extremes requires the consideration of extreme values of phenomena for, inter alia, precipitation, temperature, evaporation and atmospheric pressure [52]. An approach that uses a sequence of observations extracted from equal periods, such as a maximum from monthly totals or a minimum from monthly precipitation totals for a given year, is widely used in modelling extreme values. Similarly, for a maximum from mean temperatures or a minimum from mean temperatures for a given year, it assumes that the set of extremes is independent and identically distributed, being fitted to a probability distribution model such as the generalised extreme value distribution (GEV). As the impact of climate change has become a significant issue, many efforts have been made to account for non-stationarity in hydrological applications. One popular approach is to apply different non-stationary models to non-stationary data and select an appropriate model based on model diagnostics. Due to its adaptability to changes in the data structure, maximum-likelihood estimation of non-stationary model parameters is usually used for this purpose [50,51,53,54]. To date, this approach has been widely studied and can be described as a ‘user-friendly’ method. Such an approach was used in this study.
The generalised extreme value distribution (GEV) was used in the calculations [55,56,57].
F x = 1 σ exp ⁡ − 1 + k x − μ σ − 1 k 1 + k x − μ σ − 1 − 1 k ,   f o r   k ≠ 0 1 σ exp ⁡ − x − μ σ − e x p − x − μ σ − 1 k ,   f o r   k = 0
The parameters k , σ , μ refer to the shape parameter, scale and position [55].

2.3. Shannon Entropy

The concept of entropy has been used in the study of physical systems, and was defined on the occasion of the second law of thermodynamics. The measure of entropy defined by C.E. Shannon on the basis of information theory has been applied in subsequent years in many scientific fields, including statistics and computer science [12,26,47,58]. Today, information theory is still mainly concerned with communication systems, but applications of the concept of entropy in the analysis of the behavior of a variety of systems, including economic and social systems, financial systems, climate systems are emerging, and subsequent years have brought numerous generalizations of Shannon’s measure of entropy [12,59,60].
Shannon entropy is based on the probability distribution of the data. If this distribution is poorly estimated, the entropy can give erroneous results. Therefore, it is important to understand and model the data distribution well in order to obtain accurate entropy results.
In information theory, a measure of the entropy of a random variable X with a discrete distribution {   p ( x 1   ) ,   p ( x 2   ) , . . . ,   p ( x n   ) } has been defined [61].
The probabilities p x i   satisfy the normalisation and singular sum conditions:
0 ≤ p x i   ≤ 1 ∑ i = 1 n p x i   = 1
The Shannon entropy function expressed in units of [bits] takes the form [61]:
H S X = H S p ( x 1   ) ,   p ( x 2   ) , . . . ,   p ( x n   ) = ∑ i = 1 n p x i   log 2 ⁡ 1 p x i  
The entropy H S X   is a measure of the uncertainty associated with the probability distribution {   p ( x 1   ) ,   p ( x 2   ) , . . . ,   p ( x n   ) } , with which the values { x 1 , x 2 , … , x n } of the discrete variable X occur.
Despite the frequent use of this measure, it is important to mention the drawbacks and dangers associated with its use. Several limitations associated with Shannon entropy should be noted:
  • Measurement scale: this is sensitive to the measurement scale, meaning that the measurement units can affect the entropy results. It is important to accurately define the measurement units and adjust the scale so that the results are interpretable,
  • Even distribution: this is greatest when all possible results are evenly distributed. In the case of meteorological data such as precipitation and temperature, where there are natural limitations at the extremes (e.g., precipitation cannot be negative), even distribution may not be an adequate representation. This can lead to lower entropy values than in reality, which can introduce error in the interpretation of results.
  • Lack of consideration of correlations: Shannon entropy does not take into account correlations between data. In fact, in meteorological data, there are often correlations between different variables such as temperature and precipitation – ignoring these correlations may lead to a simplified model that does not take into account the full complexity of atmospheric phenomena.
  • Data discretisation: this assumes that the data are discretised, meaning that the data are divided into categories or compartments. The choice of discretisation can affect the entropy results, so it is important to adjust the discretisation appropriately to the characteristics of the data.
In the present study, Shannon entropy values were calculated for extreme monthly precipitation totals and extreme monthly mean temperatures. The sequences thus created constituted the data for further analyses related to the assessment of entropy variability. Knowing the criticisms of the Shannon entropy measure, calculations were planned to avoid the limitations of its use. Units were standardised, the selection of GEV distribution parameters was performed using ADT tests and a constant discretisation was assumed for all analysed cases.

2.4. Variability of Entropy

In the paper, entropy was calculated separately for minimum values and maximum values. A measure was proposed to take into account the variability of distributions describing extreme values. The evaluation of the variability of Shannon entropy was made on the basis of the values of calculated trends. A measure of the Euclidean norm was proposed here [62,63,64].
The Euclidean norm can be written as:
v e c t o r = { a ,   b }   ; v e c t o r = N o r m v e c t o r = a 2 + b 2
where:
a , b - coordinates of the vector
In this study, variability was determined based on Shannon entropy trends separately in the form of distributions describing minimum values and distributions describing maximum values. Finally, it also allowed calculating the resultant variability of Shannon’s entropy by taking the entropy trends for precipitation phenomena and temperature phenomena separately as vector coordinates. Finally, a measure was proposed that takes into account the variability of both precipitation and temperature extremes.
d y n H S P = t r e n d ( H S P m i n ) 2 + t r e n d ( H S P m a x ) 2 d y n H S T = t r e n d ( H S T m i n ) 2 + t r e n d ( H S T m a x ) 2 d y n H S = d y n H S P 2 + d y n H S T 2
where:
t r e n d ( H S P m i n ) – Shannon entropy trend for minimum rainfall values,
t r e n d ( H S P m a x ) – Shannon’s entropy trend for maximum rainfall values,
t r e n d ( H S T m i n ) – Shannon’s entropy trend for minimum temperature values,
t r e n d ( H S T m a x ) – Shannon’s entropy trend for maximum temperature values,
d y n H S P – variation of Shannon’s entropy for extreme precipitation values,
d y n H S T – variation of Shannon’s entropy for extreme temperature values,
d y n H S – variation of Shannon’s entropy for extreme values of precipitation and temperature.
All magnitudes of the analysed component trends and resultant Shannon entropy are expressed in the unit [bit/year].
The Euclidean norm is one of many ways to measure the dynamics of climate variability, and its calculation based on Shannon entropy trends for temperature and precipitation extremes can help understand climate variability. It can be used to compare different time periods and geographic regions to assess whether the dynamics of climate variability are increasing, decreasing, or remaining constant. However, the Euclidean norm itself does not provide insight into the causes of these changes, but only informs about the degree of variability itself. It is worth noting that calculating the Euclidean norm from Shannon’s entropy trends for minimum and maximum temperature and precipitation values is one of many possible ways to analyse climate entropy variability, and should be considered as a complement to other research methods and not as the only method of analysis.

3. Data Preparation for Analysis

The paper relies on grid data of monthly precipitation totals from the Global Precipitation Climatology Center (GPCC) released products and grid data of monthly mean temperatures from National Oceanic and Atmospheric Administration (NOAA) products. The data correspond to a spatial resolution of 0.5°x 0.5° and are consistent with regard to spatial and temporal factors. Products from both GPCC and NOAA are made available via the Internet [65,66,67,68]. These data are not made available in real time.
This paper examines global Shannon entropy trends of monthly precipitation totals and monthly mean temperatures from an area of 377 river basins distributed over all continents. A total of 377 river basins were selected based on data that was made available by GRDC and characterised as areas at risk of extreme events [68].
Assuming 509.9 million square kilometres of land area, 12.76% of the land area is included in the analysis. Table 1 shows the areas covered by the analysis.
GPCC and NOAA data, were converted to catchment areas. This yielded a sequence of monthly precipitation and temperatures, which became the subject of the analyses presented in this article. The analyses covered the years 1901 to 2010.

3.1. Tatistical Tests Used

In evaluating the form of entropy trends for both precipitation and temperature, a bootstrap resampling technique was used to create sequences for calculating Shannon entropy and estimating GEV distribution parameters. The form of the trends was verified with the Mann-Kendall test (MKT) at the 5% significance level. In addition, entropy trend change points were determined using the Pettitt change point test (PCPT) at the 5% significance level. If the change point was positively verified at the 5% level of significance, a new trend form was determined for the new sub-series using the MKT test. For each sequence of extreme values analyzed, the applicability of the GEV distribution was determined by the AD test performed at the 5% significance level.
To examine the trend in a given time series, the MKT test was used [69,70]. This test is independent of the type of distribution and we do not need to assume any special form of data distribution function [71]. This test has been widely recommended by the World Meteorological Organization for public use; moreover, it has been used in many scientific papers to evaluate the trend of water resources data [19,28,70]. The magnitude of the trend is estimated using a nonparametric median-based slope estimator proposed by Sen [72] and extended by Hirsch [73]. In this study, this test was used to examine the Shannon entropy trend.
A number of methods [19,38,70,74,75] can be used to determine time series change points. In this analysis, the nonparametric Pettitt change point test [76] was used to detect the occurrence of change. The Pettitt change point test (PCPT) is a nonparametric abrupt change test in a time sequence. It is used to detect the turning point at which a sudden change occurred, the so-called “spike” in the time sequence. The TP involves comparing the sum of the ranks of two subsets of data, which are divided by a threshold value, to determine whether there is a statistically significant change in the time sequence. This test can be used to analyse data with any distribution, and the test result does not depend on the assumption of normality of the data. The result of the Pettitt test is the value of the test statistic, which is compared with the critical value for the significance level to determine whether the null hypothesis of no abrupt change in the time sequence can be rejected.
PCPT is widely used to detect changes in observed climatic as well as hydrological time series [19,77,78,79]. In the present study, the existence of change points in the Shannon entropy time series for extreme values of monthly precipitation totals and monthly mean temperatures was checked. For time series showing a significant change point, the trend test is applied to the sub-series, and if the change point is not significant, the trend test is applied to the entire time series [19].

3.2. Analysis of Shannon’s Entropy Trend Variation

This paper focuses on the variability of Shannon entropy in long-term sequences of precipitation and temperature to assess the polarity of climate phenomena. Shannon entropy was used as a measure of the indeterminacy and unpredictability of climate phenomena - precipitation and temperature - which allowed the study of the degree of variability of these sequences over time. An increase in Shannon entropy in precipitation sequences indicates increased variability in precipitation and potentially extreme weather events such as intense rains or droughts. Conversely, an increase in Shannon entropy in temperature sequences signals increased temperature variability and the potential for extreme events such as heat waves or extreme cold. Analysis of the variability of Shannon entropy enables the identification of areas where the climate becomes more polarised. Higher entropy values indicate greater climate variability and unpredictability, which can lead to significant changes in the local environment. These changes include shifts in the distribution of plant and animal species, changes in weather patterns and changes in sea level [80].
The variability of entropy trends can be one of the key indicators of climate change, and its analysis can facilitate the understanding of future changes in precipitation and temperature. A decrease in entropy trends for precipitation may suggest that the region is experiencing periods of drought or extreme precipitation, which may result in flooding. An increase in precipitation entropy trends may indicate greater variability in the amount and timing of precipitation, which can lead to difficulties in managing water resources. Variability in temperature entropy trends can affect plant development, biological processes and animal migratio [81,82]. A decrease in temperature entropy trends may suggest a more stable climate but at the same time may lead to a lack of adaptation of organisms to changing conditions. An increase in temperature entropy trends may indicate increasingly unstable climatic conditions, which may lead to a risk of extreme weather events such as heat waves or storms.
The assessment of Shannon entropy trends of extreme precipitation and temperature values is an important tool in studies of climate variability [83,84]. The analysis of historical observations allows the variability of precipitation and temperature to be accurately assessed according to the observed period and enables the form of the directions of these occurring changes to be determined [85]. The study of Shannon entropy allows the detection of trends and changes in these trends in extreme data. The application of statistical techniques, such as Shannon entropy trend analysis, can enable these effects to be predicted more accurately and appropriate preventive action to be taken. Finally, the application of statistical techniques in climate variability studies is particularly important in the context of predicting the variability of extreme events [27,86,87,88,89,90,91,92].
The study of the entropy trend change point, i.e., a change in the direction or nature of precipitation and temperature trends, can be the result of various atmospheric factors and phenomena. This study does not analyse the causes of changes in the direction or nature of trends. However, it is possible to note in general terms what may cause this change:
  • Climate cycles: multi-year and decadal climate cycles, such as El Niño and La Niña, the North Atlantic Oscillation (NAO) or the South-North Pacific Oscillation (ENSO), affect regional and global precipitation patterns; changes in these cycles can cause a switch in precipitation trends [93,94,95],
  • Changes in atmospheric circulation: changes in atmospheric circulation, such as changes in winds, atmospheric currents or high and low pressure systems, can affect local precipitation patterns [96],
  • Changes in ocean surface temperature: ocean surface temperature is an important factor affecting regional precipitation patterns and ocean temperature anomalies such as El Niño and La Niña can affect precipitation changes [97],
  • Urbanisation: urban development and land use changes can affect local precipitation patterns through the so-called “heat island effect” and changes in air circulation [98],
  • Global climate change: climate changes related to human activities, such as greenhouse gas emissions and global warming, can affect changes in precipitation patterns on both global and regional scales [98],
  • Topography: landforms such as mountains and valleys can affect local precipitation patterns through the so-called “orographic effect” [32,98],
  • Ocean-atmosphere interactions: changes in ocean-atmosphere interactions, such as ocean currents and the phenomenon of deep ocean upwelling, can affect regional precipitation patterns [98],
  • Industrial development: the growth of industrial activities, particularly greenhouse gas emissions and air pollution associated with industrial activities, can affect climate change and precipitation patterns. Emissions of greenhouse gases such as carbon dioxide (CO2) and methane (CH4) cause global warming, which can affect regional precipitation patterns, in addition, air pollutants emitted by industry can affect cloud formation and rain [99],
  • Agricultural development, in particular changes in land use, can affect local precipitation patterns. Excessive deforestation and changes in soil use can affect air circulation and moisture, which can affect local precipitation patterns in addition to fertilization and irrigation practices in agriculture [98,99],
  • Melting of glaciers and ice caps: a reduction in the earth’s glaciers and ice caps affects albedo, or the ability of the surface to reflect solar radiation; a smaller ice cap leads to greater heat absorption by the earth, which contributes to global warming [98,99,100],
  • Changes in solar activity: fluctuations in solar activity can affect the amount of solar radiation reaching the earth, which affects climate and surface temperatures [98,99,101],
  • Volcanism: volcanic eruptions introduce large amounts of dust and gases into the atmosphere, which can affect global short-term temperature changes [100,102],
  • Other natural factors: in some cases, changes in temperature trends can be the result of natural climate changes, such as solar-magnetic cycles and changes in ocean circulation [103].

4. Results of the Analyses and Discussion

In the present study, Shannon entropy trends were investigated based on long-term sequences of monthly precipitation totals and monthly mean temperatures for 377 catchments within six WMO regions. From the analysed data, sequences of minimum and maximum values of precipitation and temperatures were extracted. In assessing the form of the entropy trends for both precipitation and temperature, the bootstrap resampling technique was used to create Shannon entropy sequences and estimate GEV distribution parameters. The form of the trends was verified with the MKT test at the 5% significance level. In addition, entropy trend change points were determined using the PCPT test at the 5% significance level. If the change point was positively verified at the 5% significance level, a new trend form was determined for the new sub-series using the MKT test. The applicability of the GEV distribution, for each analysed sequence of extreme values, was assessed using the ADT test at the 5% significance level. The results of the analyses are presented graphically. Graphical presentations of each aspect of the analysis performed enable the trend of change to be seen more easily and precisely.
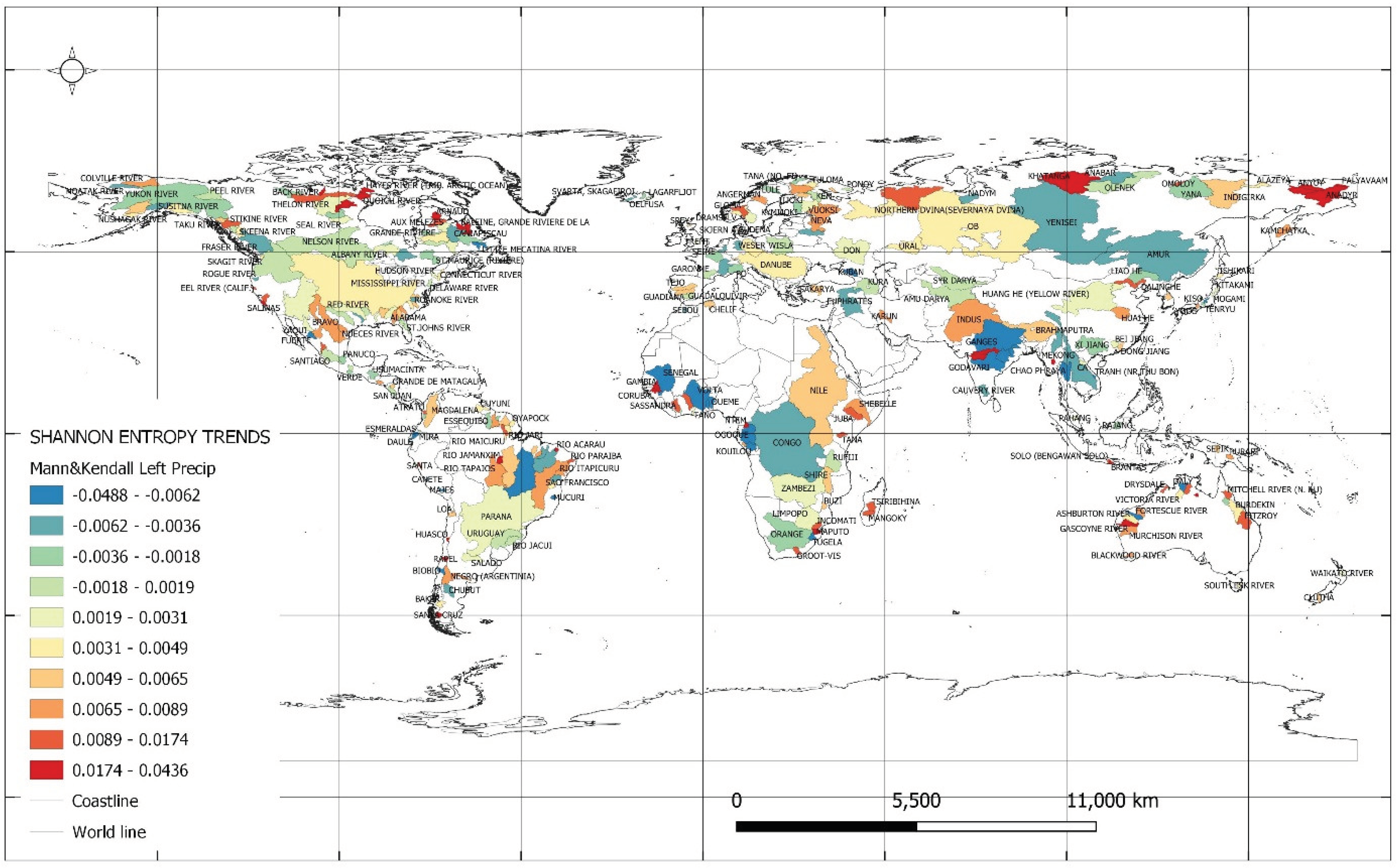
Figure 2 shows the Shannon entropy trends for the values of minimum monthly precipitation totals. The least negative values of entropy trends for minimum monthly precipitation values occurred in the river catchments shown in Table 2. It should be emphasised that in the catchment of the Daule River, Ecuador, the decreasing trend worsens, almost doubling from a value of (-0.040) to (-0.074). The nineteen-eighties is a period of changing trends. Fewer extreme drought or intense rainfall events can be expected in these catchments, which can have a positive impact on agriculture and water resources. Lower entropy for minimum precipitation may indicate more predictable precipitation patterns, which facilitates the planning and management of water resources.
The largest values of entropy trends for the minimum values of monthly precipitation occurred in the river catchments shown in Table 3. It should be noted that in the catchment of the Anyuy River, Russian Federation, there is a decrease of more than four times the Shannon entropy from the value of 0.036 to 0.008 in 1990. The beginning of the nineteen=nineties was a period of changing trends. In the case of the catchment area of the Khatanga River, Russian Federation, there is a trend reversal from a value of 0.033 to a value of (-0.002). The trend collapse occurred in 1990. In these catchments, the increase in entropy for minimum precipitation means greater variability and instability of atmospheric conditions, which can lead to longer periods of drought. This is particularly unfavourable for agriculture, as it causes a decrease in crop yields and worsens the food situation.
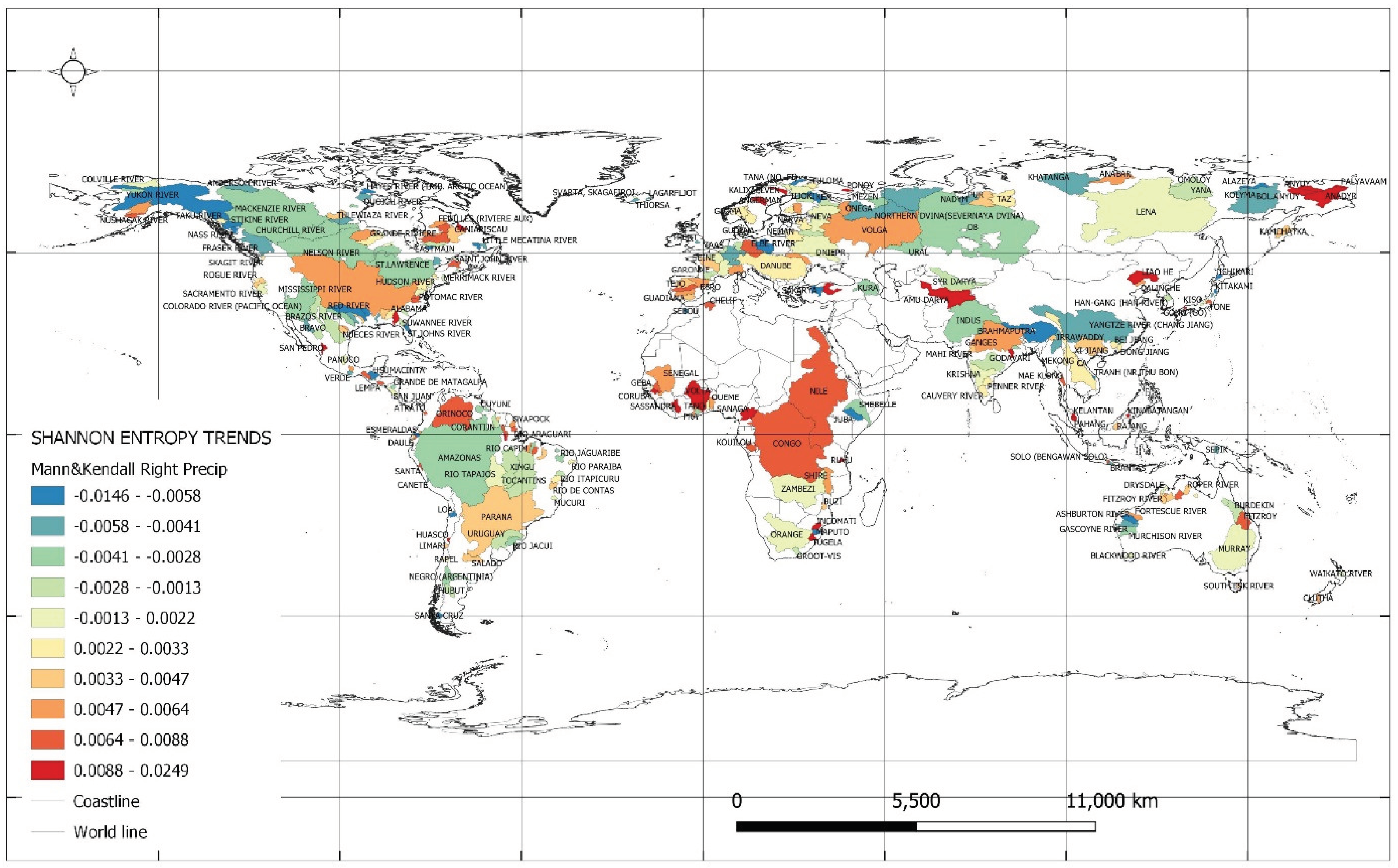
Figure 3 shows Shannon entropy trends for the values of maximum monthly precipitation totals. The lowest values of entropy trends for the maximum values of monthly precipitation occurred in the river catchments shown in Table 4. In the case of the catchment of the St. Johns River: United States, a twofold deepening of the trend is shown, from a value of (-0.010) to (-0.020) in 1994. In the catchment of the Santa Cruz River, Argentina, there is an almost fourfold deepening of the trend, from a value of (-0.008) to a value of (-0.022) in 1997. The following can be expected in these catchments: a reduction in variability in rainfall intensity, which can affect water cycles and natural processes that are important for ecosystem health. However, an increase in the stability of high-intensity precipitation may at the same time lead to flooding, which can have serious consequences for infrastructure and human life and health.
The largest entropy trend values for maximum monthly precipitation values occurred in the river catchments presented in Table 5. In the catchment of the Volta River: Ghana, a twofold decrease in trend values from 0.014 to 0.008 in 1990 is shown, and similarly in the Anyuy Russian Federation river catchment from 0.025 to 0.013 in 1990. The processes in these catchments indicate an increase in rainfall variability. This can affect water cycles and natural processes that are important for ecosystem health. On the one hand, an increase in maximum precipitation can benefit the ecosystems of dry regions, which need more water. On the other hand, increased maximum precipitation can lead to flooding and soil erosion. In that case, reducing the variability of maximum precipitation would be beneficial to the health of ecosystems. In the context of climate change, increased maximum precipitation is one of the expected effects of global warming.
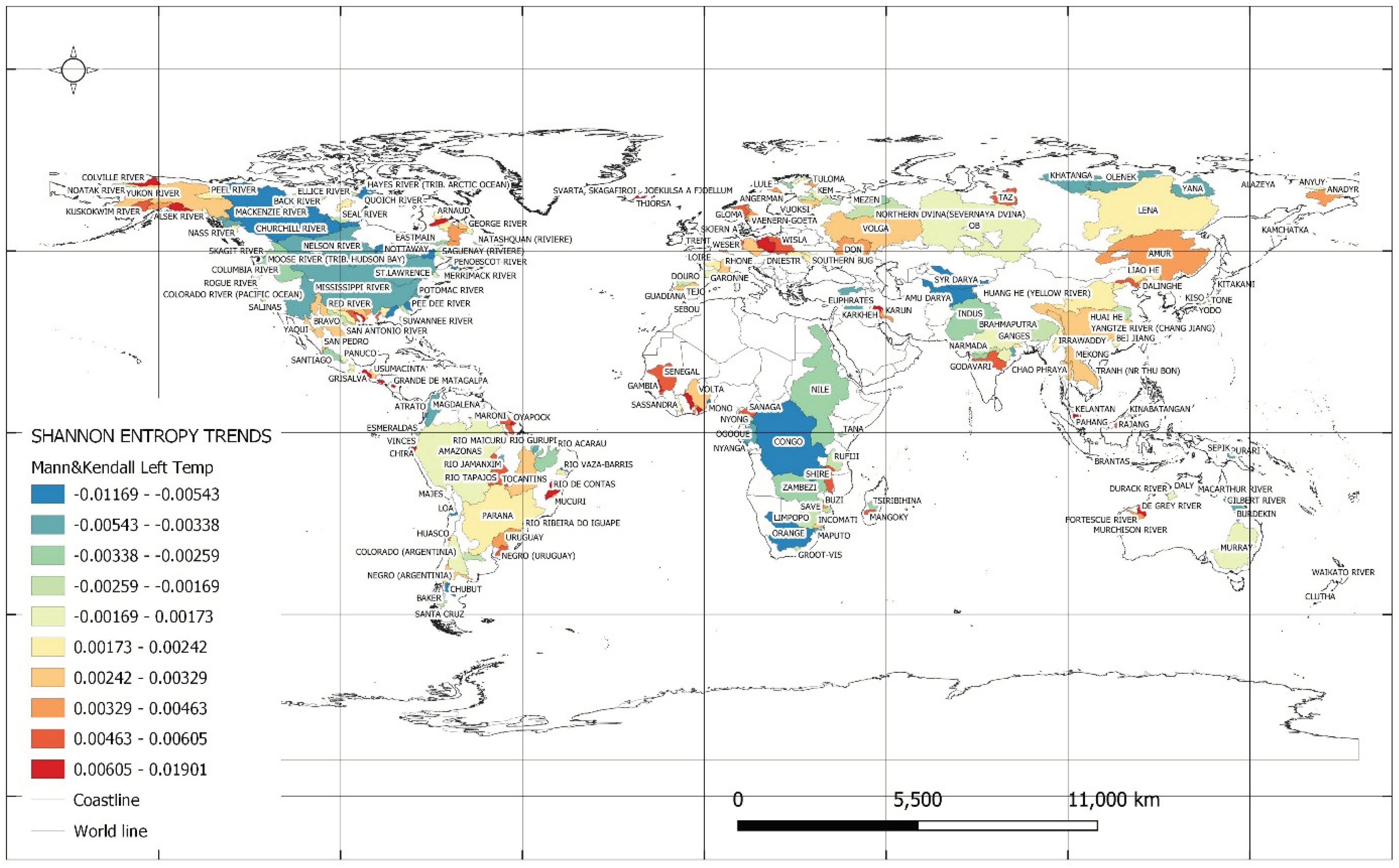
Figure 4 shows the Shannon entropy trends for the values of minimum monthly average temperatures. The lowest values of entropy trends for minimum monthly average temperatures occurred in the catchments shown in Table 6. The Churchill River catchment in Canada showed a twofold increase in trend from a value of (-0.007) to (-0.003) in 1987. In these catchments, the direction of the change in temperature entropy may suggest that temperature variability is less comparable with the past, so the climate is becoming more stable.
The largest entropy trend values for minimum monthly average temperatures occurred in the catchments presented in Table 7. The three catchments of Svarta, Skagafiroi, Iceland, Thjorsa, Iceland and Joekulsa A Fjoellu, Iceland, showed the largest trend values of 0.016 to 0.019. For the first two catchments, there was a threefold decrease in trend values to a magnitude of 0.006 to 0.005. For the third catchment, a year of trend change (1988) was shown, while the value of the new trend at the 5% significance level was not determined. An increase in temperature entropy can increase extreme weather conditions such as droughts, heat waves, hurricanes and storms, which can have negative effects on human, animal and environmental health. Increasing the entropy of minimum temperatures may be beneficial for agriculture and vegetation growth. However, more research is needed to better understand the effects of changes in temperature entropy and develop strategies to adapt to climate change.
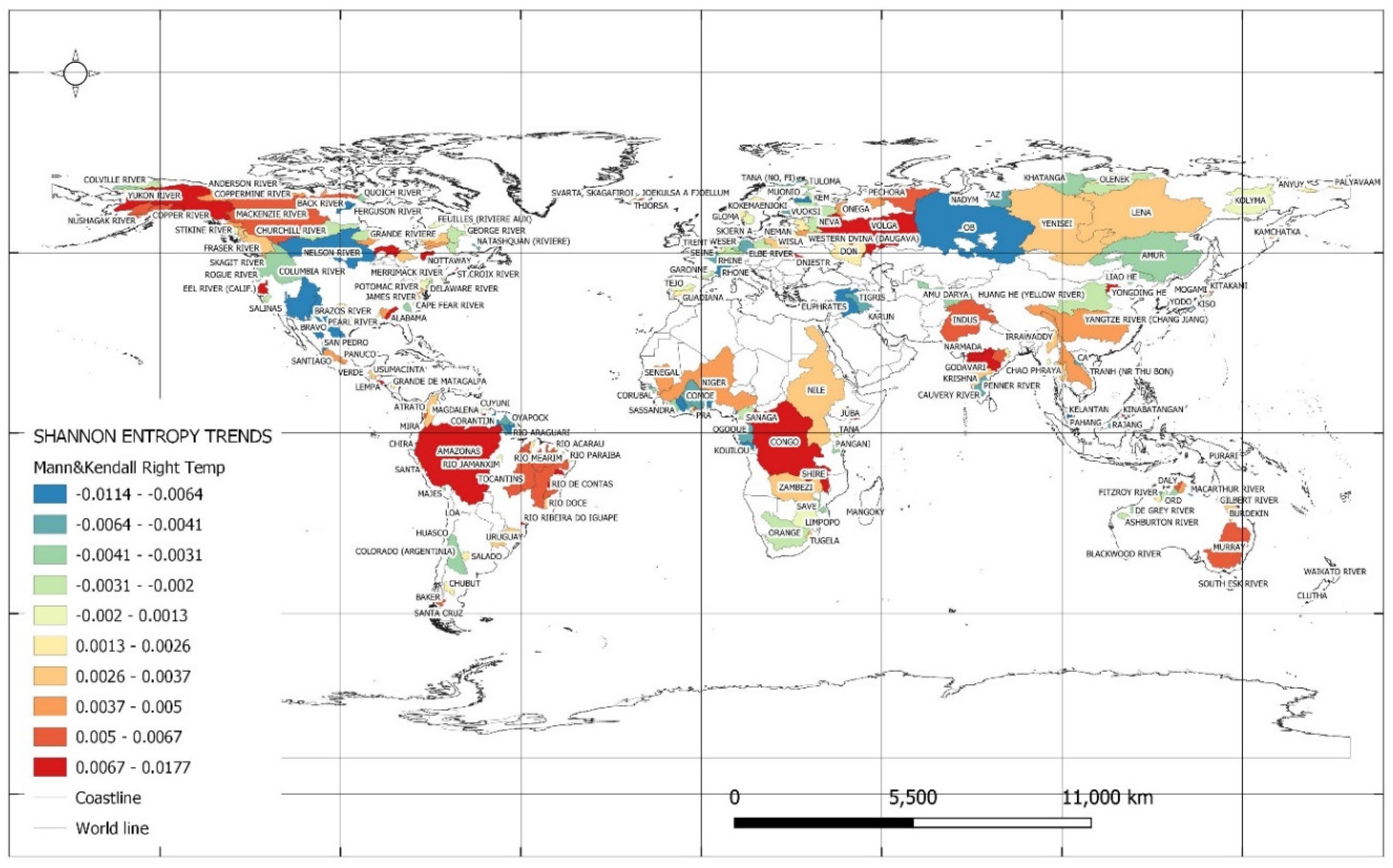
Figure 5 shows Shannon entropy trends for the values of maximum monthly average temperatures. The lowest values of entropy trends for maximum monthly average temperatures occurred in the catchments presented in Table 8. In the case of the catchment of the Nadym River, Russian Federation, a doubling of the trend from a value of (-0.011) to a value of (-0.021) in 1991 is shown. In the catchment of the Loa River, Chile, there is a reversal of the weather pattern and a change in the direction of the trend from a value of (-0.011) to a value of 0.003 in 1983. In these catchments, the trend of maximum temperature entropy is decreasing and this means that the variability in high temperatures is decreasing, which may suggest that extreme heat becomes less common. This could have a beneficial effect on human health but could also affect ecosystems, including plants, animals and microorganisms that are adapted to certain temperatures.
The largest entropy trend values for maximum monthly average temperatures occurred in the catchments presented in Table 9. The catchment of the Juba River, Somalia has a twofold decrease in trend values from 0.010 to a value of 0.005 in 1990. An increase in temperature entropy can increase extreme weather conditions such as droughts, heat waves, hurricanes and storms, which can have negative effects on human, animal and environmental health.
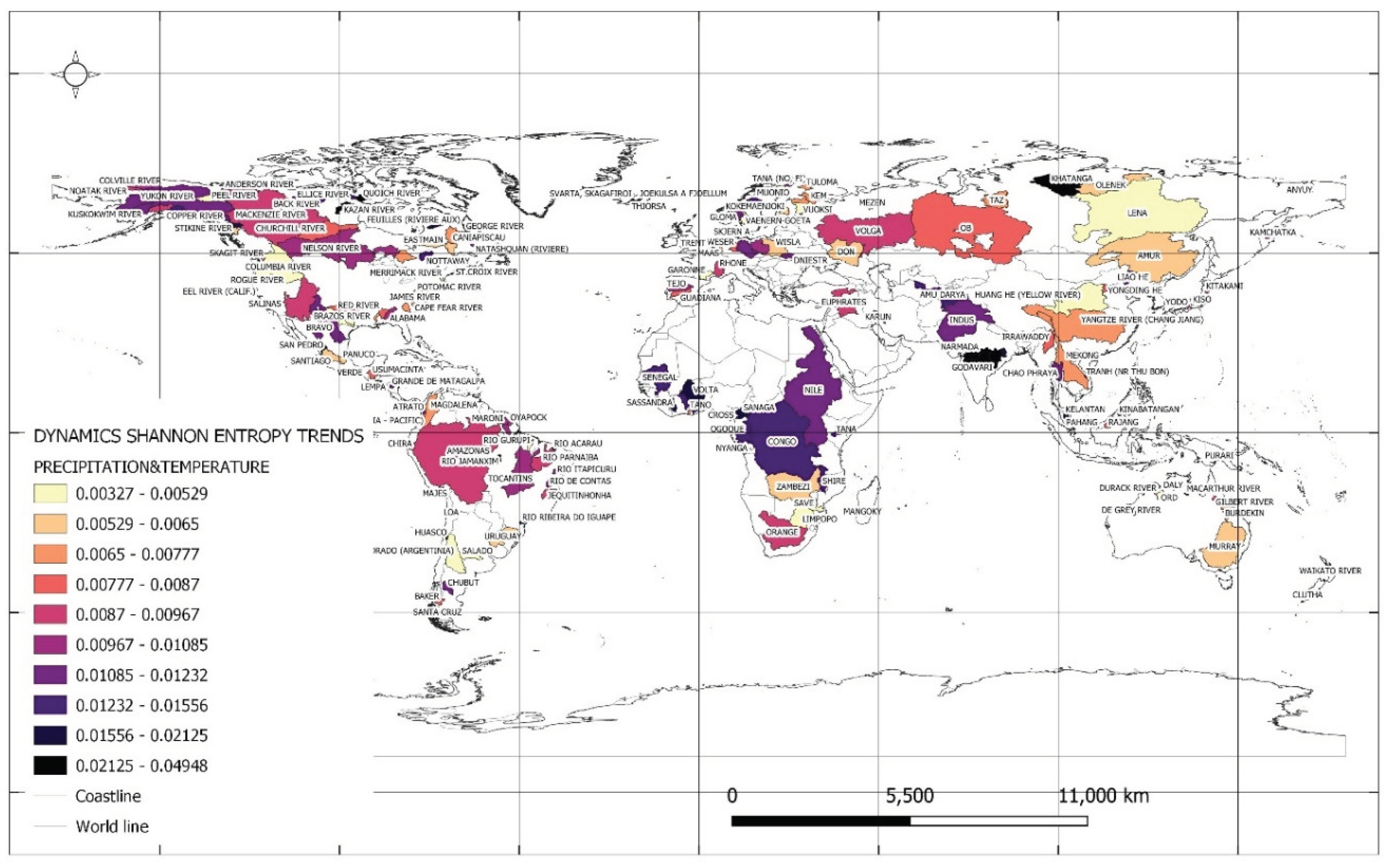
Figure 6 shows the spatial location of the catchments in which the greatest dynamics of Shannon entropy trends for minimum and maximum values of precipitation and temperature were identified at the 5% significance level. The maximum values of the norm take the magnitude of 0.049 [bit/year] for the Daly river catchment, Australia, the smallest 4e-16 [bit/year] for the Kovda river catchment, Russian Federation, Table 10. Note that the dynamics of Shannon entropy for minimum and maximum monthly average precipitation compared to the dynamics of Shannon entropy for minimum and maximum monthly average temperatures is greater than 1 and takes values from 2.0 to 19.8, Table 10. The almost twenty-times-greater dynamics in the Anyuy river catchment, Russian Federation, in the area of precipitation compared to the dynamics of temperature means that the variability of extreme precipitation values in this catchment is much greater than the variability of extreme temperature values. In other words, extreme precipitation events are more varied and extreme than extreme temperature events. This may indicate that the area experiences more extreme and varied precipitation-related weather conditions, such as floods, storms, heavy rains, droughts, etc., than temperature-related conditions, such as heat waves and freezing temperatures.

5. Summary

This study demonstrates the applicability of the Shannon entropy measure in the analysis of climate change by allowing the degree of disorder and complexity of distributions describing climate variables in the form of precipitation and temperature to be measured. Catchment areas were identified where Shannon entropy trends were identified at a 5% level of significance in both temperature and precipitation. Possible weather patterns were also identified, as well as their directions due to changes in these trends. A bootstrap method was used to evaluate the entropy trends. As a result, Shannon entropy trend values were obtained to assess the variability of climatic conditions in the 377 catchment areas. The presented analysis was based on annual minimum and maximum values calculated from mean values. Analysis of averages is statistically more stable, allows for a larger number of observations and better reflects typical values, which is important for detecting persistent trends and ongoing changes.
The trend relationships of Shannon entropy in extreme precipitation and extreme temperature defined in this study can be characterised as follows:
  • An increase in the entropy of extreme precipitation can be related to increased variability in precipitation occurrence and intensity, which can affect extreme weather events such as downpours, floods or droughts.
  • A decrease in the entropy of extreme precipitation may indicate reduced variability in the occurrence of extreme precipitation, which may imply more stable precipitation patterns in an area.
  • An increase in the entropy of extreme temperature may reflect greater variability in temperature extremes, such as heat waves or sudden temperature drops.
  • A decrease in extreme temperature entropy may indicate less variability in extreme temperatures, which may suggest more stable thermal conditions in a given area.
  • A positive correlation between the entropy of extreme precipitation and the entropy of extreme temperature may indicate that changes in precipitation and temperature are occurring in similar patterns, which may be due to the influence of the same climatic factors.
  • A negative correlation between the entropy of extreme precipitation and the entropy of extreme temperature may indicate that variations in these two variables occur in opposite directions, which may be due to different factors influencing precipitation and temperature.
  • An increase in the entropy of extreme precipitation with a decrease in the entropy of extreme temperature may indicate variability in the occurrence of precipitation without much change in extreme temperature.
  • A decrease in the entropy of extreme precipitation with a simultaneous increase in the entropy of extreme temperature may indicate less variability in precipitation with greater variability in temperature.
  • The lack of a relationship between trends in the entropy of extreme precipitation and trends in the entropy of extreme temperature may suggest that the variability in these two variables is independent of each other and due to different factors.
Noting the variability and relationships between the entropy trends of minimum and maximum precipitation and temperature can facilitate the analysis of climate change and forecasting extreme weather events. The analyses documented the conditions of climate variability in the area of precipitation and temperature, and these are key factors affecting the environment and water resources, which is particularly relevant for predicting the effects of hydrological floods and droughts, which have serious consequences for humanity and the environment.
Shannon’s entropy measures the indeterminacy and unpredictability of information. In the case of climate change, entropy can facilitate the analysis of the various drivers of climate change and predict future impacts. It can help identify changes in atmospheric conditions, such as changes in temperature, precipitation and pressure, which may affect climate change. Entropy can also help analyse the complex interactions between different climate factors, such as atmospheric circulation, ocean circulation and the amount of solar radiation. It can also be used to assess the risk of climate change in assessing the probability of different climate change scenarios and in determining the degree of uncertainty associated with these scenarios. In addition, entropy can help identify different patterns of climate change, such as climate cycles in which periodic changes in solar radiation and ocean circulation influence climate change. Entropy can also be used to identify the complexity of climate and its systems, which can help us to understand how different factors influence climate change. Finally, entropy analysis can help develop strategies to manage the risks associated with climate change, which is particularly important in view of the increasing number of climate change-related disasters such as hurricanes, floods and droughts. Shannon’s entropy is appropriate for climate change analysis by enabling the measurement of the degree of disorder and the complexity of climate change distributions. It can help identify trends, cyclicity, fluctuations and anomalies in climate data, as well as forecasting future changes based on historical data. It can be used to analyse a variety of climate factors and to assess the effectiveness of measures to reduce the impact of human activities on the climate.

References

  1. Rummukainen, M. Changes in climate and weather extremes in the 21st century. Wiley Interdiscip. Rev. Clim. Chang. 2012, 3, 115–129. [Google Scholar] [CrossRef]
  2. Viner, D.; Ekstrom, M.; Hulbert, M.; Warner, N.K.; Wreford, A.; Zommers, Z. Understanding the dynamic nature of risk in climate change assessments—A new starting point for discussion. Atmos. Sci. Lett. 2020, 21, 1–8. [Google Scholar] [CrossRef]
  3. Lal, P.N. et al., National systems for managing the risks from climate extremes and disasters 9781107025. 2012. [CrossRef]
  4. Elahi, E.; Khalid, Z.; Tauni, M.Z.; Zhang, H.; Lirong, X. Extreme weather events risk to crop-production and the adaptation of innovative management strategies to mitigate the risk: A retrospective survey of rural Punjab, Pakistan. Technovation, 2022; 117, 102255. [Google Scholar] [CrossRef]
  5. Waseem, M.; Khurshid, T.; Abbas, A.; Ahmad, I.; Javed, Z. Impact of meteorological drought on agriculture production at different scales in Punjab, Pakistan. J. Water Clim. Chang. 2022, 13, 113–124. [Google Scholar] [CrossRef]
  6. Ogbuabor, J.E.; Egwuchukwu, E.I. The impact of climate change on the Nigerian economy. Int. J. Energy Econ. Policy 2017, 7, 217–223. [Google Scholar]
  7. G. Stephan, “Intergenerational Fairness and Climate Change Adaptation Policy: An Economic Analysis,” Green Low-Carbon Econ., Mar. 2023. [CrossRef]
  8. Zhang, X. et al. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
  9. Metz, B.; Meyer, L.; Bosch, P. Climate change 2007 mitigation of climate change. Clim. Chang. 2007 Mitig. Clim. Chang. 2007, 9780521880114, 1–81. [Google Scholar] [CrossRef]
  10. Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Hegerl, G.C. Changes in temperature and precipitation extremes in the IPCC ensemble of global coupled model simulations. J. Clim. 2007, 20, 1419–1444. [Google Scholar] [CrossRef]
  11. Wanson, K.L.; Tsonis, A.A. Has the climate recently shifted? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
  12. Williams, J.M. Entropy shows that global warming should cause increased variability in the weather. Glob. Warm. 1.5.2, no. c, 2000.
  13. Liu, B.; Chen, X.; Lian, Y.; Wu, L. Entropy-based assessment and zoning of rainfall distribution. J. Hydrol. 2013, 490, 32–40. [Google Scholar] [CrossRef]
  14. Ramirez-Villegas, J. Climate analogues: finding tomorrow’s agriculture today. Work. Pap. 2011, 12, 40. [Google Scholar]
  15. M. H.; Thornton, A.J.C.P.K., Ed.; Ericksen, P.J. Climate variability and vulnerability to climate change : a review. pp. 3313–3328, 2014. [Google Scholar] [CrossRef]
  16. Pfleiderer, P.; Schleussner, C.F.; Mengel, M.; Rogelj, J. Global mean temperature indicators linked to warming levels avoiding climate risks. Environ. Res. Lett. no. 6. 2018, 13. [Google Scholar] [CrossRef]
  17. 17. G. Y. Lenny Bernstein, Peter Bosch, Osvaldo Canziani, Zhenlin Chen, Renate Christ, Ogunlade Davidson, William Hare, Saleemul Huq, David Karoly, Vladimir Kattsov, Zbigniew Kundzewicz, Jian Liu, Ulrike Lohmann, Martin Manning, Taroh Matsuno, Bettina Menne, Bert M, “Climate Change 2007 : An Assessment of the Intergovernmental Panel on Climate Change,” Change, vol. 446, no. November, pp. 12–17, 2007, [Online]. Available: http://www.ipcc.ch/pdf/assessment-report/ar4/syr/ar4_syr.pdf. /.
  18. Hussain, A. Spatiotemporal temperature trends over homogenous climatic regions of Pakistan during 1961–2017. Theor. Appl. Climatol. 2023, 153, 397–415. [Google Scholar] [CrossRef]
  19. Jaiswal, R.K.; Lohani, A.K.; Tiwari, H.L. Statistical Analysis for Change Detection and Trend Assessment in Climatological Parameters. Environ. Process. 2015, 2, 729–749. [Google Scholar] [CrossRef]
  20. Katz, R. Statistics of Extremes in Climatology and Hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
  21. Hussain, A. et al. Assessment of precipitation extremes and their association with NDVI, monsoon and oceanic indices over Pakistan. Atmos. Res. 2023, 292. [Google Scholar] [CrossRef]
  22. Hussain, A. et al. Ocean-atmosphere circulation coherences associated with temperature increase in Pakistan. Environ. Res. Lett. 2023, 18. [Google Scholar] [CrossRef]
  23. Su, L.; Miao, C.; Duan, Q.; Lei, X.; Li, H. Multiple-Wavelet Coherence of World’s Large Rivers With Meteorological Factors and Ocean Signals. J. Geophys. Res. Atmos. 2019, 124, 4932–4954. [Google Scholar] [CrossRef]
  24. Saha, S.; Chattopadhyay, S. Exploring of the summer monsoon rainfall around the Himalayas in time domain through maximization of Shannon entropy. Theor. Appl. Climatol. 2020, 141, 133–141. [Google Scholar] [CrossRef]
  25. de P, V.; Filho, A.F.B.; Almeida, R.S.R.; de Holanda, R.M.; da Cunha Campos, J.H.B. Shannon information entropy for assessing space-time variability of rainfall and streamflow in semiarid region. Sci. Total Environ. 2016, 544, 330–338. [Google Scholar] [CrossRef]
  26. Guntu, R.K.; Agarwal, A. Investigation of Precipitation Variability and Extremes Using Information Theory. p. 14, 2021. [CrossRef]
  27. Romanowicz, R.J. Climate Change Impact on Hydrological Extremes: Preliminary Results from the Polish-Norwegian Project. Acta Geophys. 2016, 64, 477–509. [Google Scholar] [CrossRef]
  28. Palaniswami, S.; Muthiah, K. Change point detection and trend analysis of rainfall and temperature series over the vellar river basin. Polish J. Environ. Stud. 2018, 27, 1673–1682. [Google Scholar] [CrossRef] [PubMed]
  29. Groves, D.G.; Yates, D.; Tebaldi, C. Developing and applying uncertain global climate change projections for regional water management planning. Water Resour. Res. 2008, 44, 1–16. [Google Scholar] [CrossRef]
  30. Heim, R.R. An overview of weather and climate extremes - Products and trends. Weather Clim. Extrem. 2015, 10, 1–9. [Google Scholar] [CrossRef]
  31. Ziernicka-Wojtaszek, A.; Kopcińska, J. Variation in atmospheric precipitation in Poland in the years 2001-2018. Atmosphere (Basel). 2020, 11. [Google Scholar] [CrossRef]
  32. Singh, P.; Gupta, A.; Singh, M. Hydrological inferences from watershed analysis for water resource management using remote sensing and GIS techniques. Egypt. J. Remote Sens. Sp. Sci. 2014, 17, 111–121. [Google Scholar] [CrossRef]
  33. Gómez, J.D.; Etchevers, J.D.; Monterroso, A.I.; Gay, C.; Campo, J.; Martínez, M. Spatial estimation of mean temperature and precipitation in areas of scarce meteorological information. Atmosfera 2008, 21, 35–56. [Google Scholar]
  34. Zhang, X.; Vincent, L.A.; Hogg, W.D.; Niitsoo, A. Temperature and precipitation trends in Canada during the 20th century. Atmos. - Ocean 2000, 38, 395–429. [Google Scholar] [CrossRef]
  35. Tabari, H.; Madani, K.; Willems, P. The contribution of anthropogenic influence to more anomalous extreme precipitation in Europe. Environ. Res. Lett. 2020, 15, 104077. [Google Scholar] [CrossRef]
  36. Tabari, H.; Willems, P. Lagged influence of Atlantic and Pacific climate patterns on European extreme precipitation. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef]
  37. Venegas-Cordero, N.; Kundzewicz, Z.W.; Jamro, S.; Piniewski, M. Detection of trends in observed river floods in Poland. J. Hydrol. Reg. Stud. 2022, 41. [Google Scholar] [CrossRef]
  38. Radziejewski, M.; Bardossy, A.; Kundzewicz, Z.W. Detection of change in river flow using phase randomization. Hydrol. Sci. J. 2000, 45, 547–558. [Google Scholar] [CrossRef]
  39. Twaróg, B. ASSESSING THE POLARIZATION OF CLIMATE PHENOMENA BASED ON LONG-TERM PRECIPITATION AND TEMPERATURE SEQUENCES. 2023.
  40. Cardona, O.D. et al. Determinants of risk: Exposure and vulnerability. Manag. Risks Extrem. Events Disasters to Adv. Clim. Chang. Adapt. Spec. Rep. Intergov. Panel Clim. Chang. 2012, 9781107025, 65–108. [Google Scholar] [CrossRef]
  41. Sillmann, J. et al. Understanding, modeling and predicting weather and climate extremes: Challenges and opportunities. Weather Clim. Extrem. 2017, 18, 65–74. [Google Scholar] [CrossRef]
  42. Chai, Y. et al. Homogenization and polarization of the seasonal water discharge of global rivers in response to climatic and anthropogenic effects. Sci. Total Environ. 2020, 709, 136062. [Google Scholar] [CrossRef]
  43. Kundzewicz, Z.W.; Robson, A. Detecting Trend and Other Changes in Hydrological Data. World Clim. Program. - Water, no. May, p. 158, 2000, [Online]. Available: http://water.usgs.gov/osw/wcp-water/detecting-trend.pdf.
  44. Christensen, J.H. et al. Climate phenomena and their relevance for future regional climate change. Clim. Chang. 2013 Phys. Sci. Basis Work. Gr. I Contrib. to Fifth Assess. Rep. Intergov. Panel Clim. Chang. 2013, 9781107057, 1217–1308. [Google Scholar] [CrossRef]
  45. Easterling, D.R.; Kunkel, K.E.; Wehner, M.F.; Sun, L. Detection and attribution of climate extremes in the observed record. Weather Clim. Extrem. 2016, 11, 17–27. [Google Scholar] [CrossRef]
  46. Singh, K.; Xie, M. Bootstrap Method. Int. Encycl. Educ. Third Ed. 2010, 46–51. [Google Scholar] [CrossRef]
  47. DeDeo, S.; Hawkins, R.X.D.; Klingenstein, S.; Hitchcock, T. Bootstrap methods for the empirical study of decision-making and information flows in social systems. Entropy 2013, 15, 2246–2276. [Google Scholar] [CrossRef]
  48. Ng, J.L.; Aziz, S.A.; Huang, Y.F.; Mirzaei, M.; Wayayok, A.; Rowshon, M.K. Uncertainty analysis of rainfall depth duration frequency curves using the bootstrap resampling technique. J. Earth Syst. Sci. 2019, 128, 1–15. [Google Scholar] [CrossRef]
  49. MATLAB Documentation. Available online: https://www.mathworks.com/help/matlab/ (accessed on 19 March 2021).
  50. Chowell, G.; Luo, R. Ensemble bootstrap methodology for forecasting dynamic growth processes using differential equations: application to epidemic outbreaks. BMC Med. Res. Methodol. 2021, 21, 34. [Google Scholar] [CrossRef]
  51. Huser, R.; Davison, A.C. Space-time modelling of extreme events. J. R. Stat. Soc. Ser. B Stat. Methodol. 2014, 76, 439–461. [Google Scholar] [CrossRef]
  52. Coles, S., An Introduction to Statistical Modeling of Extreme V (llues. Department of Mathematics, Bristol: Springer, 2016.
  53. Ross, S.M., Introduction to Probability and Statistics, no. 5. Academic Press is an imprint ofElsevier, 2014.
  54. Kim, H.; Kim, T.; Shin, J.Y.; Heo, J.H. Improvement of Extreme Value Modeling for Extreme Rainfall Using Large-Scale Climate Modes and Considering Model Uncertainty. Water (Switzerland) 2022, 14. [Google Scholar] [CrossRef]
  55. 55. “MATLAB ® Mathematics R2021a,” 1984, Accessed: May 04, 2023. [Online]. Available: www.mathworks.com. 04 May.
  56. De Michele, C.; Avanzi, F. Superstatistical distribution of daily precipitation extremes: A worldwide assessment. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
  57. Kolokytha, E.; Oishi, S.; Teegavarapu, R.S.V. Sustainable water resources planning and management under climate change. 2016.
  58. Vajapeyam, S. Understanding Shannon’s Entropy metric for Information. no. March, pp. 1–6, 2014, [Online]. Available: http://arxiv.org/abs/1405.2061.
  59. Aubry, N.; Chauve, M.P.; Guyonnet, R. Transition to turbulence on a rotating flat disk. Phys. Fluids 1994, 6, 2800–2814. [Google Scholar] [CrossRef]
  60. Aubry, N.; Guyonnet, R.; Lima, R. Spatiotemporal analysis of complex signals: Theory and applications. J. Stat. Phys. 1991, 64, 683–739. [Google Scholar] [CrossRef]
  61. Chakrabarti, C.G.; Chakrabarty, I. Shannon entropy: Axiomatic characterization and application. Int. J. Math. Math. Sci. 2005, 2005, 2847–2854. [Google Scholar] [CrossRef]
  62. Rapp, B.E. Vector Calculus. Microfluid. Model. Mech. Math. 2017, 137–188. [Google Scholar] [CrossRef]
  63. Rohat, G.; Goyette, S.; Flacke, J. Characterization of European cities’ climate shift – an exploratory study based on climate analogues. Int. J. Clim. Chang. Strateg. Manag. 2018, 10, 428–452. [Google Scholar] [CrossRef]
  64. Lindfield, G.; Penny, J. Linear Equations and Eigensystems. Numer. Methods 2019, 73–156. [Google Scholar] [CrossRef]
  65. T. C. P.; Vose, R.S. An overview of the global historical climatology network-daily database. Bull. Am. Meteorol. Soc. 1997, 78, 897–910. [CrossRef]
  66. Donat, M.G. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
  67. Becker, A. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901-present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
  68. Rudolf, B.; Beck, C.; Grieser, J.; Schneider, U. Global Precipitation Analysis Products of the GPCC. Internet Pbulication, pp. 1–8, 2005, [Online]. Available: ftp://ftp-anon.dwd.de/pub/data/gpcc/PDF/GPCC_intro_products_2008.pdf. 2005; 8. [Google Scholar]
  69. Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
  70. Salarijazi, M. Trend and change-point detection for the annual stream-flow series of the Karun River at the Ahvaz hydrometric station. African J. Agric. Reseearch 2012, 7, 4540–4552. [Google Scholar] [CrossRef]
  71. Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
  72. Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
  73. Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
  74. Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
  75. Gupta, A.K.; Chen, J. Parametric Statistical Change Point Analysis. Angew. Chemie Int. Ed. 2021, 6, 951–952. [Google Scholar] [CrossRef]
  76. Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. Ser. C (Applied Stat.） 1979, 28, 126–135. [Google Scholar] [CrossRef]
  77. Verstraeten, G.; Poesen, J.; Demarée, G.; Salles, C. Long-term (105 years) variability in rain erosivity as derived from 10-min rainfall depth data for Ukkel (Brussels, Belgium): Implications for assessing soil erosion rates. J. Geophys. Res. Atmos. 2006, 111, 1–11. [Google Scholar] [CrossRef]
  78. Kundzewicz, Z.W.; Radziejewski, M. Methodologies for trend detection. IAHS-AISH Publ. 2006, 308, 538–549. [Google Scholar]
  79. Conte, L.C.; Bayer, D.M.; Bayer, F.M. Bootstrap Pettitt test for detecting change points in hydroclimatological data: case study of Itaipu Hydroelectric Plant, Brazil. Hydrol. Sci. J. 2019, 64, 1312–1326. [Google Scholar] [CrossRef]
  80. Persson, J. et al. No polarization-expected values of climate change impacts among European forest professionals and scientists. Sustain. 2020, 7, 2659. [Google Scholar] [CrossRef]
  81. Iverson, L.R.; McKenzie, D. Tree-species range shifts in a changing climate: Detecting, modeling, assisting. Landsc. Ecol. 2013, 28, 879–889. [Google Scholar] [CrossRef]
  82. Franklin, J. Mapping Species Distributions: Spatial Inference and Prediction. Oryx 2010, 44, 615–615. [Google Scholar] [CrossRef]
  83. Herschy, R.W. The world’s maximum observed floods. Flow Meas. Instrum. 2002, 13, 231–235. [Google Scholar] [CrossRef]
  84. Blöschl, G. et al. Twenty-three unsolved problems in hydrology (UPH)–a community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
  85. Dankers, R.; Hiederer, R. Extreme Temperatures and Precipitation in Europe: Analysis of a High-Resolution Climate Change Scenario. JRC Sci. Tech. Reports 2008, 82. [Google Scholar]
  86. Mudelsee, M.; Börngen, M.; Tetzlaff, G.; Grünewald, U. Extreme floods in central Europe over the past 500 years: Role of cyclone pathway ‘Zugstrasse Vb. J. Geophys. Res. D Atmos. 2004, 109, 1–21. [Google Scholar] [CrossRef]
  87. Vavrus, S.J.; Notaro, M.; Lorenz, D.J. Interpreting climate model projections of extreme weather events. Weather Clim. Extrem. 2015, 28, 10–28. [Google Scholar] [CrossRef]
  88. Angélil, O. et al. Comparing regional precipitation and temperature extremes in climate model and reanalysis products. Weather Clim. Extrem. 2016, 13, 35–43. [Google Scholar] [CrossRef]
  89. Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
  90. Das, N.; Bhattacharjee, R.; Choubey, A.; Ohri, A.; Dwivedi, S.B.; Gaur, S. Time series analysis of automated surface water extraction and thermal pattern variation over the Betwa river, India. Adv. Sp. Res. 2021, 68, 1761–1788. [Google Scholar] [CrossRef]
  91. Reinking, R.F. An approach to remote sensing and numerical modeling of orographic clouds and precipitation for climatic water resources assessment. Atmos. Res. 1995, 35, 349–367. [Google Scholar] [CrossRef]
  92. López-Bermeo, C.; Montoya, R.D.; Caro-Lopera, F.J.; Díaz-García, J.A. Validation of the accuracy of the CHIRPS precipitation dataset at representing climate variability in a tropical mountainous region of South America. Phys. Chem. Earth, Parts A/B/C 2022, 127, 103184. [Google Scholar] [CrossRef]
  93. Duan, Q.; Duan, A. The energy and water cycles under climate change. Natl. Sci. Rev. 2020, 7, 553–557. [Google Scholar] [CrossRef] [PubMed]
  94. Allan, R.P.; Soden, B.J. Atmospheric warming and the amplification of precipitation extremes. Science 2008, 321, 1481–1484. [Google Scholar] [CrossRef] [PubMed]
  95. Froyland, G.; Giannakis, D.; Lintner, B.R.; Pike, M.; Slawinska, J. Spectral analysis of climate dynamics with operator-theoretic approaches. Nat. Commun. 2021, 12, 1–21. [Google Scholar] [CrossRef] [PubMed]
  96. Li, Z.; Shi, Y.; Argiriou, A.A.; Ioannidis, P.; Mamara, A.; Yan, Z. A Comparative Analysis of Changes in Temperature and Precipitation Extremes since 1960 between China and Greece. Atmosphere 2022, 13, 1824. [Google Scholar] [CrossRef]
  97. Smith, T.M.; Reynolds, R.W.; Peterson, T.C.; Lawrimore, J. Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880-2006). J. Clim. 2008, 21, 2283–2296. [Google Scholar] [CrossRef]
  98. R. K., P.; Team, C.W. Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change., no. 2. 2014.
  99. Mahmoud, S.H.; Gan, T.Y. Impact of anthropogenic climate change and human activities on environment and ecosystem services in arid regions. Sci. Total Environ. 2018, 633, 1329–1344. [Google Scholar] [CrossRef] [PubMed]
  100. Stocker, T.F. et al. Physical Climate Processes and Feedbacks. Clim. Chang. 2001 Sci. Bases. Contrib. Work. Gr. I to Third Assess. Rep. Intergov. Panel Clim. Chang., p. 881, 2001.
  101. Pitt, M.A. Increased Temperature and Entropy Production in the Earth’s Atmosphere: Effect on Wind, Precipitation, Chemical Reactions, Freezing and Melting of Ice and Electrical Activity. J. Mod. Phys. 2019, 10, 966–973. [Google Scholar] [CrossRef]
  102. Mills, T.C. Applied Time Series Analysis: A Practical Guide to Modeling and Forecasting. 2019.
  103. Delgado-Bonal, A.; Marshak, A.; Yang, Y.; Holdaway, D. Analyzing changes in the complexity of climate in the last four decades using MERRA-2 radiation data. Sci. Rep. 2020, 10, 1–8. [Google Scholar] [CrossRef]
Preprints 100252 g001
Figure 1. Schematic of the bootstrap process for estimating Shannon entropy at the 5% significance level for a selected catchment for a seventy-element sequence.
Figure 1. Schematic of the bootstrap process for estimating Shannon entropy at the 5% significance level for a selected catchment for a seventy-element sequence.
Preprints 100252 g001
Preprints 100252 g002
Figure 2. Shannon entropy trends for values of minimum monthly precipitation totals.
Figure 2. Shannon entropy trends for values of minimum monthly precipitation totals.
Preprints 100252 g002
Preprints 100252 g003
Figure 3. Shannon entropy trends for values of maximum monthly precipitation totals.
Figure 3. Shannon entropy trends for values of maximum monthly precipitation totals.
Preprints 100252 g003
Preprints 100252 g004
Figure 4. Shannon entropy trends for minimum values of monthly average temperatures.
Figure 4. Shannon entropy trends for minimum values of monthly average temperatures.
Preprints 100252 g004
Preprints 100252 g005
Figure 5. Shannon entropy trends for maximum values of monthly average temperatures.
Figure 5. Shannon entropy trends for maximum values of monthly average temperatures.
Preprints 100252 g005
Preprints 100252 g006
Figure 6. Catchments in which the greatest dynamics of Shannon entropy trends for extremes of precipitation and temperature were recognized at the 5% significance level.
Figure 6. Catchments in which the greatest dynamics of Shannon entropy trends for extremes of precipitation and temperature were recognized at the 5% significance level.
Preprints 100252 g006
Table 1. Areas covered in the WMO regions analysis [39].
Table 1. Areas covered in the WMO regions analysis [39].
Region Continent Lands area Area catchment Coverage of the continents
WMO mln km2 mln km2 %
1 Africa 30.3 8.43 27.83%
2 Asia 44.3 20.3 45.86%
3 South America 17.8 12.6 70.57%
4 North America 24.2 13.0 53.87%
5 Australia and Oceania 8.5 1.1 13.07%
6 Europe 10.5 6.7 64.10%
Antarctica 13.1 0.0 0.00%
Lands together 148.7 65.1 43.77%
Earth, total 509.9 65.1 12.76%
Table 2. River basins in which the smallest decreasing values of Shannon entropy trends were found for minimum monthly precipitation values at the 5% level of significance.
Table 2. River basins in which the smallest decreasing values of Shannon entropy trends were found for minimum monthly precipitation values at the 5% level of significance.
Name of river Name of country Area catchment Slope of Shannon entropy, min values Year of change of slope of Shannon entropy min values Slope of Shannon entropy, min values -subseries
[km2] [bit/year] [bit/year]
Daly Australia 47000 -0.049 1990 -0.025
Daule Ecuador 8690 -0.040 1988 -0.074
Mahanadi River India 132090 -0.036 1986 -0.006
Canete Peru 4900 -0.033 1990 -0.017
Fuerte Mexico 34247 -0.026 1990 -0.009
Vinces Ecuador 4400 -0.023 1990 -0.014
Little Mecatina River Canada 19100 -0.017 1989
Kouilou Congo 55010 -0.015 1984
Biobio Chile 24029 -0.014 1989 -0.012
Esmeraldas Ecuador 18800 -0.014 1991 -0.010
Table 3. River catchments in which the largest increasing values of Shannon entropy trends were found for minimum monthly precipitation values at the 5% level of significance.
Table 3. River catchments in which the largest increasing values of Shannon entropy trends were found for minimum monthly precipitation values at the 5% level of significance.
Name of river Name of country Area catchment Slope of Shannon entropy, min values Year of change of slope of Shannon entropy min values Slope of Shannon entropy, min values -subseries
[km2] [bit/year] [bit/year]
Sittang River Myanmar 14660 0.044 1990 0.031
Quoich River Canada 30100 0.040 1990 0.016
Macarthur River Australia 10400 0.039 1990 0.032
Bol. Anyuy Russian Feder. 49600 0.038 1990 0.011
Ellice River Canada 16900 0.037 1989 0.019
Anyuy Russian Feder. 30000 0.036 1990 0.008
Baleine, Grande River Canada 29800 0.035 1990 0.014
Khatanga Russian Feder. 275000 0.033 1990 -0.002
Tapti River India 61575 0.030 1991 0.006
Narmada India 89345 0.029 1992 0.001
Ferguson River Canada 12400 0.029 1990 0.031
Table 4. River basins in which the smallest decreasing values of Shannon entropy trends were found for maximum monthly precipitation values at the 5% level of significance.
Table 4. River basins in which the smallest decreasing values of Shannon entropy trends were found for maximum monthly precipitation values at the 5% level of significance.
Name of river Name of country Area catchment Slope of Shannon entropy, max values Year of change of slope of Shannon entropy max values Slope of Shannon entropy, max values -subseries
[km2] [bit/year] [bit/year]
Sakarya Turkey 55322 -0.015 1987 -0.025
Stikine River United States 51593 -0.014 1987
Brahmaputra Bangladesh 636130 -0.010 1988 -0.005
St. Johns River United States 22921 -0.010 1994 -0.020
Juba Somalia 179520 -0.009 1994 -0.004
Loa Chile 33570 -0.009 1990
Tana (No, Fi) Norway 14165 -0.009 1992 -0.013
Ashburton River Australia 70200 -0.008 1995
Tranh (Nr Thu Bon) Viet Nam 9153 -0.008 1994 -0.020
Santa Cruz Argentina 15550 -0.008 1997 -0.022
Table 5. River catchments in which the largest increasing values of Shannon entropy trends were found for monthly precipitation maxima at the 5% significance level.
Table 5. River catchments in which the largest increasing values of Shannon entropy trends were found for monthly precipitation maxima at the 5% significance level.
Name of river Name of country Area catchment Slope of Shannon entropy, max values Year of change of slope of Shannon entropy max values Slope of Shannon entropy, max values -subseries
[km2] [bit/year] [bit/year]
Anyuy Russian Feder. 30000 0.025 1990 0.013
Rio Maicuru Brazil 17072 0.018 1984
Bol. Anyuy Russian Feder. 49600 0.018 1990
San Pedro Mexico 25800 0.017 1995
Brahmani River India 39033 0.016 1990 0.017
Anadyr Russian Feder. 156000 0.016 1990 0.007
Sassandra Cote D’ivoire 62000 0.016 1990 0.005
Kinabatangan Malaysia 10800 0.016 1988
Ponoy Russian Feder. 15200 0.016 1989 0.010
Volta Ghana 394100 0.014 1990 0.008
Table 6. River catchments in which the smallest decreasing values of Shannon entropy trends were found for minimum monthly average temperatures at the 5% level of significance.
Table 6. River catchments in which the smallest decreasing values of Shannon entropy trends were found for minimum monthly average temperatures at the 5% level of significance.
Name of river Name of country Area catchment Slope of Shannon entropy, min values Year of change of slope of Shannon entropy min values Slope of Shannon entropy, min values -subseries
[km2] [bit/year] [bit/year]
Rio Ribeira Do Igu Brazil 12450 -0.012 1990
Chubut Argentina 16400 -0.010 1987
Ellice River Canada 16900 -0.008 1994
Orange South Africa 850530 -0.008 1986 -0.011
Gilbert River Australia 11800 -0.008 1998 -0.010
Penobscot River United States 19464 -0.008 1991
Loa Chile 33570 -0.008 1997 -0.009
Syr Darya Kazakhstan 402760 -0.007 1989 -0.009
Churchill River Canada 287000 -0.007 1987 -0.003
Mono Benin 21575 -0.007 1987 -0.010
Table 7. River basins in which the largest increasing values of Shannon entropy trends were found for minimum monthly average temperatures at the 5% level of significance.
Table 7. River basins in which the largest increasing values of Shannon entropy trends were found for minimum monthly average temperatures at the 5% level of significance.
Name of river Name of country Area catchment Slope of Shannon entropy, min values Year of change of slope of Shannon entropy min values Slope of Shannon entropy, min values -subseries
[km2] [bit/year] [bit/year]
Svarta, Skagafiroi Iceland 393 0.019 1990 0.006
Thjorsa Iceland 7380 0.016 1988 0.005
Joekulsa A Fjoellu Iceland 7074 0.016 1988
Lempa El Salvador 18176 0.013 1989 0.011
Pra Ghana 22714 0.013 1987 0.010
Thames United Kingdo 9948 0.010 1991 0.007
Grande De Matagalp Nicaragua 14646 0.009 1990 0.011
Comoe Cote D’ivoire 69900 0.009 1990 0.012
Grisalva Mexico 37702 0.009 1988
Sabine River United States 24162 0.009 1991 0.007
Table 8. River basins in which the smallest decreasing values of Shannon entropy trends were found for maximum monthly average temperatures at the 5% level of significance.
Table 8. River basins in which the smallest decreasing values of Shannon entropy trends were found for maximum monthly average temperatures at the 5% level of significance.
Name of river Name of country Area catchment Slope of Shannon entropy, max values Year of change of slope of Shannon entropy max values Slope of Shannon entropy, max values -subseries
[km2] [bit/year] [bit/year]
Nadym Russian Feder. 48000 -0.011 1991 -0.021
Loa Chile 33570 -0.011 1983 0.003
Ferguson River Canada 12400 -0.011 1983
Kouilou Congo 55010 -0.011 1986 -0.018
Pahang Malaysia 19000 -0.009 1993
Kelantan Malaysia 11900 -0.009 1998
Karun Iran, Islamic 60769 -0.009 1984
San Pedro Mexico 25800 -0.008 1987 -0.006
Nelson River Canada 1060000 -0.008 1992
Rhone France 95590 -0.008 1989 -0.003
Table 9. River basins in which the largest increasing values of Shannon entropy trends were found for maximum monthly average temperatures at the 5% level of significance.
Table 9. River basins in which the largest increasing values of Shannon entropy trends were found for maximum monthly average temperatures at the 5% level of significance.
Name of river Name of country Area catchment Slope of Shannon entropy, max values Year of change of slope of Shannon entropy max values Slope of Shannon entropy, max values -subseries
[km2] [bit/year] [bit/year]
Godavari India 299320 0.018 1991 0.014
Tapti River India 61575 0.014 1988 0.008
Mahi River India 33670 0.013 1990 0.016
Lempa El Salvador 18176 0.013 1990
Rio Ribeira Do Igu Brazil 12450 0.012 1992 0.012
Narmada India 89345 0.011 1987
Sacramento River United States 60885.7 0.010 1991 0.017
Juba Somalia 179520 0.010 1990 0.005
Nottaway Canada 57500 0.010 1991 0.008
Dniestr Moldova, Repu 66100 0.009 1990 0.014
Table 10. River basins with the highest dynamics calculated from Shannon entropy trend values for minimum and maximum monthly average precipitation and minimum and maximum monthly average temperatures at the 5% significance level.
Table 10. River basins with the highest dynamics calculated from Shannon entropy trend values for minimum and maximum monthly average precipitation and minimum and maximum monthly average temperatures at the 5% significance level.
Name of river Name of country Area catchment Dynamic of Shannon entropy of precipitation Dynamic of Shannon entropy of temperature Multiplicity of entropy dynamics of precipitation to temperature Total dynamic of Shannon entropy
[km2] [bit/year] [bit/year] [bit/year]
Daly Australia 47000 0.049 0.008 5.8 0.049
Anyuy (Trib. Kolym Russian Feder. 30000 0.044 0.002 19.8 0.044
Quoich River Canada 30100 0.041 0.007 5.7 0.041
Macarthur River Australia 10400 0.039 0.008 4.8 0.040
Ellice River Canada 16900 0.037 0.010 3.9 0.039
Mahanadi River (Ma India 132090 0.036 0.006 6.4 0.037
Khatanga Russian Feder. 275000 0.034 0.006 5.7 0.034
Tapti River India 61575 0.030 0.015 2.0 0.033
Narmada India 89345 0.029 0.011 2.7 0.031
Santa Cruz Argentina 15550 0.026 0.007 3.8 0.027
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated