Prerpints.org logo
Preprint
Review

Modelling of Biomass Gasification: From Thermodynamic to Process Simulations

Altmetrics

Downloads

589

Views

74

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

03 August 2023

Posted:

04 August 2023

You are already at the latest version

Alerts
Abstract
Biomass gasification acquired great interest over the past decades as an effective and trustable technology to produce energy and fuels with net-zero carbon emissions. Moreover, using biomass waste as feedstock enables to recycle organic wastes and to fit the circular economy goals thus reducing the environmental impacts of waste management. Even if many studies have been already carried on, this kind of process must still be investigated and optimized with the final aim to develop industrial plants for different applications, from the hydrogen production to net-negative emission strategies. Modeling and developing of process simulations became an important tool to investigate the chemical and physical behavior of the plant, allowing to make a first raw optimization of the process and to define heat and material balances of the plant as well as to define optimal geometrical parameters with cost and time effective approaches. The present review paper focuses on the main literature models developed until now to describe biomass gasification process, and in particular on kinetic models, thermodynamic models, and computational fluid dynamic models. The aim of this study is to point out the strengths and the weakness of those models, comparing them and indicating in which situation is better to use an approach instead of another. Moreover, theoretical shortcut models and software simulations, not explicitly addressed by prior reviews, are taken into account. For researchers and designers this review provides a detailed methodology characterization as a guide to develop innovative study or project.
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

During the Anthropocene, the pressure on environment is increasing exponentially along with global warming. On the other hand, the need for each country to be energy-independent and to find low-price solution for energy production, represent an actual challenge.
In order to deal with those problems, many researchers pointed out that it is possible to make an energetic transition from fossil fuels to renewable energy sources. Among the most investigated renewable energy sources, biomass is confirmed as the most favourable one, since it is the widest source of energy after coal, oil, and natural gas [1,2,3,4]. Using biomass as feedstock for energy production allows to achieve both green energy production and national energy security goal. Moreover, using biomass waste instead of energetic culture accomplish the request for circular economy to reuse those organic wastes that otherwise would be dispose polluting soil and air and also avoiding the fuel vs. food issue [5,6,7].
During the last years, many processes for biomass conversion into energy were investigated, and gasification was highlighted as one of the most efficacious [8,9,10]. Gasification is a thermo-chemical technology to convert biomass into a combustible gas mixture by the partial oxidation of the biomass at high temperature (750-950 °C) in presence of a gasifying agent [11,12,13,14]. Fluidized bed reactor was confirmed as the most suitable as gasifier reactor due to the excellent thermal and mixing properties that ensure high heat transfer rates, high efficiency, low combustion temperature and low pollutant emissions [15,16]. The gas mixture produced by gasification process is called syngas and it is mainly made of H2, CO, CO2, CH4, H2O, along with organic and inorganic contaminants [17]; the quantity of each produced component depends on feedstock characteristics, gasifying agent, operative conditions of the process, reactor design, etc. [18,19].
To investigate biomass waste gasification process, modelling approaches and simulation software provide useful tools to investigate different operative conditions, to make a first raw optimization of the process obtaining the most suitable syngas for the desired uses and to scale-up lab-scale and pilot apparatus. Results coming from simulative models must be the base for the realization of pilot plant, allowing to reduce cost, avoiding risk for human health as well as to interpret the experimental data and build the foundations of knowledge necessary for the realization of a project [20]. Both mathematical and numerical simulative models are suitable for those purposes since they both are able to predict the performance of the process and to give a good representation of the chemical and physical phenomena occurring, in order to optimize the process with swift time and minimal cost [21]. Then, it is also possible to choose to simulate the process in steady state condition (time independent) or in dynamic condition (time dependent), according to what is the focus of the investigation. Kinetic, thermodynamic, Computational Fluid Dynamic (CFD), and Artificial Neural Network (ANN) models have been adapted and implemented for the study of syngas production from a wide variety of feedstocks [22,23,24,25].
Kinetic models take into account the kinetic of the gasification reactions given the reactor properties (residence time, operative temperature, and pressure). They predict the syngas yield, the produced syngas composition after a finite time, or in a finite volume in a flowing medium. These models, after a proper validation, allow to predict the process performances for a specific operating conditions and reactor design [26,27].
Since kinetic models depend on the specific fluid-dynamics and geometry of the case study, their applicability is restricted to specific reactor configurations. Complex configuration of the reactors enhances the complexity of the describing model.
Thermodynamic models predict the syngas composition based on the assumption that the reactants react in a fully mixed condition for an infinite time, so to reach the thermodynamic equilibrium [28]. The main advantage of those models is the independency from the gasifier design [29], that means thermodynamic models can be used to describe a wide range of plants, without any particular restrictions, despite kinetic models.
CFD models describe the gasification process based on the conservation of mass, momentum, species, and energy into a certain portion [28,30]. Those models are able to predict a very accurate syngas composition when coupled with a well-known fluid-dynamic of the gasifier and are especially suitable for fluidized bed reactors, in which they provide important information about temperature profiles and species concentration.
Black-box approaches, including algorithms of Artificial Intelligence as ANN, are considered a relatively new approach for modelling biomass gasification process. They have the great merit to not require the formulation of a complex mathematical equations and also to be able to understand and identify non-linear relations [31]. Therefore, ANN modelling is acquiring great interest when the aim of the study is to investigate biomass gasification process there complex non-linearities occur in the dataset [32].
The aim of the present paper is to investigate the most recent simulative models and results from scientific literature, in order to provide a critic review that is able to indicate which is the best approach, among kinetic, thermodynamic, CFD, Multivariate Data Analysis (MVDA) and ANN to describe a biomass gasification process according to the specifications and the desired goal.

2. Biomass gasification principle and technology

Gasification is a partial thermal oxidation, occurring at high temperature (in the range 750-900 °C) in presence of a gasifying agent (steam, air, oxygen, or a mixture of them) that reacts with biomass producing a gaseous product mainly composed of H2, CO, CH4, CO2 along with small quantities of solid product (char), inorganic contaminants (mainly H2S and HCl), and organic contaminants (tar). The amount of final inorganic compounds depends on biomass inlet properties, for instance, it is recommended to take as low as possible the inlet concentrations of S and Cl. The gasifying agent influences the final gas composition (see Table 1), steam provides the highest H2 content and the highest Low Heating Value (LHV), while air provides a lower quality syngas due to the bigger amount of inlet N2.
The chemistry of biomass gasification is quite complex. The reactions involved in the process are listed in Table 2, while the gasification stages can be summarized as follow [8,33]:
○
Drying. Occurring at 100-200 °C, drying stage reduces the moisture content of biomass below 5%.
○
Devolatilization (pyrolysis). In this step, the thermal decomposition of biomass occurs, in absence of oxygen or air. The volatile matter is decreased, releasing hydrocarbon gases from biomass, which is then reduced to solid charcoal.
○
Oxidation. In this stage, CO2 is produced from the reaction of solid carbonized biomass and oxygen in the air. H2 present in the biomass is oxidized to produce water. Then, if oxygen is present in sub-stoichiometric quantities, partial oxidation of carbon may happen, producing CO.
○
Reduction. At high temperature (800-950 °C) several reduction reactions occur in the absence (or sub-stoichiometric presence) of oxygen. Those reactions are water-gas reaction, Boudouard reaction, water-gas shift reaction and methane reaction.

2. Thermodynamic models

Thermodynamic models describe the thermodynamic equilibrium (temperature, pressure, and composition), achieved by perfect mixing and infinite reaction time. The system is time-invariant and not depending on kinetic factors such as the design of reactor and fluid dynamics [29]. This property makes the models at thermodynamic equilibrium very flexible to use and suitable for a wide variety of process without any specific constraints. Indeed, they provide information about limit gas yield, gas composition, and even if they apply under many rescripted assumptions, still they provide insights about unit operation, process optimization, energy recovery and also life-cycle assessment and techno-economic analysis [2,36,37,38]. Equilibrium models have a wide range of applicability since usually gasification process is driven close to equilibrium [29]. Thermodynamic equilibrium models can be classified into [39,40,41]:
  • Stoichiometric models, which are based on equilibrium constants: the specific chemical reactions of the process must be declared;
  • Non-stoichiometric models, which are based on minimisation of the Gibbs free energy, neglecting the chemical reactions involved. Only the definition of a set of chemical compounds that are expected at equilibrium is needed.
Stoichiometric models and non-stoichiometric models, even if built with a completely different mathematical implementation, were demonstrated to reach close results if some conditions are satisfied [42]. Even if stoichiometric models are based on simple mathematical formulation, they have not been widely utilized in literature, while non-stoichiometric models are used in approximately 73% of equilibrium simulations in literature, while 27% of literature relies on stoichiometric ones [39].
Stoichiometric models include mass balances and the calculation of equilibrium constants at a given temperature. The mathematical model combines the conservation laws of atomic species with those of thermodynamic equilibrium by referring to the global gasification reaction starting from reactants and inert compounds in the feed. The result is a tool to predict the composition of the produced gas, once the characteristics of the feed to be gasified are known (proximate and ultimate analysis), such as the operating conditions in terms of pressure, temperature, and steam/feed ratio. Mass and energy balances result into a system of non-linear algebraic equations for each reaction, whose unknown variables are the extent of each reaction; the solution is found applying the classic methods to evaluate the roots of non-linear algebraic equations, such as the Newton-Rapson one. Once computed the extents of all reactions at equilibrium, it is possible to compute the equilibrium composition of the products at a given temperature. If the temperature is unknown, it is necessary to couple an energy balance taking into account the enthalpies of the reactants and products, thus increasing the complexity of the system. These models are commonly based on the following assumptions [43]:
a)
all the reactions considered are at thermodynamic equilibrium equivalent to an infinite residence time;
b)
all the carbon is gasified and is not present among the reaction products;
c)
the products leaving the gasifier, except for the ashes in the solid phase, are in the gaseous phase and consist of CO, CO2, H2O, H2, CH4, N2;
d)
among the reaction products there is no tar.
The mass balances in presence of the equilibrium reaction require the molar concentrations and the molar ratios of components in the feedstock. Since the solid feedstock (solid biomass) is often a complex mixture, it is described by a brute formula derived from the ultimate analysis of dry and ash-free biomass samples. Thus, the feedstock is represented as a single component CHmOpNq reacting as:
C H m O p N q + w H 2 O   → a C O + b C O 2 + c H 2 + d   C H 4 + e H 2 O + f N 2
K e q = e − ∆ G T 0 R T
∆ G T 0 R T = ∆ G 298 0 R   · 298.15 − ∫ 298.15 T ∆ H T 0 R T 2   d T
∆ H T 0 = ∆ H 298.15 0 + ∑ ∫ 298.15 T 2 v i C p , i ( T ) d T
∆ H 298.15 0 = ∑ v i H 298.15   p r o d u c t s 0 − ∑ v i H 298.15   r e a c t a n t s 0
∆ G 298.15 0 = ∑ v i G 298.15   p r o d u c t s 0 − ∑ v i G 298.15   r e a c t a n t s 0
C p , i T = a + b T + c T 2 + d T 3 + e T 2 + f T 0.5
∆ G 0 and ∆ H 0 are the variation of standard Gibbs free energy and enthalpy formation, respectively.
Assuming to know the composition of the biomass and the characterization of the reactants, including the biomass moisture and the gasifying agent (steam), it is possible to develop the model taking into account two chemical reactions: water-gas shift (9) and steam reforming (10). The solving system is represented by the four mass balance equations and the two chemical equilibrium equations (21)-(26).
1 = a + b + c
m + 2w = 2c + 4d + 2e
q = 2f
p + w = a + 2b + e
K 1 = P C O 2 P 0 · P H 2 P 0 P C O P 0 · P H 2 O P 0 = b · c a · e
K 2 = P C O P 0 · P H 2 P 0 3 P H 2 O P 0 · P C H 4 P 0 = a · c 3 d · e · n T 2
P0 represents the system operative pressure, while PCH4, PH2, PH2O, and PCO2 are the partial pressures of CH4, H2, H2O, and CO2, respectively. nT are the total moles of produced gas.
In Table 3 are listed the values of coefficient a, b, c ,d, e, and f, following the Hougen-Watson approach [44]. In Table 4 are listed the values of standard Gibbs free energy and enthalpy formation.
These models are of rapid use and are based on solid theoretical foundations widely developed in chemical engineering and reactor engineering textbooks. On the other hand, they often generate a non-negligible error due to the following reasons: the reactions really occurring are only partially known, they describe only the gaseous phase, at a given fixed temperature where all reactions are in equilibrium.
Non-stoichiometric models demonstrated their reliability over the years since were successfully used in modelling the gasification process, especially in fluidised-bed gasifiers [40,45,46], allowing to evaluate the effect of temperature, equivalence ratio, steam to biomass ratio, moisture content of feedstock on the gasification process.
Non-stoichiometric equilibrium models may be upgraded into the so called quasi-equilibrium approach, that is a compromise between equilibrium thermodynamic models and experimental data in reaction conditions close to the equilibrium [9,29], providing more accurate results about syngas composition.
The non-stoichiometric equilibrium modelling approach is founded on the direct minimization of the Gibbs free energy of reaction species. This methodology can be used to find equilibrium compositions "virtually" including unknown reaction paths. On the other hand, the minimization of the Gibbs free energy can be stopped in non-equilibrium conditions as explained in our previous works [43,47] and in some cases referred to as quasi-equilibrium temperature (QET) approach. This latter is actually considered the most effective way to model the gasification process [48] and have also been adopted by commercial process simulators as mentioned in the next chapters. The final composition is derived by setting a QET for each reaction that occurs into the gasifier. In this way each reaction occurs at its equilibrium temperature instead of the gasification temperature set for the gasifier block [49]. On the other hand, the minimization can be stopped by introducing other criteria. For instance, in our previous work [47] we defined an algorithm based on the minimization of the error model predictions and experimental data. In this way it is possible to train a quasi-equilibrium model and then use it as a scaling-up tool. We report below the formulation of a non-stoichiometric model based on the minimization of Gibbs free energy (G) for the previously selected set of reactions: steam reforming and water gas shift. It must be premised that this type of modelling starts following a first devolatilization defining the composition of the gaseous state that participates in the reaction. This preliminary phase is often trained on experimental data to get a more realistic description of the formation of ash, char, and tar. In fixed temperature and pressure conditions, the function G depends only on the extent of the reactions α and β , expressed as an extensive variable as follows:
G ( α , β ) T , P = ∑ i n i ( α , β ) · μ i ( α , β , T )
μ i = μ i 0 T + R T l n P i
P i = n i ( α , β ) n T O T ( α , β ) P
μ i = μ i 0 T 0 T T 0 − T ∫ T 0 T H i T T 2 d T + R T l n P i
where i = CO, CO2, H2O, H2, CH4, N2, H2S. The partial pressure Pi is written by assuming an ideal mixture of gases. ni is the number of moles of the i-component; µi is the chemical potential; Hi is the standard molar enthalpy of the component i in the gaseous phase, calculated at the temperature T of the system. μ i 0 T is the standard chemical potential of the i-component at temperature T. R is the universal constant of gas and Pi is the partial pressure of i-component.
Once the chemical potentials of the components present in the system have been defined, at a given temperature, it is possible to evaluate the total free energy of the system at fixed G ( α , β ) T , P in equation (27) as function of two independent variables α , β . In other words, the free energy G ( α , β ) T , P   is as a surface in the space ( α , β ,   G ) and is characterized by the presence of a minimum which corresponds exactly to the equilibrium conditions of the system. The Gibbs Free Energy Gradient Method Model (GMM) exploits the thermodynamic principle stating that a system always reaches the equilibrium conditions starting from initial conditions by minimizing the energy value. The minimum energy value corresponds to the condition of all reactions being at the equilibrium simultaneously. From a theoretical point of view, the equilibrium condition is reached after an infinite time.
In practice, real systems can reach, even in very low time, conditions so close to the equilibrium that the difference lies within the error threshold of the current measurement methods, entering a kind of “grey zone”, not observable.
In an industrial equipment, the system will reach this “grey zone” if the residence time is large enough, according to the reactor geometry and operating conditions. Among the infinite routes between the initial point (α = β = 0) and the equilibrium point, the system chooses the path that offers the maximum gradient ∇G(α, β) [43,47]. Through a purposed set of experiments, it is possible to train the model by comparing the simulated with the experimental states. 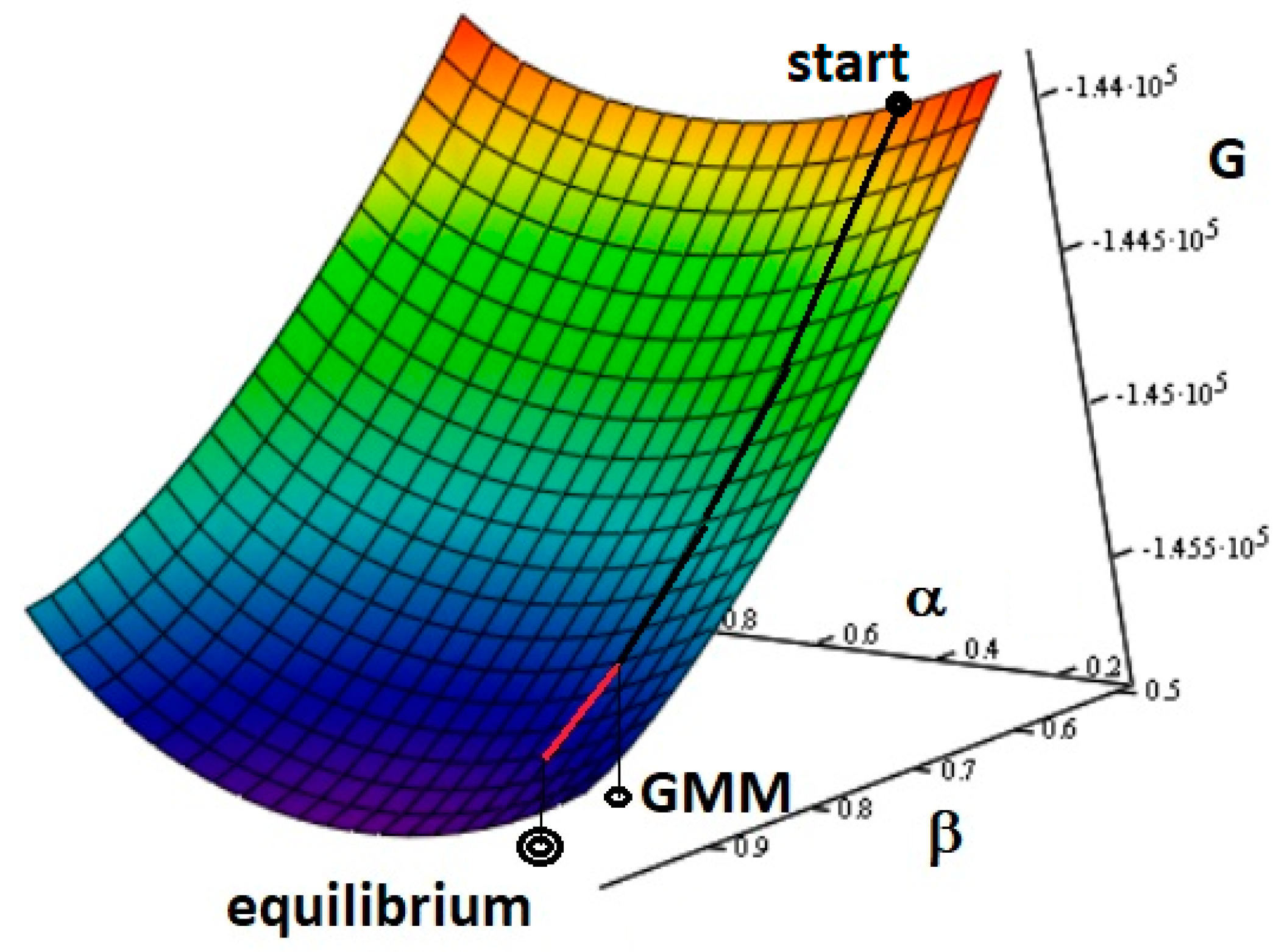Figure 1 reports a comparison of trajectories following the ∇G(α, β) between the GMM method and the final equilibrium state in a given experiment [43,46].
Even if some studies over the past decades focused on the improvement of the evaluation of the QET by means of a data-fit made by experimental data [50,51,52], there is still a lack of comprehensive studies applied to fluidised-bed gasifier taking into account the use of different gasifying agents and also the undesired by-products (organic and inorganic compounds). Marcantonio et. al [29] proposed a process simulation study that tried to overcome this issue by developing a quasi-equilibrium model that includes air/steam/oxygen biomass-gasification in presence of organic and inorganic by-products. The results were in good agreement with experiments, and it was also possible to make an optimization of the process investigating the effect of gasification temperature and S/B ratio on the gas composition for different gasifying agents.
The most common properties whose experimental observation mostly deviates from ideal equilibrium prediction are the concentration of methane and the amount of unreacted char. The under or over prediction of methane is an ordinary issue in equilibrium models [53]. Indeed, in real case the conversion of methane is kinetically limited, so the final methane concentration is controlled by non-equilibrium factors and it is not possible to obtain a good prediction by means of equilibrium model [54]. The unreacted char issue is best dealt with and avoided by only computing the equilibrium of the volatile gas-phase components rather than the complete heterogeneous equilibrium or otherwise setting as input the specific amount of unreacted char from experimental results. Loha et al. [55,56] compared an equilibrium model of steam gasification in a fluidized-bed reactor with the correspondent experimental data. They showed that the actual deviation of methane increases at higher temperature, against the “general rule” stating that at higher temperatures reduce the gap between equilibrium model and experimental case. Applying a QET approach to simulate the syngas concentration at 750 °C Loha et al. found that the experimental molar dry concentration of methane was 4.2% against the simulated 2%. Many other studies in literature confirmed this trend of methane to be even twice in experimental case compared with equilibrium simulation [57]. As for the other main syngas components (hydrogen, carbon monoxide, carbon dioxide, steam) there is a good agreement between the simulations in QET conditions and corresponding experimental data, whit poor deviations (within 5% molar fraction) [58]. More in general, however, thermodynamic equilibrium model poorly applies to specific gasifier conformations and under some operating conditions, in particular for reactors operating at low temperatures [8,59,60].

2. Kinetic models

Kinetic models are commonly used in chemical reactor engineering to predict non-equilibrium product distributions, evolution of the system over time as a function of temperature and residence time. For their nature, they should be also accompanied by thermal energy and momentum balance. In order to obtain the information listed above, the kinetic equations must be very accurate, that means the reaction mechanism and the kinetic constant of the process must be validated on a wide range of experimental conditions. For these reasons, the kinetic model developed is strictly dependent on the geometry of the reactor and on the characteristic of the specific process and, if used to simulate other processes with different specifications, it can result an unpredictable error. The majority of kinetic models in literature is built to calculate the kinetic parameters to predict biomass feedstock conversion, syngas yield and composition.
Castello and Fiori [61] proposed a simplified model for hydrothermal gasification of methanol, they adapted the kinetic model according to elementary equations of combustion. They pointed out the relevance of two reactions among others: water-gas shift and CO methanation, which mostly influence the process. Another way to simplify the kinetic modelling of gasification process is through the lumped method, considering a pseudo-mono-component for the intermediate products and assuming that the syngas is produced from the decomposition of this single component [62]. Resende and Savage [63] developed a lumped first-order kinetic model to describe the gasification of cellulose and lignin fitting the experimental results in order to adjust the output. The model was able predict gas yield and syngas composition for different feeds. The results from this kinetic model were compared with those from a thermodynamic equilibrium model, adopting Gibbs free energy minimization method, found a good agreement. Guan et al. [64] studied hydrothermal gasification of algae by means of a lumped first-order kinetic model, which was able to give the precise gas yield and also the effect of water density and biomass inlet on the final gas composition. Jin et al. [65] investigated the gasification of lignite by means of lumped method; they were able to predict the gas yield in good agreement with experimental data obtained by means of a micro quartz tube reactor.
Even if the lumped first-order method seems promising in estimating gas yield and gas composition, it is not flexible for all processes. For instance, it is not suitable to predict the syngas composition in supercritical water gasification, whose reaction conditions strongly depend on structures and distributions of pores in the feedstock material, which vary their structure along with the gasification process in turn affecting the reaction rate [66,67]. For this reason, some authors proposed a kinetic alternative model based on random pore size distribution. Vostrikov et al. [68] proposed a kinetic model based on random pore size distribution for the investigation of supercritical water gasification of coal. The study confirmed that the model is suitable for describing the rate of coal conversion dependent upon the coal conversion degree. Moreover, it was highlighted that random pore size distribution model is not trustable when catalytic effects occurred in non-uniform way.
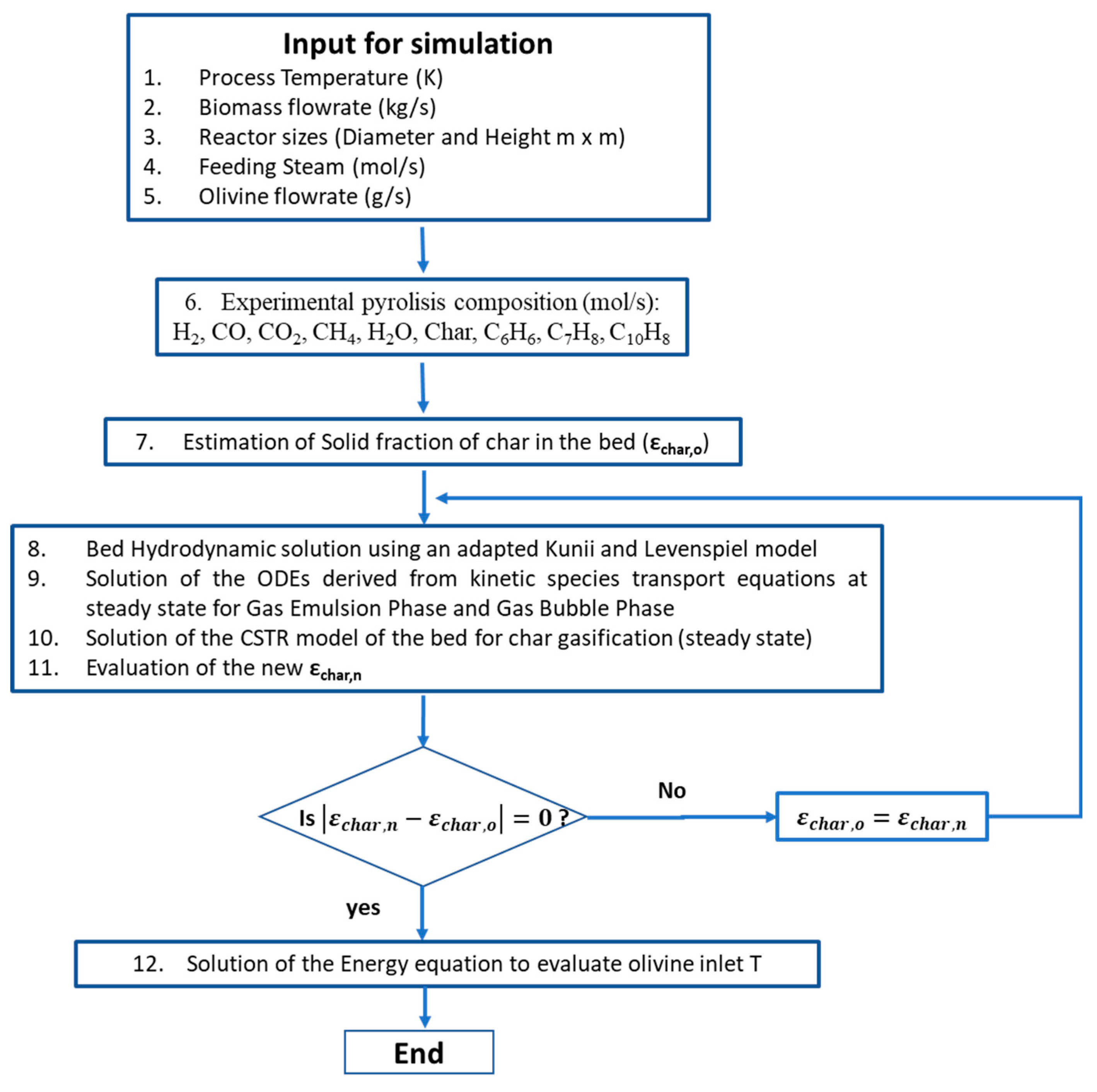
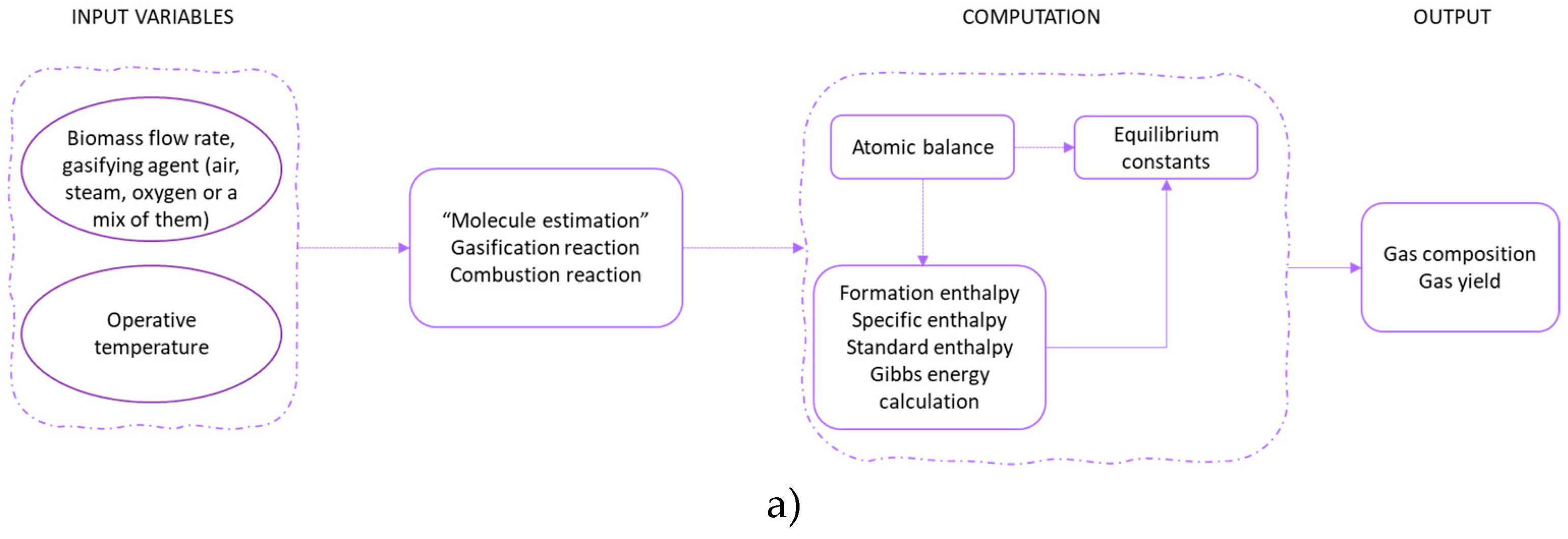
Di Carlo et al. [69] developed a semi-empirical kinetic model for steam gasification via fluidized-bed gasifier. The reactor was a cylinder, and the model was based on a mono-dimensional modelling of the mass and energy balance in order to calculate the syngas composition along the axis of the cylinder. The corresponding algorithm flowchart implemented by the authors is shown in Figure 2. Kunii and Levenspiel [70] developed a hydrodynamic model in order to describe the multiphase (bubble and emulsion) nature of reacting mixture phases and their interaction.
The kin-semi approach helps simplifying the complexity of kinetic models by assuming local equilibrium for specific reactions and/or gasifier zones, while concentrations and temperatures of the other reactions and/or zones are kinetically controlled [71,72,73]. The most common choice for the kin-semi model is to consider homogenous gas-phase equilibrium of reacting components from the step of pyrolysis; the equilibrium compositions is computed through three equilibrium constants or by minimizing Gibbs free energy.
Then, the produced gas mixture is mixed with the gasifying agent and char and became the inlet of a kinetic module were the final gas composition is computed using kinetic models [74,75]. Kin-semi approach are easier to use compared with kin-total one, indeed it need less kinetic information and parameters, while kin-total model describes with kinetic reaction rates both the volatile and char gasification reactions. For this reason, kin-semi model provides more precises output results when the gas phase is near to the chemical equilibrium.
To come to the point, kinetic models have the potential to indicate which reaction route or pathway is responsible for the production of a particular gaseous product and are also able to give precise output results only if the reaction rates, kinetic constant and gasifier geometry are well-known. However, this means that these models are not flexible to use, since it must be developed precisely on a specific process with given conditions, and moreover it is also though to develop since the required input information is not easy to reach and scientific literature is still struggled to obtain them. On the other, it is possible to use simplified kinetic models providing quite accurate results for gas yield and gas composition. However, the simplified models are not able to identify which reaction route or pathway is responsible for the production of a particular gaseous product, so when such information is needed it is possible to overcome the limitation of the simplified models coupling them with a CFD model.

4. CFD models

CFD modeling is based on fluid mechanics principles and the use of numerical methods to solve the Navier-Stokes equations [76,77]. It is a powerful tool to simulate the interaction among fluids that have surfaces inside specific boundary conditions. In literature, there are several examples of CFD models to simulate biomass conversion processes such as thermochemical gasification [23,78,79] and pyrolysis [80,81]. CFD models are widely used to optimize the design of fluidized-bed reactor since they are able to predict inert material concentration of in-bed gasifier, emissions, operational parameters, fuel mixing efficiency, temperature profiles, heat flux, etc. [82,83].
It is possible to classify the CFD numerical approaches into three classes:
▪
Eulerian-Lagrangian Discrete Particle Model (DPM), which considers gas as continuous and particle as discrete phase. It is used where there are diluted particle conditions, such as freeboard of reactor. CFD DPM models consider particles trajectory in a continuous phase of fluid and take into account the interaction between particles by means of the heat and mass transfer as the governing phenomena [84,85]. The main advantage is the simple accounting of the particle size, allowing to track the changes in physic-chemical characteristics of the biomass particles during conversion along their path through the reactor.
▪
Eulerian-Eulerian Two Fluid Models (TFM), which is used to investigate both the gaseous and solid (particle) phase. Interaction of granular and continuous phase is considered via momentum transfer contribution based on drag models [86]. The CFD TFM approach has the disadvantages of high computational demand when a wide range of particle sizes have to be investigated because each size fraction of the distribution is accounted as a separated phase. Moreover, another drawback of these models is they are poor in recognizing the discrete character of the particle phase, so they are consequently poor in modeling flows of particles with a wide size and in tracking movement and conversion of single particles.
▪
Eulerian-Eulerian Discrete Element Model (DEM) within Eulerian-Lagrangian framework, which uses Eulerian method for gas phase and discrete element method for particle phase, tracking individually each particle and associating it with multiple physical (size, density, composition, and temperature) and thermo-chemical (reactive or inert) properties [87,88]. The main disadvantages of this method is the extremely small required time-steps, making this approach highly computationally demanding thus practically avoiding for design and optimization of industrial scale facilities [89].
In literature many studies [90,91,92,93,94] investigated coal gasification in fluidized-bed by means of CDF TFM approach. Those studies showed great potential in modelling gasification process, but at the same time the still need to be improved in describing chemical reactions, especially pyrolysis step.
Adnan et al. [95] made a comparison between CDF TFM and CFD DPM model, showing similar results for the fluid dynamics of a fluidized-bed gasifier. More in general, DPM models are more suitable for large-scale applications, where there is more independency from grids.
Ramos et al. [30] investigated results from a CFD TFM and CFD DEM model, concluding that the latter gives a more accurate prediction. However, when the prediction is given for a local discrete temperature value, TFM models were demonstrated to be more accurate compared with DEM model. Moreover, DEM approach requires about twice the time needed to execute TFM model.

5. Process modelling

Process modelling is a sequential approach in which each process is divided into unit operation and a series of equations are solved by means of kinetic or thermodynamic models. The most used software in this field is Aspen Plus [1,21,96]. Developed by Massachusetts Institute of Technology (MIT), Aspen Plus is a chemical engineering process optimization software that utilizes unit operation blocks, such as reactors, pumps, columns, heat exchangers, etc. Unit blocks are connected to each other through mass and energy streams, and this is represented in terms of a flowchart of the whole process. The software is based on a sub-sequential modular approach and the simulation calculations use the in-built physical properties database [48]. The main advantage of Aspen Plus is that each unit can be analyzed independently and the properties of the outlet stream of each unit depends only on its inlet stream properties. In order to evaluate all physical properties of conventional components in the gaseous phase of the gasification process, the most suitable description is provided by the Peng-Robinson equation of state, with the Boston-Mathias (PR-MB) modification [29], present in the default simulation setting of the Aspen Plus software. The evaluation of the enthalpy and density of the non-conventional components (biomass and ash), is obtained choosing the modules HCOALGEN and DCOALGEN, for enthalpy and density, respectively [29]; those settings are meant for the general coal model, but they are now used for other non-conventional feedstock too, despite the reported deviations in the estimated heating value of biomass [97].
The main merits of process modelling are [12,27,39]:
  • the whole process is taken into account (e.g., separators, mixers, heat exchangers, pumps, etc.) and not only the reaction unit.
  • overall energy duty of the process is estimated.
  • optimization to improve CAPEX and OPEX are allowed.
The main assumptions for process modelling in Aspen Plus are:
  • process is steady-state and isothermal [98];
  • volatile products are H2, CO, CO2, CH4 and H2O [99];
  • char is 100% carbon [100];
  • all gas mixtures are supposed to behave as perfect gases;
  • pressure drops and heat losses are neglected.
When process modelling is based on thermodynamic modelling, it is possible to obtain a QET approach also in process models, with the same benefits listed in paragraph 2. Thermodynamic models.
Several authors investigated biomass gasification process by means of Aspen Plus, demonstrating that it is a powerful tool to describe biomass gasification [12,101,102,103,104]. However, in literature there is a lack of scientific articles that point out the basic understanding of each model type and its applicability for designing a common biomass gasification process. In order to fill that gap, in Table 5 are shown the basic unit that make up the gasification model, considering both the thermodynamic equilibrium and the kinetic approach.
The units listed in Table 5 are the strictly required three units needed to develop a thermodynamic or kinetic process model by means of Aspen Plus software. Beyond the kinetic approach reported in Table 3, the semi-kinetic method using a DECOMP block (yield reactor) provide a simpler approach to convert the non-conventional inlet stream of biomass into its conventional components (carbon, hydrogen, oxygen, sulphur, nitrogen, and ash). 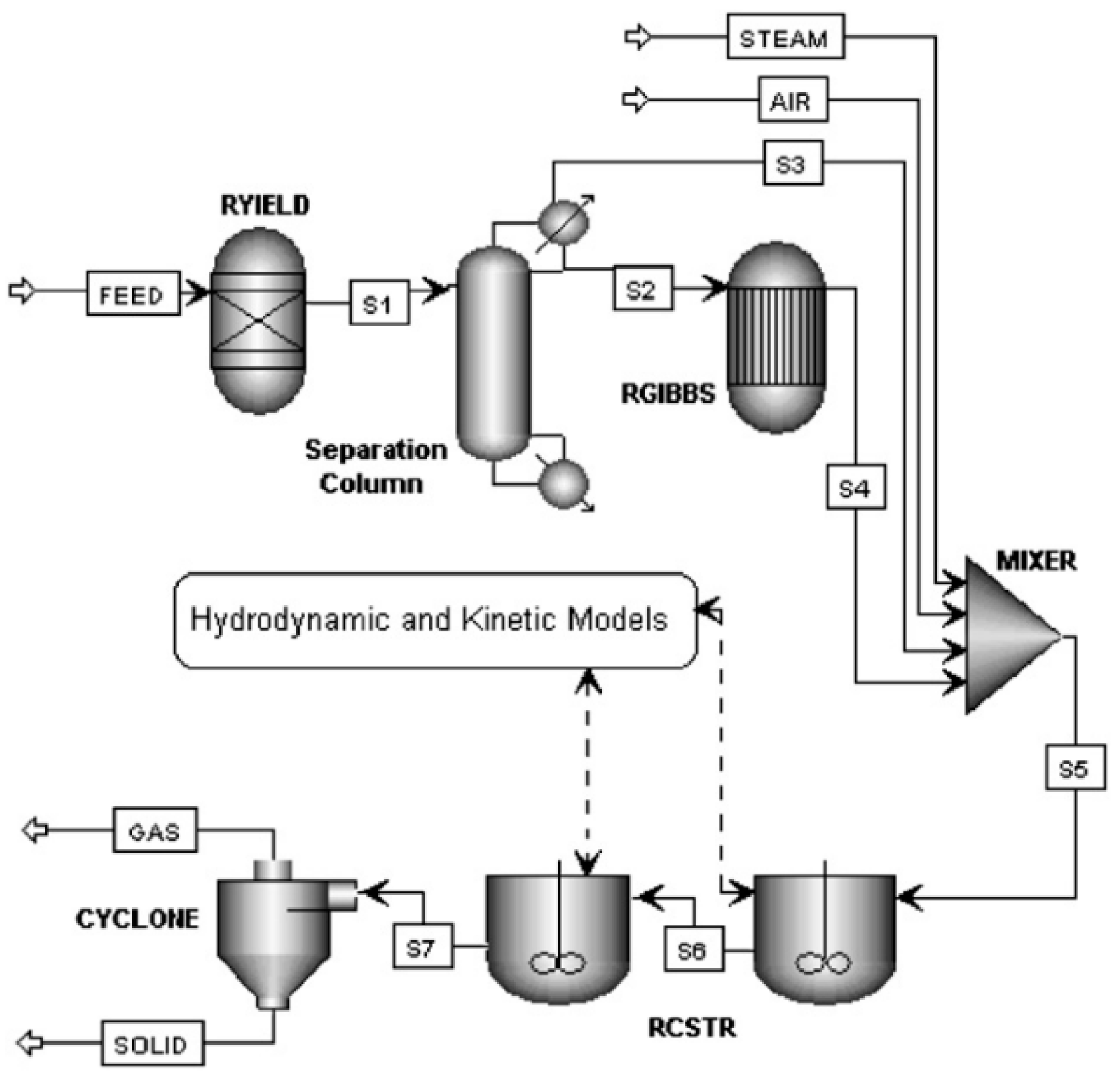The biomass ultimate analysis provides information to specify the yield distribution, the char gasification is performed in a CSTR introducing the reaction kinetics written through an external FORTRAN module [71] (see Figure 3). The separation column separates the volatile matter and solid matter, followed by a RGibbs reactor where the volatile combustion occurs, according to the hypothesis that reactions in gaseous phase occurs at Gibbs equilibrium. Moreover, the authors implemented hydrodynamic parameters to divide the gasifier in two parts: bed and freeboard, both modelled as CSTR reactors. Using FORTRAN code, each RCSTR is divided into a series of CSTR reactors with equal volume. The number of the elemental reactors depends on residence time, reactor dimensions, and operational conditions. Char gasification was performed in the RCSTR by means of kinetic reactions introduced through an external Fortran module. The model is used to predict the results of lab-scale gasification of pine with air and steam and gave results in good agreement with experimental data.
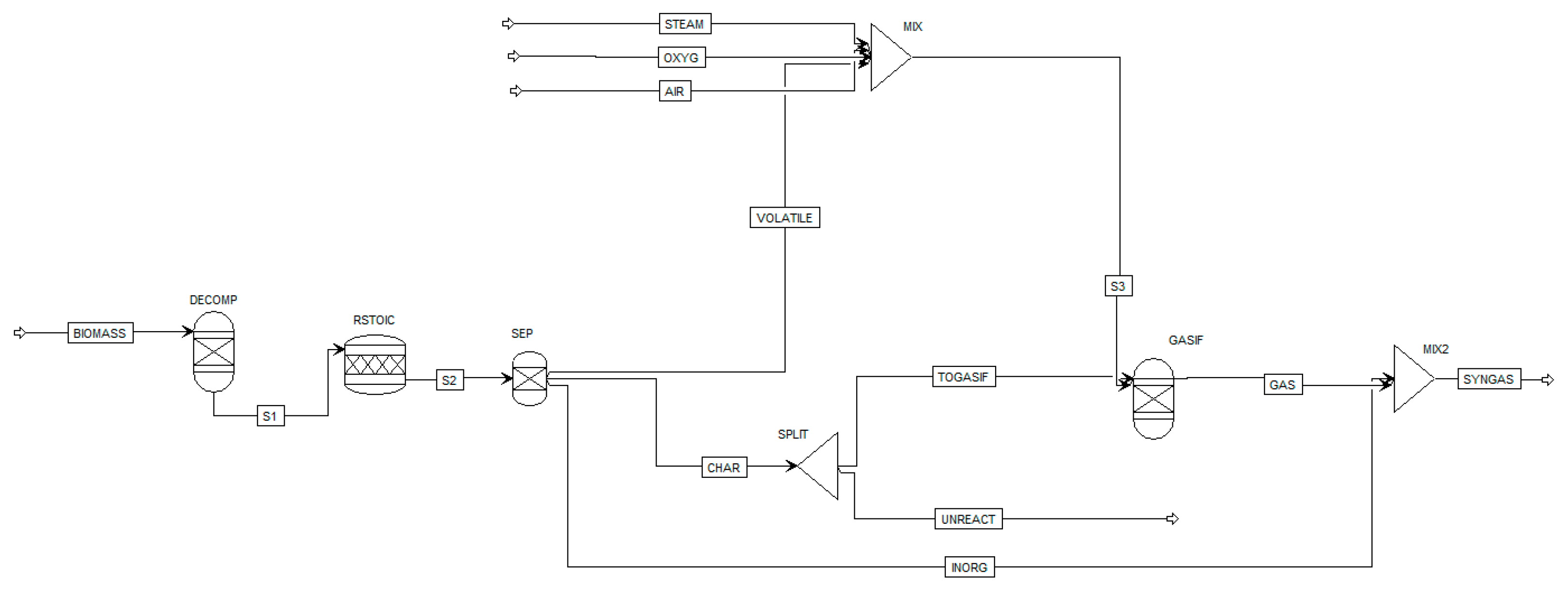
An example of basic equilibrium process model, developed by Marcantonio et al. [53] by means of Aspen Plus software, is shown in Figure 4. The modelling was done using the main units reported in Table 5 and adding a mixer to mix the biomass volatile stream with gasifying agent stream (oxygen, steam, air, or a mix of them). Moreover, the total amount of char was splitted according to literature experimental data and only 89% went to the gasifier while 11% was unreacted [104]. The simulative process was validated against experimental data showing good correlation between simulations and experiments. The maximum error for the concentration of hydrogen, the main product of the gasification process, was 16.3%.
Process models, as thermodynamic models, are not accurate at low temperature or at large scale. To overcome such limitations, some authors suggested to improve the equilibrium model with adjustable parameters and semi-empirical correlations [47].

6. Multivariate Data Analysis (MVDA) and Model Validation

In the ever-evolving fields of process and chemical engineering, managing and interpreting vast amounts of data is critical for optimizing processes, ensuring product quality, and making informed decisions [108,109]. In the area of biomass valorization and biorefinery processes, the process control is particularly challenging due to the high variability of biomass (feed) properties [110,111]. For instance, Williams et al. [110] reviewed the effect of biomass properties variability in different processes of energy conversion - fermentation, hydrothermal liquefaction, pyrolysis, and direct combustion - with a special focus on ligno-cellulosic feedstock. They underlined the relevance of some parameters, such as biomass moisture, in all process stages and on its performance, even hindering the large-scale use of biomass as carbon-neutral source for energy production.
Statistical methods can be used to manage the biomass variability [112]. Multivariate Data Analysis (MVDA) is a classical tool to extract meaningful insights from complex datasets, providing engineers with a deeper understanding of their systems and enabling them to enhance efficiency, reduce costs, and improve overall performance [109,113]. Multivariate Data Analysis (MVDA) focuses on uncovering the connections among variables by leveraging correlation patterns. In broader terms, MVDA enables the following [114]:
  • Reducing the number of variables while maintaining the system's descriptive capacity.
  • Grouping variables into categories.
  • Utilizing correlations between variables to characterize system behavior.
The simplest MVDA tool relies on the Pearson correlation coefficient, which establishes direct correlations between pairs of variables. However, in complex systems, this approach may not yield a definitive response, as a high correlation coefficient (close to unity in absolute value) does not always indicate a genuine causal relationship between the two variables. For instance, such a correlation might be the result of a third variable's influence, which is independently highly correlated with both. Therefore, additional methods are necessary to elucidate the true interdependencies between variables.
Principal Component Analysis (PCA) [115] offers a solution by transforming the original variables dataset into a new set of orthogonal variables known as Principal Components (PC). Principal Components (PCs) are linear combinations of the initial dataset. Let X = {〖x〗_1 ,〖x〗_2 ,...,〖x〗_m } represent the original dataset with m variables (LCA outputs), recorded on n samples (statistical units). PCA transforms X into a new set of variables, PC = {P〖C〗_1 ,P〖C〗_2 ,...,P〖C〗_k }, where k ≤ m. PCs are mutually orthogonal and ordered based on the descending values of explained variance. Given the PC set, the loadings matrix L = {〖λ〗_((i,j)) } reports the correlation coefficient between the i-th original variable, 〖x〗_(i ), and the j-th principal component P〖C〗_j, where each 〖λ〗_((i,j)) represents a generic element in the matrix. Another tool of MVDA is the Canonical Correlation Analysis (CCA) [116]. CCA relies on initially dividing the entire dataset into two or more categories. Variables within each category are then combined linearly to generate k variables, known as Canonical Variables (CVs). The value of k corresponds to the minimum rank (number of variables) among all categories. The scores obtained through linear combinations aim to maximize the Pearson correlation coefficient between variables. As a result, CCA calculates the correlations between different classes (categories) of variables, effectively describing the system's behavior. Consequently, a high correlation coefficient between the first canonical variables of two categories indicates a strong interdependency between the variables in those respective categories. Similarly, in the loading’s matrix L={〖λ〗_((i,j)) }, the generic element 〖λ〗_((i,j)) denotes the correlation between the i-th canonical variable of a given category and the j-th variable from the original dataset. The complexity of the gasification reactions produces a large number of variables required to describe the kinetic and thermodynamic properties of the reacting phases. MVDA is an elective tool for the analysis of the resulting data set; several works deal with the MVDA application to gasifiers, providing unique information for their optimization [105,117,118,119,120,121,122,123,124].
Gil et al. [125] adopted a multifaceted Multivariate Analysis of the data of gasification of ten different biomasses (almond shells, chestnut sawdust, torrefied chestnut sawdust, cocoa shells, grape pomace, olive stones, pine leaves, pine sawdust, torrefied pine sawdust and pine kernel shells). The experimental data were collected in a bubbling fluidized-bed gasifier under an air-steam atmosphere. The analysis was carried out on the variables of the gasification outlet streams and biomass properties. The analysis included different MVDA methods, including PCA: the ten different biomasses were classified into two groups according to their gasification products. The findings revealed that gasification of pine kernel shells, pine leaves, torrefied pine sawdust, olive stones, and pine sawdust resulted in substantial quantities of combustible gaseous products, including CO and CH. Additionally, their gasification exhibited high conversion rates and cold gas efficiency. Thus, it was inferred that C and H contents and the HHV of the biomass are the most important biomass properties for promoting the gas production, calorific value of the product gas, gasification conversion and energy efficiency. On the other hand, gasification of cocoa shells and grape pomace produced high H2 concentration and H2/CO molar ratio in the gas product, mainly due to the higher H/O ratio and K2O ash content of the biomass. Through a simple correlation analysis, the H2 concentration in the product gas were found negatively correlated to the O and volatile matter contents of the biomass.
All in all, this study demonstrated the potentiality of the MVDA in analyzing the gasification data, so as to reach valuable insight about the influence of the biomass properties on the gasification results.
Similarly, Dellavedova et al. [121] analyzed biomass characterization, gasification process conditions and obtained syngas properties from literature data by means of Principal Component Analysis, showing again biomass can be characterized and classified on the basis of its properties; this study showed that the most important variables for this model are the equivalence ratio (ER, i.e. the actual air fuel ratio divided by the stoichiometric air fuel ratio), the steam to biomass ratio (SB, i.e. the weight ratio between the amount of vapor used in the process and the biomass treated), the high heating value HHV, the carbon content and temperature.
It was observed a strong direct correlation between SB and the syngas characteristics. On the other hand, a negative correlation was found between syngas features and ER.
These two models show the potentiality of the MVDA in providing a data-driven description of gasification processes and, more in general, of complex reacting systems where the detailed description of all reactions and the characterization of the reactants can be very challenging.

6.1. Black-box approaches

Artificial Neural Networks models are inspired by natural neurons: they are composed of a wide number of strictly interconnected processing elements, called neurons or nodes, working all together at the same time to solve a given problem [126,127]. The nodes are organized in separated layers and interconnected with a given architecture. Each layer has a weight matrix, a bias vector, and an output vector [128].
This kind of model does not require physical description of the phenomena and is able to approximate arbitrary non-linear functions, that is why it was found a suitable approach to simulate and up-scale complex biomass gasification process [32].
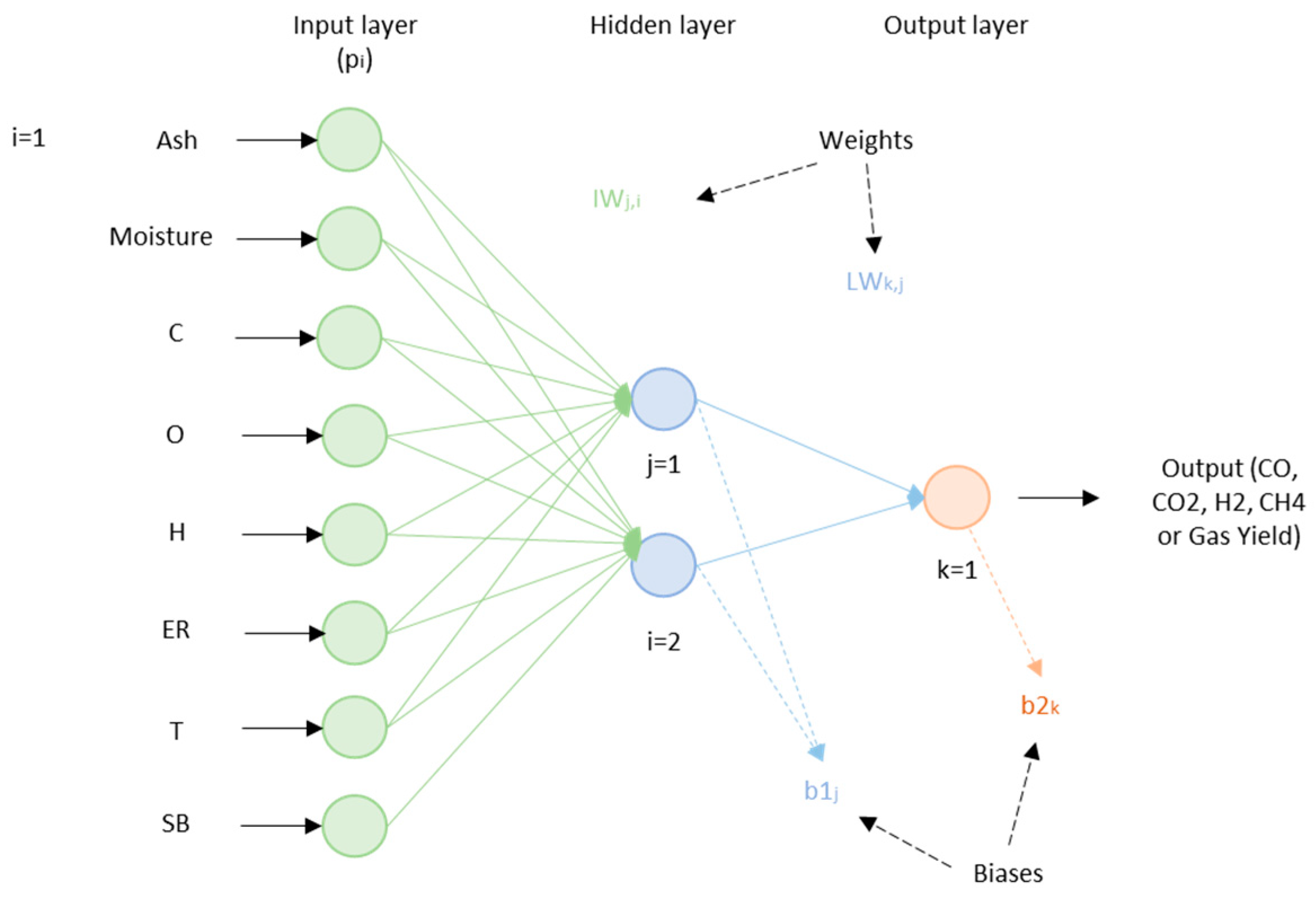
Puig-Arnavat et al. [32] proposed a model to predict gas composition and gas yield from biomass gasification in a fluidized-bed gasifier. The model structure developed by the authors is shown in Figure 5.
Input and output variables used by Puig-Arnavat el al. [32] in their developed model are shown in Table 6.
Results from the computational implementation of the ANN model were demonstrated to be in a good agreement with experiments.
Brown et al. [129] integrated an ANN approach with an equilibrium model for biomass gasification in a fluidized-bed. The authors performed a non-linear regression with ANN to compute temperature changes, fuel composition and operational variables. They demonstrated that the application of the ANN model improved the accuracy of the equilibrium model and, consequently, the quantity of required input data decreased.
Sreejith et al. [130] developed an ANN model to predict the output gas composition, the heat content, and the temperature profile in a fluidized-bed gasifier. Results obtained from the model were in good agreement with experimental data: at steam to biomass of 2.5 the simulative results of H2 concentration was found to be 28.2 %, while the experimental result was 29.1 %.
Although the application of ANN method has yielded positive results in biomass gasification, it remains a scarcity of studies on the subject in the current literature. It is important to emphasize that ANN models are limited to the range of operating conditions used in their previous training study. To enhance the effectiveness of ANN predictions, expanding the experimental database with a broader range of operating conditions could be highly beneficial.

7. Discussion

Table 7 shows features, pros, and cons of the three modelling approaches discussed in the previous paragraphs.
The choice of the model depends on the objectives and the experimental information available.
A first raw prediction of gasification process performance is well given by thermodynamic modelling, easy to implement and flexible to use thanks to the independence of geometry. However, this approach does not give a realistic representation of the process at low temperature; and, moreover, it is not able to predict gasification process far from equilibrium (controlling kinetics and fluid dynamics phenomena, such as unconverted solid carbon and the formation of gaseous hydrocarbons).
Kinetic modelling gives a more accurate description of phenomena, but it requires a complete description of the reaction mechanisms, often unknown or only poorly known.
The main limitation of both kinetic and thermodynamic modelling in the investigation of gasification process is related to the interaction between solid and gas phases reactions, highly undescribed. In order to overcome this issue, CFD modelling is used to answer about interaction between solid and gas phases reactions involving a combined solution of mass, momentum, energy balances, including turbulence regimes and multiphase hydrodynamics. In turn, the CFD computational complexity is very high, so it is reasonably used if some reliable experimental data are known and used as reference. The black box approaches do not require any preliminary understanding and description of the physical phenomena.
Compared with other modeling approaches, ANN copes non-linearity in a superior manner. Moreover, it does not require any mathematical or physical description of the phenomena and is able to adapt and learn, for those reasons ANN modelling makes the computational tool able to update itself. On the other hand, it works only within the specific range of operational conditions it was trained on.
Finally, MVA and more in general statistical methods provide insight about the correlation patterns of variables in gasification process: this information is particularly valuable in the case of systems controlled by a large number of variables, such as in the case of gasification. High correlation may infer a causal link between variables, worth to be explored through more detailed physical descriptions.
Additionally, the correlation analysis is the basis for the sensitivity analysis, which guides the optimization methods for process engineering.
In summary, it is possible to affirm that black-box models with some empirical constraints are enough for preliminary predictions (e.g., quasi-equilibrium model).
In Figure 6 (a)-(e) is briefly reported a schematic approach of each modelling.

8. Conclusions

A review of the most important and recent gasification modelling approaches was presented. Even if the most appropriate choice of model depends on factors such as the scope of the simulation, the type of gasifier, the feedstock, and operational parameters several general observations can be made.
Equilibrium models are the simplest and easiest to develop and implement and have the advantage of being independent of gasifier design. They are able to predict the maximum achievable yield of a desired product from a reacting system and the gas composition. But they lost their accuracy at low temperature. Unlike equilibrium models, kinetic models predict the progress and product composition at different positions along a reactor, also providing a useful design aid in evaluating the possible limiting behavior of a system that is difficult or unsafe to reproduce experimentally. However, kinetic models are strictly dependent on the geometry, and they cannot be used for system different from the ones they are built for. CFD model results showed a good agreement with experimental data in many cases. However, CFD models are computationally intensive and still have many approximations as well as assumptions and there are many aspects of fluidized-bed reactor where the application of CFD modeling still needs to be explored (i.e., fuel combustion/gasification behavior during feeding, mixing of fuel in the dense bed, ash sintering, fuel characteristics, char reactivity, fragmentation of fuel in dense bed). In order to avoid complex processes and develop the simplest possible model that incorporates the principal gasification reactions and the gross physical characteristics of the reactor, process simulation models were developed, using the process simulator Aspen Plus. Process simulation models are able to give a first raw evaluation of the overall energy duty and economic of the system, bust they have all the pros and cons of the modelling they are based on (thermodynamic or kinetic modelling). ANN models offer some contribution to research in gasification process. Literature results show how the percentage composition of the main four gas species (H2, CO, CO2 and CH4) in producer gas and producer gas yield for a fluidized-bed gasifier can be successfully predicted by applying a neural network. However, ANN models still need to be trained and improved, for this reason it is necessary to enlarge the literature database adding more experimental data. MVA analysis provides a good prediction of both dynamic behavior and equilibrium conditions, requiring a minimal computational burden, but it does not add any physical interpretation of the phenomena occurring.

Author Contributions

Conceptualization, M.C.; methodology, M.C. and L.D.P.; formal analysis, V.M.; investigation, V.M.; data curation, V.M., M.C and L.D.P.; writing—original draft preparation, V.M. and L.D.P.; writing—review and editing, L.D.P, M.C. and M.D.F.; visualization, V.M.; supervision, M.C.. All authors have read and agreed to the published version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Nomenclature

Acronyms
ANN Artificial Neural Network GMM Gibbs Free Energy Gradient Method Model
CCA Canonical Correlation Analysis LHV Low Heating Value
CFD Computational Fluid Dynamics MVDA Multivariate Data Analysis
CSTR Continuous-flow Stirred-Tank Reactor QET Quasi-Equilibrium Temperature
DEM Discrete Element Method PCA Principal Component Analysis
DPM Discrete Particle Model TFM Two Fluid Model
Symbols Unit Description
Cp,i J/(mol·k) Specific heat at constant pressure of the i-component
H kJ/mol Enthalpy
∆ H 0 kJ/mol Enthalpy formation
G kJ/mol Gibbs free energy
∆ G 0 kJ/mol Gibbs energy formation
ni mol Number of moles of the i-component
nT mol Total moles of produced gas
P Pa Pressure
Pi Pa Partial pressure of i-component
P0 Pa Operative pressure of the system
R J/(mol·k) Universal constant of gas
T K Temperature
Greek letters
α Reaction coordinate of water gas shift reaction
β Reaction coordinate of steam reforming reaction
µi Chemical potential
μ i 0 T Standard chemical potential of the i-component

References

  1. Pala, L.P.R.; Wang, Q.; Kolb, G.; Hessel, V. Steam gasification of biomass with subsequent syngas adjustment using shift reaction for syngas production: An Aspen Plus model. Renew. Energy 2017, 101, 484–492. [Google Scholar] [CrossRef]
  2. Chang, W.-R.; Hwang, J.-J.; Wu, W. Environmental impact and sustainability study on biofuels for transportation applications. Renew. Sustain. Energy Rev. 2017, 67, 277–288. [Google Scholar] [CrossRef]
  3. Biagini, E.; Barontini, F.; Tognotti, L. Gasification of agricultural residues in a demonstrative plant: Vine pruning and rice husks. Bioresour. Technol. 2015, 194, 36–42. [Google Scholar] [CrossRef]
  4. Ritslaid, K.; Küüt, a; Olt, J. State of the Art in Bioethanol Production. Agron. Res. 2010, 8, 236–254. [Google Scholar]
  5. Kuchler, M.; Linnér, B. Challenging the food vs. fuel dilemma : Genealogical analysis of the biofuel discourse pursued by international organizations. Food Policy 2012, 37, 581–588. [Google Scholar] [CrossRef]
  6. Antizar-Ladislao, B.; Turrion-Gomez, J.L. Second-generation biofuels and local bioenergy systems. Biofuels, Bioprod. Biorefining 2008, 2, 455–469. [Google Scholar] [CrossRef]
  7. Oliveira, W.E.; Franca, A.S.; Oliveira, L.S.; Rocha, S.D. Untreated coffee husks as biosorbents for the removal of heavy metals from aqueous solutions. J. Hazard. Mater. 2008, 152, 1073–1081. [Google Scholar] [CrossRef]
  8. Puig-Arnavat, M.; Bruno, J.C.; Coronas, A. Review and analysis of biomass gasification models. Renew. Sustain. Energy Rev. 2010, 14, 2841–2851. [Google Scholar] [CrossRef]
  9. Marcantonio, V.; De Falco, M.; Capocelli, M.; Bocci, E.; Colantoni, A.; Villarini, M. Process analysis of hydrogen production from biomass gasification in fluidized bed reactor with different separation systems. Int. J. Hydrogen Energy 2019, 44. [Google Scholar] [CrossRef]
  10. Marcantonio, V.; De Falco, M.; Bocci, E. Non-Thermal Plasma Technology for CO2 Conversion—An Overview of the Most Relevant Experimental Results and Kinetic Models. Energies 2022, 15, 7790. [Google Scholar] [CrossRef]
  11. Ramzan, N.; Ashraf, A.; Naveed, S.; Malik, A. Simulation of hybrid biomass gasification using Aspen plus : A comparative performance analysis for food, municipal solid and poultry waste. Biomass and Bioenergy 2011, 35, 3962–3969. [Google Scholar] [CrossRef]
  12. Liao, C.; Summers, M.; Seiser, R.; Cattolica, R.; Herz, R. Simulation of a pilot-scale dual-fluidized-bed gasifier for biomass. Environ. Prog. Sustain. Energy 2014, 33, 732–736. [Google Scholar] [CrossRef]
  13. Baldinelli, A.; Cinti, G.; Desideri, U.; Fantozzi, F. Biomass integrated gasifier-fuel cells: Experimental investigation on wood syngas tars impact on NiYSZ-anode Solid Oxide Fuel Cells. Energy Convers. Manag. 2016, 128, 361–370. [Google Scholar] [CrossRef]
  14. Arteaga-Pérez, L.E.; Casas-Ledón, Y.; Pérez-Bermúdez, R.; Peralta, L.M.; Dewulf, J.; Prins, W. Energy and exergy analysis of a sugar cane bagasse gasifier integrated to a solid oxide fuel cell based on a quasi-equilibrium approach. Chem. Eng. J. 2013. [Google Scholar] [CrossRef]
  15. Stemmler, M.; Tamburro, A.; Müller, M.; Ud Din, Z.; Zainal, Z.A.; Meng, X.; De Jong, W.; Pal, R.; Verkooijen, A.H.M.; Husmann, M.; et al. Effects of loading methods and oxidation degree of support on the tar reforming activity of char-supported Ni catalyst using toluene as a model compound. Fuel 2020, 3, 536–546. [Google Scholar] [CrossRef]
  16. Parvez, A.M.; Hafner, S.; Hornberger, M.; Schmid, M.; Scheffknecht, G. Sorption enhanced gasification (SEG) of biomass for tailored syngas production with in-situ CO2 capture: Current status, process scale-up experiences and outlook. Renew. Sustain. Energy Rev. 2021, 141, 110756. [Google Scholar] [CrossRef]
  17. Dascomb, J.; Krothapalli, A.; Fakhrai, R. Thermal conversion efficiency of producing hydrogen enriched syngas from biomass steam gasification. Int. J. Hydrogen Energy 2013, 38, 11790–11798. [Google Scholar] [CrossRef]
  18. Villarini, M.; Marcantonio, V.; Colantoni, A.; Bocci, E.; Villarini, M.; Marcantonio, V.; Colantoni, A.; Bocci, E. Sensitivity Analysis of Different Parameters on the Performance of a CHP Internal Combustion Engine System Fed by a Biomass Waste Gasifier. Energies 2019, 12, 688. [Google Scholar] [CrossRef]
  19. Marcantonio, V.; Müller, M.; Bocci, E. A review of hot gas cleaning techniques for hydrogen chloride removal from biomass-derived syngas. Energies 2021, 14. [Google Scholar] [CrossRef]
  20. Hamel, S.; Krumm, W. Mathematical modelling and simulation of bubbling fluidised bed gasifiers. Powder Technol. 2001, 120, 105–112. [Google Scholar] [CrossRef]
  21. Ahmed, T.Y.; Ahmad, M.M.; Yusup, S.; Inayat, A.; Khan, Z. Mathematical and computational approaches for design of biomass gasification for hydrogen production: A review. Renew. Sustain. Energy Rev. 2012, 16, 2304–2315. [Google Scholar] [CrossRef]
  22. Patra, T.K.; Sheth, P.N. Biomass gasification models for downdraft gasifier: A state-of-the-art review. Renew. Sustain. Energy Rev. 2015, 50, 583–593. [Google Scholar] [CrossRef]
  23. Canneto, G.; Freda, C.; Braccio, G. Numerical simulation of gas-solid flow in an interconnected fluidized bed. Therm. Sci. 2015, 19, 317–328. [Google Scholar] [CrossRef]
  24. Ajorloo, M.; Ghodrat, M.; Scott, J.; Strezov, V. Recent advances in thermodynamic analysis of biomass gasification: A review on numerical modelling and simulation. J. Energy Inst. 2022, 102, 395–419. [Google Scholar] [CrossRef]
  25. Mazaheri, N.; Akbarzadeh, A.H.; Madadian, E.; Lefsrud, M. Systematic review of research guidelines for numerical simulation of biomass gasification for bioenergy production. Energy Convers. Manag. 2019, 183, 671–688. [Google Scholar] [CrossRef]
  26. Basu, P. Biomass gasification and pyrolysis : practical design and theory; Academic Press, 2010; ISBN 0080961622. [Google Scholar]
  27. Ahmed, A.M.A.; Salmiaton, A.; Choong, T.S.Y.; Azlina, W.A.K.G.W. Review of kinetic and equilibrium concepts for biomass tar modeling by using Aspen Plus. Renew. Sustain. Energy Rev. 2015, 52, 1623–1644. [Google Scholar] [CrossRef]
  28. Baruah, D.; Baruah, D.C. Modeling of biomass gasification: A review. Renew. Sustain. Energy Rev. 2014, 39, 806–815. [Google Scholar] [CrossRef]
  29. Marcantonio, V.; Bocci, E.; Monarca, D. Development of a chemical quasi-equilibrium model of biomass waste gasification in a fluidized-bed reactor by using Aspen plus. Energies 2019, 13. [Google Scholar] [CrossRef]
  30. Ramos, A.; Monteiro, E.; Rouboa, A. Numerical approaches and comprehensive models for gasification process: A review. Renew. Sustain. Energy Rev. 2019, 110, 188–206. [Google Scholar] [CrossRef]
  31. Li, Y.; Yan, L.; Yang, B.; Gao, W.; Farahani, M.R. Simulation of biomass gasification in a fluidized bed by artificial neural network (ANN). 2018, 40, pp. 544–548. [CrossRef]
  32. Puig-Arnavat, M.; Hernández, J.A.; Bruno, J.C.; Coronas, A. Artificial neural network models for biomass gasification in fluidized bed gasifiers. Biomass and Bioenergy 2013, 49, 279–289. [Google Scholar] [CrossRef]
  33. Review of Technologies for Gasification of Biomass and Wastes Final report. 2009.
  34. Bridgwater, T. Biomass for energy. J. Sci. Food Agric. 2006, 86, 1755–1768. [Google Scholar] [CrossRef]
  35. Puig-Gamero, M.; Argudo-Santamaria, J.; Valverde, J.L.; Sánchez, P.; Sanchez-Silva, L. Three integrated process simulation using aspen plus®: Pine gasification, syngas cleaning and methanol synthesis. Energy Convers. Manag. 2018, 177, 416–427. [Google Scholar] [CrossRef]
  36. Eisavi, B.; Chitsaz, A.; Hosseinpour, J.; Ranjbar, F. Thermo-environmental and economic comparison of three different arrangements of solid oxide fuel cell-gas turbine (SOFC-GT) hybrid systems. Energy Convers. Manag. 2018, 168, 343–356. [Google Scholar] [CrossRef]
  37. Collings, P.; Yu, Z.; Wang, E.; Ozgur Colpan, C.; Ibrahim, D.; Feridun, H.; Sadaka, S.; Johnson, D.M.; Guo, C.; Du, X.; et al. Optimization on pinch point temperature difference of ORC system based on AHP-Entropy method. Energy 2016, 98, 790–797. [Google Scholar] [CrossRef]
  38. Wan, W.; Engvall, K.; Yang, W. Model investigation of condensation behaviors of alkalis during syngas treatment of pressurized biomass gasification. Chem. Eng. Process. - Process Intensif. 2018, 129, 28–36. [Google Scholar] [CrossRef]
  39. Safarian, S.; Unnþórsson, R.; Richter, C. A review of biomass gasification modelling. Renew. Sustain. Energy Rev. 2019, 110, 378–391. [Google Scholar] [CrossRef]
  40. Li, X.T.; Grace, J.R.; Lim, C.J.; Watkinson, A.P.; Chen, H.P.; Kim, J.R. Biomass gasification in a circulating fluidized bed. Biomass and Bioenergy 2004, 26, 171–193. [Google Scholar] [CrossRef]
  41. Aydin, E.S.; Yucel, O.; Sadikoglu, H. Numerical and experimental investigation of hydrogen-rich syngas production via biomass gasification. Int. J. Hydrogen Energy 2018, 43, 1105–1115. [Google Scholar] [CrossRef]
  42. Fiori, L.; Castello, D. Thermodynamic Analysis of the Supercritical Water Gasification of Biomass. 2014, 99–129. [Google Scholar] [CrossRef]
  43. Barba, D.; Prisciandaro, M.; Salladini, A.; Mazziotti Di Celso, G. The Gibbs Free Energy Gradient Method for RDF gasification modelling. Fuel 2011, 90, 1402–1407. [Google Scholar] [CrossRef]
  44. Langmuir-Hinshelwood-Hougen-Watson(LHHW) model.
  45. Doherty, W.; Reynolds, A.; Kennedy, D. Aspen Plus Simulation of Biomass Gasification in a Steam Blown Dual Fluidised Bed. Book/b. Chapters 2013.
  46. Marcantonio, V.; De Falco, M.; Capocelli, M.; Bocci, E.; Colantoni, A.; Villarini, M. Process analysis of hydrogen production from biomass gasification in fluidized bed reactor with different separation systems. Int. J. Hydrogen Energy 2019, 44, 10350–10360. [Google Scholar] [CrossRef]
  47. Barba, D.; Capocelli, M.; Cornacchia, G.; Matera, D.A. Theoretical and experimental procedure for scaling-up RDF gasifiers: The Gibbs Gradient Method. Fuel 2016, 179, 60–70. [Google Scholar] [CrossRef]
  48. Patra, T.K.; Sheth, P.N. Biomass gasification models for downdraft gasifier: A state-of-the-art review. Renew Sustain Energy Rev 2015, 50, 583–593. [Google Scholar] [CrossRef]
  49. Gumz, W. Gas producers and blast furnaces; 1950. [Google Scholar]
  50. Doherty, W.; Reynolds, A.; Kennedy, D.; Doherty, W.; Reynolds, A.; Kennedy, D. Simulation of a Circulating Fluidised Bed Biomass Gasifier using ASPEN Plus : a Performance Analysis Simulation of a Circulating Fluidised Bed Biomass Gasifier Using ASPEN Plus – A Performance Analysis. 2008, 1241–1248. [Google Scholar]
  51. Mckeen, L.W.; Taylor, J.W. A study of the input data selection on the qet calculated intensities of ethylene and propane ions. Int. J. Mass Spectrom. Ion Phys. 1980, 33, 167–185. [Google Scholar] [CrossRef]
  52. Marcantonio, V.; Monforti Ferrario, A.; Di Carlo, A.; Del Zotto, L.; Monarca, D.; Bocci, E. Biomass Steam Gasification: A Comparison of Syngas Composition between a 1-D MATLAB Kinetic Model and a 0-D Aspen Plus Quasi-Equilibrium Model. Computation 2020, 8, 86. [Google Scholar] [CrossRef]
  53. Marcantonio, V.; Bocci, E.; Monarca, D. Development of a chemical quasi-equilibrium model of biomass waste gasification in a fluidized-bed reactor by using Aspen plus. Energies 2019, 13. [Google Scholar] [CrossRef]
  54. Buekens, A.G.; Schoeters, J.G. Modelling of Biomass Gasification. In; Overend, R.P., Milne, T.A., Mudge, L.K., Eds.; Springer Netherlands, 1985; pp. 619–689.
  55. Loha, C.; Chatterjee, P.K.; Chattopadhyay, H. Performance of fluidized bed steam gasification of biomass - Modeling and experiment. Energy Convers. Manag. 2011, 52, 1583–1588. [Google Scholar] [CrossRef]
  56. Loha, C.; Chattopadhyay, H.; Chatterjee, P.K. Thermodynamic analysis of hydrogen rich synthetic gas generation from fluidized bed gasification of rice husk. Energy 2011, 36, 4063–4071. [Google Scholar] [CrossRef]
  57. Kaya, E.; Koksal, M. Investigation of the predicting ability of single-phase chemical equilibrium modeling applied to circulating fluidized bed coal gasification. J. Energy Resour. Technol. Trans. ASME 2016, 138. [Google Scholar] [CrossRef]
  58. Ramanan, M.V.; Lakshmanan, E.; Sethumadhavan, R.; Renganarayanan, S. Modeling and Experimental Validation of Cashew Nut Shell Char Gasification Adopting Chemical Equilibrium Approach. Energy and Fuels 2008, 22, 2070–2078. [Google Scholar] [CrossRef]
  59. Bridgwater, A. V. The technical and economic feasibility of biomass gasification for power generation. Fuel 1995, 74, 631–653. [Google Scholar] [CrossRef]
  60. Basu, P.; Kaushal, P. Modeling of pyrolysis and gasification of biomass in fluidized beds: A review. Chem. Prod. Process Model. 2009, 4. [Google Scholar] [CrossRef]
  61. Castello, D.; Fiori, L. Kinetics modeling and main reaction schemes for the supercritical water gasification of methanol. J. Supercrit. Fluids 2012, 69, 64–74. [Google Scholar] [CrossRef]
  62. Ranzi, E.; Dente, M.; Goldaniga, A.; Bozzano, G.; Faravelli, T. Lumping procedures in detailed kinetic modeling of gasification, pyrolysis, partial oxidation and combustion of hydrocarbon mixtures. Prog. Energy Combust. Sci. 2001, 27, 99–139. [Google Scholar] [CrossRef]
  63. Resende, F.L.P.; Savage, P.E. Kinetic model for noncatalytic supercritical water gasification of cellulose and lignin. AIChE J. 2010, 56, 2412–2420. [Google Scholar] [CrossRef]
  64. Guan, Q.; Wei, C.; Savage, P.E. Kinetic model for supercritical water gasification of algae. Phys. Chem. Chem. Phys. 2012, 14, 3140–3147. [Google Scholar] [CrossRef]
  65. Jin, H.; Guo, L.; Guo, J.; Ge, Z.; Cao, C.; Lu, Y. Study on gasification kinetics of hydrogen production from lignite in supercritical water. Int. J. Hydrogen Energy 2015, 40, 7523–7529. [Google Scholar] [CrossRef]
  66. Iwaszenko, S.; Howaniec, N.; Smoliński, A. Determination of random pore model parameters for underground coal gasification simulation. Energy 2019, 166, 972–978. [Google Scholar] [CrossRef]
  67. Experimental Investigation on the Gasification Kinetic Model of a Char Particle in Supercritical Water. n.d. Available online: https://agris.fao.org/agris-search/search.do?recordID=US201700052980 (accessed on 19 May 2023).
  68. Vostrikov, A.A.; Psarov, S.A.; Dubov, D.Y.; Fedyaeva, O.N.; Sokol, M.Y. Kinetics of coal conversion in supercritical water. Energy and Fuels 2007, 21, 2840–2845. [Google Scholar] [CrossRef]
  69. Di Carlo, A.; Borello, D.; Bocci, E. Process simulation of a hybrid SOFC/mGT and enriched air/steam fluidized bed gasifier power plant. Int. J. Hydrogen Energy 2013, 38, 5857–5874. [Google Scholar] [CrossRef]
  70. Kunii, D.; Levenspiel, O. Fluidized reactor models. 1. For bubbling beds of fine, intermediate, and large particles. 2. For the lean phase: freeboard and fast fluidization. Ind. Eng. Chem. Res. 1990, 29, 1226–1234. [Google Scholar] [CrossRef]
  71. Nikoo, M.B.; Mahinpey, N. Simulation of biomass gasification in fluidized bed reactor using ASPEN PLUS. Biomass and Bioenergy 2008, 32, 1245–1254. [Google Scholar] [CrossRef]
  72. Roy, P.C.; Datta, A.; Chakraborty, N. Assessment of cow dung as a supplementary fuel in a downdraft biomass gasifier. Renew. Energy 2010, 35, 379–386. [Google Scholar] [CrossRef]
  73. Roy, P.C.; Datta, A.; Chakraborty, N. An assessment of different biomass feedstocks in a downdraft gasifier for engine application. Fuel 2013, 106, 864–868. [Google Scholar] [CrossRef]
  74. Jia, J.; Xu, L.; Abudula, A.; Sun, B. Effects of operating parameters on performance of a downdraft gasifier in steady and transient state. Energy Convers. Manag. 2018, 155, 138–146. [Google Scholar] [CrossRef]
  75. Kaushal, P.; Tyagi, R. Advanced simulation of biomass gasification in a fluidized bed reactor using ASPEN PLUS. Renew. Energy 2017, 101, 629–636. [Google Scholar] [CrossRef]
  76. Lu, Y.; Huang, J.; Zheng, P. Fluid hydrodynamic characteristics in supercritical water fluidized bed: A DEM simulation study. Chem. Eng. Sci. 2014, 117, 283–292. [Google Scholar] [CrossRef]
  77. Gómez-Barea, A.; Leckner, B. Modeling of biomass gasification in fluidized bed. Prog. Energy Combust. Sci. 2010, 36, 444–509. [Google Scholar] [CrossRef]
  78. Xue, Q.; Fox, R.O. Reprint of: Multi-fluid CFD modeling of biomass gasification in polydisperse fluidized-bed gasifiers. Powder Technol. 2014, 265, 23–34. [Google Scholar] [CrossRef]
  79. Hassen, W.; Dhrioua, M.; Kolsi, L.; Anbumalar, V.; Al-Rashed, A.A.A.A.; Borjini, M.N. CFD modeling of gas-particles flow in a circulating fluidized G-Volution gasification reactor. Int. J. Mech. Sci. 2018, 144, 438–451. [Google Scholar] [CrossRef]
  80. Papadikis, K.; Gu, S.; Bridgwater, A. V.; Gerhauser, H. Application of CFD to model fast pyrolysis of biomass. Fuel Process. Technol. 2009, 90, 504–512. [Google Scholar] [CrossRef]
  81. Xue, Q.; Dalluge, D.; Heindel, T.J.; Fox, R.O.; Brown, R.C. Experimental validation and CFD modeling study of biomass fast pyrolysis in fluidized-bed reactors. Fuel 2012, 97, 757–769. [Google Scholar] [CrossRef]
  82. Nguyen, T.D.B.; Seo, M.W.; Lim, Y. Il; Song, B.H.; Kim, S.D. CFD simulation with experiments in a dual circulating fluidized bed gasifier. Comput. Chem. Eng. 2012, 36, 48–56. [Google Scholar] [CrossRef]
  83. Herce, C.; Cortés, C.; Stendardo, S. Numerical simulation of a bubbling fluidized bed reactor for sorption-enhanced steam methane reforming under industrially relevant conditions: Effect of sorbent (dolomite and CaO-Ca 12 Al 14 O 33 ) and operational parameters. Fuel Process. Technol. 2019, 186, 137–148. [Google Scholar] [CrossRef]
  84. Barik, H.; Bhattacharya, S.; Bose, M. CFD-DPM-based numerical simulation for char gasification in an entrained flow reactor: Effect of residence time distribution. Can. J. Chem. Eng. 2023, 101, 2286–2306. [Google Scholar] [CrossRef]
  85. Salem, A.M.; Paul, M.C. CFD modelling of spatiotemporal evolution of detailed tar species in a downdraft gasifier. Biomass and Bioenergy 2023, 168, 106656. [Google Scholar] [CrossRef]
  86. von Berg, L.; Anca-Couce, A.; Hochenauer, C.; Scharler, R. Multi-scale modelling of fluidized bed biomass gasification using a 1D particle model coupled to CFD. Fuel 2022, 324, 124677. [Google Scholar] [CrossRef]
  87. Wang, S.; Luo, K.; Fan, J. CFD-DEM coupled with thermochemical sub-models for biomass gasification: Validation and sensitivity analysis. Chem. Eng. Sci. 2020, 217, 115550. [Google Scholar] [CrossRef]
  88. Ku, X.; Li, T.; Løvås, T. CFD–DEM simulation of biomass gasification with steam in a fluidized bed reactor. Chem. Eng. Sci. 2015, 122, 270–283. [Google Scholar] [CrossRef]
  89. Lungu, M.; Siame, J.; Mukosha, L. Comparison of CFD-DEM and TFM approaches for the simulation of the small scale challenge problem 1. Powder Technol. 2021, 378, 85–103. [Google Scholar] [CrossRef]
  90. Yu, L.; Lu, J.; Zhang, X.; Zhang, S. Numerical simulation of the bubbling fluidized bed coal gasification by the kinetic theory of granular flow (KTGF). Fuel 2007, 86, 722–734. [Google Scholar] [CrossRef]
  91. Armstrong, L.M.; Gu, S.; Luo, K.H. Parametric Study of Gasification Processes in a BFB Coal Gasifier. Ind. Eng. Chem. Res. 2011, 50, 5959–5974. [Google Scholar] [CrossRef]
  92. Armstrong, L.M.; Gu, S.; Luo, K.H. Effects of limestone calcination on the gasification processes in a BFB coal gasifier. Chem. Eng. J. 2011, 168, 848–860. [Google Scholar] [CrossRef]
  93. Yang, S.; Liu, X.; Wang, S. CFD simulation of air-blown coal gasification in a fluidized bed reactor with continuous feedstock. Energy Convers. Manag. 2020, 213, 112774. [Google Scholar] [CrossRef]
  94. Xia, Z.; Fan, Y.; Wang, T.; Guo, X.; Chen, C. A TFM-KTGF jetting fluidized bed coal gasification model and its validations with data of a bench-scale gasifier. Chem. Eng. Sci. 2015, 131, 12–21. [Google Scholar] [CrossRef]
  95. Adnan, M.; Sun, J.; Ahmad, N.; Wei, J.J. Comparative CFD modeling of a bubbling bed using a Eulerian–Eulerian two-fluid model (TFM) and a Eulerian-Lagrangian dense discrete phase model (DDPM). Powder Technol. 2021, 383, 418–442. [Google Scholar] [CrossRef]
  96. Doherty, W.; Reynolds, A.; Kennedy, D.; Doherty, W.; Reynolds, A.; Kennedy, D. Aspen Plus Simulation of Biomass Gasification in a Steam Blown Dual Fluidised Bed Recommended Citation Aspen plus simulation of biomass gasification in a steam blown dual fluidised bed; n.d.
  97. Mutlu, Ö.Ç.; Zeng, T. Challenges and Opportunities of Modeling Biomass Gasification in Aspen Plus: A Review. Chem. Eng. Technol. 2020, 43, 1674–1689. [Google Scholar] [CrossRef]
  98. Ye, G.; Xie, D.; Qiao, W.; Grace, J.R.; Lim, C.J. Modeling of fluidized bed membrane reactors for hydrogen production from steam methane reforming with Aspen Plus. Int. J. Hydrogen Energy 2009, 34, 4755–4762. [Google Scholar] [CrossRef]
  99. Sadaka, S.S.; Ghaly, A.E.; Sabbah, M.A. Two phase biomass air-steam gasification model for fluidized bed reactors: Part I—model development. Biomass and Bioenergy 2002, 22, 439–462. [Google Scholar] [CrossRef]
  100. Demirbaş, A. Carbonization ranking of selected biomass for charcoal, liquid and gaseous products. Energy Convers. Manag. 2001, 42, 1229–1238. [Google Scholar] [CrossRef]
  101. Jang, D.H.; Kim, H.T.; Lee, C.; Kim, S.H.; Doherty, W.; Reynolds, A.; Kennedy, D.; Kong, X.; Zhong, W.; Du, W.; et al. Gasification of hazelnut shells in a downdraft gasifier. Energy 2002, 27, 415–427. [Google Scholar] [CrossRef]
  102. Batista, F.R.M.; Follegatti-Romero, L.A.; Bessa, L.C.B.A.; Meirelles, A.J.A. Computational simulation applied to the investigation of industrial plants for bioethanol distillation. Comput. Chem. Eng. 2012, 46, 1–16. [Google Scholar] [CrossRef]
  103. Detchusananard, T.; Ponpesh, P.; Saebea, D.; Authayanun, S.; Arpornwichanop, A. Modeling and analysis of sorption enhanced chemical looping biomass gasification. Chem. Eng. Trans. 2017, 57, 103–108. [Google Scholar] [CrossRef]
  104. Marcantonio, V.; De Falco, M.; Capocelli, M.; Amado-Fierro, Á.; Centeno, T.A.; Bocci, E. Modelling and assessment of a sorption enhanced gasification system coupled with hydrothermal carbonization, hot gas cleaning, and plasma to produce pure H2 from biomass. Int. J. Hydrogen Energy 2023. [Google Scholar] [CrossRef]
  105. Dang, Q.; Zhang, X.; Zhou, Y.; Jia, X. Prediction and optimization of syngas production from a kinetic-based biomass gasification process model. Fuel Process. Technol. 2021, 212, 106604. [Google Scholar] [CrossRef]
  106. Peters, J.F.; Banks, S.W.; Bridgwater, A. V.; Dufour, J. A kinetic reaction model for biomass pyrolysis processes in Aspen Plus. Appl. Energy 2017, 188, 595–603. [Google Scholar] [CrossRef]
  107. Di Blasi, C. Modeling chemical and physical processes of wood and biomass pyrolysis. Prog. Energy Combust. Sci. 2008, 34, 47–90. [Google Scholar] [CrossRef]
  108. Krijnen, W.P.; Wit, E. Computational and statistical methods for chemical engineering; ISBN 9781032013244.
  109. Ge, Z.; Song, Z. Process Monitoring Based on Independent Component Analysis−Principal Component Analysis (ICA−PCA) and Similarity Factors. Ind. Eng. Chem. Res. 2007, 46, 2054–2063. [Google Scholar] [CrossRef]
  110. Williams, C.L.; Westover, T.L.; Emerson, R.M.; Tumuluru, J.S.; Li, C. Sources of Biomass Feedstock Variability and the Potential Impact on Biofuels Production. Bioenergy Res. 2016, 9, 1–14. [Google Scholar] [CrossRef]
  111. Resch, M.G.; Ladisch, M.R. Analysis, Impacts, and Solutions to Biomass Variability for Production of Fuels and Value-Added Products. ACS Sustain. Chem. Eng. 2020, 8, 15375–15377. [Google Scholar] [CrossRef]
  112. González Martínez, M.; Floquet, P.; Dupont, C.; da Silva Perez, D.; Meyer, X. mi Assessing the impact of woody and agricultural biomass variability on its behaviour in torrefaction through Principal Component Analysis. Biomass and Bioenergy 2020, 134, 105474. [Google Scholar] [CrossRef]
  113. MULTIVARIATE STATISTICAL PROCESS CONTROL AND INDUSTRIAL APPLICATIONS - ProQuest. n.d. Available online: https://www.proquest.com/openview/207b6bafd5110b23915b2f4994723514/1?pq-origsite=gscholar&cbl=39817 (accessed on 31 July 2023).
  114. Clark, V. Multivariate data analysis in industrial practice: by Paul J. LEWI John Wiley and Sons, Chichester, 1982 (256 pp., $29.95/£13.75, ISBN 0471 10466 3). Comput. Stat. Data Anal. 1983, 1, 289–290. [Google Scholar] [CrossRef]
  115. Principal Component Analysis for Special Types of Data. Princ. Compon. Anal. 2002, 338–372. [CrossRef]
  116. Canonical Correlation Analysis: Uses and Interpretation - Bruce Thompson - Google Libri. n.d. Available online: https://books.google.it/books?hl=it&lr=&id=Dk0XINOvsw8C&oi=fnd&pg=PA11&dq=Canonical+correlation+analysis:+uses+and+interpretation+1984&ots=3bDu3-ZXuh&sig=cAomz5x1Xjj3nzyA0aIVRKT6ZD8#v=onepage&q=Canonical correlation analysis%3A uses and interpretation 1984&f=false (accessed on 31 July 2023).
  117. Nachtergaele, P.; Thybaut, J.; De Meester, S.; Drijvers, D.; Saeys, W.; Dewulf, J. Multivariate Analysis of Industrial Biorefinery Processes: Strategy for Improved Process Understanding with Case Studies in Fatty Acid Production. Ind. Eng. Chem. Res. 2020, 59, 7732–7745. [Google Scholar] [CrossRef]
  118. Li, J.; Xu, K.; Yao, X.; Chen, S. Prediction and optimization of syngas production from steam gasification: Numerical study of operating conditions and biomass composition. Energy Convers. Manag. 2021, 236, 114077. [Google Scholar] [CrossRef]
  119. Meuzelaar, H.L.C.; Hoesterey, B.L.; Windig, W.; Hill, G.R. Prediction and modeling of coal conversion reactions by pyrolysis mass spectrometry and multivariate statistical analysis. Fuel Process. Technol. 1987, 15, 59–70. [Google Scholar] [CrossRef]
  120. Tiong, L.; Komiyama, M. Statistical analysis of microalgae supercritical water gasification: Reaction variables, catalysis and reaction pathways. J. Supercrit. Fluids 2022, 183, 105552. [Google Scholar] [CrossRef]
  121. Dellavedova, M.; Derudi, M.; Biesuz, R.; Lunghi, A.; Rota, R. On the gasification of biomass: Data analysis and regressions. Process Saf. Environ. Prot. 2012, 90, 246–254. [Google Scholar] [CrossRef]
  122. Motta, I.L.; Marchesan, A.N.; Maciel Filho, R.; Wolf Maciel, M.R. Correlating biomass properties, gasification performance, and syngas applications of Brazilian feedstocks via simulation and multivariate analysis. Ind. Crops Prod. 2022, 181, 114808. [Google Scholar] [CrossRef]
  123. Baggio, P.; Baratieri, M.; Fiori, L.; Grigiante, M.; Avi, D.; Tosi, P. Experimental and modeling analysis of a batch gasification/pyrolysis reactor. Energy Convers. Manag. 2009, 50, 1426–1435. [Google Scholar] [CrossRef]
  124. Adeyemi, I.; Janajreh, I.; Arink, T.; Ghenai, C. Gasification behavior of coal and woody biomass: Validation and parametrical study. Appl. Energy 2017, 185, 1007–1018. [Google Scholar] [CrossRef]
  125. Gil, M. V.; González-Vázquez, M.P.; García, R.; Rubiera, F.; Pevida, C. Assessing the influence of biomass properties on the gasification process using multivariate data analysis. Energy Convers. Manag. 2019, 184, 649–660. [Google Scholar] [CrossRef]
  126. Obafemi, O.; Stephen, A.; Ajayi, O.; Nkosinathi, M. A survey of Artificial Neural Network-based Prediction Models for Thermal Properties of Biomass. Procedia Manuf. 2019, 33, 184–191. [Google Scholar] [CrossRef]
  127. George, J.; Arun, P.; Muraleedharan, C. Assessment of producer gas composition in air gasification of biomass using artificial neural network model. Int. J. Hydrogen Energy 2018, 43, 9558–9568. [Google Scholar] [CrossRef]
  128. Ranade, N. V.; Nagarajan, S.; Sarvothaman, V.; Ranade, V. V. ANN based modelling of hydrodynamic cavitation processes: Biomass pre-treatment and wastewater treatment. Ultrason. Sonochem. 2021, 72, 105428. [Google Scholar] [CrossRef] [PubMed]
  129. Brown, D.; Fuchino, T.; Maréchal, F. Solid fuel decomposition modelling for the design of biomass gasification systems. Comput. Aided Chem. Eng. 2006, 21, 1661–1666. [Google Scholar] [CrossRef]
  130. Sreejith, C.C.; Muraleedharan, C.; Arun, P. Performance prediction of fluidised bed gasification of biomass using experimental data-based simulation models. Biomass Convers. Biorefinery 2013, 3, 283–304. [Google Scholar] [CrossRef]
Preprints 81460 g001
Figure 1. - GMM training pathway: 2-D representation in the α, β plan and highlights on the equilibrium and non-equilibrium coordinates [46].
Figure 1. - GMM training pathway: 2-D representation in the α, β plan and highlights on the equilibrium and non-equilibrium coordinates [46].
Preprints 81460 g001
Preprints 81460 g002
Figure 2. – Model algorithm flowchart developed by [69].
Figure 2. – Model algorithm flowchart developed by [69].
Preprints 81460 g002
Preprints 81460 g003
Figure 3. – A basic kinetic model for biomass gasification [71].
Figure 3. – A basic kinetic model for biomass gasification [71].
Preprints 81460 g003
Preprints 81460 g004
Figure 4. - A basic thermodynamic equilibrium model for biomass gasification [53].
Figure 4. - A basic thermodynamic equilibrium model for biomass gasification [53].
Preprints 81460 g004
Preprints 81460 g005
Figure 5. - ANN model structure to predict producer gas composition and gas yield from biomass gasification in a fluidized-bed gasifier [32].
Figure 5. - ANN model structure to predict producer gas composition and gas yield from biomass gasification in a fluidized-bed gasifier [32].
Preprints 81460 g005
Preprints 81460 g006aPreprints 81460 g006bPreprints 81460 g006c
Figure 6. – Basic input/output diagram of (a) thermodynamic equilibrium modelling, (b) kinetic modelling, (c) CFD modelling, (d) ANN modelling, (e) process modelling for biomass gasification process.
Figure 6. – Basic input/output diagram of (a) thermodynamic equilibrium modelling, (b) kinetic modelling, (c) CFD modelling, (d) ANN modelling, (e) process modelling for biomass gasification process.
Preprints 81460 g006aPreprints 81460 g006bPreprints 81460 g006c
Table 1. Effect of gasifying agents on the composition of gas products [25].
Table 1. Effect of gasifying agents on the composition of gas products [25].
Gasifying agent H2 (%mol) CO2 (%mol) CO (%mol) CH4 (%mol) N2 (%mol) LHV (MJ/kg)
Air 3-13 10-18 5-28 0-7 40-50 4-6
Oxygen 20-30 25-40 20-30 5-10 0-1 7-8
Steam 30-50 8-25 20-40 6-15 0-1 9-11
Table 2. – Chemical reactions of gasification process [8,34,35].
Table 2. – Chemical reactions of gasification process [8,34,35].
Oxidation reaction
Volatiles Char
C O + 1 2 O 2 ⇿ C O 2   (1)
ΔH= - 283 kJ/mol		 C + 1 2 O 2 ⇿ C O   (3)
ΔH= - 111 kJ/mol
H 2 + 1 2 O 2 ⇿ H O 2   (2)
ΔH= - 242 kJ/mol		 C + O 2 ⇿ C O 2 ..   (4)
ΔH= - 394 kJ/mol
Boudouard reaction
C + C O 2 ⇿ 2 C O  (5)   ΔH= - 172 kJ/mol
Water-Gas reaction
Primary Secondary
C + H 2 O ⇿ C O + H 2   (6)
ΔH= - 131 kJ/mol		 C + 2 H 2 O ⇿ C O 2 + 2 H 2 (7)
ΔH= - 90 kJ/mol
Methanation reaction
C + 2 H 2 ⇿ C H 4  (8)  ΔH= - 75 kJ/mol
Water-Gas shift reaction
C O 2 + H 2 ⇿ C O + H 2 O  (9)  ΔH= - 41 kJ/mol
Steam Reforming reaction
C H 4 + H 2 O ⇿ C O + 3 H 2  (10)
ΔH= 206 kJ/mol
C n H + n H 2 O ⇿ n C O + n + m 2 H 2   (11)
Dry Reforming reaction
C H 4 + C O 2 ⇿ 2 C O + 2 H 2  (12)
ΔH= 247 kJ/mol
C n H m + n C O 2 ⇿ 2 n C O + m 2 H 2  (13)
Table 3. – Coefficients for the computation of the specific heat at constant pressure [44].
Table 3. – Coefficients for the computation of the specific heat at constant pressure [44].
Compound a b c d e f
CH4 4.75 1.200E-02 3.030E-06 -2.63E-09 0 0
H2O(gas) 6.97 3.464E-03 -4.833E-07 0 0 0
CO 6.48 1.566E-03 -2.387E-07 0 0 0
CO2 18.036 -4.474E-05 0 0 0 -158.08
H2 6.424 1.039E-03 -7.804E-08 0 0 0
N2 6.50 1.00E-03 0 0 0 0
H2O(liquid) 18 0 0 0 0 0
Table 4. - Standard Gibbs free energy and molar enthalpy formation [43].
Table 4. - Standard Gibbs free energy and molar enthalpy formation [43].
Compound H 0 (kcal/mol) G 0 (kcal/mol)
CH4 -17.810 -12.057
H2O(gas) -57.7979 -54.6351
CO -26.416 -32.808
CO2 -94.052 -94.26
H2 0 0
C(solid) 0 0
Table 5. – Basic blocks for gasification process in Aspen Plus.
Table 5. – Basic blocks for gasification process in Aspen Plus.
Aspen Plus Block Name Description
Thermodynamic equilibrium approach [53,104]
RYield
Preprints 81460 i001 		Usually called DECOMP block (DECOMP stays for decomposition), it is a yield reactor which converts the non-conventional inlet stream of biomass into its conventional components (carbon, hydrogen, oxygen, sulphur, nitrogen, and ash) by specifying the yield distribution according to the biomass ultimate analysis.
RStoic
Preprints 81460 i002 		Stoichiometric reactor, used to simulate the production of inorganic compounds. Indeed, DECOMP block creates N, Cl and S as elemental components that are known to produce mainly HCl, NH3 and H2S, and the results of the real fractional conversion model are closer to the experimental data than that of the chemical equilibrium. This is the reason why a stoichiometric reactor is needed to simulate the production of H2S, NH3 and HCl specifying the proper reactions and the fractional conversion for S, Cl2 and N.
RGibbs
Preprints 81460 i003 		Gibbs free energy reactor, which simulates drying, pyrolysis, partial oxidation, and gasification. It is possible to let the software individuate all the possible products without specifying any reactions or products by means of the option “Calculate phase equilibrium and chemical equilibrium”. Otherwise, it is also possible using the QET approach of the specified reactions to set the syngas composition by specifying a temperature approach for individual reactions by means of the option “Restrict chemical equilibrium – specify temperature approach or reaction extents”.
Total kinetic approach [105,106]
RYield
Preprints 81460 i004 		Yield reactor represents the virtual reaction step that decomposes the biomass into its three principal biochemical building blocks: cellulose, hemicellulose, and lignin. This reaction step does not represent any part of the actual pyrolysis reaction mechanism but is necessary for the following interlinked reaction model. The yields are calculated iteratively by an embedded Excel worksheet which determines the cellulose, hemicellulose, and lignin composition of the biomass according to its elemental composition.
RCSTR or RBatch
Preprints 81460 i005 		In the second phase, a kinetic reaction model is implemented for the primary pyrolysis reactions. It is an interlinked model of individual decomposition reactions of cellulose, hemicellulose and lignin, according to [62,107]. The reactor type can be chosen according to the pyrolysis reactor that wants to be modelled. For fast pyrolysis, the RCStir reactor is used, while the RBatch-type reactor is more suitable for slow pyrolysis modelling.
RYield
Preprints 81460 i006 		The secondary vapor reactions at longer residence times are implemented in Aspen Plus as an embedded Excel sheet which determines the yields of the RYield type secondary reactions reactor. The complete methodology and the corresponding equations
Table 6. - Input and output variables in the ANN model of [32].
Table 6. - Input and output variables in the ANN model of [32].
Range
Input variables
Ash content of dry biomass (g/kg) 5.5-11.0
Moisture content of wet biomass (g/kg) 62.8-25.0
Carbon content of dry biomass (g/kg) 458.9-505.4
Oxygen content of dry biomass (g/kg) 411.1-471.8
Hydrogen content of dry biomass (g/kg) 56.4-70.8
Equivalence ratio (ER) 0.19-0.47
Gasification temperature (T) (°C) 700-900
Steam to dry biomass ratio (SB) (kg/kg) 0-0.04
Output variables
Gas yield (m3/kg) 1.17-3.42
H2 volume fraction, dry basis (%) 4.97-26.17
CO volume fraction, dry basis (%) 10-29.47
CO2 volume fraction, dry basis (%) 9.82-18.60
CH4 volume fraction, dry basis (%) 2.40-6.07
Table 7. – Description of gasification modelling approaches.
Table 7. – Description of gasification modelling approaches.
Approach Features Pros Cons
Kinetic modelling
  • Finite time or volume
  • Explicitly accounts reactions kinetic, system hydrodynamics and particle size distribution
  • Accurate and detailed results even at low temperatures
  • Able to predict the spatial distribution of products in the reactor
  • ∙
  • Computationally intensive
  • Dependent on geometric parameters, so the applicability is limited to the specific plant the model is built for
  • Complete reaction mechanisms are often unknown or only partially known
  • Sensitive to gas-solid contacting process
Thermodynamic modelling
  • Assumption: the reactants react in a fully mixed condition for an infinite period of time
  • Zero dimensional
  • No chemical reactions or conversion mechanisms are needed
  • Can be improved by using the coefficients for equilibrium constants or yields distribution
  • Simple and easy to develop and implement
  • Independent of gasifier design, so the applicability is not restricted, and the model is flexible for various feedstocks and process parameters
  • Good prediction of maximum yield
  • Equilibrium condition may not be reached in real cases, especially at low temperatures
  • Over-under estimations of the amount of produced methane and char
CFD modelling
  • Based on mass, momentum, and heat balances in presence of gasification reactions
  • It applies the principles of fluid dynamics, numerical methods, and different algorithms to solve Navier-Stokes equations
  • It produces temperature, pressure, and velocity profile across the reactor at a steady or transient state
  • It can predict the flow pattern of reactants through the reactor together with the heat and mass transfer
  • Accurate prediction of syngas yield
  • Special software are often used for analysis, most of which are expensive
  • Large number of experimental data are required
  • Huge computational power is needed
MVA analysis
  • It applies the statistics principles to understand and exploit the correlation patterns between gasification variables
  • It is able to strongly reduce the number of variable to be monitored
  • It provides prediction of both dynamic behavior and equilibrium conditions
  • It requires a light computational burden
  • It does not add any physical interpretations of correlation
Process Simulation modelling with commercial software
  • The process is represented by means of single unit operations
  • A series of equations are solved based on kinetic or equilibrium models.
  • It takes into account the global process (i.e., exchangers, pumps, reactors, etc.) and not only the reaction step
  • It allows the estimation of the overall energy duty and economics of the system
  • Based on thermodynamic or kinetic modelling, it takes all their pros and cons. So, process simulation based on kinetic model is more complex to be developed, but more accurate, while when based on thermodynamic model is easier to develop but less trustable
  • Purposed and expensive software is required, such as Aspen Plus, Chemcad, Aspen HYSYS, etc.
Artificial neural network modelling
  • The model is trained on syngas composition and other experimental parameters
  • It is able to represent non-linearity
  • It accurately predicts experimental data used for the training set
  • Required a wide dataset of experimental data
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated