Induced Electrostatic Fields in the Presence of Conductors and Dielectrics: A Purely Laplace Equation-Based Treatment

Preprint

Article

Induced Electrostatic Fields in the Presence of Conductors and Dielectrics: A Purely Laplace Equation-Based Treatment

Altmetrics

Downloads

172

Views

Comments

George Bjornsen^*

This version is not peer-reviewed

Submitted:

19 February 2024

Posted:

20 February 2024

You are already at the latest version

Alerts

Abstract

This article studies electrostatic fields and potentials in the presence of conductors and point charges under the framework of solving Laplace’s equation with specifi ed boundary conditions. The results demonstrate that many problems posed and solved in elementary electrostatics through various heuristics such as the method of images, can be more rigorously treated under the solution framework of Laplace’s equation.

Keywords:

Subject: Physical Sciences - Mathematical Physics

1. Introduction

Since the times when electricity was studied by rubbing objects like amber and pith [1], empirical formulas [2] have been proposed for the electric force created by a charge at a given distance. By the 18th century, several prominent mathematicians and natural scientists were already aware of the inverse square dependence of the force, and in 1785, French physicist Charles–Augustin de Coulomb published his famous papers [3,4] stating the law now commonly referred to as Coulomb’s law. In modern terminology and notation, the law states that the electric field E produced at a point r due to a stationary charge q placed at the origin, is given by

\begin{matrix} E (r) = \frac{q}{4 π ϵ_{0} r^{2}} \hat{r}, \end{matrix}

or due to a volume charge density

ρ (r^{'})

distributed over a set

r^{'} \in D

\begin{matrix} E (r) = \int_{D} \frac{ρ}{4 π ϵ_{0} {∥r - r^{'}∥}^{3}} (r - r^{'}) d V^{'} . \end{matrix}

(1)

This formulation provided considerable mathematical advances in electrostatics [5], and mathematician Carl Friedrich Gauss used Coulomb’s law to formulate the so-called Gauss’s law or Gauss’s flux theorem [4,6], which states that the electric flux through a closed surface is proportional to the total charge enclosed by the surface, or, equivalently in differential form,

\nabla \cdot E = ρ / ϵ_{0},

where

ρ

is the electrostatic charge density and

\nabla \cdot A

for a vector field

A (r) \equiv A_{x} (r) \hat{x} + A_{y} (r) \hat{y} + A_{z} (r) \hat{z}

is defined as

\nabla \cdot A : = \frac{\partial A_{x}}{\partial x} + \frac{\partial A_{y}}{\partial y} + \frac{\partial A_{z}}{\partial z} .

With Maxwell’s unification of electromagnetism [7], it was proved that Gauss’s law is more general than Coulomb’s law, and continues to hold beyond electrostatics, even for time-varying fields and charge distributions, and ultimately, from the point of view of modern quantum electrodynamics [8,9,10], is a limitation on the degrees of freedom of the photon, the fundamental particle carrying the electromagnetic field.

An electrostatic field satisfying Coulomb’s law (1) is known to be conservative, i.e., the line integral of

E

from a point A to a point B depends only on the vector

r_{A \to B}

from A to

B .

Potential theory then tells us [11] that any such electrostatic field

E

can be expressed as

E = - \nabla V

for some differentiable scalar field

V .

Combining this with Gauss’s law yields the Poisson equation [12]

\nabla^{2} V = - ρ / ϵ_{0} .

If a region of space has no net charge density, Poisson’s equation reduces to

\nabla^{2} V = 0,

which is the so-called Laplace’s equation [13] arising in diverse application areas such as fluid flow [14], gravitation, electrodynamics [15], and general relativity and cosmology [16]. Due to the broad application and richness of Laplace’s equation, it has spawned a new mathematical field of harmonic functions [17]. In this work, we examine some solutions of Laplace’s equation with various boundary conditions in the context of calculating electric fields and potentials produced by static charge distributions.

2. Laplace’s Equation and Electric Fields

We will solve Laplace’s equation

\nabla^{2} V = 0

with various boundary conditions to determine the electric potentials (and thereby, the electric fields) produced by various charge distributions and conductors and dielectrics [18]. Since the boundary conditions and charge distributions we will consider will typically have some sort of spherical symmetry, it will be easier to solve Laplace’s equation in the spherical polar coordinates rather than Cartesian coordinates. To facilitate the solution, we first state the following lemma on the form of the Laplace operator in spherical polar coordinates.

Lemma 1.

The Laplacian operator

\nabla^{2}

can be represented in spherical polar coordinates

(r, θ, ϕ)

\begin{matrix} \nabla^{2} \equiv \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial}{\partial r}) + \frac{1}{r^{2} sin θ} \frac{\partial}{\partial θ} (sin θ \frac{\partial}{\partial θ}) + \frac{1}{r^{2} {sin}^{2} θ} \frac{\partial^{2}}{\partial ϕ^{2}} . \end{matrix}

(2)

For completeness, we provide the proof of Lemma 1 in the Appendix.

Remark 1.

Similar to Lemma 1, one can readily establish that the Laplacian operator

\nabla^{2}

can be written in the cylindrical coordinates

(ρ, ϕ, z)

\begin{matrix} \nabla^{2} \equiv \frac{1}{ρ} \frac{\partial}{\partial ρ} (ρ \frac{\partial}{\partial ρ}) + \frac{1}{ρ^{2}} \frac{\partial^{2}}{\partial ϕ^{2}} + \frac{\partial^{2}}{\partial z^{2}} . \end{matrix}

(3)

We now establish the solution of Laplace’s equation in spherical coordinates with spherical boundary conditions.

Proposition 1.

Consider Laplace’s equation

\nabla^{2} V = 0

with one or more boundary conditions of the form

\begin{matrix} V (r_{i}, θ, ϕ) \equiv f_{i} (θ), \end{matrix}

(4)

\begin{matrix} \frac{\partial V}{\partial r} |_{r = r_{j}} \equiv g_{j} (θ), \end{matrix}

(5)

for piecewise continuous functions

{f_{i} : [0, π] \to R}_{i}

and

{g_{j} : [0, π] \to R}_{j} .

Then, the solution, if it exists, is of the form

V (r, θ, ϕ) = \sum_{l = 0}^{\infty} (A_{l} r^{l} + \frac{B_{l}}{r^{l + 1}}) P_{l} (cos θ),

where the constants

{A_{l}}_{l = 0}^{\infty}

and

{B_{l}}_{l = 0}^{\infty}

are determined by the functions

{f_{i}}_{i}

and

{g_{j}}_{j},

and the function

P_{l} (\cdot)

is the

l^{th}

order Legendre polynomial given as [19]

P_{l} (t) = \frac{1}{2^{l} l!} \frac{d^{l}}{d t^{l}} ({(t^{2} - 1)}^{l}) .

In order to prove Proposition 1, we need 2 additional lemmas, whose proofs are omitted.

Lemma 2

([20]). The solution to the Laplace equation

\nabla^{2} V = 0

with boundary conditions

V (r_{0}, θ, ϕ) = f (θ, ϕ)

is uniquely determined by the function f and the radius

r_{0}

(

> 0

). The solution to the Laplace equation with boundary conditions

{\partial V / \partial r |}_{r = r_{0}} = g (θ, ϕ)

is uniquely determined by the function g and the radius

r_{0}

(

> 0

), up to an additive constant.

Lemma 3

([21]). Given any piecewise continuous function

f (x)

with finitely many discontinuities in the interval

[- 1, 1],

consider the sequence of sums

f_{n} (x) = \sum_{l = 0}^{n} a_{l} P_{l} (x),

where

P_{l} (x)

is theLegendre polynomialdefined as

P_{l} (t) = \frac{1}{2^{l} l!} \frac{d^{l}}{d t^{l}} ({(t^{2} - 1)}^{l}) .

Then, we have

lim_{n \to \infty} \int_{- 1}^{1} {| f_{n} (x) - f (x) |}^{2} d x = 0,

provided we take

a_{l} = \frac{2 l + 1}{2} \int_{- 1}^{1} f (x) P_{l} (x) d x .

Proof

(Proof of Proposition 1). To solve Laplace’s equation with the stated boundary conditions [22], we will use the so-called separation of variables method [23]. We note that the setting of Proposition 1 is similar to that of Lemma 2, except that the functions

f_{i}

and

g_{j}

are now functions of

θ

only; therefore, by Lemma 2, if we can find a solution

V (r, θ, ϕ) \equiv V (r, θ)

matching the boundary conditions, then that would be the unique solution, at most up to an additive constant. To this end, let us define a trial solution of Laplace’s equation of the form

V (r, θ) \equiv R (r) Θ (θ),

where

R : R^{+} \to R

and

Θ : [0, π] \to R

are twice differentiable functions. Using (2), the Laplace equation then reduces to

\begin{matrix} \frac{Θ}{r^{2}} \frac{d}{d r} (r^{2} R^{'} (r)) + \frac{R}{r^{2} sin θ} \frac{d}{d θ} (sin θ \cdot Θ^{'} (θ)) & = 0, \end{matrix}

\begin{matrix} \frac{1}{R} \frac{d}{d r} (r^{2} R^{'} (r)) + \frac{1}{Θ \cdot sin θ} \frac{d}{d θ} (sin θ \cdot Θ^{'} (θ)) & = 0 . \end{matrix}

(6)

Now, Equation (6) has to hold for every

(r, θ)

in the domain, therefore, we must have

\frac{1}{R} \frac{d}{d r} (r^{2} R^{'} (r)) = - \frac{1}{Θ \cdot sin θ} \frac{d}{d θ} (sin θ \cdot Θ^{'} (θ)) = K,

where K is a constant independent of the coordinates

(r, θ) .

Examining the

θ

equation first, we obtain, through a slight rearrangement,

\frac{d}{d θ} (sin θ \cdot Θ^{'} (θ)) + K Θ \cdot sin θ = 0 .

Writing

ξ (cos θ) : = Θ (θ)

enables us to write

Θ^{'} (θ) = - ξ^{'} (cos θ) sin θ,

and the equation therefore reduces to

- \frac{d}{d θ} ({sin}^{2} θ ξ^{'} (cos θ)) + K ξ (cos θ) sin θ = 0 .

Now, dividing throughout by

sin θ,

writing

u : = cos θ,

and noting that

- \frac{1}{sin θ} \frac{d}{d θ} ({sin}^{2} θ ξ^{'} (cos θ)) = \frac{d}{d u} ({sin}^{2} θ ξ^{'} (u)) = \frac{d}{d u} ((1 - u^{2}) ξ^{'} (u)),

the

θ

equation becomes, in terms of

u : = cos θ

as the independent variable,

\begin{matrix} \frac{d}{d u} ((1 - u^{2}) θ ξ^{'} (u)) + K ξ (u) = 0 . \end{matrix}

(7)

Equation (7) is the Legendre equation [19] with

K = l (l + 1) .

For non-integer

l \in R,

the solutions to Legendre’s equation are power series with radius of convergenece smaller than

1 .

For the current problem, however, the domain is

u \in [- 1, 1] .

Therefore, the only possible solutions to (7) that would make the trial solution valid, should be polynomials. Through the application of Sturm–Liouville theory (see, for example, [21]), we can conclude that the solutions are indeed polynomials when l is a non-negative integer. Therefore, for the trial solution to be valid, we must have

K = l (l + 1)

for a non-negative integer

l,

and the corresponding solution of the

θ

equation becomes

\begin{matrix} Θ_{l} (θ) = P_{l} (cos θ) \end{matrix}

(8)

up to a multiplicative constant. To tackle the r equation, writing

ζ (log r) : = R (r)

enables us to write

ζ^{'} (log r) = r R^{'} (r),

and a change of independent variable to

v : = log r

enables us to write the v equation as

\frac{d}{d r} (r ζ^{'} (v)) - l (l + 1) ζ (v) = 0,

and replacing r with

e^{v}

leads to

e^{- v} \frac{d}{d v} (e^{v} ζ^{'} (v)) - l (l + 1) ζ (v) = 0,

which simplifies to

\begin{matrix} ζ^{''} (v) + ζ^{'} (v) - l (l + 1) ζ (v) = 0 . \end{matrix}

(9)

From elementary calculus, Equation (9) has the general solution of the form

ζ (v) = A \cdot exp (α v) + A \cdot exp (β v),

where

α

and

β

are solutions of the quadratic equation

x^{2} + x - l (l + 1) = 0 .

We immediately obtain

α = l

and

β = - (l + 1),

which yields the solution

ζ (v) = A \cdot exp (l v) + B \cdot exp (- (l + 1) v),

and the solution to the r equation then becomes

\begin{matrix} R_{l} (r) = A_{l} r^{l} + \frac{B_{l}}{r^{l + 1}} . \end{matrix}

(10)

Finally, noting that since the Laplace equation is linear, any linear combination of a set of valid solutions will also be a solution, we come up with the largest set of soltuions that the trial solution enables us to get, by combining (10) and (8):

\begin{matrix} V (r, θ, ϕ) = \sum_{l = 0}^{\infty} (A_{l} r^{l} + \frac{B_{l}}{r^{l + 1}}) P_{l} (cos θ) . \end{matrix}

(11)

Now, by uniqueness (Lemma 2), if we can find constants

{A_{l}, B_{l}}

matching the boundary conditions (4) and/or (5), then (11) with the determined constants will be the unique solution to the problem. Let us now focus on the boundary conditions (4). The result will similarly follow for the boundary conditions (5). Since

f_{i}

is a piecewise continuous function, by the completeness of Legendre polynomials (Lemma 3), there exist constants

{A_{l}, B_{l}}

for which

f_{i} (θ) = \sum_{l = 0}^{\infty} (A_{l} r_{i}^{l} + \frac{B_{l}}{r_{i}^{l + 1}}) P_{l} (cos θ) .

More specifically, we have, in this case,

\begin{matrix} A_{l} r_{i}^{l} + \frac{B_{l}}{r_{i}^{l + 1}} = \frac{2 l + 1}{2} \int_{0}^{π} f_{i} (θ) P_{l} (cos θ) sin θ d θ . \end{matrix}

(12)

Note that at least 2 such boundary conditions are needed to uniquely determine the constants

A_{l}

and

B_{l} .

For such consistent boundary conditions, (11) with the constants

A_{l}

and

B_{l}

determined by the boundary conditions (12) is the unique solution to the Laplace equation. □

We will now directly use Proposition 1 to calculate electric potentials (and, thereby, electric fields) rigorously for various electrostatics problems commonly posed in many textbooks (see, for example, [15]).

2.1. Conducting Sphere in Uniform Electric Field

Consider a conducting sphere of radius

a > 0

(with center at the origin) placed in a uniform electric field

E_{0} .

Without loss of generality, let

E_{0} = E_{0} \hat{z} = E_{0} cos θ \hat{r} - E_{0} sin θ \hat{θ} .

If a unique solution exists in the region

r > a,

it must only be determined by the vector

E_{0},

and therefore,

V (r, θ, ϕ)

must be independent of

ϕ .

(This property is referred to as azimuthal symmetry.) We can then write a trial solution as

V (r, θ, ϕ) = \sum_{l = 0}^{\infty} (A_{l} r^{l} + \frac{B_{l}}{r^{l + 1}}) P_{l} (cos θ),

which yields

\frac{\partial V}{\partial r} = \sum_{l = 0}^{\infty} (l A_{l} r^{l - 1} - \frac{(l + 1) B_{l}}{r^{l + 2}}) P_{l} (cos θ) .

Since the conductor is finite, the distortion caused by it to the electric field [24,25] is local and therefore, as

r \to \infty,

the electric field must approach

E_{0} .

We thus have

{lim}_{r \to \infty} \partial V / \partial r = - E_{0} cos θ,

which is only possible if

A_{l} = 0

for

l \geq 2,

and

A_{1} = - E_{0} .

The solution then becomes

\begin{matrix} V (r, θ, ϕ) = A_{0} + \frac{B_{0}}{r} + (\frac{B_{1}}{r^{2}} - E_{0} r) cos θ + \sum_{l = 2}^{\infty} \frac{B_{l}}{r^{l + 1}} P_{l} (cos θ) \end{matrix}

(13)

for some constants

A_{0}, B_{0}, B_{1}, \dots .

Now, for a conductor, the electric field at the surface is purely along the normal to the surface, and therefore, we have

\frac{\partial V}{\partial θ} |_{r = a} = 0,

which, combining with (13), yields

(\frac{B_{1}}{a^{2}} - E_{0} a) sin θ + sin θ \sum_{l = 2}^{\infty} \frac{B_{l}}{a^{l + 1}} P_{l}^{'} (cos θ) = 0

for

θ \in [0, π] .

This is satisfied if

B_{1} = E_{0} a^{3}

and

B_{l} = 0

for

l \geq 2,

and the solution therefore becomes

V (r, θ, ϕ) = A_{0} + \frac{B_{0}}{r} + (\frac{a^{3}}{r^{2}} - r) E_{0} cos θ,

which yields the electric field

\begin{matrix} E (r, θ, ϕ) & = - \nabla V \\ = - \frac{\partial V}{\partial r} \hat{r} - \frac{1}{r} \frac{\partial V}{\partial θ} \hat{θ} \\ = (\frac{B_{0}}{r^{2}} + (\frac{2 a^{3}}{r^{3}} + 1) E_{0} cos θ) \hat{r} + (\frac{a^{3}}{r^{3}} - 1) E_{0} sin θ \hat{θ} \\ = E_{0} + \frac{a^{3}}{r^{3}} (2 (E_{0} \cdot \hat{r}) \hat{r} - (E_{0} \cdot \hat{θ}) \hat{θ}) + \frac{B_{0}}{r^{2}} \hat{r} \\ = E_{0} + \frac{a^{3}}{r^{3}} (2 (E_{0} \cdot \hat{r}) \hat{r} - [E_{0} - (E_{0} \cdot \hat{r}) \hat{r}]) + \frac{B_{0}}{r^{2}} \hat{r} \\ = E_{0} + \frac{a^{3}}{r^{3}} (3 (E_{0} \cdot \hat{r}) \hat{r} - E_{0}) + \frac{B_{0}}{r^{2}} \hat{r} \\ = (1 - \frac{a^{3}}{r^{3}}) E_{0} + (\frac{3 a^{3}}{r^{3}} (E_{0} \cdot \hat{r}) + \frac{B_{0}}{r^{2}}) \hat{r} . \end{matrix}

(14)

Note that (14) satisfies

{lim}_{r \to \infty} E (r, θ, ϕ) = E_{0},

as required. However, the constant

B_{0}

is still undetermined. It is a measure of the state of the conductor, as can be seen from the following. From (14), we have

\begin{matrix} E_{r} (a, θ, ϕ) & = 3 (E_{0} \cdot \hat{r}) + \frac{B_{0}}{a^{2}} \\ = 3 E_{0} cos θ + \frac{B_{0}}{a^{2}} . \end{matrix}

(15)

Since the electric field inside a conductor is zero, we have that the surface charge density induced on the sphere is given by

σ (θ, ϕ) = ϵ_{0} E_{r} (a, θ, ϕ) = 3 ϵ_{0} E_{0} cos θ + \frac{ϵ_{0} B_{0}}{a^{2}} .

The total charge on the conductor is then given by

\begin{matrix} Q & = a^{2} \int_{0}^{π} \int_{0}^{2 π} σ (θ, ϕ) sin θ d θ d ϕ \\ = 4 π ϵ_{0} B_{0}, \end{matrix}

(16)

which enables us to finally write the electric field in terms of the physical invariants of the system as

E = (1 - \frac{a^{3}}{r^{3}}) E_{0} + (\frac{3 a^{3}}{r^{3}} (E_{0} \cdot \hat{r}) + \frac{Q}{4 π ϵ_{0} r^{2}}) \hat{r} .

This essentially says that the total net charge on the conductor gets distributed in such a way as to produce the same field (outside the conductor) as a point charge placed at the center. In particular, if we place an uncharged conductor inside a uniform electrostatic field

E_{0},

then the final electrostatic field will be given by

\begin{matrix} E = (1 - \frac{a^{3}}{r^{3}}) E_{0} + \frac{3 a^{3}}{r^{3}} (E_{0} \cdot \hat{r}) \hat{r} . \end{matrix}

(17)

We finally note that this expression for the electric field is “coordinate free” in the sense that it is only a function of the vector

E_{0}

and the radius vector

r

at each point, the latter of which essentially encodes the position of the sphere.

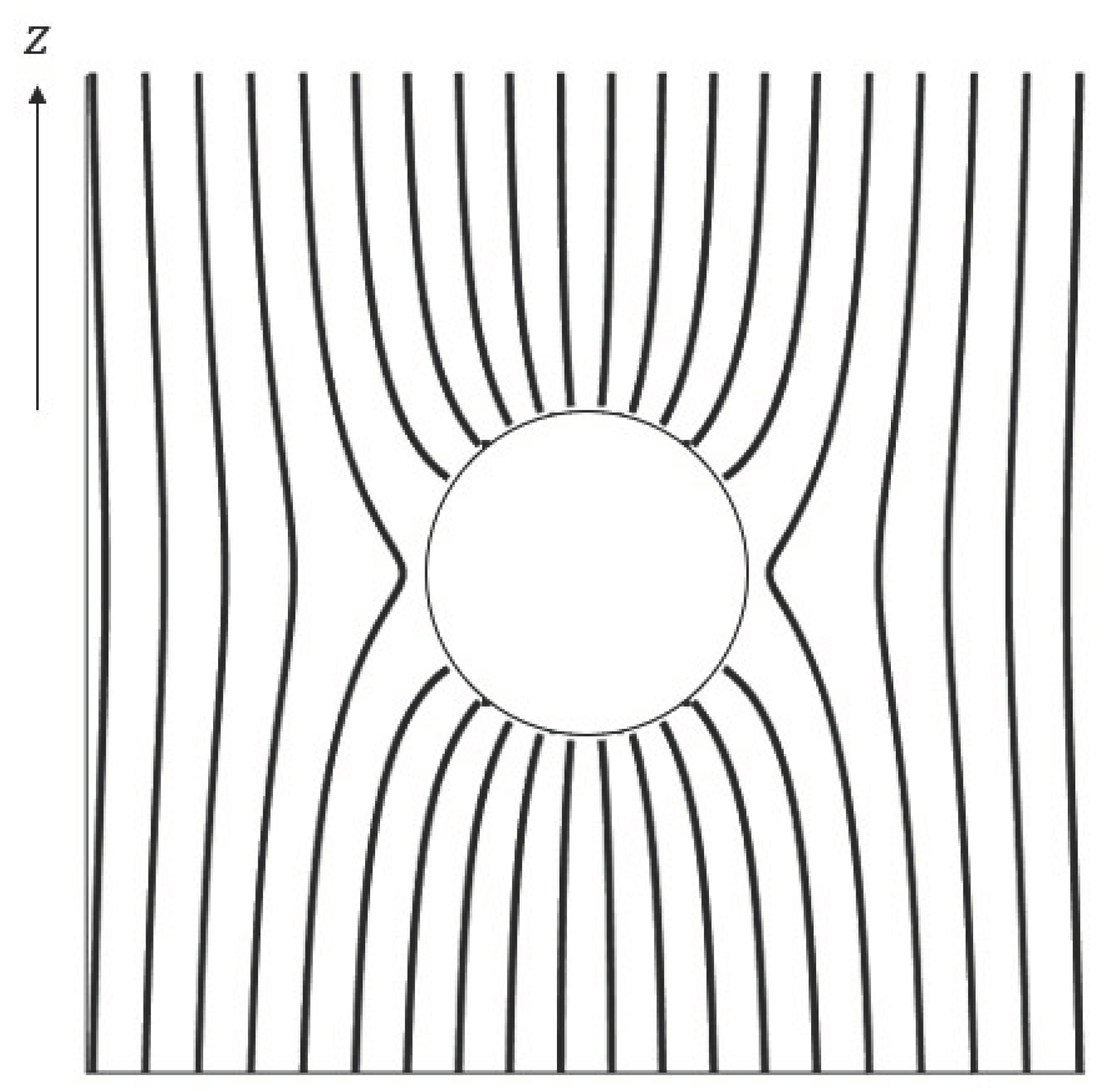
Figure 1 illustrates the electric field lines on a vertical plane (i.e., containing the z axis) obtained from the electric field in (17). As expected, far away from the sphere, the lines are vertical, while close by, they are “distorted” by the presence of the conductor. We also note that the field lines always enter and leave the sphere normally, and field abruptly drops to 0 as soon as we cross the boundary into the conductor. Finally, the field lines are seen to be the densest around the poles of the conductor (

r = a, θ = 0, π

), which can also be verified analytically from Equation (17). An analytical derivation yields a maximum field strength of

3 E_{0} .

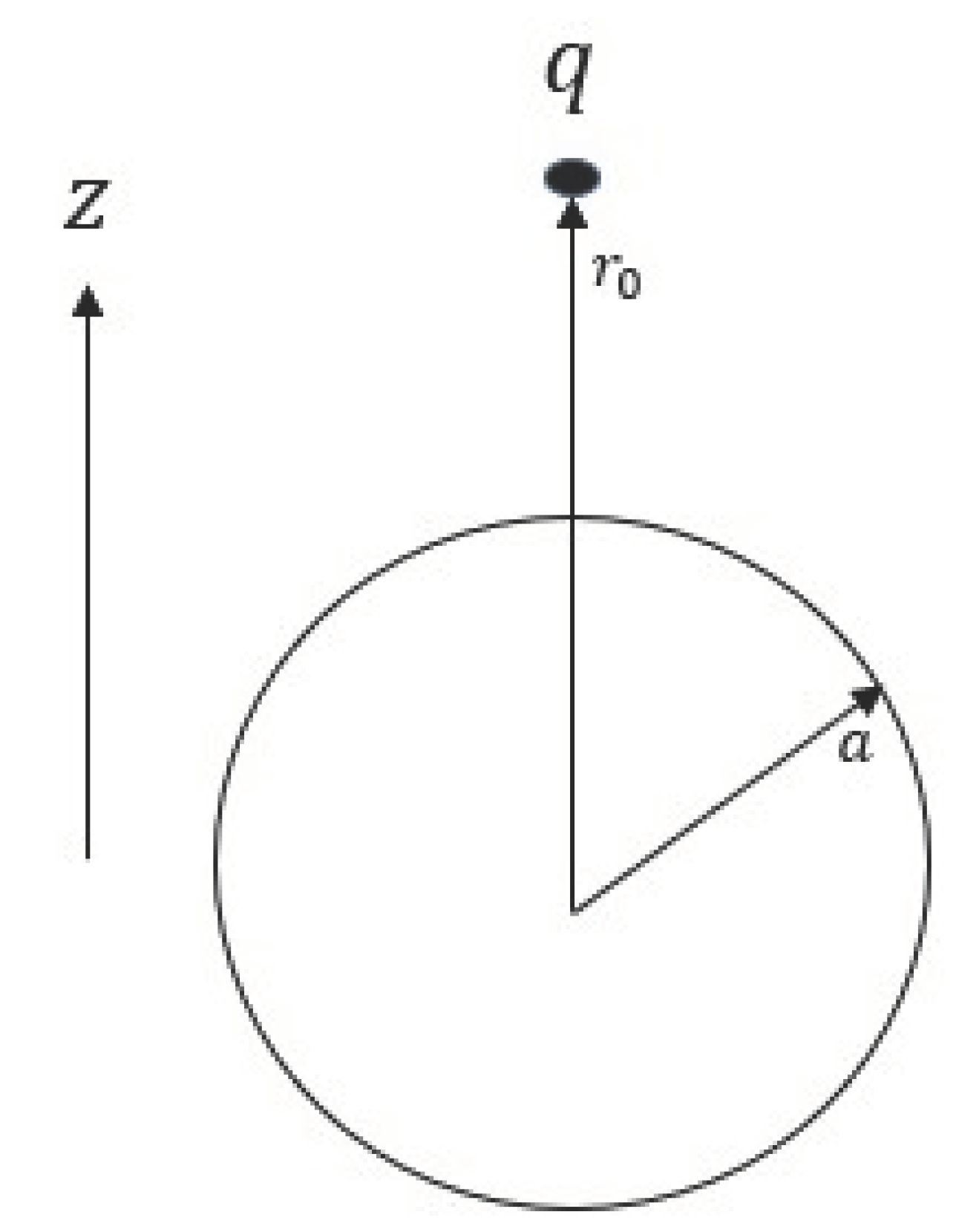
2.2. Conducting Sphere Near a Point Charge

Consider a conducting sphere of radius

a > 0

(with center at the origin) placed near a point charge q located at

r_{0} \hat{z}

with

r_{0} > a

(see Figure 2). Since the conducting sphere is an equipotential, let it be at potential

V_{0} .

The overall potential

V (r, θ, ϕ)

[26] for

r > a

can be written as

V (r, θ, ϕ) = V_{q} (r, θ, ϕ) + \tilde{V} (r, θ, ϕ),

where

V_{q}

is the potential due to the charge q and

\tilde{V}

satisfies Laplace equation with appropriate boundary conditions.

To determine these boundary conditions, we note that the potential due to the charge q at a point

(a, θ, ϕ)

on the sphere (assuming the boundary conditions

{lim}_{r \to \infty} V (r, θ, ϕ) = 0

) is given by Coulomb’s law as

V_{q} (a, θ, ϕ) = \frac{q}{4 π ϵ_{0}} \cdot \frac{1}{{(r_{0}^{2} - 2 r_{0} a cos θ + a^{2})}^{1 / 2}} .

Therefore,

\tilde{V}

satisfies the boundary condition

\begin{matrix} \tilde{V} (a, θ, ϕ) & = V_{0} - \frac{q}{4 π ϵ_{0}} \cdot \frac{1}{{(r_{0}^{2} - 2 r_{0} a cos θ + a^{2})}^{1 / 2}} \\ = V_{0} - \frac{q}{4 π ϵ_{0} r_{0}} \cdot \frac{1}{{(1 - 2 \frac{a}{r_{0}} cos θ + \frac{a^{2}}{r_{0}^{2}})}^{1 / 2}} . \end{matrix}

(18)

Writing a trial solution

\tilde{V}

\tilde{V} (r, θ, ϕ) = \sum_{l = 0}^{\infty} (A_{l} r^{l} + \frac{B_{l}}{r^{l + 1}}) P_{l} (cos θ),

we observe that since we have the boundary conditions

{lim}_{r \to \infty} \tilde{V} (r, θ, ϕ) = 0,

we must have

A_{l} = 0

for all

l \geq 0 .

To obtain the coefficients

B_{l}

using (18), we need the following lemma.

Lemma 4

([13]). The series

\sum_{l = 0}^{\infty} P_{l} (x) t^{l}

converges absolutely for

x \in [- 1, 1]

and

t \in (0, 1),

and

\begin{matrix} \sum_{l = 0}^{\infty} P_{l} (x) t^{l} = \frac{1}{{(1 - 2 t x + t^{2})}^{1 / 2}} . \end{matrix}

(19)

Remark 2.

The expansion (19) is the basis for the so-called “multi-pole” expansion (see, for example, [27]).

Since we have

| cos θ | \leq 1

and

a < r_{0},

we can use Lemma 4 to rewrite (18) as

\begin{matrix} \tilde{V} (a, θ, ϕ) & = V_{0} - \frac{q}{4 π ϵ_{0} r_{0}} \sum_{l = 0}^{\infty} {(\frac{a}{r_{0}})}^{l} P_{l} (cos θ) \\ = V_{0} - \frac{q a / r_{0}}{4 π ϵ_{0}} \sum_{l = 0}^{\infty} {(\frac{a^{2}}{r_{0}})}^{l} \frac{1}{a^{l + 1}} P_{l} (cos θ) . \end{matrix}

(20)

Therefore, by the uniqueness theorem (Lemma 2), the coefficients

{B_{l}}_{l}

are given by

\begin{matrix} B_{0} & = a V_{0} - \frac{q a}{4 π ϵ_{0} r_{0}}, \end{matrix}

(21)

\begin{matrix} B_{l} & = - \frac{q a}{4 π ϵ_{0} r_{0}} {(\frac{a^{2}}{r_{0}})}^{l} for l \geq 1 . \end{matrix}

(22)

The general solution

\tilde{V}

is thus given by

\begin{matrix} \tilde{V} (r, θ, ϕ) = \frac{a V_{0}}{r} - \frac{q a}{4 π ϵ_{0} r_{0}} \sum_{l = 0}^{\infty} {(\frac{a^{2}}{r_{0}})}^{l} \frac{1}{r^{l + 1}} P_{l} (cos θ) \end{matrix}

(23)

for

r > a .

Equation (23) can be written in a more illuminating form as

\begin{matrix} \tilde{V} (r, θ, ϕ) & = \frac{a V_{0}}{r} - \frac{q a / r_{0}}{4 π ϵ_{0} r} \sum_{l = 0}^{\infty} {(\frac{a^{2}}{r r_{0}})}^{l} P_{l} (cos θ) \\ \overset{t o 0 p t ()}{=} \frac{a V_{0}}{r} - \frac{q a / r_{0}}{4 π ϵ_{0} r} \cdot \frac{1}{{(1 - \frac{2 a^{2}}{r r_{0}} cos θ + {(\frac{a^{2}}{r r_{0}})}^{2})}^{1 / 2}} \\ = \frac{a V_{0}}{r} - \frac{q a / r_{0}}{4 π ϵ_{0}} \cdot \frac{1}{{(r^{2} - 2 r \cdot \frac{a^{2}}{r_{0}} cos θ + {(\frac{a^{2}}{r_{0}})}^{2})}^{1 / 2}} . \end{matrix}

(24)

The overall potential is then given by

\begin{matrix} V (r, θ, ϕ) & = V_{q} (r, θ, ϕ) + \tilde{V} (r, θ, ϕ) \\ = \frac{q}{4 π ϵ_{0}} \cdot \frac{1}{{(r^{2} - 2 r r_{0} cos θ + r_{0}^{2})}^{1 / 2}} - \frac{q a / r_{0}}{4 π ϵ_{0}} \cdot \frac{1}{{(r^{2} - 2 r \cdot \frac{a^{2}}{r_{0}} cos θ + {(\frac{a^{2}}{r_{0}})}^{2})}^{1 / 2}} + \frac{a V_{0}}{r} . \end{matrix}

(25)

The potential (25) is the same as that produced by the charge q at

z = r_{0},

together with “virtual” charges

- q a / r_{0}

z = a^{2} / r_{0}

and

4 π ϵ_{0} a V_{0}

at the center of the conducting sphere [28]. This can also be obtained through the so-called method of images as used in many treatments of this topic [15]. Equation (25) also enables us to write the surface charge density on the sphere as

\begin{matrix} σ (θ, ϕ) & = - ϵ_{0} \frac{\partial V}{\partial r} |_{r = a} \\ = {[\frac{q}{4 π} \cdot \frac{r - r_{0} cos θ}{{(r^{2} - 2 r r_{0} cos θ + r_{0}^{2})}^{3 / 2}} - \frac{q a / r_{0}}{4 π} \cdot \frac{r - \frac{a^{2}}{r_{0}} cos θ}{{(r^{2} - 2 r \cdot \frac{a^{2}}{r_{0}} cos θ + {(\frac{a^{2}}{r_{0}})}^{2})}^{3 / 2}} + \frac{a ϵ_{0} V_{0}}{r^{2}}]}_{r = a} \\ = (\frac{q}{4 π} \cdot \frac{a - r_{0} cos θ}{{(a^{2} - 2 a r_{0} cos θ + r_{0}^{2})}^{3 / 2}}) - (\frac{q a / r_{0}}{4 π} \cdot \frac{a - \frac{a^{2}}{r_{0}} cos θ}{{(a^{2} - 2 a \cdot \frac{a^{2}}{r_{0}} cos θ + {(\frac{a^{2}}{r_{0}})}^{2})}^{3 / 2}}) + \frac{ϵ_{0} V_{0}}{a} \\ = (\frac{q}{4 π} \cdot \frac{a - r_{0} cos θ}{{(a^{2} - 2 a r_{0} cos θ + r_{0}^{2})}^{3 / 2}}) - (\frac{q r_{0}^{2}}{4 π a^{2}} \cdot \frac{a - \frac{a^{2}}{r_{0}} cos θ}{{(a^{2} - 2 a r_{0} cos θ + r_{0}^{2})}^{3 / 2}}) + \frac{ϵ_{0} V_{0}}{a} \\ = \frac{ϵ_{0} V_{0}}{a} - (\frac{q}{4 π a^{2}} \cdot \frac{a^{2} (r_{0} cos θ - a) + a r_{0} (r_{0} - a cos θ)}{{(a^{2} - 2 a r_{0} cos θ + r_{0}^{2})}^{3 / 2}}) \\ = \frac{ϵ_{0} V_{0}}{a} - (\frac{q}{4 π a} \cdot \frac{r_{0}^{2} - a^{2}}{{(a^{2} - 2 a r_{0} cos θ + r_{0}^{2})}^{3 / 2}}) . \end{matrix}

(26)

The charge density (26) can be integrated to obtain the total charge on the sphere as

\begin{matrix} Q_{tot} & = a^{2} \int_{0}^{π} \int_{0}^{2 π} σ (θ, ϕ) sin θ d ϕ d θ \\ = 4 π ϵ_{0} a V_{0} - \frac{a q}{2} \int_{0}^{π} \frac{(r_{0}^{2} - a^{2})}{{(a^{2} - 2 a r_{0} cos θ + r_{0}^{2})}^{3 / 2}} sin θ d θ . \end{matrix}

(27)

Writing

u : = {(a^{2} - 2 a r_{0} cos θ + r_{0}^{2})}^{1 / 2},

we have

\begin{matrix} u \frac{d u}{d θ} = a r_{0} sin θ . \end{matrix}

(28)

We can then continue (27) as

\begin{matrix} Q_{tot} & = 4 π ϵ_{0} a V_{0} - \frac{q (r_{0}^{2} - a^{2})}{2 r_{0}} \int_{r_{0} - a}^{r_{0} + a} \frac{1}{u^{2}} d u \\ = 4 π ϵ_{0} a V_{0} - \frac{q a}{r_{0}} . \end{matrix}

(29)

Equation (29) is often interpreted (see, for example, [15,27]) as the sum of the image charges

- \frac{q a}{r_{0}}

and

4 π ϵ_{0} a V_{0} .

2.3. Uniform Dielectric Sphere in Uniform Electric Field

Consider a sphere of radius

a > 0,

made of a linear deielectric material of electric susceptibility

χ

(with center at the origin) placed in a uniform electric field

E_{0} .

Without loss of generality, let

E_{0} = E_{0} \hat{z} = E_{0} cos θ \hat{r} - E_{0} sin θ \hat{θ} .

We now wish to find the field both inside and outside the sphere. As we shall see later (cf. Remark 4), this situation can be thought of as a generalization to the problem studied in Section 2.1. As argued in Section 2.1, this problem exhibits azimuthal symmetry since the boundary conditions are independent of

ϕ .

We can then write trial solutions for the potentials inside and outside the sphere as

\begin{matrix} V^{in} (r, θ, ϕ) & = \sum_{l = 0}^{\infty} (A_{l}^{in} r^{l} + \frac{B_{l}^{in}}{r^{l + 1}}) P_{l} (cos θ), \end{matrix}

(30)

\begin{matrix} V^{out} (r, θ, ϕ) & = \sum_{l = 0}^{\infty} (A_{l}^{out} r^{l} + \frac{B_{l}^{out}}{r^{l + 1}}) P_{l} (cos θ), \end{matrix}

(31)

We will now discuss the boundary conditions to this problems, which are what will turn out to cause the crucial differences in the solutions for this case. First, as argued in Section 2.1, the electric field must approach

E_{0}

r \to \infty,

and we therefore conclude that

A_{l}^{out} = 0

for

l \geq 2,

and

A_{1}^{out} = - E_{0} .

Further, since the field inside the sphere is finite,

V^{in}

must have finite derivatives as

r \to 0,

and (30) then leads us to conclude that

B_{l}^{in} = 0

for all

l .

Equations (30) and (31) then enable us to write down a global trial solution as

\begin{matrix} V (r, θ, ϕ) = \{\begin{matrix} \sum_{l = 0}^{\infty} A_{l}^{in} r^{l} P_{l} (cos θ), & r < a, \\ A_{0}^{out} + \frac{B_{0}^{out}}{r} + (\frac{B_{1}^{out}}{r^{2}} - E_{0} r) cos θ + \sum_{l = 2}^{\infty} \frac{B_{l}^{out}}{r^{l + 1}} P_{l} (cos θ), & r > a . \end{matrix} \end{matrix}

(32)

By the continuity of V at the surface of the dielectric, the two expressions in (32) must match at

r = a .

Rearrangement leads to

\begin{matrix} (A_{0}^{out} + \frac{B_{0}^{out}}{a} - A_{0}^{in}) + (\frac{B_{1}^{out}}{a^{2}} - E_{0} a - A_{1}^{in} a) cos θ + \sum_{l = 2}^{\infty} (\frac{B_{l}^{out}}{a^{l + 1}} - A_{l}^{in} a^{l}) P_{l} (cos θ) = 0 . \end{matrix}

(33)

Using the completeness of Legendre polynomials (Lemma 3) and noting that

P_{1} (cos θ) = cos θ,

Equation (33) enables us to write

\begin{matrix} A_{0}^{out} + \frac{B_{0}^{out}}{a} & = A_{0}^{in} = : V_{0}, \end{matrix}

(34)

\begin{matrix} A_{1}^{in} & = \frac{B_{1}^{out}}{a^{3}} - E_{0}, \end{matrix}

(35)

\begin{matrix} A_{l}^{in} & = \frac{B_{l}^{out}}{a^{2 l + 1}}, l \geq 2 . \end{matrix}

(36)

Finally, we come to the behavior of the electric field at the surface of the dielectric, which will yield additional boundary conditions and will be determined by the properties of the dielectric. The surface density of bound charges on the dielectric can be written as

\begin{matrix} σ (θ, ϕ) = ϵ_{0} {[\frac{\partial V^{in}}{\partial r} - \frac{\partial V^{out}}{\partial r}]}_{r = a} . \end{matrix}

(37)

This bound charge density, however, is also given by the radial component of the polarization vector

P,

i.e.,

σ (θ, ϕ) = {[P \cdot \hat{r}]}_{r = a} .

Finally, since the material is a linear dielectric, we have

P (r) = χ ϵ_{0} E (r)

for

∥r∥ < a .

We therefore have

\begin{matrix} σ (θ, ϕ) = - χ ϵ_{0} \cdot \frac{\partial V^{in}}{\partial r} |_{r = a} . \end{matrix}

(38)

Equations (37) and (38) enable us to write

\begin{matrix} {[(1 + χ) \frac{\partial V^{in}}{\partial r} - \frac{\partial V^{out}}{\partial r}]}_{r = a} = 0 . \end{matrix}

(39)

Using Lemma 3 again, the boundary condition (39) enables us to write

\begin{matrix} B_{0}^{out} & = 0, \end{matrix}

(40)

\begin{matrix} A_{1}^{in} & = - \frac{1}{1 + χ} (\frac{2 B_{1}^{out}}{a^{3}} + E_{0}), \end{matrix}

(41)

\begin{matrix} A_{l}^{in} & = - \frac{(l + 1) B_{l}^{out}}{l (1 + ξ) a^{2 l + 1}}, l \geq 2 . \end{matrix}

(42)

For

l \geq 2,

(36) and (42) can simultaneously hold only if

A_{l}^{in} = B_{l}^{out} = 0 .

Moreover, (35) and (41) enable us to solve for

B_{1}^{out}

\frac{B_{1}^{out}}{a^{3}} - E_{0} = - \frac{1}{1 + χ} (\frac{2 B_{1}^{out}}{a^{3}} + E_{0}),

i.e.,

B_{1}^{out} = a^{3} \frac{(1 - \frac{1}{1 + χ}) E_{0}}{1 + \frac{2}{1 + χ}} = \frac{χ}{χ + 3} a^{3} E_{0} .

This immediately yields

A_{1}^{in} = - \frac{3}{χ + 3} E_{0},

and we can finally write down the full solution (32) as

\begin{matrix} V (r, θ, ϕ) = \{\begin{matrix} V_{0} - \frac{3}{χ + 3} E_{0} r cos θ, & r < a, \\ V_{0} + ((\frac{χ}{χ + 3}) \frac{a^{3}}{r^{2}} - r) E_{0} cos θ, & r > a . \end{matrix} \end{matrix}

(43)

The potential (43) yields the electric field

\begin{matrix} E (r, θ, ϕ) & = - \nabla V \\ = - \frac{\partial V}{\partial r} \hat{r} - \frac{1}{r} \frac{\partial V}{\partial θ} \hat{θ} \\ = \{\begin{matrix} (\frac{3}{χ + 3}) E_{0} cos θ \hat{r} - (\frac{3}{χ + 3}) E_{0} sin θ \hat{θ}, & r < a \\ (1 + \frac{2 χ a^{3}}{(χ + 3) r^{3}}) E_{0} cos θ \hat{r} + ((\frac{χ}{χ + 3}) \frac{a^{3}}{r^{3}} - 1) E_{0} sin θ \hat{θ}, & r \geq a . \end{matrix} \end{matrix}

The electric field inside can then be written as

\begin{matrix} E^{in} = (\frac{3}{χ + 3}) E_{0} (cos θ \hat{r} - sin θ \hat{θ}) = (\frac{3}{χ + 3}) E_{0}, \end{matrix}

(44)

which turns out to be uniform. The field outside can be written as

\begin{matrix} E^{out} & = E_{0} + \frac{a^{3}}{r^{3}} (2 (\frac{χ}{χ + 3}) (E_{0} \cdot \hat{r}) \hat{r} - (\frac{χ}{χ + 3}) (E_{0} \cdot \hat{θ}) \hat{θ}) \\ = E_{0} + \frac{a^{3}}{r^{3}} (\frac{χ}{χ + 3}) (2 (E_{0} \cdot \hat{r}) \hat{r} - [E_{0} - (E_{0} \cdot \hat{r}) \hat{r}]) \end{matrix}

(45)

\begin{matrix} = E_{0} + \frac{a^{3}}{r^{3}} (\frac{χ}{χ + 3}) (3 (E_{0} \cdot \hat{r}) \hat{r} - E_{0}) \end{matrix}

(46)

\begin{matrix} = (1 - \frac{χ a^{3}}{(χ + 3) r^{3}}) E_{0} + (\frac{3 χ a^{3}}{(χ + 3) r^{3}} (E_{0} \cdot \hat{r})) \hat{r} . \end{matrix}

(47)

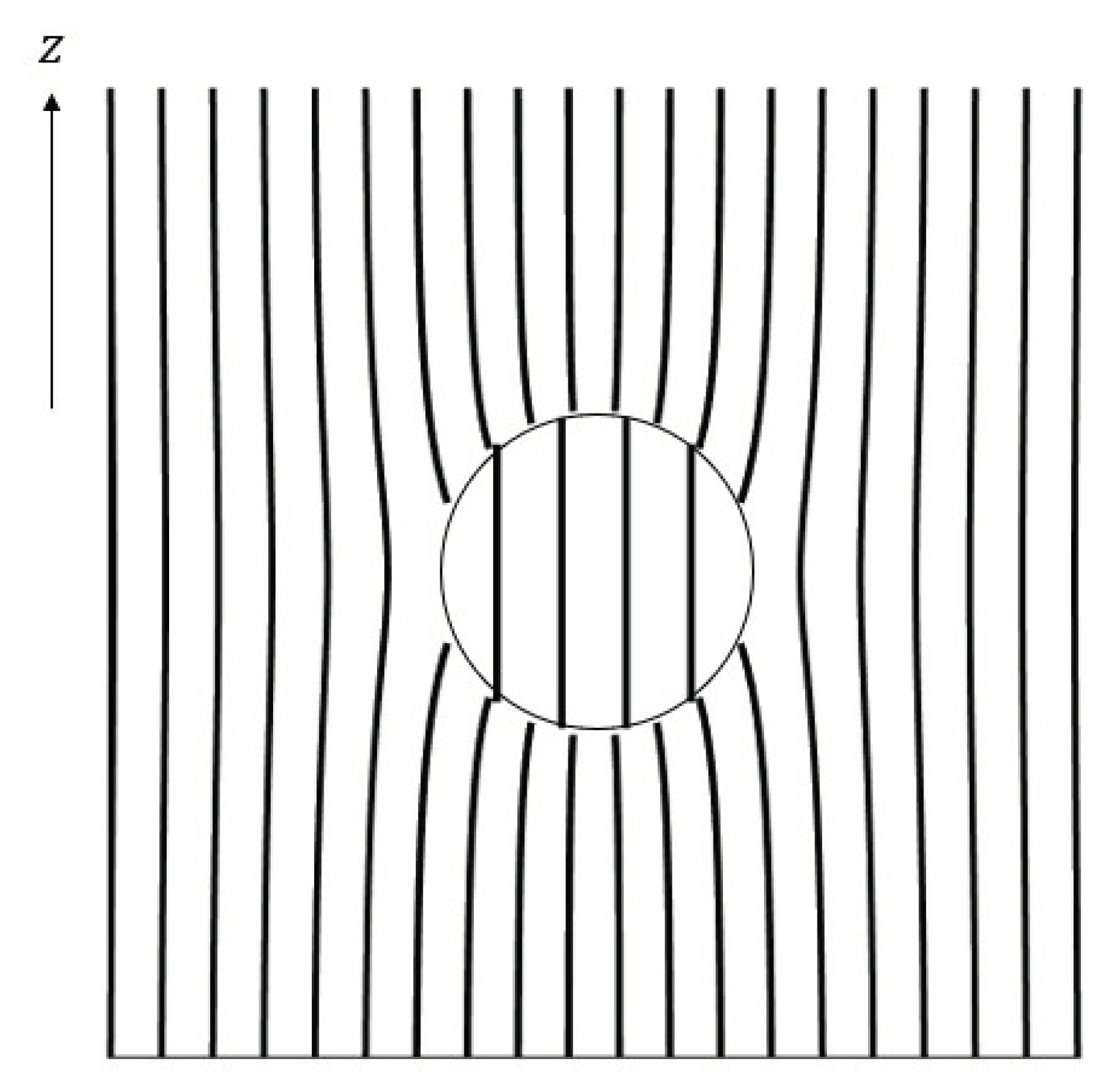
Figure 3 illustrates the electric field lines on a vertical plane (i.e., containing the z axis) obtained from the electric field in (46) and (44). As expected, far away from the sphere, the lines are vertical, while close by, they are “distorted” by the presence of the dielectric. We also note that there is a discontinuity of the field at the boundary of the dielectric, but unlike Figure 1 in Section 2.1, the field inside the dielectric is nonzero. Finally, the field lines are no longer orthogonal to the surface of the dielectric; the field can have a tangential component and electrostatic conditions can still be maintained.

Remark 3.

We note that the field when an uncharged conductor is placed in a uniform electric field (cf. (17) in Section 2.1) can also be written as

\begin{matrix} E = E_{0} + \frac{a^{3}}{r^{3}} (3 (E_{0} \cdot \hat{r}) \hat{r} - E_{0}) . \end{matrix}

(48)

Both (48) and (45) can be compared to the field of a dipole

p

placed at the origin (see, for example, [15]):

E = \frac{1}{4 π ϵ_{0} r^{3}} (3 (p \cdot \hat{r}) \hat{r} - p) .

This suggests that a sphere made of a conductor or a linear dielectric material placed in an uniform electrostatic field acquires a dipole moment equal to

\begin{matrix} p^{cond} . = 4 π ϵ_{0} a^{3} E_{0}, \\ p^{diel} . = 4 π ϵ_{0} a^{3} (\frac{χ}{χ + 3}) E_{0} . \end{matrix}

The polarization

P

is defined as dipole moment per unit volume, therefore this suggests that the spheres acquire polarizations

P^{cond} . = 3 ϵ_{0} E_{0}

and

P^{diel} . = 3 (χ / (χ + 3)) ϵ_{0} E_{0} .

The electric susceptibility

χ,

therefore, can be interpreted as a parameter quantifying the amount of “freedom of movement” of charges inside a metrial – in a conductor they have perfect freedom of movement (i.e., ability to polarize), enabling complete cancellation of the electric field, but in a dielectric sphere, the polarization is

χ / (χ + 3)

times relative to a conductor.

Remark 4.

We note that all results in Section 2.1 follow from those in this section by taking

χ \to \infty .

This shows that in electrostatics, in many situations a conductor can be thought of as a dielectric within infinite susceptibility. Taking this limit for (44) for the field inside the dielectric immediately recovers the result that the field is zero inside the conductor.

Remark 5.

Note that in this section, we tacitly assumed that the dielectric is uncharged when we equated (37) and (38). The dielectric, in fact, could have a “free” surface charge density

σ_{f} (θ, ϕ)

which would then have to be taken into account at that step. However, because charges cannot move about freely in a dielectric, unlike in a conductor, the complete charge density

σ_{f} (θ, ϕ)

would have to be specified for this problem to have a unique solution.

3. Discussions

The general setup described in this work can be used to find potentials and fields for a wide range of charge distributions commonly used to demonstrate the “method of images” in electrostatics texts. A popular and elementary problem setup not explored in this work is the infinite conducting plane near a point charge

q,

which can be similarly solved, but in the cylindrical coordinates using (3). For a detailed account of the history and development of Laplace’s equation and solution techniques in the context of electrostatics, we refer the reader to [1].

Appendix A Proofs

Proof

(Proof of Lemma 1). We first establish some preliminary results that will make the proof considerably easier. The relations between Cartesian and spherical polar coordinates can be written [29] as

\begin{matrix} (r, θ, ϕ) \mapsto (x, y, z) : & \{\begin{matrix} x & = r sin θ cos ϕ \\ y & = r sin θ sin ϕ \\ z & = r cos θ \end{matrix} \end{matrix}

(A1)

and

\begin{matrix} (x, y, z) \mapsto (r, θ, ϕ) : & \{\begin{matrix} r & = \sqrt{x^{2} + y^{2} + z^{2}} \\ θ & = acos (\frac{z}{\sqrt{x^{2} + y^{2} + z^{2}}}) \\ ϕ & = atan 2 (y, x), \end{matrix} \end{matrix}

(A2)

where

atan 2 (y, x)

is the four-quadrant inverse tangent defined as the real number

λ

satisfying

cos λ = x / \sqrt{x^{2} + y^{2}}

and

sin λ = y / \sqrt{x^{2} + y^{2}} .

Treating the spherical unit vectors

\hat{r},

\hat{θ}

and

\hat{ϕ}

as functions of

(r, θ, ϕ),

we can then write

\begin{matrix} \hat{r} & = \frac{r}{r} \\ = \frac{x \hat{x} + y \hat{y} + x \hat{z}}{r} \\ = sin θ cos ϕ \hat{x} + sin θ sin ϕ \hat{y} + cos θ \hat{z}, \end{matrix}

(A3)

\begin{matrix} \hat{θ} & = \frac{\frac{\partial \hat{r}}{\partial θ}}{∥\frac{\partial \hat{r}}{\partial θ}∥} \\ = cos θ cos ϕ \hat{x} + cos θ sin ϕ \hat{y} - sin θ \hat{z}, \end{matrix}

(A4)

and

\begin{matrix} \hat{ϕ} & = \hat{r} \times \hat{θ} \\ = - sin ϕ \hat{x} + cos ϕ \hat{y} . \end{matrix}

(A5)

Equations (A3)–(A5) can be easily inverted to yield

\begin{matrix} \hat{x} & = sin θ cos ϕ \hat{r} + cos θ cos ϕ \hat{θ} - sin ϕ \hat{ϕ}, \\ \hat{y} & = sin θ sin ϕ \hat{r} + cos θ sin ϕ \hat{θ} + cos ϕ \hat{ϕ}, \\ \hat{z} & = cos θ \hat{r} - sin θ \hat{θ}, \end{matrix}

or, more compactly,

\begin{matrix} [\begin{matrix} \hat{x} \\ \hat{y} \\ \hat{z} \end{matrix}] & = [\begin{matrix} sin θ cos ϕ & cos θ cos ϕ & - sin ϕ \\ sin θ sin ϕ & cos θ sin ϕ & cos ϕ \\ cos θ & - sin θ & 0 \end{matrix}] [\begin{matrix} \hat{r} \\ \hat{θ} \\ \hat{ϕ} \end{matrix}] \\ = : M (r, θ, ϕ) \cdot [\begin{matrix} \hat{r} \\ \hat{θ} \\ \hat{ϕ} \end{matrix}] . \end{matrix}

(A6)

One can verify that the matrix M is orthogonal, i.e.,

M^{- 1} = M^{T} .

Finally, the infinitesimal line element can be written in spherical spherical polar coordinates as

\begin{matrix} d r & = d (r \hat{r}) \\ = d r \hat{r} + r \frac{\partial \hat{r}}{\partial θ} d θ + r \frac{\partial \hat{r}}{\partial ϕ} d ϕ \\ \overset{t o 0 p t (a)}{=} d r \hat{r} + r d θ \hat{θ} + r sin θ d ϕ \hat{ϕ}, \end{matrix}

(A7)

where

(a)

follows from Equations (A3)–(A5). This also leads us to conclude immediately, that the infinitesimal volume element (since

\hat{r},

\hat{θ},

and

\hat{ϕ}

are orthonormal) is given by

d V = r^{2} sin θ \cdot d r \cdot d θ \cdot d ϕ .

Now, with these preliminaries established, let f be a differentiable scalar field. We have

\begin{matrix} d f = \frac{\partial f}{\partial r} d r + \frac{\partial f}{\partial θ} d θ + \frac{\partial f}{\partial ϕ} d ϕ . \end{matrix}

(A8)

Now, writing

\nabla f \equiv g^{(r)} (r, θ, ϕ) \hat{r} + g^{(θ)} (r, θ, ϕ) \hat{θ} + g^{(ϕ)} (r, θ, ϕ) \hat{ϕ}

and using the gradient theorem [11]

d f = \nabla f \cdot d r,

(A7), and (A8), we have

g^{(r)} (r, θ, ϕ) d r + (r g^{(θ)} (r, θ, ϕ)) d θ + (r sin θ \cdot g^{(ϕ)} (r, θ, ϕ)) d ϕ \equiv \frac{\partial f}{\partial r} d r + \frac{\partial f}{\partial θ} d θ + \frac{\partial f}{\partial ϕ} d ϕ .

This implies that

\begin{matrix} \nabla f & = \frac{\partial f}{\partial r} \hat{r} + \frac{1}{r} \frac{\partial f}{\partial θ} \hat{θ} + \frac{1}{r sin θ} \frac{\partial f}{\partial ϕ} \hat{ϕ} . \end{matrix}

(A9)

Equation (A9) also implies that

[\begin{matrix} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} & \frac{\partial f}{\partial z} \end{matrix}] [\begin{matrix} \hat{x} \\ \hat{y} \\ \hat{z} \end{matrix}] = [\begin{matrix} \frac{\partial f}{\partial r} & \frac{1}{r} \frac{\partial f}{\partial θ} & \frac{1}{r sin θ} \frac{\partial f}{\partial ϕ} \end{matrix}] [\begin{matrix} \hat{r} \\ \hat{θ} \\ \hat{ϕ} \end{matrix}],

or in other words,

\begin{matrix} [\begin{matrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \\ \frac{\partial f}{\partial z} \end{matrix}] = M \cdot [\begin{matrix} \frac{\partial f}{\partial r} \\ \frac{1}{r} \frac{\partial f}{\partial θ} \\ \frac{1}{r sin θ} \frac{\partial f}{\partial ϕ} \end{matrix}] . \end{matrix}

(A10)

We can write (A10) as the three scalar equations

\begin{matrix} \frac{\partial f}{\partial x} & = \frac{\partial f}{\partial r} sin θ cos ϕ + \frac{1}{r} \frac{\partial f}{\partial θ} cos θ cos ϕ - \frac{1}{r sin θ} \frac{\partial f}{\partial ϕ} sin ϕ, \end{matrix}

(A11)

\begin{matrix} \frac{\partial f}{\partial y} & = \frac{\partial f}{\partial r} sin θ sin ϕ + \frac{1}{r} \frac{\partial f}{\partial θ} cos θ sin ϕ + \frac{1}{r sin θ} \frac{\partial f}{\partial ϕ} cos ϕ, \end{matrix}

(A12)

\begin{matrix} \frac{\partial f}{\partial z} & = \frac{\partial f}{\partial r} cos θ - \frac{1}{r} \frac{\partial f}{\partial θ} sin θ . \end{matrix}

(A13)

Now, let

A

be a differentiable vector field. We have

\begin{matrix} A & = [\begin{matrix} A_{x} & A_{y} & A_{z} \end{matrix}] [\begin{matrix} \hat{x} \\ \hat{y} \\ \hat{z} \end{matrix}] \\ \overset{t o 0 p t (a)}{=} [\begin{matrix} A_{x} & A_{y} & A_{z} \end{matrix}] \cdot M \cdot [\begin{matrix} \hat{r} \\ \hat{θ} \\ \hat{ϕ} \end{matrix}] \\ \equiv [\begin{matrix} A_{r} & A_{θ} & A_{ϕ} \end{matrix}] [\begin{matrix} \hat{r} \\ \hat{θ} \\ \hat{ϕ} \end{matrix}], \end{matrix}

which leads to

[\begin{matrix} A_{x} & A_{y} & A_{z} \end{matrix}] = [\begin{matrix} A_{r} & A_{θ} & A_{ϕ} \end{matrix}] \cdot M^{- 1},

or, since M is orthogonal,

\begin{matrix} [\begin{matrix} A_{x} \\ A_{y} \\ A_{z} \end{matrix}] = M \cdot [\begin{matrix} A_{r} \\ A_{θ} \\ A_{ϕ} \end{matrix}] . \end{matrix}

(A14)

We can write (A14) as the three scalar equations

\begin{matrix} A_{x} & = A_{r} sin θ cos ϕ + A_{θ} cos θ cos ϕ - A_{ϕ} sin ϕ, \end{matrix}

(A15)

\begin{matrix} A_{y} & = A_{r} sin θ sin ϕ + A_{θ} cos θ sin ϕ + A_{ϕ} cos ϕ, \end{matrix}

(A16)

\begin{matrix} A_{z} & = A_{r} cos θ - A_{θ} sin θ . \end{matrix}

(A17)

Using Equations (A11)–(A13) and (A15)–(A17), collecting terms, and simplifying, we obtain

\begin{matrix} \nabla \cdot A & = \frac{\partial A_{x}}{\partial x} + \frac{\partial A_{y}}{\partial y} + \frac{\partial A_{z}}{\partial z} \\ = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} A_{r}) + \frac{1}{r sin θ} \frac{\partial}{\partial θ} (sin θ A_{θ}) + \frac{1}{r sin θ} (\frac{\partial A_{ϕ}}{\partial ϕ}) . \end{matrix}

(A18)

Combining (A9) and (A18), we can then write, for a twice differentiable scalar field

f,

\begin{matrix} \nabla^{2} f & = \nabla \cdot (\nabla f) \\ \overset{t o 0 p t ()}{=} \nabla \cdot (\frac{\partial f}{\partial r} \hat{r} + \frac{1}{r} \frac{\partial f}{\partial θ} \hat{θ} + \frac{1}{r sin θ} \frac{\partial f}{\partial ϕ} \hat{ϕ}) \\ \overset{t o 0 p t (a)}{=} \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial f}{\partial r}) + \frac{1}{r sin θ} \frac{\partial}{\partial θ} (sin θ \frac{1}{r} \frac{\partial f}{\partial θ}) + \frac{1}{r sin θ} (\frac{\partial}{\partial ϕ} (\frac{1}{r sin θ} \frac{\partial f}{\partial ϕ})) \\ = \frac{1}{r^{2}} \frac{\partial}{\partial r} (r^{2} \frac{\partial f}{\partial r}) + \frac{1}{r^{2} sin θ} \frac{\partial}{\partial θ} (sin θ \frac{\partial f}{\partial θ}) + \frac{1}{r^{2} {sin}^{2} θ} \frac{\partial^{2} f}{\partial ϕ^{2}}, \end{matrix}

(A19)

where

(a)

follows from (A18), by using

A_{r} \leftrightarrow \partial f / \partial r,

A_{θ} \leftrightarrow (1 / r) \partial f / \partial θ,

A_{ϕ} \leftrightarrow (1 / r sin θ) \partial f / \partial ϕ .

Equation (A19) establishes the result. □

References

Brian Baigrie, Electricity and Magnetism: A Historical Perspective (Greenwood Press, 2007), pp. 7–8.
Pratik B. Vyas, Ninad Pimparkar, Robert Tu, Wafa Arfaoui, Germain Bossu, Mahesh Siddabathula, Steffen Lehmann, Jung-Suk Goo, and Ali B. Icel, “Reliability-Conscious MOSFET Compact Modeling with Focus on the Defect-Screening Effect of Hot-Carrier Injection”, 2021 IEEE International Reliability Physics Symposium (IRPS), pp. 1-4, 2021.
Charles–Augustin de Coulomb, “Premier mémoire sur l’électricité et le magnétisme”, Histoire de l’Académie Royale des Sciences, 1785.
Charles–Augustin de Coulomb, “Second mémoire sur l’électricité et le magnétisme”, Histoire de l’Académie Royale des Sciences, pp. 578–611, 1785.
Pratik B. Vyas, Maarten L. Van de Put, and Massimo V. Fischetti, “Master-Equation Study of Quantum Transport in Realistic Semiconductor Devices Including Electron-Phonon and Surface-Roughness Scattering”, Phys. Rev. Appl. 13, pp. 014067, 2020.
Carl F. Gauss, “Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata”, Gauss, Werke V, p. 1.
James Clerk Maxwell(1865), “A dynamical theory of the electromagnetic field”, Philosophical Transactions of the Royal Society of London, 155, pp. 459–512.
P. B. Vyas, C. Naquin, H. Edwards, M. Lee, W. G. Vandenberghe, and M. V. Fischetti, “Theoretical simulation of negative differential transconductance in lateral quantum well nMOS devices”, Journal of Applied Physics 121, pp. 044501, 2017.
Pratik B. Vyas, Maarten L. Van de Put, and Massimo V. Fischetti, “Simulation of Quantum Current in Double Gate MOSFETs: Vortices in Electron Transport”, 2018 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), pp. 1-4, 2018.
Richard P. Feynman, “Space–Time Approach to Quantum Electrodynamics”, Phys. Rev. 76(6), pp. 769–789, 1949.
P. R. Garabedian and M. Schiffer, “On existence theorems of potential theory and conformal mapping”, Annals of Mathematics 52(1), pp. 164–187, 1950.
Siméon Denis Poisson, “Mémoire sur la théorie du magnétisme en mouvement”, Mémoires de l’Académie Royale des Sciences de l’Institut de France 6, pp. 441–570, 1823.
R. Courant and D. Hilbert, “Methods of Mathematical Physics”, Interscience, New York, 1966.
Richard P. Feynman, Robert B. Leighton, and Matthew Sands, The Feynman Lectures on Physics, Vol. 2, Chap. 12 (Addison-Wesley, 1964).
David J. Griffiths, Introduction to Electrodynamics (Boston:Pearson, 2013).
S. Persides, “The Laplace and Poisson equations in Schwarzschild’s space–time”, Journal of Mathematical Analysis and Applications 43(3), pp. 571–578, 1973.
David Gilbarg and Neil S. Trudinger, Elliptic Partial Differential Equations of Second Order (Berlin: Springer, 2015).
Pratik B. Vyas, Charisse Zhao, Sefa Dag, Ashish Pal, El Mehdi Bazizi, and Buvna Ayyagari-Sangamalli, “Next Generation Gate-all-around Device Design for Continued Scaling Beyond 2 nm Logic”, 2023 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), pp. 57-60, 2023.
George B. Arfken and Hans J. Weber, Mathematical Methods for Physicists (Elsevier Academic Press, 2005).
G. Barton, Elements of Green’s Functions and Propagation: Potentials, Diffusion and Waves (Oxford: Oxford Science Publications, 1989).
Augusto B. d’Oliveira, Ed Gerck, and Jason A. C. Gallas, “Solution of the Schrödinger equation for bound states in closed form”, Phys. Rev. A 26:1(1), June 1982.
Pratik B. Vyas, Maarten L. Van de Putt, and Massimo V. Fischetti, “Quantum Mechanical Study of Impact of Surface Roughness on Electron Transport in Ultra- Thin Body Silicon FETs”, 2018 IEEE 13th Nanotechnology Materials and Devices Conference (NMDC), pp. 1-4, 2018.
Erwin Kreyszig, Advanced Engineering Mathematics (3rd ed.) (New York: Wiley, 1972).
P. Zhao, P. B. Vyas, S. Mcdonnell, P. Bolshakov-Barrett, A. Azcatl, C. L. Hinkle, P. K. Hurley, R. M. Wallace and C. D. Young, “Electrical characterization of top-gated molybdenum disulfide metal-oxide-semiconductor capacitors with high-k dielectrics”, Microelectronic Engineering 147, pp. 151-154, 2015.
Ali Saadat, Pratik B. Vyas, Maarten L. Van de Put, Massimo V. Fischetti, Hal Edwards, and William G. Vandenberghe “Channel Length Scaling Limit for LDMOS Field-Effect Transistors: Semi-classical and Quantum Analysis”, 2020 32nd International Symposium on Power Semiconductor Devices and ICs (ISPSD), pp. 443-446, 2020.
Pratik B. Vyas, Charisse Zhao, Sefa Dag, Ashish Pal, El Mehdi Bazizi, and Buvna Ayyagari-Sangamalli, “Modeling of SiC transistor with counter-doped channel”, Solid State Electronics 200, pp. 108548, 2023.
J. D. Jackson, Classical Electrodynamics (3rd ed.) (New York:Wiley, 1999).
Pratik B. Vyas, Ashish Pal, Gregory Costrini, Plamen Asenov, Sarra Mhedhbi, Charisse Zhao, Victor Moroz, Benjamin Colombeau, Bala Haran, El Mehdi Bazizi, and Buvna Ayyagari-Sangamalli, “Materials to System Co-optimization (MSCO^TM) for SRAM and its application towards Gate-All-Around Technology”, 2023 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), pp. 53-56, 2023.
P. M. Morse and H. Feshbach, Methods of Theoretical Physics, Part I (New York: McGraw–Hill, 1953), p. 658.
Richard Courant, Differential and Integral Calculus, Vol. 1 (London: Blacktie & Son Limited, 1961).

Figure 1. Electric field lines.

Figure 2. Conducting sphere near a point charge.

Figure 3. Electric field lines.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Induced Electrostatic Fields in the Presence of Conductors and Dielectrics: A Purely Laplace Equation-Based Treatment

Abstract

1. Introduction

2. Laplace’s Equation and Electric Fields

2.1. Conducting Sphere in Uniform Electric Field

2.2. Conducting Sphere Near a Point Charge

2.3. Uniform Dielectric Sphere in Uniform Electric Field

3. Discussions

Appendix A Proofs

References

MDPI Initiatives

Important Links

Subscribe