Prerpints.org logo
Preprint
Article

A Concrete Core Void Imaging Approach for Concrete-Filled Steel Tube Members and Parameter Analysis with Travel Time Tomography

Altmetrics

Downloads

97

Views

43

Comments

0

This version is not peer-reviewed

Submitted:

07 August 2023

Posted:

08 August 2023

You are already at the latest version

Alerts
Abstract
Concrete-filled steel tube (CFST) members have been widely used in the field of civil engineering due to their advanced superior mechanical properties. However, internal defects such as concrete core voids and interface debonding are likely to weaken the load-carrying capacity and stiffness of these members, which affects safety and serviceability of CFST structures. Visualizing the inner defects of concrete core in CFST members have been a critical need in civil engineering construction, a travel time tomography (TTT) is introduced to quantitatively identify and visualize the sizes and positions of CFST members in this paper. Moreover, a parameter analysis is performed to investigate the relationship between TTT imaging qualities and influence factors, e.g. inversion parameters, defect sizes and positions. The effectiveness and accuracy of the TTT algorithm are verified by several numerical examples and the results demonstrate that TTT can identify the sizes and positions of concrete core void defects in CFST members efficiently and several inversion parameters including model weighting matrix and inversion grid size really pose a significant impact on the imaging results of CFST members. In addition, several optimum parameters are recommended to benefit the future study of the promising TTT approach for CFST members.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

With the development of building materials, construction technology and computational theory, large-scale structures spring up in the past decades. For example, concrete filled steel tube (CFST) structures have attracted more and more attention in super high-rise buildings, long-span bridges, harbor engineering, subway stations and other large-scale structures due to their excellent mechanical properties and convenient constructions when compared with reinforced concrete (RC) or steel structures [1,2,3]. Although CFST structural systems have the potential to provide cost-effective alternatives to traditional steel or RC structures, they are prone to yield defects such as interface debonding and concrete core voids under various factors, e.g. concrete shrinkage and creep, complex loads, temperature variation and etc. Existing studies show that the ultimate load-carrying capacity and stiffness of CFST members are dramatically weakened due to the loss of confinement effect of steel tube on concrete core and the existence of voids in concrete core, even structural failure and catastrophic accidents probably happen [4,5,6,7,8,9]. Therefore, it is vital and urgent to explore a non-destructive inspection and health assessment technique for CFST members.
As a classic non-destructive testing technology, stress wave analysis for large CFST structures has become one of hot spots in the area of damage detection in recent years [10]. For example, Xu et al., Chen et al. and Wang et al. [11,12,13,14,15,16] carried out theoretical and experimental studies to investigate the feasibility and the principle of defect detection approaches for CFST members using stress wave measurements with Piezoelectric lead zirconate titanate (PZT) actuators and sensors embedded in concrete or mounted on the outer surface of steel tube of CFST members. The proposed detection approaches work for both interface debonding and concrete core void defects in CFST members. In addition to the PZT based methods, scanning analysis approaches, e.g. time or frequency analysis [17,18], wavelet analysis [19], travel time analysis [20,21] and etc., are also capable of determining whether there are defects in concrete. Moreover, they enable the estimation of the approximate area where the defects appear through feature extractions of stress wave signals and previous engineering experiences. However, scanning analysis methods still struggle to quantitatively identify the sizes and positions of the internal defects of CFST members. Therefore, it is desired to develop defect imaging technologies to detect the defects of CFST members quantitatively and in a visualization way.
Tomography techniques, including attenuation tomography (AT) [22] and travel time tomography (TTT) [23,24], are able to detect defects in concrete structures composed of a sole material. However, strong scattering attenuation may be trigged by the concrete inhomogeneity at the scale of ultrasonic wavelength, which will hinder the application of AT in large-scale engineering structures such as CFST members in high-rise buildings or long-span bridges. By contrast, TTT gets rid of such restrictions and has been widely applied to subsurface medium detection. For instance, a crosshole tomography method is proposed based on the straight ray tracing algorithm [25]. Although it is quite suitable when the medium of the cross-section changes slightly, a big imaging error may be yielded if it is treated as a homogeneous material for the case that the medium of the measured cross-section changes greatly. To overcome this shortcoming, Clement et al. [26] proposed a crosshole radar TTT algorithm based on curved ray tracing method. This method is essentially an iterative inversion scheme based on two-dimensional ray tracing technique and it successfully provides a 2-D image of the subsurface along a transect through a wellfield designed to support hydrologic and geophysical research. Compared with the straight ray tracing approach, the accuracy of the calculated ray path via curved ray tracing way is greatly promoted. Therefore, the curved ray tracing based TTT method has been widely accepted and it gradually extends from geophysical exploration to non-destructive inspection of civil engineering structures [27,28,29,30,31,32]. However, current TTT case studies mostly focus on concrete structures [33,34] and few attention has been paid on CFST members composed of two different kinds of materials with different structural properties [35]. Actually, the travel velocity of stress waves depends on the elastic modulus and density of propagation mediums. Due to this, the propagation process of stress waves through CFST members is more complicated when compared with traditional concrete structures with sole concrete material. In addition, the thickness of the surrounding steel tube only shares a few parts of the whole ray path, resulting in that the imaging of the steel tube remains not well resolved. Therefore, how to accurately track the travel paths inside steel tube and concrete core and acquire the travel velocity distributions becomes a critical issue for the quantification of internal defects inside CFST members.
To address these issues mentioned above, TTT is introduced in this paper to carry out concrete core void defect imaging for CSFT members. The results demonstrate that the curved ray theory based TTT algorithm is capable of identifying the position and size of the void defects in concrete core effectively. Moreover, a parameter analysis is performed to investigate the relationship between TTT imaging qualities and inversion parameters, defect size and position. Due to this, several optimum parameters are recommended to benefit the future study of this promising TTT approach for inner concrete core voids imagination of CFST members.
The outline of this paper is as follows. The TTT algorithm is detailed in Section 2 while the multi-physics coupling finite element model of PZT-CFST is established in Section 3. The analysis of inversion imaging parameters and generality of the proposed imaging approach for CFST members considering concrete core void size, position and number are investigated in Section 4 and Section 5, respectively. Concluding remarks are drawn in Section 6.

2. Travel Time Tomography for Concrete Core Voids Imagination of CFST Members

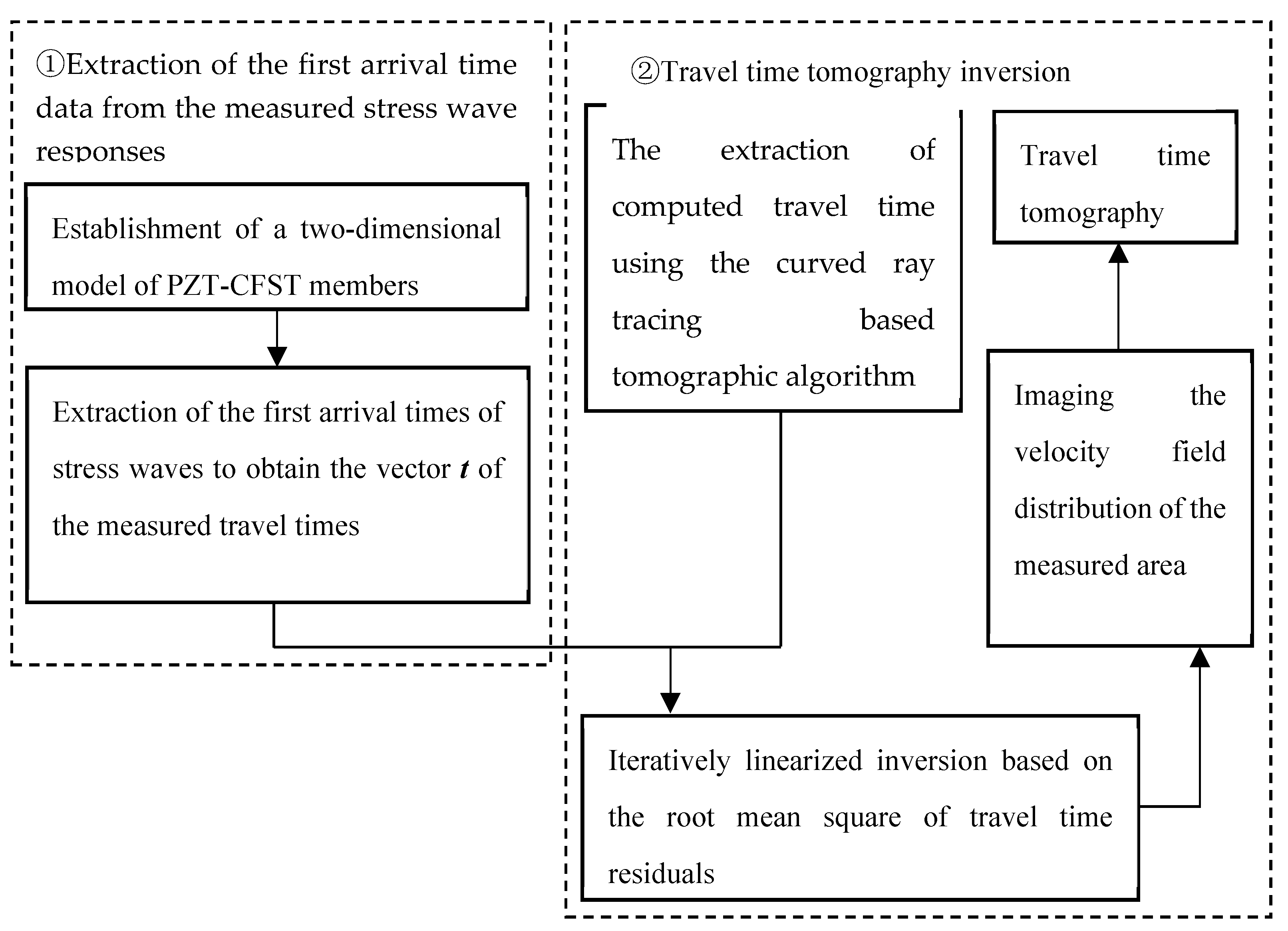
Travel time tomography (TTT) is a method that applies first arrival time of stress waves to inverse velocity/slowness distributions between the actuators and sensors mounted on the outer surface of CFST members. The flowchart of TTT is plotted in Figure 1. As shown in Figure 1, a ray tracing technique is required in TTT. Typically, the propagation medium of the stress wave is assumed to be homogeneous. Therefore, we can approximately assume that the ray path between an arbitrary actuator and sensor is a straight ray. 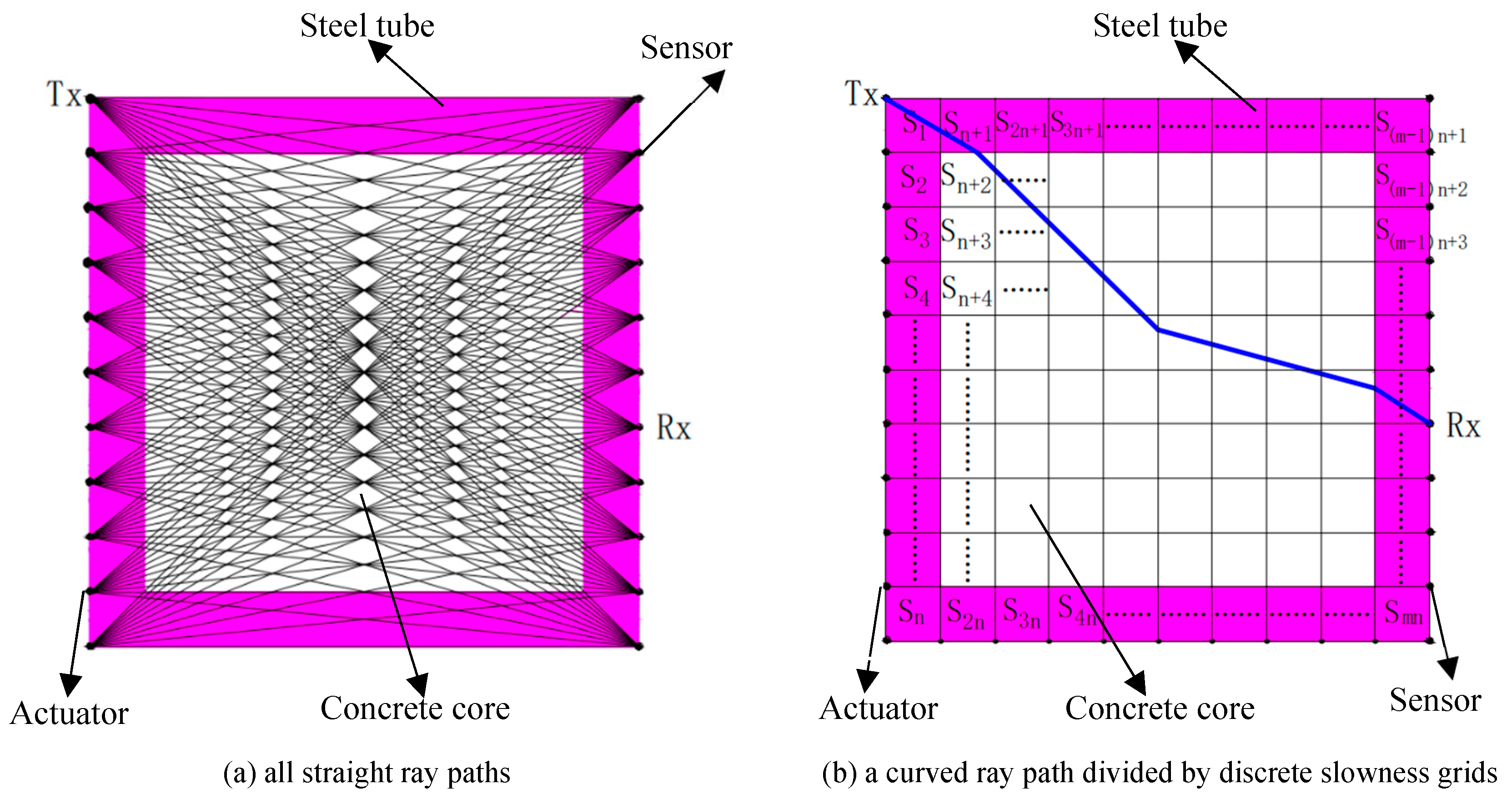It is shown in Figure 2(a) that n actuators and sensors are mounted on the two sides of cross section of a CFST member. Tx and Rx represent actuators and sensors, respectively. If an excitation signal is generated from an arbitrary actuator, all n sensors on the opposite side will receive a stress wave that travels through the CFST member and as a result n straight rays are yielded. Similarly, n×n straight rays will be received if all n excitation signals are generated. Nevertheless, traditional straight ray theorem is no longer suitable for simulating the transmission of stress waves inside CFST members with concrete core void defects due to the different structural properties of steel and concrete. Moreover, void defects in concrete core also create challenge for the straight ray tracing method. To be specific, stress waves are likely to bypass the internal concrete core void defects/abnormal low-velocity areas and turn to travel along the path with least time. By contrast, the curved ray tracing theory provides a more real ray tracing path than the typical straight ray method for CFST members and yields a more accurate velocity distribution as well.
According to the principle of TTT, an arbitrary curved ray path can be regarded as a sum of several straight rays when the path is divided by discrete slowness grids of a cross section of a CFST member as illustrated in Figure 2(b). Actually, the discrete slowness grids are square areas that are yielded by meshing the cross section of CFST members with an equivalent interval and surface-mounted actuators and sensors are located at the nodes. Here, slowness indicates the reciprocal of velocity. That is to say, the size of a slowness grid, e.g. S1, equals the distance between adjacent actuators/sensors. As a result, the travel time of stress wave along the curved ray path can be obtained by summing up the counterparts of all straight rays that constitutes it. For example, the time travelling along the i-th curved ray, expressed as t i , is calculated according to Equation (1).
t i = ∑ j = 1 m l j i s j
where i and j denote the i-th curved ray and the j-th grid, respectively. m represents the total number of grids that the i-th ray passes through. Here, s j is the slowness inside the j-th grid, while l j i represents the length of the i-th curved ray within in the j-th grid.
If n actuators and n sensors are both arranged on the two opposite sides (left and right sides in Figure 2) of CFST members, the total number of rays will equal n×n. Then, the measured travel time matrix as expressed in Equation (2) can be established on a basis of Equation (1).
t n × n = L n × m S m × n
where t , and s represent matrices of travel time and slowness, respectively. Here, L is a coefficient matrix containing the lengths of the curved ray paths that passing through the slowness grids. Each element in L denotes the length of the ray path inside a slowness grid.
After that, Equation (2) can be rewritten as Equation (3) by pre-multiplying L − 1 .
s = L − 1 t
where L − 1 represents the inverse matrix of the matrix L .
Due to L is usually a sparse matrix, it has the possibility to be a singular matrix, which implies the inverse matrix of L − 1 does not exist. In order to address this issue, Tikhonov regularization function [36] is introduced to define the objective function in Equation (4).
Ф s = W d t − L s 2 + 2 W m s − s 0 2
where
is weighting factor. W d and W m represent data and model weighting matrices, respectively. s and s 0 separately represent the slowness vector to be solved and the initial slowness vector defined in advance. As symmetric matrices, the priori information contained in W d and W m can effectively guarantee the uniqueness of the solution to the nonlinear equation as shown in Equation (4).
It can be seen from Equation (4) that the coefficient matrix L is actually a function of the slowness matrix s on condition that t is solved by employing the first arrival time of the stress wave as mentioned before. Therefore, L s can be expressed as d ( s ) and then is defined as the theoretical travel time vector as well. After that, it can be solved by the finite difference method. To minimize Equation (4), the partial derivative of s with respect to time is calculated and hence Equation (4) can be expressed as
λ 2 W m T W m s − s 0 = J T W d T W d t − d ( s )
where J = ∂ d ( s ) / ∂ s denotes the Jacobian matrix, while the subscript of T indicates transposed matrix.
With a consideration of the nonlinear properties of d ( s ) , J cannot be obtained directly and the initial Jacobian matrix J 0 can only be solved by knowing the initial slowness vector s 0 in advance. Hence, an iterative algorithm is required to solve Equation (5). Typically, a linear iteration method is used to take a Taylor series expansion on d ( s ) and the first order term is retained alone, leading to d s as illustrated in Equation (6).
d s ≈ d s 0 + J 0 s − s 0
As such, Equation (5) becomes
J 0 T W d T W d J 0 + 2 W m T W m s − s 0 = J 0 T W d T W d t − d ( s 0 )
It should be noted here that J is replaced by J 0 in Equation (7) due to it only denotes the initial iteration step.
After that, Equation (7) can be rewritten in the iterative form and shown as Equation (8).
J k T W d T W d J k + 2 W m T W m s k + 1 − s k = J k T W d T W d t − d s k , k = 0 ， 1 ， 2 ， 3 ⋯
where k represents the number of iterations.
The updated slowness vector s k can be solved according to Equation (8). Normally, it will be iterated repeatedly until the error between the theoretical travel time vector d ( s k ) and the observed travel time vector t reaches a determined threshold or the number of iterations that exceeds the number defined beforehand. Thus, the final updated slowness vector s k + 1 can be regarded as the actual slowness field inside the CFST member.
To enhance the efficiency of solving Equation (8), the least square algorithm is used instead of applying the above mentioned iterative approach alone. Due to this, Equation (8) is equivalent to Equation (9) and the process of solving Equation (9) by the least square method is called least square iterative linear inversion algorithm.
W d J k W m s k + 1 − s k = W d t − d ( s k ) 0 , （ k = 0 ， 1 ， 2 ， 3 ）
where W d , W m , and λ represent data weighting matrix, model weighting matrix and weighting factor, respectively.
J = ∂ d ( s ) ∂ s = ∂ L s ∂ s = L
As seen in Equation (10), the Jacobian matrix J equals the coefficient matrix L according to the curved ray theory based TTT method. Therefore, the Jacobian matrix J can be established by calculating the ray length of the i-th ray within j-th grid, that is, l j i .

3. Multi-Physics Finite Element Model for Stress Wave Travelling Time Determination of PZT-CFST Coupling System

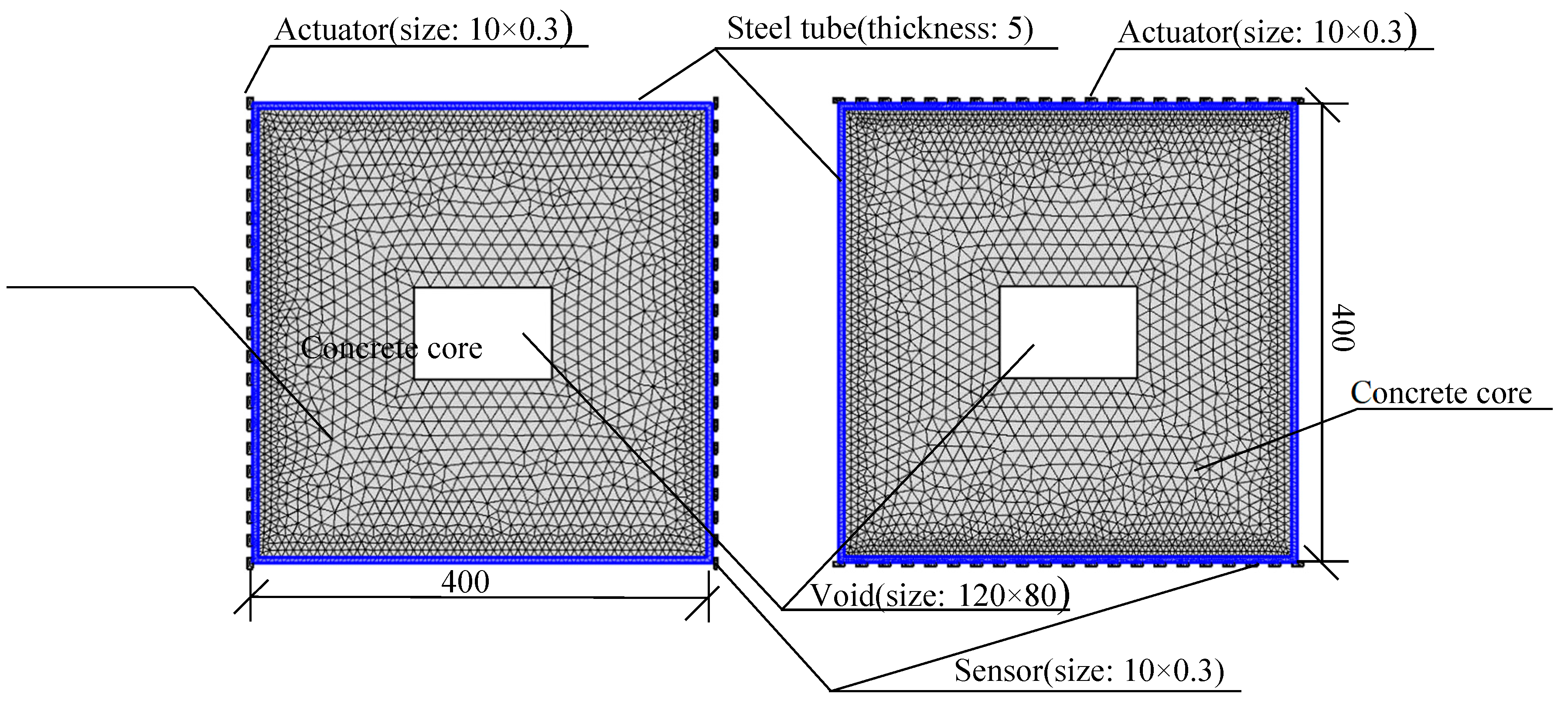
A multi-physics coupling finite element model of PZT-CFST is established in Figure 3 with the assumption of homogeneous material. As shown in Figure 3, the sizes of the square CFST model and the concrete core void defects are separately 400mm×400mm and 120mm×80mm, while the thickness of the surrounding steel tube is 5mm. 21 PZT patches with a definition of actuators are arranged with an equal interval of 20mm (0.02m) on the left/upper side of the outer wall of the steel tube, while other 21 PZT patches, used as sensors, are laid out on the opposite side. The plane size of each PZT patch is 10mm×10mm and the thickness is 0.3mm. Here, the employed PZT patches is compressive type and its polarization direction is along the thickness direction. The material properties of the PZT-CFST coupling model are illustrated in Table 1.
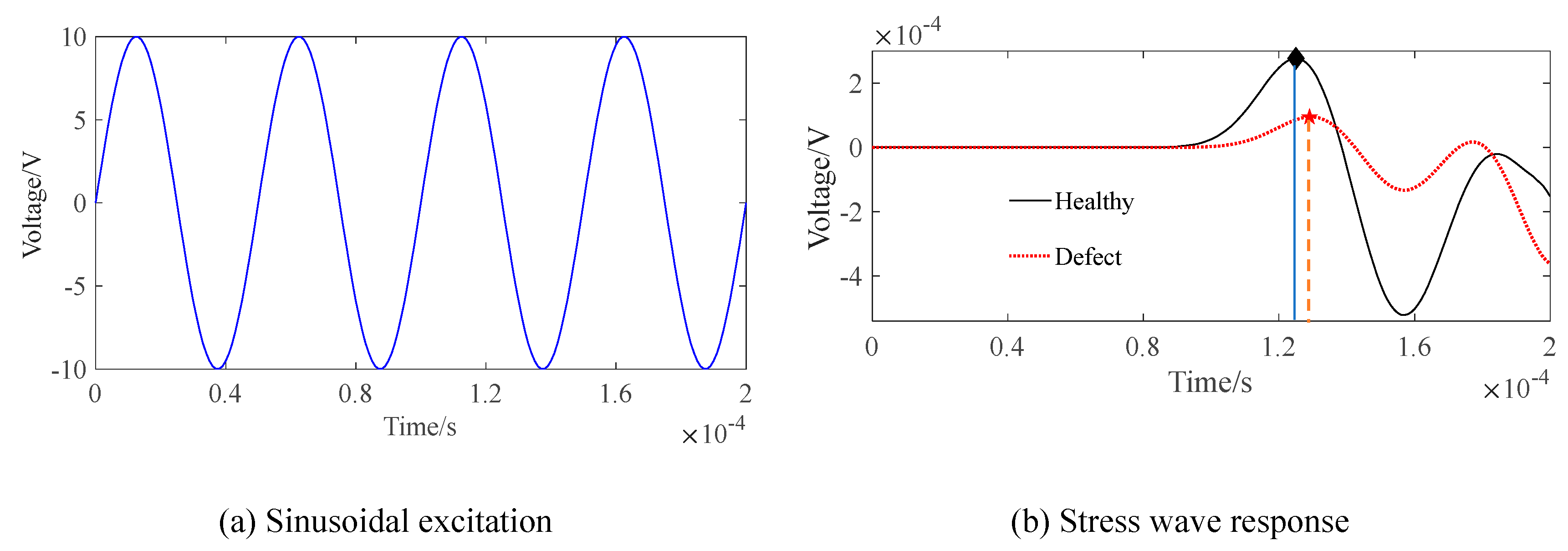
At first, a sinusoidal signal with a frequency of 20 kHz and an amplitude of 10 V is set as the excitation and its waveform is plotted in Figure 4(a). Here, four cycles of the excitation signal are selected for signal processing, that is to say, the excitation signal at least has a time duration of 4×1/20=0.2ms. After that, the stress wave is going to propagate in the CFST section with a concrete core void defect under the excitation and the resultant response signal as shown in Figure 4(b) is received by a sensor. In order to extract the first wave peak time from the measured response signal more effectively, the peak picking method is used. As seen in Figure 4(b), the red dashed line indicates the received response signal after the stress wave travels through the cross section of the CFST model with a concrete core void defect, and the red pentagram represents the first wave peak time of the received stress wave response signal. Compared with the first wave peak time under the healthy condition (black diamond), the counterpart under defect case (red pentagram) is slightly delayed and the amplitude decreases to an extent as well. The reason for this phenomenon is that the travel path will be changed when the stress wave encounters the concrete core void defect. In other words, the stress wave is likely to propagate along the edge of the concrete core void instead of traveling through the concrete core void itself. As a result, the travel path becomes relatively longer, leading to a delayed travel time and an energy attenuation as well.
Following the extraction of the first wave peak time, the time interval between the first wave peak time of the response signal and that of the excitation signal is defined as the first wave arriving time. Since 21 actuators and sensors are separately arranged on the left and right sides of the cross section, 441 travel paths (21×21=441) will be yielded and hence the same number of first wave arriving times needs to be extracted accordingly. After that, the 441 extracted first wave arriving time data constitutes a measured travel time matrix ( t ) as shown in Equation (11) and then the TTT algorithm is introduced to yield a defect imaging result. Similarly, another defect imaging result will be yielded when 21 actuators and sensors are mounted on the upper and lower sides of the cross section, respectively. To reduce the errors caused by the sparsity of the rays located at the four edges of CFST cross section, the two obtained defect imaging results are comprehensively considered and hence an algorithm of average is used for getting a better cross section imaging result.
t = t 11 ⋯ t 1 n ⋮ ⋱ ⋮ t n 1 ⋯ t n n
where t n n represents the first wave arriving time between the n-th actuator and the n-th sensor.

4. Analysis of Inversion Imaging Parameters

In TTT, the default inversion algorithm is the least square QR (LSQR). According to Equation (9), the inversion parameters of W d , W m and λ are artificially defined and hence the selection of the W d , W m and λ is likely to pose a great impact on the results of TTT. In addition, the inversion grid size (d) not only affects the computational efficiency of TTT, but also applies influence on the accuracy of the imaging results to an extent. Unfortunately, few attention has been paid on the influence caused by the four parameters mentioned above and hence it deserves an extensive study.

4.1. Selection of Inversion Parameters

As mentioned before, W d , W m and λare the three inversion parameters that pose impacts on the imaging results. Normally, the unit matrix operator is used for W d , which indicates the data is uniformly weighted. Due to this, W d does not affect the imaging results too much and hence its effect is no longer considered here. By contrast, the influence of other inversion parameters including the model weighting matrix ( W m ) and weighting factor (λ) are investigated in addition to the inversion grid size (d).
In order to better understand the influence of W m , λ and d on the TTT results of the concrete core void defects inside the CFST section, the PZT-CFST coupling model as illustrated in Figure 3 is investigated and seven cases are preset as shown in Table 2.

4.2. Model Weighting Matrix

Since the model weighting matrix W m contains prior information to reduce the multiple solutions of inversion problems, its selection is vital for concrete core void defects imaging by TTT. Three types of model weighting matrices, including unit matrix operator, first-order difference operator and second-order difference operator, are selected in this section to perform TTT.
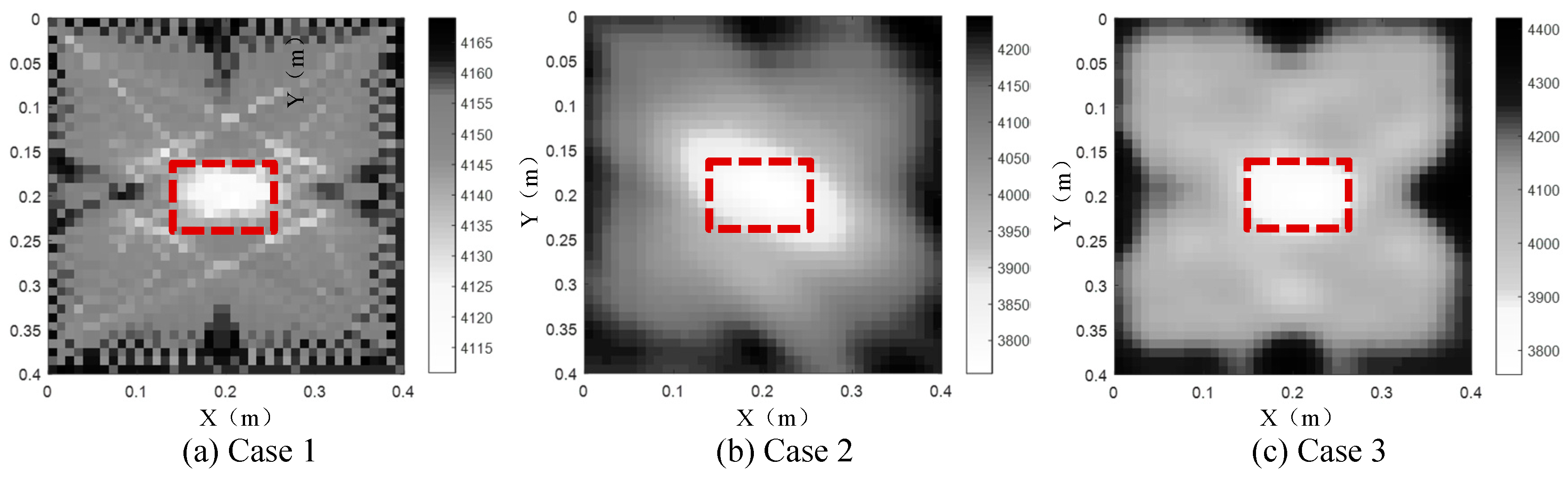
By using TTT, the concrete core void defect of the CFST model is inverted and illustrated in Figure 5. It is noted here that all void defect imaging results in the rest sections of this paper are plotted in the style of grey-scale map. That is to say, the white color in the grey-scale maps represents the concrete core void defects, while the grey and black colors denote concrete cores and steel tubes, respectively. X and Y in the grey-scale map separately represent the horizontal and vertical coordinates of the cross section. In addition, the number on the color bar denotes the inverted velocity (Unit: m/s).
As shown in Figure 5(a), the position of the concrete core void defect basically agrees with the theoretical result when the unit matrix operator is selected, however, the steel tube, concrete core and the size of the concrete core void defect are not accurately imaged in Case 1. When the first-order difference operator is employed (Case 2), the size of the inverted concrete core void defect is larger than that of the actual model. In addition to this, the imaged shape of the concrete core void defect is also distorted in Case 2. It can be seen from Figure 5(c) that the position and size of the concrete core void defect agree with the theoretical result best in Case 3 when compared with Figure 5(a) and (b). Moreover, the surrounding steel tube can also be effectively imaged even though it is slightly thicker than the counterpart of the actual model when the second-order difference operator is selected in Case 3. The reason for this phenomenon is that the curved rays in TTT cannot ensure a good coverage for the four sides of the cross section. In contrast, the concrete core region is covered very well by the curved rays and hence can be imaged effectively. In a word, the TTT has the potential to accurately image CFST members on condition that the second-order difference operator is selected and both actuators and sensors are mounted on the four sides of CFST cross sections.

4.3. Weighting Factor

In addition to model weighting matrix, the weighting factor (λ) also plays an important role on TTT. As the name implies, λ controls the weight between data space and model space. If λ is too small, it cannot smooth the model very well. Otherwise, excessive smoothness will be caused for a big λ. Therefore, an optimum λ needs to be determined during the TTT inversion process. As suggested in [30], the L-curve method is recommended to decide the optimum value range of λ (usually 2~20). For simplicity, λ =2 (Case 4), λ =5 (Case 3) and λ =10 (Case 5) are investigated in this study.
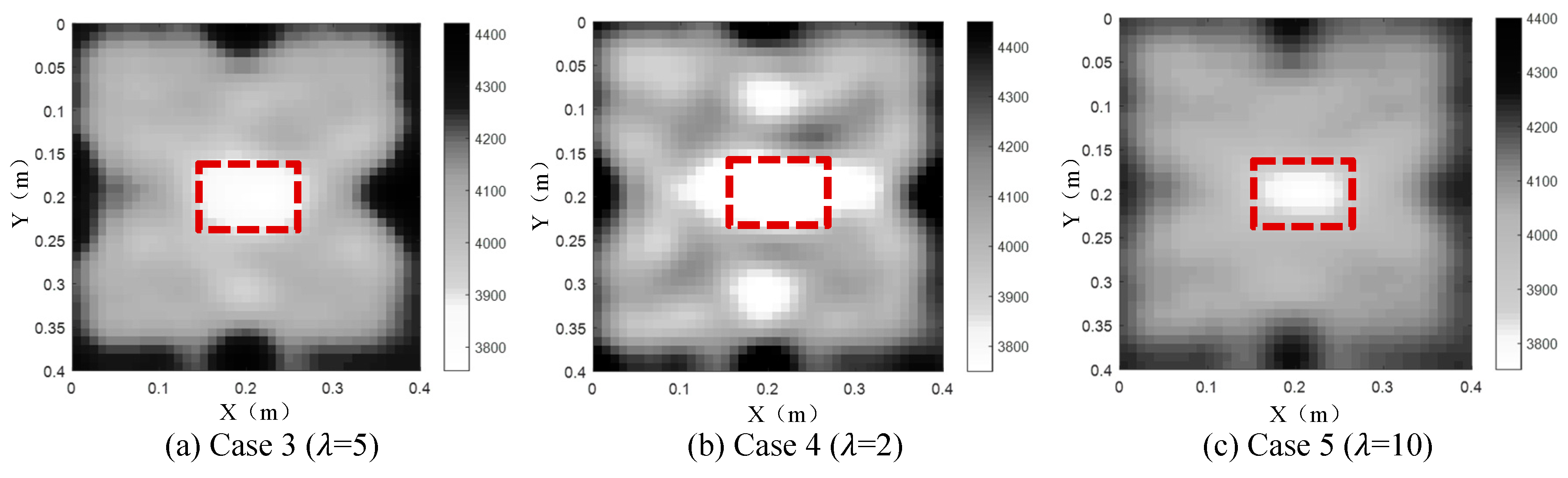
The imaging results under Cases 3, 4 and 5 are plotted in Figure 6. It can be seen from Figure 6 that the concrete core void defect imaging result inside the CFST section does not agree with the real concrete core void defect well in Case 4 ( λ =2). Moreover, two fake concrete core void images appear on the upper and lower sides of the central concrete core void defect inside the CFST section. By contrast, the imaging results of the concrete core void defect is consistent with the real size and position of the concrete core void defect if λ =5 (Case 3). Compared with Case 3, the images effect in Case 5 ( λ =10) is worse due to the size of the imaged concrete core void defect is smaller than the actual size. The reason for this phenomenon is that the model is smoothed excessively for a big weighting matrix (e.g. λ =10), which probably leads to an obvious reduction of fake images. However, the inverting error of the whole velocity field inside the CFST section is likely to increase accordingly due to a big λ . By contrast, fake images will be yielded if a small λ is selected. In a word, the TTT inversion result in Case 3 agrees with the true velocity field distribution best, and hence λ =5 can be thought as the optimum value for this numerical example.

4.4. Inversion Grid Size

During the process of TTT, the selection of inversion grid size (d) depends on what kind of accuracy you require. Usually, the inversion grid size is determined according to the distance of actuators/sensors. In other words, d is often set to be equal to or smaller than the distance of actuators/sensors to reach a relatively accurate inverted image. If the inversion grid size is large, the number of discrete grids in the inverted region will decrease greatly, and the accuracy of the theoretical/calculated travel time and curved ray tracing is going to be reduced. Moreover, the inversion accuracy of the slowness/velocity field inside the CFST section is affected. On the contrary, the number of discrete grids divided in the inversion region will increase dramatically while the inversion grid size is small.
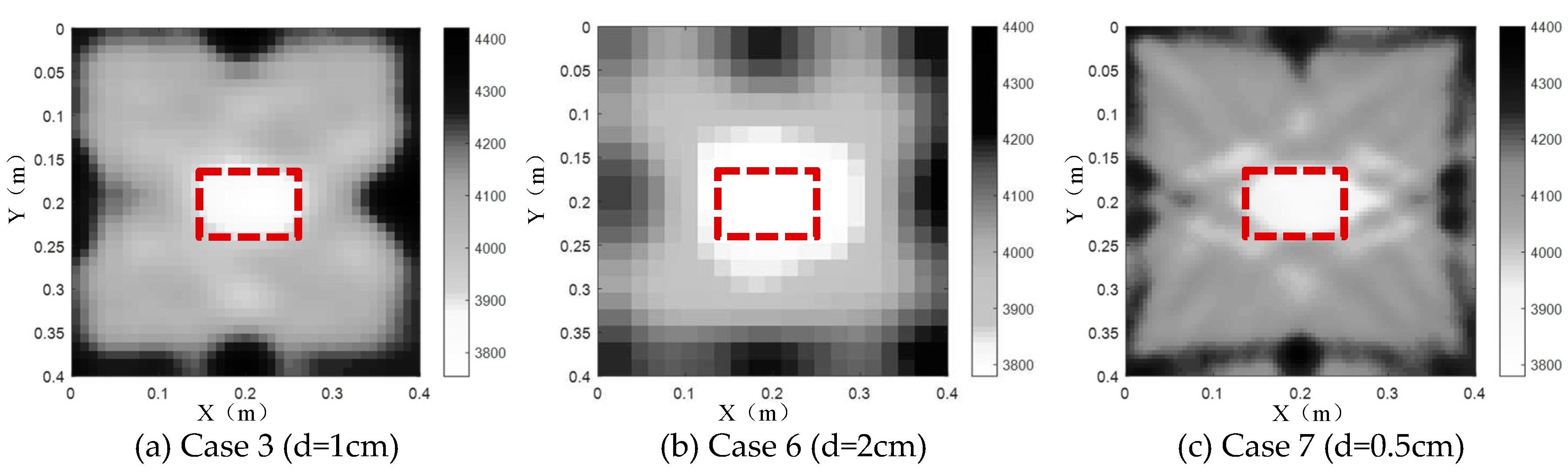
In order to investigate the impact of the inversion grid size on the imaging results of TTT, three kinds of inversion grid size (d) are considered, that is, 2cm (Case 6), 1cm (Case 3) and 0.5cm (Case 7). As shown in Figure 7(b), the position of the concrete core void defect inside the CFST section is effectively imaged when d equals 2cm (Case 6), however, the inversion quality of the size of the concrete core void defect, the concrete core and the steel tube can be thought as the worst in Case 6. The reason accounting for this phenomenon is that a large d will cause the reduction of the inversion accuracy. Hence, false abnormal velocity distribution areas are prone to be generated. When the inversion grid size is 1cm (Case 3), the imaging quality of the CFST section is going to be better. That is to say, the inverted position and size of the concrete core void defect agrees with the real model well in Case 3. Nevertheless, the defect imaging effect is not promoted for Case 7 (d=0.5cm). Figure 7 (c) also illustrates that a few fake images appear due to the interferences from more large angle rays, which implies the imaging effect of the concrete core void defects are decreased to an extent. In addition to a worse concrete core void imaging result than the counterpart in Figure 7 (a), the computing efficiency is also reduced in Case 7. Therefore, too large or small inversion grid size probably leads to a bad inversion imaging effect and hence an appropriate inversion grid size is required. Here, d=1cm is recommended in this numerical example according to the imaging results illustrated in Figure 7.

5. Generality of the Proposed Imaging Approach for Concrete Core Void of CFST Members Considering Void Size, Position and Number

In this section, both void defect size and position are investigated to demonstrate their imaging effect on the simulated CFST members.

5.1. Imaging Results Considering Different Concrete Core Void sizes

In order to investigate the imagining results of concrete core void defects with different sizes using the proposed TTT approach, three concrete core void defect sizes are simulated at the center of the multi-physics finite element model of PZT-CFST coupling system. The dimensions of the considered concrete core void defects are 120mm×80mm, 100mm×60mm, 80mm×40mm, respectively, which indicates the concrete core void ratios are 6%, 3.75% and 2%, respectively. Based on the analysis results of the inversion imaging parameters in Section 4, the second-order difference operator, 5 and 1cm are separately selected for W m , λ and the inversion grid size. After that, TTT is performed on the established finite element model to yield the imaging results as illustrated in Figure 8.
It can be seen from Figure 8 that the position and size of the three concrete core void defects inverted by TTT are in good accordance with the theoretical results shown by the red dash lines. Therefore, if a single defect is located at the center of the section, the inversion accuracy is almost unaffected whatever the size or the concrete core void ratio is.

5.2. Imaging Results Considering Different Concrete Core Void Defect Positions

To further investigate the feasibility of the proposed imaging approach for concrete core void defect in CFST members, imaging results for three CFST members with concrete core void defects at different locations are considered. With the premise that the size of a single concrete core void defect is 100mm×60mm (concrete core void ratio=3.75%), three different defect positions are investigated, that is, the center, the neighborhoods of the actuator side and the sensor side. After that, the TTT algorithm is employed to invert the concrete core void defects and the results are plotted in Figure 9.
As shown in Figure 9, the sizes and positions inverted by TTT agree with the counter-parts inside the CFST section well whatever the concrete core void defect is located at the center or the actuator/ sensor side. Therefore, a conclusion can be drawn that a single concrete core void defect can be imaged with acceptable accuracy using the proposed TTT approach for CFST members.
However, it should be noted that multiple concrete core void defects usually appear in actual CFST members. As such, the subsequent analysis will focus on the imaging results for CFST members with two concrete core void defects at different locations. To be specific, the two concrete core void defects have an identical size of 100mm×60mm, and both of them are located at the actuator side, sensor side and the diagonal line of the cross section, respectively. After that, the TTT algorithm is applied to analyze the above mentioned three cases and the results are shown in Figure 10.
It can be seen from Figure. 10 that the two concrete core void defect positions inverted by TTT are in good accordance with the exact positions defined beforehand whatever the two concrete core void defects are close to the actuator side or the sensor side. TTT is also capable of inverting the sizes of the two concrete core void defects effectively when they are located at the diagonal line of the cross section, however, there is a small offset to the actuator/left side for the two concrete core void defects. The reason for this phenomenon is that large angle rays are possible to bring in some interferences to the inverted imaging results. In a word, TTT can identify the positions and sizes of multiple concrete core void defects effectively, even though there is a slight deviation between the inverted results and the theoretical counterparts.

6. Concluding Remarks

This paper introduces the TTT algorithm to image the sizes and positions of concrete core void defects in CFST members using surface-mounted PZT actuating and sensing technology. In addition, a parameter analysis is also performed to reflect how the inversion parameters, defect sizes and positions affect the imaging results via TTT. In order to verify the effectiveness and accuracy of the TTT algorithm, several numerical examples are investigated. The results demonstrate that TTT has the potential to identify the sizes and positions of the concrete core void defects, the steel tube and concrete core effectively. Moreover, the inversion imaging quality will be the best if the second-order difference operator is selected as model weighting matrix ( W m ). In addition to W m , weighting factor (λ) and inversion grid size (d) also have a significant impact on the imaging results and their optimum values are suggested in this paper. Due to the TTT algorithm is verified via several numerical examples alone in this study, future work will be devoted to its application on scale CFST models with mimicked concrete core void defects in lab and real CFST structural members in engineering structures.

Author Contributions

Conceptualization, Bin Xu; methodology, Wen-Ting Zheng and Jiang Wang; writing—original draft preparation, Wen-Ting Zheng; writing-review and editing, Jing-Liang Liu and Bin Xu.

Funding

This research was funded by the National Natural Science Foundation of China (NSFC) under Grants No. 51878305 and 51608122.

Acknowledgments

We really thank Prof. Hai Liu of Guangzhou University for helping us on the understanding the TTT theory.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Liu, X.; Xu, C.; Liu, J.; et al. Research on special-shaped concrete-filled steel tubular columns under axial compression. J. Constr. Steel Res. 2018, 147, 203–223. [Google Scholar] [CrossRef]
  2. Alatshan, F.; Osman, S.A.; Hamid, R.; et al. Stiffened concrete-filled steel tubes: A systematic review. Thin-Walled Structures. 2020, 148, 106590. [Google Scholar] [CrossRef]
  3. Chen, B.; Han, L.; Qin, D.; et al. Life-cycle based structural performance of long-span CFST hybrid arch bridge: A study on arch of Pingnan Third Bridge. J. Constr. Steel Res. 2023, 207, 107939. [Google Scholar] [CrossRef]
  4. Lin, X.; Zhang, Y.X. Novel composite beam element with bond-slip for nonlinear finite-element analyses of steel/FRP–reinforced concrete beams. J. Struct. Eng. 2013, 139, 1–5. [Google Scholar] [CrossRef]
  5. Majdi, Y.; Hsu, C.T.T.; Punurai, S. Local bond-slip behavior between cold-formed metal and concrete. Eng. Struct. 2014, 69, 271–284. [Google Scholar] [CrossRef]
  6. Chen, L.; Dai, J.; Jin, Q.; Chen, L. Refining bond–slip constitutive relationship between checkered steel tube and concrete. Constr. Build. Mater. 2015, 79, 153–164. [Google Scholar] [CrossRef]
  7. Chen, D.; Montano, V.; Huo, L.; et al. Detection of subsurface voids in concrete-filled steel tubular (CFST) structure using percussion approach. Constr. Build. Mater. 2020, 262, 119761. [Google Scholar] [CrossRef]
  8. Lu, Z.; Guo, C.; Li, G. Air void and ring gap effect on CFST arch bridges dynamic performance. J. Constr. Steel Res. 2021, 177, 106418. [Google Scholar] [CrossRef]
  9. Huang, Y.; Li, W.; Lu, Y.; et al. Behavior of CFST slender columns strengthened with steel tube and sandwiched concrete jackets under axial loading. J. Build. Eng. 2022, 45, 103613. [Google Scholar] [CrossRef]
  10. Stojić, D.; Nestorović, T.; Marković, N.; et al. Detection of damage to reinforced-concrete structures using piezoelectric smart aggregates. Građevinar 2016, 68, 371–380. [Google Scholar]
  11. Xu, B.; Chen, H.; Xia, S. Numerical study on the mechanism of active interfacial debonding detection for rectangular CFSTs based on wavelet packet analysis with piezoceramics. Mech. Syst. Signal Process. 2017, 86, 108–121. [Google Scholar] [CrossRef]
  12. Xu, B.; Chen, H.; Mo, Y.L.; et al. Dominance of debonding defect of CFST on PZT sensor response considering the meso-scale structure of concrete with multi-scale simulation. Mech. Syst. Signal Process. 2018, 107, 515–528. [Google Scholar] [CrossRef]
  13. Xu, B.; Luan, L.; Chen, H.; et al. Experimental study on active interface debonding detection for rectangular concrete-filled steel tubes with surface wave measurement. Sensors 2019, 19, 1–14. [Google Scholar] [CrossRef]
  14. Chen, H.; Xu, B.; Wang, J.; et al. XFEM-based multiscale simulation on monotonic and hysteretic behavior of reinforced concrete columns. Appl. Sci. 2020, 10, 7899. [Google Scholar] [CrossRef]
  15. Wang, J.; Xu, B.; Chen, H.; et al. Mesoscale numerical analysis and test on the effect of debonding defect of rectangular CFSTs on wave propagation with a homogenization method. Mech. Syst. Signal Process. 2022, 163, 108135. [Google Scholar] [CrossRef]
  16. Wang, J.; Xu, B.; Liu, Q.; et al. Multi-physics mesoscale substructure analysis on stress wave measurement within CFST-PZT coupling models for interface debonding detection. Sensors 2022, 22, 1039. [Google Scholar] [CrossRef] [PubMed]
  17. Hoegh, K.; KhazanovichL. Extended synthetic aperture focusing technique for ultrasonic imaging of concrete. NDT E Int. 2015, 74, 33–42. [Google Scholar] [CrossRef]
  18. Cosmes-López, M.F.; Castellanos, F.; Cano-Barrita, P.F. Ultrasound frequency analysis for identification of aggregates and cement paste in concrete. Ultrasonics 2017, 73, 88–95. [Google Scholar] [CrossRef]
  19. Xu, B.; Zhang, T.; Song, G.; et al. Active interface debonding detection of a concrete-filled steel tube with piezoelectric technologies using wavelet packet analysis. Mech. Syst. Signal Process. 2013, 36, 7–17. [Google Scholar] [CrossRef]
  20. Luo, M.; Li, W.; Hei, C.; et al. Concrete infill monitoring in concrete-filled FRP tubes using a PZT-based ultrasonic time-of-flight method. Sensors 2016, 16, 1–11. [Google Scholar] [CrossRef]
  21. Liu, H.; Chen, Z.; Liu, Y.; et al. Interfacial debonding detection for CFST structures using an ultrasonic phased array: Application to the Shenzhen SEG building. Mech. Syst. Signal Process. 2023, 192, 110214. [Google Scholar] [CrossRef]
  22. Chai, H.K.; Momoki, S.; Kobayashi, Y.; et al. Tomographic reconstruction for concrete using attenuation of ultrasound. NDT E Int. 2011, 44, 206–215. [Google Scholar] [CrossRef]
  23. Behnia, A.; Chai, H.K.; Yorikawa, M.; et al. Integrated non-destructive assessment of concrete structures under flexure by acoustic emission and travel time tomography. Constr. Build. Mater. 2014, 67, 202–215. [Google Scholar] [CrossRef]
  24. Stefanov, P.; Uhlmann, G.; Vasy, A.; et al. Travel time tomography. Acta Math. Sin. Engl. Ser. 2019, 1085–1114. [Google Scholar] [CrossRef]
  25. Tronicke, J.; Tweeton, D.R.; Dietrich, P.; et al. Improved crosshole radar tomography by using direct and reflected arrival times. J. Appl. Geophys. 2001, 47, 97–105. [Google Scholar] [CrossRef]
  26. Clement, W.P.; Barrash, W. Crosshole radar tomography in a fluvial aquifer near Boise, Idaho. J. Environ. Eng. Geophys. 2006, 11, 171–184. [Google Scholar] [CrossRef]
  27. Becht, A.; Bürger, C.; Boris, K.o.s.t.i.c.; et al. High-resolution aquifer characterization using seismic cross-hole tomography: An evaluation experiment in a gravel delta. J. Hydrol. 2007, 336, 171–185. [Google Scholar] [CrossRef]
  28. Musil, M.; Maurer, H.R.; Green, A.G. Discrete tomography and joint inversion for loosely connected or unconnected physical properties: Application to crosshole seismic and georadar data sets, Geophys. J. R. Astron. Soc. 2010, 153, 389–402. [Google Scholar] [CrossRef]
  29. Zhu, K.; Huang, Y.; Wang, J. Curved ray tracing method for one-dimensional radiative transfer in the linear-anisotropic scattering medium with graded index. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 377–383. [Google Scholar] [CrossRef]
  30. Wang, F.; Liu, S.; Qu, X. Crosshole radar traveltime tomographic inversion using the fast marching method and the iteratively linearized scheme. J. Environ. Eng. Geophys. 2014, 19, 229–237. [Google Scholar] [CrossRef]
  31. Huang, G.; Zhou, B.; Li, H.; et al. Seismic travel time inversion based on tomographic equation without integral terms. Comput. Geosci. 2017, 104, 29–34. [Google Scholar] [CrossRef]
  32. Khairi, M.T.M.; Ibrahim, S.; Yunus, M.A.M.; el, al. Ultrasound computed tomography for material inspection: Principles, design and applications. Measurement 2019, 146, 490–523. [Google Scholar] [CrossRef]
  33. Qi, X.; Zhao, X.; Xie, J. Improved iterative algorithm based on Snell law and disturbance ray tracing for ultrasonic computerized tomography on concrete. J. Inf. Comput. Sci. 2014, 11, 2965–2974. [Google Scholar] [CrossRef]
  34. Jiang, W.; Zelt, C.A.; Zhang, J. Detecting an underground tunnel by applying joint traveltime and waveform inversion. J. Appl. Geophys. 2020, 174, 103957. [Google Scholar] [CrossRef]
  35. Liu, H.; Xia, H.; Zhuang, M.; et al. Reverse time migration of acoustic waves for imaging based defects detection for concrete and CFST structures. Mech. Syst. Signal Process. 2019, 117, 210–220. [Google Scholar] [CrossRef]
  36. Gerth, D. A new interpretation of (Tikhonov) regularization. Inverse Probl. 2021, 37, 064002. [Google Scholar] [CrossRef]
Preprints 81746 g001
Figure 1. The flowchart of TTT.
Figure 1. The flowchart of TTT.
Preprints 81746 g001
Preprints 81746 g002
Figure 2. Schematic diagram of ray path tracing for a cross section of a CFST member.
Figure 2. Schematic diagram of ray path tracing for a cross section of a CFST member.
Preprints 81746 g002
Preprints 81746 g003
Figure 3. Multi-physics coupling finite element model of PZT-CFST system (Unit: mm).
Figure 3. Multi-physics coupling finite element model of PZT-CFST system (Unit: mm).
Preprints 81746 g003
Preprints 81746 g004
Figure 4. Sinusoidal excitation and stress wave response signal.
Figure 4. Sinusoidal excitation and stress wave response signal.
Preprints 81746 g004
Preprints 81746 g005
Figure 5. Inversion results of concrete core void defects of a CFST model under various model weighting matrices.
Figure 5. Inversion results of concrete core void defects of a CFST model under various model weighting matrices.
Preprints 81746 g005
Preprints 81746 g006
Figure 6. Inversion results of concrete core void defects of a CFST model under various weighting factors: (a) Case3; (b) Case 4; (c) Case 5.
Figure 6. Inversion results of concrete core void defects of a CFST model under various weighting factors: (a) Case3; (b) Case 4; (c) Case 5.
Preprints 81746 g006
Preprints 81746 g007
Figure 7. Inversion results of concrete core void defects of a CFST model under various grid sizes.
Figure 7. Inversion results of concrete core void defects of a CFST model under various grid sizes.
Preprints 81746 g007
Preprints 81746 g008
Figure 8. The tomography results of a single concrete core void defect of a CFST model with various void defect sizes/ratios.
Figure 8. The tomography results of a single concrete core void defect of a CFST model with various void defect sizes/ratios.
Preprints 81746 g008
Preprints 81746 g009
Figure 9. The tomography results of a single concrete core void defect located at different positions.
Figure 9. The tomography results of a single concrete core void defect located at different positions.
Preprints 81746 g009
Preprints 81746 g010
Figure 10. The tomography results of two concrete core void defects located at different positions.
Figure 10. The tomography results of two concrete core void defects located at different positions.
Preprints 81746 g010
Table 1. The material properties of the PZT-CFST coupling model.
Table 1. The material properties of the PZT-CFST coupling model.
Number Material Elastic modulus (GPa) Poisson ratio Density(kg/m³)
1 Steel 206 0.30 7850
2 Concrete 30.0 0.17 2400
3 PZT5A --- --- 7500
Table 2. The seven cases of selecting different inversion parameters.
Table 2. The seven cases of selecting different inversion parameters.
Cases W m λ d
Case 1 Unit matrix operator 5 1cm
Case 2 first-order difference operator 5 1cm
Case 3 second-order-difference operator 5 1cm
Case 4 second-order-difference operator 2 1cm
Case 5 second-order-difference operator 10 1cm
Case 6 second-order-difference operator 5 2cm
Case 7 second-order-difference operator 5 0.5cm
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated