Prerpints.org logo
Preprint
Article

Binary Black Hole Mirror Explosion

This version is not peer-reviewed.

Submitted:

03 August 2023

Posted:

08 August 2023

You are already at the latest version

Abstract
When two black holes form a binary system, each black hole observes an event horizon and a curved distorted space-time region around the other black hole. In this space-time, two such regions are formed, and another black hole forms in the second region from the initial black hole, which may be termed the “image” of the first black hole. The same event occurs for the other black hole also, and an extra image of it is formed. In these conditions, the energy of the system divides between the two black holes and their images. These four new black holes that are formed interact with each other again and produce new horizons and new distorted regions. Each black hole produces an image of all the other black holes and detects the background of six black holes instead of three. Consequently, for four black holes, 24 new black holes arise. The energy of the system will be divided amongst all 24 black holes. This story continues and black holes interact with one another and produce new images. Finally, very light black holes are formed each of which is so weak that it cannot produce strong distortions of space-time. The radiated gravitational waves from these weak black holes could be detected by LIGO as well as the signature of these binary black holes. However, detected waves are only a part of very strong gravitational waves. Each time a part of these waves escapes from the system and reaches the earth, they may be regarded as emitted waves from a new binary black hole. The time between radiated signals decreases, and it may be interpreted that a new supermassive binary black hole is radiating. If radiated signals combine, an explosion of the very strong binary system could be detected.
Keywords: 
Subject: 
Physical Sciences  -   Astronomy and Astrophysics

1. Introduction

One of best sources of gravitational waves is a binary black hole system. Like binary stars, two black holes attract each other and move or accelerate around each other. To date, several observations have been made by collaborations like the Laser Interferometer Gravitational-Wave Observatory (LIGO):
  • On September 14, 2015 at 09:50:45 UTC, the two detectors of LIGO simultaneously observed a transient gravitational-wave signal. The signal sweeps upwards in frequency from 35 to 250 Hz with a peak gravitational-wave strain of 1.0×10-21. These changes belong to a binary black hole whose total mass is 62 M⊙ and the masses of the black holes in this system are 36 M⊙ and 29 M⊙ [1].
  • Also, this detector reported the observation of a gravitational-wave signal produced by the coalescence of two stellar-mass black holes on December 26, 2015 at 03:38:53 UTC. The initial black hole masses are 14.2 M⊙ and 7.5 M⊙ and the final black hole mass is 20.8 M⊙ [2].
  • Another signal was measured on January 4, 2017 at 10:11:58.6 UTC by the twin advanced detectors of LIGO during its second observing run, with a network signal-to-noise ratio of 13 and a false alarm rate of less than 1 in 70,000 years. The inferred component black hole masses were 31.2 M⊙ and 19.4 M⊙ (at the 90% credible level) [3].
  • Also, on June 8, 2017 at 02:01:16.49 UTC, a gravitational-wave signal from the merger of two stellar-mass black holes was observed by the two Advanced LIGO detectors with a network signal-to-noise ratio of 13. This system was the lightest black hole binary so far observed, with component masses 12 M⊙ and 7 network [4].
  • Another research reported the observation of a compact binary coalescence during LIGO and Virgo’s third observing run on August 14, 2019 at 21:10:39 UTC involving a 22.2–24.3 M⊙ black hole and a compact object with a mass of 2.50–2.67 M⊙. This had a signal-to-noise ratio of 25 in the three-detector network (all measurements quoted at the 90% confidence level) [5].
  • On the other hand, on May 21, 2019 at 03:02:29 UTC Advanced LIGO and Virgo observed a new short duration gravitational-wave signal, GW190521, with a three-detector network signal-to-noise ratio of 14.7, and an estimated false-alarm rate of 1 in 4900 years using a search sensitive to generic transients. If GW190521 was from a quasi-circular binary inspiral, then the detected signal would be consistent with the merger of two black holes with masses of 85 M⊙ and 66 M⊙ [6].
To date, many models have been proposed for binary black holes, e.g., long-term simulations of orbiting black holes became possible when three groups independently developed ground-breaking new methods to model the inspiral merger and ring-down of binary black holes in 2005. [7,8,9]. Also, differences between binary Schwarzschild and Kerr black holes have been considered in some articles [10,11], whereas some other papers have investigated the shape of binary black holes [12].
Now the question that arises is what is the effect of the background of a black hole on the other black hole in a binary system? We answer this question, and show that interactions between the black hole backgrounds cause the formation of new black holes similar to mirror images.

2. A model for a Black Hole Mirror

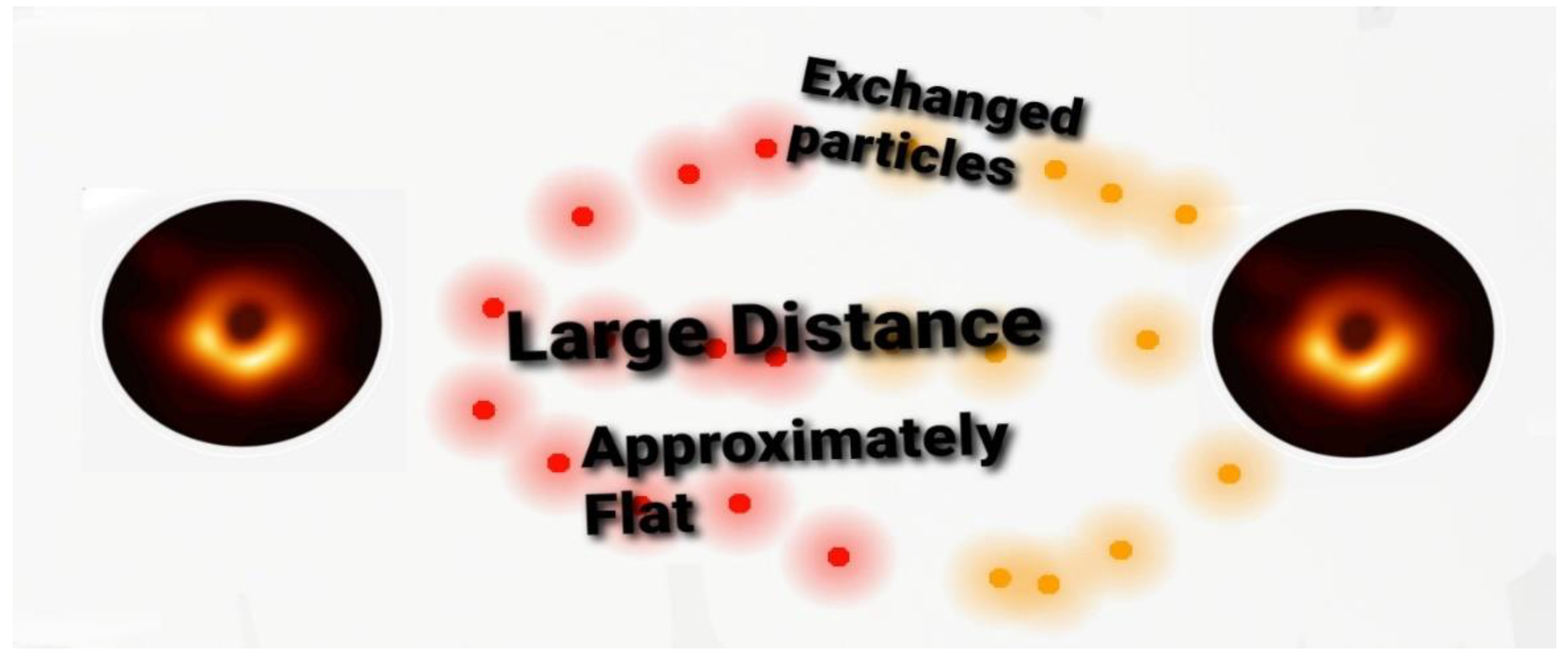
When two black holes are relatively distant from each other, space-time is approximately flat (See Figure 1).
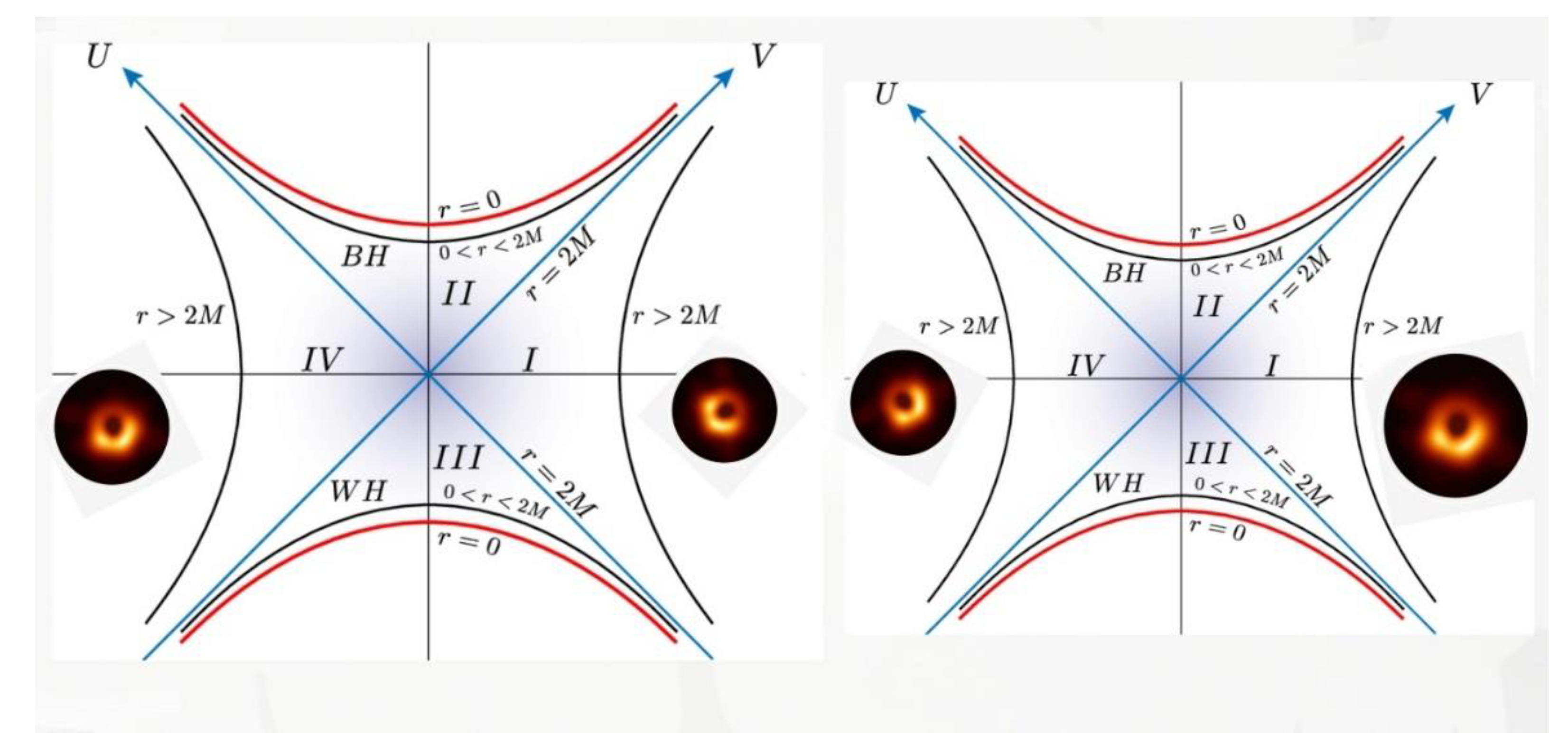
In these conditions, black holes could interact via different types of fields like scalar, Dirac and graviton fields. Eventually, black holes come close to each other, and their backgrounds have direct effects on each other. In these conditions, two type of distorted curved space-time regions emerge. One region is related to the first black hole and the other corresponds to the second black hole. Each background includes four regions which are disconnected by the event horizon. A black hole in region I will have a so-called image in region IV. Thus, a black hole divides into two black holes, and the two initial black holes in a binary system convert to four black holes (See Figure 2).

System

Summing over the masses of these black holes should be equal to summing over the masses of the two initial black holes. Each of these four black holes again produces a backgound for each of the other black holes, and produces an image for each of them. In fact, each black hole creates three backgrounds for each of the other three black holes, and in each back ground, an extra image from each black hole is created. Thus, each black hole creates six new black holes. Since there are four black holes interacting with each other, they form 24 new black holes. Summing over the masses of these new black holes is equivalent to summing over the masses of the initial two black holes. So, by any interaction, a lighter black hole is created. These interactions between the black holes and the backgrounds, and the formation of lighter black holes and images continue until the formation of very light black holes. This event is similar to putting two mirrors face to face and the creation of many images–see Figure 3. However, there are two main differences between the black holes and the analogy with the mirrors. The first difference is that in contrast to the mirrors, black hole images are real and take a portion of the black hole mass. Consequently, a massive black hole divides into lighter black holes. The second difference is that the number of images in the mirrors have no bound but the number of images in a black hole binary system continues until the formation of extremely light black holes. These black holes are so light that they have weaker gravitational waves and backgrounds. Objects with masses lighter then these black holes have no event horizons.

3. Observations

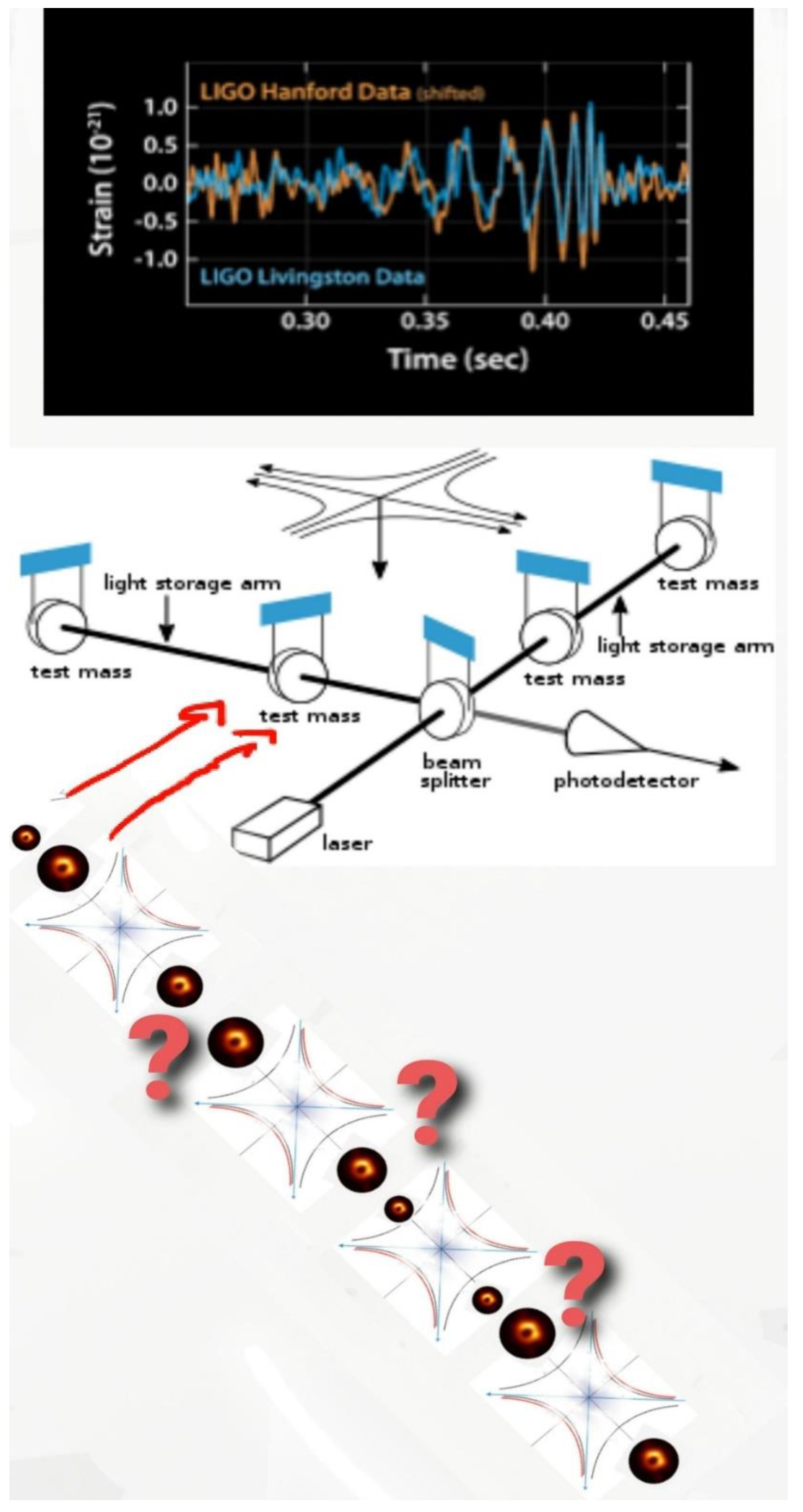
The question that arises is whether we could detect the signature of such a binary black hole mirror. Firstly, if there exists this type of gravitational mirror, we should have a string of gravitational wave detections in which the time separation between signals decreases, and the amplitude of the measured waves increase. This is because initially, weak gravitational waves of two very light black holes or images may be detected, while most of the energies are confined within the binary system. This huge amount of energy is confined within the event horizon and could not escape fast enough. However, later, this energy is released and the power of the gravitational strain increases and time between two signals decreases. These gravitational waves enter a detector and force photons to change their direction towards photodetectors (See Figure 4).
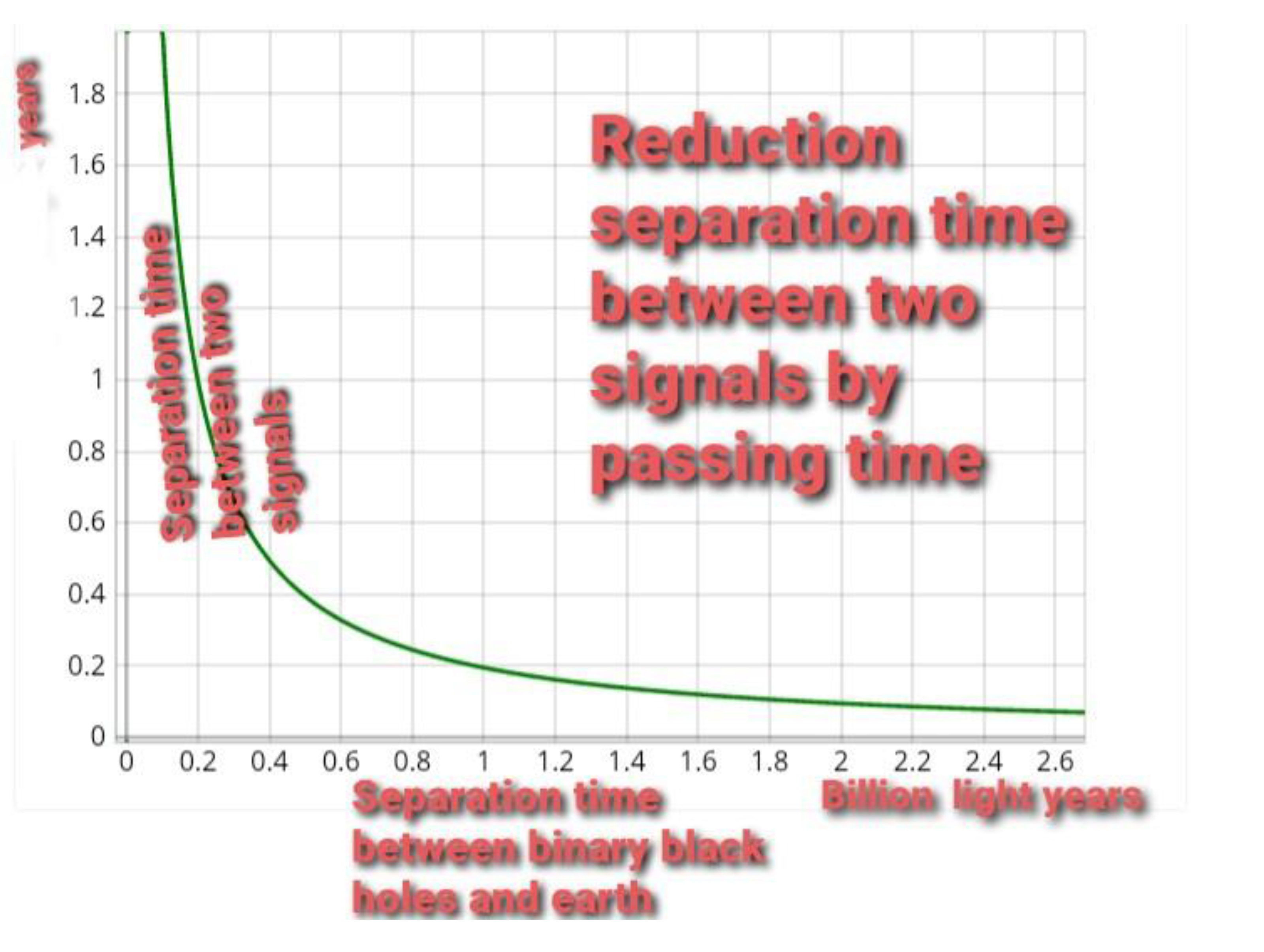
In Figure 5, we assume that gravitational fields escape from a binary black hole following an exponential pattern. It is clear that initially, the separation time between two signals may be very large. However, after any emission, the ability of a binary system to confine energy decreases and more energy can escape. Consequently, the time internal between two events decreases.
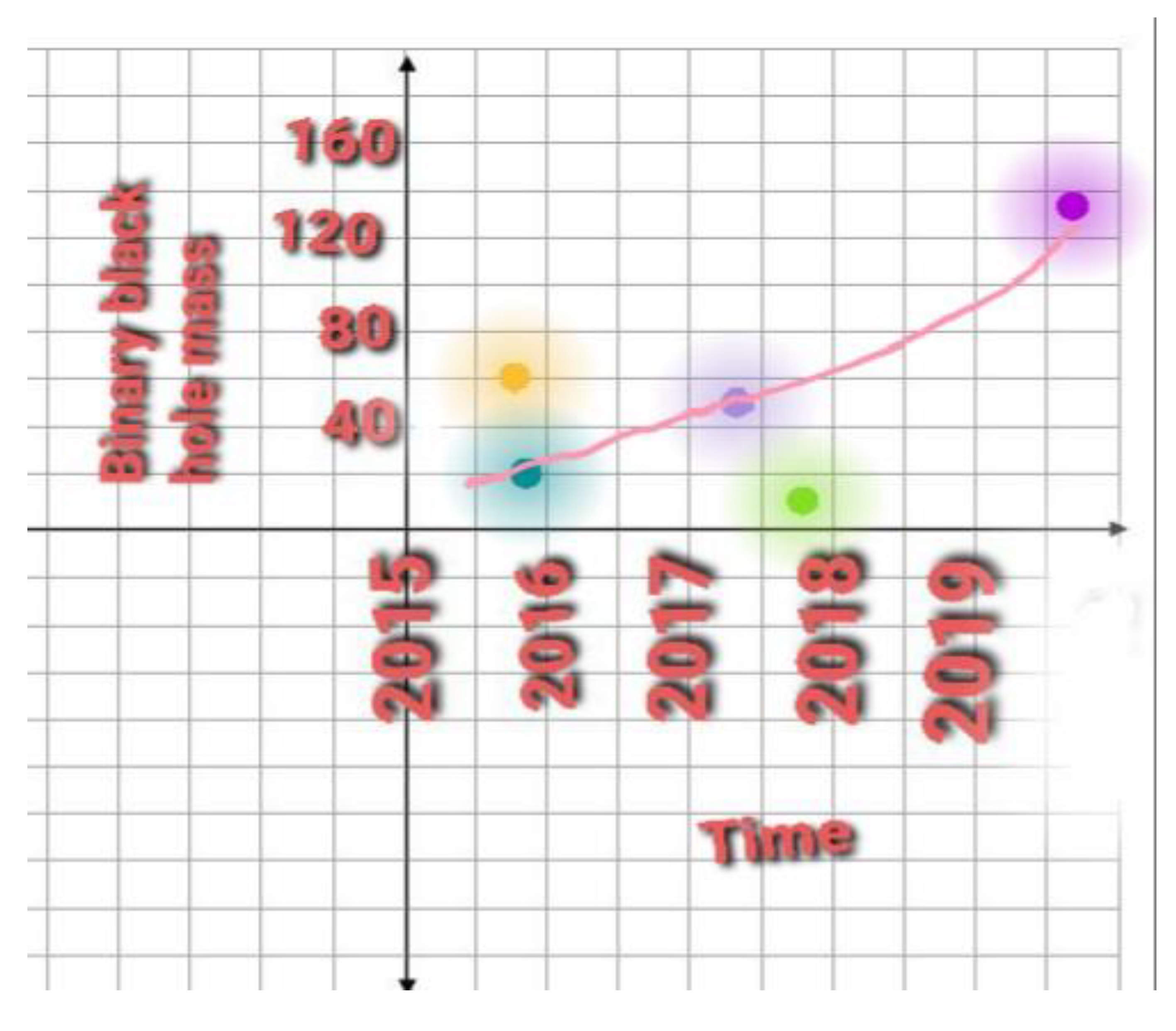
In Figure 6, we collect the results of LIGO for the different years from 2015 to 2021. It is clear that the detected masses increase with later detections. For example, the first detections in 2015 were related to black hole binaries with a mass of 62 M⊙ or less, while the final detections were related to binaries with a mass of 150 M⊙ or more. If all these detections are related to a binary mirror, we can expect a huge increase in detected gravitational waves.

4. Results and Discussion

The physics of a black hole mass is equivalent to the physics of the acceleration of a non-inertial frame. In fact, approximately any formula in an accelerating frame could be applied in a black hole frame by replacing the acceleration (a) by the inverse of the black hole mass (M -1). On the other hand, when two black holes propagate around each other, they accelerate. Thus, we can define the total acceleration for a binary black hole system as:
a = k   ( M B B ) − 1 + a r o t a t e ,
where a is the total acceleration, M B B is the mass and a r o t a t e is the angular acceleration. For this acceleration, there is a direct relationship between the coordinates in flat space time and the binary black hole [13]:
t 1 = a 1 − 1   e a 1 R 1 sinh ⁡ ( a 1 T 1 ) ,
and
r 1 = a 1 − 1   e a 1 T 1 cosh ⁡ ( a 1 R 1 ) ,
where t and r are coordinates in flat space-time and R and T are the coordinates in the black hole binary system.
To obtain the distance between the solar system and the binary black hole, we write:
r 1 − r 0 = a 1 − 1   e a 1 T 1 cosh ⁡ ( a 1 R 1 ) − R 0 ,
or by replacing a 1 in equation (4) with
a 1 = k ( M 1 , B B ) − 1 + a a 1 ,   r o t a t e ,
we get:
r 1 − r 0 = [ k ( M 1 , B B ) − 1 + a a 1 ,   r o t a t e ]   e a 1 T 1 cosh ⁡ [ { a 1 k ( M 1 , B B ) − 1 + a a 1 ,   r o t a t e } R 1 ] − R 0 ,
where r 0 and R 0 are the positions of the solar system in the flat and binary systems, respectively. Since we are very distant from a binary system, we have r 0 = R 0 . The above equation shows that the estimated position of a binary system depends on the black hole masses and acceleration. Any small change in the black hole masses or acceleration will change separation.
Let us consider that a binary system emits a particle with energy E p , 0 . The binary mass after this radiation becomes:
M B B , p , 0 = M B B − E p , 0   ,
For this new mass, the distance from a binary system to our solar system becomes:
r 1 , p . o − r 0 = [ k ( M 1 , B B − E p , 0 ) − 1 + a a 1 ,   r o t a t e ]   e a 1 T 1 c o s h ⁡ [ { k ( M 1 , B B − E p , 0 ) − 1 + a a 1 ,   r o t a t e } R 1 ] − R 0
The above equation shows that as a result of the first emission, the estimated distance between the binary system and the solar system changes. After n radiations this separation then becomes:
r 1 , p , n − r 0 = [ k ( M 1 , B B − E p , n − E p , n − 1 − … − E p , 0 ) − 1 + a a 1 ,   r o t a t e ] e a 1 T 1 c o s h ⁡ [ { a 1 k ( M 1 , B B − E p , n − E p , n − 1 − … − E p , 0 ) − 1 + a a 1 ,   r o t a t e } R 1 ] − R 0
Thus the real separation may be different from what detectors predict. Detectors usually make use of redshift and ignore these types of actions. Thus, we cannot count on the correctness of those results.
In addition to this factor, there is another factor also. Two black holes in a binary system could interact with each other and distort their curved space-times in different ways. For example, the second black hole could see a curved space time which belongs to the first black hole. In these conditions, the coordinates change again and new coordinates should be defined. We have:
t 2 = a 2 − 1   e a 2 r 1 sinh ⁡ a 2 t 1 = a 2 − 1   e a 2 r 1 s i n h ⁡ [ a 2 a 1 − 1 e a 1 R 1 sinh ⁡ ( a 1 T 1 ) ] ,
and
r 2 = a 2 − 1   e a 2 t 1 cosh ⁡ a 2 r 1 = a 2 − 1   e a 2 t 1 c o s h ⁡ [ a 2 a 1 − 1 e a 1 T 1 cosh ⁡ ( a 1 R 1 ) ]
For these new coordinates; the separation becomes:
r 2 , n , n − r 0 = [ k ( M 2 , B B − E p , n − … − E p , 0 ) − 1 + a 2 , r o t a t e ] − 1 e a 2 t 1 c o s h ⁡ [ { k ( M 2 , B B − E p , n − … − E p , 0 ) − 1 + a 2 , r o t a t e } r 1 ] − R 0 = [ k ( M 2 , B B − E p , 0 − … − E p , 0 ) − 1 + + a 2 , r o t a t e ] − 1 e a 2 t 1 c o s h ⁡ [ { k ( M 2 , B B − E p , n − … − E p , 0 ) − 1 + a 2 , r o t a t e } { k ( M 1 , B B − E p , n − … − E p , 0 ) − 1 + a 2 , r o t a t e } { k ( M 1 , B B − E p , n − … − E p , 0 ) − 1 + a 1 , r o t a t e } − 1   x   e a 1 T 1 cosh ⁡ k M 1 , B B − E p , n − … − E p , 0 ) − 1 + a 1 , r o t a t e R 1 − R 0
This process may be repeated, and by any interaction between black holes or any radiation, the distance between the binary system and our solar system changes.
The above results indicate that the different signals which have been detected may be from one big black hole binary system and not different ones. If this is true, we should expect the detection of a big explosion of a binary black hole.

5. Conclusions

In this research, we have studied a binary black hole system, and provide an alternative description of the system. It is well-known that the space time around a black hole is distorted. We show that the initial two black holes of the system produce a further two black holes, and this process continues until the furthest black holes cause very little distortions of the spacetime. This process is similar to the infinite images seen via mirrors as shown in Figure 3. Hence, we may interpret black hole binaries as face to face mirrors which divide the initial energies up to very light ones. We discussed the possible observation of such an interpretation. The time interval between the signals from binary black holes that have been detected have been illustrated in a diagram (Figure 5). The data is compatible with signals from a single binary black hole initially that divides into many other black holes by the process illustrated similar to the images that we can see via mirrors. In addition, we have also shown in Figure 6 that the masses associated with the detected black holes over time is increasing. Again this is also compatible with our interpretation. Our system emits a weak gravitational wave at first, and most of energy cannot be detected. However, as the system evolves, it cannot save its energy, and a portion of it escapes. This causes the amplitude of the observed gravitational waves to increase, and eventually, a big explosion may be seen. This is one of the predictions from our alternative description which could be detected in future

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Abbott, B.P.; et al. (LIGO Scientific Collaboration and Virgo Collaboration). Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
  2. Abbott, B.P.; et al. (LIGO Scientific Collaboration and Virgo Collaboration). Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
  3. Abbott, B.P. et al. (LIGO Scientific and Virgo Collaboration). Erratum: GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2 [Phys. Rev. Lett. 2017, 118, 221101] 2018, 121, 129901Author 1, A.; Author 2, B. Title of the chapter. In Book Title, 2nd ed.; Editor 1, A., Editor 2, B., Eds.; Publisher: Publisher Location, Country, 2007; Volume 3, pp. 154–196.
  4. Abbott, B.P.; et al. (LIGO Scientific and Virgo Collaboration). GR170608: Observation of a 19-solar-mass Black Hole Coalescence. Ap. J. Lett. 2017, 851, L35. [Google Scholar]
  5. Abbott, R.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Ap. J. Lett. 2020, 896. L44 (20 pp.). [Google Scholar] [CrossRef]
  6. Abbott, R.; et al. GW190521: A Binary Black Hole Merger with a total mass of 150 Phys. Rev. Lett. 2020, 125, 110102. [Google Scholar] [CrossRef] [PubMed]
  7. Pretorius, F. Evolution of Binary Black-Hole Spacetimes. Phys. Rev. Lett. 2005, 95, 121101. [Google Scholar] [CrossRef] [PubMed]
  8. Campanelli, M.; Lousto, C.O.; Marronetti, P.; Zlochower, Y. Accurate Evolutions of Orbiting Black-Hole binaries without Excision. Phys. Rev. Lett. 2006, 96, 111101. [Google Scholar] [CrossRef] [PubMed]
  9. Baker, J.G.; Centralla, J.; Choi, D-Il. ; Koppitz, M; van Meter, J. Gravitational-Wave Extraction from an Inspiring Configuration of Merging Black Holes. Phys. Rev. Lett. 2006, 96, 111102. [Google Scholar] [CrossRef] [PubMed]
  10. Smarr, L; Cadez, A. ; DeWitt, B.; Eppley, K. Collision of two Black Holes: Theoretical Framework. Phys. Rev. D 1976, 14, 2443. [Google Scholar] [CrossRef]
  11. Nichols, D.A.; Yanbei, C. Hybrid method for understanding black-hole mergers: Inspiralling case. Phys. Rev. D 2012, 85, 044035. [Google Scholar] [CrossRef]
  12. Cohen, M.I.; Kaplan, J.D.; Scheel, M.A. On Toroidal Horizons in Binary Black Hole Inspirals. Phys. Rev. D, 2012, 85, 024031. [Google Scholar] [CrossRef]
  13. Fuentes-Schuller, I; Mann, R. B. Alice Falls into a Black Hole: Entanglement in Noninertial Frames. Phys. Rev. Lett., 2005, 95, 120404. [Google Scholar] [CrossRef] [PubMed]
  14. Author 1, A.B.; Author 2, C. Title of Unpublished Work. Abbreviated Journal Name year, phrase indicating stage of publication (submitted; accepted; in press).
  15. Author 1, A.B. (University, City, State, Country); Author 2, C. (Institute, City, State, Country). Personal communication, 2012.
  16. Author 1, A.B.; Author 2, C.D.; Author 3, E.F. Title of Presentation. In Proceedings of the Name of the Conference, Location of Conference, Country, Date of Conference (Day Month Year).
  17. Author 1, A.B. Title of Thesis. Level of Thesis, Degree-Granting University, Location of University, Date of Completion.
  18. Title of Site. Available online: URL (accessed on Day Month Year).
Preprints 81526 g001
Figure 1. Two distant black holes.
Figure 1. Two distant black holes.
Preprints 81526 g001
Preprints 81526 g002
Figure 2. Two initial black holes mixing with their images in the back ground of a binary.
Figure 2. Two initial black holes mixing with their images in the back ground of a binary.
Preprints 81526 g002
Preprints 81526 g003
Figure 3. Analogy of a binary black hole with two mirrors face to face.
Figure 3. Analogy of a binary black hole with two mirrors face to face.
Preprints 81526 g003
Preprints 81526 g004
Figure 4. Signature of a black hole mirror in gravitational waves.
Figure 4. Signature of a black hole mirror in gravitational waves.
Preprints 81526 g004
Preprints 81526 g005
Figure 5. Reduction of time interval between two signals against distance between binary black hole and earth.
Figure 5. Reduction of time interval between two signals against distance between binary black hole and earth.
Preprints 81526 g005
Preprints 81526 g006
Figure 6. An increase in detected black hole mass against time.
Figure 6. An increase in detected black hole mass against time.
Preprints 81526 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated