Decentralized QFT Controller Design Based on the Equivalent Subsystems Method

1. Introduction

Since its come up in the 70´s, decentralized control has been an important practice-oriented advanced control approach. Various decentralized control methodologies have been developed to deal with the challenge of controlling complex and/or spatially distributed systems with multiple inputs and multiple outputs (MIMO systems) such as chemical plants, interconnected electrical power systems with strong interactions, water treatment plants, etc.

Typically, complex systems are made up of several mutually interacting subsystems whereby each subsystem operates relatively independently having its own sub-objective contributing to the global objective of the overall system. In complex systems control, major problems arise due to interactions among subsystems; if they are strong, multivariable controllers have to be used. Due to practical reasons, restrictions on the controller structure may be reasonable and even inevitable. In the extreme case, when the multivariable controller of the overall system splits into individual local feedback loops it becomes a decentralized controller. Generally, such constraints on controller structure bring about a certain performance deterioration compared with centralized controllers, however counterbalanced by significant practical benefits such as simplicity of controller design as well as hardware, operation, and reliability improvements. Decentralization and decomposition are effective tools to overcome difficulties specific for complex systems namely high dimensionality, information structure constraints and uncertainty [3].

Decentralization has gained a foothold throughout the development of modern control systems. Distributed control systems (DCS) are used in the innovative process industries as an extension of traditional controllers. Their major concept is derived from the idea of decentralizing the control unit and establishing a common network between the engineering stations with autonomous controllers distributed throughout the system with a central operator supervisory control [4]. Since the 80’s as microprocessors became more powerful and cheaper, they could have been embedded in remote devices and components to perform dedicated specific functions including control ones in a communications network close to the processes they control. In the last few years, convergence of the cyber and the physical spaces has further transformed traditional embedded systems into cyber-physical systems (CPS) characterized by tight integration and coordination between computation and physical processes by means of networking. Examples of CPS include a wide range of large-scale engineered systems such as avionics, healthcare, transportation, and smart grid systems [5]. In general, the use of distributed information and control structures such as networked systems, embedded systems, or cyber-physical systems requires to synthesize control laws in a constrained (decentralized) information structure.

Decentralized control has been the most common control scheme for MIMO systems since the 70’s. Various design approaches and techniques have been developed both in the time and the frequency domains. The first major frequency domain multivariable design techniques were based on a generalization of the classical SISO concepts. In the 80’s, robust approach to the decentralized control design was commonly used. Key theoretical results in the seminal paper [6] show how classical SISO statements of the feedback design problem in face of uncertainties can be generalized to MIMO systems. Based on how the interactions between subsystems are handled in the design process, the developed design techniques have been classified as 1. fully coordinated design (simultaneous) design, 2. sequential design, and 3. independent design [7,8,9,10]. According to the first approach, diagonal controllers are designed simultaneously, and the result is theoretically optimal but offering only few of the decentralized control benefits. The second approach allows to design local controllers sequentially applying time decomposition; fast loops are closed first, and the previously designed controllers must be considered when closing subsequent slower loops. This approach, however, does not guarantee failure tolerance. By the third approach, each local controller is designed based on the respective decoupled subsystem such that each local control loop is stable. The resulting diagonal controller guarantees stability and a proper operation of individual parts of the system, however at the cost of conservative sufficient stability conditions to be met. Usually, off-diagonal interactions cannot be simply neglected but have to be appropriately considered in the local designs. In the industrial practice, decentralized controllers are frequently used with decouplers to minimize interaction or to make the system diagonal dominant prior to designing local controllers [11,12,13].

In the frequency domain, stability with respect to model uncertainty (robust stability) is usually assessed by means of stability margins and sensitivity peaks. However, only a limited number of works address MIMO controller tuning in terms of gain and phase margins, mostly just for two input-two output systems and simplified models of decoupled subsystems [14,15]. The Equivalent Subsystems Method (ESM) is a Nyquist-based decentralized controller design method for specified performance [16,22,23] further augmented to integrate the general robust stability condition into local designs [1,10,17,18]. The method is applicable for uncertain square MIMO systems with arbitrary number of subsystems modelled using non-parametric uncertainty. As the method is based upon frequency plots, individual subsystems can be of any order even with unstable zeros and time delays. The design procedure is similar for SISO and MIMO systems and both continuous and discrete-time controllers. According to the principal modification proposed in this article, local controllers of equivalent subsystems are designed using the standard QFT method [19]. Combination of the ESM and the QFT methods brings about surprising benefits, mainly reduced design conservatism as well as possibility to specify arbitrary performance requirements for the overall system and ensure their fulfillment by translating them into frequency domain specifications for equivalent subsystems.

The article is organized as follows: Section 2 provides a concise theoretical background on the topic and formulation of the problem to be solved. In Section 3, principles of the Equivalent Subsystems Method (ESM) and the standard QFT compensator design are presented; these two methods are the core of the proposed enhancement of the unified robust decentralized controller design method presented in Section 4. The developed design procedure is demonstrated in detail and verified on a case study on the robust decentralized controller design for the quadruple tank process [2] in Section 5. Discussion on achieved results is in Section 6.

2. Preliminaries and Problem Formulation

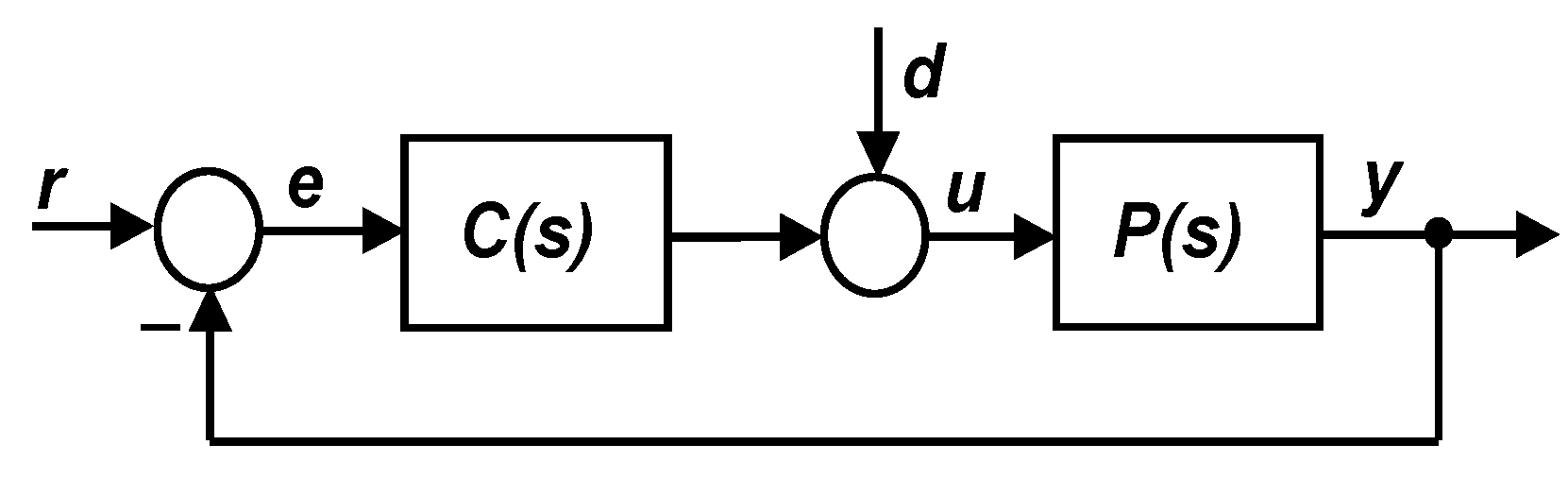
Consider the standard closed- loop in Figure 1 where P(s) is a  $m\times m$  transfer function matrix modelling the MIMO controlled plant with m inputs and m outputs,  $\mathrm{m}\ge 1,$  and C(s) is a  $m\times m$  transfer function matrix of a controller; r, e, u, y and d denote respectively the reference, control error, control action, output and input disturbance variables.

Necessary and sufficient stability conditions for the MIMO closed loop are expressed in the Generalized Nyquist Stability Theorem.

Theorem 1. (Generalized Nyquist Stability Theorem, [7])

Suppose that P(s) and C(s) are minimal realizations of a MIMO controlled system and the controller, respectively. Then, the closed-loop inFigure 1 is internally stable if and only if  $\forall s\in \mathcal{D}:$ 

$$1. \det \left[\mathrm{I}+\mathrm{Q}\left(\mathrm{s}\right)\right]\ne 0$$

(1)

$$2.\mathrm{N}\left\{0,\det \left[\mathrm{I}+\mathrm{Q}\left(\mathrm{s}\right)\right]\right\}=\sum _{\mathrm{i}=1}^{\mathrm{m}}\mathrm{N}\left\{0,\left[1+{\mathrm{q}}_{\mathrm{i}}\left(\mathrm{s}\right)\right]\right\}={\mathrm{n}}_{\mathrm{q}},$$

(2)

where  $Q\left(s\right)=P\left(s\right)C\left(s\right)$  is the open-loop transfer function with no internal right half-plane pole-zero cancellations between  $P\left(s\right)$  and  $C\left(s\right); N\left\{0,\mathit{det}\left[I+Q\left(s\right)\right]\right\}$  is the number of anticlockwise encirclements of (0,0j) by $\mathit{det}\left[I+Q\left(s\right)\right];{ n}_q$  is the number of unstable poles of  $Q\left(s\right);$   $\mathcal{D}$  is the Nyquist contour; I is the identity matrix;  $q_i\left(s\right), i=1,\dots , m$  are characteristic functions of  $Q\left(s\right)$  defined as:

$$\det \left[{\mathrm{q}}_{\mathrm{i}}\left(s\right)\mathrm{I}-\mathrm{Q}\left(\mathrm{s}\right)\right]=0, \mathrm{i}=1,\dots ,\mathrm{m}.$$

(3)

Remark 1:

The Nyquist contour  $\mathcal{D}$  is a large contour in the complex plain consisting of the imaginary axis  $s=j\omega , \omega ϵ<-\alpha , \alpha >$ , where  $\alpha$  is a radius of a semicircle in the right half-plane large enough to encircle unstable poles of  $Q\left(s\right)$ ; if there are any poles on the imaginary axis,  $\mathcal{D}$  is intended to the left-half plane to include them.

Remark 2:

Characteristic loci (CL)  $q_i\left(j\omega \right), i=1,\dots , m$  are traced out in the complex plane by characteristic functions of Q(s) as s traverses the Nyquist contour  $\mathcal{D}$ .

Let the mathematical description of an uncertain MIMO plant with equal number of inputs and outputs be given as a set of square transfer matrices; such a specification is used if the MIMO system has been identified in several (N) working points.

The set  $\mathsf{\Pi }$  of transfer matrices is given as:

$$\mathsf{\Pi }≔\left\{{\mathrm{P}}^{\mathrm{k}}\left(\mathrm{s}\right)\right\},\mathrm{k}=1,\dots ,\mathrm{N},$$

(4)

where

$${\mathrm{P}}^{\mathrm{k}}\left(\mathrm{s}\right)=\left\{{\mathrm{P}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}\left(\mathrm{s}\right)\right\},\mathrm{i},\mathrm{j}=1,\dots ,\mathrm{m},\mathrm{m}\ge 1,$$

(5)

and individual entries of the transfer matrix (5) are in the general form:

$${\mathrm{P}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}\left(\mathrm{s}\right)=\frac{{\mathrm{B}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}\left(\mathrm{s}\right)}{{\mathrm{A}}_{\mathrm{i}\mathrm{j}}^{\mathrm{k}}\left(\mathrm{s}\right)}=\frac{\sum _{\mathrm{q}=0}^{\mathrm{r}}{\mathrm{b}}_{\mathrm{i}\mathrm{j}\mathrm{q}}^{\mathrm{k}}{\mathrm{s}}^{\mathrm{q}}}{\sum _{\mathrm{p}=0}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{i}\mathrm{j}\mathrm{p}}^{\mathrm{k}}{\mathrm{s}}^{\mathrm{p}}}, \mathrm{q}=1,\dots ,\mathrm{r};\mathrm{p}=1,\dots ,\mathrm{n};\mathrm{r}<\mathrm{n}.$$

(6)

The uncertain system (4) can be modelled using the nominal model and a suitable uncertainty model that properly quantifies the difference between the real and the nominal system dynamics. The nominal model

$${\mathrm{P}}^0\left(\mathrm{s}\right)=\left\{{\mathrm{P}}_{\mathrm{i}\mathrm{j}}^0\left(\mathrm{s}\right)\right\},\mathrm{i},\mathrm{j}=1,\dots ,\mathrm{m},$$

(7)

is usually obtained as a mean value parameter model [1,7,8] or can simply be selected as any from the set of transfer matrices (4), [19].

The uncertainty can be described as parametric (structured) or nonparametric (unstructured) [7]. When nonparametric uncertainty is considered, the set  $\mathsf{\Pi }$  is generated using any of 6 types of unstructured uncertainty models [1,7] and the upper bound on its spectral norm. In case of parametric uncertainty, knowledge of the structure of all elements of  $\mathsf{\Pi }$  is assumed while their parameters may vary within a given compact set.

Using parametric uncertainty, the uncertain SISO system is described by (4) where individual entries (6) have a uniform structure ( $\mathrm{i}=1,\mathrm{j}=1,\mathrm{m}=1$ and the superscript k is omitted for readability):

$$\mathrm{P}\left(\mathrm{s}\right)=\frac{\mathrm{B}\left(\mathrm{s}\right)}{\mathrm{A}\left(\mathrm{s}\right)}=\frac{{\mathrm{a}}_0+{\mathrm{a}}_1\mathrm{s}+{\mathrm{a}}_2{\mathrm{s}}^2+...+{\mathrm{a}}_{\mathrm{n}}{\mathrm{s}}^{\mathrm{n}}}{{\mathrm{b}}_0+{\mathrm{b}}_1\mathrm{s}+{\mathrm{b}}_2{\mathrm{s}}^2+...+{\mathrm{b}}_{\mathrm{m}}{\mathrm{s}}^{\mathrm{m}}}, {\mathrm{a}}_{\mathrm{n}}\ne 0,{\mathrm{b}}_{\mathrm{m}}\ne 0,\mathrm{m}\le \mathrm{n},$$

(8)

with varying coefficients of numerator and denominator polynomials.

By defining interval polynomials of the numerator and denominator using the lower and upper limits of their uncertain coefficients as follows:

$$\begin{array}{c}\mathrm{D}\left(\mathrm{s}\right)=\left\{\mathrm{A}\left(\mathrm{s}\right):{\mathrm{a}}_0+...+{\mathrm{a}}_{\mathrm{n}}{\mathrm{s}}^{\mathrm{n}},{\mathrm{a}}_{\mathrm{k}}\in 〈\underset{\_}{{\mathrm{a}}_{\mathrm{k}}},\overline{{\mathrm{a}}_{\mathrm{k}}}〉,\mathrm{k}=\mathrm{0,1},2,\dots ,\mathrm{n}\right\}\\ \mathrm{N}\left(\mathrm{s}\right)=\left\{\mathrm{B}\left(\mathrm{s}\right):{\mathrm{b}}_0+...+{\mathrm{b}}_{\mathrm{m}}{\mathrm{s}}^{\mathrm{m}},{\mathrm{b}}_{\mathrm{k}}\in 〈\underset{\_}{{\mathrm{b}}_{\mathrm{k}}},\overline{{\mathrm{b}}_{\mathrm{k}}}〉,\mathrm{k}=\mathrm{0,1},2,\dots ,\mathrm{m}\right\},\end{array}$$

(9)

the corresponding interval system reads as:

$$\mathrm{P}\left(\mathrm{s}\right):=\left\{\mathrm{P}\left(\mathrm{s}\right)=\frac{\mathrm{n}\left(\mathrm{s}\right)}{\mathrm{d}\left(\mathrm{s}\right)}:\mathrm{n}\left(\mathrm{s}\right)\mathsf{ϵ}\mathrm{N}\left(\mathrm{s}\right),\mathrm{d}\left(\mathrm{s}\right)\mathsf{ϵ}\mathrm{D}\left(\mathrm{s}\right)\right\}$$

(10)

A controller that guarantees closed-loop stability over the whole uncertainty region as defined by the set of uncertain plant models (4) and modelled using a selected type of uncertainty (parametric uncertainty in our case) is called a robust controller. Being designed for the nominal model selected from the set (4), the robust controller has to guarantee nominal stability first. Thus, nominal stability is a prerequisite for robust stability.

Main results on parametric approach in robust control evolve from the Kharitonov’s theorem which gives a necessary and sufficient robust stability condition of an interval family of polynomials. An overview of the robust analysis results, generalization of the Kharitonov’s theorem, the Edge theorem and related results can be found e.g. in [20].

The frequency-domain QFT controller design methodology presented e.g. in [19] and references therein allows to synthesize a compensator that guarantees closed-loop robust stability of the interval system (10) while respecting bounds imposed by performance requirements as well. In the sequel, we will build on this approach.

Consider the uncertain MIMO system (4) which is an interconnection of  $\mathrm{m}$  subsystems and has  $\mathrm{m}$  inputs and  $\mathrm{m}$  outputs. This type of uncertain MIMO systems can be modelled as a set of square transfer function matrices (5) having the form:

$${\mathrm{P}}^{\mathrm{k}}\left(\mathrm{s}\right)=\left[\begin{array}{cccc}{\mathrm{P}}_{11}^{\mathrm{k}}\left(\mathrm{s}\right)& {\mathrm{P}}_{12}^{\mathrm{k}}\left(\mathrm{s}\right)& \cdots & {\mathrm{P}}_{1\mathrm{m}}^{\mathrm{k}}\left(\mathrm{s}\right)\\ {\mathrm{P}}_{21}^{\mathrm{k}}\left(\mathrm{s}\right)& {\mathrm{P}}_{22}^{\mathrm{k}}\left(\mathrm{s}\right)& \cdots & {\mathrm{P}}_{2\mathrm{m}}^{\mathrm{k}}\left(\mathrm{s}\right)\\ ⋮& ⋮& ⋮& ⋮\\ {\mathrm{P}}_{\mathrm{m}1}^{\mathrm{k}}\left(\mathrm{s}\right)& \cdots & \cdots & {\mathrm{P}}_{\mathrm{m}\mathrm{m}}^{\mathrm{k}}\left(\mathrm{s}\right)\end{array}\right],\mathrm{k}=,1,\dots ,\mathrm{N};\mathrm{m}\ge 1.$$

(11)

To design a robust decentralized controller, the transfer matrices (11) have to be recast into a single transfer matrix which entries are in form of interval systems (8-10).

To design a decentralized controller, all transfer matrices (11) will be split according to regular splitting [21] as follows (the superscript  $\mathrm{k}$  is omitted for simplicity):

$$\mathrm{P}\left(\mathrm{s}\right)={\mathrm{P}}_{\mathrm{d}}\left(\mathrm{s}\right)+{\mathrm{P}}_{\mathrm{n}}\left(\mathrm{s}\right),$$

(12)

where the nonsingular diagonal matrix

$${\mathrm{P}}_{\mathrm{d}}\left(\mathrm{s}\right)=\left[\begin{array}{cccc}{\mathrm{P}}_{11}\left(\mathrm{s}\right)& 0& \cdots & 0\\ 0& {\mathrm{P}}_{22}\left(\mathrm{s}\right)& \cdots & 0\\ ⋮& ⋮& ⋮& ⋮\\ 0& \cdots & \cdots & {\mathrm{P}}_{\mathrm{m}\mathrm{m}}\left(\mathrm{s}\right)\end{array}\right]$$

(13)

describes the dynamics of decoupled subsystems, and the off-diagonal entries collected in  ${\mathrm{P}}_{\mathrm{n}}\left(\mathrm{s}\right)=\mathrm{P}\left(\mathrm{s}\right)-{\mathrm{P}}_{\mathrm{d}}\left(\mathrm{s}\right)$  correspond to interactions.

2.1. Problem Formulation

Consider an uncertain MIMO system with  $\mathrm{m}$  inputs and  $\mathrm{m}$  outputs consisting of m subsystems,  $\mathrm{m}\ge 1,$  given as a set of  $\mathrm{N}$  transfer function matrices (4). Let each transfer function matrix can be split into the diagonal and the off-diagonal transfer matrices  ${\mathrm{P}}_{\mathrm{d}}^{\mathrm{k}}\left(\mathrm{s}\right)$  and  ${\mathrm{P}}_{\mathrm{n}}^{\mathrm{k}}\left(\mathrm{s}\right)$ , respectively:

$${\mathrm{P}}^{\mathrm{k}}\left(\mathrm{s}\right)={\mathrm{P}}_{\mathrm{d}}^{\mathrm{k}}\left(\mathrm{s}\right)+{\mathrm{P}}_{\mathrm{n}}^{\mathrm{k}}\left(\mathrm{s}\right), \mathrm{k}=1,\dots \mathrm{N}$$

(14)

here  ${\mathrm{P}}_{\mathrm{d}}^{\mathrm{k}}\left(\mathrm{s}\right)$  and  ${\mathrm{P}}_{\mathrm{m}}^{\mathrm{k}}\left(\mathrm{s}\right)$  are respectively transfer matrices of decoupled subsystems and interactions among them.

A decentralized (diagonal) controller (15)

$$\mathrm{C}\left(\mathrm{s}\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{{\mathrm{C}}_{\mathrm{i}}\left(\mathrm{s}\right)\right\},\mathrm{i}=1,\dots ,\mathrm{m};\det \mathrm{C}\left(\mathrm{s}\right)\ne 0,\forall \mathrm{s}$$

(15)

is to be designed to guarantee closed-loop stability and required performance over the whole operating range of the uncertain system (4).

The design problem will be solved in the frequency domain as independent design based on the Equivalent Subsystems Method [1] to allow considering parametric uncertainty in the design of local controllers as well as properly formulated performance requirements.

3. Methods Applied in the Solution

To solve the robust decentralized controller design problem as formulated in Section 2.1, a design procedure has been developed based on two frequency-domain design methodologies:

• the Equivalent Subsystem Method (ESM), which provides a framework for the independent design of local controllers constituting the decentralized controller to guarantee closed-loop stability of the overall system; and
• the Quantitative Feedback Theory (QFT), to design a minimum structure local compensators guaranteeing robust stability of uncertain SISO systems with parametric uncertainty as well as fulfillment of properly specified performance requirements.

Both methods are graphical and based on nonparametric models of the controlled system and related frequency dependencies. The design procedure is thus graphical, insightful, and interactive and even intermediate results have an immediate visual interpretation.

3.1. The Equivalent Subsystems Method

The Equivalent Subsystems Method (ESM) is a Nyquist-based decentralized controller design method for stability and specified performance. It relies on the factorization of the closed-loop characteristic polynomial of the feedback system in Figure 1:

$$\mathrm{d}\mathrm{e}\mathrm{t}\left[\mathrm{I}+\mathrm{P}\left(\mathrm{s}\right)\mathrm{C}\left(\mathrm{s}\right)\right]=\mathrm{d}\mathrm{e}\mathrm{t}\left[{\mathrm{C}}^{-1}\left(\mathrm{s}\right)+{\mathrm{P}}_{\mathrm{d}}\left(\mathrm{s}\right)+{\mathrm{P}}_{\mathrm{n}}\left(\mathrm{s}\right)\right]\mathrm{d}\mathrm{e}\mathrm{t}\mathrm{C}\left(\mathrm{s}\right)$$

(16)

where  $\mathrm{C}\left(\mathrm{s}\right)$  is a decentralized (diagonal) controller (15).

Characteristic functions  ${\mathrm{g}}_{\mathrm{i}}\left(\mathrm{s}\right),\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{m}$ of  ${\mathrm{P}}_{\mathrm{n}}\left(\mathrm{s}\right)$  are defined as follows:

$$\mathrm{d}\mathrm{e}\mathrm{t}\left[{\mathrm{g}}_{\mathrm{i}}\left(\mathrm{s}\right)\mathrm{I}-{\mathrm{P}}_{\mathrm{n}}\left(\mathrm{s}\right)\right]=0,\mathrm{i}=1,\dots ,\mathrm{m}.$$

(17)

In terms of stability,  ${\mathrm{P}}_{\mathrm{n}}\left(\mathrm{s}\right)$  can be replaced by its characteristic function matrix in the sense of the Cayley-Hamilton Theorem:

$${\mathrm{P}}_{\mathrm{n}}\left(\mathrm{s}\right)={\mathrm{g}}_{\mathrm{k}}\left(\mathrm{s}\right)\mathrm{I},\mathrm{k}\in \left\{1,\dots ,\mathrm{m}\right\},$$

(18)

where  ${\mathrm{g}}_{\mathrm{k}}\left(\mathrm{s}\right),\mathrm{k}\in \left\{1,\dots ,\mathrm{m}\right\}$  is one (arbitrary) selected characteristic function.

As a result, (16) modifies to:

$$\mathrm{N}\left\{0,\mathrm{d}\mathrm{e}\mathrm{t}\left[\mathrm{I}+\mathrm{P}\left(\mathrm{s}\right)\mathrm{C}\left(\mathrm{s}\right)\right]\right\}=\mathrm{N}\left\{0,\mathrm{d}\mathrm{e}\mathrm{t}\left[{\mathrm{C}}^{-1}\left(\mathrm{s}\right)+{\mathrm{P}}_{\mathrm{d}}\left(\mathrm{s}\right)+{\mathrm{g}}_{\mathrm{k}}\left(\mathrm{s}\right)\mathrm{I}\right]\mathrm{d}\mathrm{e}\mathrm{t}\mathrm{C}\left(\mathrm{s}\right)\right\}.$$

(19)

Using the following notation in the bracketed term on the right-hand side:

$${\mathrm{P}}_{\mathrm{k}}^{\mathrm{e}\mathrm{q}}\left(\mathrm{s}\right):={\mathrm{P}}_{\mathrm{d}}\left(\mathrm{s}\right)+{\mathrm{g}}_{\mathrm{k}}\left(\mathrm{s}\right)\mathrm{I}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{{\mathrm{P}}_{\mathrm{i}\mathrm{k}}^{\mathrm{e}\mathrm{q}}\left(\mathrm{s}\right)\right\},\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{m}; \mathrm{k}\in \left\{1,\dots ,\mathrm{m}\right\},$$

(20)

the diagonal matrix of equivalent subsystems is defined by (20).

As the analytical calculation of characteristic functions is not straightforward and sometimes even unfeasible, they are computed frequency-by-frequency; as a result, individual equivalent subsystems are generated according to:

$${\mathrm{P}}_{\mathrm{i}\mathrm{k}}^{\mathrm{e}\mathrm{q}}\left(\mathrm{j}\mathsf{\omega }\right)={\mathrm{P}}_{\mathrm{i}\mathrm{i}}\left(\mathrm{j}\mathsf{\omega }\right)+{\mathrm{g}}_{\mathrm{k}}\left(\mathrm{j}\mathsf{\omega }\right),\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{m},\mathrm{k}\in \left\{\mathrm{1,2},\dots ,\mathrm{m}\right\},\forall \mathrm{j}\mathsf{\omega }\in \mathcal{D}$$

(21)

which are frequency responses of individual decoupled subsystems shaped by a selected characteristic locus of the matrix of interactions.

Substituting (20) into (19) after a small manipulation yields the key result:

$$\mathrm{N}\left\{0,\mathrm{d}\mathrm{e}\mathrm{t}\left[\mathrm{I}+\mathrm{P}\left(\mathrm{s}\right)\mathrm{C}\left(\mathrm{s}\right)\right]\right\}=\mathrm{N}\left\{0,\mathrm{d}\mathrm{e}\mathrm{t}\left[\mathrm{I}+{\mathrm{P}}_{\mathrm{k}}^{\mathrm{e}\mathrm{q}}\left(\mathrm{s}\right)\mathrm{C}\left(\mathrm{s}\right)\right]\right\}.$$

(22)

Considering (21), a further manipulation of the r.h.s. of (22) results in:

$$\mathrm{N}\left\{0,\mathrm{d}\mathrm{e}\mathrm{t}\left[\mathrm{I}+{\mathrm{P}}_{\mathrm{k}}^{\mathrm{e}\mathrm{q}}\left(\mathrm{s}\right)\mathrm{C}\left(\mathrm{s}\right)\right]\right\}=\sum _{\mathrm{i}=1}^{\mathrm{m}}\mathrm{N}\left\{-1,\left[{\mathrm{P}}_{\mathrm{i}\mathrm{i}}\left(\mathrm{s}\right)+{\mathrm{g}}_{\mathrm{k}}\left(\mathrm{s}\right)\right]{\mathrm{C}}_{\mathrm{i}}\left(\mathrm{s}\right)\right\}={\mathrm{n}}_{\mathrm{q}}$$

(23)

From (22) and (23) results that necessary and sufficient closed-loop stability condition for the overall system under a decentralized controller is guaranteed if and only if each closed-loop equivalent subsystem under its related local controller is stable. The above development is summarized in Theorem 2 which reformulates the conditions of the Generalized Nyquist stability theorem (Theorem 1) for a MIMO system under a decentralized controller.

Theorem 2. (MIMO stability under a decentralized controller [1])

The closed loop in Fig. 1 comprising a MIMO system (13) and a decentralized controller (14) is stable if and only if there exists  $g_k\left(j\omega \right)$  such that  $\forall s=j\omega \in \mathcal{D}$ 

$$\begin{array}{c}1.\mathrm{d}\mathrm{e}\mathrm{t}\left[{\mathrm{g}}_{\mathrm{k}}\left(\mathrm{j}\mathsf{\omega }\right)\mathrm{I}-{\mathrm{P}}_{\mathrm{n}}\left(\mathrm{j}\mathsf{\omega }\right)\right]=0,\mathrm{k}\in \left\{\mathrm{1,2},\dots ,\mathrm{m}\right\}\\ 2. \sum _{i=1}^m\mathrm{N}\left\{-1,\left[{\mathrm{P}}_{\mathrm{i}\mathrm{i}}\left(\mathrm{j}\mathsf{\omega }\right)+{\mathrm{g}}_{\mathrm{k}}\left(\mathrm{j}\mathsf{\omega }\right)\right]{\mathrm{C}}_{\mathrm{i}}\left(\mathrm{j}\mathsf{\omega }\right)\right\}={\mathrm{n}}_{\mathrm{q}}.\end{array}$$

(24)

From the Theorem 2 follows that a decentralized controller guaranteeing stability of the overall closed-loop system is composed from local controllers independently designed for individual equivalent subsystem using any SISO design. The ESM-based decentralized controller design is applicable for square MIMO systems of any dimension with stable interactions. By integrating robust stability conditions into the local controller designs it can be extended to design robust controllers.

Since equivalent subsystems are generated in the form of frequency characteristics, it is recommended to use following frequency domain design methods:

• The Neymark D-partition method [22,23] is suitable if performance requirements for the overall system are specified in terms of its degree-of-stability; the same degrees-of-stability must be achieved in equivalent subsystems. Using this SISO design, robust stability conditions cannot be directly incorporated in the design of local controllers, they can only be checked additionally which makes the robust controller design iterative.
• Standard Bode diagram design [10,17] or the Nyquist diagram design [16]. Performance requirements for the overall system specified in terms of maximum overshoot and settling time and have to be translated into respective frequency performance measures (stability margins) to be achieved in individual equivalent subsystems. Robust stability conditions for systems with unstructured uncertainty can be easily incorporated into local designs [1,10].
• Nichols diagram-based SISO design known as a well-elaborated QFT design technique is the next option allowing to consider uncertain systems with parametric uncertainty.

3.2. QFT Design

The Quantitative Feedback Theory, QFT is a frequency domain engineering method to design robust controllers developed by is Isaac Horowitz [24], founder of an important scientific school. This robust feedback compensator synthesis methodology is based on classical feedback control theory and allows simultaneously 1. to reduce the impact of model uncertainty, while 2. satisfying properly specified performance requirements for each realization from a given set of uncertain systems.

QFT solves the above problems by designing a single (robust) compensator capable to simultaneously achieve multiple desired performance specifications (including stability, rejection of input and output disturbances, limitation of control variable, reference variable tracking, damping of oscillation, etc.) for every plant within the existing model uncertainty. It highlights the trade-off (quantification) among simplicity of the controller structure, minimization of the ‘cost of feedback’ (bandwidth), model uncertainty (parametric and non-parametric) and the achievement of the desired performance specifications at every frequency of interest [25]. As a frequency method, QFT uses frequency tools that are illustrative and understandable by practitioners at each step of the design process.

The standard SISO QFT controller design procedure has the following steps [19]:

• Plant modelling which includes specification of the interval model and appropriate frequency range.
• Definition of a discrete number of plants, choice of the nominal model.
  By gridding each uncertain parameter of the interval model between its minimum and maximum values, another set of uncertain plant realizations is generated from all combinations of uncertain parameters values. The task is simplified if the uncertain parameters are interrelated with each other. Any model from the generated plant realizations can be selected as the nominal one; the final QFT controller will be the same no matter what nominal plant is chosen [19].
• Calculation of QFT templates.
  QFT templates are projection of the transfer function  $\mathrm{P}\left(\mathrm{j}\mathsf{\omega }\right)$  onto the Nichols diagram considering each parameter within the uncertainty and at each frequency  of interest.
• Stability specifications.
  Instead of using classical gain and phase stability margins,  ${\mathrm{M}}_{\mathrm{c}}$  circles are used as a more general stability measure representing the loci of constant closed-loop magnitudes  ${\mathrm{W}}_{\mathrm{s}}$  in the Nichols diagram.
• Performance specifications.
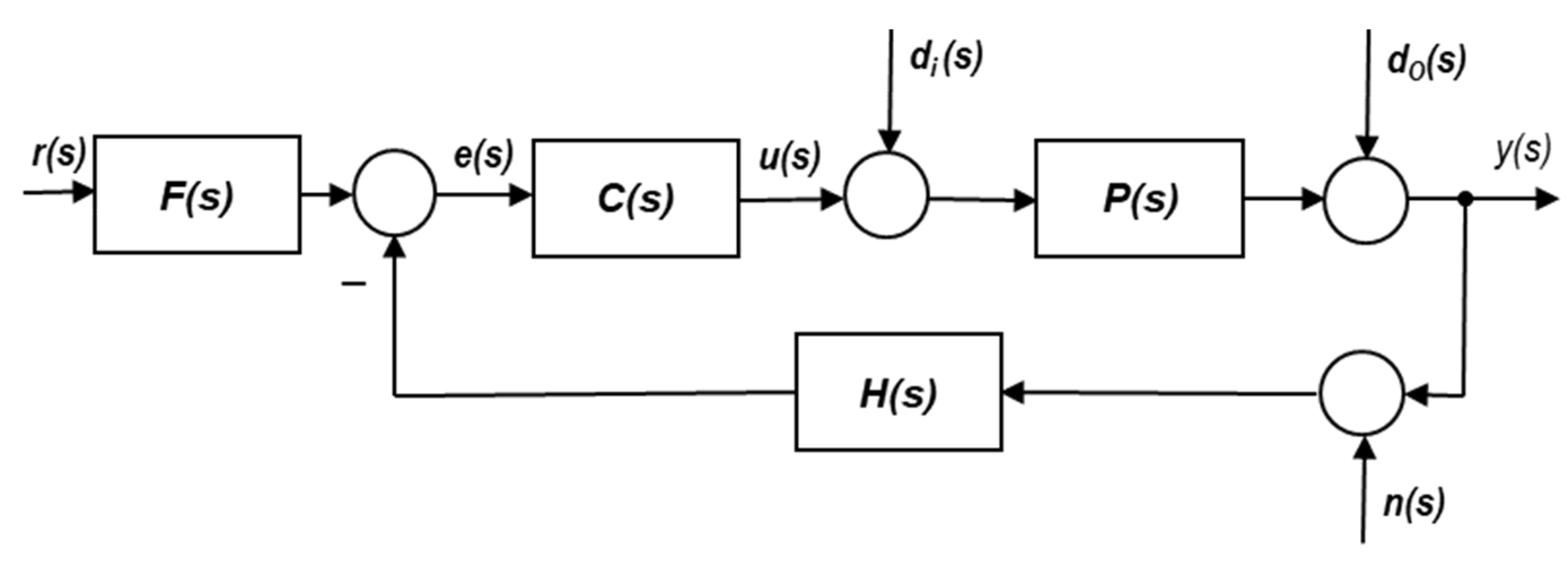
  Stability and performance requirements are specified in terms of frequency-domain inequalities based on transfer functions between the inputs and outputs of a classical two-degree of freedom closed-loop in Figure 2.

Frequency-domain performance specifications have a general form:

$$\left\{\left|{\mathrm{T}}_{\mathrm{k}}\left(\mathrm{j}{\mathsf{\omega }}_{\mathrm{i}}\right)\right|\le {\mathsf{\delta }}_{\mathrm{k}}\left({\mathsf{\omega }}_{\mathrm{i}}\right),{\mathsf{\omega }}_{\mathrm{i}}\mathsf{ϵ}{\mathrm{\Omega }}_{\mathrm{k}},\mathrm{k}=\mathrm{1,2},\dots ;\mathrm{i}=\mathrm{1,2},\dots \right\}$$

(25)

where  ${\mathrm{T}}_{\mathrm{k}}\left(\mathrm{j}{\mathsf{\omega }}_{\mathrm{i}}\right)$  is the considered transfer function and  ${\mathsf{\delta }}_{\mathrm{k}}\left({\mathsf{\omega }}_{\mathrm{i}}\right)$  is the upper limit of its magnitude and  ${\mathrm{\Omega }}_{\mathrm{k}}$  is the set of frequencies from a selected range.

The individual inequality specification types include:

Type 1 – Stability specification

Type 2 – Complementary sensitivity specification

Type 3 – Sensitivity or plant output disturbance specification

Type 4 – Plant input disturbance specification

Type 5 – Control action reduction specification

Type 6 – Reference tracking specification.

6.

Calculation of QFT bounds.

Every plant in the  ${\mathsf{\omega }}_{\mathrm{i}}$  template as well as the compensator can be expressed in their respective polar form:

$$\mathrm{P}\left(\mathrm{j}{\mathsf{\omega }}_{\mathrm{i}}\right)=\mathrm{p}{\mathrm{e}}^{\mathrm{j}\mathsf{\theta }}=\mathrm{p}\mathrm{⦟}\mathsf{\theta }\mathrm{C}\left(\mathrm{j}{\mathsf{\omega }}_{\mathrm{i}}\right)=\mathrm{c}{\mathrm{e}}^{\mathrm{j}\mathsf{\phi }}=\mathrm{c}\mathrm{⦟}\mathsf{\phi }$$

(26)

QFT bounds are calculated from the control specifications and considering model uncertainty. By substituting the polar forms (26) into individual selected performance specification types, they can be rearranged into quadratic inequalities in the form:

$${\mathrm{l}}_{{\mathsf{\omega }}_{\mathrm{i}}}^{\mathrm{k}}\left(\mathrm{p},\mathsf{\varphi },{\mathsf{\delta }}_{\mathrm{k}},\mathsf{\theta }\right)=\mathrm{a}{\mathrm{c}}^2+\mathrm{b}\mathrm{c}+\mathrm{f}\ge 0$$

(27)

where the coefficients  $\mathrm{a},\mathrm{b},\mathrm{f}$  are functions of  $\mathrm{p},\mathsf{\varphi },\mathsf{\theta }$  and  ${\mathsf{\delta }}_{\mathrm{k}}$ .

Using an appropriate algorithm [19], the quadratic inequalities (27) are solved and translated into a set of curves in the Nichols diagram for each frequency and specification type. Thus, at each frequency  ${\mathsf{\omega }}_{\mathrm{i}}$  and for each specification  $\mathrm{k}$ there is a bound  ${\mathrm{B}}_{\mathrm{k}}\left(\mathrm{j}{\mathsf{\omega }}_{\mathrm{i}}\right)$  which can be dashed or solid, depending on whether the area satisfying the bound is above or below the line.

7.

Calculation of intersection of the QFT bounds and checking for their compatibility.

If more than one performance specification is considered, it is necessary to find the intersection of all bounds at each frequency.

8.

Controller design by loop shaping in the Nichols diagram.

After plotting the bounds in the Nichols diagram, it is sufficient to deal just with a single (nominal plant) to find a controller that meets the bounds. Hence, QFT provides elegant and practical solution by integrating information associated with the model uncertainty and all control specifications in a set of simple curves. The loop shaping design is carried out by adding poles and zeros until the nominal loop lies near its bounds (optimally on the top of the bounds at each frequency).

The QFT compensator has a general form:

$$\mathrm{C}\left(\mathrm{s}\right)={\mathrm{k}}_{\mathrm{C}}\frac{{\prod }_{\mathrm{i}=1}^{{\mathrm{n}}_{\mathrm{r}\mathrm{z}}}\left(\left(\frac{\mathrm{s}}{{\mathrm{z}}_{\mathrm{i}}}\right)+1\right){\prod }_{\mathrm{i}=1}^{{\mathrm{n}}_{\mathrm{c}\mathrm{z}}}\left(\left(\frac{{\mathrm{s}}^2}{{\mathsf{\omega }}_{\mathrm{n}\mathrm{i}}^2}\right)+\left(\frac{2{\mathsf{\xi }}_{\mathrm{i}}}{{\mathsf{\omega }}_{\mathrm{n}\mathrm{i}}}\right)\mathrm{s}+1\right)}{{\mathrm{s}}^{\mathrm{r}}{\prod }_{\mathrm{j}=1}^{{\mathrm{m}}_{\mathrm{r}\mathrm{p}}}\left(\left(\frac{\mathrm{s}}{{\mathrm{p}}_{\mathrm{j}}}\right)+1\right){\prod }_{\mathrm{j}=1}^{{\mathrm{m}}_{\mathrm{c}\mathrm{p}}}\left(\left(\frac{{\mathrm{s}}^2}{{\mathsf{\omega }}_{\mathrm{n}\mathrm{j}}^2}\right)+\left(\frac{2{\mathsf{\xi }}_{\mathrm{j}}}{{\mathsf{\omega }}_{\mathrm{n}\mathrm{j}}}\right)\mathrm{s}+1\right)},$$

(28)

where  $\mathrm{z}$  denotes the zeros,  $\mathrm{p}$  the poles,  ${\mathsf{\omega }}_{\mathrm{n}}$  is the natural frequency,  $\mathsf{\xi }$  is the relative damping and  ${\mathrm{k}}_{\mathrm{C}}$  is the gain.

9.

Prefilter design.

A prefilter is used to solve the reference tracking problem.

10.

Analysis and validation.

This step includes:

-

frequency domain analysis of each specification for all the significant plants within the model uncertainty,

-

time domain simulation for linear and nonlinear system.

To easily apply the QFT theory in practical tasks, a QFT Control Design Toolbox in MATLAB has been developed in 1995 and is being continuously improved since then [26,27,28]. In another version available commercially, the latest QFT techniques are implemented within a user friendly and interactive environment [19].

4. Robust Decentralized QFT Controller Design Based on the Equivalent Subsystems Method (“ESM – QFT” method)

Development of the innovative robust decentralized controller design method based on the combination of the Equivalent Subsystems Method and the QFT method (ESM-QFT) is the main result of this article.

ESM provides the basic framework to implement the independent design of local controllers for uncertain equivalent subsystems guaranteeing fulfillment of the necessary and sufficient stability conditions according to the Theorem 2. Using the QFT method to independently design SISO controllers for uncertain equivalent subsystems guarantees robust stability and required performance of the overall uncertain system.

The proposed ESM-QFT design procedure evolves from the results given in the Theorem 2 and the QFT SISO design procedure as described in subsection 3.2.

The ESM-QFT design procedure has the following steps:

I. 

Modelling the uncertain MIMO system

The uncertain MIMO system consisting of  $\mathrm{m}$  interconnected subsystems can be given either as

• a set of  $\mathrm{m}\times \mathrm{m}$  transfer matrices (4), or
• a single transfer matrix with entries having interrelated uncertain parameters.

In the latter case, the set of uncertain plant realizations is generated by gridding the uncertain parameters between their minimum and maximum values and considering all their (feasible) combinations. Then  $\mathrm{N}$  corresponds to the number of all feasible combinations of uncertain parameters.

One (any) of the realizations (4) can be chosen as a nominal system denoted as:

$${\mathrm{P}}^0\left(\mathrm{s}\right)=\left\{{\mathrm{P}}_{\mathrm{i}\mathrm{j}}^0\left(\mathrm{s}\right)\right\},\mathrm{i},\mathrm{j}=1,\dots ,\mathrm{m}.$$

(29)

II. 

Generation of uncertain equivalent subsystems

Each transfer function matrix (5) from the set (4) can be split into the diagonal and the off-diagonal transfer matrices  ${\mathrm{P}}_{\mathrm{d}}^{\mathrm{r}}\left(\mathrm{s}\right)$  and ${\mathrm{P}}_{\mathrm{n}}^{\mathrm{r}}\left(\mathrm{s}\right)$  , respectively:

$${\mathrm{P}}^{\mathrm{r}}\left(\mathrm{s}\right)={\mathrm{P}}_{\mathrm{d}}^{\mathrm{r}}\left(\mathrm{s}\right)+{\mathrm{P}}_{\mathrm{n}}^{\mathrm{r}}\left(\mathrm{s}\right), \mathrm{r}=1,\dots \mathrm{N}.$$

(30)

For each  ${\mathrm{P}}_{\mathrm{n}}^{\mathrm{r}}\left(\mathrm{s}\right), \mathrm{r}=1,\dots \mathrm{N}$ , the  $\mathrm{N}\times \mathrm{m}$  characteristic functions are calculated frequency-by-frequency and corresponding m sets of N characteristic loci  ${\mathrm{g}}_{\mathrm{i}}^{\mathrm{r}}, \mathrm{i}=1,\dots ,\mathrm{m};\mathrm{r}=1,\dots ,\mathrm{N}$  are plotted.

Using one selected  $\left({\mathrm{k}}^{\mathrm{t}\mathrm{h}}\right)$  from the m sets of characteristic functions  ${\mathrm{g}}_{\mathrm{k}}^{\mathrm{r}}, \mathrm{k}\in \{1,\dots ,\mathrm{m}\};\mathrm{r}=1,\dots ,\mathrm{N}$ ; respective sets of N equivalent subsystems are calculated according to (21) as follows:

$${\mathrm{P}}_{\mathrm{i}\mathrm{k}}^{\mathrm{e}\mathrm{q}\_\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right)={\mathrm{P}}_{\mathrm{i}\mathrm{i}}^{\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right)+{\mathrm{g}}_{\mathrm{k}}^{\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right),\mathrm{i}=\mathrm{1,2},\dots ,\mathrm{m};\mathrm{k}\in \left\{\mathrm{1,2},\dots ,\mathrm{m}\right\};\mathrm{r}=1,\dots ,\mathrm{N}.$$

(31)

III. 

Calculation of QFT templates of equivalent subsystems

For one chosen  $\mathrm{k}\in \left\{\mathrm{1,2},\dots ,\mathrm{m}\right\}$  and the respective set of uncertain equivalent subsystems (30), corresponding QFT templates are calculated and plotted in  $\mathrm{m}$  Nichols diagrams.

IV. 

Independent design of SISO local controllers for uncertain equivalent subsystems

Independent design of local controllers for individual equivalent subsystems consists of m parallel designs according to the steps 4-9 of the QFT design procedure in 3.2. For each equivalent subsystem it includes:

-

stability specification,

-

performance specification,

-

calculation of QFT bounds, of their intersection and compatibility checking,

-

controller design by loop shaping of the nominal equivalent subsystem in the Nichols diagram.

V. 

Analysis in the frequency and time domains

The resulting decentralized controller  $\mathrm{C}\left(\mathrm{s}\right)=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left\{{\mathrm{C}}_{\mathrm{i}}\left(\mathrm{s}\right)\right\},\mathrm{i}=1,\dots ,\mathrm{m}$  is composed of the individual local controllers designed for respective uncertain equivalent subsystems.

Frequency-domain analysis is carried out at the equivalent subsystem levels and includes verification of the required stability performance specifications.

Time-domain analysis relates to the overall system level when the decentralized controller is implemented in real subsystems; it is based on simulations for linear/nonlinear models under various simulation scenarios.

5. Case Study

The proposed design method was verified on a benchmark case study dealing with the design of a robust decentralized level control in a quadruple tank process [1,2,10]. The freely available toolbox [26,27,28] with necessary modifications performed was used to perform the independent QFT designs for uncertain equivalent subsystems.

5.1. Description of the Controlled Plant

The quadruple-tank process (Figure 1) is a laboratory plant suitable to analyze and demonstrate different approaches to control a two input-two output MIMO system in either minimum and/or nonminimum phase configurations [2].

Level control in the two lower tanks is performed using two pumps, their voltages  ${\mathrm{v}}_1,$   ${\mathrm{v}}_2 \left[\mathrm{V}\right]$  are the inputs. Levels in the lower tanks ${\mathrm{h}}_1$ , ${\mathrm{h}}_2 \left[\mathrm{c}\mathrm{m}\right]$  are the controlled outputs. Pump voltages define corresponding inflows  ${\mathrm{F}}_{\mathrm{i}}={\mathrm{k}}_{\mathrm{i}}{\mathrm{v}}_{\mathrm{i}},\mathrm{i}=\mathrm{1,2}$ . Parameters  ${\mathsf{\gamma }}_{\mathrm{i}}, \mathrm{i}=\mathrm{1,2}$  denote valve settings, i.e. relative ratios of pump flows into the lower and upper diagonal tanks (tanks 1 and 4 for  ${\mathsf{\gamma }}_1,$ and tanks 2 and 3 for  ${\mathsf{\gamma }}_2$ ), hence  ${\mathsf{\gamma }}_1,{\mathsf{\gamma }}_2\mathsf{ϵ}<\mathrm{0,1}>$ .

The first principles nonlinear state space model of the device has the form:

$$\begin{array}{c}\frac{{\mathrm{d}\mathrm{h}}_1}{\mathrm{d}\mathrm{t}}=-\frac{{\mathrm{a}}_1}{{\mathrm{A}}_1}\sqrt{{2\mathrm{g}\mathrm{h}}_1}+\frac{{\mathrm{a}}_3}{{\mathrm{A}}_1}\sqrt{{2\mathrm{g}\mathrm{h}}_3}+\frac{{\mathsf{\gamma }}_1{\mathrm{k}}_1}{{\mathrm{A}}_1}{\mathrm{v}}_1\\ \frac{{\mathrm{d}\mathrm{h}}_2}{\mathrm{d}\mathrm{t}}=-\frac{{\mathrm{a}}_2}{{\mathrm{A}}_2}\sqrt{{2\mathrm{g}\mathrm{h}}_2}+\frac{{\mathrm{a}}_4}{{\mathrm{A}}_2}\sqrt{{2\mathrm{g}\mathrm{h}}_4}+\frac{{\mathsf{\gamma }}_2{\mathrm{k}}_2}{{\mathrm{A}}_2}{\mathrm{v}}_2\\ \frac{{\mathrm{d}\mathrm{h}}_3}{\mathrm{d}\mathrm{t}}=-\frac{{\mathrm{a}}_3}{{\mathrm{A}}_3}\sqrt{{2\mathrm{g}\mathrm{h}}_3}+\frac{(1-{\mathsf{\gamma }}_2){\mathrm{k}}_2}{{\mathrm{A}}_3}{\mathrm{v}}_2\\ \frac{{\mathrm{d}\mathrm{h}}_4}{\mathrm{d}\mathrm{t}}=-\frac{{\mathrm{a}}_4}{{\mathrm{A}}_4}\sqrt{{2\mathrm{g}\mathrm{h}}_4}+\frac{\left(1-{\mathsf{\gamma }}_1\right){\mathrm{k}}_1}{{\mathrm{A}}_4}{\mathrm{v}}_1,\end{array}$$

(32)

where  ${\mathrm{A}}_{\mathrm{i}}$  and  ${\mathrm{a}}_{\mathrm{i}},\mathrm{i}=1,\dots ,4$  are cross-sections of individual tanks and of their outlet holes respectively;  ${\mathrm{h}}_{\mathrm{i}},\mathrm{i}=1,\dots ,4$  are levels in individual tanks; g is the gravitational acceleration.

The plant model can be configured as a minimum or nonminimum phase one depending on the relative ratios of the pump flows  ${\mathsf{\gamma }}_{1,}{\mathsf{\gamma }}_2.$ For the minimum-phase configuration the following condition is satisfied:

$$1<{\mathsf{\gamma }}_1+{\mathsf{\gamma }}_2<2,$$

(33)

and the nonminimum-phase condition is:

$$0<{\mathsf{\gamma }}_1+{\mathsf{\gamma }}_2<1.$$

(34)

By linearization of (33) around a selected working point specified by the levels in individual tanks  ${\mathrm{h}}_{\mathrm{i}0},\mathrm{i}=1,\dots ,$ 4, the corresponding transfer function matrix is obtained [2]:

$$\mathrm{P}(\mathrm{s})=\left[\begin{array}{cc}\frac{{\mathrm{c}}_1{\mathsf{\gamma }}_1}{{\mathrm{T}}_1\mathrm{s}+1}& \frac{{\mathrm{c}}_1(1-{\mathsf{\gamma }}_2)}{{(\mathrm{T}}_3\mathrm{s}+1\left)\right({\mathrm{T}}_1\mathrm{s}+1)}\\ \frac{{\mathrm{c}}_2(1-{\mathsf{\gamma }}_1)}{{(\mathrm{T}}_4\mathrm{s}+1\left)\right({\mathrm{T}}_2\mathrm{s}+1)}& \frac{{\mathrm{c}}_2{\mathsf{\gamma }}_2}{{\mathrm{T}}_2\mathrm{s}+1}\end{array}\right]$$

(35)

where

$$\begin{array}{c}{\mathrm{T}}_{\mathrm{i}}=\frac{{\mathrm{A}}_{\mathrm{i}}}{{\mathrm{a}}_{\mathrm{i}}}\sqrt{\frac{2{\mathrm{h}}_{\mathrm{i}}^0}{\mathrm{g}}},\mathrm{i}=1,\dots ,4\\ {\mathrm{c}}_{\mathrm{i}}=\frac{{\mathrm{T}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{i}}{\mathrm{k}}_{\mathrm{c}}}{{\mathrm{A}}_{\mathrm{i}}}\sqrt{\frac{2{\mathrm{h}}_{\mathrm{i}}^0}{\mathrm{g}}},\mathrm{i}=\mathrm{1,2}\end{array}$$

(36)

Values of individual plant parameters were taken from [24] and are shown in Table 1.

5.2. Control Problem Statement

For the quadruple tank system, the aim is to control levels in the two lower tanks (h₁, h₂) by means of the flows delivered by the two pumps (v₁, v₂) in the operating range specified by valves settings ( ${\mathsf{\gamma }}_1,$   ${\mathsf{\gamma }}_2$ ) which represent uncertain parameters interrelated depending on the specific plant configuration (33) or (34). Hence, the plant has  $\mathrm{m}=2$  subsystems, the minimum phase configuration is considered, and the decentralized control structure is to be employed.

5.3. Robust Decentralized Controller Design

The ESM-QFT design procedure described in Section 4 was used to design the robust decentralized controller.

I. 

Modelling the uncertain MIMO system

The linearized model of the uncertain plant based on parameter values in Table 1 is:

$$\mathrm{P}\left(\mathrm{s}\right)=\left[\begin{array}{cc}\frac{0.747{\mathsf{\gamma }}_1}{62.044\mathrm{s}+1}& \frac{0.747\left(1-{\mathsf{\gamma }}_2\right)}{\left(22.992\mathrm{s}+1\right)\left(62.044\mathrm{s}+1\right)}\\ \frac{0.949\left(1-{\mathsf{\gamma }}_1\right)}{\left(29.995\mathrm{s}+1\right)\left(90.031\mathrm{s}+1\right)}& \frac{0.949{\mathsf{\gamma }}_2}{90.031\mathrm{s}+1}\end{array}\right].$$

(37)

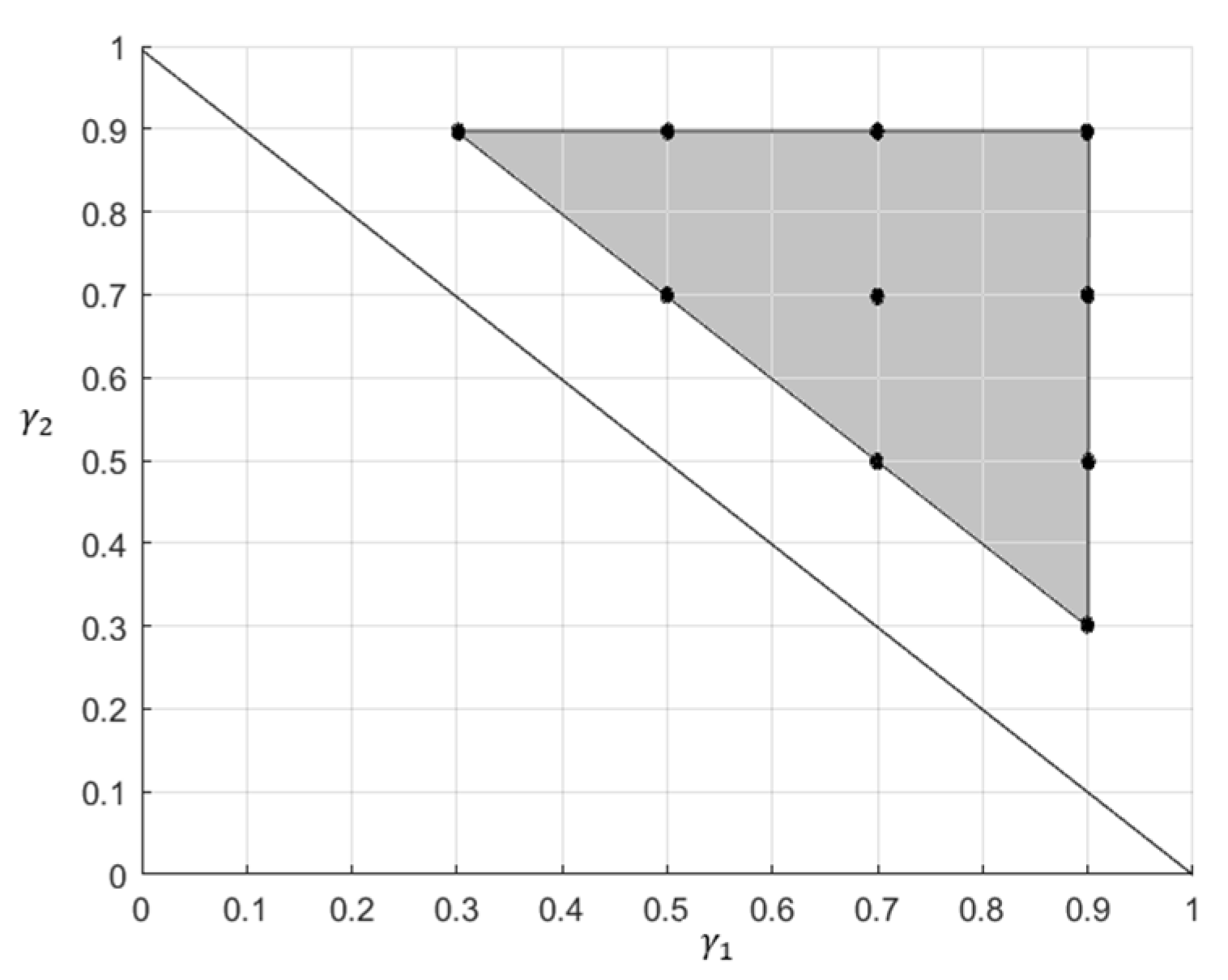
When considering the minimum phase plant configuration, the two uncertain parameters  ${\mathsf{\gamma }}_1,$   ${\mathsf{\gamma }}_2\in <0, 1>$ are interrelated according to (33). The set of realizations of the uncertain plant was generated by gridding  ${\mathsf{\gamma }}_1,$   ${\mathsf{\gamma }}_2\in <0.3, 0.9>$ and considering all their combinations that meet (33). The number of all feasible combinations is  $\mathrm{N}=10$ . 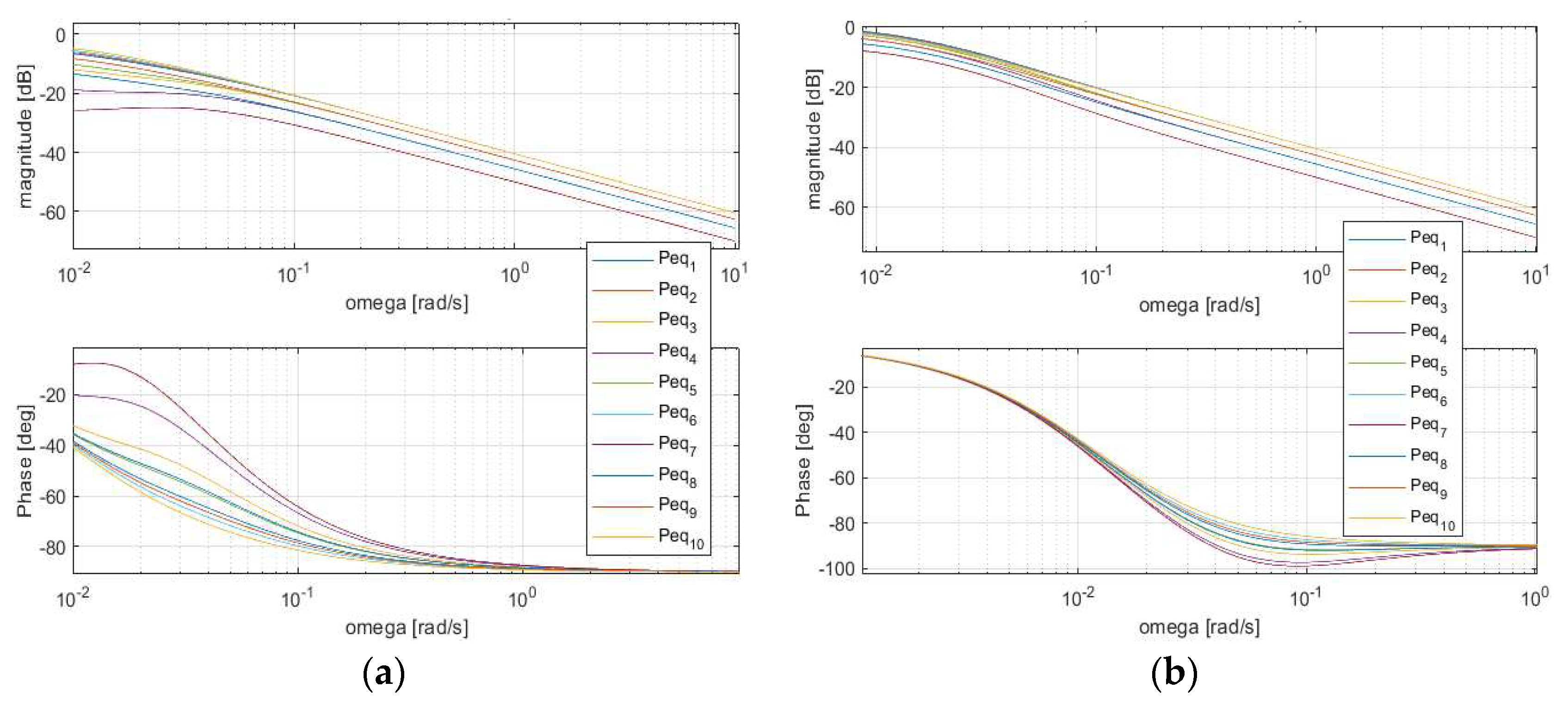The corresponding combinations specifying the considered uncertainty region are depicted in Figure 4. The nominal model was selected as (37) evaluated in  ${\mathsf{\gamma }}_1=$   ${\mathsf{\gamma }}_2=0.7.$ 

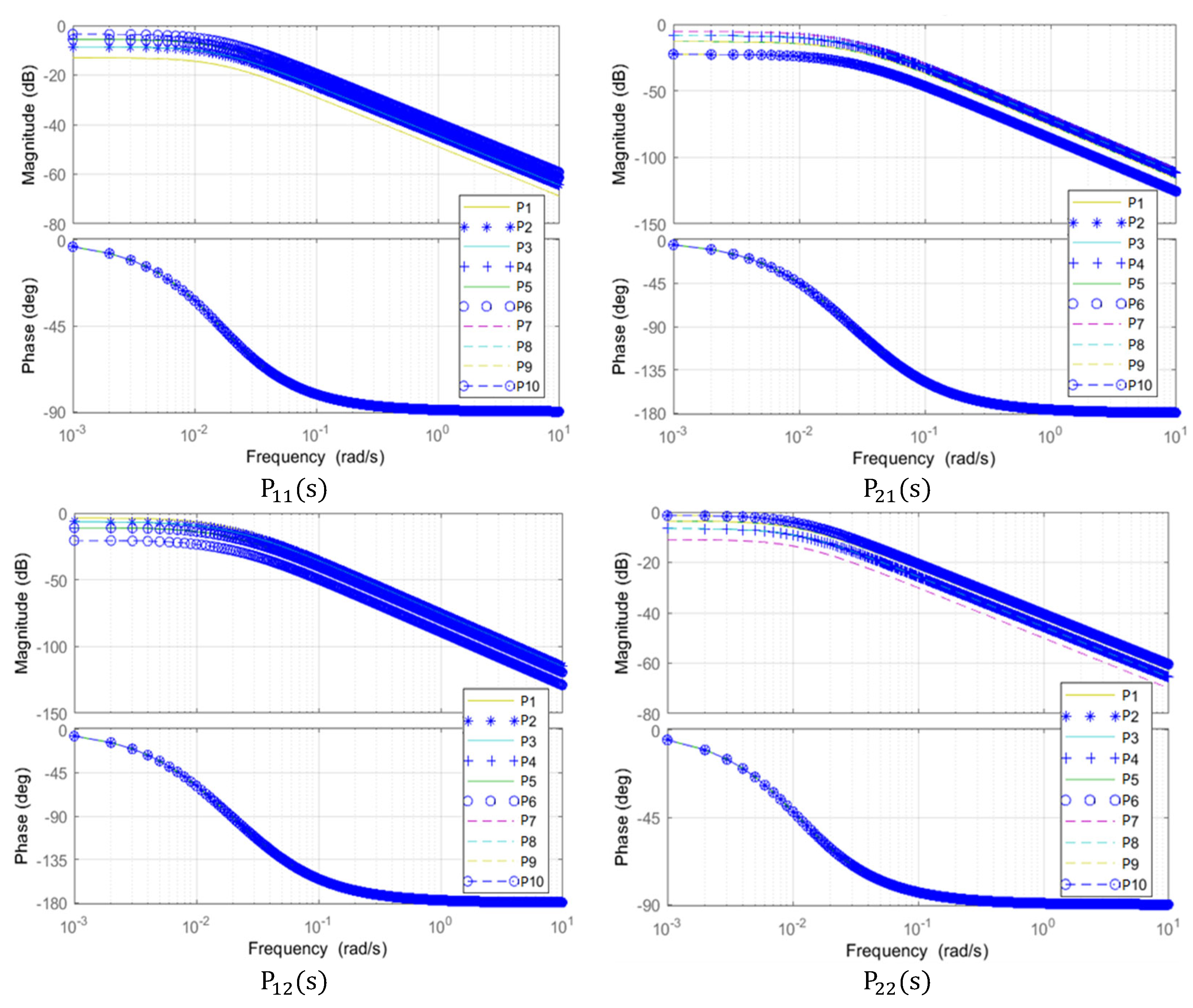
To appropriately choose the frequency range to be considered in the controller design, Bode diagrams of individual entries of the transfer matrix (37) have been depicted in Figure 5.

II. 

Generation of uncertain equivalent subsystems

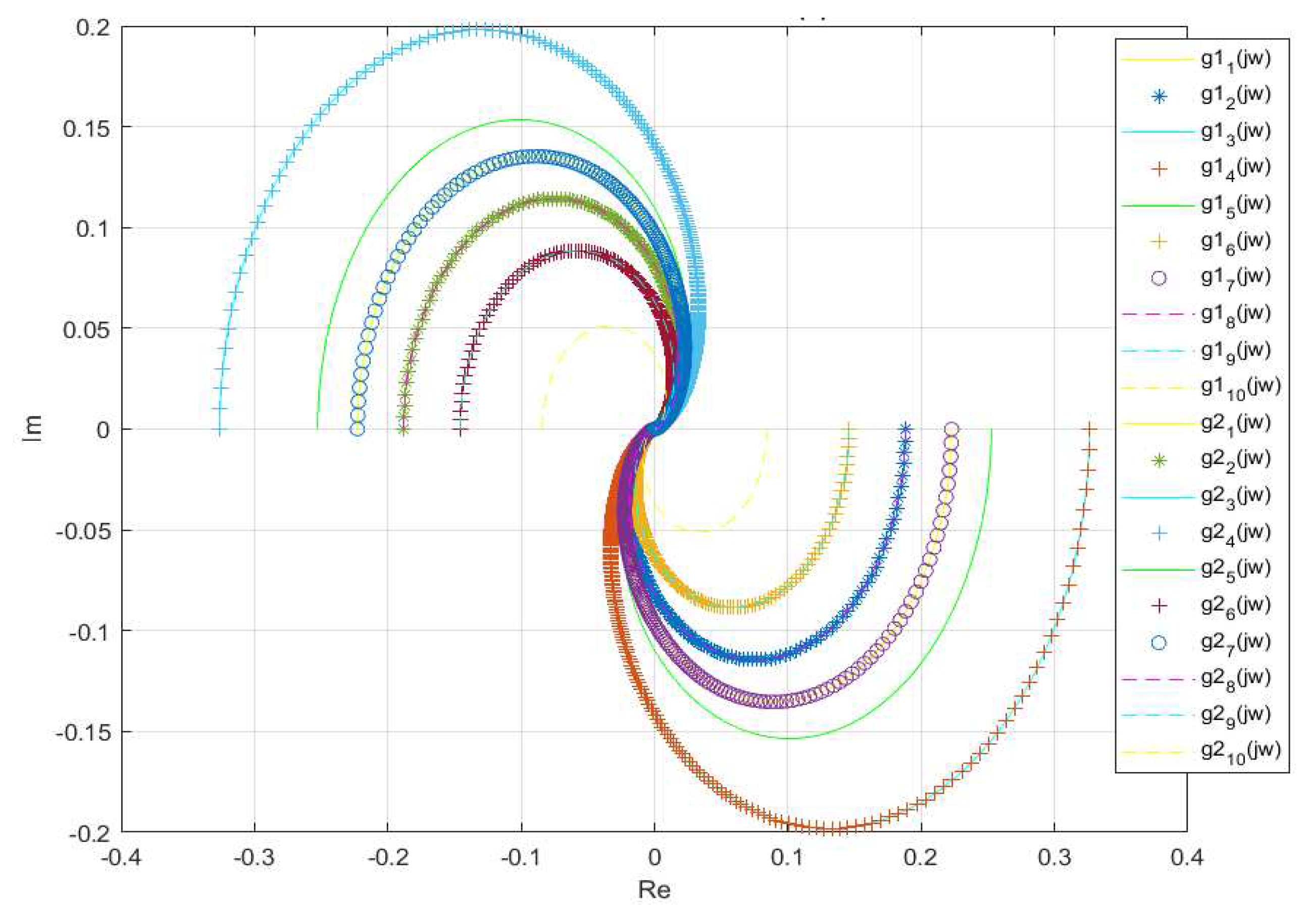
Characteristic loci of the matrices of interactions  ${\mathrm{P}}_{\mathrm{n}}^{\mathrm{r}}\left(\mathrm{s}\right), \mathrm{r}=1,\dots 10$  for all realizations are depicted in Figure 6.

Equivalent subsystems were generated according to (21) using the characteristic loci  ${\mathrm{g}}_2^{\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right),\mathrm{r}=1,\dots ,10$ :

$${\mathrm{P}}_{\mathrm{i}2}^{\mathrm{e}\mathrm{q}\_\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right)={\mathrm{P}}_{\mathrm{i}\mathrm{i}}^{\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right)+{\mathrm{g}}_2^{\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right),\mathrm{i}=\mathrm{1,2};\mathrm{r}=\left\{\mathrm{1,2},\dots ,10\right\},$$

(38)

respective Bode diagrams are shown in Figure 7.

III. 

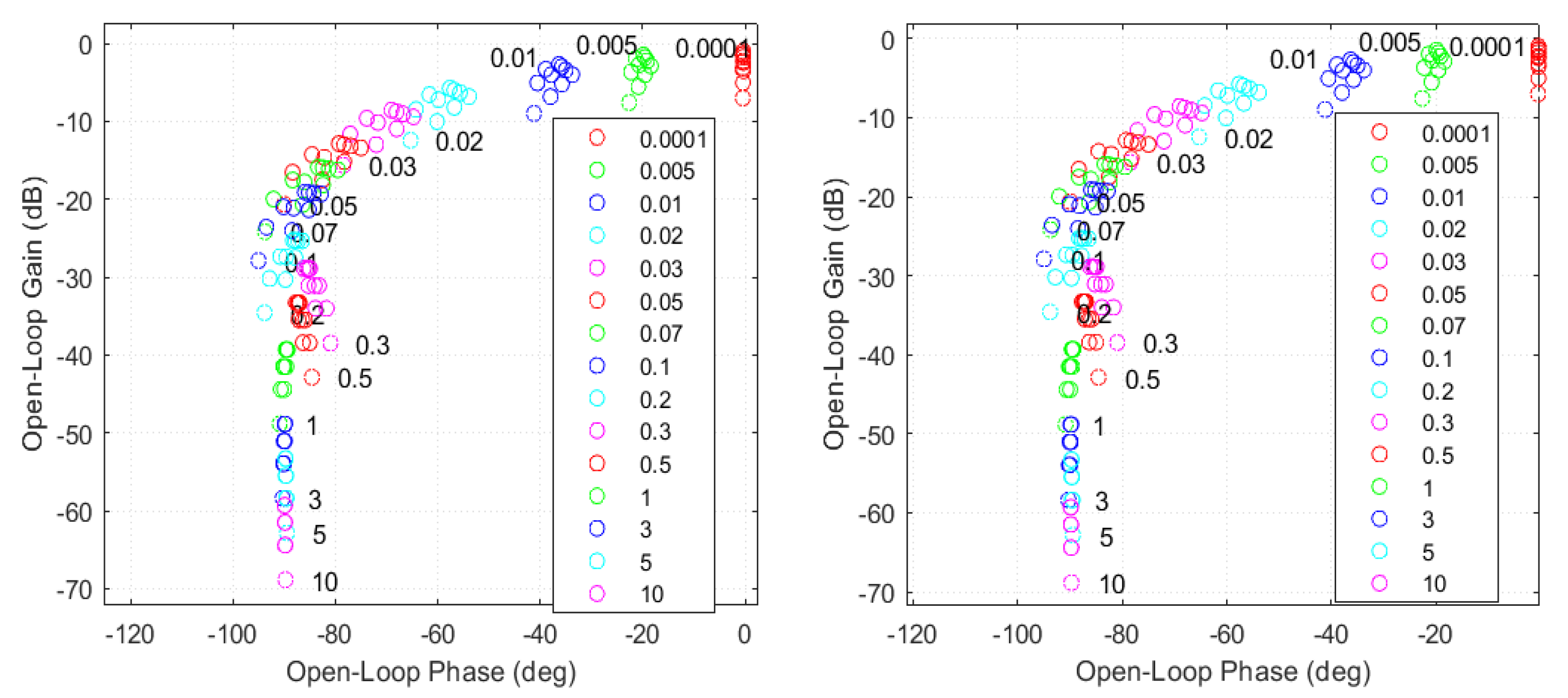
Calculation of QFT templates of equivalent subsystems

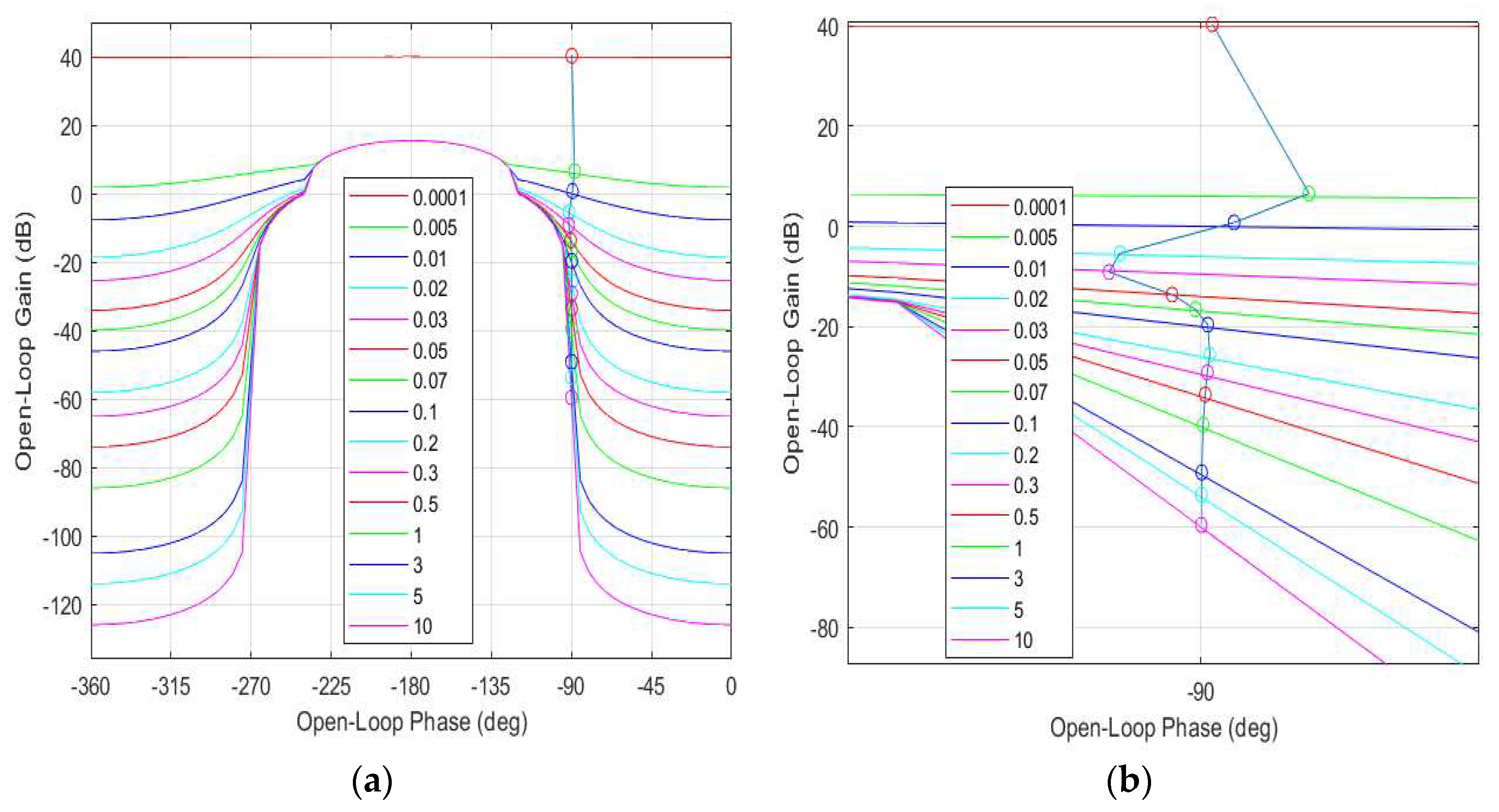
For the set of uncertain equivalent subsystems (38), corresponding QFT templates were calculated and plotted in the Nichols diagrams (Figure 8) for the selected frequencies  $\mathsf{\omega }=\{0.0001 0.005 0.01 0.02 0.03 0.05 0.07 0.01 0.2 0.3 0.5 1 3 5 10\}.$ 

IV. 

Independent design of SISO local controllers  $C_i\left(s\right)=\mathrm{1,2}$ for uncertain equivalent subsystems

Time-domain performance requirements for the overall system usually specified in terms time-domain measures (maximum overshoot, settling time) had to be interpreted into frequency domain measures; two following out of eight QFT stability and performance specifications [19] similar for both equivalent subsystems were selected:

• Stability specification (determines 20% maximum overshoot of output responses):

  $$\left|{\mathrm{T}}_1\left(\mathrm{j}\mathsf{\omega }\right)\right|=\left|\frac{{\mathrm{P}}_{\mathrm{i}2}^{\mathrm{e}\mathrm{q}\_\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right){\mathrm{C}}_i\left(\mathrm{j}\mathsf{\omega }\right)}{1+{\mathrm{P}}_{\mathrm{i}2}^{\mathrm{e}\mathrm{q}\_\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right){\mathrm{C}}_i\left(\mathrm{j}\mathsf{\omega }\right)}\right|\le {\mathrm{W}}_{\mathrm{s}\mathrm{i}}=1.2, \mathrm{i}=\mathrm{1,2}.$$

  (39)
• Performance specification (sensitivity constraint), determines bandwidth which is a measure of speed of response like time domain measures such as rise time or peak time [30]:

  $$\left|{\mathrm{T}}_3\left(\mathrm{j}\mathsf{\omega }\right)\right|=\left|\frac{1}{1+{\mathrm{P}}_{\mathrm{i}2}^{\mathrm{e}\mathrm{q}\_\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right){\mathrm{C}}_{\mathrm{i}}\left(\mathrm{j}\mathsf{\omega }\right)}\right|\le {\mathsf{\delta }}_{3\mathrm{i}}=\frac{\left(\mathrm{s}/{\mathrm{a}}_{\mathrm{d}\mathrm{i}}\right)}{\left(\mathrm{s}/{\mathrm{a}}_{\mathrm{d}\mathrm{i}}\right)+1}, \mathrm{i}=\mathrm{1,2}$$

  (40)

where  ${\mathrm{a}}_{\mathrm{d}\mathrm{i}}=0.01, \mathrm{i}=\mathrm{1,2}$ .

Based on performance specifications and QFT templates, the QFT bounds were calculated, their intersection was plotted in the Nichols diagram (Figure 9).

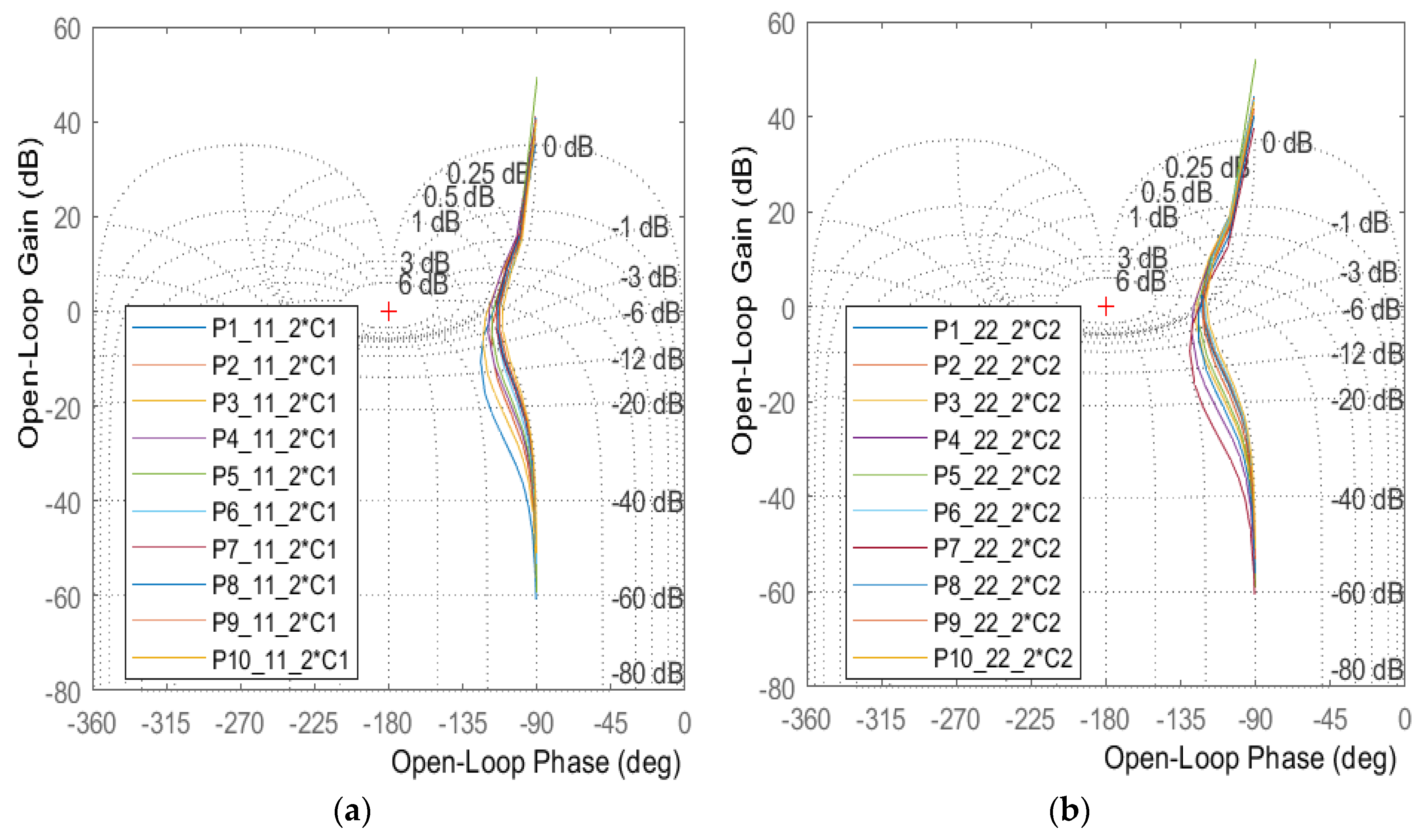
Local controllers  ${\mathrm{C}}_{\mathrm{i}}\left(\mathrm{s}\right)=\mathrm{1,2}$  were designed by loop shaping of nominal open loops  ${\mathrm{L}}_{0\mathrm{i}}\left(\mathrm{j}\mathsf{\omega }\right)={\mathrm{P}}_{\mathrm{i}2}^{\mathrm{e}\mathrm{q}\_5}\left(\mathrm{j}\mathsf{\omega }\right){\mathrm{C}}_{\mathrm{i}}\left(\mathrm{j}\mathsf{\omega }\right), \mathrm{i}=\mathrm{1,2}$  in the respective Nichols diagrams with depicted QFT bounds (Figure 10 and Figure 11).

Local controllers designed for equivalent subsystems constitute the resulting decentralized controller to be implemented for the real system:

$$\mathrm{C}\left(\mathrm{s}\right)=\left[\begin{array}{cc}{\mathrm{C}}_1\left(\mathrm{s}\right)& 0\\ 0& {\mathrm{C}}_2\left(\mathrm{s}\right)\end{array}\right]=\left[\begin{array}{cc}1.2485+\frac{0.0384}{\mathrm{s}}& 0\\ 0& 1.4582+\frac{0.04487}{\mathrm{s}}\end{array}\right],$$

(41)

V. 

Analysis in the frequency and time domains

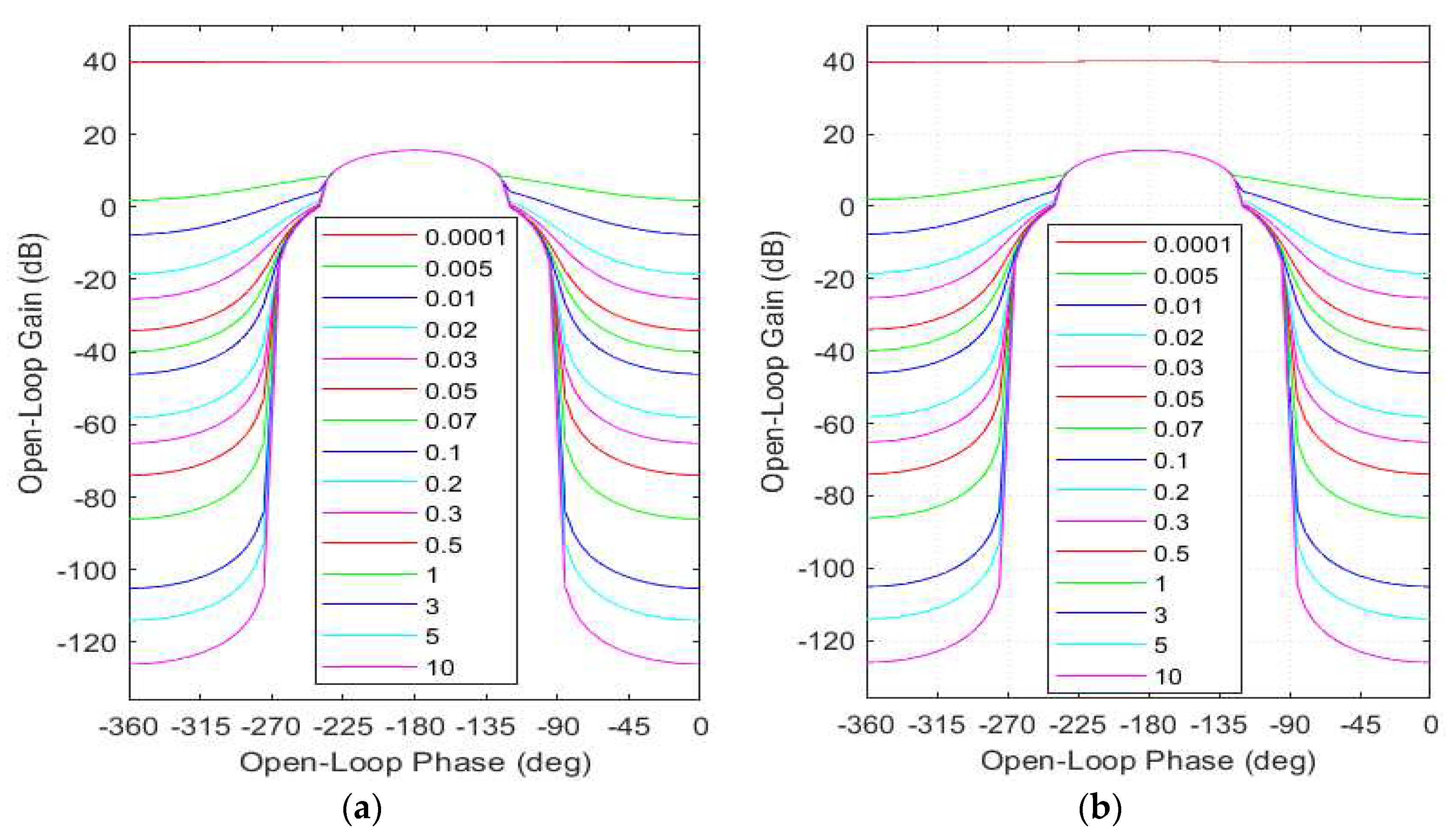
Frequency domain analysis includes:

• verification of the fulfillment of performance requirements in equivalent subsystems by plotting Nichols plots of open-loop equivalent subsystems  ${{\mathrm{P}}_{\mathrm{i}2}^{\mathrm{e}\mathrm{q}\_\mathrm{r}}\left(\mathrm{j}\mathsf{\omega }\right)\mathrm{C}}_{\mathrm{i}}\left(\mathrm{j}\mathsf{\omega }\right),\mathrm{i}=\mathrm{1,2}$  for r=1, …,10 to (Figure 12);
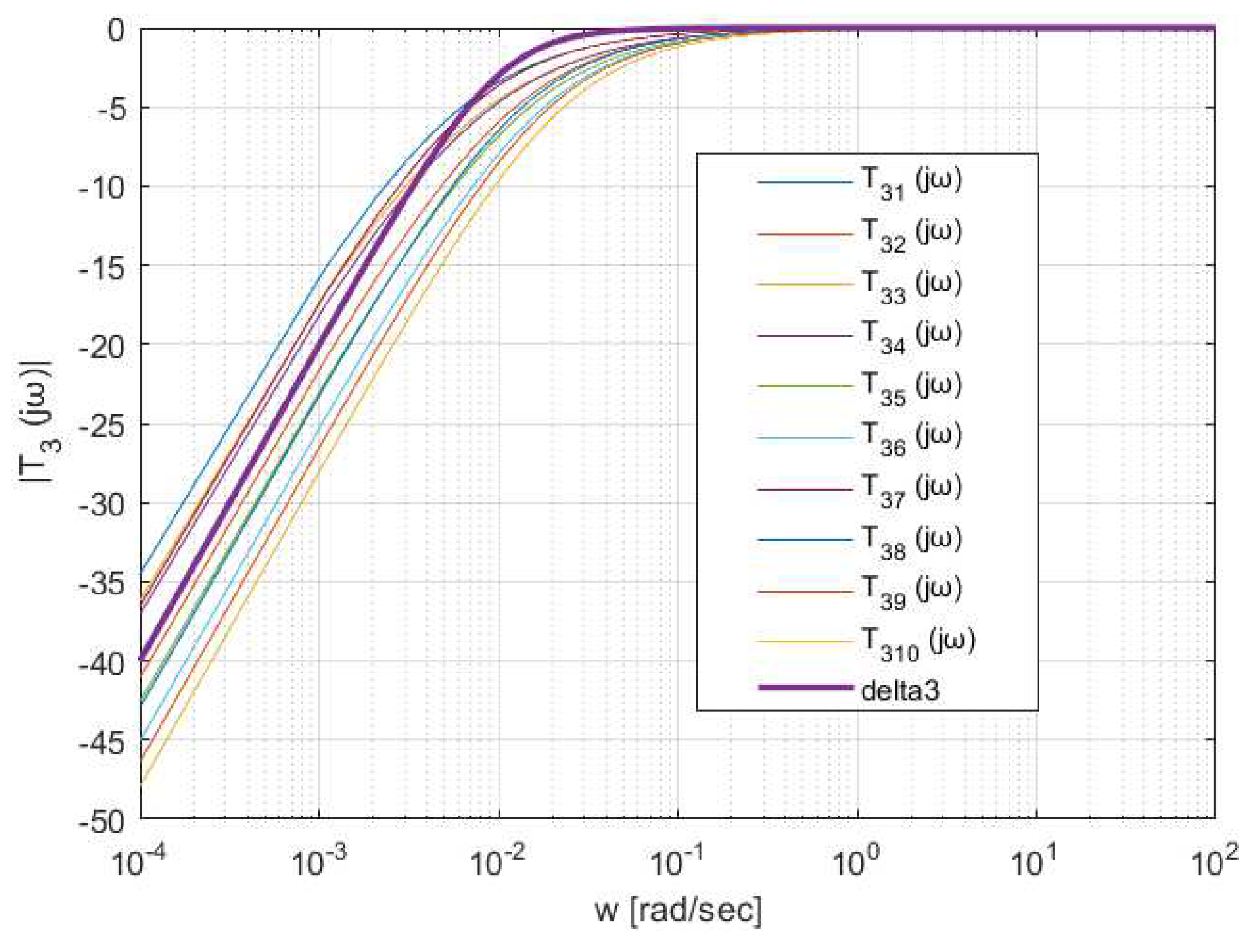
• investigation of the fulfillment of performance requirements on the level of the overall closed-loop system by plotting the sensitivity module of the overall system under the decentralized controller (Figure 13);
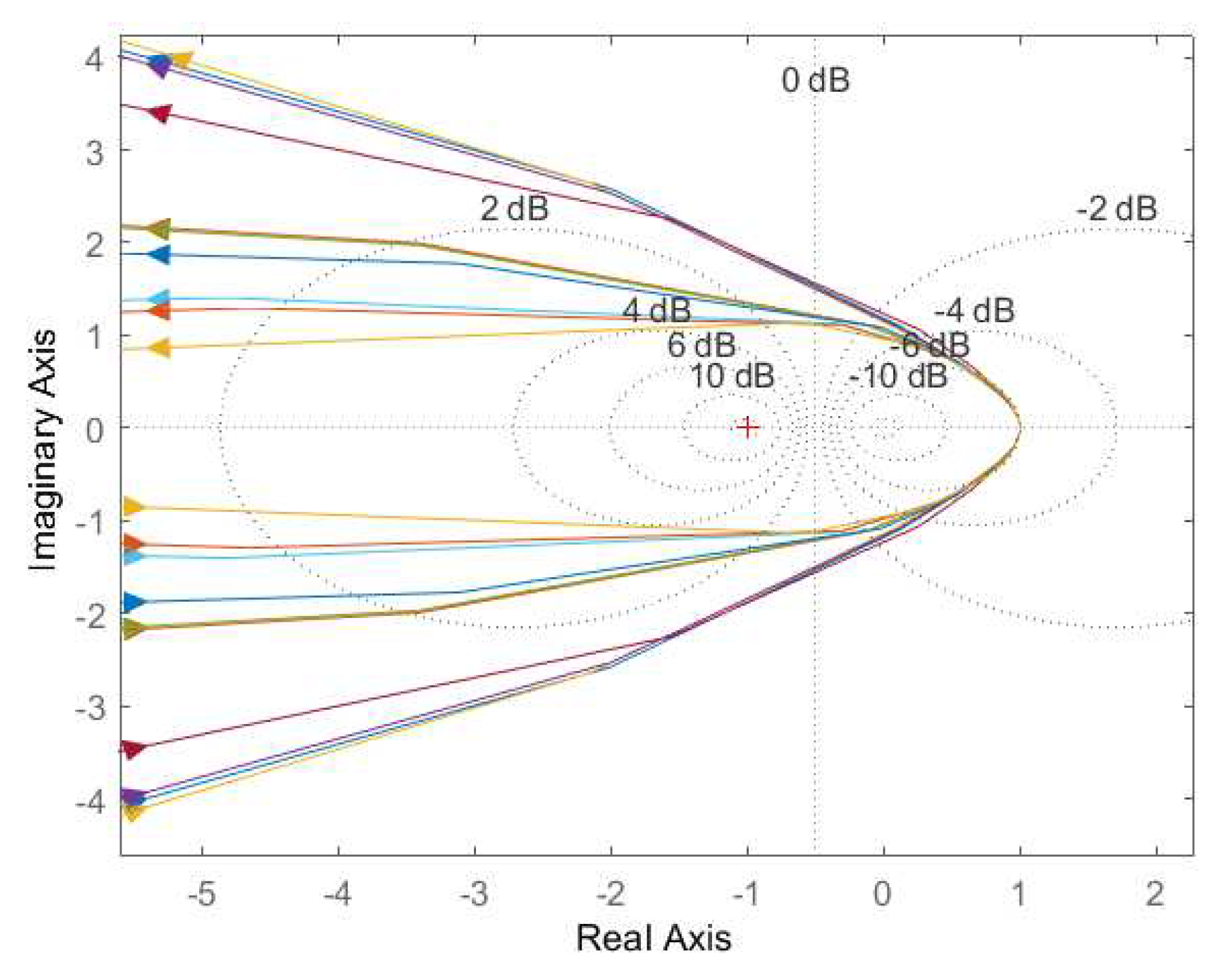
• closed-loop stability verification using the generalized Nyquist stability criterion (2) (Figure 14).

For both equivalent subsystems, Nichols diagrams in Figure 12 prove stability and fulfillment of the Type 1 specification (39) as neither of the depicted Nichols plots intersects or touches the curve of the value  $20\log \left(1.2\right)=1.58 \mathrm{d}\mathrm{B}$  corresponding to  ${\mathrm{W}}_{\mathrm{s}}=1.2$   $.$ The required minimum bandwidth specified for equivalent subsystems by the Type 3 performance specification (40) is kept for all realizations of the overall system (Figure 13,  ${\mathsf{\delta }}_3\left(\mathsf{\omega }\right)$ is depicted in bold), the minimum bandwidth achieved is  ${\mathsf{\omega }}_{\mathrm{B}\mathrm{W}}=0.008{ s}^{-1}$ .

The overall closed-loop system under the decentralized controller is stable as ` $\mathrm{N}\left[0,\mathrm{d}\mathrm{e}\mathrm{t}\left[\mathrm{I}+\mathrm{Q}\left(\mathrm{s}\right)\right]\right]={\mathrm{n}}_{\mathrm{q}}=0$  for all 10 plant realizations considered (Figure 14).

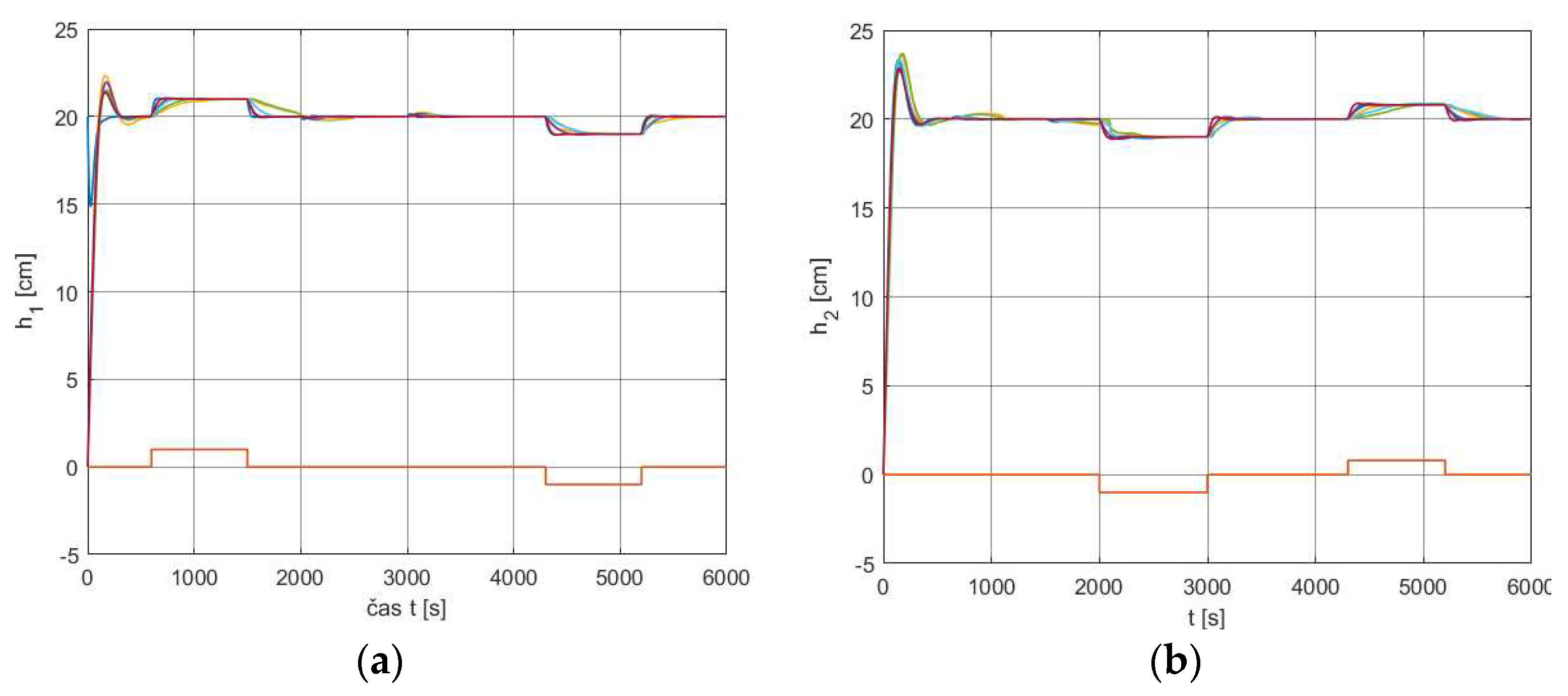
Time domain analysis is based on simulations of step changes in references of the lower tanks according to scenarios depicted in the lower parts of the charts in Figure 15 and Figure 16. Simulations were performed using both the linear and the nonlinear models (35), (32) respectively, in the specified working point given by  ${\mathrm{h}}_{\mathrm{i}}^0, \mathrm{i}=1, \dots , 4$  for all 10 valve settings  ${\mathsf{\gamma }}_1,$   ${\mathsf{\gamma }}_2$  according to Table 2. Respective output responses are depicted in Figure 15 (linear model) and Figure 16 (nonlinear model); the performance on individual charts is of interest only after the variables have first settled at the respective working points.

Responses in Figure 15 and Figure 16 are another proof of the fulfillment of the Type 1 specification (39), as the overshoots of the responses  ${\mathrm{h}}_1\left(\mathrm{t}\right)$  a  ${\mathrm{h}}_2\left(\mathrm{t}\right)$  are  ${\mathsf{\eta }}_{\mathrm{m}\mathrm{a}\mathrm{x}}<20\mathrm{\%}$ .

6. Discussion

The proposed ESM-QFT frequency domain method is suitable to design robust decentralized controllers for uncertain MIMO systems consisting of interconnected subsystems given as a set of square transfer function matrices. Combination of the Equivalent Subsystems Method (ESM) and the standard QFT design allows to exploit the assets of both methods.

Using the ESM, local controllers are independently designed for individual equivalent subsystems and subsequently implemented on true subsystems as a decentralized controller guaranteeing fulfillment of the necessary and sufficient stability condition according to the generalized Nyquist stability theorem. The independent design carried out for equivalent subsystems does not introduce conservatism compared with standard independent designs based on decoupled subsystems [8].

Design of local SISO controllers for individual equivalent subsystems based on the QFT is advantageous in that it uses sets of equivalent subsystems generated directly from the transfer function matrices of the uncertain MIMO system with no need to additionally specify the unstructured uncertainty as e.g., in [1]. Moreover, performance requirements imposed on the overall uncertain system are usually specified in the time-domain; according to the ESM-QFT method, their fulfillment is guaranteed if they are translated into frequency domain performance specifications and their fulfillment in the equivalent subsystems is ensured.

The ESM-QFT method uses nonparametric models of the controlled plant and related frequency dependencies, hence the design procedure is graphical, insightful, and interactive, and may be applied for continuous and discrete, minimum- and non-minimum phase systems as well as for systems with delays. Future research will encompass application of the developed method for these various types of MIMO systems and case studies.