IRS Assisted Hybrid Secret Key Generation

Preprint

Article

IRS Assisted Hybrid Secret Key Generation

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 August 2023

Posted:

09 August 2023

You are already at the latest version

Alerts

Abstract

Physical layer secret key (SK) generation is known to be an efficient means to achieve high secrecy rate, on the condition that dynamic channel state information (CSI) is provided. For this reason, the secrecy performance is highly degraded in a static environment. The intelligent reflecting surface (IRS) is a promising solution to create dynamic randomness, and thus lead to enhanced secrecy performance regardless of the user environments. This paper proposes an IRS-assisted physical layer SK generation scheme, by efficiently combing phase information of the direct and reflected channel information in a hybrid way. In particular, the initial SKs are obtained by adopting efficient phase quantization method with symmetric bit allocation to complex numbered channel estimates. Simulation results show that the proposed hybrid phase quantization (PQ) can improve the SK generation rate and the key disagreement probability in a static environment.

Keywords:

Subject: Engineering - Telecommunications

1. Introduction

Physical layer secret key (SK) generation technology is a promising technique for achieving one-time-pad encryption approach in wireless communication systems. This is possible due to the reciprocity, space-time uniqueness, and fast time-varying nature of the wireless channel. With this approach, both legitimate communication parties can independently generate SKs in real-time using the wireless channel features as a random source, without the need for key transmission [1]. SK generation techniques rely on time-varying characteristic of the wireless channel. Therefore, in static environments, the keys cannot be updated quickly, which can eventually result in lower security protection.

The intelligent reflecting surface (IRS) has received a lot of attention in recent years, due to its capability of ameliorating the wireless channel environment through software-controlled reflections [2]. Specifically, the IRS consists of a large number of low-cost passive reflecting elements, each can independently make changes to the incident signal [2,3], and thus it has great potential to increase the SK generation rate in real time [4,5,6,7]. Most of the current research works on IRS-assisted SK generation focused on optimization problems to maximize the SK generation rate or SK capacity at the legitimate user by optimizing the phase shift coefficients or using random phase shifting of IRS [5,6,7].

For example, an IRS-assisted SK generation scheme was proposed in order to overcome the problem of low SK rate in a static environment, by using discrete phase shift [5]. This scheme maximized the SK rate by optimizing the IRS phase switching time, but there was no implementation details such as quantization method for the estimated channel state information (CSI). On the other hand, phase shift optimization schemes for the IRS were proposed [6,7]. A lower bound on the SK capacity was derived for an IRS-assisted wireless network with multiple eavesdroppers, and an IRS reflection coefficient optimization framework was introduced [6]. The design principle of IRS-assisted SK generation was proposed, and its performance improvement in SK rate was verified [7].

However, both of the above two schemes incurred complexity compared with the random phase shifting scheme. Furthermore, a technique to maximize the SK capacity was introduced for SK generation process based on CSI, by adjusting the layout of the IRS elements [8]. It also proposed the process of SK generation based on CSI, but there was no detailed description for each step.

On the other hand, a number of studies reported quantization methods used during the SK generation process [9,10,11,12,13,14]. Although binary quantization method is simple and easy to implement [9], it can only generate a single SK bit. Multi-level equiprobable quantization methods were utilized to increase bit generation rate [10,11]. In this case, selecting the appropriate quantization levels and interval partitioning are crucial issues that require a trade-off between information preservation and SK length. For example, previous studies presented multi-level phase quantization (PQ) methods to increase SK generation rate [12,13,14]. However, the complexity of quantization process is also increasing as the number of quantized bits. This is because the number of quantization levels is exponentially increasing with the number of quantized bits.

As a solution to the above mentioned problems of the existing works, this paper proposes an efficient IRS-assisted SK generation scheme with a computationally efficient PQ method. The first novelty of the proposed scheme lies in the hybrid method of extracting CSI for initial key generation. Phase information is first extracted from the direct channel, and then extracted from the combined channels with the IRS. This is because the IRS usually changes the phase of the reflecting signals almost without amplitude variations. This way of hybrid extraction of CSI from different channels will contribute to increasing the randomness of key generation, and eventually lead to the increment in SK generation rate. The second novelty of the proposed scheme is utilization of a new and computationally efficient PQ method to generate SK from the extracted CSI. We first form a new complex number by using the amplitude and phase information extracted from the proposed hybrid method, and then quantize the phase in the complex plane. This paper presents the details of extracting phase information from the estimated CSI of the proposed hybrid method. The proposed method is universally applicable to any m-level quantization method, and the quantization level can be adaptively regulated.

The remainder of this paper is organized as follows. Section 2 describes the related works including the system model for an IRS-assisted SK generation and the conventional quantization methods. Section 3 first presents the hybrid way of extracting CSI, and then details the proposed PQ method. In order to verify the merits of the proposed scheme, Section 4 first presents a number of performance measures, and then provides the simulation results. Finally, the paper is concluded in Section 5.

2. Related Works

2.1. System Model

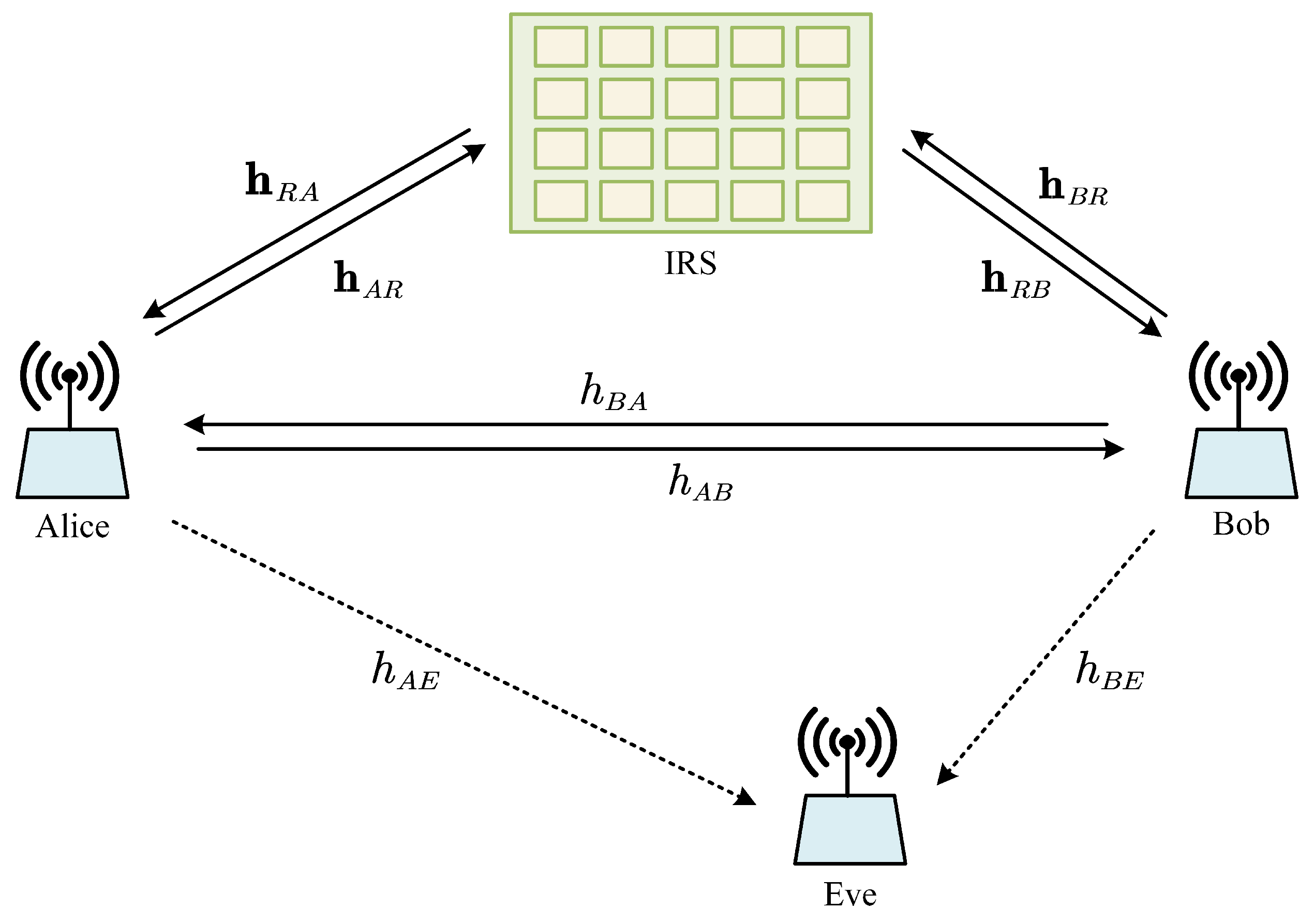
Figure 1 shows a system model for an IRS-assisted wireless communication system, where data transmission is encrypted with SK generated with the aid of IRS in order to achieve secure communications [4]. The legitimate communication parties Alice and Bob send probe signals to each other in time-division duplex (TDD) mode, and extract SK from their correlated measurements before encrypted data transmission. Because the block fading channel remains constant during a long coherence time, an IRS is adopted to increase for randomness by configuring its phase shift. Each of N reflecting elements receives a superimposed multipath signal from the sender and then reflects the signal in random phase, with a diagonal IRS phase shifting matrix

Θ = diag (e^{j θ_{1}}, e^{j θ_{2}}, \dots, e^{j θ_{N}})

, where

θ_{n} \in [0, 2 π)

is the phase shift of the n-th element. The eavesdropper Eve is assumed to be a few wavelengths away from the legitimate users, so that Eve taps an eavesdropping channel that is independent of the legitimate channel. They are equipped with a single antenna.

In each block, Alice and Bob send the probe pilots alternatively to generate the SK during the first L time slots of the coherence time. After key generation, the data is encrypted with the generated keys before its transmission during the remaining coherence time. The received signals at Alice and Bob in each probe round can be expressed as follows, respectively [4,15]:

\begin{matrix} \begin{matrix} y_{A} & = (h_{B A} + h_{R A}^{H} Θ h_{B R}) x + n_{A}, \\ y_{B} & = (h_{A B} + h_{R B}^{H} Θ h_{A R}) x + n_{B}, \end{matrix} \end{matrix}

(1)

where

h_{A B} \in C^{1 \times 1}

and

h_{B A} \in C^{1 \times 1}

are the CSIs of the direct channel from Alice to Bob and Bob to Alice, respectively,

h_{A R}

and

h_{B R} \in C^{N \times 1}

are the CSI vectors from Alice and Bob to the IRS, and

h_{R A}

and

h_{R B} \in C^{N \times 1}

are the reflected CSI vectors from the IRS to Alice and Bob, respectively. In addition,

x \sim C N (0, I)

is the probing signal vector sent by Bob and Alice, and

n_{A} \sim C N (0, σ_{A}^{2} I)

and

n_{B} \sim C N (0, σ_{B}^{2} I)

denote the complex additive white Gaussian noise (AWGN) at Alice and Bob, where

I

is the identity matrix.

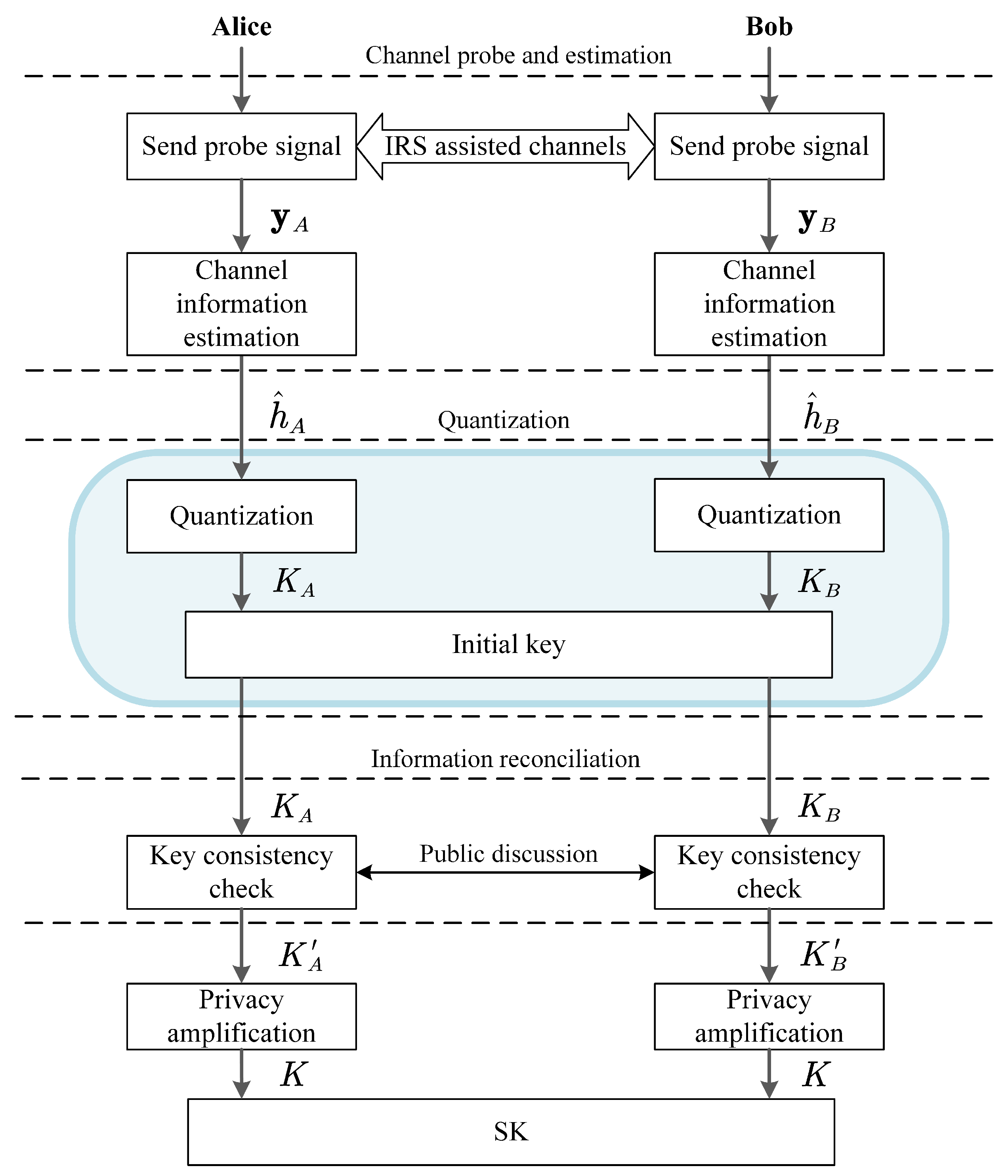
In this case, the channel estimates at Alice and Bob can be calculated from their reciprocally combined channels of the direct and reflected channels as follows:

\begin{matrix} \begin{matrix} {\hat{h}}_{A} & = h_{B A} + h_{R A}^{H} Θ h_{B R} + {\hat{n}}_{A}, \\ {\hat{h}}_{B} & = h_{A B} + h_{R B}^{H} Θ h_{A R} + {\hat{n}}_{B}, \end{matrix} \end{matrix}

(2)

where

{\hat{n}}_{A} = x^{H} n_{A} / {∥ x ∥}^{2}

and

{\hat{n}}_{B} = x^{H} n_{B} / {∥ x ∥}^{2}

denote the estimation errors at Alice and Bob, respectively. These channel estimates are used to generate SK at the quantization process, and the generated keys are used for information reconciliation as shown in Figure 2. Finally, the privacy amplification algorithm based on hash function is applied to avoid information leakage [8]. Through the above process, both communication parties complete the same key establishment.

2.2. Quantization of CSI

Based on the above channel estimates of

{\hat{h}}_{A}

and

{\hat{h}}_{B}

, the initial key value is generated by converting the estimated value to binary bits. There have been binary quantization methods, namely absolute value-based quantization (AVQ) and difference value-based quantization (DVQ) [9]. Since these methods converts the channel estimates in to a single bit, SK rate becomes low.

Multi-level quantization methods can be used to increase SK rate [10,11,12,13,14]. For example, an equiprobable quantization method was proposed [10], given the probability density function (PDF) of the input signal x, the decision thresholds for the m-level quantization method was determined as follows:

\begin{matrix} \int_{- \infty}^{{\bar{q}}_{i}} p (x) d x = \frac{i}{m}, \end{matrix}

(3)

where

p (x)

is the PDF of x,

{\bar{q}}_{i}

is the i-th decision threshold,

i = 1, 2, \dots, m - 1

. By this way, each of m quantization regions, i.e.,

(- \infty, {\bar{q}}_{1}], ({\bar{q}}_{1}, {\bar{q}}_{2}], \dots, ({\bar{q}}_{m - 1}, \infty)

is selected with equal probability, and it is mapped to

{log}_{2} m

bits using Gray coding. Furthermore, a method to improve bit agreement ratio was proposed by inserting guard bands between two consecutive quantization levels [11]. We note that the complex numbered CSI does not have a uniform distribution, and thus

{\bar{q}}_{i}

cannot be simply determined. This eventually leading to a complex quantization problem.

Since the phase information of the CSI has uniform PDF, quantization of the phase may lead to a simple quantization process. A PQ method was proposed by using a uniform quantization method for a phase information of the channel estimates [12]. Furthermore, a phase shift quantization method which is similar to phase shift keying (PSK) demodulation method was proposed [13]. This method quantized the phase value,

ϕ

with a m-level uniform quantizer as follows [14]:

\begin{matrix} f (ϕ) = j if ϕ \in [\frac{2 π (j - 1)}{m}, \frac{2 π j}{m}), \end{matrix}

(4)

for

j = 1, 2, \dots, m

. Therefore, the quantization of each phase value generates

{log}_{2} m

secret bits. In order to extract

{log}_{2} m

bits, the above quantization method requires of 1 to m comparison operations, and thus average

m / 2

operations per extracted CSI.

3. Proposed Methods

3.1. SK Generation Protocol

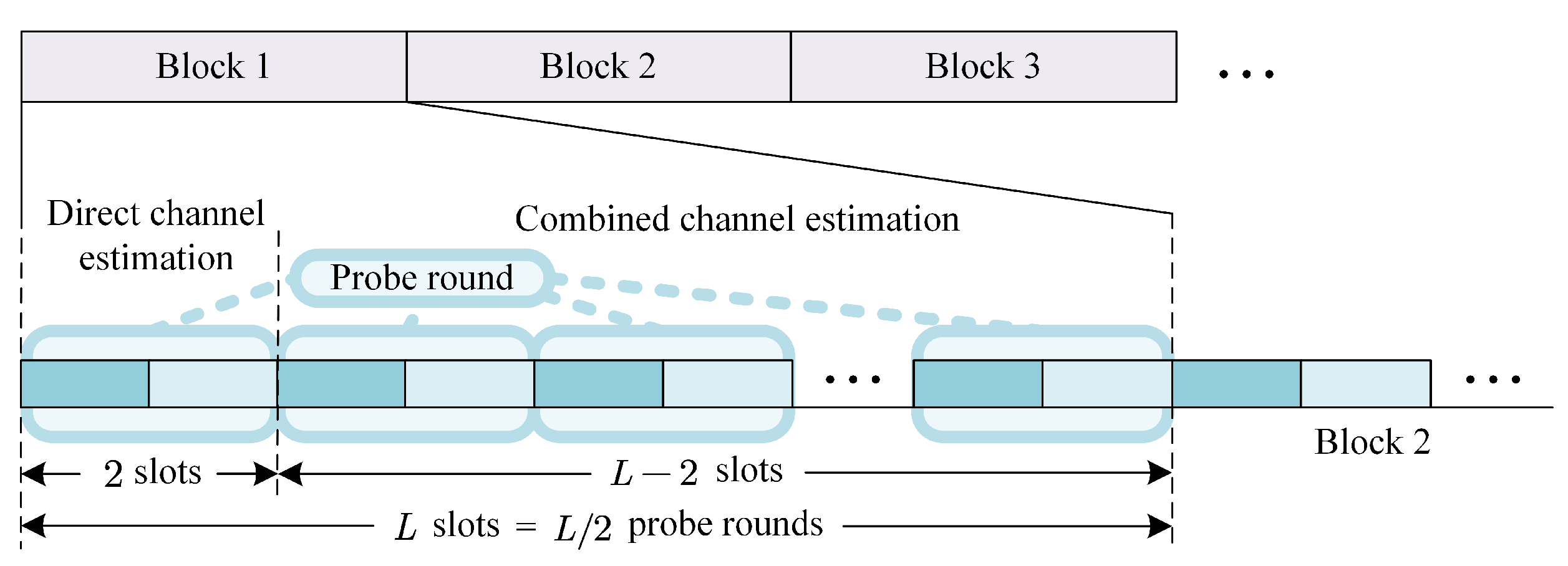
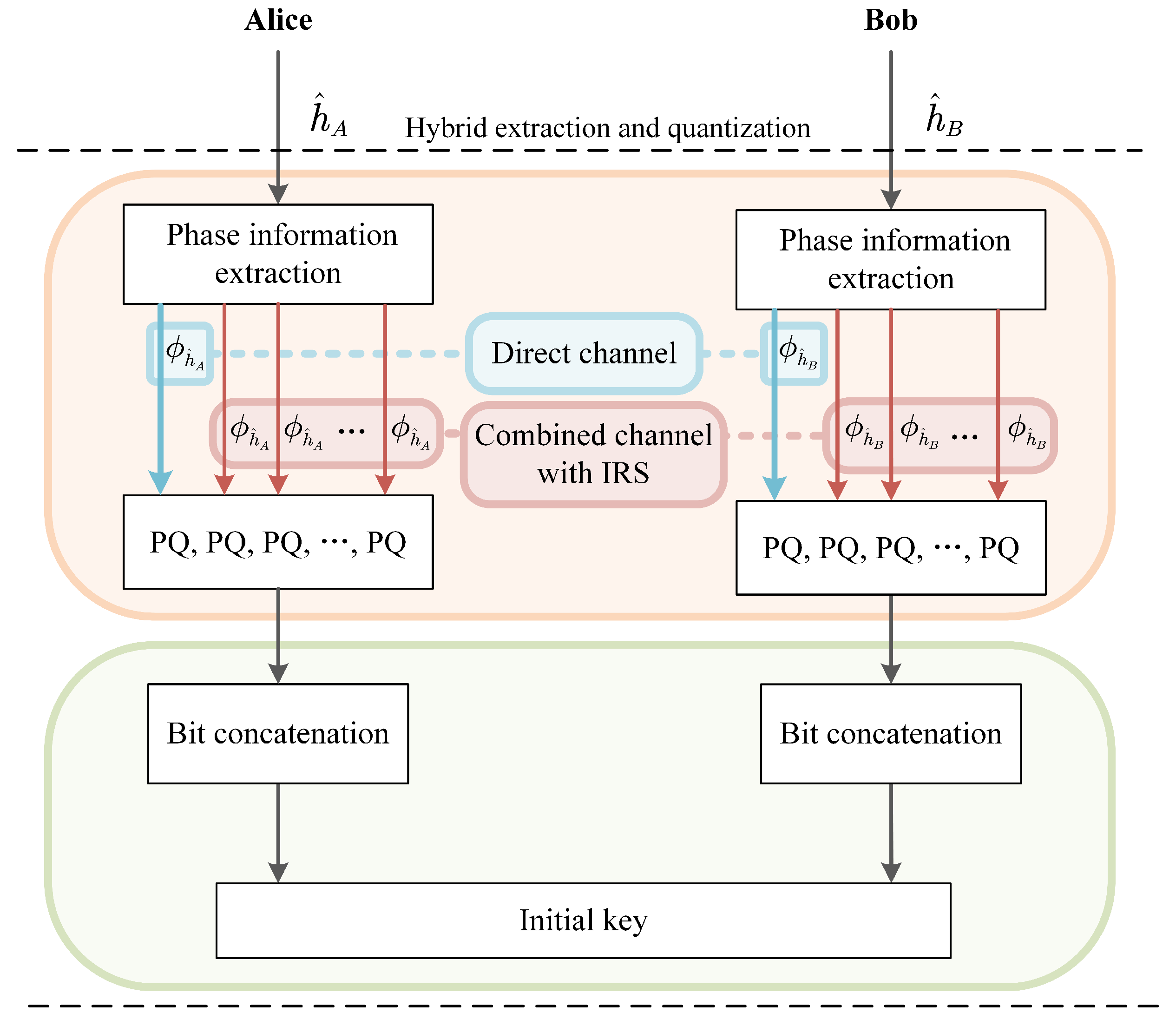
In order to fully exploit the randomness, we propose a hybrid approach to extracting CSI in order to generate the SK, as shown in Figure 3. In each block, there are total L time slots, and we assume that the channel does not change within a block, i.e., the length of each block is equivalent to the coherence time of the channel. In addition, Alice and Bob alternatively send probe signals every two time slots, and thus there are total

L / 2

probe rounds in each block. Specifically, in the first probe round, Alice and Bob alternatively send probe signals while the IRS is turned off. Then, the received signals at Alice and Bob can be expressed as follows, respectively:

\begin{matrix} \begin{matrix} y_{A} & = h_{B A} x + n_{A}, \\ y_{B} & = h_{A B} x + n_{B} . \end{matrix} \end{matrix}

(5)

Upon receiving

y_{A}

and

y_{B}

in (5) at Alice and Bob, respectively, channel estimations are conventionally performed using the least square (LS) method, and the channel estimates at Alice and Bob can be presented as follows [6]:

\begin{matrix} \begin{matrix} {\hat{h}}_{A} & = h_{B A} + {\hat{n}}_{A}, \\ {\hat{h}}_{B} & = h_{A B} + {\hat{n}}_{B} . \end{matrix} \end{matrix}

(6)

The phase information of these channel estimates will be jointly quantized to form the initial key bit sequence.

Afterwards, Alice and Bob alternatively extract the channel estimates from the combined channels which are composed of the direct and reflected channels, using (2) during the subsequent

L - 2

time slots. In this case,

Θ

is randomly switched at every 2 time slots to impose randomness. Similarly, the phase information of these channel estimates with linear normalization will be jointly quantized to generate the initial key bit sequence. The detailed process of the quantization for the proposed method is explained in the next section.

3.2. Compact Phase Quantization Method

We propose a new efficient

2^{p}

-level PQ method using the phase information of

{\hat{h}}_{A}

and

{\hat{h}}_{B}

in (2) and (6) to generate p quantized bits, respectively, as shown in Figure 4. We set quantization thresholds which equally divide the complex plane into

2^{p}

regions, and allocate p bits in each region by using the Gray coding, which allows to extract p bits from the phase information.

We note that the main purpose of the proposed hybrid CSI extraction is to compensate low SK rate during the static environment, by using an efficient quantization method. Since we assume low amplitude variation of

h_{A B}

, the IRS is activated to impose phase dynamics of the CSI. This implies that it is not necessary to allocate multiple bits to amplitude in the channel probing stage. Instead, multiple bit allocation to phase information obtained from IRS would contribute to increase the dynamics of the CSI. In addition, phase information is uniformly distributed from 0 to

2 π

, PQ would provide better randomness than AQ to secrete key information. Therefore, we extract phase information in the total time slots. It is also important to have computationally efficient quantization methods, i.e., a compact and easily extendable method. Considering the above facts, we refer to the constellation diagrams of PSK. modulation scheme with Gray coding and its soft demapping principle introduced in [16], and tailor them for our purpose.

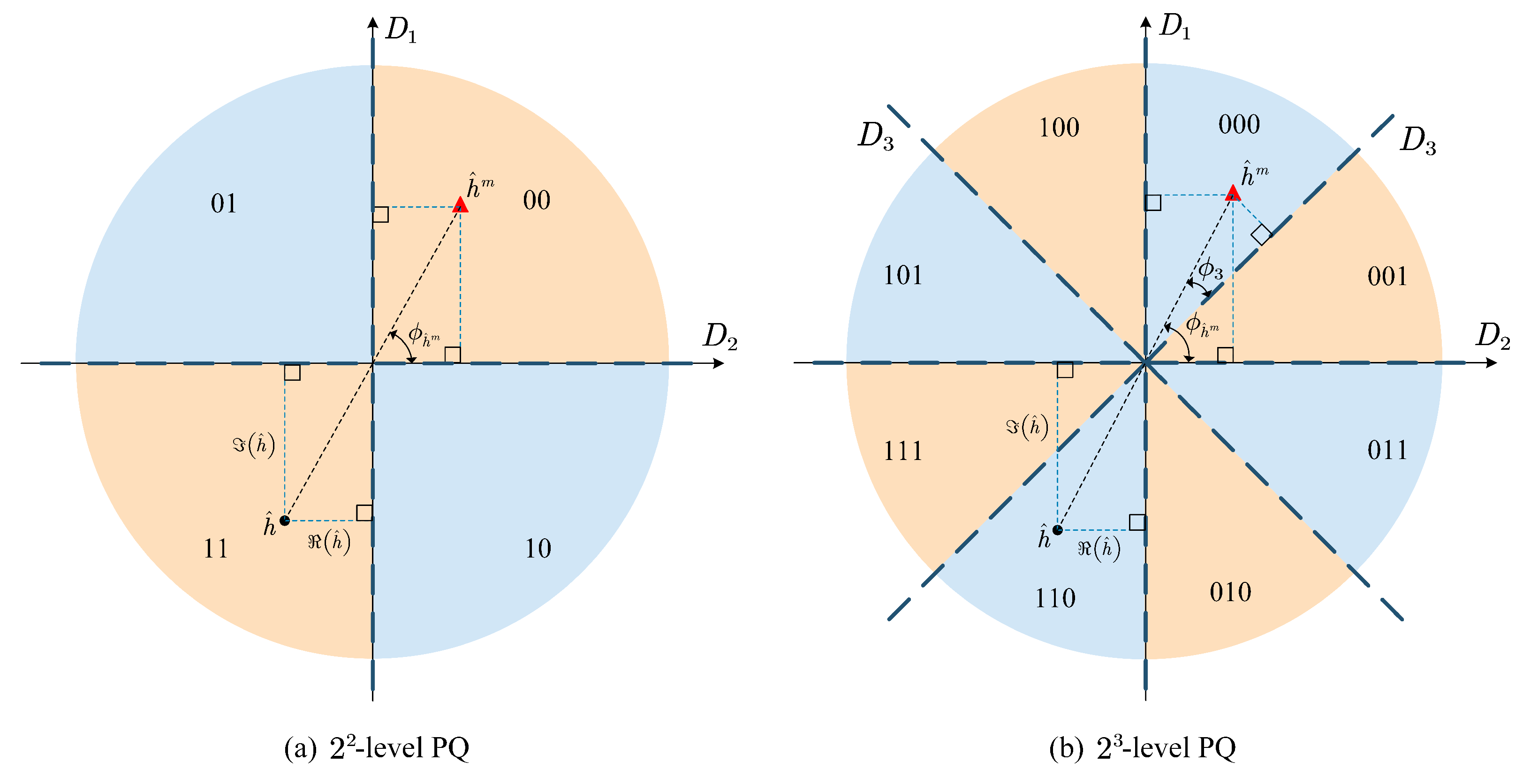
In order to visualize the PQ, we represent the extracted CSI of

{\hat{h}}_{A}

and

{\hat{h}}_{B}

{\hat{h}}_{A} = | {\hat{h}}_{A} | e^{j ϕ_{{\hat{h}}_{A}}} = ℜ ({\hat{h}}_{A}) + j ℑ ({\hat{h}}_{A})

and

{\hat{h}}_{B} = | {\hat{h}}_{B} | e^{j ϕ_{{\hat{h}}_{B}}} = ℜ ({\hat{h}}_{B}) + j ℑ ({\hat{h}}_{B})

, respectively, where

| x |

is the amplitude,

ϕ_{x}

is the phase,

ℜ (x)

is the real part, and

ℑ (x)

is the imaginary part of the complex number x, respectively. We equally divide the complex plane into

2^{p}

separated phase regions. In the following sections, we present the proposed PQ examples of 4 to 32 levels, and this can be extendable to any

2^{p}

-level schemes.

3.3. Examples of 4 to 32 Level PQ

For a

2^{p}

-level PQ, the quantization bit mapping is made by Gray coding principle. For convenience, here we denote the estimated CSI of either Alice or Bob as

\hat{h}

, because the quantization processes for

{\hat{h}}_{A}

and

{\hat{h}}_{B}

are the same. Figure 5 shows the bit mapping and decision threshold lines for

2^{2}

and

2^{3}

-level PQ methods for the estimated CSI,

\hat{h}

in the complex plane, where

D_{i}

indicates the decision threshold for the i-th quantized bit

b_{i}, i = 1, \dots, p

Referring to Figure 5, we can find that the first and second bits can be estimated by taking the signs of real and imaginary parts of

\hat{h}

, i.e.,

b_{1} = sign (ℜ (\hat{h}))

and

b_{2} = sign (ℑ (\hat{h}))

. Then, these

b_{1}

and

b_{2}

provides sufficient information on in which quadrant of the complex plain

\hat{h}

locates. By using this, we map

\hat{h}

in the first quadrant of the complex plain, that is

{\hat{h}}^{m} = | \hat{h} | e^{j ϕ_{{\hat{h}}^{m}}}

, where

ϕ_{{\hat{h}}^{m}} = {tan}^{- 1} (| ℑ (\hat{h}) / ℜ (\hat{h}) |)

, so that its phase value is in the region of 0 to

π / 2

. This makes the third bit of

2^{3}

-level PQ can be estimated by taking the sign of the distance between the threshold line

D_{3}

{\hat{h}}^{m}

located in the first quadrant, that is,

\begin{matrix} \begin{matrix} b_{3} & = sign (| {\hat{h}}^{m} | sin (- (ϕ_{{\hat{h}}^{m}} - π / 4))) \\ = sign (- (ϕ_{{\hat{h}}^{m}} - π / 4)) . \end{matrix} \end{matrix}

(7)

The above principle, then can be extended to any

2^{p}

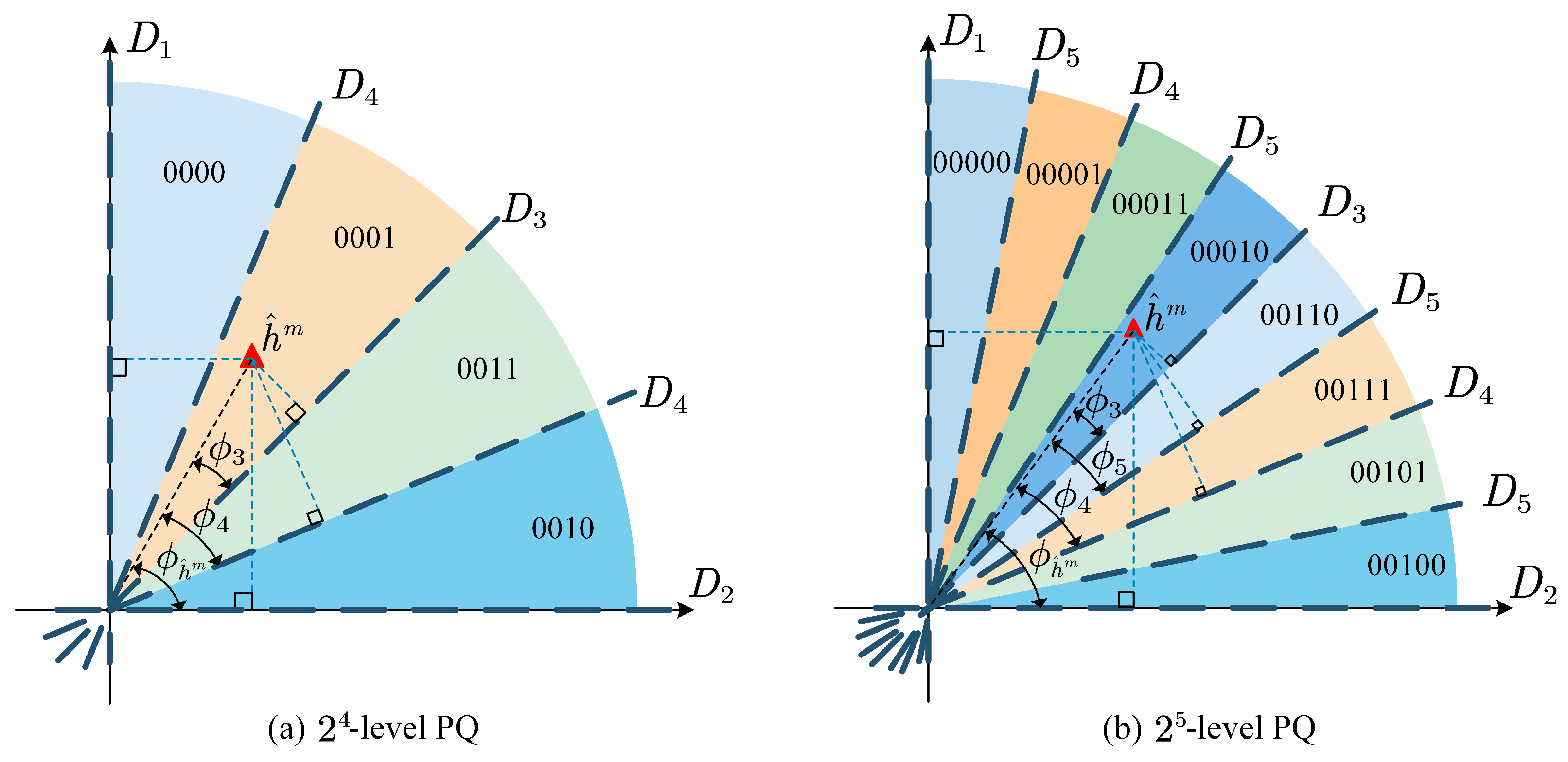
-level PQ. Figure 6 shows the bit mapping with Gary coding and decision threshold lines for

2^{4}

and

2^{5}

-level PQ methods, where

{\hat{h}}^{m}

is mapped in the first quadrant of the complex plane. It is clear that

b_{1}

b_{3}

can be estimated exactly the same way as in the above

2^{2}

and

2^{3}

-level PQ method. In addition, the remaining bits can be estimated recursively by using the previously estimated information. For example,

b_{4} = sign (| - (ϕ_{{\hat{h}}^{m}} - π / 4) | - π / 8)

By generalizing the above principle to

2^{p}

-level PQ, we can have the following recursive equation:

\begin{matrix} \begin{matrix} b_{1} & = sign (ℜ (\hat{h})), \\ b_{2} & = sign (ℑ (\hat{h})), \\ b_{i} & = sign (- ϕ_{i}), \\ ϕ_{i} & = {(- 1)}^{i} (| ϕ_{i - 1} | - π / 2^{i - 1}), 2 < i \leq p, \end{matrix} \end{matrix}

(8)

where

ϕ_{2} = ϕ_{{\hat{h}}^{m}}

. The following Algorithm 1 describes the proposed PQ method. After the quantization process, the quantized bits are concatenated together to obtain the initial key bit sequence for Alice and Bob, respectively.

Algorithm 1:Proposed PQ

Input: $\hat{h}$ % Estimated CSI
Output: $b$ % Initial key bit vector

1:: $ϕ_{{\hat{h}}^{m}} = {tan}^{- 1} (| ℑ (\hat{h}) / ℜ (\hat{h}) |)$
2:: $ϕ_{2} = ϕ_{{\hat{h}}^{m}}$
3:: $b_{1} = sign (ℜ (\hat{h}))$
4:: $b_{2} = sign (ℑ (\hat{h}))$
5:: for $i \leftarrow 3 t o p$ do
6:: $ϕ_{i} = {(- 1)}^{i} (| ϕ_{i - 1} | - π / 2^{i - 1})$
7:: $b_{i} = sign (- ϕ_{i})$
8:: end for

We note that the proposed PQ in Algorithm 1 can be applied any p bit PQ scheme, and thus a single quantizer can be universally applied to various multi-level quantization systems. In particular, when we adopt an adaptive quantization scheme to generate a time-varying p bits, the proposed scheme may have a strong advantage for its universal applicability.

4. Secrecy Performance

4.1. Performance Measures

We evaluate the proposed SK generation scheme in terms of a number of secrecy performance measures including the SK capacity, SK randomness, initial key disagreement probability, and effective key length. All of the above performance measures of the proposed schemes are compared with those of the conventional schemes.

The SK capacity, C is defined as

C = min {I ({\hat{h}}_{A}; {\hat{h}}_{B}), I ({\hat{h}}_{A}; {\hat{h}}_{B} ∣ {\hat{h}}_{E})}

, where

{\hat{h}}_{E}

denotes the estimated CSI at Eve. Since the channel estimates in different probe rounds are independent random variables [4], the SK capacity in the s-th probe round,

C_{s}

is also a random variable. Assuming the eavesdropper Eve is a wavelength or more away from either Alice or Bob, the SK capacity in the first probe round without IRS,

C_{1}

is upper bounded by the mutual information [10,17]:

\begin{matrix} \begin{matrix} C_{1} & \leq I ({\hat{h}}_{A}; {\hat{h}}_{B} ∣ {\hat{h}}_{E}) = I ({\hat{h}}_{A}; {\hat{h}}_{B}) \\ = {log}_{2} (1 + \frac{σ_{{\hat{h}}_{B A}}^{2}}{σ_{{\hat{n}}_{A}}^{2} + σ_{{\hat{n}}_{B}}^{2} + \frac{σ_{{\hat{n}}_{A}}^{2} σ_{{\hat{n}}_{B}}^{2}}{σ_{{\hat{h}}_{B A}}^{2}}}) . \end{matrix} \end{matrix}

(9)

In this case, due to the channel reciprocity within the coherent time, we have

σ_{h_{B A}}^{2} = σ_{h_{A B}}^{2}

. In addition, we can assume that

{\hat{n}}_{A}

and

{\hat{n}}_{B}

are independent and identically distributed random variables without loss of generality, and thus

σ_{{\hat{n}}_{A}}^{2} = σ_{{\hat{n}}_{B}}^{2}

. Therefore, (9) can be simplified as:

\begin{matrix} \begin{matrix} C_{1} & \leq {log}_{2} (1 + \frac{σ_{h_{B A}}^{4} / σ_{{\hat{n}}_{A}}^{4}}{1 + 2 σ_{h_{B A}}^{2} / σ_{{\hat{n}}_{A}}^{2}}) . \end{matrix} \end{matrix}

(10)

The SK capacity in the remaining probe rounds with IRS,

C_{s}, s = 2, 3, \dots, S

S = L / 2

, is upper bounded by the conditional mutual information [10,17]. In this case, we have

σ_{h_{B A}}^{2} + \sum_{n = 1}^{N} σ_{h_{B R A}^{n}}^{2}

, where

σ_{h_{B R A}^{n}}^{2}

is the variance of the n-th reflected channel. Thus,

C_{s}

can be derived as follows [8]:

\begin{matrix} \begin{matrix} C_{s} & \leq I ({\hat{h}}_{A}; {\hat{h}}_{B} ∣ {\hat{h}}_{E}) = I ({\hat{h}}_{A}; {\hat{h}}_{B}) \\ = {log}_{2} (1 + \frac{{(σ_{h_{B A}}^{2} + \sum_{n = 1}^{N} σ_{h_{B R A}^{n}}^{2})}^{2} / σ_{{\hat{n}}_{A}}^{4}}{1 + 2 (σ_{h_{B A}}^{2} + \sum_{n = 1}^{N} σ_{h_{B R A}^{n}}^{2}) / σ_{{\hat{n}}_{A}}^{2}}), \\ 2 \leq s \leq S . \end{matrix} \end{matrix}

(11)

The above derivation result shows that the SK capacity of the proposed system is certainly dependent on

σ_{h_{B R A}^{n}}^{2}

, and it is proportional to N. Therefore, we can expect the enhanced SK capacity in the proposed system due to the increased randomness introduced by the IRS.

Finally, the SK capacity of the proposed scheme,

C_{p}

across all L slots is upper bounded as follows [15]:

\begin{matrix} \begin{matrix} C_{p} & \leq \frac{1}{S} \sum_{s = 1}^{S} C_{s} \\ = \frac{1}{S} [C_{1} + \sum_{s = 2}^{S} C_{s}] \\ = \frac{1}{S} [C_{1} + (S - 1) C_{s}] . \end{matrix} \end{matrix}

(12)

On the other hand, the SK capacity of the conventional scheme without IRS, is upper bounded by

C_{c} = C_{1}

The second performance measure to be investigated is the SK randomness which is defined as the proportion of ’1’ in the generated binary initial key bit sequence, thus we have:

r = \frac{\sum^{n_{q}} \sum_{i = 1}^{p} [b_{i} = 1]}{n_{q} p},

(13)

where

n_{q}

is the total number of investigated probe rounds for the estimation. The closer to 0.5 the r, the better the randomness of the key. In other word, when the proportion of ’1’ and ’0’ in the key sequence is uniform, the randomness of the key is better.

The third performance measure is the initial key disagreement probability. Suppose that Alice and Bob convert each of their estimations

{\hat{h}}_{A}

and

{\hat{h}}_{B}

(b_{A, 1}, b_{A, 2}, \dots, b_{A, p})

and

(b_{B, 1}, b_{B, 2}, \dots, b_{B, p})

, respectively, then the initial key disagreement probability,

p_{d}

is the probability of inconsistent bits between Alice and Bob. Therefore, it is defined as the ratio of the number of inconsistent bits to the key sequence length as follows:

p_{d} = \frac{\sum^{n_{q}} \sum_{i = 1}^{p} b_{A, i} \oplus b_{B, i}}{n_{q} p} .

(14)

The last performance measure is effective key length

K_{l}

(bits/block). It describes the length of error-free SK that can be generated per block, and it can be represented as follows:

K_{l} = p (1 - p_{d}) \frac{L}{2} .

(15)

4.2. Simulation Results and Discussions

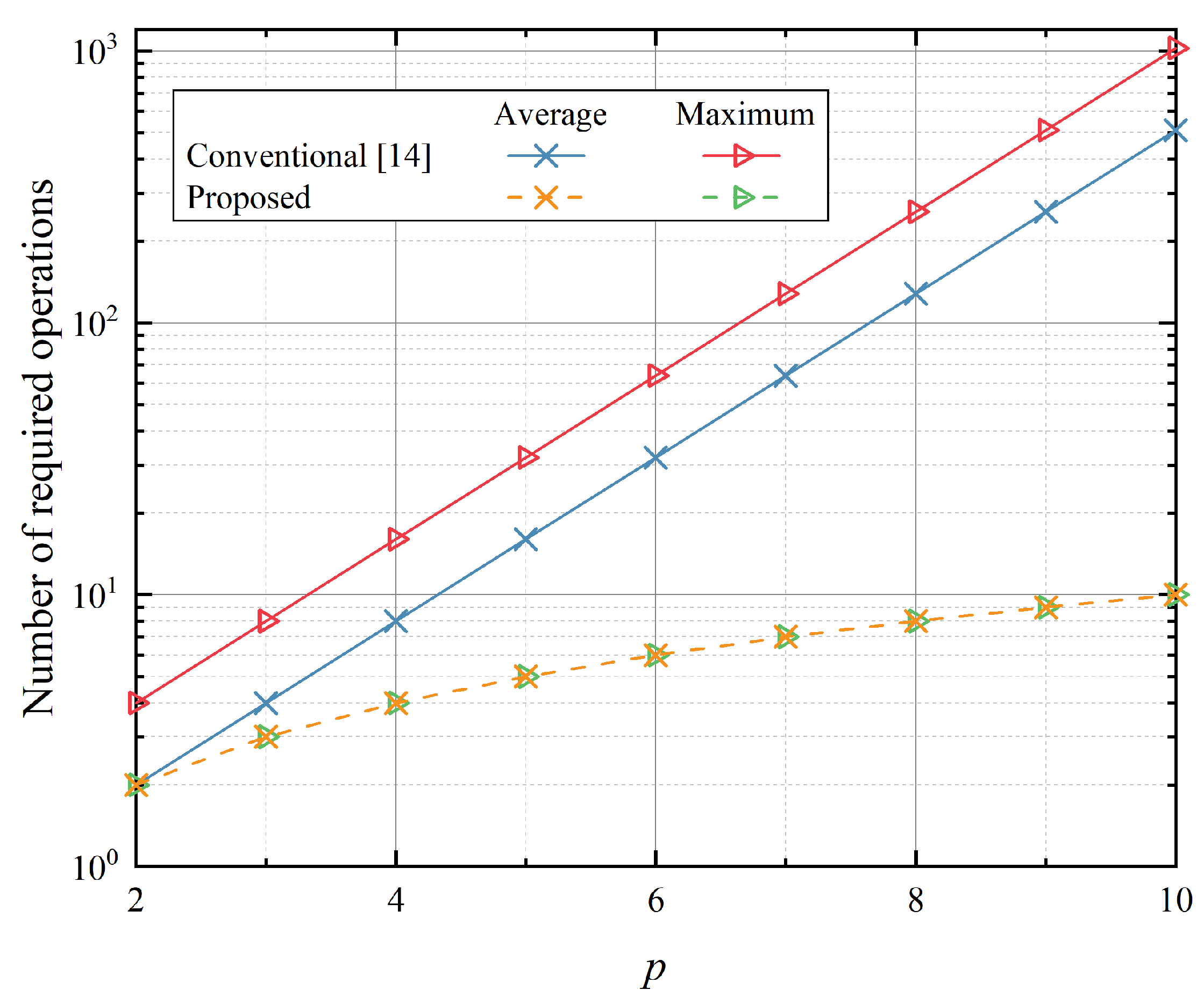
Before we compare the secrecy performance measures presented in the previous section, the computational complexities of the proposed and conventional PQ methods are compared in terms of the number of the required operations for PQ. As shown in Table 1 the proposed method requires linearly increasing complexity by p, and it requires a constant number of operations regardless of the estimated CSI value. On the other hand, the conventional PQ method requires exponentially increasing complexity by p, and it requires one to maximum of

2^{p}

comparisons, resulting in

(2^{p} / 2)

comparisons on average. Figure 7 illustrates this.

We simulate the secrecy rate of various quantization method, as shown in Fig. **/Table **.

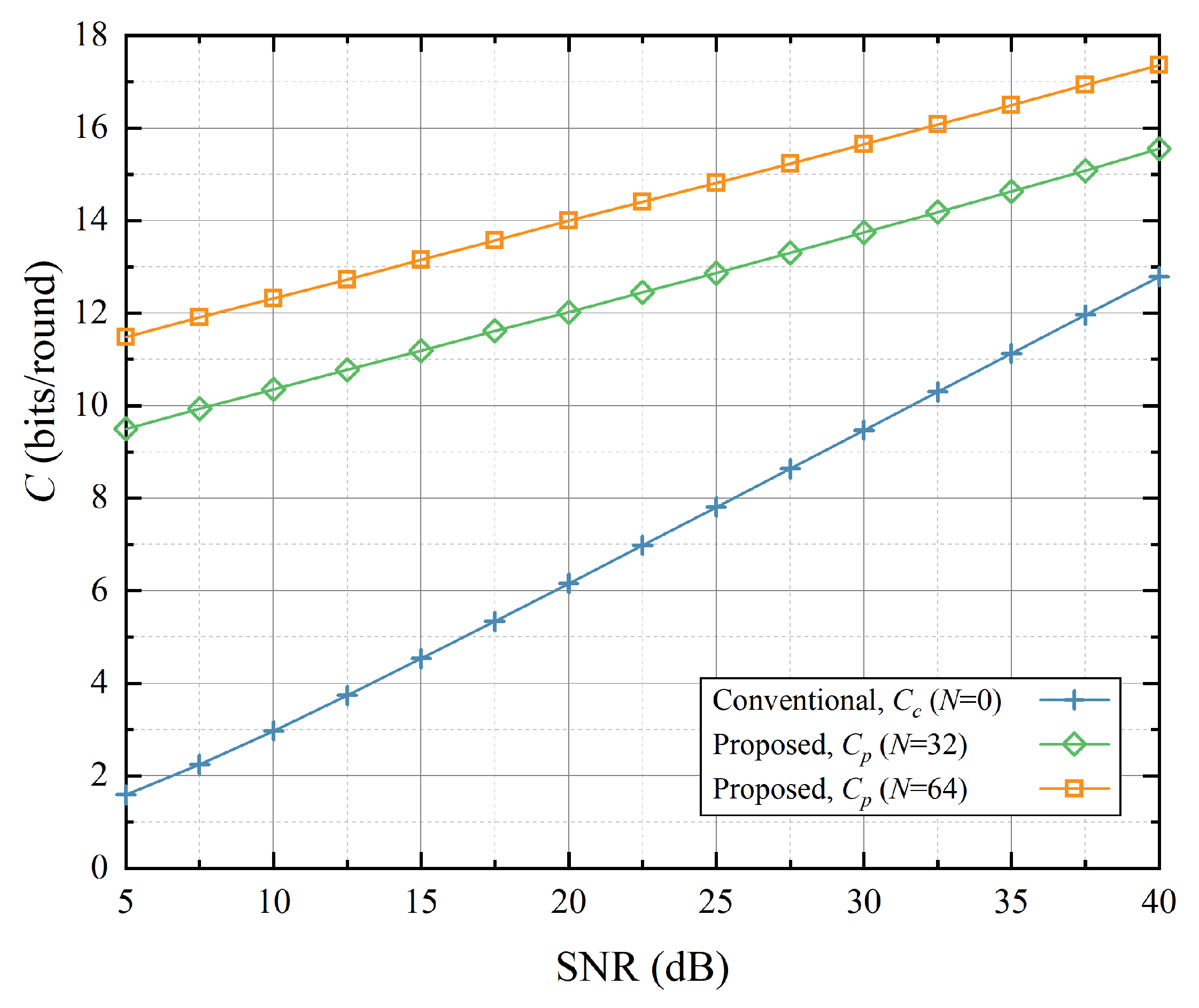
Next, we compare performance simulation results of the proposed scheme to that of the conventional schemes. First, Figure 8 shows the SK capacity variation by signal-to-noise ratio (SNR). It is evident that the SK capacity of the proposed scheme with IRS assistance is higher than the conventional one, and the SK capacity increases with an increase in the number of IRS elements N.

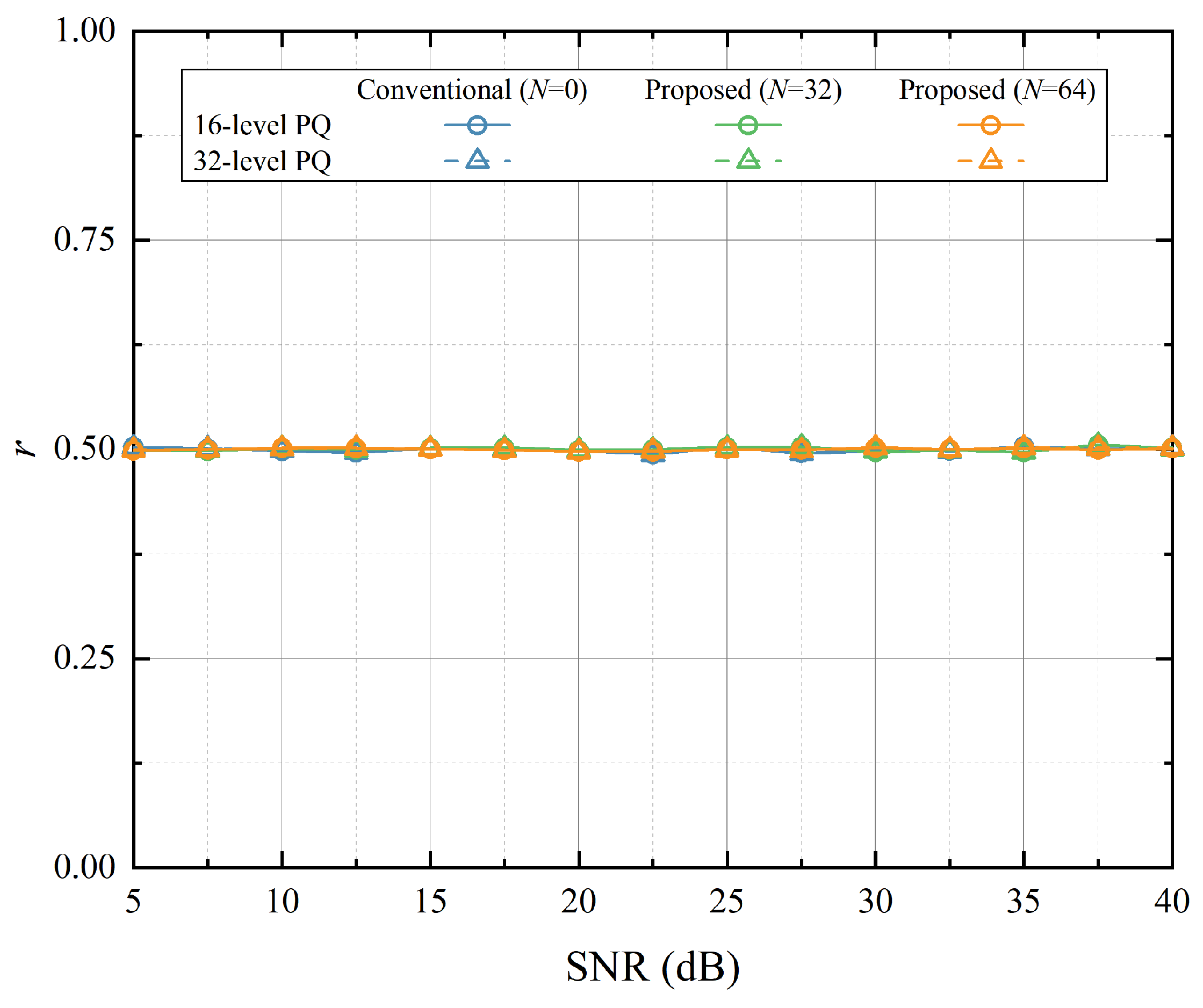
Second, Figure 9 compares the SK randomness, r. We can see that the SK randomness of the all PQ methods remains stable, showing almost a constant value of about 0.5 across all the investigated SNR ranges. In other words, the assistance of IRS in the proposed mehtod does not alter randomness performance. This is primarily due to the property of PQ having a uniform PDF and its quantization regions being equally probable and uniformly distributed. Consequently, both ’1’ and ’0’ are uniformly quantized, leading to the preservation of SK randomness.

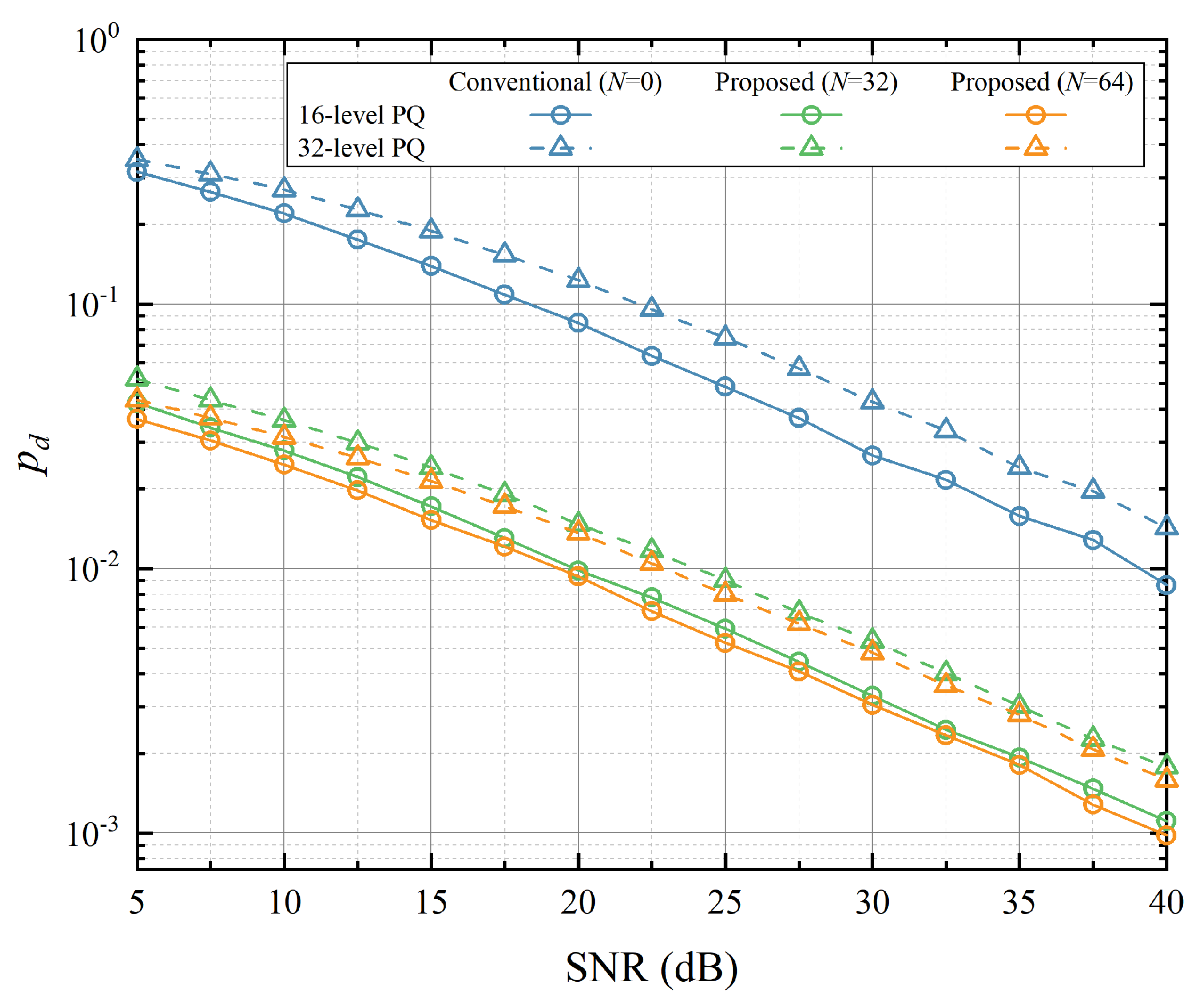
Figure 10 compares the initial key disagreement probabilities. As shown in the figure, the lower the quantization level, the smaller the initial disagreement probability. Giving the quantization level, the proposed PQ outperforms the conventional PQ method without IRS. It can also be seen that as the number of IRS elements N increases, the disagreement probability decreases.

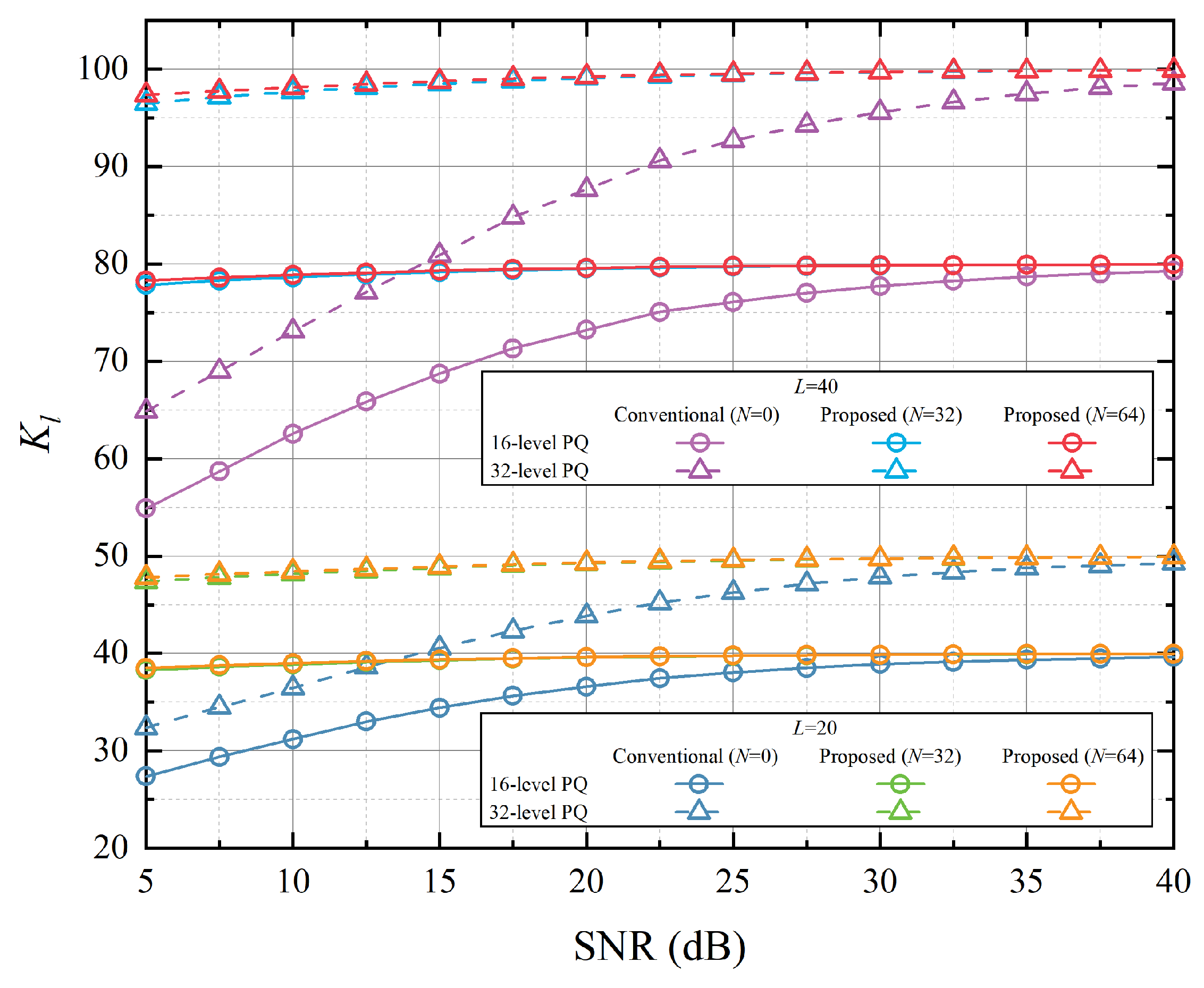
Figure 11 compares the effective key length,

K_{l}

of the proposed method with that of the conventional method, when the number of probe rounds is set to 10 and 20, i.e.,

L = 20

and

L = 40

. It is evident that higher quantization levels result in longer effective key length. Furthermore, when compared to the conventional PQ without IRS, as L increases, our proposed scheme with IRS demonstrates superior performance, with its effective key length increasing with the rise of N. In the static environment, the channel features extracted by Alice and Bob have low correlation and high initial key disagreement rate, thus affecting the effectiveness of the subsequent information reconciliation stage. Configuring the IRS as a new random source and extracting phase information means that our proposed scheme can obtain initial keys with a lower key disagreement probability, making information reconciliation easier to achieve during SK generation.

5. Conclusions

In this paper, we proposed an efficient IRS-assisted physical layer SK generation scheme with random phase shifts in static environment. By extracting the phase information from the combined channel estimation from both sides of the legitimate communication parties, a better random key sequence can be generated. Specifically, this paper proposed a simple and computationally efficient PQ method by using a symmetric bit allocation, which can be easily extended to any

2^{p}

-level quantization scheme and can be universally applied. Simulation results demonstrated that the proposed scheme can improve various performance measures including the SK capacity, effective key length, and the SK disagreement probability, without sacrificing the randomness.

Funding

This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2021R1A2C1003121).

Data Availability Statement

Not applicable.

Acknowledgments

The authors extend their appreciation to the Yangzhou University Graduate International Academic Exchange Fund Project (YZUF2022204) and the Young Backbone Teachers Project of Yangzhou University.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

SK	Secret key
CSI	Channel state information
IRS	Intelligent reflecting surface
PQ	Phase quantization
TDD	Time-division duplex
AWGN	Additive white Gaussian noise
AVQ	Absolute value-based quantization
DVQ	Difference value-based quantization
PDF	Probability density function
PSK	Phase shift keying
LS	Least square
SNR	Signal-to-noise ratio

References

Maurer, U.M. Secret key agreement by public discussion from common information. IEEE Trans. Inf. Theory. May. 1993, 39, 733–742. [Google Scholar] [CrossRef]
Wu, Q.; Zhang, R. Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Commun. Mag. Jan. 2019, 58, 106–112. [Google Scholar] [CrossRef]
Wu, Q.; Zhang, R. Beamforming optimization for wireless network aided by intelligent reflecting surface with discrete phase shifts. IEEE Trans. Commun. Mar. 2019, 68, 1838–1851. [Google Scholar] [CrossRef]
Ji, Z.; Yeoh, P.L.; Chen, G.; Pan, C.; Zhang, Y.; He, Z.; Yin, H.; Li, Y. Random shifting intelligent reflecting surface for OTP encrypted data transmission. IEEE Wireless Commun. Lett. Jun. 2021, 10, 1192–1196. [Google Scholar] [CrossRef]
Hu, X.; Jin, L.; Huang, K.; Sun, X.; Zhou, Y.; Qu, J. Intelligent reflecting surface-assisted secret key generation with discrete phase shifts in static environment. IEEE Wireless Commun. Lett. Sep. 2021, 10, 1867–1870. [Google Scholar] [CrossRef]
Ji, Z.; Yeoh, P.L.; Zhang, D.; Chen, G.; Zhang, Y.; He, Z.; Yin, H.; et al. Secret key generation for intelligent reflecting surface assisted wireless communication networks. IEEE Trans. Veh. Technol. Jan. 2021, 70, 1030–1034. [Google Scholar] [CrossRef]
Liu, Y.; Wang, M.; Xu, J.; Gong, S.; Hoang, D.T.; Niyato, D. Boosting secret key generation for IRS-assisted symbiotic radio communications. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring). IEEE; 2021; pp. 1–6. [Google Scholar]
Lu, X.; Lei, J.; Shi, Y.; Li, W. Intelligent reflecting surface assisted secret key generation. IEEE Signal Process. Lett. 2021, 28, 1036–1040. [Google Scholar] [CrossRef]
Zhang, J.; Rajendran, S.; Sun, Z.; Woods, R.; Hanzo, L. Physical layer security for the Internet of Things: Authentication and key generation. IEEE Wireless Commun. 2019, 26, 92–98. [Google Scholar] [CrossRef]
Ye, C.; Reznik, A.; Shah, Y. Extracting secrecy from jointly Gaussian random variables. In Proceedings of the 2006 IEEE International Symposium on Information Theory. IEEE; 2006; pp. 2593–2597. [Google Scholar]
Zeng, K.; Wu, D.; Chan, A.; Mohapatra, P. Exploiting multiple-antenna diversity for shared secret key generation in wireless networks. In Proceedings of the 2010 Proceedings IEEE INFOCOM. IEEE; 2010; pp. 1–9. [Google Scholar]
Sayeed, A.; Perrig, A. Secure wireless communications: Secret keys through multipath. In Proceedings of the 2008 IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE; 2008; pp. 3013–3016. [Google Scholar]
Shehadeh, Y.E.H.; Alfandi, O.; Tout, K.; Hogrefe, D. Intelligent mechanisms for key generation from multipath wireless channels. In Proceedings of the 2011 Wireless Telecommunications Symposium (WTS). IEEE; 2011; pp. 1–6. [Google Scholar]
Wang, Q.; Su, H.; Ren, K.; Kim, K. Fast and scalable secret key generation exploiting channel phase randomness in wireless networks. In Proceedings of the 2011 Proceedings IEEE INFOCOM. IEEE; 2011; pp. 1422–1430. [Google Scholar]
Lu, T.; Chen, L.; Zhang, J.; Cao, K.; Hu, A. Reconfigurable Intelligent Surface Assisted Secret Key Generation in Quasi-Static Environments. IEEE Commun. Lett. 2021, 26, 244–248. [Google Scholar] [CrossRef]
Zhang, M.; Kim, S. Universal soft demodulation schemes for M-ary phase shift keying and quadrature amplitude modulation. IET Communications 2016, 10, 316–326. [Google Scholar] [CrossRef]
F. Rottenberg, T. Nguyen, J.D.F.H.; Louveaux, J. CSI-Based Versus RSS-Based Secret-Key Generation Under Correlated Eavesdropping. IEEE Trans. Commun. 2021, 69, 1868–1881. [CrossRef]

Figure 1. System model for an IRS-assisted wireless communication system.

Figure 2. Conventional SK generation protocol with IRS.

Figure 3. Channel probing stage of IRS-assisted SK generation.

Figure 4. Proposed hybrid quantization with IRS.

Figure 5. Bit mapping and decision thresholds for

2^{2}

-level PQ and

2^{3}

-level PQ.

Figure 5. Bit mapping and decision thresholds for

2^{2}

-level PQ and

2^{3}

-level PQ.

Figure 6. Bit mapping and decision thresholds for

2^{4}

-level PQ and

2^{5}

-level PQ.

Figure 6. Bit mapping and decision thresholds for

2^{4}

-level PQ and

2^{5}

-level PQ.

Figure 7. Comparison of computations for quantization in terms of the number of required operations.

Figure 8. Comparison of SK capacity, C.

Figure 9. Comparison of SK randomness, r.

Figure 10. Comparison of initial key disagreement probability,

p_{d}

Figure 10. Comparison of initial key disagreement probability,

p_{d}

Figure 11. Comparison of effective key length,

K_{l}

Figure 11. Comparison of effective key length,

K_{l}

Table 1. Comparisons of computations required for quantization.

$2^{p}$ -level PQ methods	Required operations (average, maximum)
Conventional PQ [14]	comparisons (( $2^{p} / 2$ ), $2^{p}$ )
Proposed PQ	p linear operations in (8) (p,p)

Table 2. Comparisons of minimum SNR for

P_{d} = 10^{- 2}

required by various quantization methods

Table 2. Comparisons of minimum SNR for

P_{d} = 10^{- 2}

required by various quantization methods

Quantization scheme	$a + p = 4$	$a + p = 5$
Conv. [10]
4+12-APQ
4+12+16-APQ

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

IRS Assisted Hybrid Secret Key Generation

Abstract

1. Introduction

2. Related Works

2.1. System Model

2.2. Quantization of CSI

3. Proposed Methods

3.1. SK Generation Protocol

3.2. Compact Phase Quantization Method

3.3. Examples of 4 to 32 Level PQ

4. Secrecy Performance

4.1. Performance Measures

4.2. Simulation Results and Discussions

5. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe