Predicting Multiple Numerical Solutions to the Duffing Equation Using Machine Learning

1. Introduction

The Duffing equation is a significant nonlinear second-order differential equation commonly employed to model general oscillations in nonlinear systems. This equation captures various nonlinear vibration phenomena, including those that arise in circuits with specific inductance and capacitance configurations when subjected to electric current. It also describes dynamic friction effects, such as in oscillator systems, where nonlinearity leads to divergent behavior from linear systems at large vibration amplitudes. Furthermore, the Duffing equation finds application in analyzing vibrations in aircraft wings and automobiles, which, if severe, may cause damage to machine components. Therefore, estimating and understanding the vibration conditions is crucial for preventing potential harm. Among the studies related to the Duffing equation, Feng [1] employed the variational method and the theoretical approach of Dimensional Analysis to derive a novel analytical frequency function. This analytical function accurately describes the vibration frequency of the undamped Duffing equation. The validity and effectiveness of this frequency solution were confirmed through numerical simulations and experiments, providing a deeper understanding of the oscillation characteristics of the Duffing equation without damping. In another study, Rao [2] investigated the behavior of the Duffing equation in undamped free vibration and damped forced vibration scenarios. For undamped free vibration, Rao explained that varying initial conditions lead to convergence results switching between 1 and -1 within a specific interval, exhibiting irregular changes. In the case of damped forced vibration, when specific initial conditions are fixed, the solution of the Duffing equation demonstrates various convergence patterns, such as single-cycle, double-cycle, and four-cycle, among others. Akhmet et al. [3] studied the Bifurcation behavior of Duffing Oscillator in damped forced vibration, and used Bifurcation diagram and Lyapunov exponent to analyze the chaotic phenomenon of the system when the external force amplitude increased. Then the Ott-Grebogi-Yorke (OGY) control method was used to stabilize the chaotic behavior and reduce its amplitude. They demonstrated the effectiveness of the OGY control method with numerical simulations, and confirmed that the types of multiple solutions in nonlinear equations have the potential to be studied. Therefore, this research is inspired to explore the types of various solutions of the Duffing equation. Compared with general analytical or numerical analysis, since the nonlinear solution takes a lot of computing time, this research will try to use machine learning to judge the value of multiple solutions of the Duffing equation.

Machine learning has experienced significant growth and has become widely utilized in various domains, leading to its rapid development in modern times. This powerful technology finds applications in diverse fields such as image recognition, search engines, industrial analysis, and artificial intelligence itself. The utilization of machine learning, along with the advancements in artificial intelligence, has shown substantial improvement in recent years, as indicated by statistics from Hao [4]. The trend of artificial intelligence application has evolved over time, progressing from the use of code command systems to the impact of machine learning and the widespread adoption of neural networks in the late 1990s and early 2000s. The continuous development of sophisticated algorithms and architectures, such as the three-layered model proposed by Hinton et al. [5], has paved the way for the progress of machine learning and artificial intelligence as a whole. In 2007, Hinton [6] introduced deep learning as an addition to the backpropagation method, enabling the adjustment of weights for improved training effectiveness. While this development brought significant advancements in weight updates and training, it did not fully address the issue of overfitting. To tackle this problem, Hinton et al. [7,8] proposed Dropout in 2012. This technique involves randomly dropping out neurons during the learning process, preventing excessive reliance on specific neurons and effectively mitigating overfitting. In 2015, Kingma et al. [9] presented the Adam optimizer, which combines the strengths of various previous optimizers. This method guides the training of each parameter in the loss function towards the most favorable direction, thus avoiding obstacles like saddle points and enhancing training speed and accuracy significantly. Furthermore, in 2018, Potdar et al. [10] conducted a study evaluating six different encoding techniques across six diverse datasets. These techniques included binary encoding, label encoding, and One-hot encoding, among others. The performance of each technique was assessed based on classification accuracy, and the impact of dataset size and the number of categories on each technique's performance was analyzed.

In 1995, Mathia et al. [11] used Multilayer perceptron (MLP) and Hopfield Neural Network (HNN) to find approximate solutions to approximate nonlinear equations by means of forward propagation. Predictions are made by a Recurrent Neural Networks (RNN) model. Not only has there been a great breakthrough in finding approximate solutions to nonlinear equations, but also the method of supervised learning has made great contributions to the prediction of nonlinear solutions. This also strengthens the confidence of using machine learning to analyze the solution of the Duffing equation in this study. Hochreiter and Schmidhuber [12] proposed the Long short term memory (LSTM) method. They improved RNN and improved the short-term memory ability of the original RNN to be able to deal with long-term and short-term memory problems. It not only improves the training speed, but also solves more complex and long-term dependent problems. In the area of high-dimensional partial differential equations, Han et al. [13] proposed a new method for solving high-dimensional partial differential equations (PDEs) using deep neural networks. In the study of Wang et al. [14], the flutter speed was analyzed by the K-method, and the deep learning method of machine learning was used to predict the occurrence of flutter. They compared the performance of DNN and LSTM methods for flutter speed prediction, and attempted to predict aeroelastic phenomena in various flight conditions. Gawlikowski et al. [15] first gave an overview of various sources of uncertainty in deep learning, including data noise, model error, and model structure uncertainty. Applications of uncertainty estimation to deep learning were also discussed, including applications to active learning, decision making, etc... Hua et al. [16] used time series forecasting in fields such as finance, weather forecasting and traffic forecasting. They highlighted the potential of LSTM networks for time series forecasting and provided insights into the design and optimization of LSTM networks for their task. Hwang et al. [17] proposed a method called Single Stream RNN (SS-RNN). SS-RNN achieves single-stream parallelization by using a single GPU stream at each time step to process multiple sequences. They also proposed a method called Blockwise Inference for efficiently performing inference of RNNs on GPUs. In addition, Zheng et al. [18] proposed a compiler called Echo, which aims to reduce GPU memory usage during LSTM RNN training. Echo also provides an optimization method based on calculation graphs to reduce the number of data transmissions.Tariq et al. [19] proposed a method using multivariate convolutional LSTM (MC-LSTM) and mixed probabilistic principal component analysis (MPPCA) to detect anomalies in spatiotemporal data collected from space. This method was based on the LSTM model, and by adding convolutional layers, spatial and temporal features can be extracted from spatiotemporal data. Memarzadeh and Keynia [20] proposed a short-term electricity load and price forecasting algorithm based on LSTM-Neural Network (LSTM-NN). That algorithm was based on the combination of LSTM and Neural Network, and improved the prediction performance by optimizing the parameters of LSTM and Neural Network.

The present work used Duffing equation to simulate the general nonlinear vibration situation and divided it into the special case of undamped free vibration and the condition of damped forced vibration. When the Duffing equation is in undamped free vibration, with the different initial conditions, the convergence result changes between 1 or -1 within a certain interval, and such changes are irregular. In addition, when the Duffing equation is in damped forced vibration, its solution will vary depending on the initial conditions, external forces, etc., and the final vibration condition will be different, and there may be multiple solutions. This study will observe the single-cycle convergent solution of the Duffing equation, especially the periodic solution of this system when the convergent trajectory is a single closed curve.

In order to collect the convergence results of the Duffing equation with two different types, this study uses the fourth-order Runge-Kutta method to collect the results of two different types, and changes the initial conditions and other parameters for analysis. Then, using the supervised learning method in machine learning, the undamped free vibration type is guided by the Labeled method to guide the machine to analyze the target object cognitively. This study uses data preprocessing, training and validation to analyze the problem, and selects two algorithms to predict this nonlinear vibration phenomenon to analyze its accuracy. The two algorithms are: Deep Neural Networks (DNN) and Long short term memory model (LSTM). Among them, DNN is a supervised learning method, which is suitable for processing Labeled data. LSTM is a branch of Recurrent Neural Networks (RNN), which solves the performance of time recurrent neural networks in long sequences, and also solves the problems of gradient disappearance and gradient explosion, and is suitable for dealing with problems highly related to time series. Finally, use the Long short term memory model to add a small number of neuron hidden layers (LSTM-NN) to find the best learning model. This study aims to explore suitable learning models for predicting convergence results of nonlinear vibration equations in specific cases. To accomplish this, two different types of the Duffing equation will be examined as examples. The goal is to identify a learning model that can effectively predict the convergence outcomes of these nonlinear vibration equations.

2. Theoretical Analysis

This study focuses on the Duffing equation, a representative nonlinear second-order differential equation commonly employed to simulate general nonlinear excited vibration systems. The equation describes various nonlinear vibration phenomena applicable to aircraft wing and automobile vibrations. Specifically, this research delves into the undamped free vibration type of the Duffing equation. When the linear and nonlinear elastic coefficients are identical, the solution converges to either +1 or -1. On the other hand, for the damped forced vibration type, the solution exhibits chaotic behavior in certain cases, while others converge to a limit cycle oscillation (LCO) result. For this situation, there is no analytical solution available so far. To address these phenomena, we numerically collect results for the +1 or -1 solutions in the undamped free vibration of the Duffing equation, along with the maximum and minimum displacements and velocities in the limit cycle oscillation of the damped forced vibration. Subsequently, we utilize deep learning methods to predict multiple solutions.

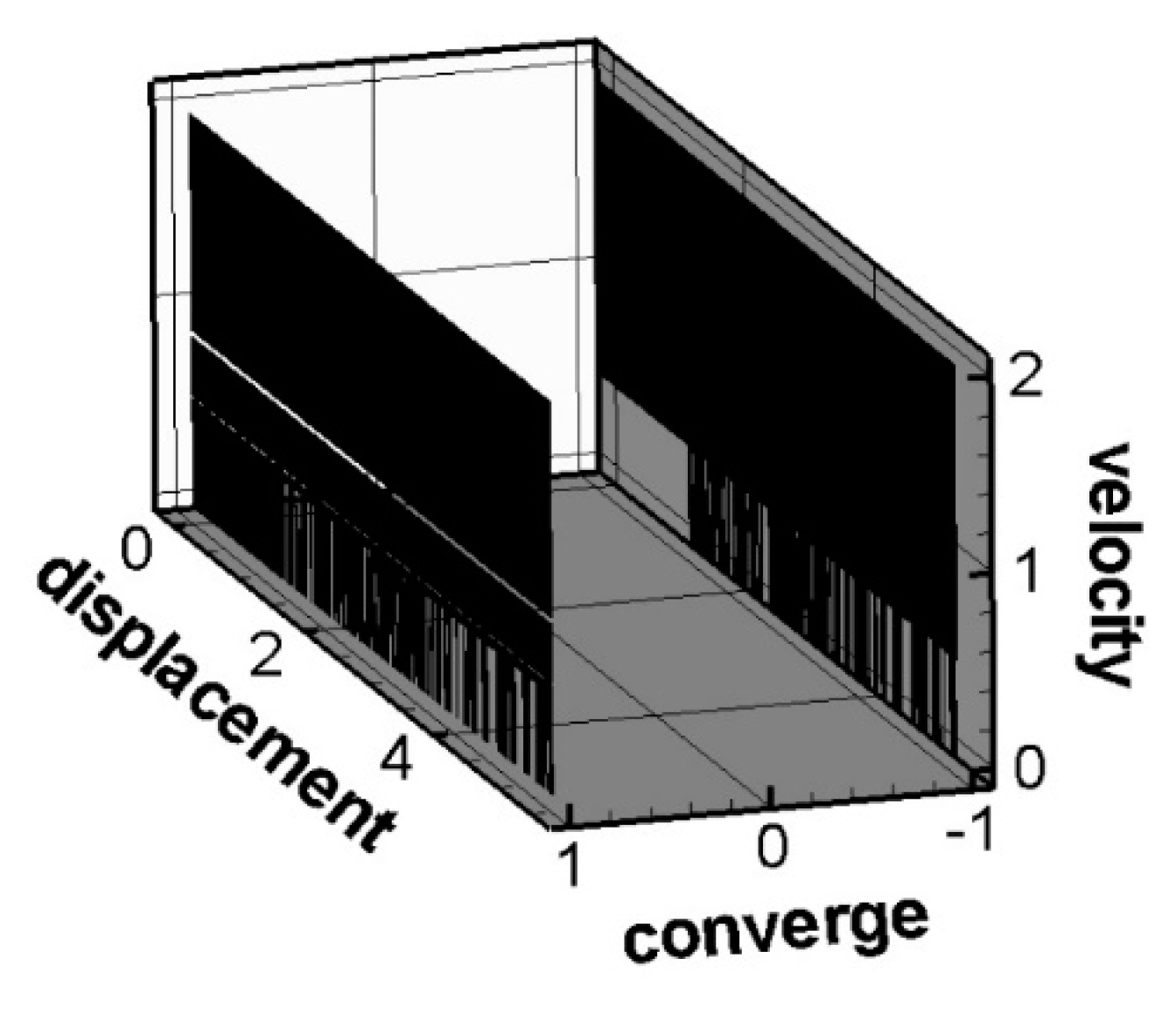
2.1. Duffing equation

Duffing equation can be written as follows:

$$m\ddot{x}+\mu \dot{x}\pm kx\pm \beta x^3=F\cos (\omega t)$$

(1)

where m is the mass, $\mu$ is the damping coefficient, k and $\beta$ are the linear and nonlinear spring constant, respectively. $F\cos (\omega t)$ is the external force, $(\stackrel{•}{})$ represents differentiate with respect to time, and $\omega$ is the vibration frequency. The undamped free vibration form of the Duffing equation is:

$$m\ddot{x}+kx+\beta x^3=0$$

(2)

Equation (2) can be divided into two forms k>0 and k<0, when k<0, the solution of Eq. (2) contains two forms $\pm 1$. However, when k>0, Eq. (2) can be obtained by “Dimensional Analysis method” to obtain a high-order approximate solution [1]. Once the analytical solution is obtained, it does not need to be estimated by machine learning methods for this case.

2.2. Numerical solution of fourth-order Runge-Kutta method

We use the fourth-order Runge-Kutta (RK-4) numerical method to solve the Duffing equation, and choose the coefficient of Eq. (2) as k/m =$\beta$/m = n:

$$\ddot{x}-nx+n{x}^3=0$$

(3)

In the case of changing different n, when the spring constants are equal, the displacement will happen to converge at two points +1 or -1, and when n is different, the displacement convergence results are not the same, and there is no analytical solution, so it is worthy of further study. Figure 1 shows different initial displacements, initial velocities, and their convergence results for k/m=$\beta$/m = 0.5. These results will be collected for subsequent analysis.

Then we collect the data of the numerical solutions of the damped forced vibration type of the Duffing equation. This type will cause chaos under certain conditions. For example: m=1, $\mu =0.2,$k= -1, $\beta =1.0,F_0=0.3,\omega =1.29$, $x_0=0.15,\dot{x}=1.2$. The result is shown in Figure 2. In some cases, Limit Cycle Oscillation will appear, and its convergent trajectory is a single closed curve, for example: m=1, $\mu =0.2,$k=1, $\beta =1.0,F_0=0.3,\omega =0.8$, $x_0=0.1,\dot{x}=0.5$. This solution corresponds to the periodic solution of the system, and forms a closed curve as shown in Figure 3. In addition, there are double loops or quadruple loops, etc. The trajectory of convergence is a closed curve composed of two cycles or four cycles. In this study, the fourth-order Runge-Kutta numerical method is used to collect data of different initial conditions, and only a single cycle solution is considered, and the maximum and minimum values of displacement and velocity of this closed curve will be recorded.

3. Deep Learning

3.1. Database establishment

The chosen machine learning method for our study is supervised learning, which involves performing feature labeling actions on the data and input labels. Initially, we focus on the Duffing equation without damping and external force, as described in Eq. (2). The initial conditions of this equation serve as data features, and we utilize the RK-4 method to calculate the convergence results of the equation. These results are then transformed into data labels using the One-Hot Encoding method, a widely-used tagging technique. Although the One-Hot Encoding method demands significant memory space and computation time, it provides substantial improvements in accuracy and an excellent training rate, particularly at lower values. The parameters utilized in our study include initial displacements and initial velocities. Table 1 presents the parameters and label data utilized in our database, which consists of a collection of 117,432 data sets.

The next step is to collect data on the single-cycle convergence results when the Duffing equation contains damping and external force terms. The parameters used are the initial displacements, initial velocities, natural vibration frequencies, damping coefficients, and external forces in Eq. (1). In the process of collecting parameters, only single-cycle parameters and convergence data are kept, and the maximum and minimum displacements and velocities of single-cycle convergence results are used as prediction objects. Finally, 557,346 sets of data are collected as training and verification sets. Table 2 is the ranges of the parameters we chose, and Table 3 is the ranges of the results.

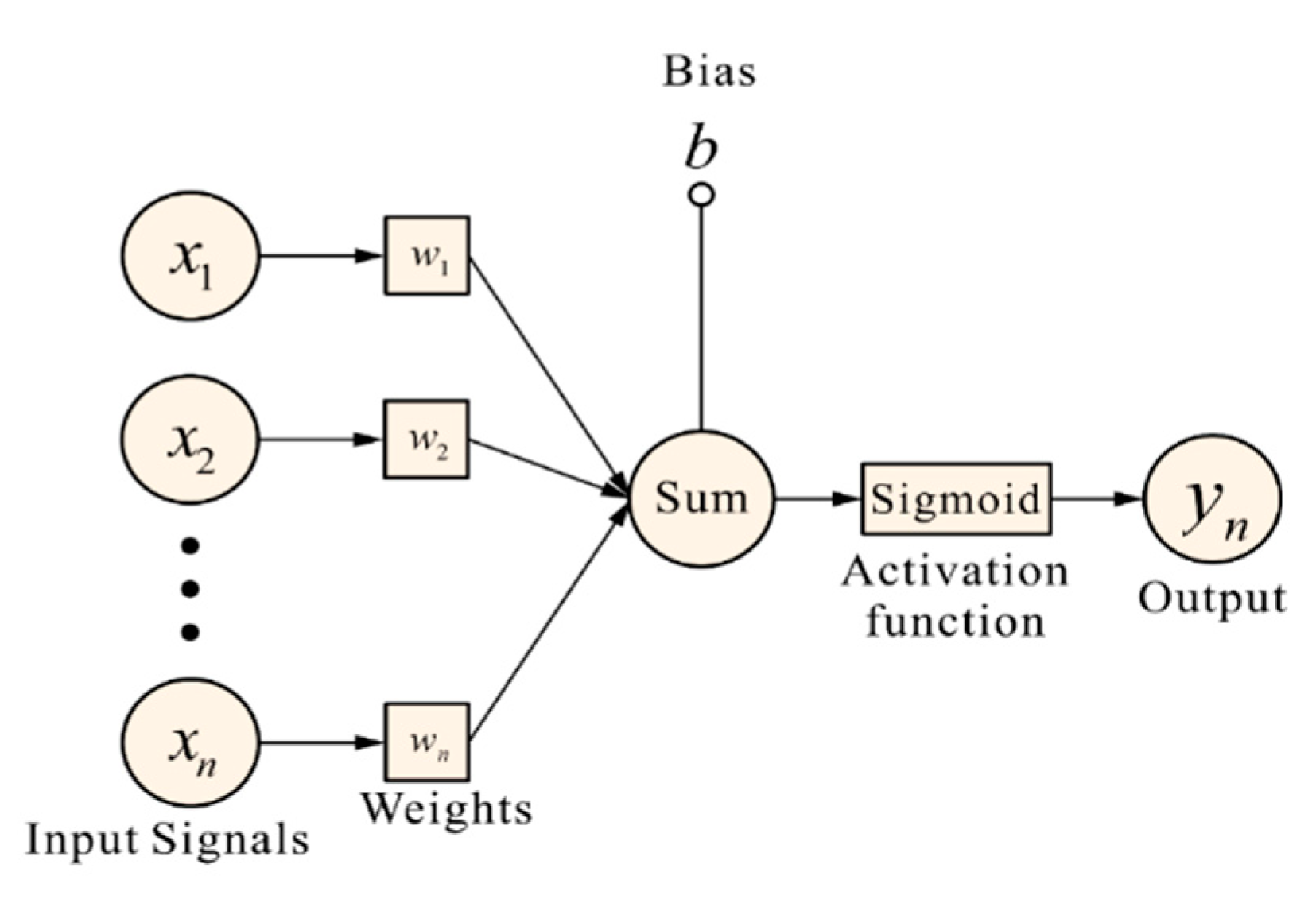
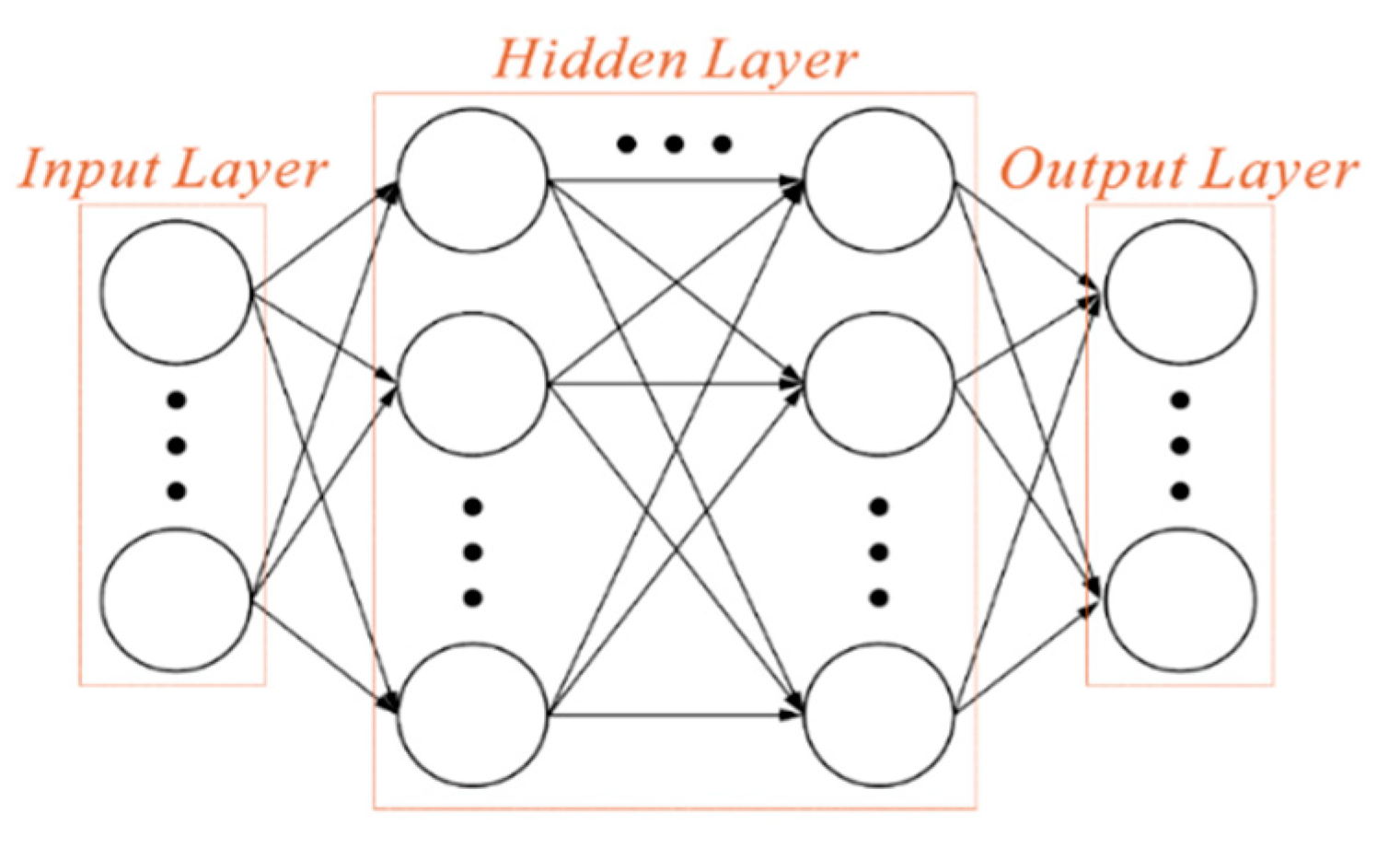
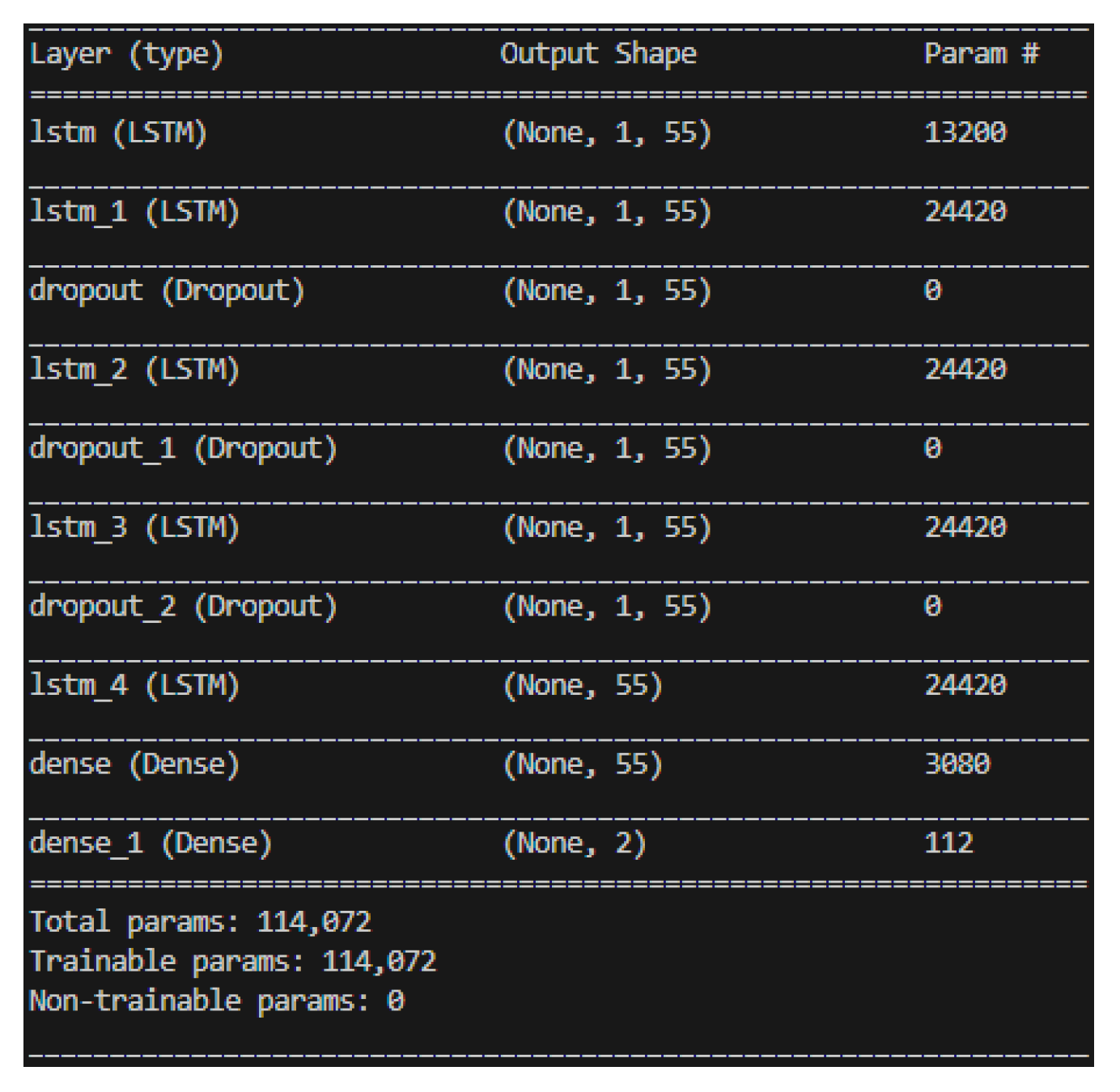
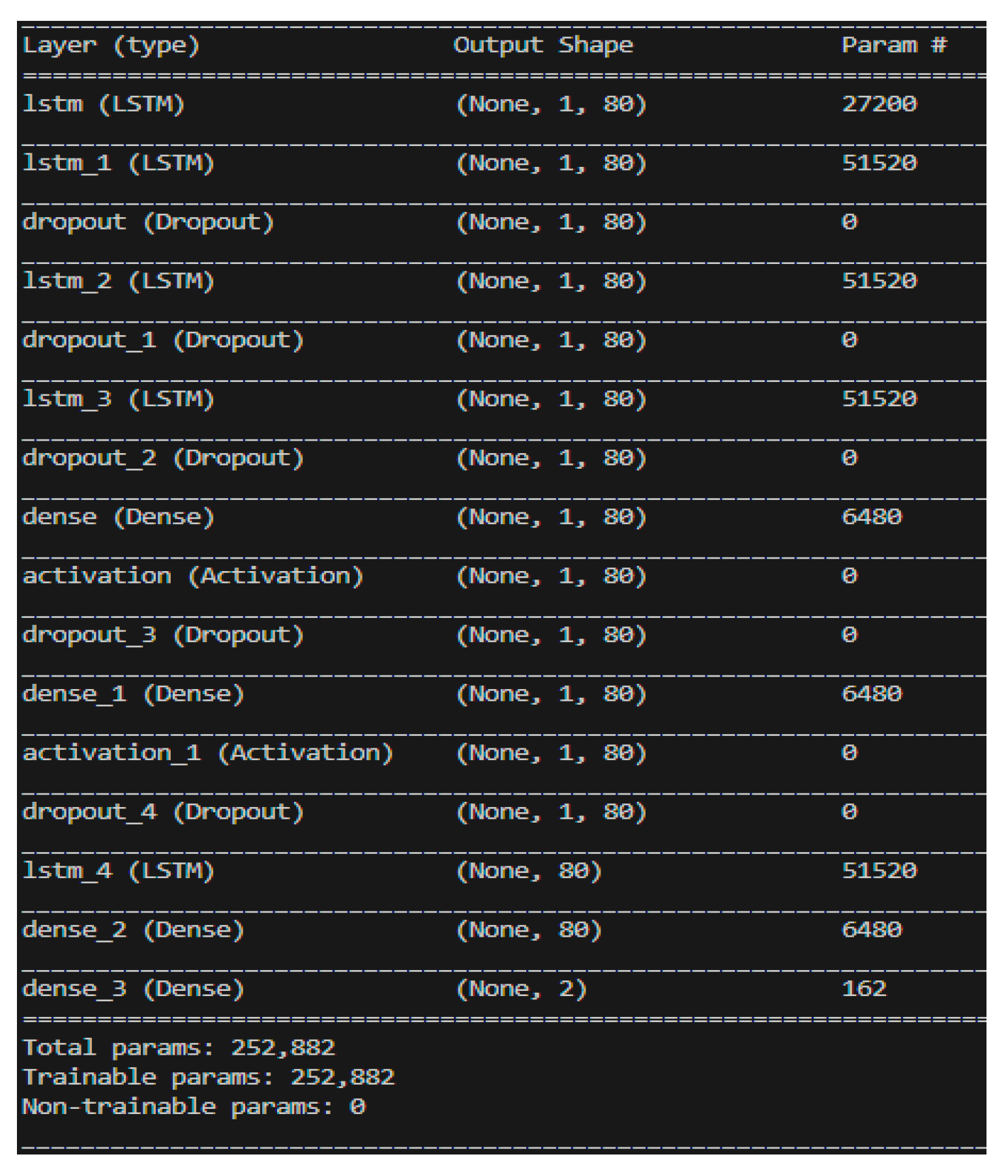
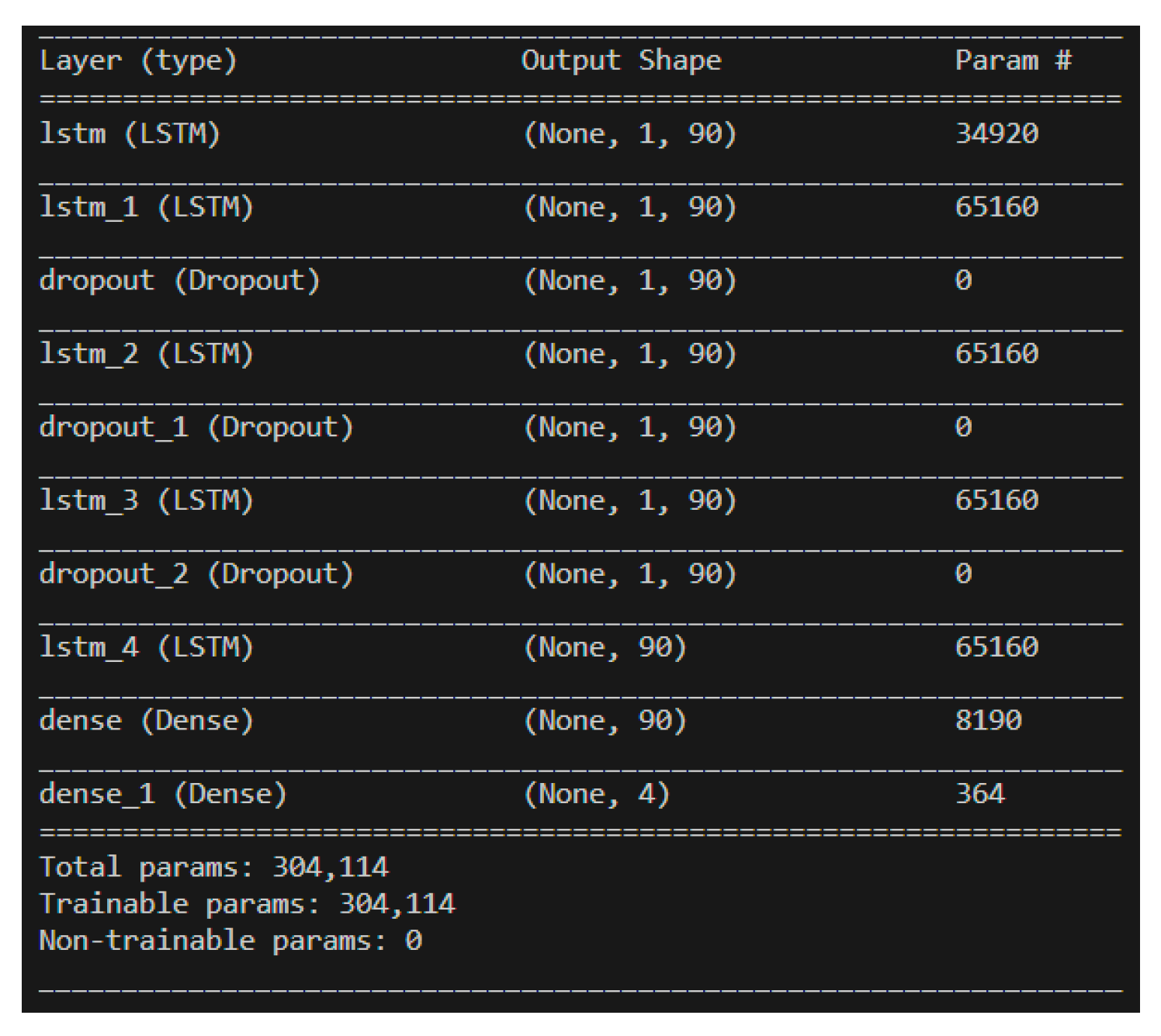
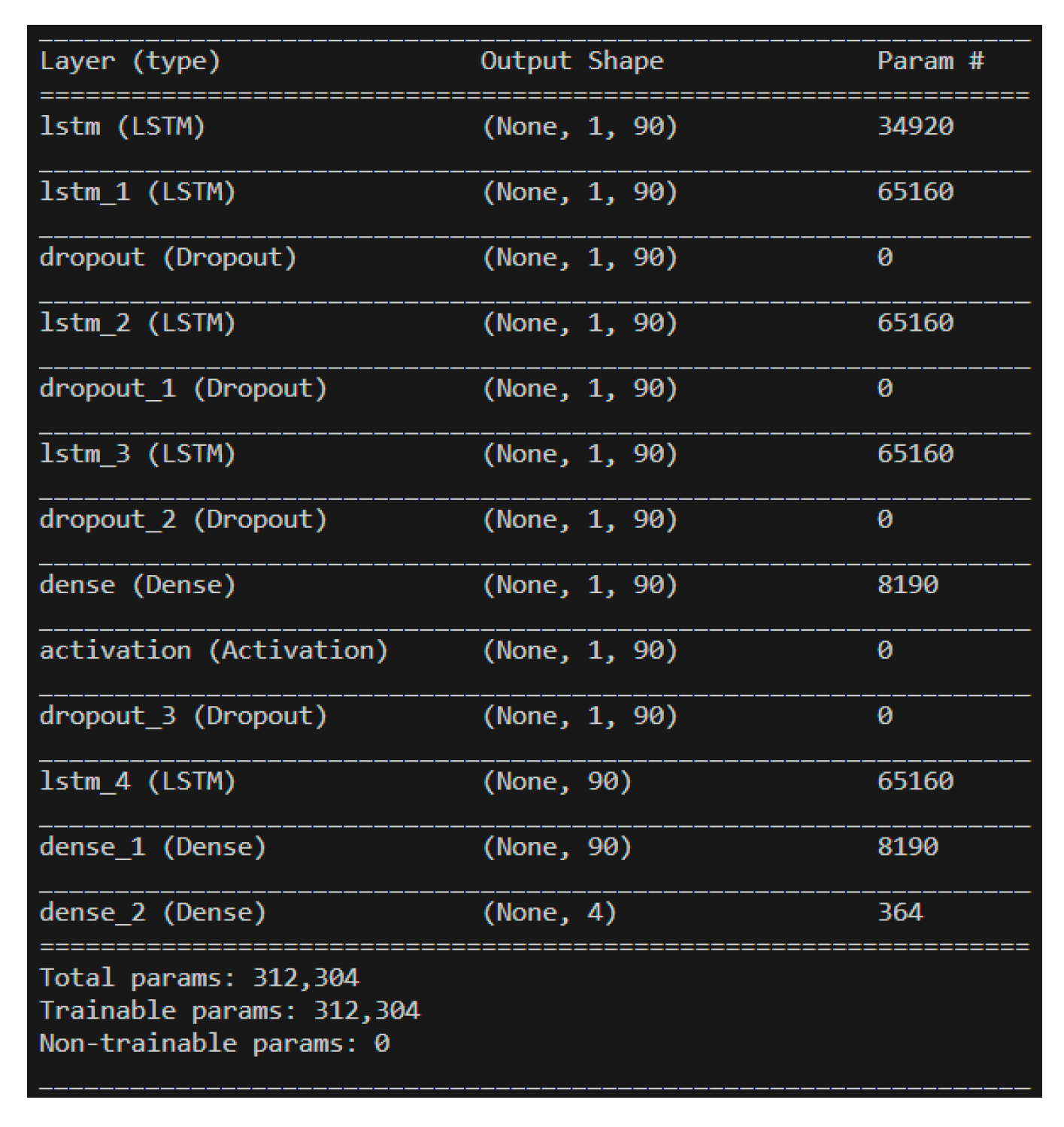
3.2. Deep Neural Network Architecture

Deep Neural Networks are the deeper Artificial Neural Networks (ANNs). The human brain can transmit and analyze information through the interconnection of neurons and make relative feedback. The neural network is composed of a large number of artificial neurons, and the artificial neurons are represented by Eq. (4) and Figure 4.

$$y=\sigma ({\displaystyle \sum _{i=1}^n{w}_i{x}_i+b})$$

(4)

Among them, x represents the value of neuron input, and w is the “weight”. Neurons and nearby neurons will influence each other, and the greater the weight, the greater the influence. If the weight of the input value is zero, any change of the current neuron has nothing to do with the output value. Therefore, different weight combinations will affect the overall output and then affect the overall accurate value. Additionally, the bias value (b), also known as Bias, introduces a deviation factor to the neural network. and $\sigma$ is the activation function. After the input value has been processed by the weight value and deviation value, it needs to be transformed by an activation function (Activation Function). The activation function is used to transform the weighted sum of each input of the neuron to obtain the output signal. The architecture of deep neural network is divided into three parts, namely input layer, output layer and hidden layer. There are multiple hidden layers between the input layer and the output layer. Each layer contains a plurality of neurons, which are respectively connected from the input layer to the hidden layer, and then respectively connected to the output layer from the hidden layer, as shown in Figure 5.

Most of the algorithms in machine learning require a maximum or minimum function or index, which is called the object function, and the objective function of deep learning is usually a loss function. We choose categorical cross-entropy, which is more commonly used in classification problems, as the loss function of our deep neural network architecture. The operation of categorical cross-entropy is shown in Eq. (5).

$$E_D=-{\displaystyle \sum _i^n{y}_i\log (p_i)}$$

(5)

Among them, E_D refers to the loss function, while n represents the number of classification categories. The variable y_i corresponds to the labeled data, and p_i denotes the accuracy rate of the classifier in predicting the convergence result of the Duffing equation. When employing the classification cross-entropy loss function, the activation function for the output layer is selected as Softmax. The equations presented above correspond to the forward propagation phase, which can be visualized as a series of operations performed from left to right. The input passes through the weights and bias values, undergoes function transformations, and progresses until reaching the output. On the other hand, the backpropagation algorithm is a more efficient variant of the gradient descent method. It calculates the gradient by means of partial differentiation and adjusts the weights to minimize the error. By leveraging the chain rule, the backpropagation method combines the gradient descent approach and serves as an optimization algorithm. Notably, the backpropagation process is the reverse of the forward propagation. Eq. (6) demonstrates that the backpropagation method employs the loss to compute the gradient of the loss function in each layer.

$$\frac{\partial E_D}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial y}{\partial z}\frac{\partial E_D}{\partial y}$$

(6)

where y is the value of the weighted product transformed by the activation function.

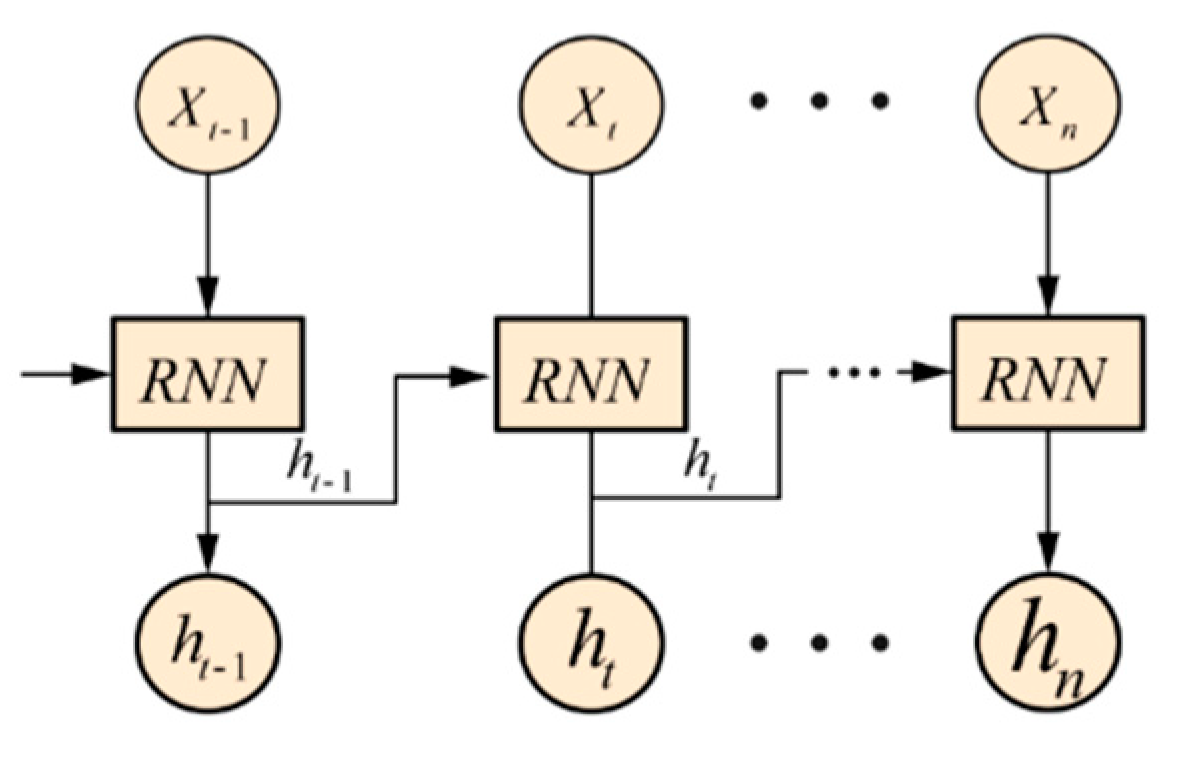
3.3. The basic structure of LSTM

A temporal recurrent neural network is a specific type of neural network that processes information sequentially in one direction. It possesses connections between hidden layers, known as recurrent connections, which enable the network to retain past information while incorporating new information. These connections allow for information to flow and facilitate short-term memory capabilities. Figure 6 illustrates the architecture of a temporal recurrent neural network. During the operation of the long-term short-term memory unit state, it undergoes calculations similar to a deep neural network. It involves multiplying the input with a weight, adding a bias value, and subsequently updating the state using a control gate. The unit state and control gate are transformed using activation functions. In this case, the unit state employs a hyperbolic tangent function as its activation function, while the control gate employs a sigmoid function as its activation function.

In LSTM networks, an objective function is essential for training. Mean Square Error (MSE) is a commonly used loss function in regression problems. MSE calculates the average of the squared differences between the predicted values and the actual values. It focuses solely on the magnitude of the errors and disregards their direction, quantifying the error based on the deviation distance. Assuming there are q records, the calculation formula for MSE can be represented as Eq. (7),

$$MSE=\frac{1}{q}{\displaystyle \sum _{i=1}^q{(y_i-{\widehat{y}}_i)}^2}$$

(7)

where y_i is the actual value after labeling, and ${\widehat{y}}_i$ is the predicted result.

During the training process, the loss function is evaluated across the entire training set. However, to effectively minimize the loss function, it is crucial to employ an optimizer that guides the parameters in the right direction. Optimizers play a vital role in deep learning, as they enhance training efficiency, help avoid getting stuck in saddle points, and mitigate overfitting issues. In this study, we refer to [8] and select the Adam optimizer for training purposes. The Adam optimizer combines the strengths of the Adagrad and Momentum optimizers. Adagrad adjusts the learning rate to improve training efficiency. Eq. (8) represents the basic concept of Adagrad algorithm.

$${\theta }_{t+1,i}={\theta }_{t,i}-\frac{\eta }{\sqrt{G_{t,ii}+\epsilon }}\cdot g_{t,i}$$

(8)

In the equations, $\theta$ represents the weight, $\eta$ denotes the learning rate, g signifies the gradient of ${\theta }_t$, G_t,ii is the sum of the squared gradients from previous steps, and ɛ is a smoothing term. The purpose of changing the learning rate using G_t is to address issues such as overfitting and slow training. Initially, with smaller values of G_t, a higher learning rate is employed, resulting in faster training efficiency. As G_t increases over time, the learning rate decreases to mitigate overfitting concerns. The smoothing term (ɛ) prevents the denominator from becoming zero. However, in cases where the Adagrad optimizer has a large value in later stages, the learning rate may become excessively low, resulting in slow training. On the other hand, the Momentum optimizer adjusts the learning rate based on the gradient direction. When the gradients align in the same direction, the learning rate gradually accelerates, whereas it decreases when the gradients are in the opposite direction. Eqs. (9) and (10) depict the concept of the Momentum algorithm.

$$\theta =\theta -v_t$$

(9)

$$v_t=\gamma v_{t-1}+\eta \cdot \frac{\partial L}{\partial \theta }$$

(10)

If v_t represents the previous term, it gradually grows larger, leading to an increase in the weight value. However, the Momentum method is unable to anticipate certain situations. If we have prior knowledge of the upcoming direction, we can make necessary preparations. The Adam (Adaptive Moment Estimation) optimizer combines the capability of the Momentum algorithm to adjust speed based on past gradient directions with the ability of the Adagrad algorithm to update the learning rate.

Eqs. (11) and (12) represent the Adam algorithm, which encompasses these combined functionalities.

$$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$$

(11)

$$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t{}^2$$

(12)

Among them, both m_t and v_t require correction for deviation to prevent them from being initialized as zero vectors, which would cause them to gravitate towards zero. We utilize Eqs. (13) and (14) to calculate the bias correction and counteract any bias present.

$${\widehat{m}}_t=\frac{m_t}{1-{\beta }_1{}^t}$$

(13)

$${\widehat{v}}_t=\frac{v_t}{1-{\beta }_2{}^t}$$

(14)

After correcting Eqs. (13) and (14), the gradient update rule of Adam algorithm is shown in Eq. (15).

$${\theta }_{t+1}={\theta }_t-\eta \frac{{\widehat{m}}_t}{\sqrt{{\widehat{v}}_t}+\epsilon }$$

(15)

In parameter setting, the learning rate $\eta$ is set to 0.003, the default value of ${\beta }_1$is 0.9, while ${\beta }_2$ is 0.999, and $\epsilon$ is 1e-08. When selecting an activation function, different activation functions need to be selected according to different states. The activation functions we use for training include Simgoid function, Hyperbolic tangent function, Softmax function, etc... Sigmoid is a synthetic function of natural exponents, which can convert the input into a number between 0 and 1. Eq. (16) is the mathematical definition of the Sigmoid function:

$$Sigmoid=\frac{1}{1+e^{-x}}$$

(16)

Hyperbolic tangent function is more commonly used in time-recurrent neural network architecture, and its value range is [-1,1]. Eq. (17) is the mathematical definition of Hyperbolic tangent function:

$$\tanh =\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

(17)

The Softmax function, as defined by Eq. (18), ensures that its output falls within the interval [0,1].

$$y_i=\frac{e^{x_i}}{{\displaystyle \sum _{i=0}^n{e}^{x_i}}}$$

(18)

4. Deep learning training analysis

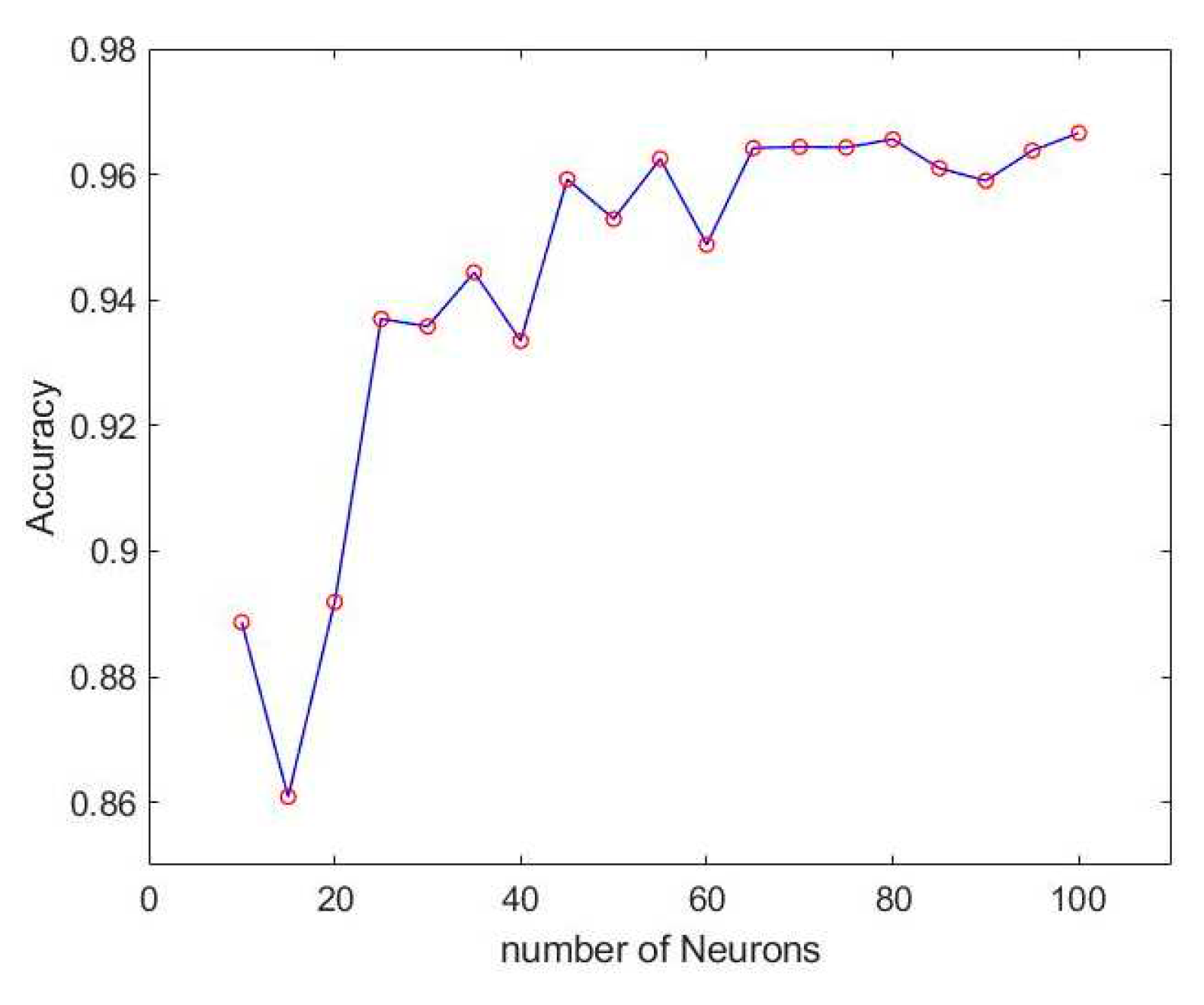
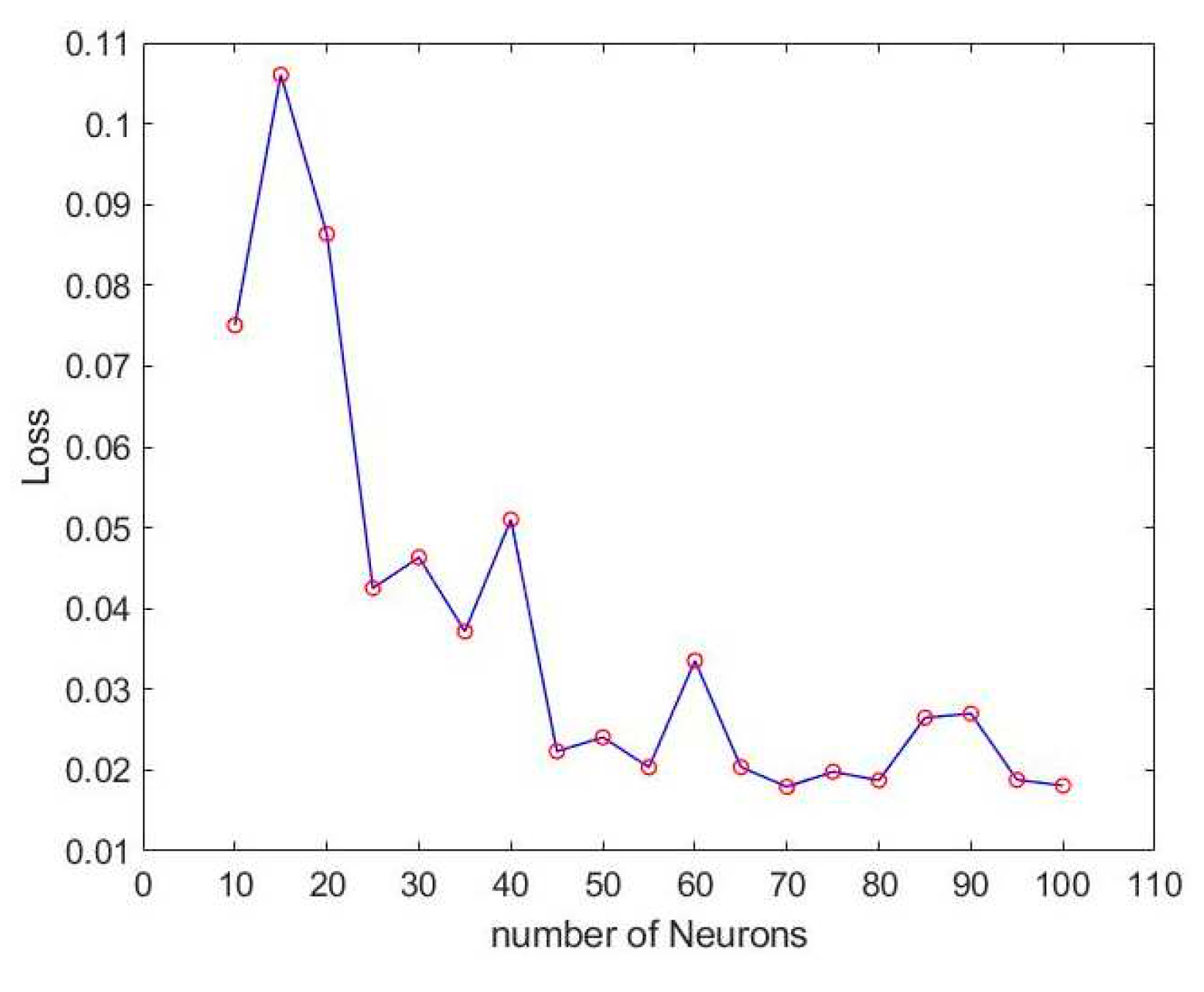
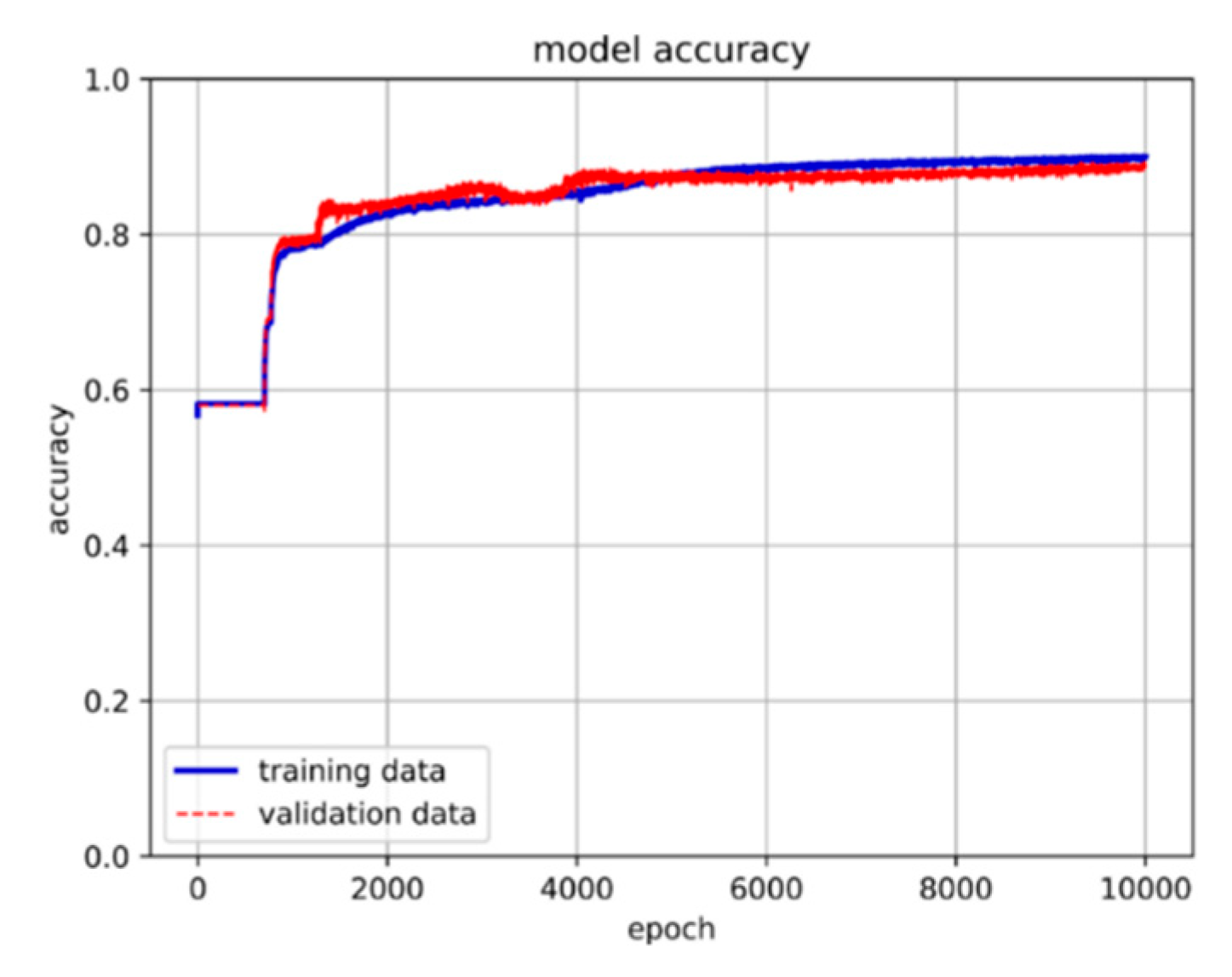
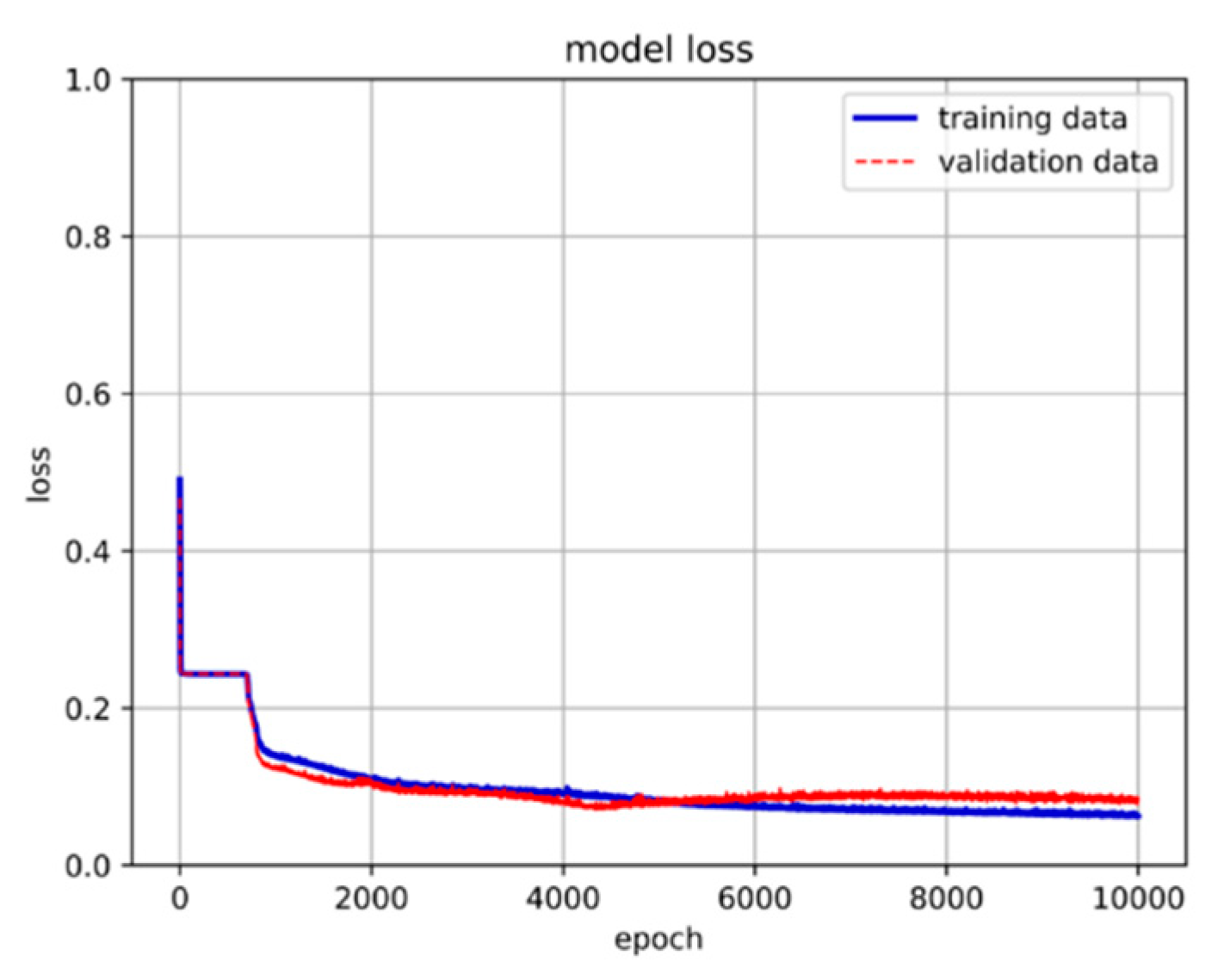
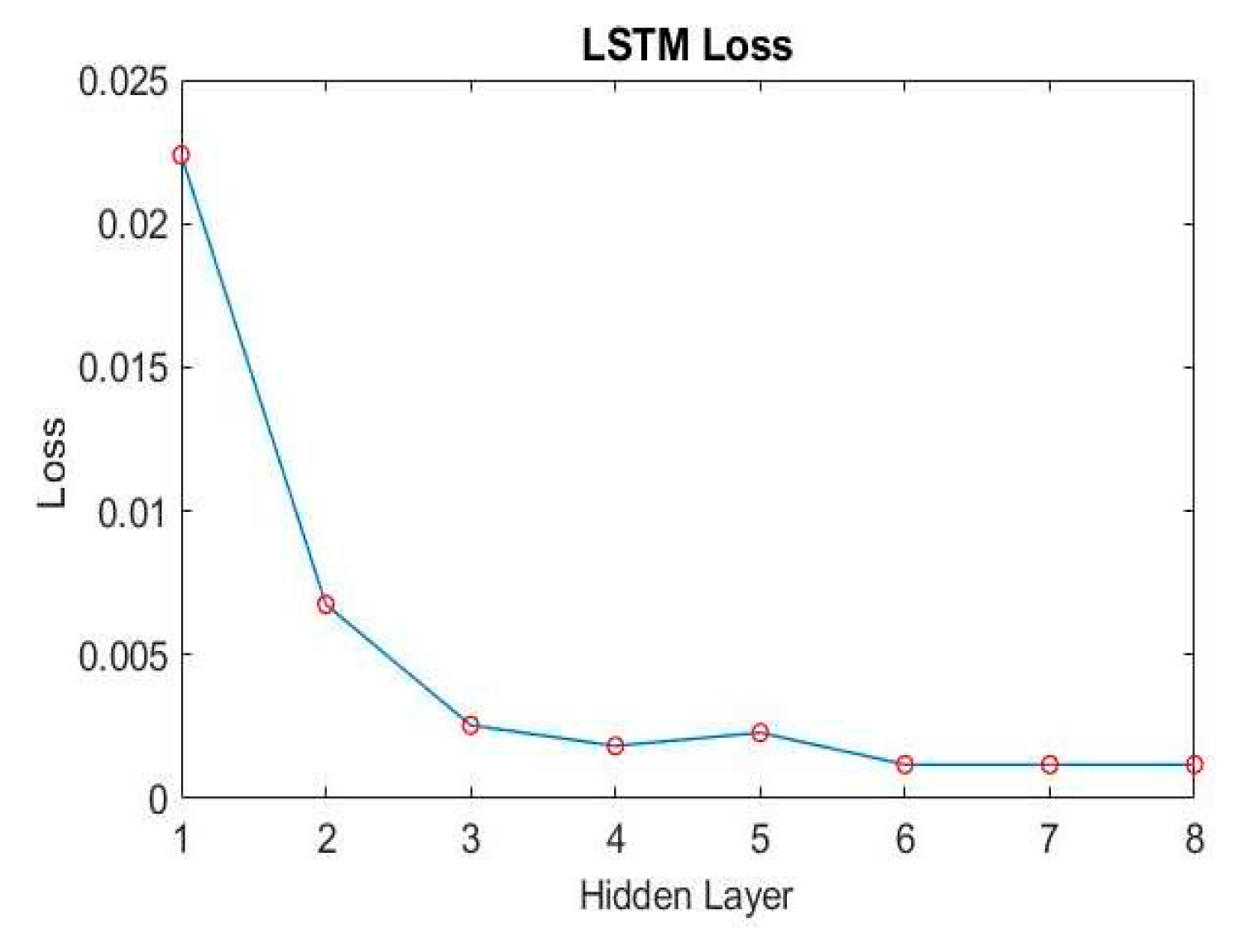
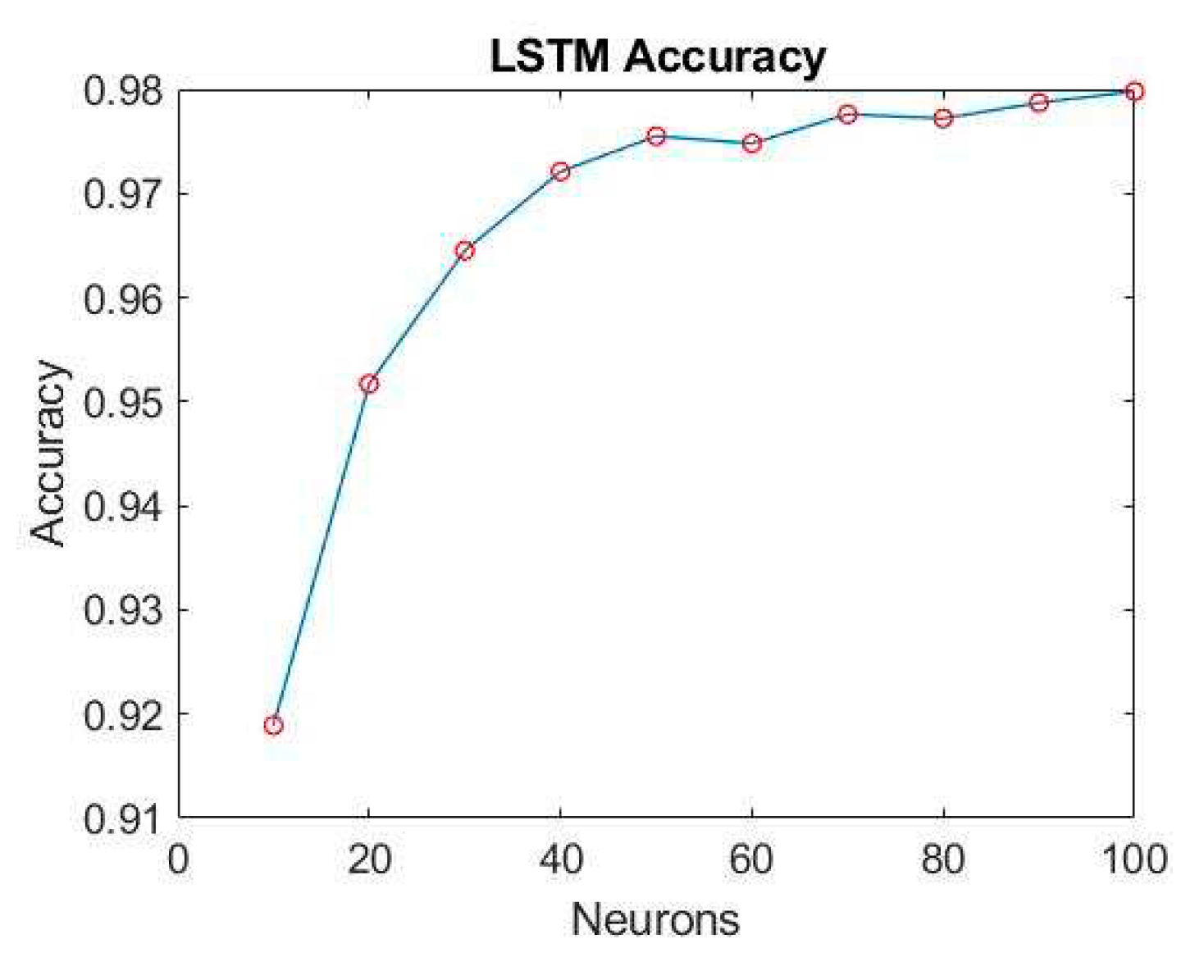
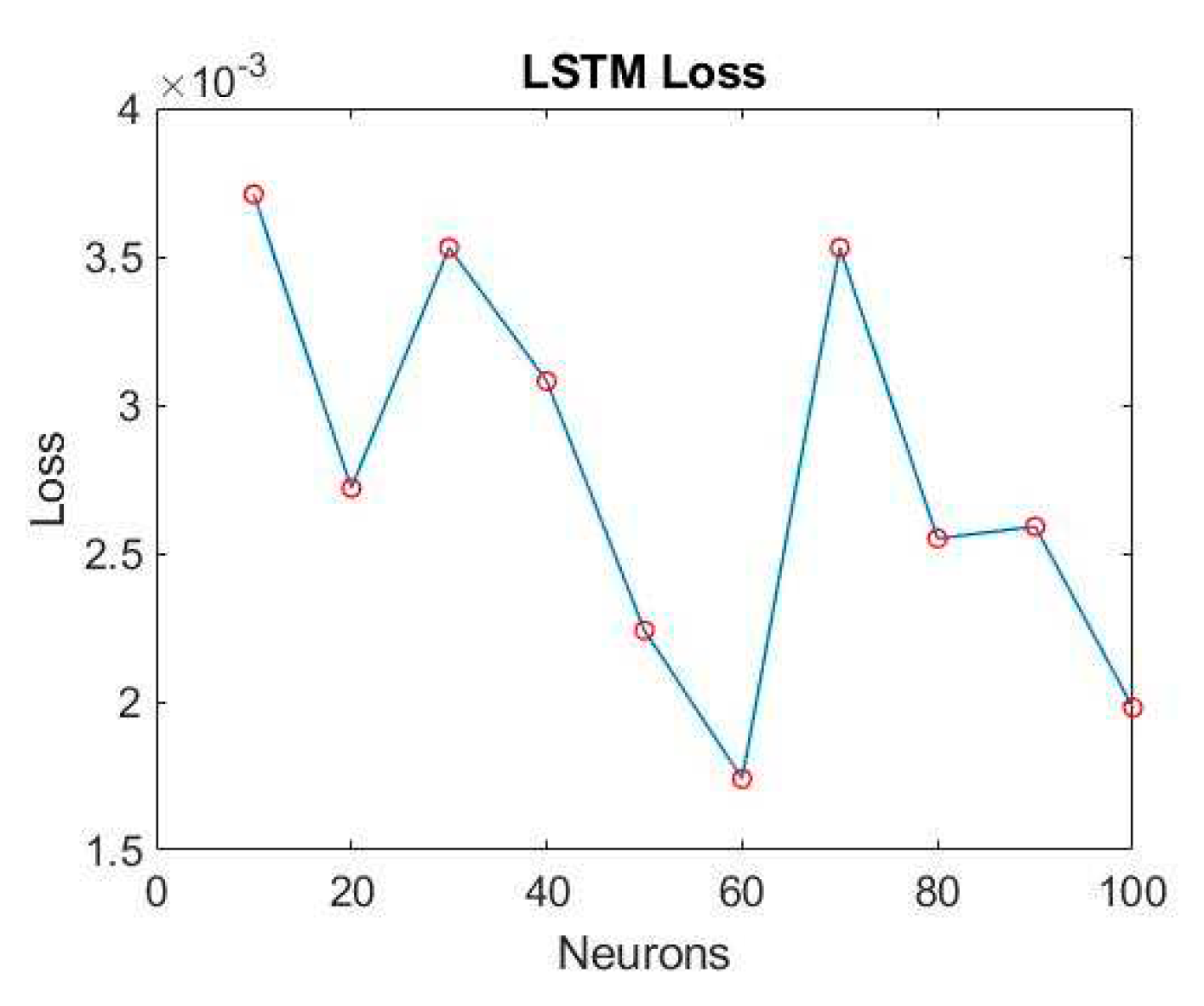
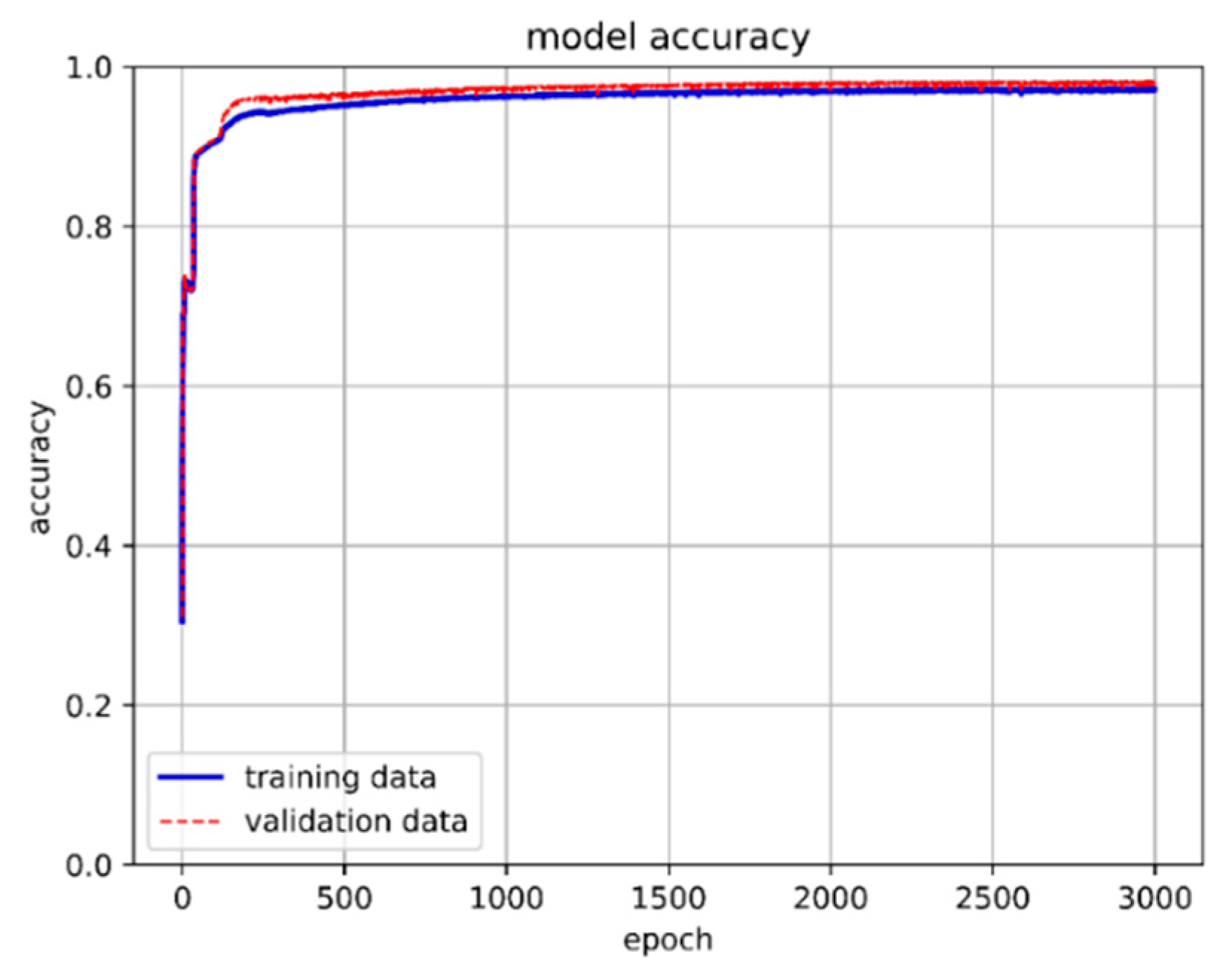
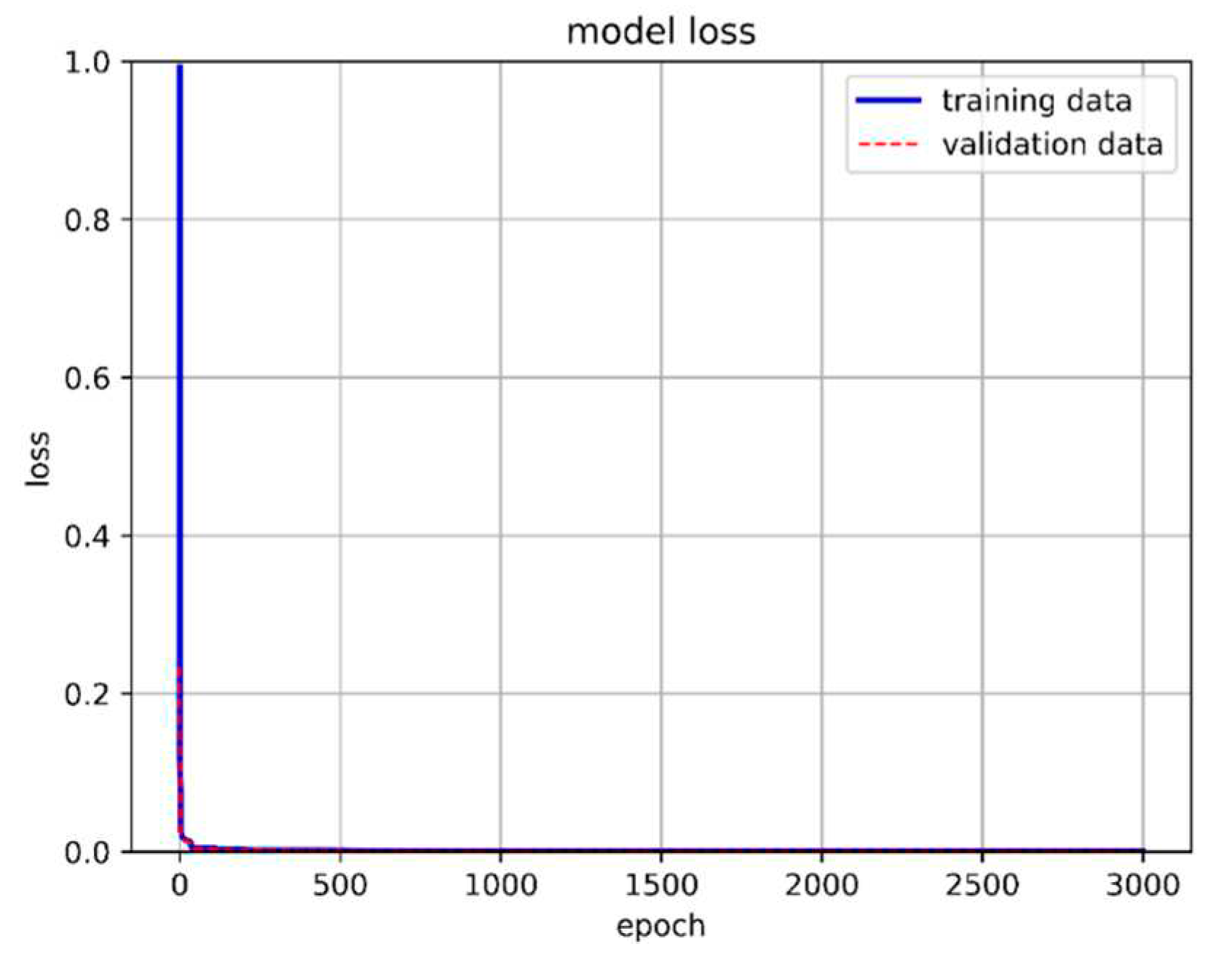
4.1. Duffing equation undamped free vibration type - by LSTM model

We use the LSTM method to predict the convergence outcome of the undamped free vibration type of the Duffing equation. The dataset comprises a total of 117,432 records. Initially, we construct an LSTM framework capable of training this data and partition it into three sets. The training set consists of 65% of the total data, the validation set contains 30%, and the remaining 5% is allocated as the prediction set. The model's input parameters consist of initial displacement, initial velocity, nonlinear and linear spring constants, while the output dataset consists of the convergence values of the equation's solution. After establishing the fundamental structure of the LSTM model for data training, we utilize two hidden layers with 10 neurons each. We conduct 10,000 epochs with a batch size of 16,284. The training results are presented in Figure 7.

Once we employ the One-hot encoding technique to label the output, we can distinguish the output values across different dimensions. This method proves particularly effective when the output values are limited in range. In the case of the undamped free vibration mode of the Duffing equation, where only two convergence types (+1 or -1) exist, we find this approach suitable and employ it. To address concerns regarding overfitting, we incorporate dropout layers in each hidden layer. To determine the optimal configuration for the hidden layers, we conduct tests with varying numbers of layers. The accuracy and loss results for different hidden layer configurations are illustrated in Figure 8 and Figure 9, respectively.

According to the accuracy and loss of LSTM method mentioned above, the best number of hidden layers can be found to be three. We then adjust the number of neurons to find the best result. The accuracy and loss of different numbers of neurons are shown in Figure 10 and Figure 11.

From Figure 12 of the training results, it can be concluded that when the number of neurons is 55, the training result has reached 96% accuracy, and the loss is only 2%. But it was also found that there will be instability when using LSTM. There are almost 5% unstable oscillations in the accuracy rate. The unstable situation is shown in Figure 13 and Figure 14.

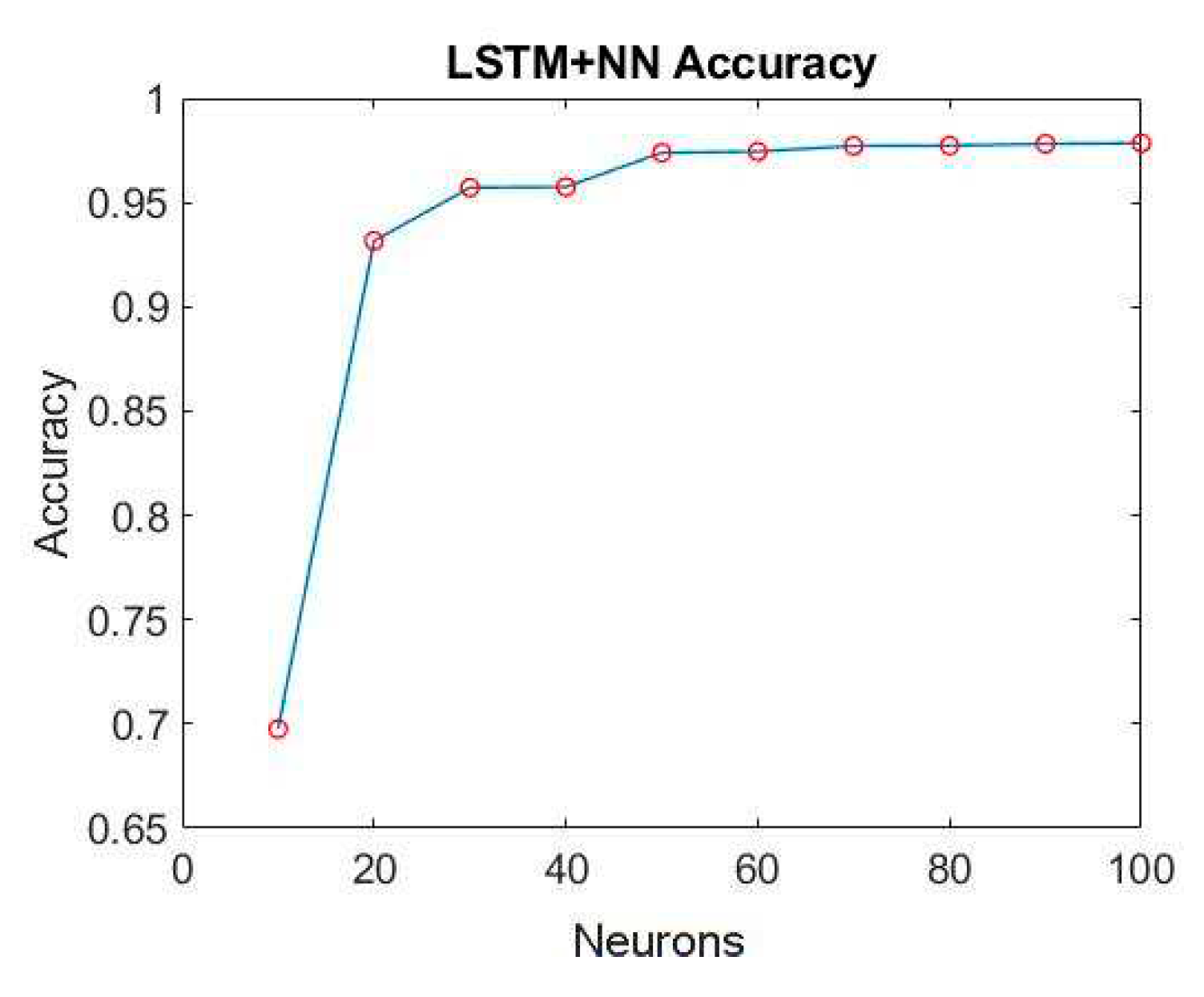
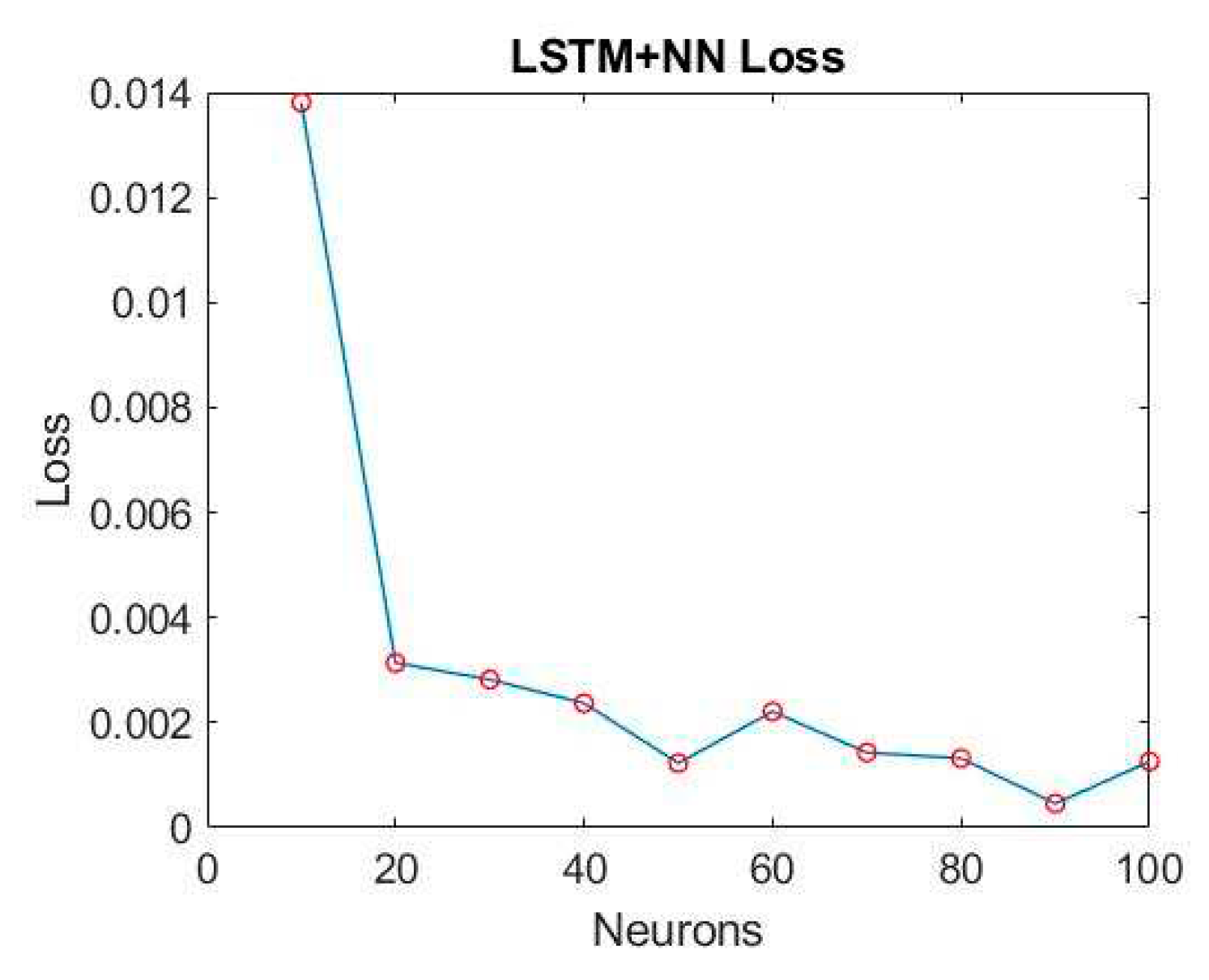
4.2. Duffing equation undamped free vibration type - by LSTM-NN model

When training the LSTM model for the undamped free vibration type of the Duffing equation, it was observed that the accuracy rate after training exhibited instability. To address this issue and enhance the prediction results, we introduced deep neural network hidden layers while modifying the activation function. Using the same dataset, we initially established an LSTM framework capable of training this data. Following the approach described in Section 4.1, we divided the data into three parts: the Training set (comprising 65% of the total data), the Validation set (30%), and a separate 5% as the prediction set. The number of neurons was initially set to 30. Table 4 presents the accuracy and loss values for different hidden layers.

After evaluating the accuracy, loss, and stability of various architectures, this study ultimately adopts a model architecture consisting of three hidden layers of LSTM and two hidden layers of neural networks. Subsequently, adjustments were made to the activation function. Initially, we experimented with replacing the previously used ReLU function with the sigmoid function in search of the optimal learning model. However, the use of the sigmoid function did not yield better results. Consequently, the final model architecture for this research consists of three layers of LSTM hidden layers and two layers of neural network hidden layers, utilizing the ReLU activation function, as illustrated in Figure 15. The training results are presented in Figure 16 and Figure 17.

After finding the best learning model architecture, we changed the number of neurons in each layer to find the best training model. The results after training are shown in Figure 18 and Figure 19.

According to training accuracy, loss and stability among different neurons, the optimal number of neurons is 80. Its stability is significantly better than the model using only LSTM. And it has excellent performance in accuracy and loss. The accuracy of the training results is 96% and the loss is 2.1%, and the accuracy is unstable with only 1% fluctuation. The training model is shown in Figure 20 and the results are shown in Figure 21 and Figure 22.

4.3. Duffing equation damped and forced vibration type - by LSTM model

In this study, we apply the method described in Section 2 to gather convergence results of the damped forced vibration type of the Duffing equation. The dataset is created by collecting the maximum and minimum values of displacement and velocity from the convergence outcomes. This data is then split into a 65% training set, a 30% validation set, and the remaining 5% is used as the prediction set. The model's input parameters consist of initial displacement, initial velocity, damping coefficient, natural vibration frequency, and external force. Initially, we train the model using 557,346 data values, employing a model architecture with one hidden layer comprising 80 neurons. We conduct 3,000 epochs with a batch size of 16,384. However, we observe underfitting in the validation set, indicated by an upward trend in the loss around the 500th epoch. Figure 23 illustrates the training results. To tackle overfitting, we include a dropout layer during the training process. Additionally, unlike in Section 4.1, where the One-hot encoding method was used to label the target parameters, in the case of training multiple numerical solutions, we directly use the original values as labels to ensure the credibility of the target parameter predictions.

According to the method in Section 4.1, we first adjust the number of different hidden layers to find out the training results of each layer. As shown in Figure 24 and Figure 25, it can be seen that when training to three hidden layers, better results can be obtained. Subsequent hidden layers with different numbers do not grow very well, and the training time is longer. So we choose 3 hidden layers as the architecture of the training model.

After establishing the LSTM training model, we proceed to fine-tune the number of neurons, exploring different configurations at intervals of every 10 neurons. The training results for various neuron counts are presented in Figure 26 and Figure 27. Notably, when utilizing 60 neurons, the model achieves exceptional performance with a minimal loss of only 0.17% and an outstanding accuracy rate of 97.5%. As a result, this study selects 60 neurons as the optimal number within the final LSTM model architecture, as illustrated in Figure 28.

4.4. Duffing equation damped and forced vibration type - by LSTM-NN model

The dataset of 557,346 records was divided into approximately 65% for the training set, 30% for the validation set, and 5% for the prediction set. The model utilized 80 neurons, underwent 3000 epochs, and used a batch size of 16,384. The training method was based on the target parameters described in Section 4.2, where training and prediction employed the original values to ensure result credibility. Table 5 presents the training results for different hidden layers. Notably, when the LSTM hidden layer consisted of three layers combined with one neural network hidden layer utilizing the ReLU activation function, the model achieved an exceptional accuracy rate of 98.14% with a loss of 0.07%. Training accuracy and loss are depicted in Figure 29 and Figure 30, respectively.

After choosing a model architecture for training, its number of hidden layer neurons is adjusted. We started with 10 neurons as the minimum number and increased by 10 units each time to 100. The epoch is adjusted to 5000 according to the downward trend of its loss, and its accuracy and loss are collected. Figure 31 and Figure 32 are the training results of different numbers of neurons.

When the number of neurons reaches more than 50, its training accuracy is as high as 97.5%. When the number of neurons is 90, the loss is only 0.046%. So, the number of hidden layer neurons in the final model architecture is set to 90. Figure 33 shows the final selected model architecture.

5. Deep learning prediction results and model comparison

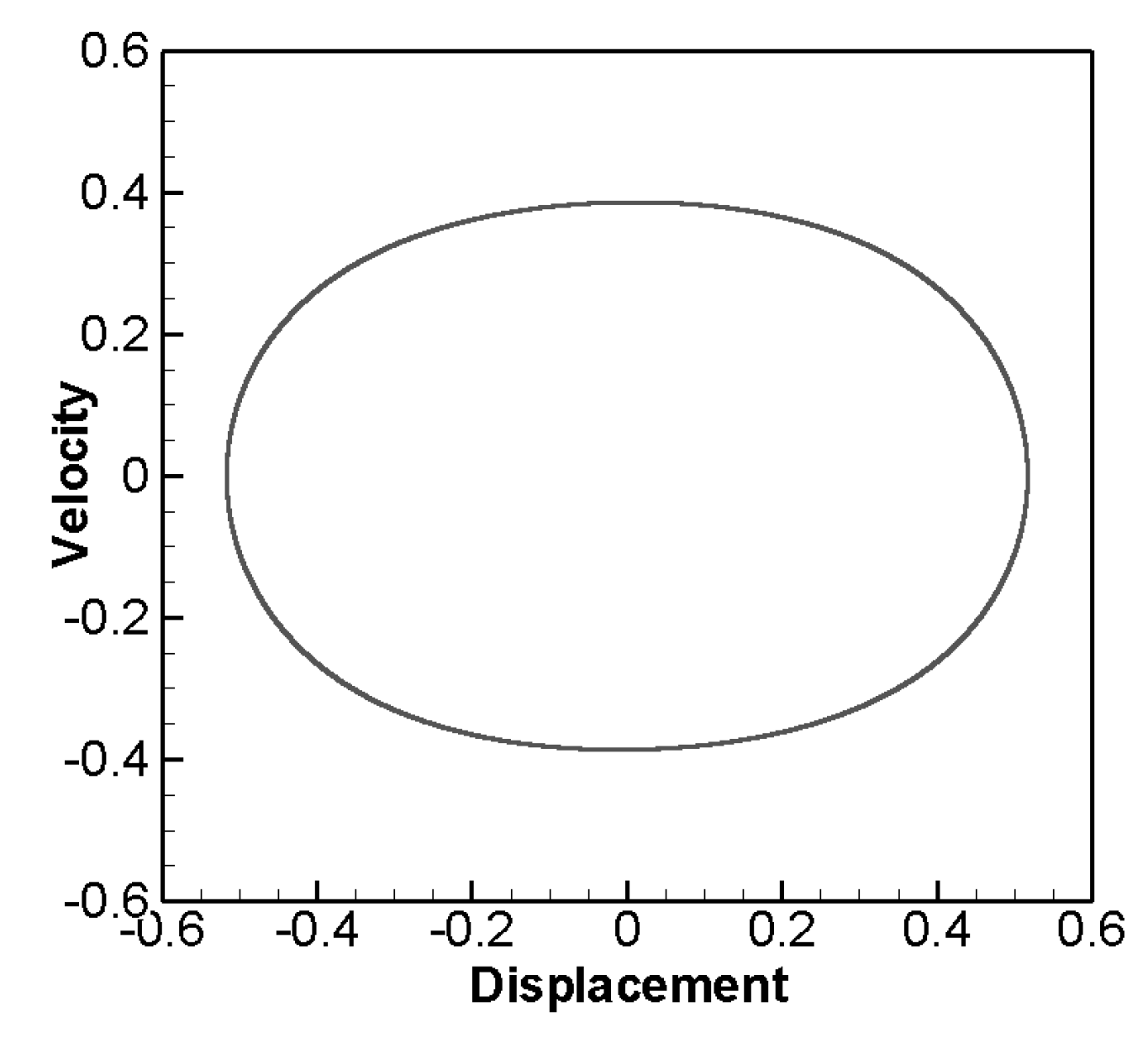
5.1. Duffing equation undamped free vibration type

Before making predictions, it is necessary to evaluate the performance of the model being used. We assess the training time using both CPU and GPU and compare the results. Figure 34 illustrates the training time for the first five epochs when using CPU, while Figure 35 shows the training time when using GPU for the same model.

From Figure 34 and Figure 35, it is evident that the GPU significantly outperforms the CPU in terms of training time. This discrepancy can be attributed to the GPU's superior computing power and memory bandwidth, enabling more efficient parallel computing and faster model training. As a result, GPUs are well-suited for training deep learning models.

Based on the training results presented in Section 4.1 and Section 4. 2, the LSTM & LSTM-NN training model is selected for prediction. The prediction data employs the last 5% of the dataset as the prediction set. Figure 36 and Figure 37 display the prediction results, while Figure 38 and Figure 39 illustrate the training time for the first five epochs, respectively.

The prediction results indicate that when the LSTM model predicts a value of -1, the accuracy rate reaches 96% compared to the true value. However, when both the predicted and actual values are 1, the accuracy drops to 86%. On the other hand, the LSTM-NN model achieves an accuracy rate of 87% for a predicted value of -1, while reaching 98% when both the predicted and actual values are 1.

Figure 36 and Figure 37 demonstrate that the model with a hidden layer of neurons in the prediction process attains higher accuracy. Throughout the training process, the LSTM-NN model exhibits better and more stable performance compared to the LSTM model. Figure 38 and Figure 39 illustrate that the LSTM-NN model has a longer training time than LSTM due to the inclusion of a larger number of hidden layers and neurons. While the LSTM model offers the advantage of faster training speed, its performance in handling binary classification datasets can be enhanced by incorporating hidden layers of neurons, leading to the LSTM-NN model. This modification improves the training and prediction outcomes significantly.

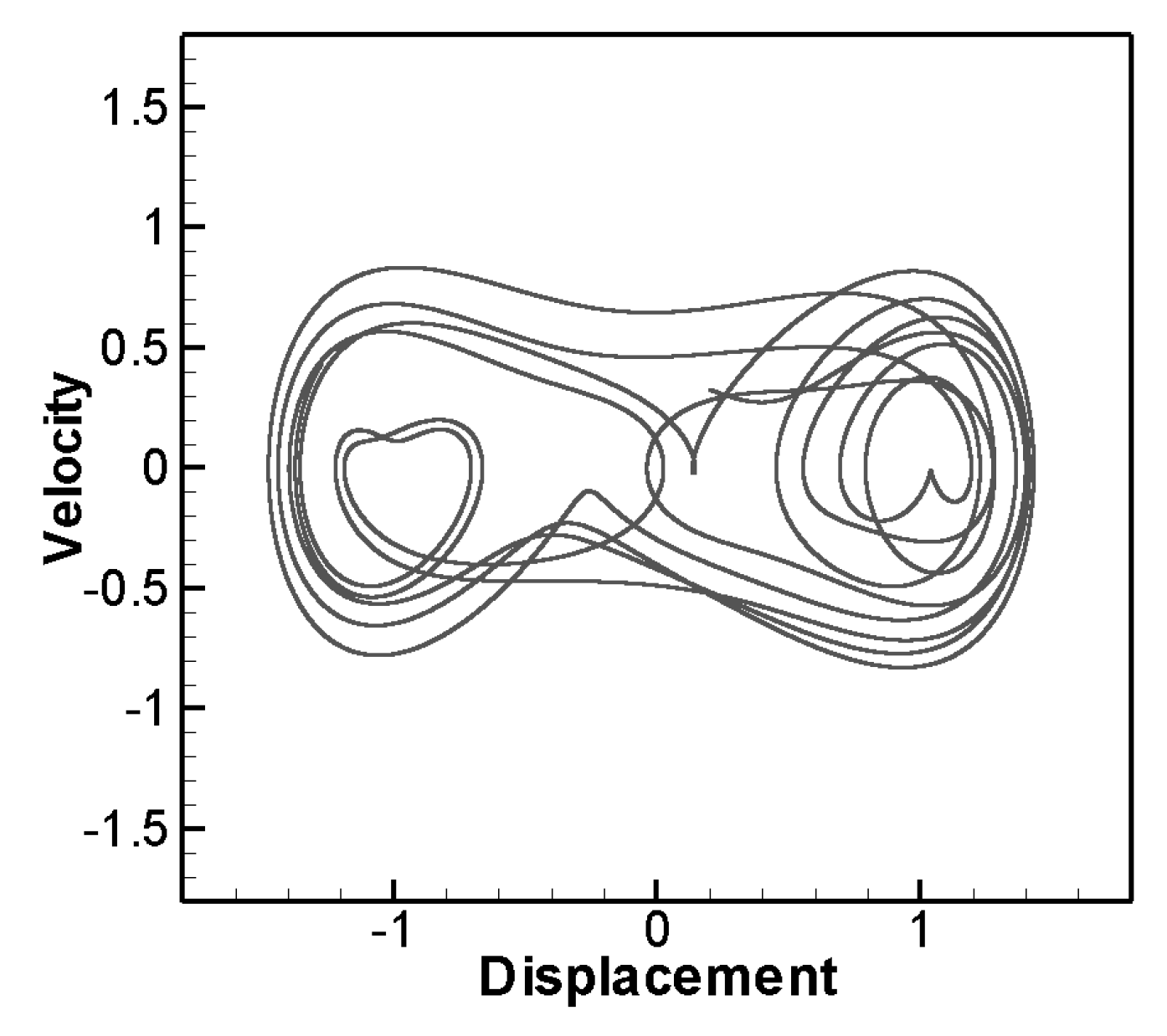
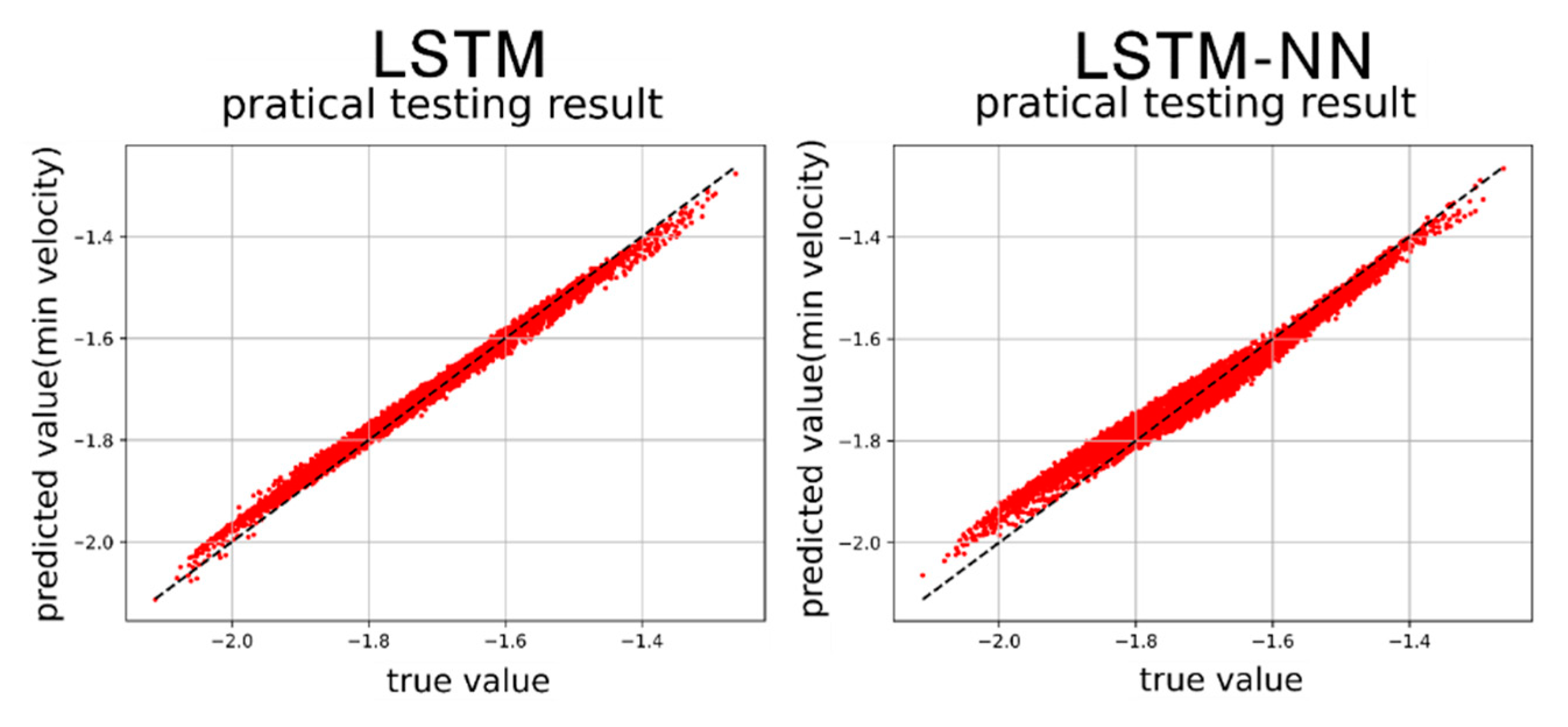
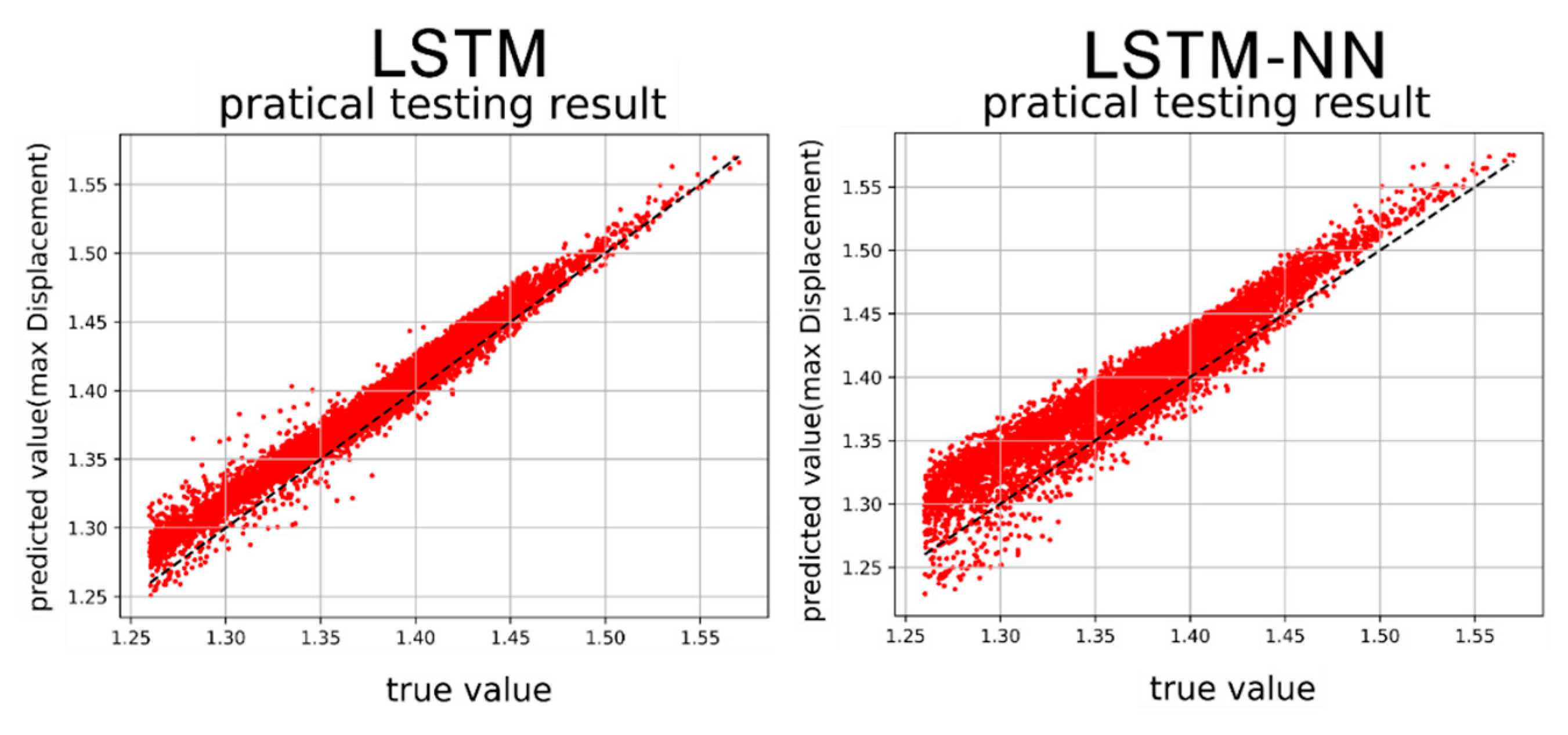
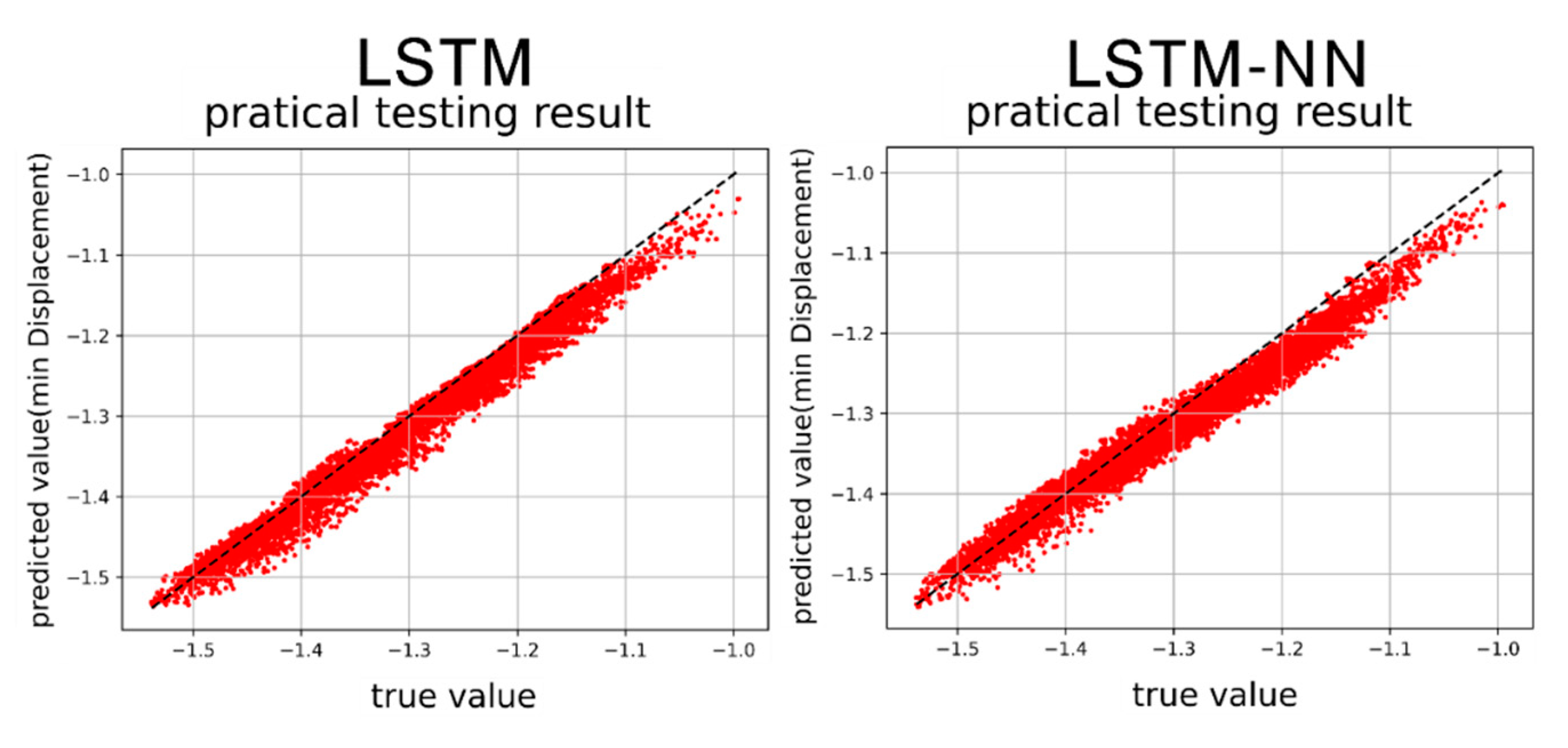
5.2. Duffing equation damped and forced vibration type

After training the models in Section 4.3 and Section 4.4, we proceed to predict the single-cycle convergence results in the Duffing equation dataset containing damping and external force, using the prediction set. Both the LSTM model and the LSTM-NN model are utilized for this prediction. Figure 40, Figure 41, Figure 42 and Figure 43 display the results of predicting the maximum velocity, minimum velocity, maximum displacement, and minimum displacement using the LSTM and LSTM-NN models, respectively.

Figure 40, Figure 41, Figure 42 and Figure 43 present the prediction graphs, with the horizontal axis representing the actual value and the vertical axis representing the predicted value. The dashed line represents the baseline where the actual value is equal to the predicted value. These figures provide an overview of the prediction results for the two models. Upon analyzing the training phase, it becomes evident that the LSTM-NN model performs better during training. However, the prediction results are not as satisfactory, indicating an overfitting problem during training for the LSTM-NN model. Notably, the prediction accuracy for velocity is noticeably higher compared to displacement. This discrepancy may arise due to the model's insensitivity in capturing the data characteristics of displacement or the presence of poor-quality displacement data, resulting in inferior prediction performance. Between the two models, the LSTM model demonstrates superior accuracy compared to the LSTM-NN model. Furthermore, the training time for both models can be observed in Figure 44 and Figure 45.

Based on the comparison of prediction accuracy and training time presented in Figure 44 and Figure 45, it becomes evident that the LSTM model offers the advantages of shorter training time and high prediction accuracy. However, one drawback of LSTM models is that they may exhibit large fluctuations in training accuracy. On the other hand, the LSTM-NN model showcases stable training accuracy without significant ups and downs. However, when it comes to prediction accuracy, the LSTM-NN model falls short compared to the general LSTM model, particularly when dealing with multiple solutions. In summary, while the LSTM model excels in terms of training time and prediction accuracy, it is prone to fluctuations in training accuracy. Conversely, the LSTM-NN model maintains stable training accuracy but exhibits less accurate predictions, particularly for multiple solutions.

6. Conclusions

This study investigates the convergence results of the Duffing equation in two scenarios: undamped free vibration and damped forced vibration. The RK-4 method is utilized to collect data and mark the convergence results for undamped free vibration. Subsequently, the long short-term memory (LSTM) and LSTM-Neural Network (LSTM-NN) methods are employed for training and prediction to identify the best results. Moving on, the study examines the convergence results of the Duffing equation for damped forced vibration, considering various convergence characteristics, particularly focusing on the range of single-cycle convergence results. The collected data is compiled into a dataset, and LSTM and LSTM-NN models are established to train and predict multiple solutions for the Duffing equation with damped forced vibration. From this study, several conclusions are drawn:

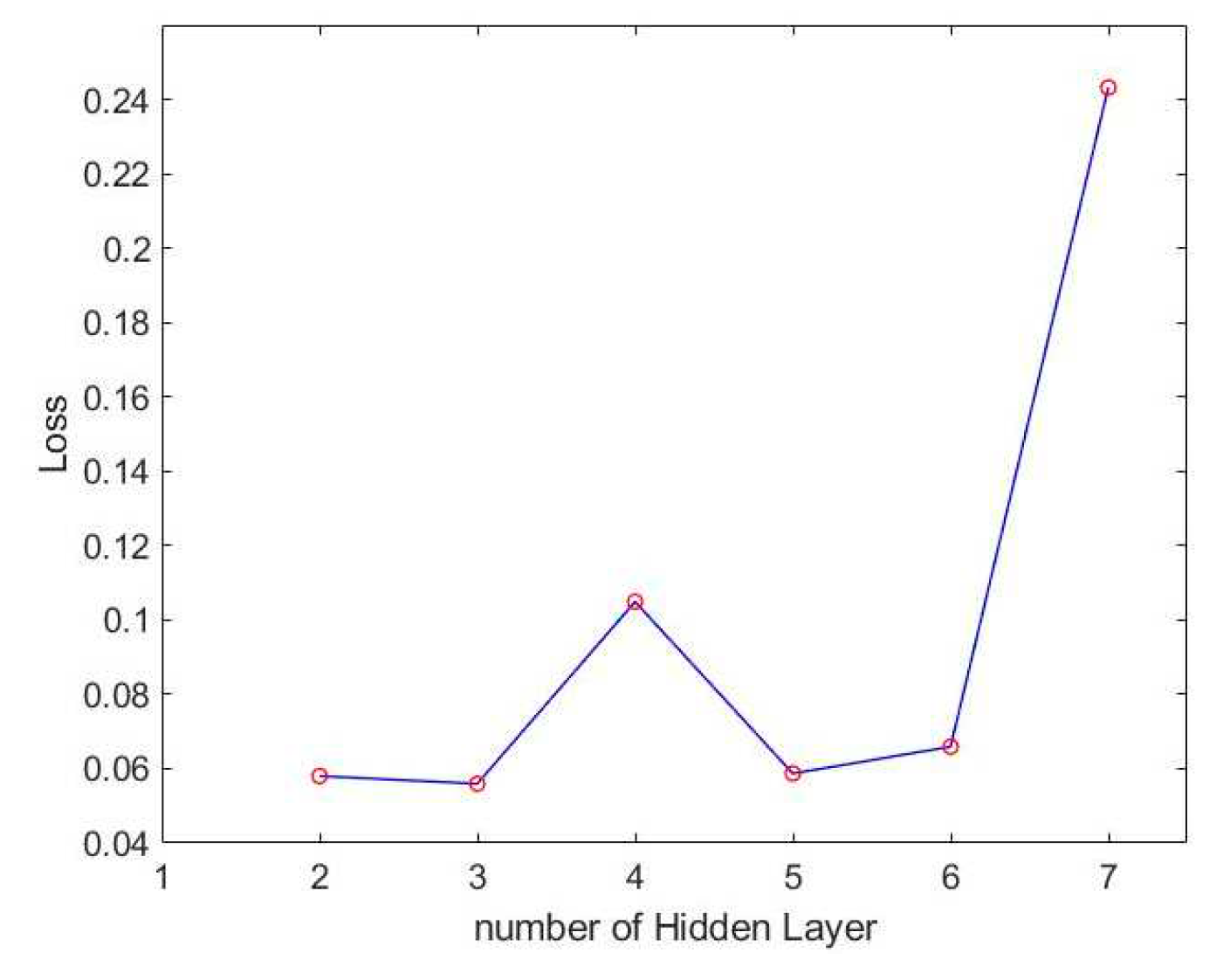
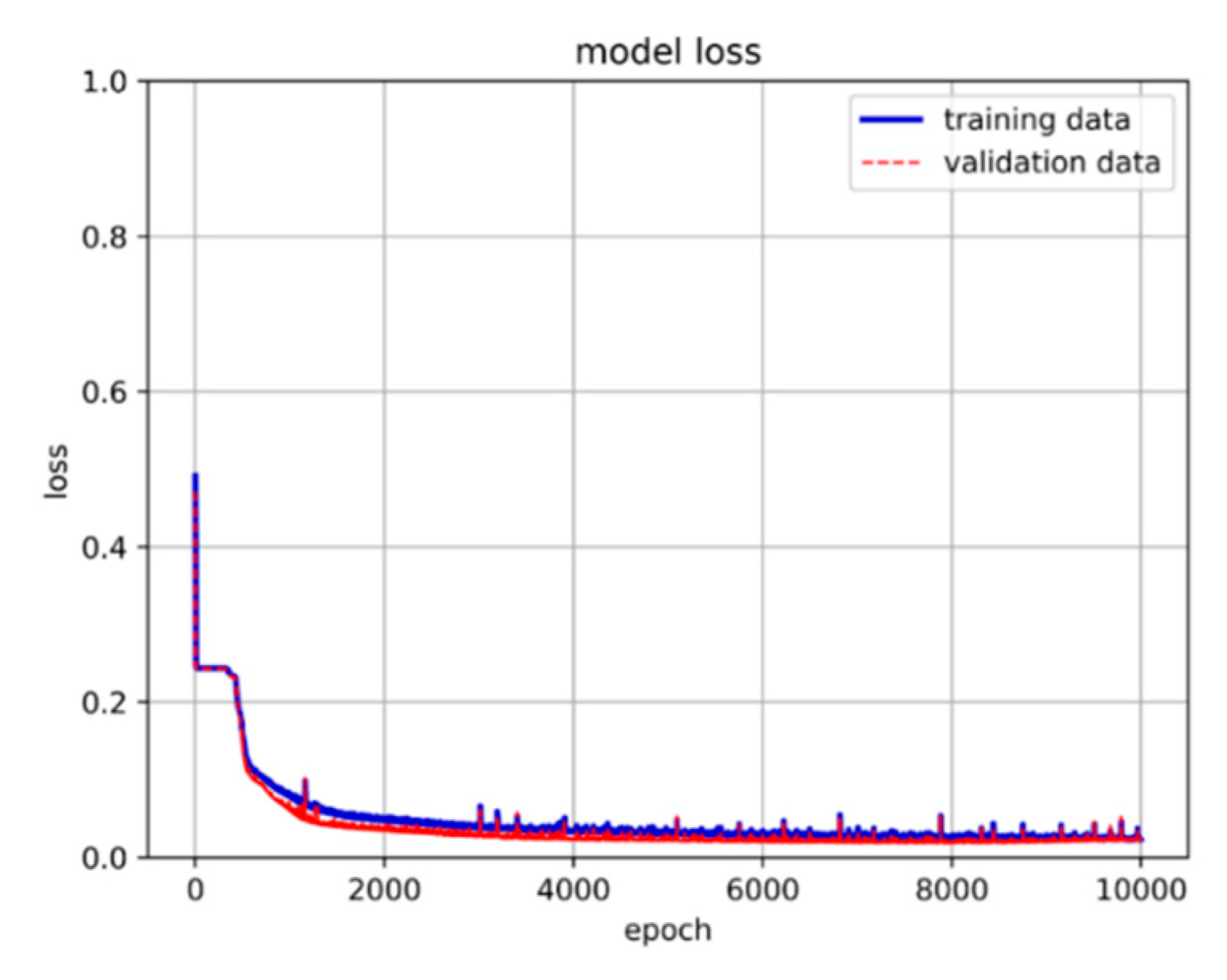
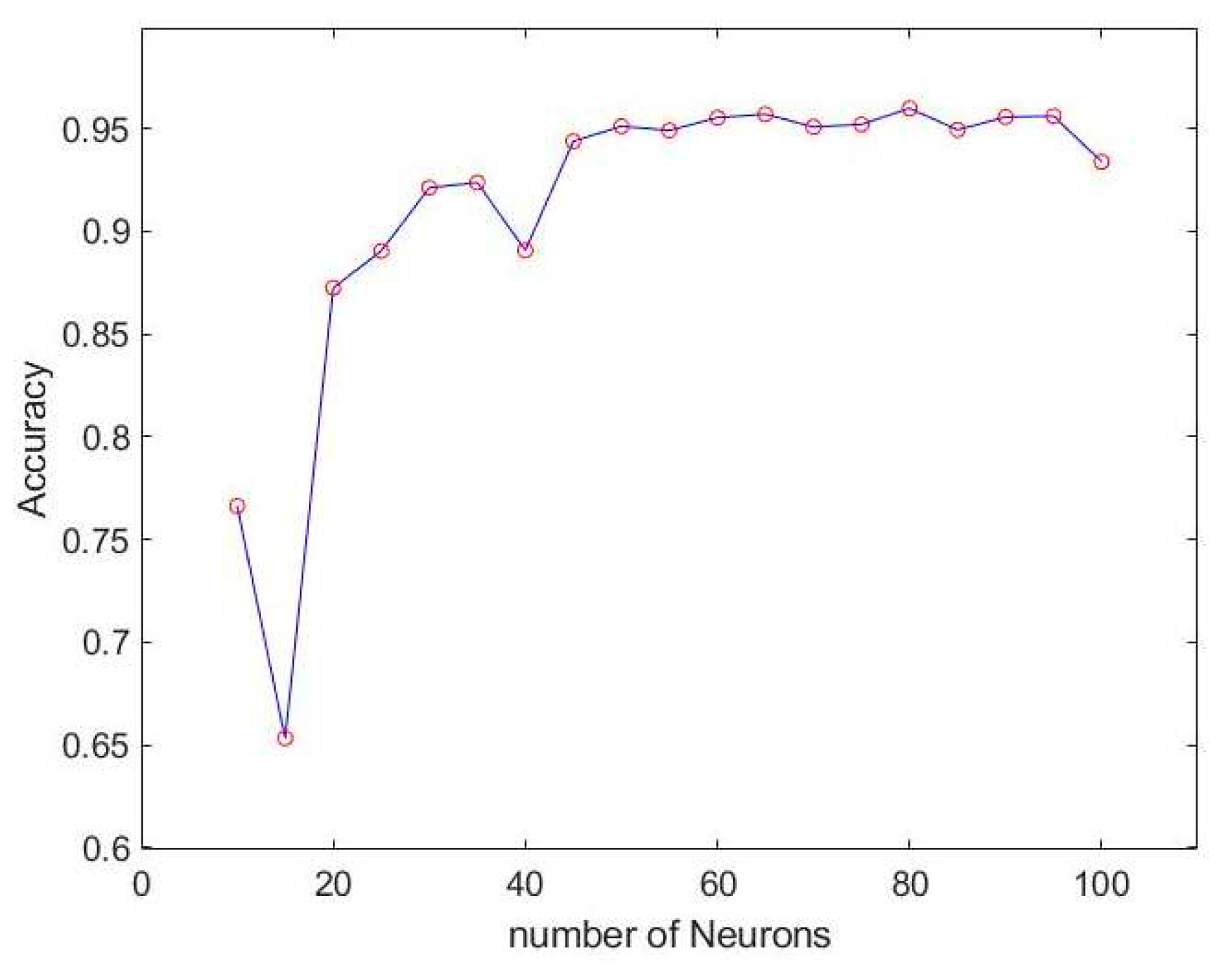
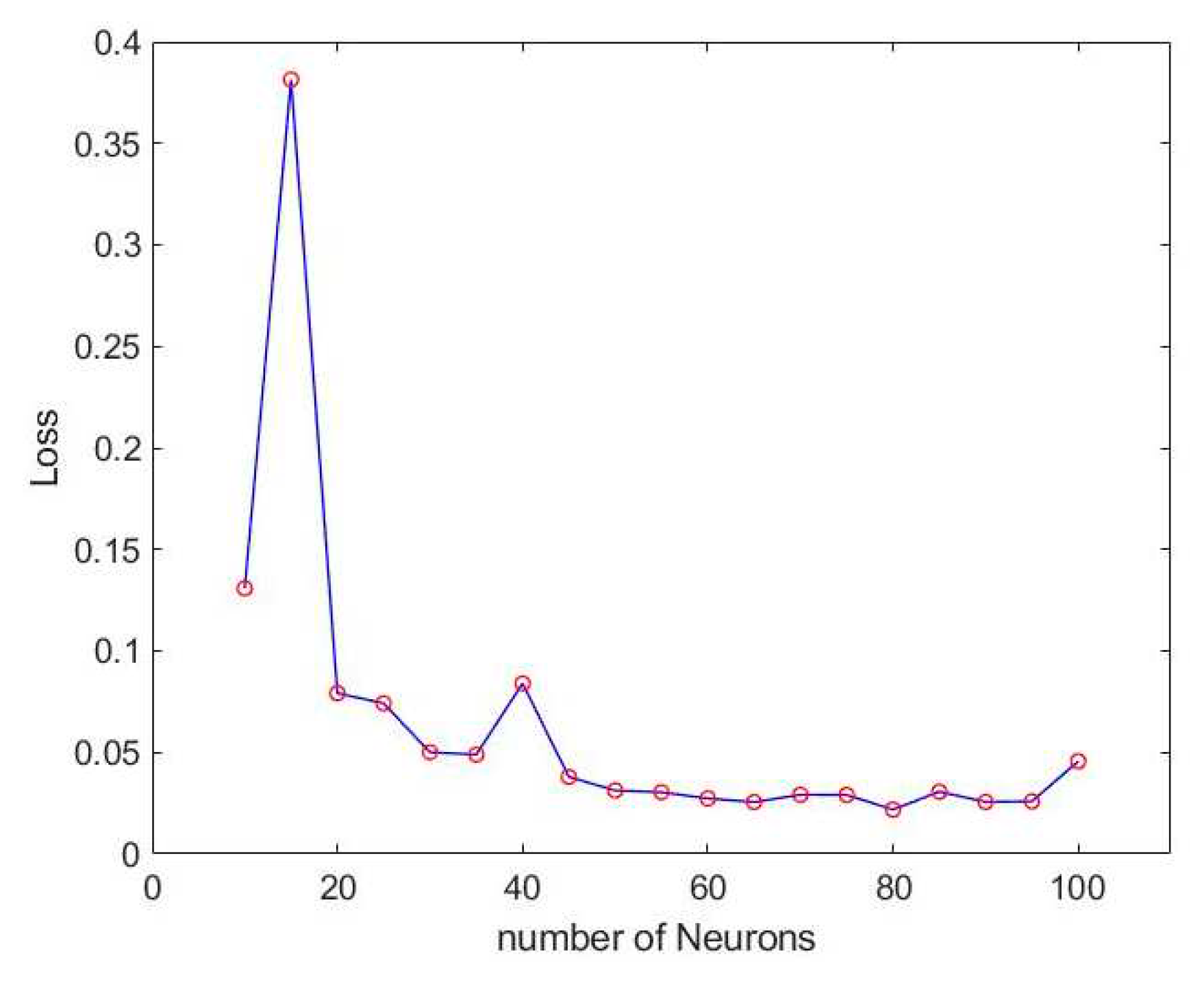
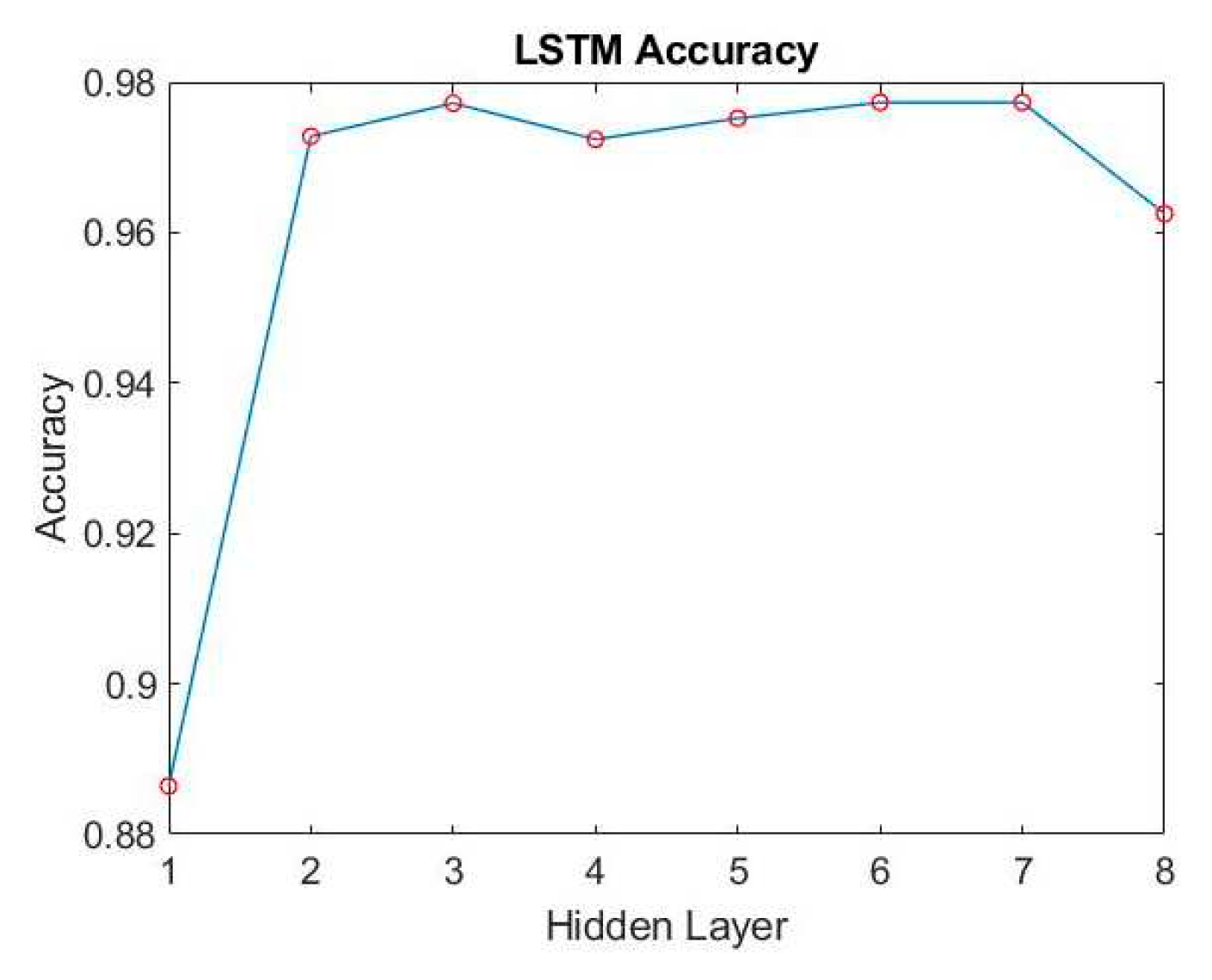
• When training the LSTM model, careful consideration must be given to the number of hidden layers, neurons, and epochs. While increasing these parameters may lead to improvements on the training set, there is a risk of overfitting on the validation set. Therefore, selecting the optimal number of layers, neurons, and epochs is essential to ensure efficient training and optimal performance on both the training and validation sets.
• To address the issue of over-reliance on training data and mitigate overfitting, incorporating a dropout layer into the basic model structure is recommended. The dropout layer enhances training stability by preventing excessive dependence on specific neurons, reducing the risk of overfitting.
• When selecting computing hardware for LSTM model training, using a GPU can significantly reduce the training time. GPUs are equipped with more cores and higher memory bandwidth, facilitating parallel execution of multiple matrix operations. This characteristic makes GPUs highly suitable for training deep learning models, efficiently handling the extensive computations involved in these models. Consequently, opting for GPU acceleration can lead to substantial time savings during LSTM model training.
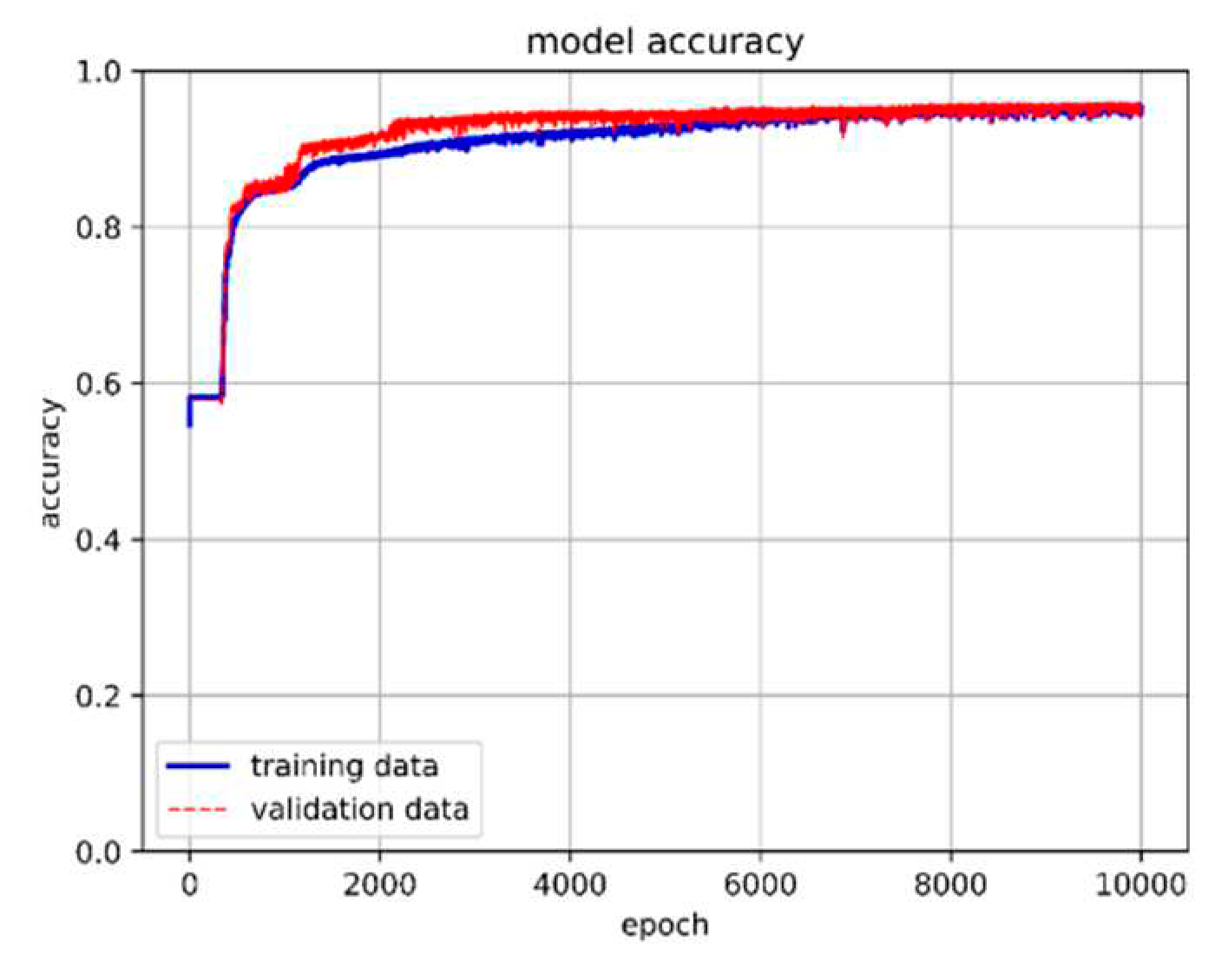
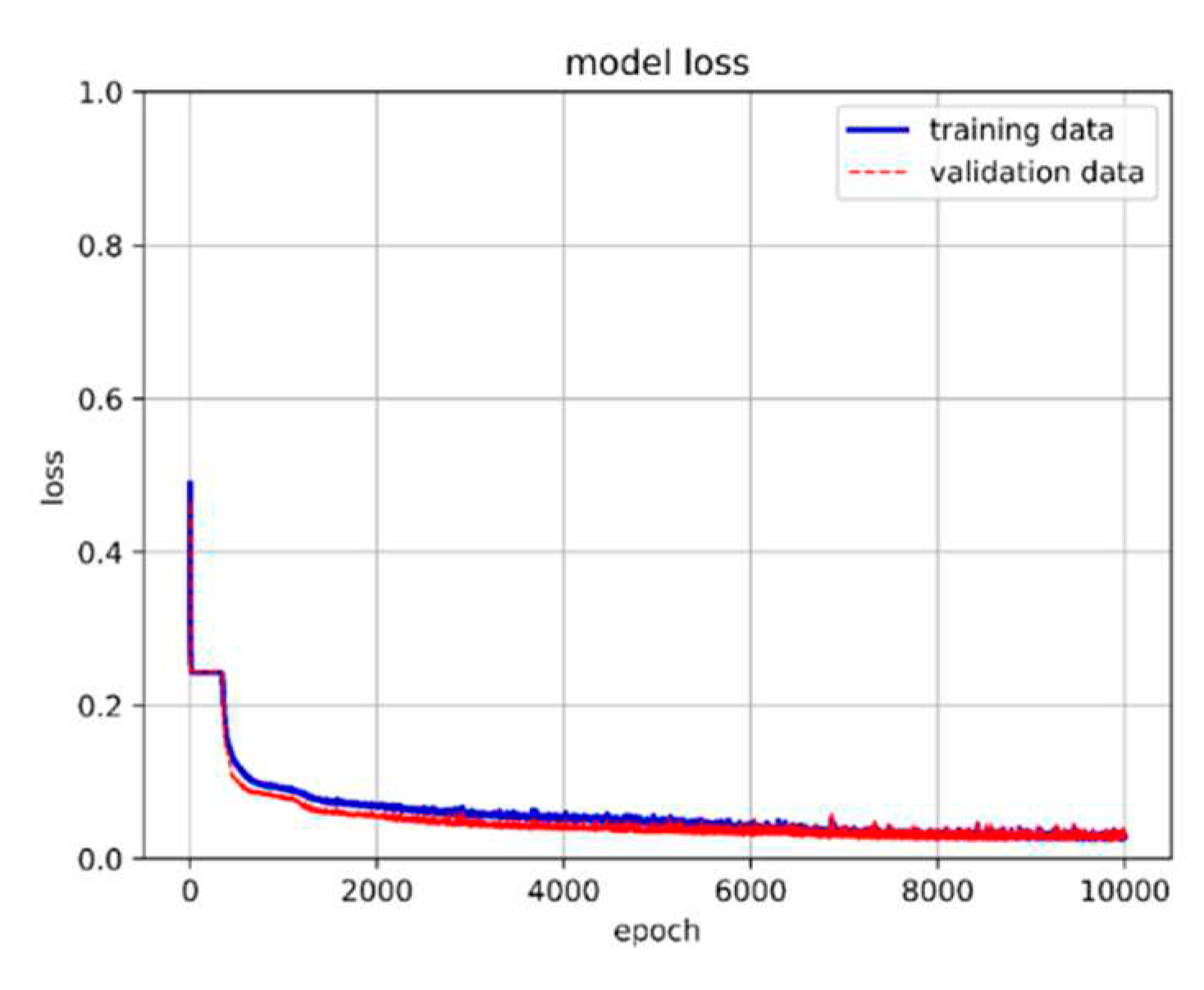
• In this study, LSTM models were employed to train a specific dataset of undamped and unforced Duffing equation convergence results. The achieved accuracy was 95%, although it exhibited some fluctuations. To address this, neural network hidden layers were incorporated into the LSTM model, creating the LSTM-NN model. This modification improved the accuracy to 96% and mitigated the issue of accuracy fluctuations. However, it is worth noting that the increased number of hidden layers resulted in longer training times.
• In this study, the LSTM model was utilized to train a dataset containing convergence results of the Duffing equation with damping and external forces, focusing on single-cycle solutions. The accuracy achieved was 97.5% with fast training speed. By incorporating hidden layers of neurons (LSTM-NN), the training accuracy increased to 98% with lower loss. However, it is important to acknowledge that training time was prolonged due to the inclusion of a larger number of hidden layers.
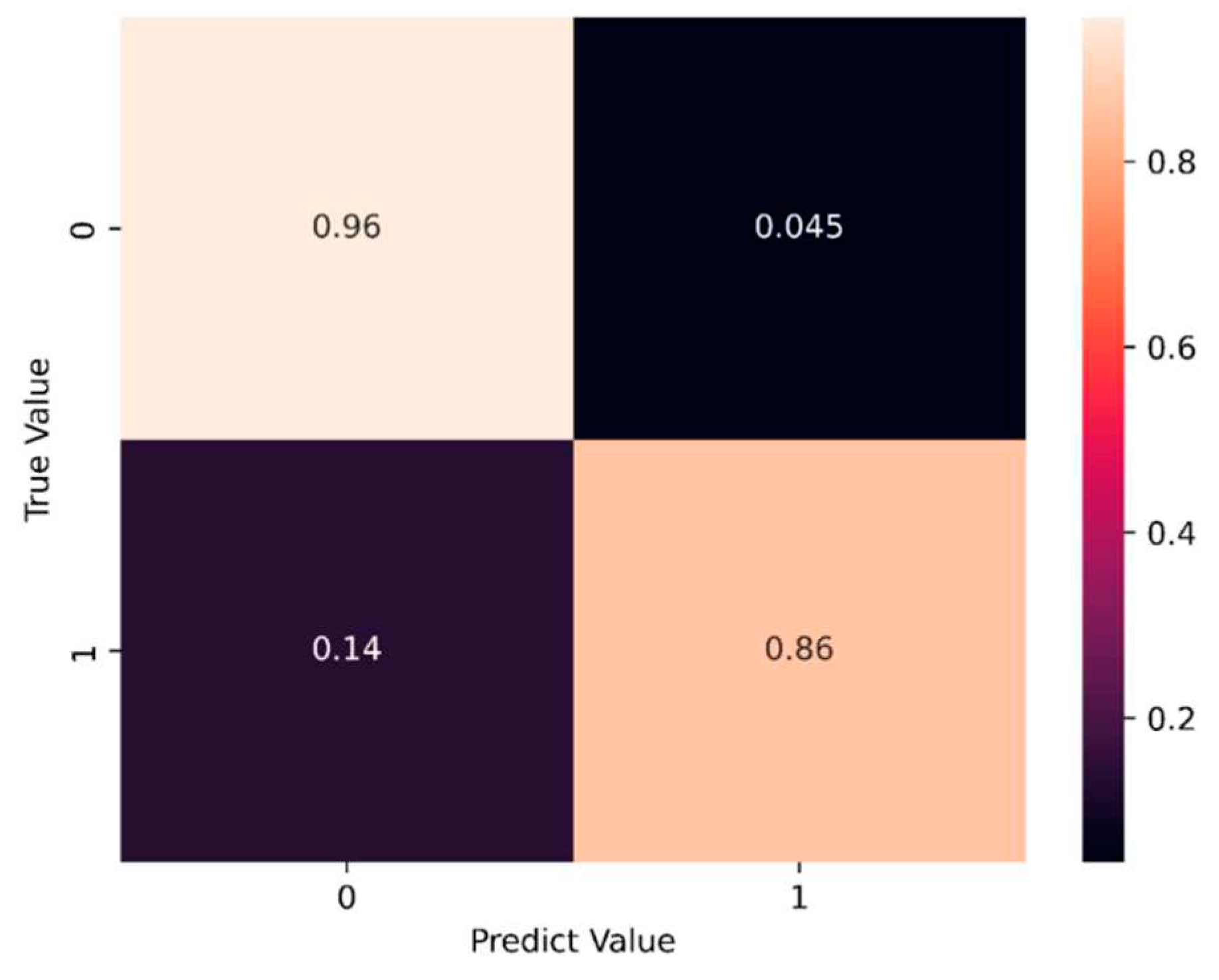
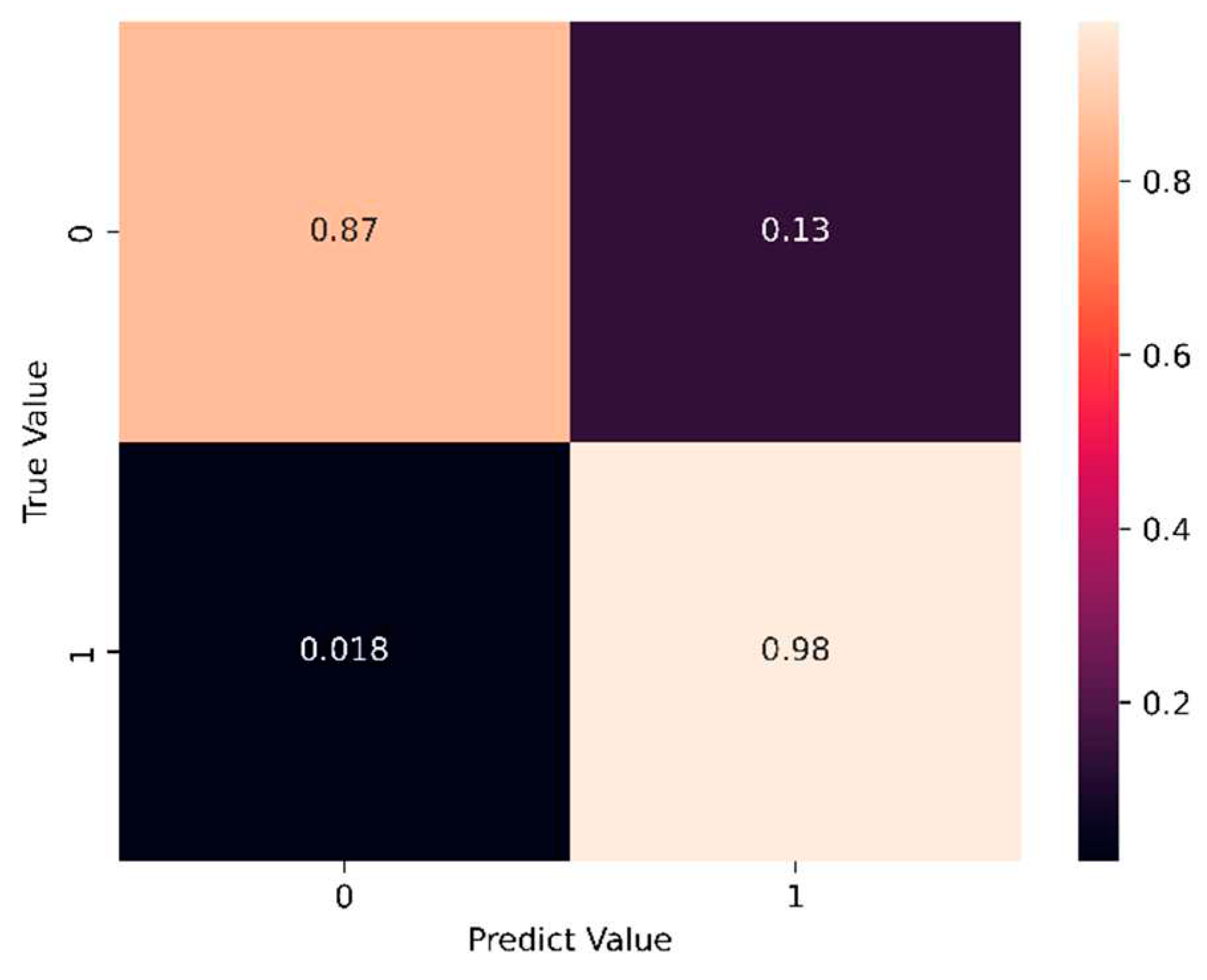
• The LSTM model established in this study can predict the special case of the convergence result of the Duffing equation without damping and no external force. When the predicted value is +1, the accuracy reaches 96%, and when the value is -1, the accuracy also reaches 86%. The model with a hidden layer of neurons was 87% accurate on +1 predictions and 98% accurate on -1 predictions. The LSTM model after adding the hidden layer of neurons (LSTM-NN) is more suitable for predicting binary data sets.
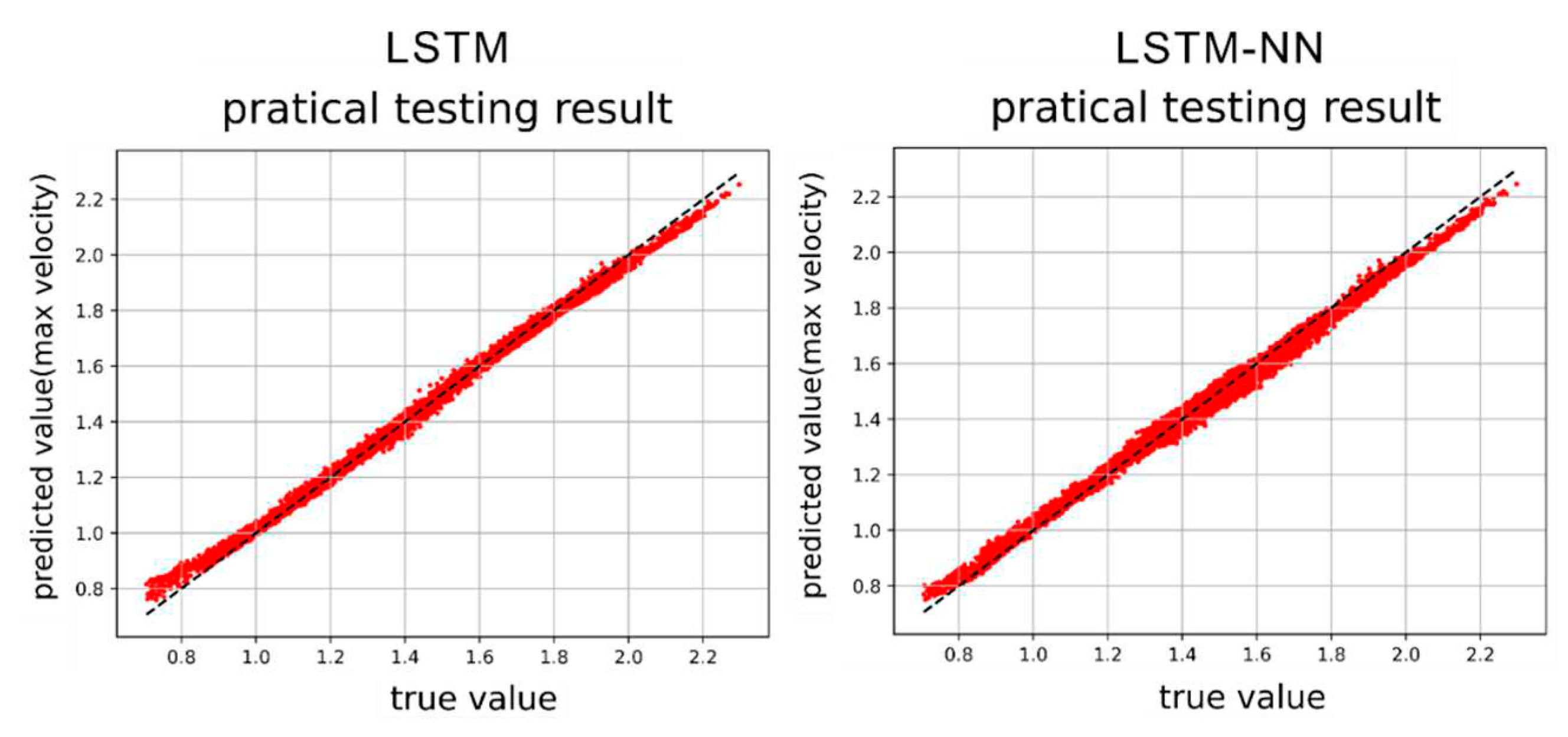
• The LSTM model established in this study has a large deviation in the predicted displacement range when predicting the convergence range of the single-cycle Duffing equation containing damping and external forces, but has better performance in predicting the range of velocity (the case of multi-solution prediction). The model after adding the neuron hidden layer (LSTM-NN) also has the same situation, but the prediction accuracy is lower than that of the general LSTM model.