Prerpints.org logo
Preprint
Article

An Adaptive Partial Least Square Regression Approach for Classifying Chicken Egg Fertility by Hyperspectral Imaging

Altmetrics

Downloads

114

Views

45

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

09 August 2023

Posted:

10 August 2023

You are already at the latest version

Alerts
Abstract
Partial least square (PLS) regression is a well-known chemometric method used for predictive modelling, especially in the presence of many variables. Although PLS was not initially developed as a technique for classification tasks, scientists have reportedly used this approach successfully for discrimination purposes. Whereas some non-supervised learning approaches including but not limited to PCA, and k-means clustering do well in identifying/understanding grouping and clustering patterns in multidimensional data, they are limited when the end target is discrimination, making PLS a preferable alternative. A total of fertilized 672 chicken egg hyperspectral imaging data, consisting of 336 white eggs and 336 brown eggs were used in this study. Hyperspectral images in the NIR region of 900-1700 nm wavelength range were captured prior to incubation on day 0 and on days 1-4 after incubation. Eggs were candled on incubation day 5 and broken out on day 10 to confirm fertility. While a total number of 312 and 314 eggs were found to be fertile in the brown and white egg batches respectively, total numbers of non-fertile eggs in the same set of batches were 23 and 21 respectively. Spectral information was extracted from a segmented region of interest (ROI) of each hyperspectral image and spectral transmission characteristics were obtained by averaging the spectral information. A moving-thresholding technique was implemented for discrimination based on PLS regression results on the calibration set. With true positive rates (TPR) of up to 100% obtained at selected threshold values of between 0.50-0.85 and on different days of incubation, the results indicated that the proposed PLS technique can accurately discriminate between fertile and non-fertile eggs. The adaptive PLS approach was thereby presented as suitable for handling hyperspectral imaging-based chicken egg fertility data
Keywords: 
Subject: Engineering  -   Bioengineering

1. Introduction

Out of 13.1 billion hatching eggs produced in the U.S. egg industry for the year 2005, the ratio of layer to broiler eggs produced was reported to be around 12:1, creating different degrees of discriminating tasks to both layers and broilers industries. With fertility rates in the range of 60 to 90% (Lawrence et al., 2007; NASS, 2006), there could be about 1.3 billion to over 5 billion infertile eggs being incubated yearly. According to the Agriculture and Agri-Food Canada report 2013, total hatching egg product was set at 798.3 million, resulting in a minimum of about 80 million non-fertile eggs being incubated annually in Canada alone which is worth a whopping sum of about $27.6 million being lost annually. Furthermore, discarding of non-hatching eggs has consistently posed significant disposal problems for the hatcheries, especially in the case of exploder eggs in hatching cabinet, resulting in high tendency of molds and bacteria infestation to other eggs (Lawrence et al., 2007). Thus, identification and isolation of infertile eggs from fertile eggs have significant economic and safety implications for commercial broiler breeders.
Recent researches indeed have supported the great potential applications of Hyperspectral imaging as a non-destructive method for assessing fertility/hatchability, embryo development and mortality rates in chicken eggs. These studies have however reported mostly on fertility detection of white-shelled chicken eggs with scanty reports on brown eggs and where available, results were not as promising as with white eggs. Also, samples considered in earlier studies were small (Lawrence et al., 2007; Liu and Ngadi, 2013; Smith et al., 2008). Smith et al. (2008) reported low validation and verification accuracies for fertility detection in brown eggs (Validation data sets: 71% for Day 0; 63% for Day 1, 65% for Day 2, 83% for Day 3; Verification data sets: 51% for Day 0 and 50% for Day 3). It was concluded that the Mahalanobis Distance (MD)/Principal Component Analysis (PCA) model used was not adequate for the discrimination. This is of a great concern for the poultry industry as this means large number of fertile eggs would end up being discarded based on such model. Hence, there is indeed an urgent need for more appropriate discrimination technique for egg fertility assessment.
Partial least square (PLS) regression, also commonly known as the Projection to Latent Structure (Swarbrick, 2012) is a widely used technique that have found useful applications in various domains including but not limited to the engineering, medicine, and agriculture. The PLS approach is particularly known for building predictive models with many variables rather than explaining underlying correlations between variables (Yu, 2000). PLS was not initially developed as an approach for statistical classification tasks except for regression; nonetheless, scientists have reportedly used this approach successfully for discrimination purposes (Barker and Rayens, 2003; Briandet et al., 1996; Gottfries et al., 1995; Iizuka and Aishima, 1997; Ortiz et al., 1996). Even though principal component analysis (PCA) is a well-known chemometric method that has recorded notable success as a pre-classification procedure, this success has been reported to be only possible in various application domains because of its favourable disposition to consider the among-groups variability rather than the within-groups variability (Barker and Rayens, 2003). This mode of PCA implementation therefore do not address situation in which the within-groups variability in data, is also of a major concern due to existence of several sub-clusters in a single class, not having the same number of samples (Japkowicz, 2001). The within-class variability occurrence has been reported to have unfavourable consequence on learning algorithms (Yoon and Kwek, 2007). In such situation, PCA has been observed to perform less optimally and thereby presenting PLS as the next applicable alternative. According to (Barker and Rayens, 2003), PLS was reported to have potential of outperforming PCA when within-groups variability dominates the among-groups variability. Additionally, PLS has been judged versatile in solving data structural problems like skew distributions, multicollinearity, and missing regressors condition- all which are peculiar characteristics of hyperspectral imaging data (Cassel et al., 1999).
(Liu and Ngadi, 2013) reported a perfect classification accuracy using PCA and k-means clustering. However, these approaches being non-supervised learning techniques need further confirmation using standard supervised learning algorithm(s). Although some non-supervised learning approaches like the PCA, k-means, k-medians, and hierarchical cluster analysis are superb with identifying/understanding grouping and clustering patterns in multidimensional data, they are limited when the end target is discrimination (Barker and Rayens, 2003). Furthermore, unsupervised classification is always the starting point in any discrimination problem and should necessarily be followed by supervised classification (Abdel-Nour et al., 2009), towards an industrial adoptability consideration.
In view of the foregoing, this study has therefore considered and tested, the suitability of an adaptive supervised learning PLS regression approach, together with a threshold-moving technique, in handling chicken egg fertility hyperspectral imaging data. Classification accuracy have been based on the confusion matrix evaluation criterion at the expense of the more general overall accuracy computation, which has been shown to be inappropriate when dealing with data containing a rare class (Liao, 2008) as with the non-fertile eggs in chicken egg fertility data.

2. Materials and Methods

2.1. Samples

A total of 336 Brown shell eggs and 336 White shell eggs were received from a commercial fertile egg producer (Simetin Hatchery; www.couvoir.com) in 14 batches (48 eggs per batch) over a period of 3 months. There were 7 batches of eggs collected in each group of brown and white egg sets. Table 1 shows the details of the overall egg samples available for analysis on each day of incubation for both brown and white eggs. Out of the total 336 eggs received for both brown and white eggs, the number of total available eggs eventually used for analysis varied with incubation time due to egg breakage during handling. While 2 eggs (1, day 0; 1, day1) were broken from the brown egg batch, a total of 3 eggs (1, day 0; 2, day 3) were broken from the white egg batch. This variation in total available eggs during analysis results into a slightly different degree of imbalance from one day of incubation to another. The ratio of non-fertile to fertile eggs in this study is estimated from Table 1 to be 1:13 and 1:15 for both brown and white eggs respectively.

2.2. Image acquisition and processing

A laboratory near-infrared (NIR) hyperspectral imaging system used in this project comprised of an InGaAs camera, a conveyor (Donner 2200 series, Donner Mfg. Corp., USA) driven by a stepping motor (MDIP22314, Intelligent motion system Inc., USA), a line-scan spectrograph (HyperspecTM, Headwall Photonics Inc. USA) with a NIR spectral wavelength range from 900 to 1700 nm and a spectral resolution of 4.79 nm, a tungsten halogen lamp (50 W) providing back illumination to eggs, an enclosure supporting the system, a data acquisition and pre-processing software (Hyperspec, Headwall Photonics Inc. USA) and a PC. All eggs were first imaged by the hyperspectral imaging system on Day 0 (just prior to incubation) and immediately after imaging, the eggs were incubated in an Ova-Easy 190 Advance Series II Cabinet Incubator (Brinsea Products Inc., Florida, USA) at 37.78°C (100°F) and 55% relative humidity. The eggs were automatically turned every hour. On days 1, 2, 3, and 4 of incubation, eggs were removed for imaging in sequence and then immediately returned into the incubator, in a process of about 1 min.
After 10 days of incubation, eggs were candled and broken out to determine fertility. The output hypercube image obtained is 800 rows x 320 columns x 167 bands. The region of interest (ROI) of obtained spectral images was individual egg of each sample image. The ROI was selected at maximum wavelength band 37 (1071 nm) and punched through other wave bands. A mask was created for each individual egg to segment it from the original spectral image that normally included four eggs. Segmented individual eggs were then used for calculating mean spectra, following standard procedures.

2.3. Spectral transmission and feature extraction

Spectral transmission characteristic namely Mean Spectral, MS and extracted features based on thresholding were used in this study for further data analysis. MS stands for the mean value of all pixels in ROI for the current wavelength over the spectral range of 900-1700 nm. Threshold-moving method has been used in cost-sensitive neural networks learning with reported good effectiveness even with highly imbalanced data sets. More detailed explanation of this method is as described by (Longadge and Dongre, 2013; Williams et al., 2009). Threshold (TR) values considered for extraction of features in the present work ranged between 0.50 - 0.85. The purpose of adopting thresholding technique in conjunction with PLS algorithm was to extract useful spectral features to facilitate the discrimination of fertile eggs from non-fertile eggs. With the choice of an appropriate threshold value, a new set of features with the potential of achieving optimal classification accuracy is extracted for analysis, and discrimination performance was then evaluated using the confusion matrix evaluation criterion. All operations were performed in the MATLAB R2014a (The MathWorks, Inc., MA, USA) platform.

2.4. Partial least square regression analysis

For the different days of egg incubation, a PLS code written in the MATLAB R2014a environment was used for data analysis and full cross validation was later employed as a means of internal validation in all cases. Unlike the popular multiple linear regression (MLR) which is prone to the problem of over-fitting in the presence of too many factors, PLS analysis do adjust to over- fitting problem by extracting only the latent factors accounting for majority of the manifest factor variation (Tobias, 1995). Not only this, PLS is well known for analyzing data with strongly collinear (correlated), noisy, and numerous X-variables. The PLS analysis as adopted in this study models both the X- and Y-matrices simultaneously (thereby maximizing the covariance between X and Y) to reveal the latent variables in X, having the potential of predicting accurately the latent variables in Y (Wold et al., 2001). Unlike the PCA, which decomposes X to obtain components that explains most variability in X, PLS seeks to identify components from X that best predict Y (Abdi, 2010).

2.4.1. Choice of optimal number of PLS components (PCs)

PLS modelling process is greatly influenced by only few underlying (latent) variables; whereas, the appropriate number of these latent variables is usually unknown. One major aim of PLS analysis therefore was to estimate this number (Wold et al., 2001) and in doing so, it becomes very critical to identify an optimum value for the user- defined number “n” of PLS components (PCs). which is directly related to the selection of informative features required for accurate discrimination process. This study have followed the full (leave one out) cross-validation (CV) procedure reported by (Wold et al., 2001) in testing the predictive performance of PLS components and stopping when adding more components tends to reduce performance. Detailed explanation of this procedure has been described elsewhere (Clark and Cramer, 1993; Höskuldsson, 1988, 1996; Wakeling and Morris, 1993; Wold et al., 1993). Nevertheless, because the end goal in this study is discrimination and not regression, the traditional interpretation of the CV procedure cannot be applied directly in entirety and the reason why the confusion matrix criterion was adopted for evaluating discrimination performance. PCs ranging from n = 5 to n = 50 (in interval of 5) were tested for classification accuracy before arriving at an optimum value for “n”. The threshold for initial feature extraction was chosen to be 0.80 from preliminary trial and error analysis. This threshold was subsequently used in predictive performance testing for determining optimum number of PCs.

2.4.2. Criteria for evaluating discrimination performance

Overall accuracy has been presented as inappropriate for measuring classifier performance in the situation consisting of a rare class data (Liao, 2008; Nguyen et al., 2009). The present study has therefore adopted the confusion matrix evaluation criterion for a binary-class egg fertility discrimination problem. In a binary class classification situation, the particular class with very few training samples but with high identification importance is commonly referred to as the positive class and the other as the negative class (Sun et al., 2009). This definition however seems not to be directly applicable to most Agricultural and food processing operations. Even though non-fertile eggs in this research belongs to the rare class (very few training examples), fertile eggs of the majority class are of higher identification importance, from the hatchery industries point of view. Therefore, Agricultural and food processing applications might not fit in directly to the definition of positive class being the class with very few training samples and simultaneously of higher recognition importance. Nonetheless, in this first study, we have maintained taking non-fertile eggs as the positive class not only because they fall into the minority class, but also that the future industrial instrumentation for egg fertility assessment might be much more economically built and viable to reject non-fertile eggs (fewer samples) than accepting fertile eggs (larger number of samples). The choice of our true positive class in this first study is critical to be able to examine our results while maintaining conventional consistency. The confusion matrix employed for the interpretation of the PLS analysis and hence determining classification accuracy is as shown in Table 2, where TPR, FPR, TNR, and FNR represent the rate in percentage of true positive examples, the rate in percentage of false positive examples, the rate in percentage of true negative examples, and the rate in percentage of false negative examples, respectively. If TP = True positive (number of non-fertile eggs classified as non-fertile), TN= True negative (number of fertile eggs classified as fertile), FP= False positive (number of fertile eggs classified as non-fertile), and FN=False negative (number of non-fertile eggs classified as fertile), the following equations as reported in (François, 2006; Sokolova and Lapalme, 2009; Sun et al., 2009) can be obtained and the traditional overall accuracy (OVA), including the error rate (ERR) can also be computed as:
TPR = TP/ (TP+FN) * 100
TNR = TN/(TN+FP) * 100
FPR = FP/ (FP+TN) * 100
FNR = FN/ (FN+TP) * 100
OVA = (TP+TN)/ (TP+FN+FP+TN) * 100
ERR = (FP+FN)/ (TP+FN+FP+TN) * 100

2.5. Results and Discussion

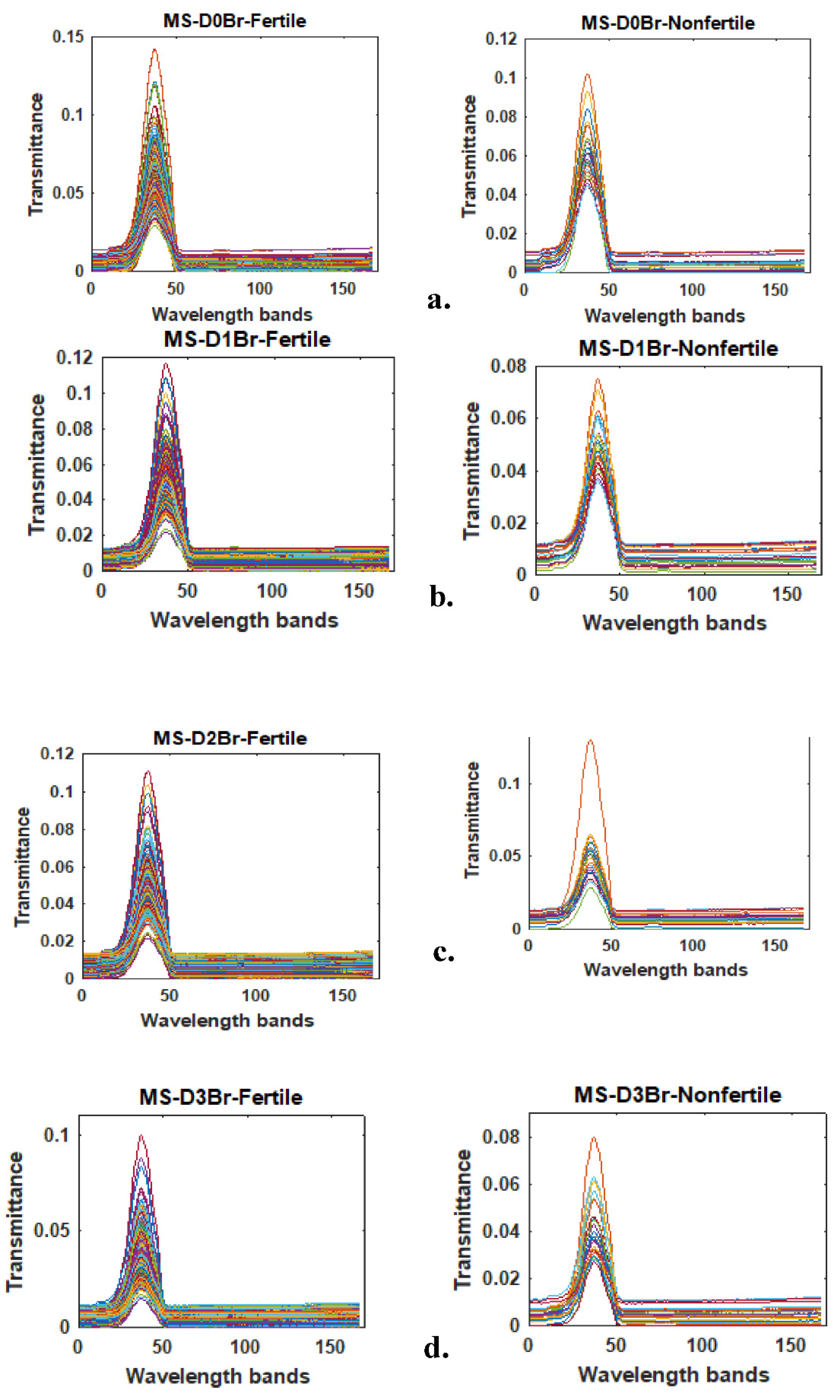
While a total number of 312 and 314 eggs were found to be fertile (F) in the brown and white egg batches respectively, total numbers of non-fertile (NF) eggs in the same set of batches were 23 and 21 respectively (see Table 1), at the start of our analysis. Figure 1 showed typical transmittance MS profiles of brown eggs, on different days of incubation. It was observed from Figure 1 that fertile eggs maximum transmittance intensity decreases as incubation period increases from day 0 through day 3. This observation seems related to the onset of active molecular activities from meiotic and mitotic cell divisions in the fertile eggs. Knowing that the proportion of light absorbed by any material is dependent on the quantity of molecules involved in molecular interaction, fertile eggs tend to absorb more light at different wavelengths as incubation period progresses, and hence the amount of light being transmitted decreases accordingly. Non-fertile eggs transmission intensity over the considered incubation periods did not follow a definite trend. The initial decrease in maximum transmittance intensity from day 0 to day 1 might as well be related to the molecular interactions from meiotic cellular division. As meiosis process terminated in the non-fertile eggs, further cell division also ceased, since there was no fertilization to trigger on the onset of mitotic cell division. Therefore, subsequent egg maximum intensity increase, and later decrease can be attributed to the degree of albumen-yolk solution concentration, and this is dependent on the rate of yolk dissolution into the albumen under incubation conditions. From Beer’s law, solution concentration is directly proportional to light’s absorption (Norris, 1996; Williams and Norris, 1987) up to a specific level, as the law failed at some higher concentrations.
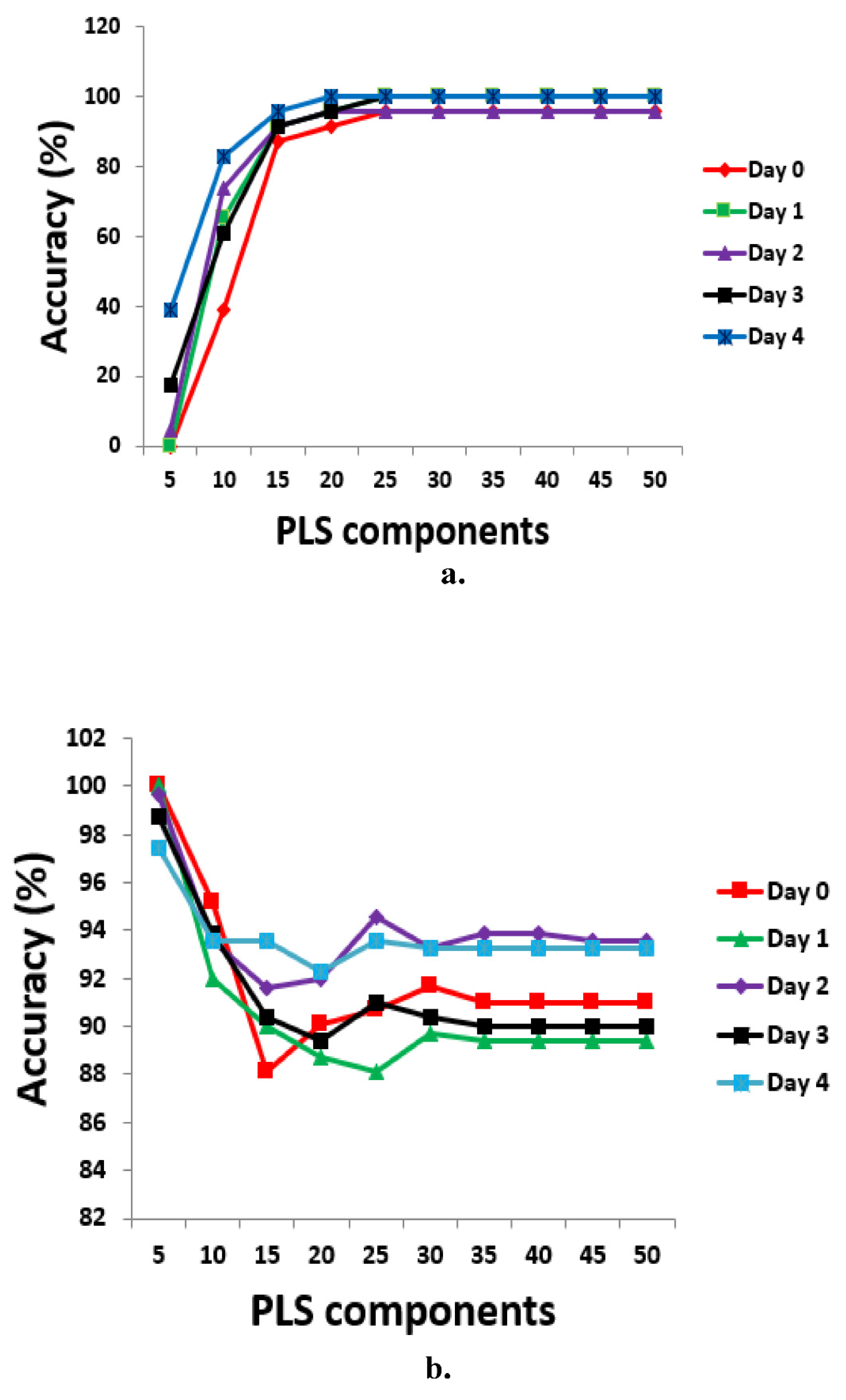
Using brown eggs data, Figure 2 shows the predictive performance chart for determining optimum number of PLS components for different days of egg incubation. The TPR performance chart (Figure 2a) showed that adding more components above 25 does not bring any further improvement in classification accuracy. 25 PLS components were then chosen for feature extraction and subsequent discrimination based on the TPR performance results. However, if TNR is of greater or equal interest, only the first 5 PLS components will suffice for further feature extraction (see Figure 2b). In the light of the above, further analysis in this study have used both 25 and 5 PLS components at various selected thresholds between 0.50 to 0.80 for feature extraction and eventual classification. Table 3 showed evaluation metrics at threshold point 0.80 for both brown and white eggs, on different days of incubation, and with associated misclassification error rates. 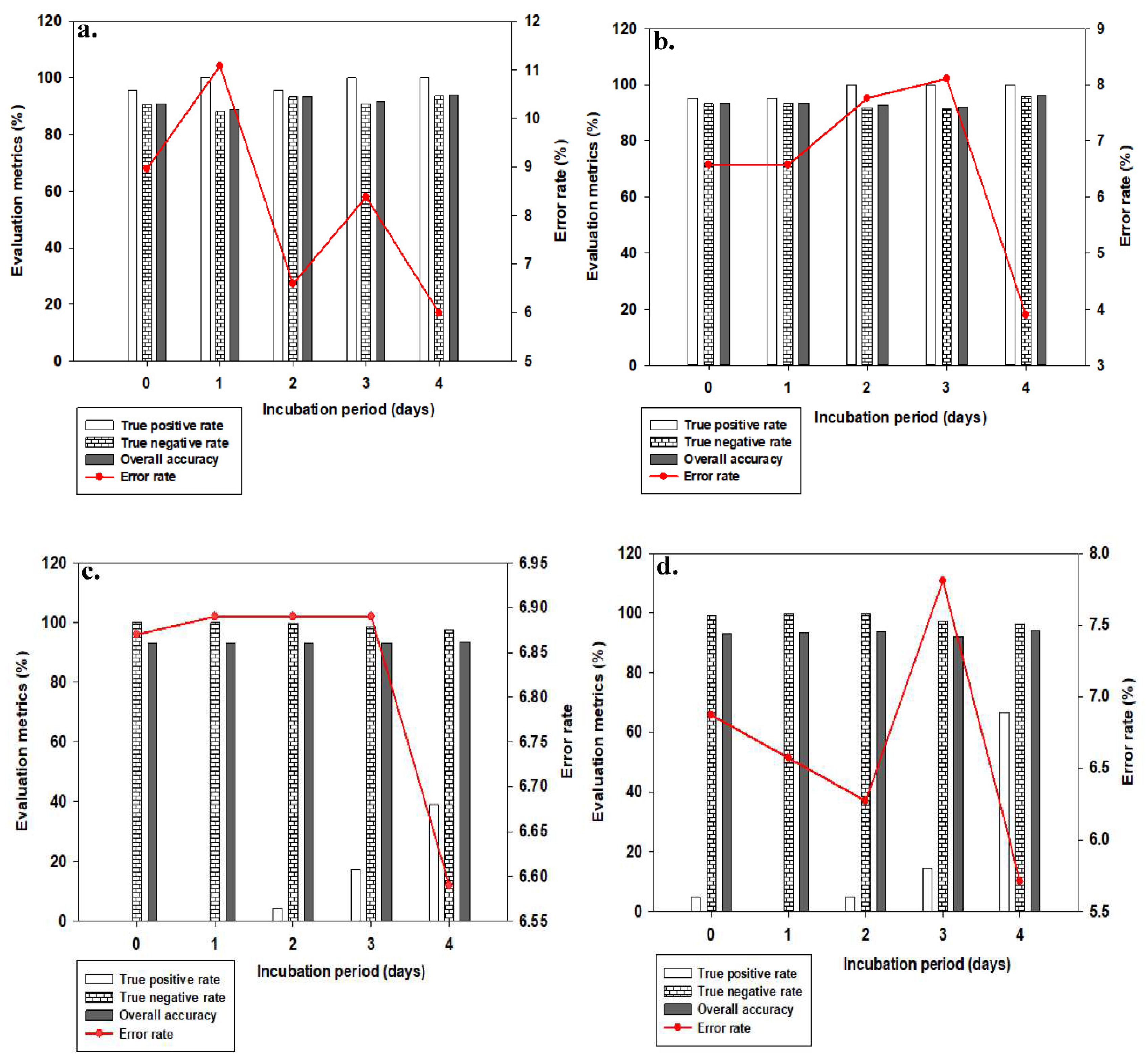Figure 3 showed evaluation metrics at threshold point 0.80 for both brown and white eggs, on different days of incubation, and with associated misclassification error rates.
From Figure 3a,b at 25 PCs, both brown and white eggs achieved 100% TPR accuracy on days 3 and 4. While none of the two sets of eggs achieved 100% TPR accuracy on day 0 incubation, 100% TPR accuracy was also obtained for both brown and white eggs respectively on incubation days 1 and 2. At 5 PCs (Figure 3c,d), none of the two sets of eggs achieved perfect TPR accuracy of 100% on all incubation days considered. 100% TNR accuracy was however obtained on days 0 and 1 for brown eggs, but also at a detrimental 0% TPR corresponding accuracies. Hence, the classifier despite classifying all fertile eggs as fertile, will also end up misclassifying all non-fertile eggs as fertile on these two days of incubation. The least misclassification error rates for the classes of eggs at both number of PCs considered were on day 4 incubation, but this day is already becoming too late for early recognition and classification, leaving us to consider earlier days (especially day 0) more critically. We indeed need a classifier mode that will perform at much closer margin of TPR and TNR accuracies and at the same time using much lesser number of PCs.
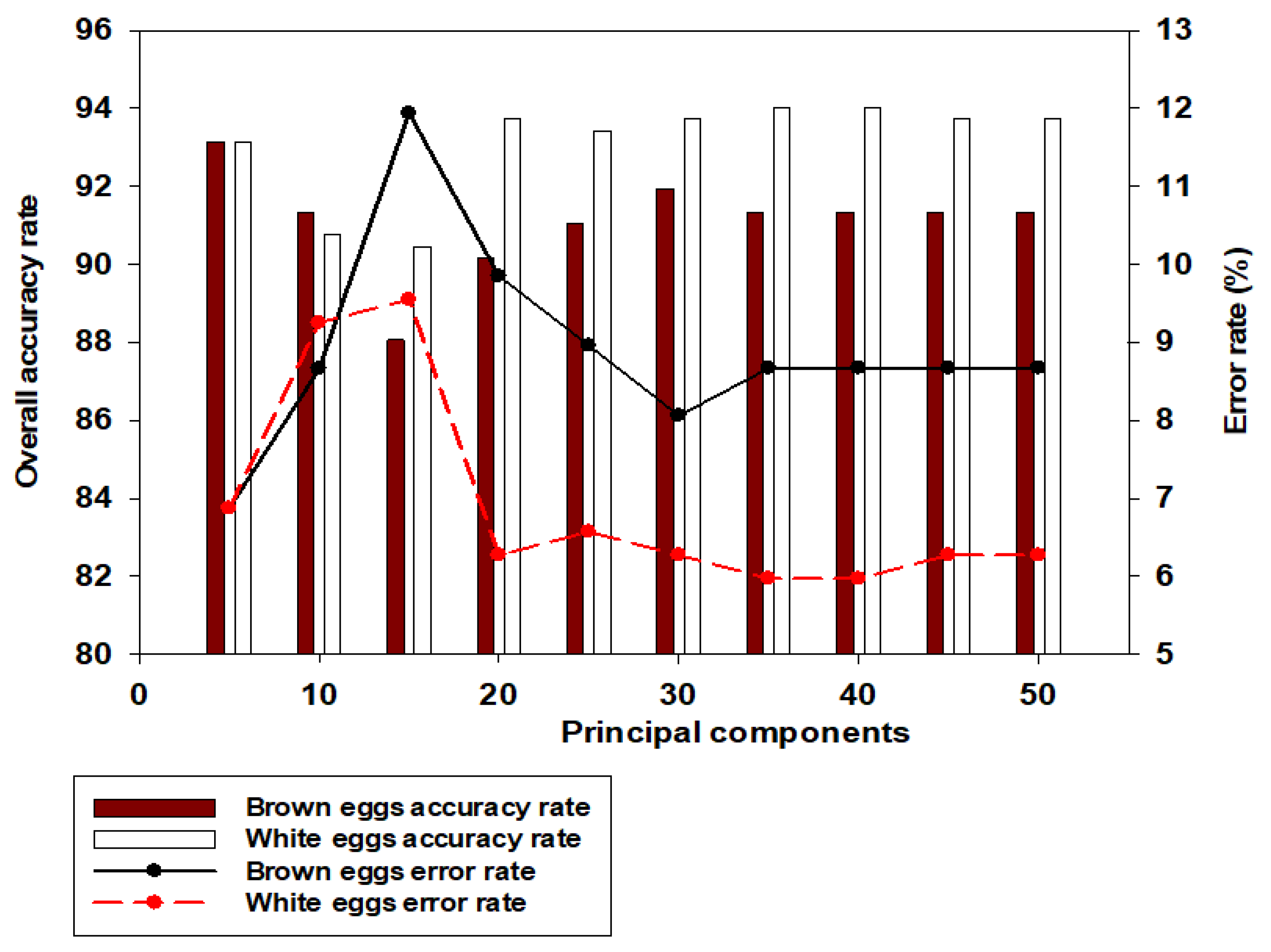
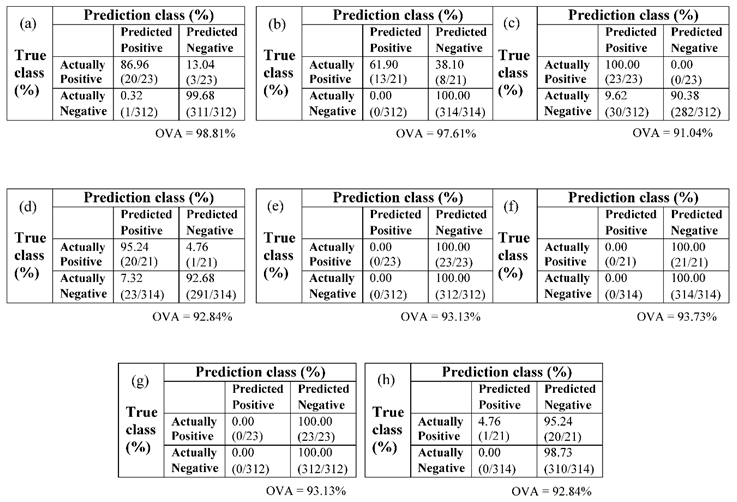
Figure 4 showed model accuracies and error rates on day 0 incubation, for all PCs considered from 5 to 50. It was observed that using PCs above 5 poses risk to model’s robustness, as the misclassification error rates are found to increase after 5PCs. Table 4 showed typical day 0 incubation confusion matrix results at some other selected thresholds 0.81 and 0.55, for both brown and white eggs. Detailed values used for the computation of the confusion matrices is as shown in appendix A. On day 0 of incubation for brown eggs (Table 3.4c), TPR of 100% was achieved at threshold value of 0.81; whereas white eggs achieved TPR classification accuracy of 95.24% at this same threshold (Table 3.4d). Detailed percent classification accuracy information for both brown and white eggs are as shown in appendices A1- A4, for both 25 and 5 PCs respectively. The same TPR classification accuracy of 95.24% was also achieved at TR 0.80 for white eggs, in which only one non-fertile egg was misclassified as fertile (see appendix A2). None of the threshold values considered between 0.50 to 0.85 for the white eggs, on day 0 incubation achieved 100% classification accuracy considering the TPR values. Considering the true negative rates (TNR) however, white eggs achieved accuracy of 100% at four threshold values of 0.5, 0.55, 0.60 and 0.65; whereas brown eggs achieved 99.68, 99.68, 99.68 and 99.04%, respectively at these same thresholds (Appendices A1, A2, and Tables 3.4a, b). For the brown eggs, only one fertile egg was misclassified as non-fertile at thresholds 0.5, 0.55 and 0.60, but three fertile eggs were misclassified as non-fertile at threshold value of 0.65. These results showed that the PLS algorithm used can discriminate both brown and white fertile eggs from non- fertile eggs prior to incubation using any of the thresholds identified.
Table 4. Typical confusion matrix for selected egg models at different thresholds and PCs (a) brown, TR 0.55, PC 25 (b) white, TR 0.55, PC 25 (c) brown, TR 0.81, PC 25 (d) white, TR 0.81, PC 25 (e) brown, TR 0.55, PC 5 (f) white, TR 0.55, PC 5 (g) brown, TR 0.81, PC 5 (h) white, TR 0.81, PC 5.
Table 4. Typical confusion matrix for selected egg models at different thresholds and PCs (a) brown, TR 0.55, PC 25 (b) white, TR 0.55, PC 25 (c) brown, TR 0.81, PC 25 (d) white, TR 0.81, PC 25 (e) brown, TR 0.55, PC 5 (f) white, TR 0.55, PC 5 (g) brown, TR 0.81, PC 5 (h) white, TR 0.81, PC 5.
Preprints 81999 i001
The results shown specifically in Table 4a–d at 25 PCs are promising for both brown and white eggs, considering closer margin of TPR and TNR accuracies. However, models built with 5 PCs as shown in Table 4e–h are much in favour of the prevalent class as can be seen in the TNR perfect accuracies as against the TPR lowest accuracies. This observation has been reported in literatures to be related to imbalanced data phenomenon (He and Garcia, 2009; Mani and Zhang, 2003; Sun et al., 2009) in the considered data sets. Therefore, despite the overall percentage accuracy (OVA) obtained for brown eggs on day 0 incubation at various thresholds from 0.50 through 0.75 at 25 PCs were much higher than that at thresholds 0.80 and 0.81 (see Appendix A1), the final accepted model might not be based on this overall accuracy due to the imbalanced data phenomenon, shifting the overall accuracy performance in favour of the majority class at the expense of the minority class. This is the reason why performance is better judged based on the true positive and/or true negative rates. In the specific situation under discussion, it might be more appropriate to adopt a model based on the 0.81 TR (TPR value of 100%, OVA of 91.04%), than a model based on 0.55 TR (TPR value of 86.96% but OVA of 98.81%). Notwithstanding, if the majority class is also of equal or greater interest, the reverse choice might be preferable in which a model based on the 0.55 TR (TNR 99.68%, OVA 98.81%) would be adopted over that based on TR 0.81 (TNR 90.38%, OVA 91.04). Also see Table 4a,c. Our study has clearly shown that the adapted PLS regression algorithm is adequate for handling chicken egg classification task. There is however a need to improve its present implementation mode, in relation to handling imbalanced data, towards achieving a better trade off between TPR and TNR accuracies, and at the same time favouring the use of lesser number of PLS components.

2.6. Conclusion

This paper has presented the details of a study carried out to investigate the appropriateness of a PLS regression-based technique to classify chicken egg fertility data. Up to ten different set of features were extracted based on threshold selections. PLS regression (with an internal full cross validation procedure) analysis was implemented and tested for discrimination accuracy using the confusion matrix evaluation criterion. While 25 PCs were found suitable for accurate classification based on the true positive rates computation, only 5 PCs proved appropriate using the true negative and misclassification error rate computations. The analysis results showed that the adapted PLS regression algorithm can discriminate both brown and white fertile eggs from non-fertile eggs prior to incubation and on different days of incubation using the moving thresholding selection technique. It was further observed that recognising appropriately non-fertile eggs (TPR of 100%) with an acceptable matching up recognition accuracy of fertile eggs would need up to 25 PCs. However, models built with 5 PCs shifted recognition accuracies to be mostly in favour of the majority fertile egg class at the expense of the rare class non-fertile eggs. This scenario has been widely reported in literatures to be related to imbalanced data problem. We therefore need a classifier mode that will perform at much closer margin of TPR and TNR accuracies and at the same time using much lesser number of PCs. This study has clearly shown that the adapted PLS regression algorithm is adequate for handling chicken egg classification task, there is however a need to improve its present implementation mode, in relation to handling imbalanced data, towards achieving a better tradeoff between TPR and TNR accuracies, and at the same time optimizing the use of adequate number of PCs. Addressing the limitation in the present research outcome would be the major focus of our subsequent study.

Appendix A

Table A1. Percent classification accuracy for brown eggs based on 25 PLS components.
Table A1. Percent classification accuracy for brown eggs based on 25 PLS components.
INC. DAY TR FP FN TP TN TPR (%) TNR (%) OVA (%)
Day 0 0.5 1 8 15 311 65.22 99.68 97.31
F = 312 0.55 1 3 20 311 86.96 99.68 98.81
NF = 23 0.60 1 3 20 311 86.96 99.68 98.81
T = 335 0.65 3 3 20 309 86.96 99.04 98.21
0.70 12 3 20 300 86.96 96.15 95.52
0.75 14 1 22 298 95.65 95.51 95.52
0.80 29 1 22 283 95.65 90.71 91.04
0.81 30 0 23 282 100 90.38 91.04
Day 1 0.5 0 10 13 311 56.52 100 97.01
F = 311 0.55 0 8 15 311 65.22 100 97.6
NF = 23 0.60 1 4 19 310 82.61 99.68 98.5
T = 334 0.65 3 2 21 308 91.3 99.04 98.5
0.70 6 1 22 305 95.65 98.07 97.9
0.75 16 1 22 295 95.65 94.86 94.91
0.79 32 1 22 279 95.65 89.71 90.12
0.80 37 0 23 274 100 88.1 88.92
Day 2 0.5 0 4 19 311 82.61 100 98.8
F = 311 0.55 0 3 20 311 86.96 100 99.1
NF = 23 0.60 0 1 22 311 95.65 100 99.7
T = 334 0.65 0 1 22 311 95.65 100 99.7
0.70 2 1 22 309 95.65 99.36 99.1
0.75 8 1 22 303 95.65 97.43 97.31
0.79 18 1 22 293 95.65 94.21 94.31
0.80 21 1 22 290 95.65 93.25 93.41
Day 3 0.5 0 7 16 311 69.57 100 97.9
F = 311 0.55 0 7 16 311 69.57 100 97.9
NF = 23 0.60 0 6 17 311 73.91 100 98.2
T = 334 0.65 1 4 19 310 82.61 99.68 98.5
0.70 5 3 20 306 86.96 98.39 97.6
0.75 15 2 21 296 91.3 95.18 94.91
0.79 25 0 23 286 100 91.96 92.51
0.80 28 0 23 283 100 91 91.62
Day 4 0.5 0 6 17 311 73.91 100 98.2
F = 311 0.55 0 5 18 311 78.26 100 98.5
NF = 23 0.60 0 5 18 311 78.26 100 98.5
T = 334 0.65 1 3 20 310 86.96 99.68 98.8
0.70 4 0 23 307 100 98.71 98.8
0.75 13 0 23 298 100 95.82 96.11
0.79 17 0 23 294 100 94.53 94.91
0.80 20 0 23 291 100 93.57 94.01
Table A2. Percent classification accuracy for white eggs based on 25 PLS components.
Table A2. Percent classification accuracy for white eggs based on 25 PLS components.
INC. DAY TR FP FN TP TN TPR (%) TNR (%) OVA (%)
Day 0 0.5 0 10 11 314 52.38 100 97.01
F = 314 0.55 0 8 13 314 61.9 100 97.61
NF = 21 0.60 0 7 14 314 66.67 100 97.91
T = 335 0.65 0 6 15 314 71.43 100 98.21
0.70 2 3 18 312 85.71 99.36 98.51
0.75 7 3 18 307 85.71 97.77 97.01
0.80 21 1 20 293 95.24 93.31 93.43
0.81 23 1 20 291 95.24 92.68 92.84
Day 1 0.5 0 5 16 314 76.19 100 98.51
F = 314 0.55 0 3 18 314 85.71 100 99.1
NF = 21 0.60 1 3 18 313 85.71 99.68 98.81
T = 335 0.65 2 2 19 312 90.48 99.36 98.81
0.70 6 2 19 308 90.48 98.09 97.61
0.75 10 1 20 304 95.24 96.82 96.72
0.80 21 1 20 293 95.24 93.31 93.43
0.81 26 1 20 288 95.24 91.72 91.94
Day 2 0.5 0 8 13 314 61.9 100 97.61
F = 314 0.55 0 5 16 314 76.19 100 98.51
NF = 21 0.60 0 3 18 314 85.71 100 99.1
T = 335 0.65 2 1 20 312 95.24 99.36 99.1
0.70 3 1 20 311 95.24 99.04 98.81
0.75 10 1 20 304 95.24 96.82 96.72
0.80 26 0 21 288 100 91.72 92.24
0.81 31 0 21 283 100 90.13 90.75
Day 3 0.5 0 4 17 312 80.95 100 98.8
F = 312 0.55 0 3 18 312 85.71 100 99.1
NF = 21 0.60 0 3 18 312 85.71 100 99.1
T = 333 0.65 1 2 19 311 90.48 99.68 99.1
0.70 3 2 19 309 90.48 99.04 98.5
0.75 10 1 20 302 95.24 96.79 96.7
0.79 23 0 21 289 100 92.63 93.09
0.80 27 0 21 285 100 91.35 91.89
Day 4 0.5 0 5 16 312 76.19 100 98.5
F = 312 0.55 0 5 16 312 76.19 100 98.5
NF = 21 0.60 1 3 18 311 85.71 99.68 98.8
T = 333 0.65 2 0 21 310 100 99.36 99.4
0.70 3 0 21 309 100 99.04 99.1
0.75 5 0 21 307 100 98.4 98.5
0.79 12 0 21 300 100 96.15 96.4
0.80 13 0 21 299 100 95.83 96.1

References

  1. Abdel-Nour, N., Ngadi, M., Prasher, S., Karimi, Y., 2009. Combined Maximum R2 and partial least squares method for wavelengths selection and analysis of spectroscopic data. International Journal of poultry science 8, 170-178. [CrossRef]
  2. Abdi, H., 2010. Partial least squares regression and projection on latent structure regression (PLS Regression). Wiley Interdisciplinary Reviews: Computational Statistics 2, 97-106. [CrossRef]
  3. Barker, M., Rayens, W., 2003. Partial least squares for discrimination. Journal of chemometrics 17, 166-173.
  4. Briandet, R., Kemsley, E.K., Wilson, R.H., 1996. Discrimination of Arabica and Robusta in instant coffee by Fourier transform infrared spectroscopy and chemometrics. Journal of agricultural and food chemistry 44, 170-174. [CrossRef]
  5. Cassel, C., Hackl, P., Westlund, A.H., 1999. Robustness of partial least-squares method for estimating latent variable quality structures. Journal of applied statistics 26, 435-446. [CrossRef]
  6. Clark, M., Cramer, R.D., 1993. The probability of chance correlation using partial least squares (PLS). Quantitative Structure-Activity Relationships 12, 137-145. [CrossRef]
  7. François, D., 2006. Binary classification performances measure cheat sheet. Journal of Machine Learning Research 7, 1-30.
  8. Gottfries, J., Blennow, K., Wallin, A., Gottfries, C., 1995. Diagnosis of dementias using partial least squares discriminant analysis. Dementia and Geriatric Cognitive Disorders 6, 83-88. [CrossRef]
  9. He, H., Garcia, E.A., 2009. Learning from imbalanced data. Knowledge and Data Engineering, IEEE Transactions on 21, 1263-1284.
  10. Höskuldsson, A., 1988. PLS regression methods. Journal of chemometrics 2, 211-228.
  11. Höskuldsson, A., 1996. Prediction methods in science and technology. 1. Basic theory. Thor Publ.
  12. Iizuka, K., Aishima, T., 1997. Soy sauce classification by geographic region based on NIR spectra and chemometrics pattern recognition. Journal of food science 62, 101-104. [CrossRef]
  13. Japkowicz, N., 2001. Concept-learning in the presence of between-class and within-class imbalances, Advances in Artificial Intelligence. Springer, pp. 67-77. [CrossRef]
  14. Lawrence, K., Smith, D., Windham, W., Heitschmidt, G., Park, B., Yoon, S., 2007. Egg embryo development detection with hyperspectral imaging. International Journal of Poultry Science 5, 964-969. [CrossRef]
  15. Liao, T.W., 2008. Classification of weld flaws with imbalanced class data. Expert Systems with Applications 35, 1041-1052. [CrossRef]
  16. Liu, L., Ngadi, M.O., 2013. Detecting Fertility and Early Embryo Development of Chicken Eggs Using Near-Infrared Hyperspectral Imaging. Food and Bioprocess Technology 6, 2503-2513. [CrossRef]
  17. Longadge, R., Dongre, S., 2013. Class Imbalance Problem in Data Mining Review. arXiv preprint arXiv:1305.1707.
  18. Mani, I., Zhang, I., 2003. kNN Approach to Unbalanced Data Distributions: A Case Study involving Information Extraction, Proc. ICML’03 Workshop on Learning from Imbalanced Data Sets, Washington, DC.
  19. NASS, U., 2006. Statistical Highlights of US Agriculture, 2005-2006. Nguyen, G., Bouzerdoum, A., Phung, S., 2009. Learning pattern classification tasks with imbalanced data sets, In: Yin, P. (Ed.), Pattern recognition. INTECH Open Access Publisher, Vukovar, Croatia, pp. 193-208.
  20. Norris, K., 1996. History of NIR. Journal of Near Infrared Spectroscopy 4, 31-38.
  21. Ortiz, M.C., Sarabia, L.A., Symington, C., Santamaría, F., Íñiguez, M., 1996. Analysis of ageing and typification of vintage ports by partial least squares and soft independent modelling class analogy. Analyst 121, 1009-1013. [CrossRef]
  22. Smith, D., Lawrence, K., Heitschmidt, G., 2008. Fertility and embryo development of broiler hatching eggs evaluated with a hyperspectral imaging and predictive modeling system. International journal of poultry science 7, 1001-1004.
  23. Sokolova, M., Lapalme, G., 2009. A systematic analysis of performance measures for classification tasks. Information Processing & Management 45, 427-437. [CrossRef]
  24. Sun, Y., Wong, A., Kamel, M., 2009. Classification of imbalanced data: A review. International Journal of Pattern Recognition and Artificial Intelligence 23, 687-719.
  25. Tobias, R.D., 1995. An introduction to partial least squares regression, Proc. Ann. SAS Users Group Int. Conf., 20th, Orlando, FL, pp. 2-5.
  26. Wakeling, I.N., Morris, J.J., 1993. A test of significance for partial least squares regression. Journal of Chemometrics 7, 291-304. [CrossRef]
  27. Williams, D.P., Myers, V., Silvious, M.S., 2009. Mine classification with imbalanced data. Geoscience and Remote Sensing Letters, IEEE 6, 528-532. [CrossRef]
  28. Williams, P., Norris, K., 1987. Near-infrared technology in the agricultural and food industries. American Association of Cereal Chemists, Inc.
  29. Wold, S., Johansson, E., Cocchi, M., 1993. PLS: partial least squares projections to latent structures.
  30. Wold, S., Sjöström, M., Eriksson, L., 2001. PLS-regression: a basic tool of chemometrics. Chemometrics and intelligent laboratory systems 58, 109-130.
  31. Yoon, K., Kwek, S., 2007. A data reduction approach for resolving the imbalanced data issue in functional genomics. Neural Computing and Applications 16, 295-306. [CrossRef]
  32. Yu, C.H., 2000. An overview of remedial tools for collinearity in SAS, Proceedings of 2000 Western Users of SAS Software Conference, pp. 196-201.
Preprints 81999 g001
Figure 1. Typical transmittance mean spectra (MS) profiles of brown eggs, on different days of incubation (a), prior incubation (b), day 1 incubation (c), day 2 incubation (d) day 3 incubation.
Figure 1. Typical transmittance mean spectra (MS) profiles of brown eggs, on different days of incubation (a), prior incubation (b), day 1 incubation (c), day 2 incubation (d) day 3 incubation.
Preprints 81999 g001
Preprints 81999 g002
Figure 2. Determining the optimum number of PLS components for brown eggs based on (a), TPR and (b), TNR.
Figure 2. Determining the optimum number of PLS components for brown eggs based on (a), TPR and (b), TNR.
Preprints 81999 g002
Preprints 81999 g003
Figure 3. Evaluation metrics (%) for built models on different days of incubation (a) brown eggs, 25 PCs (b) white eggs, 25 PCs (c) brown eggs, 5 PCs (d) white eggs, 5 PCs.
Figure 3. Evaluation metrics (%) for built models on different days of incubation (a) brown eggs, 25 PCs (b) white eggs, 25 PCs (c) brown eggs, 5 PCs (d) white eggs, 5 PCs.
Preprints 81999 g003
Preprints 81999 g004
Figure 4. Model accuracies and error rates for all PCs from 5 to 50 on day 0 incubation.
Figure 4. Model accuracies and error rates for all PCs from 5 to 50 on day 0 incubation.
Preprints 81999 g004
Table 1. Overall egg sample specifications for (a), brown and (b), white eggs.
Table 1. Overall egg sample specifications for (a), brown and (b), white eggs.
a.
Incubation period Egg received Broken Total Eggs used Fertile (F) Non-fertile (NF)
Day 0 336 1 335 312 (93.13%) 23 (6.87%)
Day 1 335 1 334 311 (93.11%) 23 (6.89%)
Day 2 334 - 334 311 (93.11%) 23 (6.89%)
Day 3 334 - 334 311 (93.11%) 23 (6.89%)
Day 4 334 - 334 311 (93.11%) 23 (6.89%)
b.
Incubation period Egg received Broken Total Eggs used Fertile (F) Non-fertile (NF)
Day 0 336 1 335 314 (93.73%) 21 (6.27%)
Day 1 335 - 335 314 (93.73%) 21 (6.27%)
Day 2 335 - 335 314 (93.73%) 21 (6.27%)
Day 3 335 2 333 312 (93.69%) 21 (6.31%)
Day 4 333 - 333 312 (93.69%) 21 (6.31%)
Table 2. Confusion matrix.
Table 2. Confusion matrix.
Prediction class
True class Predicted as Positive Predicted as Negative
Actually Positive TPR FNR
Actually Negative FPR TNR
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated