Prerpints.org logo
Preprint
Article

Remaining Life Prediction of Rolling Bearings Based on Grey Wolf Optimized Network

Altmetrics

Downloads

73

Views

25

Comments

0

Submitted:

27 July 2023

Posted:

10 August 2023

You are already at the latest version

Alerts
Abstract
In order to assess the degradation state of rolling bearings and accurately grasp the remaining life information of rolling bearings, a bearing remaining life prediction method based on the grey wolf optimization algorithm to improve the BP neural network model is proposed. The method consists of two steps, firstly, using the craggy value and root mean square value to determine the first failure time of rolling bearings so as to approximate the input features, and secondly, using the Grey Wolf optimization algorithm to optimize the BP neural network to construct the degradation model of the bearings through machine learning. The method reduces the prediction error compared with conventional techniques, indicating that the method can effectively simulate the bearing degradation process and predict the remaining useful life (RUL) of the bearing.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Rolling bearings are widely used in a variety of rotating machinery, and used as key components1. However, with the development of modern industry, electromechanical equipment gradually presents the development trend of automation and complexity, which often puts mechanical equipment in a continuous working condition of variable working conditions and high load2. This makes the parts of mechanical equipment more prone to failure, which in turn increases the difficulties and challenges for the initial reliability design of mechanical equipment, the convenience of maintenance during use and the management of health inspection after use3. At the same time, the probability of malfunction and functional failure gradually increases due to the increase in the number of components and influencing factors of mechanical systems. Therefore, mechanical system fault diagnosis and maintenance have become the focus of researchers' attention4-5. According to statistics, in rotating mechanical equipment using rolling bearings, roughly 30% of mechanical failures are directly related to bearing damage. The performance, life and reliability of rolling bearings play a decisive role in the safe and stable operation of the whole rotating machinery system6. The performance, life and reliability of rolling bearings play a decisive role in the safe and stable operation of the entire rotating machinery system.
Liu7 Establishment of a contact fatigue remaining life prediction model based on data-driven technique. Qiu8 A residual life prediction method for bearings based on correlation coefficient and BP neural network model is proposed. Huang9 proposed a new method for predicting the remaining life of rolling bearings based on self-organizing mapping and BP neural network. Jin10 A particle swarm optimization BP neural network based method for extracting the characteristic frequency of bearing faults is proposed. The BP algorithm was optimized in different ways, but there were some problems in the accuracy of prediction and the applicability under different working conditions. Therefore, this paper proposes an improved BP neural network based on the Grey wolf optimization algorithm for accurate prediction of the remaining service life of rolling bearings under different operating conditions.

2. Data Processing

2.1. Feature Extraction

One of the main difficulties in the process of bearing remaining life prediction is how to establish feature indicators representing the degraded state for assessing health from the effective features. In order to accurately predict the remaining life of bearings, this paper selects several feature indicators from the time domain, frequency domain and time-frequency domain as sample inputs to the model. These feature indicators reflect the operational status and development trend of bearings in different degrees, and the failure-sensitive features are selected for life prediction.
Firstly, the root mean square value, mean value, standard deviation, square root magnitude, absolute mean magnitude, peak value, peak-to-peak value, skewness, kurtosis, skewness factor, kurtosis factor, peak factor, pulse factor, waveform factor and margin factor are extracted from the original data as time domain features. Then the fast Fourier transform of the original data extracted to the center of gravity frequency, frequency domain amplitude mean frequency standard deviation and root mean square frequency as the frequency domain features, and finally through the three-layer wavelet packet decomposition to get eight sub-band energy ratios as the eight time-frequency domain features.

2.2. Feature Dimensionality Reduction

The top 10 features are obtained as the sensitive feature set by comprehensively evaluating the above extracted 27 features in terms of monotonicity, robustness, correlation with time and recognizability, and the data are downscaled by principal component analysis (PCA) to obtain a low-dimensional sensitive degraded feature dataset for subsequent prediction.

2.3. Time to First Failure Judgment

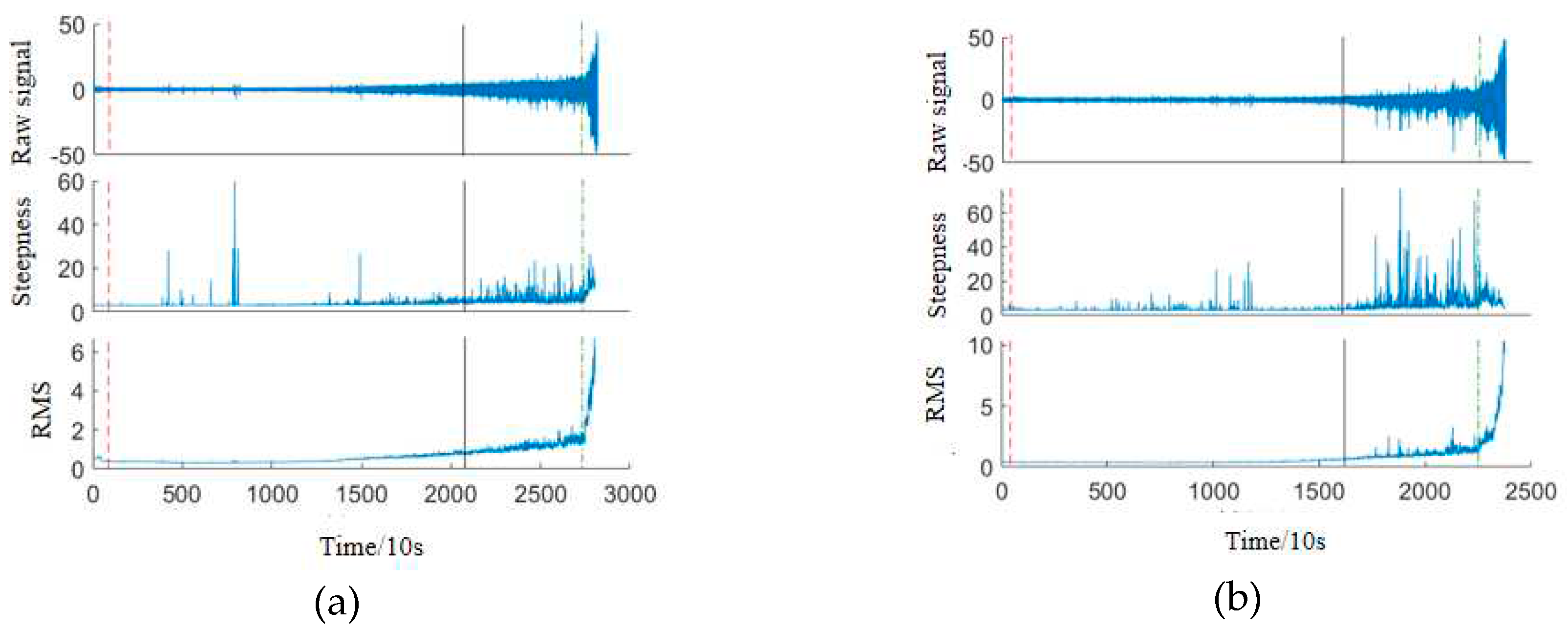
In order to test the performance of the adaptive index first failure time judgment method used in this paper, the existing full-life vibration signals of rolling bearings are utilized for the first failure time judgment. As can be seen from Figure 1, the RMS value has been at a low level in the early stage of the degradation process, and only in the late stage of the degradation process does it show an exponential upward trend. And the change of the cliff value is very obvious when there is interference noise. So when a single root mean square value or crag value is used to judge the first fault point, delayed judgment or premature judgment will occur.
The time of the first failure of the three rolling bearings shown in Figure 1a,b is at the moment when the failure has just started to appear, i.e., when the amplitude of the vibration signals and their RMS values start to increase, but the increase is not significant. This shows that the crag value is more sensitive to the early fault information in the degradation process. However, the crag value is very sensitive to noise. When the crag value is used as the only indicator for determining the time of first failure, the first failure time chosen is often too early to correctly determine the true time of first failure. To overcome the effect of noise on the detection method of the crag value indicator, Li10 chose the method of repeatedly judging the craggy value indicator in multiple consecutive samples. However, this method will lead to a delay in the detection time and cannot meet the needs of real-time detection.
Prior to the selection of the first failure time, the crag values of the bearing signals, as shown in Figure 1a,b, increased significantly. The reason why this time point cannot be recognized as the first failure time is because its RMS value corresponding to the original bearing signal is still in the normal range. According to WANG11 's method, using the RMS metric to determine the first failure time has better robustness to noise than the crag metric, but the RMS metric cannot capture transient shocks, so this paper uses an adaptive combined metric of the RMS and crag values.
As can be seen in Figure 1, by appropriately setting the normal ranges for the root mean square and crag values, the first fault time selection method used is able to detect faults at an early stage while avoiding interference due to noise.

3. BP Neural Network

3.1. Introduction to BP Neural Networks

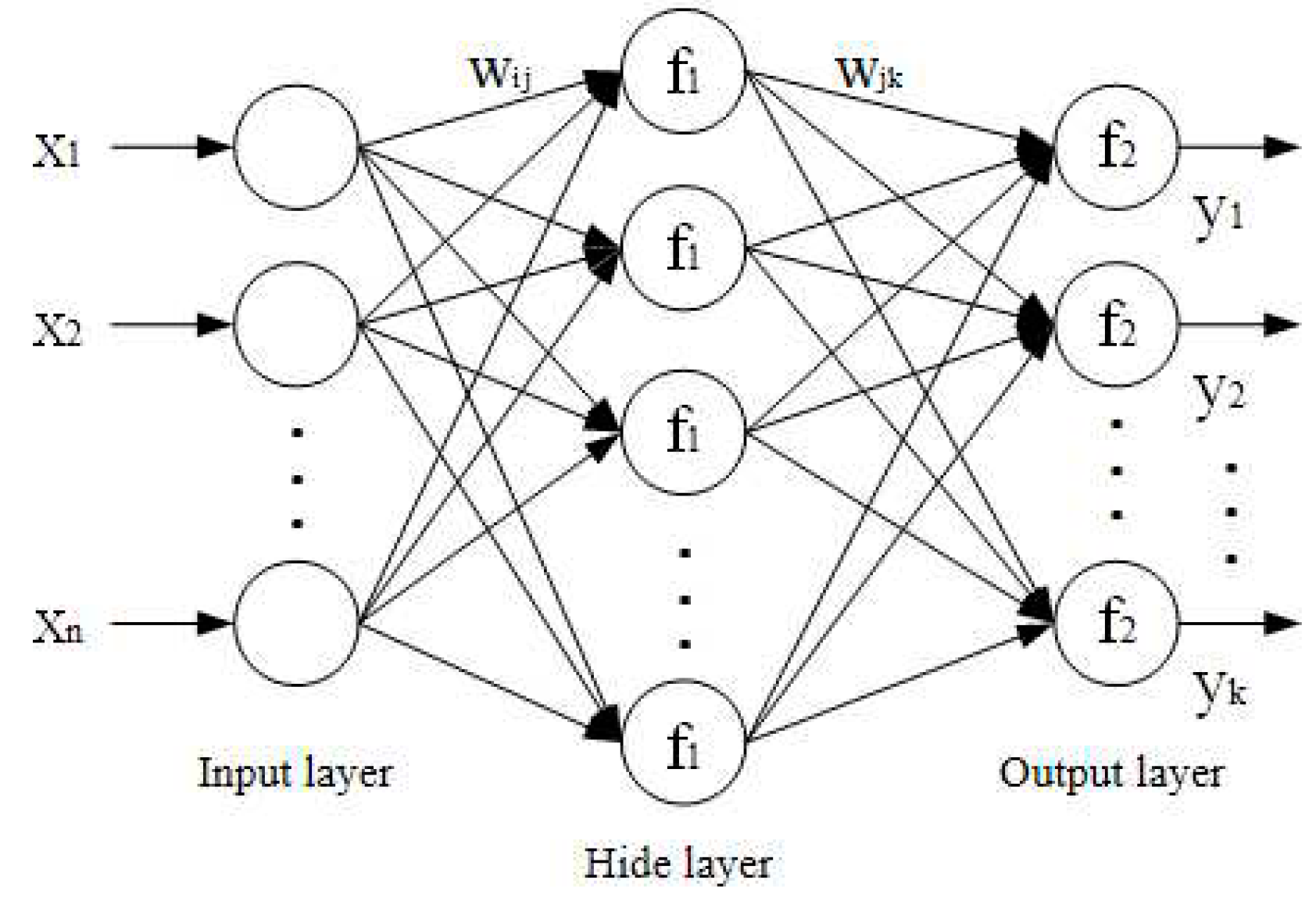
BP neural network was proposed in 1986, which is one of the commonly used neural networks with the advantages of nonlinear mapping, robustness, etc12. It is applied in the field of bearing residual life prediction and occupies an important position in the field of equipment failure prediction. In its topology, the artificial neurons are organized into layers and the signal flows forward while the error propagates backward. The input signal is processed layer by layer through the input layer, the hidden layer and the output layer, and the network weights and thresholds are continuously adjusted according to the error between the predicted output and the desired output until the algorithm converges to get the prediction result that approximates the desired output. As long as there are enough nodes in the hidden layer of the BP network, the network can approximate any nonlinear mapping relationship, and this global approximation approach of the BP network has a better generalization ability. The three-layer structure of this network is shown in Figure 2. This section may be divided by subheadings. It should provide a concise and precise description of the experimental results, their interpretation, as well as the experimental conclusions that can be drawn.

3.2. Grey Wolf Optimization Algorithm

The main idea of the Grey wolf optimization algorithm is to simulate the collective hunting nature of the wolf pack. There is a strict hierarchy in the grey wolf group, in which a small number of grey wolves with absolute voice lead the remaining grey wolves to move forward to the prey. Collective hunting is a kind of social behavior of grey wolves, and social hierarchy plays an important role in the collective hunting process, and the predation process is completed under the leadership of the head wolf. It mainly consists of three steps, the first step is to stalk and approach the prey; the second step is to pursue and surround the prey until it stops moving; and the third step is to attack the prey.
In order to hunt efficiently, grey wolf packs are divided into four classes known as α-wolves, β-wolves, δ-wolves, and ω-wolves. There are three kinds of wolves in the pack, α-wolf, β-wolf and δ-wolf, as the leaders of hunting, where α-wolf is the king of wolves, β-wolf and δ-wolf are ranked second and third, respectively, and both β-wolf and δ-wolf have to obey α-wolf, and δ-wolf has to listen to β-wolf and δ-wolf. These three wolves guide the other wolves (i.e., ω-wolves) in their search for prey. The process of wolves searching for prey is the process of finding our optimal solution. Each of the four wolves has a different role. α wolf's role is to act as the highest leader in the population and is responsible for leading the whole wolf pack to hunt prey, i.e. the optimal solution in the optimization algorithm. β wolf's role is to be responsible for assisting α wolf, i.e. the sub-optimal solution in the optimization algorithm. δ wolf listens to the commands and decisions of α and β wolves, and is responsible for scouting, sentinel duty and so on. Poorly adapted α-wolves and β-wolves are relegated to δ-wolves. ω-wolves act as the lowest level wolves of the pack, which surround the α-wolves, β-wolves or δ-wolves, and their role is to perform positional updating to get closer to the prey.
To mathematically model the social hierarchy of grey wolves in GWO, the top 3 best wolves (optimal solutions) are corresponded to α-wolves, β-wolves, and δ-wolves, which guide the other wolves in their search towards the goal. The remaining wolves (candidate solutions) are defined as ω wolves, which update their positions around α wolves, β wolves or δ wolves.
Grey wolves let their prey approach them gradually and surround them, and the mathematical model of this behavior is as follows:
D = C ⋅ X p t − X t
X ( t + 1 ) = X p ( t ) − A ⋅ D
In Eq. (1), D denotes the distance between the grey wolf and the prey, Eq. (2) is the position update formula for the grey wolf, Xp and X are the position vector of the prey and the position of the grey wolf, respectively, and t is the current number of iterations. a and C are the coefficients of determination, whose computations are shown in the formulas (3) and (4), respectively.
A = 2 a ⋅ r 1 − a
C = 2 r 2
Where, r1 and r2 are two uniformly distributed one-dimensional random components with values ranging from random numbers within [0,1], A is used to simulate the attack behavior of the grey wolf on its prey, and its value is affected by a. a is called the convergence factor, which is a key parameter balancing the ability of exploration and exploitation in the grey wolf optimization algorithm. It takes a value that shows a linear decrease from 2 to 0 as the number of iterations increases.
a = 2 − 2 t T
where Tmax is the maximum number of iterations. From Eq. (6) to Eq. (9), the prey position can be approximated by the three lead wolves stored in each iteration, thus mathematically modeling the hunting style of grey wolves.
D α = C 1 ∗ X α − X D β = C 2 ∗ X β − X D δ = C 3 ∗ X δ − X
Where , D α 、 D β and D δ denote the distance of from ω wolf to α-wolf, β-wolf and δ-wolf, respectively.
X 1 = X α − A 1 ∗ D α X 2 = X β − A 2 ∗ D β X 3 = X δ − A 3 ∗ D δ
The position of ω wolf at the (t+1)th iteration is calculated from the positions of X1 , X2 and X3 as shown in equation(8).
X t + 1 = X 1 + X 2 + X 3 3
In summary, GWO starts with the creation of a random initial grey wolf population (solution). α wolves, β wolves, and δ wolves estimate the location of the prey in an iterative process. The distance between the prey and each candidate solution is updated based on the exploratory or exploitative ability of the parameter |A| value. ω wolves approach or flee from dominant wolves such as α wolves, β wolves, and δ wolves. Depending on the value of the parameter |A| in each iteration, the movement strategy of the wolf is decided. In order to improve the exploration ability in the first few iterations and the exploitation ability in the later iterations, the parameter a is reduced from 2 to 0. Therefore, if |A| > 1, the grey wolf will escape from the dominant wolf, which means that ω-wolf will run away from the prey and explore the new region in the hope of having a better search space. If |A|<1, it is said to be valid and the ω-wolf will approach the dominant wolf, which means that the ω-wolf will follow the dominant wolf in approaching the prey, which is referred to as local search in optimization. The parameter C can provide an increasingly random weight for the prey, which facilitates local optimal avoidance and encourages some exploratory behavior. When |C|>1, the wolf has more influence on approaching the prey, and when |C|<1, the wolf has less influence on the prey. In this way, grey wolves complete their hunting activities by repeating the steps of circling and hunting.

4. Experimental Verification

4.1. Experimental Platform

The PRONOSTIA platform is used to test and validate bearing health assessment, fault diagnosis and failure prediction models13. The platform is capable of accelerating bearing degradation and collecting real-world experimental data describing bearing degradation patterns in just a few hours. The PRONOSTIA platform is designed to provide bearing degradation data under a variety of operating conditions14.
The degradation of the bearings is characterized by two types of sensors mounted on the test rig: an accelerometer and a temperature sensor. The inner ring of the bearing follows the shaft in rotational motion, while the outer ring remains fixed. The two accelerometers are mounted in the horizontal and vertical positions of the bearing outer ring to collect vibration information from the horizontal and vertical directions, respectively. The sampling frequency of the acceleration sensors is 25.6 kHz. Under this experimental platform, the life acceleration experiments of the bearings are carried out under three different working conditions, and the rotational speed as well as the load information of each working condition is shown in Table 1.

4.2. Evaluation Indicators

In order to comprehensively analyze whether the selected method is effective or not, this paper chooses three indicators, root mean square error (RMSE), mean absolute error (MAE) and correlation coefficient (R2), to determine whether the prediction is accurate or not. Mean Absolute Mean Error (MAE) is applicable when the error between the predicted value and the actual observed value is more obvious, while Root Mean Square Error (RMSE) is applicable when the prediction error is not very obvious. The correlation coefficient is a comprehensive evaluation index used to measure the degree of explanation of each variable on the changes of the dependent variable, the closer the correlation coefficient is to 1, the higher the degree of explanation. The formulas for the three evaluation indicators are shown below.
R M S E = 1 n ∑ i = 1 n y i − y i ^ 2
M A E = 1 n ∑ i = 1 n y i − y i ^
R 2 = C o v y i , y i ^ y i y i ^
In Eq. (9) to Eq. (11), and represent the actual remaining life and predicted remaining life, respectively, and n represents the number of sample samples. The smaller the root mean square error and the mean absolute mean error, and the correlation coefficient close to 1, the more accurate the prediction performance of the neural network.

4.3. Optimization Steps

The input and output are first normalized to set the parameters of the initial BP neural network. The initial dimension represents the initial weight and bias of the BP neural network, and the initial dimension is initialized to [-1,1], and then substituted into the BP neural network for training, and according to the fitness function Eq. (6), the fitness value of each grey wolf is computed and sorted from smallest to largeest, from which the three grey wolves with the smallest fitness value in the first generation are selected, and labeled as α-wolf, β-wolf, and δ-wolf, respectively. Update the position of each individual grey wolf according to Eq. (6) and Eq. (7), construct a new BP neural network and train it, calculate the fitness function value of each grey wolf, and select the new α-wolf, β-wolf and δ-wolf, and then update the position of each grey wolf. Determine whether the maximum number of iterations of the grey wolf optimization algorithm is reached. If the maximum number of iterations is not reached, return to calculate the fitness function and update α-wolf, β-wolf and δ-wolf, and if the maximum number of iterations is reached, record the initial weights and bias of the BP neural network corresponding to the optimal grey wolf individual α-wolf. According to the derived optimized initial weights and biases, substitute them into the BP neural network training, and stop the training of the network when the training error meets the requirements. The test set is substituted into the trained BP neural network.

4.4. Analysis of Results

Bearing 1-7, 2-7 and 3-7 data are used as the test set, and the rest of the bearing data are used as the training set, and the ratio of training and validation data in the training set is 0.7 and 0.3, respectively.
In this paper, the three working conditions are trained and predicted separately, utilizing the obtained sensitive feature datasets, which are used as network inputs.
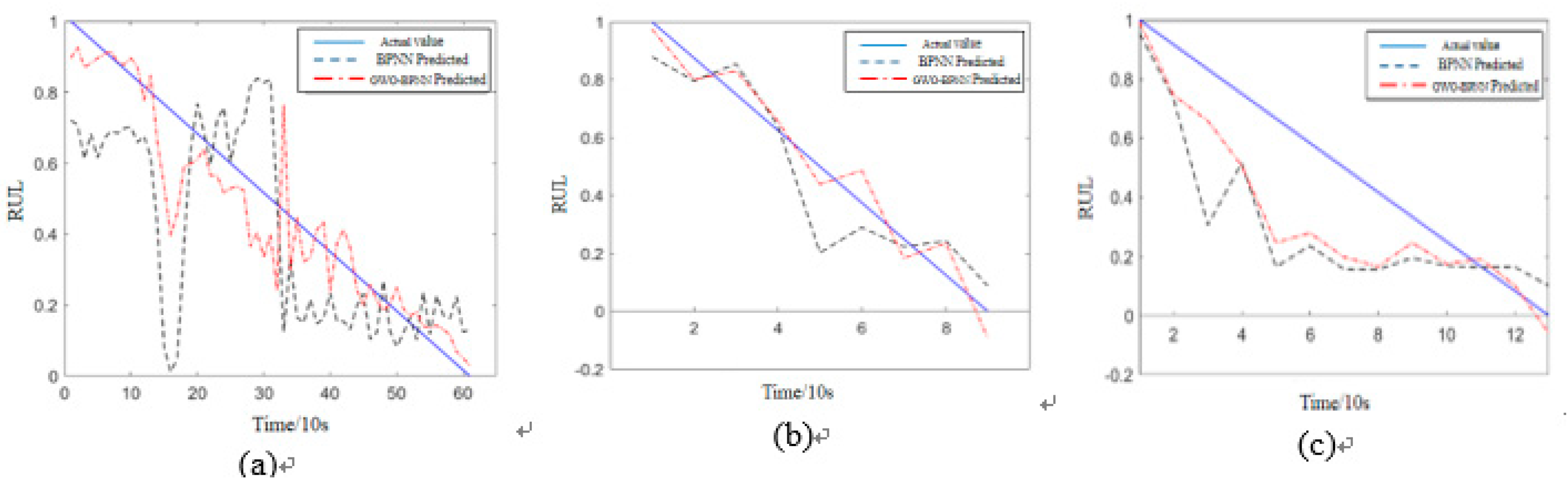
Preprints 80736 g003
Figure 3. BP neural networks and GWO-BP prediction results of bearings 1-7, 2-7, 3-3.
Figure 3. BP neural networks and GWO-BP prediction results of bearings 1-7, 2-7, 3-3.
Preprints 80736 g003
From Table 2, it can be seen that the optimized GWO-BP neural network of the Grey Wolf optimization algorithm performs better than the unoptimized base BP neural network under all three working conditions. In Case 1, the correlation coefficient is improved from 0.692 to 0.938, the root mean square error is decreased by 55%, and the average absolute mean error is decreased by 58%. Under condition two, the root mean square error decreases by 39.5%, the average absolute mean error decreases by 29.8%, and the correlation coefficient is improved accordingly. In Case 3, the root mean square error decreases by 23.8%, the average absolute mean error decreases by 24.7%, and the correlation coefficient also improves considerably.
In summary, the optimized GWO-BP neural network can more accurately predict the degradation trend of the remaining life of rolling bearings compared with the basic BP neural network under the three working conditions.

5. Conclusion

BP neural network was used to carry out the rolling bearing life prediction under three kinds of working conditions, and concluded that BP neural network can predict the remaining life degradation trend of rolling bearings, but there is a certain amount of error, and it is affected by the noise, in the three middle kinds of conditions, the root mean square error of BP neural network prediction is 0.234, 0.129 and 0.273, respectively, and the average absolute mean error is 0.190, 0.104 and 0.219, and the correlation coefficients are 0.692, 0.921 and 0.780, respectively;
(2) In order to predict the remaining life of rolling bearings more accurately, the weights and biases of the basic BP neural network are optimized using the Grey Wolf optimization algorithm, and the GWO-BP neural network is constructed, and the same data are imported into the GWO-BP neural network, and the remaining life is predicted for three kinds of working conditions. The root-mean-square errors of the GWO-BP neural network prediction were 0.108, 0.078 and 0.208, and the average absolute mean errors were 0.079, 0.073 and 0.165, with the correlation coefficients of 0.938, 0.971 and 0.901, respectively, under the three middle operating conditions;
(3) The prediction results of BP neural network and GWO-BP neural network are compared. the prediction results of GWO-BP neural network are closer to the actual values of the setting, and the root mean square error is reduced by 55%, 39.5% and 23.8%, and the average absolute mean error is reduced by 58%, 29.8% and 24.7%, respectively, for the three working conditions. It is known that the prediction accuracy of GWO-BP neural network is higher than that of BP neural network.
This section is not mandatory but can be added to the manuscript if the discussion is unusually long or complex.

Data Availability Statement

No data was used for the research described in the article.

Acknowledgments

This research was funded by the Shandong Province Natural Science, grant number ZR2021ME242.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Kang S Q, Wang Y J, Jiang Y C, et al. Fault classification of rolling bearings based on multi-class support vector machine with superball center spacing[J]. Proceedings of the CSEE, 2014, 34(14) : 2319-2325. [CrossRef]
  2. Ren L, Sun Y, Wang H, et al. Prediction of Bearing Remaining Useful Life With Deep Convolution Neural Network[J]. IEEE Access, 2018:13041-13049. [CrossRef]
  3. Rezamand M, Kordestani M, Carriveau R, et al. An integrated feature-based failure prognosis method for wind turbine bearings[J]. IEEE/ASME Transactions on Mechatronics, 2020, 25(3): 1468-1478. [CrossRef]
  4. Wang Y L, Pan Z F, Yuan X F, et al. A novel deep learning based fault diagnosis approach for chemical process with extended deep belief network[J]. ISA Transactions, 2020, 96(C): 457-467. [CrossRef]
  5. Li X, Jia X, Wang Y L, et al. Industrial Remaining Useful Life Prediction by Partial Observation Using Deep Learning with Supervised Attention [J]. IEEE/ASME Transactions on Mechatronics, 2020, 25(5): 2241-2251. [CrossRef]
  6. Wu J, Tang T, Chen M, et al. A study on adaptation lightweight architecture based deep learning models for bearing fault diagnosis under varying working conditions [J]. Expert Systems with Applications, 2020, 160: 113710. [CrossRef]
  7. Liu Y, Liu Y B, Liu Z Y. Construction and validation of contact fatigue residual life prediction model[J]. Journal of Machine Design, 2022, 39(11): 17-25.
  8. Huang R Q, Xi L F, Li X L, et al. Residual life predictions for ball bearings based on self-organizing map and back propagation neural network methods[J]. Mechanical Systems and Signal Processing.2005,21(1): 193-207. [CrossRef]
  9. Jin Y J, Zhang D, Sui W T, et al. Residual life prediction of rolling bearings based on particle swarm optimization neural network[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2020, No. 558(8): 64-66+70. [CrossRef]
  10. Li N, Lei Y G, Lin J, et al. An Improved Exponential Model for Predicting Remaining Useful Life of Rolling Element Bearings.[J]. IEEE Trans. industrial Electronics, 2015, 62(12): 7762-7773. [CrossRef]
  11. 11. Wang W B. A model to predict the residual life of rolling element bearings given monitored condition information to date[J]. IMA Journal of Management Mathematics,2002,13(1): 3-16. [CrossRef]
  12. Runmelhart D E, Hinton G E, Williams R J. Learning representations by back-propagating errors[J]. Nature, 1986, 323(6088): 533-536. [CrossRef]
  13. Mirjalili S, Mirjalili S M, Lewis A. Grey Wolf Optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. [CrossRef]
  14. Nectoux P, Gouriveau, Medjaher K, et al. Pronostia: an experiment platform for bearings accelerated degradation tests[C]. Proceedings of IEEE International Conference on Prognostics and Health Management, 2012: 1-8.
Preprints 80736 g001
Figure 1. First failure time judgment.
Figure 1. First failure time judgment.
Preprints 80736 g001
Preprints 80736 g002
Figure 2. Schematic diagram of BP neural network structure.
Figure 2. Schematic diagram of BP neural network structure.
Preprints 80736 g002
Table 1. Speed and load under various working conditions.
Table 1. Speed and load under various working conditions.
working condition Speed (rpm) Load (N)
Working condition I 1800 4000
Working condition II 1650 4200
Working condition Ⅲ 1500 5000
Table 2. Prediction results of BP neural network and GWO-BP neural network.
Table 2. Prediction results of BP neural network and GWO-BP neural network.
working condition Evaluation indicators BP neural network GWO-BP neural network
Working condition I RMSE 0.243 0.108
MAE 0.190 0.079
R2 0.692 0.938
Working condition II RMSE 0.129 0.078
MAE 0.104 0.073
R2 0.921 0.971
Working condition Ⅲ RMSE 0.273 0.208
MAE 0.219 0.165
R2 0.780 0.901
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated