Submitted:
09 August 2023
Posted:
11 August 2023
You are already at the latest version
Abstract
Keywords:
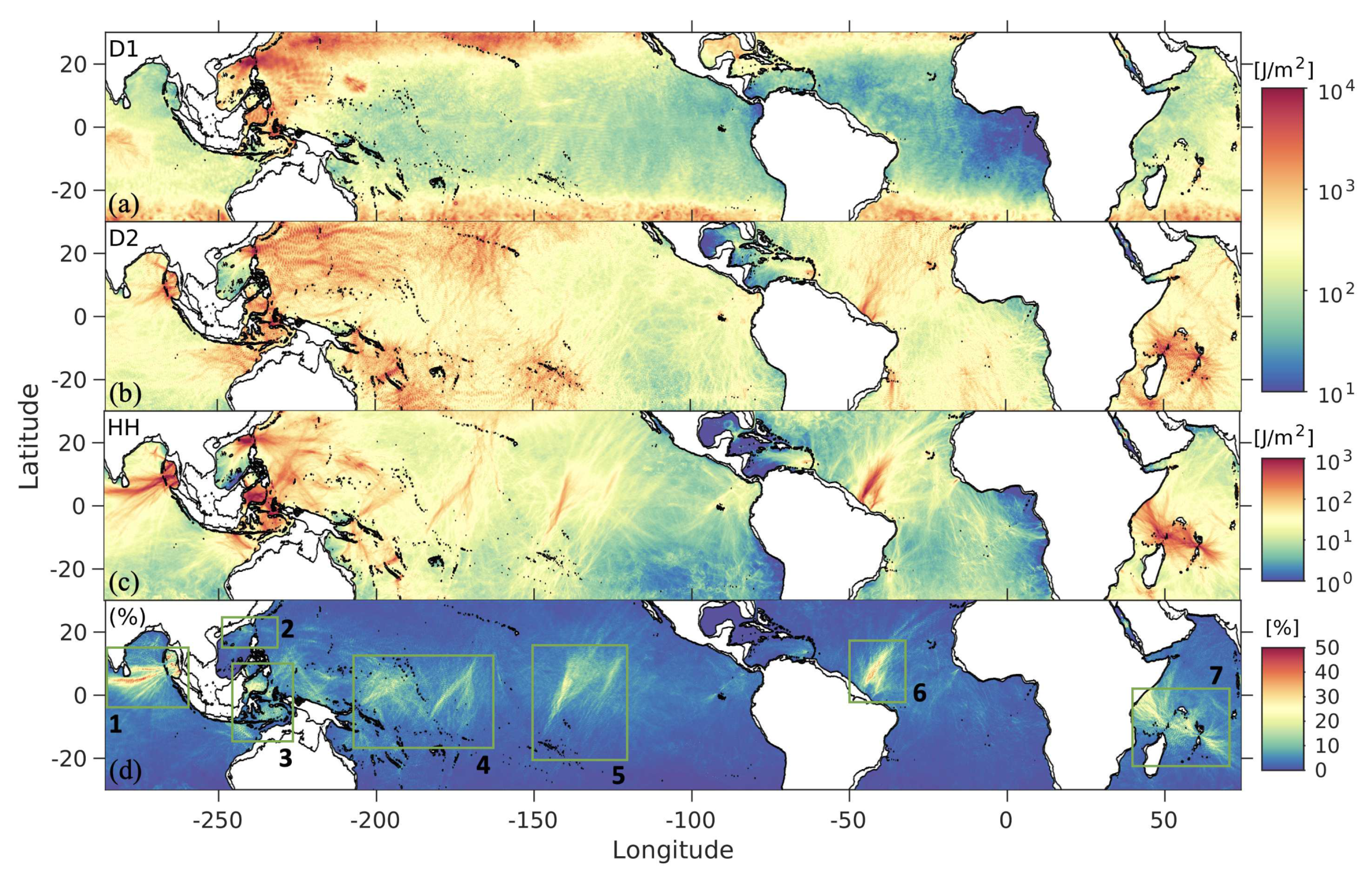
- Supertidal energy as a fraction of the tidal energy is elevated at low latitudes, making up to 50% of total tidal energy in some regions
- Supertidal flux divergence and surface tidal energy reveal banding pattern due to interaction of mode 1 and mode 2 internal tides
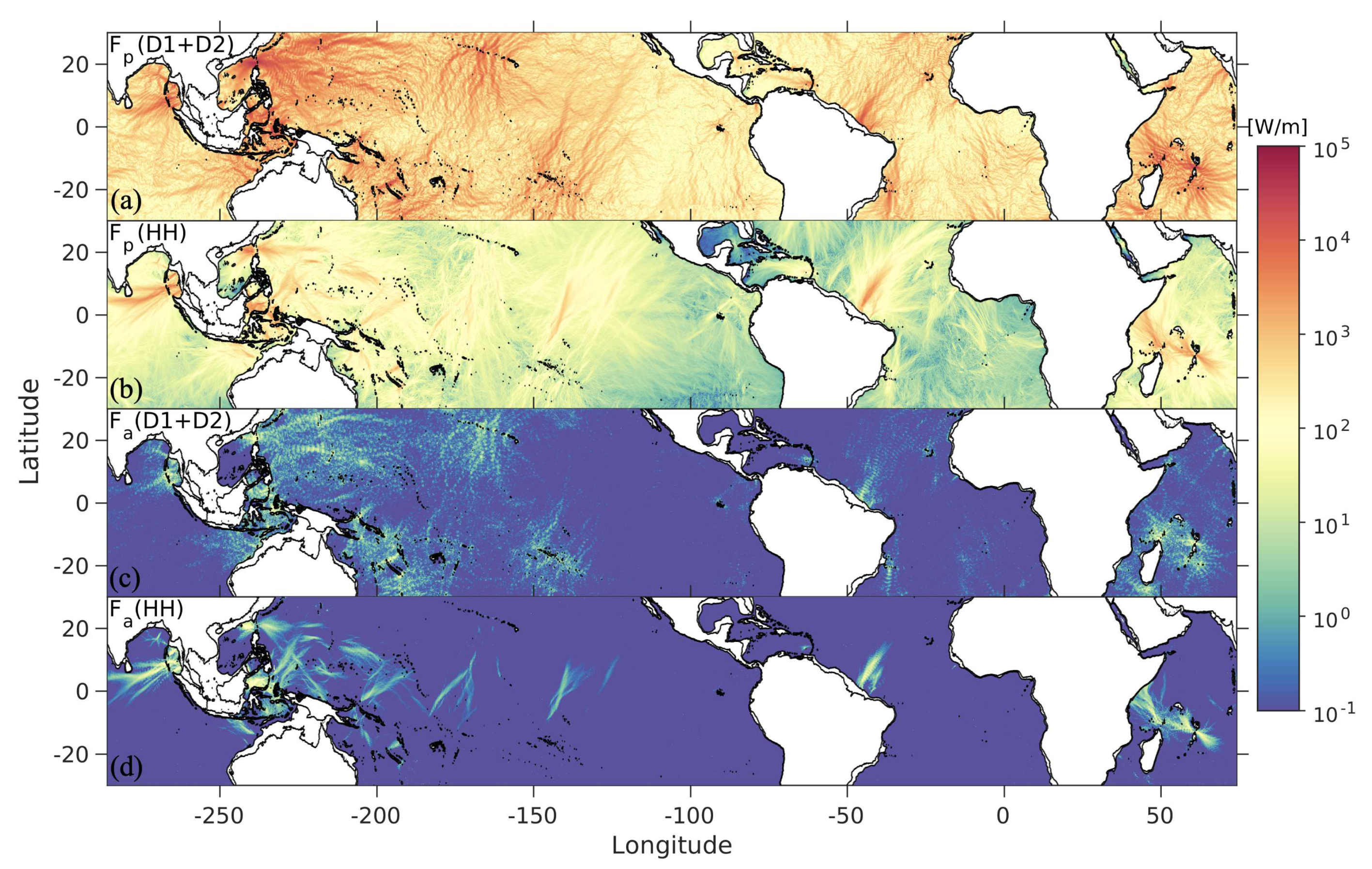
- Supertidal flux divergence is due to energy transfer from internal tides to higher-harmonic frequencies as computed with coarse-graining
Plain Language Summary
1. Introduction
2. Model and Methods
2.1. Model
2.2. Filtering
2.3. Internal Wave Energetics
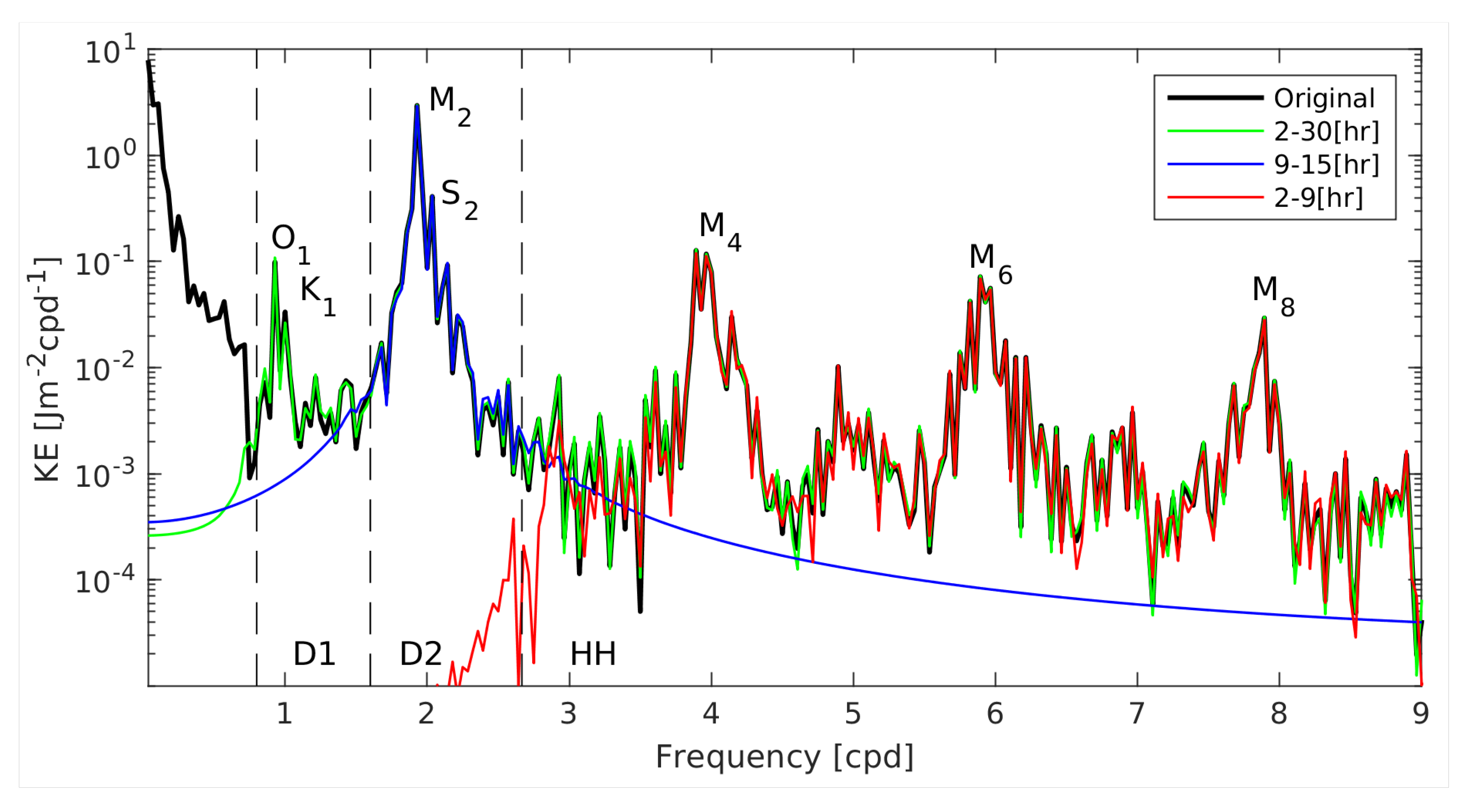
3. Results
3.1. Global internal tide energetics
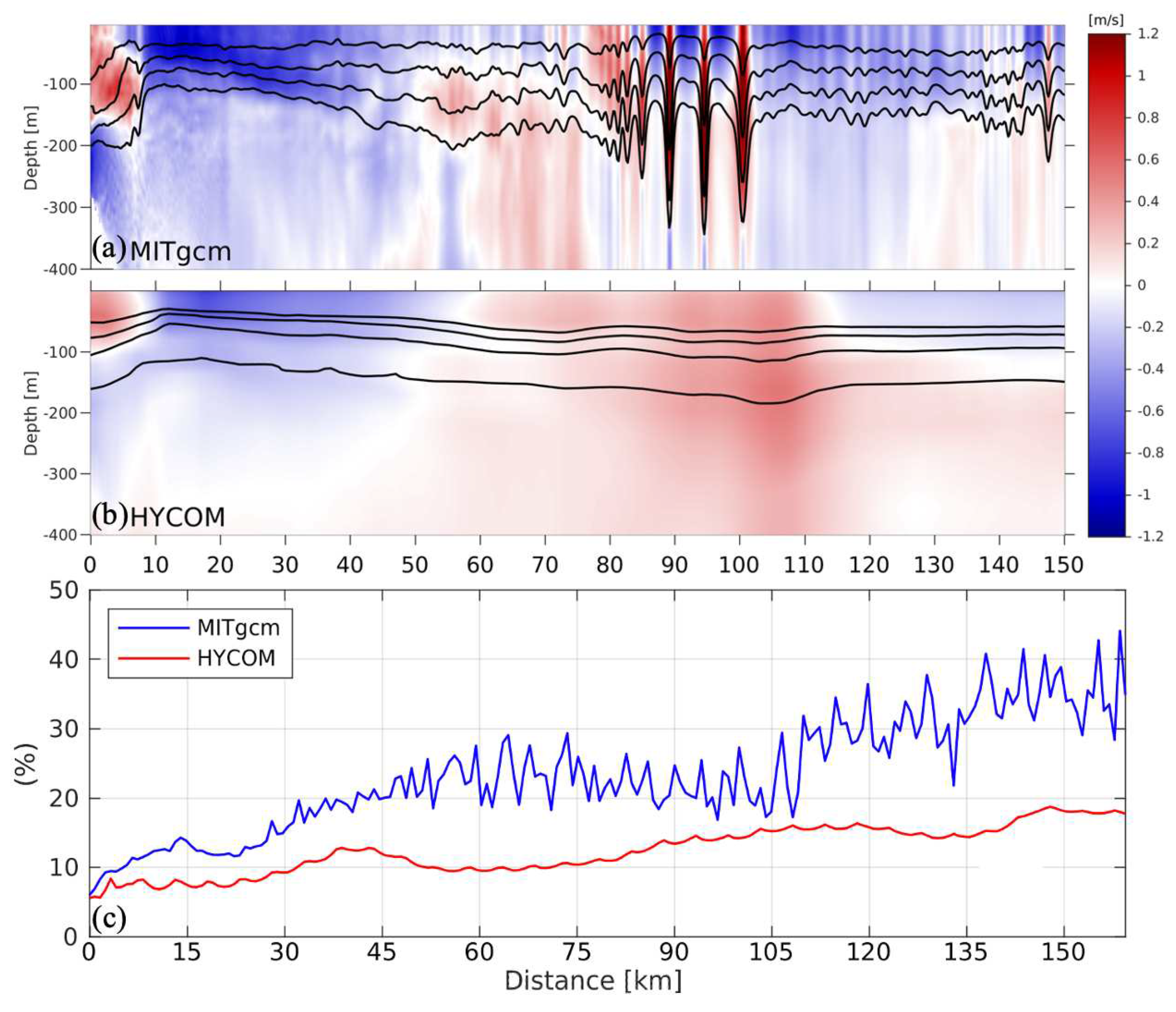
3.2. Nonlinear internal tides at the Amazon shelf
3.3. Solitary-like waves in HYCOM
4. Discussion
4.1. Solitary NLIW in global HYCOM
4.2. Nonlinear energy cross-scale transfer
4.3. Spatial modulation of nonlinear energy transfer
4.4. Temporal modulation of nonlinear energy transfer
4.5. Synthesis
5. Summary and Conclusions
Acknowledgments
Appendix A. Effect of horizontal grid resolution
References
- Egbert.; Ray. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 2000, 405, 775–778. [CrossRef] [PubMed]
- Egbert.; Ray. Estimates of M2 tidal energy dissipation from TOPEX/Poseidon altimeter data. Journal of Geophysical Research 2001, 106, 475–497. [CrossRef]
- Wunsch, C.; Ferrari, R. Vertical mixing, energy and the general circulation of the oceans. Annual Review of Fluid Mechanics 2004, 36, 281–314. [CrossRef]
- Melet, A.; Hallberg, R.; Legg, S.; Polzin, K. Sensitivity of the Ocean State to the Vertical Distribution of Internal-Tide-Driven Mixing. Journal of Physical Oceanography 2013, 43, 602 – 615. [CrossRef]
- Waterhouse, A.F.; Mackinnon, J.A.; Nash, J.D.; Alford, M.H.; Kunze, E.; Simmons, H.L.; Polzin, K.L.; Laurent, L.C.; Sun, O.M.; Pinkel, R.; Talley, L.D.; Whalen, C.B.; Huussen, T.N.; Carter, G.S.; Fer, I.; Waterman, S.; Garabato, A.C.N.; Sanford, T.B.; Lee, C.M. Global patterns of diapycnal mixing from measurements of the turbulent dissipation rate. Journal of Physical Oceanography 2014, 44, 1854–1872. [CrossRef]
- Vic, C.; Garabato, A.C.N.; Green, J.A.; Waterhouse, A.F.; Zhao, Z.; Melet, A.; de Lavergne, C.; Buijsman, M.C.; Stephenson, G.R. Deep-ocean mixing driven by small-scale internal tides. Nature Communications 2019, 10. [CrossRef]
- Zhao, Z., M. Alford, J. Girton, L. Rainville, and H. Simmons. 2016. Global observations of open-ocean mode-1 M2 internal tides. Journal of Physical Oceanography 46: 1657–1684. [Google Scholar] [CrossRef]
- Shriver, J.F.; Arbic, B.K.; Richman, J.G.; Ray, R.D.; Metzger, E.J.; Wallcraft, A.J.; Timko, P.G. An evaluation of the barotropic and internal tides in a high-resolution global ocean circulation model. Journal of Geophysical Research: Oceans 2012, 117. [CrossRef]
- Muller, M., J. Cherniawsky, M. Foreman, and J. von Storch. 2012. Global M2 internal tide and its seasonal variability from high resolution ocean circulation and tide modeling. Geophysical Research Letters 39: L19607. [Google Scholar] [CrossRef]
- Buijsman, M.C.; Stephenson, G.R.; Ansong, J.K.; Arbic, B.K.; Green, J.A.; Richman, J.G.; Shriver, J.F.; Vic, C.; Wallcraft, A.J.; Zhao, Z. On the interplay between horizontal resolution and wave drag and their effect on tidal baroclinic mode waves in realistic global ocean simulations. Ocean Modelling 2020, 152. [CrossRef]
- Johnston, T.M.S.; Merrifield, M.A. Internal tide scattering at seamounts, ridges, and islands. Journal of Geophysical Research: Oceans 2003, 108, 1–17. [CrossRef]
- Lamb, K.G. Nonlinear interaction among internal wave beams generated by tidal flow over supercritical topography. Geophysical Research Letters 2004, 31. [CrossRef]
- Mathur, M.; Carter, G.S.; Peacock, T. Topographic scattering of the low-mode internal tide in the deep ocean. Journal of Geophysical Research: Oceans 2014, 119, 2165–2182. [CrossRef]
- Kelly, S.M.; Lermusiaux, P.F.; Duda, T.F.; Haley, P.J. A coupled-mode shallow-water model for tidal analysis: Internal tide reflection and refraction by the gulf stream. Journal of Physical Oceanography 2016, 46, 3661–3679. [CrossRef]
- Dunphy, M.; Ponte, A.L.; Klein, P.; Gentil, S.L. Low-Mode Internal Tide Propagation in a Turbulent Eddy Field. Journal of Physical Oceanography 2017, 47, 649 – 665. [CrossRef]
- Savage, A.C.; Waterhouse, A.F.; Kelly, S.M. Internal Tide Nonstationarity and Wave–Mesoscale Interactions in the Tasman Sea. Journal of Physical Oceanography 2020, 50, 2931–2951. [CrossRef]
- Legg, S. Scattering of Low-Mode Internal Waves at Finite Isolated Topography. Journal of Physical Oceanography 2014, 44, 359 – 383. [CrossRef]
- Klymak, J.M.; Simmons, H.L.; Braznikov, D.; Kelly, S.; MacKinnon, J.A.; Alford, M.H.; Pinkel, R.; Nash, J.D. Reflection of Linear Internal Tides from Realistic Topography: The Tasman Continental Slope. Journal of Physical Oceanography 2016, 46, 3321–3337. [CrossRef]
- Olbers, D.J. Nonlinear energy transfer and the energy balance of the internal wave field in the deep ocean. Journal of Fluid Mechanics 1976, 74, 375–399. [CrossRef]
- Varma, D.; Mathur, M. Internal wave resonant triads in finite-depth non-uniform stratifications. Journal of Fluid Mechanics 2017, 824, 286–311. [CrossRef]
- Eden, C.; Pollmann, F.; Olbers, D. Numerical evaluation of energy transfers in internal gravity wave spectra of the ocean. Journal of Physical Oceanography 2019, 49, 737–749. [CrossRef]
- Baker, L.E.; Sutherland, B.R. The evolution of superharmonics excited by internal tides in non-uniform stratification. Journal of Fluid Mechanics 2020, 891, R1. [CrossRef]
- Sutherland, B.R.; Dhaliwal, M.S. The nonlinear evolution of internal tides. Part 1: the superharmonic cascade. Journal of Fluid Mechanics 2022, 948, A21. [CrossRef]
- Mackinnon, J.A.; Alford, M.H.; Sun, O.; Pinkel, R.; Zhao, Z.; Klymak, J. Parametric subharmonic instability of the internal tide at 29°N. Journal of Physical Oceanography 2013, 43, 17–28. [CrossRef]
- Ansong, J.K.; Arbic, B.K.; Simmons, H.L.; Alford, M.H.; Buijsman, M.C.; Timko, P.G.; Richman, J.G.; Shriver, J.F.; Wallcraft, A.J. Geographical distribution of diurnal and semidiurnal parametric subharmonic instability in a global ocean circulation model. Journal of Physical Oceanography 2018, 48, 1409–1431. [CrossRef]
- Helfrich, K.R.; Grimshaw, R.H.J. Nonlinear Disintegration of the Internal Tide. Journal of Physical Oceanography 2008, 38, 686 – 701. [CrossRef]
- Ostrovsky, L., and Y.A. Stepanyants. 1989. Do internal solitons exist in the ocean? Review of Geophysics 27: 293–310. [Google Scholar] [CrossRef]
- Farmer, D.; Li, Q.; Park, J. Internal wave observations in the South China Sea: The role of rotation and non-linearity. Atmosphere-Ocean 2009, 47, 267–280. [CrossRef]
- Maxworthy, T. A note on the internal solitary waves produced by tidal flow over a three-dimensional ridge. Journal of Geophysical Research: Oceans 1979, 84, 338–346. [CrossRef]
- New, A.L.; Pingree, R.D. Large-amplitude internal soliton packets in the central Bay of Biscay. Deep Sea Research Part A. Oceanographic Research Papers 1990, 37, 513–524. [CrossRef]
- New, A.L.; Pingree, R.D. Local generation of internal soliton packets in the central bay of Biscay. Deep Sea Research Part A. Oceanographic Research Papers 1992, 39, 1521–1534. [CrossRef]
- Gerkema, T. Internal and interfacial tides: Beam scattering and local generation of solitary waves.
- Grisouard, N.; Staquet, C.; Gerkema, T. Generation of internal solitary waves in a pycnocline by an internal wave beam: a numerical study. Journal of Fluid Mechanics 2011, 676, 491–513. [CrossRef]
- Mercier, M.J.; Mathur, M.; Gostiaux, L.; Gerkema, T.; MagalhÃes, J.M.; Silva, J.C.D.; Dauxois, T. Soliton generation by internal tidal beams impinging on a pycnocline: Laboratory experiments. Journal of Fluid Mechanics 2012, 704, 37–60. [CrossRef]
- Gerkema, T.; Staquet, C.; Bouruet-Aubertot, P. Non-linear effects in internal-tide beams, and mixing. Ocean Modelling 2006, 12, 302–318. [CrossRef]
- Alpers, W. Theory of radar imaging of internal waves. Nature 2018, 314, 245–247. [CrossRef]
- Jackson, C.R.; da Silva, J.C.; Jeans, G. The generation of nonlinear internal waves. Oceanography 2012, 25, 108–123. [CrossRef]
- Jackson, C.R.; da Silva, J.; Jeans, G.; Alpers, W.; Caruso, M. Nonlinear Internal Waves in Synthetic Aperture Radar Imagery. Oceanography 2013, 26, 68–79. [CrossRef]
- Jackson, C. Internal wave detection using the Moderate Resolution Imaging Spectroradiometer (MODIS). Journal of Geophysical Research: Oceans 2007, 112. [CrossRef]
- Simmons, H., M.H. Chang, Y.T. Chang, S.Y. Chao, O. Fringer, C.R. Jackson, and D.S. Ko. 2011. Modeling and Prediction of Internal Waves in the South China Sea. Oceanography 24: 88–99. [Google Scholar] [CrossRef]
- Alford, M.H.; Peacock, T.; Mackinnon, J.A.; Nash, J.D.; Buijsman, M.C.; Centuroni, L.R.; Chao, S.Y.; Chang, M.H.; Farmer, D.M.; Fringer, O.B.; Fu, K.H.; Gallacher, P.C.; Graber, H.C.; Helfrich, K.R.; Jachec, S.M.; Jackson, C.R.; Klymak, J.M.; Ko, D.S.; Jan, S.; Johnston, T.M.; Legg, S.; Lee, I.H.; Lien, R.C.; Mercier, M.J.; Moum, J.N.; Musgrave, R.; Park, J.H.; Pickering, A.I.; Pinkel, R.; Rainville, L.; Ramp, S.R.; Rudnick, D.L.; Sarkar, S.; Scotti, A.; Simmons, H.L.; Laurent, L.C.S.; Venayagamoorthy, S.K.; Wang, Y.H.; Wang, J.; Yang, Y.J.; Paluszkiewicz, T.; Tang, T.Y. The formation and fate of internal waves in the South China Sea. Nature 2015, 521, 65–69. [CrossRef]
- Konyaev, K.; Sabinin, K.; Serebryany, A. Large-amplitude internal waves at the Mascarene Ridge in the Indian Ocean. Deep Sea Research Part I: Oceanographic Research Papers 1995, 42, 2075–2091. [CrossRef]
- da Silva, J.C.; Buijsman, M.C.; Magalhaes, J.M. Internal waves on the upstream side of a large sill of the Mascarene Ridge: A comprehensive view of their generation mechanisms and evolution. Deep-Sea Research Part I: Oceanographic Research Papers 2015, 99, 87–104. [CrossRef]
- Osborne, A.R.; Burch, T.L. Internal Solitons in the Andaman Sea. Science 1980, 208, 451–460. [CrossRef]
- Jensen, T.G.; Magalhães, J.; Wijesekera, H.W.; Buijsman, M.; Helber, R.; Richman, J. Numerical modelling of tidally generated internal wave radiation from the Andaman Sea into the Bay of Bengal. Deep-Sea Research Part II: Topical Studies in Oceanography 2020, 172. [CrossRef]
- Magalhaes, J.M.; da Silva, J.C.; Buijsman, M.C. Long lived second mode internal solitary waves in the Andaman Sea. Scientific Reports 2020, 10. [CrossRef]
- Ivanov, V.; Ivanov, L.; Lisichenok, A. Redistribution of energy of the internal tidal wave in the North Equatorial Countercurrent region. Soviet Journal of Physical Oceanography 1990, 1, 383–386. [CrossRef]
- Magalhaes, J.M.; Silva, J.C.D.; Buijsman, M.C.; Garcia, C.A. Effect of the North Equatorial Counter Current on the generation and propagation of internal solitary waves off the Amazon shelf (SAR observations). Ocean Science 2016, 12, 243–255. [CrossRef]
- van Aken, H.M.; van Haren, H.; Maas, L.R.M. The high-resolution vertical structure of internal tides and near-inertial waves measured with an ADCP over the continental slope in the Bay of Biscay. Deep-Sea Research Part I: Oceanographic Research Papers 2007, 54, 533–556. [CrossRef]
- Yu, X.; Ponte, A.L.; Elipot, S.; Menemenlis, D.; Zaron, E.D.; Abernathey, R. Surface Kinetic Energy Distributions in the Global Oceans From a High-Resolution Numerical Model and Surface Drifter Observations. Geophysical Research Letters 2019, 46, 9757–9766. [CrossRef]
- Moum, J.N.; Farmer, D.M.; Smyth, W.D.; Armi, L.; Vagle, S. Structure and Generation of Turbulence at Interfaces Strained by Internal Solitary Waves Propagating Shoreward over the Continental Shelf. Journal of Physical Oceanography 2003, 33, 2093–2112. [CrossRef]
- Carter, G.S.; Gregg, M.C.; Lien, R.C. Internal waves, solitary-like waves, and mixing on the Monterey Bay shelf. Continental Shelf Research 2005, 25, 1499–1520. [CrossRef]
- Shroyer, E.L.; Moum, J.N.; Nash, J.D. Energy transformations and dissipation of nonlinear internal waves over New Jersey’s continental shelf. Nonlinear Processes in Geophysics 2010, 17, 345–360. [CrossRef]
- Zhang, X.; Huang, X.; Yang, Y.; Zhao, W.; Wang, H.; Yuan, C.; Tian, J. Energy cascade from internal solitary waves to turbulence via near N-waves in the northern South China Sea. Journal of Physical Oceanography 2023. [CrossRef]
- Buijsman, M.C.; Kanarska, Y.; McWilliams, J.C. On the generation and evolution of nonlinear internal waves in the South China Sea. Journal of Geophysical Research: Oceans 2010, 115. [CrossRef]
- Vitousek, S.; Fringer, O.B. Physical vs. numerical dispersion in nonhydrostatic ocean modeling. Ocean Modelling 2011, 40, 72–86. [CrossRef]
- Müller, M.; Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Kunze, E.L.; Scott, R.B.; Wallcraft, A.J.; Zamudio, L. Toward an internal gravity wave spectrum in global ocean models. Geophysical Research Letters 2015, 42, 3474–3481. [CrossRef]
- Savage, A.C.; Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Alford, M.H.; Buijsman, M.C.; Farrar, J.T.; Sharma, H.; Voet, G.; Wallcraft, A.J.; Zamudio, L. Frequency content of sea surface height variability from internal gravity waves to mesoscale eddies. Journal of Geophysical Research: Oceans 2017, 122, 2519–2538. [CrossRef]
- Luecke, C.A.; Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Alford, M.H.; Ansong, J.K.; Bassette, S.L.; Buijsman, M.C.; Menemenlis, D.; Scott, R.B.; Timko, P.G.; Voet, G.; Wallcraft, A.J.; Zamudio, L. Statistical Comparisons of Temperature Variance and Kinetic Energy in Global Ocean Models and Observations: Results From Mesoscale to Internal Wave Frequencies. Journal of Geophysical Research: Oceans 2020, 125, e2019JC015306. [CrossRef]
- Arbic, B.; Elipot, S.; Brasch, J.M.; Menemenlis, D.; Ponte, A.L.; Shriver, J.F.; Yu, X.; Zaron, E.D.; Alford, M.H.; Buijsman, M.C.; Abernathey, R.; Garcia, D.; Guan, L.; Martin, P.E.; Nelson, A.D. Near-Surface Oceanic Kinetic Energy Distributions From Drifter Observations and Numerical Models. Journal of Geophysical Research: Oceans 2022, 127, e2022JC018551. [CrossRef]
- Müller, M. On the space- and time-dependence of barotropic-to-baroclinic tidal energy conversion. Ocean Modelling 2013, 72, 242–252. [CrossRef]
- Buijsman, M.C.; Ansong, J.K.; Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Timko, P.G.; Wallcraft, A.J.; Whalen, C.B.; Zhao, Z. Impact of parameterized internal wave drag on the semidiurnal energy balance in a global ocean circulation model. Journal of Physical Oceanography 2016, 46, 1399–1419. [CrossRef]
- Li, Z.; von Storch, J.S. M2 Internal-Tide Generation in STORMTIDE2. Journal of Geophysical Research: Oceans 2020, 125, e2019JC015453. [CrossRef]
- Raja, K.J.; Buijsman, M.C.; Shriver, J.F.; Arbic, B.K.; Siyanbola, O. Near-Inertial Wave Energetics Modulated by Background Flows in a Global Model Simulation. Journal of Physical Oceanography 2022, 52, 823 – 840. [CrossRef]
- Bleck, R. An oceanic general circulation model framed in hybrid isopycnic-Cartesian coordinates. Ocean Modelling 2002, 4, 55–88. [CrossRef]
- Metzger, E.J., O.M. Smedstad, P.G. Thoppil, H.E. Hurlburt, J.A. Cummings, A.J. Wallcraft, L. Zamudio, D.S. Franklin, P.G. Posey, M.W. Phelps, P.J. Hogan, F.L. Bub, and C.J. Dehaan. 2014. US Navy Operational Global Ocean and Arctic Ice Prediction Systems. Oceanography 27: 32–43. [Google Scholar] [CrossRef]
- Hogan, T.F., M. Liu, J.A. Ridout, M.S. Peng, T.R. Whitcomb, B.C. Ruston, C.A. Reynolds, S.D. Eckermann, J.R. Moskatiis, N.L. Baker, J.P. McCormack, K.C. Viner, J.G. McLay, M.K. Flatau, L. Xu, C. Chen, and S.W. Chang. 2014. The Navy Global Environmental Model. Oceanography 27: 116–125. [Google Scholar] [CrossRef]
- Ngodock, H.E.; Souopgui, I.; Wallcraft, A.J.; Richman, J.G.; Shriver, J.F.; Arbic, B.K. On improving the accuracy of the M2 barotropic tides embedded in a high-resolution global ocean circulation model. Ocean Modelling 2016, 97, 16–26. [CrossRef]
- Jayne, S.R.; St. Laurent, L.C. Parameterizing tidal dissipation over rough topography. Geophysical Research Letters 2001, 28, 811–814. [CrossRef]
- Kang, D.; Fringer, O. Energetics of barotropic and baroclinic tides in the Monterey Bay area. Journal of Physical Oceanography 2012, 42, 272–290. [CrossRef]
- Kelly, S.M. The vertical mode decomposition of surface and internal tides in the presence of a free surface and arbitrary topography. Journal of Physical Oceanography 2016, 46, 3777–3788. [CrossRef]
- Pan, Y.; Haley, P.J.; Lermusiaux, P.F. Interactions of internal tides with a heterogeneous and rotational ocean. Journal of Fluid Mechanics 2021, 920, A18. [CrossRef]
- Barkan, R.; Srinivasan, K.; Yang, L.; McWilliams, J.C.; Gula, J.; Vic, C. Oceanic Mesoscale Eddy Depletion Catalyzed by Internal Waves. Geophysical Research Letters 2021, 48, e2021GL094376. [CrossRef]
- Kang, D.; Fringer, O. On the calculation of available potential energy in internal wave fields. Journal of Physical Oceanography 2010, 40, 2539–2545. [CrossRef]
- Nash.; Alford, M.H.; Kunze, E. Estimating Internal Wave Energy Fluxes in the Ocean. Journal of Atmospheric and Oceanic Technology 2005, 22, 1551–1570. [CrossRef]
- Venayagamoorthy, S.K.; Fringer, O.B. Nonhydrostatic and nonlinear contributions to the energy flux budget in nonlinear internal waves. Geophysical Research Letters 2005, 32. [CrossRef]
- Tchilibou, M.; Koch-Larrouy, A.; Barbot, S.; Lyard, F.; Morel, Y.; Jouanno, J.; Morrow, R. Internal tides off the Amazon shelf during two contrasted seasons: Interactions with background circulation and SSH imprints. Ocean Science Discussions 2022, 2022, 1–38. [CrossRef]
- Eyink, G.L.; Aluie, H. Localness of energy cascade in hydrodynamic turbulence. I. Smooth coarse graining. Physics of Fluids 2009, 21, 115107. [CrossRef]
- Aluie, H.; Hecht, M.; Vallis, G.K. Mapping the Energy Cascade in the North Atlantic Ocean: The Coarse-Graining Approach. Journal of Physical Oceanography 2018, 48, 225–244. [CrossRef]
- Pollmann, F.; Eden, C.; Olbers, D. Evaluating the Global internal wave model IDEMIX using finestructure methods. Journal of Physical Oceanography 2017, 47, 2267–2289. [CrossRef]
- Buijsman, M.C.; Solano, M.; Shriver, J.F. Variance in vertical modes across frequency bands in a global ocean simulation. Ocean Modelling in preparation.
- Eden, C.; Olbers, D. An Energy Compartment Model for Propagation, Nonlinear Interaction, and Dissipation of Internal Gravity Waves. Journal of Physical Oceanography 2014, 44, 2093 – 2106. [CrossRef]
- de Lavergne, C.; Falahat, S.; Madec, G.; Roquet, F.; Nycander, J.; Vic, C. Toward global maps of internal tide energy sinks. Ocean Modelling 2019, 137, 52–75. [CrossRef]
- Nelson, A.D.; Arbic, B.K.; Menemenlis, D.; Peltier, W.R.; Alford, M.H.; Grisouard, N.; Klymak, J.M. Improved Internal Wave Spectral Continuum in a Regional Ocean Model. Journal of Geophysical Research: Oceans 2020, 125, e2019JC015974. [CrossRef]
- Zaron, E.D. Mapping the nonstationary internal tide with satellite altimetry. Journal of Geophysical Research: Oceans 2017, 122, 539–554. [CrossRef]
- Buijsman, M.C.; Arbic, B.K.; Richman, J.G.; Shriver, J.F.; Wallcraft, A.J.; Zamudio, L. Semidiurnal internal tide incoherence in the equatorial Pacific. Journal of Geophysical Research 2017, 122, 5286–5305. [CrossRef]
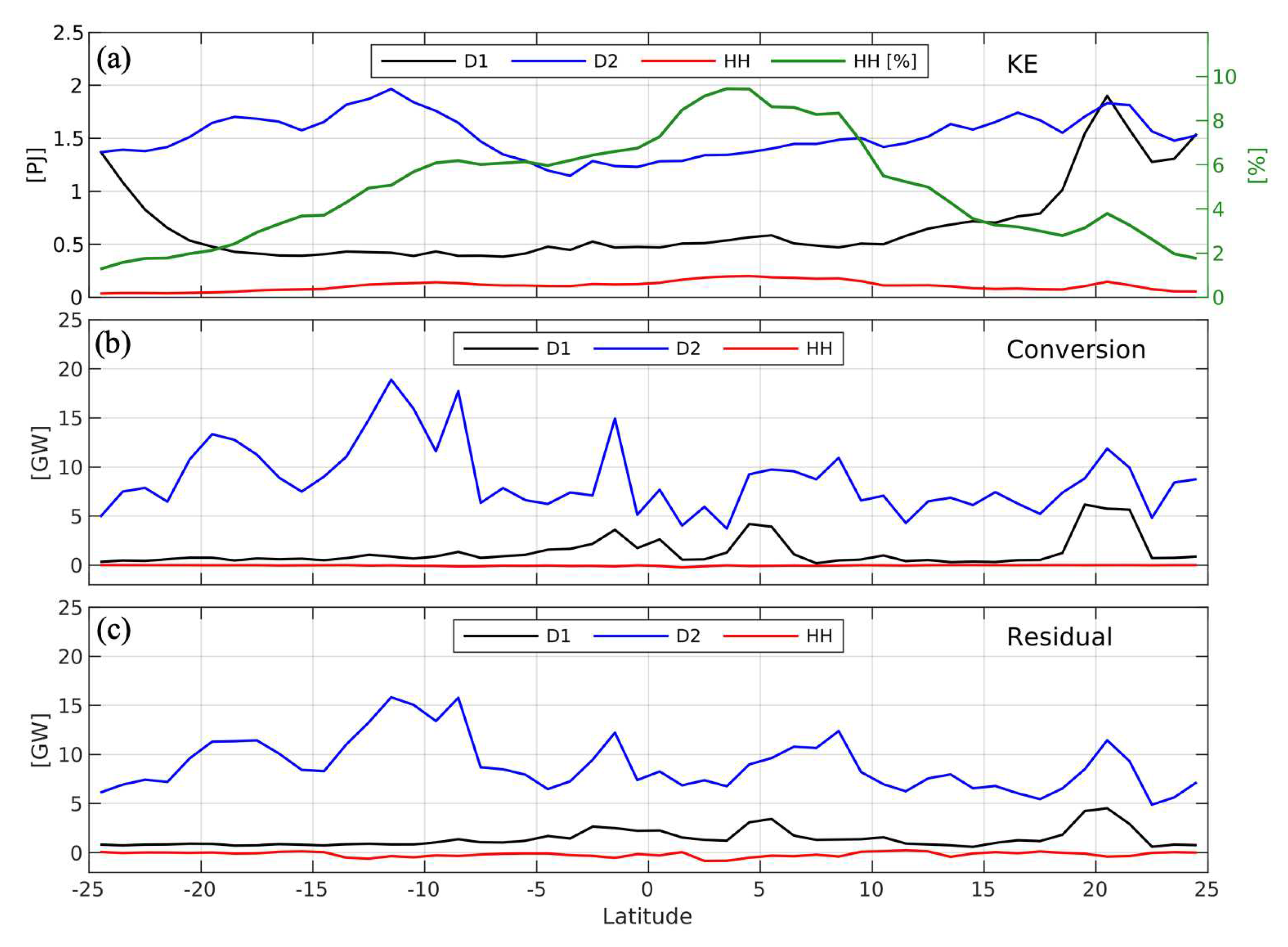
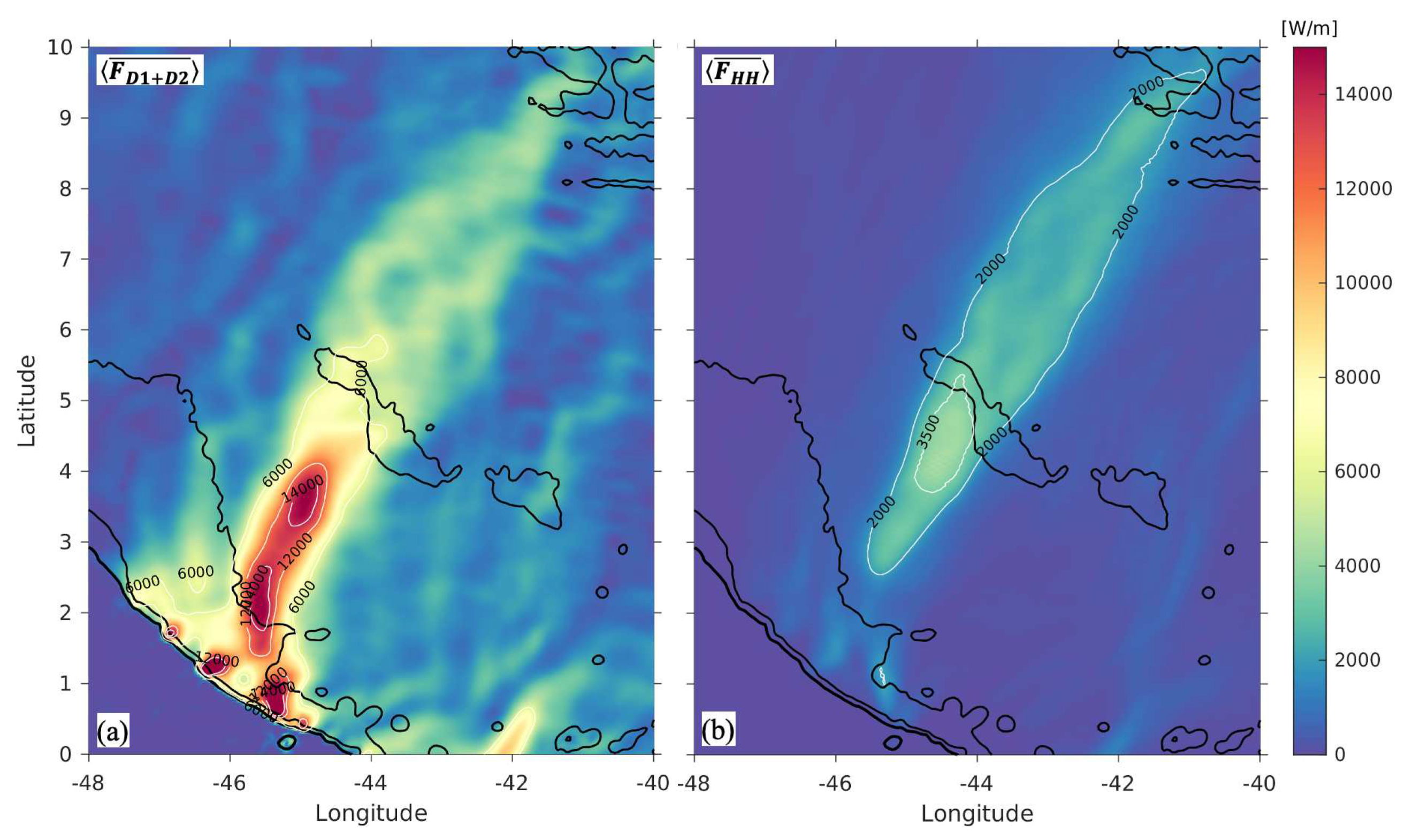
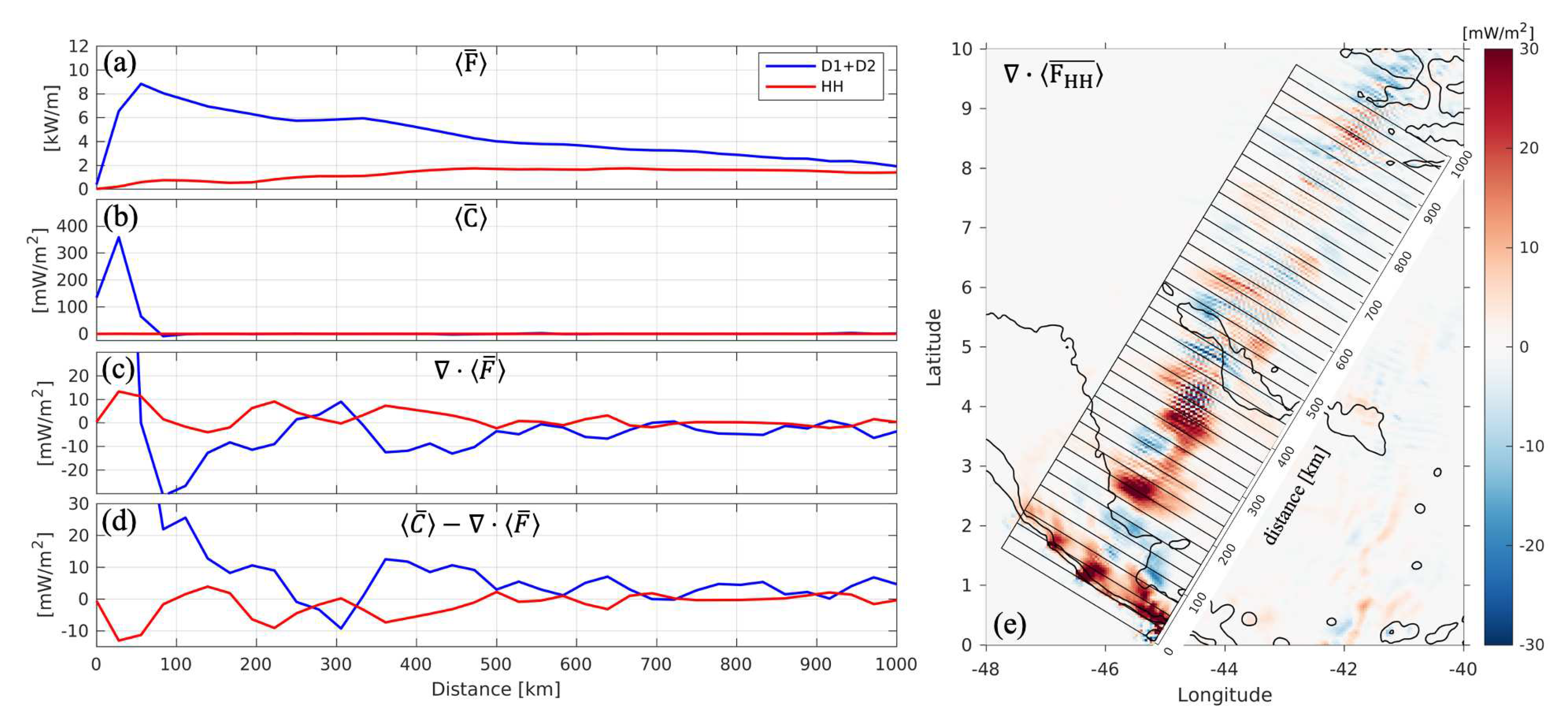
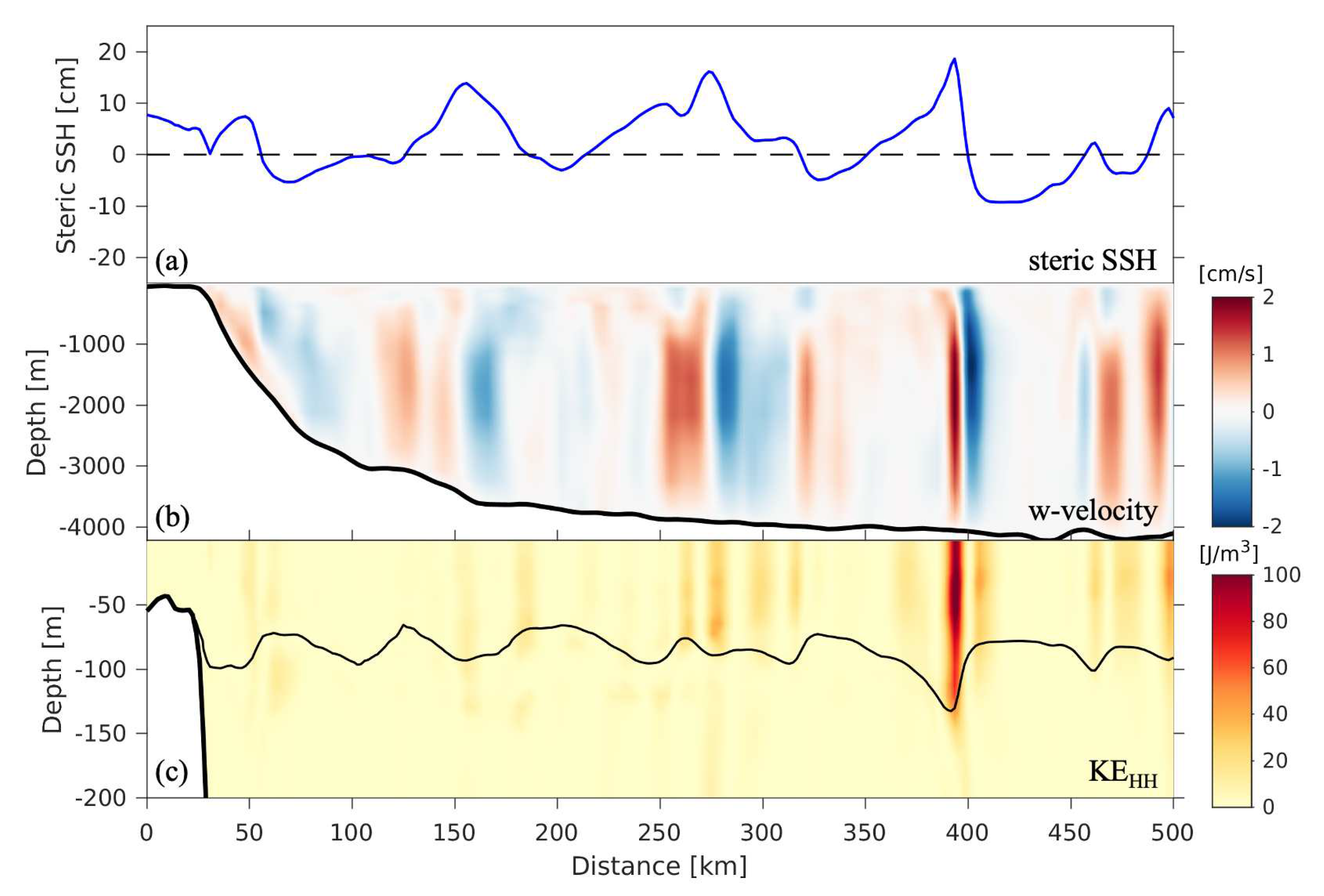
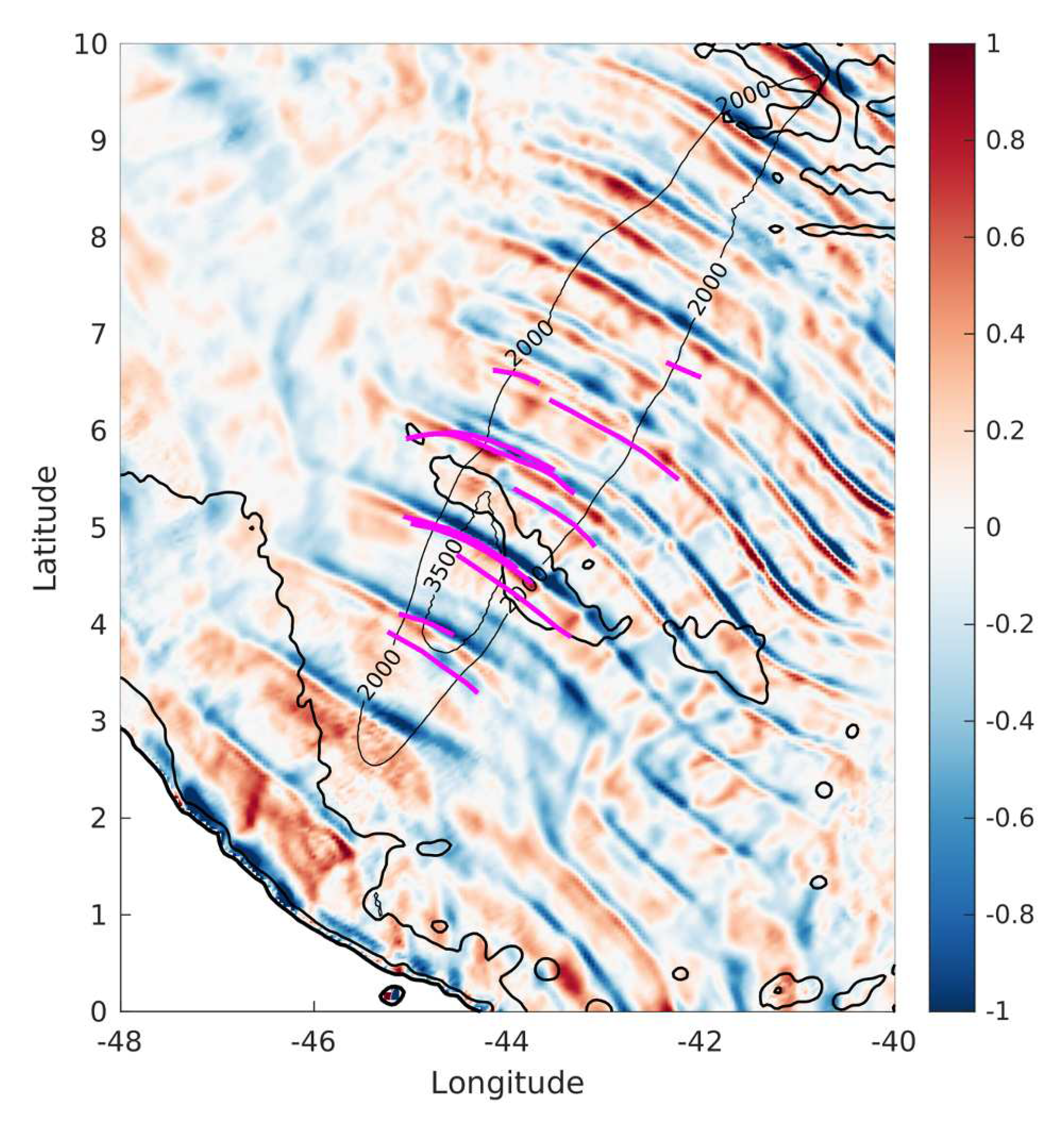
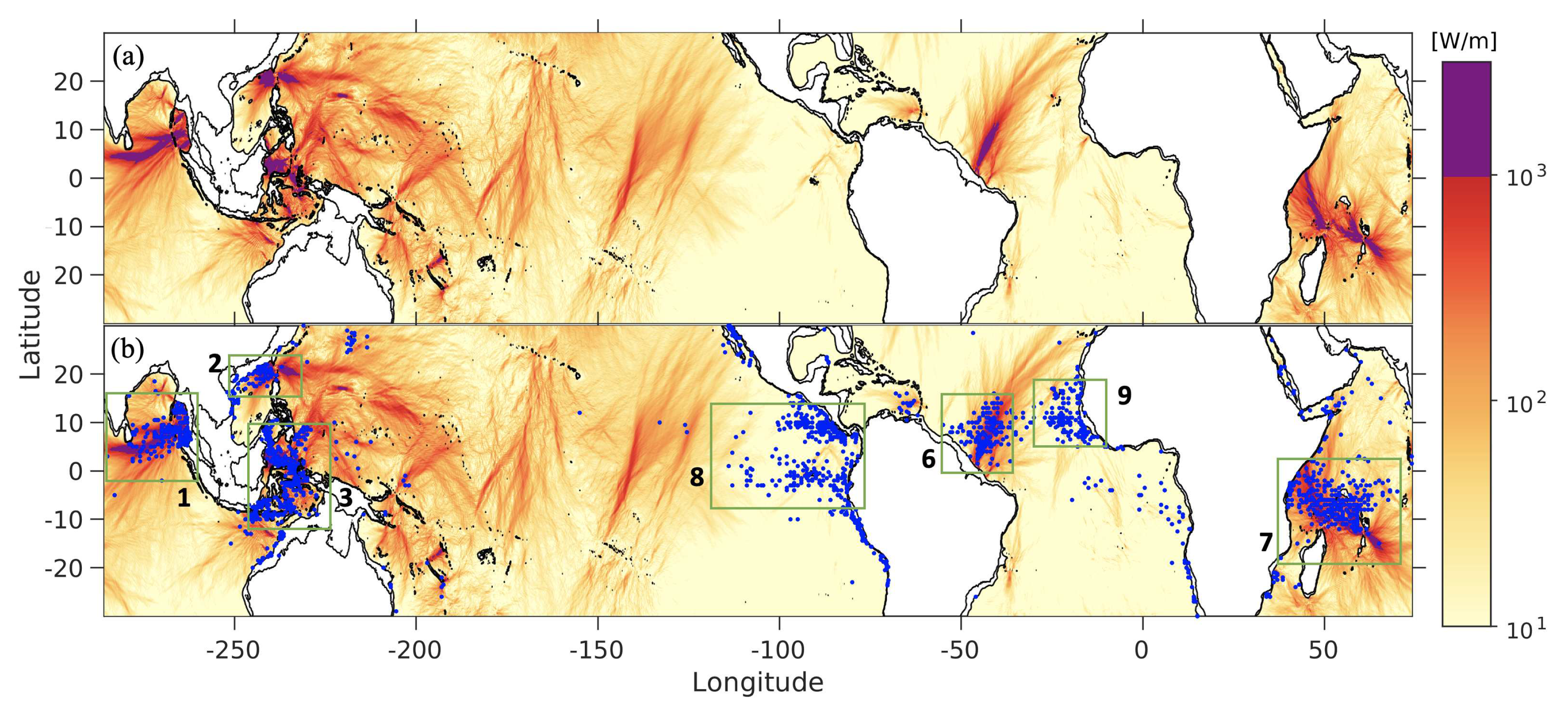
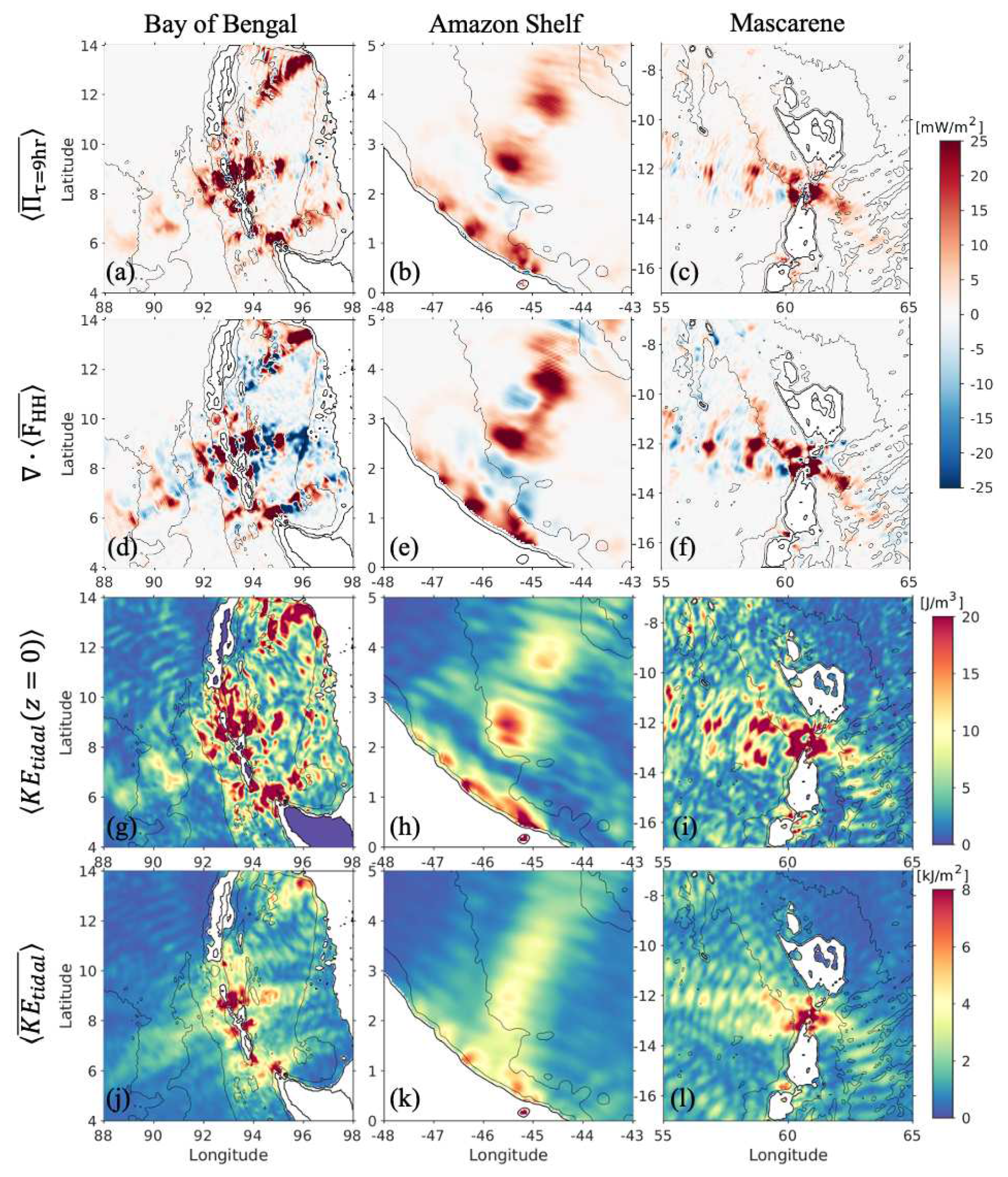
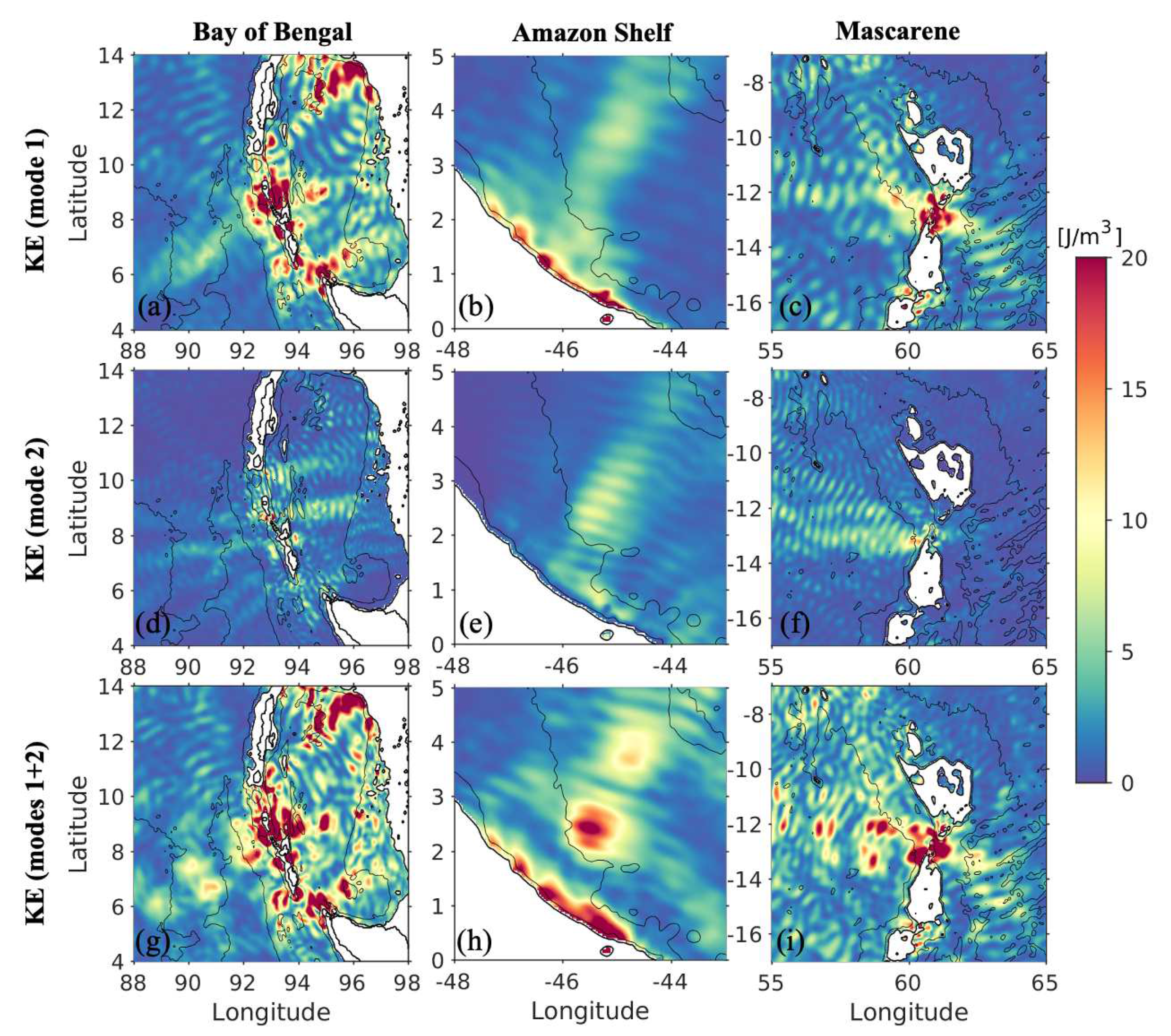
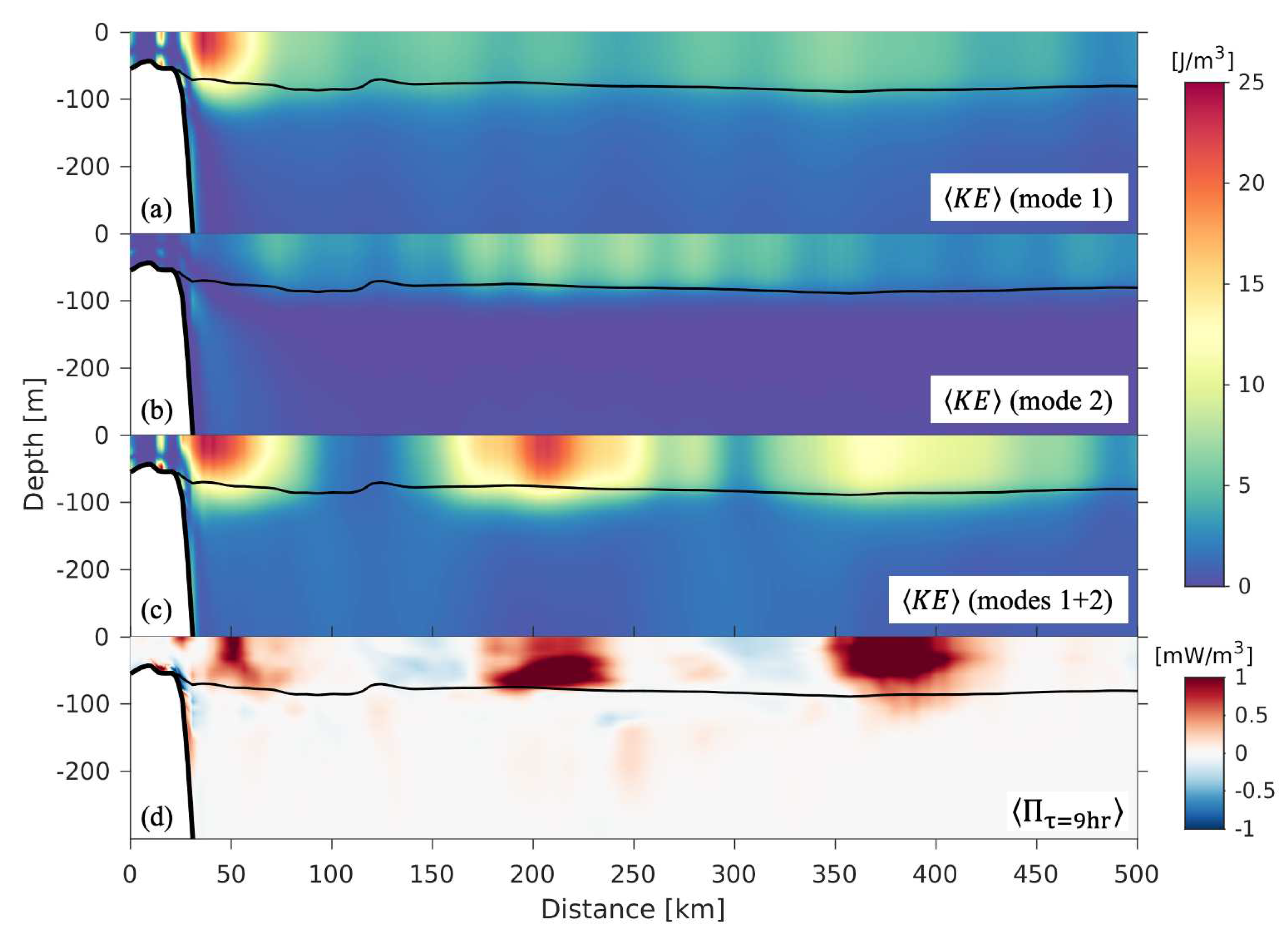
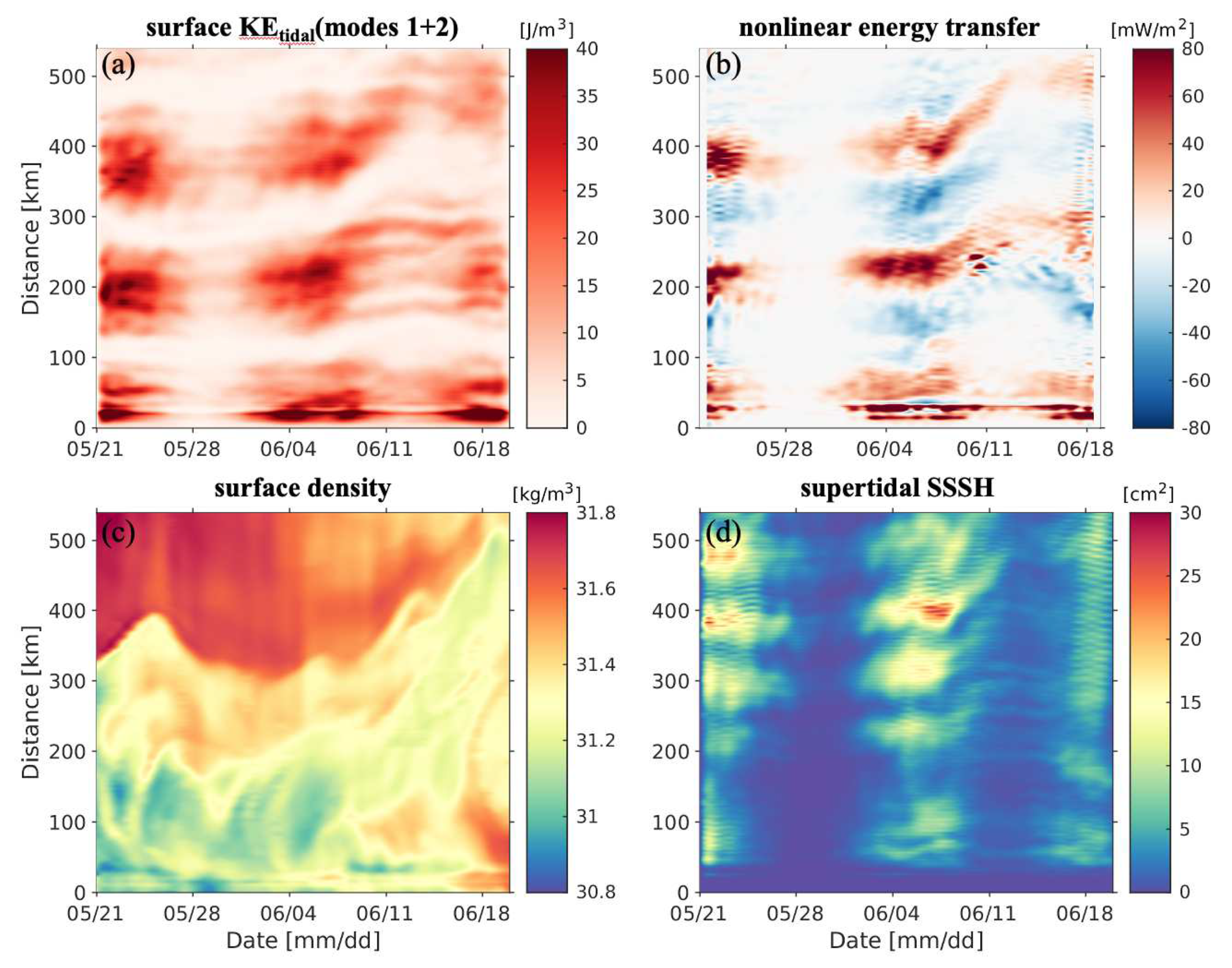
| area | [km] | [km] | [ms] | [ms] | [km] | [km] |
|---|---|---|---|---|---|---|
| Bay of Bengal | 216 | 210 | 2.79 | 1.75 | 125 | 78 |
| Amazon Shelf | 180 | 177 | 2.42 | 1.50 | 108 | 67 |
| Mascarene Ridge | 190 | 185 | 2.95 | 1.72 | 132 | 77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





