Prerpints.org logo
Preprint
Article

Explosion and Dynamic Transparency of Low-Density Structured Polymeric Targets Irradiated by a Long-Pulse KrF Laser

Altmetrics

Downloads

97

Views

16

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

09 August 2023

Posted:

11 August 2023

You are already at the latest version

Alerts
Abstract
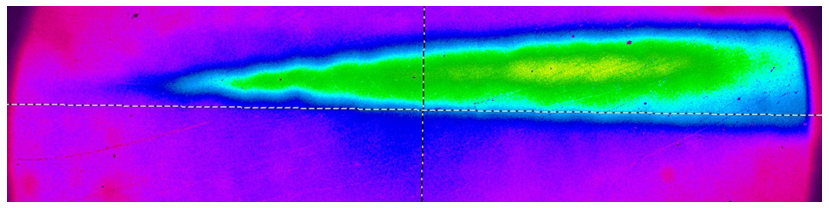
The hydrodynamics of plasma formed in the interaction of 100-ns UV KrF laser pulses with foam targets with volume densities from 5 to 500 mg/cm3 was studied. Initial and dynamic transmittance at 248-nm wavelength have been measured. At intensities about 1012 W/cm2, the propagation rates of radiation through foam targets reached 80 km/s, while plasma stream velocities from both front and rear sides of targets were approximately the same ~ 75 km/s, which confirms a volumetric absorption of radiation within the target thickness and the explosive nature of the plasma formation and expansion.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

The idea of Basov and Krokhin to fire with a laser thermonuclear (TN) reaction between deuterium and tritium (D−T) during a short time compared to the hydrodynamic expansion of heated plasma, i.e., to obtain the inertial confinement fusion (ICF) in the micro explosion [1], is currently under a comprehensive investigation. It is either in a direct-drive irradiation of a shell target with TN fuel by laser light [2], or in the indirect scheme with converting laser radiation into X-rays in the cylindrical capsule with a target inside [3]. Nowadays, when the ignition of TN reaction has been already achieved in the indirect-drive at NIF Nd: glass laser facility [4], it is quite obvious from a prolonged experimental run [5,6,7,8] that the main obstacle on the path to ignition are hydrodynamic instabilities. From initial perturbations caused by either target imperfections or X-ray irradiation asymmetry they rapidly develop into the turbulent phase during shell acceleration, as well as its deceleration afore the target collapse.
In the direct-drive scheme initial small-scale perturbations besides a roughness of the shell surface are mainly caused by speckles typical for irradiation by a coherent light. A large-scale asymmetry arises either because of a limited number of laser beams even in the advanced ICF laser facilities (e.g., about 200 for the biggest ones NIF [9] and LMJ [10]) or energy misbalance between the beams. The latter originates from energy exchange in a course of nonlinear laser interaction with underdense outer plasma corona [11]. The small-scale hydrodynamic perturbations are seeded via "laser imprinting" at the very beginning of target irradiation, before plasma corona being formed: light inhomogeneities are directly transformed into inhomogeneous profile of the ablation front moving inward the shell [12]. The growth of instabilities and their transition into the turbulence lead to mixing of the TN fuel and shell material followed by temperature and density decrease in the target core which results in a sharp fall of the TN reaction rate and prevents the TN fuel burning.
To uniform the distribution of laser radiation over a target surface, many optical methods have been developed (they are described e.g., in the review [11]) that are random phase plates, phased zone plates, and kinoform phase plates. As well an optical smoothing was demonstrated by angular dispersion of frequency-modulated laser light, induced spatial incoherence (ISI) produced by echelons. To reduce the effect of laser imprinting, in addition to optical methods, there are various hydrodynamic methods based on the creation of a plasma layer in front of the target with a density gradient towards the target before the arrival of the main heating pulse. Such absorbing plasma with a density somewhat higher than the critical one evens out the irradiation inhomogeneities due to transverse thermal diffusion [13]. It can be created by ionizing a gas [14] or a porous medium, i.e., a foam with a low volume density placed in front of the plastic ablator by a low-energy prepulse [15,16]. A near-critical-density (NCD) preheated foam plasma can be also produced by X-ray radiation from a nearby laser-plasma source [17,18], or by using a thin (<1000 Å) layer of a high-Z material, which is deposited on the target surface or incorporated into the foam facing the laser [19,20,21]. In the latter case, laser-heated high-Z plasma effectively re-radiates in the soft X-ray range, causing uniform ablation of the target. As a result, the distance between the absorption zone of laser radiation nearby the critical plasma density and the ablation front increases, which leads to smoothing of the laser imprint.
Laser-foam interaction including ionization dynamics of foams have been studied experimentally and theoretically in many works mostly with Nd: glass lasers at wavelength λ = 1060 nm, sometimes at second (2ω) or third (3ω) harmonics (see, for example, [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]). It is commonly assumed that foams are initially transparent for laser radiation and plasma is originated from evaporation and ionization of pore septa. Meantime, compared with a Nd: glass laser, KrF laser looks more attractive in the role of ICF driver, and especially for the production of the Inertial Fusion Energy (IFE), as it can be scaled to required sub-megajoule pulse energy, operate with overall efficiency up to 7% at rep-rate 5−10 Hz and be arranged by a focal spot zooming synchronously with a target implosion [39,40]. As KrF fundamental radiation UV wavelength λ = 248 nm is one and a half times less than the 3ω Nd: glass laser, it has a number of important advantages in laser-target interaction: higher ablation pressure and efficiency of laser energy transfer into the kinetic energy of the imploding target, higher thresholds of laser-plasma instabilities (LPI) in the plasma corona and, accordingly, less amount of harmful fast “superthermal” electrons preheating the dense target core before the collapse. The effective echelon-free ISI smoothing of a broad-bandwidth radiation with a noncoherent master oscillator was implemented on Nike KrF laser facility [41]. An overlapping of 44 noncoherent beams with a total energy about 1.7 kJ in 4-ns pulses produced on a planar target intensity I ~ 1014 W/cm2 with the highest ever achieved uniformity with an rms deviation ~ 0.15% within the spot of 500−1000 μm. A stepwise laser pulse-form used in early experiments [42,43] and supposed for the ICF-scale target design [44] had a low-intensity “foot” of 3 to 5 ns length with I = 1012−1013 W/cm2, which sets the required compression adiabat of the imploding target. In such conditions laser imprinted perturbations were still observed for polystyrene (СH) targets with rms roughness < 30 Å, while hydrodynamic smoothing reduced them by an order of magnitude.
Among other foam applications, experiments at the 5-beam Shenguang III 3ω Nd: glass laser facility could be mentioned [45] where a homogenous long-scale NCD plasma was produced by 4 laser beams with total energy 3.2 kJ in 1-ns pulses and intensity I ≈ 8×1014 W/cm2 from uniformly irradiated foam with a density ~ 10 mg/cm3. Interaction of the fifth delayed beam at intensity I ~ 1015 W/cm2 with the plasma was investigated which modeled the LPI development in the ICF-scale conditions. Thick NCD foam targets were used by Romsej et al. for direct laser acceleration (DLA) of electrons at relativistic intensity of 1019 W/cm2 in homogeneous plasma channel of sub-mm length preformed by a nanosecond laser pulse with intensity I ≈ 5×1013 W/cm2 [46,47]. Long foam plasma gave a significant advantage in the DLA compared with a short-scale plasma produced in a conventional laser-foil interaction.
The present studies with low-density foam targets performed with a long-pulse GARPUN KrF laser at relatively low peak intensity ~ 1012 W/cm2 were motivated by our previous experiments [48,49] where in a specific two-dimensional (2D) geometry high-aspect-ratio capillary channels were obtained in semitransparent polymeric materials, e.g., polymethyl methacrylate (PMMA) and they revealed obvious features of the UV radiation waveguide. A direct electron acceleration in a self-produced, or preliminary drilled capillaries was observed up to a few hundred keV [50], being associated with a longitudinal component of the electric field in a corrugated waveguide which retarded the light in phase with electrons [51]. It is expected that the 2D hydrodynamics of low-density foam targets for 100-ns laser pulse would be rather different from the case of 1D geometry typical for the most laser-foam interaction studies [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] carried out with ns-scale laser pulses. In addition, the most plastic materials have a steep rise in absorbance around KrF laser wavelength [49], which should decrease the plasma formation time for foams. So, we believe that mm-scale plasma channels could be obtained with long KrF laser pulses.

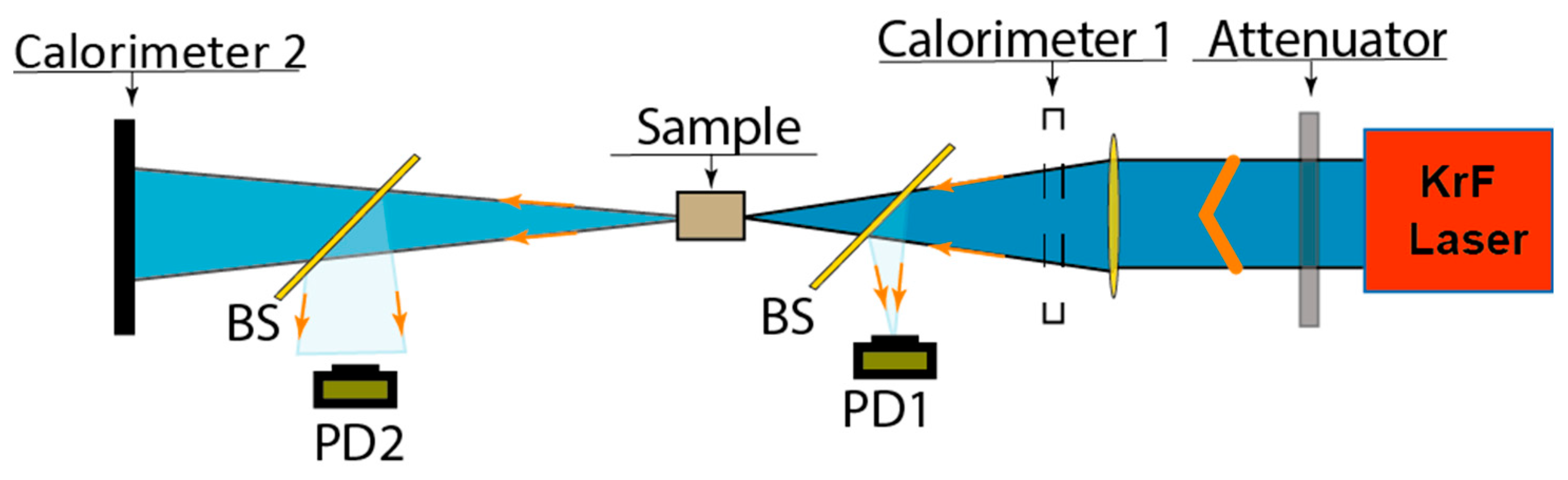
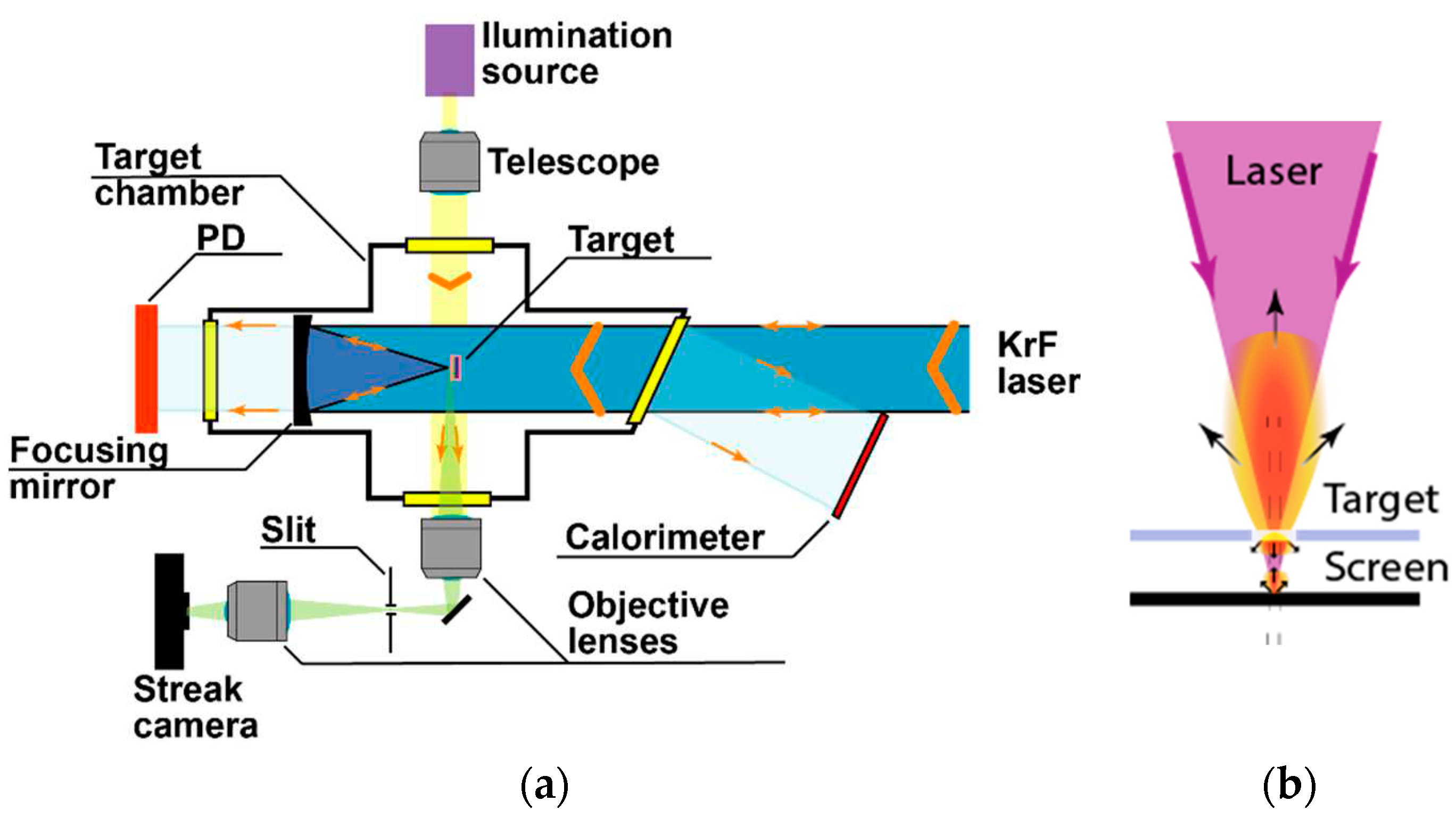
2. Experimental setup

2.1. GARPUN KrF laser description and performance of experiments

Two sets of experiments were performed at GARPUN KrF laser facility with foam targets. Firstly, an initial foam transparency was measured at low laser intensity I ≤ 106 W/cm2 below the plasma formation threshold. After that, the dynamic transparency of foams was investigated in the intensity range I = (1÷6)×1010 W/cm2 when targets became evaporated during the action of the laser pulse. A discharge-pumped Lambda Physik EMG 150 TMSC laser was used in these measurements which generated pulses of a bell-like form with maximal energy Emax = 250 mJ, temporal width τ = 20 ns at FWHM, and beam divergence ~ 0.2 mrad. By using a step-wise diffraction attenuator DVA-22-250 (Inst. of Automation and Electrometry, Siberian Branch of RAS), the energy was varied in the range E = (0.01÷0.94)×Emax before being focused by a lens with F = 1 m on the samples (see Figure 1). Energy of incident and transmitted radiation was measured by calorimeters PESO-SH-V2 with NOVA II display (Ophir Photonics) and pulse shapes by photodiodes (PD) Thorlabs DET10A and TDS 2024 200 MHz (Tektronix) oscilloscope with ~2 ns temporal resolution. The radiation distribution in a focal plane was measured with Spiricon SP620U profiler (Ophir Photonics), while K8 glass plate was used to convert UV laser light into green fluorescence [49]. The focal distribution had a Gaussian-like symmetric central part of 60-μm diameter at the FWHM and broad low-intensity wings, originated from a temporal evolution of laser light in the unstable resonator cavity of the laser [50].
The initial sample transparency was measured in the same scheme, but the focusing lens was replaced by a diaphragm with a diameter of 1 mm which allowed to probe small samples with a uniform intensity distribution quite below plasma formation.
The second set of experiments was carried out at a large-volume GARPUN KrF laser with a two-side e-beam pumping. It was equipped with an unstable telescopic resonator (magnification parameter M = 6) and generated in the injection-controlled operation mode 100-J & 100-ns trapezoidal pulses with a rise front of 20 ns. EMG 150 TMSC laser was used as a master oscillator, which pulses were distributed between 4 laser-triggered switches in high-voltage pulsed power supply of e-beam cold-cathode guns while a rest small fraction was injected into the resonator cavity of the GARPUN laser thus providing a quasi-steady divergence of output radiation ~2×10-4 (for other details see [48]). A slightly convergent output laser beam with initial cross section of 14×18 cm2 was directed into the vacuum chamber and focused by a spherical mirror with F=400 mm in a spot of 150 µm diameter (at 0.1 level of the maximum), which contained 75% of the whole energy [48]. The peak intensity in the center of the focal spot was about 1012 W/cm2 in present experiments.
Various foam targets were placed in the vacuum chamber at the adjustable suspension. The layout of plasma imaging in visible light is shown in Figure 2a (see also [50]). A plasma plume was imaged with an objective with F = 210 mm onto the intermediate plane, where an optical slit cut out a narrow strip oriented parallel to the incident laser beam. A time scanning of the strip was obtained by the “Agat” streak-camera with time resolution ~ 100 ps. A “burn-through” time when laser radiation penetrated through the tested target was measured with an additional thick Al screen placed behind the target (Figure 2b). When the tested target became transparent, plasma was created on the screen which allow to find the ablation front velocity inside the target. Preliminary target alignment on the streak camera screen was carried out in the “static mode” (without temporal scanning of the image) using a collimated probe beam produced by a telescope from an additional light source in the absence of a laser “shot”. By using a lens an image from the camera screen was displayed on the profilometer.

2.2. Foam target preparation

Structured polymer low-density materials (PLDM) based on super-crosslinked polymers have been manufactured for experiments on the GARPUN KrF laser facility using a technology developed in [52,53]. Linear polymers − polystyrene, poly-alpha-methylstyrene, polyacenaphthylene, polyvinyl naphthalene, polyvinylcarbazole, oligomethylphenylsiloxane − were used as starting polymers for the production of PLDM with the elemental composition of C-H, C-H–Si-O, C-H-N. High-molecular samples were synthesized by low-temperature cation polymerization. Super-crosslinked polymers in the form of organo-gels were obtained by crosslinking polymer macrochains in the Friedel-Crafts reaction in an organic solvent medium with chlorine-containing cross-agents, p-xylenedihloride and bis(chloromethyl)biphenyl. The synthesized polymer meshes have a rigid spatial structure, since they contain repeatedly connected benzene rings. In such a polymer, short interstitial fragments form a volumetric molecular framework with nanoscale cavities – micropores. On the other hand, a structurally rigid molecular mesh is formed in a dilute polymer solution. As a result of drying, larger cavities are formed – mesopores and macropores. Due to such a special molecular architecture, the obtained materials have a developed pore system with a specific surface area of up to 1800 m2/g and a low volume density.
Detailed studies of the porous structure were carried out using the method of low-temperature adsorption of nitrogen at 77 K and carbon dioxide at 273 K at the NovaTouch facility (Quantachrome, USA). The main characteristics of the porous structure of the PLDM were determined ‒ specific surface area, pore volume, parameters of the fractional composition of the pore system-surface, volume and size of pores, pore size distribution functions, etc. The density of the obtained materials was determined by hydrostatic weighing.
Several types of PLDM targets were selected for present laser experiments, differing in composition and manufacturing technology, as well as volume density and shape (Figure 3). The highest density among them were targets made of CH polymer ρ = 150−500 mg/cm3 made in the form of cylinders with a diameter of up to several millimeters (a). The lowest density down to ρ ~ 5 mg/cm3 with a thickness l of hundreds of microns had PLDM from CHO polymer (b). It was formed by drying the gel on special copper hoop which thickness set the thickness of the foam target. The plasma glow in the direction perpendicular to the laser beam was registered through the slot made in the hoop. SiO2 aerogel targets obtained by the method of supercritical drying of a colloidal silica gel solution in methanol had a volumetric density in the range ρ = 100−150 mg/cm3 and a different shape with a thickness of l up to several millimeters (c, d).
The PLDM targets were fixed in the interaction chamber at the suspension holder, and adjusted so that their frontal surface was in the focal plane of the focusing mirror. An additional screen for recording the burn-through time of the target was located a few millimeters behind a foam target (Figure 3 c).

3. PLDM transmittance

3.1. Initial PLDM transmittance at 248-nm wavelength

The initial transmittance of PLDM targets was measured at the wavelength λ=248 nm with a discharge-pumped KrF laser at low intensities of UV radiation I ≤ 106 W/cm2 quite below the threshold of target evaporation. An aperture of 1-mm cut out a collimated probe beam which passed through the samples. Pulses of incident and transmitted radiation reflected by beam-splitters (BS) were registered by two PDs (Figure 1a). With the help of a diffraction attenuator, the energy of the incident radiation could be varied by two orders of magnitude. Preliminarily PDs calibration relative each other has been done in the absence of a target. Within the measurement accuracy, the PLDM targets made of CH polymer completely absorbed UV radiation. The initial transmittance of targets made of CHO foam with a thickness of l ≈150 μm and SiO2 aerogel (l ≈ 3 mm) was, respectively, T = 15−20 and 5−8% and it did not depend on the incident intensity. For the given thicknesses of these targets differed by more than an order of magnitude, we obtain that SiO2 aerogel has the lowest effective (taking into account scattering in matter) absorption coefficient α = (1/l)ln(100/T[%]) ≈ 10 cm-1 among the tested PLDM targets. In CHO foam it was α ≈ 102 cm-1.

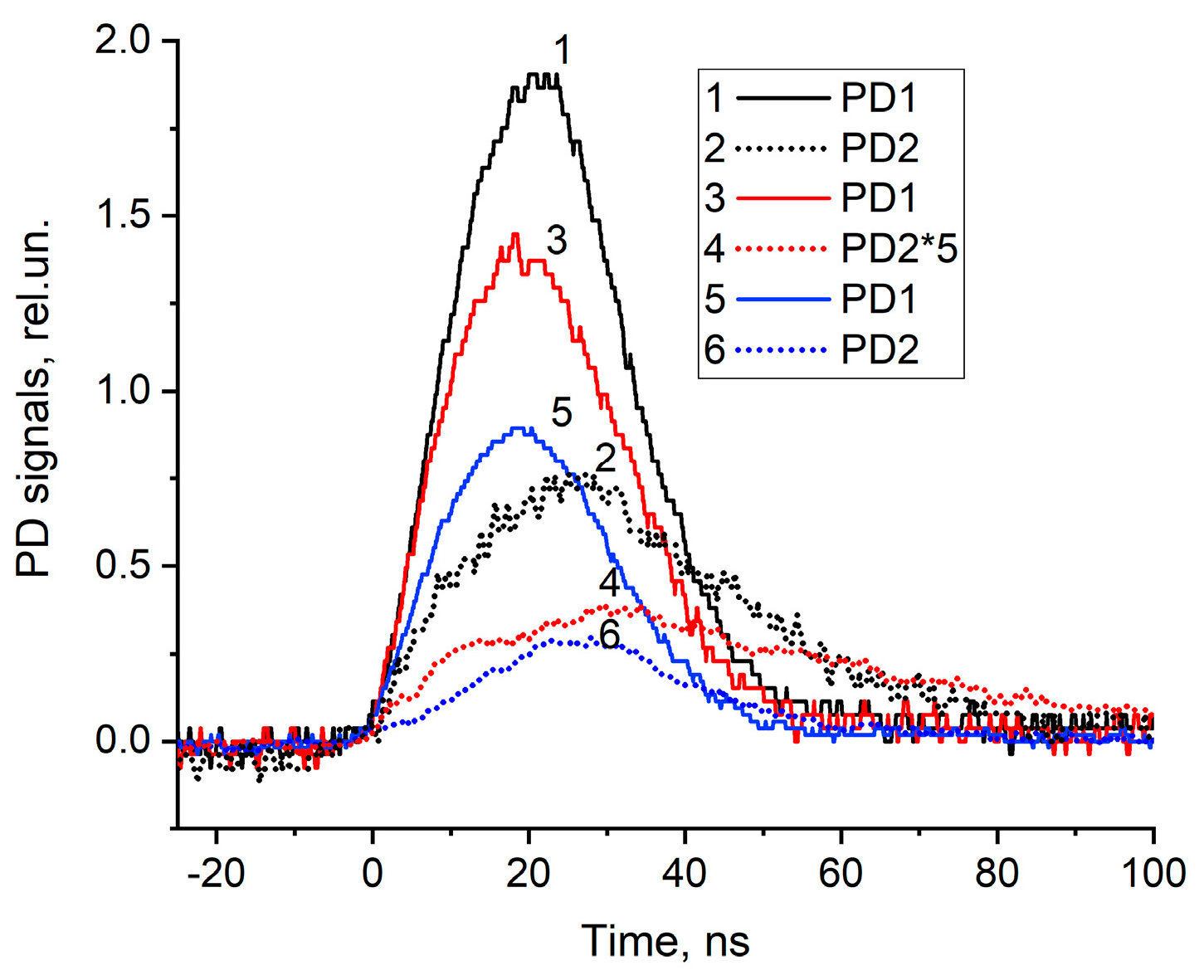
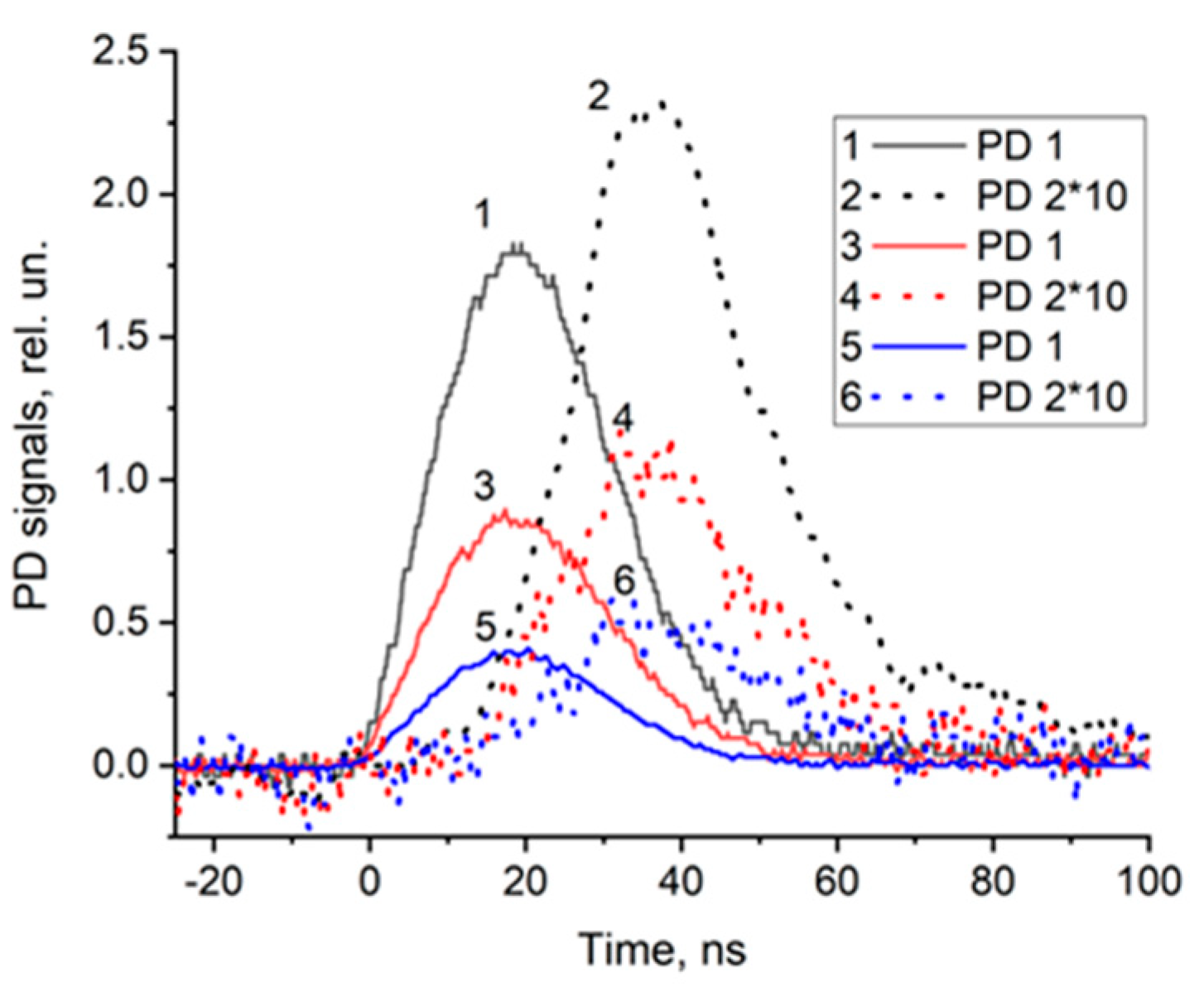
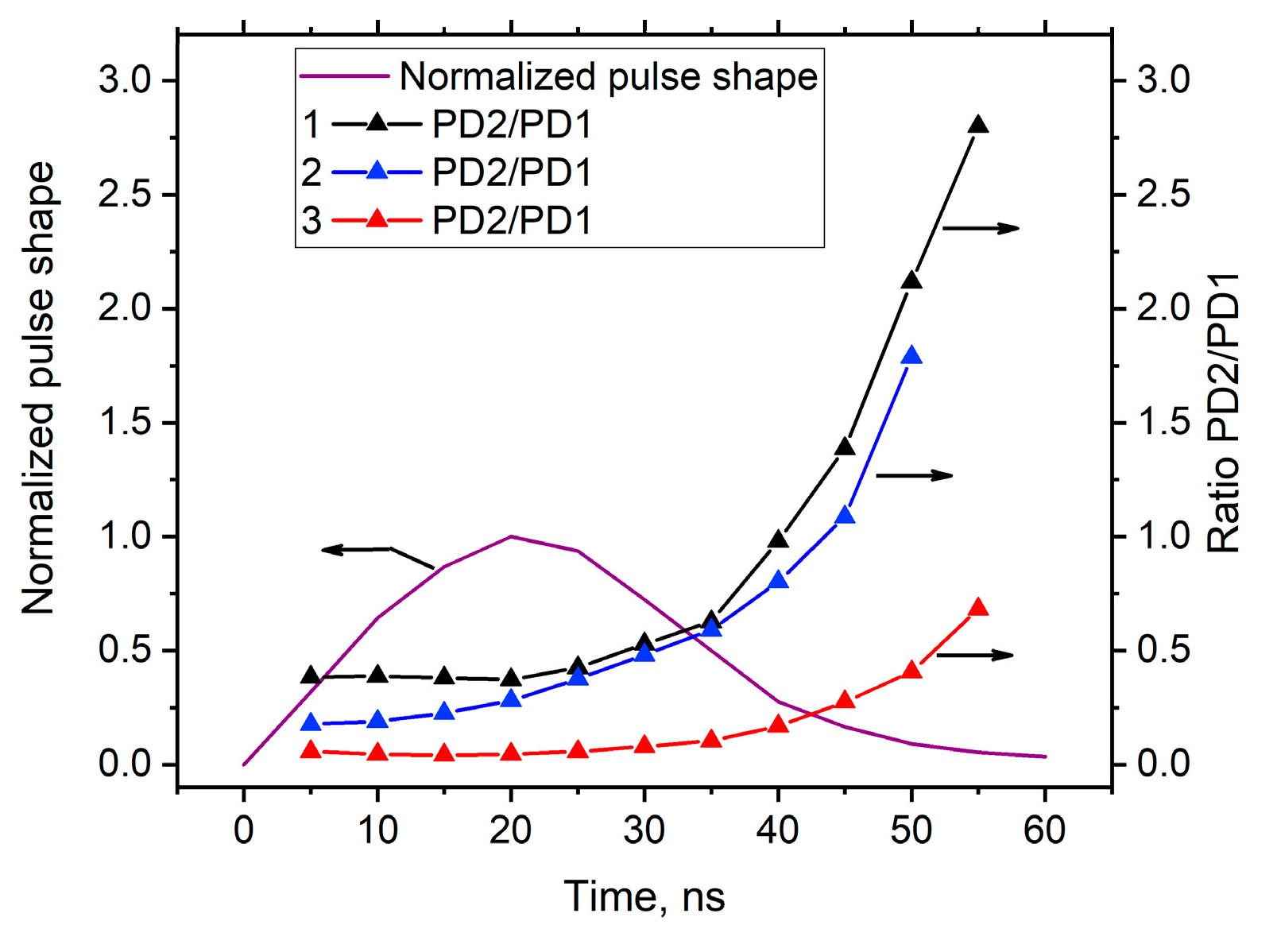
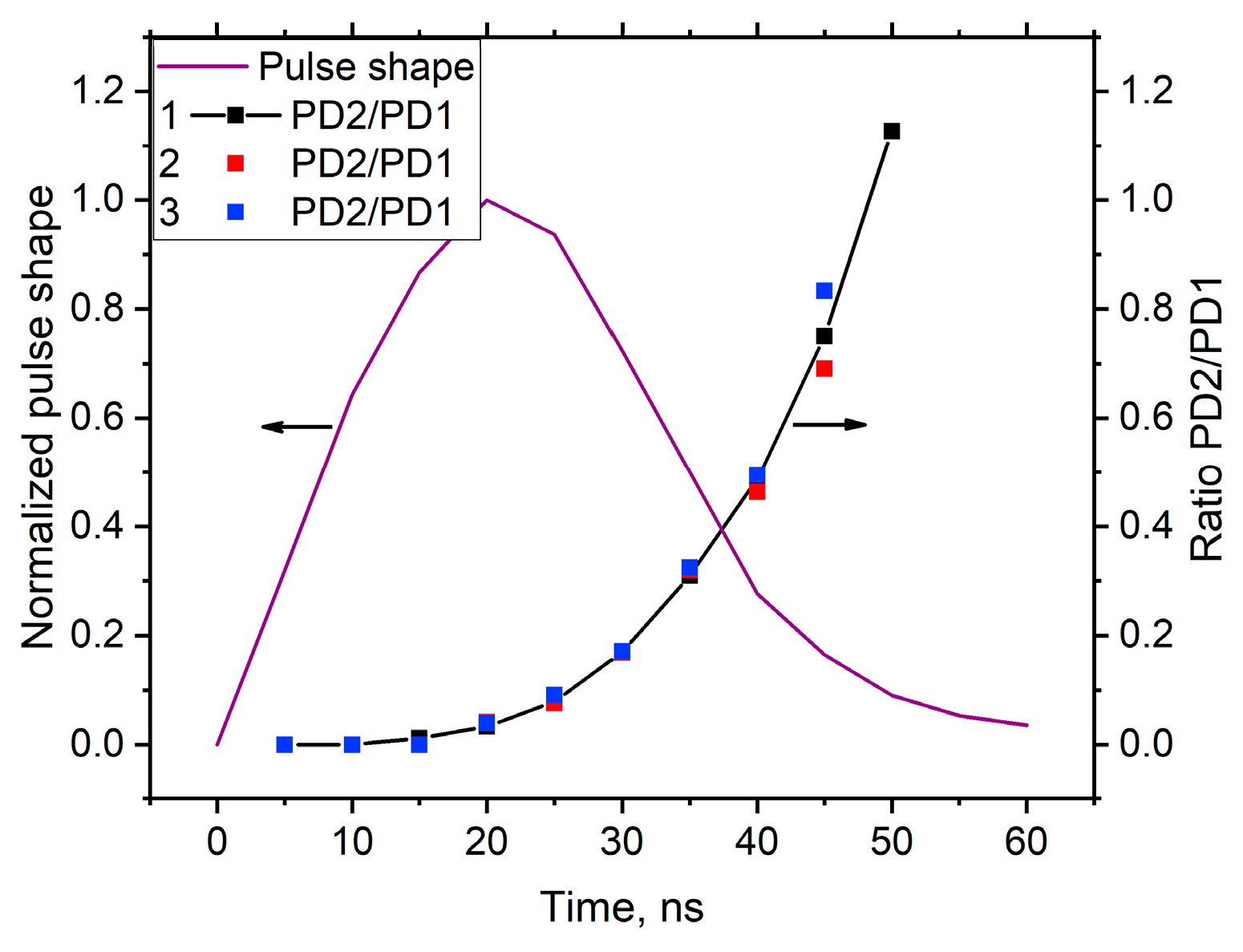
3.2. Dynamic PLDM transmittance during thermal explosion

A thin CH film with a thickness l = 0.9 μm and a density of ρ ≈ 1 g/cm3 was chosen for comparison with PLDM targets. Its areal density ρl ≈ 10-4 g/cm2 is comparable to thin CHO foam targets (ρl ~ 10-4 g/cm2) and much less than that of PLDM targets made of CH polymer (ρl = 5×10-2-1.5×10-1 g/cm2), and aerogel SiO2 (ρl = (3−5)×10-2 g/cm2). Typical oscilloscope traces of incident and transmitted radiation measured in the layout of Figure 1 are shown for different foams and intensities in Figure 4 and for CH film in Figure 5. It is seen that transmitted radiation through the foams (PD2 signals) appears synchronously with the beginning of the laser pulse (PD1 signals), while PD2 maximum is delayed by about 7 ns relative to the PD1 one. For CH-films PD2 signals start by ~ 15 ns later than PD1 with the maximum delayed by ~ 15 ns.
Figure 6 demonstrates a ratio of PD2 to PD1 signals for foams being found from Figure 4. The same dependence for a CH film in Figure 7 was obtained from Figure 5.
Initial transmittance of foams i.e., a ratio PD2/PD1 could be found. It depended on the individual foam thickness: For thinner CHO foam (1) it was about 0.38, while for the thicker one (3) ~0.18−0.2. The latter is in agreement with low-intensity measurements for the 150-μm foam. The SiO2 aerogel had initial transmittance 0.04−0.05 in agreement with a low-intensity value. Radiation energy absorbed in the foams caused their thermal explosion and ionization which was manifested by a rapid growth of the PD2/PD1 ratio. The same PD2/PD1 growing behavior was observed for CH films. Remarkably, that for CHO foams the ratio PD2/PD1 overcame 1 and reached the value 2.8. This might be explained by the fact that the laser pulse formed a narrow plasma channel in the foam where radiation was redistributed in a waveguide manner which resulted in a somewhat focusing on PD2 (taking into account that photodiode receiving area is very small).

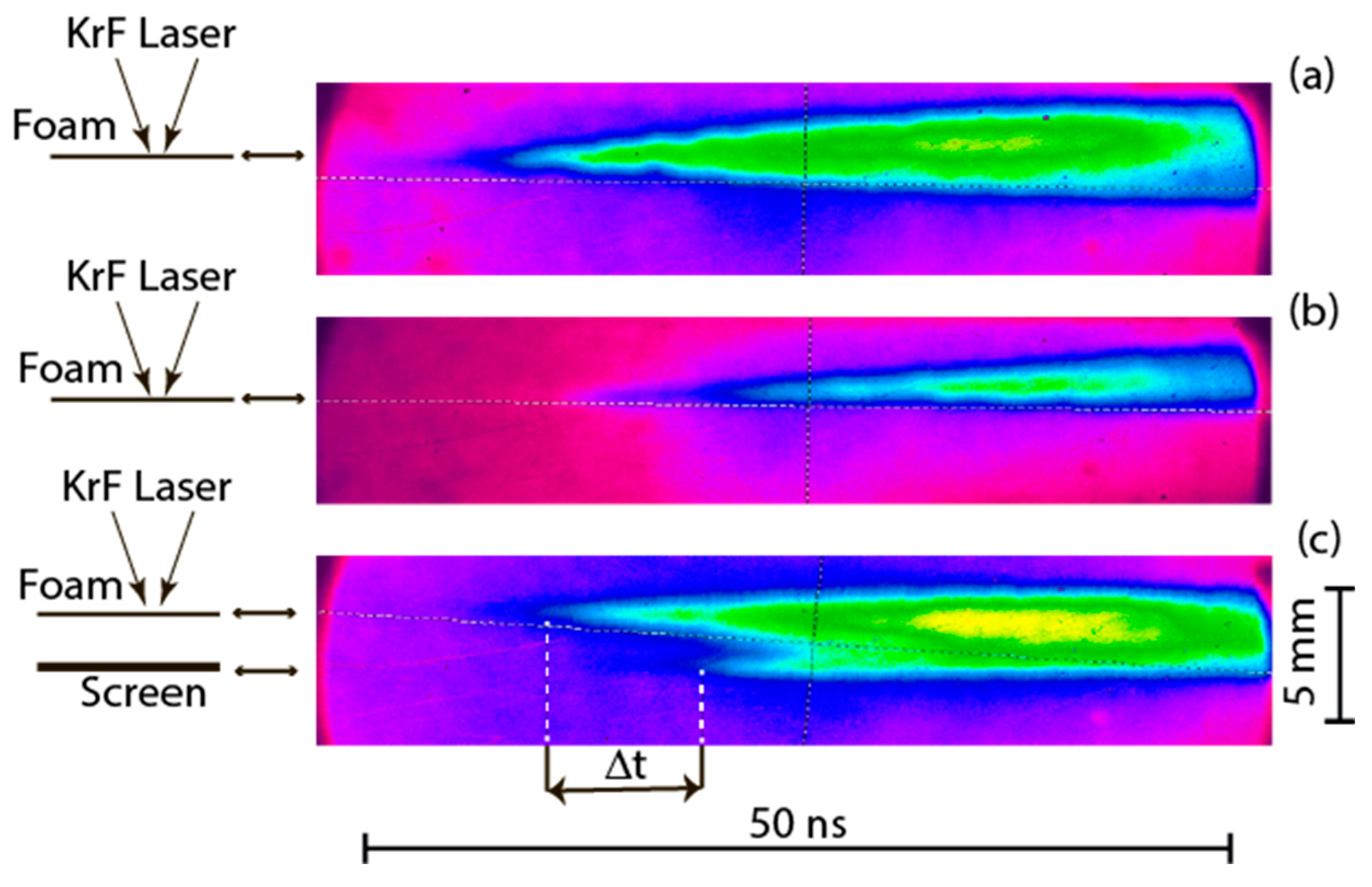
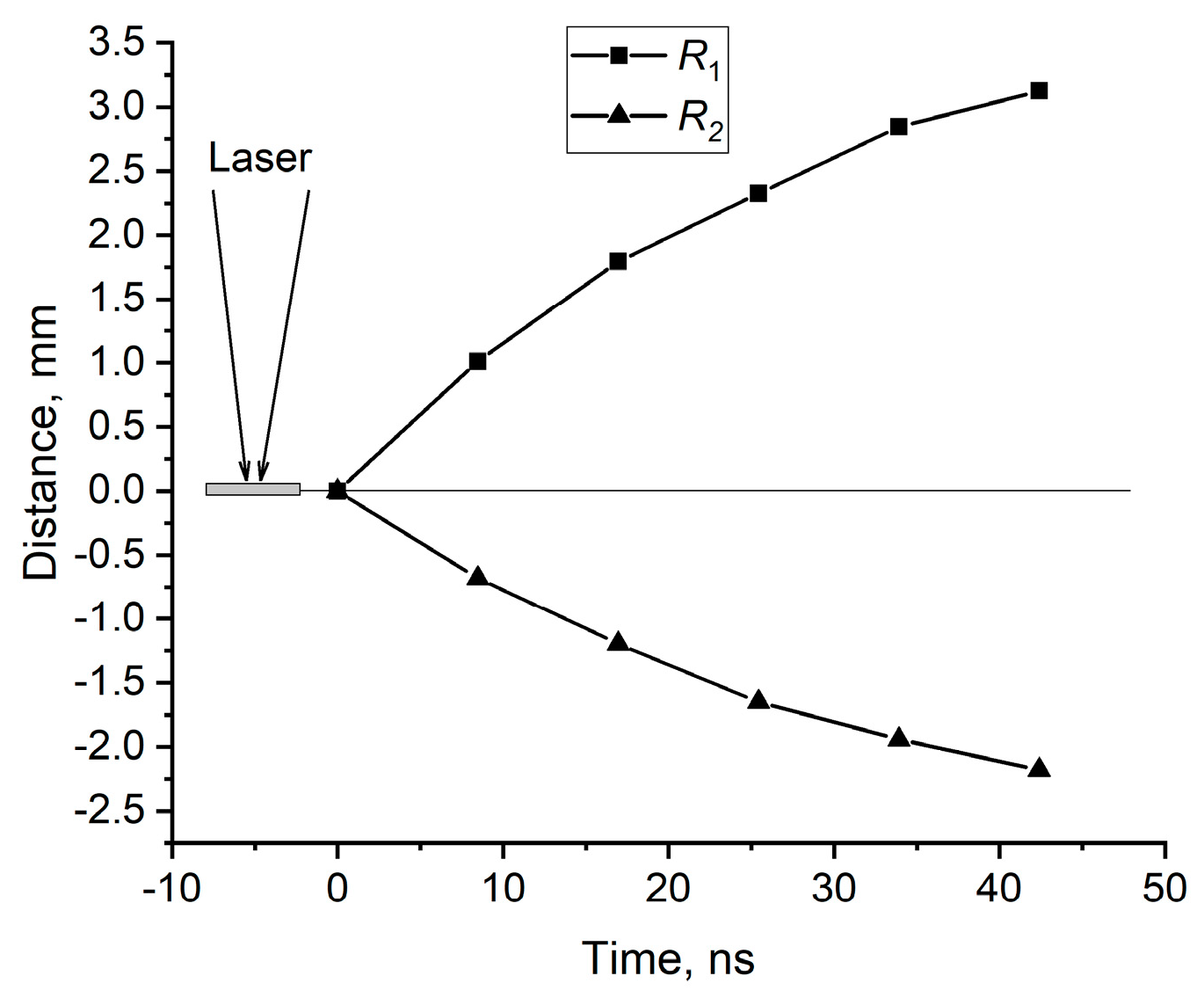
4. PLDM hydrodynamics

Typical hydrodynamic picture of high-energy 100-ns pulse interaction with foam targets at GARPUN laser is illustrated in Figure 8. At irradiation intensity I ≈ 1012 W/cm2 the plasma produced from a CHO foam of the thickness l = 200 μm and density ρ = 20 mg/cm3 expanded from a front side of the target towards incident radiation and from a back side in the laser beam direction with approximately equal velocities v ≈ 75 km/s (a). A rapid volumetric absorption of radiation inside the foam determined the explosive nature of plasma formation. When the pulse energy E (and, accordingly, the intensity) were reduced by 4.8 times, the plasma expansion velocity decreased down to v ≈ 55 km/s (b). It means that the dependance of plasma front velocity on laser energy v ∝ E 1 5 formally coincides with Sedov–von Neumann–Taylor blast wave solution for the radius R and velocity v [54]:
R = α E 0 1 5 t 2 5 ,     v = 2 5 α E 0 1 5 t − 3 5
Here E is the energy release, ρ0 medium density, α coefficient depending on the adiabatic index γ; for γ=1.4 in air α ≈ 1.
Formula (1) is exactly valid for a strong instantaneous point massless explosion. It was also used to estimate energy load in foam explosion produced by a nanosecond pulse [31]. In our case of a long 100-ns laser pulse, which was comparable with a hydrodynamic time scale, after a rapid foam explosion the produced plasma cloud quickly became transparent for UV radiation, and only a small fraction of the laser energy was released in the foam.
However, a finite time of the foam explosion and a finite focal spot size resulted in a different R(t) dependence (Figure 9) compared with the formula (1). Only for the later time t ≥35 ns the plasma blow-up velocity follows a relation R ∝ t 2 5 . By this moment the mass of surrounded air involved into the blast wave (for a residual pressure in the interaction chamber ~ 0.1 Torr) became comparable with the evaporated foam mass.
Measurements of the burn-through time performed with CHO foam of l = 400 μm, ρ = 20 mg/cm3 and with an additional screen behind a target illustrated in Figure 8 c confirm very fast foam explosion. The CHO foam became transparent with a delay Δt ≈ 10 ns after the beginning of the laser pulse. In the case of a thick SiO2 aerogel with l = 2.5 mm and ρ = 100−150 mg/cm3, the radiation passed through the plasma after ~ 30 ns. Thus, the measured burn-through rates are vb ≈ 40 km/s in CHO foam and vb ~ 80 km/s in SiO2 aerogel. These measurements correspond to effective mass ablation rates m ˙ = l / ρ v b : 8×104 and ~106 g/cm2‧s, respectively. A difference in m ˙ by an order of magnitude obviously originates from a tenfold difference in CHO foam and SiO2 aerogel absorption coefficients for laser radiation (see above, section 3.2).
Ablation rates m ˙ in Al foil and graphite targets were measured in a similar layout earlier in the intensity range I = (1−5)×1012 W/cm2 [55]. Very high velocities were obtained for 100-ns pulses which exceeded by an order of magnitude the measured ones for nanosecond pulses. They were mostly caused by a hydrodynamic radial displacement of matter by a megabar-scale ablation pressure. An approximation formula for m ˙ was obtained:
m ˙ = 2.6 × 10 6 I 10 13 1 2 ,
where m ˙ is in [g/cm2‧s] and I in [W/cm2].
In this regard, Al foils were used in present experiments to compare with foam targets. For peak radiation intensity I ≈ 1012 W/cm2, burn-through times of 10−50 ns have been measured for foils of l = 20−110 μm thicknesses (Figure 10), which corresponds to the burn-through rate in aluminum vb ≈ 2.2 km/s and effective mass ablation rate m ˙ ≈ 6×105 g/cm2‧s. These values coincide with our previous above-mentioned measurements. Plasma expansion velocity towards incident radiation was v ≈ 80 km/s, i.e., approximately the same as for the foam targets with a volume absorption.

5. Summary

The present study filled a niche in the use of polymer low-density materials (PLDM) for the ICF applications and waveguide-like NCD plasma channel formation for electron acceleration, as the most of previous research have been carried out for laser wavelengths longer than 350 nm, whereas KrF laser with a 248-nm UV wavelength is considered as a promising driver for the ICF. Two PLDMs, namely, CHO foam with volume density ρ = 5−20 mg/cm3 and SiO2 aerogel with ρ = 100−150 mg/cm3 were investigated with 20-ns laser pulses in regard of the initial (at low laser intensity I ≤ 106 W/cm2) and dynamic transmittance during foam plasma formation in the intensity range I = (1÷6)×1010 W/cm2. The latter measurements were compared with a dynamic transmittance of the initially opaque 0.9-μm CH film. Low-intensity absorption coefficients were found to be α ≈ 102 cm-1 in CHO foam and α ≈ 101 cm-1 in SiO2 aerogel. An obvious feature of a waveguide-like plasma channel formation was revealed in abnormal increase of the laser light transmitted through the CHO foam.
An explosive character of plasma formation was demonstrated in the interaction of high-energy 100-ns laser pulses with CHO and SiO2 PLDM. Plasma expansion velocity for CHO foam reached v ≈ 75 km/s, being accompanied by a fast propagation of laser radiation through the foam thickness with the velocity vb ≈ 40 km/s which corresponded to effective mass ablation rate m ˙ = 8×104 g/cm2‧s. Even faster propagation with vb ≈ 80 km/s and m ˙ = 106 g/cm2‧s was obtained in SiO2 aerogel, being associated with by an order of magnitude less absorption coefficient. It was found that the experimental energy dependence v ∝ E 1 5 satisfied the blast wave solution for a strong instantaneous point massless explosion, while the measured temporal dependence approaches the theoretical one R ∝   t 2 5 , when the mass of residual air involved into the blast wave was comparable with the evaporated foam mass.

Author Contributions

Conceptualization, V.D.Z.; methodology, V.D.Z., N.G.B.; PLDM targets development, N.G.B, K.S.P.; investigation, V.D.Z., N.N.U., A.V.S., N.G.B.; writing—original draft preparation, V.D.Z.; writing—review and editing, N.N.U., A.V.S., and N.G.B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Ministry of Science and Higher Education of the Russian Federation in the framework of the research contract # 023-2019-0002.

Acknowledgments

The work was carried out under the auspices of the scientific program of the National Center for Physics and Mathematics in the frame of the State Contract No. Н4c.241.4Д.23.1085. We are grateful to Veliev P.V. and Metreveli G.E. from P. N. Lebedev Physical Institute—for their assistance in experiments.

Conflicts of Interest

The authors declare no conflict of interest. Any other persons had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Basov, N.G.; Krokhin, O.N. Condition for heating up of a plasma by the radiation from an optical generator. Sov. Phys. JETP 1964, 19, 123–125. [Google Scholar]
  2. Nuckolls, J.; Wood, L.; Thiessen, A. and Zimmerman, G. Laser compression of matter to super-high densities: Thermonuclear (CTR) applications. Nature 1972, 239, 139–142. [Google Scholar] [CrossRef]
  3. Lindl, J. Development of the indirect drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasmas 1995, 2, 3933–4024. [Google Scholar] [CrossRef]
  4. National Ignition Facility achieves fusion ignition. https://llnl.gov/news/national-fusion-facility-achievs ignition; https://energy.gov/articles/doe-national-laboratory-makes-history-achieving-fusion-ignition.
  5. Kritcher, A.; HIBRYD-E ICF team. Initial results from HYBRID-E DT experiment N210808 with >1.3 MJ yield. IFSA virtual meeting, September 2021. LLNL-PRES-826367.
  6. Lindl, J.; Landen, O.; Edwards, J.; Moses, E.; NIC Team. Review of the National Ignition Campaign 2009-2012. Phys. Plasmas 2014, 21, 020501. [Google Scholar] [CrossRef]
  7. Montgomery, D.S. Two decades of progress in understanding and control of laser plasma instabilities in indirect drive inertial fusion. Phys. Plasmas 2016, 23, 055601. [Google Scholar] [CrossRef]
  8. Robey, H.F.; Smalyuk, V.A.; Milovich, J.L.; Döppner, T.; Casey, D.T.; et al. Performance of indirectly driven capsule implosions on the National Ignition Facility using adiabat-shaping. Phys. Plasmas 2016, 23, 056303. [Google Scholar] [CrossRef]
  9. Haynam, C.A.; Wegner, P.J.; Auerbach, J.M.; Bowers, M.W.; Dixit, S.N.; et al. National Ignition Facility laser performance status. Appl. Opt. 2007, 46, 3276–3303. [Google Scholar] [CrossRef]
  10. Miquel, J.-L.; Lion, C.; Vivini, P. The Laser Mega-Joule: LMJ & PETAL status and program overview. J. Phys.: Conf. Ser. 2016, 688, 012067. [Google Scholar] [CrossRef]
  11. Craxton, R.S.; Anderson, K.S.; Boehly, T.R.; Goncharov, V.N.; Harding, D.R.; et al. Direct-drive inertial confinement fusion: A review. Phys. Plasmas 2015, 22, 110501. [Google Scholar] [CrossRef]
  12. Desselberger, M.; Afshar-rad, T.; Khattak, F.; Viana, S. and Willi, O. Nonuniformity imprint on the ablation surface of laser-irradiated targets. Phys. Rev. Lett. 1992, 68, 1539–1542. [Google Scholar] [CrossRef] [PubMed]
  13. Emery, M.H.; Gardner, J.H.; Lehmberg, R.H. and Obenschain, S.P. Hydrodynamic target response to an induced spatial incoherence-smoothed laser beam. Phys. Fluids B: Plasma Phys. 1991, 3, 2640–2651. [Google Scholar] [CrossRef]
  14. Malka, V.; Faure, J.; Huller, S.; Tikhonchuk, V.T.; Weber, S. and Amiranoff, F. Enhanced spatiotemporal laser-beam smoothing in gas-jet plasmas. Phys. Rev. Lett. 2003, 90, 075002. [Google Scholar] [CrossRef]
  15. Dunne, M.; Borghesi, M.; Iwase, A.; Jones, M.W.; Taylor, R.; et al. Evaluation of a foam buffer target design for spatially uniform ablation of laser-irradiated plasmas. Phys. Rev. Lett. 1995, 75, 3858–3861. [Google Scholar] [CrossRef] [PubMed]
  16. Metzler, N.; Velikovich, A.L.; Schmitt, A.J.; Gardner, J.H. Laser imprint reduction with a short shaping laser pulse incident upon a foam-plastic target. Phys. Plasmas 2002, 9, 5050–5058. [Google Scholar] [CrossRef]
  17. Desselberger, M.; Jones, M.W.; Edwards, J.; Dunne, M.; Willi, O. Use of X-ray preheated foam layers to reduce beam structure imprint in laser-driven targets. Phys. Rev. Lett. 1995, 74, 2961–2964. [Google Scholar] [CrossRef]
  18. Nishikino, M.; Shiraga, H.; Miyanaga, N.; Ohnishi, N.; Shigemori, K.; et al. Imprint reduction in a plasma layer preformed with x-ray irradiation. Phys. Plasmas 2002, 9, 1381–1391. [Google Scholar] [CrossRef]
  19. Hu, S.X.; Fiksel, G.; Goncharov, V.N.; Skupsky, S.; Meyerhofer, D.D.; Smalyuk, V.A. Mitigating laser imprint in direct-drive inertial confinement fusion implosions with high-Z dopants. Phys. Rev. Lett. 2012, 108, 195003. [Google Scholar] [CrossRef]
  20. Karasik, M.; Weaver, J.L.; Aglitskiy, Y.; Oh, J.; Obenschain, S.P. Suppression of laser nonuniformity imprinting using a thin high-Z coating. Phys. Rev. Lett. 2015, 114, 085001. [Google Scholar] [CrossRef]
  21. Karasik, M.; Oh, J.; Obenschain, S.P.; Schmitt, A.J.; Aglitskiy, Y.; Stoeckl, C. Order-of-magnitude laser imprint reduction using pre-expanded high-Z coatings on targets driven by a third harmonic Nd: glass laser. Phys. Plasmas 2021, 28, 032710. [Google Scholar] [CrossRef]
  22. Koenig, M.; Benuzzi, A.; Philippe, F.; Batani, D.; Hall, T.; et al. Equation of state data experiments for plastic foams using smoothed laser beams. Phys. Plasmas 1999, 6, 3296–3301. [Google Scholar] [CrossRef]
  23. Batani, D.; Nazarov, W.; Hall, T.; Lower, T.; Koenig, M. Foam-induced smoothing studied through laser-driven shock waves. Phys. Rev. E. 2000, 62, 8573–8582. [Google Scholar] [CrossRef] [PubMed]
  24. Gus’kov, S.Yu.; Gromov, A.I.; Merkul’ev, Yu.A.; Rozanov, V.B.; Nikishin, V.V.; et al. Nonequilibrium laser-produced plasma of volume-structured media and ICF applications. Laser Part. Beams 2000, 18, 1–10. [Google Scholar] [CrossRef]
  25. Nishimura, H.; Shiraga, H.; Azechi, H.; Miyanaga, N.; Nakai, M.; et al. Indirect–direct hybrid target experiments with the GEKKO XII laser. Nucl. Fusion 2000, 40, 547–556. [Google Scholar] [CrossRef]
  26. Willi, O.; Barringer, L.; Bell, A.; Borghesi, M.; Davies, J.; et al. Inertial confinement fusion and fast ignitor studies. Nucl. Fusion 2000, 40, 537–545. [Google Scholar] [CrossRef]
  27. Hall, T.; Batani, D.; Nazarov, W.; Koenig, M. and Bennuzzi, A. Recent advances in laser–plasma experiments using foams. Laser Part. Beams 2002, 20, 303–316. [Google Scholar] [CrossRef]
  28. Limpouch, J.; Demchenko, N.N.; Gus'kov, S.Yu.; Kalal1, M.; Kasperczuk, A.; et al. Laser interactions with plastic foam-metallic foil layered targets. Plasma Phys. Control. Fusion 2004, 46, 1831–1841. [Google Scholar] [CrossRef]
  29. Jiang, S.; Xu, Y.; Ding, Y.; Lai, D.; Zheng, Z.; et al. Experimental investigation of supersonic radiation propagation in low-density plastic and copper-doped foams. Science in China Ser. G Physics, Mechanics & Astronomy 2005, 48, 549–558. [Google Scholar] [CrossRef]
  30. Tanabe, M., Nishimura, H., Ohnishi, N., Fournier, K.B., Fujioka, S.; et al. Characterization of heat-wave propagation through laser-driven Ti-doped underdense plasma. High Energy Density Physics 2010, 6, 89–94. [CrossRef]
  31. Rozanov, V.B.; Barishpol’tsev, D.V.; Vergunova, G.A.; Demchenko, N.N.; Ivanov, E.M.; et al. Interaction of laser radiation with a low-density structured absorber. JETP 2016, 122, 256–276. [Google Scholar] [CrossRef]
  32. Cipriani, M.; Gus’kov, S.Yu.; De Angelis, R.; Consoli, F.; Rupasov, A.A.; et al. Laser-driven hydrothermal wave speed in low-Z foam of overcritical density. Phys. Plasmas 2018, 25, 092704. [Google Scholar] [CrossRef]
  33. Cipriani, M.; Gus’kov, S.Yu.; De Angelis, R.; Consoli, F.; Rupasov, A.A.; et al. Laser-supported hydrothermal wave in low-dense porous substance. Laser Part. Beams 2018, 36, 121–128. [Google Scholar] [CrossRef]
  34. Belyaev, M.A.; Berger, R.L.; Jones, O.S.; Langer, S.H. and Mariscal D.A. Laser propagation in a subcritical foam: Ion and electron heating. Phys. Plasmas 2018, 25, 123109. [Google Scholar] [CrossRef]
  35. Batani, K.; Aliverdiev, A.; Benocci, R.; Dezulian, R.; Amirova, A.; et al. Shock dynamics and shock collision in foam layered targets. High Power Laser Science and Engineering 2021, 9, e47. [Google Scholar] [CrossRef]
  36. Roycroft, R.; Bradley, P.A.; McCary, E.; Bowers, B.; Smith, H.; et al. Experiments and simulations of isochorically heated warm dense carbon foam at the Texas Petawatt Laser. Matter Radiat. Extremes 2021, 6, 014403. [Google Scholar] [CrossRef]
  37. Tikhonchuk, V.T.; Gong, T.; Jourdain, N.; Renner, O.; Condamine, F.P.; et al. Studies of laser-plasma interaction physics with low-density targets for direct-drive inertial confinement fusion on the Shenguang III prototype. Matter Radiat. Extremes 2021, 6, 025902. [Google Scholar] [CrossRef]
  38. Karasik, M.; Oh, J.; Obenschain, S.P.; Schmitt, A.J.; Aglitskiy, Y.; Stoeckl, C. Order-of-magnitude laser imprint reduction using pre-expanded high-Z coatings on targets driven by a third harmonic Nd:glass laser. Phys. Plasmas 2021, 28, 032710. [Google Scholar] [CrossRef]
  39. Aglitskiy, Y.; Zulick, C.; Oh, J.; Velikovich, A.L.; Schmitt, A.J.; Obenschain, S.P.; Karasik, M.; Weaver, J.L. Plasma hydrodynamic experiments on NRL Nike KrF laser. High Energy Density Phys. 2020, 37, 100866. [Google Scholar] [CrossRef]
  40. Bodner, S.E.; Schmitt, A.J. and Sethian, J.D. Laser requirements for a laser fusion energy power plant. High Power Laser Science and Engineering 2013, 1, 2–10. [Google Scholar] [CrossRef]
  41. Obenschain, S.; Lehmberg, R.; Kehne, D.; Hegeler, F.; Wolford, M.; et al. High-energy krypton fluoride lasers for inertial fusion. Appl. Opt. 2015, 34, F103–F122. [Google Scholar] [CrossRef]
  42. Obenschain, S.P.; Bodner, S.E.; Colombant, D.; Gerber, K.; Lehmberg, R.H.; et al. The Nike KrF laser facility: Performance and initial target experiments. Phys. Plasmas 1996, 3, 2098–2107. [Google Scholar] [CrossRef]
  43. Pawley, C.J.; Gerber, K.; Lehmberg, R.H.; McLean, E.A.; Mostovych, A.N.; et al. Measurements of laser-imprinted perturbations and Rayleigh–Taylor growth with the Nike KrF laser. Phys Plasmas 1997, 4, 1969–1977. [Google Scholar] [CrossRef]
  44. Obenschain, S.P.; Colombant, D.G.; Karasik, M.; Pawley, C.J.; Serlin, V.; et al. Effects of thin high-Z layers on the hydrodynamics of laser-accelerated plastic targets. 2002, 9, 2234–2243. [Google Scholar] [CrossRef]
  45. Schmitt, A.J.; Bates, J.W.; Obenschain, S.P.; Zalesak, S.T.; Fyfe, D.E.; Betti, R. Direct drive fusion energy shock ignition designs for sub-MJ lasers. Fusion Sci. Technol. 2009, 56, 377–383. [Google Scholar] [CrossRef]
  46. Tikhonchuk, V.T.; Gong, T.; Jourdain, N.; Renner, O.; Condamine, F.P.; et al. Studies of laser-plasma interaction physics with low-density targets for direct-drive inertial confinement fusion on the Shenguang III prototype. Matter Radiat. Extremes 2021, 6, 025902. [Google Scholar] [CrossRef]
  47. Rosmej, O.N.; Andreev, N.E.; Zaehter, S.; Zahn, N.; Christ, P.; Borm, B.; et al. Interaction of relativistically intense laser pulses with long-scale near critical plasmas for optimization of laser-based sources of MeV electrons and gamma-rays. New J. Phys. 2019, 21, 043044. [Google Scholar] [CrossRef]
  48. Rosmej, O.N.; Gyrdymov, M.; Günther, M.M.; Andreev, N.E.; Tavana, P.; et al. High-current laser-driven beams of relativistic electrons for high energy density research. Plasma Phys. Control. Fusion 2020, 62, 115024. [Google Scholar] [CrossRef]
  49. Zvorykin, V.D.; Lebo, I.G.; Shutov, A.V.; Ustinovskii, N.N. Self-focusing of UV radiation in 1 mm scale plasma in a deep ablative crater produced by 100 ns, 1 GW KrF laser pulse in the context of ICF. Matter Radiat. Extremes 2020, 5, 035401. [Google Scholar] [CrossRef]
  50. Smetanin, I.V.; Shutov, A.V.; Ustinovskii, N.N.; Veliev, P.V.; Zvorykin, V.D. A new insight into high-aspect-ratio channel drilling in translucent dielectrics with a KrF laser for waveguide applications. Materials 2022, 15, 8347. [Google Scholar] [CrossRef] [PubMed]
  51. Zvorykin, V.D.; Arlantsev, S.V.; Shutov, A.V.; Ustinovskii, N.N.; Veliev, P.V. Deep penetration of UV radiation into PMMA and electron acceleration in long plasma channels produced by 100 ns KrF laser pulses. Symmetry 2021, 13, 1883. [Google Scholar] [CrossRef]
  52. Tadjima, T. High-energy laser plasma accelerators. Laser Part. Beams 1985, 3(part 4), 351–413. [Google Scholar] [CrossRef]
  53. Pastukhov, A.V. Mesoporous polymer systems based on divinylbenzenecopolymers modified with linear rubbers. Eur. Polymer J. 2020, 124, 109480. [Google Scholar] [CrossRef]
  54. Kovalev, A.I.; Pastukhov, A.V.; Tkachenko, E.S.; Klemenkova, Z.S.; Kuvshinov, I.R.; Khotina, I.A. Polyphenylenes with Phen-1,3,5-triyl branching moieties based on p-Diacetylbenzene: synthesis and study of porosity and heat resistance. Polymer Sci., Ser C. 2020, 62, 205–213. [Google Scholar] [CrossRef]
  55. Sedov, L.I. Similarity and dimensional methods in mechanics; Academic Press: New York-London, 1959; pp. 363 p. [Google Scholar]
  56. Zvorykin, V.D.; Bakaev, V.G.; Lebo, I.G. and Sychugov, G.V. Hydrodynamics of plasma and shock waves generated by the high-power GARPUN KrF laser. Laser Part. Beams 2004, 22, 51–57. [Google Scholar] [CrossRef]
Preprints 82025 g001
Figure 1. Layout of transmittance measurements.
Figure 1. Layout of transmittance measurements.
Preprints 82025 g001
Preprints 82025 g002
Figure 2. Optical scheme for (a) studying the laser-target interaction and (b) measuring the burn-through time of targets.
Figure 2. Optical scheme for (a) studying the laser-target interaction and (b) measuring the burn-through time of targets.
Preprints 82025 g002
Preprints 82025 g003
Figure 3. Photos of foam targets made of (a) CH polymer in the form of a cylinder, (b) CHO film on the hoop, (c) SiO2 aerogel in the form of a parallelepiped.
Figure 3. Photos of foam targets made of (a) CH polymer in the form of a cylinder, (b) CHO film on the hoop, (c) SiO2 aerogel in the form of a parallelepiped.
Preprints 82025 g003
Preprints 82025 g004
Figure 4. Oscilloscope traces of incident (PD1) and transmitted (PD2) radiation for different foams and peak intensities: (1,2) CHO foam, I = 6×1010 W/cm2; (3,4) SiO2 aerogel, I = 4.5×1010 W/cm2; (5,6) CHO foam, I = 2.8×1010 W/cm2. PD2 signal (4) is multiplied by 5.
Figure 4. Oscilloscope traces of incident (PD1) and transmitted (PD2) radiation for different foams and peak intensities: (1,2) CHO foam, I = 6×1010 W/cm2; (3,4) SiO2 aerogel, I = 4.5×1010 W/cm2; (5,6) CHO foam, I = 2.8×1010 W/cm2. PD2 signal (4) is multiplied by 5.
Preprints 82025 g004
Preprints 82025 g005
Figure 5. Oscilloscope traces of incident (PD1) and transmitted (PD2) radiation for CH-film at peak intensities: (1,2) I = 6×1010 W/cm2; (3,4) I = 2.7×1010 W/cm2; (5,6) I = 1.3×1010 W/cm2. All PD2 signal were multiplied by 10.
Figure 5. Oscilloscope traces of incident (PD1) and transmitted (PD2) radiation for CH-film at peak intensities: (1,2) I = 6×1010 W/cm2; (3,4) I = 2.7×1010 W/cm2; (5,6) I = 1.3×1010 W/cm2. All PD2 signal were multiplied by 10.
Preprints 82025 g005
Preprints 82025 g006
Figure 6. A normalized laser pulse shape and PD2/PD1 ratio obtained for (1) CHO foam, I = 6×1010 W/cm2; (2) CHO foam, I = 2.8×1010 W/cm2; (3) SiO2 aerogel, I = 4.5×1010 W/cm2.
Figure 6. A normalized laser pulse shape and PD2/PD1 ratio obtained for (1) CHO foam, I = 6×1010 W/cm2; (2) CHO foam, I = 2.8×1010 W/cm2; (3) SiO2 aerogel, I = 4.5×1010 W/cm2.
Preprints 82025 g006
Preprints 82025 g007
Figure 7. A normalized laser pulse shape and PD2/PD1 ratio obtained for CH films at (1) I = 6×1010; (2) I = 2.7×1010; (3) I = 1.3×1010 W/cm2.
Figure 7. A normalized laser pulse shape and PD2/PD1 ratio obtained for CH films at (1) I = 6×1010; (2) I = 2.7×1010; (3) I = 1.3×1010 W/cm2.
Preprints 82025 g007
Preprints 82025 g008
Figure 8. Streak images of CHO foam with density ρ = 20 mg/cm3, different thicknesses l and peak irradiation intensities I: (a) l = 200 μm, I≈1012 W/cm2; (b) l = 200 μm and I≈0.21×1012 W/cm2; (c) l = 400 μm and I≈0.93×1012 W/cm2 with Al screen behind.
Figure 8. Streak images of CHO foam with density ρ = 20 mg/cm3, different thicknesses l and peak irradiation intensities I: (a) l = 200 μm, I≈1012 W/cm2; (b) l = 200 μm and I≈0.21×1012 W/cm2; (c) l = 400 μm and I≈0.93×1012 W/cm2 with Al screen behind.
Preprints 82025 g008
Preprints 82025 g009
Figure 9. Time evolution of the blast wave distances from the front R1 and from the back side R2 of the CHO foam (ρ = 20 mg/cm3, l = 200 μm, I≈1012 W/cm2).
Figure 9. Time evolution of the blast wave distances from the front R1 and from the back side R2 of the CHO foam (ρ = 20 mg/cm3, l = 200 μm, I≈1012 W/cm2).
Preprints 82025 g009
Preprints 82025 g010
Figure 10. (a) A burn-through measurements for Al foils: (a) a static target image with an additional screen; streak images for I≈1012 W/cm2 and different thicknesses l (b) l = 20, (c) 50 and (d) 110 μm.
Figure 10. (a) A burn-through measurements for Al foils: (a) a static target image with an additional screen; streak images for I≈1012 W/cm2 and different thicknesses l (b) l = 20, (c) 50 and (d) 110 μm.
Preprints 82025 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated