Submitted:
09 August 2023
Posted:
14 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
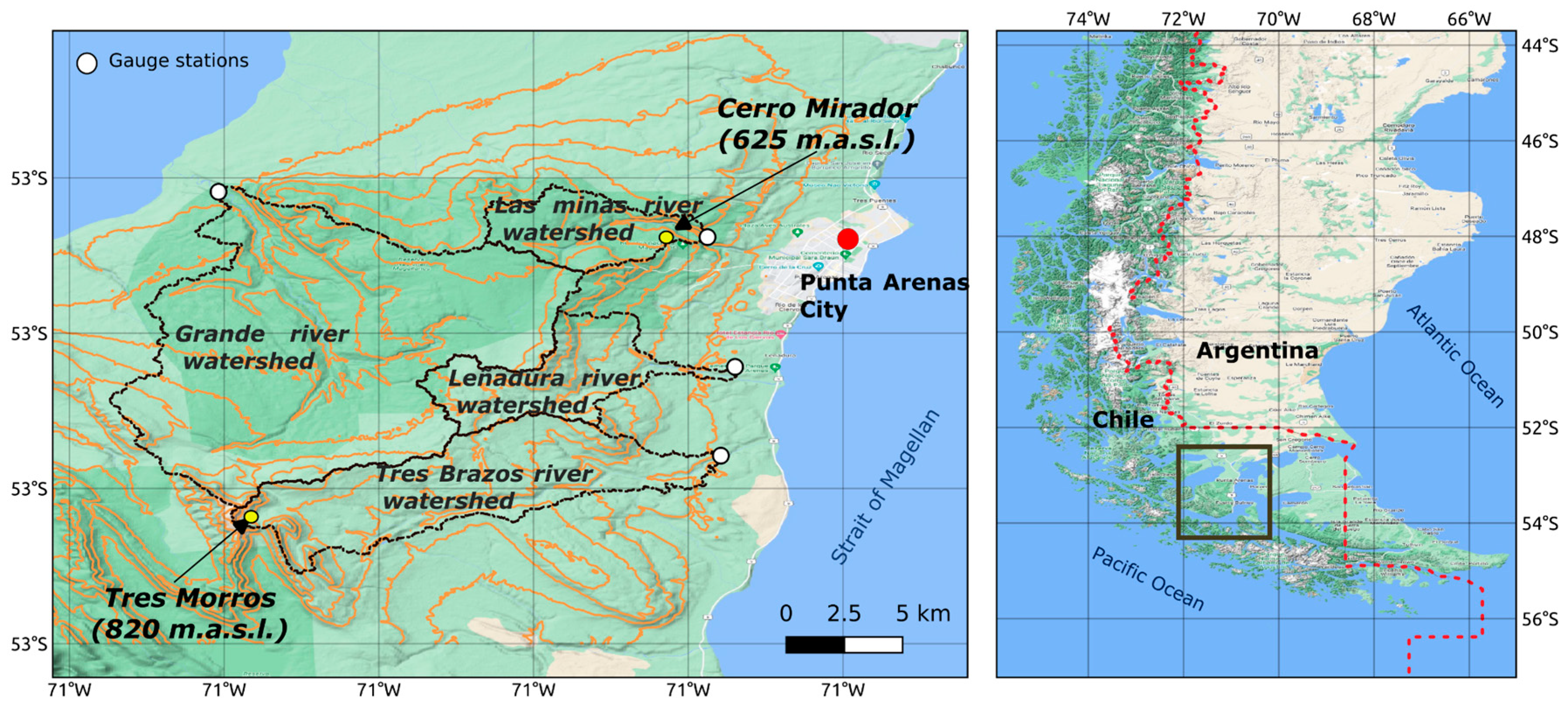
2. Study Area
3. Data and Methods
3.1. Data
- a)
- Satellite sensor data
- b)
- Weather stations
3.2. Methods
3.2.1. Downscaling and Spectral Fusion
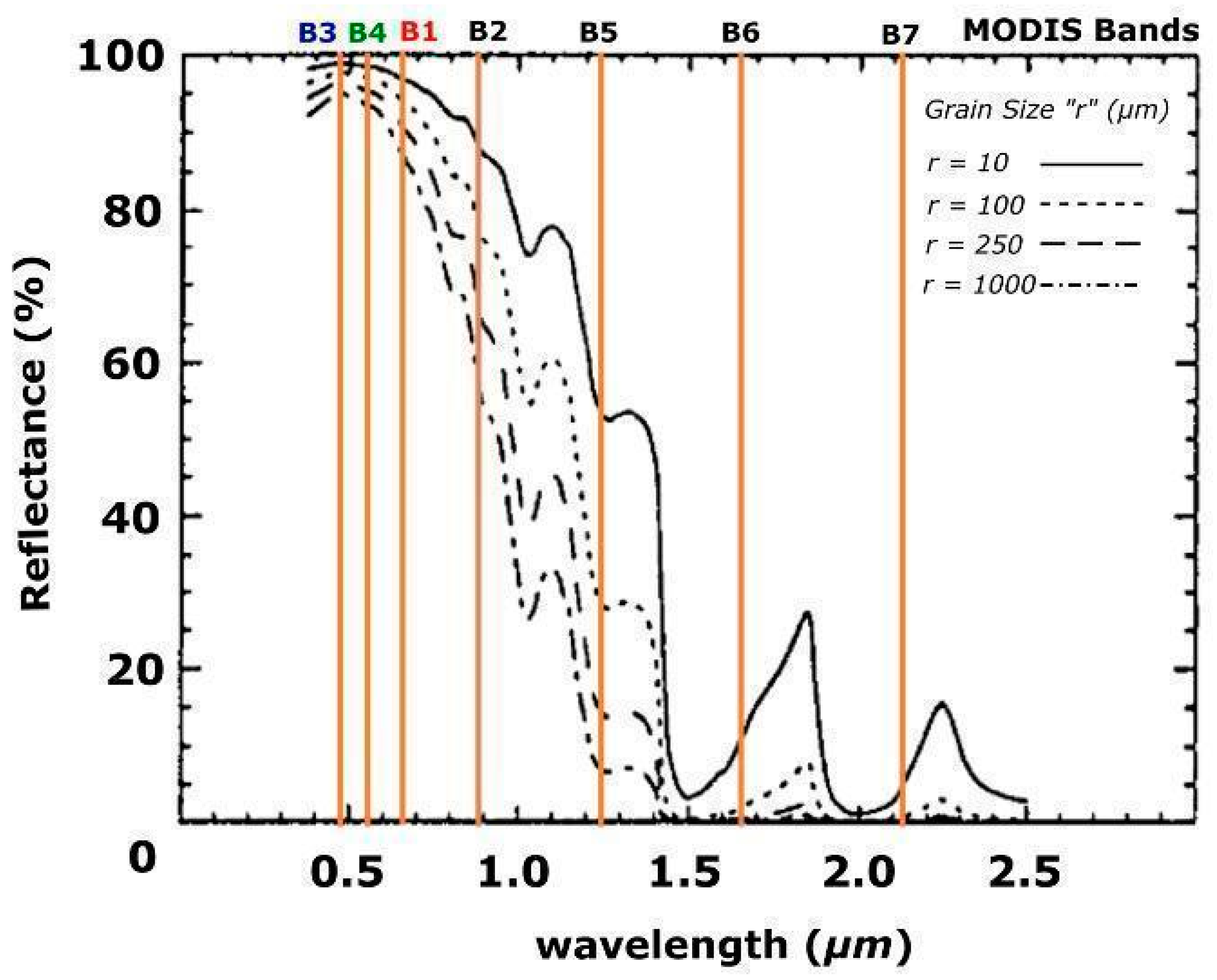
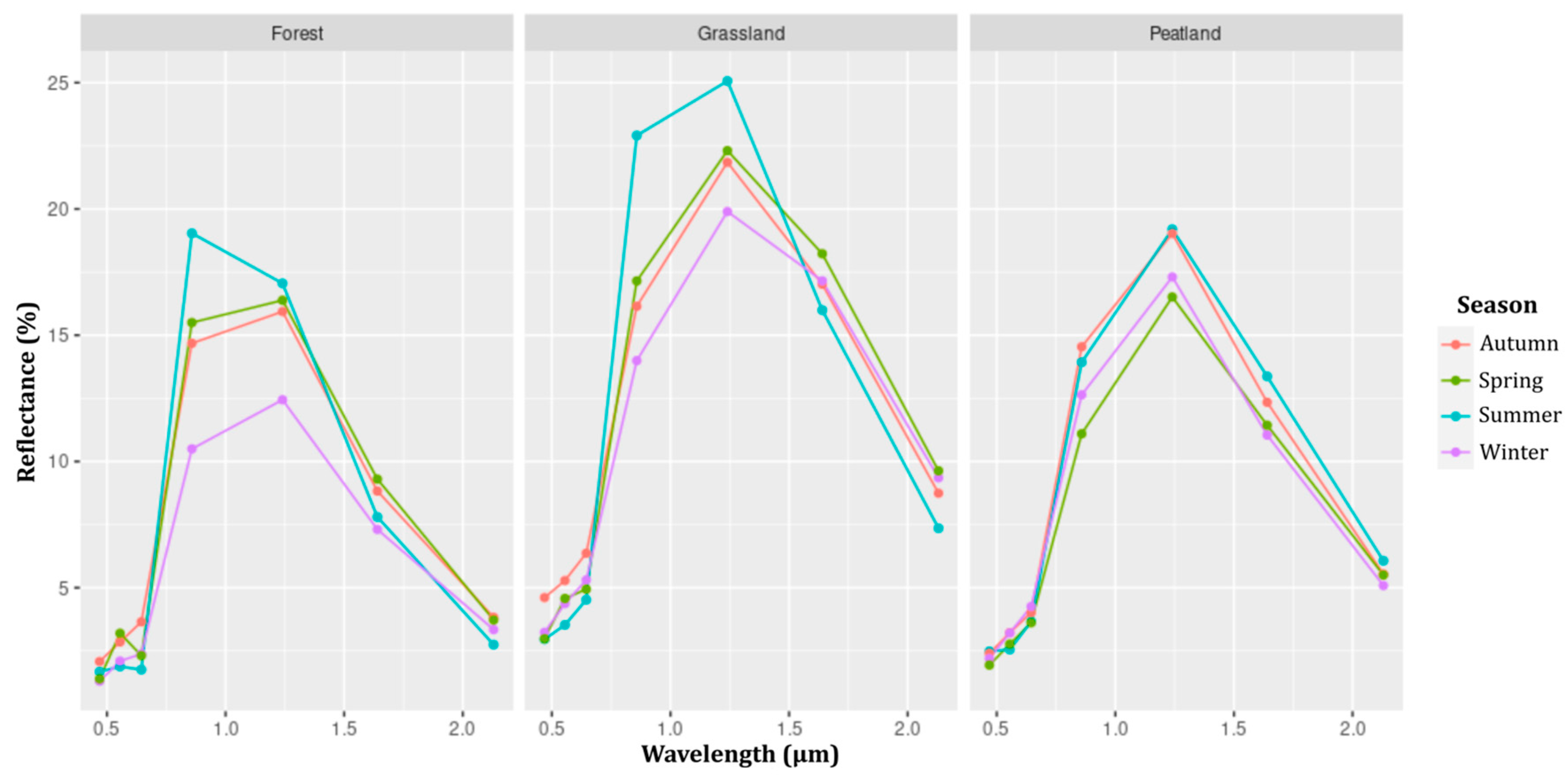
3.2.2 Spectral Mixture Analysis
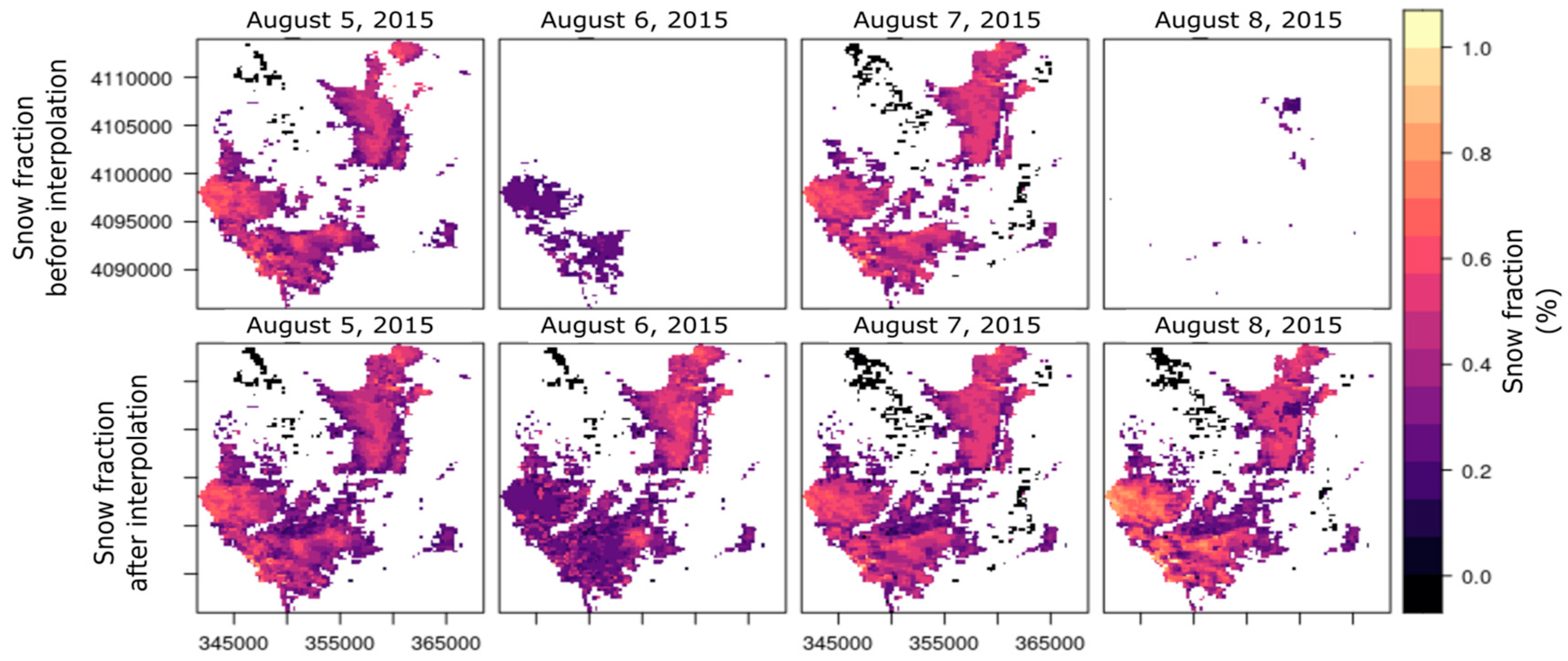
3.2.3. Spatio-Temporal Snow Reconstruction
- a)
- Cloud and snow masks
- b)
- Temporal interpolation
3.2.4. Ground Validation
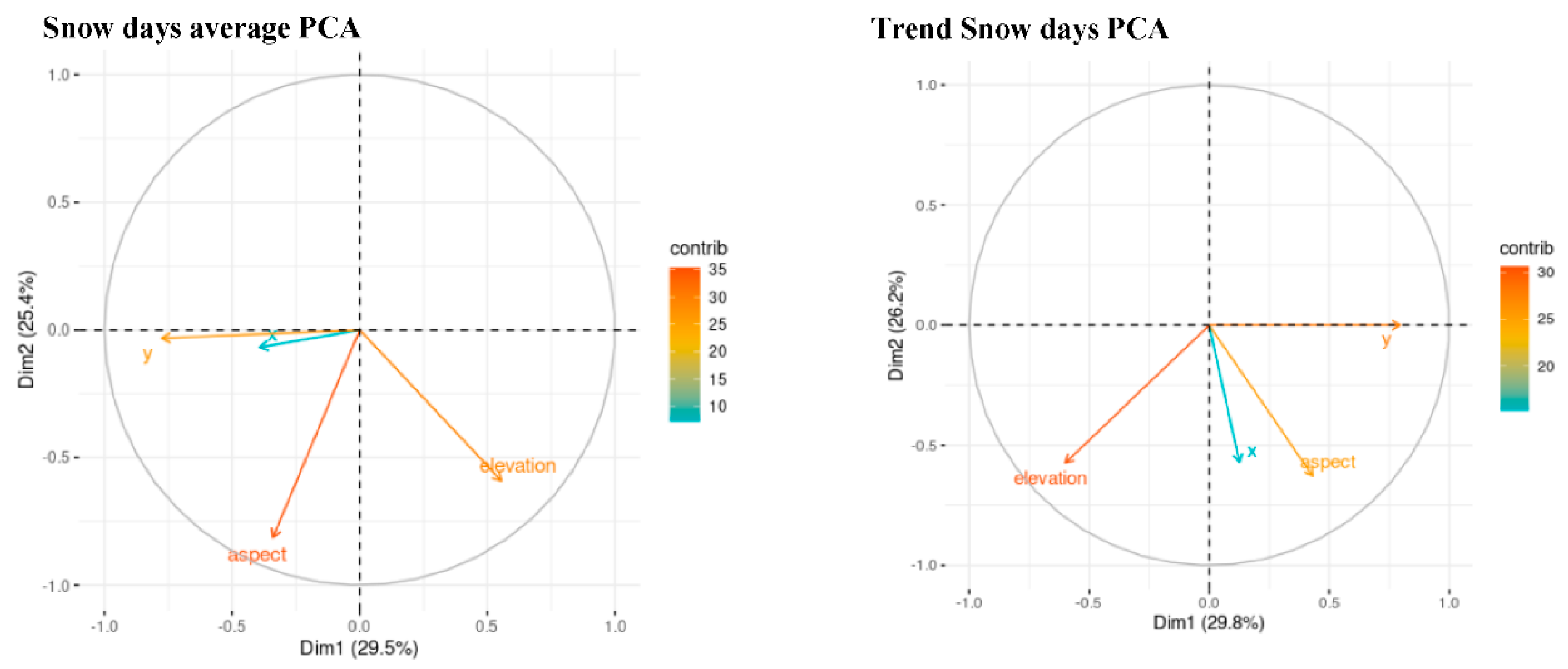
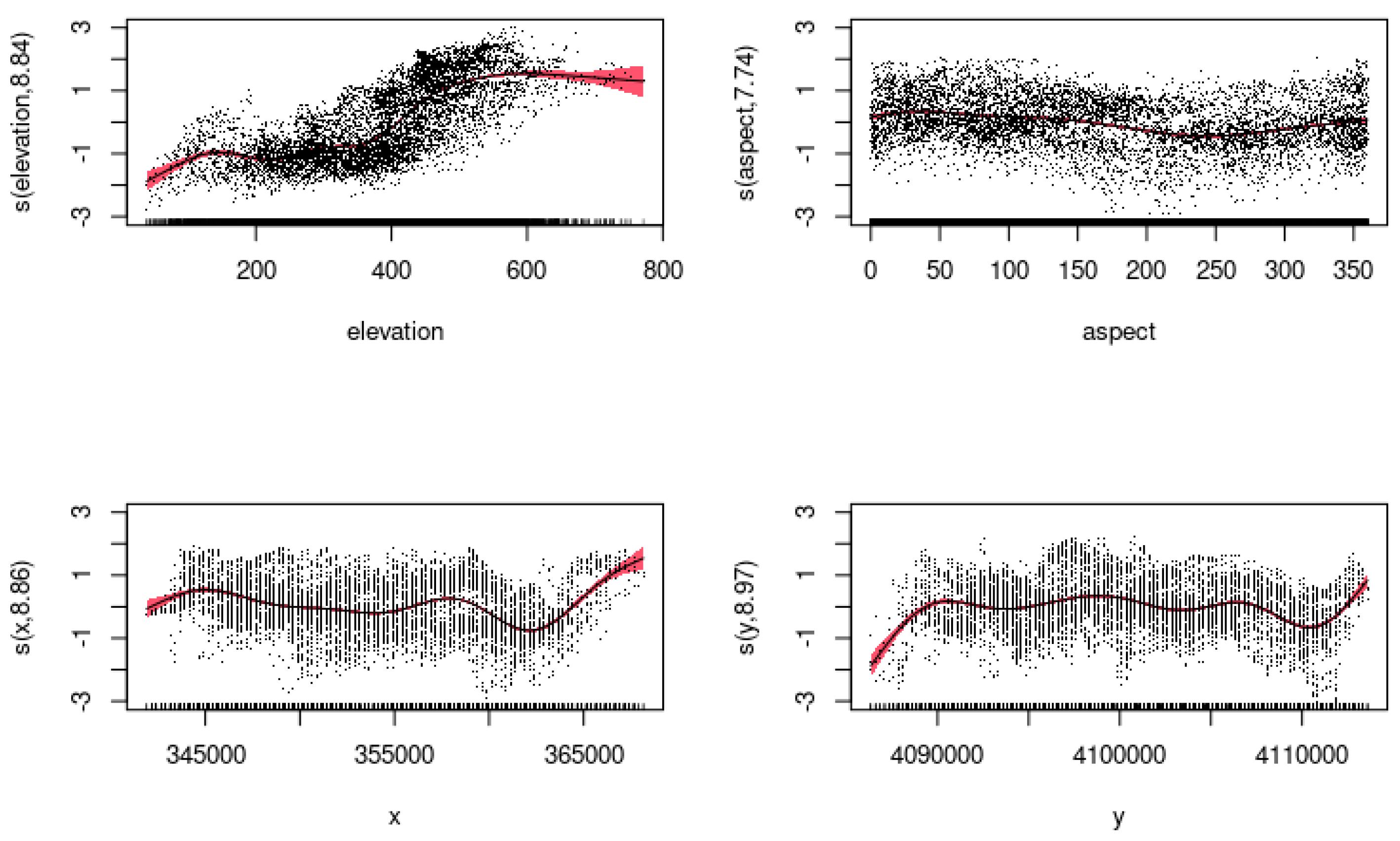
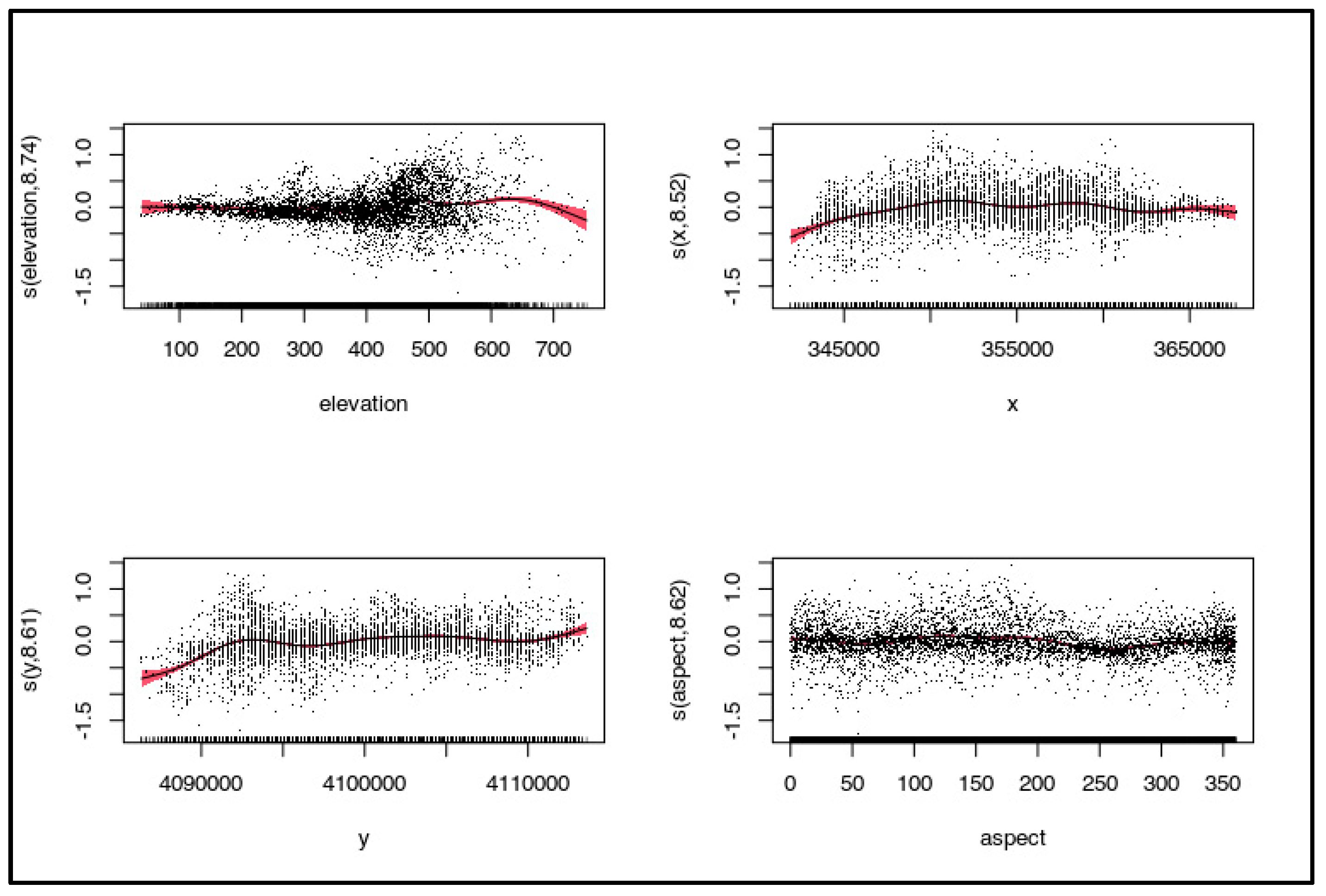
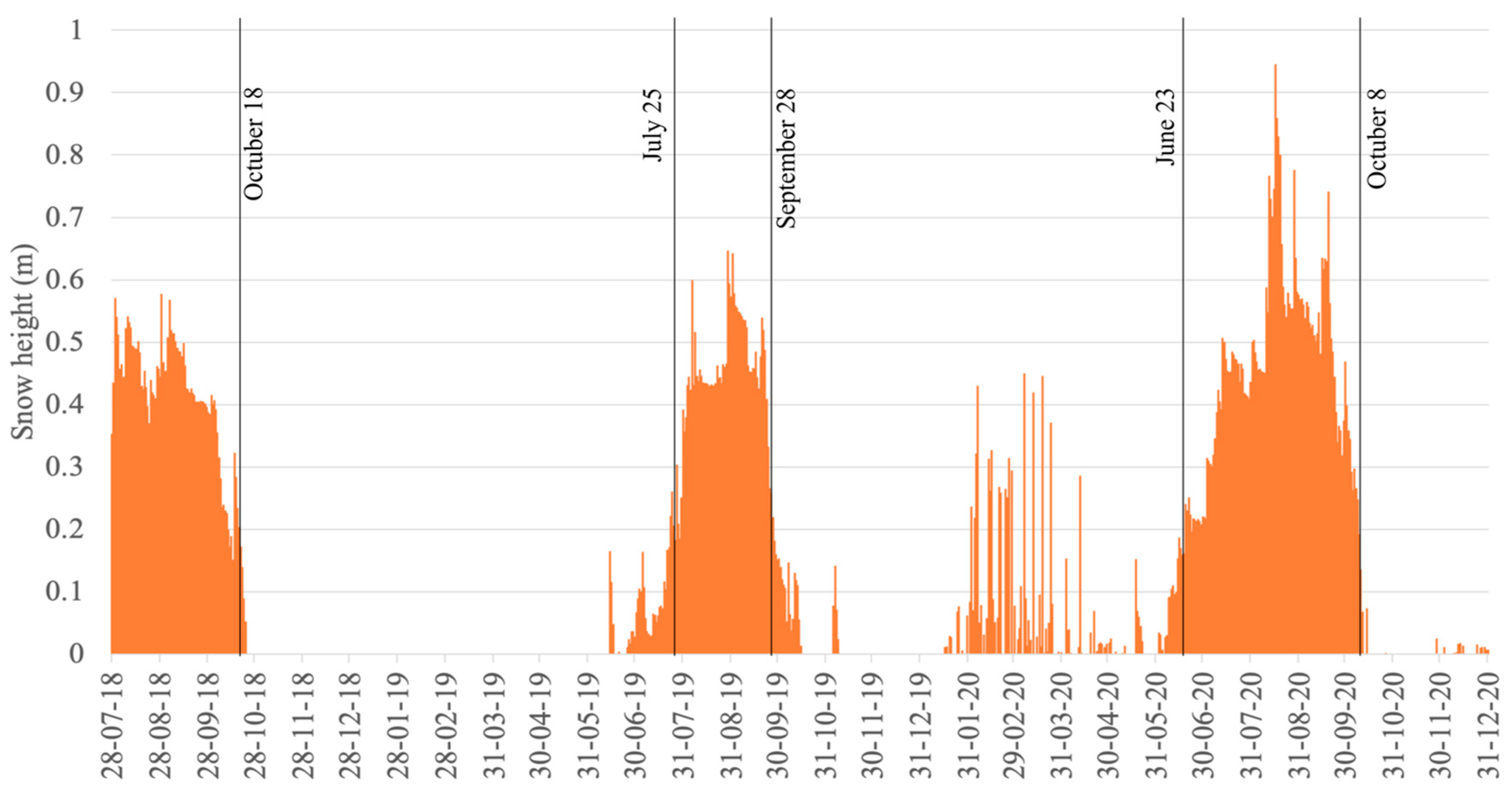
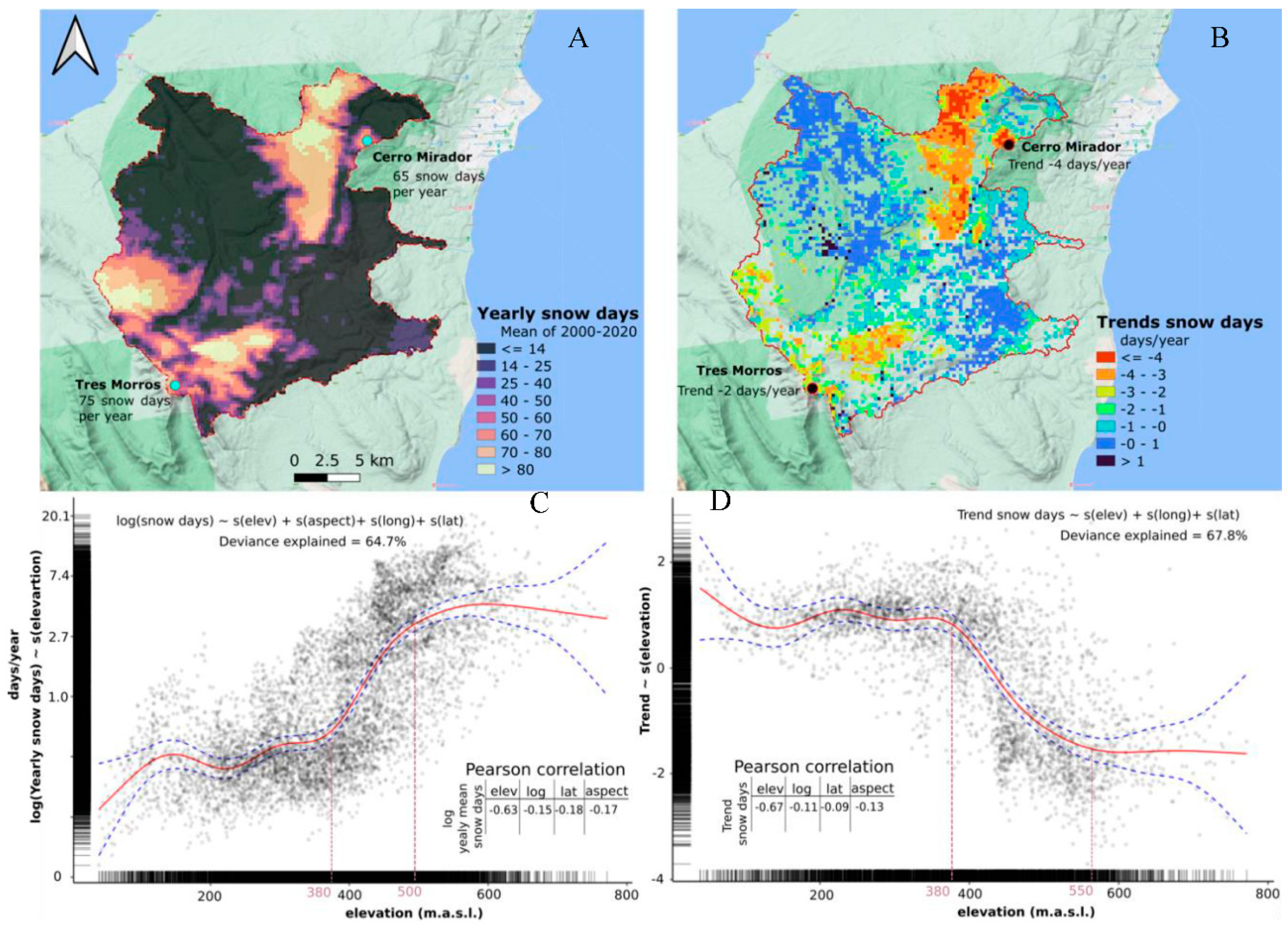
3.2.5. Snow Cover Variability
4. Results
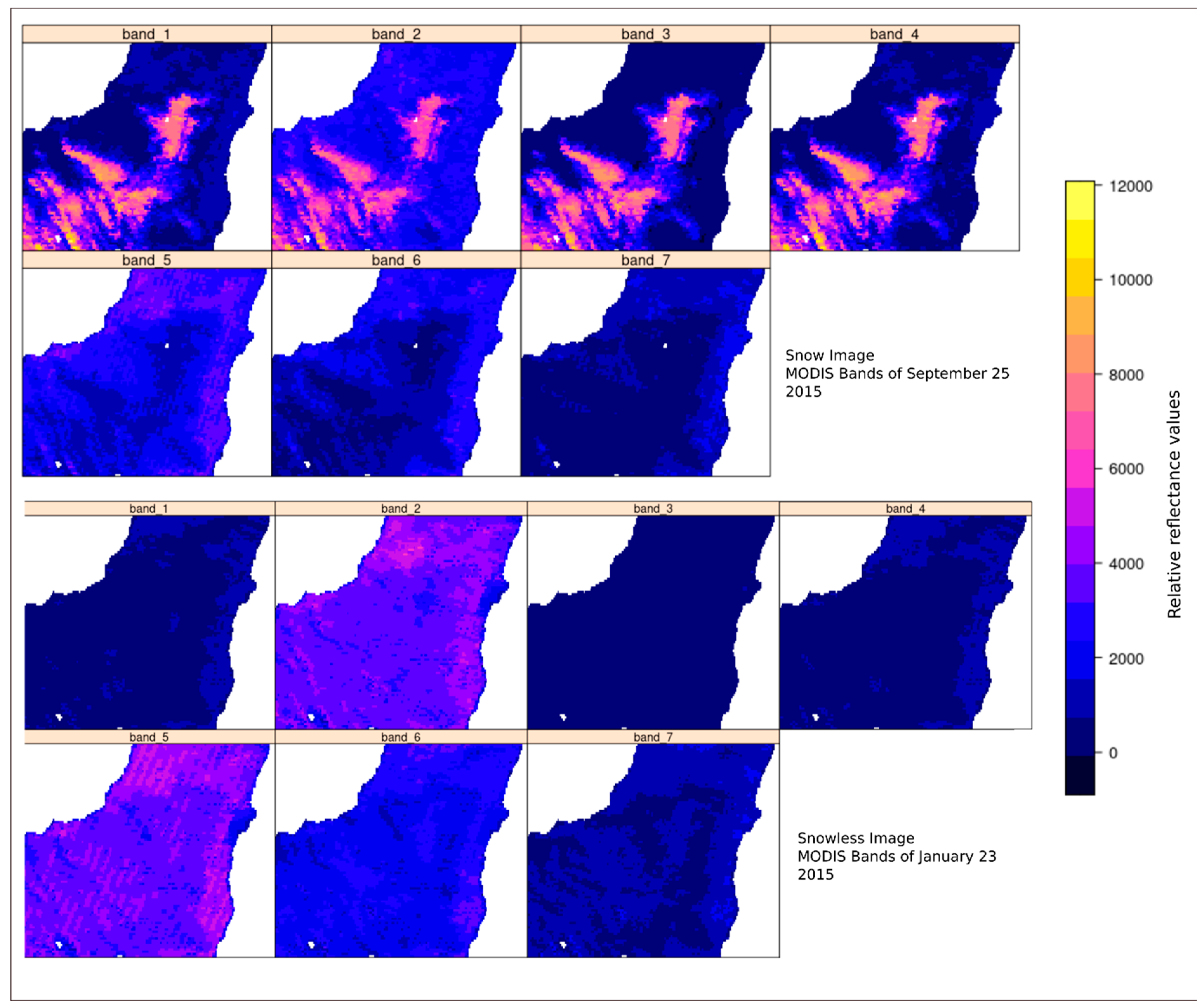
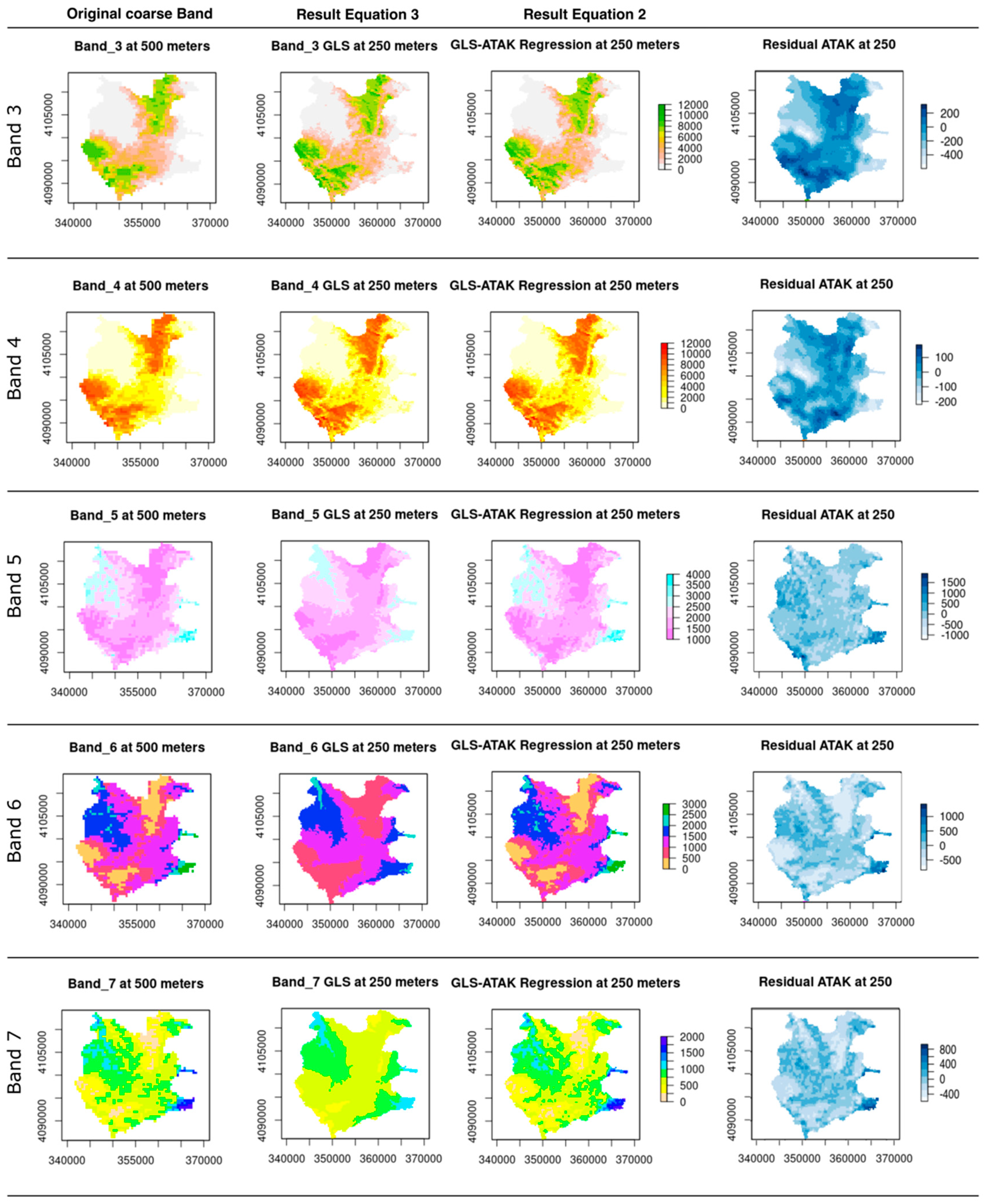
4.1. Spectral Fusion
4.1.1. The First-Term of Spectral Fusion, the Linear Relationship
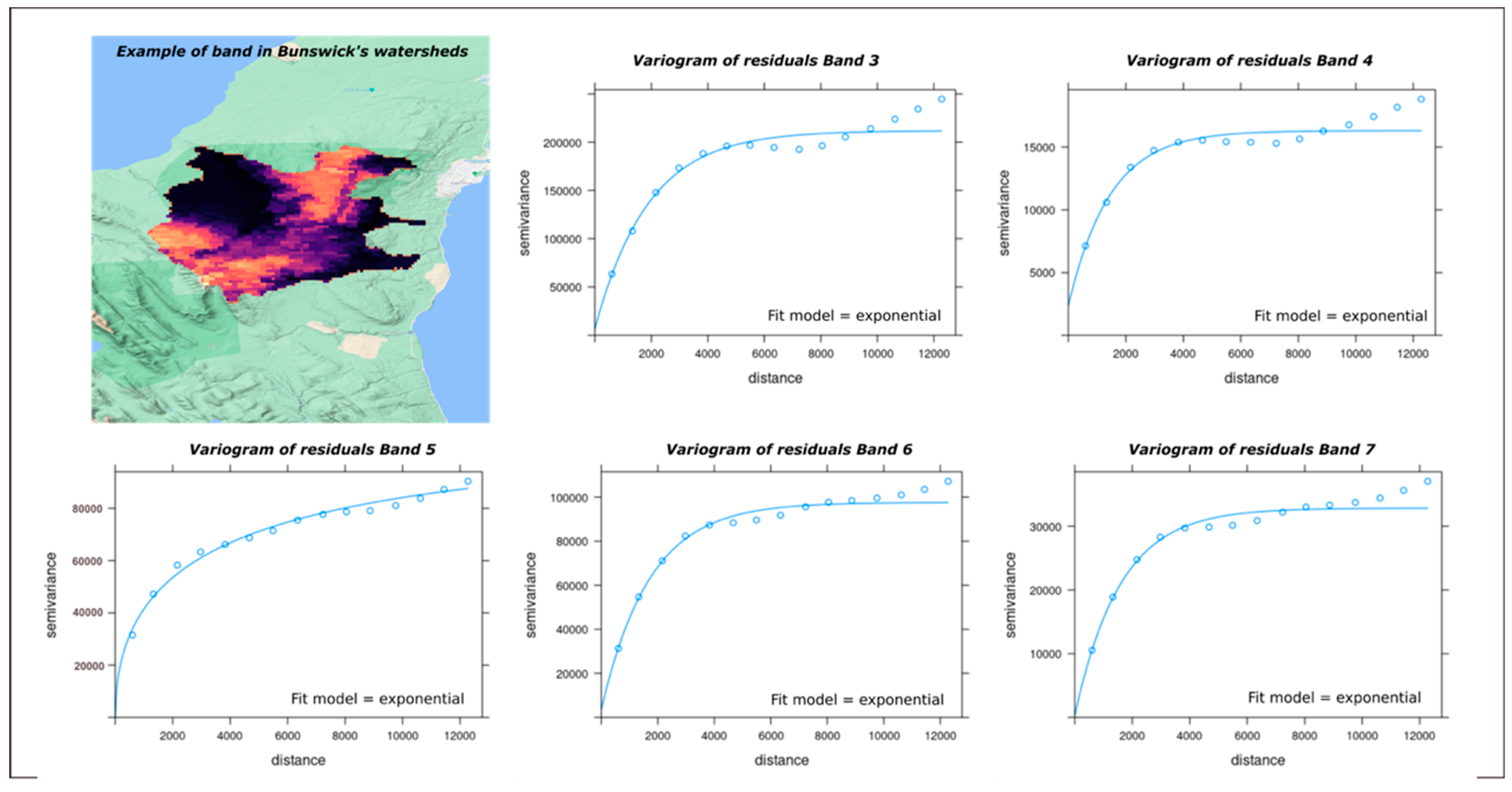
4.1.2. The Second Term of Spectral Fusion, Kriging Interpolation
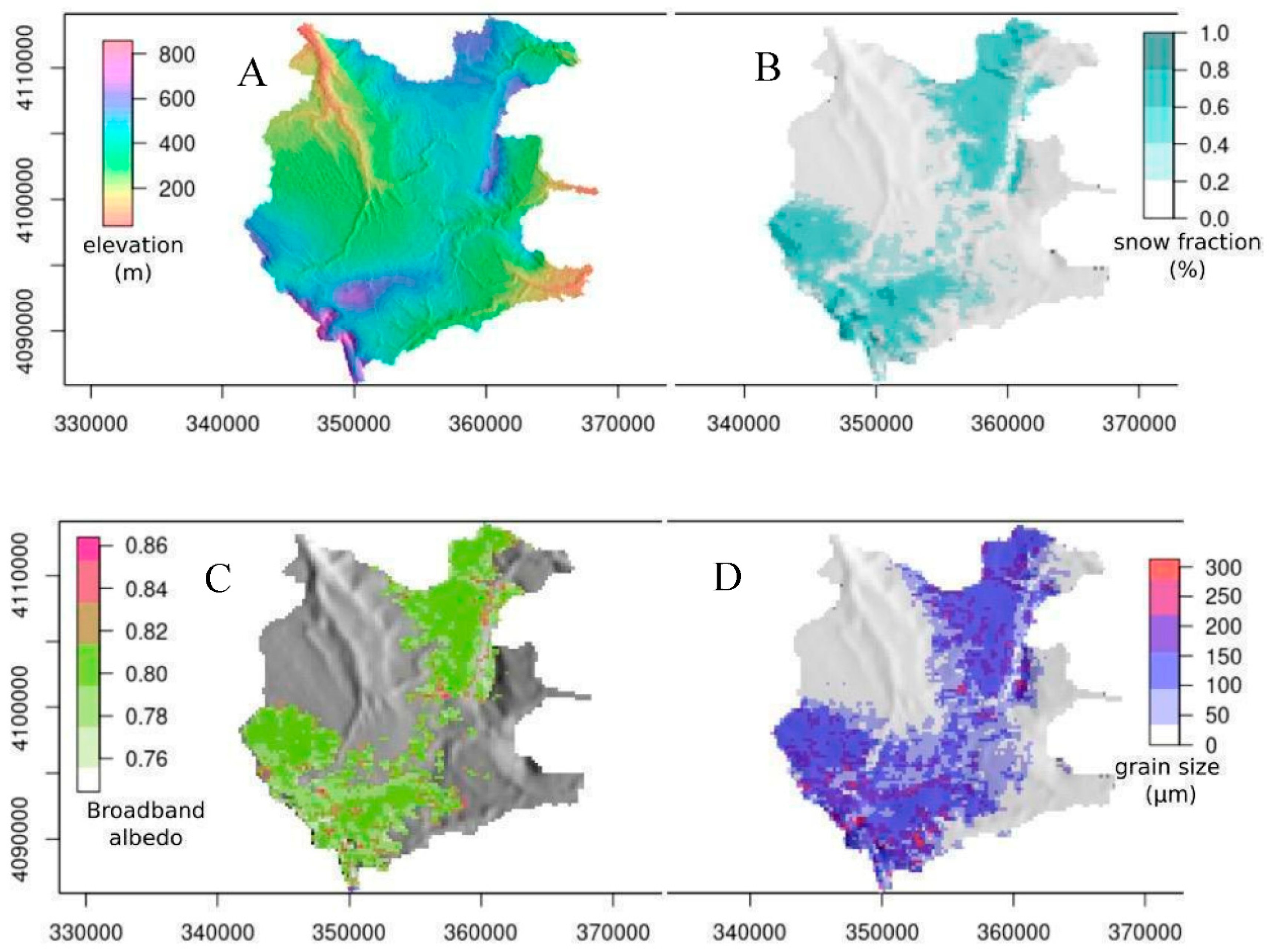
4.2. SMA
4.3. Spatio-Temporal Snow Reconstruction
4.3.1. Cloud and Snow Masks
4.3.2. Temporal Interpolation
4.4 Ground Validation with AWS Data
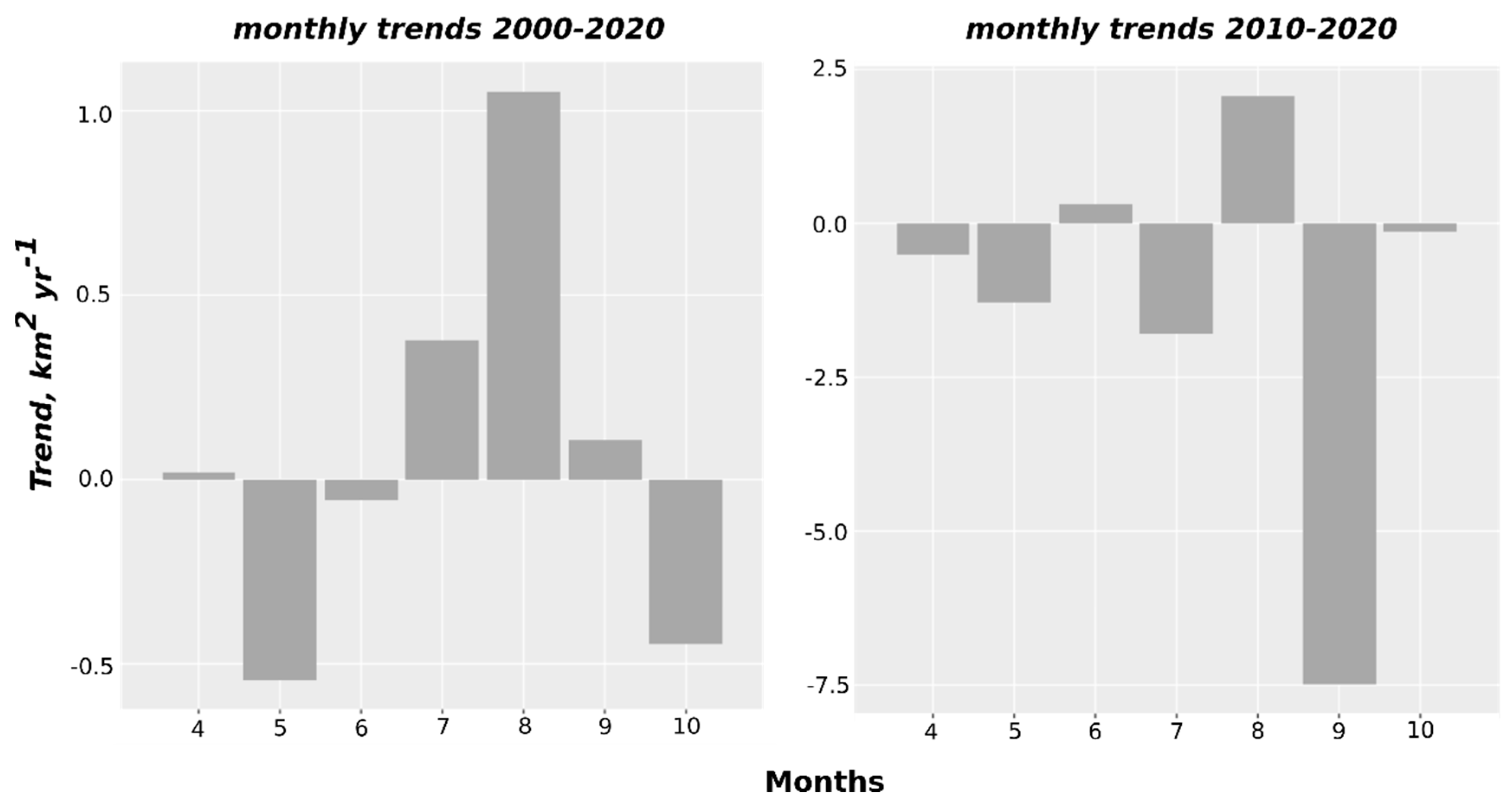
4.5 Reconstructed Snow Cover Variability at Brunswick Peninsula
5 Discussion
5.1 Method Improvement
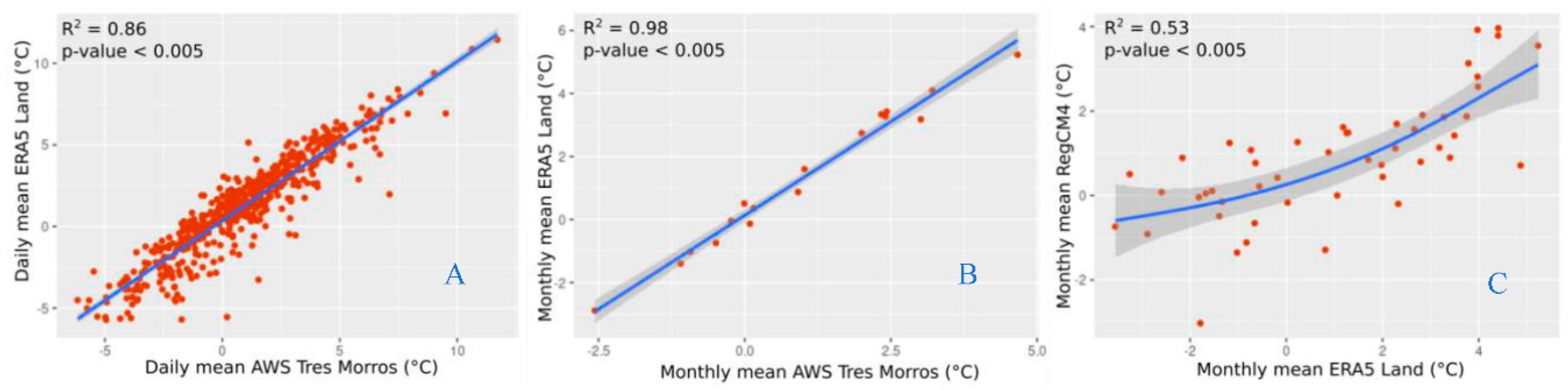
5.2 Climate Forcing
| ERA5 climate variables | Liquid precipitation | Solid precipitation | Mean temperature | Maximum temperature | Minimum temperature | Degree-hours |
|---|---|---|---|---|---|---|
| Cross Pearson correlation with MODIS snow cover area | -0.49 | 0.48 | -0.70 | -0.65 | -0.60 | -0.70 |
6. Conclusions
Acknowledgments
Appendix A. Supplementary data and codes
References
- Chen, X.; Long, D.; Liang, S.; He, L.; Zeng, C.; Hao, X.; Hong, Y. Developing a Composite Daily Snow Cover Extent Record over the Tibetan Plateau from 1981 to 2016 Using Multisource Data. Remote Sens Environ 2018, 215, 284–299. [Google Scholar] [CrossRef]
- Frei, A.; Tedesco, M.; Lee, S.; Foster, J.; Hall, D.K.; Kelly, R.; Robinson, D.A. A Review of Global Satellite-Derived Snow Products. Advances in Space Research 2012, 50, 1007–1029. [Google Scholar] [CrossRef]
- Aguirre, F.; Carrasco, J.; Sauter, T.; Schneider, C.; Gaete, K.; Garín, E.; Adaros, R.; Butorovic, N.; Jaña, R.; Casassa, G. Snow Cover Change as a Climate Indicator in Brunswick Peninsula, Patagonia. Front Earth Sci (Lausanne) 2018, 6, 130. [Google Scholar] [CrossRef]
- Hughes, L. Climate Change and Australia: Trends, Projections and Impacts. Austral Ecol 2003, 28, 423–443. [Google Scholar] [CrossRef]
- Beniston, M.; Farinotti, D.; Stoffel, M.; Andreassen, L.M.; Coppola, E.; Eckert, N.; Fantini, A.; Giacona, F.; Hauck, C.; Huss, M.; et al. The European Mountain Cryosphere: A Review of Its Current State, Trends, and Future Challenges. Cryosphere 2018, 12, 759–794. [Google Scholar] [CrossRef]
- IPCC Summary for Policymakers. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, 2013; 33. [CrossRef]
- Mernild, S.H.; Liston, G.E.; Hiemstra, C.A.; Malmros, J.K.; Yde, J.C.; McPhee, J. The Andes Cordillera. Part I: Snow Distribution, Properties, and Trends (1979-2014). International Journal of Climatology 2017, 37, 1680–1698. [Google Scholar] [CrossRef]
- Walker, D.A.; Halfpenny, J.C.; Walker, M.D.; Wessman, C.A. Long-Term Studies of Snow-Vegetation Interactions. Bioscience 1993, 43, 287–301. [Google Scholar] [CrossRef]
- Lillesand, T.M.; Kiefer, R.W.; Chipman, J.W. Remote Sensing and Image Interpretation; Seventh.; John Wiley & Sons, 2015. ISBN 9781118343289.
- Tedesco, M. Electromagnetic Properties of Components of the Cryosphere. In Remote sensing of the cryosphere; Tedesco, M., Knight, P., Eds.; Wiley-Blackwell: Oxford, UK, 2015; pp. 17–29. ISBN 9781118368862. [Google Scholar]
- Cortés, G.; Girotto, M.; Margulis, S.A. Analysis of Sub-Pixel Snow and Ice Extent over the Extratropical Andes Using Spectral Unmixing of Historical Landsat Imagery. Remote Sens Environ 2014, 141, 64–78. [Google Scholar] [CrossRef]
- Painter, T.H.; Rittger, K.; McKenzie, C.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of Subpixel Snow Covered Area, Grain Size, and Albedo from MODIS. Remote Sens Environ 2009, 113, 868–879. [Google Scholar] [CrossRef]
- Rittger, K.; Painter, T.H.; Dozier, J. Assessment of Methods for Mapping Snow Cover from MODIS. Adv Water Resour 2013, 51, 367–380. [Google Scholar] [CrossRef]
- Hall, D.K.; Frei, A.; Dery, S. Remote Sensing of Snow Extent. In Remote sensing of the cryosphere; Tedesco, M., Knight, P., Eds.; Wiley-Blackwell: Oxford, UK, 2014; pp. 31–47. ISBN 9781118368862. [Google Scholar]
- Hall, D.K.; Riggs, G.A. Accuracy Assessment of the MODIS Snow Products. Hydrol Process 2007, 21, 1534–1547. [Google Scholar] [CrossRef]
- Riggs, G.; Hall, D. MODIS Snow Products User Guide to Collection 6. 2017.
- Hall, D.K.; Riggs, G.A. Normalized-Difference Snow Index (NDSI). In Encyclopedia of snow, ice and glaciers; Singh, V.P. (Vijay P.), Singh, P. (Hydrologist), Haritashya, U.K., Eds.; Springer, Dordrecht: Zurich, Switzerland, 2011; pp. 779–780. [Google Scholar]
- Frei, A.; Lee, S. A Comparison of Optical-Band Based Snow Extent Products during Spring over North America. Remote Sens Environ 2010, 114, 1940–1948. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V. V; DiGirolamo, N.E.; Bayr, K.J. MODIS Snow-Cover Products. Remote Sens Environ 2002, 83, 181–194. [Google Scholar] [CrossRef]
- Lopez, P.; Sirguey, P.; Arnaud, Y.; Pouyaud, B.; Chevallier, P. Snow Cover Monitoring in the Northern Patagonia Icefield Using MODIS Satellite Images (2000–2006). Glob Planet Change 2008, 61, 103–116. [Google Scholar] [CrossRef]
- Sirguey, P.; Mathieu, R.; Arnaud, Y. Subpixel Monitoring of the Seasonal Snow Cover with MODIS at 250 m Spatial Resolution in the Southern Alps of New Zealand: Methodology and Accuracy Assessment. Remote Sens Environ 2009, 113, 160–181. [Google Scholar] [CrossRef]
- Musselman, K.N.; Molotch, N.P.; Brooks, P.D. Effects of Vegetation on Snow Accumulation and Ablation in a Mid-Latitude Sub-Alpine Forest. Hydrol Process 2008, 22, 2767–2776. [Google Scholar] [CrossRef]
- Varhola, A.; Coops, N.C.; Weiler, M.; Moore, R.D. Forest Canopy Effects on Snow Accumulation and Ablation: An Integrative Review of Empirical Results. J Hydrol (Amst) 2010, 392, 219–233. [Google Scholar] [CrossRef]
- Sirguey, P.; Mathieu, R.; Arnaud, Y. Subpixel Monitoring of the Seasonal Snow Cover with MODIS at 250 m Spatial Resolution in the Southern Alps of New Zealand: Methodology and Accuracy Assessment. Remote Sens Environ 2009, 113, 160–181. [Google Scholar] [CrossRef]
- Dumont, M.; Gardelle, J.; Sirguey, P.; Guillot, A.; Six, D.; Rabatel, A.; Arnaud, Y. Linking Glacier Annual Mass Balance and Glacier Albedo Retrieved from MODIS Data. Cryosphere 2012, 6, 1527–1539. [Google Scholar] [CrossRef]
- GCOS, G. Systematic Observation Requirements for Satellite-Based Data Products for Climate 2011 Update: Supplemental Details to the Satellite-Based Component of the “Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC (2010 Upd. In Tech. rep; World Meteorological Organisation (WMO) 7 bis, 2011.
- Dozier, J.; Painter, T.H. MULTISPECTRAL AND HYPERSPECTRAL REMOTE SENSING OF ALPINE SNOW PROPERTIES. Annu Rev Earth Planet Sci 2004, 32, 465–494. [Google Scholar] [CrossRef]
- Painter, T.H.; Rittger, K.; McKenzie, C.; Slaughter, P.; Davis, R.E.; Dozier, J. Retrieval of Subpixel Snow Covered Area, Grain Size, and Albedo from MODIS. Remote Sens Environ 2009, 113, 868–879. [Google Scholar] [CrossRef]
- Pérez, T.; Mattar, C.; Fuster, R. Decrease in Snow Cover over the Aysén River Catchment in Patagonia, Chile. Water (Basel) 2018, 10, 619. [Google Scholar] [CrossRef]
- Stehr, A.; Aguayo, M. Snow Cover Dynamics in Andean Watersheds of Chile (32.0–39.5° S) during the Years 2000–2016. Hydrol Earth Syst Sci 2017, 21, 5111–5126. [Google Scholar] [CrossRef]
- Malmros, J.K.; Mernild, S.H.; Wilson, R.; Tagesson, T.; Fensholt, R. Snow Cover and Snow Albedo Changes in the Central Andes of Chile and Argentina from Daily MODIS Observations (2000–2016). Remote Sens Environ 2018, 209, 240–252. [Google Scholar] [CrossRef]
- Mernild, S.H.; Beckerman, A.P.; Yde, J.C.; Hanna, E.; Malmros, J.K.; Wilson, R.; Zemp, M. Mass Loss and Imbalance of Glaciers along the Andes Cordillera to the Sub-Antarctic Islands. Glob Planet Change 2015, 133, 109–119. [Google Scholar] [CrossRef]
- Garreaud, R.; Lopez, P.; Minvielle, M.; Rojas, M.; Garreaud, R.; Lopez, P.; Minvielle, M.; Rojas, M. Large-Scale Control on the Patagonian Climate. J Clim 2013, 26, 215–230. [Google Scholar] [CrossRef]
- Rozzi, R.; Massardo, F.; Gallardo, M.R.; Plana, J. La Reserva de Biosfera Cabo de Hornos: Un Desafío Para La Conservación de La Biodiversidad e Implementación Del Desarrollo Sustentable En El Extremo Austral de América. Environ Res 2007, 35, 55–70. [Google Scholar]
- Aguirre, F.; Squeo, F.A.; López, D.; Grego, R.D.; Buma, B.; Carvajal, D.; Jaña, R.; Casassa, G.; Rozzi, R. Gradientes Climáticos y Su Alta Influencia En Los Ecosistemas Terrestres de La Reserva de La Biosfera Cabo de Hornos, Chile. In Proceedings of the Anales del Instituto de la Patagonia; 2021; Vol. 49. [Google Scholar]
- Aravena, J.C.; Luckman, B.H. Spatio-Temporal Rainfall Patterns in Southern South America. International Journal of Climatology 2009, 29, 2106–2120. [Google Scholar] [CrossRef]
- Davies, B.J.; Darvill, C.M.; Lovell, H.; Bendle, J.M.; Dowdeswell, J.A.; Fabel, D.; García, J.L.; Geiger, A.; Glasser, N.F.; Gheorghiu, D.M.; et al. The Evolution of the Patagonian Ice Sheet from 35 Ka to the Present Day (PATICE). Earth Sci Rev 2020, 204, 103152. [Google Scholar] [CrossRef]
- Kilian, R.; Lamy, F. A Review of Glacial and Holocene Paleoclimate Records from Southernmost Patagonia (49–55°S). Quat Sci Rev 2012, 53, 1–23. [Google Scholar] [CrossRef]
- Markgraf, V.; Huber, U.M. Late and Postglacial Vegetation and Fire History in Southern Patagonia and Tierra Del Fuego. Palaeogeogr Palaeoclimatol Palaeoecol 2010, 297, 351–366. [Google Scholar] [CrossRef]
- Villalba, R.; Grosjean, M.; Kiefer, T. Long-Term Multi-Proxy Climate Reconstructions and Dynamics in South America (LOTRED-SA): State of the Art and Perspectives. Palaeogeogr Palaeoclimatol Palaeoecol 2009, 281, 175–179. [Google Scholar] [CrossRef]
- Mayewski, P.A.; Meredith, M.P.; Summerhayes, C.P.; Turner, J.; Worby, A.; Barrett, P.J.; Casassa, G.; Bertler, N.A.N.; Bracegirdle, T.; Naveira Garabato, A.C.; et al. State of the Antarctic and Southern Ocean Climate System. Reviews of Geophysics 2009, 47, RG1003. [Google Scholar] [CrossRef]
- Marshall, G.J. Trends in the Southern Annular Mode from Observations and Reanalyses. J Clim 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
- Sauter, T. Revisiting Extreme Precipitation Amounts over Southern South America and Implications for the Patagonian Icefields. Hydrol Earth Syst Sci 2020, 24, 2003–2016. [Google Scholar] [CrossRef]
- Carrasco, J.F.; Casassa, G.; Rivera, A. Meteorological and Climatological Aspects of the Southern Patagonia Icefield. In; Springer, Boston, MA, 2002; pp. 29–41.
- Schneider, C.; Glaser, M.; Kilian, R.; Santana, A.; Butorovic, N.; Casassa, G. Weather Observations Across the Southern Andes at 53°S. Phys Geogr 2003, 24, 97–119. [Google Scholar] [CrossRef]
- Garreaud, R.; Lopez, P.; Minvielle, M.; Rojas, M. Large-Scale Control on the Patagonian Climate. J Clim 2013, 26, 215–230. [Google Scholar] [CrossRef]
- Weidemann, Stephanie. ; Sauter, T.; Kilian, R.; Steger, D.; Butorovic, N.; Schneider, C. A 17-Year Record of Meteorological Observations Across the Gran Campo Nevado Ice Cap in Southern Patagonia, Chile, Related to Synoptic Weather Types and Climate Modes. Front Earth Sci (Lausanne) 2018, 6, 53. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Mendoza, P.A.; Boisier, J.P.; Addor, N.; Galleguillos, M.; Zambrano-Bigiarini, M.; Lara, A.; Cortes, G.; Garreaud, R.; McPhee, J. The CAMELS-CL Dataset: Catchment Attributes and Meteorology for Large Sample Studies-Chile Dataset. Hydrol Earth Syst Sci 2018, 22, 5817–5846. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Reviews of Geophysics 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Pohl, C.; Van Genderen, J. Remote Sensing Image Fusion: A Practical Guide; Crc Press, 2017. ISBN 1498730035.
- Canty, M.J. Image Analysis, Classification and Change Detection in Remote Sensing: With Algorithms for Python; Fourth.; CRC Press, 2019. ISBN 0429875347.
- Shettigara, V.K. A Generalized Component Substitution Technique for Spatial Enhancement of Multispectral Images Using a Higher Resolution Data Set. Photogramm Eng Remote Sensing 1992, 58, 561–567. [Google Scholar]
- Nunez, J.; Otazu, X.; Fors, O.; Prades, A.; Pala, V.; Arbiol, R. Multiresolution-Based Image Fusion with Additive Wavelet Decomposition. IEEE Transactions on Geoscience and Remote Sensing 1999, 37, 1204–1211. [Google Scholar] [CrossRef]
- Ranchin, T.; Aiazzi, B.; Alparone, L.; Baronti, S.; Wald, L. Image Fusion—the ARSIS Concept and Some Successful Implementation Schemes. ISPRS Journal of Photogrammetry and Remote Sensing 2003, 58, 4–18. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Context-Driven Fusion of High Spatial and Spectral Resolution Images Based on Oversampled Multiresolution Analysis. IEEE Transactions on Geoscience and Remote Sensing 2002, 40, 2300–2312. [Google Scholar] [CrossRef]
- Sales, M.H.; Souza, C.M.; Kyriakidis, P.C. Fusion of MODIS Images Using Kriging With External Drift. IEEE Transactions on Geoscience and Remote Sensing 2013, 51, 2250–2259. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, W.; Atkinson, P.M.; Zhao, Y. Downscaling MODIS Images with Area-to-Point Regression Kriging. Remote Sens Environ 2015, 166, 191–204. [Google Scholar] [CrossRef]
- Gao, F.; Kustas, W.; Anderson, M. A Data Mining Approach for Sharpening Thermal Satellite Imagery over Land. Remote Sens (Basel) 2012, 4, 3287–3319. [Google Scholar] [CrossRef]
- Hu, M.; Huang, Y. Atakrig: An R Package for Multivariate Area-to-Area and Area-to-Point Kriging Predictions. Comput Geosci 2020, 139, 104471. [Google Scholar] [CrossRef]
- Pardo-Iguzquiza, E.; Atkinson, P.M.; Chica-Olmo, M. DSCOKRI: A Library of Computer Programs for Downscaling Cokriging in Support of Remote Sensing Applications. Comput Geosci 2010, 36, 881–894. [Google Scholar] [CrossRef]
- Jin, Y.; Ge, Y.; Wang, J.; Heuvelink, G.; Wang, L. Geographically Weighted Area-to-Point Regression Kriging for Spatial Downscaling in Remote Sensing. Remote Sens (Basel) 2018, 10, 579. [Google Scholar] [CrossRef]
- Zuur, A.; Ieno, E.N.; Walker, N.; Saveliev, A.A.; Smith, G.M. Dealing with Heterogeneity. In Mixed effects models and extensions in ecology with R; Springer Science & Business Media, 2009; pp. 71–101. ISBN 0387874585.
- Hijmans, R.J.; van Etten, J. Raster: Geographic Data Analysis and Modeling. R package version 2016, 2. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; Heisterkamp, S.; Van Willigen, B.; Maintainer, R. Package ‘Nlme. ’ Linear and nonlinear mixed effects models, version 2017, 3. [Google Scholar]
- Pebesma, E.J. Multivariable Geostatistics in S: The Gstat Package. Comput Geosci 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel: An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. J Stat Softw 2013, 63, 1–50. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A Universal Image Quality Index. IEEE Signal Process Lett 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Alparone, L.; Aiazzi, B.; Baronti, S.; Garzelli, A.; Nencini, F.; Selva, M. Multispectral and Panchromatic Data Fusion Assessment without Reference. Photogramm Eng Remote Sensing 2008, 74, 193–200. [Google Scholar] [CrossRef]
- Somers, B.; Asner, G.P.; Tits, L.; Coppin, P. Endmember Variability in Spectral Mixture Analysis: A Review. Remote Sens Environ 2011, 115, 1603–1616. [Google Scholar] [CrossRef]
- Roberts, D.A.; Gardner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, R.O. Mapping Chaparral in the Santa Monica Mountains Using Multiple Endmember Spectral Mixture Models. Remote Sens Environ 1998, 65, 267–279. [Google Scholar] [CrossRef]
- Leutner, B.; Horning, N.; Schwalb-Willmann, J.; Hijmans, R.J. RStoolbox: Tools for Remote Sensing Data Analysis. R package version 0.2.6 2019. [Google Scholar]
- Painter, T.H.; Roberts, D.A.; Green, R.O.; Dozier, J. The Effect of Grain Size on Spectral Mixture Analysis of Snow-Covered Area from AVIRIS Data. Remote Sens Environ 1998, 65, 320–332. [Google Scholar] [CrossRef]
- Dudley, K.L.; Roth, K.L.; Coates, A.R. A Multi-Temporal Spectral Library Approach for Mapping Vegetation Species across Spatial and Temporal Phenological Gradients. Remote Sens Environ 2015, 167, 121–134. [Google Scholar] [CrossRef]
- Congedo, L. Semi-Automatic Classification Plugin Documentation. Release 2016, 4, 29. [Google Scholar]
- QGIS Development-Teams QGIS Geographic Information System. Open Source Geospatial Foundation Project 2020.
- Dozier, J.; Painter, T.H.; Rittger, K.; Frew, J.E. Time-Space Continuity of Daily Maps of Fractional Snow Cover and Albedo from MODIS. Adv Water Resour 2008, 31, 1515–1526. [Google Scholar] [CrossRef]
- Redpath, T.A.N.; Sirguey, P.; Cullen, N.J. Characterising Spatio-Temporal Variability in Seasonal Snow Cover at a Regional Scale from MODIS Data: The Clutha Catchment, New Zealand. Hydrol Earth Syst Sci 2019, 23, 3189–3217. [Google Scholar] [CrossRef]
- Chylek, P.; McCabe, M.; Dubey, M.K.; Dozier, J. Remote Sensing of Greenland Ice Sheet Using Multispectral Near-Infrared and Visible Radiances. J Geophys Res 2007, 112, D24S20. [Google Scholar] [CrossRef]
- Bormann, K.J.; McCabe, M.F.; Evans, J.P. Satellite Based Observations for Seasonal Snow Cover Detection and Characterisation in Australia. Remote Sens Environ 2012, 123, 57–71. [Google Scholar] [CrossRef]
- Medeiros, E.S. de; de Lima, R.R.; Olinda, R.A. de; Dantas, L.G.; Santos, C.A.C. dos Space–Time Kriging of Precipitation: Modeling the Large-Scale Variation with Model GAMLSS. Water (Basel) 2019, 11, 2368. [Google Scholar] [CrossRef]
- Wang, Y. Smoothing Splines: Methods and Applications; CRC press, 2011. ISBN 1420077562.
- Pebesma, E. Spacetime: Spatio-Temporal Data in R. J Stat Softw 2012, 51, 1–30. [Google Scholar] [CrossRef]
- Easterling, D.R.; Kunkel, K.E.; Wehner, M.F.; Sun, L. Detection and Attribution of Climate Extremes in the Observed Record. Weather Clim Extrem 2016, 11, 17–27. [Google Scholar] [CrossRef]
- Mudelsee, M. Trend Analysis of Climate Time Series: A Review of Methods. Earth Sci Rev 2019, 190, 310–322. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.R. Updating a Land Surface Model with MODIS-Derived Snow Cover. J Hydrometeorol 2004, 5, 1064–1075. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R 2 An Introduction with R. Generalized Additive Models 2017, 10, 9781315370279. [Google Scholar]
- Mann, B.H. Non-Parametric Test Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J Am Stat Assoc 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Helsel, D.R.; Hirsch, R.M. Echniques of Water Resources Investigations, Book 4, Chapter A3; U.S. Geological Survey., 2002. ISBN 0444814639/9780444814630.
- Rosenbluth, B.N.; Fuenzalida, H.A.; Aceituno, P. RECENT TEMPERATURE VARIATIONS IN SOUTHERN SOUTH AMERICA. INTERNATIONAL JOURNAL OF CLIMATOLOGY Int. J. Climatol 1997, 17, 67–85. [Google Scholar] [CrossRef]
- Hyndman, R.; Koehler, A.B.; Ord, J.K.; Snyder, R.D. Forecasting with Exponential Smoothing: The State Space Approach; Springer Science & Business Media, 2008. ISBN 3540719180.
- Chatfield, C. The Analysis of Time Series : An Introduction, Sixth Edition. The Analysis of Time Series 2003. [Google Scholar] [CrossRef]
- Jassby, A.D.; Cloern, J.E. Wq: Exploring Water Quality Monitoring Data 2017.
- Frey, R.A.; Ackerman, S.A.; Liu, Y.; Strabala, K.I.; Zhang, H.; Key, J.R.; Wang, X. Cloud Detection with MODIS. Part I: Improvements in the MODIS Cloud Mask for Collection 5. J Atmos Ocean Technol 2008, 25, 1057–1072. [Google Scholar] [CrossRef]
- Wachter, P.; Beck, C.; Philipp, A.; Höppner, K.; Jacobeit, J. Spatiotemporal Variability of the Southern Annular Mode and Its Influence on Antarctic Surface Temperatures. Journal of Geophysical Research: Atmospheres 2020, 125, e2020JD033818. [Google Scholar] [CrossRef]
- Clem, K.R.; Renwick, J.A.; McGregor, J.; Fogt, R.L. The Relative Influence of ENSO and SAM on Antarctic Peninsula Climate. Journal of Geophysical Research: Atmospheres 2016, 121, 9324–9341. [Google Scholar] [CrossRef]
- Garreaud, R. Record-Breaking Climate Anomalies Lead to Severe Drought and Environmental Disruption in Western Patagonia in 2016. Clim Res 2018, 74, 217–229. [Google Scholar] [CrossRef]
- Turner, J.; Lu, H.; White, I.; King, J.C.; Phillips, T.; Hosking, J.S.; Bracegirdle, T.J.; Marshall, G.J.; Mulvaney, R.; Deb, P. Absence of 21st Century Warming on Antarctic Peninsula Consistent with Natural Variability. Nature 2016, 535, 411–415. [Google Scholar] [CrossRef] [PubMed]
- Schneider, C.; Gies, D. Effects of El Niño–Southern Oscillation on Southernmost South America Precipitation at 53°S Revealed from NCEP–NCAR Reanalyses and Weather Station Data. International Journal of Climatology 2004, 24, 1057–1076. [Google Scholar] [CrossRef]
- Srur, A.M.; Villalba, R.; Rodríguez-Catón, M.; Amoroso, M.M.; Marcotti, E. Climate and Nothofagus Pumilio Establishment at Upper Treelines in the Patagonian Andes. Front Earth Sci (Lausanne) 2018, 6, 57. [Google Scholar] [CrossRef]
- Sato, K.; Inoue, J. Comparison of Arctic Sea Ice Thickness and Snow Depth Estimates from CFSR with in Situ Observations. Clim Dyn 2018, 50, 289–301. [Google Scholar] [CrossRef]
- Wang, C.; Graham, R.M.; Wang, K.; Gerland, S.; Granskog, M.A. Comparison of ERA5 and ERA-Interim near-Surface Air Temperature, Snowfall and Precipitation over Arctic Sea Ice: Effects on Sea Ice Thermodynamics and Evolution. Cryosphere 2019, 13, 1661–1679. [Google Scholar] [CrossRef]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A State-of-the-Art Global Reanalysis Dataset for Land Applications. Earth Syst Sci Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Bravo, C.; Ross, A.N.; Quincey, D.J.; Cisternas, S.; Rivera, A. Surface Ablation and Its Drivers along a West–East Transect of the Southern Patagonia Icefield. Journal of Glaciology 2021, 1–14. [Google Scholar] [CrossRef]
- Quilodrán, C.S.; Sandvig, E.M.; Aguirre, F.; de Aguilar, J.R.; Barroso, O.; Vásquez, R.A.; Rozzi, R. The Extreme Rainfall Gradient of the Cape Horn Biosphere Reserve and Its Impact on Forest Bird Richness. Biodivers Conserv 2022, 1–15. [Google Scholar] [CrossRef]
- Schaefer, M.; Machguth, H.; Falvey, M.; Casassa, G. Modeling Past and Future Surface Mass Balance of the Northern Patagonia Icefield. J Geophys Res Earth Surf 2013, 118, 571–588. [Google Scholar] [CrossRef]
- Bozkurt, D.; Rojas, M.; Boisier, J.P.; Rondanelli, R.; Garreaud, R.; Gallardo, L. Dynamical Downscaling over the Complex Terrain of Southwest South America: Present Climate Conditions and Added Value Analysis. Clim Dyn 2019, 53, 6745–6767. [Google Scholar] [CrossRef]

| year | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
| season length | 78 | 85 | 65 | 76 | 57 | 95 | 10 | 0 | 30 | 30 | Closed due to pandemic |
| Snow Image | Snowless Image | |
| Bandi | Bandi ~ Band1 | Bandi ~ Band1 |
| Band3 | R2 = 0.96 RMSE = 0.229 |
R2 = 0.91 RMSE = 0.066 |
| Band4 | R2 = 0.99 RMSE = 0.094 |
R2 = 0.84 RMSE = 0.074 |
| Band5 | R2 = 0.39 RMSE = 0.264 |
R2 = 0.22 RMSE = 0.165 |
| Band6 | R2 = 0.54 RMSE = 0.229 |
R2 = 0.73 RMSE = 0.133 |
| Band7 | R2 = 0.41 RMSE = 0.409 |
R2 = 0.93 RMSE = 0.075 |
| OLS Regression | ||
| Band 3 | R2 = 0.96 RMSE = 0.230 |
|
| Band 4 | R2 = 0.99 RMSE = 0.094 |
|
| Band 5 | R2 = 0.52 RMSE = 0.234 |
|
| Band 6 | R2 = 0.68 RMSE = 0.319 |
|
| Band 7 | R2 = 0.61 RMSE = 0.333 |
| OLS500 | GLS500 | GWR500 | OLS_ATAK250 | GLS_ATAK250 | GWR_ATAK250 | |
|---|---|---|---|---|---|---|
| Band_3500 | R2 = 0.97 RMSE = 0.230 AIC = -175 |
R2 = 0.97 RMSE = 0.372 AIC = -2877 |
R2 = 0.99 RMSE = 0.110 AIC = -2500 |
UQI= 0.92 | UQI= 0.94 | UQI= 0.93 |
| Band_4500 | R2 = 0.993 RMSE = 0.085 AIC = -3713 |
R2 = 0.993 RMSE = 0.101 AIC = -6053 |
R2 = 0.99 RMSE = 0.038 AIC = -6296 |
UQI= 0.93 | UQI= 0.93 | UQI= 0.93 |
| Band_5500 | R2 = 0.64 RMSE = 0.152 AIC = -1654 |
R2 = 0.63 RMSE = 0.153 AIC =-1727 |
R2 = 0.97 RMSE = 0.047 AIC = -5404 |
UQI= 0.89 | UQI= 0.98 | UQI= 0.89 |
| Band_6500 | R2 = 0.69 RMSE = 0.304 AIC = 822 |
R2 = 0.65 RMSE = 0.392 AIC = 222 |
R2 = 0.98 RMSE = 0.074 AIC = -3838 |
UQI= 0.96 | UQI= 0.99 | UQI= 0.91 |
| Band_7500 | R2 = 0.58 RMSE = 0.302 AIC = 794 |
R2 = 0.53 RMSE = 0.359 AIC = 498 |
R2 = 0.97 RMSE = 0.080 AIC = -3545 |
UQI= 0.97 | UQI= 0.99 | UQI= 0.89 |
| Ds | 0.042 | 0.043 | 0.039 | |||
| Dγ | 0.015 | 0.009 | 0.016 | |||
| QNR Index | 0.943 | 0.949 | 0.946 |
| Season | Image date |
|---|---|
| Summer | January 17 2015 January 16 2016 |
| Autumn | April 29 2016 May 05 2016 |
| Winter | September 03 &11 2016 |
| Spring | October 16 & 18 2016 |
| Relations evaluated | |
|---|---|
|
Linear SF_Rec ~ aws_sh |
R2 = 0.30 RMSE = 0.113 AIC = -199.8 |
|
GAM SF_Rec ~ s(aws_sh) |
R2 = 0.55 RMSE = 0.089 AIC = -252.4 |
|
GAM 20 cm SF_Rec ~ s(aws_sh) |
R2 = 0.05 RMSE = 0.066 AIC = - 251.6 |
| 1 | |
| 2 | QGIS
Geographic Information System. QGIS Team (2017). QGIS Geographic Information
System. Open Source Geospatial Foundation Project. Available Online at:
https://qgis.org
|
| 3 | |
| 4 | |
| 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





