Peculiarities of the Spatial and Electronic Structure of 2-aryl-1,2,3-triazol-5-carboxylic Acids and Their Salts on the Basis of Spectral Studies and DFT Calculations

Preprint

Article

Peculiarities of the Spatial and Electronic Structure of 2-aryl-1,2,3-triazol-5-carboxylic Acids and Their Salts on the Basis of Spectral Studies and DFT Calculations

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Supplementary Material

supplementary.pdf (2.04MB )

Mauricio Alcolea Palafox^*,

Nataliya P. Belskaya,

Irena P. Kostova

Mauricio Alcolea Palafox^*,

Nataliya P. Belskaya,

Irena P. Kostova

This version is not peer-reviewed

Submitted:

13 August 2023

Posted:

14 August 2023

You are already at the latest version

Alerts

Abstract

The molecular structure and vibrational spectra of six 1,2,3-triazoles-containing molecules with possible anticancer activity were investigated. In two of them, the optimized geometry was determined in the monomer, cyclic dimer and staking forms using the B3LYP, M06-2X and MP2 methods. The effect of the para-substitution in the aryl ring was evaluated based on the changes in the molecular structure and atomic charge distribution of the triazole ring. Several relationships were obtained that could facilitate the selection of the substituents on the triazole ring for their further synthesis. The observed IR and Raman bands in the solid state of two of these compounds were accurately assigned according to the functional calculations on the monomer and dimer forms, together with the polynomic scaling equation procedure (PSE).

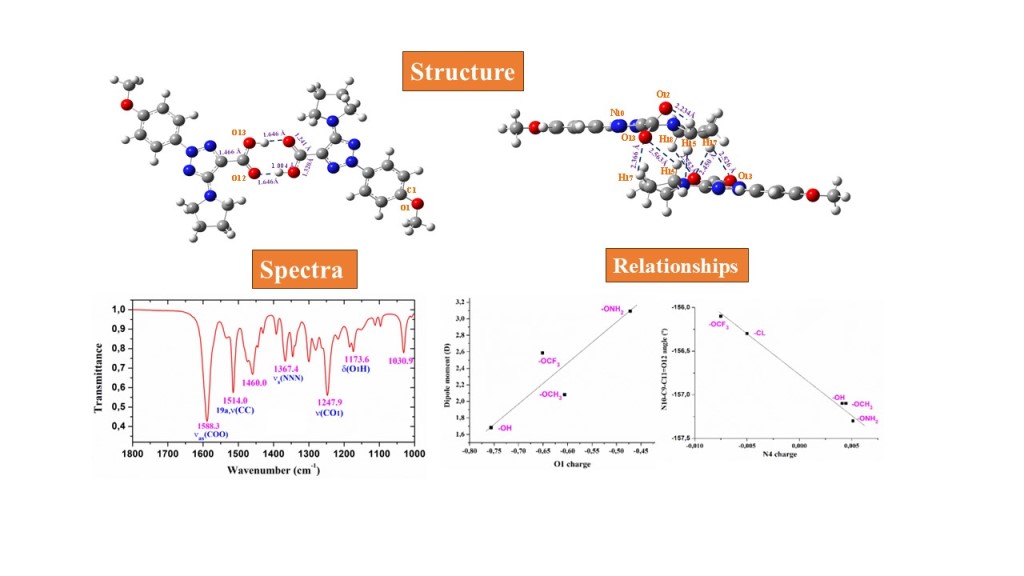
Keywords:

Subject: Medicine and Pharmacology - Pharmacy

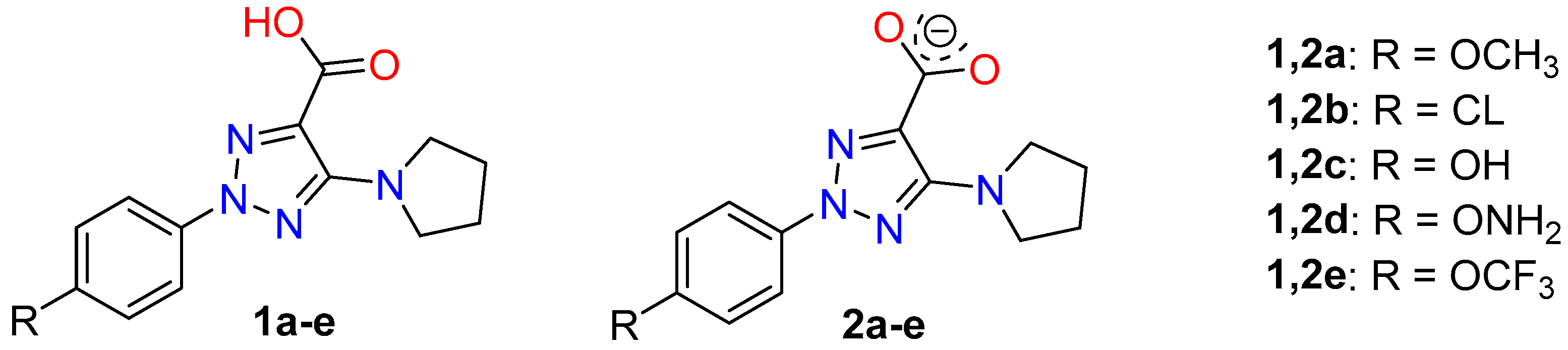
1. Introduction

Triazole-containing molecules with anticancer activity are being widely synthesized and extensively tested [1,2]. 1,2,3-triazole is a privileged moiety and one of the most important classes of nitrogen-rich heterocyclic scaffolds. Their derivatives have also shown a profound activity to inhibit cancer cell proliferation and to induce cell cycle arrest and apoptosis. It is due to the 1,2,3-triazole ring can readily interact with diverse enzymes and receptors in organisms through weak interactions. Moreover, it can not only be acted as a linker to different pharmacophores but also serve as an alone pharmacophore [3]. This fact allows the potential use of these compounds in medicinal chemistry [1].

Previously, the synthesis of a series of new 1,2,3-triazole derivatives with different substituents at N2-aryl ring, with the carboxylic (or carboxylate) group, in addition to the pyrrolidine group was reported by us [3], two of which are now in the focus of detailed study from theoretical and experimental spectroscopy points of view. It is well known that the molecular architecture in biological active compounds affect to its binding force to the active sites of receptors or targeting molecules, and therefore determines its selectivity and cytotoxicity degree. Therefore, the knowledge of the electronic density distribution in a molecule, the greatness of its charges on the nucleophilic and electrophilic centres, and its dipole moment, magnitudes that are calculated in the present work, will be very important to predict its biological effects and to design new candidates with improved properties.

The selected molecules were 2-(4-methoxyphenyl)-5-(pyrrolidin-1-yl)-2H-1,2,3-triazole-4-carboxylic acid (molecule 1a) and its sodium salt (molecule 2a), Figure 1. These molecules can have special properties, due to the liposolubility to the structure provided by the aromatic ring that facilitate the cell membrane penetration, and its hydrosolubility provided by the carboxylic group or its anionic form. In addition to these compounds, several derivatives (1c-e and 2c-e) with electron-donating group in para-position at the aryl ring were optimized and the effect of the substituent electronic nature on the structural parameters of the triazole ring was evaluated, which will be useful in further synthesis.

In these molecules, intramolecular and intermolecular non-bonded interactions are weak, but they build a fine supramolecular structure, which will later affect to many properties that will allow their pharmacological application. We will report the differences between the geometry and electronic characteristics of the dimers and their separate molecules of thiazole acid and its salt, and we will try to clarify the dependence of these characteristics on the electronic nature of the substituent at the aryl fragment.

Vibrational FTIR spectra of related triazole molecules have been reported [4], although not in such detailed form as presented here, nor using accurate scaling procedures. For this purpose, the crystal unit cell in the solid state of 1a and 2a was simulated as a dimer form and optimized. Therefore, an improvement in the theoretical spectra was raised, which facilitates the assignment of the experimental ones.

2. Results and Discussion

One of the goals of the present manuscript was to know the effect of several substituents on the molecular structure and atomic charge distribution of the triazole ring. Its acknowledgement will facilitate the selection of the substituents on the triazole ring for synthesis of new bioactive compounds. In the present paper, we have tested few substituents in para-position of the aryl ring, Figure 1. Of these compounds, 2-aryltriazole acids, 1a and 1b, and their corresponding anionic forms were synthesized previously and studied their NMR and fluorescent properties [3]. The molecular structure and vibrational spectra of 1a (R = OCH₃) and its anion form 2a was interpretated in detail in the present manuscript, including their dimer forms

2.1. Molecular Geometries in the Monomer form of 1a and 2a

In the monomer form, four conformers appear stable in 1a by rotation of both, the methyl group around the C₁-O bond and the -COOH group. The most stable one (conformer 1) is that plotted in Figure 2 and their values were only discussed in the present manuscript. By rotation around C₁-O bond we obtain conformer 2, which was included in Figure 1-SUP (Supplementary Material). The energy difference between both conformers is very small, 0.01 kJ/mol at MP2 level. However, the rotation around the -COOH group leads to a larger difference, 10.6 kJ/mol, conformers 3 and 4. To this feature contributes the increases of the out-of-planarity of this COOH group with a torsional angle C₈-C₉-C₁₁=O₁₂ of 28.2º. Because their lower stability, these conformers were not analyzed in the present work.

Several selected optimized geometrical parameters, namely bond lengths, bond angles and torsional angles calculated using the B3LYP and MP2 methods and the 6-31G(d,p) basis set are collected in Table 1 for 1a and 2a, as well as with all the molecules of Figure 1, but only at the MP2 level for simplicity. In Table 1-SUP is collected more geometrical parameters. The optimized structure in the neutral form 1a and its anion form 2a are shown in Figure 2, while those corresponding to molecules 1b (R = CL) substitution), 1c (R = OH), 1d (R = ONH₂), and 1e (R = OCF₃) are included in Figure 3. The label of the atoms is in accordance to that reported in a previous study [3]. Few values of several bond lengths of interest are also included in these figures. In the bottom of each Figure 2 is shown the total energy (E) values, which includes the ZPE (zero-point vibrational energy) correction, and the Gibbs energy (G). In Figure 3, the energy values by MP2 were only included, for simplicity.

Figure 2. Labeling of the atoms and plot of the structure of: (a) 2-(4-methoxyphenyl)-5-(pyrrolidin-1-yl)-2H-1,2,3-triazole-4-carboxylic acid (in short 1a). (b) sodium 2-(4-methoxyphenyl)-5-(pyrrolidin-1-yl)-2H-1,2,3-triazole-4-carboxylate (in short 2a), with front and lateral views forms. Several bond lengths and intramolecular H-bond values of interest calculated at the MP2/6-31G(d,p) level are included in the figure. The energy values correspond to the B3LYP and MP2 methods, 1 AU = 2625.5 kJ/mol.

In general, comparing the geometric parameters of the most stable forms of 1a and 2a, it is noted that the change of –COOH in 1a (neutral form) by –COO in 2a (anion form) leads to large differences in the whole molecular structure. These differences are noticeable larger than if different substituents are inserted in the para-position (on C₁) of the aryl ring, molecules 1b to 1e.

Figure 3. Two views of the optimized structure in the neutral form of 1b (with chlorine substitution), 1c (with hydroxyl substitution), 1d (with the oxo-amino group), and 1e (with the oxo-trifluoromethyl group). The MP2 energy value was included in the bottom of each figure.

In these molecules both the aryl and triazole rings show a full planar structure, as can be seen from the side views of these figures. However, the pyrrolidine ring is clearly non-planar as it expected. This non-planarity measured in the torsional angle N₁₄-C₁₅-C₁₆-C₁₇ is higher in 7.5˚ (B3LYP) and 17.8˚ (MP2) in the neutral 1a than in the anionic form 2a.

The substituents on the triazole ring are not coplanar with it. Thus, the aryl ring appears noticeable rotated related to the triazole ring, with values of the torsional angle C₅-C₄-N₄-N₁₀ remarkably higher in the neutral form 1a (-14.2º by MP2) than in the anionic form 2a (-3.0º). B3LYP fails in the calculation of this angle with very low values. The pyrrolidine ring plane is also out of the triazole ring plane with values of the torsional angle C₉-C₈-N₁₄-C₁₈ of 26.4º by MP2 in 1a and 35.6º in 2a. B3LYP also fails in the calculation of this angle with lower values. This non-coplanarity of the triazole substituents was also observed in molecules 1b to 1e with small differences in the torsional angles, around 2-3º.

The carboxylic group appears remarkably rotated related to the triazole ring, while the coplanar form corresponds to a saddle point. This rotation is especially large in the anionic form 2a with a value by MP2 of the torsional angle C₈-C₉-C=O₁₂ of 26.5º, vs 15.0º in 1a. This feature can be explained by a larger flexibility of the carboxylic oxygens in 2a form with a longer C=O₁₂ bond length of 1.268 Å vs 1.225 Å in 1a. This flexibility is regulated by a strong O₁₂···H₁₈ H-bond, which is shortening in the anionic form compared to the neutral form by 0.151 Å (Figure 2). This hydrogen bond little changes in the triazoles 1b-e. However, this non-planarity of the structure is expected to be reduced in the solid state because of the intermolecular H-bonds and packing forces of the crystal will tend to compress the structure.

Table 1. Several selected optimized geometrical parameters calculated in the monomer form with the 6-31G(d,p) basis set. Bond lengths (r) in Å, bond angles and dihedral angles (∠) in degrees.

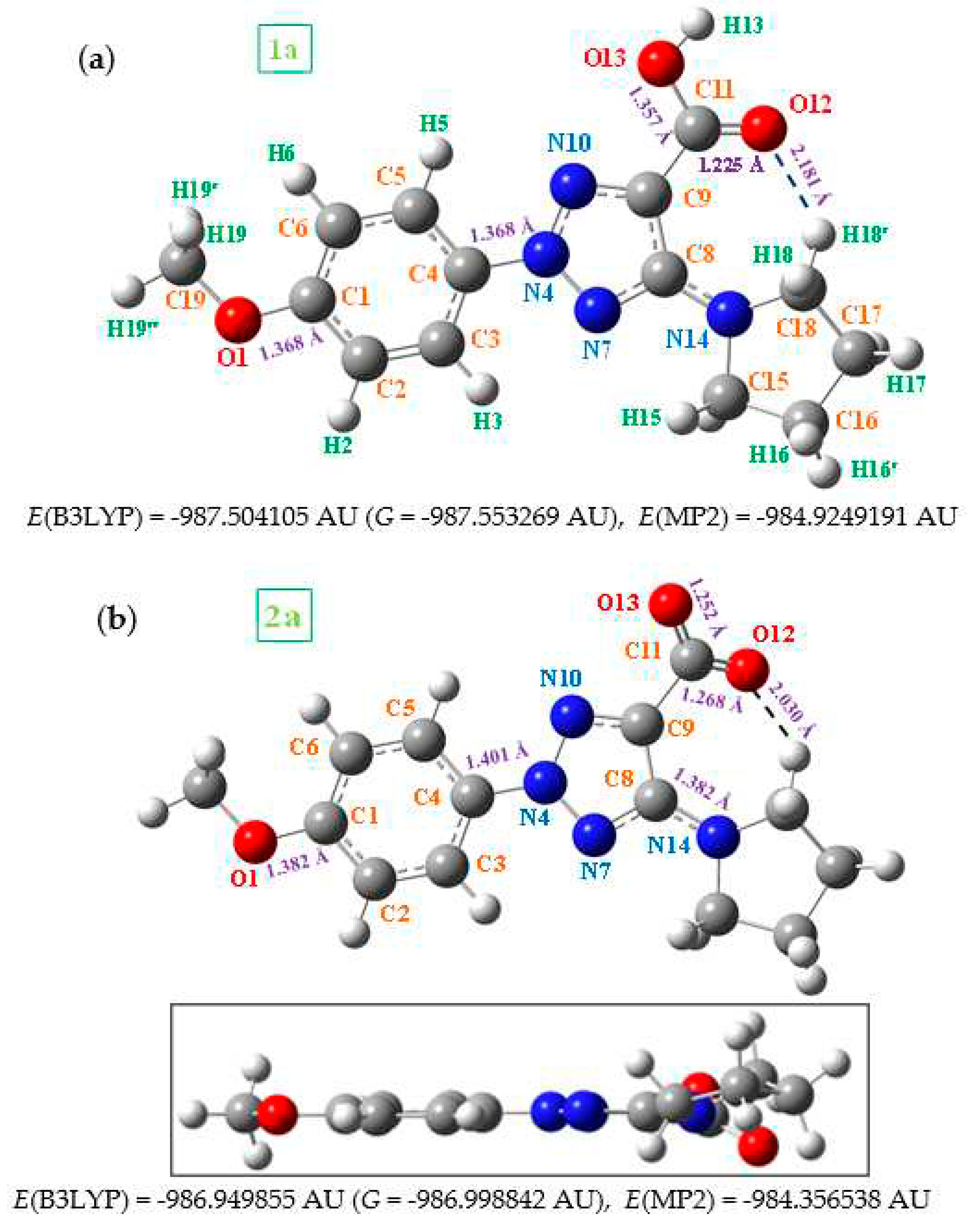
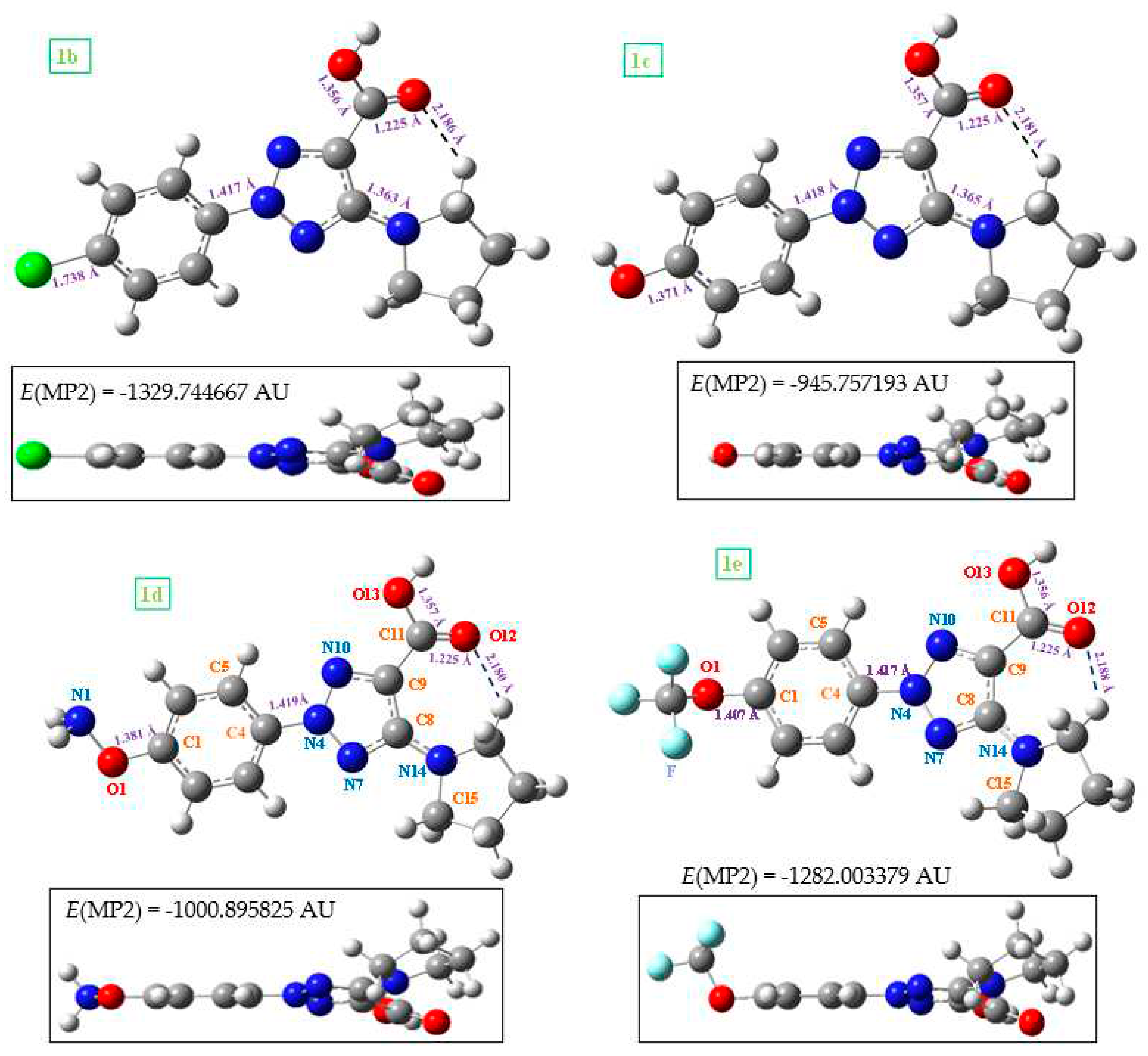
Parameters	-OCH₃				-CL	-OH	-ONH₂	-OCF₃
	B3LYP		MP2		MP2	MP2	MP2	MP2
	1a	2a	1a	2a	1b	1c	1d	1e
r(C₄-N₄) r(N₄-N₇) r(N₄-N₁₀) r(C₈-C₉) r(C₉-N₁₀) r(C₉-C₁₁) O₁₂…H₁₈ ∠(C₄-N₄-N₁₀) ∠N-N-N) ∠(N₁₀-C₉-C₁₁) ∠(C₉-C₈-N₁₄) ∠(C₉-C₁₁=O₁₂) ∠(C₉-C₁₁-O₁₃) ∠(O=C=O) ∠(C₅-C₄-N₄-N₁₀) ∠(N₄-N₁₀-C₉-C₁₁) ∠(N₁₀-N₄-N₇-C₈) ∠(N₁₀-C₉-C=O₁₂) ∠(N₁₀-C₉-C-O₁₃) ∠(C₈-C₉-C=O₁₂) ∠(C₁₁-C₉-C₈-N₁₄) ∠(C₉-C₈-N₁₄-C₁₈) ∠(C₈-N₁₄-C₁₅-C₁₆) ∠(N₁₄-C₁₅-C₁₆-C₁₇)	1.421 1.349 1.311 1.440 1.347 1.465 2.152 122.5 115.9 119.7 133.2 126.1 112.4 121.4 -1.6 175.6 -0.4 -165.9 13.0 9.6 4.8 19.7 -163.0 -21.5	1.398 1.357 1.343 1.448 1.329 1.549 1.980 122.7 115.0 121.0 131.0 113.9 115.7 130.3 -1.1 175.3 -1.1 -145.7 32.8 29.1 4.4 22.2 -169.6 -14.0	1.418 1.340 1.334 1.422 1.358 1.466 2.181 121.7 116.7 119.2 132.6 125.7 111.9 122.4 -14.2 173.6 -0.9 -157.1 21.9 15.0 8.0 26.4 -151.8 -22.9	1.401 1.348 1.350 1.427 1.350 1.541 2.030 122.0 116.1 120.7 131.0 113.6 115.3 131.0 -3.0 176.1 -1.4 -149.3 29.8 26.5 2.5 35.6 -163.7 -5.1	1.417 1.340 1.334 1.423 1.357 1.467 2.186 121.7 116.8 119.2 132.7 125.6 111.8 122.6 -10.3 173.7 -0.8 -156.3 22.6 16.0 8.0 24.9 -152.0 -23.6	1.418 1.340 1.334 1.422 1.358 1.466 2.181 121.7 116.7 119.2 132.6 125.7 111.9 122.4 -13.7 173.6 -0.9 -157.1 21.9 15.0 8.0 26.4 -151.8 -22.9	1.419 1.340 1.334 1.422 1.358 1.466 2.180 121.8 116.7 119.3 132.6 125.7 111.9 122.4 -14.9 173.6 -0.9 -157.3 21.7 14.7 8.1 27.0 -151.7 -22.6	1.417 1.340 1.334 1.424 1.356 1.468 2.188 121.7 116.8 119.2 132.7 125.6 111.8 122.6 -10.7 173.7 -0.8 -156.1 22.9 16.4 8.0 24.4 -152.0 -23.8

The loose of the H₁₃ proton in the anionic form leads to a noticeable effect on the molecular structure. Indeed, the loss of the H₁₃ proton in the anionic form leads to a noticeable effect on the structure of the molecule. It is confirmed by the charge values on the carboxylic group atoms, with larger negative charge localization on the oxygen atoms O₁₂ (-0.889e) and O₁₃ (-0.843e), with arrangement of C₁₁-O₁₃ (1.252 Å) and C₁₁-O₁₂ (1.268 Å) bonds and increase of C₉-C₁₁ bond length up to 1.549 Å and with a higher flexibility of this group (Table 1 and Table 2). This lengthening of the C₉-C₁₁ bond in the anionic form leads to an increment of the double bond character of N₇=C₈ and C₉=N₁₀ of the triazole ring and consequently the C₄-N₄, N-N and C₈-N₁₄ bonds are lengthened. This feature modifies in ca. 2º the bond angles of this triazole ring and in special the torsional angles and the non-planarity with its substituents, Table 1.

In the neutral form of these molecules the highest negative charge corresponds to the hydroxyl oxygen O₁₃ (-0.776e), Table 2. O₁₂ and O₁ oxygens have also a large negative charge and they can take part in the binding of these molecules with biological targets. The negative charge on the nitrogen atoms N₇ and N₁₄ is lower (-0.188e and -0.388e, respectively) but it is expected that they can also affect the biological behavior of these molecules. By contrast, the highest positive charge appears in the carbon atoms C₈ and C₁₁ because they are bonded to large negative atoms.

Table 2. Natural atomic charges (in e) calculated in the monomer form at the MP2/6-31G(d,p) level.

	-OCH₃		-CL	-OH	-ONH₂	-OCF₃
atom	1a	2a	1b	1c	1d	1e
O₁ C₁ C₄ N₄ N₇ C₈ C₉ N₁₀ C₁₁ =O₁₂ O₁₃ N₁₄ C₁₈ H₁₈	-0.606 0.378 0.117 0.004 -0.380 0.458 -0.099 -0.188 0.979 -0.724 -0.776 -0.561 -0.211 0.263	-0.615 0.332 0.167 -0.064 -0.398 0.409 0.019 -0.240 0.956 -0.889 -0.843 -0.558 -0.219 0.297	-0.012* -0.052 0.160 -0.005 -0.381 0.462 -0.091 -0.183 0.979 -0.720 -0.775 -0.560 -0.211 0.263	-0.756 0.385 0.115 0.004 -0.380 0.458 -0.099 -0.188 0.979 -0.724 -0.776 -0.561 -0.211 0.263	-0.472 0.368 0.117 0.005 -0.380 0.457 -0.101 -0.185 0.979 -0.725 -0.776 -0.561 -0.211 0.263	-0.651 0.288 0.163 -0.007 -0.381 0.462 -0.089 -0.182 0.978 -0.719 -0.775 -0.560 -0.211 0.263

*With CL.

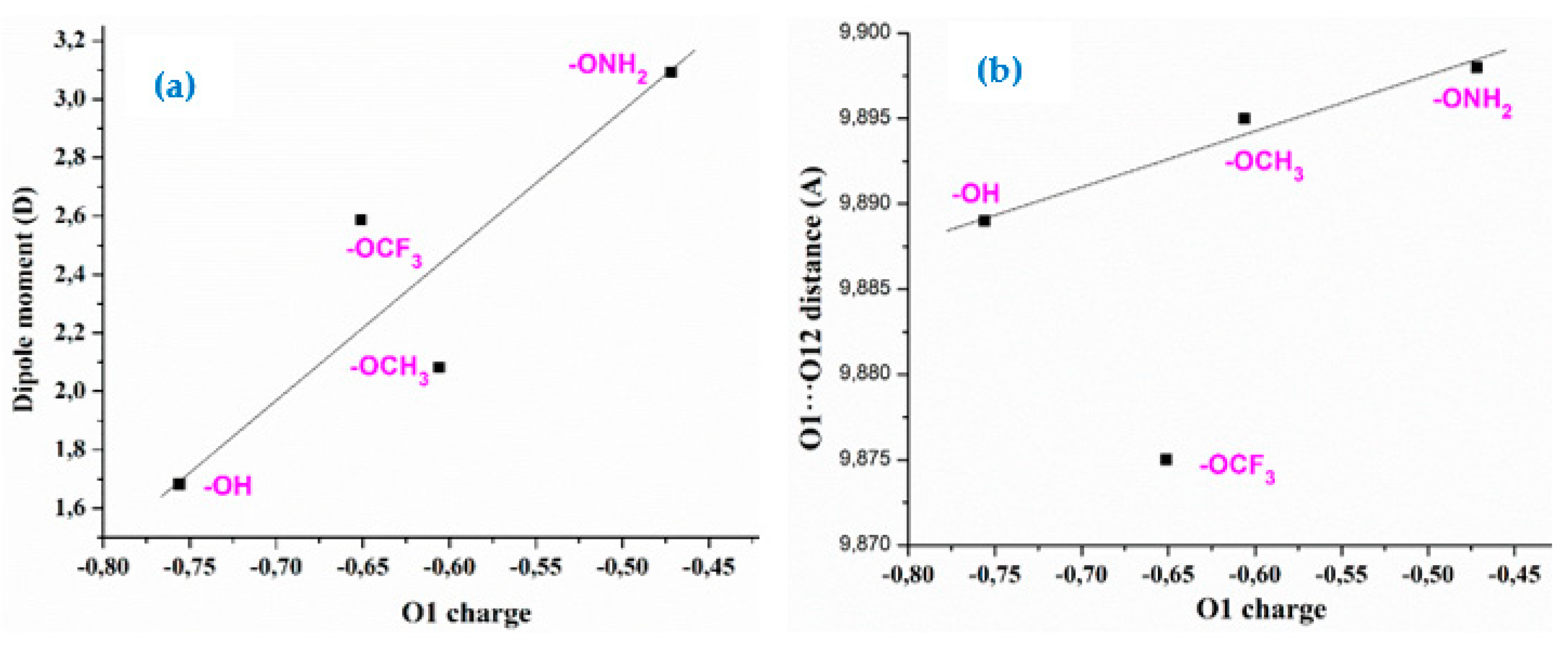
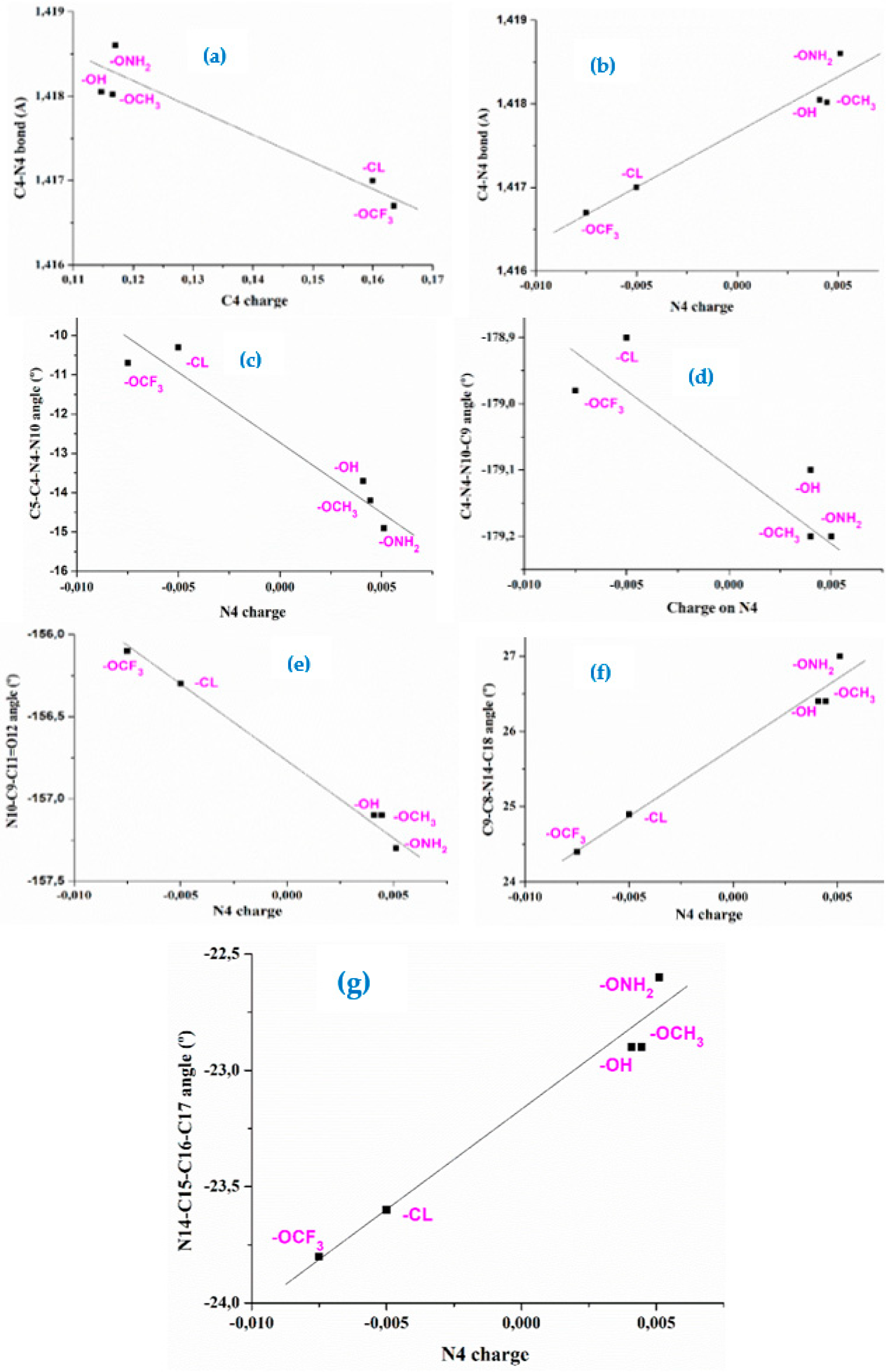
2.2. Relationships Stablished between the Molecular Parameters

Several relationships were stablished with the optimized values of the five neutral compounds shown in Figure 1. The different para-substituents on the phenyl ring leads to a noticeable change in the negative NBO natural atomic charge of O1 oxygen, which is large with the hydroxyl group, and lower with the oxo-amino group, Table 2. The lowest value corresponds to the chlorine substituent 1b. With the exception of this substituent, their values appear linear related to the dipole moment of the molecule, Figure 4a. A decrease in its negative value leads to an increment in the dipole moment, as it is expected due to the large negative charge of the other side of the molecule with the -COOH group.

With the exception of 1b (R = CL) and 1e (R = OCF₃), a decrease in the negative charge on O1 leads to a slight increment in the intramolecular distance of the most reactive O1 and O12 atoms, Figure 4b. If this distance is increased, it could affect to its arrangement and further interaction with the protein cavity aminoacids, and therefore its anticancer activity and selectivity.

A change in the negative charge on O₁ with the different para-substituents on the aryl ring leads to a change in the positive charge on the C₁ bonded atom. The exception is 1b with a negative charge on C₁ due to there is a chlorine atom instead of O₁. This feature leads to a redistribution of the aryl group charge, which affect its aromaticity and the positive charge value on C₄. An increment in its positive value appears linear related to a shortening of the C₄-N₄ bond length, Figure 5a. Although this change in 1b (R = CL) and 1e (R = OCF₃) looks small, it is enough to give rises to a decrease of 4º in the rotation of the aryl ring plane related to the triazole ring plane, the C₅-C₄-N₄-N₁₀ torsional angle. This decrease is lower in the anionic forms.

An increase in the positive charge on C₄ give rises to an increment in the charge on N₄ of the triazole ring, which is negative in 1b and 1e, and become very small positive or almost null in the other molecules 1a, 1c and 1d, Figure 5b, and it is also related to the C₄-N₄ bond length. The variations in the N₄ charge appears to have a significant effect in the torsional angles of the triazole substituents. Therefore, an increment in its positive value is linear related to a decrease in the torsional angles C₅-C₄-N₄-N₁₀ (Figure 5c), C₄-N₄-N₁₀-C₉ (Figure 5d) and N₁₀-C₉-C₁₁=O₁₂ (Figure 5e), and an increment in the C₉-C₈-N₁₄-C₁₈.

(Figure 5f) and N₁₄-C₁₅-C₁₆-C₁₇ (Figure 5g). All these results show how the different substituents affect the triazole ring structure. Although the changes observed appear small, they could be of importance in the sensitivity of these molecules to external stimulus in microenvironments, including their biological behavior.

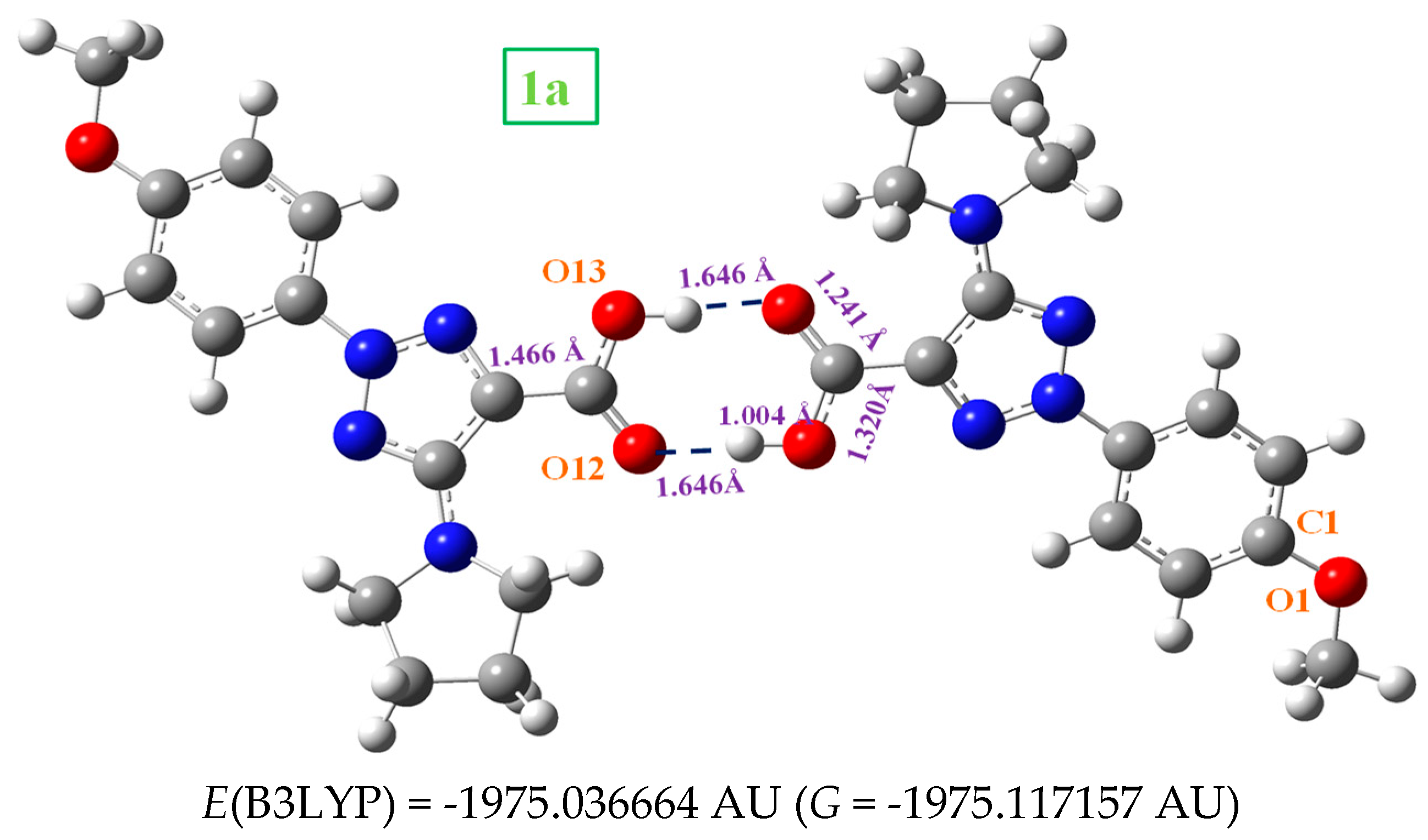
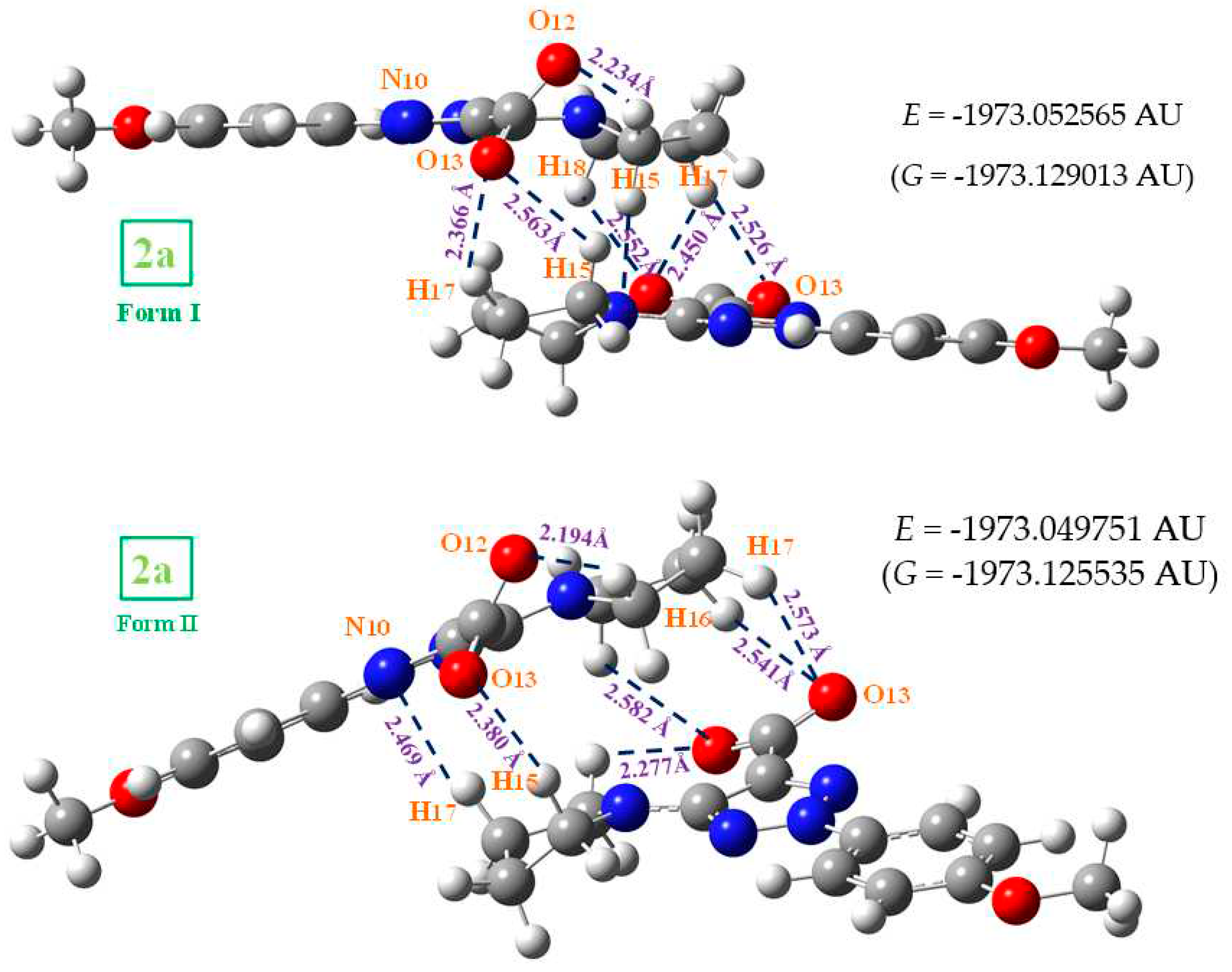
2.3. Molecular Geometries in the Dimer Forms

In the solid state, 1a is expected to be symmetric H-bonded in a cyclic dimer form through the –COOH group as in related molecules with the carboxylic group [5]. Thus, its dimeric structure was optimized and plotted in Figure 6. This optimized dimer form predicted for the crystal unit cell was confirmed by comparison of the carboxylic vibrations of their IR and Raman spectra with those obtained experimentally in the solid state sample. Both molecules of dimer are almost planar, and they are H-bonded with the same bond length, 1.646 Å by B3LYP. This H-bond value is slightly longer than that reported in benzoic acid (BA) dimer, 1.616 Ǻ [5], which can be explained be the slight decrease in the negative charge on =O₁₂ in 1a as compared to BA. A longer C=O bond (1.241 Ǻ vs 1.237 Ǻ in BA) and consequently a shorter C₉-C₁₁ bond length (1.466 Ǻ vs 1.487 Ǻ in BA) is calculated. As it is expected, a lengthening of the acceptor C=O bond (1.225 Å in monomer vs. 1.241 Å in dimer) and a shortening of the donor C-OH bond (1.357 Å in monomer vs 1.320 Å in dimer) is observed on dimer H-bond formation. This shortening in the C-OH bond is proportional to the intermolecular H-bond length [6].

The anion 2a cannot be in cyclic dimer form in the crystal through an O-H···O bond as in 1a. Thus, several staking forms between two molecules were optimized as a simplified model, with interaction of both -COO and NNN moieties as well as π-π interactions. Figure 7 shows the calculated two best optimum stable forms with the M06-2X method, since B3LYP fails in the staking interactions [7]. The most stable one corresponds to form I, and only for this form was studied the vibrational spectra. This staking form was confirmed in the further comparison of its theoretical scaled vibrational spectra with the corresponding experimental one, especially in the stretching vibrations of the -COO and NNN modes.

Form I appears stabilized by several weak H-bonds/interactions through the oxygen atoms and the out-of-plane methyl hydrogens of the pyrrolidine ring. An increment in the twist of the –COO group is observed to facilitate these intermolecular H-bonds/interactions. A high planarity appears between both monomers of this dimer form, and because of that, this structure is expected in the crystal unit cell. Form II is slightly less stable than form I, and it is also stabilized by weak H-bonds/interactions C-H···O between the –COO group and the hydrogens of the pyrrolidine ring. In addition, a weak C-H···N H-bond/interaction is observed. However, the planarity between both monomers is remarkable reduced in this dimer and thus it is expected that the crystal packing forces modify this structure. Other dimer forms were tried to be optimized with several H-bonds/interactions through the nitrogen atoms, but they were not stable.

The interaction energies were calculated in 1a and 2a dimers. Its calculation appears describe in detail in the Supplementary Material Section. The deformation energy E^def in the 1a dimers, 18.6 kJ/mol, is slightly lower than in the most stable form of 2a, 21.8 kJ/mol. It is because of the staking interaction, although weak in the 2a dimer, affect to a larger number of atoms than in 1a dimer. This deformation energy has similar value in the I and II forms of 2a. The CP corrected interaction energy of the

∆ E_{}^{C P}

is -82.8 kJ/mol in 1a, in accordance to that reported in the cyclic dimer of benzoic acid, -81.7 kJ/mol [5].

2.4. Molecular Properties

Several thermodynamic parameters, rotational constants and dipole moments were also calculated for dimer forms and compared to those for individual molecules (monomers). These data obtained in the global minimum were included in Table 3. In general, the computed values by B3LYP are close to those by M06-2X, with small differences. In the dimer form, the rotational constants values are remarkably reduced, around five times lower than those in the monomer form. By contrast, the values of C_v and entropy (S) are ca. twice higher in the dimer form than in its monomer. The values of these parameters appear similar with the other molecules under study.

However, the dipole moment value in the anion form 2a is remarkably higher, ca. 10 times, than in its neutral form 1a. It is the main difference among these molecules. This feature is in accordance to a higher solubility in water of 2a. By contrast the value in 1a is too low and it has not water solubility. In the dimer forms, the dipole moment value is slightly lower in 1a than in its monomer, but in 2a anion it is remarkably lower in its dimer in accordance to the arrangement of the –COO groups.

2.5. Scaling the Wavenumbers

Because theoretical methods do not adequately reproduce all the experimental patterns of wavenumbers with enough accuracy, the use of scaling procedures is necessary to improve the results remarkably [8,9]. The linear scaling equation procedure [10], using one (LSE) or two equations (TLSE) (for high and low wavenumbers) represents a compromise between accuracy and simplicity, and therefore they were the main procedures used to assign the experimental bands. In addition, the polynomic scaling equation procedure (PSE) was also used. These procedures use the equations calculated in simpler building molecules, which in the present study the results used were those of the benzene molecule at the same level of theory. The calculated wavenumber by the theoretical method is represented by ν^cal, and the wavenumber scaled obtained by v^scal. Thus, with the LSE equation [10] is:

ν^scal = 22.1 + 0.9543 · ν^cal at B3LYP/6-31G(d,p) level

The equations corresponding to the TLSE procedure are:

ν^scal = 29.7 + 0.9509 · ν^cal at B3LYP/6-31G(d,p) level for the 1000-3700 cm^-1 range

ν^scal = -16.0 + 1.0009 · ν^cal at B3LYP/6-31G(d,p) level for the 0-1000 cm^-1 range

Finally, the scaling equation used by the PSE procedure is:

ν^scal = -4.2 + 0.9909 · ν^cal - 0.00000929· (ν^cal )² at B3LYP/6-31G(d,p) level

ν^scal = 6.5 + 0.9694 · ν^cal - 0.00000612· (ν^cal )² at M06-2X/6-31G(d,p) level

The equation corresponding to the M06-2X/6-31G(d,p) level was only used for the dimer form of 2a, because the lower accuracy [10] of this M06-2X method than B3LYP in the scaled wavenumbers.

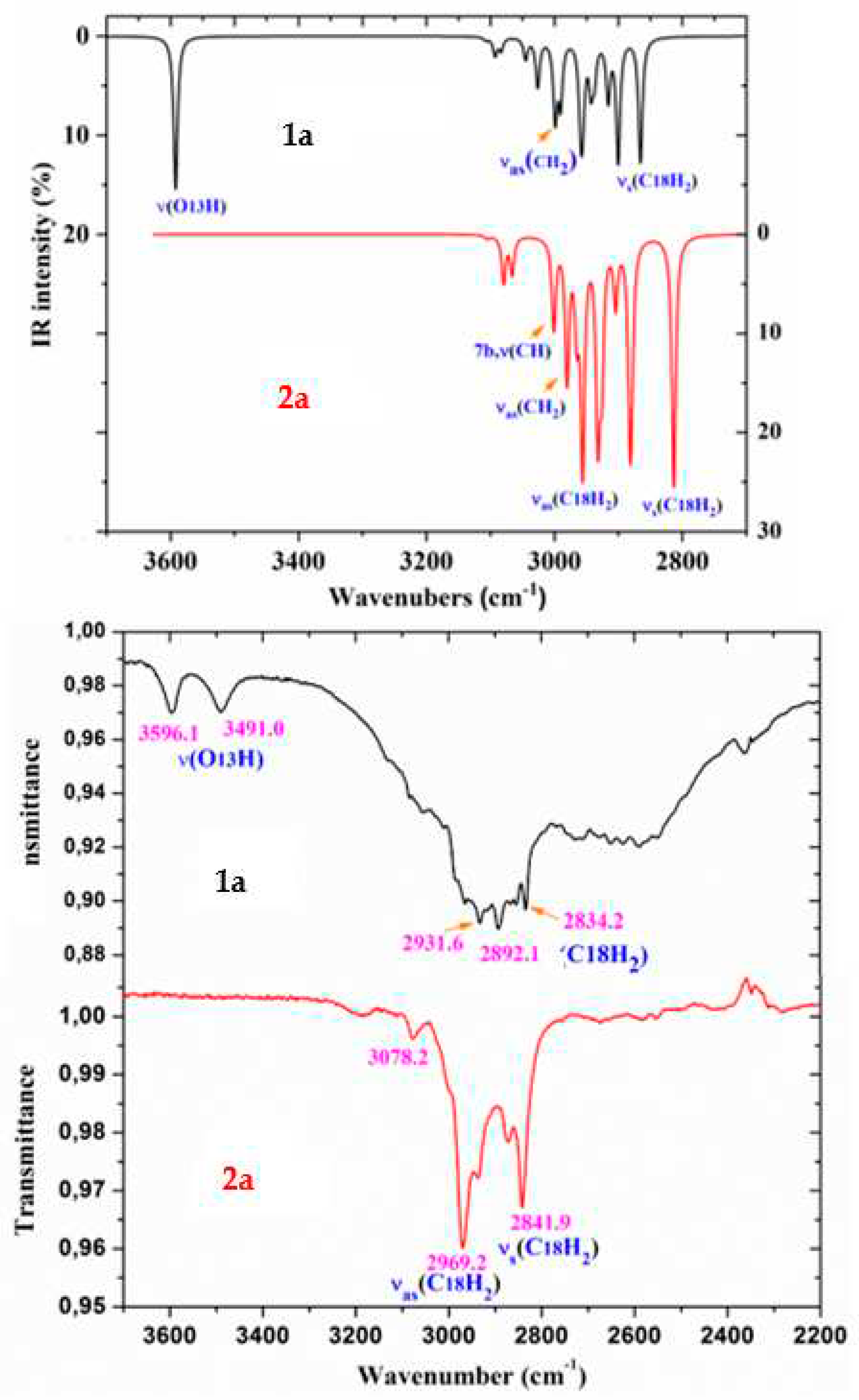
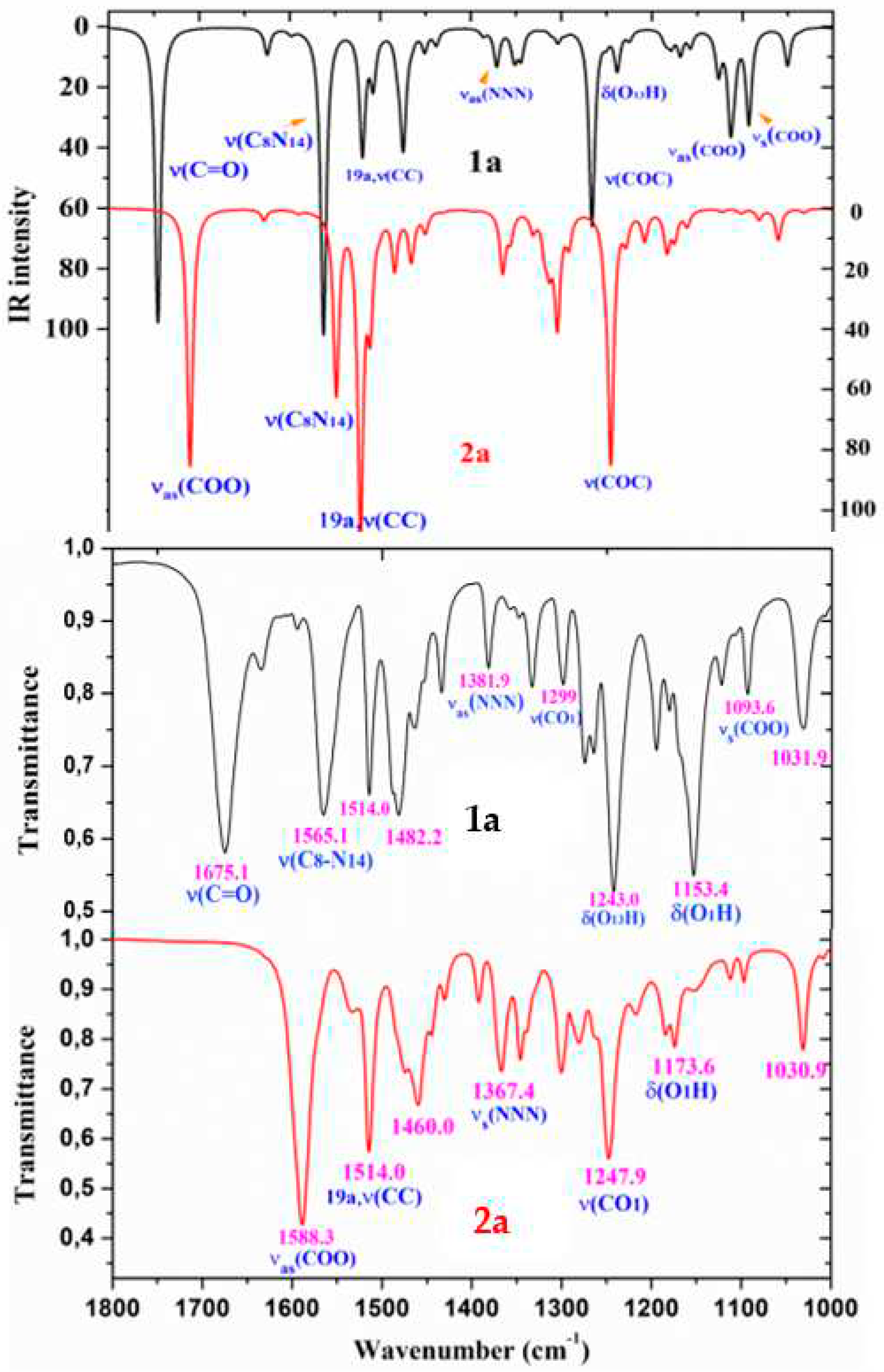
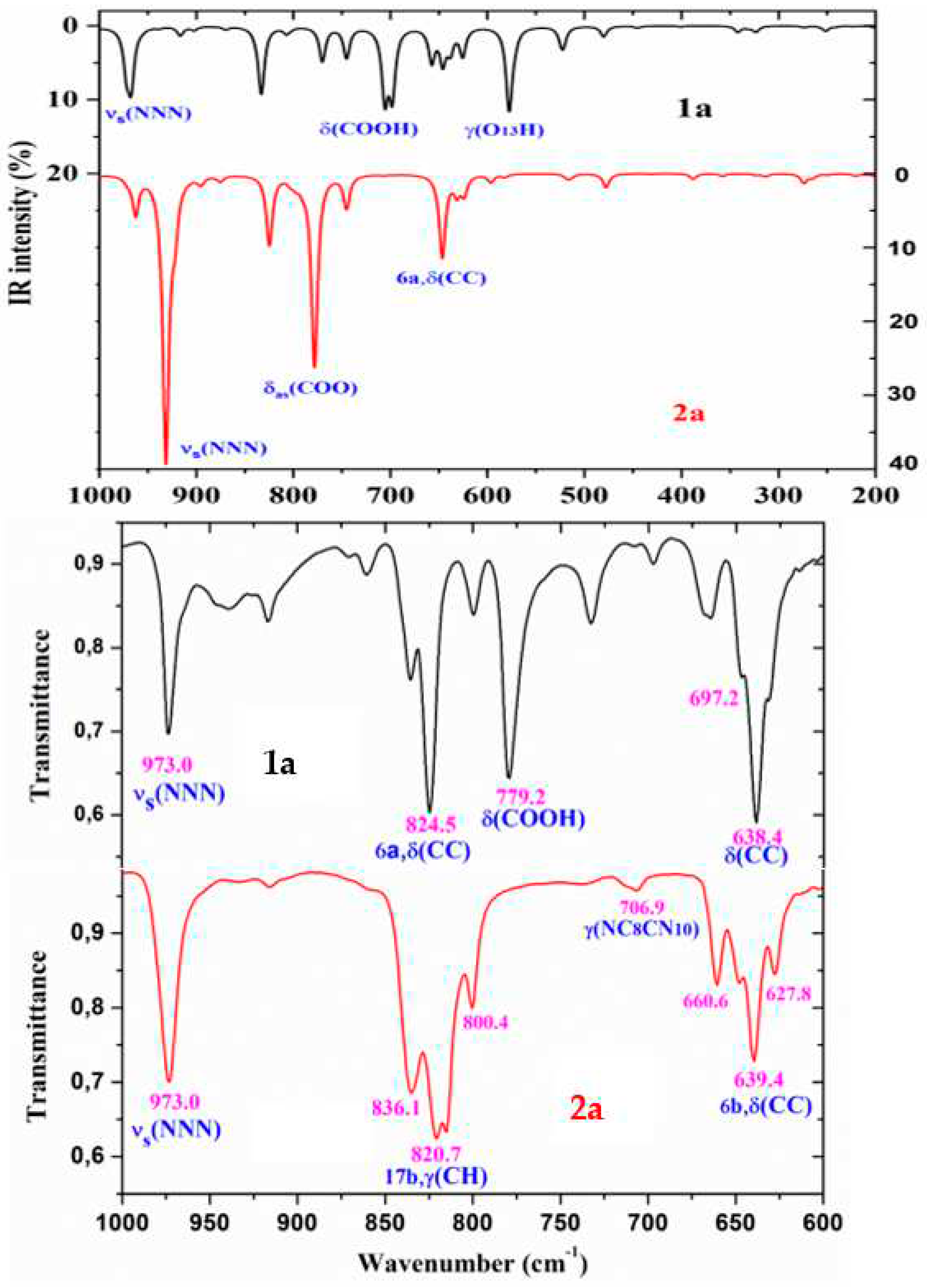
2.6. Vibrational Analysis of 1a and 2a

All the calculated wavenumbers in the most stable form I are collected in Table 2-SUP (Supplementary Material). A short resume of the most important values is shown in Table 4 and Table 5. Because the geometrical values and vibrational wavenumbers of form 2 are almost the same than those of the form 1, they were not included in the tables. Only the wavenumbers with high IR or Raman intensity, or those characteristics of the molecular structure were included. The scaled wavenumbers by two methods, the relative (%) computed IR and Raman intensities, the experimental values observed in the spectra and the main characterization of the vibrations with their % contribution of the different modes to a computed value (PEDs) are also included in the Tables. Contributions in general lower than 10% are not included. The relative intensities are obtained by normalizing each calculated value to the intensity of the strongest one.

The scaled IR and Raman spectra were mainly carried out using the TLSE and PSE scaling procedures. The LSE procedure is the worst, while the PSE procedure leads to the best results, with errors in general lower than 3%. The scaled wavenumbers are slightly worse using the LSE and TLSE procedures than the PSE. Thus, all the scaled spectra shown in the present manuscript were done with this PSE procedure, as well as the discussion with the scaled values.

A comparison of the whole FTIR experimental spectra of 1a and 2a with those corresponding to the theoretical scaled spectra by the PSE procedure in the monomer form were plotted in Figure 2-SUP, while the comparison with the Raman values is shown in Figure 3-SUP. For a better analysis and comparison of the different experimental and scaled vibrational wavenumbers of these figures, the spectra are divided in three regions, such as: 3700-2700 cm^-1, 1800-1000 cm^-1, and 1000-0 cm^-1 (or 1000-600 cm^-1). The IR spectra of these figures are shown in Figure 8, Figure 9 and Figure 10, while for simplicity the Raman spectra are included as Supplementary Material, Figure 4, Figure 5 and Figure 6-SUP. The assignment of the most intense and characteristic IR wavenumbers is included in these figures.

In a general comparison of the IR spectra of Figure 2-SUP is observed the following: (i) A large difference between the spectra of 1a and 2a. This difference is in agreement with a significant change in the geometric parameters and charges between both molecules. Although acid and salt having almost the same chemical structure, they can differ significantly in biological effect, since they differ greatly in electronic and geometric characteristics both in the form of individual molecules and in the form of dimers. This can be manifested in their affinity to specific receptor site and in value of the effect and selectivity. (ii) The noticeable accordance between the scaled wavenumbers in the monomer form with the experimental ones, with only few significant differences. (iii) The scaled spectra in the dimer or staking forms reduce the differences theory-experiment.

It is noted that most of the modes in the compounds under study appear in the expected ranges. Due to this feature and because the difference in the observed and scaled values of most of the fundamentals is very small, the assignments in general could be considered correct. This assignment of the vibrational bands was carried out through a detailed comparison of the experimental with the scaled spectra. This assignment was discussed under the following sections: (i) The COOH and COO group modes, (ii) the OH group modes, (iii) the triazole ring modes, (iv) the phenyl ring modes, and (v) the methoxy O-CH₃ modes. The discussion was carried out mainly focused on (i) and (ii) sections because they involved the most reactive groups.

2.6.1. The Carboxylic COOH Group Modes in Molecule 1a

The displacement vectors for the characterization of these modes are similar for the monomer and dimer forms, although for each dimer vibration two wavenumbers appear, one corresponds to the in-phase mode (Raman active) and another one to the out-of-phase mode (IR active). Table 5 collects a resume of the calculated (scaled) wavenumbers, together with the experimental ones and the main characterization with the %PED. The full Table is included as Table 3-SUP. The theoretical values mainly correspond to the monomer form of the molecules, and only when noticeable differences appear with the dimer they are included in this Table.

The experimental IR spectra of Figure 10 are characterized by a broad and complex spectral structure around 2850 cm^-1 which is characteristic of the carboxylic acid association by hydrogen bonding. Only the internal modes of the COOH and COO groups were discussed under the following sections:

The C=O modes: The C=O stretching was calculated in the monomer form with very strong IR intensity and scaled by PSE at 1745 cm^-1. However, this value noticeable differs (ca. 70-100 cm^-1) of that observed at lower values in the experimental IR and Raman spectra, which is due to intermolecular H-bonds present in the solid state through the carboxylic –COOH group. In our dimer simulation, this mode was scaled at 1695 cm^-1 with very strong IR intensity also. This value is slightly higher than 1675.1 cm^-1 found experimentally. This feature indicates an intermolecular H-bond slightly stronger in our calculated dimer form than in the experimental sample of 1a. It is that expected and in accordance to additional intermolecular interactions with other dimer form present in staking form in the solid state crystal that slight lengthening the C=O bond length.

Another ν(C=O) stretching vibration is predicted at 1655 cm^-1 in our optimized form of 1a, but with the displacement vectors of the stretch motion appearing in-phase between both monomer forms of dimer. This kind of motion leads to an active Raman band with very strong intensity, but inactive in IR. Our predicted wavenumber in Raman is in good accordance to the experimental Raman line at 1643.2 cm^-1. In the solid state of BA this mode has been reported experimentally [5] at 1693 cm^-1 (IR) and 1635 cm^-1 (Raman), in accordance to our results.

The C=O in-plane bending appears strongly coupled with the δ(C-OH) mode, and therefore it can be better denoted as δ(COOH) in Table 5. It is predicted in the monomer form at 699 cm^-1. However, in the dimer form it is scaled at 780 cm^-1 (IR, out-of-phase motion) with medium IR intensity and at 761 cm^-1 (Raman, in-phase motion) with weak value, in excellent accordance to the very strong experimental IR band at 779.2 cm^-1 and to the medium intensity Raman line at 768.0 cm^-1. The discussion of the out-of-plane modes is included in the Supplementary Material Section.

The C-O₁₃ modes: The displacement vectors correspond to the COO group instead of an isolated C-O bond and therefore it was characterized as ν_as(COO) in Table 5. In the monomer form its stretching mode appeared scaled with strong IR intensity at 1113 cm^-1 and it could be related to the experimental bands at 1122.5 cm^-1 (IR) and 1120.6 cm^-1 (Raman). In the dimer form they were predicted with very weak IR and Raman intensities, and therefore they were not detected in the spectra. This stretching mode in 1a appears noticeable coupled with ν_s(NNN) and δ(C-H) modes and thus their experimental wavenumbers differ of that assigned to this mode in BA at 1347 cm^-1 (IR) [11].

The ν_s(COO) mode appears strongly coupled with the ν(NNN) stretching of the triazole ring that difficult its identification. It was characterized in the scaled wavenumber of the monomer form at 1093 cm^-1 appearing with medium-strong IR intensity and thus it was well related to the IR band with medium intensity at 1093.6 cm^-1. In Raman it was predicted with weak intensity and it was related to the Raman line at 1096.5 cm^-1. In the dimer form this mode was predicted with very weak and almost null intensity and therefore it was not related to experimental band.

The O₁₃-H modes: The stretching ν(O-H) of free hydroxyl groups (monomer form) appears scaled at 3592 cm^-1 with medium IR and Raman intensity and they were related to the weak experimental IR bands at 3596.1 and 3491.0 cm^-1, and to the Raman line at 3504.2 cm^-1. It means, that free COOH groups appears in 1a, in accordance to the experimental IR band reported at 3553.3 cm^-1 in p-methoxybenzoic acid [12]. These features are also in accordance to that reported in BA [5], where the monomer form is calculated by B3LYP/6-31G(d,p) at 3763 cm^-1 (scaled by PSE at 3593 cm^-1), at almost the same wavenumber that to our value in 1a at 3592 cm^-1. Although, a medium intensity band at 3567 cm^-1 has been found [13,14] in the experimental IR spectrum of BA molecule, which appears at slightly lower wavenumber than in 1a at 3596.1 cm^-1, perhaps due to a lengthening of the OH bond by weak interactions in the solid state. A weak and broad IR band is also detected in 1a at 3491.0 cm^-1 (at 3504.2 cm^-1 in Raman) which can be only due to the stretching of free O-H groups weakly intermolecular H-bonded to other molecules.

In H-bonded hydroxyl groups (cyclic dimer form through this group) the OH stretching wavenumber is red shifted (scaled) at 3035 cm^-1 (IR) and 2943 cm^-1 (Raman) and it is predicted with the strongest intensity of the spectra. This highest intensity in the dimer form appear in accordance to that calculated in the dimer of BA [5], and to that reported in carboxylic acids [15,16], where it is usually identified by a broad stretching band near 3000 cm^-1. However, bands with strong or very strong intensity have not been observed in the stretching region of the experimental IR and Raman spectra. Perhaps due to they are included in the very broad band with weak-medium intensity observed in the IR spectrum at 3054.1 cm^-1, closely to our calculations in the dimer form. This feature, together with the red shifted of the ν(C=O) wavenumber in the dimer form and the experimental bands assigned to the δ(C=O) mode, indicates that in the solid state most of the molecules appear H-bonded in cyclic dimer forms through the COOH group but there are also molecules that remain free of H-bonds.

The in-plane bending δ(O-H) appears strongly coupled with CN and C-H modes, as well as with other modes. In the monomer form it appears scaled at 1238 cm^-1, in accordance to the experimental IR band observed at 1243.1 cm^-1 and the Raman line at 1243.0 cm^-1. In BA it was calculated at 1218 cm^-1 (scaled at 1189 cm^-1), slightly lower than our calculations and to the experimental IR value [13,14] at 1169 cm^-1. In the dimer form of 1a this mode appears spread out in many calculated wavenumbers, especially at 1540, 1454 and 1371 cm^-1. Because this mode does not represent the main contribution in the calculated wavenumber, their values were not included in Table 5.

The out-of-plane bending γ(O-H) mode appears clearly characterized as an almost pure mode (81% PED) and scaled at 578 cm^-1, in accordance to the weak Raman line at 570.9 cm^-1. In the dimer form it was scaled at 998 and 942 cm^-1 but with almost null intensity. Thus, only the very weak Raman line at 932.5 cm^-1 could be tentatively assigned to this mode. In BA it was reported at 628 cm^-1 (in free O-H) and at 960 cm^-1 (in O-H bonded) [5,13,14] in accordance to our results, as well as in p-methoxybenzoic acid [11] which was observed at 546 cm^-1.

2.6.2. The Carboxylate COO Group Modes in 2a

The ν_as(COO) stretching mode was predicted (scaled) with very strong IR intensity in the monomer form at 1710 cm^-1, but in the experimental IR spectrum was not detected bands in the 1590-2200 cm^-1 range, and the most closely band appears at 1588.3 cm^-1 with very strong intensity, which was related to this mode. This large red shifted to lower wavenumbers in the experimental spectra can be interpreted because of strong intermolecular interactions of these molecules through the COO group that lengthened the CO bond. This feature is in accordance to the strong IR absorption near 1600-1560 cm^-1 reported for the carboxylate group (COO^-) and corresponding to asymmetric stretching vibrations of solid state samples [15,16].

Because planar structures cannot be formed in 2a molecules, stacking forms were optimized at the M06-2X/6-31G(d,p) level, which were stabilized by several interactions/H-bonds of this COO group, Figure 7. These interactions in the stacking form shifts the scaled wavenumbers of this mode, but not enough, and they are also far away of the experimental ones. This feature indicates that the packing crystal forces in the solid state are stronger than that in our simplified optimized model, with a shortening in the distance between planes that increase the COO group interactions and a lengthening of their CO bond lengths. Under a stronger packing, the wavenumbers will be closer to the experimental ones.

The symmetric ν_s(COO) stretching mode appears spread out and strongly coupled with other modes. The highest contribution was determined in the scaled wavenumber at 1304 cm^-1 with medium-strong IR intensity, in accordance to the IR band observed with medium intensity at 1299.9 cm^-1, and the very weak shoulder at 1348 cm^-1. However, our values also appear in strong disagreement with the IR absorption near 1420-1400 cm^-1 reported for this symmetric stretching in solid state samples of related compounds [15,16].

2.6.3. The Triazole Ring Modes

The NNN modes: The ν_s(NNN) stretching appears strongly coupled with the ν(C₄-N) mode as well as with other ring modes and it is scaled at 1386 cm^-1 in 1a. Because the very weak IR intensity predicted for this mode, it could not be related to an observed band in the experimental spectrum. However, it was predicted with strong Raman intensity and thus it was related to the strong line at 1383.8 cm^-1. Similar wavenumber was calculated in the dimer form of 1a because the small effect of the dimer structure on the triazole ring. A large contribution of this mode was also observed in the scaled wavenumber at 1372 cm^-1, whose mayor contribution corresponds to the C₄-N stretching.

In 2a this mode was predicted with weak-medium IR intensity at 1356 cm^-1 and almost null Raman intensity, and therefore it was well related to the experimental IR band with medium intensity at 1346.2 cm^-1 and to the weak Raman line at 1356.8 cm^-1. In the staking form, this mode is slight red shifted because the weak π-π interaction of this triazole ring with the COO group. This feature confirms the weak effect on the triazole ring of our staking optimized structure. Large contributions of this mode appear in the scaled wavenumbers at 1399 and 1319 cm^-1 that were assigned to the C4-N stretching as the main contribution.

The C₈-N₁₄ modes: The stretching mode is predicted with the highest IR intensity and medium Raman activity in 1a is accordance to the very strong band observed in the IR spectrum and to the medium intensity line in Raman. It was scaled at 1562 cm^-1 and good related to the IR band at 1565.1 cm^-1 and Raman line at 1561.2 cm^-1. Our scaled wavenumber remains almost unchanged in its dimer form. In 2a it is predicted with strong IR intensity at 1549 cm^-1 but the closest experimental IR band appears at 1533.3 cm^-1 and with weak intensity. This discrepancy can be due to the staking interactions of the solid state. Thus, in the staking form of 2a it was predicted at with strong intensity at 1587 and 1596 cm^-1 and they can be inside of the very strong IR band at 1588.3 cm^-1.

2.6.4. The Aryl Ring Modes

The assignments for several phenyl ring modes are obvious and require no further discussion, therefore the attention was focused only on some important modes here. To avoid a lengthened of the manuscript, this discussion is included in the Supplementary Material Section. For the assignments of the ring modes was followed the Varsanyi notation [17] for a 1,4-disubstituted benzene.

2.6.5. The Methoxy OCH₃ Modes

In general, the calculated wavenumbers of the methyl group, namely ν_as, ν_s, δ_as, δ_s, γ_as, γ_s agree well with the experimental values. The stretching modes are calculated as pure modes (100% PED) and with weak IR intensity, as well as the antisymmetric in-plane deformations. The symmetric in-plane mode appears as almost pure (87% PED), as well as the γ_as modes. However, the symmetric out-of-plane mode appears spread out in many calculated vibrations.

The C₁-O₁ stretching is predicted strongly coupled with phenyl ring modes. By the displacement vectors of the phenyl atoms in 2a it was assigned as mode 7a. It is predicted at 1266 cm^-1 in 1a and at 1245 cm^-1 in 2a with strong-very strong IR intensity in accordance to strong IR band observed at 1274.9 cm^-1 and to the very strong band at 1247.9 cm^-1, respectively. This mode was predicted in Raman weak-very weak intensity.

3. Experimental Details

Triazoles 1a and 2a were obtained by alkaline hydrolysis of 2-(4-methoxyphenyl)-5-(pyrrolidin-1-yl)-2H-1,2,3-triazole-4-carbonitrile according to previously developed procedures [18,19]. The IR spectra in the powder form were recorded in the 400-4000 cm^–1 range on a Brüker IFS-66 FTIR spectrometer equipped with a Globar source, Ge/KBr beam splitter and a TGS detector. For the spectrum acquisition, 50 interferograms were collected. The Raman spectrum was registered in the 50-4000 cm⁻¹ range on a Brüker IFS 66 optical bench with an FRA106 Raman module attachment interfaced to a microcomputer. The sample was mounted in the sample illuminator using optical mount without sample pre-treatment. To excite the spectrum, the 1064 nm line from an Nd:YAG laser was utilized. The laser power was set at 250 mW and the spectrum was recorded over 1000 scans at room temperature.

4. Computational Details

Density Functional methods (DFT) [20] were mainly used for the calculations, which provide adequate compromise between the computer time and power required for the computations and the desired chemical accuracy of the results. In biomolecules, DFT calculations have provided results which are quantitatively in good accordance to those raised at MP2 level [21,22], and even better for the vibrational wavenumber calculations [8,23,24]. The B3LYP/6-31G(d,p), M06-2X/6-31G(d,p) and MP2/6-31G(d,p) theoretical levels were used for geometry optimisations and NBO atomic charges computations [25], while the B3LYP/6-31G(d,p) was mainly used [26,27] in the calculation of the harmonic IR and Raman vibrational wavenumbers. All optimized structures show only positive harmonic vibrations (local energy minima). B3LYP is one of the most cost-effective DFT methods [14,28] and it has been used satisfactory in many studies of biomolecules [29,30,31] and in the drug design field [32,33]. The M06-2X method was used to optimize the dimer structures in staking form of 2a, because it shows good results in non-covalent interactions with broad applicability in chemistry [34]. The MP2 method was also used to confirm the stability of all optimized structures. The 6-31G(d,p) basis set was mainly used in all calculations since it appears as the most cost-effective one. All these methods and basis set are implemented in the GAUSSIAN-16 program package [35]. The UNIX version with standard parameters of this package was running in the Brigit computer of the University Complutense of Madrid. Berny optimisation under the TIGHT convergence criterion was used.

5. Summary and Conclusions

Six 1,2,3-triazoles derivatives with possible anticancer activity were analyzed in detail, from the structural and spectroscopy points of view, especially two of them with the methoxy substituent. The most important findings of this study were the following:

(1): A conformational study at the MP2 level was carried out in the molecules under study. By rotation on the C-O₁ bond length the conformers differ less than 1 kJ/mol, while by rotation on the C₉-C₁₁ bond it is about 10 kJ/mol. This feature means a large flexibility of the substituents bonded to the triazole ring and variability of its spatial arrangements.
(2): The ionization of neutral carboxylic acid and formation of anionic form demonstrated larger effect on the triazole ring structure and its charges than the electronic nature of different substituents on the aryl ring.
(3): The effect of five substituents in para-position of the aryl ring on the molecular structure of the triazole and on its atomic charge distribution was determined and several relationships were stablished. Therefore, an increment in the positive N4 charge is linear related to a decrease of both, the aryl ring and the carboxylic group rotation respect to the triazole ring, and by contrast, an increment in the pyrrolidine ring rotation.
(4): The FT-IR and FT-Raman spectra in the solid state of 1a and 2a were recorded, and an accurate assignment of all bands observed was carried out for the first time. For this task the calculated wavenumbers were improved by two main scaling procedures, leading the PSE to the best results, with errors less than 3%. The scaled wavenumbers were slightly worse using the LSE procedure than the TLSE.
(5): The scaled wavenumbers in the acid 1a dimer and staking forms of triazole 2a were in better accordance to the experimental bands than those with monomer, which confirms our simplified optimized system for the crystal unit cell of the solid state.
(6): In the experimental IR spectrum of 1a appears weak bands at 3596.1 and 3491.0 cm^-1 that can be only assigned to ν(O-H) in free COOH groups. The large red-shift of the ν(C=O) mode to 1675.1 cm^-1 indicates that strong H-bonds in dimer form appear in the solid state through this group. These features mean that in the solid state free and H-bonded COOH groups exist simultaneously.
(7): A cyclic dimer form through the carboxylic –COOH group was optimized in 1a, while several staking forms were determined in 2a. A comparison of the scaled and experimental wavenumbers confirms these features for the solid state, with free and H-bonded COOH groups in 1a, and staking forms in 2a.
(8): The experimental values in the solid state of 1a also indicate that the –COOH group in cyclic dimer form, in addition it interacts slightly with the neighbor dimer forms present in staking form in the solid state crystal.

The structural and spectroscopic characterization of two triazole derivatives with possible anticancer activity as well as the relationships stablished with other derivatives could manage the selection of substituents on the triazole ring for the design of new type of antitumor compounds.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Funding

This work was financially supported by the European Union-Next Generation EU, through the National Recovery and Resilience Plan of the Republic of Bulgaria (BG-RRP-2.004-0004-C01), and by the Russian Science Foundation (project 20-13-00089).

Declaration of interests

The authors declare that they have no known competing interests on personal relationships that could have appeared to influence the work reported in this paper.

References

Mahboob Alam, M. 1,2,3-Triazole hybrids as anticancer agents: A review. Archiv der Pharmazie, 2022, 355(1), 2100158. [CrossRef]
Slavova, K.I.; Todorov, L.T.; Belskaya, N.P.; Alcolea Palafox, M.; Kostova. I.P. Developments in the Application of 1,2,3-Triazoles in Cancer Treatment. Recent Patents Anti-Cancer Drug Discov. 2020, 15, 92-112. [CrossRef]
Safronov, N.E.; Kostova, I.P.; Alcolea Palafox, M.; Belskaya, N.P. Combined NMR Spectroscopy and Quantum-Chemical Calculations in Fluorescent 1,2,3-Triazole-4-Carboxylic Acids Fine Structures Analysis. Int. J. Mol. Sci. 2023, 24, 8947-8966. [CrossRef]
Hrimla, M.; Oubella, A.; Laamari, Y.; Lahoucine, B.; Ghaleb, A.; Ait Itto, M.Y.; Auhmani, A.; Morjani, H.; Julve, M.; Stiriba, S.-E. Click Synthesis, Anticancer Activity, and Molecular Docking Investigation of some Functional 1,2,3-triazole Derivatives. Biointerface Res. Appl. Chem. 2021, 12(6), 7633-7667. [CrossRef]
Alcolea Palafox, M.; Núñez, J.L.; Gil, M. Theoretical Quantum Chemical Study of Benzoic Acid: Geometrical Parameters and Vibrational Wavenumbers. Int. J. Quantum Chem. 2002, 89(1), 1-24. [CrossRef]
Jeffrey, G.A.; Saenger, W. Hydrogen bonding in biological structures. Springer-Verlag, Berlin, 1991; Chapter 5.
Alcolea Palafox, M. Effect of the Sulphur Atom on S2 and S4 Positions of the Uracil Ring in different DNA:RNA Hybrid Microhelixes with three Nucleotide Base Pairs. Biopolym. 2019, 110(3), 1-25, e23247. [CrossRef]
Alcolea Palafox, M.; Iza, N.; Gil, M. The hydration effect on the uracil frequencies: an experimental and quantum chemical study. J. Mol. Struct. (Theochem) 2002, 585 (1-3), 69-92. [CrossRef]
Alcolea Palafox, M. Scaling factors for the prediction of vibrational spectra. I. Benzene molecule. Int. J. Quantum Chem. 2000, 77, 661-684. [CrossRef]
Alcolea Palafox, M. DFT computations on vibrational spectra: Scaling procedures to improve the wavenumbers. In Density Functional Theory: Advances in Applications (Book). Ramasami, P. (Ed.). Walter de Gruyter, Inc., Boston, USA, 2019; chapter 10, pp. 147-191.
Sanchez de la Blanca, E.; Núñez, J. L.; Martinez, P. An. Quim Ser A, 1986, 82(3), 480.
Alcolea Palafox, M.; Gil, M.; Núñez, J.L. Spectroscopy of p-methoxybenzoic acid: An AM1 and ab initio study. Appl. Spectrosc. 1994, 48(1), 27-36. [CrossRef]
Reva, I.D.; Stepanian, S.G. An infrared study on matrix-isolated benzoic acid. J. Mol. Struct. 1995, 349, 337-340. [CrossRef]
Stepanian, S.G.; Reva, I.D.; Radchenko, E.D.; Sheina, G.G. Infrared spectra of benzoic acid monomers and dimers in argon matrix. Vibrat. Spectrosc. 1996, 11(2), 123-133. [CrossRef]
Socrates, G. Infrared and Raman characteristic group frequencies, 3rd ed; Wiley, NewYork, 2001.
George, S. Infrared and Raman Characteristic Group Wavenumbers, Tables and Charts, 3rd ed, Wiley: Chichester, U.K, 2001.
17. Varsányi G, Assignment for Vibrational Spectra of Seven Hundred Benzene derivatives, Adam Hilder; London, 1974; Volume 1 and 2.
Gavlik, K.D.; Lesogorova, S.G.; Sukhorukova, E.S.; Subbotina, J.O.; Slepukhin, P.A.; Benassi, E.; Belskaya, N.P. Synthesis of 2-Aryl-1,2,3-triazoles by Oxidative Cyclization of 2-(Arylazo)ethene-1,1-diamines: A One-Pot Approach. Eur. J. Org. Chem. 2016, 15, 2700-2710. DOI:10.1002/ejoc.201600256. [CrossRef]
Safronov, N.E.; Fomin, T.O.; Minin, A.S.; Todorov, L.; Kostova, I.; Benassi, E.; Belskaya, N.P. 5-Amino-2-aryl-1,2,3-triazol-4-carboxylic acids: Synthesis, photophysical properties, and application prospects. Dye. Pigm. 2020, 178, 108343. [CrossRef]
Seminario, J.M.; Politzer, P. (Eds), Modern Density Functional Theory: a tool for chemistry, Elsevier, Amsterdam, volume 2, 1995.
Alcolea Palafox, M.; Iza, N. Tautomerism of the Natural Thymidine Nucleoside and the Antiviral Analogue D4T. Structure and influence of an Aqueous Environment Using MP2 and DFT Methods. Phys. Chem. Chem. Phys. 2010, 12(4), 881-893. [CrossRef]
Brovarets’, O.O.; Hovorun, D.M. Prototropic tautomerism and basic molecular principles of hypoxanthine mutagenicity: an exhaustive quantum-chemical analysis. J. Biomol. Struct. Dyn. 2013, 31(8), 913-936. [CrossRef]
Alcolea Palafox, M.; Nielsen, O.F.; Lang, K.; Garg, P.; Rastogi, V.K. Geometry and vibrational spectra of 5-substituted uracils. Asian Chem. Letts. 2004, 8(1), 81-93.
Rastogi, V.K.; Alcolea Palafox, M. Vibrational spectra, Tautomerism and Thermodynamics of anticarcinogenic Drug: 5-Fluorouracil. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2011, 79(5), 970-977. [CrossRef]
Carpenter, J.E.; Weinhold, F. Analysis of the geometry of the hydroxymethyl radical by the “different hybrids for different spins” natural bond orbital procedure. J. Mol. Struct. (Theochem) 1988, 169, 41-62. [CrossRef]
Szafran, M.; Ostrowska, K.; Katrusiak, A.; Dega-Szafran, Z. Spectral and structural studies of dimethylphenyl betaine hydrate. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2014, 128, 844-851. [CrossRef]
Arjunan, V.; Devi, L.; Subbalakshmi, R.; Rani, T.; Mohan, S. Synthesis, vibrational, NMR, quantum chemical and structure-activity relation studies of 2-hydroxy-4- methoxyacetophenone. Spectrochim. Acta Part A: Mol. Biomol. Spectrosc. 2014, 130, 164-177. [CrossRef]
Rastogi, V.K.; Palafox, M.A.; Mittal, L.; Peica, N.; Kiefer, W.; Lang, K.; Ojha, S. P. FTIR and FT-Raman spectra and density functional computations of the vibrational spectra, molecular geometry and atomic charges of the biomolecule: 5-Bromouracil. J. Raman Spectrosc. 2007, 38(10), 1227-1241. [CrossRef]
Ponomareva, A.G.; Yurenko, Y.P.; Zhurakivsky, R.O.; van Mourik, T.; Hovorun, D.M. Complete conformational space of the potential HIV-1 reverse transcriptase inhibitors d4U and d4C. A quantum chemical study. Phys. Chem. Chem. Phys. 2012, 14, 6787-6795. [CrossRef]
Shishkin, O.V.; Gorg, L.; Zhikol, O.A.; Leszczynski, J. Conformational Analysis of Canonical 2-Deoxyribonucleotides. 2. Purine Nucleotides. J. Biomol. Struct. Dyn. 2004, 22, 227-243. [CrossRef]
Brovarets’, O.O.; Hovorun, D.M. Can tautomerization of the A·T Watson–Crick base pair via double proton transfer provoke point mutations during DNA replication? A comprehensive QM and QTAIM analysis. J. Biomol. Struct. Dyn. 2014, 32, 127-154. [CrossRef]
Alcolea Palafox, M. Molecular structure differences between the antiviral Nucleoside Analogue 5-iodo-2´-deoxyuridine and the natural nucleoside 2´-deoxythymidine using MP2 and DFT methods: Conformational analysis, crystal simulations, DNA pairs and possible behaviour. J. Biomol. Struct. Dyn. 2014, 32(5), 831-851. [CrossRef]
Alcolea Palafox, M.; Posada-Moreno, P.; Villarino-Marín, A. L.; Martinez-Rincon, C.; Ortuño-Soriano, I.; Zaragoza-García, I. DFT Calculation of four new potential agents muscarinic of bispyridinium type: structure, synthesis, biological activity, hydration, and relations with the potents W84 and DUO-3O. J. Computer-Aided Mol. Design 2011, 25(2), 145-161. [CrossRef]
Zhao, Y.; Truhlar, D. G. Applications and validations of the Minnesota density functionals. Chem. Phys. Lett. 2011, 502(1-3), 1-13. [CrossRef]
Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019.

Figure 1. Structures of the triazoles under investigation with its notation.

Figure 4. Relationships stablished between the atomic charge on O₁ with: a) the dipole moment. b) the intramolecular O₁···O₁₂ distance.

Figure 5. Relationships stablished between the atomic charges on C₄ and N₄ with the geometric parameters involved in the triazole ring structure.

Figure 6. The two optimized dimer forms of 2a. Several bond lengths and intra- and intermolecular H-bond values of interest calculated at the M06-2X/6-31G(d,p) level are included in the figure.

Figure 7. The two optimized dimer forms of 2a. Several bond lengths and intra- and intermolecular H-bond values of interest calculated at the M06-2X/6-31G(d,p) level are included in the figure.

Figure 8. Comparison of the scaled IR spectra of 1a and 2a molecules by the PSE procedure in the 3700-2700 cm^-1 range with the experimental ones in the 3700-2200 cm^-1 range.

Figure 9. Comparison of the scaled IR spectra of 1a and 2a molecules by the PSE procedure with the experimental ones in the 1800-1000 cm^-1 range.

Figure 10. Comparison of the scaled IR spectra of 1a and 2a molecules by the PSE procedure in the 1000-200 cm^-1 range with the experimental ones in the 1000-600 cm^-1 range.

Table 3. Molecular properties calculated at the B3LYP/6-31G(d,p) and M06-2X/6-31G(d,p) (values in parentheses) levels corresponding to 1a and 2a molecules.

Form	Molecular properties	1a	2a
monomer	Rotational constants: A (GHz) B C	0.616 0.142 0.116	0.647 0.140 0.116
	C_v (cal/mol·K) S (cal/mol·K)	70.04 144.58	69.04 144.01
	Dipole moment (Debye)	1.632	12.775
dimer	Rotational constants: A (GHz) B C	0.114 0.024 0.021	(0.169) (0.034) (0.032)
	C_v (cal/mol·K) S (cal/mol·K)	143.7 252.9	(141.8) (241.5)
	Dipole moment (Debye)	0.751	(9.734)

Table 4. Calculated harmonic wavenumbers (ν, cm^-1), relative infrared intensities (A, %) and relative Raman scattering activities (S, %), obtained at the B3LYP/6-31G(d,p) level in 1a and 2a. Scaled (ν, cm^-1) wavenumbers were obtained with the linear scaling equation procedure (LSE) and the polynomic scaling equation procedure (PSE). The main characterization of the different experimental bands was included. The number of the ring mode corresponds to Wilson’s notation [17].

ν^cal 1a	TLSE	PSE	A	S	Experimental 1a		Characterization of 1a
ν^cal 1a	ν^scal	ν^scal	A	S	IR	Raman	Characterization of 1a
1670 1643 1605 1561 1515 1513 1476 1422 1407 1389 1298 1282 1269 1215 1207 1154 1075 995 990 825 672 652 640 591	1618 1592 1556 1514 1470 1468 1433 1382 1368 1351 1264 1249 1236 1185 1177 1127 1052 980 975 810 657 637 625 576	1625 1599 1562 1520 1476 1474 1438 1386 1372 1354 1266 1251 1238 1186 1178 1127 1050 973 968 807 657 638 626 578	9 2 100 40 22 17 5 2 12 2 64 3 13 3 5 14 12 5 7 1 4 3 4 11	100 6 17 48 6 10 1 57 46 0 0 2 2 0 1 0 0 9 11 0 0 1 1 1	1634.6 w 1594.0 vw 1565.1 vs 1514.0 vs 1482.2 vs 1463.9 s 1434.0 m 1381.9 m 1357.8 vw 1274.9 s 1265.2 s 1243.1 vs 1194.8 s 1153.4 vs 973.0 s 824.5vs 664.4 m 638.4 vs 614.3 vvw	1615.2 vs 1594.0 m 1561.2 m 1511.1 s 1485.1 w 1472.5 w 1420.5 m 1383.8 s 1362.6 vw 1357.8 vw 1262.0 m 1246.9 w 1243.0 w 1201.6 vw 1175.5 sh 1140.8 w 972.1 s 965.3 m 813.0 w 662.5 vw 639.2 m 631.7 m 570.9 w	8a, ν(C=C) (96) 8b, ν(C=C) (97) ν(C₈-N₁₄) (65) + ν_s(N₇CC) (20) 19a, ν(CC)(87) + δ_s(CH) in pyrrolidine (11) δ_s(C-H) out-of-phase pyrrolidine (83) δ_s(C-H) out-of-phase pyrrolidine (75) 19b, ν(CC,CH) in aryl (72) ν_s(NNN)(35) + ν_s(C₄N) (28) + ν(COO)(25) ν(C₄N) (28) + ν(NNN)(22) + δ(COO) (18) ν(C₉N)(32) + δ(COO)(25) + δ_s(pyrrolidine) (23) ν(C-O1)(65) + 14, ν(CC) in aryl (22) γ_as(C-H) in pyrrolidine (78) ν(NN)(53) + γ_as(C-H) in pyrrolidine (33) γ_as(C-H) in pyrrolidine (88) γ_as(C-H) in pyrrolidine (82) + δ(O₁₃H) (14) ν_s(COOH)(45) + δ_as(CH) in pyrrolidine (42) ν(O1-CH₃) (83) ν_as(NNN)(42)+δ(CN₁₄)(24)+ γ(CC) pyrrolid(22) ν_s(NNN)(38) + 12, δ(CC)(34) + δ(CC,CN)(24) 10a, γ(C-H) in aryl (97) γ_s(triazole) (78) + γ(O13-H) (15) 6b, δ(CC) (42) + δ(triazole) (24) Γ(triazole)(34) + 6b, δ(CC) in aryl (33) γ(O₁₃-H) (81)
ν^cal 2a	TLSE	PSE	A	S	Experimental 2a		Characterization of 2a
ν^cal 2a	ν^scal	ν^scal	A	S	IR	Raman	Characterization of 2a
1674 1634 1591 1563 1514 1505 1435 1400 1391 1276 1213 1203 1085 994 953 722 638 610	1622 1583 1543 1516 1469 1461 1394 1361 1352 1243 1183 1174 1061 975 936 716 636 610	1629 1590 1549 1522 1475 1466 1399 1365 1356 1245 1184 1174 1060 972 932 706 624 597	3 1 58 100 1 15 0 19 8 79 8 8 10 1 32 0 2 1	100 2 12 23 2 13 20 7 0 1 0 1 4 2 6 0 0 0	1588.3 vs 1533.3 w 1514.0 vs 1474.5 m 1460.0 s 1392.5 w 1367.4 m 1346.2 m 1247.9 vs 1184.2 m 1173.6 m 973.0 m 933.4 vvw 706.9 vw 627.8 w 613.3 vvw	1610.4 vs 1592.1 m 1535.2 w 1515.9 vs 1476.4 m 1466.7 m 1393.4 vs 1372.2 vs 1356.8 w 1251.7 vw 1175.5 m 1063.7 w 975.0 vs 927.7 vw 707.9 w 627.8 w 607.6 w	8a, ν(C=C) (95) 8b, ν(C=C) (89) ν(C₈-N₁₄) (72) + ν_s(N7CC) (15) 19a, ν(CC) (76) + δ_s(CH) in pyrrolidine (18) δ_s(C-H) out-of-phase in pyrrolidine (92) ν_s(C₈C₉N)(62) + δ_s(CH₂) (16) + ν(NN)(15) ν(C₄N)(41) + ν(NNN)(25) + 19a, ν(CC)(15) γ_s(C-H) in-phase in pyrrolidine (87) ν_s(NNN)(38)+ γ_s(C-H)pyrrolidine(30)+ν(C₈C)(25) 7a,ν(COC)(62) + δ(CH) aryl (25) +γ_as(CH₃) (11) δ(triazole)(73) + γ (CC,CN) in pyrrolidine (16) γ_as(C-H) in pyrrolidine (68) + δ(triazole) (15) ν_as(COC)(62) + 15, δ(CH)(17) + γ_s(CH₃)(15) ν_as(NNN)(32) + δ(CN₁₄)(29)+ δ(CC) pyrrolidi(25) ν_s(NNN)(44) + ν(C₈C)(20) + 10b, γ (CH)(18) γ (NC₈CN10) (53) + γ_s(COO) (38) Γ(triazole) (38) + δ(CC) in aryl (25) γ_s(NNN) (55) + γ (COO) (18)

^†Observed frequencies characterized by notation: vs= very strong, s= strong, m= medium, w=weak band, vw= very weak, vvw= very very weak, ν_as: anti-symmetric stretching, ν_s: symmetric stretching, δ: in-plane bending, γ: out-of-plane bending.

Table 5. Calculated harmonic wavenumbers (ν, cm^-1), relative infrared intensities (A, %), relative Raman intensities (S, %) and scaled values (ν, cm^-1) in the COOH (1a) and COO (2a) groups.

Group	Mode		A	S	TLSE	PSE	IR	Raman	Characterization
Group	Mode	ν^cal	A	S	ν^scal	ν^scal	IR	Raman	Characterization
COOH	ν(O-H) δ(O-H) γ(O-H)	3762 3161 1269 591	15 100 13 11	17 0 2 1	3607 3035 1236 576	3592 3035 1238 578	3596.1 w 3491.0 w 1243.1 vs	3504.2 vw 1243.0 w 570.9 w	ν(O-H) (100) Dimer: ν(O-H) out-of-phase δ(O-H)(52) + ν(CN)(25) + γ_as(CH) pyrrolidine (16) γ(O-H) (81)
	ν(C=O)	1743 1702	80 0	0 70	1687 1648	1695 1655	1675.1 vs	1643.2 m	Dimer: ν(C=O) out-of-phase Dimer: ν(C=O) in-phase
	ν(C-O)	1140 1119	29 30	0 3	1114 1094	1113 1093	1122.5 m 1093.6 m	1120.6 w 1096.5 w	ν_as(COO)(33) + ν_s(NNN)(31) + 15, δ(CH)(28) ν_s(COO) (45) + δ(NNN) (38)
	δ(C=O)	714 796 777	9 15 0	0 0 8	699 782 763	699 780 761	697.2 w 779.2 vs	696.3 w 768.0 m	δ(COOH) (46) + γ(triazole) (38) Dimer: δ(COOH) out-of-phase + ν(CC) Dimer: δ(COOH) in-phase
	γ(C=O)	721	9	1	706	705	707.8 vvw	705.9 w	γ(COOH)(62) + γ(NC₈C)(21) + γ (CN₁₄)(16)
COO	ν_as ν_s δ_as γ_s	1759 1337 795 808	83 35 25 1	2 4 1 1	1702 1301 786 798	1710 1304 778 790	1588.3 vs 1299.9 m	1629.7 vw 1307.6 vw 774.4 w 783.1 vw	ν_as(COO) (96) ν_s(COO)(34)+ν(triazole)(32)+ γ(CH)pyrrolidine (18) δ_as(COO) (58) + δ_as(C-H) in pyrrolidine (15) γ_s(CCOO)(55) + γ(C₈C)(30) + 6a, δ(CC) (27)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Peculiarities of the Spatial and Electronic Structure of 2-aryl-1,2,3-triazol-5-carboxylic Acids and Their Salts on the Basis of Spectral Studies and DFT Calculations

Abstract

1. Introduction

2. Results and Discussion

2.1. Molecular Geometries in the Monomer form of 1a and 2a

2.2. Relationships Stablished between the Molecular Parameters

2.3. Molecular Geometries in the Dimer Forms

2.4. Molecular Properties

2.5. Scaling the Wavenumbers

2.6. Vibrational Analysis of 1a and 2a

2.6.1. The Carboxylic COOH Group Modes in Molecule 1a

2.6.2. The Carboxylate COO Group Modes in 2a

2.6.3. The Triazole Ring Modes

2.6.4. The Aryl Ring Modes

2.6.5. The Methoxy OCH3 Modes

3. Experimental Details

4. Computational Details

5. Summary and Conclusions

Supplementary Materials

Funding

Declaration of interests

References

MDPI Initiatives

Important Links

Subscribe

2.6.5. The Methoxy OCH₃ Modes