Prerpints.org logo
Preprint
Brief Report

Modelisation of the Biomethane Accumulation in Anaerobic Co-digestion of Whey and Sugarcane Molasse Mixtures

Altmetrics

Downloads

80

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

12 August 2023

Posted:

14 August 2023

You are already at the latest version

Alerts
Abstract
The biomethane accumulation of several combinations of whey and sugarcane molasses, inoculated with sludge from a treatment facility of one of the dairy enterprises of Imbabura, was assessed in the current experiment at a concentration of 0.5 g/l COD. The whey: molasses (W: M) ratios for each treatment were 0:100, 25:75, 50:50, 75:25, and 100:0, with a constant temperature of 37°C and an initial pH adjustment of 7.5. Half a litre of total mixes was used for each treatment in duplicate. Six kinetic models were evaluated to account biomethane accumulation in anaerobic co-digestion processes in batch of whey and sugarcane molasses. Five of these have been tested by other researchers, and one was developed by modifying a first-order model to consider changes in the biomethane accumulation profile. This proposed model, along with the modified two-phase Gompertz model, resulted in the ones that were best able to adjust the experimental data, obtaining in all cases an R² ≥ 0.949, indicating the accuracy of both models. In addition, the proposed here model has five parameters, one less than the modified two-phase Gompertz model, making it more straightforward and robust.
Keywords: 
Subject: Engineering  -   Chemical Engineering

1. Introduction

The world's population has grown steadily over the past centuries, reaching 7.9 billion inhabitants today (Population Growth - Our World in Data). Alongside this, demand for food and energy is also growing, and pressure on arable land and ecosystems is increasing [1]. With the increase in food production, there is also, logically, an increase in the waste generated. In contrast, the incessant increase in energy demand makes it essential to explore other renewable sources of energy to provide a future response to the depletion of traditional non-renewable sources, which will inexorably occur in the not-too-distant future.
In this sense, Ecuador, and specifically Zone 1 (formed by the provinces of Imbabura, Carchi, Esmeraldas, and Sucumbíos), is characterised by an active agricultural economy, which includes the daily production of more than 50% of Ecuador's milk production [2]. An essential part of this production is destined for cheese production, which generates significant quantities of cow-whey. In 2017, it was estimated that in the provinces of Imbabura and Carchi alone, more than 120 m3 of whey was generated daily [3]. About 70% of this whey is used for pig feed, but the rest must be treated in treatment plants due to its high polluting power [3].
On the other hand, one of the central sugar mills in the country is in the province of Imbabura, which generates sugar cane molasses as waste [4]. In this sense, agro-industrial waste could be studied as possible sources of raw material for biogas generation [5], an alternative to the circular economy for local industries.
Finally, modelling the complex fermentative processes that take place within anaerobic co-digestion [6,7], mediated by complex consortia of bacteria and yeast, including acetogenic and methanogenic bacteria and diverse sources of carbon and nitrogen, is of utmost importance for the design of treatment processes for bioremediation and as a source of renewable biomethane these agriculture or agro-industrial wastes [8,9].
The present work aims to evaluate the anaerobic digestion of cow's whey and sugarcane molasse, alone or formed by different mixtures, and to fit different kinetics models for the biomethane accumulation reported by other authors. A modified first-order model in two stages, not reported before, has also been evaluated.

2. Materials and Methods

2.1. Raw materials used

The whey used in this study came from the Ibarra branch of the company Floralp S.A. (Princesa Paccha 5-163, Caranqui, Ibarra, Imbabura, Ecuador, https://floralp-sa.com). The company's waste treatment plant supplied the sludge. The sugar cane molasses was purchased on the local market from the Ingenio Azucarero del Norte (Panamericana Norte, km 25 vía Tulcán, Imbabura, Ecuador, www.tababuela.com).

2.2. Physico-chemical characterisation

The total and volatile solids were determined according to the methods described in APHA 2540 B and APHA 2540 E, respectively [10]. For the determination of COD, the method described in APHA 5520 D was used [10].
A known volume was weighed to determine the density and pH, and the pH was measured in a conventional pH meter, previously adjusted between pH 4 and pH 10.

2.3. Experimental procedure

Each experimental unit had a total volume of approximately 200 ml, and six 250 ml Schoot flasks were used, the lids of which were pierced, and a rubber stopper was placed. The flasks were placed in a thermostatically controlled bath, maintaining the temperature at 37 ± 1°C. The experimental setup consists of six 500-mL flasks, where anaerobic digestion occurs discontinuously, which are connected to six 250-mL flasks, which act as a trap to capture the CO2 produced. Each trap flask was connected to 250-ml test tubes, inverted, and filled with the same solution as the traps (0.375 M NaOH + phenolphthalein), allowing the measurement of methane gas by liquid displacement, as described by other authors [6,11,12]. All test tubes were placed in a cuvette, partially filled with the same alkaline solution (Figure 1).
Before this, the sludge was adapted for 15 days, with similar amounts as in the whey and cane molasses mixture evaluation being supplied every 2-3 days, and when an appreciable decrease in gas bubbling was observed. The sludge was inoculated into the reactors once the fizzing had ceased after the last addition of the substrate.
Experimental blocks with six variants in each maintained a constant ratio of Total COD/SVinoculum equal to 0.5.

2.4. Kinetic model for the anaerobic co-digestion mixes of whey and molasses

To kinetically characterise the process and model the generation of the primary metabolite, methane, the modified first-order in two-stage model (Equation (2)) was used together with other traditional models described by other authors [7], like the modified two-phase Gompertz model (Equation (3)), the multi-stage first-order model (Equation (4)), all conceived to describe the accumulative biomethane production obtained from complex substrates in which the diauxic growth has been observed.
Additionally, the three simplest models with three parameters each were also evaluated. The Fitzhugh model (Equation (5)), the transference-function model (Equation (6)), and Cone’s model (Equation (7)), despite their simplicity, in most cases, as will demonstrate further, adjust the experimental values accurately.
The model used here is based on the first-order model and was conceived for anaerobic digestions of substrate mixtures and where the phenomenon of diauxic is observed. For this, we should estimate t d i when a change in the methane accumulation profile is observed. Therefore, it is a modified first-order model for mixtures of many substrates and multi-stages are available.
G = G m 1 1 − e − k 0 1 t   f o r   0 ≤ t < t d 1 G m 2 1 − e − k 0 2 t − t d 1   f o r   t d 1 ≤ t < t d 2 G m 3 1 − e − k 0 3 t − t d 2   f o r   t d 2 ≤ t ≤ t d 3 ⋮ G m n 1 − e − k 0 n t − t d n − 1   f o r   t d n − 1 ≤ t ≤ t f
For only two stages above model will transform in:
G = G m 1 1 − e − k 0 1 t   f o r   0 ≤ t < t d 1 G m 2 1 − e − k 0 2 t − t d 1   f o r   t d 1 ≤ t < t f
Where Gm1 and Gm2 are the maximum accumulated value of methane in each stage, in Nml CH4; k01 and k02 are the first-order constants of the kinetics of biomethane accumulation, in d-1; td and tf are the times where diauxic phenomenon and end of the anaerobic co-digestion process are observed in days.
The two-phase modified Gompertz model was suggested to represent the accumulation of biomethane in AD processes, where the phenomenon of diauxic growth is observed [13]. This model is based on six parameters (Gm1, Gm2, Rm1, Rm2, λ1 and λ2) (f = 6).
G = G m 1 e − e R m 1 ∙ e ∙ λ 1 − t / G m 1 + 1 + G m 2 e − e R m 2 ∙ e ∙ λ 2 − t / G m 2 + 1
The Gm1, Gm2, Rm1, Rm2, λ1 and λ2 parameters that can be obtained, like that of the rest of the models, experimentally from having experimental data relating to G vs t, and employing a non-linear regression analysis, represent the maximum values of biomethane accumulation (Gm1 and Gm2, in Nml CH4), biomethane generation rate (Rm1 and Rm2, in Nml CH4/d) and the duration of the lag phase (λ1 and λ2, in days), for each of the two phases of diauxic growth.
The multi-stage first-order model was conceived to model the production of biomethane in the presence of complex substrates formed by various sources of carbon, and their interactions, which lead to anaerobic digestion passing through different stages [14].
G = G m 1 1 − e − k 0 1 t + G m 2 1 − e − k 0 2 t + G m 12 1 − k 0 2 ∙ e − k 0 1 t k 0 2 − k 0 1 − k 0 1 ∙ e − k 0 2 t k 0 1 − k 0 2
It is a five-factor (f = 5) model (Gm1, Gm2, Gm12, k01 and k02), where Gm1, Gm2 and Gm12 represent the maximum accumulation of biomethane (Nml CH4) in the stages "1", "2" and during the interaction of both substrates ("12"), whereas k01, and k02, represent the first-order kinetic constants in the states "1" and "2", respectively.
The last three models to be analyzed are simple models formed by only three factors (f = 3).
The Fitzhugh model, initially developed to monitor the production of biomethane by the action of microorganisms present in livestock rumen [15,16], has also been successfully used by other researchers to co-digest food waste with activated sludge [17]. It is a simple three-factor model (Gm, k0 and n, f = 3), where n represents the presence (if n ≥ 1) or the absence (If n < 1) of a lag phase in the anaerobic process.
G = G m 1 − e − k 0 t n
Gm, k0 and n (f = 3), represent the maximum accumulation of biomethane (in Nml CH4), the first order kinetic constant (in d-1), and a dimensional constant, related to the existence or not of a lag phase in the anaerobic digestion (AD) process, respectively.
Additionally, the transference function model was also assessed (Equation 6). In some cases, this model has been used to describe anaerobic digestion [18].
G = G m 1 − e − R m / G m ∙ t − λ
Cone’s empirical model, like others here, was initially developed to quantify methane production by the rumen microorganisms by metabolizing the grass [19].
G = G m 1 + k t − n
The values that need to be adjusted are Gm, k and n, representing the maximum cumulative amount of methane (in Nml CH4), the first-order kinetic constant (d-1), and a nondimensional number, respectively.
The experimental data (N = 19) for each mix was fitted by the least squares method and using the generalized reduced gradient (GRG) method [20], a nonlinear numerical optimization algorithm provided by the MS Office-365 Excel Solver tool.

2.5. Statistical Comparison of Models

Three known formulas will be used to judge whether the models represent the observed experimental data sufficiently well: the square regression coefficient (R², -; Equation (8)), the normalized root mean square error (NRMSE, %; Equation (9)) and the corrected Akaike information criterion (AICC, -; Equation (10)) [14,17,21].
R 2 = 1 − ∑ i = 1 19 G e x p − G m o d e l i 2 ∑ i = 1 19 G e x p − G − e x p i 2
And
N R M S E = ∑ i = 1 19 G e x p − G m o d e l i 2 N G e x p m a x − G e x p m i n × 100
The correction that is introduced in the nondimensional Akaike Information Criterion (the last term on right in Equation (9)) [22] is recommended when the values obtained from AIC are small, and the number N of experimental data is not too large, as is the present case [23].
A I C C = N ∙ ln ⁡ ∑ i = 1 19 G e x p − G m o d e l i 2 N + 2 f + 2 f f + 1 N − f − 1
Where N represents the number of experimental points used to construct each model (N = 19), and f represents the number of factors the model possesses.
In this case, models with R² values closer to one and with lower NRMSE and AICC values are considered the most appropriate models to represent the observed experimental data.

3. Results and Discussion

For whey, sugarcane molasse and activated sludge, the values of volatile solids were 164.24, 726.94, and 7.73 g VS/l, respectively. The total solids were 237.70, 824.70, and 12.96 g TS/l, respectively, while the DQO reached values of 0.64, 8.14, and 1.56 g COD/l in the same order. Additionally, the density was 0.98, 1.20, and 0.98 g/ml, while the initial pH that was had was of 6.90, 5.60, and 3.90, respectively.
According to the characterisation of the substrates in terms of volatile solids, total solids, and COD, it can be concluded that molasses has 4.4, 3.4 and 12.7 times more, respectively than whey, suggesting a priori that molasses have a higher potential than whey for methane production.
The methane yield values are shallow, so it is suggested in further studies to raise the Total COD/SVinoc. ratio to values ≥ 1.
The average values of each two-mixture treatment were used to represent the models for accumulative methane production. The models were charted alongside the observed experimental data, separating the five- and six-parameter models (Figure 2, a1-a5) from the simpler three-factor models (Figure 2, b1-b5).
The R², NRMSE, and AICC values of the five- and six-factor models exhibit better results, especially in those cases where changes in the methane accumulation profile are observed, and within these modified first-order model and two-phase modified Gompertz model have shown higher performance than multi-stage first-order model (Table 1).
Except for mixing (W: M) 50:50 in three-parameter models (f = 3), for the rest of the cases, all models showed good performance, with R² > 0.89.
In the present study, only the modified first-order (f = 5) and the two-phase modified Gompertz (f = 6) models were able to represent all the experimental values of the mixtures adequately and in which notable results were consistently obtained as demonstrated by the R² ≥ 0.949, and values of NRMSE ≤ 5.59%, and AICC ≤ 102.75, for all the mixes.
It should be noted that the modified two-phase Gompertz model has been used successfully to represent the accumulation of methane and its yield, in numerous studies of anaerobic digestion [24,25,26,27], both in the single substrate and in mixtures, where the phenomenon of diauxic growth has often been observed [13].
Both models quite accurately represent the experimental data obtained. The modified first order model, however, does so with one factor less, which makes that, for equal values of R², as is the case for mixing (W: M) 25:75 (see Figure 2(a2) and Table 1), the AICC value of the modified second order model is lower, and therefore better, than the one obtained for the two-phase modified Gompertz model.

4. Conclusions

In the study presented here, we managed to model the cumulative production of biomethane from various mixtures of whey and sugarcane molasse, using various models reported elsewhere. In addition, a new model was suggested that accurately predicts the observed experimental behaviour and is less complex than the best of the models used here. Further studies are in progress to evaluate and validate this model for other anaerobic co-digestion processes.

Author Contributions

Conceptualization. I.P.R and J.M.P.C.; methodology. I.P.R., J.M.P.C. and H.P.A.G.; software. J.M.P.C.; validation. R.C.E.V., and M.V.L.F.; formal analysis. J.N.P.; investigation. H.P.A.G. and J.M.P.C.; resources. R.C.E.V.; data curation. J.N.P.; writing—original draft preparation. H.P.A.G.; writing—review and editing. J.M.P.C.; visualization. I.P.R.; supervision. I.P.R.; project administration. M.V.L.F.; funding acquisition. R.C.E.V. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

The authors of the work wish to express their gratitude to the dean, Marcelo Cevallos, of the FICAYA, for the support given to this research.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Araújo, R.G.; Chavez-Santoscoy, R.A.; Parra-Saldívar, R.; Melchor-Martínez, E.M.; Iqbal, H.M.N. Agro-food systems and environment: Sustaining the unsustainable. Curr. Opin. Environ. Sci. Heal. 2023, 31. [Google Scholar] [CrossRef]
  2. Peralta, A. Eficiencia en la producción lechera. In Proceedings of the VIII Foro del Sector Lechero Ecuatoriano. Estrategias para mejorar el consumo de lácteos en la población.; Centro de la Industria Láctea (CIL): Quito, 2017; p. 20. [Google Scholar]
  3. Pais Chanfrau, J.M.; Núñez Pérez, J.; Lara Fiallos, M. V; Rivera Intriago, L.M.; Abril Porras, V.H.; Cuaran Guerrero, M.J.; Trujillo Toledo, L.E. Milk whey-from a problematic byproduct to a source of valuable products. Prensa Med. Argent 2017, 103, 1. [Google Scholar]
  4. Sánches, A.; Vayas, T.; Mayorga, F.; Freire, C. Sector Azucarero del Ecuador. Obs. Econ. y Soc. Tunguragua 2018. [Google Scholar]
  5. Alghoul, O.; El-Hassan, Z.; Ramadan, M.; Olabi, A.G. Experimental investigation on the production of biogas from waste food. Energy Sources, Part A Recover. Util. Environ. Eff. 2019, 41. [Google Scholar] [CrossRef]
  6. López González, L.M.; Pereda Reyes, I.; Romero Romero, O. Anaerobic co-digestion of sugarcane press mud with vinasse on methane yield. Waste Manag. 2017, 68. [Google Scholar] [CrossRef] [PubMed]
  7. Zeller, V.; Lavigne, C.; D’Ans, P.; Towa, E.; Achten, W.M.J. Assessing the environmental performance for more local and more circular biowaste management options at city-region level. Sci. Total Environ. 2020, 745. [Google Scholar] [CrossRef]
  8. Ardolino, F.; Parrillo, F.; Arena, U. Biowaste-to-biomethane or biowaste-to-energy? An LCA study on anaerobic digestion of organic waste. J. Clean. Prod. 2018, 174. [Google Scholar] [CrossRef]
  9. Rao, P.V.; Baral, S.S.; Dey, R.; Mutnuri, S. Biogas generation potential by anaerobic digestion for sustainable energy development in India. Renew. Sustain. Energy Rev. 2010. [Google Scholar] [CrossRef]
  10. Rice, E.; Baird, R.; Eaton, A.; Clesceri, L. Standard Methods for the Examination of Water and Wastewater. Stand. Methods 2012. [Google Scholar]
  11. Pagés Díaz, J.; Pereda Reyes, I.; Lundin, M.; Sárvári Horváth, I. Co-digestion of different waste mixtures from agro-industrial activities: Kinetic evaluation and synergetic effects. Bioresour. Technol. 2011, 102. [Google Scholar] [CrossRef] [PubMed]
  12. Montesdeoca-Pichucho, N.B.; Garibaldi-Alcívar, K.; Baquerizo-Crespo, R.J.; Gómez-Salcedo, Y.; Pérez-Ones, O.; Pereda-Reyes, I. Synergistic and antagonistic effects in anaerobic co-digestion. Analysis of the methane yield kinetics. Rev. Fac. Ing. Univ. Antioquia 2022. [Google Scholar] [CrossRef]
  13. Gomes, C.S.; Strangfeld, M.; Meyer, M. Diauxie studies in biogas production from gelatin and adaptation of the modified gompertz model: Two-phase gompertz model. Appl. Sci. 2021, 11. [Google Scholar] [CrossRef]
  14. Lima, D.R.S.; Adarme, O.F.H.; Baêta, B.E.L.; Gurgel, L.V.A.; de Aquino, S.F. Influence of different thermal pretreatments and inoculum selection on the biomethanation of sugarcane bagasse by solid-state anaerobic digestion: A kinetic analysis. Ind. Crops Prod. 2018, 111. [Google Scholar] [CrossRef]
  15. Pitt, R.E.; Cross, T.L.; Pell, A.N.; Schofield, P.; Doane, P.H. Use of in vitro gas production models in ruminal kinetics. Math. Biosci. 1999, 159. [Google Scholar] [CrossRef] [PubMed]
  16. Venkateshkumar, R.; Shanmugam, S.; Veerappan, A. Anaerobic co-digestion of cow dung and cotton seed hull with different blend ratio: experimental and kinetic study. Biomass Convers. Biorefinery 2022, 12. [Google Scholar] [CrossRef]
  17. Jhunjhunwala, U.; Padhi, S.K.; Pattanaik, L.; Sharma, D.; Kumar, A.; Chaudhary, P.; Saxena, V. Anaerobic co-digestion of food waste and waste activated sludge for methane production: Evaluation of optimum ratio, microbial analysis, and kinetic modeling. Biomass Convers. Biorefinery 2023. [Google Scholar] [CrossRef]
  18. Redzwan, G.; Banks, C. The use of a specific function to estimate maximum methane production in a batch-fed anaerobic reactor. J. Chem. Technol. Biotechnol. 2004, 79. [Google Scholar] [CrossRef]
  19. Groot, J.C.J.; Cone, J.W.; Williams, B.A.; Debersaques, F.M.A.; Lantinga, E.A. Multiphasic analysis of gas production kinetics for in vitro fermentation of ruminant feeds. Anim. Feed Sci. Technol. 1996, 64, 77–89. [Google Scholar] [CrossRef]
  20. Lasdon, L.S.; Fox, R.L.; Ratner, M.W. Nonlinear optimization using the generalized reduced gradient method. RAIRO Oper. Res. 1974, 8, 73–103. [Google Scholar] [CrossRef]
  21. Morais, N.W.S.; Coelho, M.M.H.; de Oliveira, M.G.; Mourão, J.M.M.; Pereira, E.L.; dos Santos, A.B. Kinetic Study of Methanization Process Through Mathematical Modeling in Biochemical Methane Potential Assays from Four Different Inoculants. Water. Air. Soil Pollut. 2021, 232. [Google Scholar] [CrossRef]
  22. Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 1974, 19. [Google Scholar] [CrossRef]
  23. Chai, A.; Wong, Y.S.; Ong, S.A.; Lutpi, N.A.; Sam, S.T.; Kee, W.C.; Eng, K.M. Kinetic model discrimination on the biogas production in thermophilic co-digestion of sugarcane vinasse and water hyacinth. Environ. Sci. Pollut. Res. 2022, 29. [Google Scholar] [CrossRef] [PubMed]
  24. Roubinek, O.K.; Wilinska-Lisowska, A.; Jasinska, M.; Chmielewski, A.G.; Czerwionka, K. Production of Biogas from Distillation Residue as a Waste Material from the Distillery Industry in Poland. Energies 2023, 16. [Google Scholar] [CrossRef]
  25. AL-Huqail, A.A.; Kumar, V.; Kumar, R.; Eid, E.M.; Taher, M.A.; Adelodun, B.; Abou Fayssal, S.; Mioč, B.; Držaić, V.; Goala, M.; et al. Sustainable Valorization of Four Types of Fruit Peel Waste for Biogas Recovery and Use of Digestate for Radish (Raphanus sativus L. cv. Pusa Himani) Cultivation. Sustain. 2022, 14. [Google Scholar] [CrossRef]
  26. Hassan, M.; Anwar, M.; Sarup Singh, R.; Zhao, C.; Mehryar, E. Co-digestion of chicken manure with goose manure and thermo-oxidative-treated wheat straw in CSTR: co-digestion synergistics and OLR optimization through kinetic modeling. Biomass Convers. Biorefinery 2022. [Google Scholar] [CrossRef]
  27. Khatun, M.L.; Nime, J.; Nandi, R.; Alam, M.M.; Saha, C.K. Co-digestion of poultry droppings and banana waste for maximizing biogas production in Bangladesh. Fuel 2023, 346. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements. opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas. methods. instructions or products referred to in the content.
Preprints 82269 g001
Figure 1. The experimental facility used in the research. (A). Thermostated water-bath with recirculation; (B). Anaerobic digester flasks; (C). Bubbling traps for CO2 capture; (D). Immersion cuvette; (E). Inverted test tubes for methane measurement.
Figure 1. The experimental facility used in the research. (A). Thermostated water-bath with recirculation; (B). Anaerobic digester flasks; (C). Bubbling traps for CO2 capture; (D). Immersion cuvette; (E). Inverted test tubes for methane measurement.
Preprints 82269 g001
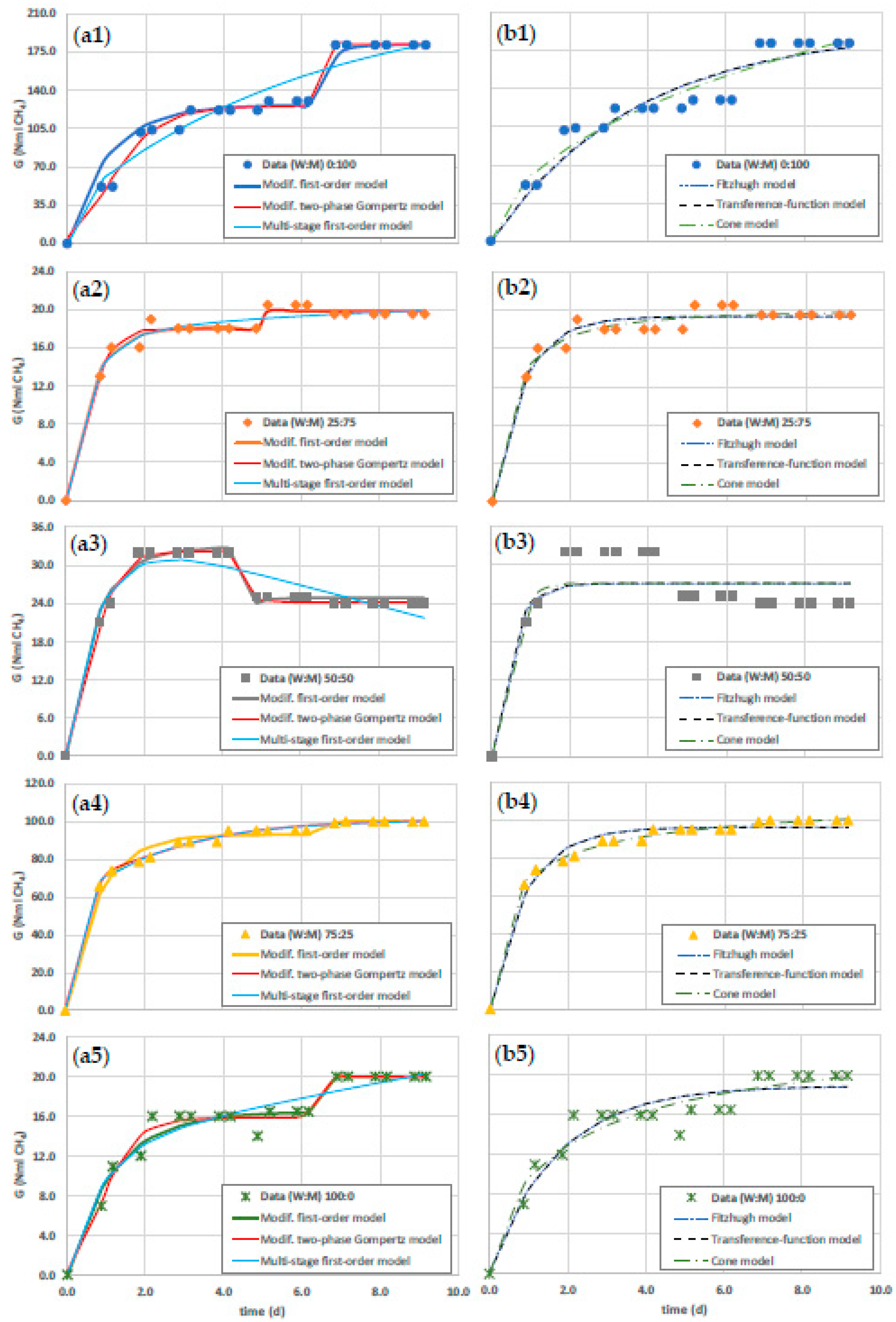
Preprints 82269 g002
Figure 2. Biomethane accumulation kinetics for different mixtures of whey and sugarcane molasse. On the left side, of (a1)-(a5), are represented the three models that have between 5 and 6 factors, being from (a1) to (a5), the ratio of whey and molasse (W: M): 0:100; 25:75; 50:50; 75:25; and 100:0, respectively. On the right side, of (b1)-(b5), the three most straightforward, three-factor models were charted, being of (b1) to (b5), the ratios (W: M): 0:100;25:75; 50:50; 75:25, and 100:0, respectively.
Figure 2. Biomethane accumulation kinetics for different mixtures of whey and sugarcane molasse. On the left side, of (a1)-(a5), are represented the three models that have between 5 and 6 factors, being from (a1) to (a5), the ratio of whey and molasse (W: M): 0:100; 25:75; 50:50; 75:25; and 100:0, respectively. On the right side, of (b1)-(b5), the three most straightforward, three-factor models were charted, being of (b1) to (b5), the ratios (W: M): 0:100;25:75; 50:50; 75:25, and 100:0, respectively.
Preprints 82269 g002
Table 1. Parameters of the kinetic models analysed in the present study and their respective statistical values of adjustment goodness.
Table 1. Parameters of the kinetic models analysed in the present study and their respective statistical values of adjustment goodness.
Models Parameters Mix (W:M)
0:100 25:75 50:50 75:25 100:0
Modif. first-order
(f = 5)
Equation (2)		 Gm1, Nml CH4 127.00 18.21 32.90 92.86 16.47
k01, d-1 0.95 1.55 1.37 1.25 0.86
Gm2, Nml CH4 182.00 19.83 24.90 100.00 20.00
k02, d-1 3.92 32.18 4.72 12.53 12.65
td, d 6.17 4.80 4.17 6.51 6.21
R², - 0.949 0.983 0.979 0.986 0.966
NRMSE, % 5.59% 2.84% 3.17% 2.62% 4.48%
AICC, - 102.75 -5.95 15.12 51.24 10.44
Modif. two-phase Gompertz
(f = 6)
Equation (3)		 Gm1, Nml CH4 125.71 1.90 32.30 66.89 15.90
Rm1, Nml CH4·d-1 59.39 35.66 28.95 159.11 10.80
λ1, d 0.13 4.88 0.16 0.39 0.20
Gm2, Nml CH4 56.31 17.94 -8.02 33.45 4.10
Rm2, Nml CH4·d-1 251.23 20.22 -13.43 6.90 18.10
λ2, d 6.16 0.18 4.20 0.00 6.14
R², - 0.990 0.983 0.993 0.995 0.975
NRMSE, % 2.66% 2.81% 1.86% 1.48% 3.85%
AICC, - 78.94 -2.02 -0.68 33.90 9.11
Multi-stage first-order
(f = 5)
Equation (4)		 Gm1, Nml CH4 193.22 3.99 36.66 47.91 49.88
k01, d-1 0.16 0.15 1.20 0.42 0.02
Gm2, Nml CH4 1.10 10.22 1013.16 25.60 6.38
k02, d-1 3.50 1.67 0.00 6.37 1.13
Gm12, Nml CH4 32.5 6.70 1144.77 27.5 6.4
R², - 0.926 0.968 0.921 0.996 0.932
NRMSE, % 7.15% 3.84% 5.88% 1.46% 6.22%
AICC, - 112.11 5.56 38.63 28.88 22.91
Fitzhugh
(f = 3)
Equation (5)		 Gm, Nml CH4 194.38 19.29 27.14 96.39 18.89
k0, d-1 0.16 0.99 1.79 1.09 0.48
n, - 1.65 1.28 1.19 0.99 1.21
R², - 0.915 0.960 0.667 0.971 0.898
NRMSE, % 8.09% 4.33% 10.93% 3.83% 7.75%
AICC, - 109.80 3.05 55.18 58.63 24.25
Transference function
(f = 3)
Equation (6)		 Gm, Nml CH4 194.40 19.30 27.14 96.39 18.89
Rm, Nml CH4·d-1 52.63 24.47 58.03 104.96 10.99
λ, d 0.00 0.00 0.00 0.00 0.00
R², - 0.915 0.960 0.672 0.971 0.898
NRMSE, % 8.09% 4.33% 10.93% 3.83% 7.75%
AICC, - 109.80 3.05 55.18 58.63 24.25
Cone
(f = 3)
Equation (7)		 Gm, Nml CH4 746.80 20.24 27.18 116.36 26.06
k, d-1 0.02 2.00 1.40 1.76 0.48
n, - 0.61 1.26 5.78 0.67 0.77
R², - 0.933 0.968 0.688 0.996 0.919
NRMSE, % 6.91% 3.85% 10.72% 1.42% 6.81%
AICC, - 103.79 -1.40 54.44 20.93 19.32
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated