A Novel Symmetrical Active-Switched Coupled-Inductor High-Step-Up DC/DC Converter

This paper proposes a novel symmetrical active-switched coupled-inductor high-step-up DC/DC converter. A new active-switched coupled inductor is used to allow much higher voltage gain of the proposed converter. The symmetrical circuit structure of the proposed converter evenly divides large input currents and reduce input current ripple by operating in interleaved mode so power density is increased. The switches also have low voltage stress. The operating principle and design considerations for the converter topology are described. The proposed converter with an input voltage of 40 V, an output voltage of 400 V and an output of 1000 W at a switching frequency of 50 kHz is implemented. The simulations and experimental results are thus depicted to verify the theoretical analysis. The highest efficiency is 95.5% at 200 W measured by using a HIOKI 3390. Consequently, the proposed converter is suitable for renewable energy generation systems that require high power, high voltage gain and high efficiency.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

Due to the energy crisis caused by the problem of global warming, energy saving and carbon reduction become much more important. Renewable energy applications, including solar, wind or fuel cells, are thus emphasized because they have zero carbon emissions. For a single-phase 220 Vac generated from a DC-AC inverter in a distributed power grid system with renewable energy, a high dc voltage of 380~420 V is required to offer to the inverter. However, the output voltage of a solar array module is about 36 ~ 48 V for domestic applications, so a step-up DC-DC converter with a high voltage gain is needed to convert the voltage level.

In general, the ideal traditional boost DC-DC converter with a near unity duty cycle can achieve high voltage gain, but the presence of parasitic resistances in circuit components greatly limits the voltage gain and conversion efficiency [1]. Therefore, for obtaining a high voltage gain and improving the conversion efficiency, many high step-up techniques have been presented and applied to propose a lot of high step-up converter structures [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26].

Switched-capacitor techniques [2,3,4,5,6,7] and voltage-lift techniques [8,9,10,11,12,13,14,15,16] have been widely used to achieve high step-up voltage gain. The main purpose for these step-up techniques is to create voltages across the capacitors. Therefore, the induced capacitor voltages can be positively series at output side for a very high output voltage, but some of the high step-up converters [3,8,17] have the drawback of no common ground involving the load, switches, and the input voltage source in order to cascode the voltages from the equivalent circuit structure deformed by component displacement. On the other hand, the capacitor voltages can also be set as a negative voltage against output voltage in the path of releasing energy for the inductor when the switch is off to be able to derive a much higher output voltage based on volt–second balance principle to inductors. However, if the voltage gain needs to be increased in advance, much more diodes and capacitors will be required and result in more cost and power losses. On the other hand, the high charging currents will also exist and flow through the main switches and rectified diodes, and that will increase more power dissipation.

In order to increase the voltage conversion ratio of a dc–dc converter, the other common solution is to use the turns ratio of the coupled inductor or transformer [17,18,19]. These high step-up converters have an extra design freedom degree, which is the turns ratio. High voltage gain can thus be achieved for these converters with high turns ratio. However, a large turns ratio increases leakage inductance, which may cause high voltage spikes and increases voltage stresses on the switches and diodes. Therefore, several non-isolated converters have been proposed, such as switched-inductor applications [20,21,22,23,24,25,26].

In [26], a symmetrical dual-switch converter with synchronous switching mode is presented. It has a simple circuit configuration and can achieve a high voltage gain based on the switched-inductor boost technique. But a high voltage stresses of switches, high input current ripple and just one degree of design freedom are the main drawbacks. 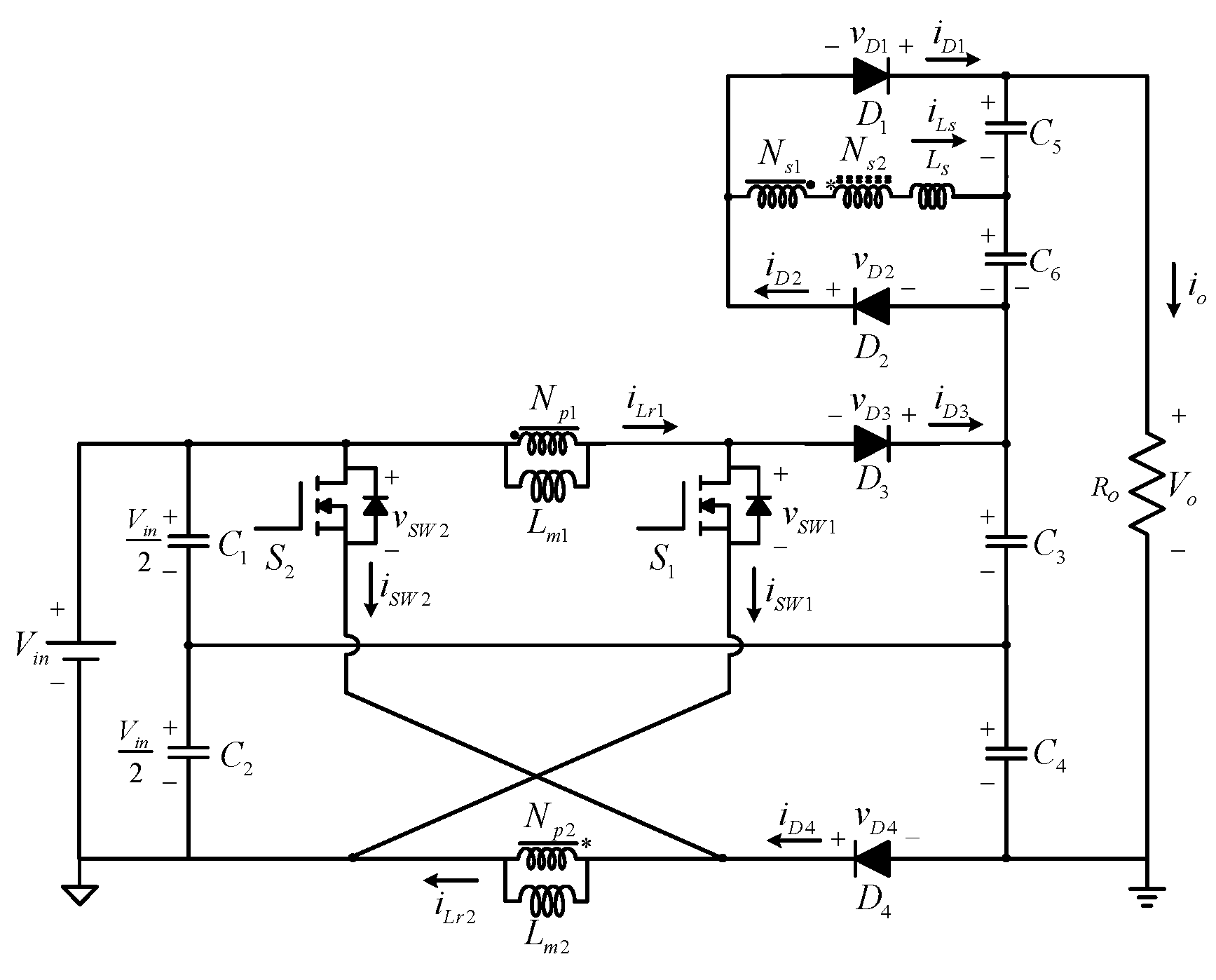However, in this paper, an active-switched coupled-inductor can be proposed and applied in this symmetrical dual-switch circuit structure, and thus a voltage multiplier [17,18,20,23] can also be used to achieve much higher voltage gain and decrease the voltage stresses of the switches and diodes in the proposed active-switched coupled-inductor high-step-up DC/DC converter as shown in Figure 1. On the other hand, the proposed converter operated in interleaved mode can also obtain the lower input current ripple. The advantages of the proposed converters are thus demonstrated as follows.

(1): Simple and innovative topology: The symmetrical circuit structure is simple and the components are few. The new active-switched coupled-inductor boost technology features both switching inductor and coupled inductor boost characteristics so the converter can be easier to achieve a higher voltage gain.
(2): High voltage gain: The converter has a high boost voltage conversion ratio without an extremely large duty cycle and the turns ratio $n$ is used to allows a high voltage gain and much freedom of design.
(3): High-power applications: For renewable energy power generation systems, the input voltage is usually low so there is a large input current for the high-power applications. The symmetric structure of the proposed converter using an interleaved operation can share the large input current and reduce input current ripple, simultaneously. This paper proposes a converter with an output power of 1 kW.
(4): Low voltage stress: For a specific power application, due to the symmetrical circuit structure and the active-switched coupled-inductor high-step-up technique for the proposed converter, the voltage stress on the switches is much less than the output voltage of 400 V.
(5): High efficiency: The interleaved operation and symmetrical structure reduces the voltage and current stress on the switches and diodes, so switches with low ON-resistance and diodes with low forward voltage are used to reduce conduction losses and increase overall efficiency. The maximum efficiency for the converter is 95.5%.

2. Proposed Converter and Operating Principle

The proposed converter is shown in Figure 1.

S_{1}

and

S_{2}

are power switches,

L_{m 1}

and

L_{m 2}

are magnetizing inductors and

N_{p 1}

N_{p 2}

N_{s 1}

and

N_{s 2}

are the number of turns in the primary and secondary coils, respectively.

D_{1}

and

D_{2}

are voltage-doubling diodes,

D_{4}

and

D_{5}

are clamping diodes,

C_{1}

and

C_{2}

are input capacitors,

C_{3}

and

C_{4}

are clamping capacitors,

C_{5}

and

C_{6}

are voltage-doubling capacitors,

V_{i n}

is the input voltage,

V_{o}

is the output voltage and

R_{o}

is the output load.

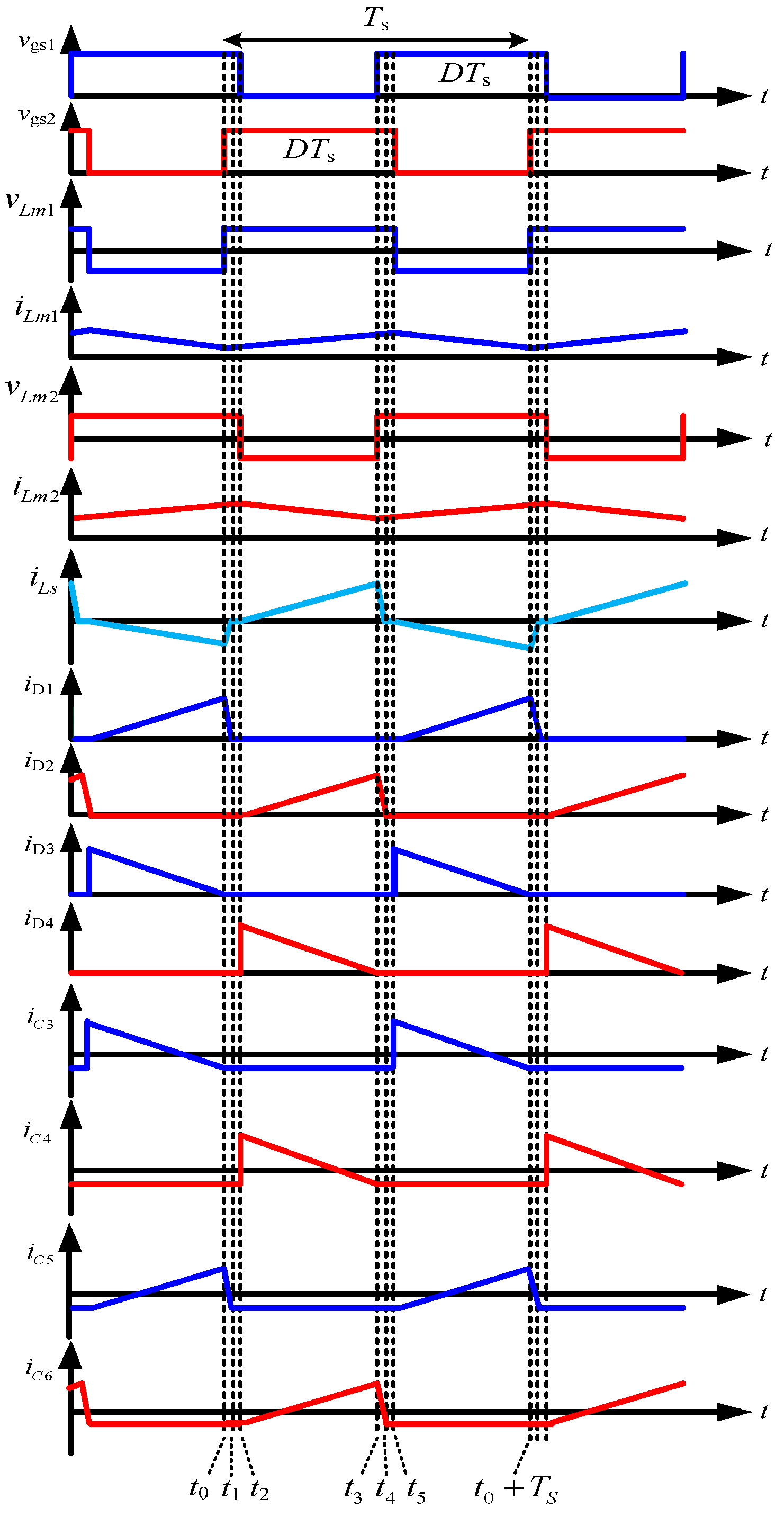
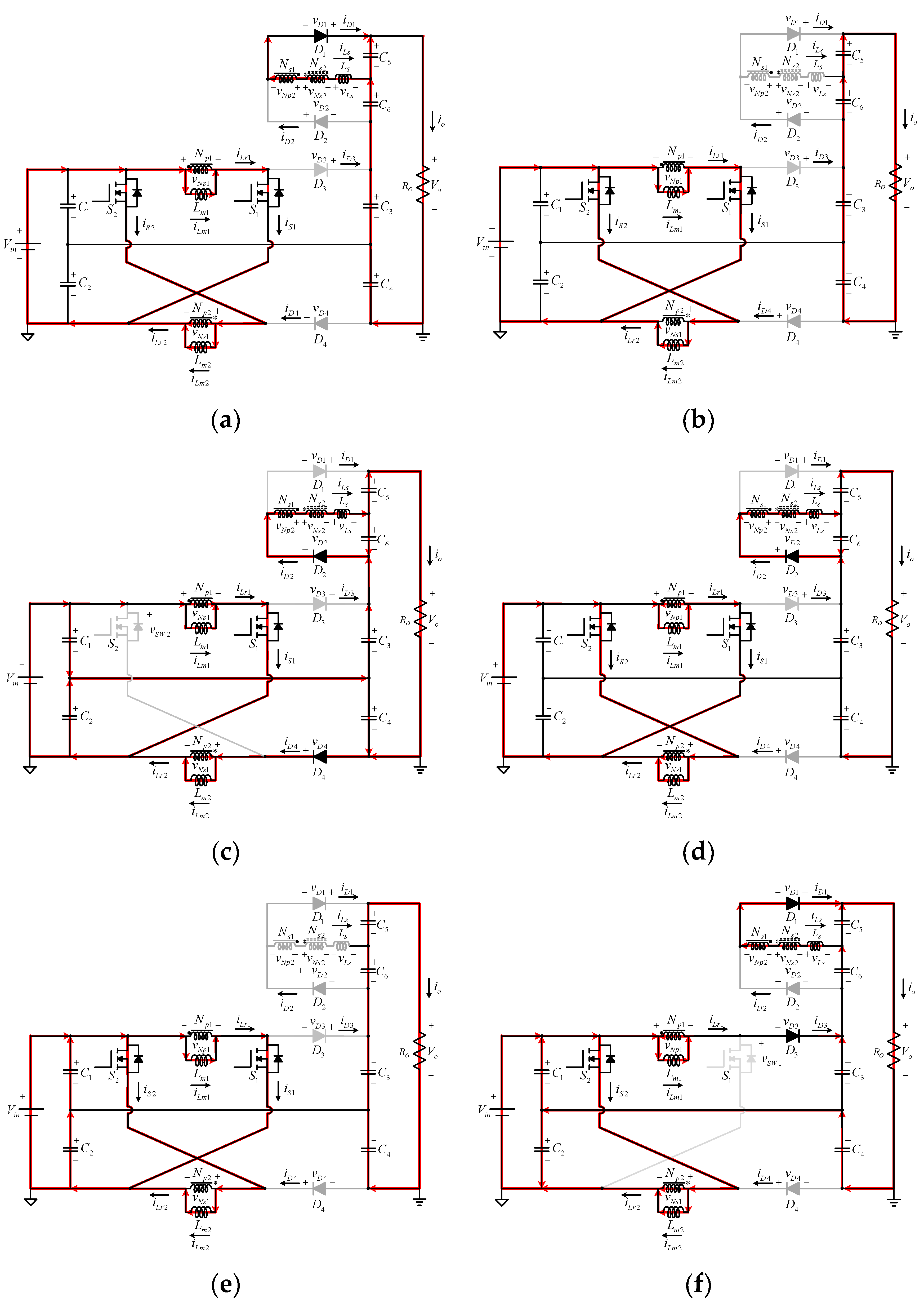
The theoretical key waveforms for proposed converter operating in continuous conduction mode (CCM) are shown in Figure 2. The proposed converter has six linear stages during one switching cycle. The equivalent circuits for these stages are shown in Figure 3.

The following assumptions are made before the theoretic analyzing.

(1): The converter is operating in a steady-state.
(2): The magnetizing inductors $L_{m 1}$ and $L_{m 2}$ are assumed to be sufficiently large to allow the magnetizing inductor current to operate in continuous conduction mode (CCM).
(3): Inductors, capacitors, power switches and diodes are ideal.
(4): $C_{1}$ , $C_{2}$ , $C_{3}$ , $C_{4}$ , $C_{5}$ , and $C_{6}$ are sufficiently large that the voltage is regarded as constant within one switching cycle.

Stage 1 [

t_{0} ~ t_{1}

]: This stage starts at

t = t_{0}

, when power switches

S_{1}

and

S_{2}

are turned on. Diodes

D_{2}

D_{3}

and

D_{4}

are turned off due to the reverse-bias. Diode

D_{1}

remains on due to discharge of the leakage inductor current

i_{L s}

. The path for current flow is shown in Figure 3a. The voltages across the inductors at this stage are:

{\begin{cases} v_{L m 1} = V_{i n} \\ v_{L m 2} = V_{i n} \end{cases}

(1)

v_{L s} = v_{N p 2} - v_{N s 2} + V_{C 5} = n v_{N p 1} - n v_{N s 1} + V_{C 5} = V_{C 5}

(2)

Inductor currents

i_{L m 1}

i_{L m 2}

and

i_{L s}

all increase linearly and the reverse-bias for diodes

D_{2}

D_{3}

and

D_{4}

is:

{\begin{cases} v_{D 2} = V_{C 5} + V_{\begin{array}{l} C 6 \end{array}} \\ v_{D 3} = V_{C 3} + V_{\begin{array}{l} C 2 \end{array}} \\ v_{D 4} = V_{C 4} + V_{C 1} \end{cases}

(3)

As the leakage inductor current

i_{L s}

increases to zero at

t = t_{1}

D_{1}

is turned off and the next stage begins.

Stage 2 [

t_{1} ~ t_{2}

]: This stage starts at

t = t_{1}

. Power switches

S_{1}

and

S_{2}

are still on. Diodes

D_{1}

D_{2}

D_{3}

and

D_{4}

become reverse-bias. The path for current flow is shown in Figure 3b. The voltages across inductors at this stage are:

{\begin{cases} v_{L m 1} = V_{i n} \\ v_{L m 2} = V_{i n} \end{cases}

(4)

v_{L s} = 0

(5)

Inductor currents

i_{L m 1}

and

i_{L m 2}

both increase linearly and

i_{L s}

remains at zero. The voltages across diodes

D_{1}

D_{2}

D_{3}

, and

D_{4}

are:

{\begin{cases} v_{D 1} = V_{\begin{array}{l} C 5 \end{array}} \\ v_{D 2} = V_{\begin{array}{l} C 6 \end{array}} \\ v_{D 3} = V_{C 3} + V_{\begin{array}{l} C 2 \end{array}} \\ v_{D 4} = V_{C 4} + V_{C 1} \end{cases}

(6)

t = t_{2}

, power switch

S_{2}

is turned from on to off and this stage ends.

Stage 3 [

t_{2} ~ t_{3}

]: This stage starts at

t = t_{2}

. Power switch

S_{2}

is turned off, and the power switch

S_{1}

still on. Diodes

D_{1}

and

D_{3}

are still off due to the reverse-bias. The magnetizing inductor current

i_{L m 2}

decreases and inductor

L_{m 2}

is discharged to the load through

D_{2}

and

D_{4}

so the diodes

D_{2}

and

D_{4}

are forced to conduct. The path for current flow is shown in Figure 3c. The voltages across the inductors at this stage are:

{\begin{cases} v_{L m 1} = V_{i n} \\ v_{L m 2} = \frac{V_{i n}}{2} - V_{C 4} < 0 \end{cases}

(7)

v_{L s} = v_{N p 2} - v_{N s 2} - V_{C 6} = n v_{N p 1} - n v_{N s 1} - V_{C 6} = n V_{i n} - n (\frac{V_{i n}}{2} - V_{C 4}) - V_{C 6} > 0

(8)

Inductor currents

i_{L m 1}

and

i_{L s}

still increase linearly and

i_{L m 2}

decreases linearly. At this stage, the voltage across power switch

S_{2}

is:

v_{S 2} = V_{C 1} + V_{C 4}

(9)

The reverse-bias voltages for diodes

D_{1}

and

D_{3}

are:

{\begin{cases} v_{D 1} = V_{C 5} + V_{C 6_{_{}}} \\ v_{D 3} = V_{C 2} + V_{C 3} \end{cases}

(10)

t = t_{3}

, power switch

S_{2}

is turned on again and this stage ends and the next stage begins.

Stage 4 [

t_{3} ~ t_{4}

]: This stage starts at

t = t_{3}

, when power switch

S_{2}

is turned on and power switch

S_{1}

remains on. At this time, diode

D_{4}

is turned off due to the reverse-bias. The path for current flow is shown in Figure 3d. The voltages across the inductors at this stage are:

{\begin{cases} v_{L m 1} = V_{i n_{_{}}} \\ v_{L m 2} = V_{i n} \end{cases}

(11)

v_{L s} = v_{N p 2} - v_{N s 2} - V_{C 6} = n v_{N p 1} - n v_{N s 1} - V_{C 6} = - V_{C 6} < 0

(12)

Inductor currents

i_{L m 1}

and

i_{L m 2}

increase linearly and

i_{L s}

decreases linearly. At this time, the reverse-bias voltages across diodes

D_{1}

D_{3}

and

D_{4}

are:

{\begin{cases} v_{D 1} = V_{C 5} + V_{\begin{array}{l} C 6 \end{array}} \\ v_{D 3} = V_{C 3} + V_{\begin{array}{l} C 2 \end{array}} \\ v_{D 4} = V_{C 4} + V_{C 1} \end{cases}

(13)

t = t_{4}

, the leakage inductor current

i_{L s}

is reduced to zero so

D_{2}

is turned off and the next stage begins.

Stage 5 [

t_{4} ~ t_{5}

]: This stage starts at

t = t_{4}

. Power switches

S_{1}

and

S_{2}

remain on, and diodes

D_{2}

D_{3}

and

D_{4}

are off. The path for current flow is shown in Figure 3e. The operation for this stage is exactly the same as that for Stage 2, so it is not described in detail again at this stage. At

t = t_{5}

, power switch

S_{1}

is turned off and this stage ends and the next begins.

Stage 6 [

t_{5} ~ t_{0} + T_{S}

]: This stage starts at

t = t_{5}

. Power switch

S_{1}

is turned off, power switch

S_{2}

remains on, and diodes

D_{2}

and

D_{4}

are both off. The magnetizing inductor current

i_{L m 1}

begins to decrease and inductor

L_{m 1}

is discharged to the load through

D_{1}

and

D_{3}

so diodes

D_{1}

and

D_{3}

are forced to conduct. The path for current flow is shown in Figure 3f. The voltage across the inductors at this stage is:

{\begin{cases} v_{L m 1} = \frac{V_{i n}}{2} - V_{C 3} < 0 \\ v_{L m 2} = V_{i n} \end{cases}

(14)

v_{L s} = - v_{N p 2} + v_{N s 2} + V_{C 5} = - n v_{N p 1} + n v_{N s 1} + V_{C 5} = - n (\frac{V_{i n}}{2} - V_{C 3}) n V_{i n} + V_{C 5} < 0

(15)

Inductor currents

i_{L m 1}

and

i_{L s}

decrease linearly and

i_{L m 2}

increases linearly. At this stage, the voltage across power switch

S_{1}

is:

v_{S 1} = V_{C 2} + V_{C 3}

(16)

The voltage across diodes

D_{2}

and

D_{4}

is:

{\begin{cases} v_{D 2} = V_{C 5} + V_{C 6_{_{}}} \\ v_{D 4} = V_{C 1} + V_{C 4} \end{cases}

(17)

When

t = t_{0} + T_{S}

, power switch

S_{1}

is turned on again to complete one switching cycle for the circuit.

3. Steady-State Analysis

This section analyzes the converter's voltage gain ratio, component voltage stress and the design conditions for inductors and capacitors in a steady state. At last, the performance comparison with some high step-up converters in literature is also presented herein.

3.1. Voltage Gain Ratio Derivation

Applying the volt–second balance principle to magnetizing inductors

L_{m 1}

and

L_{m 2}

, the voltage across capacitors

C_{3}

and

C_{4}

is:

{\begin{cases} {〈 v_{L m 1} 〉}_{T_{s}} = 0 \\ {〈 v_{L m 2} 〉}_{T_{s}} = 0 \end{cases} \Rightarrow {\begin{cases} D V_{i n} + (1 - D) (\frac{V_{i n}}{2} - V_{C 3}) = 0 \\ D V_{i n} + (1 - D) (\frac{V_{i n}}{2} - V_{C 4}) = 0 \end{cases} \Rightarrow V_{C 3} = V_{C 4} = \frac{1 + D}{1 - D} \frac{V_{i n}}{2}

(18)

To simplify the analysis, the leakage inductor is ignored for Stages 3 and 6, so the voltage across capacitors

C_{5}

and

C_{6}

is:

{\begin{cases} V_{C 6} = v_{N p 2} - v_{N s 2} = n V_{i n} - n (\frac{V_{i n}}{2} - V_{C 4}) \\ V_{C 5} = v_{N p 2} - v_{N s 2} = n V_{i n} - n (\frac{V_{i n}}{2} - V_{C 3}) \end{cases}

(19)

Substituting (18) into (19) gives:

V_{C 5} = V_{C 6} = \frac{n}{(1 - D)} V_{i n}

(20)

By using Equations (18) and (20), the voltage gain ratio for the converter is calculated as:

M = \frac{V_{o}}{V_{i n}} = \frac{V_{C 3} + V_{C 4} + V_{C 5} + V_{C 6}}{V_{i n}} = \frac{(1 + D) + 2 n}{1 - D}

(21)

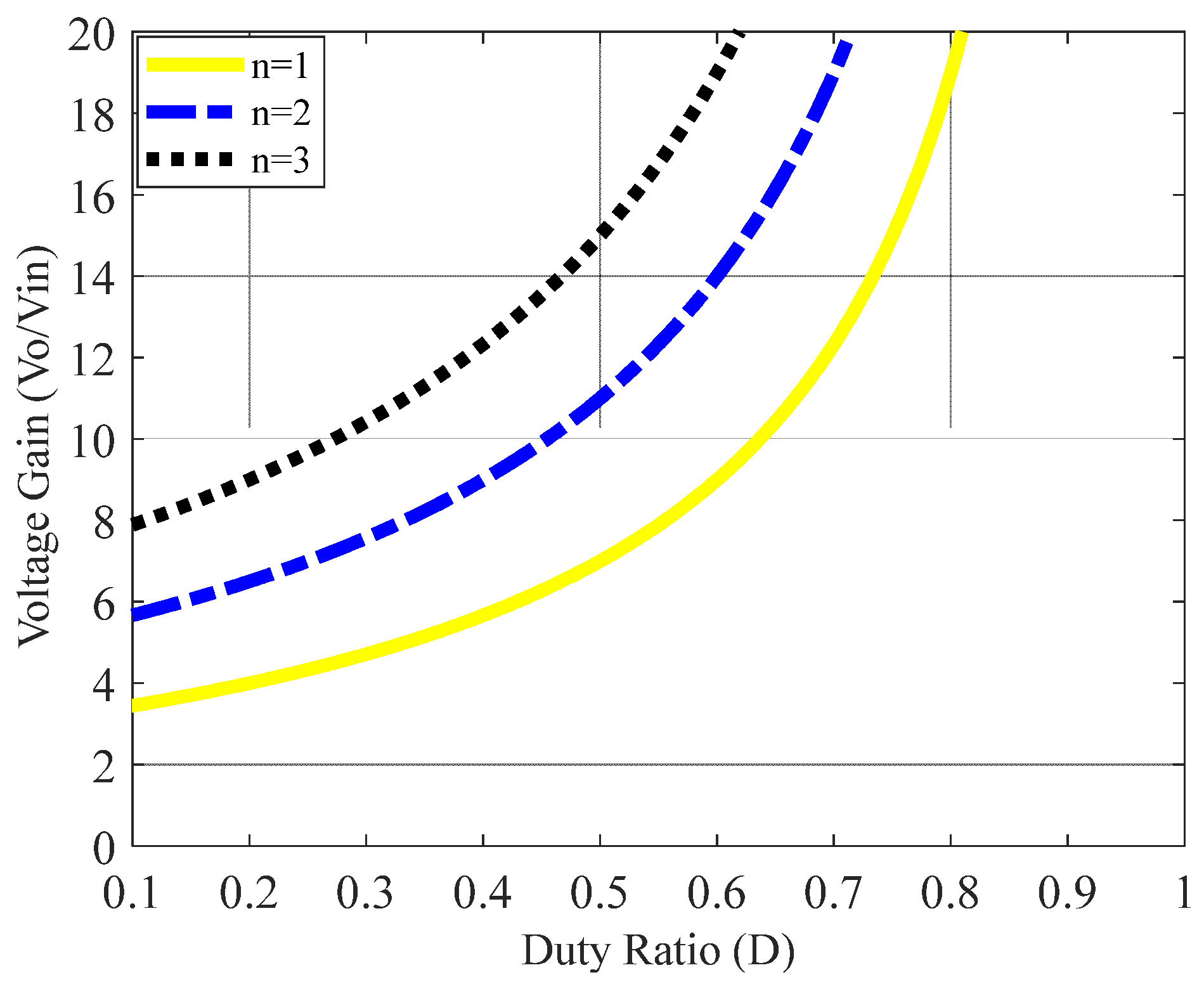
There are two design conditions that affect the voltage gain for the converter: the coupled turns ratio

n

and the duty cycle

D

. There are two degrees of freedom in the voltage-gain design. Appropriate values for

n

and

D

ensure that there is a high voltage gain without using a extremely duty cycle.

The voltage gain curve for the proposed converter is shown in Figure 4. If either the duty cycle or the turns ratio is increased, the voltage gain increases. If the turns ratio of the coupled inductor is

n = 1

, the voltage gain is 10 with

D = 0.636

and if the turns ratio for the coupled inductor is

n = 3

, the voltage gain can achieve 20 with

D = 0.619

3.2. Voltage Stresses on Semiconductor Devices

When power switches

S_{1}

and

S_{2}

are off, the voltage stresses are calculated as:

v_{S 1 (v o t a g e - s t r e s s)} = V_{C 2} + V_{C 3} = \frac{1}{(1 - D)} V_{i n} = \frac{1}{(1 + D) + 2 n} V_{o}

(22)

v_{S 2 (v o t a g e - s t r e s s)} = V_{C 1} + V_{C 4} = \frac{1}{(1 - D)} V_{i n} = \frac{1}{(1 + D) + 2 n} V_{o}

(23)

When the diodes are off, the voltage stresses are:

v_{D 1 (v o t a g e - s t r e s s)} = V_{C 5} + V_{C 6} = \frac{2 n}{(1 - D)} V_{i n} = \frac{2 n}{(1 + D) + 2 n} V_{o}

(24)

v_{D 2 (v o t a g e - s t r e s s)} = V_{C 5} + V_{C 6} = \frac{2 n}{(1 - D)} V_{i n} = \frac{2 n}{(1 + D) + 2 n} V_{o}

(25)

v_{D 3 (v o t a g e - s t r e s s)} = V_{C 2} + V_{C 3} = \frac{1}{(1 - D)} V_{i n} = \frac{1}{(1 + D) + 2 n} V_{o}

(26)

v_{D 4 (v o t a g e - s t r e s s)} = V_{C 1} + V_{C 4} = \frac{1}{(1 - D)} V_{i n} = \frac{1}{(1 + D) + 2 n} V_{o}

(27)

3.3. Design of Inductors

Assuming the current sharing is achieved, the currents of magnetizing inductors

L_{m 1}

and

L_{m 2}

are the same after one of those currents are shifted half switching period.

I_{L m}

is the average current of magnetizing inductors

L_{m 1}

and

L_{m 2}

, and

Δ i_{L m}

is the inductor ripple current. When the converter operates in CCM. It shows that

I_{L m} > \frac{1}{2} Δ i_{L m}

(28)

The average magnetizing inductor current is half of the average input current. It yields

I_{L m} = I_{L m 1} = I_{L m 2} = \frac{P_{o}}{2 V_{i n}}

(29)

where

P_{o}

is the average output power. The inductor current ripple

Δ i_{L m}

is written as:

Δ i_{L m} = \frac{V_{i n} D T_{s}}{L_{m}}

(30)

Substituting (29)-(30) into (28) gives the design condition for inductor

L_{m}

as:

L_{m} > \frac{V_{i n}^{2} \cdot R_{o} \cdot D T_{s}}{V_{o}^{2}}

(31)

3.4. Design of Capacitors

Based on the charges for capacitors through the circuit in Figure 2, it gives:

{\begin{cases} C_{3} Δ V_{C 3} = \frac{V_{o} (1 - D) T_{s}}{R_{o}} \\ C_{4} Δ V_{C 3} = \frac{V_{o} D T_{s}}{R_{o}} \\ C_{5} Δ V_{C 3} = \frac{V_{o} (1 - D) T_{s}}{R_{o}} \\ C_{6} Δ V_{C 3} = \frac{V_{o} D T_{s}}{R_{o}} \end{cases}

(32)

The capacitances are calculated using Equation (32) as:

{\begin{cases} C_{3} = \frac{V_{o} (1 - D) T_{s}}{R_{o} Δ V_{C 3}} \\ C_{4} = \frac{V_{o} D T_{s}}{R_{o} Δ V_{C 4}} \\ C_{5} = \frac{V_{o} (1 - D) T_{s}}{R_{o} Δ V_{C 5}} \\ C_{6} = \frac{V_{o} D T_{s}}{R_{o} Δ V_{C 6}} \end{cases}

(33)

Equations (18), (20) and (21) are substituted into this equation (33) to get:

{\begin{cases} C_{3} = \frac{2 (1 + D + 2 n) (1 - D) T_{s}}{(1 + D) \cdot R_{o_{_{}}} \cdot (Δ V_{C 3} / V_{C 3})} \\ C_{4} = \frac{2 (1 + D + 2 n) D T_{s}}{(1 + D) \cdot R_{o_{_{}}} \cdot (Δ V_{C 4} / V_{C 4})} \\ C_{5} = \frac{(1 + D + 2 n) (1 - D) T_{s}}{n R_{o} \cdot {(Δ V_{C 5} / V_{C 5})}_{_{}}} \\ C_{6} = \frac{(1 + D + 2 n) D T_{s}}{n R_{o} \cdot (Δ V_{C 6} / V_{C 6})} \end{cases}

(34)

3.5. Performance Comparison

In this paper, a comparison with three high step-up converters [19,20,21] is given. The comparison shown in Table 1 includes voltage gain, the value of voltage gain at n=1 and D=0.6, voltage stresses of switches and diodes, number of switches, diodes, capacitors, cores and winding, input current sharing ability, and efficiency at 200-250 W. It shows that the proposed converter has the higher voltage gain of 9 than 7 of converter in [20] and 6.25 of converter in [21]. In order to obtain the same voltage gain, the converters in [20] and [21] are required larger turn ratios or duty cycles, which thereby increase power losses. It also can see that the efficiency 95.5 % of the proposed converter at 200 W is higher than those 94.3 % and 92 % of the converters in [20] and [21], respectively. In addition, the proposed converter and the converter in [20] have the current sharing ability, but the converter in [21] does not have. It reveals that the current flowing through the components of the converter in [21] is larger than those of the proposed converter and converter in [20], so the converter in [21] has higher conduction losses and worse power efficiency.

On the other hand, by comparing with the proposed converter and the converter in [19], it gives that they can offer the same high voltage gain but the proposed converter has fewer components, resulting in a smaller volume, higher power density, and fewer magnetic cores, reducing volume and magnetic core losses. Moreover, the proposed converter exhibits lower power switch and diode voltage stresses compared to converters [19,20,21]. Therefore, low conduction resistance switches can be used to reduce conduction losses and costs. This is the reason why the efficiency of the proposed converter is also higher than that of the converter in [19].

4. Controller Design

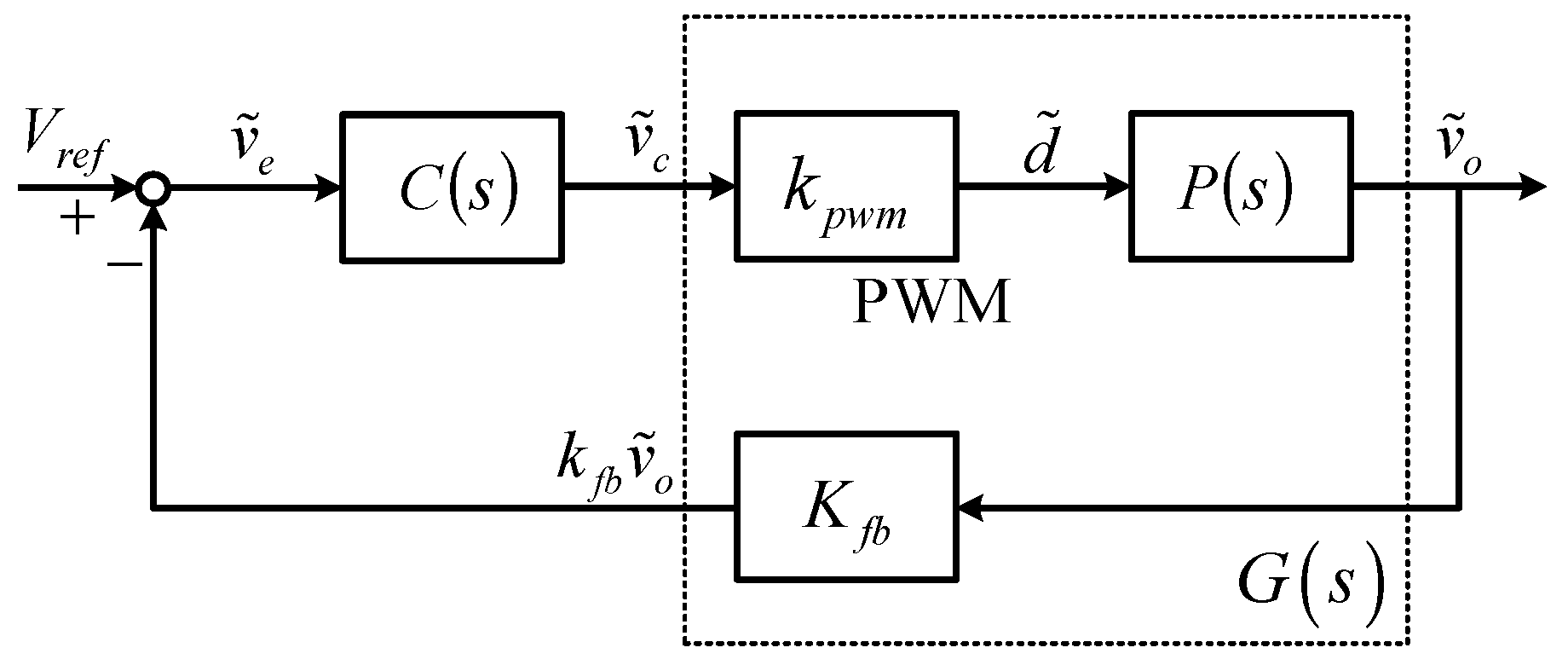
A controller is designed to regulate the output voltage of the proposed converter with variations in input voltage and load. The control block diagram is shown in Figure 5. T The transfer function

G (s)

is obtained from the control signal

{\tilde{v}}_{c}

to the output voltage divider signal

K_{f b} {\tilde{v}}_{o}

. It is written as:

G (s) = K_{f b} P (s) K_{p w m}

(35)

where the equivalent gain for the PWM (pulse width modulation) circuit is

K_{p w m}

, the transfer function of proposed converter is

P (s)

K_{f b}

is the feedback voltage gain. Moreover,

C (s)

is a controller that needs to be designed.

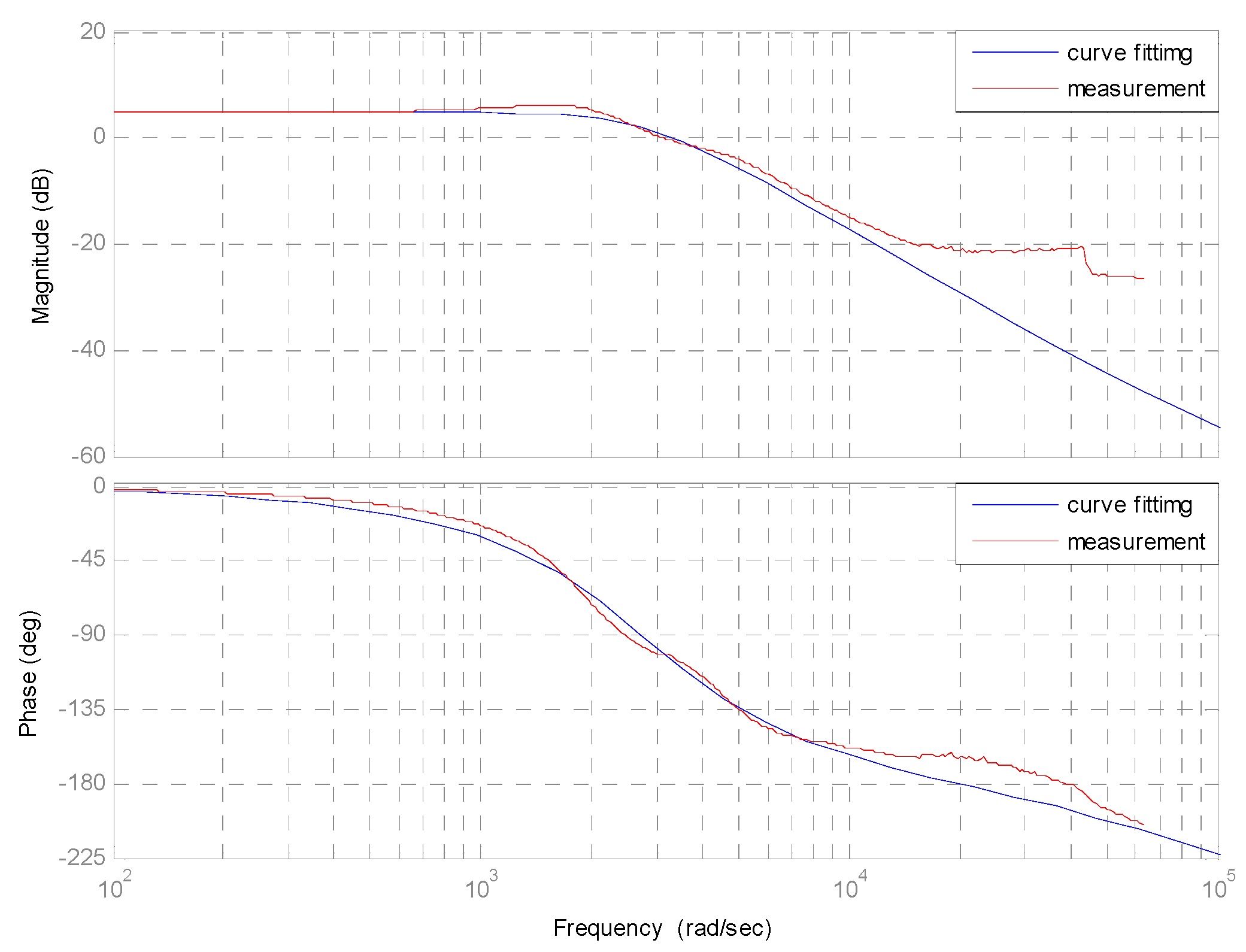
A prototype converter was constructed and tested. The specifications of the proposed converter and component parameters derived from the design considerations are shown in Table 2. A frequency response analyzer (FRA51602) was used to measure the Bode plots of the plant

G (s)

for an output power of 500 W. The result is shown in Figure 6. The red curves are the measured results and the blue curves are derived by curve fitting using MATLAB software. It shows that the two curves are similar in terms of gain and phase. Therefore, the small-signal transfer function for the proposed converter is obtained as:

G (s) = 1 . 74 \frac{(1 - \frac{s}{100000})}{(\frac{1}{2800^{2}} s^{2} + \frac{2 \times 0.7}{2800} s + 1)}

(36)

Based on (36), the voltage feedback controller is designed by the K-factor method [27]. A 45° phase margin at a crossover frequency of 1 kHz is given that a Type III controller is designed as

C (s) = 174825 \times \frac{(s + 2083) (s + 2222)}{s (s + 19230) (s + 20202)}

(37)

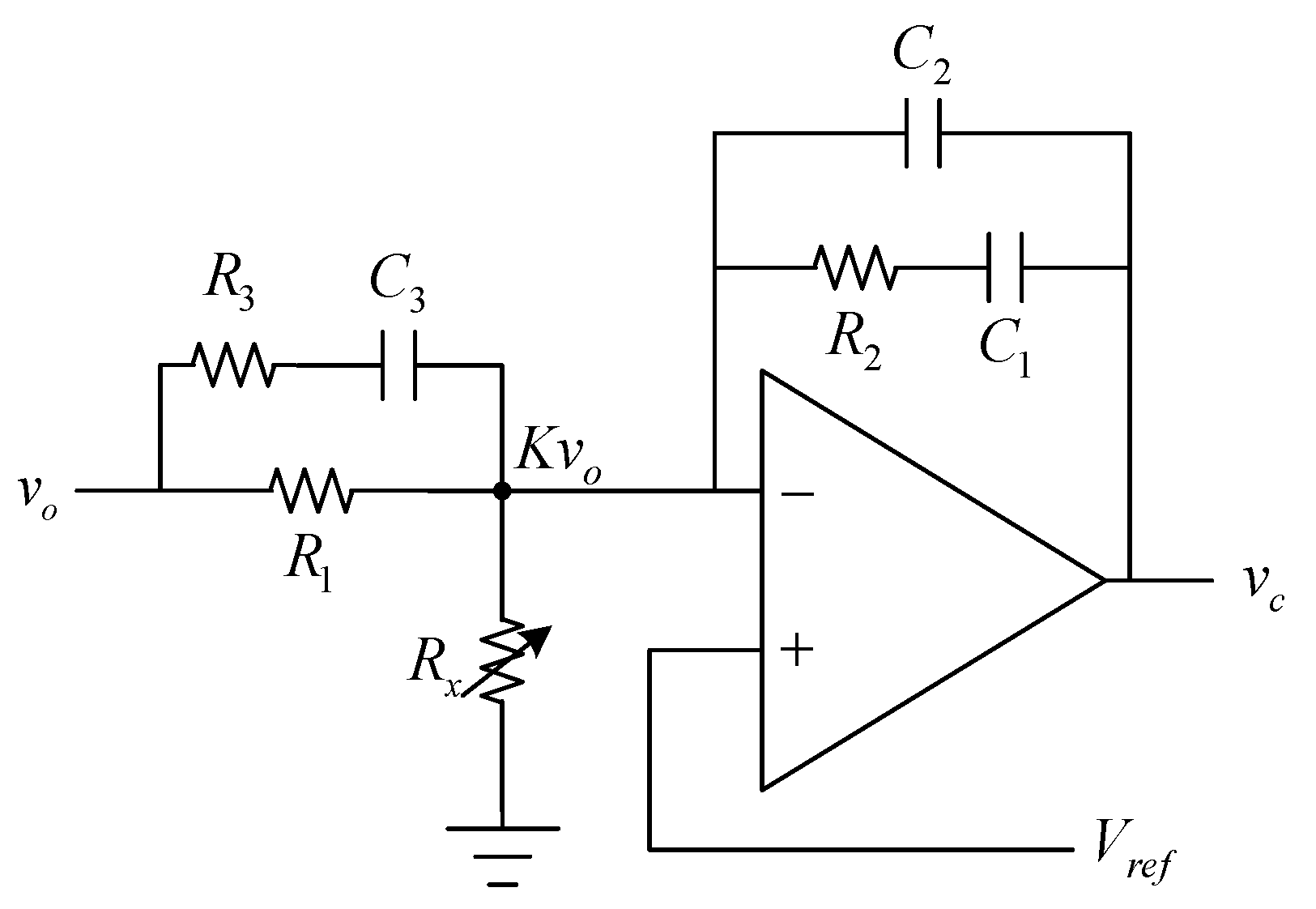
The Type III controller is implemented using an operational amplifier circuit shown in Figure 7, and the transfer function of the proposed Type-III controller is presented as

\frac{{\tilde{v}}_{c} (s)}{K {\tilde{v}}_{o} (s)} = - \frac{R_{1} + R_{3}}{R_{1} R_{3} C_{2}} \frac{(s + \frac{1}{R_{2} C_{1}}) (s + \frac{1}{(R_{1} + R_{3}) C_{3}})}{s (s + \frac{1}{R_{2} C_{1} C_{2} / (C_{1} + C_{2})}) (s + \frac{1}{R_{3} C_{3}})}

(38)

From (37) and (38), the passive components of the Type III controller in Figure 7 can be calculated and used to realize the designed controller, where it yields

R_{1} = 100 k Ω 、 R_{2} = 100 k Ω 、 R_{3} = 11 k Ω 、 C_{1} = 4.8 nF 、 C_{2} = 0.52 nF 、 C_{1} = 4.5 nF

(39)

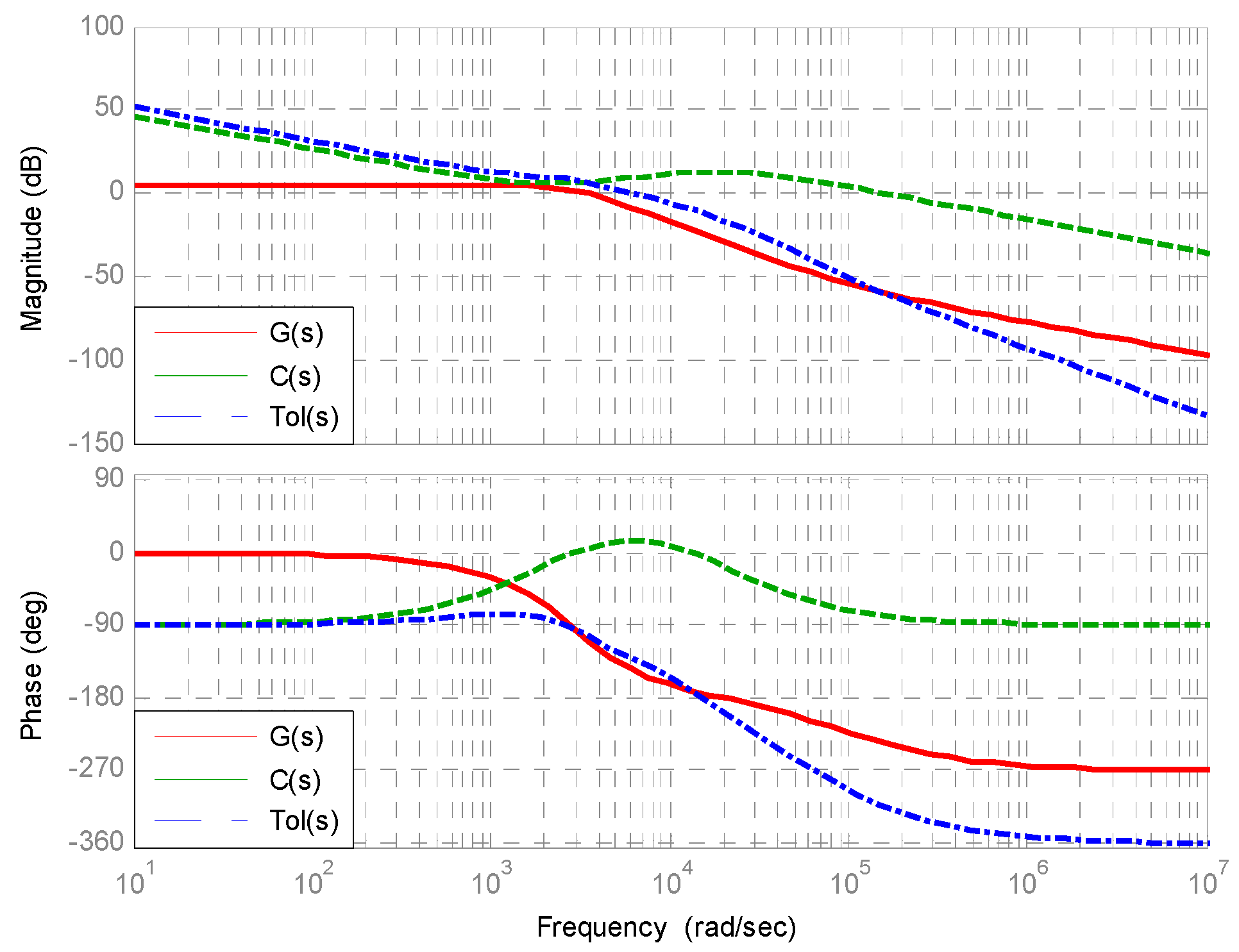
Finally, the Bode plots for plant

G (s)

, the Bode plots for the controller

C (s)

and the Bode plots for the open-loop system

T o l (s) = G (s) C (s)

can be drawn and shown in Figure 8. It reveals that a 45° phase margin at a crossover frequency of 1 kHz is achieved.

5. Simulations and Experimental Results

This paper simulates and implements a proposed converter operating at 200-1000 W. Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 show the waveforms for the Is-Spice simulations and experimental results for the proposed converter at 1 kW in the steady state.

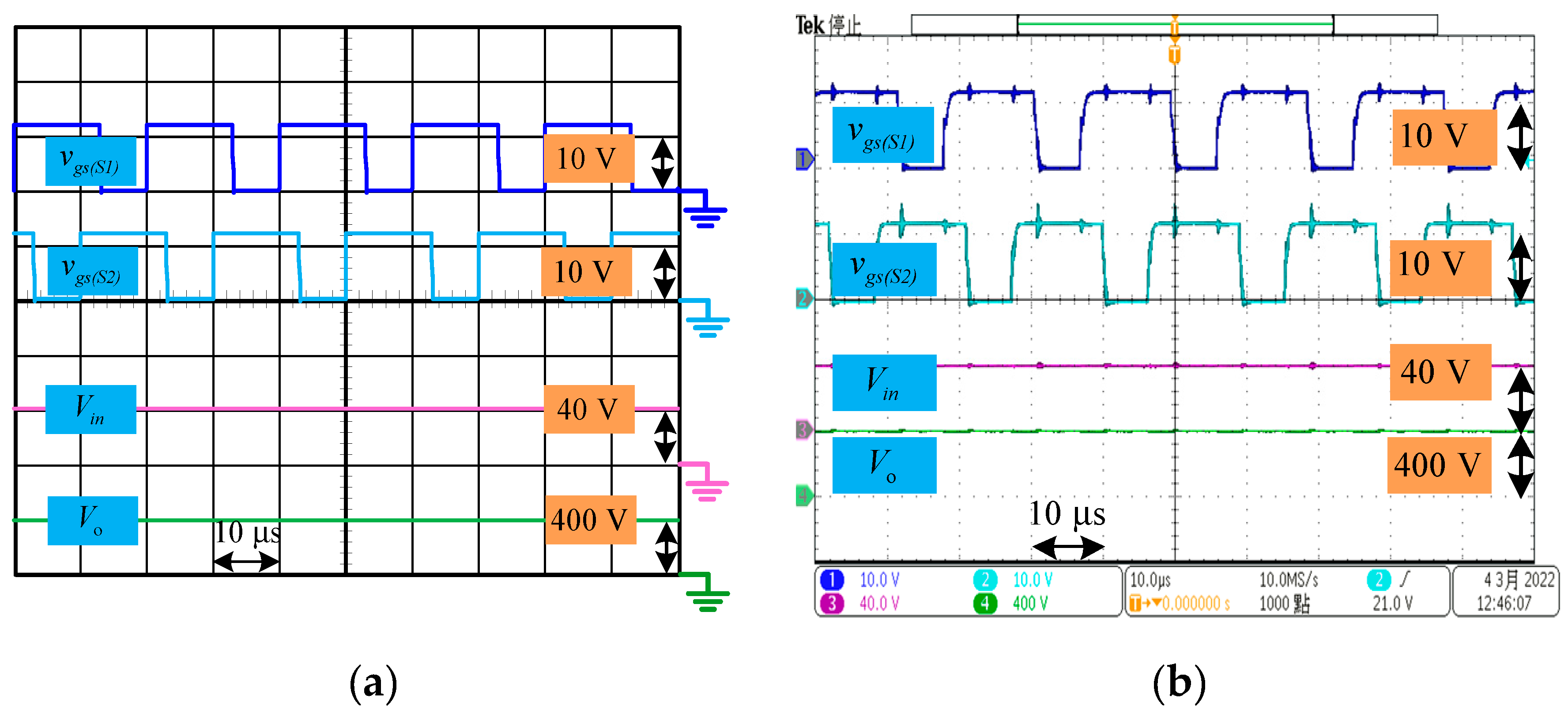
Figure 9 shows that the input voltage

V_{i n}

is 40 V and the output voltage

V_{o}

is 400 V. The high voltage gain of 10 is achieved herein. From the drive signals for the switches, it shows that the duty cycle for simulation is 0.643, for experimental result is 0.67. The duty cycle for theoretical value is 0.636 calculated form (21). There is a significant reduction in voltage drop in practice because the actual components are not ideal, so the duty cycle for experimental result is slightly higher than those for simulation and the theoretical result.

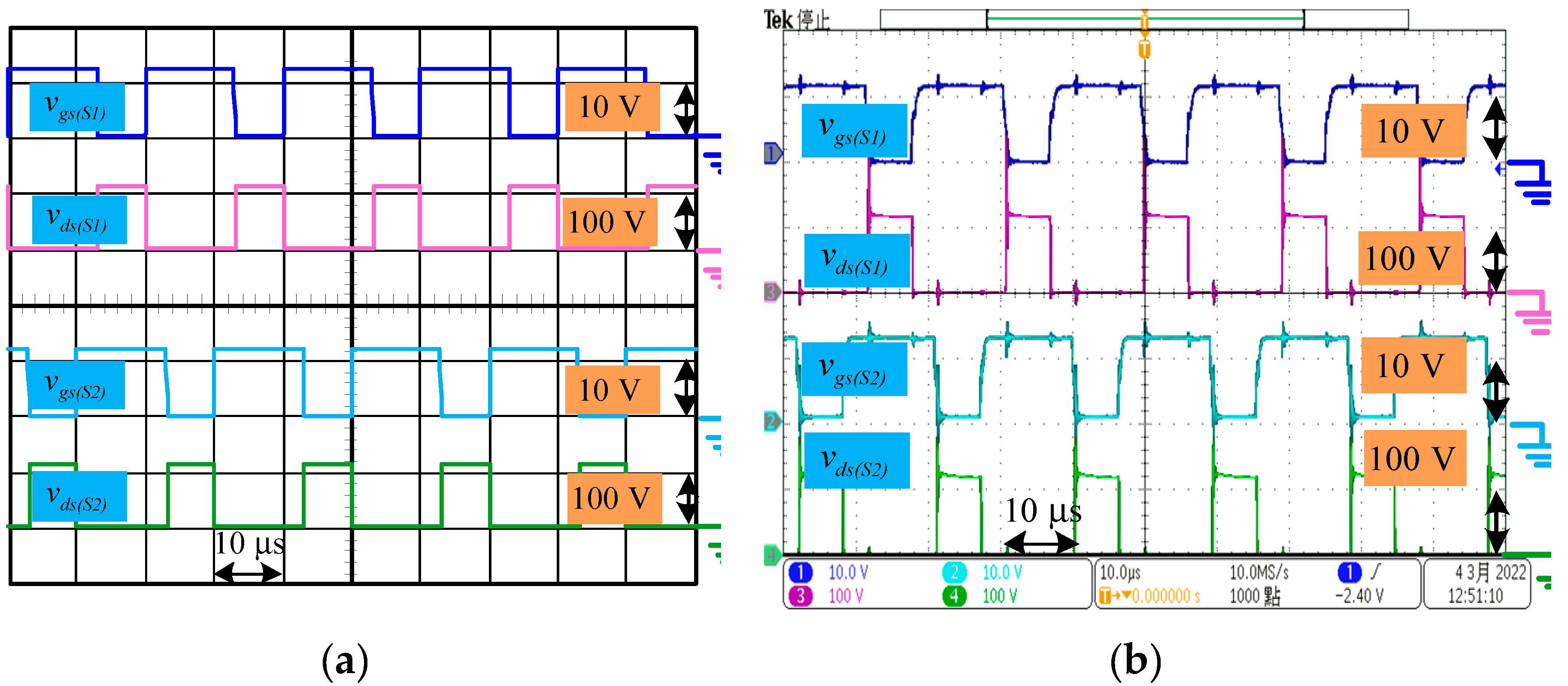
The waveforms for voltages

v_{d s 1}

and

v_{d s 2}

across power switches

S_{1}

and

S_{2}

are shown in Figure 10. The simulations and experimental results of voltage stresses

v_{d s 1}

and

v_{d s 2}

in steady state are 114 V and 112 V, respectively. Both of them are close to the theoretical results of 110 V. Therefore, the switches for the proposed converter have low voltage stress.

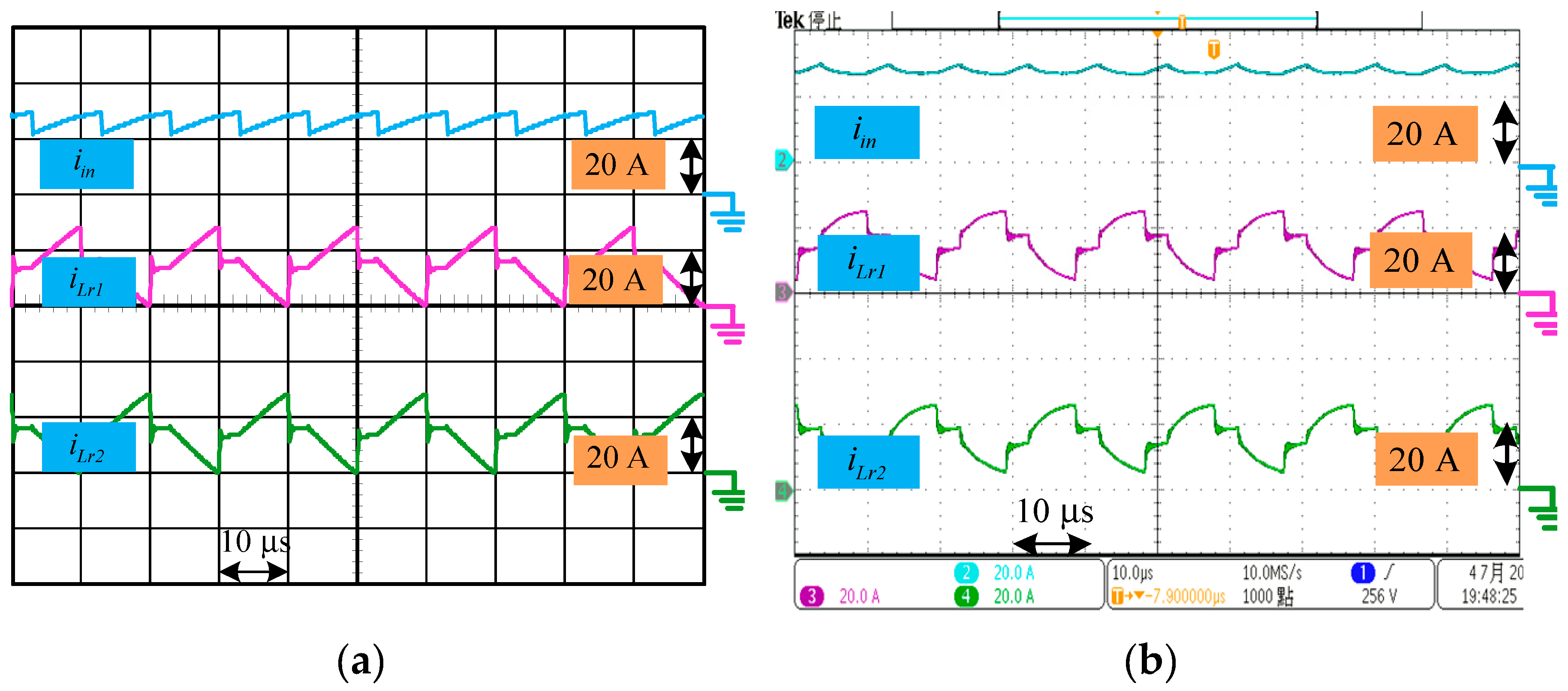
The converter is a symmetrical structure and current

i_{L r 1}

is similar to

i_{L r 2}

but interleaved with a

180 °

phase shift. The waveforms for input current

i_{i n}

, currents

i_{L r 1}

and

i_{L r 2}

are shown in Figure 11. The average currents of

i_{L r 1}

and

i_{L r 2}

are the same of 14.2 A for the simulation results and are 14.42 A and 14.52 A respectively for the experiment results. Therefore, the converter features the performance of current sharing. Moreover, it reveals from Figure 11 that the current ripples of the input current

i_{i n}

are 7.74 A and 3.95 A for simulation and experimental result respectively. They become much smaller than the current ripples of

i_{L r 1}

and

i_{L r 2}

, which are 27.8 A and 21.4 A for simulation and experimental result respectively.

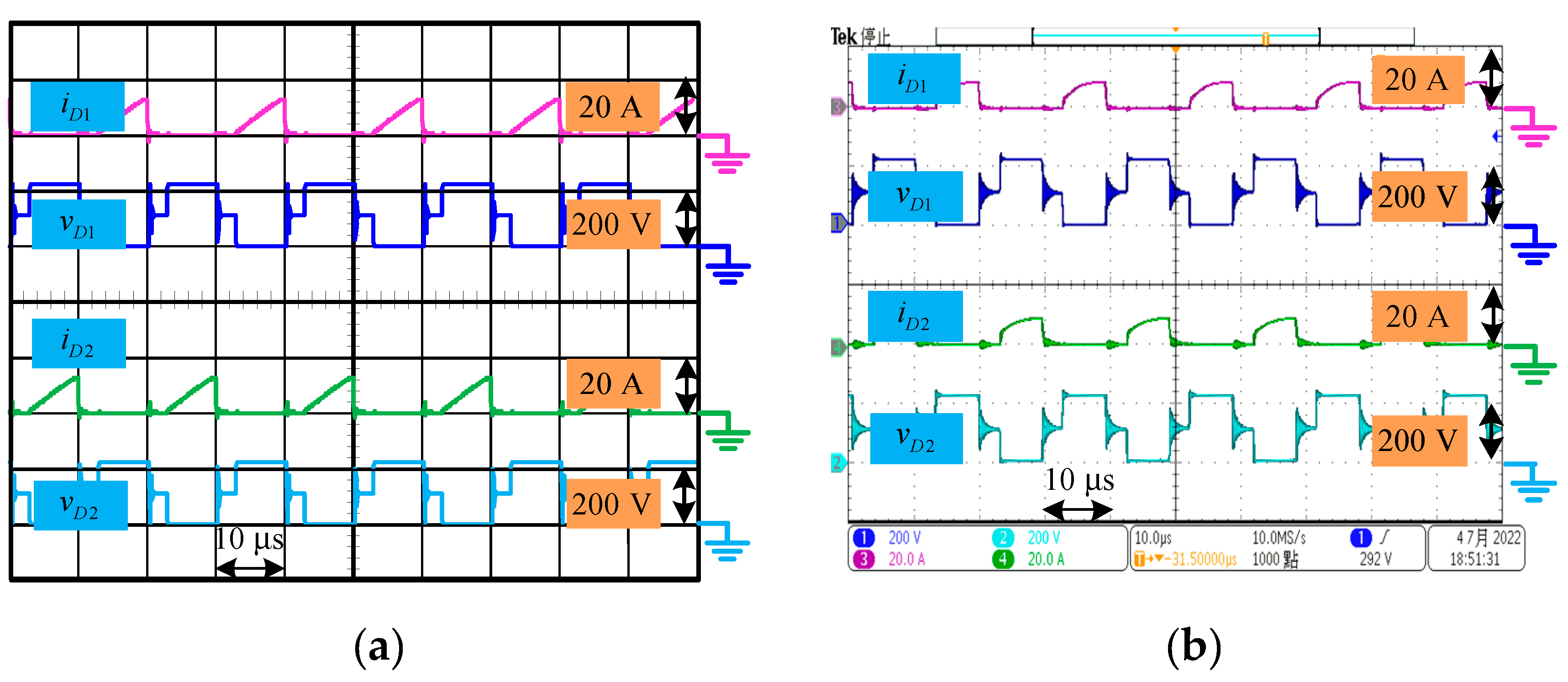
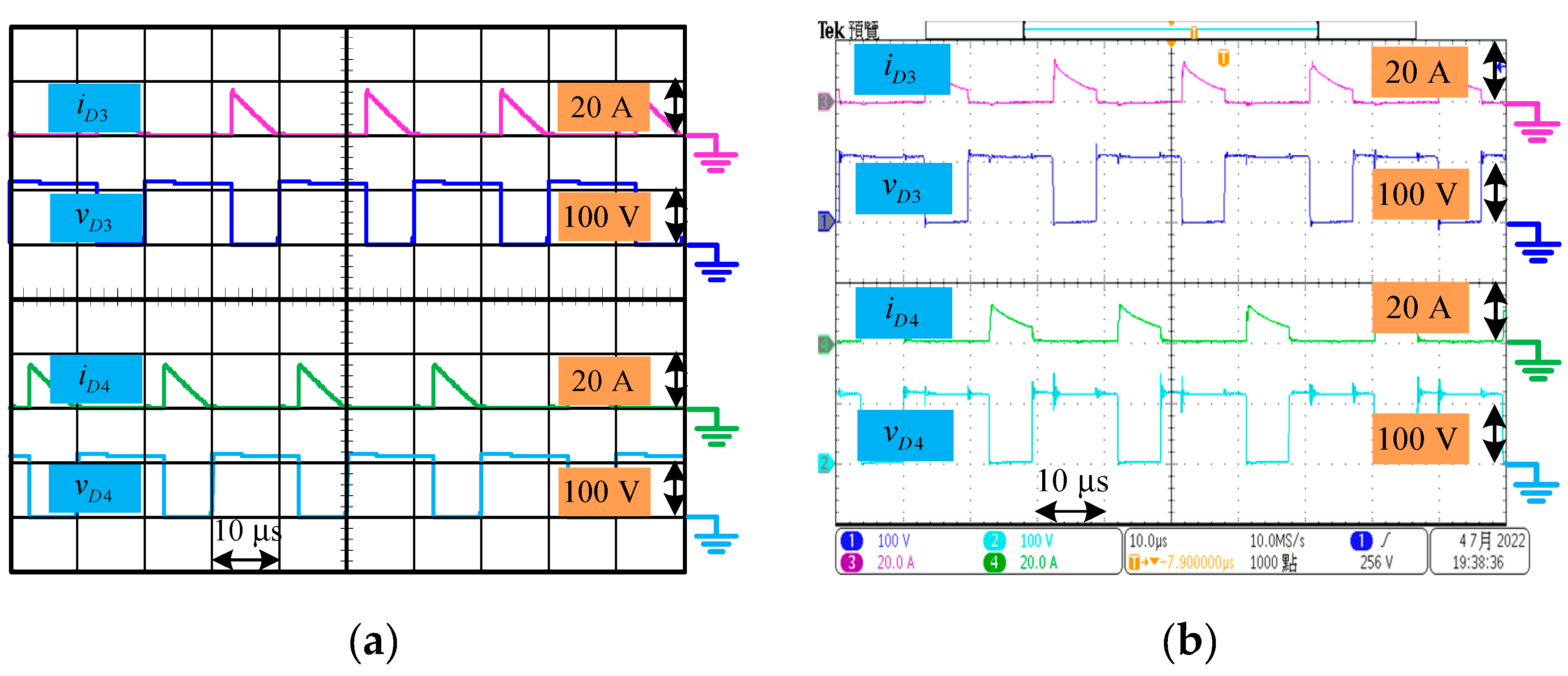
The current and voltage waveforms for diodes

D_{1}

and

D_{2}

are shown in Figure 12. The current and voltage waveforms for diodes

D_{3}

and

D_{4}

are shown in Figure 13. It shows that there is no reverse-recovery problem for all the diodes as diode is turned from on to off. Moreover, it also gives that the maximum voltages across diodes

D_{1}

D_{2}

are 220 V, which is about

V_{o}

/2 , and the maximum voltages across diodes

D_{3}

and

D_{4}

are 110 V, which is about

V_{o}

/4 . It means that all of the diodes

D_{1}

, ,

D_{3}

and

D_{4}

have low voltage stress.

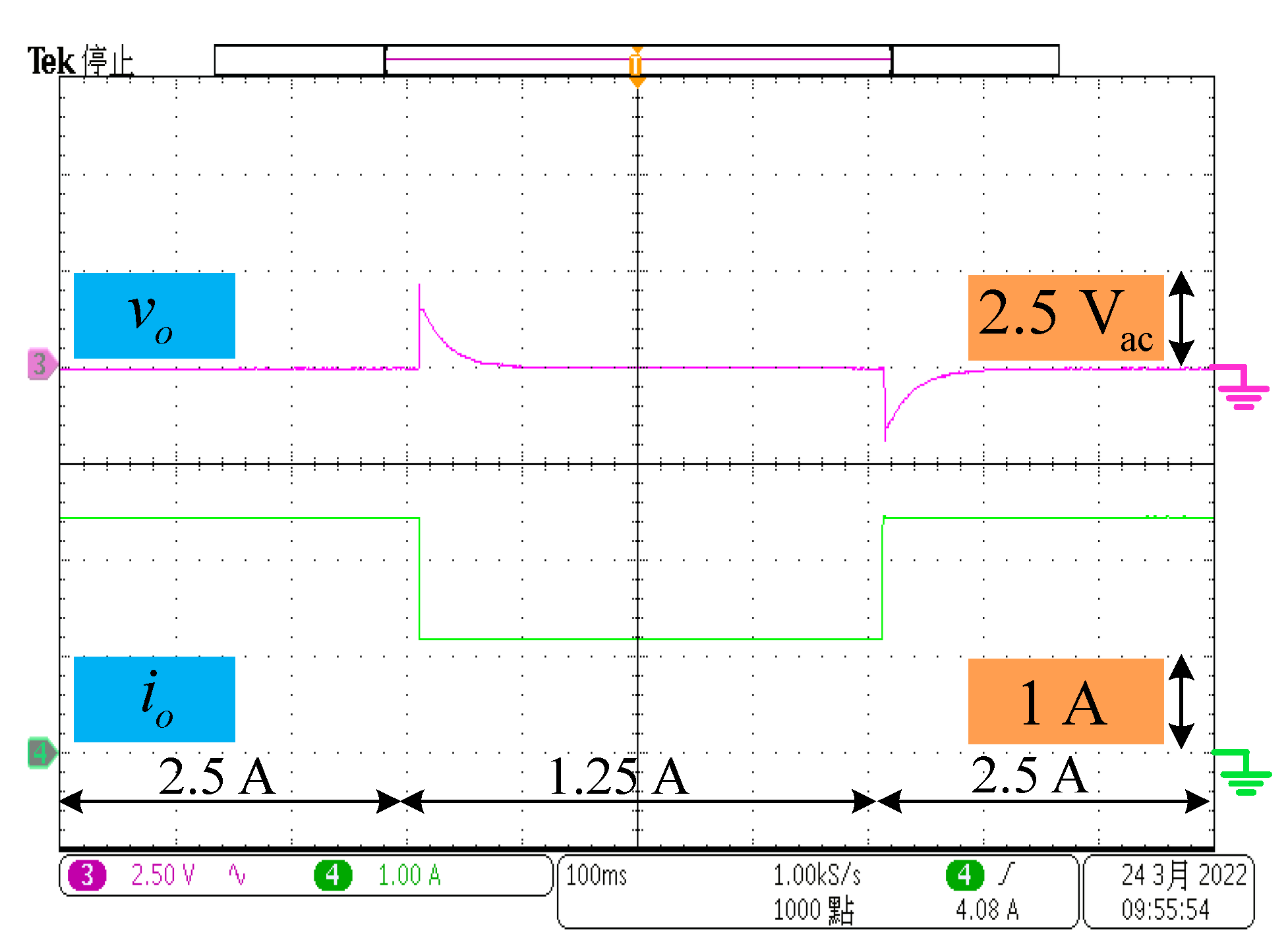
Figure 14 shows the dynamic response for the output voltage when there is a step change in the output load from

200 W

1000 W

and then to

200 W

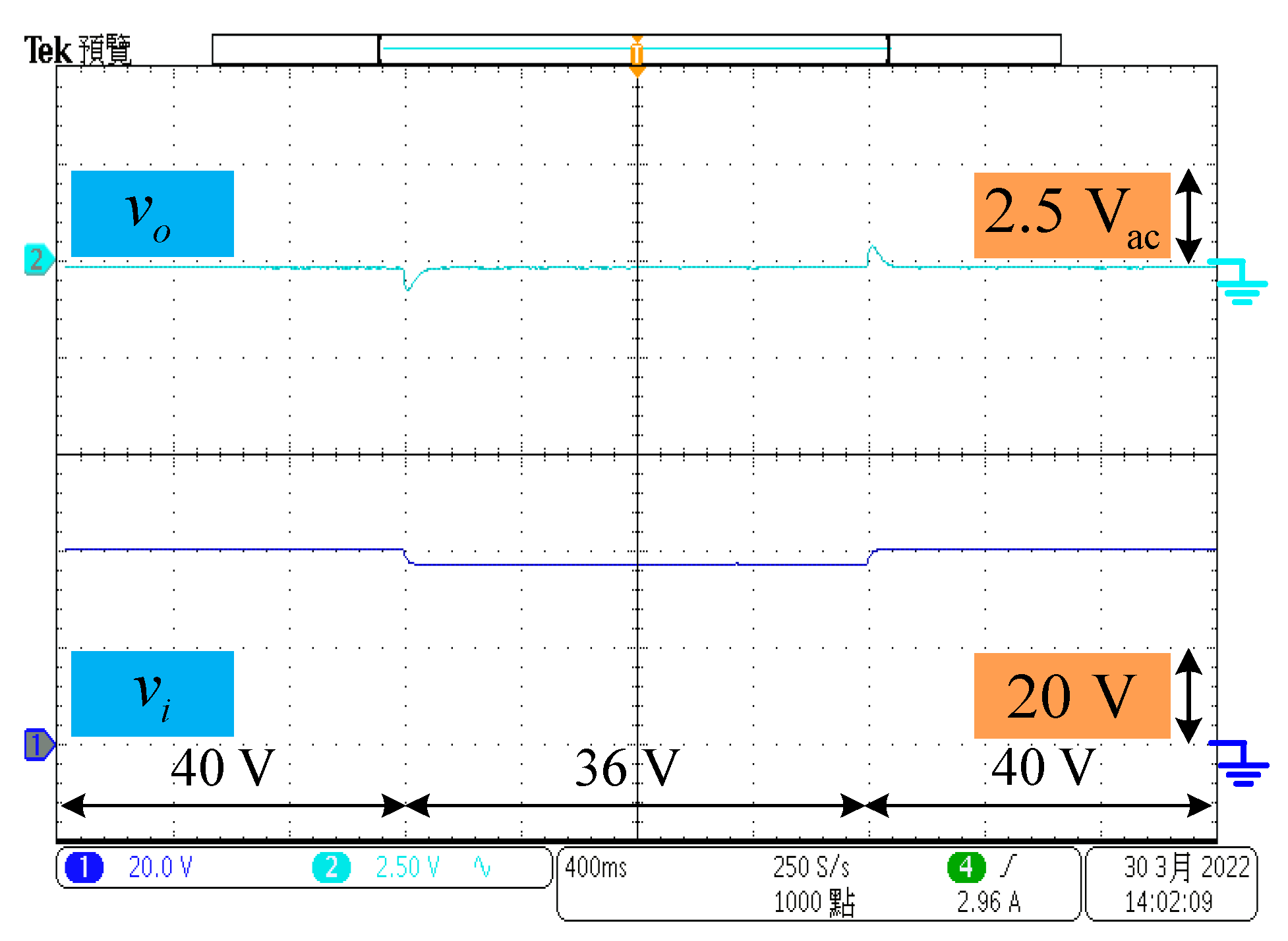
. It has a voltage overshoot of 2.3 V, which is much less than the output voltage of 400 V. Figure 15 shows the dynamic response for the output voltage when there is a step change in the input voltage from 40 V to 36 V and then to 40 V. The output voltage overshoot is 0.71 V, which is quite smaller than the output voltage of 400 V. The results in these two figures show that the output voltage can be regulated under input voltage and output load variations. It means that the overall system is very robust.

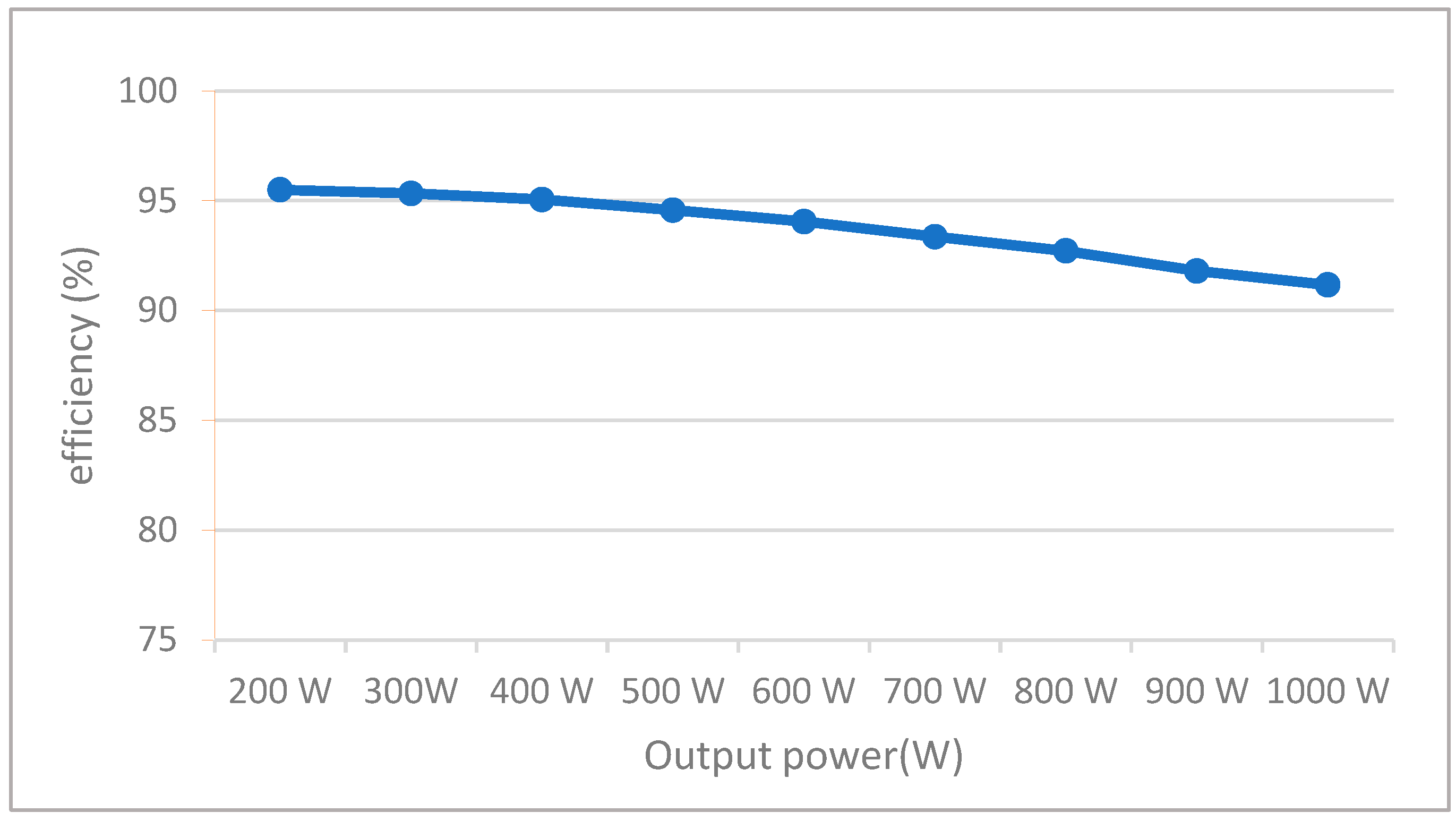
In this paper, the conversion efficiency of the proposed converter for output powers from 200 W to 1000 W was measured by a HIOKI 3390 and the results are shown in Figure 16. The converter has a maximum efficiency of 95.5 % at a light load of 200 W. A heavy load of 1000 W results in the efficiency of 91.16 %, which is still more than 90 %. Moreover, the picture of the experimental prototype for power stage is also presented in Figure 17. It shows that the proposed converter has a simple circuit structure with fewer components.

6. Conclusion

This paper proposes a novel symmetrical active-switched coupled-inductor high-step-up DC/DC converter. The new active-switched coupled-inductor boost technology features both switching inductor and coupled inductor boost characteristics so the converter can be easier to achieve a higher voltage gain with two design freedom of the turn ratio and the duty cycle and operated without a large duty cycle. Moreover, the voltage stresses on the switches and diodes in the converter are much lower than the output voltage. It gives that the power switches with a smaller ON-resistance and diodes with smaller forward voltage can applied to reduce conduction losses. So the overall efficiency of the proposed converter can be further increased. A steady-state analysis, component design considerations, dynamics and controller design are also presented herein. Finally, a 200-1000 W with 40 V input and 400 V output at 50 kHz switching frequency prototype is implemented. The simulations and experimental results are thereby given to validate the theoretic results. It reveals that the proposed converter exhibits a high voltage gain of 10, low voltage stresses of power switches and diodes, output voltage regulation despite of input voltage and output load variations, and high efficiency of 95.5 % at 200 W. As a result, the proposed converter with high voltage gain, low voltage stress, high efficiency and simple circuit topology can be used for a rectifier giving a 400 V dc bus in a renewable energy generation system.

References

Tofoli, F.L.; Pereira, D.d.C.; Josias de Paula, W.; Oliveira Junior, D.d.S. Survey on non-isolated high-voltage step-up dc–dc topologies based on the boost converter. IET Power Electronics. 2015, 8, 2044–2057. [Google Scholar] [CrossRef]
Zhu, B.; Ding, F.; Vilathgamuwa, D.M. Coat Circuits for DC–DC Converters to Improve Voltage Conversion Ratio. IEEE Trans Power Electronics. 2020, 35, 3679–3687. [Google Scholar] [CrossRef]
Alzahrani, A.; Ferdowsi, M.; Shamsi, P. High-voltage-gain dc-dc step-up converter with bifold dickson voltage multiplier Cells. IEEE Trans Power Electronics. 2019, 34, 9732–9742. [Google Scholar] [CrossRef]
Ye, Y.; Peng, W.; Jiang, B. High step-up dc-dc converter with multi-winding CL and switched capacitor. IET Power Electronics. 2018, 11, 2232–2240. [Google Scholar] [CrossRef]
Zhao, J.; Chen, D. Switched-Capacitor High Voltage Gain Z-Source Converter with Common Ground and Reduced Passive Component. IEEE Access. 2021, 9, 21395–21407. [Google Scholar] [CrossRef]
Lei, H.; Hao, R.; You, X.; Li, F. Nonisolated High Step-Up Soft-Switching DC–DC Converter with Interleaving and Dickson Switched-Capacitor Techniques. IEEE Journal of Emerging and Selected Topics in Power Electronics 2019, 8, 2007–2021. [Google Scholar] [CrossRef]
Zeng, T.; Wu, Z.; He, L. An interleaved soft switching high step-up converter with low input current ripple and high efficiency. IEEE Access. 2019, 7, 93580–93593. [Google Scholar] [CrossRef]
Akhlaghi, B.; Molavi, N.; Fekri, M.; Farzanehfard, H. High Step-Up Interleaved ZVT Converter with Low Voltage Stress and Automatic Current Sharing. IEEE Trans Industrial Electronics. 2018, 65, 291–299. [Google Scholar] [CrossRef]
Axelrod, B.; Beck, Y.; Berkovich, Y. High step-up DC-DC converter based on the switched-coupled-inductor boost converter and diode-capacitor multiplier: steady state and dynamics. IET Power Electronics. 2015, 8, 1420–1428. [Google Scholar] [CrossRef]
Moradpour, R.; Ardi, H.; Tavakoli, A. Design and Implementation of a New SEPIC-Based High Step-Up DC/DC Converter for Renewable Energy Applications. IEEE Trans on Industrial Electronics. 2018, 65, 1290–1297. [Google Scholar] [CrossRef]
Luo, P.; Liang, T.J.; Chen, K.H.; Chen, S.M. Design and Implementation of a High Step-Up DC-DC Converter with Active Switched Inductor and Coupled Inductor. In Proceedings of the 2022 International Power Electronics Conference (IPEC-Himeji 2022- ECCE Asia), Himeji, Japan, 15–19 May 2022; pp. 1670–1676. [Google Scholar]
Tseng, K.C.; Cheng, C.A.; Chen, C.T. High Step-Up Interleaved Boost Converter for Distributed Generation Using Renewable and Alternative Power Sources. IEEE Journal Emerging and Selected Topics in Power Electronics. 2017, 5, 713–722. [Google Scholar] [CrossRef]
Ardi, H.; Ajami, A. Study on a High Voltage Gain SEPIC-Based DC-DC Converter with Continuous Input Current for Sustainable Energy Applications. IEEE Tran Power Electronics, 2018, 33, 10403–10409. [Google Scholar] [CrossRef]
Molavi, N.; Adib, E.; Farzanehfard, H. Soft-switching bidirectional DC–DC converter with high voltage conversion ratio. IET Power Electronics. 2018, 11, 33–42. [Google Scholar] [CrossRef]
Ajami, A.; Ardi, H.; Farakhor, A. A novel high step-up DC/DC converter based on integrating coupled inductor and switched-capacitor techniques for renewable energy applications. IEEE Trans Power Electronics. 2015, 30, 4255–4263. [Google Scholar] [CrossRef]
Seo, S.W.; Ryu, J.H.; Kim, Y.; Choi, H.H. Non-Isolated High Step-Up DC/DC Converter with Coupled Inductor and Switched Capacitor. IEEE Access. 2022, 8, 217108–217122. [Google Scholar] [CrossRef]
Seo, S.W.; Ryu, J.H.; Kim, Y.; Lee, J.B. Ultra-High Step-Up Interleaved Converter with Low Voltage Stress. IEEE Access. 2021, 9, 37167–37178. [Google Scholar] [CrossRef]
Luo, P.; Liang, T.J.; Chen, K.H.; Chen, S.M. High Step-up DC-DC Converter with Active Switched Inductor and Voltage Double Based on Three-winding Coupled Inductor. In Proceedings of the 2022 IEEE Applied Power Electronics Conference and Exposition(APEC), Houston, TX, USA, 20–24 March 2022; pp. 1–6. [Google Scholar]
Guepfrih, M.F.; Waltrich, G.; Lazzarin, T.B. High Step-Up DC-DC Converter Using Built-In Transformer Voltage Multiplier Cell and Dual Boost Concepts. IEEE Journal of Emerging and Selected Topics in Power Electronics. 2021, 9, 6700–6712. [Google Scholar] [CrossRef]
Vaghela, M.A.; Mulla, M.A. High Step-Up Gain Converter Based on Two-Phase Interleaved Coupled Inductor Without Right-Hand Plane Zero. IEEE Transactions on Power Electronics. 2023, 38, 5911–5927. [Google Scholar] [CrossRef]
Lopez-Santos, O.; Mayo-Maldonado, J.C.; Rosas-Caro, J.C.; Valdez-Resendiz, J.E.; Zambrano-Prada, D.A. Ruiz-Martinez, O.F. Quadratic boost converter with low-output-voltage ripple. IET Power Electronics. 2020, 13, 1605–1612. [Google Scholar] [CrossRef]
Li, F.; Yao, Y.; Wang, Z.; Liu, H. Coupled-inductor-inverse high step-up converter. IET Power Electronics. 2018, 11, 902–911. [Google Scholar] [CrossRef]
Henn, G.A.L.; Silva, R.N.A.L.; Praca, P.P.; Barreto, L.H.S.C.; Oliveira, D.S. Interleaved-Boost Converter with High Voltage Gain. IEEE Trans power electronics. 2010, 25, 2753–2761. [Google Scholar] [CrossRef]
Alateeq, A.; Almalaq, Y.; Matin, M. A Switched-Inductor Model for a Non-Isolated Multilevel Boost Converter. In Proceedings of the 2017 North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–5. [Google Scholar]
Jose, M.P.; Paulose, S.; John, N.; Paul, B.; Eldo, H.S. CD-Cell Switched Inductor Based Fifth Order Boost Converter. In Proceedings of the 2021 International Conference on Communication, Control and Information Sciences (ICCISc), Idukki, India, 16–18 June 2021; pp. 1–5. [Google Scholar]
Tang, Y.; Tong, H.; Kan, J.; Zhang, Y.; Xu, K. Symmetric Dual-Switch Converter. IEEE Transactions on Power Electronics. 2020, 35, 11955–11964. [Google Scholar] [CrossRef]
Venable, D. The K factor: a new mathematical tool for stability analysis and synthesis. Proceedings Powercon 1983, 10. [Google Scholar]

Figure 1. Proposed converter

Figure 2. Theoretical key waveform for the proposed converter operating in CCM

Figure 3. Equivalent circuits for: (a) Stage 1, (b) Stage 2, (c) Stage 3, (d) Stage 4, (e) Stage 5 and (f) Stage 6.

Figure 4. Voltage gain for the proposed converter versus turns ratio

n

and duty cycle

D

Figure 4. Voltage gain for the proposed converter versus turns ratio

n

and duty cycle

D

Figure 5. Control block diagram for the overall system.

Figure 6. Bode plots for the measurement result (red) and curve fitting result (blue).

Figure 7. Type III Controller circuit.

Figure 8. Bode plots for the plant, controller and open-loop system.

Figure 9. Waveforms for

v_{g s 1}

v_{g s 2}

V_{i n}

and

V_{o}

: (a) Simulation results. (b) Experimental results.

Figure 9. Waveforms for

v_{g s 1}

v_{g s 2}

V_{i n}

and

V_{o}

: (a) Simulation results. (b) Experimental results.

Figure 10. Waveforms for

v_{g s 1}

v_{g s 2}

v_{d s 1}

and

v_{d s 2}

: (a) Simulation results. (b) Experimental results.

Figure 10. Waveforms for

v_{g s 1}

v_{g s 2}

v_{d s 1}

and

v_{d s 2}

: (a) Simulation results. (b) Experimental results.

Figure 11. Waveforms for

i_{i n}

i_{L r 1}

and

i_{L r 2}

: (a) Simulation results. (b) Experimental results.

Figure 11. Waveforms for

i_{i n}

i_{L r 1}

and

i_{L r 2}

: (a) Simulation results. (b) Experimental results.

Figure 12. Waveforms for

i_{D 1}

v_{D 1}

i_{D 2}

and

v_{D 2}

: (a) Simulation results. (b) Experimental results.

Figure 12. Waveforms for

i_{D 1}

v_{D 1}

i_{D 2}

and

v_{D 2}

: (a) Simulation results. (b) Experimental results.

Figure 13. Waveforms for

i_{D 3}

v_{D 3}

i_{D 4}

and

v_{D 4}

.: (a) Simulation results (b) Experimental results.

Figure 13. Waveforms for

i_{D 3}

v_{D 3}

i_{D 4}

and

v_{D 4}

.: (a) Simulation results (b) Experimental results.

Figure 14. Dynamic response for output voltage for a step change in load (

200 W - 1000 W - 200 W

Figure 14. Dynamic response for output voltage for a step change in load (

200 W - 1000 W - 200 W

Figure 15. Dynamic response for output voltage for a change in input voltage (

40 V - 36 V - 40 V

Figure 15. Dynamic response for output voltage for a change in input voltage (

40 V - 36 V - 40 V

Figure 16. Measured efficiency of the proposed converter.

Figure 17. Experimental prototype for power stage.

Table 1. Comparison of the proposed converter with other previously presented converters.

Parameter	[19]	[20]	[21]	Proposed converter
Voltage gain(M)	$\frac{1 + D + 2 n}{1 - D}$	$\frac{1}{1 - D} + 2 n$	$\frac{1}{{(1 - D)}^{2}}$	$\frac{1 + D + 2 n}{1 - D}$
M for n=1, D=0.6	9	7	6.25	9
Voltage stress of switch (V_S/V_in)	$\frac{M}{1 + D + 2 n}$	$\frac{M}{1 + 2 n - 2 n D}$	$M$	$\frac{M}{1 + D + 2 n}$
Maximum voltage stress of diodes (V_D/V_in)	$\frac{(n + 1) M}{1 + D + 2 n}$	$\frac{n M}{1 + 2 n - 2 n D}$	$M$	$\frac{2 n M}{1 + D + 2 n}$
Number of elements Switches/diodes/ capacitors/cores/ winding	2/4/6/4/4	2/4/3/2/4	2/2/2/2/2	2/4/6/2/4
Input current sharing	Yes	Yes	No	Yes
Efficiency	93.2% @200 W	94.3% @200 W	92% @250 W	95.5% @200 W

Table 2. Specifications and parameters for the proposed converter.

Parameter/Description	Specification/Value
Input voltage V_in	40 V
Output voltage V_o	400 V
Rated output power P_o	1000 W
Switching frequency f_s	50 kHz
Magnetizing inductance L_m	140 µH
Turns ratio n	1
Power switches S₁ and S₂	NTHL020N090SC1
Diodes D₁, D₂, D₃, D₄	STTH3003CW
Capacitor C₁, C₂, C₃, C₄, C₅, C₆	100 µF

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Novel Symmetrical Active-Switched Coupled-Inductor High-Step-Up DC/DC Converter

Abstract

1. Introduction

2. Proposed Converter and Operating Principle

3. Steady-State Analysis

3.1. Voltage Gain Ratio Derivation

3.2. Voltage Stresses on Semiconductor Devices

3.3. Design of Inductors

3.4. Design of Capacitors

3.5. Performance Comparison

4. Controller Design

5. Simulations and Experimental Results

6. Conclusion

References

MDPI Initiatives

Important Links

Subscribe