Prerpints.org logo
Preprint
Article

Comparing the Performance of RF Photonic Transversal Signal Processors Based on Microcombwith Discrete Components and Integrated Chips

Altmetrics

Downloads

121

Views

28

Comments

0

This version is not peer-reviewed

Submitted:

14 August 2023

Posted:

15 August 2023

You are already at the latest version

Alerts
Abstract
RF photonic transversal signal processors, which combine reconfigurable electrical digital signal processing and high-bandwidth photonic processing, provide a powerful solution for achieving adaptive high-speed information processing. Recent progress in optical microcomb technology provides compelling multi-wavelength sources with compact footprint, yielding a variety of microcomb-based RF photonic transversal signal processors implemented by either discrete or integrated components. Although operating based on the same principle, processors in these two forms exhibit distinct performance. This letter presents a comparative investigation into their performance. First, we compare the performance of state-of-the-art processors, focusing on the processing accuracy. Next, we analyze various factors that contribute to the performance differences, including tap number and imperfect response of experimental components. Finally, we discuss the potential for future improvement. These results provide a comprehensive comparison of microcomb-based RF photonic transversal signal processors implemented using discrete and integrated components and provide insights for their future development.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

Ⅰ. Introduction

Driven by the exponential growth of data capacity, there has been a rapid increase in the demand for high-speed information processing. Radio-frequency (RF) photonics, which utilize photonic hardware and technologies to process high-bandwidth RF signals, provides speed advantages over electrical signal processing with intrinsic bandwidth limitations [1]. Among the various schemes to implement RF photonic processors, RF photonic transversal signal processors have garnered significant interest due to their exceptional reconfigurability, allowing for the realization of diverse processing functions without the need for changing any hardware [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36].
In RF photonic transversal signal processors, a number of wavelength channels are needed to facilitate high reconfigurability and ensure high processing accuracy. In addition, a wide channel spacing between these wavelength channels is necessary to ensure a large operational bandwidth. Recent advances in optical microcomb technology provide a competitive solution to meet these requirements by generating a substantial number of widely spaced wavelengths from a micro-scale resonator, together with added benefits of significantly reduced device footprint, power consumption, and complexity [37]. In contrast, conventional multi-wavelength sources, such as discrete laser arrays [38], fiber Bragg grating arrays [39], laser frequency combs generated by electro-optic (EO) modulation [40], and mode-locked fiber lasers [41] suffer from limitations in one form or another, such as a limited number of wavelength channels and insufficient channel spacings.
Early implementations of microcomb-based RF photonic transversal signal processors simply replaced conventional multi-wavelength sources with optical microcombs while retaining all other components as discrete devices [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Although this already yields significant benefits, there is much more to be gained by increasing the level of integration for the entire processing system, particularly with respect to the system size, power consumption, and cost. Recently, several processors comprised entirely of integrated components have also been demonstrated [42,43]. Despite based on the same operation principle, the processors implemented by discrete and integrated components present different processing performance.
In this paper, we provide a comparative study of the performance of microcomb-based RF photonic transversal signal processors implemented by discrete and integrated components. First, we compare the performance of state-of-the-art processors, focusing on the processing accuracy. Next, we conduct analysis of multiple factors that induce the performance differences, including tap number and imperfect response of experimental components. Finally, we discuss the potential for future development. These results provide a comprehensive comparison and valuable perspectives for these processors with high reconfigurability for diverse signal processing applications.

Ⅱ. Microcomb-based rf photonic transversal signal processors

RF transversal signal processors are implemented based on the transversal filter structure in digital signal processing, which features a finite impulse response and has found applications in a wide range of signal processing functions [1]. Implementing these processors by using RF photonic technology can yield significantly higher processing bandwidth compared to their electronic counterparts [1], and the use of optical microcombs provides a powerful multiwavelength source that is critical for the RF photonic system. Figure 1(a) illustrates the operation principle of a microcomb-based RF photonic transversal signal processor. The processor employs an optical microcomb as a multiwavelength source, which simultaneously generates numerous wavelength channels as discrete taps. Input RF signal is modulated onto each wavelength channel via EO modulation, producing multiple RF replicas. Next, optical spectral shaping is applied to weight these modulated replicas, and time delay is introduced between adjacent wavelength channels. Finally, the weighted and delayed RF replicas are added together through photodetection to generate the final RF output of the processor. After going through the processing flow in Figure 1(a), the output RF signal s(t) can be given by [1].
s ( t ) = ∑ M - 1 n = 0 a n f ( t   –   n Δ T ) ,
where f(t) is the input RF signal, M is the tap number, an (n = 0, 1, 2, …, M-1) is the tap weight of the nth tap, and ΔT is the time delay between adjacent wavelength channels. Therefore, the system’s impulse response can be expressed as [1].
h ( t ) = ∑ M - 1 n = 0 a n δ ( t   –   n Δ T ) ,
After Fourier transformation from Eq. (2), the spectral transfer function of the processor can be described as
H ( ω ) = FT   [ h ( t ) ] = ∑ M - 1 n = 0 a n e - j ω n Δ T ,
According to Eqs. (1) ‒ (3), different processing functions can be realized by appropriately setting the tap coefficients an (n = 0, 1, 2, …, M-1) without changing the hardware, which allows for a high reconfigurability for the processor.
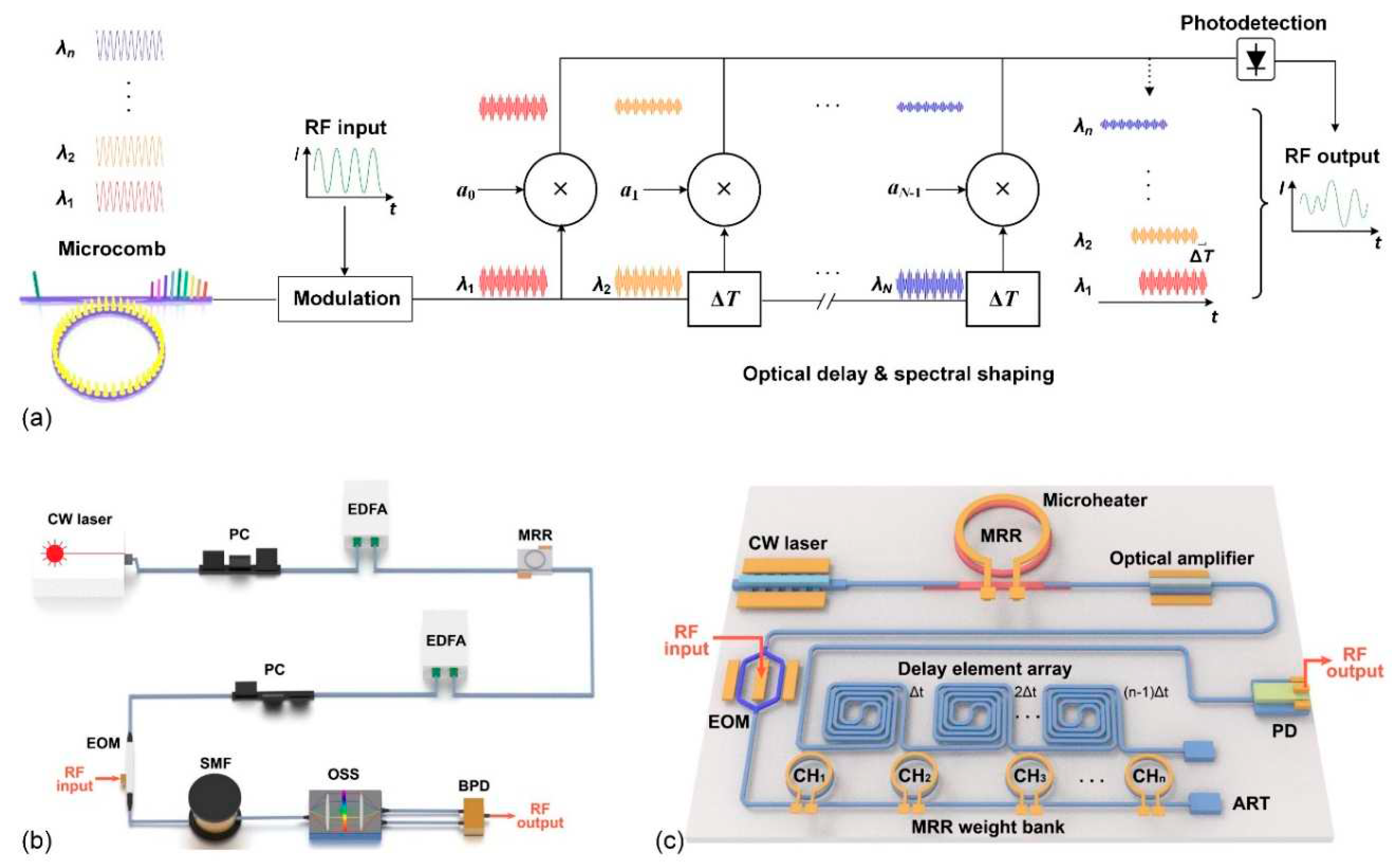
Preprints 82344 g001
Figure 1. (a) Schematic illustration of the operation principle of a microcomb-based RF photonic transversal signal processor. (b) Schematic of a microcomb-based RF photonic transversal signal processor implemented by discrete components. (c) Schematic of an on-chip microcomb-based RF photonic transversal signal processor implemented by integrated components. EOM: electro-optic modulator. RF: radio frequency. PD: photodetector. CW laser: continuous-wave laser. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. SMF: single-mode fibre. OSS: optical spectral shaper. BPD: balanced photodetector. BPD: balanced photodetector. ART: anti-reflection termination.
Figure 1. (a) Schematic illustration of the operation principle of a microcomb-based RF photonic transversal signal processor. (b) Schematic of a microcomb-based RF photonic transversal signal processor implemented by discrete components. (c) Schematic of an on-chip microcomb-based RF photonic transversal signal processor implemented by integrated components. EOM: electro-optic modulator. RF: radio frequency. PD: photodetector. CW laser: continuous-wave laser. EDFA: erbium-doped fibre amplifier. PC: polarization controller. MRR: microring resonator. SMF: single-mode fibre. OSS: optical spectral shaper. BPD: balanced photodetector. BPD: balanced photodetector. ART: anti-reflection termination.
Preprints 82344 g001
Based on the operation principle in Figure 1(a), microcomb-based RF photonic transversal signal processors can be practically implemented into two forms. The first form is illustrated in Figure 1(b), where all the components are discrete devices except for an integrated microring resonator (MRR) used to generate optical microcombs. The second is comprised entirely of integrated components, as shown in Figure 1(c). To simplify our discussion, we will refer to the processors implemented in these two forms as discrete and integrated processors. Early microcomb-based RF photonic transversal signal processors were in the form of discrete processors [1,2], while more recently, some integrated processors have been demonstrated [42,43]. Although the operation principle remains consistent across these two forms, their different components result in distinct performance. In the following, we compare their performance in Section Ⅲ and discuss their potential for improvement in Section Ⅳ.

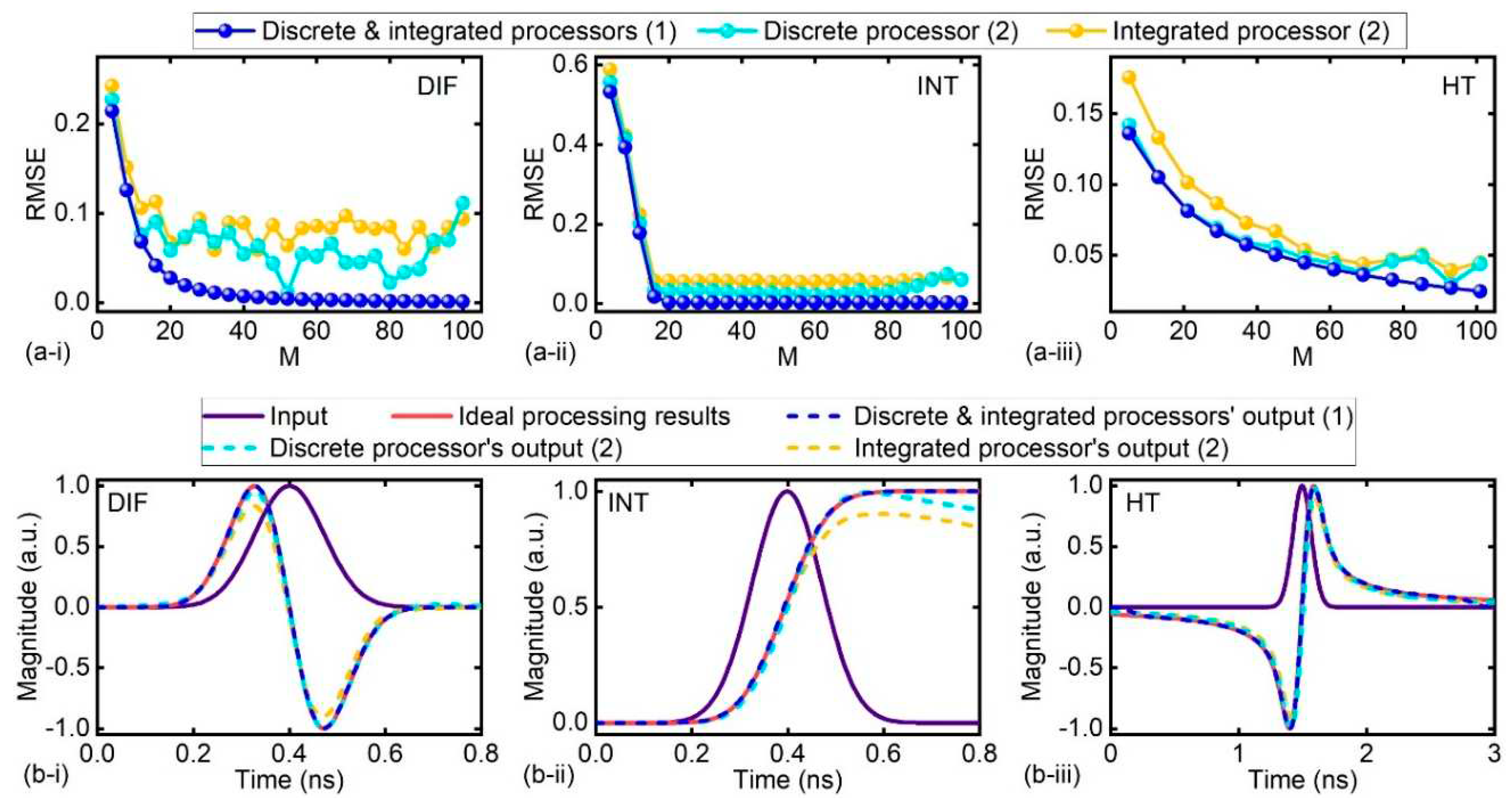
Ⅲ. Performance comparison of discrete and integrated processors

In this section, we compare the performance of discrete and integrated processors shown in Figure 1(b) and (c), respectively. Although the size, weight, and power consumption (SWaP) of integrated processors are greatly reduced compared with the discrete processors, the state-of-the-art integrated processors suffer from limited tap numbers due to the restrictions imposed by the integrated components. Currently, integrated processors with only 8 [42] and 12 taps [43] have been demonstrated, whereas discrete processors have been implemented with up to 80 taps [1,44]. The difference in the tap numbers results in a difference in the processing accuracy [44]. In addition, the imperfect response of experimental components also induces processing errors. These mainly include noise of microcombs, chirp of the EOM, errors in the delay element, and errors of the spectral shaping module [44].
Table 1 summarizes parameters of the components in the three processors that we investigate, including a discrete processor (Processor 1) and two integrated processors (Processors 2 and 3). There are two integrated processors: one with the same tap number as that in Ref. [42] and the other with an increased tap number to demonstrate the potential for improvement. To characterize the errors induced by imperfect experimental components, optical signal-to-noise ratios (OSNRs), chirp parameters (α), error of the delay element (tv), and random tap coefficient errors (RTCEs) are introduced. These parameters are all set based on the real processors in Refs. [43,44,45,46,47]. For comparison, we assume that the three processors employ the same microcomb with a comb spacing of 0.4 nm (~50 GHz). We also assume that the time delay between adjacent taps in Eq. (3) is ∆T = 33.4 ps to ensure the same operation bandwidth.
Compared with discrete EOM, the integrated EOM has a relatively high chirp parameter in Table 1, mainly because achieving an accurate bias point and precise electrode placement is more challenging for integrated devices [47]. The lower accuracy for the delay element in the discrete processor is mainly caused by the high-order dispersion of the dispersive medium (e.g., optical fibre), which results in non-uniform time delays between adjacent wavelength channels [44]. In contrast, in integrated processors time delay is introduced by integrated optical delay lines (e.g., Si spiral waveguides), which exhibit a higher accuracy owing to the precise control over the amount of delay achieved by designing specific length and refractive index profile [48]. The accuracy differences between the integrated and discrete spectral shaping modules are more noticeable. Although the integrated spectral shaping modules have much lower tap numbers, they have lower spectral shaping accuracy compared to their discrete counterparts. This is due to the fact that commercial discrete waveshapers based on mature liquid crystal on silicon (LCoS) technology offer much better accuracy for amplitude and phase control, as well as inter-channel synchronization [49].
In our following analysis, three typical signal processing functions including first-order differentiation (DIF), integration (INT), and Hilbert transform (HT) are taken as examples to compare the accuracy of discrete and integrated processors. The tap numbers required to achieve these processing functions are designed based on our previous work in Refs. [1]. To quantify the comparison of processing accuracy, the root mean square error (RMSE) is introduced to compare the deviation between the processors’ outputs and the ideal results, which is expressed as
RMSE = ∑ k i = 1 ( Y i   –   y i ) 2 k    
where k is the number of sampled points, Y1, Y2, …, Yn are the values of the ideal result, and y1, y2, …, yn are the values of the output of the processors.
Figure 2(a) – (c) show the outputs of Processors 1 – 3 in Table 1 that perform DIF, INT, and HT, respectively. The input RF signal is a Gaussian pulse with a full-width-at-half-maximum (FWHM) of ~0.17 ns. Here we show the processors’ outputs with errors induced by (1) only limited tap numbers and (2) both limited tap numbers and experimental errors. The ideal processing results are also shown for comparison. Deviations between the processors’ outputs and the ideal results are observed for all three functions, and the deviations become more significant when taking into account the experimental errors.
Figure 3 compares RMSEs of the processors in Figure 2. The higher processing accuracy of the discrete processor, compared to the integrated processors, is reflected by the lower RMSEs of Processor 1 for all three processing functions. In addition, the RMSEs of Processor 3 are lower compared to Processor 2, which indicates a higher processing accuracy achieved by increasing the tap number. According to the results in Figure 3, the primary factor that contributes to the degradation of accuracy for integrated processors is the limited tap number. Whereas for discrete processors with a sufficiently large tap number, the processing inaccuracy is mainly induced by the imperfect response of experimental components. We also note that the differences in RMSEs among Processors 1 – 3 are more prominent for the INT than the other two processing functions, indicating a higher requirement for a greater number of taps to improve the processing accuracy of INT. In addition, experimental errors have a substantial impact on the RMSEs of DIF, whereas their impact on HT is very small.

Ⅳ. Potential for improvement

In this section, we discuss the potential for improvement for both the discrete and integrated processors. In Figure 4(a), we quantitively analyze the influence of tap number M on the processing accuracy, where the parameters of the input signal and the processor components are kept the same as those in Figure 2. Similar to that in Figure 2 and Figure 3, we show the results with errors induced by (1) only limited tap numbers and (2) both limited tap numbers and experimental errors. It is evident that when assuming no experimental errors, both discrete and integrated processors exhibit the same RMSE values at the same M, as they possess identical comb spacing and time delay. When experimental errors are considered, the RMSEs no longer exhibit a monotonic decrease with the tap number M as observed when assuming no experimental errors. This can be attributed to the accumulated experimental errors as M increases, such as increased shaping errors in both discrete and integrated processors, as well as the increased errors of time delay induced by higher-order dispersion in discrete processors [44].
When considering experimental errors, DIF, INT, and HT require a tap number of 20, 20, and 80 to achieve a RMSE of ~0.05, respectively. Although this can be easily achieved by the discrete processor, it is challenging for the state-of-the-art integrated processors due to the significantly increased complexity and degraded processing accuracy for M ≥ 20. The increased complexity results from the increased numbers of MRRs, micro-heaters, and spiral waveguides in Figure 1(c). Although integrated processors have the advantage of monotonically integrating a large number of these building blocks, achieving their precise tuning and control can be challenging, especially when dealing with a large number of taps. On the other hand, fabrication errors, additional loss, and thermal drifts in these building blocks degrade the cooperative operation of different wavelength channels, and the processing errors resulting from these factors increase super linearly with the tap number.
Figure 4(b) compares the output waveforms of both discrete and integrated processors with the same tap number M = 80. Compared to the discrete processor, the experimental errors have more significant influence on the processing accuracy of the integrated processor. Note that we have not taken into account any additional processing errors resulting from factors that may degrade the cooperative operation of different wavelength channels, as discussed earlier. Considering these factors could lead to even higher errors.
To reduce the errors induced by imperfect response of experimental components, employing advanced mode-locking approaches [1] to reduce the noise of microcombs could be beneficial for both discrete and integrated processors. For integrated processors, the chirp of silicon EOM can be mitigated by using push-pull configurations as well as p-n depletion mode structure [47], and proper methods to calibrate the bias point [43]. The shaping errors of integrated spectral shapers can be alleviated via calibration procedures and gradient-descent control [43]. Integrated delay elements introduce additional loss especially when using a waveguide with high propagation loss, and adiabatic Euler bends can be employed to achieve low-loss and low-crosstalk waveguide bends [48]. The use of a wavelength-addressable serial integration scheme can also enable large-scale integration [50]. On the other hand, for discrete processors, there is still room for improving the processing accuracy. Errors of delay elements induced by higher-order dispersion can be reduced by using programmable phase characteristics of optical spectral shapers (OSSs), and the shaping errors can be minimized through employing feedback control [44]. These results have significant implications for all microwave photonics devices based on microcomb sources. [51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97]

Ⅴ. Conclusion

In summary, we provide a comparative study of the performance between microcomb-based RF photonic transversal signal processors implemented by discrete and integrated components. We first compare the performance of state-of-the-art processors, especially the processing accuracy. Next, analysis of multiple factors that contribute to the performance differences is conducted, including tap number and imperfect response of experimental components. Finally, we discuss the potential for future improvement. Our results show that although current integrated processors are attractive in providing significantly reduced system size, power consumption, and cost, their processing accuracy is not as high as the discrete processors. In addition, there is still room for improvement for both the discrete and integrated processors. The results offer valuable insights for microcomb-based RF photonic transversal signal processors with high reconfigurability for diverse applications.

References

  1. Sun, Y.; Wu, J.; Tan, M.; Xu, X.; Li, Y.; Morandotti, R.; Mitchell, A.; Moss, D.J. Applications of optical microcombs. Adv. Opt. Photon- 2023, 15, 86. [Google Scholar] [CrossRef]
  2. Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef] [PubMed]
  3. Weiwei Han, Zhihui Liu, Yifu Xu, Mengxi Tan, Yuhua Li, Xiaotian Zhu, Yanni Ou, Feifei Yin, Roberto Morandotti, Brent E. Little, Sai Tak Chu, Xingyuan Xu, David J. Moss, and Kun Xu, “Dual-polarization RF Channelizer Based on Microcombs”, Journal of Lightwave Technology (2023).
  4. Mengxi Tan, Xingyuan Xu, Andreas Boes, Bill Corcoran, Thach G. Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Jiayang Wu, Arnan Mitchell, and David J. Moss, “Photonic signal processor for real-time video image processing at 17 Tb/s based on a Kerr microcomb”, Nature Communications Engineering 2 (2023).
  5. Yang Li, Yang Sun, Jiayang Wu, Guanghui Ren, Roberto Morandotti, Xingyuan Xu, Mengxi Tan, Arnan Mitchell, and David J. Moss, “Performance analysis of microwave photonic spectral filters based on optical microcombs”, Optics and Lasers in Engineering (2023).
  6. Yang Sun, Jiayang Wu, Yang Li, Xingyuan Xu, Guanghui Ren, Mengxi Tan, Sai Tak Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Optimizing the performance of microcomb based microwave photonic transversal signal processors”, Journal of Lightwave Technology 41 (2023).
  7. Sun, Y.; Wu, J.; Li, Y.; Tan, M.; Xu, X.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Quantifying the Accuracy of Microcomb-Based Photonic RF Transversal Signal Processors. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1–17. [Google Scholar] [CrossRef]
  8. Bai, Y.; Xu, X.; Tan, M.; Sun, Y.; Li, Y.; Wu, J.; Morandotti, R.; Mitchell, A.; Xu, K.; Moss, D.J. Photonic multiplexing techniques for neuromorphic computing. Nanophotonics 2022, 12, 795–817. [Google Scholar] [CrossRef]
  9. Xu, X.; Han, W.; Tan, M.; Sun, Y.; Li, Y.; Wu, J.; Morandotti, R.; Mitchell, A.; Xu, K.; Moss, D.J. , Neuromorphic computing based on wavelength-division multiplexing. IEEE Journal of Selected Topics in Quantum Electronics Special Issue on Optical Computing 2023, 29, 7400112. [Google Scholar] [CrossRef]
  10. Prayoonyong, C.; Boes, A.; Xu, X.; Tan, M.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J.; Corcoran, B. Frequency comb distillation for optical superchannel transmission. J. Light. Technol. 2021, 39, 1–1. [Google Scholar] [CrossRef]
  11. Tan, M.; Xu, X.; Wu, J.; Corcoran, B.; Boes, A.; Nguyen, T.G.; Chu, S.T.; E Little, B.; Morandotti, R.; Mitchell, A.; et al. Integral order photonic RF signal processors based on a soliton crystal micro-comb source. J. Opt. 2021, 23, 125701. [Google Scholar] [CrossRef]
  12. Tan, M.; Xu, X.; Boes, A.; Corcoran, B.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Lowery, A.J.; Morandotti, R.; et al. Highly Versatile Broadband RF Photonic Fractional Hilbert Transformer Based on a Kerr Soliton Crystal Microcomb. J. Light. Technol. 2021, 39, 7581–7587. [Google Scholar] [CrossRef]
  13. Li, Y.; Kang, Z.; Zhu, K.; Ai, S.; Wang, X.; Davidson, R.R.; Wu, Y.; Morandotti, R.; Little, B.E.; Moss, D.J.; Chu, A.S.T. All-optical RF frequency spectrum analyzer with a 5 Terahertz bandwidth based on CMOS-compatible high-index doped silica waveguides. Optics Letters 2021, 46, 1574–1577 . [Google Scholar] [CrossRef]
  14. Tan, M.; Xu, X.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Orthogonally polarized Photonic Radio Frequency single sideband generation with integrated micro-ring resonators. IOP Journal of Semiconductors 2021, 42, 041305. [Google Scholar] [CrossRef]
  15. Tan, M.; Xu, X.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Photonic radio frequency channelizers based on Kerr optical micro-combs. J. Semicond. 2021, 42. [Google Scholar] [CrossRef]
  16. Tan, M.; Xu, X.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. RF and microwave photonic temporal signal processing with Kerr micro-combs. Adv. Physics: X 2020, 6. [Google Scholar] [CrossRef]
  17. Tan, M.; Xu, X.; Boes, A.; Corcoran, B.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Photonic RF Arbitrary Waveform Generator Based on a Soliton Crystal Micro-Comb Source. J. Light. Technol. 2020, 38, 6221–6226. [Google Scholar] [CrossRef]
  18. Xu, X.; Tan, M.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Broadband photonic radio frequency channelizer with 90 channels based on a soliton crystal microcomb. Journal of Lightwave Technology 2020, 38, 5116–5121. [Google Scholar] [CrossRef]
  19. Bill Corcoran, Mengxi Tan, Xingyuan Xu, Andrew Boes, Jiayang Wu, Thach Nguyen, Sai T. Chu, Brent E. Little, Roberto Morandotti, Arnan Mitchell, and David J. Moss, “Ultra-dense optical data transmission over standard fiber with a single chip source”, Nature Communications 11 Article number: 2568 (2020). [CrossRef]
  20. X.Xu, M.Tan, J.Wu, A.Boes, B.Corcoran, T.G. Nguyen, S.T. Chu, B.E. Little, R.Morandotti, A.Mitchell, and D. J. Moss, “Photonic RF and microwave integrator with soliton crystal microcombs”, IEEE Transactions on Circuits and Systems: Express Briefs, Volume: 67, Issue: 12, pp. 3582–3586 (2020). [CrossRef]
  21. Tan, M.; Xu, X.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. Photonic RF and microwave filters based on 49 GHz and 200 GHz Kerr microcombs. Opt. Commun. 2020, 465, 125563. [Google Scholar] [CrossRef]
  22. Xu, X.; Tan, M.; Wu, J.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Corcoran, B.; Hicks, D.; Moss, D.J. Photonic perceptron based on a Kerr microcomb for scalable high speed optical neural networks. Laser and Photonics Reviews 2020, 14, 2000070. [Google Scholar] [CrossRef]
  23. Tan, M.; Xu, X.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. RF and Microwave Fractional Differentiator Based on Photonics. IEEE Trans. Circuits Syst. II: Express Briefs 2020, 67, 2767–2771. [Google Scholar] [CrossRef]
  24. Xu, X.; Tan, M.; Wu, J.; Boes, A.; Corcoran, B.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; et al. Photonic RF Phase-Encoded Signal Generation With a Microcomb Source. J. Light. Technol. 2020, 38, 1722–1727. [Google Scholar] [CrossRef]
  25. Xu, X.; Wu, J.; Tan, M.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Broadband microwave frequency conversion based on an integrated optical micro-comb source. Journal of Lightwave Technology 2020, 38, 332–338. [Google Scholar] [CrossRef]
  26. Tan, M.; Xu, X.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Broadband microwave and RF photonic fractional Hilbert transformer based on a 50GHz integrated Kerr micro-comb. Journal of Lightwave Technology 2019, 37, 6097–6104. [Google Scholar] [CrossRef]
  27. Xu, X.; Tan, M.; Wu, J.; Morandotti, R.; Mitchell, A.; Moss, D.J. Microcomb-based photonic RF signal processing. IEEE Photonics Technology Letters 2019, 31, 1854–1857. [Google Scholar] [CrossRef]
  28. Xu, X.; Tan, M.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Advanced adaptive photonic RF filters based on an optical micro-comb source with 80 taps. Journal of Lightwave Technology 2019, 37, 1288–1295. [Google Scholar] [CrossRef]
  29. Xu, X.; Tan, M.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. High performance RF filters via bandwidth scaling with Kerr micro-combs. APL Photon- 2019, 4, 026102. [Google Scholar] [CrossRef]
  30. Moss, D.J.; Xu, X.; Wu, J.; Mitchell, A.; Morandotti, R.; Little, B.E.; Chu, S.T. Integrated Kerr micro-comb sources for photonic microwave applications. 2018, 10518, 105180B. [CrossRef]
  31. Xu, X.; Wu, J.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Broadband RF Channelizer Based on an Integrated Optical Frequency Kerr Comb Source. J. Light. Technol. 2018, 36, 4519–4526. [Google Scholar] [CrossRef]
  32. Xu, X.; Wu, J.; Nguyen, T.G.; Moein, T.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Photonic microwave true time delays for phased array antennas using a 49 GHz FSR integrated optical micro-comb source [Invited]. Photon- Res. 2018, 6, B30–B36. [Google Scholar] [CrossRef]
  33. Wu, J.; Xu, X.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. RF photonics: An optical micro-combs’ perspective. IEEE Journal of Selected Topics in Quantum Electronics 2018, 24, 6101020. [Google Scholar] [CrossRef]
  34. Xu, X.; Wu, J.; Nguyen, T.G.; Shoeiby, M.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Advanced RF and microwave functions based on an integrated optical frequency comb source. Opt. Express 2018, 26, 2569–2583. [Google Scholar] [CrossRef]
  35. Xu, X.; Wu, J.; Shoeiby, M.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Reconfigurable broadband microwave photonic intensity differentiator based on an integrated optical frequency comb source. APL Photon- 2017, 2. [Google Scholar] [CrossRef]
  36. Nguyen, T.G.; Shoeiby, M.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Integrated frequency comb source based Hilbert transformer for wideband microwave photonic phase analysis. Opt. Express 2015, 23, 22087–22097. [Google Scholar] [CrossRef] [PubMed]
  37. Chang, L.; Liu, S.; Bowers, J.E. Integrated optical frequency comb technologies. Nat. Photon- 2022, 16, 95–108. [Google Scholar] [CrossRef]
  38. Zhang, J.; Yao, J. Photonic True-Time Delay Beamforming Using a Switch-Controlled Wavelength-Dependent Recirculating Loop. J. Light. Technol. 2016, 34, 3923–3929. [Google Scholar] [CrossRef]
  39. Yu, G.; Zhang, W.; Williams, J. High-performance microwave transversal filter using fiber Bragg grating arrays. IEEE Photon- Technol. Lett. 2000, 12, 1183–1185. [Google Scholar] [CrossRef]
  40. Supradeepa, V.R.; Long, C.M.; Wu, R.; Ferdous, F.; Hamidi, E.; Leaird, D.E.; Weiner, A.M. Comb-based radiofrequency photonic filters with rapid tunability and high selectivity. Nat. Photon- 2012, 6, 186–194. [Google Scholar] [CrossRef]
  41. Ortigosa-Blanch, A.; Mora, J.; Capmany, J.; Ortega, B.; Pastor, D. Tunable radio-frequency photonic filter based on an actively mode-locked fiber laser. Opt. Lett. 2006, 31, 709–711. [Google Scholar] [CrossRef]
  42. Shu, H.; Chang, L.; Tao, Y.; Shen, B.; Xie, W.; Jin, M.; Netherton, A.; Tao, Z.; Zhang, X.; Chen, R.; et al. Microcomb-driven silicon photonic systems. Nature 2022, 605, 457–463. [Google Scholar] [CrossRef]
  43. Bai, B.; Yang, Q.; Shu, H.; Chang, L.; Yang, F.; Shen, B.; Tao, Z.; Wang, J.; Xu, S.; Xie, W.; et al. Microcomb-based integrated photonic processing unit. Nat. Commun. 2023, 14, 1–10. [Google Scholar] [CrossRef]
  44. Sun, Y.; Wu, J.; Li, Y.; Tan, M.; Xu, X.; Chu, S.T.; Little, B.E.; Morandotti, R.; Mitchell, A.; Moss, D.J. Quantifying the Accuracy of Microcomb-Based Photonic RF Transversal Signal Processors. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1–17. [Google Scholar] [CrossRef]
  45. Iii, C.E.R.; Carini, J.L.; Pechkis, J.A.; Gould, P.L. Characterization and compensation of the residual chirp in a Mach-Zehnder-type electro-optical intensity modulator. Opt. Express 2010, 18, 1166–1176. [Google Scholar] [CrossRef]
  46. Tait, A.N.; de Lima, T.F.; Nahmias, M.A.; Shastri, B.J.; Prucnal, P.R. Continuous Calibration of Microring Weights for Analog Optical Networks. IEEE Photon- Technol. Lett. 2016, 28, 887–890. [Google Scholar] [CrossRef]
  47. Sinatkas, G.; Christopoulos, T.; Tsilipakos, O.; Kriezis, E.E. Electro-optic modulation in integrated photonics. J. Appl. Phys. 2021, 130, 010901. [Google Scholar] [CrossRef]
  48. Ji, X.; Liu, J.; He, J.; Wang, R.N.; Qiu, Z.; Riemensberger, J.; Kippenberg, T.J. Compact, spatial-mode-interaction-free, ultralow-loss, nonlinear photonic integrated circuits. Commun. Phys. 2022, 5, 1–9. [Google Scholar] [CrossRef]
  49. Tait, A.N.; Jayatilleka, H.; De Lima, T.F.; Ma, P.Y.; Nahmias, M.A.; Shastri, B.J.; Shekhar, S.; Chrostowski, L.; Prucnal, P.R. Feedback control for microring weight banks. Opt. Express 2018, 26, 26422–26443. [Google Scholar] [CrossRef] [PubMed]
  50. Kuramochi, E.; Nozaki, K.; Shinya, A.; Takeda, K.; Sato, T.; Matsuo, S.; Taniyama, H.; Sumikura, H.; Notomi, M. Large-scale integration of wavelength-addressable all-optical memories on a photonic crystal chip. Nat. Photon- 2014, 8, 474–481. [Google Scholar] [CrossRef]
  51. Murphy, M.T.; Udem, T.; Holzwarth, R.; Sizmann, A.; Pasquini, L.; Araujo-Hauck, C.; Dekker, H.; S. D'Odorico; Fischer, M.; Hänsch, T.W.; Manescau, A. High-precision wavelength calibration of astronomical spectrographs with laser frequency combs. Monthly Notices of the Royal Astronomical Society 2007, 380, 839–847. [Google Scholar] [CrossRef]
  52. Steinmetz, T.; Wilken, T.; Araujo-Hauck, C.; Holzwarth, R.; Hänsch, T.W.; Pasquini, L.; Manescau, A.; S. D'Odorico; Murphy, M.T.; Kentischer, T.; Schmidt, W.; Udem, T. Laser Frequency Combs for Astronomical Observations. Science 2008, 321, 1335–1337. [Google Scholar] [CrossRef]
  53. Li, C.H.; Benedick, A.J.; Fendel, P.; Glenday, A.G.; Kärtner, F.X.; Phillips, D.F.; Sasselov, D.; Szentgyorgyi, A.; Walsworth, R.L. A laser frequency comb that enables radial velocity measurements with a precision of 1 cm s-1. Nature 2008, 452, 610–612. [Google Scholar] [CrossRef]
  54. Zhu, S.; Li, M.; Wang, X.; Zhu, N.H.; Cao, Z.Z.; Li, W. Photonic generation of background-free binary phase-coded microwave pulses. Opt. Lett. 2018, 44, 94–97. [Google Scholar] [CrossRef]
  55. Li, Z.; Li, W.; Chi, H.; Zhang, X.; Yao, J. Photonic Generation of Phase-Coded Microwave Signal With Large Frequency Tunability. IEEE Photon- Technol. Lett. 2011, 23, 712–714. [Google Scholar] [CrossRef]
  56. Liu, W.; Gao, L.; Yao, J. Photonic generation of triangular waveforms based on a polarization modulator in a Sagnac loop. 2013, 68–71. [CrossRef]
  57. Hillerkuss, D.; Schmogrow, R.; Schellinger, T.; Jordan, M.; Winter, M.; Huber, G.; Vallaitis, T.; Bonk, R.; Kleinow, P.; Frey, F.; et al. 26 Tbit s−1 line-rate super-channel transmission utilizing all-optical fast Fourier transform processing. Nat. Photon- 2011, 5, 364–371. [Google Scholar] [CrossRef]
  58. Ataie, V.; Temprana, E.; Liu, L.; Myslivets, E.; Kuo, B.P.-P.; Alic, N.; Radic, S. Ultrahigh Count Coherent WDM Channels Transmission Using Optical Parametric Comb-Based Frequency Synthesizer. J. Light. Technol. 2015, 33, 694–699. [Google Scholar] [CrossRef]
  59. Weimann, C.; Schindler, P.C.; Palmer, R.T.; Wolf, S.T.; Bekele, D.A.; Korn, D.; Pfeifle, J.; Koeber, S.; Schmogrow, R.M.; Alloatti, L.; et al. Silicon-organic hybrid (SOH) frequency comb sources for terabit/s data transmission. [CrossRef]
  60. Chou, J.; Han, Y.; Jalali, B. Adaptive RF-photonic arbitrary waveform generator. IEEE Photon- Technol. Lett. 2003, 15, 581–583. [Google Scholar] [CrossRef]
  61. Cundiff, S.T.; Weiner, A.M. Optical arbitrary waveform generation. Nat. Photon- 2010, 4, 760–766. [Google Scholar] [CrossRef]
  62. Rashidinejad, A.; Li, Y.; Weiner, A.M. Recent Advances in Programmable Photonic-Assisted Ultrabroadband Radio-Frequency Arbitrary Waveform Generation. IEEE J. Quantum Electron. 2015, 52, 1–17. [Google Scholar] [CrossRef]
  63. Sano, T. Kobayashi, S. Yamanaka, A. Matsuura, H. Kawakami, Y. Miyamoto, K. Ishihara, and H. Masuda, "102.3-Tb/s (224 × 548-Gb/s) C- and extended L-band all-Raman transmission over 240 km using PDM-64QAM single carrier FDM with digital pilot tone," in OFC/NFOEC(2012), pp. 1–3.
  64. G.694.1 : Spectral grids for WDM applications: DWDM frequency grid," https://www.itu.int/rec/T-REC-G.694.1-202010-I/en.
  65. Pfeifle, J.; Vujicic, V.; Watts, R.T.; Schindler, P.C.; Weimann, C.; Zhou, R.; Freude, W.; Barry, L.P.; Koos, C. "Flexible terabit/s Nyquist-WDM super-channels using a gain-switched comb source. Opt. Express 2015, 23, 724–738. [Google Scholar] [CrossRef] [PubMed]
  66. Barry, J.; Lee, E. Performance of coherent optical receivers. Proc. IEEE 1990, 78, 1369–1394. [Google Scholar] [CrossRef]
  67. W. Freude, R. W. Freude, R. Schmogrow, B. Nebendahl, M. Winter, A. Josten, D. Hillerkuss, S. Koenig, J. Meyer, M. Dreschmann, M. Huebner, C. Koos, J. Becker, and J. Leuthold, "Quality metrics for optical signals: Eye diagram, Q-factor, OSNR, EVM and BER," in 2012 14th International Conference on Transparent Optical Networks (ICTON)(2012), pp. 1–4.
  68. Mazur, M.; Suh, M.G.; Fülöp, A.; Schröder, J.; Company, V.T.; Karlsson, M.; Vahala, K.; Andrekson, P. High Spectral Efficiency Coherent Superchannel Transmission With Soliton Microcombs. Journal of Lightwave Technology 2021, 39, 4367–4373. [Google Scholar] [CrossRef]
  69. Geng, Y.; Zhou, H.; Han, X.; Cui, W.; Zhang, Q.; Liu, B.; Deng, G.; Zhou, Q.; Qiu, K. Coherent optical communications using coherence-cloned Kerr soliton microcombs. Nat. Commun. 2022, 13, 1–8. [Google Scholar] [CrossRef]
  70. Capmany, J.; Novak, D. Microwave photonics combines two worlds. Nat. Photon- 2007, 1, 319–330. [Google Scholar] [CrossRef]
  71. Yao, J. Microwave Photonics. Journal of Lightwave Technology 2009, 27, 314–335. [Google Scholar] [CrossRef]
  72. T. Okoshi, and K. Kikuchi, Coherent optical fiber communications (Springer Science & Business Media, 1988).
  73. Li, G. Recent advances in coherent optical communication. Adv. Opt. Photon- 2009, 1, 279–307. [Google Scholar] [CrossRef]
  74. Schmogrow, R.; Nebendahl, B.; Winter, M.; Josten, A.; Hillerkuss, D.; Koenig, S.; Meyer, J.; Dreschmann, M.; Huebner, M.; Koos, C.; et al. Error Vector Magnitude as a Performance Measure for Advanced Modulation Formats. IEEE Photon- Technol. Lett. 2011, 24, 61–63. [Google Scholar] [CrossRef]
  75. Xie, X.; Dai, Y.; Ji, Y.; Xu, K.; Li, Y.; Wu, J.; Lin, J. Broadband Photonic Radio-Frequency Channelization Based on a 39-GHz Optical Frequency Comb. IEEE Photon- Technol. Lett. 2012, 24, 661–663. [Google Scholar] [CrossRef]
  76. Wang, W.; Davis, R.; Jung, T.; Lodenkamper, R.; Lembo, L.; Brock, J.; Wu, M. Characterization of a coherent optical RF channelizer based on a diffraction grating. IEEE Trans. Microw. Theory Tech. 2001, 49, 1996–2001. [Google Scholar] [CrossRef]
  77. Dutt, A.; Joshi, C.; Ji, X.; Cardenas, J.; Okawachi, Y.; Luke, K.; Gaeta, A.L.; Lipson, M. On-chip dual-comb source for spectroscopy. Sci. Adv. 2018, 4, e1701858. [Google Scholar] [CrossRef]
  78. Bao, C.; Yuan, Z.; Wang, H.; Wu, L.; Shen, B.; Sung, K.; Leifer, S.; Lin, Q.; Vahala, K. Interleaved difference-frequency generation for microcomb spectral densification in the mid-infrared. Optica 2020, 7, 309–315. [Google Scholar] [CrossRef]
  79. Coddington, I.; Swann, W.; Newbury, N. Coherent dual-comb spectroscopy at high signal-to-noise ratio. Phys. Rev. A 2010, 82. [Google Scholar] [CrossRef]
  80. Zou, X.; Lu, B.; Pan, W.; Yan, L.; Stöhr, A.; Yao, J. Photonics for microwave measurements. Laser Photon- Rev. 2016, 10, 711–734. [Google Scholar] [CrossRef]
  81. Coddington, I.; Newbury, N.; Swann, W. Dual-comb spectroscopy. Optica 2016, 3, 414–426. [Google Scholar] [CrossRef]
  82. Bao, C.; Yuan, Z.; Wu, L.; Suh, M.-G.; Wang, H.; Lin, Q.; Vahala, K.J. Architecture for microcomb-based GHz-mid-infrared dual-comb spectroscopy. Nat. Commun. 2021, 12, 1–8. [Google Scholar] [CrossRef]
  83. Jang, Y.-S.; Liu, H.; Yang, J.; Yu, M.; Kwong, D.-L.; Wong, C.W. Nanometric Precision Distance Metrology via Hybrid Spectrally Resolved and Homodyne Interferometry in a Single Soliton Frequency Microcomb. Phys. Rev. Lett. 2021, 126, 023903. [Google Scholar] [CrossRef]
  84. Lamb, E.S.; Carlson, D.R.; Hickstein, D.D.; Stone, J.R.; Diddams, S.A.; Papp, S.B. Optical-Frequency Measurements with a Kerr Microcomb and Photonic-Chip Supercontinuum. Phys. Rev. Appl. 2018, 9, 024030. [Google Scholar] [CrossRef]
  85. Wang, B.; Yang, Z.; Zhang, X.; Yi, X. Vernier frequency division with dual-microresonator solitons. Nat. Commun. 2020, 11, 1–7. [Google Scholar] [CrossRef]
  86. Wang, R.; Chen, L.; Hu, H.; Zhao, Y.; Zhang, C.; Zhang, W.; Zhang, X. Precise dynamic characterization of microcombs assisted by an RF spectrum analyzer with THz bandwidth and MHz resolution. Opt. Express 2021, 29, 2153–2161. [Google Scholar] [CrossRef]
  87. Tan, T.; Yuan, Z.; Zhang, H.; Yan, G.; Zhou, S.; An, N.; Peng, B.; Soavi, G.; Rao, Y.; Yao, B. Multispecies and individual gas molecule detection using Stokes solitons in a graphene over-modal microresonator. Nat. Commun. 2021, 12, 1–8. [Google Scholar] [CrossRef]
  88. Minoshima, K.; Matsumoto, H. High-accuracy measurement of 240-m distance in an optical tunnel by use of a compact femtosecond laser. Appl. Opt. 2000, 39, 5512–5517. [Google Scholar] [CrossRef]
  89. Coddington, I.; Swann, W.C.; Nenadovic, L.; Newbury, N.R. Rapid and precise absolute distance measurements at long range. Nat. Photon- 2009, 3, 351–356. [Google Scholar] [CrossRef]
  90. Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.N.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C.; et al. Autonomous driving in urban environments: Boss and the Urban Challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef]
  91. Behroozpour, B.; Sandborn, P.A.M.; Wu, M.C.; Boser, B.E. Lidar System Architectures and Circuits. IEEE Commun. Mag. 2017, 55, 135–142. [Google Scholar] [CrossRef]
  92. Cui, M.; Zeitouny, M.G.; Bhattacharya, N.; Berg, S.A.v.D.; Urbach, H.P. Long distance measurement with femtosecond pulses using a dispersive interferometer. Opt. Express 2011, 19, 6549–6562. [Google Scholar] [CrossRef]
  93. Berg, S.A.v.D.; van Eldik, S.; Bhattacharya, N. Mode-resolved frequency comb interferometry for high-accuracy long distance measurement. Sci. Rep. 2015, 5, 14661. [Google Scholar] [CrossRef]
  94. McCracken, R.A.; Charsley, J.M.; Reid, D.T. A decade of astrocombs: recent advances in frequency combs for astronomy [Invited]. Opt. Express 2017, 25, 15058–15078. [Google Scholar] [CrossRef] [PubMed]
  95. Yang, Q.-F.; Yi, X.; Yang, K.Y.; Vahala, K. Counter-propagating solitons in microresonators. Nat. Photon- 2017, 11, 560–564. [Google Scholar] [CrossRef]
  96. Ferrera, M.; Reimer, C.; Pasquazi, A.; Peccianti, M.; Clerici, M.; Caspani, L.; Chu, S.T.; Little, B.E.; Morandotti, R.; Moss, D.J. CMOS compatible integrated all-optical radio frequency spectrum analyzer. Opt. Express 2014, 22, 21488–98. [Google Scholar] [CrossRef] [PubMed]
  97. Li, Y.; Kang, Z.; Zhu, K.; Ai, S.; Wang, X.; Davidson, R.R.; Wu, Y.; Morandotti, R.; Little, B.E.; Moss, D.J.; et al. All-optical RF spectrum analyzer with a 5 THz bandwidth based on CMOS-compatible high-index doped silica waveguides. Opt. Lett. 2021, 46, 1574–1577. [Google Scholar] [CrossRef]
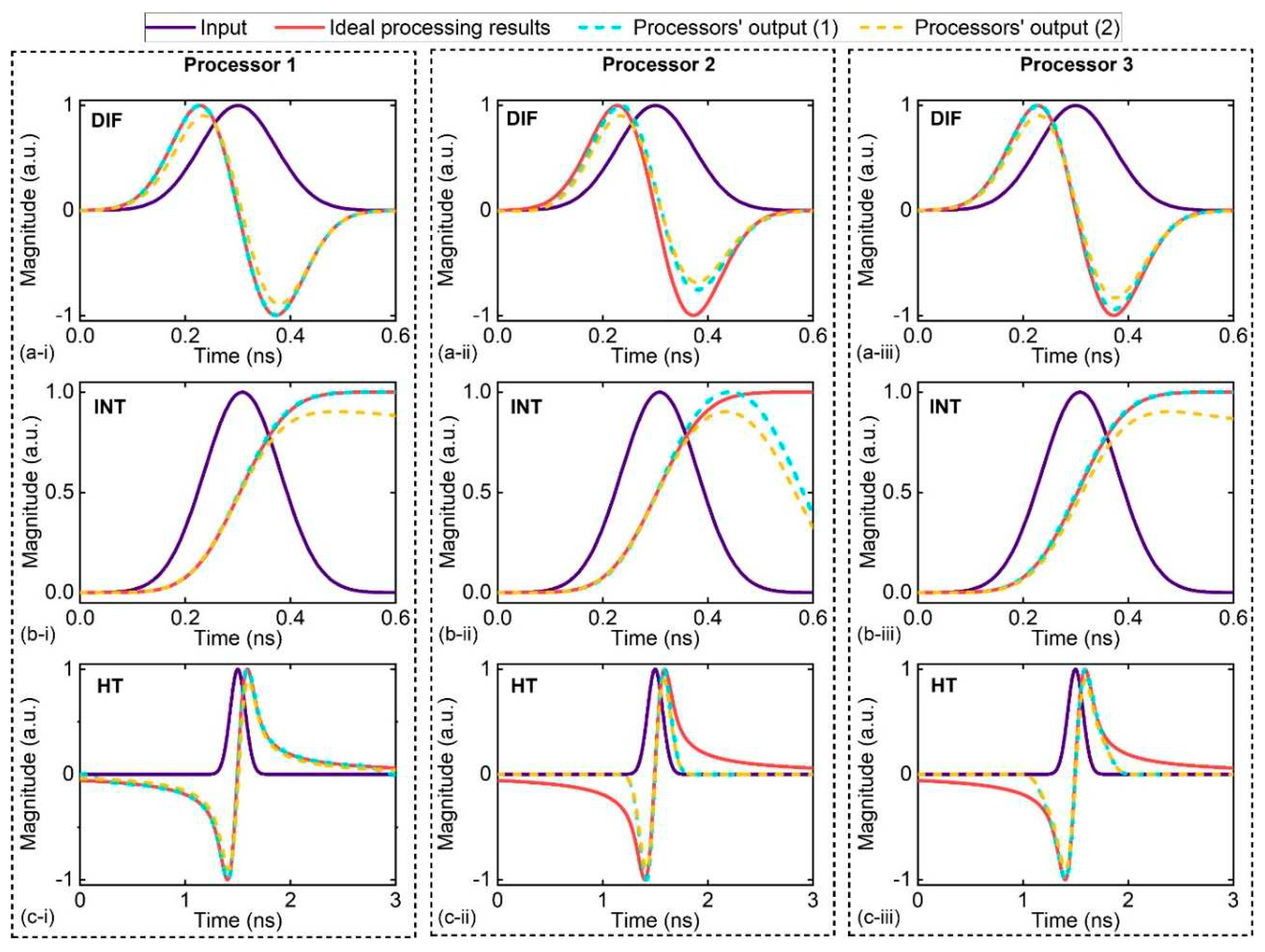
Preprints 82344 g002
Figure 2. Temporal waveform of Gaussian input pulse and output waveforms from Processors 1 – 3 that perform (a) differentiation (DIF), (b) integration (INT), and (c) Hilbert transform (HT). The processors’ outputs with errors induced by (1) only limited tap numbers and (2) both limited tap numbers and experimental errors are shown, together with the ideal processing result for comparison.
Figure 2. Temporal waveform of Gaussian input pulse and output waveforms from Processors 1 – 3 that perform (a) differentiation (DIF), (b) integration (INT), and (c) Hilbert transform (HT). The processors’ outputs with errors induced by (1) only limited tap numbers and (2) both limited tap numbers and experimental errors are shown, together with the ideal processing result for comparison.
Preprints 82344 g002
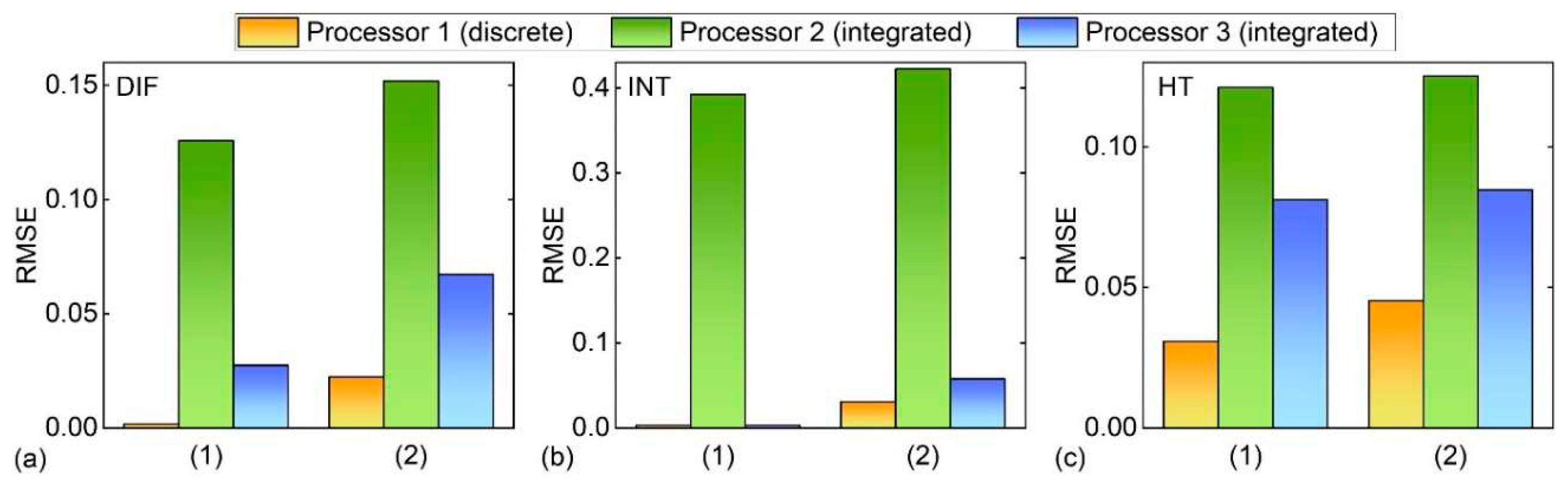
Preprints 82344 g003
Figure 3. Comparison of root mean square errors (RMSEs) of Processors 1 – 3 that perform (a) DIF, (b) INT, and (c) HT. The RMSEs of processors’ outputs with errors induced by (1) only limited tap numbers and (2) both limited tap numbers and experimental errors are shown.
Figure 3. Comparison of root mean square errors (RMSEs) of Processors 1 – 3 that perform (a) DIF, (b) INT, and (c) HT. The RMSEs of processors’ outputs with errors induced by (1) only limited tap numbers and (2) both limited tap numbers and experimental errors are shown.
Preprints 82344 g003
Preprints 82344 g004
Figure 4. Influence of the tap number and experimental errors on processing accuracy of the discrete and integrated processors. (a) RMSEs of processors that perform (i) DIF, (ii) INT, and (iii) HT as a function of tap number M. The RMSEs of processors’ outputs with errors induced by (1) only limited tap numbers and (2) both limited tap numbers and experimental errors are shown. (b) Temporal waveform of Gaussian input pulse and output waveforms of discrete and integrated processors that perform (i) DIF, (ii) INT, and (iii) HT. The processors’ outputs with errors induced by (1) limited tap number and (2) both the limited tap number and experimental errors are shown, together with the ideal processing result for comparison.
Figure 4. Influence of the tap number and experimental errors on processing accuracy of the discrete and integrated processors. (a) RMSEs of processors that perform (i) DIF, (ii) INT, and (iii) HT as a function of tap number M. The RMSEs of processors’ outputs with errors induced by (1) only limited tap numbers and (2) both limited tap numbers and experimental errors are shown. (b) Temporal waveform of Gaussian input pulse and output waveforms of discrete and integrated processors that perform (i) DIF, (ii) INT, and (iii) HT. The processors’ outputs with errors induced by (1) limited tap number and (2) both the limited tap number and experimental errors are shown, together with the ideal processing result for comparison.
Preprints 82344 g004
Table 1. Comparison of components’ parameters in discrete and integrated processors.
Table 1. Comparison of components’ parameters in discrete and integrated processors.
Discrete
processor		 No. Tap No. OSNR of microcombs Chirp parameter of the EOM Errors of the delay element RTCE of the spectral shaping module
1 M = 80 [44] OSNR : 20 dB [44] α : 0.1 [47] tv : 4% [44] RTCE : 5% [44]
Integrated
processors		 No. Tap No. OSNR of microcombs Chirp parameter of the EOM Error of the delay element RTCE of the spectral shaping module
2 M = 8 [42] OSNR : 20 dB [44] α : 0.8 [45] tv : 3% [43] RTCE : 9% [46]
No. Tap No. OSNR of microcombs Chirp parameter of the EOM Error of the delay element RTCE of the spectral shaping module
3 M = 20 OSNR : 20 dB [44] α : 0.8 [45] tv : 3% [43] RTCE : 9% [46]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated