Preprint

Article

Self-Interactions, Self-Energy and the Electromagnetic Contribution to the Anomalous g-Factor

Altmetrics

Downloads

255

Views

328

Comments

A peer-reviewed article of this preprint also exists.

Miroslav Georgiev^*

This version is not peer-reviewed

Submitted:

24 October 2023

Posted:

25 October 2023

You are already at the latest version

Alerts

Abstract

The present paper reports an exact approach quantifying the electromagnetic contribution to the anomalous magnetic moment occurring in isolated system comprised of non-composite particle carrying elementary electric charge. Essential averaging procedure and regularization of the electromagnetic field potentials necessary when quantifying the electromagnetic self-interactions and when deriving equations of motion without singularities and obeying the conservation laws are thoroughly discussed. The study shows that the dynamics of the considered system is associated to unique classical transcendental equations of motion satisfied by the particle's velocity and the electromagnetic contribution to the anomalous $g$-factor known from the quantum electrodynamics. The equations of motion lead to an exact analytical expression for the anomalous $g$-factor that provides more accurate result than that calculated with the aid of quantum electrodynamics. It matches the experimentally measured value reported in the literature to a one part per trillion. We obtain a_e=0.00115965218000(65) thus reveling the potential of non-perturbative, non-probability methods in predicting the electron's anomalous g-factor.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

The anomalous magnetic moment and the intrinsic dynamics of non-composite particles have been considered as unique features of the quantum field theory since the beginning of its elaboration [1,2,3,4,5]. The electron’s anomalous magnetic moment and its fundamental properties are the first to be studied and realized. With the aid of quantum electrodynamics the value of corresponding g-factor was predicted with a stunning accuracy [6,7,8,9,10,11,12,13], leaving no space for mistrusting its effectiveness. Determining with high accuracy the dynamics of the two remaining massive leptons carrying elementary charge, the muon and tau, is an active field of research. The muon’s anomalous magnetic moment [14,15] is still puzzling the community aiming to reduce the gap between theory and experiment [16,17,18,19,20,21,22], recently known to be of about

0.58

%. On the other hand, having a very short lifetime and being the massive among all leptons, measuring and predicting tau anomalous magnetic moment is a challenging task requiring great efforts [23,24,25,26,27,28,29]. Although, there is a serious discrepancy between theory and experiment, such efforts may have the potential to shed more light on the contribution of high order hadronic terms thus aiding in resolving the inconsistency in the muon data.

The microscopic electrodynamics underlying the occurrence of anomalous component in the intrinsic magnetic moment of the elementary particles is indispensably related to a singularity-free radial dependence of the effective mass density and corresponding self-energy [1,30,31,32,33,34,35]. The latter are believed to be uniquely addressable by the regularization and renormalization methods of quantum theory [36,37,38,39,40,41], with no classical analog. Yet, even within the standard methods of quantum mechanics, the evaluation of self-Coulomb energy in multi-electron systems still poses a challenge [42,43].

The quantum and classical theories are believed to have no interconnection pertaining to the occurrence of anomalous magnetic moment in the dynamics of non-composite particles and to the corresponding self-energy divergence problem. Therefore, a classical method with the potential to quantify the above mentioned anomalous magnetic moment and self-energy in the absence of singularities and electromagnetic radiation may contribute significantly in establishing a better interrelationship between both theories.

The present paper propose an exact approach quantifying the electromagnetic contribution to the anomalous g-factor and related dynamics of isolated non-composite particle carrying elementary electric charge. The approach build on the methods of classical electrodynamics in studying the microscopic dynamics of self-symmetric systems, like the considered one, by removing all singular points. It incorporates a particular spatial averaging procedure and regularization of the electromagnetic field potentials confining the field to the particle itself. Accordingly, the effect of self-repulsion is accounted for without singularity, or violation of the conservation laws, allowing a complete microscopic description of the system’s energy state. Two types of self-interactions are predicted, the self-Coulomb and self-Zeeman ones. Essentially, the considered approach results in a system of transcendental equations of motion satisfied by the particle’s velocity and the anomalous g-factor of electromagnetic origin. The derived system of equations ensure fast and accurate computational results and predicts the value of anomalous g-factor with the same success the perturbative approach of quantum electrodynamics does. In the present work, the computations are carried out with accuracy matching one prat in a billion.

The rest of the paper is organized as follows. The mathematical notation of all fundamental physical quantities characterizing the system under consideration along with essential interrelationships between the introduced observables are presented in Section 2. Furthermore, the section discusses the occurrence of self-interactions and their explicit representation. Lagrangian and Hamiltonian density representations are also given. The main results are outlined in Section 3, with computations carried out on Wolfram Mathematica. Section 4 summarizes the used approach and obtained results.

2. Theoretical background

2.1. General considerations

In the present study all representations are restricted to the mathematical framework of the classical relativistic mechanics and electrodynamics, overlooking all relevant quantum mechanical representations except the ones of immense significance. For the sake of clarity, all physical quantities and equations of motion are represented within the standard three-dimensional vector formalism. The four-vector convention is omitted, since the representation in Minkowski space with the relevant Lorentz group is straightforward [44,45,46].

Consider an isolated system composed of single non-composite particle of type q, with rest frame of reference

R

, rest mass

m_{q}

and electric charge

e_{q}^{\pm} = \pm e

\forall q

, where e denotes the elementary charge. Let

r_{c q} = α {\bar{λ}}_{c q}

be the particle’s electromagnetic radius at rest, where

α

and

{\bar{λ}}_{c q}

are the fine structure constant and reduced Compton wavelength, respectively. Let

u_{q}

, with

| u_{q} | = u_{q}

, be the velocity associated to the considered particle and

p_{q} = γ_{q} m_{q} u_{q}

the corresponding momentum in the observer’s rest frame

O

, where

γ_{q}

is the corresponding Lorentz factor. Furthermore, let

r_{q} = {\bar{λ}}_{q}

, with

λ_{q} = λ_{c q}

\sqrt{β_{q}^{- 2} - 1}

, be the particle’s electromagnetic radius in

O

, where

λ_{q}

is the particle’s intrinsic wavelength,

β_{q} = u_{q} c^{- 1}

and c denotes the light speed in vacuum. Since the particle alone represents the only center of symmetry in the system,

r_{q}

and

p_{q}

are conjugate intrinsic quantities, satisfying

r_{q} p_{q} = {\bar{λ}}_{c q} m_{q} c

. Accordingly, we have

u_{q} \equiv {\bar{λ}}_{q} ω_{q}

, where

ω_{q}

is the particle’s intrinsic frequency.

Let

ρ_{| e_{q}^{\pm} |}

and

ρ_{m_{q}}

, with

ρ_{s} = \frac{2}{V_{c q}} \int_{0}^{\infty} s δ (\bar{λ} - α {\bar{λ}}_{c q}) d \bar{λ}, s = {| e_{q}^{\pm} |, m_{q}},

be the charge and rest mass densities, respectively, such that

V_{c q} = 8 π \int_{0}^{\infty} \int_{0}^{\bar{λ}} δ (\bar{λ} - α {\bar{λ}}_{c q}) r^{2} d r d \bar{λ},

(1)

and

e_{q}^{\pm} = \pm \int_{Ω_{c q}} ρ_{| e_{q}^{\pm} |} d v, m_{q} = \int_{Ω_{c q}} ρ_{m_{q}} d v,

(2)

where the spatial domain

Ω_{c q} \in R^{3}

, with a boundary

\partial Ω_{c q}

, is such that

V_{c q} = \int_{Ω_{c q}} d v

Let for all q the system is characterized by an effective rest mass given by

M_{q} = \int_{Ω_{c q}} ρ_{M_{q}} d v,

(3)

where the corresponding density

ρ_{M_{q}} = ρ_{M_{q}} (r)

is a smooth function over

r \in (0, + \infty)

The system posses intrinsic angular momentum

f_{q}

and a corresponding magnetic one

μ_{q}

, with magnitudes

f_{q}

and

μ_{q}

, respectively. In accordance to Equation (3), we have

f_{q} = \int_{Ω_{c q}} r_{q} \times j_{m_{q}} d v, μ_{q} = \frac{1}{2} \int_{Ω_{c q}} r_{q} \times G_{q} j_{e_{q}^{\pm}} d v,

(4)

where

j_{m_{q}} = γ_{q} ρ_{m_{q}} u_{q}

and

j_{e_{q}^{\pm}} = \pm γ_{q} ρ_{| e_{q}^{\pm} |} u_{q}

are the system’s mass and charge density currents, respectively. Here,

G_{q}

is the integrand g-factor, where the latter reads

g_{e} = \frac{2}{V_{c q}} \int_{Ω_{c q}} G_{q} d v, G_{q} = \frac{| e_{q}^{\pm} | ρ_{M_{q}}}{m_{q} ρ_{| e_{q}^{\pm} |}} .

(5)

We further have

g_{e} = 2 (1 + a_{e})

, where

a_{e}

is the electromagnetic contribution to the anomalous g-factor.

Let us point out that according to Equation (5) the fraction

M_{q} m_{q}^{- 1}

is a constant for all q. We would like to stress, furthermore, that

f_{q}

is not an orbital angular momentum, since the system does not posses a center of symmetry independent from the particle. In the vector diagram sketching the dynamics of the considered system, the position vector

r_{q}

associated to the density currents will remain conjugate to the particle’s momentum for an infinite time, with

f_{q}

being an invariant. In other words, the dynamics related to both physical quantities given in Equation (4) is not time and space independent event for an observer in

O

and hence it cannot be associated to a free spinning sphere of radius

r_{c q}

, or

r_{q}

2.2. Field observables

Since the system is isolated,

{\dot{u}}_{q}

is a zero vector and the particle posses elementary electric charge confined within the time independent spatial domain

Ω_{c q}

, the resulting electric current and its density are time and spatially independent. Accordingly, the electric

E_{q}

and magnetic

B_{q}

components of the corresponding electromagnetic field in

O

are time independent and spatially conjugated to the particle’s momentum. Thus, we have the relations

E_{q} = - \nabla φ_{q}

and

B_{q} = \nabla \times A_{q}

, where

φ_{q} = φ_{q} (r)

and

A_{q} = A_{q} (r)

are the scalar and vector potentials of the electromagnetic field in

O

. In particular, we have

φ_{q} = γ_{q} ϕ_{q}, A_{q} = γ_{q} \frac{u_{q}}{c^{2}} ϕ_{q}, B_{q} = \frac{1}{c^{2}} (u_{q} \times E_{q}),

(6)

where the function

ϕ_{q} = ϕ_{q} (r)

, given with respect to the observer’s rest frame, is regularized to the origin of

R

and reads

ϕ_{q} (r) = \frac{e_{q}^{\pm}}{4 π ε_{o} r} (1 - e^{- \frac{γ_{q} r}{(1 + a_{e}) λ_{c q}}}),

(7)

with

ε_{o}

denoting the vacuum permittivity. The function given in Equation (7) is solution to the superposition of Poisson and Helmholtz equations, with constant of integration equal to zero at the limit

r \to \infty

and minimal wavelength associated to the electromagnetic field equal to

(1 + a_{e}) λ_{c q}

\sqrt{1 - β_{q}^{2}}

r \to 0

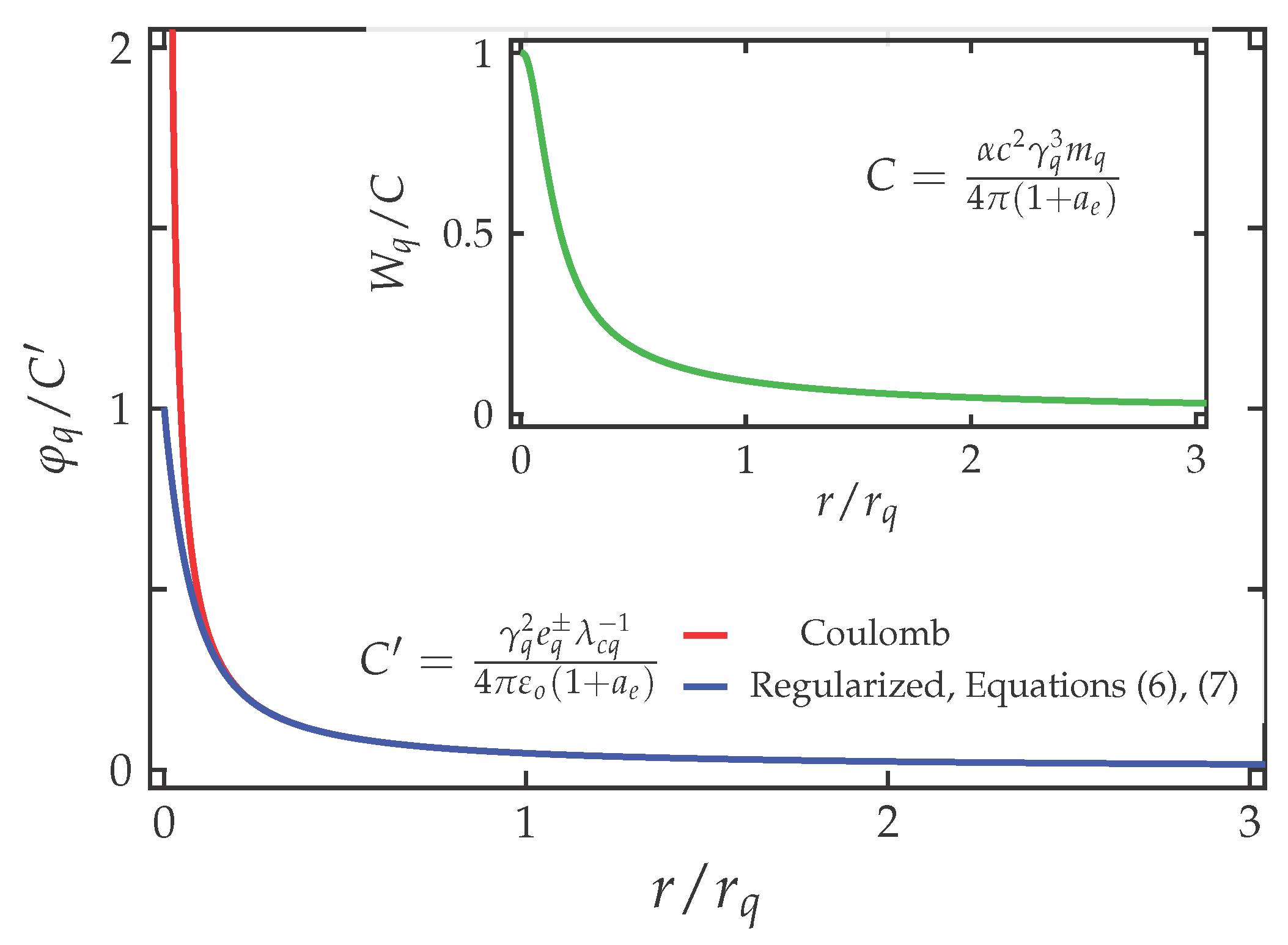
. Graphical representation of the difference between the Coulomb potential and the one given in Equation (7) is shown in Figure 1.

We would like to note that in Cartesian coordinates, the components of the vector potential given in Equation (6) read

A_{q}^{τ} = γ_{q} c^{- 2} u_{q}^{τ} ϕ_{q} (β, ν)

, where

τ \neq β \neq ν = {x, y, z}

and

u_{q}^{τ}

are the components of

u_{q}

. The potentials given in Equation (6) satisfy trivially both choices of gauge the Coulomb and Lorenz one.

Owing to Equation (7), we obtain the analytical expression of the electromagnetic field’s energy, with density

ε_{o} E_{q}^{2}

, for all q. Thus, integrating over

R^{3}

, we get

W_{q} (r) = α c^{2} γ_{q}^{2} m_{q} \frac{{\bar{λ}}_{c q}}{2 r} (2 - 4 e^{\frac{γ_{q} r}{(1 + a_{e}) λ_{c q}}} + 2 e^{2 \frac{γ_{q} r}{(1 + a_{e}) λ_{c q}}} + \frac{γ_{q} r}{(1 + a_{e}) λ_{c q}}) e^{- 2 \frac{γ_{q} r}{(1 + a_{e}) λ_{c q}}},

(8)

where the constant of integration is fixed at

r \to \infty

. Graphical representation is depicted in the inset in Figure 1.

From Equations (7) and (8), we obtain two important limits. We have,

lim_{r \to 0} φ_{q} (r) = \frac{γ_{q}^{2} e_{q}^{\pm}}{4 π ε_{o} (1 + a_{e}) λ_{c q}} and lim_{r \to 0} W_{q} (r) = \frac{α c^{2} γ_{q}^{3} m_{q}}{4 π (1 + a_{e})},

respectively. These results point out that the energy of generated electromagnetic field does not vanish at

r \to 0

and the potential energy is a constant ensuring that the self-interactions do not vanish at the given limit and do not associate to singularity points. Hence, on any gradient surface, including all points on the boundary

\partial Ω_{c q}

, the presence of electromagnetic field appears as a steady electromagnetic veil making the particle to appear as a very round object [47,48]. In addition, for the corresponding Umov-Poynting vector, we have

μ_{o}^{- 1} (E_{q} \times B_{q}) = ε_{o} E_{q}^{2} u_{q}

, where

μ_{o}

is the vacuum magnetic permeability.

Note that, the discussed electromagnetic field is consistently confined to the particle. It depends exclusively on the particle’s intrinsic characteristics and does not obey the Liénard-Wiechert representation [46,49,50,51]. Hence, the electromagnetic field does not propagate at speed c independently from the particle and does not classify as an on shell coupling between the electric and magnetic field components. We neither observe spontaneous emission nor absorption of photons. In this regard, the steady presence of electromagnetic field around the particle can be considered as a classical analog of the foam of virtual photons presented in quantum electrodynamics.

2.3. Electromagnetic self-energy and self-interactions

Since the system is closed, with the action of no additional fields, the particle exhibits no exchange of energy and hence momentum. Accordingly, neither external nor net self-forces [46,52,53] are acting on the particle and the energy of the system remains purely kinetic. However, the considered system definitely exhibits two types of self-interactions of electromagnetic nature, with average energy depending only on

u_{q}

The Hamiltonian describing the total energy of electromagnetically self-interacting particle reads

H_{q} = γ_{q} m_{q} c^{2} + Σ_{q} + Z_{q},

(9)

where the energy terms

Σ_{q}

and

Z_{q}

are associated to the self-Coulomb and self-Zeeman interactions, respectively.

The self-Coulomb term is the spatial average over the domain

Ω_{c q}

of the interaction energy between the particle’s charge and its own electromagnetic field. It reads

Σ_{q} = γ_{q} c^{2} \int_{Ω_{c q}} ρ_{M_{q}} - ρ_{m_{q}} d v,

(10)

where

ρ_{M_{q}} = ρ_{m_{q}} (1 + η_{q} \frac{r_{c q}}{r} (1 - e^{- \frac{γ_{q} r}{(1 + a_{e}) λ_{c q}}})),

(11)

η_{q} = 1 + β_{q}^{2}

. Here, we take into account the relation

ρ_{m_{q}} c^{2} = | e_{q}^{\pm} | ρ_{| e_{q}^{\pm} |} {(4 π ε_{o} r_{c q})}^{- 1}

The self-Zeeman term represents the spatial average over the domain

Ω_{c q}

of the interaction energy between the system’s intrinsic magnetic moment presented in Equation (4) and the induced magnetic field given in Equation (6). Since the self-Zeeman interaction is time independent, the corresponding integrand satisfies

- μ_{q} \cdot B_{q} = - μ_{q} B_{q}

, where in accordance to Equation (6), we have

B_{q} = c^{- 2} γ_{q} u_{q} | \nabla ϕ_{q} |

. Thus, taking into account Equation (4), according to which

μ_{q} = e {\bar{λ}}_{c q} c \frac{M_{q}}{2 m_{q}} and f_{q} = {\bar{λ}}_{c q} m_{q} c,

(12)

we obtain

Z_{q} = - \frac{{\bar{λ}}_{c q} c M_{q} p_{q}}{2 m_{q}^{2} η_{q}} \int_{Ω_{c q}} | \nabla ρ_{M_{q}} | d v .

(13)

The self-energy terms given in Equations (10) and (13) are intrinsic to the considered particle and hence invariant to an external influence. Therefore, represented in terms of quantum theory they will remain invariant with respect to the particle’s orbital state in many-body systems. That may be of benefit to the researchers studying multi-electron systems with the aid of computational methods that fail to account for the self-interactions without generating errors, see for example the case of Kohn-Sham density functional theory [43,54,55].

2.4. The Lagrangian and Hamiltonian density

In Section 2.3 we discuss the two allowed by the conservation laws types of electromagnetic self-interactions that take place only within the domain

Ω_{c q}

and have particular energy densities.

In general, the Hamiltonian (9) has a corresponding density and Lagrangian. The latter reads

L_{q} = p_{q} \cdot {\tilde{u}}_{q} - γ_{q} c^{2} ρ_{M_{q}} + \frac{M_{q} p_{q}^{3}}{2 m_{q}^{3} η_{q}} κ_{q} \cdot \nabla_{p} ρ_{M_{q}},

(14)

where

{\tilde{u}}_{q} = \frac{2}{V_{c q}} \int_{0}^{\infty} u_{q} (\bar{λ}) δ (\bar{λ} - {\bar{λ}}_{q}) d \bar{λ}

(15)

is the generalized velocity,

κ_{q}

is the unit vector of the particle’s velocity and

ρ_{M_{q}} = ρ_{m_{q}} (1 + \frac{η_{q}}{m_{q}} \frac{α}{c} p_{q} (1 - e^{- \frac{γ_{q} m_{q} c}{2 π (1 + a_{e}) p_{q}}}))

(16)

is the momentum representation of the effective mass density. Here, we take into account that

κ_{q} \cdot \nabla_{p} ρ_{M_{q}} \in R_{+}

for all q, such that

| \nabla ρ_{M_{q}} (r_{q}) | \to p_{q}^{2} {(λ_{c q} c m_{q})}^{- 1} κ_{q} \cdot \nabla_{p} ρ_{M_{q}} (p_{q})

For the corresponding Hamiltonian density, we have

H_{q} = γ_{q} c^{2} ρ_{M_{q}} - \frac{M_{q} p_{q}^{3}}{2 m_{q}^{3} η_{q}} κ_{q} \cdot \nabla_{p} ρ_{M_{q}},

(17)

where the Hamiltonian’s equations read

{\tilde{u}}_{q} = \nabla_{p} H_{q}, and {\dot{p}}_{q} = 0 .

(18)

3. Results and Discussion

3.1. Equations of motion

Following the Hamiltonian’s equations (18), the generalized velocity representation (15) and (5), we obtain the system’s equations of motion.

Working with the magnitude of the particle’s velocity for convenience, we have

u_{q} = \int_{Ω_{c q}} κ_{q} \cdot \nabla_{p} H_{q} d v .

(19)

Integrating over the domain

Ω_{c q}

, we obtain one of the equations. It is a transcendental equation and its quadratic form reads

α c γ_{q} {\tilde{η}}_{q} (u_{q} - (u_{q} + \frac{c}{2 π (1 + a_{e})}) e^{- \frac{c}{2 π (1 + a_{e}) u_{q}}}) - \frac{α c u_{q} γ_{q}^{2}}{8 π^{2} (1 + a_{e})} e^{- \frac{c}{2 π (1 + a_{e}) u_{q}}} - u_{q}^{2} = 0,

(20)

where

{\tilde{η}}_{q} = η_{q} + 1.5 (1 + a_{e}) γ_{q} β_{q}^{2}

On the other hand, taking into account the explicit representation of the effective mass density (11), from (5) we obtain second equation. For all q, we have

3 η_{q} (\frac{1}{2} - (\frac{1 - e^{- \frac{γ_{q} α}{2 π (1 + a_{e})}} (1 + \frac{γ_{q} α}{2 π (1 + a_{e})})}{{(\frac{γ_{q} α}{2 π (1 + a_{e})})}^{2}})) - a_{e} = 0 .

(21)

The transcendental equations (20) and (21) represent the system’s equations of motion. By solving these equations, we obtain the exact value of the particle’s energy represented by the Hamiltonian (9) and essentially to that of the electromagnetic contribution to the anomalous g-factor. In particular, for all q,

m_{q}

and

t \in [0, + \infty)

, we have

u_{q} = u_{e}

, where

u_{e}

is an invariant.

3.2. Effective mass-energy equivalence

Taking into account the contribution only of the electric part of the self-interactions in (9), we obtain the effective mass-energy relation. Accounting for the first two terms on the right hand side after the corresponding equality symbol, we obtain

E_{q} = γ_{e} M_{q} c^{2},

(22)

where for the self-Coulomb energy term we get

Σ_{q} = a_{e} γ_{e} m_{q} c^{2}

and for the effective rest mass we have

M_{q} = m_{q} (1 + a_{e})

. Here,

γ_{e}

is a constant, with

β_{e} = α

for all q, obtained by solving Equations (20) and (21), see Section 3.1. We would like to point out once more that within the considered mathematical framework if

∄ e

, then

∄ a_{e}

, the transformations given in Equation (Section 3.4) are no longer applicable and the particle can be at rest with respect to any observer. Thus, the energy of a free electrically charged non-composite particle of rest mass

m_{q}

is always higher than the energy of a free electrically neutral non-composite particle of the same rest mass. Furthermore, according to Equation (22) the former will always be characterized by an effective momentum given by

P_{q} = γ_{e} M_{q} u_{e}

yielding to the effective energy-momentum representation

E_{q} = \sqrt{M_{q}^{2} c^{4} + P_{q}^{2} c^{2}} .

(23)

The effective rest mass, energy and momentum related by Equation (23) are physical characteristics of the spinor field

Ψ_{q} (x_{μ})

that effectively account for the self-Coulomb energy of the q-th particle and satisfies the Dirac equation

(i ℏ γ^{μ} \partial_{μ} - M_{q} c) Ψ_{q} (x_{μ}) = 0 .

(24)

Here, the free-particle representation of the corresponding field holds ensuing that at the quantum limit the system under consideration remains isolated and hence the conservation laws are not violated. Moreover, Equation (24) accounts for the electromagnetic contribution to the particle’s anomalous g-factor, predicting

g_{e} = 2 (1 + a_{e})

for all q.

3.3. Observation and velocities

Prior to any observation of the system under consideration the particle is in its highest symmetry state. The associated electric field is centrally symmetric, the surface defined by all points with position vector

r_{q}

is spherically symmetric, the particle’s momentum at each of these points and at the origin of

R

is a zero net vector quantity and the system’s energy is observable only as an averaged in space quantity. In this regard, it is worth mentioning that by solving Equations (20) and (21), for the observed electromagnetic radius of the electron, we obtain

r_{e l} = r_{b}

, where

r_{b}

is the Bohr radius and

q \to e l

. Here, we take into account that

r_{e l}

and

p_{e l}

are conjugate quantities. This result points out that if the particle is confined by an external centrally symmetric electric field, with energy of the same magnitude as the corresponding self-Coulomb one (see Equation (10)) and tailored to the origin of

R

, then the particle will remain in its highest symmetry state. Without an external influence the resulting system will neither exchange energy and momentum nor acquire an orbital angular momentum. It will remain stable for an infinite time. Prominent example of such a system is the hydrogen atom at its ground state.

When an observation takes place at a particular point in space-time, the four-vector quantities characterizing the particle obey the Lorentz transformations. Such an act of observation reduces the particle’ manifesting symmetry thus making its behavior directionally specific. For the considered system, we have

u_{q} = u_{e} κ_{q}

, with

{\dot{κ}}_{q} = 0

and

{\bar{λ}}_{q} ω_{q} = u_{e}

for all q. The unit vector

κ_{q}

is time independent and the particle’s spatial degrees of freedom are reduced to two. The axis parallel to this unit vector is the symmetry one and specifies the spatial direction at which the observation takes place. Accordingly, the dynamics associated to the particle is expanded in a cylindrically symmetric space, with corresponding time dependent unit vectors

ρ_{q}

and

ϕ_{q} = {\dot{ρ}}_{q} ω_{q}^{- 1}

representing a plane of isotropy. We have

u_{q} = {\bar{λ}}_{q} ω_{q}

, where

ω_{q} = ω_{q} κ_{q}

is the corresponding angular velocity. The latter is neither related to a rotation nor spinning of the particle’s electric charge and mass, since both are not coupled to a specific point in space outside the domain

Ω_{c q}

. It is associated to a circularly polarized matter wave with magnitude

r_{q}

and phase speed

{\bar{λ}}_{q} ω_{q}

, such that

ω_{q} = (ρ_{q} \times {\dot{ρ}}_{q})

. We would like to point out that the frame of reference

R

remains inertial and the electromagnetic field discussed in Section 2.2 remains confined to the particle abiding by the resultant cylindrical symmetry. The inherent vector quantities given in Equation (4) and their magnitudes (see Equation (12)) are time independent. The particle’s magnetic moment now have a specific direction determined by the relation

(r_{q} \times u_{q}) = {\bar{λ}}_{q}^{2} ω_{q}

. In particular, we have

μ_{q} = \pm \frac{1}{2} g_{e} μ_{b} κ_{q},

where

μ_{b}

is the Bohr magneton. Here, we take into account that

f_{q} \equiv ℏ

for all q. The plus-minus sign results from the charge conjunction.

3.4. Transformation of velocities

Consider a second observer with frame of reference

O^{'}

moving relative to

O

with velocity

V

. The particle’s velocity in

O^{'}

reads

u_{q}^{'} = {\bar{λ}}_{q} ω_{q}^{'}

. Accordingly, we have

ω_{q} = w_{q} + {\tilde{w}}_{q}

and

ω_{q}^{'} = w_{q}^{'} + {\tilde{w}}_{q}^{'}

, where

w_{q}

w_{q}^{'}

and

{\tilde{w}}_{q}

{\tilde{w}}_{q}^{'}

are the respective longitudinal and transverse to the direction of

V

components. The magnitudes of these components,

w_{q}

w_{q}^{'}

and

{\tilde{w}}_{q}

{\tilde{w}}_{q}^{'}

, respectively, represent the directionally specific frequencies, satisfying

ω_{q} = \sqrt{w_{q}^{2} + {\tilde{w}}_{q}^{2}}, w_{q} = \frac{w_{q}^{'} + ω_{q} \frac{V}{u_{e}}}{1 + \frac{w_{q}^{'}}{ω_{q}} \frac{V}{u_{e}}}, {\tilde{w}}_{q} = \frac{{\tilde{w}}_{q}^{'}}{1 + \frac{w_{q}^{'}}{ω_{q}} \frac{V}{u_{e}}} \sqrt{1 - \frac{V^{2}}{u_{e}^{2}}}

(25a)

and

ω_{q} = \sqrt{{(w_{q}^{'})}^{2} + {({\tilde{w}}_{q}^{'})}^{2}}, w_{q}^{'} = \frac{w_{q} - ω_{q} \frac{V}{u_{e}}}{1 - \frac{w_{q}}{ω_{q}} \frac{V}{u_{e}}}, {\tilde{w}}_{q}^{'} = \frac{{\tilde{w}}_{q}}{1 - \frac{w_{q}}{ω_{q}} \frac{V}{u_{e}}} \sqrt{1 - \frac{V^{2}}{u_{e}^{2}}},

(25b)

where V is the magnitude of the relative velocity. Equations (Section 3.4) demonstrate that for different observers the particle will have different behavior in space. The most illustrative case follows for

u_{e} ≳ V

and

w_{q}^{'} \to 0

. In this case, for an observer in

O^{'}

making observation on the same direction the primed frame of reference is moving relative to the unprimed one the particle will appear as a slowly moving point-like object. Making an observation on the transverse direction, however, the same observer will reckon a wave-like behavior, with frequency

{\tilde{w}}_{q}^{'} \to ω_{q}

. On the other hand, for an observer in

O

the observation of point-like and wave-like behavior will appear the other way around, with

w_{q} \to ω_{q}

In the case

u_{e} < V < c

, the transformations in Equations (Section 3.4) does not hold, since the particle is not the center of symmetry in the system. The corresponding boost will be the Lorentz one and for all q,

u_{q}

will be a relative quantity, with

u_{q} \neq u_{e}

. Note that

u_{e}

remains invariant and the occurrence of orbital angular momentum is expected.

3.5. The anomalous g-factor

The computations of the electromagnetic component of the particle’s anomalous g-factor and its speed are carried out for

c = 2.997924584 \times 10^{8}

{ms}^{- 1}

and

α = 137 . 0359990849^{- 1}

. Note that according to NIST [56] the value of fine structure constant is

α = 137 . 035999084^{- 1}

. Solving the transcendental equation (20), we get

u_{e} \to α c

. As a consequence, from Equation (21), we obtain the analytical expression

a_{e} = 3 (1 + α^{2}) (\frac{1}{2} - (\frac{1 - e^{- \frac{α}{2 π (1 + a_{e}) \sqrt{1 - α^{2}}}} (1 + \frac{α}{2 π (1 + a_{e}) \sqrt{1 - α^{2}}})}{{(\frac{α}{2 π (1 + a_{e}) \sqrt{1 - α^{2}}})}^{2}})) .

(26)

Compared to the experimentally obtained [12] and calculated with the aid of quantum electrodynamics [8,9] electron’s anomalous g-factor, the numerical value obtained by solving Equation (26), with the given value of the fine structure constant, is accurate to a one part per trillion, see Table 1. To the best of our knowledge, the result given in the second row of Table 1 is the most accurate evaluation of the electron’s anomalous g-factor reported to the present days. We would like to point out that for

α = 137 . 035999206^{- 1}

[57] the result for

a_{e}

is accurate only to a one part per billion.

4. Summary

With the aid of essential regularization (Section 2.2) of the electromagnetic field potentials and spatial averaging procedure (Section 2.3), elaborated within the formalism of classical electrodynamics, the present paper reports an exact approach quantifying on a microscopic level the electrodynamics of isolated system comprised of non-composite particle of arbitrary rest mass and possessing elementary electric charge. The proposed approach overcomes all singularities arising in the conventional methods of classical electrodynamics thus uncovering in details the physical nature of electromagnetic self-interactions and the occurrence of anomalous magnetic moment in the system. It quantifies the particle’s dynamics exactly through system of transcendental equations of motion obtained in the absence of any approximations and at the classical limit, see Section 3.1. Essentially, the solutions of these equations give the exact values of the particle’s observable radius, intrinsic magnetic moment, velocity and the electromagnetic contribution to the anomalous g-factor (see Section 3.3 and Section 3.5). The derived transcendental equations ensure fast computations and provide highly accurate results competitive to the perturbative method of quantum electrodynamics, see the comparison in Table 1.

In general, the proposed approach may be build on and integrated into the mathematical framework of the classical and quantum field theories. In that regard, more contributions to the particle’s magnetic moment may be calculated exactly. With the appropriate gauge fields and regularization one may introduce additional self-interactions and generalize the system of transcendental equations discussed in Section 3.1.

In conclusion, it appears that the present study supports the thesis pointing out that the anomalous magnetic moment may not be a unique feature to the quantum theory and its occurrence may have a solid classical description. Moreover, it may be the case that the perturbative method of quantum field theory is not unique to that feature and in addition there exist an exact method for its calculation. On that account, pushing the boundaries of classical or quantum field theories further to test the possibility for the exact calculation of even higher contributions in the anomalous magnetic moment of non-composite particles is worth a shot. The proposed regularization to the scalar potential and the related self-Coulomb and self-Zeeman interactions, furthermore, may significantly facilitate the optimization of some computational methods in solid state physics making them self-consistent. Especially these methods studying multi-electron systems that fail to address the self-interactions without the consideration of additional corrections.

Author Contributions

Not applicable.

Funding

This work was supported by National Program “Young scientists and postdoctoral researchers-2” of the Ministry of Education and Science, Bulgaria, approved by DCM 206 / 07.04.2022.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data generated within this research is included in the paper.

Conflicts of Interest

Not applicable.

References

Heisenberg, W. The self-energy of the electron. In Early Quantum Electrodynamics, 1 ed.; Miller, A.I., Ed.; Cambridge University Press, 1994; pp. 121–128. [CrossRef]
Roberts, B.L.; Marciano, W.J. Lepton Dipole Moments; Vol. 20, Advanced Series on Directions in High Energy Physics, World Scientific, 2009. [CrossRef]
Keshavarzi, A.; Khaw, K.S.; Yoshioka, T. Muon g-2: A review. Nucl. Phys. B 2022, 975, 115675. [Google Scholar] [CrossRef]
Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press, 2013. [CrossRef]
Melnikov, K.; Vainshtein, A. Theory of the muon anomalous magnetic moment; Springer tracts in modern physics, Springer: Berlin : New York, 2006. [Google Scholar]
Vogel, M. The anomalous magnetic moment of the electron. Contemp. Phys. 2009, 50, 437–452. [Google Scholar] [CrossRef]
Kataev, A.L. Analytical eighth-order light-by-light QED contributions from leptons with heavier masses to the anomalous magnetic moment of electron. Phys. Rev. D 2012, 86, 013010. [Google Scholar] [CrossRef]
Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. Tenth-Order QED Contribution to the Electron g-2 and an Improved Value of the Fine Structure Constant. Phys. Rev. Lett. 2012, 109, 111807. [Google Scholar] [CrossRef] [PubMed]
Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. Tenth-order electron anomalous magnetic moment: Contribution of diagrams without closed lepton loops. Phys. Rev. D 2015, 91, 033006. [Google Scholar] [CrossRef]
Aoyama, T.; Kinoshita, T.; Nio, M. Theory of the Anomalous Magnetic Moment of the Electron. Atoms 2019, 7, 28. [Google Scholar] [CrossRef]
Lin, F.; Huang, M. Magnetic correction to the anomalous magnetic moment of electrons. Commun. Theor. Phys. 2022, 74, 055202. [Google Scholar] [CrossRef]
Fan, X.; Myers, T.; Sukra, B.; Gabrielse, G. Measurement of the Electron Magnetic Moment. Phys. Rev. Lett. 2023, 130, 071801. [Google Scholar] [CrossRef]
Volkov, S. Calculation of lepton magnetic moments in quantum electrodynamics: a justification of the flexible divergence elimination method 2023. Publisher: arXiv Version Number: 2. 2. [CrossRef]
Jegerlehner, F.; Nyffeler, A. The muon g-2. Physics Reports 2009, 477, 1–110. [Google Scholar] [CrossRef]
Jegerlehner, F. The Anomalous Magnetic Moment of the Muon; Vol. 274, Springer Tracts in Modern Physics, Springer International Publishing: Cham, 2017. [CrossRef]
Morte, M.D.; Francis, A.; Gülpers, V.; Herdoíza, G.; Von Hippel, G.; Horch, H.; Jäger, B.; Meyer, H.B.; Nyffeler, A.; Wittig, H. The hadronic vacuum polarization contribution to the muon g-2 from lattice QCD. J. High Energ. Phys. 2017, 2017, 20. [Google Scholar] [CrossRef]
Logashenko, I.B.; Eidelman, S.I. Anomalous magnetic moment of the muon. Phys.-Usp. 2018, 61, 480–510. [Google Scholar] [CrossRef]
Westin, A.; Kamleh, W.; Young, R.; Zanotti, J.; Horsley, R.; Nakamura, Y.; Perlt, H.; Rakow, P.; Schierholz, G.; Stüben, H. Anomalous magnetic moment of the muon with dynamical QCD+QED 2020. 245, 06035. [CrossRef]
Aoyama, T.; Asmussen, N.; Benayoun, M.; Bijnens, J.; Blum, T.; Bruno, M.; Caprini, I.; Carloni Calame, C.; Cé, M.; Colangelo, G.; et al. The anomalous magnetic moment of the muon in the Standard Model. Physics Reports 2020, 887, 1–166. [Google Scholar] [CrossRef]
Gérardin, A. The anomalous magnetic moment of the muon: status of lattice QCD calculations. Eur. Phys. J. A 2021, 57, 116. [Google Scholar] [CrossRef] [PubMed]
Leutgeb, J.; Mager, J.; Rebhan, A. Holographic QCD and the muon anomalous magnetic moment. Eur. Phys. J. C 2021, 81, 1008. [Google Scholar] [CrossRef] [PubMed]
Nedelko, S.; Nikolskii, A.; Voronin, V. Soft gluon fields and anomalous magnetic moment of muon. J. Phys. G: Nucl. Part. Phys. 2022, 49, 035003. [Google Scholar] [CrossRef]
Eidelman, S.; Passera, M. Theory of the τ lepton anomalous magnetic moment. Mod. Phys. Lett. A 2007, 22, 159–179. [Google Scholar] [CrossRef]
González-Sprinberg, G.A.; Vidal, J. Tau magnetic moment. J. Phys.: Conf. Ser. 2017, 912, 012001. [Google Scholar] [CrossRef]
Özgüven, Y.; Billur, A.A.; İnan, S.C.; Bahar, M.K.; Köksal, M. Search for the anomalous electromagnetic moments of tau lepton through electron–photon scattering at CLIC. Nucl. Phys. B 2017, 923, 475–490. [Google Scholar] [CrossRef]
Chen, X.; Wu, Y. Search for the Electric Dipole Moment and anomalous magnetic moment of the tau lepton at tau factories. J. High Energ. Phys. 2019, 2019, 89. [Google Scholar] [CrossRef]
Arroyo-Ureña, M.A.; Hernández-Tomé, G.; Tavares-Velasco, G. Anomalous magnetic and weak magnetic dipole moments of the τ lepton in the simplest little Higgs model. Eur. Phys. J. C 2017, 77, 227. [Google Scholar] [CrossRef]
Dyndał, M.; Kłusek-Gawenda, M.; Szczurek, A.; Schott, M. Anomalous electromagnetic moments of τ lepton in γγ →τ+τ- reaction in Pb+Pb collisions at the LHC. Phys. Lett. B 2020, 809, 135682. [Google Scholar] [CrossRef]
Tran, H.M.; Kurihara, Y. Tau g-2 at e^-e⁺ colliders with momentum-dependent form factor. Eur. Phys. J. C 2021, 81, 108. [Google Scholar] [CrossRef]
Datzeff, A. On the classical self-energy of the electron. Physics Letters A 1971, 34, 167–168. [Google Scholar] [CrossRef]
Vilenkin, A. Correspondence principle in the self-energy problem. Ann. Phys. 1979, 120, 471–477. [Google Scholar] [CrossRef]
Malenfant, J. Renormalized Coulomb-gauge self-energy function. Phys. Rev. D 1987, 35, 1525–1527. [Google Scholar] [CrossRef] [PubMed]
Frolov, V.P.; Zelnikov, A. Classical self-energy and anomaly. Phys. Rev. D 2012, 86, 044022. [Google Scholar] [CrossRef]
Borges, L.H.C.; Barone, F.A.; Ferrari, A.F. The point-charge self-energy in a nonminimal Lorentz-violating Maxwell electrodynamics. EPL 2018, 122, 31002. [Google Scholar] [CrossRef]
Sebens, C.T. Eliminating Electron Self-repulsion. Found. Phys. 2023, 53, 65. [Google Scholar] [CrossRef]
Fetter, A.L.; Walecka, J.D. Quantum theory of many-particle systems; Dover Publications: Mineola, N.Y, 2003.
Weinberg, S. The Quantum Theory of Fields; Vol. 1, Cambridge University Press, 1995. [CrossRef]
Weinberg, S. The Quantum Theory of Fields; Vol. 2, Cambridge University Press, 1996. [CrossRef]
Desai, B.R. Quantum Mechanics with Basic Field Theory, 1 ed.; Cambridge University Press, 2009. [CrossRef]
Pollock, M.D. On the electron self-energy. Eur. Phys. J. Plus 2018, 133, 132. [Google Scholar] [CrossRef]
Collins, J.C. Renormalization: An Introduction to Renormalization, the Renormalization Group and the Operator-Product Expansion, 1 ed.; Cambridge University Press, 2023. [CrossRef]
Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
Bao, J.L.; Gagliardi, L.; Truhlar, D.G. Self-Interaction Error in Density Functional Theory: An Appraisal. J. Phys. Chem. Lett. 2018, 9, 2353–2358. [Google Scholar] [CrossRef] [PubMed]
Hehl, F.W.; Obukhov, Y.N. Foundations of Classical Electrodynamics: Charge, Flux, and Metric; Birkhäuser Boston: Boston, MA, 2003. [Google Scholar] [CrossRef]
Shanahan, D. A Case for Lorentzian Relativity. Found. Phys. 2014, 44, 349–367. [Google Scholar] [CrossRef]
Griffiths, D.J. Introduction to Electrodynamics, 4 ed.; Cambridge University Press, 2017. [CrossRef]
Moskowitz, C. Electron appears spherical, squashing hopes for new physics theories. Nature, 2013. [Google Scholar] [CrossRef]
Roussy, T.S.; Caldwell, L.; Wright, T.; Cairncross, W.B.; Shagam, Y.; Ng, K.B.; Schlossberger, N.; Park, S.Y.; Wang, A.; Ye, J.; et al. An improved bound on the electron’s electric dipole moment. Science 2023, 381, 46–50. [Google Scholar] [CrossRef]
Greiner, W. Classical Electrodynamics; Theoretical Physics, Springer New York: New York, NY, 1998. [Google Scholar] [CrossRef]
Jackson, J.D. From Lorenz to Coulomb and other explicit gauge transformations. Am. J. Phys. 2002, 70, 917–928. [Google Scholar] [CrossRef]
Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Photons and atoms: Introduction to quantum electrodynamics; Physics textbook, Wiley-VCH: Weinheim, 2004. [Google Scholar]
Rohrlich, F. The self-force and radiation reaction. Am. J. Phys. 2000, 68, 1109–1112. [Google Scholar] [CrossRef]
Gratus, J. Maxwell-Lorentz without self-interactions: conservation of energy and momentum. J. Phys. A: Math. Theor. 2022, 55, 065202. [Google Scholar] [CrossRef]
Lonsdale, D.R.; Goerigk, L. The one-electron self-interaction error in 74 density functional approximations: a case study on hydrogenic mono- and dinuclear systems. Phys. Chem. Chem. Phys. 2020, 22, 15805–15830. [Google Scholar] [CrossRef] [PubMed]
Zope, R.R.; Yamamoto, Y.; Diaz, C.M.; Baruah, T.; Peralta, J.E.; Jackson, K.A.; Santra, B.; Perdew, J.P. A step in the direction of resolving the paradox of Perdew-Zunger self-interaction correction. J. Chem. Phys. 2019, 151, 214108. [Google Scholar] [CrossRef]
2018 CODATA Value: fine-structure constant. The NIST Reference on Constants, Units, and Uncertainty. NIST 2019.
Morel, L.; Yao, Z.; Cladé, P.; Guellati-Khélifa, S. Determination of the fine-structure constant with an accuracy of 81 parts per trillion. Nature 2020, 588, 61–65. [Google Scholar] [CrossRef]

Figure 1. Graphical representations of the regularized electromagnetic scalar potential considered in the present study and the conventional (Coulomb) one depicted for comparison. For the sake of clarity both potentials are normalized by

C^{'}

. The energy of corresponding electromagnetic field as a function of the distance from the origin of particle’s rest frame of reference is depicted in the inset.

C^{'}

. The energy of corresponding electromagnetic field as a function of the distance from the origin of particle’s rest frame of reference is depicted in the inset.

Table 1. Theoretical and experimental values of the anomalous g-factor of electromagnetic origin. Second, third and fourth rows show the theoretical results, with prediction of classical electrodynamics (CED) discussed in the present study (see Section 3.5) and some of the recent results based on renormalized quantum electrodynamics (QED). The last row shows the most recent experimental result, with measurements carried out on electrons.

Methods	$a_{e}$	Ref.
Exact CED	$0.00115965218000 (65)$ 2	(26)
Perturbative QED	$0.00115965218178 (77)$	[8]
Perturbative QED	$0.001159652181643 (25)$	[9]
Experimental	$0.00115965218059 (13)$	[12]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Self-Interactions, Self-Energy and the Electromagnetic Contribution to the Anomalous g-Factor

Abstract

1. Introduction

2. Theoretical background

2.1. General considerations

2.2. Field observables

2.3. Electromagnetic self-energy and self-interactions

2.4. The Lagrangian and Hamiltonian density

3. Results and Discussion

3.1. Equations of motion

3.2. Effective mass-energy equivalence

3.3. Observation and velocities

3.4. Transformation of velocities

3.5. The anomalous g-factor

4. Summary

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe