Prerpints.org logo
Preprint
Article

The Influence of Reverse Yielding on the Plastic Conditioning of Interference Fits in the Power Transmission Engineering

Altmetrics

Downloads

274

Views

718

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

14 August 2023

Posted:

16 August 2023

You are already at the latest version

Alerts
Abstract
Interference fits are a very common shaft-hub connection due to their low manufacturing cost and excellent technical properties. Plastic Conditioning of this machine element is a new and not very well known method. By exploiting residual stresses and the associated increase in the yield point, these components can absorb operating loads such as rotating bending moments, torsion, temperature changes and centrifugal forces purely elastically and avoid plastic deformation during operation. Compared to conventionally joined interference fits, the load bearing capacity in the elastic range can be increased by almost 200% and a specifically defined additional safety against plastic deformation in the elastic-plastic range can be ensured. This paper examines the effects of Reverse Yielding on the technology of Plastic Conditioning of Interference Fits in Power Transmission Engineering. Based on the Shear Stress Hypothesis (SH), the Plane Stress State (PSS) and the ideal plastic behavior of materials, the stress-mechanical relationships are explained, the influencing parameters are examined and conclusions are drawn for the plastic conditioning process. Taking into account the theoretical knowledge according to the state of the art, modified material behavior assumptions (isotropic hardening) and the Von Mises Yield Criterion (VMYC) are also considered. In addition, the method of plastic conditioning of interference fits is introduced and its basic principles are briefly explained. Along with computational suggestions to avoid Reverse Yielding, open issues requiring further research are identified.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

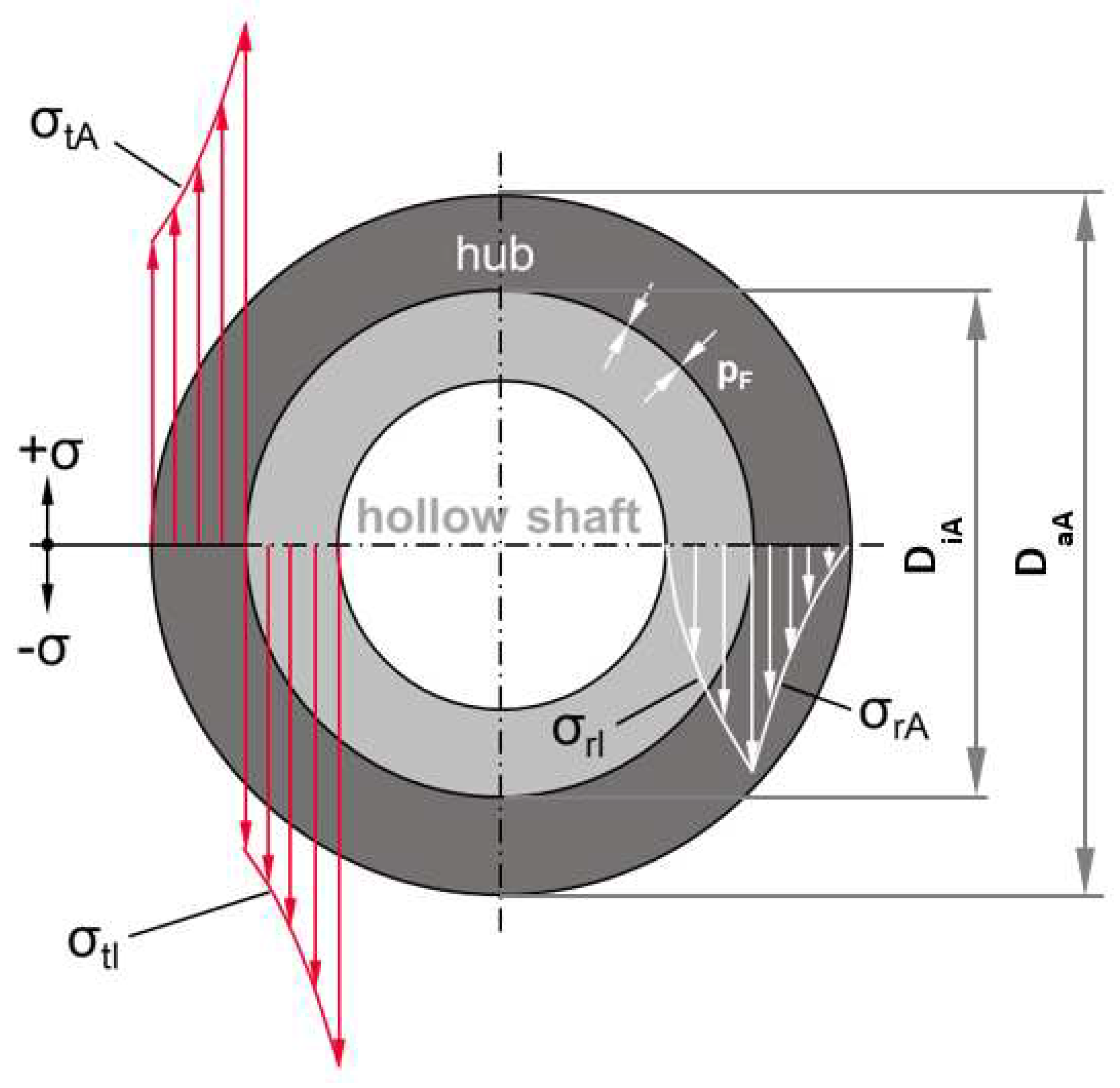
Frictional shaft-hub connections in the form of interference fits are commonly used in power transmission applications. These connections are based on the transmission of forces and moments by frictional contact between the inner part (shaft) and the outer part (hub), which generates compressive stress in their contact zone. Figure 1 shows such a connection between a hub and a hollow shaft in cross section, where the hub represents a hollow cylinder under internal pressure and the hollow shaft represents one under external pressure. The distribution of radial and tangential stresses (principal stresses) over the cross-sections of the hub and hollow shaft is shown in Figure 1. For the hub, which is the subject of this study, these stresses are calculated according to Equation (1) (pi = pF).
σ r A ( d ) = − p i 1 − Q A 2 ⋅ D i A d 2 − Q A 2 σ t A ( d ) = p i 1 − Q A 2 ⋅ D i A d 2 + Q A 2
From the stress curves in the cross section, it can be seen that for both components, the greatest stresses occur at the respective inner diameters and that the onset of plastic stresses is always found here. If the joint is designed purely elastically, the high stress gradients mean that the rest of the component cross section remains purely elastic, which in many cases can lead to unfavorable material utilization.
In order to save material, space, weight and increase load capacity, the stress limits of these components have been extended beyond their elastic limits into the plastic region [1,2,3,4,5,6]. Herebey partially plastic components with plastic stressed inner zones are permitted. However, when the outer part is subjected to plastic deformation, it can experience additional plastic deformation in the opposite direction in certain stress relief situations, known as Reverse Yielding [7,8,9,10].
This paper focuses on the effect of Reverse Yielding on the Plastic Conditioning of interference fits (especially in the outer part / hub) in Power Transmission Engineering. We discuss the current understanding of Reverse Yielding and the stress-mechanical principles of Plastic Conditioning.
The phenomenon of Reverse Yielding of elastically-plastically loaded interference fits was investigated in detail by Kollmann and Önöz [11] on the basis of the Shear Stress Hypothesis (SH), the associated flow rule according to Melan, Prager and Koiter [12], the Plane Stress State (PSS) and ideal plastic material behavior. Corresponding calculation principles were derived analytically.
The question of the occurrence of Reverse Yielding during deceleration of a rotating interference fit with a plastified hub and the calculation of residual stresses at standstill is addressed in the work of Gamer [13]. The occurrence of Reverse Yielding in rotating thick-walled hollow cylinders with elastic-idealplastic material and free ends after a reduction of the angular velocity is described by Mack in [14].
Extensive work has been done on Reverse Yielding in the context of autofretting technology [7,8,9,10]. The main objective of autofretting is to improve the strength properties and fatigue life (from a fracture mechanics point of view) of tubular components / pressure vessels under high internal pressure loading, such as those used in nuclear reactors, reciprocating compressors or common rail applications. In addition to improving the strength properties, the use of Plastic Conditioning Technology for interference fits must take into account much more complex loading situations both in the components and in their contact zones. Important aspects are shape stability and functional reliability, even under dynamic loads.
When considering multiple interference fits, the complexity of the parameters increases with the number of joining partners. Such interference fits are very common in industrial applications in the form of clamp connections, such as clamping elements. An example of this can be found in wind turbines, where the connection between the gear shaft and the rotor shaft of the wind turbine is joined using clamping elements, and where material stress reserves are often sought in industrial practice because of the reduced strength limit due to the Geometric size effect.
Initial studies on the effects of Reverse Yielding on Plastic Conditioning Technology have been conducted by Schierz [15]. The purpose of this study is to investigate how Reverse Yielding affects Plastic Conditioning technology by examining analytical relationships based on the Shear Stress Hypothesis (SH) and the Plane Stress State (PSS) in the context of the physical principles of Plastic Conditioning. Of particular interest are the conditions under which Reverse Yielding can occur and how to calculate them. The main focus is on the diameter ratio QA (Equation (2)) and the maximum achievable internal pressures pi or radial stresses σr. The study also examines how these conditions change under the Von Mises Yield Criterion (VMYC), with hardening of the material, and by considering the Bauschinger effect. Ultimately, this research aims to develop a reliable calculation system for practical use.
σ t = − m ⋅ σ r   w i t h   m = 1 + Q A 2 1 − Q A 2 = − tan α = tan 180 ° − α       a n d   Q A = D i A D a A

2. Plastic Conditioning of Interference Fits; Stress-mechanical principles

The fundamental idea of the Plastic Conditioning Method was based on the fact that an elastic-plastic pretreatment of the joining partners of an interference fit is carried out before or during the joining process, e.g., by applying a conditioning pressure pK to a hub (pK = pi see also Figure 7 in Chapter 4). During the subsequent elastic relief and, if necessary, reloading of these joining partners, a purely elastic stress state can be established in such a way that all additional stresses to be expected on the hub during operation, such as rotating bending moments, torsion, temperature changes and centrifugal forces, result exclusively in purely elastic stress changes. This property is also required for other frictionally engaged joints, such as bolted joints, because plastic deformation due to operating loads usually results in a reduction of transmittable forces and moments. In addition, several articles have been published on the Plastic Conditioning method [15,16,17].
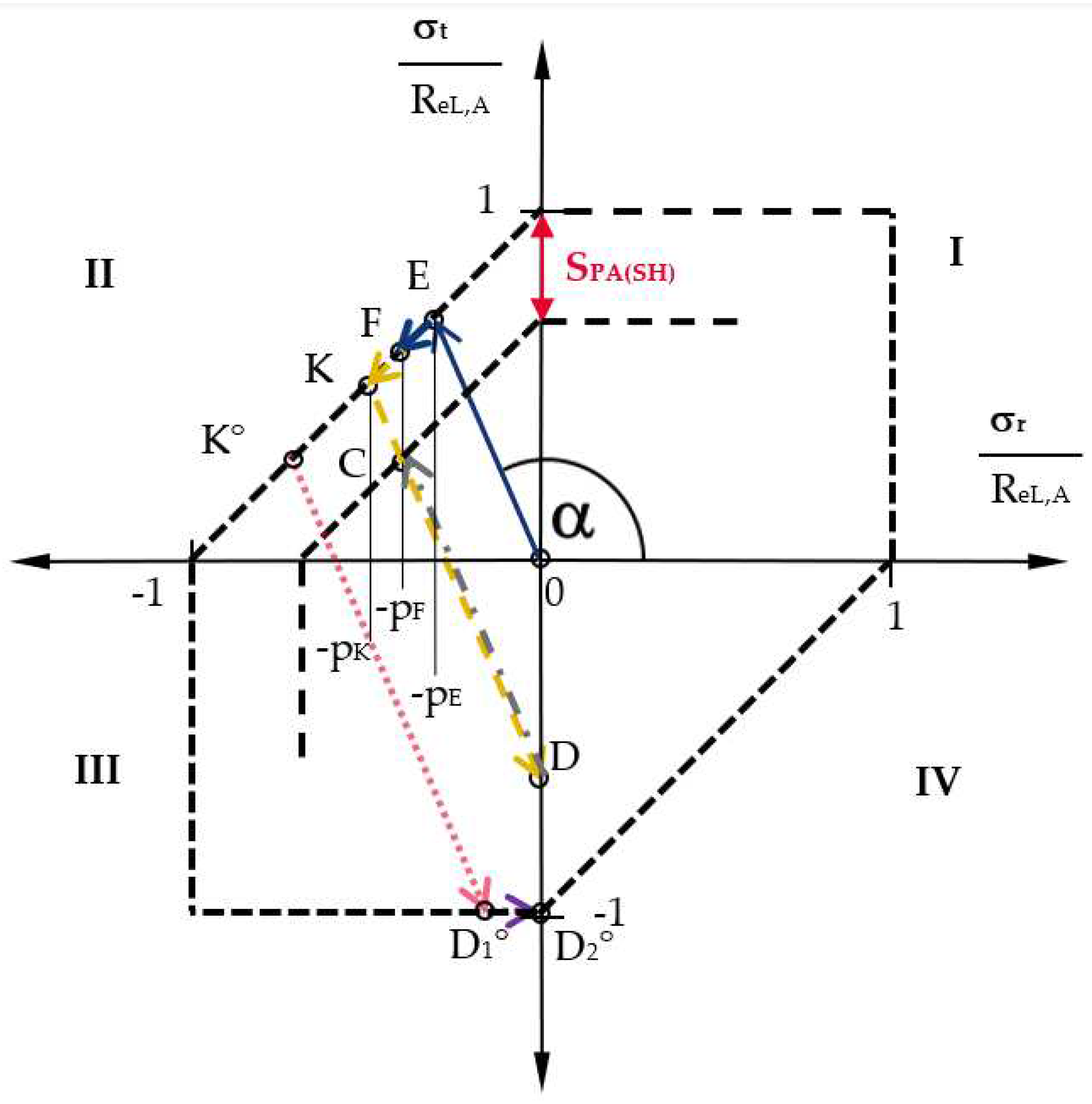
The stress curves during the conditioning process are shown in Figure 2. It shows the changes in stress on the inner diameter DiA of an outer part (hub) under internal pressure in the principal stress plane, assuming the Plane Stress State (PSS). Its axes are formed by the radial stress σr on the abscissa and the tangential stresses σt on the ordinate. The closed dashed line in Figure 2 represents the ideal plastic yield strength of the material according to the Shear Stress Hypothesis (SH) used and is calculated with reference to Equation (1) as follows.
σ v = max σ t − σ r   ;   σ r   ;   σ t
The production of elastically-plastically joined interference fits with an internal plastic zone, as described in Chapter 1, has so far been carried out in practice according to Figure 2 along the load path 0 E ¯   −   E F ¯ (blue arrow / solid line). According to Kollmann, the angle of inclination α of the straight line 0 E ¯   is determined exclusively by the diameter ratio QA of the component according to Equation (2).
When point E in Figure 2 is reached, the stress state is at the yield point. As the negative radial stress continues to increase, the associated stress states can only develop along the yield curve (e.g., along the load path E F ¯ ).
Point F then marks the stress state at the inner diameter DiA of the outer part of the interference fit after completion of the joining process for conventional elastically-plastically joined hubs.
When producing a conditioned hub with the same joint pressure but with an additional safety SPA(SH) (see Figure 2 red double arrow) against plastic deformation, the radial stress is further increased up to the conditioning pressure at point K in Figure 2. There is then complete elastic relief (σr = 0) to point D, which illustrates the remaining tangential residual stresses and where the end of the conditioning process is reached. Point D can be calculated for the Shear Stress Hypothesis as follows (Equation (4)).
D σ t S H = − 2 ⋅ p K − p E 1 − Q A 2           D σ r S H = 0   ;
From a technical point of view, the conditioning of a hub can be carried out in a simple manner, for example, by means of clamping elements or, in the case of hubs for conical interference fits, by means of a corresponding cone. In these cases, the interference in the hub bore generates a surface pressure corresponding to the radial stress in Figure 2.
The subsequent reloading along the straight line D C ¯   (gray arrow / dashed-dotted-line) leads to the final joined state of the interference fit at stress point C. Here, the joint pressure pF is identical to that of conventional elastically–plastically joined interference fits at point F, but with the above-mentioned safety SPA(SH). Additional stresses caused by operating loads can thus be absorbed by a conditioned interference fit in a purely elastic manner and, after they have subsided, it always returns unchanged to its original state.
The safety against plastic deformation SPA(SH) (at point C relative to point K in Figure 2) achieved by conditioning is calculated as follows (Equation (5)).
S P A ( S H ) = 1 1 − Δ p K R e L , A ⋅ 1 + 1 + Q A 2 1 − Q A 2     with     Δ p K = p K − p F
A description of the items in Figure 2 is as follows:
E: Purely elastic state at the yield strength
F: Elastic-plastic state (conventionally joined according to DIN 7190-1 [18])
K: Stress state at yield curve due to conditioning
C: Joined final state of the conditioned interference fit
D: Stress state after complete relief (tangential residual stresses)

3. Reverse Yielding

3.1. Occurrence of Reverse Yielding in Plastic Conditioning

Reverse Yielding is a mechanical process that occurs when plastically stressed parts (hubs) in interference fits undergo elastic relief, resulting in renewed plastic stress in the opposite direction.
In the example of Figure 2, the stress point D at the end of the conditioning process is located in the elastic region within the yield curve. Under certain conditions, which will be explained in more detail below, the relief straight line K ° D 1 ¯ °   (pink dotted line) may intersect the yield curve at point D1°. In this case, the material will return to a plastic state and the stress will inevitably continue to follow the yield curve until it is completely relieved at point D2°. This process is known as Reverse Yielding. This shows that the area between D1° and D2° can no longer contribute to conditioning. For the maximum usable conditioning pressure pKond,max, therefore, only those values are meaningful whose elastic relief straight lines end at point D2°. If Reverse Yielding is induced beyond this point, this will only result in unnecessary plastic deformation and compromise the desired residual stress state.
It should be mentioned at this point that Reverse Yielding cannot occur in hollow cylinders under external pressure, in principle (see Figure 1). In the case of interference fits, for example, this applies to hollow shafts which, in principle, can also be subjected to elastic-plastic stresses. Solid shafts can only be subjected to purely elastic stresses due to the stress-mechanical principles that apply. Since hollow shafts are subject to compressive stresses only, their stress states are generally in the IIIrd quadrant (see Figure 2) and their relief straight lines always end in the elastic region of the ordinate. More detailed information about this can be found in Kollmann and Önöz [11].

3.2. Influence parameters for Reverse Yielding

This section deals with the conditions under which Reverse Yielding can occur. Assuming the Shear Stress Hypothesis (SH), the associated flow rule according to Melan, Prager and Koiter [12], the Plane Stress State (PSS) and an ideal plastic material behavior, Kollmann and Önöz [11] found the following equation as a necessary condition for the critical pressure pkrit that must be generated at the inner diameter DiA of the hub in order for Reverse Yielding to occur with subsequent elastic relief.
p k r i t ,   S H = R e L , A ⋅ 1 − Q A 2
It is also shown that this pressure can only occur in hubs with a diameter ratio QA < 0.45076. For larger diameter ratios, the maximum possible fully plastic state of the hub according to Equation (7) [11], which should be avoided for ideal plastic material, is reached before the critical pressure pkrit.
p max ,   S H = − R e L , A ⋅ ln Q A
For information only, it should be noted that for diameter ratios QA < 0.368 (so-called “thick-walled hubs”) the fully plastic state cannot be achieved and the maximum achievable pressure is equal to the yield strength.
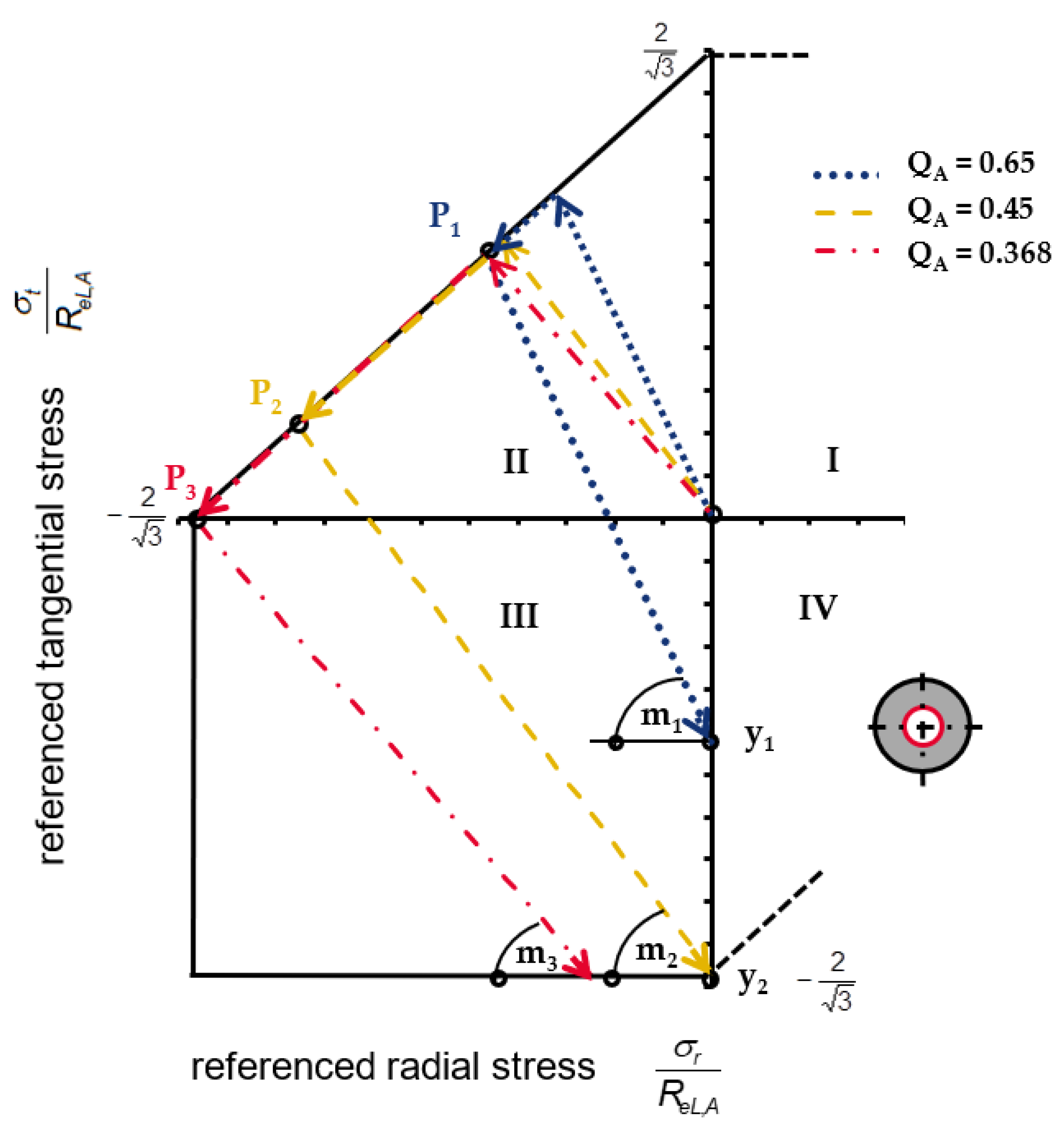
Figure 3 illustrates these relationships using the example of relief straight lines with maximum possible pressures pmax,MSH (Equation (8)) of three characteristic diameter ratios QA at the inner diameters of the respective hubs in the principal stress plane.
The yield curve here corresponds to the Modified Shear Stress Hypothesis (MSH), for which Equations (6) and (7) has been adapted as follows.
p max ,   ​   M S H = − R e L A ⋅ 2 3   ⋅   ln   Q A
p k r i t ,   M S H = 2 3 ⋅ R e L , A ⋅ 1 − Q A 2
The relief straight lines in the elastic region of quadrants II and III of Figure 3 are calculated according to Equation (10), where their gradients mn are calculated from Equation (2) using QA and y determines the points of intersection of the relief straight lines with the ordinate and thus the tangential residual stresses at the inner diameter after complete relief (Figure 3).
σ t R e L , A   =   −   m ⋅ σ r R e L , A − y R e L , A
The points of intersection (P1 bis P3) of the relief straight lines with the yield curve in the IInd quadrant mark the stress states at the inner diameter at maximum plastic loading of the component according to Kollmann and are defined analytically only for the SH and MSH (see also Equations (7) and (8)).
It can clearly be seen that the relief straight lines for QA > 0.45076 (and σr = 0) always end in the elastic region of the principal stress plane (dotted line for QA = 0.65). Only when QA < 0.45076 do the relief straight lines intersect the yield curves again and Reverse Yielding occurs (dashed line for QA = 0.45 and dashed dotted line for QA = 0.368).
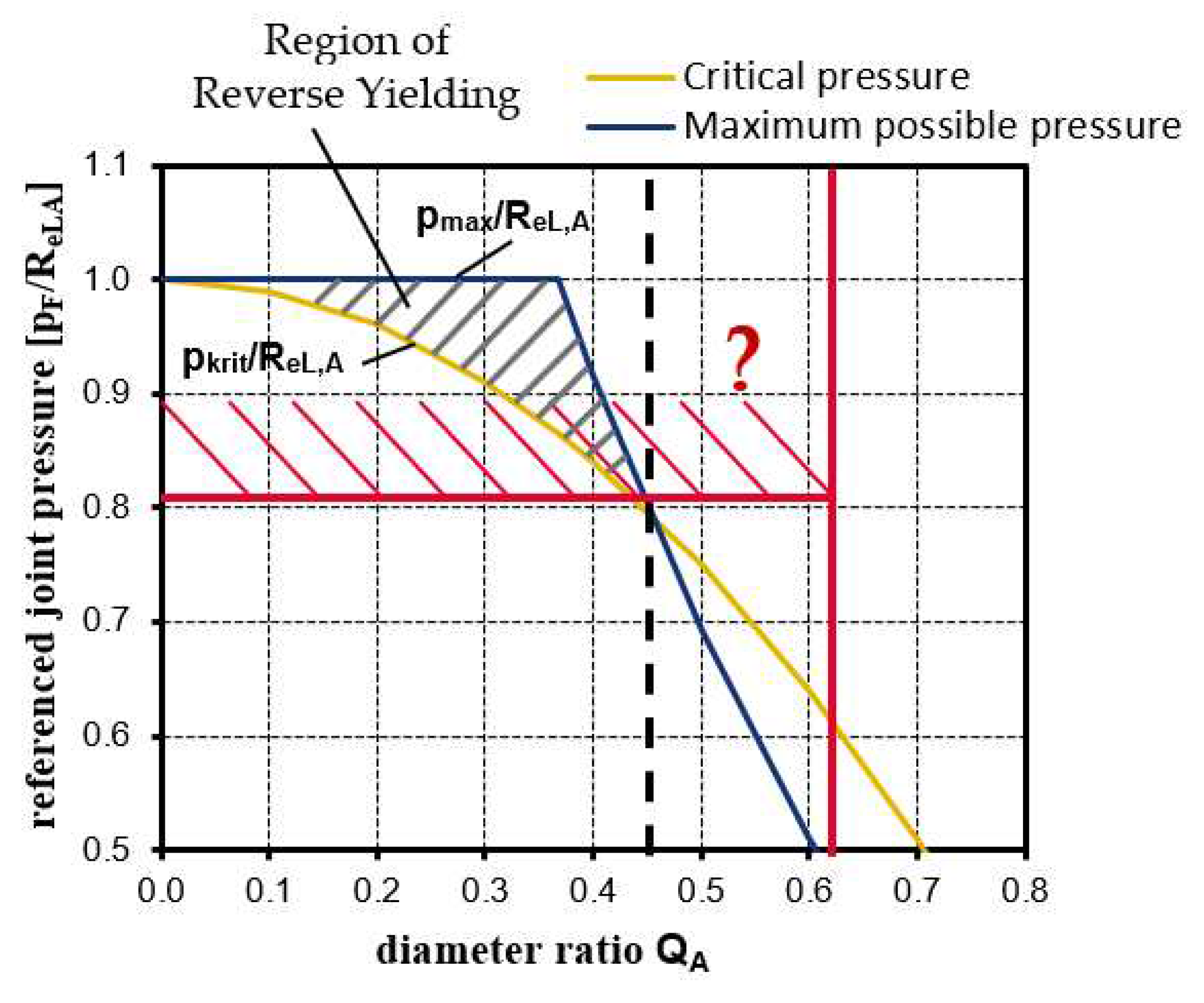
In the diagram in Figure 4, the referenced internal pressures pF/ReL,A are plotted against the diameter ratios QA of the outer parts (hubs) of an interference fit. The black shaded area marks the range of possible pressures and diameter ratios at which Reverse Yielding can occur. It can be seen that, under the above conditions, Reverse Yielding occurs mainly with so-called thick-walled hubs. These in turn are of particular interest for Plastic Conditioning as they offer the greatest potential for this technology [15].
To prevent Reverse Yielding after complete stress relief during conditioning, the condition given in Equation (11) must be satisfied for all relief straight lines with QA < 0.45. The maximum conditioning joint pressure pKond,max, at which the residual stress state at the inner diameter DiA after complete stress relief is just not at the yield curve, is identical to the negative radial stress - σr according to
y =   −   m ⋅ σ r − σ t   < R e L , A

4. Calculation Results

4.1. Results under MSH and ideal plastic material behavior assumptions

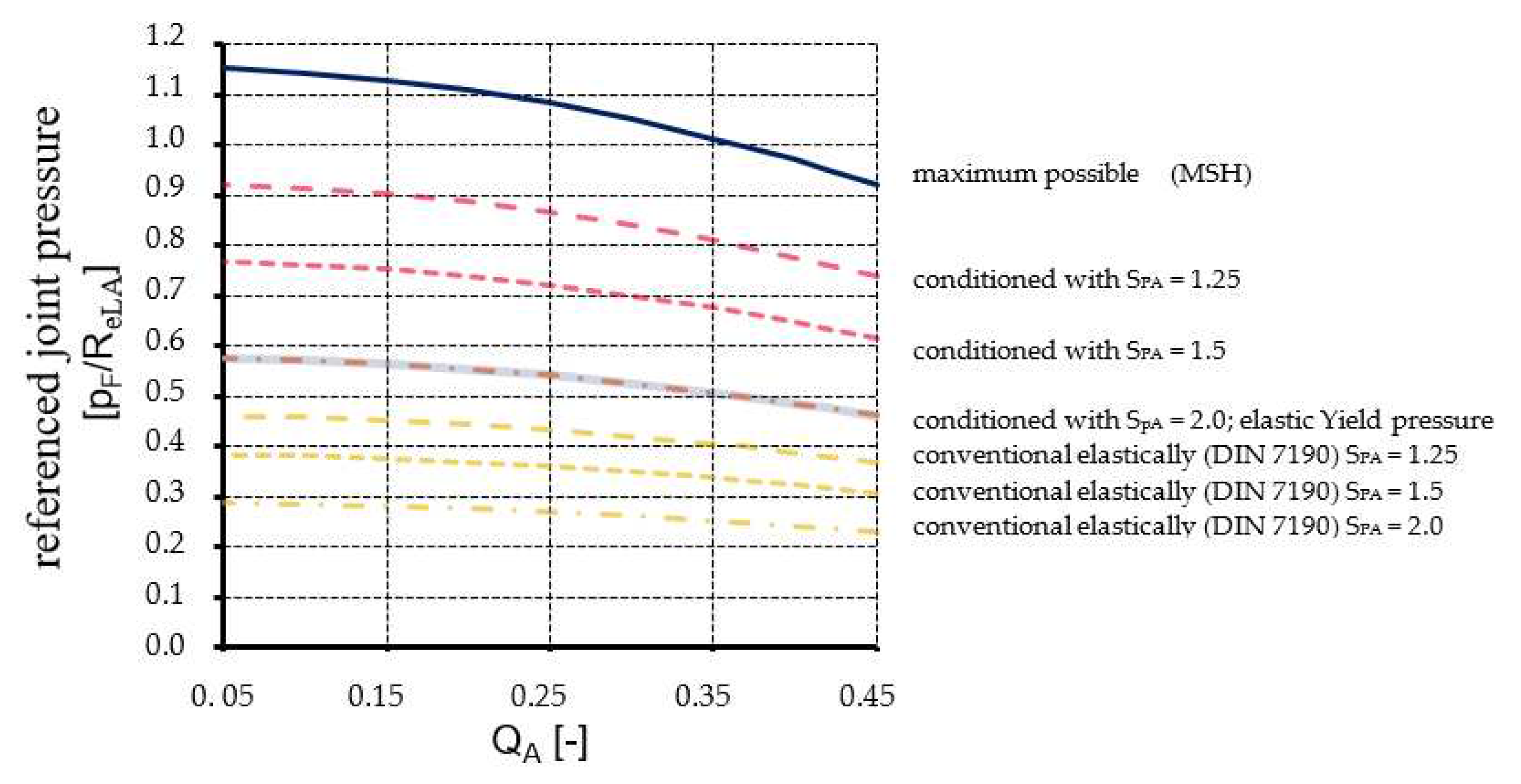
Figure 5 illustrates the maximum joint pressures (calculated using Equations (3) and (10) when y = 1,1547·ReL,A) that can be achieved by Plastic Conditioning, assuming MSH and ideal plastic material behavior, when Reverse Yielding is avoided and the specified safety factors SPA are met. The maximum achievable joint pressures are compared with those of conventional, purely elastically joined interference fits according to DIN 7190 [18].
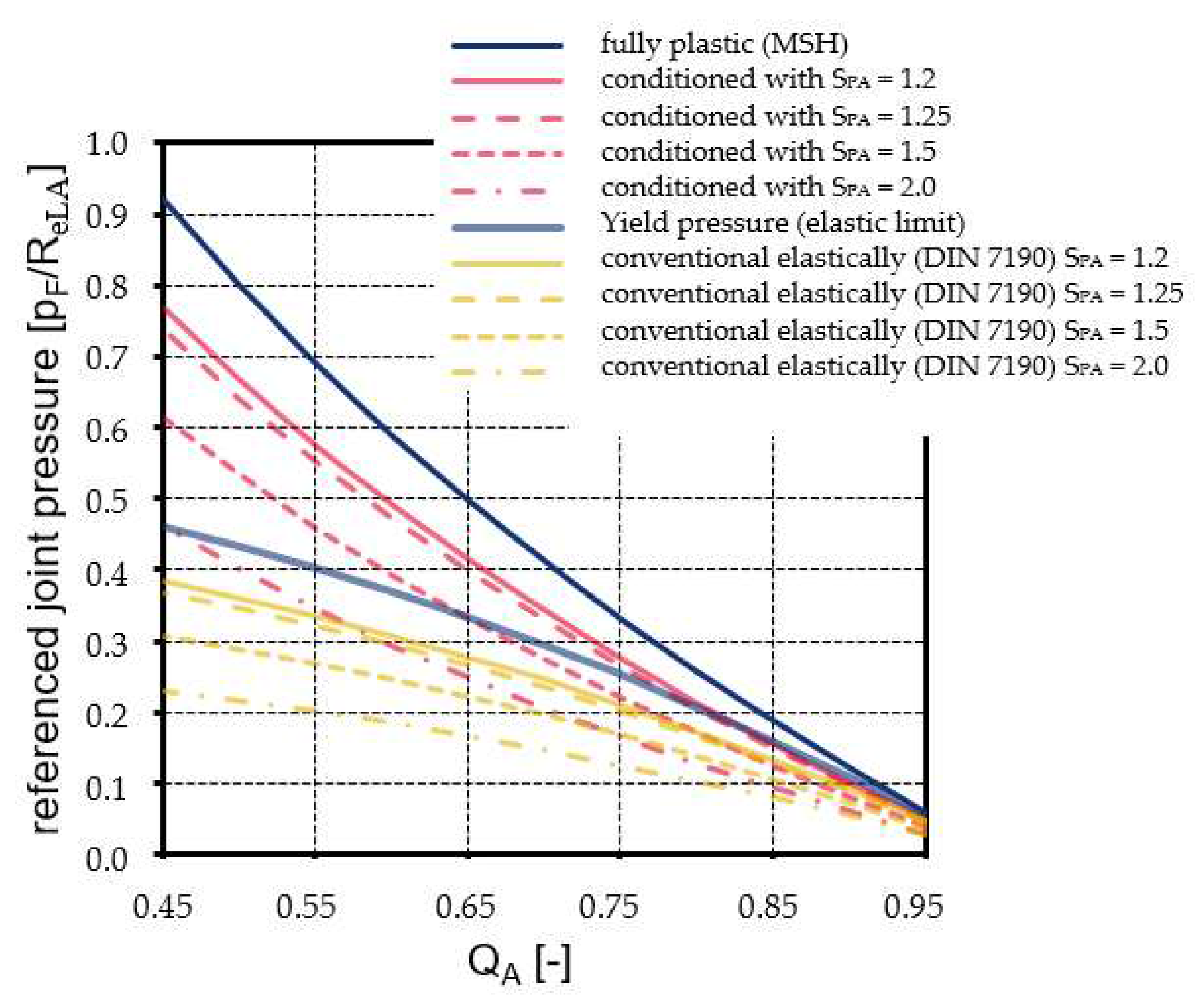
In Figure 6 we compare the highest possible pressures that can be achieved in joints that are not affected by Reverse Yielding and have a QA value above 0.45. These joints have safety factors built in to prevent plastic deformation during assembly and in service. We compare the pressure achieved by purely elastic joints according to DIN 7190 with the pressure achieved by interference fits with prior conditioning. The maximum pressure that can be tolerated during conditioning based on the MSH is called the fully plastic joint pressure (see Equation (8)) and is the reference point for this comparison. The previous explanations were based on the Shear Stress Hypothesis (SH / MSH) and ideal plastic material behavior. Our own numerical investigations based on the Von Mises Yield Criterion (VMYC) and an isotropically hardening material have shown that there is a potential risk of Reverse Yielding beyond the limits described so far (red shaded area in Figure 4).

4.2. Results regarding VMYC and hardening material behavior

Contrary to ideal plastic material behavior, real hardening materials do not exhibit unrestricted flow in the region of uniform elongation of the tensile test stress-strain curve that is of interest for interference fits. Plastic deformation during strengthening is limited by the inhibition of lattice dislocations and the resulting increase in yield strength. This means that the maximum joint pressure is not determined by the yield strength as in the ideal plastic approach, because the inner diameter of a hub or an outer part can now theoretically be loaded at least up to the limit of uniform elongation of the tensile test stress-strain curve. As a result, fully plastic states are theoretically possible even for “thick-walled hubs”, and for hubs with QA > 0.45076 the fully plastic state is only reached at higher pressures than for ideal plastic material according to Equations (7) and (8).
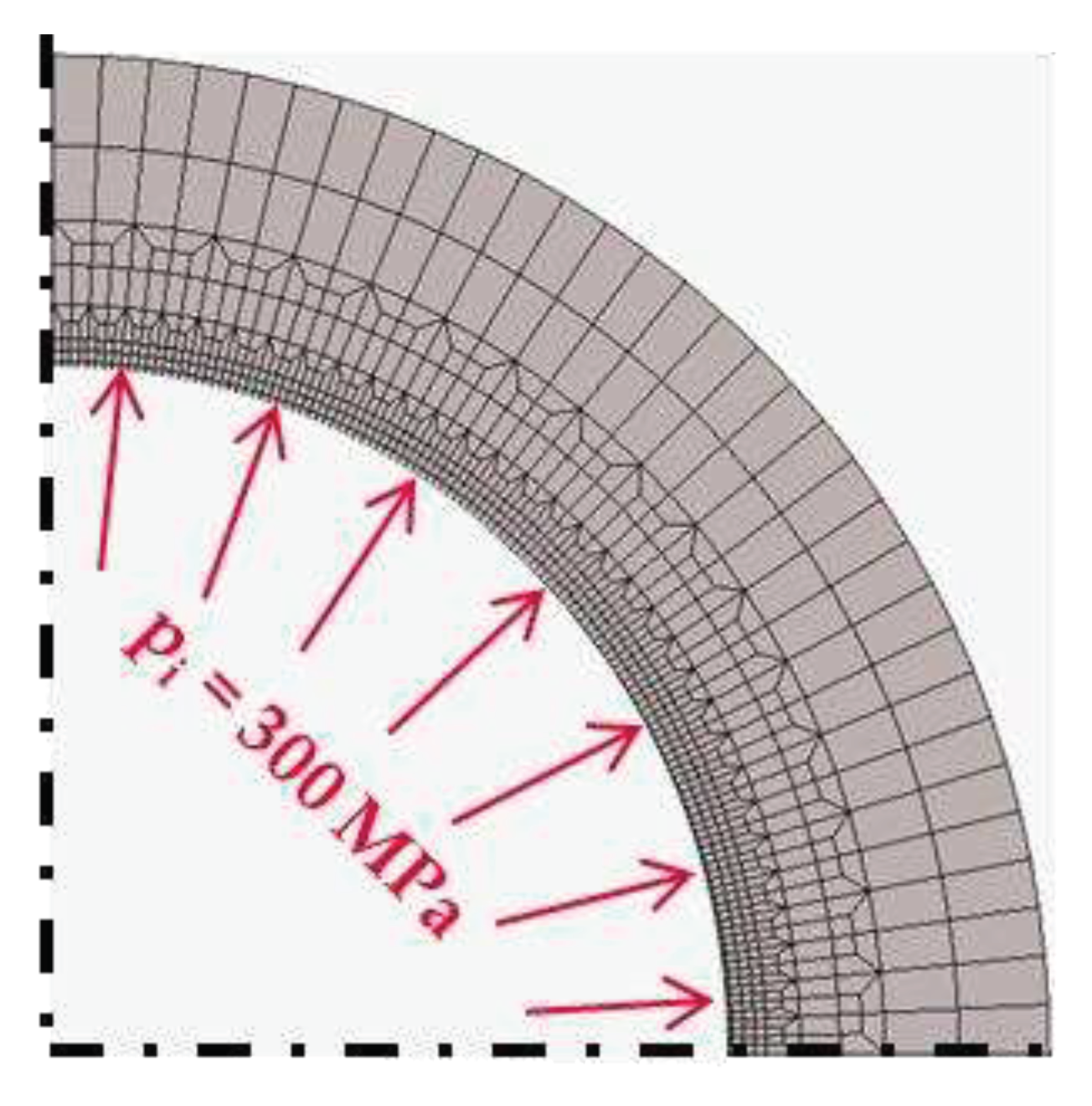
In addition to a significant increase in the joint pressure and the maximum plasticity diameter for “thick-walled hubs”, the range of Reverse Yielding as a function of the diameter ratio according to Kollmann and Önöz [11] is also extended by taking into account material hardening. This was shown by investigations on a two-dimensional FE model corresponding to Figure 7 with a diameter ratio of QA = 0.625 and a pressure of pi = 300 MPa (corresponding to point K in Figure 2) applied to the inner diameter DiA. The pressure was then completely released (corresponding to point D in Figure 2). The hardening behavior was modeled on the basis of tensile tests for the material C45 according to Table 1.
Preprints 82357 g007
Figure 7. Quarter section of the meshed FE model of a hub with QA = 0.625.
Figure 7. Quarter section of the meshed FE model of a hub with QA = 0.625.
Preprints 82357 g007
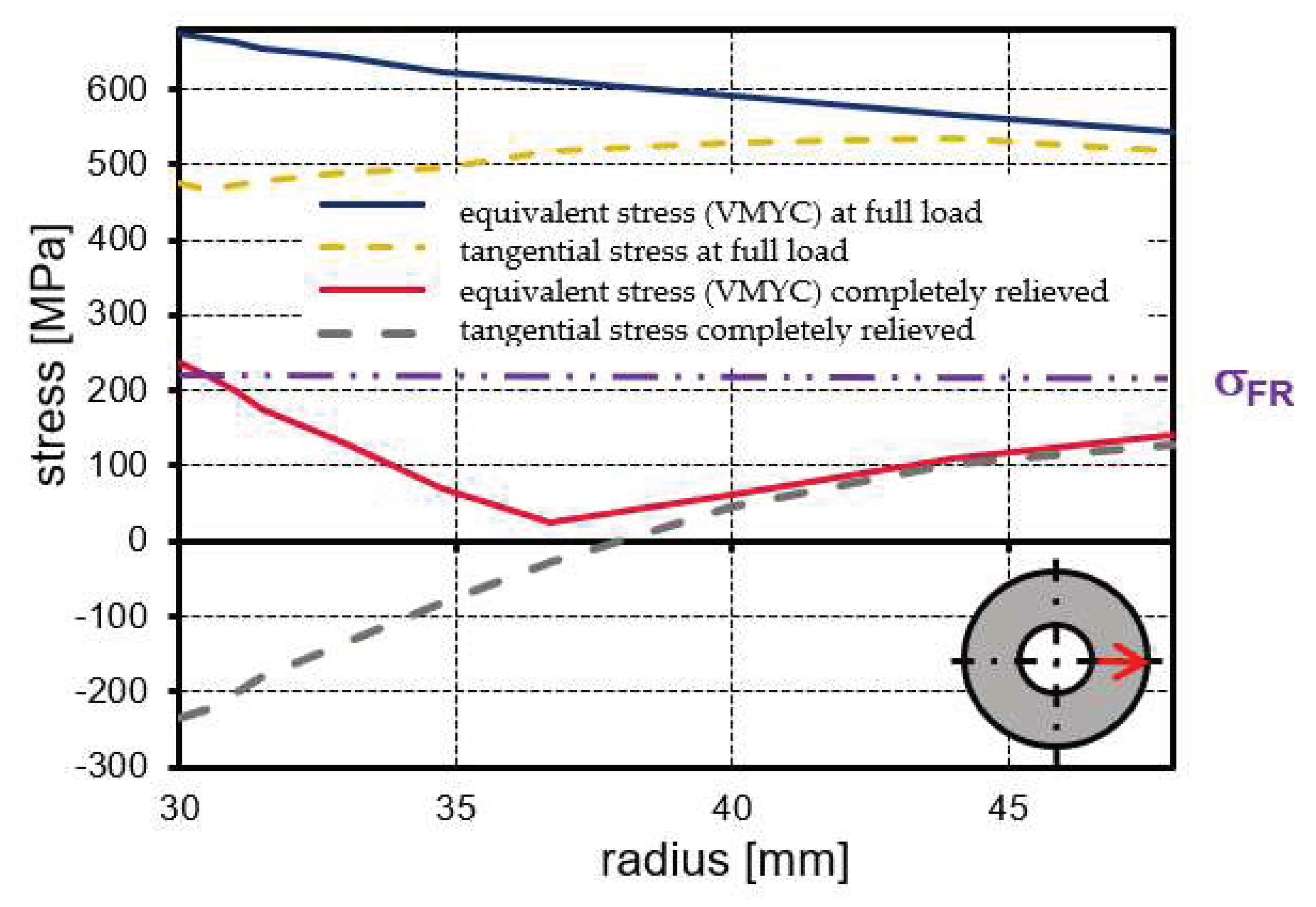
When the component is completely relieved by reducing the internal pressure, the plastic deformation will produce a residual stress state as shown in Figure 8. The blue solid line and the yellow dashed line in Figure 8 show the stress profile in the cross section of the FE model (see red arrow in sketch) at full load. The red solid line and the gray dashed line show the residual stress state after complete unloading.
The equivalent stress curve after complete unloading indicates in the area of the inner diameter that the relief will produce compressive residual stresses of an order of magnitude that will again exceed the yield strength and cause Reverse Yielding if the load history is in the opposite direction. To verify this, the residual stresses were compared to the reverse yield strength, shown in Figure 8 as a purple dash-dot-dot line.
According to Chapter 3.2, this means that, depending on the maximum load and the hardening behavior of the material, Reverse Yielding can also occur in hubs with hardening material if they have a larger diameter ratio (see red line at QA = 0.625 in Figure 4) than that marked in Figure 4 by the dashed line at QA = 0.45 [11] for ideal plastic material.

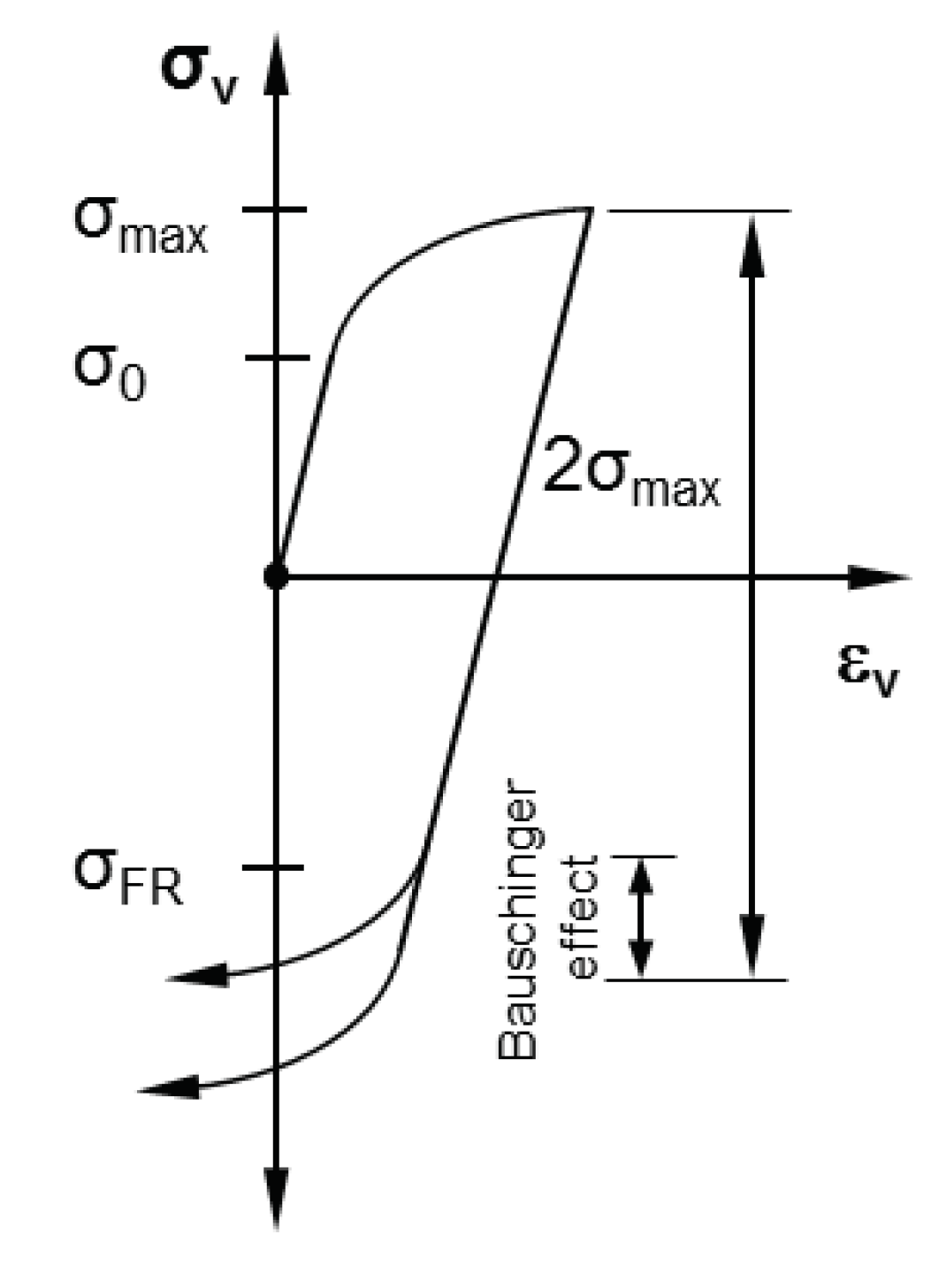
4.3. Results with respect to the Bauschinger effect

The reverse yield strength in Figure 8 shows a significant reduction from the original yield strength before work hardening due to the Bauschinger effect. The influence of the Bauschinger effect on the reduction of yield strength is highly dependent on material and technological factors and can be simplified defined by the Bauschinger Stress Parameter (Equation (12)) [19].
β B S = σ max σ F R  
In this equation, σmax is the maximum stress achieved by plastic deformation as a result of hardening and σFR is the reverse yield strength that is reached when the material is subsequently stressed in the reverse direction (Figure 9).
The C45 steel considered here has a large Bauschinger effect. Therefore, the reverse yield strength in this calculation example was determined to be σFR = 227 MPa, assuming a Bauschinger stress parameter of βBS = 2.95. As can be seen in Figure 8, the equivalent stress at the inner diameter DiA of the hub (red line at radius 30 mm) exceeds this new yield point and plastic stresses reappear.
Therefore, the only way to prevent Reverse Yielding of at-risk components is either to relieve the stress only until it reaches σFR, or to select σmax so that the stresses do not reach σFR after complete relief.
It should be noted that Equation (12) is primarily considered from a fracture mechanics point of view [19]. It does not take into account the dependence of the reverse yield strength on the magnitude of the plastic strains. For this purpose, a number of investigations on autofrettaged cylinders made of higher-strength steels using different approaches have also focused on the influence of the Bauschinger effect [20,21,22,23]. The deviations of the respective results clearly show the decisive influence of the material models used. For larger plastic deformations, a nonlinear unloading behavior was found for the higher-strength steels investigated.
The results of this work highlight the need for research regarding to the Plastic Conditioning of Interference Fits and the materials commonly used in this process.

4.4. Technological Avoidance of Reverse Yielding

Reverse Yielding can also be avoided technologically by integrating Plastic Conditioning into the joining process, which does not require relieving the components in the reverse yielding area. Such an approach is conceivable, for example, in the case of conical interference fits [24] or the use of clamping elements, as shown in Figure 10 (RING-SPANN GmbH).
In these cases, however, it should be borne in mind that Reverse Yielding may also occur in outer (tensile stressed) parts during the disassembly of joints subjected to such plastic stresses. When reassembling such components, there is a risk that the original joint pressures will not be achieved.

5. Conclusions

This paper examines in detail the phenomenon of Reverse Yielding of elastically-plastically loaded interference fits and its influencing parameters.
Going beyond the state of the art, the effects of Reverse Yielding on the plastic conditioning process were investigated and other equivalent stress hypotheses (VMYC) and material models (strain hardening) were included in the investigations.
The extended influencing parameters compared to Autofretting were shown and discussed.
It has been shown that it is important to avoid Reverse Yielding during Plastic Conditioning as it limits the intended residual stress states and the extension of the elastic stress range. We defined the associated parameters, such as diameter ratio QA and maximum pressure pmax, as well as their limits of influence, and identified the components at risk. We also analytically presented possible methods to prevent Reverse Yielding, assuming an ideal plastic material and the Shear Stress Hypothesis.
Since our own numerical investigations for hardening materials based on the Von Mises Yield Criterion (VMYC) have shown an extension of the hazard potential with respect to larger diameter ratios QA and lower pressures pi (or lower amounts of radial stress │σr│), there is a need for further numerical and experimental research on these prerequisites. In this context, material models that represent the Bauschinger effect as realistically as possible should also be used. This is important because previous results have shown that the Bauschinger effect significantly increases the risk of Reverse Yielding, and thus ignoring it can lead to severe miscalculations. The main task here is to determine the extent to which nonlinear unloading behavior [10,21] must be taken into account for the materials used and the common plastic strains.
With the results of this research, the influencing parameters and their range limits for avoiding Reverse Yielding during Plastic Conditioning can be described more precisely, for larger ranges of validity, and prepared in a way that is manageable for users in engineering practice.
The research results in this publication have been collected analytically and numerically. Therefore, another important concern of this work was to identify the need for further research activities in order to be able to plan the necessary resources. This mainly concerns the experimental verification of the analytical and numerical results and the determination of appropriate material models as well as data acquisition and calculation methods. This also includes investigations of the fatigue strength of plastically conditioned interference fits.
For components with larger diameter ratios made of hardening material, investigations beyond the fully plastic state are also of interest. Due to material hardening, for diameter ratios QA > 0.45076, stress states can be achieved before reaching the fully plastic state, resulting in Reverse Yielding after complete unloading, which is not possible with ideal plastic material. Especially for such diameter ratios, it is interesting to investigate conditioning pressures that exceed the fully plastic loading of the component cross-section, since this could significantly intensify the performance increase by conditioning for these components. Special attention is paid to the load limits as a function of the yield strength and stress-strain curve of the material, as well as the increasing risk of Reverse Yielding.

Abbreviations

Abbreviation Unit Meaning
d mm Diameter coordinate (control variable)
DaA mm Outer diameter of the outer part
DF mm Joint diameter (nominal)
DiA mm Inner diameter of the outer part
DPA mm Plasticity diameter of the outer part
Dσr(SH),Dσt(SH) MPa Stress values at point D in the principal stress plane for Shear Stress Hypothesis (SH)
m - Factor for determining the angle of inclination
pi MPa Internal pressure of the disc
pE MPa Elastic joint pressure at the yield strength
pF MPa Joint pressure
pK MPa Conditioning pressure
pKond,max MPa Maximum joint pressure when conditioning
pkrit,SH MPa Critical pressure for Reverse Yielding according to Shear Stress Hypothesis (SH)
pkrit,MSH MPa Critical pressure for Reverse Yielding according to Modified Shear Stress Hypothesis (MSH)
pmax,SH MPa Maximum possible pressure before the fully plastic state of the hub for ideal plastic material according to Shear Stress Hypothesis (SH)
pmax,MSH MPa Maximum possible pressure before the fully plastic state of the hub for ideal plastic material according to Modified Shear Stress Hypothesis (MSH)
QA - Diameter ratio of the outer part
ReL,A MPa Lower yield strength of the outer part
SPA - Safety against plastic deformation of the outer part
SPA(SH) - Safety against plastic deformation of the outer part achieved by conditioning
y MPa Intersection of the relief straight line with the ordinate (tangential residual stress after complete relief)
α ° Inclination angle for load line and relief straight line
BS ° Bauschinger Stress Parameter
εv - Equivalent strain
σFR MPa yield strength that is reached when the material is subsequently subjected to stress in the opposite direction
σmax MPa Maximum stress achieved by plastic deformation as a result of hardening
σr MPa Radial stress
σt MPa Tangential stress
σv MPa Equivalent stress
AT Outer part of the Interference fit
PSS Plane stress state
FE Finite elements
FEM Finite element method
VMYC Von Mises Yield Criterion
SH Shear Stress Hypothesis according to TRESCA
IKAT Institute of Construction and Drive Technology (TU Chemnitz)

References

  1. Rees D W A (1999) Elastic-Plastic Stresses in Rotating Discs by von Mises and Tresca. ZAMM·Z.Angew. Math. Mech., Vol 79, No. 4, 281 - 288.
  2. Jiang J F, Bi Y B (2019) An Elastic-Plastic Analysis of Interference Fit Connection, IOP Conference Series: Materials Science and. Engineering, vol. 504, no. 1. [CrossRef]
  3. Torabnia S, Aghajani S, Hemati M (2019) An analytical investigation of elastic-plastic deformation of FGM hollow rotors under a high centrifugal effect. International Journal of Mechanical and Materials Engineering, 14, Article number:16. [CrossRef]
  4. Lätzer M, Leidich E (2011) FVA-Nr. 566 I-Heft 993-Übertragungsfähigkeit von Klemmverbindungen Unter Besonderer Berücksichtigung Plastischer Verformungen; Abschlussbericht, Forschungsvereinigung Antriebstechnik e.V, Frankfurt, Germany.
  5. Laghzale N, Bouzid A (2016) Analytical Modelling of Elastic-Plastic Interference Fit Joints. International Review on Modelling and Simulations. 9 (3), 191-199, 10.15866/iremos.v9i3.8703.
  6. Baldanzini N (2004) A General Formulation for Designing lnterference-Fit Joints with Elastic-Piastic Components. Journal of Mechanical Design. 126 (4), 737-743. [CrossRef]
  7. Chen P C T (1985) The bauschinger and hardening effect on residual stresses in an autofrettaged thick-walled cylinder. Journal of Pressure Vessel Technology 108, 108-112.
  8. Parker A P, Underwood J H, Kendall D P (1999) Bauschinger Effect Design Procedures for Autofrettaged Tubes Including Material Removal and Sachs’ Method. ASME J. Pressure Vessel Technol., 121, 430–437.
  9. Ghorbanpour A, Loghman A, Khademizadeh H, Moradi M (2003) The Bauschinger and hardening effect on residual stresses in thick-walled cylinders of SUS 304. Transactions of the Canadian Society for Mechanical Engineering. 26 (4), 361-372, 10.1139/tcsme-2002-0021.
  10. Jahed H, Dubey R N (1997) An Axisymmetric Method of Elastic-Plastic Analysis Capable of Predicting Residual Stress Field, ASME J. Pressure Vessel Technol., 119, 264-273. [CrossRef]
  11. Kollmann F G, Önöz E (1979) Die Eigenspannungen in den Ringen eines elastisch-plastisch beanspruchten Querpreßverbandes nach der Entlastung. Forschung im Ingenieurwesen. Bd. 45 (6), 169-177.
  12. Koiter T W (1960) General theorems for elastic-plastic solids. Progress in Solid Mechanics, Vol. I. Amsterdam: North Holland Publishing Comp.
  13. Gamer U (1987) Die Spannungen im elastisch-plastischen Preßverband nach Rotation. Forschung im Ingenieurwesen Bd. 53, 97-100.
  14. Mack, W (1992) Entlastung und sekundares Fließen in rotierenden elastisch-plastischen Hohlzylindern. ZAMM. Z. angew. Math. Mech. 72, 65-68.
  15. Schierz M (2018) Steigerung des elastischen Potenzials von Pressverbindungen durch plastische Konditionierung der Fügepartner. Dissertation, Technische Universität Chemnitz, Chemnitz.
  16. Schierz M, Leidich E, Ziaei M (2018) Plastisch konditionierte Pressverbindungen. In: VDI (Hrsg) Welle-Nabe-Verbindungen. VDI-Berichte Nr. 2337.
  17. Schierz, M (2022) Increase in Elastic Stress Limits by Plastic Conditioning: Influence of Strain Hardening on Interference Fits. Applied Mechanics 3, no. 2, 375-389. [CrossRef]
  18. DIN 7190-1:2017: Pressverbände - Teil 1: Berechnungsgrundlagen und Gestaltungsregeln (2017).
  19. Buciumeanu M, Palaghian L, Miranda A S, Silva F (2011) Fatigue life predictions including the Bauschinger effect. International Journal of Fatigue, Vol. 33 Issue 2, 145-152. [CrossRef]
  20. Parker A P (2001) Bauschinger Effect Design Procedures for Compound Tubes Containing an Autofrettaged Layer. ASME. J. Pressure Vessel Technol, 123(2), 203–206. [CrossRef]
  21. Loffredo M (2018) Measurement and modelling of Bauschinger effect for low-level plastic strains on AISI 4140 steel. Procedia Structural Integrity, Volume 8, 265-275. [CrossRef]
  22. Jahed H, Faritus M R, Jahed Z (2012) Residual Stress Measurements in an Autofrettage Tube Using Hole Drilling Method. ASME. J. Pressure Vessel Technol. 12, 134(5). 20 October. [CrossRef]
  23. Huang X P, Cui W (2006) Effect of Bauschinger Effect and Yield Criterion on Residual Stress Distribution of Autofrettaged Tube. Journal of Pressure Vessel Technology-transactions of The Asme - J PRESSURE VESSEL TECHNOL. 128. 10.1115/1.2172621.
  24. DIN 7190-2:2017: Pressverbände - Teil 2: Berechnungsgrundlagen und Gestaltungsregeln für kegelige, selbsthemmende Pressverbände (2017).
Preprints 82357 g001
Figure 1. Cross section of an interference fit (hub and hollow shaft) with principal stresses.
Figure 1. Cross section of an interference fit (hub and hollow shaft) with principal stresses.
Preprints 82357 g001
Preprints 82357 g002
Figure 2. Principal stresses at the inner diameter DiA of the outer part of an interference fit with the ideal plastic yield strength according to the Shear Stress Hypothesis (SH) during Plastic Conditioning.
Figure 2. Principal stresses at the inner diameter DiA of the outer part of an interference fit with the ideal plastic yield strength according to the Shear Stress Hypothesis (SH) during Plastic Conditioning.
Preprints 82357 g002
Preprints 82357 g003
Figure 3. Stress states at any point of the inner diameter DiA (marked in red) of three characteristic diameter ratios QA in the principal stress plane (ideal plastic material) during conditioning with maximum conditioning joint pressure pKond,max and subsequent stress relief.
Figure 3. Stress states at any point of the inner diameter DiA (marked in red) of three characteristic diameter ratios QA in the principal stress plane (ideal plastic material) during conditioning with maximum conditioning joint pressure pKond,max and subsequent stress relief.
Preprints 82357 g003
Preprints 82357 g004
Figure 4. Region of Reverse Yielding in an outer part.
Figure 4. Region of Reverse Yielding in an outer part.
Preprints 82357 g004
Preprints 82357 g005
Figure 5. Maximum achievable joint pressures (MSH) for plastic conditioned interference fits (0.05 ≤ QA ≤ 0.45) compared with those of conventional, purely elastically joined according to DIN 7190 with specified safety against plastic deformation SPA and avoidance of Reverse Yielding.
Figure 5. Maximum achievable joint pressures (MSH) for plastic conditioned interference fits (0.05 ≤ QA ≤ 0.45) compared with those of conventional, purely elastically joined according to DIN 7190 with specified safety against plastic deformation SPA and avoidance of Reverse Yielding.
Preprints 82357 g005
Preprints 82357 g006
Figure 6. Maximum achievable joint pressures (MSH) for plastic conditioned interference fits (0.45 ≤ QA ≤ 0.95) compared with those of conventional, purely elastically joined according to DIN 7190 with specified safety against plastic deformation SPA and avoidance of Reverse Yielding.
Figure 6. Maximum achievable joint pressures (MSH) for plastic conditioned interference fits (0.45 ≤ QA ≤ 0.95) compared with those of conventional, purely elastically joined according to DIN 7190 with specified safety against plastic deformation SPA and avoidance of Reverse Yielding.
Preprints 82357 g006
Preprints 82357 g008
Figure 8. Stress states of a C45 hub with QA = 0.625 loaded with an internal pressure of pi = 300 MPa and relieved by Reverse Yielding.
Figure 8. Stress states of a C45 hub with QA = 0.625 loaded with an internal pressure of pi = 300 MPa and relieved by Reverse Yielding.
Preprints 82357 g008
Preprints 82357 g009
Figure 9. Bauschinger effect.
Figure 9. Bauschinger effect.
Preprints 82357 g009
Preprints 82357 g010
Figure 10. Shaft–hub connection with a cone clamping element (hub clamped on the inside) from RINGSPANN GmbH (Image source: RINGSPANN GmbH).
Figure 10. Shaft–hub connection with a cone clamping element (hub clamped on the inside) from RINGSPANN GmbH (Image source: RINGSPANN GmbH).
Preprints 82357 g010
Table 1. Data from the tensile test for C45 (IKAT).
Table 1. Data from the tensile test for C45 (IKAT).
σv εv
(MPa) (-)
370.00 0.00171
390.00 0.00182
400.00 0.00189
410.00 0.01303
420.00 0.01417
430.00 0.01549
440.00 0.01665
470.00 0.02075
500.00 0.02543
530.00 0.03097
560.00 0.03775
590.00 0.04612
620.00 0.05967
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated