Prerpints.org logo
Preprint
Article

Hybrid BBO-Firefly algorithm for parameter optimization of bidirectional reflection distribution function model

Altmetrics

Downloads

101

Views

33

Comments

0

This version is not peer-reviewed

Submitted:

15 August 2023

Posted:

16 August 2023

You are already at the latest version

Alerts
Abstract
We designed a bidirectional reflection distribution function (BRDF) measurement system to research the characteristics of space target materials. This system measures the BRDF data of an aluminum plate and gold foil. A hybrid biogeography-based optimization-firefly (BBO-Firefly) algorithm was proposed to optimize the five-parameter BRDF model. To check the performance of the hybrid BBO-Firefly algorithm, we set up a contrast experiment to optimize the BRDF parameters using the BBO algorithm, Firefly algorithm, and hybrid BBO-Firefly algorithm. The experimental results prove that the hybrid BBO-Firefly algorithm surpasses the BBO algorithm and Firefly algorithm in convergence speed and precision in the same situation and has a better optimization effect. Finally, we substitute the optimization results of the hybrid BPO-Firefly algorithm into the BRDF model to analyze the reflection characteristics of an aluminum plate and gold foil.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

BRDF is a physical quantity that characterizes the reflection characteristics of the target surface space. It is widely used in computer graphics[1,2,3,4], remote sensing[5,6,7,8,9], and Lidar[10,11,12]. BRDF models were divided into the analytical model[13,14,15,16,17] and the empirical model[18,19,20,21,22] according to different modeling methods. The analysis model is based on theoretical analysis and corresponding physical derivation, which can precisely simulate the physical process of the reflection of the target material. Torrance-Sparrow(T-S) model[13] is the most representative analysis model based on the microplate theory. The T-S model fully considers the occlusion and shadow effect between adjacent microplates. Cook and Torrance optimized the Fresnel formula in the T-S model and proposed Cook-Torrance(C-T) reflection model[14] for rough surfaces. Wu proposed a five-parameter BRDF model[15] based on the C-K model, which has a good optimization effect on composite materials and has been widely studied and applied. The empirical model mainly carries out a mass of experimental measurements on the target material and optimizes the model parameters according to the experimental results. The Phong model[22] is the most typical BRDF empirical model, which simplifies the T-S model and consists of specular reflection and diffuse reflection in the form of higher cosine. The Phong model is widely used in computer graphics rendering because of its high computational efficiency and accurate image expression. Analytical and empirical models have their characteristics, and appropriate BRDF models can be selected according to different material types to research the target characteristics.
In practice, BRDF parameters of the same material may vary significantly due to different surface roughness. Therefore, it is an effective research method to collect BRDF experimental data on materials and optimize model parameters through experimental data. Wu used a genetic algorithm (GA) to optimize the uncertain parameters in the BRDF model[15] of cement, steel plate, and other rough materials. GA algorithm has strong global search ability, but its disadvantages contain slow convergence, weak local search ability, and long running time. Wang proposed a hybrid artificial bee colony algorithm[23], which improved the algorithm's local search ability and efficiency, but the algorithm was prone to fall into the optimal local solution. To solve the above problems, we proposed a hybrid BBO-Firefly algorithm to optimize the parameters of the BRDF model. The BBO algorithm is a newly developed natural heuristic algorithm based on biogeography theory. The BBO algorithm has shown better optimization strategies and effects in numerous experimental scenarios than other meta-heuristic algorithms in the initial iteration process. However, it needs to be competitive enough to discover the optimal solution when the number of iterations increases. The Firefly algorithm is a natural optimization algorithm based on fireflies' flicker patterns and behavior. Compared with other optimization algorithms, it can find the optimal solution better. Therefore, the core idea of the hybrid BBO-Firefly algorithm is to combine the fast global search ability of the BBO algorithm with the optimal exploration and development ability of the Firefly algorithm. When the two algorithms are combined, the hybrid BBO-Firefly algorithm can explore to the maximum extent.

2. BRDF measurement system

2.1. Five-Parameter BRDF Model

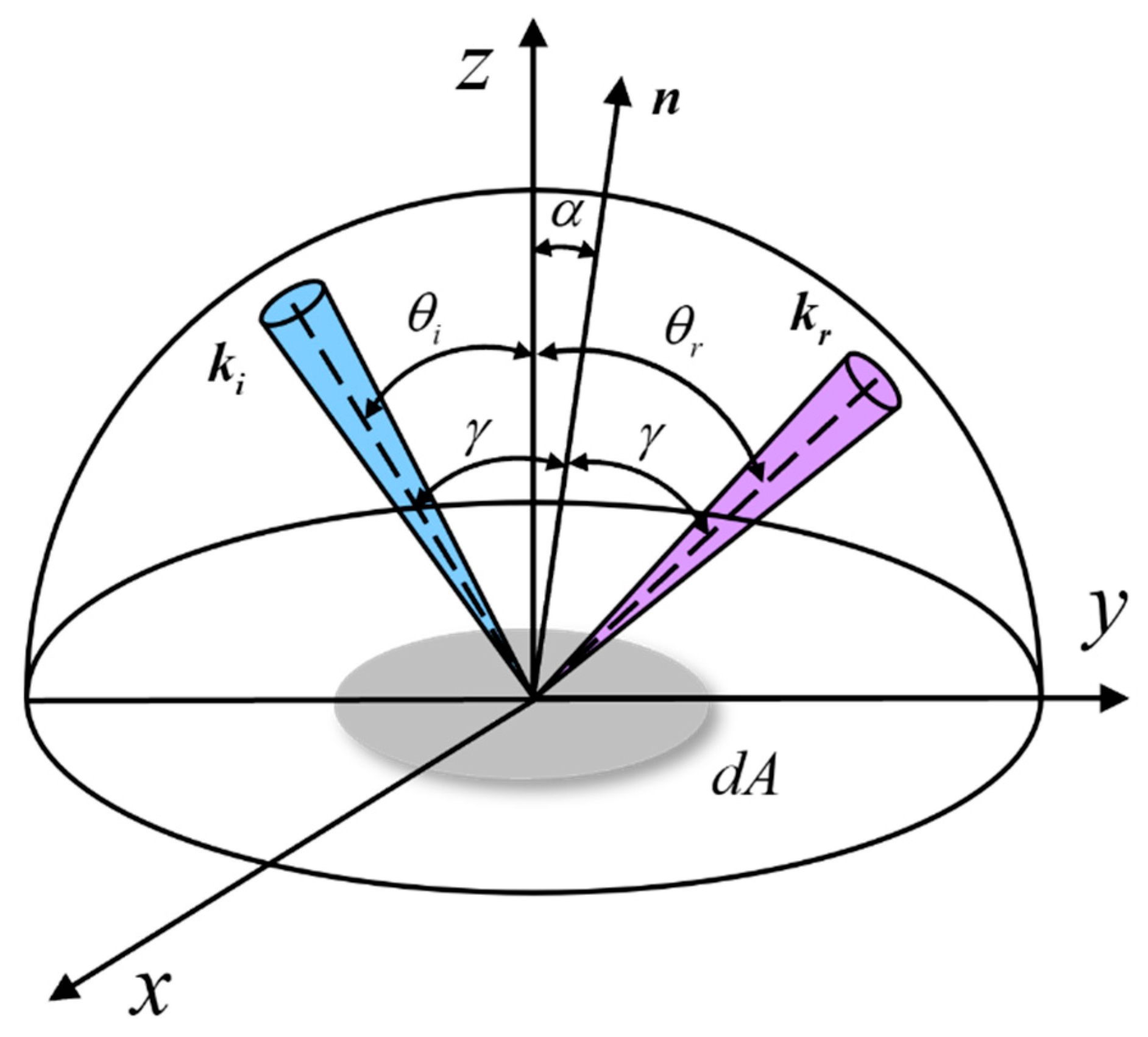
This paper researches the reflection characteristics of aluminum plates and gold foil in the five-parameter BRDF model. This model considers the material surface to be composed of many small surface elements, and the reflection of each surface element follows Fresnel's reflection law.
Figure 1 presents a diagram of the BRDF model of the microelement. The o z axis is the normal direction of the macroscopic object surface, and the n axis is the normal direction of the microfacet. γ is the angle between the incident light's direction and the microfacet's normal direction. The incident wave vector k i illuminates the material's surface, k r is the reflected wave vector. ( θ i , φ i ) is the incident angle, ( θ r , φ r ) is the scattering angle, α is the included angle between n axis and z axis, α and γ can be represented as:
cos α = cos θ i + cos θ r 2 cos γ
cos 2 γ = 1 2 cos θ i cos θ r + sin θ i sin θ r cos φ r + 1
According to the principle of geometric optics and probability, the five-parameter model can be expressed as:
f r θ i , θ r cos θ i = k b k r 2 cos α 1 + k r 2 − 1 cos α exp b ⋅ 1 − cos γ a ⋅ G θ i , θ r cos θ i cos θ r + k d cos θ i
where, k b , k d , k r , a , and b are unknown parameters. k b and k d are specular reflection coefficient and diffuse reflection coefficient, respectively. k r is related to the roughness of the material surface. a and b depend on the refractive index of the material. f r θ i , θ r is the BRDF measured value, G θ i , θ r is the shadow shading function of the BRDF model, which can be expressed as:
G θ i , θ r = 1 + ω p tan θ i p tan θ r p 1 + σ r tan β p 1 + ω p tan 2 θ i p 1 + ω p tan 2 θ r p
ω p = σ p 1 + u p sin α sin α + v p cos α tan θ i p = tan θ i sin θ i + sin θ r cos φ r 2 sin α cos β tan θ r p = tan θ r sin θ r + sin θ i cos φ r 2 sin α cos β tan β p = cos θ i − cos β 2 sin α cos β
where σ p , σ r , u p and v p are the experimental parameters related to the surface roughness and refractive index of the material. Generally, we set the following empirical values to: σ p =0.0136, σ r =0.0136, u p =9.0, v p =1.0.

2.2. Experimental equipment and methods

In order to obtain the actual data of the target material, we independently designed a set of multi-azimuth irradiance measurement systems to research the BRDF characteristics of the aluminum plate and gold foil. Figure 2 presents a diagram of the measurement system. The measuring system comprises a laser light source, an electric rotary table system, and a high-sensitivity laser power meter. Using a rotating arm for the laser light source, another for the laser power meter, and two corresponding independent rotary motors makes material surface measurement possible. Adjust the height of the lifting platform so that the axis of the two rotating arms is the same height as the material's surface to be measured. The system can complete high-precision measurements under the setting of an electric rotary table.
The measured value of BRDF can be expressed by the ratio of radiated illumination reflected by the target to irradiance irradiated on the target surface[24] :
B R D F θ i , φ i , θ r , φ r = d L r θ i , φ i , θ r , φ r d E θ i , φ i
where, θ and φ represent zenith angle and azimuth angle, respectively, and subscripts i and r represent incidence and reflection, respectively, d E ( θ i , φ i ) is the irradiance radiated to the target surface, and d L r ( θ i , φ i ; θ r , φ r ) is the irradiance reflected by the target surface.
In the actual measurement of BRDF, factors such as experimental environment and measuring equipment may cause changes in measured values, which is called experimental uncertainty. We assume that experimental uncertainty is mainly related to the laboratory environment, detector, laser light source and the rotation device. The measurement uncertainty model of the BRDF measuring system can be expressed as:
U B R D F = U E 2 + U D 2 + U L 2 + U T 2
The experiment was conducted in an opaque dark room, and a laser light source（ λ =650nm） supplied stable collimated illumination. A 5-h test indicated that the output power error of the laser light source was within 3%. The high-precision power meter used in the experimental is Thorlabs S120-FC, and the product test report shows that the measurement uncertainty is within 3% under the condition of wavelength of 440-980nm. The experimental measurement error was 0.03 μ W / m 2 of the irradiance under dark conditions in the laboratory, the uncertainty introduced by the laboratory environment is about 0.15%. The accuracy of incidence angle and reflection angle is mainly affected by the rotation arms, and the uncertainty of the rotation arm is 0.3%. Therefore, according to the calculation of the Formula (7), the uncertainty of the BRDF measuring system we designed is 3.6%. It should be noted that the experiment ignored the uncertainty caused by non-ideal factors such as the operating error and the laboratory temperature.
This paper measured the BRDF of the Lambertian plate shown in Figure 3a to further verify our measuring system before measuring the BRDF of the target material. Zenith angle and azimuth angle are set θ i = φ i = 0 ° due to the isotropy of the Lambertian plate, and the reflection angle ranges from 0°to 90° with an interval of 5°. Experimental measurement and theoretical values are shown in Figure 3b.
The experimental measurement is in good agreement with the theoretical values. The reflection error of the Lambertian plate is less than 0.53%, which indicates that our experimental device is accurate and reliable.
The aluminum sheet and gold leaf samples are placed on a horizontal platform. The incidence angle of the laser light source is changed by controlling the angle of the light source arm, and the incidence angles were 15°, 30°, 45°, and 60°, respectively. For each angle of incidence, the detector automatically rotates from -90° to 90° to collect the reflected beam in the plane. The experimental test results will be used to optimize the BRDF model parameters.

3. Hybrid BBO-Firefly optimization algorithm

After obtaining the BRDF data of the target material through the self-designed experimental system, the unknown parameters of the BRDF model need to be optimized by algorithms. In order to accurately describe the characteristics of the target material, the hybrid BBO-Firefly algorithm is proposed to solve the parameter optimization problem of the BRDF model. The Hybrid BBO-Firefly algorithm is a new joint optimization algorithm combining the BBO and Firefly algorithms. It not only guarantees the global search characteristic of the BBO algorithm but also plays the fast search characteristic of the Firefly algorithm.

3.1. BBO algorithm

The biogeography-based optimization (BBO) algorithm[25] is based on the biogeography theory proposed by Dan Simon in 2009. The algorithm simulates the migration and variation process in biogeography to evolve the population and solve the optimization problem continuously. The algorithm can be understood as N organisms surviving in the geographical environment. Affected by external conditions such as rainfall and environmental temperature, some organisms in the population will migrate to adapt better to the environment. is the habitat where the population resides in the migration process. Each habitat represents a potential solution to the optimization problem, and the habitat quality is represented by the habitat suitability index (HIS). HSI is related to factors such as rainfall, vegetation diversity, geomorphic features, land area, temperature, and humidity, called Suitability Index Variables (SIV). When the habitat population number exceeds the habitat fitness function value , the population will emigrate. The habitat renewal process of a population can be expressed as follows:
x i = x i + α ( x n e w − x i )
where, x n e w is the new habitat selected by the population to immigrate. α is the immigration coefficient.
Population variation will occur due to natural disasters or abnormal climate changes, resulting in significant changes in the number of species in the habitat. Population habitat change caused by variation can be expressed as:
x i = x i + δ ⋅ r a n d n
where, δ is the variation coefficient, and r a n d n is the random variation range of the population.
Through the above two processes of migration and variation, the population can update its position and optimize the scheme.

3.2. Firefly algorithm

The Firefly algorithm[26] is a natural heuristic optimization algorithm proposed by Yang in 2010. The algorithm simulates the luminescence mechanism and behavior mode of tropical fireflies in nature. It stimulates the search and position updating process in the optimization process into the mutual attraction and movement process among fireflies. The objective function is simulated as the luminance information of an individual firefly, and the optimal solution is found by iteration. Assume that the position of the firefly is x i , and the brightness of the firefly determines its attractiveness. Firefly with low brightness moves towards the brighter firefly, and its movement process can be expressed as:
x i = x i + β 0 e γ ⋅ r i j 2 ( x j − x i ) + α ε
where, β 0 is the attraction coefficient between fireflies, γ is the light absorption coefficient, r i j is the distance between firefly i and firefly j , and α ε is a random term.
The position of firefly is updated by iteration, and the optimal solution is used as the optimization scheme of the Firefly algorithm.

3.3. Hybrid BBO-Firefly algorithm

The hybrid BBO-Firefly algorithm introduces the Firefly operator into the BBO algorithm, improving the local searching ability and solving precision. The basic steps of the hybrid BBO-Firefly can be summarized as the pseudocode shown in Table 1.
According to the pseudocode implementation steps in Table 1, the experimental data was optimized to verify the algorithm's feasibility.

4. Experimental result

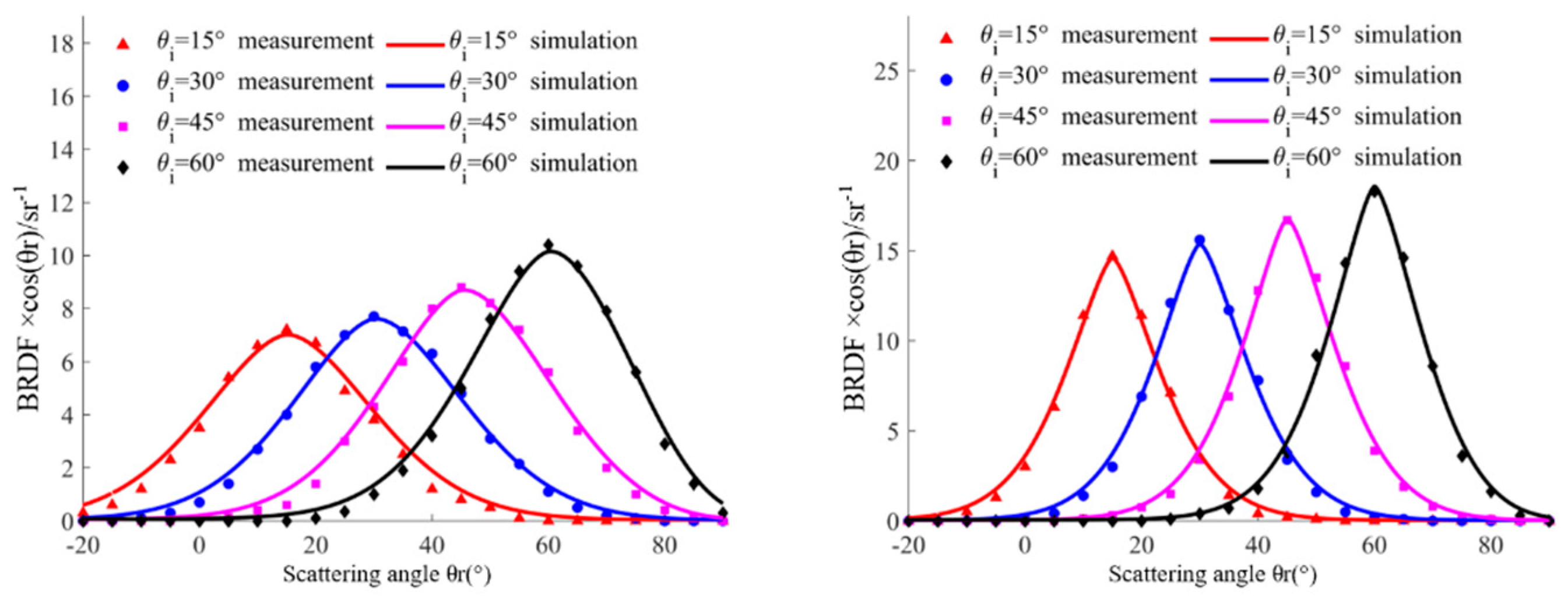
The BRDF measurement system obtains BRDF data values of aluminum plate and gold foil. Unknown parameters in the five-parameter BRDF model are optimized by the BBO-Firefly algorithm. BRDF-measured values and optimization curves were plotted, as shown in Figure 4. The incidence angles are 15°, 30°, 45°, and 60° respectively, and the observed angles vary from -20° to 90°. Figure 4 (a) and (b) show the changes in BRDF measurements and fitting values of aluminum plate and gold foil with the observation angle, respectively. According to the optimization effect of the algorithm, the BRDF characteristics of different materials are different. BRDF peak positions of the same material are different at different incident angles. The peak value of BRDF is in the direction of the same observation angle as the incident angle. As a result, BRDF consists of diffuse and specular reflection. In the same case, the BRDF value of Figure 4b is greater than that of Figure 4a, so gold foil's specular reflection is stronger than aluminum plate's. The optimization results indicate that the model curve calculated by BBO -Firefly algorithm is certainly consistent with the experimental data.
This paper sets up three control experiments to accurately measure the optimization effect of the BBO-Firefly algorithm. In the same situation, the optimization effect of the three groups of algorithms is compared, and the algorithm's optimization error is evaluated using the MSE function. The objective function is defined as:
M S E = 1 n ∑ i = 1 n f model k b , k d , k r , a , b − f measured   k b , k d , k r , a , b 2
The BRDF model parameters of the BBO algorithm, Firefly algorithm, and hybrid BBO-Firefly algorithm are calculated, and the MSE function of each algorithm is calculated and written in Table 2.
According to the optimization results in Table 2, the incidence angles are 15°, 30°, 45°, and 60°, respectively. When the material is an aluminum plate, the MSE of the BBO-Firefly algorithm is reduced to 14%, 7%, 10%, and 11% compared with the original BBO algorithm, and the MSE is reduced to 14%, 7%, 12%, 15% compared with the original Firefly algorithm. When the material is gold foil, the MSE of the BBO-Firefly algorithm is reduced to 17%, 18%, 12%, and 11% compared with the original BBO algorithm, and the MSE is reduced to 15%, 24%, 28%, 32% compared with the original Firefly algorithm. The results show that the optimization precision of the BBO-Firefly algorithm is much higher than that of the BBO algorithm and Firefly algorithm, and it has better stability performance.
For intelligent optimization algorithms, iteration speed determines the efficiency of the algorithm. Figure 5 shows the convergence curve of the BBO-Firefly algorithm, BBO algorithm, and Firefly algorithm when optimizing the BRDF model of aluminum plate.
As shown in Figure 5, After 50 iterations, the BBO-Firefly algorithm tends to be horizontal. Compared with the BBO algorithm and the Firefly algorithm, the BBO-Firefly algorithm has stronger convergence ability and can search for the optimal solution quickly.
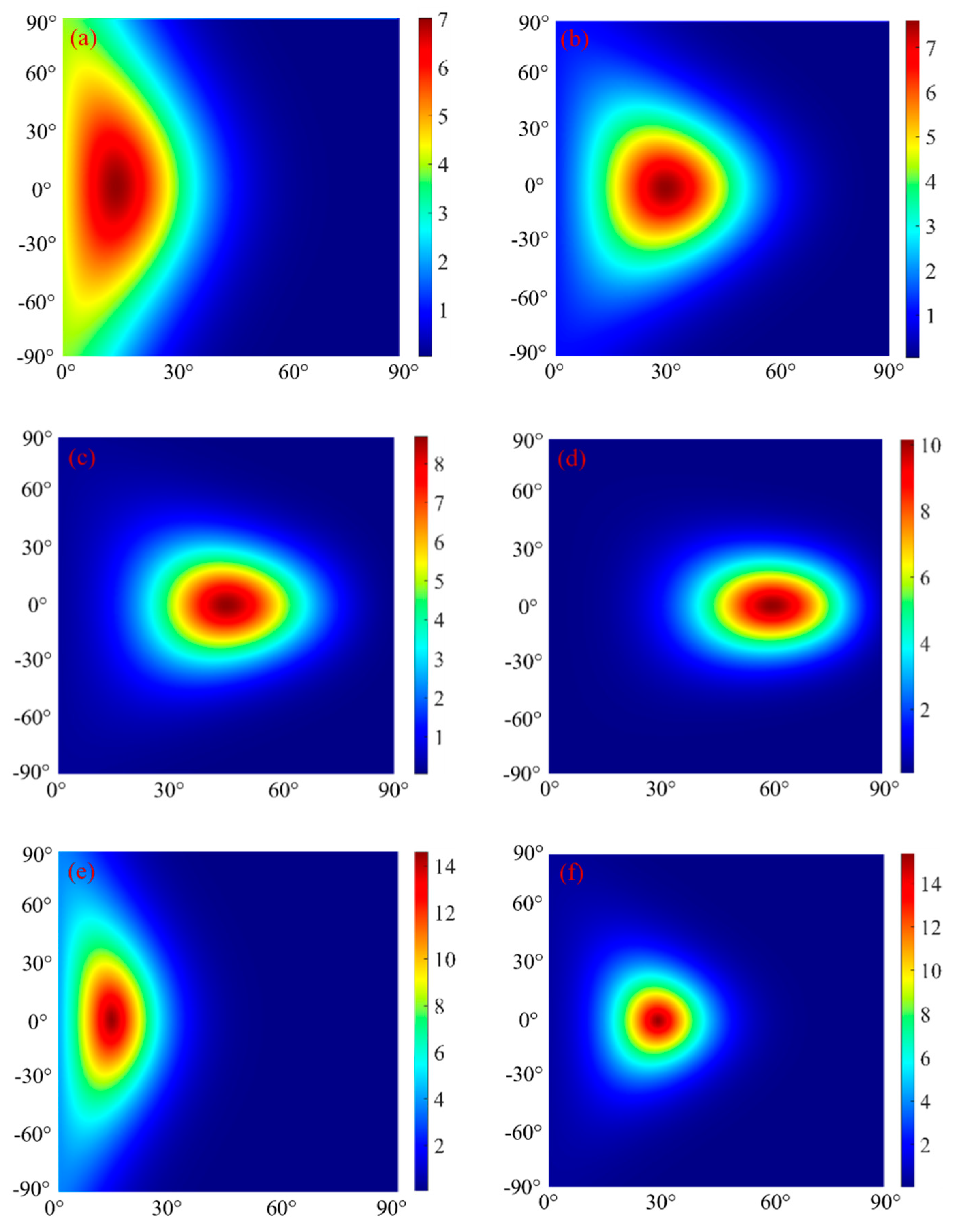
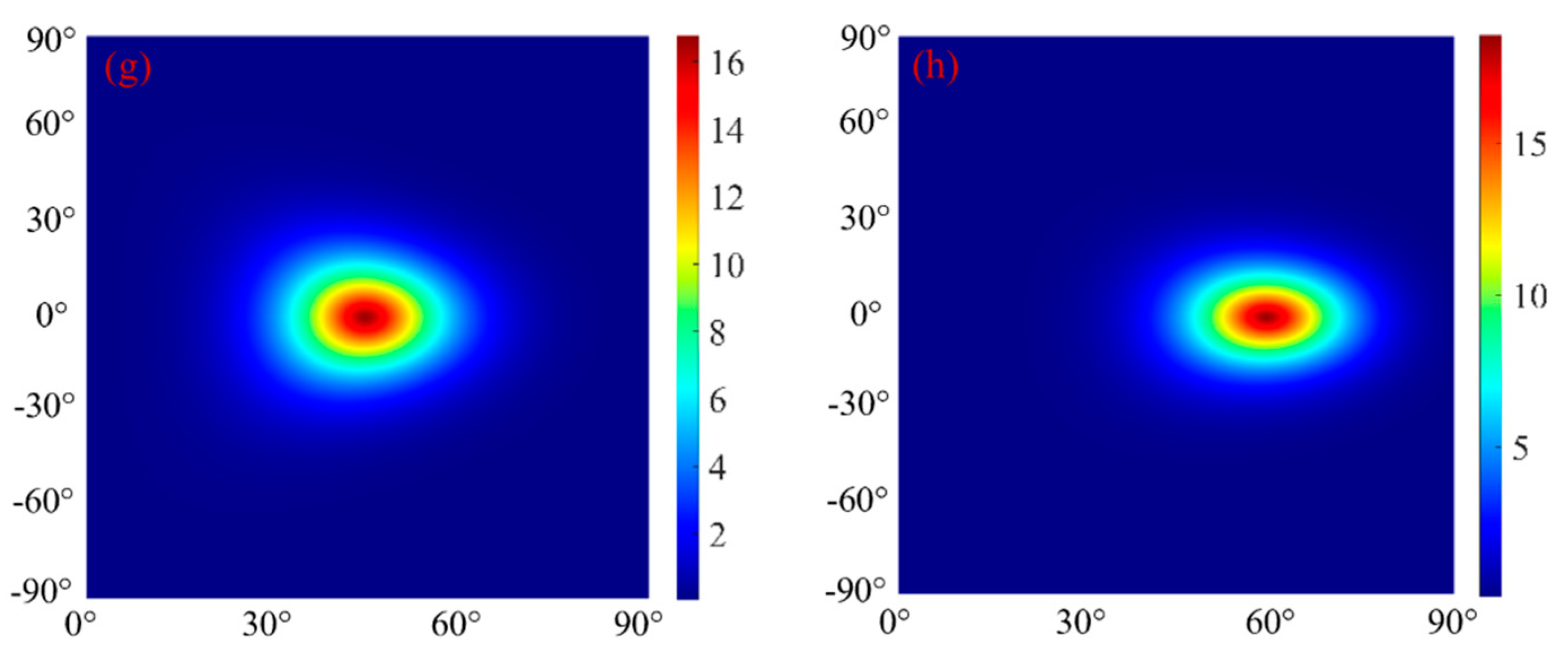
Figure 6 is a false-color image simulating BRDF measurements of aluminum plate and gold foil. Figure 6a–d shows the BRDF distribution of aluminum plate with incident angles of 15°, 30°, 45°, and 60°, respectively. Figure 6 e–h shows the BRDF distribution of the gold foil, with incidence angles of 15°, 30°, 45°, and 60°. The results show a distinct difference in reflection characteristics between the two samples.

5. Conclusion

In this paper, the BRDF data of aluminum plate and gold foil is measured by the self-designed BRDF measurement system. A hybrid BBO-Firefly algorithm is proposed to optimize the parameters of the five-parameter BRDF model. The hybrid BBO-Firefly algorithm introduces the Firefly operator into the BBO algorithm, the local searching ability and solving precision are improved, and the optimal solution is searched quickly. To demonstrate the performance of the BBO-Firefly algorithm, we measured the irradiance of materials under different incident angles and observation angles and calculated its BRDF value. The experimental results show that the model parameters obtained by the hybrid BBO-Firefly algorithm coincides with the experimental data. The optimization speed and precision of the hybrid BBO-Firefly algorithm are significantly improved compared with the BBO algorithm and Firefly algorithm. Moreover, this algorithm can be used to inverse other space target materials and the BRDF parameter model, which provides a technical scheme for researching space target characteristics.

6. Patents

The relevant content of the article has applied for a national invention patent, the patent name is a BRDF parameter fitting method and system for material surface based on lidar imaging, patent number: ZL 2023 1 0531474.8.

Author Contributions

All experiments were carried out and analyzed by all authors. H.S. wrote the manuscript, which was discussed by all authors. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data that support this study are proprietary in nature and may
only be provided with restrictions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Da Silva Nunes, M. ;F. Melo Nascimento;G. Florêncio Miranda Jr;B. Trinchão Andrade. Techniques for BRDF evaluation. The Visual Computer.
  2. Sun, T. ;H. W. Jensen;R.J.A.T.o.G. Ramamoorthi. Connecting measured BRDFs to analytic BRDFs by data-driven diffuse-specular separation. 2018, 37, 1–15. [Google Scholar]
  3. Sztrajman, A. ;G. Rainer;T. Ritschel;T. Weyrich. Neural BRDF Representation and Importance Sampling. Computer Graphics Forum.
  4. Lavoué, G. ;N. Bonneel;J.-P. Farrugia;C. Soler. Perceptual quality of BRDF approximations: dataset and metrics. Computer Graphics Forum.
  5. Zhang, H. ;Z. Jiao;Y. Dong;P. Du;Y. Li;Y. Lian;T. Cui. Analysis of Extracting Prior BRDF from MODIS BRDF Data. 2016, 8, 1004. [Google Scholar]
  6. Zhang, X.; Z. Jiao;C. Zhao;S. Yin;L. Cui;Y. Dong;H. Zhang;J. Guo;R. Xie;S. Li;Z. Zhu;Y. Tong. Retrieval of Leaf Area Index by Linking the PROSAIL and Ross-Li BRDF Models Using MODIS BRDF Data. 2021, 13, 4911. [Google Scholar]
  7. Wise, J.E.; J. C. Mars. Field Reflectance Measurements at Night of Beach and Desert Sands within a Particulate BRDF Model. Remote Sensing 2022, 14, 5020. [Google Scholar] [CrossRef]
  8. Yang, J.; Y. Shuai;J. Duan;D. Xie;Q. Zhang;R. Zhao. Impact of BRDF Spatiotemporal Smoothing on Land Surface Albedo Estimation. Remote Sensing 2022, 14, 2001. [Google Scholar] [CrossRef]
  9. Saulquin, B. BRDF Estimations and Normalizations of Sentinel 2 Level 2 Data Using a Kalman-Filtering Approach and Comparisons with RadCalNet Measurements. Remote Sensing 2021, 13, 3373. [Google Scholar] [CrossRef]
  10. Sun, J. ;X. Zhou;Z. Fan;Q.J.I.p. Wang;technology. Investigation of light scattering properties based on the modified Li-Liang BRDF model. 2022, 120.
  11. Cao, Y.; Y. Cao;W. Li;L. Bai;Z. Wang. Optimization of ray tracing algorithm for Laser Radar Cross Section calculation based on material Bidirectional Reflection Distribution Function. Optics Communications 2021, 127207. [Google Scholar] [CrossRef]
  12. Zhang, Y. ;S. Li;J. Sun;X. Zhang;R. Zhang. Detection of the near-field targets by non-coaxial underwater single-photon counting lidar. Optik: Zeitschrift fur Licht- und Elektronenoptik: = Journal for Light-and Electronoptic.
  13. Torrance, K.E. ;E.M. Sparrow. Theory for off-specular reflection from roughened surfaces. Journal of the Optical Society of America (, 1967; ,57. [Google Scholar]
  14. Cook, R.L.; K. E. Torrance. A reflectance model for computer graphics. Acm Siggraph Computer Graphics 1981, 15, 307–316. [Google Scholar] [CrossRef]
  15. Sciences, S.O.; X. University;X. An;Hefei. Modeling Reflectance Function from Rough Surface and Algorithms. Acta Optica Sinica 2002, 22, 000897–901. [Google Scholar]
  16. Beckmann, P.; A. Spizzichino. The Scattering of Electromagnetic Waves From Rough Surfaces. 1987. [Google Scholar]
  17. He, X.D.; K. E. Torrance;F.X. Sillion;D.P. Greenberg. A Comprehensive Physical Model for Light Reflection. ACM SIGGRAPH Computer Graphics 1991, 25, 175–186. [Google Scholar] [CrossRef]
  18. Maxwell, J.R. ;J. Beard;S. Weiner;D. Ladd;S. Ladd. Bidirectional Reflectance Model Validation and Utilization. Bidirectional Reflectance Model Validation & Utilization.
  19. Sandford., B.P. Sandford., B.P.;D.C. Robertson. Infrared reflectance properties of aircraft paints.
  20. Robert; R. ;Lewis. Making Shaders More Physically Plausible. in CROSSREF. 1994. [Google Scholar]
  21. Neumann, L.; A. Neumann. A New Class of BRDF Models with Fast Importance Sampling. Rendering Seminar Dagstuhl 1997. [Google Scholar]
  22. Phong, B.T. Illumination for Computer Generated Pictures. Communications of the ACM 1998, 18, 311–317. [Google Scholar] [CrossRef]
  23. Wang, Q.; J. Zhao;Y. Gong;Q. Hao;Z. Peng. Hybrid artificial bee colony algorithm for parameter optimization of five-parameter bidirectional reflectance distribution function model. Applied Optics 2017, 56, 9165–9170. [Google Scholar] [CrossRef] [PubMed]
  24. Nicodemus, F.E. Directional Reflectance and Emissivity of an Opaque Surface. Applied Optics 1965, 4, 767–773. [Google Scholar] [CrossRef]
  25. Dan, S. Biogeography-Based Optimization. IEEE Transactions on Evolutionary Computation 2009, 12, 702–713. [Google Scholar]
  26. Yang; S. Xin. Firefly Algorithm, Stochastic Test Functions and Design Optimisation. International Journal of Bio-Inspired Computation 2010, 2, 78–84. [Google Scholar] [CrossRef]
Preprints 82461 g001
Figure 1. Five-parameter BRDF.
Figure 1. Five-parameter BRDF.
Preprints 82461 g001
Preprints 82461 g002
Figure 2. BRDF measurement system.
Figure 2. BRDF measurement system.
Preprints 82461 g002
Preprints 82461 g003
Figure 3. (a): Lambertian plate;(b): Experimental measurement and theoretical values.
Figure 3. (a): Lambertian plate;(b): Experimental measurement and theoretical values.
Preprints 82461 g003
Preprints 82461 g004
Figure 4. BRDF measurements and fitting curves.
Figure 4. BRDF measurements and fitting curves.
Preprints 82461 g004
Preprints 82461 g005
Figure 5. BEDF parameter optimization convergence curve.
Figure 5. BEDF parameter optimization convergence curve.
Preprints 82461 g005
Preprints 82461 g006aPreprints 82461 g006b
Figure 6. BRDF simulation measurement.
Figure 6. BRDF simulation measurement.
Preprints 82461 g006aPreprints 82461 g006b
Table 1. Pseudocode for the hybrid BBO-Firefly algorithm.
Table 1. Pseudocode for the hybrid BBO-Firefly algorithm.
Preprints 82461 i001
Table 2. Optimization Results of the BBO algorithm, Firefly algorithm, and hybrid BBO-Firefly algorithm.
Table 2. Optimization Results of the BBO algorithm, Firefly algorithm, and hybrid BBO-Firefly algorithm.
k b k d k r a b MSE
15° 30° 45° 60°
BBO-Firefly 6.7790 0.0389 0.9479 0.8818 -38.8936 0.0636 0.0266 0.0485 0.0566
BBO 6.8690 0.0342 0.9471 0.9347 -34.1335 0.4653 0.3572 0.5103 0.5035
Firefly 6.9765 0.0358 0.8963 0.9439 -35.8712 0.4633 0.3244 0.4199 0.3765
BBO-Firefly 14.3215 0.0293 0.8364 0.7327 -45.6591 0.0478 0.0652 0.0598 0.0758
BBO 14.2614 0.0281 0.8166 0.6657 -41.4935 0.2885 0.3699 0.4826 0.6994
Firefly 15.3142 0.0278 0.7532 0.7118 -36.7565 0.3208 0.2733 0.2172 0.2262
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated