Optimzation Of Fuzzy PI-Fractional Using GA For Enhacement Of The Quality Energy In The Electrical Smart Grid

Preprint

Article

Optimzation Of Fuzzy PI-Fractional Using GA For Enhacement Of The Quality Energy In The Electrical Smart Grid

Altmetrics

Downloads

Views

Comments

This version is not peer-reviewed

Submitted:

15 August 2023

Posted:

16 August 2023

You are already at the latest version

Alerts

Abstract

Recently, new advanced techniques have been proposed to improve the quality of smart grids that use intermittent renewable energy sources. One of the most effective techniques is active filtering, which utilizes a power electronic converter in the smart load. This technique has the potential to enhance the power quality of the supply voltage by minimizing current harmonics, which is crucial. In this article, we propose a new command intelligence system based on Fuzzy PI fractional (fuzzy FOPI) and GA to control the harmonic currents generated by an active filter powered by a wind system.

Keywords:

Subject: Engineering - Control and Systems Engineering

1. Introduction

Currently, the main priority of modern power system infrastructure is to reduce the use of fossil fuels and energy resources due to related issues. Saving electrical energy is also a crucial factor [1]. Therefore, generating electricity using renewable energy sources is preferred as it is beneficial for the environment. To meet the ever-increasing global energy needs, there is a need for more significant adoption of alternative green energy based on renewable resources. Currently, wind and solar energies are the dominant sources of renewable electricity production worldwide [2].

After the 1960s, the power grid underwent a significant transformation known as the second generation. This expansion involved the implementation of larger units capable of handling ultra-high-voltage transmission and the interconnection of large-scale power grids. Unfortunately, the emergence of nonlinear, unbalanced, and impact loads has had adverse effects on the grid [3]. As we move forward, one of the biggest challenges we face is ensuring energy sustainability in light of the rapidly increasing demand for energy and the global decline of fossil fuel reserves expected within the next few decades.

Power quality is a crucial aspect in the context of renewable energy resources and their frequent connection to distribution systems [4]. When energy-consuming loads, especially non-linear loads, are connected to the electrical network, they can cause voltage and current distortion, which can affect other devices connected to the same network. To address this issue, both classical and modern filtering systems are employed to eliminate harmonics. Researchers are continuously working on innovative solutions to tackle this problem.

The Integration of wind energy into an existing power system poses technical challenges, which require careful consideration of voltage regulation, stability, and power quality problems [5].

Among the advanced techniques of current filtering, we find the active filter. The SAPF, also called pure active filter, responds to global specifications and constitutes the optimal solution for filtering harmonics because it is viable and economical for industrial companies with low to medium kVA loads where the system engineering effort represents a large part of the overall cost [6,7]. This system can dampen the propagation of harmonics in a distribution feeder or between two distribution feeders; it can also compensate the reactive power in the electrical grid [8].

In this article, we introduce a novel control strategy that utilizes fuzzy FOPI adapted by GA. This intelligent control system combines two other smart controls, namely fractional fuzzy PI (fuzzy FOPI) and GA, with the goal of regulating the inverse harmonic currents produced by a DC storage system.

Why use this combination? The fractional-order PI controller (PI

λ

) includes an integrator of order

λ \in ℜ^{+}

. Studies have shown that this type of controller performs well compared to the conventional PI [9]. Furthermore, the addition of fuzzy logic to optimize the FOPI has been proven to improve results for various types of systems. This is because it provides additional flexibility to the design, as demonstrated in numerous studies [10,11,12].

Genetic algorithms (GA) are a specific type of evolutionary algorithm. They are based on principles from evolutionary biology, including inheritance, mutation, natural selection, and crossover. These principles were first established by Darwin’s theory of evolution [13].

The main role of GA is to adjust the normalization gains in the fuzzy FOPI controller input (error and error variation), optimize the speech universe and thus the membership functions for (Kp, Ki and

λ

) [11]. All the processes of this calculation are based on evolutionary algorithms whether in GA or fuzzy FOPI, so this work is very modern and considered as a scientific research contribution. The results obtained are compared with the results of the classical PI regulator.

2. System composition and modeling

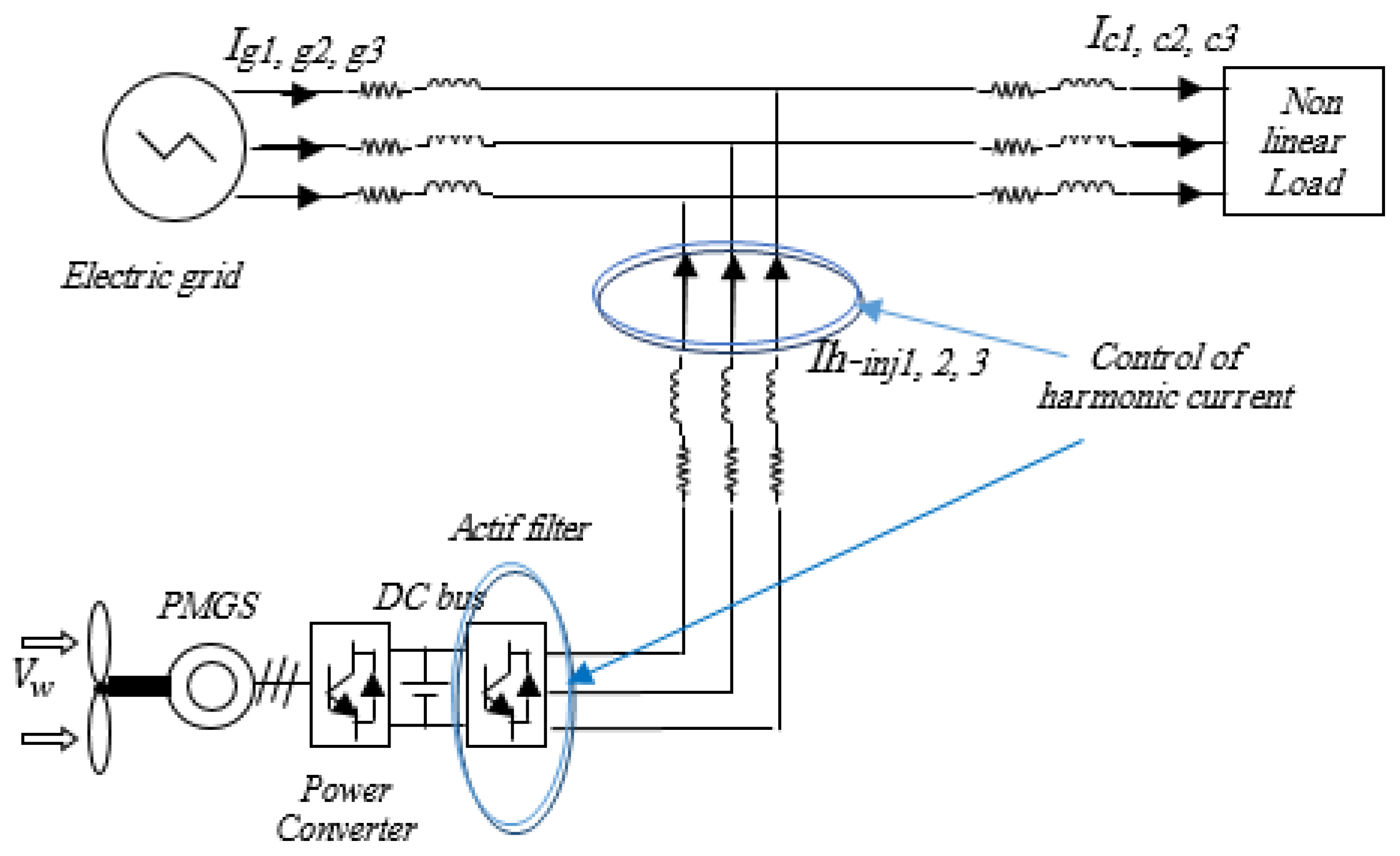
In Figure 1; the overall system contains an electrical network which is supplied by a non-linear load, this mechanism is connected in parallel by a wind chain which has the objective of supplying the active filtering system.

In this example, we take advantage of the existence of a two-level inverter not only to ripple the currents and voltages but also to provide the reverse harmonic currents to eliminate the distortion of the electrical currents caused by the non-linear load.

2.1. Real and Imaginary Instantaneous Powers Theory

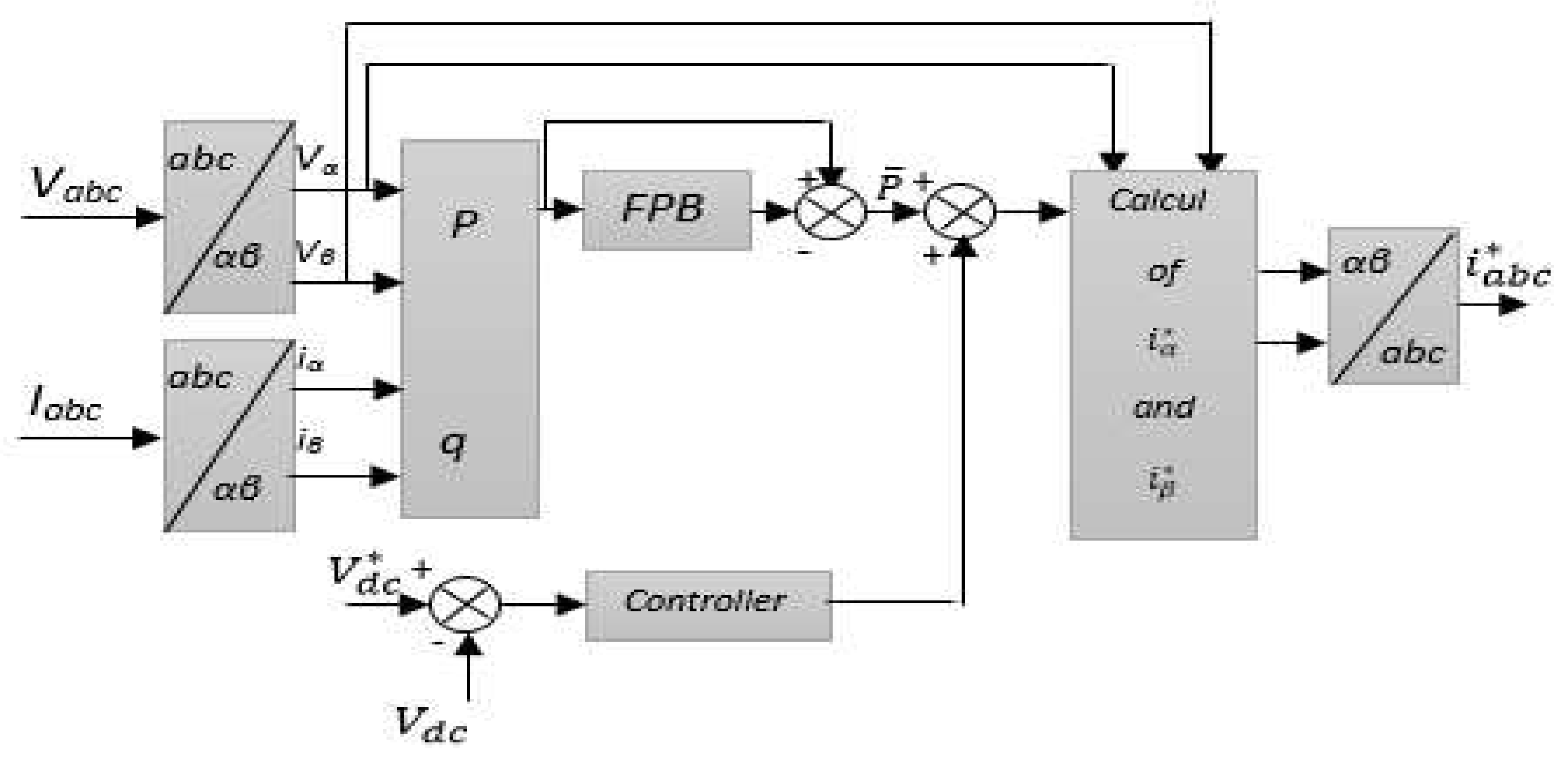
The Real and Imaginary Instantaneous Powers theory determines the harmonic distortion from the calculation of the instantaneous power in a three-phase system, with the aim of applying it to the control of active power filters. It first applies an algebraic transformation (Clarke’s transformation) of the voltages and load of the three-phase system currently in the coordinate’s a-b-c to the coordinates

α

β

by and then we can from them calculate the p and q by the relations [14,15]:

(\begin{matrix} p \\ q \end{matrix}) = (\begin{matrix} V_{α} & V_{β} \\ - V_{β} & V_{α} \end{matrix}) (\begin{matrix} i_{α} \\ i_{β} \end{matrix})

(1)

where p is the instantaneous real power. q is the instantaneous imaginary power. By observing the formulations of p and q, it is possible to put them in the following form in Equation 2:

\{\begin{matrix} P = \bar{P} + \tilde{P} \\ q = \bar{q} + \tilde{q} \end{matrix}

(2)

(\begin{matrix} i_{α} \\ i_{β} \end{matrix}) = \frac{1}{V_{α}^{2} + V_{β}^{2}} (\begin{matrix} V_{α} & - V_{β} \\ V_{β} & V_{α} \end{matrix}) (\begin{matrix} P \\ q \end{matrix})

(3)

(\begin{matrix} i_{α} \\ i_{β} \end{matrix}) = \underset{A c t i v e c u r r e n t}{\underset{︸}{\frac{1}{Δ} (\begin{matrix} V_{α} & - V_{β} \\ V_{β} & V_{α} \end{matrix}) (\begin{matrix} \bar{P} \\ 0 \end{matrix})}} + \underset{R e a c t i v e c u r r e n t}{\underset{︸}{\frac{1}{Δ} (\begin{matrix} V_{α} & - V_{β} \\ V_{β} & V_{α} \end{matrix}) (\begin{matrix} 0 \\ \bar{q} \end{matrix})}} + \underset{H a r m o n i c c u r r e n t}{\underset{︸}{\frac{1}{Δ} (\begin{matrix} V_{α} & - V_{β} \\ V_{β} & V_{α} \end{matrix}) (\begin{matrix} \tilde{P} \\ \tilde{q} \end{matrix})}}

(4)

Finally, it is possible to calculate the reference currents, in the

α

–

β

coordinates by applying equations 4. The reference currents are then translated into the a-b-c coordinates through the following inverse Clarke transform:

(\begin{matrix} I_{r e f 1} \\ I_{r e f 1} \\ I_{r e f 1} \end{matrix}) = \sqrt{\frac{2}{3}} (\begin{matrix} 1 & 0 \\ - \frac{1}{2} & \frac{\sqrt{3}}{2} \\ - \frac{1}{2} & - \frac{\sqrt{3}}{2} \end{matrix}) (\begin{matrix} I_{α} \\ I_{β} \end{matrix})

(5)

To compensate for current harmonics generated by nonlinear loads, the reference signal of the shunt APF must include the values of

\tilde{p}

and

\tilde{q}

. The diagram in Figure 2 illustrates the different steps for obtaining the harmonic components of the current of a non-linear load.

3. Meta heuristics controllers

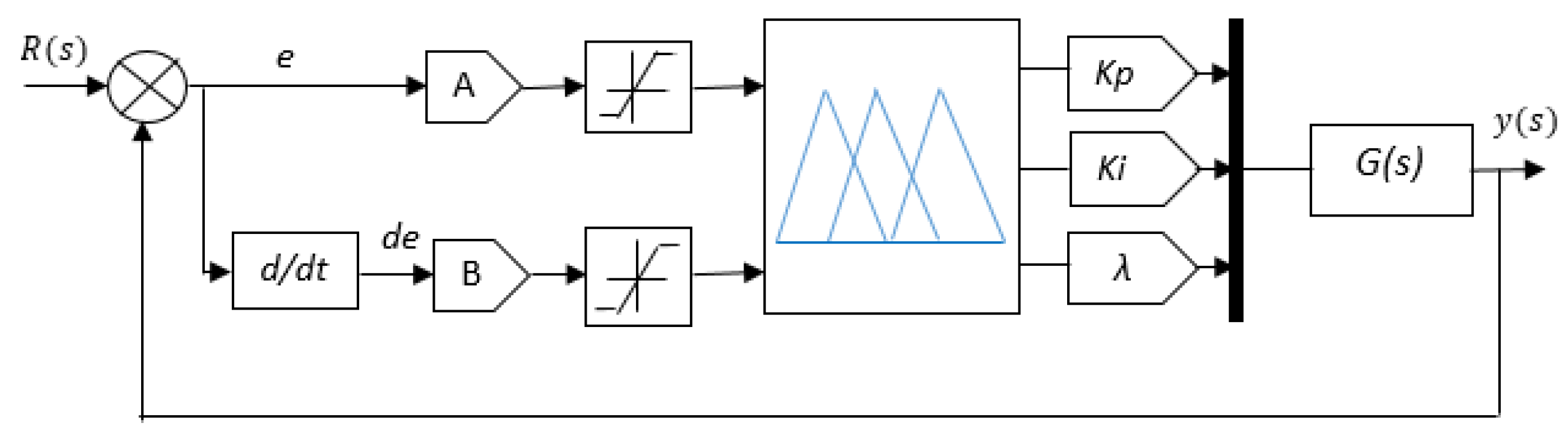
3.1. Fuzzy PI fractional controller and structure

The fuzzy PI Fractional is combines fuzzy logic with fractional order PI (FOPI) control to improve the system’s performance. The fractional order calculus provide more flexibility in designing the controller to meet specific system requirements. The transfer function for the FOPI controller can be expressed as shown in Equation 6 [16]:

C (s) = K p + \frac{K i}{s^{λ}}

(6)

The Fuzzy FOPI controller is characterized by five unknown parameters, namely

K p

K i

λ

, A, and B.

K p

and

K i

represents successively the proportional and the integral gain,

λ

represents the fractional-order integral. A and B are the error gain and error rate gain, respectively. The structure of a Fuzzy FOPI controller is depicted in Figure 3.

The fuzzy FOPI structure utilized in this study takes in two inputs: the error and its derivative (e,

Δ e

). It generates three outputs, namely

K p

K i

, and

λ

. Fuzzy logic is an AI-based command that we have implemented in this research through a fuzzy FOPI algorithm. We can obtain output values from this algorithm and easily modify universes of speech and fuzzy rules in the algorithm script. Adding the fractional order

λ

enhances the effectiveness of fuzzy FOPI command. However, selecting universes of discourse for the inputs (e,

Δ e

) and outputs (

K p

K i

, and

λ

) is the most challenging aspect of this process.

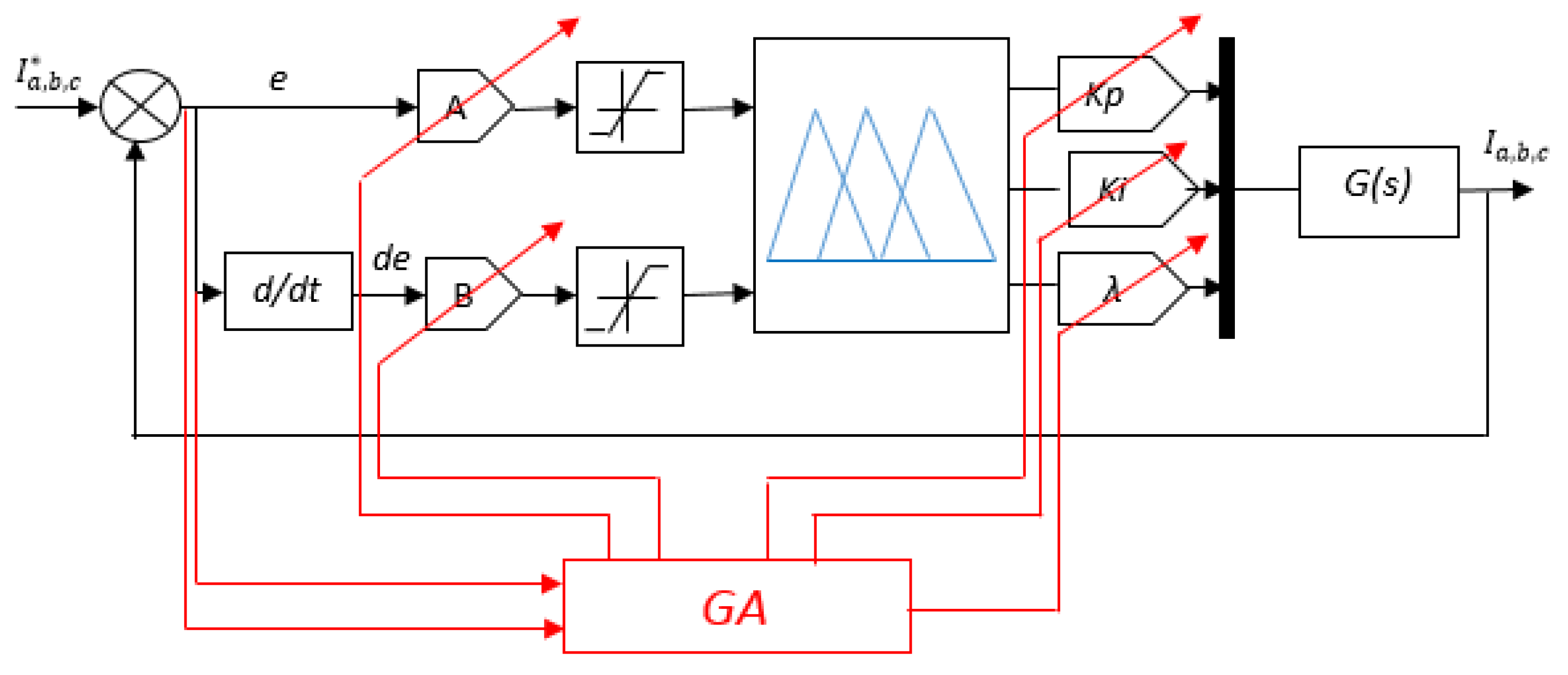
To address this issue, we proposed an evolutionary control solution utilizing genetic algorithms. This approach contributes to optimization and represents a valuable research contribution.

3.2. Optimization algorithm using GA

To optimize both the FOPI and fuzzy-FOPI controllers, we use an intelligent meta-heuristic technique called the Genetic Algorithm. This technique is based on biological concepts of natural selection and reproduction, and is used in computing to find solutions to search problems. The Genetic Algorithm was invented by John Holland in 1960, and was further developed by his colleagues and students at the University of Michigan [17].

Outline of the basic Genetic Algorithm is given as follows:

Algorithm: Genetic algorithm (GA)

(1)

Start: Generate random population of N chromosomes (suitable solutions for the problem).

(2)

Fitness: Evaluate the fitness (or cost function) f(x) of each chromosome x in the population.

(3)

New population: Create a new population by repeating the following steps until the new population is complete.

Selection: Select two parent chromosomes from a population according to their fitness (the better fitness, the bigger chance to be selected).
Crossover: With a crossover probability cross over the parents to form new offspring (children). If no crossover was performed, offspring is the exact copy of parents.
Mutation: With a mutation probability, mutate new offspring at each locus (position in chromosome).
Accepting: Place new offspring in the new population.

(4)

Replace: Use new generated population for a further run of the algorithm.

(5)

Test: If the end condition is satisfied, stop, and return the best solution in current population.

(6)

Loop: go to step 2.

3.3. GA-Fuzzy FOPI

The combination between the two fuzzy commands FOPI and the GA is described in Figure 4. The global objective of GA is to adjust the normalization gains A and B and consequently to optimize the output’s parameters of the fuzzy FOPI. The GA is we help also to determine the universes of discourse for that the objective function is minimal.

4. Optimization problem

The Integral Time Absolute Errors (

I T A E

) fitness function as shown in Equation 7 is used to evaluate the performance of the system’s output response. The

I T A E

index presents very good performance compared to other performance indices

I A E

I S E

, and

I T S E

[18,19].

e = I A T E = \int_{0}^{t_{s i m}} t . |e (t)| d t

(7)

where

t_{s i m}

is total simulation time and the typical ranges of the optimized parameters are given by:

A_{m i n} \leq A \leq A_{m a x}

B_{m i n} \leq B \leq B_{m a x}

K p_{m i n} \leq K p \leq K p_{m a x}

K i_{m i n} \leq K i \leq K i_{m a x}

The harmonic currents transfer functions are presented in the following equations:

G (s) = \frac{1}{L f . s + R f}

(8)

The setting of the PI controller parameters

K p

K i

, and

λ

is based on finding the point of optimization by the GA over an interval [0 0 0] to [300 300 1]. The sampling period

t_{s i m}

is 0.001s.

5. Result calculus, simulation and discussion

In this section, we will go over the calculation details and simulation results for the GA-FOPI and GA-fuzzy FOPI system and tune parameters controller. The simulation was conducted using MATLAB Simulink, while the software for the genetic algorithm and fuzzy FOPI was written in MATLAB.

The optimization process involves two steps. Firstly, we initiate the GA to explore the optimization points of the FOPI controller for the parameters (

K p

K i

, and

λ

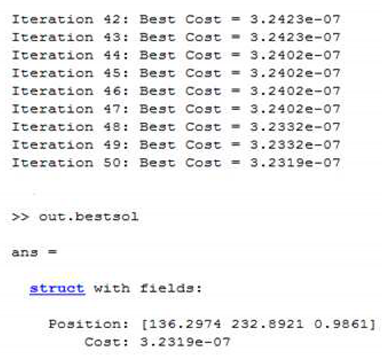
). After 50 calculation iterations, we will obtain the following results: Preprints 82468 i001

Table 1 shows the results parameters of regulators GA-FOPI.

We will use the error values and their variations, which were calculated by the GA, in a fuzzy FOPI algorithm. Upon completion of the calculation process, we will receive the results of the fuzzy rule along with the values of the parameters (

K p

K i

, and

λ

) for the fuzzy regulator FOPI.

Table 2. This is a table caption. Tables should be placed in the main text near to the first time they are cited.

Fuzzy rules
ans = (1) If (error is negative) or (error variation is negative) then (Kp is PS)(Ki is PM)(lamda is PB) (1). (2) If (error is negative) or (error variation is zeros) then (Kp is PS)(Ki is PM)(lamda is PB) (1). (3) If (error is negative) or (error variation is positive) then (Kp is PS)(Ki is PL)(lamda is PB) (1). (4) If (error is zeros) or (error variation is negative) then (Kp is PMS)(Ki is PL)(lamda is PB) (1). (5) If (error is zeros) or (error variation is zeros) then (Kp is PM)(Ki is PL)(lamda is PB) (1). (6) If (error is zeros) or (error variation is positive) then (Kp is PM)(Ki is PL)(lamda is PB) (1). (7) If (error is pozitive) or (error variation is negative) then (Kp is PM)(Ki is PB)(lamda is PB) (1). (8) If (error is pozitive) or (error variation is zeros) then (Kp is PM)(Ki is PB)(lamda is PB) (1). (9) If (error is pozitive) or (error variation is positive) then (Kp is Pl)(Ki is PB)(lamda is PB) (1). Out = 136.3083 232.8977 0.9832.

Fuzzy rules

ans =

(1): If (error is negative) or (error variation is negative) then (Kp is PS)(Ki is PM)(lamda is PB) (1).
(2): If (error is negative) or (error variation is zeros) then (Kp is PS)(Ki is PM)(lamda is PB) (1).
(3): If (error is negative) or (error variation is positive) then (Kp is PS)(Ki is PL)(lamda is PB) (1).
(4): If (error is zeros) or (error variation is negative) then (Kp is PMS)(Ki is PL)(lamda is PB) (1).
(5): If (error is zeros) or (error variation is zeros) then (Kp is PM)(Ki is PL)(lamda is PB) (1).
(6): If (error is zeros) or (error variation is positive) then (Kp is PM)(Ki is PL)(lamda is PB) (1).
(7): If (error is pozitive) or (error variation is negative) then (Kp is PM)(Ki is PB)(lamda is PB) (1).
(8): If (error is pozitive) or (error variation is zeros) then (Kp is PM)(Ki is PB)(lamda is PB) (1).
(9): If (error is pozitive) or (error variation is positive) then (Kp is Pl)(Ki is PB)(lamda is PB) (1).

Out =
136.3083 232.8977 0.9832.

¹ Tables may have a footer.

The following Table 3 presents these results.

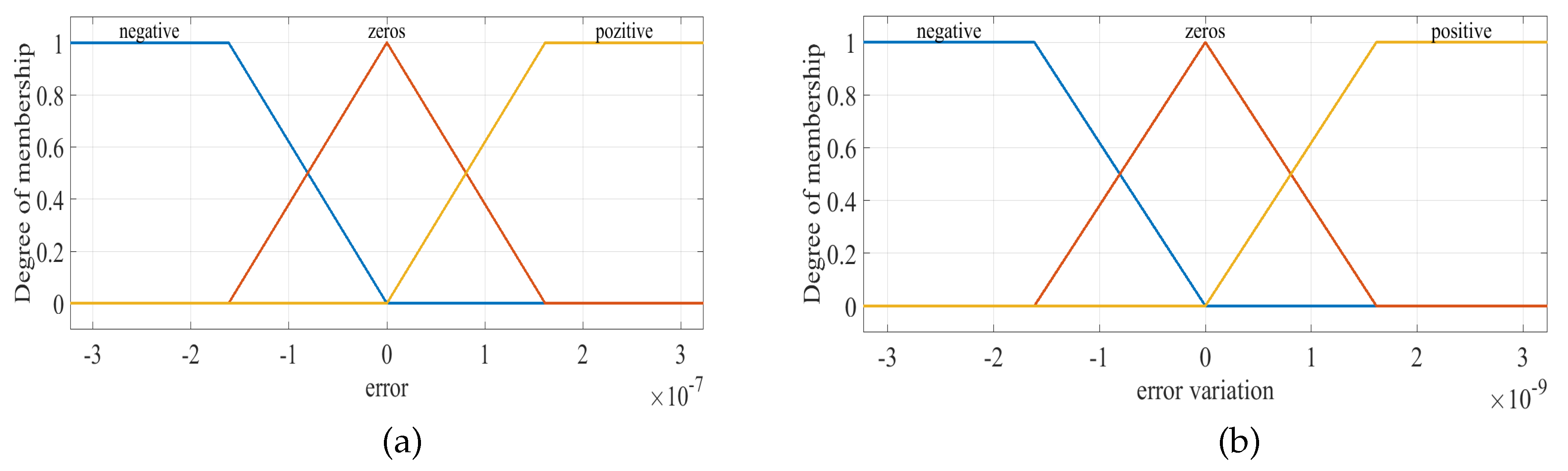
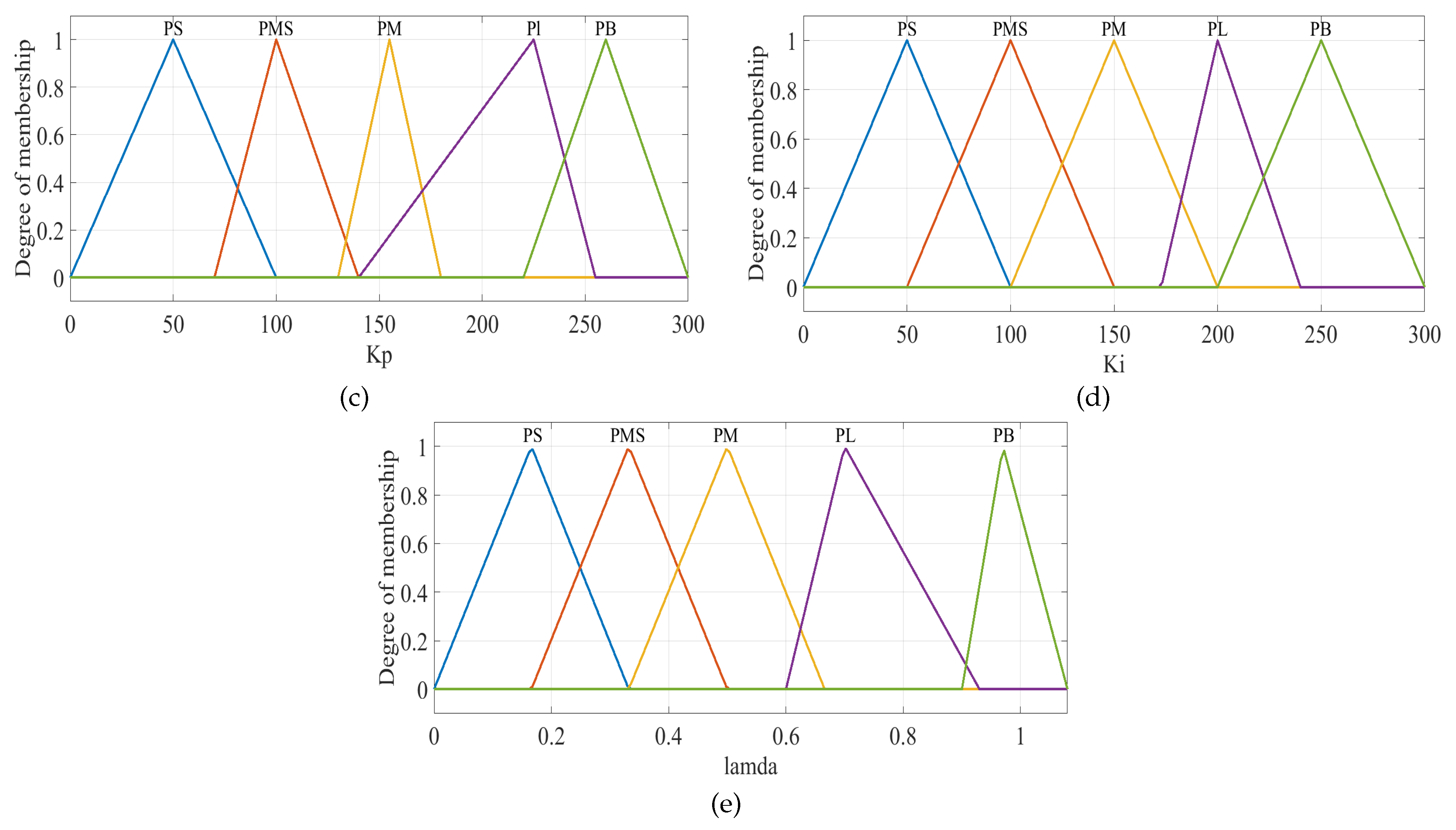
These figures show the membership functions for the inputs and outputs of the GA-fuzzy FOPI regulator, which were obtained by using fuzzy FOPI algorithms. The membership is represented using trapezoidal and triangular fuzzy types.

Figure 5. (a),(b) Inputs MFs of FLC.

Figure 6. (c),(d),(e) outputs MFs for FLC.

This section focuses on simulating various controllers, including GA-fuzzy FOPI, GA-FOPI, and traditional PI controller, to evaluate their effectiveness. MATLAB Simulink is used to implement the redundant dynamic model, controller, and desired trajectory. These controllers are utilized to regulate the reverse harmonic currents injected into the electrical network, addressing the issue of current distortion. 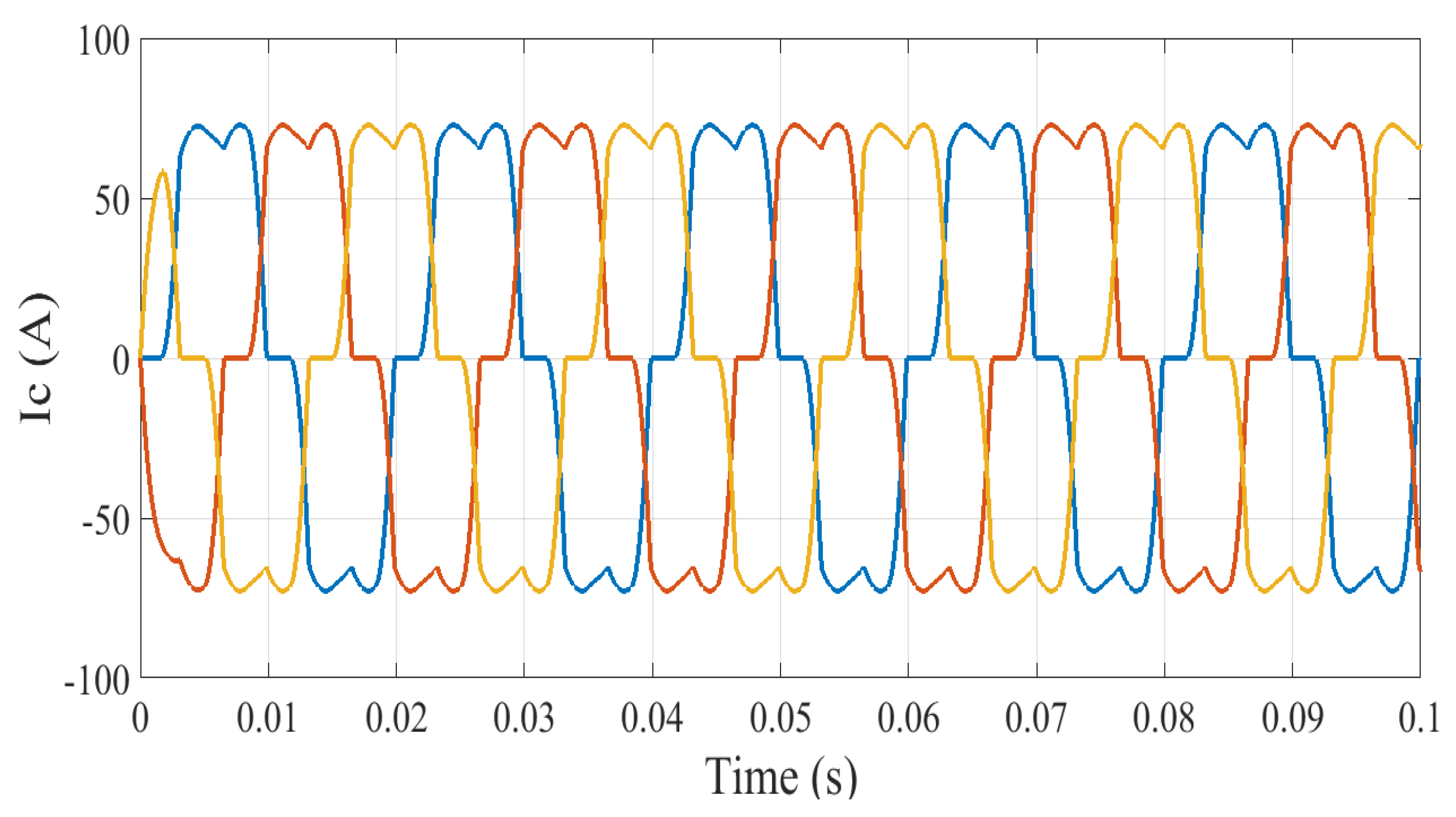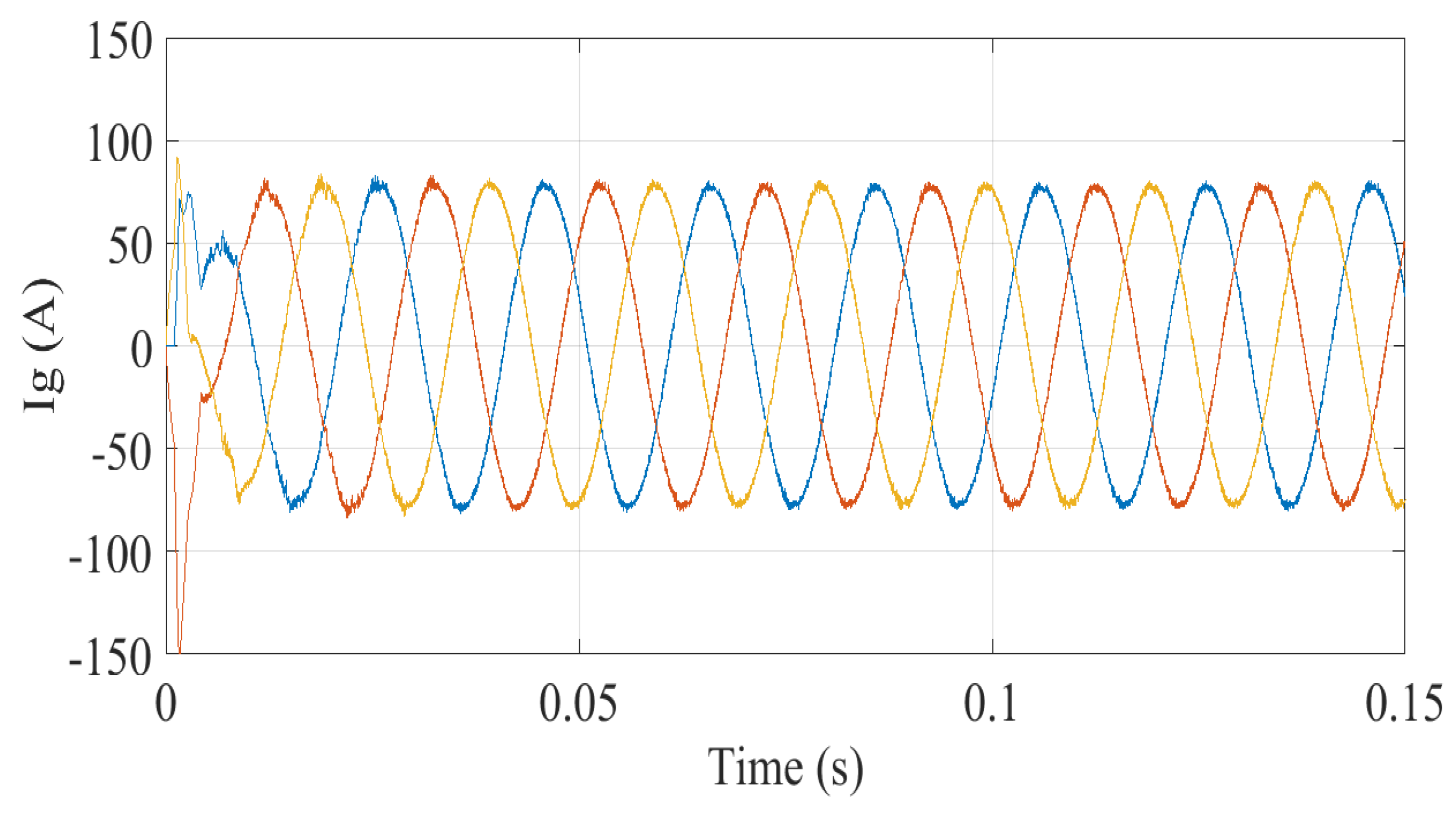Figure 7 displays the waveform of the currents before the insertion of the active filter.

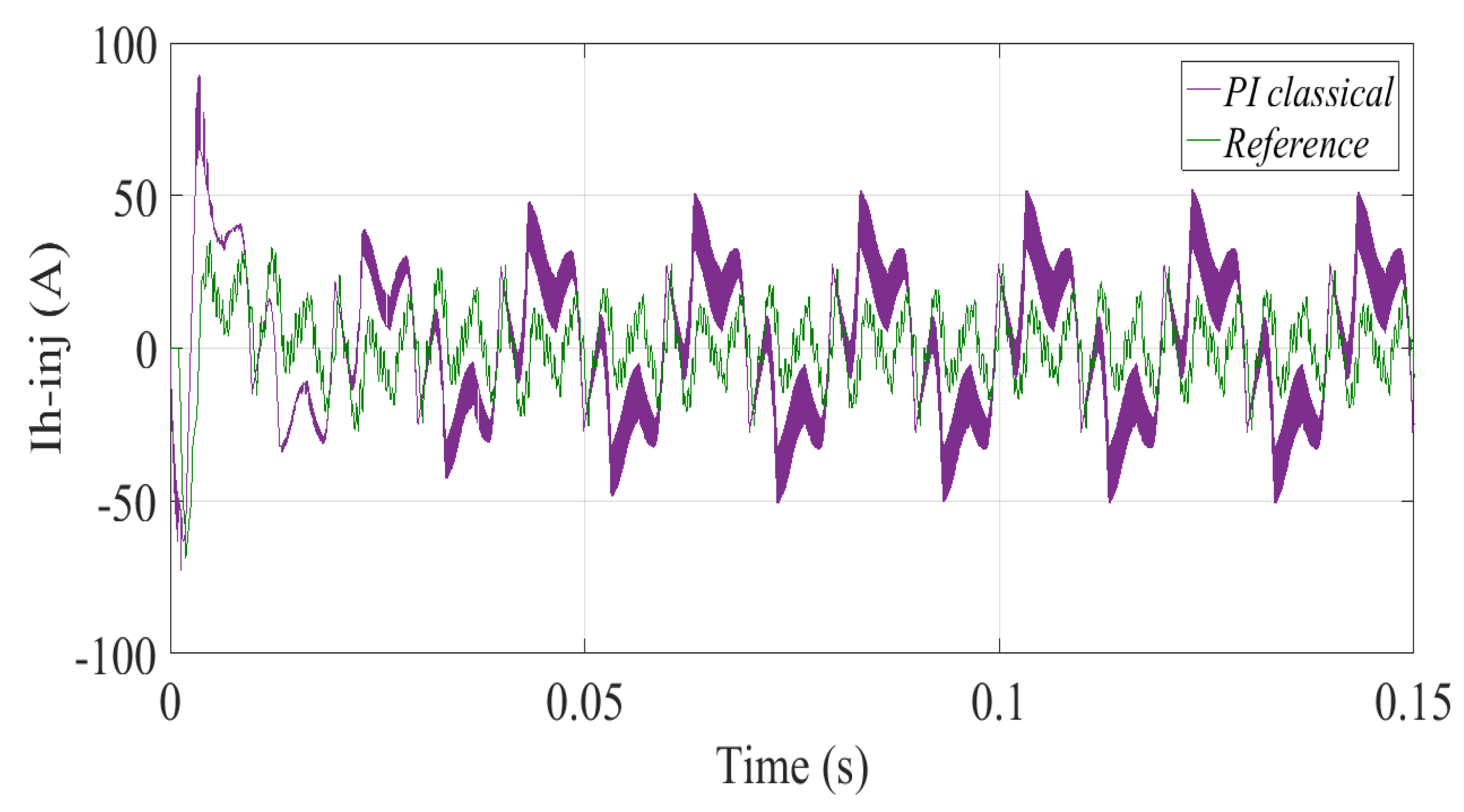
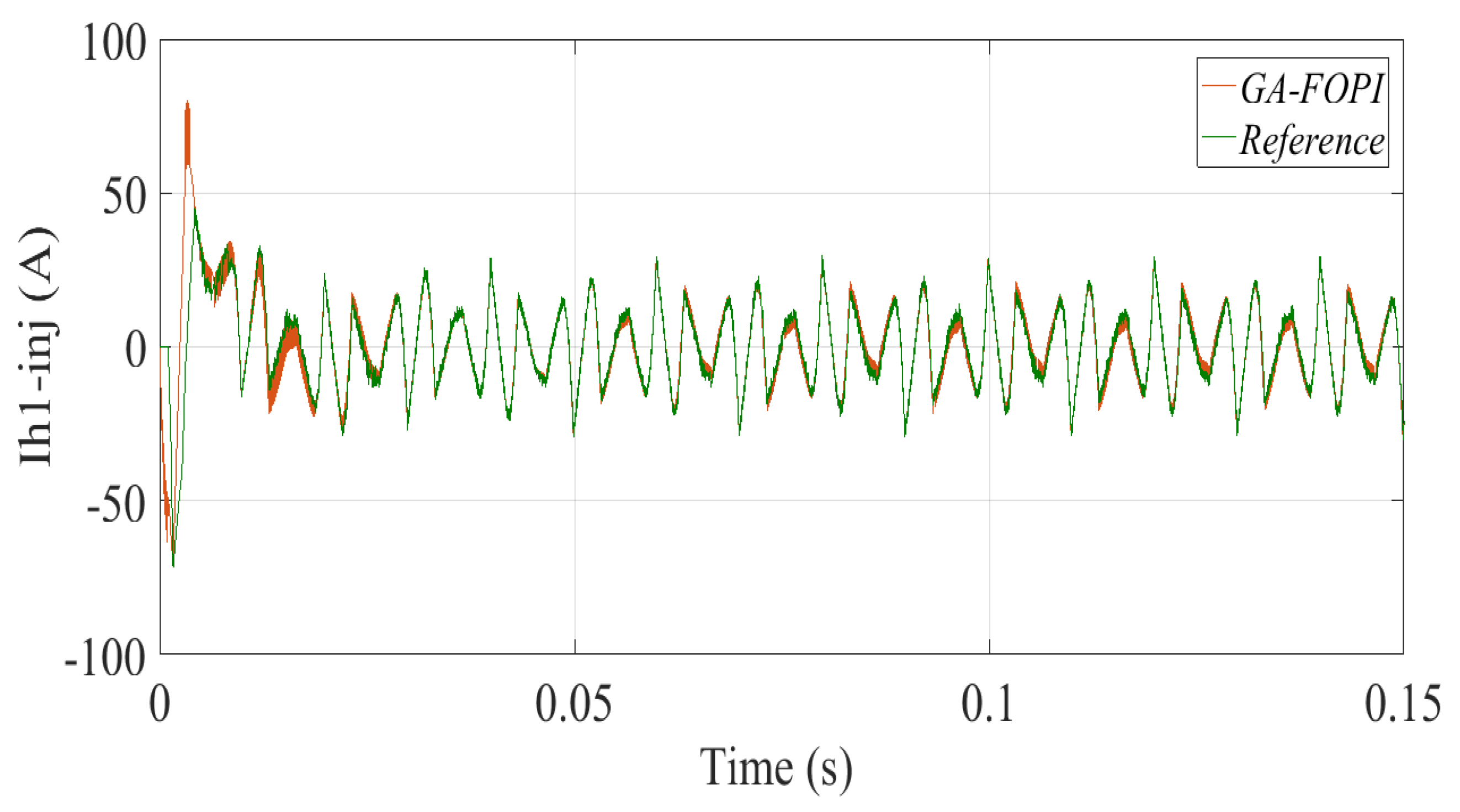
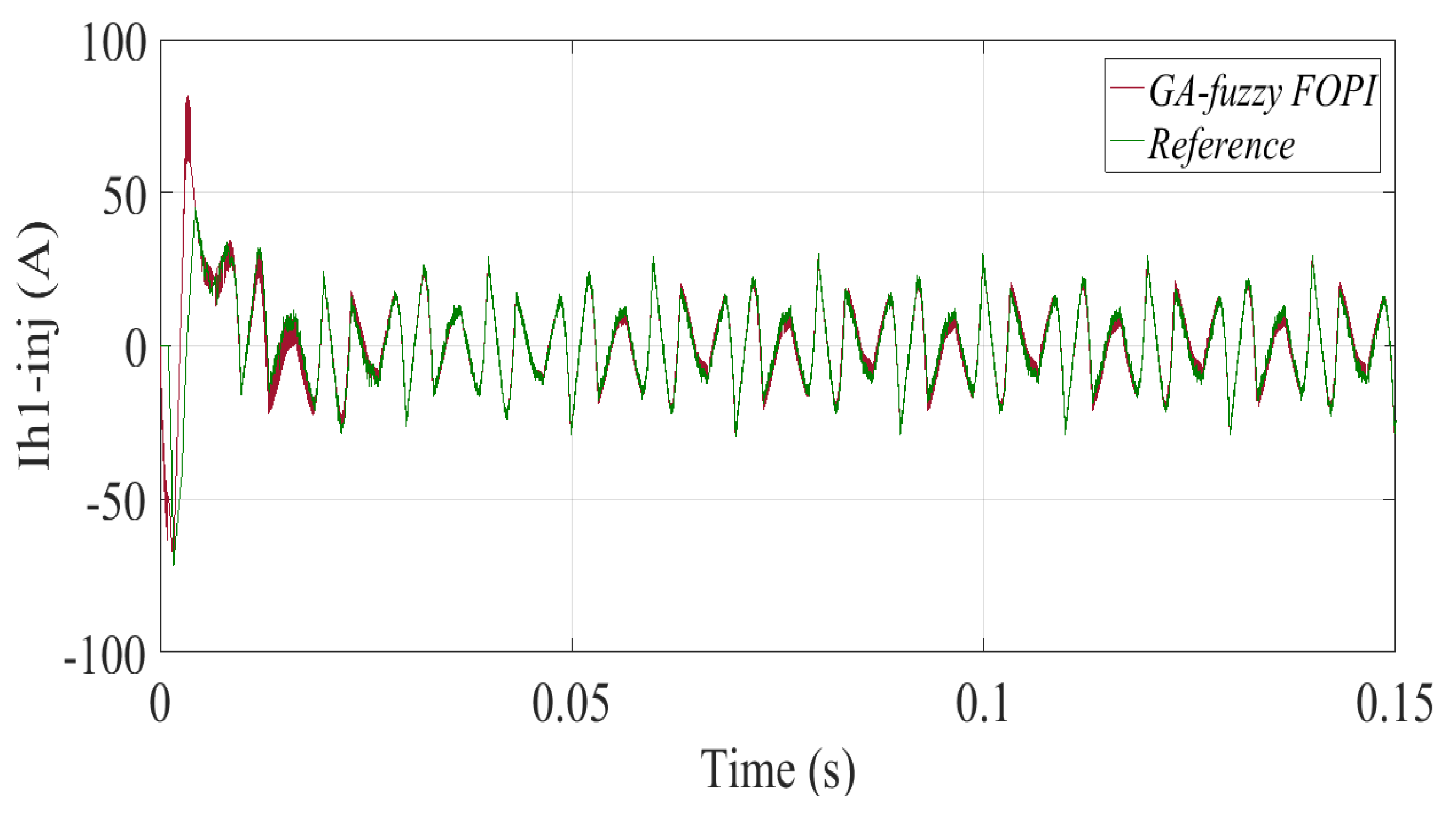
The Figure 8, Figure 9 and Figure 10 represent respectively the regulation of inverse harmonic currents using: classical PI, GA-FOPI, GA-fuzzy FOPI regulators.

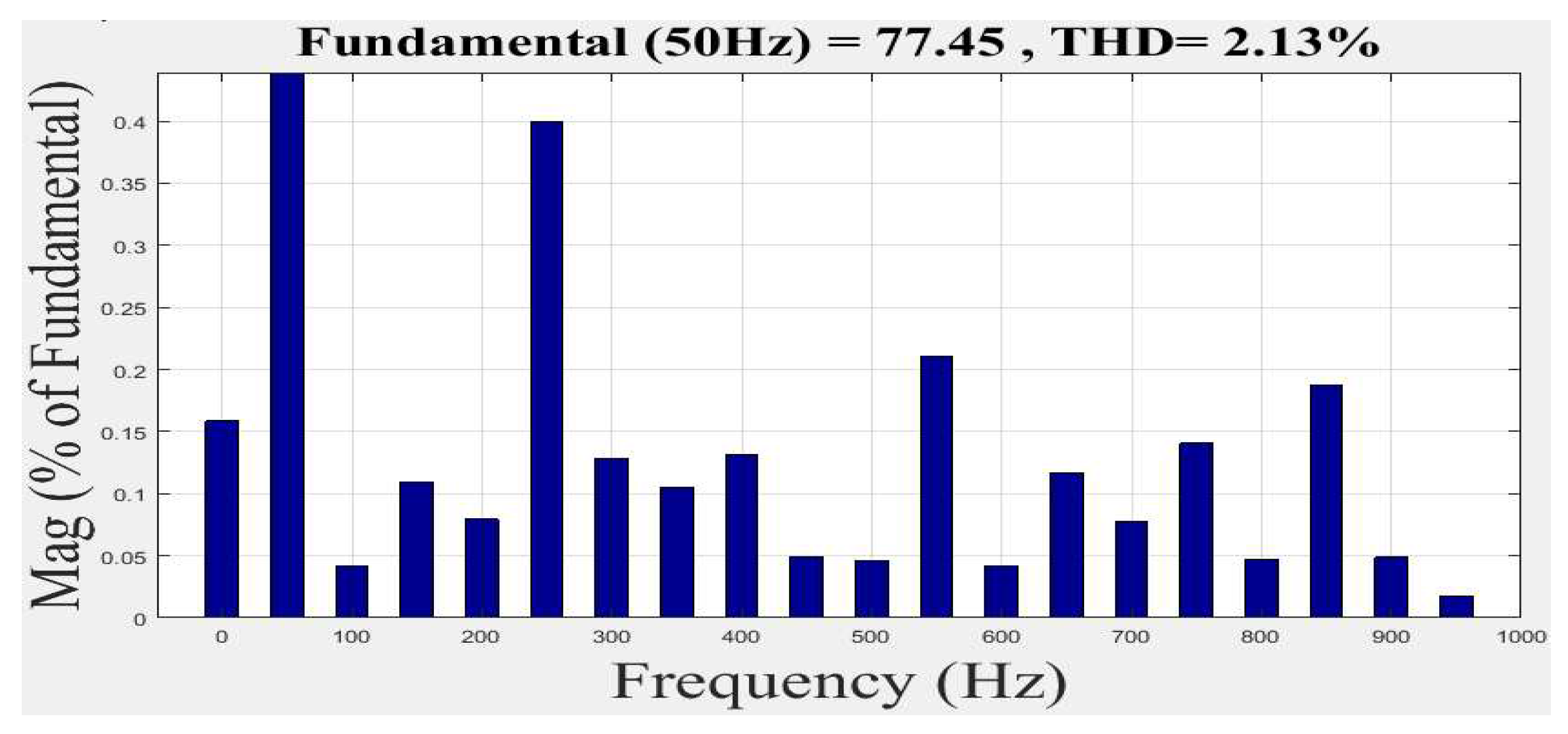
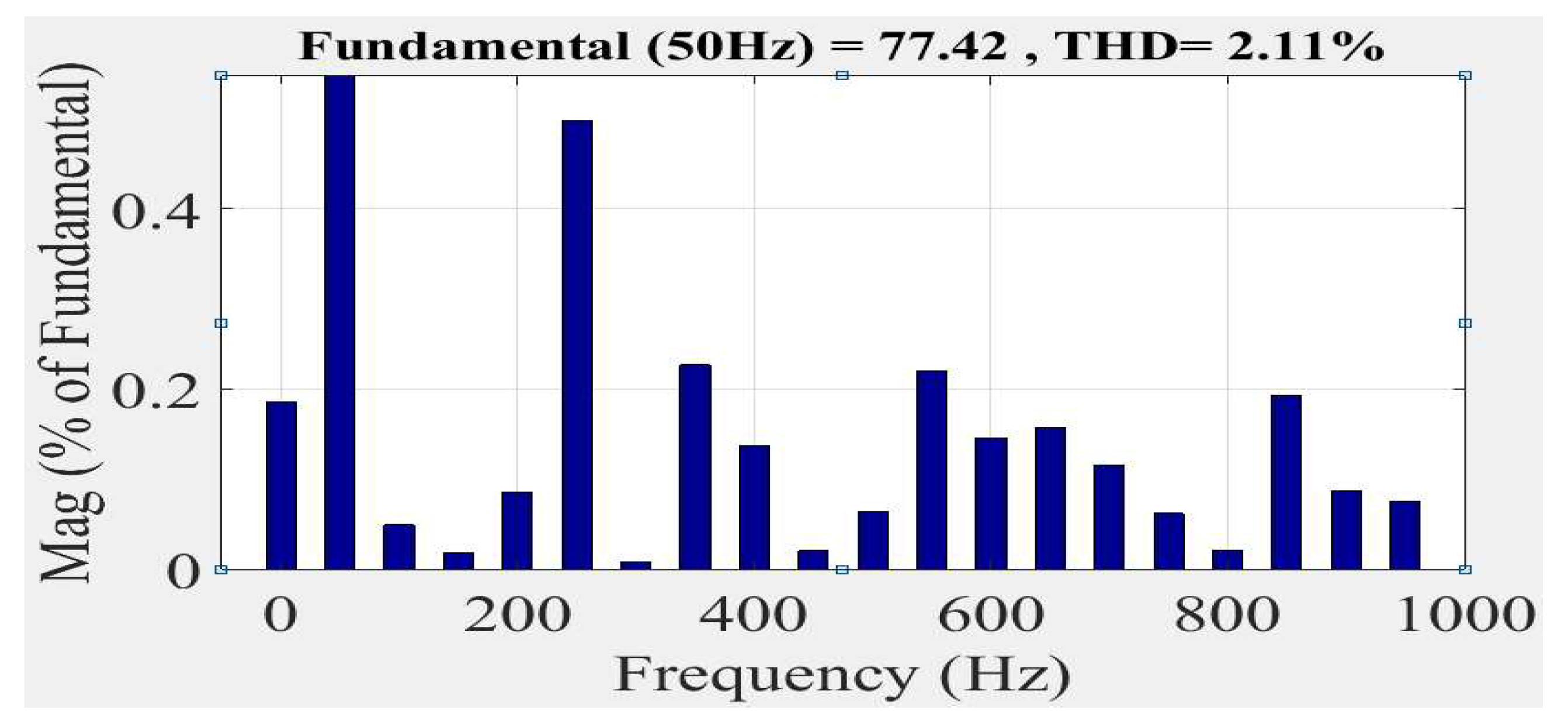
Based on the previous figures, it is evident that the two controllers GA-FOPI and GA-fuzzy FOPI are very efficient compared to the classic PI; in view of which is the best; the occurrence of this superiority is illustrated in the figures of the harmonic analysis; the THD in Figure 11 when we used GA-FOPI is: 2.13 and in Figure 12 is: 2.11 when we used GA-fuzzy FOPI.

We conclude that the active filter acts very well on the quality of energy in the electrical network (show Figure 13) and especially that we use the GA-fuzzy FOPI.

6. Conclusions

In this article, a fuzzy FOPI controller has been developed and optimized by GA to regulate inverse harmonic currents that are injected into the electrical network via an active filtering system. The main objective of this regulation is to eliminate current distortion in the electrical network. In order to achieve good regulation, it is important to use a highly efficient control system. Therefore, the combination of fuzzy FOPI and GA controllers has been found to be more effective than classic PI and even GA-optimized FOPI controllers. The efficiency of the GA-fuzzy FOPI controller has been demonstrated through the optimization of normalization gains, speech universe, and output parameters of the fuzzy FOPI regulator. This optimization was achieved by adjusting the fuzzy rules and MFs. The study concludes that the GA-fuzzy FOPI controller is more robust and efficient than conventional controllers when it comes to trajectory tracking problems.

Acknowledgments

This research was conducted at the Laboratory of Exegetical and Computer Engineering (L2GEGI) at the University of Tiaret - Algeria.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:

SAPF	Shunt Active Power Filter
MFs	Membership Functions

References

Bajaj, Mohit 1, Aggarwal, Surbhi 2, Singh, Amit Kumar 3, Power quality concerns with integration of RESs into the smart power grid and associated mitigation techniques. 9th power India international conference (PIICON) 2020, IEEE, 1–6.
Merabet Boulouiha, Houari 1, Khodja, Mohamed 2, Rahiel, Djelloul 3, Allali, Ahmed 4, Kaddour, Fouad 5, Denai Mouloud 6, Power quality enhancement in electricity grids with wind energy using multicell converters and energy storage. Journal of Renewable and Sustainable Energy 2019, 1, Vol–11.
Zhang, Jingyue 1, Research on power quality problems based on smart grid and new energy generation. book:AIP Conference Proceedings.
Rao, Sivakavi Naga Venkata Bramareswara 1, Kumar, Yellapragada Venkata Pavan 2, Pradeep, Darsy John 3, Reddy, Challa Pradeep 4, Flah, Aymen, Kraiem, Habib 5, Al-Asad, Jawad F 6,Power quality improvement in renewable-energy-based microgrid clusters using fuzzy space vector PWM controlled inverter, Journal of Sustainability-MDPI 2022, 8, 4663, Vol 14. 4663.
Mundackal, JohnsonAbraham 1, Varghese, Alan C 2, Sreekala, P, Reshmi, V 3, Grid power quality improvement and battery energy storage in wind energy systems, 2013 Annual International Conference on Emerging Research Areas and 2013 International Conference on Microelectronics, Communications and Renewable Energy 2013, 10, 1–6, IEEE. 10.
Chaoui, Abdelmadjid 1, Gaubert, Jean-Paul 2, Krim, Fateh 3, Rambault, Laurent 4, On the design of shunt active filter for improving power quality, IEEE International Symposium on Industrial Electronics 2008, 31–37, IEEE. 31–37.
Ravinder, Kumar 1, Bansal, Hari Om 2, Investigations on shunt active power filter in a PV-wind-FC based hybrid renewable energy system to improve power quality using hardware-in-the-loop testing platform, Electric Power Systems Research 2019, 105957, vol177, Elsevier journal. Elsevier journal.
Tey, LH 1, So, PL 2, Chu, YC 3, Improvement of power quality using adaptive shunt active filter, IEEE transactions on power delivery 2005, 1558–1568, 2, IEEE. 2.
Jesus, Isabel S 1, Barbosa, Ramiro S 2, Genetic optimization of fuzzy fractional PD+ I controllers, Isa Transactions, 2015, 220–230, 2, vol57, Elsevier journal. vol57.
Swethamarai, P 1, Lakshmi, P 2, Gokul Prassad, S 3, Whale-optimized fuzzy-fractional order controller-based automobile suspension model, Isa Transactions, 2022, 1110–1130, 7, vol54, Engineering Optimization. Engineering Optimization.
2022; 1. [CrossRef]
Ali, Moetasem 1, Kotb, Hossam 2, AboRas, M Kareem 3, Abbasy, H Nabil 4, Frequency regulation of hybrid multi-area power system using wild horse optimizer based new combined Fuzzy Fractional-Order PI and TID controllers, Alexandria Engineering Journal, 2022, 12187–12210, 12,vol61, Elsevier. 12.
Sarir, Noureddine 1, Morsli, Sebaa 2 Allaoui, Tayeb 3, Denai, Mouloud 3, Optimal fractional-order pi control design for a variable speed PMSG-based wind turbine, Journal Europèen des Systèmes Automatisés, 2021.
Buyuk, Mehmet 1, Inci, Mustafa 2, Tan, Adnan 3, Tumay, Mehmet 4, Improved instantaneous power theory based current harmonic extraction for unbalanced electrical grid conditions, Electric Power Systems Research, 2021, 106014,vol177, Elsevier. vol177.
Eskandarian, Nasser 1, Beromi, Yousef Alinejad 2, Farhangi, Shahrokh 3, Improvement of dynamic behavior of shunt active power filter using fuzzy instantaneous power theory, Journal of power Electronics, 2014, 1303–1313,6, vol14. 6.
Mohamed Naji Muftah 1, Ahmad Athif Mohd Faudzi 2, Shafishuhaza Sahlan 3, Shahrol Mohamaddan 4, Fuzzy Fractional Order PID Tuned via PSO for a Pneumatic Actuator with Ball Beam (PABB) System; Fractal Fract journal, fractalfract journal, 2023, 7(6),416, doi.org/10.3390/fractalfract7060416.
2017; 1. [CrossRef]
Nie, Yonghui 1, Zhang, Yidan 2, Zhao, Yan 3, Fang, Binbin 4, Zhang, Lili 5, Wide-area optimal damping control for power systems based on the ITAE criterion, International Journal of Electrical Power and Energy Systems, 2019, 192–200, vol106, Elsevier. vol106.
Rao, C Sankar 1, Santosh, Simi 2, others 3, Tuning optimal PID controllers for open loop unstable first order plus time delay systems by minimizing ITAE criterion, IFAC-PapersOnLine, 2020, 123–128, vol53, 1, Elsevier. vol53.

Figure 1. global system composition.

Figure 2. performance of GA-fuzzy FOPI.

Figure 3. Structure of the fractional order fuzzy PI controller.

Figure 4. Block diagram for the GA-Fuzzy control system.

Figure 7. Waveform of the currents before insertion of the active filter.

Figure 8. Performance of classical PI regulator.

Figure 9. performance of GA-FOPI.

Figure 10. performance of GA-fuzzy FOPI.

Figure 11. Spectral analysis of currents for GA-FOPI.

Figure 12. Spectral analysis of currents for GA-FOPI.

Figure 13. Waveform of the currents after insertion of the active filter.

Table 1. Results parameters of FOPI controller obtained by GA algorithm.

GA algorithm	$K p$	$K i$	$λ$	Error (output)	Error variation (output)
PI Rang [0 0 0] to [300 300 1]	136.2974	232.8921	0.9861	3.2319e-07	3.2319e-09 (50 iter)

Table 3. Results parameters of FOPI controller obtained by GA algorithm..

GA algorithm	$K p$	$K i$	$λ$	Error (intput)	Error variation (input)
PI Rang [0 0 0] to [300 300 1]	136.3083	232.8977	0.9832	3.2319e-07	3.2319e-09

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimzation Of Fuzzy PI-Fractional Using GA For Enhacement Of The Quality Energy In The Electrical Smart Grid

Abstract

1. Introduction

2. System composition and modeling

2.1. Real and Imaginary Instantaneous Powers Theory

3. Meta heuristics controllers

3.1. Fuzzy PI fractional controller and structure

3.2. Optimization algorithm using GA

3.3. GA-Fuzzy FOPI

4. Optimization problem

5. Result calculus, simulation and discussion

6. Conclusions

Acknowledgments

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe