Prerpints.org logo
Preprint
Article

Distinction between Effects of IR-Drop and Negative Capacitance of Fast Cyclic Voltammograms

Altmetrics

Downloads

87

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

15 August 2023

Posted:

16 August 2023

You are already at the latest version

Alerts
Abstract
Diffusion-controlled cyclic voltammograms at fast scan rates show peak shifts as well as decreases in the peak currents from the predicted diffusion-controlled currents especially when currents are large in low concentration of supporting electrolyte. This has been conventionally recognized as an IR-drop effect by solution resistance on the peaks as well as heterogeneous kinetics. It is also brought about by negatively capacitive currents associated with charge transfer reactions. The reaction product generates dipoles with counterions to yield a capacitance, of which current flows oppositely to that of the double layer capacitance. The three effects are specified here in the oxidation of a ferrocenyl derivative by fast scan voltammetry. The expression for voltammograms complicated with IR-drop is derived analytically, and yields deformed voltammograms. The peak shift is approximately linear with the IR-term, but exhibits a convex variation. Dependence of some parameters on the peaks by the IR-drop is compared with those by the negative capacitance. The latter is more conspicuous than the former under conventional conditions. The two effects cannot be distinguished specifically except for variations of conductance of the solution.
Keywords: 
Subject: Chemistry and Materials Science  -   Electrochemistry

1. Introduction

Linear sweep cyclic voltammetry has been conventionally made at scan rates v ranging 0.01 < v < 0.2 V s–1. The slowest scan has been used on the assumption of the steady state for hydrodynamic voltammetry [1] and microelectrode voltammetry [2]. It often provides a well-defined voltammogram but takes a long period of a few minutes. An advantage of the slow scan rates is to distinguish faradaic, diffusion-controlled currents from background currents by a double layer capacitance (DLC). For example, the diffusion current at concentration 0.5 mM (M = mol dm–3) redox species is roughly Id = 3v1/2 μA at a 1 mm2 planar electrode for v in the unit of V s–1. In contrast, a DLC of a platinum electrode in aqueous solutions, being C = 30 μF cm–2, provides the capacitive current Ic = 0.3v μA. Since the ratio is Ic/Id = 0.1 v1/2, the diffusion currents at v = 0.2 V s–1 can be distinguished from the background with 5 % errors. A disadvantage is a time-consumed measurement, during which redox species might be altered through chemical complications. If faradaic reactions occur under an adsorbed state, the advantage is not perceptive because the background current has the same v-dependence as Ic. Slow responses fail to detect kinetic properties.
Study on homogeneous and heterogeneous kinetics requires such a wide range of v that reaction rates can be covered. A range of the kinetics is often much wider than the conventional scan rates (0.01 – 0.2 V s–1), and hence fast scan voltammetry is desirable for kinetic work principally [3,4,5,6,7,8,9,10] and practically [11,12,13,14] for applications to neurotransmitter detection. Unfortunately, the increase in scan rates is associated with at least five problems to be considered. (A) IR-drop, in which applied voltage is lost by solution resistance, makes voltammograms deformed and shifted in a scanned direction [15,16]. (B) Even if difference in v-dependence of Id and of Ic enables us to evaluate Id accurately [17], the adsorption-controlled current, Ia, prohibits the extraction of Ia from the observed current because of the same v-dependence as Ic. (C) A delay of a potentiostat underestimates true currents at short time [7,8,17]. (D) Heterogeneous kinetics represented by the Butler-Volmer equation makes the peak potential shifted and the peak current deviated lower than the predicted diffusion-controlled peak current [18] with an increase in v. (E) Fast scans more than 0.5 V s–1 generate the negatively capacitive current, which is caused by formation of dipoles of a reaction product with counterions at an electrode [19,20,21,22,23].
A level of these problems depends on magnitude of v. We suggest three classes; v < 0.2 V s–1, v < 5 V s–1 and v < 500 V s–1. Advantages and possible risks for each class are listed in Table 1.
The usage of fast scan rates prevents clear distinction of faradaic reactions from backgrounds. The difficulty in the distinction in class III has been overcome with efforts of trial and error, as exemplified with the rapid detection of neurotransmitters,[11–13]. The developed techniques are specific to given redox species under limited conditions. In contrast, those in class II have been carried out on the theoretical base of the difference in the v-dependence when faradaic reactions proceed in diffusion-control. If problems (A)-(E) are intertwined complicatedly, corrections are not enough sufficient for finding expected behavior of the faradaic waves. For class I, the intertwinement is largely solved except for adsorption in the v-dependence.
We examine here subjects (A)-(E) carefully. Since no stereotyped redox species has been found for the Butler-Volmer kinetics yet [24], (D) may be excluded from the present work on ferrocenyl derivatives [25,26,27]. If we pay attention only to diffusion-controlled currents under category (II), subjects (B) and (C) have been automatically resolved. Both (A) and (E), being necessarily involved in fast scan voltammetry, exhibit similar behavior in spite of different concepts. We examine in this work how voltammetric peak potentials and currents belonging to class (II) are varied with controlling parameters for (A) and (E) by use of fast scan voltammetry of a ferrocenyl derivative. Unfortunately, effects of IR-drop (A) have not been discussed systematically yet. Thus, we present here the experimental results and the theory.

2. Materials and Methods

2.1. Chemicals

All the chemicals were of analytical grade. Solutions were prepared in doubly distilled water prepared by CPW-100 (Advance, Tokyo, Japan). Aqueous solutions with different concentrations of KCl (0.005, 0.05, 0.1, 0.5 and 5 M) were prepared at the aim of varying solution resistance. The electrochemical charge transfer species was 1 mM (ferrocenylmethyl)trimethyl ammonium (FcTMA).

2.2. Voltammetry

Voltammetry was made in a three-electrode cell equipped with a working platinum wire electrode 0.03 mm, 0.5 mm in diameter or a 1.6 mm disk electrode. The tip of the wire was inserted into the solution by a given length (ca. 1 mm) which was measured with a microscope. The wire was not sealed with any insulator to expose an active area in order to avoid floating capacitance at crevices of electrode|insulator. The electrode was pretreated by being socked in the mixed acid (0.26 M acetic + 0.33 M nitric acid + 0.73 M phosphoric acid) for 1 min to clean the surface. A counter electrode was a platinum coil. A reference electrode was a homemade Ag|AgCl (x M KCl). A columnar porous glass was fixed to a tip of taper glass tube with a heat shrink tube, into which a Ag|AgCl wire was inserted together with x M KCl solution. In order to detect any leakage of chloride ions during the experiment, we measured the resistance values of the solution before and after the experimental test, which were almost the same.
A delay of the potentiostat, Compactstat by Ivium (Netherlands), was examined by using a carbon resistance 1 kΩ for a dummy cell by applying the voltage with 1 V. The maximum difference in the currents at the forward and the reverse scan was 3% at 8 V s–1. Our voltammetry for FcTMA and various concentrations of KCl was made at scan rate less than 7 V s–1. Ac-impedance was made for the 10 mV amplitude and frequency domain from 1 Hz to 10 kHz. All measurements were made at temperature of 25 ± 1 ℃.

3. Results

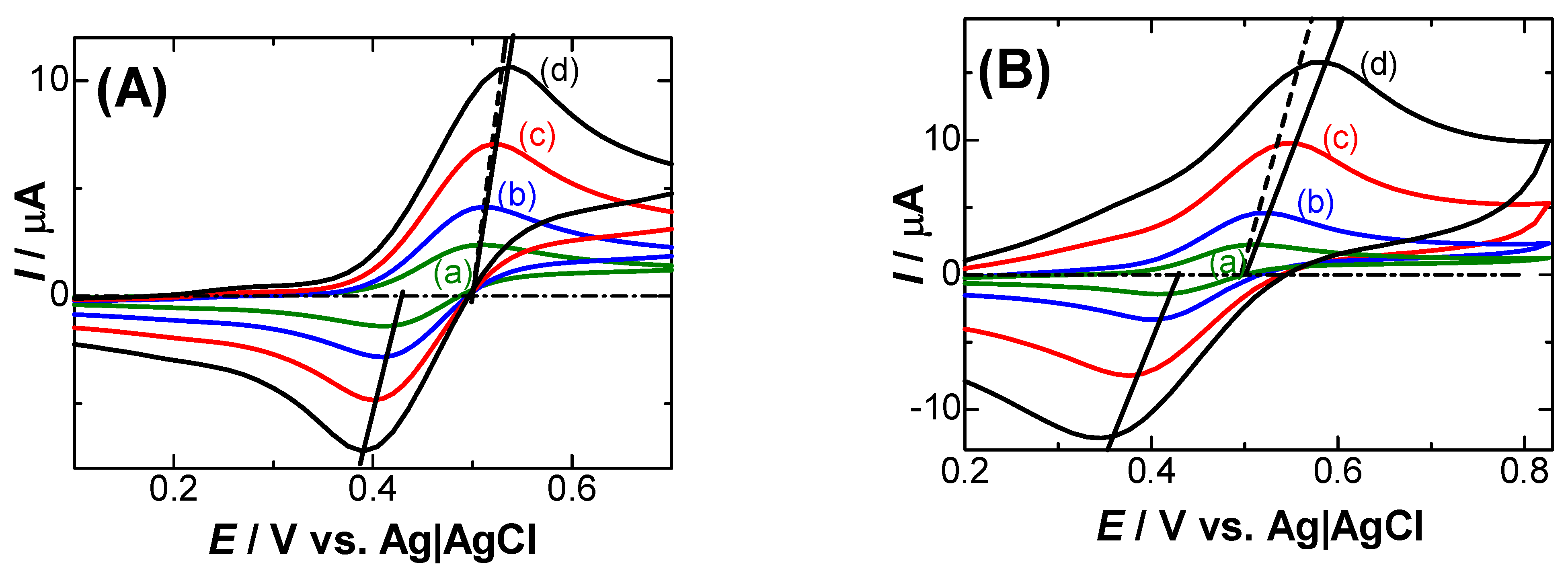
Figure 1A shows voltammograms at the 0.5 mm platinum wire electrode inserted in 1 mm length in the solution of 1.0 mM FcTMA + 5 mM KCl for several scan rates. FcTMA or related ferrocenyl derivatives have been recognized as such fast charge transfer reacting species that voltammetric peak potentials, Ep, may be independent of voltammetric scan rates [19,24,28,29,30]. However, the peak potential in Figure 1A shifted in the forward direction at the fast scan rates. The potential shift has often been attributed to the IR-drop. The resistance values were estimated from the inverse slope of the line connecting the peaks (solid lines) [18,28]. The slope for the anodic waves was the same as that for the cathodic one. This equality partially supports the effect of IR-drop on the potential shift. The inverse slope was close to the resistance (2.7 kΩ) obtained through Nyquist plots by ac-impedance. The potential at which the lines are extrapolated to zero current can be regarded as the peak potential without IR-drop. The difference between the extrapolated anodic potential and the cathodic one was 60 mV, indicating the diffusion- controlled behavior [18]. The voltammograms in Figure 1B at the disk electrode 1.6 mm in diameter were drawn out to exhibit the peak-connecting line with the inverse slope of 5.5 kΩ, which was larger than the resistance value of 4.2 kΩ by ac-impedance. Except for this point, the behavior was almost the same as in (A).
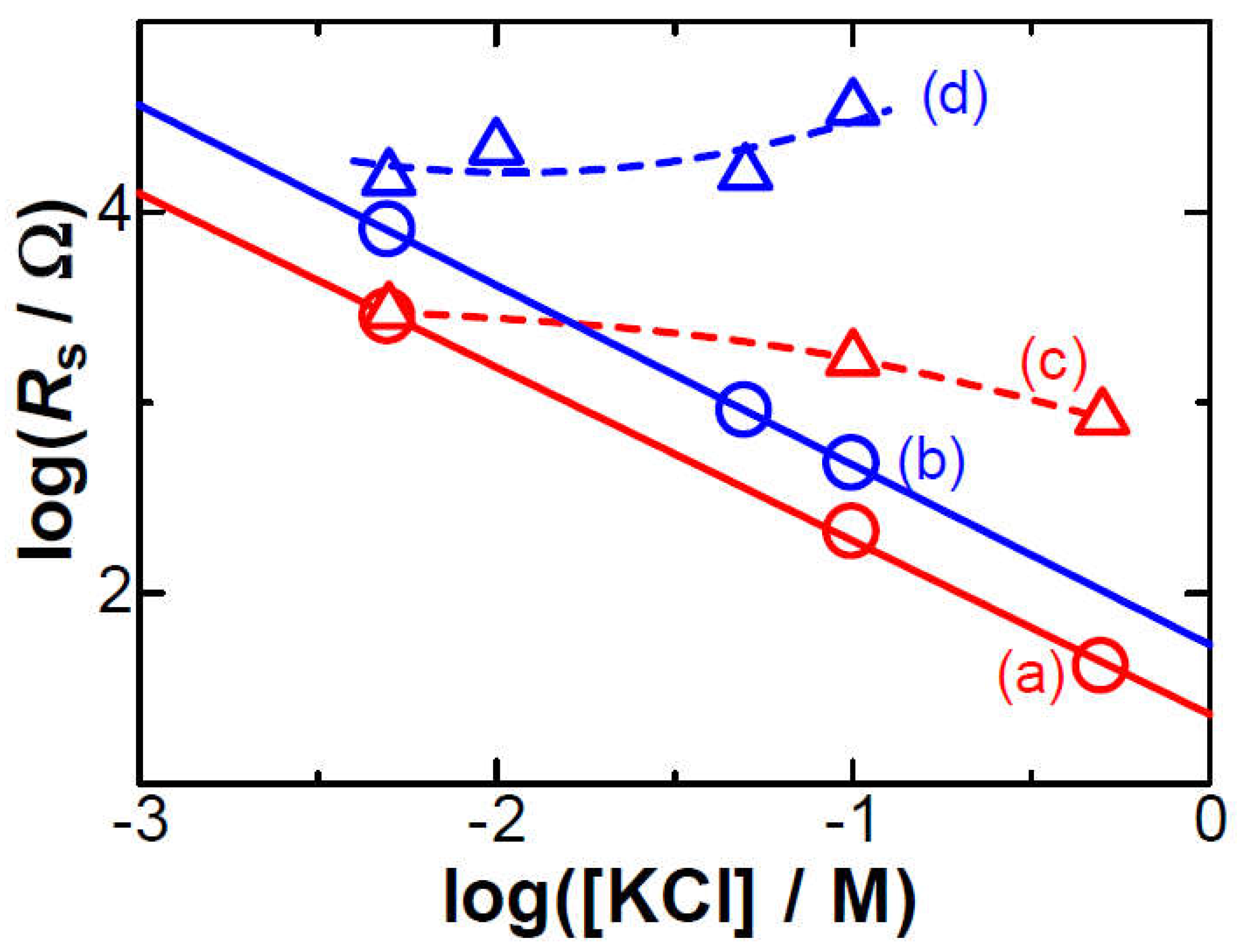
There may be a reason for the larger values of the slopes of voltammetric peaks than the Rs-values by ac-impedance. Figure 2 shows logarithmic plots of two kinds of the resistance against concentrations of KCl. Rs-values (a, b) by ac-impedance were linear with the logarithmic form of [KCl] with the slope –0.91, independent of the electrode geometry. The approximately inverse proportion of Rs to [KCl] agrees with the concept of ionic mobility by electric field [31]. The deviation of the slope (–0.91) from the ideal one (–1.0) can be attributed to the frequency dispersion of the double layer capacitance, of which values increase slightly with salt concentrations [23,32,33]. It can be understood in terms of an upward shift of Nyquist plots with an increase in salt concentrations [33]. It is noteworthy to pay attention to the invalidity of simple RC-relaxation of the double layer capacitances [8,9]. In contrast, the resistances evaluated from voltammetric peaks (c, d) were kept almost constant for the low salt concentrations. They are provided through the oxidation current of FcTMA rather than the capacitive currents of the electric double layer. The potential-shifts only caused by faradaic reactions can be attributed to effects of (i) electric migration [34,35,36], (ii) the heterogeneous kinetics for the charge transfer reaction [18], (iii) following chemical reactions [37,38], and (iv) the negative capacitance associated with the charge transfer reaction [19,20,21,22,23]. We attempt to estimate these effects briefly here.
(i) The flux of a uni-valent cationic redox species controlled both with diffusion and electric migration is expressed by the Nernst-Planck equation, j/F = –Ddc/dx – (DF/RT)c(dφ/dx) [39], where c is its concentration, D is the diffusion coefficient, and φ is the potential in solution at a distance from the electrode x. It can be approximated to be j/F = –Dc*/δ – (DF/RT)c*(Δφ/δ), on the basis of a concept of diffusion layer [40]. Here, its thickness at the peak current, Ip, is given by δ = Dc*FA/Ip, where A is the electrode area. The ratio of the current component of the migration to that of diffusion is (F/RT)Δφ. When Δφ is replaced by RsIp, the ratio becomes less than 0.5 % under our experimental conditions. Therefore, migration has no contribution to the potential shift in our case.
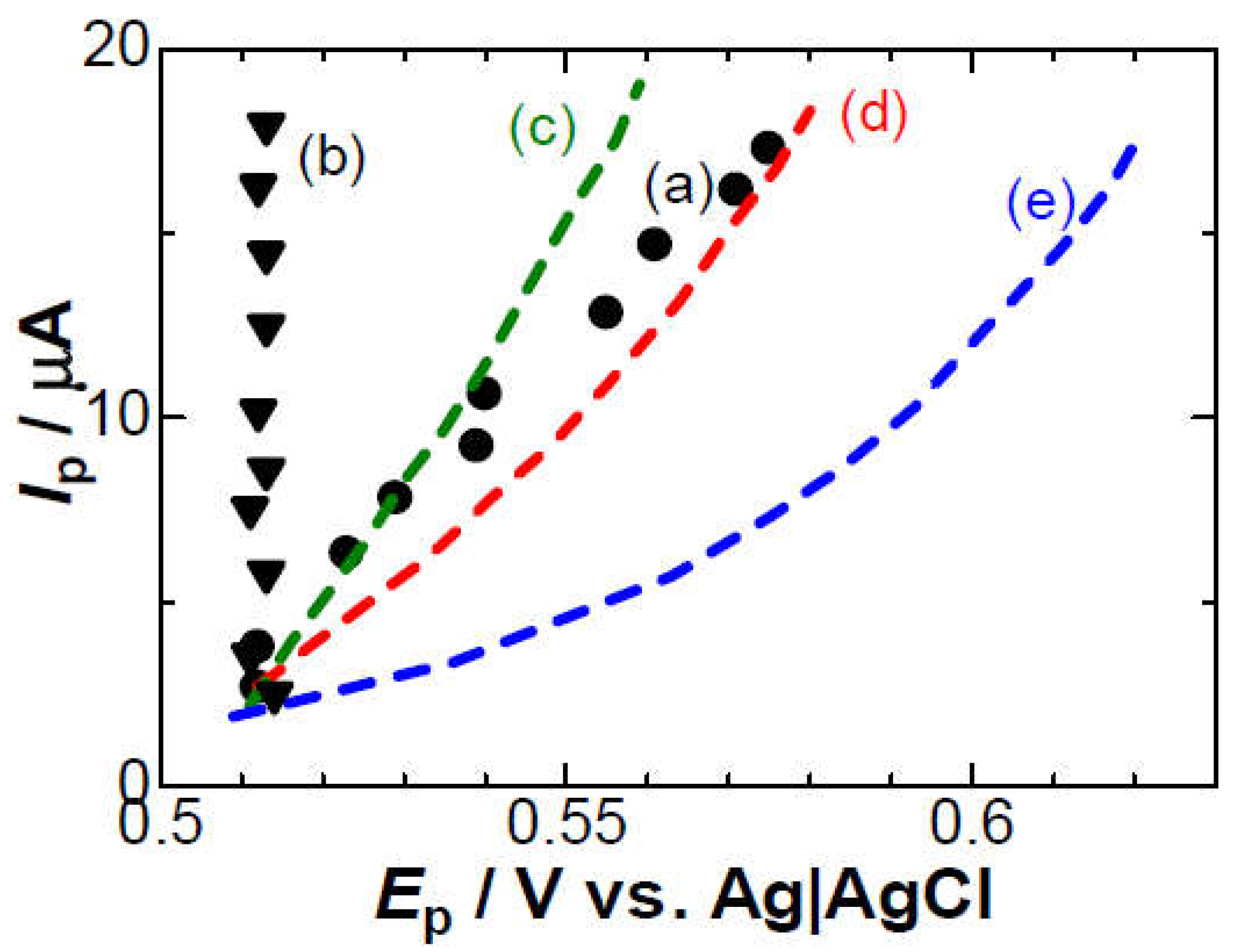
(ii) The electrode kinetics has often caused potential shifts. A quantitatively accessible kinetics is represented by the Butler-Volmer equation. The theoretical peak currents and potentials for different scan rates can be obtained from the analytical equation at a given transfer coefficient α and a heterogeneous rate constant k0 [18]. Figure 3c–e shows the variation of Ip with Ep for several scan rates at the α = 0.5 and some values of k0 by use of our software of the kinetics so that Ip vs. Ep were close to the experimental ones (a). However, the experimental plots (a) is different from theoretical variations for any different values of k0. The inconsistency was also applied to other values of Rs (b). Since no potential shift was found in 0.1 M KCl solution (b), it is not reasonable to explain the shift in terms of the heterogeneous kinetics. However, the explanation only by the kinetics has often been reported [3,[3–,4,5,6,7,8,9,10].
(iii) A following chemical reaction causes a potential shift, as can be understood from the Nernst equation for reaction rates faster than voltammetric rates. Ferrocenyl compounds, however, are not satisfied with the condition of the rates, and hence, item (iii) is unsuitable of explaining the present potential shifts.
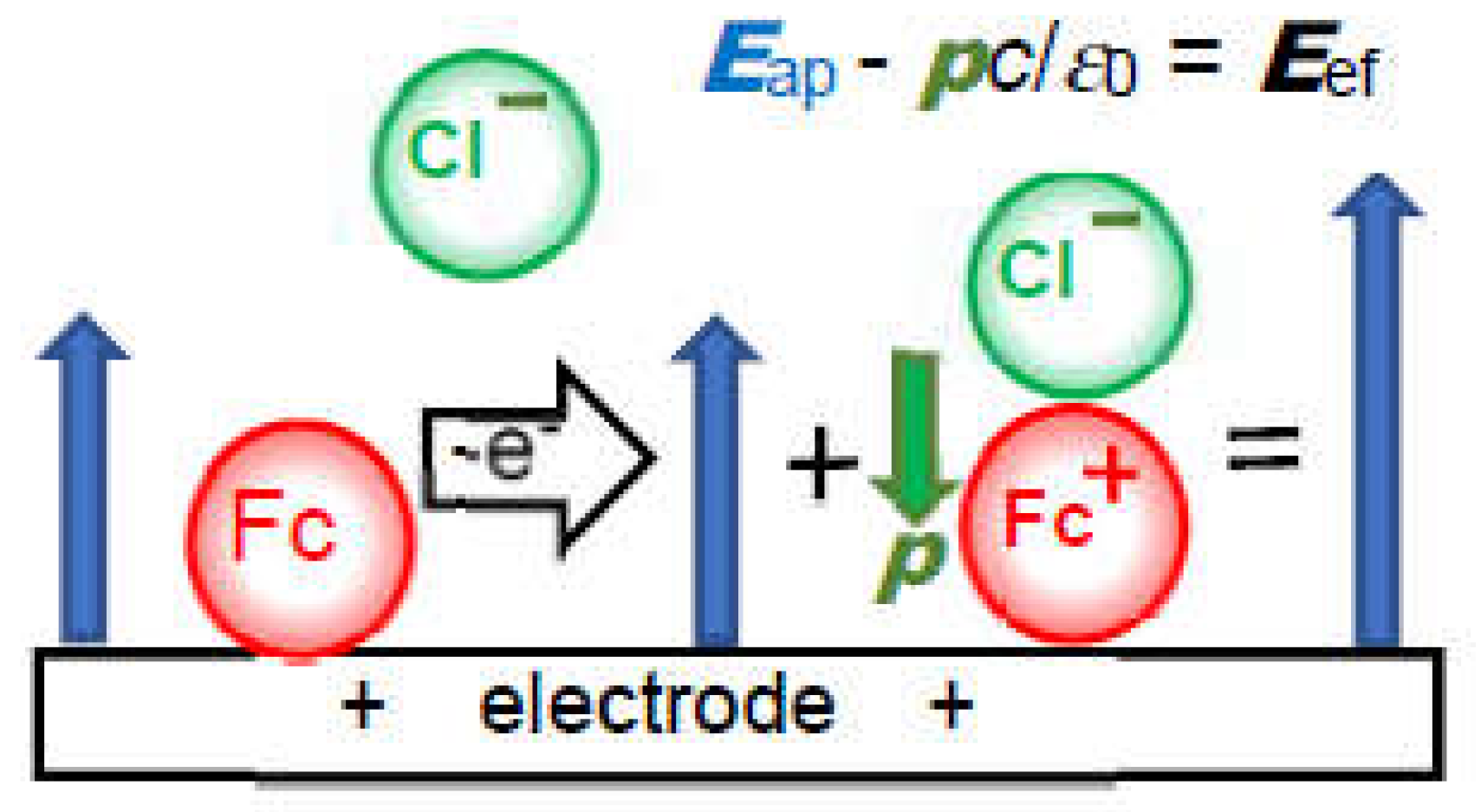
(iv) The negative capacitance is brought about through the following steps in Figure 4: a charge transferred redox species (Fc) is coupled with a counterion (Cl–) for electric neutrality by responding to the externally applied field Eap to yield an electric dipole(Fc+-Cl–); the dipole with the dipole moment p is oriented in the direction for enhancing the external field by -pc/ε0 to yield the effective field Eef, which generates a capacitance with a sign opposite to a double-layer capacitance [17,41]. The negative capacitance has been obtained for ferrocenyl derivative [19,20], ruthenium complex, iridium complex [20] and hemin [41] by ac-impedance. Since the voltammetric current from the negative capacitance is proportional to the scan rate, it depresses the diffusion tail to cause the potential shift [17]. The negative capacitance varies with electrode areas and scan rates, as the IR-drop does. The similarity in the properties stimulates us to distinguish their properties theoretically.

4. Theory of effects of IR-drop

The electrode reaction here is a simple Nernstian charge-transfer reaction with the mass transfer controlled by x-directional diffusion. The diffusion coefficient of the reduced species, D, is assumed to have a common value to the oxidized species. Letting the solution resistance between a working electrode and a reference one be Rs, the scan rate be v and the initial potential be Ein, we can express the linearly scanned potential participating efficiently in the oxidation for the current I as E(t) = Ein + vt – I(t)Rs at the time t. The common value of D implies that the sum of concentrations of both species is equal to the bulk concentration, c*, in any time and any location. Thus, the Nernst equation for the reduced species tends to
cx=0 = c*/{1 + exp((Ein + vt – I(t)Rs)F/RT)}
On the other hand, the surface concentration is given by a solution of the diffusion equation [18] as a function of the current density j
cx=0 = c* – F–1(πt) –1/2∫0t j(t – u)u–1/2du
Inserting this equation into Equation (1) and extracting j by the technique previously described [42] yields
j/c*FD1/2 = d∫0t (πu) –1/2{1 + exp[– (E(t–u)F/RT]} –1du / dt
Application of Leibniz's theorem [43] makes the combination of the integral and the differentiation be reduced to
I/Ac*FD1/2 = (1/4)∫0t {π(t – u)} –1/2{sech2(E(u)F/2RT)}{v – RsdI(u)/du)}(F/RT) du
where A is the area of the electrode.
We replace the time by the potential through y = (Ein + vu)F/RT, and define the dimensionless current as
f(t) = I(t)/Ip0
where Ip0 is the peak current without solution resistance, given by Ip0 =0.446Ac*F(FDv /RT)1/2. The current has the dimensionless parameter for the resistance
ρ = Ip0RsF/RT
and can be rewritten as
f(t) = π–1/2∫ζinζap (ζap – y)–1/2g(y – 2.24ρf(y)){1 – ρdf(y)/dy} dy
where g(x) = (1/4)sech2(x/2), and ζin and ζap are the dimensionless initial voltage EinF/RT and the dimensionless applied voltage (Ein+vt)F/RT, respectively. Function f was evaluated by numerical computation by discretization of ζap –ζin = nh for a small value of h, as was described in the supporting information.
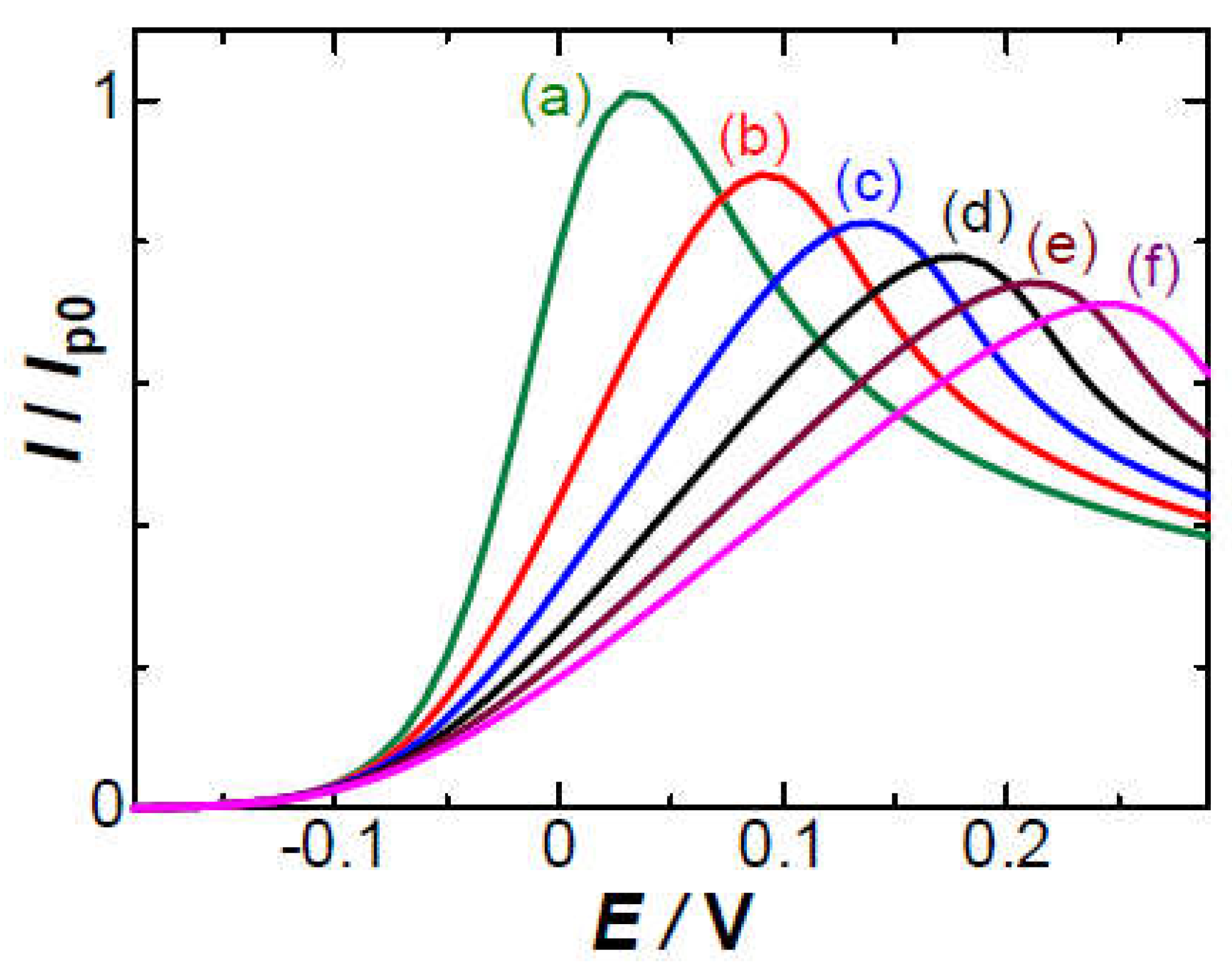
Figure 5 shows dimensionless voltammograms for several values of resistance parameter ρ (Equation (4)). With an increase in the values of ρ, voltammograms shift in the positive direction accompanied with a decrease in the peak currents. An exemplified value of ρ = 4 corresponds to Ip0 = 0.1 mA, Rs = 1 kΩ.
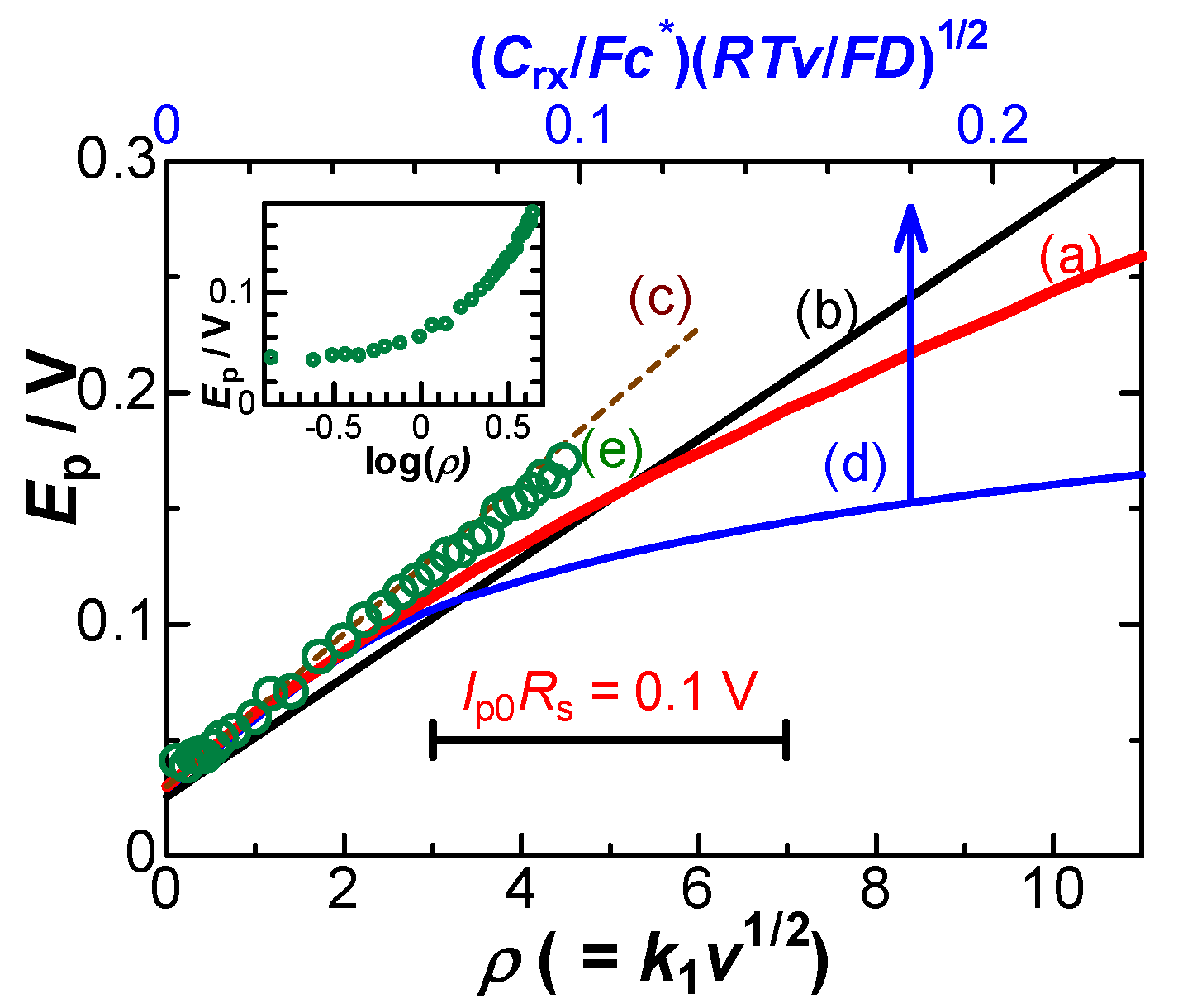
Peaks were calculated for various values of ρ. The Ep increased from 0.029 V convexly with ρ, as shown in Figure 6a. The intuitively predicted increase in Ep is Ip0Rs or (26 mV)ρ,
(Ep)IR,prdct = Ip0Rs + 0.026 V
as shown in the line of Figure 6b. The tangent line at ρ = 0 has the slope, 33 mV (Figure 6c). The slight shift from 26 mV is ascribed to the smaller decrease in the current for E > Ep than that for E < Ep (see Figure 5) owing to the diffusion tail. Consequently, the Ep-values calculated from Equation (5) for ρ < 3 are larger than the line (Equation (6)). Since the variable ρ is proportional to v1/2 through Ip0, the effect of IR-drop on the voltammograms is approximately exhibited in the form of the linearity of Ep to v1/2 rather than log v.
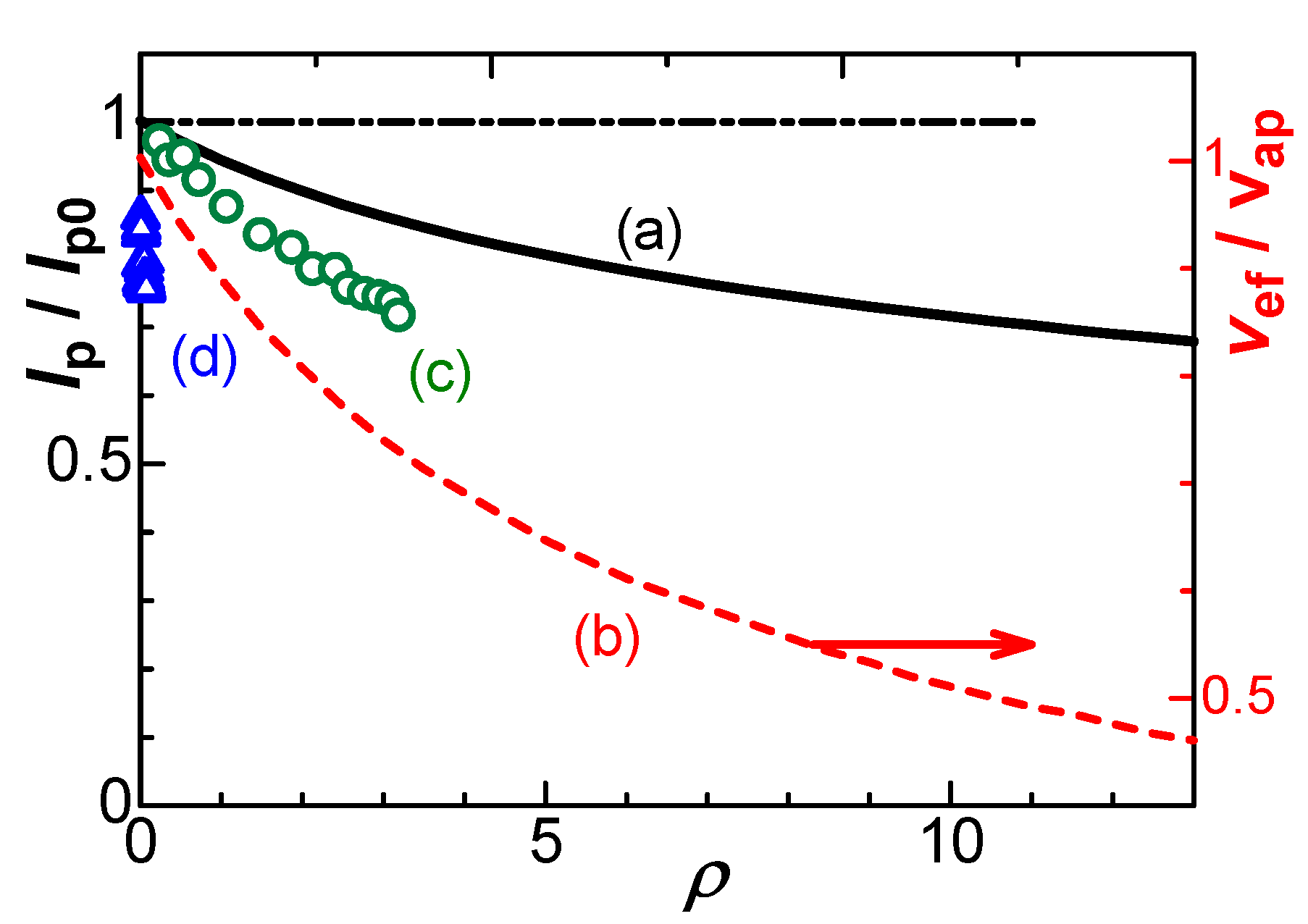
The peak current normalized with the theoretically diffusion-controlled one decreased with an increase in the resistance, as shown in Figure 7. The decrease can be explained in terms of the following reasons: the shift of the peak potential delays the arrival at the peak; the delay is equivalent to a substantial decrease in the applied scan rate, vap, which leads a decrease in Ip so that Ip < Ip0 = k1vap1/2, where k1 = 0.446Ac*F(FD/RT)1/2. By letting the effective scan rate, vef, be Ip = kvef1/2, vef decreases with ρ, as shown on the right ordinate in Figure 7b. It varies linearly with ρ1/2. The effective rate becomes less than a half for ρ > 10 or Ip0Rs > 0.25 V. The difference, 0.446– (Ip/Ac*F)(RT/FDvap)1/2, was approximately proportional to ρ1/2. As a result, the peak current at any value of Rs can be approximated as
Ip/Ip0 = 1 – 0.09ρ1/2
This is a new insight for the IR-drop effect that has not been reported yet [8,9]. Since ρ is proportional to v1/2 through Ip0 (Equation (4)), the peak current for the IR-drop can be approximated as Ip = kv1/2 – k1v3/4.
It is interesting to compare the effects of IR-drop on Ip and Ep with those of the negative capacitance (NC), Crx. The Ep due to Crx has varied linearly with log[(σ*/c*)2(v/FRTD)] [17] for Ep – Eo > 0.06 V, where σ* is the sum of the surface charge density of the oxidized and the reduced species, and c* is the bulk concentration of FcTMA. In contrast, its variation for Ep – Eo < 0.1 V is linear with (σ*/c*)(v/FRTD)1/2, as shown in Figure 6 on the upper abscissa, which was scaled so that the line may be overlapped with the line for the IR-drop. The line can be approximated as 0.0217(σ*/c*)(v/FRTD)1/2 + 0.03 in the unit of V for Ep – Eo > 0.06 V. The empirical equality, Crx = 0.16(F/RT)σ*, in Equation (13) of ref. 17 can substitute Crx for σ* to give
(Ep)NC, <0.10V / V = 0.135(Crx/Fc*)(RTv/FD)1/2 + 0.03
When potential shift is small, the observed shift is the sum of the shifts for the IR-drop and the negative capacitance,
(Ep)<0.10V / V = 0.135(Crx/Fc*)(RTv/FD)1/2 + 1.15Ip0Rs + 0.03
Rs varies with geometry of electrodes at given conductivity of solution. A disk electrode makes Rs be 1/4Λ[KCl]a = (π/A)1/2/4Λ[KCl] [44] for the molar conductivity Λ of KCl. Rs at a wire electrode, on the other hand, is inversely proportional to A. Some variables that control Ep are summarized in Table 2 for comparing these two effects.
The IR-drop contribution normalized with Ip0 is
(Ip0 – Ip)/Ip0 ≡ XIR = 0.09(Ip0RsF/RT)1/2
On the other hand, the negatively capacitive peak current is given by INC = Ip0 – ACrxv. The normalized contribution is given by
XNC = ACrxv/ Ip0
Eliminating Ip0 from Equations (10) and (11) yields
XIR = 0.09(ARsCrxvF/RTXNC)1/2
Especially, the relation for the disk is given by
(XIR)disk = 0.06A1/4(CrxvF/RTΛ[KCl]XNC)1/2
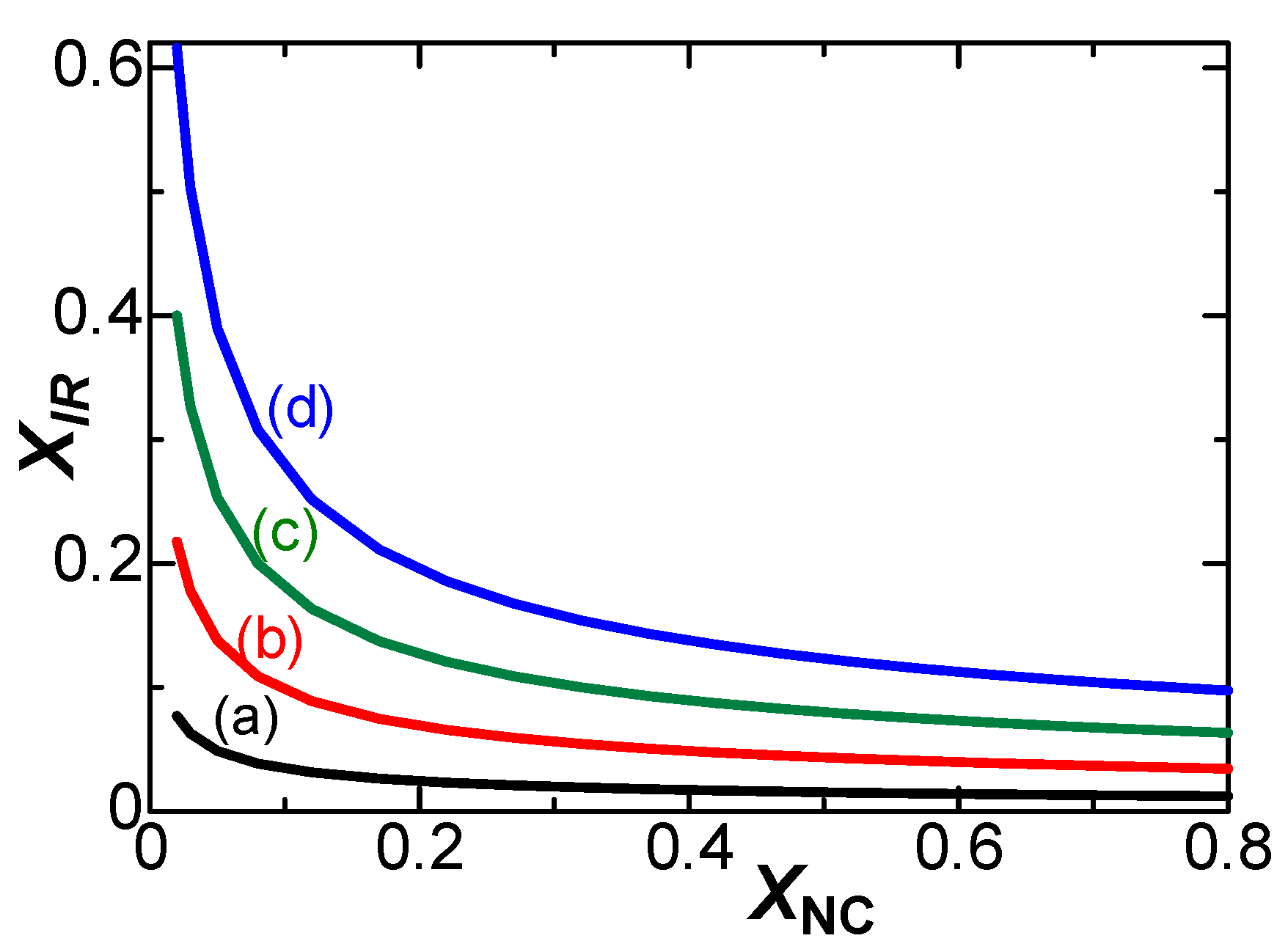
Figure 8 shows variations of (XIR)disk with XNC for some electrode areas at conventionally experimental conditions of v, κ (=Λ[KCl]) and Crx. The constant of XIR2XNC indicates that the effect of the negative capacitance is predominant to that of the IR-drop. Furthermore, high scan rates at large electrodes in low salt concentration should enhance both the IR-drop and the negative capacitance.

5. Discussion

Experimental values of Ep in the solution of 1 mM FcTMA + 5 mM KCl were plotted against ρ (= IpRsF/RT) in Figure 6e, where the value of Rs for ρ was obtained from the Nyquist plot. They were on a line, deviated upward from the theoretical curve Figure 6a of the IR-drop, and hence the potential shift cannot be ascribed only to the IR-drop. The plot of the experimental Ep vs. log v is shown in the inset of Figure 6, as is often plotted. The non-linearity indicates that the conventionally observed linearity should not explain any IR-drop effect. Addition of voltages does not agree with that of processes because of non-linear relation to voltages in electrochemical processes. The experimentally obtained ratio, Ip/Ip0, decreased with an increase in v, as shown in Figure 7c,d at two values of Rs. The variation of the triangular marks is close to that of the circles if ρ-axis is expanded. The experimental values (c,d) lower than the theory (a) were caused by the effect of the negative capacitance.
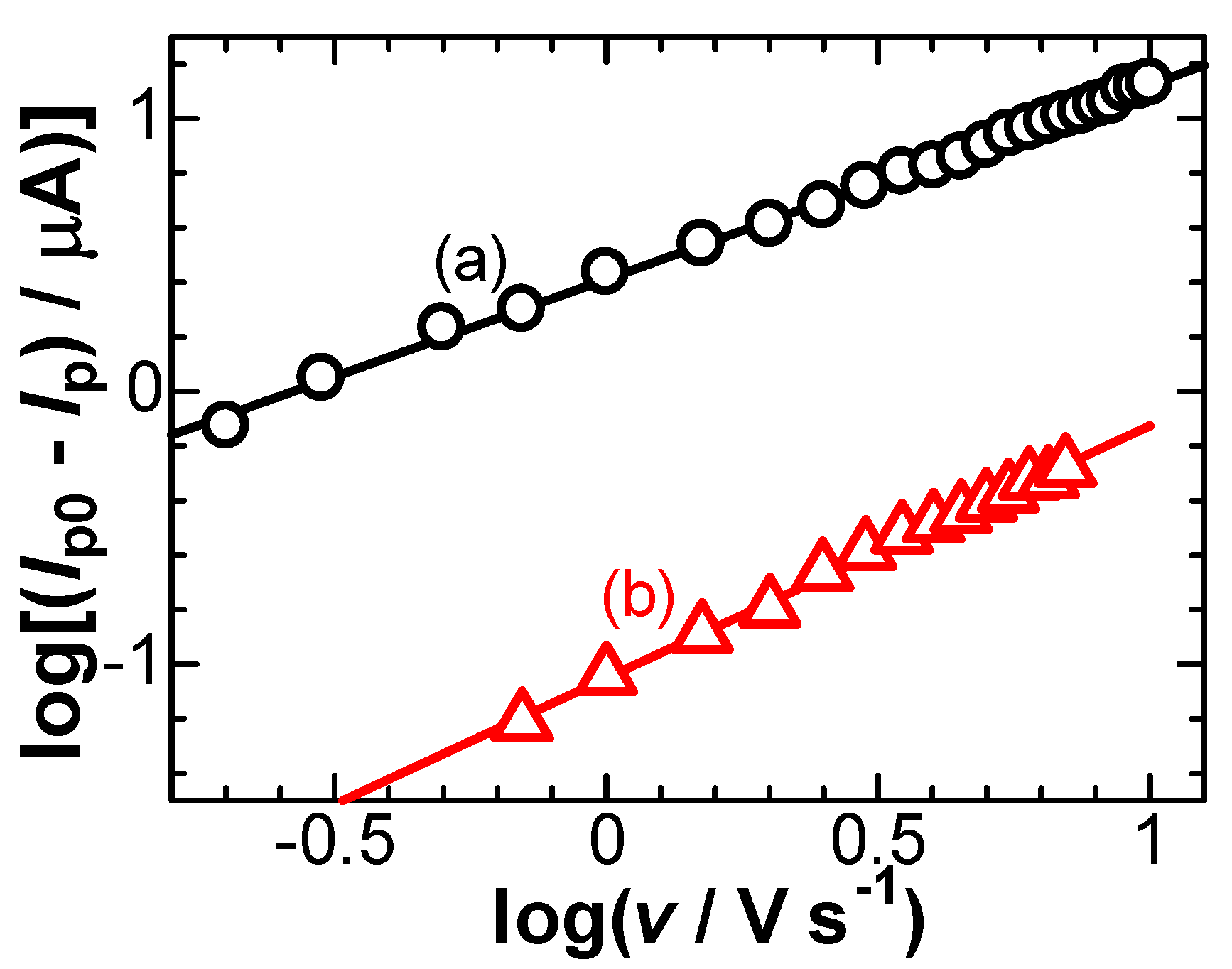
It is current that can make arithmetic operations possible through an addition of current at a parallel process or of inverse currents at a series one. In order to confirm the dependence of the IR-drop contribution on the scan rates, we plotted Ip0–Ip in solution of 1 mM FcTMA + 5 mM KCl against v logarithmically in Figure 9a. The plot shows a line with the slope, 0.71, which is close to the theoretical value, 3/4, in Table 2. The value of the slope suggests the control of the IR-drop. On the other hand, the currents at the 0.03 mm wire in 0.1 M KCl (in Figure 2d) did not contain any IR-drop effect, as demonstrated in Figure 3b. The logarithmic plots of Ip0–Ip vs. v shows a line with slope of 0.92 in Figure 9b. The value of the slope is close to unity, and hence it should belong to the negative capacitance.

6. Conclusion

Fast scan for a diffusion-controlled voltammogram makes the peak potential shifted and the peak current decreased from the theoretical values. The deviation is not caused by the Butler-Volmer typed kinetics but is caused by combinations of IR-drop of solution resistance and the negative capacitance associated with electrode reactions. The two effects are hardly discriminated in terms of scan rate-dependence, but the distinction can be made with variation of concentrations of electrolytes or size of electrodes. The effect of the negative capacitance is likely to appear more strongly than the IR-drop effect in voltammetric peaks. Wire electrodes less than 0.05 mm in diameter are suitable for suppressing the IR-drop effects even in low concentrations of electrolytes.
The expression for voltammograms complicated by the IR-drop is given by a non-linear integral equation as a function of Ip0Rs. The evaluation has to relay on numerical computation through digitization. The peak potential shifts intuitively by Ip0Rs. However, the theory predicts that it shows a non-linear relation with Ip0Rs, because of asymmetric waveform near the peak. Calculated potential shifts over 0.2 V are smaller than the values of Ip0Rs. The potential shift retards the time reaching the peak, yielding a decrease in the actual scan rate. As a result, the peak current is observed to be suppressed.

6. Supporting information

This section informs numerical computation of
f(t) = π–1/2∫ζinζap (ζap – y)–1/2g(y – 2.24ρf(y)){1–ρdf(y)/dy} dy
Discretization of ζap–ζin = nh with an equal width h rewrites Equation (5)
f(t) =π–1/2Σk=0n–1 ∫ζin+khζin+(k+1)h (ζap–y)–1/2g(y – 2.24ρf(y)){1 – ρdf(y)/dy} dy
It is assumed that g(y – 2.24ρf(y)) and {1 – 2.24ρdf(y)/dy} are constant at each discretized domain, g(y – 2.24ρf(y)) ≈ g(yk – 2.24ρf(yk)) = g(yk – 2.24ρfk)
1– 2.24ρdf(y)/dy} ≈ 1 – 2.24ρ(yk+1 – yk–1)/2h
Then (S1) becomes
fn =π–1/2Σk=0n–1 g(yk – 2.24ρfk){1 – 2.24ρ(fk+1 – fk–1)/2h} ∫ζin+khζin+(k+1)h (ζap – y)–1/2dy
The integral provides
∫ζin+khζin+(k+1)h (ζap – y)–1/2dy = ∫(n–k–1)h (n–k)h x–1/2dx = 2h1/2{(n–k)1/2– (n–k–1)1/2}
Then, (S2) can be rewritten as
fn =2(h/π)1/2 Σk=0n–1Hk,n
Hk,n = g(yk – 2.24ρfk){1 – 2.24ρ(fk+1 – fk–1)/2h}{(n–k)1/2– (n–k–1)1/2}
We attempted to calculate fn successively starting for n = 1 on the assumption of replacing fn in Hn,n as fn–1, we found that values of fn diverged before a voltammetric peak. The assumption was refined by by extracting fn from Hn,n to rewrite the following form:
fn =2(h/π)1/2 [g(yn–1 – 2.24ρfn–1){1 – 2.24ρ(fn–fn–2)/2h} + Σk=0n–2Hk,n]
Solving Equation (S3) with respect to fn yields
fn =2(h/π)1/2[g(yn–1 – 2.24ρfn–1){1+2.24ρfn–2/2h}+ Σk=0n–2Hk,n]
/ [1+(πh) –1/22.24ρ g(yn–1 – 2.24ρfn–1)]
The initial value was f0 = 0 for y0=ζin and f–1 = 0 because of no current.

References

  1. A.J. Bard. L.R. Faulkner, Electrochemical Methods; Fundamentals and Applications, John Wiley & Sons, New York, 2nd. Ed., 2001, pp. 331–332.
  2. A.J. Bard. L.R. Faulkner, Electrochemical Methods; Fundamentals and Applications, John Wiley & Sons, New York, 2nd. Ed., 2001, pp. 170–176.
  3. J.O. Howell, J.M. Goncalves, C. Amatore, L. Klasinc, R.M. Wightman, J.K. Kochi, J. Am. Chem. Sot., 1984, 106, 3968.
  4. C. Amatore, C. Lefrou, J. Electroanal. Chem., 1990, 296, 335–358.
  5. M.I. Montenegro, D. Pletcher, J. Electroanal. Chem., 1986, 200, 371.
  6. A. Fitch, D.H. Evans, J. ElectroanaI. Chem., 1986, 202, 83.
  7. C. Amatore, E. Maisonhaute, G. Simonneau, Electrochem. Commun., 2000, 2, 81–84.
  8. C.P. Andrieux, D. Garreau, P. Hapiot, J. Pinson, J.M. Saveant, J. Eleetroanal. Chem., 1988, 243, 321–335.
  9. G. Wosiak, D. Coelho, E. B. Carneiro-Neto, E. C. Pereira, M. C. Lopes, Anal. Chem., 2020, 92, 15412-15419.
  10. C. Amatore, A. Oleinick, I. Svir, Anal. Chem., 2008, 80, 7947-7956.
  11. J.G. Roberts, L.A. Sombers, Anal. Chem. 2018, 90, 490–504.
  12. J.E. Baur, E.W. Kristensen, L.J. May, D.J. Wiedemann, R.M. Wightman, Anal. Chem., l988, 60, 1268–1272.
  13. B.J. Venton, Q. Cao, Analyst, 2020, 145, 1158.
  14. P. Puthongkham, B.J. Venton, Analyst, 2020, 145, 1087–1102.
  15. BioLogic, EC-Lab – Application Note #41, 07/2012, CV Sim: Simulation of the simple redox reaction (E) Part II: The effect of ohmic drop and double layer capacitance.
  16. K.J. Aoki, J. Chen, Tips of Voltammetry, IntehOpen, 2018, pp. 1–19.
  17. K.J. Aoki, J. Chen, Y. Liu, B.Jia, J. Electroanal. Chem., 2020, 856, 113609.
  18. H. Matsuda, Y. Ayabe, Z. Elektrochmie. 1955, 59, 494–503.
  19. K.J Aoki, J. Chen, X. Zeng, Z. Wang, RSC Adv. 2017, 7, 22501–22501.
  20. K.J. Aoki, J. Chen. P. Tang, J. Phys. Chem. C, 2018, 122, 16727–16732.
  21. K.J. Aoki, J. Chen, R. Wang, Electroanalysis, 2019, 31, 1–9.
  22. K.J. Aoki, T. Peng, J. Chen, Am. J. Anal. Chem., 2019, 10, 286–295.
  23. R. Wang, K.J. Aoki, J. Chen, Electrochem, 2022, 3, 397–406.
  24. K.J. Aoki, C. Zhang, J. Chen, T. Nishiumi, J. Electroanal. Chem., 2013, 706, 40–47.
  25. P. Sun, M.V. Mirkin, Anal. Chem., 2006, 78, 6526–6534.
  26. J. Velmurugan, P. Sun, M. V. Mirkin, J. Phys. Chem. C, 2009, 113, 459–464.
  27. J. F. Smalley, S. W. Feldberg, C. E. D. Chidsey, M. R. Linford, M. D. Newton, Y.-P. Liu, J. Phys. Chem., 1995, 99, 13141–13149.
  28. N. Nioradze, J. Kim, S. Amemiya, Anal. Chem., 2011, 83, 828–835.
  29. Y. Li, D. Bergman, B. Zhang, Anal. Chem., 2009, 81, 5496–5502.
  30. Y. Zhang, J. Zhou, L. Lin, Z. Lin, Electroanal., 2008, 20, 1490–1494.
  31. P. Atkins, J.de Paula, Atkin's Physical Chemistry, 10th ed., Oxford University Press, pp, 799–802.
  32. K. J. Aoki, R. He, J. Chen, Electrochem, 2021, 2, 71–82.
  33. K.J. Aoki, R. He, J. Chen, Electrochem, 2021, 2, 631–642.
  34. Y. Zhou, P. Yang, C. Yuan, Y. Huo, Chem. Eng. Trans., 2013, 33, 559–564.
  35. R.S. Sorbello, Mater. Res. Soc. Conference Proceedings 1996, 427, 73–81.
  36. B.R. Putra, K.J. Aoki, J. Chen, F. Marken, Langmuir, 2019, 35, 2055–2065.
  37. P. Song, A.C. Fisher, J.D. Wadhawan, J.J. Cooper, H.J. Ward, N.S. Lawrence, RSC Adv., 2016, 6, 70237–70242.
  38. H. M. Nassef, A.-E. Radi, C.K. O'Sullivan, Electrochem. Commun., 2006, 8, 1719–1725.
  39. A.J. Bard. L.R. Faulkner, Electrochemical Methods; Fundamentals and Applications, John Wiley & Sons, New York, 2nd. Ed., 2001, pp. 29.
  40. A.Molina, J. Gonzalez, E. Laborda, R.G. Compton, Phys. Chem. Chem. Phys., 2013, 15, 2381–2388.
  41. K.J Aoki, S. Taniguchi, J. Chen, Omega ACS, 2020, 5, 29447–29452.
  42. K. Aoki, Electroanalysis, 2005, 17, 1379–1383.
  43. M. Abramowitz, I.A. Stegun, Handbook of Mathematical Functions, National Bureau of Standards, 1964, pp. 11, 3.3.7.
  44. J.S. Newman, Electrochemical Systems, Prentice-Hall Inc. Englewood Cliff, N. J. Chapter 18, pp. 340–345.
Preprints 82475 g001
Figure 1. Voltammograms in 1.0 mM FcTMA + 5 mM KCl at the (A) Pt wire 0.5 mm in diameter and 1 mm long, (B) 1.6 mm disk Pt for v = (a) 0.03, (b) 0.1, (c) 0.3 and (d) 0.7 V s –1. The solid lines are connecting lines on the peaks, while the dashed lines are drawn from the solution resistance by ac-impedance.
Figure 1. Voltammograms in 1.0 mM FcTMA + 5 mM KCl at the (A) Pt wire 0.5 mm in diameter and 1 mm long, (B) 1.6 mm disk Pt for v = (a) 0.03, (b) 0.1, (c) 0.3 and (d) 0.7 V s –1. The solid lines are connecting lines on the peaks, while the dashed lines are drawn from the solution resistance by ac-impedance.
Preprints 82475 g001
Preprints 82475 g002
Figure 2. Logarithmic dependence of the solution resistance, Rs on [KCl] at Pt wires (a, c) 0.5 mm and (b, d) 0.03 mm in diameter 1 mm in length. Rs (a, b) were obtained by ac-impedance at the polarized potential, whereas (c, d) were obtained from slopes of lines connecting voltammetric peaks in Figure 1.
Figure 2. Logarithmic dependence of the solution resistance, Rs on [KCl] at Pt wires (a, c) 0.5 mm and (b, d) 0.03 mm in diameter 1 mm in length. Rs (a, b) were obtained by ac-impedance at the polarized potential, whereas (c, d) were obtained from slopes of lines connecting voltammetric peaks in Figure 1.
Preprints 82475 g002
Preprints 82475 g003
Figure 3. Variations of Ip against Ep at the 0.5 mm Pt wire electrode 1 mm long in the solution of 1.0 mM FcTMA + (a) 0.005 M and (b) 0.1 M KCl at 0.03 < v < 3 V s–1. The other plots were calculated from the Butler-Volmer typed kinetic equation for the k0 = (c) 0.01, (d) 0.005 and (e) 0.001 cm s-1 and α = 0.5.
Figure 3. Variations of Ip against Ep at the 0.5 mm Pt wire electrode 1 mm long in the solution of 1.0 mM FcTMA + (a) 0.005 M and (b) 0.1 M KCl at 0.03 < v < 3 V s–1. The other plots were calculated from the Butler-Volmer typed kinetic equation for the k0 = (c) 0.01, (d) 0.005 and (e) 0.001 cm s-1 and α = 0.5.
Preprints 82475 g003
Preprints 82475 g004
Figure 4. Illustration of generation of a dipole with Cl- just after the oxidation of the ferrocenyl molecule.
Figure 4. Illustration of generation of a dipole with Cl- just after the oxidation of the ferrocenyl molecule.
Preprints 82475 g004
Preprints 82475 g005
Figure 5. Voltammograms computed from Equation (5) for ρ = (a) 0, (b) 2, (c) 4, (d) 6, (e) 8 and (f) 10.
Figure 5. Voltammograms computed from Equation (5) for ρ = (a) 0, (b) 2, (c) 4, (d) 6, (e) 8 and (f) 10.
Preprints 82475 g005
Preprints 82475 g006
Figure 6. Variations of the peak potential by (a) the IR-drop with the resistance parameter, (b) the intuitive IR-drop by Ip0Rs, (c) the tangent line of (a) at ρ = 0, (d) the negative capacitance with (Crx/c*)(v/RTFD)1/2, and (e) experimental variations of Ep with ρ where Rs = 2.7 kΩ in 1mM FcTMA + 5 mM KCl at the 0.5 mm wire electrode.
Figure 6. Variations of the peak potential by (a) the IR-drop with the resistance parameter, (b) the intuitive IR-drop by Ip0Rs, (c) the tangent line of (a) at ρ = 0, (d) the negative capacitance with (Crx/c*)(v/RTFD)1/2, and (e) experimental variations of Ep with ρ where Rs = 2.7 kΩ in 1mM FcTMA + 5 mM KCl at the 0.5 mm wire electrode.
Preprints 82475 g006
Preprints 82475 g007
Figure 7. Variations of (a) the peak current (b) the ratio of effective scan rate and (c) the experimental peak current with the dimensionless resistance ρ at (circles) Rs=2.7 kΩ and (triangles) Rs= 80 Ω.
Figure 7. Variations of (a) the peak current (b) the ratio of effective scan rate and (c) the experimental peak current with the dimensionless resistance ρ at (circles) Rs=2.7 kΩ and (triangles) Rs= 80 Ω.
Preprints 82475 g007
Preprints 82475 g008
Figure 8. Variations of the fraction of the IR-drop, XIR (= (Ip0 – Ip)/Ip0), with that of the negative capacitance, XNC, for A = (a) 0.01, (b) 0.04, (c) 0.09 and (d) 0.16 mm2 at v = 0.1 V s–1, κ = 0.133 S m–1 corresponding to [KCl] = 10 mM, and Crx = 50 μF cm–2.
Figure 8. Variations of the fraction of the IR-drop, XIR (= (Ip0 – Ip)/Ip0), with that of the negative capacitance, XNC, for A = (a) 0.01, (b) 0.04, (c) 0.09 and (d) 0.16 mm2 at v = 0.1 V s–1, κ = 0.133 S m–1 corresponding to [KCl] = 10 mM, and Crx = 50 μF cm–2.
Preprints 82475 g008
Preprints 82475 g009
Figure 9. Logarithmic variation of Ip0-Ip with v in the solution of (a) 1 mM FcTMA + 0.005 M KCl at the 0.5 mm wire electrode (b) 1 mM FcTMA + 0.1 M KCl at the 0.03 mm wire electrode.
Figure 9. Logarithmic variation of Ip0-Ip with v in the solution of (a) 1 mM FcTMA + 0.005 M KCl at the 0.5 mm wire electrode (b) 1 mM FcTMA + 0.1 M KCl at the 0.03 mm wire electrode.
Preprints 82475 g009
Table 1. Advantages and risks for three classes for the levels
Table 1. Advantages and risks for three classes for the levels
Range of v Advantages Risks
(I)
< 0.2 V s-1 		Small background currents
Easy extraction of diffusion currents
Usage of low-cost potentiostats
Possibility of theoretical analysis		 Misleading kinetic reaction mechanisms
Time consumption
(II)
< 5 V s-1 		Possibility of subtraction of IR-drop
Possibility of determining reaction mechanisms
Evaluation of heterogeneous kinetics
Comparison of the results with those by other rapid electrochemical methods
Commercially available potentiostats		 Discussion required for peak shifts
Deformation of waveform
Limitation to microelectrodes in order to prevent large currents
(III)
< 500 V s-1 		Detection of kinetics with milli-second orders such as neurotransmitters Empirical search for detecting conditions
A loss of theoretical support
Table 2. Variations of Ep and Ip0- Ip with four variables.
Table 2. Variations of Ep and Ip0- Ip with four variables.
variables Ep Ip0- Ip
IR NC IR NC
c* c* 1 c*3/2 c*
A(disk) A1/2 1 A5/4 A
v v1/2 v1/2 v3/4 v
Rs Rs 1 Rs1/2 1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated