Prerpints.org logo
Preprint
Communication

Anomalous Interactions of Airy Solitons Modulated by Fundamental Gaussian Beam and Fourth-Order Diffraction

Altmetrics

Downloads

79

Views

33

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

16 August 2023

Posted:

16 August 2023

You are already at the latest version

Alerts
Abstract
We investigate numerically the interactions of in-phase Airy beams modulated by a fundamental Gaussian beam and fourth-order diffraction in Kerr nonlinear media. Directly numerical simulations show that normal (anomalous) fourth-order diffractions and in-phase (out-of-phase) Gaussian beam affect the interactions of solitons generated from Airy beams in unique manners. Different from previous results that interactions between in-phase (out-of-phase) conventional beams are always attractive (repulsive), many anomalous interactions of Airy beams are obtained. Stable bound states of breathing Airy soliton pairs can be formed with the help of fourth-order diffraction and fundamental Gaussian beam.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction

During the past decades, investigation of Airy beams [1,2,3,4,5,6,7,8,9] have been one of the hot topics in the area of optics due to their novel propagation properties, e.g., ballistic motion [10,11], self-healing [12], etc. In linear regime, mechanisms of Airy beams are widely used in particle clearing [13], light bullets [14], surface plasmons [15,16,17], and electron beams [18,19]. On the contrary, nonlinear manipulation of Airy beams is another novel problem, including nonlinear generation of Airy beams [20,21], propagation of Airy beams in nonlinear media [22,23,24,25,26,27,28,29], solitons generated form Airy beams [30] and spatiotemporal Airy light bullets [31,32,33].
In nonlinear media, interactions between Airy beams have also been extensively studied in recent years. In particular, interactions of Airy beams were studied in photorefractive crystal [34,35,36,37,38,39], Kerr media [40,41,42], optical fiber [43,44,45], quadratic nonlinear medium [46], fractional media [47,48], photonic lattices [49], as well as nonlocal nonlinear media [50,51,52,53]. Compared with interactions of conventional beams [54], many anomalous interactions of Airy beams have been reported [51,52,53].
In nonlinear media, besides nonlinear self-focusing effect, linear diffraction is another effect induced by optical beams themselves during propagation [55]. Apart from quadratic diffraction, high-order diffraction should not be neglected [56]. In particular, fourth-order diffraction has deep impacts on nonlinear optics, e.g., self-similar propagation of optical pulses [57], modulation instability [58], pure-quartic soliton laser [59], and soliton states [60,61,62,63,64,65], etc.
The effects of third-order [66,67] and fourth-order [68,69,70] diffraction/dispersion on the propagation of Airy pulses/beams have been investigated in detail. In our previous work, we have also studied interactions of Airy beams in local Kerr, saturable, and nonlocal media with fourth-order diffraction [71]. We demonstrated that stable bound states of Airy solitons pairs can be obtained in nonlocal medium with fourth-order diffraction which are always repulsive in local media [71].
In this paper, based on our previous works [52,71], we demonstrate that the interactions of solitons generated from two in-phase Airy beams in Kerr nonlinear media can be controlled by a fundamental Gaussian beam and fourth-order diffraction. Numerical results with split-step Fourier transform method reveal the interactions of Airy beam are sensitive to the beam intervals, coupling constant of fourth-order diffraction as well as the relative phase and amplitude of the fundamental Gaussian beam. In particular, many anomalous interactions are obtained and physical mechanisms are explained in detail. Stable bound states of breathing Airy soliton pairs can be formed with appropriate beam parameters and coupling constants of fourth-order diffraction.

2. Physical model and basic equations

Considering the propagation of an optical beams in nonlinear media with fourth-order diffraction, the slowly varying envelope of the beam ψ ( x , z ) is described by the following normalized nonlinear Schrödinger equation[61,62],
i ∂ ψ ∂ z + 1 2 ∂ 2 ψ ∂ x 2 − β ∂ 4 ψ ∂ x 4 + δ n ( I ) ψ = 0 ,
here x and z denote transverse and longitude spatial coordinates [40,41], and β represents the strength of fourth-order diffraction [61,62,63], respectively. When β > 0 , the fourth-order diffraction is normal, whereas, it is anomalous when β < 0 [61,62,63]. The nonlinear refractive index change of the Kerr media δ n ( I ) can be written as
δ n ( I ) = | ψ | 2 .
In this work, we concentrate on the manipulation of interactions of Airy beams with the help of a fundamental Gaussian beam and fourth-order diffraction. Thus we assume the incident beam is composed of two in-phase shifted counter propagating Airy beams, but with an additional fundamental Gaussian beam located in the middle with a relative phase between them [52],
ψ ( x ) = A { A i [ ( x − B ) ] exp [ a ( x − B ) ] + A i [ − ( x + B ) ] exp [ − a ( x + B ) ] } + exp ( i ρ π ) C exp ( − x 2 / 2 ) ,
where A represents the amplitude of the Airy beams and we set A = 3 to ensure solitons can be generated from Airy beams, B is the parameter controlling the beam separations (intervals), C denotes the amplitude of the fundamental Gaussian beam [52], and a = 0.2 is the decaying factor of the Airy beams [1], respectively. ρ is the parameter controlling the phase shift, in particular, ρ = 0 ( ρ = 1 ) describes Airy beams and fundamental Gaussian beam are in-phase (out of phase) [52].
The interactions of the beams can be investigated numerically by integrating Eq. (1) directly with split-step Fourier transform method. In the following, with fourth-order diffraction, we will demonstrated the interactions of Airy beams modulated by in-phase and out-of-phase fundamental Gaussian beams, respectively.

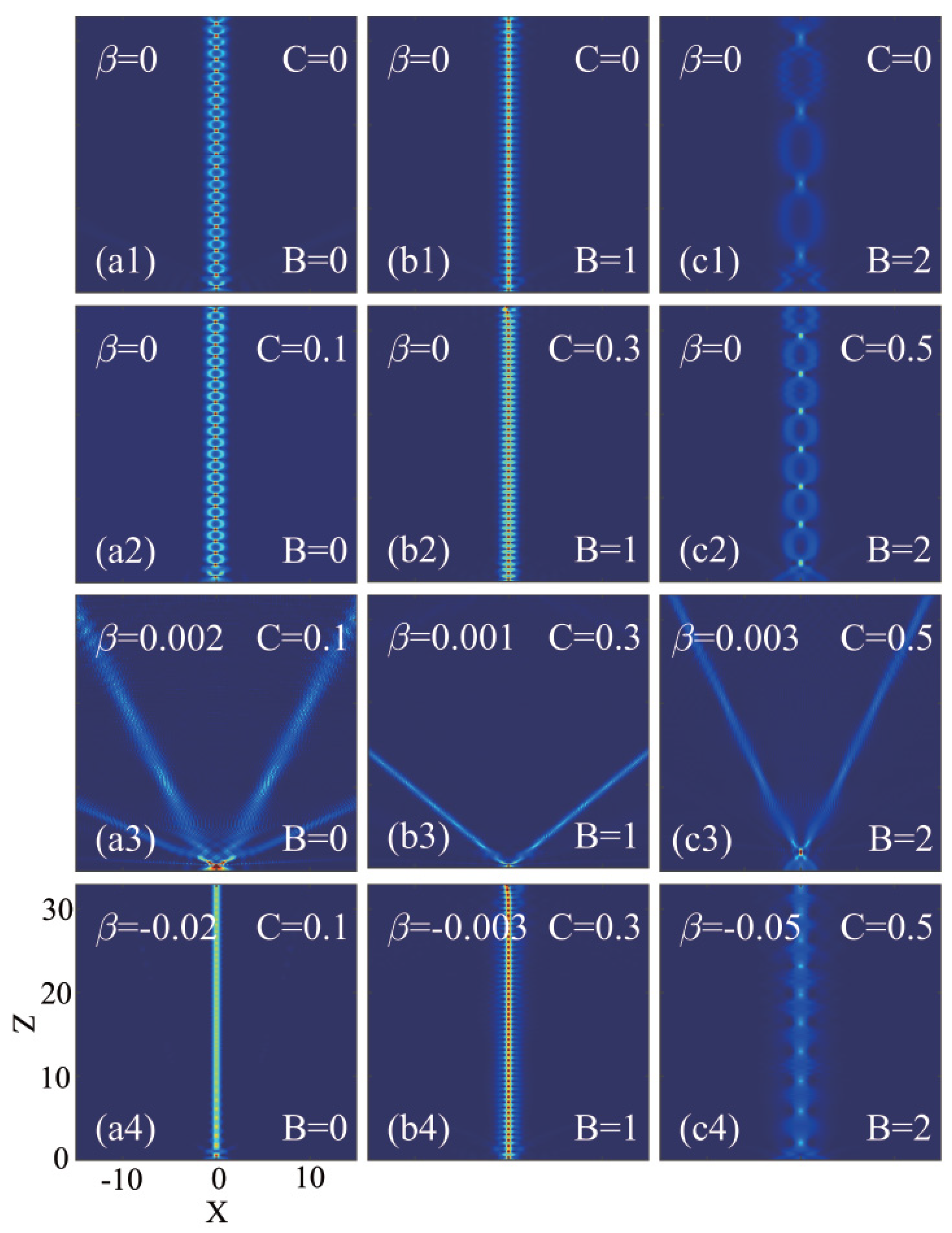
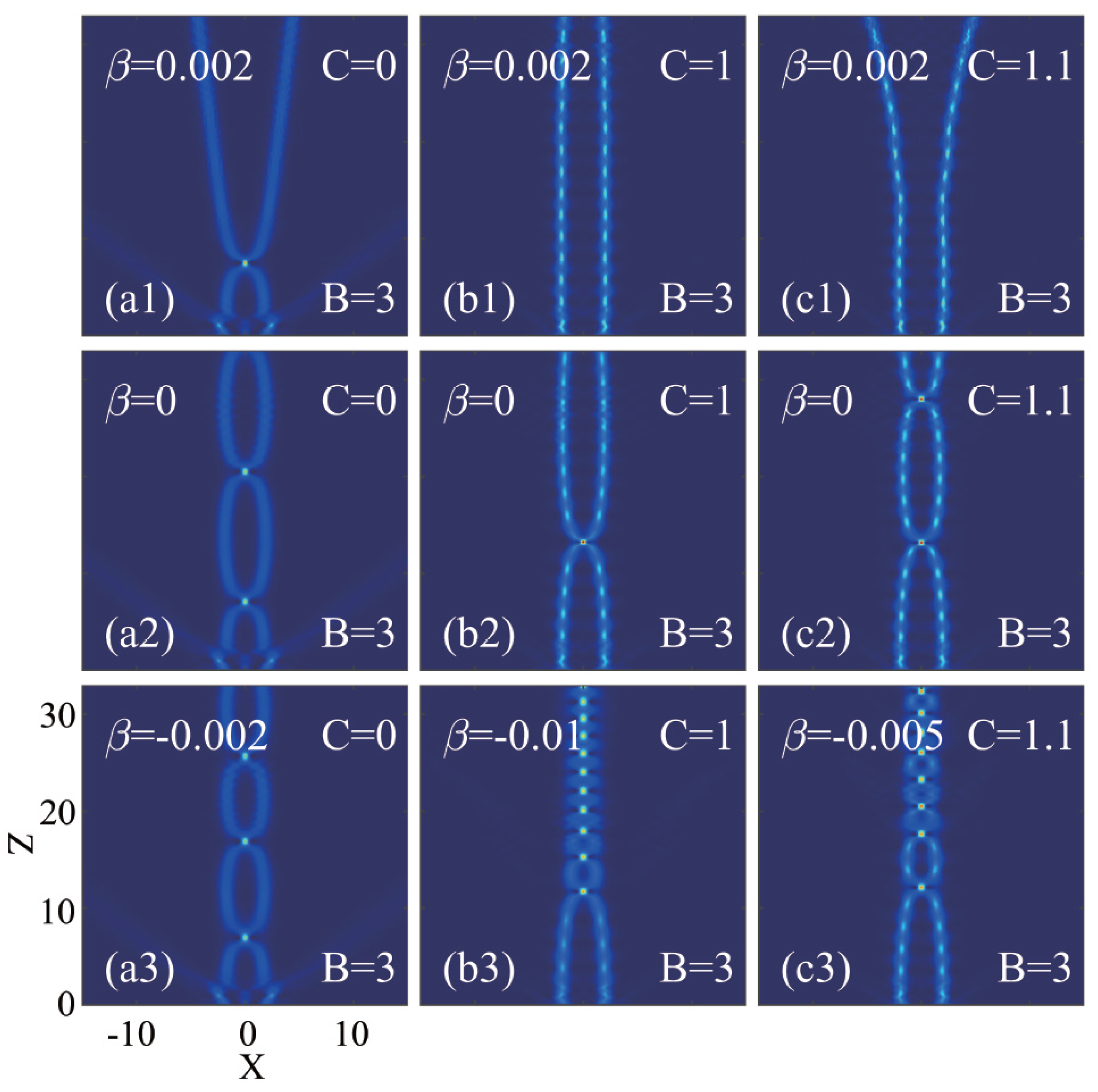
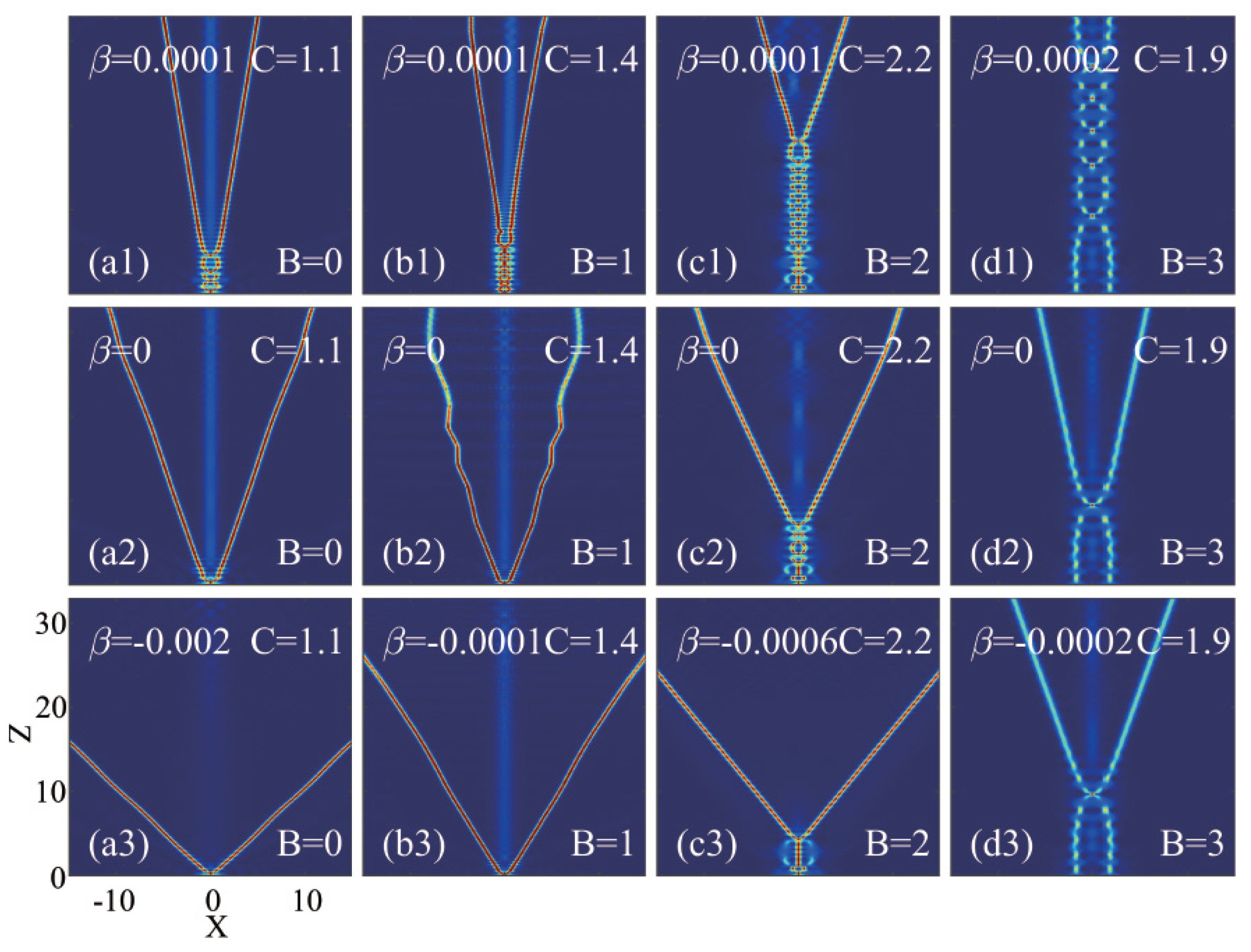
3. Interactions of Airy beams with in-phase Gaussian beam and fourth-order diffraction

Firstly, we consider the interactions of Airy beams and in-phase ( ρ = 0 ) Gaussian beam with fourth-order diffraction. In Figure 1, we display the numerical results of the interactions with some different beam intervals B = 0 , 1 , 2 and fourth-order diffraction coupling constants β in the case of weak Gaussian beam ( C < < A ). Previous work has shown that dynamics of interactions depend crucially on the amplitude of the Gaussian beam [52].
For comparison, we also re-do some previous results. When β = 0 and C = 0 , it represents the interactions of two in-phase Airy beams in Kerr media with only quadratic diffraction [40,41,51,52,71] and attractions between beams are always dominant. It is obvious that bound states of breathing soliton pairs with different breathing periods are obtained [Figure 1(a1-c1)]. The strongest attraction occurs at B = 1 [Figure 1(b1)] due to strong self-trapping effect [40,41,51,52]. With a in-phase ( ρ = 0 ) weak fundamental Gaussian beam ( C < < A ), the attraction between Airy beams are enhanced and the corresponding breathing periods are reduced significantly [Figure 1(a2-c2)]. The physical mechanisms for above results have been explained extensively in previous works [52].
The dynamics of bound states can be modulated by fourth-order diffraction. In particular, without fundamental Gaussian beam (C=0), the interactions between both in-phase and out-of-phase Airy beams under fourth-order diffraction have been studied previously [71]. Thus in this paper we focus on the condition of C ≠ 0 when fourth-order diffraction is taken into account ( β ≠ 0 ). For normal fourth-order diffraction ( β > 0 ), with an in-phase Gaussian beam, as shown in Figure 1(a3-c3), the interactions of Airy beams exhibit repulsions for all beam intervals due to the fact that the diffraction effect of the beams is enhanced. The nonlinearity is unable to overcome the strong diffraction induced by normal fourth-order diffraction, and therefore no stable bound state can be formed [71]. On the other hand, when fourth-order diffraction is anomalous ( β < 0 ), situations become different. Comparing with case without fourth-order diffraction β = 0 [Figure 1(a2-c2)], the attractions between Airy beams are significantly strengthened with breathing periods of all the bound states become smaller [Figure 1(a4-c4)]. The reason is that the diffraction effect of the beams is weakened with anomalous fourth-order diffraction, so nonlinearity will reinforce the interactions between Airy beams [71].
In general, the beam interval B is an important parameter in controlling the interactions of Airy beams. When B is larger, e.g., B = 4 , only two parallel solitons can be generated from two well-separated Airy beams [40,41]. Apart from the results obtained above, anomalous interactions happen when B = 3 . As illustrated in Figure 1, an in-phase fundamental Gaussian beam always enhances the attractions of two in-phase Airy beams when B = 0 , 1 , 2 . When increasing the amplitude C gradually, attraction between the Airy beams with B = 3 decreases firstly and subsequently increases [52], as shown in Figure 2(a2-c2). This interesting phenomena can be explained as follow: the nonlinearity induced by the intensity of the incident beam [Eq. (3)] decreases firstly and then increases subsequently, leading to the weakness and then enhancement of the attractions [52]. Similar with Figure 1, normal ( β > 0 ) and anomalous ( β < 0 ) fourth-order diffraction will weaken and strengthen the attractions of the Airy beams, result in the repulsions [Figure 2(a1-c1)] and bound states [Figure 2(a3-c3)] with smaller breathing periods, respectively.
When the Gaussian beam is strong light, the amplitude of the fundamental Gaussian beam C is large enough. Similarly, we show in Figure 3 interactions of airy beams with different beam intervals B = 0 , 1 , 2 , 3 and fourth-order diffraction coupling constants β . When β = 0 , a single solitons generated from fundamental Gaussian beam is located in the cental of two solitons shedding from Airy beams [Figure 3(a2-d2)]. Different from the case of enhancement of the attractions with in-phase weak light Gaussian beam [Figure 1(a2-c2)], repulsions appear for all beam intervals [Figure 3(a2-d2)]. For smaller beam intervals B = 0 [Figure 3(a2)] and B = 1 [Figure 3(b2)], repulsions appear after a very short propagation distance. Although bound states are formed initially, for larger beam intervals B = 2 [Figure 3(c2)] and B = 3 [Figure 3(d2)], repulsions overcome attractions eventually [41,52].
Surprisingly, fourth-order diffraction plays an unique role in the interactions of Airy beam with an in-phase strong light Gaussian beam. As shown in Figure 3, repulsions are weakened for β > 0 [Figure 3(a1-d1)] and strengthened for β < 0 [Figure 3(a3-d3)]. This interesting result is quite different with the case of weak light Gaussian beam [Figure 1 and 2], where normal (anomalous) fourth-order diffraction always strengthen (weaken) the repulsions. The anomalous phenomena is very similar with the interactions of two in-phase Airy beams in saturable nonlinear media with fourth-order diffraction [71].

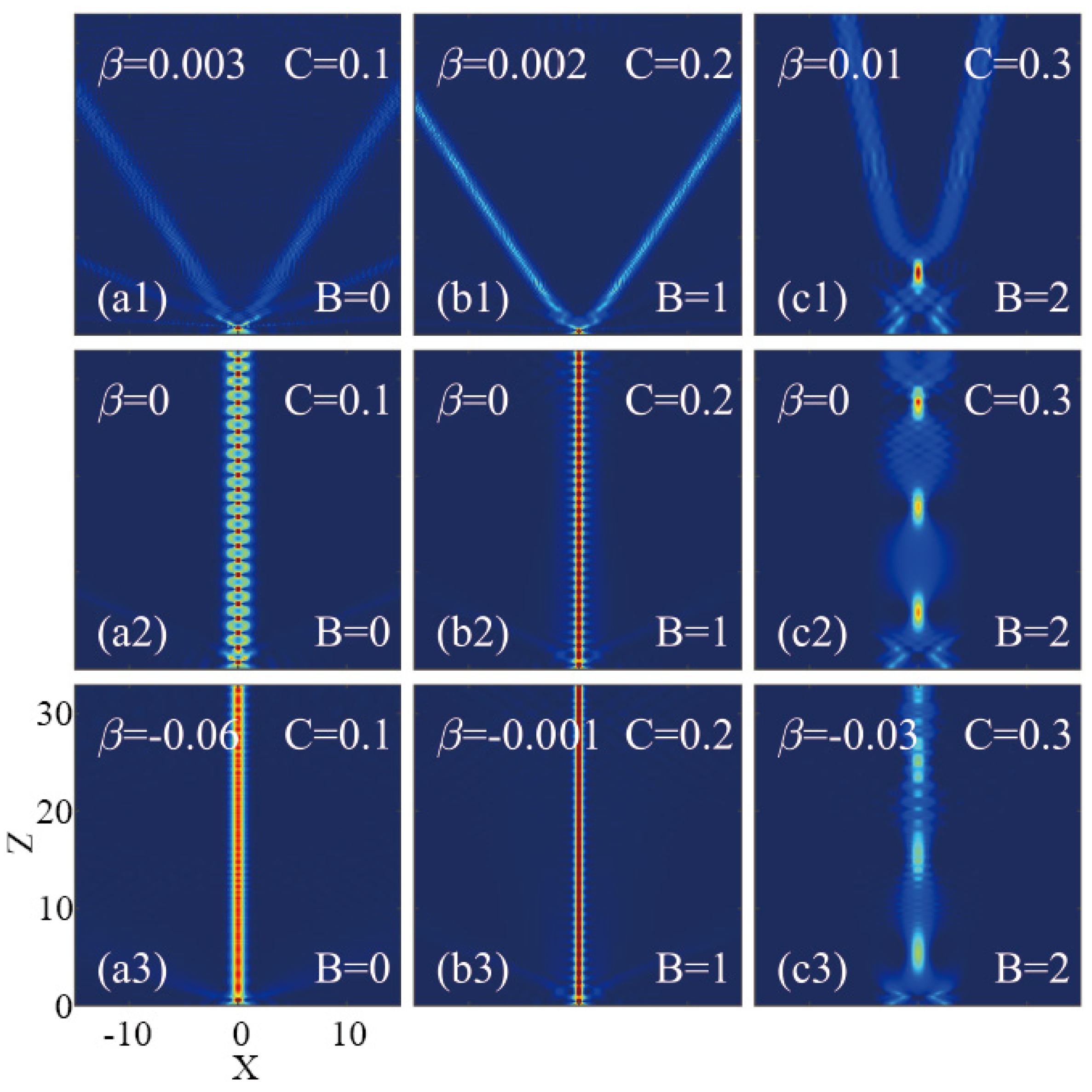
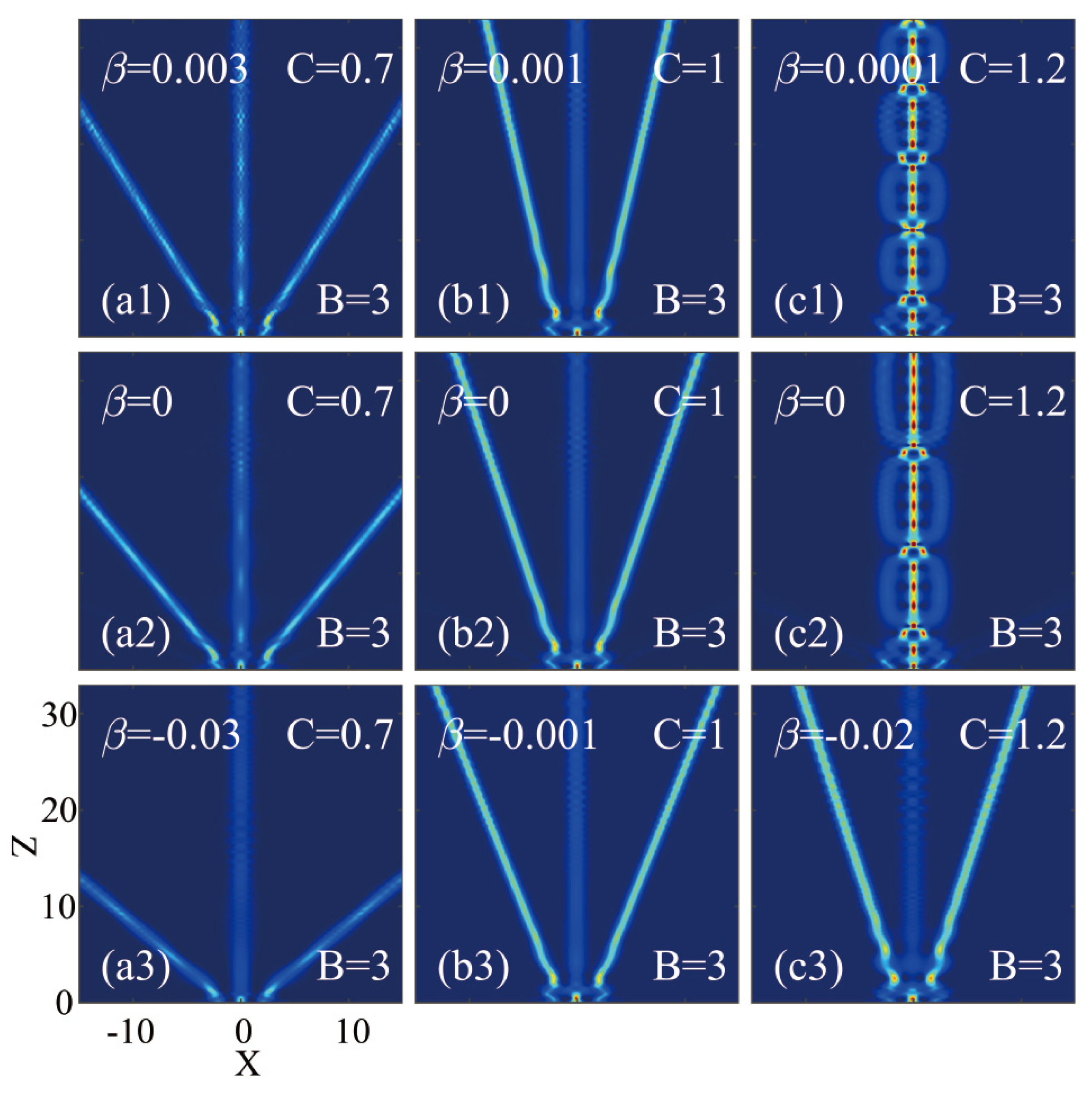
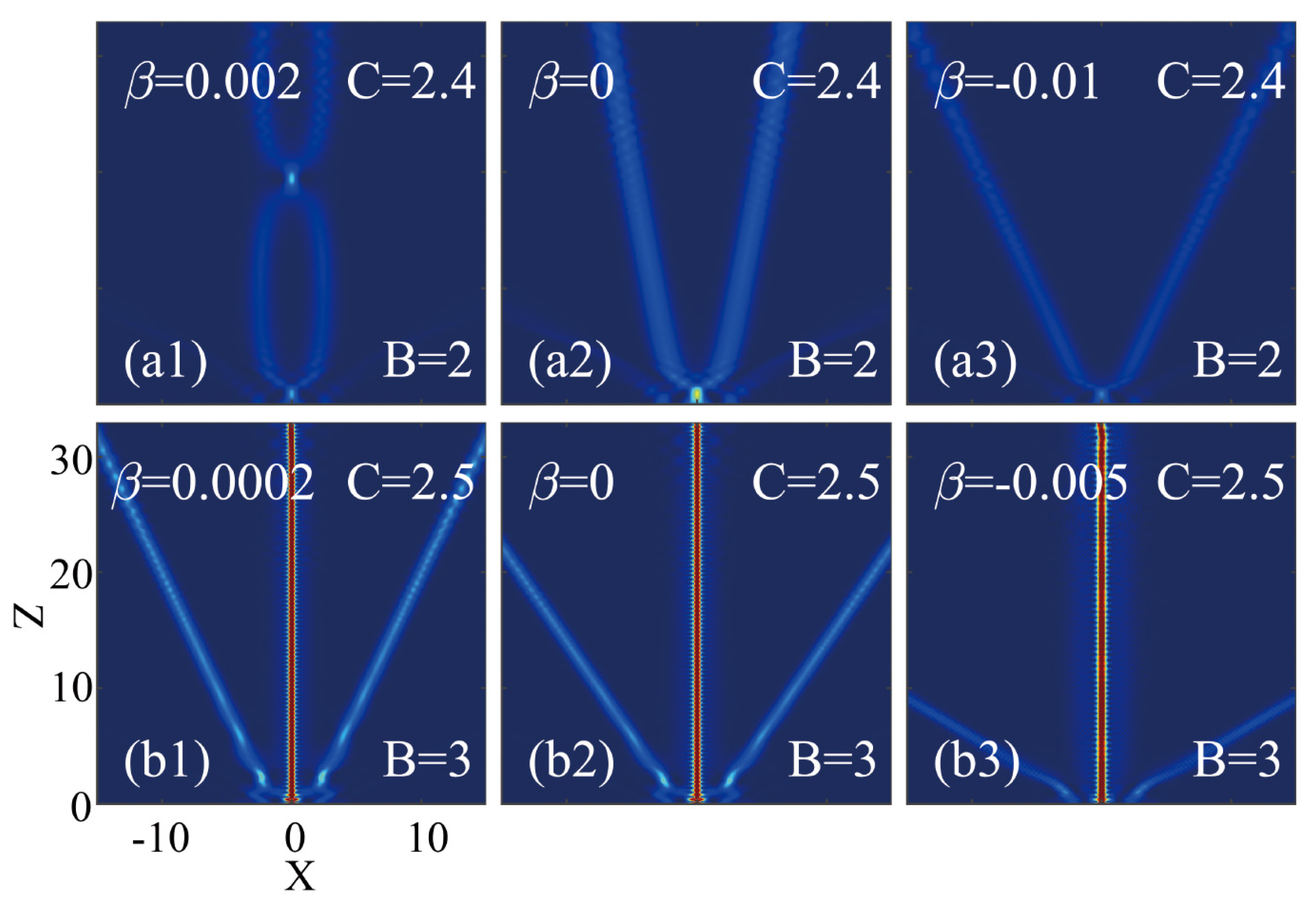
4. Interactions of Airy beams with out-of-phase Gaussian beam and fourth-order diffraction

Next, we study the interactions of Airy beams and out-of-phase ( ρ = 1 ) fundamental Gaussian beam in nonlinear Kerr media with fourth-order diffraction. Comparing Figure 1(a1-c1), when beam intervals are smaller ( B = 0 , 1 , 2 ) and without fourth-order diffraction ( β = 0 ), weak light out-of-phase fundamental Gaussian beam weakens the attractions of Airy beams with breathing periods increase obviously [52], as shown in Figure 4(a2-c2). This is the general case that out-of-phase Gaussian beam provides a repulsive force between Airy beams [52].
Similar with results of Figure 1 and 3, dynamics of interactions of Airy beams are shown in Figure 4(a1-c1) and 4(a3-c3) when normal and anomalous fourth-order diffraction is used, respectively. Specifically, with normal fourth-order diffraction ( β > 0 ), attractions become weaker and repulsions appear for all the beam intervals. On the contrary, attractions become stronger and breathing periods of the bound states decrease for anomalous fourth-order diffraction ( β < 0 ).
In the case of the beam interval B = 3 , without fourth-order diffraction ( β = 0 ) and fundamental Gaussian beam ( C = 0 ), stationary bound state of two in-phase Airy beams is formed [Figure 2(a2)]. When an out-of-phase Gaussian beam with amplitude C = 0.7 is added, repulsion appears between the two Airy beams and one fundamental solitons generated from Gaussian beam is located in the center, as shown in Figure 5(a2). However, repulsion will be weakened [Figure 5(b2)] when the amplitude of Gaussian beam C increases, and bound state of breathing mode can be even formed [Figure 5(c2)] with appropriate intensity of Gaussian beam. We emphasize that the anomalous interaction demonstrated in Figure 5(c2) is different from conventional interactions between out-of-phase beams, where repulsions are always dominant [54].
Similar with the interactions of Airy beam with an in-phase strong light Gaussian beam shown in Figure 3 or interactions of two in-phase Airy beams in saturable nonlinear media [71], fourth-order diffraction plays the same role in the interactions between Airy beam and out-of-phase weak light Gaussian beam when the beam interval is B = 3 . As shown in Figure 5(a1-b1), repulsions are also weakened (or attractions are enhanced) and breathing period decreases for C = 1.2 [Figure 5(c1)] when fourth-order diffraction is normal. On the other hand, repulsions are enhanced for all the interactions with anomalous fourth-order diffraction [Figure 5(a3-c3)].
In the case of out-of-phase strong light Gaussian beam, for beam intervals B = 0 and B = 1 , similar with Figure 4(a2-b2), we numerically check that the breathing periods of the bound states become larger (not shown). When B = 2 , as shown in Figure 6(a2), repulsion appears instead of attraction [Figure 4(c2)] when C = 2.4 . Similar result happens to the case of B = 3 , repulsion emerges again [Figure 6(b2)] despite of bound state can be formed with appropriate out-of-phase fundamental Gaussian beam [Figure 5(c2)].
Similar with Figure 3 and 5, anomalous fourth-order diffraction ( β < 0 ) strengthens the repulsions of the interactions, as shown in Figure 6(a3) and 6(b3). However, normal fourth-order diffraction ( β > 0 ) weakens the repulsions for B = 3 [Figure 6(b1)], and stationary bound state can even be formed for B = 2 [Figure 6(a1)]. These impacts of fourth-order diffraction are different with outcomes obtained in Figure 1, 2 and 4.

5. Conclusions

In conclusion, interactions of in-phase Airy beams modulated by a fundamental Gaussian beam and fourth-order diffraction in Kerr nonlinear media were investigated numerically with split-step Fourier transform method. Attractions and repulsions between the Airy beams with different beam intervals can be controlled flexibly by normal (anomalous) fourth-order diffractions and in-phase (out-of-phase) Gaussian beam. We demonstrated properties of both normal and anomalous interactions of Airy beams in detail. For the sake of the formation of stable bound states of breathing Airy soliton pairs, the parameters of fourth-order diffraction and fundamental Gaussian beam should be adjusted properly. Our results may have potential applications in the areas of all optical interconnect, optical switch and guided wave optics.

Author Contributions

Conceptualization, L.G. and M.S.; Software, W.Z.; All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (No. 61975109).

Data Availability Statement

Not applicable.

Conflicts of Interest

The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979–981. [Google Scholar] [CrossRef] [PubMed]
  2. Siviloglou, G. A.; Broky, J.; Dogariu, A.; Christodoulides, D. N. Observation of accelerating Airy beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
  3. Bandres, M. A. Accelerating beams. Opt. Lett. 2009, 34, 3791–3793. [Google Scholar] [CrossRef] [PubMed]
  4. Efremidis, N. K.; Christodoulides, D. N. Abruptly autofocusing waves. Opt. Lett. 2010, 35, 4045–4047. [Google Scholar] [CrossRef] [PubMed]
  5. Greenfield, E.; Segev, M.; Walasik, W.; Raz, O. Accelerating light beams along arbitrary convex trajectories. Phys. Rev. Lett. 2011, 106, 213902. [Google Scholar] [CrossRef] [PubMed]
  6. Kaminer, I.; Bekenstein, R.; Nemirovsky, J.; Segev, M. Nondiffracting accelerating wave packets of Maxwell’s equations. Phys. Rev. Lett. 2012, 108, 163901. [Google Scholar] [CrossRef] [PubMed]
  7. Aleahmad, P.; Miri, M. A.; Mills, M. S.; Kaminer, I.; Segev, M.; Christodoulides, D. N. Fully vectorial accelerating diffraction-free Helmholtz beams. Phys. Rev. Lett. 2012, 109, 203902. [Google Scholar] [CrossRef]
  8. Zhang, P.; Hu, Y.; Li, T.; Cannan, D.; Yin, X.; Morandotti, R.; Chen, Z.; Zhang, X. Nonparaxial Mathieu and Weber accelerating beams. Phys. Rev. Lett. 2012, 109, 193901. [Google Scholar] [CrossRef]
  9. Efremidis, N.K.; Chen, Z.; Segev, M.; Christodoulides, D.N. Airy beams and accelerating waves: an overview of recent advances. Optica 2019, 6, 686–701. [Google Scholar] [CrossRef]
  10. Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D. N. Ballistic dynamics of Airy beams. Opt. Lett. 2008, 33, 207–209. [Google Scholar] [CrossRef]
  11. Hu, Y.; Zhang, P.; Lou, C.; Huang, S.; Xu, J.; Chen, Z. Optimal control of the ballistic motion of Airy beams. Opt. Lett. 2010, 35, 2260–2262. [Google Scholar] [CrossRef] [PubMed]
  12. Broky, J.; Siviloglou, G.A.; Dogariu, A.; Christodoulides, D.N. Self-healing properties of optical Airy beams. Opt. Express 2008, 16, 12880–12891. [Google Scholar] [CrossRef] [PubMed]
  13. Baumgartl, J.; Mazilu, M.; Dholakia, K. Optically mediated particle clearing using Airy wavepackets. Nat. Photon. 2008, 2, 675–678. [Google Scholar] [CrossRef]
  14. Chong, A.; Renninger, W.H.; Christodoulides, D. N.; Wise, F. W. Airy–Bessel wave packets as versatile linear light bullets. Nat. Photon. 2010, 4, 103–106. [Google Scholar] [CrossRef]
  15. Polynkin, P.; Kolesik, M.; Moloney, J.V.; Siviloglou, G. A.; Christodoulides, D. N. Curved plasma channel generation using ultraintense Airy beams. Science 2009, 324, 229–232. [Google Scholar] [CrossRef]
  16. Minovich, A.; Klein, A.E.; Janunts, N.; Pertsch, T.; Neshev, D. N.; Kivshar, Y.S. Generation and near-field imaging of Airy surface plasmons. Phys. Rev. Lett. 2011, 107, 116802. [Google Scholar] [CrossRef] [PubMed]
  17. Dolev, I.; Epstein, I.; Arie, A. Surface-plasmon holographic beam shaping. Phys. Rev. Lett. 2012, 109, 203903. [Google Scholar] [CrossRef] [PubMed]
  18. Shiloh, R.; Tsur, Y.; Remez, R.; Lereah, Y.; Malomed, B. A.; Shvedov, V.; Hnatovsky, C.; Krolikowski, W.; Arie, A. Unveiling the orbital angular momentum and acceleration of electron beams. Phys. Rev. Lett. 2015, 114, 096102. [Google Scholar] [CrossRef]
  19. Voloch-Bloch, N.; Lereah, Y.; Lilach, Y.; Gover, A.; Arie, A. Generation of electron Airy beams. Nature 2013, 494, 331–335. [Google Scholar] [CrossRef]
  20. Ellenbogen, T.; Voloch-Bloch, N.; Ganany-Padowicz, A.; Arie, A. Nonlinear generation and manipulation of Airy beams. Nat. Photon. 2009, 3, 395–398. [Google Scholar] [CrossRef]
  21. Zhang, P.; Hu, Y.; Cannan, D.; Salandrino, A.; Li, T.; Morandotti, R.; Zhang, P.; Chen, Z. Generation of linear and nonlinear nonparaxial accelerating beams. Opt. Lett. 2012, 37, 2820–2822. [Google Scholar] [CrossRef] [PubMed]
  22. Jia, S.; Lee, J.; Fleischer, J. W.; Siviloglou, G. A.; Christodoulides, D. N. Diffusion-trapped Airy beams in photorefractive media. Phys. Rev. Lett. 2010, 104, 253904. [Google Scholar] [CrossRef] [PubMed]
  23. Hu, Y.; Huang, S.; Zhang, P.; Lou, C.; Xu, J.; Chen, Z. Persistence and breakdown of Airy beams driven by an initial nonlinearity. Opt. Lett. 2010, 35, 3952–3954. [Google Scholar] [CrossRef] [PubMed]
  24. Chen, R.; Yin, C.; Chu, X.; Wang, H. Effect of Kerr nonlinearity on an Airy beam. Phys. Rev. A 2010, 82, 043832. [Google Scholar] [CrossRef]
  25. Kaminer, I.; Segev, M.; Christodoulides, D. N. Self-accelerating self-trapped optical beams. Phys. Rev. Lett. 2011, 106, 213903. [Google Scholar] [CrossRef]
  26. Lotti, A.; Faccio, D.; Couairon, A.; Papazoglou, D. G.; Panagiotopoulos, P.; Abdollahpour, D.; Tzortzakis, S. Stationary nonlinear Airy beams. Phys. Rev. A 2011, 84, 021807. [Google Scholar] [CrossRef]
  27. Dolev, I.; Kaminer, I.; Shapira, A.; Segev, M.; Arie, A. Experimental observation of self-accelerating beams in quadratic nonlinear media. Phys. Rev. Lett. 2012, 108, 113903. [Google Scholar] [CrossRef]
  28. Chen, R.P.; Chew, K. H.; He, S. Dynamic control of collapse in a vortex Airy beam. Scientific Reports 2013, 3, 1406. [Google Scholar] [CrossRef]
  29. Driben, R.; Meier, T. Nonlinear dynamics of Airy-vortex 3D wave packets: emission of vortex light waves. Opt. Lett. 2014, 39, 5539–5542. [Google Scholar] [CrossRef]
  30. Allayarov, I. M.; Tsoy, E. N. Dynamics of Airy beams in nonlinear media. Phys.Rev. A 2014, 90, 023852. [Google Scholar] [CrossRef]
  31. Fattal, Y.; Rudnick, A.; Marom, D. M. Soliton shedding from Airy pulses in Kerr media. Opt. Express 2011, 19, 17298–17307. [Google Scholar] [CrossRef] [PubMed]
  32. Abdollahpour, D.; Suntsov, S.; Papazoglou, D. G.; Tzortzakis, S. Spatiotemporal airy light bullets in the linear and nonlinear regimes. Phys. Rev. Lett. 2010, 105, 253901. [Google Scholar] [CrossRef] [PubMed]
  33. Panagiotopoulos, P.; Papazoglou, D.G.; Couairon, A.; Tzortzakis, S. Sharply autofocused ring-Airy beams transforming into non-linear intense light bullets. Nature Communications 2013, 4, 2622. [Google Scholar] [CrossRef] [PubMed]
  34. Zhang, M.; Huo, G.; Zhong, H.; Hui, Z. Interactions between self-accelerating beams in photorefractive media. Opt. Express 2017, 25, 22104–22112. [Google Scholar] [CrossRef] [PubMed]
  35. Zhang, M.Z.; Zhang, T. Y.; Huo, G. W.; Hui, Z.Q.; Duan, Z. L.; Zha, X. W. Temporal analysis of Airy beam propagation in photorefractive media. Commun. Nonlinear Sci. Numer. Simulat. 2019, 76, 45–50. [Google Scholar] [CrossRef]
  36. Wiersma, N.; Marsal, N.; Sciamanna, M.; Wolfersberger, D. All-optical interconnects using Airy beams. Opt. Lett. 2014, 39, 5997–6000. [Google Scholar] [CrossRef]
  37. Wiersma, N.; Marsal, N.; Sciamanna, M.; Wolfersberger, D. Spatiotemporal dynamics of counterpropagating Airy beams. Scientific Reports 2015, 5, 13463. [Google Scholar] [CrossRef]
  38. Marsal, N.; Wiersma, N.; Sciamanna, M.; Wolfersberger, D. Counterpropagating interactions of self-focusing Airy beams. Scientific Reports 2019, 9, 5004. [Google Scholar] [CrossRef]
  39. Diebel, F.; Bokić, B. M.; Timotijević, D. V.; Jović Savić, D. M.; Denz, C. Soliton formation by decelerating interacting Airy beams. Opt. Express 2015, 23, 24351–24361. [Google Scholar] [CrossRef]
  40. Zhang, Y.; Belic, M.; Wu, Z.; Zheng, H.; Lu, K.; Li, Y.; Zhang, Y. Soliton pair generation in the interactions of Airy and nonlinear accelerating beams. Opt. Lett. 2013, 38, 4585–4588. [Google Scholar] [CrossRef]
  41. Zhang, Y.; Belić, M. R.; Zheng, H.; Chen, H.; Li, C.; Li, Y.; Zhang, Y. Interactions of Airy beams, nonlinear accelerating beams, and induced solitons in Kerr and saturable nonlinear media. Opt. Express 2014, 22, 7160–7171. [Google Scholar] [CrossRef] [PubMed]
  42. Driben, R.; Konotop, V. V.; Meier, T. Coupled Airy breathers. Opt. Lett. 2014, 39, 5523–5526. [Google Scholar] [CrossRef] [PubMed]
  43. Rudnick, A.; Marom, D. M. Airy-soliton interactions in Kerr media. Opt. Express 2011, 19, 25570–25582. [Google Scholar] [CrossRef]
  44. Zhang, X.; Pierangeli, D.; Conti, C.; Fan, D.; Zhang, L. Control of soliton self-frequency shift dynamics via Airy soliton interaction. Opt. Express 2018, 26, 32971–32980. [Google Scholar] [CrossRef] [PubMed]
  45. Zhang, X.; Chen, L.; Cheng, K.; Yao, N.; Sheng, J. Generation of single or double parallel breathing soliton pairs, bound breathing solitons, moving breathing solitons, and diverse composite breathing solitons in optical fibers. Opt. Express 2018, 26, 15683–15692. [Google Scholar] [CrossRef]
  46. Mayteevarunyoo, T.; Malomed, B. A. The interaction of Airy waves and solitons in a three-wave system. J. Opt. 2017, 19, 085501.
  47. Zhang, L.; Zhang, X.; Wu, H.; Li, C.; Pierangeli, D.; Gao, Y.; Fan, D. Anomalous interaction of Airy beams in the fractional nonlinear Schrödinger equation. Opt. Express 2019, 27, 27936–27945. [Google Scholar] [CrossRef] [PubMed]
  48. Chen, W.; Lian, C.; Luo, Y. Interaction of Airy beams modeled by the fractional nonlinear cubic-quintic Schrödinger equation. Phys. Scr. 2021, 96, 125256. [Google Scholar] [CrossRef]
  49. Shi, Z.; Xue, J.; Zhu, X.; Xiang, Y.; Li, H. Interaction of Airy-Gaussian beams in photonic lattices with defects. Phys. Rev. E 2017, 95, 042209. [Google Scholar] [CrossRef]
  50. Bekenstein, R.; Schley, R.; Mutzafi, M.; Rotschild, C.; Segev, M. Optical simulations of gravitational effects in the Newton-Schrodinger system. Nature Physics 2015, 11, 872–878. [Google Scholar] [CrossRef]
  51. Shen, M.; Gao, J.; Ge, L. Solitons shedding from Airy beams and bound states of breathing Airy solitons in nonlocal nonlinear media. Scientific Reports 2015, 5, 9814. [Google Scholar] [CrossRef]
  52. Shen, M.; Li, W.; Lee, R.-K. Control on the anomalous interactions of Airy beams in nematic liquid crystals. Opt. Express 2016, 24, 8501–8511. [Google Scholar] [CrossRef] [PubMed]
  53. Shen, M.; Wu, L.; Gao, M.; Li, W. Incoherent interactions of Airy beams in nonlocal nonlinear media. J. Phys. B: At. Mol. Opt. Phys. 2018, 51, 165401.
  54. Stegeman, G.I.; Segev, M. Optical Spatial Solitons and Their Interactions: Universality and Diversity. Science 1999, 286, 1518–1523. [Google Scholar] [CrossRef] [PubMed]
  55. Kivshar, Yuri S.; Agrawal, G. P. Optical Solitons: From Fibers to Photonic Crystals, 2003.
  56. Roy, S.; Bhadra, S. K.; Agrawal, G. P. Dispersive waves emitted by solitons perturbed by third-order dispersion inside optical fibers. Phys. Rev. A 2009, 79, 023824. [Google Scholar] [CrossRef]
  57. Runge, A. F. J.; Alexander, T. J.; Newton, J.; Alavandi, P. A.; Hudson, D. D.; Blanco-Redondo, A.; Martijn de Sterke, C. Self-similar propagation of optical pulses in fibers with positive quartic dispersion. Opt. Lett. 2020, 45, 3365–3368. [Google Scholar] [CrossRef]
  58. Zambo Abou,ou, M. N.; Tchofo Dinda, P.; Ngabireng, C. M.; Pitois, S.; Kibler, B. Impact of fourth-order dispersion in the spectra of polarization-modulational instability in highly nonlinear fibers. Phys. Rev. A 2013, 87, 033803.
  59. Runge, A. F. J.; Hudson, D. D.; Tam, K. K. K.; Martijn de Sterke, C.; Blanco-Redondo, A. The pure-quartic soliton laser. Nature Photonics 2020, 14, 492–497. [Google Scholar] [CrossRef]
  60. Alexander, T. J.; Tsolias, G. A.; Demirkaya, A.; Decker, R. J.; Martijn de Sterke, C.; Kevrekidis, P. G. Bright optical soliton in the presence of fourth-order dispersion. Opt. Lett. 1996, 21, 845–847. [Google Scholar]
  61. Cole J., T.; Musslimani, Z. H. Band gaps and lattice solitons for the higher-order nonlinear Schrödinger equation with a periodic potential. Phys. Rev. A 2014, 90, 013815. [Google Scholar] [CrossRef]
  62. Ge, L.; Shen, M.; Ma, C.; Zang, T.; Dai, L. Gap solitons in PT-symmetric optical lattices with higher-order diffraction. Opt. Express 2014, 22, 29435–29444. [Google Scholar] [CrossRef]
  63. Li, J.; Zhang, Y.; Zeng, J. Dark gap solitons in one-dimensional nonlinear periodic media with fourth-order dispersion. Chaos, Solitons and Fractals 2022, 157, 111950.
  64. Blanco-Redondo, A.; Martijn de Sterke, C.; Sipe, J. E.; Krauss, T. F.; Eggleton, B. J.; Husko, C. Pure-quartic solitons. Nature Communications 2016, 7, 10427. [Google Scholar] [CrossRef]
  65. Alexander, T. J.; Tsolias, G. A.; Demirkaya, A.; Decker, R. J.; Martijn de Sterke, C.; Kevrekidis, P. G. Dark solitons under higher-order dispersion. Opt. Lett. 2022, 47, 1174–1177. [Google Scholar] [CrossRef]
  66. Driben, R.; Hu, Y.; Chen, Z.; Malomed, B. A.; Morandotti, R. Inversion and tight focusing of Airy pulses under the action of third-order dispersion. Opt. Lett. 2013, 38, 2499–2501. [Google Scholar] [CrossRef] [PubMed]
  67. Zhang, L.; Zhang, J.; Chen, Y.; Liu, A.; Liu, G. Dynamic propagation of finite-energy Airy pulses in the presence of higher-order effects. J. Opt. Soc. Am. B 2014, 31, 889–897. [Google Scholar] [CrossRef]
  68. Mandeng, L. M.; Tchawa, C.; Tagwo, H.; Zghal, M.; Cherif, R.; Mohamadou, A. Role of the input profile asymmetry and the chirp on the propagation in highly dispersive and nonlinear fibers. Journal of Lightwave Technology. 2016, 34, 5635–5641. [Google Scholar] [CrossRef]
  69. Zhang, L.; Zhang, X.; Pierangeli, D.; Li, Y.; Fan, D.; Conti, C. Synchrotron resonant radiation from nonlinear self-accelerating pulses. Opt. Express 2018, 26, 14710–14717. [Google Scholar] [CrossRef] [PubMed]
  70. Singh Gaur, D.; Purohit, A.; Kumar Mishra, A. Soliton shedding from Airy pulses in a highly dispersive and nonlinear medium. J. Opt. Soc. Am. B 2021, 38, 3729–3736. [Google Scholar] [CrossRef]
  71. Zhao, W.; Ge, L.; Shen, M. Interactions of Airy beams in nonlinear media with fourth-order diffraction. Opt. Express 2023, 31, 14715–14725. [Google Scholar] [CrossRef]
Preprints 82541 g001
Figure 1. (Color online) The intensity trajectories of interactions between Airy beams and in-phase ( ρ = 0 ) weak light Gaussian beams. The beam intervals are B=0 (a1-a4), B=1 (b1-b4), and B=2 (c1-c4). The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a3-c3), (a1-c2), and (a4-c4), respectively. The amplitudes are A = 3 .
Figure 1. (Color online) The intensity trajectories of interactions between Airy beams and in-phase ( ρ = 0 ) weak light Gaussian beams. The beam intervals are B=0 (a1-a4), B=1 (b1-b4), and B=2 (c1-c4). The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a3-c3), (a1-c2), and (a4-c4), respectively. The amplitudes are A = 3 .
Preprints 82541 g001
Preprints 82541 g002
Figure 2. (Color online) The intensity trajectories of interactions between Airy beams and in-phase ( ρ = 0 ) weak light Gaussian beams. The beam intervals are B=3. The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-c1), (a2-c2), and (a3-c3), respectively. The amplitudes are A = 3 .
Figure 2. (Color online) The intensity trajectories of interactions between Airy beams and in-phase ( ρ = 0 ) weak light Gaussian beams. The beam intervals are B=3. The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-c1), (a2-c2), and (a3-c3), respectively. The amplitudes are A = 3 .
Preprints 82541 g002
Preprints 82541 g003
Figure 3. (Color online) The intensity trajectories of interactions between Airy beams and in-phase ( ρ = 0 ) strong light Gaussian beams. The beam intervals are B=0 (a1-a3), B=1 (b1-b3), B=2 (c1-c3) and B=3 (d1-d3). The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-d1), (a2-d2), and (a3-d3), respectively. The amplitudes are A = 3 .
Figure 3. (Color online) The intensity trajectories of interactions between Airy beams and in-phase ( ρ = 0 ) strong light Gaussian beams. The beam intervals are B=0 (a1-a3), B=1 (b1-b3), B=2 (c1-c3) and B=3 (d1-d3). The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-d1), (a2-d2), and (a3-d3), respectively. The amplitudes are A = 3 .
Preprints 82541 g003
Preprints 82541 g004
Figure 4. (Color online) The intensity trajectories of interactions between Airy beams and out-of-phase ( ρ = 1 ) weak light Gaussian beams. The beam intervals are B=0 (a1-a3), B=1 (b1-b3), and B=2 (c1-c3). The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-c1), (a2-c2), and (a3-c3), respectively. The amplitudes are A = 3 .
Figure 4. (Color online) The intensity trajectories of interactions between Airy beams and out-of-phase ( ρ = 1 ) weak light Gaussian beams. The beam intervals are B=0 (a1-a3), B=1 (b1-b3), and B=2 (c1-c3). The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-c1), (a2-c2), and (a3-c3), respectively. The amplitudes are A = 3 .
Preprints 82541 g004
Preprints 82541 g005
Figure 5. (Color online) The intensity trajectories of interactions between Airy beams and out-of-phase ( ρ = 1 ) weak light Gaussian beams. The beam intervals are B=3. The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-c1), (a2-c2), and (a3-c3), respectively. The amplitudes are A = 3 .
Figure 5. (Color online) The intensity trajectories of interactions between Airy beams and out-of-phase ( ρ = 1 ) weak light Gaussian beams. The beam intervals are B=3. The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-c1), (a2-c2), and (a3-c3), respectively. The amplitudes are A = 3 .
Preprints 82541 g005
Preprints 82541 g006
Figure 6. (Color online) The intensity trajectories of interactions between Airy beams and out-of-phase ( ρ = 1 ) strong light Gaussian beams. The beam intervals are B=2 (a1-a3) and B=3 (b1-b3). The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-b1), (a2-b2), and (a3-b3), respectively. The amplitudes are A = 3 .
Figure 6. (Color online) The intensity trajectories of interactions between Airy beams and out-of-phase ( ρ = 1 ) strong light Gaussian beams. The beam intervals are B=2 (a1-a3) and B=3 (b1-b3). The fourth-order diffraction coupling constants are β > 0 , β = 0 , and β < 0 for (a1-b1), (a2-b2), and (a3-b3), respectively. The amplitudes are A = 3 .
Preprints 82541 g006
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated