A Posterior p-Value for Homogeneity Testing of the Three Sample Problem

Preprint

Article

A Posterior p-Value for Homogeneity Testing of the Three Sample Problem

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 August 2023

Posted:

18 August 2023

You are already at the latest version

Alerts

Abstract

In this paper we study a special kind of finite mixture model. The sample drawn from the model consisits of three parts. The first two parts are drawn from specified distributions f1 and f2, while the third one is drawn from the mixture. A problem of interest is whether the two distributions f1 and f2 are the same. To test this hypothesis, we first define the regular location and scale family of distributions and assume that f1 and f2 are regular denisty functions. Then the hypothesis transforms to the equalities of the location and scale parameters, respectively. To utilize the information in the sample, we use Bayes’ theorem to obtain the posterior distribution and give the sampling method. Then we propose the posterior p-value to test the hypothesis. The simulation studies show that our posterior p-value largely improves the power in both normal and logistic cases while nicely controls the Type-I error. A real halibut dataset is used to illustrate the validity of our method.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

In this paper we focus on the model proposed by Hosmer [1], which is used to study the halibut data. There are two different sources of halibut data. One is from the research cruises, where the sex, age and length of the halibut are available while another comes from the commercial catch where only age and length can be obtained since the fish have been cleaned before the boats returned to the port. The length distribution of an age class of halibut is closely approximated by a mixture of two normal distributions, which is

\begin{matrix} X_{i} \overset{i i d}{\sim} f_{1} (y), i = 1, \dots, n_{1} \\ Y_{j} \overset{i i d}{\sim} f_{2} (y), j = 1, \dots, n_{2} \\ Z_{k} \overset{i i d}{\sim} λ f_{1} (y) + (1 - λ) f_{2} (y), k = 1, \dots, n_{3}, \end{matrix}

(1)

where

f_{1}

and

f_{2}

are the probability density functions of the normal distributions and

λ

is the proportion of the male halibut in the commercial catches. Hosmer [1] estimated the parameters of the two distributions using the iterative maximum likelihood estimate method. Murray and Titterington [2] summarized the techniques for maximum likelihood estimation and Bayesian analysis. Anderson [3] proposed a semiparametric modeling assumption known as the exponential tilt mixture model. The estimating of the proportion is done by a general method based on direct estimation of the likelihood ratio. The estimation of the model is further studied by Qin [4], who extended Owen ’s [5] empirical likelihood to the semiparametric model. Qin gave the asymptotic variance formula for the maximum semiparametric likelihood estimation. Later, Zou et al. [6] showed that the partial profile empirical likelihood also worked well with realistic sample size. An EM algorithm for this semiparametric model is further given by Zhang [7]. Furthermore, Inagaki and Komaki [8] and Tan [9] respectively modified the profile likelihood function and provided better estimators for the parameters.

Except for the estimation of parameters, another important issue is to test the homogeneity of the model. Thus the null hypothesis is

H_{0} : f_{1} = f_{2} .

To test the null hypothesis, Liang and Rathouz [10] proposed a score test and applied it to genetic linkage. Lemdani and Pons [11] suggested using likelihood ratio tests(LRT) under modified likelihood function since classical results on LRT may be invalid. Chen et al. [12,13] proposed a modified LRT with a general parametric kernel distribution family and they proved that the modified LRT has a

χ

-type of null limiting distribution and is asymptotically most powerful under local alternatives. Chen and Li [14] proposed an EM approach for the normal mixture models. Li et al. [15] used a high-order expansion to establish a nonstandard convergence rate

N^{- 1 / 4}

for the odds ratio parameter estimator and solved the problem of degeneration of the Fisher information. These works are applied to a variety of genetic mixture model in real applications. For example, genetic imprinting and quantitative trait locus mapping, see Li et al. [16] and Liu et al. [17].

Most mixture models discribed above mainly consider the case when

f_{1}

and

f_{2}

are normal distributions. In this paper, we want to extend the conclusion to more general cases. Similar question has been researched by Ren et al. [18]. In their paper a two-block Gibbs sampling method are proposed to obtain the samples of the generalized pivot quantities of the parameters. They studied both cases when

f_{1}

and

f_{2}

are normal and logistic distributions. In our paper, we assume that

f_{1}

and

f_{2}

are in a specified location-scale family with location parameter

μ

and scale parameter

σ

. We propose a posterior p-value based on the posterior distribution to test the homogeneity. To sample from the posterior distirbutions, we propose to use approximate Bayesian computation (ABC) method for the case when

f_{1}

and

f_{2}

are normal distributions, which is different from the cases when

f_{1}

and

f_{2}

are general distributions. This is because the posterior distirbution of the normal case can be regard as using the information contained in the first two samples as prior distribution and updating it via the third one without loss of information. We find in our simulation that this method is promising and efficient even we use the simplest reject-sampling. For the general case, since ABC method is no longer available, we use MCMC method such as Metropolis-Hastings sampling method proposed by Hannig et al. [19] and the two-block Gibbs sampling proposed by Ren et al. [18] to sample from the posterior distribution.

The paper is organized as follow. In Section 2 we first define the regular location-scale family and give some properties of the family. Then we propose our posterior p-value for testing the homogeneity. We further introduce the sampling method for different cases. A real data of the halibut is studied in Section 3 to illustrate the validity of our method. The simulation study is given in Section 4 while the conclusion is given in Section 5.

2. Test Procedure

In this section we consider model (1) where the distributions are in a certain regular location-scale family. Thus, we first give the definition in the following subsection.

2.1. Regular Location-Scale Family

In this section we first give the definition of the regular location-scale family.

Definition 1 (regular location-scale family).

Let

f (x)

be a probability density function. If

f (x)

satisfies

(1): $f (x) > 0$ , $- \infty < x < \infty$ ;
(2): $f^{″} (x)$ is continous;
(3): $lim_{x \to - \infty} x^{2} f^{'} (x) = lim_{x \to + \infty} x^{2} f^{'} (x) = 0$ ;
(4): $\int_{- \infty}^{+ \infty} x^{2} \frac{{[f^{'} (x)]}^{2}}{f (x)} d x < \infty$ .

Then

f (x)

is defined as a regular density function, and

R_{f} = \{\frac{1}{σ} f (\frac{x - μ}{σ}); μ \in (- \infty, + \infty), σ \in (0, + \infty)\}

is defined as the regular location-scale family.

It is easy to verify that many families of distributions are regular location-scale families. For example, let

f_{1} (x) = \frac{1}{\sqrt{2 π}} e^{- \frac{x^{2}}{2}}, f_{2} (x) = \frac{e^{- x}}{{(1 + e^{- x})}^{2}} .

Then

f_{1} (x)

and

f_{2} (x)

are regular density functions. The families of distributions that constructed by

f_{1} (x)

and

f_{2} (x)

are regular, which are the families of normal distributions and logistic distibutions, respectively. The two families of distributions are concerned in the paper later.

The following lemma highlights some properties of this family.

Lemma 1.

f (x)

is a regular density function, then we have

(1): $lim_{x \to - \infty} x f (x) = lim_{x \to + \infty} x f (x) = 0$ ;
(2): $\int_{- \infty}^{+ \infty} f^{'} (x) d x = 0$ ;
(3): $\int_{- \infty}^{+ \infty} x f^{'} (x) d x = - 1$ ;
(4): $\int_{- \infty}^{+ \infty} f^{″} (x) d x = 0$ ;
(5): $\int_{- \infty}^{+ \infty} x f^{″} (x) d x = 0$ ;
(6): $\int_{- \infty}^{+ \infty} x^{2} f^{″} (x) d x = 0$ .

The proof of this lemma is given in Appendix.

We further calculate the Fisher information matrix of the regular location-scale family with the following proposition.

Proposition 1.

Assume that

f (x; ξ) = \frac{1}{σ} f (\frac{x - μ}{σ})

is in the regular location-scale family, where

ξ = {(μ, σ)}^{⊤}

. The parameter space

Ω = {(μ, σ) : - \infty < μ < \infty, σ > 0}

. Let

l (ξ, X) = log f (X; ξ)

. Then

(1): The score function satisfies

$E_{ξ} [\frac{\partial l (X; ξ)}{ξ}] = 0;$
(2): The Fisher information matrix satisfies

$0 < I_{f} (ξ) = E_{ξ} {[(\frac{\partial l (X; ξ)}{\partial ξ}) (\frac{\partial l (X; ξ)}{\partial ξ})]}^{⊤} = \frac{1}{σ^{2}} C (f) = \frac{1}{σ^{2}} (\begin{matrix} C_{11} (f) & C_{12} (f) \\ C_{21} (f) & C_{22} (f) \end{matrix}) < \infty,$

where

$\begin{matrix} C_{11} (f) & = \int_{- \infty}^{\infty} \frac{{[f^{'} (y)]}^{2}}{f (y)} d y \\ C_{12} (f) & = C_{21} (f) = \int_{- \infty}^{\infty} y \frac{{[f^{'} (y)]}^{2}}{f (y)} d y \\ C_{22} (f) & = \int_{- \infty}^{\infty} {(1 + y \frac{f^{'} (y)}{f (y)})}^{2} f (y) d y = \int_{- \infty}^{\infty} y^{2} \frac{{[f^{'} (y)]}^{2}}{f (y)} d y - 1 \end{matrix}$
(3): The Fisher information matrix is given by

$I_{f} (ξ) = - E_{ξ} [\frac{\partial^{2} f (X, ξ)}{\partial ξ \partial ξ^{⊤}}] .$

The proof is given in Appendix.

Proposition 2.

Assume that

0 < λ_{0} < 1

and

f (\cdot)

is regular. Then

{g (x; θ) : θ \in Ω}

given by

g (x, θ) = \frac{λ_{0}}{σ_{1}} f (\frac{x - μ_{1}}{σ_{1}}) + \frac{1 - λ_{0}}{σ_{2}} f (\frac{x - μ_{2}}{σ_{2}}),

(2)

where

θ = {(μ_{1}, μ_{2}, σ_{1}, σ_{2})}^{⊤}

and

Ω = R^{2} \times {R^{+}}^{2}

, has following properties.

(1): $E_{θ} [\frac{\partial log g (x, θ)}{\partial θ}] = 0;$
(2): $I (θ) = E {[(\frac{\partial log g (x, θ)}{\partial θ}) (\frac{\partial log g (x, θ)}{\partial θ})]}^{⊤} < \infty;$
(3): $I (θ) = - E_{θ} [\frac{\partial^{2} log g (x; θ)}{\partial θ \partial θ^{⊤}}] .$

The proof is given in Appendix.

We then give the Fisher information matrix of the normal and logistic distribution. For the normal distribution, we have

\begin{matrix} C_{11} (f) & = \int_{- \infty}^{\infty} \frac{1}{\sqrt{2 π}} e^{- \frac{y^{2}}{2}} y^{2} d y = 1 \\ C_{12} (f) & = C_{21} (f) = \int_{- \infty}^{\infty} \frac{1}{\sqrt{2 π}} e^{- \frac{y^{2}}{2}} y^{3} d y = 0 \\ C_{22} (f) & = \int_{- \infty}^{\infty} \frac{1}{\sqrt{2 π}} e^{- \frac{y^{2}}{2}} y^{4} d y - 1 = 2 \end{matrix}

Thus the Fisher information matrix of normal distribution is

I_{f} (ξ) = \frac{1}{σ^{2}} (\begin{matrix} 1 & 0 \\ 0 & 2 \end{matrix})

Similarly, for the logistic distribution,

\begin{matrix} C_{11} (f) & = \int_{- \infty}^{\infty} \frac{e^{- y} {(e^{- y} - 1)}^{2}}{{(1 + e^{- y})}^{4}} d y = 1 / 3 \\ C_{12} (f) & = C_{21} (f) = \int_{- \infty}^{\infty} \frac{e^{- y} {(e^{- y} - 1)}^{2}}{{(1 + e^{- y})}^{4}} d y = 0 \\ C_{22} (f) & = \int_{- \infty}^{\infty} \frac{e^{- y} {(e^{- y} - 1)}^{2}}{{(1 + e^{- y})}^{4}} d y = \frac{1}{3} + \frac{π^{2}}{9} \end{matrix}

Thus the Fisher information matrix of logistic distribution is

I_{f} (ξ) = \frac{1}{σ^{2}} (\begin{matrix} \frac{1}{3} & 0 \\ 0 & \frac{1}{3} + \frac{π^{2}}{9} \end{matrix})

2.2. A Posterior p-Value

Now we consider testing the homogeneity of model (1) where

f_{1}

and

f_{2}

are in

R_{f}

f_{1} = \frac{1}{σ_{1}} f (\frac{x - μ_{1}}{σ_{1}}), f_{2} = \frac{1}{σ_{2}} f (\frac{x - μ_{2}}{σ_{2}}) .

This is equivalent to testing equality of the parameters of the two density functions, that is,

H_{0} : μ_{1} = μ_{2}, σ_{1} = σ_{2} v . s . H_{1} : μ_{1} \neq μ_{2} or σ_{1} \neq σ_{2} .

(3)

Consider the density function

g (x; θ) = \frac{λ}{σ_{1}} f (\frac{x - μ_{1}}{σ_{1}}) + \frac{λ}{σ_{2}} f (\frac{x - μ_{2}}{σ_{2}}),

where

θ = {(μ_{1}, μ_{2}, σ_{1}, σ_{2}, λ)}^{⊤}

is the unknown parameter.

f (x)

is the regular density function, then the Fisher information matrix is

I_{g} (θ) = E_{θ} [\frac{\partial log g (x; θ)}{\partial θ}] {[\frac{\partial log g (x; θ)}{\partial θ}]}^{⊤},

where

\frac{\partial log g (x; θ)}{\partial θ} = (\begin{matrix} \frac{1}{g (x; θ)} [- \frac{λ}{σ_{1}^{2}} f^{'} (\frac{x - μ_{1}}{σ_{1}})] \\ \frac{1}{g (x; θ)} [- \frac{1 - λ}{σ_{2}^{2}} f^{'} (\frac{x - μ_{2}}{σ_{2}})] \\ \frac{1}{g (x; θ)} [- \frac{λ}{σ_{1}^{2}} f^{'} (\frac{x - μ_{1}}{σ_{1}}) - \frac{λ}{σ_{1}^{3}} f^{'} (\frac{x - μ_{1}}{σ_{1}})] \\ \frac{1}{g (x; θ)} [- \frac{1 - λ}{σ_{2}^{2}} f^{'} (\frac{x - μ_{2}}{σ_{2}}) - \frac{1 - λ}{σ_{2}^{3}} f^{'} (\frac{x - μ_{2}}{σ_{2}})] \\ \frac{1}{g (x; θ)} [\frac{1}{σ_{1}} f (\frac{x - μ_{1}}{σ_{1}}) - \frac{1}{σ_{2}} f (\frac{x - μ_{2}}{σ_{2}})] \end{matrix})

When

μ_{1} = μ_{2}, σ_{1} = σ_{2}

\frac{\partial log g (x; θ)}{\partial λ} = 0,

the last row and column of

I_{g} (θ)

is zero, which means that

| I_{g} (θ) | = 0

and is non-definite. Thus, we may encounter some difficulties when using some traditional test methods, such as the likelihood ratio test.

We suggest a solution here. First we assume that

λ = λ_{0}

is known. Then there are 4 parameters and we still denote them by

θ = {(μ_{1}, μ_{2}, σ_{1}, σ_{2})}^{⊤}

. We use the estimate of

λ

instead since

λ

is unknown. This is because that when the homogeneity hypothesis holds, the distribution of the population is irrelative to

λ

. So the level of the test is irrelative to the estimate of

λ

. We then give the inference on

θ

below. For the first two samples, the fiducial density of

(μ_{1}, σ_{1})

and

(μ_{2}, σ_{2})

are

(μ_{1}, σ_{1}) \propto [\prod_{i = 1}^{n_{1}} \frac{1}{σ_{1}} f (\frac{x_{1 i} - μ_{1}}{σ_{1}})] \frac{1}{σ_{1}}, (μ_{2}, σ_{2}) \propto [\prod_{j = 1}^{n_{2}} \frac{1}{σ_{2}} f (\frac{x_{2 j} - μ_{2}}{σ_{2}})] \frac{1}{σ_{2}},

(4)

where “∝” denote “proportion to”, see the example 3 of Hannig et al. [19]. Then to combine (4) with the third sample, we regard (4) as the prior distribution. By the Bayes’ theorem

\begin{matrix} θ \propto & \prod_{k = 1}^{n_{3}} [\frac{λ_{0}}{σ_{1}} f (\frac{x_{3 k} - μ_{1}}{σ_{1}}) + \frac{1 - λ_{0}}{σ_{2}} f (\frac{x_{3 k} - μ_{2}}{σ_{2}})] \\ \cdot & [\prod_{i = 1}^{n_{1}} \frac{1}{σ_{1}} f (\frac{x_{1 i} - μ_{1}}{σ_{1}})] \frac{1}{σ_{1}} \cdot [\prod_{j = 1}^{n_{2}} \frac{1}{σ_{2}} f (\frac{x_{2 j} - μ_{2}}{σ_{2}})] \frac{1}{σ_{2}} \end{matrix}

(5)

Denote the probability measure on the parameter space determined by (5) by

P^{Θ | x}

, where

x = (x_{1}^{⊤}, x_{2}^{⊤}, x_{3}^{⊤})

x_{1} = {(x_{11}, x_{12}, \dots, x_{1 n_{1}})}^{⊤}

x_{2} = {(x_{21}, x_{22}, \dots, x_{2 n_{2}})}^{⊤}

x_{3} = {(x_{31}, x_{32}, \dots, x_{3 n_{3}})}^{⊤}

Θ

denotes the random variable. We can see from the expression (5) that

P^{Θ | x}

is the posterior distribution under the prior distribution

d θ = \frac{1}{σ_{1} σ_{2}} d μ_{1} d μ_{2} d σ_{1} σ_{2} .

Let

A = [\begin{matrix} 1 & - 1 & 0 & 0 \\ 0 & 0 & 1 & - 1 \end{matrix}], b = {[0, 0]}^{⊤} .

Then the hypotheses (3) is equivalent to

H_{0} : A θ = b v . s . H_{1} : A θ \neq b .

(6)

where

θ = {(μ_{1}, μ_{2}, σ_{1}, σ_{2})}^{⊤}

To establish Bernstein-von Mises theorem for multiple samples, we first introduce some necessary assumptions below. Let

l_{i} (θ)

be the log-likelihood function of the ith sample, where

i = 1, 2, 3

Assumption 1.

Given any

ε > 0

, there exists

δ > 0

such that in the expansion

l_{i} (θ) = l_{i} (θ_{0}) + {(θ - θ_{0})}^{⊤} l_{i}^{'} (θ_{0}) - \frac{1}{2} {(θ - θ_{0})}^{⊤} [n I_{i} (θ_{0}) + R_{n_{i}} (θ)] (θ - θ_{0}), i = 1, 2, 3,

where

θ_{0}

is the true value of the parameter.

I_{i} (θ_{0})

is the Fisher Information matrix. The probability of the following event

sup \{\frac{1}{n} λ_{max} [R_{n_{i}} (θ)] : ∥ θ - θ_{0} ∥ \leq δ\} \geq ε

tends to 0 as

n \to \infty

, where

∥ \cdot ∥

is the Euclidean norm and

λ_{max} (A)

denotes the largest absolute eigenvalues of a square matrix A.

Assumption 2.

For any

δ > 0

, there exists

ε > 0

such that the probability of the event

sup \{\frac{1}{n_{i}} [l_{i} (θ) - l_{i} (θ_{0})] : ∥ θ - θ_{0} ∥ \geq δ\} \leq - ε

tends to 1 as

n \to \infty

Assumption 3.

Under the prior π, there exist

k_{0}

such that the integral of

∥ θ ∥

below exists,

{\int ∥ θ ∥}^{2} \prod_{i = 1}^{k_{0}} [\frac{1}{σ_{1}} f (\frac{x_{1 i} - μ_{1}}{σ_{1}})] \prod_{j = 1}^{k_{0}} [\frac{1}{σ_{2}} f (\frac{x_{2 i} - μ_{2}}{σ_{2}})] π (θ) d θ < \infty .

Assumption 4.

When

n = n_{1} + n_{2} + n_{3} \to \infty

\frac{n_{i}}{n} \to r_{i} \in (0, 1), i = 1, 2, 3 .

Then we give the Berstein-von Mises theorem for multiple samples as follow.

Theorem 1.

Denote the posterior density of

t = \sqrt{n} (θ - T_{n})

π^{*} (t | x)

, where

T_{n} = θ_{0} + \frac{1}{n} I^{- 1} (θ_{0}) l^{'} (θ_{0}) .

If the Assumption 1, 2 and 4 hold, then

\int_{Ω} |π^{*} (t | x) - {(2 π)}^{- \frac{k}{2}} {|I (θ_{0})|}^{\frac{1}{2}} e^{- \frac{1}{2} t^{⊤} I (θ_{0}) t}| d t \overset{P}{\to} 0 .

Furthermore, if Assumption 3 holds, then

\int_{Ω} (1 + {∥ t ∥}^{2}) |π^{*} (t | x) - {(2 π)}^{- \frac{k}{2}} {|I (θ_{0})|}^{\frac{1}{2}} e^{- \frac{1}{2} t^{⊤} I (θ_{0}) t}| d t \overset{P}{\to} 0 .

Then we can define the posterior p-value as follow

Definition 2.

Let

\begin{matrix} p (x) = P^{Θ | x} ( & {(Θ - θ_{B})}^{⊤} A^{⊤} {(A Σ_{B} A^{⊤})}^{- 1} A (Θ - θ_{B}) \\ ⩾ {(b - A θ_{B})}^{⊤} {(A Σ_{B} A^{⊤})}^{- 1} (b - A θ_{B})), \end{matrix}

(7)

where

P^{Θ | x} (\cdot)

is the probability under the posterior distribution.

θ_{B}

is the posterior mean and

Σ_{B}

is the posterior covariance matrix. We call

p (x)

as a posterior p-value.

The theorem below gurantees the validity of the posterior p-value.

Theorem 2.

Under the assumption of Theorem 1, the p-value define by (7) satisfies

p (X) \overset{d}{⟶} U (0, 1) .

where

“ {\overset{d}{^{'}}}^{'}

is the convergence in distribution and

U (0, 1)

is the uniform distribution on the internal

(0, 1)

The proof is given in Appendix. Then for a given significance level

α

, we may reject the null hypothesis if the p-value is less than

α

2.3. Sampling Method

The posterior mean

θ_{B}

and the posterior variance

Σ_{B}

in equation (7) can be estimated by the sample mean and variance, respectively. Now the remain problem is how to sample from the posterior distribution. When

λ

is unknown, we first propose an EM algorithm to estimate

λ

, then we sample from the posterior distribution where

λ

is fixed to the estimate of

λ

. The Markov Chain Monte Carlo (MCMC) method are commonly used. However, as we have mentioned earlier, MCMC method needs to discard a large number of samples in the burn-in period to gurantee the samples accepted sufficiently close to the ones from the real distribution. Fortunately, when

f_{1}

and

f_{2}

are normal distributions, we find that the posterior distribution can be transformed and sampled by using the approximate Bayesian computation (ABC) method. However, when

f_{1}

and

f_{2}

are some more common distributions, such as the logistic distributions, the two-block Gibbs sampling proposed by Ren et al. [18] can be an appropriate substitution. We will discuss the details in the following subsection.

2.3.1. Em Algorithm for $λ$

In this subsection we propose the EM alogorithm for estimating

λ

The log-likelihood function of the model is

L (x; θ, λ) = \sum_{i = 1}^{n_{1}} log [f_{1} (x_{1 i}; θ)] + \sum_{j = 1}^{n_{2}} log [f_{2} (x_{2 j}; θ)] + \sum_{k = 1}^{n_{3}} log [p (x_{3 k}; θ, λ)],

where

f_{1}

and

f_{2}

are in the same regular location-scale family

R_{f}

, with parameters

(μ_{1}, σ_{1})

and

(μ_{2}, σ_{2})

respectively.

p (x_{3 k}; θ, λ)

in the log-likelihood function of the third sample is

p (x_{3 k}; θ, λ) = λ f_{1} (x_{3 k}; θ) + (1 - λ) f_{2} (x_{3 k}; θ) .

The EM algorithmis is first proposed by Dempster et al. [20] and broadly applied to a wide variety of parametric models, see McLachlan and Krishnan [21] for a better review.

Assume that we have obtain the estimate of the parameters after m times of iterative, denote them by

θ^{(m)} = {(μ_{1}^{(m)}, σ_{1}^{(m)}, μ_{2}^{(m)}, σ_{2}^{(m)})}^{⊤}

and

λ^{(m)}

. We introduce the latent variable

γ = {(γ_{1}, γ_{2}, \dots, γ_{n_{3}})}^{⊤}

, the component

γ_{k}

indicates which distribution the sample

x_{3 k}

is drawn from.

γ_{k} = 1

when it is drawn from the first distribution

f_{1} (x_{3 k}; θ)

, otherwise,

γ_{k} = 0

. Then we have

P (γ_{k} = 1) = λ, P (γ_{k} = 0) = 1 - λ, k = 1, 2, \dots, n_{3}

The density of the joint distribution of

X_{1}, X_{2}, X_{3}, γ

\prod_{i = 1}^{n_{1}} f_{1} (x_{1 i}; θ) \prod_{j = 1}^{n_{2}} f_{2} (x_{2 j}; θ) \prod_{k = 1}^{n_{3}} {[λ f_{1} (x_{3 k}; θ)]}^{γ_{k}} {[(1 - λ) f_{2} (x_{3 k}; θ)]}^{1 - γ_{k}} .

Given

X_{1} = x_{1}, X_{2} = x_{2}, X_{3} = x_{3}

, the conditional distribution of

γ_{k}

{[\frac{λ f_{1} (x_{3 k}; θ)}{λ f_{1} (x_{3 k}; θ) + (1 - λ) f_{2} (x_{3 k}; θ)}]}^{γ_{k}} {[\frac{(1 - λ) f_{2} (x_{3 k}; θ)}{λ f_{1} (x_{3 k}; θ) + (1 - λ) f_{2} (x_{3 k}; θ)}]}^{1 - γ_{k}},

where

γ_{k} = 0, 1

k = 1, 2, \dots, n_{3}

. Thus the conditional expectation of

γ_{k}

E_{(θ, λ)} γ_{k} = P_{(θ, λ)} (γ_{k} = 1) = \frac{λ f_{1} (x_{3 k}; θ)}{λ f_{1} (x_{3 k}; θ) + (1 - λ) f_{2} (x_{3 k}; θ)} .

When

θ = θ^{(m)}

and

λ = λ^{(m)}

, the conditional expectation of

γ_{k}

can be the estimate of

γ_{k}

{\hat{γ}}_{k} (θ^{(m)}, λ^{(m)}) = \frac{λ^{(m)} f_{1} (x_{3 k}; θ^{(m)})}{λ^{(m)} f_{1} (x_{3 k}; θ^{(m)}) + (1 - λ^{(m)}) f_{2} (x_{3 k}; θ^{(m)})},

k = 1, 2, \dots, n_{3}

The log likelihood function is

\begin{matrix} \sum_{i = 1}^{n_{1}} log f_{1} (x_{1 i}; θ) + \sum_{j = 1}^{n_{2}} log f_{2} (x_{2 j}; θ) + \sum_{k = 1}^{n_{3}} γ_{k} log f_{1} (x_{3 k}; θ,) \\ + \sum_{k = 1}^{n_{3}} (1 - γ_{k}) log f_{2} (x_{3 k}; θ,) + (\sum_{k = 1}^{n_{3}} γ_{k}) log λ + (n_{3} - \sum_{k = 1}^{n_{3}} γ_{k}) log (1 - λ) . \end{matrix}

Since the latent variable is unknown, we use its conditional expectation. Besides, the MLE of

λ

λ^{(m + 1)} = \frac{\sum_{k = 1}^{n_{3}} {\hat{γ}}_{k} (θ^{(m)}, λ^{(m)})}{n_{3}} .

Then in the E-step, we calculate the expectation of new parameters conditional on

(θ^{(m)}, λ^{(m)})

\begin{matrix} Q (θ, λ | θ^{(m)}, λ^{(m)}) = & \sum_{i = 1}^{n_{1}} log f_{1} (x_{1 i}; θ) + \sum_{j = 1}^{n_{2}} log f_{2} (x_{2 j}; θ) \\ + \sum_{k = 1}^{n_{3}} {\hat{γ}}_{k} ((θ^{(m)}, λ^{(m)})) log f_{1} (x_{3 k}; θ,) \\ + \sum_{k = 1}^{n_{3}} (1 - {\hat{γ}}_{k} ((θ^{(m)}, λ^{(m)}))) log f_{2} (x_{3 k}; θ,) . \end{matrix}

Let

{\hat{γ}}_{k} = {\hat{γ}}_{k} (θ^{(m)}, λ^{(m)})

, then

\begin{matrix} Q (θ, λ | θ^{(m)}, λ^{(m)}) = & \sum_{i = 1}^{n_{1}} [- log σ_{1} + log f (\frac{x_{1 i} - μ_{1}}{σ_{1}})] \\ + \sum_{j = 1}^{n_{2}} [- log σ_{2} + log f (\frac{x_{2 j} - μ_{2}}{σ_{2}})] \\ + \sum_{k = 1}^{n_{3}} {\hat{γ}}_{k} [- log σ_{1} + log f (\frac{x_{3 k} - μ_{1}}{σ_{1}})] \\ + \sum_{k = 1}^{n_{3}} (1 - {\hat{γ}}_{k}) [- log σ_{2} + log f (\frac{x_{3 k} - μ_{2}}{σ_{2}})] . \end{matrix}

In the M-step we compute the simultaneous equations below to maximize

Q (θ, λ | θ^{(m)}, λ^{(m)})

. The solutions are the new parameters

(θ^{(m + 1)}, λ^{(m + 1)})

. We give the equations of

(μ_{1}, σ_{1})

, similarly can we get

(μ_{1}, σ_{1})

\{\begin{matrix} 0 = \sum_{k = 1}^{n_{3}} \frac{γ_{k}}{λ f_{1} + (1 - λ) f_{2}} f^{'} (\frac{x_{3 k} - μ_{1}}{σ_{1}}) + \sum_{i = 1}^{n_{1}} [\frac{1}{f_{1}} f^{'} (\frac{x_{1 i} - μ_{1}}{σ_{1}})] \\ 0 = \sum_{k = 1}^{n_{3}} \frac{γ_{k}}{λ f_{1} + (1 - λ) f_{2}} [σ_{1}^{2} f_{1} + f^{'} (\frac{x_{3 k} - μ_{1}}{σ_{1}}) (x_{3 k} - μ_{1})] + \sum_{i = 1}^{n_{1}} [σ_{1}^{2} + (x_{1 i} - μ_{1}) f^{'} (\frac{x_{1 i} - μ_{1}}{σ_{1}}) \frac{1}{f_{1}}] \\ λ = \frac{1}{n_{3}} \sum_{k = 1}^{n_{3}} γ_{k} \end{matrix}

In the simulation study we consider the normal and logistic cases. Then the maximization step of the normal case can be simplified as

\begin{matrix} μ_{1} & = \frac{\sum_{k = 1}^{n_{3}} γ_{k} x_{3 k} + \sum_{i = 1}^{n_{1}} x_{1 i}}{\sum_{k = 1}^{n_{3}} γ_{k} + n_{1}}, \\ σ_{1}^{2} & = \frac{\sum_{k = 1}^{n_{3}} γ_{k} {(x_{3 k} - μ_{1})}^{2} + \sum_{i = 1}^{n_{1}} {(x_{1 i} - μ_{1})}^{2}}{\sum_{k = 1}^{n_{3}} γ_{k} + n_{1}}, \end{matrix}

while that of the logistic case is

\{\begin{matrix} 0 = \sum_{k = 1}^{n_{3}} γ_{k} (\frac{e^{\frac{x_{3 k} - μ_{1}}{σ_{1}}} - 1}{e^{\frac{x_{3 k} - μ_{1}}{σ}} + 1}) + \sum_{i = 1}^{n_{1}} \frac{e^{\frac{x_{1 i} - μ_{1}}{σ}} - 1}{e^{\frac{x_{1 i} - μ_{1}}{σ_{1}}} + 1} \\ 0 = \sum_{k = 1}^{n_{3}} [γ_{k} (\frac{x_{3 k} - μ_{1}}{σ_{1}} \frac{e^{\frac{x_{3 k} - μ_{1}}{σ_{1}}} - 1}{e^{\frac{x_{3 k} - μ_{1}}{σ_{1}}} + 1} - 1)] + \sum_{i = 1}^{n_{1}} [\frac{x_{1 i} - μ_{1}}{σ_{1}} (\frac{e^{\frac{x_{1 i} - μ_{1}}{σ_{1}}} - 1}{e^{\frac{x_{1 i} - μ_{1}}{σ_{1}}} + 1}) - 1] . \end{matrix}

The two steps are repeated sufficiently to gurantee the convergence. Then we can get the MLE of the parameters.

2.3.2. Normal Case

When the estimate of

λ

is obtained, the posterior distribution (5) can be rewritten as

\begin{matrix} π (θ | X_{1}, X_{2}, X_{3}) & = (\frac{1}{σ_{1}} \prod_{i = 1}^{n_{1}} f (X_{1 i}; μ_{1}, σ_{1})) \times (\frac{1}{σ_{2}} \prod_{j = 1}^{n_{2}} f (X_{2 j}; μ_{2}, σ_{2})) \\ \times \prod_{k = 1}^{n_{3}} [\hat{λ} f (X_{3 k}; μ_{1}, σ_{1}) + (1 - \hat{λ}) f (X_{3 k}; μ_{2}, σ_{2})] . \end{matrix}

(8)

This means that the posterior distribution is equivalent to using the first two terms on the right side of the equation as the “prior distribution” and the third term as the likelihood function. For the first term we have

\frac{1}{σ_{1}} \prod_{i = 1}^{n_{1}} f (X_{i}; μ_{1}, σ_{1}) = \frac{1}{σ_{1}} {(\frac{1}{\sqrt{2 π} σ_{1}})}^{n} exp [- \frac{\sum_{i = 1}^{n_{1}} {(X_{i} - μ_{1})}^{2}}{2 σ_{1}^{2}}] .

Denote the sample mean and variance by

\bar{X}

and

S_{1}^{2}

, respectively, we have

\bar{X_{1}} = \frac{1}{n_{1}} \sum_{i = 1}^{n_{1}} X_{1 i}, S_{1}^{2} = \frac{1}{n - 1} \sum_{i = 1}^{n_{1}} {(X_{1 i} - \bar{X_{1}})}^{2},

which follows a normal and

χ^{2} (n_{1} - 1)

distribution respectively, that is,

\bar{X_{1}} \sim N (μ_{1}, \frac{σ_{1}^{2}}{n_{1}}), \frac{(n_{1} - 1) S_{1}^{2}}{σ_{1}^{2}} \sim χ^{2} (n_{1} - 1) .

Let

U \sim N (0, 1)

and

V \sim χ^{2} (n_{1} - 1)

be two independent random variables. Then

\bar{X_{1}} = μ_{1} + \frac{σ_{1}}{\sqrt{n_{1}}} U, (n_{1} - 1) S_{1}^{2} = σ_{1}^{2} V .

Given

\bar{X_{1}} = \bar{x_{1}}

and

S_{1}^{2} = s_{1}^{2}

, then

μ_{1}

and

σ_{1}

can be regard as the functions of U and V

μ_{1} = \bar{x_{1}} - \frac{σ_{1}}{\sqrt{n_{1}}} U, σ_{1}^{2} = \frac{(n_{1} - 1) s_{1}^{2}}{V} .

The joint distribution of

(U, V)

\frac{1}{\sqrt{2 π}} e^{- \frac{u^{2}}{2}} \frac{v^{\frac{n_{1} - 1}{2} - 1}}{Γ (\frac{n_{1} - 1}{2}) 2^{\frac{n_{1} - 1}{2}}} e^{- \frac{v}{2}} .

Then the joint distribution of

(μ_{1}, σ_{1})

can be calculated as

π (μ_{1}, σ_{1} | x_{o b s}) = \frac{\sqrt{n_{1}}}{\sqrt{2 π} σ_{1}} e^{- \frac{n_{1} {(\bar{x_{1}} - μ_{1})}^{2}}{2 σ_{1}^{2}}} \frac{{(s_{1}^{2})}^{\frac{n_{1} - 1}{2}} {(n_{1} - 1)}^{\frac{n_{1} - 1}{2}}}{Γ (\frac{n_{1} - 1}{2}) 2^{\frac{n_{1} - 1}{2}}} {(\frac{1}{σ_{1}^{2}})}^{\frac{n_{1} - 1}{2} - 1 + \frac{3}{2}} e^{- \frac{(n_{1} - 1) s_{1}^{2}}{2 σ_{1}^{2}}},

(9)

where

{x_{1}}_{o b s} = {(x_{1}, x_{2}, \dots, x_{n_{1}})}^{⊤}

. This coincides with the joint fiducial density proposed by Fisher [22], which means that the fiducial distribution of

(μ_{1}, σ_{1})

μ_{1} | σ_{1}^{2} \sim N (\bar{x_{1}}, \frac{σ_{1}^{2}}{n_{1}}), \frac{1}{σ_{1}^{2}} \sim \frac{χ^{2} (n_{1} - 1)}{(n_{1} - 1) s_{1}^{2}} .

(10)

Similarly can we get

μ_{2} | σ_{2}^{2} \sim N (\bar{x_{2}}, \frac{σ_{2}^{2}}{n_{1}}), \frac{1}{σ_{2}^{2}} \sim \frac{χ^{2} (n_{2} - 1)}{(n_{2} - 1) s_{2}^{2}},

(11)

where

\bar{x_{2}}

and

s_{2}^{2}

are the sample mean and variance of the second sample and

{x_{2}}_{o b s} = {(x_{21}, x_{22}, \dots, x_{2 n_{2}})}^{⊤}

With the conclusion above, sampling from the posterior distribution (5) can be done by sampling first from the fiducial distribution of the parameters and then combine the information with the likelihood function of the third sample from the mixture model (1). This can be done simply using the approximate Bayesian computation (ABC) method. In this case, we regard the fiducial distributions of

{(μ_{1}, σ_{1}, μ_{2}, σ_{2})}^{⊤}

as the prior distribution. After we drawn samples of parameters from (10) and (11), denote by

{(μ_{1}^{*}, σ_{1}^{*}, μ_{2}^{*}, σ_{2}^{*})}^{⊤}

, we generate simulations from the model below and denote them by

{x_{3}}_{s i m} = {(x_{31}, x_{32}, \dots, x_{3 n_{3}})}^{⊤}

\hat{λ} f (x; μ_{1}^{*}, σ_{1}^{*}) + (1 - \hat{λ}) f (x; μ_{2}^{*}, σ_{2}^{*})

where

\hat{λ}

is the MLE of

λ

estimated aforehand using the EM algorithm proposed in the last subsection. Then we calculate the distance between the simulations and the observation and accept those whose distance is below a given threshold

ε

. The algorithm is given below.

Compute the sample mean and variance of the first two samples and denote them by $\bar{x}$ , $s_{1}^{2}$ , $\bar{y}$ and $s_{2}^{2}$ . Calculate the MLE of $λ$ using EM algorithm and denote it by $\hat{λ}$
Sample $U_{1}$ and $U_{2}$ from the standard normal distribution, $V_{1}$ from the $χ^{2} (n_{1} - 1)$ distribution and $V_{2}$ from $χ^{2} (n_{2} - 1)$ . respectively. To sample from the fiducial distributions of the parameters, we calculate $μ_{1}$ , $σ_{1}$ , $μ_{2}$ and $σ_{2}$ using

$\begin{matrix} μ_{1} = \bar{x_{1}} - \frac{U_{1}}{V_{1} / \sqrt{n_{1} - 1}} \frac{s_{1}}{\sqrt{n_{1}}}, σ_{1}^{2} = \frac{(n_{1} - 1) s_{1}^{2}}{V_{1}^{2}}, \\ μ_{2} = \bar{x_{2}} - \frac{U_{2}}{V_{2} / \sqrt{n_{2} - 1}} \frac{s_{2}}{\sqrt{n_{2}}}, σ_{2}^{2} = \frac{(n_{2} - 1) s_{2}^{2}}{V_{2}^{2}} . \end{matrix}$

We denote the samples of the parameters by $θ^{*} = {(μ_{1}^{*}, μ_{2}^{*}, σ_{1}^{*}, σ_{2}^{*})}^{⊤}$ .
Generate a simulation of size $n_{3}$ from

$\hat{λ} f (x; μ_{1}^{*}, σ_{1}^{*}) + (1 - \hat{λ}) f (x; μ_{2}^{*}, σ_{2}^{*}) .$

The simulation is represented by ${x_{3}}_{s i m} = {(x_{31}^{*}, x_{32}^{*}, \dots, x_{3 n_{3}}^{*})}^{⊤}$ .
Calculate the Euclidean distance between the order statistics of the observation $Z_{1}, Z_{2}, \dots, Z_{n_{3}}$ and the simulation $z_{1}^{*}, z_{2}^{*}, \dots, z_{n_{3}}^{*}$ . We accept the parameters if the distance is below a given threshold $ε$ . Otherwise we reject the parameters.
The procedure is repeated until we accept a certain number of parameters.

A remark that should be noted in this algorithm is that the samples we get from is an approximation to the posterior distribution

()

. We actually samples from

π (θ, ε | {x_{1}}_{o b s}, {x_{2}}_{o b s}, x) \propto π (θ | {x_{1}}_{o b s}, {x_{2}}_{o b s}, {x_{3}}_{o b s}) I (∥ x - {x_{3}}_{o b s} ∥ \leq ε),

(12)

where

I

is the indicator function.

ε

controls the proximity of (12) to (5) and can be adjusted to balance the accuracy and computational cost.

2.3.3. General Case

When

f_{1}

and

f_{2}

are not normal distributions, to sample from the posterior (8), it is natural to use the Markov chain Monte Carlo (MCMC) method. Metropolisi-Hastings (MH) sampling method and Gibbs sampling method are commonly used. An early version of MH algorithm was given by Metropolis et al. [23] in a statistical physics context, with subsequent generalization by Hastings [24], who focused on statistical problems. Some computational problem and solutions can be further see in Owen and Glynn [25].

The initial values of the parameters can be determined by the EM algorithm mentioned above. For the proposal distribution, we choose

\begin{matrix} q (μ_{k} | μ_{k}^{(τ)}) = N (\cdot; μ_{k}^{(τ)}, 1) \\ q (σ_{k} | σ_{k}^{(τ)}) = G a (\cdot; σ_{k}^{(τ)}, 1) \end{matrix}

(13)

where

G a (\cdot)

and

N (\cdot)

denote the gamma distribution and normal distribution respectively.

k = 1, 2

and

μ_{k}^{(τ)}

σ_{k}^{(τ)}

denotes the parameters accepted in the

τ

th loop. After we get

θ^{(τ)} = {(μ_{1}^{(τ)}, σ_{1}^{(τ)}, μ_{2}^{(τ)}, σ_{2}^{(τ)})}^{⊤}

, we can further obtain

θ^{(τ + 1)}

via the following two-step algorithm.

Sample ${(μ_{1}^{*}, σ_{1}^{*}, μ_{2}^{*}, σ_{2}^{*})}^{⊤}$ respectively from the proposal distribution $(13)$ . Compute

$\begin{matrix} log Q (θ^{*} | θ^{τ}) & = log q (μ_{1}^{*} | μ_{1}^{(τ)}) + log q (μ_{2}^{*} | μ_{2}^{(τ)}) + log q (σ_{1}^{*} | σ_{1}^{(τ)}) + log q (σ_{2}^{*} | σ_{2}^{(τ)}) \\ + \sum_{i = 1}^{n_{1}} log f (x_{i}; μ_{1}^{*}, σ_{1}^{*}) + \sum_{i = 1}^{n_{2}} log f (y_{i}; μ_{2}^{*}, σ_{2}^{*}) \\ + \sum_{i = 1}^{n_{3}} [\hat{λ} f (z_{i}; μ_{1}^{*}, σ_{1}^{*}) + (1 - \hat{λ}) f (z_{i}; μ_{2}^{*}, σ_{2}^{*})] - log (σ_{1}^{*} σ_{2}^{*}) . \end{matrix}$
Accept $θ^{*}$ with probability

$P (θ^{*}, θ^{(τ)}) = exp \{min [0, log Q (θ^{*} | θ^{τ}) - log Q (θ^{(τ)} | θ^{*})]\} .$

and let $θ^{(τ + 1)} = θ^{*}$ . Otherwise we reject the parameters and return to the first step.

The algorithm should be repeated sufficiently before obtain the samples from the posterior distribution. This cost much more time compare with the ABC algorithm for the normal case. What’s more, in our simulation we found that the MH algorithm may be too conservative. A better subsititution can be the two-block Gibbs sampling proposed by Ren et al. [18]. In this sampling method,

λ

is first estimiated using the EM algorithm, then for each loop, the parameters are updated by the conditional generalized pivotal quantities.

3. Real Data Example

In this section we apply the proposed posterior p-value to the real halibut dataset studied by Hosmer [1], which is given by International Halibut Commission in Seattle, Washington. This dataset consists of the lengths of 208 halibut caught on one of their research cruises, in which 134 are female while the rest 74 are male. The data is summarized by Karunamuni and Wu [26] and given in Table 1. We follow their method and randomly select 14 males and 26 females from the samples and regard them as the first and second sample of the mixture model 1. Then the remain male proportion of 60/168 is approximately indentical to the original male proportion of 74/208, which is 0.3558. 100 replications is generated with the same procedure. Hosmer [1] pointed out that the component for the dataset can be fitted by the normal distribution. A problem of interest is whether the sex effects the length of the halibut.

To test the homogeneity, for each replication we first use the EM algorithm to estimate

λ

, then we use the reject-ABC method to generate 8000 samples. We choose a moderate threshold

ε

to balance the accuracy and the computational cost. For the 100 replications, the mean of estimate of the male proportion

λ

is 0.3381, with the mean squared error 0.0045, which illustrate the accuracy of our EM algorithm The estimates of the location and scale parameter of the male halibut are

\hat{μ_{1}} = 96.655

and

\hat{σ_{1}} = 12.983

while that of the female ones are

\hat{μ_{2}} = 118.806

and

\hat{σ_{2}} = 9.077

. This is close to the estimates of Ren et al. [18]. As with the hypothesis testing

f_{1} = f_{2}

, we calculate the posterior p-value of the 100 replications. Given the significance level

α = 0.05

, all the p-values are less than

α

. Thus the null hypothesis is rejected, which indicates that there exists association between the sex and length of the halibut.

4. Simulation Study

In this section we give the simulation study of the cases discussed above. We compare the results of the posterior p-value (7) using different sampling methods and the generalized fiducial method proposed by Ren et al. [18]. As we can see from the simulations, the posterior p-value we proposed largely improves the testing of homogeneity.

4.1. Normal Case

When

f_{1}

and

f_{2}

are normal distributions, we compare the results of three different tests. The first two are the posterior p-value we proposed, but using two-block Gibbs sampling and reject-ABC sampling method, respectively. The last one is the generalized fiducial method proposed by Ren et al. [18]. In the following tables, the first two are denoted by “

T_{G}

” and “

T_{R}

”, while the last is denoted by “G”. We fix

f_{1}

N (0, 1)

while

f_{2}

is set to be

N (0, 1)

N (1, 1)

N (0, 1 . 5^{2})

and

N (1, 1 . 5^{2})

. For each

f_{1}

and

f_{2}

we consider

λ = 0.3, 0.5, 0.7

and different sample sizes for

n_{1}, n_{2}

and

n_{3}

. We simulate

N = 10000

repetitions for each case. For the Gibbs sampling, we accept 3000 samples after burning in the first 2000. For the reject-ABC sampling method, we first calculate the estimate of

λ

and accept 4000 parameters with

ε

set to

\sqrt{n_{3}} / 2

. Then we calculate the posterior p-value using the samples. We set the significance level to

a l p h a = 0.05

and reject the null hypothesis when the posterior p-value is below

α

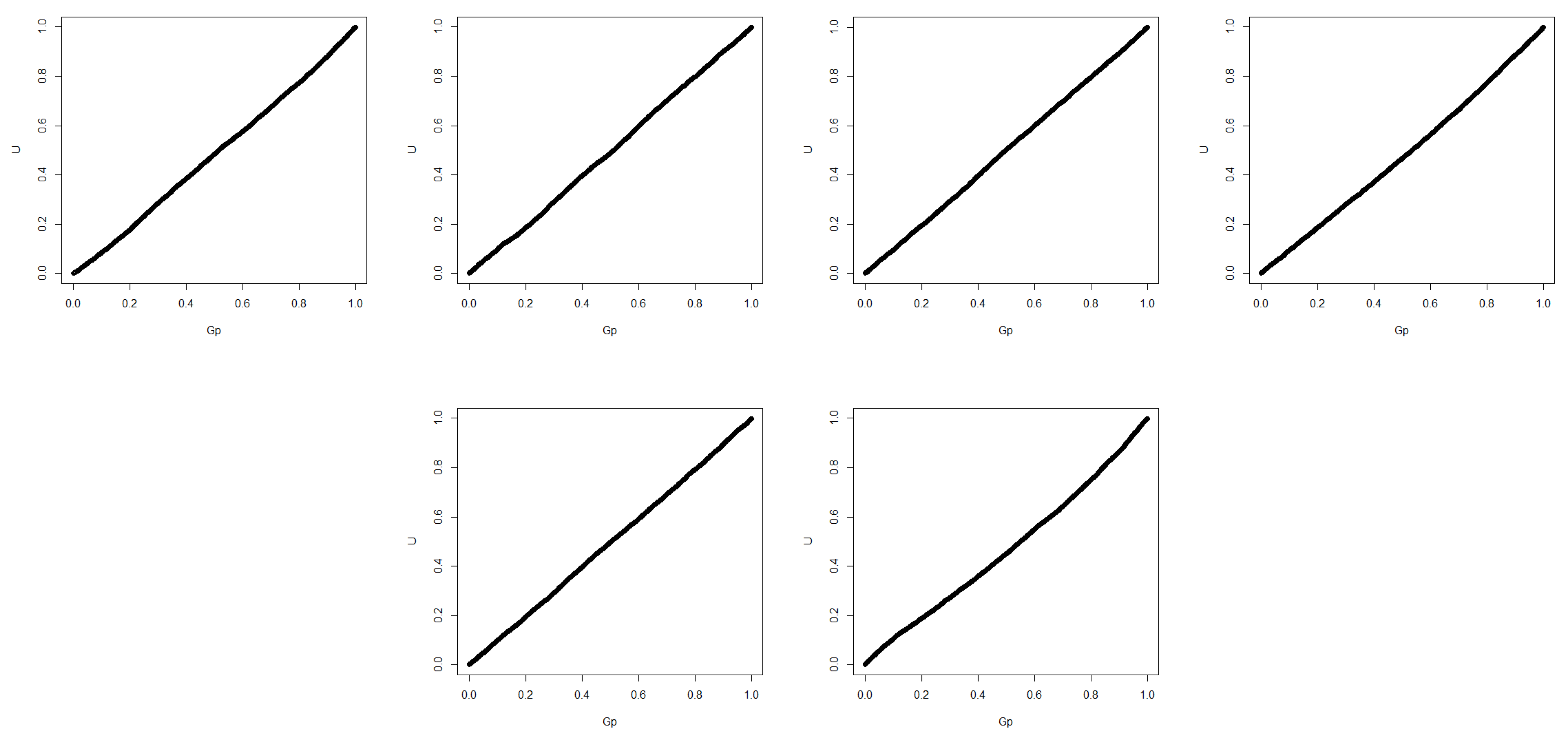
. The results are shown in Table 2, Table 3, Table 4 and Table 5. We further give the QQ-plot of

T_{R}

in Figure 1, which indicates the correctness of Theorem 2. The first row are the cases of

(n_{1}, n_{2}, n_{3})

(10, 10, 10)

(20, 20, 20)

and

(30, 30, 30)

, while the second row are the cases of

(10, 20, 30)

(30, 20, 10)

and

(15, 25, 150)

We can see from the results that the posterior p-value largely improves the testing of homogeneity in normal cases. The Type-I error is controlled as well as the generalized fiducial methods. Moreover, our method significantly improves the power of testing homogeneity, especially when

σ

is different. The reject-ABC sampling method has the advantage of lower computational cost, comparing with the two-block Gibbs sampling method. However, the power of using reject-ABC sampling method is smaller than using two-block Gibbs sampling when

n_{3}

is much larger than

n_{1}

and

n_{2}

. Thus, we can use reject-ABC sampling method when the sample size is small or moderate and two-block Gibbs sampling when the sample size is large.

4.2. General Case

For general case we assume that

f_{1}

and

f_{2}

are logistic distributions. The location and scale parameters of

f_{1}

and

f_{2}

are set the same as that of the normal case. We simulate 10000 repetitions for each sample size. We propose three methods in this simulation. The first two are the generalized fiducial method proposed by Ren et al. [18] and our posterior p-value using two-blocks Gibbs sampling. They are denoted by “G” and “

T_{G}

” as last simulation. The last one is the posterior p-value using M-H algorithm, which is denoted by “

T_{M}

”. First we calculate the MLE of

λ

using the EM algorithm. Then we propose the Metropolis-Hastings algorithm to obtain 12000 samples after first burn-in 8000 ones. To avoid the dependency between the samples, we choose the first one in every three samples, which leaves us 4000 samples. Then we use these samples to calculate the posterior p-value. The algorithm is natural and seems to be feasible. However, from the Table 6 we can see that with this sampling method the results are rather conservative. Given the significance level

α = 0.05

, the type-I error of

T_{M}

is always much more smaller than 0.05, which makes the power of

T_{M}

also smaller than the rest two when

f_{1} \neq f_{2}

. However, We find that the two-block Gibbs sampling method can successfully solve the problem. It can be seen that the type-I error of

“ T_{G}^{″}

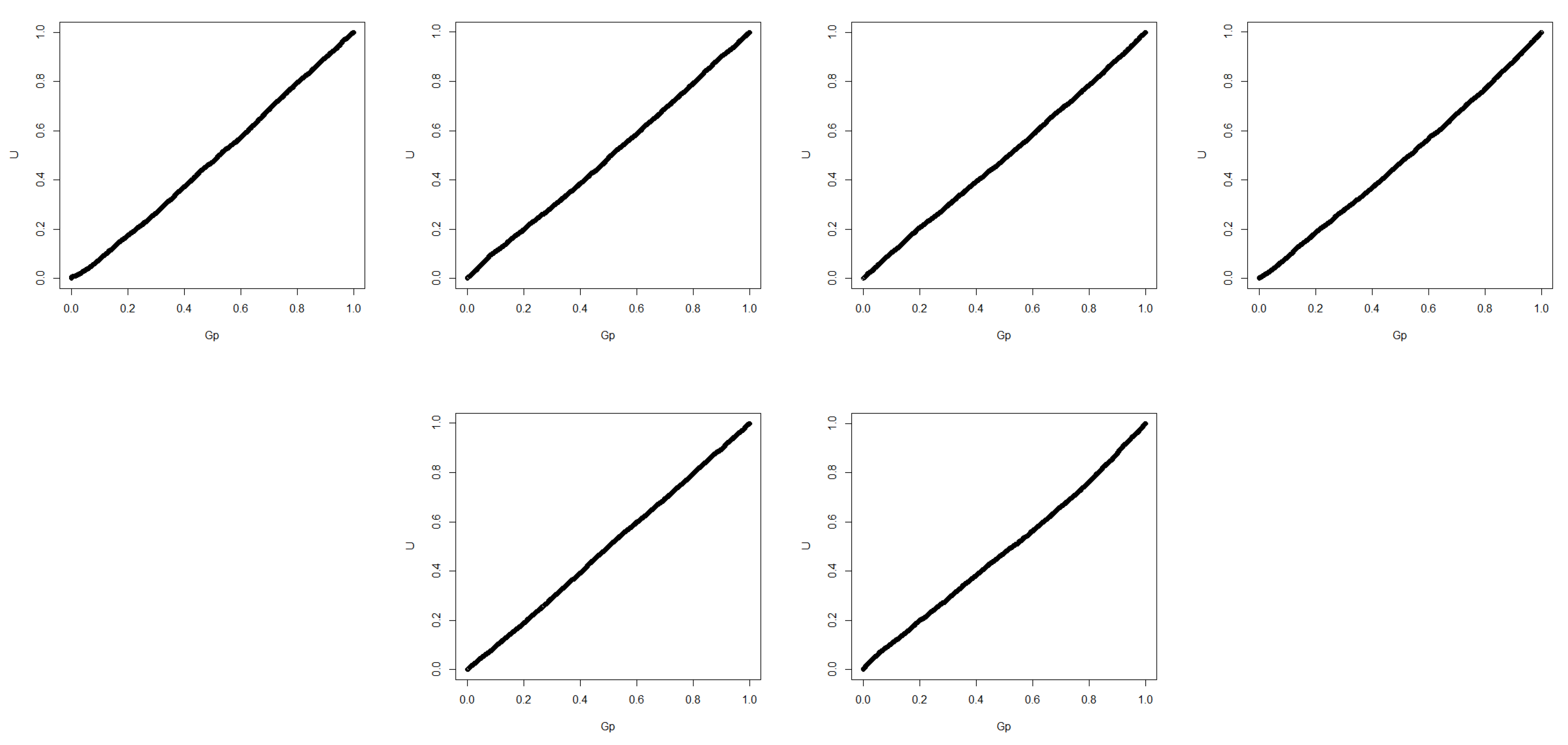
can be controlled well while the power is largerly improved, compares with the genralized fiducial method. The results are shown in Table 7, Table 8 and Table 9. We also give the QQ-plot of

“ T_{G}^{″}

in Figure 2.

5. Conclusions

In this paper, we propose a new posterior p-value for testing the homogeneity of the three-sample problem. We define the regular location-scale family and assume that both

f_{1}

and

f_{2}

are in the same family. Then testing the homogeneity is equivalent to testing the equality of the location and scale parameters. We use the Bayes’ theorem to obtain the posterior distribution of the parameters and propose the Bernstein-von Mises theorem for multiple samples. Then we propose the posterior p-value for testing the equality of the parameters. To sample from the posterior distribution, we compare different sampling methods. The simulation studies illustrate that reject-ABC sampling method may be a good choice for the normal case while the two-block Gibbs sampling is better for the general ones. It should be noticed that we transform the hypotheses of homogeneity to the hypotheses (6). Then with different matrix

A

, we can generate our method to a variety of hypotheses.

Author Contributions

Conceptualization, X.X.; methodology, X.X.; software, Y.W.; validation, Y.W. and X.X.; formal analysis, Y.W. and X.X.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W.; visualization, Y.W.; supervision, X.X.; project administration, X.X.; funding acquisition, X.X. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China under Grant No.11471035.

Institutional Review Board Statement

The study did not require ethical approval.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The author is very grateful to the referees and to the assistant editor for their kind and professional remarks.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Appendix A

Proof of lemma 1.

(1) First we show that

lim_{x \to - \infty} f (x) = lim_{x \to + \infty} f (x) = 0 .

(A1)

By the third condition in Definition 1, there exists a

M > 0

such that when

| x | > M

x^{2} | f^{'} (x) | < 1

. Let

{x_{n}, n = 1, 2, \dots}

be a sequence satisfies

lim_{n \to \infty} x_{n} = - \infty

and let

a_{n} = f (x_{n})

. Then for sufficiently large m and n such that

| x_{n} | > M

and

| x_{m} | > M

, we have

| a_{m} - a_{n} | = | f (x_{m}) - f (x_{n}) | = | \int_{x_{m}}^{x_{n}} f^{'} (x) d x | \leq | \int_{x_{n}}^{x_{m}} \frac{1}{x^{2}} d x | = | \frac{1}{x_{m}} - \frac{1}{x_{n}} | .

This indicates that when

m, n \to \infty

| a_{m} - a_{n} | \to 0

. Thus

{a_{n}, n = 1, 2, \dots}

is a Cauchy sequence, which must be convergence. Since

{x_{n}, n = 1, 2, \dots}

is an arbitrary sequence, then the limit

lim_{x \to - \infty} f (x)

exists. Notice that

f (x)

is a continuous density function, so

lim_{x \to - \infty} f (x) = 0 .

Similarly can we show that

lim_{x \to + \infty} f (x) = 0 .

By condition (3) in Definition 1, for arbitrary

ε > 0

, there exists a number B such that when

| x | > B

x^{2} | f^{'} (x) | < ε

. Then by (A1) we have

| x f (x) | = | x \int_{- \infty}^{x} f^{'} (t) d t | \leq | x | \int_{- \infty}^{x} | f^{'} (t) | d t \leq | x | \int_{- \infty}^{x} \frac{ε}{t^{2}} d t = ε .

This means that

lim_{x \to + \infty} x f (x) = 0

. In the same way can we obtain

lim_{x \to - \infty} x f (x) = 0

(2) From (A1) we can get

\int_{- \infty}^{\infty} f^{'} (x) d x = f (x) |_{- \infty}^{\infty} = 0 .

(3) As we can see

\int_{- \infty}^{\infty} x f^{'} (x) d x = x f (x) |_{- \infty}^{\infty} - \int_{- \infty}^{\infty} f (x) d x .

Then by the lemma we just proved and the fact that

f (x)

is a density function,

\int_{- \infty}^{\infty} x f^{'} (x) d x = - 1 .

(A2)

(4) Since

lim_{x \to - \infty} f^{'} (x) = lim_{x \to + \infty} f (x) = 0 .

Then it is easy to get

\int_{- \infty}^{\infty} f^{″} (x) d x = f^{'} (x) |_{- \infty}^{\infty} = 0 .

(5)

lim_{x \to - \infty} x f^{'} (x) = lim_{x \to + \infty} x f^{'} (x) = 0

\int_{- \infty}^{+ \infty} x f^{″} (x) d x = x f^{'} (x) |_{- \infty}^{\infty} - \int_{- \infty}^{\infty} f^{'} (x) d x = 0 - f (x) |_{- \infty}^{\infty}

Then by (A1)

\int_{- \infty}^{\infty} x f^{″} (x) d x = 0 .

(6)

\int_{- \infty}^{\infty} x^{2} f^{″} (x) d x = x^{2} f^{'} (x) |_{- \infty}^{\infty} - \int_{- \infty}^{\infty} 2 x f^{'} (x) d x = - 2 \int_{- \infty}^{\infty} x f^{'} (x) d x

Then by (A2), we have

\int_{- \infty}^{\infty} x^{2} f^{″} (x) d x = 2

□

Proof of Proposition 1.

(1) The log likelihood function

l (ξ, x)

l (ξ, x) = log f (x, ξ) = - log σ + log f (\frac{x - μ}{σ}) .

Then we can get the derivatives as below

\begin{matrix} \frac{\partial l (ξ, x)}{\partial μ} & = - \frac{1}{σ} f^{'} (\frac{x - μ}{σ}) / f (\frac{x - μ}{σ}) \\ \frac{\partial l (ξ, x)}{\partial σ} & = - \frac{1}{σ} - \frac{1}{σ} \frac{x - μ}{σ} f^{'} (\frac{x - μ}{σ}) / f (\frac{x - μ}{σ}) \end{matrix}

Using the second term in Lemma 1, we can get the expectation of the first derivatives

\begin{matrix} E_{ξ} [\frac{\partial l (ξ, x)}{\partial μ}] & = - \frac{1}{σ^{2}} \int_{- \infty}^{\infty} f^{'} (\frac{x - μ}{σ}) d x = - \frac{1}{σ} \int_{- \infty}^{\infty} f^{'} (y) d y = 0 \\ E_{ξ} [\frac{\partial l (ξ, x)}{\partial σ}] & = 0 . \end{matrix}

(2) The elements of the Fisher information matrix are computed as

\begin{matrix} E_{ξ} {[\frac{\partial l (ξ, x)}{\partial μ}]}^{2} & = \int_{- \infty}^{\infty} \frac{1}{σ^{2}} \frac{{[f^{'} (\frac{x - μ}{σ})]}^{2}}{f^{2} (\frac{x - μ}{σ})} \cdot \frac{1}{σ} f (\frac{x - μ}{σ}) d x \\ = \frac{1}{σ^{2}} \int_{- \infty}^{\infty} \frac{{[f^{'} (y)]}^{2}}{f (y)} d y = \frac{C_{11} (f)}{σ^{2}}, \end{matrix}

\begin{matrix} E_{ξ} [\frac{\partial l (ξ, x)}{\partial μ} \frac{\partial l (θ, x)}{\partial σ}] & = \int_{- \infty}^{\infty} \frac{1}{σ} \frac{f^{'} (\frac{x - μ}{σ})}{f (\frac{x - μ}{σ})} [\frac{1}{σ} + \frac{1}{σ} \frac{x - μ}{σ} \frac{f^{'} (\frac{x - μ}{σ})}{f (\frac{x - μ}{σ})}] \frac{1}{σ} f (\frac{x - μ}{σ}) d x \\ = \frac{1}{σ^{2}} \int_{- \infty}^{\infty} [f^{'} (y) + y {[f^{'} (y)]}^{2} / f (y)] d y \\ = \frac{1}{σ^{2}} \int_{- \infty}^{\infty} y \frac{{[f^{'} (y)]}^{2}}{f (y)} d y = \frac{C_{12} (f)}{σ^{2}}, \end{matrix}

\begin{matrix} E_{ξ} {[\frac{\partial l (ξ, x)}{\partial σ}]}^{2} & = \frac{1}{σ^{2}} \int_{- \infty}^{\infty} {[1 + \frac{x - μ}{σ} \frac{f^{'} (\frac{x - μ}{σ})}{f (\frac{x - μ}{σ})}]}^{2} \frac{1}{σ} f (\frac{x - μ}{σ}) d x \\ = \frac{1}{σ^{2}} \int_{- \infty}^{\infty} {[1 + y \frac{f^{'} (y)}{f (y)}]}^{2} f (y) d y \\ = \frac{1}{σ^{2}} [1 + 2 \int_{- \infty}^{\infty} y f^{'} (y) d y + \int_{- \infty}^{\infty} y^{2} \frac{{[f^{'} (y)]}^{2}}{f (y)} d y] \\ = \frac{1}{σ^{2}} [\int_{- \infty}^{\infty} y^{2} [\frac{f^{'} {(y)}^{2}}{f (y)} d y - 1] = \frac{C_{22} (f)}{σ^{2}} . \end{matrix}

So the equation holds. By the fourth condition in Definition 1, we can prove that

I_{f} (ξ) = \frac{1}{σ^{2}} C (f) < \infty .

Now we show that

C (f) > 0

. Suppose that

| C (f) | = 0

, then there exists a nonzero vector

a = {(a_{1}, a_{2})}^{⊤}

such that

a^{⊤} C a = 0

, which also means that

a^{⊤} \frac{\partial l (ξ, x)}{\partial θ} |_{ξ = {(0, 1)}^{⊤}} = 0, a . e . f (x) .

Since

f (x) > 0

, we have

{a^{⊤} \frac{\partial l (ξ, x)}{\partial θ}|}_{ξ = {(0, 1)}^{⊤}} = - a_{1} \frac{f^{'} (x)}{f (x)} + a_{2} (- 1 - x \frac{f^{'} (x)}{f (x)}) = 0, a . e . L

where L is the Lebesgue measure. Because

a

is nonzero, so

a_{2} \neq 0

, then

(x + b) \frac{f^{'} (x)}{f (x)} + 1 = 0,

where

b = a_{1} / a_{2}

. When

x > - b

\begin{matrix} {(log f (x))}^{'} = \frac{f^{'} (x)}{f (x)} = - \frac{1}{x + b}, \\ log f (x) = - ln (x + b) + D, \end{matrix}

where D is a constant. Then

f (x) = e^{D} / (x + b)

, this is contradict to the first equation in Lemma 1. Thus the assumption of

| C (f) | = 0

is not true, then

I (θ) > 0

. (3) We first calculate the second derivatives of the parameters.

\begin{matrix} \frac{\partial^{2} l (ξ, x)}{\partial μ^{2}} = \frac{1}{σ^{2}} [\frac{f^{″} (\frac{x - μ}{σ})}{f (\frac{x - μ}{σ})} - \frac{{(f^{'} (\frac{x - μ}{σ}))}^{2}}{f^{2} (\frac{x - μ}{σ})}], \\ \frac{\partial^{2} l (ξ, x)}{\partial μ \partial σ} = \frac{1}{σ^{2}} [\frac{f^{'} (\frac{x - μ}{σ})}{f (\frac{x - μ}{σ})} + \frac{x - μ}{σ} \frac{f^{″} (\frac{x - μ}{σ})}{f (\frac{x - μ}{σ})} - \frac{x - μ}{σ} \frac{{(f^{'} (\frac{x - μ}{σ}))}^{2}}{f^{2} (\frac{x - μ}{σ})}], \\ \frac{\partial^{2} l (ξ, x)}{\partial σ^{2}} = \frac{1}{σ^{2}} + \frac{2 (x - μ)}{σ^{3}} \cdot \frac{f^{'} (\frac{x - μ}{σ})}{f (\frac{x - μ}{σ})} + \frac{{(x - μ)}^{2}}{σ^{4}} \frac{f^{″} (\frac{x - μ}{σ})}{f (\frac{x - μ}{σ})} - \frac{{(x - μ)}^{2}}{σ^{4}} \frac{{(f^{'} (\frac{x - μ}{σ}))}^{2}}{{(f (\frac{x - μ}{σ}))}^{2}} . \end{matrix}

Then by Lemma 1, we have

\begin{matrix} E_{ξ} [\frac{\partial^{2} l (ξ, x)}{\partial μ^{2}}] = - \frac{C_{11} (f)}{σ^{2}}, \\ E_{ξ} [\frac{\partial^{2} l (ξ, x)}{\partial μ \partial σ}] = - \frac{C_{12} (f)}{σ^{2}}, \\ E_{ξ} [\frac{\partial^{2} l (ξ, x)}{\partial σ^{2}}] = - \frac{C_{22} (f)}{σ^{2}} . \end{matrix}

□

Proof of Proposition 2.

(1) First we calculate the derivatives as follow.

\begin{matrix} \frac{\partial log g (x, θ)}{\partial μ_{1}} = - \frac{λ_{0}}{σ_{1}^{2}} f^{'} (\frac{x - μ_{1}}{σ_{1}}) / g (x; θ); \\ \frac{\partial log g (x, θ)}{\partial μ_{2}} = - \frac{1 - λ_{0}}{σ_{2}^{2}} f^{'} (\frac{x - μ_{2}}{σ_{2}}) / g (x; θ); \\ \frac{\partial log g (x, θ)}{\partial σ_{1}} = [- \frac{λ_{0}}{σ_{1}^{2}} f (\frac{x - μ_{1}}{σ_{1}}) - \frac{λ_{0}}{σ_{1}} \frac{x - μ_{1}}{σ_{1}^{2}} f^{'} (\frac{x - μ_{1}}{σ_{1}})] / g (x; θ); \\ \frac{\partial log g (x, θ)}{\partial σ_{2}} = [- \frac{1 - λ_{0}}{σ_{2}^{2}} f (\frac{x - μ_{2}}{σ_{2}}) - \frac{1 - λ_{0}}{σ_{2}} \frac{x - μ_{2}}{σ_{2}^{2}} f^{'} (\frac{x - μ_{2}}{σ_{2}})] / g (x; θ) . \end{matrix}

Then by the second equation in Lemma 1, we have

E_{θ} [\frac{\partial log g (x; θ)}{\partial μ_{1}}] = - \frac{λ_{0}}{σ_{1}^{2}} \int_{- \infty}^{\infty} f^{'} (\frac{x - μ_{1}}{σ}) d x = - \frac{λ_{0}}{σ} \int_{- \infty}^{\infty} f (y) d y = 0

By Lemma 1(3),

\begin{matrix} E_{θ} [\frac{\partial log g (x; θ)}{\partial σ_{1}}] & = \int_{- \infty}^{+ \infty} [- \frac{λ_{0}}{σ_{1}^{2}} f (\frac{x - μ_{1}}{σ_{1}}) - \frac{λ_{0}}{σ_{1}} \frac{x - μ_{1}}{σ_{1}^{2}} f^{'} (\frac{x - μ_{1}}{σ_{1}})] d x \\ = \int_{- \infty}^{\infty} [- \frac{λ_{0}}{σ_{1}} f (y) - \frac{λ_{0}}{σ_{1}} y f (y)] d y \\ = - \frac{λ_{0}}{σ_{1}} [1 + \int_{- \infty}^{\infty} y f (y) d y] = 0 . \end{matrix}

Similarly can we prove that

E_{θ} [\frac{\partial log g (x) θ)}{\partial σ_{2}}] = 0 .

(2) First we calculate the derivatives on the location parameter as

\begin{matrix} E_{θ} {[\frac{\partial log g (x; θ)}{\partial μ_{1}}]}^{2} & = \int_{- \infty}^{\infty} \frac{λ_{0}^{2}}{σ_{1}^{4}} {[f^{'} (\frac{x - μ_{1}}{σ_{1}})]}^{2} / g (x; θ) d x \\ \leq \int_{- \infty}^{\infty} \frac{λ_{0}^{4}}{σ_{1}^{2}} {[f^{'} (\frac{x - μ_{1}}{σ_{1}})]}^{2} / [\frac{λ_{0}}{σ_{1}} f (\frac{x - μ_{1}}{σ_{1}})] d x \\ = \frac{λ_{0}}{σ_{1}^{2}} \int_{- \infty}^{\infty} \frac{{(f^{'} (y))}^{2}}{f (y)} d y \\ = \frac{λ_{0}}{σ_{1}^{2}} C_{11} (f) < \infty . \end{matrix}

Similarly we have

E_{θ} {[\frac{\partial log g (x; θ)}{\partial μ_{2}}]}^{2} \leq \frac{1 - λ_{0}}{σ_{2}^{2}} C_{11} (f) < \infty

Then as with the scale parameter, we have

\begin{matrix} E_{θ} {[\frac{\partial log g (x; θ)}{\partial σ_{1}}]}^{2} & = \frac{λ_{0}^{2}}{σ_{1}^{2}} \int_{- \infty}^{\infty} {[\frac{1}{σ_{1}} f (\frac{x - μ_{1}}{σ_{1}}) + \frac{x - μ_{1}}{σ_{1}^{2}} f^{'} (\frac{x - μ_{1}}{σ_{1}})]}^{2} / g (x; θ) d x \\ \leq \frac{λ_{0}^{2}}{σ_{1}^{2}} \int_{- \infty}^{\infty} {[\frac{1}{σ_{1}} f (\frac{x - μ_{1}}{σ_{1}}) + \frac{x - μ_{1}}{σ_{1}^{2}} f^{'} (\frac{x - μ_{1}}{σ_{1}})]}^{2} / \frac{λ_{0}}{σ_{1}} f (\frac{x - μ_{1}}{σ_{1}}) d x \\ = \frac{λ_{0}}{σ_{1}^{2}} \int_{- \infty}^{\infty} {[1 + y \frac{{(f^{'} (y))}^{2}}{f (y)}]}^{2} f (y) d y \\ = \frac{λ_{0}}{σ_{1}^{2}} C_{22} (f) < \infty \end{matrix}

E_{θ} {[\frac{\partial log g (x; θ)}{\partial σ_{2}}]}^{2} = \frac{1 - λ_{0}}{σ_{2}^{2}} C_{22} (f) < \infty .

Then

I (θ) < \infty

(3)

\frac{\partial^{2} log g (x; θ)}{\partial μ_{1}^{2}} = \frac{\frac{λ_{0}}{σ_{1}^{3}} f^{''} (\frac{x - μ_{1}}{σ_{1}})}{g (x; θ)} - \frac{\frac{λ_{0}^{2}}{σ_{1}^{4}} {(f^{'} (\frac{x - μ_{1}}{σ_{1}}))}^{2}}{{(g (x; θ))}^{2}}

Then by the fourth equation in Lemma 1 can we get

E_{θ} \frac{\partial^{2} log g (x; θ)}{\partial μ_{1}^{2}} = - E_{θ} \frac{\frac{λ_{0}^{2}}{σ_{1}^{4}} {(f^{'} (\frac{x - μ_{1}}{σ_{1}}))}^{2}}{g {(x; θ)}^{2}} = - E_{θ} {(\frac{\partial log g (x, θ)}{\partial μ_{1}})}^{2}

The same procedure can be applied to the rest 9 equations to show that the conclusion holds. □

Proof of Theorem 1.

First we give the Bernstein-von Mises theorem for multiple samples, see the Theorem 2 in Long and Xu [27]. Besides the Assumption 1 to 4 in the context, there are some other assumptions below

Assumption 5.

For all

i = 1, 2, \dots, k

, the density function

f_{i} (x | θ)

of the population

G_{i}

satisfies the following conditions:

(a) The parameter space of θ contains an open subset

ω \subset Ω

, in which the true value is included.

(b) The set

A_{i} = {x : f_{i} (x | θ) > 0}

is independent of θ.

x \in A_{i}

f_{i} (x | θ)

as a function of θ admits continous second derivatives

\frac{\partial^{2}}{\partial θ_{j} \partial θ_{h}} f_{i} (x | θ)

j, h = 1, 2, \dots, d

, for all

θ \in ω

(d) Denote by

I^{(i)} (θ)

the Fisher’s information matrix of

f_{i} (x | θ)

. The first and second derivatives of the logarithm of

f_{i} (x | θ)

satisfy the equations

\begin{matrix} E_{θ} [\frac{\partial}{\partial θ_{j}} l o g f_{i} (x | θ)] = 0, j = 1, \dots, d, \\ I_{j h}^{(i)} (θ) = E_{θ} [\frac{\partial}{\partial θ_{j}} l o g f_{i} (x | θ) \cdot \frac{\partial}{\partial θ_{h}} l o g f_{i} (x | θ)] \\ = E_{θ} [- \frac{\partial^{2}}{\partial θ_{j} \partial θ_{h}} l o g f_{i} (x | θ)], j, h = 1, 2, \dots, d . \end{matrix}

(e) Suppose the sample size

n_{i}

G_{i}

satisfies that when

n \to \infty

n_{i} / n \to r_{i} \in (0, 1)

. Let

I (θ) = \sum_{i = 1}^{k} r_{i} I^{(i)} (θ) .

We assume that all entries of

I (θ)

are finite, and

I (θ)

is positive definite.

Then, by Definition 1, Proposition 1 and 2 and Assumption A1- A5, the Theorem 1 holds. It should be noticed that since the prior is

π (θ) = 1 / σ_{1} σ_{2}

, its second moment doesn’t exist. So we draw

k_{0}

samples from the first two density functions and combine them with

π (θ)

, thus we get the new prior. This is a trick in the research of big data. □

Proof of Theorem 2.

First we give two conclusions

\sqrt{n} (θ_{B} - T_{n}) \overset{P}{\to} 0, n Σ_{B} \overset{P}{\to} I^{- 1} (θ_{0}) .

Let

E_{p} g (θ)

be the expectation of

g (θ)

under distribution P. Then

\sqrt{n} (θ_{B} - T_{n}) = \sqrt{n} (E_{π} θ - T_{n}) = E_{π} [\sqrt{n} (θ - T_{n})] = E_{π^{*}} θ - E_{N (0, I^{- 1} (θ_{0}))} θ .

\begin{matrix} ∥ \sqrt{n} (θ_{B} - T_{n}) ∥ & = ∥ E_{π^{*}} θ - E_{N (0, I^{- 1} (θ_{0}))} θ ∥ \\ \leq \int ∥ θ ∥ | π^{*} (θ | x) - {(2 π)}^{- \frac{4}{2}} {| I (θ_{0}) |}^{\frac{1}{2}} e^{- θ^{⊤} I (θ_{0}) θ} | d θ . \end{matrix}

By the Theorem 1, the above equation converges in probability to 0.

\begin{matrix} n Σ_{B} & = n E_{π} (θ - θ_{B}) {(θ - θ_{B})}^{⊤} \\ = n E_{π} (θ - T_{n} + T_{n} - θ_{b}) {(θ - T_{n} + T_{n} - θ_{b})}^{⊤} \\ = n E_{π} (θ - T_{n}) {(θ - T_{n})}^{⊤} + n E_{π} (θ - T_{n}) {(T_{n} - θ_{B})}^{⊤} \\ + n (T_{n} - θ_{B}) E_{π} (θ - T_{n}) + n (T_{n} - θ_{B}) (T_{n} - θ_{B}) \\ = E_{π^{*}} θ θ^{⊤} + E_{π^{*}} θ \sqrt{n} {(T_{n} - θ_{B})}^{⊤} + \sqrt{n} (T_{n} - θ_{B}) E_{π^{*}} θ + [\sqrt{n} (T_{n} - θ_{B})] {[\sqrt{n} (T_{n} - θ_{B})]}^{⊤} . \end{matrix}

From the conclusion above we have

\sqrt{n} (T_{n} - θ_{B}) \overset{P}{⟶} 0, E_{π^{*}} θ \overset{P}{⟶} 0,

then by Theorem 1,

E_{π^{*}} (θ θ^{⊤}) \to I^{- 1} (θ_{0}) .

thus,

n Σ_{B} \overset{P}{⟶} I^{- 1} (θ_{0}) .

Then we can get

\begin{matrix} {(θ - θ_{B})}^{⊤} A^{⊤} {(A Σ_{B} A^{⊤})}^{- 1} A (θ - θ_{B}) \\ = & {[\sqrt{n} (θ - θ_{B})]}^{⊤} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A [\sqrt{n} (θ - θ_{B})] \\ = & {[\sqrt{n} (θ - T_{n}) - \sqrt{n} (θ_{B} - T_{n})]}^{⊤} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A [\sqrt{n} (θ - T_{n}) - λ_{n} (θ_{B} - T_{n})) \\ = & t^{⊤} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A t - 2 t^{⊤} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A [\sqrt{n} (θ_{B} - T_{n})] \\ + {[\sqrt{n} (θ_{B} - T_{n})]}^{⊤} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A [\sqrt{n} (θ_{B} - T_{n})] . \end{matrix}

The expression above should have the same asymptotic distribution as

t^{⊤} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A t

, where

t \sim N_{p} (0, I^{- 1} (θ_{0}))

and

A t \sim N_{k} (0, A I^{- 1} (θ_{0}) A^{⊤})

. From the conclusion above we have

A (n Σ_{B}) A^{⊤} \overset{P}{\to} A I^{- 1} (θ_{0}) A^{⊤}

, thus we can get

t^{⊤} A^{⊤} {[A (n Σ B) A^{⊤}]}^{- 1} A t ⟶ χ^{2} (k),

where k is the degree of freedom and also the rows of matrix A. Thus

{(θ - θ_{B})}^{⊤} A^{⊤} {(A Σ_{B} A^{⊤})}^{- 1} A (θ - θ_{B}) \overset{d}{\to} χ^{2} (k)

Under the null hypothesis,

\begin{matrix} {(b - A θ_{B})}^{⊤} {(A Σ_{B} A^{⊤})}^{- 1} (b - A θ_{B}) \\ = & {[b - A T_{n} - A (θ B - T_{n})]}^{- 1} {(A Σ_{B} A^{⊤})}^{- 1} {[b - A T_{n} - A (θ_{B} - T_{n})]}^{- 1} \\ = & {(b - A T_{n})}^{⊤} {(A Σ_{B} A^{⊤})}^{- 1} (b - A T_{n}) + {(θ_{B} - T_{n})}^{⊤} A^{⊤} {(A Σ_{B} A^{⊤})}^{- 1} A (θ_{B} - T_{n}) \\ - 2 {(b - A T_{n})}^{⊤} {(A Σ_{B} A)}^{- 1} A (θ_{B} - T_{n}) . \end{matrix}

Since

b = A θ_{0}

, the expression above is equalivalent to

\begin{matrix} {(\frac{1}{n} I^{- 1} (θ_{0}) l^{'} (θ_{0}))}^{⊤} A^{⊤} {(A Σ_{B} A^{⊤})}^{- 1} A (\frac{1}{n} I^{''} (θ_{0}) l^{'} (θ_{0})) \\ + & {[\sqrt{n} (θ_{B} - T_{n})]}^{- 1} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A [\sqrt{n} (θ_{B} - T_{n})] \\ + & 2 {(\frac{1}{\sqrt{n}} I^{- 1} (θ_{0}) ℓ^{1} (θ_{0}))}^{⊤} A^{⊤} {[A (n Σ_{B}) A]}^{- 1} A [\sqrt{n} (θ_{B} - T_{n})] . \end{matrix}

The first term can be rewritten as

{(\frac{1}{\sqrt{n}} I^{- 1} (θ_{0}) l^{'} (θ_{0}))}^{⊤} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A (\frac{1}{\sqrt{n}} I^{- 1} (θ_{0}) l^{'} (θ_{0})) .

This asypototically follows the

χ^{2} (k)

distribution. The second and third terms tend to 0 in probability. Thus

p (x) - F_{k} [1 - {(\frac{1}{\sqrt{n}} I^{- 1} (θ_{0}) l^{'} (θ_{0}))}^{⊤} A^{⊤} {[A (n Σ_{B}) A^{⊤}]}^{- 1} A (\frac{1}{n} I^{- 1} (θ_{0}) l^{'} (θ_{0}))] \overset{P}{\to} 0 .

Where

F_{k}

is the cumulative distribution function of

χ^{2} (k)

. Then by the asymptotic property, we have

p (x) \overset{d}{⟶} U (0, 1) .

□

References

Hosmer, D.W. A Comparison of Iterative Maximum Likelihood Estimates of the Parameters of a Mixture of Two Normal Distributions Under Three Different Types of Sample. Biometrics 1973, 29, 761–770. [Google Scholar] [CrossRef]
Murray, G.D.; Titterington, D.M. Estimation Problems with Data from a Mixture. Journal of the Royal Statistical Society. Series C (Applied Statistics) 1978, 27, 325–334. [Google Scholar] [CrossRef]
Anderson, J.A. Multivariate logistic compounds. Biometrika 1979, 66, 17–26. [Google Scholar] [CrossRef]
Qin, J. Empirical likelihood ratio based confidence intervals for mixture proportions. The Annals of Statistics 1999, 27, 1368–1384. [Google Scholar] [CrossRef]
Owen, A. Empirical Likelihood Ratio Confidence Regions. The Annals of Statistics 1990, 18. [Google Scholar] [CrossRef]
Zou, F.; Fine, J.P.; Yandell, B.S. On empirical likelihood for a semiparametric mixture model. Biometrika 2002, 89, 61–75. [Google Scholar] [CrossRef]
Zhang, B. Assessing goodness-of-fit of generalized logit models based on case-control data. Journal of Multivariate Analysis 2002, 82, 17–38. [Google Scholar] [CrossRef]
Inagaki, K.; Komaki, F. A modification of profile empirical likelihood for the exponential-tilt model. Statistics and Probability Letters 2010, 80, 997–1004. [Google Scholar] [CrossRef]
Tan, Z. A note on profile likelihood for exponential tilt mixture models. Biometrika 2009, 96, 229–236. [Google Scholar] [CrossRef]
Liang, K.Y.; Rathouz, P.J. Hypothesis Testing Under Mixture Models: Application to Genetic Linkage Analysis. Biometrics 1999, 55, 65–74. [Google Scholar] [CrossRef]
Lemdani, M.; Pons, O. Likelihood Ratio Tests in Contamination Models. Bernoulli 1999, 5, 705. [Google Scholar] [CrossRef]
Chen, H.; Chen, J.; Kalbfleisch, J.D. A Modified Likelihood Ratio Test for Homogeneity in Finite Mixture Models. Journal of the Royal Statistical Society Series B: Statistical Methodology 2002, 63, 19–29. [Google Scholar] [CrossRef]
Chen, H.; Chen, J.; Kalbfleisch, J.D. Testing for a Finite Mixture Model with Two Components. Journal of the Royal Statistical Society Series B: Statistical Methodology 2003, 66, 95–115. [Google Scholar] [CrossRef]
Chen, J.; Li, P. Hypothesis test for normal mixture models: The EM approach. The Annals of Statistics 2009, 37. [Google Scholar] [CrossRef]
Li, P.; Liu, Y.; Qin, J. Semiparametric Inference in a Genetic Mixture Model. Journal of the American Statistical Association 2017, 112, 1250–1260. [Google Scholar] [CrossRef]
Li, S.; Chen, J.; Guo, J.; Jing, B.Y.; Tsang, S.Y.; Xue, H. Likelihood Ratio Test for Multi-Sample Mixture Model and Its Application to Genetic Imprinting. Journal of the American Statistical Association 2015, 110, 867–877. [Google Scholar] [CrossRef]
Liu, G.; Li, P.; Liu, Y.; Pu, X. Hypothesis testing for quantitative trait locus effects in both location and scale in genetic backcross studies. Scandinavian Journal of Statistics 2020, 47, 1064–1089. [Google Scholar] [CrossRef]
Ren, P.; Liu, G.; Pu, X. Generalized fiducial methods for testing the homogeneity of a three-sample problem with a mixture structure. Journal of Applied Statistics 2023, 50, 1094–1114. [Google Scholar] [CrossRef] [PubMed]
Hannig, J.; Iyer, H.; Lai, R.C.S.; Lee, T.C.M. Generalized Fiducial Inference: A Review and New Results. Journal of the American Statistical Association 2016, 111, 1346–1361. [Google Scholar] [CrossRef]
Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. Roy. Statist. Soc. Ser. B 1977, 39, 1–38. [Google Scholar] [CrossRef]
McLachlan, G.J.; Krishnan, T. The EM algorithm and extensions; Wiley Series in Probability and Statistics: Applied Probability and Statistics, John Wiley & Sons, Inc., New York, 1997. [Google Scholar]
Fisher, R.A. The fiducial argument in statistical inference. Annals of Eugenics 1935, 6, 391–398. [Google Scholar] [CrossRef]
Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. The Journal of Chemical Physics 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
Hastings, W.K. Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
Owen, A.B.; Glynn, P.W. (Eds.) Monte Carlo and Quasi-Monte Carlo Methods; Springer International Publishing, 2018.
Karunamuni, R.; Wu, J. Minimum Hellinger distance estimation in a nonparametric mixture model. Journal of Statistical Planning and Inference 2009, 139, 1118–1133. [Google Scholar] [CrossRef]
Long, Y.; Xu, X. Bayesian decision rules to classification problems. Aust. N. Z. J. Stat. 2021, 63, 394–415. [Google Scholar] [CrossRef]

Figure 1. The QQ-plot of the normal cases.

Figure 2. The QQ-plot of the logistic cases.

Table 1. Frequency distribution of the lengths in centimeters of 11 year old male and female halibut caught on Western Trip I, April

1957 .

Table 1. Frequency distribution of the lengths in centimeters of 11 year old male and female halibut caught on Western Trip I, April

1957 .

	75	80	85	90	95	100	105	110	115	120	125	130	135
Males	2	7	8	6	7	11	10	9	9	3	2	0	0
Females	0	1	0	0	4	2	7	18	22	29	28	13	10

Table 2. Type-I errors(%) of the three methods in normal cases.

$n_{1}, n_{2}, n_{3}$	G	$T_{G}$	$T_{R}$
$(10, 10, 10)$	$3.89$	$3.92$	$4.47$
$(20, 20, 20)$	$4.63$	$4.84$	4.72
$(30, 30, 30$ )	4.63	4.75	5.42
$(10, 20, 30)$	$4.36$	4.85	4.36
$(30, 20, 10)$	$4.46$	4.46	4.79
$(10, 10, 100)$	3.92	4.64	4.77
$(15, 25, 150)$	$4.64$	5.65	4.51

Table 3. Power comparison(%) of the cases when

f_{1} = N (0, 1)

and

f_{2} = N (1, 1)

Table 3. Power comparison(%) of the cases when

f_{1} = N (0, 1)

and

f_{2} = N (1, 1)

	0.3			0.5			0.7
	G	$T_{G}$	$T_{R}$	G	$T_{G}$	$T_{R}$	G	$T_{G}$	$T_{R}$
(10, 10, 10)	32.2	33.9	36.8	32.2	33.9	36.5	33.3	35.9	36.5
(20, 20, 20)	70.6	74.2	76.3	70.3	74.0	76.0	72.3	76.2	75.6
(30, 30, 30)	90.2	93.3	92.1	89.2	91.2	92.2	90.7	92.2	92.0
(10, 20, 30)	46.3	50.9	46.4	51.3	56.1	45.6	56.8	63.2	45.6
(30, 20, 10)	84.3	85.8	85.3	81.3	83.3	85.4	82.8	84.3	85.2
(10, 10, 100)	35.4	43.0	41.8	33.1	41.9	41.7	34.3	44.5	41.2
(15, 25, 150)	63.5	70.7	71.5	66.8	75.1	74.0	75.8	82.3	72.6

Table 4. Power comparison(%) of the cases when

f_{1} = N (0, 1)

and

f_{2} = N (0, 1 . 5^{2})

Table 4. Power comparison(%) of the cases when

f_{1} = N (0, 1)

and

f_{2} = N (0, 1 . 5^{2})

	0.3			0.5			0.7
	G	$T_{G}$	$T_{R}$	G	$T_{G}$	$T_{R}$	G	$T_{G}$	$T_{R}$
(10, 10, 10)	11.8	20.8	22.5	13.9	22.3	22.8	14.0	24.3	22.4
(20, 20, 20)	28.4	39.9	43.8	29.7	41.6	44.6	32.8	44.5	43.4
(30, 30, 30)	42.2	57.1	58.5	44.1	56.3	58.3	45.5	57.4	58.5
(10, 20, 30)	14.3	23.8	26.3	15.5	26.8	26.5	20.9	33.5	26.8
(30, 20, 10)	38.4	50.5	50.1	38.6	49.8	51.3	38.9	49.2	50.7
(10, 10, 100)	9.4	18.0	25.2	14.4	22.2	23.7	18.5	27.6	25.4
(15, 25, 150)	20.9	35.4	35.6	28.2	42.5	37.7	35.3	48.8	38.4

Table 5. Power comparison(%) of the cases when

f_{1} = N (0, 1)

and

f_{2} = N (1, 1 . 5^{2})

Table 5. Power comparison(%) of the cases when

f_{1} = N (0, 1)

and

f_{2} = N (1, 1 . 5^{2})

	0.3			0.5			0.7
	G	$T_{G}$	$T_{R}$	G	$T_{G}$	$T_{R}$	G	$T_{G}$	$T_{R}$
(10, 10, 10)	38.9	42.6	46.6	38.2	42.1	41.7	42.0	46.2	42.6
(20, 20, 20)	77.3	79.7	82.3	75.2	78.0	80.6	80.0	82.6	80.8
(30, 30, 30)	93.6	94.2	95.5	93.8	94.0	93.3	93.9	94.5	94.4
(10, 20, 30)	47.2	50.0	55.2	55.4	59.6	57.2	62.1	66.0	56.1
(30, 20, 10)	88.4	89.0	88.9	85.8	87.2	86.5	86.3	87.6	85.3
(10, 10, 100)	46.0	48.9	49.1	53.8	56.9	45.9	59.1	64.6	48.6
(15, 25, 150)	77.1	78.6	78.1	83.9	84.8	74.4	89.6	91.5	75.1

Table 6. Type-I errors(%) of the three methods in logistic cases.

$n_{1}, n_{2}, n_{3}$	G	$T_{G}$	$T_{M}$
$(10, 10, 10)$	$4.15$	$3.34$	$2.98$
$(20, 20, 20)$	$4.81$	$4.83$	2.81
$(10, 20, 30)$	$4.18$	3.85	2.67
$(30, 20, 10)$	$4.73$	4.61	2.31
$(30, 30, 30)$	4.72	4.92	3.41
$(10, 10, 100)$	4.16	4.92	2.58
$(15, 25, 150)$	$5.06$	5.96	2.91

Table 7. Power comparison(%) of the cases when

f_{1} = L o g i s (0, 1)

and

f_{2} = L o g i s (1, 1)

Table 7. Power comparison(%) of the cases when

f_{1} = L o g i s (0, 1)

and

f_{2} = L o g i s (1, 1)

	0.3			0.5			0.7
	G	$T_{G}$	$T_{M}$	G	$T_{G}$	$T_{M}$	G	$T_{G}$	$T_{M}$
(10, 10, 10)	12.2	12.0	13.2	12.6	13.3	14.5	13.2	13.0	13.7
(20, 20, 20)	29.4	30.3	26.2	28.3	29.9	26.4	28.9	30.2	26.0
(30, 30, 30)	43.2	45.4	36.6	43.1	45.2	35.9	43.9	46.5	37.3
(10, 20, 30)	17.5	18.1	15.1	19.3	20.2	16.9	22.2	23.2	18.7
(30, 20, 10)	35.4	36.6	31.8	33.9	35.8	32.4	33.5	35.1	30.4
(10, 10, 100)	13.8	17.8	12.7	13.8	17.1	11.8	13.9	16.6	11.9
(15, 25, 150)	24.4	29.3	20.1	25.3	30.0	22.7	30.9	38.1	24.1

Table 8. Power comparison(%) of the cases when

f_{1} = L o g i s (0, 1)

and

f_{2} = L o g i s (0, 1.5)

Table 8. Power comparison(%) of the cases when

f_{1} = L o g i s (0, 1)

and

f_{2} = L o g i s (0, 1.5)

	0.3			0.5			0.7
	G	$T_{G}$	$T_{M}$	G	$T_{G}$	$T_{M}$	G	$T_{G}$	$T_{M}$
(10, 10, 10)	10.3	13.5	16.2	10.5	14.7	16.3	11.2	15.9	15.9
(20, 20, 20)	20.8	32.4	23.6	21.7	33.3	23.7	23.0	33.4	24.1
(30, 30, 30)	32.4	44.7	33.3	33.8	44.9	33.2	34.9	46.2	34.1
(10, 20, 30)	9.6	15.3	12.1	11.1	18.0	15.2	14.2	21.9	17.9
(30, 20, 10)	27.4	37.1	21.9	27.1	36.7	22.4	27.1	36.3	22.3
(10, 10, 100)	8.9	14.8	10.6	10.2	16.3	12.2	12.7	18.4	16.8
(15, 25, 150)	15.1	26.2	20.6	21.1	32.0	20.7	24.2	35.6	22.0

Table 9. Power comparison(%) of the cases when

f_{1} = L o g i s (0, 1)

and

f_{2} = L o g i s (1, 1.5)

Table 9. Power comparison(%) of the cases when

f_{1} = L o g i s (0, 1)

and

f_{2} = L o g i s (1, 1.5)

	0.3			0.5			0.7
	G	$T_{G}$	$T_{M}$	G	$T_{G}$	$T_{M}$	G	$T_{G}$	$T_{M}$
(10, 10, 10)	17.4	17.9	18.1	18.3	21.7	18.8	18.5	22.6	19.6
(20, 20, 20)	43.7	49.4	36.3	43.7	49.3	36.2	45.2	51.3	37.7
(30, 30, 30)	62.9	67.3	58.1	62.2	67.2	57.9	63.6	68.4	59.6
(10, 20, 30)	20.6	24.2	21.3	24.1	29.4	26.2	30.1	35.8	35.8
(30, 20, 10)	52.7	57.0	37.6	51.7	55.9	39.7	51.5	56.0	38.8
(10, 10, 100)	19.9	24.1	18.7	23.1	27.3	19.8	23.5	30.2	19.7
(15, 25, 150)	36.7	43.1	40.4	44.6	51.5	40.7	51.0	57.8	40.1

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Posterior p-Value for Homogeneity Testing of the Three Sample Problem

Abstract

1. Introduction

2. Test Procedure

2.1. Regular Location-Scale Family

2.2. A Posterior p-Value

2.3. Sampling Method

2.3.1. Em Algorithm for λ

2.3.2. Normal Case

2.3.3. General Case

3. Real Data Example

4. Simulation Study

4.1. Normal Case

4.2. General Case

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe

2.3.1. Em Algorithm for $λ$