Prerpints.org logo
Preprint
Article

Experimental Study on Methane Diffusion Characteristics of Different Metamorphic Deformed Coals Based on Counter Diffusion Method

Altmetrics

Downloads

89

Views

13

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

20 August 2023

Posted:

22 August 2023

You are already at the latest version

Alerts
Abstract
The diffusion coefficient (D) is a key parameter characterizing gas transport in coal seams. Usually, the D is calculated from the desorption curve of particle coal, which cannot accurately reflect the diffusion characteristics under the stress constraint conditions of in-situ coal seams. In this paper, based on Fick's law of counter diffusion, different metamorphic deformed coals of medium and high coal rank are taken as the research object. The change laws of D under different confining pressure, gas pressure, and temperature conditions are tested and analyzed, and the influencing mechanisms on the D are discussed. The results show that the D of different metamorphic deformed coals decreases exponentially with the increase of confining pressure, and increases exponentially with the increase of gas pressure and temperature. There is a limit diffusion coefficient. The influence of confining pressure on the D is essentially determined by the change of effective stress, and the D has a negative effect of effective stress similar to permeability. The effect of gas pressure on the D involves two mechanisms, namely, mechanical and adsorption effects, which are jointly restricted by effective stress and coal particle shrinkage and expansion deformation. The effect of temperature on the D is mainly achieved by changing the root mean square speed and average free path of gas molecules. Under the same temperature and pressure conditions, the D increases first and then decreases with the increase of deformation degree, and the D of fragmented coal is the largest. Under similar deformation conditions, the D of high-rank anthracite is greater than that of medium-rank fat coal. It is considered that porosity is the key factor affecting the change of D in different metamorphic deformed coals.
Keywords: 
Subject: Environmental and Earth Sciences  -   Geophysics and Geology

1. Introduction

Improving the efficiency of coalbed methane development and utilization can effectively alleviate the dependence on high-carbon energy, particularly coal, and accelerate the achievement of China's "carbon peak" and "carbon neutrality" goals. Against the backdrop of China's vigorous promotion of ecological civilization construction, the urgent need to rapidly develop clean coalbed methane resources as a substitute for coal, which has severe impacts on national life safety and the natural environment, is increasingly prominent [1,2]. China's coalbed methane resources rank third in the world, reaching about 10.87×1012 m3, demonstrating a huge potential for coalbed methane resource development [3,4]. However, except for the Qinshui Basin and the Ordos Basin, other regions face issues such as low single well yield, poor production stability, and poor technical replicability in the process of coalbed methane resource development. The core reason lies in the features of China's coalbed methane reservoirs, including low gas saturation, low permeability, low reservoir pressure, and widespread development of tectonic deformed coal [5,6,7]. Coal is an extremely complex porous organic rock. According to the dual porosity structure model of coal (Warren-Root model), the internal space of coal is composed of pores in the coal matrix and fractures around the coal matrix [8,9]. The pores and fractures in coal are not only the storage space for coalbed methane but also the channels for its migration [10,11]. It is generally believed that due to the differences in the causes, forms, and scales of pores and fractures in coal, methane has different migration mechanisms in pore and fracture channels, which can be divided into pore diffusion and fracture seepage [12,13]. One is the seepage through the cleavage and fracture system in the coal body, driven by pressure difference, following Darcy's Law [14,15]; the other is diffusion within the coal matrix pores and micro-fractures, driven by concentration difference, following Fick's Law [16,17]. The production rate of coalbed methane mainly depends on the diffusion rate and seepage rate. When the diffusion rate is insufficient to provide conditions for seepage, the production rate is mainly controlled by the diffusion rate [18]. As the exploration and development of coalbed methane continue, the diffusion of methane in coal reservoirs has increasingly received attention. For coalbed diffusion media, there are two types of diffusion processes in in-situ coalbeds: columnar coal sample diffusion and particle coal sample diffusion [19,20]. In terms of diffusion state, under certain temperature and pressure conditions, the three types of gas inside the coal matrix block that is not affected by mining are in a relative equilibrium state. The driving force of diffusion is the chemical gradient, which belongs to self-diffusion [21]. If the reservoir pressure decreases, the diffusion develops towards desorption, such as pressure relief gas extraction and coal drop gas gushing; if the reservoir pressure increases, the diffusion develops towards adsorption, such as N2/CO2 displacement technology. The driving force for these two types of diffusion is the concentration gradient, which belongs to transfer diffusion [22,23]. Therefore, there are two types of diffusion media and three types of diffusion processes in coalbeds under actual formation conditions, and different diffusion processes can coexist and convert into each other.
The diffusion coefficient (D) is one of the key parameters controlling the gas transport dynamics in the coal matrix. Existing methane diffusion coefficient measurement techniques include the particle method, steady-state flow method, and counter diffusion method, studies have shown that these methods all have a certain degree of limitations and applicability [4,18,24]. Different experimental means, from the process analysis, describe different diffusion processes. The particle method is a transient method measuring the non-steady-state release of gas after the adsorption equilibrium pressure drops to atmospheric pressure, and the diffusion coefficient is obtained by inverse calculation from the coal gas desorption curve using the desorption model [24,25]. This method uses particle coal samples for testing, usually without the influence of confining pressure, mainly used for gas content measurement (estimating the amount of gas lost during sampling), prediction of gas outburst from coal drops, etc [26,27]. The steady-state flow method is similar to the steady-state flow method for measuring the permeability of methane in coal, using cylindrical coal samples for the experiment, maintaining a constant methane pressure difference at both ends of the coal sample, and calculating the methane diffusion coefficient in the coal when the flow is stable according to the methane flow rate [18,28]. This method has not been widely used, only Thimons and Sevenster have measured the methane diffusion coefficient in coal using the steady-state flow method [29,30]. To solve the problems of long test time and difficulty in avoiding methane seepage in the coal with the steady-state flow method, Smith and Williams proposed to measure the diffusion coefficient of methane in coal using the constant pressure counter diffusion method [31,32]. The counter diffusion method still uses cylindrical coal samples for the experiment, placing methane and non-adsorptive nitrogen at both ends of the coal sample and ensuring equal pressure. Since the gas pressure at both ends of the coal sample is equal, methane and nitrogen do not porous flow in the form of seepage, but diffuse with each other driven by the concentration gradient. The methane concentration at both ends of the coal sample can be measured after a period of time to calculate the methane diffusion coefficient in the coal [29,31]. Mutual diffusion experiments can simultaneously apply confining pressure and gas pressure, use Fick's law to calculate the diffusion coefficient after data collection, and are mainly used for predicting and evaluating the diffusion rate in the original coal seam, coalbed methane production planning, and economic reserve estimation, etc. [33,34]. Scholars at home and abroad have done a lot of exploratory work in the measurement of gas diffusion coefficients, but there are significant differences in the experimental methods and results of different scholars in measuring the diffusion coefficient of methane in coal [26]. The methane diffusion coefficients in coal measured by different experimental methods vary greatly, with numerical ranges from 10-7 m2/s to 10-15 m2/s. The differences in the testing principles and conditions of different methods cause these techniques to lack comparability with each other [35,36].
Under the effect of long geological history, diffusion becomes an important mechanism for the underground migration and loss of gas in coal seams, and it is also one of the important ways for coalbed gas to accumulate and store under original stratum conditions. There are many factors that affect the diffusion of gas in coal (coal particles), including the characteristics of the diffusion medium (coal itself, such as the state of matter, degree of metamorphism, degree of destruction, microstructure, etc.), the characteristics of the diffusion phase (methane, such as gas concentration, molecular polarity of the gas, etc.) and the external environment (temperature, gas pressure, confining pressure, etc.) [29,36-39]. At present, most of the diffusion coefficients reported in the literature are derived from the adsorption data of particle coal based on the classical homogeneous spherical Fick diffusion mathematical model [4,30,36,40]. The diffusion coefficient or adsorption time obtained using the particle method to evaluate the diffusion of gas in coal leads to significant deviations in the gas diffusion characteristics and extraction rate obtained from the actual situation [34,41]. In recent years, some scholars have begun to use columnar coal samples to measure the diffusion coefficient. Meng et al. [29] used the mutual diffusion method to test the diffusion coefficient of low-high rank original structure coal, and found that from low rank to medium rank coal, as the degree of coal metamorphism increases, the methane diffusion coefficient decreases in a negative exponential function. From medium rank to high rank coal, as the degree of coal metamorphism increases, the methane diffusion coefficient increases exponentially. Under the same temperature, gas pressure and confining pressure conditions, as the degree of coal metamorphism increases, the methane gas diffusion coefficient in coal shows a trend of rapid decline followed by slow rise. Xu et al. [18] used thin slices of coal matrix instead of coal particles as the test samples and found that the diffusion coefficient of methane in the coal matrix showed a "U" trend of first decreasing and then increasing with the increase in coal rank. An et al. [35] compared the diffusion coefficient measured by the steady-state method with the anthracite diffusion coefficient obtained from the classical model and the time-variable diffusion coefficient model, and found that the magnitudes of the obtained diffusion coefficients were the same, the sizes could differ by several times, and the diffusion coefficient changed differently with the increase in methane pressure. Dong et al. [31] used the particle method and counter diffusion method to measure the transient and quasi-steady-state diffusion characteristics of bituminous coal, and the results showed that the quasi-steady-state diffusion coefficient was higher than the transient diffusion coefficient. The difference may be related to the influence of adsorbed methane surface diffusion, suggesting that the transient diffusion coefficient should be used to calculate the coal and gas outburst risk evaluation index in gas extraction engineering. Liu et al. [34] studied the effects of confining pressure and pore pressure on the diffusion of methane in columnar coal samples. The results showed that with the increase of confining pressure and the decrease of pore pressure, the effective diffusion coefficient gradually decreased. It is suggested that in future research, block coal with a complete internal structure under constraints should be used to study the diffusion behavior of gas in situ coal seams. Cai et al. [42] observed the shape of coal fragments after crushing and sieving a large number of coal samples, and found that most of the crushed particle coal was cylindrical or rectangular, with a particle size generally of 0.20～0.25 mm, and a small amount of particle coal was spherical. Baatar et al. [33] obtained the change in the coal body diffusion coefficient with confining pressure and gas pressure from reverse diffusion experiments, and believed that the internal pore/crack structure of the coal body has an important impact on the diffusion coefficient.
Although the diffusion coefficient is a key parameter characterizing the diffusion ability of methane in coal seams, the physical meaning, numerical magnitude, and changes of this parameter vary under different laboratory test method conditions. During gas extraction, methane diffuses in coal in two typical situations. The first is the diffusion of methane in coal particles, which is a transient diffusion process due to a high methane concentration gradient. The second is the diffusion process of methane in the coal matrix, where the methane concentration gradient is smaller and can be regarded as a quasi-steady-state diffusion process. In-situ coal seams are generally under stress constraints, but laboratories often use granular coal to study the dynamic characteristics of methane diffusion, where the coal sample cannot withstand stress. Therefore, it is debatable whether the laboratory test results of granular coal can reflect the gas diffusion behavior in in-situ coal seams. Moreover, there are few reports in the literature on the determination of the methane diffusion coefficient of different metamorphic deformed coal intact core samples in the laboratory using the counter diffusion method. To solve these problems, this paper takes medium-high rank original structure coal and a series of tectonic deformed coal as research objects, and carries out methane diffusion experiments on original coal columnar coal samples under different confining pressures, gas pressures, and temperature conditions using the counter diffusion method. The influence of confining pressure, gas pressure, and temperature on the methane diffusion characteristics of the original coal under stratum conditions is discussed, and its relationship with porosity and the coal hardiness coefficient of outburst prevention is analyzed. This is of great scientific significance for enriching and improving the gas migration of coal seam gas in the in-situ coal seam, CO2-ECBM, and geological sequestration of CO2.

2. Experiment Design

2.1. Experimental Platform Construction

The counter diffusion method methane diffusion coefficient tester can simulate actual stratum conditions and achieve the determination of the methane diffusion coefficient of the original coal seam under certain confining pressure, temperature, and gas injection pressure conditions. The diffusion coefficient determination device mainly consists of a coal core holder, a pressure control system, a temperature control system, a vacuum pump system, a gas supply system, a gas sampling device, and a data collection system (Figure 1). The coal core holder is used to fix the coal sample and provides a place for the tested coal core to simulate stratum pressure and temperature; the pressure control system provides the circumferential and axial pressure required by the coal core for the experiment; the temperature control system provides the temperature required by the coal core for the experiment and maintains it constant; the gas supply system supplies CH4 and N2 to the two gas chambers at both ends of the holder respectively; the vacuum pump system provides a vacuum environment for the entire experimental system to ensure that there is no influence of other gases in the system. The gas sampling device is used to collect gas samples for gas chromatography analysis after the experiment is completed, and the data collection system mainly collects experimental data such as the circumferential pressure, axial pressure, gas injection pressure, and temperature of the coal sample during the test. The principle of the experiment is based on the principle of gas freely diffusing through the coal sample under a concentration gradient. CH4 is injected at one end and N2 at the other end of the diffusion chamber at both ends of the coal sample holder, and there is no pressure difference between the two ends. Under the specified temperature and pressure conditions, the gas concentration changes with time. Then the volume fraction values of each component of the gas in the diffusion chamber at both ends at different time periods are measured, and the methane diffusion coefficient of different metamorphic deformed coals is calculated based on Fick's law.

2.2. Experimental samples

During the complex geological history and evolution process, coal seams have undergone a series of metamorphic and deformation processes and can be divided into original structure coal and a series of tectonic deformed coal in terms of coal body structure types [3,43]. The experimental coal samples were collected from the mine areas in the central and southern part of North China where the late Paleozoic Shanxi Group coal seams, original structure coal, and tectonic deformed coal (fractured coal, granular coal, mylonite coal) are well developed, namely anthracite from Zhongmacun Mine in Jiaozuo mining area, Henan Province, and fat coal from No.12 mine in Pingdingshan mining area, Henan Province. According to underground observations, the main coal seam in Zhongmacun Mine, Coal 2-1, shows an interlayered distribution of four types of coal body structure, mainly developed in fractured coal and granular coal. The main coal seam in the No.12 mine, Coal 2-1, is mainly granular coal and mylonite coal, with local development of original-fractured structural coal. The collected coal samples are numbered as: WYM-1, WYM-2, WYM-3, WYM-4, FM-1, FM-2, FM-3, FM-4. According to national standards GB/T6948-2008, GB/T212-2008, GB/T23561.4-2009, GB/T 23561.12-2010, etc., 300g of air-dried base coal samples with a size of 0.17-0.25 mm were selected for each, and maximum vitrinite reflectance, industrial analysis, true density, apparent density, porosity, and coal hardiness coefficient parameters were determined. The results of the parameter determination are shown in Table 1.
The experiment used original cylindrical coal samples as the coal samples. The four types of coal body structures were prepared in different ways according to their different hardness. The method and steps for making original coal isostatic pressing cylindrical coal samples of strongly tectonic deformed coals are given in author's reference [44]. The coal sample specifications are Φ25mm×50mm. During the sample preparation process, the adverse effects of different internal structures of the sample and processing errors on the test results should be avoided as much as possible. At the same time, the samples made from the same piece of coal should be selected by statistical classification and surface crack photography observation method to select the complete, compact ones, and those without obvious exogenous cracks as experimental samples. After the sample preparation is completed, it also needs to be dried in a drying oven for 24 hours. The original coal samples of the original structural coal and the tectonic deformed coal columnar coal samples are shown in Figure 2.

2.3. Experimental conditions

Generally speaking, under the combined action of geothermal and overburden pressure, the temperature and pressure of the coal seam are linearly positively correlated with the depth, and the geothermal gradient and reservoir pressure gradient are important parameters reflecting this regular change. Reference [45] has compiled the geothermal gradient and reservoir pressure gradient of the main coal-bearing formations in our country, including the Jiaozuo mining area and Pingdingshan mining area in North China. The maximum geothermal gradient is 4.49℃/100m, the minimum is 0.40℃/100m, and the average is 2.12℃/100m. The maximum reservoir pressure gradient is 1.293MPa/100m, the minimum is 0.402MPa/100m, and the average is 0.862MPa/100m. The geothermal gradient and reservoir pressure gradient of the Zhongmacun Mine and the No.12 Pingdingshan Coal Mine do not have any anomalies in geothermal and geopressure and are basically at the average level of North China. Therefore, the temperature and pressure conditions of the coal seam at depths of 600 to 1300m were predicted according to the average geothermal gradient and average reservoir pressure gradient of the coal-bearing strata in North China, and the predicted results of the original coal seam temperature and pressure are shown in Table 2.
Based on the actual geological conditions such as the temperature, reservoir pressure, and gas pressure during the exploration period of the in-situ coal seam, combined with the research purpose of this experiment and the pressure resistance of the coal samples. To study the effect of single variables (such as variable confining pressure, variable gas pressure, and variable temperature) on the CH4 diffusion law of columnar coal samples, an orthogonal experimental design was made according to Table 2. Conditions for measuring diffusion coefficient are shown in Table 3, starting with the analysis of single influencing factors affecting the diffusion law, and finally comprehensive analysis.

2.4. Calculation models

The key parameter to measure the diffusion capacity and speed of methane in coal is the diffusion coefficient D (cm2/s). If the diffusion speed per unit area per unit time is proportional to the volume fraction gradient, and the diffusion speed only depends on distance, irrespective of time, it is called quasi-steady-state diffusion, which follows Fick's first law. If the diffusion flux of methane in the coal seam varies with both time and distance, it is called non-steady-state diffusion, which can be described by Fick's second law. Therefore, the diffusion coefficient of methane in the experiment is calculated using Fick's second law (Equation 1):
D = ln ( Δ C 0 / Δ C i ) B ( t i − t 0 )
where: Δ C i = C 1 i − C 2 i , B = A ( 1 / V 1 + 1 / V 2 ) / L , D is the diffusion coefficient of methane in the coal sample, unit: cm2/s; Δ C 0 is the volume fraction difference of methane gas in the diffusion chamber at both ends at the initial moment, %; Δ C i is the volume fraction difference of methane gas in the diffusion chamber at both ends at the i-th moment, %; t i is the i-th moment, s; t 0 is the initial moment, s; C 1 i is the volume fraction of methane gas in the methane diffusion chamber at the i-th moment, %; C 2 i is the volume fraction of methane gas in the nitrogen diffusion chamber at the i-th moment, %; A is the cross-sectional area of the coal sample, cm2; L is the length of the coal sample, cm; V1, V2 are the volumes of the methane diffusion chamber and the nitrogen diffusion chamber respectively, unit: cm3.

3. Results and discussion

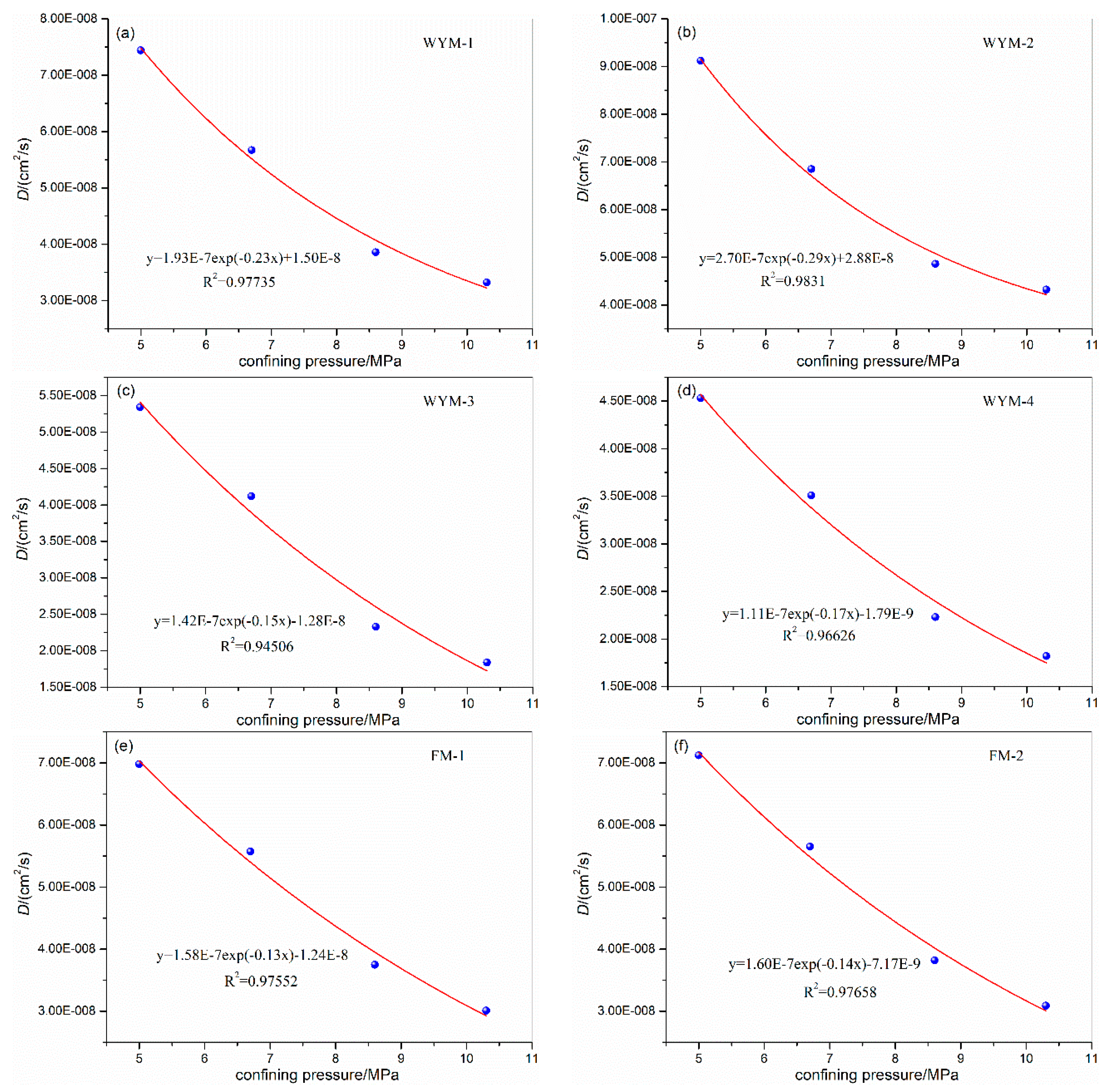
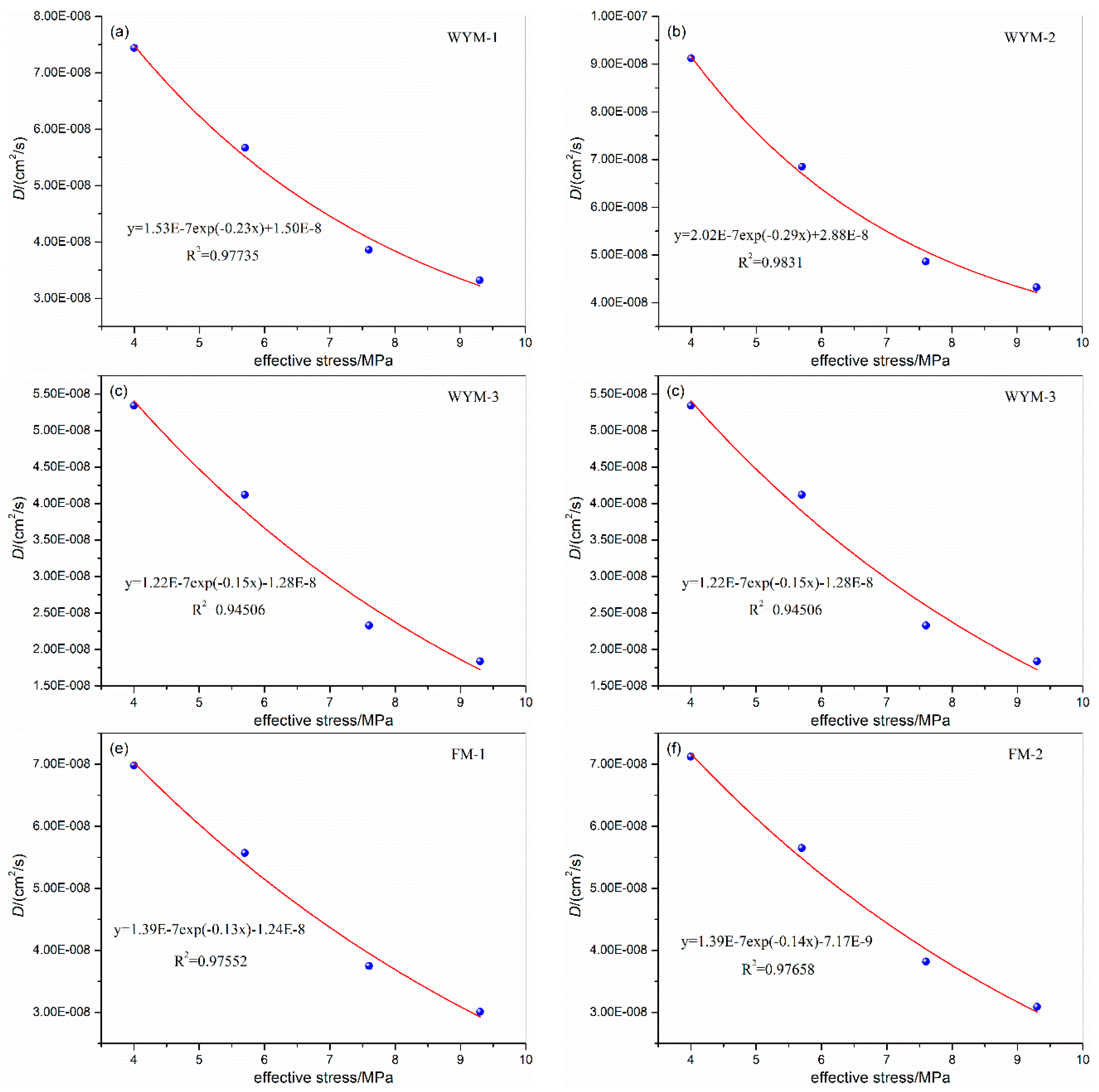
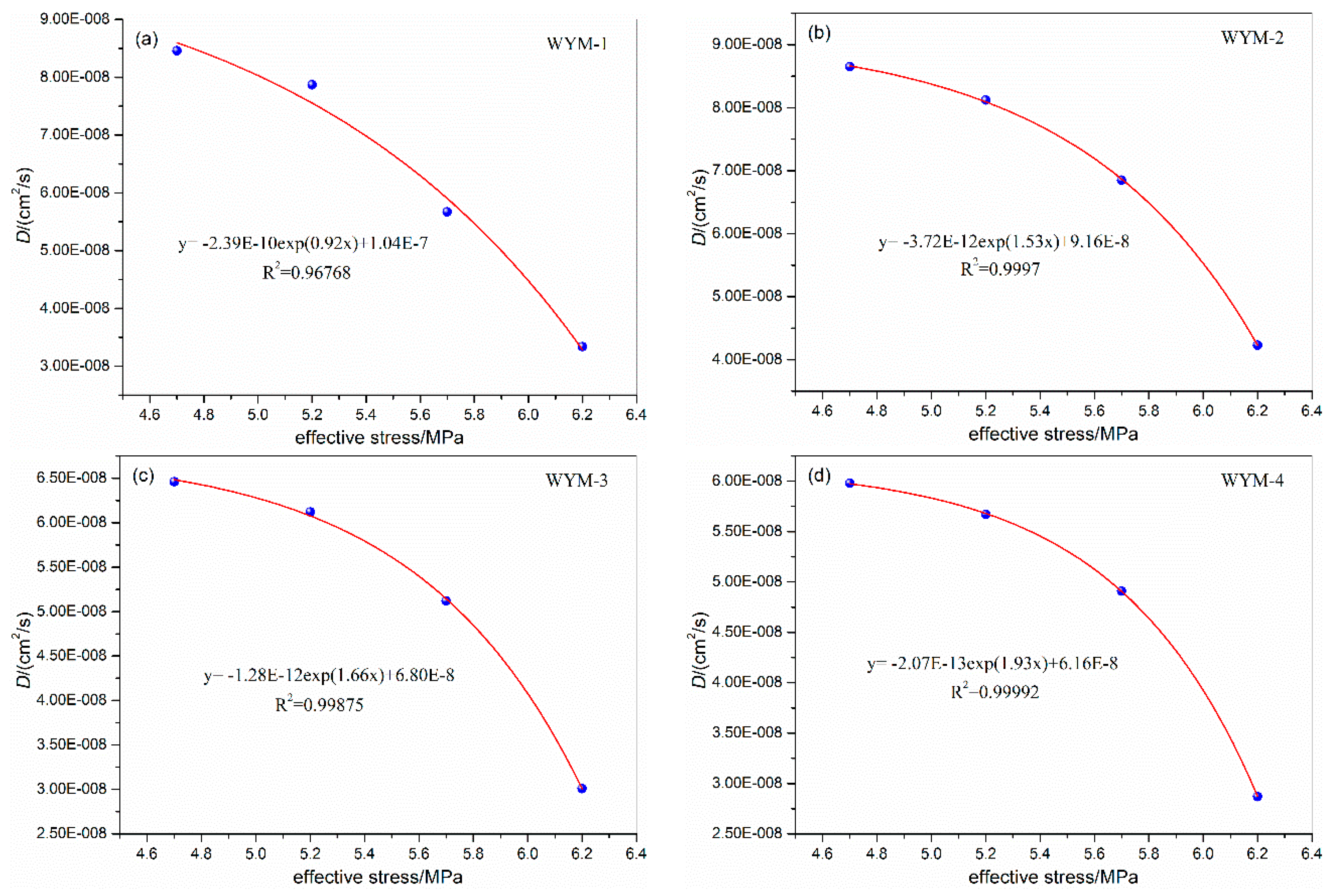
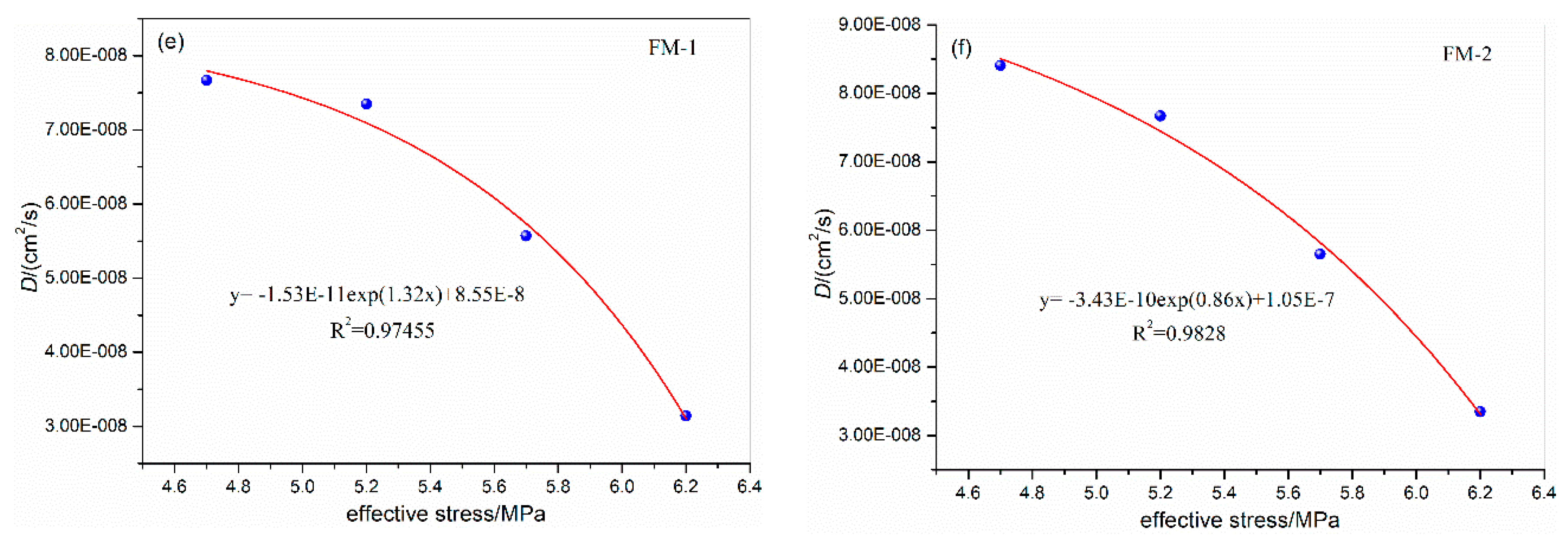
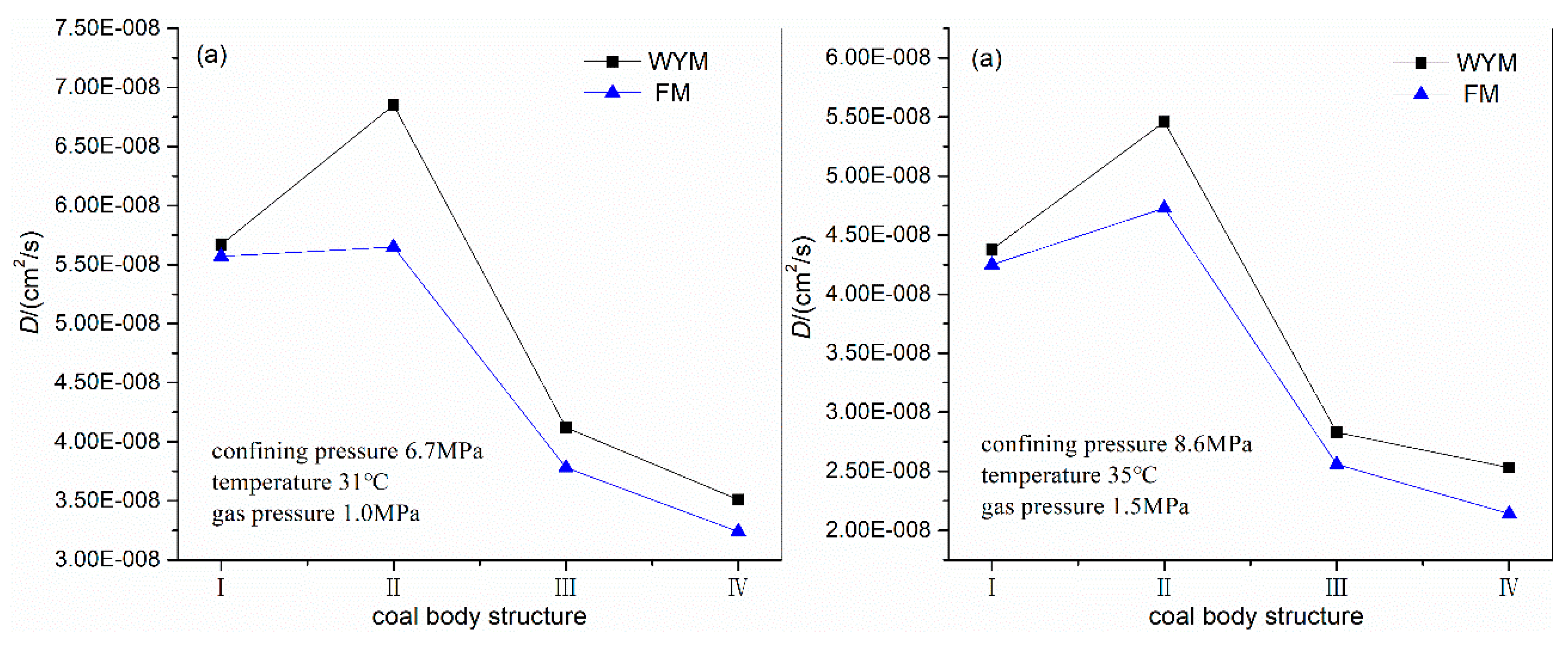
3.1. Influence of Confining Pressure on Diffusion Coefficient

The coal reservoir is a three-dimensional geological body stored underground at a certain depth, and its reservoir physical characteristics, especially diffusion and permeability, are closely related to the confining pressure [29,34]. Under natural conditions, the geostress field acts on coal seam pores, forming the confining pressure on coal seam pores, which inevitably affects the pore-fracture system of the coal seam, and thus affects the fluid migration laws in the coal seam. The confining pressure change diffusion coefficient measurement used WYM-1, WYM-2, WYM-3, WYM-4, FM-1, FM-2, six original columnar coal samples as experimental samples. The experiments were conducted under conditions where the confining pressure was set to 5.0MPa, 6.7MPa, 8.6MPa, 10.3MPa, the temperature was 31℃, and the gas pressure was 1.0MPa to explore the impact of confining pressure changes on the diffusion coefficient. The experimental conditions and results are shown in Table 4.
According to the experimental measurement results in Table 4, the relationship between the diffusion coefficient and the increase in confining pressure is plotted (Figure 3). As shown in Figure 3, under the same temperature and gas pressure conditions, the methane diffusion coefficient decreases exponentially with the increase in confining pressure, and the speed of decrease slows slightly as the confining pressure continues to rise. In the case of no damage to the experimental coal samples, the confining pressure of this variable confining pressure diffusion experiment was carried out to the limit of 10.3MPa, without a clear slowdown in the rate of decline. It is speculated that when the confining pressure continues to increase, the diffusion coefficient will tend to stabilize and no longer decrease.
Effective stress refers to the difference between the confining pressure acting on the coal reservoir and the fluid pressure in its pores and fractures [26,34]. According to the data in Table 4, the relationship between the diffusion coefficient and the effective stress generated by the change in confining pressure is plotted (Figure 4). As can be seen, the diffusion coefficient decreases exponentially with the increase in effective stress, and the speed of decrease slightly slows as the effective stress increases. It is believed that the exponential decrease in the diffusion coefficient with the increase in confining pressure is essentially determined by the change in effective stress. According to the theory of material mechanics [46,47], coal deformation always increases with the increase in stress. Therefore, under the condition that other conditions remain unchanged, as the confining pressure increases and the pore pressure (gas pressure) remains constant, the effective stress of the coal body will continue to increase, causing the coal body deformation to increase continuously. The pores and pore throats in the coal are contracted and deformed under the action of the effective stress, ultimately leading to a decrease in the porosity of the coal body and a decrease in the diffusion coefficient. It can be seen that the diffusion coefficient, like permeability [12,48], also has a negative effect of effective stress.

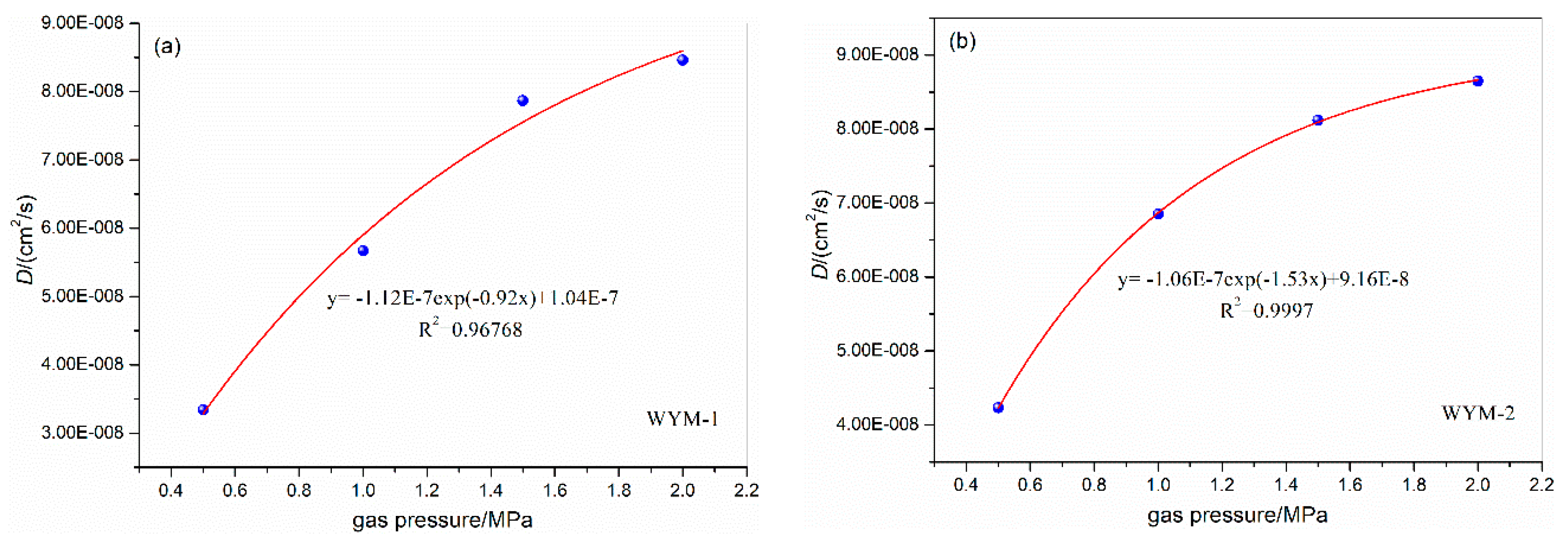
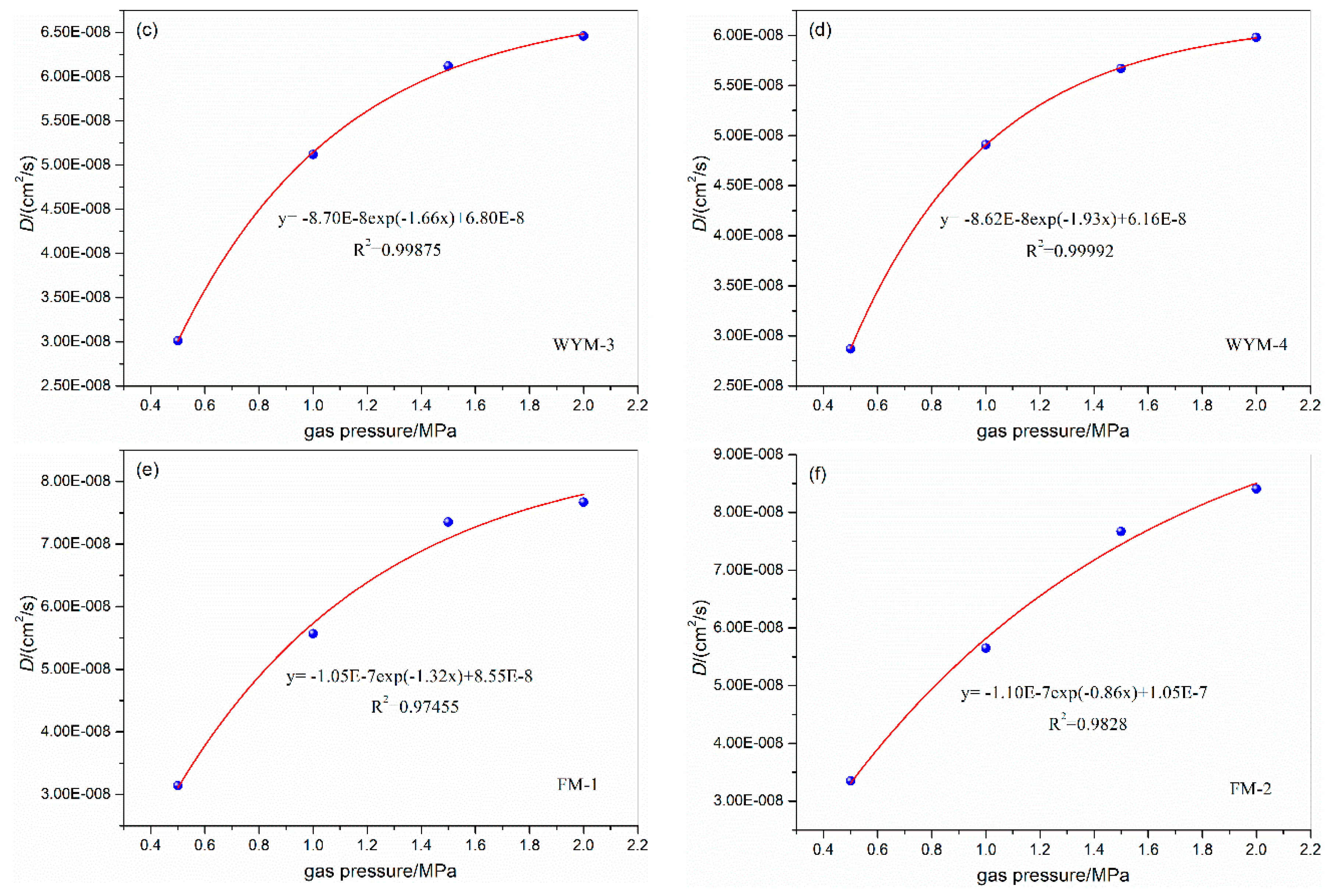
3.2. Influence of gas pressure on the diffusion coefficient

To explore the influence of gas pressure changes on the diffusion coefficient, the change in gas pressure diffusion coefficient was measured using WYM-1, WYM-2, WYM-3, WYM-4, FM-1, FM-2, six original columnar coal samples as experimental samples. According to Table 3, the gas pressure was set to 0.5MPa, 1.0MPa, 1.5MPa, 2.0MPa, the temperature was set to 31℃, and the confining pressure was set to 6.7MPa for the diffusion experiment. The variable gas pressure experimental conditions and measurement results are shown in Table 5.
According to the experimental results in Table 5, a graph of the relationship between variable gas pressure and the diffusion coefficient was drawn (Figure 5). As shown in Figure 5, under the same temperature and confining pressure conditions, as the gas pressure increased from 0.5MPa to 2.0MPa, the change pattern of the CH4 diffusion coefficient of the six groups of measured original coal columnar coal samples was opposite to that of the confining pressure, gradually increasing in an exponential relationship, and the speed of increase slowed down as the gas pressure increased. It is speculated that when the gas pressure continues to increase, the diffusion coefficient will tend to stabilize and no longer increase, therefore there exists a limit diffusion coefficient for the original coal columnar coal samples.
At the same time, based on the experimental results in Table 5, a graph of the relationship between the diffusion coefficient and the effective stress generated by the change in gas pressure was drawn (Figure 6). As can be seen, the CH4 diffusion coefficient of the original coal increases exponentially with the decrease in effective stress (Figure 6), and the speed of increase slightly slows down as the effective stress decreases. It can be seen that the exponential increase of the CH4 diffusion coefficient of the original coal columnar samples with the increase in gas pressure is essentially also determined by the change in effective stress.
Previous research has confirmed [49,50] that as the pressure of CH4 gas in coal increases, coal's adsorption of CH4 gas molecules strengthens. Under external constraint conditions, the adsorption expansion stress increases, leading to a decrease in the effective stress of the coal. As analyzed in the aforementioned Section 3.1, a decrease in effective stress will lead to an increase in the diffusion coefficient (Figure 4 and Figure 6). On the other hand, during the diffusion process of CH4, the coal matrix exerts an adsorption effect on CH4, with part of the adsorption expansion volume being converted into expansion stress at the contact points, and another part being converted into inward adsorption expansion strain that changes the pore volume. As the pressure of CH4 gas increases, the inward adsorption deformation of the coal matrix increases, the coal matrix expands, porosity decreases, and the diffusion coefficient decreases; conversely, when pore pressure decreases, the coal matrix contracts, porosity increases, and the diffusion coefficient increases. Therefore, compared to the influence of confining pressure on the diffusion coefficient, the influence of gas pressure on the diffusion coefficient involves two mechanisms: mechanical action and adsorption action.
The experimental results of the variable gas pressure on original coal columnar coal samples show that as the gas pressure increases, the diffusion coefficient also increases. This indicates that the control effect of gas pressure on CH4 diffusion in coal is jointly constrained by the effective stress and the shrinking/expanding deformation of the coal matrix. These two factors may bring opposite results, but the final relationship between gas pressure and the diffusion coefficient will be constrained by the dominant factor.

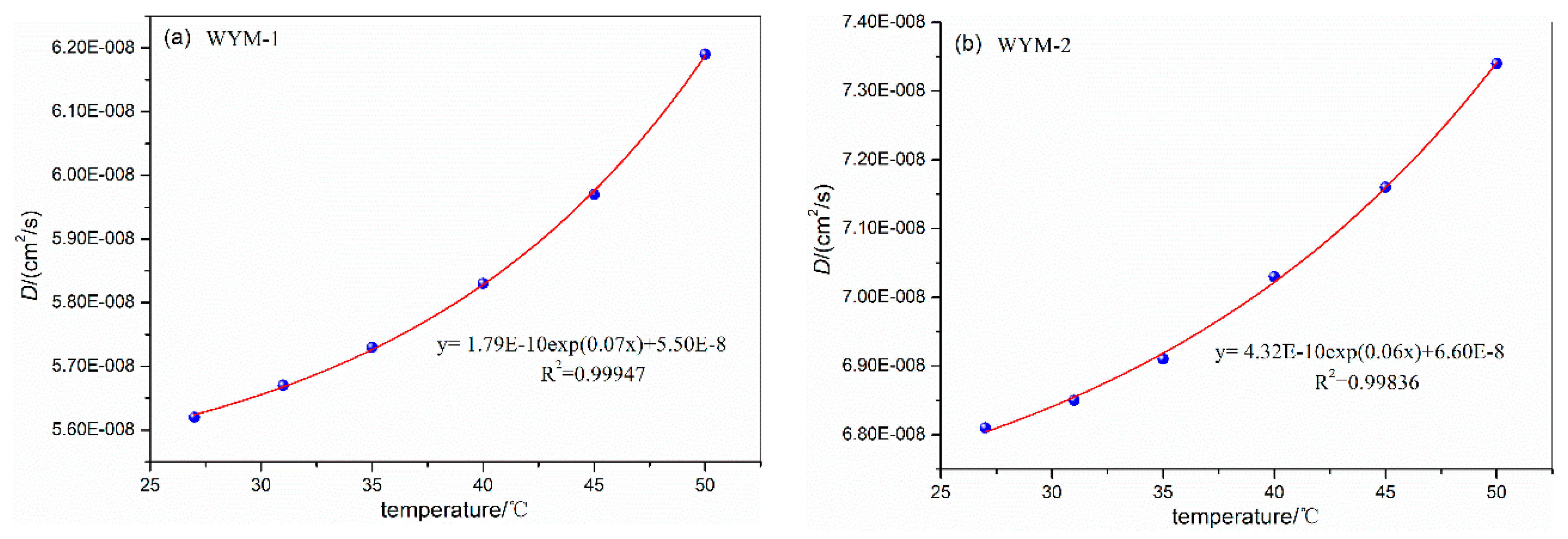
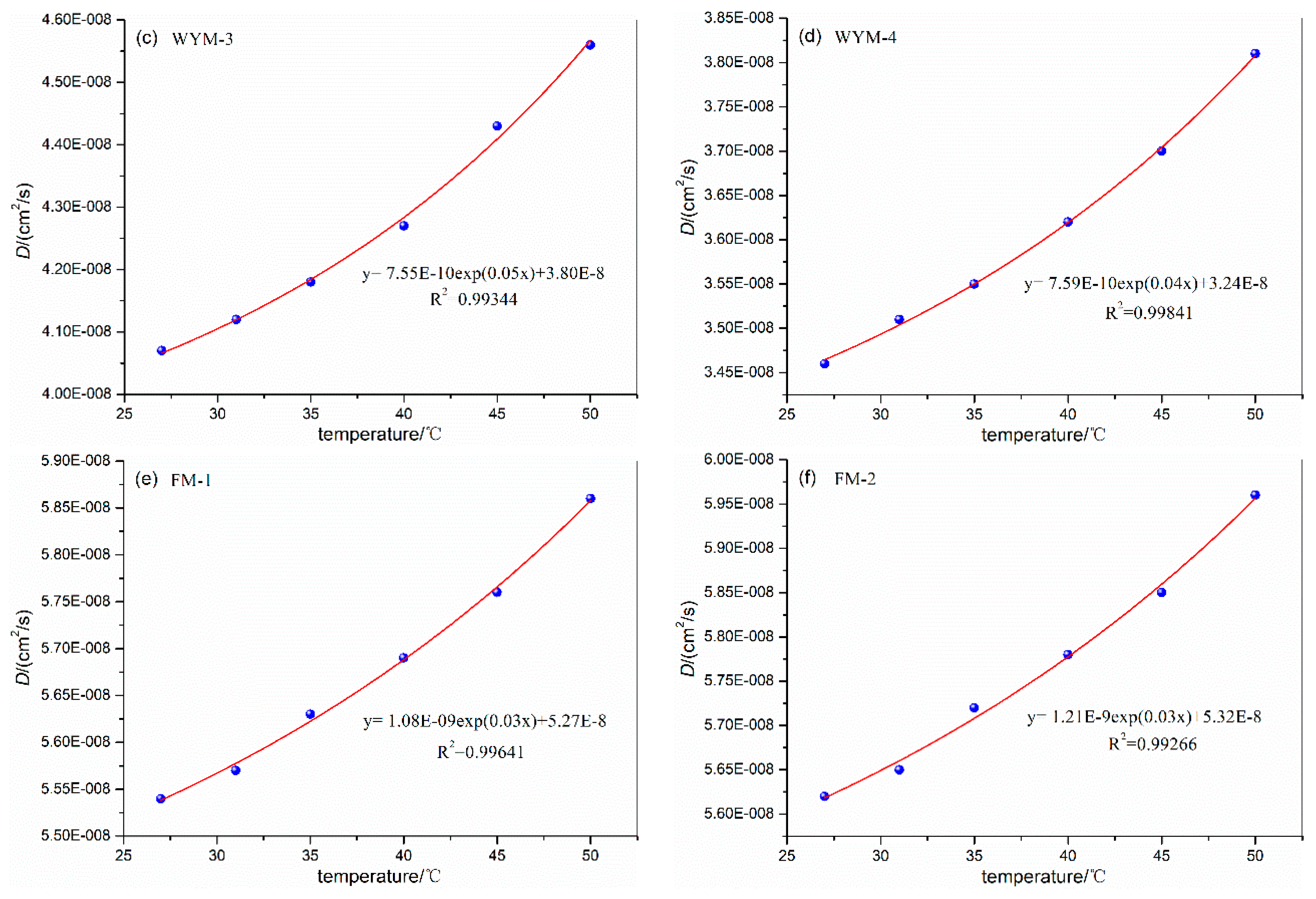
3.3. Influence of Temperature on Diffusion Coefficient

To explore the influence of temperature changes on the diffusion coefficient, the diffusion coefficient measurement of columnar coal samples under variable temperature conditions was carried out with WYM-1, WYM-2, WYM-3, WYM-4, FM-1, FM-2, a total of 6 original columnar coal samples as experimental samples. The temperature was set at 27℃, 31℃, 35℃, 40℃, 45℃, 50℃, with confining pressure at 6.7MPa and gas pressure at 1.0MPa for the diffusion experiment. The experimental conditions and results are shown in Table 6. According to the data in Table 6, a graph depicting the relationship between the diffusion coefficient and temperature is shown in Figure 7.
As shown in Figure 7, under the same gas pressure and confining pressure conditions, as the temperature rises from 27℃ to 40℃, the variation pattern of the CH4 diffusion coefficient in the measured six coal samples gradually rise in an exponential relationship. Furthermore, as the temperature rises, the rate of increase slightly accelerates.
According to the theory of gas molecular motion [51,52], the impact of temperature on gas molecular diffusion mainly changes the root mean square speed and the average free path of the gas molecules. The molecular motion theory in material science clarifies that the temperature of a gas is a sign of the average kinetic energy of the molecules [29,53]. With the increase in temperature, the amplitude and frequency of molecular vibration can be increased, the speed of molecular motion increases, the vigor of molecular movement increases, and the speed of movement from high concentration to low concentration increases. This in turn speeds up the diffusion, ultimately causing the diffusion coefficient to show an increasing trend.

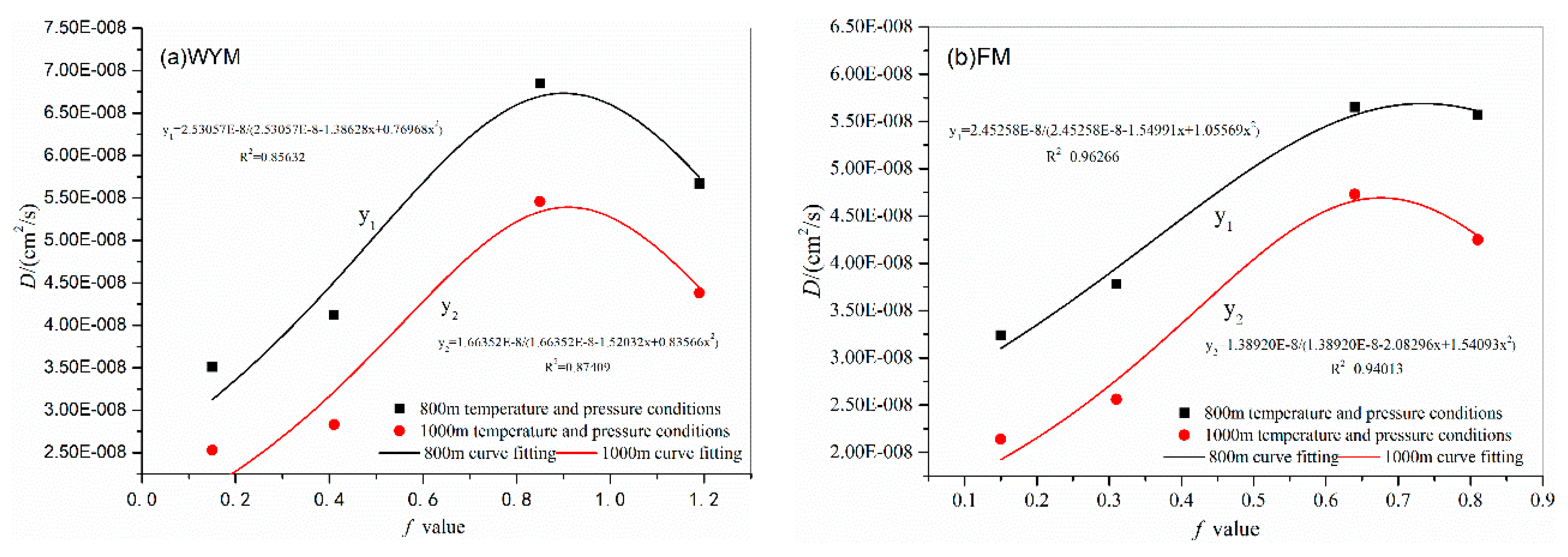
3.4. Influence of Degree of Metamorphism and Deformation on Diffusion Coefficient

To explore the influence of the degree of metamorphism and deformation on the diffusion coefficient, the testing of original coal columnar coal samples with different degrees of metamorphism and deformation was carried out with WYM-1, WYM-2, WYM-3, WYM-4, FM-1, FM-2, FM-3, FM-4, a total of eight original coal samples as experimental samples. The confining pressure was set at 6.7MPa, the temperature at 31℃, and the gas pressure at 1.0MPa (simulating a coal seam buried 800m deep), and the confining pressure was 8.6MPa, the temperature 35℃, and the gas pressure 1.5MPa (simulating a coal seam buried 1000m deep) for the experiment. The experimental conditions and results are shown in Table 7.
According to the data in Table 7, a graph of the change in the diffusion coefficient with different degrees of metamorphism and deformation in coal methane diffusion coefficients (Figure 8) has been plotted. As shown in Figure 8, under the same confining pressure, temperature, and gas pressure conditions, the same degree of metamorphism coal (anthracite, fat coal) shows an increase first and then a decrease trend with the increase in the degree of deformation, with the diffusion coefficient of fragmented coal being the largest. The coal with similar degrees of deformation shows an increasing trend with the increase in the degree of metamorphism, i.e., under the same degree of deformation conditions, the diffusion coefficient of anthracite is greater than the diffusion coefficient of fat coal. The diffusion coefficient measured by the granular method in literature [13,54] shows a continuous increase with the increase in the degree of coal deformation, which is significantly different from the rule obtained by the mutual diffusion experiment of different degrees of metamorphism and deformation columnar coal samples.
The solidity coefficient of coal (f value) is an indicator of the solidity of coal. In China, the drop hammer method is commonly used to measure it. The measurement principle is based on the fact that brittle materials follow the area force energy theory when they break, and it is assumed that the work A consumed by broken coal is directly proportional to the surface area S of the broken material, and the surface area is inversely proportional to the particle diameter. The solidity of coal can be expressed by the crushing ratio, the harder the coal, the higher its strength, the larger the f value, and vice versa.
The hardiness coefficient of coal (f value) is an index reflecting the ability of coal to resist external force damage. The f value of coal with different coal body structural types has a certain value range and a relatively dense value range interval, i.e., the common value range. Therefore, the hardiness coefficient of coal f value can be used as an index for classifying coal structures. According to Table 1 and Table 7, the relationship between the diffusion coefficient D of different coal structure coal and the hardiness coefficient f value is fitted into a curve, as shown in Figure 9.
As shown in Figure 9, the quantitative changes between the two can be expressed by the following function relationship between the diffusion coefficient D and the f value:
D = a / ( a + b · f + c · f 2 )
where D is the diffusion coefficient, cm2/s; f is the hardiness coefficient of coal, dimensionless; a, b, c are undetermined coefficients, dimensionless.
This shows that the diffusion coefficient D and the f value have good correlation, with determination coefficient R2 all above 85%, so the hardiness coefficient f value of coal can be used to predict the diffusion coefficient of coal. The coal body structure changes from simple to complex, the diffusion coefficient first increases and then decreases, showing a Holliday nonlinear function relationship.
According to the data in Table 1 and Table 7, the change in relationship between the diffusion coefficient of different metamorphic deformed coal and porosity under simulated confining pressure, temperature, and gas pressure conditions at a burial depth of 800m and 1000m has been plotted respectively (Figure 10). As shown in Figure 10, the diffusion coefficient D and porosity of coal with different metamorphic deformations basically show the same trend. That is, under the same coal rank condition, with the increase of deformation degree, the diffusion coefficient D and porosity both show a trend of increasing first and then decreasing. Under the same coal rank condition, the porosity and diffusion coefficient of fragmented coal are the highest, followed by original structure coal, granular coal, and the diffusion coefficient of granulated coal is the smallest. Under the same deformation degree, the porosity and diffusion coefficient of anthracite are greater than that of fat coal.
The effects of metamorphism and deformation are inseparable in the coal-forming process of the same coal seam. The porosity of coal refers to the ratio of voids (including micropores and microfractures) in coal to its total volume (GB/T23561.4-2009) [55]. The porosity measurement results of coal samples from Table 1 show that under the same metamorphic conditions, the porosity of different coal grades is the highest in fragmented coal, and with the increase of deformation degree, the porosity shows a trend of increasing first and then decreasing. This is because in coal-bearing strata near the same location, the coalification history and coalification process that the coal seam has experienced are almost the same, the degree of coal metamorphism is basically the same, and the confining pressure conditions it bears are also similar. That is, under the same stratum pressure condition, the coal seam with a greater degree of deformation (granular coal, mylonitic coal) is more likely to be compacted and solidified, resulting in a smaller macro porosity; on the contrary, the coal seam with a smaller degree of deformation (original structure coal, fragmented coal) has stronger ability to maintain the original skeleton, is less likely to be compacted, and the original pores and microfractures are better preserved, so the porosity of fragmented coal is relatively high. Generally speaking, the higher the porosity, the lower the displacement pressure, indicating that there are more coarse throats, the better the pore structure, and the more conducive to diffusion; on the contrary, the worse the pore structure, the more unfavorable for diffusion [8,27,37]. It is analyzed that the diffusion coefficient measured in the columnar coal sample in the counter diffusion experiment is mainly controlled by the porosity, and the large pores and microfractures play a leading role. Existing research shows [43,47,48] that microfractures mostly constitute important channels for connected pores and endogenous fractures and layer fractures, and the existence of microfractures shortens the distance of coal seam methane diffusion. In addition to diffusing in micropores and flowing in endogenous fractures, coal seam methane also diffuses or flows in microfractures. The macro manifestation is that the permeability of soft coal (granular coal, mylonite coal) under reservoir conditions is worse than that of hard coal, which can reasonably explain why soft coal is more difficult to extract, the effect of gas injection displacement is poor, and the macro transformation of hydraulic fracturing is difficult, etc. Therefore, it is suggested that in future research, columnar coal samples of different metamorphic deformed coal under the action of effective stress should be used to study the diffusion behavior of in-situ coal seam gas. The diffusion coefficients measured by particle method and counter diffusion method cannot be simply substituted for application.

4. Conclusions

(1) The methane diffusion coefficient of raw coal cylindrical samples decreases in an exponential relationship as the confining pressure increases, and the decrease slightly slows down with the increase of the confining pressure. The decrease of the diffusion coefficient with the increase of the confining pressure, which is essentially determined by the changes in effective stress, also shows an exponential relationship. The methane diffusion coefficient of cylindrical coal samples is similar to permeability, both showing negative effects under effective stress.
(2) The change in the methane diffusion coefficient of raw coal cylindrical samples with gas pressure is opposite to that with confining pressure, increasing gradually in an exponential relationship, and the rate of increase slows down with the rise of gas pressure. The diffusion coefficient also increases exponentially with the reduction of effective stress caused by changes in gas pressure, and the rate of increase slows down slightly with the reduction of effective stress. There is a limit to the diffusion coefficient under in-situ geological conditions. The impact of gas pressure on the diffusion coefficient differs slightly from that of confining pressure, involving two mechanisms of mechanical action and adsorption, which are jointly constrained by effective stress and changes in coal particle shrinkage/expansion. The two mechanisms lead to opposite results, but are ultimately restricted by the main controlling factor, the mechanical effect of effective stress.
(3) The methane diffusion coefficient of raw coal cylindrical samples gradually increases in an exponential relationship as the temperature rises, and the rate of increase slightly grows with the temperature. The influence of temperature on diffusion is mainly achieved by changing the root mean square speed and mean free path of gas molecules.
(4) Under the same confining pressure, temperature, and gas pressure conditions, for coal samples with the same degree of metamorphism, the methane diffusion coefficient presents a trend of increasing first and then decreasing with the increase of deformation degree, with the maximum diffusion coefficient in fractured coal. The diffusion coefficient and the firmness coefficient value present a Holliday nonlinear function variation, and the diffusion coefficient first increases and then decreases as the coal structure changes from simple to complex. Under similar deformation conditions, the diffusion coefficient of anthracite is greater than that of fat coal. The porosity is the key factor affecting the change in the methane diffusion coefficient of different metamorphic and deformed coals.

Author Contributions

Jiangang Ren: Methodology, Visualization, Data Curation, Formal analysis, Writing-Original Draft, Writing-Review & Editing, Funding acquisition; Liang Gao: Methodology, Data Curation, Formal analysis; Zhihui Wen: Supervision, Investigation, validation; Hongbo Weng: Data Curation, Formal analysis; Jianbao Liu: Supervision, Investigation; Runsheng Lv: Supervision, Investigation; Yanwei Qu: Supervision, Investigation; Zhimin Song: Conceptualization, Methodology, Supervision, Funding acquisition; Yongwang Zhang: data curation; Bing Li: Data Curation, Formal analysis, Writing-Review & Editing, Funding acquisition; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Natural Science Foundation of China (Grant Nos. 42002185, 41972177 and 42172189), the Natural Science Foundation of Henan province (No. 202300410099), the Key Scientific and Technological Project of Henan Province (No. 192102310464), the Key Research Project of Higher Education in Henan Province (No. 18A440008) and the Doctoral Scientific Fund Project of Henan University of Engineering (No. D2017010).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The experimental data used to support the results of this study are available from the corresponding authors upon request.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Wang, X.L.; Pan, J.N.; Wang, K.; Mou, P.W.; Li, J.X. Fracture variation in high-rank coal induced by hydraulic fracturing using X-ray computer tomography and digital volume correlation. International Journal of coal geology 2022, 252, 103942. [Google Scholar] [CrossRef]
  2. Wang, Q.W.; GUO, B.; Song, M.; Yan, Q. Construction and application of “coal-water-environment” coordinated development evaluation index system: A case study of Sihe Minefield. Coal Geology & Exploration 2022, 50, 98–105. [Google Scholar]
  3. Ren, J.G.; Song, Z.M.; Li, B.; Liu, J.B.; Lv, R.S.; Liu, G.F. Structure feature and evolution mechanism of pores in different metamorphism and deformation coals. Fuel. 2021, 283, 119292. [Google Scholar] [CrossRef]
  4. Zhao, W.; Cheng, Y.P.; Pan, Z.J.; Wang, K.; Liu, S.M. Gas diffusion in coal particles: A review of mathematical models and their applications. Fuel 2019, 252, 77–100. [Google Scholar] [CrossRef]
  5. Zhang, Q.G.; Li, Q.S.; Fan, X.Y.; Liu, C.; Ge, Z.L.; Jiang, Z.G.; Peng, X.L.; Li, X.C.; Zhu, S.Y.; Zhao, S.L.; Zhao, P.F.; Chen, Y.F. Current situation and development trend of theories and technologies for coal and CBM co-mining in China. Natural Gas Industry 2022, 42, 130–145. [Google Scholar]
  6. Wang, Z.Z.; Fu, X.H.; Hao, M.; Li, G.F.; Pan, J.N.; Niu, Q.H.; Zhou, H. Experimental insights into the adsorption-desorption of CH4/N2 and induced strain for medium-rank coals. Journal of Petroleum Science and Engineering 2021, 204, 108705. [Google Scholar] [CrossRef]
  7. Tao, S.; Pan, Z.J.; Tang, S.L.; Chen, S.D. Current status and geological conditions for the applicability of CBM drilling technologies in China: A review. International Journal of Coal Geology 2019, 202, 95–108. [Google Scholar] [CrossRef]
  8. Hu, B.; Cheng, Y.P.; Pan, Z.J. Classification methods of pore structures in coal: A review and new insight. Gas Science and Engineering 2023, 110, 204876. [Google Scholar] [CrossRef]
  9. Zhou, H.; Wu, C.F.; Pan, J.N.; Wang, Z.Z.; Niu, Q.H.; Du, M.Y. Research on Molecular Structure Characteristics of Vitrinite and Inertinite from Bituminous Coal with FTIR, Micro-Raman, and XRD Spectroscopy. Energy & Fuel 2021, 35, 1322–1335. [Google Scholar]
  10. Mou, P.W.; Pan, J.N.; Niu, Q.H.; Wang, Z.Z.; Li, Y.B.; Song, D.Y. Coal Pores: Methods, Types, and Characteristics. Energy & Fuel 2021, 35, 7467–7484. [Google Scholar]
  11. Liu, D.; Wang, Y.; Ni, X.; Tao, C.; Fan, J.; Wu, X.; Zhao, S. Classification of Coal Structure Combinations and Their Influence on Hydraulic Fracturing: A Case Study from the Qinshui Basin, China. Energies 2020, 13, 4559. [Google Scholar] [CrossRef]
  12. Li, Z.Q.; Li, P.F.; Wang, L.; Liu, Y.W.; Li, L. Experiment, Model, and Mechanism of Multiscale Dynamic Diffusion–Permeability in Coal under Different Fluids. ACS Omega 2023, 8, 1606–1617. [Google Scholar] [CrossRef] [PubMed]
  13. Ren, J.G.; Wang, Z.Z.; Li, B.; Chen, F.; Liu, J.B.; Liu, G.F.; Song, Z.M. Fractal-Time-Dependent Fick Diffusion Model of Coal Particles Based on Desorption–Diffusion Experiments. Energy & Fuel 2022, 36, 6198–6215. [Google Scholar]
  14. Li, Z.Q.; Peng, J.S.; Li, L.; Qi, L.L.; Li, W. Novel Dynamic Multiscale Model of Apparent Diffusion Permeability of Methane through Low-Permeability Coal Seams. Energy & Fuel 2021, 35, 7844–7857. [Google Scholar]
  15. Pan, Z.J.; Connell, L.D.; Camilleri, M.; Connelly, L. Effects of matrix moisture on gas diffusion and flow in coal. Fuel 2010, 89, 3207–3217. [Google Scholar] [CrossRef]
  16. Wen, Z.H.; Wang, Q.; Ren, J.G.; Zhang, L.L.; Yuan, Y.W. Dynamic Gas Diffusion Model of Capillary Pores in a Coal Particle Based on Pore Fractal Characteristics. Transport in Porous Media 2021, 140, 581–601. [Google Scholar] [CrossRef]
  17. Wang, Y.; Liu, S.M. Estimation of Pressure-Dependent Diffusive Permeability of Coal Using Methane Diffusion Coefficient: Laboratory Measurements and Modeling. Energy & Fuel 2016, 30, 8968–8976. [Google Scholar]
  18. Xu, H.; Tang, D.Z.; Zhao, J.L.; Li, S.; Tao, S. A new laboratory method for accurate measurement of the methane diffusion coefficient and its influencing factors in the coal matrix. Fuel 2015, 158, 239–247. [Google Scholar] [CrossRef]
  19. Liu, J.J.; Cheng, D.Q.; Li, Y.L.; Zhao, K.; Kou, Q.Q. Quantitative evaluation of the influence of coal particle size distribution on gas diffusion coefficient by image processing method. Fuel 2022, 314, 122946. [Google Scholar] [CrossRef]
  20. Liu, Z.D.; Lin, X.S.; Cheng, Y.P.; Chen, R.; Zhao, L.Y.; Wang, L.; Li, W.; Wang, Z.Y. Experimental investigation on the diffusion property of different form coal: Implication for the selection of CO2 storage reservoir. Fuel 2022, 318, 123691. [Google Scholar] [CrossRef]
  21. Sander, R.; Connell, L.D.; Camilleri, M.C.; Pan, Z.J. CH4, CO2, N2 diffusion in Bowen Basin (Australia) coal: Relationship between sorption kinetics of coal core and crushed coal particles. Journal of Natural Gas Science and Engineering 2020, 81, 103468. [Google Scholar] [CrossRef]
  22. Bai, Y.; Lin, H.F.; Li, S.G.; Long, H.; Yan, M.; Li, Y.; Qin, L.; Zhou, B. Experimental study on kinetic characteristics of gas diffusion in coal under nitrogen injection. Energy 2022, 254, 124251. [Google Scholar] [CrossRef]
  23. Tan, Y.L.; Pan, Z.J.; Liu, J.S.; Kang, J.H.; Zhou, F.B.; Connell, L.D.; Yang, Y.X. Experimental study of impact of anisotropy and heterogeneity on gas flow in coal. Part I: Diffusion and adsorption. Fuel 2018, 232, 444–453. [Google Scholar] [CrossRef]
  24. Liu, Q.Q.; Wang, J.; Liu, J.J.; Yang, Q.Q.; Huang, W.Y.; Liu, Y.Y.; Wang, L. Determining diffusion coefficients of coal particles by solving the inverse problem based on the data of methane desorption measurements. Fuel 2022, 308, 122045. [Google Scholar] [CrossRef]
  25. Lu, S.Q.; Li, M.J.; Sa, Z.Y.; Liu, J.; Wang, S.C.; Qu, M. Discrimination of gas diffusion state in intact coal and tectonic coal: Model and experiment. Fuel 2022, 325, 124916. [Google Scholar] [CrossRef]
  26. An, F.H.; Jia, H.F.; Feng, Y. Effect of stress, concentration and temperature on gas diffusion coefficient of coal measured through a direct method and its model application. Fuel 2022, 312, 122991. [Google Scholar] [CrossRef]
  27. Li, Y.D.; Pan, J.N.; Cheng, N.N.; Wang, Z.Z.; Zhang, L.; Liu, W.Q. Relationship Between Micropore Structure of Different Coal Ranks and Methane Diffusion. Natural Resources Research volume 2022, 31, 2901–2917. [Google Scholar] [CrossRef]
  28. Lu, X.; Armstrong, R.T.; Mostaghimi, P. Analysis of gas diffusivity in coal using micro-computed tomography. Fuel 2020, 261, 116384. [Google Scholar] [CrossRef]
  29. Meng, Y.; Li, Z.P. Experimental study on diffusion property of methane gas in coal and its influencing factors. Fuel 2016, 185, 219–228. [Google Scholar] [CrossRef]
  30. Cheng, Y.P.; Pan, Z.J. Reservoir properties of Chinese tectonic coal: A review. Fuel 2020, 260, 116350. [Google Scholar] [CrossRef]
  31. Dong, J.; Cheng, Y.P.; Pan, Z.J. Comparison of transient and pseudo-steady diffusion of methane in coal and implications for coalbed methane control. Journal of Petroleum Science and Engineering 2020, 184, 106543. [Google Scholar] [CrossRef]
  32. Thimons, E.D.; Kissell, F.N. Diffusion of methane through coal. Fuel 1973, 52, 274–280. [Google Scholar] [CrossRef]
  33. Baatar, L.; Mostaghimi, P.; Yuan, M.; Armstrong, R.T.; Adler, L.; Canbulat, I.; Si, G.Y.; Gaidarov, B.; Jing, Y. Multiscale measurements of gas diffusion coefficient of coal using counter-diffusion and image-based methods. International Journal of Coal Geology 2023, 265, 104155. [Google Scholar] [CrossRef]
  34. Liu, T.; Lin, B.Q.; Fu, X.H.; Gao, Y.B.; Kong, J.; Zhao, Y.; Song, H.R. Experimental study on gas diffusion dynamics in fractured coal: A better understanding of gas migration in in-situ coal seam. Energy 2020, 195, 117005. [Google Scholar] [CrossRef]
  35. Qin, Y.J.; An, F.H.; Su, W.W.; Jia, H.F.; Chen, X.J. Direct determination of the diffusion coefficient variation of cylindrical coal based on Fick’s law and model construction. Coal Science and Technology 2023, 51, 1–10. [Google Scholar]
  36. Yi, M.H.; Wang, L.; Cheng, Y.P.; Wang, C.H.; Hu, B. Calculation of gas concentration-dependent diffusion coefficient in coal particles: Influencing mechanism of gas pressure and desorption time on diffusion behavior. Fuel 2022, 320, 123973. [Google Scholar] [CrossRef]
  37. Fang, X.L.; Liu, D.L.; Zhou, Y.F.; Liu, X.B.; Cai, Y.D. Factors influencing methane diffusion behaviors in micro-nano coal pores: A comprehensive study. Frontiers of Earth Science 2023, 17, 71–86. [Google Scholar] [CrossRef]
  38. Song, H.R.; Lin, B.Q.; Zhong, Z.; Liu, T. Experimental study on methane diffusion kinetics in three typical metamorphic coals. Fuel 2022, 311, 122601. [Google Scholar] [CrossRef]
  39. Yang, X.; Wang, G.D.; Zhang, J.Y.; Ren, T. The Influence of Sorption Pressure on Gas Diffusion in Coal Particles: An Experimental Study. Processes 2019, 7, 219. [Google Scholar] [CrossRef]
  40. Zang, J.; Wang, K.; Liu, A. Phenomenological over-parameterization of the triple-fitting-parameter diffusion models in evaluation of gas diffusion in coal. Processes 2019, 7, 241. [Google Scholar] [CrossRef]
  41. Liu, Q.Q.; Huang, W.Y.; Lv, B.; Ma, X.H.; Lu, X.D.; Wang, J.; Wang, L. Decoupling experiments for CH4 “diffusion-seepage” in coal columns to effectively measure sorption time. International Journal of Coal Geology 2022, 261, 104074. [Google Scholar] [CrossRef]
  42. Cai, Y.Y.; Cheng, J.S.; Cheng, B. Study on the gas emission law of circular column cinder based on time－varying diffusion coefficient. Mining Safety & Environmental Protection 2020, 47, 32–36. [Google Scholar]
  43. Song, Y.; Jiang, B.; Li, M.; Hou, C.L.; Xu, S.C. A review on pore-fractures in tectonically deformed coals. Fuel 2020, 278, 118248. [Google Scholar]
  44. Ren, J.G.; Weng, H.B.; Song, Z.M.; Li, B.; Lv, R.S. Method of Making Raw Coal Isostatic Pressing Columnar Coal Samples for Heavily Tectonically Deformed Coal. Safety in Coal Mines 2018, 49, 66–69. [Google Scholar]
  45. Liu, G.F. Mechanism and model of coal adsorption gas in high temperature and pressure and three-phase medium. Doctoral Thesis, Henan Polytechnic University, Jiaozuo, China, 2011. [Google Scholar]
  46. Zhu, W.C.; Liu, S.Y.; Zhang, X.F.; Wei, C.H. Coupled coal–gas interaction during CBM and CO2-ECBM recovery in coal seams: A critical review. Geomechanics and Geophysics for Geo-Energy and Geo-Resources 2022, 8, 195. [Google Scholar] [CrossRef]
  47. Liu, Z.D.; Lin, X.S.; Wang, Z.Y.; Zhang, Z.; Chen, R.; Wang, L.; Li, W. Modeling and experimental study on methane diffusivity in coal mass under in-situ high stress conditions: A better understanding of gas extraction. Fuel 2022, 321, 124078. [Google Scholar] [CrossRef]
  48. Niu, Q.H.; Cao, L.W.; Sang, S.X.; Zhou, X.Z.; Wang, W.; Yuan, W.; Ji, Z.M.; Wang, H.C.; Nie, Y. Study on the anisotropic permeability in different rank coals under influences of supercritical CO2 adsorption and effective stress and its enlightenment for CO2 enhance coalbed methane recovery. Fuel 2020, 262, 116515. [Google Scholar] [CrossRef]
  49. Ji, X.F.; Song, D.Y.; Shi, W.F.; Li, Y.F. Influence of Nanopore Structure Deformation on Gas Migration in Coal. ACS Omega 2021, 29, 19115–19126. [Google Scholar] [CrossRef]
  50. Wang, Z.Z.; Fu, X.H.; Pan, J.N.; Deng, Z. Effect of N2/CO2 injection and alternate injection on volume swelling/shrinkage strain of coal. Energy 2023, 275, 127377. [Google Scholar] [CrossRef]
  51. Zhao, D. Study on the behavior and mechanism of methane desorption-diffusion for multi-scale coal samples under multi-temperature conditions. Fuel 2022, 328, 125332. [Google Scholar] [CrossRef]
  52. Qin, Y. Modeling of Gas Desorption and Diffusion Kinetics in a Coal Seam Combined with a Free Gas Density Gradient Concept. Energy & Fuel 2022, 36, 10052–10063. [Google Scholar]
  53. Liu, S.; Wei, C.; Zhu, W.; Zhang, M. Temperature- and pressure-dependent gas diffusion in coal particles: Numerical model and experiments. Fuel 2020, 266, 117054. [Google Scholar] [CrossRef]
  54. Liu, Y.W.; Du, Y.; Li, Z.Q.; Zhao, F.J.; Zuo, W.Q.; Wei, J.P.; Mitri, H. A rapid and accurate direct measurement method of underground coal seam gas content based on dynamic diffusion theory. International Journal of Mining Science and Technology 2020, 30, 799–810. [Google Scholar] [CrossRef]
  55. Lu, S.Q.; Wang, C.F.; Li, M.J.; Sa, Z.Y.; Zhang, Y.L.; Liu, J.; Wang, H.; Wang, S.C. Gas time-dependent diffusion in pores of deformed coal particles: Model development and analysis. Fuel 2021, 295, 120566. [Google Scholar] [CrossRef]
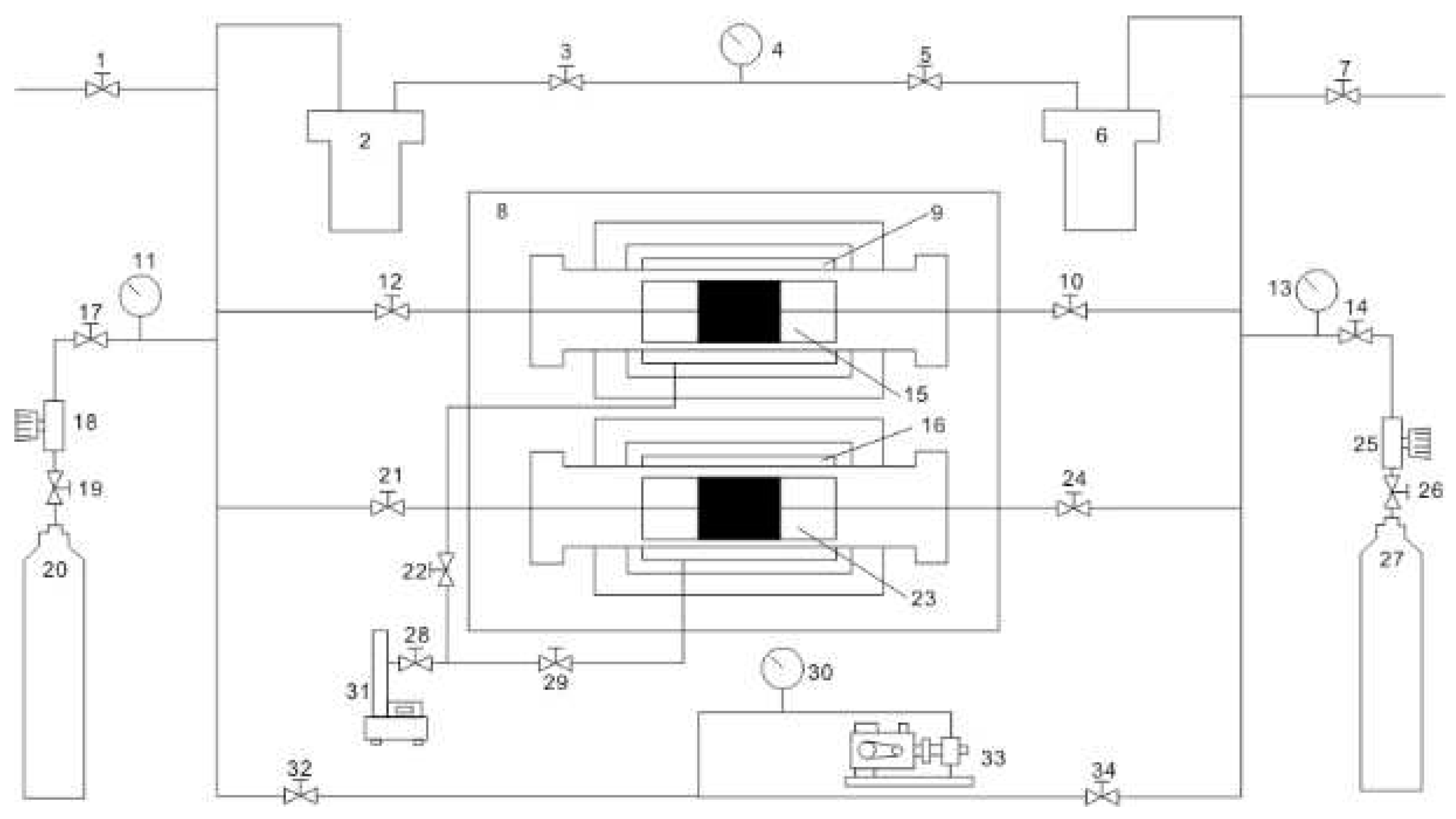
Preprints 82865 g001
Figure 1. Methane diffusion coefficient determination device by counter diffusion method. annotations: 1,3,5,7,10,12,14,17,19,21,22,24,26,28,29,32,34 - Shut-off valves; 2 - Methane chamber; 4 - Differential pressure transmitter; 6 - Nitrogen chamber; 8 - Coal core holder; 9,16 - Confining pressure systems; 11,13 - Pressure gauges; 15,23 - Coal samples; 18,25 - Pressure reducing valves; 20 - Methane; 27 - Nitrogen; 30 - Vacuum gauge; 31 - Confining pressure pump; 33 - Vacuum pump.
Figure 1. Methane diffusion coefficient determination device by counter diffusion method. annotations: 1,3,5,7,10,12,14,17,19,21,22,24,26,28,29,32,34 - Shut-off valves; 2 - Methane chamber; 4 - Differential pressure transmitter; 6 - Nitrogen chamber; 8 - Coal core holder; 9,16 - Confining pressure systems; 11,13 - Pressure gauges; 15,23 - Coal samples; 18,25 - Pressure reducing valves; 20 - Methane; 27 - Nitrogen; 30 - Vacuum gauge; 31 - Confining pressure pump; 33 - Vacuum pump.
Preprints 82865 g001
Preprints 82865 g002
Figure 2. Original coal samples of the four types of coal used in the diffusion experiment. a. Original structural coal samples b. Fractured coal samples c. Granular coal samples d. Mylonite coal samples.
Figure 2. Original coal samples of the four types of coal used in the diffusion experiment. a. Original structural coal samples b. Fractured coal samples c. Granular coal samples d. Mylonite coal samples.
Preprints 82865 g002
Preprints 82865 g003
Figure 3. Relationship between Diffusion Coefficient and Confining Pressure.
Figure 3. Relationship between Diffusion Coefficient and Confining Pressure.
Preprints 82865 g003
Preprints 82865 g004
Figure 4. Relationship between Diffusion Coefficient and Effective Stress (Variable Confining Pressure).
Figure 4. Relationship between Diffusion Coefficient and Effective Stress (Variable Confining Pressure).
Preprints 82865 g004
Preprints 82865 g005aPreprints 82865 g005b
Figure 5. Relationship between Diffusion Coefficient and Gas Pressure.
Figure 5. Relationship between Diffusion Coefficient and Gas Pressure.
Preprints 82865 g005aPreprints 82865 g005b
Preprints 82865 g006aPreprints 82865 g006b
Figure 6. Relationship between Diffusion Coefficient and Effective Stress (Variable Gas Pressure).
Figure 6. Relationship between Diffusion Coefficient and Effective Stress (Variable Gas Pressure).
Preprints 82865 g006aPreprints 82865 g006b
Preprints 82865 g007aPreprints 82865 g007b
Figure 7. Relationship between Diffusion Coefficient and Temperature.
Figure 7. Relationship between Diffusion Coefficient and Temperature.
Preprints 82865 g007aPreprints 82865 g007b
Preprints 82865 g008
Figure 8. Change diagram of diffusion coefficient of different metamorphic deformation coal.
Figure 8. Change diagram of diffusion coefficient of different metamorphic deformation coal.
Preprints 82865 g008
Preprints 82865 g009
Figure 9. Relationship Between Diffusion Coefficient and f Value of Coal with Different Metamorphic Deformation.
Figure 9. Relationship Between Diffusion Coefficient and f Value of Coal with Different Metamorphic Deformation.
Preprints 82865 g009
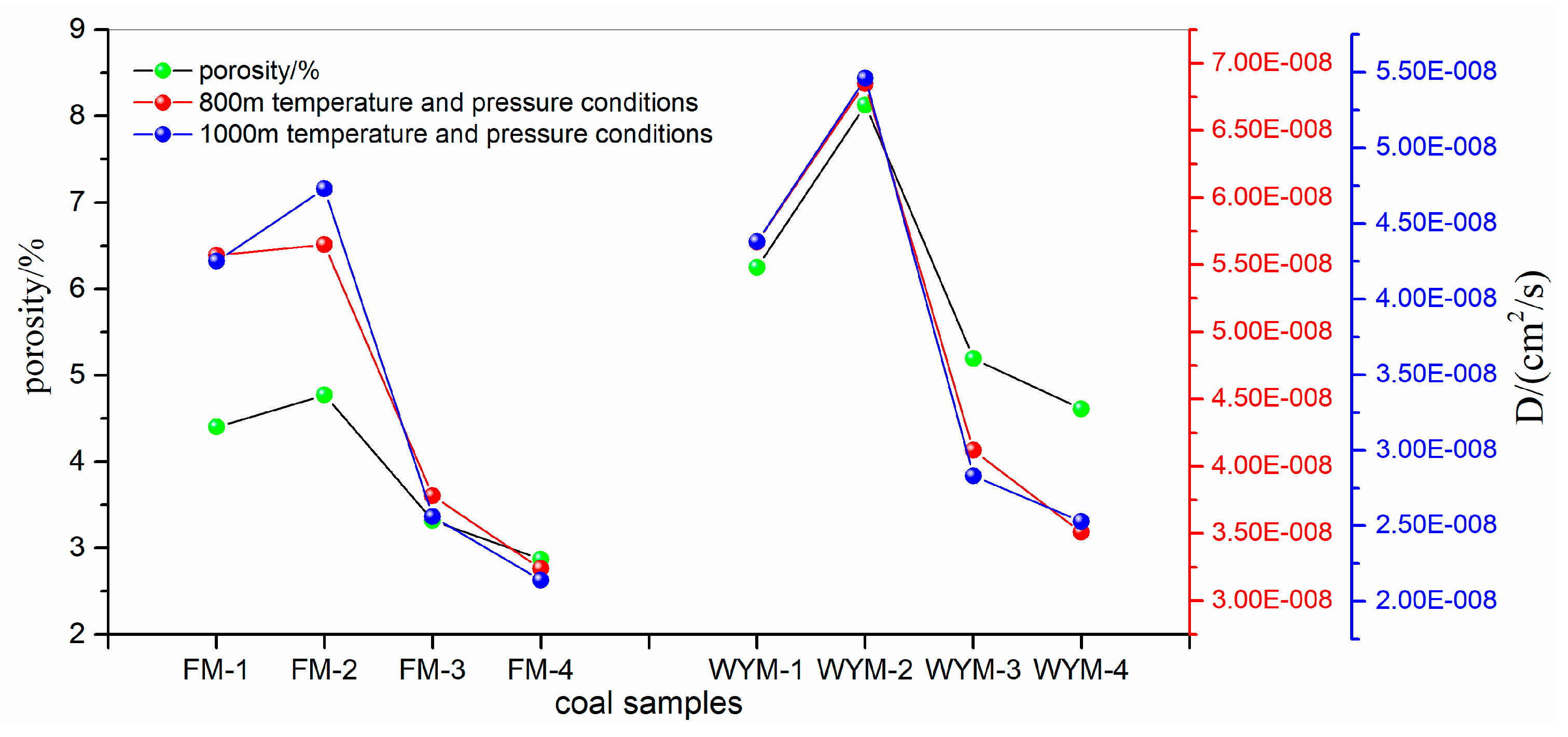
Preprints 82865 g010
Figure 10. Relationship Between Diffusion Coefficient and Porosity of Coal with Different Metamorphic Deformation.
Figure 10. Relationship Between Diffusion Coefficient and Porosity of Coal with Different Metamorphic Deformation.
Preprints 82865 g010
Table 1. Basic Parameter Measurement Results of Coal Samples.
Table 1. Basic Parameter Measurement Results of Coal Samples.
Samples Coal structure Ro,max(%) Mad (%) Ad (%) Vdaf (%) FCd (%) Porosity /% f value
WYM-1 Original structure coal 3.38 2.94 8.41 5.50 83.15 6.25 1.19
WYM-2 Fragmented coal 3.41 2.93 8.41 5.49 83.17 8.13 0.85
WYM-3 Flax seed coal 3.39 2.67 8.36 5.63 83.22 5.19 0.41
WYM-4 Mylonitized coal 3.44 2.53 8.57 5.71 83.19 4.61 0.15
FM-1 Original structure coal 1.14 1.42 10.10 11.03 70.65 4.40 0.81
FM-2 Fragmented coal 1.16 1.44 8.70 10.52 69.99 4.77 0.64
FM-3 Flax seed coal 1.14 1.21 8.65 10.79 70.52 3.32 0.31
FM-4 Mylonitized coal 1.15 1.06 8.77 10.21 70.32 2.87 0.15
Table 2. Predicted Results of Original Coal Seam Temperature and Pressure.
Table 2. Predicted Results of Original Coal Seam Temperature and Pressure.
Coal seam burial depth
/m		 Predicted coal seam temperature/℃ Average value/℃ Predicted reservoir pressure/MPa Average value
/MPa
Minimum/Maximum Minimum/Maximum
600 22/32 27 2.4/7.7 5.0
700 24/34 29 2.8/9.0 5.9
800 26/36 31 3.2/10.3 6.7
900 28/38 33 3.6/11.6 7.6
1000 30/40 35 4.0/12.9 8.6
1100 32/43 37.5 4.4/14.2 9.5
1200 34/46 40 4.8/15.5 10.3
1300 36/49 42.5 5.2/16.8 11.0
Table 3. Conditions for measuring diffusion coefficient by interdiffusion method.
Table 3. Conditions for measuring diffusion coefficient by interdiffusion method.
Simulated burial depth/m Confining pressure/MPa Gas pressure/MPa Temperature/℃ Remarks
600 5.0 0.5 27 Orthogonal experiment designed accordingly
800 6.7 1.0 31
1000 8.6 1.5 35
1200 10.3 2.0 40
Table 4. Variable Confining Pressure Diffusion Experiment Conditions and Results.
Table 4. Variable Confining Pressure Diffusion Experiment Conditions and Results.
Samples Experimental conditions Effective stress/MPa CH4 diffusion coefficient D/(cm2/s) Samples Experimental conditions Effective stress/MPa CH4 diffusion coefficient D/(cm2/s)
Confining pressure /MPa Temperature /℃ Gas pressure /MPa Confining pressure /MPa Temperature /℃ Gas pressure /MPa
WYM-1 5.0 31 1.0 4.0 7.44E-08 WYM-3 5.0 31 1.0 4.0 5.34E-08
6.7 5.7 5.67E-08 6.7 5.7 4.12E-08
8.6 7.6 3.86E-08 8.6 7.6 2.33E-08
10.3 9.3 3.32E-08 10.3 9.3 1.84E-08
WYM-2 5.0 31 1.0 4.0 9.12E-08 WYM-4 5.0 31 1.0 4.0 4.53E-08
6.7 5.7 6.85E-08 6.7 5.7 3.51E-08
8.6 7.6 4.86E-08 8.6 7.6 2.23E-08
10.3 9.3 4.32E-08 10.3 9.3 1.82E-08
FM-1 5.0 31 1.0 4.0 6.98E-08 FM-2 5.0 31 1.0 4.0 7.12E-08
6.7 5.7 5.57E-08 6.7 5.7 5.65E-08
8.6 7.6 3.75E-08 8.6 7.6 3.82E-08
10.3 9.3 3.01E-08 10.3 9.3 3.09E-08
Table 5. Variable Gas Pressure Diffusion Experiment Conditions and Results.
Table 5. Variable Gas Pressure Diffusion Experiment Conditions and Results.
Samples Experimental conditions Effective stress/MPa CH4 diffusion coefficient D/(cm2/s) Samples Experimental conditions Effective stress/MPa CH4 diffusion coefficient D/(cm2/s)
Gas pressure /MPa Temperature /℃ Confining pressure /MPa Gas pressure /MPa Temperature /℃ Confining pressure /MPa
WYM-1 0.5 31 6.7 6.2 3.34E-08 WYM-3 0.5 31 6.7 6.2 3.01E-08
1.0 5.7 5.67E-08 1.0 5.7 4.12E-08
1.5 5.2 7.87E-08 1.5 5.2 6.12E-08
2.0 4.7 8.46E-08 2.0 4.7 6.46E-08
WYM-2 0.5 31 6.7 6.2 4.23E-08 WYM-4 0.5 31 6.7 6.2 2.87E-08
1.0 5.7 6.85E-08 1.0 5.7 3.51E-08
1.5 5.2 8.12E-08 1.5 5.2 5.67E-08
2.0 4.7 8.65E-08 2.0 4.7 5.98E-08
FM-1 0.5 31 6.7 6.2 3.14E-08 FM-2 0.5 31 6.7 6.2 3.35E-08
1.0 5.7 5.57E-08 1.0 5.7 5.65E-08
1.5 5.2 7.35E-08 1.5 5.2 7.67E-08
2.0 4.7 7.67E-08 2.0 4.7 8.41E-08
Table 6. Variable Temperature Experimental Conditions and Results.
Table 6. Variable Temperature Experimental Conditions and Results.
Samples Experimental conditions CH4 diffusion coefficient D/(cm2/s) No. Experimental conditions CH4 diffusion coefficient D/(cm2/s)
Temperature/℃ Confining pressure/MPa Gas pressure/MPa Temperature/℃ Confining pressure/MPa Gas pressure/MPa
WYM-1 27 6.7 1.0 5.62E-08 WYM-3 27 6.7 1.0 4.07E-08
31 5.67E-08 31 4.12E-08
35 5.73E-08 35 4.18E-08
40 5.83E-08 40 4.27E-08
45 5.97E-08 45 4.43E-08
50 6.19E-08 50 4.56E-08
WYM-2 27 6.7 1.0 6.81E-08 WYM-4 27 6.7 1.0 3.46E-08
31 6.85E-08 31 3.51E-08
35 6.91E-08 35 3.55E-08
40 7.03E-08 40 3.62E-08
45 7.16E-08 45 3.70E-08
50 7.34E-08 50 3.81E-08
FM-1 27 6.7 1.0 5.54E-08 FM-2 27 6.7 1.0 5.62E-08
31 5.57E-08 31 5.65E-08
35 5.63E-08 35 5.72E-08
40 5.69E-08 40 5.78E-08
45 5.76E-08 45 5.85E-08
50 5.86E-08 50 5.96E-08
Table 7. Experimental Conditions and Results for Coal Samples of Different Metamorphic and Deformation Degrees.
Table 7. Experimental Conditions and Results for Coal Samples of Different Metamorphic and Deformation Degrees.
Samples f value Experimental conditions CH4 diffusion coefficient D/(cm2/s) Simulated coal seam burial depth/m
Confining pressure /MPa Temperature /℃ Gas pressure /MPa
WYM-1 1.19 6.7 31 1.0 5.67E-08 800m
WYM-2 0.85 6.7 31 1.0 6.85E-08
WYM-3 0.41 6.7 31 1.0 4.12E-08
WYM-4 0.15 6.7 31 1.0 3.51E-08
FM-1 0.81 6.7 31 1.0 5.57E-08
FM-2 0.64 6.7 31 1.0 5.65E-08
FM-3 0.31 6.7 31 1.0 3.78E-08
FM-4 0.15 6.7 31 1.0 3.24E-08
WYM-1 1.19 8.6 35 1.5 4.38E-08 1000m
WYM-2 0.85 8.6 35 1.5 5.46E-08
WYM-3 0.41 8.6 35 1.5 2.83E-08
WYM-4 0.15 8.6 35 1.5 2.53E-08
FM-1 0.81 8.6 35 1.5 4.25E-08
FM-2 0.64 8.6 35 1.5 4.73E-08
FM-3 0.31 8.6 35 1.5 2.56E-08
FM-4 0.15 8.6 35 1.5 2.14E-08
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated