1. Introduction
Detecting jumps in a series of real numbers and determining their number and locations is known in statistics as a change-point problem. This is usually solved by testing for the stationarity of the series and estimating the change locations when the null hypothesis of stationarity is rejected.
Change-point problems can be encountered in a wide range of disciplines, such as quality control, genetic data analysis and bio informatics (see, e.g., [
1,
2]) and financial analysis (see, e.g., [
3,
4,
5]). The study of conditional variations in financial and economic data receives a particular attention as a result of its interest in hedging strategies and risk management.
The literature on change-points is vast. Parametric or non-parametric approaches are used for independent and identically distributed (iid) data as well as for dependent data. The pioneering works of [
6] and [
7] proposed tests for identifying a deviation in the mean of iid Gaussian variables from industrial quality control. [
8] proposed a test for detecting change in mean. This criterion was leter generalized by [
9], which envisioned a much more general model allowing incremental changes. [
10,
11,
12] presented a documentary analysis of several non-parametric procedures.
A popular alternative to using the likelihood ratio test was employed in [
13] and [
14]. [
15] reviewed the asymptotic behavior of likelihood ratio statistics for testing a change in the mean in a series of iid Gaussian random variables. [
16] came up with statistics based on linear rank statistical processes with quantum scores. [
17] looked at detection tests and change-point estimation methods for models based on the normal distribution. The contribution of [
18] is related to the change in mean and variance. [
19] proposed permutation tests for the location and scale parameters of a law. [
20] developed a change-point test using the empirical characteristic functions. [
21] proposed several CUSUM approaches. [
22] proposed tests for change detection in the mean, variance, and autoregressive parameters of a
p-order autoregressive model. [
23] used a weighted CUSUM procedure to identify a potential change in the mean and covariance structure of linear processes.
There are several types of changes depending on the temporal behavior of the series studied. The usual ones are abrupt change, gradual change, and intermittent change. These are studied in the frameworks of
on-line or
off-line data. In this paper, we focus abrupt change in the conditional variance of
off-line data issue from a class of CHARN models (see [
24] and [
25]). These models are of the most famous and significant ones in finance, which include many financial time series models. We suggest an hybrid estimation procedure which combines CLS and non-parametric methods to estimate the change location. Indeed, conditional least-squares estimators own a computational advantage and require no knowledge of the innovation process.
The rest of the paper is organized as follows.
Section 2 presents the class of models studied, the notation, the main assumptions and the main result on the CLS estimators of the parameters.
Section 3 presents the change-point test and the change location LS estimation. The asymptotic distribution of the test statistic under the null hypothesis is investigated. The consistency rates are obtained for the change location estimator and its limit distribution is derived.
Section 4 presents the simulation results from a few simple time series models. The results are also applied to a real data set. This section ends with a conclusion on our work. The proofs and auxiliary results are given in the last section.
2. Model and assumptions
2.1. Notation and Assumptions
Let
l and
r be positive integers. For given real functions
defined on a non-empty subset of
,
and
defined on a non-empty subset of
, we denote:
For a vector or matrix function
, we denote by
, the transpose of
. We define:
All along the text, the notations
and
denote respectively, the weak convergence in functional spaces and the convergence in distribution.
We place ourselves in the framework where the observations at hand are assumed to be issued from the following CHARN(
) model:
where
;
and
are two real-valued functions of known forms depending on unknown parameters
and
respectively; for all
,
;
is a sequence of stationary random variables with
and
such that
is independent of the
algebra
. The case
is treated in [
26,
27,
28]) where the stationarity and the ergodicity of the process
is studied. Although we restrict to
, all the results stated here also hold for
.
Let
, the vector of the parameters of the model (
1) and
the true parameter vector. Denote by
an appropriate norm of a vector or a matrix
M. We assume that all the random variables in the whole text are defined on the same probability space
. We make the following assumptions:
- (A1)
The common fourth order moment of the ’s is finite.
- (A2)
-
The function is twice continuously differentiable a.e., with respect to in some neighborhood of .
The function is twice continuously differentiable a.e., with respect to in some neighborhood of .
There exists a positive function
such that
, and
- (A3)
There exists a positive function
such that
, and for all
, and
,
- (A4)
-
The sequence is stationary and satisfies either of the following two conditions:
-mixing with mixing coefficient satisfying and for some ;
-mixing with mixing coefficient satisfying and for some .
2.2. Parameter estimation
2.2.1. Conditional least-squares estimation
The conditional mean and the conditional variance of
are given respectively by
=
and
. From these, one has that for all
,
Therefore, for any bounded measurable functions
and
, we have
Without loss of generality, in the following we take, for all
. Now, given
with
, we let
and consider the sequences of random functions
We have the following theorem:
Theorem 1. Under assumptions (A1)-(A3), there exists a sequence of estimators such that almost surely, and for any , there exists an event E with , and a non negative integer such that on E, for ,
and attains a relative minimum at ;
assuming fixed, and attains a relative minimum at .
Proof. This result is an extension of [
29] to the case
is a mixing martingale difference. The proof can be handled in the same lines and is left to the reader. □
3. Change-point study
3.1. Change-point test and change location estimation
We essentially use the techniques of [
30], who studied the estimation of the shift in the mean of a linear process by a LS method. We first consider the model (
1) for known
, and
, for some known positive real-valued function
defined on
and for an unknown positive real number
. We wish to test
against
where
and
are unknown parameters.
We are also interested in estimating
and the change location
, when
is rejected. It is assumed that
for some
, with
standing for the integer part of any real number
x. From (
1), one can easily check that
from which we define the LS estimator
of
as follows:
where
. Thus, the change location is estimated by minimizing the sum of squares of residuals among all possible sample slits.
Letting
it is easily seen that for some
k, the LS estimator of
and
are
and
respectively, and that (
3) can be written as
Let
. A simple algebra gives
where
From (
4) and (
5), we have
From (
6), a simple algebraic computation gives the following alternative expression for
:
It results from (
7) and (
8) that
Writing
, it is immediate that
Simple computations give
from which we have
The test statistic we use for testing
against
is a scale version of
.
One can observe that under some conditions (e.g.,
i.i.d. with
), this statistic is the equivalent likelihood based test statistic for testing
against
(see, e.g., [
31]).
Let
By simple calculations, we obtain
where
is a positive weight function defined for any
by
.
3.2. Asymptotics
3.2.1. Asymptotic distribution of the test statistic
The study of the asymptotic distribution of the test statistic under
, is based on that of the the process
defined for any
by
where
where we recall that
is the integer part of
. For some
and for any
s in
, we define
where
and
is any consistent estimator of
For
, we denote by
the space of all right continuous functions with left limits on
endowed with the Skorohod metric. It is clear that
and
.
Theorem 2. Assume that the assumptions (A1)–(A4) hold. Then under , we have
;
,
where is a Brownian Bridge on .
It is worth noting that if the change occurs at the very beginning or at the very end of the data, we may not have sufficient observations to obtain consistent LSE estimators of the parameters or these may not be unique. This is why we stress on the truncated version of the test statistic given in [
21] that we recall:
By Theorem 2, it is easy to see that for any
,
which yields the asymptotic null distribution of the test statistic. With this, at level of significance
,
is rejected if
, where
is the
-quantile of the distribution of the above limit. This quantile can be computed by observing that under
, for larger values of
n one has
From the following relation (1.3.26) of [
32], for each
, and for larger real number
x, we have
which gives an approximation of the tail distribution of
. Thus, using
, an estimation of
can be obtained from this approximation. Monte Carlo simulations are often carried out to obtain accurate approximations of
. In this purpose, it is necessary to do a good choice of
. We selected
as our option, which we found to be a suitable choice for all the cases we examined. But, to avoid the difficulties associated with the computation of
, a decision can also be taken by using the
p-value method as in [
33]. That is using the approximation (
16), reject
if
This idea is used in the simulation section.
3.2.2. Rate of convergence of the change location estimator
For the study of the estimator
, we let
and assume without loss of generality that
(see, e.g., [
34]) and that the unknown change point
depends on the sample size
n. We have the following result:
Theorem 3.
Assume that (A4) is satisfied, for some , for some and as , and Then we have
where denotes a "big-O" of Landau in probability.
3.2.3. Limit distribution of the location estimator
In this section we study the asymptotic behavior of the location estimator. We make the additional assumptions that
and that as
,
By (
10), we have
To derive the limiting distribution of
, we study the behavior of
for those
k’s in the neighborhood of
such that
, where
r varies in an arbitrary bounded interval
. In this purpose, we define
where
. In addition, we define the two-sided standard Wiener process
as follows:
where
are two independent standard Wiener processes defined on
with
.
First, we identify the limit of the process on for every given . We denote by the space of all continuous functions on endow with the uniform metric.
Proposition 1. Assume that (A4) holds, that for some and that as , . Then for every , the process converges weakly in to the process , where is the two sided standard Winer process defined above.
The above results make it possible to achieve a weak convergence result for and then apply the Argmax-Continuous Mapping Theorem (Argmax-CMT). We have:
Theorem 4.
Assume that (A4) is satisfied, that for some and as , . Then we have
where .
This result yields the asymptotic distribution of the change location estimator. [
35,
36] and [
37] investigated the density function of the random variable
(see the Lemma 1.6.3 of [
32] for more details). They also showed that
has a symmetric (with respect to 0) probability density function
defined for any
by
where
is the cumulative distribution function of the standard normal variable. From this result, a confidence interval for the change-point location can be obtained, if one has consistent estimates of
and
. With
, consistent estimates of
and
are given respectively by
Thus a consistent estimate of
is given by
A consistent estimator of
that we denote by
, can be easily obtained by taking its empirical counterpart. So, at risk
, letting
be the quantile of order
of the distribution of the random variable
, an asymptotic confidence interval for
is given by
Remark 1.
In the case that the parameter ρ is unknown, it can be estimated by the CLS method (see Section 2.2.1), and be substituted for its estimator in . Indeed, one can easily show that
where for any , and is the conditional least squares estimators of ρ obtained from Theorem 1. Hence, the same techniques as in the case where ρ is known can be used.
4. Practical consideration
In this section we do numerical simulations to evaluate the performances of our methods and these are applied to two sets of real data. We start with the presentation of the results of numerical simulations done with the software R. The trials are based on 1000 replications of observations of lengths
, 1000, 5000 and 10000 generated from the model (
1) for
=
with
=
and
;
is a white noise with density function
f. We also assume the sufficient condition
, to ensure the strict stationarity and ergodicity of the process
(see, e.g., Theorem 3.2.11 of [
38], p. 86 and [
39], p. 5). The noise densities
f that we employed was Gaussian.
4.1. Example 1
We consider the model (
1) for
,
,
=
,
,
and
. The resulting model is an ARCH(1). The change location estimators are calculated for
at the locations
for
. In each case, we compute the bias and the standard error SE
1 of the change location estimator.
Table 1 shows that the bias declines rapidly as
increases. Also, as the sample size
n increases, the bias and the SE decrease. This tends to show the consistency of
, as expected from the asymptotic results.
We also consider the case
, where
. It is easy to check that with this
is stationary and strongly mixing, and that
and
. In this case, we only study the SE for
and the results are compared to those obtained for
, for the same values of
as above but for
and
. These results listed in
Table 2 show that for
, the location estimator is more accurate and the SE decreases slightly compared to the case
. It seems from these results that the nature of the white noise
does not affect much the location estimator for larger values of
n and
.
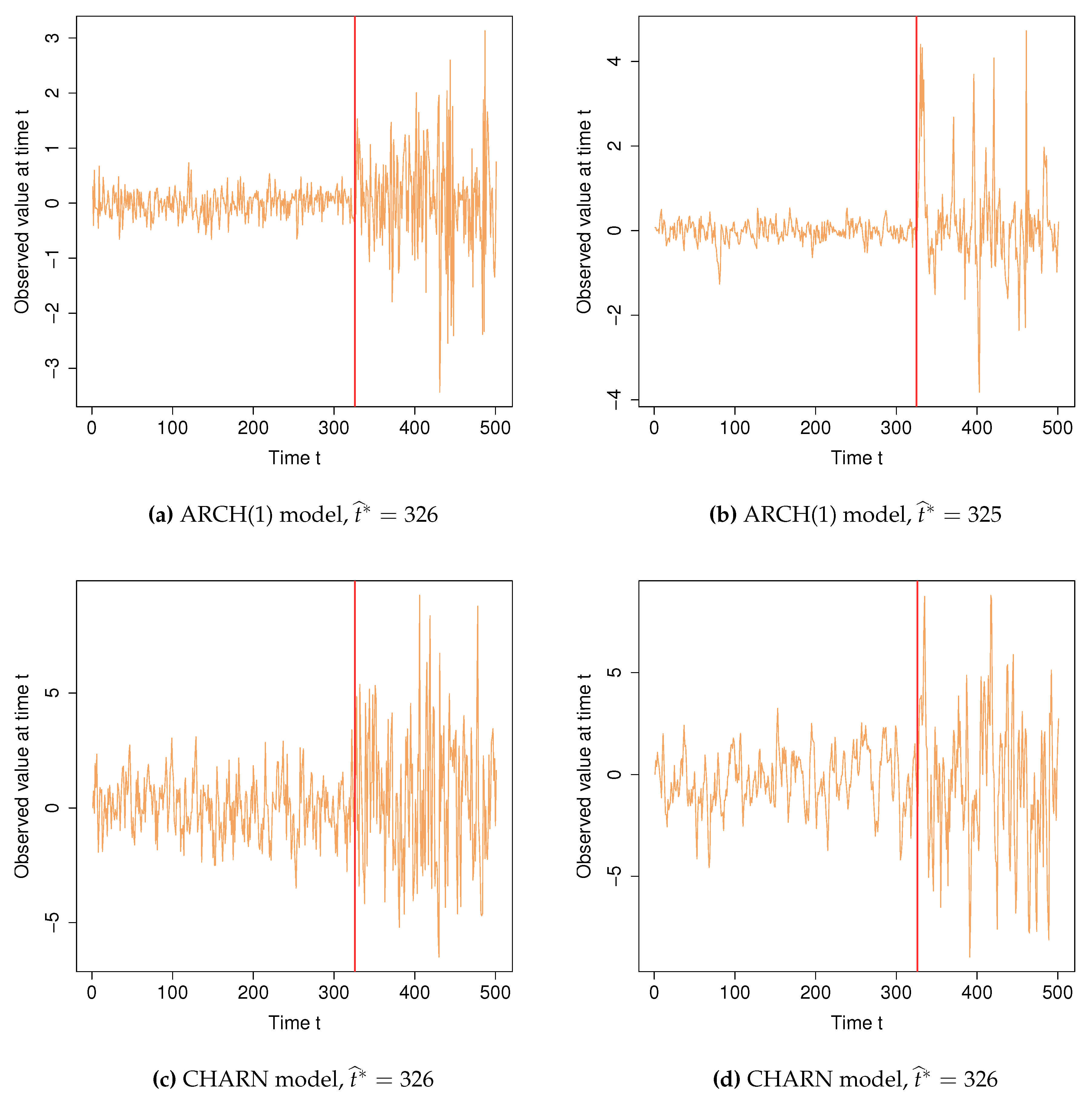
We present two graphs showing a change in volatility at a time
. This is indicated by a vertical red line on both graphics where one can easily see the evolution of the time series before and after the change location estimator
. The series in both figures are obtained for
,
,
and
. That in
Figure 1(a) is obtained for standard iid Gaussian
’s. In this case, using our method, the change location
is estimated by
. The time series in
Figure 1(b) is obtained with
AR(1). In this case,
is estimated by
.
4.2. Example 2
We generate
n observations from the model (
1) for
and
,
,
,
and
. We assume
is unknown and estimated by CLS method and
is a function unknown which depends on the unknown parameter
. We made 1000 replications for the lengths
from this model. The change location estimator, its bias and SE are calculated for the same values of
and locations
as in the preceding example. The results given in
Table 3 are very similar to those displayed in
Table 1.
As in the previous example, we present two graphs illustrating our method’s ability to detect the change-point in the time series considered. On both graphics one can easily see the evolution of the time series before and after the change location estimator. The series in both figures are obtained for
,
,
and
. That in
Figure 1(c) is obtained for standard i.i.d. Gaussian
’s. In this case, using our method, the change location
is estimated by
. The time series in
Figure 1(d) is obtained with AR(1)
’s. In this case,
is estimated by
.
When performing our test, we used the
p-value method. In other words, for the nominal level
, we simulated 1000 samples each of length
and 1000 from the model (
1) for
and
,
,
,
and
. We then calculated
and counted the number of samples for which
and we divided this number by 1000. This ratio corresponds to the empirical power of our statistical test for change in volatility. The results obtained are listed in
Table 4. We can clearly see that, when
, the empirical power of the test is almost the same as the nominal level
for all
n sizes (see
Table 4).
4.3. Application to real data
In this section, we apply our procedure to two sets of genuine time series, namely, the USA stock market prices and the Brent crude oil prices. As these have large values, we take their logarithms and differentiate the resulting series to remove their trends.
4.3.1. USA stock market
These data of length 2022 from the American stock market were recorded daily from January 2nd, 1992 to December 31st, 1999. They represent the daily stock prices of the S&P 500 stock market (SPX). They are among the most closely followed stock market indices in the world and are considered as an indicator of the USA economy. They have also been recently examined by [
40] and can be found at: (
www.investing.com).
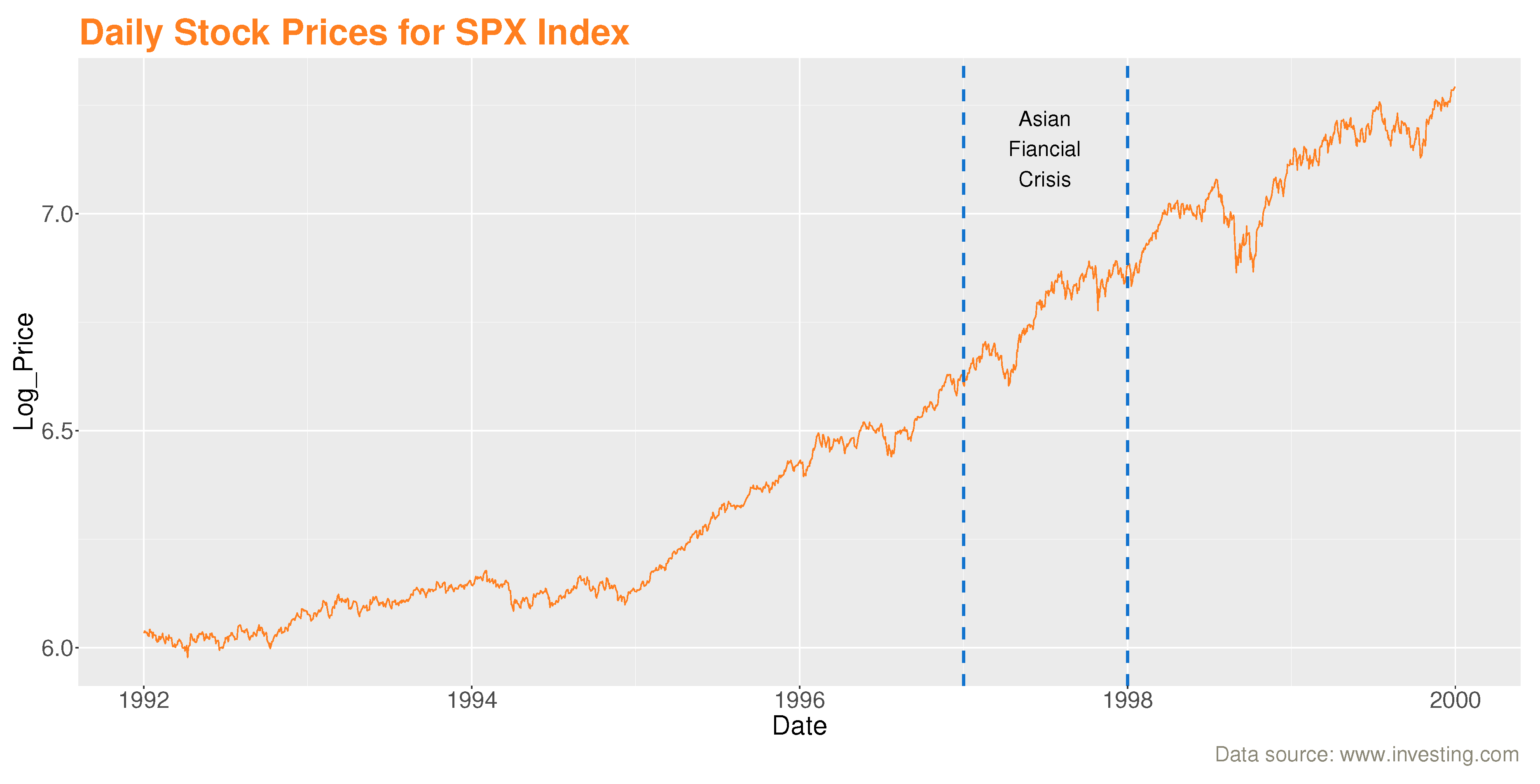
On
Figure 2, we observe that the trend of the SPX daily stock price series is not constant over time. We also observe that stock prices have fallen sharply, especially in the time interval between the two vertical dashed blue lines (the period of the 1997-1998 Asian financial crisis).
Denote by
the value of the stock price for SPX index at day
t, and the first difference of the logarithm of stock price,
as
is the logarithmic return of stock price for SPX index at day
t.
The series
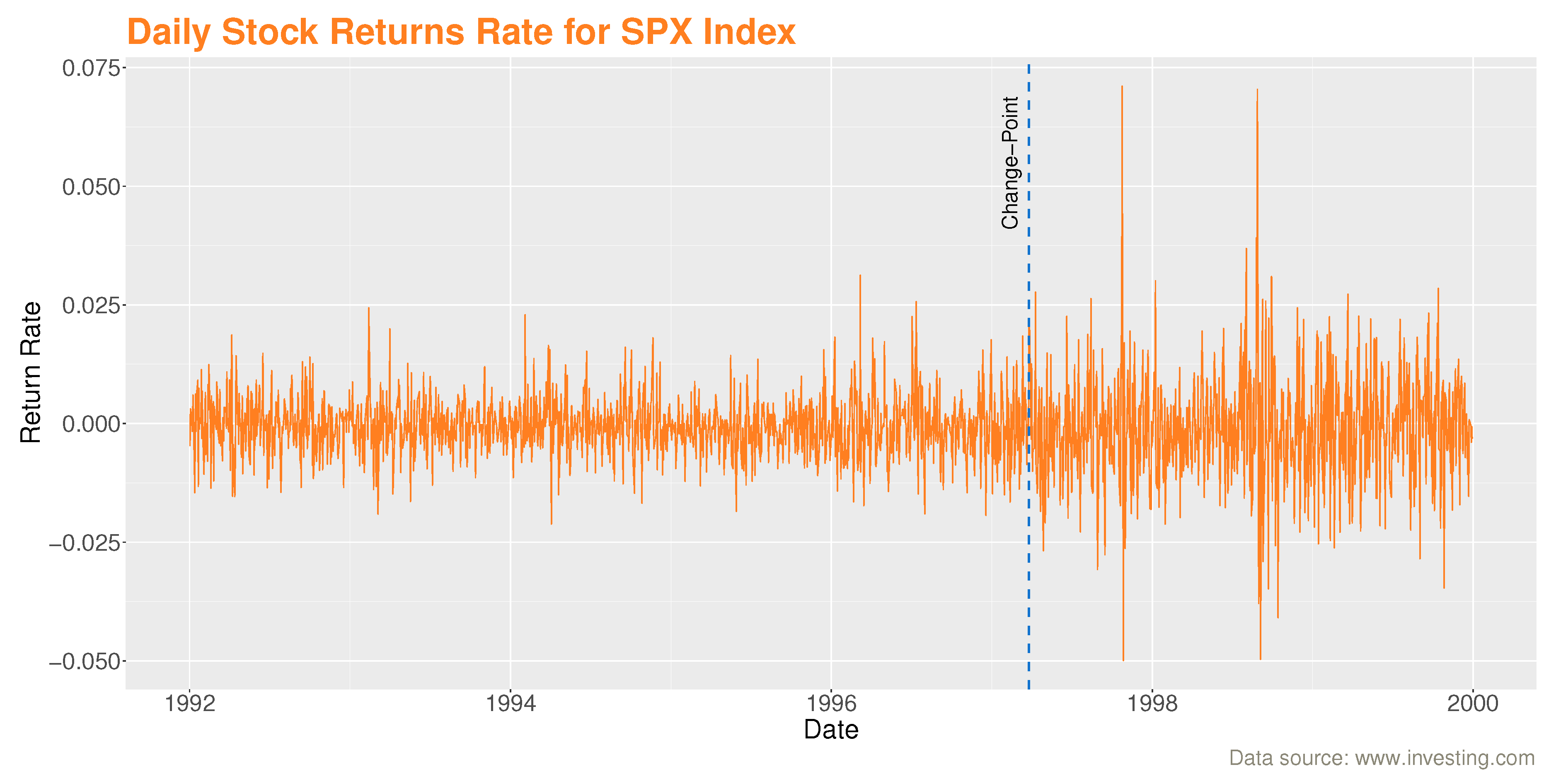
is approximately piece-wise stationary on two segments and symmetric around zero (see
Figure 3). This brought us to consider a CHARN model with
,
for
,
and
estimated by CLS described in
Section 2.
Using our procedure, we found an important change point in stock price volatility in March 26, 1997, which is consistent with the date found by [
40] (see
Figure 3).
The vertical dashed blue line of
Figure 3, represents the date at which the change occurred. It should be noted that the change in volatility coincides with the Asian crisis in 1997 when Thailand devalued its currency, the baht, against the US dollar. This decision led to a fall in the currencies and financial markets of several countries in its surroundings. The crisis then spread to other emerging countries with important social and political consequences and repercussions on the world economy.
4.3.2. Brent crude oil
These data of length 585 are based on Brent oil futures. They represent the prices of Brent oil (USD/barrel) on a daily basis between January 4th, 2021 and April 6th, 2023. They are available at: (
www.investing.com).
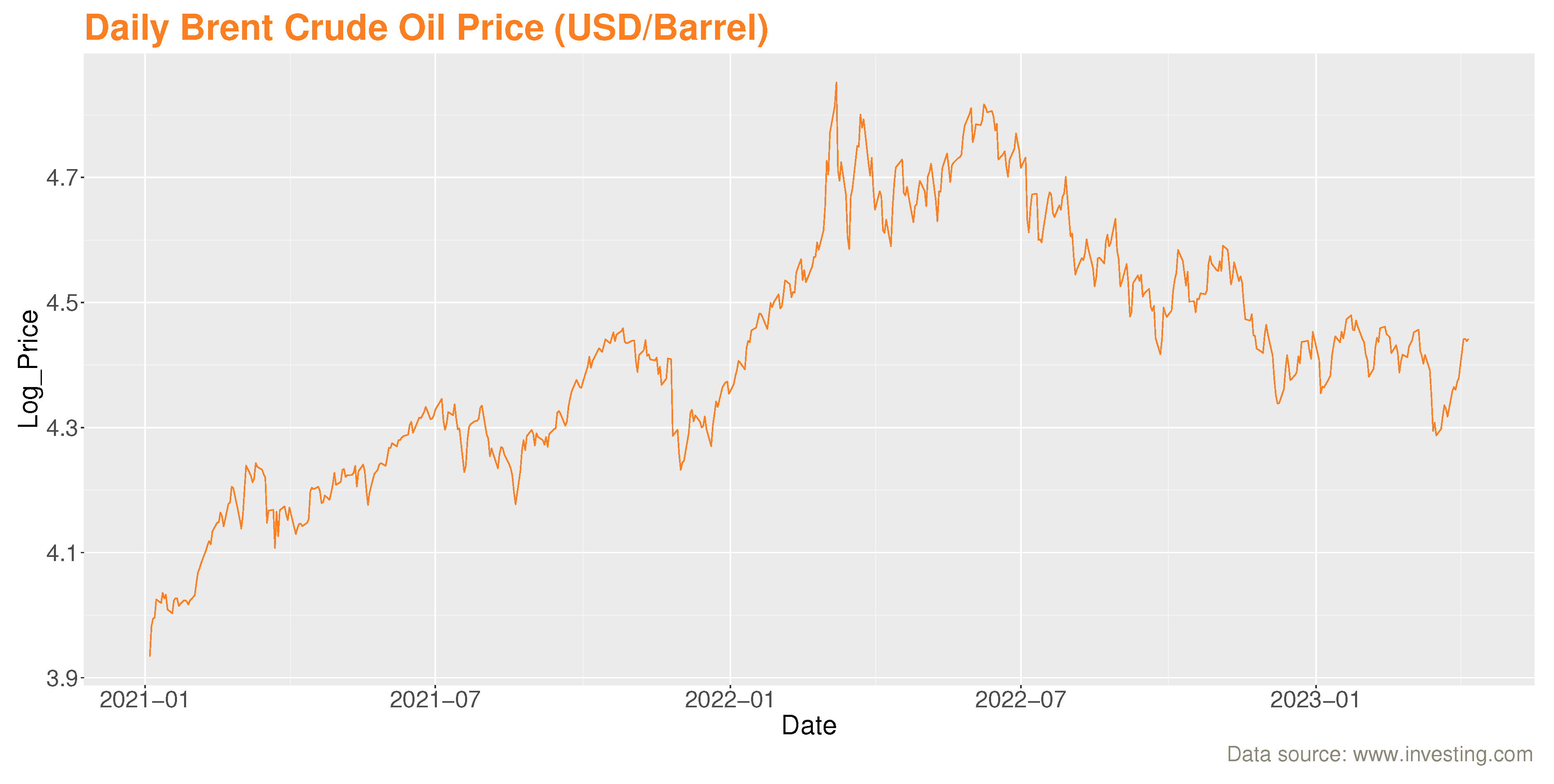
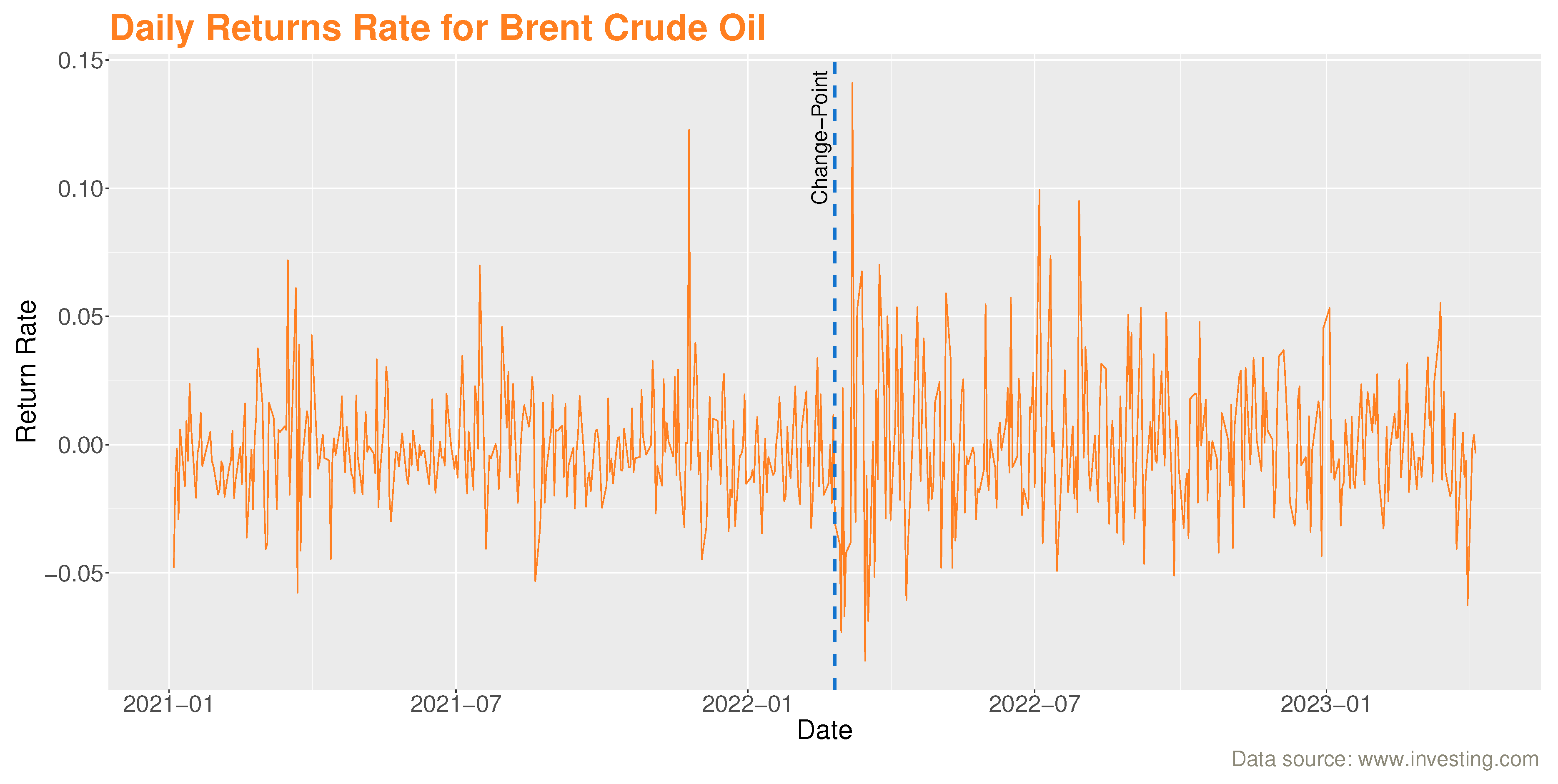
Figure 4, shows that the evolution of the daily series of Brent oil prices is non-stationary. It also shows that stock prices fell sharply, especially in early March 2022 (the date of the conflict between OPEC and Russia, when the latter refused to reduce its oil production in the face of declining global demand caused by the Covid-19 pandemic).
We follow the same procedure as in the previous example and obtain the logarithmic transformation of the daily rate of return series for Brent oil (see
Figure 5 below). Proceeding as for the first data, the application of our procedure allows to find a change at February 25, 2022. The break date is marked by a dashed blue vertical line (see
Figure 5).
It also performs well on these data. Indeed, oil volatility was very high in March 2022 due to the Covid-19 pandemic and the conflict between OPEC and Russia. The health crisis led to a significant drop in global oil demand, while Russia refused to cut oil production as proposed by OPEC, which caused oil prices to fall. Brent crude oil fell from over 60 dollars a barrel to less than 20 dollars in a month.
5. Conclusions
In this article, we have presented a CUSUM test based on a least-squares statistics for detecting an abrupt change in the volatility of CHARN models. We have shown that the test statistic converges to supremum of a weighted standard Brownian Bridge. We have constructed a change location estimator and obtained its rate of convergence its limiting distribution whose density function is given. A simulation experiment shows that our procedure performs well on the examples tested. This procedure is applied to real equity price data and real Brent crude oil data, and has led to finding change locations found in the literature. The next step to this work is its extension to the detection of multiple changes in volatility of multivariate CHARN models.
Author Contributions
Conceptualization, M.S.E.A., E.E. and J.N.-W.; Methodology, M.S.E.A., E.E. and J.N.-W.; Software, M.S.E.A., E.E. and J.N.-W.; Validation, E.E. and J.N.-W.; Writing—original draft preparation, M.S.E.A., E.E. and J.N.-W.; Writing—review and editing, M.S.E.A., E.E. and J.N.-W.; Supervision, E.E. and J.N.-W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We express our gratitude to the referees for their comments and suggestions, which have been instrumental in improving this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
This section is devoted to the proofs of the results. Here, recalling that for any
,
, the sequence
is the process defined for any
by
We first recall some definitions and preliminary results.
Appendix A.1. Preliminary results
Recall that
is a probability space. Let
be a sequence of random variables (not necessarily stationary). For
, define the
field
and for each
, define the following
mixing coefficients:
The random sequence
X is said to be "strongly mixing" or "
-mixing " if
as
, "
-mixing " if
as
. One shows that
, so that an
-mixing sequence of random variables is also
-mixing. The following corollary serves to prove Lemma A1 below.
Corollary A1 ([
41]).
Let be a sequence of ϕ-mixing random variables with
and a positive non-decreasing real number sequence. For any and positive integers , then there exists a constant such that,
where .
Lemma A1.
We assume (A4) is satisfied, then there exists a constant , such that for every and , we have
Proof. By substituting
by
k,
by
in Corollary A1, for any
and positive integers
, we obtain
Since
we have
which in turn implies that for any
, there exists a real number
such that
From (
A2) and (
A3), we have
This proves Lemma A1 for
. □
Remark A1.
Taking and and proceeding as in the proof of Lemma A1, one has by (A2) and (A3), for some ,
from which it follows that,
Lemma A2.
We assume that (A4) is satisfied, and for some , then for every , there exists and such that, for all , the estimator satisfies
Proof. For proving the consistency of an estimator obtained by maximizing an objective function, we must assert that the objective function converges uniformly in probability to a non-stochastic function which has a unique global maximum. More often than not, it is to show that the objective function is close to its mean function. Our problem’s objective function is
,
. It results from (
10), that
where we recall that
It is possible to simplify the problem by working with
without the absolute sign. We thus show that the expected value of
has a unique maximum at
and that
, is uniformly small in
k for a large
n.
We have
In order to simplify without losing generality, it is assumed that
is an integer equal to
, i.e.
. Let
and demonstrate first that
for some
, where
such that
.
For this it is sufficient to consider the case where
due to the symmetry. Then from (
A5) and according
, we obtain
In particular,
, therefore we obtain
Let
, then through (
A8), we have shown that
We clearly see that the previous inequality indicates that
achieves its maximum at
.
From (
A6), (
A9) and
, immediately by replacing
d by
, we obtain
and
From (
A10) and (
A11), we obtain
From (
A5), we obtain
It results that,
From (
A4), we deduce that the right side of the inequality (
A14) is
uniformly in
k. It follows from (
A12), (
A14) and (
A4), that
As a result, for all
, there exists
and
such that, for all
, we obtain
Which completes the proof of Lemma A2. □
Appendix A.2. Proof of Theorems
Appendix A.2.1. Proof of Theorem 2
Proof. Under (i.e., ), by simple will of simplicity we take .
Let and With this, and from simple computations, .
Since
,
. This result is guaranteed by assumption
(see, e.g., [
42], p.172). It is possible to use weak invariance principles for the sum of the underlying errors (see, e.g., [
43]). Let
be the random variable defined from the partial sums
. For points
in
, we set
and for the remaining points
s of
,
is defined by a linear interpolation, that is, for any
, and for any
s in
,
Since
if
, we may define the random function
more concisely by:
Under assumption
and by using a generalization of Donsker’s theorem in [
42], we have
where
denotes the standard Brownian motion on
. We can also prove this outcome by using Theorem 20.1 of [
42].
So
where
, stands for the Brownian Bridge on
.
Let
, then
Since
we have
It is easy to check that
From (
A15) and (
A16), it follows that
Hence,
from which the proof of Part 1 handled. Note that this proof could be done using Theorem 2.1 of [
44]. For the proof of Part 2, by the continuous mapping theorem, it follows from (
A17) that
Whence, as
is consistent to
, from (
15) and (
A18), we obtain easily
This completes the proof of Part 2 and that of the Theorem 2. □
Appendix A.2.2. Proof of Theorem 3
Proof. We need only prove that . For this, we use Lemmas A1 and A2. From Lemma A2, we have , which implies , which in turn is equivalent to .
As, , as , it is clear that , which shows that is consistent to .
Since
for some
, using the above results, it is clear that for all
,
for larger
n. Thus, it suffices to investigate the behavior of
for
. In this purpose, we prove that for all
,
for larger
n and for some sufficiently large real number
.We have
where
. We study the first term in the right-hand side of (A20). For this, it is easy to see that
where
and
.
As
, it is obvious that
Then
From (
A13), we have
Then,
where
. As
for all
, we can write
From (A22) and Lemma A1, there exists
and
such that,
which implies that as
,
Now we turn to the study of
. Observing that
and that from (
A9)
it results from (
A13) that
where
and
By (A24), (A25) and (A26), we can observe that
From above, we obtain
It is suffices to consider the case where
and
due to the symmetry. Specifically, we restrict to the values of
k such that
.
From (A27),
can be rewritten as follows:
As
,
, one can easily verify that
From (A30), (A31) and
, one obtains
According to the previous inequality and the fact that
, one obtains
Inequality (A33) implies that
Which implies that
From Lemma A1, all the three terms
,
and
tends to 0 for larger
n and for some sufficiently large real number
. This implies that for larger values of
n and for all
,
and
. It easily follows from these that for larger values of
n,
It follows from (A35), (A29), (A23) and (A21), that
Thus, for larger values of
n and for some sufficiently large real number
, from (A36) and (A20), we can conclude that, for all
,
, that is
, equivalently
Which completes the proof of Theorem 3. □
Appendix A.2.3. Proof of Theorem 4
Proof. It suffices to use Proposition 1 and apply the functional Continuous Mapping Theorem (CMT). Let
, be the subset of continuous functions in
for which the functions reach their maximum at a unique point in
, equipped with the uniform metric. It makes no doubt that Proposition 1, implies that the process
converges weakly in
to
. Now, from (
17), we define
Since the Argmax functional is continuous on
, by the Continuous Mapping Theorem,
Since
and
have the same distribution for every
, by the change of variable
, it is easy to show that
and it follows that
Clearly, almost surely, there is a unique random variable
, such that
and
, where
is an almost surely unique random variable such that,
Hence,
and the proof of Theorem 4 is completed. □
Appendix A.3. Proof of Propositions
Appendix A.3.1. Proof of Proposition 1
Proof. We just study the case where
r is negative. The other case can be handled in the same way by symmetry. Let
be the set defined by
We have
We first show that the first two in the right-hand side of the above equality are negligible on
. As from (
A14),
is stochastically bounded, it is therefore sufficient to show that
is negligible over
. For this, we write
where
and
are defined by (A27) and (A28) respectively, and prove that each of the right-hand terms of the above last inequality converges uniformly to 0 on
. Notice that if
then
and there exists
such that
. Thus the inequality (A32) holds and we have
On the one hand, for
, we can write
uniformly in
k, where
denotes a "little-o" of Landau in probability. This is due (
A4) and to the fact that as
,
. In a similar way, we have
uniformly in
k. On the other hand, if
, there exists
such that
. Consequently, we have
uniformly in
k, and we have proved that
uniformly on
. Based on the same reasoning and the same way, we can establish that
uniformly on
.
From (
A7), we have
From (A31), since
, it is obvious that
uniformly in
k. Thus, we have proved that
uniformly on
.
Now study the asymptotic behavior of
for
. For this, we write,
For the sake of simplicity, we assume that
and
are integers. Then, from (A26), we have
where
is given by (A30). Using the same reasoning as the one which led to (A39), one can prove easily that the first two terms of (A30) multiplied by
are negligible on
, and that
A functional central limit theorem (invariance principle) is applied to
(see, e.g., [
45]). Thus, we have
where
is a standard Wiener process defined on
with
. It is clear that if
, then
converges to
and
converges to
. Consequently,
By the same reasoning one can show that
and that
From (
A7) and (
A8), we have
Using the fact that for
and
converges to
, we find
and
From (A40), (A41), (A42) and (A43), we conclude that
From the previous result and (A37), we find that
which writes again
By the same reasoning, one can prove that
where
is a standard Wiener process defined on
with
.
Given that
and
are two independent standard Wiener processes defined on
,
where
is a two sided standard Wiener process. This completes the proof of Proposition 1. □
References
- Hocking, T.D.; Schleiermacher, G.; Janoueix-Lerosey, I.; Boeva, V.; Cappo, J.; Delattre, O.; Bach, F.; Vert, J.P. Learning smoothing models of copy number profiles using breakpoint annotations. BMC bioinformatics 2013, 14, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Wright, A.; Hauskrecht, M. Change-point detection method for clinical decision support system rule monitoring. Artificial intelligence in medicine 2018, 91, 49–56. [Google Scholar] [CrossRef] [PubMed]
- Lavielle, M.; Teyssiere, G. Adaptive detection of multiple change-points in asset price volatility. In Long memory in economics; Springer, 2007; pp. 129–156. [Google Scholar]
- Frick, K.; Munk, A.; Sieling, H. Multiscale change point inference. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2014, 76, 495–580. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Estimating and Testing Linear Models with Multiple Structural Changes. Econometrica 1998, 66, 47–78. [Google Scholar] [CrossRef]
- Page, E.S. Continuous inspection schemes. Biometrika 1954, 41, 100–115. [Google Scholar] [CrossRef]
- Page, E. A test for a change in a parameter occurring at an unknown point. Biometrika 1955, 42, 523–527. [Google Scholar] [CrossRef]
- Pettitt, A.N. A non-parametric approach to the change-point problem. Journal of the Royal Statistical Society: Series C (Applied Statistics) 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Lombard, F. Rank tests for changepoint problems. Biometrika 1987, 74, 615–624. [Google Scholar] [CrossRef]
- Scariano, S.M.; Watkins, T.A. Nonparametric point estimators for the change-point problem. Communications in Statistics-Theory and Methods 1988, 17, 3645–3675. [Google Scholar] [CrossRef]
- Bryden, E.; Carlson, J.B.; Craig, B. Some Monte Carlo results on nonparametric changepoint tests; Citeseer, 1995. [Google Scholar]
- Bhattacharya, P.; Zhou, H. Nonparametric Stopping Rules for Detecting Small Changes in Location and Scale Families. In From Statistics to Mathematical Finance; Springer, 2017; pp. 251–271. [Google Scholar]
- Hinkley, D.V. Inference about the change-point in a sequence of random variables 1970.
- Hinkley, D.V. Time-ordered classification. Biometrika 1972, 59, 509–523. [Google Scholar] [CrossRef]
- Yao, Y.C.; Davis, R.A. The asymptotic behavior of the likelihood ratio statistic for testing a shift in mean in a sequence of independent normal variates. Sankhyā: The Indian Journal of Statistics, Series A 1986, 339–353. [Google Scholar]
- Csörgö, M.; Horváth, L. Nonparametric tests for the changepoint problem. Journal of Statistical Planning and Inference 1987, 17, 1–9. [Google Scholar] [CrossRef]
- Chen, J.; Gupta, A. Change point analysis of a Gaussian model. Statistical Papers 1999, 40, 323–333. [Google Scholar] [CrossRef]
- Horváth, L.; Steinebach, J. Testing for changes in the mean or variance of a stochastic process under weak invariance. Journal of statistical planning and inference 2000, 91, 365–376. [Google Scholar] [CrossRef]
- Antoch, J.; Hušková, M. Permutation tests in change point analysis. Statistics & probability letters 2001, 53, 37–46. [Google Scholar]
- Hušková, M.; Meintanis, S.G. Change point analysis based on empirical characteristic functions. Metrika 2006, 63, 145–168. [Google Scholar] [CrossRef]
- Zou, C.; Liu, Y.; Qin, P.; Wang, Z. Empirical likelihood ratio test for the change-point problem. Statistics & probability letters 2007, 77, 374–382. [Google Scholar]
- Gombay, E. Change detection in autoregressive time series. Journal of Multivariate Analysis 2008, 99, 451–464. [Google Scholar] [CrossRef]
- Berkes, I.; Gombay, E.; Horváth, L. Testing for changes in the covariance structure of linear processes. Journal of Statistical Planning and Inference 2009, 139, 2044–2063. [Google Scholar] [CrossRef]
- Härdle, W.; Tsybakov, A. Local polynomial estimators of the volatility function in nonparametric autoregression. Journal of econometrics 1997, 81, 223–242. [Google Scholar] [CrossRef]
- Härdle, W.; Tsybakov, A.; Yang, L. Nonparametric vector autoregression. Journal of Statistical Planning and Inference 1998, 68, 221–245. [Google Scholar] [CrossRef]
- Bardet, J.M.; Wintenberger, O. Asymptotic normality of the Quasi Maximum Likelihood Estimator for multidimensional causal processes. Annals of Statistics 2009, 37, 2730–2759. [Google Scholar] [CrossRef]
- Bardet, J.M.; Kengne, W.; Wintenberger, O. Multiple breaks detection in general causal time series using penalized quasi-likelihood. Electronic Journal of Statistics 2012, 6, 435–477. [Google Scholar] [CrossRef]
- Bardet, J.M.; Kengne, W. Monitoring procedure for parameter change in causal time series. Journal of Multivariate Analysis 2014, 125, 204–221. [Google Scholar] [CrossRef]
- Ngatchou-Wandji, J. Estimation in a class of nonlinear heteroscedastic time series models. Electronic Journal of Statistics 2008, 2, 40–62. [Google Scholar] [CrossRef]
- Bai, J. Least squares estimation of a shift in linear processes. Journal of Time Series Analysis 1994, 15, 453–472. [Google Scholar] [CrossRef]
- Hawkins, D.M. Testing a sequence of observations for a shift in location. Journal of the American Statistical Association 1977, 72, 180–186. [Google Scholar] [CrossRef]
- Csörgö, M.; Horváth, L. Limit theorems in change-point analysis 1997.
- Joseph, N.W.; Echarif, E.; Harel, M. On change-points tests based on two-samples U-Statistics for weakly dependent observations. Statistical Papers 2022, 63, 287–316. [Google Scholar]
- Antoch, J.; Hušková, M.; Veraverbeke, N. Change-point problem and bootstrap. Journal of Nonparametric Statistics 1995, 5, 123–144. [Google Scholar] [CrossRef]
- Bhattacharya, P.K. Maximum likelihood estimation of a change-point in the distribution of independent random variables: General multiparameter case. Journal of Multivariate Analysis 1987, 23, 183–208. [Google Scholar] [CrossRef]
- Picard, D. Testing and estimating change-points in time series. Advances in applied probability 1985, 17, 841–867. [Google Scholar] [CrossRef]
- Yao, Y.C. Approximating the distribution of the maximum likelihood estimate of the change-point in a sequence of independent random variables. The Annals of Statistics 1987, 1321–1328. [Google Scholar] [CrossRef]
- Taniguchi, M.; Kakizawa, Y. Asymptotic theory of estimation and testing for stochastic processes. In Asymptotic Theory of Statistical Inference for Time Series; Springer, 2000; pp. 51–165. [Google Scholar]
- Ngatchou-Wandji, J. Checking nonlinear heteroscedastic time series models. Journal of Statistical Planning and Inference 2005, 133, 33–68. [Google Scholar] [CrossRef]
- Kouamo, O.; Moulines, E.; Roueff, F. Testing for homogeneity of variance in the wavelet domain. Dependence in Probability and Statistics 2010, 200, 175. [Google Scholar]
- Gan, S.; Qiu, D. On the Hájek-Rényi inequality. Wuhan University Journal of Natural Sciences 2007, 12, 971–974. [Google Scholar] [CrossRef]
- Billingsley, P. Convergence of probability measures John Wiley. New York 1968. [Google Scholar]
- Doukhan, P.; Portal, F. Principe d’invariance faible pour la fonction de répartition empirique dans un cadre multidimensionnel et mélangeant. Probab. math. statist 1987, 8, 117–132. [Google Scholar]
- Wooldridge, J.M.; White, H. Some invariance principles and central limit theorems for dependent heterogeneous processes. Econometric theory 1988, 4, 210–230. [Google Scholar] [CrossRef]
- Hall, P.; Heyde, C.C. Martingale limit theory and its application; Academic press, 1980. [Google Scholar]
| 1 |
SE=SD, where SD denotes the standard deviation. |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).