Cumulative Entropy of Past Lifetime for Coherent Systems at the System Level

Preprint

Article

Cumulative Entropy of Past Lifetime for Coherent Systems at the System Level

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

21 August 2023

Posted:

23 August 2023

You are already at the latest version

Alerts

Abstract

In this paper, we investigate the cumulative historical entropy of the lifetime of an n-component coherent system under the assumption that all system components have failed at time t. Using the system signature, we can calculate the cumulative historical entropy of the system’s lifespan, which is an important aspect in determining a system’s predictability. This research produces a number of significant results, including expressions, bounds, and ordering aspects for this measure. In addition, we offer a method for finding a preferred system based on cumulative Kullback-Leibler discriminating information that is closely related to the parallel system. These findings provide important insights into the predictability and dependability of coherent systems, emphasizing the importance of this field.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

MSC: 60E05; 62B10; 62N05; 94A17

1. Introduction

The Shannon differential entropy has gained widespread adoption as a measure across various fields of research. It was introduced by Shannon in his article [1], and since then, it has become a cornerstone of probability theory. Suppose we have a non-negative random variable X, which is absolutely continuous with a probability density function

f (x)

. If the expected value of the logarithm exists, then the expression

H (X) = - E [log f (X)]

is referred to as the Shannon differential entropy. This is the situation being described in this scenario. This definition allows us to quantify the uncertainty associated with the random variable X by measuring the amount of information required to describe it. Owing to its adaptability and usefulness, this metric has gained widespread adoption in a multitude of research domains, making it an essential tool for any researcher looking to explore probability distributions.

While differential entropy has many advantages, a fascinating substitute for conventional entropy was suggested by Rao and colleagues in their paper [2], which they called cumulative residual entropy (CRE). Unlike differential entropy, which uses

f (x)

, CRE uses

S (x) = P (X > x)

to obtain a measure of entropy. The definition of CRE is given by

CE (X) = - \int_{0}^{\infty} S (x) log S (x) d x .

(1)

With its ability to capture the residual uncertainty of a distribution, CRE is particularly useful in situations where the tails of the distribution are of interest. The CRE has emerged as the preferred measure for characterizing information dispersion in problems related to reliability theory, which is robust metric has been extensively employed in numerous studies, such as those carried out by [3,4,5,6,7,8], to name a few. A representation of the cumulative entropy (CE), which is an information measure similar to equation (1), is provided by Di Crescenzo and Longobardi in their work [9] given by

CE (X) = - \int_{0}^{\infty} F (x) log F (x) d x,

(2)

where

F (\cdot)

is the cumulative distribution function (cdf) of a random variable

X .

Like CRE, CE is nonnegative and

CE (X) = 0

if and only if X is a constant.

Several measures of dynamic information have been proposed to characterize the uncertainty in suitable functionals of the random lifetime X of a system. We review two such measures, namely the dynamic cumulative residual entropy (introduced by Asadi and Zohrevand [10]) and the cumulative past entropy (proposed by Di Crescenzo and Longobardi in [11]), which are defined as the dynamic cumulative entropy of

X^{t} = [X | X > t]

and

X_{t} = [X | X \leq t]

, respectively. In this case, the dynamic cumulative residual entropy is defined as

\begin{matrix} E (X^{t}) & = & - \int_{t}^{\infty} {\bar{F}}_{t} (x) log {\bar{F}}_{t} (x) d x \end{matrix}

(3)

\begin{matrix} = & - \int_{t}^{\infty} \frac{\bar{F} (x)}{\bar{F} (t)} log \frac{\bar{F} (x)}{\bar{F} (t)} d x, t > 0, \end{matrix}

(4)

where

{\bar{F}}_{t} (x) = \bar{F} (x) / \bar{F} (t), x > t,

is the survival function of

X^{t} = [X | X > t]

. Di Crescenzo and Longobardi [11] pointed out that in many realistic scenarios, uncertainty is not necessarily related to the future. For example, if a system that starts operating at time 0 is only observed at predetermined inspection times and is found to be "down" at time t, then the uncertainty is dependent on the specific moment within

(0, t)

at which it failed. When faced with such scenarios, the cumulative past entropy proves to be a valuable metric. It is defined as follows:

\begin{matrix} CE (X_{t}) & = & - \int_{0}^{t} F_{t} (x) log F_{t} (x) d x \\ = & - \int_{0}^{t} (\frac{F (x)}{F (t)}) log (\frac{F (x)}{F (t)}) d x, \end{matrix}

(5)

where

F_{t} (x) = F (x) / F (t), 0 < x \leq t,

is the cdf of

X_{t} = [X | X \leq t]

Numerous researchers have demonstrated a strong inclination toward investigating the information characteristics of coherent systems which can be seen in [8,12,13,14,15,16], and the references therein. Recently, Kayid [17] investigated the Tsallis entropy of coherent systems when all components are alive at time

t .

Mesfioui et al. [18] have also delved into the Tsallis entropy such systems, adding to the current body of captivating research in this area. More recently, Kayid and Shrahili [19,20] investigated the Shannon differential and Renyi entropy of coherent systems when all components have failed at time

t .

The aim of this study is to examine the uncertainty properties of the lifetimes of coherent systems, with a particular focus on the cumulative past entropy. In fact, when all components have failed at time

t,

we focus on coherent systems consisting of n components by utilizing the system signature.

Therefore, the result of this paper is organized as follows: In Section 2, we provide an expression for the CE of a coherent system’s lifetime when component lifetimes are independent and identically distributed, given that all components of the system have failed at time t by implementing the concept of system signature. In Section 3, some useful bounds are presented. A new criterion is represented to choose a preferable among coherent systems in Section 4. Some concluding remarks are also given in Section 5.

2. CE of the past lifetime

In this section, we present by applying the system signature concept to define the past lifetime CE of a coherent system, which can have an arbitrary structure. To this aim, we assume that at a specific time

t,

all components of the system have failed and employ the concept of system signature which is described by an n-dimensional vector

p = (p_{1}, \dots, p_{n}),

where the i-th element is defined as

p_{i} = P (T = X_{i : n}), i = 1, 2, \dots, n .

(see [21]).

Consider a coherent system whose component lifetimes

X_{1}, \dots, X_{n}

are independent and identically distributed (i.i.d.), and whose signature vector

p = (p_{1}, \dots, p_{n})

is known. Assuming that the coherent system have failed at time t, we can represent the past lifetime of the system as

T_{t} = [t - T | X_{n : n} \leq t] .

Khaledi and Shaked [22] have established results that allow us to express the cumulative distribution function of

T_{t}

in terms of their findings as

F_{T_{t}} (x) = \sum_{i = 1}^{n} p_{i} F_{T_{t}^{i}} (x),

(6)

where

\begin{matrix} F_{T_{t}^{i}} (x) & = & P (t - X_{i : n} \leq x | X_{n : n} \leq t) \\ = & \sum_{k = 0}^{i - 1} (\binom{n}{k}) {(\frac{F (t - x)}{F (t)})}^{k} {(1 - \frac{F (t - x)}{F (t)})}^{n - k}, 0 < x < t, \end{matrix}

denotes the cdf of

T_{t}^{i} = [t - X_{i : n} | X_{n : n} \leq t], i = 1, 2, \dots, n .

It is important to note that

T_{t}^{i}, i = 1, 2, \dots, n,

represents the elapsed time since the failure of the component with a lifetime of

X_{i : n}

in the system, given that the system has failed at or before time

t .

Furthermore, according to (6),

T_{t}^{i}

corresponds to the ith order statistic of n i.i.d. components with a cumulative distribution function of

\frac{F (t - x)}{F (t)}, 0 < x < t .

Hereafter, we provide a formula for computing the cumulative entropy of

T_{t}

. For this purpose, we define

F_{t} (x) = \frac{F (x)}{F (t)}, 0 < x < t

, and use

V = F_{t} (T_{t})

, which is essential to our approach. Using this transformation, we can express the cumulative entropy of

T_{t}

in terms of V, as shown in the upcoming theorem.

Theorem 1.

We can express the CE of

T_{t}

as follows

CE (T_{t}) = \int_{0}^{1} \frac{ψ (S_{V} (v))}{f_{t} (F_{t}^{- 1} (v))} d v,

(7)

where

ψ (v) = - v log v, 0 < v < 1,

for all

t > 0

and

S_{V} (v) = \sum_{i = 1}^{n} p_{i} S_{i} (v), 0 \leq u \leq 1,

(8)

represents the survival function of

V = F_{t} (T_{t})

such that

S_{i} (v) = \sum_{k = 0}^{i - 1} (\binom{n}{k}) v^{k} {(1 - v)}^{n - k}, 0 < v < 1 .

(9)

is the survival function of i-th order statistics where lifetimes are uniformly distributed. Moreover,

F_{t}^{- 1} (u) = inf {x; F_{t} (x) \geq u}

is the quantile function of

F_{t} (x) .

Proof.

Substituting

z = t - x

and using equations (5) and (6), we obtain:

\begin{matrix} CE (T_{t}) & = & \int_{0}^{t} ψ (F_{T_{t}} (x)) d x \\ = & \int_{0}^{t} ψ (\sum_{i = 1}^{n} p_{i} F_{T_{t}^{i}} (x)) d x \\ = & \int_{0}^{t} ψ (\sum_{i = 1}^{n} p_{i} \sum_{k = 0}^{i - 1} (\binom{n}{k}) {(\frac{F (t - x)}{F (t)})}^{k} {(1 - \frac{F (t - x)}{F (t)})}^{n - k}) d u, \\ = & \int_{0}^{t} ψ (\sum_{i = 1}^{n} p_{i} \sum_{k = 0}^{i - 1} (\binom{n}{k}) {(\frac{F (x)}{F (t)})}^{k} {(1 - \frac{F (x)}{F (t)})}^{n - k}) d u, \\ = & \int_{0}^{1} \frac{ψ (\sum_{i = 1}^{n} p_{i} \sum_{k = 0}^{i - 1} (\binom{n}{k}) u^{k} {(1 - u)}^{n - k})}{f_{t} (F_{t}^{- 1} (u))} d u, \\ = & \int_{0}^{1} \frac{ψ (\sum_{i = 1}^{n} p_{i} S_{i} (v))}{f_{t} (F_{t}^{- 1} (u))} d u, \end{matrix}

where the last equality is obtained by using the change of variables

u = F_{t} (x) .

Furthermore,

S_{i} (v)

represents the survival function of

U_{i : n} = F_{t} (T_{t}^{i})

as given in (9). By utilizing (8), we can derive the relationship (7), which serves to conclude the proof. □

Suppose we examine an i-out-of-n system with a system signature of

p = (0, \dots, 0, 1_{i}, 0, \dots, 0)

, where

i = 1, 2, \dots, n .

Them, we obtain a special case of Equation (7), which reduces to

CE (T_{t}^{i}) = \int_{0}^{1} \frac{ψ (S_{i} (u))}{f_{t} (F_{t}^{- 1} (u))} d u, t > 0 .

(10)

The following theorem is a direct consequence of Theorem 1 and characterizes the aging properties of the system’s components. It is noteworthy to mention that a random variable X is said to have a decreasing reversed hazard rate (DRHR) if its reversed hazard rate function

τ (x) = f (x) / F (x)

declines for

x > 0

Theorem 2.

If X is DRHR, then

CE (T_{t})

is increasing in t.

Proof.By noting that

f_{t} (F_{t}^{- 1} (x)) = x τ_{t} (F_{t}^{- 1} (x)),

Equation (7) can be rewritten as

\begin{matrix} CE (T_{t}) = \int_{0}^{1} \frac{ψ (S_{V} (u))}{u τ_{t} (F_{t}^{- 1} (u))} d u, \end{matrix}

(11)

for all

t > 0 .

We can easily confirm that

F_{t}^{- 1} (u) = F^{- 1} (u F (t))

holds for all

0 < u < 1

. Therefore, we obtain:

\begin{matrix} τ_{t} (F_{t}^{- 1} (u)) & = & τ (F^{- 1} (u F (t))), 0 < u < 1 . \end{matrix}

t_{1} \leq t_{2}

, then

F^{- 1} (u F (t_{1})) \leq F^{- 1} (u F (t_{2}))

. Therefore, if X has a DRHR property, then:

\begin{matrix} \int_{0}^{1} \frac{ψ (S_{V} (u))}{u τ_{t_{1}} (F_{t_{1}}^{- 1} (u))} d u & = & \int_{0}^{1} \frac{ψ (S_{V} (u))}{u τ (F^{- 1} (u F (t_{1}))} d u \\ \geq (\leq) & \int_{0}^{1} \frac{ψ (S_{V} (u))}{u τ (F^{- 1} (u F (t_{2}))} d u d u \\ = & \int_{0}^{1} \frac{ψ (S_{V} (u))}{u τ_{t_{2}} (F_{t_{2}}^{- 1} (u))} d u . \end{matrix}

By utilizing Equation (11), we can infer that

CE (T_{t_{1}}) \geq (\leq) CE (T_{t_{2}})

for all

t_{1} \leq t_{2}

, thus completing the proof. □

We provide an example to demonstrate the applications of Theorems 1 and 2 in engineering systems. This example highlights how these theorems can be utilized for analyzing the CE of a failed coherent system and for investigating the aging characteristics of a system.

Example 1.

Suppose we have a coherent system with a system signature

p = (1 / 4, 1 / 4, 1 / 2, 0)

. To compute the precise value of

CE (T_{t})

using equation (7), we require the lifetime distributions of the system components. For this purpose, let us assume the following lifetime distributions.

(i) Let X follow the uniform distribution in

[0, 1] .

From (7), we immediately obtain

CE (T_{t}) = 0.2245 t, t > 0 .

The analysis indicates that the cumulative entropy of

T_{t}

increases as time t increases, which aligns with previous research on the behavior of cumulative entropy for specific categories of random variables. For instance, it is established that the uniform distribution has a DRHR property, indicating that the CE of

T_{t}

should increase as time t increases, as per Theorem 2.

(b) Let’s examine a random variable X, whose cdf is defined as follows:

F (x) = e^{- x^{- k}}, x > 0, k > 0 .

After performing some algebraic manipulations, we have

CE (T_{t}) = \int_{0}^{1} \frac{ψ (S_{V} (v))}{k u {(t^{- k} - log u)}^{\frac{k + 1}{k}}} d u, t > 0 .

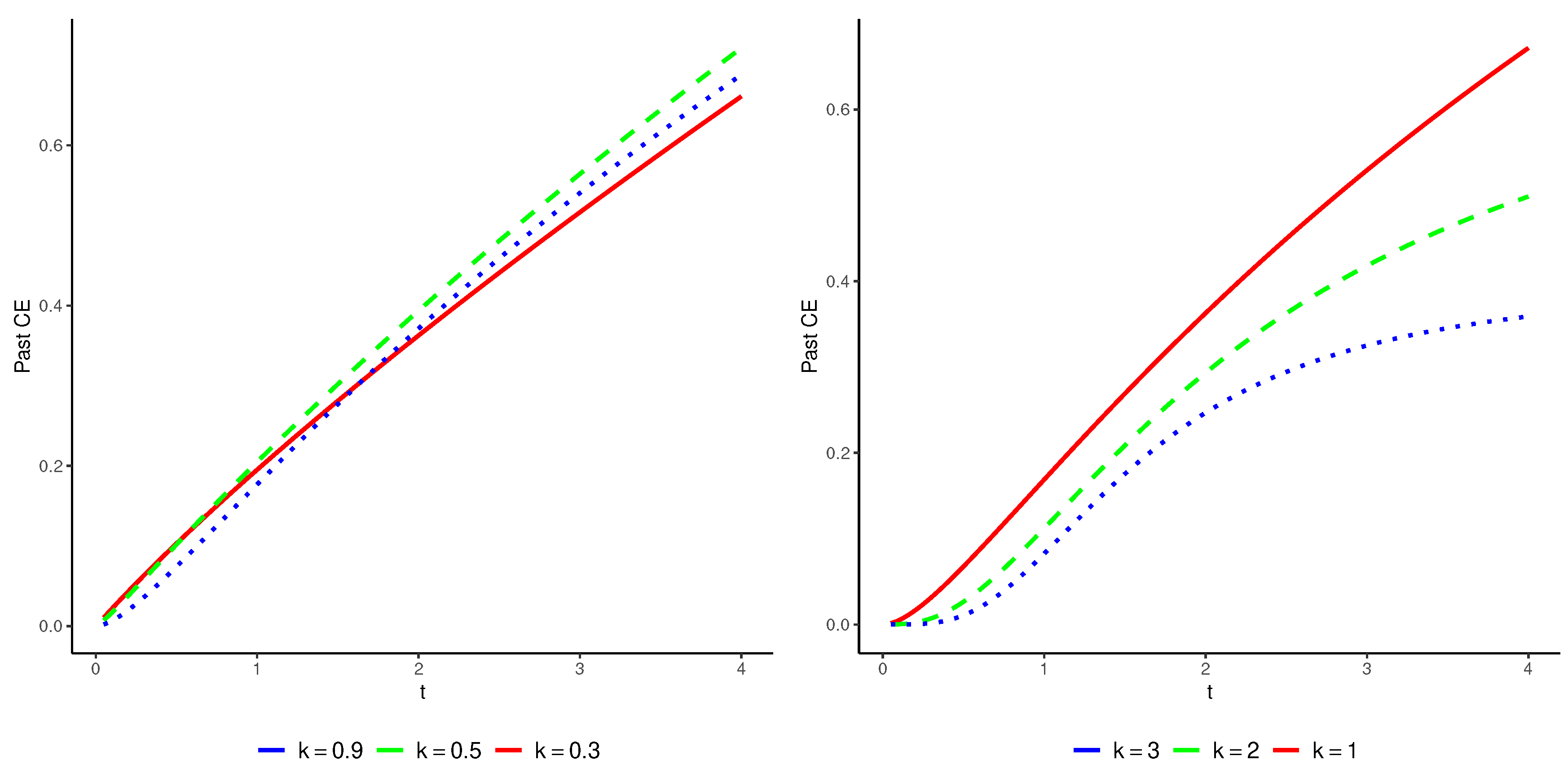
Calculating this relationship explicitly is challenging, thus we must rely on numerical methods to proceed. In Figure 2, we illustrate the cumulative entropy of

T_{t}

for different values of k. It is evident that X exhibits a DRHR property for all

k > 0

. Referring back to Theorem 2, we can see that

CE (T_{t})

rises with increasing t when

k > 0

Figure 1. A coherent system with signature

p = (1 / 4, 1 / 4, 1 / 2, 0) .

Figure 1. A coherent system with signature

p = (1 / 4, 1 / 4, 1 / 2, 0) .

Figure 2. Cumulative entropy of

T_{t}

with respect to t for various values of

k > 0

, using the cdf Part (b) from Example 1.

Figure 2. Cumulative entropy of

T_{t}

with respect to t for various values of

k > 0

, using the cdf Part (b) from Example 1.

The example above provides insight into the complex interplay between the CE of a random variable and time, emphasizing the significance of accounting for the decreasing reversed hazard rate property when analyzing such systems. The results suggest that the DRHR property of X is a critical factor in determining the temporal dynamics of the CE of

T_{t}

, which could have significant consequences in various areas of research including the study of intricate systems and the development of efficient data compression methods.

The notion of duality is a valuable tool in engineering reliability to reduce the computational workload of computing the signatures of all coherent systems of a given magnitude by roughly half (as demonstrated, for instance, in Kochar et al. [23]). Particularly, if

T_{t}

stands for lifetime of a coherent system with signature

p = (p_{1}, \dots, p_{n}),

then its dual system with lifetime

{T_{t}}^{D, n}

has a signature

p^{D} = (p_{n}, \dots, p_{1})

. By utilizing the principle of duality, we have the following theorem which facilitates the computational intricacy entailed in calculating the past cumulative entropy of

T_{t} .

Theorem 3.

f_{t} (F_{t}^{- 1} (u)) = f_{t} (F_{t}^{- 1} (1 - u))

holds true for all

0 < u < 1

and t, then, for all

p

and

n,

we can conclude that

CE (T_{t}) = CE ({T_{t}}^{D}) .

Proof.

It is crucial to emphasize that the equation

S_{i} (1 - u) = S_{n - i + 1} (u)

valids for all

i = 1, \dots, n

and

0 < u < 1

. Furthermore, since

f_{t} (F_{t}^{- 1} (u)) = f_{t} (F_{t}^{- 1} (1 - u))

holds for all

0 < u < 1

, we can leverage (7) to derive the subsequent expression:

\begin{matrix} CE ({T_{t}}^{D}) & = & \int_{0}^{1} \frac{ψ (\sum_{i = 1}^{n} p_{n - i + 1} S_{i} (u))}{f_{t} (F_{t}^{- 1} (u))} d u \\ = & \int_{0}^{1} \frac{ψ (\sum_{r = 1}^{n} p_{r} S_{n - r + 1} (u))}{f_{t} (F_{t}^{- 1} (u))} d u \\ = & \int_{0}^{1} \frac{ψ (\sum_{r = 1}^{n} p_{r} S_{r} (1 - u))}{f_{t} (F_{t}^{- 1} (1 - u))} d u \\ = & \int_{0}^{1} \frac{ψ (\sum_{r = 1}^{n} p_{r} S_{r} (u))}{f_{t} (F_{t}^{- 1} (u))} d u \\ = & CE (T_{t}), \end{matrix}

and this completes the proof. □

3. Bounding the Cumulative Entropy of Past Lifetime

When working with extremely intricate systems that consist of numerous components, calculating

CE (T_{t})

can be a difficult undertaking. To handle this difficulty, investigators have newly proposed uncertainty bounds for the component lifetimes in coherent systems. This approach is explored in works such as [16,19,20] and related literature. In the next theorem, we obtain bounds for

CE (T_{t})

based on the CE of the parent distribution

CE (X_{t})

. These bounds can be useful in certain circumstances, particularly when calculating the precise cumulative past entropy is challenging.

Proposition 1.

T_{t} = [t - T | X_{n : n} \leq t]

denotes the past lifetime of the system, then

\begin{matrix} B_{1} CE (X_{t}) \leq CE (T_{t}) \leq B_{2} CE (X_{t}) \end{matrix}

where

B_{1} = {inf}_{u \in (0, 1)} \frac{ψ (S_{V} (u))}{ψ (u)}

B_{2} = {sup}_{u \in (0, 1)} \frac{ψ (S_{V} (u))}{ψ (u)}

and

ψ (u) = - u log (u)

Proof.

The upper bound is given by:

\begin{matrix} CE (T_{t}) & = & \int_{0}^{1} \frac{ψ (S_{V} (u))}{f_{t} (F_{t}^{- 1} (u))} d u \\ = & \int_{0}^{1} \frac{ψ (S_{V} (u))}{ψ (u)} \frac{ψ (u)}{f_{t} (F_{t}^{- 1} (u))} d u \\ \leq & sup_{u \in (0, 1)} \frac{ψ (S_{V} (u))}{ψ (u)} \int_{0}^{1} \frac{ψ (u)}{f_{t} (F_{t}^{- 1} (u))} d u \\ = & B_{2} CE (X_{t}) . \end{matrix}

The constant

B_{2}

is dependent on the distribution of V. Using the same method, we can also derive a lower bound for

CE (T_{t})

. □

It is worth noting that

B_{1}

in the aforementioned theorem is obtained by computing the infimum of

ψ (S_{V} (u)) / ψ (u)

for

u \in (0, 1)

and

B_{2}

is obtained by computing the supremum of the same ratio. The given bounds offer valuable means of approximating

CE (T_{t})

based on

CE (X_{t}) .

Remark 1.

It is worth noting that the lower bound

B_{1}

in Proposition 1 equals zero for all coherent systems that satisfy either

p_{1} = 0

p_{n} = 0

. This is especially true for coherent systems with more than one i.i.d. component, as outlined in [8].

Proposition 2.

The lower bound for the CE of

T_{t}

is given by

CE (T_{t}) \geq {CE}_{L} (T_{t}),

(12)

where

{CE}_{L} (T_{t}) = \sum_{i = 1}^{n} p_{i} CE (T_{t}^{i}) .

Proof.

Utilizing (7) and the concavity of the function

ψ (u) = - u log (u)

, we can derive the following lower bound:

\begin{matrix} CE (T_{t}) & = \int_{0}^{1} \frac{ψ (S_{V} (u))}{f_{t} (F_{t}^{- 1} (u))} d u \\ \geq \int_{0}^{1} \frac{\sum_{i = 1}^{n} p_{i} ψ (S_{i : n} (u))}{f_{t} (F_{t}^{- 1} (u))} d u \\ = \sum_{i = 1}^{n} p_{i} CE (T_{t}^{i}), \end{matrix}

where

CE (T_{t}^{i})

is the cumulative entropy of

T_{t}^{i}

. □

Notice that equality in (12) holds for i-out-of-n systems in the sense that we have

p_{j} = 0

, for

j \neq i,

and

p_{j} = 1

, for

j = i

and then

CE (T_{t}) = CE (T_{t}^{i})

. When the lower bounds in both parts of Theorems 1 and 2 can be computed, one may use the maximum of the two lower bounds.

Example 2.

In this example, we analyze a coherent system with the signature

p = (0, \frac{3}{10}, \frac{5}{10}, \frac{2}{10}, 0)

, consisting of

n = 5

i.i.d. component lifetimes drawn from a uniform distribution in the interval

[0, 1]

. If

T_{t} = [t - T | X_{5 : 5} \leq t]

denotes the past lifetime of this system, Remark 1 yields

B_{1} = 0

, while

B_{2} = 1.25

and

CE (X_{t}) = \frac{t}{4}, 0 < t < 1 .

As per Theorem 1, we deduce that

CE (T_{t})

is bounded accordingly:

0 \leq CE (T_{t}) \leq 1.25 t, 0 < t < 1 .

(13)

Moreover, as

\sum_{i = 1}^{n} p_{i} CE (U_{i : n}) = 0.164

, we can represent the lower bound provided in (12) as:

CE (T_{t}) \geq 0.164 t, 0 < t < 1 .

(14)

Recalling the lower bound (14) and the upper bound (13), we have the following inequality

0.164 t \leq CE (T_{t}) \leq 1.25 t,

for all

0 < t < 1 .

This inequality supplies a precise and secure boundary for the conditional CE of

T_{t}

over the entire interval

(0, 1)

4. Preferable system

Hereafter, we consider two nonnegative random variables, X and Y, that represent the lifetimes of two items having the same supports

(0, \infty) .

For any given time

t > 0

, we define their respective past lifetimes as

X_{t} = [X | X \leq t]

and

Y_{t} = [Y | Y \leq t]

. To this end, we also introduce the distribution functions of

X_{t}

and

Y_{t}

F_{t} (x) = \frac{F (x)}{F (t)}, S_{t} (x) = \frac{G (x)}{G (t)}, 0 \leq x \leq t,

(15)

respectively. In their groundbreaking work, Di Crescenzo and Longobardi [24] introduced a novel concept that utilizes the mean past lifetimes of nonnegative random variables X and Y with cdfs F and G, by

μ_{X} (t) = E [t - X | X \leq t]

and

μ_{Y} (t) = E [t - Y | Y \leq t],

respectively. They proposed a past version of the cumulative Kullback-Leibler information measure that is defined as a function of the mean past lifetimes of X and Y as follows:

\begin{matrix} CE (X_{t}, Y_{t}) & = & \int_{0}^{t} F_{t} (x) log \frac{F_{t} (x)}{S_{t} (x)} d x + μ_{X} (t) - μ_{Y} (t), \end{matrix}

(16)

provided that

F_{t} (x) = 0

whenever

S_{t} (x) = 0 .

In order to advance our findings, we define a novel measure of distance that is symmetric and applicable to two distributions. This measure is called Symmetric Past Cumulative (SPC) Kullback-Leibler divergence and is denoted by the shorthand

SPC (X_{t}, Y_{t})

Definition 1.

Consider two non-negative past random variables,

X_{t}

and

Y_{t}

, with shared support and cumulative distribution functions

F_{t}

and

S_{t}

, respectively. In this case, we introduce the SPC Kullback-Leibler divergence as a measure of distance between the two variables as follows:

\begin{matrix} SPC (X_{t}, Y_{t}) & = & CE (X_{t}, Y_{t}) + CE (X_{t}, Y_{t}) = \int_{0}^{t} [F_{t} (x) - S_{t} (x)] log \frac{F_{t} (x)}{S_{t} (x)} d x, \end{matrix}

(17)

for all

t > 0 .

The proposed measure, defined as (17), possesses several desirable properties. First and foremost, it is nonnegative and symmetric. Moreover, the value of

SPC (X_{t}, Y_{t})

is equal to zero if and only if

F_{t} (x)

and

S_{t} (x)

are almost everywhere equal. In addition to these properties, we also observe the following.

Lemma 1.Suppose we have three random variables,

X_{t}

Y_{t}

, and

Z_{t}

, each with cumulative distribution functions

F_{t}

S_{t}

, and

H_{t}

, respectively. If the stochastic ordering

X_{t} \leq_{s t} Y_{t} \leq_{s t} Z_{t}

holds, then the following statement is true

(i): $0 \leq SPC (X_{t}, Y_{t}) \leq SPC (X_{t}, Z_{t}),$
(ii): $0 \leq SPC (Y_{t}, Z_{t}) \leq SPC (X_{t}, Z_{t}),$

for all

t > 0 .

Proof. Given that the function

(x - 1) log (x)

is decreasing in the interval

(0, 1)

and increasing in

(1, \infty)

, we can make an important inference from the condition

F_{t} (x) \geq S_{t} (x) \geq H_{t} (x)

for

0 \leq x \leq t

. Specifically, we can conclude that

(i): $[S_{t} (x) - F_{t} (x)] log \frac{S_{t} (x)}{F_{t} (x)} \leq [H_{t} (x) - F_{t} (x)] log \frac{H_{t} (x)}{F_{t} (x)}, 0 \leq x \leq t,$
(ii): $0 \leq [S_{t} (x) - H_{t} (x)] log \frac{S_{t} (x)}{H_{t} (x)} \leq [F_{t} (x) - H_{t} (x)] log \frac{F_{t} (x)}{H_{t} (x)}, 0 \leq x \leq t .$

By integrating both sides of the descriptions (i) and (ii), we can obtain the desired result. □

T_{t}^{1} \leq_{s t} T_{t} \leq_{s t} T_{t}^{n}

holds for any coherent system, from Lemma 1, we have the following theorem.

Theorem 4.If

T_{t}

is the lifetime of a coherent system based on

X_{1}, \dots, X_{n}

, then:

(i): $0 \leq SPC (T_{t}, T_{t}^{1}) \leq SPC (T_{t}^{1}, T_{t}^{n})$ ,
(ii): $0 \leq SPC (T_{t}, T_{t}^{n}) \leq SPC (T_{t}^{1}, T_{t}^{n})$ .

Traditional stochastic ordering may not be sufficient for pairwise comparisons of system performance, particularly for certain system structures. In some cases, pairs of systems remain incomparable using stochastic orders. In this case, alternative metrics for comparing system performance are being explored. Hereafter, we will introduce a new method to choose a preferable system. It is worth to note that engineers typically favor those that offer extended operational time. As a result, it is crucial to ensure that the systems being compared possess comparable attributes. Furthermore, assuming that all other attributes are equal, we can choose parallel system lifetime since it has a longer past lifetime than alternative systems. In other words, from (6), we have

\begin{matrix} F_{T_{t}^{1}} (x) \geq F_{T_{t}} (x) \geq F_{T_{t}^{n}} (x), x > 0 . \end{matrix}

Rather than relying on comparisons between two systems at a time

t,

we can explore a system that has a structure or distribution that is more similar to that of the parallel system. Essentially, our goal is to determine which of these systems is more similar or closer in configuration to the parallel system, while also having a dissimilar configuration from that of the series system. To this aim, one can employ the idea of SPC given in Definition 1. Consequently, we put forth the following Symmetric Past Divergence (SPD) measure for

T_{t}

SPD (T_{t}) = \frac{SPC (T_{t}, T_{t}^{1}) - SPC (T_{t}, T_{t}^{n})}{SPC (T_{t}^{1}, T_{t}^{n})} .

(18)

Theorem 3 establishes that

- 1 \leq SPD (T_{t}) \leq 1

. It is evident that

SPD (T_{t}) = 1

if and only if

T_{t} =_{s t} T_{t}^{n}

and

SPD (T_{t}) = - 1

if and only if

T_{t} =_{s t} T_{t}^{1}

. Put simply, we can deduce that if

SPD (T_{t})

is closer to 1, the distribution of

T_{t}

is more akin to the parallel system’s distribution. On the other hand, if

SPD (T_{t})

is closer to

- 1

, the distribution of

T_{t}

is more similar to the series system’s distribution. Based on this, we suggest the subsequent definition.

Definition 2.

Consider two coherent systems, each with n component lifetimes that are independent and identically distributed, alongside signatures

p_{1}

and

p_{2}

. Let

T_{1, t}

and

T_{2, t}

represent their respective past lifetimes. At time t, we assert that

T_{2, t}

is more desirable than

T_{1, t}

with regard to the Symmetric Past Distance (SPD) measure, indicated by

T_{1, t} \leq_{S P D} T_{2, t}

, if and only if

SPD (T_{1, t}) \leq SPD (T_{2, t})

for all

t > 0 .

It is important to note that the equivalence of

SPD (T_{1, t})

and

SPD (T_{2, t})

does not always mean that

T_{1, t} =_{s t} T_{2, t}

. In accordance with Definition 2, we can define

PD (T) = SPC (T, T_{t}^{1}) - SPC (T, T_{t}^{n})

. From equation (17) and the aforementioned conversions, we obtain

\begin{matrix} SPC (T_{t}, T_{t}^{i}) & = & \int_{0}^{1} \frac{S_{V} (u) - S_{i : n} (u)]}{f_{t} (F_{t}^{- 1} (u))} log \frac{S_{V} (u)}{S_{i : n} (u)} d u, \end{matrix}

(19)

for

i = 1, n

. Then, from (19), we get

PD (T) = \int_{0}^{1} \frac{[S_{V} (u) - S_{1 : n} (u)]}{f_{t} (F_{t}^{- 1} (u))} log \frac{S_{V} (u)}{S_{1 : n} (u)} d u - \int_{0}^{1} \frac{[S_{V} (u) - S_{n : n} (u)]}{f_{t} (F_{t}^{- 1} (u))} log \frac{S_{V} (u)}{S_{n : n} (u)} d u,

SPC (T_{t}^{1}, T_{t}^{n}) = \int_{0}^{1} \frac{[S_{n : n} (u) - S_{1 : n} (u)]}{f_{t} (F_{t}^{- 1} (u))} log \frac{S_{n : n} (u)}{S_{1 : n} (u)} d u .

If we assume that the components are i.i.d., we can derive the equations

ψ (S_{1 : n} (u)) = u^{n}

and

ψ (S_{n : n} (u)) = 1 - {(1 - u)}^{n}

. By referencing Theorem 4, we can arrive at an intriguing result.

Proposition 3.

T_{t}

is the lifetime of a coherent system based on

X_{1}, \dots, X_{n}

, then

SPC (T_{t}, T_{t}^{i}) \leq SPC (T_{t}^{1}, T_{t}^{n})

, for

i = 1, n

The next theorem is readily apparent.

Theorem 5.

Assuming the conditions outlined in Definition 2, if the

X_{1}

is exponentially distributed, then the SPD measure is independent of time

t .

In other words,

SPD (T_{t}) = SPD (T)

holds true for all

t > 0 .

Proof.

Using the memoryless property, we can deduce that

f_{t} (F_{t}^{- 1} (u)) = f (F^{- 1} (u))

holds true for all

t > 0

. Consequently, we can conclude that the result holds true. □

Example 3.

Consider two coherent systems with past lifetimes

T_{1, t}

and

T_{2, t}

, in which the component lifetimes are exponentially distributed with cdf

F (x) = 1 - e^{- x}, x > 0

. The signatures of these systems are given by

p_{1} = (1 / 4, 1 / 4, 1 / 2, 0)

and

p_{2} = (0, 2 / 3, 1 / 3, 0),

respectively. Although these systems are not comparable using traditional stochastic orders, so, we can compare them by the SPD measure. By using numerical computation, we obtain

SPD (T_{1, t}) = 0.0914

and

SPD (T_{2, t}) = 0.1179 .

This indicates that the system with lifetime

T_{1, t}

is less similar to the parallel system than the system with lifetime

T_{2, t}

Theorem 6.

Suppose that

T_{1, t}

and

T_{2, t}

denote the lifetimes of two coherent systems with signatures

p_{1}

and

p_{2}

, respectively, based on n i.i.d. components with the same cdf F. If

p_{1} \leq_{s t} p_{2}

, we can assert that

T_{1, t} \leq_{S P D} T_{2, t}

Proof.

We can derive the desired outcome from Theorem 2.3 of Khaledi and Shaked [22]. Specifically, if we have two probability vectors denoted

p_{1}

and

p_{2}

, where

p_{1} \leq_{s t} p_{2}

, then we have

T_{t}^{1} \leq_{s t} T_{1, t} \leq_{s t} T_{2, t} \leq_{s t} T_{t}^{n}

. By applying Lemma 1, we can obtain

SPC (T_{1, t}, T_{t}^{1}) \leq SPC (T_{2, t}, T_{t}^{1})

and

SPC (T_{1, t}, T_{t}^{n}) \geq SPC (T_{2, t}, T_{t}^{n})

. These relations enable us to arrive at the desired outcome due to the relation defined in equation (18). □

An exciting discovery is that the comparison based on SPD can perform as a necessary condition for the usual stochastic order. Let us assume we have two coherent systems, denoted by

T_{1, t}

and

T_{2, t}

, each composed of several components with lifetimes

X_{1}, \dots, X_{n}

. If we find that

T_{1, t}

is less reliable than

T_{2, t}

in the stochastic order, denoted as

T_{1, t} \leq_{s t} T_{2, t}

, we can conclude that the system

T_{1, t}

is also less reliable than

T_{2, t}

in the SPD order, i.e.,

T_{1, t} \leq_{S P D} T_{2, t}

. This comparison of systems through the SPD order can be useful when comparing systems that are difficult to assess otherwise. It is worth noting that if we find that two systems

T_{1, t}

and

T_{2, t}

are equally reliable in the stochastic order, i.e.,

T_{1, t} =_{s t} T_{2, t}

, then they are also equivalently reliable in the SPD order, i.e.,

T_{1, t} =_{S P D} T_{2, t}

. This highlights the potential power of the SPD order in system analysis.

5. Conclusion

In the past few years, there has been a growing interest in quantifying the uncertainty related to the lifetime of engineering systems. Hence, this criterion can be used to predict the uncertainty of the lifetime of the system. The measurement of CE is an extension of Shannon’s entropy, making it a highly useful tool in these types of situations. This paper presented the CE presentation for the system’s lifetime if all components of the system have failed at time t. In addition, we have studied the properties of the proposed metrics including expressions and bounds in terms of CE uncertainties using the concept of system signature. We presented a series of examples to demonstrate our findings. In conclusion, we introduced criteria based on relative CE to identify a preferred system that is more akin to the parallel system.

Author Contributions

Conceptualization, M.S.; methodology, M.S.; software, M.K.; validation, M.S. and M.K.; formal analysis, M.S.; investigation, M.K.; resources, M.K.; writing—original draft preparation, M.S.; writing—review and editing, M.S. and M.K.; visualization, M.K.; supervision, M.K.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Researchers Supporting Project number (RSP2023R464), King Saud University, Riyadh, Saudi Arabia.

Data Availability Statement

No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Acknowledgments

The authors acknowledge financial support from the Researchers Supporting Project number (RSP2023R464), King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest

The authors declare no conflict of interest.

References

Shannon, C.E. A mathematical theory of communication. The Bell system technical journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: a new measure of information. IEEE transactions on Information Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
Rao, M. More on a new concept of entropy and information. Journal of Theoretical Probability 2005, 18, 967–981. [Google Scholar] [CrossRef]
Asadi, M.; Zohrevand, Y. On the dynamic cumulative residual entropy. Journal of Statistical Planning and Inference 2007, 137, 1931–1941. [Google Scholar] [CrossRef]
Baratpour, S. Characterizations based on cumulative residual entropy of first-order statistics. Communications in Statistics—Theory and Methods 2010, 39, 3645–3651. [Google Scholar] [CrossRef]
Baratpour, S.; Rad, A.H. Testing goodness-of-fit for exponential distribution based on cumulative residual entropy. Communications in Statistics-Theory and Methods 2012, 41, 1387–1396. [Google Scholar] [CrossRef]
Navarro, J.; del Aguila, Y.; Asadi, M. Some new results on the cumulative residual entropy. Journal of Statistical Planning and Inference 2010, 140, 310–322. [Google Scholar] [CrossRef]
Toomaj, A.; Zarei, R. Some new results on information properties of mixture distributions. Filomat 2017, 31, 4225–4230. [Google Scholar] [CrossRef]
Di Crescenzo, A.; Longobardi, M. On cumulative entropies. Journal of Statistical Planning and Inference 2009, 139, 4072–4087. [Google Scholar] [CrossRef]
Asadi, M.; Ebrahimi, N. Residual entropy and its characterizations in terms of hazard function and mean residual life function. Statistics & probability letters 2000, 49, 263–269. [Google Scholar]
Di Crescenzo, A.; Longobardi, M. Entropy-based measure of uncertainty in past lifetime distributions. Journal of Applied probability 2002, 39, 434–440. [Google Scholar] [CrossRef]
Abdolsaeed, T.; Doostparast, M. A note on signature-based expressions for the entropy of mixed r-out-of-n systems. Naval Research Logistics (NRL) 2014, 61, 202–206. [Google Scholar]
Toomaj, A.; Doostparast, M. On the Kullback Leibler information for mixed systems. International Journal of Systems Science 2016, 47, 2458–2465. [Google Scholar] [CrossRef]
Asadi, M.; Ebrahimi, N.; Soofi, E.S.; Zohrevand, Y. Jensen–Shannon information of the coherent system lifetime. Reliability Engineering & System Safety 2016, 156, 244–255. [Google Scholar]
Toomaj, A. Renyi entropy properties of mixed systems. Communications in Statistics-Theory and Methods 2017, 46, 906–916. [Google Scholar] [CrossRef]
Toomaj, A.; Chahkandi, M.; Balakrishnan, N. On the information properties of working used systems using dynamic signature. Applied Stochastic Models in Business and Industry 2021, 37, 318–341. [Google Scholar] [CrossRef]
Kayid, M.; Alshehri, M.A. Tsallis entropy of a used reliability system at the system level. Entropy 2023, 25, 550. [Google Scholar] [CrossRef]
Mesfioui, M.; Kayid, M.; Shrahili, M. Renyi Entropy of the Residual Lifetime of a Reliability System at the System Level. Axioms 2023, 12, 320. [Google Scholar] [CrossRef]
Kayid, M.; Shrahili, M. Rényi Entropy for Past Lifetime Distributions with Application in Inactive Coherent Systems. Symmetry 2023, 15, 1310. [Google Scholar] [CrossRef]
Kayid, M.; Shrahili, M. On the Uncertainty Properties of the Conditional Distribution of the Past Life Time. Entropy 2023, 25, 895. [Google Scholar] [CrossRef]
Samaniego, F.J. System signatures and their applications in engineering reliability; Vol. 110, Springer Science & Business Media, 2007.
Khaledi, B.E.; Shaked, M. Ordering conditional lifetimes of coherent systems. Journal of Statistical Planning and Inference 2007, 137, 1173–1184. [Google Scholar] [CrossRef]
Kochar, S.; Mukerjee, H.; Samaniego, F.J. The “signature” of a coherent system and its application to comparisons among systems. Naval Research Logistics (NRL) 1999, 46, 507–523. [Google Scholar] [CrossRef]
Di Crescenzo, A.; Longobardi, M.; others. Some properties and applications of cumulative Kullback-Leibler information. Applied stochastic models in business and industry 2015, 31, 875–891. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Cumulative Entropy of Past Lifetime for Coherent Systems at the System Level

Abstract

1. Introduction

2. CE of the past lifetime

3. Bounding the Cumulative Entropy of Past Lifetime

4. Preferable system

5. Conclusion

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe