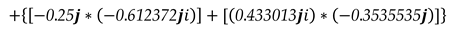Spinors and Spatial Vectors Are Part of the Number System; They Are Extensions of Complex Numbers into Three-Dimensional Space

Preprint

Article

Spinors and Spatial Vectors Are Part of the Number System; They Are Extensions of Complex Numbers into Three-Dimensional Space

Altmetrics

Downloads

281

Views

103

Comments

Srinivasa Mugeraya^*

This version is not peer-reviewed

Submitted:

29 August 2023

Posted:

30 August 2023

You are already at the latest version

Alerts

Abstract

Spinors are used for the computation of probability in quantum mechanics. They are treated as elements of a complex vector space in contrast to a real vector space. Spinor theory is abstract mathematics with an ambiguous interpretation. The overall phase of spinors does not affect the computation of probability in quantum mechanics. If two spinors have an overall phase of imaginary number i, then they can be treated like vectors in a real vector space. The square of the magnitude of the number, which is the sum of dot product and the term having basis vector i of cross product of two such vectors, is equal to the probability computed using the corresponding spinors. Therefore, the geometry of such spinors can be easily depicted in a three-dimensional space like vectors in a real vector space. Spinors are not isotropic vectors in Hilbert space. The sum of dot product and cross product of two complex numbers is equivalent to the quotient of the division of one complex number by another. Similarly, the sum of dot product and cross product of two vectors is the quotient of the division of one vector by another. Using the rules of division of vectors, we can find the rules of multiplication of vectors. The rules of multiplication and division of basis vector i match the rules of multiplication and division of imaginary number i. Therefore, basis vector i is nothing but imaginary number i. Multiplication of dot and cross product of two vectors to the second vector will give us the components of the first vector that are parallel and orthogonal to the second vector. Vectors are also made up of complex numbers like spinors. The reason for finding dot product of complex numbers in the process of computing the probability is to ignore the overall phase in contrast to the phase difference. This is misconstrued as complex vector space in quantum mechanics. 3-D number which is nothing but a spinor with new notation is an extension of vector algebra. It can have a real number as a term in addition to the terms i, j and k. In all other respects, it is a vector. 3-D numbers are part of the number system like real numbers and complex numbers. The real numbers are one dimensional numbers, the complex numbers are two-dimensional numbers and the 3-D numbers as well as vectors and spinors are three-dimensional numbers. As polarisation and spin are one and the same, we can straight away apply 3-D numbers to polarisation of light. 3-D numbers will greatly simplify the study of areas of science where three-dimensional space is involved.

Keywords:

Subject: Physical Sciences - Mathematical Physics

1. Introduction

Spinors are treated as elements of a complex vector space in contrast to a real vector space. Spinors are used in quantum mechanics to compute the probability of finding a particle. An introduction to spinors for beginners is given in Appendix I.

Spinor theory is abstract mathematics with an ambiguous interpretation. The geometrical significance of spinors is a mystery. The major issues flagged by mathematicians and physicists concerning spinors are given in Appendix II. There is no clarity about the spinor except for the fact that probabilities computed using spinors match the experimental results in quantum mechanics. A table of notations and symbols used in this article is given in Appendix VIII for reference. We will try to understand the spinor and simplify its notation.

2. Spinor notation

A general spin

\frac{1}{2}

superposition state vector

| ѱ ⟩

can be expressed as a combination of the basis kets

| + ⟩

and

| - ⟩

. If

θ

is the angle between kets

| + ⟩

and

|-⟩

and

φ

is the angle of phase difference, then the general spin

\frac{1}{2}

superposition state vector can be expressed as follows⁽¹⁾:

a): vector in the spin up direction

{| + ⟩}_{n} = c o s \frac{θ}{2} |+⟩ + s i n \frac{θ}{2} e^{i φ} |-⟩

[2.1]

b): vector in the spin down direction

{| - ⟩}_{n} = s i n \frac{θ}{2} |+⟩ - c o s \frac{θ}{2} e^{i φ} |-⟩

[2.2]

Instead of the above equations, two basis kets can be expressed as a column vector

S_{+ n} = [\begin{array}{l} c o s \frac{θ}{2} \\ s i n \frac{θ}{2} e^{i φ} \end{array}]

The above column vector is commonly known as a spinor. In this form, basis kets

| + ⟩

and

| - ⟩

are not expressly stated but implied.

The above equations are based on the convention of choosing the first coefficient to be real and positive. The overall phase of a quantum state spinor is not physically relevant. Only the relative phase between different components of the spinor is physically measurable. Hence, we are free to choose one coefficient of each spinor to be real and positive without any loss of generality.^(2),(6)

If the said convention is not followed then:

{| + ⟩}_{n} = c o s \frac{θ}{2} e^{i δ} | + ⟩ + s i n \frac{θ}{2} e^{i φ} e^{i δ} | - ⟩ {| - ⟩}_{n} = s i n \frac{θ}{2} e^{i δ} |+⟩ - c o s \frac{θ}{2} e^{i φ} e^{i δ} | - ⟩

where

δ

is the angle of the overall phase or phase factor.

3. New Spinor notation

We can skip

|+⟩

ket identification and

|-⟩

ket can be replaced by

j

{| + ⟩}_{n} = c o s \frac{θ}{2} + s i n \frac{θ}{2} j e^{i φ}

[3.1]

{| - ⟩}_{n} = s i n \frac{θ}{2} - c o s \frac{θ}{2} j e^{i φ}

[3.2]

If the term does not have

j

as its factor, then it is the term of basis ket

|+⟩

and if the term has

j

as its factor then it is the term of basis ket

|-⟩

.The division of angle

θ

by 2 is done in spinor theory due to the representation of

θ

2 θ

in the Bloch sphere (refer to Section 17). Therefore, replacing

θ

instead of

\frac{θ}{2}

{| + ⟩}_{n} = c o s θ + s i n θ j e^{i φ}

[3.3]

{| - ⟩}_{n} = s i n θ - c o s θ j e^{i φ}

[3.4]

Spinors under the new notation may be termed as ‘spin-numbers’. Different forms of spin-numbers are:

Form	spin-number with equal phase	spin-number with phase difference
trigonometric	$r \{c o s θ e^{i δ} + s i n θ j e^{i δ}\}$	$r \{c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ}\}$
factorised	$r {(x + y j) (a + b i)}$	$r {x (a + b i) + y j (c + d i)}$
Expanded	${a x + b x i + a y j + b y j i}$	${a x + b x i + c y j + d y j i}$
Expanded simplified	${a + b i + c j + d j i}$	${a + b i + c j + d j i}$

where

a, b, c, d, x & y

are real numbers.

θ

is the degree of polarisation, which is the same as in optics;

δ

the overall phase angle;

φ

is the phase difference; and

r

is the magnitude (or modulus or amplitude) of a spin-number. A spin-number may have one term each of a real number, an imaginary number

i

, new numbers

j a n d j i

. The number

j i

is the product of two numbers, one being an imaginary number and the other being the new number

j

. The new number

j

has all the properties of an imaginary number

i

. Note that any reference to an angle of the circle in this article shall be construed as the central angle of the circle in a sphere.

If the spin-number is in trigonometric form, then the same can be converted to expanded form as shown below:

S = r \{c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ}\} S = r \{c o s θ c o s δ + c o s θ s i n δ i + s i n θ c o s δ c o s φ j + s i n θ s i n δ s i n φ j i\}

4. Computing probability in Quantum mechanics using Spin-numbers

4.1: Let us compute the probability of finding the particle using spin-numbers. Let

{| + ⟩}_{A}

be the output state spin-number and

{| + ⟩}_{B}

be the input state spin-number.

{| + ⟩}_{A} = c o s α + s i n α j e^{i β}

[4.1]

{| + ⟩}_{B} = c o s θ + s i n θ j e^{i φ}

[4.2]

We will find the inner product

{_{A} 〈 + | + ⟩}_{B}

using the rules applicable to spinors. While taking the inner product under the spinor method, we have to change the complex number term of the output spin-number to its conjugate. Then the complex number and real number factors in each term of the output spin-number have to be multiplied with the complex number and real number factors of the corresponding term of the input spin-number. We will use the symbol small circle ‘

\circ

’ to denote inner product operation on spinors.

{_{A} 〈 + | + ⟩}_{B} = (c o s α + s i n α j e^{i β}) \circ (c o s θ + s i n θ j e^{i φ})

{_{A} 〈 + | + ⟩}_{B} = (c o s α + s i n α j e^{- i β}) (c o s θ + s i n θ j e^{i φ})

{_{A} 〈 + | + ⟩}_{B} = c o s α c o s θ + s i n α {s i n θ e}^{i (φ - β)}

[4.3]

In spinor mathematics, the inner product is the sum of a real number and an imaginary number. Therefore, it is more appropriate to term it as ‘complex dot product’.

The probability of finding a particle is given by multiplying the complex dot product, which is a complex number, with its complex conjugate.

P_{+ A | + B} = (c o s α c o s θ + s i n α {s i n θ e}^{i (φ - β)}) * (c o s α c o s θ + s i n α {s i n θ e}^{i (β - φ)})

P_{+ A | + B} = c o s α c o s θ c o s α c o s θ + c o s α c o s θ s i n α {s i n θ (e}^{i (φ - β)} + e^{i (β - φ)}) + s i n α {s i n θ e}^{i (φ - β)} s i n α {s i n θ e}^{i (β - φ)}

P_{+ A | + B} = {c o s}^{2} α {c o s}^{2} θ + c o s α c o s θ s i n α {s i n θ (e}^{i (φ - β)} + e^{i (β - φ)}) + {s i n}^{2} α {s i n}^{2} θ

\{e^{i (β - φ)}\}

is the conjugate of

\{e^{i (φ - β)}\}

. The sum of a complex number and its conjugate will always be two times the real part of that complex number. Here,

(φ - β)

is the phase difference.

P_{+ A | + B} = {c o s}^{2} α {c o s}^{2} θ + (2 c o s α c o s θ s i n α s i n θ \cos [φ - β]) + {s i n}^{2} α {s i n}^{2} θ

Theorem 1

: The probability of finding input spin-number

\{{| + ⟩}_{B} = c o s θ + s i n θ j e^{i φ}\}

in output state spin-number

\{{| + ⟩}_{A} = c o s α + s i n α j e^{i β}\}

is given by

P_{+ A | + B} = {c o s}^{2} α {c o s}^{2} θ + (2 c o s α c o s θ s i n α s i n θ \cos [φ - β]) + {s i n}^{2} α {s i n}^{2} θ

[4.4]

4.2: Let us compute the probability of finding a particle using spin-numbers when the first term is an imaginary number and not a real number. To do so, we have to change the overall phase to

e^{i (\frac{π}{2})}

. Therefore, we will multiply the spin-numbers [4.1] and [4.2] with the imaginary number

i

{| + ⟩}_{A} = (c o s α + s i n α j e^{i β}) * i

{| + ⟩}_{B} = (c o s θ + s i n θ j e^{i φ}) * i

{| + ⟩}_{A} = c o s α i + s i n α j e^{i (β + \frac{π}{2})}

{| + ⟩}_{B} = c o s θ i + s i n θ j e^{i (φ + \frac{π}{2})}

\{β + \frac{π}{2}\}

and

\{φ + \frac{π}{2}\}

will be replaced by

β

and

φ

for the time being.

{| + ⟩}_{A} = c o s α i + s i n α j e^{i β}

[4.5]

{| + ⟩}_{B} = c o s θ i + s i n θ j e^{i φ}

[4.6]

Let us find the complex dot product

{_{A} 〈 + | + ⟩}_{B}

{_{A} 〈 + | + ⟩}_{B} = (c o s α i + s i n α j e^{i β}) \circ (c o s θ i + s i n θ j e^{i φ})

{_{A} 〈 + | + ⟩}_{B} = (- c o s α i + s i n α j e^{- i β}) (c o s θ i + s i n θ j e^{i φ})

{_{A} 〈 + | + ⟩}_{B} = c o s α c o s θ + s i n α {s i n θ e^{- i β} e}^{i φ}

[4.7]

P_{+ A | + B} = (c o s α c o s θ + s i n α {s i n θ e^{- i β} e}^{i φ}) * (c o s α c o s θ + s i n α {s i n θ e^{i β} e}^{- i φ})

P_{+ A | + B} = c o s α c o s θ c o s α c o s θ + c o s α c o s θ s i n α {s i n θ e^{- i β} e}^{i φ} + c o s α c o s θ s i n α {s i n θ e^{i β} e}^{- i φ} + s i n α {s i n θ e^{- i β} e}^{i φ} s i n α {s i n θ e^{i β} e}^{- i φ}

P_{+ A | + B} = {c o s}^{2} α {c o s}^{2} θ + c o s α c o s θ s i n α {s i n θ (e^{- i β} e}^{i φ} + {e^{i β} e}^{- i φ}) + {s i n}^{2} α {s i n}^{2} θ

P_{+ A | + B} = {c o s}^{2} α {c o s}^{2} θ + c o s α c o s θ s i n α {s i n θ (e}^{i (φ - β)} + e^{i (β - φ)}) + {s i n}^{2} α {s i n}^{2} θ

{∴ P}_{+ A | + B} = {c o s}^{2} α {c o s}^{2} θ + (2 c o s α c o s θ s i n α s i n θ \cos [φ - β]) + {s i n}^{2} α {s i n}^{2} θ

Replacing back

\{β + \frac{π}{2}\}

and

\{φ + \frac{π}{2}\}

{∴ P}_{+ A | + B} = {c o s}^{2} α {c o s}^{2} θ + (2 c o s α c o s θ s i n α s i n θ \cos [(φ + \frac{π}{2}) - (β + \frac{π}{2})]) + {s i n}^{2} α {s i n}^{2} θ

{∴ P}_{+ A | + B} = {c o s}^{2} α {c o s}^{2} θ + (2 c o s α c o s θ s i n α s i n θ \cos [φ - β]) + {s i n}^{2} α {s i n}^{2} θ

[4.8]

{_{A} 〈 + | + ⟩}_{B}

in [4.3] and

P_{+ A | + B}

in [4.4] are equal to

{_{A} 〈+| +⟩}_{B}

in [4.7] and

P_{+ A | + B}

in [4.8].

It may be noted that multiplying the spin-number with imaginary number

i

has not made any difference on the probability.

Theorem 2

: If spin-numbers are multiplied by the imaginary number

i

, then the complex dot product and the probability of spin-numbers after such multiplication will be same as the complex dot product and probability of spin-numbers before such multiplication.

4.3: We will find the complex dot products and the probabilities of all permutations of spin-up numbers

+ ⟩_{A}

and

+ ⟩_{B}

in equations [4.5] and [4.6] and their spin-down numbers.

{_{A} 〈 + | + ⟩}_{B} = (c o s α i + s i n α j e^{i β}) \circ (c o s θ i + s i n θ j e^{i φ})

{_{A} 〈 + | - ⟩}_{B} = (c o s α i + s i n α j e^{i β}) \circ (s i n θ i - c o s θ j e^{i φ})

{_{A} 〈 - | + ⟩}_{B} = (s i n α i - c o s α j e^{i β}) \circ (c o s θ i + s i n θ j e^{i φ})

{_{A} 〈 - | - ⟩}_{B} = (s i n α i - c o s α j e^{i β}) \circ (s i n θ i - c o s θ j e^{i φ})

{_{B} 〈 + | + ⟩}_{A} = (c o s θ i + s i n θ j e^{i φ}) \circ (c o s α i + s i n α j e^{i β})

{_{B} 〈 + | - ⟩}_{A} = (c o s θ i + s i n θ j e^{i φ}) \circ (s i n α i - c o s α j e^{i β})

{_{B} 〈 - | + ⟩}_{A}) = (s i n θ i - c o s θ j e^{i φ}) \circ (c o s α i + s i n α j e^{i β})

{_{B} 〈 - | - ⟩}_{A}) = (s i n θ i - c o s θ j e^{i φ}) \circ (s i n α i - c o s α j e^{i β})

We know that

P_{{_{A} 〈 + | + ⟩}_{B}} + P_{{_{A} 〈 + | - ⟩}_{B}} = 1

P_{{_{A} 〈 - | + ⟩}_{B}} + P_{{_{A} 〈 - | - ⟩}_{B}} = 1

P_{{_{B} 〈 + | + ⟩}_{A}} + P_{{_{B} 〈 + | - ⟩}_{A}} = 1

and

P_{{_{B} 〈 - | + ⟩}_{A}}

P_{{_{B} 〈 - | - ⟩}_{A}} = 1

We can prove the following theorems by finding the probabilities of the above complex dot products.

Theorem 3:

P_{{_{A} 〈 + | + ⟩}_{B}} = P_{{_{A} 〈 - | - ⟩}_{B}} {= P}_{{_{B} 〈 + | + ⟩}_{A}} = P_{{_{B} 〈 - | - ⟩}_{A}}

Theorem 4:

P_{{_{A} 〈 + | - ⟩}_{B}} = P_{{_{A} 〈 - | + ⟩}_{B}} = P_{{_{B} 〈 + | - ⟩}_{A}} = P_{{_{B} 〈 - | + ⟩}_{A}}

5. Computing probability using Vectors

We will compute the probability of finding a particle by treating spin-numbers as Euclidean vectors or spatial vectors

\vec{a}

and

\vec{b}

of real vector space, hereafter referred to as ‘vectors’. We will use the star symbol (*) for multiplication, dot (

\cdot)

for dot product and cross (

\times

) for cross product. In physics, Standard basis vectors are denoted by

i, j a n d k

. While converting spin-number to vector, we will treat imaginary number

i

as basis vector

i

and treat

j i

as basis vector

k

(refer to Section8 for the proof).

Let us convert the spin-numbers [4.5] and [4.6] to vector form.

{| + ⟩}_{A} = c o s α i + s i n α j e^{i β}

{| + ⟩}_{A} = c o s α i + s i n α c o s β j + s i n α s i n β k

Converting to vector form by treating

i, j a n d k

as basis vectors,

\vec{a} = (a_{1} i + a_{2} j + a_{3} k)

[5.1]

{| + ⟩}_{B} = c o s θ i + s i n θ j e^{i φ}

{| + ⟩}_{B} = c o s θ i + s i n θ c o s φ j + s i n θ s i n φ k

Converting to vector form,

\vec{b} = (b_{1} i + b_{2} j + b_{3} k)

[5.2]

\vec{a} \cdot \vec{b} = (a_{1} i + a_{2} j + a_{3} k) \cdot (b_{1} i + b_{2} j + b_{3} k)

\vec{a} \cdot \vec{b} = {(a}_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3})

\vec{a} \times \vec{b} = (a_{1} i + a_{2} j + a_{3} k) \times (b_{1} i + b_{2} j + b_{3} k)

As per the vector method, dot product is a real number. As per the spinor method, inner product is the sum of a real number and an imaginary number. Let us check whether the term with basis vector

i

in cross product of vectors corresponds to the required imaginary number.

{(\vec{a} \times \vec{b})}_{} = {(a}_{2} b_{3} j k + a_{3} b_{2} k j) + \dots

{(\vec{a} \times \vec{b})}_{} = {(a}_{2} b_{3} {- a}_{3} b_{2}) i + \dots

Let us add

\{\vec{a} \cdot \vec{b}\}

and term having basis vector

i

of cross product

\{\vec{a} \times \vec{b}\}

which will be represented by the new notation

\{A \circ B\}

and the same may be called complex dot product as in the case of spinors (the symbol small circle ‘

\circ

’ denotes complex dot product).

A \circ B = {(a}_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) + {(a}_{2} b_{3} {- a}_{3} b_{2}) i

[5.3]

We will treat the above number as a complex number.

Converting to trigonometric form,

A \circ B = [(c o s α c o s θ + s i n α c o s β s i n θ c o s φ + s i n α s i n β s i n θ s i n φ) + (s i n α c o s β s i n θ s i n φ - s i n α s i n β s i n θ c o s φ) i]

A \circ B = c o s α c o s θ + s i n α (c o s β - s i n β i) s i n θ (c o s φ + s i n φ i)

A \circ B = (c o s α c o s θ + s i n α {s i n θ e}^{- i β} e^{i φ})

[5.4]

Comparing the complex dot product of spin-numbers in [4.7] and that of vectors in [5.4], we can see that

\{A \circ B\}

is equal to

\{{_{A} 〈 + | + ⟩}_{B}\}

|A \circ B|^{2} = (c o s α c o s θ + s i n α {s i n θ e}^{- i β} e^{i φ}) (c o s α c o s θ + s i n α {s i n θ e}^{i β} e^{- i φ})

|A \circ B|^{2} = {c o s}^{2} α {c o s}^{2} θ + (2 c o s α c o s θ s i n α s i n θ \cos [φ - β]) + {s i n}^{2} α {s i n}^{2} θ

[5.5]

The probability as per the spinor method in equations [4.4] and [4.8] are equal to the probability as per the vector method in equation [5.5].

|A \circ B|^{2} = P_{{_{A} 〈 + | + ⟩}_{B}}

[5.6]

It may be noted that replacing back

\{β + \frac{π}{2}\}

and

\{φ + \frac{π}{2}\}

is unnecessary as it will not make any difference to the result.

Theorem 5

: The sum of dot product and term having basis vector

i

of cross product of two vectors is the complex dot product of vectors.

Theorem 6

: The probability of finding an input vector in an output vector using the complex dot product is equal to the probability of corresponding spin-numbers using the spinor method.

Illustrations on computing probabilities in quantum mechanics using the spinor method, vector method and spin-number method are given in Appendix IV.

It may be noted that the mathematical procedure for the complex dot product of spinors is different from that of vectors. In the case of Spinors, we multiply the complex numbers of first term of two spinors followed by the complex numbers of second term of two spinors and the sum of the results is taken as the complex dot product. On the other hand, in the case of vectors, the sum of dot product of two vectors and the term with basis vector

i

in cross product of vectors is the complex dot product.

6. Geometry of Spinors

6.1: In Section 5, spin-numbers were treated like vectors of real vector space and we arrived at probability that is equal to the probability under the spin-number method in Section 4.2.

About the spinor mystery, Gerrit Coddens has stated as follows: “…. a thorough understanding of the ideas behind the mathematics is absolutely necessary if one wants to overcome the conceptual difficulties inherent to quantum mechanics. …. It would be futile to try to search for a physical explanation of some difficult point if the difficulty in question is in reality purely mathematical. ……. Spinors occur in the representation SU(2) of the three dimensional rotation group in

R^{3}

. As it uses spinors, which seem particularly difficult to understand, SU(2) appears to be a mystery representation of the three-dimensional rotation group. Now here is the question: How on Earth can it be that there is something mysterious about the three-dimensional rotation group? Is it not mere Euclidean geometry? This seems to suggest that there might be something simple that we have overlooked and that has escaped our attention.”⁽⁵⁾.

It is indeed true that we have missed a crucial point as discussed hitherto. However, Gerrit Coddens states that spinors do not build a vector space but a curved manifold and tries to demystify spinors using group theory. However, we have proved that spinor is indeed in vector space.

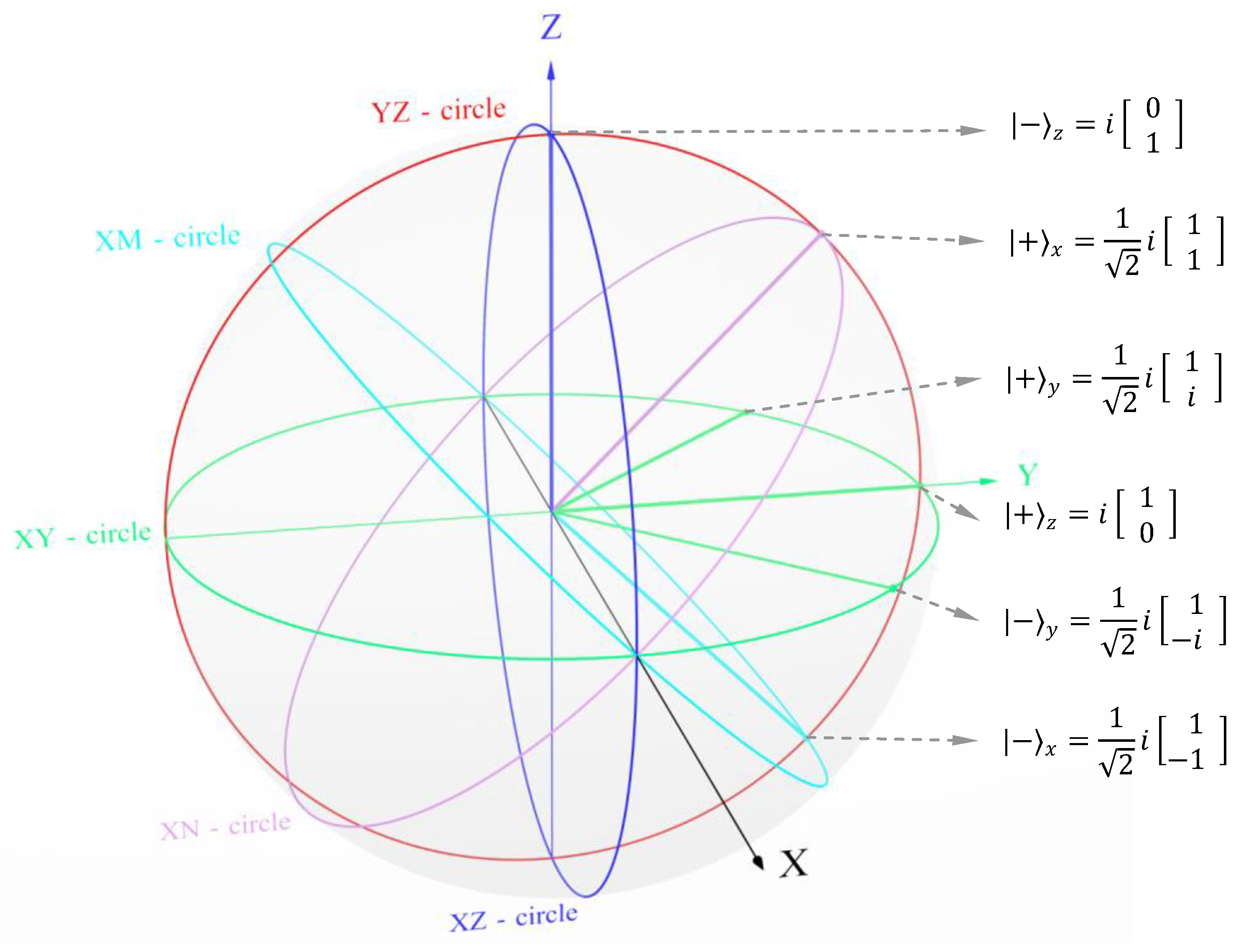
Gerrit Coddens has highlighted 0 = 1 paradox in quantum mechanics. The Dirac equation can be derived from a reasoning based on the isotropic vector (X, Y, Z), but afterwards, in the calculations, one identifies this isotropic vector with a position vector (x, y, z)⁽⁴⁾. Considering our findings in Section 5, we can safely say that spinors are in spatial vector space. Spinors are not isotropic vectors in Hilbert space. If two spinors have an overall phase equal to imaginary number

i

, then they can be treated like vectors in a real vector space. Therefore, the geometry of such spinors can be easily depicted in a three-dimensional space like vectors in a real vector space. Plotting the spin-numbers in a unit sphere is explained in detail in Section 11 and 16.

Figure 1. Spinor Geometry.

7. Projection of Complex Numbers

7.1: In linear algebra, dot product is the magnitude of one vector that is parallel to the other vector. The dot product is a measure of similarity of two vectors. If the vectors are perpendicular, the dot product will be zero. The cross product measures how different two vectors are, rather than how similar they are.

We will try to do the projection of one complex number over another. We will consider only unit complex numbers for the projections. Let

A

and

B

be unit complex numbers.

A = (a_{1} + a_{2} i) B = (b_{1} + b_{2} i)

Projection of

B o v e r A

will give us a dot product. It can be found by using vector rules by multiplying the real numbers of matching terms.

A \cdot B = a_{1} b_{1} + a_{2} b_{2}

We know that cross product involves the amount of a vector that is perpendicular to the other vector. We will apply the same rule to complex numbers. We will find the perpendicular complex number (

B_{⟂}

) of

B

By multiplying

B

with imaginary number

i

will turn

B

into its perpendicular position.

B_{⟂} = (b_{1} + b_{2} i) * i = (- b_{2} + b_{1} i)

Now, we will get dot product

\{A \cdot B_{⟂}\}

A \cdot B_{⟂} = (a_{1} + a_{2} i) \cdot (- b_{2} + b_{1} i)

A \cdot B_{⟂} = (a_{2} b_{1} - a_{1} b_{2})

This can be termed as ‘Orthogonal dot product’. To get cross product, we have to multiply the same by imaginary number

i

∴ A \times B = (A \cdot B_{⟂}) i

[7.1]

A \times B = (a_{2} b_{1} {- a}_{1} b_{2}) i

With the above results in hand, we will divide the

A

B

and find the relationship between dot product and division.

A \div B = (a_{1} + a_{2} i) \div (b_{1} + b_{2} i) = (a_{1} + a_{2} i) * (b_{1} - b_{2} i)

A \div B = (a_{1} b_{1} + a_{2} b_{2}) + (a_{2} b_{1} {- a}_{1} b_{2}) i

Let

C

be the quotient of the division of

A

B

∴ A \div B = C = (A \cdot B) + (A \times B)

[7.2]

A \div B = C

then

A B^{- 1} = C

and

A = C B

∴ A = [(A \cdot B) * B] + [(A \times B) * B]

[7.3]

It can be seen that scalar term of

C

is dot product

\{A \cdot B\}

and second term is cross product

\{A \times B\}

. Therefore, dot product and cross product method is an alternative to division.

Theorem 7

: The sum of dot product and cross product of complex numbers is equivalent to the quotient of the division of first complex number with the second complex number.

Theorem 8

: Dot product of complex numbers is a scalar part of the quotient of the division of first complex number with the second complex number.

7.2: The dot products

\{A \cdot B\}

and

\{A \cdot B_{⟂}\}

are real numbers. These two real numbers can be multiplied to

B

and

B_{⟂}

to arrive at

A

. Let us see whether it is true.

A = \{(A \cdot B) * B\} + \{(A \cdot B_{⟂}) * B_{⟂}\}

[7.4]

A \cdot B * B = (a_{1} b_{1} + a_{2} b_{2}) * (b_{1} + b_{2} i) = (a_{1} b_{1} b_{1} + a_{2} b_{2} b_{1} + a_{1} b_{1} b_{2} i + a_{2} b_{2} b_{2} i)

A \cdot B_{⟂} * B_{⟂} = (- a_{1} b_{2} + a_{2} b_{1}) * (- b_{2} + b_{1} i) = (a_{1} b_{2} b_{2} - a_{2} b_{1} b_{2} - a_{1} b_{2} b_{1} i + a_{2} b_{1} b_{1} i)

A = (a_{1} b_{1} b_{1} + a_{2} b_{1} b_{2} + a_{1} b_{1} b_{2} i + a_{2} b_{2} b_{2} i) + (a_{1} b_{2} b_{2} - a_{2} b_{1} b_{2} - a_{1} b_{1} b_{2} i + a_{2} b_{1} b_{1} i)

A = (b_{1} b_{1} + b_{2} b_{2}) a_{1} + (b_{1} b_{1} + b_{2} b_{2}) a_{2} i

As dot product of a unit vector with itself is just 1,

∴ b_{1} b_{1} + b_{2} b_{2} = 1

A = a_{1} + a_{2} i

Thus the two dot products

\{A \cdot B\}

and

\{A \cdot B_{⟂}\}

are magnitudes of

B

and

B_{⟂}

A

. Therefore, [7.4] is true.

Theorem 9

: If

A a n d B

are two complex numbers and

B_{⟂}

is perpendicular complex number of

B

, then the dot products

\{A \cdot B\}

and

\{A \cdot B_{⟂}\}

are real numbers. These two real numbers can be multiplied to

B

and

B_{⟂}

to arrive at

A

. The dot products

\{A \cdot B\}

and

\{A \cdot B_{⟂}\}

are magnitudes of

B

and

B_{⟂}

A

8. Multiplication of Vectors is a Division in disguise

8.1: While finding the probability in Section 5, we encountered a strange phenomenon. Spin-numbers were treated as vectors and we arrived at a probability that is equal to the probability under the spinor method. However, spinors and spin-numbers are constructed using the complex numbers. Further, while converting a spin-number to a vector, we had treated the imaginary number

i

as basis vector

i

. By re-converting the sum of dot product and vector term having basis vector

i

of cross product as a complex number, we were able to arrive at probability as that of a spin-number. Therefore, we must admit that basis vector

i

and imaginary number

i

are one and the same. However, we know that

i ∙ i = 1

for basis vector

i

. We need to find an explanation for the same.

In Section 7, it has been shown that projection of complex numbers is an alternative method of the division of complex numbers. We need to consider whether projection of vectors is also an alternative method of division of vectors.

Let us consider the vectors in [5.1] and [5.2].

\vec{a} = (a_{1} i + a_{2} j + a_{3} k) and \vec{b} = (b_{1} i + b_{2} j + b_{3} k)

We will simply multiply the two vectors term by term.

\vec{a} * \vec{b} = (a_{1} b_{1} i^{2} + a_{2} b_{2} j^{2} + a_{3} b_{3} k^{2}) + {(a_{2} b_{3} - a_{3} b_{2}) j k + (a_{3} b_{1} - a_{1} b_{3}) k i + (a_{1} b_{2} - a_{2} b_{1}) i j}

Applying the vector product rules,

i ∙ i = j . j = k . k = 1

and

i \times j = k; j \times k = i; k \times i = j

\vec{a} * \vec{b} = \{a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}\} + {(a_{2} b_{3} - a_{3} b_{2}) i + (a_{3} b_{1} - a_{1} b_{3}) j + (a_{1} b_{2} - a_{2} b_{1}) k}

We know that a dot product is

\{\vec{a} \cdot \vec{b} = (a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3})\}

and cross product is

\vec{a} \times \vec{b} = {(a_{2} b_{3} - a_{3} b_{2}) i + (a_{3} b_{1} - a_{1} b_{3}) j + (a_{1} b_{2} - a_{2} b_{1}) k}

Therefore, it looks like

\{\vec{a} * \vec{b} = \vec{a} \cdot \vec{b} + \vec{a} \times \vec{b}\}

. However, as per equation [7.2] and theorem 7 of complex numbers,

A \div B = (A \cdot B) + (A \times B)

Therefore, there is a contradiction. As per theorem 7, it should be the division of two complex numbers, whereas in vectors, we have treated it as the multiplication. If we treat it as a division of vectors, this contradiction can be avoided.

∴ \vec{a} \div \vec{b} = \vec{a} \cdot \vec{b} + \vec{a} \times \vec{b}

[8.1]

Aninterestingpoint to be noted here is that the term-by-term product is equal tothesum of dot product and cross product. Therefore, a dot product can be added to a cross product which means that a real number can be added to a vector.

Other important points to be considered here are;

a): We know that $\{i \cdot i = j \cdot j = k \cdot k = 1\}$ . If we divide any number by itself then we get unity. On the other hand if we multiply any number with itself, then the result is the square of the number. Therefore, projection of vectors must be division of vectors. As a consequence, dot product of basis vectors must be a division of basis vectors.
b): In Section 5, we have proved that basis vector $i$ behaves exactly like an imaginary number.
c): While taking the inner product under the spinor method, we have to change the complex number term, if any, of the output state spinor to its conjugate. Complex numbers are conjugated only in a division operation. Therefore, inner product of two spinors is a projection as well as a division. Here, the output state spinor is the numerator and the input state spinor is the denominator of the division. It must be noted that the output spinor is conjugated, instead of input spinor being the denominator. The reason is the impact of $j$ on these complex numbers as can be seen from the vector complex dot product in Section 5.
d): Vectors are not part of the number system but vector dot product results in real numbers. This creates difficulty in defining the relationship between a real number and a vector. If we treat dot product as a part of division, then the relationship between a real number and a vector will be clear.
e): When vector product is defined, vector division is treated as undefined and does not exist. Division is the inverse of multiplication. If multiplication is possible, then division should also be possible.
f): In Sections 8.2 to 8.4, we will show that multiplication of vectors can be done by treating vector projection as division and it is shown that, $i * i = - 1$ for multiplication of vectors.
g): In the case of complex numbers, in [7.2] and [7.3], we have proved that

$A \div B = (A \cdot B) + (A \times B)$ ;

$A = [(A \cdot B) * B] + [(A \times B) * B]$

Therefore, the sum of dot product and cross product is the quotient of the division. In Section 8.3, for vectors, we will prove that $\{\vec{a} = [(\vec{a} \cdot \vec{b}) * \vec{b} + (\vec{a} \times \vec{b}) * \vec{b}]\}$ . Therefore, projection of vectors is division of vectors.
h): In Section 8.8, we will show that the multiplication of dot and cross product of two vectors to the second vector will give us the components of the first vector that are parallel and orthogonal to second vector. Therefore, dot product should be part of the quotient of the division of two vectors.

Therefore, vector projection is nothing but division.

8.2: The rules of vector multiplication can be found by treating the rules of dot product and cross product as properties of division.

a): Dot product:

We know that basis vector dot products and cross products are:

i \cdot i = j \cdot j = k \cdot k = 1,

i \times j = k; j \times k = i; k \times i = j

and

j \times i = - k; k \times j = - i; i \times k = - j

If vector dot and cross products are part of division, then

i \div i = j \div j = k \div k = 1

i \div j = k; j \div k = i; k \div i = j; j \div i = - k; k \div j = - i; i \div k = - j

[8.1]

To convert it to multiplication, we have to multiply the inverse:

i * j^{- 1} = k; j * k^{- 1} = i; k * i^{- 1} = j j * i^{- 1} = - k; k * j^{- 1} = - i; i * k^{- 1} = - j

[8.3]

j * i^{- 1} = - k; k * j^{- 1} = - i; i * k^{- 1} = - j

[8.4]

Using the first equation of [8.3] and [8.4],

i * j^{- 1} = - (j * i^{- 1})

Multiplying both sides with

j^{- 1}

i * j^{- 1} j^{- 1} = - j * i^{- 1} j^{- 1}

Using

\{j * i^{- 1} = - k\}

in [8.4]

i * j^{- 1} j^{- 1} = k * j^{- 1}

Using

\{k * j^{- 1} = - i\}

in [8.4]

i * j^{- 1} * j^{- 1} = - i

j^{- 1} * j^{- 1} = - 1

1 = - 1 * j * j

j * j = - 1

Similarly,

i * i = - 1

k * k = - 1

Therefore, dot product on multiplication is:

i i = - 1, j j = - 1, k k = - 1,

[8.5]

b): Cross product:

Using

[8.3]

i * j^{- 1} = k; j * k^{- 1} = i; k * i^{- 1} = j

Shifting the

j^{- 1}

to the other side,

i = k j; j = i k; k = j i

j i = k; k j = i; i k = j

[8.6]

Using

\{j * i^{- 1} = - k\}

in [8.4] and using

\{j i = k\}

in [8.6],

j i^{- 1} = - j i

i^{- 1} = - i

, similarly for

j, k

{∴ i}^{- 1} = - i; j^{- 1} = - j; k^{- 1} = - k

[8.7]

We have arrived at

\{j i = k\}

in [8.6] on the multiplication of basis vectors. In Section 5.1, while converting spin-numbers to vectors, we have assumed that

\{j i = k\}

. In a spin-number,

j i m e a n s \{j * i\}

. Therefore, our assumption that

\{j i = k\}

was correct.

8.3: Let us consider the vectors in [5.1] and [5.2],

\vec{a} = (a_{1} i + a_{2} j + a_{3} k)

and

\vec{b} = (b_{1} i + b_{2} j + b_{3} k)

Applying dot product rule of vectors,

\vec{a} \cdot \vec{b} = (a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3})

Applying cross product rule of vectors,

\vec{a} \times \vec{b} = {(a_{2} b_{3} - a_{3} b_{2}) i + (a_{3} b_{1} - a_{1} b_{3}) j + (a_{1} b_{2} - a_{2} b_{1}) k}

In equation [8.1], we have already proved that

\vec{a} \div \vec{b} = \vec{c} = (\vec{a} \cdot \vec{b}) + (\vec{a} \times \vec{b})

\vec{c} = \{(a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) + (a_{2} b_{3} - a_{3} b_{2}) i + (a_{3} b_{1} - a_{1} b_{3}) j + (a_{1} b_{2} - a_{2} b_{1}) k\}

[8.8]

\vec{a} \div \vec{b} = \vec{c}

\vec{a} = \vec{c} \vec{b}

We will use the multiplication rules stated in Section 8.2 to find

\{\vec{c} \vec{b}\}

\vec{c} \vec{b} = [(a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) * (b_{1} i + b_{2} j + b_{3} k)] + {[(a_{2} b_{3} - a_{3} b_{2}) i + (a_{3} b_{1} - a_{1} b_{3}) j + (a_{1} b_{2} - a_{2} b_{1}) k] * (b_{1} i + b_{2} j + b_{3} k)} = {[(a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) b_{1} i + (a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) b_{2} j + (a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) b_{3} k] + [(a_{1} b_{2} - a_{2} b_{1}) b_{2} i - (a_{3} b_{1} - a_{1} b_{3}) b_{3} i + (a_{2} b_{3} - a_{3} b_{2}) b_{3} j - (a_{1} b_{2} - a_{2} b_{1}) b_{1} j + (a_{3} b_{1} - a_{1} b_{3}) b_{1} k - (a_{2} b_{3} - a_{3} b_{2}) b_{2} k]}

= \{a_{1} b_{1} b_{1} i + a_{2} b_{1} b_{2} i + a_{3} b_{1} b_{3} i + a_{1} b_{1} b_{2} j + a_{2} b_{2} b_{2} j + a_{3} b_{2} b_{3} j + a_{1} b_{1} b_{3} k + {i a u n i t 3 - D n u m b e r, a}_{2} b_{2} b_{3} k + {a_{3} b_{3} b}_{3} k\} + {a_{1} b_{2} b_{2} i - a_{2} b_{1} b_{2} i - a_{3} b_{1} b_{3} i + a_{1} b_{3} b_{3} i + a_{2} b_{3} b_{3} j - a_{3} b_{2} b_{3} j {- a}_{1} b_{1} b_{2} j + a_{2} b_{1} b_{1} j + a_{3} b_{1} b_{1} k - a_{1} b_{1} b_{3} k - a_{2} b_{2} b_{3} k + {a_{3} b_{2} b}_{2} k}

= {a_{1} b_{1} b_{1} i + a_{2} b_{1} b_{1} j + a_{3} b_{1} b_{1} k {+ a}_{1} b_{2} b_{2} i + a_{2} b_{2} b_{2} j + {a_{3} b_{2} b}_{2} k + {a_{3} b_{3} b}_{3} k + a_{1} b_{3} b_{3} i + a_{2} b_{3} b_{3} j}

= \{{b_{1} b_{1} (a}_{1} i + a_{2} j + a_{3} k {) + b_{2} b_{2} (a}_{1} i + a_{2} j + a_{3} k) + {b_{3} b_{3} (a}_{1} i + a_{2} j + a_{3} k)}

= {\{a_{1} i + a_{2} j + a_{3} k\} (b}_{1} b_{1} + b_{2} b_{2} + b_{3} b_{3})

\vec{c} \vec{b} = \{a_{1} i + a_{2} j + a_{3} k\} ({b_{1}}^{2} + {b_{2}}^{2} + {b_{3}}^{2})

{b_{1}}^{2} + {b_{2}}^{2} + {b_{3}}^{2} = 1

∴ \vec{c} \vec{b} = (a_{1} i + a_{2} j + a_{3} k) = \vec{a}

∴ \vec{a} = (\vec{a} \div \vec{b}) * \vec{b}

[8.9]

\{\vec{a} = \vec{c} \vec{b}\}

is true,

(\vec{a} \div \vec{b}) = (\vec{a} \cdot \vec{b}) + (\vec{a} \times \vec{b})

[8.10]

and \vec{a} = {(\vec{a} \cdot \vec{b}) * \vec{b} + (\vec{a} \times \vec{b}) * \vec{b}}

[8.11]

In Geometric Algebra, dot product and wedge product are summed up to get geometric product. In Section 15.2, we will show that the wedge product is similar to cross product. Therefore, adding a scalar to cross product is correct.

Theorem 10

: Dot product of vectors,

\{\vec{a} \cdot \vec{b}\}

, is nothing but dot product part of the quotient,

\{\vec{a} \div \vec{b}\}

. In other words, it is a scalar part of the quotient of the division of one vector by another. Cross product of two vectors,

\{\vec{a} \times \vec{b}\}

, is cross product part of the quotient,

\{\vec{a} \div \vec{b}\}

Theorem 11

: The sum of dot product and cross product of two vectors is equivalent to the quotient of a the division of one vector by another.

Theorem 12

: Vector

\vec{a}

is equivalent to the quotient of the division of vector

\vec{a}

by vector

\vec{b}

\{\vec{a} \div \vec{b}\}

multiplied by vector

\vec{b}

. In other words,

\{\vec{a} = (\vec{a} \div \vec{b}) * \vec{b}\}

Theorem 13

: Vector

\vec{a}

is equivalent to the sum of dot product and cross product of vector

\vec{A}

and vector

\vec{b}

multiplied by vector

\vec{b}

. In other words,

{\vec{a} = [(\vec{a} \cdot \vec{b}) * \vec{b} + (\vec{a} \times \vec{b}) * \vec{b}]}

8.4: As per vector rules,

\{i \cdot i = 1\}

. We know that dot product is part of division. Therefore,

\{i \div i = 1\}

, which means,

\{i * i^{- 1} = 1\}

. Similarly,

\{j * j^{- 1} = 1\}

\{k * k^{- 1} = 1\}

. This leads us to assume that the inverse of

\{\vec{b} = (b_{1} i + b_{2} j + b_{3} k)\}

{\vec{b}}^{- 1} = (- b_{1} i - b_{2} j - b_{3} k)

[8.12]

\vec{a} = (a_{1} i + a_{2} j + a_{3} k)

, then

\vec{a} \div \vec{b} = \vec{a} * {\vec{b}}^{- 1}

\vec{a} * {\vec{b}}^{- 1} = (a_{1} i + a_{2} j + a_{3} k) * (- b_{1} i - b_{2} j - b_{3} k)

\vec{a} * {\vec{b}}^{- 1} = (a_{1} i + a_{2} j + a_{3} k) * (- b_{1} i - b_{2} j - b_{3} k)

\vec{a} * {\vec{b}}^{- 1} = \{(a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) + (a_{2} b_{3} - a_{3} b_{2}) i + (a_{3} b_{1} - a_{1} b_{3}) j + (a_{1} b_{2} - a_{2} b_{1}) k\}

[8.13]

\{\vec{a} * {\vec{b}}^{- 1}\}

is equal to

\{\vec{a} \div \vec{b}\}

in [8.8] and therefore, equal to the sum of dot product and cross product of two vectors.

Therefore,

\{{\vec{b}}^{- 1} = (- b_{1} i - b_{2} j - b_{3} k)\}

is correct.

Theorem 14

: If

\{\vec{b} = (b_{1} i + b_{2} j + b_{3} k)\}

then it’s inverse

\{{\vec{b}}^{- 1} = (- b_{1} i - b_{2} j - b_{3} k)\}

and

\{\vec{a} * {\vec{b}}^{- 1}\}

is equal to

\{\vec{a} \div \vec{b}\}

8.5: As per the modified rules of vector multiplication and division given in equations [8.1], [8.5] and [8.7],

\{i i = - 1\}

\{i^{- 1} = - i\}

\{i \div i = 1\}

. These rules exactly match the rules of imaginary number

i

. Therefore, basis vector

i

is nothing but imaginary number

i

8.6: A vector can be split into two terms. Let us split vector in equation [5.1].

\vec{a} = (a_{1} i + a_{2} j + a_{3} k)

In equation [8.6], we have proved that

\{j i = k\}

∴ \vec{a} = [a_{1} i + j (a_{2} + a_{3} i)]

The first term is an imaginary number and the second term consists of two factors,

j

and

\{a_{2} + a_{3} i\}

. Therefore,

\{j + k = j (1 + i)\}

[8.14]

A vector is also made up of complex numbers like a spinor. Therefore, the vector must be equal to the spinor.

Converting the vector to a spin number;

A = [a_{1} i + j (a_{2} + a_{3} i)]

A = [a_{1} i + a_{2} j {+ a}_{3} j i]

8.7: We can take the complex dot product of vectors like spinors. We will restate the vectors in equations [5.1] and [5.2] by separating the complex numbers as described in Section 8.6.

\vec{a} = (a_{1} i + a_{2} j + a_{3} k) a n d \vec{b} = (b_{1} i + b_{2} j + b_{3} k)

[8.15]

\vec{a} = [a_{1} i + j (a_{2} + a_{3} i)] a n d \vec{b} = [b_{1} i + j (b_{2} + b_{3} i)]

We will take the complex dot product of the two vectors using the same approach as that of spinors described in Section 4.1.

\vec{a} \circ \vec{b} = [a_{1} i + j (a_{2} + a_{3} i)] \circ [b_{1} i + j (b_{2} + b_{3} i)]

\vec{a} \circ \vec{b} = [{- a}_{1} i + j (a_{2} - a_{3} i)] [b_{1} i + j (b_{2} + b_{3} i)]

\vec{a} \circ \vec{b} = {(a}_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) + {(a}_{2} b_{3} {- a}_{3} b_{2}) i

[8.16]

In equation [5.3], which is given below, we have found the complex dot product using the vector product method which is equal to equation [8.16].

A \circ B = {(a}_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3}) + {(a}_{2} b_{3} {- a}_{3} b_{2}) i

In Section 5, we have converted the spin-numbers in equations [4.5] and [4.6] to vector form and arrived at vectors in equations [5.1] and [5.2]. The spin numbers in equations [4.5] and [4.6] are reproduced below.

{| + ⟩}_{A} = c o s α i + s i n α c o s β j + s i n α s i n β k

{| + ⟩}_{B} = c o s θ i + s i n θ c o s φ j + s i n θ s i n φ k

Converting the equation [8.16] into trigonometric form,

A \circ B = (c o s α c o s θ + s i n α c o s β s i n θ c o s φ + s i n α s i n β s i n θ s i n φ) + (s i n α c o s β s i n θ s i n φ - s i n α s i n β s i n θ c o s φ) i

A \circ B = c o s α c o s θ + s i n α s i n θ (c o s β c o s φ + s i n β s i n φ + c o s β s i n φ i - s i n β c o s φ i)

A \circ B = c o s α c o s θ + s i n α s i n θ (c o s β - s i n β i) (c o s φ + s i n φ i)

A \circ B = c o s α c o s θ + s i n α {s i n θ e^{- i β} e}^{i φ}

[8.17]

The complex dot product of spin-numbers as arrived at in equation [4.7] is given below.

{_{A} 〈 + | + ⟩}_{B} = c o s α c o s θ + s i n α {s i n θ e^{- i β} e}^{i φ}

The result in equation [8.17] exactly matches the result in equation [4.7].

8.8: In vector algebra, if we resolve

\vec{a}

into components parallel and orthogonal to

\vec{b}

, then the sum of the component parallel to

\vec{b}

and component orthogonal to

\vec{b}

will be equal to

\vec{a}

⁽²⁶⁾. Further, the component of

\vec{a}

parallel to

\vec{b}

is given by

\{(\vec{a} \cdot \vec{b}) * \vec{b}\}

⁽²⁷⁾. The component of

\vec{a}

orthogonal to

\vec{b}

is given by

\vec{a}

minus component of

\vec{a}

parallel to

\vec{b}

⁽²⁸⁾.

In Section 8.1, we have proved that

{\vec{a} = [(\vec{a} \cdot \vec{b}) * \vec{b} + (\vec{a} \times \vec{b}) * \vec{b}]}

. If component of

\vec{a}

parallel to

\vec{b}

is given by

\{(\vec{a} \times \vec{b}) * \vec{b}\}

as stated in the previous paragraph, the component of

\vec{a}

orthogonal to

\vec{b}

should be equal to

\{(\vec{a} \times \vec{b}) * \vec{b}\}

Theorem 15

: The component of

\vec{a}

orthogonal to

\vec{b}

is equal to

\{(\vec{a} \times \vec{b}) * \vec{b}\}

9. Vector and Probability in Quantum Mechanics

9.1: We can use the vector algebra stated in Section 8 to find the probability in quantum mechanics. Let

{| + ⟩}_{A}

be the output state spin-number and

{| + ⟩}_{B}

be the input state spin-number.

{| + ⟩}_{A} = c o s \frac{2 π}{9} i + s i n \frac{2 π}{9} j e^{i \frac{7 π}{18}}

[9.1]

{| + ⟩}_{B} = c o s \frac{5 π}{36} i + s i n \frac{5 π}{36} j e^{i \frac{7 π}{36}}

[9.2]

We can convert the above two spin-numbers into vectors using the method described in Section 5.

\vec{a} = (0.76604 i + 0.21985 j + 0.60402 k)

\vec{b} = (0.90631 i + 0.34619 j + 0.24240 k)

\vec{a} \div \vec{b} = (0.76604 i + 0.21985 j + 0.60402 k) \div (0.90631 i + 0.34619 j + 0.2424 k)

\vec{a} \div \vec{b} = (0.9168 - 0.15581 i + 0.36174 j + 0.06595 k)

[9.3]

We will multiply each term of

(\vec{a} \div \vec{b})

\vec{b}

one by one using the multiplication rules of vectors stated in Section 8.2.

0.91680 * (0.90631 i + 0.34619 j + 0.2424 k) = (0.00000 + 0.83090 i + 0.31739 j + 0.22223 k)

[9.4]

- 0.15581 i * (0.90631 i + 0.34619 j + 0.2424 k) = (0.14122 + 0.00000 i - 0.03777 j + 0.05394 k)

[9.5]

S u m o f [9.4] a n d [9.5] = (0.14122 + 0.83090 i + 0.27962 j + 0.27617 k)

[9.6]

0.36174 j * (0.90631 i + 0.34619 j + 0.2424 k) = (- 0.12523 - 0.08769 i + 0.00000 j + 0.32785 k)

[9.7]

0.06595 k * (0.90631 i + 0.34619 j + 0.2424 k) = (- 0.01599 + 0.02283 i - 0.05977 j + 0.00000 k)

[9.8]

S u m o f [9.7] a n d [9.8] = (- 0.14122 - 0.06486 i - 0.05977 j + 0.32785 k)

[9.9]

\vec{a} = s u m o f [9.6] & [9.9] = (0.00000 + 0.76604 i + 0.21985 j + 0.60402 k)

[9.10]

Equation	Magnitude	Probability	Projection direction
[9.4]	0.9168	84.05%	$r e a l$ number
[9.5]	0.1558	02.43%	$i$
[9.6]	0.9299	86.48%	$r e a l n u m b e r + i$

[9.7]	0.3617	13.09%	$j$
[9.8]	0.0659	0. 43%	$k$
[9.9]	0.3677	13.52%	$j + k$
[9.10]	1.0000	100%
Table 9.1

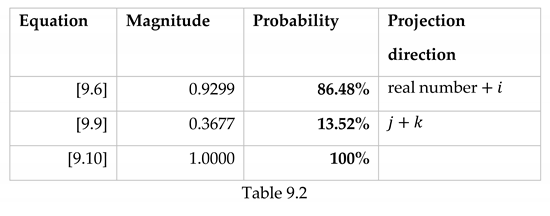
The sum of equations in [9.4], [9.5], [9.7] and [9.8] is equal to vector

\vec{a}

in [9.10]. The reason is that

\{\vec{a} = (\vec{a} \div \vec{b}) * \vec{b}\}

which has already been proved in [8.9]. The sum of probabilities of equations in [9.4], [9.5], [9.7] and [9.8] is equal to 1 being the square of the magnitude of vector

\vec{a}

(Table 9.1).

The magnitude of the number in [9.6] is 0.9299 and the probability is 86.48%. The sum of the probabilities of equations in [9.4] and [9.5] is equal to the probability of equation in [9.6] (Table 9.1). A simple summation of the probabilities of the real number case and the imaginary number case will yield the probability of the complex number case [9.6]. This is for the reason that in the case of a complex number

\{a + b i\}

, the square of the magnitude is

\{a^{2} + b^{2}\}

As stated in Section 8.8, if we resolve

\vec{a}

into components parallel and orthogonal to

\vec{b}

, then the sum of component parallel to

\vec{b}

and component orthogonal to

\vec{b}

will be equal to

\vec{a}

. In the example above, [9.4] is a component of

\vec{a}

which is parallel to

\vec{b}

. The component of

\vec{a}

which is orthogonal to

\vec{b}

is given below;

s u m o f [9.5], [9.7] & [9.8] = - 0.06486 i - 0.09754 j + 0.38179 k

[9.11]

Therefore,

\vec{a}

is the sum of [9.4] and [9.11].

\vec{a} = 0.76604 i + 0.21985 j + 0.60402 k

[9.12]

In vector algebra, dot product of two vectors is the magnitude of the component of vector

\vec{a}

that is parallel to the vector

\vec{b}

. On multiplication of dot product in

\{\vec{a} \div \vec{b}\}

to vector

\vec{b}

, we get vector in [9.4].

The co-efficient of

i

term of cross product of two vectors is the magnitude of the component of vector

\vec{a}

that is perpendicular in the

i

direction to the vector

\vec{b}

. On multiplication of said

i

term in

\{\vec{a} \div \vec{b}\}

to vector

\vec{b}

, we get vector in [9.5]. The equation in [9.5] is reframed below.

- 0.15581 i * (0.90631 i + 0.34619 j + 0.2424 k) = 0.15581 * (- i) * (0.90631 i + 0.34619 j + 0.2424 k)

- 0.15581 i * \vec{B} = - 0.15581 * i * \vec{B}

i \vec{b} = (- 0.90631 + 0.2424 k - 0.34619 k)

[9.13]

- 0.15581 i \vec{b} = - 0.15581 * (- 0.90631 + 0.2424 k - 0.34619 k)

[9.14]

Here, 0.15581 is the magnitude. The minus sign indicates that the projection is in the opposite direction of the vector in [9.13].

Similarly, the co-efficient of

j

k

term of cross product of two vectors is the magnitude of the component of vector

\vec{a}

that is perpendicular in the

j

k

direction to the vector

\vec{b}

. On multiplication of said

j

k

term in

\{\vec{a} \div \vec{b}\}

to vector

\vec{b}

, we get vector in [9.7] or [9.8].

It is pertinent to note that even though a real number is not a term in vector

\vec{a}

,real numbers are terms of equations in [9.5], [9.7] & [9.8]. However, their net sum is zero. We have already proved that the real number being a dot product has to be added to arrive at

\{\vec{a} \div \vec{b}\}

Toconclude, vector multiplication will help us to decompose a vector in terms of another vector and real numbers are essential for vector algebra.

9.2: Let us find

{| - ⟩}_{B}

using

{| + ⟩}_{B}

at [9.2].

{| - ⟩}_{B} = s i n \frac{5 π}{36} i - c o s \frac{5 π}{36} j e^{i \frac{7 π}{36}}

Converting the above spin-number into vectors using the method described in Section 5,

{\vec{b}}_{⟂} = 0.42262 i - 0.74241 j - 0.51984 k

\vec{a} \div {\vec{b}}_{⟂} = (0.76604 i + 0.21985 j + 0.60402 k) \div (0.42262 i - 0.74241 j - 0.51984 k)

\vec{a} \div {\vec{b}}_{⟂} = (- 0.15346 + 0.33414 i + 0.65349 j - 0.66163 k)

Projection direction	Magnitude	Probability	Spinor notation
$r e a l n u m b e r + i$	0.3677	13.52%	$P_{{_{A} 〈 + \| - ⟩}_{B}}$
$j + k$	0.9299	86.48%
	1.0000	100%
Table 9.2

9.3: Similarly, we can find the probabilities of different permutations of

\vec{a}

and

\vec{b}

Spinor notation	Magnitude	Probability
$P_{{_{A} 〈 + \| - ⟩}_{B}} o r P_{{_{A} 〈 - \| + ⟩}_{B}} o r P_{{_{B} 〈 + \| - ⟩}_{A}} o r P_{{_{B} 〈 - \| + ⟩}_{A}}$	0.3677	13.52%
$P_{{_{A} 〈 + \| + ⟩}_{B}} o r P_{{_{A} 〈 - \| - ⟩}_{B}} {o r P}_{{_{B} 〈 + \| + ⟩}_{A}} o r P_{{_{B} 〈 - \| - ⟩}_{A}}$	0.9299	86.48%
Table 9.3

The reason for the probabilities being equal for different products is already given in theorems 3 and 4.

9.4 Significance of complex numbers in computing probability: In Section 9.1, we have demonstrated that vector division and multiplication can be used to compute the probability in quantum mechanics. The probability of

\{{_{A} 〈 + | - ⟩}_{B}\}

computed using the spinor inner product method will be equal to the probability computed in Section 9.1. In [9.5], we are multiplying the magnitude of the component of vector

\vec{a}

that is orthogonal in the

i

direction of

\vec{b}

. In [9.6], we are summing up [9.4] and [9.5] and finding the component of vector

\vec{a}

that is parallel to the vector

\vec{b}

and perpendicular in the

i

direction to the vector

\vec{b}

. Therefore, the sum of the probabilities of [9.4] and [9.5] as shown in Table 9.1 is the probability we are seeking in quantum mechanics.

The reason for summing up of probabilities of [9.4] and [9.5] is to ignore the overall phase in contrast to the phase difference. As stated earlier, the overall phase of a quantum state spinor is not physically relevant and only the relative phase between different components of the spinor is physically measurable ^(2),(6). The Stern-Gerlach analyzer of quantum mechanics is not equipped to measure the overall phase. It is only measuring the angle between kets

| + ⟩

and

|-⟩

and angle resulting in a phase difference. If vector

\vec{a}

is the output state and vector

\vec{b}

is the input state, particles in the parallel direction to vector

\vec{b}

and particles in the perpendicular direction of

i

to the vector

\vec{b}

will go in the spin-up direction of the analyser. Therefore, the sum of the probabilities of [9.4] and [9.5] as shown in Table 9.1 is the probability of getting particles in the spin-up direction of the analyser. Particles in the perpendicular direction of

j

and

k

to the vector

\vec{b}

will go in the spin-down direction of the analyser. As the sum of the probabilities of [9.4] and [9.5] is required, the quantum mechanics requires the probability of a complex number. This is misconstrued as complex vector space in quantum mechanics. Therefore, treating spinors as elements of a complex vector space in contrast to a real vector space is wrong. This assumption was made due to a lack of understanding of the reasons for the presence of complex numbers in probability computation.

As the Stern-Gerlach analyzer of quantum mechanics is not able to account for the overall phase, the underlying mathematics should also ignore the phase. Therefore, in spinor mathematics, we multiply the complex numbers ignoring the effect of

|-⟩

ket. In vector product, the impact of

j

is also considered along with the complex number. Therefore, when two vectors do not have the same overall phase, we have to convert vectors to have equal overall phases. Otherwise, when two vectors do not have the same overall phase, the probability result will be different as normal vector division or multiplication will cover the effect of phase. Alternatively, we have to ignore the impact of

j

like in spinor mathematics by splitting the basis vector

k

by treating

k

j i

, and separating complex number in

\{j + k\}

9.5: Probability is not essential in quantum mechanics: In quantum mechanics, we are describing the probability of an ensemble of particles and not individual particles. Instead of finding probability, we can find the magnitude and describe the results of the Stern-Gerlach experiment. In table 9.2, the magnitudes of equations [9.6] and [9.9] are reproduced from table 9.1.

In the case of a vector, dot product itself is the magnitude of the component of vector

\vec{a}

that is parallel to the vector

\vec{b}

which is given in equation [9.4]. The same is used in physics without converting it to probability. Similarly, the magnitude, instead of probability, of the equation [9.6], which is the sum of the two components of vector

\vec{a}

given in equations [9.4] and [9.5], can be used in quantum mechanics.

9.6: In vector algebra, a real term is not one of the basis vectors and is not part of a vector. We restrict the complex numbers to their imaginary number positions only. However, we have shown that spatial vectors are part of the number system. We can have one division which will give us both dot product and cross product.

We have seen that in vector algebra, a real number is not part of the vector. This results in severe restrictions on its operations and use. For example;

▪ Vector division is not defined.
▪ Results of dot and cross product cannot be added together.
▪ Dot product of a non-unit vector is not defined.
▪ A vector cannot be used when first term is a real number.
▪ A real number cannot be added to a vector.

However, a real number pops up in dot product. In vector algebra, reasons as to why it should be kept aside are not given. Again, the same dot product is used to revert back and arrive at the original vector as shown in Sections 8.3 and 9.1.

In Section 8.8, we have shown that multiplication of dot and cross product of two vectors to the second vector will give us the components of the first vector that are parallel and orthogonal to second vector. Therefore, dot product should be part of the quotient of the division of two vectors.

We need to note that

a): the basis vector $i$ behaves exactly like an imaginary number as proved in Section 8.5.
b): toarriveat probability, we have to addbasis vector $i$ to dot product.
c): the vector is equal to spinor when overall phase is $e^{i (\frac{π}{2})}$ .

Therefore, the basis vector

i

should be the imaginary number

i

. In Section 8.6, it is shown that a vector is also made up of complex numbers like spinor. Therefore, the vector must be a spinor.

Theorem 16

: The basis vector

i

and the imaginary number

i

are one and the same. Vectors are spinors with an overall phase of imaginary number

i

Restricting the first term to basis vector

i

and not allowing a real number as part of vector has led to the development of alternative mathematical models like the Jones vector which is used in optics and the spinor which is used in quantum mechanics. Even though vector algebra is suitable to represent oriented objects, it cannot account for the rotation of an oriented object due to the exclusion of the real number as a term in a vector. Euler angles and Rodrigues’ rotation formula, which encodes rotation in three dimensional space, do not have good algebraic properties. Therefore, they are not equipped to handle even basic arithmetical operations like multiplication.

10. Basic properties of 3-D numbers

Spin-number which is nothing but a spinor with new notation is an extension of vector algebra. It can have a real number as a term in addition to the terms in a vector being

i

j

and

k

. In all other respects, it is a vector. Therefore, it is more appropriate to refer it as 3 dimensional number or ‘3-D number’. All spatial vectors are 3-D numbers but not vice versa. The sum of the complex dot product and cross product of two vectors is a 3-D number.

The rules of multiplication of terms of 3-D numbers are the same as those of multiplication of vectors as described in Section 8.2. The basic properties of terms of 3-D numbers are the same as those of basis vectors. However,

j i

is kept as it is without being replaced by

k

. This is useful while decomposing the 3-D number into trigonometric form and understanding the geometry of the 3-D number.

a): Four basis numbers in a 3-D number - real number, i, j and ji.
b): i is an imaginary number.
c): j will obey the exponential rules of i.

j^{2} = - 1; j^{3} = - j; j^{4} = 1

d): ji is the product of j & i and its square is a unity

{(j i)}^{2} = - 1

e): The numbers i & j will satisfy the commutative and associative laws of addition, the associative law of multiplication and the distributive laws of multiplication over addition.
f): Anti-commutative law of multiplication is applicable when numbers i & j are factors of a term in a 3-D number.

j i = - i j; i j = - j i; i j i = j; j i j = i;

g): A 3-D number can be represented in trigonometric form.

h): In trigonometric form, when j number and complex number are factors, when changing the order of the operands, we have to change the complex number to its conjugate. In such cases, the commutative law of multiplication is subject to conjugation. Proof of the same is given in Section 14.6.

11. 3-D number in Three-dimensional space

11.1: The complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system. In the said system,

X

-axis is formed by the real numbers and the

Y

-axis is formed by the imaginary numbers. Geometrically, 3-D numbers extend the concept of the two-dimensional complex plane into three-dimensional space.

Figure 2. Three-dimensional space.

11.2: We know that a unit circle can be considered as a circle formed by the complex numbers of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane. The unit circle is the set of complex numbers whose magnitude is one. Similarly, a unit sphere is the sphere formed by 3-D numbers of radius one centered at the origin in the three-dimensional Cartesian coordinate system in Euclidean space. In the said sphere, there are three unit circles.

a): The first circle joins $X$ and $Y$ axes and is in a horizontal state and the same can be named as $X Y$ circle. This is a normal unit circle formed by complex numbers with the imaginary number $i$ .
b): The second circle joins $X$ and $Z$ axes and the same can be named as $X Z$ circle. It is in a vertical state and is perpendicular to first circle. A complex number in this circle will behave like a complex number in a normal unit circle.
c): The third circle joins $Y$ and $Z$ axes and the same can be named as $Y Z$ circle. It is a vertical circle that binds the other two circles. It is perpendicular to other two circles. It is formed by a number like a complex number but its imaginary number is $j$ which may be referred to as ‘ $j$ -complex number’.

Thus there are two normal complex numbers in a unit sphere and one

j

-complex number. Each circle is formed by the numbers having a radius of unity centred at the origin.

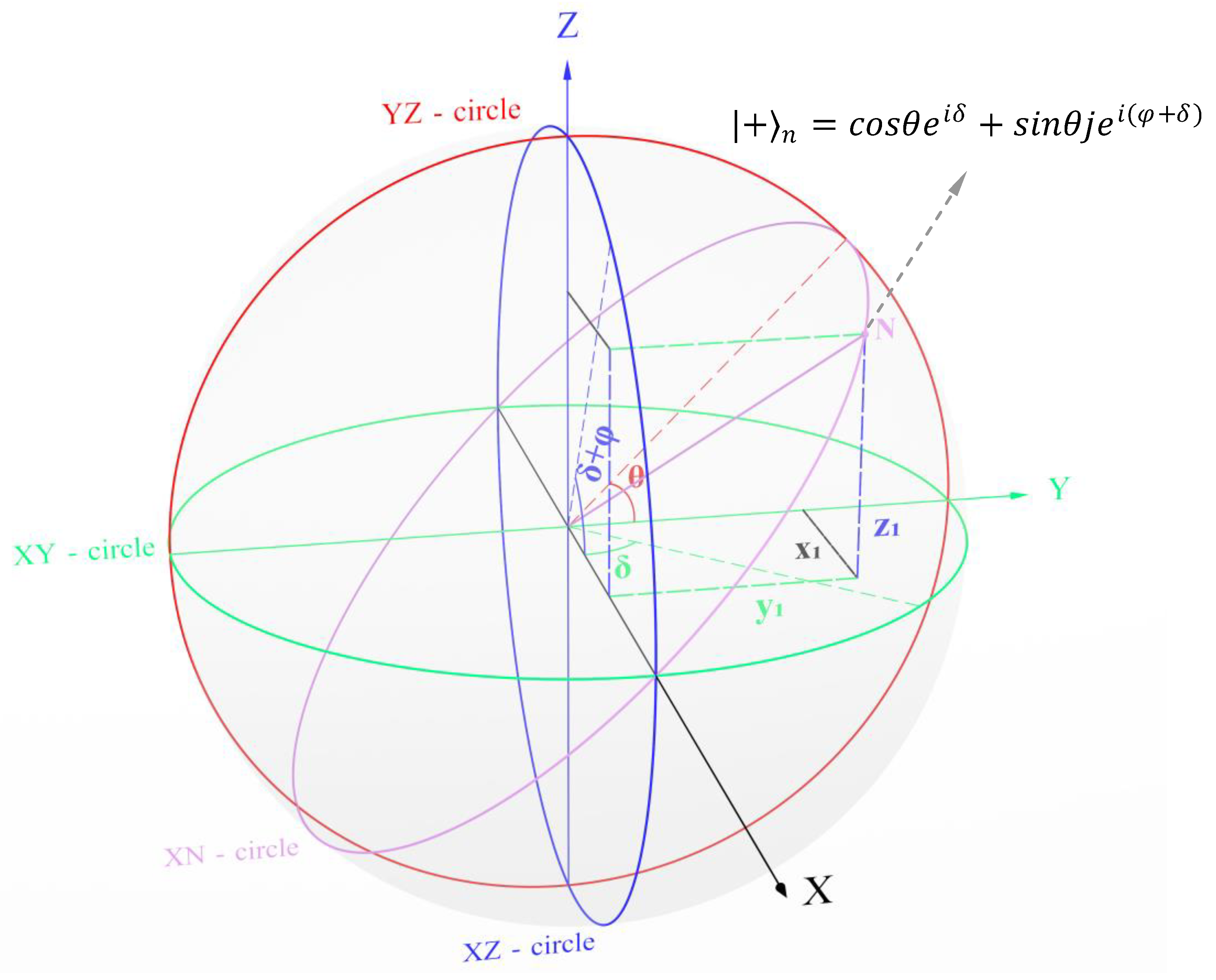
General spin

\frac{1}{2}

superposition state spinors are represented through spin-numbers [3.1] and [3.2],

{| + ⟩}_{n} = c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ}

{| - ⟩}_{n} = s i n θ e^{i δ} - c o s θ j e^{i φ} e^{i δ}

Replacing

e^{i φ} e^{i δ}

with

e^{i (φ + δ)}

{| + ⟩}_{n} = c o s θ e^{i δ} + s i n θ j e^{i (φ + δ)}

{| - ⟩}_{n} = s i n θ e^{i δ} - c o s θ j e^{i (φ + δ)}

Where,

δ

is the angle formed between axes

X

and

Y

or the angle of the complex number in

X Y

circle.

φ + δ

is the angle formed between axes

X

and

Z

or the angle of the complex number in

X Z

circle.

θ

is the angle formed between axes

Y

and

Z

or the angle of the

j

-complex number in

Y Z

circle.

φ

is the phase difference between the complex number in

X Y

circle and the complex number in

X Z

circle.

r

is the magnitude or modulus or amplitude of a 3-D number.

A 3-D number may have once term each of a real number, an imaginary number

i

, new numbers

j a n d j i,

which is a product of the two imaginary numbers and new number

j

. The new number

j

has all the properties of

i

except that it is in

Y Z

circle.

There are two complex numbers in a 3-D number with δ angle and

\{φ + δ\}

angle. The third number, i.e.,

j

-complex number, has θ angle and is formed with number

j

. This number is similar to a complex number but has number

j

in place of imaginary number

i

. A 3-D number is the sum of two complex numbers bound by a

j

-complex number.

Note: References to an angle of the circle in this article shall be construed as central angles of the circle.

3-D number

{| + ⟩}_{n}

can be decomposed into the following three numbers:

1): Complex number $e^{i δ}$ of $X Y$ circle
2): Product of two complex numbers $e^{i φ} e^{i δ}$ which is the complex number of $X Z$ circle
3): $j$ -complex number $\{c o s θ + s i n θ j\}$ of $Y Z$ circle

Algebraic form of the 3-D number is [refer to Section 3]:

S = x (a + b i) + y j (c + d i) o r S = a x + b x i + c y j + d y j i

3-D number

S

can be decomposed into the following three numbers:

1): Complex number $\{a + b i\}$ of $X Y$ circle
2): complex number $\{c + d i\}$ of $X Z$ circle
3): $j$ -complex number $\{x + y j\}$ of $Y Z$ circle

The magnitude (r) of a 3-D number:

r = \sqrt{{(a x)}^{2} {+ (b x)}^{2} + {(c y)}^{2} {+ (d y)}^{2}}

11.3 Unit 3-D number: The unit circle is the set of complex numbers

i

whose magnitude is one. Similarly, a unit sphere is a set of 3-D numbers whose magnitude is one and such numbers may be referred to as unit 3-D numbers. The

X Y

unit circle of a sphere is formed by the imaginary number

i

and its exponentiation. This is a horizontal circle. In

X Z

unit circle is made up of the imaginary number

i

and its exponentiation and it will be a vertical circle. The two will be perpendicular to each other and both will have the same origin. In between these two unit circles there will be several unit circles formed by the addition of these two circles. We will denote these circles as

X N

circles. All unit 3-D numbers will fall in one of these circles. Thus each unit 3-D number represents a point in the unit sphere. Unit 3-D numbers falling in one unit circle will have the same

θ

. The complex number falling in a

X N

circle may be denoted by

\{m + n i\}

11.4 Length of axes of 3-D number having equal phase: Length of axes of

X, Y a n d Z

dimensions of a unit 3-D number without phase difference, which is in a

X N

circle, can be found using the formulae given below.

(1) 3-D numbers with equal phases in factorised and expanded forms given in Section 3 are

S = {(x + y j) (a + b i)}

S = {a x + b x i + a y j + b y j i}

We will find the values of

m

and

n

in complex number

\{m + n i\}

X N

circle:

m = \sqrt{{(a x)}^{2} + {(a y)}^{2}}

m = \sqrt{{a^{2} (x}^{2} + y^{2})}

’ S ’

is a unit 3-D number,

\{x + y j\}

is a

j

-complex number similar to a unit complex number. The

j

-complex number

\{x + y j\}

is equal to

\{c o s θ + s i n θ j\}

(refer to Section 11.2).

{∴ x}^{2} + y^{2} = 0

∴ m = a

Similarly,

n = b

Therefore, complex number in

X N

circle is

\{a + b i\}

which is equal the complex number in

X Y

circle and

X Z

circle also.

X N

circle is in between

X Y

circle and

X Z

circle. Therefore, the length of

Y & Z

axes can be found by splitting the

n

value using

x

and

y

values in

\{x + y j\}

. The length of axes of

X, Y a n d Z

dimensions is given below:

X = m = a

Y = n x = b x

Z = n y = b y

(2) 3-D number with equal phase in trigonometric form given in Section 3 is reproduced below.

{| + ⟩}_{n} = c o s θ e^{i δ} + s i n θ j e^{i δ}

{| + ⟩}_{n} = \{c o s θ c o s δ + c o s θ s i n δ i + s i n θ c o s δ j + s i n θ s i n δ j i\}

m = c o s δ

n = s i n δ

X = m = c o s δ

Y = n c o s θ = s i n δ c o s θ

Z = n s i n θ = s i n δ s i n θ

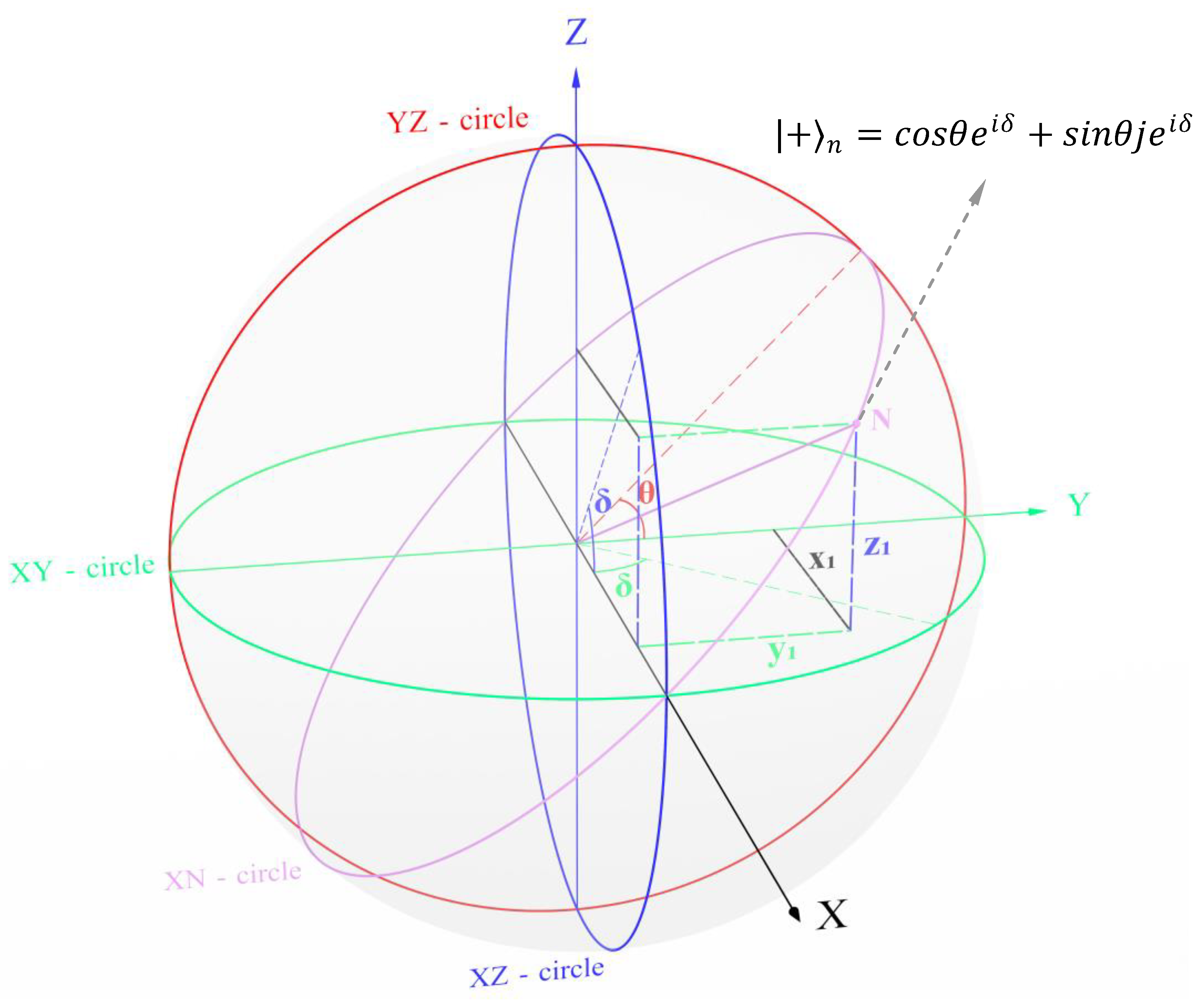
Figure 3. A 3-D number with equal phase in a unit sphere.

11.5 Length of axes of a 3-D number with phase difference: Length of axes of

X, Y a n d Z

dimensions of a unit 3-D number with phase difference, which is in a

X N

circle, can be found using the formulae given below. A 3-D number in trigonometric form is as follows:

{| + ⟩}_{n} = c o s θ e^{i δ} + s i n θ j e^{i (φ + δ)}

3-D number with phase difference in factorised form given in Section 3 is reproduced below:

S = x (a + b i) + y j (c + d i)

S = a x + b x i + c y j + d y j i

We will find the values of

m

and

n

of complex number

\{m + n i\}

X N

circle:

(1): If $a x a n d c y$ have the same sign:

m = \sqrt{{(a x)}^{2} + {(c y)}^{2}} (T h e s q u a r e r o o t w i l l h a v e t h e s i g n o f a x o r c y)

n = \sqrt{{(b x)}^{2} + {(d y)}^{2}} (The square root will have the sign of b x o r d y)

(2): If $a x a n d c y$ have opposite signs:

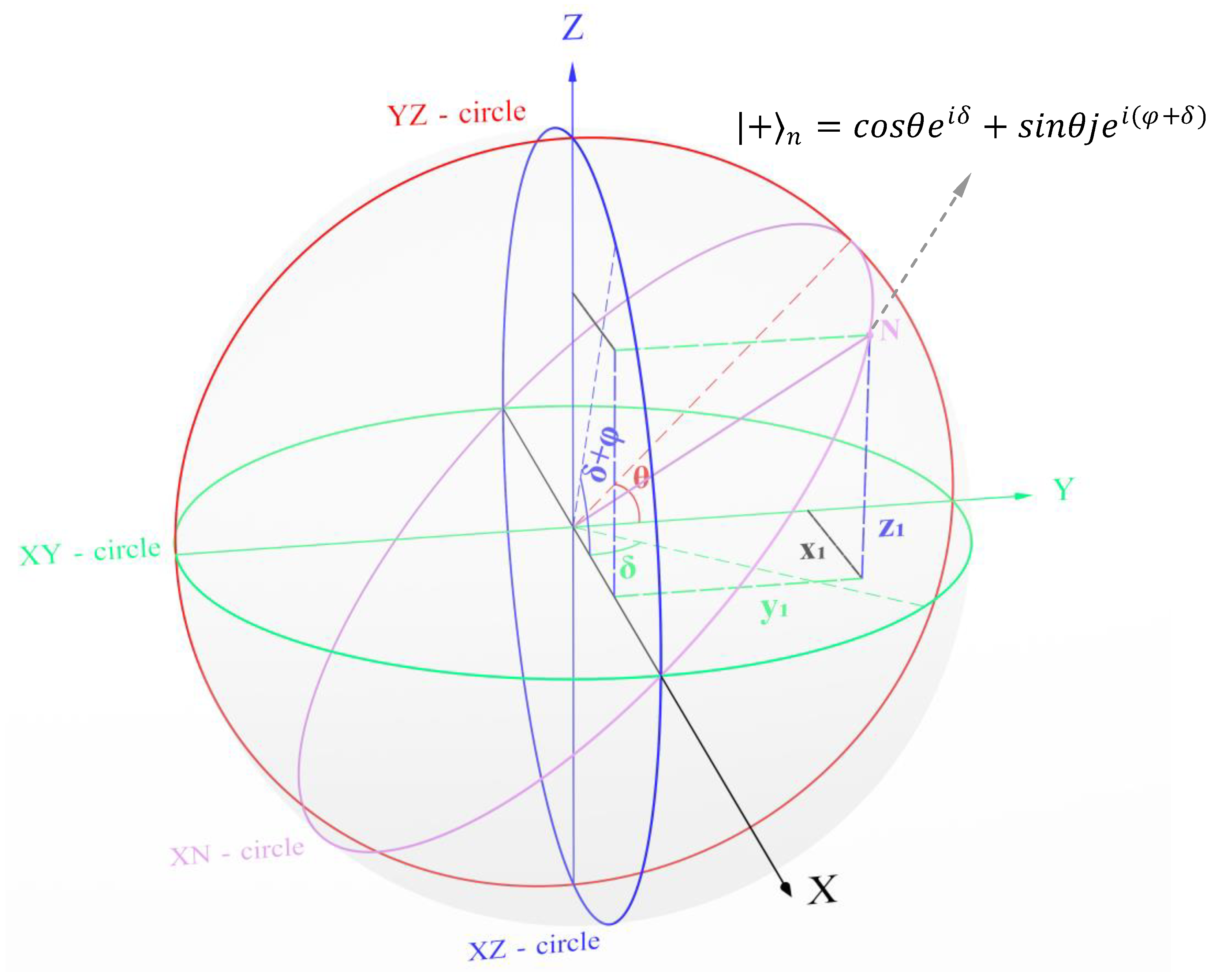
In the case of a 3-D number with phase difference, the real term of complex number may be the positive number and that of

j

-complex number may be the negative number or vice versa. In such cases, the two complex numbers in

X Y

circle and

X Z

circle are not on the same side of the

Y Z

circle in the sphere. Therefore, the position of the number will be in the middle of these two complex numbers.

If $|a x| > |c y|$ ,

m = \sqrt{{(a x)}^{2} - {(c y)}^{2}} (T h e s q u a r e r o o t w i l l h a v e t h e s i g n o f a x)

As we have deducted

{(c y)}^{2}

instead of adding it to the square of magnitude of

m

, we have to add

\{{2 (c y)}^{2}\}

to the square of magnitude of

n

in order to preserve magnitude.

n = \sqrt{{(b x)}^{2} + {(d y)}^{2} + {2 (c y)}^{2}}

If $|a x| < |c y|$ ,

m = \sqrt{{(c y)}^{2} - {(a x)}^{2}} (T h e s q u a r e r o o t w i l l h a v e t h e s i g n o f c y)

n = \sqrt{{(b x)}^{2} + {(d y)}^{2} + {2 (a x)}^{2}}

X N

circle is in between

X Y

circle and

X Z

circle. Therefore, the length of

Y & Z

axes can be found by splitting the

n

value using

x

and

y

values in

\{x + y j\}

. The length of axes of

X, Y a n d Z

dimensions is given below:

X = m Y = n x Z = n y

Figure 4. A 3-D number with phase difference in a unit sphere.

11.6: 3-D numbers are part of the number system like real numbers and complex numbers. If the real number is a one dimensional number, the complex number is a two-dimensional number and the 3-D number is a three-dimensional number. Note that the real number is part of the complex number and the complex number is part of the 3-D number. We know that a real number

x

can be regarded as a complex number

\{x + 0 i\}

, whose imaginary part is 0. Similarly, the real number

x

can be regarded as a 3-D number

\{x + 0 i + 0 j + 0 j i\}

and the complex number can be regarded as a 3-D number

\{x + y i + 0 j + 0 j i\}

. A vector can be converted into trigonometric form which will result in a better understanding of the geometry of vector.

11.7: Spin-up number and spin-down number relationship: The general state spinor in spin-number notation is [2.1] and [2.2],

{| + ⟩}_{n} = c o s θ + s i n θ j e^{i φ}

{| - ⟩}_{n} = s i n θ - c o s θ j e^{i φ}

We know that

\{s i n θ = c o s (θ - \frac{π}{2})\}

and

\{c o s θ = s i n (θ + \frac{π}{2})\}

{| - ⟩}_{n} = \cos (θ - \frac{π}{2}) + s i n (θ - \frac{π}{2}) j e^{i φ}

Therefore, if we rotate

j

-complex number of

y z

circle of a spin-up number by

\frac{π}{2}

in the reverse direction, then we will get a spin-down number.

12. Operations on 3-D numbers

12.1 Arithmetic operations of addition, subtraction, multiplication, division and exponentiation on 3-D numbers are fairly simple and are similar to those of quaternion.

3-D numbers share the same axioms as complex numbers apart from multiplication, where they do not commute. The basic axioms are stated below with the help of three 3-D numbers

A, B a n d C

Axioms of addition:

Commutative

A + B = B + A

Associative

(A + B) + C = A + (B + C)

Axioms of multiplication:

Associative

(A B) C = A (B C)

Non-commutative

A B \neq B A

The operations on 3-D numbers are explained in detail hereinafter:

12.2 Addition and Subtraction:

Addition or subtraction has to be made term wise (Illustrations 1 & 2)

(a_{1} + a_{2} i + a_{3} j {+ a}_{4} j i) + (b_{1} + b_{2} i + b_{3} j {+ b}_{4} j i) = {(a}_{1} {+ b}_{1}) + (a_{2} + b_{2}) i + {(a}_{3} {+ b_{3}) j + (a}_{4} {+ b}_{4}) j i

12.3 Multiplication:

Multiplication can be done by multiplying each term of the first complex number with each term of the second complex number. Commutative law does not apply to the multiplication of 3-D numbers. (Illustration 3)

(a_{1} + a_{2} i + a_{3} j {+ a}_{4} j i) * (b_{1} + b_{2} i + b_{3} j {+ b}_{4} j i) = = (+ a_{1} b_{1} + a_{2} b_{1} i + a_{3} b_{1} j + a_{4} b_{1} j i) + (- a_{2} b_{2} + a_{1} b_{2} i - a_{4} b_{2} j + a_{3} b_{2} j i) + (- a_{3} b_{3} + a_{4} b_{3} i + a_{1} b_{3} j - a_{2} b_{3} j i) + (- a_{4} b_{4} - a_{3} b_{4} i + a_{2} b_{4} j + a_{1} b_{4} j i)

12.4 Conjugation:

The conjugate of a 3-D number

A

is denoted by

\bar{A}

. If

A

is a unit 3-D number,

A \bar{A} = \bar{A} A = 1

i): If we change the signs of each term of a 3-D number except the real number term, we will get the conjugate of that 3-D number.
ii): If the 3-D number is in trigonometric form, then the complex number of $X Y$ circle and $j$ - $c o m p l e x n u m b e r$ of $Y Z$ circle should be conjugated. If the complex number and the number $j$ are factors of a term, conjugation of the complex number is not required and conjugation of the number $j$ alone is sufficient as that itself will result in conjugation of the entire number.

Examples of conjugates are given below:

A = \{a x + b x i + c y j + d y j i\}

\bar{A} = {a x - b x i - c y j - d y j i}

B = \{2 + 3 i + 4 j + 5 j i\},

\bar{B} = {2 - 3 i - 4 j - 5 j i}

{C = j e}^{i θ}

\bar{C} {= - j e}^{i θ}

{C = j e}^{i θ} e^{i φ}

\bar{C} {= - j e}^{i θ} e^{i φ}

B = c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ}

B = c o s θ e^{- i δ} - s i n θ j e^{i φ} e^{i δ}

12.5 Multiplicative inverse:

If we divide conjugate with square of the magnitude, we get the multiplicative inverse.

A

is 3-D number, the multiplicative inverse is

A^{- 1}

{\bar{A} A A}^{- 1} = A^{- 1} A \bar{A} = \bar{A}

Multiplicative inverse

A^{- 1} = \frac{\bar{A}}{A \bar{A}}

A \bar{A}

is the square of magnitude.

When

A

is a unit 3-D number

, A \bar{A} = 1

{∴ A}^{- 1} = \bar{A}

12.6 Multiplication and commutative law

i)

The commutative law of multiplication will not be applicable for 3-D numbers. However, the following identities will be applicable when changing the order of operands.

If $A, B a n d C$ are unit 3-D numbers and $A B = C$ , using $A \bar{A} = \bar{A} A = 1$
$A B = C$ , $A \bar{A} C = C$ $∴ B = \bar{A} C$
$A B = C$ , $C \bar{B} B = C$ $∴ A = C \bar{B}$
$B = \bar{A} C$ , $B \bar{C} C = B$ $∴ \bar{A} = B \bar{C}$
Similarly, $\bar{C} = \bar{B} \bar{A}$ $\bar{B} = \bar{C} A$

The above identities will be useful in division too.

ii): If $A, B a n d C$ are non-unit 3-D numbers, then replace conjugate with multiplicative inverse in the above identities.

If $\{A B = C\}$ , then $\{B = A^{- 1} C\}$ and so on.
iii): The anti-commutative law of multiplication is applicable when number $i a n d j$ are factors of a term in a 3-D number. However, if complex number and number $j$ are factors of a term in a 3-D number, then, on changing the order of operands (factors), the conjugate of complex number has to be multiplied and not the opposite number. The opposite and conjugate of an imaginary number are equal but those of a complex number are different.

Illustration 1:

{j e}^{i θ} {j e}^{i α} = {- e^{- i θ} e}^{i α}

Proof:

{j e}^{i θ} {j e}^{i α} = (c o s θ j + s i n θ j i) * (c o s α j + s i n α j i)

{j e}^{i θ} {j e}^{i α} = (c o s θ j c o s α j + s i n θ j i c o s α j) + (c o s θ j s i n α j i + s i n θ j i s i n α j i)

{j e}^{i θ} {j e}^{i α} = (c o s θ c o s α j j + s i n θ c o s α j i j) + (c o s θ s i n α j j i + s i n θ s i n α j i j i)

{j e}^{i θ} {j e}^{i α} = (- c o s θ c o s α + s i n θ c o s α i) + (- s i n θ s i n α - c o s θ s i n α i)

{j e}^{i θ} {j e}^{i α} = {- e^{- i θ} e}^{i α}

Illustration 2: If

{X = j e}^{i θ} e^{i φ}

and

{Y = j e}^{i α} e^{i β}

{X Y = j e}^{i θ} e^{i φ} {j e}^{i α} e^{i β}

{X Y = - e}^{- i θ} e^{- i φ} e^{i α} e^{i β}

12.7 Division:

The division of a 3-D number is similar to that of a complex number. We have to multiply both the numerator and denominator by the multiplicative inverse of the denominator. By doing so, the denominator will result in a real number (Illustration 4). Commutative law does not apply to the division of 3-D numbers.

Where $A$ and $B$ are 3-D numbers,

\frac{A}{B} = A B^{- 1}

A a n d B

are unit 3-D numbers, then as

B \bar{B} = 1

\frac{A}{B} = A \bar{B}

If $A, B a n d C$ are unit 3-D numbers and $A \div B = A \bar{B} = C$ , using $A \bar{A} = \bar{A} A = 1$ and

▪

$A \bar{B} = C$ , $A \bar{A} C = C$ $∴ \bar{B} = \bar{A} C$

▪

$A \bar{B} = C$ , $C B \bar{B} = C$ $∴ A = C B$

▪

$\bar{B} = \bar{A} C$ , $\bar{B} \bar{C} C = \bar{B}$ $∴ \bar{A} = \bar{B} \bar{C}$

▪

Similarly, $B \bar{A} = \bar{C}$ , $\bar{B} \bar{C} = \bar{A}$ , $\bar{C} A = B$

12.8 Rotation of a 3-D number from one position to another:

To rotate a 3-D number from one position to another, first multiply the multiplicative inverse and then multiply the 3-D number of the new position. This rule may be referred to as the rotation rule.

1): If $A, B a n d C$ are unit 3-D numbers, to rotate from position B to position A.

L e t B C = A

. We have to find C.

B \bar{B} A = A

∵ B \bar{B} = 1

∴ C = \bar{B} A

(Illustration 6 in Appendix VII)

2): Where $A, B$ and $C$ are unit 3-D numbers, i $f \{A \div C = B\}$ and $A a n d B$ is known, then to find $C,$

A \div C = B

∴ A = B C

Therefore, this problem is the same as the previous one.

∴ C = \bar{B} A

12.9 Conversion to trigonometric form:

Steps to convert a 3-D number to trigonometric form:

1): Separate the magnitude of the 3-D number
2): Separate the magnitude of complex numbers in $X Y$ circle and $X Z$ circle
3): Convert the complex numbers in $X Y$ circle and $X Z$ circle into trigonometric form
4): Convert the $j$ -complex number in $Y Z$ circle into trigonometric form

(Illustration 5 in Appendix VII)

Illustrations of different operations on 3-D numbers are given in Appendix VII.

13. Projection of 3-D numbers

13.1: In the complex number system, a dot product is a projection of one complex number over another. We will try to project one 3-D number over another. We will use a star (*) for normal multiplication and the symbol ‘

\times

’ for cross product to avoid confusion. We will consider only unit 3-D numbers for the projections. Consider the 3-D numbers in trigonometric form with real number as first term as given in equations [4.1] and [4.2].

A = c o s α + s i n α j e^{i β}

B = c o s θ + s i n θ j e^{i φ}

In the case of a complex number, there are only two dimensions with one angle between them. Projection requires a perpendicular number and as there is only one angle, there is only one perpendicular number. Therefore, there is only one projection possibility.

We have already proved that dot and cross product method of the complex numbers is nothing but an alternative method of division. In the case of dot and cross product of a complex number, real numbers are multiplied with each other to get the result. While taking the product of the 3-D numbers, we will encounter complex numbers. In such cases, we will use the traditional complex number division method under which we will multiply complex conjugates.

Complex dot product:

A \circ B = (c o s α + s i n α j e^{i β}) \circ (c o s θ + s i n θ j e^{i φ})

A \circ B = (c o s α - s i n α j e^{i β}) (c o s θ + s i n θ j e^{i φ})

(3-D number

A

is conjugated on changing the sign to multiplication while taking a complex dot product)

Term-to-term multiplication excluding cross multiplication is done by applying the multiplication rules of the 3-D numbers;

A \circ B = c o s α c o s θ - s i n α j e^{i β} s i n θ j e^{i φ}

A \circ B = c o s α c o s θ - s i n α {s i n θ j e}^{i β} {j e}^{i φ} (∵ s i n θ

is a real number)

A \circ B = c o s α c o s θ + s i n α {s i n θ e}^{- i β} e^{i φ}

[14.1]

(∵ e^{i β} j = {j e}^{- i β} and j j = - 1)

A \circ B = c o s α c o s θ + s i n α {s i n θ e}^{i (φ - β)}

[14.2]

The equation in

[14.2]

is equal to the equation in

[4.3]

. The input and output spinors of equation in

[4.3]

are equal to input and output 3-D numbers used to arrive at equation in

[14.2]

. Therefore,

\{{_{A} 〈 + | + ⟩}_{B} = A \circ B\}

Conjugation of the denominator is the correct approach: In spinor algebra, output spin number has to be conjugated before taking the complex dot product. In the division operation of complex numbers, the denominator has to be conjugated for multiplication. However, even if we conjugate input spin number being the denominator, the complex dot product result will not change. When conjugation operation is done on a unit complex number, it will result in an inverse. Therefore, in a division operation of two numbers, the denominator has to be conjugated on multiplication. Therefore, hereafter we will conjugate the denominator.

Cross product: To get cross product, perpendicular 3-D number of

B

is required. A 3-D number has three dimensions and three complex numbers with three angles. Cross product can be taken from all angles or from any angle. For the time being, we will consider cross product only in the angle θ of 3-D number

B

. To find the perpendicular number of

B

θ

angle being

B_{⟂}

, we will take assistance from spinor theory. In spinor theory, for every

{| + ⟩}_{n}

[3.3] there exists a

{| - ⟩}_{n}

[3.4].

{| + ⟩}_{n} = c o s θ + s i n θ j e^{i φ}

{| - ⟩}_{n} = s i n θ - c o s θ j e^{i φ}

Here,

{| + ⟩}_{n} = B

. Let us assume that

{| - ⟩}_{n} = B_{⟂}

. The proof of this assumption is given in Section 14.2.

B_{⟂} = s i n θ - c o s θ j e^{i φ}

[14.3]

If we multiply

s i n θ j e^{i φ}

with

\{- j e^{i φ}\},

we will get

s i n θ

\{- j e^{i φ}\}

is conjugate of

j e^{i φ}

. By multiplying

B

with

\{- j e^{i φ}\}

, we will get

B_{⟂}

Now, we will try to get the complex dot product of 3-D numbers

A

and

B_{⟂}

A \circ B_{⟂} = (c o s α + s i n α j e^{i β}) \circ (s i n θ - c o s θ j e^{i φ})

A \circ B_{⟂} = (c o s α + s i n α j e^{i β}) (s i n θ + c o s θ j e^{i φ})

A \circ B_{⟂} = (c o s α s i n θ - s i n α c o s θ e^{- i β} e^{i φ})

[14.4]

It is an orthogonal complex dot product. To get vector cross product, we have to multiply

\{A . B_{⟂}\}

with

[14.4]

with

\{- j e^{i φ}\}

. This is similar to the multiplication done in the case of complex number projection in [7.1].

A \times B = (c o s α s i n θ - s i n α c o s θ e^{- i β} e^{i φ}) * - j e^{i φ})

∴ A \times B = (s i n α c o s θ {j e}^{i β} - c o s α s i n θ j e^{i φ})

[14.5]

With the above result in hand, we will find a shortcut to arrive at complex dot product and cross product.

Let

\{A \div B = C\}

, then

\{C = A \bar{B}\}

(identity in 13.7)

\bar{B} = c o s θ - s i n θ j e^{i φ}

C = (c o s α + s i n α j e^{i β}) * (c o s θ - s i n θ j e^{i φ})

C = (c o s α c o s θ + s i n α s i n θ e^{- i β} e^{i φ}) + (s i n α c o s θ j e^{i β} - c o s α s i n θ j e^{i φ})

C

is the sum of [14.1] and [14.5]

C = (A \circ B) + (A \times B)

A \div B = (A \circ B) + (A \times B)

Therefore,

C

is truly the quotient of the division. It can be seen that first part of

C

is the complex dot product

\{A \circ B\}

and second part is cross product

\{A \times B\}

Theorem 17

: The sum of the complex dot product and cross product of two 3-D numbers, applying the formula of inner product and cross product of a spinor, is equivalent to the quotient of a division. The complex dot product and cross product method is an alternative method of division of 3-D numbers.

Theorem 18

: The complex dot product

\{A \circ B\}

of 3-D numbers is nothing but the complex dot product part of the quotient of the division of 3-D numbers.

13.2: The complex dot products

\{A \circ B\}

and

\{A \circ B_{⟂}\}

are the complex numbers. These numbers can be multiplied with

B

and

B_{O}

to arrive at

A

A = {(A \circ B) * B} + {(A \circ B_{⟂}) * B_{⟂}}

(A \circ B) * B = (c o s α c o s θ + s i n α {s i n θ e}^{- i β} e^{i φ}) * (c o s θ + s i n θ j e^{i φ})

(A \circ B) * B = (c o s α c o s θ c o s θ + c o s α {c o s θ s i n θ j e}^{i φ} + s i n α {c o s θ s i n θ e}^{- i β} e^{i φ} + s i n α {s i n θ s i n θ j e}^{i β})

A \circ B_{⟂} * B_{⟂} = (c o s α s i n θ - s i n α c o s θ e^{- i β} e^{i φ}) * (s i n θ - c o s θ j e^{i φ})

A \circ B_{⟂} * B_{⟂} = (c o s α s i n θ s i n θ - c o s α c o s θ s i n θ j e^{i φ} - s i n α c o s θ s i n θ e^{- i β} e^{i φ} + s i n α c o s θ c o s θ j e^{i β})

A = {(A \circ B) * B} + {(A \circ B_{⟂}) * B_{⟂}}

A = (c o s α c o s θ c o s θ + c o s α c o s θ s i n θ j e^{i φ} + s i n α {c o s θ s i n θ e}^{- i β} e^{i φ} + s i n α {s i n θ s i n θ j e}^{i β}) + (c o s α s i n θ s i n θ - c o s α c o s θ s i n θ j e^{i φ} - s i n α c o s θ s i n θ e^{- i β} e^{i φ} + s i n α c o s θ c o s θ j e^{i β})

A = c o s α c o s θ c o s θ + s i n α {s i n θ s i n θ j e}^{i β} + c o s α s i n θ s i n θ + s i n α c o s θ c o s θ j e^{i β}

A = c o s α (c o s θ c o s θ + s i n θ s i n θ) + s i n α j e^{i β} (c o s θ c o s θ + s i n θ s i n θ)

A = c o s α + s i n α j e^{i β}

In Section 14.1, we have assumed that

\{{| - ⟩}_{B} = B_{⟂}\}

. We have proved that

A = {(A \circ B) * B} + {(A \circ B_{⟂}) * B_{⟂}}

. Therefore,

{| - ⟩}_{B} = B_{⟂}

is proved.

A a n d B

are two 3-D numbers,

B_{⟂}

is the perpendicular number of

B

y z

circle and

A_{⟂}

is perpendicular number of

A

y z

circle, then the complex dot products

\{A \circ B\}

\{A \circ B_{⟂}\}

\{A_{⟂} \circ B_{⟂}\}

and

\{A_{⟂} \circ B\}

are complex numbers. Now, the following theorems emerge.

Theorem 19

: Complex numbers

\{A \circ B\}

and

\{A \circ B_{⟂}\}

can be multiplied with

B

and

B_{⟂}

to arrive at

A

. The complex numbers

\{A \circ B\}

and

\{A \circ B_{⟂}\}

are magnitudes of

B

and

B_{⟂}

A

Theorem 20

: The state spinor in the spin down direction is the perpendicular 3-D number

B_{⟂}

of a state spinor

B

which is in the spin up direction.

Theorem 21

: If the input state to the Stern-Gerlach analyser is

B

and the output state is

A

, then the complex dot products

\{A \circ B\}

and

\{A \circ B_{⟂}\}

are magnitudes of

B

and

B_{⟂}

A

Theorem 22

{_{A} 〈 + | + ⟩}_{B}

is the bra-ket notation of the complex dot product of two spinors

A

a n d

B,

when B is in the input state.

{_{A} 〈 + | + ⟩}_{B} = A \circ B

|{_{A} 〈 + | + ⟩}_{B}|^{2} = |A \circ B|^{2}

|A \circ B|^{2}

is the probability of finding input state

B

in output state

A

Theorem 23

{_{A} 〈 + | - ⟩}_{B}

is the bra-ket notation of the complex dot product of

A

a n d

B_{⟂}, w h e n B_{⟂}

is the input state.

{_{A} 〈 + | - ⟩}_{B} = A \circ B_{⟂}

|{_{A} 〈 + | - ⟩}_{B}|^{2} = |A \circ B_{⟂}|^{2}

|A \circ B_{⟂}|^{2}

is the probability of input state

B_{⟂}

in output state

A

As a corollary, we can add the following two theorems.

Theorem 24

{_{A} 〈 - | - ⟩}_{B}

is the bra-ket notation of the complex dot product of

A_{⟂}

a n d

B_{⟂}, w h e n B_{⟂}

is the input state.

{_{A} 〈 - | - ⟩}_{B} = A_{⟂} \circ B_{⟂}

|{_{A} 〈 - | - ⟩}_{B}|^{2} = |A_{⟂} \circ B_{⟂}|^{2}

|A_{⟂} \circ B_{⟂}|^{2}

is the probability of finding input state

B_{⟂}

in output state

A_{⟂}

Theorem 25

{_{A} 〈 - | + ⟩}_{B}

is the bra-ket notation of the complex dot product of

A_{⟂}

a n d

B, w h e n B

is the input state.

{_{A} 〈 - | + ⟩}_{B} = A_{⟂} \circ B

|{_{A} 〈 - | + ⟩}_{B}|^{2} = |A_{⟂} \circ B|^{2}

|A_{⟂} \circ B|^{2}

is the probability of input state

B

in output state

A_{⟂}

We have found the probability of a 3-D number with an imaginary number

i

as the overall phase of both input and output 3-D numbers. Projection of 3-D numbers having an overall phase, which is a complex number, and the computation of probability of such numbers is given in Appendix VI. Illustrations on computing probabilities using 3-D numbers are given in Appendix V. If two 3-D numbers do not have the same overall phase, then we have to convert them to get an equal overall phase which is similar to the case of vectors as discussed in Section 9.3.

13.3: We will find the probability considering that spinor

B

is the input state and spinor

A

is the output state.

{| + ⟩}_{A} = c o s \frac{2 π}{3} + s i n \frac{2 π}{3} j e^{i \frac{π}{4}}

{| + ⟩}_{B} = c o s \frac{π}{3} + s i n \frac{π}{3} j e^{i \frac{π}{8}}

{| + ⟩}_{A} = - 0.5 + 0.866025 j (0.707107 + 0.707107 i)

{| + ⟩}_{A} = - 0.5 + 0.612372 j + 0.612372 j i

{| + ⟩}_{B} = c o s \frac{π}{4} + s i n \frac{π}{4} j e^{i \frac{π}{3}}

{| + ⟩}_{B} = 0.5 + 0.866025 j (0.382683 + 0.923880 i)

{| + ⟩}_{B} = 0.5 + 0.331413 j + 0.800103 j i

Considering the above two spinors as spin numbers or 3-D numbers,

A \circ B = (- 0.5 + 0.612372 j + 0.612372 j i) \circ (0.5 + 0.331413 j + 0.800103 j i)

A \circ B = (- 0.5 + 0.612372 j + 0.612372 j i) (0.5 - 0.331413 j - 0.800103 j i)

(3-D number

B

is conjugated on changing the sign to multiplication while taking a complex dot product)

= \{[- 0.5 * 0.5] + [0.612372 j * (- 0.331413 j)] + (0.612372 j i) * (- 0.800103 j i)]\} + \{[0.612372 j * (- 0.800103 j i)] + [(0.612372 j i) * (- 0.331413 j)]\}

(While taking the complex dot product, we will find only terms having real number and

i

as a factor)

= \{- 0.25 + 0.202948 + 0.489961\} + \{0.489961 i - 0.202948 i\}

A \circ B = 0.442909 + 0.287013 i

P_{{_{A} 〈 + | + ⟩}_{B}} = 27.854 %

We will find the result of

A \div B

A \div B = \{- 0.5 + 0.612372 j + 0.612372 j i\} \div \{0.5 + 0.331413 j + 0.800103 j i\}

A \div B = \{- 0.5 + 0.612372 j + 0.612372 j i\} * \{0.5 - 0.331413 j - 0.800103 j i\}

14. Quaternions and 3-D numbers

14.1: Quaternions form a 4-dimensional vector space over the reals. There are just four independent ‘basis’ quantities

\{1, i, j, k\}

that span the entire space of quaternions.

Quaternion form:

q = a + b i + c j + d k, i^{2} = j^{2} = k^{2} = i j k = - 1 i j = k; j k = i; k i = j

where a, b, c and d are real numbers, defines the general quaternion.

These quantities satisfy all the normal laws of algebra except the commutative law of multiplication. Hamilton found that

i j = - j i, j k = - k j, k i = - i k

Quaternion satisfies the commutative and associative laws of addition, the associative law of multiplication and the distributive laws of multiplication over addition.

14.2: A 3-D number is similar to a quaternion except for the following differences.

(a): In quaternion, last basis quantity is $k$ which is equal to $i j$ . Whereas, in a 3-D number, last basis quantity is $j i$ .
(b): A quaternion has four dimensions whereas 3-D number has only three dimensions.
(c): A 3-D number can be factorised and represented in trigonometric form.
(d): In mathematics and physics, the role of quaternion is undefined ⁽⁷⁾.

Note that in quaternion rules,

\{i j = k\}

whereas we have arrived at

\{j i = k\}

in vector multiplication in Section 8. In other respects, vector multiplication rules are equal to quaternion multiplication rules.

14.4: Both quaternion and vector were discovered around the middle of the 19^th century. By the end of the 19th century, vectors have gained prominence over quaternions. According to W. Thompson (1892), “Quaternions came from Hamilton after his really good work had been done; and, though beautifully ingenious, have been an unmixed evil to those who have touched them in any way, including Clerk Maxwell.”⁽¹⁶⁾. Oliver Heaviside (1893) has summed up as follows: “…the quaternion was not only not required, but was a positive evil of no inconsiderable magnitude; and that by its avoidance the establishment of vector analysis was made quite simple and its working also simplified, and that it could be conveniently harmonised with ordinary Cartesian work.” ⁽²⁵⁾. Quaternion was discarded by physicists because it was mysterious.

15. Geometric Algebra and 3-D numbers

15.1:Geometric Algebra

Let us consider the vectors in [5.1] and [5.2]

\vec{A} = (a_{1} i + a_{2} j + a_{3} k)

and

\vec{B} = (b_{1} i + b_{2} j + b_{3} k)

Now, let us compute the cross product.

\vec{A} \times \vec{B} = {(a_{2} b_{3} - a_{3} b_{2}) i + (a_{3} b_{1} - a_{1} b_{3}) j + (a_{1} b_{2} - a_{2} b_{1}) k}

If we take their wedge product (∧) in geometric algebra,

\vec{A} \land \vec{B} = {(a_{2} b_{3} - a_{3} b_{2}) (j \land k) + (a_{3} b_{1} - a_{1} b_{3}) (k \land i) + (a_{1} b_{2} - a_{2} b_{1}) (i \land j)}

We know that

\{i \times j = k; j \times k = i; k \times i = j\}

in vector algebra. If the same is true in geometric algebra too, then

\{\vec{A} \land \vec{B}\}

will be equal to

\{\vec{A} \times \vec{B}\}

. However, in geometric algebra

\{i \land j \neq k\}

\{i \land j\}

is treated as a bi-vector. The wedge product of two basis vectors is not equal to a basis vector that is perpendicular to the first two basis vectors. This is the fundamental difference between vector algebra and geometric algebra.

15.2: In geometric algebra, we may write the geometric product of any two vectors as the sum of a dot product and a wedge product:

\vec{A} \vec{B} = \vec{A} \cdot \vec{B} + \vec{A} \land \vec{B}

[15.1]

In equation [ 8.10], we have already found that

(\vec{A} \div \vec{B}) = (\vec{A} \cdot \vec{B}) + (\vec{A} \times \vec{B})

Equations

[15.1]

and [8.10] will be equal if a bi-vector is treated as a vector and a vector product is a division of vectors.

In geometric algebra, an expression may comprise of scalars, basis vectors and bi-vectors. In 3-D numbers, an expression may comprise of scalars and basis vectors. The foundation of geometric algebra is based on the assumption that basis vector product is multiplication. In geometric algebra, basis vectors and bi-vectors are different as square of a basis vector is 1 whereas square of a bi-vector is

- 1

. We have proved that a vector product is a division of vectors (Section 8). Multiplication or division of two basis vectors results in another basis vector. There is no need of bi-vector at all. Further, the square of basis vector is

- 1

and not 1. Therefore, geometric algebra is incorrect.

16. Geometry of 3-D number

15.1: One would wonder how a number with four terms in it would fit into a three-dimensional sphere. Quaternion, which has four terms, was considered by default as having four dimensions. The geometrical meaning of spinor, which is also having four terms in it, is obscure and no one fully understands spinors ^(17),(18). The vector dot product was treated as an operation separate from the vector cross product precisely due to the fear of fourth dimension and the difficulty of comprehension in the fourth dimension. The key here is to break the assumption that each term corresponds to a distinct dimension. A 3-D number overcomes this difficulty by splitting the four terms into two complex numbers which are tied by the third

j

-complex number. Now we are able to understand the geometry of the number in a sphere. In the Argand plane, we are positioning a complex number in between the real number term and the imaginary number term. Similarly, the position of 3-D number is in between the positions of two complex numbers. The positioning of 3-D numbers with equal phases is relatively easy. Length of axes of a 3-D number without phase difference can be found using the formulae in Section 11.5. The position of a 3-D number in a sphere is depicted in the figure given below:

Figure 5. A 3-D number with a phase difference in a unit sphere.

We have already noted that a unit sphere is a set of 3-D numbers whose magnitude is one and such numbers may be referred to as unit 3-D numbers. A unit sphere can be divided into two parts: the right and left hemispheres. The positive 3-D numbers lie in the right hemisphere and the negative 3-D numbers lie in the left hemisphere.

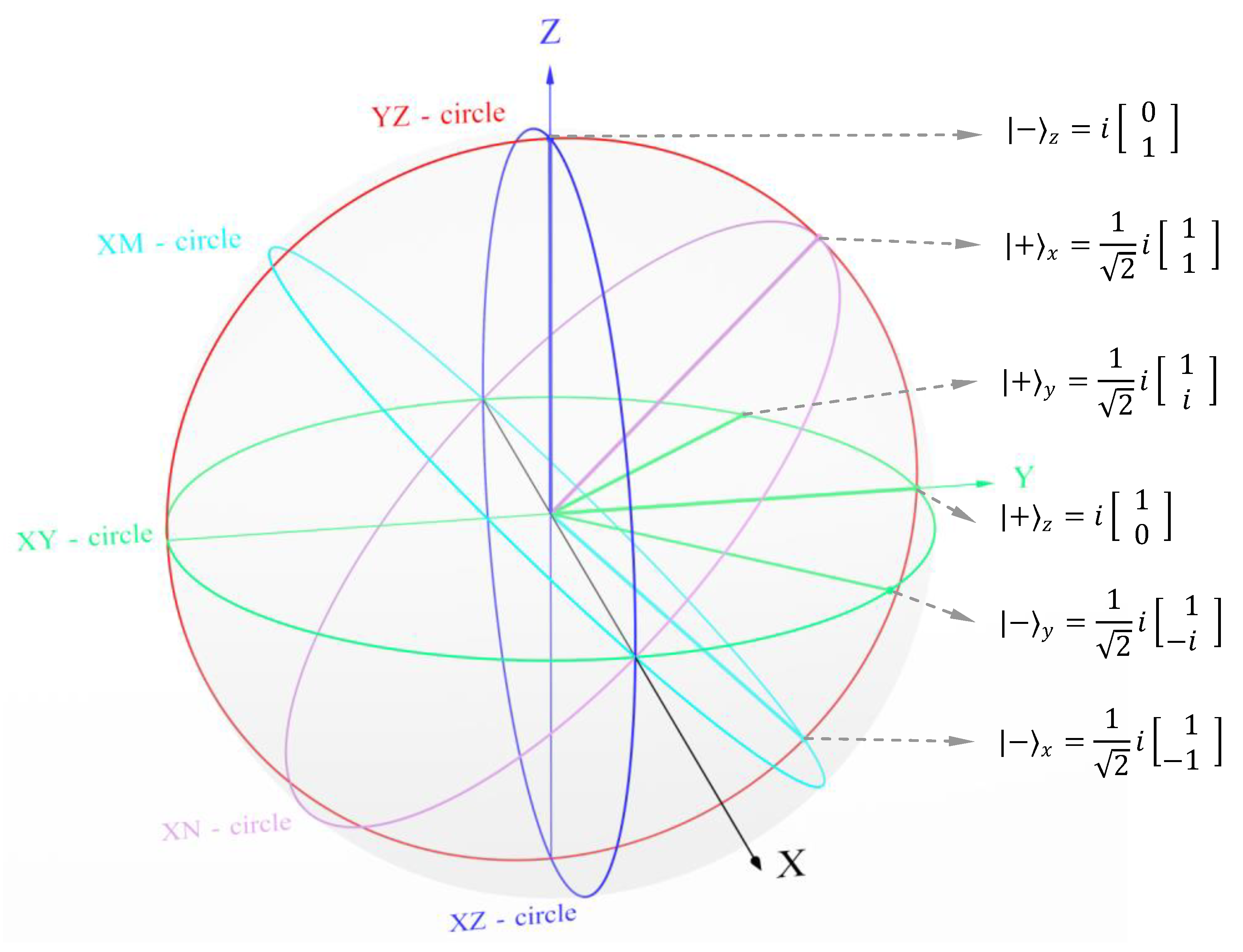
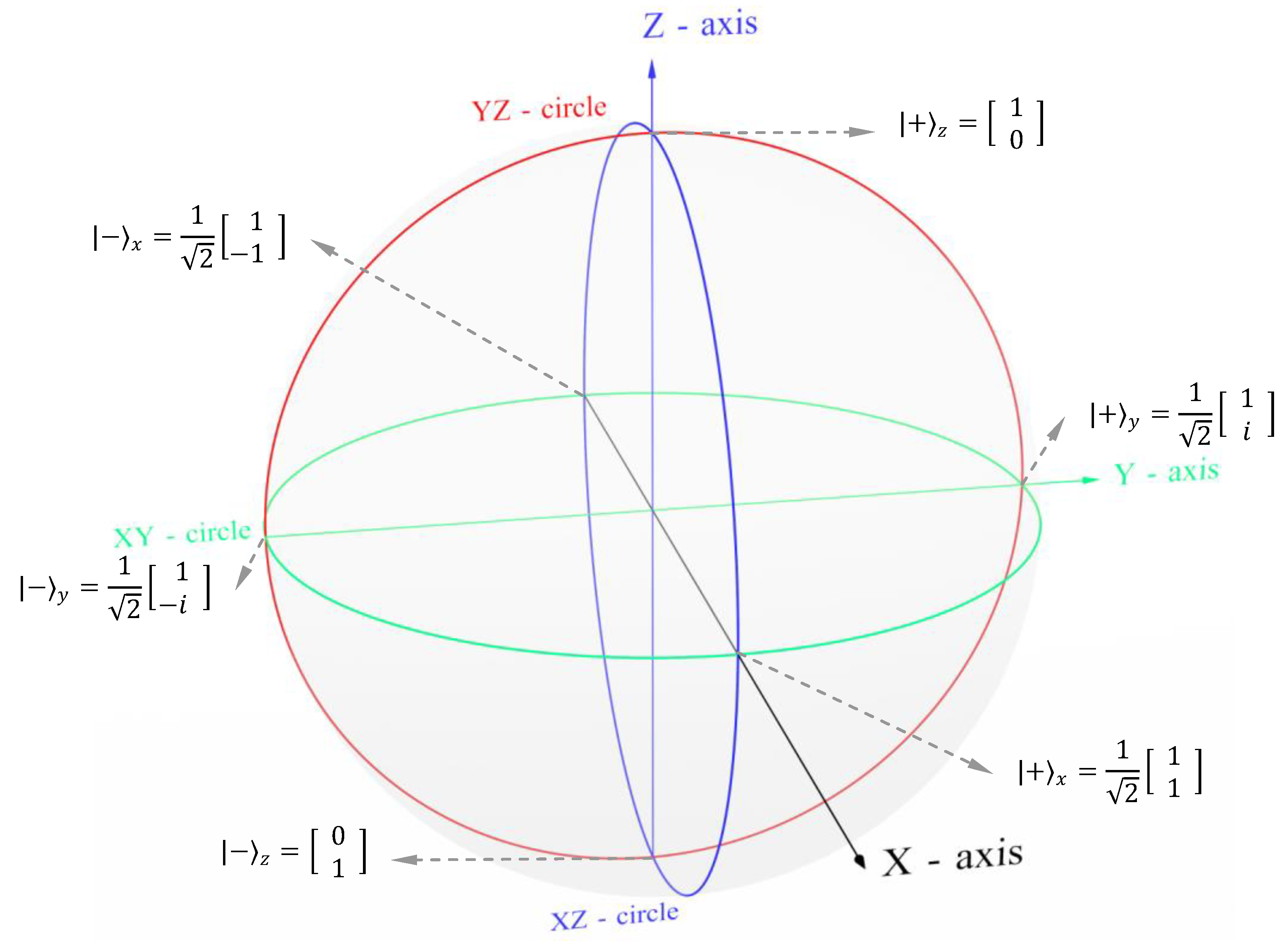
15.2: Relation to the geometry of quantum mechanics: In the Stern-Gerlach device, we can measure the spin component of particles along the Z-axis, X-axis or Y-axis. The spinors for the

X, Y & Z

dimensions in quantum mechanics are given below.

{| + ⟩}_{x} = \frac{1}{\sqrt{2}} [\begin{matrix} 1 \\ 1 \end{matrix}]

{| - ⟩}_{x} = \frac{1}{\sqrt{2}} [\begin{matrix} 1 \\ - 1 \end{matrix}]

{| + ⟩}_{y} = \frac{1}{\sqrt{2}} [\begin{matrix} 1 \\ i \end{matrix}]

{| - ⟩}_{y} = \frac{1}{\sqrt{2}} [\begin{matrix} 1 \\ - i \end{matrix}]

{| + ⟩}_{z} = [\begin{matrix} 1 \\ 0 \end{matrix}]

{| - ⟩}_{z} = [\begin{matrix} 0 \\ 1 \end{matrix}]

The general state spinors in spin-number notation are given in equations [2.1] and [2.2]. They are;

{| + ⟩}_{n} = c o s θ + s i n θ j e^{i φ}

{| - ⟩}_{n} = s i n θ - c o s θ j e^{i φ}

If the overall phase is the imaginary number

i

{| + ⟩}_{x} = \frac{1}{\sqrt{2}} i [\begin{matrix} 1 \\ 1 \end{matrix}]

{| - ⟩}_{x} = \frac{1}{\sqrt{2}} i [\begin{matrix} 1 \\ - 1 \end{matrix}]

{| + ⟩}_{y} = \frac{1}{\sqrt{2}} i [\begin{matrix} 1 \\ i \end{matrix}]

{| - ⟩}_{y} = \frac{1}{\sqrt{2}} i [\begin{matrix} 1 \\ - i \end{matrix}]

{| + ⟩}_{z} = i [\begin{matrix} 1 \\ 0 \end{matrix}]

{| - ⟩}_{z} = i [\begin{matrix} 0 \\ 1 \end{matrix}]

{| + ⟩}_{n} = \frac{1}{\sqrt{2}} i [\begin{matrix} c o s θ \\ s i n θ e^{i φ} \end{matrix}]

{| - ⟩}_{n} = \frac{1}{\sqrt{2}} i [\begin{matrix} s i n θ \\ - c o s θ e^{i φ} \end{matrix}]

The

X, Y & Z

dimensions in quantum mechanics do not match with dimensions of a 3-D number as the 4π rotation is required in the Bloch sphere of quantum mechanics for rotation to bring it to its original position whereas the same is 2π in the case of 3-D number. We will address this issue in Section 17.

Figure 6. Spinors in 3-D number geometry.

17. Is 4π of rotation required to bring the state spinor to its original position?

In spinor mathematics, basis kets

| + ⟩

and

|-⟩

are orthogonal. Therefore,

〈+| -⟩ = 0

and

〈-| +⟩ = 0

. If so, basis kets

| + ⟩

and

|-⟩

are apart by

90 °

and not

180 °

Figure 7. Bloch sphere.

The Bloch sphere is a geometrical representation of pure state space. The north and south poles of the Bloch sphere correspond to the standard basis kets {\displaystyle |0\rangle }

|+⟩

and

| - ⟩

{\displaystyle |1\rangle } respectively, which in turn correspond to the spin-up and spin-down states of an electron. Now, both states are on the same line and not orthogonal. One explanation offered is that they are spatially parallel but in Hilbert space they are orthogonal. According to Roger Penrose, orthogonal in Hilbert space does not correspond to ‘at right angles’ in space but ‘opposite’ ⁽⁸⁾. However, geometry of Hilbert space is unknown ^{(20), (21)}. It is really surprising that the mathematical orthogonality of the kets is simply ignored in quantum mechanics. In Section 6, we have shown that spinors are in spatial vector space and Hilbert space construction is not required for spinors. According to Roger Penrose, the complex numbers that appear in quantum-state formalism are not completely abstract things; they are intimately related to geometrical and dynamical behaviour ⁽⁸⁾. However, in Section 8.6, we have shown that complex numbers are hidden in spatial vectors as well. Therefore, Hilbert space is unnecessary for spinors.

In optics, The Poincaré sphere represents different types of polarisations. Wharton et al,⁽⁹⁾ have given a classical analogy for the electron spin state. According to them, 2π rotation around the Poincaré sphere merely corresponds to a π rotation of the electromagnetic polarisation in physical space. And this is equivalent to a π phase shift in the resulting wave; it would now interfere destructively with an identical unrotated wave. Of course, this is also the observed effect for a 2π rotation of a quantum spin state around the Bloch sphere, although in the latter case the net geometric phase shift is generally thought to be inexplicable from a classical perspective. The classical polarisation analogy demonstrates that such behaviour does indeed have a straightforward classical interpretation, because the geometrical phase of the spin state is directly analogous to the overall phase of the physical electromagnetic wave. The key is that the Poincaré sphere does not map to physical space, so a 2π rotation need not return the electromagnetic wave to its original state. The Classical polarisation analogy therefore advocates the viewpoint that the Bloch sphere should not map to physical space, even for an electron spin state.

The general spin

\frac{1}{2}

superposition state vector in spin up direction [2.1]:

{| + ⟩}_{n} = c o s \frac{θ}{2} |+⟩ + s i n \frac{θ}{2} e^{i φ} |-⟩

The Poincare mapping involves twice the geometrical angle between the planes of polarisation i.e., plane of horizontally polarised light and plane of vertically polarised light ⁽¹¹⁾. Therefore, in the state spinor of quantum mechanics, θ is divided by 2 to cover up the doubling of angle in the Bloch sphere. This is done precisely for the reason that a hemisphere in space is projected onto a sphere by doubling the angle θ. It is interesting to note that phase angle

φ

is not doubled in both optics and quantum mechanics. This confirms the projection of a hemisphere onto a sphere. If the reason for doubling was mathematical, both θ and

φ

should have been doubled. Therefore, 2π rotation is required to bring the state spinor to its original position and not 4π rotation. A 4π rotation is required to bring the state spinor to its original position when θ is divided by 2 in the state spinor. Thus, it is clear that the Bloch sphere is a geometrical representation of the hemisphere of space rather than the sphere.

18. Polarisation of Light and Spinors

Despite the conventional view of quantum spin as being an inherently non-classical phenomenon, there is a rich history of exploring classical analogy for spin-1/2 systems in particular ⁽¹⁰⁾. The connection between the coherency matrix, the Stokes parameters, and the Pauli spin matrices was pointed out by U. Fano in 1954 ^(12)(29). The connection between Jones vectors and the Poincar´e sphere on the one hand and spinors is derived by Gori at al ⁽¹³⁾.

The state of polarisation of a wave is usually specified using the Stokes parameters or the Jones vector. The Stokes parameters can be expressed in terms of the two-component spinor and the Jones vector is essentially this spinor. The identification of the Jones vector with a spinor will facilitate the representation of the Jones vector by a tangent vector to the Poincaré sphere, in terms of which, among other things, the Pancharatnam phase can be visualised. The Jones vector is a two-component spinor on which the rotations on the Poincaré sphere act through the spin-1/2 representation ⁽¹⁴⁾.

The polarisation of a beam of light is exactly the same kind of thing as the spin of a beam of electrons, the differences in terminology reflecting only the accidents of the historical order of discovery ⁽¹⁵⁾.

As polarisation and spin are one and the same, we can straight away apply the mathematics of 3-D numbers to polarisation of light. Such an application will save us from the complications involved in the use of Jones vectors and matrices in optics. Further, the 3-D number will simplify the study of optics.

19. Conclusion

The 3-D number helps us to present the spinor in geometry. This will in turn lead to greater clarity in quantum mechanics and resolve many outstanding issues. A 3-D number is in a three-dimensional space. It can be applied to optics, quantum mechanics and other areas of physics. It can replace vectors, quaternions, spinors, geometric algebra, Jones vectors & matrices, etc. 3-D numbers will greatly simplify the study of areas of science where three-dimensional space is involved.

Appendix I

Introduction to the Spinors

David H. McIntyre has given a lucid introduction to the spinors. The description given in Section 1.2 of his book⁽¹⁾ is summarised below. McIntyre has used the term quantum state vector or simply vector (it is not a spatial vector) instead of spinor. A similar approach can also be found in the book by John S. Townsend ⁽³⁰⁾.

In vector space of a spin-1/2 system, kets

| + ⟩

and

| - ⟩

form basis. General quantum state vector

| ѱ ⟩

is a linear combination of the two basis kets:

|ѱ⟩ = a |+⟩ + b | + ⟩

where

a

and

b

are complex numbers. This addition of two kets yields another ket in the same abstract space. On taking the inner product of one vector with another, the complex numbers of first vector are conjugated and that vector is called bra.

〈 ѱ | = \bar{a} 〈 + | + \bar{b} 〈 - |

where

\bar{a}

and

\bar{a}

are complex conjugates. Quantum mechanics stipulates that kets are to be used for a mathematical description of a quantum mechanical system. These kets are abstract entities that obey many of the rules you know about ordinary spatial vectors. Hence they are called quantum state vectors. These vectors must employ complex numbers in order to properly describe quantum mechanical systems. Quantum state vectors are part of a vector space called Hilbert space. Because the quantum state vectors are abstract, it is hard to say much about what they are, other than how they behave mathematically and how they lead to physical predictions.

For the spin basis kets

| + ⟩

and

| - ⟩

, there is no spatial geometry involved. Rather, the spin basis kets

| + ⟩

and

| - ⟩

are orthogonal in the mathematical sense and the inner product

〈+| -⟩ = 0

. It is assumed that a well-behaved basis set obeys orthogonality. Though there is no geometry in this property for quantum mechanical basis vectors, the fundamental idea of orthogonality is the same and if a general vector “points” in the direction of a basis vector, then there is no component in the “direction” of the other unit vectors. In quantum mechanics, all vectors are normalised:

\{〈+| +⟩ = 1\}

and

\{〈-| -⟩ = 1\}

. Further, the orthogonal product

\{〈+| -⟩ = 0\}

and

\{〈-| +⟩ = 0\}

In a Stern-Gerlach experiment, if the input state vector is

|ѱ_{i n}⟩

and output state vector (vector of the direction in which output is aligned) is

|ѱ_{o u t}⟩

then,

〈ѱ_{o u t}| ѱ_{i n}⟩

is the inner product of two vectors and the probability of the outcome is given by

{| 〈ѱ_{o u t}| ѱ_{i n}⟩ |}^{2}

. This is the crucial element of spinor mathematics in quantum mechanics.

Appendix II

Mysteries of Spinors

The geometrical significance of spinors is mysterious

Michael Atiyah, mathematician specialising in geometry, winner of the Fields Medal in 1966 and the Abel Prize in 2004:

“No one fully understands spinors. Their algebra is formally understood but their general significance is mysterious. In some sense they describe the ‘square root’ of geometry and, just as understanding the square root of -1 took centuries, the same might be true of spinors".

“The reason is that the geometrical significance of spinors is still very mysterious. Unlike differential forms, which are related to areas and volumes, spinors have no such simple explanation. They appear out of some slick algebra, but the geometrical meaning is obscure as is illustrated by the global obstruction referred to earlier.”⁽¹⁸⁾.

2.: Nobody understands quantum mechanics

Richard Feynman, recipient of the Nobel Prize of Physics in 1965:

“I think that I can safely say that nobody understands quantum mechanics."⁽¹⁷⁾.

3.: Even Physicists Don’t Understand Quantum Mechanics.

“Even Physicists Don’t Understand Quantum Mechanics. Worse, they don’t seem to want to understand it.” Dr. Sean Carroll ⁽¹⁹⁾.

4.: Paradox: Does quantum mechanics tacitly imply that 0 = 1?⁽⁴⁾

“… to define a spinor in the rotation group one uses isotropic vectors (X, Y, Z)∈C³, for which

X^{2} + Y^{2} + Z^{2} = 0

. These spinors code rotations, i.e. group elements. Of course, these complex quantities cannot be particle coordinates (x, y, z)∈R³, since for particle coordinates one has

x^{2} + y^{2} + z^{2} = r^{2} \neq 0, \forall (x, y, z) \neq (0, 0, 0)

. A position vector of a particle is something very different from a rotation or a group element. To follow a particle under rotations we could take

r = 1

. Following a particle with

r = 1

this way can be done with 3×3 rotation matrices in R³. But in SU(2) things are not that way; the paradigm is completely different. When Cartan says physicists use spinors like vectors, he pinpoints the fact that they act as though (X, Y,Z) = (x, y, z). Now |(X, Y,Z)| = 0, while |(x, y, z)| = 1. The Dirac equation can be derived from a reasoning based on the isotropic vector (X, Y,Z), but afterwards, in the calculations, one identifies this isotropic vector with a position vector (x, y, z). This happens in the solution of the wave equation for the hydrogen atom, when one introduces spherical coordinates and harmonic polynomials. In other words, physicists are acting all the time as though 0 = 1, which is, admittedly, a well-known fact of elementary mathematics. This is only one example of a mathematical paradox; there are scores of others. ……… There is also really nothing to be sarcastic about. Because, miraculously, these calculations, despite all the confusion about the 1 = 0 issue and other paradoxes, turn out the right physical answers with amazing precision.”

5.: Mysterious Hilbert space

“…the (pure) state of a quantum system is represented by a vector in a Hilbert space, a formalism that has proved high successful at the empirical level. Basically, Hilbert space is a complex vector space on which an inner product is defined (Wallace-Garden 1984, 7). …. However, the Hilbert space representation is very different from the way that the state of a physical system is characterised in classical mechanics where the system’s state may be represented by a point in a phase space. Why have a physical theory that uses abstract (Hilbert) vector spaces?” Peter Riggs ⁽²⁰⁾

“The erection of the Hilbert space edifice and the subsequent development of operator algebras (extending now into non-commutative (NC) geometry) has an air of magic. It works but exactly why it works and what it really represents remain shrouded in ambiguity.” Robert Carroll ⁽²¹⁾

6.: What is spin?

“Spin … differs from what we usually … mean by spin. Spin is really something very queer …” Karl Popper ⁽²²⁾

“Pauli’s theory does not explain the origin of the spin, nor does it give any reason for its magnitude. It merely provides a method for incorporating it into quantum mechanics.” Lindsay and Margenau ⁽²³⁾

7.: Shut up and calculate

“If I were forced to sum up in one sentence what copenhegan interpretation says to me it would be ‘shut up and calculate!’. But I wont shutup. I would rather celebrate the strangeness of quantum theory than deny it…….” N D Mermin ⁽²⁴⁾

8.: Abstract mathematics

“Because the quantum state vectors are abstract, it is hard to say much about what they are, other than how they behave mathematically and how they lead to physical predictions…… For the spin basis kets

| + ⟩

and

| - ⟩

, there is no spatial geometry involved.” David H. McIntyre ⁽³⁾

Appendix III

Vectors

Vectorsaregeometrical entities that have magnitude and direction.

1.: Basic properties of vectors

Dot product:

i ∙ i = j . j = k . k = 1, i ∙ j = j . k = k . i = 0

i, j a n d k

are mutually orthogonal, the dot product of each basis vector with other basis vector is zero.

Cross Product:

i \times i = j \times j = k \times k = 0,

i \times j = k; j \times k = i; k \times i = j

j \times i = - k; k \times j = - i; i \times k = - j

2.: Projection of Vectors

Scalar Product or dot product: Projection of one vector onto another or the amount of a given vector that points along the other vector. Dot product of a vector with itself is the square of the magnitude of that vector. Mutually orthogonal, so dot products with each other are zero. The vectors used here are normalised and therefore are unit vectors.

\vec{a} \cdot \vec{b} = (a_{1} i + a_{2} j + a_{3} k) . (b_{1} i + b_{2} j + b_{3} k) = (a_{1} b_{1} + a_{2} b_{2} + a_{3} b_{3})

It is a real number.

Cross product or Vector product: If dot product involves the amount of one vector that is parallel to the other vector, then cross product involves the amount of a vector that is perpendicular to the other vector.

\vec{a} \times \vec{b} = (a_{1} i + a_{2} j + a_{3} k) \times (b_{1} i + b_{2} j + b_{3} k) \vec{a} \times \vec{b} = {(a_{2} b_{3} - a_{3} b_{2}) i + (a_{3} b_{1} - a_{1} b_{3}) j + (a_{1} b_{2} - a_{2} b_{1}) k}

Dot product is a measure of similarity of two vectors. If the vectors are perpendicular, dot product will be zero. Cross product is a sort of dual to dot product. It measures how different two vectors are, rather than how similar they are. Cross product provides a way to measure orthogonality.

\{\vec{a} \times \vec{b}\}

is orthogonal to both

\vec{a} a n d \vec{b}

Appendix IV

Illustrations on computing probabilities using different methods

a): Let us compute the probability considering the spin-numbers as vectors. Let output and input state spin-number as

{| + ⟩}_{A} = c o s \frac{π}{3} i + s i n \frac{π}{3} j e^{i \frac{5 π}{3}}

{| + ⟩}_{B} = c o s \frac{π}{4} i + s i n \frac{π}{4} j e^{i \frac{π}{3}}

Now applying the vector method,

{| + ⟩}_{A} = 0.5 i + 0.866025 j (0.5 - 0.866025 i)

\vec{a} = 0.5 i + 0.433013 j - 0.75 k

{| + ⟩}_{B} = 0.707107 i + 0.707107 j (0.5 + 0.866025 i)

\vec{b} = 0.707107 i + 0.3535535 j + 0.612372 k

Dot product of two vectors:

\vec{a} \cdot \vec{b} = \{0.5 i + 0.433013 j - 0.75 k\} \cdot \{0.707107 i + 0.3535535 j + 0.612372 k\}

\vec{a} \cdot \vec{b} = \{[0.5 i * 0.707107 i] + [0.433013 j * (0.3535535 j)] + (- 0.75 k) * (0.612372 k)]\}

\vec{a} \cdot \vec{b} = 0.04737

Cross product of two vectors:

\vec{a} \times \vec{b} = \{0.5 i + 0.433013 j - 0.75 k\} \times \{0.707107 i + 0.3535535 j + 0.612372 k\}

\vec{a} \times \vec{b} = \{[0.433013 j \times (0.612372 k)] + [(- 0.75 k) \times (0.3535535 j)]\} + \{[0.5 i \times 0.612372 k] + [(- 0.75 k) \times 0.707107 i]\} + {[0.5 i \times 0.3535535 j] + [0.433013 j \times 0.707107 i]}

\vec{a} \times \vec{b} = {[0.265165 i + 0.265165 i] + [- 0.30619 j - 0.53033 j] + [0.17678 k - 0.30619 k]

}

\vec{a} \times \vec{b} = {+ 0.53033 i - 0.89052 j - 0.12941 k}

(\vec{a} \cdot \vec{b}) + (\vec{a} \times \vec{b}) = {0.047367 + 0.53033 i - 0.83652 j - 0.12941 k}

To get a complex dot product, we have to take the sum of

(\vec{a} \cdot \vec{b})

and cross product term which is a factor of imaginary number

i

which is denoted by

A \circ B

A \circ B = 0.047367 + 0.53033 i

P_{{_{A} 〈 + | + ⟩}_{B}} = (0.047367 + 0.53033 i) * (0.047367 - 0.53033 i)

P_{{_{A} 〈 + | + ⟩}_{B}} = 28.349 %

b): We will compute the probability as per the traditional spinor method using new notation of spin-number.

{| + ⟩}_{A} = c o s \frac{π}{3} i + s i n \frac{π}{3} j e^{i \frac{5 π}{3}}

{| + ⟩}_{B} = c o s \frac{π}{4} i + s i n \frac{π}{4} j e^{i \frac{π}{3}}

{_{A} 〈 + | + ⟩}_{B} = c o s α c o s θ + s i n α {s i n θ e}^{- i β} e^{i φ}

{_{A} 〈 + | + ⟩}_{B} = (c o s \frac{π}{3} i + s i n \frac{π}{3} j e^{i \frac{5 π}{3}}) \circ (c o s \frac{π}{4} i + s i n \frac{π}{4} j e^{i \frac{π}{3}})

{_{A} 〈 + | + ⟩}_{B} = (c o s \frac{π}{3} c o s \frac{π}{4} [- i] * i) + (s i n \frac{π}{3} {s i n \frac{π}{4} e^{- i \frac{5 π}{3}} e^{i \frac{π}{3}}}^{})

{_{A} 〈 + | + ⟩}_{B} = (0.35355) + (0.61237 {e^{- i \frac{4 π}{3}}}^{})

{_{A} 〈 + | + ⟩}_{B} = (0.04736 + 0.53033 i)

P_{{_{A} 〈 + | + ⟩}_{B}} = (0.04736 + 0.53033 i) * (0.04736 - 0.53033 i)

P_{{_{A} 〈 + | + ⟩}_{B}} = 28.349 %

The probability found using spin-numbers is the same as the probability found using vectors.

c): Let us apply a shortcut to compute the probability by using the formula in $[4.4]$ found in Section 4.1.

{| + ⟩}_{A} = 0.5 i + 0.866025 j (0.5 - 0.866025 i)

{| + ⟩}_{B} = 0.707107 i + 0.707107 j (0.5 + 0.866025 i)

P_{{_{A} 〈 + | + ⟩}_{B}} = {c o s}^{2} α {c o s}^{2} θ + (2 c o s α c o s θ s i n α s i n θ \cos [φ - β]) + {s i n}^{2} α {s i n}^{2} θ

P_{{_{A} 〈 + | + ⟩}_{B}} = {(0.5 * 0.707107)}^{2} + [2 * 0.5 * 0.707107 * 0.866025 * 0.707107 * - 0.5] + {(0.866025 * 0.707107)}^{2}

P_{{_{A} 〈 + | + ⟩}_{B}} = 28.349 %

We are getting the same probability as that of other two methods. Thus the formula in

[4.4]

is correct.

d): We will find out the probability $P_{- A}$ by using vector method

{| - ⟩}_{A} = s i n \frac{π}{3} i - c o s \frac{π}{3} j e^{i \frac{5 π}{3}}

{| - ⟩}_{A} = 0.866025 i - 0.25 j + 0.433013 k

{| + ⟩}_{B} = c o s \frac{π}{4} i + s i n \frac{π}{4} j e^{i \frac{π}{3}}

{| + ⟩}_{B} = 0.707107 i + 0.3535535 j + 0.612372 k

\vec{a_{⟂}} \cdot \vec{b} = \{0.866025 i - 0.25 j + 0.433013 k\} \cdot \{0.707107 i + 0.3535535 j + 0.612372 k\}

\vec{a_{⟂}} \cdot \vec{b} = \{[0.866025 i * 0.707107 i] + [- 0.25 j * (0.3535535 j)] + 0.433013 k * (0.612372 k)]\}

\vec{a_{⟂}} \cdot \vec{b} = \{0.612372 - 0.088388 + 0.265165\}

\vec{a_{⟂}} \cdot \vec{b} = 0.789149

\vec{a_{⟂}} \times \vec{b} = \{0.866025 i - 0.25 j + 0.433013 k\} \times \{0.707107 i + 0.3535535 j + 0.612372 k\}

\vec{a_{⟂}} \times \vec{b} = \{[- 0.25 j * 0.612372 k] + [0.433013 k * 0.3535535 j]\} + \{[0.866025 i * 0.612372 k] + [(0.433013 k) * 0.707107 i]\} + {[0.866025 i * 0.3535535 j] + [(- 0.25 j) * 0.707107 i]}

\vec{a_{⟂}} \times \vec{b} = {- 0.306186 i - 0.224143 j + 0.48296 k}

(\vec{a_{⟂}} \cdot \vec{b}) + (\vec{a_{⟂}} \times \vec{b}) = {0.789149 - 0.306186 i - 0.224143 j + 0.48296 k}

We are interested only in cross product term having imaginary number

i

as its factor. If a complex dot product like spinor method is taken,

Appendix V

Illustrations on computing probabilities using 3-D numbers

1): The output state in the Stern-Gerlach analyzer is aligned along the direction $A$ defined by the angles $θ = \frac{π}{3} a n d φ = \frac{5 π}{3}$ .

{| + ⟩}_{A} = c o s \frac{π}{3} + s i n \frac{π}{3} j e^{i \frac{5 π}{3}}

{| - ⟩}_{A} = s i n \frac{π}{3} - c o s \frac{π}{4} j e^{i \frac{5 π}{3}}

The input state to the Stern-Gerlach analyzer is aligned along the direction

B

defined by the angles

θ = \frac{π}{4} a n d φ = \frac{π}{3}

{| + ⟩}_{B} = c o s \frac{π}{4} + s i n \frac{π}{4} j e^{i \frac{π}{3}}

{| - ⟩}_{B} = s i n \frac{π}{4} - c o s \frac{π}{4} j e^{i \frac{π}{3}}

When

A

is the output state,

{_{A} 〈 + | + ⟩}_{B} = A \circ B

and

{_{A} 〈 + | - ⟩}_{B} = A \circ B_{⟂}

{| + ⟩}_{B} = B

and

{| - ⟩}_{B} = B_{⟂}

A \circ B = \{c o s \frac{π}{3} + s i n \frac{π}{3} j e^{i \frac{5 π}{3}}\} \circ \{c o s \frac{π}{4} + s i n \frac{π}{4} j e^{i \frac{π}{3}}\}

B

is conjugated while taking the complex dot product

A \circ B = \{c o s \frac{π}{3} + s i n \frac{π}{3} j e^{i \frac{5 π}{3}}\} \{c o s \frac{π}{4} - s i n \frac{π}{4} j e^{i \frac{π}{3}}\}

= \{c o s \frac{π}{3} c o s \frac{π}{4} - s i n \frac{π}{3} j e^{i \frac{5 π}{3}} s i n \frac{π}{4} j e^{i \frac{π}{3}}\}

= \{c o s \frac{π}{3} c o s \frac{π}{4} - s i n \frac{π}{3} {s i n \frac{π}{4} j e}^{i \frac{5 π}{3}} j e^{i \frac{π}{3}}\}

∵ s i n \frac{π}{4}

is a real number

= \{c o s \frac{π}{3} c o s \frac{π}{4} + s i n \frac{π}{3} s i n \frac{π}{4} {e^{- i \frac{5 π}{3}} e}^{i \frac{π}{3}}\}

∵ e^{i \frac{5 π}{3}} j

becomes

j e^{- i \frac{5 π}{3}}

and

j j = - 1

= (0.35355) - 0.30619 + 0.53033 i

A \circ B = 0.04736 + 0.53033 i

A \bar{A}

is the square of magnitude of a 3-D number.

Probability of B in A,

P_{{_{A} 〈 + | + ⟩}_{B}} = (0.04736 + 0.53033 i) * (0.04736 - 0.53033 i)

P_{{_{A} 〈 + | + ⟩}_{B}} = 28.349 %

2): Now, we will convert $A a n d B$ into expanded form and then find out the probability.

{| + ⟩}_{A} = c o s \frac{π}{3} + s i n \frac{π}{3} j e^{i \frac{5 π}{3}}

{| + ⟩}_{A} = 0.5 + 0.866025 j (0.5 - 0.866025 i)

{| + ⟩}_{A} = 0.5 + 0.433013 j - 0.75 j i

{| + ⟩}_{B} = c o s \frac{π}{4} + s i n \frac{π}{4} j e^{i \frac{π}{3}}

{| + ⟩}_{B} = 0.707107 + 0.3535535 j + 0.612372 j i

Considering the above two spinors as spin numbers or 3-D numbers,

A \circ B = \{0.5 + 0.433013 j - 0.75 j i\} \circ \{0.707107 + 0.3535535 j + 0.612372 j i\}

A \circ B = \{0.5 + 0.433013 j - 0.75 j i\} \{0.707107 - 0.3535535 j - 0.612372 j i\}

(3-D number

B

is conjugated on changing the sign to multiplication while taking a complex dot product)

= \{[0.5 * 0.707107] + [0.433013 j * (- 0.3535535 j)] + (- 0.75 j i) * (- 0.612372 j i)]\}

+ \{[0.433013 j * (- 0.612372 j i)] + [(- 0.75 j i) * (- 0.3535535 j)]\}

(While taking the complex dot product like a spinor, we will find only terms having a real number and

i

as a factor. We will not find out the results of terms having

j

and

j i

as factors.)

= \{0.3535535 + 0.153093 - 0.459279\} + \{0.265165 i + 0.265165 i\}

A \circ B = 0.04736 + 0.53033 i

P_{{_{A} 〈 + | + ⟩}_{B}} = 28.349 %

3): We will compute the probability of finding ${| + ⟩}_{B} i n {| - ⟩}_{A}$ , i.e., $P_{- A}$ .

{| - ⟩}_{A} = s i n \frac{π}{3} - c o s \frac{π}{3} j e^{i \frac{5 π}{3}}

{| - ⟩}_{A} = 0.866025 - 0.25 j + 0.433013 j i

We know that

{| - ⟩}_{A} = A_{⟂}

{| + ⟩}_{B} = c o s \frac{π}{4} + s i n \frac{π}{4} j e^{i \frac{π}{3}}

{| + ⟩}_{B} = 0.707107 + 0.3535535 j + 0.612372 j i

Considering the above two spinors as 3-D numbers,

A_{⟂} \circ B = \{0.866025 - 0.25 j + 0.433013 j i\} \circ \{0.707107 + 0.3535535 j + 0.612372 j i\}

A_{⟂} \circ B = \{0.866025 - 0.25 j + 0.433013 j i\} \{0.707107 - 0.3535535 j - 0.612372 j i\}

= \{[0.866025 * 0.707107] + [- 0.25 j * (- 0.3535535 j)] + [(0.433013 j i) * (- 0.612372 j i)]\}

Appendix VI

Projection of a 3-D number with an overall phase

1) Consider the 3-D number trigonometric form with an overall phase of

e^{i γ}

for 3-D number

A

and

e^{i δ}

for 3-D number

B

A = c o s α e^{i γ} + s i n α j e^{i β} e^{i γ}

B = c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ}

A \circ B = (c o s α e^{i γ} + s i n α j e^{i β} e^{i γ}) \circ (c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ})

A \circ B = (c o s α e^{i γ} + s i n α j e^{i β} e^{i γ}) \circ (c o s θ e^{- i δ} - s i n θ j e^{i φ} e^{i δ})

(∵

B

is conjugated before taking the complex dot product

)

A \circ B = c o s α {c o s θ e}^{i γ} e^{- i δ} - s i n α {s i n θ j e}^{i β} e^{i γ} {j e}^{i φ} e^{i δ}

(∵ s i n θ

is a real number and multiplication obeys the commutative property)

A \circ B = c o s α {c o s θ e}^{i γ} e^{- i δ} + s i n α {s i n θ e}^{- i β} e^{- i γ} e^{i φ} e^{i δ}

(

∵ e^{i β} e^{i γ} j = {j e}^{- i β} e^{- i γ}

and

j j = - 1

)

To find the perpendicular number of

B

being

B_{⟂}

θ

angle, we need to change

θ

angle. In spinor theory, for every

{| + ⟩}_{n}

there exists a

{| - ⟩}_{n}

{| + ⟩}_{n} = c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ}

{| - ⟩}_{n} = s i n θ e^{i δ} - c o s θ j e^{i φ} e^{i δ}

{| - ⟩}_{n} = B_{⟂}

B_{⟂} = s i n θ e^{i δ} - c o s θ j e^{i φ} e^{i δ}

To get

B_{⟂}, θ

angle should be

{- 90}^{0}

. To change the

θ

angle by

{- 90}^{0}

, the

j

-complex number in

B

should be separated.

j

-complex number

= c o s θ + s i n θ j

. Now, this number should be multiplied with

- j

(c o s θ + s i n θ j) * (- j) = s i n θ - c o s θ j

This is the perpendicular number of

j

-complex number in

y z

circle of a right handed unit sphere.

Replacing

j

-complex number in

B

with its perpendicular number, i.e.,

s i n θ - c o s θ j

, we will get

B_{⟂}

. However, we are not able to do so by simple multiplication as both terms of the

j

-complex number are factors of complex numbers. Therefore, we need to find out a number by multiplying which, we will get

B_{⟂}

To find

B_{⟂},

we have to find a number so that by multiplying it with a number to

s i n θ j e^{i φ} e^{i δ}

which is second term of

B_{⟂}

, we will get

s i n θ e^{i δ}

which is first term of

B_{⟂}

Using the identity given in Section 13, if

A B = C

, then

B = A^{- 1} C

∴

D E = F

, then

E = D^{- 1} F

s i n θ j e^{i φ} e^{i δ} * ? = s i n θ e^{i δ}

Here

D = s i n θ j e^{i φ} e^{i δ}, F = s i n θ e^{i δ}

and we have to find

E = \bar{D} F

E = (- s i n θ j e^{i φ} e^{i δ}) \frac{1}{{s i n}^{2} θ} * s i n θ e^{i δ} {∵ A}^{- 1} = \frac{\bar{A}}{A \bar{A}}

E = - (j e^{i φ} e^{i δ} e^{i δ}

)

Therefore, if we multiply

s i n θ j e^{i φ} e^{i δ}

with

- (j e^{i φ} e^{i δ} e^{i δ}),

we will get

s i n θ e^{i δ}

. Now, multiplying

B

with

- (j e^{i φ} e^{i δ} e^{i δ})

B_{⟂} = (c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ}) * [- (j e^{i φ} e^{i δ} e^{i δ})]

B_{⟂} = (- c o s θ e^{i δ} j e^{i φ} e^{i δ} e^{i δ} - s i n θ j e^{i φ} e^{i δ} j e^{i φ} e^{i δ} e^{i δ})

B_{⟂} = (- s i n θ j j {e^{- i φ} e^{- i δ} e}^{i φ} e^{i δ} e^{i δ} - c o s θ e^{i δ} e^{- i δ} j e^{i φ} e^{i δ})

B_{⟂} = s i n θ e^{i δ} - c o s θ j e^{i φ} e^{i δ}

A \circ B_{⟂} = (c o s α e^{i γ} + s i n α j e^{i β} e^{i γ}) \circ (s i n θ e^{i δ} - c o s θ j e^{i φ} e^{i δ})

A \circ B_{⟂} = (c o s α e^{i γ} + s i n α j e^{i β} e^{i γ}) (s i n θ e^{- i δ} + c o s θ j e^{i φ} e^{i δ})

A \circ B_{⟂} = (c o s α s i n θ e^{i γ} e^{- i δ} - s i n α c o s θ e^{- i β} e^{- i γ} e^{i φ} e^{i δ})

This is cross product in true sense. It is an orthogonal complex dot product. To get vector cross product, we have to multiply

A . B_{⟂}

with

{e^{- i φ} e}^{- i δ} j e^{i δ}

which is the conjugate of

- (e^{- i φ} e^{- i δ} j e^{i δ})

A \times B = (c o s α s i n θ e^{i γ} e^{- i δ} - s i n α c o s θ e^{- i β} e^{- i γ} e^{i φ} e^{i δ}) * {(e^{- i φ} e}^{- i δ} j e^{i δ})

∴ A \times B = (s i n α c o s θ {j e}^{i β} e^{i γ} e^{- i δ} - c o s α s i n θ j e^{- i γ} e^{i φ} e^{i δ})

With the above result in hand, we will find a shortcut to arrive at the result. Let

A \div B = C

C = A \bar{B}

\bar{B} = c o s θ e^{- i δ} - s i n θ j e^{i φ} e^{i δ}

C = (c o s α e^{i γ} + s i n α j e^{i β} e^{i γ}) * (c o s θ e^{- i δ} - s i n θ j e^{i φ} e^{i δ})

C = (c o s α {c o s θ e}^{i γ} e^{- i δ} + s i n α s i n θ e^{- i β} e^{- i γ} e^{i φ} e^{i δ}) + (s i n α c o s θ j e^{i β} e^{i γ} e^{- i δ} - c o s α {s i n θ j e}^{- i γ} e^{i φ} e^{i δ})

Therefore,

C

is truly the quotient of the division. It can be seen that first part of

C

is the complex dot product

(A \circ B)

and second part is cross product

(A \times B)

∴ A \div B = (A \circ B) + (A \times B)

2) If

A \div B = C

then

A = C B

The complex dot products

A \circ B

and

A \circ B_{⟂}

are the complex numbers. These numbers can be multiplied with

B

and

B_{⟂}

to arrive at

A

A = {(A \circ B) * B} + {(A \circ B_{⟂}) * B_{⟂}}

(A \circ B) * B = (c o s α {c o s θ e}^{i γ} e^{- i δ} + s i n α {s i n θ e}^{- i β} e^{- i γ} e^{i φ} e^{i δ}) * (c o s θ e^{i δ} + s i n θ j e^{i φ} e^{i δ})

(A \circ B) * B = (c o s α {c o s θ c o s θ e}^{i γ} + c o s α {c o s θ s i n θ j e}^{- i γ} e^{i δ} e^{i φ} e^{i δ} + s i n α {c o s θ s i n θ e}^{- i β} e^{- i γ} e^{i φ} e^{i δ} e^{i δ} + s i n α {s i n θ s i n θ j e}^{i β} e^{i γ})

A \circ B_{⟂} * B_{⟂} = (c o s α s i n θ e^{i γ} e^{- i δ} - s i n α c o s θ e^{- i β} e^{- i γ} e^{i φ} e^{i δ}) * (s i n θ e^{i δ} - c o s θ j e^{i φ} e^{i δ})

A \circ B_{⟂} * B_{⟂} = (c o s α s i n θ {s i n θ e}^{i γ} - c o s α c o s θ s i n θ {j e}^{- i γ} e^{i δ} e^{i φ} e^{i δ} - s i n α c o s θ s i n θ e^{- i β} e^{- i γ} e^{i φ} e^{i δ} e^{i δ} + s i n α c o s θ c o s θ j e^{i β} e^{i γ})

A = {(A \circ B) * B} + {(A \circ B_{⟂}) * B_{⟂}}

A = (c o s α {c o s θ c o s θ e}^{i γ} + c o s α {c o s θ s i n θ j e}^{- i γ} e^{i δ} e^{i φ} e^{i δ} + s i n α {c o s θ s i n θ e}^{- i β} e^{- i γ} e^{i φ} e^{i δ} e^{i δ} + s i n α {s i n θ s i n θ j e}^{i β} e^{i γ}) + (c o s α s i n θ {s i n θ e}^{i γ} - c o s α c o s θ s i n θ {j e}^{- i γ} e^{i δ} e^{i φ} e^{i δ} - s i n α c o s θ s i n θ e^{- i β} e^{- i γ} e^{i φ} e^{i δ} e^{i δ} + s i n α c o s θ c o s θ j e^{i β} e^{i γ})

A = c o s α {c o s θ c o s θ e}^{i γ} + s i n α {s i n θ s i n θ j e}^{i β} e^{i γ} + c o s α s i n θ {s i n θ e}^{i γ} + s i n α c o s θ c o s θ j e^{i β} e^{i γ}

A = c o s α e^{i γ} (c o s θ c o s θ + s i n θ s i n θ) + s i n α j e^{i β} e^{i γ} (c o s θ c o s θ + s i n θ s i n θ)

A = c o s α e^{i γ} + s i n α j e^{i β} e^{i γ}

In the beginning, we have assumed that

{| - ⟩}_{B} = B_{⟂}

. We have proved that

A = {(A \circ B) * B} + {(A \circ B_{⟂}) * B_{⟂}}

Therefore,

{| - ⟩}_{B} = B_{⟂}

is proved.

Appendix VII

Illustrations of operations on 3-D numbers

Illustrations of the different operations on 3-D numbers are given below.

1): Addition:

Illustration 1:

{2 + 3 i + 4 j + 5 j i}

{6 + 7 i + 8 j + 9 j i}

{8 + 10 i + 12 j + 14 j i}

2): Subtraction:

Illustration 2:

\{6 + 7 i + 8 j + 9 j i\}

- {2 + 3 i + 4 j + 5 j i}

{4 + 4 i + 4 j + 4 j i}

3): Multiplication:

Illustration 3:

\{0.70 + 0.51 i + 0.40 j + 0.29 j i\} * \{0.48 + 0.82 i + 0.15 j + 0.27 j i\}

= (\{0.70 + 0.51 i + 0.40 j + 0.29 j i\} * 0.48) +

(\{0.70 + 0.51 i + 0.40 j + 0.29 j i\} * 0.82 i) +

(\{0.70 + 0.51 i + 0.40 j + 0.29 j i\} * 0.15 j)

(\{0.70 + 0.51 i + 0.40 j + 0.29 j i\} * 0.27 j i)

(+ 0.3360 + 0.2448 i + 0.1920 j + 0.1392 j i) +

(- 0.4182 + 0.5740 i - 0.2378 j + 0.328 j i) +

(- 0.0600 + 0.0435 i + 0.1050 j - 0.0765 j i) +

(

- 0.0783 - 0.108 i + 0.1377 j + 0.1890 j i

)

{- 2205 + 0.7543 i + 0.1969 j + 0.5797 j i}

4): Division:

Illustration 4:

\frac{\{4 - 44 i - 22 j + 100 j i\}}{\{2 + 3 i + 4 j + 5 j i\}} = \{4 - 44 i - 22 j + 100 j i\} * \frac{{2 - 3 i - 4 j - 5 j i}}{54}

= \frac{\{144 - 305 i + 230 j + 35 j i\}}{27}

5): Conversion to trigonometric form:

Illustration 5:

s = {(\sqrt{3} + i) + j (1 + \sqrt{3} i)}

Find the magnitude,

r = \sqrt{{(a x)}^{2} {+ (b x)}^{2} + {(c y)}^{2} {+ (d y)}^{2}}

r = {\sqrt{3} + i + j + \sqrt{3} j i}

r = \sqrt{{(\sqrt{3})}^{2} {+ (1)}^{2} + {(1)}^{2} {+ (\sqrt{3})}^{2}}

r = 2 \sqrt{2}

Taking out the magnitude,

S = 2 \sqrt{2} \{(\sqrt{3} \frac{\sqrt{2}}{4} + \frac{\sqrt{2}}{4} i) + j (\frac{\sqrt{2}}{4} + \frac{\sqrt{2}}{4} \sqrt{3} i)\} ∵ \frac{1}{2 \sqrt{2}} = \frac{\sqrt{2}}{4}

Find out the magnitude of

(\sqrt{3} \frac{\sqrt{2}}{4} + \frac{\sqrt{2}}{4} i)

and

(\frac{\sqrt{2}}{4} j + \frac{\sqrt{2}}{4} \sqrt{3} j i)

parts separately

Magnitude of

(\sqrt{3} \frac{\sqrt{2}}{4} + \frac{\sqrt{2}}{4} i)

as well as

(\frac{\sqrt{2}}{4} + \frac{\sqrt{2}}{4} \sqrt{3} i)

\sqrt{2}

. Taking this magnitude outside the respective terms,

S = 2 \sqrt{2} \{\frac{\sqrt{2}}{2} (\frac{\sqrt{3}}{2} + 0.5 i) + \frac{\sqrt{2}}{2} j (0.5 + \frac{\sqrt{3}}{2} i)\}

Converting the same into trigonometric form

s = r \{c o s α e^{i γ} + s i n α j e^{i β} e^{i γ}\}

Then,

α = 45 °

γ = 30 °

β + γ = 60 °

β = 30 °

6): Rotation:

Illustration 6:

\{\frac{\sqrt{2}}{2} (1 + i)\} * ?

\{\frac{\sqrt{2}}{2} j (1 + i)\}

Conjugate of

\{\frac{\sqrt{2}}{2} (1 + i)\}

\{\frac{\sqrt{2}}{2} (1 - i)\}

Multiplying the conjugate and further multiplying with

\{\frac{\sqrt{2}}{2} j (1 + i)\},

\{\frac{\sqrt{2}}{2} (1 + i)\} * \{\frac{\sqrt{2}}{2} (1 - i)\} * \{\frac{\sqrt{2}}{2} j (1 + i)\} = \{\frac{\sqrt{2}}{2} j (1 + i)\}

\{\frac{\sqrt{2}}{2} (1 - i)\} * \{\frac{\sqrt{2}}{2} j (1 + i)\} = \{(\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} i)\} * \{j (\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} i)\}

= \{(\frac{\sqrt{2}}{2} - \frac{\sqrt{2}}{2} i) j (\frac{\sqrt{2}}{2} + \frac{\sqrt{2}}{2} i)\}

= j i

∴ \{\frac{\sqrt{2}}{2} (1 + i)\} * j i

\{\frac{\sqrt{2}}{2} j (1 + i)\}

Appendix VIII

Table of Notations and Symbols

$\| + ⟩$ , $\| - ⟩$	Basis kets of complex vector space. ‘+’ denotes spin-up and ‘-’ denotes spin-down direction
$\|ѱ⟩$	General quantum state vector which is a linear combination of two basis kets
$〈 + \|$ , $〈 - \|$	‘Bra’ is a conjugate of ket. To get a conjugate, change the complex number factor of bra to its conjugate
$〈 ѱ \|$	General quantum state vector which is a linear combination of two basis bras
${\| + ⟩}_{n} {, \| - ⟩}_{n}$	General spin $\frac{1}{2}$ superposition state vector in spin-up direction and spin-down direction
$θ$	Angle between $\| + ⟩$ ket and $\|-⟩$ ket
$φ$	Angle of phase difference of a spinor or 3-D number. The difference between angles of $\| + ⟩$ ket and $\|-⟩$ ket
$δ$	Angle of overall phase of a spinor or 3-D number
$r$	Magnitude of spinor or 3-D number
$j$	Alternative notation to $\|-⟩$ ket. If $j$ is used for $\|-⟩$ ket, $\|+⟩$ ket identification is skipped
${\| + ⟩}_{A}$	Spinor A in the spin-up direction
${\| - ⟩}_{B}$	Spinor B in the spin-down direction
${_{A} 〈 + \| + ⟩}_{B}$	Inner product of spinor A (output spinor) and spinor B (input spinor) under spinor method
$P_{+ A \| + B}$	Probability of getting input spinor B in the direction of output spinor A.
$\|{_{A} 〈 - \| + ⟩}_{B}\|^{2}$	The square of magnitude of inner product under spinor method which is equivalent to $P_{+ A \| + B}$
$\vec{a}$ , $\vec{b}$	Vector a, Vector b
${\vec{a}}^{- 1}$	Inverse of vector a
$A$ , $B$	3-D number A and 3-D number B. 3-D number is new notation for representing spinor as a number. Alternative name for 3-D number is spin-number.
$B_{⟂}$	3-D number which is perpendicular in the direction of $θ$ angle to 3-D number B
*	The star symbol for multiplication
$\cdot$	Dot symbol for dot product of two vectors
$\circ$	The small Circle symbol is for ▪ taking the dot product of complex numbers in two spinors by conjugating the first spinor ▪ taking the sum of dot product of two vectors and $i$ term in cross product of two vectors ▪ taking the sum of the real number term and $i$ term in the result of division of two 3-D numbers The final result is named as complex dot product.
×	Cross symbol for taking cross product of two vectors

References

McIntyre, D. H.; 2012, Quantum Mechanics, A Paradigms Approach; Pearson, ISBN 13: 978-0-321-76579-6; p. 41.
Ibid., p. 18.
Ibid., p. 11.
Coddens, G. 2015, From Spinors to Quantum Mechanics; Imperial College Press, London, ISBN 978-1-78326-636-4, p. 5.
Coddens, G. 2021, The Geometrical Meaning of Spinors Lights the Way to Make Sense of Quantum Mechanics. Symmetry 13, 659. , p. 2. [CrossRef]
Dirac, P. A. M. 1967, The Principles of Quantum Mechanics, Oxford University Press, London. p. 22, 74.
Penrose, R. 2004, The Road to Reality; Jonathan Cape, London, p. 206.
Ibid. p. 555-556.
Wharton, K.B. et al, 2011, A classical analog for the electron spin state; arXiv:1111.3348v2, p. 5.
Ibid., p. 2.
Fano, U., 1949, Remarks on the Classical and Quantum-Mechanical Treatment of Partial Polarisation; Journal of The Optical Society Of America; v. 39, p. 861.
Fano, U. 1954, A Stokes-Parameter Technique for the Treatment of Polarisation in Quantum Mechanics; Phys. Rev. 93, 121 . [CrossRef]
Gori, F. et al, 1997, An elementary approach to spinors; Eur. J. Phys. 18, 256.
Torres del Castillo G.F. et al, 2013, The Jones vector as a spinor and its representation on the Poincaré sphere; arXiv:1303.4496, p.12.
Park, D., 1974, Introduction to the quantum theory, McGraw-Hill, p. 32.
Thompson, S. P. (1910). The life of William Thomson (Vol. 2); Macmillan, London. p. 1138.
Farmelo, G. 2009, The Strangest Man. In The Hidden Life of Paul Dirac: Quantum Genius; Faber and Faber; p. 430.
Atiyah, M., 1998, Paul Dirac-The Man and His Work; Cambridge University Press, p. 113-114.
Carroll, S. 2019, Even Physicists Don’t Understand Quantum Mechanics https://www.nytimes.com/2019/09/07/opinion/sunday/quantum-physics.html.
Riggs, P. J. 2009, Quantum Causality. Springer, DOI , p. 24-25. [CrossRef]
Carroll, R. 2004, Remarks on the Schrödinger Equation. arXiv:quant-ph/0401082, p. 1.
Popper, K.R. 1982, Quantum Theory and the Schism in Physics. Unwin and Hyman, London, p. 24.
Lindsay, R.B. and Margenau, H. 1957, Foundations of Physics. Dover, New York, p. 487.
Mermin N. D. 1989, Physics Today 42, 4, 9; [CrossRef]
Heaviside, O. (1893), Electromagnetic Theory. Vol. I. London, UK; The Electrician Printing and Publishing Company, pp. 134–135.
Chisholm J. S. R. 1978, Vectors in Three-Dimensional Space. Cambridge University Press, Cambridge, p. 60, equation 3.8.
Ibid. p. 35, equation 2.23.
Ibid. p. 36, equation 2.26.
Goldstein, D. 2003, Polarized Light, Marcel Dekker, Inc; ISBN: 0-8247-4053-X, Section 4.7.
Townsend J. S. 2000, A Modern Approach to Quantum Mechanics. University Science Books, California, chapter 1.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Spinors and Spatial Vectors Are Part of the Number System; They Are Extensions of Complex Numbers into Three-Dimensional Space

Abstract

1. Introduction

2. Spinor notation

3. New Spinor notation

4. Computing probability in Quantum mechanics using Spin-numbers

5. Computing probability using Vectors

6. Geometry of Spinors

7. Projection of Complex Numbers

8. Multiplication of Vectors is a Division in disguise

9. Vector and Probability in Quantum Mechanics

10. Basic properties of 3-D numbers

11. 3-D number in Three-dimensional space

12. Operations on 3-D numbers

13. Projection of 3-D numbers

14. Quaternions and 3-D numbers

15. Geometric Algebra and 3-D numbers

16. Geometry of 3-D number

17. Is 4π of rotation required to bring the state spinor to its original position?

18. Polarisation of Light and Spinors

19. Conclusion

Appendix I

Appendix II

Appendix III

Appendix IV

Appendix V

Appendix VI

Appendix VII

Appendix VIII

References

MDPI Initiatives

Important Links

Subscribe