Prerpints.org logo
Preprint
Article

Cubic Nonlinearity of Graphene-Oxide Monolayer

Altmetrics

Downloads

92

Views

18

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

22 August 2023

Posted:

23 August 2023

You are already at the latest version

Alerts
Abstract
The cubic nonlinearity of graphene oxide (GO) monolayer was characterized by open and closed Z-scan using a nano-second laser of 10 Hz repetition rate with a Gaussian spatial beam profile. The reverse saturable absorption or positive nonlinearity from open Z-scan and valley-peak traces or positive nonlinearity from closed Z-scan was displayed. The reverse saturable absorption could be from a two-photon or two-step excitation process due to the larger absorption in the lower visible and upper UV wavelength region compared with the excitation source. The nonlinear absorption and nonlinear refraction coefficient were estimated to be ~ 2.62x10-8 m/W and 3.9x10-15 m2/W, respectively. This study also reveals the effect of nonlinear absorption on nonlinear refraction traces.
Keywords: 
Subject: Physical Sciences  -   Optics and Photonics

1. Introduction (cross green, should be remove red)

Successful extraction of a Graphene single layer through mechanical cleavage in 2004 has triggered an explosion of academic research interest in two-dimensional (2D) materials [1]. Due to the optical nonlinearities of Graphene with remarkable Kerr effect and high nonlinear absorption coefficient, it has been perceived as a promising material for application in optoelectronics [2,3]. However, the high nonlinear absorption coefficient was accompanied by zero bandgap through the strong two-photon absorption (TPA) process which might not only be from the two-step excitation but also due to an undesired free-carrier absorption (FCA) and free-carrier dispersion (FCD) [4]. Currently, Graphene oxide (GO) has been recognized as a rising material in the Graphene family due to its tunable bandgap [5]. One intriguing property is that its optical and electrical properties can be tuned by manipulating the content and location of oxygen-containing groups through either chemical or physical reduction [6]. These reduction processes transform GO from an insulator to a semiconductor and to a metal-like state, in the form of graphene. In addition, GO is a hydrophilic and water-soluble material due to the existence of the oxygen-containing group which makes it easier in the fabrication process.
The third-order nonlinear optical properties of GO are stable under high-power illumination [7] which makes GO a strong candidate for a variety of applications such as pulse compression, mode-locking to Q-switching, and optical limiting (OL), and all-optical switching [5,8,9,10,11,12,13,14,15,16,17,18,19,20]. The third-order optical nonlinearity includes the polarity and magnitude of NLA and nonlinear refraction (NLR) of the optical medium, which is a prime factor for prospective technical applications in optoelectronics. For example, the saturable absorption (SA) of negative nonlinearity materials is used for the lasers as Q-switching elements [21] and the reverse saturable absorption (RSA)of positive nonlinearity materials is applicable for two-photon microscopy and optical limiters [22]. Therefore, the “Z-scan technique” is used to investigate the polarity and magnitude of NLA and NLR coefficient which is comparatively simple and more accurate compared to other third-order nonlinear characterization techniques [14,23]. Kang et al, revealed that Graphene Oxide (GO) exhibits strong and broadband NLO properties owing to its wide optical band structure which results in the optical power limiting for a wide spectral range of wavelength [24]. It obviously meets the demands for upcoming photonic applications to overcome the OL behavior at certain wavelengths via metallic nanomaterials (zinc ferrites nanoparticles [25], gold clusters [26]). However, the magnitude of third-order susceptibility (χ3) was estimated to be ~ 8.97x10-18 m2/V2 which is relatively lower than our estimation. In addition, the nonlinear optical response exhibits SA at the short wavelength and RSA at the longer wavelength which may result in varying magnitude of third-order susceptibility based on the wavelength-dependent nonlinear optical transition [24]. The magnitude and polarity of nonlinearity are modified by excitation processes such as resonant and non-resonant nonlinear processes. For example, the magnitude of nonlinearity via resonant excitation is relatively larger, and the nonlinear optical process is relatively slower than the magnitude of nonlinearity from non-resonant excitation [27]. Also, the OL actions of few-layered GO dispersed in an organic solvent displayed the OL actions by Z-scan at 532 nm [28]. GO nanosheets dispersed in the de-ionized water demonstrated the broadband NLO and OL properties at 1064 nm [29]. The tunable OL properties of GO in ethanol solution were studied at 1550 nm [30]. In moving towards the application of GO in optical limiters in the visible region, the third-order nonlinear optical susceptibility χ3 is a crucial parameter that needs to be evaluated. Since the complex χ3 of GO has a strong relationship with its nonlinear refraction and absorption, the imaginary part directly verbalizes the information about the saturable absorption (SA) and reversed saturable absorption (RSA), which are important bases for the OL applications.
Ebrahimi et al. reported the imaginary (Im) χ3 value of GO in ethanol at 532 nm was 2.17x10-14 m2/V2 [31]. The values of Imχ3 changes with GO dispersion in different solvents at 532 nm that varied from 1.0x10-19 to 5.1x10-19 m2/V2 [28]. In addition, Khanzadeh revealed the χ3 of GO was 5.12x10-16 m2/V2. In the same wavelength, Kang et al. demonstrated the χ3 value of GO is 8.97x10-18 m2/V2 [24]. It implies that the different magnitude of χ3 arises from the number of oxygen content in the sample, types of solvent used, and the applied wavelength. Our estimation of χ3 in a single wavelength is one order higher than the characterized by continuous wavelength range from 450 to 750 nm as per the literature review [24]. The positive nonlinear absorption coefficient at 532 nm wavelength indicates that the excited state absorption is higher than that in the ground state, and GO exhibits RSA behavior, which can be utilized in the optical limiters. In addition, due to the highly intense laser beam used in the nonlinearity, results from Z-scan might include a thermal effect as well. It is well known that the thermal effect is significantly dominant in certain laser specifications such as ultrafast and continuous laser (CW) systems due to the pico-second thermal relaxation rate in GO. Therefore, this article presented the polarity and magnitude of nonlinear absorption and nonlinear refraction coefficient of GO in Di-water using a nanosecond laser at a visible wavelength of 532 nm through the Z-scan.

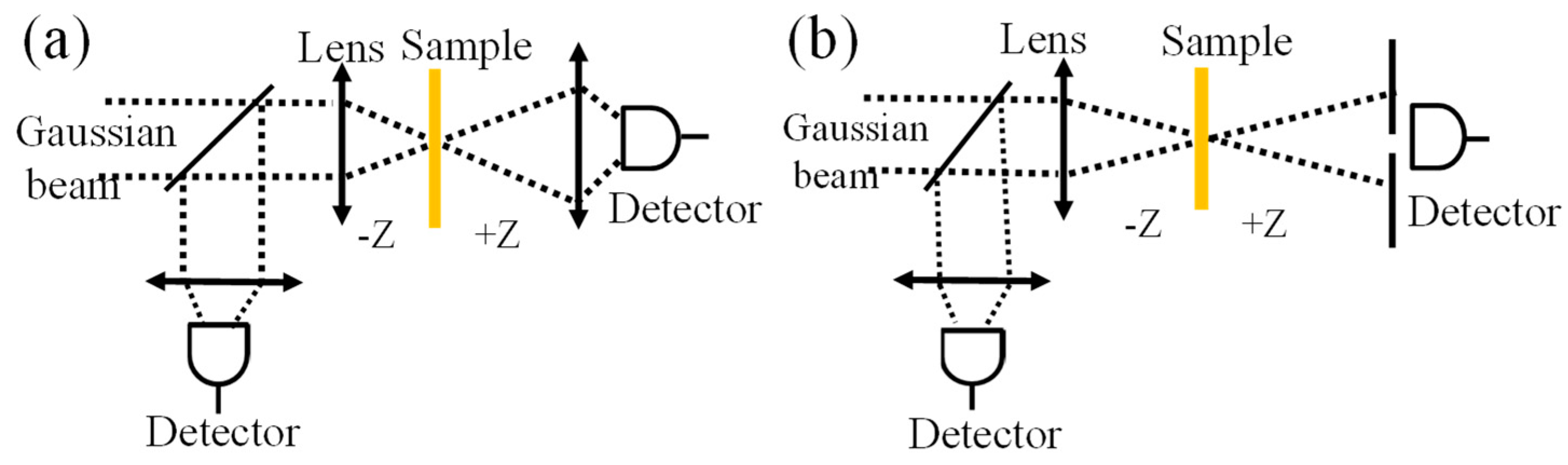
2. Materials and Methods

The Graphene Oxide (GO) nanoflakes in aqueous solution were purchased from a Graphene laboratory [32]. The ultra-high GO concentration of 6.2 g/L has > 80% monolayer of concentration with 0.5 -5 microns nanoflakes size. The cubic nonlinear optical properties of GO nanoflakes were characterized using Z-scan in a 1-mm quartz cuvette. The excitation source for Z-scan was a pulsed laser at 532 nm, 10-Hz repetition rate, and ~6-ns temporal pulse width with the gaussian beam [33]. The effective focal length of the focusing lens for the Z-scan was ~125 mm. The radius of the beam waist (wo) at the focal point was ~15.1 µm. The Rayleigh length ( z 0 = k w 0 2 / 2 ) was ~2.02 mm which was larger than the sample thickness (1 mm). The Gaussian beam at the focusing lens was ~2.8 mm at FWHM and was prepared using two irises. All optical nonlinearity measurements were conducted within the system linearity to avoid any additional nonlinear contributions from the electronic devices and the optics used in the experiments. Also, the third-order optical nonlinearity of both the base solution and the GO atomic layer in the base solution were separately scanned to remove the nonlinearity from the base solution.
All the experiments were conducted within the linearity of a system to avoid the nonlinear contribution from electronic devices and optics used in an experiment. Both base solution and GO atomic layer in base solution were scanned in higher peak intensity region separately which shows the absence of nonlinearity from base solution. For reference, the nonlinear refraction of CS2 was utilized with the closed Z-scan [33]. The schematic drawings of open and closed Z-scan setups are shown in Figure 1 (a) and (b) respectively [23].

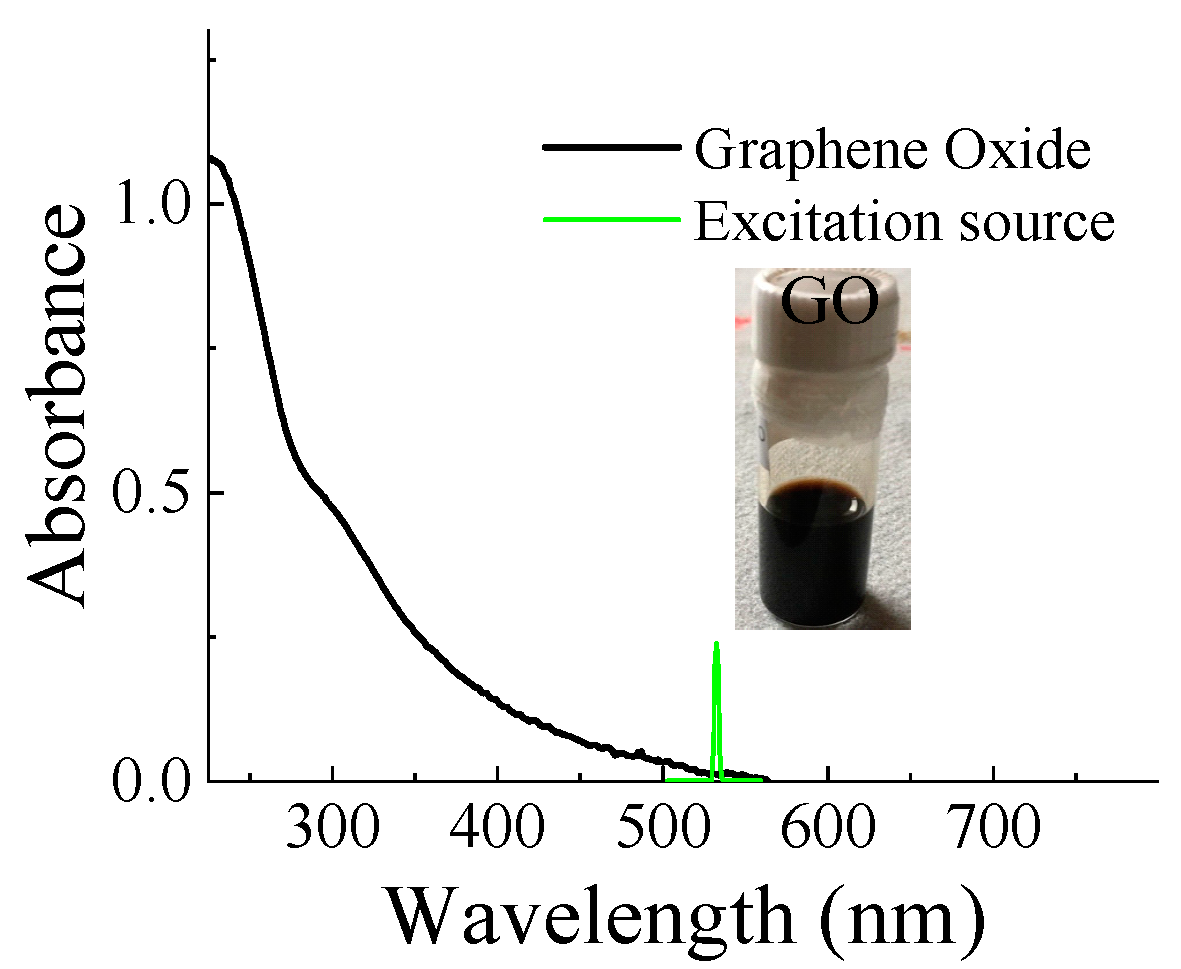
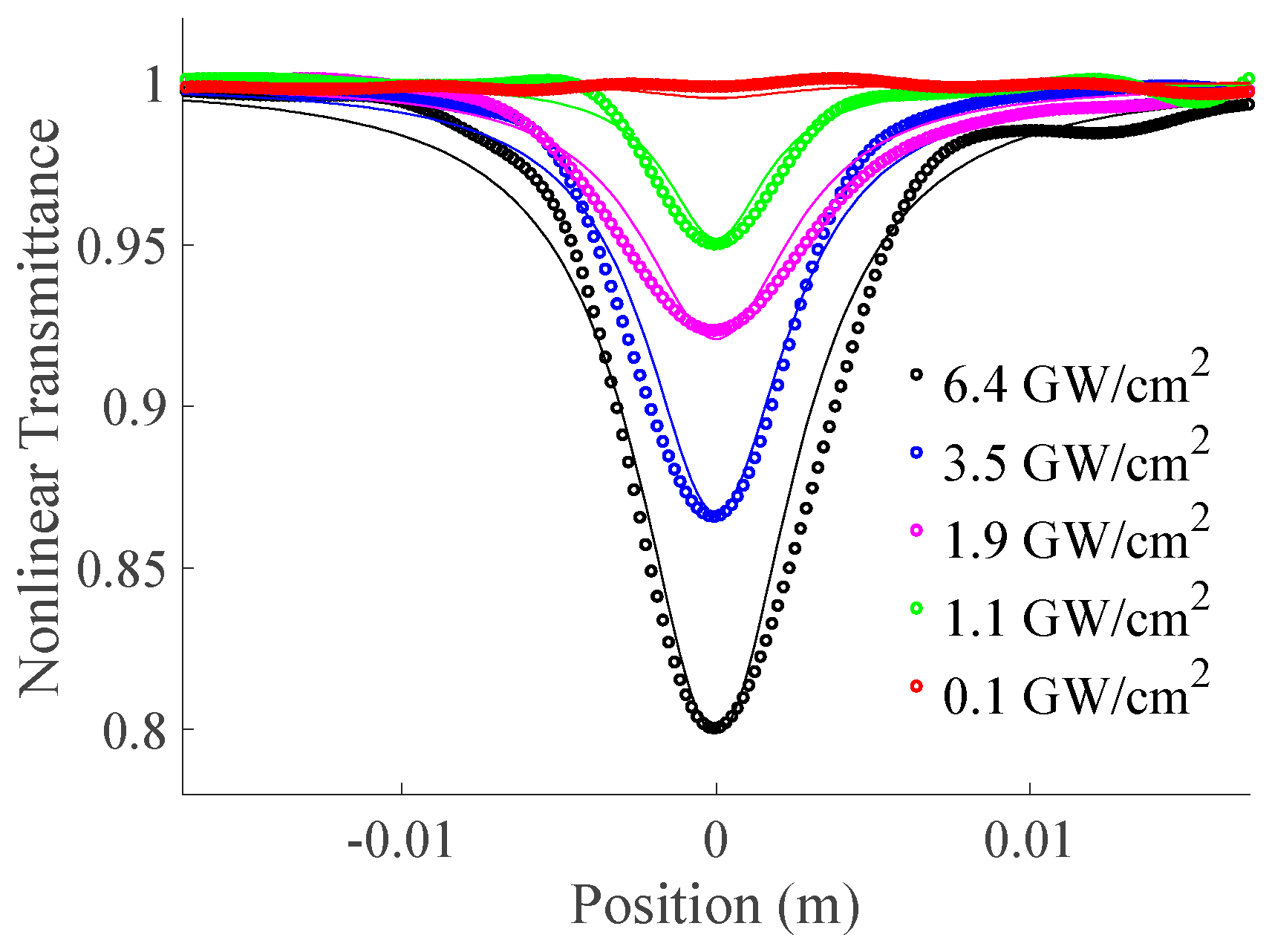
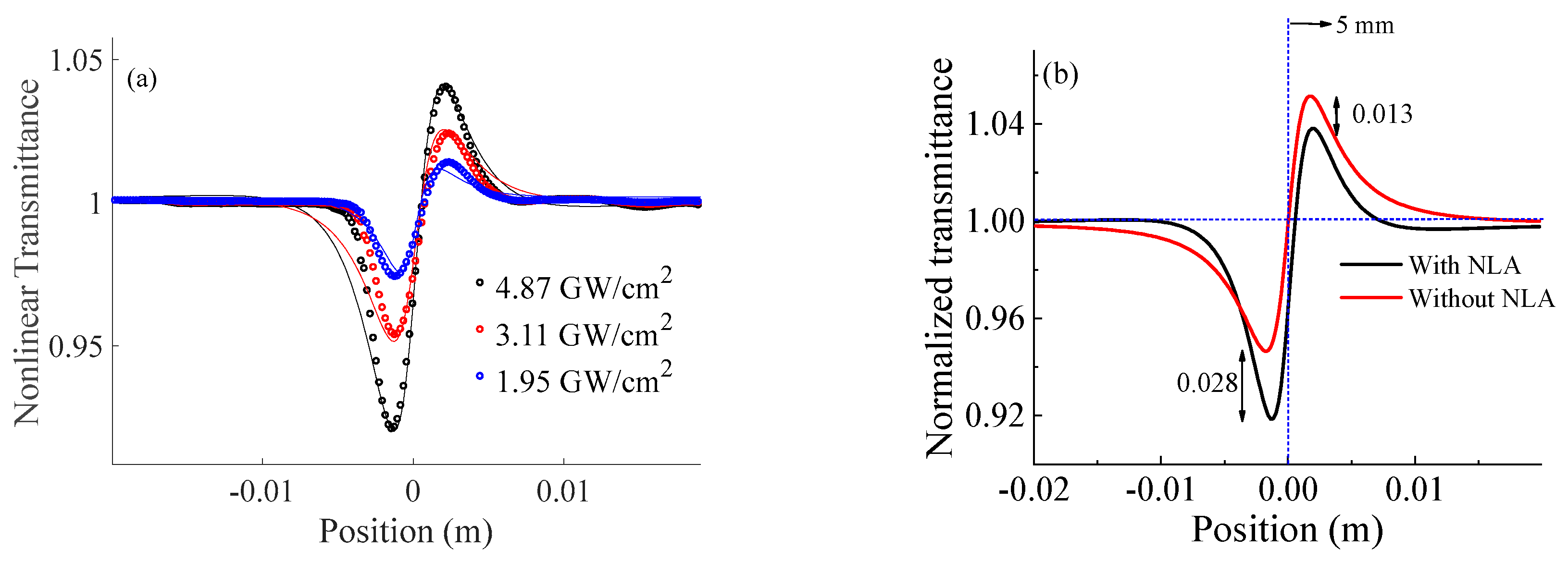
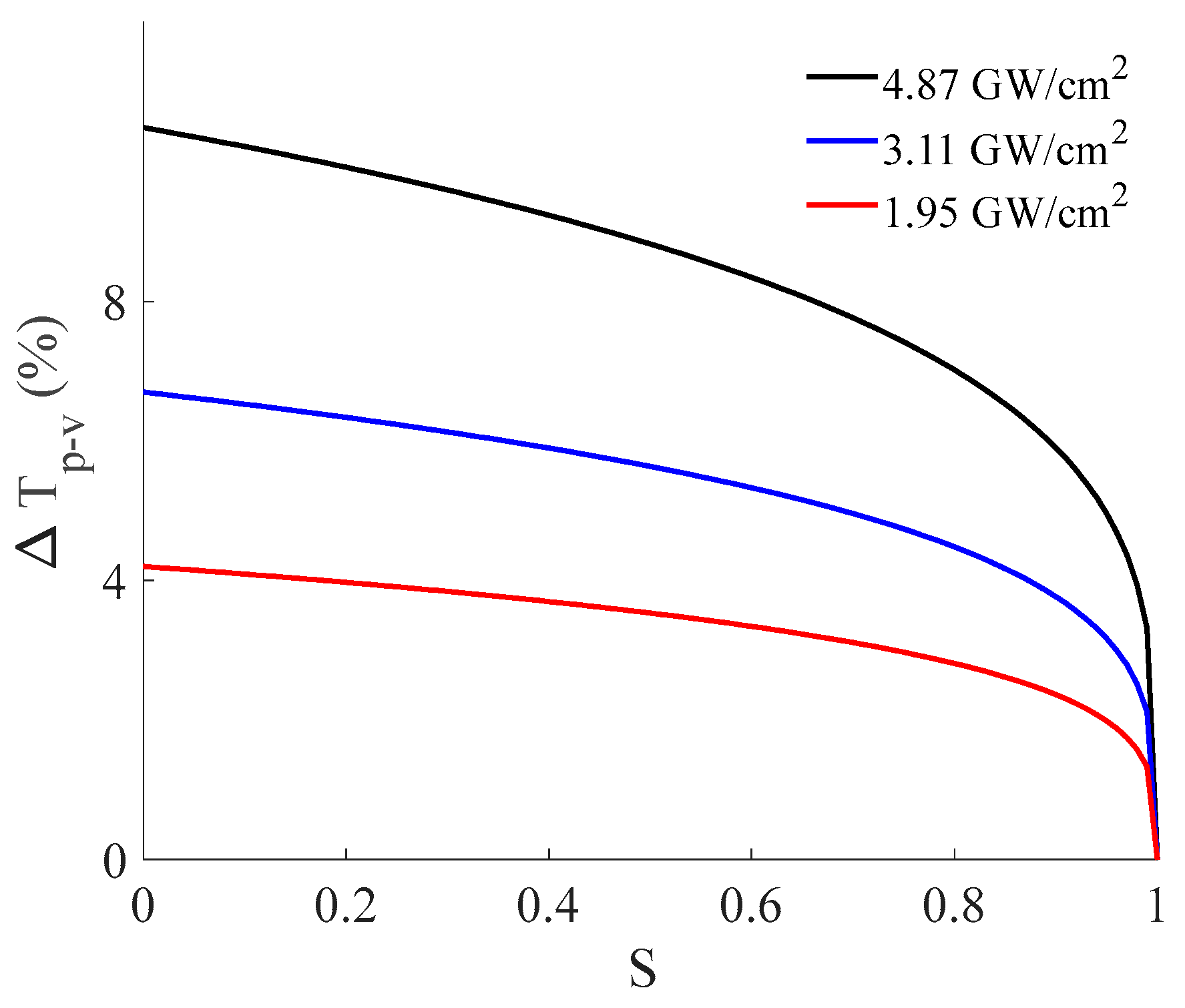
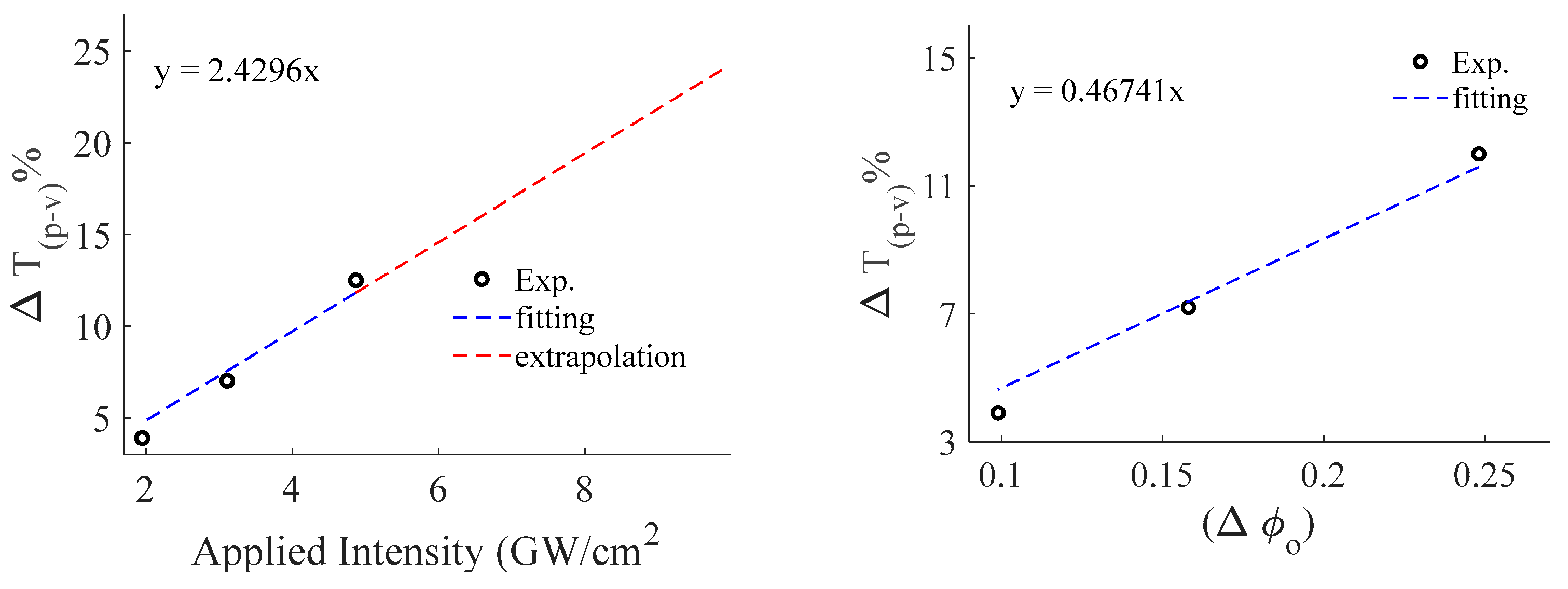
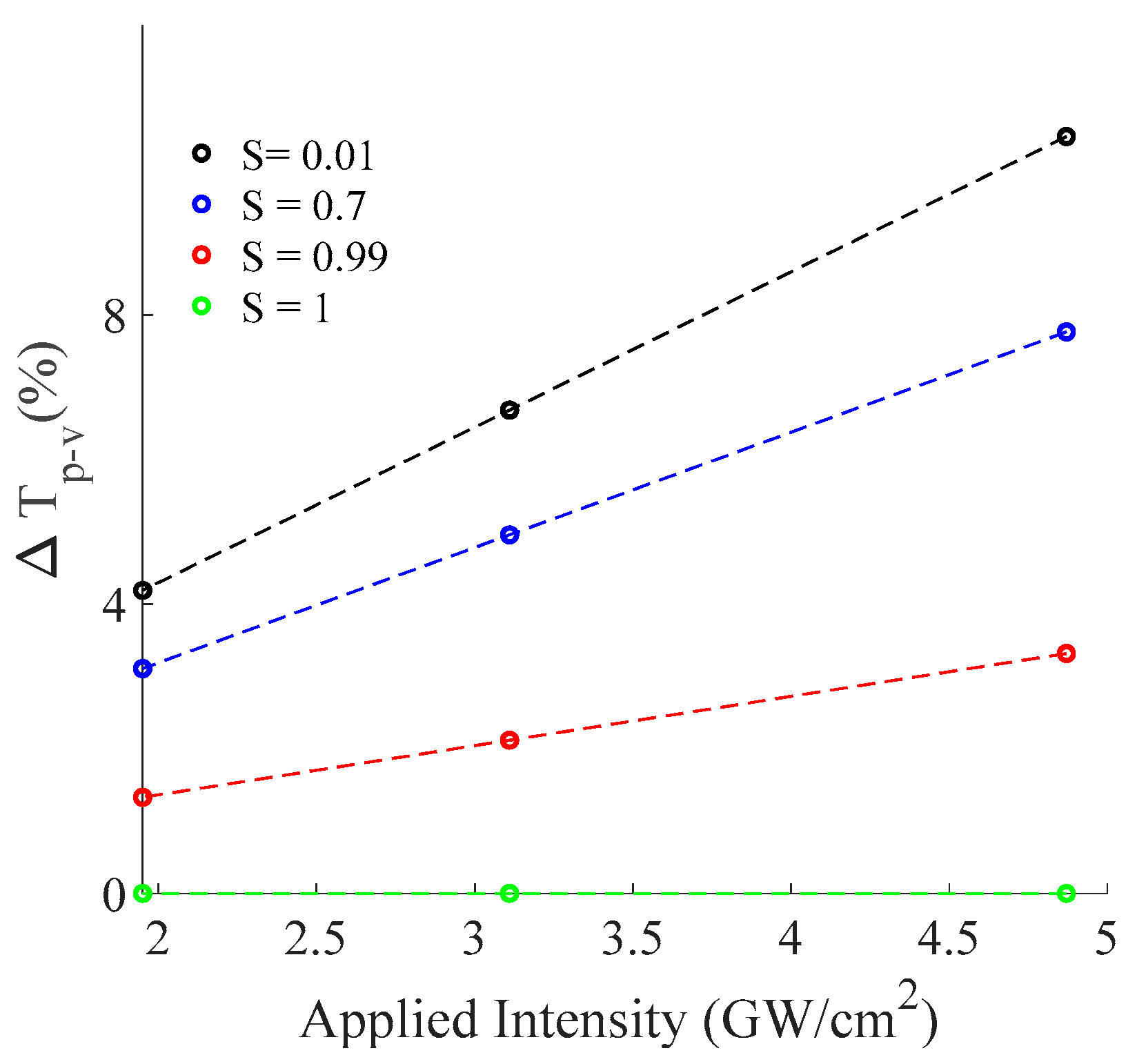
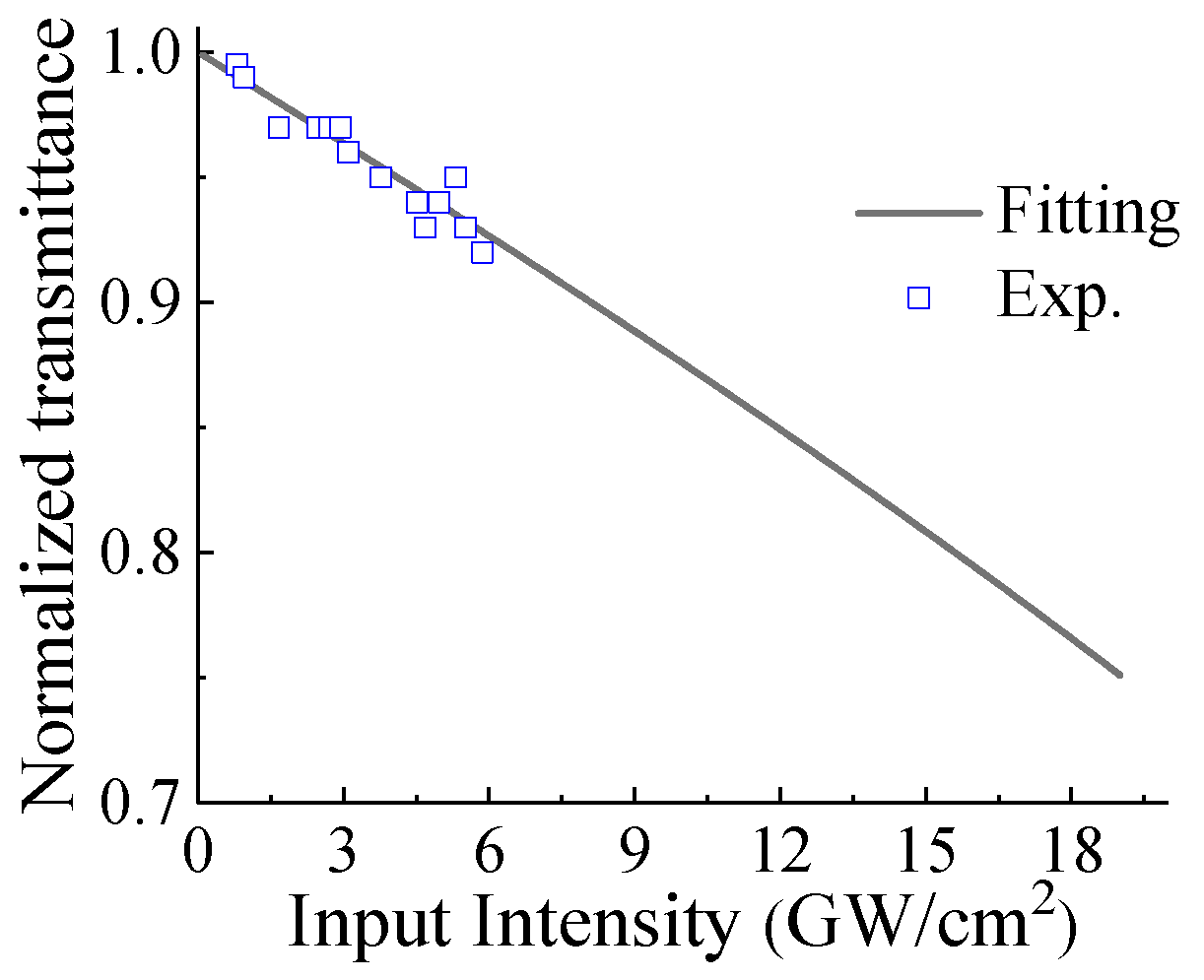
3. Results and Discussion

Figure 2 displayed the absorption spectrum of GO nanoflakes in a base solution of DI water using a UV-Vis absorption spectrometer. It revealed that the absorption peaks are located at around 230 nm and 300 nm and the electronic transitions in the ultraviolet (UV), with their tail extending into the visible region. The p orbitals of carbon can be combined either in-phase or out of phase, producing bonding and anti-bonding combinations. This gives rise to π and π* orbitals, where the π orbital is lower in energy than the π*, allowing for a photon- induced transition between π and π* [34]. The first peak is related to π-π* transition of the C=C bond and the latter one corresponds to π-π* transition of the C=O bonds of GO [35].
To characterize the nonlinear absorption of GO nanoflakes in the water, the open Z-scan technique was used. Figure 3 shows the nonlinear transmittance as a function of sample position (z) for the different peak excitation intensities of ~6.4 GW/cm2, 3.5 GW/cm2, 1.9 GW/cm2, 1.1 GW/cm2, and 0.1 GW/cm2 at the focus plane at z= 0 mm. The nonlinear transmittance at both negative and positive z-positions was normalized to 1. The nonlinear transmittance traces of GO nanoflakes displayed a reverse saturable absorption (RSA) with a positive nonlinearity [12]. It implies that the absorption cross-section at the excited state is larger than the absorption cross-section at the ground state. The excitation source being on the edge of absorption spectra and larger absorption in lower wavelength regions than the excitation source may also facilitate the two-photon excitation or two-photon absorption process. The nonlinear transmittance with open Z-scan for a Gaussian beam is given by [14],
T ( z , S = 1 ) = ∑ m = 0 ∞ ( − q 1 + ( z / z o ) 2 ) m ( 1 + m ) 3 / 2
where z is the sample position, S = 1 − exp ( − 2 r a 2 / w 0 2 ) = 1 is the unit linear transmittance indicating no aperture in front of the detector in the open Z-scan, ra is the radius of a finite aperture in front of an optical detector, q(r,z,t) = βIoLeff < 1 is the requirement for nonlinear absorption characterization with the negligible nonlinear phase distortion of Δ Ψ o ( t ) = β I o ( t ) L e f f / 2 , L e f f = ( 1 − exp ( − α o L ) ) / α o L is the effective sample length, L is the sample thickness, Io is the peak intensity of excitation beam, αo is the linear absorption coefficient, and β is the nonlinear absorption coefficient. The nonlinear absorption coefficient of GO was extracted to be ~ 2.62 ×10-8 m/W after fitting with equation 1.
Again, the nonlinear refraction coefficient was characterized by closed Z-scan techniques using a far-field condition of an aperture (d ~ 2.0 >> zo). The radius (ra) of a finite aperture in front of the diameter was ~ 0.75 mm which results in the linear transmittance of finite aperture (S) ~ 0.01 <1 [33]. The normalized transmittance as a function of sample position displayed the valley-peak traces as shown in Figure 4. It prevails over the self-focusing characteristics or positive nonlinear refraction of GO nanoflakes. The nonlinear transmittance of a closed Z-scan with a Gaussian beam is given by [23,36],
T ( S < < 1 ) = 1 − 4 Δ φ 0 x + q ( 3 + x 2 ) ( 1 + x 2 ) ( 9 + x 2 ) − 4 Δ φ 0 2 ( 5 − 3 x 2 ) − 8 Δ φ 0 q x ( 9 + x 2 ) − q 2 ( 40 + 17 x 2 + x 4 ) ( 1 + x 2 ) ( 9 + x 2 ) ( 25 + x 2 ) + ..
where wa is the radius of beam waist at the focal plane, q ( r , z , t ) = β I o L e f f < 1 , Δ φ o = k γ I o L e f f < 1 is the phase distortion for the symmetric peak-valley nonlinear transmittance trace, γ is the nonlinear refraction coefficient, and x = − ( 1 / z o ) ( z + ( z o 2 + z 2 ) / d − z ) ~ z / z o for the far-field condition of an aperture (d >> zo) where d is the distance between the focal plane and the aperture. The nonlinear refraction (γ) was estimated to be ~ 3.9 x 10-15 m2/W from fitting equation 2. Looking into the valley-peak transmittance, the valley is much deeper (~ 0.028 Tv-p) than the valley-peak symmetry. It might be the absorption of 532 nm laser by GO nanoflakes [37].
The NLR curve described by equation 2 results in transmittance variation between normalized peak and valley transmittance Tp-v = 0.4| Δϕo | and a peak–valley separation of zp-v = 1.79z0. Also, ΔTp-v depends on the magnitude of the nonlinear phase shift (Δϕo) and linear transmittance of finite aperture (S). For smaller phase shift (Δϕo ≤ π), which resembles this experiment, the ΔTp-v follows the equation within ±2% variation is [14],
∆ T p − v ≈ 0.406 1 − S 0.25 | ∆ ϕ o |
For an applied Intensity, the phase shift is constant. Therefore, this article is focused on investigating the effect of S on ΔTp-v using the estimated nonlinear refraction coefficient for given three different applied peak intensities.
Figure 5 reveals that the magnitude of the peak-valley difference is lower if the applied input intensity is smaller which is obviously expected. Also, as the linear transmittance of finite aperture gets higher, the peak difference is lower which finally reaches zero for S = 1. Note that S = 1 is the no aperture condition which is used to measure the nonlinear absorption phenomenon utilizing the open Z-scan technique. It suggests that keeping the value of S smaller is the ideal condition to study the Nonlinear refraction phenomenon. The experiment was conducted under three different applied intensities, which results in corresponding phase differences for a given S = 0.01. Figure 6 shows the magnitude of peak-valley difference as a function of applied intensity (left) with its fitting (red dotted) and nonlinear phase shift (right).
Furthermore, calculated Tp-v as a function of the phase shift at the focus results in a linear coefficient of 0.46 which agrees well with a numerical solution to verify the accuracy of Z-scan data as shown in Figure 6 [14]. In addition, calculated Tp-v as a function of the applied intensity demonstrates that the linear coefficient (slope) decreases if aperture size is increased, which is expected for the Z-scan result as shown in Figure 7 [14].
Since the nonlinear absorption and nonlinear refraction coefficients are associated with the imaginary and real parts of cubic nonlinear susceptibility respectively, the modulus of cubic nonlinear susceptibility is given by,
| χ ( 3 ) | = | Re χ ( 3 ) | 2 + | Im χ ( 3 ) | 2
where Re χ ( 3 ) = ( 4 / 3 ) n o 2 ε o c γ and Im χ ( 3 ) = ( 1 / 3 π ) n o 2 ε o c λ β are real and imaginary components of cubic nonlinearity, no is the linear refractive index [36], εo is the dielectric constant of the vacuum, and c is the velocity of light. The nonlinear transmittance Equations (1) and (2) are for the field of the Gaussian beam. Using these equations, the cubic nonlinear susceptibility of GO monolayer in aqueous solution was estimated to be |χ(3)| ~ 9.55 x 10-17 m2/V2 which is one order higher (~ 8.97 x 10-18 m2/V2) than the GO in Di-water [24] and one order lower (~ 5.12 x 10-16 m2/V2) than the GO in ethanol [28].
The rise time of a thermal lens in an aqueous liquid is determined by the acoustic transit time, τ = wo/vs [14] where vs ≈ 1437 m/s [38], is the velocity of sound in the water at room temperature. We obtain τ ~ 10.1 ns, which is almost double the pulse width (~6 ns). Therefore, both electronic (Kerr effect) and thermal effects could contribute to γ in closed-aperture Z-scans. The polarity of the nonlinear refraction coefficient could be further verified using the I-scan technique which investigates the nonlinear transmittance as a function of the input intensity. The normalized transmittance depends on several parameters such as the intensity, the nonlinear absorption, the nonlinear refraction, the position of the sample, the Rayleigh range, the effective length of the sample, and the distance between the sample and the aperture [39]. Therefore, the GO dispersion was placed at the valley of closed Z-scan traces. It shows that the normalized transmittance decreases with the peak intensity increases as shown in Figure 8. This is because the transmittance beam through the optical medium is diffracted further and further with higher peak intensity which also confirms the negative nonlinearity or defocusing effect of GO nanoflakes. In the valley position, the intensity-dependent total absorption (α(I) = αo + βI) and the total refraction (n(I) = no + γI) contributed the laser power shielded capacity for the optical power limiter. It implies that the GO nanoflakes are very useful materials for the optical power limiting to protect the eyes and sensor from high power radiation.

4. Conclusions

The cubic nonlinearity of graphene oxide (GO) was studied through the Z-scan technique using a single wavelength at 532 nm laser source. The positive nonlinear (reverse saturable) absorption and nonlinear (valley-peak) refraction properties were observed through the open Z-scan and closed Z-scan techniques, respectively. Due to the linear absorption spectra below the 500 nm region, the excitation source of 532 nm in this study might be facilitated by either two-photon excitation or a two-excitation process that results in reverse saturable absorption. It implies that the excited state absorption is higher than that in the ground state, and GO exhibits RSA behavior, which can be utilized in the optical limiters. The nonlinear absorption and nonlinear refraction coefficient were estimated to be ~ 2.62x10-8 m/W and 3.9x10-15 m2/W respectively. Decreased transmittance was observed for higher intensities via an I-scan, which can pave the way for the application of Graphene Oxide in power-limiting devices in future technology.

Author Contributions

Conceptualization, F.J.S. and W.-J.K.; methodology, T.N. and U.P.; formal analysis, T.N. and U. P; resources, F.J.S.; writing—original draft preparation, T.N. and U. P.; writing—review and editing, F.J.S., B.T., T.N., U. P. and W.-J.K.; visualization, T.N.; supervision, F.J.S. and B.T.; funding acquisition, F.J.S. All authors have read and agreed to the published version of the manuscript.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Acknowledgments

This work was supported at Hampton by NASA NNX15AQ03A and ARO W911NF-15-1-0535; at UNC-Pembroke by North Carolina Collaboratory (collab_368); and at K1 Solution R&D Center by …….

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Geim, A. K.; Novoselov, K.S. The rise of graphene. Nat Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
  2. Zhang, H.; Virally, S.; Bao, Q.; Ping, L. K.; Massar, S.; Godbout, N.; Kockaert, P. Z-scan measurement of the nonlinear refractive index of graphene. Opt. Lett. 2012, 37, 1856–1858. [Google Scholar] [CrossRef] [PubMed]
  3. Bao, Q.; Zhang, H.; Wang, Y.; Ni, Z.; Yan, Y.; Shen, Z.; Loh, K. P.; Tang, D.Y. Atomic-Layer Graphene as a Saturable Absorber for Ultrafast Pulsed Lasers. Adv. Funct. Mater. 2009, 19, 3077–3083. [Google Scholar] [CrossRef]
  4. Mizrahi, V.; Delong, K. W.; Stegeman, G. I.; Saifi, M. A.; Andrejco, M.J. Two-photon absorption as a limitation to all-optical Switching. Opt. Lett. 1982, 14, 1140–1142. [Google Scholar] [CrossRef]
  5. Chantharasupawong, P.; Philip, R.; Narayanan, N. T.; Sudeep, P. M.; Mathkar, A.; Ajayan, P. M.; Thomas, J. Optical Power Limiting in Fluorinated Graphene Oxide: An Insight into the Nonlinear Optical Properties. J. Phys. Chem. C. 2012, 116, 25955–25961. [Google Scholar] [CrossRef]
  6. Zhu, Y.; Murali, S.; Cai, W.; Li, X.; Sul, J. W.; Potts, J. R.; Ruoff, R. S. Graphene and Graphene Oxide: Synthesis, Properties, and Applications. Adv Mater 2010, 22, 3906–3924. [Google Scholar] [CrossRef]
  7. Ren, J.; Zheng, X.; Tian, Z.; Li, D.; Wang, P.; Jia, B. Giant third-order nonlinearity from low-loss electrochemical graphene oxide film with a high-power stability. Appl. Phys. Lett 2016, 109, 221105. [Google Scholar] [CrossRef]
  8. Loh, K. P.; Bao, Q.; Eda, G.; Chhowalla, M. ; Graphene oxide as a chemically tunable platform for optical applications. Nat. Chem 2010, 2, 1015–1024. [Google Scholar] [CrossRef]
  9. Jiang, X. F.; Polavarapu, L.; Neo, S. T.; Venkatesan, T.; Xu, Q.H. Graphene Oxides as Tunable Broadband Nonlinear Optical Materials for Femtosecond Laser Pulses. J. Phys. Chem. Lett. 2012, 3, 785–790. [Google Scholar] [CrossRef]
  10. Xu, X.; Zheng, X.; He, F.; Wang, Z.; Subbaraman, H.; Wang, y.; Jia, B.; Chen, R.T. Observation of Third-order Nonlinearities in Graphene Oxide Film at Telecommunication Wavelengths. Sci. Rep. 2017, 7, 9646. [Google Scholar] [CrossRef]
  11. Burkins, P.; Kuis, R.; Basaldua, I.; Johnson, A. M.; Swaminathan, S. R.; Zhang, D.; Trivedi, S. Thermally managed Z-scan methods investigation of the size-dependent nonlinearity of graphene oxide in various solvents. JOSAB 2016, 33, 2395–2401. [Google Scholar] [CrossRef]
  12. Krishna, M. B. M.; Venkatramaiah, N.; Venkatesan, R.; Rao, D. N. Synthesis and structural, spectroscopic and nonlinear optical measurements of graphene oxide and its composites with metal and metal free porphyrins. J. Mater. Chem. 2010, 22, 3059. [Google Scholar] [CrossRef]
  13. Shan, Y.; Tang, J.; Wu, L.; Lu, S.; Dai, X.; Xiang, Y. Spatial self-phase modulation and all-optical switching of graphene oxide dispersions. J. Alloys Compd. 2019, 771, 900–904. [Google Scholar] [CrossRef]
  14. Bahae, M. S.; Said, A. A.; Wei, T. H.; Hagan, D. J.; Stryland, E.W. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
  15. Durbin, S. D.; Arakelian, S. M.; Shen, Y.R. Laser-induced diffraction rings from a nematic-liquid-crystal film. Opt. Lett. 1981, 6, 411–413. [Google Scholar] [CrossRef]
  16. Callen, W. R.; Huth, B. G.; Pantell, R.H. Optical Patterns of Thermally Self-Defocused Light. Appl. Phys. Lett. 1967, 11, 103–105. [Google Scholar] [CrossRef]
  17. Kean, P. N.; Smith, K.; Sibbett, W. Spectral and temporal investigation of self-phase modulation and stimulated Raman scattering in a single-mode optical fibre. IEE Proceeding 1987, 134, 163–167. [Google Scholar] [CrossRef]
  18. Neupane, T.; Wang, H.; Yu, W. W.; Tabibi, B.; Seo, F. J. Second order hyperpolarizability and all-optical-switching of intensity-modulated spatial self-phase modulation in CsPbBr1.5I1.5 perovskite quantum dot. Opt. Laser Technol. 2021, 140, 107090. [Google Scholar] [CrossRef]
  19. Neupane, T.; Tabibi, B.; Kim, W.-J.; Seo, F.J. Spatial Self-Phase Modulation in Graphene-Oxide Monolayer. Crystals 2023, 13, 271. [Google Scholar] [CrossRef]
  20. Neupane, T.; Tabibi, B. ; Kim, Seo, F.J. Spatial Self-Phase Modulation in Ws2 and MoS2 atomic layer. Opt. Mater. Express, 2020, 8, 831–842.
  21. Woodward, R. I.; Kelleher, E. J. R.; Howe, R. C. T.; Hu, G.; Torrisi, F.; Hasan, T.; Popov, S.V.; Taylor, J.R. Tunable Q-switched fiber laser based on saturable edge-state absorption in few-layer molybdenum disulfide (MoS2). Opt. Express 2014, 22, 31113–31122. [Google Scholar] [CrossRef]
  22. Wang, J.; Gu, B.; Wang, H. T.; Ni, X.W. Z-scan analytical theory for material with saturable absorption and two photon absorption. Opt. Commun. 2010, 283, 3525–3528. [Google Scholar] [CrossRef]
  23. Bahae, M. S.; Said, A. A.; Stryland, E. W. High-sensitivity, single-beam n2 measurements, Opt. Lett. 1989, 14, 955–957. [Google Scholar]
  24. Kang, L.; Sato, R. Zhang, B.; Takeda, Y.; Tang, J. Experimental dispersion of the third-order optical susceptibility of graphene oxide. Opt. Mater. Express 2020, 10, 3041–3050. [Google Scholar] [CrossRef]
  25. Chantharasupawong, P.; Philip, R.; Endo, T. ; Thomas, J Enhanced optical limiting in nanosized mixed zinc ferrites. Appl. Phys. Lett. 2012, 100, 221108. [Google Scholar] [CrossRef]
  26. Philip, R.; Chantharasupawong, P.; Qian, H.; Jin, R.; Thomas, J. Evolution of nonlinear optical properties: From gold atomic clusters to plasmonic nanocrystals. Nano Lett. 2012, 12, 4661–4667. [Google Scholar] [CrossRef] [PubMed]
  27. Seo, J. T.; Ma, S. M.; Yang, Q.; Creekmore, L.; Battle, R.; Brown, H.; Jackson, A.; Skyles, T.; Tabibi, B.; Yu, W.; Jung, S. S.; Namkung, M. Large resonant third-order optical nonlinearity of CdSe nanocrystal quantum dots. J. Phys. Conf. Ser. 2006, 38, 91–95. [Google Scholar] [CrossRef]
  28. Liaros, N.; Iliopoulos, K.; Stylianakis, M. M.; Koudoumas, E.; Couris, S. Optical limiting action of few layered graphene oxide dispersed in different solvents. Opt. Mater. 2013, 36, 112–117. [Google Scholar] [CrossRef]
  29. Feng, M.; Zhan, H.; Chen, Y. Nonlinear optical and optical limiting properties of graphene families. Appl. Phys. Lett. 2010, 96, 033107. [Google Scholar] [CrossRef]
  30. Fang, C.; Dai, B.; Hong, R.; Tao, C.; Wang, Q.; Wang, X.; Zhang, D.; Zhuang, S. Tunable optical limiting optofluidic device filled with graphene oxide dispersion in ethanol. Sci. Rep. 2015, 5, 15362. [Google Scholar] [CrossRef]
  31. Ebrahimi, M.; Zakery, A.; Karimipour, M.; Molaei, M. Nonlinear optical properties and optical limiting measurements of graphene oxide - Ag@TiO2 compounds. Opt. Mater. 2016, 57, 146–152. [Google Scholar] [CrossRef]
  32. Coleman, J. N.; Khan, U.; Young, K.; Gaucher, A.; De, S.; Smith, R. J.; Shvets, I. V.; Arora, S. K.; Stanton, G.; Kim, H.; Lee, K.; Kim, G. T.; Duesberg, G.S.; Hallam, T.; Boland, J. J.; Wang, J. J.; Donegan, J. F.; Grunlan, J. C.; Moriarty, G.; Shmeliov, A.; Nicholls, R. J.; Perkins, J. M.; Grieveson, E. M.; Theuwissen, K.; Mccomb, D. W.; Nellist, P. D.; Nicolosi, V. Two-Dimensional Nanosheets Produced by Liquid Exfoliation of Layered Materials. Science 2011, 331, 568–571. [Google Scholar] [CrossRef] [PubMed]
  33. Neupane, T.; Yu, S.; Rice, Q.; Tabibi, B.; Seo, F.J. Third-order optical nonlinearity of tungsten disulfide atomic layer with resonant excitation. Opt. Mat. 2019, 96, 109271. [Google Scholar] [CrossRef]
  34. Shang, J.; Li, J.; Ai, W.; Yu, T.; Gurzadyan, G.G. The Origin of Fluorescence from Graphene Oxide. Sci Rep. 2012, 2, 792. [Google Scholar] [CrossRef] [PubMed]
  35. Kimiagar, S.; Abrinaei, F. Effect of temperature on the structural, linear, and nonlinear optical properties of MgO-doped graphene oxide nanocomposites. Nanophotonics 2017, 7, 243. [Google Scholar] [CrossRef]
  36. Neupane, T.; Rice, Q.; Jung, S.; Tabibi, B. ; Kim, Seo, F.J. Cubic Nonlinearity of Molybdenum Disulfide Nanoflakes. J. nanoscience and nanotechnology 2020, 20, 4373–4375. [Google Scholar] [CrossRef] [PubMed]
  37. Kwak, C. H.; Lee, Y. L.; Kim, S. G. ; Analysis of asymmetric Z-scan measurement for large optical nonlinearities in an amorphous As2S3 thin film. J. Opt. Soc. Am B 1999, 16, 600–604. [Google Scholar] [CrossRef]
  38. Martin, K.; Spinks, D. Measurement of the speed of sound in ethanol/water mixture. Ultrasound Med. Biol. 2001, 27, 289–291. [Google Scholar] [CrossRef]
  39. Seo, J. T.; Yang, Q.; Creekmore, S.; Temple, D.; Yoo, K. P.; Kim, S. Y.; Jung, S. S.; Mott, A. Large pure refractive nonlinearity of nanostructure silica aerogel at near infrared wavelength. Appl Phys Lett. 2003, 82, 4444–4446. [Google Scholar] [CrossRef]
Preprints 83066 g001
Figure 1. Schematic diagram of open (a) and closed (b) Z-scan setups for characterizing the magnitude and polarity of nonlinear absorption and nonlinear refraction.
Figure 1. Schematic diagram of open (a) and closed (b) Z-scan setups for characterizing the magnitude and polarity of nonlinear absorption and nonlinear refraction.
Preprints 83066 g001
Preprints 83066 g002
Figure 2. The absorption spectrum of GO nanoflakes in water. The green spectrum indicates the laser excitation for nonlinear optical characterizations.
Figure 2. The absorption spectrum of GO nanoflakes in water. The green spectrum indicates the laser excitation for nonlinear optical characterizations.
Preprints 83066 g002
Preprints 83066 g003
Figure 3. Nonlinear transmittance as a function of the sample position along the open Z-scan for different input peak intensities.
Figure 3. Nonlinear transmittance as a function of the sample position along the open Z-scan for different input peak intensities.
Preprints 83066 g003
Preprints 83066 g004
Figure 4. Normalized transmittance as a function of sample position (z) for the closed Z-scan technique (a) experimental and their fitting traces and (b) comparing traces with and without NLA coefficient for the 4.87 GW/cm2.
Figure 4. Normalized transmittance as a function of sample position (z) for the closed Z-scan technique (a) experimental and their fitting traces and (b) comparing traces with and without NLA coefficient for the 4.87 GW/cm2.
Preprints 83066 g004
Preprints 83066 g005
Figure 5. Difference between the normalized peak and valley transmittance as a function of linear transmittance of finite aperture (S) for different applied intensities.
Figure 5. Difference between the normalized peak and valley transmittance as a function of linear transmittance of finite aperture (S) for different applied intensities.
Preprints 83066 g005
Preprints 83066 g006
Figure 6. Percentage difference between the normalized peak and valley transmittance as a function of nonlinear phase shift (Δϕo) for linear transmittance of finite aperture (0.01).
Figure 6. Percentage difference between the normalized peak and valley transmittance as a function of nonlinear phase shift (Δϕo) for linear transmittance of finite aperture (0.01).
Preprints 83066 g006
Preprints 83066 g007
Figure 7. Percentage difference between the normalized peak and valley transmittance as a function of applied intensity for various linear transmittance of finite aperture (S).
Figure 7. Percentage difference between the normalized peak and valley transmittance as a function of applied intensity for various linear transmittance of finite aperture (S).
Preprints 83066 g007
Preprints 83066 g008
Figure 8. Normalized transmittance as a function of applied peak intensity at the valley position of valley-peak of closed Z-scan traces.
Figure 8. Normalized transmittance as a function of applied peak intensity at the valley position of valley-peak of closed Z-scan traces.
Preprints 83066 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated