1. Introduction
The group
offers particular interest in physics as it is the configuration space for the motion of a rigid body fixed in a point. It is also of interest in signal analysis and processing. The rigid rotor is a classic problem in classical and quantum mechanics, describing the dynamics of a rigid body with its center of mass held fixed [
1,
2,
3,
4]. On the quantum level, it allows a consistent description of the rotational spectra of molecules [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17]. Moreover, using
as a configuration manifold leads to several applications including texture analysis [
18,
19,
20], protein-protein docking [
21,
22], air tempertature control [
23], structure of interest rates (in economics) [
24], attitude of rigid body [
25,
26,
27,
28,
29,
30], quantum information [
31] or spherical image analysis [
32,
33].
This work can be viewed as the direct continuation of a previous ones devoted to the semi-discrete cylinder [
34,
35]. We also draw our inspiration from the insightful works by Mukunda et al [
36,
37,
38]. These authors were concerned by the finding of a consistent Wigner function for compact Lie groups, and they illustrate their approach with the example of SU
, the double covering of SO
. For more recent related works, see for instance [
39,
40] and references therein.
Here, we investigate the so-called covariant integral quantization of functions or distributions on the phase space
, where
is the discrete set
labelling the matrix elements of the unitary irreducible representations (UIR) of SO
with respect to the spherical harmonic Hilbertian basis of
. In
Section 2 we briefly introduce the general concept of covariant integral quantization, and in
Section 3 we apply it to the quantum description of motion of a particle on the
manifold. In
Section 4 we derive the (non-unitary) Weyl-Gabor operator
U acting on the Hilbert space
of square integrable functions on the manifold
equipped with its Haar measure. This operator leads to a decomposition of the identity on space
. In
Section 5, we first define our quantization tools, namely a weight function
defined on the phase space and the related integral operator
acting on the representation space. We then define the quantization map which transforms a function or distribution
f on the phase space
into an operator
acting on
. We compute the quantization of separable functions in position and momentum, in momentum only, and position only. In
Section 6 we compute the so-called semi-classical portrait (or lower symbol) of the operator
and study how much they are closed to the original
f. In
Section 7, we give examples of quantum operators obtained through coherent state quantization. In
Section 8 we introduce a Wigner function built from what we define as the
squaring rotation operator. In the concluding
Section 9, we present some appealing investigations in the continuation of the present work and we give some insights about the application of our formalism to the analysis of signals defined on the manifold
. Interesting formulae are given in Appendix A.
2. Resolution of the identity as the common guideline
Here we give an outline of integral quantization. Detailed presentations can be found in [
41,
42], and more recently in [
43,
44,
45] with references therein.
Given a measure space
and a (separable) Hilbert space
, an operator-valued function
resolves the identity operator
in
with respect the measure
if
holds in a weak sense.
In Signal Analysis,
analysis and
reconstruction are grounded in the application of (
1) on a signal,
i.e., a vector in
In quantum formalism,
integral quantization is grounded in the linear map of a function on
X to an operator in
2.1. Probabilistic content of integral quantization: semi-classical portraits
If the operators
in
are nonnegative,
i.e.,
for all
, one says that they form a (normalised) positive operator-valued measure (POVM) on
X.
If they are further unit trace-class,
i.e. for all
,
i.e., if the
’s are density operators, then the map
is a local averaging of the original
(which can very singular, like the Dirac defined in (
8) below) with respect to the probability distribution on
X,
This averaging, or semi-classical portrait of the operator
, is in general a regularisation, depending of course on the topological nature of the measure space
and the functional properties of the
’s.
2.2. Classical limit
Consider a set of parameters
and corresponding families of POVM
solving the identity
One says that the classical limit
holds at
if
where the convergence
is defined in the sense of a certain topology.
Otherwise said,
tends to
where
is a Dirac measure with respect to
,
Of course, these definitions should be given a rigorous mathematical sense, and nothing guarantees the existence of such a limit.
3. Overview: Scalar fields on the rotation group SO, Fourier and Gabor transform
3.1. Quantum formalism on SO
An element of SO can be parametrised in several ways.
- a)
-
In the Euler angles parametrization with ZYZ convention,
and
are rotation angles about the 3rd axis and
is a rotation angle about the 2nd axis, with
,
, and
. The corresponding rotation matrix reads en terms of these one-dimensional matrices as:
The related (non normalised) Haar measure is given by
which yields Vol
.
- b)
-
In the axis-angle parametrization,
is the anticlockwise (or right-hand rule) rotation angle about the oriented axis
determined by the usual angular spherical coordinates
,
.
The matrix representation of
is given by
where
is the orthogonal projector on
,
and
is linearly acts on
as
The related unnormalized Haar measure is:
We now consider the Hilbert space
of square integrable functions
on the rotation group SO
, that is, functions satisfying the condition,
The group multiplication on the left induces the unitary action of the operator
on
,
The 3 basic generators (angular momentum components) of this action in the Euler angles parametrization (
9) are given by [
46]:
One can decompose any function
using the Wigner
-functions
, with
, and
. Hence, these functions form an Hilbertian basis of
, and the set of triplets of integers
form the Fourier dual of
. The Wigner
-functions
are matrix elements of the irreducible unitary representation of SO
with respect to the Hilbertian basis of normalised spherical harmonics
in
. Our convention concerning the latter is that one given by Edmonds [
46]:
where the
are the associated Legendre functions [
47].
In the Euler angle parametrization the Wigner
-functions appear in the expansion [
5,
46]:
and are given by
In this expression the functions
are expressed in terms of the Jacobi polynomials for
and
[
47]:
The other cases give similar expressions after using symmetries of indexes for these polynomials. More precisely, from the general expression of the Jacobi polynomials
with
one can derive the Fourier series expansion of the Wigner
d-functions (not trivial!):
where
[
48,
49]. In terms of its matrix elements, the unitarity of the
-matrix at fixed
l read
and so
while the orthogonality relations obeyed by these
-matrix elements read
Let us introduce the Dirac distribution
on SO
as having its support at the group identity
for all test functions in some dense subspace of
, e.g., infinitely differentiable. For any
and from the
invariance of the measure, we have
which entails the definition of the Dirac distribution
with support at any point
:
Using Dirac notations, we introduce kets
and their dual bras
, both labeled by the points
, as obeying the following orthogonality and normalization (in the distributional sense) and resolution of the unity in
From its construction, we derive the invariance property of the Dirac distribution on SO
:
With these notations, one can write for any
(or for suitably defined distributions)
With this formalism at hand the completeness of the Hilbertian basis
in
reads:
On the other hand, as matrix elements of the unitary operator
( irreducibly acting in the
-dimensional subspace
of
) they are uniformly bounded by
We now define the SO
Fourier transform of
as the orthogonal projection of
on the basis
, that is its Fourier coefficient:
and its inverse is consistently the Fourier series expansion:
3.2. Phase space formalism
Inspired by the Mukunda et al’s approach [
36,
37] we now consider the rotation
as an element of the configuration space SO
and the triple
of its unitary (∼ Fourier) dual
as
momentum or
frequency variables. Hence, we denote in the following
with orthogonality relations and resolution of the identity
With these shortened notations, we write the Hilbertian basis as:
The completeness relation (
39), Fourier transform (
41), and its inverse (
42), take the simplest forms:
3.3. SO-Weyl-Gabor operator, coherent states and Gabor transform
3.3.1. SO-Weyl-Gabor operator
Besides the unitary representation operator
introduced in (
16) we define the non-unitary modulation operator by the momentum variable
as the non-Hermitian bounded multiplication operator:
Note that it is the sum of unitary operators due to (
23) and (
27):
Its adjoint
is defined by:
where the transpose
of
means
Combining these operators leads to the (non-unitary) “SO
-Weyl-Gabor” operator
acting on
as
Its adjoint
acts on
as:
We then have the following actions on
:
In particular, the lack of unitarity of
and
is obvious from the fact that
and
are nontrivial bounded multiplication operators:
3.3.2. Coherent states
Let us pick a normalised vector
in
and consider the family of family of states labelled by the elements of the phase space
:
These states will be named
-coherent states with
fiducial vector
for the reason that they solve the identity in
, as asserted in the following.
Proposition 3.1.
Let us equip the phase space Γ with the measure
Then the states resolve the identity in with respect to this measure:
Proof. Pick
,
and compute
First performing the sum on
yields
by application of (
46). By integrating the latter and using the invariance of the Haar measure
we end with
□
3.3.3. Gabor transform
The Gabor transform, denoted by
, maps
to a function
in the Hilbert space
of square integrable functions on the phase space
equipped with the measure
:
Proposition 3.2. The map satisfies the following properties:
- (i)
- (ii)
it can be inverted on its range:
- (iii)
the closure of the range of is a reproducing kernel Hilbert space:
Proof. All statements are straighforward consequence of the resolution of the identity (
61). □
Proposition 3.3.
We have the following trace formulas for the SO-Weyl-Gabor operator:
Proof. For (
66), using (
46) and the orthonormality of the
’s,
□
3.4. Example of fiducial vectors and coherent states
As seen above, for any square integrable function on SO, including the completely non localized function on the manifold SO, is a fiducial vector, our coherent states form the family of transported through the SO-Weyl-Gabor operator. It is, of course, interesting to consider fiducial vectors that are well “localized” in position and momentum. Although it is not the main purpose of this paper, we present a few fiducial vectors that can be of interest. Some of these examples are extracted from signal processing on SO as related to probability densities.
- 1.
-
Eigenfunctions of certain operators [
50]. The first example is the free rotor fiducial vector which is the eigenfunction of
.
The second example is the highest fiducial vector for
which is cancelled by
, that is:
- 2.
-
Some radial fiducial vectors. Below, we give examples of fiducial vectors depending only on
which defines a metric on
. Details about this metric can be found in [
22],
- (a)
-
The
-dependent von Mises-Fisher Kernel fiducial vectors
[
22], their derivatives with respect to
and
, and their difference at two different
:
where
,
denotes the modified Bessel functions of first kind.
In
Appendix B, we give plots of these fiducial vectors in
and
variables at a fixed
and for a few values of
(Figures B.1. and B.2.).
- (b)
The Abel-Poisson fiducial vector
[
22]:
4. Quantization operators and the quantization map
Following previous works [
43,
44,
45], we pick a function
, called weight (but not necessarily positive), on the phase space
. We then define the operator
by
and we choose the weight such that the operator
is bounded and symmetric,
i.e., is self-adjoint on the Hilbert
of “physical states”.
In what follows, we compute the kernel of this operator and the related trace.
Proposition 4.1.
-
(i)
-
The operator is the integral operator:
where the kernel is given by:
Here, is the partial inverse discrete Fourier transform (48) of ϖ with respect to the discrete variables.
-
(ii)
The operator is symmetric if and only the weight satisfies;
-
(iii)
The trace of is given by
Proof.
- (i)
-
The action of
on
is given by:
Using the change of variable
, the invariance of the Haar measure
, and the partial inverse discrete Fourier transform (
48), we get the expected kernel (
77).
- (ii)
-
The action of
on
is given by:
Using the change of variable
, the invariance of the Haar measure
, and the partial discrete Fourier transform (
47) we formally get (
78) by comparison with (
77).
- (iii)
The relation (
79) trivially results from (
66).
□
In turn,we show in the following proposition that one retrieves the weight from the quantization operator through a tracing operation.
Proposition 4.2.
The trace of the operator is given by:
Proof. This relation trivially results from (67). □
As a first example, let us examine the case
. Then the operator
is determined through its action on basis elements
:
Let us introduce the
squaring rotation operator defined by
With this definition we precisely get from (
81):
where
is the transpose of
and we remind that
. This operator plays the central role in our definition of the Wigner-like function within the present context (see
Section 8). Other examples of weights will be considered in the rest of the paper.
5. SO-covariant integral quantization from weight function
5.1. General results
We now establish general formulas for the integral quantization issued from a weight function
on
yielding the bounded self-adjoint operator
defined in (
75). This allows us to build a family of operators obtained from SO
Weyl-Gabor operator transport of
:
Then, the corresponding integral quantization is given by the linear map:
We have the following result.
Proposition 5.1.
is the integral operator on
and its kernel is given by
with a weighted version of the completeness relation:
The condition that be mapped to the unit operator imposes that the follow normalization for ϖ holds:
Proof. The calculation of the kernel of the integral operator
goes through the following steps which follow from the expressions (
84) and (57).
We then proceed with the change of variable
and use the SO
invariance of the measures
to obtain the form
with
We then proceed with the change of variables
to obtain
which is (
87) with the notation (
88).
Putting
in the above expression and using the completeness relation (
46) give
and yield (
89).
□
5.2. Particular quantizations
In what follows, we compute the quantized operators of the various simplifications of
. Let us first introduce the function:
It obeys
We also introduce the notations:
In Appendix we give examples of such calculations in the case of coherent states.
Of course,
or, equivalently,
should be understood as
and
means the Euler angle
of the rotation
, etc. We will also need the integral formulae (with suitable conditions on functions appearing in the integrand)
5.2.1. Separable functions
In this case
in the integral factorises as
with the notation
Hence,
5.2.2. Univariate function
In this case the above (
101) simplifies to:
Hence, the quantization of
is the multiplication operator.
where the (noncommutative) convolution
on the group SO
is defined by
Let us give the quantizations of some basic Fourier or trigonometric functions
. In the sequel we put
.
For
we get
where:
For
,
where:
For
,
where:
For
,
where:
5.2.3. Univariate function
The integral kernel reads in this case:
We know that the values of
are constrained in a forward rectangular discrete pyramid, which is the momentum space. We here work with Euler angle parameters:
,
. We will omit them for simplicity and explicitly put them when needed. Let us present the quantization of a few elementary functions
.
6. Semi-classical portrait
Given a function
on the phase space
, normalised at
, and yielding a non-negative unit trace operator,
i.e., a density operator,
, the quantum phase space portrait of an operator
A on
is defined as:
The most interesting aspect of this notion in terms of probabilistic interpretation holds when the operator
A is precisely the integral quantized version
of a classical
with the same function
(actually we could define the transform with 2 different ones, one for the “analysis” and the other for the “reconstruction”). Then, with the use of the composition rule let us compute the transform:
Using the partial Fourier transform
of
, we get:
Hence we can write:
where the kernel is given by
Using the adjointness condition for
, one gets:
where:
Hence we can conclude with the following result:
Proposition 6.1.
The semi-classical portrait of the operator : with respect to the weight ϖ is given by:
where the kernel is given by:
This kernel satisfies the property:
Below we give the kernels and semi-classical portraits for two specific weights.
- (i)
-
For the unit weight
the kernel reads:
where:
- (ii)
-
For the squaring rotation map weight
,
and:
For the univariate functions
and
:
A third example of weight, namely that one corresponding to coherent states, is given in the next section.
7. Quantization and semi-classical portraits with coherent states with non-unit fiducial states
7.1. CS quantization
In this section, we consider the quantization yielded by the weight which corresponds through Proposition 8.2 to the one-rank density operator , , .
Proposition 7.1.
Given a fiducial vector ϕ and the projector , the trace of the operator is given by (with the notations of (59)):
In addition, we have:
-
(i)
the partial inverse Fourier transform of with respect to is given by:
-
(ii)
-
the kernel of the related quantum operator is given by:
with the notations of (88).
In what follows, we compute the kernels or/and the corresponding operators for various simple cases of .
- a)
For
,
- b)
-
For
,
Hence, the quantized of
is the multiplication operator.
- c)
For
7.2. Semi-classical portraits through CS
For the coherent state weight
the kernel is the probability distribution on the phase space:
Hence
is the local averaging of the original
:
8. Squaring rotation operator for Wigner function
In preamble to this section, let us consider the following phase portrait of a state
,
where the operator
is requested to yield marginality properties
à la Wigner for
:
Let us assume that
acts on
through some differentiable transformation of the group manifold
, namely
where the factor
has also to be determined.
With (
54), (
55), and the above definitions, we have
The completeness relation (
46) combined with the above integral and change of variable
allows to write
The condition for getting marginality with regard to summing on
, namely
thus imposes on the action
and the function
the following conditions
Besides the constraint
possible solutions for
are
since the group structure imposes that
,
i.e.,
should be one of the
roots of the unity in SO
. The most natural choice for
n is obviously
:
and we will keep it in the sequel. Let us now examine the condition for getting marginality with regard to integrating on
, namely
where we remind that
is the Fourier transform of
:
With the solution (142) at hand, let us evaluate the l.h.s. of (
143), assuming that inverting the order of integrations is legitimate.
Now, after changing the variable in the second integral
and using the invariance of the measure
, one obtains
In order to get marginality with regard to integrating on
the only possibility is that
. Then, we get (
143), and
is precisely the squaring rotation operator introduce in (
82),
In summary, and extending the above properties to mixed states in
, we state the following.
Proposition 8.1. To any density operator in the squaring rotation operator associates its Wigner-like function on the phase space defined by
This function obeys the marginality properties:
-
(i)
-
where the are the matrix elements of in the basis .
-
(ii)
-
(iii)
For a pure state these formulae simplify to
-
(iv)
It results from these two marginal properties the normalisation of as a complex-valued quasi-distribution on the phase space:
Let us tell more about the properties of the squaring rotation operator.
Proposition 8.2.
- (i)
The operator is unit trace.
- (ii)
The weight function giving rise to through (75), i.e., , is given by the trace of the operator :
- (iii)
-
The inverse partial Fourier transform of the weight with respect to the momentum is given by:
and the kernel of the related quantum operator is given by:
with the notations of (88).
Proof.
- (i)
Using the completeness property (
46) and (
36), we get:
- (ii)
where we again have used the completeness property (
46) and (
36) after changing the variable
.
- (iii)
The proof is direct.
□
In what follows, we compute the kernels or/and the corresponding operators for various simple cases of .
- a)
For
,
- b)
-
For
,
Hence, the quantized of
is the multiplication operator.
- c)
For
9. Conclusion
In this paper, we have established a covariant integral quantization for systems whose phase space is the so-called semi-discrete hypercylinder , i.e., whose configuration space is , and where . This extends our previous work on the discrete cylinder for the motion of particle on circle . Although the phase space is not a coset arising from a group, we have shown that the Weyl-Gabor formalism applies.
First, we have established the concomitant resolution of the identity and subsequent properties such as the Gabor transform on and its inversion, the reproducing kernel and the fact that any square integrable function on the groupe is fiducial vector. The decomposition of the identity allows to define an integral operator from weight function defined on the phase space.
There are noticeable results related to the quantization of a point
in the phase space according to two standard choices of the weight.
In a follow up studies, we plan to extend the results of this work in several directions.
Extend the work to all rotation groups
, and also to the related Spheres
. Also look into the quantization of continuation phase space related to the Euclidean groups
,
, [
51,
52].
Extend the work to full configuration space of the rigid body that is the Euclidean motion group in three dimensions .
Extend the formalism to the case where the configuration space is a non-compact group, for example, or .
Explore the possibility of covariant integral quantization in the situation where the phase space is
This phase space is used in the context of quantum loop gravity [
53,
54].
Apply to signal analysis on SO(3). We will investigate the robustness of the phase space of representation
of signal
in capturing salient futures in the signal. Various tools will be used. These include: visualization of various partial energy densities of the Gabor transform, quantum operators related to various fiducial vectors, Husimi distributions, the Wigner distribution, entropy, and sampling/frames on
[
48,
55].
Author Contributions
Conceptualization, J.-P. Gazeau and R. Murenzi; methodology, J.-P. Gazeau and R. Murenzi; validation, J.-P. Gazeau and R. Murenzi; formal analysis, J.-P. Gazeau and R. Murenzi; investigation, J.-P. Gazeau and R. Murenzi; writing—original draft preparation, R. Murenzi; writing—review and editing, J.-P. Gazeau and R. Murenzi. Both authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
J.-P. Gazeau thanks the ICTP Trieste for financial support and hospitality. We acknowledge discussions with Mladen Victor Wickerhauser
Conflicts of Interest
The authors declare no conflict of interest. The ideas and opinions expressed in this article are those of the authors and do not necessary represent the view of UNESCO.
Abbreviations
The following abbreviations are used in this manuscript:
| POVM |
Positive operator-valued measure |
| UIR |
Unitary irreducible representation |
| CS |
Coherent state |
Appendix A. Some formulas for CS quantization
In this appendix, we compute
, for the coherent state weight
, for
, using the following summation formulae [
56],
We therefore have:
Let us now two types of fiducial vectors.
Appendix B. Plot of Von Mise fiducial vector and derivative
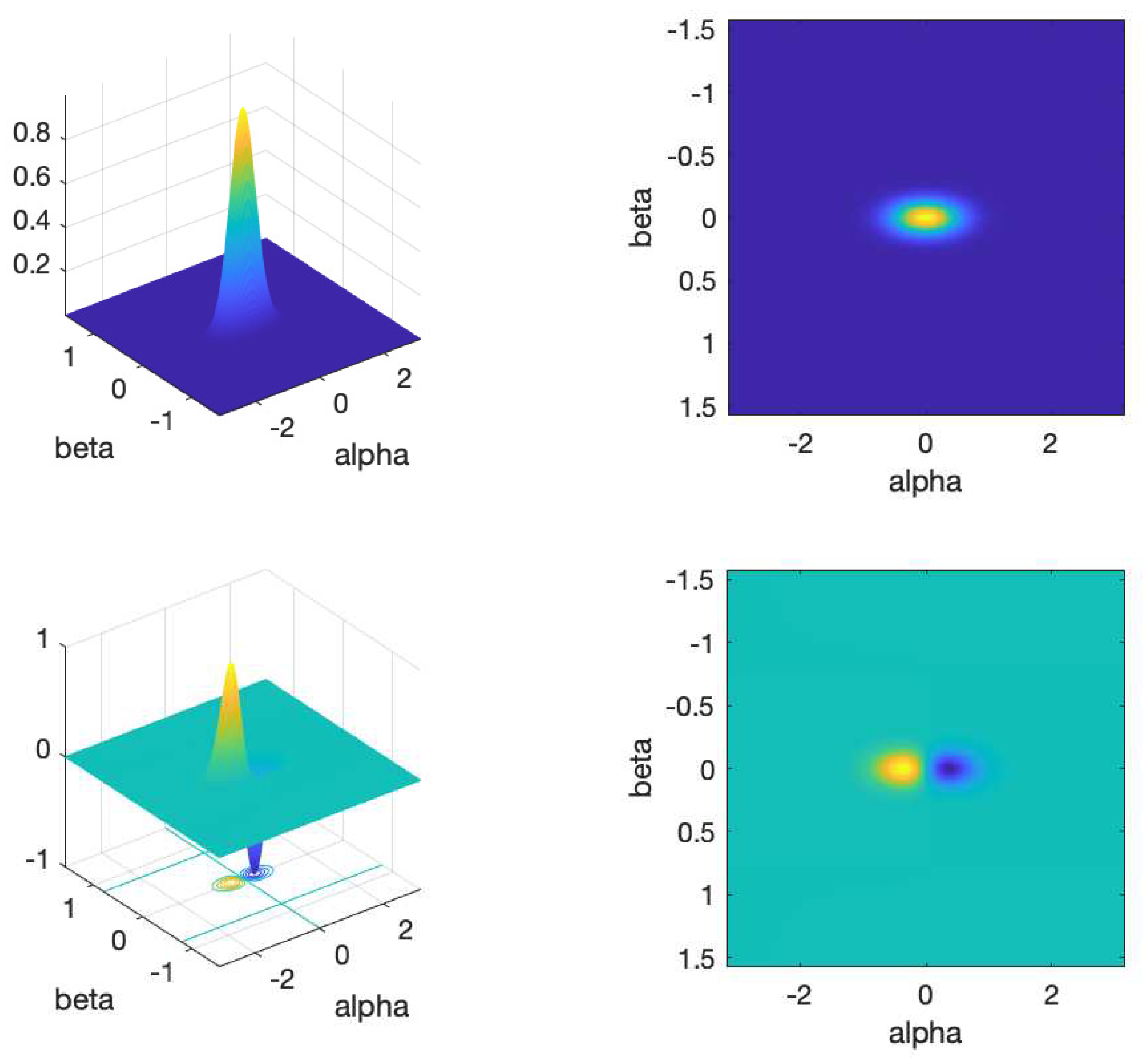
Figure B.1.
Top left and right: Von Mises Fiducial vector in () variables at ; bottom left and right: derivative with respect to of the Von Mises Fiducial vector in () variables at
Figure B.1.
Top left and right: Von Mises Fiducial vector in () variables at ; bottom left and right: derivative with respect to of the Von Mises Fiducial vector in () variables at
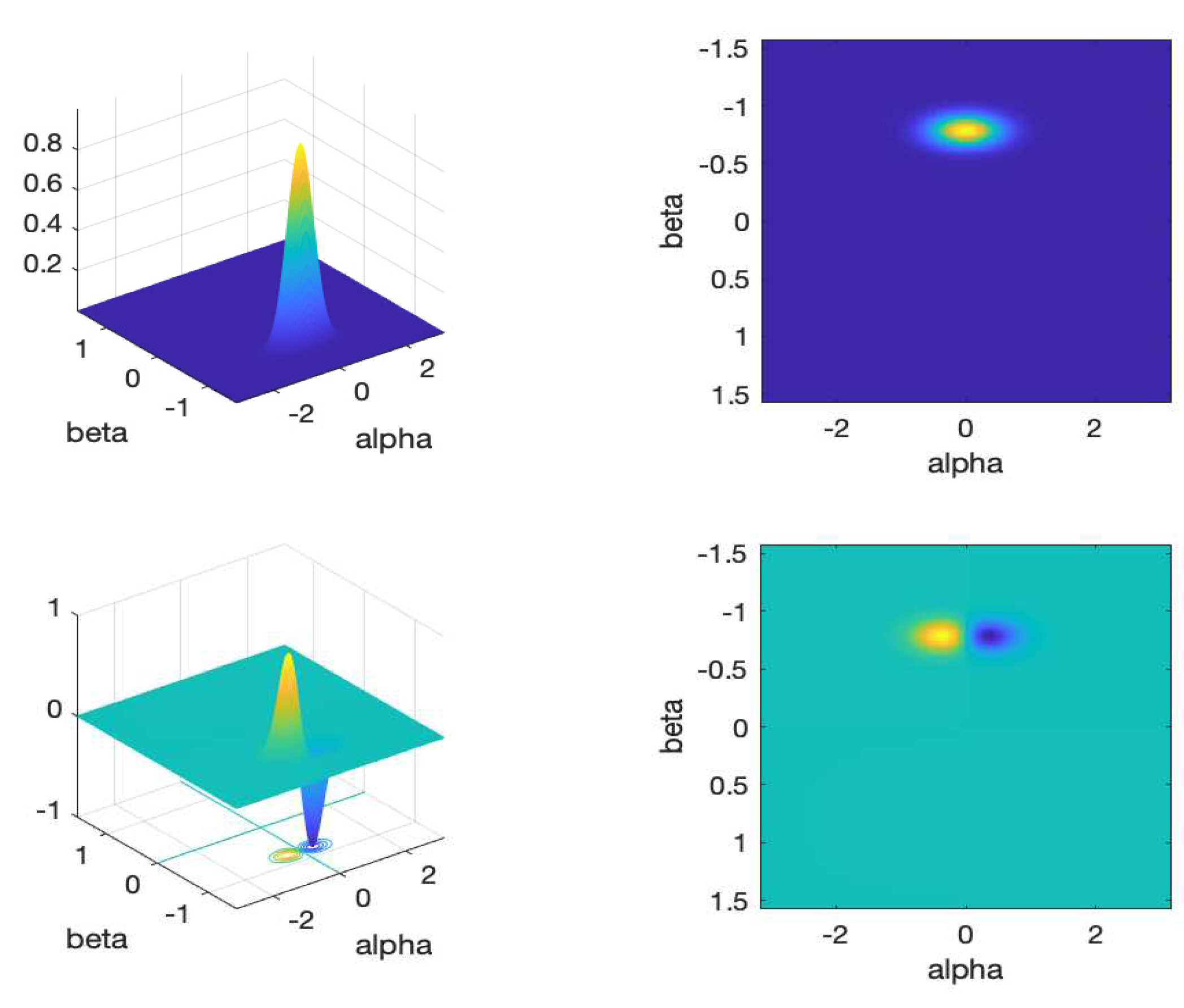
Figure B.2.
Top left and right: Von Mises Fiducial vector in () variables at ; bottom left and right: derivative with respect to of the Von Mises Fiducial vector in () variables at
Figure B.2.
Top left and right: Von Mises Fiducial vector in () variables at ; bottom left and right: derivative with respect to of the Von Mises Fiducial vector in () variables at
References
- Marle, C-M. On Mechanical Systems with a Lie Group as Configuration Space, in Jean Leray ’99 Conference Proceedings, the Karlskrona Conference in Honor of Jean Leray, 1999, edited by Maurice de Gosson, Springer-Science+Business Media, B.V. pp183–203.
- Prieto, C. T. Quantization and spectral geometry of a rigid body in a magnetic monopole field. Differential Geometry and its Applications 2001, 14, 157–179. [Google Scholar] [CrossRef]
- Khatua, S.; Ganesh, R. Berry phase in the rigid rotor: Emergent physics of odd antiferromagnets. Phys. Rev. B 2022, 105, 184401. [Google Scholar] [CrossRef]
- Casimir, H. Rotation of a rigid body in quantum mechanics. Ph.D. thesis, University of Leiden, 1931.
- Breev, A.; Gitman, D. New Exact Solutions Describing Quantum Asymmetric Top. Symmetry 2023, 15, 503. [Google Scholar] [CrossRef]
- Wells, T; Raston, P. L. Concerning the asymmetric top rotational partition function in astronomical spectroscopy. Journal of Molecular Spectroscopy 2020, 370, 111292. [Google Scholar] [CrossRef]
- Karczmarek, J.; Wright, J.; Corkum, P.; Ivanov, M. Optical Centrifuge for Molecules, Phys. Rev. Lett. 1999, 26, 3420–3423. [Google Scholar] [CrossRef]
- Makito, O. Revisiting the Concept of Nuclear Rotation: Quantum and Classical Viewpoints. Bulgarian Journal of Physics 2022, 49, 97–107. [Google Scholar]
- Boscain, U.; Pozzoli, E.; Sigalotti, M. Classical and quantum controllability of a rotating 3D symmetric molecule. SIAM Journal on Control Optimization 2021, 59, 156–184. [Google Scholar] [CrossRef]
- Koch, C. P.; Lemeshko, M.; Sugny, D. Quantum control of molecular rotation. Rev. Mod. Phys. 2019, 91, 035005–36. [Google Scholar] [CrossRef]
- Thiamova, G.; Rowe, D.J.; Caprio, M.A. The relationship between the interacting boson model and the algebraic version of Bohr’s collective model in its triaxial limit. Nuclear Physics A 2012, 895, 20–32. [Google Scholar] [CrossRef]
- Bohr, A.; Mottelson, B. R. Collective Nuclear Motion and the Unified Model, Chapter XVII, pp 468–493 in book Beta and Gamma Ray Spectroscopy, 1955, North Holland Publishing Co., Amsterdam, Kai Siegbahn, Editor.
- Dudek, J.; Gozdz, A.; Curien, D.; Pangona, V.; Schunc, N. Nuclear Tetrahedral Symmetry and Collective Rotation. Acta Physica Polonica Series B 2006, 38, 1389–1404. [Google Scholar]
- Bohm, A.; Teese, R. B. Spectrum generating group of the symmetric top molecule, J. Math. Phys. 1976, 17, 94. [Google Scholar] [CrossRef]
- Bozic, M.; Arsenovic, D. Quantum magnetic top. In the book: Quantization and Infinite-Dimensional Systems, Editors:J-P. Antoine, S. Twareque Ali, W. Lisiecki, I. M. Mladenov, A. Odzijewicz, Springer 1994.
- Toth, J.A. Eigenfunction localization in the quantized rigid, J. Diferential geometry 1996, 43, 844–858. [Google Scholar]
- Prie, C. T. Quantization and spectral geometry of a rigid body in a magnetic monopole field, Differential Geometry and its Applications 2001, 14, 157-179.
- Yashnikov, V.P.; Bunge, H.J. Geometrical Foundations of Texture Analysis. Geodesic Curves and Motions in the group Space of Three-Dimensional Rotations. Textures and Microstructures, 1997, 30, 1–42. [Google Scholar] [CrossRef]
- Man, C-S. Crystallographic Texture and Group Representations, Journal of Elasticity 2022, 149, 3–445.
- Savyolova, T.I.; Filatov, S.V. About normal distribution on SO(3) group in texture analysis. J. Phys.: Conf. Ser. 2017, 937, 012045. [Google Scholar] [CrossRef]
- Chirikjian, G. S.; Kyatkin, A. B. Engineering Applications of Noncommutative Harmonic Analysis With Emphasis on Rotation and Motion Groups. Boca Raton, FL, USA: CRC Press, 2000.
- Vollrath, A. The Nonequispaced Fast SO(3) Fourier Transform, Generalisations and Applications. Thesis, Lübeck University, 2010.
- Uçan, Y.; Bildirici, M. Air temperature measurement based on lie group SO(3). Thermal Science 2022, 26, 3089–3095. [Google Scholar] [CrossRef]
- Bildirici, M; Ucan, Y; Lousada, S. Interest Rate Based on The Lie Group SO(3) in the Evidence of Chaos. Mathematics 2022, 10, 3998. [Google Scholar] [CrossRef]
- Markley, F. Attitude Filtering on SO(3). The Journal of the Astronautical Sciences 2006, 54, 391–413. [Google Scholar] [CrossRef]
- Lee, T.; Leok, M.; McClamroch, N. H. Optimal Attitude Control of a Rigid Body Using Geometrically Exact Computations on SO(3). Journal of Dynamical and Control Systems volume 2008, 14, 465–487. [Google Scholar] [CrossRef]
- Lee, T.; Leok, M.; McClamroch, N.H. Global Symplectic Uncertainty Propagation on SO(3). Proceedings of the 47th IEEE Conference on Decision and Control Cancun, Mexico, 2008.
- Berkane, S. Hybrid Attitude Control and Estimation On SO(3). PHD Thesis, The University of Western Ontario, 2017.
- Lee, T. Bayesian Attitude Estimation With the Matrix Fisher Distribution on SO(3). IEEE Transactions on Automatic Control 2018, 63, 18. [Google Scholar] [CrossRef]
- Berkane, S.; Tayebi, A. Construction of Synergistic Potential Functions on SO(3) With Application to Velocity-Free Hybrid Attitude Stabilization. IEEE Transactions on Automatic Control 2017, 62, 495–501. [Google Scholar] [CrossRef]
- Albert, V.V.; Covey, J.P.; Preskill, J. Robust encoding of a qubit in a molecule. Phys. Rev. X 2020, 10, 031050. [Google Scholar] [CrossRef]
- Kazhdan, M.; Funkhouser, T.; Rusinkiewicz, S. Rotation invariant spherical harmonic representation of 3D shape descriptors, in Eurographics Symposium on Geometry Processing, L. Kobbelt, P. Schroder, H. Hoppe (Editors), 2003, 156–164.
- Hoover, R. C.; Maciejewski, A. A.; Roberts, R. G. Hoover, R. C.; Maciejewski, A. A.; Roberts, R. G. Pose detection of 3-D objects using images sampled on SO(3) spherical harmonics, and Wigner-D matrices, in Proc. IEEE Int. Conf. Automation Science and Engineering, CASE 2008., 2008, 47-52.
- Gazeau, J.-P.; Murenzi, R. Integral Quantization for the Discrete Cylinder. Quantum Reports 2022, 4, 362–379. [Google Scholar] [CrossRef]
- Fabre, N.; Klimov, A.B.; Murenzi, R.; Gazeau, J-P. ; Sanchez-Soto, L. L. Majorana stellar representation of twisted photons. Phys. Rev. Research 2023, 5, L032006. [Google Scholar] [CrossRef]
- Mukunda, N.; Arvind, S.; Chaturvedi, S.; Simon, R. ; Wigner distributions and quantum mechanics on Lie groups: The case of the regular representation. J. Math. Phys. 2004, 45, 114–148. [Google Scholar] [CrossRef]
- Mukunda, N.; Marmo, G.; Zampini, A.; S. Chaturvedi, S.; Simon, R. Wigner Weyl isomorphism for quantum mechanics on Lie groups. J. Math. Phys. 2005, 46, 012106-1–21. [Google Scholar] [CrossRef]
- Chaturvedi, Marmo, G. ; S; Mukunda, N; Simon, R., Zampini, A.; The Schwinger Representation of a Group: Concept and Applications. Reviews in Mathematical Physics 2006, 18, 887–912. [Google Scholar] [CrossRef]
- Fischer, T.; Gneiting, C.; Hornberger, K. Wigner function for the orientation state. New Journal of Physics 2013, 15, 063004-1–10. [Google Scholar] [CrossRef]
- Grigorescu, M. Coherent distributions for the rigid rotator. J. Math. Phys. 2016, 57, 062702. [Google Scholar] [CrossRef]
- Bergeron, H.; Gazeau, J.P. Integral quantizations with two basic examples. Ann. Phys. 2014, 344, 43–68. [Google Scholar] [CrossRef]
- Ali, S.T.; Antoine, J.-P.; Gazeau, J.-P. Coherent States, Wavelets and their Generalizations, 2nd ed.; Theoretical and Mathematical Physics; Springer: New York, NY, USA, 2014; chapter 11. [Google Scholar]
- Gazeau, J.-P.; Murenzi, R. Covariant Affine Integral Quantization(s). J. Math. Phys. 2016, 57, 052102-1-22. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Koide, T.; Murenzi, R. 2-D Covariant Affine Integral Quantization(s). Adv. Oper. Theory 2020, 5, 901–935. [Google Scholar] [CrossRef]
- Gazeau, J.-P.; Koide, T.; Murenzi, R. Correction to: 2-D Covariant Affine Integral Quantization(s). Adv. Oper. Theory 2022, 7, 22. [Google Scholar] [CrossRef]
- Edmonds, A. R. Angular Momentum in Quantum Mechanics, Princeton University Press, Princeton, N.J., 1957.
- Magnus, W.; Oberhettinger, F.; Soni, R. P. Formulas and Theorems for the Special Functions of Mathematical Physics, Springer-Verlag, Berlin, Heidelberg and New York, 1966.
- McEwen, J.D.; Buttner, M.; Boris Leistedt, B.; Peiris, H.V.; Wiaux, Y. A. novel sampling theorem on the rotation group, IEEE Signal Processing Letters, 2005, 22, 2425–2429.
- Risbo, T. Fourier transform summation of Legendre series and D-functions. J. Geodesy 2020, 70, 383–396. [Google Scholar] [CrossRef]
- Biedenharn, L. C. ; D. Louck, J.D. Standard Treatment of Angular Momentum in Quantum Mechanics in book Angular Momentum in Quantum Physics, Theory and Application. Cambridge University Press, 1984.
- Torresani, B. Position-frequency analysis for signals defined on spheres. Signal Processing 1995, 43, 341–346. [Google Scholar] [CrossRef]
- Fresneda, R.; Gazeau, J-P. ; Noguera, D. Quantum localisation on the circle. J. Math. Phys. 2018, 59, 052105. [Google Scholar] [CrossRef]
- Oriti, D.; Raasakka, M. Quantum Mechanics on SO(3) via Non-commutative Dual Variables. Phys. Rev. D 2011, 84, 025003. [Google Scholar] [CrossRef]
- Freidel, L.; Livine, E. R. Ponzano-Regge model revisited III: Feynman diagrams and Effective field theory. Class. Quantum Grav. 2006, 23, 2021–2061. [Google Scholar] [CrossRef]
- Murenzi, R. Ondelettes multidimensionnelles et applications à l’analyse d’images. PHD Thesis, Catholic University of Louvain, 1990.
- Lai, S-T. ; Palting, P.; Chiu, Y-N.; Silverstone, H. J. On the summations involving Wigner rotation matrix elements. Journal of Mathematical Chemistry 1998, 24, 123–132. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).